北航计算机研究生课程-算法设计与分析-HomeWork-1
北航计算机考研参考书

北航计算机考研参考书摘要:1.北航计算机考研的招生专业和方向2.初试科目和复试内容3.参考书目4.考研难度和录取情况5.北航计算机考研与北邮计算机考研的比较正文:对于想要报考北京航空航天大学计算机相关专业的考生来说,了解北航计算机考研的招生专业和方向是十分重要的。
根据相关资料,北航计算机考研的主要专业和方向包括计算机软件与理论、人工智能与普适计算、数据科学与知识工程等。
在初试阶段,考生需要参加的科目有思想政治理论、英语一、数学一和计算机学科专业基础综合。
其中,计算机学科专业基础综合是北航自2021 年起首次实行的考试科目,考生需要对此做好充分的准备。
复试阶段主要包括专业英语、实验部分、面试部分以及计算机笔试,如数据结构和计算机体系结构等。
在准备北航计算机考研的过程中,参考书目是必不可少的。
以下是一些建议的参考书目:《数据结构》严蔚敏著,清华大学出版社;《计算机操作系统(修订版)》汤子瀛著,西安电子科技大学出版社;《计算机组成原理》唐朔飞著,高等教育出版社;《计算机网络(第五版)》谢希仁著,电子工业出版社。
当然,这些参考书目只是建议,具体的复习资料还需要考生根据自己的实际情况进行选择。
在考研难度方面,北航计算机考研具有一定的难度,但难度并不是不可逾越的。
考生需要在英语、数学和专业课等方面进行全面的复习,并在复习过程中不断提高自己的实际能力。
据了解,考研320 分左右的成绩是有可能考上北航计算机专业的,但具体还需要看考生的整体表现和竞争对手的情况。
最后,对于许多考生关心的北航计算机考研与北邮计算机考研的比较,可以从以下几个方面进行考虑。
首先,北航计算机考研更偏重软件方面,而北邮则偏重网络和通信方面。
其次,两个学校在这方面都有国家重点实验室,因此具有较高的研究水平。
最后,北邮的就业前积极准备的氛围较为浓厚,而北航则在就业方面略逊一筹。
计算机学院-北航研究生院-北京航空航天大学

计算机学院计算机科学与技术(0812)博士研究生培养方案一、适用学科计算机科学与技术(0812)二、培养目标1.坚持党的基本路线,热爱祖国,遵纪守法,品行端正,诚实守信,身心健康,具有良好的科研道德和敬业精神。
2.在计算机科学与技术方面具有坚实宽广的理论基础和系统深入的专门知识,全面了解学科发展动向;具有独立从事科学研究的能力;具有良好的综合素质;能够独立地、创造性地从事科学研究工作,或具有主持较大型科研、技术开发项目,或解决经济、社会发展问题的能力;至少能熟练运用一门外国语撰写科技论文和进行国际学术交流。
3.在科学或专门技术上做出创造性的成果。
三、培养方向按计算机科学与技术一级学科统一招生,按计算机系统结构、计算机软件与理论、计算机应用技术、计算机网络与信息安全等培养博士研究生。
学科培养方向包括:1.计算机系统结构:具体研究方向包括高性能计算机体系结构、嵌入式与容错计算技术、网络体系结构、分布式计算机系统、计算机存储技术、并行计算技术、分布式计算技术、新概念计算技术等;2.计算机软件与理论:具体研究方向计算复杂性理论、计算系统建模理论、算法理论、智能计算理论、程序的形式化理论与编程模型、程序变换方法与技术、新型程序设计方法、可计算性理论、海量信息的理论与方法、软件中间件技术等;3.计算机应用技术:具体研究方向数据库应用技术、多媒体技术、数字图像及音视频处理、虚拟现实技术与系统、计算机视觉、模式识别、计算机仿真技术、嵌入式系统应用、物联网应用、云计算应用、服务计算、社会计算、大规模计算机应用工程化等;4.计算机网络与信息安全:具体研究方向计算机网络理论、网络传输技术、网络管理技术、网络计算技术、计算机网络应用技术、计算机安全技术、软件安全技术、网络安全技术、信息对抗技术、内容安全技术、行为安全技术、信息隐藏与检测以及可信计算技术等。
四、培养模式及学习年限本学科博士研究生主要按一级学科培养,鼓励开展国际联合培养,实行导师或联合导师负责制,负责制订研究生个人培养计划、指导科学研究和学位论文。
北航研究生课程_程序语言设计原理教程_第01章

第4页
1 单主机计算
30年大致可分为以下三个时代。
• 程序设计时代 • 结构化程序设计时代 • 软件工程时代
第5页
程序设计时代
• 55-65头十年是单主机计算形成期。此时的硬件是CPU、内、 外存储器、各种外设。软件的操作系统成熟、并有少量的 库函数和系统支持程序。应用方式是编程计算。应用领域 是大型科学计算和大量数据处理。 • 编译理论、技术成熟、大量高级语言涌现。 • 数据结构算法、可计算理论完善。 • 高级程序设计语言的出现实现了系统程序员和应用程序员 的第一次分工。 • 计算机是科学家的工具,开始人工智能研究。
第22页
续
• 96年网络计算机NC(Network Computer)问世,NC机只 有一个简单的操作系统有接各种多媒体的接口,快 CPU,大内存,好显示器。不设硬盘,不用维护、升 级个人拥有的系统软件和应用软件,可节省大量维护 费。 • 客户端的客户程序越来越简单。除了写一个程序头和 程序尾之外,中间嵌入若干对各种服务器的请求,程 序就编写完了。善于将各服务器的各种功能组织到本 专业的应用(即目标系统)上,提出合理解决方案 (Solution)是网络计算时代应用者的基本素质。
续
• 多媒体与网络通信技术结合为新兴领域发展提供可能, 为基于卫星定位系统和地理信息系统的城市交通控制、 汽车驾驶自动化;停机坪调度;交通安全;军事侦察。 • 多媒体与计算机模拟的综合应用是虚拟现实(Virtual Reality)技术。它使人与虚拟事物交互。虚拟大学、 虚拟商场、虚拟银行、虚拟…将从根本上改变人们的 生活工作方式。
第19页
续
• Internet上有几十万个各种各样的服务器。有些服务器只 提供专用的计算,另一些服务器在全网上提供用户使用 网络的服务。 • 万维网WWW是在Internet网上装上了Web服务器,使每 个站点都认识、传递标准化的主页,使信息畅通无阻。 • 客户与服务器之间遵照超文本传输协议(HTTP)传递信 息。用户要查询某个信息或作计算,他向本机的浏览器 (Browser)指定主页(Homepage)的URL地址,向相应 的Web服务器提出请求。HTTP把URL换成所在服务器上 的文件路径名,并按名找到服务器的主页。如果查出该 名是所在服务器上为客户提供的HTML主页,则Web服务 器把该主页传回客户机。用户即可在自己的屏幕上看到 结果。如果按文件路径名查出的是通用网关接口(CGI)文 件。则该文件由Web服务器“执行”。Web服务器将执行 第20页 结果(以HTML格式)传回请求的客户。
北航国家精品课程嵌入式系统ARM_homeowork

ARM汇编作业具体要求如下:
1.在Linux下编写汇编程序和C程序,或者是内嵌汇编的C程序;然后编译连接成ARM可运行的二进制文件,最后把该二进制文件下载到目标机(教学试验平台)上运行,查看运行结果是否正确。
2.在C程序main函数中,接收用户输入(用户任意输入9个整数),然后在main中调用使用ARM汇编编写的函数(在该函数中完成对这9个整数的排序功能),然后再在C程序main函数中输出这9个排好顺序的整数。
3.作业的提交:把源程序和ARM二进制文件打包成一个zip文件,把该文件提交到课程ftp网站上的homework_1目录下。
文件的命名规则为:学号_1.zip,例如SY0506101_1.zip。
4.作业请务必在5月1日前提交,切记相互之间不要抄袭;否则一经发现将扣除本次作业的分数。
说明:Linux环境下的交叉编译环境(包含ARM汇编连接工具)已放在课程FTP 网站上,同学们可自由下载。
同学们也可以首先在课程ftp网站上下载ADS集成开发环境,在Windows平台上通过软件仿真调试该程序(此时不需要教学试验平台)。
北航计算机考研科目

北航(北京航空航天大学)计算机考研科目包含以下内容,具体要求可能会有一定的变化,建议在报名前查阅北航的招生信息和考试大纲,以获取最新的考试科目和要求。
1.计算机组成原理:涉及计算机硬件系统的结构和功能,包括数字逻辑、处理器设计、存储器层次结构、输入输出系统等。
2.操作系统:重点学习操作系统的基本原理、进程管理、内存管理、文件系统、设备管理、死锁处理等。
3.数据结构与算法:包括常见数据结构(如数组、链表、栈、队列、树、图等)的基本概念、实现方式和常用算法(如排序、查找、图算法等)的设计与分析。
4.计算机网络:涵盖计算机网络的基本概念、协议体系结构、局域网与广域网技术、传输层协议(如TCP和UDP)、网络安全等。
5.数据库系统:学习数据库的基本概念、关系数据库理论、SQL语言、数据库设计与管理、事务处理与并发控制、数据仓库与数据挖掘等。
6.软件工程:重点涉及软件开发过程、需求分析与建模、软件设计原则与方法、软件测试与质量保证、软件项目管理等。
此外,北航计算机考研还可能包括一些选修科目,如人工智能、机器学习、图像处理、编译原理等。
在备考过程中,您可以参考相关教材和资料,系统学习每个科目的基本概念、原理和应用。
北航计算机组成原理讲义-1

指令周期:指令执行的时间,包括取指令、
分析指令、执行指令所需的时间。
机器周期:指令周期按功能分成几个不同的
阶段,每个阶段所需的时间,称为一个机器
周期。比如取指周期,取数周期等。
节拍周期:也是时钟周期,微操作执行的时
间。
时钟脉冲信号:计算机系统的基本定时信号,
是其他时序信号的基准
一个指令周期 = N 个机器周期
Memory)
•运算器+控制器=CPU(Central Process Unit)
计算机组成(2)
存储器
保存程序和数据 存储单元(bit, Byte, Word) 地址的概念(每一个字节单元一个唯一的地址) 存储器的工作方式:读、写 组成:存储体+地址缓冲部件+数据缓冲部件+读写控制部件 存储器的层次:Cache + RAM + Disk + Tape
L64852 MBus control
M-S Adapter
SBus
SBus
DMA
SCSI Ethernet
SBus Cards
STDIO
serial kbd mouse audio RTC
Floppy
计算机的工作原理
❖机器指令:计算机硬件可以执行的表示一种基本操作的 二进制代码。
➢指令格式:操作码 + 操作数(操作数地址) ➢操作码:指明指令的操作性质 ➢操作数(地址):指令操作数的位置(或操作数本身)
指令的执行过程:微操作
Q AC Q
Q 微Q操作:计算机可以完成的最基D 本
B的D操作,一条机器指令的执行可以
AND
AC + B
AC
解释为一系列的微操作的执行
A B 操AN作D 性质:对数据进行某种处ALU理
北航研究生数值分析编程大作业1

数值分析大作业一、算法设计方案1、矩阵初始化矩阵[]501501⨯=ij a A 的下半带宽r=2,上半带宽s=2,设置矩阵[][]5011++s r C ,在矩阵C 中检索矩阵A 中的带内元素ij a 的方法是:j s j i ij c a ,1++-=。
这样所需要的存储单元数大大减少,从而极大提高了运算效率。
2、利用幂法求出5011λλ,幂法迭代格式:0111111nk k k k kk T k k k u R y u u Ay y u ηηβ------⎧∈⎪⎪=⎪=⎨⎪=⎪⎪=⎩非零向量 当1210/-≤-k k βββ时,迭代终止。
首先对于矩阵A 利用幂法迭代求出一个λ,然后求出矩阵B ,其中I A B λ-=(I 为单位矩阵),对矩阵B 进行幂法迭代,求出λ',之后令λλλ+'='',比较的大小与λλ'',大者为501λ,小者为1λ。
3、利用反幂法求出ik s λλ,反幂法迭代格式:0111111nk k k k kk T k k k u R y u Au y y u ηηβ------⎧∈⎪⎪=⎪=⎨⎪=⎪⎪=⎩非零向量 当1210/-≤-k k βββ时,迭代终止,1s k λβ=。
每迭代一次都要求解一次线性方程组1-=k k y Au ,求解过程为:(1)作分解LU A =对于n k ,...,2,1=执行[][]s k n r k k k i c c c c c n s k k k j c cc c k s ks k t k s k r i t t s t i k s k i k s k i js j t k s j r k t t s t k j s j k j s j k <+++=-=++=-=+++----=++-++-++-++----=++-++-++-∑∑);,min(,...,2,1/)(:),min(,...,1,:,1,11),,1max(,1,1,1,11),,1max(,1,1,1(2)求解y Ux b Ly ==,(数组b 先是存放原方程组右端向量,后来存放中间向量y))1,...,2,1(/)(:/:),...,3,2(:,1),min(1.1.11),1max(,1--=-===-=+++-++-+--=++-∑∑n n i c x c b x c b x n i b c b b i s t n s i i t t s t i i i ns n n ti r i t t s t i i i使用反幂法,直接可以求得矩阵按模最小的特征值s λ。
北航计算机研究生考试科目

北航计算机研究生考试科目
北航计算机研究生考试科目包括以下几个科目:
1. 数学:包括高等数学和线性代数等数学基础知识。
2. 英语:包括英语阅读、写作、听力和口语等英语能力测试。
3. 数据结构与算法:测试考生对数据结构和算法的理解和应用能力。
4. 操作系统:测试考生对操作系统原理、进程管理、内存管理和文件系统等知识的掌握程度。
5. 计算机网络:测试考生对计算机网络的基本原理、协议和网络安全等方面的理解。
6. 数据库:测试考生对数据库基本概念、SQL语言、数据库
设计和数据处理等知识的掌握程度。
7. 编程语言:测试考生对一种或多种编程语言的掌握程度,如
C、C++、Java等。
8. 计算机组成原理:测试考生对计算机硬件组成和工作原理的了解。
9. 软件工程:测试考生对软件工程的基本概念、软件开发流程和项目管理等知识的理解。
10. 数据挖掘和机器学习:测试考生对数据挖掘和机器学习的
基本概念、算法和应用等方面的了解。
具体考试科目可能根据不同学校和不同专业的要求有所差异。
考生在复习备考时应结合招生简章和考试大纲进行全面的准备。
北航计算机研究生专业课考试大纲

北航计算机研究生专业课考试大纲
卓越考研
/ 卓而优越则成
一、考试组成
961计算机专业技术基础共包括三门课程的内容:计算机组成原理、操作系统、计算机网络技术,分别占60分,50分、40分。
二、计算机组成原理部分的考试大纲(60分)
(一)指定参考书
1、计算机组成与设计—硬件/软件接口,中文第3版,郑伟民等译,机械工业出版社,2007.4,ISBN 978-7-111-20214-1。
(二)复习内容
1. 理解单处理器计算机系统中各部件的内部工作原理、组成结构以及相互连接方式,具有
完整的计算机系统的整机概念。
2. 理解计算机系统层次化结构概念,熟悉硬件与软件之间的界面,
掌握以MIPS为代表的R
ISC指令集体系结构的基本知识。
3. 能够对有关计算机硬件系统中的理论和实际问题进行计算与分析;能根据指令语义进行
单周期/多周期数据通路及其控制器的简单设计;能对MIPS汇编程序设计语言的相关问题进行分析。
一、计算机系统概述
(一)计算机系统层次结构
1. 计算机系统的基本组成
2. 计算机硬件的基本组成
3. 计算机软件和硬件的关系
4. 计算机的工作过程
(二)计算机性能指标
吞吐量、响应时间、带宽、延迟;CPU时钟周期、主频、CPI、CPU执行时间;MIPS、MFLOPS、GFLOPS、TFLOPS、PFLOPS。
二、数据的表示和运算
(一)数制与编码
1. 进位计数制及其相互转换
2. 真值和机器数
1。
北京航空航天大学算法设计与分析试题答案(软件)

2006-2007学年第二学期《计算机算法设计与分析》试题院系:软件学院专业:软件工程年级:2004级一.简答题(共10分)略二.计算题(35分)1. (6 分)对下列各组函数f(n)和g(n),确定f(n)=O(g(n))或f(n)= Q(g(n))或f(n)=8 (g(n))。
(1)f(n)=3n, g(n)=2n2(2)f(n)=log n + 5, g(n)=log n(3)f(n)=log n, g(n尸J n咨:(1)f(n) = Q(g(n)) (2 分)(2)f(n) = 9(g(n)) (2 分)(3)f(n) = O(g(n)) (2 分)2. (8分)采用动态规划策略,计算a= {5,-37-4,-5,9,-2,10,-3,2}的最大子段和, 并给出这个最大子段和的起始下标和终止下标。
[设数组a中的元素下标从1开始。
]要求给出过程。
答:b[1]=5;b[2]=max{b[1]+a[2] , a[2]}=max{2,-3}=2b[3]=max{b[2]+a[3] , a[3]}=max{9,7}=9b[4]=max{b[3]+a[4] , a[4]}=max{5,-4}=5b[5]=max{b[4]+a[5] , a[5]}=max{0,-5}=0b[6]=max{b[5]+a[6] , a[6]}=max{9,9}=9b[7]=max{b[6]+a[7] , a[7]}=max{7,-2}=7b[8]=max{b[7]+a[8] , a[8]}=max{17,10}=17b[9]=max{b[8]+a[9] , a[9]}=max{14,-3}=14b[10]=max{b[9]+a[10] , a[10]}=max{16,2}=16(上述每两行1分,共5分)最大子段和为17 (1分)(若数组下标从1开始)起始下标:6 (1分),终止下标:8 (1分)(若数组下标从0开始)起始下标:5 ( 0.5分),终止下标:7 (0.5分)3 .(11分)设有3件工作分配给3个人,将工作i分配给第j个人所花的费用为C ij,现将为每一个人都分配1件不同的工作,并使总费用达到最小。
北航研究生数值分析作业第二题

北航研究生数值分析作业第二题北航研究生数值分析作业第二题:一、算法设计方案1.按照题目给出的矩阵定义对矩阵A赋初值:对应的函数为a_init();2.对矩阵A进行householder变换,使其拟上三角化:对应的函数为householder();3.输出拟上三角化后的A:对应的函数为aout(int);4.对拟上三角化后的矩阵A使用带双步位移的QR分解法逐次迭代(最大迭代次数L=500),逐个求出其特征值,对应的函数为eigen_a();中间包含两个子程序:calc_mk()和qr_analyze(),分别用来计算矩阵M k和对M k进行QR 分解并得到A k+1;5.输出QR分解过程完毕后的A及求得的特征向量:对应的函数为aout()和eigenvalout();6.对于在第三步中求得的每个实特征值,使用带原点平移的反幂法求出其对应的特征向量,对应的函数为eigenvec();其中包含一个解方程(A-μI)=y k-1的程序段。
这部分也用迭代完成,仍然将最大迭代次数L设置为500;7.输出矩阵A的特征向量,结束计算:对应的函数为eigenvecout()。
算法编译环境:vlsual c++6.0二、源程序如下:#include#include#define N 10 //矩阵阶数;#define EPSL 1.0e-12 //迭代的精度水平;#define L 500 //迭代最大次数;#define OUTPUTMODE 1 //输出格式:0--输出至屏幕,1--输出至文件double a[N][N], a2[N][N], eigen[N][N]; //声明矩阵A;double sa_re[N] = {0}, sa_im[N] = {0}; //声明矩阵的特征值数组;double u_init[N] = {2,1,2,1,2,1,2,1,2,1}; //定义反幂法中使用的初始向量u;//主程序开始;int main(){FILE *p;void a_init();void householder();void equal_zero(double matrix[N][N], int);void eigenvec();int eigen_a();void aout(int);void eigenvalout(int);void eigenvecout(int);if(OUTPUTMODE){p = fopen("Result.txt", "w+");fprintf(p, "计算结果:\n");fclose(p);}a_init(); //对矩阵A进行初始化;householder(); //对矩阵A进行拟上三角化;equal_zero(a, N); //对矩阵A的元素进行归零处理,消除误差;aout(OUTPUTMODE); //输出A;if(eigen_a()) printf("迭代超过最大次数,特征值求解结果可能不正确。
算法设计与分析_北京航空航天大学中国大学mooc课后章节答案期末考试题库2023年

算法设计与分析_北京航空航天大学中国大学mooc课后章节答案期末考试题库2023年1.对如下所示连通无向图【图片】,其最小生成树的权重为【图片】参考答案:232.对如下所示有向图,从【图片】点开始进行深度优先搜索(DFS),搜索时按照字典序遍历某一节点的相邻节点。
在得到的深度优先搜索树中,包含如下哪些类别的边(多选)【图片】参考答案:树边_前向边_后向边_横向边3.在0-1背包问题中,若背包容量为20,5个物品的体积分别为【图片】,价格分别为【图片】。
则该背包能容纳物品的最大总价格为____参考答案:254.设计动态规划算法的一般步骤为____参考答案:问题结构分析→递推关系建立→自底向上计算→最优方案追踪5.给定两个序列分别为“algorithm”和“glorhythm”。
则以下分别为两序列的最长公共子序列和最长公共子串的选项是____参考答案:gorthm thm6.在最长公共子串问题的递推式中,【图片】表示____参考答案:和中以和结尾的最长公共子串的长度7.在支持插入、删除、替换三种操作的最小编辑距离问题中,用【图片】数组来记录编辑方案。
则【图片】数组中的"L","U","LU"分别代表哪种操作___参考答案:插入删除替换/空操作8.字符串“algorithm”到字符串“altruistic”的最小编辑距离为___参考答案:69.数组【图片】中的逆序对个数为____参考答案:510.在上题中,均不在搜索树中的边有哪些____(多选)参考答案:_11.在扇形图(Fan Graph)【图片】中,其邻接表和结构如下第一张图所示。
从顶点【图片】开始进行广度优先搜索(BFS),搜索时按照邻接表顺序遍历某一节点的相邻节点。
得到搜索树如下第二张图,该搜索树并未画全,应从虚线中选择____补全。
(多选)【图片】【图片】参考答案:①_②12.同上题,在扇形图(Fan Graph)【图片】中,其邻接表和结构如下图所示。
北航硕士研究生数值分析大作业一

数值分析—计算实习作业一学院:17系专业:精密仪器及机械姓名:张大军学号:DY14171142014-11-11数值分析计算实现第一题报告一、算法方案算法方案如图1所示。
(此算法设计实现完全由本人独立完成)图1算法方案流程图二、全部源程序全部源程序如下所示#include <iostream.h>#include <iomanip.h>#include <math.h>int main(){double a[501];double vv[5][501];double d=0;double r[3];double uu;int i,k;double mifayunsuan(double *a,double weiyi);double fanmifayunsuan(double *a,double weiyi);void yasuo(double *A,double (*C)[501]);void LUfenjie(double (*C)[501]);//赋值语句for(i=1;i<=501;i++){a[i-1]=(1.64-0.024*i)*sin(0.2*i)-0.64*exp(0.1/i);}//程序一:使用幂方法求绝对值最大的特征值r[0]=mifayunsuan(a,d);//程序二:使用幂方法求求平移λ[0]后绝对值最大的λ,得到原矩阵中与最大特征值相距最远的特征值d=r[0];r[1]=mifayunsuan(a,d);//比较λ与λ-λ[0]的大小,由已知得if(r[0]>r[1]){d=r[0];r[0]=r[1];r[1]=d;}//程序三:使用反幂法求λr[2]=fanmifayunsuan(a,0);cout<<setiosflags(ios::right);cout<<"λ["<<1<<"]="<<setiosflags(ios::scientific)<<setprecision(12)<<r[0]<<endl;cout<<"λ["<<501<<"]="<<setiosflags(ios::scientific)<<setprecision(12)<<r[1]<<endl;cout<<"λ[s]="<<setiosflags(ios::scientific)<<setprecision(12)<<r[2]<<endl;//程序四:求A的与数u最接近的特征值for(k=1;k<40;k++){uu=r[0]+k*(r[1]-r[0])/40;cout<<"最接近u["<<k<<"]"<<"的特征值为"<<setiosflags(ios::scientific)<<setprecision(12)<<fanmifayunsuan(a,uu)<<endl;}//程序五:谱范数的条件数是绝对值最大的特征值除以绝对值最小的特征值的绝对值cout<<"cond(A)2="<<fabs(r[0]/r[2])<<endl;//程序六:A的行列式的值就是A分解成LU之U的对角线的乘积yasuo(a,vv);LUfenjie(vv);uu=1;for(i=0;i<501;i++){uu=uu*vv[2][i];}cout<<"Det(A)="<<uu<<endl;return 1;}double mifayunsuan(double *a,double weiyi){int i,k;double b=0.16;double c=-0.064;double ee,w,v1,v2,mm,sum;double u[501];double y[505]={0};for(i=0;i<501;i++)u[i]=1;//给u赋初值if (weiyi!=0){for (i=0;i<501;i++)a[i]-=weiyi;}ee=1;k=0;//使得初始计算时进入循环语句while(ee>1e-12){mm=0;for(i=0;i<501;i++){mm=mm+u[i]*u[i];}w=sqrt(mm);for(i=0;i<501;i++){y[i+2]=u[i]/w;//注意此处编程与书上不同,之后会解释它的巧妙之处1 }for(i=0;i<501;i++){u[i]=c*y[i]+b*y[i+1]+a[i]*y[i+2]+b*y[i+3]+c*y[i+4];//1显然巧妙之处凸显出来}sum=0;for(i=0;i<501;i++){sum+=y[i+2]*u[i];}v1=v2;v2=sum;//去除特殊情况,减少漏洞if(k==0){k++;}else{ee=fabs(v2-v1)/fabs(v2);}}if (weiyi!=0){for (i=0;i<501;i++)a[i]+=weiyi;}//还原A矩阵return (v2+weiyi);}double fanmifayunsuan(double *a,double weiyi){int i,k;double b=0.16;double c=-0.064;double ee,w,v1,v2,mm,sum;double u[501];double y[501];double C[5][501];void yasuo(double *A,double (*C)[501]);void LUfenjie(double (*C)[501]);void qiuU(double (*C)[501],double *y,double *u);//把A阵压缩到C阵中for(i=0;i<501;i++)u[i]=1;//给u赋初值if (weiyi!=0){for (i=0;i<501;i++)a[i]-=weiyi;}yasuo(a,C);LUfenjie(C);ee=1;k=0; //使得初始计算时进入循环语句while(ee>1e-12){mm=0;for(i=0;i<501;i++){mm=mm+u[i]*u[i];}w=sqrt(mm);for(i=0;i<501;i++){y[i]=u[i]/w;}qiuU(C,y,u);sum=0;for(i=0;i<501;i++){sum+=y[i]*u[i];}v1=v2;v2=sum;//去除特殊情况,减少漏洞if(k==0){k++;}else{ee=fabs(1/v2-1/v1)/fabs(1/v2);}}if (weiyi!=0){for (i=0;i<501;i++)a[i]+=weiyi;}//还原A矩阵return (1/v2+weiyi);}void yasuo(double *A,double (*C)[501]){double b=0.16;double c=-0.064;int i;for(i=0;i<501;i++){C[0][i]=c;C[1][i]=b;C[2][i]=A[i];C[3][i]=b;C[4][i]=c;}}void LUfenjie(double (*C)[501]){int k,t,j;int r=2,s=2;double sum;int minn(int ,int );int maxx(int ,int );for(k=0;k<501;k++){for(j=k;j<=minn(k+s,501-1);j++){if(k==0)sum=0;else{sum=0;for(t=maxx(k-r,j-s);t<k;t++){sum=sum+C[k-t+s][t]*C[t-j+s][j];}}C[k-j+s][j]=C[k-j+s][j]-sum;}for(j=k+1;j<=minn(k+r,501-1);j++){if(k<501-1){if(k==0)sum=0;else{sum=0;for(t=maxx(j-r,k-s);t<k;t++){sum=sum+C[j-t+s][t]*C[t-k+s][k];}}C[j-k+s][k]=(C[j-k+s][k]-sum)/C[s][k];}}}}void qiuU(double (*C)[501],double *y,double *u){int i,t;double b[501];double sum;int r=2,s=2;int minn(int ,int );int maxx(int ,int );for(i=0;i<501;i++){b[i]=y[i];}for(i=1;i<501;i++){sum=0;for(t=maxx(0,i-r);t<i;t++){sum=sum+C[i-t+s][t]*b[t];}b[i]=b[i]-sum;}u[500]=b[500]/C[s][500];for(i=501-2;i>=0;i--){sum=0;for(t=i+1;t<=minn(i+s,500);t++){sum=sum+C[i-t+s][t]*u[t];}u[i]=(b[i]-sum)/C[s][i];}}int minn(int x,int y){int min;if(x>y)min=y;elsemin=x;return min;}int maxx(int b,int c){int max;if(b>c){if(b>0)max=b;elsemax=0;}else{if(c>0)max=c;elsemax=0;}return max;}三、特征值以及的值λ[1]=-1.070011361502e+001 λ[501]=9.724634098777e+000λ[s]=-5.557910794230e-003最接近u[1]的特征值为-1.018293403315e+001最接近u[2]的特征值为-9.585707425068e+000最接近u[3]的特征值为-9.172672423928e+000最接近u[4]的特征值为-8.652284007898e+000最接近u[5]的特征值为-8.0934********e+000最接近u[6]的特征值为-7.659405407692e+000最接近u[7]的特征值为-7.119684648691e+000最接近u[8]的特征值为-6.611764339397e+000最接近u[9]的特征值为-6.0661********e+000最接近u[10]的特征值为-5.585101052628e+000最接近u[11]的特征值为-5.114083529812e+000最接近u[12]的特征值为-4.578872176865e+000最接近u[13]的特征值为-4.096470926260e+000最接近u[14]的特征值为-3.554211215751e+000最接近u[15]的特征值为-3.0410********e+000最接近u[16]的特征值为-2.533970311130e+000最接近u[17]的特征值为-2.003230769563e+000最接近u[18]的特征值为-1.503557611227e+000最接近u[19]的特征值为-9.935586060075e-001最接近u[20]的特征值为-4.870426738850e-001最接近u[21]的特征值为2.231736249575e-002最接近u[22]的特征值为5.324174742069e-001最接近u[23]的特征值为1.052898962693e+000最接近u[24]的特征值为1.589445881881e+000最接近u[25]的特征值为2.060330460274e+000最接近u[26]的特征值为2.558075597073e+000最接近u[27]的特征值为3.080240509307e+000最接近u[28]的特征值为3.613620867692e+000最接近u[29]的特征值为4.0913********e+000最接近u[30]的特征值为4.603035378279e+000最接近u[31]的特征值为5.132924283898e+000最接近u[32]的特征值为5.594906348083e+000最接近u[33]的特征值为6.080933857027e+000最接近u[34]的特征值为6.680354092112e+000最接近u[35]的特征值为7.293877448127e+000最接近u[36]的特征值为7.717111714236e+000最接近u[37]的特征值为8.225220014050e+000最接近u[38]的特征值为8.648666065193e+000最接近u[39]的特征值为9.254200344575e+000cond(A)2=1.925204273902e+003 Det(A)=2.772786141752e+118四、现象讨论在大作业的程序设计过程当中,初始向量的赋值我顺其自然的设为第一个分量为1,其它分量为0的向量,计算结果与参考答案存在很大差别,计算结果对比如下图2所示(左侧为正确结果,右侧为错误结果),导致了我花了很多的时间去检查程序算法。
东北大学《算法设计与分析( 一)》期末考试必备通关指导

东北大学继续教育学院算法设计与分析(一)复习题一、选择题1.算法的复杂性是()的度量,是评价算法优劣的重要依据。
A.时间效率B.算法效率C.空间效率D.输出效率2.衡量一个算法好坏的标准是()。
A.运行速度快B.占用空间少C.时间复杂度低D.代码短3.算法分析的两个主要方面是()。
A.空间复杂度和时间复杂度B.正确性和简单性C.可读性D.程序复杂度4.计算机算法指的是()。
A.计算方法B.排序方法C.解决问题的方法和过程D.调度方法5.多阶段决策问题就是要在可以选择的那些策略中间选取一个()策略使在预定的标准下达到最好的效果。
A.最优B.最差C.平衡D.任意6.下列关于算法的说法中正确的有()个。
(1)求解某一类问题的算法是唯一的;(2)算法必须在有限步操作后停止;(3)算法的每一步操作是明确的,不能有歧义或含义模糊;(4)算法执行后一定产生确定的结果。
7.( )是指算法执行时所需计算机资源的多少,包括运行时间和存储空间两个方面的要求。
A.正确性B.可读性C.效率D.健壮性8.对于简单的输入,输出和赋值语句,执行时间为()。
(1) (n) (n*n) D.都不对9.算法点的空间复杂度是指()。
A.算法在执行过程中所需的计算机存储空间B.算法所处理的数据量C.算法程序中的语句或指令的条数D.算法在执行过程中所需要的临时工作单元数10.算法点的时间复杂度是指()。
A.算法的执行时间B.算法所处理的数据量C.算法程序中的语句或指令的条数D.算法在执行过程中所需要的基本运算次数11.下列哪一种算法不是随机化算法()。
A.遗传算法B.模拟退火算法C.动态规划算法D.模特卡罗算法12.下面不是动态规划算法基本步骤的是()。
A.找出最优解的性质B.构造最优解C.算出最优解D.定义最优解13.下列是动态规划算法基本要素的是()。
A.定义最优解B.构造最优解C.算出最优解D.子问题重叠性质14.采用广度优先策略搜索的算法是()。
北航研究生 算法设计与分析大作业一
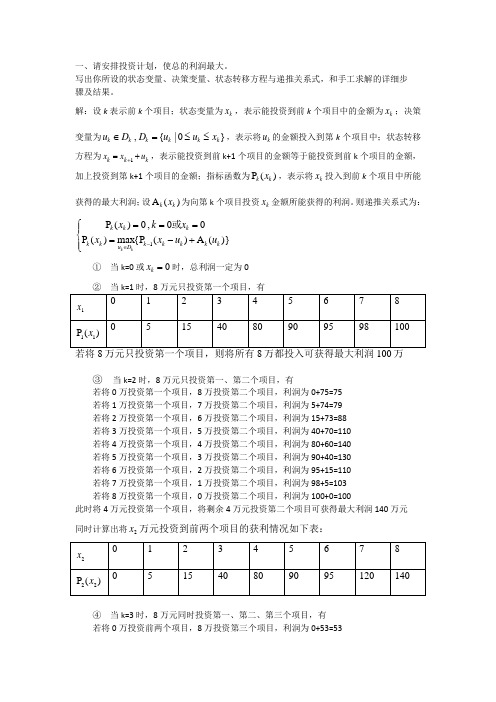
一、请安排投资计划,使总的利润最大。
写出你所设的状态变量、决策变量、状态转移方程与递推关系式,和手工求解的详细步 骤及结果。
解:设k 表示前k 个项目;状态变量为k x ,表示能投资到前k 个项目中的金额为k x ;决策变量为}0|{ , k k k k k k x u u D D u ≤≤=∈,表示将k u 的金额投入到第k 个项目中;状态转移方程为k k k u x x +=+1,表示能投资到前k+1个项目的金额等于能投资到前k 个项目的金额,加上投资到第k+1个项目的金额;指标函数为)(P k k x ,表示将k x 投入到前k 个项目中所能获得的最大利润;设)(A k k x 为向第k 个项目投资k x 金额所能获得的利润。
则递推关系式为:⎪⎩⎪⎨⎧+-====-∈)}(A )({P max )(P 00 , 0)(P 1k k k k k D u kk k k k u u x x x k x k k 或① 当k=0或0=k x 时,总利润一定为0③ 当k=2时,8万元只投资第一、第二个项目,有若将0万投资第一个项目,8万投资第二个项目,利润为0+75=75若将1万投资第一个项目,7万投资第二个项目,利润为5+74=79 若将2万投资第一个项目,6万投资第二个项目,利润为15+73=88 若将3万投资第一个项目,5万投资第二个项目,利润为40+70=110 若将4万投资第一个项目,4万投资第二个项目,利润为80+60=140 若将5万投资第一个项目,3万投资第二个项目,利润为90+40=130 若将6万投资第一个项目,2万投资第二个项目,利润为95+15=110 若将7万投资第一个项目,1万投资第二个项目,利润为98+5=103 若将8万投资第一个项目,0万投资第二个项目,利润为100+0=100此时将4万元投资第一个项目,将剩余4万元投资第二个项目可获得最大利润140万元 同时计算出将2x 万元投资到前两个项目的获利情况如下表:④ 当k=3时,8万元同时投资第一、第二、第三个项目,有 若将0万投资前两个项目,8万投资第三个项目,利润为0+53=53若将1万投资前两个项目,7万投资第三个项目,利润为5+52=57若将2万投资前两个项目,6万投资第三个项目,利润为15+51=66若将3万投资前两个项目,5万投资第三个项目,利润为40+50=90若将4万投资前两个项目,4万投资第三个项目,利润为80+45=125若将5万投资前两个项目,3万投资第三个项目,利润为90+40=130若将6万投资前两个项目,2万投资第三个项目,利润为95+26=121若将7万投资前两个项目,1万投资第三个项目,利润为120+4=124若将8万投资前两个项目,0万投资第三个项目,利润为140+0=140此时将4万元投资第一个项目,将剩余4万元投资第二个项目,第三个项目投资0元,可获得最大利润140万元。
北航算法分析研究生课程3

• Algorithm B
To find a minimum-weight spanning tree T in a weighted, connected network G with N vertices and M edges.
[Initialize] Label all vertices ―unchosen‖; set T ← a network with N vertices and no edges; choose an arbitrary vertex and label it ―chosen‖. Step 1. [Iterate] While there is an unchosen vertex do step 2 od; STOP. Step 2. [Pick a lightest edge] Let (U, V) be a lightest edge between any chosen vertex U and any unchosen vertex V; label V as ―chosen‖; and set T ← T + (U, V). Step 0.
Does it work?
• There are several questions we should ask about this algorithm;
1. Does it always STOP? 2. When it STOPs, is T always a spanning tree of G? 3. Is T guaranteed to be a minimum-weight spanning tree? 4. Is it self-contained (or does it contain hidden, or implicit, sub-algorithms)? 5. Is it efficient?
北航计算机研究生课程-算法设计与分析-HomeWork-1

一、已知下列递推式:C(n) = 1 若n =1= 2C (n/2) + n – 1 若n ≥ 2请由定理1 导出C(n)的非递归表达式并指出其渐进复杂性。
定理1:设a,c 为非负整数,b,d,x 为非负常数,并对于某个非负整数k, 令n=c k , 则以下递推式f(n) =d 若 n=1=af(n/c)+bn x 若 n>=2的解是f(n)= bn x log c n + dn x 若 a=c x f(n)= x x xa x xn c a bc n c a bc d c ⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-+log若 a ≠c x解:令F(n) = C(n) – 1则 F(n) = 0 n=1F(n) = 2C(n/2) + n – 2 n>=2= 2[F(n/2) + 1] + n – 2= 2F(n/2) + n利用定理1,其中:d=0,a=2,c=2,b=1,x=1,并且a=c x所以 F(n) = nlog 2n所以 C(n) = F(n) + 1 = nlog 2n + 1C(n)的渐进复杂性是O(nlog 2n)二、由于Prim 算法和Kruskal 算法设计思路的不同,导致了其对不同问题实例的效率对比关系的不同。
请简要论述:1、如何将两种算法集成,以适应问题的不同实例输入;2、你如何评价这一集成的意义?答:1、Prim 算法基于顶点进行搜索,所以适合顶点少边多的情况。
Kruskal 从边集合中进行搜索,所以适合边少的情况。
根据输入的图中的顶点和边的情况,边少的选用kruskal 算法,顶点少的选用prim 算法2、没有一个算法是万能的,没有一个算法是对所有情况都适合的。
这一集成体现了针对具体问题选用最适合的方法,即具体问题具体分析的哲学思想。
三、分析以下生成排列算法的正确性和时间效率:HeapPermute (n )//实现生成排列的Heap 算法//输入:一个正正整数n和一个全局数组A[1..n]//输出:A中元素的全排列if n = 1write Aelsefor i ←1 to n doHeapPermute(n-1)if n is oddswap A[1]and A[n]else swap A[i]and A[n]解:n=1时,输出a1n=2时,输出a1a2,a2a1n=3时,(1)第一次循环i=1时,HeapPermute(2)将a1a2做完全排列输出,记为[a1a2]a3,并将A变为a2a1a3,并交换1,3位,得a3a1a2(2)第二次循环i=2时,HeapPermute(2)输出[a3a1]a2,并将A变为a1a3a2,交换1,3位,得a2a3a1(3)第三次循环i=3时,HeapPermute(2)输出[a2a3]a1,并将A变为a3a2a1,交换1,3位,得a1a2a3,即全部输出完毕后数组A回到初始顺序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、已知下列递推式:
C(n) = 1若n =1
= 2C (n/2) + n – 1 若n ≥ 2
请由定理1 导出C(n)的非递归表达式并指出其渐进复杂性。
定理1:设a,c 为非负整数,b,d,x 为非负常数,并对于某个非负整数k, 令n=c k , 则以下递推式
f(n) =d 若 n=1
=af(n/c)+bn x 若 n>=2
的解是
f(n)= bn x log c n + dn x 若 a=c x f(n)= x x x
a x x
n c a bc n c a bc d c ⎪⎪⎭
⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-+log 若 a ≠c x 解:令F(n) = C(n) – 1
则 F(n) = 0 n=1
F(n) = 2C(n/2) + n – 2 n>=2
= 2[F(n/2) + 1] + n – 2
= 2F(n/2) + n
利用定理1,其中:
d=0,a=2,c=2,b=1,x=1,并且a=c x
所以 F(n) = nlog 2n
所以 C(n) = F(n) + 1 = nlog 2n + 1
C(n)的渐进复杂性是O(nlog 2n)
二、由于Prim 算法和Kruskal 算法设计思路的不同,导致了其对不同问题实例的效率对比关系的不同。
请简要论述:
1、如何将两种算法集成,以适应问题的不同实例输入;
2、你如何评价这一集成的意义?
答:
1、Prim 算法基于顶点进行搜索,所以适合顶点少边多的情况。
Kruskal 从边集合中进行搜索,所以适合边少的情况。
根据输入的图中的顶点和边的情况,边少的选用kruskal 算法,顶点少的选用prim 算法
2、没有一个算法是万能的,没有一个算法是对所有情况都适合的。
这一集成体现了针对具体问题选用最适合的方法,即具体问题具体分析的哲学思想。
三、分析以下生成排列算法的正确性和时间效率:
HeapPermute (n )
//实现生成排列的Heap 算法
//输入:一个正正整数n 和一个全局数组A [1..n ]
//输出:A 中元素的全排列
if n = 1
write A
else
for i ←1 to n do
HeapPermute (n -1)
if n is odd
swap A[1]and A[n]
else swap A[i]and A[n]
解:
n=1时,输出a1
n=2时,输出a1a2,a2a1
n=3时,
(1)第一次循环i=1时,HeapPermute(2)将a1a2做完全排列输出,记为
[a1a2]a3,并将A变为a2a1a3,并交换1,3位,得a3a1a2
(2)第二次循环i=2时,HeapPermute(2)输出[a3a1]a2,并将A变为a1a3a2,
交换1,3位,得a2a3a1
(3)第三次循环i=3时,HeapPermute(2)输出[a2a3]a1,并将A变为a3a2a1,
交换1,3位,得a1a2a3,即全部输出完毕后数组A回到初始顺序。
n=4时,
(1)i=1时,HeapPermute(3)输出[a1a2a3]a4,并且a1a2a3顺序不变,交换
1,4位,得a4a2a3a1
(2)i=2时,HeapPermute(3)输出[a4a2a3]a1,并且a4a2a3顺序不变,交换
2,4位,得a4a1a3a2
(3)i=3时,HeapPermute(3)输出[a4a1a3]a2,并且a4a1a3顺序不变,交换
3,4位,得a4a1a2a3
(4)i=4时,HeapPermute(3)输出[a4a1a2]a3,并且a4a1a2顺序不变,交换
4,4位,得a4a1a2a3,即全部输出完毕后数组A循环右移一位。
由以上分析可得出结论:
当n为偶数时,HeapPermute(n)输出全排列后数组元素循环右移一位。
当n为奇数时,HeapPermute(n)输出全排列后数组元素顺序保持不变。
所以由归纳法证明如下:
(1)i=1时,显然成立。
(2)i=k为偶数时,假设输出的是全排列,则i=k+1(奇数)时,k+1次循环中,
每次前k个元素做全排列输出后循环右移一位,所以对换swap A[1]and A[n]可以保证每次将前k个元素中的一个换到k+1的位置,所以k+1次循环后输出的是A[1…k+1]的全排列。
(3)i=k为奇数时,假设输出的是全排列,则i=k+1(偶数)时,k+1次循环中,
每次前k个元素做全排列输出后顺序保持不变,所以对换swap A[i]and A[n]可以保证每次将前k个元素中的一个换到k+1的位置,所以k+1次循环后输出的是A[1…k+1]的全排列。
证毕。
时间复杂度递推公式为T(n) = 1 n=1
= n[ T(n-1)+2 ] n>1
化简得T(n) = n! + O(n n-1)
所以时间复杂度为O(n!) + O(n n-1)
四、对于求n 个实数构成的数组中最小元素的位置问题,写出你设计的具有减治思想算法的伪代码,确定其时间效率,并与该问题的蛮力算法相比较。
解:
(1)算法思想:将n分为[n/2],n-[n/2]([]表示向下取整)两部分,分别找
出其中的最小元及其位置,比较这两个元素的大小,得出总的最小元素的位置。
(2)伪代码:
(x,i) = FindLeastElement(a,b)
//从数组A[a…b]中找出最小元x,及其位置i
//输入:全局实数数组A[1…n],搜索起始位置a,结束位置b
//输出:最小元素x及其位置i
if a==b
return(A[a],a)
else
(x1,i) = FindLeastElement(1,[n/2]);
(x2,j) = FindLeastElement([n/2]+1,n);
if x1<x2
return (x1,i)
else
return (x2,j)
(3)算法复杂度递推公式:F(n) = 1 n=1
= 2F(n/2) n>1
化简:F(n) = 2F(n/2) + 1
= 2[2F(n/22)+1] + 1
= 22F(n/22) + 2 + 1
…
= 2k F(2k/2k) + 1 + 2 + … + 2k-1 ( n=2k)
= 2n-1
所以复杂度为O(2n-1)
蛮力法的复杂度为O(n),所以此方法还没有蛮力法效率高,因为减治后会增加比较次数。
五、请给出约瑟夫斯问题的非递推公式J(n),并证明之。
其中,n 为最初总人数,J(n) 为最后幸存者的最初编号。
解:已知幸存者号码的递推公式:J(1) = 1;
J(2k) = 2J(k) – 1; n=2k
J(2k+1) = 2J(k) + 1; n=2k+1
幸存者号码非递推公式:设n = 2m + b,J(n) = 2*b+1 (0<=b<2m,m>=0)
证明(数学归纳法):
(1)i=1时,m=0,b=0,J(1)=2*b+1=1,成立。
(2)i>1时,
当i为偶数时,设k = i/2时成立,即k = 2m + b,则J(k) = 2b+1,
此时,i = 2k = 2m+1 + 2b
J(i) = J(2k) = 2J(k) – 1 = 2(2b+1) – 1 = 4b + 1 = 2(2b) + 1,
即k=i时成立。
当i为奇数时,设k = (i-1)/2时成立,即k = 2m + b,则J(k) = 2b+1,
此时,i = 2k + 1 = 2m+1 + 2b+1
J(i)= J(2k+1) = 2J(k)+1 = 2(2b+1)+1 = 4b+3 = 2(2b+1)+1,即k=i时成立。
证毕。
