北航研究生算法(2018精心整理)
北京航空航天大学招收攻读2018年博士学位研究生工作管理办法

北京航空航天大学招收攻读2018年博士学位研究生工作管理办法为加强对北京航空航天大学(以下简称北航)招收攻读2018年博士学位研究生(以下简称博士生)工作的管理,提高博士生选拔质量,确保招生工作科学、规范、公平和安全,依据《中华人民共和国教育法》、《中华人民共和国高等教育法》和《中华人民共和国学位条例》,参照《教育部办公厅关于做好2017年招收攻读博士学位研究生工作的通知》(教学厅〔2017〕2号)和《2014年招收攻读博士学位研究生工作管理办法》(教学〔2014〕4号)有关规定,制定本管理办法。
第一章总则第一条北航招收攻读博士学位研究生是为了培养德智体全面发展、掌握本学科坚实宽广的基础理论和系统深入的专门知识、具有独立从事科学研究工作能力、在科学或专门技术上做出创造性成果的高级专门人才。
第二条博士生招生应坚持社会主义办学方向,为培养社会主义合格建设者和可靠接班人挑选好苗子;坚持科学选拔,积极探索并遵循高层次专业人才选拔规律,采用多样化的考察方式方法,确保生源质量;坚持公平公正,做到政策透明、程序公正、结果公开、监督机制健全,维护考生的合法权益;坚持以人为本,增强服务意识,耐心解释招生政策、认真回答考生问题;统筹考虑学校发展及学科布局,坚持绩效优先的原则,优先保证生源充足、培养质量高、绩效好的学科专业和研究方向招生。
第三条招生专业及导师以学校公布的招生专业目录为准。
第四条招生对象为符合有关学籍、学历、学位要求的中华人民共和国公民。
第五条博士录取类别按就业方式分为定向就业和非定向就业两种,按学习方式分为全日制和非全日制两种,工程博士与高级研修中心专项博士学习方式为非全日制。
第六条博士生招生考试分为初试和复试两个阶段,初试和复试都是博士研究生招生考试的重要组成部分。
招生方式包括本科直博、硕博连读、申请考核与普通招考。
本科直博是指具有推荐免试攻读研究生资格的优秀应届本科毕业生,免除初试,直接进行复试考核的招生方式。
北航研究生数值分析作业第一题

北航研究⽣数值分析作业第⼀题北航研究⽣数值分析作业第⼀题:⼀、算法设计⽅案1.要求计算矩阵的最⼤最⼩特征值,通过幂法求得模最⼤的特征值,进⾏⼀定判断即得所求结果;2.求解与给定数值接近的特征值,可以该数做漂移量,新数组特征值倒数的绝对值满⾜反幂法的要求,故通过反幂法即可求得;3.反幂法计算时需要⽅程求解中间过渡向量,需设计Doolite分解求解;4.|A|=|B||C|,故要求解矩阵的秩,只需将Doolite分解后的U矩阵的对⾓线相乘即为矩阵的Det。
算法编译环境:vlsual c++6.0需要编译函数:幂法,反幂法,Doolite分解及⽅程的求解⼆、源程序如下:#include#include#include#includeint Max(int value1,int value2);int Min(int value1,int value2);void Transform(double A[5][501]);double mifa(double A[5][501]);void daizhuangdoolite(double A[5][501],double x[501],double b[501]); double fanmifa(double A[5][501]); double Det(double A[5][501]);/***定义2个判断⼤⼩的函数,便于以后调⽤***/int Max(int value1,int value2){return((value1>value2)?value1:value2);}int Min(int value1,int value2){return ((value1}/*****************************************//***将矩阵值转存在⼀个数组⾥,节省空间***/void Transform(double A[5][501],double b,double c){int i=0,j=0;A[i][j]=0,A[i][j+1]=0;for(j=2;j<=500;j++)A[i][j]=c;i++;j=0;A[i][j]=0;for(j=1;j<=500;j++)A[i][j]=b;i++;for(j=0;j<=500;j++)A[i][j]=(1.64-0.024*(j+1))*sin(0.2*(j+1))-0.64*exp(0.1/(j+1)); i++;for(j=0;j<=499;j++)A[i][j]=b;A[i][j]=0;i++;for(j=0;j<=498;j++)A[i][j]=c;A[i][j]=0,A[i][j+1]=0;}/***转存结束***///⽤于求解模最⼤的特征值,幂法double mifa(double A[5][501]){int s=2,r=2,m=0,i,j;double b2,b1=0,sum,u[501],y[501];for (i=0;i<=500;i++){u[i] = 1.0;}do{sum=0;if(m!=0)b1=b2;m++;for(i=0;i<=500;i++)sum+=u[i]*u[i];for(i=0;i<=500;i++)y[i]=u[i]/sqrt(sum);for(i=0;i<=500;i++){u[i]=0;for(j=Max(i-r,0);j<=Min(i+s,500);j++)u[i]=u[i]+A[i-j+s][j]*y[j];}b2=0;for(i=0;i<=500;i++)b2=b2+y[i]*u[i];}while(fabs(b2-b1)/fabs(b2)>=exp(-12));return b2;}//带状DOOLITE分解,并且求解出⽅程组的解void daizhuangdoolite(double A[5][501],double x[501],double b[501]) { int i,j,k,t,s=2,r=2;double B[5][501],c[501];for(i=0;i<=4;i++){for(j=0;j<=500;j++)B[i][j]=A[i][j];}for(i=0;i<=500;i++)c[i]=b[i];for(k=0;k<=500;k++){for(j=k;j<=Min(k+s,500);j++){for(t=Max(0,Max(k-r,j-s));t<=k-1;t++)B[k-j+s][j]=B[k-j+s][j]-B[k-t+s][t]*B[t-j+s][j]; }for(i=k+1;i<=Min(k+r,500);i++){for(t=Max(0,Max(i-r,k-s));t<=k-1;t++)B[i-k+s][k]=B[i-k+s][k]-B[i-t+s][t]*B[t-k+s][k]; B[i-k+s][k]=B[i-k+s][k]/B[s][k];}}for(i=1;i<=500;i++)for(t=Max(0,i-r);t<=i-1;t++)c[i]=c[i]-B[i-t+s][t]*c[t];x[500]=c[500]/B[s][500];for(i=499;i>=0;i--){x[i]=c[i];for(t=i+1;t<=Min(i+s,500);t++)x[i]=x[i]-B[i-t+s][t]*x[t];x[i]=x[i]/B[s][i];}}//⽤于求解模最⼤的特征值,反幂法double fanmifa(double A[5][501]){int s=2,r=2,m=0,i;double b2,b1=0,sum=0,u[501],y[501];for (i=0;i<=500;i++){u[i] = 1.0;}do{if(m!=0)b1=b2;m++;sum=0;for(i=0;i<=500;i++)sum+=u[i]*u[i];for(i=0;i<=500;i++)y[i]=u[i]/sqrt(sum);daizhuangdoolite(A,u,y);b2=0;for(i=0;i<=500;i++)b2+=y[i]*u[i];}while(fabs(b2-b1)>=fabs(b1)*exp(-12));return 1/b2;}//⾏列式的LU分解,U的主线乘积即位矩阵的DET double Det(double A[5][501]) {int i,j,k,t,s=2,r=2;for(k=0;k<=500;k++){for(j=k;j<=Min(k+s,500);j++){for(t=Max(0,Max(k-r,j-s));t<=k-1;t++)A[k-j+s][j]=A[k-j+s][j]-A[k-t+s][t]*A[t-j+s][j];}for(i=k+1;i<=Min(k+r,500);i++){for(t=Max(0,Max(i-r,k-s));t<=k-1;t++)A[i-k+s][k]=A[i-k+s][k]-A[i-t+s][t]*A[t-k+s][k];A[i-k+s][k]=A[i-k+s][k]/A[s][k];}}double det=1;for(i=0;i<=500;i++)det*=A[s][i];return det;}void main(){double b=0.16,c=-0.064,p,q;int i,j;double A[5][501];Transform(A,b,c); //进⾏A的赋值cout.precision(12); //定义输出精度double lamda1,lamda501,lamdas;double k=mifa(A);if(k>0) //判断求得最⼤以及最⼩的特征值.如果K>0,则它为最⼤特征值值,//并以它为偏移量再⽤⼀次幂法求得新矩阵最⼤特征值,即为最⼤ //与最⼩的特征值的差{lamda501=k;for(i=0;i<=500;i++)A[2][i]=A[2][i]-k;lamda1=mifa(A)+lamda501;for(i=0;i<=500;i++)A[2][i]=A[2][i]+k;}else //如果K<=0,则它为最⼩特征值值,并以它为偏移量再⽤⼀次幂法//求得新矩阵最⼤特征值,即为最⼤与最⼩的特征值的差{lamda1=k;for(i=0;i<=500;i++)A[2][i]=A[2][i]-k;lamda501=mifa(A)+lamda1;for(i=0;i<=500;i++)A[2][i]=A[2][i]+k;}lamdas=fanmifa(A);FILE *fp=fopen("result.txt","w");fprintf(fp,"λ1=%.12e\n",lamda1);fprintf(fp,"λ501=%.12e\n",lamda501);fprintf(fp,"λs=%.12e\n\n",lamdas);fprintf(fp,"\t要求接近的值\t\t\t实际求得的特征值\n");for(i=1;i<=39;i++) //反幂法求得与给定值接近的特征值{p=lamda1+(i+1)*(lamda501-lamda1)/40;for(j=0;j<=500;j++)A[2][j]=A[2][j]-p;q=fanmifa(A)+p;for(j=0;j<=500;j++)A[2][j]=A[2][j]+p;fprintf(fp,"µ%d: %.12e λi%d: %.12e\n",i,p,i,q);}double cond=fabs(mifa(A)/fanmifa(A));double det=Det(A);fprintf(fp,"\ncond(A)=%.12e\n",cond);fprintf(fp,"\ndetA=%.12e\n",det);}三、程序运⾏结果λ1=-1.069936345952e+001λ501=9.722283648681e+000λs=-5.557989086521e-003要求接近的值实际求得的特征值µ1: -9.678281104107e+000 λi1: -9.585702058251e+000µ2: -9.167739926402e+000 λi2: -9.172672423948e+000µ3: -8.657198748697e+000 λi3: -8.652284007885e+000µ4: -8.146657570993e+000 λi4: -8.0934********e+000µ5: -7.636116393288e+000 λi5: -7.659405420574e+000µ6: -7.125575215583e+000 λi6: -7.119684646576e+000µ7: -6.615034037878e+000 λi7: -6.611764337314e+000µ8: -6.104492860173e+000 λi8: -6.0661********e+000µ9: -5.593951682468e+000 λi9: -5.585101045269e+000µ10: -5.0834********e+000 λi10: -5.114083539196e+000µ11: -4.572869327058e+000 λi11: -4.578872177367e+000µ12: -4.062328149353e+000 λi12: -4.096473385708e+000µ13: -3.551786971648e+000 λi13: -3.554211216942e+000µ14: -3.0412********e+000 λi14: -3.0410********e+000µ15: -2.530704616238e+000 λi15: -2.533970334136e+000µ16: -2.020*********e+000 λi16: -2.003230401311e+000µ17: -1.509622260828e+000 λi17: -1.503557606947e+000µ18: -9.990810831232e-001 λi18: -9.935585987809e-001µ19: -4.885399054182e-001 λi19: -4.870426734583e-001µ20: 2.200127228676e-002 λi20: 2.231736249587e-002µ21: 5.325424499917e-001 λi21: 5.324174742068e-001µ22: 1.043083627697e+000 λi22: 1.052898964020e+000µ23: 1.553624805402e+000 λi23: 1.589445977158e+000µ24: 2.064165983107e+000 λi24: 2.060330427561e+000µ25: 2.574707160812e+000 λi25: 2.558075576223e+000µ26: 3.0852********e+000 λi26: 3.080240508465e+000µ27: 3.595789516221e+000 λi27: 3.613620874136e+000µ28: 4.106330693926e+000 λi28: 4.0913********e+000µ29: 4.616871871631e+000 λi29: 4.603035354280e+000µ30: 5.127413049336e+000 λi30: 5.132924284378e+000µ31: 5.637954227041e+000 λi31: 5.594906275501e+000µ32: 6.148495404746e+000 λi32: 6.080933498348e+000µ33: 6.659036582451e+000 λi33: 6.680354121496e+000µ34: 7.169577760156e+000 λi34: 7.293878467852e+000µ35: 7.680118937861e+000 λi35: 7.717111851857e+000µ36: 8.190660115566e+000 λi36: 8.225220016407e+000µ37: 8.701201293271e+000 λi37: 8.648665837870e+000µ38: 9.211742470976e+000 λi38: 9.254200347303e+000µ39: 9.722283648681e+000 λi39: 9.724634099672e+000cond(A)=1.925042185755e+003detA=2.772786141752e+118四、分析如果初始向量选择不当,将导致迭代中X1的系数等于零.但是,由于舍⼊误差的影响,经若⼲步迭代后,.按照基向量展开时,x1的系数可能不等于零。
北航计算机研究生课程算法设计及解析总结

一、解:第 k 月的需求量 Nk(k=1,2,3,4)状量 Xk:第 k 月初的存量, X1=X5=0,0≤Xk≤ Nk+⋯+N4决策量 Uk:第 k 月的生量, max{0, Nk-Xk} ≤ Uk≤min{6 ,Nk+⋯+N4 - Xk}状移方程: X = Uk + Xk – Nkk+1第 k 月的成本 Vk = *(Xk - Nk) Uk=03 + Uk + *(Uk + Xk - Nk) Uk ≠ 0F k(Xk) 是由第 k 月初的存量 Xk 开始到第 4 月份束段的最成本F k(Xk) = min{Vk + F k+1(X k+1 )}1≤k≤4= min{ 3 + Uk + *(Uk + Xk - Nk) + F k+1(Uk + Xk - Nk) }Uk≠0min{ *(Xk - Nk) + F k+1(Xk - Nk) }Uk=0F5(X5)=0四个月内的最成本F1 (X1)=F 1(0)算步以下:(1) k=40≤X4≤4,max{0,4 - X4}≤U4≤min{6,4-X4}X4 U4 X5 V4 F5(X5) V4 + F5(X5)0 4 0 7 0 7=F4(0)1 3 0 6 0 6=F4(1)2 2 0 5 0 5=F (2)43 1 04 0 4=F4(3)4 0 0 0 0 0=F4(4)即于状 X4 的每个取,都有唯一确定的决策量U4 使得 F4(X4) 最(2) k=30≤X3≤6,max{0,2 - X3} ≤U3≤min{6 , 6-X3}X3 U3 X4 V3 F4(X4) V3 + F4(X4) 0 2 0 5 7 123 1 64 2 85 135 3 46 4 11 0 11=F3(0)1 1 0 4 7 112 1 63 2 7 5 124 3 42 5 4 10 0 10=F3(1) 0 0 0 7 7=F (2)31 1 62 2 6 5 113 3 43 4 4 9 0 90 1 6 =F (3)31 2 5 5 102 3 44 3 4 8 0 80 2 1 5 6=F (4)31 3 42 4 7 0 75 0 3 4 =F3 (5)1 4 6 0 66 0 4 3 0 2=F3(6)(3) k=2 时0≤X2≤9,max{0,3 - X2}≤U2≤min{6,9-X2}X2 U2 X3 V2 F3(X3) V2 + F 3(X3) 0 3 0 6 11 174 1 105 2 9 7 16=F (0)26 3 171 2 0 5 11 163 1 104 2 8 7 15=F2(1)5 3 166 4 11 6 172 1 0 4 11 152 1 103 2 7 7 14=F (2)24 3 155 4 106 166 5 173 0 0 0 11 11=F (3)21 1 102 2 6 7 133 3 144 4 9 6 155 5 166 6 12 2 144 0 1 10 =F (4)21 2 5 7 132 3 133 4 8 6 144 5 155 6 11 2 135 0 2 1 7 8=F (5)21 3 122 4 7 6 133 5 144 6 10 2 126 0 3 8=F (6)21 4 6 6 122 5 133 6 9 2 117 0 4 2 6 8=F (7)21 5 122 6 8 2 108 0 5 8=F2(8)9 1 6 7 2 90 6 3 2 5=F (9)2(4) k=1X1=0,max{0,2} ≤U1≤min{6 , 11}X1 U1 X2 V1 F2(X2) V1 + F2(X2) 0 2 0 5 16 213 1 154 2 8 14 225 3 11 =F1 (0)6 4 11由以上算可得, 4 个月的最成本 F (0) = ( 千元 )1从 k=1 回溯,可得最果中各段的状量Xk 和决策量 Uk 以下表:月份 k 量 Uk 月初存量 Xk 需求量 Nk 每个月成本Vk1 5 0 22 03 3 03 6 0 2 114 0 4 4 0二、解:1、变量设定段 k:已遍 k 个点, k=1,2 ⋯ 6,7 。
2018北京航空航天大学计算机学院考研复试通知复试时间复试分数线复试经验

2018北京航空航天大学计算机学院考研复试通知复试时间复试分数线复试经验启道考研网快讯:2018年考研复试即将开始,启道教育小编根据根据考生需要,整理2017年北京航空航天大学计算机学院考研复试细则,仅供参考:一、复试科目(启道考研复试辅导班)二、复试通知(启道考研复试辅导班)三、复试分数线(启道考研复试辅导班)四、复试流程(启道考研复试辅导班)关于考研复试流程及调剂,启道考研复试辅导班老师解析如下图:五、初试高分为何被刷?初试定资格,复试定结果。
考研初试高分除了保证你能进复试之外,录取是根本无法保证的,这也凸显了复试的重要性。
启道考研复试辅导班建议大家熟读复试注意事项,避免高分被刷情况发生。
1、导师喜欢综合能力更强的学生不少初试高分落榜者会认为“复试有黑幕,存在暗箱操作”。
其实不然,启道考研辅导班帮你找找个人原因。
学生的综合素质对其未来发展是很重要的,面试的目的其实就是想通过直接接触学生来全面地权衡学生的综合素质。
在面试的过程中,评委老师主要会有以下几个考察点:专业知识、运用专业知识的能力、分析研究问题的潜力、逻辑思维能力、语言表达能力以及非语言表达能力。
因为复试直接是人与人打交道,因此高分落榜有很大的人为因素,这种人为因素主要体现在学生的思维活跃性、课外阅读量以及知识延展等方面,“导师一想到你以后将与他三年共事,哪怕你考试考得再好,但你是个书呆子,他怎么会要你?2、复试权重高于初试初试定资格,复试定结果。
换言之,过了笔试线,只是给了你一张船票,但它并不能送你走到最后。
随着研究生招生录取的不断改革,复试的权重越来越高于初试,2017年很多学校的复试比例在1:1.2-1:1.6之间,有些专业硕士甚至达到1:3,这意味着如果录取10人的话,面试者可能是30人,导师的选择性也越来越大。
因此考生在备考时,必须得努力拓展自己的专业知识面。
为了避免各位机械工程学院考研生出现高分被刷的遗憾,启道考研复试辅导班带领大家一起熟悉考研复试的五大禁忌:一、全面了解复试内容大学复试前招生院校会有通知,复试内容一般包括专业课笔试、外语听说能力等,不少院校也将心理测评放到复试的内容当中,与此同时,举止表达和礼仪等方面也在考查范围之内。
北航计算机考研经验

北航计算机考研经验我报的是计算机专硕,不分方向。
初试347分,其中政治72,英语67,数学114,专业课94。
2018年专硕复试线290分/学硕310分;我347分排在第60多名(ps:由于非全日制满足校线的才两人,所以专硕划分比较低,同时由于专硕报名人数多,导致后面复试会刷掉很多专硕,以及分数较低的会调剂到非全日制)。
首先谈初试,北航计算机无论学硕还是专硕考试科目都是一样的。
公共课为英语一、数学一、政治;专业课代码是961,包含组成原理,操作系统和计算机网络三门。
数学一:我大概2017年寒假就下定决心考研了,寒假的时候就在家里看高数书,记笔记。
作为过来人,我不推荐学弟学妹刚开始复习时就自己啃高数书,首先是这些知识点是大一学的,很多都记不清了,自己看书理解可能不会很深刻,其次是高数书比较无聊,会出现看不下去的情况,导致复习时事倍功半。
但是我当时没有及时发现这个问题,直到5月份参加了一次数学模考,发现自己做题时根本就不懂题目考点,在请教一些同学后才开始改过来,在5、6、7月开始疯狂地补数学视频,重新做数学笔记。
所以我的第一个经验就是:学习数学时,最好一边看数学辅导视频,一边做笔记,看完一章后,做相应的辅导习题(高数十八讲、全书等)。
数学150分,是一个特别容易拉分的学科,也是整个考研期间不间断学习的学科,整体时间分配大概是暑假前完成高数十八讲以及线性代数和概率论的基础。
暑假期间属于高数强化阶段做1000题或者660题,并弄清每个题目的考点。
然后9月开始(最迟10月,不然真题训练量不够)开始做数学真题、8套卷、四套卷,并可以将真题的错误记录在改错本上。
同时留出3套左右的试卷,以便在11、12月份自己进行模拟考试。
数学考试在考研第二天08:30~11:30,三个小时的时间。
所以学弟学妹们在学习数学时,也尽量拿上午的时间来学习。
英语一:英语是我的弱项,我英语四级考了两次才过。
但是学弟学妹们不要慌,只要把英语的得分点弄明白然后专攻得分点,也能拿到不错的成绩。
北航机械工程及自动化学院2018年研究生招生方案

北航机械工程及自动化学院2018年研究生招生方案一、机械学院复试资格基本线根据2018年硕士研究生招生初试成绩统计结果和各学科招生规模情况,经机械学院研究生招生工作领导小组讨论决定,2018年硕士研究生招生复试资格基本线如下:考试方式一志愿报考专业[专业代码]总分单科单科(满分=100分)(满分>100分)全国统考(不含少数民族骨干计划和退役大学生计划)机械工程[080200]3104060材料加工工程[080503]3104060航空宇航制造工程[082503]3104060机械工程(专业学位)[085201]2904060强军计划无退役大学生计划说明:初试各项成绩(包括总分、政治、外国语、业务课1和业务课2)达到报考第一志愿专业:机械学院复试资格基本线的考生可参加机械学院复试。
机械学院不接收一志愿未报考本院考生的调剂申请。
上线学生自动获得一志愿报考专业复试资格,学院不再单独通知,名单见附件4。
二、机械学院硕士研究生复试工作小组组长:丁希仑副组长:蔡军成员:边宇枢、李刘合、李东升、陈华伟、杨民、刘静华、陈殿生、郑联语秘书:乐悦三、机械学院硕士研究生思政考核工作小组由学院分党委委员、党员系所主任、系所党支部书记组成,名单如下:组长:邓怡成员:丁希仑、蔡军、周正干、李东升、于靖军、从保强、边宇枢、吴琼、李刘合、郭伟、孟宝、陈华伟、彭翀、杨民、文力、刘静华、宫浩钦、陈殿生、王巍、郑联语、杜福洲四、体检通知复试考生由北航校医院统一组织体格检查,详情查询北航校医院主页公告通知栏:体检表由校医院统一发放,请带好现金131元、一寸照片与签字笔。
校医院安排机械学院考生在3月17日体检。
因北航全校上线考生较多,报考机械学院的在京考生推荐在3月11日(周日)参加体检,尽量避开体检高峰。
考生体检报告收取时间:3月19日-3月21日,地点:新主楼A828,体检不合格者不予录取。
五、复试资格审查机械学院按照北航研招网上公布的“2018年硕士研究生招生复试资格基本线及复试规定”要求,对考生的复试资格进行严格审查。
(完整word版)北航研究生算法设计与分析Assignment_2

用分支定界算法求以下问题:某公司于乙城市的销售点急需一批成品,该公司成品生产基地在甲城市。
甲城市与乙城市之间共有n 座城市,互相以公路连通。
甲城市、乙城市以及其它各城市之间的公路连通情况及每段公路的长度由矩阵M1 给出。
每段公路均由地方政府收取不同额度的养路费等费用,具体数额由矩阵M2 给出。
请给出在需付养路费总额不超过1500 的情况下,该公司货车运送其产品从甲城市到乙城市的最短运送路线。
具体数据参见文件:m1.txt: 各城市之间的公路连通情况及每段公路的长度矩阵(有向图); 甲城市为城市Num.1,乙城市为城市Num.50。
m2.txt: 每段公路收取的费用矩阵(非对称)。
思想:利用Floyd算法的基本方法求解。
程序实现流程说明:1.将m1.txt和m2.txt的数据读入两个50×50的数组。
2.用Floyd算法求出所有点对之间的最短路径长度和最小费用。
3.建立一个堆栈,初始化该堆栈。
4.取出栈顶的结点,检查它的相邻的所有结点,确定下一个当前最优路径上的结点,被扩展的结点依次加入堆栈中。
在检查的过程中,如果发现超出最短路径长度或者最小费用,则进行”剪枝”,然后回溯。
5.找到一个解后,保存改解,然后重复步骤4。
6.重复步骤4、5,直到堆栈为空,当前保存的解即为最优解。
时间复杂度分析:Floyd算法的时间复杂度为3O N,N为所有城市的个数。
()该算法的时间复杂度等于DFS的时间复杂度,即O(N+E)。
其中,E为所有城市构成的有向连通图的边的总数。
但是因为采用了剪枝,会使实际运行情况的比较次数远小于E。
求解结果:算法所得结果:甲乙之间最短路线长度是:464最短路线收取的费用是:1448最短路径是:1 3 8 11 15 21 23 26 32 37 39 45 47 50C源代码(注意把m1.txt与m2.txt放到与源代码相同的目录下,下面代码可直接复制运行):#include<stdlib.h>#include<stdio.h>#include<time.h>#include<string.h>#define N 50#define MAX 52void input(int a[N][N],int b[N][N]);void Floyd(int d[N][N]);void fenzhi(int m1[N][N],int m2[N][N],int mindist[N][N],int mincost[N][N]);int visited[N],bestPath[N];void main(){clock_t start,finish;double duration;int i,j,mindist[N][N],mincost[N][N],m1[N][N],m2[N][N]; /* m1[N][N]和m2[N][N]分别代表题目所给的距离矩阵和代价矩阵*/// int visited[N],bestPath[N];FILE *fp,*fw;// system("cls");time_t ttime;time(&ttime);printf("%s",ctime(&ttime));start=clock();for(i=0;i<N;i++){visited[i]=0;bestPath[i]=0;}fp=fopen("m1.txt","r"); /* 把文件中的距离矩阵m1读入数组mindist[N][N] */if(fp==NULL){printf("can not open file\n");return;}for(i=0;i<N;i++)for(j=0;j<N;j++)fscanf(fp,"%d",&mindist[i][j]);fclose(fp); /* 距离矩阵m1读入完毕*/fp=fopen("m2.txt","r"); /* 把文件中的代价矩阵m2读入数组mincost[N][N] */if(fp==NULL){printf("can not open file\n");return;}for(i=0;i<N;i++)for(j=0;j<N;j++)fscanf(fp,"%d",&mincost[i][j]);fclose(fp); /* 代价矩阵m2读入完毕*/input(m1,mindist); /* mindist[N][N]赋值给m1[N][N],m1[N][N]代表题目中的距离矩阵*/input(m2,mincost); /* mincost[N][N]赋值给m2[N][N],m2[N][N]代表题目中的代价矩阵*/for(i=0;i<N;i++) /* 把矩阵mindist[i][i]和mincost[i][i]的对角元素分别初始化,表明城市到自身不连通,代价为0 */{mindist[i][i]=9999;mincost[i][i]=0;}Floyd(mindist); /* 用弗洛伊德算法求任意两城市之间的最短距离,结果存储在数组mindist[N][N]中*//*fw=fopen("1.txt","w");for(i=0;i<N;i++){for(j=0;j<N;j++)fprintf(fw,"%4d ",mindist[i][j]);fprintf(fw,"\n");}fclose(fw);// getchar();//*/Floyd(mincost); /* 用弗洛伊德算法求任意两城市之间的最小代价,结果存储在数组mincost[N][N]中*//*fw=fopen("2.txt","w");for(i=0;i<N;i++){for(j=0;j<N;j++)fprintf(fw,"%4d ",mincost[i][j]);fprintf(fw,"\n");}fclose(fw);// getchar();//*/fenzhi(m1,m2,mindist,mincost); /* 调用分支定界的实现函数,寻找出所有的可行路径并依次输出*/finish=clock();duration = (double)(finish - start) / CLOCKS_PER_SEC;printf( "%f seconds\n", duration );//*/}void Floyd(int d[N][N]) /* 弗洛伊德算法的实现函数*/{int v,w,u,i;for(u=0;u<N;u++){for(v=0;v<N;v++){for(w=0;w<N;w++)if(d[v][u]+d[u][w]<d[v][w]){//printf("v,w,u,d[v][u],d[u][w],d[v][w] %d %d %d %d %d %d",v+1,w+1,u+1,d[v][u],d[u][w],d[v][ w]);getchar();d[v][w]=d[v][u]+d[u][w];}}}}void input(int a[N][N],int b[N][N]) /* 把矩阵b赋值给矩阵a */{int i,j;for(i=0;i<N;i++)for(j=0;j<N;j++)a[i][j]=b[i][j];}void fenzhi(int m1[N][N],int m2[N][N],int mindist[N][N],int mincost[N][N]){int stack[MAX],depth=0,next,i,j; /* 定义栈,depth表示栈顶指针;next指向每次遍历时当前所处城市的上一个已经遍历的城市*/int bestLength,shortestDist,minimumCost,distBound=9999,costBound=9999;int cur,currentDist=0,currentCost=0; /* cur指向当前所处城市,currentDist和currentCost分别表示从甲城市到当前所处城市的最短距离和最小代价,currentDist和currentCost初值为0表示从甲城市出发开始深度优先搜索*/stack[depth]=0; /* 对栈进行初始化*/stack[depth+1]=0;visited[0]=1; /* visited[0]=1用来标识从甲城市开始出发进行遍历,甲城市已被访问*/while(depth>=0) /* 表示遍历开始和结束条件,开始时从甲城市出发,栈空,depth=0;结束时遍历完毕,所有节点均被出栈,故栈也为空,depth=0 *//* 整个while()循环体用来实现从当前的城市中寻找一个邻近的城市*/{cur=stack[depth]; /* 取栈顶节点赋值给cur,表示当前访问到第cur号城市*/ next=stack[depth+1]; /* next指向当前所处城市的上一个已经遍历的城市*/for(i=next+1;i<N;i++) /* 试探当前所处城市的每一个相邻城市*/{if((currentCost+mincost[cur][N-1]>costBound)||(currentDist+mindist[cur][N-1]>=distBound)){ /* 所试探的城市满足剪枝条件,进行剪枝*///printf("here1 %d %d %d %d %d %d %d\n",cur,currentCost,mincost[cur][49],costBound,curre ntDist,mindist[cur][49],distBound); getchar();//printf("%d %d %d %d %d %d",cur,i,m1[cur][i],currentCost,mincost[cur][49],costBound); getchar();continue;}if(m1[cur][i]==9999) continue; /* 所试探的城市不连通*/if(visited[i]==1) continue; /* 所试探的城市已被访问*/if(i<N) break; /* 所试探的城市满足访问条件,找到新的可行城市,终止for循环*/ }if(i==N) /* 判断for循环是否是由于搜索完所有城市而终止的,如果是(i==N),进行回溯*/{// printf("here");getchar();depth--;currentDist-=m1[stack[depth]][stack[depth+1]];currentCost-=m2[stack[depth]][stack[depth+1]];visited[stack[depth+1]]=0;}else /* i!=N,表示for循环的终止是由于寻找到了当前城市的一个可行的邻近城市*/{//printf("%d %d %d %d %d %d\n",cur,i,m1[stack[depth]][i],m2[stack[depth]][i],currentCost,curre ntDist);//getchar();currentDist+=m1[stack[depth]][i]; /* 把从当前所处城市到所找到的可行城市的距离加入currentDist */currentCost+=m2[stack[depth]][i]; /* 把从当前所处城市到所找到的可行城市的代价加入currentCost */depth++; /* 所找到的可行城市进栈*/stack[depth]=i; /* 更新栈顶指针,指向所找到的可行城市*/stack[depth+1]=0;visited[i]=1; /* 修改所找到的城市的访问标志*/if(i==N-1) /* i==N-1表示访问到了乙城市,完成了所有城市的一次搜索,找到一条通路*/{// printf("here\n");for(j=0;j<=depth;j++) /* 保存当前找到的通路所经过的所有节点*/ bestPath[j]=stack[j];bestLength=depth; /* 保存当前找到的通路所经过的所有节点的节点数*/shortestDist=currentDist; /* 保存当前找到的通路的距离之和*/minimumCost=currentCost; /* 保存当前找到的通路的代价之和*///costBound=currentCost;distBound=currentDist; /* 更新剪枝的路径边界,如果以后所找到的通路路径之和大于目前通路的路径之和,就剪枝*/if(minimumCost>1500) continue; /* 如果当前找到的通路的代价之和大于1500,则放弃这条通路*/printf("最短路径:%3d,路径代价:%3d,所经历的节点数目:%3d,所经历的节点如下:\n",shortestDist,minimumCost,bestLength+1); /* 输出找到的通路的结果*/bestPath[bestLength]=49;for(i=0;i<=bestLength;i++) /* 输出所找到的通路所经过的具体的节点*/ printf("%3d ",bestPath[i]+1);(完整word版)北航研究生算法设计与分析Assignment_2 printf("\n");depth--; /* 连续弹出栈顶的两个值,进行回溯,开始寻找新的可行的通路*/currentDist-=m1[stack[depth]][stack[depth+1]];currentCost-=m2[stack[depth]][stack[depth+1]];visited[stack[depth+1]]=0;depth--;currentDist-=m1[stack[depth]][stack[depth+1]];currentCost-=m2[stack[depth]][stack[depth+1]];visited[stack[depth+1]]=0;// getchar();}}}}。
北航研究生数值分析编程大作业1

数值分析大作业一、算法设计方案1、矩阵初始化矩阵[]501501⨯=ij a A 的下半带宽r=2,上半带宽s=2,设置矩阵[][]5011++s r C ,在矩阵C 中检索矩阵A 中的带内元素ij a 的方法是:j s j i ij c a ,1++-=。
这样所需要的存储单元数大大减少,从而极大提高了运算效率。
2、利用幂法求出5011λλ,幂法迭代格式:0111111nk k k k kk T k k k u R y u u Ay y u ηηβ------⎧∈⎪⎪=⎪=⎨⎪=⎪⎪=⎩非零向量 当1210/-≤-k k βββ时,迭代终止。
首先对于矩阵A 利用幂法迭代求出一个λ,然后求出矩阵B ,其中I A B λ-=(I 为单位矩阵),对矩阵B 进行幂法迭代,求出λ',之后令λλλ+'='',比较的大小与λλ'',大者为501λ,小者为1λ。
3、利用反幂法求出ik s λλ,反幂法迭代格式:0111111nk k k k kk T k k k u R y u Au y y u ηηβ------⎧∈⎪⎪=⎪=⎨⎪=⎪⎪=⎩非零向量 当1210/-≤-k k βββ时,迭代终止,1s k λβ=。
每迭代一次都要求解一次线性方程组1-=k k y Au ,求解过程为:(1)作分解LU A =对于n k ,...,2,1=执行[][]s k n r k k k i c c c c c n s k k k j c cc c k s ks k t k s k r i t t s t i k s k i k s k i js j t k s j r k t t s t k j s j k j s j k <+++=-=++=-=+++----=++-++-++-++----=++-++-++-∑∑);,min(,...,2,1/)(:),min(,...,1,:,1,11),,1max(,1,1,1,11),,1max(,1,1,1(2)求解y Ux b Ly ==,(数组b 先是存放原方程组右端向量,后来存放中间向量y))1,...,2,1(/)(:/:),...,3,2(:,1),min(1.1.11),1max(,1--=-===-=+++-++-+--=++-∑∑n n i c x c b x c b x n i b c b b i s t n s i i t t s t i i i ns n n ti r i t t s t i i i使用反幂法,直接可以求得矩阵按模最小的特征值s λ。
北航招收2018年学历硕士研究生招生简章

北航招收2018年学历硕士研究生招生简章一、拟招生人数2018年北京航空航天大学(以下简称北航)拟计划招收约6400名各类学历硕士研究生,其中全日制学习方式约3400名,非全日制学习方式约3000名,最终名额以教育部下达为准。
我校硕士研究生拟接收校内外推荐免试生约1700名,以最终实际录取人数为准。
招生工作坚持“公开、公平、公正”、全面衡量、择优录取、宁缺毋滥的基本原则。
二、报考条件与要求报考我校考生须符合《2018年全国硕士研究生招生工作管理规定》(教学〔2017〕9号)的规定(可登录/查询),且满足以下相应的的报考条件及要求。
(一)推荐免试经本科毕业学校(具有开展推免工作资格的高校)选拔并确认资格的推免生,需按照《北航接收推荐免试攻读2018年研究生(含直博生)相关要求》完成各项流程。
(二)全国统考1.学业水平符合下列条件之一的考生,可报考北京航空航天大学并且参加全国统一考试:(1)具有国家承认的大学本科毕业学历的人员(截止到现场确认前,须在“中国高等教育学生信息网”(网址/)可查询本科毕业的学历信息)。
(2)国家承认学历的应届本科毕业生(含普通高校、成人高校、普通高校举办的成人高等学历教育应届本科毕业生)及自学考试和网络教育届时可毕业的本科生,必须在2018年9月1日前取得国家承认的本科毕业证书。
(3)已获硕士学位或博士学位的人员。
(4)已经获得国家承认学历的本科结业生(即现场确认前登录/,在中国高等教育学生信息网查询结果为本科结业),可按本科毕业生同等学力身份报考。
(5)获得国家承认的高职高专毕业学历,经2年或2年以上(2016年9月1日以前获得国家承认学历的高职高专毕业证书),并同时满足以下两个条件的考生,可按大学本科毕业生同等学力资格报考:a.在全日制普通高等学校辅修过所报专业本科的全部主干课程(需加盖辅修学校教务处公章);b.在所报考专业领域的有关核心期刊上以第一作者发表过一篇(含)以上文章。
考研攻略——北京航空航天大学软件学院考研初试总结

考研攻略——北京航空航天大学软件学院考研初试总结本人本科北航软院,2018考研,报考北航软院学硕,总分375,政治56,英语一68,数学一114,专业课137,比起各400分大佬还差了不少,不过考研过程中也算是有点总结,希望分享出来给大家做做参考,如有不妥之处请指出。
闲话不多说,直接进入正题。
数学相信大家都知道数学在考研中的地位,基本上得数学者得高分吧,毕竟150的总分在那里摆着,我就是因为数学只有114才没能得到高分。
数学复习主要有以下几点:尽早开始(大三下期尽可能把第一遍过完,推荐用李永乐)套题很重要!速度很重要!训练后期训练以套题为主。
刷真题!(凡是真题中出现过的知识点,不会的或是记得不清的,一定要去复习清楚)除了李永乐,张宇的教材也建议买(我想很多人报班上万都舍得,多买几本书应该是没有问题的),因为个人感觉张宇的教材在某些知识点有独特的讲解很有收获。
但是张宇那三本不用全刷,在后续的复习过程中,一旦有某块知识有问题,就把张宇和李永乐的对应内容都可以看看,加深印象。
从九月份开始就可以进入刷套题的阶段了,严格控制时间非常有必要,因为考场环境下因为各种因素你的做题速度很可能比不上平时的状态。
平时尽量训练到自己能在两个半小时内完成套题,或者说训练自己在两个半小时内使自己的分数最大化。
这时候可以根据个人能力选择几天一套题,我才开始大概是两天一套,第一天早上做,第二天早上复习做错的知识点。
大概用了一个多月把数一的所有考研真题刷完了。
后面还做了李永乐和张宇的各种模拟题卷试卷的完成顺序也可以根据自己的擅长进行调整,比如我就觉得概率最容易做,其次高数,最后线代,所以我的试卷完成顺序是选题题—–>概率大题—–>高数大题—–>线代大题这个顺序只是提供参考,但是有时候好的顺序真的能帮你多拿分,就比如我高考那一年的理综,我一般做理综先生物后化学最后物理,事实证明是非常正确的,因为14年的四川理综卷,物理题很难,最后一道大题全省只有两三个人得了满分。
2018年北京航空航天大学考研复试-北航人文社会科学学院考研复试科目复试分数线复试参考书复试经验

2018年北京航空航天大学考研复试-北航人文社会科学学院考研复试科目复试分数线复试参考书复试经验启道考研网快讯:2018年考研复试即将开始,启道教育小编根据根据考生需要,整理2017年北京航空航天大学人文社会科学学院考研复试细则,仅供参考:一、复试科目(启道考研复试辅导班)考试科目单元考试科目代码考试科目名称第一门考试科目101 思想政治理论第二门考试科目201 英语一第三门考试科目713 自然辩证法概论第四门考试科目813 科学技术史二、复试通知(启道考研复试辅导班)一、复试组织管理在学校研究生招生工作领导小组领导下,学院成立研究生招生复试工作小组(以下简称“学院工作小组”),负责制订学院复试工作具体方案并组织实施,指导复试小组进行相应考核工作。
组长:郑晓齐副组长:李亚梅赵世奎张德辉吴铭心成员:雷庆、胡象明、方卫华、徐治立、沈映春、邓丽芳、章琰、谢凌玲秘书:李厚之按照专业类别,成立复试小组,在学院工作小组指导下具体实施笔试、面试考核工作。
二、复试工作原则坚持社会主义办学方向,坚持科学选拔,坚持公平公正,坚持全面考查、突出重点,坚持客观评价,坚持以人为本、增强服务意识。
三、复试资格基本线和拟录取人数根据学校相关规定和我院各学科专业招生规模情况,经学院研究生招生工作小组讨论决定,四、复试时间和地点各专业具体复试时间如下:公共管理专业硕士(MPA)复试考生, 3 月 19 日上午 8:00到教学区主M楼402报到,交验相关材料,通知笔试和面试地点。
其他专业所有复试考生,复试当天上午8:00到教学区图书馆西配楼二层(高等教育研究院)报到,交验相关材料,通知笔试和面试地点。
五、复试内容复试采取差额形式,差额比例一般不低于120%。
复试包括笔试和面试。
各专业面试内容均包括思想政治情况考核、英语口语和听力测试、专业素质考察三部分。
每名复试考生的面试时间总计不少于20分钟,其中,思想政治情况考核5分钟,英语口语和听力测试5分钟,专业素质考察不少于10分钟。
北航研究生历年分数线

北航研究生历年分数线北京航空航天大学(简称北航)是国内一所著名的理工类综合性大学,其在研究生招生中也是众多院校中的佼佼者。
每年,多数考生都会考虑申请北航研究生,实习和就业市场普遍需要北航毕业生,使得北航成为各类考生的向往之地。
然而,要想申请到这样的一所学校,首先要了解北航研究生的分数线,以便安排自己的学习安排。
那今天,我们就一起梳理一下北航研究生历年分数线的变化情况吧。
写作练习一、2018年2018年北航研究生录取专业分数线在历年上有所变化,有些是向上提高,有些则是下降,具体如下:1.理科学与工程:本科学分总分不低于3.3,专业学分不低于3.0;2.空宇航学:本科学分总分不低于3.2;3.制理论与控制工程:本科学分总分不低于3.0,专业学分不低于2.8;4.进制造工程:本科学分总分不低于3.0,专业学分不低于2.8;5.能机器人:本科学分总分不低于3.2,专业学分不低于2.8;6.算机自动化:本科学分总分不低于3.2,专业学分不低于2.8;7.空航天科学与技术:本科学分总分不低于3.2,专业学分不低于2.8。
二、2019年2019年,北航研究生的分数线有所变化,与2018年相比,有些分数线有所提高,有些分数线有所降低,具体如下:1.理科学与工程:本科总分不低于3.5,专业学分不低于3.2;2.空宇航学:本科学分总分不低于3.4;3.制理论与控制工程:本科学分总分不低于3.2,专业学分不低于3.0;4.进制造工程:本科学分总分不低于3.2,专业学分不低于3.0;5.能机器人:本科学分总分不低于3.4,专业学分不低于3.0;6.算机自动化:本科学分总分不低于3.4,专业学分不低于3.0;7.空航天科学与技术:本科学分总分不低于3.4,专业学分不低于3.0。
三、2020年2020年,由于新型冠状病毒的爆发,原定的研究生招生计划也受到一定的影响,北航研究生的分数线也有所改变,与2019年的分数线相比,有些分数率得到提高以及下降,具体如下:1.理科学与工程:本科总分不低于3.6,专业学分不低于3.3;2.空宇航学:本科学分总分不低于3.3;3.制理论与控制工程:本科学分总分不低于3.2,专业学分不低于3.1;4.进制造工程:本科学分总分不低于3.3,专业学分不低于3.1;5.能机器人:本科学分总分不低于3.3,专业学分不低于3.1;6.算机自动化:本科学分总分不低于3.3,专业学分不低于3.1;7.空航天科学与技术:本科学分总分不低于3.3,专业学分不低于3.1。
北京航空航天大学2018年MPAcc(非全日制)复试

北京航空航天大学2018年MPAcc(非全日制)复试北航经济管理学院始建于1956年,是我国理工科大学中最早成立的管理类院系之一。
学院设有9个系、5个校级研究中心,科研实力雄厚;是全国唯一拥有2个省部级重点实验室、3个省部级实验基地、首个拥有973首席科学家的管理学院。
经历60年的黾勉发展,经济管理学院形成了“尚学敏行、求真拓新”为核心的文化价值观,积累了雄厚的科研实力,在学科建设和人才培养等多方面取得了卓越的成果。
北航会计硕士专业学位(Master of Professional Accounting,简称MPAcc,专业代码:125300会计)教育旨在培养适应我国社会主义市场经济发展和经济全球化的需要,具备良好的政治思想素质和高尚的会计职业道德素养,系统掌握现代会计学基本理论及相关领域的知识和技能,具有开阔的国际视野、较强的专业实战能力、能够创造性的适应大中型企业、政府事业等决策部门需要的应用型高级会计专门人才。
依托我校管理科学工程学术优势、工商管理学科的案例教学与开发特色,会计硕士专业学位主要设置“财务会计与信息化”和“公司理财与资本运营”两个研究专业方向,并根据专业方向开设相应的特色课程。
复试北航为自主确定复试分数线的学校。
初试(即联考)成绩满足北航复试基本要求的考生须参加复试。
复试采取差额形式,差额比例一般不低于120%。
,复试不合格考生不予录取。
1.复试时间:通常在3月中下旬左右进行。
2.复试具体要求:请于2017年3月上旬登录北航研究生招生信息网、北航经管学院官网查询。
3.复试内容:①政治笔试。
②专业课笔试,闭卷。
考试执行MPAcc教指委专业课复试阶段指导性大纲(含中高级财务会计学、财务管理学和审计学),具体考试范围和考试参考书目可于2018年1月初上北航经管学院官网进行查询。
③英语听力和英语口语面试。
④面试:对考生的综合素质和能力进行测评(个人面试)。
4.考生在复试时除复试通知书(北航研究生招生信息网上下载,无须盖章)外,还须携带以下材料(请考生按照以下顺序装订成册),材料齐全方可参加面试及复试:(1)本人第二代居民身份证(应届本科毕业生还需持本人学生证)原件及复印件三份(正反面请复印在同一张A4纸上);(2)体格检查表。
北航计算机研究生课程-算法设计与分析-HomeWork-1

一、已知下列递推式:C(n) = 1 若n =1= 2C (n/2) + n – 1 若n ≥ 2请由定理1 导出C(n)的非递归表达式并指出其渐进复杂性。
定理1:设a,c 为非负整数,b,d,x 为非负常数,并对于某个非负整数k, 令n=c k , 则以下递推式f(n) =d 若 n=1=af(n/c)+bn x 若 n>=2的解是f(n)= bn x log c n + dn x 若 a=c x f(n)= x x xa x xn c a bc n c a bc d c ⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-+log若 a ≠c x解:令F(n) = C(n) – 1则 F(n) = 0 n=1F(n) = 2C(n/2) + n – 2 n>=2= 2[F(n/2) + 1] + n – 2= 2F(n/2) + n利用定理1,其中:d=0,a=2,c=2,b=1,x=1,并且a=c x所以 F(n) = nlog 2n所以 C(n) = F(n) + 1 = nlog 2n + 1C(n)的渐进复杂性是O(nlog 2n)二、由于Prim 算法和Kruskal 算法设计思路的不同,导致了其对不同问题实例的效率对比关系的不同。
请简要论述:1、如何将两种算法集成,以适应问题的不同实例输入;2、你如何评价这一集成的意义?答:1、Prim 算法基于顶点进行搜索,所以适合顶点少边多的情况。
Kruskal 从边集合中进行搜索,所以适合边少的情况。
根据输入的图中的顶点和边的情况,边少的选用kruskal 算法,顶点少的选用prim 算法2、没有一个算法是万能的,没有一个算法是对所有情况都适合的。
这一集成体现了针对具体问题选用最适合的方法,即具体问题具体分析的哲学思想。
三、分析以下生成排列算法的正确性和时间效率:HeapPermute (n )//实现生成排列的Heap 算法//输入:一个正正整数n和一个全局数组A[1..n]//输出:A中元素的全排列if n = 1write Aelsefor i ←1 to n doHeapPermute(n-1)if n is oddswap A[1]and A[n]else swap A[i]and A[n]解:n=1时,输出a1n=2时,输出a1a2,a2a1n=3时,(1)第一次循环i=1时,HeapPermute(2)将a1a2做完全排列输出,记为[a1a2]a3,并将A变为a2a1a3,并交换1,3位,得a3a1a2(2)第二次循环i=2时,HeapPermute(2)输出[a3a1]a2,并将A变为a1a3a2,交换1,3位,得a2a3a1(3)第三次循环i=3时,HeapPermute(2)输出[a2a3]a1,并将A变为a3a2a1,交换1,3位,得a1a2a3,即全部输出完毕后数组A回到初始顺序。
北京航空航天大学2018年学历硕士研究生各招收专业、学院、学制、学习方式及学费标准
2.5 2.5 2.5 2.5 2.5 2.5 2.5ห้องสมุดไป่ตู้2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5
全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制
8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000 8000
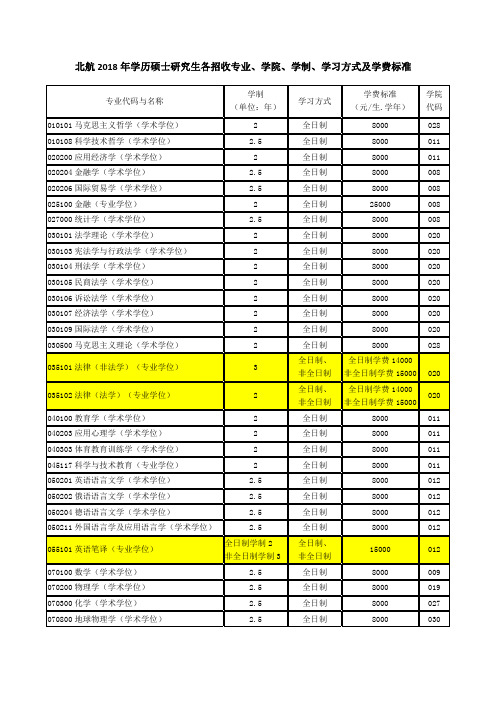
北航 2018 年学历硕士研究生各招收专业、学院、学制、学习方式及学费标准
专业代码与名称 010101 马克思主义哲学(学术学位) 010108 科学技术哲学(学术学位) 020200 应用经济学(学术学位) 020204 金融学(学术学位) 020206 国际贸易学(学术学位) 025100 金融(专业学位) 027000 统计学(学术学位) 030101 法学理论(学术学位) 030103 宪法学与行政法学(学术学位) 030104 刑法学(学术学位) 030105 民商法学(学术学位) 030106 诉讼法学(学术学位) 030107 经济法学(学术学位) 030109 国际法学(学术学位) 030500 马克思主义理论(学术学位) 035101 法律(非法学)(专业学位) 035102 法律(法学)(专业学位) 040100 教育学(学术学位) 040203 应用心理学(学术学位) 040303 体育教育训练学(学术学位) 045117 科学与技术教育(专业学位) 050201 英语语言文学(学术学位) 050202 俄语语言文学(学术学位) 050204 德语语言文学(学术学位) 050211 外国语言学及应用语言学(学术学位) 055101 英语笔译(专业学位) 070100 数学(学术学位) 070200 物理学(学术学位) 070300 化学(学术学位) 070800 地球物理学(学术学位) 学制 (单位:年) 2 2.5 2 2.5 2.5 2 2.5 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2.5 2.5 2.5 2.5 全日制学制 2 非全日制学制 3 2.5 2.5 2.5 2.5 学习方式 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制、 非全日制 全日制、 非全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制 全日制、 非全日制 全日制 全日制 全日制 全日制 学费标准 (元/生.学年) 8000 8000 8000 8000 8000 25000 8000 8000 8000 8000 8000 8000 8000 8000 8000 全日制学费 14000 非全日制学费 15000 全日制学费 14000 非全日制学费 15000 8000 8000 8000 8000 8000 8000 8000 8000 15000 8000 8000 8000 8000 020 020 011 011 011 011 012 012 012 012 012 009 019 027 030 学院 代码 028 011 011 008 008 008 008 020 020 020 020 020 020 020 028
北航算法分析研究生课程3

• Algorithm B
To find a minimum-weight spanning tree T in a weighted, connected network G with N vertices and M edges.
[Initialize] Label all vertices ―unchosen‖; set T ← a network with N vertices and no edges; choose an arbitrary vertex and label it ―chosen‖. Step 1. [Iterate] While there is an unchosen vertex do step 2 od; STOP. Step 2. [Pick a lightest edge] Let (U, V) be a lightest edge between any chosen vertex U and any unchosen vertex V; label V as ―chosen‖; and set T ← T + (U, V). Step 0.
Does it work?
• There are several questions we should ask about this algorithm;
1. Does it always STOP? 2. When it STOPs, is T always a spanning tree of G? 3. Is T guaranteed to be a minimum-weight spanning tree? 4. Is it self-contained (or does it contain hidden, or implicit, sub-algorithms)? 5. Is it efficient?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一:判断题1、一个正确的算法,对于每个合法输入,都会在有限的时间内输出一个满足要求的结果。
(对)2、NP完全问题比其他所有NP问题都要难。
(错)3、回溯法用深度优先法或广度优先法搜索状态空间树。
(错,仅深度优先)4、在动态规划中,各个阶段所确定的策略就构成一个策略序列,通常称为一个决策。
(错)5、P类和NP类问题的关系用P⊂NP来表示是错误的。
(错)6、若近似算法A求解某极小化问题一实例的解为Sa,且已知该问题的最优解为Sa/3,则该近似算法的性能比为3。
(错)7、通常来说,算法的最坏情况的时间复杂行比平均情况的时间复杂性容易计算。
(对)8、若P2多项式时间转化为(polynomial transforms to)P1,则P2至少与P1一样难。
(错)9、快速排序算法的平均时间复杂度是O(nlogn),使用随机化快速排序算法可以将平均时间复杂度降得更低。
(错)10、基于比较的寻找数组A[1,…,n]中最大元素的问题下届是Ω(n/3)。
(错)11、O(f(n))+O(g(n))=O(min{f(n),g(n)})(错)12、若f(n)=Ω(g(n)),g(n)=Ω(h(n)),则f(n)=Ω(h(n))(对)13、若f(n)=O(g(n)),则g(n)=Ω(f(n))(对)14、贪婪技术所做的每一步选择所产生的部分解,不一定是可行性的。
(错)15、LasVegas算法只要给出解就是正确的。
(对)16、一个完全多项式近似方案是一个近似方案{Aε},其中每一个算法Aε在输入实例I的规模的多项式时间内运行。
(错)二:简答1、二叉查找树属于减治策略的三个变种中的哪一个的应用?什么情况下二叉查找树表现出最差的效率?此时的查找和插入算法的复杂性如何?答:减治策略有3个主要的变种,包括减常量、减常数因子和减可变规模。
(1) 二叉查找树属于减可变规模变种的应用。
(2) 当先后插入的关键字有序时,构成的二叉查找树蜕变为单支树,树的深度等于n,此时二叉查找树表现出最差的效率,(3) 查找和插入算法的时间效率都属于Θ(n)。
2、何谓伪多项式算法?如何将一Monte Carlo算法转化为Las Vegas算法?答:若一个数值算法的时间复杂度可以表示为输入数值N的多项式,但其运行时间与输入数值N的二进制位数呈指数增长关系,则称其时间复杂度为伪多项式时间。
Las Vegas算法不会得到不正确的解。
一旦用拉斯维加斯算法找到一个解,这个解就一定是正确解。
但有时用拉斯维加斯算法找不到解。
Monte Carlo算法每次都能得到问题的解,但不保证所得解的准确性转化:可以在Monte Carlo算法给出的解上加一个验证算法,如果正确就得到解,如果错误就不能生成问题的解,这样Monte Carlo算法便转化为了Las Vegas算法。
3、构造AVL树和2-3树的主要目的是什么?它们各自有什么样的查找和插入的效率?答:(1)当先后插入的关键字有序时,构成的二叉查找树蜕变为单支树,树的深度等于n,此时二叉查找树表现出最差的效率,为了解决这一问题,可以构造AVL树或2-3树,使树的深度减小。
一棵AVL树要求它的每个节点的左右子树的高度差不能超过1。
2-3树和2-3-4树允许一棵查找树的单个节点不止包含一个元素。
(2) AVL树在最差情况下,查找和插入操作的效率属于Θ(lgn)。
2-3树无论在最差还是平均情况下,查找和插入的效率都属于Θ(log n)。
4、写出0/1背包问题的一个多项式等价(Polynomial Equivalent)的判定问题,并说明为什么它们是多项式等价的。
答:0/1背包问题:从M件物品中,取出若干件放在空间为W的背包里,给出一个能获得最大价值的方案。
每件物品的体积为W1,W2……Wn,与之相对应的价值为P1,P2……Pn。
+判定问题I:从M件物品中,取出若干件放在空间为W的背包里,是否存在一个方案,所获价值≥P*?。
每件物品的体积为W1,W2……Wn,与之相对应的价值为P1,P2……Pn。
若判定问题I存在多项式时间的解法,则反复调用该算法就可以在多项式时间内解决0/1背包的优化问题。
因而这个判定问题与原问题多项式等价。
5、下面问题是否属于NP问题?为什么?问题表述:给定图中的两个点、,整数和,图中每条边的长度及便利这条边的时间,问图中是否存在一条由到的路径,使得其长度大于,且遍历时间小于?答:这个问题属于NP问题。
因为若给出该问题的一个解,可以在多项式时间内检验这个解的正确性。
如给出一条由p到q的路径,可以在多项式时间内计算出它的长度及遍历时间,然后分别与C和t进行比较,从而可以判断这个解的对错。
分治题1.写出一个求解下列问题的分治算法,推导其时间复杂性并与蛮力法相比较。
给定互不相等的n个数的一个序列,若其中某两个数和的关系为:且,则称和是逆序的。
要求计算该序列中的逆序个数,即具有逆序关系的元素对的总数目。
解:/** *求解n个数的一个序列,具有逆序关系的元素对的总数目*/count = 0; //逆序元素对的全局计数变量mergeInvertedPairs(A,low,mid,high) {i = low;j = mid+1;k = low;tmp[n]; //用于归并排序的辅助数组while i <= mid && j <= high {if (A[i] > A[j]) {tmp[k] = A[j++];count += (mid-i+1); //相比归并排序,就多了这一条语句} else {tmp[k] = A[i++];}k++;}while i <= mid {tmp[k++] = A[i++];}while j <= high {tmp[k++] = A[j++];}for (j = low; j <= high; j++) {A[j] = tmp[j];}}findInvertedPairs(A[], low, high) {if (low < high) {mid = (low+high) / 2;findInvertedPairs(A,low,mid);findInvertedPairs(A,mid+1,high);mergeInvertedPairs(A,low,mid,high);}算法思路:以归并排序为基础,在两两集合合并的时候如果前一个集合的元素a[i]>a[j],那么说明需要调整次序,逆序数num=num+mid-i。
时间复杂度的迭代公式为11;(n)2(n/2)(n)n1;nTT O=⎧=⎨+>⎩因此算法的时间复杂度为T(n)=O(nlogn);蛮力法的时间复杂度为O(n2),当n数目较大时,分治法计算规模远小于蛮力法。
2.为一个整数序列,中的整数如果在中出现次数多余,那么称为多数元素。
例如,在序列中3是多数元素,因为出现了4次,大于。
求A的多数元素问题的蛮力算法复杂性如何?设计一个具有变治思想的算法,提高蛮力算法的效率,写出伪代码并分析其事件复杂性。
2. num <- src[0];count <-0;for i <-0 to n-1do{if(num == src[i]){count++;}else{count--;if(count <0){num <- src[i];count = 0;}}}采用减治的思想每一个减去一个元素,时间复杂度为O(n),蛮力法的时间复杂度为O(n2)。
动态规划题1.某工厂调查了解市场情况,估计在今后四个月内,市场对其产品的需求量如下表所示。
已知:对每个月来讲,生产一批产品的固定成本费为3(千元),若不生成,则为零。
每生产单位产品的成本费为1(千元)。
同时,在任何一个月内,生产能力所允许的最大生产批量为不超过6个单位。
又知:每单位产品的库存费用为每月0.5(千元),同时要求在第一个月开始之初,及在第四个月末,均无产品库存。
问:在满足上述条件下,该厂应如何安排各个时期的生产与库存,使所花的总成本费用最低?写出你所设的状态变量、决策变量、状态转移方程与递推关系式,和手工求解的详细步骤及结果。
解:设阶段序数k表示月份,状态变量x k为第k个月初拥有的单位产品数量,亦为第k-1月末时的单位产品数量,决策变量u k为第k个月生产的单位产品数量,c k为第k月份需要的产品数量,这里x k和u k均取离散变量。
状态转移方程为: , k =1,2,3,4; 且x1=0。
k段允许决策集合为: k = 1,2,3;当k=4时,。
设为第k月的成本费,单位为(千元),则,故指标函数为令表示为由出发采用最优生产方案到第4个月结束这段期间的产品成本。
根据最优化原理,则有递推公式:其中:逆序计算的详细步骤如下:(1)当k=4时,(2)当k=3时,因为,且所以有:当此时在处取得最小值。
当,此时在处取得最小值。
当,此时在处取得最小值。
当,此时,在处取得最小值。
当,此时,在处取得最小值。
当,此时,在处取得最小值。
当,此时,在处取得最小值。
(3)当k=2时,因为,且所以有:当时,,在处取得最小值。
当时,,且在处取得最小值。
当时,,在处取得最小值。
当时,,且在处取得最小值。
当时,,且在处取得最小值。
当时,,且在处取得最小值。
当时,,且在处取得最小值。
(4)当k=1时,因为,所以有:当,,且在处取得最小值。
综上所述,最优的库存方案为:第一月生产5单位产品,第二月和第四月不生产,第三月生产6单位产品。
2.用动态规划方法手工求解以下问题有8万元的投资可以投给3个过目,每个项目在不同筒子数额下(以万元为单位)的利润如下表请安排投资计划,使总的利润最大。
写出你所设的状态变量、决策变量、状态转移方程与递推关系式和手工求解的详细步骤及结构。
解:状态变量:x k 表示留给项目k..n的投资额,其中n为项目总个数,k=1..n.决策变量:u k 表示投给项目k的投资额.允许决策集合:状态转移方程:递推关系式:其中,表示项目k的投资额为u k时的盈利.针对本题,n = 3,x k最大取8手工详解过程:1.初始化k = 32.k = 23.k = 1最终结果:给项目1投资4万元,项目2投资4万元,项目3不投资,将获得最大利润140万元.线路题的某种深搜解法:1)可以根据线路(l1,l2,...,lm)的取舍构建一棵m层二叉搜索树。
第i层的所有左分支表示铺设线路li,右分支则表示不铺设。
如果存在可行解,遍历此二叉搜索树即可找到最优解。
2)前进:当前节点未被剪枝并且仍有子节点即可继续前进。
分支:先遍历左分支,后遍历右分支。
回溯:左右分支都被遍历时返回父节点。
剪枝:剪枝条件如下:1。
