理论物理导论-李卫1-3章习题解答完整详解
普通物理学习题问题详解全

实用文档
实用文档
第七章 电磁感应 电磁场理论
实用文档
7-2
实用文档
7-5
实用文档
7-7
7-14
7-15
实用文档
7-16
实用文档
实用文档
第一章 力和运动
1-2
实用文档
1-4
实用文档
实用文档
1-5
1-6
实用文档
1-9
1-14
实用文档
实用文档
1-14 题解:
a(t
)
10
2t 5(t
5)
0 t 5 且 v(0) 0,
5 t 7
x(0) 0
t
t2
0 t 5
v(t) v(0)
第五章 静止电荷的电场 ................. - 25 -
5-1................................................................. - 25 5-5................................................................. - 26 5-7................................................................. - 26 5-13................................................................ - 27 5-15................................................................ - 28 5-17................................................................ - 30 5-26................................................................ - 31 5-29................................................................ - 32 5-30................................................................ - 33 5-31................................................................ - 33 -
(完整版)理论力学习题集册答案解析
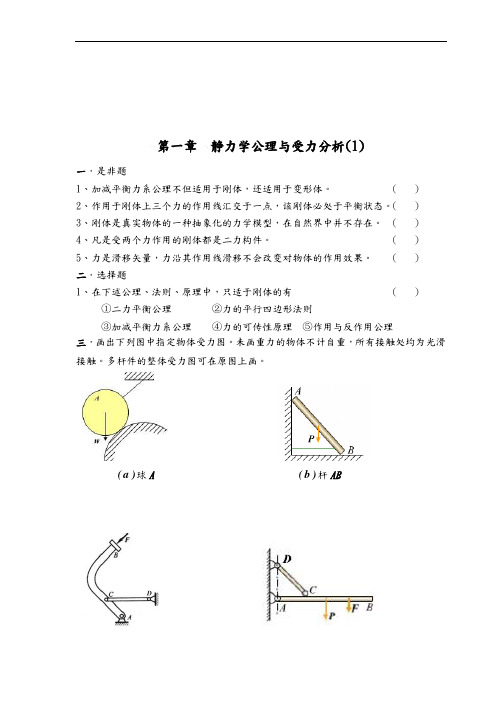
第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
()4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
()二.选择题1、在下述公理、法则、原理中,只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
b(杆AB)a(球A )d(杆AB、CD、整体)c(杆AB、CD、整体))e(杆AC、CB、整体)f(杆AC、CD、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体第一章 静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体 )b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体 )d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体第二章平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F= - F’,所以力偶的合力等于零。
()2、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
()3、力偶矩就是力偶。
()二.电动机重P=500N,放在水平梁AC的中央,如图所示。
2 理论物理导论-第一章2
m2g
y1
3、应用动力学普遍方程
FIA δxA FIB δxB m1 g δy A m1 g δyB m2 g δyC 0
O1 rA FIA m1g l
C
x1
l l
A
x A l cos y A l sin xB l cos yB l sin yC 2l sin
x
解:自由度 k 2 , 选x和θ为广义坐标。
m A r
30
vA
m
l
C
L T V
3 2 1 2 l 2 l m x ( θ) 2 x θ sin θ mx 4 2 2 2 1 ml 2 1 mgl sin θ 2 12 2
2
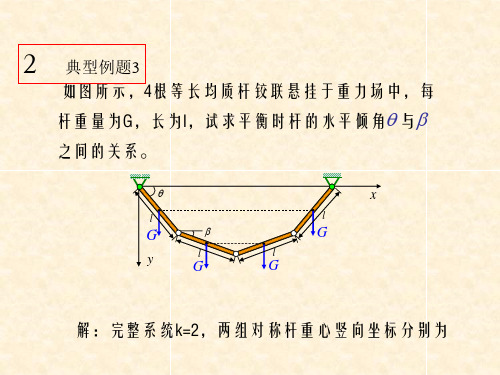
典型例题3 如图所示,4根等长均质杆铰联悬挂于重力场中,每
杆重量为G,长为l,试求平衡时杆的水平倾角 与 之间的关系。
x
l
l
G
y
G G
l
G
l
解:完整系统k=2,两组对称杆重心竖向坐标分别为
l l y1 sin , y2 l sin sin 2 2
给对称虚位移:
y1
x
1 2 l 2 V kl (1 cos ) mg cos 2 2
dV 由 0 ,有 dθ
k
A
mg [kl (1 cos ) ]sin 0 2 故 0, 1
mg
B
再由
mg 2 arccos(1 ) 53.8 2kl d2 V mg 2 2 kl (cos cos sin ) cos 2 d 2
物理学第3版习题解答-第1章流体的运动

第1章 流体的运动1-1 横截面是4 m 2的水箱,下端装有一个导管,水以2 m ·s -1的速度由这个导管流出。
如果导管的横截面是10 cm 2,那么水箱内水面下降时的速度是多大?解:根据连续性原理,得s m s m S v S v /105/410102442112--⨯=⨯⨯== l-2 有一水管,如图所示,设管中的水作稳定流动。
水流过A 管后,分B 、C 两支管流出。
已知三管的横截面积分别为S A =100 cm 2,S B =40 cm 2,S C =80 cm 2。
A 、B 两管中的流速分别为v A =40 cm ·s -1及v B =30 cm ·s -1。
则C 管中的流速v C 等于多少?解:根据连续性原理,得C C B B A A v S v S v S +=所以 s cm s cm S v S v S V C B B A A C /35/80304040100=⨯-⨯=-=1-3 水平放置的自来水管,粗处的直径是细处的2倍。
若水在粗处的流速和压强分别为1.0 m ·s -1和1.96×105 Pa ,那么水在细处的流速和压强各是多少? 解:4)2()2(2121222121===d dr r S S ππππ 根据连续性方程,得s m s m v S S v /4/141212=⨯== 根据伯努利方程,222212112121gh v p gh v p ρρρρ++=++得:Pa Pa v v p p 5223522211210885.1)41(10211096.1)(21⨯=-⨯⨯+⨯=-+=ρ 1-4 灭火水枪每分钟喷出60 m 3的水,若喷口处水柱的截面积为1.5 cm 2,问水柱喷到2m 高时的截面积有多大?解: s m s m St V v /1067.6/60105.160341⨯=⨯⨯==- 根据伯努利方程 222212121gh v v ρρρ+= 得 s m gh v v /1067.62102)1067.6(23232212⨯=⨯⨯-⨯=-=根据连续性原理,得 225.1cm S =题l-21-5 水在粗细不均匀的水平管中稳定流动,已知截面S 1处的压强为110 Pa ,流速为0.2 m ·s -1;在截面S 2处的压强为5 Pa ,求S 2处的流速。
理论力学第三版课后答案第3章
r 由式(1)在 τ 向的坐标式,可得点 B 的速度 r τ : vB = vO + rω = 2rω
aw .
re vω B r vO
r n
(1)
co
τ
r
m
固定圆弧纯滚动由点 O′ 到点O,有 AD = AD′ ,即 r (φ + θ ) = Rθ ,得 rφ = (R − r )θ ,两边对时
∩
∩
ww w
r 公共基 e 的坐标式为 rA = rB + A1 ρBA ,展开,考虑到图
r x2 r x3
r y3
C
3-2Ca 有
网
θ3
案
0 ⎛ xA ⎞ ⎛ ⎞ ⎛ cos φ1 ⎜ ⎜y ⎟ ⎟=⎜ ⎜ l sin (α − φ )⎟ ⎟+⎜ ⎜ 1 ⎠ ⎝ sin φ1 ⎝ A⎠ ⎝
− sin φ1 ⎞⎛ l cos α ⎞ ⎟⎜ ⎟ ⎜ ⎟ cos φ1 ⎟ ⎠⎝ 0 ⎠
aw .
r y2
B
r r 连体基 e 2 相对于与连体基 e 1 的位形为
r y
co
A
(1)
m
r y1 r x1
φ1 α
r r r r (2)对于连体基 e 1 ,由图 3-2Ca 有 rA = rB + ρ BA 在
.k hd
ρ = (0 − l sin α ) , θ 3 =
1 C T
π
2
−α
(2)
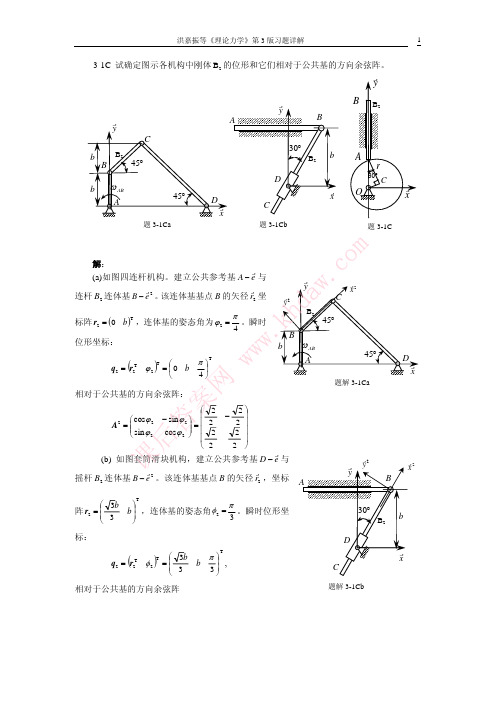
洪嘉振等《理论力学》第 3 版习题详解
1
3-1C 试确定图示各机构中刚体 B2 的位形和它们相对于公共基的方向余弦阵。
r y
r y r y
C b
B2
大物习题册答案全套

练习一 力学导论 参考解答1. (C); 提示:⎰⎰=⇒=t3x9vdt dxtd xd v2. (B); 提示:⎰⎰+=R20y 0x y d F x d F A3. 0.003 s ; 提示:0t 3104400F 5=⨯-=令 0.6 N·s ; 提示: ⎰=003.00Fdt I2 g ; 提示: 动量定理0mv 6.0I -==3. 5 m/s 提示:图中三角形面积大小即为冲量大小;然后再用动量定理求解 。
5.解:(1) 位矢 j t b i t a r ρρρωωsin cos += (SI)可写为 t a x ωcos = , t b y ωsin =t a t x x ωωsin d d -==v , t b ty ωωcos d dy -==v 在A 点(a ,0) ,1cos =t ω,0sin =t ω E KA =2222212121ωmb m m y x =+v v由A →B ⎰⎰-==0a 20a x x x t cos a m x F A d d ωω=⎰=-022221d a ma x x m ωω⎰⎰-==b 02b 0y y t sin b m y F A dy d ωω=⎰-=-b mb y y m 022221d ωω6. 解:建立图示坐标,以v x 、v y 表示小球反射速度的x 和y 分量,则由动量定理,小球受到的冲量的x,y 分量的表达式如下: x 方向:x x x v v v m m m t F x 2)(=--=∆ ① y 方向:0)(=---=∆y y y m m t F v v ② ∴ t m F F x x ∆==/2v v x =v cos a∴ t m F ∆=/cos 2αv 方向沿x 正向.根据牛顿第三定律,墙受的平均冲力 F F =' 方向垂直墙面指向墙内.ααmmOx y练习二 刚体的定轴转动 参考解答1.(C) 提示: 卫星对地心的角动量守恒2.(C) 提示: 以物体作为研究对象P-T=ma (1);以滑轮作为研究对象 TR=J β (2)若将物体去掉而以与P 相等的力直接向下拉绳子,表明(2)式中的T 增大,故β也增大。
理论物理整理习题答案

2 0
1 r / a0 1 d 2 d r / a0 2 e [r (e )]r sin drd d 3 2 a0 r dr dr
2
2 a
2
3 0
3 0
0
sin d d
0
2
0
r 2 2r 2r / a0 ( 2 )e dr a0 a0
2
d 2 (r ) 可改写为 Er 2 2 dr
2
令f (r ) r
代入上式,得
d 2 f (r ) Ef (r ) 2 2 dr
2
令k
2
2 E
2
上式可化为
d 2 f (r ) 2 k f (r ) 0 2 dr 方程的通解为 f (r ) A sin(kr ) B cos(kr )
d2 1 2 2 [ x ] ( x) 2 2 dx 2
2 4 2 2
2
利用
2
1 ( x 5 ) ( x) 2 x 2 ( x) 2 2 5 5 ( x ) 则此态下能量的本征值为 2 2
3.解(1)动能的平均值
2 1 ˆ ˆ2 T p 2 2 2
+ 1
=
+
-
d 1 ( ) 2 d dx
不是厄米算符
(3)设ψ1和ψ2为任意波函数
2 2 d + d 2 d - 1 dx2 2 = dydz - 1 dx2 dx +
d d 2 = dydz ( )dx - dx dx d 2 + + d d 2 1 = dydz 1 dx
大学物理课后习题答案(全册)

《大学物理学》课后习题参考答案习题11-1. 已知质点位矢随时间变化函数形式为)ωtsin ωt(cos j i R r其中为常量.求:(1)质点轨道;(2)速度和速率。
解:1)由)ωtsin ωt(cos j i R r知t cos R x ωtsin R yω消去t 可得轨道方程222Ryx2)jr vt Rcos sin ωωt ωR ωdtd iRωt ωR ωt ωR ωv2122])cos ()sin [(1-2. 已知质点位矢随时间变化的函数形式为j ir )t 23(t 42,式中r 的单位为m ,t 的单位为s .求:(1)质点的轨道;(2)从0t到1t 秒的位移;(3)0t 和1t 秒两时刻的速度。
解:1)由j ir)t 23(t 42可知2t 4x t23y消去t 得轨道方程为:2)3y(x2)jir v 2t 8dtd jij i v r 24)dt2t 8(dt101Δ3)jv 2(0)jiv 28(1)1-3. 已知质点位矢随时间变化的函数形式为j ir t t 22,式中r 的单位为m ,t 的单位为s .求:(1)任一时刻的速度和加速度;(2)任一时刻的切向加速度和法向加速度。
解:1)ji r v2t 2dtd iv a2dtd 2)212212)1t(2]4)t 2[(v1tt 2dtdv a 2t22221nta aat 1-4. 一升降机以加速度a 上升,在上升过程中有一螺钉从天花板上松落,升降机的天花板与底板相距为d ,求螺钉从天花板落到底板上所需的时间。
解:以地面为参照系,坐标如图,升降机与螺丝的运动方程分别为20121att v y (1)图 1-420221gttv h y (2)21y y (3)解之2d tg a 1-5. 一质量为m 的小球在高度h 处以初速度0v 水平抛出,求:(1)小球的运动方程;(2)小球在落地之前的轨迹方程;(3)落地前瞬时小球的td dr ,td dv ,tv d d .解:(1)t v x 0式(1)2gt21hy 式(2)jir )gt 21-h (t v (t)20(2)联立式(1)、式(2)得22v 2gx hy (3)ji r gt -v td d 0而落地所用时间gh 2t所以j i r 2gh -v t d d 0jv g td d 2202y2x)gt (vvvv 211222222[()](2)g ghg t dv dtvgt vgh 1-6. 路灯距地面的高度为1h ,一身高为2h 的人在路灯下以匀速1v 沿直线行走。
理论物理导论答案

理论物理导论答案【篇一:杭州电子科技大学2011年1月理论物理导论期末考试卷(参考答案)2】xt>???考虑双粒子体系,整个体系是反对称的,定义总自旋算符为s?s1?s2.波函数为:?(q1,q2)??(r1,r2)?(sz1,sz2)???的本征值,和总自旋z方a卷的问题:如果空间部分波函数是对称的.写出总自旋平方算符s2?的本征值. 向分量算符sz?的本征值,和总自旋zb卷的问题: :如果空间部分波函数是反对称的.写出总自旋平方算符s2?的本征值. 方向分量算符sz解:由量子力学相关知识可知,?2和s?的共同本征函数系是:?(s)和?(s). 对单粒子体系而言,s1z1zz22?2?和s?的共同本征函数系是:???(s)?(s) 对双粒子体系而言,s1,11z11z2z22?1,0??1(sz1)?1(sz2)??1(sz1)?1(sz2)]??2222?2?2?1,?1??1(sz1)?1(sz2) ?0,0??1(sz1)?1(sz2)??1(sz1)?1(sz2)]??22221??m?(后面。
szs2?2?s(s?1)?2(后面是本征值).量子数s只能取对单粒子体系而言。
s是本征值).ms只能取?1 2??m?(后面是?2?s(s?1)?2(后面是本征值).量子数s能取1,0。
s对双粒子体系而言,szs本征值).ms能取1,-1,0 .上面四种组合方式中,?s,ms(sz1,sz2)的前三种是对称行,后一种是反对称。
a题解:所以,如果空间部分波函数是对称的,那么意味着自选部分是反对称的。
?的本征值是0.反对称的自 ?2?s(s?1)?2,s反对称的自旋角动量量子数s 只能取0.所以s2b题解:??m?,s?的本征值是0. 旋角动量z方向上分量的量子数ms取0,所以szsz如果空间部分波函数是反对称的,那么意味着自选部分是对称的。
对称的自旋波函数有三种形式,分别对应的量子数是不同的??m?= ?2?s(s?1)?2=2?2,s?1,1??1(sz1)?1(sz2)这个波函数对应的s=1, ms=1. szs22??1,0??1(sz1)?1(sz2)??1(sz1)?1(sz2)]这个波函数对应的量子数s=1,ms=0.对应??2222的本征值??m?=0 ?2?s(s?1)?2=2?2.sszs?1,?1??1(sz1)?1(sz2)这个波函数对应的量子数s=1, ms=-1.对应的本征值?2?2??m?=?? ?2?s(s?1)?2=2?2,sszs6.(氦原子零级近似波函数)忽略与自旋相关的相互作用,写出he原子体系(这是个双电子体系),的零级近似波函数。
(完整word版)理论力学教程思考题答案第三版.doc

第一章思考题解答1.1答:平均速度是运动质点在某一时间间隔内位矢大小和方向改变的平均快慢速度,其方向沿位移的方向即沿对应的轨迹割线方向;瞬时速度是运动质点在某时刻或某未知位矢和方向变化的快慢程度其方向沿该时刻质点所在点轨迹的切线方向。
在的极限情况,二者一致,在匀速直线运动中二者也一致的。
1.2答:质点运动时,径向速度和横向速度的大小、方向都改变,而中的只反映了本身大小的改变,中的只是本身大小的改变。
事实上,横向速度方向的改变会引起径向速度大小大改变,就是反映这种改变的加速度分量;经向速度的方向改变也引起的大小改变,另一个即为反映这种改变的加速度分量,故,。
这表示质点的径向与横向运动在相互影响,它们一起才能完整地描述质点的运动变化情况1.3答:内禀方程中,是由于速度方向的改变产生的,在空间曲线中,由于恒位于密切面内,速度总是沿轨迹的切线方向,而垂直于指向曲线凹陷一方,故总是沿助法线方向。
质点沿空间曲线运动时,z 何与牛顿运动定律不矛盾。
因质点除受作用力,还受到被动的约反作用力,二者在副法线方向的分量成平衡力,故符合牛顿运动率。
有人会问:约束反作用力靠谁施加,当然是与质点接触的周围其他物体由于受到质点的作用而对质点产生的反作用力。
有人也许还会问:某时刻若大小不等,就不为零了?当然是这样,但此时刻质点受合力的方向与原来不同,质点的位置也在改变,副法线在空间中方位也不再是原来所在的方位,又有了新的副法线,在新的副法线上仍满足。
这反映了牛顿定律得瞬时性和矢量性,也反映了自然坐标系的方向虽质点的运动而变。
1.4答:质点在直线运动中只有,质点的匀速曲线运动中只有;质点作变速运动时即有。
1.5答:即反应位矢大小的改变又反映其方向的改变,是质点运动某时刻的速度矢量,而只表示大小的改变。
如在极坐标系中,而。
在直线运动中,规定了直线的正方向后,。
且的正负可表示的指向,二者都可表示质点t t t ∆+→t ∆0→∆t r V θV r a r &&r V θa θθ&&&r r +θV θV r V 2θ&r -r V θV θ&&r 2θ&&&r r a r -=.2θθθ&&&&r r a +=n a a v n a v n a 0,0≠=b b F a F R 0=+b b R F 0=b a b b R F 与b a b a 00==+b b b a R F 即n a a 而无ττa a n 而无n t a a 又有dt d r r dtdr r j i r θ&&r r dt d +=r dt dr &=dt d dt dr r =dt dr dt d r的运动速度;在曲线运动中,且也表示不了的指向,二者完全不同。
理论物理导论-李卫1-3章习题解答完整详解

P(x) (x) (x) 43x e2 2x
(3)在极值点,由一阶导数
dP(x) 0 dx
可得方程
x(1 x)e2x 0
而方程的根
x 0 ; x ; x 1/
即为极值点。几率密度在极值点的值
P(0) 0;lim P(x) 0;P(1/ ) 4e2 x
由于P(x)在区间(0,1/)的一阶导数大于零,是升函数; 在区间(1/,)的一阶导数小于零,是减函数,故几率密
其中Hn (x)
(-1)n e(x)2
d
dn
x
n
(e-(x)2 ),n
0,1,2
En
(n
1 ),
2
n
0,1,2
当取n=2时,得到
2(x)
1
e2
2x2
(2
2
x2
1)
2
即题中所给的本征态。
所以此时
En
E2
(2
1 )
2
5 2
3.解:氢原子电子势能 U (r) e2
4 0r
(r,
,)
(a03
3.设把宽为 a的一维无限深势阱的坐标原点取在势阱中点,有
U
(x)
0, ,
(| x | a / 2) (| x | a / 2)
试通过具体解定态方程,证明势阱中粒子的波函数为
2 n
n
(
x)
cos x, aa
2 sin n x,
aa
n 1,3,5, n 2,4,6,
粒子的能量为
En
22 2a 2
(1)归一化因子A;
(2)粒子的几率密度;
(3)粒子出现在何处的几率最大?
现代物理导论第一章至第九章思考题答案

现代物理导论第一章至第九章思考题答案第一章至第九章思考题第一讲文明的曙光1人类文明如何从自然演化中产生?2埃及文明、两河流域文明与希腊文明有什么关系?3比较一下东西方文明诞生与发展的规律。
4在古代,东西方文化有过什么交流,相互有过什么影响?5谈谈你对历史传说、考古研究的看法。
第二章远古的辉煌1苏格拉底、柏拉图与亚历士多德思想有何传承关系?2亚历山大科学院对文明和科学的发展有什么作用?3欧几里得几何对西方文化发展有何影响?4描述古代宇宙观的发展。
5古希腊文明与阿拉伯文明有什么关系?第三章科学的诞生1地理大发现、文艺复兴和宗教改革对人类文明的发展有什么作用?2为什么郑和下西洋未对世界产生重大影响,而哥伦布、麦哲伦等人的“地理大发现”则对世界产生了重大影响?3中国的四大发明对近代自然科学的诞生有什么作用?4从哥白尼日心说的诞生过程看,宗教对科学的作用是推动还是阻碍?5对开普勒三定律的发现,你有哪些体会?第四章物理的初创1简述伽利略对力学的几个重要贡献,惯性定律,自由落体定律和相对性原理2牛顿对时间、空间有什么看法?3开普勒三定律与牛顿万有引力定律有什么关系?4有哪些实验证实了万有引力定律?5经典力学最基本的内容有哪些?第五章热学与统计1简述热力学的四条定律。
2热力学第二定律有哪些主要表达方式?3熵的物理意义是什么?4谈谈你所了解的负温度。
5麦克斯韦妖能破坏热力学第二定律吗?6什么是耗散结构?第六章认识电与光1牛顿对光的颜色理论有什么贡献?2双缝干涉实验的光为什么必须来自同一光源?3如何理解真空中的光速值是一个“约定”?4从法拉第与麦克斯韦的成功,你悟出了什么道理?5最基本的电磁规律有哪些?什么实验启发麦克斯韦推测光波就是电磁波?第七章走近相对论1爱因斯坦如何把普朗克的量子说推进为光子说?二者差异在何处?2洛伦兹理论与爱因斯坦相对论的主要区别是什么?3相对论建立在哪两个假设的基础之上?4相对论有哪些重要结论?5谈谈你对质能关系式的理解。
理论物理导论习题及解答

2.9 秋千何以能越荡越高?这时能量的增长是从 哪里来的?
答:秋千受绳的拉力和重力的作用,在运动中绳的拉力 提供圆弧运动的向心力,此力不做功,只有重力做功。 重力是保守力,故重力势能与动能相互转化。当秋千荡 到铅直位置向上去的过程中,人站起来提高系统重心的 位置,人克服重力做功使系统的势能增加;当达到最高 点向竖直位置折回过程中,人蹲下去,内力做功降低重 心位置使系统的动能增大,这样循环往复,系统的总能 不断增大,秋千就可以越荡越高。 这时能量的增长是人体内力做功,消耗人体内能转
2 3 2
又
把 y 2px 两边对时间求导得:
2
yy x p
v2 2 y y2 1 2 p
y 又因为 v x
2 2
2
所以
( y 1
v2
y p2
2
)
1
2
所以
可化为 对等式两边积分 所以
v ue
k
2.7选用质心坐标系,在动量定理中是否需要计入 惯性力?
y
m
M
u
O
题2.7.1图
x
MV mvx
m相对于地固连的坐标系Oxy的绝对速度 V V V 绝对 相 牵
V绝对 V相 V牵
V相 为m相对M的运动速度
y
m
u a
故水平方向 vx u cos V 竖直方向
②
③
V
M
O
题2.7.1图
u
x
vy u sin
④
在下滑过程中,只有保守力(重力)做功,系统机械能守恒:
答:设质心的速度Vc,第i个质点相对质心的速度Vi’, 则v i v c vi ,代入质点组动量定理可得
大学物理一二三章习题讲解

a1
m1
T
T T T
对m1
T m1a m1a
F
y
a
N
m2
m2 g
N
T m2 g m2 (a) 对m2 N m2 a 0
a2
对M F N T Ma 0
4个未知数,4个方程
第(2)问,a 0 , F 未知,同样是 4个未知数,4米。若按宽度一定、 厚度均匀的薄片计算,旋翼以400r/min的转速旋转时,其 根部受到的拉力为其重力的几倍?
在一质量为 M 的小车上放一质量为 m1 的物块。它用细绳通 过固定在小车上的滑轮与质量为 m2的物块相连,物块 m2 靠在小 车的前壁上而使悬线垂直,忽略所有摩擦及滑轮的质量。 (1)当用水平力 F 推小车使之沿桌面加速前进时,小车的加 速度多大?(2)如果要保持 m2 的高速不变,力 F 应多大? 第(1)问:在小车系(非惯性系)
L
dr
分割成质元,每个质元圆周运动都 需要向心力,质点系水平方向的合外力 就是所有质元向心力的合。连续分布, 求和等于积分。先求小量再积分。
r
质元质量
dm Sdr
L
为密度,S是截面积
质元所需向心力 dF dm an Sdr 2r
1 1 2 2 2 积分 F dF S rdr S L m L 2 2 0 F 2L 534 mg 2 g
a3
分别对每个物体受力分析,应用牛顿第二定律
m1g T1 m1a1
m2 g T2 m2 a2
m3 g T2 m3a3
绳长不可伸长,B和C相对动滑轮的加速度大小相等,加速度存 在关系(不同参照系间加速度的变换)
物理学导论-试题及课后答案

21.(本题5分)(1652)假想从无限远处陆续移来微量电荷使一半径为R 的导体球带电.(1) 当球上已带有电荷q 时,再将一个电荷元d q从无限远处移到球上的过程中,外力作多少功? (2) 使球上电荷从零开始增加到Q 的过程中,外力共作多少功?22.(本题5分)(2654)如图所示,有两根平行放置的长直载流导线.它们的直径为a ,反向流过相同大小的电流I ,电流在导线内均匀分布.试在图示的坐标系中求出x 轴上两导线之间区域]25,21[a a 内磁感强度的分布. 23.(本题5分)(2303)图示相距为a 通电流为I 1和I 2的两根无限长平行载流直导线.(1) 写出电流元11d l I 对电流元22d l I的作用力的数学表式;(2) 推出载流导线单位长度上所受力的公式.24.(本题10分)(2150)如图所示,两条平行长直导线和一个矩形导线框共面.且导线框的一个边与长直导线平行,他到两长直导线的距离分别为r 1、r 2.已知两导线中电流都为t I I ωsin 0=,其中I 0和ω为常数,t 为时间.导线框长为a 宽为b ,求导线框中的感应电动势.22.(本题5分)(2442)将细导线弯成边长d =10 cm 的正六边形,若沿导线流过电流强度为I =25 A 的电流,求六边形中心点的磁感强度B .(μ0 =4π×10-7 N ·A -2 )23.(本题5分)(2548)在氢原子中,电子沿着某一圆轨道绕核运动.求等效圆电流的磁矩m p与电子轨道运动的动量矩L大小之比,并指出m p和L方向间的关系. (电子电荷为e ,电子质量为m )Ia aI xO2aI 1I 211d l I22d l Ia12rIIOxr 1r 2 ab24.(本题10分)(2737)两根平行无限长直导线相距为d,载有大小相等方向相反的电流I,电流变化率d I /d t =α >0.一个边长为d的正方形线圈位于导线平面内与一根导线相距d,如图所示.求线圈中的感应电动势ε,并说明线圈中感应电流是顺时针还是逆时针方向.dII7-3 计算和证明题7-3-1解Q22004lπε+=,求得Q =- 7-3-2解场强大小为20044()a ladx lE dE x a a l λλπεπε+===+⎰⎰,沿带电直线方向. 7-3-3解 如图建立坐标系,正负电荷关于x 对称,它们在O 点产生的场强沿y 轴负向,在圆上取dl=Rd φdq=λdl=R λd φ,它在O 点产生场强大小为 dE=204RRd πεϕλ方向沿半径向外 则 dE x =dEsin φ=ϕϕπελd Rsin 40dE y =dEcos(π-φ)=R04πελ-cos φd φ积分 2002sin 04x E d Rπλϕϕπε==⎰2220002cos 42y qE d RR R πλλϕϕπεπεπε-==-=-⎰ 方向沿y 轴负向. 7-3-4解xθdEOx dE如图所示,dq dl Rd λλθ==,它在圆心O 点产生 的场强200cos 44Rd A d dE R Rλθθθπεπε==其在x 轴上的场强为cos()x x E dE dE πθ==+⎰⎰22000cos 44A d AR Rπθθπεε=-=-⎰方向沿x 轴负向,其在y 轴上的场强为sin()y y E dE dE πθ==+⎰⎰200cos sin 04A d Rπθθθπε=-=⎰7-3-5解小球受力如图所示,由图可知,qE mgtg θ= 即 02qmgtg σθε=, 有 06202308.010/mgtg C m qεσ-==⨯7-3-6解在r R >处取一细圆环,其带电量2dq dS rdr σσπ==,根据教材例7-2-4结果可知,圆环在轴线上P 点产生的场强大小223/2223/2223/200024()4()2()xdq x rdr x rdrdE x r x r x r σπσπεπεε===+++22223/2223/200()2()4()RR x rdr x d x r E x r x r σσεε∞∞+==++⎰⎰qE7-3-7解(1)11122222(2)(21) 1.05/e bd S b d S bd d N m C Φ=-⋅+⋅=-⋅=⋅(2)由高斯定理可得,1209.2910ie iqC ε-=Φ=⨯∑7-3-8解半圆柱薄筒的横截面如图所示,建立直角坐标系Oxy ,沿弧长方向 取一宽度为dl 的细条,此细条单位长度上的带电量为dl Rd d R R ϕλϕλλλπππ'===, 此细条等同于无限长均匀带电直线,因此它在O 点产生的场强为20022d dE R Rλλϕπεπε'==, 20cos cos()2x d dE dE Rλϕϕπϕπε=+=-, 20sin sin()2y d dE dE Rλϕϕπϕπε=+=-,20cos 02x x d E dE Rπλϕϕπε==-=⎰⎰, 22000sin 2y y d E dE R Rπλϕϕλπεπε==-=-⎰⎰, 20x y y E E i E j E j j Rλπε=+==-7-3-9解(1)以地面为高斯面,由高斯定理可得2111114ne i Si E dS E S E R q πε=Φ=⋅=-=-=∑⎰⎰,所以2510149.0310nii qE R C πε==-=-⨯∑(2)如下图,由高斯定理 01()e SE dS E E S nSh εΦ=⋅=-=⎰⎰下上,dEdl所以有 122120 1.0610/E E E E n C m h hε---===⨯下上7-3-10解我们可以设想不带电空腔内分布着体密度相同的正负电荷.由电场的叠加原理可知,有空腔的带电球体的电场,可以看作一个半径为R 电荷体密度为ρ的均匀带正电球体和一个半径为r 电荷体密度为ρ-的均匀带负电球体所激发电场的叠加.即000E E E +-=+由高斯定理可求出00E +=,302004343a a E a πρρπεε-⋅==, 所以O 点的场强大小为0003a E E ρε-==,方向沿OO '. 同理,O '点的场强大小为 00003a E E E ρε'''+-=+=,方向仍沿OO '. 7-3-11解由电荷的轴对称性分析可知,场强也具有轴对称性,可利用高斯定理求场强. (1) 在r R <处,作一同轴圆柱形高斯面,由高斯定理所以 0E =(2) 在12R r R ≤≤处,类似(1),有102lrlE λπε=nnE 下1120ne iSi E dS rlE qπε=Φ=⋅===∑⎰⎰所以 102E rλπε=(3) 在2r R >处,类似(1),有122rlE l λλπε+=所以 1202E rλλπε+=7-3-12解(1)A点电势为104A q U rπε=B点电势为B U =,63.610J -=⨯ 注 式中90210q C -=⨯ (2)C点电势为204C q U rπε=,D 点电势为1202D q q U dπε+=,2120000())42CD C D q q qA q U U q r dπεπε+=-=- 63.610J -=-⨯ 7-3-13解(1)00E =,9493104104910 2.881040.05iO i iq U V r πε-=⨯==⨯⨯⨯=⨯∑(2)9360()010 2.8810 2.8810O O A q U U J --∞∞=-=-⨯⨯=-⨯,1000()(4AB A B q A q U U q r πε=-=311110191436410 1.610910q U R C πε--=⋅=⨯⨯⨯=⨯⨯0q 电势能的改变为60 2.8810O W A J -∞=-=⨯ (3)60 2.8810O W W A J -∞∞-==-⨯ 7-3-14解(1)雨滴的电势为11014q U R πε=,有(21,这时雨滴表面电势为9112202574q U V R πε-=== 7-3-15解根据电势叠加原理,O 点的电势可看作直线AB 、DE 和半圆周BCD 所带电荷在O 点产生电势的叠加,AB 、DE 在O 点产生的电势为 21300ln 244RRdx U U x λλπεπε===⎰,半圆周BCD 在O 点产生的电势为22000444q R U RR λπλπεπεε⋅===所以O 点产生的电势为 1230(2ln 2)4U U U U λππε=++=+ 7-3-16解 金核表面的电势为,金核中心的电势为7-3-17解 由高斯定理可求得Ⅰ、Ⅱ、Ⅲ区域的场强大小分别为9197115091079 1.610 1.61047.010qU V R πε--⨯⨯⨯⨯===⨯⨯72132000033 2.41044242RR qr q q U dr dr U V R r R πεπεπε∞=+===⨯⎰⎰12121122200044R R rR R q q q dr dr drr r πεπε∞+=++⎰⎰⎰10E =,12204q E r πε=123204q q E rπε+=设1P 、2P 、3P 分别为Ⅰ、Ⅱ、Ⅲ区域内任一点, (1) Ⅰ区域内任一点1P 的电势由电势的定义式计算,有11P U E dl ∞=⋅⎰1212123R R rR R E dl E dl E dl ∞=⋅+⋅+⋅⎰⎰⎰12121()4q q R R πε=+ (2) Ⅱ区域内任一点2P 的电势由电势的定义式计算,有 22P U E dl ∞=⋅⎰2223R rR E dl E dl ∞=⋅+⋅⎰⎰22112220044R rR q q q dr dr r r πεπε∞+=+⎰⎰1221()4q q r R πε=+ (3) Ⅲ区域内任一点3P 的电势由电势的定义式计算,有 33P U E dl ∞=⋅⎰3rE dl ∞=⋅⎰12204rq q dr r πε∞+=⎰1204q q rπε+=7-3-18解 两“无限长”共轴圆柱面之间场强可由高斯定理求得为 02E rλπε=式中λ为单位长度上所带电量.由电势差的定义,两圆柱面之间的电势差为00[ln ln()]ln 2l a a l a x l x aλλπεπε--=--= 212001ln 22BR AB AR R U E dl dr r R λλπεπε=⋅==⎰⎰, 则 809212450 2.0810/102910ln ln 3AB U C m R R πελ-===⨯⨯⨯⨯7-3-19 解 由高斯定理可得场强分布为a x a -<< 0E σε=-; x a <- 或x a > 0E =;由电势的定义式计算电势分布 在x a <-区域,0000a xxaU Edx dx dx a σσεε--==+-=-⎰⎰⎰ 在a x a -<<区域, 000xx U Edx dx x σσεε==-=⎰⎰ 在a x ≤<∞区域,0000axxaU Edx dx dx a σσεε==+-=⎰⎰⎰ 电势U 随在x 分布如图所示7-3-20解 设坐标原点在左边导线轴线上,x 轴通过两导线并与之垂直.在两导线之间,坐标为x 的任一点P 的场强为 0022()E x l x λλπεπε=+-, 所以两导线间电势差为 00()22()l aAB aU dx x l x λλπεπε-=+-⎰U7-3-21解(1)在带电直线上取电荷元dq dx λ=,它在P 点的电势为 004()4()dq dxdU r x r x λπεπε==++整个带电直线在P 点的电势为 000ln4()4lP r lU dx r x rλλπεπε+==+⎰(2)根据场强与电势的微分关系dUE dr=-,有 04()lE r r l λπε=+7-3-22解 由高斯定理可求得均匀带电球体内外的场强分布为 r R ≤,103r E ρε=; r R >,32203R E rρε= (1)r R >,33220033r rrR R U E dr dr r rρρεε∞∞===⎰⎰(2)r R =,320033R R R U R ρρεε==(3)r R <,322122000(2)336RRr rRrR r R U E dr E dr dr dr R r r ρρρεεε∞∞=+=+=-⎰⎰⎰⎰7-3-23 解(1)r R <处,在圆柱体内任取一点,该点到轴线距离为r ,过该点作一半径为r ,高为l 的同轴闭合圆柱形高斯面,由高斯定理 11ne iSi E dS qε=Φ=⋅=∑⎰⎰,可得312223ral rlE ar rldr r πππεε=⋅=⎰求得 23ar E ε=内,方向沿径向向外.对r R >,同理由高斯定理可得312223Ral rlE ar rldr R πππεε=⋅=⎰求得 30 3aR E rε=外(2)设1r m =处为电势零参考位置且假设该点在圆柱体外,则在r R >区域内,33110ln 33r r aR aR U E dr dr r r εε===-⎰⎰外外在r R <区域内,23110033RRrRrR ar aR U E dr E dr dr dr r εε=+=+⎰⎰⎰⎰外内内33300()ln 93a aR R r R εε=-- 8-3 计算和证明题8-3-1解 请参见教材P342题8-3-1图(1)由于静电感应,球壳内表面带电量为q -,外表面带电量为q +;球壳电势为 33200344R R q q U E dl dr rR πεπε∞∞=⋅==⎰⎰3(2)内表面带电量为q -,外表面带电量为0;球壳电势为 0U =3(3)内球接地时,内球的电势0U =1,设内球此时带电量为q '+,则球壳内表面带电量为q '-;外表面带电量为q q '-,空间场强分布为: 12R r R <<,1204q E r πε'=;23R r R <≤,20E =; 3r R >,3204q qE r πε'-=;因此,内球的电势 231231123R R R R R U E dr E dr E dr ∞=++⎰⎰⎰213220044R R R q q q dr dr r r πεπε∞''-=+⎰⎰0120311()044q q qR R R πεπε''-=-+=求得12122313R R qq R R R R R R '=+-球壳的电势为3123303012231344R R R q q qU E dr R R R R R R R πεπε∞'--'===⋅+-⎰电势的改变为12333012231304R R q U U U U R R R R R R πε-''∆=-=-=⋅+-8-3-2解 请参见教材P342题8-3-2图(1)设导体球上的感应电量为q ',这些感应电荷到球心O 点的距离都为R ,因此感应电荷q '在O 点产生的电势为04q R πε',点电荷q 在O 点产生的电势为042qRπε⋅,故O 点的电势为000048q q U R Rπεπε'=+= (导体球接地), 求得2q q '=-(2)因O 点场强为零,故q '在O 点产生的场强大小等于q 在O 点产生的场强大小,方向相反,即为00q q E E E '=+= 所以 2016q q E R πε'=8-3-3解请参见教材P342题8-3-3图(1)设A 板两表面中左侧表面带电量为1q ,右侧表面带电量为2q ,其电荷面密度分别为11q S σ=,22qSσ=,由于B 、C 板都接地,故有 AC AB U U =AC AC ABAB E d E d =写成1200AC AB d d σσεε= 有12002q qS Sεε= ① 又 12q q Q += ② 由①②解得 12/3q Q =,2/3q Q =因此C 板带电为712/3 2.010()C q q Q C -=-=-=-⨯,72/3 1.010()B q q Q C -=-=-=-⨯(2)3200 2.2610()3A AB AB AB q Q U U d d V S Sεε====⨯ 8-3-4解设导体片C 插入后,AC 间场强为1E ,CB 间场强为2E ,并 假设0q >,则各板带电分布如图所示,并作如图所示的高斯 面,两底面与板平行,由高斯定理可得120Sq SE dS E S E S Sε∆⋅=-∆+∆=⎰⎰即有 210qE E Sε-= ① 由题意得 2122d dU E E =⋅+⋅ ② 由①②解得 20224C CB d U qdU U E Sε==⋅=+8-3-5解对于半径为R 的金属球,不论是实心还是空心,当带电量为q 时,其电势均为04q U Rπε=,则电容为04qC R Uπε==,可见电容是相同的. 对于地球,711C F μ= 8-3-6解(1)设内、外金属膜圆筒半径分别为1R 和2R ,高度均为L ,其上分别带电量为Q ±,则玻璃内的场强为12R r R << , 02r Q E Lrπεε=内外圆筒之间的电势差为21201ln2R R r R Q U E dl LR πεε∆=⋅=⎰ 莱顿瓶的电容为 90212 2.2810ln r L q C F R U R πεε-===⨯∆(2)圆柱形电容器两金属膜之间靠近内膜处场强为最大,令该处场强等于击穿场强,即 101()2r Q E R E LR πεε==击穿所以 5012 6.6710r Q LR E C πεε-==⨯击穿 8-3-7解 (1)由123111AB C C C C =++,求得 3.75AB C F μ=(2)总电量43.7510AB AB Q C U C -==⨯ 因为1C 和2C 并联,故有1212Q Q C C = 即有 122Q Q = ①又 12Q Q Q += ② 由①②求得2C 带电量为4211.25103Q Q C -==⨯,2C 上的电压22225Q U V C == (3)3100U U V ==,4333510Q C U C -==⨯8-3-8解(1)作一高斯面,使其两底面分别在板中和介质中且平行于板面,由介质中的高斯定理1ni Si D dS q =⋅=∑⎰⎰可得0D S S σ∆=∆ 求得 0Q D Sσ==又 0()[()]r U E d t Et d t t E ε=-+=-+ 求得 ()r UE d t tε=-+因此 00()r r r U D E d t tεεεεε==-+(2)由上面结果可知 00()r r US Q S DS d t tεεσε===-+(3)0()r r S QC U d t tεεε==-+ 8-3-9解(1)由题意极板间带电量Q 不变,00000SQ Q C U U d ε===(2)电位移00S Q D S d εσ===,介质中的场强000r U D E dεεε== (3)电容大小与带电量多少无关,由题意可知 0()r r S C d t tεεε=-+8-3-10解设单位长度带电量为λ,则两极板间场强2E rλπε=,击穿场强0E 一定时,02rE λπε=最大,电容器两极板电压为 0ln ln 2RrR R U Edr rE r rλπε===⎰式中r 是变量,适当选择r 的值,可使U 有极大值,即令00ln 0dU RE E dr r =-=, 求得0Rr e=故当0Rr e=时,电容器可能承受的最大电压为 0max 000ln 147RE R U r E KV r e=== 8-3-11解(1)当1R r R <<,由介质中的高斯定理可得0SD dS Q ⋅=⎰⎰,即有204r D Q π= 求得 024Q D rπ=, 所以有 012004rr Q DE r εεπεε==当2R r R <<,02204Q DE rεπε==(2)电势差为 2112RR R RU E dr E dr ∆=+⎰⎰2100220044RR R Rr Q Q dr dr r r πεεπε=+⎰⎰001211()4r rrQ R R R εεπεε-=+-(3)001221124()()r r Q RR R C U R R R R R R πεεε==∆-+- (4)2122220102114422RR r R R W E r dr E r dr εεπεπ=⋅+⋅⎰⎰ 2001211()8r rrQ R R R εεπεε-=+- (5)00211(1)(1)4rrQ R σσεπε'=-=- 8-3-12解(1)在12R r R <<区域内作以r 为半径,长为l 的同轴柱面为高斯面,则由介质中的高斯定理222220000041121()()222142312r Q Q Q Q C U C C C C ε=+-=+-=+()1ni Si D dS q =⋅=∑⎰⎰,有2rlD l πλ=所以 2D rλπ=又 0r D E εε=我们得到离轴线距离为r 处的场强为 02r E rλπεε=, 方向沿径向向外(2)22112001ln 22R R R R r r R U Edr dr r R λλπεεπεε∆===⎰⎰(3)2122200112ln 24R r R r R W E rdr R λεεππεε=⋅=⎰8-3-13解(1)282014.410/2e w E J m ε-==⨯ (2)3354[()]7.6103e W R h R w J π=+-=⨯式中R 为地球半径并取6370R km =8-3-14解(1)浸入煤油后,电容器电容增加为原来的r ε倍,即002r C C C ε==,而电量不变.能量损失为2222210200000111(1)9109002222444Q Q Q Q W C U C C C C -∆=-=-===⨯⨯⨯ 41.8210J -=⨯(2)若将两电容器并联,则要发生电荷转移,但电荷总量不变,仍为2Q .并联后总电容为 001r C C C C ε=+=+总(), 两电容器并联后总能量为22024221rQ Q W C C ε'==+总()() 并联后能量损失为0W W W W ''∆=+-() 56.110J -=⨯ 8-3-15解K 接到1处,1C 带电为641108101209.610()Q CU C --==⨯⨯=⨯;再将K 接到2后,1C 和2C 总带电量仍为1Q ,两电容器电压为4169.6108010Q U V C --⨯===⨯总(8+4)电容器1C 中的能量2622111181080 2.561022W C U J --==⨯⨯⨯=⨯ 电容器2C 中的能量22221 1.28102W C U J -==⨯8-3-16解据题意,把电子看作电荷均匀分布在外表面上,其静电能为222200200111()422424R e e W E dV r dr r Rεεππεπε∞==⋅=⋅⎰⎰ 在估计电子半径的数量级时,一般可以略去上式中的系数,因此204e W Rπε=,据题意2204e e m C Rπε=,我们可以求得21520 2.8104e e R m m Cπε-==⨯ 8-3-17解当介质板插入x 距离时,电容器的电容为 000()[(1)]r x r a x a xaaC a x dddεεεεε-=+=+-此时电容器储能为220()22[(1)]x r Q Q dW x C a a x εε==+- 电介质未插入时,电容器储能为22020022Q Q dW C aε== 当电介质插入x 时,电场力F 对电介质板所作的功等于电容器储能的减少量,即0()W W x -,电场力为当插入一半时,2ax =,则电场力为 2020[()](1)2[(1)]r r W W x Q d F x a a x εεε∂--==∂+-,方向平行极板向右.8-3-18解(1)因电压U 不变,拉开前的静电能为 222001111222SS W C U U U d d εε==⋅= 拉开后的静电能为 2220022112224SS W C U U U d dεε==⋅= 则系统静电能的改变为 222000210424SSSW W W U U U dddεεε∆=-=-=-<结果表明当极板拉开后,系统的静电能减少.(2)当保持电压一定时,电场对电源作功为 A U Q =-∆两板距离从d 拉开到2d 时,极板上电荷的增量Q ∆为0002121()22S S SQ Q Q C U C U U U d d dεεε∆=-=-=-=- 因此 200()022S S A U Q U U U d dεε=-∆=--=>结果表明当极板拉开后,在保持U 不变时,电场对电源作正功.(3)外力F 对极板作的功为 2222222000211()22224ddd ddd SU SU SU CU A F dl dx dx x d d d dεεε'=⋅===-=⎰⎰⎰外力F 对极板作的功,也可由功能关系得到 222000()424SU SU SU A W A dddεεε'=∆+=-+=所得结果相同.8-3-19解(1)令无限远处电势为零,则带电荷为q 的导体球,其电势为04q U Rπε=,将dq 从无限远处搬到球上的过程中,外力作的功等于该电荷元在球上所具有的电势能 04q dA dW dq Rπε==(2)外力作功为23302(1)()2(1)r r Q d aF a εεε-=+200048Qq Q A dA dq RRπεπε===⎰⎰8-3-20解因为电荷保持不变,故有、无介质时,电场中各点的电位移矢量D 不变,电场能量密度为2000111222e e r r rw D D w DE D εεεεε==⋅==电场总能量为e rW W ε=9-3计算题9-3-1. 解:(1)导线水平段在P 点产生的磁感应强度为零, 因此P 点的磁感应强度由竖直段产生, 即,4)90cos 0(cos 400aIa I B πμπμ=︒-︒=根据右手定则可判断其方向垂直纸面向外. (2)两水平段半长直导线在P 点产生的磁场方向相同,因此相当于一无限长直导线. 所以P 点的磁场为一无限长直导线和半圆共同产生的,即,4200rIr I B μπμ+=方向垂直纸面向里. (3)三边在P 点产生的磁场完全相同,因此P 点的磁感应强度为,29)150cos 30(cos 3024300a Itg a I B πμπμ=︒-︒︒=方向垂直纸面向里.9-3-2. 解: O 点磁感应强度大小为部分圆弧和直线段共同产生,且它们的方向相同,所以),222(4)22cos(22cos 4222000ϕϕππμϕπϕπμπϕπμtg R I R I R I B B B BA ACB +-=-••+-•=+=方向垂直纸面向里. 9-3-3. 解:导线可分为四段,其中水平部分在O 点不产生磁场,因此O 点的磁场为两半圆和竖直向下半无限长直导线共同产生的,即磁感应强度大小为,444202010R IR IR IB πμμμ-+=方向垂直纸面向里. 9-3-4. 解:取薄金属板上宽度为dx 的长直电流元,其电流为,aIdxdI =到P 点的距离为x ,该线电流在点P 激发的磁感应强度大小为.,20方向垂直纸面向外xdIdB πμ=因所有线电流在点P 激发的磁场方向均相同,故点P 的磁感应强度为⎰⎰+===ab bdx axIdB B πμ20,ln20b b a a I +πμ方向垂直纸面向外.9-3-5. 解:环心O 在两根通电直导线的延长线上,故它们在O 点产生的磁场为零,长为l 的载流圆弧在其圆心处的磁场为2001422r Ilr l r I B πμπμ==,设左右两段圆弧的弧长分别为21,l l ,则两者在O 点的磁感应强度分别为,方向垂直纸面向里。
物理学概论习题答案(1)

物理学概论习题答案(1)第二章习题答案1.什么情况下你可将物体视为质点?从“质点模型”你能获得一种研讨问题的什么方法?解:质点是指只有质量而无大小、形状的点。
例如研究地球绕太阳公转时,地球的大小和形状就可以忽略,从而可以把地球看成是一个“点”,但考察地球自转问题时就不能把地球看成一个“质点”了。
从方法论上叫做建立模型,简称建模,即将复杂问题简单化;从哲学上说叫抓主要矛盾。
3.你能表明描写运动的四个物理量——位矢、位移、速度、加速度的物理含义及单位吗?解:位矢物理含义:由坐标原点向质点所在位置画一个有向线段r 来表示质点所在的位置,这个有向线段称为位矢。
单位是米,符号m 。
位移的物理含义:由t 时刻质点位置指向t t ?+时刻质点位置的一个矢量。
单位是米,符号m 。
速度的物理含义:无限小位移r d 和经历此小位移的无限小时间t d 的比值,称为瞬时速度,简称速度。
单位是米每秒,符号m/s 。
加速度的物理含义:无限小速度变化量v d 与对应的无限小时间t d 的比值,称为瞬时加速度,简称加速度。
单位是米每二次方秒,符号2s m 。
4. 知道了在平面上运动质点在s 21=t 时刻的坐标为(3m ,8m),在4s 2=t 时刻的坐标为(7m ,14m),试分别确定在2,4秒时的位矢和这段时间内的位移及平均速度。
解:对于平面运动,位置矢量表达式为)(m j y i x r +=s 21=t 时,位矢为)(831m j i r +=。
4s 2=t 时,位矢为)(1472m j i r +=。
这段时间内的位移)(648)-14(3)-7(12m j i j i r r r +=+=-=? 平均速度)(m/s 322464j i j i t r v +=-+=??=6. 平均速度等于零,是否物体一定静止?解:不一定。
根据平均速度表达式tr v ??= 可知,若该时间内位移r ?为零,则若平均速度 v 一定为零,但物体不一定静止。
理论物理导论-第一章1

i ) 由此得到: d ( T ) d (mi xi ) m d ( x i mi x i i dt x dt dt i ,由(1-1)式,正等于 X i ,于是: x 而 mi
U 再结合(1-3)式 X i , xi
17
d T ( ) Xi i dt x
分析力学初步
第一章 拉格朗日方程 与哈密顿方程
低速宏观运动的基本原理,除了牛顿 三定律表述外,还有拉格朗日表述方式和 哈密顿表述方式。这些表述方式实质内容 相同,只是表达形式有差别。拉氏表述和 哈氏对客观规律的本质反映得更清楚,而 且便于推广到高速和微观情况。
1
§1-1 自由度 约束与广义坐标
约束方程的一般形式
不稳定约束:约束方程中明显地含有时间变量 t 例:一个质点被约束在一个不断变化的球面上运动 约束方程的一般形式
6
可解约束,不可解约束 不可解约束:约束始终不能解除 例:一个质点连结刚性的杆子 质点到连结点的距离只能是杆长,即始终不 能脱离约束
可解约束:约束在某范围内可以被解除 例:一个质点连结在不可伸长的软绳上 质点到连结点的距离不能大于绳长, 但可接近连结点,即不大于 r 的范围 内脱离了约束
独立坐标变量 x,y 或独立参量
都可以作为广义坐标 9
例如,对约束在空间固定曲线上运动的 质点,可用自始点计量的路程s作广义坐 标;
再例如,用细杆约束在竖直平面内摆动 的质点,可用杆与铅垂线的夹角θ作广义 坐标。
10
讨论: 1)广义坐标不限于长度量纲,也可以是:角度 电量q,面积A,体积V,电位移矢量,磁化强度 2)自由度对一个系统是唯一确定的,广义坐标 则可多种选取。 例: 3)广义坐标已经体现出约束方程的要求,就不 必再列出约束方程,约束越多,广义坐标的个数 越少,原则上说,问题变得越简单,广义坐标的 这些特点具有很大的优越性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P(x) (x) (x) 43x e2 2x
(3)在极值点,由一阶导数
dP(x) 0 dx
可得方程
x(1 x)e2x 0
而方程的根
x 0 ; x ; x 1/
即为极值点。几率密度在极值点的值
P(0) 0;lim P(x) 0;P(1/ ) 4e2 x
由于P(x)在区间(0,1/)的一阶导数大于零,是升函数; 在区间(1/,)的一阶导数小于零,是减函数,故几率密
k
。
h
A
1
mv2
3、用来解释光电效应的爱因斯坦公式为
2
。
4、戴微孙-革末 实验验证了德布罗意波的存在,德布罗意关系
为
E
,
p
k
。
3.两个质量为m1、m2的质点固定于一长为R的轻杆两端,杆 的质量可以忽略不计,这个系统在重力作用下,在一铅直面 内运动,请分别用拉式方程和哈氏方程分析其运动。
解:设杆在水平方向的位移为x,在竖直方向的位移为y.
0
k
2e 2 d
2 0
k
2
1 2
e 2
0
0
e
2
d
k 1 e 2 d
2 2 0
k 1 2 2 2
k
4
2
将
k
2 、 2
代入,可得
U
1
4
1 2
E0
是总能量的一半,由能量守恒定律
E0 T U
可知动能平均值
T
E0
U
1 2
E0
U
和势能平均值相等,也是总能量的一半。
)
(m1gy1
m2
gy2)]
m1x12 m1 y12 m2 x22 m2 y22
代入哈氏方程:
H x1
p x1
H y1
p y1
H
p
可解得与(1)相同结果
5.对本章1-3节所举的两个小球的振动,给出初始条件如下:
t
0,{ x1 x2
a; x1 0; x2
0 0
试求a1,a2,δ1,δ2,并讨论两球各自的位移与时间的关系。 解:
x1 a1 cos(w1t 1) a2 cos(w2t 2 )
x2 a1 cos(w1t 1) a2 cos(w2t 2x2
a; 0;
x1 x2
0 0
解得:
1 2 0
a1
a2
a 2
所以:
x1
a 2 [cos(w1t)
c os (w2t ) ]
x2 x1 R sin,y2 y1 R cos
(1)拉式方程分析:
U (- m1gy1 m2 gy2)
T
1 2
m1 ( x12
y12 )
1 2
m2 (x22
y22
)
则有
L
T
-
U
1 2
m1 ( x12
y12
)
1 2
m2
( x22
y22
)
(m1gy1
m2
gy2)
由拉式方程:
d L L dt x1 x1 0
度的最大值为 4e2 ,出现在 x 1/ 处。
2. 一维线性谐振子处于状态
1 2 x 2 1 it
(x,t) Ae 2 2
(1)求归一化因子A;
(2)求谐振子坐标 x 的平均值;
(3)求谐振子势能的平均值。
解:(1) dx A2 e 2x2 dx
2 A2 e 2 x2 dx 0
(1)归一化因子A;
(2)粒子的几率密度;
(3)粒子出现在何处的几率最大?
解:(1) (x) (x)dx A2 x2e2xdx 令 2x ,则
0
A2
x2e2xdx
0
A2
83
2e d
0
A2
83
(3)
A2
83
2!
A2
43
由归一化的定义
(x) (x)dx 1
得 A 23/ 2
3.设把宽为 a的一维无限深势阱的坐标原点取在势阱中点,有
U
(x)
0, ,
(| x | a / 2) (| x | a / 2)
试通过具体解定态方程,证明势阱中粒子的波函数为
2 n
n
(
x)
cos x, aa
2 sin n x,
aa
n 1,3,5, n 2,4,6,
粒子的能量为
d dt
L x2
L x2
0
d dt
L y 1
L y1
0
d dt
L y 2
L y2
0
解得:
x1 x2 0, y1 y2 g
该系统在水平方向加速度为0,在竖直方向加速度为g.
(2)哈氏方程分s 析:
H L p j q j
j 1
-[1 2
m1 ( x12
y12
)
1 2
m2
( x22
y22
x2
a 2
[c
os
(w1t
)
c
os
(w2t
)]
第二章 薛定谔方程 习题解答
第二章 薛定谔方程
本章要求: 1 .了解波粒二象性假设的物理意义及其主要实验事实, 2 .熟练掌握波函数的标准化条件:有限性、连续性和单值性。深入理解波函数的 概率解释。 3 .理解态叠加原理以及任何波函数按不同动量的平面波展开的方法及其物理意 义. 4 .熟练掌握薛定谔方程的建立过程。深入了解定态薛定谔方程,定态与非定态波 函数的意义及相互关系。了解连续性方程的推导及其物理意义。
2A2 e 2 d A2
由归一化的定义 0
dx 1
得
A
(2) x xP(x)dx A2 xe 2x2 dx
因被积函数是奇函数,在对称区间上积分应为0,故
x 0
(3)U U (x)P(x)dx
1 kx2 e 2x2 dx
2
k x2e 2x2 dx
第一章 拉格朗日方程与哈密顿方程 习题解答
本章要求:
1. 熟练掌握自由度、约束和广义坐标基本概念 2. 熟练掌握拉格朗日方程的形式 3. 熟练掌握哈密顿方程的形式及其物理意义 4. 基本掌握应用拉格朗日方程和哈密顿方程解
决力学问题
填 空:
1、玻尔的量子化条件为 L n
2、德布罗意关系为
E
,
p
填 空:
1、波函数的标准条件为 单值,连续,有限 。
2、 (x, y, z,t) 2 的物理意义: 发现粒子的几率密度与之成正比 。
3、 (r, ,) 2r 2dr 表示 在 r—r+dr 单位立体角的球壳内发现粒子的几率。
1. 一维运动粒子处于
(
x)
Axe
x
的状态,式中 >0,求
0
(x 0) (x 0)
第二章 薛定谔方程
本章要求:(二)一维势场中的粒子 1 .熟练掌握一维薛定谔方程边界条件的确定和处理方法。 2 .熟练掌握一维无限深方势阱的求解方法及其物理讨论,掌握一维有限深方势阱 束缚态问题的求解方法。 3 .熟练掌握势垒贯穿的求解方法及隧道效应的解释。掌握一维有限深方势阱的反 射、透射的处理方法及共振现象的发生。 4 .熟练掌握一维谐振子的能谱及其定态波函数的一般特点及其应用。
