湖北省武汉市北水湖备考2020九年级元调模拟题 (二)Word解析版
湖北省武汉市新观察2020年九年级数学元月调考复习交流卷(二) 解析版

湖北省武汉市新观察2020年九年级数学元月调考复习交流卷(二)一、选择题(共10小题,每小题3分,共30分)1.(3分)下列方程是一元二次方程的是()A.ax2+bx+c=0 B.x+=2 C.2(x﹣1)2=4 D.x3+x=12.(3分)将抛物线y=x2向左平移2个单位,再向下平移1个单位,所得抛物线为()A.y=(x﹣2)2﹣1 B.y=(x﹣2)2+1 C.y=(x+2)2﹣1 D.y=(x+2)2+1 3.(3分)下列关于事件的说法,错误的是()A.“通常温度降到0℃以下时,纯净的水结冰”是必然事件B.“随意翻到一本书的某页,这页的页码是奇数”是随机事件C.“从地面发射1枚导弹,未击中目标”是不可能事件D.“购买一张彩票,中奖”是随机事件4.(3分)下列图案中,既是中心对称图形又是轴对称图形的是()A.B.C.D.5.(3分)如图是一个隧道的横截面,它的形状是以O为圆心的圆的一部分,CM=DM=2,MO交圆于E,EM=6,则圆的半径为()A.4 B.2C.D.6.(3分)若x1,x2是一元二次方程x2﹣3x+2=0的两根,则x1+x2+x1x2的值是()A.﹣1 B.﹣5 C.5 D.17.(3分)一个不透明的袋中有四张完全相同的卡片,把它们分别标上数字1、2、3、4.随机抽取两张卡片,则两次抽取的卡片上数字之积为偶数的概率是()A.B.C.D.8.(3分)已知⊙O的半径等于8cm,圆心O到直线l上某点的距离为8cm,则直线1与⊙O 的公共点的个数为()A.0 B.1或0 C.0或2 D.1或29.(3分)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角DA和DC(两边足够长),再用28m长的篱笆围成一个面积为192m2矩形花园ABCD(篱笆只围AB、BC两边),在P处有﹣棵树与墙CD、AD的距离分别是15m和6m,现要将这棵树也围在花园内(含边界,不考虑树的粗细),则AB的长为()A.8或24 B.16 C.12 D.16或12 10.(3分)如图,BC为⊙O直径,弦AC=2,弦AB=4,D为⊙O上一点,I为AD上一点,且DC=DB=Dl,AI长为()A.B.C.D.二、填空题(共6小题,每小题3分,共18分)11.(3分)已知﹣2是方程x2﹣c=0的一个根,c=.12.(3分)如表记录了一名球员在罚球线上投篮的结果投篮次数n50 100 150 200 250 300 500投中次数m28 60 78 104 123 152 251投中频率(精确到0.01)0.56 0.60 0.52 0.52 0.49 0.51 0.50 由此估计这名球员在罚球线上投中篮的概率约是.(精确到0.01)13.(3分)我国古代南宋数学家杨辉在1275年提出了一个问题:直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少12步),问阔及长各几步(问宽和长各多少步).“如果设矩形田地的宽为x步,则可列出方程再化为一般形式为.14.(3分)正八边形半径为2,则正八边形的面积为.15.(3分)圆锥的侧面展开图是一个扇形,扇形的弧长为10πcm,扇形面积为65πcm2,则圆锥的高为.16.(3分)一元二次方程ax2﹣2ax+c=0有一个根为x=3,且y=ax2﹣2ax+c过(2,﹣3),则不等式ax2﹣2ax+c≤﹣x﹣1的解为.三、解答题(共8题,共72分)17.(8分)解方程:2x2﹣2x﹣1=0.18.(8分)如图,A、B、C、D是⊙O上四点,且AB=CD,求证:AD=BC.19.(8分)把三张形状、大小完全相同但画面不同的风景图片,都按同样的方式剪成相同的三段,然后将上、中、下三段分别装入甲、乙、丙三个盒子中,从三个盒子中各抽取一张,求所抽取图片恰好组成一张完整的风景图片的概率.20.(8分)如图,在8×8网格上,已知A(﹣2,2)、B(1,1).(1)将B绕A顺时针旋转90°,画出B点对应点D的位置并求其坐标.(2)若A绕某点旋转90°可与B重合,画出旋转中心C的位置并求其坐标.(3)直接写出网格上使∠APB=45°的格点P的个数.21.(8分)如图I,四边形ADBC内接于⊙O,E为BD延长线上一点,AD平分∠EDC,(1)求证:AB=AC;(2)如图2,若CD为直径,过A点的圆的切线交BD延长线于E,若DE=1,AE=2.求⊙O的半径.22.(10分)系统找不到该试题23.(10分)已知△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,M为CE中点.(1)如图1,若D点在BA延长线上,直接写出BM与DM的数量关系与位置关系不必证明.(2)如图2,当C,E,D在同直线上,连BE,探究BE与AB的的数量关系,并加以证明.(3)在(2)的条件下,若AB=AE=2.求BD的长.24.(12分)如图1,抛物线y=x2+bx+c的顶点P在直线y=2x+4上移动,直线y=2x+4与y轴交于点A.(1)若点P的模坐标为﹣1,求b,c的值;(2)当b何值时,c有最小值,求此时抛物线的解析式;(3)如图2,若抛物线的顶点在x轴上,E为线段OA上一点,H(﹣1,a)在抛物线上,直线EH交抛物线于另一点F,连接AF,若FA=FE,求点E的坐标.参考答案与试题解析一、选择题(共10小题,每小题3分,共30分)1.(3分)下列方程是一元二次方程的是()A.ax2+bx+c=0 B.x+=2 C.2(x﹣1)2=4 D.x3+x=1【分析】根据一元二次方程必须同时满足三个条件:①整式方程,即等号两边都是整式;方程中如果有分母,那么分母中无未知数;②只含有一个未知数;③未知数的最高次数是2进行分析即可.【解答】解:A、因为a可能为0,所以不一定是一元二次方程,故此选项错误;B、因为含有分式,所以不是一元二次方程,故此选项错误;C、因为符合一元二次方程的定义,所以是一元二次方程,故此选项正确;D、因为最高是三次,所以不是一元二次方程,故此选项错误;故选:C.2.(3分)将抛物线y=x2向左平移2个单位,再向下平移1个单位,所得抛物线为()A.y=(x﹣2)2﹣1 B.y=(x﹣2)2+1 C.y=(x+2)2﹣1 D.y=(x+2)2+1 【分析】根据二次函数图象的平移规律(左加右减,上加下减)进行解答即可.【解答】解:原抛物线的顶点为(0,0),向左平移2个单位,再向下平移1个单位,那么新抛物线的顶点为(﹣2,﹣1).可设新抛物线的解析式为:y=﹣3(x﹣h)2+k,代入得:y=(x+2)2﹣1,化成一般形式得:y=﹣3x2﹣6x﹣5.故选:C.3.(3分)下列关于事件的说法,错误的是()A.“通常温度降到0℃以下时,纯净的水结冰”是必然事件B.“随意翻到一本书的某页,这页的页码是奇数”是随机事件C.“从地面发射1枚导弹,未击中目标”是不可能事件D.“购买一张彩票,中奖”是随机事件【分析】直接利用随机事件以及必然事件的定义进而分析得出答案.【解答】解:A、“通常温度降到0℃以下时,纯净的水结冰”是必然事件,正确,不合题意;B、“随意翻到一本书的某页,这页的页码是奇数”是随机事件,正确,不合题意;C、“从地面发射1枚导弹,未击中目标”是随机事件,原说法错误,符合题意;D、“购买一张彩票,中奖”是随机事件,正确,不合题意;故选:C.4.(3分)下列图案中,既是中心对称图形又是轴对称图形的是()A.B.C.D.【分析】根据轴对称图形与中心对称图形的概念进行判断即可.【解答】解:A、是轴对称图形,也是中心对称图形,故正确;B、不是轴对称图形,不是中心对称图形,故错误;C、是轴对称图形,不是中心对称图形,故错误;D、是轴对称图形,不是中心对称图形,故错误.故选:A.5.(3分)如图是一个隧道的横截面,它的形状是以O为圆心的圆的一部分,CM=DM=2,MO交圆于E,EM=6,则圆的半径为()A.4 B.2C.D.【分析】因为M是⊙O弦CD的中点,根据垂径定理,EM⊥CD,则CM=DM=2,在Rt△COM 中,有OC2=CM2+OM2,进而可求得半径OC.【解答】解:连接OC,∵M是⊙O弦CD的中点,根据垂径定理:EM⊥CD,设圆的半径是x米,在Rt△COM中,有OC2=CM2+OM2,即:x2=22+(6﹣x)2,解得:x=,所以圆的半径长是.故选:D.6.(3分)若x1,x2是一元二次方程x2﹣3x+2=0的两根,则x1+x2+x1x2的值是()A.﹣1 B.﹣5 C.5 D.1【分析】利用根与系数的关系可得x1+x2=3,x1x2=2,代入x1+x2+x1x2,计算即可.【解答】解:∵x1,x2是一元二次方程x2﹣3x+2=0的两根,∴x1+x2+x1x2=3+2=5.故选:C.7.(3分)一个不透明的袋中有四张完全相同的卡片,把它们分别标上数字1、2、3、4.随机抽取两张卡片,则两次抽取的卡片上数字之积为偶数的概率是()A.B.C.D.【分析】画树状图展示所有6种等可能的结果数,再找出两次抽取的卡片上数字之积为偶数的结果数,然后根据概率公式求解.【解答】解:画树状图为:共有6种等可能的结果数,其中两次抽取的卡片上数字之积为偶数的结果数为5,所以两次抽取的卡片上数字之积为偶数的概率=故选:D.8.(3分)已知⊙O的半径等于8cm,圆心O到直线l上某点的距离为8cm,则直线1与⊙O 的公共点的个数为()A.0 B.1或0 C.0或2 D.1或2【分析】利用直线与圆的位置关系的判断方法得到直线l和⊙O相离,然后根据相离的定义对各选项进行判断.【解答】解:∵⊙O的半径等于8cm,圆心O到直线l的距离为8cm,即圆心O到直线l的距离小于或等于圆的半径,∴直线l和⊙O相切或相交,∴直线l与⊙O公共点的个数为1或2.故选:D.9.(3分)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角DA和DC(两边足够长),再用28m长的篱笆围成一个面积为192m2矩形花园ABCD(篱笆只围AB、BC两边),在P处有﹣棵树与墙CD、AD的距离分别是15m和6m,现要将这棵树也围在花园内(含边界,不考虑树的粗细),则AB的长为()A.8或24 B.16 C.12 D.16或12【分析】设AB=xm,则BC=(28﹣x)m,根据矩形的面积公式结合矩形花园ABCD的面积,即可得出关于x的一元二次方程,解之取其较小值即可得出结论.【解答】解:设AB=xm,则BC=(28﹣x)m,依题意,得:x(28﹣x)=192,解得:x1=12,x2=16.∵P处有一棵树与墙CD、AD的距离分别是15m和6m,∴x2=16不合题意,舍去,∴x=12.故选:C.10.(3分)如图,BC为⊙O直径,弦AC=2,弦AB=4,D为⊙O上一点,I为AD上一点,且DC=DB=Dl,AI长为()A.B.C.D.【分析】如图,连接IC,作IE⊥AC于E,IF⊥AB于F,IG⊥BC于G.首先证明点I是△ABC的内心,再利用面积法求出IE的长即可解决问题.【解答】解:如图,连接IC,作IE⊥AC于E,IF⊥AB于F,IG⊥BC于G.∵DB=DC,∴=,∠DBC=∠DCB,∴∠BAD=∠CAD,∵DI=DC,∴∠DIC=∠DCI,∵∠DIC=∠DAC+∠ACI,∠DCI=∠DCB+∠ICB,∠DBC=∠DAC,∴∠ICA=∠ICB,∴点I为△ABC内心,∴IE=IF=IG,∵BC是直径,∴∠BAC=90°,∴BC===2,∵S△ABC=•AB•AC=•IE•(AB+AC+BC),∴IE=3﹣,∵∠IAE=∠AIE=45°,∴AI=IE=3﹣,故选:D.二、填空题(共6小题,每小题3分,共18分)11.(3分)已知﹣2是方程x2﹣c=0的一个根,c= 4 .【分析】将x=﹣2代入求解可得.【解答】解:将x=﹣2代入,得:4﹣c=0,解得c=4,故答案为:4.12.(3分)如表记录了一名球员在罚球线上投篮的结果投篮次数n50 100 150 200 250 300 500投中次数m28 60 78 104 123 152 251 投中频率(精确到0.01)0.56 0.60 0.52 0.52 0.49 0.51 0.50 由此估计这名球员在罚球线上投中篮的概率约是0.50 .(精确到0.01)【分析】根据频率估计概率的方法结合表格数据可得答案.【解答】解:由频率分布表可知,随着投篮次数越来越大时,频率逐渐稳定到常数0.50附近,∴这名球员在罚球线上投篮一次,投中的概率为0.50,故答案为:0.50.13.(3分)我国古代南宋数学家杨辉在1275年提出了一个问题:直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少12步),问阔及长各几步(问宽和长各多少步).“如果设矩形田地的宽为x步,则可列出方程再化为一般形式为x2+12x﹣864=0 .【分析】直接利用长乘以宽=864进而得出答案.【解答】解:设矩形田地的宽为x步,根据题意可得:x(x+12)=864,整理得:x2+12x﹣864=0.故答案为:x2+12x﹣864=0.14.(3分)正八边形半径为2,则正八边形的面积为16.【分析】首先根据正八边形的性质得出中心角度数,进而得出AC的长,从而计算出△ABO 的面积,最后乘以8即可求得正八边形的面积.【解答】解:连接OA,OB,作AC⊥BO于点C,∵⊙O的半径为2,则⊙O的内接正八边形的中心角为:=45°,∴AC=CO=2,∴S△ABO=OB•AC=×2×2=2,∴S正八边形=8S△ABO=16,故答案为:16.15.(3分)圆锥的侧面展开图是一个扇形,扇形的弧长为10πcm,扇形面积为65πcm2,则圆锥的高为12 .【分析】圆锥的侧面积=×弧长×母线长,把相应数值代入即可求解可得圆锥的母线长,然后可以利用勾股定理求得圆锥的高.【解答】解:设母线长为R,由题意得:65π=×10π×R,解得R=13cm.设圆锥的底面半径为r,则10π=2πr,解得:r=5,故圆锥的高为:=12故答案为:12.16.(3分)一元二次方程ax2﹣2ax+c=0有一个根为x=3,且y=ax2﹣2ax+c过(2,﹣3),则不等式ax2﹣2ax+c≤﹣x﹣1的解为﹣1≤x≤2 .【分析】先把(2,﹣3)代入y=ax2﹣2ax+c得到c=﹣3,把x=3代入ax2﹣2ax﹣3=0得a=1,则抛物线为y=x2﹣2x﹣3,通过解方程x2﹣2x﹣3=x﹣1得抛物线为y=x2﹣2x﹣3与直线y=x﹣1的交点的横坐标分别为然后利用函数图象写出直线不在抛物线下方的部分对应的自变量的范围即可.【解答】解:把(2,﹣3)代入y=ax2﹣2ax+c得4a﹣4a+c=﹣3,即c=﹣3,把x=3代入ax2﹣2ax+c=0得9a﹣6a+c=0,解3a﹣3=0,解得a=1,所以抛物线为y=x2﹣2x﹣3,解方程x2﹣2x﹣3=﹣x﹣1,解得x1=﹣1,x2=2,∴抛物线为y=x2﹣2x﹣3与直线y=﹣x﹣1的交点的横坐标分别为﹣1和2,即不等式ax2﹣2ax+c≤﹣x﹣1的解为﹣1≤x≤2,故答案为:﹣1≤x≤2.三、解答题(共8题,共72分)17.(8分)解方程:2x2﹣2x﹣1=0.【分析】此题可以采用配方法和公式法,解题时要正确理解运用每种方法的步骤.【解答】解法一:原式可以变形为,,,∴,∴,.解法二:a=2,b=﹣2,c=﹣1,∴b2﹣4ac=12,∴x==,∴x1=,x2=.18.(8分)如图,A、B、C、D是⊙O上四点,且AB=CD,求证:AD=BC.【分析】想办法证明=即可.【解答】证明:∵AB=CD,∴=,∴+=+,∴=,∴AD=BC.19.(8分)把三张形状、大小完全相同但画面不同的风景图片,都按同样的方式剪成相同的三段,然后将上、中、下三段分别装入甲、乙、丙三个盒子中,从三个盒子中各抽取一张,求所抽取图片恰好组成一张完整的风景图片的概率.【分析】把三张风景图片用甲、乙、丙来表示,根据题意画树形图,数出可能出现的结果利用概率公式即可得出答案.【解答】解:把三张风景图片用甲、乙、丙来表示,根据题意画如下的树形图:从树形图可以看出,所有可能出现的结果共有27种,这些结果出现的可能性相等.其中恰好组成一张完整风景图片的有3种,所以所抽取图片恰好组成一张完整风景图片的概率为=.20.(8分)如图,在8×8网格上,已知A(﹣2,2)、B(1,1).(1)将B绕A顺时针旋转90°,画出B点对应点D的位置并求其坐标.(2)若A绕某点旋转90°可与B重合,画出旋转中心C的位置并求其坐标.(3)直接写出网格上使∠APB=45°的格点P的个数.【分析】(1)利用网格特点和旋转的性质画出B点的对称点D,从而得到D点坐标;(2)以AB为斜边作等腰直角三角形得到C点和C′点的坐标;(3)分别以C点和C′为圆心,CA为半径作圆,然后再优弧AB上找出格点的个数即可.【解答】解:(1)如图,点D为所作,D(﹣3,﹣1);(2)如图,点C为所作,C点坐标为(3,0)或(﹣1,0);(3)P点的个数为10个.21.(8分)如图I,四边形ADBC内接于⊙O,E为BD延长线上一点,AD平分∠EDC,(1)求证:AB=AC;(2)如图2,若CD为直径,过A点的圆的切线交BD延长线于E,若DE=1,AE=2.求⊙O的半径.【分析】(1)根据圆内接四边形的性质得到∠EDA=∠ACB,根据圆周角定理得到∠CDA =∠ABC,根据等腰三角形的判定定理证明;(2)连接AO并延长交BC于H,AM⊥CD于M,根据角平分线的性质得到DM=DE=1,AE =AM=2,证明Rt△ABE≌Rt△ACM,得到CM=BE,根据勾股定理列式计算得到答案.【解答】(1)证明:∵四边形ADBC内接于⊙O,∴∠EDA=∠ACB,由圆周角定理得,∠CDA=∠ABC,∵AD平分∠EDC,∴∠EDA=∠CDA,∴∠ABC=∠ACB,∴AB=AC;(2)解:连接AO并延长交BC于H,AM⊥CD于M,∵AB=AC,∴AH⊥BC,又AH⊥AE,∴AE∥BC,∵CD为⊙O的直径,∴∠DBC=90°,∴∠E=∠DBC=90°,∴四边形AEBH为矩形,∴BH=AE=2,∴BC=4,∵AD平分∠EDC,∠E=90°,AM⊥CD,∴DE=DM=1,AE=AM=2,在Rt△ABE和Rt△ACM中,∴Rt△ABE≌Rt△ACM(HL),∴BE=CM,设BE=x,CD=x+2,在Rt△BDC中,x2+42=(x+2)2,解得,x=3,∴CD=5,∴⊙O的半径为2.5.22.(10分)系统找不到该试题23.(10分)已知△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,M为CE中点.(1)如图1,若D点在BA延长线上,直接写出BM与DM的数量关系与位置关系不必证明.(2)如图2,当C,E,D在同直线上,连BE,探究BE与AB的的数量关系,并加以证明.(3)在(2)的条件下,若AB=AE=2.求BD的长.【分析】(1)连接AM,则CM=AM,可证明△BCM≌△BAM,可得∠MBA=45°,同理可得∠MDA=45°,则结论得证;(2)延长BM到N,使BM=MN,连EN,DN,BD,BE,则△CBM≌△ENM,再证△DEN≌△ABD,可得DB=DN,DB⊥DN,则结论得证;(3)连BE,BD交AE于N,证明BD为AE的垂直平分线,则EN=AN=,可得BN=,求出BD=+.【解答】解:(1)BM=DM,BM⊥DM;如图1,连接AM,∵△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,∴∠BAC=∠EAD=45°,∴∠CAE=90°,∵M为CE中点.∴CM=AM,∵BM=BM,BC=BA,∴△BCM≌△BAM(SSS),∴∠CBM=∠MBA=45°,同理可得∠MDA=45°,∴∠BMD=90°,∴BM=DM,BM⊥DM;(2)如图2,延长BM到N,使BM=MN,连EN,DN,BD,BE,∵∠CMB=∠EMN,CM=ME,∴△CBM≌△ENM(SAS),∴BC=EN,∠BCM=∠MEN,∴EN=AB,∵∠CBA=∠ADE=90°,∴∠BCM+∠BAD=180°,∵∠NED+∠MEN=180°,∴∠NED=∠BAD,又∵AD=DE,∴△DEN≌△ABD(SAS),∴DB=DN,DB⊥DN,∴DM⊥BN,∴BE=EN=BC=AB;(3)如图3,连BE,BD交AE于N,∵BE=AE=AB=2,DE=DA=2,∴BD为AE的垂直平分线,∴EN=DN=AN=,∴BN==,∴BD=+.24.(12分)如图1,抛物线y=x2+bx+c的顶点P在直线y=2x+4上移动,直线y=2x+4与y轴交于点A.(1)若点P的模坐标为﹣1,求b,c的值;(2)当b何值时,c有最小值,求此时抛物线的解析式;(3)如图2,若抛物线的顶点在x轴上,E为线段OA上一点,H(﹣1,a)在抛物线上,直线EH交抛物线于另一点F,连接AF,若FA=FE,求点E的坐标.【分析】(1)设点P(m,2m+4),m=﹣1,则点P(﹣1,2),则抛物线的表达式为:y =(x+1)2+2=x2+x+,即可求解;(2)抛物线的对称轴为:x=﹣b,则点P(﹣b,4﹣2b),将点P的坐标代入抛物线表达式得:b2﹣b2+c=4﹣2b,即c=(b﹣2)2+2,即可求解;(3)FA=FE,则AG=GE,即(2k2﹣2k+)=2k2﹣2k+﹣(k+),解得:k=或﹣,即可求解.【解答】解:(1)设点P(m,2m+4),m=﹣1,则点P(﹣1,2),则抛物线的表达式为:y=(x+1)2+2=x2+x+,故b=1,c=;(2)抛物线的对称轴为:x=﹣b,则点P(﹣b,4﹣2b),将点P的坐标代入抛物线表达式得:b2﹣b2+c=4﹣2b,即c=(b﹣2)2+2,∵0,故c有最小值,此时b=2,故抛物线的表达式为:y=x2+x+4;(3)过点F作FG⊥y轴于点G,∵点P在x轴上,故点P(﹣2,0),则抛物线的表达式为:y=(x+2)2…①,令x=0,则y=4,即点A(0,4),设过点H的直线表达式为:y=kx+k+…②,联立①②并解得:x=2k﹣3,故点F(2k﹣3,2k2﹣2k+),∵FA=FE,∴AG=GE,∴(2k2﹣2k+)=2k2﹣2k+﹣(k+),解得:k=或﹣,故直线EF的表达式为:y=x+或y=﹣x,故点E(0,0)或(0,).。
武汉2020届九年级元调语文模拟试卷

武汉2020届九年级元调语文模拟试卷第Ⅰ卷(选择题共30分)一、(共12分,每小题3分)1.下列各组词语中,注音和字形有错误...的一组是()A.诓骗自欺欺人舍(shě)身求法怀(huái)古伤今B.流俗不攻自破孜孜(zī)不倦埋(mái)头苦干C.视察不足为剧前仆(pú)后继持之以恒(héng)D.停滞轻而易举不言而喻(yù)根深蒂(dì)固2.依次填入下面横线处的词语,恰当..的一组是()著名教学论专家杨启亮先生的话震撼心灵:“每每看到越来越多的学生不喜欢写字,不喜欢汉语言文学,不喜欢千古传诵的诗词歌赋,无知于中国传统文化,就像看到黄河一样,会感慨却欲哭无泪,这真是令人的语文教学的命运,因为汉语是母语,母语是母亲说的话……”A.茫然截流凄然心灰B.凄然截流茫然心碎C.凄然断流茫然心灰D.茫然断流凄然心碎3.下列句子中,有语病的....一项是()A.如何才能富起来呢?关键在于知识。
知识的贫乏必然造成财富的贫乏,财富的充足是以知识的充足为前提的。
B.汉字书写大赛、非遗保护等文化现象引人注目,传统文化的重要性已越来越为国人所知。
C.为加大文化进校园的宣传力度,学校开展了丰富多彩的读书活动,学生在活动中陶冶了情操。
D.文化自信,对于行进在实现自己伟大梦想中的民族、国家意义重大,对于实现潜能、追求幸福的个体更是不可或缺。
4.下面标点符号使用不正确.....的一项是()A.在最伟大的人物中间,巴尔扎克是名列前茅者;在最优秀的人物中间,巴尔扎克是佼佼者。
他才华卓越,至善至美,他的成就不是眼下说得尽的。
B.我今天要是没有看见这些,一切也都在进行之中。
我今天偶然瞥见了他们,一切也都没有被打乱,偶遇也就是这么普通,也是这么惊心。
C.他的所有作品形成了一部书,一部有生命的、光亮的、深刻的书。
我们在这里看见整个现代文明的走向,带着我们说不清楚的、同现实打成一片的惊惶与恐怖。
2020武汉元调数学试卷及答案(Word精校版)

第1页 / 共12页2019-2020学年度武汉市部分学校九年级元月调考数学试卷一、选择题(共10小题,每小题3分,共30分)1.将一元二次方程2514x x 化成一般形式后,二次项系数和一次项系数分别是( ) A .5,-1 B .5,4 C .5,-4 D .5,12.下列四张扑克牌的牌面,不是中心对称图形的是( )A .B .C .D .3.抛物线22y x 与22yx 相同的性质是( ) A .开口向下 B .对称轴是y 轴 C .有最低点 D .对称轴是x 轴4.一个不透明的袋子中只有4个黑球,2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )A .至少有1个球是黑球B .至少有1个球是白球C .至少有2个球是黑球D .至少有2个球是白球5.已知O 的半径等于3cm ,圆心O 到点P 的距离为5cm ,那么点P 与O 的位置关系是( ) A .点P 在O 内 B . 点P 在O 外 C .点P 在O 上 D .无法确定6.要将抛物线2y x 平移后得到抛物线223y x x ,下列平移方法正确的是( ) A .向左平移1个单位,再向上平移2个单位 B .向左平移1个单位,再向下平移2个单位 C .向右平移1个单位,再向上平移2个单位 D .向右平移1个单位,再向下平移2个单位7.如图,将△ABC 绕顶点C 逆时针旋转角度得到A B C ,且点B 刚好落在A B 上,若∠A =28°,BCA =43°,则等于( )A .36°B .37°C .38°D .39°8.小明上学要经过三个十字路口,每个路口遇到红灯、绿灯的可能性都相等,小明上学经过三个路口时,不全是红灯的概率是( )A .38 B . 12 C . 58 D . 789.如果m 、n 是一元二次方程24x x +=的两个实数根,那么多项式222n mn m --的值是( )A .16B .14C .10D .610.如图,△ABC 的两个顶点A ,B的O 上,∠A =60°,∠B =30°.若固定点A ,点B 在O 上运动,则OC 的最小值是( )A第2页 / 共12页A .B .C .D .二、填空题(本大题共6个小题,每小题3分,共18分)11.在平面直角坐标系中,点P (1,2)关于原点对称的点坐标是________. 12. 一个盒子中有10枚黑棋子和若干枚白棋子,这些棋子除颜色外无其他差别,从盒中随机取出一枚棋子,记下颜色,再放回盒子中,不断重复上述过程,一共取了300次,其中有100次取到黑棋子,由此估计盒中约有________枚白棋子.13.如图,四边形ABCD 是⊙O 的内接四边形,∠BOD =100°,∠BCD 的大小是 .14.为响应全民阅读活动,某校面向社会开放图书馆,自开放以来,进馆人次逐月增加,第一个月进馆200人次,前三个月累计进馆872人次,若进馆人次的月增长率相同,为求进馆人次的月增长率,设进馆人次的月增长率为x ,依题意可列方程为 .15.已知二次函数()20y ax bx c c =++<的图像开口向上,对称轴为直线1x =,下列结论中,一定正确的 是 (填序号即可).①0b <; ②420a b c ++<; ③a c b +>; ④()a b t at b +≤+(t 是一个常数).16.我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的周长,进而确定圆周率,某圆半径为R ,其内接正十二边形的周长为C . 若R ,则C = ,2CR≈ ,(结果精确到0.01 2.449≈ 1.414≈).三、解答题(共8题,共72分)17.(本题8分)若关于x 的一元二次方程x 2+2x +m =0有两个相等的实数根,求m 的值及此时方程的根.B第3页 / 共12页18. (本题8分)如图,A .B .C 三点在半径为1的O 上,四边形ABCD 是菱形,求的长.19. (本题8分)在5种同型号的产品中,有1件不合格品和4件合格品. (1)从这5件产品中随机选取1件,直接写出抽到合格品的概率; (2)从这5件产品中随机选取2件,求抽到都是合格品的概率.20.(本题8分)请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹(用虚线表示画图过程,实线表示画图结果). (1)如图(1),P 是平行四边形ABCD 边AD 上一点,过点P 画一条直线把这个四边形分成面积相等的两部分; (2)如图(2),五边形ABCDE 是正五边形,画一条直线把这个五边形分成面积相等的两部分; (3)如图(3),△ABC 的外接圆的圆心是点O ,D 是的中点,画一条直线把△ABC 分成面积相等的两部分.(1)(2)(3)AED CBAD21.(如图8分)如图,P A,PB 分别与O相切于A,B两点,AC 是O的直径,AC=AP,连接OP交AB于点D,连接PC 交O于点E,连接DE.(1)求证:△ABC≌△PDA;(2)求BDDE的值.22.(本题10分)某公司经过市场调查,整理出来某种商品在某个月的第x天的销售价与销售量的相关信息如(1)求y与x的函数关系式;(2)问销售该商品第几天时,日销售利润为2250元?(3)问在当月有多少天的日销售利润不低于2400元,请直接写出结果.第4页 / 共12页23.(本题10分)问题背景:如图(1),在四边形ABCD中,若BC=CD,∠BAD=∠BCD=90°,则AC平分∠BAD,小明为了证明这个结论,将△ABC绕点C顺时针旋转90°,请帮助小明完成他的作图.迁移应用:如图(2),在五边形ABCDE中,∠A=∠C=90°,AB=BC,AE+CD=DE,求证:BD平分∠CDE.联系拓展:如图(3),在Rt△ABC中,AC=BC,若点D满足1013AD AB,BD=AB,点P是AD的中点,直接写出PCAB的值.(1) (2) (3)BB第5页 / 共12页24.(本题12分)如图,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(m,2m+4)(m>-2),且与x轴相切于点B.y与x之间存在一种确定的函数关系,其图象是一条常见的曲线,记做曲线F.(1)如图(1),①当y=32时,直接写出P的半径;②当m=-1,x=-2时,直接写出P的半径.(2)求曲线F最低点的坐标(用含有m的式子表示);(3)如图(2),若曲线F最低点总在直线y=12x+3的下方,点C(-2,y1),D(1,y2)都在曲线F上,试比较y1与y2的大小.3第6页 / 共12页第7页 / 共12页2019-2020学年度武汉市部分学校九年级元月调考数学试卷参考答案9.答案:B 解析:∵m ,n 为方程x ²+x =4的解∴m +n =-1;mn =-4,且代n 到原式,得n ²=4-n∴原式=2(4-n )-mn -2m =8-2n -2m -mn =8-2(m +n )-mn =8+2+4 =1410.答案:A 解析:延长BC 交圆O 与D ,连O D .取AD 的中点E ,连OE ,连CE ∵ ∠B =30°,∴∠DOA =60°,∴△DAO 为等边三角形 ∵3OA ,∴3AD∵∠DCA =90°,∴点C 在以点E为半径的圆上运动∵OC OE CE ,∴3322OC ,故答案选A二、填空题(本大题共6个小题,每小题3分,共18分) 11. ()1,2-- 12.20 13.130°14.()()220020012001872x x ++++=15.①②④16.答案:24; 3.1116.解析:过C 作CD ⊥AB 于D , 正十二边形中心角∠CAD =30°B第8页 / 共12页∴12CD AC ==AD ==,BD AB AD =- 在Rt △CDB中,2CB =,∴24C =, 3.112CR≈三、解答题(共8题,共72分) 17. m =1,方程的根为x 1=x 2=-118. 23π19.(1)45;(2)3520. (1)(2)(作法不唯一)(3)21. 证明:(1)∵P A 为O 切线,∴∠P AO =90° ∵AC 为O 直径,∴∠ABC =90°∴∠BAC +∠ACB =∠BAC +∠P AD ,∴ ∠ACB =∠P ADBE第9页 / 共12页∵P A ,PB 为O 切线,∴P A =PB∵OA =OB ,P A =PB ,∴OP ⊥AB ,∴∠ADP =90° 在△ABC 和△PDA 中 ∠=∠=⎧⎪⎨⎪⎩=∠∠ACB PAD AC PA ABC PDA ∴△ABC ≌△PDA (AAS )解:(2)连接AE ,连接BE 交DP 于点F ∵∠ADO =∠ABC =90°,∴OP ∥BC ,∴∠BCE =∠FPE ,∵AC 为直径,∴∠AEC =90°, ∵∠P AO =90°,AC =AP ,∴∠ACE =45°,CE =PE 在△CEB 和△PEF 中 ∠=∠=∠⎧⎪⎨⎩=∠⎪BCE FPE CE PECEB PEF ∴△CEB ≌△PEF (ASA ) ∴BE =FE∵∠ABE =∠ACE =45°,∠BDP =∠ADP =90°,∴BD =DF 在Rt △BDF 中,222+=BD DF BF ,∴222=BD BF ,∴BF∵BE =EF ,∴BDDE22. 解:(1)y =[(x +40)-20](100-2x ) ,∴y =-2x 2+60x +2000 (2)由(1)知y =-2x 2+60x +2000当日销售利润为2250元时,有-2x 2+60x +2000=2250 解得:x 1=5; x 2=25故该销售商品第5天或第25天时,日销售利润为2250元. (3)11天当销售利润为2400时,有-2x 2+60x +2000=2400 解得:x 1=10; x 2=20 由二次函数图像性质可知:共有11天(第10天到第20天),销售利润不低于2400元.23. (1) 解:第10页 / 共12页(2) 证明:延长DC 至点F ,使CF =AE ,连接BE ,BF在△ABE 和△CBF 中 ==BCF =AB BC A AE CF ⎧⎪⎨⎪⎩∠∠ ∴△ABE ≌△CBF (SAS ),∴BE =BF 又∵DE =AE +CD 且AE =CF ,∴DE =DF 在△BDE 和△BDF 中 BE BF DE DF BD BD =⎧⎪=⎨⎪=⎩∴△BDE ≌△BDF (SSS )∴∠BDE =∠BDF ,∴BD 平分∠CDE (3)①当D 在AB 左侧时连接CP ,过点C 作CE ⊥CP ,交DA 的延长线于E 点∵AB =BD ,且P 是AD 的中点,∴BP ⊥AD ,即∠CBP =∠CAE∵AD =1013AB ,∴AP =12AD =513AB ,BP1213AB∵=ACE PCB ∠∠,在△BCP 和△ACE 中第11页 / 共12页CBP CAE BC ACBCP ACE =⎧⎪=⎨⎪=⎩∠∠∠∠ ∴△BCP ≌△ACE (ASA )∴AE =PB =1213AB ,PE =AP +AE =1713AB ∵PC =CE ,PC ⊥CE ,∴△PCE 为等腰直角三角形PCPE,即PC AB ②当D 在AB 右侧时连接CP ,过点C 作CQ ⊥CP 交BP 于点Q由①可知:∠APB =∠ACB =90°,AP =513AB ,PB =1213AB ∵PC ⊥CQ ,∴∠PCQ =∠ACB =90°,∴∠ACP =∠BCQ ∵∠APB =∠ACB ,∴∠CAP =∠CBQ在△ACP 和△BCQ 中CAP CBQ AC BCACP BCQ =⎧⎪=⎨⎪=⎩∠∠∠∠ ∴△ACP ≌△BCQ (ASA )∴BQ =AP =513AB PQ =BP -BQ =713AB ,PC =PQ ∵PC ⊥CQ ,∴△PCQ 为等腰直角三角形∴PCPQAB ,即PC = 综上所述:PC AB =24.解:(1)①32②54(2)依题意得:PB =P Ay = B D第12页 / 共12页 ()()22224y y m x m ---=-,∴()()21242y x m m m =-+++, 即顶点(m ,m +2)(3)方法一:顶点(m ,m +2)在直线y =x +2运动 又∵最低点一直在132y x =+下方,x +2<132x +,即m <2,∴-2<m <2 ∵C (-2,y 1),D (1,y 2),∴()()212242m y m m +=+++,()()221242m y m m =+++- ()()()()()2212213214242m m m y y m m +--+-==++,令y 1=y 2,解得12m =- ①当-2<m <12-时,()()32142m m ++<0 ,即y 1-y 2<0,故y 1<y 2; ②当12m =-时,()()32142m m ++=0,y 1=y 2; ③当-12<m <2时,()()32142m m ++>0,y 1>y 2. 综上①当-2<m <12-时,y 1<y 2;②当12m =-时,y 1=y 2;③当-12<m <2时,y 1>y 2. 方法二:(3)函数值的大小可以比较点到对称轴的距离当m =12-时,y 1=y 2 ;当-2<m <12-时,y 1<y 2 ;当-12<m <2时,y 1>y 2.。
(湖北卷) 2020年中考数学第二次模拟考试-数学(参考答案)

2020届九年级第二次模拟考试【湖北卷】数学·参考答案12345678910CABBDBCD AA11.212.2.1×10813.–214.215.16.417.【解析】(a +2b )(a ﹣2b )+(a ﹣2b )2﹣2a (a ﹣b )=a 2﹣4b 2+a 2﹣4ab +4b 2﹣2a 2+2ab =﹣2ab ,∵a =6,b =13,∴原式=﹣2×6×13=﹣4.18.【解析】(1)∵AC BD ⊥,EF BD ⊥,∴ABC ∆和EDF ∆为直角三角形,∵CD BF =,∴CF BF CF CD +=+,即BC DF =,在Rt ABC ∆和Rt EDF ∆中,AB DE BC DF =⎧⎨=⎩,∴()Rt ABC Rt EDF HL ∆≅∆;(2)由(1)可知ABC EDF ∆≅∆,∴B D ∠∠=,∴//AB DE .19.【解析】(1)∵了解很少的有30人,占50%,∴接受问卷调查的学生共有:30÷50%=60(人);∴扇形统计图中“基本了解”部分所对应扇形的圆心角为:1560×360°=90°;故答案为60,90;(2)60﹣15﹣30﹣10=5;补全条形统计图得:(3)根据题意得:900×15560+=300(人),则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为300人.20.【解析】(1)证明:在AB 上截取BH ,使BH BE =,连接EH ,∵四边形ABCD 是正方形,∴AB BC =,90ABC BCD ∠=∠=︒,45BDC ∠=︒,∴45BHE BEH ∠=∠=︒,∴135+∠=∠∠=︒AHE ABC BEH ,∵//CF BD ,∴45DCF BDC ∠=∠=︒,∴135+∠=∠∠=︒ECF BCD DCF ,∴AHE ECF ∠=∠,∵90ABC AEF ∠=∠=︒,∴90BAE AEB CEF AEB ∠+∠=∠+∠=︒,∴BAE CEF ∠=∠,∵AB BC =,BH BE =,∴AB BH BC BE -=-,即AH EC =.在AHE 和ECF △中,BAE CEF AH ECAHE ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴≅ AHE ECF (ASA ),∴AE EF =;(2)//CF EG 且=CF EG ;证明:∵90ABC ∠=︒,∴90CBG ABC ∠=∠=︒,在ABE △和CBG 中,AB BC ABC CBG BE BG =⎧⎪∠=∠⎨⎪=⎩,∴≅ ABE CBG (SAS ),∴BAE BCG ∠=∠,AE CG =,∵BAE CEF ∠=∠,AE EF =,∴BCG CEF ∠∠=,CG EF =,∴//CG EF ,∴四边形CFEG 是平行四边形,∴//CF EG 且=CF EG .21.【解析】(1)证明:连接O C.∴OA =OC ,∴∠ACO =∠BAC .∵CD ⊥AB ,CG ⊥AE ,∴∠CGA =∠CFA =90°,∵CG =CF ,AC =AC ,∴Rt △ACG ≌Rt △ACF ,∴∠CAG =∠CAB ,∴∠ACO =∠CAG ,∴OC ∥AG ,∴∠OCG +∠G =180°,∵∠CGA =90°,∴∠OCG =90°,即OC CG ⊥,∴CG 是⊙O 的切线.(2)过点O 作OM ⊥AE ,垂足为M ,则AM =ME =12AE =1,∠OMG =∠OCG =∠G =90°.∴四边形OCGM 为矩形,∴OC =MG =ME +EG =2.在Rt △AGC 和Rt △AFC 中,CG CFAC AC =⎧⎨=⎩,∴Rt △AGC ≌Rt △AFC ,∴AF =AG =AE +EG =3,∴OF =AF -OA =1,在Rt △COF 中,∵cos ∠COF =OF OC =12.∴∠COF =60°,CF =OC ·sin ∠COF =2×2∴S 弓形BC =2602360π⋅⋅-1223π-.22.【解析】(1)设每个A 型垃圾箱x 元,B 型垃圾箱y 元,依题意有3254032160x y y x +=⎧⎨-=⎩,解得100120x y =⎧⎨=⎩.故每个A 型垃圾箱100元,B 型垃圾箱120元;(2)设购买B 型垃圾箱m 个,则购买A 型垃圾箱(20﹣m )个,依题意有120m +100(20﹣m )≤2100,解得m ≤5.故该小区最多可以购买B 型垃圾箱5个.(3)由题知3≤m ≤5,故方案一:A 买17个,B 买3个,费用为:17×100+3×120=2060元;方案二:A 买16个,B 买4个,费用为:16×100+4×120=2080元;方案三:A 买15个,B 买5个,费用为:15×100+5×120=2100元;∴最省钱方案是A 买17个,B 买3个,费用2060元.23.【解析】(1)2(3)0b +-=,∴10a +=,30b -=,∴1a =-,3b =;(2)如图1所示,过M 作CE ⊥x 轴于E ,∵1a =-,3b =,∴A (–1,0),B (3,0),∴OA =1,OB =3,∴AB =4,∵在第三象限内有一点M (–2,m ),∴ME m m ==-,∴S △ABM =12AB ×ME =12×4×(m -)=2m -;(2)当32m =-时,点M 的坐标为(2-,32-),S △ABM =3232⎛⎫-⨯-= ⎪⎝⎭,∴PBM ABM 2236S S ==⨯= ,设直线BM 交y 轴于C 点,①当点P 在y 轴上时,如图:∵PBM MPC BPC 11PC 2PC 3622S S S =+=⨯+⨯= ,解得:PC =125,设直线BM 的解析式为y kx d =+,把点M (2-,32-),B (3,0)代入得:32203k d k d ⎧-=-+⎪⎨⎪=+⎩,解得:310910k d ⎧=⎪⎪⎨⎪=-⎪⎩,∴直线BM 的解析式为391010y x =-,当0x =时,910y =-,∴点C 的坐标为(0,910-),∴OC =910,当点P 在点C 的下方时,点P 的坐标为(0,129510--),即P (0,3310-),当点P 在点C 的上方时,点P 的坐标为(0,129510-),即1P (0,1510),②当P 在x 轴上且在点A 的左侧时,设P 点的坐标为(x ,0),如图:∵PBM ABM 2236S S ==⨯= ,∴PB =2AB ,∵B (3,0),AB =4,∴38x -=,∴5x =-,∴P 点的坐标为(5-,0),当P 在x 轴上且在点B 的D 右侧时,设P 点的坐标为(x ,0),如图:同理,PB =2AB ,∵B (3,0),AB =4,∴38x -=,∴11x =,∴P 点的坐标为(11,0),综合上述:P 点的坐标为(5-,0)或(11,0)或(0,3310-)或(0,1510).24.【解析】(1)∵抛物线y =ax 2+bx +2经过A (﹣1,0),B (4,0)两点,∴2016420a b a b -+=⎧⎨++=⎩,解得:1232a b ⎧=-⎪⎪⎨⎪=⎪⎩.∴抛物线解析式为213y x x 222=-++.当y =2时,213x x 2222-++=,解得:x 1=3,x 2=0(舍去).∴点D 坐标为(3,2).(2)A ,E 两点都在x 轴上,AE 有两种可能:①当AE 为一边时,AE ∥PD ,∴P 1(0,2).②当AE 为对角线时,根据平行四边形对顶点到另一条对角线距离相等,可知P 点、D 点到直线AE (即x 轴)的距离相等,∴P 点的纵坐标为﹣2.代入抛物线的解析式:213x x 2222-++=-,解得:123x x 22-==.∴P点的坐标为(2,﹣2),(32,﹣2).综上所述:P 1(0,2);P 2(2,﹣2);P 3(32-,﹣2).(3)存在满足条件的点P ,显然点P 在直线CD 下方.设直线PQ 交x 轴于F ,点P 的坐标为(213222a a a -++,),①当P 点在y 轴右侧时(如图1),CQ =a,PQ =2213132a a 2=a a 2222⎛⎫--++- ⎪⎝⎭.又∵∠CQ ′O +∠FQ ′P =90°,∠COQ ′=∠Q ′FP =90°,∴∠FQ ′P =∠OCQ ′,∴△COQ ′∽△Q ′FP ,∴Q 'C Q 'P =CO FQ ',即213a aa 22= 2FQ '-,解得FQ ′=a ﹣3∴OQ ′=OF ﹣FQ ′=a ﹣(a ﹣3)=3,CQ=CQ 此时a,点P 的坐标为().②当P 点在y 轴左侧时(如图2)此时a <0,,213a a 222-++<0,CQ =﹣a ,(无图)PQ =2213132a a 2=a a 2222⎛⎫--++- ⎪⎝⎭.又∵∠CQ ′O +∠FQ ′P =90°,∠CQ ′O +∠OCQ ′=90°,∴∠FQ ′P =∠OCQ ′,∠COQ ′=∠Q ′FP =90°.∴△COQ ′∽△Q ′FP .∴Q 'C Q 'P =CO FQ ',即213a aa 22= 2FQ '--,解得FQ ′=3﹣A .∴OQ ′=3,CQ=CQ .此时a =,点P的坐标为(92--,).综上所述,满足条件的点P 坐标为(),(92--,).。
2020年湖北省武汉市模拟中考题2(含答案和解析)

2020年武汉中考模拟考试2英语第I卷(选择题共85分)第一部分听力部分一、听力测试(共三节)第一节(共5小题,每小题1分,满分5分)听下面4个问题。
每个问题后有三个答语,从题中所给的A、B、C三个选项中选出最佳选项。
听完每个问题后,你都有5秒钟的时间来作答和阅读下一小题。
每个问题仅读一遍。
1. A. A teacher. B. In the office. C. Pretty well.2. A. It’s new. B. Beside the television. C. Ninety dollars.3. A. Four years old. B. He lives far C. Very active.4. A. It’s a football. B. The group leader. C. That’s dangerous.第二节(共7小题,每小题1分,满分7分)听下面8段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段対话后,你都有10秒钟的时间来作答有关小题和阅读下一小題。
每段对话仅读一遍。
5. Where are probably the two speakers?A.In a store.B. At school.C. In a hospital.6. What is probably the relationship between the speakers?A. Mother and son.B. Policewoman and driver.C. Teacher and student.7. Who are the two speakers?A. Mother and son.B. Teacher and student.C. Husband and wife.8. Where is the penA. On the desk.B. Beside the phone.C. Under the book.9. What’s Tom’s telephone number?A.502-4561.B.502-4516.C.502-4461.10. What’s the weather like today?A. Rainy.B. Sunny.C. Cloudy.11. What do you think the man is?A. A hotel guest.B. A cook.C. A waiter.12. When will they arrive at the mountains?A. July 22nd.B. July 20th.C. July 18th.第三节(共13小題,每小题l分,满分l3分)听下面4段对话或独自,每段対话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟,听完后,各小题将给出5秒钟的作答时间,每段对话或独白读两遍。
最新武汉市2019—2020学年元月调考模拟考试九年级数学试卷(二)

最新武汉市2019—2020学年元月调考模拟考试九年级数学试卷(二)一、选择题(共10小题,每小题3分,共30分)1.方程3x 2+1=6x 的二次项系数和一次项系数分别为( )A .3和6B .3和-6C .3和-1D .3和12.下列事件中,必然发生的事件是( )A .随意翻到一本书的某页,这页的页码是奇数B .通常温度降到0℃以下,纯净的水结冰C .地面发射一枚导弹,未击中空中目标D .测量某天的最低气温,结果为-150℃3.将抛物线y =-x 2向上平移3个单位,再向左平移2个单位,那么得到的抛物线解析式为( )A .y =-(x +2)2+3B .y =-(x -2)2+3C .y =-(x +2)2-3D .y =-(x -2)2-34.方程09242=+-x x 的根的情况是( )A .有两个不相等实根B .有两个相等实根C .无实根D .以上三种情况都有可能5.下列说法正确的是( ) A .掷两枚骰子,面朝上的点数和是偶数的概率为21 B .连续摸了两次彩票都中奖的概率为21 C .投两次硬币,朝上的面都为正面的概率为21 D .任何人连续投篮两次,投中的概率为21 6.如图,A 、B 、C 三点都在⊙O 上,∠ABO =50°,则∠ACB =( )A .50°B .40°C .30°D .25°7.如图,在下面的网格中,每个小正方形的边长均为1,△ABC 的三个顶点都是网格线的交点.已知A (-2,2)、C (-1,-2),将△ABC 绕着点C 顺时针旋转90°,则点A 对应点的坐标为( )A .(2,-2)B .(-5,-3)C .(2,2)D .(3,-1)8.某树主干长出若干数目的支干,每个支干又长出同样数目小分支,主干、支干和小分支总数共73.若设主干长出x 个支干,则可列方程是( )A .(1+x )2=73B .1+x +x 2=73C .(1+x )x =73D .1+x +2x =739.二次函数y =x 2+mx +1的图象的顶点在坐标轴上,则m 的值( )A .0B .2C .±2D .0或±210.若二次函数y =ax 2+bx +c 的图象的顶点在第一象限,且过点(0,1)和(-1,0),则s =a +b +c的值的变化范围是( )A .0<s <1B .0<s <2C .1<s <2D .-1<s <2二、填空题(本大题共6个小题,每小题3分,共18分)11.点A (-2,5)关于原点的对称点B 的坐标是___________;12.抛物线y =x 2-2x -2的顶点坐标是___________.13.方程3x 2-1=2x +5的两根之和为___________.14.如图,有一块长30m 、宽20m 的矩形田地,准备修筑同样宽的三条直路,把田地分成六块,种植不同品种的蔬菜,并且种植蔬菜面积为矩形田地面积的5039,则道路的宽为___________.15.如图,在矩形ABCD 中,AB =4,AD =3,以顶点D 为圆心作半径为r 的圆.若要求另外三个顶点A 、B 、C 中至少有一个点在圆内,且至少有一个点的圆外,则r 的取值范围是 .16.如图,正方形ABCD 的边长为2,P 为BC 上一动点,将DP 绕P 逆时针旋转90°,得到PE ,连接EA ,则△PAE 面积的最小值为__________.三、解答题(共8题,共72分)17.(本题8分)已知关于x 的方程x 2+2x +a -2=0(1) 若该方程有两个不相等的实数根,求实数a 的取值范围;(2) 当该方程的一个根为1时,求a 的值及方程的另一根.18.(本题8分)如图,菱形ABCD 和Rt △ABE ,∠AEB =90°,将△ABE 绕点O 旋转180°得到△CDF .(1)在图中画出点O 和△CDF ;(2)若∠ABC =130°,直接写出∠AEF 的度数.A B CDE19.(本题8分)如图,⊙O 中,直径CD ⊥弦AB 于M ,AE ⊥BD 于E ,交CD 于N ,连AC(1)求证:AC =AN ;(2)若OM ∶OC =3∶5,AB =5,求⊙O 的半径;20.(本题8分)老师和小明玩游戏,老师取出一个不透明口袋,口袋中装有三张分别标有数字1、2、3的卡片,卡片除数字外其余都相同.老师要求小明两次随机摸取一张卡片(第一次取出后放回),并计算两次抽到卡片上的数字之积是奇数的概率.求小明两次抽到卡片上的数字之积是奇数的概率21.(本题8分)一个涵洞成抛物线形,它的截面如图,现测得:当水面宽AB=1.6 m时,涵洞顶点与水面的距离为2.4 m,离开水面1.5 m处是涵洞宽ED;(1)求抛物线的解析式;(2)求ED的长;22.(本题10分)如图所示,为了改造小区环境,某小区决定要在一块一边靠墙(墙的最大可使用长度13 m)的空地上建造一个矩形绿化带.除靠墙一边(AD)外,用长为36 m的栅栏围成矩形ABCD,中间隔有一道栅栏(EF).设绿化带宽AB为x m,面积为S m2(1)求S与x的函数关系式,并求出x的取值范围(2)绿化带的面积能达到108 m2吗?若能,请求出AB的长度;若不能,请说明理由(3)当x为何值时,满足条件的绿化带面积最大E D C B A N M D C B A23.(本题10分)已知等边△ABC ,点D 和点B 关于直线AC 轴对称.点M (不同于点A 和点C )在射线CA 上,线段DM 的垂直平分线交直线BC 的于N ,(1)如图1,过点D 作DE ⊥BC ,交BC 的延长线于E ,若CE =5,求BC 的长;(2)如图2,若点M 在线段AC 上,求证:△DMN 为等边三角形;(3)连接CD ,BM ,若3S ABM DMC S △△,直接写出MBNMCN S △△S .图1 图224.(本题12分)已知抛物线y =ax 2-2amx +am 2+2m +4的顶点P 在一条定直线l 上.(1)直接写出直线l 的解析式;(2)若存在唯一的实数m ,使抛物线经过原点.①求此时的a 和m 的值;②抛物线的对称轴与x 轴交于点A ,B 为抛物线上一动点,以OA 、OB 为边作□OACB ,若点C 在抛物线上,求B 的坐标.(3)抛物线与直线l 的另一个交点Q ,若a =1,直接写出△OPQ 的面积的值或取值范围.BBACA BDBDB10. 将点(0,1)和(-1,0)分别代入抛物线解析式,得c=1,a=b-1,∴S=a+b+c=2b ,由题设知,对称轴x=-错误!>0且a <0,∴2b >0.又由b=a+1及a <0可知2b=2a+2<2.∴0<S <2.故本题答案为:0<S <2. 11. (2,-5) 12. (1,-3) 13. 错误!14. 2 15. 3<r<5 16. 错误! 16. 过E 作EF ⊥BC 于F ,EG ⊥AD 于G ,设GE=a ,可证AG=2-a ,EFP AGE AGFP AEP S S S S △△梯△--==错误!(a-1)2+错误!,当a=1时,AEP S △=错误!17. (1)a<3 (2)a=-1;-318. 65°,AEBO 共圆19. (1)连AC ,△AMN ≌△AMC ;(2)连OA ,设OM=3x ,OC=5x ,r=错误!20. 错误!21. (1)y=-错误!x 2 (2)562 22. (1)S=-3x 2+36x (错误!≤x<12)(2)不能 (3)错误!23. (1)连CD ,∠DCE=60°,CD=BC=10;(2)∠DCA=60°,连CD ,过N 作NG ⊥CD 于G ,NH ⊥AC 于H ,∠GCN=60°,∴∠NCH=60°,∴NG=NH ,∴Rt △MNH ≌Rt △DNG (HL ),∴∠CMQ=∠NDG ,∴∠MCQ=∠MND=60°,∴△DMN 为等边三角形;(3)连AD ,BD 交AC 于P ,BP=PB ,△ADM ≌△CND ≌△ABM ,∵3S =ABM DMC S △△,∴31=MC AM ,MBN MCN S △△S =51=BN CN ;当M 在CA 延长线上时,MBN MCN S △△S =1;答案:51或1. 24.(1) y=a (x-m )2+2m+4,P (m ,2m+4),∴y=2x+4;(2) ①将x=0,y=0代入,∴am 2+2m+4=0∴△=0,a=错误!,m=-4;②B 、C 关于对称轴对称,∴B 的横坐标为-2,y=错误!(x+4)2-4,∴B (-2,-3);(3) y=2x+4与x 轴交于点B (-2,0),交y 轴于点A (0,4),作OM ⊥AB 于M.∴AB=2,5 ,∴OM=554,y=2x+4代入抛物线解析式y= 2-2mx +m 2+2m +4,解得x=m 或x=m+2,∴P(m ,m+2),Q (m+2,2m+8),PQ=2,17 ,OPQ S △=错误!·PQ ·OM=8554.。
2020武汉市中考数学模拟试题2参考答案及评分标准(WORD版)

=t(k-n)+2(k+n) =-2t+2(k-n)=-2t ∴k-n=0④……………………10 分 ∴联立③④: k=-1,n=1 ∴直线 BP 的解析式为 y=x-2 代入抛物线: x1=0,x2=1(舍) ∴P(0,-2)…………………………12 分
40 故答案为:40,108°,……………………2 分 (2)补全条形统计图如图所示:
……4 分 (3)2500× 16 =1000(人).……6 分
40 答:该校 2500 名学生中 D 类的约有 1000 人.…………8 分 20.解:(1)(2) …………………………5 分 (3) 3 65 - 5 …………8 分
=4n8÷4n8……………………4 分 =1……………………8 分 18.解:(1)∵AB=AC, ∴∠ABC=∠C∵BC 平分∠ABD, ∴∠ABC=∠CBD, ∴∠C=∠CBD,∴AC∥BD, ∵∠A=100°,∴∠ABD=180°﹣∠A=80°, ∴∠CBD=40°故答案为:40°.………………………………3 分 (2)AC∥BD,理由如下: ∵AB=AC,∴∠ABC=∠C…………………………5 分 ∵BC 平分∠ABD,∴∠ABC=∠CBD,…………………………7 分 ∴∠C=∠CBD,∴AC∥BD.………………………………8 分 19.解:(1)8÷20%=40(人),C 组人数为 40﹣4﹣8﹣16=12(人),360°× 12 =108°,
设 AD=m,AC=4m=BC,构造△PED∽△CEB,由于 BE 4 ,EC=8,得 PE=10, DE 5
PD=5m,PC=8m,PA=PC;倍长 AQ=AE,得 PQ=CE=8,∠EPQ=60°,解三角形△EPQ 解得 EQ= 2 21 ,AE= 21 …………10 分
模拟卷2:2020武汉市中考数学模拟卷(二)—解析版

模拟卷2:2020武汉市中考数学模拟卷(二)—解析版2020年武汉市中考模拟卷(二)—解析版数学试卷(考试时间:120分钟满分:120分)一.选择题(共12小题,每小题3分,共36分) 1. 6.1亿用科学记数法表示为().A .6.1×101B .0.61×109C .6.1×108D .61×107【解答】C .2. 式子1a +有意义,则实数a 的取值范围是()A .a ≥﹣1B .a ≠0C .a >﹣1D .a >0【解答】A .3. 军运会设计运动中,运动员每次射击击中靶的环数为1到10,不考虑脱靶的情况下,下列事件为随机事件的是()A .某运动员两次射击总环数大于1B .某运动员两次射击总环数等于1C .某运动员两次射击总环数大于20D .某运动员两次涉及总环数等于20 【解答】D . 4. 下列图形中不是轴对称图形的是()A .B .C .D .【解答】B .5. 下列图形都是由大小相同的正方体搭成的,其三视图都相同的是()A .B .C .D .【解答】C .6. 将一箱苹果分给若干个小朋友,若每位小朋友分5个苹果,则还剩12个苹果;若每位小朋友分8个苹果,则有一个小朋友分到苹果但不到8个苹果.求这一箱苹果的个数与小朋友的人数.若设有x 人,则可列不等式为()A .8(1)5128x x -<+<B .05128x x <+<C .05128(1)8x x <+--<D .85128x x <+< 【解答】C 7. 根据规定,我市将垃圾分为了四类:可回收物、易腐垃圾、有害垃圾和其他垃圾四大类.现有投放这四类垃圾的垃圾桶各1个,若将用不透明垃圾袋分类打包好的两袋不同垃圾随机投进两个不同的垃圾桶,投放正确的概率是()A .16B .18C .112D .116【解答】C 8. 已知点M (2,3)是一次函数y =kx +1的图象和反比例函数my x=的图象的交点,当一次函数的值大于反比例函数的值时,x 的取值范围是()A .x <﹣3或0<x <2B .x >2C .﹣3<x <0或x >2D .x <﹣3 【解答】C9.如图,在⊙O中,直径CD垂直弦AB于点E,且OE=DE.点P为?BC上一点(点P不与点B,C重合),连结AP,BP,CP,AC,BC.过点C作CF⊥BP于点F.给出下列结论:①△ABC是等边三角形;②在点P从B→C的运动过程中,CFAP BP-的值始终等于32.则下列说法正确的是()A.①,②都对B.①对,②错C.①错,②对D.①,②都错【解答】A【解析】如图,作CM⊥AP于M,连接AD.∵AE⊥OD,OE=DE,∴AO=AD,∵OA=OD,∴AO=AD=OD,∴△AOD是等边三角形,∴∠D=∠ABC=60°,∵CD⊥AB,∴AE=EB,∴CA=CB,∴△ABC是等边三角形,故①正确,∵∠CP A=∠ABC=60°,∠APB=∠ACB=60°,∴∠CPF=180°﹣60°﹣60°=60°,∵∠CPM=∠CPF=60°,CF⊥PF,CM⊥P A,∴CF=CM,∵PC=PC,∠CFP=∠CMP,∴Rt△CPF≌Rt△CPM(HL),∴PF=PM,∵AC=BC,CM=CF,∠AMC=∠CFB=90°,∴Rt△AMC≌Rt△BFC(HL),∴AM=BF,∴AP﹣PB=PM+AM﹣(BF﹣PF)=2PM=2PF,∴12PFPA PB=-,在Rt△CPF中,∵∠CPF=60°,∠CFP=90°,tan603CF PF PF∴=?=g,3PF CF∴=,∴3CFPA PB=-,故②正确,10.现有一列数a1,a2,a3,…,a98,a99,a100,其中a3=2020,a7=﹣2018,a98=﹣1,且满足任意相邻三个数的和为常数,则a1+a2+a3+…+a98+a99+a100的值为()A.1985 B.﹣1985 C.2019 D.﹣2019 【解答】B【解析】∵任意相邻三个数的和为常数,∴a1+a2+a3=a2+a3+a4,a2+a3+a4=a3+a4+a5,a3+a4+a5=a4+a5+a6,∴a1=a4,a2=a5,a3=a6,∵a7=﹣2018,a98=﹣1,7÷3=2…1,98÷3=32…2,∴a1=﹣2018,a2=﹣1,∴a1+a2+a3=﹣2018+(﹣1)+2020=1,∵100÷3=33…1,∴a100=a1=﹣2018,∴a1+a2+a3+…+a98+a99+a100=(a1+a2+a3)+…+(a97+a98+a99)+a100=1×33+(﹣2018)=﹣1985.二.填空题(共12小题,每小题3分,共36分)11.计算:32736-+==.【解答】3.12.某公司招聘职员,公司对应聘者进行了面试和笔试(满分均为100分),规定笔试成绩占60%,面试成绩占40%,应聘者小菁的笔试成绩和面试成绩分别为95分和90分,她的最终得分是分.【解答】93.13. 化简:2221a ab a b---的结果是.【解答】1a b+ 14. 在△ABC 中,D 、E 是边BC 上的两点,DC =DA ,EA =EB ,∠DAE =40°,则∠BAC 的度数是.【解答】70?或110? 15. 已知实数a ,b ,c 满足a ≠0,且a ﹣b +c =0,9a +3b +c =0,则抛物线y =ax 2+bx +c 图象上的一点(﹣2,4)关于抛物线对称轴对称的点为.【解答】(4,4). 16. 如图,在菱形ABCD 中,∠ABC =120°,将菱形折叠,使点A 恰好落在对角线BD 上的点G 处(不与B 、D 重合),折痕为EF ,若DG =2,BG =6,则BE 的长为.【解答】2.8【解析】作EH ⊥BD 于H ,由折叠的性质可知,EG =EA ,BD =DG +BG =8,∵四边形ABCD 是菱形,∴AD =AB ,1602ABD CBD ABC ∠=∠=∠=?,∴△ABD 为等边三角形,∴AB =BD =8,设BE =x ,则EG =AE =8﹣x ,在Rt △EHB 中,12BH x =,3EH x =,在Rt △EHG 中,EG 2=EH 2+GH 2,即22231(8)()(6)2x x x -=+-,解得,x =2.8,即BE =2.8,三.解答题(共8小题,共72分)17. 计算:8a 6÷2a 2+4a 3?2a ﹣(3a 2)2 【解答】解:原式=4a 4+8a 4﹣9a 4=3a 4.18. 如图,直线AB ∥直线CD ,直线EF 分别交AB 、CD 于E 、F 两点,EM 、FN 分别平分∠BEF 、∠CFE ,求证:EM ∥FN .【解答】证明:∵直线AB ∥直线CD ,∴∠BEF =∠CFE ,又∵EM 、FN 分别平分∠BEF 、∠CFE ,∴∠FEM =∠EFN ,∴EM ∥FN .19.某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:(1)本次调查的样本为,样本容量为;(2)在频数分布表中,a=,b=,并将频数分布直方图补充完整;(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?【解答】解:(1)20÷0.1=200(人),所以本次调查的样本为200名初中毕业生的视力情况,样本容量为200;(2)a=200×0.3=60,b=10÷200=0.05;如图,故答案为200名初中毕业生的视力情况,200;60,0.05;(3)5000×(0.35+0.3+0.05)=3500(人),估计全区初中毕业生中视力正常的学生有3500人.20.如图,在平面直角坐标系中,点A(0,4)、B(﹣3,0),将线段AB沿x轴正方向平移n个单位得到菱形ABCD.(1)画出菱形ABCD,并直接写出n的值及点D的坐标;(2)已知反比例函数kyx=的图象经过点D,?ABMN的顶点M在y轴上,N在kyx=的图象上,求点M的坐标;(3)若点A、C、D到某直线l的距离都相等,直接写出满足条件的直线解析式.【解答】解:(1)如图,∵点A(0,4)、B(﹣3,0),∴AO=4,BO =3∴AB=5∵四边形ABCD是菱形,∴AB=BC=CD=AD=5∵将线段AB沿x轴正方向平移n个单位得到菱形ABCD.∴n=5,点C坐标为(2,0),点D坐标为(5,4),(2)∵反比例函数kyx=的图象经过点D,∴k=4×5=20∵N在20yx=的图象上,∴设点20(,)N aa,如图,过点N作NH⊥OA于点H,∵四边形ABMN是平行四边形,∴AN=BM,AN∥BM,∴∠BMA =∠NAM∴∠BMO=∠NAH,且AN=BM,∠BOM=∠NHA=90°,∴△ANH≌△MBO(AAS)∴HN=BO=3,MO=AH∴HN=a=3,20203HOa==,83OM AH HO AO∴==-=,∴点8 (0,)3 M(3)∵点A、C、D到某直线l的距离都相等,∴直线l是△ACD的中位线所在直线,如图所示:若直线l过线段AC,CD中点,∴直线l 的解析式为:y=2若直线l过线段AD,AC中点,即直线l过点(5(2,4),点(1,2)设直线l的解析式为:y=mx+n ∴5 422m nm n=+=+,解得:43m=,23n=,∴直线l的解析式为:4233y x=+若直线l过线段AD,CD中点,即直线l过点(5( 2,4),点(7(2,2)设直线l解析式为:y=kx+b∴542722k bk b=+=+,解得:k=﹣2,b=9,∴直线l的解析式为:y=﹣2x+921.如图,AB为⊙O的直径,点P在AB的延长线上,点C在⊙O 上,且PC2=PB?P A.(1)求证:PC是⊙O的切线;(2)已知PC=20,PB=10,点D是?AB的中点,DE⊥AC,垂足为E,DE交AB于点F,求EF 的长.【解答】(1)证明:连接OC,如图1所示:∵PC2=PB?P A,即PA PCPC PB=,且∠P=∠P,∴△PBC∽△PCA,∴∠PCB=∠P AC,∵AB为⊙O的直径,∴∠ACB=90°,∴∠A+∠ABC=90°,∵OC=OB,∴∠OBC=∠OCB,∴∠PCB+∠OC B=90°,即OC⊥PC,∴PC是⊙O的切线;(2)解:连接OD,如图2所示:∵PC=20,PB=10,PC2=PB?P A,22204010PCPAPB∴===,∴AB=P A﹣PB=30,∵△PBC∽△PCA,∴2AC PABC PC==,设BC=x,则AC=2x,在Rt△ABC中,x2+(2x)2=302,解得:x=65x=BC=65x=∵点D是?AB AB为⊙O∴∠AOD=90°,∵DE⊥AC,∴∠AEF=90°,∵∠ACB =90°,∴DE ∥BC ,∴∠DFO =∠ABC ,∴△DOF ∽△ACB ,∴12OF BC OD AC ==,11522OF OD ∴==,即15AF =,∵EF ∥BC ,∴14EF AF BC AB ==,1354EF BC ∴=.22. 农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p (千克)与销售价格x (元/千克)之间的关系,经过市场调查获得部分数据如下表:销售价格x (元/千克) 30 35 40 45 50 日销售量p (千克)600 450 300 150 0(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p 与x 之间的函数表达式;(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?(3)若农经公司每销售1千克这种农产品需支出a 元(a >0)的相关费用,当40≤x ≤45时,农经公司的日获利的最大值为2430元,求a 的值.(日获利=日销售利润﹣日支出费用)【解答】解:(1)假设p 与x 成一次函数关系,设函数关系式为p =kx +b ,则3060040300k b k b +=??+=?,解得:k =﹣30,b =1500,∴p =﹣30x +1500,检验:当x =35,p =450;当x =45,p =150;当x =50,p =0,符合一次函数解析式,∴所求的函数关系为p =﹣30x +1500;(2)设日销售利润w =p (x ﹣30)=(﹣30x +1500)(x ﹣30)即w =﹣30x 2+2400x ﹣45000,∴当2400402(30)x =-=?-时,w 有最大值3000元,故这批农产品的销售价格定为40元,才能使日销售利润最大;(3)日获利w =p (x ﹣30﹣a )=(﹣30x +1500)(x ﹣30﹣a ),即w =﹣30x 2+(2400+30a )x ﹣(1500a +45000),对称轴为2400301402(30)2a x a +=-=+?-,①若a >10,则当x =45时,w 有最大值,即w =2250﹣150a <2430(不合题意);②若a <10,则当1402x a =+时,w 有最大值,将1402x a =+代入,可得2130(10100)4w a a =-+,当w =2430时,21243030(10100)4a a =-+,解得12a =,238a =(舍去),综上所述,a 的值为2.23. (1)在△ACB 中,∠ACB =90°,CD ⊥AB 于D ,点E 在AC 上,BE 交CD 于点G ,EF ⊥BE 交AB 于点F .①如图1,AC =BC ,点E 为AC 的中点,求证:EF =EG ;②如图2,BE 平分∠CBA ,AC =2BC ,试探究EF 与EG 的数量关系,并证明你的结论;(2)如图3,在△ABC 中,若3tan 3B =,点E 在边AB 上,点D 在线段BC 的延长线上,连接DE 交AC 于M ,∠CMD =60°,DE =2AC ,33CD =,直接写出BE 的长.【解答】(1)①证明:如图1,过E 作EM ⊥AB 于M ,EN ⊥CD 于N ,∵∠ACB =90°,AC =BC ,∴∠A =∠ABC =45°,∴AD =CD ,∵点E 为AC 的中点,CD ⊥AB ,EN ⊥DC ,12EN AD ∴=,12EM CD ∴=,∴EN =EM ,∵∠FEB =90°,∠MEN =90°,∴∠NEG =∠FEM ,在△EFM 和△EGN 中,NEG FEMEN EM ENG EMF ∠=∠??=??∠=∠?,∴△EFM ≌△EGN (ASA ),∴EF =EG ;②解:5EF EG =,理由如下:如图2,作EP ⊥AB 于点P ,EQ ⊥CD 于点Q ,易证:△EFP ∽△EGQ ,∴EF EPEG EQ=,∵BE 平分∠ABC ,EC ⊥BC ,EP ⊥AB ,∴EC =EP ,∵EQ ∥AB ,∴∠CEQ =∠A ,∵∠EQC =∠ACB ,∴△ECQ ∽△ABC ,∴2EQ ACCQ BC==,设CQ =a ,EQ =2a ,则5EC EP a ==,∴55EF a EG ==,(2)解:如图3,过C 作CF ∥DE ,过A 作AF ⊥AC ,交CF 于F ,连接EF ,3tan B =Q ,∴∠ABC =30°,∵CF ∥DE ,∴∠ACF =∠DMC =60°,∴∠AFC =30°,∵∠CAF =90°,∴CF =2AC ,∵DE =2AC ,∴DE =CF ,∴四边形EFCD 是平行四边形,∴EF ∥CD ,33EF CD ==,∴∠ABC =∠BEF =30°,∵∠AFC =∠ABC =30°,∴A 、F 、B 、C 四点共圆,∴∠FBC +∠CAF =180°,∴∠FBC =90°,∵EF ∥BC ,∴∠BFE =90°,3cos cos30EF BEF BE ∠=?==,23363BE ?∴==.24. 在平面直角坐标系中,抛物线214y x =沿x 轴正方向平移后经过点A (x 1,y 2),B (x 2,y 2),其中x 1,x 2是方程x 2﹣2x =0的两根,且x 1>x 2,(1)如图1.求A ,B 两点的坐标及平移后抛物线的解析式;(2)平移直线AB 交抛物线于M ,交x 轴于N ,且14AB MN =,求△MNO 的面积;(3)如图2,点C 为抛物线对称轴上顶点下方的一点,过点C 作直线交抛物线于E 、F ,交x 轴于点D ,探究CD CDCE CF+的值是否为定值?如果是,求出其值;如果不是,请说明理由.【解答】解:(1)解方程x 2﹣2x =0得x 1=2,x 2=0.∴点A 坐标为(2,0),抛物线解析式为21(2)4y x =-.把x =0代入抛物线解析式得y =1.∴点B 坐标为(0,1).(2)如图,过M 作MH ⊥x 轴,垂足为H∵AB ∥MN ∴△ABO ∽△NMH ,∴14BO HN AB MH AO MN ===,∴MH =4,HN =8 将y =4代入抛物线21(2)4y x =-,可得x 1=﹣2,x 2=6∴M 1(﹣2,4),N 1(6,0),M 2(6,4),N 2(14,0)11164122M N O S =??=V ,221144282M N O S =??=V(3)设C (2,m ),设直线CD 为y =kx +b将C (2,m )代入上式,m =2k +b ,即b =m ﹣2k .∴CD 解析式为y =kx +m ﹣2k ,令y =0得kx +m ﹣2k =0,∴点D 为(2(k mk-,0)联立221(2)4y kx m k y x =+-=-??,消去y 得,212(2)4kx m k x +-=-,化简得,x 2﹣4(k +1)x +4﹣4m +8k =0 由根与系数关系得,x1+x 2=4k +4,x 1?x 2=4﹣4m +8k .过E 、F 分别作EP ⊥CA 于P ,FQ ⊥CA 于Q ,∴AD ∥EP ,AD ∥FQ ,∴CD CD AD AD EP FQAD CE CF EP FQ EP FQ ++=+=g g 121212()42(2)2(4)x x k m k x x x x +--=-?-++g (44)4(448)2(44)4m k k m k k -+-=-+-++g =1 ∴CD CD CE CF+为定值,定值为1。
2020届九年级语文模拟考试试题(二)(含解析)

2020届九年级语文模拟考试试题注意事项:1.答卷前,考生务必将自己的姓名、考试号填写在试卷和答题卡上,并将考试号条型码粘贴在答题卡上指定位置。
2.选择题每小题选出答案后,用2B铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,答在试题卷上无效。
3.非选择题用0.5毫米的黑色墨水签字笔或黑色墨水钢笔直接答在答题卡上每题对应的答题区域内,答在试题卷上无效.作图一律用2B铅笔或0.5毫米黑色签字笔。
4.考试结束后,请将本试题卷和答题卡一并上交。
一.语言的积累与运用(34分)1.(3分)将下面句子组成语意连贯的一段话,填写在横线处,排列最合适的一项是()。
如果不能互相救助,反而互相争夺,那么,谁也存活不了。
因此,存活之道,繁衍之道,发展之道,必然包含着大爱之道、善良之道。
①当这种痕迹集中起来,“文化”也就是人类在特定时间和空间上的生态共同体。
②过去的解释是,能生存,只因为强大。
③回溯远古历史,最早所说的“文化”,就是指人活动的痕迹。
④但是,这样的共同体应该很多,为什么只有很少几个能在极其恶劣的条件下生存下来,而其他却不能?⑤其实只要稍稍研究一下比较严重的自然灾害和传染病疫就能明白,人类在巨大而突发的破坏力面前,一时的所谓强大并没有用。
A.⑤①④③②B.③①④②⑤C.③⑤①④②D.③④⑤②①2.(3分)下面各项中加点字的注音完全正确的一项是()A.诅.咒(zǔ)腻.味(nì)蔫.巴(niān)溢.于言表(yì)B.摩挲.(sūo)殷.红(yīn)蹊.跷(qī)万事俱.备(jǜ)C.剔.透(tì)撺掇.(duo)宁.可(nìn)明眸.善睐(mó)D.遴.选(líng)卷帙.(zhì)摒.弃(bìng)果实累.累(lěi)3.(3分)下列各句中加点成语运用正确的一项是()A.不可理喻....,在创造的宇宙里,贝多芬、爱因斯坦、莎士比亚都是光辉灿烂的明星。
2020年湖北省武汉市九年级元月调考数学模拟试卷(二)(解析版)

2020年湖北省武汉市九年级元月调考数学模拟试卷(二)一、选择题(共10小题,每小题3分,共30分)1.(3分)将方程3x2+1=6x化成一元二次方程的一般形式,其中二次项系数、一次项系数和常数项分别是()A.3,﹣6,1B.3,6,1C.3,1,﹣6D.3,1,62.(3分)下列图形中是中心对称图形的是()A.B.C.D.3.(3分)将抛物线y=x2先向右平移2个单位长度,再向上平移4个单位长度,得到的新的抛物线的解析式为()A.y=(x+2)2+4B.y=(x+2)2﹣4C.y=(x﹣2)2+4D.y=(x﹣2)2﹣4 4.(3分)投掷两枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,掷一次骰子.则下列事件属于随机事件的是()A.两枚骰子向上一面的点数之和等于6B.两枚骰子向上一面的点数之和大于13C.两枚骰子向上一面的点数之和等于1D.两枚骰子向上一面的点数之和大于15.(3分)已知⊙O的直径为12cm,圆心到直线L的距离5cm,则直线L与⊙O的公共点的个数为()A.2B.1C.0D.不确定6.(3分)在我国古代数学著作《九章算术》的第九章《勾股》中记载了这样的一个问题:“今天有开门去阔一尺,不合二寸,问门广几何?”意思是:如图,推开两扇门(AD和BC),门边缘D,C两点到门槛AB的距离是1尺,两扇门的间隙CD为2寸,则门宽AB长是()寸.(1尺=10寸)A.101B.100C.52D.967.(3分)假定鸟卵孵化后,雏鸟为雌与雄的概率相同.如果三枚卵全部成功孵化,则三只雏鸟中恰有两只雌鸟的概率是()A .B .C .D .8.(3分)如图,扇形OAB 中,∠AOB =90°,将扇形OAB 绕点B 逆时针旋转,得到扇形BDC ,若点O 刚好落在弧AB 上的点D 处,则的值为( )A .B .C .D .9.(3分)欧几里得在《几何原本》中,记载了用图解法解方程x 2+ax =b 2的方法,类似地可以用折纸的方法求方程x 2+x ﹣1=0的一个正根,如图,裁一张边长为1的正方形的纸片ABCD ,先折出BC 的中点E ,再折出线段AE ,然后通过折叠使EB 落在线段EA 上,折出点B 的新位置F ,因而EF =EB ,类似地,在AB 上折出点M 使AM =AF ,表示方程x 2+x ﹣1=0的一个正根的线段是( )A .线段BMB .线段AMC .线段BED .线段AE10.(3分)如图,直线y =2x 与直线x =2相交于点A ,将抛物线y =x 2沿线段OA 从点O 运动到点A ,使其顶点始终在线段OA 上,抛物线与直线x =2相交于点P ,则点P 移动的路径长为( )A .4B .3C .2D .1二、填空题(本大题共6个小题,每小题3分,共18分)11.(3分)已知3是一元二次方程x2+m=0的一个根,则该方程的另一个根是.12.(3分)在平面直角坐标系中,已知点P的坐标为(3,﹣4),则点P关于原点对称的点的坐标为.13.(3分)一个口袋中有6个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,…,不断重复上述过程.小明共摸了100次,其中60次摸到白球.根据上述数据,小明可估计口袋中的白球大约有个.14.(3分)要为一幅矩形照片配一个镜框,如图,要求镜框的四条边宽度都相等,且镜框所占面积是照片本身面积的四分之一,已知照片的长为21cm,宽为10cm,求镜框的宽度.设镜框的宽度为xcm,依题意列方程,化成一般式为.15.(3分)如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加m.16.(3分)如图,正方形ABCD中,AB=4,E,F分别是边AB,AD上的动点,AE=DF,连接DE,CF交于点P,过点P作PK∥BC,且PK=2,若∠CBK的度数最大时,则BK 长为.三、解答题(共8题,共72分)17.(8分)解方程:x2﹣4x+1=0.18.(8分)如图,已知A、B、C、D是⊙O上的四点,延长DC、AB相交于点E.若BC =BE.求证:△ADE是等腰三角形.19.(8分)某学校初中英语口语听力考试即将举行,准备了A、B、C、D四份听力材料,它们的难易程度分别是易、中、难、难;另有a、b是两份口语材料,它们的难易程度分别是易、难.(1)从四份听力材料中,任选一份是难的听力材料的概率是;(2)用树状图形或列表法,求出听力、口语两份材料都是难的一套模拟试卷的概率.20.(8分)如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(0,1),B(1,3),C(4,3).(1)将△ABC平移得到△A1B1C1,且C1的坐标是(0,﹣1),画出△A1B1C1;(2)将△ABC绕点A逆时针旋转90°得到△A2B2C2,画出△A2B2C2;(3)小娟发现△A1B1C1绕点P旋转也可以得到△A2B2C2,请直接写出点P的坐标.21.(8分)在⊙O中,直径AB⊥弦CD于点F,点E是弧AD上一点,连BE交CD于点N,点P在CD的延长线上,PN=PE.(1)求证:PE是⊙O的切线;(2)连接DE,若DE∥AB,OF=3,BF=2,求PN的长.22.(10分)某商场销售一种成本为每件30元的商品,销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=﹣10x+600,商场销售该商品每月获得利润为w(元).(1)求w与x之间的函数关系式;(2)如果商场销售该商品每月想要获得2000元的利润,那么每月成本至少多少元?(3)若销售价不低于40元且不高于55元,请直接写出每月销售新产品的利润w的取值范围.23.(10分)在△ABC中,∠ABC=120°,线段AC绕点C顺时针旋转60°得到线段CD,连接BD.(1)如图1,若AB=BC,求证:BD平分∠ABC;(2)如图2,若AB=2BC,①求的值;②连接AD,当S=时,直接写出四边形ABCD的面积为.△ABC24.(12分)已知抛物线y=ax2﹣2ax+3与x轴交于点A、B(A左B右),且AB=4,与y轴交于C点.(1)求抛物线的解析式;(2)如图,证明:对于任意给定的一点P(0,b)(b>3),存在过点P的一条直线交抛物线于M、N两点,使得PM=MN成立;(3)将该抛物线在0≤x≤4间的部分记为图象G,将图象G在直线y=t上方的部分沿y =t翻折,其余部分保持不变,得到一个新的函数的图象,记这个函数的最大值为m,最小值为n,若m﹣n≤6,求t的取值范围.2020年湖北省武汉市九年级元月调考数学模拟试卷(二)参考答案与试题解析一、选择题(共10小题,每小题3分,共30分)1.(3分)将方程3x2+1=6x化成一元二次方程的一般形式,其中二次项系数、一次项系数和常数项分别是()A.3,﹣6,1B.3,6,1C.3,1,﹣6D.3,1,6【分析】方程整理后为一般形式,找出二次项系数与一次项系数即可.【解答】解:方程整理得:3x2﹣6x+1=0,二次项系数为3;一次项系数为﹣6,常数项为1,故选:A.【点评】此题考查了一元二次方程的一般形式,一元二次方程的一般形式是:ax2+bx+c =0(a,b,c是常数且a≠0)特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.2.(3分)下列图形中是中心对称图形的是()A.B.C.D.【分析】根据中心对称图形的概念即可求解.【解答】解:A、不是中心对称图形,不符合题意;B、不是中心对称图形,不符合题意;C、不是中心对称图形,不符合题意;D、是中心对称图形,符合题意.故选:D.【点评】本题考查了中心对称的概念,中心对称图形是要寻找对称中心,旋转180度后两部分重合,难度一般.3.(3分)将抛物线y=x2先向右平移2个单位长度,再向上平移4个单位长度,得到的新的抛物线的解析式为()A.y=(x+2)2+4B.y=(x+2)2﹣4C.y=(x﹣2)2+4D.y=(x﹣2)2﹣4【分析】根据二次函数图象左加右减,上加下减的平移规律进行求解.【解答】解:抛物线y=x2先向右平移2个单位长度,得:y=(x﹣2)2;再向上平移4个单位长度,得:y=(x﹣2)2+4.故选:C.【点评】主要考查的是函数图象的平移,用平移规律“左加右减,上加下减”直接代入函数解析式求得平移后的函数解析式.4.(3分)投掷两枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,掷一次骰子.则下列事件属于随机事件的是()A.两枚骰子向上一面的点数之和等于6B.两枚骰子向上一面的点数之和大于13C.两枚骰子向上一面的点数之和等于1D.两枚骰子向上一面的点数之和大于1【分析】根据必然事件、不可能事件、随机事件的概念以及事件发生的可能性大小判断即可.【解答】解:A、两枚骰子向上一面的点数之和等于6是随机事件,正确;B、两枚骰子向上一面的点数之和大于13是不可能事件,错误;C、两枚骰子向上一面的点数之和等于1是不可能事件,错误;D、两枚骰子向上一面的点数之和大于1是必然事件,错误;故选:A.【点评】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.5.(3分)已知⊙O的直径为12cm,圆心到直线L的距离5cm,则直线L与⊙O的公共点的个数为()A.2B.1C.0D.不确定【分析】先求出圆的半径,圆心到直线的距离与半径比较即可判断出直线和圆的位置关系,从而确定公共点的个数.【解答】解:∵⊙O的直径为12cm,∴⊙O的半径为6cm,∵圆心到直线L的距离为5cm,∴直线L与圆是相交的位置关系,∴直线L与⊙O的公共点的个数为2个.故选:A.【点评】直线和圆的位置关系的确定一般是利用圆心到直线的距离与半径比较来判断.若圆心到直线的距离是d,半径是r,则①d>r,直线和圆相离,没有交点;②d=r,直线和圆相切,有一个交点;③d<r,直线和圆相交,有两个交点.6.(3分)在我国古代数学著作《九章算术》的第九章《勾股》中记载了这样的一个问题:“今天有开门去阔一尺,不合二寸,问门广几何?”意思是:如图,推开两扇门(AD和BC),门边缘D,C两点到门槛AB的距离是1尺,两扇门的间隙CD为2寸,则门宽AB长是()寸.(1尺=10寸)A.101B.100C.52D.96【分析】画出直角三角形,根据勾股定理即可得到结论.【解答】解:过点D作DE⊥AB,垂足为E,设单门的宽度AO是x寸,则AE=x﹣1,DE=10寸,根据勾股定理,得:AD2=DE2+AE2,则x2=102+(x﹣1)2,解得:x=50.5,故AB=101寸,故选:A.【点评】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.7.(3分)假定鸟卵孵化后,雏鸟为雌与雄的概率相同.如果三枚卵全部成功孵化,则三只雏鸟中恰有两只雌鸟的概率是()A.B.C.D.【分析】画树状图得出所有等可能的情况数,找出恰有两只雌鸟的情况数,即可求出所求的概率.【解答】解:画树状图,如图所示:所有等可能的情况数有8种,其中三只雏鸟中恰有两只雌鸟的情况数有3种,则P=.故选:B.【点评】此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.8.(3分)如图,扇形OAB中,∠AOB=90°,将扇形OAB绕点B逆时针旋转,得到扇形BDC,若点O刚好落在弧AB上的点D处,则的值为()A.B.C.D.【分析】如图,连OD、AB、BC,延长AD交BC于H点,由旋转的性质可得BD=BO =OD=CD=OA,∠BDC=90°,可证△ABC是等边三角形,由线段垂直平分线的性质可得AH垂直平分BC,由等腰直角三角形的性质和等边三角形的性质可得AC=2CH,AD=CH﹣CH,即可求解.【解答】解:如图,连OD、AB、BC,延长AD交BC于H点,∵将扇形OAB绕点B逆时针旋转,得到扇形BDC,若点O刚好落在弧AB上的点D处,∴BD=BO=OD=CD=OA,∠BDC=90°∴∠OBD=60°,即旋转角为60°,∴∠ABC=60°,又可知AB=BC,∴△ABC是等边三角形,∵AB=AC,BD=CD,∴AH垂直平分BC,∴∠CAH=30°,∴AC=2CH,AH=CH,∵BD=CD,∠BDC=90°,DH⊥BC,∴DH=CH,∴AD=CH﹣CH,∴=.故选:A.【点评】本题考查了旋转的性质,等边三角形的性质,利用CH表示AC和AD是本题的关键.9.(3分)欧几里得在《几何原本》中,记载了用图解法解方程x2+ax=b2的方法,类似地可以用折纸的方法求方程x2+x﹣1=0的一个正根,如图,裁一张边长为1的正方形的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置F,因而EF=EB,类似地,在AB上折出点M使AM=AF,表示方程x2+x﹣1=0的一个正根的线段是()A.线段BM B.线段AM C.线段BE D.线段AE【分析】设正方形的边长为1,AF=AM=x,根据勾股定理即可求出答案.【解答】解:设正方形的边长为1,AF=AM=x,则BE=EF=,AE=x+,在Rt△ABE中,∴AE2=AB2+BE2,∴(x+)2=1+()2,∴x2+x﹣1=0,∴AM的长为x2+x﹣1=0的一个正根,故选:B.【点评】本题考查一元二次方程,解题的关键是根据勾股定理列出方程,本题属于中等题型.10.(3分)如图,直线y=2x与直线x=2相交于点A,将抛物线y=x2沿线段OA从点O 运动到点A,使其顶点始终在线段OA上,抛物线与直线x=2相交于点P,则点P移动的路径长为()A.4B.3C.2D.1【分析】根据点M在y=2x上可得相应坐标,即可用顶点式表示出相应的二次函数解析式,求出点P的坐标,利用二次函数的性质解决问题即可.【解答】解:∵设抛物线的顶点M的横坐标为m,且在线段OA上移动,∴y=2m(0≤m≤2).∴当抛物线运动到A点时,顶点M的坐标为(m,2m),∴抛物线函数解析式为y=(x﹣m)2+2m.∴当x=2时,y=(2﹣m)2+2m=m2﹣2m+4(0≤m≤2),∴点P的坐标是(2,m2﹣2m+4).∵对于二次函数y′=m2﹣2m+4=(m﹣1)2+3当0≤m≤2时,∴m=1时,y′有最小值3,当m=0或2时,y′的值为4,∴点P移动的路径长为2×(4﹣3)=2,故选:C.【点评】本题考查轨迹,二次函数的性质等知识,解题的关键是学会利用参数,构建二次函数解决问题,属于中考填空题中的压轴题.二、填空题(本大题共6个小题,每小题3分,共18分)11.(3分)已知3是一元二次方程x2+m=0的一个根,则该方程的另一个根是﹣3.【分析】根据方程的解求出m的值,再利用直接开平方法解方程可得答案.【解答】解:将x=3代入方程,得:9+m=0,则m=﹣9,∴方程为x2﹣9=0,解得x=±3,∴方程的另一个根为﹣3,故答案为:﹣3.【点评】本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.12.(3分)在平面直角坐标系中,已知点P的坐标为(3,﹣4),则点P关于原点对称的点的坐标为(﹣3,4).【分析】根据平面直角坐标系中任意一点P(x,y),关于原点的对称点是(﹣x,﹣y),即关于原点的对称点,横纵坐标都变成相反数.【解答】解:∵点P的坐标为(3,﹣4),∴点P关于原点对称的点的坐标为:(﹣3,4).故答案为:(﹣3,4).【点评】本题主要考查了关于原点的对称点的性质,正确把握横纵坐标的关系是解题关键.13.(3分)一个口袋中有6个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,…,不断重复上述过程.小明共摸了100次,其中60次摸到白球.根据上述数据,小明可估计口袋中的白球大约有9个.【分析】设口袋中有x个白球,根据利用频率估计概率得到估计摸到白球的概率为=,然后根据概率公式得到=,再解方程即可.【解答】解:设口袋中有x个白球,因为摸了100次,其中60次摸到白球,则估计摸到白球的概率为=,所以=,解得x=9,即可估计口袋中的白球大约有9个.故答案为9.【点评】本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.14.(3分)要为一幅矩形照片配一个镜框,如图,要求镜框的四条边宽度都相等,且镜框所占面积是照片本身面积的四分之一,已知照片的长为21cm,宽为10cm,求镜框的宽度.设镜框的宽度为xcm,依题意列方程,化成一般式为8x2+124x﹣105=0.【分析】设镜框的宽度为xcm,根据镜框所占面积是照片本身面积的四分之一,即可得出关于x的一元二次方程,此题得解.【解答】解:设镜框的宽度为xcm,依题意,得:21×10=4[(21+2x)(10+2x)﹣21×10],整理,得:8x2+124x﹣105=0.故答案为:8x2+124x﹣105=0.【点评】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.15.(3分)如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加(4﹣4)m.【分析】根据已知建立平面直角坐标系,进而求出二次函数解析式,再通过把y=﹣2代入抛物线解析式得出水面宽度,即可得出答案.【解答】解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,抛物线以y轴为对称轴,且经过A,B两点,OA=OB=AB=2米,抛物线顶点C坐标为(0,2),通过以上条件可设顶点式y=ax2+2,其中a可通过将A点坐标(﹣2,0)代入抛物线解析式可得出:a=﹣0.5,所以抛物线解析式为y=﹣0.5x2+2,当水面下降2米,通过抛物线在图上的观察可转化为:当y=﹣2时,对应的抛物线上两点之间的距离,也就是直线y=﹣2与抛物线相交的两点之间的距离,可以通过把y=﹣2代入抛物线解析式得出:﹣2=﹣0.5x2+2,解得:x=±2,所以水面宽度增加到4米,比原先的宽度当然是增加了(4﹣4)米,故答案为:4﹣4.【点评】此题主要考查了二次函数的应用,根据已知建立坐标系从而得出二次函数解析式是解决问题的关键.16.(3分)如图,正方形ABCD中,AB=4,E,F分别是边AB,AD上的动点,AE=DF,连接DE,CF交于点P,过点P作PK∥BC,且PK=2,若∠CBK的度数最大时,则BK 长为6.【分析】根据全等三角形的性质得到∠ADE=∠DCF,求得∠CPD=90°,得到点P在以CD为直径的半圆上运动,取CD的中点O,过O作OM⊥CD,且点M在CD的右侧,MO=2,连接OP,KM,推出四边形POMK是菱形,于是得到点K在以M为圆心,半径=2的半圆上运动,当BK与⊙M相切时,∠CBK最大,根据勾股定理即可得到结论.【解答】解:∵正方形ABCD中,AD=CD,∠A=∠CDA=90°,∵AE=DF,∴△ADE≌△DCF(SAS),∴∠ADE=∠DCF,∵∠ADE+∠CDE=90°,∴∠DCF+∠CDE=90°,∴∠CPD=90°,∴点P在以CD为直径的半圆上运动,取CD的中点O,过O作OM⊥CD,且点M在CD的右侧,MO=2,连接OP,KM,∵PK∥BC,BC⊥CD,∴PK⊥CD,∴PK∥OM,PK=OM=2,∴四边形POMK是平行四边形,∵CD=AB=4,∴OP=CD=2,∴OP=OM,∴四边形POMK是菱形,∴点K在以M为圆心,半径=2的半圆上运动,当BK与⊙M相切时,∠CBK最大,∴∠BKM=90°,∵BM==2,∴BK==6,故答案为:6.【点评】本题考查了切线的性质,正方形的性质,全等三角形的判定和性质,菱形的判定和性质,圆周角定理,正确的作出辅助线是解题的关键.三、解答题(共8题,共72分)17.(8分)解方程:x2﹣4x+1=0.【分析】根据配方法可以解答此方程.【解答】解:x2﹣4x+1=0x2﹣4x+4=3(x﹣2)2=3x﹣2=∴x1=2+,x2=2﹣;【点评】本题考查解一元二次方程﹣配方法,解答本题的关键是会用配方法解方程的方法.18.(8分)如图,已知A、B、C、D是⊙O上的四点,延长DC、AB相交于点E.若BC =BE.求证:△ADE是等腰三角形.【分析】求出∠A=∠BCE=∠E,即可得出AD=DE,从而判定等腰三角形.【解答】证明:∵A、D、C、B四点共圆,∴∠A=∠BCE,∵BC=BE,∴∠BCE=∠E,∴∠A=∠E,∴AD=DE,即△ADE是等腰三角形.【点评】考查了圆内接四边形的性质、等腰三角形的判定的知识,属于基础题,相对比较简单.19.(8分)某学校初中英语口语听力考试即将举行,准备了A、B、C、D四份听力材料,它们的难易程度分别是易、中、难、难;另有a、b是两份口语材料,它们的难易程度分别是易、难.(1)从四份听力材料中,任选一份是难的听力材料的概率是;(2)用树状图形或列表法,求出听力、口语两份材料都是难的一套模拟试卷的概率.【分析】(1)直接根据概率公式求解即可;(2)根据题意列出图表得出所有等可能的结果数和听力、口语两份材料都是难的一套模拟试卷的情况数,然后根据概率公式即可得出答案.【解答】解:(1)∵A、B、C、D四份听力材料的难易程度分别是易、中、难、难,∴从四份听力材料中,任选一份是难的听力材料的概率是;故答案为:;(2)列表如下:由列表可知:共有8种可能出现的结果,且每种结果出现的可能性相等,其中听力、口语均为难的结果有2种,所以P(两份材料都难)==.【点评】本题主要考查了利用树状图或列表法求概率,当有两个元素时,可用树形图列举,也可以列表列举.随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.20.(8分)如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(0,1),B(1,3),C(4,3).(1)将△ABC平移得到△A1B1C1,且C1的坐标是(0,﹣1),画出△A1B1C1;(2)将△ABC绕点A逆时针旋转90°得到△A2B2C2,画出△A2B2C2;(3)小娟发现△A1B1C1绕点P旋转也可以得到△A2B2C2,请直接写出点P的坐标.【分析】(1)根据C1的坐标是(0,﹣1),即可画出△A1B1C1;(2)根据△ABC绕点A逆时针旋转90°得到△A2B2C2,即可画出△A2B2C2;(3)连接两对对应点,分别作两条连线的垂直平分线,其交点P即为所求,进而得出坐标.【解答】解:(1)如图所示,△A1B1C1即为所求;(2)如图所示,△A2B2C2即为所求;(3)如图所示,点P即为所求,点P的坐标为(﹣4,1).【点评】本题主要考查了利用平移变换以及旋转变换作图,旋转作图有自己独特的特点,决定图形位置的因素较多,旋转角度、旋转方向、旋转中心,任意不同,位置就不同,但得到的图形全等.21.(8分)在⊙O中,直径AB⊥弦CD于点F,点E是弧AD上一点,连BE交CD于点N,点P在CD的延长线上,PN=PE.(1)求证:PE是⊙O的切线;(2)连接DE,若DE∥AB,OF=3,BF=2,求PN的长.【分析】(1)连接OE,由等腰三角形的性质得出∠PEN=∠PNE=∠BNF,∠OEB=∠OBE.证出∠OEB+∠PEN=90°,即PE⊥OE,即可得出结论;(2)连接CE,证出CE为⊙O的直径.由垂径定理得出CF=DF,得出DE=2OF=6.求出OC=OB=5,CE=10,由勾股定理得出CD=8.设PD=x,则PC=x+8.在Rt△PDE和Rt△PCE中,由勾股定理得出方程,解方程求出PD=,由勾股定理即可得出答案.【解答】(1)证明:连接OE,如图1所示:∵PN=PE,∴∠PEN=∠PNE=∠BNF,∵OE=OB,∴∠OEB=∠OBE.∵AB⊥CD,∴∠OBE+∠BNF=90°,∴∠OEB+∠PEN=90°,即∠OEP=90°,∴PE⊥OE,∴PE是⊙O的切线.(2)解:连接CE,如图2所示:∵DE∥AB,AB⊥CD,∴∠EDC=90°∴CE为⊙O的直径.∵AB⊥CD,∴CF=DF,∴DE=2OF=6.∵OF=3,BF=2,∴OC=OB=5,CE=10,∴CD===8,由(1)知PE⊥CE.设PD=x,则PC=x+8.在Rt△PDE和Rt△PCE中,由勾股定理,得:PD2+DE2=PE2=PC2﹣CE2,即x2+62=(x+8)2﹣102,解得:x=,∴PD=.∴PE===,∴PN=PE=.【点评】本题考查切线的判定、勾股定理、圆周角定理、等腰三角形的性质、解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.22.(10分)某商场销售一种成本为每件30元的商品,销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=﹣10x+600,商场销售该商品每月获得利润为w(元).(1)求w与x之间的函数关系式;(2)如果商场销售该商品每月想要获得2000元的利润,那么每月成本至少多少元?(3)若销售价不低于40元且不高于55元,请直接写出每月销售新产品的利润w的取值范围.【分析】(1)根据月利润=(销售单价﹣成本价)×销售量,从而列出关系式;(2)令w=2000,然后解一元二次方程,从而求出销售单价,再根据:月成本=成本价×销售量可得答案;(3)将(2)中w的解析式配方,根据二次函数的性质及售价的范围,可得答案.【解答】解:(1)w=(x﹣30)(﹣10x+600)=﹣10x2+900x﹣18000.(2)由题意得,﹣10x2+900x﹣18000=2000,解得:x1=40,x2=50,当x=40时,成本为30×(﹣10×40+600)=6000(元),当x=50时,成本为30×(﹣10×50+600)=3000(元),∴每月想要获得2000元的利润,每月成本至少3000元;(3)∵w=(x﹣30)(﹣10x+600)=﹣10x2+900x﹣18000=﹣10(x﹣45)2+2250∴当x=45时,w取得最大值2250∵销售价不低于40元且不高于55元,55离对称轴x=45远,∴当x=55时,w取得最小值,最小值为1250∴销售价不低于40元且不高于55元时,每月销售新产品的利润w的取值范围为:1250≤w≤2250.【点评】本题考查了把实际问题转化为二次函数,再利用二次函数的性质进行实际应用.根据题意分情况建立二次函数的模型是解题的关键.23.(10分)在△ABC中,∠ABC=120°,线段AC绕点C顺时针旋转60°得到线段CD,连接BD.(1)如图1,若AB=BC,求证:BD平分∠ABC;(2)如图2,若AB=2BC,①求的值;②连接AD,当S=时,直接写出四边形ABCD的面积为.△ABC【分析】(1)连接AD,证△ACD是等边三角形,再证△ABD≌△CBD,推出∠CBD=∠ABD,即得出结论;(2)①连接AD,作等边三角形ACD的外接圆⊙O,证点B在⊙O上,在BD上截取BM,使BM=BC,证△CBA≌△CMD,设BC=BM=1,则AB=MD=2,BD=3,过点C作CN⊥BD于N,可求出BN=BC=,CN=BC=,ND=BD﹣BN=,CD=,即可求出==;②分别过点B,D作AC的垂线,垂足分别为H,Q,设CB=1,AB=2,CH=x,则由①知,AC=,AH=﹣x,在Rt△BCH与Rt△BAH中利用勾股定理求出BH的值,再求出DQ的值,求出=,因为AC为△ABC与△ACD的公共底,所以=,可求出△ACD的面积,进一步求出四边形ABCD的面积.【解答】(1)证明:连接AD,由题意知,∠ACD=60°,CA=CD,∴△ACD是等边三角形,∴CD=AD,又∵AB=CB,BD=BD,∴△ABD≌△CBD(SSS),∴∠CBD=∠ABD,∴BD平分∠ABC;(2)解:①连接AD,作等边三角形ACD的外接圆⊙O,∵∠ADC=60°,∠ABC=120°,∴∠ADC+∠ABC=180°,∴点B在⊙O上,∵AD=CD,∴,∴∠CBD=∠CAD=60°,在BD上截取BM,使BM=BC,则△BCM为等边三角形,∴∠CMB=60°,∴∠CMD=120°=∠CBA,又∵CB=CM,∠BAC=∠BDC,∴△CBA≌△CMD(AAS),∴MD=AB,设BC=BM=1,则AB=MD=2,∴BD=3,过点C作CN⊥BD于N,在Rt△BCN中,∠CBN=60°,∴∠BCN=30°,∴BN=BC=,CN=BC=,∴ND=BD﹣BN=,在Rt△CND中,CD===,∴AC=,∴==;②如图3,分别过点B,D作AC的垂线,垂足分别为H,Q,设CB=1,AB=2,CH=x,则由①知,AC=,AH=﹣x,在Rt△BCH与Rt△BAH中,BC2﹣CH2=AB2﹣AH2,即1﹣x2=22﹣(﹣x)2,解得,x=,∴BH==,在Rt△ADQ中,DQ=AD=×=,∴==,∵AC为△ABC与△ACD的公共底,∴==,=,∵S△ABC=,∴S△ACD=+=,∴S四边形ABCD故答案为:.【点评】本题是一道几何综合题,考查了等边三角形的性质,圆的有关性质,勾股定理,三角形的面积等,解题关键是能够构造ACD的外接圆.24.(12分)已知抛物线y=ax2﹣2ax+3与x轴交于点A、B(A左B右),且AB=4,与y轴交于C点.(1)求抛物线的解析式;(2)如图,证明:对于任意给定的一点P(0,b)(b>3),存在过点P的一条直线交抛物线于M、N两点,使得PM=MN成立;(3)将该抛物线在0≤x≤4间的部分记为图象G,将图象G在直线y=t上方的部分沿y =t翻折,其余部分保持不变,得到一个新的函数的图象,记这个函数的最大值为m,最小值为n,若m﹣n≤6,求t的取值范围.【分析】(1)抛物线y=ax2﹣2ax+3的对称轴为x=1,又AB=4,由对称性得A(﹣1,0)、B(3,0),即可求解;(2)证明△PMG≌△NMH(AAS),y G+y H=2y M,即可求解;(3)分当D′在点H(4,﹣5)上方、点D′在点H(4,﹣5)下方两种情况,分别求解即可.【解答】解:(1)抛物线y=ax2﹣2ax+3的对称轴为x=1,又AB=4,由对称性得A(﹣1,0)、B(3,0).把A(﹣1,0)代入y=ax2﹣2ax+3,得a+2a+3=0,∴a=﹣1.∴抛物线的解析式为y=﹣x2+2x+3.(2)如图,过M作GH⊥x轴,PG∥x轴,NH∥x轴,由PM=MN,则△PMG≌△NMH(AAS),∴PG=NH,MG=MH.设M(m,﹣m2+2m+3),则N(2m,﹣4m2+4m+3),。
鄂教版2020届九年级下学期语文中考二模试卷(II)卷

( 3) 李贺的《雁门太守行》中写敌人兵临城下,战云笼罩,使人透不过气来,而战士整装待发,士气还很高 昂的诗句是: ________, ________。
( 4) 富贵不能淫, ________, ________。(《富贵不能淫》 )
( 5) 请将《渡荆门送别》一诗补充完整。
渡远荆门外,来从楚国游。 ________, ________。 ________, ________。仍怜故乡水,万里送行舟。
? 父亲又是高兴,又是流泪,说:“儿子,爸对不起你,爸老了,不中用了!你找工作的事,我只会着急,却 一点儿也帮不上你。我不该整天喝闷酒,总想着你去世的妈妈。爸知道你想我,可爸更想你呀。你离家出走的这些 天,爸每天都在四处寻找你,爸知道你会给我打电话的,怕错过了你的电话,就开通了‘来电显示’和‘录音’功 能,这不,爸一接到你的电话,就立刻来看你了。”
________的氛围。
( 2) 本诗尾联与王维《竹里馆》“深林人不知,明月来相照”在情感表达上相似,请加以赏析。
第 1页 共 9页
三、 文言文阅读 ( 共 2 题;共 16 分)
3. ( 12 分) (2019 九上·中山期末 ) 阅读下面的文言文,完成下列小题。
【甲】
至若春和景明,波澜不惊,上下天光,一碧万顷,沙鸥翔集,锦鳞游泳,岸芷汀兰,郁郁青青。而或长烟一空, 皓月千里,浮光跃金,静影沉璧,渔歌互答,此乐何极!登斯楼也,则有心旷神怡,宠辱偕忘,把酒临风,其喜洋 洋者矣。
(选自《青年文摘》 ,有删改)
( 1) 父与子是一对天生的冤家,然而冲突之中有挚爱,分开之时有牵挂。阅读文章,填写表格。
我的言行
父亲的表现
第 5页 共 9页
①________ 我不告而别去他乡租房找工作 ③________ 我天南海北地忙业务
(湖北武汉卷) 2020年九年级化学第二次模拟大联考(全解全析)
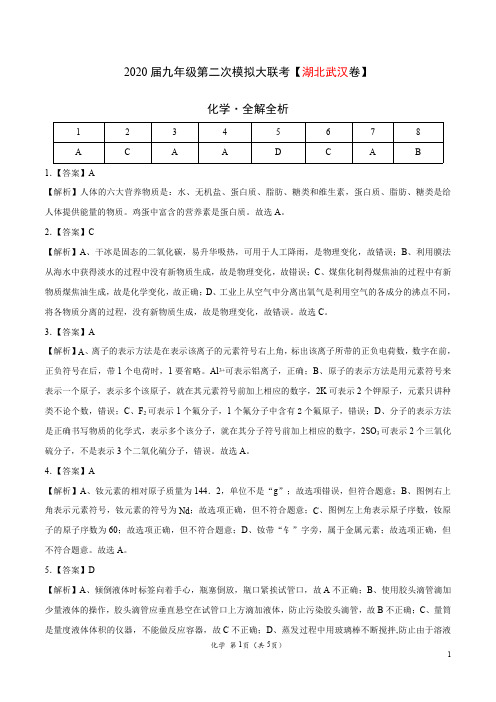
2020届九年级第二次模拟大联考【湖北武汉卷】化学·全解全析12345678A C A A D C AB 1.【答案】A【解析】人体的六大营养物质是:水、无机盐、蛋白质、脂肪、糖类和维生素,蛋白质、脂肪、糖类是给人体提供能量的物质。
鸡蛋中富含的营养素是蛋白质。
故选A。
2.【答案】C【解析】A、干冰是固态的二氧化碳,易升华吸热,可用于人工降雨,是物理变化,故错误;B、利用膜法从海水中获得淡水的过程中没有新物质生成,故是物理变化,故错误;C、煤焦化制得煤焦油的过程中有新物质煤焦油生成,故是化学变化,故正确;D、工业上从空气中分离出氧气是利用空气的各成分的沸点不同,将各物质分离的过程,没有新物质生成,故是物理变化,故错误。
故选C。
3.【答案】A【解析】A、离子的表示方法是在表示该离子的元素符号右上角,标出该离子所带的正负电荷数,数字在前,正负符号在后,带1个电荷时,1要省略。
Al3+可表示铝离子,正确;B、原子的表示方法是用元素符号来表示一个原子,表示多个该原子,就在其元素符号前加上相应的数字,2K可表示2个钾原子,元素只讲种类不论个数,错误;C、F2可表示1个氟分子,1个氟分子中含有2个氟原子,错误;D、分子的表示方法是正确书写物质的化学式,表示多个该分子,就在其分子符号前加上相应的数字,2SO3可表示2个三氧化硫分子,不是表示3个二氧化硫分子,错误。
故选A。
4.【答案】A【解析】A、钕元素的相对原子质量为144.2,单位不是“g”;故选项错误,但符合题意;B、图例右上角表示元素符号,钕元素的符号为Nd;故选项正确,但不符合题意;C、图例左上角表示原子序数,钕原子的原子序数为60;故选项正确,但不符合题意;D、钕带“钅”字旁,属于金属元素;故选项正确,但不符合题意。
故选A。
5.【答案】D【解析】A、倾倒液体时标签向着手心,瓶塞倒放,瓶口紧挨试管口,故A不正确;B、使用胶头滴管滴加少量液体的操作,胶头滴管应垂直悬空在试管口上方滴加液体,防止污染胶头滴管,故B不正确;C、量筒是量度液体体积的仪器,不能做反应容器,故C不正确;D、蒸发过程中用玻璃棒不断搅拌,防止由于溶液局部温度过高,造成液体飞溅,故D正确。
元调模拟最新版2

2019~2020学年度武汉市部分学校九年级调研测试物理试题(2)说明:本试卷分第Ⅰ卷和第Ⅱ卷。
第Ⅰ卷为选择题题,第Ⅱ卷为非选择题。
全卷满分70分,考试时间70分钟。
用到的物理量:天然气的热值为3×107J/m 3 C水=4.2×103J/(Kg•℃)汽油的热值为4.5×107J/kg第Ⅰ卷(选择题共36分)一.选择题((共12小题每,小题只有一个选项符合题意。
每小题3分,共36分))9. 下列对生活中的现象解释正确的是A.“破镜难重圆”----分子间存在斥力B.铁棒很难被压缩----固体内分子之间只有斥力C.海边昼夜温差变化比沙漠中大----水的比热容比沙石的比热容大D.火箭的助推剂选用氢气做燃料----氢气的热值较高10.关于内能、温度和热量,下列说法正确的是A.温度高的物体内能一定大B.做功也可以改变物体的内能C.物体温度升高,一定吸收了热量D.物体放出了热量,温度一定降低11.下图各实例中,属于通过做功的方式使物体内能增大的是12.下图是四冲程汽油机的剖面图,下列关于汽油机工作过程描述错误的是A.如图正在进行的是做功冲程B.若该汽油机的效率为20%,则完全燃烧100g汽油放可以获得约9×105J的有用功C.做功冲程中,燃料释放的能量绝大部分转化为机械能D.在汽油机的四个冲程中,排出废气带走的那部分能量最多13.如图所示,小明同学用塑料梳子在头发上摩擦几下后,塑料梳子能够吸引碎纸片。
上述过程中塑料梳子所带的电荷和同毛皮摩擦过的橡胶棒所带的电荷相同,这个现象说明A.摩擦时,同时发生了正、负电荷的转移,头发带负电,塑料梳子带正电B.摩擦时,同时发生了正、负电荷的转移,头发带正电,塑料梳子带负电C.摩擦时,只发生了正电荷的转移,使塑料梳子带了正电D.摩擦时,头发上的电子向塑料梳子转移,使塑料梳子带了负电14.下列电路图中,与实物图对应的是15.如图所示为常用电热暖手宝。
(word版)2019-2020学年湖北省武汉市部分学校上学期九年级数学元调模拟试题 答案

2019—2020学年度上学期九年级数学元调模拟试题一、选择题(共10小题,每小题3分,共30分)1.一元二次方程3x 2-x -2=0的二次项系数是3,它的一次项系数是() A .-1B .-2C .1 D .0 答案A2.下列图形中,既是轴对称图形,又是中心对称图形的是()A .B .C .D . 答案B3.下列事件中,必然事件是()A .任意掷一枚均匀的硬币,正面朝上B .从一副扑克牌中,随意抽出一张是大王C .通常情况下,抛出的篮球会下落D .三角形内角和为360° 答案C4.抛物线y =2(x +3)2+5的顶点坐标是()A .(3,5)B .(-3,5)C .(3,-5)D .(-3,-5) 答案B5.关于x 的一元二次方程x 2+(2k +1)x +k 2=0有两个不相等的实数根,则k 的取值范围为() A .k >-14B .k >4C .k <-1D .k <4答案A6.在Rt △ABC 中,∠C =90°,∠B =30°,AB =4,以点C 为圆心2为半径作⊙C ,直线AB 与⊙C 的位置关系是()A .相离B .相切C .相交D .相切或相交 答案C7.将抛物线y =2x 2向左平移2个单位后所得到的抛物线解析式为() A .y =2x 2-2B .y =2x 2+2C .y =2(x -2)2 D .y =2(x +2)2 答案D8.如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果:下面由三个推断,合理的是()①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;②随着试验次数的增加,“正面向上”的频率总是在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45. A .①B .②C .①②D .①③ 答案B9.如图,AB 为⊙O 的直径,点C 、D 在O 上,若∠AOD =30°, 则∠BCD 的度数是() A .100°B .105° C .110°D .115° 答案B10.已知二次函数y =ax 2+2ax +3a 2+3(其中x 是自变量),当x ≥2时,y 随x 的增大而增大,且-2≤x ≤1时,y 的最大值为9,则a 的值为() A .1或-2B .2C .-2或2D .1 答案D二、填空题(本大题共6个小题,每小题3分,共18分)11.已知x =-1是一元二次方程x 2+mx +1=0的一个根,那么m 的值是. 答案212.已知电流在一定时间段内正常通过某一个电子元件的概率是0.5,则在如图所示的电路中,在一定时间段内,A 、B 之间电流能够正常通过的概率是. 答案3413.九年级学生在毕业前夕,某班每名同学都为其他同学写一段毕业感言,全班共写了2256段毕业感言,如果该班有x 名同学,根据题意列出方程为. 答案(1)2256x x -=14.已知圆锥的侧面积是其底面积的3倍,这个圆锥的侧面展开图的扇形角的度数为___. 答案120°15.如图,⊙O 的半径为2,正八边形ABCDEFGH 内接于⊙O ,对角线CE 、DF 相交于点M ,则△MEF 的面积是.答案216.如图,⊙O 的半径为42,点B 是圆上一动点,点A 为⊙O 内一定点,OA =4,将AB 绕A 点顺时针方向旋转120°到AC ,以AB 、BC 为邻边作□ABCD ,对角线AC 、BD 交于E ,则OE 的最大值为.答案三、解答题(共8题,共72分) 17.(本题8分)解方程:x 2-2x -3=0. 解:(1)(3)0x x +-=11x ∴=-,23x =18.(本题8分)已知AB 是⊙O 的直径,C 是圆上的点,D 是优弧ABC 的中点. (1)若∠AOC =100°,则∠D 的度数为, ∠A 的度数为,(2)求证:∠ADC =2∠DAB . 解(1)50°,25°;(2)证明:连OD ,∵⌒AD =⌒CD ∴AD =CD 在△AOD 与△COD 中,OD ODAO CO AD CD =⎧⎪=⎨⎪=⎩∴△AOD ≌ △COD ∴∠1=∠2,∴∠ADC=2∠1∵AO =OD ,∴∠1=∠DAB,∴∠ADC =2∠DAB19.(本题8分)武汉市某中学进行九年级理化实验考查,有A 和B 两个考查实验,规定每位学生只参加一个实验的考查,并由学生自己抽签决定具体的考查实验,小孟、小柯、小刘都要参加本次考查. (1)用列表或画树状图的方法求小孟、小柯都参加实验A 考查的概率; (2)他们三人中至少有两人参加实验B 的概率(直接写出结果) . 解:(1)由题意列树状图如下:共有8种结果,每种结果出现的可能性相等,其中小明和小丽都参加A 考查有:AAA,AAB 共2种。
武汉市2020年九年级元调试卷附答案

2019-2020学年度武汉市部分学校九年级质量检测语文试卷武汉市教育科学研究院命制 2020.1.8亲爱的同学,在你答题前,请认真阅读下面的注意事项:1.本试卷由第I卷(选择题)和第1卷(非选择题)两部分组成。
全卷共8页,七大题,满分120分。
考试用时150分钟。
2.答题前,请将你的姓名、准考证号填写在“答题卡”相应位置,并在“答题卡”背面左上角填写姓名和座位号。
3.答第I卷(选择题)时,选出每小题答案后,用2B铅笔把“答题卡”上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案。
答在“试卷”上无效。
4.答第卷(非选择题)时,答案用0.5毫米黑色笔迹签字笔书写在“答题卡”上。
答在“试卷”上无效。
5.认真阅读答题卡上的注意事项。
预祝你取得优异成绩!第I卷(选择题共30分)一、(共9分,每小题3分)1.依次填人下面横线处的词语,恰当的一组是( )在双方难分伯仲的实力较量中,若能赢得竞争固然是一件的事情,然而更的是,赢得友谊和尊重一赢得对手的心,贏得世人的,贏在“灵魂的卓越”。
A.激动人心重要感动B.大快人心关键感动C.大快人心重要感激D.激动人心关键感激2.下列各句中有语病的一项是( )A.不少市民特意购买首发车票,目的是第一时间感受汉十高铁带来的速度与便利。
B.全年减税降费的政策红利,让企业不但可以轻装上阵,也点燃了投资者的热情。
C.中国支持世贸组织进行改革,希望它在扩大开放促进发展方面发挥更大作用。
D.面对百年未有之大变局,我们应顺应时代潮流,在追求发展的道路上矢志不移。
3.下列各向标点符号使用不规范的一项是( )A.不同国家地区、民族,不同历史宗教、习俗,彼此交相辉映,相因相生,共同擘画出这个精彩纷呈的世界。
B.故事一定要贯穿节目的每一个环节:从标题、片子开场,到主持人,评论员的每一个问题,都要跟这个故事配套。
C.灿烂的阳光一扫冬日的阴霾,天空顿时湛蓝如洗。
山川河流早已解冻,泥土中散发出草芽萌发的新鲜气息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020元月调考人教版九年级数学模拟试卷(二)一.选择题(共10小题)1.将方程3x2+1=6x化成一元二次方程的一般形式,其中二次项系数、一次项系数和常数项分别是()A.3,﹣6,1 B.3,6,1 C.3,1,﹣6 D.3,1,62.下列图形中,是中心对称图形的是()A.B.C.D.3.将抛物线y=x2向右平移两个单位,再向下平移4个单位,所得抛物线是()A.y=(x+2)2+4 B.y=(x﹣2)2﹣4 C.y=(x﹣2)2+4 D.y=(x+2)2﹣4 4.投掷两枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,掷一次骰子,设两枚骰子向上一面的点数之和为S,则下列事件属于随机事件的是()A.S=6 B.S>13 C.S=1 D.S>15.已知⊙O的直径为12cm,圆心到直线L的距离5cm,则直线L与⊙O的公共点的个数为()A.2 B.1 C.0 D.不确定6.在我国古代数学著作《九章算术》“勾股”章有一题:“今有开门去阃(kǔn)一尺,不合二寸,问门广几何.”大意是说:如图,推开双门(AD和BC),门边缘D、C两点到门槛AB距离为1尺(1尺=10寸),双门间的缝隙CD为2寸,那么门的宽度(两扇门的和)AB为()A.100寸B.101寸C.102寸D.103寸7.假定鸟卵孵化后,雏鸟为雌与雄的概率相同.如果三枚卵全部成功孵化,则三只雏鸟中恰有两只雌鸟的概率是()A.B.C.D.8.如图,扇形OAB中,∠AOB=90°,将扇形OAB绕点B逆时针旋转,得到扇形BDC,若点O刚好落在弧AB上的点D处,则的值为()A.B.C.D.9.我们可以用折纸的方法求方程x2+x﹣1=0的一个正根.如图,裁一张边长为1的正方形纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置F,因而EF=EB,类似地,在AB上折出点M,使AM=AF,表示方程x2+x﹣1=0的一个正根的线段是()A.线段BM B.线段AM C.线段BE D.线段AE10.如图,直线y=2x与直线x=2相交于点A,将抛物线y=x2沿线段OA从点O运动到点A,使其顶点始终在线段OA上,抛物线与直线x=2相交于点P,则点P移动的路径长为()A.4 B.3 C.2 D.1二.填空题(共6小题)11.已知3是一元二次方程x2+m=0的一个根,则该方程的另一个根是.12.在平面直角坐标系xOy中,点(3,﹣4)关于原点对称的点的坐标为.13.一个口袋中有6个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,…,不断重复上述过程.小明共摸了100次,其中60次摸到白球.根据上述数据,小明可估计口袋中的白球大约有个.14.要为一幅矩形照片配一个镜框,如图,要求镜框的四条边宽度都相等,且镜框所占面积是照片本身面积的四分之一,已知照片的长为21cm,宽为10cm,求镜框的宽度.设镜框的宽度为xcm,依题意列方程,化成一般式为.15.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加m.16.如图,正方形ABCD中,AB=4,E,F分别是边AB,AD上的动点,AE=DF,连接DE,CF交于点P,过点P作PK∥BC,且PK=2,若∠CBK的度数最大时,则BK长为.三.解答题(共8小题)17.解方程:x2﹣4x+1=0.18.已知A,B,C,D是⊙O上的四点,延长DC,AB相交于点E,若BC=BE.求证:△ADE是等腰三角形.19.某学校初中英语口语听力考试即将举行,准备了A、B、C、D四份听力材料,它们的难易程度分别是易、中、难、难;另有a、b是两份口语材料,它们的难易程度分别是易、难.(1)从四份听力材料中,任选一份是难的听力材料的概率是;(2)用树状图形或列表法,求出听力、口语两份材料都是难的一套模拟试卷的概率.20.如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(0,1),B(1,3),C(4,3).(1)将△ABC平移得到△A1B1C1,且C1的坐标是(0,﹣1),画出△A1B1C1;(2)将△ABC绕点A逆时针旋转90°得到△A2B2C2,画出△A2B2C2;(3)小娟发现△A1B1C1绕点P旋转也可以得到△A2B2C2,请直接写出点P的坐标.21.在⊙O中,直径AB⊥弦CD于点F,点E是弧AD上一点,连BE交CD于点N,点P在CD 的延长线上,PN=PE.(1)求证:PE是⊙O的切线;(2)连接DE,若DE∥AB,OF=3,BF=2,求PN的长.22.某商场销售一种成本为每件30元的商品,销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=﹣10x+600,商场销售该商品每月获得利润为w(元).(1)求w与x之间的函数关系式;(2)如果商场销售该商品每月想要获得2000元的利润,那么每月成本至少多少元?(3)若销售价不低于40元且不高于55元,请直接写出每月销售新产品的利润w的取值范围.23.在△ABC中,∠ABC=120°,线段AC绕点C顺时针旋转60°得到线段CD,连接BD.(1)如图1,若AB=BC,求证:BD平分∠ABC;(2)如图2,若AB=2BC,①求的值;②连接AD,当S△ABC=时,直接写出四边形ABCD的面积为.24.已知抛物线y=ax2﹣2ax+3与x轴交于点A、B(A左B右),且AB=4,与y轴交于C 点.(1)求抛物线的解析式;(2)如图,证明:对于任意给定的一点P(0,b)(b>3),存在过点P的一条直线交抛物线于M、N两点,使得PM=MN成立;(3)将该抛物线在0≤x≤4间的部分记为图象G,将图象G在直线y=t上方的部分沿y =t翻折,其余部分保持不变,得到一个新的函数的图象,记这个函数的最大值为m,最小值为n,若m﹣n≤6,求t的取值范围.参考答案与试题解析一.选择题(共10小题)1.将方程3x2+1=6x化成一元二次方程的一般形式,其中二次项系数、一次项系数和常数项分别是()A.3,﹣6,1 B.3,6,1 C.3,1,﹣6 D.3,1,6【分析】方程整理后为一般形式,找出二次项系数与一次项系数即可.【解答】解:方程整理得:3x2﹣6x+1=0,二次项系数为3;一次项系数为﹣6,常数项为1,故选:A.2.下列图形中,是中心对称图形的是()A.B.C.D.【分析】根据中心对称图形的概念即可求解.【解答】解:A、不是中心对称图形,不符合题意;B、不是中心对称图形,不符合题意;C、不是中心对称图形,不符合题意;D、是中心对称图形,符合题意.故选:D.3.将抛物线y=x2向右平移两个单位,再向下平移4个单位,所得抛物线是()A.y=(x+2)2+4 B.y=(x﹣2)2﹣4 C.y=(x﹣2)2+4 D.y=(x+2)2﹣4 【分析】先确定出原抛物线的顶点坐标,然后根据向右平移横坐标加,向下平移纵坐标减求出新图象的顶点坐标,然后写出即可.【解答】解:抛物线y=x2的顶点坐标为(0,0),向右平移2个单位,再向下平移4个单位后的图象的顶点坐标为(2,﹣4),所以,所得图象的解析式为y=(x﹣2)2﹣4,故选:B.4.投掷两枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,掷一次骰子,设两枚骰子向上一面的点数之和为S,则下列事件属于随机事件的是()A.S=6 B.S>13 C.S=1 D.S>1【分析】根据必然事件、不可能事件、随机事件的概念以及事件发生的可能性大小判断即可.【解答】解:A、两枚骰子向上一面的点数之和S等于6是随机事件,符合题意;B、两枚骰子向上一面的点数之和S大于13是不可能事件,不合题意;C、两枚骰子向上一面的点数之和S等于1是不可能事件,不合题意;D、两枚骰子向上一面的点数之和S大于1是必然事件,不合题意;故选:A.5.已知⊙O的直径为12cm,圆心到直线L的距离5cm,则直线L与⊙O的公共点的个数为()A.2 B.1 C.0 D.不确定【分析】先求出圆的半径,圆心到直线的距离与半径比较即可判断出直线和圆的位置关系,从而确定公共点的个数.【解答】解:∵⊙O的直径为12cm,∴⊙O的半径为6cm,∵圆心到直线L的距离为5cm,∴直线L与圆是相交的位置关系,∴直线L与⊙O的公共点的个数为2个.故选:A.6.在我国古代数学著作《九章算术》“勾股”章有一题:“今有开门去阃(kǔn)一尺,不合二寸,问门广几何.”大意是说:如图,推开双门(AD和BC),门边缘D、C两点到门槛AB距离为1尺(1尺=10寸),双门间的缝隙CD为2寸,那么门的宽度(两扇门的和)AB为()A.100寸B.101寸C.102寸D.103寸【分析】画出直角三角形,根据勾股定理即可得到结论.【解答】解:设OA=OB=AD=BC=r,过D作DE⊥AB于E,则DE=10,OE=CD=1,AE=r﹣1.在Rt△ADE中,AE2+DE2=AD2,即(r﹣1)2+102=r2,解得2r=101.故门的宽度(两扇门的和)AB为101寸.故选:B.7.假定鸟卵孵化后,雏鸟为雌与雄的概率相同.如果三枚卵全部成功孵化,则三只雏鸟中恰有两只雌鸟的概率是()A.B.C.D.【分析】画树状图得出所有等可能的情况数,找出恰有两只雌鸟的情况数,即可求出所求的概率.【解答】解:画树状图,如图所示:所有等可能的情况数有8种,其中三只雏鸟中恰有两只雌鸟的情况数有3种,则P=.故选:B.8.如图,扇形OAB中,∠AOB=90°,将扇形OAB绕点B逆时针旋转,得到扇形BDC,若点O刚好落在弧AB上的点D处,则的值为()A.B.C.D.【分析】如图,连OD、AB、BC,延长AD交BC于H点,由旋转的性质可得BD=BO=OD =CD=OA,∠BDC=90°,可证△ABC是等边三角形,由线段垂直平分线的性质可得AH 垂直平分BC,由等腰直角三角形的性质和等边三角形的性质可得AC=2CH,AD=CH ﹣CH,即可求解.【解答】解:如图,连OD、AB、BC,延长AD交BC于H点,∵将扇形OAB绕点B逆时针旋转,得到扇形BDC,若点O刚好落在弧AB上的点D处,∴BD=BO=OD=CD=OA,∠BDC=90°∴∠OBD=60°,即旋转角为60°,∴∠ABC=60°,又可知AB=BC,∴△ABC是等边三角形,∵AB=AC,BD=CD,∴AH垂直平分BC,∴∠CAH=30°,∴AC=2CH,AH=CH,∵BD=CD,∠BDC=90°,DH⊥BC,∴DH=CH,∴AD=CH﹣CH,∴=.故选:A.9.我们可以用折纸的方法求方程x2+x﹣1=0的一个正根.如图,裁一张边长为1的正方形纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置F,因而EF=EB,类似地,在AB上折出点M,使AM=AF,表示方程x2+x﹣1=0的一个正根的线段是()A.线段BM B.线段AM C.线段BE D.线段AE【分析】设AM=AF=x,根据勾股定理即可求出答案.【解答】解:设AM=AF=x,由题意知EF=BE=,在Rt△ABE中,AB2+BE2=AE2,即1+()2=(x+)2,整理得x2+x﹣1=0,即AM为方程x2+x﹣1=0的一个正数根.故选:B.10.如图,直线y=2x与直线x=2相交于点A,将抛物线y=x2沿线段OA从点O运动到点A,使其顶点始终在线段OA上,抛物线与直线x=2相交于点P,则点P移动的路径长为()A.4 B.3 C.2 D.1【分析】根据点M在y=2x上可得相应坐标,即可用顶点式表示出相应的二次函数解析式,求出点P的坐标,利用二次函数的性质解决问题即可.【解答】解:∵设抛物线的顶点M的横坐标为m,且在线段OA上移动,∴y=2m(0≤m≤2).∴当抛物线运动到A点时,顶点M的坐标为(m,2m),∴抛物线函数解析式为y=(x﹣m)2+2m.∴当x=2时,y=(2﹣m)2+2m=m2﹣2m+4(0≤m≤2),∴点P的坐标是(2,m2﹣2m+4).∵对于二次函数y′=m2﹣2m+4=(m﹣1)2+3当0≤m≤2时,∴m=1时,y′有最小值3,当m=0或2时,y′的值为4,∴点P移动的路径长为2×(4﹣3)=2,故选:C.二.填空题(共6小题)11.已知3是一元二次方程x2+m=0的一个根,则该方程的另一个根是﹣3 .【分析】根据方程的解求出m的值,再利用直接开平方法解方程可得答案.【解答】解:将x=3代入方程,得:9+m=0,则m=﹣9,∴方程为x2﹣9=0,解得x=±3,∴方程的另一个根为﹣3,故答案为:﹣3.12.在平面直角坐标系xOy中,点(3,﹣4)关于原点对称的点的坐标为(﹣3,4).【分析】根据关于原点对称的点,横坐标与纵坐标都互为相反数解答.【解答】解:点(3,﹣4)关于原点对称的点的坐标是(﹣3,4).故答案为:(﹣3,4).13.一个口袋中有6个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,…,不断重复上述过程.小明共摸了100次,其中60次摸到白球.根据上述数据,小明可估计口袋中的白球大约有9 个.【分析】设口袋中有x个白球,根据利用频率估计概率得到估计摸到白球的概率为=,然后根据概率公式得到=,再解方程即可.【解答】解:设口袋中有x个白球,因为摸了100次,其中60次摸到白球,则估计摸到白球的概率为=,所以=,解得x=9,即可估计口袋中的白球大约有9个.故答案为9.14.要为一幅矩形照片配一个镜框,如图,要求镜框的四条边宽度都相等,且镜框所占面积是照片本身面积的四分之一,已知照片的长为21cm,宽为10cm,求镜框的宽度.设镜框的宽度为xcm,依题意列方程,化成一般式为8x2+124x﹣105=0 .【分析】设镜框的宽度为xcm,根据镜框所占面积是照片本身面积的四分之一,即可得出关于x的一元二次方程,此题得解.【解答】解:设镜框的宽度为xcm,依题意,得:21×10=4[(21+2x)(10+2x)﹣21×10],整理,得:8x2+124x﹣105=0.故答案为:8x2+124x﹣105=0.15.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加(4﹣4)m.【分析】根据已知建立平面直角坐标系,进而求出二次函数解析式,再通过把y=﹣2代入抛物线解析式得出水面宽度,即可得出答案.【解答】解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,抛物线以y轴为对称轴,且经过A,B两点,OA=OB=AB=2米,抛物线顶点C坐标为(0,2),通过以上条件可设顶点式y=ax2+2,其中a可通过将A点坐标(﹣2,0)代入抛物线解析式可得出:a=﹣0.5,所以抛物线解析式为y=﹣0.5x2+2,当水面下降2米,通过抛物线在图上的观察可转化为:当y=﹣2时,对应的抛物线上两点之间的距离,也就是直线y=﹣2与抛物线相交的两点之间的距离,可以通过把y=﹣2代入抛物线解析式得出:﹣2=﹣0.5x2+2,解得:x=±2,所以水面宽度增加到4米,比原先的宽度当然是增加了(4﹣4)米,故答案为:4﹣4.16.如图,正方形ABCD中,AB=4,E,F分别是边AB,AD上的动点,AE=DF,连接DE,CF交于点P,过点P作PK∥BC,且PK=2,若∠CBK的度数最大时,则BK长为 6 .【分析】根据全等三角形的性质得到∠ADE=∠DCF,求得∠CPD=90°,得到点P在以CD为直径的半圆上运动,取CD的中点O,过O作OM⊥CD,且点M在CD的右侧,MO=2,连接OP,KM,推出四边形POMK是菱形,于是得到点K在以M为圆心,半径=2的半圆上运动,当BK与⊙M相切时,∠CBK最大,根据勾股定理即可得到结论.【解答】解:∵正方形ABCD中,AD=CD,∠A=∠CDA=90°,∵AE=DF,∴△ADE≌△DCF(SAS),∴∠ADE=∠DCF,∵∠ADE+∠CDE=90°,∴∠DCF+∠CDE=90°,∴∠CPD=90°,∴点P在以CD为直径的半圆上运动,取CD的中点O,过O作OM⊥CD,且点M在CD的右侧,MO=2,连接OP,KM,∵PK∥BC,BC⊥CD,∴PK⊥CD,∴PK∥OM,PK=OM=2,∴四边形POMK是平行四边形,∵CD=AB=4,∴OP=CD=2,∴OP=OM,∴四边形POMK是菱形,∴点K在以M为圆心,半径=2的半圆上运动,当BK与⊙M相切时,∠CBK最大,∴∠BKM=90°,∵BM==2,∴BK==6,故答案为:6.三.解答题(共8小题)17.解方程:x2﹣4x+1=0.【分析】根据配方法可以解答此方程.【解答】解:x2﹣4x+1=0x2﹣4x+4=3(x﹣2)2=3x﹣2=∴x1=2+,x2=2﹣;18.已知A,B,C,D是⊙O上的四点,延长DC,AB相交于点E,若BC=BE.求证:△ADE是等腰三角形.【分析】根据圆内接四边形的性质得到∠A=∠BCE,根据等腰三角形的判定和性质定理证明.【解答】证明:∵A,B,C,D是⊙O上的四点,∴∠A=∠BCE,∵BC=BE,∴∠E=∠BCE,∴∠A=∠E,∴DA=DE,即△ADE是等腰三角形.19.某学校初中英语口语听力考试即将举行,准备了A、B、C、D四份听力材料,它们的难易程度分别是易、中、难、难;另有a、b是两份口语材料,它们的难易程度分别是易、难.(1)从四份听力材料中,任选一份是难的听力材料的概率是;(2)用树状图形或列表法,求出听力、口语两份材料都是难的一套模拟试卷的概率.【分析】(1)直接根据概率公式求解即可;(2)根据题意列出图表得出所有等可能的结果数和听力、口语两份材料都是难的一套模拟试卷的情况数,然后根据概率公式即可得出答案.【解答】解:(1)∵A、B、C、D四份听力材料的难易程度分别是易、中、难、难,∴从四份听力材料中,任选一份是难的听力材料的概率是;故答案为:;(2)列表如下:A易B中C难D难a易易,易中,易难,易难,易b难易,难中,难难,难难,难由列表可知:共有8种可能出现的结果,且每种结果出现的可能性相等,其中听力、口语均为难的结果有2种,所以P(两份材料都难)==.20.如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(0,1),B(1,3),C(4,3).(1)将△ABC平移得到△A1B1C1,且C1的坐标是(0,﹣1),画出△A1B1C1;(2)将△ABC绕点A逆时针旋转90°得到△A2B2C2,画出△A2B2C2;(3)小娟发现△A1B1C1绕点P旋转也可以得到△A2B2C2,请直接写出点P的坐标.【分析】(1)根据C1的坐标是(0,﹣1),即可画出△A1B1C1;(2)根据△ABC绕点A逆时针旋转90°得到△A2B2C2,即可画出△A2B2C2;(3)连接两对对应点,分别作两条连线的垂直平分线,其交点P即为所求,进而得出坐标.【解答】解:(1)如图所示,△A1B1C1即为所求;(2)如图所示,△A2B2C2即为所求;(3)如图所示,点P即为所求,点P的坐标为(﹣4,1).21.在⊙O中,直径AB⊥弦CD于点F,点E是弧AD上一点,连BE交CD于点N,点P在CD 的延长线上,PN=PE.(1)求证:PE是⊙O的切线;(2)连接DE,若DE∥AB,OF=3,BF=2,求PN的长.【分析】(1)连接OE,由等腰三角形的性质得出∠PEN=∠PNE=∠BNF,∠OEB=∠OBE.证出∠OEB+∠PEN=90°,即PE⊥OE,即可得出结论;(2)连接CE,证出CE为⊙O的直径.由垂径定理得出CF=DF,得出DE=2OF=6.求出OC=OB=5,CE=10,由勾股定理得出CD=8.设PD=x,则PC=x+8.在Rt△PDE和Rt △PCE中,由勾股定理得出方程,解方程求出PD=,由勾股定理即可得出答案.【解答】(1)证明:连接OE,如图1所示:∵PN=PE,∴∠PEN=∠PNE=∠BNF,∵OE=OB,∴∠OEB=∠OBE.∵AB⊥CD,∴∠OBE+∠BNF=90°,∴∠OEB+∠PEN=90°,即∠OEP=90°,∴PE⊥OE,∴PE是⊙O的切线.(2)解:连接CE,如图2所示:∵DE∥AB,AB⊥CD,∴∠EDC=90°∴CE为⊙O的直径.∵AB⊥CD,∴CF=DF,∴DE=2OF=6.∵OF=3,BF=2,∴OC=OB=5,CE=10,∴CD===8,由(1)知PE⊥CE.设PD=x,则PC=x+8.在Rt△PDE和Rt△PCE中,由勾股定理,得:PD2+DE2=PE2=PC2﹣CE2,即x2+62=(x+8)2﹣102,解得:x=,∴PD=.∴PE===,∴PN=PE=.22.某商场销售一种成本为每件30元的商品,销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=﹣10x+600,商场销售该商品每月获得利润为w(元).(1)求w与x之间的函数关系式;(2)如果商场销售该商品每月想要获得2000元的利润,那么每月成本至少多少元?(3)若销售价不低于40元且不高于55元,请直接写出每月销售新产品的利润w的取值范围.【分析】(1)根据月利润=(销售单价﹣成本价)×销售量,从而列出关系式;(2)令w=2000,然后解一元二次方程,从而求出销售单价,再根据:月成本=成本价×销售量可得答案;(3)将(2)中w的解析式配方,根据二次函数的性质及售价的范围,可得答案.【解答】解:(1)w=(x﹣30)(﹣10x+600)=﹣10x2+900x﹣18000.(2)由题意得,﹣10x2+900x﹣18000=2000,解得:x1=40,x2=50,当x=40时,成本为30×(﹣10×40+600)=6000(元),当x=50时,成本为30×(﹣10×50+600)=3000(元),∴每月想要获得2000元的利润,每月成本至少3000元;(3)∵w=(x﹣30)(﹣10x+600)=﹣10x2+900x﹣18000=﹣10(x﹣45)2+2250∴当x=45时,w取得最大值2250∵销售价不低于40元且不高于55元,55离对称轴x=45远,∴当x=55时,w取得最小值,最小值为1250∴销售价不低于40元且不高于55元时,每月销售新产品的利润w的取值范围为:1250≤w≤2250.23.在△ABC中,∠ABC=120°,线段AC绕点C顺时针旋转60°得到线段CD,连接BD.(1)如图1,若AB=BC,求证:BD平分∠ABC;(2)如图2,若AB=2BC,①求的值;②连接AD,当S△ABC=时,直接写出四边形ABCD的面积为.【分析】(1)连接AD,证△ACD是等边三角形,再证△ABD≌△CBD,推出∠CBD=∠ABD,即得出结论;(2)①连接AD,作等边三角形ACD的外接圆⊙O,证点B在⊙O上,在BD上截取BM,使BM=BC,证△CBA≌△CMD,设BC=BM=1,则AB=MD=2,BD=3,过点C作CN⊥BD 于N,可求出BN=BC=,CN=BC=,ND=BD﹣BN=,CD=,即可求出==;②分别过点B,D作AC的垂线,垂足分别为H,Q,设CB=1,AB=2,CH=x,则由①知,AC=,AH=﹣x,在Rt△BCH与Rt△BAH中利用勾股定理求出BH的值,再求出DQ 的值,求出=,因为AC为△ABC与△ACD的公共底,所以=,可求出△ACD的面积,进一步求出四边形ABCD的面积.【解答】(1)证明:连接AD,由题意知,∠ACD=60°,CA=CD,∴△ACD是等边三角形,∴CD=AD,又∵AB=CB,BD=BD,∴△ABD≌△CBD(SSS),∴∠CBD=∠ABD,∴BD平分∠ABC;(2)解:①连接AD,作等边三角形ACD的外接圆⊙O,∵∠ADC=60°,∠ABC=120°,∴∠ADC+∠ABC=180°,∴点B在⊙O上,∵AD=CD,∴,∴∠CBD=∠CAD=60°,在BD上截取BM,使BM=BC,则△BCM为等边三角形,∴∠CMB=60°,∴∠CMD=120°=∠CBA,又∵CB=CM,∠BAC=∠BDC,∴△CBA≌△CMD(AAS),∴MD=AB,设BC=BM=1,则AB=MD=2,∴BD=3,过点C作CN⊥BD于N,在Rt△BCN中,∠CBN=60°,∴∠BCN=30°,∴BN=BC=,CN=BC=,∴ND=BD﹣BN=,在Rt△CND中,CD===,∴AC=,∴==;②如图3,分别过点B,D作AC的垂线,垂足分别为H,Q,设CB=1,AB=2,CH=x,则由①知,AC=,AH=﹣x,在Rt△BCH与Rt△BAH中,BC2﹣CH2=AB2﹣AH2,即1﹣x2=22﹣(﹣x)2,解得,x=,∴BH==,在Rt△ADQ中,DQ=AD=×=,∴==,∵AC为△ABC与△ACD的公共底,∴==,∵S△ABC=,∴S△ACD=,∴S四边形ABCD=+=,故答案为:.24.已知抛物线y=ax2﹣2ax+3与x轴交于点A、B(A左B右),且AB=4,与y轴交于C 点.(1)求抛物线的解析式;(2)如图,证明:对于任意给定的一点P(0,b)(b>3),存在过点P的一条直线交抛物线于M、N两点,使得PM=MN成立;(3)将该抛物线在0≤x≤4间的部分记为图象G,将图象G在直线y=t上方的部分沿y =t翻折,其余部分保持不变,得到一个新的函数的图象,记这个函数的最大值为m,最小值为n,若m﹣n≤6,求t的取值范围.【分析】(1)抛物线y=ax2﹣2ax+3的对称轴为x=1,又AB=4,由对称性得A(﹣1,0)、B(3,0),即可求解;(2)证明△PMG≌△NMH(AAS),y G+y H=2y M,即可求解;(3)分当D′在点H(4,﹣5)上方、点D′在点H(4,﹣5)下方两种情况,分别求解即可.【解答】解:(1)抛物线y=ax2﹣2ax+3的对称轴为x=1,又AB=4,由对称性得A(﹣1,0)、B(3,0).把A(﹣1,0)代入y=ax2﹣2ax+3,得a+2a+3=0,∴a=﹣1.∴抛物线的解析式为y=﹣x2+2x+3.(2)如图,过M作GH⊥x轴,PG∥x轴,NH∥x轴,由PM=MN,则△PMG≌△NMH(AAS),∴PG=NH,MG=MH.设M(m,﹣m2+2m+3),则N(2m,﹣4m2+4m+3),∵P(0,b),GM=MH,∴y G+y H=2y M,即b+(﹣4m2+4m+3)=2(﹣m2+2m+3),∴2m2=b﹣3,∵b>3,∴关于m的方程总有两个不相等的实数根,此即说明了点M、N存在,并使得PM=MN.证毕;(3)图象翻折前后如右图所示,其顶点分别为D(1,4)、D′(1,2t﹣4).①当D′在点H(4,﹣5)上方时,2t﹣4≥﹣5,∴t≥﹣,此时,m=t,n=﹣5,∵m﹣n≤6,∴t+5≤6,∴t≤1,∴﹣≤t≤1;②当点D′在点H(4,﹣5)下方时,同理可得:t<﹣,m=t,n=2t﹣4,由m﹣n≤6,得t﹣(2t﹣4)≤6,∴t≥﹣2,∴﹣2≤t<﹣.综上所述,t的取值范围为:﹣2≤t≤1.。
