回归方程求法Microsoft Word 文档
回归直线方程计算
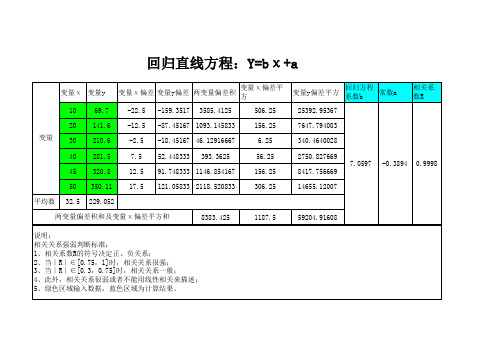
两变量偏差积和及变量χ偏差平方和
说明: 相关关系强弱判断标准: 1、相关系数R的符号决定正、负关系; 2、当∣R∣∈[0.75,1]时,相关关系很强; 3、当∣R∣∈[0.3,0.75]时,相关关系一般; 4、此外,相关关系很弱或者不能用线性相关来描述; 5、绿色区域输入数据,蓝色区域为计算结果。
yba变量变量y变量偏差变量y偏差变量偏差平方变量y偏差平方回归方程系常数a相关系数r两变量偏差积和及变量偏差平方和说明
回归直线方程: 回归直线方程:Y=bχ+a
变量χ 变量y 10 20 变量 30 40 45 50 平均数 32.5 210.6 281.5 320.8 350.11 229.052 8383.425 1187.5 59204.91608 -2.5 7.5 12.5 17.5 -18.45167 46.12916667 52.448333 393.3625 6.25 56.25 156.25 306.25 340.4640028 2750.827669 7.0597 91.748333 1146.854167 121.05833 2118.520833 8417.756669 14655.12007 -0.3894 0.9998 69.7 141.6 变量χ偏差 变量y偏差 两变量偏差积 -22.5 -12.5 -159.3517 3585.4125 变量χ偏差平 方 506.25 156.25 变量y偏差平方 25392.95367 7647.794003 回归方程 常数a 系数b 相关系 数R
实验(二)多变量线性回归模型Microsoft Word 文档

实验(二)多变量回归模型及面板数据初步处理【实验目的】掌握多变量线性回归模型的参数估计及相关内容【实验内容】建立多变量线性回归模型,回归参数估计,散点图,残差图等。
建立面板数据库并处理数据。
【实验步骤】实验步骤一:如何在数据表删除某一列数据,或在两列数据中插入一列数据,在数据表删除某一列数据的操作:双击数据组标示→打开数据组表→编辑一组数据→点击鼠标右键→拉出一菜单→点击Remove Series。
在两列数据中插入一列数据:双击数据组标示→打开数据组表→编辑一组数据→点击鼠标右键→拉出一菜单→点击Insert Series。
实验步骤二:建立面板数据库并处理数据。
向EViews6.0中输入截面数据名称的时候,应先建立一个合并数据(Pool)对象。
★选择EViews6.0主菜单Object→New Object→Pool★在Pool中输入_BJ_TJ_HB_LN_SHH_JS_ZHJ_FJ_SHD_GD_HN★在Pool窗口点击name,保存。
★在Pool窗口点击sheet,打开一个窗口,输入GDP?,RENKOU?,GSH?,GZH?。
就得到一个东部地区GDP,RENKOU,GSH,GZH的Poolsheet(面板数据表)。
★在Pool窗口点击define,回到Pool的标示窗口;点击Pool的标示窗口sheet,打开一个窗口,输入GDP?,RENKOU?,GSH?,GZH?。
得到GDP,RENKOU,GSH,GZH的Poolsheet (面板数据表)。
★Pool序列的序列名使用的是基本名和“?”占位符。
例如,GDP?代表:GDP_BJ——北京GDPGDP_TJ——天津GDPGDP_HB——河北GDPGDP_LN——辽宁GDPGDP_SHH——上海GDPGDP_JS——江苏GDPGDP_ZHJ——浙江GDPGDP_FJ——福建GDPGDP_SHD——山东GDPGDP_GD——广东GDPGDP_HN——海南GDP★还可以通过Pool窗口中的PoolGenerate,通过公式可以生成以面板数据为基础的新数据。
线性回归方程公式_数学公式

线性回归方程公式_数学公式线性回归方程公式线性回归方程公式:b=(x1y1+x2y2+...xnyn-nXY)/(x1+x2+...xn-nX)。
线性回归方程公式求法:第一:用所给样本求出两个相关变量的(算术)平均值:x_=(x1+x2+x3+...+xn)/ny_=(y1+y2+y3+...+yn)/n第二:分别计算分子和分母:(两个公式任选其一)分子=(x1y1+x2y2+x3y3+...+xnyn)-nx_Y_分母=(x1^2+x2^2+x3^2+...+xn^2)-n__x_^2第三:计算b:b=分子/分母用最小二乘法估计参数b,设服从正态分布,分别求对a、b的偏导数并令它们等于零。
其中,且为观测值的样本方差.线性方程称为关于的线性回归方程,称为回归系数,对应的直线称为回归直线.顺便指出,将来还需用到,其中为观测值的样本方差。
先求x,y的平均值X,Y再用公式代入求解:b=(x1y1+x2y2+...xnyn-nXY)/(x1+x2+...xn-nX)后把x,y的平均数X,Y代入a=Y-bX求出a并代入总的公式y=bx+a得到线性回归方程(X为xi的平均数,Y为yi的平均数)线性回归方程的应用线性回归方程是回归分析中第一种经过严格研究并在实际应用中广泛使用的类型。
这是因为线性依赖于其未知参数的模型比非线性依赖于其位置参数的模型更容易拟合,而且产生的估计的统计特性也更容易确定。
线性回归有很多实际用途。
分为以下两大类:如果目标是预测或者映射,线性回归可以用来对观测数据集的和X的值拟合出一个预测模型。
当完成这样一个模型以后,对于一个新增的X值,在没有给定与它相配对的y的情况下,可以用这个拟合过的模型预测出一个y值。
给定一个变量y和一些变量X1,...,Xp,这些变量有可能与y相关,线性回归分析可以用来量化y与Xj之间相关性的强度,评估出与y不相关的Xj,并识别出哪些Xj的子集包含了关于y的冗余信息。
求回归方程公式

求回归方程公式
回归方程公式为:
y = β0 + β1*x1 + β2*x2 + … + βn*xn + ε
其中,y表示被解释变量(或因变量),x1、x2、…、xn表示解
释变量(或自变量),β0表示截距,β1、β2、…、βn表示自变量
的系数,ε表示误差项。
回归方程是一个用自变量来预测因变量的方程,它可以用来解释
因变量(y)与自变量(x)之间的关系。
回归方程可以用来进行预测、掌握因变量如何受自变量影响、预测因变量在不同自变量取值下的可
能取值等。
在实际应用中,回归方程可以用来分析各种关系,例如:影响销
售额的各种因素(例如广告费用、产品价格等)、影响学生成绩的各
种因素(例如考试成绩、学习时间、家庭背景等)、影响医疗费用的
各种因素(例如年龄、性别、体重指数等)等等。
除了上述基本回归方程外,还有一些其他类型的回归方程,例如:多元非线性回归方程、广义线性回归方程等,在实际应用中可以根据
具体需求选择合适的回归方程模型。
线性回归方程的求法

高考统计部分的两个重要公式 具体如何应用第一公式:线性回归方程为ˆˆˆybx a =+的求法: (1) 先求变量x 的平均值,即1231()n x x x x x n=+++⋅⋅⋅+ (2) 求变量y 的平均值,即1231()n y y y y y n=+++⋅⋅⋅+ (3) 求变量x 的系数ˆb,有两个方法 法1 121()()ˆ()niii nii x x y y bx x ==--=-∑∑(题目给出不用记忆)[]112222212()()()()...()()()()...()n n n x x y y x x y y x x y y x x x x x x --+--++--=⎡⎤-+-++-⎣⎦(需理解并会代入数据)法2 1221ˆni ii nii x y n x ybxn x==-⋅⋅=-⋅∑∑(题目给出不用记忆)[]1122222212...,...n n n x y x y x y n x y x x x n x++-⋅⋅=⎡⎤+++-⋅⎣⎦(这个公式需要自己记忆,稍微简单些)(4) 求常数ˆa,既ˆˆa y bx =- 最后写出写出回归方程ˆˆˆybx a =+。
可以改写为:ˆˆy bx a =- 例.已知,x y 之间的一组数据:求y 与x 的回归方程:解:(1)先求变量x 的平均值,即(0123) 1.54x =+++= (2)求变量y 的平均值,即1(1357)44y =+++=(3)求变量x 的系数ˆb,有两个方法 []11223344222212342222()()()()()()()()ˆ1()()()()(0 1.5)(14)(1 1.5)(34)(2 1.5)(54)(3 1.5)(74)57(0 1.5)(1 1.5)(2 1.5)(3 1.5)x x y y x x y y x x y y x x y y bx x x x x x x x --+--+--+--=⎡⎤-+-+-+-⎣⎦--+--+--+--==⎡⎤-+-+-+-⎣⎦法法2 ˆb =[][]112222222222212...011325374 1.5457...01234 1.5n n n x y x y x y nx y x x x nx++-⋅⨯+⨯+⨯+⨯-⨯⨯==⎡⎤⎡⎤+++-+++-⨯⎣⎦⎣⎦ (4) 求常数ˆa,既525ˆˆ4 1.577a y bx =-=-⨯= 最后写出写出回归方程525ˆˆˆ77ybx a x =+=+第二公式:独立性检验两个分类变量的独立性检验:注意:数据a 具有两个属性1x ,1y 。
回归方程公式

回归方程公式回归方程是一种特殊的统计关系,它允许你使用数学表达式来预测变量之间的关系。
使用一个或多个自变量(例如年龄,收入,教育,种族等)来预测另一个变量,例如财富或健康状况。
归方程使用变量之间的数据来确定回归系数以及预测结果。
回归方程的公式是什么?回归方程的公式通常形式为:Y=a+bX,其中a是回归系数,b是X变量的系数,X是被预测变量,Y是预测结果。
例如,假设您正在预测财富与年龄之间的关系,则回归方程可能是Y = a + bX,其中Y 表示财富,X表示年龄,a和b表示回归系数。
求解回归方程的方法回归方程的求解分为两个主要步骤。
先,使用X变量的数据集(例如,年龄)拟合一个数学拟合曲线,称为回归曲线。
外,需要使用回归曲线对Y变量(例如,财富)求和平方差,以得出回归系数a和b。
回归曲线可以分为线性回归曲线和非线性回归曲线。
性回归曲线是具有确定性系数的线性关系,它可以明确地预测变量之间的关系。
线性回归曲线是具有不确定性系数的非线性关系,它不能明确地预测变量之间的关系。
为了求解回归方程,需要使用数据拟合技术,例如最小二乘法,线性回归和非线性回归。
小二乘法可以用来拟合线性模型,同时确定模型中每个变量的权重。
性回归可以用来拟合线性模型,而非线性回归可以用来拟合非线性模型。
由于每种拟合技术的方法不同,因此可能需要使用不同的算法来求解每种类型的回归方程。
例如,使用最小二乘法拟合线性回归模型时,可以使用最小二乘法的梯度下降算法来求解回归方程;而使用非线性回归模型时,可以使用多项式回归,神经网络或其他类似的算法来求解该方程。
回归方程的应用回归方程是统计学中常用的工具,它可以用来研究变量之间的关系,特别是当变量之间存在某种可能的统计关系时,回归方程可以帮助我们对变量之间的关系进行更详细的分析。
例如,可以使用回归方程来研究收入与教育程度之间的关系,或研究冠状动脉病变(CVD)和高血压之间的关系等。
此外,回归方程可能还可以用于模拟和预测变量之间的关系,例如通过模拟股票价格的变化,预测经济增长,或者预测政治事件对市场的影响等。
回归直线方程

组数据 x1, y1 , x2, y2 , x3, y3 ,… xn, yn , 所求回
归方程是 yˆ bx a(其中a,b是待定系数).
回归方程 yˆ bx a 的斜率与截距的一般公式:
n
n
xi x yi y xi yi nxy
(3)90-(0.7×100+0.35)=19.65(t) ∴降低了19.65吨.
回归直线方程
【典型例题】
分析:对于两个变量,在确定具有线性相关关系后,可以利
用“最小二乘法”来求回归方程.用“最小二乘法”求回归
直线方程的关键在于正确地利用回归方程中系数公式
n
xi yi n x y
b
i 1 n
xi2
2
nx
,a
y bx,
求出系数 a,b,这样回归方程也就
171.6
i 1
因而所求得回归直线方程为:
∴a y b x 67.01 0.4646 66.8 35.975
当x=78时,yˆ 0.4646 78 35.975 72.2138 所以当父亲的身高为78英寸时,估计儿子的身高约为 72.2138英寸.
回归44842.4
xi2 44794, yi2 44941.93, 代入公式
i 1 10
i 1
b
xi yi nx y
i 1
n
xi2
2
nx
44842.4 10 66.8 67.01 79.72
44974 10 66.82
0.4646
知识点——
回归直线方程
回归直线方程
回归方程 Microsoft Word 文档1
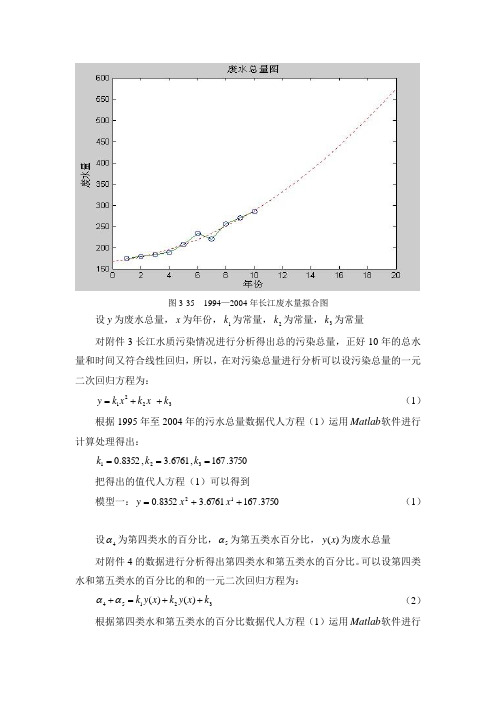
图3-35 1994—2004年长江废水量拟合图设y 为废水总量,x 为年份,1k 为常量,2k 为常量,3k 为常量对附件3长江水质污染情况进行分析得出总的污染总量,正好10年的总水量和时间又符合线性回归,所以,在对污染总量进行分析可以设污染总量的一元二次回归方程为:3221k x k x k y ++= (1)根据1995年至2004年的污水总量数据代人方程(1)运用Matlab 软件进行计算处理得出:3750.167,6761.3,8352.0321===k k k把得出的值代人方程(1)可以得到模型一:3750.1676761.38352.012++=x x y(1)设4α为第四类水的百分比,5α为第五类水百分比,)(x y 为废水总量对附件4的数据进行分析得出第四类水和第五类水的百分比。
可以设第四类水和第五类水的百分比的和的一元二次回归方程为:32154)()(k x y k x y k ++=+αα (2)根据第四类水和第五类水的百分比数据代人方程(1)运用Matlab 软件进行计算处理得出:6459.181,64489.1,0033.0321-==-=k k k把得出的值代人方程(1)可以得出:模型一:()()6459.18164489.10033.0254-+-=+x y x y αα (2)则根据曲线拟合我们可到废水排放总量图3-36长江未来10年废水排放总量示意图设6α为第六类水的百分比,)(x y 为废水总量对附件4的数据进行分析得出第六类水的百分比,可以设第六类水与废水总量关系的一元一次回归方程为:216)(k x y k +=α (3)根据第六类水百分比值的数据代人方程(1)可以得出:3838.11,0625.021-==k k把1k 和2k 的值代人方程(1)可以得出:模型一:3838.11)(0625.06-=x y α (3)。
回归经验方程公式

回归经验方程公式
回归经验方程公式是一种用来建模和预测现象或事件的数学表达式。
它基于经验数据和统计方法,通过拟合数据点到一个数学函数或曲线上,以确定变量之间的关系。
回归经验方程公式的一般形式可以表示为:
Y = β0 + β1X1 + β2X2 + ... + βnXn + ε
其中,Y表示因变量(要预测的变量),X1、X2、...、Xn表示自变量(用来预测的变量),β0、β1、β2、...、βn表示回归系数,ε表示误差项。
回归经验方程公式的建立过程通常分为以下几个步骤:
1. 数据收集:收集与研究对象相关的数据,包括因变量和自变量的观测值。
2. 数据预处理:对数据进行清洗、缺失值处理、异常值处理等。
3. 模型选择:根据研究问题和数据特点选择适当的回归模型,如线性回归、多项式回归、逻辑回归等。
4. 模型拟合:利用统计方法,对选定的回归模型进行参数估计和模型拟合,即确定回归系数。
5. 模型评估:通过检验回归模型的合理性和拟合效果,评估模型的准确性和可靠性。
6. 预测和应用:利用建立的回归经验方程公式,对未知自变量的值进行预测,以便进行决策和应用。
回归经验方程公式在许多领域都有广泛的应用,包括经济学、金融学、市场营销、医学、工程等。
它可以帮助我们了解变量之间的关系,预测未来的趋势和结果,为决策提供科学依据。
同时,回归经验方程公式也有其局限性,如对数据的依赖性较强、模型假设的前提条件等,需要在实际应用中慎重考虑和验证。
求回归直线方程

求回归直线方程在统计学中,回归分析是指通过建立一个数学模型来分析与预测自变量和因变量的关系。
回归分析是一种多元统计方法,可用于描述一组数据之间的关系以及预测未来数据的趋势。
在回归分析中,回归直线是非常重要的,它是通过拟合数据点确定的一条直线,用于描述自变量和因变量之间的关系。
回归直线方程的基本形式为:y = mx + b其中,y是因变量,x是自变量,m是斜率,b是截距。
斜率表示因变量y随着自变量x的变化而变化的比率,截距表示当自变量为0时,因变量的值。
回归直线方程的求解可以通过最小二乘法进行,最小二乘法是一种通过求解平方误差最小化模型的方法。
计算平方误差的公式可以表示为:SS = Σ(y - ŷ)²其中,SS是平方误差,y是实际的因变量值,ŷ是回归预测的因变量值。
通过最小化平方误差,可以得到最优的回归直线。
求解回归直线方程的步骤如下:1. 收集数据:首先需要收集自变量和因变量的一组数据,这些数据需要符合要求,如数据需要是连续的、随机分布的等。
2. 确定自变量和因变量:确定自变量和因变量的关系,例如,自变量为气温,因变量为销售量。
3. 绘制散点图:利用收集到的数据,绘制出自变量与因变量的散点图,从而观察出它们之间的数量关系。
4. 确定回归方程类型:根据数据的关系,确定回归方程类型,如线性回归、非线性回归等。
5. 拟合回归直线:根据最小二乘法,对散点图进行回归分析,得到回归直线的方程,从而通过方程进行预测和分析。
6. 检验拟合优度:通过拟合优度检验方法,检验回归模型的效应,以确定该模型是否适用于实际场景。
总之,在求回归直线方程的过程中,需要收集数据、确定自变量和因变量、绘制散点图、拟合回归直线和检验拟合优度等步骤。
通过这些步骤,可以得到回归直线方程,从而预测和分析自变量和因变量之间的关系,这对于许多应用领域都是非常有用的。
求回归直线方程的步骤

求回归直线方程的步骤
嘿,咱今儿就来唠唠求回归直线方程的那些事儿!你说这求回归直线方程啊,就像是搭积木,一块一块得放对地方才行呢!
先得收集一堆数据,就好像是准备一堆各种各样的积木块儿。
这些数据可重要啦,它们就像是搭积木的基础材料呢!然后呢,得计算平均数啥的,这就好比是给这些积木块找个中心位置,让它们能围绕着这个中心来搭建。
接下来就是关键的一步啦,要找到那个最合适的斜率!你想想,这斜率就像是积木塔的倾斜度,要是找不对,那整个塔可就歪啦!这可得仔细着点儿,一点点地算,一点点地琢磨。
再然后呢,根据找到的斜率和平均数这些,就能求出截距啦!这截距呀,就像是给积木塔找个稳稳的落脚点,让它能立得住。
哎呀,你说这求回归直线方程不就跟搭个漂亮的积木塔一样嘛!得精心挑选材料,找好角度,放对位置。
要是哪一步马虎了,那可就全乱套咯!
你看啊,要是数据收集得不对,那不就跟拿了些奇奇怪怪的积木块一样,怎么可能搭出好看的塔呢!要是计算平均数的时候出了错,那塔的中心位置就歪了呀,还怎么立得稳呢!还有那斜率和截距,一个不对,整个塔要么歪歪扭扭,要么直接就倒啦!
所以啊,求回归直线方程可不能小瞧了它,每一步都得认真对待,就跟对待宝贝似的。
咱得有耐心,有细心,才能求出那准确又好用的回归直线方程呀!
你说是不是这个理儿?咱可别嫌麻烦,别嫌累,好好地把这每一步都走踏实了。
等求出了准确的回归直线方程,那感觉,就像是自己搭出了一个超级棒的积木塔一样,心里可得意啦!
这就是求回归直线方程的步骤啦,虽然听起来好像有点复杂,但只要咱一步一步来,肯定能搞得定!加油吧,朋友们!让我们一起把这回归直线方程求个明明白白!。
线性回归方程求法

实际
样本
抽样
y = f(x)
分析
y = f(x)
模拟
y = f(x)
线性回归方程求法
现实生活中两个变量间的关系有哪些呢? 不相关
两个变量的关系
函数关系
相关 关系
线性相关 非线性相关
线性回归方程求法
思考:相关关系与函数关系有怎样的不同?
函数关系中的两个变量间是一种确定性关系 相关关系是一种非确定性关系 函数关系是一种理想的关系模型 相关关系在现实生活中大量存在,是更一 般的情况
一般而言,父辈身高者,其子辈身高也高,依此推论,祖祖辈辈遗传下来,身 高必然向两极分化,而事实上并非如此,显然有一种力量将身高拉向中心,即子辈 的身高有向中心回归的特点。“回归”一词即源于此。
虽然这种向中心回归的现象只是特定领域里的结论,并不具有普遍性,但从它 所描述的关于X为自变量,Y为不确定的因变量这种变量间的关系看,和我们现在的 回归含义是相同的。
(2)请根据上表提供的数据,用最小二乘法求出y关于x的
性回归方程 y bˆx aˆ
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准 煤,试根据(2)求出的线性回归方程,预测生产100 吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3 2 . 5 4 3 5 4 6 4 . 5 6 6 . 5 )
9. 利用线性回归模型解决一类 非线性回归问题
10. 正确理解分析方法与结果
线性回归方程求法
什么是回归分析:
“回归”一词是由英国生物学家F.Galton在研究人体身高的遗传问题时首先提出的。
根据遗传学的观点,子辈的身高受父辈影响,以X记父辈身高,Y记子辈身高。 虽然子辈身高一般受父辈影响,但同样身高的父亲,其子身高并不一致,因此, X和Y之间存在一种相关关系。
(完整word版)线性回归方程的求法(需要给每个人发)

耿老师总结的高考统计部分的两个重要公式的具体如何应用ˆ+a ˆ=bx ˆ的求法:第一公式:线性回归方程为y(1)先求变量x 的平均值,既x =(2)求变量y 的平均值,既y =1(x 1+x 2+x 3+⋅⋅⋅+x n )n 1(y 1+y 2+y 3+⋅⋅⋅+y n )n ˆ,有两个方法(3)求变量x 的系数bˆ=法1b∑(x -x )(y -y )iii =1n∑(x -x )ii =1n(题目给出不用记忆)2(x1-x )(y 1-y )+(x 2-x )(y 2-y )+...+(x n-x )(y n-y )][(需理解并会代入数据)=222⎡⎤(x -x )+(x -x )+...+(x -x )2n ⎣1⎦nˆ=法2b∑(x -x )(y -y )iii =1∑(x -x )ii =1n(题目给出不用记忆)2=[x 1y1+x 2y 2+...x ny n]-nx ⋅y,(这个公式需要自己记忆,稍微简单些)2222⎡⎣x 1+x 2+...+x n ⎤⎦-nx ˆˆ=y -bx ˆ,既a (4)求常数aˆ+a ˆ-a ˆ=bx ˆ。
可以改写为:y =bx ˆ(y ˆ与y 不做区分)最后写出写出回归方程y例.已知x ,y 之间的一组数据:x0123y1357求y 与x 的回归方程:解:(1)先求变量x 的平均值,既x =(2)求变量y 的平均值,既y =1(0+1+2+3)=1.541(1+3+5+7)=44ˆ,有两个方法(3)求变量x 的系数b2222⎡⎤(x -x )+(x -x )+(x -x )+(x -x )1234⎣⎦ˆ法1b=(0-1.5)(1-4)+(1-1.5)(3-4)+(2-1.5)(5-4)+(3-1.5)(7-4)5==22227⎡⎣(0-1.5)+(1-1.5)+(2-1.5)+(3-1.5)⎤⎦(x1-x )(y 1-y )+(x 2-x )(y 2-y )+(x 3-x )(y 3-y )+(x 4-x )(y 4-y )][=ˆ=法2b[x 1y1+x 2y 2+...x ny n]-nx ⋅y=[0⨯1+1⨯3+2⨯5+3⨯7]-4⨯1.5⨯4=52222⎡⎤x +x +...+x -nx 12n ⎣⎦2222⎡⎤0+1+2+3⎣⎦7ˆ=4-ˆ=y -bx ˆ,既a (4)求常数aˆ+a ˆ=bx ˆ=最后写出写出回归方程y第二公式:独立性检验两个分类变量的独立性检验:525⨯1.5=77525x +77y1a ca +cy2b d总计x 1a +b c +d a +b +c +d注意:数据a 具有两个属性x 1,y 1。
wps最小二乘法求回归方程

wps最小二乘法求回归方程使用WPS最小二乘法求回归方程回归分析是统计学中一种常用的分析方法,用于研究变量之间的关系。
最小二乘法是回归分析中常用的一种方法,用于求解回归方程。
WPS作为一款功能强大的办公软件,提供了最小二乘法的求解功能,在进行回归分析时可以便捷地使用该方法求解回归方程。
最小二乘法是一种通过最小化误差平方和来拟合数据的方法。
在回归分析中,我们希望找到一个函数,使得该函数与实际观测到的数据之间的误差最小。
最小二乘法通过调整函数的参数,使得误差平方和最小化。
具体而言,对于一个简单线性回归模型,假设我们有n组数据,其中自变量为x,因变量为y,回归方程可以表示为y = β0 + β1x,其中β0和β1是回归系数。
使用WPS进行最小二乘法求解回归方程的步骤如下:1. 打开WPS软件,选择“数据分析”功能。
在数据分析功能中,可以找到“回归”选项。
2. 在回归选项中,选择“最小二乘法”求解方法。
在输入数据的区域,填入自变量x和因变量y的数据。
3. 确定回归方程的形式。
在最小二乘法中,可以选择线性回归、多项式回归等不同形式的回归方程。
根据实际情况选择合适的回归方程形式。
4. 点击“确定”按钮,WPS会自动计算出回归方程的系数。
根据计算结果,可以得到回归方程的具体形式。
最小二乘法求解回归方程的优点在于可以通过最小化误差平方和来拟合数据,得到较为准确的回归方程。
通过回归方程,我们可以对未知的自变量对应的因变量进行预测。
这在实际应用中具有重要的意义,可以帮助我们理解变量之间的关系,进行预测和决策。
需要注意的是,最小二乘法的应用需要满足一些前提条件。
首先,自变量与因变量之间应该存在一定的线性关系。
其次,误差项应该满足独立同分布的假设,即误差项之间应该没有相关性。
最后,误差项应该满足正态分布的假设,即误差项的分布应该服从正态分布。
总结起来,使用WPS最小二乘法求解回归方程是一种便捷而准确的方法。
通过回归分析,我们可以找到变量之间的关系,进行预测和决策。
回归方程公式

回归方程公式
回归方程是统计学中常用的一种数学方程,它用于研究两个变量之间的关系,对于了解一个变量如何受另一个变量的影响,回归方程是一种有效的方法。
回归方程可以简单地用一个数学公式来代表变量之间的关系,因此它可以帮助我们更好地理解变量之间的关系。
回归方程可以表示为一个标准的一元线性方程,其公式如下:
tY = bX+a
其中,Y代表被研究变量,X代表研究变量,a代表Y中在X为0时的偏移量,b代表X和Y的系数,也称为斜率。
使用回归方程,我们可以用X来预测Y的值,具体的计算方法是:首先,根据X的值,计算出Y的偏移,然后用Y的偏移加上X的系数,即可得到方程的解。
使用回归方程,我们还可以检验两个变量之间的关系是线性的,也就是说,Y的值的变化程度与X的值是成正比的。
如果拟合的线性关系满足一定的统计要求,我们可以根据给定的X来预测Y的值,从而得出结论,即不同X对应不同Y之间存在着一定的联系。
当我们使用回归方程来研究变量之间的关系时,我们需要对数据进行解释。
这种解释可以使用一个概念叫做“R方”来反映。
R方指数可以反映拟合度,即X和Y变量之间的拟合程度,R方指数是0到1之间的数字,越接近1,表明X和Y之间的关系越接近线性,反之,如果R方指数接近0,则表明X和Y之间的关系不太线性。
回归方程可以帮助我们更好地了解变量之间的关系,从而更加有
效地进行研究。
它可以用来预测Y的值,以及检验X和Y之间是否存在线性关系。
总的来说,回归方程具有很多使用价值,是研究变量之间关系的重要工具。
回归方程的公式

回归方程的公式回归方程是数理统计学中的一种重要方法,用于建立自变量与因变量之间的关系模型。
其公式为:Y = β0 + β1X1 + β2X2 + … + βkXk + ε,其中Y是因变量,X1、X2、…、Xk是自变量,β0、β1、β2、…、βk是回归系数,ε是误差项。
在回归方程中,回归系数β用于衡量自变量对因变量的影响程度。
其中,β0是截距项,表示当自变量都取0时,因变量的值。
而β1、β2、…、βk则分别表示当对应的自变量增加1单位时,因变量增加的值。
这些系数可以通过最小二乘法来估计。
回归方程可以建立线性和非线性关系模型。
线性回归方程是指因变量和自变量之间呈现线性关系的模型,其回归方程为Y = β0 + β1X1 + ε。
非线性回归方程则是指因变量和自变量之间呈现非线性关系的模型,其回归方程为Y = β0 + β1f(X1) + ε,其中f(X1)是非线性的函数。
回归方程的建立需要满足一些假设条件。
首先,因变量和自变量之间要呈现一定的相关性。
其次,误差项必须满足独立同分布的假设条件。
最后,自变量之间不能存在多重共线性,即自变量之间不能存在高度的相关性。
在实际应用中,回归方程可以用于预测和控制因变量的值。
例如,在销售预测中,可以根据历史数据建立回归方程,预测未来的销售量。
在生产控制中,可以根据回归方程,调整生产计划,以达到最优的生产效益。
然而,回归方程也存在一些局限性。
首先,回归方程只能建立自变量和因变量之间的关系模型,而不能确定因果关系。
其次,回归方程只能建立线性或非线性关系模型,而不能建立其他复杂的关系模型。
最后,回归方程建立的结果只是基于样本数据,不能完全代表总体数据,因此需要进行适当的统计推断。
回归方程是一种重要的数理统计学方法,可以用于建立自变量和因变量之间的关系模型,进行预测和控制。
在实际应用中,需要满足一定的假设条件,并注意其局限性。
