矩阵(ch1.7)
1.7 矩阵的秩
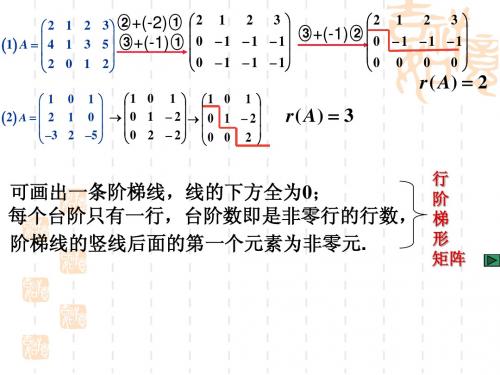
行最简形矩阵
1.梯矩阵中非零行的行数称为矩阵的秩, 记作 r(A)=r 2. Th 1.9 矩阵经初等变换后,其秩不变 . 1)当A= O时, 规定 r ( A ) 0 2) 0 ≤r≤min (m, n), r(A)=r(AT) 3)当 r(A)= min (m, n)时, 称A为满秩矩阵. 则A一定滿秩. 4) 若A为非奇异矩阵,或A 是可逆矩阵, A的不等于0的子式的最高阶为 n A 0 A可逆 r(A)= n 二、矩阵秩的求法 1.利用初等变换; 2.根据定义求. 利用 k 阶子式
4 . 初等变换不改变矩阵的
秩 . 当 P , Q 是初等矩阵时,
r ( A ) r ( PA ) r ( AQ ) r ( PAQ ) 5. r ( A ) r 存在可逆矩阵
6. r ( A B) r ( A) r ( B).
A 6. O O A B O
1 5 4 3 0
0 10 5 7 2
r(A)=2
三、矩阵的秩的性质
1. r ( A ) 0 A 0
2. r ( A ) r ( A );
T
3 . 若 A ( a ij ) n n 可逆, 则 r ( A ) r ( A
1
) n
1 2 4 0 0 4 9 0
1 1 0 0
2 1 0 0
1 1 2 0
4 0 6 0
行阶梯形矩阵
1 0 0 0
0 1 0 0
1 1 0 0
0 0 1 0
4 3 3 0
求矩阵A的秩
1 0 2 4
0
4 1 1 3
1
矩阵的定义及其运算规则

矩阵的定义及其运算规则1、矩阵的定义一般而言,所谓矩阵就是由一组数的全体,在括号()内排列成m行n 列(横的称行,纵的称列)的一个数表,并称它为m×n阵。
矩阵通常是用大写字母A 、B …来表示。
例如一个m 行n 列的矩阵可以简记为:,或。
即:(2-3)我们称(2-3)式中的为矩阵A的元素,a的第一个注脚字母,表示矩阵的行数,第二个注脚字母j(j=1,2,…,n)表示矩阵的列数。
当m=n时,则称为n阶方阵,并用表示。
当矩阵(a ij)的元素仅有一行或一列时,则称它为行矩阵或列矩阵。
设两个矩阵,有相同的行数和相同的列数,而且它们的对应元素一一相等,即,则称该两矩阵相等,记为A=B。
2、三角形矩阵由i=j的元素组成的对角线为主对角线,构成这个主对角线的元素称为主对角线元素。
如果在方阵中主对角线一侧的元素全为零,而另外一侧的元素不为零或不全为零,则该矩阵叫做三角形矩阵。
例如,以下矩阵都是三角形矩阵:,,,。
3、单位矩阵与零矩阵在方阵中,如果只有的元素不等于零,而其他元素全为零,如:则称为对角矩阵,可记为。
如果在对角矩阵中所有的彼此都相等且均为1,如:,则称为单位矩阵。
单位矩阵常用E来表示,即:当矩阵中所有的元素都等于零时,叫做零矩阵,并用符号“0”来表示。
4、矩阵的加法矩阵A=(a ij)m×n和B=(b ij)m×n相加时,必须要有相同的行数和列数。
如以C=(c ij)m ×n表示矩阵A及B的和,则有:式中:。
即矩阵C的元素等于矩阵A和B的对应元素之和。
由上述定义可知,矩阵的加法具有下列性质(设A、B、C都是m×n矩阵):(1)交换律:A+B=B+A(2)结合律:(A+B)+C=A+(B+C)5、数与矩阵的乘法我们定义用k右乘矩阵A或左乘矩阵A,其积均等于矩阵中的所有元素都乘上k之后所得的矩阵。
如:由上述定义可知,数与矩阵相乘具有下列性质:设A、B都是m×n矩阵,k、h为任意常数,则:(1)k(A+B)=kA+kB(2)(k+h)A=kA+hA(3)k(hA)=khA6、矩阵的乘法若矩阵乘矩阵,则只有在前者的列数等于后者的行数时才有意义。
矩阵(Matrix)的定义

a11 a12
A
a21
a22
am1 am1
a1n
a2n
amn
系数矩阵
线性变换与矩阵之间存在着一一对应关系.
第二节 矩阵的运算
主要内容
矩阵的加法 数与矩阵相乘 矩阵的乘法 方阵的幂
矩阵乘积的意义 矩阵的转置 方阵的行列式
一、矩阵的加法
1.定义:设有两个 m×n 矩阵 A = (aij),B = (bij) ,那么矩 阵 A 与 B 的和记作 A+B,规定为
a11 b11
A
B
a21
b21
am1 bm1
a12 b12 a22 b22
am2 bm2
a1n b1n
a2n
b2n
amn bmn
说明:只有当两个矩阵是同型矩阵时,才能进行加法运算.
2.矩阵加法的运算规律
a, b, c R
设 A、B、C 是同型矩阵
交 换 abba 律
A(B C) AB AC (B C)A BA CA
(iv) 单位矩阵在矩阵乘法中的作用类似于数1,即
Em Amn Amn En A
推论:矩阵乘法不一定满足交换律,但是纯量阵 lE 与任何
同阶方阵都是可交换的.
(l En ) An l An An (l En )
纯量阵不同 于对角阵
1 2 4 3 9 8 5 2 , 4 2 1 0
1 2 3 0
9
8
.
5 1
3
5
行列式
a11 a12
a1n
a21 a22
a2n
矩阵
a11 a12
a1n
a21 a22
a2n
第一章 第二讲 矩阵及矩阵初等变换2

第二讲 矩阵及初等变换(4节)在上一讲中,我们简单介绍了n 元线性方程组的求解过程是如何用数表的形式来表达的思想,这种既能简化求解方程组的过程又使得求解形式简单明了的数表,我们称之为矩阵。
矩阵是线性代数中重要的概念之一,它的理论与方法在数学、经济、工程技术等方面都有较广泛的应用。
著名的列昂节夫投入—产出模型就是利用矩阵这一数学工具建立起来的。
因此掌握矩阵这一数学工具是非常必要的。
本讲的主要内容就是给出矩阵的概念及运算性质,为下一步更好地利用矩阵理论与方法讨论线性方程组提供有力的理论支撑。
1.2.1矩阵的概念定义2.1 由m n ⨯个数i j a (=1,2,,i m ;=1,2,j n )排成了m 行n 列的矩形数表111212122212n n m m m na a a a a a a a a称其为m 行n 列矩阵,记作111212122212n nm m m n m na a a a a a a a a ⨯⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭。
其中称ij a 是矩阵的第i 行第j 列元素。
矩阵常用大写字母m n A ⨯,m n B ⨯… ...表示,或简记m n A ⨯=()ij m n a ⨯,m n B ⨯=()ij m n b ⨯… … 等.注意:矩阵的行数m 与列数n 可以不相等,行列相同的矩阵称为方阵. 例如 2行3列矩阵 232310-2=25-3A ⨯⨯⎛⎫⎪⎝⎭ , 2行2列矩阵 222221=16B ⨯⨯⎛⎫⎪-⎝⎭。
例2.1例:给个具体的矩阵表示实例1.2.2矩阵的运算矩阵也有加、减、数乘、乘法等基本运算法则,以及转置运算等.由于矩阵是个数表,所以它的运算法则与数之间的运算法则有本质上的区别。
下面我们先给出矩阵的基本的运算.定义2.2 若两个行列相同的矩阵()(),ij ij m nm nA aB b ⨯⨯==其对应元素相等,即()ijm na ⨯=()ij m nb ⨯则称矩阵A 与B 相等,记作A B =。
矩阵理论知识点整理

欢迎来主页下载---精品文档精品文档三、矩阵的若方标准型及分解λ-矩阵及其标准型定理1 λ-矩阵()λA 可逆的充分必要条件是行列式()λA 是非零常数引理2λ-矩阵()λA =()()n m ij ⨯λa 的左上角元素()λ11a 不为0,并且()λA 中至少有一个元素不能被它整除,那么一定可以找到一个与()λA 等价的()()()nm ij ⨯=λλb B 使得()0b 11≠λ且()λ11b 的次数小于()λ11a 的次数。
引理3任何非零的λ-矩阵()λA =()()nm ij⨯λa 等价于对角阵()()()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0...0.....d 21λλλr d d ()()()λλλr 21d ,....d ,d 是首项系数为1的多项式,且()()1......3,2,,1,/d 1-=+r i d i i λλ引理4等价的λ-矩阵有相同的秩和相同的各阶行列式因子推论5 λ-矩阵的施密斯标准型是唯一的由施密斯标准型可以得到行列式因子 推论6两个λ-矩阵等价,当且仅当它们有相同的行列式因子,或者相同的不变因子推论7λ-矩阵()λA 可逆,当且仅当它可以表示为初等矩阵的乘积推论8两个()()λλλB A m 与矩阵的-⨯n 等价当且仅当存在一个m 阶的可逆λ-矩阵()λP 和一个n 阶的λ-矩阵()λQ 使得()()()()λλλλQ A P =B精品文档推论9两个λ-矩阵等价,当且仅当它们有相同的初等因子和相同的秩定理10设λ-矩阵()λA 等价于对角型λ-矩阵()()()()⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=λλλλn h h .....21h B ,若将()λB 的次数大于1的对角线元素分解为不同的一次因式的方幂的乘积,则所有这些一次因式的方幂(相同的按照重复的次数计算)就是()λA 的全部初等因子。
行列式因子不变因子初等因子初等因子被不变因子唯一确定但,只要λ-矩阵()λA 化为对角阵,再将次数大于等于1的对角线元素分解为不同的一次方幂的乘积,则所有这些一次因式的方幂(相同的必须重复计算)就为()λA 的全部初等因子,即不必事先知道不变因子,可以直接求得初等因子。
矩阵(ch1.6)

kai1
kain
1 am1
amn am1
amn
12
1
1k
1
a11
ai1
a
j1
a1n ain a jn
ai1
a11 ka j1 a j1
a1n
ain
ka
jn
a jn
1 am1
amn am1
amn
13
例:矩阵
3 0 1 A 1 1 2
A1
24
例 解
1 2 3
求
A
2
2
1
的逆矩阵。
3 4 3
1 2 3 1 0 0
A
E
2
2
1
0
1
0
3 4 3 0 0 1
1 2 3 1 0 0
r2 2r1
r3 3r1
0
2
5
2
1
0
0 2 6 3 0 1
25
1 0 2 1 1 0
r1 r2
r3 r2
0
2
5
2
1
0
0 0 1 1 1 1
4 1
2 1
3
0
1 2 1 1 2 3
1 r12r2 1 0 1 1 0 r1r3 1 0 1 1 4 3
r3 r2
r1 r2
0 0
4 1
3 1
2 0
0 3
3 3
r2 4r3
r2 r3
0 0
1 0
1 1
0 2
3 12
3
9
1 r1r3 0 0 3 8 6
r2 r3
( 1) r3
1.7 简化阶梯形矩阵--线性代数PPT

1.7 简化阶梯形矩阵
.T 设是阶梯形矩阵,一个非零元⎪⎪⎪⎪⎪⎭
⎫ ⎝⎛---00000310003011040101⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---000003100001110
41211定义T 如果的主元所在列只有.T 简化阶则为梯形矩阵称
,A 对任意矩阵4定理A T 与是行等价的,T 化为简化阶梯形矩阵0,T A 设为的阶梯形证明12,,,.
r j j j 标号为01,2,
,1,T r r 将的第行乘以适当常数加到第行.
r j 可使第列上主元以外的元素都为零使得,T 存在简化阶梯形矩阵(A 或者可以经有限次初等行变换).T A 称为的简化阶梯形0,T r 有个主元主元所在列的
1,2,
,2,r -第行.
都为零,.A T 依此类推就可以得到的简化阶梯形证毕1r -然后将所得矩阵的第行乘以适当常数加到1r j -使得第列上主元以外的元素
11214246482311236979A -⎛⎫ ⎪- ⎪= ⎪-- ⎪-⎝⎭
12140110000300000111-⎛⎫ ⎪- ⎪- ⎪ ⎪⎝⎭
阶梯形 −−→
12070103000300000111-⎛⎫ ⎪- ⎪- ⎪ ⎪⎝⎭
−−−−→−+-+-2313)1()1(R R R R 01040103.000300001110-⎛⎫ ⎪- ⎪- ⎪ ⎪⎝⎭
−−−−→−+-12)1(R R 简化阶梯形 ▌ 12140110000300000111-⎛⎫ ⎪- ⎪- ⎪ ⎪⎝⎭
任意矩阵的简化阶梯形是唯一的
.。
矩阵基础知识

矩阵基础知识贺国宏 编为了学好测绘工程专业的核心课程〈测量平差基础〉,必须掌握以下所述矩阵的基础知识,同时,学习这些知识,对于学习测绘工程的其它课程,以及以后的深造,都是重要的。
1、矩阵的秩定义:矩阵A 的最大线性无关的行(列)向量的个数r ,称为矩阵A 的行(列)秩。
由于矩阵的行秩等于列秩,故统称为矩阵的秩,记为R(A)。
对于矩阵的秩有性质:{})(),(m in )(B R A R AB R ≤(1)2、矩阵的迹定义:方阵A 的主对角元素之和称为该方阵的迹,记为∑==ni ii a A tr 1)((2)对于矩阵的迹有下面的性质:(1) tr (A T )=tr (A)(3) (2) tr (A+B)=tr (A)+tr (B) (4) (3) tr (kA)=k tr (A) (5) (4) tr (AB)=tr (BA)(6)3、矩阵的特征值和特征向量定义:对于n 阶方阵A ,若存在非零向量χ,使得x x λ=A(7)则称常数λ为矩阵A 的特征值(或特征根),而χ称为矩阵A 属于特征值λ的特征向量。
由此可得=-χ)(A E λ0(8)因此,该齐次线性方程有非零解的条件是0)(0111=++++=-=--a a a A E f n n n λλλλλΛ(9)称λE-A 为矩阵A 的特征矩阵,而f (λ)为矩阵A 的特征多项式。
显然,矩阵A 的特征根),,2,1(n i i Λ=λ为特征方程(9)的根。
应该指出,对于一般的实矩阵A ,特征根可能是复数,从而特征向量也是复数。
以后将会看到,对于实对称矩阵,其特征根和特征向量都是实的。
这一点是很重要的。
特征值和特征向量具有下列性质:(1) 设n λλλ,,,21Λ为n 阶方阵A 的n 个特征值,则:A K 的特征值为kn k k λλλ,,,21Λ A -1的特征值为11211,,,---n λλλΛ(2) tr (A)=n λλλ+++Λ21 =A n λλλΛ21⋅(3) 矩阵A 的属于不同特征值的特征向量是线性无关的。
矩阵(Matrix)PPT课件

a11 a12
A
a21
a22
am1 am2
a1n x1 b1
a2n
,
x
x2
,
b
b2
amn xn bn
ai1x1 ai2 x2 ain xn bi
则方程组又可表示为 Ax b.
x1ai1 x2ai2 xnain bi
a11 a21
定义成
a11 a21
x1 x1
a12 x2 a22 x2
x1
a11
a21
x2
a12
a22
x1 1 x2 2
e2
(a12 , a22 )
2
1
y ( y1, y2 )
2
A和x的乘法实质给出了 向量y在A坐标系(β1Oβ2) 下的刻划方法。
e1
(a11,1a21 )
y y1e1 y2e2
ai1b1 j ai 2b2 j a b b 1j is sj
a a a i1 i2
b2 j is
注:A的列数和B的行数相等时 b,sj AB才有意义。
• 例3 设矩阵
1 0 1
A
1
1
3
,
求乘积 AB.
解
1 0
C
AB
1
1
0 3 4 B 1 2 1
3 1 1
B
a12
a22
a1n a2n
am1
am2
y (x1, x2, , xn )
c (b1,b2, ,bm)
amn nm
则方程组又可表示为 yB c.
矩阵向量乘法意义之二:为刻划向量提供了坐标系
根据矩阵乘法定义,m n 阶矩阵A与n维列向
矩阵分析理论的基础知识

前言 1、自我介绍2、矩阵分析理论是在线性代数的基础上推广的3、矩阵分析理论的组成:四部分:基础知识(包括书上的前三章内容)难点:约当标准形与移项式矩阵矩阵分析(第四章:矩阵函数及其应用) 矩阵特征值的估算(第五章) 非负矩阵(第六章)第一部:矩阵分析理论的基础知识§1 线性空间与度量空间一、线性空间:1.数域:Df 1:若复数的一个非空集合P 含有非零的数,且其中任意两数的和、差、积商(除数不为0)仍在这个集合中,则称数集P 为一个数域eg 1:Q (有理数),R (实数),C (复数),Z (整数),N (自然数)中哪些是数域?哪些不是数域?2.线性空间—设P 是一个数域,V 是一个非空集合,若满足:<1> 可加性—指在V 上定义了一个二元运算(加法)即:V ∈∀βα, 经该运算总存在唯一的元素V ∈γ与之对应,称γ为α与β的和,记βαγ+= 并满足:① αββα+=+② )()(γβαγβα++=++ ③ 零元素—=有θαθααθ+∈∀∈∃Vt s V .④ αβαβθβααβ-+∈∀∈∃=记的负元素为=有对V V<2> 数积:(数乘运算)—在P 与V 之间定义了另一种运算。
即V P k ∈∈∀α,经该运算后所得结果,仍为V 中一个唯一确定的元素。
存在唯一确定的元素V ∈δ与之对应,称δ为k 与α的乘积。
记为αδk = 并满足:①αα=⋅1② P l k ∈∀, αα)()(kl l k = ③ P l k ∈∀, αααl k l k +=+)( ④ γβα∈∀, βαβαk k k +=+)(则称V 为数域P 上的线性空间(向量空间)记为)...(∙+P V 习惯上V 中的元素—向量, θ—零向量, 负元素—负向量结论:可以证明,线性空间中的零向量是唯一的,负元素也是唯一的,且有:θα=⋅0 θθ=⋅k αα-=⋅-)1( )(βαβα-+=-eg2:}{阶矩阵是n m A A V ⨯= P —实数域R按照矩阵的加法和数与矩阵的乘法,就构成实数域R 上的线性空间,记为:n m R ⨯ 同样,若V 为n 维向量,则可构成R 上的n 维向量空间n R —线性空间。
矩阵的总结知识点

矩阵的总结知识点一、矩阵的基本概念1. 矩阵的定义矩阵是一个按照矩形排列的数学对象。
矩阵的概念最早出现在线性代数理论中,它是由m行n列的数字排成的矩形阵列。
通常表示为一个大写字母,比如A,而矩阵中的元素通常用小写字母表示,比如a_ij,表示在第i行第j列的元素。
2. 矩阵的类型根据矩阵的形状和性质不同,可以将矩阵分为多种类型,比如方阵、对称矩阵、对角矩阵、三角矩阵等。
方阵是指行数和列数相等的矩阵,对称矩阵是指矩阵关于主对角线对称,对角矩阵是指除了主对角线上的元素外,其他元素都为零,而三角矩阵是指上三角或下三角矩阵。
3. 矩阵的运算矩阵的运算包括矩阵的加法、减法、数乘、矩阵的乘法等。
其中,矩阵的加法和减法要求相加的矩阵具有相同的形状,即行数和列数相同;而矩阵的数乘是指矩阵中的每个元素都乘以一个标量;矩阵的乘法是指矩阵A的列数等于矩阵B的行数时,可以进行矩阵乘法运算。
4. 矩阵的转置和逆矩阵矩阵的转置是指将矩阵的行和列对调得到一个新的矩阵,记作A^T。
而逆矩阵是指如果一个矩阵A存在逆矩阵A^(-1),使得A*A^(-1)=I,其中I是单位矩阵,则称矩阵A可逆,否则称矩阵A为奇异矩阵。
二、矩阵的应用1. 线性方程组的求解矩阵可以用来表示和求解线性方程组,线性方程组可以表示成AX=B的形式,其中A是系数矩阵,X是未知数矩阵,B是常数矩阵。
通过矩阵的基本变换和行列式的计算,可以求解线性方程组的解。
2. 数据处理和分析在数据处理和分析领域,矩阵可以用来表示和处理大规模的数据集。
比如,在机器学习算法中,可以通过矩阵的运算和矩阵分解来进行数据的降维和特征的提取。
3. 控制理论在控制理论中,矩阵可以用来描述线性系统的状态方程和控制方程,通过对状态矩阵和控制矩阵的计算和分析,可以得到系统的稳定性和控制性能。
4. 计算机图形学在计算机图形学中,矩阵可以用来描述和处理图形的旋转、平移、缩放等变换,通过矩阵的运算和矩阵乘法,可以实现图形的变换和动画效果。
CH矩阵特征值问题计算实用

第5页/共41页
乘幂法的基本思想是取初始向量v(0)Rn,作迭代 v(k+1) =Av(k) =Ak+1v(0) , k=0,1,2,…
产生迭代序列v(k).
由于x1,xv2(,0…) =xan1线x1+性a2无x2关+…, 从+a而nx有n
(2) A(1)
n
i
2i
x
i
i 1
………
当k 充分大时,有
(k )
1k
1
x1
,
(k 1)
1k
1
1
x1
(((k(k1) )))i i 1
第4页/共41页
§1.1 乘幂法
乘幂法是用来求矩阵A按模最大的特征值和相应的特征向量的方法.
设A是单构矩阵, 即A有n个线性无关的特征向量.
A的n个特征值为 |1 2 n
1 ,
x
0;
(2)
1
max
xRn , x 0
( Ax, x) ;
(x, x)
(3)
n
min
xRn , x 0
( Ax, x) . (x, x)
1 n为A
第3页/共41页
§1 乘幂法和反幂法
计算矩阵的主特征根及对应的特征向量
➢ 原始幂法
条件:关A 的有特特征征向根量|1x|>1 ,
|2|
... ,
定理(Schur定理)设A Rnn,则存在酉矩阵U 使
r11 r12
UH
AU
r22
r1n
r2 n
R
rnn
其中rii (i 1, 2, , n)为A的特征值.
标准阶梯形矩阵

标准阶梯形矩阵阶梯形矩阵是线性代数中一个非常重要的概念,它在矩阵的运算和求解线性方程组中起着至关重要的作用。
本文将详细介绍标准阶梯形矩阵的定义、性质和应用。
1. 定义。
首先,我们来看一下标准阶梯形矩阵的定义。
一个矩阵如果满足以下条件,则称之为标准阶梯形矩阵:(1)矩阵的第一个非零行的首个非零元素为1;(2)每一行的首个非零元素所在的列在前一行首个非零元素所在的列的右边;(3)除了首个非零元素外,每一行的其他元素都为0;(4)所有全为0的行都在矩阵的底部。
2. 性质。
标准阶梯形矩阵具有一些重要的性质,这些性质对于矩阵的运算和求解线性方程组都有着重要的意义。
(1)标准阶梯形矩阵的行最简形是唯一的。
(2)标准阶梯形矩阵的行秩等于它的非零行数。
(3)标准阶梯形矩阵的列秩等于它的首个非零元素所在的列数。
(4)标准阶梯形矩阵的秩等于它的行秩和列秩。
(5)对于任意的m×n矩阵A,存在m阶可逆矩阵P和n阶可逆矩阵Q,使得P-1AQ是标准阶梯形矩阵。
3. 应用。
标准阶梯形矩阵在线性代数中有着广泛的应用,特别是在矩阵的运算和求解线性方程组中。
(1)矩阵的运算,标准阶梯形矩阵可以简化矩阵的运算,特别是在矩阵的乘法和求逆运算中,可以大大减少计算量。
(2)线性方程组的求解,通过将系数矩阵化为标准阶梯形矩阵,可以利用矩阵的性质快速求解线性方程组,避免了繁琐的计算过程。
(3)矩阵的秩和线性相关性,标准阶梯形矩阵可以帮助我们判断矩阵的秩和线性相关性,从而更好地理解矩阵的性质和应用。
总结。
标准阶梯形矩阵是线性代数中一个重要的概念,它具有独特的定义和重要的性质,对于矩阵的运算和求解线性方程组有着重要的应用价值。
通过深入理解标准阶梯形矩阵的定义、性质和应用,我们可以更好地掌握线性代数的基本理论和方法,为进一步深入学习和应用线性代数奠定坚实的基础。
矩阵的标准型怎么求

矩阵的标准型怎么求矩阵的标准型是线性代数中一个重要的概念,它可以帮助我们更好地理解和分析矩阵的性质和特点。
那么,矩阵的标准型怎么求呢?接下来,我们将详细介绍求解矩阵标准型的方法。
首先,我们需要了解什么是矩阵的标准型。
矩阵的标准型是指将一个矩阵通过一系列相似变换,转化为一种特殊的形式,这种形式通常是对角线上有特定的数值,其余位置都是0的形式。
通过将矩阵转化为标准型,我们可以更清晰地看出矩阵的特征和性质。
接下来,我们来介绍求解矩阵标准型的具体步骤。
首先,我们需要找到矩阵的特征值和特征向量。
具体来说,对于一个n阶矩阵A,我们需要求解它的特征值和对应的特征向量。
这一步通常可以通过求解矩阵A的特征多项式,并解特征多项式的根来获得矩阵A的特征值。
然后,我们可以通过代入这些特征值到特征方程中,求解对应的特征向量。
接下来,我们将特征值和特征向量组合成矩阵的形式。
具体来说,我们可以将特征向量按列排列成一个矩阵P,而特征值则按对角线排列成一个矩阵D。
这样,我们就可以得到矩阵A的特征分解形式A=PDP^(-1)。
最后,我们需要进一步对特征分解形式进行变换,使得矩阵A转化为标准型。
具体来说,我们可以通过对P和P^(-1)进行一系列相似变换,将矩阵A转化为对角线上有特定数值,其余位置都是0的形式。
这样,我们就得到了矩阵的标准型。
总结一下,求解矩阵的标准型的具体步骤包括,求解矩阵的特征值和特征向量,将特征值和特征向量组合成特征分解形式,进一步对特征分解形式进行相似变换,得到矩阵的标准型。
在实际操作中,求解矩阵的标准型可能会比较复杂,需要进行一系列繁琐的计算。
因此,我们通常会借助计算机软件来进行求解,比如MATLAB、Python等。
这些软件提供了丰富的矩阵运算函数,可以帮助我们快速、准确地求解矩阵的标准型。
总之,矩阵的标准型是一个重要的概念,它可以帮助我们更好地理解和分析矩阵的性质和特点。
通过求解矩阵的标准型,我们可以更清晰地看出矩阵的特征和性质。
矩阵 简介

矩阵是数学中的一个重要概念,它是由数字按照矩形排列而成的二维数据结构。
矩阵通常用方括号[] 或圆括号() 表示,其中包含了行和列。
例如,一个常见的矩阵可以表示为:
A = [1 2 3]
[4 5 6]
[7 8 9]
在这个示例中,矩阵A 是一个3x3的矩阵,它有3行和3列。
每个数字在矩阵中被称为一个元素,可以通过行号和列号来唯一标识。
例如,A的第二行第三列的元素是6。
矩阵在数学和科学领域中有广泛的应用,包括线性代数、统计学、物理学、工程学等等。
它们可以用来表示和处理各种类型的数据,如向量、多维数据、转换操作等。
矩阵运算包括加法、减法、乘法、求逆等,它们在各种领域中都有着重要的作用。
等价标准形矩阵的定义

等价标准形矩阵的定义
等价标准形矩阵是一种用于描述和比较不同维度或特征的对象的工具。
它是一个n×n 的矩阵,其中n是对象的数量。
等价标准形矩阵的元素表示两个对象之间的等价关系或相对价值。
具体地说,在等价标准形矩阵中,每个元素(aij)表示对象i与对象j之间的等价关系或相对价值,其中aij的取值范围通常为[0,1]。
矩阵的对角线元素(aii)通常是1,表示每个对象与自身的等价关系或相对价值为最高。
等价标准形矩阵的构建通常需要依靠专家判断、主观评价或经验数据。
专家根据对被比较对象的理解和评估,根据事先设定的等价标准,将对象之间的等价关系或相对价值转化为矩阵元素的取值。
这些取值可以是可度量的具体数值,如比例值或评分,也可以是由专家主观判断的相对大小关系。
等价标准形矩阵可以在多个领域和应用中使用。
在多属性决策分析中,等价标准形矩阵可以用于确定不同属性之间的相对重要程度,从而帮助决策者进行权衡和选择。
在定性研究中,等价标准形矩阵可以用于对不同概念、变量或主题进行关联和分类。
在市场调研中,等价标准形矩阵可以用于对产品特征或服务质量进行评估和比较。
等价标准形矩阵是一种用于描述和比较对象的工具,它通过矩阵元素的设定,反映了对象之间的等价关系或相对价值。
这种矩阵在多个领域和应用中都具有实用的价值,可以帮助人们进行决策、分类和评估。
七点法求基础矩阵

基础矩阵是计算机视觉中的一个重要概念,它用于解决双目视觉、三维重建等问题。
七点法是一种求解基础矩阵的经典方法,步骤如下:
1. 根据已知的匹配点对(即两张图像中对应的特征点),构造齐次坐标向量x'和x。
2. 将x'和x分别进行归一化处理,即去除它们的均值并将它们缩放到单位尺度,得到新的向量x''和x'''。
3. 构造一个7x9的矩阵A,每行由向量x''和x'''按列拼接而成。
共有7个这样的方程。
4. 对A进行奇异值分解,得到其最小奇异值对应的右奇异向量v。
5. 将v重新排列成3x3的矩阵F,并强制使得F的秩为2,即通过奇异值分解将F的最小奇异值设为0。
6. 反归一化F,即将F转换为原始坐标系下的基础矩阵。
需要注意的是,七点法只能从7对匹配点对中求解基础矩阵,因此需要保证匹配点对数量不少于7对。
同时,由于匹配点对中可能存在误匹配或噪声,因此需要进行一些预处理或后处理工作,如RANSAC算法等,以提高基础矩阵的准确性和鲁棒性。
以上是七点法求解基础矩阵的基本步骤,希望能对你有所帮助。
h-矩阵的一些性质

h-矩阵的一些性质1、可交换律若定义矩阵A和矩阵B相乘,则有A×B=B×A,可交换律表示矩阵相乘顺序可以交换,无论怎么组合结果都是相同的。
2、结合律若定义矩阵A、矩阵B和矩阵C,则:A×(B×C)=(A×B)×C,结合律表明在矩阵相乘时,括号的顺序可以任意改变而不影响结果。
3、矩阵的结果的转置若定义矩阵A和矩阵B,则:(A×B)T=BTA。
表示矩阵相乘的结果的转置等于B的转置与A的相乘。
4、交换矩阵当所有元素取正负号时,矩阵不变。
5、单位矩阵具有对角线全为1,其余元素全为零的m×m阶方阵被称为单位矩阵,它具有将任意矩阵乘以它的结果始终为它原来的值的性质。
6、可加性若定义矩阵A、B、C,则有A+B+C=A+(B+C),表示矩阵之间可以进行加法运算,加法的可交换性不受顺序影响。
7、可乘性若定义矩阵A、B、C,则有A×(B×C)=(A×B)×C,表示矩阵之间可以进行乘法运算,乘法的可交换性不受顺序影响。
8、矩阵乘法可分配律若定义矩阵A、B、C、D,则有A×(B+C)=(A×B)+(A×C),表示矩阵乘法可以同时对加法和减法运算进行分配,不受运算顺序影响。
9、乘法结合律若定义矩阵A、B、C,则有A×(B×C)=(A*B)*C,表示矩阵乘法同样可以进行分配,不受运行顺序影响。
10、矩阵的幂定律若定义二阶矩阵A,则当n≥2时,有A^n=(A^(n-1))×A,表示二阶矩阵的幂定律,可递推计算出关于矩阵A的任何n次方的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
−1 1 1 −2 1 0 r1−r2 0 0 → r −r3 0 0 1 1 0 0 0 0 0 0 −2 0 1 1 0 2 0 0 1 0 0 0
0 −2 0 2 1 0 0 0 1 0 0 0
称为行最简形矩阵 特点:各阶第一个非零元都 是1且所在列其余元素均为0.
12
3 1 2 3 r3 − r2 1 2 r2 −2r 1 解 A→ 0 −2 −5→ 0 −2 −5 : r −3r 3 1 0 0 −1 0 −2 −6
所以 r( A) = 3.
10
1 −2 2 −1 0 2 −4 8 例 A = ( aij ) = 4×5 −2 4 −2 3 3 −6 0 −6
3
注: 1. 当A = O时, 规定r (A) = 0 时 规定r 2. 0 ≤ r ( A) ≤ min(m, n) 3. 当 r ( A) = min(m, n) 时, 称矩阵A为满秩矩阵 称矩阵A 4. r ( A) = r ( AT ) 5. 若 A = ( aij )n×n , 则r (A) = n 的充分必要条件是 A ≠ 0 r
§ 1. 7 矩阵的秩
在矩阵A 定义: 定义: 设 A = ( aij ) 是一个 m × n 矩阵,则在矩阵A中任取 ( k行k列 i1 , i2 ,L, ik 行, j1 , j2 , L , jk 列), 位于这些行和 列相交处的 k 2 个元素按照原来相应位置所构成的 k 阶行列式:
a i1 j1 a i2 j1 L a i k j1 a i1 j 2 a i2 j 2 L a ik j 2 L L L L a i1 j k a i2 j k L a ik j k
6
1
2
三. 求秩方法
例
解
行阶梯形矩阵 特点: 特点: 横线下方全是0; 横线下方全是 ; 每阶只有一行, 每阶只有一行,阶数即 非零行数; 非零行数; 竖线后面第一个元素为 非零元. 非零元
7
定理1.8: 定理1.8: 任意一个 m × n 矩阵,均可以经过一系列行 矩阵, 梯矩阵. 初等变换化为 m × n梯矩阵. 定理1.9: 任一矩阵A经过有限次初等变换后其秩不变. 定理1.9: 任一矩阵A经过有限次初等变换后其秩不变. 包括( 互换两行( ),其秩不变 其秩不变; 包括(1)互换两行(列),其秩不变; 非零数k乘以第 ),其秩不变 其秩不变; (2)非零数k乘以第i行(列),其秩不变; 非零数k (3)非零数k 乘以 第i 行(列)加到第 j 行(列), 其秩不变. 其秩不变.
1 2 −1 4 r3 − r2 1 2 −1 4 r2 −2r 1 0 0 5 −3 解 A→ 0 0 5 −3→ r +r 3 1 0 0 0 0 0 0 5 −3
所以
r ( A) = 2.
9
1 2 3 例 A = ( aij ) = 2 2 1, ( ) r 求 A. 3×3 3 4 3
为二阶子式;
2 2 4 1 2 为三阶子式. 3
−3 , 1 −2 4
2
思考m ×n矩阵A的 k 阶子式共有多少个?
共C ⋅ C 个 .
k m k n
二. 矩阵的秩 A 定义: 定义: 设 A = ( aij ) 是一个 m × n 矩阵,如果A中不等于零 的子式的最高阶数为r, 的子式的最高阶数为r, 即存在一个 r 阶子式不 为零, 而任何r +1阶子式皆为零, 则称 r 为矩阵A 零 而任何r 零 为矩阵A 的秩, 记作秩( 的秩, 记作秩(A) = r 或 r (A) = r .
1 2 , () 求 A. r 3 4
1 −2 2 −1 r2 − 2 r1 0 0 4 2 解: A → 0 2 1 r3 + 2 r1 0 r4 −3 r1 0 0 −6 −3
1 −2 r −5r4 3 0 0 → 0 r ↔r4 0 3 0 0 2 −1 1 2 1 0 , 0 0 1 0 0 0
初等变换求矩阵秩的方法: 初等变换求矩阵秩的方法:把矩阵用初等行变换 变成行阶梯形矩阵, 变成行阶梯形矩阵,行阶梯形矩阵中非零行的行 数就是矩阵的秩. 数就是矩阵的秩
8
1 2 −1 4 r 求 A. 例 A = ( aij )3×4 = 2 4 3 5 , ( ) −1 −2 6 −7
一. 矩阵的 k 阶子式 (定义1.9 )书P25
叫做A的一个k阶子式. 叫做A的一个k阶子式.
1
例 A = ( aij )3×4
3 = 1 4
2 2 4
1 −3 2 −2 3 1
其中 −3 , 1 为一阶子式;
1 4
3 1 4
2 3 , 4 1
2 2 4 1
1 −3
3ቤተ መጻሕፍቲ ባይዱ
4
例 求 A = ( aij )3×4
3 2 1 1 = 0 0 0 0 的秩. 4 4 −2 3
矩阵A 三阶子式共有4个 解 矩阵A 的三阶子式共有 个:
3 3 2 1 3 2 1 0 0 0 = 0, 0 0 0 = 0, 0 4 4 −2 4 4 3 4
1 1 2 1 1 0 0 = 0, 0 0 0 = 0, −2 3 4 −2 3
3 2 4 4 = 4 ≠ 0,
矩阵A 的二阶子式共有18个, 其中 矩阵A 二阶子式共有 个 所以 r ( A) = 2.
5
例 求 A = ( aij )3×4
1 = 2 3
1 2 3
1 2 3
2 4的秩 的秩. 6
矩阵A 三阶子式共有4个 解 矩阵A 的三阶子式共有 个: 1 1 1 1 1 2 1 1 2 1 1 2 2 2 2 = 0, 2 2 4 = 0, 2 2 4 = 0, 2 2 4 = 0, 3 3 3 3 3 6 3 3 6 3 3 6 矩阵A 二阶子式共有18个均为零 个均为零: 矩阵A 的二阶子式共有 个均为零 2 4 = 0,L 一阶子式|1|≠ 0, 所以r ( A) = 1.
1 0 5 1
1 −2 0 0 → 0 0 r3 −r2 r4 +3r2 0 0
1 r2 2
2 −1 1 2 1 0 0 0 5 0 0 1
所以 r( A) = 3.
11
1 −2 2 0 0 2 0 0 0 0 0 0 1 −2 1 r2 2 0 0 → 0 0 0 0
