初中数学奥林匹克竞赛解题方法大全(配PDF版)-第11章-相似形与面积问题
2023年初中数学奥林匹克竞赛解题方法大全配版四边形的趣味问题

第十章四边形旳趣味问题第一节四边形旳分类与鉴定【知识点拨】1.四边形旳性质: 四边形旳内角和等于3600。
2、四边形旳旳分类: (1)对边平行;(2)对边不平行。
本节研究是对边不平行旳四边形。
没用措施是转化为三角形进行研究。
【赛题精选】例2.如图: 求∠A+∠B+∠C+∠D+∠E+∠F旳度数。
(1999年重庆市竞赛题)【阐明】探索存在型问题是指在一定条件下, 判断与否存在某个结论。
解答此类问题, 先假设结论存在, 从假设出发, 根据题设条件及有关性质进行推理论证, 若推出矛盾, 则不定假设, 若推出合理旳成果, 则阐明假设对旳。
这种措施叫“假设法”。
【阐明】对于四边形, 作对角是常用旳辅助线!【针对训练】第二节平行四边形旳问题【知识点拨】1.平行四边形性质: 对边平行且相等、对角相等、邻角互补、对角线互相平分。
2.矩形性质: 矩形除具有平行四边形旳性质外, 还具有对角线相等、四个角是直角。
3、菱形性质:除具有平行四边形旳性质外, 尚有四条边相等、对角线互相垂直、且每一条对角线平分一组对角。
4、平行四边形问题旳处理措施:(1)转化为三角形问题来处理;(2)常用平行四边形旳性质来处理。
【赛题精选】例2.凸四边形ABCD中, AB∥CD, 且AB+BC=CD+AD求证: ABCD是平行四边形。
(1990年芜湖市竞赛题)例3.平面上有三个正△ABD.△ACE、△BCF, 两两共有一种顶点。
求证: CD与EF互相平分。
(1990年芜湖市竞赛题)例4.在Rt△ABC中, ∠ACB=900, CD⊥AB于D, AE平分∠BAC, 交CD于K, 交BC 于E、, F是BE上一点, 且BF=CE。
求证: FK∥AB。
(大连市第八届“育英杯”竞赛题)例6.矩形ABCD中, AB=20cm, BC=10cm, 若在AC.AB上各取一点M、N, 使BM+MN旳值最小, 求这个最小值。
(1998年北京市竞赛题)例7、设P为等腰三角形ABC斜边AB上任意一点, PE⊥AC于点E, PF⊥BC于点F, PG⊥EF于G, 延长GP并在其延长线上取一点D, 使得PD=PC。
初中数学奥林匹克竞赛解题方法大全(配PDF版)一元一次方程及汇总

第四章一元一次方程及其应用第一节一元一次方程例1、在解方程的过程中,为了使得到的方程和原方程同解,可在原方程的两边()A、乘以同一个数B、乘以同一个整式C、加上同一个代数式D、都加上同一个数例2、方程甲3(x-4)=3x与方程乙x-4=4x同解,其根据是() 4A、甲方程两边都加上了同一个整式B、甲方程两边都乘以了4/3xC、甲方程两两边都乘以了4/3D、甲方程两边都乘以了3/4例3、方程1⎧1⎡1⎛1⎫⎤⎫x-1⎪-1⎥-1⎬-1=2001的根x=__________。
⎨⎢2⎩2⎣2⎝2⎭⎦⎭例4、1992+1994+1996+1998=5000- 成立,则中应当填的数是()A、5B、-900C、-1900D、-2980例5、若P、Q都是质数,以X为未知数的方程PX+5Q=97的根是1。
则P2-Q=____。
例6、有理数111xz、、8恰是下列三个方程的根,则-=________。
25yx(1)2x-110x+12x+1-=-1 (2)3(2y+1)=2(1+y)+3(y+3) 3124(3)1⎡1⎤2z-(z-1)=(z-1) ⎥2⎢2⎣⎦327例7、解方程:x-=1990的去处时,某同学误将3.57 错写成3.57,结果与正确答案例8、在计算一个正数乘以3.57相差1.4,求正确的乘积应是多少? 2829第二节列方程解应用题例1、海滩上有一堆核桃,第一天猴子吃了这堆核桃的2/5,又将4个扔到大海里;第二天猴子吃掉的核桃数加上3个就是第一天所剩核桃数的5/8。
若第二天剩下6个核桃。
问海滩上原有多少个核桃?(20个)例2、古希腊数学家丢番图的墓志铭上记载:“坟中安葬着丢番图,多幺令人惊讶,它忠实地记录了所经历的道路。
上帝给予的童年占六分之一,又过十二分之一,两颊长胡,再过七分之一,点燃起结婚的蜡烛。
五年之后天赐贵子,可怜迟到的宁馨儿,享年仅及其父之半,便进入冰冷的墓。
悲伤只有用数论的研究去弥补,又过四年,他也走完了人生的旅途。
初中数学奥林匹克竞赛解题方法大全(配PDF版)--二次方程与方程组

第八章 二次方程与方程组第一节 一元二次方程【赛题精选】§1、一元一次方程的解法主要有:直接开平方法、因式分解法、配方法、公式法。
例1、利用直接开平方法解下列关于x 的方程。
(1)0)1(9)2(22=+--x x (2))0(0)22()(22>=+-+a a x a x(3))21(2142222nx n x n x x ++=++例2、利用因式分解法解下列关于x 的方程。
(1)(5x+2)(x-1)=(2x+11)(x-1) (2)0452=+-x x(3)02_23()12(2=++-+x x (4)0)()(22222=-++-q p pq x q p x(5)x m x m x x m )1()1()1(2222-=--+-例3、用配方法解下列关于x 的方程。
(1))0(02≠=++a c bx ax (2)03)12()1(2=-+-+-m x m x m(3)01333223=-+++x x x§2、根的判别式、根与系数的关系韦达定理:若)0(02≠=++a c bx ax 的两个根为1x 、2x ,那么1x 、2x 与a 、b 、c的关系为:两根之和a b x x -=+21;两根之积ac x x =21。
例4、若首项系数不相等的两个二次方程02)2()1(222=+++--a a x a x a (1)、02)2()1(222=+++--b b b x b (2)(其中a 、b 均为正整数)有一个公共根。
求ab ab b a b a --++的值。
例5、已知方程02=++c bx x 与02=++b cx x 各有两个根1x 、2x 及'1x 、'2x ,且1x 2x >0,'1x '2x >0。
求证:(1)1x <0,2x <0,'1x <0,'2x <0;(2)b-1≤c ≤b+1;(3)求b 、c 所有可能的值。
奥林匹克数学竞赛因式分解

奥林匹克数学竞赛因式分解因式分解是多项式乘法的逆向运算,是代数恒等变形的基础,体现了一种化归的思想.提取公因式法、公式法、二次三项式的十字相乘法、分组分解法是因式分解的基本方法,下面是为你整理的奥林匹克数学竞赛因式分解,一起来看看吧。
奥林匹克数学竞赛因式分解十二种方法1、提公因法如果一个多项式的各项都含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式。
例1、分解因式x-2x-x(2003淮安市中考题)x-2x-x=x(x-2x-1)2、应用公式法由于分解因式与整式乘法有着互逆的关系,如果把乘法公式反过来,那么就可以用来把某些多项式分解因式。
例2、分解因式a+4ab+4b(2003南通市中考题)解:a+4ab+4b=(a+2b)3、分组分解法要把多项式am+an+bm+bn分解因式,可以先把它前两项分成一组,并提出公因式a,把它后两项分成一组,并提出公因式b,从而得到a(m+n)+b(m+n),又可以提出公因式m+n,从而得到(a+b)(m+n)例3、分解因式m+5n-mn-5m解:m+5n-mn-5m=m-5m-mn+5n=(m-5m)+(-mn+5n)=m(m-5)-n(m-5)=(m-5)(m-n)4、十字相乘法对于mx+px+q形式的多项式,如果a×b=m,c×d=q且ac+bd=p,则多项式可因式分解为(ax+d)(bx+c)例4、分解因式7x-19x-6分析:1-3722-21=-19解:7x-19x-6=(7x+2)(x-3)5、配方法对于那些不能利用公式法的多项式,有的可以利用将其配成一个完全平方式,然后再利用平方差公式,就能将其因式分解。
例5、分解因式x+3x-40解x+3x-40=x+3x+()-()-40=(x+)-()=(x++)(x+-)=(x+8)(x-5)6、拆、添项法可以把多项式拆成若干部分,再用进行因式分解。
奥林匹克数学的解题方法

奥林匹克数学的解题方法(上篇)有固定求解模式的问题不属于奥林匹克数学,通常的情况是,在一般思维规律的指导下,灵活运用数学基础知识去进行探索与尝试、选择与组合。
这当中,经常使用一些方法和原理(如探索法,构造法,反证法,数学归纳法,以及抽屉原理,极端原理,容斥原理……),同时,也积累了一批生气勃勃、饶有趣味的奥林匹克技巧。
在2-1曾经说过:“竞赛的技巧不是低层次的一招一式或妙手偶得的雕虫小技,它既是使用数学技巧的技巧,又是创造数学技巧的技巧,更确切点说,这是一种数学创造力,一种高思维层次,高智力水平的艺术,一种独立于史诗、音乐、绘画的数学美。
”奥林匹克技巧是竞赛数学中一个生动而又活跃的组成部分。
2-7-1 构造它的基本形式是:以已知条件为原料、以所求结论为方向,构造出一种新的数学形式,使得问题在这种形式下简捷解决。
常见的有构造图形,构造方程,构造恒等式,构造函数,构造反例,构造抽屉,构造算法等。
例2-127 一位棋手参加11周(77天)的集训,每天至少下一盘棋,每周至多下12盘棋,证明这棋手必在连续几天内恰好下了21盘棋。
证明:用n a 表示这位棋手在第1天至第n 天(包括第n 天在内)所下的总盘数(1,2,77n =…),依题意 127711211132a a a ≤<<≤⨯=…考虑154个数:12771277,,,21,21,21a a a a a a +++…,又由772113221153154a +≤+=<,即154个数中,每一个取值是从1到153的自然数,因而必有两个数取值相等,由于i j ≠时,i i a a ≠ 2121i j a a +≠+故只能是,21(771)i j a a i j +≥>≥满足 21i j a a =+ 这表明,从1i +天到j 天共下了21盘棋。
这个题目构造了一个抽屉原理的解题程序,并具体构造了154个“苹果”与153个“抽屉”,其困难、同时也是精妙之处就在于想到用抽屉原理。
初三奥林匹克数学竞赛方法思路讲解及经典题型分析-第11套题

初三奥林匹克数学竞赛方法思路讲解及经典题型分析…………第十一节…………圆、圆和直线的位置关系解题技巧及典型题目类型1 (第六届江苏省初中数学竞赛试题)如图,NS是⊙O的直径,弦AB和NS垂直,且交NS于M,P 为优弧ANB上异于N的任意一点,PS交AB于R,PM的延长线交⊙O于Q,求证:RS>MQ。
2 (第九届江苏省初中数学竞赛试题)如图,在Rt△ABC中,∠ACB=90o,M是AB上一点,且AM2+BM2+CM2=2AM+2BM+2CM-3。
若P是线段AC上的一个动点,⊙O是过P、M、C三点的圆,过P作PD∥AB交⊙O于D。
(1)求证:M是AB的中点。
(2)求PD的长。
3(00年北京市初中数学竞赛试题)如图,以△ABC的边AB为直径画圆,与边AB交于M,与边BC交于N,已知△ABC的面积是△CMN面积的4倍,△ABC中有一个内角度数是另一个内角度数的2倍,求△ABC的三个内角的度数。
4(第十二届江苏省初中数学竞赛试题)如图,已知A、B、C、D顺次在⊙O上,AB=BD,BM⊥AC 于M,求证:AM=DC+CM。
5(01年河北省初中数学竞赛试题)如图,在半径为r的⊙O中,AB为直径,C为弧AB的中点,D 为弧BC的三分之一点,且弧BD的长是弧CD的长的2倍,连结AD并延长交⊙O的切线CE于点E(C为切点)。
求AE长。
6(02年太原初中数学竞赛试题)如图,已知AB为⊙O的直径,C为⊙O上一点,延长BC至D,使CD=BC,CE⊥AD,垂足为E,BE交⊙O于F,AF交CE于P,求证:PE=PC。
7(00年全国理科班招生题)如图,PA、PB是⊙O的两条切线,PEC是一条割线,D是AB与PC的交点,若PE的长为2 ,CD=1,求DE的长。
8 锐角△ABC 的外接圆在B 和C 处的切线相交于P ,M 为BC 的中点,求证:BAC cos APAM ∠=。
初中数学奥林匹克竞赛解题方法大全(配PDF版)-第09章-三角形基本问题
107第九章 三角形基本问题第一节 三角形内角和【知识点拨】三角形内角和定理:三角形三个内角和为1800。
推论:(1)三角形的一个外角等于和它不相邻的两个内角之和。
(2)三角形的一个外角大于任何一个和它不相邻的内角。
凸n 边形的内角和为(n -2)×1800,凸n 边形的外角和为3600。
【赛题精选】例1、在△ABC 中,∠B =320,∠C =250,AD ⊥BC ,AE 平分∠BAC 。
求:∠DAE 的度数。
例2、如图,求∠1+∠2+∠3+∠4+∠5的度数。
【说明】如图中,很容易推出∠1+∠2=∠3+∠4的结论,这个结论经常会用到!例3、如图,∠DEA 的平分线与∠BCA 的平分线相交于点F 。
求证:∠F =21(∠B +∠D )。
108例4、试证明“三角形中的最大角不小于600,最小角不大于600。
”例5、平面上有四个点A 、B 、C 、D ,其中任何三点都不共线。
求证:△ABC 、△ABD 、△ACD 、△BCD 中至少一个内角不超过45°。
例6、P 为△ABC 内一点,求证∠BPC >∠BAC 。
例7、如图,B 、C 、D 三点在同一直线上,∠ABC 的平分线与∠ACD 的平分线交于点E 。
109求证:∠E =21∠A 。
例8、∠AEB 、∠AFD 的平分线相交于O 点。
求证∠EOF =21(∠DAB +∠BCD )。
例9、如图E 是△ABC 中AC 边延长线上一点,∠BCE 的平分线交AB 延长线于D 。
若∠CAB =400,∠CBD =680。
求CDB 的度数。
例10、证明:凸n 边形中锐角的个数不超过3个。
110【针对训练】A 组1、如右图,在△ABC 中,∠A =700,∠B 、∠C 的平分线交于点O ,求∠BOC 的度数。
2、试证明三角形中直角或钝角的个数不能多于一个。
3、在△ABC 中,∠A ≥1200,试证明∠B 、∠C 中至少有一个不超过300。
4、如右图,在△ABC 中,∠BAC =420,∠B 、∠C 的三等分线分别交于D 、E ,求∠BDC 、∠BEC 的度数。
初中数学奥林匹克赛题解析知识点整理

初中数学奥林匹克赛题解析知识点整理数学奥林匹克赛是一项旨在培养学生数学思维能力和解决问题能力的比赛。
它涵盖了初中数学的各个领域,并且难度较高,需要学生具备一定的数学基础和解题技巧。
在本文中,我们将解析一些常见的初中数学奥林匹克赛题,并整理出一些涉及的重要知识点,帮助学生更好地准备和应对这类比赛。
1. 方程的解析解法在初中数学奥林匹克赛中,经常会出现一些复杂的方程问题。
要解决这类问题,我们首先要掌握方程的基本概念和解法。
一般来说,方程的解就是使得方程两边相等的未知数值。
我们可以通过消元、配方法、因式分解等一系列的运算步骤,得出方程的解。
对于一些复杂的方程,我们还可以利用图形解法、特殊解法等方法求解。
2. 几何图形的性质分析几何问题是初中数学奥林匹克赛中的重要题型之一。
在解答几何题时,我们需要掌握各类几何图形的性质和定理。
例如,矩形的对角线相等、平行四边形的对边平行等。
同时,我们要善于利用图形的特殊性质来解决问题,比如利用对称性、相似性等特点进行推理。
3. 数列的性质和求解方法数列是数学奥林匹克赛中的常见题型。
学生要能够分析数列的性质并运用相关的公式和定理。
例如,等差数列的通项公式为an=a1+(n-1)d,等比数列的通项公式为an=a1*q^(n-1)。
我们还需要熟练掌握数列的求和公式,如等差数列的前n项和Sn=n/2*(a1+an)。
4. 不等式的求解技巧不等式在初中数学奥林匹克赛中也是常见的题型。
要解决不等式问题,我们需要利用各种不等式的性质和定理。
例如,对于一元一次不等式ax+b>0,如果a>0,那么解集为x>-b/a;如果a<0,那么解集为x<-b/a。
此外,我们还要善于进行不等式的加减乘除操作,以求得不等式的解。
5. 组合数学的运算方法组合数学是数学奥林匹克赛中的一道难题。
学生要能够灵活运用组合数学的技巧和公式。
例如,排列组合的计算公式为C(n,m)=n!/m!(n-m)!,其中n为总数,m 为选择个数。
初中数学竞赛教程及练习之面积法附答案

面积法一、内容提翼.因为面积公式是用线段的代数式表示的,所以面积与线段可以互相转换。
运用面积公式及有关面积性质定理解答儿何题是常用的方法,简称面积法。
.面积公式(略)两个三角形的面积比定理.等高(底)的两个三角形的面积比,等于它们对应的底(高)的比.有一个角相等或互补的两个三角形面积的比等于夹这个角两边的乘积的比.相似三角形面积的比等于它们的相似比的平方.有公共边的两个三角形面积的比等于它们的第三顶点连线被公共边分成的两条线段的比(内分比或外分比K a A如图△ABC和AADC有公共边AC,氽M内分BD o第三顶点连线BD被公共边AC/l\/\内分或外分于点M,//X.则』空十尸汶4。
‘△ADC MD定理④是以公共边为底,面积的比等于它们的对应高的比换成对应线段的比二、例题.求证有一个30度角的菱形,边长是两条对角线的比例中项已知:菱形ABCD中,ZDAC=30°求证:ab2=acxbd证明:作高DE,VZDAE=30°.•.de=L ad=L ab S22S菱形abcd=ACXBD./.AB2=ACXBD.求证:等边三角形内任一点到各边的距离的和是一个定值已知:AABC中,AB=BC=AC,D是形内任一点,DE±BC.DF_LAC,DG±AB,E, F.G是垂足求证:DE+DF+DG是一个定值证明:连结DA,DB.DC,设边长为a,‘△abc=S mbc+S adca+S adabC lah a=-J-a(DE+DF+DG)22.•.DE+DF+DGf...等边三角形的高h,是一个定值,...DE+DF+DG是一个定值本题可推广到任意正n边形,其定值是边心距的n倍f aAD BE CF 1已知:AABC 中,——=——=——=-AB BC CA 3求:萨虬的值'△ABCBE (本题可推广到:1—,---=—,m BC n 竺=顼CA p'△DEh mn P + "1 + 〃 + p - mn - nip - np )S A abc mnP如图RtAABC 被斜边上的高CD 和直角平分线CE 分成3个三角形,已知其中两个面积的值标在图中,求第三个三角形的面积X 。
初中数学奥林匹克竞赛解题方法大全(配PDF版)-第06章-几何基础知识

第六章几何基础知识第一节线段与角的推理计算【知识点拨】掌握七条等量公理:1、同时等于第三个量的两个量相等。
2、等量加等量,和相等。
3、等量减等量,差相等。
4、等量乘等量,积相等。
5、等量除以等量(0除外),商相等。
6、全量等于它的各部分量的和。
7、在等式中,一个量可以用它的等量来代替(等量代换)。
【赛题精选】例1、如图,∠AOB=∠COD,求证:∠AOC=∠BOD。
例2、C、D为线段AB上的两点,AD=CB,求证:AC=DB。
例3、AOB是一条直线,∠AOC=600,OD、OE分别是∠AOC和∠BOC的平分线。
问图中互为补角关系的角共有多少对?例4、已知B、C是线段AD上的任意两点,M是AB的中点,N是CD的中点,若MN=a,BC=b,求CD的长。
例5、已知OM是∠AOB的平分线,射线OC在∠BOM内部,ON是∠BOC的平分线,且∠AOC=800。
求∠MON的度数。
例6、已知A、O、B是一条直线上的三个点,∠BOC比∠AOC 大240,求∠BOC、∠AOC的度数。
例7、如图,AE=8.9CM,BD=3CM。
求以A、B、C、D、E这5个点为端点的所有线段长度的和是多少?例8、线段AB上的P、Q两点,已知AB=26CM,AP=14CM,PQ=11CM。
求线段BQ的长。
例9、已知∠AOC=∠BOD=1500,∠AOD=3∠BOC。
求∠BOC的度数。
例10、已知C是AB上的一点,D是CB的中点。
若图中线段的长度之和为23CM,线段AC的长度与线段CB 的长度都是正整数。
求线段AC的长度是多少厘米?【针对训练】第二节相交线与平行线【知识点拨】平行公理:经过直线外一点,有且只有一条直线和已知直线平行。
相交线性质:两直线相交,对顶角相等。
平行线性质定理平行线的判定定理两直线平行,同位角相等。
同位角相等,则两直线平行。
两直线平行,内错角相等。
内错角相等,则两直线平行。
两直线平行,内旁内角互补。
同旁内角互补,则两直线平行。
相似三角形与面积有关的问题-含详细参考答案

中考数学复习之相似三角形有关的面积问题(学案)知识与方法梳理 处理面积问题的三种方法 1. 公式法2. 割补法(分割求和,补形作差)3. 转化法(相似类、同底类、共高或等高类)利用常见结构进行转化是在复杂背景下处理面积问题的通常思路,在转化过程中需要结合背景的特点.动态背景:要抓住变化过程中所求面积不变的特征;函数背景:优先考虑公式法,或者割补之后采用公式法,也可结合几何特征进行转化; 探索规律背景:根据结构特征确定第一项的处理办法,后续进行类比. 面积问题中的常见结构举例例1:如图,在Rt ABC △中,1D 是斜边AB 的中点.过1D 作11D E AC ⊥于E 1,连接1BE 交1CD 于2D ,过2D 作22D E AC ⊥于2E ,连接2BE 交1CD 于3D ,过3D 作33D E AC ⊥于3E ,连接3BE 交1CD 于4D …如此继续.11E BD 1S S ∆=22E BD 2S S ∆=33E BD 3S S ∆=nn E BD n S S ∆=则n S =____________ABC S △(用含n 的代数式表示).32E 1D 4D 3D 2D 1CBA分析:题目中的相似三角形非常之多,三角形的面积关系也非常之多,这是面积问题同学们需要面对的第一大难题,处理好这些关系,才能最终解决问题; 解:1.易知E 1为AC 的中点,S ∆ABE1=12S ∆ABC ,D1为AB 的中点,S ∆BD1E1=12S ∆ABE1,故S ∆BDE =14S ∆ABC ;2. D 1E 1||BC ,1112D E AC =,故E 2为E 1C 的三等分点,12113BE E BCE S S ∆∆=,D 2为BE 1的三等分点,故222123BD E BE E S S ∆∆=,112BE C ABC S S ∆∆=,故2219BD E ABC S S ∆∆=3. 易知221123D E D E =,111AC 2D E =,故221AC 3D E =,D 3为BE 2的四等分点,231211212BE E BE E ABC S S S ∆∆∆==,,而33116BD E ABC S S ∆∆=;综合上述,猜想S n =21(1)ABCS n ∆+练习题1. 如图,△ABC 的面积为63cm 2,D 是BC 上的一点,且BD :CD =2:1,DE △AC 交AB 于点E ,延长DE 到F ,使FE :ED =2:1,连接CF ,则△CDF 的面积为 .FED CBA2. 如图,在△ABC 中,D ,E 分别是边AB ,AC 的中点,G 为EC 的中点,连接DG 并延长交BC 的延长线于点F ,BE 与DF 交于点O .若△ADE 的面积为S ,则四边形BOGC 的面积为_______.G ODCAE BF3. 如图,在梯形ABCD 中,AB △CD ,AB =3CD ,对角线AC ,BD 交于点O ,中位线EF 与AC ,BD 分别交于点M ,N ,则图中阴影部分的面积是梯形ABCD 面积的( ) A .12 B .13 C .14 D .474. 如图,点A 1,A 2,A 3,A 4在射线OA 上,点B 1,B 2,B 3在射线OB 上,且A 1B 1△A 2B 2△A 3B 3,A 2B 1△A 3B 2△A 4B 3.若△A 2B 1B 2,△A 3B 2B 3的面积分别为1,4,则图中阴影部分的面积为_______.12345.如图,点D是△ABC的边AB的延长线上一点,点F是边BC上的一个动点(不与点B重合).以BD,BF为邻边作平行四边形BDEF,又AP△BE,且AP=BE(点P,E在直线AB的同侧),若14BD AB,则△PBC的面积与△ABC的面积的比值是___________.ABCD EFPG6.如图,已知直线l1:y=23x+83与直线l2:y=-2x+16相交于点C,直线l1,l2分别交x轴于A,B两点,矩形DEFG的顶点D,E分别在l1,l2上,顶点F,G都在x轴上,且点G与点B重合,那么S矩形DEFG:S△ABC=____________.7.已知:如图,DE是△ABC的中位线.点P是DE的中点,连接CP并延长交AB于点Q,那么S△DPQ:S△ABC=_________.QP EDC BA8.如图,在△ABC中,CE:EB=1:2,DE△AC.若△ABC的面积为S,则△ADE的面积为____________.9.如图,已知△ABC△△DCE△△HEF,三条对应边BC,CE,EF在同一条直线上,连接BH,分别交AC,DC,DE于点P,Q,K.若△DQK的面积为2,则图中阴影部分的面积为__________.10.如图,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连接DN,EM交于点F.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分的面积为___________.参考答案1.422.7 4 S3.C4.21 25.3 46.8:9 7.1:248.2 9 S9.26 10.30cm2。
初中数学重点梳理:面积问题的解决方法
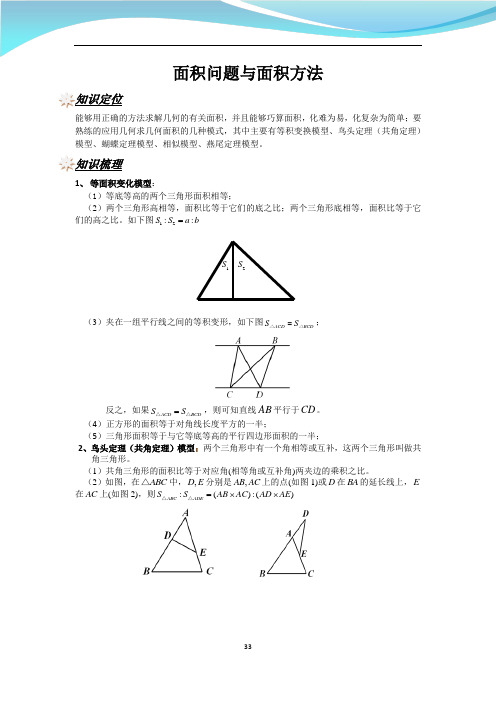
面积问题与面积方法知识定位能够用正确的方法求解几何的有关面积,并且能够巧算面积,化难为易,化复杂为简单;要熟练的应用几何求几何面积的几种模式,其中主要有等积变换模型、鸟头定理(共角定理)模型、蝴蝶定理模型、相似模型、燕尾定理模型。
知识梳理1、 等面积变化模型:(1)等底等高的两个三角形面积相等;(2)两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如下图12::S S a b =(3)夹在一组平行线之间的等积变形,如下图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD 。
(4)正方形的面积等于对角线长度平方的一半;(5)三角形面积等于与它等底等高的平行四边形面积的一半;2、鸟头定理(共角定理)模型:两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
(1)共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
(2)如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△1S 2S3、蝴蝶定理模型:任意四边形中的比例关系。
蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
① 1243::S S S S =1324S S S S ⨯=⨯ ② ()()1243::AO OC S S S S =++ 4、相似模型:相似三角形:相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:(1)相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; (2)相似三角形的面积比等于它们相似比的平方。
非学科数学学培训-相似与面积(资料附答案)

自学资料一、相似三角形综合复习【知识探索】1.面积的计算方法:(1)规则图形:运用公式直接计算;(2)不规则图形:割补法。
二、相似三角形判定与性质综合【知识探索】1.面积问题:(1)规则图形:直接运用公式计算即可;(2)不规则图形:割补法求面积。
【错题精练】例1.如图,在△ABC中,∠A=36∘,AC=AB=2,将△ABC绕点B逆时针方向旋转得到△DBE,使点E在边AC上,DE交AB于点F,则△AFE与△DBF的面积之比等于()第1页共40页自学七招之日计划护体神功:每日计划安排好,自学规划效率高非学科培训A. √5−1;2B. √5−1;4C. 3−√5;2.D. 3−√54【答案】C例2.如图,已知D、E分别是△ABC的AB,AC边上的点,DE∥BC,且S△ADE:S四边形DBCE=1:8,那么AE:AC等于()A. 1:9B. 1:3C. 1:8D. 1:2【答案】B例3.如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中阴影部分)的面积分别是4,9和49.则△ABC的面积是__________第2页共40页自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌非学科培训【解答】【答案】144例4.如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为1,4,则图中三个阴影三角形面积之和为__________第3页共40页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训【解答】【答案】10.5例5.如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以3cm/s的速度向A点运动.设运动时间为x(s).(1)当x为何值时,PQ//BC;(2)当△APQ与△CQB相似时,AP的长为_________;(3)当S△BCQ:S△ABC=1:3,求S△APQ:S△ABQ的值.第4页共40页自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌非学科培训【解答】【答案】见解析例6.如图,等腰△ABC中,BA=BC,AO=3CO=6,动点F在BA上以每分钟5个单位长度的速度从第5页共40页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训B点出发向A点移动,过F作FE∥BC交AC边于E点,连结FO、EO.(1)求A、B两点的坐标;(2)证明:当△EFO面积最大时,△EFO∽△CBA;(3)在(2)的基础上,BC边上是否还存在一个点D,使得△EFD≌△FEO?若存在,请求出D点的坐标;若不存在,试说明理由.【解答】(1)解:∵AO=3CO=6,∴CO=2.∴C(2,0),A(0,6).设BO=x,且x>0,则BC2=(2+x)2,AB2=AO2+OB2=36+x2,又∵BC=AB,∴(2+x)2=36+x2.解得x=8,∴B(-8,0).(2)解:如图1,过F点作FK⊥BC于K,可设F点移动的时间为t,且0<t<2,则:BF=5t,TO=FK=3t,∴AT=6−3t.又∵FE∥BC,∴△AFE∽△ABC.而AO⊥BC交EF于T,则:EFBC =ATAO,∴EF10=6−3t6.即EF=10−5t,故S△EFO=12EF×TO=12(10−5t)×3t,即S△EFO=−152(t−2)t,∴当t=1时,△EFO的面积达到最大值.此时BF=FA,EF恰好为△ABC的中位线,则:EFBC =12,又有AO⊥BC于O,第6页共40页自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌非学科培训则:FOAB =EOAC=12,∴FOAB =EOAC=FEBC.∴△EFO∽△CBA.(3)解:在(2)的基础上,E、F分别是AC、AB的中点,若使D为BC的中点时,FOAB =EOAC=FEBC=12,又∵FOAB =EOAC=FEBC,∴FO=ED,EO=FD,EF=FE.∴△EFD≌△FEO.故:存在满足条件的D点,其坐标为(-3,0).【答案】(1)(-8,0);(2)略;(3)(-3,0).例7.如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向A点运动,设运动时间为x秒.(1)x为何值时,PQ//BC;(2)是否存在某一时刻,使△APQ∽△CQB?若存在,求出此时AP的长;若不存在,请说明理由;(3)当时,求的值.第7页共40页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训【解答】第8页共40页自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌非学科培训【答案】见解析例8.如图所示,△ABC中,∠B=90°,点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B 点开始沿BC边向点C以2cm/s的速度移动.(1)如果P,Q分别从A,B同时出发,经几秒,使△PBQ的面积等于8cm2?(2)如果P,Q分别从A,B同时出发,并且P到B后又继续在BC边上前进,Q到C后又继续在CA 边上前进,经过几秒,使△PCQ的面积等于12.6cm2?第9页共40页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训【解答】【答案】见解析例9.如图,在△ABC中,已知AB=BC=AC=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s,点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为t(s),(1)求t为何值时,PQ⊥AC;(2)当0<t<2时,求证:AD平分△PQD的面积;(3)当0<t<2时,求△PQD面积的最大值.第10页共40页自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌非学科培训【解答】【答案】见解析例10.如图,已知A、B两点的坐标分别为(40,0)和(0,30),动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动、动直线EF从x轴开始以每1个单位的速度向上平行移动(即EF//x轴),并且分别与y轴、线段AB交于点E、F,连接EP、FP,设动点P与动直线EF同时出发,运动时间为t秒.(1)求t=15时,△PEF的面积;(2)直线EF、点P在运动过程中,是否存在这样的t,使得△PEF的面积等于160(平方单位)?若存在,请求出此时t的值;若不存在,请说明理由.(3)当t为何值时,△EOP与△BOA相似.【解答】【答案】见解析例11.如图,已知△ABC中,AB=AC=a,BC=10,动点P沿CA方向从点C向点A运动,同时,动点Q沿CB方向从点C向点B运动,速度都为每秒1个单位长度,P、Q中任意一点到达终点时,另一点也随之停止运动.过点P作PD//BC,交AB边于点D,连接DQ.设P、Q的运动时间为t.(1)直接写出BD的长;(用含t的代数式表示)(2)若a=15,求当t为何值时,△ADP与△BDQ相似;(3)是否存在某个a的值,使P、Q在运动过程中,存在S△BDQ:S△ADP:S梯形CPDQ=1:4:4的时刻,若存在,求出a的值;若不存在,请说明理由.【解答】【答案】见解析例12.如图,抛物线y=x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0).(1)求该抛物线的解析式.(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.【答案】解:(1)把点C(0,﹣4),B(2,0)分别代入y= x2+bx+c中,(3)△OMD为等腰三角形,可能有三种情形:(I)当DM=DO时,如答图①所示.DO=DM=DA=2,∴∠OAC=∠AMD=45°,∴∠ADM=90°,∴M点的坐标为(﹣2,﹣2);(II)当MD=MO时,如答图②所示.过点M作MN⊥OD于点N,则点N为OD的中点,∴DN=ON=1,AN=AD+DN=3,又△AMN为等腰直角三角形,∴MN=AN=3,∴M点的坐标为(﹣1,﹣3);(III)当OD=OM时,∵△OAC为等腰直角三角形,【举一反三】1.如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为()A.B.C.D.【解答】【答案】D2.如图,在Rt△ABC中,∠C=90°,P是BC边上不同于B,C的一动点,过点P作PQ⊥AB,垂足为Q,连接AP.若AC=3,BC=4,则△AQP的面积的最大值是()A.B.C.D.【解答】【答案】C3.如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HE•HB=,BD、AF 交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=;④若BE平分∠DBC,则正方形ABCD的面积为4.其中正确的结论个数有()A. 1个B. 2个C. 3个D. 4个【解答】【答案】D4.如图,正方形ABCD中,O为BD中点,以BC为边向正方形内作等边△BCE,连接并延长AE交CD于F,连接BD分别交CE、AF于G、H,下列结论:①∠CEH=45°;②GF∥DE;③2OH+DH=BD;④BG=DG;⑤.其中正确的结论是()A. ①②③B. ①②④C. ①②⑤D. ②④⑤【解答】【答案】C5.如图,在△ABC中,AB=AC=10,BC=12,AD⊥BC于点D,点E在边AB上运动,过点E作EF∥BC与边AC交于点F,连结FD,以EF、FD为邻边作▱EFDG,当▱EFDG与△ABC重叠部分为△ABC的面积的时,线段EF的长为__________ .【解答】【答案】6.如图,在平面直角坐标系中,点C(﹣3,0),点A、B分别在x轴、y轴的正半轴上,且满足.(1)求点A、B的坐标;(2)若点P从点C出发,以每秒1个单位的速度沿射线CB运动,连接AP.设△ABP的面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量t的取值范围.(3)在(2)的条件下,是否存在点P,使以点A、B、P为顶点的三角形与△AOB相似?若存在,直接写出点P坐标;若不存在,说明理由.【解答】【答案】见解析7.在△ABC中,AB=AC=5,BC=6,点D在边AB上,DE⊥AB,点E在边BC,点F在边AC上,且∠DEF=∠B.(1)求证:△FCE∽△EBD;(2)当点D在线段AB上运动时,是否有可能使S△FCE=4S△EBD?如果有可能,那么求出BD的长;如果不可能,请说明理由.【解答】【答案】见解析8.如图,在等腰△ABC中,AB=AC=5cm,BC=6cm,点P从点B开始沿BC边以每秒1cm的速度向点C运动,点Q从点C开始沿CA边以每秒2 cm的速度向点A运动,DE保持垂直平分PQ,且交PQ于点D,交BC于点E.点P,Q分别从B,C两点同时出发,当点Q运动到点A时,点Q、P停止运动,设它们运动的时间为x cm.(1)当x=____秒时,射线DE经过点C;(2)当点Q运动时,设四边形ABPQ的面积为ycm2,求y与x的函数关系式(不用写出自变量取值范围);(3)当点Q运动时,是否存在以P、Q、C为顶点的三角形与△PDE相似?若存在,求出x的值;若不存在,请说明理由.【解答】【答案】见解析9.已知:如图①在▱ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速运动,速度为1cm/s,当点P与点C 重合时△PNM停止平移,点Q也停止运动.如图②设运动时间为t(s).解答下列问题:(1)当t为_____S时,点P与点C重合;(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;(3)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.【解答】【答案】见解析10.如图,Rt△ABC的两条直角边AB=4cm,AC=3cm,点D沿AB从A向B运动,速度是1cm/秒,同时,点E沿BC从B向C运动,速度为2cm/秒.动点E到达点C时运动终止.连接DE、CD、AE.(1)当动点运动几秒时,△BDE与△ABC相似?(2)设动点运动t秒时△ADE的面积为s,求s与t的函数解析式;(3)在运动过程中是否存在某一时刻t,使CD⊥DE?若存在,求出时刻t;若不存在,请说明理由.【解答】【答案】见解析11.如图,抛物线y=ax2+bx+c经过点A(﹣6,0),B(2,0),C(0,﹣6).(1)求抛物线的解析式;(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.【答案】1.如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△CEF:S四边形BCED的值为()A. 1:3B. 2:3C. 1:4D. 2:5【解答】【答案】A2.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.则下列结论:①若∠MFC=130°,则∠MAB=40°;②∠MPB=90°﹣∠FCM;③△ABM∽△CEF;④S四边形AMED﹣S△EFC;=2S△MFC′.正确的是()A. ①②④B. ①③④C. ②③D. ①②③④【解答】【答案】D3.如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为()A.B.C.D.【解答】【答案】C4.如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.(1)求证:△AOD∽△BOC;(2)若cos∠ABO=,S△BOC=18,求S△AOD的值.【答案】5.如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC 的方向匀速运动,速度为2cm/秒;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/秒,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).(1)当t为何值时,PM∥BC?(2)设四边形PQCM的面积为ycm²,求y与t之间的函数关系式;(3)已知某一时刻t,有S四边形PQCM=S△ABC成立,请你求出此时t的值.【答案】。
初中奥数常用的解题方法

初中奥数常用的解题方法初中奥数常用的解题方法【配方法】所谓配方,就是把一个解析式利用恒等变形的方法,把其中的某些项配成一个或几个多项式正整数次幂的和形式。
通过配方解决数学问题的方法叫配方法。
其中,用的最多的是配成完全平方式。
配方法是数学中一种重要的恒等变形的方法,它的应用十分非常广泛,在因式分解、化简根式、解方程、证明等式和不等式、求函数的极值和解析式等方面都经常用到它。
【因式分解法】因式分解,就是把一个多项式化成几个整式乘积的形式。
因式分解是恒等变形的基础,它作为数学的一个有力工具、一种数学方法在代数、几何、三角等的解题中起着重要的作用。
因式分解的方法有许多,除中学课本上介绍的提取公因式法、公式法、分组分解法、十字相乘法等外,还有如利用拆项添项、求根分解、换元、待定系数等等。
【换元法】换元法是数学中一个非常重要而且应用十分广泛的解题方法。
我们通常把未知数或变数称为元,所谓换元法,就是在一个比较复杂的数学式子中,用新的变元去代替原式的一个部分或改造原来的式子,使它简化,使问题易于解决。
【判别式法与韦达定理】一元二次方程ax2+bx+c=0(a、b、c属于R,a≠0)根的判别,△=b2-4ac,不仅用来判定根的性质,而且作为一种解题方法,在代数式变形,解方程(组),解不等式,研究函数乃至几何、三角运算中都有非常广泛的应用。
韦达定理除了已知一元二次方程的一个根,求另一根;已知两个数的和与积,求这两个数等简单应用外,还可以求根的对称函数,计论二次方程根的符号,解对称方程组,以及解一些有关二次曲线的问题等,都有非常广泛的.应用。
【待定系数法】在解数学问题时,若先判断所求的结果具有某种确定的形式,其中含有某些待定的系数,而后根据题设条件列出关于待定系数的等式,最后解出这些待定系数的值或找到这些待定系数间的某种关系,从而解答数学问题,这种解题方法称为待定系数法。
它是中学数学中常用的方法之一。
【构造法】在解题时,我们常常会采用这样的方法,通过对条件和结论的分析,构造辅助元素,它可以是一个图形、一个方程(组)、一个等式、一个函数、一个等价命题等,架起一座连接条件和结论的桥梁,从而使问题得以解决,这种解题的数学方法,我们称为构造法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一章相似形与面积问题第一节相似三角形【知识点拨】1、相似三角形的判定:(1)两角对应相等,两个三角形相似;(2)两边对应成比例且夹角相等,两个三角形相似;(3)三边对应成比例,两个三角形相似;(4)如果两个直角三角形的斜边和一条直角边对应成比例,这两个直角三角形相似。
2、相似三角形的性质(1)相似三角形的对应角相等,对应边成比例;(2)相似三角形的对应高的比、对应中线的比、对应角平分线的比、对应周长的比都等于相似比;(3)相似三角形的面积比等于相似比的平方。
3、涉及的问题及解题思路:证线段成比例、线段相等、线段的和差倍分、角相等;证平行、计算线段长;求三角形的面积。
解题时,要注意抓住题设、结论的特点,设法将问题设法与证两个三角形相似联系。
【赛题精选】例1、已知正方形ABCD的边长是5厘米,EF=FG,FD=DG。
求△ECG的面积。
(2003年河北省竞赛题)Array【说明】在相似形中,计算线段长的主要方法是由线段成比例定理(如平行线分线段成比例定理、相似三角形的性质等)列出含待求线段的比例式,再设法求出待求线段的长。
154155例2、已知在平行四边形ABCD 中,M 、N 为AB 的三等分点,DM 、DN 交于AC 于P 、Q 两点。
求AP :PQ :QC 的值。
(2001年河北省竞赛题)【说明】解线段a :b :c 的问题,可根据相关的性质将a 、b 、c 用同一条线段表示出来,再求几条线段的比。
若a 、b 、c 正好可组成一条线段,常用这条线段表示这三条线段。
例3、正方形ABCD 中,E 是对角线AC 上一点,F 是边AB 上一点,且AE =2EC ,FB =2AF 。
求∠EDF 的度数(2002年河南省竞赛题)例4、如图,四边形ABCD 中,AC 与BD 交于点O ,直线l ∥BD ,且与AB 、DC 、BC 、AD 及AC 的延长线分别相交于点M 、N 、R 、S 和P 。
求证:P M ·PN =PR ·PS 。
(1999年山东竞赛题)【说明】证明线段成比例的方法有:证两个三角形相似、等线代换法、等比代换法。
对于等积式的证明,常将其改证比例式,若比例式不能用上述三种方法证明时,可证等积式两边都等于第三个某两条线段的乘积。
156例5、正方形ABCD 中,M 、N 分别在AB 、BC 边上,且BM =BN ,又BP ⊥MC 于P 。
求证:PD ⊥PN 。
(1990年四川省竞赛题)【说明】要证相等的两角是两个三角形的角,若能证这两个三角形相似,且两角是对应角,则达到两角相等。
此种方法是证角相等的常用方法。
例6、在△ABC 中,∠A :∠B :∠C =1:2:4。
求证:BC AC AB 111=+。
【说明】要证明形如c b a 111=+几何题的常用方法有: (1) 比例法:将原等式变形为c ab b a 1=+、cb a b a =+,故构造以a +b 、b 为边且与a 、c 所在三角形相似的三角形;(2) 通分法:先将原等式变形为1=+bc a c 。
利用相关定理将两个比通分,即证出d m a c 1=、dm b c 2=,且d m m =+21,则原式成立。
157例7、在△ABC 中,∠ACB =2∠ABC 。
求证:BC AC AC AB ∙+=22。
(按图示辅助线以两种方法证明)【说明】证明ef cd ab ±=型命题常用以下方法:(1) 利用提公因式或平方差公式,将原式转化为等积式,再利用三角形相似加以证明;(2) 要证ef cd ab ±=,可在线段b 所在的直线上取一点,则21b b b ±=,则ef cd b b a ±=±)(21,再证cd ab =1、ef ab =2即可。
例8、在△ABC 中,D 、E 分别是BC 、AB 上一点,且∠1=∠2=∠3,如果△ABC 、△EBD 、△ADC 的周长依次是m 、1m 、2m 。
求证:4521≤+m m m (1989年全国联赛题)158例9、在△ABC 中,BC >AC ,CH 是AB 上的高,且BH AH BCAC 22。
试证明∠A +∠B =900或∠A -∠B =900。
(2001年全国初中数学联赛武汉选拨赛题)【针对训练】1、在△ABC中,已知AB=3、AC=4、BC=5,现将它折叠,使B、C两点重合,则折痕长是__________. (2003年全国初中联合竞赛题)159160161第二节 角平分线定理【知识点拨】1、三角形内角平分线的性质定理:三角形内角的平分线内分对边所成的两条线段和相邻两边对应成比例。
(试证明)2、三角形外角平分线性质定理:三角形外角平分线分对边所得的两条线段和相邻的两边对应成比例。
3、常见问题对于涉及角平分线的相关计算,常由角平分线性质定理列出比例式进行计算,对于关于角平分线的证明题,常由角平分线性质定理列出比例式进行代换,达到证明的目的。
【赛题精选】例1、在△ABC 中,∠C =900,CD 是∠C 的平分线,且CA =3,CB =4。
求CD 的长。
例2、若PA =PB ,∠APB =2∠ACB ,AC 与PB 相交于点D ,且PB =4,PD =3。
求A D ·DC 的值。
(2001年全国竞赛题)【说明】角平分线性质定理又提供计算线段的方法,解题时要注意应用。
计算时要注意对应关系,正确书写比例式。
对于求线段ab 的值的题目,常由相关定理证出等积式ab =cd ,求出cd 的值即可。
162例3、I 是△ABC 内角平分线的交点,AI 交对应边于D 。
求证:BCAC AB ID AI +=。
例4、Rt △ABC 中,∠ACB =900,CD ⊥AB 于D ,AF 平分∠CAB 交CD 于E ,交CB 于F ,且EG ∥AB 交CB 于G 。
试求:CF 与GB 的大小关系如何?(1998年“希望杯”邀请赛题)【说明】欲证线段a =b ,由线段成比例定理得出含a 、b 的比例式,111n m x a =、222n m x b =, 然后证2211n m n m =,从而得到21x b x a =,再证21x x =,从而得到a =b 。
本题证法较多,如过点E 作EH ∥BC 交AB 于H ,则EH =GB ,再证EH =EC 、EC =CF ;或过F 作FM ⊥AB 于M ,证Rt △CEG ≌Rt △FMB 。
163 例5、在△ABC 中,AD 平分∠BAC ,CE ⊥AD 交AB 于G ,AM 是BC 边的中线,交CG 于F 。
求证:AC ∥DF 。
【说明】三角形角平分线的性质为比例关系的转化提供了新的方法,从而开阔了解题思路,另外在证明几何题时,还应注意合比、等比性质的应用。
本题是由线段成比例证明两条直线平行的,这是证两条直线平行的新方法,对于题设中有平行、角平分线条件证平行的题目,常用此方法证明。
例6、在△ABC 中,A 、B 、C 的对边分别是a 、b 、c ,且a >b >c ,AS 、AS ’为∠A 的平分线与外角的平分线,BT 、BT ’为∠B 的平分线与外角平分线,CU 、CU ’为∠C 的平分线及外角平分线。
求证:T T U U S S '='+'111。
(1990年上海市竞赛题)【说明】通过本题的求解,我们得到cb a 111=+型几何题的又一种解法,即分别计算出a 、b 、c 的值,再验证等式两边相等。
【针对训练】164165第三节 面积证题初步【知识点拨】1、用面积证题就是利用面积关系建立线段之间的关系,或根据面积有关性质将线段关系转化为面积关系,通过解方程或适当变形,从而解决线段有关问题。
2、对于由面积关系建立线段关系常用几种方法:(1)利用一个图形的面积的几种不同的等积表示;(2)利用面积相等;(3)利用一个图形的面积等于几个图形的面积的和或倍数。
而证明面积相等常用的方法是:等底等高的三角形面积相等。
3、对于涉及线段比,常用以下性质将线段比转化为面积比;(1)两个等高的三角形的两底之比,等于两个三角形的面积之比;两个等底的三角形的两高之比,等于两个三角形的面积比。
(2)相似三角形的面积比等于相似比的平方。
【赛题精选】例1、设△ABC 的面积是1,D 是BC 上一点,且DC =2BD (BD/DC =1/2),若在AC 上取一点E ,使四边形ABDE 的面积为4/5。
求AE/EC 的值。
(2003年全国初中数学竞赛天津赛区初赛题)例2、在直角梯形ABCD 中,底AB =13、CD =8,AD ⊥AB ,且AD =12。
求A 到BC 的距离。
(2003年全国初中竞赛联合竞赛初赛题)166例3、设△ABC 的三边a 、b 、c ,三边上的高分别为h 1、h 2、h 3,三边满足2b =a +c 。
求证:ca b h h h 112+=。
(1996年山东省初中数学竞赛题)例4、在矩形ABCD 中,已知AD =12,AB =5,P 是AD 边上任意一点,PE ⊥BD ,PF ⊥AC ,E 、F 分别是垂足。
求PE +PF 的值。
(1998年全国竞赛题)【说明】对于垂线段的和差问题,常利用一个三角形的面积等于几个三角形的面积的和差来求。
已知直角三角形的三边,求斜边上的高,由面积法来求比较方便。
例5、平行四边形ABCD 中,M 、N 分别是AD 、AB 上的点,且BM =DN ,其交战为P ,设∠CPB =α,∠CPD =β,则 ( )A 、α=βB 、α>βC 、α<βD 、α、β大小无法确定(1993年哈尔滨市竞赛题)【说明】欲证明两线段相等,可证它们所在的三角形的面积相等,进而得出两个三角形的底、高的关系式。
若两高相等,则两底相等;反之则两高相等。
167例6、设P 、Q 为线段BC 上两点,且BP =CQ ,A 为BC 外一点,当点A 运动到使∠BAP =∠CAQ 时,△ABC 是什么三角形,并证明。
(1986年全国联赛题)【说明】证明线段的等积式时,要注意等积式的特点,若两线段乘积与某个图形的面积有关,则等积式可由面积公式证得。
例7、已知△PQR 、△P ’Q ’R ’是两个全等的等边三角形,六边形ABCDEF 的边长分别记为:AB =a 1、BC =a 2、CD =a 3、DE =b 1、EF =b 2、FA =b 3。
求证:a 12+a 22+a 32=b 12+b 22+b 32。
(1998年全国联赛题)【说明】继勾股定理后,证明线段的平方关系,也可利用相似三角形的面积比等于相似比的平方来证。
由题设容易得到相似三角形多用这个定理。
168例8、已知直线PQR 交△ABC 的边AB 于P ,交AC 于Q ,交BC 的延长线于R 。
