2017年美国辛辛那提大学数学专业介绍
数学(0701)介绍

数学(0701)一、学科简介本学科为数学一级学科硕士点,包括基础数学、计算数学、概率论与数理统计、应用数学、运筹学与控制论五个二级学科。
本学科前期积累坚实,起步早,1978年开始招收硕士生,2003年建成宁夏大学首个一级学科硕士点,形成了完整的数学学科硕士研究生培养体系,已培养20余届硕士生,拥有“应用数学”、“信息与计算科学”两个省级重点学科和国家“211工程”重点建设学科“数学力学与工程技术科学计算”。
现有包括5位博导在内的17位教授和16位具有博士学位的中青年骨干教师;6位有海外留学经历,其中2位获国外博士学位。
1人入选国家“百千万人才工程”,1人入选宁夏“313人才计划”。
学科点队伍结构合理,优势明显,具有丰富的高层次人才培养经验。
近5年来完成及在研国家自然科学基金项目10余项,“973”前期专项1项,国家科技支撑计划子项目2项。
获省部级科技进步二等奖2项。
在国内外有重要影响的学术期刊发表论文500余篇,其中SCI, EI和ISTP收录90余篇。
本学科点经过长期的建设与积累,其研究方向各具特色,相互促进。
既与围绕该学科长期储备形成的学科队伍现状相吻合,也是宁夏大学数学、力学与材料、环境、能源等学科交叉具有新的增长点的基础学科,具有充分发挥宁夏大学在高层次人才培养、服务宁夏经济等方面的综合优势。
二、培养目标1.认真学习掌握辩证唯物主义和历史唯物主义的基本原理,树立科学的世界观与方法论,具有集体主义精神以及追求真理、献身科学事业的精神。
2. 在本学科内掌握坚实的基础理论和系统的专业知识;具有从事科学研究工作、教学工作或独立担负专门技术工作的能力;知识结构应达到能够读懂本专业学术论文;应具有熟练运用本专业常用实验方法、计算方法、分析方法等研究方法的实践能力;应具有参加完整科研过程的科研能力。
3.掌握一门外国语,能运用该门外国语比较熟练地阅读本专业外文资料。
4.身心健康。
三、培养方式硕士研究生培养方式灵活多样,充分发挥导师指导硕士研究生的主导作用,建立和完善有利于发挥学术群体作用的培养机制。
美国大学数学教材中文版

美国大学数学教材中文版
1.《数学分析》(Calculus),作者:詹姆斯·萨维奇(James Stewart)
2.《线性代数》(Linear Algebra),作者:弗朗西斯·费舍尔(Francis J. Flanigan)
3.《概率论和统计学》(Probability and Statistics),作者:查
尔斯·贝尔(Charles M. Bell)
4.《微积分》(Calculus),作者:约翰·科恩(John C. Kern)
5.《抽象代数》(Abstract Algebra),作者:约翰·拉德贝克(John B. Ladue)
6.《数学分析:实变函数与复变函数》(Real and Complex Analysis),作者:罗伯特·科尔曼(Robert L. Coleman)
7.《数学分析:积分与微分方程》(Integral and Differential Equations),作者:伊恩·米勒(Ian Miller)
8.《几何学》(Geometry),作者:罗伯特·科尔曼(Robert L. Coleman)
9.《数学分析:空间解析几何》(Analytic Geometry),作者:罗伯特·科尔曼(Robert L. Coleman)
10.《数论》(Number Theory),作者:约翰·科恩(John C. Kern)。
美国学科专业目录
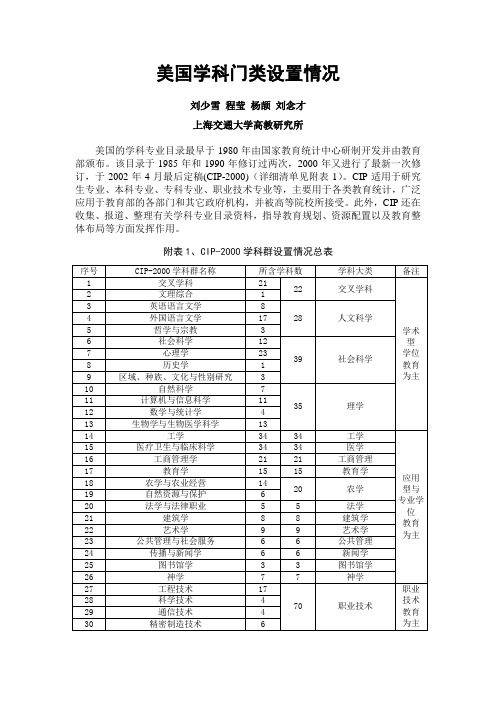
美国学科门类设置情况刘少雪程莹杨颉刘念才上海交通大学高教研究所美国的学科专业目录最早于1980年由国家教育统计中心研制开发并由教育部颁布。
该目录于1985年和1990年修订过两次,2000年又进行了最新一次修订,于2002年4月最后定稿(CIP-2000)(详细清单见附表1)。
CIP适用于研究生专业、本科专业、专科专业、职业技术专业等,主要用于各类教育统计,广泛应用于教育部的各部门和其它政府机构,并被高等院校所接受。
此外,CIP还在收集、报道、整理有关学科专业目录资料,指导教育规划、资源配置以及教育整体布局等方面发挥作用。
附表1、CIP-2000学科群设置情况总表注:“学科群”和“学科”分别是CIP目录中两位数和四位数代码表示的学科领域。
“学科大类”根据美国的国家教育统计中心、国家自然科学基金会和国家科学院等权威机构统计口径及世界著名大学的院系设置统计等划分。
附表2、CIP-2000学科专业目录表—交叉学科类附表3、CIP-2000学科专业目录表—人文科学类注:“------”表示该学科所含的专业未全部列出,下同。
附表4、CIP-2000学科专业目录表—社会科学类附表4、CIP-2000学科专业目录表—社会科学类(续)附表5、CIP-2000学科专业目录表—理学类附表5、CIP-2000学科专业目录表—理学类(续)附表6、CIP-2000学科专业目录表—工学类附表7、CIP-2000学科专业目录表—医学类附表8、CIP-2000学科专业目录表—工商管理类附表9、CIP-2000学科专业目录表—教育学类附表10、CIP-2000学科专业目录表—农学类附表11、CIP-2000学科专业目录表—法学类附表12、CIP-2000学科专业目录表—建筑学类附表13、CIP-2000学科专业目录表—艺术学类附表14、CIP-2000学科专业目录表—公共管理类附表15、CIP-2000学科专业目录表—新闻学类附表16、CIP-2000学科专业目录表—图书馆学类CIP-2000学科专业目录表—神学类附表17、附表18、CIP-2000学科专业目录表—职业技术类附表18、CIP-2000学科专业目录表—职业技术类(续)。
金融工程和金融数学两者的区别是什么

金融工程和金融数学两者的区别是什么金融工程和金融数学在美国留学生圈中一直是两个比较热门的专业,因为这两个专业的就业前景也是很不错的,今天店铺小编就给大家介绍金融工程和金融数学之间的区别是什么,如果对这个话题感兴趣的话,欢迎点击。
金融工程和金融数学之间的区别一、专业介绍金融工程和金融数学一直都是美国硕士申请的热门项目,很多申请纯金融学的学生也会考虑申请金融工程和金融数学(简称金工和金数)。
金工和金数都是新兴学科,专注于利用数学工具来建立金融市场模型和解决金融问题,主要的性质是运用数学算法和计算机等技能去计算金融交易中会产生的风险并有效的去管理和降低它们所能带来的亏损,提高回报率。
金工和金数之间有什么区别呢?金工是分别运用数学与统计、金融与经济、计算机科学这三种不同领域的知识去解决金融上遇到的问题。
除了强调数学方面的知识以外,该专业还非常注重计算机和编程等能力。
随着计算机和人工智能的飞速发展,金工也越来越依靠统计学,大数据,机器学习和深度学习等能力去实现更好的金融决策。
总体来说,金工是一门熟练使用先进的计算机科学技术将数学和统计学应用于金融市场研究的专业。
金数的主旨和金工一样,而它们之间的区别就在于它们教学的侧重点不同。
相较于金工,金数会更加注重数学方面的理论知识以及如何把数学运用到金融市场上去解决问题;金数的课程也有比较少的金融经济管理类的课程,加入了更多数学类的课程,相对来说实践领域会较少于金工。
二、院校介绍Baruch College巴鲁克学院NO.1巴鲁克学院归属纽约市立大学,毗邻美国金融中心华尔街,其毕业生一直以来都是华尔街众多企业招聘的重点对象。
该校的金融工程硕士(MFE)项目以顶尖的就业资源和校友网络强势突围,常年占据QuantNet 金融工程项目排名榜首,在华尔街金融企业中几乎家喻户晓。
此外,每年的校招开始得非常早,华尔街各大公司在招聘季往往第一波就是去巴鲁克学院,学生在就业上占尽天时地利人和。
最出名的美国高等数学教材

最出名的美国高等数学教材美国是世界上数学研究和教育水平最高的国家之一。
在高等数学领域,美国拥有许多优秀的教材,被广泛应用于大学和研究机构。
本文将介绍几本最出名的美国高等数学教材,它们对于数学教育的发展起到了重要的推动作用。
1.《微积分》(Calculus),James Stewart《微积分》是一本广泛使用的高等数学教材,由加拿大数学家James Stewart编写。
这本教材以其清晰的文字、严谨的推导和丰富的例题而闻名。
它包含了单变量和多变量微积分的内容,并覆盖了微积分的基本原理、技巧和应用。
《微积分》被许多大学选作本科生微积分课程的教材,对于培养学生的数学思维和问题解决能力起到了积极的作用。
2.《实变函数与泛函分析》(Real Analysis and Functional Analysis),Elias M. Stein and Rami Shakarchi《实变函数与泛函分析》是一本权威性和深度的高级数学教材,由两位杰出的数学家Elias M. Stein和Rami Shakarchi合著。
这本教材以其严谨的逻辑和精确的证明而著称,涵盖了实变函数和泛函分析的核心理论和应用。
《实变函数与泛函分析》适合于研究生和高年级本科生,对于培养学生的数学分析能力和创新思维具有重要意义。
3.《代数结构导论》(Introduction to Algebraic Structures),Joseph Landin《代数结构导论》是一本经典的代数学教材,由Joseph Landin编写。
这本教材系统地介绍了代数学的基本概念、原理和方法,包括群论、环论、域论等内容。
它以其简洁明了的讲解和充满意义的例子而受到广大学生和教师的喜爱。
《代数结构导论》不仅适合于代数学专业的学生,也适用于理工科和计算机科学等相关专业的学生。
4.《偏微分方程》(Partial Differential Equations),Lawrence C. Evans《偏微分方程》是一本全面介绍偏微分方程理论和应用的教材,由Lawrence C. Evans编写。
美本高等数学教材目录

美本高等数学教材目录以下是美本高等数学教材的目录:第一章:微积分基础1.1 实数与数轴1.2 函数与映射1.3 极限与连续1.4 导数与微分1.5 中值定理与导数的应用第二章:高等微积分2.1 不定积分与定积分2.2 微积分基本定理与换元积分法2.3 定积分的应用2.4 曲线的长度、曲率与曲边梯形法2.5 多重积分与重心坐标法2.6 广义积分与反常积分第三章:级数与收敛性3.1 数列的极限3.2 数列的收敛性与敛散性判定3.3 黎曼和与积分3.4 级数的收敛性与敛散性判定3.5 幂级数与泰勒级数第四章:微分方程4.1 常系数线性微分方程4.2 变系数线性微分方程4.3 高阶线性齐次微分方程4.4 高阶线性非齐次微分方程4.5 欧拉方程与二阶线性方程4.6 线性方程组与矩阵方程第五章:多元函数与矢量分析5.1 多元函数的极限与连续5.2 偏导数与全微分5.3 多元函数的导数与链式法则5.4 隐函数与隐函数的微分5.5 多元函数的极值与条件极值5.6 多元函数积分与曲线积分5.7 曲面积分与格林公式第六章:多元函数微分学6.1 方向导数与梯度6.2 多元函数泰勒公式6.3 多元函数的最小二乘法6.4 多元函数的泛函极值6.5 多元函数的约束优化问题6.6 多元函数积分的应用第七章:常微分方程7.1 初等方程的解法与初值问题7.2 高阶常微分方程7.3 常系数线性齐次微分方程7.4 常系数线性非齐次微分方程7.5 高阶常微分方程组7.6 线性微分方程与矩阵第八章:变分法与特殊函数8.1 函数的极值与最优化8.2 随机函数与最优随机过程8.3 欧拉方程与变分法8.4 贝塞尔方程与贝塞尔函数8.5 雅各比方程与雅各比函数8.6 数学物理方程与特殊函数第九章:傅里叶级数与变换9.1 傅里叶级数与周期函数9.2 傅里叶级数的收敛性与性质9.3 傅里叶级数与一般函数9.4 波的传播与振动现象9.5 傅里叶变换与拉普拉斯变换9.6 傅里叶变换与偏微分方程第十章:复变函数10.1 复数与复平面10.2 复变函数的极限与连续10.3 复变函数的导数与全纯函数10.4 保解析函数与解析函数10.5 全纯映射与有限变射10.6 复积分与柯西定理以上是美本高等数学教材的目录,本教材全面系统地介绍了微积分、级数与收敛性、微分方程、多元函数与矢量分析、常微分方程、变分法与特殊函数、傅里叶级数与变换、复变函数等数学知识点,旨在帮助学生打好数学基础,提升数学应用能力。
美国大学应用数学专业排名

美国大学应用数学专业排名美国大学应用数学专业排名在应用数学专业,你将系统学习各种数学课程,以及你所选择的应用领域。
应用领域包括计算机和信息科学,作业研究,系统工程,控制论和统计学。
以下是店铺为大家搜索整理的.美国大学应用数学专业排名,仅供参考,希望能给大家带来帮助!美国大学应用数学本科2017排名:1 New York University纽约大学2 Massachusetts Institute of Technology麻省理工学院3 California Institute of Technology加州理工学院4 University of California Los Angeles加州大学洛杉机分校5 University of Minnesota Twin Cities明尼苏达大学Twin Cities 分校6 Brown University布朗大学7 Princeton University普林斯顿大学8 Stanford University斯坦福大学The University of T exas at Austin德克萨斯大学奥斯汀分校10 University of California Berkeley加州大学伯克利分校11 Carnegie Mellon University卡内基美隆大学12 University of Maryland College Park马里兰大学帕克分校13 Georgia Institute of Technology佐治亚理工学院The University of Arizona亚利桑那大学15 Cornell University康乃尔大学University of Michigan Ann Arbor密西根大学-安娜堡分校17 Northwestern University西北大学The University of Chicago芝加哥大学University of Washington华盛顿大学20 Rensselaer Polytechnic Institute伦斯勒理工学院21 Harvard University哈佛大学22 University of Colorado Boulder科罗拉多大学波尔得分校23 North Carolina State University,Raleigh北卡罗来纳州立大学Rice University莱斯大学25 The University of Utah犹他大学数学与应用数学专业培养掌握数学科学的基本理论与基本方法,具备运用数学知识、使用计算机解决实际问题的能力,受到科学研究的初步训练,能在科技、教育和经济部门从事研究、教学工作或在生产经营及管理部门从事实际应用、开发研究和管理工作的高级专门人才。
大学数学类专业课程大全

大学数学类专业课程大全一、高等数学1. 微积分微积分是数学中最基础的一门课程,通过学习微积分可以更好地理解函数、极限、导数、积分等概念。
2. 线性代数线性代数是一门关于线性方程组、行列式、向量空间与线性变换等内容的课程,其在几何学、计算机科学、物理学等领域都有广泛的应用。
3. 概率论与数理统计概率论与数理统计是一门基础课程,其通过介绍随机事件、随机变量、概率分布、统计推断等概念,让学生深入了解随机性的规律与应用。
二、工程数学1. 工程数学分析工程数学分析是一门介绍基本数学概念,如极限、连续性、微积分等内容,并通过实例让学生了解这些概念在工程领域的应用。
2. 微分方程微分方程是一门介绍微分方程理论与方法的课程,内容包括常微分方程、偏微分方程、数值方法等,并讲授微分方程在工科和自然科学中的应用。
3. 数值计算方法数值计算方法是一门计算数学的课程,其重点介绍各种数值算法,如数值积分、数值解线性方程组、非线性方程组、微分方程初值问题、边值问题等。
三、应用数学1. 微分几何微分几何是一门介绍流形、张量场、黎曼流形等内容,并讨论这些概念在物理和工程中的应用。
2. 数学建模数学建模是一门将数学理论与实际问题相结合的课程,其内容包括数据收集、分析、建模、验证及方案评估等。
3. 图论与组合优化图论与组合最优化是一门介绍图论、组合优化、算法设计、计算复杂性等概念的课程,重点讲解在领域和工程中的应用。
四、统计学1. 因子分析与聚类分析因子分析与聚类分析是一门介绍统计模型和分析方法的课程,包括因子分析、聚类分析、判别分析等相关概念和方法,这些方法都广泛应用于数据分析和统计处理。
2. 时间序列分析时间序列分析是一门介绍时间序列概念、程序方法、模型检验等方法的课程,这些方法广泛应用于金融、宏观经济和自然灾害等领域。
3. 非参数统计非参数统计是一门介绍绝对差、秩、核估计、分位数等方法的课程,这些方法广泛应用于数据分析和统计推断。
数学专业介绍英文

数学专业介绍英文Mathematics is a versatile and highly respected field of study that plays a crucial role in various aspects of our daily lives. A major in mathematics provides students with a strong foundation in logical reasoning, problem-solving skills, and critical thinking abilities. The curriculum typically includes courses in calculus, algebra, geometry, statistics, and differential equations, among others. Students also have the opportunity to explore more advanced topics such as number theory, mathematical analysis, and mathematical modeling.One of the key benefits of studying mathematics is the development of analytical skills that are highly sought after in a wide range of industries. Mathematics majors are equipped with the ability to analyze complex problems, formulate logical arguments, and devise innovative solutions. These skills are applicable in fields such as finance, engineering, computer science, and data analysis, making mathematics graduates highly marketable in today'scompetitive job market.Furthermore, a mathematics major opens up a diverse range of career opportunities for graduates. Many mathematics majors pursue careers in academia as professors or researchers, while others find employment in industries such as finance, technology, consulting, and government. The analytical and problem-solving skills gained through a mathematics degree are transferable to various professions, making mathematics graduates valuable assets in any workplace.In addition to its practical applications, mathematics is also a deeply theoretical and abstract field of study that appeals to those with a passion for pure mathematics. The beauty of mathematics lies in its elegant theories, complex structures, and profound connections to other disciplines such as physics, computer science, and economics. Students who are drawn to the theoretical aspects of mathematics can delve into topics such as topology, abstract algebra, and mathematical logic, exploring the fundamental principles that underpin themathematical universe.Moreover, studying mathematics can also lead to personal growth and intellectual fulfillment. The process of solving challenging mathematical problems, proving theorems, and exploring new mathematical concepts can be intellectually stimulating and rewarding. Mathematics majors develop a strong sense of discipline, perseverance, and creativity as they grapple with complex mathematical ideas and push the boundaries of their understanding. The pursuit of knowledge in mathematics is a journey of self-discovery that can lead to a deeper appreciation of the beauty and power of mathematics.Overall, a major in mathematics offers students a unique opportunity to cultivate their analytical skills, explore the theoretical foundations of mathematics, and pursue diverse career paths in academia, industry, and beyond. Whether you are interested in applying mathematics to real-world problems, delving into abstract mathematical theories, or simply seeking intellectual challenge and personal growth, a mathematics major can provide you withthe knowledge, skills, and opportunities to succeed in a variety of fields. Mathematics is not just a subject of study; it is a way of thinking, problem-solving, and understanding the world around us.。
解读美国精算专业

美国留学精算专业简单的说就是依据经济学的基本原理,运用现代数学、统计学、金融学及法学等的各种科学有效的方法,对各种经济活动中未来的风险进行分析,评估和管理,是现代保险、金融、投资实现稳健经营的基础。
精算的课程运用到应用统计、数学、财务的概念:1、应用统计:机率分配(Probability)2、数学:多变向微积分(Multi-variable Calculus)3、财务:风险管理、投资管理与时间序列美国留学精算专业设置:可能设置精算学位的系所有:1、商学院的MBA,或保险系:着重风险管理、财务管理、投资;2、应用统计系:利用统计的机率分配概念设计保险产品;3、数学系:运用时间序列计算年金保险。
专业侧重点:1、MBA:重点放在管理、财务、行销、会计等MBA必修的课程;2、.MS in Insurance:着重保险法规、保险的原理、社会责任、与道德问题。
美国留学精算专业课程介绍1、拥有4年制大学的学历2、如要报考MBA,需有GMAT的成绩;若是要修MS学位,必须考过GRE。
3、申请人最好修过相关的数理课程,如商用数学、微积分、机率分配;有很强的数理能力。
4、曾经有保险、金融、投资等相关行业的工作经历,不过这不是绝对的条件。
美国留学精算专业申请资格保险、精算是近年来相当热门的科目之一。
投入精算业的人通常具有财务、数学、统计、保险背景。
以往,亚洲地区对保险精算需求较高的地区只有日本、香港、新加坡等地;这几年由于经济成长、金融国际化,对精算、保险的需求有越来越高的趋势;尤其亚洲人口占世界的一半,因此这方面的需求,成长潜力非常惊人。
保险vs.精算精算一般而言应用在投资、保险业、金融业,这些行业都具备一个共同特色:需要风险控管、投资管理以及金融商品设计。
保险业,在亚洲绝大多数的'地方除了日本、新加坡、香港之外,都处於一个非常封闭的环境。
随着加入WTO、以及经济高速成长的影响,保险业的成长将来会非常惊人,相对地,人才需求也会大幅提升,保险精算的前景十分看好。
mit数学系培养方案

mit数学系培养方案MIT数学系培养方案MIT数学系培养方案是世界上最为著名和顶尖的数学教育计划之一。
作为国际数学研究和教育的领导者,MIT数学系的培养方案在数学领域具有举足轻重的地位。
本文将对MIT数学系的培养方案进行全面介绍,并探讨其独特之处和培养出的优秀数学家。
MIT数学系培养方案以提供全面而深入的数学教育为目标,旨在培养学生的数学思维能力和解决问题的能力。
该方案注重培养学生的数学基础,包括数学分析、代数、几何、拓扑等各个方面。
学生在学习过程中将接触到各种数学概念和技巧,并通过应用解决实际问题来提高数学能力。
MIT数学系培养方案的特点之一是注重实践和研究。
学生在学习过程中将参与到各种数学研究项目中,与导师和其他学生一起进行研究探讨。
这种实践和研究的机会使学生能够深入理解数学的本质,并培养出创新思维和科研能力。
MIT数学系培养方案还注重培养学生的团队合作能力和沟通能力。
学生将有机会参与到各种团队项目中,与其他学生合作解决复杂的数学问题。
通过与他人的合作,学生能够分享和交流自己的想法,提高团队合作和沟通能力。
MIT数学系培养方案的另一个独特之处是其开放和多样化的课程设置。
学生可以根据自己的兴趣和需求选择各种数学课程。
不仅有基础的数学课程,还有专业的高级数学课程,如微分几何、复变函数、数论等。
这种开放和多样化的课程设置使学生能够自由选择自己感兴趣的方向,并深入研究。
MIT数学系培养方案的最终目标是培养出杰出的数学家和科学家。
许多MIT数学系的毕业生都成为了世界上著名的数学家和科学家,他们在各个领域都取得了举足轻重的成就。
这些优秀的数学家不仅在学术界有很高的声誉,还在工业界和金融界等领域发挥着重要作用。
MIT数学系培养方案是一套全面而深入的数学教育计划,旨在培养学生的数学思维能力和解决问题的能力。
通过实践和研究,团队合作和沟通,以及开放和多样化的课程设置,该方案成功地培养出了许多优秀的数学家和科学家。
全球世界大学数学专业排名TOP100

306
评估申请条件
83
巴塞罗那自治大学
Spain Barcelona
62.7
167
评估申请条件
83
巴黎银行-巴黎第九大学
France Paris
62.7
167
评估申请条件
85
格拉纳达大学
Spain Granada, Granada
62.4
313
评估申请条件
85
慕尼黑大学
Germany Munich
88.3
9
评估申请条件
15
芝加哥大学
United States Chicago, IL
87.4
13
评估申请条件
16
威斯康星大学
United States Madison, WI
86.6
29
评估申请条件
17
德克萨斯农机大学-学院站
United States College Station, TX
86.2
78.7
154
评估申请条件
29
新泽西州立大学罗格斯分校
United States Piscataway Township, NJ
78.5
82
评估申请条件
30
北京师范大学
China Beijing
78
286
评估申请条件
31
上海交通大学
China Shanghai
77.8
138
评估申请条件
32
布朗大学
United States Providence, RI
63
俄亥俄州立大学
United States Columbus, OH
0701数学一级学科简介

0701数学一级学科简介一级学科(中文)名称:数学(英文)名称: Mathematics一、学科概况数学起源于人类远古时期生产、获取、分配、交易等活动中的计数、观测、丈量等需求,并很早就成为研究天文、航海、力学的有力工具。
17世纪以来,物理学、力学等学科的发展和工业技术的崛起,与数学的迅速发展形成了强有力的相互推动。
到19世纪,已形成了分析、几何、数论和代数等分支,概率已成为数学的研究对象,形式逻辑也逐步数学化。
与此同时,在天体力学、弹性力学、流体力学、传热学、电磁学和统计物理中,数学成为不可缺少的定量描述语言和定量研究工具。
20世纪中,数学科学的迅猛发展进一步确立了它在整个科学技术领域中的基础和主导地位,并形成了当代数学的三个主要特征:数学内部各学科高度发展和相互之间不断交叉、融合的趋势;数学在其他领域中空前广泛的渗透和应用;数学与信息科学技术之间巨大的相互促进作用。
数学与科学技术一直以来的密切联系,在20世纪中叶以后更是达到了新的高度。
第二次世界大战期间,数学在高速飞行、核武器设计、火炮控制、物资调运、密码破译和军事运筹等方面发挥了重大的作用,并涌现了一批新的应用数学学科。
其后,随着电子计算机的迅速发展和普及,特别是数字化的发展,使数学的应用范围更为广阔,在几乎所有的学科和部门中得到了应用。
数学技术已成为高技术中的一个极为重要的组成部分和思想库。
另一方面,数学在向外渗透的过程中,与其他学科交叉,形成了诸如计算机科学、系统科学、模糊数学、智能计算(其中相当部分也被称为软计算)、智能信息处理、金融数学、生物数学、经济数学、数学生态学等一批新的交叉学科。
在21世纪,科学技术的突破日益依赖学科界限的打破和相互渗透,学科交叉已成为科技发展的显著特征和前沿趋势,数学也不例外。
随着实验、观测、计算和模拟技术与手段的不断进步,数学作为定量研究的关键基础和有力工具,在自然科学、工程技术和社会经济等领域的发展研究中发挥着日益重要的作用。
美国大学本科数学专业的必修课及教材

8、Algebraic Geometry I : Complex Projective Varieties by David Mumford:复代数几何的经典。
8、Lie Groups, Lie Algebras, and Their Representation by V.S. Varadarajan:最重要的李群、李代数参考书;
9、Humphreys, Introduction to Lie Algebras and Representation Theory , SpringerVerlag, GTM9:标准的李代数入门教材。
3、Warner,Foundations of Differentiable manifolds and Lie groups:标准研究生微分流形教材,有相当的篇幅讲述李群;
4、Representation theory: a first course, by W. Fulton and J. Harris:李群及其表示论标准教材;
3、Algebra Hungerford:标准的研究生一年级代数教材,适合作参考书;
4、Algebra M,Artin:标准的本科生代数教材;
5、Advanced Modern Algebra by Rotman:较新的研究生代数教材,很全面;
6、Algebra:a graduate course by Isaacs:较新的研究生代数教材;
5、Commutative Algebra with a view toward Algebraic Geometry by Eisenbud:高级的代数几何、交换代数的参考书,最新的交换代数全面参考;
全面解析美国金融数学数学金融金融工程

全面解析美国金融数学数学金融金融工程美国金融数学/数学金融/金融工程专业就业前景如何,平时都学习什么课程呢?相信这是很多想申请美国金融数学/数学金融/金融工程研究生的学生想了解的内容。
下面就给大家详细解析这个专业。
金融工程Finance Enginerring:Learning methods for monitoring financial markets and evaluating financial assets and organi金融工程Finance Enginerring:Learning methods for monitoring financial markets and evaluating financial assets and organization是研究如何监督,管理,评估金融市场,金融工具以及金融机构的一门学科。
如果你缺乏一个直观的认识,那么举几个金融工程/数学金融里面的题目框架出来。
Theories and Practice of Risk Management研究风险管理(risk management)以及模拟证券投资(simulate equity investment)的基本理论.Evaluation and Measurement of Organizational Performance 依据公司的财务金融数据(股价,公司债券价格等等)研究公司(corporate) 和证券市场( security market) 的关系研究非营利机构的金融管理Methodology of Evaluation评估的方法,理论,发展。
计量金融(Quantitative Finance)专为金融市场而设的一门应用数学。
计量金融本义上与金融经济学的范畴有密切的关系,然而前者所涉及的领域比较狭隘,理念也比后者抽象。
一般而言,若金融经济学家研究一所企业当前股价的结构性原因,数学家(或计量金融学家)所做的便是利用当前股价作参考,利用或然率微积分去计算并取得相关衍生工具的公平价格(应值价格)。
美国留学数学专业课程设置概况

美国留学数学专业课程设置概况小编为大家带来美国留学数学专业课程设置概况,希望对店铺的同学有所帮助。
想了解更多留学精彩内容,为你详细解答。
一、美国留学数学专业介绍1.1专业定义广义上讲,数学是抽象的研究数量、结构、空间和变化的科学。
主要分为纯粹数学和应用数学,其中纯粹数学又称为基础数学,主要是研究从客观世界中抽象出来的数学规律的内在联系,也可以说是研究数学本身,而不以应用为目的的学问;而应用数学着眼于说明自然现象,解决实际问题,是纯粹数学与科学技术之间的桥梁。
1.2专业分支基础数学常见的研究方向包括:代数学algebra分析学analysis拓扑学topology几何学 geometry数论number theory逻辑学logic微分方程理论differential equation theory偏微分方程partial differential equation应用数学常见分支包括:运筹学和优化理论Operations Research /Optimization微分方程和动力系统Differential Equations and Dynamical Systems随机系统和控制理论stochastic control theory/stochastic systems theory精算和金融数学actuarial/Financial Mathematics数学物理Mathematical Physics生物数学Math Biology科学计算Scientific Computing概率论和统计Probability and statistics以上是美国大学数学专业常见的分支方向,但是在学校的开设中并不是每个学校都开设有这些分支,大部分的学校只有开设其中的几个分支,因此在选择学校时,应找到自己相匹配的分支方向。
二、美国留学数学专业课程设置2.1概览数学专业典型的硕士学位分为Master of Science(MS)和Master of Arts(MA)两种,博士学位以Doctor of Philosophy为主,数学作为理科中的一门学科,研究生录取以博士招生为主,尤其是基础数学领域,部分学校甚至不设置独立的硕士项目,比如哈佛大学、普林斯顿大学等。
数学最吃香的十大专业

数学最吃香的十大专业在现代社会,数学作为一门基础学科,无处不在,被广泛应用于各行各业。
因此,选择学习数学专业的学生可以说是没有错的。
然而,数学专业中也存在一些分支领域,有些领域更为独特和吃香。
下面将介绍数学最吃香的十大专业:1. 金融数学金融数学融合了数学、统计学和金融学的内容,通过数学模型和工具研究金融市场、金融产品的定价、风险管理等问题。
金融数学专业的毕业生在金融机构、投资银行等领域有着广泛的职业选择。
2. 数据科学数据科学将数学、统计学和计算机科学相结合,利用大数据分析和机器学习技术解决实际问题。
数据科学专业的毕业生在人工智能、物联网、互联网等领域有着巨大的发展空间。
3. 统计学统计学是研究收集、分析、解释数据的学科,其在医疗、市场、政府等领域有着广泛的应用。
统计学专业的毕业生可以从事数据分析、市场研究等工作。
4. 计算数学计算数学是研究数学计算方法和数值分析的分支学科,与计算机科学、应用数学等领域有着密切联系。
计算数学专业的毕业生在科研机构、高新技术企业等领域有着很好的就业前景。
5. 运筹学运筹学是研究优化问题、决策问题的学科,其应用范围非常广泛,包括生产计划、资源配置、物流管理等领域。
运筹学专业的毕业生在企业、政府部门等领域有着很好的就业机会。
6. 拓扑学拓扑学是数学的一个分支,研究空间形态、连通性等性质。
在地理信息系统、网络拓扑结构等领域有着广泛应用。
拓扑学专业的毕业生可以从事GIS工程师、网络工程师等职业。
7. 控制论控制论是研究控制系统的一门学科,包括PID控制、自适应控制等内容。
控制论的应用领域涉及航空航天、汽车工业、机器人等领域。
控制论专业的毕业生在自动化领域有着很好的就业前景。
8. 离散数学离散数学是研究离散结构、离散对象之间关系的学科,如图论、集合论、逻辑等内容。
在计算机科学、密码学等领域有着广泛应用。
离散数学专业的毕业生可以从事软件开发、密码分析等工作。
9. 数值分析数值分析是研究数学计算方法、误差分析等问题的学科,其在工程、计算机等领域有着广泛应用。
数学最吃香的十大专业排名

数学最吃香的十大专业排名在当今社会,数学作为一门古老而神秘的学科,一直以来都备受人们的尊敬和推崇。
随着科技的飞速发展和社会的进步,对于数学专业的需求也变得越来越大。
那么在诸多专业中,数学到底有多吃香呢?下面我们来看看数学最吃香的十大专业排名。
10. 统计学专业统计学作为数学的一个分支,在当今社会中有着重要的地位。
统计学专业毕业生被广泛应用于各种行业,如金融、医疗、市场营销等领域。
因此,统计学专业在就业市场上备受欢迎。
9. 金融数学专业金融数学作为数学的一个重要应用领域,深受金融行业的青睐。
金融数学专业毕业生具有数学和金融领域的双重专业背景,能够胜任各种与金融相关的工作。
8. 运筹学专业运筹学是一门研究如何通过科学的方法解决实际问题的学科,具有广泛的应用价值。
运筹专业的毕业生在企业管理和决策领域有着重要的地位,因此备受雇主的青睐。
7. 数据科学专业数据科学是近年来兴起的一门新兴学科,与数学密切相关。
数据科学专业毕业生能够通过数学和统计学知识,分析和挖掘海量数据中的规律,为企业提供决策支持。
6. 应用数学专业应用数学是将数学理论和方法应用于实际问题的学科,具有广泛的实用价值。
应用数学专业毕业生在科研、工程、经济等领域都有着广阔的就业前景。
5. 数学教育专业数学教育专业培养具有数学知识和教学能力的专业人才,在教育领域中具有重要地位。
数学教育专业毕业生能够成为中小学数学教师或教育机构的数学培训专家。
4. 理论数学专业理论数学是数学的理论基础,是最具纯粹性的数学学科之一。
理论数学专业毕业生通常从事数学研究工作,在国内外著名大学、科研院所和企业研发部门工作。
3. 数值计算专业数值计算是将数学理论用计算机数值方法进行实际计算的学科,是科学计算与数学的交叉领域。
数值计算专业毕业生在科研和工程领域都有着广泛的应用前景。
2. 应用统计学专业应用统计学是统计学的一个重要分支,将统计学理论和方法应用于各种实际问题的解决。
美国大一数学知识点

美国大一数学知识点在美国大一的数学课程中,学生将接触到多个重要的数学知识点,这些知识点是建立数学基础并深入探索更高级数学概念的关键。
本文将介绍一些美国大一数学课程中常见的知识点。
一、微积分微积分是数学中的一门基础学科,主要包括微分学和积分学。
在美国大一的数学课程中,学生将深入学习微积分的基本原理和技巧。
以下是微积分的一些重要知识点:1. 极限与连续:学生将了解极限的概念及其在计算函数的连续性和导数中的应用。
2. 导数与微分:学生将学习如何计算函数的导数和微分,并应用它们解决实际问题,如最大值和最小值的求解等。
3. 积分与定积分:学生将学习如何计算函数的不定积分和定积分,并理解积分在几何和物理中的应用,比如面积、弧长和体积的计算等。
二、线性代数线性代数是数学中的一个重要分支,研究向量空间和线性变换等概念及其性质。
在美国大一的数学课程中,学生将学习线性代数的基本理论和应用。
以下是线性代数的一些重要知识点:1. 向量与矩阵:学生将了解向量和矩阵的基本性质,并学习如何进行向量和矩阵的运算。
2. 线性方程组:学生将学习如何求解线性方程组,并了解线性方程组在实际问题中的应用。
3. 特征值与特征向量:学生将学习如何计算矩阵的特征值和特征向量,并理解它们在线性变换中的作用。
三、概率与统计概率与统计是研究随机事件及其规律性的学科,具有广泛的应用领域。
在美国大一的数学课程中,学生将学习概率与统计的基本概念和方法。
以下是概率与统计的一些重要知识点:1. 随机变量与概率分布:学生将学习随机变量的定义及其概率分布,如离散型随机变量和连续型随机变量。
2. 概率与期望:学生将了解概率的基本计算方法,并学习如何计算随机变量的期望。
3. 统计推断:学生将学习如何利用样本数据来进行参数估计和假设检验,并理解统计推断在实际问题中的应用。
以上仅是美国大一数学课程中的一部分知识点,通过学习这些知识点,学生将建立起扎实的数学基础,并为将来的学习打下坚实的基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立思辰留学360美国留学专家介绍,辛辛那提大学始建于1819年, 其商学院成立于1906年,在如今学术研究方面已经占据世界领先地位。
辛辛那提大学商学院的出色之处在于创建了不同层次的专业设置以满足不同学生的需要并帮助他们完成他们的学习目标。
商学院提供一系列本科和研究生课程,强调实习机会、国际交流以及领导才能的培养。
商学院的发展战略是发展多种渠道沟通不同的文化,以扩展全球商业的范围;创造机会融合各个领域的知识并鼓励创新;应用领先科技增强交流与合作。
美国辛辛那提大学商学院被Business Week评为最好的商学院之一,全美排名TOP 100。
Business Week 一直致力于对美国知名的商学院进行排名。
排名参数:专业设置、注册人数、考试的分数和毕业生的起薪
辛辛那提大学商学院的数量分析(Quantitative Analysis)专业是辛辛那提大学热门专业之一。
这个专业是数学和商科的完美结合—在商科课程的基础上结合应用统计学、应用数学、运筹学、管理科学和计算机应用等课程。
这些课程的设置目标是培养综合性的金融数学人才。
学生依照个人能力,最短可以在9个月(3个学期)完成这个数量分析的硕士学位(美国一般完成硕士学位需要两年时间)。
辛辛那提大学商学院职业前景
数量分析专业自1970年代开设以来,学生的就业率在辛辛那提大学众多专业中名列前茅。
该专业的绝大多数毕业生被顶尖跨国公司、金融机构录用。
辛辛那提大学商学院入学条件
·大学本科毕业或大四在读
·TOEFL(iBT) ≥100
·GRE或GMAT成绩
·大学期间GPA≥2.7
·本科期间数学方面的课程要求:微积分;且最好有线性代数(linear algebra)及计算机方面的基础知识
·两到三封大学教授或教师的推荐信。
