单链表SLNode

单链表存储结构的概念

单链表存储结构的概念单链表（Singly Linked List）是一种常见的线性数据结构，用于存储一系列具有相同类型的元素。

它由一组称为节点（Node）的对象组成，每个节点包含了数据元素和一个指向下一个节点的引用（通常称为指针或链接）。

单链表的存储结构的概念如下：1.节点（Node）：每个节点包含两个部分，一个是数据元素，用于存储实际的数据值；另一个是指向下一个节点的链接（指针），用于指示下一个节点的位置。

2.头节点（Head）：单链表的起始节点称为头节点，它不包含实际的数据元素，只是用于标识整个链表的起点。

头节点通常是第一个具有数据元素的节点的前一个节点。

3.尾节点（Tail）：单链表的结束节点称为尾节点，它是最后一个具有数据元素的节点。

尾节点的链接通常为空（null），表示链表的结束。

4.链表的连接方式：通过每个节点的链接（指针），单链表中的节点按顺序串联在一起，形成链表结构。

通过链接，可以迅速访问到链表中的下一个节点。

单链表的存储结构具有以下特点和优势：•动态性：单链表的长度可以在运行时动态改变，不需要事先指定链表的大小。

•灵活性：可以在链表中任意位置进行插入和删除操作，不需要移动其他节点的位置。

•存储效率：相对于数组，单链表可以节省存储空间，因为它不需要预留固定大小的连续存储空间。

•适用于频繁的插入和删除操作：由于链表的特点，插入和删除操作的时间复杂度为O(1)，效率较高。

然而，单链表的访问和搜索操作的效率较低，需要从头节点开始遍历整个链表。

此外，由于每个节点需要额外的指针来存储下一个节点的地址，导致存储开销相对较高。

总的说来，单链表的存储结构使得它适用于需要频繁进行插入和删除操作而不关心随机访问的场景。

写出单链表存储结构的 c 语言描述

写出单链表存储结构的 c 语言描述一、单链表的概述单链表是一种常见的数据结构，它由若干个节点组成，每个节点包含一个数据元素和一个指向下一个节点的指针。

单链表的特点是插入和删除操作效率高，但查找操作效率较低。

二、单链表的存储结构单链表的存储结构采用动态分配内存的方式，每个节点都是一个独立的内存区域，通过指针将它们连接在一起。

下面是单链表存储结构的 c 语言描述：```typedef struct Node{int data; // 数据域struct Node *next; // 指针域} ListNode, *LinkedList;```上面代码中，ListNode 表示节点类型，LinkedList 表示链表类型。

其中 data 是数据域，next 是指针域，用于存放下一个节点的地址。

三、单链表的基本操作1. 初始化操作初始化操作用于创建一个空链表。

```void InitList(LinkedList *L){*L = (ListNode*)malloc(sizeof(ListNode)); // 创建头结点(*L)->next = NULL; // 头结点指针域为空}```2. 插入操作插入操作用于在链表中插入新节点。

```int Insert(LinkedList L, int i, int x)int j = 0;ListNode *p = L;while (p && j < i - 1) // 找到第 i-1 个节点{p = p->next;j++;}if (!p || j > i - 1) // 判断 i 的范围是否合法{return 0;}ListNode *s = (ListNode*)malloc(sizeof(ListNode)); // 创建新节点s->data = x; // 赋值数据域s->next = p->next; // 新节点指向下一个节点p->next = s; // 前一个节点指向新节点 return 1;```3. 删除操作删除操作用于删除链表中的某个节点。

单链表的基本操作实验问题与对策

单链表的基本操作实验问题与对策单链表是一种非常基础且常见的数据结构，被广泛应用于计算机科学和相关领域中。

它通过使用一系列节点来存储元素，每个节点都包含一个值和一个指向下一个节点的指针。

这些节点以线性方式连接，形成了一个单向链表。

在进行单链表的基本操作实验时，可能会遇到一些常见的问题和挑战。

例如，在进行插入操作时，可能会出现指针错误或内存分配失败的问题。

在删除操作中，可能会遇到无法找到指定元素或无法正确更新节点指针的问题。

在进行查找操作时，可能会遇到查找效率低下或无法找到特定元素的问题。

而在遍历操作中，可能会遇到指针断裂或无限循环的问题。

为了解决这些问题，我们可以采取一些对策。

例如，在进行插入操作时，我们可以使用更高效的数据结构或算法来避免指针错误和内存分配失败的问题。

在删除操作中，我们可以使用更精确的查找算法来找到指定元素并正确更新节点指针。

在进行查找操作时，我们可以使用更优化的查找算法或数据结构来提高查找效率并找到特定元素。

而在遍历操作中，我们可以使用更安全的遍历算法来避免指针断裂和无限循环的问题。

总之，单链表是一种非常有用的数据结构，在进行基本操作实验时可能会遇到一些问题和挑战。

但只要我们采取适当的对策，就可以有效地解决这些问题并更好地应用单链表这种数据结构。

问题1：插入节点时如何确保正确的位置？对策：在插入节点之前，需要遍历链表以找到正确的位置。

可以使用循环来遍历链表，确保插入的位置是正确的。

另外，可以考虑维护一个指向前一个节点的指针，以便在插入时更容易操作。

问题2：如何删除节点？对策：删除节点时，需要找到待删除节点的前一个节点，并将其指针指向待删除节点的下一个节点，然后释放待删除节点的内存。

确保在删除节点之前释放内存，以避免内存泄漏。

问题3：如何遍历链表？对策：遍历链表通常需要使用循环，从链表的头节点开始，沿着指针依次访问每个节点，直到达到链表的末尾。

可以使用循环结构来实现遍历，或者使用递归方法。

数据结构课件单链表

删除节点
删除链表中的节点需要遍历至指定位置，时间复杂度为 O(n)。
查找节点
在链表中查找一个节点需要遍历整个链表，时间复杂度为 O(n)。
空间复杂度
空间占用
单链表的空间占用主要取决于链表中的节点数，因此空间复杂度为O(n)。
VS
内存分配
每个节点需要分配内存空间存储数据和指针，因此内存分配的空间复杂度也为O(n) 。
需要根据数据元素顺序进行遍历的场景，如排序算法等。
需要频繁插入、删除操作的场景，如动态规划、图算法等。
02
单链表的实现
创建单链表
定义节点结构体
首先需要定义一个节点结构体，包含数据域和指针域两个部分，数据域用于存储数据，指针域用于指向下一个节点。
初始化头节点
创建一个头节点，并将其指针域指向 NULL，表示单链表的起始位置。
05
单链表常见问题与解决方案
循环链表
总结词
循环链表是一种特殊类型的单链表，其中尾节点的指针指向头节点，形成一个闭环。
详细描述
在循环链表中，由于尾节点的指针指向头节点，因此遍历链表时需要特别注意，以避免无限循环。常见的解决方法是在遍历时记录已经访问过的节点，避免重复访问。
链表中的重复元素
总结词
链表中可能存在重复元素的问题，这会影响数据处理的正确性。
详细描述
为了解决这个问题，可以在插入节点时检查新元素是否已存在于链表中。如果存在，则不进行插入操作。另外，也可以使用哈希表等数据结构来快速查找重复元素。
链表的排序
总结词
对链表进行排序是常见的需求，但链表的排序算法通常比数组的排序算法复杂。
合并单链表
总结词
将两个已排序的单链表合并为一个新的已排序的单链表。

数据结构-链表

链表一种数据结构的链接实现是指按链式存储方式构建其存储结构，并在此链式存储结构上实现其基本运算。

线性表的常见链式存储结构有单链表、循环链表和双链表，其中最简单的单链表。

本节讨论单链表的组织方法以及线性表的基本运算在单链表上的实现。

单链表示法的基本思想是用指针表示结点间的逻辑关系。

因此单链表的一个存储结点包含两个部分，结点形式如下：其中，data部分称为数据域，用于存储线性表的一个数据元素。

next部分称为指针域或链域，用于存放一个指针，该指针指向本结点所含数据元素的直接后继所在的结点。

从上述单链表中可以联想到我们生活中的火车，还有一种火车只有火车头。

假设数据元素的类型为Datatype。

单链表的类型定义如下：typedef struct node{Datatype data;struct node * next;} node，* LinkList;struct node表示链表的结点，一个结点是由两个域数据域data和指针域next组成的记录（每个域实际上相当于一个变量），而next本身又是一个pointer类型的指针型变量。

这个定义与上面给出的单链表的结点形式一致。

单链表的简单操作：1、初始化建立一个空表。

空表由一个头指针和一个头结点（该结点同时也是尾结点）组成。

LinkList Initiate_LinkList()/* 建立一空表 */{ LinkLis head;head= malloc(sizeof(node));head -> next = NULL;return head;}2、定位：按值查找。

按从前往后的顺序，依次比较单链表中各表结点数据域的值与给定值X，第一个值与X相等的表结点的序号就是结果。

若没有这样的结点，运算结果为0。

int Locate_LinkList(LinkList head,Datatype x){ Node *p;p = head; /* 置初值 */p=p->next;j = 0; /* 置初值 */while((p!= NULL)&&(p -> data != x)){ p = p -> next;j ++;} /* 未达尾结点又未找到等于x的结点时继续扫描 */if (p -> data == x)return(j+1);elsereturn(0);}3、插入:把新的结点x插入到i结点之前。

编写算法：实现带头结点单链表的逆置算法

编写算法：实现带头结点单链表的逆置算法引言单链表是一种常见的数据结构，它由一系列节点组成，每个节点包含两部分：数据域和指针域。

其中，数据域用于存储数据，指针域用于指向下一个节点。

在单链表中，头结点是第一个节点之前的一个特殊节点，它不存储任何数据。

逆置（或反转）单链表是将原始链表中的节点顺序颠倒过来。

例如，给定一个单链表：1 -> 2 -> 3 -> 4 -> nullptr，逆置后的结果为：4 -> 3 -> 2 -> 1 -> nullptr。

本文将介绍如何实现带头结点单链表的逆置算法，并给出相应的C++代码实现。

算法思路要实现带头结点单链表的逆置算法，可以使用迭代或递归两种方法。

迭代方法迭代方法通过遍历原始链表中的每个节点，并修改其指针域来实现逆置。

具体步骤如下：1.如果链表为空或只有一个节点，则直接返回。

2.定义三个指针：prev、curr和next。

–prev指向当前节点的前一个节点（初始时为nullptr）；–curr指向当前节点；–next指向当前节点的下一个节点。

3.进行循环，直到curr指向nullptr为止：–将curr的指针域修改为prev；–将prev指向curr；–将curr指向next；–将next指向下一个节点。

4.修改头结点的指针域为nullptr，将prev作为新的头结点。

递归方法递归方法通过逐层调用函数来实现逆置。

具体步骤如下：1.如果链表为空或只有一个节点，则直接返回。

2.定义一个递归函数reverseList，该函数接收一个参数：当前节点head。

3.递归终止条件：如果当前节点或当前节点的下一个节点为空，则返回当前节点。

4.在递归调用前，先逆置从下一个节点开始的子链表，并将返回结果保存在变量newHead中。

5.将当前节点的下一个节点的指针域修改为当前节点（即将子链表的尾部连接到当前节点）。

6.将当前节点的指针域修改为空（即将当前节点作为新链表的尾部）。

数据结构--数组、单链表和双链表介绍以及双向链表

数据结构--数组、单链表和双链表介绍以及双向链表数组：数组有上界和下界，数组的元素在上下界内是连续的。

数组的特点是：数据是连续的；随机访问速度快。

数组中稍微复杂⼀点的是多维数组和动态数组。

对于C语⾔⽽⾔，多维数组本质上也是通过⼀维数组实现的。

⾄于动态数组，是指数组的容量能动态增长的数组；对于C语⾔⽽⾔，若要提供动态数组，需要⼿动实现；⽽对于C++⽽⾔，STL提供了Vector。

单向链表：单向链表(单链表)是链表的⼀种，它由节点组成，每个节点都包含下⼀个节点的指针。

表头为空，表头的后继节点是"节点10"(数据为10的节点)，"节点10"的后继节点是"节点20"(数据为10的节点)，"节点20"的后继节点是"节点30"(数据为20的节点)，"节点30"的后继节点是"节点40"(数据为10的节点)，......删除"节点30"删除之前："节点20" 的后继节点为"节点30"，⽽"节点30" 的后继节点为"节点40"。

删除之后："节点20" 的后继节点为"节点40"。

在"节点10"与"节点20"之间添加"节点15"添加之前："节点10" 的后继节点为"节点20"。

添加之后："节点10" 的后继节点为"节点15"，⽽"节点15" 的后继节点为"节点20"。

单链表的特点是：节点的链接⽅向是单向的；相对于数组来说，单链表的的随机访问速度较慢，但是单链表删除/添加数据的效率很⾼。

《数据结构C语言版》----第02章

int ListLength(SLNode *head) { SLNode *p = head; int size = 0; while(p->next != NULL) { p = p->next; size ++; } return size; }
p size=0
head
a0
a1
(a)
...
a n 1 ∧
3.顺序表操作的效率分析
时间效率分析: 算法时间主要耗费在移动元素的操作上，因此计算时间复杂度的基本操作(最深层语句频度) T(n)= O(移动元素次数) 而移动元素的个数取决于插入或删除元素的位置i. 若i=size，则根本无需移动（特别快）；若i=0，则表中元素全部要后移（特别慢）；应当考虑在各种位置插入（共n+1种可能）的平均移动次数才合理。
(3)带头结点单链表和不带头结点单链表的比较
1).在带头结点单链表第一个数据元素前插入结点
p head s p head data next a0 x
∧
a1
…
an-1
∧
(a) 插入前
data next a0
∧
a1
…
an-1
∧
s
x
(b) 插入后
2).删除带头结点单链表第一个数据元素结点
p data next head
（5）取数据元素ListGet(L,
i, x)
int ListGet(SeqList L, int i, DataType *x) { if(i < 0 || i > L.size-1) { printf("参数i不合法! \n"); return 0; } else { *x = L.list[i]; return 1; } }

单链表在实际程序中的使用

单链表在实际程序中的使用
单链表（Single Linked List）是一种常用的数据结构，它在许多实际程序中都有广泛的应用。

以下是一些常见的使用场景：
1. 动态数组：单链表可以作为动态数组的替代方案。

由于数组的大小在创建时就已经确定，如果要添加或删除元素，可能需要复制整个数组。

而单链表提供了动态添加和删除元素的能力，因此更适合需要频繁添加和删除元素的场景。

2. 历史记录或日志：单链表可以用来存储历史记录或日志。

每个节点可以包含一个事件或消息，以及指向下一个节点的指针。

这种方式可以方便地按顺序访问所有的事件或消息。

3. 文件系统：在文件系统中，目录结构可以用单链表来表示。

每个节点可以代表一个目录或文件，以及其子目录或文件的指针。

4. 图形和树形结构：单链表也可以用于表示图形和树形结构。

每个节点可以表示一个顶点或节点，而指针可以表示边或父-子关系。

5. 实现数据持久化：在需要将数据存储在磁盘或数据库中时，单链表可以作为一种实现数据持久化的方式。

每个节点可以包含一个数据项和一个指向下一个节点的指针，这样可以方便地将整个链表序列化为一个连续的字节流，然后存储在磁盘上。

6. 缓存和LRU算法：单链表也可以用于实现缓存和LRU（最近最少使用）算法。

在这种场景下，每个节点可以表示一个缓存项，包含数据和指向下一个节点的指针。

当缓存满时，最近最少使用的缓存项可以从链表中删除。

以上是一些常见的使用场景，实际上，单链表在许多其他领域也有广泛的应用，例如在算法、数据结构、操作系统、编译器设计等领域中都可以看到单链表的身影。

c语言单链表头插法

c语言单链表头插法单链表是一种常见的数据结构，是一种线性表，是由一系列节点组成的，每个节点都包含一个数据和一个指向下一个节点的指针。

在C语言中，我们可以使用结构体来定义一个节点，例如：```cstruct Node {int data;struct Node* next;};```上述代码定义了一个名为Node的结构体，它包含两个成员，一个是整型的数据data，另一个是指向下一个节点的指针next。

在使用单链表头插法创建链表时，我们首先需要定义一个头节点，它不存储任何数据，仅用作链表的标记。

然后，我们可以通过以下步骤来插入新的节点：1. 创建一个新节点，并为其分配内存空间。

```cstruct Node* newNode = (struct Node*)malloc(sizeof(struct Node));```上述代码使用malloc函数为新节点分配内存空间。

2. 将新节点的数据赋值。

```cnewNode->data = value;```上述代码将新节点的data成员设置为value。

3. 将新节点的next指针指向头节点的next指针所指向的节点。

```cnewNode->next = head->next;```上述代码将新节点的next指针指向头节点的next指针指向的节点，即将新节点插入到头节点之后。

4. 将头节点的next指针指向新节点。

```chead->next = newNode;```上述代码将头节点的next指针指向新节点，即将新节点设置为链表的第一个节点。

完整的头插法创建链表的函数如下：```cstruct Node* createList(int values[], int n) {struct Node* head = (struct Node*)malloc(sizeof(struct Node));head->next = NULL;for (int i = 0; i < n; i++) {struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));newNode->data = values[i];newNode->next = head->next;}return head;}```上述代码中的createList函数接受一个整型数组values和一个整数n作为参数，返回一个头指针。

数据结构c语言版单链表心得

数据结构c语言版单链表心得介绍在计算机科学中，数据结构是组织和存储数据的方式，目的是使数据可以高效地操作和访问。

而在C语言中，单链表是一种常见的数据结构，它由节点组成，每个节点包含数据和指向下一个节点的指针。

在本篇文章中，我将分享我对C语言版单链表的体会和心得。

什么是单链表单链表是一种线性数据结构，它由一系列节点组成。

每个节点包含两个部分：数据和指针。

数据部分用来存储具体的数据，而指针部分用来指向下一个节点。

通过使用指针，可以将各个节点连接起来，形成一个链表的结构。

单链表的设计与实现在C语言中，我们可以使用结构体来定义链表的节点类型。

每个节点包含一个数据域和一个指向下一个节点的指针域。

以下是单链表节点的定义：typedef struct Node {int data;struct Node* next;} Node;通过定义一个指向链表头节点的指针，我们可以操作链表。

以下是单链表的实现：#include <stdio.h>#include <stdlib.h>typedef struct Node {int data;struct Node* next;} Node;void insert(Node** head, int data) {Node* newNode = (Node*)malloc(sizeof(Node));newNode->data = data;newNode->next = *head;*head = newNode;}void printList(Node* head) {Node* curr = head;while (curr != NULL) {printf("%d ", curr->data);curr = curr->next;}}int main() {Node* head = NULL;insert(&head, 1);insert(&head, 2);insert(&head, 3);insert(&head, 4);printList(head);return 0;}单链表的插入操作向单链表中插入节点是一种常见的操作。

c语言中lnode的意思

在C语言中，lnode并不是一个标准的关键字或内建类型，因此其具体意义会依赖于上下文或者特定的代码库。

通常来说，lnode很可能是一个自定义的标识符，用于表示某种特定的数据结构或变量名。

以下是几种可能的解释：
1. 自定义数据结构：
在某些代码库或项目中，程序员可能定义了一个名为lnode的结构体，用于表示链表中的节点（linked list node）。

这样的结构体通常包含指向下一个节点的指针以及节点的数据。

2. 变量名或函数名：
lnode也可能被用作变量名或函数名，用于表示与链表或节点相关的某个实体。

例如：
或者
3. 特定库或框架的命名：
在某些代码库中，特定的库或框架可能使用lnode作为其内部实现的一部分，用于表示某种节点或元素。

总结：
lnode本身并没有在标准的C语言中定义，它可能是由程序员根据需要定义的一个标识符，用于表示链表节点或其他相关概念。

要理解其确切含义，需要查看代码的上下文或文档。

单链表的基本操作代码

单链表的基本操作代码单链表是一种常用的数据结构，它具有优秀的插入和删除性能，在数据存储和处理方面具有广泛的应用。

单链表的基本操作包含创建链表、插入节点、删除节点、查找节点等，下面是单链表的基本操作代码：1. 定义单链表结构体：typedef struct ListNode {int val;struct ListNode *next;} ListNode;2. 创建单链表：ListNode *createList(int arr[], int n) {ListNode *head = NULL, *tail = NULL, *p = NULL;for(int i = 0; i < n; i++) {p = (ListNode *)malloc(sizeof(ListNode));p->val = arr[i];p->next = NULL;if(head == NULL) {head = tail = p;} else {tail->next = p;tail = p;}}return head;}3. 插入节点：void insertNode(ListNode **head, int val, int pos) {ListNode *p = (ListNode *)malloc(sizeof(ListNode)); p->val = val;p->next = NULL;if(*head == NULL) {if(pos != 0) {printf("Invalid position\n");return;} else {*head = p;return;}}if(pos == 0) {p->next = *head;*head = p;} else {int i = 0;ListNode *q = *head;while(q != NULL && i < pos - 1) {q = q->next;i++;}if(q == NULL || i != pos - 1) {printf("Invalid position\n");return;}p->next = q->next;q->next = p;}}4. 删除节点：void deleteNode(ListNode **head, int pos) {if(*head == NULL) {printf("List is empty\n");return;}if(pos == 0) {ListNode *p = *head;*head = (*head)->next;free(p);} else {int i = 0;ListNode *p = *head, *q = NULL; while(p != NULL && i < pos) { q = p;p = p->next;i++;}if(p == NULL || i != pos) {printf("Invalid position\n");return;}q->next = p->next;free(p);}}5. 查找节点：ListNode *findNode(ListNode *head, int val) {ListNode *p = head;while(p != NULL) {if(p->val == val) {return p;}p = p->next;}return NULL;}单链表的基本操作是数据结构中最基础的部分，掌握好这些代码对于往后的学习和应用都会有很大的帮助。

数据结构实验二：单链表的基本操作

数据结构实验二：单链表的基本操作数据结构实验二：单链表的基本操作实验二：单链表的基本操作一、【实验目的】1、理解和掌握单链表的类型定义方法和结点生成方法。

2、掌握建立单链表和显示单链表元素的算法。

3、掌握单链表的查找、插入和删除算法二、【实验内容】1、建立一个整形数的单链表，手动输入10个数，并从屏幕显示单链表元素列表。

2、从键盘输入一个数，查找在以上创建的单链表中是否存在该数;如果存在，显示它的位置;如果不存在，给出相应提示。

3、删除上述单链表中指定位置的元素。

以下就是程序部分代码，恳请调试并补足并使之恰当运转：１．linlist.htypedefstructnode{datatypedata;structnode*next;}slnode;voidlistinitiate(slnode**head)/*初始化*/{/*如果有内存空间，申请头结点空间并使头指针head指向头结点*/if((*head=(slnode*)malloc(sizeof(slnode)))==null)exit(1);(*head)->next=null;/*置链尾标记null*/}intlistlength(slnode*head){slnode*p=head;/*p指向首元结点*/intsize=0;/*size初始为0*/while(p->next!=null)/*循环计数*/{p=p->next;size++;}returnsize;}intlistinsert(slnode*head,inti,datatypex)/*在带头结点的单链表head的数据元素ai（0≤i≤size）结点前*//*填入一个存放数据元素x的结点*/{slnode*p,*q;intj;p=head;/*p指向首元结点*/j=-1;/*j起始为-1*/while(p->next!=null&&j<i-1)/*最终让指针p指向数据元素ai-1结点*/{p=p->next;j++;}if(j!=i-1){printf(\填入边线参数弄错！\return0;}/*生成新结点由指针q指示*/if((q=(slnode*)malloc(sizeof(slnode)))==null)exit(1);q->data=x;q->next=p->next;/*给指针q->next赋值*/p->next=q;/*给指针p->next重新赋值*/return1;}intlistdelete(slnode*head,inti,datatype*x)/*删除带头结点的单链表head的数据元素ai（0≤i≤size-1）结点*//*删除结点的数据元素域值由x带回。

带结点与不带结点用头插法和尾插法创建单链表

带结点与不带结点⽤头插法和尾插法创建单链表⼀、采⽤带有头结点的头插法逆向建⽴单链表Linklist List_HeadInsert1(LinkList &L) //采⽤带有头结点的头插法逆向建⽴单链表{LNode *s; //声明⼀个临时结点int x;L=(LinkList)malloc(sizeof(LNode)); //创建头结点L->next=NULL; //初始为空链表scanf("%d",&x); //输⼊结点的值while(x!=9999){s=(LNode*)malloc(sizeof(LNode)); //创建新结点s->data=x;s->next=L->next; //将新结点插⼊表中，L为头指针L->next=s;scanf("%d",&x);}return L;}⼆、采⽤不带有头结点的头插法逆向建⽴单链表Linklist List_HeadInsert2(LinkList &L) //采⽤不带有头结点的头插法逆向建⽴单链表{LNode *s; //声明⼀个临时结点int x;L=NULL;scanf("%d",&x); //输⼊结点的值while(x!=9999){s=(LNode*)malloc(sizeof(LNode)); //创建新结点s->data=x;if(L==NULL) // 若第⼀次创建节点，则将该点设置为头节点{L=s;s->next=NULL;}else{ // 若不是第⼀次创建节点，则直接将新节点接到链表头s->next=L;L=s;}scanf("%d",&x);}return L;}三、采⽤带有头结点的尾插法正向建⽴单链表Linklist List_TailInsert1(LinkList &L) //采⽤带有头结点的尾插法正向建⽴单链表{LNode *s,*r; //s为临时结点，r为表尾指针int x;L=(LinkList)malloc(sizeof(LNode)); //创建头结点L->next=NULL; //初始为空链表r=L;scanf("%d",&x); //输⼊结点的值while(x!=9999){s=(LNode*)malloc(sizeof(LNode)); //创建新结点s->data=x;r->next=s;r=s; //r指向新的表尾结点scanf("%d",&x);}r->next=NULL; //尾结点指针为空return L;}四、⽤不带有头结点的尾插法正向建⽴单链表Linklist List_TailInsert2(LinkList &L) //采⽤不带有头结点的尾插法正向建⽴单链表{LNode *s,*r; //s为临时结点，r为表尾指针int x;L=NULL;r=L;scanf("%d",&x); //输⼊结点的值while(x!=9999){s=(LNode*)malloc(sizeof(LNode)); //创建新结点s->data=x;if(L==NULL) // 创建链表的第⼀个节点{L=s;r=s;s->next=NULL;}else{r->next=s;r=s;}scanf("%d",&x);}r->next=NULL; //尾结点指针为空return L;}。

单链表的实现及其基本操作

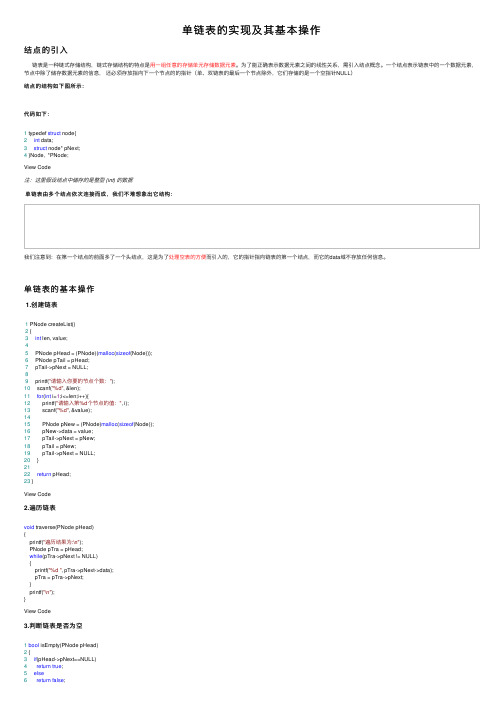
单链表的实现及其基本操作结点的引⼊链表是⼀种链式存储结构，链式存储结构的特点是⽤⼀组任意的存储单元存储数据元素。

为了能正确表⽰数据元素之间的线性关系，需引⼊结点概念。

⼀个结点表⽰链表中的⼀个数据元素，节点中除了储存数据元素的信息，还必须存放指向下⼀个节点的的指针（单、双链表的最后⼀个节点除外，它们存储的是⼀个空指针NULL）结点的结构如下图所⽰：代码如下：1 typedef struct node{2int data;3struct node* pNext;4 }Node, *PNode;View Code注：这⾥假设结点中储存的是整型 (int) 的数据单链表由多个结点依次连接⽽成，我们不难想象出它结构：我们注意到：在第⼀个结点的前⾯多了⼀个头结点，这是为了处理空表的⽅便⽽引⼊的，它的指针指向链表的第⼀个结点，⽽它的data域不存放任何信息。

单链表的基本操作1.创建链表1 PNode createList()2 {3int len, value;45 PNode pHead = (PNode)(malloc(sizeof(Node)));6 PNode pTail = pHead;7 pTail->pNext = NULL;89 printf("请输⼊你要的节点个数：");10 scanf("%d", &len);11for(int i=1;i<=len;i++){12 printf("请输⼊第%d个节点的值：", i);13 scanf("%d", &value);1415 PNode pNew = (PNode)malloc(sizeof(Node));16 pNew->data = value;17 pTail->pNext = pNew;18 pTail = pNew;19 pTail->pNext = NULL;20 }2122return pHead;23 }View Code2.遍历链表void traverse(PNode pHead){printf("遍历结果为:\n");PNode pTra = pHead;while(pTra->pNext != NULL){printf("%d ", pTra->pNext->data);pTra = pTra->pNext;}printf("\n");}View Code3.判断链表是否为空1bool isEmpty(PNode pHead)2 {3if(pHead->pNext==NULL)4return true;5else6return false;7 }View Code4.链表长度1int length(PNode pHead)2 {3int len = 0;4while(pHead->pNext!=NULL){5 pHead = pHead->pNext;6 len++;7 }8return len;910 }View Code5.插⼊结点1bool insert(PNode pHead, int pos, int val)2 {3if(pos<1 || pos>length(pHead)){4return false;5 }else{6 PNode pInsert = pHead;7for(int i=1;i<pos;i++){8 pInsert = pInsert->pNext;9 }1011 PNode pNew = (PNode)malloc(sizeof(Node));12 pNew->data = val;13 pNew->pNext = pInsert->pNext;14 pInsert->pNext = pNew;1516return true;17 }1819 }View Code6.删除结点1bool del(PNode pHead, int pos)2 {3if(pos<1 || pos>length(pHead)){4return false;5 }else{6 PNode pDel = pHead;7for(int i=1;i<pos;i++){8 pDel = pDel->pNext;9 }1011if(pos==length(pHead)){12free(pDel->pNext);13 pDel->pNext = NULL;14 }else{15 PNode pNext = pDel->pNext->pNext;16free(pDel->pNext);17 pDel->pNext = pNext;18 }1920return true;2122 }232425 }View Code7.查找节点（1）按元素值查找1 PNode locate(PNode pHead, int value)2 {3 PNode p = pHead->pNext;4while(p&&p->data!=value){ //NULL 是 05 p = p->pNext;6 }7return p;8 }View Code（2）按序号查找1 PNode get(PNode pHead, int k)2 {3 PNode p = pHead;4for(int i=1;i<=k;i++){5 p = p->pNext;6 }7return p;89 }View Code完整代码1 #include<stdio.h>2 #include<stdlib.h>3 typedef struct node{4int data;5struct node* pNext;6 }Node, *PNode;78 PNode createList();9void traverse(PNode pHead);10bool isEmpty(PNode pHead);11int length(PNode pHead);12bool insert(PNode pHead, int pos, int val);13bool del(PNode pHead, int pos);14 PNode get(PNode pHead, int k); //按序号查找15 PNode locate(PNode pHead, int value);//按值查找 1617int main(void)18 {19//test2021return0;22 }2324 PNode createList()25 {26int len, value;2728 PNode pHead = (PNode)(malloc(sizeof(Node)));29 PNode pTail = pHead;30 pTail->pNext = NULL;3132 printf("请输⼊你要的节点个数：");33 scanf("%d", &len);34for(int i=1;i<=len;i++){35 printf("请输⼊第%d个节点的值：", i);36 scanf("%d", &value);3738 PNode pNew = (PNode)malloc(sizeof(Node));39 pNew->data = value;40 pTail->pNext = pNew;41 pTail = pNew;42 pTail->pNext = NULL;43 }4445return pHead;46 }474849void traverse(PNode pHead)50 {51 printf("遍历结果为:\n");52 PNode pTra = pHead;53while(pTra->pNext != NULL)54 {55 printf("%d ", pTra->pNext->data);56 pTra = pTra->pNext;57 }58 printf("\n");59 }6061bool isEmpty(PNode pHead)62 {63if(pHead->pNext==NULL)64return true;65else66return false;67 }6869int length(PNode pHead)70 {71int len = 0;72while(pHead->pNext!=NULL){73 pHead = pHead->pNext;74 len++;75 }76return len;7778 }7980bool insert(PNode pHead, int pos, int val)81 {82if(pos<1 || pos>length(pHead)){83return false;84 }else{85 PNode pInsert = pHead;86for(int i=1;i<pos;i++){87 pInsert = pInsert->pNext;88 }8990 PNode pNew = (PNode)malloc(sizeof(Node));91 pNew->data = val;92 pNew->pNext = pInsert->pNext;93 pInsert->pNext = pNew;9495return true;96 }9798 }99100bool del(PNode pHead, int pos)101 {102if(pos<1 || pos>length(pHead)){103return false;104 }else{105 PNode pDel = pHead;106for(int i=1;i<pos;i++){107 pDel = pDel->pNext;108 }109110if(pos==length(pHead)){111free(pDel->pNext);112 pDel->pNext = NULL;113 }else{114 PNode pNext = pDel->pNext->pNext;115free(pDel->pNext);116 pDel->pNext = pNext;117 }118119return true;120121 }122123124 }125126 PNode get(PNode pHead, int k)127 {128 PNode p = pHead;129for(int i=1;i<=k;i++){130 p = p->pNext;131 }132return p;133134 }135 PNode locate(PNode pHead, int value)136 {137 PNode p = pHead->pNext;138while(p&&p->data!=value){ //NULL 是 0 139 p = p->pNext;140 }141return p;142 }View Code。

数据结构之链表

数据结构之链表链表是一种常见的数据结构，它由一系列节点组成，每个节点包含数据和指向下一个节点的指针。

相比于数组，链表具有更灵活的插入和删除操作，但访问元素的效率较低。

在计算机科学中，链表被广泛应用于各种算法和数据处理任务中。

链表的基本结构可以用以下代码表示：```pythonclass Node:def __init__(self, data):self.data = dataself.next = None```在链表中，每个节点都包含一个数据项和一个指向下一个节点的指针。

链表的头节点是链表的入口，通过头节点可以遍历整个链表。

链表的插入操作是将一个新节点插入到链表的指定位置。

例如，我们可以在链表的头部插入一个新节点：```pythondef insert_at_head(head, data):new_node = Node(data)new_node.next = headhead = new_nodereturn head```链表的删除操作是将链表中的某个节点删除。

例如，我们可以删除链表中的第一个节点：```pythondef delete_at_head(head):if head is None:return Nonehead = head.nextreturn head```链表的遍历操作是按顺序访问链表中的每个节点。

例如，我们可以遍历链表并打印每个节点的数据：```pythondef print_list(head):current = headwhile current is not None:print(current.data)current = current.next```链表的搜索操作是在链表中查找某个特定的节点。

例如，我们可以搜索链表中是否存在某个特定的数据项：```pythondef search_list(head, data):current = headwhile current is not None:if current.data == data:return Truecurrent = current.nextreturn False```链表的反转操作是将链表中的节点顺序颠倒。

使用循环单链表表示队列

使用循环单链表表示队列队列是一种常见的数据结构，它遵循先进先出（FIFO）的原则，即先进入队列的元素将先被取出。

队列通常用于需要按照顺序处理数据的场景，比如任务调度、消息传递等。

在实际应用中，我们可以使用循环单链表来表示队列。

循环单链表是一种链表结构，它与普通的单链表相比，最后一个节点的指针域不为空，而是指向链表的头结点。

这样一来，在遍历链表时可以很方便地回到链表的起始位置。

对于队列来说，使用循环单链表可以更高效地实现入队和出队的操作。

下面我们来具体讨论如何使用循环单链表来表示队列。

我们需要定义一个循环单链表节点的结构。

该结构包含一个数据域和一个指针域，分别指向下一个节点。

代码如下：```cppstruct Node {int data;Node* next;};```接下来，我们定义一个队列类，该类包含队列的基本操作，如入队、出队、判断队列是否为空等。

代码如下：```cppclass Queue {private:Node* front; // 队头指针Node* rear; // 队尾指针public:Queue() {front = rear = nullptr; // 初始化队头和队尾指针为空 }~Queue() {// 释放队列中的所有节点while (!isEmpty()) {dequeue();}}// 入队操作void enqueue(int value) {Node* newNode = new Node;newNode->data = value;newNode->next = nullptr;if (isEmpty()) {front = rear = newNode; // 队列为空，队头和队尾指针指向新节点} else {rear->next = newNode; // 将新节点链接到队尾rear = newNode; // 更新队尾指针}}// 出队操作void dequeue() {if (isEmpty()) {throw "Queue is empty!";}Node* temp = front;front = front->next; // 更新队头指针if (front == nullptr) {rear = nullptr; // 队列只有一个节点，出队后队尾指针为空}delete temp; // 释放出队节点的内存 }// 判断队列是否为空bool isEmpty() {return front == nullptr;}// 获取队头元素int getFront() {if (isEmpty()) {throw "Queue is empty!";}return front->data;}// 获取队列长度int getSize() {int size = 0;Node* current = front;while (current != nullptr) {size++;current = current->next;}return size;}};```使用循环单链表表示队列的好处是，入队和出队的时间复杂度都是O(1)，即常数时间。

单链表的基本操作

单向链表单向链表的基本操作,创建一个由6个节点组成的单向链表，显示链表中每个节点的数据,并且做增加、删除、查找节点以及计算单链表的长度等处理。

➢需求分析：1.功能(1）用尾插法创建一带头结点的由6个节点组成的单向链表：从键盘读入一组整数,作为单链表中的元素，输入完第6个结点后结束;将创建好的单链表元素依次输出到屏幕上。

（2)显示链表中每个节点的数据(3)从键盘输入一个数，查找在以上创建的单链表中是否存在该数;如果存在,显示它的位置，即第几个元素；如果不存在，给出相应提示如“No found node!”。

（4)在上述的单链表中的指定位置插入指定数据，并输出单链表中所有数据.(5)删除上述单链表中指定位置的结点,并输出单链表中所有数据.(6）求单链表的长度并输出。

2．输入要求先输入单链表中结点个数n,再输入单链表中所有数据，在单链表中需查找的数据，需插入的数据元素的位置、值，要删除的数据元素的位置。

3。

测试数据单链表中所有数据:12，23，56，21，8，10在单链表中需查找的数据：56；24插入的数据元素的位置、值：1,28;7,28；0,28要删除的数据元素的位置：6➢概要设计:1.算法思想：由于在操作过程中要进行插入、删除等操作，为运算方便，选用带头结点的单链表作数据元素的存储结构。

对每个数据元素，由一个数据域和一个指针域组成,数据域放输入的数据值，指针域指向下一个结点。

2.数据结构:单链表结点类型：typedef struct Liistnode {int data；struct Listnode *next;} NODE;3.模块划分：a)用尾插法建立带头结点的单链表*CreateList函数；b)显示链表中每个结点的数据PrintList函数；c)从键盘输入一个数,查找单链表中是否存在该数FoundList函数；d)在单链表中指定位置插入指定数据并输出单链表中所有数据InsertList函数;e)删除单链表中指定位置的结点并输出单链表中所有数据DeleteList函数；f)计算单链表的长度并在屏幕上输出LengthList函数;g)主函数main（），功能是给出测试数据值,建立测试数据值的带头结点的单链表，调用PrintList函数、FoundList函数、InsertList函数、DeleteList函数、LengthList函数实现问题要求.四、实验要求1．用C完成算法设计和程序设计并上机调试通过。

单链表逆转算法

单链表逆转算法单链表（Singly Linked List）是一种常用的数据结构，它由节点组成，每个节点由两部分组成，一部分是数据，另一部分是指向下一个节点的指针。

单链表逆转算法是将原来指向下一个节点的指针变为指向前一个节点，这样就能实现链表的逆序。

下面来分步骤阐述单链表逆转算法的实现。

第一步：定义节点类节点类是单链表的基础，它包含一个数据成员和一个指向下一个节点的指针。

在C++中，定义一个节点类可以使用如下代码：```class Node {public:int val;Node* next;Node(int val) : val(val), next(nullptr) {}};```这里定义了一个包含一个整数元素和指向下一个节点的指针的节点类。

第二步：创建链表创建单链表需要创建多个节点，并将这些节点连接起来。

这里以创建包含5个元素的单链表为例。

```Node* head = new Node(1);Node* cur = head;for (int i = 2; i <= 5; i++) {Node* node = new Node(i);cur->next = node;cur = node;}```这里定义了链表的头节点head，然后使用cur变量来指向每个新创建的节点，并将前一个节点的next指针指向它，最后将cur指向新创建的节点。

第三步：遍历链表（可选）在逆转单链表前，可以先遍历一遍链表，了解链表结构。

这里使用while循环遍历链表。

```while (head != nullptr) {cout << head->val << " ";head = head->next;}```第四步：逆转链表逆转链表需要将原来每个节点指向下一个节点的指针改为指向前一个节点的指针。

这里使用三个指针prev、cur和next，prev指向前一个节点，cur指向当前节点，next指向下一个节点。