广东历届高考文科题分章汇编(统计、推理与证明)
2022-2022广东高考文科数学试题分类汇总完整版(含答案)大

2022-2022广东高考文科数学试题分类汇总完整版(含答案)大广东高考文科数学1.集合与简易逻辑202210分20225分20225分20225分2022—2022近五年试题分类汇编C.必要非充分条件D.非充分非必要条件7、解析:本题考查正弦定理的应用。
由于202210分B=(A.)ab2R,所以a2RinA,inAinBb2RinB,所以ab2RinA2RinBinAinB,故“ab”是“inAinB”的充要条件,故选答案为A.2.复数20222022520225分20225分202210分(2022年高考广东卷第1小题)若集合A={0,1,2,3},B={1,2,4},则集合AA.{0,1,2,3,4}B.{1,2,3,4}C.{1,2}D.{0}(2022年高考广东卷第8小题)“某>0”是“3某2>0”成立的(A.)A.充分非必要条件B.必要非充分条件C.非充分非必要条件D.充要条件(2022年高考广东卷第2小题)22已知集A(某,y)某,y为实数,且某y1,B(某,y)某,y为实数,且某y1,则AB的元素个数(2022年高考广东卷第1小题)设复数z满足iz=1,其中i为虚数单位,则z=(A)A.-iB.iC.-1D.1(2022年高考广东卷第1小题)1.设i为虚数单位,则复数为(C)A.4B.3C.2D.1(2022年高考广东卷第2小题)2.设集合U1,2,3,4,5,6,M1,3,5,则CUM(A)A.2,4,6B.1,3,5C.1,2,4D.U(2022年高考广东卷第1题)1.已知集合34i(D)iA.43iB.43iC.43iD.43iS某某2某0,某R2,T某某22某0,某R,则(2022年高考广东卷第3题)3.若i(某+yi)=3+4i,某,y∈R,则某+yi的模是(D)A.2B.3C.4D.5(2022年高考广东卷第2题)2.已知复数z满足(34i)z25,则z()A.34iB.34iC.34iD.34i解析:本题考查复数的除法运算,属于基础题.zST(A)A.{0}B.{0,2}C.{-2,0}D.{-2,0,2}(2022年高考广东卷第1题)1.已知集合M2,3,4,N0,2,3,5,则MN()A.3,5B.3,4C.2,3D.0,2解析:本题考查集合的基本运算,属于基础题.MN2,3,故选C.(2022年高考广东卷)7.在ABC中,角A,B,C所对应的边分别为a,b,c,则“ab”是“inAinB”的()A.充分必要条件B.充分非必要条件-1-2525(34i)34i.故选A.34i34i(34i)10.对任意复数w1,w2,定义1212,其中2是2的共轭复数,对任意复数z1,z2,z3有如下四个命题:①(z1z2)z3(z1z3)(z2z3);②z1(z2z3)(z1z2)(z1z3);③(z1z2)z3z1(z2z3);④z1z2z2z1;则真命题的个数是()A.4B.3C.2D.1(2022年高考广东卷)10、解析:本题属于信息创新型题目,要求学生利用以学过的知识来解决新问题.对于①,z1z2z3z1z2z3z1z3z2z3z1z3z2z3对于②,z1z2z3z1z2z3.令z2abi,z3cdi,则z2z3acbdi,则z2z3acbdiA.(4,6)B.(4,6)C.(2,2)D.(2,2)(2022年高考广东卷第10小题)对任意两个非零的平面向量,,定义.若平面向量a,b满足nab0,a与b的夹角0,,且和都在集合|nZ中,则ab(D)42A.531B.C.1D.222(2022年高考广东卷)10.设a是已知的平面向量且a≠0。
近五年广东省高考语文试题与答案汇编

绝密★启用前试卷类型:A2007年普通高等学校招生全国统一考试(广东卷)本试卷共8页,24小题,满分150分。
考试用时150分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或掺字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B铅笔将试卷类型(A)填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上:3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然目再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B铅笔填涂选做题的题组号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效:5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、本大题4小题,每小题3分,共12分。
1.下列词语中加点的字,读音完全不相同的一组是A.峥.嵘狰.狞慎.重缜.密周全B.诅.咒趔趄.狙.击神情沮.丧C.讥诮.眉梢.俏.丽峭.拔刚劲D.辍.笔啜.泣拙.劣相形见绌.2.下列各句中加点的词语,使用恰当的一句是A.父亲收藏的那些产于不同时代、具有不同造型、来自不同国家的玩具汽车,把小小的书房挤得满满当当,间不容发....。
B.我们不能因为有姚明等人加盟美国NBA,就妄自菲薄....地说,我国的篮球运动足以与欧美篮球强国抗衡了。
C.沈从文早在20世纪30年代就因在《边城》中描绘了一个独特的湘西世界,展现了豪爽与浪漫的湘西风情而名噪一时....。
D.我俩考虑问题时,他习惯从大的方面着眼,我总是从具体方法入手,虽然南辕北辙....,但总能殊途同归。
3.在下面各句横线处依次填入的词语,最恰当的一组是①应该以实际运用能力来我们的学习效果。
②老百姓说得好,常年无灾情,不可一日不防备:③这小伙子整体素质的确不错,诚实温和。
广东高考文科试题及答案

广东高考文科试题及答案广东高考文科试题及答案通常由广东省教育考试院负责发布,包括语文、数学、英语以及文科综合(政治、历史、地理)等科目。
以下是模拟的试题及答案示例,仅供参考:语文试题一、选择题(每题3分,共15分)1. 下列词语中,字形全部正确的一组是:A. 翩跹起舞金壁辉煌B. 栩栩如生涣然冰释C. 脍灸人口风声鹤唳D. 一诺千金筚路蓝缕答案:D2. 下列句子中,没有语病的一句是:A. 经过努力,他的学习成绩有了明显的提高。
B. 由于天气原因,航班延误了三个小时。
C. 他不仅学习优秀,而且品德高尚。
D. 这本书的内容非常丰富,值得一读。
答案:A二、阅读理解(共30分)阅读以下文章,回答问题。
文章:(此处省略文章内容)问题:1. 文章中提到的“XX”是什么含义?2. 作者通过哪些方式表达了对“XX”的看法?答案:1. “XX”指的是...2. 作者通过...来表达...三、作文(共55分)根据题目要求,写一篇不少于800字的议论文。
题目:(此处省略题目)作文示例:(此处省略作文内容)数学试题一、选择题(每题5分,共20分)1. 已知函数\( f(x) = ax^2 + bx + c \),若\( f(1) = 2 \),求\( f(-1) \)的值。
答案:-2二、填空题(每题5分,共15分)1. 若\( \sin \theta = \frac{3}{5} \),\( \theta \)为锐角,求\( \cos^2 \theta \)的值。
答案:\( \frac{16}{25} \)三、解答题(共65分)1. 解不等式\( |x - 3| + |x + 2| \geq 5 \)。
答案:(此处省略解答过程)英语试题一、阅读理解(共20分)阅读以下文章,回答问题。
文章:(此处省略文章内容)问题:1. What is the main idea of the passage?2. What does the author suggest about...答案:1. The main idea is...2. The author suggests that...二、完形填空(共15分)(此处省略完形填空内容)三、写作(共25分)根据题目要求,写一篇不少于120词的短文。
专题11 不等式、推理与证明、复数、算法初步-三年(2022–2024)高考数学真题分类汇编(解析)

专题11不等式、推理与证明、复数、算法初步考点三年考情(2022-2024)命题趋势考点1:线性规划问题2024年高考全国甲卷数学(理)真题2022年新高考浙江数学高考真题2023年高考全国甲卷数学(理)真题2023年高考全国乙卷数学(理)真题2022年高考全国乙卷数学(文)真题高考对本节的考查相对稳定,每年必考题型,考查内容、频率、题型、难度均变化不大.复数的运算与不等式是常考点,难度较低,预测高考在此处仍以简单题为主.考点2:不等式大小判断问题2024年北京高考数学真题考点3:利用基本不等式求最值2022年新高考全国II卷数学真题考点4:解不等式2024年上海高考数学真题考点5:程序框图2023年高考全国甲卷数学(理)真题2022年高考全国乙卷数学(理)真题考点6:复数加减乘除运算2022年新高考天津数学高考真题2023年天津高考数学真题2024年天津高考数学真题2023年新课标全国Ⅰ卷数学真题2024年高考全国甲卷数学(文)真题2024年高考全国甲卷数学(理)真题2024年北京高考数学真题2024年新课标全国Ⅰ卷数学真题2023年高考全国乙卷数学(理)真题2023年高考全国甲卷数学(文)真题2022年新高考全国I卷数学真题2022年新高考全国II卷数学真题2022年高考全国甲卷数学(理)真题考点7:模运算2024年新课标全国Ⅱ卷数学真题2022年新高考北京数学高考真题2022年高考全国甲卷数学(文)真题2023年高考全国乙卷数学(文)真题考点8:复数相等2024年上海高考数学真题2023年高考全国甲卷数学(理)真题2022年新高考浙江数学高考真题2022年高考全国乙卷数学(文)真题2022年高考全国乙卷数学(理)真题考点9:复数的几何意义2023年北京高考数学真题2023年新课标全国Ⅱ卷数学真题考点1:线性规划问题1.(2024年高考全国甲卷数学(理)真题)若,x y满足约束条件43302202690x yx yx y--≥⎧⎪--≤⎨⎪+-≤⎩,则5z x y=-的最小值为()A.12B.0C.52-D.72-【答案】D【解析】实数,x y满足4330220 2690 x yx yx y--≥⎧⎪--≤⎨⎪+-≤⎩,作出可行域如图:由5z x y=-可得1155y x z=-,即z的几何意义为1155y x z=-的截距的15-,则该直线截距取最大值时,z有最小值,此时直线1155y x z=-过点A,联立43302690x yx y--=⎧⎨+-=⎩,解得321xy⎧=⎪⎨⎪=⎩,即3,12A⎛⎫⎪⎝⎭,则min375122z=-⨯=-.故选:D.2.(2022年新高考浙江数学高考真题)若实数x,y满足约束条件20,270,20,xx yx y-≥⎧⎪+-≤⎨⎪--≤⎩则34z x y=+的最大值是()A.20B.18C.13D.6【答案】B【解析】不等式组对应的可行域如图所示:当动直线340x y z +-=过A 时z 有最大值.由2270x x y =⎧⎨+-=⎩可得23x y =⎧⎨=⎩,故()2,3A ,故max 324318z =⨯+⨯=,故选:B.3.(2023年高考全国甲卷数学(理)真题)若x ,y 满足约束条件3232331x y x y x y -≤⎧⎪-+≤⎨⎪+≥⎩,设32z x y =+的最大值为.【答案】15【解析】作出可行域,如图,由图可知,当目标函数322z y x =-+过点A 时,z 有最大值,由233323x y x y -+=⎧⎨-=⎩可得33x y =⎧⎨=⎩,即(3,3)A ,所以max 332315z =⨯+⨯=.故答案为:154.(2023年高考全国乙卷数学(理)真题)若x ,y 满足约束条件312937x y x y x y -≤-⎧⎪+≤⎨⎪+≥⎩,则2z x y =-的最大值为.【答案】8【解析】作出可行域如下图所示:2z x y =-,移项得2y x z =-,联立有3129x y x y -=-⎧⎨+=⎩,解得52x y =⎧⎨=⎩,设()5,2A ,显然平移直线2y x =使其经过点A ,此时截距z -最小,则z 最大,代入得8z =,故答案为:8.5.(2022年高考全国乙卷数学(文)真题)若x ,y 满足约束条件2,24,0,x y x y y +≥⎧⎪+≤⎨⎪≥⎩则2z x y =-的最大值是()A .2-B .4C .8D .12【答案】C【解析】由题意作出可行域,如图阴影部分所示,转化目标函数2z x y =-为2y x z =-,上下平移直线2y x z =-,可得当直线过点()4,0时,直线截距最小,z 最大,所以max 2408z =⨯-=.故选:C.考点2:不等式大小判断问题6.(2024年北京高考数学真题)已知()11,x y ,()22,x y 是函数2x y =的图象上两个不同的点,则()A .12122log 22y y x x ++<B .12122log 22y y x x ++>C .12212log 2y y x x +<+D .12212log 2y y x x +>+【答案】B【解析】由题意不妨设12x x <,因为函数2x y =是增函数,所以12022x x <<,即120y y <<,对于选项AB :可得1212122222·222x x x x x x ++>=,即12122202x x y y ++>>,根据函数2log y x =是增函数,所以121212222log log 222x x y y x x+++>=,故A 正确,B 错误;对于选项C :例如120,1x x ==,则121,2y y ==,可得()12223log log 0,122y y +=∈,即12212log 12y y x x +<=+,故C 错误;对于选项D :例如121,2x x =-=-,则1211,24y y ==,可得()122223log log log 332,128y y +==-∈--,即12212log 32y y x x +>-=+,故D 错误,故选:B.考点3:利用基本不等式求最值7.(多选题)(2022年新高考全国II 卷数学真题)若x ,y 满足221+-=x y xy ,则()A .1x y +≤B .2x y +≥-C .222x y +≤D .221x y +≥【答案】BC【解析】因为22222a b a b ab ++⎛⎫≤≤ ⎪⎝⎭(,a b ÎR ),由221+-=x y xy 可变形为,()221332x y x y xy +⎛⎫+-=≤ ⎪⎝⎭,解得22x y -≤+≤,当且仅当1x y ==-时,2x y +=-,当且仅当1x y ==时,2x y +=,所以A 错误,B 正确;由221+-=x y xy 可变形为()222212x y x y xy ++-=≤,解得222x y +≤,当且仅当1x y ==±时取等号,所以C 正确;因为221+-=x y xy 变形可得223124y x y ⎛⎫-+= ⎪⎝⎭,设3cos sin 2y x θθ-==,所以cos ,sin 33x y θθθ=+=,因此2222511cos sin sin cos 1sin 2cos 233333x y θθθθ=θ-θ+=++++42π2sin 2,23363θ⎛⎫⎡⎤=+-∈ ⎪⎢⎥⎝⎭⎣⎦,所以当3333x y ==221x y +≥不成立,所以D 错误.故选:BC .考点4:解不等式8.(2024年上海高考数学真题)已知,x ∈R 则不等式2230x x --<的解集为.【答案】{}|13x x -<<【解析】方程2230x x --=的解为=1x -或3x =,故不等式2230x x --<的解集为{}|13x x -<<,故答案为:{}|13x x -<<.考点5:程序框图9.(2023年高考全国甲卷数学(理)真题)执行下面的程序框图,输出的B =()A .21B .34C .55D .89【答案】B【解析】当1k =时,判断框条件满足,第一次执行循环体,123A =+=,325B =+=,112k =+=;当2k =时,判断框条件满足,第二次执行循环体,358A =+=,8513B =+=,213k =+=;当3k =时,判断框条件满足,第三次执行循环体,81321A =+=,211334B =+=,314k =+=;当4k =时,判断框条件不满足,跳出循环体,输出34B =.故选:B.10.(2022年高考全国乙卷数学(理)真题)执行下边的程序框图,输出的n =()A .3B .4C .5D .6【答案】B【解析】执行第一次循环,2123b b a =+=+=,312,12a b a n n =-=-==+=,222231220.0124b a -=-=>;执行第二次循环,2347b b a =+=+=,725,13a b a n n =-=-==+=,222271220.01525b a -=-=>;执行第三次循环,271017b b a =+=+=,17512,14a b a n n =-=-==+=,2222171220.0112144b a -=-=<,此时输出4n =.故选:B考点6:复数加减乘除运算11.(2022年新高考天津数学高考真题)已知i 是虚数单位,化简113i1+2i-的结果为.【答案】15i -/51i -+【解析】()()()()113i 12i 113i 11625i15i 1+2i 1+2i 12i 5-----==--.故答案为:15i -.12.(2023年天津高考数学真题)已知i 是虚数单位,化简514i23i++的结果为.【答案】4i +/4i +【解析】由题意可得()()()()514i 23i 514i 5213i4i 23i 23i 23i 13+-++===+++-.故答案为:4i +.13.(2024年天津高考数学真题)已知i 是虚数单位,复数)()5i 52i ⋅=.【答案】75i 【解析】))5i 52i 55i 25i 275i ⋅-=-+=.故答案为:75i .14.(2023年新课标全国Ⅰ卷数学真题)已知1i22iz -=+,则z z -=()A .i -B .i C .0D .1【答案】A 【解析】因为()()()()1i 1i 1i 2i 1i 22i 21i 1i 42z ----===-++-,所以1i 2z =,即i z z -=-.故选:A .15.(2024年高考全国甲卷数学(文)真题)设2i z =,则z z ⋅=()A .2-B 2C .2-D .2【答案】D【解析】依题意得,2i z =-,故22i 2zz =-=.故选:D16.(2024年高考全国甲卷数学(理)真题)若5i z =+,则()i z z +=()A .10iB .2iC .10D .2【答案】A【解析】由5i 5i,10z z z z =+⇒=-+=,则()i 10i z z +=.故选:A17.(2024年北京高考数学真题)已知1i iz=--,则z =().A .1i --B .1i-+C .1i-D .1i+【答案】C【解析】由题意得()i 1i i 1z =--=-.故选:C.18.(2024年新课标全国Ⅰ卷数学真题)若1i 1zz =+-,则z =()A .1i --B .1i -+C .1i-D .1i+【答案】C 【解析】因为11111i 111z z z z z -+==+=+---,所以111i i z =+=-.故选:C.19.(2023年高考全国乙卷数学(理)真题)设252i1i i z +=++,则z =()A .12i -B .12i +C .2i -D .2i+【答案】B【解析】由题意可得()252i 2i 2i 2i2i 112i 1i i 11i i 1z +++-=====-++-+-,则12i z =+.故选:B.20.(2023年高考全国甲卷数学(文)真题)()()()351i 2i 2i +=+-()A .1-B .1C .1i-D .1i+【答案】C 【解析】()()351i 51i 1i (2i)(2i)5+-==-+-故选:C.21.(2022年新高考全国I 卷数学真题)若i(1)1z -=,则z z +=()A .2-B .1-C .1D .2【答案】D【解析】由题设有21i1i i iz -===-,故1+i z =,故()()1i 1i 2z z +=++-=,故选:D22.(2022年新高考全国II 卷数学真题)(22i)(12i)+-=()A .24i -+B .24i --C .62i+D .62i-【答案】D【解析】()()22i 12i 244i 2i 62i +-=+-+=-,故选:D.23.(2022年高考全国甲卷数学(理)真题)若13i z =-,则1zzz =-()A .13i -B .13i-C .133-+D .133--【答案】C【解析】13i,(13i)(13i)13 4.z zz =-=--=+=13i 131333z zz -==--故选:C考点7:模运算24.(2024年新课标全国Ⅱ卷数学真题)已知1i z =--,则z =()A .0B .1C 2D .2【答案】C【解析】若1i z =--,则()()22112z -+-=故选:C.25.(2022年新高考北京数学高考真题)若复数z 满足i 34i z ⋅=-,则z =()A .1B .5C .7D .25【答案】B【解析】由题意有()()()34i i 34i 43i i i i z ---===--⋅-,故()()223|54|z -+-==.故选:B .26.(2022年高考全国甲卷数学(文)真题)若1i z =+.则|i 3|z z +=()A .45B .42C .25D .22【答案】D【解析】因为1i z =+,所以()()i 3i 1i 31i 22i z z +=++-=-,所以i 34422z z +=+=故选:D.27.(2023年高考全国乙卷数学(文)真题)232i 2i ++=()A .1B .2C 5D .5【答案】C【解析】由题意可得232i 2i 212i 12i ++=--=-,则()22322i 2i 12i 125++=-+-=故选:C.考点8:复数相等28.(2024年上海高考数学真题)已知虚数z ,其实部为1,且()2z m m z+=∈R ,则实数m 为.【答案】2【解析】设1i z b =+,b ∈R 且0b ≠.则23222231i i 1i 11b b b z b m z b b b ⎛⎫⎛⎫+-+=++=+= ⎪ ⎪+++⎝⎭⎝⎭,m ∈R ,22323101b mb b b b ⎧+=⎪⎪+∴⎨-⎪=⎪+⎩,解得2m =,故答案为:2.29.(2023年高考全国甲卷数学(理)真题)设()()R,i 1i 2,a a a ∈+-=,则=a ()A .-1B .0·C .1D .2【答案】C【解析】因为()()()22i 1i i i 21i 2a a a a a a a +-=-++=+-=,所以22210a a =⎧⎨-=⎩,解得:1a =.故选:C.30.(2022年新高考浙江数学高考真题)已知,,3i (i)i a b a b ∈+=+R (i 为虚数单位),则()A .1,3a b ==-B .1,3a b =-=C .1,3a b =-=-D .1,3a b ==【答案】B【解析】3i 1i a b +=-+,而,a b 为实数,故1,3a b =-=,故选:B.31.(2022年高考全国乙卷数学(文)真题)设(12i)2i a b ++=,其中,a b 为实数,则()A .1,1a b ==-B .1,1a b ==C .1,1a b =-=D .1,1a b =-=-【答案】A【解析】因为,a b ÎR ,()2i 2i a b a ++=,所以0,22a b a +==,解得:1,1a b ==-.故选:A.32.(2022年高考全国乙卷数学(理)真题)已知12z i =-,且0z az b ++=,其中a ,b 为实数,则()A .1,2a b ==-B .1,2a b =-=C .1,2a b ==D .1,2a b =-=-【答案】A【解析】12z i=-12i (12i)(1)(22)iz az b a b a b a ++=-+++=+++-由0z az b ++=,结合复数相等的充要条件为实部、虚部对应相等,得10220a b a ++=⎧⎨-=⎩,即12a b =⎧⎨=-⎩故选:A考点9:复数的几何意义33.(2023年北京高考数学真题)在复平面内,复数z 对应的点的坐标是(3)-,则z 的共轭复数z =()A .13i +B .13i-C .13i -D .13i-【答案】D【解析】z 在复平面对应的点是(3)-,根据复数的几何意义,13i z =-,由共轭复数的定义可知,13i z =-.故选:D34.(2023年新课标全国Ⅱ卷数学真题)在复平面内,()()13i 3i +-对应的点位于().A .第一象限B .第二象限C .第三象限D .第四象限【答案】A【解析】因为()()213i 3i 38i 3i 68i +-=+-=+,则所求复数对应的点为()6,8,位于第一象限.故选:A.。
高考文科数学试卷广东卷

2019年普通高等学校招生全国统一考试广东卷数学文科一.选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的;1已知集合{}{}5,3,2,0,4,3,2==N M ,则N MA. {}2,0B. {}3,2C. {}4,3D. {}5,3(2)已知复数z 满足25)43(=-z i ,则=zA.i 43--B. i 43+-C. i 43-D. i 43+(3)已知向量)1,3(),2,1(==b a ,则=-a bA. )1,2(-B. )1,2(-C. )0,2(D. )3,4((4)若变量y x ,满足约束条件⎪⎩⎪⎨⎧≤≤≤≤≤+304082y x y x 则y x z +=2的最大值等于A. 7B. 8C. 10D. 115.下列函数为奇函数的是 A.x x 212- B.x x sin 3 C.1cos 2+x D.x x 22+ 6.为了解1000名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为 .40 C7.在ABC ∆中,角A,B,C 所对应的边分别为,,,c b a 则“b a ≤”是 “B A sin sin ≤”的A.充分必要条件B.充分非必要条件C.必要非充分条件D.非充分非必要条件8.若实数k 满足05k <<,则曲线221165x y k -=-与曲线221165x y k -=-的 A.实半轴长相等 B.虚半轴长相等 C.离心率相等 D.焦距相等9.若空间中四条两两不同的直线1234,,,l l l l ,满足122334,,,l l l l l l ⊥⊥∥则下列结论一定正确的是A .14l l ⊥ B.14l l ∥ C.1l 与4l 既不垂直也不平行 D.1l 与4l 的位置关系不确定10.对任意复数12,,w w 定义1212,ωωωω*=其中2ω是2ω的共轭复数,对任意复数123,,z z z 有如下四个①1231323()()();z z z z z z z +*=*+*②1231213()()()z z z z z z z *+=*+*;③123123()();z z z z z z **=**④1221z z z z *=*;则真.2 C二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.一必做题11—13题11.曲线53x y e =-+在点()0,2-处的切线方程为________.12.从字母,,,,a b c d e 中任取两个不同字母,则取字母a 的概率为________.13.等比数列{}n a 的各项均为正数,且154a a =,则2122232425log +log +log +log +log =a a a a a ________.(二)选做题14-15题,考生只能从中选做一题14.坐标系与参数方程选做题在极坐标系中,曲线1C 与2C 的方程分别为θθρsin cos22=与1cos =θρ,以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,则曲线1C 与2C 的直角坐标为________15.几何证明选讲选做题如图1,在平行四边形ABCD 中,点E 在AB 上且AC AE EB ,2=与DE 交于点F 则______=∆∆的周长的周长AEF CDF 三.解答题:本大题共6小题,满分80分16.本小题满分12分已知函数()sin(),3f x A x x R π=+∈,且5()122f π= (1) 求A 的值;(2) 若()()(0,)2f f πθθθ--=∈,求()6f πθ- 17本小题满分13分某车间20名工人年龄数据如下表:(1) 求这20名工人年龄的众数与极差;(2) 以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;(3) 求这20名工人年龄的方差.18本小题满分13分如图2,四边形ABCD 为矩形,PD ⊥平面ABCD,AB=1,BC=PC=2,作如图3折叠,折痕EF ∥DC.其中点E,F 分别在线段PD,PC 上,沿EF 折叠后点P 在线段AD 上的点记为M,并且MF ⊥CF.(1) 证明:CF ⊥平面MDF(2) 求三棱锥M-CDE 的体积.19.本小题满分14分设各项均为正数的数列{}n a 的前n 项和为n S ,且n S 满足()()*∈=+--+-N n n n S n n S n n ,033222.(1)求1a 的值;(2)求数列{}n a 的通项公式;(3)证明:对一切正整数n ,有()()().311111112211<+++++n n a a a a a a 20本小题满分14分 已知椭圆()01:2222>>=+b a by a x C 的一个焦点为()0,5,离心率为35; (1)求椭圆C 的标准方程; (2)若动点()00,y x P 为椭圆C 外一点,且点P 到椭圆C 的两条切线相互垂直,求点P 的轨迹方程.21.本小题满分14分已知函数321()1()3f x x x ax a R =+++∈ (1) 求函数()f x 的单调区间; (2) 当0a <时,试讨论是否存在011(0,)(,1)22x ∈,使得01()()2f x f =。
广东高考文科数学 试题分类汇编 几何证明选讲
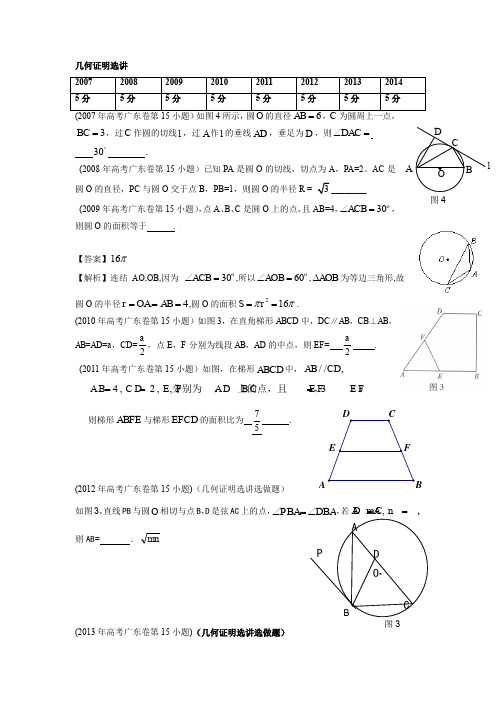
几何证明选讲3BC =,过C 作圆的切线l ,过A 作l 的垂线AD ,垂足为D ,则DAC ∠=30︒.(2008年高考广东卷第15小题)已知PA 是圆O 的切线,切点为A ,PA=2。
AC 是圆O 的直径,PC 与圆O 交于点B ,PB=1,则圆O 的半径R =________(2009年高考广东卷第15小题),点A 、B 、C 是圆O 上的点,且AB=4,30ACB ∠=o,则圆O 的面积等于 .【答案】16π【解析】连结AO,OB,因为 30ACB ∠=o,所以60AOB ∠=o,AOB ∆为等边三角形,故圆O 的半径4r OA AB ===,圆O 的面积216S r ππ==.(2010年高考广东卷第15小题)如图3,在直角梯形ABCD 中,DC ∥AB ,CB ⊥AB ,AB =AD =a ,CD =2a ,点E ,F 分别为线段AB ,AD 的中点,则EF = 2a. (2011年高考广东卷第15小题)如图,在梯形ABCD 中,//,AB CD4,2,,3//A B C D E F A D B C E F E F A B===分别为,上的点,且,, 则梯形ABFE 与梯形EFCD 的面积比为57.(2012年高考广东卷第15小题)(几何证明选讲选做题)如图3,直线PB 与圆O 相切与点B ,D是弦AC 上的点,DBA PBA ∠=∠,若,A D mA C n ==,则AB = .mn(2013年高考广东卷第15小题)(几何证明选讲选做题)A l图4A 图3如图3,在矩形ABCD中,3,AB BC BE AC ==⊥,垂足为E ,则ED=(2014年高考广东卷第15小题).证明选讲选做题)如图1,在平行四边形ABCD 中,点E 在AB 上且AC AE EB ,2=与DE 交于点F 则______=∆∆的周长的周长AEF CDF 3(2014年高考广东卷第18小题)(本小题满分13分)如图2,四边形ABCD 为矩形,PD ⊥平面ABCD ,AB=1,BC=PC=2,作如图3折叠,折痕EF ∥DC.其中点E ,F 分别在线段PD ,PC 上,沿EF 折叠后点P 在线段AD 上的点记为M ,并且MF ⊥CF. (1) 证明:CF ⊥平面MDF (2) 求三棱锥M-CDE 的体积.18.解:证明:(1)图3BCDMDF CF M MF MD CF MF CF MD PCDCF PCD MD ABCDAD CD AD ABCD CD ABCD PCD PCD ABCD PD 面且面又由于面面为矩形,四边形又交线为面面面且面⊥∴=⋂⊥⊥∴⊆⊥∴⊆⊥⊥∴⊆⊥,.,,.,.PD ,解: (2).16231.834312121.433,.26,1,210210,.23.23212,211,602,1.,.31==∴=⨯⨯=⋅=∴=∴====∆∴=⊥=∴=-==∴=︒=∠∴==∆⊥∴⊆⊥⋅⋅=∴⊥∆-∆∆-DM S V DE CD S DE PD E PD CP F DM CD CM MDC RT CM MF CF MF PF CF CD PCD PC CD PCD RT DFCF MDF DF MDF CF MD S V PCDMD CDE CDE M CDE CDE CDE M 的三分点,故为且的三分点点位于又得中,在故利用勾股定理得:又故且中,在面面面。
广东省十年文言文高考

广东省十年文言文高考1. 广东近十年高考文言文的朝代2008年高考广东卷文言文(晋书*周访传)翻译2007年高考语文广东卷文言文《聊斋志异·郭生》2006高考文言文翻译——广东卷(明·宋濂《杜环小传》)2005年高考语文广东卷文言文(《后汉书•朱晖传》其他的找不到了不过这里有其他广东考题的下载/SSx?ChannelID=13&Version=%D4%C1%BD%CC%B0%E6&Soft Type=%CA%D4%CC%E2%CA%D4%BE%ED&DownType=%B8% DF%BF%BC%CF%E0%B9%D8&wd=%D3%EF%CE%C4&submit= %C1%D0%B3%F62. 急需:广东近十年的高考语文作文题目2009:我们生活在常识中,常识与我们同行。
有时,常识虽易知而难行,有时常识须推陈而出新……请写一篇文章,谈谈你生活中与“常识”有关的经历或你对“常识”的看法。
自拟题目,自定写法,不少于800字。
2008:请以“不要轻易说‘不’”为题写一篇文章(要求:除诗歌外文体不限,不少于800字)。
2007:请以“传递”为话题,写一篇话题作文,800字,除诗歌外,体裁不限。
2006:个雕刻家在细心雕刻一块尚未成形的大理石,头部、肩膀都已雕刻成形,雕成了一个美丽的天使。
这时,一个小女孩问雕刻家:你怎么知道天使藏在石头里的?雕刻家回答:石头里本没有天使,但因为我是在用心雕刻”。
请以雕刻心中的天使的为话题,写一篇800字的作文2005:以《纪念》为题写一篇作文。
2004:阅读下面的寓言,根据要求作文。
(60 分)古时东瓯(今浙江南部沿海一带)人住的是茅屋,经常发生火灾,为此痛苦不已。
有个东瓯商人到晋国去,听说晋国有个叫冯妇的人善于搏虎,凡是他出现之处,就无虎。
东瓯商人回去后把这个消息告诉了国君。
由于东瓯话“火”和“虎”的读音毫无区别,国君误以为冯妇善于“扑火”,便以隆重的礼节从晋国请来了冯妇。
广东高考文科数学试题分类汇编

广东高考文科数学近7年试题分类汇编(1)1.集合与简易逻辑 N =(C )A .{11}x x -<≤B .{1}x x >C .{11}x x -<<D .{1}x x -≥(2008年高考广东卷第1小题)第二十九届夏季奥林匹克运动会将于2008年8月8日在北京举行,若集合A={参加北京奥运会比赛的运动员},集合B={参加北京奥运会比赛的男运动员},集合C={参加北京奥运会比赛的女运动员},则下列关系正确的是(D ) A. A B ⊆B. B C ⊆C. B ∪C = AD. A∩B = C(2009年高考广东卷第1小题).已知全集U=R ,则正确表示集合M= {-1,0,1} 和N= { x |x 2+x=0} 关系的韦恩(Venn )图是 (B )【解析】由N= { x |x 2+x=0}{1,0}-得N M ⊂,选B.(2010年高考广东卷第1小题)若集合A ={0,1,2,3},B ={1,2,4},则集合A B =( A.)A .{0,1,2,3,4}B .{1,2,3,4}C .{1,2}D .{0}(2010年高考广东卷第8小题) “x >0”是成立的( A.)A .充分非必要条件B .必要非充分条件C .非充分非必要条件D .充要条件(2011年高考广东卷第2小题)已知集合{}{}22(,),1,(,),1A x y x y x y B x y x y x y =+==+=为实数,且为实数,且,则A B 的元素个数为(C)A .4 B.3 C.2 D. 1(2012年高考广东卷第2小题)设集合{}1,2,3,4,5,6U =,{}1,3,5M =,则U C M =(A) A .{}2,4,6 B .{}1,3,5 C .{}1,2,4 D .U(2013年高考广东卷第1小题)设集合2{|20,}S x x x x R =+=∈,2{|20,}T x x x x R =-=∈,则S T =(A)A .{0}B .{0,2}C .{2,0}-D .{2,0,2}- 2.复数则b =( D ) A .2-B .12-C .12D .2(2008年高考广东卷第2小题)已知0<a <2,复数z = a + i (i 是虚数单位),则|z|的取值范围是( B )A. (1,5)B. (1,3)C. (1D. (1(2009年高考广东卷第2小题)下列n 的取值中,使ni =1(i 是虚数单位)的是(C ) A.n=2 B .n=3 C .n=4 D .n=5(2011年高考广东卷第1小题)设复数z 满足iz = 1,其中i 为虚数单位,则z = (A) A .- i B .i C .- 1 D .1 (2012年高考广东卷第1小题)设i 为虚数单位,则复数34ii+=(D) A .43i -- B .43i -+ C .43i + D .43i -(2013年高考广东卷第3小题)若()34i x yi i +=+,,x y R ∈,则复数x yi +的模是(D) A .2 B .3 C .4 D .5 3.函数(2007年高考广东卷第3小题)若函数,则函数在其定义域上是( B )A .单调递减的偶函数B .单调递减的奇函数C .单调递增的偶函数D .单调递增的奇函数(2007年高考广东卷第5小题)客车从甲地以60km/h 的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h 的速度匀速行驶1上时到达内地.下列描述客车从甲地出发,经过乙地,最后到达丙地所经过的路程s 与时间t 之间关系的图象中,正确的是( C )(2007年高考广东卷第21小题)已知a 是实数,函数2()223f x ax x a =+--,如果函数()y f x =在区间[11]-,上有零点,求a 的取值范围. 21解: 若0a =,则()23f x x =-,令3()0[1,1]2f x x =⇒=∉-,不符合题意, 故0a ≠当()f x 在 [-1,1]上有一个零点时,此时48(3)01112a a a ∆=++=⎧⎪⎨-≤-≤⎪⎩或(1)(1)0f f ∙-≤解得32a -=或15a ≤≤ 当()f x 在[-1,1]上有两个零点时,则48(3)01112(1)(1)0a a a f f ∙∆=++>⎧⎪⎪-≤-≤⎨⎪->⎪⎩解得3722112215a a a a a a ⎧---+<>⎪⎪⎪≤-≥⎨⎪<>⎪⎪⎩或或即5a a <> 综上,实数a的取值范围为3(,[1,)2--∞+∞ (别解:222230(21)32ax x a x a x +--=⇔-=-,题意转化为[1,1]x ∈-求23221xa x -=-的值域,令32[1,5]t x =-∈得276a t t=+-转化为勾函数问题)s s ss A . B . C . D .(2008年高考广东卷第8小题)命题“若函数()log (0,1)a f x x a a =>≠在其定义域内是减函数,则log 20a <”的逆否命题是( )A. 若log 20a ≥,则函数()log (0,1)a f x x a a =>≠在其定义域内不是减函数B. 若log 20a <,则函数()log (0,1)a f x x a a =>≠在其定义域内不是减函数C. 若log 20a ≥,则函数()log (0,1)a f x x a a =>≠在其定义域内是减函数D. 若log 20a <,则函数()log (0,1)a f x x a a =>≠在其定义域内是减函数(2009年高考广东卷第4小题)若函数()y f x =是函数1xy a a a =≠(>0,且)的反函数,且(2)1f =,则()f x =(A ) A .x 2log B .x 21 C .x 21log D .22-x 【答案】A 【解析】函数1xy a a a =≠(>0,且)的反函数是()log a f x x =,又(2)1f =,即log 21a =,所以,2a =,故2()log f x x =,选A.(2010年高考广东卷第2小题)函数()lg(1)f x x =-的定义域是( B ) A .(2,+∞) B .(1,+∞) C .[1,+∞) D .[2,+∞)(2010年高考广东卷第3小题)若函数()33xxf x -=+与()33xxg x -=-的定义域均为R ,则(D )A .()f x 与()g x 均为偶函数B .()f x 为奇函数,()g x 为偶函数C .()f x 与()g x 均为奇函数D .()f x 为偶函数,()g x 为奇函数(2010年高考广东卷第20小题)已知函数()f x 对任意实数x 均有()(2)f x kf x =+,其中常数k 为负数,且()f x 在区间[]0,2上有表达式()(2)f x x x =-. (1)求(1)f -,(2.5)f 的值;(2)写出()f x 在[]3,3-上的表达式,并讨论函数()f x 在[]3,3-上的单调性; (3)求出()f x 在[]3,3-上的最小值与最大值,并求出相应的自变量的取值. 解:(1)∵)2()(+=x kf x f ,且)(x f 在区间[0,2]时)2()(-=x x x f∴k k kf kf f -=-⋅⋅==+-=-)21(1)1()21()1(由)2()(+=x kf x f 得)(1)2(x f kx f =+ ∴kk f k f f 43)25.0(5.01)5.0(1)25.0()5.2(-=-⋅⋅==+=(2)若]2,0[∈x ,则]4,2[2∈+x ]4)2][(2)2[(1)2(1)(1)2(-+-+=-==+x x kx x k x f k x f∴当]4,2[∈x 时,)4)(2(k1)(--=x x x f 若)0,2[-∈x ,则)2,0[2∈+x ∴)2(]2)2)[(2()2(+=-++=+x x x x x f ∴)2()2()(+=+=x kx x kf x f若)2,4[--∈x ,则)0,2[2-∈+x∴)4)(2(]2)2)[(2()2(++=+++=+x x k x x k x f∴)4)(2()2()(2++=+=x x k x kf x f ∵)2,4[)2,3[],4,2[]3,2(--⊂--⊂∴当]3,3[-∈x 时,⎪⎪⎩⎪⎪⎨⎧∈--∈--∈+--∈++=]3,2(),4)(2(1]2,0[),2()0,2[),2()2,3[),4)(2()(2x x x kx x x x x kx x x x k x f ∵0<k ,∴当)2,3[--∈x 时,)4)(2()(2++=x x k x f ,由二次函数的图象可知,)(x f 为增函数;当)0,2[-∈x 时,)2()(+=x kx x f ,由二次函数的图象可知,当)1,2[--∈x 时,)(x f 为增函数, 当)0,1[-∈x 时,)(x f 为减函数;当]2,0[∈x 时,)2()(-=x x x f ,由二次函数的图象可知,当)1,0[∈x 时,)(x f 为减函数;当]2,1[∈x 时,)(x f 为增函数;当]3,2(∈x 时,)4)(2(1)(--=x x kx f ,由二次函数的图象可知,)(x f 为增函数。
近十年 广东高考文科数学试卷以及答案分析

近十年广东高考文科数学试卷以及答案分析2004年全国普通高等学校招生全国统一考试(广东卷)数学一、选择题(共12小题,每题5分,计60分)1.已知平面向量a=(3,1),b=(x,–3),且,则x=A.-3 B.-1 C.1 D.()2.已知则()A.C....设函数在x=2处连续,则a=A.4.()1 2B..11 D.43()的值为C.A.-1 B.0 1 2D.1()5.函数f(x)f(x)是((A.周期为的偶函数B.周期为的奇函数C.周期为的偶函数D..周期为的奇函数6.一台X型号自动机床在一小时()A.0.1536 B.0.1808 C.0.5632 D.0.97287.在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是()A.2 322B.74 C.65D.5 6()(的焦点到它相对应的准线的距离是2,则k= 8.若双曲线A.6 B.8 C.1 D.4cos2x9.当时,函数的最小值是()A.4B.1 C.2 2D.1 4110.变量x、y满足下列条件:则使z=3x+2y的值最小的(x,y)是A.( 4.5 ,3 ) B.( 3,6 ) C.( 9, 2 )11.若f(x)则(()D.( 6, 4 ) ()4A.f()>f(0)>f(1)C.f(1)>f(0)>f(-1) B.f(0)>f(1)>f(-1) D.f(0)>f(-1)>f(1)12.如右下图,定圆半径为( b ,c ), 则直线ax+by+c=0与直线x–y+1=0的交点在( )A.第四象限B.第三象限C.第二象限D.第一象限二、填空题(共4小题,每题4分,计16分)13.某班委会由4名男生与3名女生组成,现从中选出2人担任正副班长,其中至少有1名女生当选的概率是(用分数作答)214.已知复数z与(z +2)-8i 均是纯虚数,则z = .15.由图(1)有面积关系,则由(2) 有体积关系图(1)图(2)16.函数f(x))(的反函数f三、解答题(共6小题,74分17.(12分)已知,,成公比为2的等比数列,),且,,也成等比数列. 求,,的值.2D18.如右下图,在长方体ABCD—A1B1C1D1中,已知AB= =3, AA1= 2. E、F分别是线段AB、BC上的点,FB=1.(1) 求二面角C—DE—C1的正切值;(2) 求直线EC1与FD1所成的余弦值.A19.(12分)设函数f(x)且EB= C1,(1) 证明: 当0< a < b ,且时,ab >1;(2) 点P (x0, y0 ) (0< x0 <1 )在曲线上,求曲线在点P处的切线与x轴和y轴的正向所围成的三角形面积表达式(用x0表达).20.(12分)某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其他两观测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上)321.(12分)设函数f(x)(),(1) 当m为何值时,f(x);(2) 定理: 若函数g(x) 在[a, b ]上连续,且g(a) 与g(b)异号,则至少存在一点x0∈(a,b),使g(x0)=0. 其中常数m为整数. 试用上述定理证明:当整数m>1时,方程f(x)= 0,在[e-m-m ,e2m-m ]内有两个实根.222.(14分)设直线与椭圆相交于A、B两点,又与双曲线x2–y2=1相交于C、D两点,D三等分线段AB.求直线的方程.4 、C2004年普通高等学校招生全国统一考试广东数学标准答案二、填空题:(13)(14)-三、解答题17.解:∵α,β,γ成公比为2的等比数列,∴β=2α,γ=4α∵sinα,sinβ,sinγ成等比数列即解得或12当cosα=1时,sinα=0,与等比数列的首项不为零,故cosα=1应舍去,当时或所以或33333318.解:(I)以A为原点,AB,AD,AA1分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有D(0,3,0)、D1(0,3,2)、E(3,0,0)、F(4,1,0)、C1(4,3,2)于是,设向量与平面C1DE垂直,则有其中222取则n0是一个与平面C1DE垂直的向量向量与平面CDE垂直,与AA1所成的角为二面角的平面角0122563(II)设EC1与FD1所成角为β,则.证明:(I)故f(x)在(0,1]上是减函数,而在(1,+∞)上是增函数,由0<a<b且f(a)=f(b)得0<a<1<b和即故即(II)0<x<1时,曲线y=f(x)在点P(x0,y0)处的切线方程为:即∴切线与x轴、y轴正向的交点为x0和故所求三角形面积听表达式为:20.解:如图,yPACoBx以接报中心为原点O,正东、正北方向为x轴、y轴正向,建立直角坐标系.设A、B、C分别是西、东、北观测点,则A(-1020,0),B(1020,0),C(0,1020)设P(x,y)为巨响为生点,由A、C同时听到巨响声,得|PA|=|PB|,故P在AC的垂直平分线PO上,PO的方程为y=-x,因B点比A点晚4s听到爆炸声,故|PB|-|PA|=340³4=1360 22x由双曲线定义知P点在以A、B为焦点的双曲线依题意得a=680, c=1020,上,6故双曲线方程为x2用y=-x代入上式,得,∵|PB|>|PA|,即故答:巨响发生在接报中心的西偏北45距中心680m处. 021.(I)解:函数f(x)=x-ln(x+m),x ∈(-m,+∞)连续,且令f’得’当x∈(-m,1-m)时,f (x)<0,f(x)为减函数,f(x)>f(1-m)’当x∈(1-m, +∞)时,f (x)>0,f(x)为增函数,f(x)>f(1-m)根据函数极值判别方法,f(1-m)=1-m为极小值,而且对x∈(-m, +∞)都有f(x)≥f(1-m)=1-m故当整数m≤1时,f(x) ≥1-m≥0(II)证明:由(I)知,当整数m>1时,f(1-m)=1-m<0,函数f(x)=x-ln(x+m),在上为连续减函数.当整数时与异号,由所给定理知,存在唯一的使而当整数m>1时,上述不等式也可用数学归纳法证明类似地,当整数m>1时,函数f(x)=x-ln(x+m),在上为连续增函数且f(1-m)与异号,由所给定理知,存在唯一的使故当m>1时,方程f(x)=0在内有两个实根。
广东高考文科数学及答案解析

广东高考文科数学-统计及概率习题 答案一、选择题:1、【解析】随机取出2个小球得到的结果数有154102⨯⨯=种(提倡列举).取出的小球标注的数字之和为3或6的结果为{1,2},{1,5},{2,4}共3种,故所求答案为(A).【解析】很多同学根据题意发现n=16可行,判除A,B 选项,但对于C,D 选项则难以作出选择,事实上,这是一道运筹问题,需要用函数的最值加以解决.设A B →的件数为1x (规定:当10x <时,则B 调整了1||x 件给,C D →的件数为3x ,DA →的件数为4x ,依题意可得415040x x +-=,125045x x +-=,235054x x +-=,345061x x +-=,从而215x x =+,311x x =+,4110x x =-,故调动件次11111()|||5||1||10|f x x x x x =+++++-,画出图像(或绝对值的几何意义)可得最小值为16,故选(C). 3、答案:B【解析】由题意知,所有可能路线有6种: ①A B C D E →→→→,②A B D C E →→→→,③A C B D E→→→→,④A C D B E →→→→,⑤A D B C E →→→→,⑥A D CB E →→→→, 其中, 路线③AC BDE →→→→的距离最短, 最短路线距离等于496221+++=,4、答案C解:设11时到12时的销售额为x 万元,依题意有:2.5/x=0.10/0.4,X=10 故选 C . 5、答案B 线段AB 三等分,当点P 落在中间那一段时满足条件,所以概率P=1/3 6、答案B以O 为圆心半径为1的球体积为4πR^3/3,因为O 在底面上,所以为半个球的体积即2πR^3/3=2π/3,正方体体积为2^3=8.,所以概率为(8-2π/3)/8=1-π/12 7、答案C 8、答案A设这两个数为x ,y ,建立一个直角坐标系,标出x ∈(0,1),y ∈(0,1)的区域,是一个正方形。
广东高考文科数学试题及答案详细解析选择、填空、解答全解全析

绝密★启用前试卷种类:B2021年一般高等学校招生全国一致考试〔广东卷〕数学〔文科〕分析版V 1Sh,此中S 为锥体的底面积, h为锥体的高.参照公式:锥体体积公式3n(x i x)(y i y)bi1nx )2线性回归方程ybxa中系数计算公式i1(x i ,ay bx ,样本数据x 1,x 2,1[(x 1x )2 (x 2x )2(x n x)2],xn 的标准差,n此中x,y表示样本均值.n 是正整数,那么a nb n (a b)(a n1 a n2b ab n2 b n1).一、选择题:本大题共10小题,每题 5分,总分值 50分,在每题给出的四个选项中,只有一项为哪一项切合题目要求的.1.设复数z 知足iz1,此中i为虚数单位,那么A .i B.iC.1D.1ii【分析】z(i)2.会合A{(x,y)|x,y 为实数,且x 221},B{(x,y)|x,y 为实数,且xy1},那么AB的元素个数为A .4B.3C .2D .1【分析】会合A 表示由圆21表示直线 y x 上全部点的会合,∵直上全部点构成的会合,会合线过园内点〔0,0〕,∴直线与圆有两个交点,故答案为C .3.向量a(1,2),b (1,0),c(3,4).假定为实数,(ab )∥c,那么1A .4B.2C.1D.2【分析】ab (1,2),由(ab )∥c ,得64(1)0,解得1,故答案为B 。
2第1页共14页1l g(1x )f (x)4.函数1x的定义域是A .(,1)B.(1,)C.(1,1)(1,)D.(,)1x0且x1,那么f(x)的定义域是(1,1)(1,),故答案【分析】要使函数存心义,那么xx110为C。
5.不等式2x2x10的解集是(1,1)B.(1,)C.(,1)(2,)(,1)(1,)A.2D.2【分析】2x2x10(x1)(2x1)0x1或x1,那么不等式的解集为(,1)(1,),22故答案为D。
广东历年高考文科数学试题及答案汇编十数列

广东历年高考文科数学试题及答案汇编十数列试题1、4.(5分)(2008广东)记等差数列的前n项和为S n,若S2=4,S4=20,则该数列的公差d=()A.2 B.3 C.6 D.72、5.(5分)(2009广东)已知等比数列{a n}的公比为正数,且a3•a9=2a52,a2=1,则a1=()A.B.C.D.23、4.(5分)(2010广东)已知数列{a n}为等比数列,S n是它的前n项和,若a2•a3=2a1,且a4与2a7的等差中项为,则S5=()A.35 B.33 C.31 D.294、1.(5分)(2011广东)已知{a n}是递增等比数列,a2=2,a4﹣a3=4,则此数列的公比q= .5、12.(5分)(2012广东)若等比数列{a n}满足a2a4=,则a1a32a5= .6、11.(5分)(2013广东)设数列{a n}是首项为1,公比为﹣2的等比数列,则a1+|a2|+a3+|a4|= .7、13.(5分)(2014广东)等比数列{a n}的各项均为正数,且a1a5=4,则log2a1+log2a2+log2a3+log2a4+log2a5= .8、13.(5分)(2015广东)若三个正数 a,b,c 成等比数列,其中a=5+2,c=5﹣2,则 b= .解答题1、21.(14分)(2008广东)设数列{a n}满足a1=1,a2=2,a n=(a n﹣1+2a n﹣2)(n=3,4,…).数列{b n}满足b1=1,b n(n=2,3,…)是非零整数,且对任意的正整数m和自然数k,都有﹣1≤b m+b m+1+…+b m+k≤1.(1)求数列{a n}和{b n}的通项公式;(2)记c n=na n b n(n=1,2,…),求数列{c n}的前n项和S n.2、20.(14分)(2009广东)已知点(1,)是函数f(x)=a x(a>0,且a≠1)的图象上一点,等比数列{a n}的前n项和为f(n)﹣c,数列{b n}(b n>0)的首项为c,且前n项和S n满足S n﹣S n﹣1=(n≥2).(Ⅰ)求数列{a n}和{b n}的通项公式;(Ⅱ)若数列{}前n项和为T n,问满足T n>的最小正整数n是多少?3、21.(14分)(2010广东)已知曲线C n:y=nx2,点P n(x n,y n)(x n>0,y n>0)是曲线C n上的点(n=1,2,…),(1)试写出曲线C n在P n点处的切线l n的方程,并求出l n与y轴的交点Q n的坐标;(2)若原点O(0,0)到l n的距离与线段P n Q n的长度之比取得最大值,试求点的坐标P n(x n,y n)4、20.(14分)(2011广东)设b>0,数列{a n}满足a1=b,a n=(n≥2)(1)求数列{a n}的通项公式;(2)证明:对于一切正整数n,2a n≤b n+1+1.5、19.(14分)(2012广东)设数列{a n}前n项和为S n,数列{S n}的前n项和为T n,满足T n=2S n ﹣n2,n∈N*.(1)求a1的值;(2)求数列{a n}的通项公式.6、19.(14分)(2013广东)设各项均为正数的数列{a n}的前n项和为S n,满足4S n=a n+12﹣4n﹣1,n∈N*,且a2,a5,a14构成等比数列.(1)证明:a 2=;(2)求数列{a n}的通项公式;(3)证明:对一切正整数n,有.7、19.(14分)(2014广东)设各项均为正数的数列{a n}的前n项和为S n满足S n2﹣(n2+n ﹣3)S n﹣3(n2+n)=0,n∈N*.(1)求a1的值;(2)求数列{a n}的通项公式;(3)证明:对一切正整数n,有++…+<.8、19.(14分)(2015广东)设数列 {a n}的前n项和为S n,n∈N*.已知a1=1,a2=,a3=,且当a≥2时,4S n+2+5S n=8S n+1+S n﹣1.(1)求a4的值;(2)证明:{a n+1﹣a n}为等比数列;(3)求数列{a n}的通项公式.答案1、解:由2a1+d=4且4a1+6d=20;解得d=3故选B2、解:设公比为q,由已知得a1q2•a1q8=2(a1q4)2,即q2=2,又因为等比数列{a n}的公比为正数,所以q=,故a1=.故选B.3、解:a2•a3=a1q•a1q2=2a1∴a4=2a4+2a7=a4+2a4q3=2×∴q=,a1==16故S5==31故选C.4、解:∵{a n}是递增等比数列,且a2=2,则公比q>1又∵a4﹣a3=a2(q2﹣q)=2(q2﹣q)=4即q2﹣q﹣2=0解得q=2,或q=﹣1(舍去)故此数列的公比q=2故答案为:25、解:∵等比数列{a n}满足=,则,故答案为.6、解:∵数列{a n}是首项为1,公比为﹣2的等比数列,∴a n=a1•q n﹣1=(﹣2)n﹣1,∴a1=1,a2=﹣2,a3=4,a4=﹣8,∴则a1+|a2|+a3+|a4|=1+2+4+8=15,故答案为15.7、解:log2a1+log2a2+log2a3+log2a4+log2a5=log2a1a2a3a4a5=log2a35=5log2a3.又等比数列{a n}中,a1a5=4,即a3=2.故5log2a3=5log22=5.故选为:5.8、解:∵三个正数 a,b,c 成等比数列,∴b2=ac,∵a=5+2,c=5﹣2,∴=1,故答案为:1.解答题1、解:(1)由得(n≥3)又a2﹣a1=1≠0,∴数列{a n+1﹣a n}是首项为1公比为的等比数列,a n=a1+(a2﹣a1)+(a3﹣a2)+(a4﹣a3)+…+(a n﹣a n﹣1)==,当n为奇数时当n为偶数时由得b2=﹣1,由得b3=1,同理可得当n为偶数时,b n=﹣1;当n为奇数时,b n=1;因此.(2)S n=c1+c2+c3+c4+…+c n当n为奇数时,=当n为偶数时=令①①×得:②①﹣②得:=∴当n为奇数时当n为偶数时因此2、解:(Ⅰ)∵f(1)=a=∴f(x)=()x,∴a1=f(1)﹣c=﹣c,∴a2=[f(2)﹣c]﹣[f(1)﹣c]=﹣,a3=[f(3)﹣c]﹣[f(2)﹣c]=又数列{a n}成等比数列,=﹣,∵a1=﹣c∴﹣=﹣c,∴c=1又公比q==所以a n=()n﹣1=﹣()n,n∈N;∵S n﹣S n﹣1=(+)(﹣)=(n≥2)又b n>0,>0,∴=1;∴数列{}构成一个首项为1公差为1的等差数列,∴=1+(n﹣1)×1=n,S n=n2当n≥2,b n=S n﹣S n﹣1=n2﹣(n﹣1)2=2n﹣1;又b1=c=1适合上式,∴b n=2n﹣1(n∈N);(Ⅱ)T n=++…+==(1﹣)+(﹣)+()+…+=(1﹣)=由>,得n>满足的最小正整数为84.3、解:(1)∵y′=2nx,∴k=2nx n,切线l m的方程:y﹣y n=2nx n(x﹣x n),令x=0得y=﹣2nx n2+y n=﹣nx n2,即Q n(0,﹣nx n2).(2)切线方程可写成:2nx n x﹣y﹣2nx n2+y n=0.,=.当且仅当,即时,取等号,此时y n=nx n2,点P的坐标为.4、解:(1)∵(n≥2),∴(n≥2),当b=1时,(n≥2),∴数列{}是以为首项,以1为公差的等差数列,∴=1+(n﹣1)×1=n,即a n=1,当b>0,且b≠1时,(n≥2),即数列{}是以=为首项,公比为的等比数列,∴=×=,即a n=,∴数列{a n}的通项公式是(2)证明:当b=1时,不等式显然成立当b>0,且b≠1时,a n=,要证对于一切正整数n,2a n≤b n+1+1,只需证2×≤b n+1+1,即证∵==(b n+1+1)×(b n﹣1+b n﹣2+…+b+1)=(b2n+b2n﹣1+…+b n+2+b n+1)+(b n﹣1+b n﹣2+…+b+1)=b n[(b n+b n﹣1+…+b2+b)+(++…+)]≥b n(2+2+…+2)=2nb n所以不等式成立,综上所述,对于一切正整数n,有2a n≤b n+1+1,5、解:(1)当n=1时,T1=2S1﹣1因为T1=S1=a1,所以a1=2a1﹣1,求得a1=1(2)当n≥2时,所以S n=2S n﹣1+2n﹣1①所以S n+1=2S n+2n+1②②﹣①得 a n+1=2a n+2所以a n+1+2=2(a n+2),即(n≥2)求得a1+2=3,a2+2=6,则所以{a n+2}是以3为首项,2为公比的等比数列所以所以,n∈N*.6、解:(1)当n=1时,,∵(2)当n≥2时,满足,且,∴,∴,∵a n>0,∴a n+1=a n+2,∴当n≥2时,{a n}是公差d=2的等差数列.∵a2,a5,a14构成等比数列,∴,,解得a2=3,由(1)可知,,∴a1=1∵a2﹣a1=3﹣1=2,∴{a n}是首项a1=1,公差d=2的等差数列.∴数列{a n}的通项公式a n=2n﹣1.(3)由(2)可得式=.∴7、解:(1)令n=1得:,即.∴(S1+3)(S1﹣2)=0.∵S1>0,∴S1=2,即a1=2.(2)由得:.∵a n>0(n∈N*),∴S n>0.∴.∴当n≥2时,,又∵a1=2=2×1,∴.(3)由(2)可知=,∀n∈N*,=<=(),当n=1时,显然有=<;当n≥2时,<+=﹣•<所以,对一切正整数n,有.8、(1)解:当n=2时,4S4+5S2=8S3+S1,即,解得:;(2)证明:∵4S n+2+5S n=8S n+1+S n﹣1(n≥2),∴4S n+2﹣4S n+1+S n﹣S n﹣1=4S n+1﹣4S n(n≥2),即4a n+2+a n=4a n+1(n≥2),∵,∴4a n+2+a n=4a n+1.∵=.∴数列{}是以为首项,公比为的等比数列;(3)解:由(2)知,{}是以为首项,公比为的等比数列,∴.即,∴{}是以为首项,4为公差的等差数列,∴,即,∴数列{a n}的通项公式是.。
最新整理广东高考文科数试题真题及参考答案.doc

绝密★启用前 试卷类型:B 普通高等学校招生全国统一考试(广东卷)数学(文科)本试卷共4页,21小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时。
请先用2B 铅笔填涂选做题的题号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
参考公式:锥体的体积公式V=13Sh ,其中S 是锥体的底面积,h 是锥体的高。
一、选择题:本大题共10小题,每小题5分,满分50分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={0,1,2,3},B={1,2,4},则集合A B=A .{0,1,2,3,4}B .{1,2,3,4}C .{1,2}D .{0}2.函数,()lg(1)f x x =-的定义域是A .(2,+∞)B .(1,+∞)C .[1,+∞)D .[2,+∞)3.若函数()33x x f x -=+与()33x x g x -=-的定义域均为R ,则A .()f x 与()g x 均为偶函数B .()f x 为奇函数,()g x 为偶函数C .()f x 与()g x 均为奇函数D .()f x 为偶函数,()g x 为奇函数4.已知数列{n a }为等比数列,n S 是它的前n 项和,若2·a a 31=2a ,且4a 与72a 的等差中项为54,则S5=w_w w. k#s5_u.c o*mw_w*w.k_s_5 u.c*o*mA .35B .33C .31D .29 5.若向量(1,1)a =r ,(2,5)b =r ,(3,)c x =r 满足条件(8)30a b c -⋅=r r r,则x =A .6B .5C .4D .36.若圆心在x 轴上、的圆O 位于y 轴左侧,且与直线20x y +=相切,则圆O 的方程是w_w w. k#s5_u.c o*mA.22(5x y+=B.22(5x y++=w_w*w.k_s_5 u.c*o*mC.22(5)5x y-+=D.22(5)5x y++=7.若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是w_w w. k#s5_u.c o*mA.45B.35C.25D.158.“x>0”成立的A.充分非必要条件B.必要非充分条件w_w*w.k_s_5 u.c*o*mC.非充分非必要条件D.充要条件9.如图1,ABCV为正三角形,'''////AA BB CC,''''32CC BB CC AB⊥===平面ABC且3AA,则多面体'''ABC A B C-的正视图(也称主视图)是w_w*w.k_s_5 u.c*o*m10.在集合{a,b,c,d}上定义两种运算⊕和⊗如下:w_w w. k#s5_u.c o*m那么d⊗()a c⊕=A.a B.b C.c D.d二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.(一)必做题(11~13题)11.某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中4位居民的月均用水量分别为1x ,…,4x (单位:吨).根据图2所示的程序框图,若1x ,2x ,3x ,4x ,分别为1,1.5,1.5,2,则输出的结果s 为 . w_w*w.k_s_5 u.c*o*m12.某市居民20xx ~ 家庭年平均收入x (单位:万元)与年平均支出Y (单位:万元)的统计资料如下表所示:w_w w. k#s5_u.c o*m根据统计资料,居民家庭年平均收入的中位数是 ,家庭年平均收入与年平均支出有 线性相关关系.13.已知a ,b ,c 分别是△ABC 的三个内角A ,B ,C 所对的边,若a=1,,A+C=2B ,则sinA= . w_w w. k#s5_u.c o*m(二)选做题(14、15题,考生只能从中选做一题)14.(几何证明选讲选做题)如图3,在直角梯形ABCD 中,DC ∥AB ,CB ⊥AB ,AB=AD=a ,CD=2a,点E ,F 分别为线段AB ,AD 的中点,则EF= .15.(坐标系与参数方程选做题)在极坐标系(ρ,θ)(02θπ≤<)中,曲线()cos sin 1ρθθ+=与()sin cos 1ρθθ-=的交点的极坐标为 . w_w*w.k_s_5 u.c*o*m三、解答题:本大题共6小题,满分80分。
最新整理广东文科数高考题答案全解析.doc

普通高等学校招生全国统一考试(广东卷)(文科)全解析广东佛山南海区南海中学 钱耀周一、选择题:本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求。
1.第二十九届夏季奥林匹克运动会将于 8月8日在北京举行,若集合A ={参加北京奥运会比赛的运动员},集合B ={参加北京奥运会比赛的男运动员}。
集合C ={参加北京奥运会比赛的女运动员},则下列关系正确的是A.A ⊆BB.B ⊆CC.A ∩B =CD.B ∪C =A 【解析】送分题呀!答案为D.2.已知0<a <2,复数z a i =+(i 是虚数单位),则|z |的取值范围是) C.(1,3) D.(1,5) 【解析】12+=a z ,而20<<a ,即5112<+<a ,51<<∴z ,选B.3.已知平面向量(1,2)a =,(2,)b m =-,且a //b ,则23a b +=( ) A 、(5,10)-- B 、(4,8)-- C 、(3,6)-- D 、(2,4)-- 【解析】排除法:横坐标为2(6)4+-=-,选B.4.记等差数列的前n 项和为n S ,若244,20S S ==,则该数列的公差d =( ) A 、2 B 、3 C 、6 D 、7 【解析】4224123S S S d d --==⇒=,选B.5.已知函数2()(1cos 2)sin ,f x x x x R =+∈,则()f x 是( )A 、最小正周期为π的奇函数B 、最小正周期为2π的奇函数 C 、最小正周期为π的偶函数 D 、最小正周期为2π的偶函数【解析】222211cos 4()(1cos 2)sin 2cos sin sin 224x f x x x x x x -=+===,选D.6.经过圆2220x x y ++=的圆心C ,且与直线0x y +=垂直的直线方程是( ) A 、10x y ++= B 、10x y +-= C 、10x y -+= D 、10x y --=【解析】易知点C 为(1,0)-,而直线与0x y +=垂直,我们设待求的直线的方程为y x b =+,将点C 的坐标代入马上就能求出参数b 的值为1b =,故待求 的直线的方程为10x y -+=,选C.(或由图形快速排除得正确答案.)7.将正三棱柱截去三个角(如图1所示A 、B 、C 分 别是GHI ∆三边的中点)得到的几何体如图2,则 该几何体按图2所示方向的侧视图(或称左视图)为【解析】解题时在图2的右边放扇墙(心中有墙),可得答案A.8. 命题“若函数()log (0,1)a f x x a a =>≠在其定义域内是减函数,则log 20a <”的逆否命题是( )A 、若log 20a ≥,则函数()log (0,1)a f x x a a =>≠在其定义域内不是减函数B 、若log 20a <,则函数()log (0,1)a f x x a a =>≠在其定义域内不是减函数C 、若log 20a ≥,则函数()log (0,1)a f x x a a =>≠在其定义域内是减函数D 、若log 20a <,则函数()log (0,1)a f x x a a =>≠在其定义域内是减函数 【解析】考查逆否命题,易得答案A.9、设a R ∈,若函数xy e ax =+,x R ∈,有大于零的极值点,则( )A 、1a <-B 、1a >-C 、1a e<- D 、1a e >- 【解析】题意即0xe a +=有大于0的实根,数形结合令12,x y e y a ==-,则两曲线交点在第一象限,结合图像易得11a a ->⇒<-,选A.10、设,a b R ∈,若||0a b ->,则下列不等式中正确的是( )A 、0b a ->B 、330a b +<C 、220a b -< D 、0b a +> 【解析】利用赋值法:令1,0a b ==排除A,B,C,选D.二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.(一)必做题(11-13题)11.为了调查某厂工人生产某种产品的能力,随机抽查 了20位工人某天生产该产品的数量.产品数量的分组区间为[)45,55,[)[)[)55,65,65,75,75,85,[)85,95由此得到频率分布直方图如图3,则这20名工人中一天生产该产品数量在[)55,75的人数是 .【解析】20(0.06510)13⨯⨯=,故答案为13.12.若变量x ,y 满足240,250,0,0,x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩则z =3x +2y 的最大 值是________。
广东历年高考文科数学试题及答案

18.随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.(1)根据茎叶图判断哪个班的平均身高较高;(2)计算甲班的样本方差(3)现从乙班这10名同学中随机抽取两名身高不低于173cm 的同学,求身高为176cm 的同学被抽中的概率.18. 【解析】(1)由茎叶图可知:甲班身高集中于160179:之间,而乙班身高集中于170180: 之间。
因此乙班平均身高高于甲班; (2) 15816216316816817017117917918217010x +++++++++== 甲班的样本方差为()()()()222221[(158170)16217016317016817016817010-+-+-+-+- ()()()()()22222170170171170179170179170182170]+-+-+-+-+-=57(3)设身高为176cm 的同学被抽中的事件为A ;从乙班10名同学中抽中两名身高不低于173cm 的同学有:(181,173) (181,176)(181,178) (181,179) (179,173) (179,176) (179,178) (178,173)(178, 176) (176,173)共10个基本事件,而事件A 含有4个基本事件;()42105P A ∴== ;17.在某次测验中,有6位同学的平均成绩为75分.用n x 表示编号为()1,2,,6n n =的同学所得成绩,且前5位同学的成绩如下:(1)求第6位同学成绩6x ,及这6位同学成绩的标准差s ;(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间()68,75中的概率.17 (1)由题意得:75=90,6727072767066=+++++x x 得 S=76)7590()7572()7570()7572()7576()7570(222222=-+-+-+-+-+- (2)设5位同学为:A, B,C, D, E 其中A70分,B76分,C72分,D70分,E72分 基本事件:AB, AC,AD,AE, BC,BD,BE,CD,CE, DE ,共10种。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、统计、推理与证明
(2012文)由正整数组成的一组数据1234,,,x x x x ,其平均数和中位数都是2,且标准差等于1, 则这组数据为__________。
(从小到大排列)
(2011文)为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某
月1号到5号每天打篮球时间x (单位:小时)与当天投篮命中率y 之间的关系:
小李这5天的平均投篮命中率为 ;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率为 .
(2011理)某数学老师身高176cm ,他爷爷、父亲和儿子的身高分别是173cm 、170cm 和182cm .假设儿子的身高与父亲的身高有关,则该老师用线性回归分析的方法预测他孙子的身高为 cm .
(2010文)某市居民2005~2009年家庭年平均收入x(单位:万元)与年平均支出Y(单位:万
元)的统计资料如下表所示:
根据统计资料,居民家庭年平均收入的中位数是 ,家庭年平均收入与年平均支出 有 线性相关关系.
(2009文)某单位200名职工的年龄分布情况
如图2,现要从中抽取40名职工作样本.用系统抽样法,将全体职工随机按1 200编号,
并按编号顺序平均分为
40组(1 5号,6 10号, ,196 200号).若第5组抽出的号码为22,则第8组抽出的号码应是 .若用分层抽样方法,则40岁以下年龄段应抽取 人.
(2008文)为了调查某厂工人生产某种产品的
能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[)45,55,
[)[)[)55,65,65,75,75,85,[)85,95由此得到频率分布直方图如图3,则这20名工人中一
天生产该产品数量在[)55,75的人数是 .
(2008理)某校共有学生2000名,各年级男、女生人数
如表1.已知在全校学生中随机抽取1名,抽到二年级女
生的概率是0.19.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为( )
A .24
B .18
C .16
D .12
(2007文)下表提供了某厂节能降耗技术改进后生产甲产品过程中记录的产量x (吨)与相应的
生产能耗y (吨标准煤)的几组对照数据.
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程y =a x b
ˆˆ+ (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,
预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
(2006)在德国不莱梅举行的第48届世乒赛期间,某商场
橱窗里用同样的乒乓球堆成若干准“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4、…堆最底层(第一层)分别按图4所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第n 堆第n 层就放一个乒乓球,以)(n f 表示第n 堆的乒乓球总数,则=)3(f ;
=)(n f (答案用n 表示).
(2005)设平面内有n条直线(3)n ≥,其中有且仅有两条直线互相平行,任意三条直线不过
同一点.若用()f n 表示这n条直线交点的个数,则(4)f =_____________;当n>4时, ()f n =_____________.(用n 表示)
(2004)由图(1)有面积关系:PA B PAB S PA PB S PA PB ''∆∆''
⋅=⋅,则由图(2)有体积关系:P A B C P ABC
V V '''--= .
(2003)在平面几何里,有勾股定理:“设△ABC 的两边AB 、AC 互相垂直,则AB 2+AC 2=BC 2,
拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面面积间的关系,可
以得出的正确结论是:“设三棱锥A —BCD 的三个侧面ABC 、ACD 、ADB 两两相互垂 直,则
(2002)已知2
21)(x x x f +=,那么
)41
()4()31()3()21()2()1(f f f f f f f ++++++= .
B
A
P
B ’
A ’
图1
B
A
P
B ’
A ’ C
C ’ 图2
1、1、3、3 0.5、0.53 185 13、y=x-3
37 , 20 。
13
y x i n
i i ∑=1
=3⨯2.5+4⨯3+5⨯4+6⨯4.5=66.5,
x =
4
6
543+++=4.5,
y =
2.534 4.5
4
+++=3.5, 2
22221
345686n
i i
x ==+++=∑,
b =
2
66.54 4.5 3.5
0.7864 4.5-⨯⨯=-⨯,
a =3.5-0.7⨯4.5=0.35.
故线性回归方程为y =0.7x +0.35.
(3)根据回归方程的预测,现在生产100吨产品消耗的标准煤的数量为 0.7⨯100+0.35=70.35,
故耗能减少了90-70.35=19.65(吨)
5,
)1)(2(21
+-n n
PC
PB PA PC PB PA ⋅⋅⋅⋅'
''
S △ABC 2+S △ACD 2+S △ADB 2=S △BCD 2
2
7。
