(优选)第七讲散射一散射截面Ppt
散射理论PPT

有关散射的几个物理量
在研究光散射现象时,常常引入散射光强、散 射截面、吸收截面、消光截面以及相应的散射系 数、吸收系数和消光系数等描述散射现象的物理 量。这些物理量与散射颗粒的大小、折射率以及 入射光的波长等因素存在密切的关系
(1)散射截面
一个散射颗粒在单位时间内散射的全部光能量
入射光强 之I0比称为散射截面,记作
适。用米。氏粒 散子 射线 不度 同大于于瑞1利0 散的射较呈大对微称粒状散分射布称,为常米被氏用散于射
大气中滴粒分布的研究。 一、Mie 散射公式:
不考虑光波的偏振性,将光波作为标量波处理, 取散射颗粒处为坐标原点,入射光沿z 轴正方向传 播,在远离散射体处的散射光波为球面波,
其波源就是散射体。图中,r为散射光观察点与散射体 的距离,散射角为θ,观察点与Z轴组成的平面即为
众所周知,在均匀介质中,光线将沿原有的方向 传播而不发生散射现象。当光线从一均匀介质进入 另一均匀介质时,根据麦克斯韦电磁场理论,它只 能沿着折射光线的方向传播,这是由于均匀介质中 偶极子发出的次波具有与人射光相同的频率,并且 偶极子发出的次波间有一定的位相关系,它们是相 干的,在非折射光的所有方向上相互抵消,所以只 发生折射而不发生散射。
非耗散介质。波的能流为S =E×H,其传播方向即波
矢k 的方向。
当电导率
0时,
k2
2 (
i
), k
kR
ikI
为简单起见,考虑沿X轴方向传播的平面波。
波动方程为
d 2E dx2
2 (
i
)E
0
d 2H dx2
2 (
i
)H
0
其解为
E E0 exp(kI x) exp[i(kR x t)] H H0 exp(kI x) exp[i(kR x t)]
第七讲散射理论

第七讲散射理论一、散射现象的一般描述1、什么是散射?简单地说,散射就是指粒子与粒子之间或粒子与力场之间的碰撞(相互作用)过程,是一种具有重要实际意义的现象,所以散射现象也称碰撞现象,其可以示意为:粒子流散射中心如:原子物理中的α粒子散射实验。
2、散射的分类:弹性散射:一粒子与另一粒子碰撞的过程中,只有动能的交换,粒子内部状态并无改变。
非弹性散射:两粒子碰撞中粒子的内部状态有所改变(例如原子被激发或电离)。
在这里我们只讨论弹性散射,即假设碰撞过程中粒子的内部状态未变,并假设散射中心质量很大、碰撞对其运动没有影响。
3、散射的经典力学描述从经典力学来看,在散射过程中,每个入射粒子都以一个确定的碰撞参数(瞄准距离)b 和方位角0ϕ射向靶子,由于靶子的作用,入射粒子的轨道将发生偏转,沿某方向(,)θϕ出射。
例如在α粒子的散射实验中,有22cot 422M b Ze θυπε= (偏转角θ与瞄准距离之间的关系) 那些瞄准距离在b b db -和之间的α粒子,散射后,必定向着d θθθ+和之间的角度射出,如下图所示:凡通过图中所示环形面积d σ的α粒子,必定散射到角度在d θθθ+和之间的一个空心圆锥体之中。
环形面积d σ称为有效散射截面,又称微分截面。
且2222401()()4sin 2Ze d d M σθπευΩ= 然而,在散射实验中,人们并不对每个粒子的轨道感兴趣,而是研究入射粒子束经过散射后沿不同方向出射的分布。
设一束粒子流以稳定的入射流强度沿Z 轴方向射向靶粒子A ,由于靶粒子的作用,设在单位时间内有dn 个粒子沿(,)θϕ方向的立体角d Ω中射出,显然,,(,)dn Nd dn q Nd θϕ∝Ω=Ω令,即1(,)()dn q N d θϕ=Ω显然,(,)q θϕ具有面积的量纲,称为微分散射截面。
微分散射截面),(ϕθq 表示单位时间内散射到单位立体角Ωd (面积/距离平方)的粒子数占总粒子数比率,即Ω=Nd q dn ),(ϕθ。
散射一散射截面
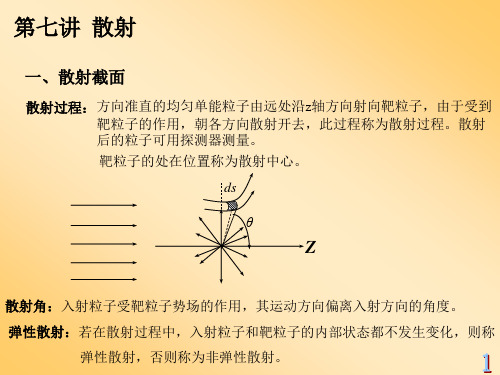
(3-2)代入(3-1),得径向方程
1 r2
d dr
r 2
dRl dr
k 2
V (r)
l
(l r2
1)
Rl
(r
)
0
令
Rl
(r)
Ul (r) r
,代入上方程
(3-3)
d 2U l dr 2
k 2
V
(r)
l
(l r2
1)
U
l
(r
)
0
(3-4)
考虑方程(3-4)在 r 情况下的极限解,,波可沿各方向散射,三维散射时,在r 处的粒子的波函数
应为入射波和散射波之和。 方程(8)有两个特解
(r, , ) f ( , )eikr
(r, , ) f ( , )eikr
因此,
2 (r, ,)
f ( , ) eikr
r
2 (r, ,)
f ( , ) eikr r
2 代表由散射中心向外传播的球面散射波, 2 代表向散射中心会聚的球面波,
究粒子间的相互作用以及其它问题。
二、散射振幅
现在考虑量子力学对散射体系的描述。设靶粒子的质量远大于散射粒子的质量,
在碰撞过程中,靶粒子可视为静止。
取散射中心A为坐标原点,散射粒子体系的定态schrödinger方程
2 2 U (r) E 2
(4)
令
k2
2E 2
V
(r)
2 2
U (r)
方程(4)改写为
弹性散射,否则称为非弹性散射。
入射粒子流密度N :单位时间内通过与入射粒子运动方向垂直的单位面积的入 射粒子数,用于描述入射粒子流强度的物理量,故又称为 入射粒子流强度。
光的散射基础内容PPT课件

8
清晨日出或
10
2019/12/23
11
米氏散射:散射粒子的线度与光波长同量级或大于光 波波长的散射
3
非均匀介质中的散射
光学性质的不均匀: (1)均匀物质中散布着折射率与它不同的大量微粒 (2)物质本身的组成部分(粒子)不规律的聚集
例:尘埃、烟、雾、悬浮液、乳状液、毛玻璃等。
特征:
杂质微粒的线度小于光波长,相互间距大于波长, 排列毫无规则,在光照下的振动无固定位相关系,任何 点可看到它们发出次波的迭加,不相消,形成散射光。
光的散射
1
定义:
光
当光通过光学性质不
的
均匀的物质时,从侧
散
向都可以看到光的现
射
象叫光的散射。
2
分 类
线性米 瑞氏 利散 散射 射: :线 线度 度ll
/ 10
非线性拉曼散射自 受发 激拉 拉曼 曼散 散射 射 布里渊散射
瑞利散射:散射粒子的线度小于光的波长的十分之一
4
散射和反射,漫射和衍射的区别
1.散射与直射、反射及折射的区别:“次波”发射中心排 列的不同,散射时无规则,而后者有规则。 2.散射与漫反射的区别:次波中心的排列仍有某些不同的 方向性 3.散射与衍射的区别:
衍射:因个别的不均匀区域(孔、缝、小障碍等)所形 成的,不均匀区域范围大小≈。
散射:大量排列不规则的非均匀小“区域”的集合所形 成的,非均匀小区域的线度<。
5
2019/12/23
6
瑞利散射
1.瑞利散射:l 的微粒对入射光的散射现象。
2.瑞利定律:散射光强度与波长的四次方成反比,
物理光学散射

I
()
1
4
此时太阳光穿过的大气层最厚,散射效应最显著。太阳光 中的短波部分几乎都侧向散射,仅剩下红光部分到达地面, 所以可以看见火红的朝阳或夕阳。
现象解释——光的散射
4.为什么云彩是白色的?
天空中的白云是大气中水滴组成的,这些水滴的线度 比可见光的波长大。根据米氏散射,各种波长的光有几乎 相同强度的散射,因而云雾呈白色。
悬浮质点的散射 瑞利散射 米氏散射
分子散射——十分纯净的液体和气体
② 散射光波长与入射光波长不等(非线性散射) 拉曼散射
布里渊散射
3.1 瑞利散射
瑞利散射——光的散射
λ
产生条件:
a
散射微粒的几何线度小于光波长 a 1
散射定律:
侧向散射光的光强反比于λ4
I
()
1
4
3.2 米氏散射
λ
米氏散射——光的散射
晴天——光的散射
白云——光的散射
阴天——光的散射
日出——光的散射
定义——光的散射
一、定义: 光通过光学性质不均匀的介质时,在偏离正常传播方
向上有光出射的现象称为散射。
光学性质不均匀: 气体中有随机运动的分子、原子或烟雾、尘埃; 液体中混入小微粒; 固体中掺入杂质或缺陷等。
散射光
散射光
定义——光的散射
产生条件:
a
散射微粒的几何线度大于等于光波长 a 1
散射规律:
散射光强度I与波长λ之间无明显关系。
散A
射瑞 光利 强区
B
米氏区
瑞利散射、米氏散射—光的散射 C
0 12
4
6
8
图 瑞利散射和米氏散射
10 a/
I
第七讲散射理论

第七讲散射理论一、散射现象的一般描述1、什么是散射?简单地说,散射就是指粒子与粒子之间或粒子与力场之间的碰撞(相互作用)过程,是一种具有重要实际意义的现象,所以散射现象也称碰撞现象,其可以示意为:粒子流散射中心如:原子物理中的α粒子散射实验。
2、散射的分类:弹性散射:一粒子与另一粒子碰撞的过程中,只有动能的交换,粒子内部状态并无改变。
非弹性散射:两粒子碰撞中粒子的内部状态有所改变(例如原子被激发或电离)。
在这里我们只讨论弹性散射,即假设碰撞过程中粒子的内部状态未变,并假设散射中心质量很大、碰撞对其运动没有影响。
3、散射的经典力学描述从经典力学来看,在散射过程中,每个入射粒子都以一个确定的碰撞参数(瞄准距离)b 和方位角0ϕ射向靶子,由于靶子的作用,入射粒子的轨道将发生偏转,沿某方向(,)θϕ出射。
例如在α粒子的散射实验中,有22cot 422M b Ze θυπε= (偏转角θ与瞄准距离之间的关系) 那些瞄准距离在b b db -和之间的α粒子,散射后,必定向着d θθθ+和之间的角度射出,如下图所示:凡通过图中所示环形面积d σ的α粒子,必定散射到角度在d θθθ+和之间的一个空心圆锥体之中。
环形面积d σ称为有效散射截面,又称微分截面。
且2222401()()4sin 2Ze d d M σθπευΩ= 然而,在散射实验中,人们并不对每个粒子的轨道感兴趣,而是研究入射粒子束经过散射后沿不同方向出射的分布。
设一束粒子流以稳定的入射流强度沿Z 轴方向射向靶粒子A ,由于靶粒子的作用,设在单位时间内有dn 个粒子沿(,)θϕ方向的立体角d Ω中射出,显然,,(,)dn Nd dn q Nd θϕ∝Ω=Ω令,即1(,)()dn q N d θϕ=Ω显然,(,)q θϕ具有面积的量纲,称为微分散射截面。
微分散射截面),(ϕθq 表示单位时间内散射到单位立体角Ωd (面积/距离平方)的粒子数占总粒子数比率,即Ω=Nd q dn ),(ϕθ。
散射散射截面
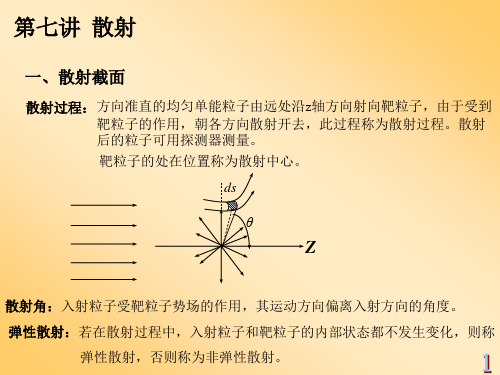
入射粒子流密度N :单位时间内通过与入射粒子运动方向垂直的单位面积的入 射粒子数,用于描述入射粒子流强度的物理量,故又称为 入射粒子流强度。
散射截面:
设单位时间内散射到(,)方向面积元ds上(立体角d内)的粒子数为dn,显 然
ds dn d
r2 dn N
处设的r 散射体时系,V的(r波) 函数0 ,。方程(5)变为
2 k 2 0
(6)
令
r
(7)
将(6)式写成
2
r 2
k 2
L情形下,此方程简化为
2 k 2 0
r 2
(8)
此方程类似一维波动方程,我们知道: 对于一维势垒或势阱的散射情况
综合之,则有:
dn Nd
或
dn q( ,)Nd
(1)
比例系数q(,)的性质:
q(,)与入射粒子和靶粒子(散射场)的性质,它们之间的相互作用,以及 入射粒子的动能有关,是,的函数。
q(,)具有面积的量纲
[q]
dn Nd
L2
故称q(,)为微分散射截面,简称为截面或角分布
如果在垂直于入射粒子流的入射方向取面积q(,),则单位时间内通过此截
面q(,)的粒子数恰好散射到(,)方向的单位立体角内。
q( ,)N dn
d
(2)
总散射截面:
2
Q q(,)d q(,)sindd
(3)
00
[由注(] 2)式知,由于N、dn 可通过实验测定,故而求得 q( ,) 。
k x Aeikx Beikx
k x ceikx
7光纤中的光散射(课堂PPT)

PB_cw(L)
exp g B
0
P0 _ cw Aeff
Leff
d
PB_cw L
2~p t 2
'2
~p t
v22~p
0
~p peiqzt c.c.
2 i ' q2 v2q2 0
2020/4/25
(r, t) ei(q.rt) c.c.
10
入射光
E(r,t)
E ei(k.r t ) 0
c.c.
极化强度变化
P(r,
t)
(r,
t)E(r,
t)
1 4E04ei
(( k
E
Core
Backward Rayleigh
Cladding
瑞利散射是一种弹性散射,其散射光的频率与入射光的 频率相同。
极化强度: P 0 E D 0E P 0 (1 )E ( )E
2020/4/25
5
B 0 E B 0
t D 0 H D 0
t
关于电场强度E的方程
ω0
散射介质
Stokes
Anti-Stokes
Rayleigh
Raman
2020/4/25
Brillouin
Brillouin
ω0
Raman
3
ω
光散射的起源
• 介质光学特性的波动
~
~
介电常数
自发散射 受激散射
2020/4/25
4
。
Rayleigh散射
Cladding
Incident light
0
2E t 2
2E
E
ln(
)
0
2
散射讲义
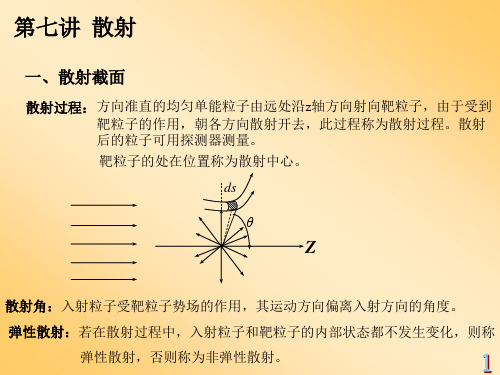
计算一个相移0 即足够了,而ka足够小,意味着入射粒子的动能较低,所以分波
法适用于低能散射,l>ka的分波散射截面可以略去。
说明:已知U(r)时,可用分波法求出低能散射的相移和散射截面,在原子核及 基本粒子问题中,作用力不清楚,也即不知道U(r)的具体形式,这时, 我们可先由实验测定散射截面和相移,然后确定势场和力的形式和性 质,这是研究原子核及基本粒子常用的一种方法。
l0
sin l
0 Pl (cos )Pl (cos )sind
2 k2
l0
(2l 1)(2l 1)ei(l l ) sin l
l0
sin l
2l
2
1
ll
4 k2
(2l 1) sin 2 l
l0
Q Ql
l 0
Ql
4
k2
(2l
1) sin 2 l
(3-16) (3-17)
(r, )r
l0
Al kr
sin kr
1 2
l
l
Pl
(cos
)
l0
A [e l
i
(
kr
1 2
l
l
)
2ikr
e
i
(
k
r
1 2
l
l
)
]Pl
(cos
)
(3-6)
另一方面,按上节的讨论,在远离散射中心处,粒子的波函数
(r, )r eikz f ( ) eikr r
(3-7)
将平面波 eikz 按球面波展开 eikz eikrcos (2l 1)il jl (kr)Pl (cos ) l0
不是散射波,应略去。
吸收截面和散射截面

吸收截面和散射截面
吸收截面和散射截面是物理学中的重要概念,它们是用来描述物体对物理现象的反应的。
吸收截面是指物体对物理现象的吸收能力,它是一个物体对物理现象的反应的度量。
它可以用来衡量物体对物理现象的吸收能力,以及物体对物理现象的敏感程度。
它可以用来衡量物体对物理现象的吸收能力,以及物体对物理现象的敏感程度。
散射截面是指物体对物理现象的散射能力,它是一个物体对物理现象的反应的度量。
它可以用来衡量物体对物理现象的散射能力,以及物体对物理现象的敏感程度。
它可以用来衡量物体对物理现象的散射能力,以及物体对物理现象的敏感程度。
吸收截面和散射截面是物理学中重要的概念,它们可以用来衡量物体对物理现象的反应能力,以及物体对物理现象的敏感程度。
它们可以用来研究物体对物理现象的反应,以及物体对物理现象的敏感程度。
它们也可以用来研究物体对物理现象的反应,以及物体对物理现象的敏感程度。
总之,吸收截面和散射截面是物理学中重要的概念,它们可以用来衡量物体对物理现象的反应能力,以及物体对物理现象的敏感程度。
它们可以用来研究物体对物理现象的反应,以及物体对物理现象的敏感程度。
它们也可以用来研究物体对物理现象的反应,以及物体对物理现象的敏感程度。
因此,吸收截面和散射截面在物理学中具有重要的意义。
散射与衍射-ReadPPT课件

Three twofold axes or mirror plane One threefold axis
One threefold axis
One threefold axis
One twofold axis or mirror plane none
Space lattices PIF
a=b=c
a=b=g=90
a=b≠c
a=b=g=90
a≠b≠c
a=b=g=90
A=b≠c a=g=90
b=120
A=b≠c a=g=90
b=120
a=b=c
a=b=g≠90
a≠b≠c
a=b=90 g≠90
a≠b≠c
a≠b≠g≠90
Essential symmetry
Four threefold axes
子顺磁共振。
红外,可见,紫外光与物质的相互作用
分子的能量由3个方面构成,
电子的能量, 核的振动能量, 分子的转动能量。 与它们相当的电磁波的波长分别为几十-几百nm,几个 m及数百m,相应的波段分别属可见-紫外区,近、中 红外区,远红外及微波区。
形成的结构分析仪器:
透射电子显微镜, 扫描电子显微镜, 低能电子衍射仪, 电子探针, 质谱仪等, 光谱仪, X射线衍射仪
~0
吸收系数 吸收与Z
较大,~10-103cm-1 随Z增加而增加
很大 无关
很小,10-1-10-3 cm-1 (B,Cd,稀土大)
随同位素而异
吸收的同位素影响
无
无
有
折射率n
非弹性散射
衍射花样、衍衬相
略<1
波长改变小,康散射 有束缚小的核外电子
总微分散射截面共84页PPT

56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
总微分散射截面
21、没有人陪你走一辈子,所以你要 适应孤 独,没 有人会 帮你一 辈子, 所以你 要奋斗 一生。 22、当眼泪流尽的时候,留下的应该 是坚强 。 23、要改变命运,首先改变自己。
24、勇气很有理由被当作人类德性之 首,因 为这种 德性保 证了所 有其余 的德性 。--温 斯顿. 丘吉尔 。 25、梯子的梯阶从来不是用来搁脚的 ,它只 是让人 们的脚 放上一 段时间 ,以便 让别一 只脚能 够再往 上登。
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d
2U l (r) dr 2
k
2U
l
(r)
0
由此求得: U l (r) Al sin(kr l)
Rl
(r)r
Al kr
sin kr
1 2
l
l
(3-5)
为了后面的方便起见,这里引入了两个新的常数
Al kAl,
l
l
2
l
将(3-5)代入(3-2),得到方程(3-1)在 r 情形下通解的渐近形式
处设的r 散射体时系,V的(r波) 函数0 ,。方程(5)变为
2 k 2 0
(6)
令
r
(7)
将(6)式写成
2
r 2
k 2
Lˆ2 r2
0
在 r 的情形下,此方程简化为
2 k 2 0
r 2
(8)
此方程类似一维波动方程,我们知道: 对于一维势垒或势阱的散射情况
k x Aeikx Beikx
[e 2
i(kr1l )
e 2 ]PL (cos )
(3-8)
(3-9) (3-10)
(3-6)和(3-10)两式右边应相等,即
e ik r
(9)
r
为方便起见,取入射平面波 eikx的系数A=1,这表明 | 1 |2 1 ,入射粒子束单
位体积中的粒子数为1。 入射波几率密度(即入射粒子流密度)
Jz
i 2
1
* 1
z
1*
1 z
i 2
(ik11*
ik1* )
k N
(10)
散射波的几率流密度
Jr
i
2
2
* 2
r
* 2
1 r2
d dr
r 2
dRl dr
k 2
V (r)
l
(l r2
1)
Rl
(r
)
0
令
Rl
(r)
Ul (r) r
,代入上方程
(3-3)
d 2Ul dr 2
k 2
V
(r
)
l
(l r2
1)
U
l
(r
)
0
(3-4)
考虑方程(3-4)在 r 情况下的极限解,令 r 方程(3-4)的极限形式
(优选)第七讲散射一散射截 面
[q]
dn Nd
L2
故称q(,)为微分散射截面,简称为截面或角分布
如果在垂直于入射粒子流的入射方向取面积q(,),则单位时间内通过此截
面q(,)的粒子数恰好散射到(,)方向的单位立体角内。
q( ,)N dn
d
(2)
总散射截面:
2
Q q(,)d q(,)sindd
取散射中心A为坐标原点,散射粒子体系的定态schrödinger方程
2 2 U(r) E 2
(4)
令
k2
2E 2
V
(r )
2 2
U (r)
方程(4)改写为
2 [k 2 V (r)] 0
(5)
由于实验观测是在远离靶的地方进行的,从微观角度看,可以认为r 。因 此,在计算时q( ,) ,仅需考虑 r 处的散射粒子的行为,即仅需考虑 r
2
r
r2
|
f
( ,) |2
(11)
单位时间内,在沿( ,) 方向d立体角内出现的粒子数为
dn
J r ds |
f ( ,) |2
r2
ds |
f ( ,) |2
Nd
比较(1)式与(12),得到
(12)
q( ,) | f ( ,) |2
(13)
由此可知,若知道了f ( ,),即可求得q( ,) ,f ( ,) 称为散射振幅,所以,
式中jl(kr)是球贝塞尔函数
jl (kr)
2kr
J
l1 2
(kr)r
1 kr
sin
kr
1 2
l
1
i(kr 1 l )
i(kr 1 l )
[e 2 e 2 ]
2ik r
利用(3-8),(3-9),可将(3-7)写成
(r,)r
f ( ) eikr r
l 0
(2l 1)il 2ikr
i(kr1l )
(r, )r
l0
Al kr
sin kr
1 2
l
l
Pl
(cos
)
l0
A [e l
i
(
kr
1 2
l
l
)
2ikr
e
i
(
k
r
1 2
l
l
)
]Pl
(cos
)
(3-6)
另一方面,按上节的讨论,在远离散射中心处,粒子的波函数
(r, )r eikz f ( ) eikr r
(3-7)
将平面波 eikz 按球面波展开 eikz eikrcos (2l 1)il jl (kr)Pl (cos ) l0
Rl (r)Pl (cos )
方程(3-1)的通解为所有特解的线性迭加
(r, ) Rl (r)Pl (cos )
l
(3-2)
Rl(r)为待定的径向波函数,每个特解称为一个分波,Rl (r)Pl (cos ) 称为第l个分 波,通常称l=0,1,2,3…的分波分别为s, p, d, f…分波
(3-2)代入(3-1),得径向方程
三、分波法
讨粒论子粒在子辏在力中场心中力的场势中能的 为U散(r射),。状态方程
2 [k 2 V (r)] 0
(3-1)
取沿粒子入射方向并通过散射中心的轴线为极轴z,显然与无关,按照§3.3.的 讨论,对于具有确定能量的粒子,方程(3-1)的特解为
Rl (r)Ylm ( , ) 由于现在与无关(m=0),所以,方程(1)的特解可写成
k x ceikx
式中 eikx 为入射波或透射波, eikx 为散射波,波只沿一方向散射。
对于三维情形,波可沿各方向散射,三维散射时,在r 处的粒子的波函数
应为入射波和散射波之和。 方程(8)有两个特解
(r, ,) f ( , )eikr
(r, , ) f ( , )eikr
因此,
(3)
00
[由注(] 2)式知,由于N、dn 可通过实验测定,故而求得 q( ,) 。
d
量子力学的任务是从理论上计算出 q( ,),以便于同实验比较,从而反过来研
究粒子间的相互作用以及其它问题。
二、散射振幅
现在考虑量子力学对散射体系的描述。设靶粒子的质量远大于散射粒子的质量,
在碰撞过程中,靶粒子可视为静止。
对于给定能量的入射粒子,速率 v 给定,于是入射粒子流密度N= v 给定,只要
知道了散射振幅 f ( ,) ,也就能求出微分散射截面,f ( ,) 的具体形式通过求
schrödinger方程(5)的解并要求在 r 时具有渐近形式(9)而得出。
下面介绍两种求散射振幅或散射截面的方法——分波法,玻恩近似方法。 分波法是准确的求散射理论问题的方法,即准确的散射理论。
2 (r, ,)
f ( , ) eikr
r
2 (r, ,)
f ( , ) eikr r
2 代表由散射中心向外传播的球面散射波, 2 代表向散射中心会聚的球面波,
不是散射波,应略去。
在 r 处,散射粒子的波函数是入射平面波 1 eikz 和球面散射波 2 之和。
即
(
