2011年陕西省中考数学试题及答案

合集下载

2011年陕西中考数学试题及答案(扫描版)

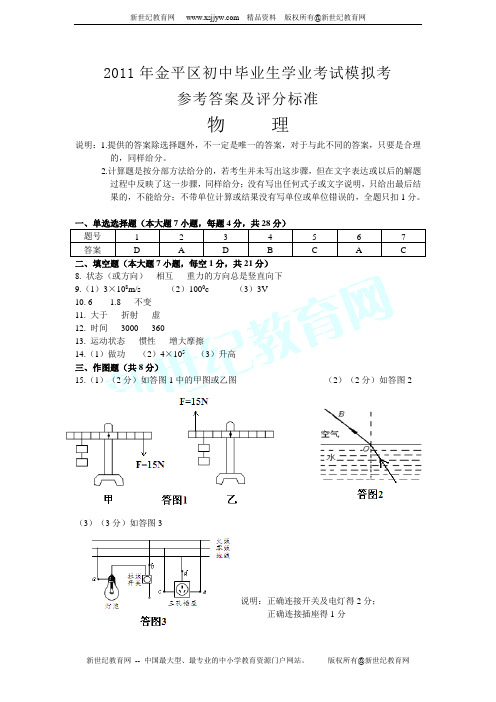
2011年金平区初中毕业生学业考试模拟考参考答案及评分标准物理说明：1.提供的答案除选择题外，不一定是唯一的答案，对于与此不同的答案，只要是合理的，同样给分。

2.计算题是按分部方法给分的，若考生并未写出这步骤，但在文字表达或以后的解题过程中反映了这一步骤，同样给分；没有写出任何式子或文字说明，只给出最后结果的，不能给分；不带单位计算或结果没有写单位或单位错误的，全题只扣1分。

一、单选选择题（本大题7小题，每题4分，共28分）题号 1 2 3 4 5 6 7 答案 D A D B C A C二、填空题（本大题7小题，每空1分，共21分）8. 状态（或方向）相互重力的方向总是竖直向下9.（1）3×108m/s （2）1000c （3）3V10. 6 1.8 不变11. 大于折射虚12. 时间3000 36013. 运动状态惯性增大摩擦14.（1）做功（2）4×105 （3）升高三、作图题（共8分）15.（1）（2分）如答图1中的甲图或乙图（2）（2分）如答图2（3）（3分）如答图3说明：正确连接开关及电灯得2分；正确连接插座得1分四、实验题（本大题3小题，共23分）16.（7分）（1）39.6 15 2.64×103 （每空1分，共3分）（2）b 0.4 5 0.8 （每空1分，共4分）17.（9分）（1）48 固液共存状态（每空1分，共2分）（2）大于物质在t5时刻从水中吸收了更多的热量，内能增大（每空1分，共2分）（3）热传递使固体受热更加均匀3×105 28.6（第一、二、三空各1分，第四空2分，共5分）18.（7分）（1）竖直匀速向上（或匀速向上）（1分）（2）60.6% （1分）（3）66.7% 同一套滑轮组所提重物越重，机械效率越高。

（第一空1分，第二空2分，共3分）（4）变大（1分）（5）不变（1分）五、计算题（本大题2小题，共16分）19.（8分）解：（1）F浮=G排=m排g=67000×103kg×10N/kg=6.7×108N （2分）（2）p=ρg h =1.1×103kg/m3×10N/kg×10m=1.1×105 Pa（2分）（3）由W=Fs 和P=W/t 得，P=Fv （1分）∴该舰的动力F=P/v=147200×103 W/16m/s=9.2×106 N （2分）∵匀速前进∴该舰所受阻力f=F=9.2×106 N （1分）答（略）20.（8分）解：（1）R1=U/I1=6V/0.3A=20Ω（2分）（2）当滑片P在A端时，滑动变阻器的阻值R2=40Ω，R1和R2串联则电流表示数I2=U/(R1+R2)=6V/(20Ω+40Ω)=0.1A （2分）电压表示数U2=I2R1=0.1A×20Ω=2V （2分）此时滑动变阻器消耗的功率P=I22R2=(0.1A)2×40Ω=0.4W （2分）答（略）六、综合能力题（本大题3小题，共24分）21.（6分）（1）①超声②音调（每空1分，共2分）（2）次声波（1分）（3）5Hz （1分）（4）声可以传递信息声可以传递能量（每空1分，共2分）22.（10分）（1）（以下答案供参考，其他答案只要合理均给分）评分说明：每空1分，共4分汽车上的装置水箱里面用水做冷却剂前方的挡风玻璃是倾斜的前排乘客必须系戴安全带汽车的方向盘涉及的物理知识水的比热容大平面镜成像原理（光的反射）惯性轮轴（简单机械）（2）C （2分）（3）D （2分）（4）A （2分）23.（8分）（1）N 丙大于（每空1分，共3分）（2）增大（1分）（3）500 1.0 （每空2分，共4分）。

2011年陕西省中考试题及答案

2011年陕西省中考试题及答案一、语文部分阅读下面短文，然后按照要求答题。

（一）他的东西让我们思考得更多，我们的文化也因此丰富多彩。

李自成（1606年—1662年），他在陕北打响了一场搅动整个大清王朝的三十年农民起义。

尽管最后他没有成功建立自己的王朝，但他的传奇经历至今仍令人赞叹不已。

李自成是一个充满了矛盾的人。

他既是一个天才的战略家，又是一个性格多疑、易怒的领导者。

他以农民为主体的农村军队走过陕北、川、鄂、豫并最终进逼中原，这在当时是一种颠覆了封建大清王朝的现象。

他治军严明，从不纵容任何懈怠和盗窃行为，还督促部下勤勉训练，始终保持军队高度战斗力。

因此，李自成军队具有很高的战斗力，给大清朝廷带来了巨大的威胁。

然而，李自成在领导方面却有许多缺点。

他喜怒无常，虐待部下，用刑过度。

他的威权颇重，经常劫掠百姓，以求财富。

这些不负责任的行为最终引起了朝廷内部的矛盾和士兵之间的不满，也是导致他失败的一个重要原因。

李自成被后人评价为一个叛逆的农民起义领袖，反叛人心的叛徒。

然而我们在了解他生活和战斗过程的同时，必须认识到，他对中国历史的影响是深远而复杂的。

他的行为触及到了权力、武力以及农民与封建地主之间的矛盾，给我们提供了重要的历史反思题材。

1. 短文中“农民起义”的含义是什么？（请用简短的话回答，不超过15个字）答案：推翻封建统治2. 短文最后作者对李自成的评价是怎样的？（请用简短的话回答，不超过15个字）答案：深远而复杂二、数学部分1. 已知函数y=3x+1，求当x等于2时，y的值为多少？答案：72. 若a:b=2:3，且a=10，求b的值。

答案：15三、英语部分阅读下面短文，并根据短文内容回答问题。

（一）My FamilyMy family is not very big. There are only three people in my family, my father, my mother, and me. My father is a teacher. He teaches English in amiddle school. He works very hard. My mother is a doctor. She works in a hospital. She is very kind and always takes care of me. I love my parents.1. How many people are there in the writer's family?答案：Three people.2. What does the writer's father do?答案：He is a teacher.四、综合部分请根据你对以上试题的回答，选择正确的选项。

2011陕西中考数学试题及答案

2011陕西中考数学试题及答案一、选择题1. 计算：$3 \times (4 + 5) - 2^2 =$ （2011陕西中考）解答：首先计算括号内的加法，得到$3 \times 9 - 2^2 =$，然后计算乘法，得到$27 - 4 =$，最后计算减法，得到$23$。

因此，答案为$23$。

2. 下列各数：$\sqrt{9}$，$\frac{12}{4}$，$(-3) \times 2^2 + 5^0$和$-1.1$中，其中不是整数的是：（2011陕西中考）A. $\sqrt{9}$B. $\frac{12}{4}$C. $(-3) \times 2^2 + 5^0$D. $-1.1$解答：$\sqrt{9}=3$，$\frac{12}{4}=3$，$(-3) \times 2^2 + 5^0=-3\times 4 + 1=-11$，$-1.1$不是整数。

因此，答案是D。

3. 用$\frac{4}{9}$表示0.4，则$\frac{41}{90}$的另一种表示是：（2011陕西中考）解答：首先计算$\frac{4}{9} \times 10$，得到$\frac{40}{9}$。

然后在$\frac{40}{9}$的基础上加上$\frac{1}{9}$，得到$\frac{41}{9}$。

最后将$\frac{41}{9}$转化为分数形式，得到$\frac{41}{9}$。

因此，答案是$\frac{41}{9}$。

4. 小花去商场选购衣服，她看中了一件原价为320元的衣服，商场正在举行打折活动，全场商品打7折。

小花还是犹豫不决，她妈妈说：“你有一张价格为20元的优惠券，使用后再打折。

”小花计算了一下，最终衣服的价格是多少元？（2011陕西中考）解答：首先计算打折后衣服的价格，$320 \times 0.7=224$。

然后将优惠券价格减去衣服价格，$20-224=-204$。

因此，最终衣服的价格是负数204元。

真题：2011年陕西中考数学试题及答案

真题：2011年陕西中考数学试题及答案
初三数学试题:图形的旋转考试题(含答案)
等可能情形下的概率计算同步练习
专题推荐：
北京精锐教育初中一对一辅导专题
初三数学试题:图形的旋转考试题(含答案)
等可能情形下的概率计算同步练习
专题推荐：
北京精锐教育初中一对一辅导专题
初三数学试题:图形的旋转考试题(含答案)
等可能情形下的概率计算同步练习
专题推荐：
北京精锐教育初中一对一辅导专题
初三数学试题:图形的旋转考试题(含答案)
等可能情形下的概率计算同步练习
专题推荐：
北京精锐教育初中一对一辅导专题
初三数学试题:图形的旋转考试题(含答案) 等可能情形下的概率计算同步练习
专题推荐：
北京精锐教育初中一对一辅导专题
初三数学试题:图形的旋转考试题(含答案) 等可能情形下的概率计算同步练习
专题推荐：
北京精锐教育初中一对一辅导专题
初三数学试题:图形的旋转考试题(含答案) 等可能情形下的概率计算同步练习
专题推荐：
北京精锐教育初中一对一辅导专题
初三数学试题:图形的旋转考试题(含答案) 等可能情形下的概率计算同步练习
专题推荐：
北京精锐教育初中一对一辅导专题。

中考数学试题汇编反比例函数

选择题每小题x 分,共y 分2011绥化市17. 若11A()x y ，,22B()x y ，,33()C x y ，是反比例函数2y x=图象上的点,且1230x x x <<<,则123y y y 、、的大小关系正确的是 AA ． 312y y y >>B ．123y y y >>C ．213y y y >>D ．321y y y >> 2011眉山市12．如图．直线(0)y x b b =-+>与双曲线(0)ky x x=>交于A 、B 两点,连接OA 、OB,AM ⊥y 轴于M ．BN ⊥x 轴于N ；有以下结论： ①OA=OB②△AOM ≌△BON． ③若∠AOB=45°．则AOB S k ∆= ④当AB=2时,ON=BN=l ；其中结论正确的个数为DA ．1B ．2C ．3 D. 42011东营10．如图,直线l 和双曲线(0)ky k x=>交于A 、B 两点,P 是线段AB 上的点不与A 、B 重合．过点A 、B 、P 分捌向x 轴作垂线,垂足分别为C 、D 、E,连接OA 、OB 、OP ．设△AOC 的面积为1S ．△BOD 的面积为2S ;△POE 的面积为3S ,则 DA ．123S S S <<B ．123S S S >>C ．123S S S =>D ．123S S S =<2011佛山8、下列函数的图像在每一个象限内,y 值随x 值的增大而增大的是 DA 、1y x =-+B 、1y x =-+C 、1y x=D 、1y x=-2011鸡西市5．若Ax 1,y 1,Bx 2,y 2,Cx 3,y 3是反比例函数y=x3图象上的点,且x 1＜x 2＜0＜x 3,则y 1、y 2、y 3的大小关系正确的是 A A y 3＞y 1＞y 2 B y 1＞y 2＞y 3 C y 2＞y 1＞y 3 D y 3＞y 2＞y 12011枣庄市8．已知反比例函数xy 1=,下列结论中不正确的是D A .图象经过点－1,－1 B .图象在第一、三象限C .当1>x 时,10<<yD .当0<x 时,y 随着x 的增大而增大2011扬州市6．某反比例函数图象经过点()16-，,则下列各点中此函数图象也经过的点是 A A ．()32-， B ．()32， C ．()23， D ．()61， 2011铜仁8．反比例函数)0(<=k xky 的大致图像是 BA B C D2011邵阳市5．已知点1,1在反比例函数y ＝错误!k 为常数,k ≠0的图象上,则这个反比例函数的大致图象是A B C D答案：C2011陕西省8．如图,过y 轴上任意一点p,作x 轴的平行线,分别与反比例函数xy x y 24=-=和的图像交于A 点和B 点,若C 为x 轴上任意一点,连接AC,BC 则△ABC 的面积为 A2011陕西省4、下列四个点,在正比例函数X Y 52-=的图像上的点是 D x yO x yO x yO x yO yo xo yx xo yyx oA 、 2, 5B 、 5, 2C 、2,-5D 、 5 , -2〔2011浙江省台州市〕9．如图,双曲线y ＝错误!与直线y ＝kx ＋b 交于点M 、N ,并且点M 的坐标为1,3,点N 的纵坐标为－1．根据图象信息可得关于x 的方程错误!＝kx ＋b 的解为 A A ．－3,1 B ．－3,3 C ．－1,1 D ．－1,32011威海市5．下列各点中,在函数6y x=-图象上的是C A ．－2,－4 B ．2,3 C ．－6,1 D ．－12,3〔2011温州市〕4、已知点P -1,4在反比例函数)0(≠=k xky 的图像上,则k 的值是 DA 、41-B 、41C 、4D 、-42011黄石市3.双曲线21k y x-=的图像经过第二、四象限,则k 的取值范围是 BA.12k >B. 12k <C. 12k = D. 不存在〔2011盐城市〕6．对于反比例函数y =错误!,下列说法正确的是C A ．图象经过点1,-1 B ．图象位于第二、四象限C ．图象是中心对称图形D ．当x ＜0时,y 随x 的增大而增大 2011茂名市6、若函数xm y 2+=的图象在其象限内y 的值随x 值的增大而增大,则m 的取值范围是 A ．2->m Ｂ．2-<m Ｃ．2>m Ｄ．2<m 〔2011广州市〕5.下列函数中,当x>0时,y 值随x 值增大而减小的是 D A.2x y = B. 1-=x y C. x y 43=D. xy 1= (1)〔2011凉山州〕二次函数2y ax bx c =++的图像如图所示,反比列函数ay x=与正比列函数y bx =在同一坐标系内的大致图像是 B2011乐山10．如图6,直线 6y x =- 交x轴、y 轴于A 、B 两点,P 是反比例函数4(0)y x x=>图象上位于直线下方的一点,过点P 作x 轴的垂线,垂足为点M,交AB 于点E,过点P 作y 轴的垂线,垂足为点N,交AB 于点F;则AF BE ⋅=ABC第18题1P 2P1A 1B2A 2B3Px yO A8 B 6 C4 D 62二、填空题每小题x 分,共y 分2011河南省9. 已知点(,)P a b 在反比例函数2y x =的图象上,若点P 关于y 轴对称的点在反比例函数k y x=的图象上,则k 的值为 -2 .2011桂林市17．双曲线1y 、2y 在第一象限的图像如图,14y x=, 过1y 上的任意一点A ,作x 轴的平行线交2y 于B ,交y 轴于C ,若1AOB S ∆=,则2y 的解析式是 26y x = ． 18. 2011山东滨州,18,4分若点Am,-2在反比例函数4y x=的图像上,则当函数值y ≥-2时,自变量x 的取值范围是___________. 答案x ≤-2或x>02011宁波18．如图,正方形1112A B PP 的顶点1P 、2P 在反比例函数2(0)y x x=>的图象上,顶点1A 、1B 分别在x 轴、y 轴的正半轴上,再在其右侧作正方形2232B A P P ,顶点3P 在反比例函数2(0)y x x=>的图象上,顶点2A 在x 轴的正半轴上,则点3P 的坐标为)13,13(-+ ▲ ．2011南充市14过反比例函数y=xkk ≠0图象上一点A,分别作x 轴,y 轴的垂线,垂足分别为B,C,如果⊿ABC 的面积为3.则k 的值为 6或—6 .2011苏州市18．如图,已知点A 的坐标为3,3,AB ⊥x 轴,垂足为B,连接OA,反比例函数ky x=k>0的图象与线段OA 、AB 分别交于点C 、D ．若AB ＝3BD,以点C 为圆心,CA 的54倍的长为半径作圆,则该圆与x 轴的位置关系是相交▲ 填“相离”、“相切”或“相交”．2011黄冈市4．如图：点A 在双曲线ky x=上,AB ⊥x 轴于B ,且△AOB 的面积S △AOB =2,则k =___-4___． 2011黄石市15.若一次函数1y kx =+的图像与反比例函数1y x=的图像没有公共点,则实数k 的取值范围是 14k <- .〔2011湖北省武汉市〕16.如图,□ABCD 的顶点A,B 的坐标分别是A-1,0,B0,-2,顶点C,D 在双曲线y=xk上,边AD 交y 轴于点E,且四边形BCDE 的面积是△ABE 面积的5倍,则k=__12___.〔2011山东省烟台市〕18、如图,在平面直角坐标系中,点O 为原点,菱形OABC 的对角线OB 在x 轴上,顶点A 在反比例函数y=的图像上,则菱形的面积为____4________;2011益阳市13．在1-,1,2这三个数中任选2个数分别作为P 点的横坐标和纵坐标,过P 点画双曲线ky x=,该双AB Oxy第4题图曲线位于第一、三象限的概率是13．〔2011福州市〕13．如图,△OPQ 是边长为2的等边三角形,若反比例函数的图象过点P ,则它的解析式是 y=x3.2011大连12．已知反比例函数k y x =的图象经过点3,－4,则这个函数的解析式为_____2y x=-______．〔2011广东省〕9．已知一次函数b x y -=与反比例函数xy 2=的图象,有一个交点的纵坐标是2,则b 的值为______-1__;11、2011·济宁反比例函数 xm y 1-=的图象在第一、三象限,则m 的取值范围是 m>1 ; 2011金华市16.如图,将一块直角三角板OAB 放在平面直角坐标系中, B 2,0,∠AOB =60°,点A 在第一象限,过点A 的双曲线为ky x=.在x 轴上取一点P ,过点P 作直线OA 的垂线l , 以直线l 为对称轴,线段OB 经轴对称变换后的像是O ′B ′. 1当点O ′与点A 重合时,点P 的坐标是4,0； ▲ ； 2设Pt ,0,当O ′B ′与双曲线有交点时,t 的取值范围是 ▲4≤t ≤25或25-≤t ≤－4 .〔2011南京市〕15．设函数2y x =与1y x =-的图象的交战坐标为a ,b ,则11a b-的值为____12-______．〔2011浙江省衢州〕15、在直角坐标系中,有如图所示的Rt △ABO,AB ⊥x 轴于点B,斜边AO ＝10,sin ∠AOB=53,反比例函数)0k (xky >= 的图象经过AO 的中点C,且与AB 交于点D,则点D 的坐标为_________8,23________；〔2011芜湖市〕15.如图,在平面直角坐标系中有一正方形AOBC,反比例函数422-的圆内切于△ABC,ky x=经过正方形AOBC 对角线的交点,半径为则k 的值为____4____;OPQxy 第13题OlB ′xyA B PO ′ 第16题图A BOC D xy第15题2011十堰市16.如图,平行四边形AOBC 中,对角线交于点E,双曲线y =kx (k >0)经过A 、E 两点,若平行四边形AOBC 的面积为18,则k ＝____6____.三、解答题：共x 分2011安徽省21. 如图函数11y k x b =+的图象与函数2k y x=x ＞0的图象交于A 、B 两点,与y 轴交于C 点.已知A 点的坐标为2,1,C 点坐标为0,3. 1求函数1y 的表达式和B 点坐标；解2观察图象,比较当x ＞0时,1y 和2y 的大小.21. 1由题意,得⎩⎨⎧==+.3,121b b k 解得⎩⎨⎧=-=.3,11b k ∴ 31+-=x y又A 点在函数x k y 22=上,所以 212k =,解得22=k 所以xy 22= 解方程组⎪⎩⎪⎨⎧=+-=x y x y 2,3 得⎩⎨⎧==.2,111y x ⎩⎨⎧==.1,222y x 所以点B 的坐标为1, 22当0＜x ＜1或x ＞2时,y 1＜y 2;当1＜x ＜2时,y 1＞y 2; 当x=1或x=2时,y 1=y 2.2011潜江市21．满分8分如图,已知直线AB 与x 轴交于点C ,与双曲线x k y =交于A 3,320、B -5,a 两点.AD ⊥x 轴于点D ,BE ∥x 轴且与y 轴交于点E . 1求点B 的坐标及直线AB 的解析式； 2判断四边形CBED 的形状,并说明理由.21．解：1∵双曲线xk y =过A 3,320,∴20=k .x 20=,第21题图得4-=a . ∴点B 的坐标是-5,-4. ………………………………2分设直线AB 的解析式为n mx y +=,将 A 3,320、B -5,-4代入得, ⎪⎩⎪⎨⎧+-=-+=nm nm 543320, 解得：38,34==n m . ∴直线AB 的解析式为：3834+=x y .………………………………… 4分 2四边形CBED 是菱形.理由如下: ………………………………… 5分点D 的坐标是3,0,点C 的坐标是-2,0. ∵ BE ∥x 轴, ∴点E 的坐标是0,-4.而CD =5, BE=5, 且BE ∥CD .∴四边形CBED 是平行四边形. ………………………………………… 6分在Rt △OED 中,ED 2＝OE 2＋OD 2, ∴ ED ＝2243+＝5,∴ED ＝CD .∴□CBED 是菱形. ……………………………………………………… 8分2011天津20本小题8分已知一次函数1y x b =+b 为常数的图象与反比例函数2ky x=k 为常数．且0k ≠ 的图象相交于点P3．1．I 求这两个函数的解析式；II 当x>3时,试判断1y 与2y 的大小．井说明理由;解 I 一次函数的解析式为12y x =-．反比例函数的解析式为23y x=． Ⅱ12y y >．理由如下：当3x =时,121y y ==．又当3x >时．一次函数1y 随x 的增大而增大．反比例函数2y 随x 的增大而减碡小, ∴当3x >时12y y >;2011江西省19.如图,四边形ABCD 为菱形,已知A 0,4,B －3,0. 1求点D 的坐标；2求经过点C 的反比例函数解析式.19．解：1 ∵(0,4),(3,0)A B -, ∴3,4,OB OA == ∴5AB =.在菱形ABCD 中,5AD AB ==, ∴1OD =, ∴D 2∵BC ∥AD , 5BC AB ==, ∴()3,5C --.设经过点C 的反比例函数解析式为k y x=. 把()3,5--代入k y x =中,得：53k -=-, ∴15k =,∴15y x=. ……6分2011北京市17. 如图注：略,在平面直角坐标系xOy 中,一次函数2y x =-的图象与反比例函数ky x=的图象的一个交点为A 1-,n ;1求反比例函数ky x=的解析式； 2若P 是坐标轴上一点,且满足PA OA =,直接写出点P 的坐标;解 1 ∵ 点A -1,n 在一次函数y= -2x 的图象上, ∴ n= -2-1=2;∴ 点A 的坐标为-1,2; ∵ 点A 在反比例函数y=xk的图象上, ∴ k= -2,∴ 反比例函数的解析式为y= -x2; 2 点P 的坐标为-2,0或0,4;2011呼和浩特市21、8分在同一直角坐标系中反比例函数x my =的图象与一次函数b kx y +=的图象相交,且其中一个交点A 的坐标为–2,3,若一次函数的图象又与x 轴相交于点B,且△AOB 的面积为6点O 为坐标原点. 求一次函数与反比例函数的解析式.21、解：将点A —2,3代入x my =中得23-=m∴ 6-=m∴x y 6-= ………………………………………………………2分又∵ △AOB 的面积为6∴ 6||||21=⋅A y OB ∴ 63||21=⋅OB∴ |OB|=4∴ B 点坐标为4,0或—4,0 ………………4分 ①当B4,0时,又∵ 点A —2,3是两函数的交点 ∴ 代入b kx y +=中得⎩⎨⎧=+-=+3204b k b k∴ ⎪⎩⎪⎨⎧=-=221b k∴221+-=x y …………………………………6分②当B —4,0时,又∵ 点A —2,3是两函数的交点 ∴ 代入b kx y +=中得⎩⎨⎧=+-=+-3204b k b k∴ ⎪⎩⎪⎨⎧==623b k∴ 623+=x y …………………………………………………8分2011重庆市潼南县23.10分如图, 在平面直角坐标系中,一次函数y kx b =+k ≠0的图象与反比例函数xmy =m ≠0的图象相交于A 、B 两点．求：1根据图象写出A 、B 两点的坐标并分别求出反比例函数和一次函数的解析式；2根据图象写出：当x 为何值时,一次函数值大于反比例函数值.23.解：1由图象可知：点A 的坐标为2,12点B 的坐标为-1,-1 --------------2分∵反比例函数x my =m ≠0的图像经过点2,12∴ m =1∴反比例函数的解析式为:1y x=---------------------4分 ∵一次函数y =kx +b k ≠0的图象经过点2,12点B-1,-1∴1221k b k b ⎧+=⎪⎨⎪-+=-⎩ 解得：k =12 b =-21 ∴一次函数的解析式为1122y x =- ----------------------6分 2由图象可知：当x ＞2 或 -1＜x ＜0时一次函数值大于反比例函数值 --------10分2011达州18、6分给出下列命题：命题1：直线x y =与双曲线x y 1=有一个交点是1,1；命题2：直线x y 8=与双曲线x y 2=有一个交点是21,4；命题3：直线x y 27=与双曲线x y 3=有一个交点是31,9；命题4：直线x y 64=与双曲线x y 4=有一个交点是41,16；…………………………………………………… 1请你阅读、观察上面命题,猜想出命题n n 为正整数； 2请验证你猜想的命题n 是真命题．18、6分解：1命题n ：直线x n y 3=与双曲线x n y =有一个交点是n1,2n …………………………………………3分2将n 1,2n 代入直线x n y 3=得：右边=231n nn =⨯,左边=2n , ∴左边=右边,∴点n 1,2n 在直线x n y 3=上,同理可证：点n 1,2n 在双曲线xny =上,∴直线x n y 3=与双曲线x n y =有一个交点是n1,2n ……………………6分〔2011浙江省义乌〕22．如图,在直角坐标系中,O 为坐标原点. 已知反比例函数y= k>0的图象经过点A 2,m ,过点A 作AB ⊥x 轴于点B ,且△AOB 的面积为 .1求k 和m 的值；2点Cx ,y 在反比例函数y= 的图象上,求当 1≤x ≤3时函数值y 的取值范围；3过原点O 的直线l 与反比例函数y= 的图象交于P 、Q 两点,试根据图象直接写出线段PQ 长度的最小值.22．解：1∵A 2,m ∴OB =2 AB =m ∴S △AOB =21OBAB =21×2×m =21 ∴m =21………………………………2分 ∴点A 的坐标为2,21 把A 2,21代入y=x k ,得21=2k∴k =1 ……………………………………………………………………………4分2∵当x =1时,y =1；当x =3时,y =31…………………………………………6分又 ∵反比例函数y =x1在x >0时,y 随x 的增大而减小…………………………7分 ∴当1≤x ≤3时,y 的取值范围为31≤y ≤1 …………………………………8分3 由图象可得,线段PQ 长度的最小值为22 ……………………………10分各位好本文件是有删节的版本你只要在淘宝网花5元钱,即可得到本人自己整理的全部49个分类的2011年中考数学试题汇编每一个汇编都按选择、填空、解答题进行分类,有答案都是word 文档,可以进行编辑;另外还送2010年的41个中考试题汇编文件请点淘宝的这个网址点击这个网址你就可免费得到两个完整的数学试卷汇编文档x k21xk xkB O A。

陕西省2011年中考数学试题(word版含答案解析)

例 2011年上海市虹口区中考模拟第25题如图，在Rt△ABC中，∠BAC＝90°，AB＝3，AC＝4，AD是BC边上的高，点E、F 分别是AB边和AC边上的动点，且∠EDF＝90°．（1）求DE∶DF的值；（2）联结EF，设点B与点E间的距离为x，△DEF的面积为y，求y关于x的函数关系式，并写出x的取值范围；（3）设直线DF与直线AB相交于点G，△EFG能否成为等腰三角形？若能，请直接写出线段BE的长；若不能，请说明理由．图1 备用图备用图动感体验请打开几何画板文件名“11虹口25”，拖动点E在AB上运动，观察△EFG的三边的垂直平分线，可以体验到，点E和点F可以落在对边的垂直平分线上，点G不可能．请打开超级画板文件名“11虹口24”，思路点拨1．本题中的直角三角形的三边比都是3∶4∶5，计算中反复用到．2．利用相似三角形的面积比等于相似比的平方求△DEF的面积比较简便．3．探究等腰△EFG，是一道非常规的等腰三角形的存在性问题，两种存在的情况各有各的算法．满分解答（1）如图2，因为∠BAC＝90°，∠EDF＝90°，AD⊥BC，所以∠1与∠C都是∠2的余角，∠3与∠4都是∠5的余角，3 tan4AD ABCCD AC∠===．所以∠1＝∠C，∠3＝∠4．所以△ADE∽△CDF．因此34 DE ADDF CD==．图2 图3 图4（2）如图3，由△BDE ∽△ADF ，得34BE BD AF AD ==．所以4433AF BE x ==．如图4，在Rt △AEF 中，AE ＝3－x ，43AF x =，由勾股定理得2224(3)()3EF x x =-+225699x x =-+．由△DEF ∽△ABC ，得S △DEF ∶S △ABC ＝EF 2∶BC 2．所以2262523654(69)25932525DEF y S x x x x ==-+=-+△． x 的取值范围为0≤x ≤3．（3）BE 的长为5425或35．考点伸展第（3）题的解题思路是这样的：①如图5，当EF ＝EG 时，∠G ＝∠6．又∠1＝∠6，所以∠G ＝∠1．从而DA ＝DG ＝DF ．于是可以得到AB ＝EF ．所以AB 2＝EF 2．解方程2259699x x =-+，得5425x BE ==． ②如图6，当FE ＝FG 时，∠G ＝∠AEF ．31tan 49935555DE DE DE DE G DG DF FG EF EF EF ∠======++⨯．443tan 33(3)x AF x AEF AE x x ∠===--．解方程1433(3)x x =-，得35x BE ==． ③不存在GE ＝GF 的可能．如图5，如图6，因为∠GEF 或∠GFE 总是钝角或者直角．图5 图6。

陕西2011中考数学(word版,含扫描答案)

例 2011年上海市闵行区中考模拟第24题如图1，已知：抛物线y＝x2＋bx－3与x轴相交于A、B两点，与y轴相交于点C，并且OA = OC．（1）求这条抛物线的解析式；（2）过点C作CE// x轴，交抛物线于点E，设抛物线的顶点为点D，试判断△CDE 的形状，并说明理由；（3）设点M在抛物线的对称轴l上，且△MCD的面积等于△CDE的面积，请写出点M的坐标（无需写出解题步骤）．图1动感体验请打开几何画板文件名“11闵行24”，拖动点A在x轴的负半轴上运动，可以体验到，△DCE的形状保持DC＝DE，当OA＝OC时，△DCE是等腰直角三角形．拖动点M在抛物线的对称轴上运动，可以体验到，△MCD与△ECD是同底的三角形，当M落在与CD平行的两条直线上时，两个三角形的面积相等，这两个点M关于点D中心对称．请打开超级画板文件名“11闵行24”，思路点拨1．求抛物线的解析式，关键是求点A的坐标，根据已知条件，数形结合．2．判断△CDE的形状是等腰直角三角形，可以方便第（3）求解点M的坐标．满分解答（1）因为抛物线y＝x2＋bx－3与y轴交于点C(0，－3)，OA＝OC，所以点A的坐标为(－3，0)．将A (－3，0)代入y＝x2＋bx－3，解得b＝2．因此抛物线的解析式为y＝x2＋2x－3．（2）由y＝x2＋2x－3＝(x＋1) 2－4，得顶点D的坐标为(－1，－4) ．因为CE // x轴，所以点C与点E关于抛物线的对称轴对称．因此CE＝2，DE＝DC．由两点间的距离公式，求得DC＝2．于是可得DE2＋DC2＝CE2．所以△CDE是等腰直角三角形．（3）M1（－1，－2），M2（－1，－6）．考点伸展第（3）题的解题思路是这样的：如图2，如图3，因为△MCD与△CDE是同底的两个三角形，如果面积相等，那么过点E作CD的平行线，与抛物线的对称轴的交点就是要探求的点M．再根据对称性，另一个符合条件的点M在点D的下方，这两个点M关于点D对称．还有更简单的几何说理方法：因为△CDE是等腰直角三角形，对于点D上方的点M，四边形CDEM是正方形，容易得到点M的坐标为（－1，－2）．再根据对称性，得到另一个点M的坐标为（－1，－6）．图2 图3。

陕西中考数学试题解析版.doc

2011年陕西省中考数学试卷一、选择题（共10小题，每小题3分，计30分．） 1、（2011•陕西）32-的倒数为（） A ． 23-B ．23C ．32D ． 32-考点：倒数。

专题：计算题。

分析：根据倒数的意义，两个数的积为1，则两个数互为倒数，因此求一个数的倒数即用1除以这个数．解答：解：32-的倒数为，1÷23⎛⎫- ⎪⎝⎭=3-2，故选：A ．点评：此题考查的是倒数，关键是由倒数的意义，用1除以这个数即是． 2、（2011•陕西）下面四个几何体中，同一个几何体的主视图和俯视图相同的共有（）A 、1个B 、2个C 、3个D 、4个考点：简单几何体的三视图。

分析：主视图、俯视图是分别从物体正面和上面看，所得到的图形．解答：解：圆柱主视图、俯视图分别是长方形、圆，主视图与俯视图不相同；圆锥主视图、俯视图分别是三角形、有圆心的圆，主视图与俯视图不相同；球主视图、俯视图都是圆，主视图与俯视图相同；正方体主视图、俯视图都是正方形，主视图与俯视图相同．共2个同一个几何体的主视图与俯视图相同．故选B ．点评：本题考查了几何体的三种视图，掌握定义是关键．注意所有的看到的棱都应表现在三视图中． 3、（2011•陕西）我国第六次人口普查显示，全国人口为1370536875人，将这个总人口数（保留三个有效数字）用科学记数法表示为（） A 、1.37×109 B 、1.37×107 C 、1.37×108 D 、1.37×1010 考点：科学记数法与有效数字。

分析：较大的数保留有效数字需要用科学记数法来表示．用科学记数法保留有效数字，要在标准形式a×10n 中a 的部分保留，从左边第一个不为0的数字数起，需要保留几位就数几位，然后根据四舍五入的原理进行取舍．解答：解：1370536875=1.370536875×109≈1.37×109，故选：A ．点评：此题主要考查了科学记数法的表示方法，以及用科学记数法表示的有效数字的确定方法． 4、（2011•陕西）下列四个点，在正比例函数的图象上的点是（）A 、（2，5）B 、（5，2）C 、（2，﹣5）D 、（5，﹣2 考点：一次函数图象上点的坐标特征。

2011年陕西中考真题及答案

2011年陕西省初中毕业学业考试(考试时间：120分钟满分：120分)第Ⅰ卷(共70分)听力部分Ⅰ. 听句子,选答语。

(共5小题,计5分)本题共有5个小题,每个小题你将听到一句话,读两遍,请从所给的三个选项中选出一个最恰当的答语。

( )1. A. I am sorry. B. OK. I will. C. I don't.( )2. A. That's all right! B. You're so kind! C. Have fun!( )3. A. Here it is. B. It's really cool. C. That sounds good.( )4. A. Nice to meet you. B. That's nothing. C. I'm sorry to hear that.( )5. A. Me, too. B. You can't. C. I can't, either.Ⅱ. 听对话,选答案。

(共10小题,计10分)本题共有10个小题,每个小题你将听到一段对话和一个问题,读两遍,请根据每段对话的内容和后面的问题,从所给的三个选项中选出最恰当的一项。

( )6. A. Green. B. Red. C. Blue.( )7. A. On the table. B. On the floor. C. In his bag.( )8. A. She was making a phone call.B. She was doing some washing.C. She was listening to music.( )9. A. For her friend. B. For herself. C. For her father.( )10. A. He is old. B. He takes exercise. C. He is young.( )11. A. This Saturday. B. Next Friday. C. Next Thursday.( )12. A. Basketball team. B. Baseball team. C. Football team.( )13. A. It's expensive. B. It's cheap. C. It's beautiful.( )14. A. It's rainy. B. It's windy. C. It's cloudy.( )15. A. A book. B. A dictionary. C. A computer.Ⅲ. 听短文,选答案。

2011年陕西省中考数学试卷答案及解析菁优网

2011年陕西省中考数学试卷2011年陕西省中考数学试卷一、选择题（共10小题，每小题3分，计30分．每小题只有一个选项是符合题意的）1．（3分）（2011?陕西）的倒数为（）A．B．C．D．2．（3分）（2011?陕西）下面四个几何体中，同一个几何体的主视图和俯视图相同的共有（）A．1个B．2个C．3个D．4个3．（3分）（2011?陕西）我国第六次人口普查显示，全国人口为1370536875人，将这个总人口数（保留三个有效数字）用科学记数法表示为（）A． 1.37×109B． 1.37×107C． 1.37×108D． 1.37×1010 4．（3分）（2011?陕西）下列四个点，在正比例函数的图象上的点是（）A．（2，5）B．（5，2）C．（2，﹣5）D．（5，﹣2）5．（3分）（2011?陕西）在△ABC中，若三边BC，CA，AB满足BC：CA：AB=5：12：13，则cosB=（）A．B．C．D．6．（3分）（2011?陕西）某校男子男球队10名队员的身高（厘米）如下：179，182，170，174，188，172，180，195，185，182，则这组数据的中位数和众数分别是（）A．181，181 B．182，181 C．180，182 D．181，1827．（3分）（2011?陕西）同一平面内的两个圆，他们的半径分别为2和3，圆心距为d，当1＜d＜5时，两圆的位置关系是（）A．外离B．相交C．内切或外切D．内含8．（3分）（2011?陕西）如图，过y轴上任意一点P，作x轴的平行线，分别与反比例函数的图象交于A点和B点，若C为x轴上任意一点，连接AC，BC，则△ABC的面积为（）A． 3 B． 4 C． 5 D． 69．（3分）（2011?陕西）如图，在?ABCD中，E、F分别是AD、CD边上的点，连接BE、AF，他们相交于G，延长BE交CD的延长线于点H，则图中的相似三角形共有（）A．2对B．3对C．4对D．5对10．（3分）（2011?陕西）若二次函数y=x2﹣6x+c的图象过A（﹣1，y1），B（2，y2），C（，y3），则y1，y2，y3的大小关系是（）A．y1＞y2＞y3 B．y1＞y3＞y2 C．y2＞y1＞y3 D．y3＞y1＞y2二、填空题（共6小题，每小题3分，计18分）11．（3分）（2011?陕西）计算：= _________ ．（结果保留根号）12．（3分）（2011?陕西）如图，AC∥BD，AE平分∠BAC交BD于点E，若∠1=64°，则∠2=_________ ．13．（3分）（2011?陕西）分解因式：ab2﹣4ab+4a= _________ ．14．（3分）（2011?陕西）一商场对某款羊毛衫进行换季打折销售，若这款羊毛衫每件原价的8折（即按照原价的80%）销售，售价为120元，则这款羊毛衫的原销售价为_________ ．15．（3分）（2011?陕西）若一次函数y=（2m﹣1）x+3﹣2m的图象经过一、二、四象限，则m的取值范围是_________ ．16．（3分）（2011?陕西）如图，在梯形ABCD中，AD∥BC，对角线AC⊥BD，若AD=3，BC=7，则梯形ABCD面积的最大值_________ ．三、解答题（共9小题，计72分．解答应写出过程）17．（5分）（2011?陕西）解分式方程：．18．（6分）（2011?陕西）在正方形ABCD中，点G是BC上任意一点，连接AG，过B，D两点分别作BE⊥AG，DF⊥AG，垂足分别为E，F两点，求证：△ADF≌△BAE．19．（7分）（2011?陕西）某校有三个年级，各年级的人数分别为七年级600人，八年级540人，九年级565人，学校为了解学生生活习惯是否符合低碳观念，在全校进行了一次问卷调查，若学生生活习惯符合低碳观念，则称其为“低碳族”；否则称其为“非低碳族”，经过统计，将全校的低碳族人数按照年级绘制成如下两幅统计图：（1）根据图①、图②，计算八年级“低碳族”人数，并补全上面两个统计图；（2）小丽依据图①、图②提供的信息通过计算认为，与其他两个年级相比，九年级的“低碳族”人数在本年级全体学生中所占的比例较大，你认为小丽的判断正确吗？说明理由．20．（8分）（2011?陕西）一天，数学课外活动小组的同学们，带着皮尺去测量某河道因挖沙形成的“圆锥形坑”的深度，来评估这些坑道对河道的影响，如图是同学们选择（确保测量过程中无安全隐患）的测量对象，测量方案如下：①先测出沙坑坑沿的圆周长34.54米；②甲同学直立于沙坑坑沿的圆周所在的平面上，经过适当调整自己所处的位置，当他位于B时恰好他的视线经过沙坑坑沿圆周上一点A看到坑底S（甲同学的视线起点C与点A，点S三点共线），经测量：AB=1.2米，BC=1.6米．根据以上测量数据，求圆锥形坑的深度（圆锥的高）．（π取3.14，结果精确到0.1米）21．（8分）（2011?陕西）2011年4月28日，以“天人长安，创意自然一一城市与自然和谐共生”为主题的世界园艺博览会在西安隆重开园，这次园艺会的门票分为个人票和团体票两大类，其中个人票设置有三种：票的种类夜票（A）平日普通票（B）指定日普通票（C）单价（元/张）60 100 150某社区居委会为奖励“和谐家庭”，欲购买个人票100张，其中B种票的张数是A种票张数的3倍还多8张，设购买A种票张数为x，C种票张数为y（1）写出y与x之间的函数关系式；（2）设购票总费用为W元，求出W（元）与X（张）之间的函数关系式；（3）若每种票至少购买1张，其中购买A种票不少于20张，则有几种购票方案？并求出购票总费用最少时，购买A，B，C三种票的张数．22．（8分）（2011?陕西）七年级五班在课外活动时进行乒乓球练习，体育委员根据场地情况，将同学分成3人一组，每组用一个球台，甲乙丙三位同学用“手心，手背”游戏（游戏时，手心向上简称“手心”，手背向上简称“手背”）来决定那两个人首先打球，游戏规则是：每人每次随机伸出一只手，出手心或者手背，若出现“两同一异”（即两手心、一手背或者两手背一手心）的情况，则出手心或手背的两个人先打球，另一人裁判，否则继续进行，直到出现“两同一异”为止．（1）请你列出甲、乙、丙三位同学运用“手心、手背”游戏，出手一次出现的所有等可能的情况（用A表示手心，B表示手背）；（2）求甲、乙、丙三位同学运用“手心、手背”游戏，出手一次出现“两同一异”的概率．23．（8分）（2011?陕西）如图，在△ABC中，∠B=60°，⊙O是△ABC外接圆，过点A作⊙O的切线，交CO的延长线于P点，CP交⊙O于D；（1）求证：AP=AC；（2）若AC=3，求PC的长．24．（10分）（2011?陕西）如图，二次函数的图象经过△AOB的三个顶点，其中A（﹣1，m），B（n，n）（1）求A、B的坐标；（2）在坐标平面上找点C，使以A、O、B、C为顶点的四边形是平行四边形．①这样的点C有几个？②能否将抛物线平移后经过A、C两点？若能，求出平移后经过A、C两点的一条抛物线的解析式；若不能，说明理由．28．（12分）（2011?陕西）如图①，在矩形ABCD中，将矩形折叠，使B落在边AD（含端点）上，落点记为E，这时折痕与边BC或者边CD（含端点）交于F，然后展开铺平，则以B、E、F为顶点的三角形△BEF称为矩形ABCD的“折痕三角形”（1）由“折痕三角形”的定义可知，矩形ABCD的任意一个“折痕△BEF”是一个_________ 三角形（2）如图①、在矩形ABCD中，AB=2，BC=4，当它的“折痕△BEF”的顶点E 位于AD的中点时，画出这个“折痕△BEF”，并求出点F的坐标；（3）如图③，在矩形ABCD中，AB=2，BC=4，该矩形是否存在面积最大的“折痕△BEF”？若存在，说明理由，并求出此时点E的坐标？若不存在，为什么？2011年陕西省中考数学试卷参考答案与试题解析一、选择题（共10小题，每小题3分，计30分．每小题只有一个选项是符合题意的）1．（3分）（2011?陕西）的倒数为（）A．B．C．D．考点：倒数．2867872专题：计算题．分析：根据倒数的意义，两个数的积为1，则两个数互为倒数，因此求一个数的倒数即用1除以这个数．解答：解：的倒数为1÷=﹣．故选：A．点评：此题考查的是倒数，关键是由倒数的意义，用1除以这个数即是．2．（3分）（2011?陕西）下面四个几何体中，同一个几何体的主视图和俯视图相同的共有（）A．1个B．2个C．3个D．4个3．（3分）（2011?陕西）我国第六次人口普查显示，全国人口为1370536875人，将这个总人口数（保留三个有效数字）用科学记数法表示为（）答：故选：A．点评：此题主要考查了科学记数法的表示方法，以及用科学记数法表示的有效数字的确定方法．4．（3分）（2011?陕西）下列四个点，在正比例函数的图象上的点是（）A．（2，5）B．（5，2）C．（2，﹣5）D．（5，﹣2）考点：一次函数图象上点的坐标特征．2867872专题：函数思想．分析：根据函数图象上的点的坐标特征，经过函数的某点一定在函数的图象上，一定满足函数的解析式．根据正比例函数的定义，知是定值．解答：解：由，得=﹣；A、∵=，故本选项错误；B 、∵=，故本选项错误；C、∵=﹣，故本选项错误；D、∵=﹣，故本选项正确；故选D．点评：本题考查了正比例函数图象上点的坐标特征，经过函数的某点一定在函数的图象上．在这条直线上的各点的坐标一定适合这条直线的解析式．5．（3分）（2011?陕西）在△ABC中，若三边BC，CA，AB满足BC：CA：AB=5：12：13，则cosB=（）A．B．C．D．考点：锐角三角函数的定义；勾股定理的逆定理．2867872专题：计算题．分析：根据三角形余弦表达式即可得出结果．解答：解：根据三角函数性质，cosB==，故选C．点评：本题主要考查了锐角三角函数的定义及比例关系，比较简单．6．（3分）（2011?陕西）某校男子男球队10名队员的身高（厘米）如下：179，182，170，174，188，172，180，195，185，182，则这组数据的中位数和众数分别是（）A．181，181 B．182，181 C．180，182 D．181，182考点：众数；中位数．2867872专题：计算题．分析：找中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数，众数是一组数据中出现次数最多的数据，注意众数可以不止一个．解答：解：在这一组数据中182是出现次数最多的，故众数是182；处于这组数据中间位置的数是180、182，那么由中位数的定义可知，这组数据的中位数是181．7．（3分）（2011?陕西）同一平面内的两个圆，他们的半径分别为2和3，圆心距为d，当1＜d＜5时，两圆的位置关系是（）8．（3分）（2011?陕西）如图，过y轴上任意一点P，作x轴的平行线，分别与反比例函数的图象交于A点和B点，若C为x轴上任意一点，连接AC，BC，则△ABC的面积为（）A． 3 B ． 4 C． 5 D． 6考点：反比例函数综合题．2867872专题：计算题．分析：先设P（0，b），由直线AB∥x轴，则A，B两点的纵坐标都为b，而A，B分别在反比例函数的图象上，可得到A点坐标为（﹣，b），B点坐标为（，b），从而求出AB的长，然后根据三角形的面积公式计算即可．解答：解：设P（0，b），∵直线AB∥x轴，∴A，B两点的纵坐标都为b，而点A在反比例函数y=﹣的图象上，∴当y=b，x=﹣，即A点坐标为（﹣，b），又∵点B在反比例函数y=的图象上，∴当y=b，x=，即B点坐标为（，b），∴AB=﹣（﹣）=，∴S△ABC=?AB?OP=?b=3．故选A．点评：本题考查了点在函数图象上，点的横纵坐标满足函数图象的解析式．也考查了与坐标轴平行的直线上的点的坐标特点以及三角形的面积公式．9．（3分）（2011?陕西）如图，在?ABCD中，E、F分别是AD、CD边上的点，连接BE、AF，他们相交于G，延长BE交CD的延长线于点H，则图中的相似三角形共有（）A．2对B．3对C．4对D．5对考点：相似三角形的判定；平行四边形的性质．2867872专题：证明题．分析：根据四边形ABCD是平行四边形，利用相似三角形的判定定理，对各个三角形逐一分析即可．解答：解：∵在?ABCD中，E、F分别是AD、CD边上的点，连接BE、AF，他们相交于G，延长BE交CD的延长线于点H，∴△AGB∽△FGH，△HED∽△HBC，△HED∽△EBA，△AEB∽△HBC，共4对．故选C．点评：此题主要考查相似三角形的判定和平行四边形的性质等知识点的理解和掌握，解答此题的关键是熟练掌握相似三角形的判定定理．10．（3分）（2011?陕西）若二次函数y=x2﹣6x+c的图象过A（﹣1，y1），B（2，y2），C（，y3），则y1，y2，y3的大小关系是（）A．y1＞y2＞y3 B．y1＞y3＞y2 C．y2＞y1＞y3 D．y3＞y1＞y2考点：二次函数图象上点的坐标特征．2867872专题：函数思想．分析：根据二次函数图象上点的坐标特征，将A（﹣1，y1），B（2，y2），C（，y3）分别代入二次函数的解析式y=x2﹣6x+c求得y1，y2，y3，然后比较它们的大小并作出选择．解答：解：根据题意，得y1=1+6+c=7+c，即y1=7+c；y2=4﹣12+c=﹣8+c，即y2=﹣8+c；y3=9+2+6﹣18﹣6+c=﹣7+c，即y3=﹣7+c；∵7＞﹣7＞﹣8，∴7+c＞﹣7+c＞﹣8+c，即y1＞y3＞y2．故选B．点评：本题主要考查了二次函数图象上点的坐标特征（图象上的点都在该函数的图象上）．解答此题时，还利用了不等式的基本性质：在不等式的两边加上同一个数，不等式仍成立．二、填空题（共6小题，每小题3分，计18分）11．（3分）（2011?陕西）计算：=．（结果保留根号）考点：实数的性质．2867872 专题：计算题．分析：本题需先判断出的符号，再求出的结果即可．解答：解：∵﹣2＜0∴=2﹣故答案为：2﹣点本题主要考查了实数的性质，在解题时要能根据绝对值得求法得出结果是本评：题的关键．12．（3分）（2011?陕西）如图，AC∥BD，AE平分∠BAC交BD于点E，若∠1=64°，则∠2=122°．考点：平行线的性质．2867872分析：由AC∥BD，根据两直线平行，同位角相等，即可求得∠B的度数；由邻补角的定义，求得∠BAC的度数；又由AE平分∠BAC交BD于点E，即可求得∠BAE的度数，根据三角形外角的性质即可求得∠2的度数．解答：解：∵AC∥BD，∴∠B=∠1=64°，∴∠BAC=180°﹣∠1=180°﹣64°=116°，∵AE平分∠BAC交BD于点E，∴∠BAE=∠BAC=58°，∴∠2=∠BAE+∠B=64°+58°=122°．故答案为：122°．点评：此题考查了平行线的性质，角平分线的定义，邻补角的定义以及三角形外角的性质．题目难度不大，注意数形结合思想的应用．13．（3分）（2011?陕西）分解因式：ab2﹣4ab+4a= a（b﹣2）2 ．14．（3分）（2011?陕西）一商场对某款羊毛衫进行换季打折销售，若这款羊毛衫每件原价的8折（即按照原价的80%）销售，售价为120元，则这款羊毛衫的原销售价为150元．15．（3分）（2011?陕西）若一次函数y=（2m﹣1）x+3﹣2m的图象经过一、二、四象限，则m的取值范围是m＜．考点：一次函数的性质．2867872专题：计算题；数形结合．分析：根据一次函数的性质进行分析：由图形经过一、二、四象限可知（2m﹣1）＜0，3﹣2m＞0，即可求出m的取值范围解答：解：∵y=（2m﹣1）x+3﹣2m的图象经过一、二、四象限∴2m﹣1＜0，3﹣2m＞0∴解不等式得：m＜，m＜∴m的取值范围是m＜．故答案为：m＜．点评：本题主要考查一次函数的性质、求不等式，关键是确定好一次函数的一次项系数和常数项16．（3分）（2011?陕西）如图，在梯形ABCD中，AD∥BC，对角线AC⊥BD，若AD=3，BC=7，则梯形ABCD面积的最大值25 ．考点：梯形；等腰三角形的性质；平行四边形的判定与性质．2867872 专题：计算题．分析：解法一、平移对角线AC后，会构造出一个直角三角形，这个直角三角形的面积就等于原梯形的面积．该三角形的斜边为3+7=10，此时，它的高越大，面积就越大．解法二、过O作ON⊥AD于N，设ON=h，AO=a，DO=ka，求出△ANO∽△AOD，得出比例式，代入求出h=，根据勾股定理得出a2+（ka）2=32，求出a2=，推出h=，只有当k=1时，即△AOD是等腰三角形时，h有最大值是1.5，同理求出△BOC边BC上的高的最大值式3.5，据梯形的面积公式代入求出即可，解答：解：解法一、过D作DE∥AC交BC延长线于E，∵AD∥BC，DE∥AC，∴四边形ACED是平行四边形，∴AD=CE，∴根据等底等高的三角形面积相等得出△ADC的面积等于△DCE的面积，即梯形ABCD的面积等于△BDE的面积，∵AC⊥BD，DE∥AC，∴∠BDE=90°，BE=3+7=10，∴此时△BDE的边BE边上的高越大，它的面积就越大，即当高是BE时最大，即梯形的最大面积是×10××10=25；解法二、过O作ON⊥AD于N，设ON=h，AO=a，DO=ka，∵∠DAO=∠DAO，∠ANO=∠AOD=90°，∴△ANO∽△AOD，∴=，∴=∴h=，而在Rt△AOD中，由勾股定理得：a2+（ka）2=32，a2=，∴h=，∵k＞0，∴只有当k=1时，即△AOD是等腰三角形时，h有最大值是1.5，同理求出△BOC边BC上的高的最大值式3.5，∴梯形ABCD的面积的最大值是：S=×（3+7）×（1.5+3.5）=25，解故答案为：25．点评：本题主要考查对梯形的性质，等腰三角形的性质等知识点的理解和掌握，求出△AOD的边AD和△BOC的边BC上的最大值是解此题的关键．三、解答题（共9小题，计72分．解答应写出过程）17．（5分）（2011?陕西）解分式方程：．考点：解分式方程．2867872专题：计算题．分析：观察两个分母可知，公分母为x﹣2，去分母，转化为整式方程求解，结果要检验．解答：解：去分母，得4x﹣（x﹣2）=﹣3，去括号，得4x﹣x+2=﹣3，移项，得4x﹣x=﹣2﹣3，合并，得3x=﹣5，化系数为1，得x=﹣，检验：当x=﹣时，x﹣2≠0，∴原方程的解为x=﹣．点评：本题考查了分式方程的解法．（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．（2）解分式方程一定注意要验根．18．（6分）（2011?陕西）在正方形ABCD中，点G是BC上任意一点，连接AG，过B，D两点分别作BE⊥AG，DF⊥AG，垂足分别为E，F两点，求证：△ADF≌△BAE．考点：正方形的性质；全等三角形的判定．2867872 专题：证明题．分析：根据正方形的性质，可以证得DA=AB，再根据同角的余角相等即可证得∠2=∠3，∠1=∠4，根据ASA即可证得两个三角形全等．解答：证明：∵四边形ABCD是正方形，∴DA=AB，∠1+∠2=90°又∵BE⊥AG，DF⊥AG∴∠1+∠3=90°，∠2+∠4=90°∴∠2=∠3，∠1=∠4又∵AD=AB∴△ADF≌△BAE．点评：本题主要考查了正方形的性质以及全等三角形的证明，正确证明∠2=∠3，∠1=∠4是解题的关键．19．（7分）（2011?陕西）某校有三个年级，各年级的人数分别为七年级600人，八年级540人，九年级565人，学校为了解学生生活习惯是否符合低碳观念，在全校进行了一次问卷调查，若学生生活习惯符合低碳观念，则称其为“低碳族”；否则称其为“非低碳族”，经过统计，将全校的低碳族人数按照年级绘制成如下两幅统计图：（1）根据图①、图②，计算八年级“低碳族”人数，并补全上面两个统计图；（2）小丽依据图①、图②提供的信息通过计算认为，与其他两个年级相比，九年级的“低碳族”人数在本年级全体学生中所占的比例较大，你认为小丽的判断正确吗？说明理由．考点：条形统计图；扇形统计图．2867872专题：数形结合．分析：（1）根据七年级的人数与所占的百分比可求出总人数，再乘以八年级对应的百分比可求出人数，九年级对应的百分比可用1减去七八年级的百分比求得，再画图即可解答．（2）分别算出三个年级的“低碳族”人数在本年级全体学生中所占的比例，再比较即可解答．解答：解：（1）由题意可知，全校“低碳族”人数为300÷25%=1200人，∴八年级“低碳族”人数为1200×37%=444人，∴九年级“低碳族”人数占全校“低碳族”人数的百分比=1﹣25%﹣37%=38%．补全的统计图如①②所示．（2）小丽的判断不正确，理由如下：∵七年级“低碳族”人数占该年级人数的百分比=×100%=50%，八年级“低碳族”人数占该年级人数的百分比=×100%≈82.2%，九年级“低碳族”人数占该年级人数的百分比=×100%≈80.7%，∴小丽的判断不正确，八年级的学生中，“低碳族”人数比例较大．点评：本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键；同时还考查了用样本来估计总体．20．（8分）（2011?陕西）一天，数学课外活动小组的同学们，带着皮尺去测量某河道因挖沙形成的“圆锥形坑”的深度，来评估这些坑道对河道的影响，如图是同学们选择（确保测量过程中无安全隐患）的测量对象，测量方案如下：①先测出沙坑坑沿的圆周长34.54米；②甲同学直立于沙坑坑沿的圆周所在的平面上，经过适当调整自己所处的位置，当他位于B时恰好他的视线经过沙坑坑沿圆周上一点A看到坑底S（甲同学的视线起点C与点A，点S三点共线），经测量：AB=1.2米，BC=1.6米．根据以上测量数据，求圆锥形坑的深度（圆锥的高）．（π取3.14，结果精确到0.1米）考点：相似三角形的应用；圆锥的计算．2867872分析：取圆锥底面圆心O，连接OS、OA，OS∥BC可得出△SOA∽△CBA，再由相似三角形的对应边成比例即可解答．解答：解：取圆锥底面圆心O，连接OS、OA，则∠O=∠ABC=90°，OS∥BC，∴∠ACB=∠ASO，∴△SOA∽△CBA，∴=，∴OS=，∵OA=≈5.5米，BC=1.6米，AB=1.2米，∴OS=≈7.3米，∴“圆锥形坑”的深度约为7.3米．故答案为：7.3米．点评：本题考查的是相似三角形在实际生活中的运用，根据题意作出辅助线，构造出相似三角形是解答此题的关键．21．（8分）（2011?陕西）2011年4月28日，以“天人长安，创意自然一一城市与自然和谐共生”为主题的世界园艺博览会在西安隆重开园，这次园艺会的门票分为个人票和团体票两大类，其中个人票设置有三种：票的种类夜票（A）平日普通票（B）指定日普通票（C）单价（元/张）60 100 150某社区居委会为奖励“和谐家庭”，欲购买个人票100张，其中B种票的张数是A种票张数的3倍还多8张，设购买A种票张数为x，C种票张数为y（1）写出y与x之间的函数关系式；（2）设购票总费用为W元，求出W（元）与X（张）之间的函数关系式；（3）若每种票至少购买1张，其中购买A种票不少于20张，则有几种购票方案？并求出购票总费用最少时，购买A，B，C三种票的张数．考点：一次函数的应用；一元一次不等式组的应用．2867872专题：优选方案问题．分析：（1）根据A、B、C三种票的数量关系列出y与x的函数关系式；（2）根据三种票的张数、价格分别算出每种票的费用，再算出总数w，即可求出W（元）与X（张）之间的函数关系式；（3）根据题意求出x的取值范围，根据取值可以确定有三种方案购票，再从函数关系式分析w随x的增大而减小从而求出最值，即购票的费用最少．解答：解：（1）由题意得，B种票数为：3x+8则y=100﹣x﹣3x﹣8化简得，y=﹣4x+92．即y与x之间的函数关系式为：y=﹣4x+92；（2）w=60x+100（3x+8）+150（﹣4x+92）化简得，w=﹣240x+14600即购票总费用W与X（张）之间的函数关系式为：w=﹣240x+14600 （3）由题意得，解得20≤x≤，∵x是正整数，∴x可取20、21、22那么共有3种购票方案．从函数关系式w=﹣240x+1460022．（8分）（2011?陕西）七年级五班在课外活动时进行乒乓球练习，体育委员根据场地情况，将同学分成3人一组，每组用一个球台，甲乙丙三位同学用“手心，手背”游戏（游戏时，手心向上简称“手心”，手背向上简称“手背”）来决定那两个人首先打球，游戏规则是：每人每次随机伸出一只手，出手心或者手背，若出现“两同一异”（即两手心、一手背或者两手背一手心）的情况，则出手心或手背的两个人先打球，另一人裁判，否则继续进行，直到出现“两同一异”为止．（1）请你列出甲、乙、丙三位同学运用“手心、手背”游戏，出手一次出现的所有等可能的情况（用A表示手心，B表示手背）；（2）求甲、乙、丙三位同学运用“手心、手背”游戏，出手一次出现“两同一异”的概率．（2）首先求得出手一次出现“两同一异”的所有情况，然后根据概率公式即可求出该事件的概率．解答：解：（1）画树状图得：∴共有8种等可能的结果：AAA，AAB，ABA，ABB，BAA，BAB，BBA，BBB；（2）∵甲、乙、丙三位同学运用“手心、手背”游戏，出手一次出现“两同一异”的有6种情况，∴出手一次出现“两同一异”的概率为：=．点评：本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．23．（8分）（2011?陕西）如图，在△ABC中，∠B=60°，⊙O是△ABC外接圆，过点A作⊙O的切线，交CO的延长线于P点，CP交⊙O于D；（1）求证：AP=AC；（2）若AC=3，求PC的长．考点：切线的性质；圆周角定理；解直角三角形．2867872 专题：几何综合题．分析：（1）连接OA，可得∠AOC=120°，所以，可得∠P=∠C=30°，即可证明；（2）AC=3，所以，PO=，所以PC=3．解答：（1）证明：连接AO，则AO⊥PA，∠AOC=2∠B=120°，∴∠AOP=60°，∴∠P=30°，又∵OA=OC，∴∠ACP=30°，∴∠P=∠ACP，∴AP=AC．（2）解：在Rt△PAO中，∠P=30°，PA=3，∴AO=，∴PO=2；∵CO=OA=，∴PC=PO+OC=3．点评：本题主要考查了直角三角形、圆周角及切线的性质定理，综合性比较强，熟记定理及性质，才是解答的关键．24．（10分）（2011?陕西）如图，二次函数的图象经过△AOB的三个顶点，其中A（﹣1，m），B（n，n）（1）求A、B的坐标；（2）在坐标平面上找点C，使以A、O、B、C为顶点的四边形是平行四边形．①这样的点C有几个？②能否将抛物线平移后经过A、C两点？若能，求出平移后经过A、C两点的一条抛物线的解析式；若不能，说明理由．考点：二次函数综合题．2867872 专题：代数几何综合题．分析：（1）把A（﹣1，m）代入函数式而解得m的值，同理解得n值，从而得到A，B的坐标；（2）①由题意可知：这样的C点有3个，②能，分别考虑函数图象经过三个点，从而得到函数方程．解答：解：（1）∵y=的图象过点A（﹣1，m）∴即m=1同理：n=解之，得n=0（舍）或n=2∴A（﹣1，1），B（2，2）（2）①由题意可知：这样的C点有3个．如图：当OA是对角线时，C是过O平行于AB的直线，以及过A平行于OB的直线的交点，设直线OB的解析式是y=kx，则2=2k，解得：k=1，设直线AC的解析式是：y=x+c，则﹣1+c=1，解得：c=2，直线的解析式是y=x+2，设直线AB的解析式是：y=mx+n，则，解得：，即直线的解析式是：y=3x+4，设直线OC的解析式是：y=3x，解方程组，解得：，则C的坐标是（﹣3，﹣1）；同理，当AB是对角线时，C的坐标是（1，3）；OB是对角线时，C的坐标是（3，1）．故：C1（﹣3，﹣1），C2（1，3），C3（3，1）．②能当平移后的抛物线经过A、C1两个点时，将B点向左平移3个单位再向下平移1个单位．使点B移到A点，这时A、C1两点的抛物线的解析式为y+1=即y=附：另两条平移后抛物线的解析式分别为：i）经过A、C2两点的抛物线的解析式为ii）设经过A、C3两点的抛物线的解析式为，OC3可看作线段AB向右平移1个单位再向下平移1个单位得到m，则C3（3，1）依题意，得，解得．故经过A、C3两点的抛物线的解析式为．点评：本题考查了二次函数的综合运用，（1）把A（﹣1，m）代入函数式而解得；（2）①由题意可知点C有几个，②分别考虑函数图象经过三个点，从而得到函数方程．也从而确定能．本题有一定难度，在图象上作好辅助线，考虑全面，而不至于漏解．28．（12分）（2011?陕西）如图①，在矩形ABCD中，将矩形折叠，使B落在边AD（含端点）上，落点记为E，这时折痕与边BC或者边CD（含端点）交于F，然后展开铺平，则以B、E、F为顶点的三角形△BEF称为矩形ABCD的“折痕三角形”（1）由“折痕三角形”的定义可知，矩形ABCD的任意一个“折痕△BEF”是一个等腰三角形（2）如图①、在矩形ABCD中，AB=2，BC=4，当它的“折痕△BEF”的顶点E 位于AD的中点时，画出这个“折痕△BEF”，并求出点F的坐标；（3）如图③，在矩形ABCD中，AB=2，BC=4，该矩形是否存在面积最大的“折痕△BEF”？若存在，说明理由，并求出此时点E的坐标？若不存在，为什么？考翻折变换（折叠问题）；勾股定理；矩形的性质；正方形的性质．2867872 点：专数形结合；分类讨论．题：分（1）由图形结合线段垂直平分线的性质即可解答；。

陕西省2011年中考数学真题及答案(纠错版)(word版含扫描答案)

例 2011年上海市虹口区中考模拟第24题如图1，在平面直角坐标系中，抛物线y＝x2＋bx＋c经过点(0，2)和点(3，5)．（1）求该抛物线的表达式并写出顶点坐标；（2）点P为抛物线上一动点，如果直径为4的⊙P与y轴相切，求点P的坐标．图1动感体验请打开几何画板文件名“11虹口24”，拖动点P在抛物线上运动，可以体验到，与y 轴相切的⊙P有两个．请打开超级画板文件名“11虹口24”，思路点拨1．⊙P与y轴相切，圆心P到y轴的距离等于圆的半径，y轴两侧各有一个点P．满分解答（1）因为抛物线y＝x2＋bx＋c经过点(0，2)和点(3，5)，所以2,93 5.cb c=⎧⎨++=⎩解得2,2.bc=-⎧⎨=⎩因此抛物线的表达式为y＝x2－2x＋2．顶点坐标为（1，1）．（2）如果⊙P与y轴相切，那么圆心P到y轴的距离等于圆的半径．已知圆的直径为4，所以圆心P到y轴的距离等于2．因此点P的横坐标为2或－2．如图2，当x＝2时，y＝x2－2x＋2＝2，此时点P的坐标为（2，2）．如图3，当x＝－2时，y＝x2－2x＋2＝10，此时点P的坐标为（－2，10）．图2 图3 图4考点伸展1．如果第（2）题的条件改为“⊙P与坐标轴相切”，那么就要分为“⊙P与y轴相切”和“⊙P与x轴相切”两种情况．因为点P在x轴上方，当⊙P与x轴相切时，y＝2．解方程x2－2x＋2＝2，得x＝0或x＝2．所以点P的坐标为（0，2）（如图4）或（2，2）（如图3）．综合两种情况，与坐标轴相切的⊙P有三个．2．在本题情景下，我们再提出几个问题：如果⊙P在坐标轴上截得的弦所对的弦心距相等，那么点P到x轴和y轴的距离相等，符合条件的圆心P有（1，1）（如图5）和（2，2）（如图3）．如图5中，弦AB所对的圆心角等于120°，那么⊙P在坐标轴上截得的弦所对的圆心角等于120°的⊙P有两个，还有一个如图6，P（－1，5）．如果⊙P在坐标轴上截得的弦所对的圆心角等于90°，那么点P有几个？点P到坐标轴的距离等于2的点有4个，其中一个如图7．图5 图6 图7。

2011年陕西省中考数学真题

2011年陕西省中考数学真题（word 版）及答案第Ⅰ卷（选择题共30分）一、选择题（共10小题，每小题3分，计30分．每小题只有一个选项是符合题意的）1．32-的倒数为【】 A ． 23- B ．23 C ．32 D ． 32-2．下面四个几何体中，同一几何体的主视图和俯视图相同的共有【】A 、1个B 、2个C 、3个D 、4个3．我国第六次人口普查显示，全国人口为人，将这个总人口数（保留三个有效数字）用科学计数法表示为【】 A 、 91037.1⨯B 、71037.1⨯ C 、81037.1⨯ D 、 101037.1⨯4、下列四个点，在正比例函数X Y 52-=的图像上的点是【】 A 、( 2, 5 ) B 、( 5, 2) C 、(2，-5)D 、 ( 5 , -2 )5．在△ABC 中，若三边BC ,CA,AB 满足 BC ：CA ：AB=5：12：13，则cosB= 【】A 、125B 、512 C 、135 D 、13126．某校男子男球队10名队员的身高（厘米）如下：179,182,170,174,188,172,180,195,185,182，则这组数据的中位数和众数分别是【】 A 、181,181 B 、182,181 C 、180,182 D 、181,1827．同一平面内的两个圆，他们的半径分别为2和3 ，圆心距为d,当51 d 时，两圆的位置关系是【】 A 、外离 B 、相交 C 、内切或外切 D 、内含正方体圆锥球圆柱（第二题图）8．如图，过y 轴上任意一点p ，作x 轴的平行线，分别与反比例函数xy x y 24=-=和的图像交于A 点和B 点，若C 为x 轴上任意一点，连接AC,BC 则△ABC 的面积为【】9、如图，在ABCD 中EF 分别是AD 、 CD 边上的点，连接BE 、AF,他们相交于G ，延长BE 交CD 的延长线于点H,则图中的全等三角形有【】 A 、2对 B 、3对 C 、4对 D 、5对10、若二次函数c x x y +-=62的图像过)321,23(),,2(),,1(Y C Y B Y A +-,则321,,y y y 的大小关系是【】 A 、321y y y B 、321y y y C 、312y y y D 、213y y y第Ⅱ卷（非选择题共90分）二、填空题（共6小题，每小题3分，计18分） 11．计算：23-= ．（结果保留根号）12．如图，AC ∥BD,AE 平分∠BAC 交BD 于点E ，若0641=∠ 则=∠1 ．13、分解因式：=+-a ab ab 442．14、一商场对某款羊毛衫进行换季打折销售，若这款羊毛衫每件原价的8折（即按照原价的80％）销售，售价为120元，则这款羊毛衫的原销售价为元15、若一次函数m x m y 23)12(-+-=的图像经过一、二、四象限，则m 的取值范围是．16、如图，在梯形ABCD 中，AD ∥BC ，对角线AC ⊥BD ，若AD=3，BC=7，则梯形ABCD 面积的最大值（第8题图）（第9题图）三、解答题（共9小题，计72分．解答应写出过程） 17．（本题满分5分）解分式方程：xx x -=--2312418．（本题满分6分）在正方形ABCD 中，点G 是BC 上任意一点，连接AG ，过B,D 两点分别作BE ⊥AG ,DF ⊥AG ,垂足分别为E,F 两点，求证：△ADF ≌△BAE 19．（本题满分7分）某校有三个年级，各年级的人数分别为七年级600人，八年级540人，九年级565人，学校为了解学生生活习惯是否符合低碳观念，在全校进行了一次问卷调查，若学生生活习惯符合低碳观念，则称其为“低碳族”；否则称其为“非低碳族”，经过统计，将全校的低碳族人数按照年级绘制成如下两幅统计图：（1）根据图①、图②，计算八年级“低碳族”人数，并补全上面两个统计图；（2）小丽依据图①、图②提供的信息通过计算认为，与其他两个年级相比，九年级的“低碳族”人数在本年级全体学生中所占的比例较大，你认为小丽的判断正确吗？说明理由。

【推荐下载】2011陕西省中考数学试题及答案解析版

[键入文字]
2011 陕西省中考数学试题及答案解析版
一、选择题（共10 小题，每小题3 分，计30 分．每小题只有一个选项是符合题意的）
1、（2011•陕西）的倒数为（）
A、B、
C、D、
考点：倒数。