有限差分法
有限差分法

有限差分法finite difference method用差分代替微分,是有限差分法的基本出发点。
是一种微分方程和积分微分方程数值解的方法。
把连续的定解区域用有限个离散点构成的网格来代替,这些离散点称作网格的节点;把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似;把原方程和定解条件中的微商用差商来近似,积分用积分和来近似,于是原微分方程和定解条件就近似地代之以代数方程组,即有限差分方程组,解此方程组就可以得到原问题在离散点上的近似解。
然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解。
如何根据问题的特点将定解区域作网格剖分;如何把原微分方程离散化为差分方程组以及如何解此代数方程组。
此外为了保证计算过程的可行和计算结果的正确,还需从理论上分析差分方程组的性态,包括解的唯一性、存在性和差分格式的相容性、收敛性和稳定性。
对于一个微分方程建立的各种差分格式,为了有实用意义,一个基本要求是它们能够任意逼近微分方程,这就是相容性要求。
另外,一个差分格式是否有用,最终要看差分方程的精确解能否任意逼近微分方程的解,这就是收敛性的概念。
此外,还有一个重要的概念必须考虑,即差分格式的稳定性。
因为差分格式的计算过程是逐层推进的,在计算第n+1层的近似值时要用到第n层的近似值,直到与初始值有关。
前面各层若有舍入误差,必然影响到后面各层的值,如果误差的影响越来越大,以致差分格式的精确解的面貌完全被掩盖,这种格式是不稳定的,相反如果误差的传播是可以控制的,就认为格式是稳定的。
只有在这种情形,差分格式在实际计算中的近似解才可能任意逼近差分方程的精确解。
最常用的方法是数值微分法,比如用差商代替微商等。
另一方法叫积分插值法,因为在实际问题中得出的微分方程常常反映物理上的某种守恒原理,一般可以通过积分形式来表示。
此外还可以用待定系数法构造一些精度较高的差分格式。
龙格库塔龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法。
有限差分法

两端都要给定边界条件(双程坐标) 。
9
(C) 双曲型方程:适当的边界条件和初始条件,与波动传 播的性质有关 如:一维对流方程
∂u ∂u +c =0 ∂t ∂x u (x ,0) = f (x )
解为 u (x , t ) = f (x − ct ) ,代表一个向右(c > 0 时)或向左 ( c < 0 时)传播的波形。必须在波形传来的一侧提供边界条 件(单程坐标) 。
10
不适定的例子:
utt + u xx = 0 u (x ,0) = u t (x ,0) = 0
拉普拉斯方程+非闭域边界条件,解为 u (x , t ) ≡ 0 。 然而,若定解条件为 u (x ,0) = 0, ut (x ,0) =
u (x , t ) = 1 sin nx ,解为 n
1 sinh nt sin nx n
(
)
n n um+1 = um −
cτ n n um +1 − um −1 2h
(
)
设计算到第 n 步时的累积误差
n ~n εn = 计算值um − 差分法精确解um m
反之
n ~n um = εn + um m
15
则第 n+1 步的计算值
~n ~ n cτ u n − u n ~ ~ um+1 = um − m +1 m −1 2h cτ n cτ n n n = um − um +1 − um −1 + εn − εm +1 − εn −1 m m 2h 2h n = um+1 + εn +1 m
uin +1 − uin −1 uin+1 − uin +1 − uin −1 − uin−1 −α =0 Lh u = τ h2 ατ 2 ⎛ ∂ 2u ⎞ τ 2 ⎛ ∂ 3u ⎞ Ti = Lh u − Lu (x i , t n ) = 2 ⎜ 2 ⎟ + ⎜ 3 ⎟ − L 截断误差 6 ⎜ ∂t ⎟i h ⎜ ∂t ⎟i ⎝ ⎠ ⎝ ⎠
有限差分法

有限差分法有限差分法(Finite Differential Method, FDM )什么是有限差分法 有限差分法是指用泰勒技术展开式将变量的导数写成变量,在不同时间或空间点值的差分形式的方法。
按时间步长和空间步长将时间和空间区域剖分成若干网格,用未知函数在网格结(节)点上的值所构成的差分近似代替所用偏微分方程中出现的各阶导数,从而把表示变量连续变化关系的偏微分方程离散为有限个代数方程,然后解此线性代数方程组,以求出溶质在各网格结(节)点上不同时刻的浓度。
有限差分法的基本步骤(1)剖分渗流区,确定离散点。
将所研究的水动力弥散区域按某种几何形状(如矩形、任意多边形等)剖分成网络系统。
(2)建立水动力弥散问题的差分方程组。
(3)求解差分方程组。
采用各种迭代法,如点逐次超松驰方法(SOR)、线逐次超松驰方法(LSOR)、迭代的交替方向隐式方法(IADI)及强隐式方法(SID)等。
(1) 现在分别对时间(从0时刻到到期日)和股票价格(S max )为可达到的足够高的股票价格)进行分割,即\triangle S=S_{max}/M,\triangle T/N,这样就分别有N+1个时间段和M+1个股票价格,建立如图(所示的坐标方格,将定解区域网格化,坐标方格上的点(i,j )对应时刻和股票价格,用变量f i ,j 表示(i,j )点的期权价格。
2.建立差分格式(1)内含的有限差分方法其步骤可分为以下几步:(1)求前向差分近似:(2) 后向差分格式:(3)将(2),(3)式平均可更加对称地求出的近似,即(4)(2)求用前向差分近似:(5)(3)求(6)(4)将(4),(5),(6)式代入(1)式可得到内含有限差分公式:+ b j f i,j−c j f i,j + 1 = f i + 1,j(7)aj f i,j− 1其中:i=0,1,…,N-1。
j=0,1…,M-1针对看跌期权和看涨期权可分别求出方程的边界条件:看跌期权:看涨期权:(5)利用边界条件和(7)式可以给出M-1个联立方程组:+ b j f N− 1,j + c j f N− 1,j + 1j=1,2…,M-1aj f N− 1,j− 1求解这M-1个联立方程组即可以求出期权价格,但对美式看跌期权时我们必须考虑其提前执行的情况。
有限差分公式

有限差分公式
有限差分是微分方程解的近似值的一种表示方法,通常用数学表达式
f(x+b)-f(x+a)来表示。
如果将有限差分除以b-a,则可以得到差商。
在微分方程数值解的有限差分方法中,特别是处理边界值问题时,有限差分导数的逼近起着关键的作用。
有限差分通常考虑三种形式:正向差分、反向差分和中心差分。
正向差分是f(x+h)-f(x),反向差分是f(x)-f(x-h),中心差分是f(x+h)-f(x-h)。
当h取为1时,正向差分除以h近似于导数。
在数值方法中,有限差分法是一种常用的数值解法,它用差商代替微分方程中的偏导数,从而得到相应的差分方程。
通过解这个差分方程,可以得到微分方程解的近似值。
以上内容仅供参考,如需更多信息,建议查阅数学类书籍或咨询数学专业人士。
工程电磁场数值分析(有限差分法)

进一步的参考书:
胡之光. 电机电磁场的分析与计算. 北京:机械工业出版 社,1989
从有限差分法看数值解的基本思想
离散解(数值解)的概念
方程的离散——化无限维问题为有限维问题 (化微分方程为代数方程组,借助计算机求解)
解的离散——离散点上的数值解
数值法的一般步骤
求解区域的离散(前处理) 方程的离散 代数方程组的求解 离散数据的分析(后处理)
h
2
F0
对所有的节点都建立一个方程,N 个 齐次第二类边界条件 节点有 N 个未知数,建立 N 个方程。
③ 求解线性代数方程组
N个方程联立成为线性代数方程组
[ A][ ] [ F ]
求解得到节点上的电位值。
④ 后处理
计算电场强度E,
Ex 0
1 3
2h
Ey
0
2 4
2h
绘制场图;计算电容、受力、能量分布等。
一些实际需要考虑的问题
精度问题与计算量
媒质交界面条件问题
边界条件处理问题
不规则网格问题
三维问题
有限差分法是最古老、最直观的一种数值方法,直至现
在仍有强大的生命力,在许多学科领域广为应用。在电磁场 领域,目前最受关注的是时域有限差分法(Finite Difference Time-Domain Method, FDTD)和有限体积法(Finite Volume Method, FVM)。
各种数值方法的不同之处
在于离散方程所依据的原
理不同,从而导致方程求
解技术、求解效率、适用 对象等的不
有限差分法(Finite Differential Method,FDM) 是基于差分原理的一种数值计算法。其基本思想是: 将场域离散为许多小网格,用差分代替微分,用差商 代替求导,将求解连续函数 的泊松方程的问题转换 为求解网格节点上 的差分方程组的问题。
有限差分法

第四章有限差分方法4.1引言有限差分法:数值求解常微分方程或偏微分方程的方法。
物理学和其他学科领域的许多问题在被分析研究之后, 往往可以归结为常微分方程或偏微分方程的求解问题。
一般说来,处理一个特定的物理问题,除了需要知道它满足的数学方程外,还应当同时知道这个问题的定解条件,然后才能设计出行之有效的计算方法来求解。
有限差分法以变量离散取值后对应的函数值来近似微分方程中独立变量的连续取值。
在有限差分方法中,我们放弃了微分方程中独立变量可以取连续值的特征,而关注独立变量离散取值后对应的函数值。
但是从原则上说,这种方法仍然可以达到任意满意的计算精度。
因为方程的连续数值解可以通过减小独立变量离散取值的间格,或者通过离散点上的函数值插值计算来近似得到。
这种方法是随着计算机的诞生和应用而发展起来的。
其计算格式和程序的设计都比较直观和简单,因而,它的实际应用已经构成了计算数学和计算物理的重要组成部分。
有限差分法的具体操作分为两个部分:(1)用差分代替微分方程中的微分,将连续变化的变量离散化,从而得到差分方程组的数学形式; (2)求解差分方程组。
在第一步中,我们通过所谓的网络分割法,将函数定义域分成大量相邻而不重合的子区域。
通常采用的是规则的分割方式。
这样可以便于计算机自动实现和减少计算的复杂性。
网络线划分的交点称为节点。
若与某个节点P 相邻的节点都是定义在场域内的节点,则P 点称为正则节点;反之,若节点P 有处在定义域外的相邻节点,则P 点称为非正则节点。
在第二步中,数值求解的关键就是要应用适当的计算方法,求得特定问题在所有这些节点上的离散近似值。
有限差分法的差分格式:一个函数在x 点上的一阶和二阶微商,可以近似地用它所临近的两点上的函数值的差分来表示。
如对一个单变量函数f(x),x 为定义在区间[a,b]的连续变量。
以步长h=Δx 将[a,b]区间离散化,我们得到一系列节点x = a , x = x + h , x = x + h = a + 212132Δx , ..., x = x + h = b , 然后求出 f(x)在这些点上的近似值。
有限差分法

对所学有限差分法的总结和其一些应用07410301班邓齐波20032471一:有限差分方法的总结有限差分方法(FDM)是计算机数值模拟最早采用的方法,至今仍被广泛运用。
该方法将求解域划分为差分网格,用有限个网格节点代替连续的求解域。
有限差分法以Taylor级数展开等方法,把控制方程中的导数用网各界点上的函数值的差商代替进行离散,从而建立以网格节点上的值为未知数的代数方程组。
该方法是一种直接将微分问题变为代数问题的近似数值解法,数学概念直观,表达简单,是发展较早且比较成熟的数值方法。
分类对于有限差分格式,从格式的精度来划分,有一阶格式、二阶格式和高阶格式。
从差分的空间形式来考虑,可分为中心格式和逆风格式。
考虑时间因子的影响,差分格式还可以分为显格式、隐格式、显隐交替格式等。
目前常见的差分格式,主要是上述几种形式的组合,不同的组合构成不同的差分格式。
差分方法主要适用于有结构网格,网格的步长一般根据实际地形的情况和柯朗稳定条件来决定。
构造差分的方法构造差分的方法有多种形式,目前主要采用的是泰勒级数展开方法。
其基本的差分表达式主要有三种形式:一阶向前差分、一阶向后差分、一阶中心差分和二阶中心差分等,其中前两种格式为一阶计算精度,后两种格式为二阶计算精度。
通过对时间和空间这几种不同差分格式的组合,可以组合成不同的差分计算格式。
在所学课程‘力学计算’中《偏微分方程数值解》,我们主要学习了一维抛物型方程、二维和三维抛物型方程、一维双曲型方程以及二维线形二阶椭圆型方程。
流体力学有限差分法与结构力学有限元法区别对于有限差分格式,从格式的精度来划分,有一阶格式、二阶格式和高阶格式。
从差分的空间形式来考虑,可分为中心格式和逆风格式。
考虑时间因子的影响,差分格式还可以分为显格式、隐格式、显隐交替格式等。
目前常见的差分格式,主要是上述几种形式的组合,不同的组合构成不同的差分格式。
差分方法主要适用于有结构网格,网格的步长一般根据实际地形的情况和柯朗稳定条件来决定。
第4章 有限差分法

可见, 对应于式(4-2)和式(4-3), 它们 都截断于 hf′(x0)项, 而把 h2项和更高幂次的 项全部略去。 换句话说, 就式(4-2)、 式 (4-3)而言, 略去余数项所引入的误差将 大致和 h 的一次方成正比。
第 4 章
有 限 差 分 法
而对于式(4-4)的一阶中心差商表达式则相当于把相应的泰勒公式
第 4 章
有 限 差 分 法
应用二元函数的泰勒公式,节点 1 的位函数值 u1 可通过 u0 表示为
同理
以 h 和 h1 分别与以上两式相乘,且相加,然后截断于 h 的二次项,便得关 于 的差分表达式为
同理可得
第 4 章
有 限 差 分 法
令 h1 =αh, h2 =βh,代入以上两式,最终再代入给定的泊松方程,即得这类 边界情况所对应的差分计算格式为
第 4 章
有 限 差 分 法
(2) 第三类边界条件的差分离散化 对此,同样需分两种情况讨论。第一种情况是在边界处引入的相应节 点恰好落在边界 L上。 这时,取决于边界 L 在该边界节点处的外法线方向 是否与网格线相重合, 对应有不同的差分离散化结果。 当边界 L 在边界节点 o 处的外法向 n 与网格线相重合时,如图 4-4 所 示,则问题在于如何用差商近似替代法向导数 。 显然, 最简洁的处
3)由所建立的差分格式(即与原定解问题对应的离散数学模型——代数方程 组),选用合适的代数方程组的解法,编制计算程序,算出待求的离散解。
有限差分法有上述大致固定的处理和计算模式,具有一定的通用性。
第 4 章
有 限 差 分 法
4.2 差分与差商
有限差分法是以差分原理为基础的一种数值计算法。它用离散的函数值 所构成的差商来近似逼近相应的偏导数, 而所谓差商则是基于差分应用的数 值微分表达式。 设一函数 f(x), 其自变量 x 得到一个很小的增量Δx = h, 则 函数 f(x)的增量 称为函数 f(x)的一阶差分。显然,只要增量 h 很小, 差分Δf与微分 df之间 的差异将很小 。 一阶差分仍是自变量 x 的函数,相类似地按式(4-1)计算一阶差分的差 分, 就得到Δ2f(x),称之为原始函数 f(x)的二阶差分。 同样, 当 h 很小时, 二阶差分Δ2f(x)逼近于二阶微分d2f。依同理,可以定义更高阶的差分。
有限差分法

1.6.1 差分格式
上页
下页
返回
结束
如图,以二维场为例,在一由边界区域L界定的二维区域 界定的二维区域D 如图 , 以二维场为例 , 在一由边界区域 界定的二维区域 电位函数φ满足拉普拉斯方程且给定为第一类边界条件: 内,电位函数φ满足拉普拉斯方程且给定为第一类边界条件
∂ 2ϕ ∂ 2ϕ ∇ 2ϕ = + 2 ∂x ∂y 2
启动 赋边界节点已知电位值 赋予场域内各节点电位初始值 累计迭代次数 N=0 N=N+1 按超松弛法进行一 次迭代,求 ϕi(,N+1) j
上页
下页
返回
结束
Y N
所有内点 相邻二次迭代值的最大误差 是否小于 W 打印 N,ϕ(i, j ) 迭代解程序框图 停机
上页
下页
返回
结束
例 一长直接地金属槽截面如图。其侧壁与底面的电位均为零, 而顶盖电位ϕ4=100。求槽内电位分布。 解: •二维场第一类边值问题。 •将二维场域划分成正方形 网格,步距h=a/4。 •场域内任一点电位ϕ应满 足二维拉普拉斯方程的差 分计算格式。
α
4
k+ k) [ϕ i(− 1,1j ) + ϕ i(,kj+ 1 ) + ϕ i(+ 1, j + ϕ i(,kj )+ 1 − 4ϕ i(,kj ) ] −1
迭代收敛的速度与 α 有明显关系: 有明显关系: 迭代收敛的速度与 收敛的速度
收敛因子(α ) 迭代次数( N) 1.0 >1000 1.7 269 1.8 1.83 1.85 1.87 1.9 174 143 122 133 171 2.0 发散
上页
下页
有限差分法

有 限 差 分 法流体运动的控制方程多为偏微分方程,在复杂的情况下不存在解析解。
但是对于一些简单的情况存在解析解,偏微分方程的解析解可用精确的数学表达式表示,该表达式给出了因变量在整个定义域中的连续变化状况。
有限差分法(Finite Difference Method ,FDM )是数值计算中比较经典的方法,由于其计算格式直观且计算简便,因此被广泛地应用在计算流体力学中。
有限差分法首先将求解区域划分为差分网格,变量信息存储在网格节点上,然后将偏微分方程的导数用差商代替,代入微分方程的边界条件,推导出关于网格节点变量的代数方程组,通过求解代数方程组,获得偏微分方程的近似解。
偏微分方程被包含离散点未知量的代数方程所替代,这个代数方程能求出离散节点处的变量,这种离散方法叫做有限差分法。
2.1有 限 差 分 逼 近2.1.1 有限差分网格 由于有限差分法求解的是网格节点上的未知量值,因此首先介绍有限差分网格。
图2.1 – 1是x-y 平面上的矩形差分网格示意图。
在x 轴方向的网格间距为△x ,在y 轴方向的网格间距为△y ,网格的交点称为节点,计算变量定义在网格节点上。
称△x 和△y 为空间步长,△x 一般不等于△y ,且△x 和△y 也可以不为常数。
取各方向等距离的网格,可以大大简化数学模型推导过程,并且经常会取得更加精确的数值解。
本章作为计算流体力学入门知识,假设沿坐标轴的各个方向网格间距分别相等,但是并不要求各方向的网格间距一致。
例如假设△x 和△y 是定值,但是不要求△x 等于△y 。
在图2.1 - 1中,网格节点在x 方向用i 表示,在y 方向用j 表示。
因此,假如(i ,j )是点P 在图2.1 – 1中的坐标,那么,点P 右边的第一个点的就可以用(i+1,j )表示;在P 左边的第一个点的就可以用(i —1,j )表示;点P 上边的第一个点的就可以用(i ,j+1)表示;点P 下边的第一个点的就可以用(i ,j —1)表示。
有限差分法
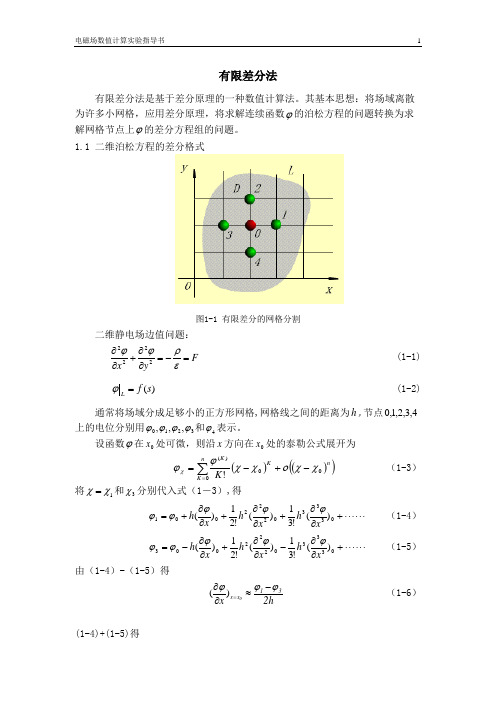
有限差分法有限差分法是基于差分原理的一种数值计算法。
其基本思想:将场域离散为许多小网格,应用差分原理,将求解连续函数ϕ的泊松方程的问题转换为求解网格节点上ϕ的差分方程组的问题。
1.1 二维泊松方程的差分格式图1-1 有限差分的网格分割二维静电场边值问题:F yx =-=∂∂+∂∂ερϕϕ2222 (1-1) )(s f L =ϕ (1-2)通常将场域分成足够小的正方形网格,网格线之间的距离为h ,节点4,3,2,1,0上的电位分别用3210,,,ϕϕϕϕ和4ϕ表示。
设函数ϕ在0x 处可微,则沿x 方向在0x 处的泰勒公式展开为()()()∑=-+-=nK n K K K 000)(!χχοχχϕϕχ (1-3)将1χχ=和3χ分别代入式(1-3),得⋅⋅⋅⋅⋅⋅+∂∂+∂∂+∂∂+=03330222001)(!31)(!21)(x h x h x h ϕϕϕϕϕ (1-4)⋅⋅⋅⋅⋅⋅+∂∂-∂∂+∂∂-=03330222003)(!31)(!21)(xh x h x h ϕϕϕϕϕ (1-5)由(1-4)-(1-5)得h2x 31x x 0ϕϕϕ-≈∂∂=)((1-6)(1-4)+(1-5)得2301x x 22h2x 0ϕϕϕϕ+-≈∂∂=)( (1-7) 同理hy y y 2)(310ϕϕϕ-≈∂∂= (1-8) 2301222)(0hy y y ϕϕϕϕ+-≈∂∂= (1-9) 将式(1-7)、(1-9)代入式(1-1),得到泊松方程的五点差分格式)(414243210204321Fh Fh -+++=⇒=-+++ϕϕϕϕϕϕϕϕϕϕ当场域中,0=ρ得到拉普拉斯方程的五点差分格式)(41044321004321ϕϕϕϕϕϕϕϕϕϕ+++=⇒=-+++1.2 边界条件的离散化处理图1-2 边界条件的离散化处理若场域离散为矩形网格(如图2-2示),差分格式为:F 2h 1h 1h 1h 10222142222121=+-+++ϕϕϕϕϕ)()()( (1-10) (1)第一类边界条件:给边界离散节点直接赋已知电位值 (2)对称边界条件:合理减小计算场域,差分格式为:)(F h 24124210-++=ϕϕϕϕ (1-11)图1-3 边界条件的离散化处理•12(3)第二类边界条件:边界线与网格线相重合的差分格式:h f f hn 2102010-ϕ=ϕ=ϕ-ϕ≈∂ϕ∂,)((1-12)(4)介质分界面衔接条件 的差分格式)1212(4143210ϕϕϕϕϕ+++++=KKK (1-13)其中b a K εε=1.3 差分方程组的求解方法(1) 高斯——赛德尔迭代法][)(,)(,)(,)(,)(,2k 1j i k j 1i 1k 1j i 1k j 1i 1k j i Fh 41-+++=+++-+-+ϕϕϕϕϕ (1-14)式中:⋅⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅=,2,1,0,2,1,k j i ,• 迭代顺序可按先行后列,或先列后行进行。
2 有限差分法

o
一阶偏导数的差分格式(P.23)
(
h1 h3 hx
二阶精度,O(h3)
3 ) 0 1 3 O (hx ) x 2hx
二阶偏导数的差分格式(P.23-23) 20 3 2 2 ( 2 )0 1 O ( h x) 2 x hx 20 4 2 2 ( 2 )0 2 O ( h ) y 2 y hy
2) df ( x ) 1 2 d 2 f ( x ) 一阶精度 ,O(h f ( x h) f ( x ) h h 2 dx 2! dx
df ( x) 2 3 d 3 f ( x) 二阶精度,O(h3) h f ( x h) f ( x h ) 2h dx 3! dx 3
由误差的泰勒展开式,如果: (7)
则称为K阶方法。
若迭代公式中ψ(x,y,h)在定义域内连续,并且关于y 满足利普希茨(Lipschitz)条件:
| ( x, y, h) ( x, z , h) | L | y z |
(8)
若截断误差满足式(7),则单步法迭代公式的误差估计式为:
同介质分界面上的差分格式)
第三步,编程计算,迭代运算或者求解方程组
二、泊松方程的有限差分格式 泊松方程:
f
2
2 2 2 f 2 x y
(1)
第一类边界条件:已知整个边界上的位函数,
|C g ( p )
n g ( p)
C
又叫Dirichlet(狄里赫利)问题。
一、有限差分法基本概念
二阶差分
2 f ( x) 1 f ( x h) f ( x) x 2 x x
(前向差分)
有限差分法

有限差分法一、有限差分法的定义有限差分法(Finite Differential Method )是基于差分原理的一种数值计算法。
其基本思想:将场域离散为许多小网格,应用差分原理,将求解连续函数ϕ的泊松方程的问题转换为求解网格节点上ϕ的差分方程组的问题。
二、有限差分法的应用例3.7.1 有一个无限长直的金属槽,截面为正方形,两侧为正方形,两侧面及底板接地,上盖板与侧面绝缘,其上的电位为ϕ=100V, 试用有限差分法计算槽内电位。
(1)用Matlab 中的有限差分法计算槽内电位;(2)对比解析法和数值法的异同点;(3)选取一点,绘制收敛曲线;(4)总的三维电位图;1、根据有限差分公式计算出电位最终近似值为1,12,13,11,22,23,21,32,33,3=7.144=9.823=7.144=18.751=25.002=18.751=42.857=52.680=42.857ϕϕϕϕϕϕϕϕϕ,,,,,,用Matlab有限差分法计算出来结果:(见附录程序一)2、解析法和数值法的异同点解析法数值法定义在分析具体问题的基础上,抽取出一个数学模型,这个数学模型能用若干个解析表达式表示出来,解决了这些表达式,问题也就得以解决。
数值法是用高性能的计算机以数值的、程序的形式解决问题,主要是指有限元法和差分法相同点都是在具体问题的基础上取一个用解析表达式表示的数学模型来解决问题;数值法是在解析法的基础上在不同尺度上进行有限元离散,离散单元尺度不同,进行有限元计算时要满足的连续性条件不同,预测结果的精确度就不同不同点解析法可以计算出精确的数值结果;可以作为近似解和数值解的检验标准;解析法过程可以观察到问题的内在和各个参数对数值结果起的作用。
但是分析过程困难又复杂使其仅能解决很少量的问题。
数值法求解过程简单,普遍性强,用户拥有的弹性大;用户不必具备高度专业化的理论知识就可以用提供的程序解决问题。
但求解结果没有解析法精确。
岩石力学-有限差分法

平衡方程 (运动方程)
新的速度和 位移
应力-应变关系 (本构方程)
新的应力或 力
显式有限差分法计算流程图
显式算法的核心概念是计算“波速”总 是超前于实际波速。
用运动方程求解静力问题,还必须采取 机械衰减方法来获得非惯性静态或准静态解, 通常采用动力松弛分法是求解给定初值和(或)边值问题 的较早数值方法之一。
有限差分法和有限元法都产生一组待解方程组。 1、有限差分基本方程 2、平面问题有限差分方程 3、显式有限差分算法-时间递步法
可以保证在被模拟的物理系统本身是非稳定的 情况下,有限差分数值计算仍有稳定解。对于非线 性材料,物理不稳定的可能性总是存在的。
有限差分方法

n
Δt
(2-2)
空间导数用一阶中心差商近似代替,即
ζ in+1 − ζ in−1 ⎛ ∂ζ ⎞ ⎜ ⎟ ≈ 2Δx ⎝ ∂x ⎠ i
则在 ( xi , t n ) 点的对流方程就可近似地写作
(2-3)
ζ in +1 − ζ in
Δt
+α
ζ in+1 − ζ in−1
2Δx
(1-11)
当然,在某些情况下也可取向前或向后的二阶差商。
9
第一节 差分原理及逼近误差/差分原理 以上是一元函数的差分与差商。多元函数f(x,y,…)的差分与 差商也可以类推。 如一阶向前差商为
Δf f ( x + Δx , y , Λ ) − f ( x , y , Λ ) = , Δx Δx
Δf f ( x, y + Δy , Λ ) − f ( x, y , Λ ) = , Δy Δy ΛΛ
(1-6)
6
第一节 差分原理及逼近误差/差分原理 函数的差分与自变量的差分之比,即为函数对自变量的 差商。 一阶向前差商为 一阶向后差商为
f ( x + Δx) − f ( x) Δy = Δx Δx
(1-7)
f ( x ) − f ( x − Δx ) Δy = Δx Δx
(1-8)
7
第一节 差分原理及逼近误差/差分原理 一阶中心差商为
15
第一节 差分原理及逼近误差/非均匀步长
图1-2 均匀和非均匀网格实例1
16
第一节 差分原理及逼近误差/非均匀步长
图1-3 均匀和非均匀网格实例2
17
第二节 差分方程 差分相应于微分,差商相应于导数。差分和差商是用有限形 式表示的,而微分和导数则是以极限形式表示的。如果将微 分方程中的导数用相应的差商近似代替,就可得到有限形式 的差分方程。现以对流方程为例,列出对应的差分方程。
有限差分法

y2 (k 2 a 2 2) y1 0 (k 2 a 2 2) y2 2 y1 0
在分点2
y3 (k 2 a 2 2) y2 y1 0
且y3=y1
由上两式得到构件的屈曲条件为
1 (k 2 a 2 2) 0 2 2 (k a 2) 2源自得 k 2a2 0.586
a
y 0 1
(a) 2 3 4
a
a
(b)
a
a
且y0=y2 =0
2P
ymax Ma 2 y1 2 2 EI (2 k a ) Ml 2 Pl 2 8EI (1 ) 8EI 8PE M 2P P 1 8PE
2P
理论值
ymax
8 PE M P 1 P 8 PE
yi 2 4 yi 1 6 yi 4 yi 1 yi 2 a4 可见曲线上任一点函数的导数是由高阶导数转化为低阶导数,直至最终形 成函数值的表达式。差分是也可用插值数y=a1x2+b1x+c1导出。如果采用更 高阶次的插值函数,可以得到更精确的差分式。 y '''i y IV i
2)第二次近似将构件分为4段,a=l/4
2 2 2 在分点1, y2 (k a 2) y1 y0 Ma / EI 0 且y0=0
y2 (k 2 a 2 2) y1 Ma 2 / EI 0 2 2 2 在分点2, y3 (k a 2) y2 y1 Ma / EI 0 且y3=y1 =0 y1 (k 2 a 2 2) y2 / 2 Ma 2 / EI
Pcr 16 0.586 EI / l 2 9.376 EI / l 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章 有限差分法2.1 引言所有的守恒方程都具有相似的结构,而且都可以看作是输运方程的特殊形式。
本章以一般输运方程在Cartesian 坐标系下的表达式为例来讲述有限差分法。
()φφφρq xx x u j jjj +⎪⎪⎭⎫⎝⎛∂∂Γ∂∂=∂∂ (2.1)在上述方程中,除外都认为是已知函数。
2.2 基本概念FD 方法的第一步是离散几何的求解域,也就是说定义数值网格。
在FD 中,网格是局部结构化的,每个网格节点都可以看作是局部坐标系的原点,网格线则是局部坐标系的坐标线。
同族的网格线两两互不相交。
每一个网格节点都可用一组指标唯一的标定。
差分形式的标量守恒方程(2.1)是FD 法的原始方程。
并被近似为以网格节点上的守恒量为未知数的代数方程系统。
代数方程组的解近似为原微分方程的解。
每一个带有未知数的节点都必须有一个代数方程,在节点以及相邻节点上的未知数之间建立联系。
这个代数方程用在接点处用有限差分近似代替偏导数的形式获得。
对于Dirichlet 边界条件,边界上不需要代数方程,,对于其他边界条件,则必须将边界条件离散以得到所需的代数方程。
有限差分的概念是从导数的定义中得到的:x x x x x i i x x i∆-∆+=⎪⎭⎫⎝⎛∂∂→∆)()(lim 0φφφ (2.2)几种常用的差分格式:向前差分(forward difference )ii ii x x x --≈∂∂++11φφφ (2.3)向后差分(backward difference )11----≈∂∂i i i i x x x φφφ (2.4)中心差分(central difference )1111-+-+--≈∂∂i i i i x x x φφφ (2.5)2.3 一阶导数的近似(2.1) 式中的对流项()xu ∂∂φρ需要对一阶导数进行离散。
2.3.1 Taylor 级数展开法任意的连续函数(x)可在x i 的领域内展开成Taylor 级数()()()()()H x n x x x x x x x x x x x x x in nni ii i i ii i +⎪⎪⎭⎫ ⎝⎛∂∂-++⎪⎪⎭⎫ ⎝⎛∂∂-+⎪⎪⎭⎫⎝⎛∂∂-+⎪⎭⎫ ⎝⎛∂∂-+=φφφφφφ!...!32)(333222(2.6)H 为高阶项,用x i -1,x i +1代替x 这些点处的函数值在x i 附近的展开式。
利用这些展开式可得一阶和高阶导数在x i 的近似表达式。
例如()()H x x x x x x x x x i i i i ii i i i +⎪⎪⎭⎫⎝⎛∂∂--⎪⎪⎭⎫ ⎝⎛∂∂----=⎪⎭⎫ ⎝⎛∂∂++++333122211162φφφφφ (2.7)或者是:()()H x x x x x x x x x i i i i i i i i i +⎪⎪⎭⎫ ⎝⎛∂∂--⎪⎪⎭⎫ ⎝⎛∂∂----=⎪⎭⎫ ⎝⎛∂∂----333122211162φφφφφ (2.8)()()()()()()H x x x x x x x x x x x x x x x x x i i i i i i i i i i i i i i i i i +⎪⎪⎭⎫ ⎝⎛∂∂--+--⎪⎪⎭⎫⎝⎛∂∂-------=⎪⎭⎫ ⎝⎛∂∂-+-+-+-+-+-+3311313122112121111162φφφφφ (2.9)当网格间距较小时,高阶项很小,在各级数中截取第一项,得:i-2 i-1 i i+1 i+2中心差分 CDS向前差分 FDS向后差分 BDS精确解i i i i i x x x --≈⎪⎭⎫ ⎝⎛∂∂++11φφφ (2.10)11----≈⎪⎭⎫⎝⎛∂∂i i i ii x x x φφφ (2.11)1111-+-+--≈⎪⎭⎫⎝⎛∂∂i i i i i x x x φφφ (2.12)上面三个公式依次是FDS (forward difference scheme ),BDS (backward difference scheme ),CDS (central difference scheme )被截去的项称为截断误差。
FDS 和BDS 为一阶精度差分格式,当网格均匀时,CDS 具有二阶精度。
2.3.2 多项式拟合法在构造差分格式时,也可以用多项式曲线(或样条曲线)来拟合函数,然后用拟合曲线的导数来近似原函数的导数。
例如采用抛物线拟合x i-1,x i ,x i+1三点,可得:()()()()[])(1122121121++++-+∆+∆∆∆∆-∆+∆+∆=⎪⎭⎫ ⎝⎛∂∂i i i i i i i i i i i i x x x x x x x x x φφφφ (2.13)采用不同的插值曲线可获得不同的差分格式,如()()32116632x O x x i i i i i∆+∆+-+=⎪⎭⎫ ⎝⎛∂∂--+φφφφφ (2.14)()()32116632x O x x i i i i i∆+∆-+--=⎪⎭⎫ ⎝⎛∂∂+++φφφφφ (2.15)()()421121288x O x x i i i i i∆+∆+-+-=⎪⎭⎫ ⎝⎛∂∂--++φφφφφ (2.16)(2.14)~(2.16)依次为三阶精度的BDS ,FDS 和4阶精度的CDS2.3.3 迎风格式对于发展方程:()⎪⎪⎩⎪⎪⎨⎧≥=≥=>≤≤=∂∂+∂∂0)(),0(0)()0,(0,100t t t u x x f x u a x x u a t uψ(2.17)方程的解为:()()⎪⎩⎪⎨⎧≤--≥--=0)(0,at x a xt at x at x f t x u ψ(2.17)当x-at=常数时,u 为常数,利用这一特性可得A n ju u =+1 (2.18)利用线性插值:()n j n j j j j A nj A u ux x x x uu 1111-------+=(2.19)由此可得差分格式:()n j nj j j j A nj n j u ux x x x u u 11111----+---+=(2.20)由于t a x x A j ∆=-,1--=∆j j x x x()()n j n j nj n j n j n j n j u u xt a u u u x t a x u u 1111---+-∆∆-=-∆∆-∆+=(2.21)整理得:()011=∆-+∆--+xu ua tu u n j n j n jn j (2.22)当a<0时,同理可得:()011=∆-+∆-++xu u at u u n jnj n jn j (2.23)结合(2.22)和(2.23)可得:()()022111=∆--+∆-++∆-+-+xu ua a xu u a a tu u n jnj nj n j njn j (2.24)j-1 j j+1n+1nA(j,n+1)(2.24)式中,a 相当于流体力学动量方程中的速度u ,差分格式(2.24)反映了上游对下游影响较大这一事实,这种差分格式称为迎风格式(upwind scheme)2.4 二阶导数的近似方程(2.1)中的扩散项⎪⎭⎫⎝⎛∂∂Γ∂∂x x φ为二阶导数项,二阶导数可以用一阶导数的差分得到,也可以用Taylor 级数法得到二阶导数的差分。
采用Taylor 级数法可得二阶导数的差分()()()()()()()()H x x x x x x x x x x x x x x x x x x ii i i i i i i i i i i i i i i i i i i i+⎪⎪⎭⎫⎝⎛∂∂----------+-=⎪⎪⎭⎫ ⎝⎛∂∂-+-+-+-++--+33111111*********2/φφφφφ (2.25)也可以用一阶偏导数的差分得到:2/)(2/)(11112/1112/1112/12/1-+---+++-+-+---Γ---Γ≈-⎪⎭⎫ ⎝⎛∂∂Γ-⎪⎭⎫ ⎝⎛∂∂Γ≈⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂Γ∂∂i i i i i ii i i i i i i i i i ix x x x x x x x x x x x φφφφφφφ(2.26)2.5 混合导数的近似混合偏导数的差分可以用一阶导数的差分得到⎪⎪⎭⎫⎝⎛∂∂∂∂=∂∂∂y x y x φφ2 (2.27)2.6 边界条件在网格的内点,用差分格式来离散PDE ,为了得到唯一的解,还需要在边界点上给出边界信息。
对于Dirichlet 边界条件,边界上的值直接给出,无需用新的方程。
对于Neumann 边界条件和混合边界条件,则需在边界上对边界条件进行离散。
对于邻近边界的内点,当采用高阶精度格式时,其差分格式也应作特殊处理。
()()4123452603310186x O x x ∆+∆-+++-=⎪⎭⎫ ⎝⎛∂∂φφφφφφ (2.28)()()31234522260147240189621x O x x ∆+∆+-++-=⎪⎪⎭⎫ ⎝⎛∂∂φφφφφφ (2.29)在边界上0012121=--⇒=⎪⎭⎫⎝⎛∂∂x x x φφφ (2.30)采用高阶差分格式()()()()[]()()()2313122122131213221231x x x x x x x x x x x x x x x --------+--≈⎪⎭⎫⎝⎛∂∂φφφφ (2.31)如果网格是均匀的,(2.31)简化为:x x ∆-+-≈⎪⎭⎫⎝⎛∂∂2341231φφφφ (2.32)2.7 有限差分法的应用实例例1.一维扩散方程()()()()()⎪⎪⎩⎪⎪⎨⎧===≥≤≤Γ=t B t l t A t x f x t l x xxt ,,0)0,(0,0φφφφφ(2.33)采用均匀网格,将直线段均匀划分为N 份,网格节点l Ni x i 1-=,1,....,2,1,0+=N i ,网格间距N l x /=∆,时间步长为t ∆。
空间扩散项采用中心差分格式:()2112x i i i xx ∆+-Γ=Γ+-φφφφ (2.32)对于时间项则分别采用三种不同格式:A :FTCS 格式(时间向前差分,空间中心差分)()21112x t t ni n i n i n i n i ni∆+-Γ=∆-≈⎪⎭⎫ ⎝⎛∂∂+-+φφφφφφ (2.33)上式中物理量的上标表示时间步。
令()2x t∆Γ∆=σ()n i n i n i n i 11121+-++-+=σφφσσφφ(2.34)边界条件:()()111111;+++++==n n N n n t B t A φφ(2.35)由于采用时间推进算法,在计算n +1时间层时,n 时间层已求解完毕,(2.34)式可以根据上一时间层的结果直接获得当前时间层的物理量而无需求解代数方程组,这样的差分格式称为显格式。
