【最新】人教版九年级数学上册22.1第5课时 二次函数y=a(x-h)2+k的图象公开课课件
九年级数学上第22章二次函数22.1二次函数的图象和性质5二次函数y=a2k的图象和性质课人教

课后训练 1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月11日星期五2022/3/112022/3/112022/3/11
2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于 独立思考的人,给那些具有锲而不舍的人。2022年3月2022/3/112022/3/112022/3/113/11/2022 3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/3/112022/3/11March 11, 2022 4、享受阅读快乐,提高生活质量。2022/3/112022/3/112022/3/112022/3/11
7.(2020·甘孜州)如图,二次函数y=a(x+1)2+k的图象与x轴 交于A(-3,0),B两点,下列说法错·误·的是( D )
A.a<0 B.图象的对称轴为直线x=-1 C.点B的坐标为(1,0) D.当x<0时,y随x的增大而增大
*8.(2020·杭州)设函数y=a(x-h)2+k(a,h,k是实数,a≠0), 当x=1时,y=1;当x=8时,y=8,( C )
解:①当 MA=MB 时,M(0,0); ②当 AB=AM 时,M(0,-3); ③当 AB=BM 时,M(0,3+3 2)或 M(0,3-3 2). 所以点 M 的坐标为(0,0),(0,-3),(0,3+3 2)或(0,3-3 2).
14.(2020·金华)如图,在平面直角坐标系中,已知二次函数 y= -12(x-m)2+4 图象的顶点为 A,与 y 轴交于点 B,异于顶点 A 的点 C(1,n)在该函数图象上.
(1)求抛物线对应的函数解析式; 解:由题意可知 h=1,则 y=a(x-1)2+k. 将点(3,0),(0,3)的坐标分别代入上式, 得4aa++kk==30,,解得ak==-4. 1, 故抛物线对应的函数解析式为 y=-(x-1)2+4.
九年级数学上册第二十二章二次函数22.1二次函数的图象和性质22.1.3二次函数y=a(x-h)2

九年级数学上册第二十二章二次函数22.1 二次函数的图象和性质22.1.3 二次函数y=a(x-h)2+k的图象和性质(第3课时)课时精讲(新版)新人教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(九年级数学上册第二十二章二次函数22.1 二次函数的图象和性质22.1.3 二次函数y=a(x-h)2+k的图象和性质(第3课时)课时精讲(新版)新人教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为九年级数学上册第二十二章二次函数22.1 二次函数的图象和性质22.1.3 二次函数y=a(x -h)2+k的图象和性质(第3课时)课时精讲(新版)新人教版的全部内容。
第3课时二次函数y=a(x-h)2+k的图象和性质1.抛物线y=a(x-h)2+k与y=ax2形状__相同___,位置__不同___,把抛物线y=ax2向上(下)和向左(右)平移,可以得到抛物线y=a(x-h)2+k,平移的方向、距离要根据__h___,__k___的值来决定.2.抛物线y=a(x-h)2+k有如下特点:①当a>0时,开口向__上___;当a<0时,开口向__下___;②对称轴是直线__x=h___;③顶点坐标是__(h,k)___.知识点1:二次函数y=a(x-h)2+k的图象1.(2014·兰州)抛物线y=(x-1)2-3的对称轴是( C)A.y轴B.直线x=-1C.直线x=1 D.直线x=-32.抛物线y=(x+2)2+1的顶点坐标是(A)A.(-2,1) B.(-2,-1)C.(2,1) D.(2,-1)3.把抛物线y=-2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为( C)A.y=-2(x+1)2+2 B.y=-2(x+1)2-2C.y=-2(x-1)2+2 D.y=-2(x-1)2-24.写出下列抛物线的开口方向、对称轴及顶点坐标:(1)y=3(x-1)2+2;解:开口向上,对称轴x=1, 顶点(1,2)(2)y=-错误!(x+1)2-5。
22.1.3 二次函数的y=a(x-h)2+k的图像和性质2024-2025学年人教版数学九年级上册

的解析式为 = −. − ,则=____
(3) 若抛物线 = + 的最小值为 4,且经过点(1,5),
则该抛物线的解析式是_________,将此抛物线向下平移
3
= +
= +
个单位,得到的新的抛物线的解析式是__________.
课堂小结
第二十二章 二次函数
22.1 二次函数的图象和性质
第3课时 二次函数的
= ( − ) +的图像和性质
第1节 二次函数 = + 的图像和性质
第2节 二次函数 = ( − ) 的图象和性质
第3节 二次函数 = ( − ) +的图象和性质
九年级上册•人教版
学习目标
中的三条抛物线分别表示桥上的三条钢梁,轴表示桥面,轴经过中
间抛物线的最高点,左右两条抛物线关于轴对称.经过测算,中间抛
物线的函数解析式为 =
−
+ .
你能计算出中间抛物线的最高点离轴的高度吗?
O
猎豹图书
x
获取新知
例1
在同一直角坐标系中,通过画出二次函数 = + ,
1 x2
y
;把抛物线
2 向右 平移 1 个单位就
得到抛物线y - 12(x-1)
2
(
− )
平移
的图象还可以由抛物线
2
个单位得到.
y
O
-4
-2
2
y - 1(x-1)
2
2
4 x
-2
2
y - 1(x+1)
2
-4
-6
-8
最新人教版初中初三九年级数学上册22.1.3二次函数y=a(x-h)2_的图象和性质精品课件

1 y ( x 2) 2 2
6 5 4
观察三条抛物线的 相互关系,并分别指 出它们的开口方向, 对称轴及顶点.
-8
y
1 2 x 2
y
1 x 2 2 2
3
2
1
-6
-4
-2
B
2
4
6
1 y ( x 2) 2 向左平移 2 2个单位
1 2 y x 2
1 y
即:
-5 -4 -3 -2 -1 o 1 2 3 4 5 x -1 -2 1 2 y ( x 1 ) -3 2 -4 -5 -6 -7 -8 -9 1 2 1 y x -10 y ( x 1) 2
2
2
在同一坐标系中作出下列二次函数:
1 2 y x 2
1 y ( x 2) 2 2
3、已知抛物线y=a(x-h)2的顶点是(-3,0)它是由 抛物线y=-4x2平移得到的,则a= -4 , h= -3 。 4、把抛物线y=(x+1)2向 右 平移 4 个 单位 后,得到抛物线y=(x-3)2 5、把抛物线y=x2+mx+n向左平移4个单位,得到抛 -10 ,n= 25 . 物线y=(x-1)2,则m=
(1)对称轴是x=h; (2)顶点是(h,0). (3)抛物线y=a(x-h)2可 以由抛物线y=ax2向左或向 右平移|h|个单位得到. h>0,向右平移; h<0,向左平移
y
x
说出抛物线的开口方向、对称轴、顶 点,最大值或最小值各是什么及增减 性如何?。
y= 2(x-3)2 y= −2(x+3)2 y= −2(x-2)2
如何平移:
22.1.3二次函数y=a(x-h)2的图象和性质 教案 2022-2023学年人教版九年级数学上册

22.1.3 二次函数y=a(x-h)^2的图象和性质教案一、教学目标本节课我们将学习二次函数y=a(x-h)^2的图象和性质,包括: - 掌握二次函数y=a(x-h)^2的图象与对称轴、顶点等特点的关系; - 能够通过二次函数的图象分析确定函数的零点与极值; - 能够应用二次函数的图象与性质解决实际问题。
二、教学内容1.二次函数y=a(x-h)^2的图象与对称轴、顶点的关系;2.二次函数的零点与极值的判断与求解;3.应用二次函数图象与性质解决实际问题。
三、教学重点1.掌握二次函数y=a(x-h)^2的图象与对称轴、顶点的关系;2.能够通过二次函数的图象分析确定函数的零点与极值。
四、教学步骤步骤一:复习二次函数的定义和基本性质•复习二次函数的定义:y=a(x-ℎ)2,其中a、h均为常数,a≠0;•复习二次函数的对称轴与顶点的概念和求解方法;•复习二次函数的开口方向和对称性。
步骤二:讲解二次函数y=a(x-h)^2的图象与对称轴、顶点的关系1.首先,通过改变a的值观察图象的变化,引导学生观察a的变化对图象的影响;2.探讨当a>0时,图象开口向上;当a<0时,图象开口向下;3.引导学生思考,当a变化时,对称轴和顶点的位置是否发生变化,通过实际计算验证结论;4.引导学生总结二次函数y=a(x-h)^2的图象与对称轴、顶点的关系。
步骤三:讲解二次函数的零点与极值的判断与求解1.引导学生回顾一元二次方程的求解方法,通过解方程y=a(x-ℎ)2=0得出零点的概念;2.讲解求解零点时利用一元二次方程求根公式,引导学生完成练习题;3.引导学生思考,当a的值变化时,零点的位置如何变化,通过实际计算验证结论;4.引导学生回顾关于函数极值的概念,讲解求解极值的方法,引导学生完成练习题;5.引导学生思考,当a的值变化时,极值的位置如何变化,通过实际计算验证结论。
步骤四:应用二次函数图象与性质解决实际问题1.给出一些实际问题,如抛物线的高度求解、拱桥的设计等,引导学生利用二次函数的图象与性质解决;2.让学生分组进行讨论和解答,培养学生的团队合作和解决问题的能力;3.每组选择一种实际问题进行展示,并进行讨论。
22.1.3.2 二次函数y=a(x-h)2的图象和性质 初中数学人教版九年级上册教学课件

yO -2
-2 -4 -6
抛物线
开口方向 对称轴 顶点坐标
y 1 x 12
2 y 1 x2
2
y 1 x 12
2
向下 向下 向下
直线x=-1 (-1,0) 直线x=0 (0,0) 直线x=1 (1,0)
2 4x
y 1 x 12
2
y 1 x2 2
探究二
二次函数y=a(x-h)2(a≠0)的性质
2
2
对称轴和顶点.
解:列表.
x
··· -3 -2 -1 0 1 2 3 ···
y 1 x 12
2
··· -2
1 2
0
1 2
-2 -4.5
-8
···
y 1 x 12
2
·ห้องสมุดไป่ตู้· -8 -4.5
-2
1 2
0
1 2
-2 ···
探究二
描点、连线,画出这两个 函数的图象.
-4
y 1 x 12
2
2
解:列表.
x
··· -3 -2 -1 0 1 2 3 ···
y 1 x2 2
9 ··· 2
2
1 2
0
1 2
2
9
2
···
y 1 ( x 2)2 2
···
25 2
8
9 2
2
1 2
0
1 2 ···
探究一
描点、连线,画出这两 个函数的图象.
y x2 6 5 4 3 2 1
y 1 x2 2
y 1 ( x 2)2
若抛物线y=3(x+ 2 )2的图象上的三个点为A(-3 2,y1),B(-1,y2), C(0,y3),则y1,y2,y3的大小关系为__y_2_<__y_3<__y_1__.
人教版数学九年级上册22.1.3二次函数y=a(x-h)2的函数图象和性质(教案)

(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《二次函数y=a(x-h)²的函数图象和性质》这一章节。在开始之前,我想先问大家一个问题:“你们在日常学习中是否遇到过需要分析抛物线形状的问题?”(如抛物线运动的轨迹)这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索二次函数的奥秘。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了二次函数y=a(x-h)²的基本概念、图象性质和实际应用。同时,我们也通过实践活动和小组讨论加深了对二次函数的理解。我希望大家能够掌握这些知识点,并在解决实际问题时灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
-二次函数的增减性、最大(小)值及其与a的正负关系;
-实际问题中二次函数的模型构建和求解。
举例:讲解a的正负对函数图象开口方向的影响,以及h对对称轴位置的影响;通过图象分析最大(小)值出现的条件及其计算方法。
2.教学难点
-理解a、h的参数变化对二次函数图象的具体影响,尤其是对图象开口大小和顶点位置的综合判断;
此外,实践活动环节,同学们在分组讨论和实验操作中表现积极,但成果展示时,部分小组的表达能力还有待提高。针对这一问题,我打算在后续的教学中,多给予同学们表达和展示的机会,以提高他们的语言组织和表达能力。
在小组讨论中,同学们对二次函数在实际生活中的应用提出了很多有趣的想法,这让我感到很欣慰。但同时,我也注意到有些同学在讨论时过于依赖教材,缺乏独立思考。为了培养同学们的创新意识,我将在今后的教学中,鼓励他们多角度、多维度地思考问题。
九年级数学上册第22章二次函数22.1二次函数的图象和性质第5课时二次函数y=a(x_h)2 k的图象课件新版新人教版

抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时, 开口向上;当a<0时,开口向下; (2)对称轴是直线x=h; (3)顶点是(h,k).
针对练一
1 )2 7 1.对于抛物线 y (x3 ,下列说法错误的是: ( D ) 2 A.开口向上 B.对称轴是x=3
C.最低点的坐标是(3,7) 向左平移3个单位,再向上平移7个单位得到 A 2 2.二次函数y=(x-1) +2的最小值是: ( ) A.2 B.1 C.-1 D.-2 D.可由抛物线
1、不是井里没有水,而是你挖的不够深。不是成功来得慢,而是你努力的不够多。 2、孤单一人的时间使自己变得优秀,给来的人一个惊喜,也给自己一个好的交代。 3、命运给你一个比别人低的起点是想告诉你,让你用你的一生去奋斗出一个绝地反击的故事,所以有什么理由不努力! 4、心中没有过分的贪求,自然苦就少。口里不说多余的话,自然祸就少。腹内的食物能减少,自然病就少。思绪中没有过分欲,自然忧就少。大悲是无泪的,同样大悟无言。缘来尽量要惜,缘尽就放。人生本来就空,对人家笑笑,对自己笑笑,笑着看天下,看日出日落, 花谢花开,岂不自在,哪里来的尘埃! 5、心情就像衣服,脏了就拿去洗洗,晒晒,阳光自然就会蔓延开来。阳光那么好,何必自寻烦恼,过好每一个当下,一万个美丽的未来抵不过一个温暖的现在。 6、无论你正遭遇着什么,你都要从落魄中站起来重振旗鼓,要继续保持热忱,要继续保持微笑,就像从未受伤过一样。 7、生命的美丽,永远展现在她的进取之中;就像大树的美丽,是展现在它负势向上高耸入云的蓬勃生机中;像雄鹰的美丽,是展现在它搏风击雨如苍天之魂的翱翔中;像江河的美丽,是展现在它波涛汹涌一泻千里的奔流中。 8、有些事,不可避免地发生,阴晴圆缺皆有规律,我们只能坦然地接受;有些事,只要你愿意努力,矢志不渝地付出,就能慢慢改变它的轨迹。 9、与其埋怨世界,不如改变自己。管好自己的心,做好自己的事,比什么都强。人生无完美,曲折亦风景。别把失去看得过重,放弃是另一种拥有;不要经常艳羡他人,人做到了,心悟到了,相信属于你的风景就在下一个拐弯处。 10、有些事想开了,你就会明白,在世上,你就是你,你痛痛你自己,你累累你自己,就算有人同情你,那又怎样,最后收拾残局的还是要靠你自己。 11、花开不是为了花落,而是为了开的更加灿烂。 12、随随便便浪费的时间,再也不能赢回来。 13、不管从什么时候开始,重要的是开始以后不要停止;不管在什么时候结束,重要的是结束以后不要后悔。 14、当你决定坚持一件事情,全世界都会为你让路。 15、只有在开水里,茶叶才能展开生命浓郁的香气。 15、如果没有人为你遮风挡雨,那就学会自己披荆斩棘,面对一切,用倔强的骄傲,活出无人能及的精彩。 16、成功的秘诀在于永不改变既定的目标。若不给自己设限,则人生中就没有限制你发挥的藩篱。幸福不会遗漏任何人,迟早有一天它会找到你。 17、一个人只要强烈地坚持不懈地追求,他就能达到目的。你在希望中享受到的乐趣,比将来实际享受的乐趣要大得多。 18、无论是对事还是对人,我们只需要做好自己的本分,不与过多人建立亲密的关系,也不要因为关系亲密便掏心掏肺,切莫交浅言深,应适可而止。 19、大家常说一句话,认真你就输了,可是不认真的话,这辈子你就废了,自己的人生都不认真面对的话,那谁要认真对待你。 20、没有收拾残局的能力,就别放纵善变的情绪。 16、成功的反义词不是失败,而是从未行动。有一天你总会明白,遗憾比失败更让你难以面对。 17、没有一件事情可以一下子把你打垮,也不会有一件事情可以让你一步登天,慢慢走,慢慢看,生命是一个慢慢累积的过程。 18、努力也许不等于成功,可是那段追逐梦想的努力,会让你找到一个更好的自己,一个沉默努力充实安静的自己。 19、你相信梦想,梦想才会相信你。有一种落差是,你配不上自己的野心,也辜负了所受的苦难。 20、生活不会按你想要的方式进行,它会给你一段时间,让你孤独、迷茫又沉默忧郁。但如果靠这段时间跟自己独处,多看一本书,去做可以做的事,放下过去的人,等你度过低潮,那些独处的时光必定能照亮你的路,也是这些不堪陪你成熟。所以,现在没那么糟,看似 生活对你的亏欠,其实都是祝愿。 10、放手如拔牙。牙被拔掉的那一刻,你会觉得解脱。但舌头总会不由自主地往那个空空的牙洞里舔,一天数次。不痛了不代表你能完全无视,留下的那个空缺永远都在,偶尔甚至会异常挂念。适应是需要时间的,但牙总是要拔,因为太痛,所以终归还是要放手,随它去。 11、这个世界其实很公平,你想要比别人强,你就必须去做别人不想做的事,你想要过更好的生活,你就必须去承受更多的困难,承受别人不能承受的压力。 12、逆境给人宝贵的磨炼机会。只有经得起环境考验的人,才能算是真正的强者。自古以来的伟人,大多是抱着不屈不挠的精神,从逆境中挣扎奋斗过来的。 13、不同的人生,有不同的幸福。去发现你所拥有幸运,少抱怨上苍的不公,把握属于自己的幸福。你,我,我们大家都可以经历幸福的人生。 14、给自己一份坚强,擦干眼泪;给自己一份自信,不卑不亢;给自己一份洒脱,悠然前行。轻轻品,静静藏。为了看阳光,我来到这世上;为了与阳光同行,我笑对忧伤。 15、总不能流血就喊痛,怕黑就开灯,想念就联系,疲惫就放空,被孤立就讨好,脆弱就想家,不要被现在而蒙蔽双眼,终究是要长大,最漆黑的那段路终要自己走完。 16、在路上,我们生命得到了肯定,一路上,我们有失败也有成功,有泪水也有感动,有曲折也有坦途,有机遇也有梦想。一路走来,我们熟悉了陌生的世界,我们熟悉了陌生的面孔,遇人无数,匆匆又匆匆,有些成了我们忘不掉的背影,有些成了我们一生的风景。我笑, 便面如春花,定是能感动人的,任他是谁。 17、努力是一种生活态度,与年龄无关。所以,无论什么时候,千万不可放纵自己,给自己找懒散和拖延的借口,对自己严格一点儿,时间长了,努力便成为一种心理习惯,一种生活方式! 18、自己想要的东西,要么奋力直追,要么干脆放弃。别总是逢人就喋喋不休的表决心或者哀怨不断,做别人茶余饭后的笑点。 19、即使不能像依米花那样画上完美的感叹号,但我们可以歌咏最感人的诗篇;即使不能阻挡暴风雨的肆虐,但我们可以左右自己的心情;即使无法预料失败的打击,但我们可以把它当作成功的一个个驿站。 20、能力配不上野心,是所有烦扰的根源。这个世界是公平的,你要想得到,就得学会付出和坚持。每个人都是通过自己的努力,去决定生活的样子。
人教版九年级数学上册课件:22.二次函数y=a(x-h)2的图象和性质共18张

y 2 x 2
向上
对称轴
直线x=3
2
3
2
y x 1
4
向上
直线x=2
向下
直线x=1
顶点坐标
( 3, 0 )
(2, 0 )
( 1, 0)
4.把抛物线y=a(x-4)2向左平移6个单位后得到抛物线y=- 3(xh)2的图象,则 a= -3 ,h= -2 .若抛物线y= a(x-4)2的顶
-2
2
4
-2
-3
y ax h
-4
2
-4
y
1
( x 1) 2
2
y
1
y x2
2
-6
1
( x 1) 2
2
探究 二
二次函数y=a(x-h)2的图象和性质
a的符号
a>0
a<0
向上
直线x=h
(h,0)
向下
直线x=h
(h,0)
h>0
图
象
h<0
开口方向
对称轴
顶点坐标
•
说出下列二次 函数图像的开口方向、对称
2.二次函数 = ( −
3
, 0)
________.
2
(
− ,可将抛物线 =
B.向下平移4个单位
D.向左平移4个单位
(
C
3
) 图象的对称轴是直线_x ___,顶点是
2
)
3.指出下列函数图象的开口方向,对称轴和顶点坐标.
抛物线
y 2 x 3
开口方向
三、探究新知,合作交流
数学人教版九年级上册22.1.3二次函数y=a(x-h)2的函数图象和性质.1.3二次函数y=a(x-h)2的函数图象和性质

(-1,0) 直线x=-1
最大值为0
当x<-1时,y随x的增大而增大; 当x&g学验证
斩获新知
二次函数y=a(x-h)2的性质与参数a,h的关系
y a ( x h )( a 0 )
2
开口 顶点: (h,0)
对称轴:直线x=h
最大(小)值为0
△增减性看开口与对称轴
y (x 1 )2
澄海集贤中学
夯实基础
3、将二次函数y=2x2的图像向右平移3个单位后得到函 y=2(x-3)2 数 的图像,其对称轴是 直线x= 3 , 顶点是 (3,0) ,当x >3 时,y随x的增大而增大; 当x <3 时,y随x的增大而减小.
4、将二次函数y= -3(x-2)2的图像向左平移3个单位后得 2 y = 3( x +1) 到函数 的图像,其顶点坐标是 (-1,0) , 对称轴是 直线x= -1 ,当x= -1 时,y有最大 值,是 0 . 5、将函数y=3(x-4)2的图象沿x轴对折后得到的函数解 y=-3(x-4)2 ;将函数y=3(x-4)2的图象沿y轴对 析式是____________ 2 y =3( x + 4) 折后得到的函数解析式是____________.
y=ax2+k
向上平移k个 (k>0)单位 h个 向右平移h个 2 2 y=a(x+h)2 向左平移 y = ax y = a ( x h ) (h>0)单位 (h>0)单位
向下平移k个 (k>0)单位
y=ax2-k
y(x 1 )2 y x 2
y(x 1 )2
y (x 1 )2 y x2
汕头澄海集贤中学
s h an t ou c h e n gh ai ji xi an middle s ch oo l
人教版九年级上数学第22章《二次函数》第5课时《二次函数y=a(x-h)2+k的图象和性质》导学案

第二十二章《二次函数》第5课时 22.1.4 二次函数y=a(x+h)2+k 的图象和性质【学习目标】: 1.会画二次函数2()y a x h k =-+的图象;2.掌握二次函数2()y a x h k =-+的性质;3.理解2y ax =与2()y a x h k =-+之间的联系。
【学习过程】:一、知识回顾说出下列函数图象的开口方向、对称轴、顶点和增减变化情况: (1). 2y x =; (2) 21y x =- (3) 22(1)y x =-二、合作探究:在同一坐标系内画出y=2x 2、y=2(x-1)2、y=2(x-1)2+1 的图象 解:列表:归纳小结:22(1)1y x =-+的图像可以由 先向 平移 个单位,再向 平移 个单位,或者先向 平移 个单位再向 平移 个单位而得到。
三、课堂练习:1.抛物线的上下平移(1)把二次函数y=(x+1)2的图像,沿y 轴向上平移3个单位,得到 的图像; (2)把二次函数_________ 的图像,沿y 轴向下平移2个单位,得到y=x 2+1的图像.1)1-+…2.抛物线的左右平移(1)把二次函数y=(x+1) 2的图像,沿x轴向左平移3个单位,得到___________的图像;(2)把二次函数_____________的图像,沿x轴向右平移2个单位,得到y=x 2+1的图像.3.抛物线的平移:(1)把二次函数y=3x 2的图像,先沿x轴向左平移3个单位,再沿y轴向下平移2个单位,得到_____________的图像;(2)把二次函数_____________的图像,先沿y轴向下平移2个单位,再沿x轴向右平移3个单位,得到y=-3(x+3) 2-2的图像。
4.对称轴是直线x=-2的抛物线是( )A.y=-2x2-2B.y=2x2-2C.y=-1/2(x+2)2-2D.y=-5(x-2)2-65.抛物线的顶点为(3,5) 此抛物线的解析式可设为( )A.y=a(x+3)2+5B.y=a(x-3)2+5C.y=a(x-3)2-5D.y=a(x+3)2-5四、典例精析:【例】.已知二次函数y=ax2+bx+c的图象如图所示求函数解析式。
人教版数学九年级上册22.1 二次函数的图象和性质(第5课时)-课件

5.小结
(1)本节课研究的主要内容是什么? (2)我们是怎么研究的(过程和方法是什么)? (3)在研究过程中你遇到的问题是什么?怎么解 决的?
6.布置作业
教科书习题 22.1 第 6题,第7 题(2).
九年级 上册
22.1 二次函数的图象和性质 (第5课时)
课件说明
• 本节课是在讨论了二次函数 y =a(x - h)2 +k 的图象和 性质的基础上对二次函数 y=ax2+bx+c 的图象和性质 进行研究.主要的研究方法是通过配方将 y=ax2+bx+c 向 y =a(x - h)2 +k 转化,体会知识之间内在联系.在 具体探究过程中,从特殊的例子出发,分别研究 a>0 和 a<0 的情况,再从特殊到一般,得出 y=ax2+bx+c 的图象和性质.
对于一般的二次函数 y = ax2 + bx + c,如果 a>0,
当 x< b 时, y 随 x 的增大而减小,当 x> b 时,
2a y 随 x 的增大而增大;如果 a<0,当 x<
b
2a 时,y 随
x 的增大而增大,当 x> b
2a 时,y 随 x 的增大而减小.
2a
4.巩固练习
(1)求出下列抛物线的开口方向,对称轴和顶点 坐标.
① y = 2x2 - 4x +5 开口向上、x = 1、(1, 3). ② y = -x2 + 2x -3 开口向下、x = 1、(1,-2).
4.巩固练习
(2)二次函数 y = -2x2 + 4x -1, 当 x <1 时, y 随 x 的增大而增大, 当 x >1 时, y 随 x 的增大而减小.
九年级数学上册 第二十二章 22.1 二次函数的图像及性质 22.1.5 二次函数y=a(x-h)2

第二十二章 22.1.5二次函数y=a(x-h)2+k的图象和性质知识点:二次函数y=a(x-h)2+k的图象及其性质二次函数y=a(x-h)2+k的图象及其性质:(1)当a>0时,图象开口向上;当a<0时,图象开口向下.(2)图象对称轴是直线x=h.(3)图象顶点坐标是(h,k).(4)当a>0时,y最小值=k,此时x=h;当a<0时,y最大值=k,此时x=h.(5)当a>0时,若x<h,则y随x的增大而减小;若x>h,则y随x的增大而增大.当a<0时,若x<h,则y随x的增大而增大;若x>h,则y随x的增大而减小.注意:因为由y=a(x-h)2+k可以直接读出图象顶点的坐标为(h,k),所以通常把y=a(x-h)2+k(a ≠0)称为二次函数的顶点式.考点1:二次函数y=a(x-h)2+k的图象【例1】已知二次函数y=(x-2a)2+a-1(a为常数),当a取不同的值时,其图象构成一个“抛物线系”.如图分别是当a=-1,a=0,a=1,a=2时二次函数的图象.它们的顶点在一条直线上,这条直线对应的函数解析式是y= .答案:x-1点拨:本题属于二次函数的图象与性质与一次函数综合题,题中给出了二次函数y=(x-2a)2+a-1和字母a的四个值,本着使计算简便的原则,可以求出当a=0,a=1时的二次函数解析式,再利用二次函数解析式求出抛物线的顶点坐标,确定出直线上两个点的坐标后,用待定系数法求得直线对应的函数解析式.此外,在已知一次函数y=kx+b的图象与y轴的交点坐标(0,-1)时,可以根据一次函数的图象的性质,设一次函数的解析式为y=kx-1,利用点(2,0)求出k的值.考点2:二次函数y=a(x-h)2+k的解析式的确定2【例2】 已知抛物线的顶点坐标是(1,3),且此抛物线经过点P(2,0),则这个抛物线对应的函数解析式为 .答案:y=-3x 2+6x点拨:如果已知抛物线对应的函数解析式的形式是y=a (x-h)2+k,我们可以写出它的顶点坐标;反过来,已知抛物线的顶点坐标为(h,k),我们也可以设其对应的函数解析式为y=a(x-h)2+k,因为抛物线的顶点坐标为(1,3),可设该解析式为y=a(x-1)2+3,把(2,0)代入解析式中求出a,可确定该解析式.考点3:二次函数图象的运动问题【例3】 如图,点A,B 的坐标分别为(1,4)和(4,4),抛物线y=a(x-m)2+n 的顶点在线段AB 上运动,与x 轴交于C,D 两点(C 在D 的左侧),点C 的横坐标最小值为-3,则点D 的横坐标最大值为( )A.-3B.1C.5D.8答案:D点拨:C,D 两点是抛物线与x 轴的交点,当取得C 的横坐标最小值为-3时,抛物线的顶点在A 处,把(-3,0)代入y=a(x-1)2+4可得0=a(-3-1)2+4,求得a=-;当抛物线的顶点在B 处时,可以取得D 的横坐标最大值,其解析式为y=-(x-4)2+4,将y=0代入解析式,解得x=0或x=8,因此点D 的横坐标最大值为8.。
【人教版】九年级上册数学教案:22.1 二次函数的图象和性质-22.1.3.2 二次函数y=a(x-h)2的图象和性质

22.1.3 二次函数y=a(x-h)2+k的图象和性质第3课时二次函数y=a(x-h)2+k的图象和性质教学目标:1.使学生理解函数y=a(x-h)2+k的图象与函数y=ax2的图象之间的关系。
2.会确定函数y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标。
3.让学生经历函数y=a(x-h)2+k性质的探索过程,理解函数y=a(x-h)2+k的性质。
重点难点:重点:确定函数y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标,理解函数y=a(x-h)2+k的图象与函数y=ax2的图象之间的关系,理解函数y=a(x-h)2+k的性质是教学的重点。
难点:正确理解函数y=a(x-h)2+k的图象与函数y=ax2的图象之间的关系以及函数y=a(x -h)2+k的性质是教学的难点。
教学过程:一、提出问题1.函数y=2x2+1的图象与函数y=2x2的图象有什么关系?(函数y=2x2+1的图象可以看成是将函数y=2x2的图象向上平移一个单位得到的)2.函数y=2(x-1)2的图象与函数y=2x2的.图象有什么关系?(函数y=2(x-1)2的图象可以看成是将函数y=2x2的图象向右平移1个单位得到的,见P10图26.2.3)3.函数y=2(x-1)2+1图象与函数y=2(x-1)2图象有什么关系?函数y=2(x-1)2+1有哪些性质?二、试一试你能填写下表吗?y=2x2向右平移的图象1个单位y=2(x-1)2向上平移1个单位y=2(x-1)2+1的图象开口方向向上对称轴y轴顶点(0,0)问题2:从上表中,你能分别找到函数y=2(x-1)2+1与函数y=2(x-1)2、y=2x2图象的关系吗? 问题3:你能发现函数y=2(x-1)2+1有哪些性质?对于问题2和问题3,教师可组织学生分组讨论,互相交流,让各组代表发言,达成共识;函数y=2(x-1)2+1的图象可以看成是将函数y=2(x-1)2的图象向上平称1个单位得到的,也可以看成是将函数y=2x2的图象向右平移1个单位再向上平移1个单位得到的。
人教版九年级上册数学精品课件 第22章 第5课时二次函数y=a(x-h)2+k(a≠0)的图象和性质

二次函数
22.1 二次函数的图象和性质
第5课时 二次函数y=a(x-h)2+k(a≠0)的图象和性质
基础过关 能力提升 核心素养
基础过关
• 知识点1 二次函数y=a(x-h)2+k(a≠0)的图象和性质
• 1.对于二次函数y=(x+3)2-5的图象,下列说法正D 确的
是
()
• A.开口向下
a3=a4=1,∴点P的坐标为(1,-4).∴当△ABP的面积是8时,点P的 坐标为(1-2 2,4)或(1+2 2,4)或(1,-4);
(3)设直线AD的解析式为y=kx+c(k≠0).将A(-1,0),D(2,-3)代
入y=kx+c,得
-k+c=0, 2k+c=-3,
解得
k=-1, c=-1,
-x2+2x+c的图象上,则y1,y2,y3的大小关系是 D( )
• A.y3>y2>y1
B.y3>y1=y2
• C.y1>y2>y3
D.y1=y2>y3
• 11.若抛物线y=(x-m)2+m+1的顶点在第一象限,则m
的取值范围为
()
• A.m>1
B.m>0
B
• C.m>-1
D.-1<m<0
12.当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,
1<0,∴当m=
1 2
时,MN取得最大值,最大值为
9 4
,此时S的值为
3 2
×
94 =
287,∴当MN的长最大时S的值为287.
包括△OAB的边界),∴4-3<m<4-32,即1<m<52.
核心素养
• 19.如图,抛物线y=(x-1)2+n与x轴交于A,B两点(A在B的左侧), 与y轴交于点C(0,-3),点D与点C关于抛物线的对称轴对称. • (1)求抛物线的解析式及点D的坐标; • (2)点P是抛物线上的一点,当△ABP的面积是8时,求出点P的坐标-1.
人教版数学九年级上册 第二十二章 二次函数 22.1 二次函数的图像和性质 二次函数y=a(xh)2
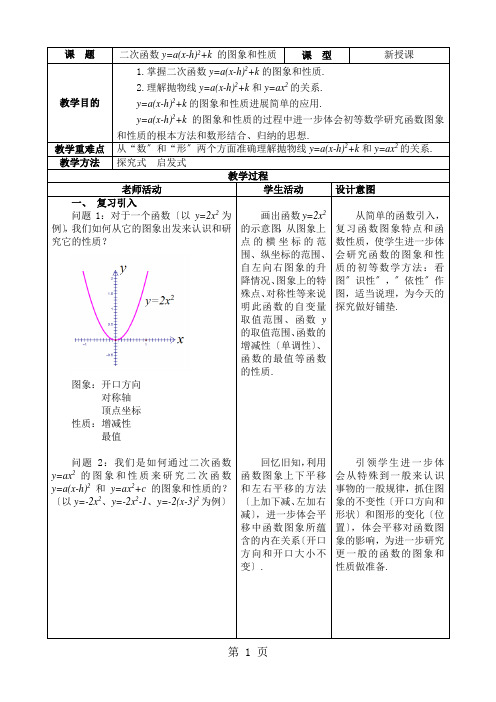
课题二次函数y=a(x-h)2+k的图象和性质课型新授课教学目的1.掌握二次函数y=a(x-h)2+k的图象和性质.2.理解抛物线y=a(x-h)2+k和y=ax2的关系.y=a(x-h)2+k的图象和性质进展简单的应用.y=a(x-h)2+k的图象和性质的过程中进一步体会初等数学研究函数图象和性质的根本方法和数形结合、归纳的思想.教学重难点从“数〞和“形〞两个方面准确理解抛物线y=a(x-h)2+k和y=ax2的关系. 教学方法探究式启发式教学过程老师活动学生活动设计意图一、复习引入问题1:对于一个函数〔以y=2x2为例〕,我们如何从它的图象出发来认识和研究它的性质?图象:开口方向对称轴顶点坐标性质:增减性最值问题2:我们是如何通过二次函数y=ax2的图象和性质来研究二次函数y=a(x-h)2和y=ax2+c的图象和性质的?〔以y=-2x2、y=-2x2-1、y=-2(x-3)2为例〕画出函数y=2x2的示意图,从图象上点的横坐标的范围、纵坐标的范围、自左向右图象的升降情况、图象上的特殊点、对称性等来说明此函数的自变量取值范围、函数y的取值范围、函数的增减性〔单调性〕、函数的最值等函数的性质.回忆旧知,利用函数图象上下平移和左右平移的方法〔上加下减、左加右减〕,进一步体会平移中函数图象所蕴含的内在关系〔开口方向和开口大小不变〕.从简单的函数引入,复习函数图象特点和函数性质,使学生进一步体会研究函数的图象和性质的初等数学方法:看图〞识性〞,〞依性〞作图,适当说理,为今天的探究做好铺垫.引领学生进一步体会从特殊到一般来认识事物的一般规律,抓住图象的不变性〔开口方向和形状〕和图形的变化〔位置〕,体会平移对函数图象的影响,为进一步研究更一般的函数的图象和性质做准备.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
合作探究 达成目标
探究点二 运用二次函数解决实际问题 例2.要修建一个圆形喷水池,在池中心竖直 安装一根水管.在水管的顶端安装一个喷水 头,使喷出的抛物线形水柱在与池中心的水 平距离为1m处达到最高,高度为3m,水柱落 地处离池中心3m,水管应多长?
解:如图建立直角坐标系, 点(1,3) y B(1,3) 是图中这段抛物线的顶点.因此可 3 设这段抛物线对应的函数是 A 2 y=a(x-1)2+3 (0≤x≤3) ∵这段抛物线经过点(3,0) 3 1 2 a= - ∴ 0=a(3-1) +3 解得: 4 因此抛物线的解析式为: 2 1 O 3 2 y=-4 (x-1) +3 (0≤x≤3) 当x=0时,y=2.25 答:水管长应为2.25m.
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时, 开口向上;当a<0时,开口向下; (2)对称轴是直线x=h; (3)顶点是(h,k).
1.对于抛物线 A.开口向上
y
1 ( x 3) 2 7 ,下列说法错误的是: ( D ) 2
B.对称轴是x=3
y 1 2 x 2 向左平移3个单
第5课时
二次函数y=a(x-h)2+k的图象
创设情境 明确目标
自主学习 指向目标
1.会用描点法画二次函数y=a(x-h)2 +k的图象. 2.理解抛物线y=ax2与y=a(x-h)2+k之间 的位置关系.
合作探究 达成目标
1
探究点一
二次函数y=a(x-h)2+k的 图象和性质
例1.画出函数 y ( x 1) 2 1 的图象.指出它的开口方向、顶 2 点与对称轴 x 1 2 … … -4 -3 -2 -1 0 解: 列表
C.最低点的坐标是(3,7) D.可由抛物线 位,再向上平移7个单位得到 2.二次函数y=(x-1)2+2的最小值是: ( A )
A.2
B.1
C.-1
D.-2
3.抛物线y=-2(x-3)2-2的开口向_____ 下 ,对称轴为____________, 直线x=3 顶点坐标为__________. (3,2)
1 2 向左平移 1 y x y ( x 1) 2 2 1个单位 2 1 向下平移 y ( x 1) 2 1 1个单位 2
-7 -8 -9 -10
2
2
2 3 4 5
x
x=-1
y
y=2(x-1)2+1
y=2x2
5 4. 3. 2. 1.
y=2(x-1)2
-3.
-2
-1
平移方法1: y 1 1 2 向下平移 1 2 y x 1个单位 y x 1 -5 -4 -3 -2 -1 o 1 -1 2 2 y 1 ( x 1) 2 1 -2 1 向左平移 2 -3 y ( x 1) 2 1 -4 1个单位 2 -5 平移方法2: -6
顶点是(-1, -1).
-5 -4 -3 -2 -1 o 1 2 3 4 5 x -1 -2 -3 -4 y 1 ( x 1) 2 1 2 -5 -6 -7 -8 -9 -10
二次函数y=a(x-h)2+k的图象
y=a(x- 开口 对称 顶 h)² +k 方向 轴 点 最值 增减情况
6.已知一条抛物线的顶点是(-1,1),且由
1 y ( x 1) 2 1 这条抛物线的解析式为______________________ 。 3
1 y ( x 1) 2 3
平移得到,
7.某广场中心标志性建筑处有高低不
同的各种喷泉,其中有一支高度为1 米的喷水管最大高度为3米,此时喷 水水平距离为1/2米,在如图所示的坐 标系中,这支喷泉的函数关系式是
C(3,0) x 3
4.已知抛物线y=3(x-h)2+k的顶点坐标是(5,6),则 5 6 h=________,k=_________.
5.已知抛物线的顶点为(3,-2),且经过坐标原点,则抛物线所
2 ( x 3) 2 2 对应的二次函数解析式为_____________________. 9 y
a>0
a<0
向上 x=h (h,k) x=h时, 有最小 值y=k 向下 x=h (h,k) x=h时, 有最大 值y=k
x<h时, y随x的增大而 减小; x>h时,y随x的增 大而增大. x<h时, y随x的增大而 增大; x>h时, y随x的增 大而减小.
|a|越大开口越小.
(2)抛物线 y 1 ( x 1) 2 1与 y 1 x 2 有什么关系?
0. -1
1.
2.
3.
x
抛物线
y=2(x-1)2 +1 与 y=2x2
有什么关系?
y
y=2x2 +1
5 4. 3. 2. 1.
y=2x2
y=2(x-1)2+1
-3.
-2
-1
0. -1
1.
2.
3.
x
抛物线
y=2(x-1)2 +1 与 y=2x2
又有什么关系?
一般地,抛物线y=a(x-h)2+k与y=ax2形状相同, 位置不同.把抛物线y=ax2向上(下)向右(左)平移,可以 得到抛物线y=a(x-h)2+k.平移的方向、距离要根据h、 k的值来决定. 平移方法: y=ax2向左(右)平移 y=a(x-h)2 向上(下)平y=a(x-h)2+k |h|个单位 移|k|个单位 或y=ax2 向上(下)平 y=ax2+k 向左(右)平 y=a(x-h)2+k 移|h|个单位 移|k|个单位
1 y ( x 1) 2 1 … -5.5 2
-3 -1.5 -1 -1.5 -3
பைடு நூலகம்
-5.5 …
描点、连线
1 (1)抛物线 y ( x 1) 2 1 2
直线x=-1
1
y
的开口方向、对称轴、顶点? 1 2 y ( x 1 ) 1 抛物线 2 的开口向下,
对称轴是直线x=-1,
1 y 8( x ) 2 3 2 ________________.
总结梳理 内化目标
达标检测 反思目标
1 y ( x 1) 2 2 2
右 2 y=x2+4x+1
3
上
解: (1)
1 y ( x 3) 2 2 2
(2)(5,0)
• 上交作业:教科书第41 页第5(3)题 .
