第二章平面问题的基本理论_第一次
2平面问题的基本理论(平面应力与应变,受力状态,圣维兰原理)

当面积 AB 无限减小而趋于 P 点时,平面 AB 上的 应力就是上述斜面上的应力。 现设斜面上的全应力p可以分解为沿坐标向的分 量( px , py ),或沿法向和切向的分量( σn , τn),如图 2-4b所示。
用n代表斜面AB的外法线方向,其方向余弦为:
cosn, x l, cosn, y m
c
0
,则有
F 0, F Mc 0
x
y
0
yx dy dy dx dx xy dy 1 ( yx dy)dx 1 yx dx 1 0 2 2 y 2 2
力矩方程化简后得到:
xy
1 xy 1 yx dx yx dy 2 x 2 y
x yx fx 0 y x xy y f 0 y x y
4.平衡微分方程适用的条件是,只要求符合连 续性和小变形假定。 5.对于平面应力问题和平面应变问题,平衡微 分方程相同。 6.由于τxy =τyx,以后只作为一个独立未知函数 处理。因此,2个独立的平衡微分方程(2-2) 中含有 3个应力未知函数。
由式(2-4)及(2-5)就可以求得经过P点的任意 斜面上的正应力 n 及切应力 n 。
3.然后,再求出主应力和应力主向
设经过P点的某一斜面上的切应力等于零,则该斜 面上的正应力称为在P点的一个主应力,而该斜面 称为在P点的一个应力主平面,该斜面的法线方向 称为在P点的一个应力主向。
(2)只在侧边上受有平行于板面且不沿厚度变化 的面力和体力,且不沿厚度变化,体力 f x , f y , o 和面 力 f x , f y , o ,只是x,y的函数,并构成平衡力系;
弹性力学-2-平面问题的基本理论

2015-1-16
4 弹性力学
2.1 平面应力问题与平面应变问题
弹性力学空间问题共有应力、应变和位
移共15个未知函数,且均为 f (x, y, z)。
弹性力学平面问题共有应力、应变和位
移8个未知函数,且均为f (x, y,)。
2015-1-16
5 弹性力学
2.1 平面应力问题与平面应变问题
什么条件下 空间问题可简化为平面问题
px n l l
py n m m
又由于:
px xl xy m p y xyl y m
32 弹性力学
2015-1-16
2.2 平面问题中一点的应力状态 问题3:若经过该点的某一斜面上的切应力为0, 求此斜面上的主应力σ和应力主方向α 从而可得
2015-1-16 25 弹性力学
2.2 平面问题中一点的应力状态 应力是与作用面有关的。σx,σy和τxy作为 基本未知函数,只是表示一点的坐标平面上的 应力分量(左图)。而校核强度时需要知道过 此点的任意斜面上的应力p。斜面上的应力p可 以按坐标轴分解为(px,py),也可沿法向和切 向分解为正应力σn和切应力τn(右图)。
z , zx , zy 0
2015-1-16 10 弹性力学
2.1 平面应力问题与平面应变问题
因此,此类问题的未知量只剩下Oxy面内 的三个应力分量: x , y , xy
所以此类问题称为平面应力问题。 由于板很薄,等厚度,外力和约束沿z 方向不变,因此应力也沿厚度z方向均匀分 布,应力x,y和xy只是坐标x, y的函数。
取如图所示的微分三角板或三棱柱
PAB,当平面AB无限接近于P点时, 该平面上的应力即为所求。
弹性力学 第二章平面问题的基本理论

体位移。
如果各点(或部分点)间的相对距离发生 变化,则物体发生了变形。这种变形一方面 表现在微线段长度的变化;另一方面表现在 微线段间夹角的变化。因此,物体变形程度 用形变分量(ε,γ)来描述。
0
A
B
0'
A'
B'
二、 几何方程
几何方程——描述任一点的微分线段 上形变分量与位移分量之间的关系。
P点的形变分量与位移分量的关系?
cos(900 1 ) cos1
m1 l1
由(a)式得:
tan1
1 x xy
设 σ2与 x 轴的夹角为α2
(b)
ta n 2
s i n 2 cos2
cos(900 2 ) cos2
m2 l2
由(a)式得:ta n 2
xy 2
y
tan1
1 x xy
ta n 2
xy 2 y
由式: σ1 +σ2 = σy +σx
作用的等厚度薄板,若板边上只受x、y方向的面力或约束且不
沿厚度变化时,其状态接近平面应力状态还是应变状态?
解:由于板面上处处受法向约束,故
z 0, z 0
不受切向面力作用,则
zx 0, zy 0,
故该薄板不属于平面应力状态。
ox y
0z y
zx 0, zy 0,
可见,其应变分量只有εx ,εy ,γxy 存在,且仅为x、y的函 数,所以其状态接近平面应变状态。
n l 1 l 2 ( 2 1 )
l 2 l 4 ( 2 1 )
1 4
(1 2
l2
)2
(
2
1
)
n
1 4
弹性力学-第二章 平面问题基本理论 (徐芝纶第五版)
平面应力问题
平面应变问题
3
1.平面应力问题
支承板
z x
y
(2) 受力特性
外力(体力、面力)和约束,仅平行于 板面作用,沿z方向不变化。
(1) 几何特性
一个方向的尺寸比另两个 方向的尺寸小得多。
——平板
4
1.平面应力问题
(3) 应力特征
由于板面上不受力,有
sx =sx(x,y)
sy =sy(x,y)
53
54
55
56
习题
57
第二章 教学参考资料 (一)本章学习要求及重点
本章系统地介绍了平面问题的基本理论: 基本方程和边界条件,及两种基本解法。这 些内容在弹性力学中具有典型性和代表性。 因此,学好平面问题的基本理论,就可以方 便地学习其他各章。为此,我们要求学生深 入地理解本章的内容,掌握好以下几点:
)
f
y
0.
68
(2)用位移表示的应力边界条件
E
1
2
[l
(
u x
v
y
)m12
(
u y
v x
)]s
fx,
E
1
2
[m(
v y
u
x
)l12
(
u y
v x
)]s
fy.
(在s 上ss)
69
(3)位移边界条件
(u)s u , (v)s v.
(在Su上)
70
4、按应力求解平面问题(平面应力问题),
应力分量 σ x , σ y ,t x必y 须满足下列全部条件:
sx =sx(x,y) sy =sy(x,y) txy =txy(x,y) sz =sz (x,y) txz =tyz =0
弹性力学第二章平面问题的基本理论

在应力约束 面上: 设 面法线与x轴正向夹角
的余玄为l,与y轴正向夹角
的余玄为m。
混合条件:
位移约束与应力约束的组合。
边界条件举例
x
y q
x
y
p
圣维南原理及其应用
圣 维 南 ( Adhémar Jean Claude Barré de Saint-Venant , 1797~1886)原理:如果把物体的一小部分边界上的面力, 变换为分布不同但静力等效的面力(主矢量相同,对于同 一点的主矩也相同),那么近处的应力分布将有显著改变, 但是远处所受的影响可以忽略不计。
— 边界条件
按位移求解平面应力问题(5)
— 小结
按位移求解平面问题需要:
1. 位移分量满足微分方程:
2.边界条件:
按位移求解平面问题(5)
— 举例
x
ρg
y=h y
按位移求解平面问题(6)
— 举例
x
ρg
y=h y
按应力求解平面应力问题(1)
— 用位移表达应变(几何方程)
形变协调方程或相容方程 连续体的形变分量不是相互独立的,它们之间必须满足 相容方程,才能保证真实的位移分量存在。
因此,由 中第一式:
最后得到:
由 中第二式:
常体力情况下的简化(5)
— 平衡方程的解
通解
特解
常体力情况下的简化(6)
— 艾里应力函数表示的相容方程
应力调和方程 代入
得到:
简写为:
常体力情况下的平面问题
常体力情况下的平面问题需要满足:
1.艾里应力函数表示的相容方程:
2.边界条件
3.位移单值条件
弹性力学第二章平面问题的基本理论
徐芝纶编《弹性力学简明教程》第四版,全部章节课后答案详解

弹性力学简明教程(第四版)课后习题解答徐芝纶第一章绪论【1-1】试举例说明什么是均匀的各向异性体,什么是非均匀的各向同性体?【分析】均匀的各项异形体就是满足均匀性假定,但不满足各向同性假定;非均匀的各向异性体,就是不满足均匀性假定,但满足各向同性假定。
【解答】均匀的各项异形体如:竹材,木材。
非均匀的各向同性体如:混凝土。
【1-2】一般的混凝土构件和钢筋混凝土构件能否作为理想弹性体?一般的岩质地基和土质地基能否作为理想弹性体?【分析】能否作为理想弹性体,要判定能否满足四个假定:连续性,完全弹性,均匀性,各向同性假定。
【解答】一般的混凝土构件和土质地基可以作为理想弹性体;一般的钢筋混凝土构件和岩质地基不可以作为理想弹性体。
【1-3】五个基本假定在建立弹性力学基本方程时有什么作用?【解答】(1)连续性假定:假定物体是连续的,也就是假定整个物体的体积都被组成这个物体的介质所填满,不留下任何空隙。
引用这一假定后,物体的应力、形变和位移等物理量就可以看成是连续的。
因此,建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。
完全弹性假定:假定物体是完全弹性的,即物体在对应形变的外力被去除后,能够完全恢复原型而无任何形变。
这一假定,还包含形变与引起形变的应力成正比的涵义,亦即两者之间是成线性关系的,即引用这一假定后,应力与形变服从胡克定律,从而使物理方程成为线性的方程,其弹性常数不随应力或形变的大小而变。
均匀性假定:假定物体是均匀的,即整个物体是由同一材料组成的,引用这一假定后整个物体的所有各部分才具有相同的弹性,所研究物体的内部各质点的物理性质都是相同的,因而物体的弹性常数不随位置坐标而变化。
各向同性假定:假定物体是各向同性的,即物体的弹性在所有各个方向都相同,引用此假定后,物体的弹性常数不随方向而变。
小变形假定:假定位移和变形是微小的。
亦即,假定物体受力以后整个物体所有各点的位移都远远小于物体原来的尺寸,而且应变和转角都远小于1。
第2章 平面问题的基本理论

例2(习题 ) (习题2-4) 按平面应变问题特征来分析, 按平面应变问题特征来分析, 本题中
ox
z
y
只有
ε x = ε x ( x, y ) ,ε y = ε y ( x, y ) ,γ xy = γ xy ( x, y )
思考题 设有厚度很大(即 向很长)的基础梁放置在地基上 的基础梁放置在地基上,如果 设有厚度很大 即 z 向很长 的基础梁放置在地基上 如果 想把它近似地简化为平面问题处理,问应如何考虑 问应如何考虑? 想把它近似地简化为平面问题处理 问应如何考虑
2、平面应变问题 (1) 几何特征: 几何特征: 常截面的柱体,长度>>截面的长 截面的长、 常截面的柱体,长度>>截面的长、宽; (2) 受力特征: ∥xy面,沿厚度不变; 受力特征: xy面 沿厚度不变; 体力f 作用于体内; 体力fx、fy作用于体内; 面力f 作用于柱面; 面力fx、fy作用于柱面; 约束u 作用于柱面。 约束u、v 作用于柱面。
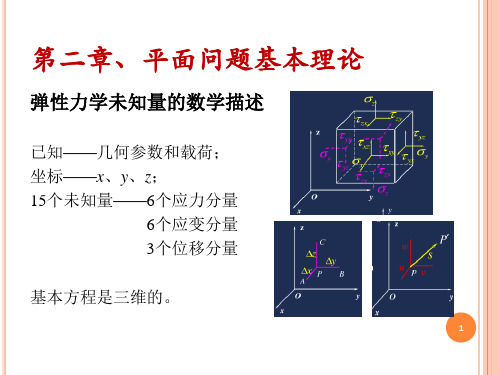
一、斜截面上的应力 求解: 边长 求解: AB=ds, PB=lds, PA=mds. AB=ds, PB=lds, PA= l=cos(n,x), m=sin(n,y) =cos(n =sin(n (1) 求(px,py)
2-3 平面问题中一点的应力状态
一、斜截面上的应力 l=cos(n,x), m=sin(n,y) =cos(n =sin(n (2) 求( σn , τn )
ω
─ 表示物体绕原点的刚体转动。 表示物体绕原点的刚体转动。
v = f 2 ( x ) = v0 + ω x
结论: 形变确定, 结论: 形变确定,位移不完全确定 : 从物理概念看, 、 确定 物体还可作刚体位移。 确定, 从物理概念看,ε、γ确定,物体还可作刚体位移。
弹性力学第二章平面问题的基本理论

圣维南定理
总结词
圣维南定理是弹性力学中的一个重要定理,它表明在弹性体的局部区域,改变内力的分布不会影响该 区域以外的应力分布。
详细描述
圣维南定理指出,在一个弹性体上施加一个集中力或分布力,只会影响该力作用点附近的应力分布, 而不会影响远离作用点的应力分布。这个定理在解决弹性力学问题时非常重要,因为它可以帮助我们 忽略某些局部细节,从而简化问题。
04
弹性力学的基本方程
平衡方程
平衡方程描述了弹性体在受力作用下的平衡状态,其数学表达式为:$frac{partial sigma_{xx}}{partial x} + frac{partial sigma_{xy}}{partial y} = 0$,其中 $sigma_{xx}$和$sigma_{xy}$分别为应力分量。
几何方程反映了物体在变形过程中满足连续性和均匀性的条 件,是解决弹性力学问题的重要基础。
本构方程
本构方程描述了应力与应变之间的关系,其数学表达式为: $sigma_{xx} = lambdaepsilon_{xx} + 2muepsilon_{xx}$, 其中$lambda$和$mu$分别为拉梅常数,$epsilon_{xx}$为 应变分量。
平面应变问题的应用场景
1 2 3
土木工程
在桥梁、建筑等土木工程结构中,常常需要考虑 平面应变问题,以分析结构的稳定性、承载能力 和抗震性能。
机械工程
在机械零件和设备的设计中,如板、壳等结构, 也需要考虑平面应变问题,以确保其在使用过程 中的安全性和稳定性。
地球科学
在地质工程、地震工程等领域,平面应变问题也 是重要的研究内容,用于分析地壳的应力分布、 地震波传播等。
弹性力学第二章平面问题的 基本理论
02《弹性力学》教案:第二章:平面问题的基本理论

二、弹性力学平面问题
弹性力学平面问题的特点有两个: ( 1) 、从几何尺寸的角度看,物体一个方向的尺寸,较之其它两个方向的尺 寸要大得多,或小得多。 ( 2) 、从受力分析的角度看,物体所受的体力分量和面力分量,以及由此产 生的应力分量、应变分量和位移分量,都与某一个坐标轴(例如 z 轴)无关。 有 两 种 典 型 情 况 , 分 别 是 平 面 应 力 问 题 ( pla ne s tre ss pr obl e m ) 和 平 面 应 变 问 题 ( pla ne stra i n pr obl e m ) 。分别讨论。 1、 平 面 应 力 问 题 几 何 尺 寸 : 物 体 是 很 薄 的 等 厚 度 平 板 , 沿 z 方 向 的 厚 度 为 t; 沿 x 方 向 和 y 方 向的尺寸,远大于厚度 t。 坐 标 系 : 以 薄 板 的 中 面 为 xoy 面 , z 轴 垂 直 于 xoy 面 。 受力特点:体力作用于板内,平行于板面且不沿厚度变化, ( X、Y) ,沿厚 度均匀分布。 面力作用于板边,平行于板面且不沿厚度变化, ( X 、Y ) ,沿厚 度均匀分布。
σ x = σ x ( x, y ) , 则 在 c d 面 上 , 由 于 长 度 增 加 了 dx , 则 c d 面 上 的 正 应 力 分 量 应 随
之 变 化 。应 力 分 量 的 这 种 变 化 可 用 泰 勒 级 数 展 开 求 得 。实 际 上 ,在 c d 面 上 ,我 们 有
σ x ( x + dx, y ) = σ x ( x, y ) +
11
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
弹性力学第二章平面问题的基本理论

位移边界条件
位移边界条件描述了物体边界上的位 移情况,即位移函数。这些条件规定 了物体在某些特定方向上的位移限制 ,例如固定、自由或受限制的位移。
位移边界条件对于确定物体的变形和 应力分布具有重要意义,特别是在解 决结构分析问题时,这些条件有助于 确定结构的刚度和稳定性。
平衡方程的数学表达式为
div F = 0,其中 F 是应力向量,div 是散度算子。
几何方程
它由两个部分组成
一部分是位移引起的形变,另一部分是应力引起的形变。
几何方程的数学表达式为
grad u = 0,其中 u 是位移向量,grad 是梯度算子。
物理方程
它由两个部分组成
一部分是线性弹性关系,另一部分是材料常数。
物理方程的数学表达式为
sigma = D*epsilon,其中 sigma 是应力矩阵,D 是弹性矩阵,epsilon 是应变矩阵。
03
平面问题的边界条件
应力边界条件
应力边界条件描述了物体边界上的应力分布情况,即应力函 数。在弹性力学中,应力边界条件通常由应力分量来表示, 这些分量与物体表面的外力有关。
近似法
近似法是通过近似的方式来 求解弹性力学平面问题的一
种方法。
1
它通常适用于无法通过解析 法和数于弹性力学的基本 方程和边界条件,通过物理 模型、经验公式等方式进行 近似求解。
近似法的优点是简便易行, 能够快速得到近似解,但缺 点是精度难以保证,可能存 在误差较大的情况。
地震工程
在地震工程中,弹性力学用于研究地震波在结构 中的传播和响应,为抗震设计和减震措施提供依 据。
弹性力学2第二章_平面问题的基本理论
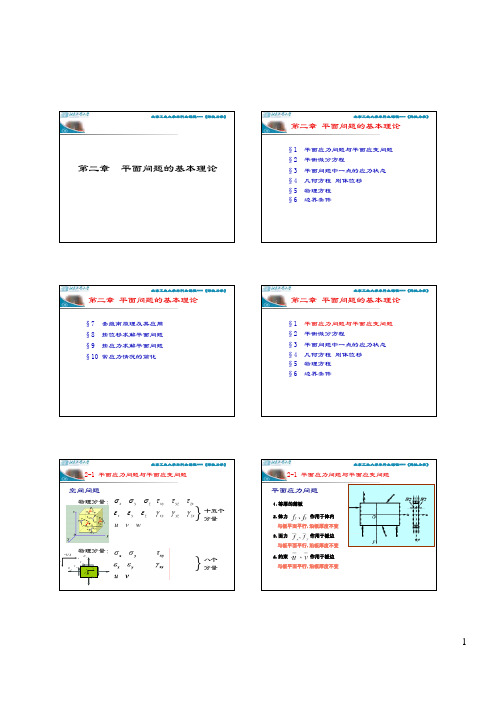
(2-4)
( ) τ n = lm σ y − σ x + (l 2 − m 2 )τ xy (2-5)
(4) τ n = 0 , 主应力和主应力方向;
(5)最大与最小切应力;
北京工业大学本科生课程---《弹性力学》
2.3 平面问题中一点的应力状态
o
τ
τ
xy
yx
σx τn
σy x
px σn
y
py p n
dy
y
方向上的位移为:
v
+
∂v ∂y
dy
切应变: γ = α + β
线段PA线应变:
εx
=
M1A1 − MA MA
=
u
+
∂u dx ∂x
dx
−u
=
∂u ∂x
北京工业大学本科生课程---《弹性力学》
2.4 几何方程(应变-位移) 刚体位移
u
P
v d y P1
dx
v
+
∂v
B dy
∂y
β
B1
u + ∂u dy ∂y
=
sin α 2 cosα 2
=
m2 l2
=
τ xy σ2 −σ y
tan α 1 ⋅ tan α 2 = −1
北京工业大学本科生课程---《弹性力学》
2.3 平面问题中一点的应力状态
(5)最大与最小切应力;
由(2-5)可以得到
τ n = lm(σ 2 − σ1)
l2 + m2 =1
τn = ±l
1− l 2 (σ 2 − σ1) = ±
北京工业大学本科生课程---《弹性力学》
弹性力学平面问题总结

P
思考题
① 试证明微分体绕 z 轴的平均转动分量是
1 2 v x u . y
② 当应变为常量时,x=a, y=b, xy=c, 试 求对应的位移分量。
第二章 平面问题的基本理论
2-1 平面应力问题与平面应变问题 2-2 平衡微分方程 2-4 几何方程 刚体位移 2-5 物理方程
物理方程
物理方程描述应力分量和应变分量之间
z
x
y
z
x
y
xy
zx
zy
1 G 1 G 1 G
xy ,
xy
) E
0,
xy ,
zx ,
zx
zy .
zy
0.
物理方程
平面应力问题的物理方程:
x
y
1 E 1 E 2(1
x
y
, ,
y
x
) E
xy
xy .
此外, z
E
x
y
,
zx
zy
0.
平面应力问题,虽然 σz=0,但一般 εz≠0。
物理方程
平面应变问题: z
0,
(在V 中)
xy 存在。
故只有平面应力 σx , σy ,
平面应力问题
(2) 由于板为等厚度,外力、约束沿 z 向不变, 故应力 x , y , xy 仅为 f x , y 。
所以归纳为平面应力问题:
a.应力中只有平面应力 x , y , xy 存在;
b.且仅为 f x , y 。
几何方程
平面问题中的几何方程:
x
u , x
y
v , y
xy
v x
u . y
当弹性体的位移分量完全确定时,应变分 量即完全确定。反之,当应变分量完全确定时, 位移分量却不能完全确定。
《弹性力学》第二章_平面问题的基本理论

o
xy
x
y
P
yx
y
A
XN
x
设AB面在xy平面内的长度为dS, 厚度为一个单位长度,N为该面的外 法线方向,其方向余弦为:
B
N
N
N
cos(N , x) l , cos(N , y) m
9
YN S
图2 - 4
斜面AB上全应力沿x轴及y轴的投影分别为XN和YN。由PAB 的平衡条件 Fx 0 可得: X N dS xldS yxmdS
2.主应力的方向
1 与 2 互相垂直。
11
§2-4
几何方程、刚体位移
在平面问题中,弹性体中各点都可能产生任意方向的位移。 通过弹性体内的任一点P,取一单元体PAB,如图2-5所示。弹性 体受力以后P、A、B三点分别移动到P′、A′、B′。 一、P点的正应变
u (u dx) u u x x dx x
二、P点的剪应变
线段PA的转角:
同理可得线段PB的转角:
u y
所以
xy
v u x y
13
因此得到平面问题的几何方程:
u x x v y y v u xy x y
由几何方程可见,当物体的位移分量完全确定时,形变 分量即可完全确定。反之,当形变分量完全确定时,位移分 量却不能完全确定。
z
E
( x y )
16
二、平面应变问题的物理方程 1 2 x ( x y ) E 1 1 2 y ( y x ) E 1 2(1 ) xy xy E 三、平面应力的应力应变关系式与平面应变的关系式之间的 变换关系 1 ( ) y 将平面应力中的关系式: x E x
第二章平面问题的基本理论

第二章平面问题的基本理论两类平面问题平面问题的基本方程平面问题的边界条件圣维南原理两种求解途径1. 两类平面问题的基本概念一般情况下,弹性力学问题都是空间问题,但是,当弹性体具有某种特殊形状,受有某种特殊的外力时,空间问题可以简化为平面问题,即弹性体的几何参数和所受的外力只是二维坐标(例如x ,y )的函数(与z 无关);只需要确定oxy 平面内的应力、应变和位移分量(且只是x 、y 的函数),其它分量或不存在、或可用oxy 平面内的分量表示出来;所得基本方程也都是二维的。
平面问题分两种情况,平面应力问题和平面应变问题。
这两类平面问题的基本特征见表2-1。
图2-1图2-2综上所述,无论是平面应力问题,还是平面应变问题,它们所具有的独立未知量是相同的,3个应力分量(xy t x τσσ,,)、3个应变分量(xy y x γεε,,)、2个位移分量(v u ,),并且都是x ,y 的函数,与z 无关。
2. 平面问题的基本方程解答弹性力学问题必须从静力学、几何学和物理学三个方面考虑,建立其基本方程。
(1)平衡微分方程 从弹性体内任一点取出微元体,建立弹性体内一点的应力分量与体力分量之间的关系。
得到平衡微分方程。
,0=+∂∂+∂∂=+∂∂+∂∂Y yxX y x y xy yxx σστσ. (2-1)(2)几何方程三个应变分量与两个位移分量之间的关系。
x v y u yv xuxy y x ∂∂+∂∂=∂∂=∂∂=γεε,,. (2-2)注意:① 从几何方程(2-2)可以看到,三个应变分量由两个位移分量表示,这说明三个应变分量之间要满足一定的协调关系,不能任意选取。
这个协调关系称为相容方程:.22222y x x y xyy x ∂∂∂=∂∂+∂∂γεε (2-3)② 对按应力求解弹性力学问题来说,由于两个平衡微分方程中含有三个应力分量,所以相容方程(2-3)是必须满足的基本方程之一。
否则,就不能由所给出的应力求出连续的位移。
第2章 平面问题的基本理论
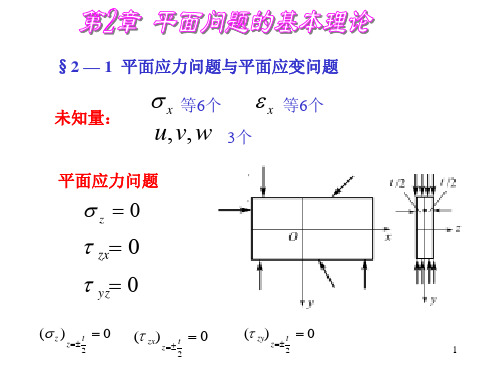
(l 2σ x + m 2σ y + 2l mτ xy ) 2
13
设经过P点的某一斜面上的切应力等于零,则该斜 面上的正应力称为P点的一个主应力,而该斜面称 为P点的一个应力主面,该斜面的法线方向(即主 应力的方向)称为P点的一个应力主向。
t x = lσ lσ x + mτ xy = lσ t y = mσ mσ y + lτ xy = mσ
,
9
∫ ∫ ∫
h/2
−h / 2 h/2
σx τ xy
x =l
dy = P dy = Q dy = M
−h / 2 h/2
x =l
−h / 2
yσ x
x =l
10
§2 — 7 按位移求解平面问题 平衡方程:
E ∂ 2u 1 − υ ∂ 2u 1 + υ ∂ 2 v ( 2 + + ) + fx = 0 2 2 2 ∂y 2 ∂x∂y 1 − υ ∂x E ∂ 2 v 1 − υ ∂ 2 v 1 + υ ∂ 2u ( 2 + + ) + fx = 0 , 2 2 2 ∂x 2 ∂x∂y 1 − υ ∂y
弹性力学:微分体平 衡 思考题: 思考题:
微分体上的应力按线性分布,试推导平衡方程 不取规则的微分体,而取任意形状脱离体 能否建立相同的平衡方程 在边界上取微分体,力矩平衡会导致什么结果
5
§2 — 3 几何方程 刚体位移
εx =
εy =
,
∂u ∂x
∂v ∂y
, ,
,
γ xy
∂v ∂u = + ∂x ∂y
平面应力问题和平面应变问题都适用 适用条件:连续性,小变形
第2章 平面问题的基本理论汇总

t= 1
平面应力:z方向应力为零。 平面应变:z方向应力自成平衡。
应用的基本假定: 连续性假定─应力用连续函数来表示。 小变形假定─用变形前的尺寸代替
变形后的尺寸。
二、平衡微分方程(平面任意力系)
合力 = 应力×面积,体力×体积; 以正向物理量来表示。
平面问题中可列出三个平衡条件:
例2(习题2-4) 按平面应变问题特征来分析, 本题中
ox z
y
只有
x x x, y , y y x, y , xy xy x, y
思考题 设有厚度很大(即 z 向很长)的基础梁放置在地基上,如果
想把它近似地简化为平面问题处理,问应如何考虑?
2-2 平面问题的平衡微分方程
将(px,py)向法向、切向投影,得
2-3 平面问题中一点的应力状态
一、斜截面上的应力
2-3 平面问题中一点的应力状态
一、斜截面上的应力
2-4 几何方程 刚体位移
一、几何方程:表示应变与位移之间的关系
x x x, y , y y x, y , xy xy x, y u u x, y,v v x, y
罗建辉
第二章
平面问题的 基本理论
2-1 平面应力问题和平面应变问题
一、弹性力学空间问题的简化
(在特定的条件下)
空间问题
平面问题
二、弹性力学平面问题
1、平面应力问题 (1) 几何特征:
等厚度的薄板,厚度<<长、宽; (2) 受力特征: ∥xy面,沿板厚不变;
体力fx、fy作用于体内; 面力fx、fy作用于板边; 约束u、v 作用于板边。
思考题
1.试检查,同一方程中的各项,其量纲必然相同(可用来 检验方程的正确性)。
《弹性力学》第二章平面问题的基本理论

平面问题研究方法
01
02
03
解析法
通过弹性力学的基本方程 和边界条件,求解出满足 条件的应力、应变和位移 分量。
数值法
利用计算机进行数值计算, 如有限元法、差分法等, 求解出弹性体的应力、应 变和位移分布。
实验法
通过实验手段,如光弹性 实验、应变电测实验等, 直接测定弹性体的应力、 应变和位移。
02 基本方程与定解条件
物理方程反映了材料的力学性质,是弹性力学中的重要基础。
03
定解条件(边界条件与初始条件)
01
02
03
定解条件是弹性力学问 题中必须满足的附加条 件,包括边界条件和初
始条件。
边界条件描述了物体边 界上的应力、位移等物 理量的已知情况,是求 解弹性力学问题的重要
依据。
初始条件描述了物体在 初始时刻的应力、位移 等物理量的已知情况, 对于动态问题和瞬态问
04 平面问题解法及实例分析
按位移求解平面问题
位移边界条件
在位移边界上,物体受到的约束可以 转化为在给定位移边界上各点的位移。
平衡微分方程
根据弹性力学的基本方程,可以建立 以位移表示的平衡微分方程。
应力边界条件
在应力边界上,物体受到的面力可以 转化为应力边界上各点的应力分量。
求解方法
通过联立平衡微分方程和应力边界条 件,可以求解出位移分量,进而求得 应力分量。
复杂应力函数求解技巧
复杂应力函数的特点
复杂应力函数可能具有复杂的数学形式和边界条件,求解难度较大。
求解技巧
针对复杂应力函数的求解,可以采用变量分离法、积分变换法、复 变函数法等数学工具进行简化处理,降低求解难度。
实例分析
以一个复杂的弹性力学问题为例,介绍如何运用上述技巧求解复杂 应力函数,并给出相应的应力分量分布图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.3 一点的应力状态和主应力 2.3 .1一点的应力状态 一点的应力状态 设 任 一 点 P 在 坐 标 轴 上 的 应 力 分 量 σx,σy,τxy 已 知 , 见 σ τ Fig.2.4(a), 试求经过该点 平行于 轴,而倾斜于 和 y 轴的任意斜面 试求经过该点, 平行于z 而倾斜于x 而倾斜于 上的应力。 上的应力。 我们取一个面AB ,平行于上述斜面 并与经过 点而垂直于 和 y 平行于上述斜面, 点而垂直于x 我们取一个面 平行于上述斜面 并与经过P点而垂直于 轴的两个平面划出一个微小的三角板或三棱柱PAB, 见图 见图2.4(b). 轴的两个平面划出一个微小的三角板或三棱柱 用 n 代表 AB面的外法线 用l 和 m 表示法线n 和 x , y 之间的角 面的外法线, 表示法线 面的外法线 度的方向余弦, 度的方向余弦
Shaft
Dam
如图2.2所示, 所示, 如图 所示 (1) 以任一横截面为 xy 面, 任一纵线为 轴, 任一纵线为z轴 则所有一切应力分量、 则所有一切应力分量、形变分量和位移分量 都不沿z方向变化 而只是x 方向变化, 的函数。 都不沿 方向变化 而只是 和 y 的函数。 (2) 由于对称性 在z轴方向上不能有任何位移和形变, 由于对称性, 轴方向上不能有任何位移和形变, 轴方向上不能有任何位移和形变 图2.2 故有w = 0 和εz = 0。 故有 。 (3) 由于对称性,应有 τ xz = 0 , τ yz = 0 . 由于对称性, 又有剪应力互等定理有
2
= 0,
(τ zy )
z =±
δ
2
= 0.
由于板很薄, 外力不沿厚度变化, 应力沿板的厚度又是连续分布, 由于板很薄 外力不沿厚度变化 应力沿板的厚度又是连续分布 因此, 因此 可以认为薄板所有的点都有
σ z = 0,
τ zx = τ xz = 0 ,
τ zy = τ yz = 0.
即,平面应力状态只有三个应力分量: σx,σy 和 τxy=τyx 平面应力状态只有三个应力分量
τ zx = 0 , τ zy = 0 .
ε z = γ zy = γ zx = 0
(4)由于胡克定律,有 γ zx = γ zy 。 由于胡克定律, 由于胡克定律 因此只有三个形变分量
{ε } = {ε x ε y γ xy }
2.2 平衡微分方程
从 图2.1的板中 或图2.2 柱形体中, 取出一个微小正平行六面体, 的板中 或图 柱形体中 取出一个微小正平行六面体 它在x 它在 方向 和y方向 的 尺寸分别是 dx and dy (见图 2.3)。为简便 方向 见图 。为简便, Z方向的尺寸取单位长度。 方向的尺寸取单位长度。 方向的尺寸取单位长度 一般地说, 的函数, 一般地说 应力分量是 x 和 y的函数 因此作用在左右两面 或 上下 的函数 两面的应力分量是不相同的. 例如, 两面的应力分量是不相同的 例如 设左侧的 正应力 是 σx , 则作用 在右侧的应力分量, 坐标的改变, 可以用Taylor’s 级数表示如 在右侧的应力分量 由于 x 坐标的改变 可以用 下: 2
两边除于dxdy, 并合并相同的项, 得
τ xy
1 ∂τ xy 1 ∂τ yx + dx = τ yx + dy 2 ∂x 2 ∂y
略去微小量, 得
τ xy = τ yx
(2.1)
其次, 以 x 轴为投影轴,列出力的平衡方程 ΣFx =0
∂σ x dx dy × 1 − σ x dy × 1 + σ x + ∂x ∂τ τ yx + yx dy dx × 1 − τ yx dx × 1 + f x dxdy × 1 = 0 ∂y
在应力主面, 由于剪应力等于零, 在应力主面 由于剪应力等于零 全应力就等于该面上的 正应力, σ,即 =p.这样 这样, 正应力 也就是主应力 σ,即σ=p.这样,它在 x 和 y 轴上的 投影为 p x = lp = lσ , p y = mp = mσ 将(2.3)代入, 即得 lσ = lσ x + mτ xy , 解出比值m/l , 得
设通过P点的某一斜面上的 剪应力 等于零, 那这个面 就叫做在 P点的应力主面 principal plane of stress), 而这 应力主面( 应力主面 个面的 主应力被叫做在P点的主应力 principal stress), 主应力( 主应力 该斜面的法线方向称为在P 点的主应力主向。 主应力主向。 主应力主向
∂σ x ∂τ yx + + f x = 0 ∂x ∂y ∂σ y ∂τ xy + + f y = 0 ∂y ∂x
在这两个方程中, 包含3个未知量 个未知量, 在这两个方程中 包含 个未知量 即 σx,σy andτxy=τyx. 因此 σ τ τ 因此, 确定应力分量的弹性问题是超静定的,要解出未知应力分量, 确定应力分量的弹性问题是超静定的,要解出未知应力分量, 还 要考虑几何和物理关系. 要考虑几何和物理关系
σy +
∂σ y ∂y dy
τ yx +
∂τ yx ∂y
dy
以通过中心点C 面的直线为轴, 列出力矩的平衡方程: 以通过中心点 并垂直于 xy 面的直线为轴 列出力矩的平衡方程: ΣMC =0
∂τ xy dx dx τ xy + dy × 1 × dx + τ xy dy × 1 × − 2 2 ∂x ∂τ yx dy dy τ yx + − τ yx dx × 1 × =0 dy dx × 1 × ∂y ∂y 2 2
2
(2.6)
从 Eqs.(2.6), 我们可推出 σ1 + σ 2 = σ x + σ y 设α1 为σ1 和 x axis 之间的夹角, 如 图 α 1 cos(90 0 − α 1 ) m1 tan α 1 = = = cos α 1 cos α 1 l1 这里 l1 and m1 是are σ1 的方向余弦. 利用公式 (a)中的第一式, 可得 σ1 − σ x tan α 1 = (a) τ
2.1.2 平面应变问题 平面应变问题(plane strain problem) 设有很长的柱形体, 它的横截面不沿长度变化, 设有很长的柱形体 它的横截面不沿长度变化 在柱面上受 有平行于横截面并且不沿长度变化的面力或约束。同时, 有平行于横截面并且不沿长度变化的面力或约束。同时 体力 也平行于横截面并且不沿长度变化, 则这种情况叫平面应变。 也平行于横截面并且不沿长度变化 则这种情况叫平面应变。
p x ds − σ x lds − τ xy mds + f x ldsmds =0 2
向分量, 趋向零, 这里 fx 是 体积力 沿x 向分量,上式除于 ds, 然后令 ds 趋向零 即得
p x = lσ x + mτ xy
同样可以由力的平衡Σ 得出一个相似的方程, 同样可以由力的平衡ΣFy =0, 得出一个相似的方程,总共得两个方 程:
工程实例
如图2.1所示,假定薄板的厚度为δ,以 所示,假定薄板的厚度为 , 如图 所示 薄板的中面为 x y面 ,以垂直于中面的任 以垂直于中面的任 因为板面上( 一直线为 z 轴. 因为板面上 不受力, 不受力 所以有
z = ±
δ
2
)
图2.1
(σ z )
z =±
δ
2
=0,
(τ zx )
z =±
δ
(2.4)
设斜面AB上的剪应力为 设斜面 上的剪应力为τn.则由 px and py 在垂直法线 n 方向上的投 则由 影得: 影得
τ n = lp y − mp x
将式(2.3)代入 即得 代入,即得 将式 代入
τ n = lm(σ y − σ x ) + (l 2 − m 2 )τ xy
(2.5)
2 .4 几何方程 刚体位移
2.4.1几何方程 现在考虑几何学方面的问题. 几何方程: 几何方程 在弹性体中的任一点 P , 沿坐标轴正方向取两个微小长度的线 段 PA=dx 和PB=dy (图2.5). 物体变形后, 点 P, A, B 移动到 P’, A’, B’. 设点P 在x 轴方向的位移是u, 则点A在x 轴方向的位移是 ∂u u+ dx ∂x 可见线段PA的线应变是 ∂u dx − u u + ∂u ∂x = εx = dx ∂x
mσ = mσ y + lτ xy
m σ −σ x = , l τ xy
τ xy m = l σ −σ y
(a)
于是得
2 (σ − σ x )(σ − σ y ) = τ xy
于是可得二次方程
2 σ 2 − (σ x + σ y )σ + (σ xσ y − τ xy ) = 0
我们知道二次方程
ax + bx + c = 0
cos(n, x) = l
cos(n, y) = m
图2.4
并用 px and py 代表斜面AB 上的全应力p在 x 和 y 轴上的投影。 代表斜面 上的全应力 在 轴上的投影。 假设AB的 长 是 ds, 则面PB 和 PA 的 长度 分别是 lds 和 mds, 而 假设 的 则面 PAB的面积 是 ldsmds/2. z 向的尺寸还取单位1, 由力的平衡ΣFx =0 的面积 向的尺寸还取单位 由力的平衡 给出
p x = lσ x + mτ xy ,
p y = mσ y + lτ xy
(2.3)
的投影得 设斜面AB上的 正应力 是σn , 则由 px and py 在法线 n 的投影得: 设斜面
σ n = lp x + mp y
