2012年全国高考文科数学考试试题-重庆卷
2012年高考试题:文科数学(全国卷)——含答案及解析

2012年普通高等学校招生全国统一考试文科数学(必修+选修Ⅰ)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷3至4页。
考试结束后,将本卷和答题卡一并交回。
第Ⅰ卷注意事项:1、答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码。
请认真核准条形码上的准考证号、姓名和科目。
2、每小题选出答案后,用2B 铅笔把答题卡上对应题目答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。
3、第Ⅰ卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项符合题目要求。
一、选择题(1)已知集合{|}{|}{|}{|}A x xB x xC x xD x x ==是平行四边形,是矩形,是正方形,是菱形,则( ).()()()()A A B B C B C D C D A D⊆⊆⊆⊆【考点】集合【难度】容易【点评】本题考查集合之间的运算关系,即包含关系。
在高一数学强化提高班上学期课程讲座1,第一章《集合》中有详细讲解,在高考精品班数学(文)强化提高班中有对集合相关知识的总结讲解。
(2)函数1(1)y x x =+-≥的反函数为( ). 2()1(0)A yx x =-≥ 2()1(1)B yx x =-≥ 2()1(0)C yx x =+≥ 2()1(1)D yx x =+≥ 【考点】反函数【难度】容易【点评】本题考查反函数的求解方法,注意反函数的定义域即为原函数的值域。
在高一数学强化提高班上学期课程讲座1,第二章《函数与初等函数》中有详细讲解,在高考精品班数学(文)强化提高班中有对函数相关知识的总结讲解。
(3)若函数()s i n [0,2]3x fx ϕϕ+=∈(π)是偶函数,则ϕ=( ).()2A π 2()3B π 3()2C π 5()3D π 【考点】三角函数与偶函数的结合【难度】中等【点评】本题考查三角函数变换,及偶函数的性质。
2012年(全国卷II)(含答案)高考文科数学

2012年普通高等学校招生全国统一考试(2全国卷)数学(文)试题一、选择题 ( 本大题 共 12 题, 共计 60 分)1.已知集合A ={x |x 是平行四边形},B ={x |x 是矩形},C ={x |x 是正方形},D ={x |x 是菱形},则( )A .AB B .CB C .DC D .AD2.函数1y x =+x ≥-1)的反函数为( ) A .y =x 2-1(x ≥0) B .y =x 2-1(x ≥1) C .y =x 2+1(x ≥0) D .y =x 2+1(x ≥1) 3.若函数()sin 3x f x ϕ+=(φ∈[0,2π])是偶函数,则φ=( ) A .π2B .2π3C .3π2D .5π34.已知α为第二象限角,3sin 5α=,则sin2α=( ) A .2425-B .1225-C .1225D .2425 5.椭圆的中心在原点,焦距为4,一条准线为x =-4,则该椭圆的方程为( )A .2211612x y += B .221128x y += C .22184x y += D .221124x y += 6.已知数列{a n }的前n 项和为S n ,a 1=1,S n =2a n +1,则S n =( )A .2n -1B .13()2n -C .12()3n -D .112n -7. 6位选手依次演讲,其中选手甲不在第一个也不在最后一个演讲,则不同的演讲次序共有( )A .240种B .360种C .480种D .720种8.已知正四棱柱ABCD -A 1B 1C 1D 1中,AB =2,122CC =E 为CC 1的中点,则直线AC 1与平面BED 的距离为( )A.2 BC .2D.19.△ABC中,AB边的高为CD.若CB=a ,CA=b,a·b=0,|a|=1,|b|=2,则AD=()A.1133-a b B.2233-a bC.3355-a b D.4455-a b10.已知F1,F2为双曲线C:x2-y2=2的左、右焦点,点P在C上,|PF1|=2|PF2|,则cos∠F1PF2=()A.14B.35C.34D.4511.已知x=ln π,y=log52,12=ez-,则()A.x<y<z B.z<x<yC.z<y<x D.y<z<x12.正方形ABCD的边长为1,点E在边AB上,点F在边BC上,AE=BF=13.动点P从E出发沿直线向F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当点P第一次碰到E时,P与正方形的边碰撞的次数为() A.8 B.6 C.4 D.3二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.13.(x+12x)8的展开式中x2的系数为__________.14.若x,y满足约束条件10,30,330, x yx yx y-+≥⎧⎪+-≤⎨⎪+-≥⎩则z=3x-y的最小值为__________.15.当函数y=sin x x(0≤x<2π)取得最大值时,x=__________.16.已知正方体ABCD-A1B1C1D1中,E,F分别为BB1,CC1的中点,那么异面直线AE与D1F所成角的余弦值为__________.三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.△ABC中,内角A,B,C成等差数列,其对边a,b,c满足2b2=3ac,求A.18.已知数列{a n}中,a1=1,前n项和23n nnS a+=.(1)求a2,a3;(2)求{a n}的通项公式.19.如图,四棱锥P-ABCD中,底面ABCD为菱形,P A⊥底面ABCD,AC=P A=2,E是PC上的一点,PE=2EC.(1)证明:PC⊥平面BED;(2)设二面角A-PB-C为90°,求PD与平面PBC所成角的大小.20.乒乓球比赛规则规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换.每次发球,胜方得1分,负方得0分.设在甲、乙的比赛中,每次发球,发球方得1分的概率为0.6,各次发球的胜负结果相互独立.甲、乙的一局比赛中,甲先发球.(1)求开始第4次发球时,甲、乙的比分为1比2的概率;(2) 求开始第5次发球时,甲得分领先的概率.21.已知函数f(x)=13x3+x2+ax.(1)讨论f(x)的单调性;(2)设f(x)有两个极值点x1,x2,若过两点(x1,f(x1)),(x2,f(x2))的直线l与x 轴的交点在曲线y=f(x)上,求a的值.22.已知抛物线C:y=(x+1)2与圆M:(x-1)2+(y-12)2=r2(r>0)有一个公共点A,且在A处两曲线的切线为同一直线l.(1)求r;(2)设m,n是异于l且与C及M都相切的两条直线,m,n的交点为D,求D到l的距离.2012年普通高等学校招生全国统一考试(2全国卷)数学(文)试题答案解析:1. B ∵正方形组成的集合是矩形组成集合的子集, ∴C B .2. A ∵1y x =+∴y 2=x +1, ∴x =y 2-1,x ,y 互换可得:y =x 2-1. 又∵10y x =+≥.∴反函数中x ≥0,故选A 项. 3.C ∵()sin3x f x ϕ+=是偶函数,∴f (0)=±1. ∴sin 13ϕ=±.∴ππ32k ϕ=+(k ∈Z).∴φ=3k π+3π2(k ∈Z). 又∵φ∈[0,2π],∴当k =0时,3π2ϕ=.故选C 项. 4.A ∵3sin 5α=,且α为第二象限角, ∴24cos 1sin 5αα=-=--.∴3424sin22sin cos 25525ααα⎛⎫==⨯⨯-=- ⎪⎝⎭.故选A 项. 5. C ∵焦距为4,即2c =4,∴c =2.又∵准线x =-4,∴24a c-=-.∴a 2=8.∴b 2=a 2-c 2=8-4=4.∴椭圆的方程为22184x y +=,故选C 项.6.B 当n =1时,S 1=2a 2,又因S 1=a 1=1,所以21 2a=,213 122S=+=.显然只有B项符合.7.C由题意可采用分步乘法计数原理,甲的排法种数为14A,剩余5人进行全排列:55A,故总的情况有:14A·55A=480种.故选C 项.8.D连结AC交BD于点O,连结OE,∵AB=2,∴AC=又1CC=AC=CC1.作CH⊥AC1于点H,交OE于点M.由OE为△ACC1的中位线知,CM⊥OE,M为C H的中点.由BD⊥AC,EC⊥BD知,BD⊥面EOC,∴CM⊥BD.∴CM⊥面BDE.∴HM为直线AC1到平面BDE的距离.又△AC C1为等腰直角三角形,∴CH=2.∴HM=1.9.D∵a·b=0,∴a⊥b.又∵|a|=1,|b|=2,∴||5AB=.∴||5CD==.∴2||25AD ==. ∴4544445()5555AD AB AB ===-=-a b a b .10. C 设|PF 2|=m ,则|PF 1|=2m , 由双曲线定义|PF 1|-|PF 2|=2a , ∴2m -m=.∴m 又24c ==, ∴由余弦定理可得cos ∠F 1PF 2=2221212||||432||||4PF PF c PF PF +-=.11. D ∵x =ln π>1,y =log 52>1log 2=,121e2z -==>=,且12e -<e 0=1,∴y <z <x . 12. B 如图,由题意:tan ∠BEF =12, ∴2112KX =,∴X 2为HD 中点,2312X D X D =,∴313X D =, 4312X C X C =,∴413X C =, 5412X H X H =,∴512X H =, 5612X A X A =,∴613X A =,∴X 6与E 重合,故选B 项. 13.答案:7 解析:∵(x +12x )8展开式的通项为T r +1=8C r x 8-r(12x)r =C r 82-r x 8-2r,令8-2r =2,解得r =3.∴x 2的系数为38C 2-3=7.14.答案:-1解析:由题意画出可行域,由z =3x -y 得y =3x -z ,要使z 取最小值,只需截距最大即可,故直线过A (0,1)时,z 最大.∴z max =3×0-1=-1. 15.答案:5π6解析:y =sin xx=1π2(sin )2sin()23x x x =-. 当y 取最大值时,ππ2π32x k -=+,∴x =2k π+5π6.又∵0≤x <2π,∴5π6x =. 16.答案:35解析:设正方体的棱长为a .连结A 1E ,可知D 1F ∥A 1E ,∴异面直线AE 与D 1F 所成的角可转化为AE 与A 1E 所成的角, 在△AEA 1中,2222213cos 5a a a a a AEA ⎛⎫⎛⎫+++- ⎪ ⎪∠==. 17.解:由A ,B ,C 成等差数列及A +B +C =180°,得B =60°,A +C =120°.由2b 2=3ac 及正弦定理得2sin 2B =3sin A sin C , 故1sin sin 2A C =.cos(A +C )=cos A cos C -sin A sin C =cos A cos C -12, 即cos A cos C -12=12-,cos A cos C =0, cos A =0或cos C =0,所以A =90°或A =30°.18.解:(1)由2243S a =得3(a 1+a 2)=4a 2,解得a 2=3a 1=3; 由3353S a =得3(a 1+a 2+a 3)=5a 3,解得a 3=32(a 1+a 2)=6. (2)由题设知a 1=1.当n >1时有a n =S n -S n -1=12133n n n n a a -++-, 整理得111n n n a a n -+=-. 于是a 1=1,a 2=31a 1,a 3=42a 2,… a n -1=2nn -a n -2,a n =11n n +-a n -1.将以上n 个等式两端分别相乘,整理得(1)2n n n a +=. 综上,{a n }的通项公式(1)2n n n a +=. 19.解法一:(1)证明:因为底面ABCD 为菱形,所以BD ⊥AC .又P A ⊥底面ABCD , 所以PC ⊥BD . 设AC ∩BD =F ,连结EF .因为AC =P A =2,PE =2EC ,故PC =3EC =,FC = 从而PC FC =,ACEC =, 因为PC ACFC EC=,∠FCE =∠PCA , 所以△FCE ∽△PCA ,∠FEC =∠P AC =90°, 由此知PC ⊥EF .PC 与平面BED 内两条相交直线BD ,EF 都垂直,所以PC ⊥平面BED .(2)在平面P AB 内过点A 作AG ⊥PB ,G 为垂足.因为二面角A -PB -C 为90°,所以平面P AB ⊥平面PBC . 又平面P AB ∩平面PBC =PB ,故AG ⊥平面PBC ,AG ⊥BC . BC 与平面P AB 内两条相交直线P A ,AG 都垂直, 故BC ⊥平面P AB ,于是BC ⊥AB ,所以底面ABCD 为正方形,AD =2,2222PD PA AD =+=. 设D 到平面PBC 的距离为d .因为AD ∥BC ,且AD 平面PBC ,BC 平面PBC ,故AD ∥平面PBC ,A ,D 两点到平面PBC 的距离相等,即d =AG 2.设PD 与平面PBC 所成的角为α,则1sin 2d PD α==. 所以PD 与平面PBC 所成的角为30°.解法二:(1)证明:以A 为坐标原点,射线AC 为x 轴的正半轴,建立如图所示的空间直角坐标系A -xyz .设C (220,0),D 2,b,0),其中b >0, 则P (0,0,2),E (23,0,23),B 2b,0). 于是PC =(220,-2),BE =(23,b ,23),DE =(23,-b ,23),从而0PC BE ⋅=,0PC DE ⋅=, 故PC ⊥BE ,PC ⊥DE .又BE ∩DE =E ,所以PC ⊥平面BDE .(2)AP =(0,0,2),AB =b,0). 设m =(x ,y ,z )为平面P AB 的法向量, 则m ·AP =0,m ·AB =0,即2z =0-by =0, 令x =b ,则m =(b,0).设n =(p ,q ,r )为平面PBC 的法向量,则n ·PC =0,n ·BE =0,即20r -=且2033bq r ++=,令p =1,则r =q b =-,n =(1,b-). 因为面P AB ⊥面PBC ,故m·n =0,即20b b-=,故b = 于是n =(1,-1),DP =(2),1cos ,2||||DP DP DP ⋅==n n n ,〈n ,DP 〉=60°. 因为PD 与平面PBC 所成角和〈n ,DP 〉互余,故PD 与平面PBC 所成的角为30°.20.解:记A i 表示事件:第1次和第2次这两次发球,甲共得i 分,i =0,1,2;B i 表示事件:第3次和第4次这两次发球,甲共得i 分,i =0,1,2; A 表示事件:第3次发球,甲得1分;B 表示事件:开始第4次发球时,甲、乙的比分为1比2;C 表示事件:开始第5次发球时,甲得分领先.(1)B =A 0·A +A 1·A , P (A )=0.4,P (A 0)=0.42=0.16,P (A 1)=2×0.6×0.4=0.48, P (B )=P (A 0·A +A 1·A )=P(A0·A)+P(A1·A)=P(A0)P(A)+P(A1)P(A)=0.16×0.4+0.48×(1-0.4)=0.352.(2) P(B0)=0.62=0.36,P(B1)=2×0.4×0.6=0.48,P(B2)=0.42=0.16,P(A2)=0.62=0.36.C=A1·B2+A2·B1+A2·B2P(C)=P(A1·B2+A2·B1+A2·B2)=P(A1·B2)+P(A2·B1)+P(A2·B2)=P(A1)P(B2)+P(A2)P(B1)+P(A2)P(B2)=0.48×0.16+0.36×0.48+0.36×0.16=0.307 2.21.解:(1)f′(x)=x2+2x+a=(x+1)2+a-1.①当a≥1时,f′(x)≥0,且仅当a=1,x=-1时,f′(x)=0,所以f(x)是R上的增函数;②当a<1时,f′(x)=0有两个根x1=-1x2=-1当x∈(-∞,-1时,f′(x)>0,f(x)是增函数;当x∈(-11时,f′(x)<0,f(x)是减函数;当x∈(-1∞)时,f′(x)>0,f(x)是增函数.(2)由题设知,x1,x2为方程f′(x)=0的两个根,故有a<1,x12=-2x1-a,x22=-2x2-a.因此f(x1)=13x13+x12+ax1=13x1(-2x1-a)+x12+ax1=13x12+23ax1=13(-2x1-a)+23ax1=23(a-1)x1-3a.同理,f(x2)=23(a-1)x2-3a.因此直线l 的方程为y =23(a -1)x -3a . 设l 与x 轴的交点为(x 0,0),得02(1)ax a =-, 22322031()[][](12176)32(1)2(1)2(1)24(1)a a a a f x a a a a a a =++=-+----. 由题设知,点(x 0,0)在曲线y =f (x )上,故f (x 0)=0, 解得a =0或23a =或34a =.22.解:(1)设A (x 0,(x 0+1)2),对y =(x +1)2求导得y ′=2(x +1), 故l 的斜率k =2(x 0+1).当x 0=1时,不合题意,所以x 0≠1. 圆心为M (1,12),MA 的斜率2001(1)21x k'x +-=-.由l ⊥MA 知k ·k ′=-1, 即2(x 0+1)·2001(1)21x x +--=-1,解得x 0=0,故A (0,1), r =|MA |=,即2r =. (2)设(t ,(t +1)2)为C 上一点,则在该点处的切线方程为y -(t +1)2=2(t +1)(x -t ),即y =2(t +1)x -t 2+1.若该直线与圆M 相切,则圆心M=化简得t 2(t 2-4t -6)=0,解得t 0=0,12t =22t =抛物线C 在点(t i ,(t i +1)2)(i =0,1,2)处的切线分别为l ,m ,n ,其方程分别为y =2x +1,①y =2(t 1+1)x -t 12+1,② y =2(t 2+1)x -t 22+1,③ ②-③得1222t t x +==. 将x =2代入②得y =-1,故D (2,-1). 所以D 到l的距离d ==.。
2012年全国高考文科数学试题及答案-新课标word版

绝密*启用前2012年普通高等学校招生全国统一考试(新课标卷)文科数学注息事项:1。
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.问答第Ⅰ卷时.选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动。
用橡皮擦干净后,再选涂其它答案标号。
写在本试卷上无效.3。
回答第Ⅱ卷时.将答案写在答题卡上。
写在本试卷上无效·4.考试结束后。
将本试卷和答且卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
1、已知集合A={x|x2-x-2〈0},B={x|-1<x<1},则(A)A错误!B (B)B错误!A (C)A=B (D)A∩B=(2)复数z=错误!的共轭复数是(A)2+i (B)2-i (C)-1+i (D)-1-i3、在一组样本数据(x1,y1),(x2,y2),…,(x n,y n)(n≥2,x1,x2,…,x n不全相等)的散点图中,若所有样本点(x i,y i)(i=1,2,…,n)都在直线y=错误!x+1上,则这组样本数据的样本相关系数为(A)-1 (B)0 (C)错误!(D)1(4)设F1、F2是椭圆E:错误!+错误!=1(a〉b〉0)的左、右焦点,P为直线x=错误!上一点,△F1PF2是底角为30°的等腰三角形,则E的离心率为()(A)错误!(B)错误!(C)错误!(D)错误!5、已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点(x,y)在△ABC内部,则z=-x+y的取值范围是(A)(1-错误!,2)(B)(0,2) (C)(错误!-1,2) (D)(0,1+错误!)(6)如果执行右边的程序框图,输入正整数N(N≥2)和实数a1,a2,…,a N,输出A,B,则(A)A+B为a1,a2,…,a N的和(B)错误!为a1,a2,…,a N的算术平均数(C)A和B分别是a1,a2,…,a N中最大的数和最小的数(D)A和B分别是a1,a2,…,a N中最小的数和最大的数(7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为(A)6(B)9(C)12(D)18(8)平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为2,则此球的体积为(A)错误!π(B)4错误!π(C)4错误!π(D)6错误!π(9)已知ω>0,0〈φ<π,直线x=错误!和x=错误!是函数f(x)=sin(ωx+φ)图像的两条相邻的对称轴,则φ=(A)错误!(B)错误!(C)错误!(D)错误!(10)等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A,B两点,|AB|=4错误!,则C的实轴长为(A)错误!(B)2错误!(C)4 (D)8(11)当0<x≤错误!时,4x<log a x,则a的取值范围是(A)(0,错误!)(B)(错误!,1)(C)(1,错误!)(D)(错误!,2)(12)数列{a n}满足a n+1+(-1)n a n=2n-1,则{a n}的前60项和为(A)3690 (B)3660 (C)1845 (D)1830第Ⅱ卷本卷包括必考题和选考题两部分.第13题—第21题为必考题,每个试题考生都必须作答,第22—24题为选考题,考生根据要求作答。
2012学年高考文科数学年重庆卷

{|1A B x x x x ⎧⎫=<-⎨⎬⎩⎭【提示】求出集合,然后直接求解A B 。
【考点】一元二次不等式的解法,交集及其运算。
【解析】10i 10i(33i (3=+210i 13i =+,在复平面内,复数【提示】由10i =1【解析】因为2||||cos 1DE CB DE DA DE DA DE DA DA ====。
故线段1A B 上存在点Q ,使1AC DEQ ⊥平面。
(2)12(1)r A d =-,22(1)r A d =-+,12(())1c A c A d ==+,32()2c A d =-- 因为10d -≤≤,所以12()()|||10|r A r A d ≥=+≥,3|)|1(0c A d ≥+≥所以)11(k A d =+≤当0d =时,)(k A 取得最大值1(3)任给满足性质P 的数表A (如下所示)a b cd e f任意改变A 三维行次序或列次序,或把A 中的每个数换成它的相反数,所得数表A *仍满足性质P ,并且 (())k A k A *=因此,不防设112()0,0()()r A c A c A ≥≥≥0,,由()k A 的定义知,112()()()()()()k A r A k A c A k A c A ≤≤≤,,,从而112()()()()3k A r A c A c A ++≤()()()a b c a d b e =++++++()()3a b c d e f a b f a b f =+++++++-=+-≤所以()k A ≤1由(2)可知,存在满足性质P 的数表A 使()k A =1,故()k A 的最大值为1.【提示】(1)根据()i r A 为A 的第i 行各数之和(1,2)i =,()j C A 为A 的第j 列各数之和1,3)(2,j =; 记()k A 为12123()|,|()|,|()|,|()|,|||()r A r A c A c A c A 中的最小值可求出所求;(2))(k A 的定义可求出)(1k A d =+,然后根据d 的取值范围可求出所求;(3)任意改变A 三维行次序或列次序,或把A 中的每个数换成它的相反数,所得数表A *仍满足性质P ,并且(())k A k A *=因此,不防设112()0,0()()r A c A c A ≥≥≥0,,然后利用不等式的性质可知112()()()()3k A r A c A c A ++≤, 从而求出)(k A 的最大值。
2012年高考新课标全国卷文科数学试题(附答案)

2012年普通高等学校招生全国统一考试(新课标全国卷)文科数学试题一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
(1)已知集合A={x |x 2−x −2<0},B={x |−1<x <1},则(A )A ⊂≠B (B )B ⊂≠A (C )A=B (D )A ∩B=∅ (2)复数z =32ii-++的共轭复数是 (A )2i + (B )2i - (C )1i -+ (D )1i --(3)在一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )(n ≥2,x 1,x 2,…,x n 不全相等)的散点图中,若所有样本点(x i ,y i )(i =1,2,…,n )都在直线112y x =+上,则这组样本数据的样本相关系数为(A )−1 (B )0 (C )12(D )1(4)设1F ,2F 是椭圆E :2222x y a b+=1(a >b >0)的左、 右焦点,P 为直线32ax =上一点,△21F PF 是底角为030的等腰三角形,则E 的离心率为 (A )12 (B )23 (C )34 D .45(5)已知正三角形ABC 的顶点A (1,1),B (1,3),顶点C 在第一象限,若点(x ,y )在△ABC内部,则z x y =-+的取值范围是(A )(1-3,2) (B )(0,2) (C )(3-1,2) (D )(0,1+3) (6)如果执行右边的程序框图,输入正整数N (N ≥2)和实数1a ,2a ,…,N a ,输出A ,B ,则 (A )A +B 为1a ,2a ,…,N a 的和 (B )2A B+为1a ,2a ,…,N a 的算术平均数 (C )A 和B 分别为1a ,2a ,…,N a 中的最大数和最小数(D )A 和B 分别为1a ,2a ,…,N a 中的最小数和最大数 (7)如图,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为 (A )6 (B )9 (C )12 (D )18(8)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为(A )6π (B )43π (C )46π (D )63π (9)已知ω>0,0ϕπ<<,直线x =4π和x =54π是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴,则ϕ=(A )π4 (B )π3 (C )π2 (D )3π4(10)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线216y x =的准线交于A 、B 两点,||AB =43,则C 的实轴长为(A )2 (B )22 (C )4 (D )8 (11)当0<x ≤12时,4log xa x <,则a 的取值范围是(A )(0,22) (B )(22,1) (C )(1,2) (D )(2,2) (12)数列{n a }满足1(1)21nn n a a n ++-=-,则{n a }的前60项和为(A )3690 (B )3660 (C )1845 (D )1830二.填空题:本大题共4小题,每小题5分。
2012年高考新课标全国卷文科数学试题附答案
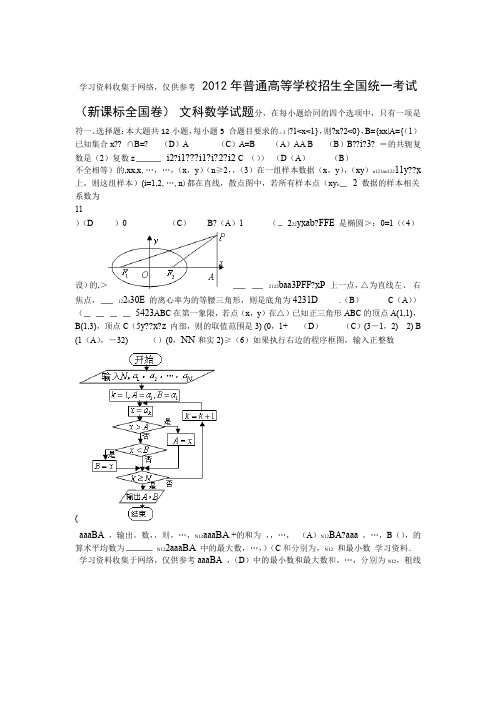
学习资料收集于网络,仅供参考 2012年普通高等学校招生全国统一考试(新课标全国卷)文科数学试题分,在每小题给同的四个选项中,只有一项是符一、选择题:本大题共12小题,每小题5 合题目要求的。
2 |?1<x<1},则?x?2<0},B={xx|A={(1)已知集合x??∩B=?(D)A (C)A=B (A)AA B (B)B??i?3?=的共轭复数是(2)复数z i2?i1???i1?i?2?i2 C ())(D(A)(B)不全相等)的,xx,x,…,…,(x,y)(n≥2,,(3)在一组样本数据(x,y),(xy)n121nn12211y??x 上,则这组样本)(i=1,2,…,n)都在直线,散点图中,若所有样本点(xy ii2数据的样本相关系数为11)(D )0 (C)B?(A)1 (222yxa b?FFE是椭圆>:0=1((4)设)的,>2122baa3PFF?x P上一点,△为直线左、右焦点,122030E的离心率为的等腰三角形,则是底角为4231D.(B)C(A))(5423ABC在第一象限,若点(x,y)在△)已知正三角形ABC的顶点A(1,1),B(1,3),顶点C(5y??x?z内部,则的取值范围是3) (0,1+ (D)(C)(3-1,2) 2) B (1(A),-32) ()(0,NN和实2)≥(6)如果执行右边的程序框图,输入正整数(aaaBA,输出,数,,则,…,N12aaa BA+的和为,,…,(A)N12BA?aaa,…,B(),的算术平均数为N122aaa BA中的最大数,…,)(C和分别为,N12和最小数学习资料.学习资料收集于网络,仅供参考aaaBA,(D)中的最小数和最大数和,…,分别为N12,粗线画出的是)如图,网格上小正方形的边长为1(7某几何体的三视图,则此几何体的体积为(A)6B)9 ()12 (C18(D)??,则此球的体积2到平面(8)平面的距离为截球O的球面所得圆的半径为1,球心O 为(D)π6C()346π(A()6πB)43π??5?????xx)x?f(?x?)?sin(0图像的两条=是函数,直线9)已知和>0,=(44?=相邻的对称轴,则3ππππ(D))(C A()(B)44322x CC x16y?A、的中心在原点,焦点在轴上,的准线交于与抛物线(10)等轴双曲线C34|AB|B两点,=,则的实轴长为2228 D))((C)4 (A)(B1x xxlog4?,则a的取值范围是(11)当0<时,≤2a222) ,)( (D1) ,(C)2(1(A)(0,,) (B)2) (22n aa1n??1)a?2a?(项和为的前,则{60}(12)数列{}满足nnn1n?1830 D)()(C1845 (A)3690 (B)36605分。
2012年普通高等学校招生全国统一考试重庆卷(数学文)

2012年普通高等学校招生统一考试(重庆卷)数学试题卷(文史类)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的(1)命题“若p 则q ”的逆命题是(A )若q 则p (B )若⌝p 则⌝ q (C )若q ⌝则p ⌝ (D )若p 则q ⌝(2)不等式102x x -<+ 的解集是为 (A )(1,)+∞ (B ) (,2)-∞- (C )(-2,1)(D )(,2)-∞-∪(1,)+∞ 【答案】:C 【解析】:10(1)(2)0212x x x x x -<⇒-+<⇒-<<+ 【考点定位】本题考查解分式不等式时,利用等价变形转化为整式不等式解. (3)设A ,B 为直线y x =与圆221x y += 的两个交点,则||AB =(A )1 (B (C (D )2 【答案】:D【解析】:直线y x =过圆221x y +=的圆心(0,0)C 则||AB =2 【考点定位】本题考查圆的性质,属于基础题. (4)5(13)x - 的展开式中3x 的系数为 (A )-270 (B )-90 (C )90 (D )270(5)sin 47sin17cos30cos17-(A)2-(B )12-(C )12 (D)2【答案】:C 【解析】:sin 47sin17cos30sin(3017)sin17cos30cos17cos17-+-=sin 30cos17cos30sin17sin17cos30sin 30cos171sin 30cos17cos172+-====【考点定位】本题考查三角恒等变化,其关键是利用473017=+ (6)设x R ∈ ,向量(,1),(1,2),a x b ==-且a b ⊥ ,则||a b += (A(B(C)(D )10 【答案】:B(7)已知2log 3log a =+,2log 9log b =-,3log 2c =则a,b,c 的大小关系是 (A ) a b c =< (B )a b c => (C )a b c << (D )a b c >> 【答案】:B【解析】:222213log 3log log 3log 3log 322a =+=+=,222213log 9log 2log 3log 3log 322b =-=-=,2322log 21log 2log 3log 3c ===则a b c => 【考点定位】本题考查对数函数运算.(8)设函数()f x 在R 上可导,其导函数()f x ',且函数()f x 在2x =-处取得极小值,则函数()y xf x '=的图象可能是【答案】:C【解析】:由函数()f x 在2x =-处取得极小值可知2x <-,()0f x '<,则()0xf x '>;2x >-,()0f x '>则20x -<<时()0xf x '<,0x >时()0xf x '>【考点定位】本题考查函数的图象,函数单调性与导数的关系,属于基础题.(9)设四面体的六条棱的长分别为1,1,1,1a 且长为a a 的取值范围是(A ) (B ) (C )(D )【答案】:A【解析】:2BE ==,BF BE <,2AB BF =【考点定位】本题考查棱锥的结构特征,考查空间想象能力,极限思想的应用,是中档题..(10)设函数2()43,()32,x f x x x g x =-+=-集合{|(())M x R f g x =∈>{|()2},N x R g x =∈<则MN 为(A )(1,)+∞ (B )(0,1) (C )(-1,1) (D )(,1)-∞ 【答案】:D【解析】:由(())0f g x >得2()4()30g x g x -+>则()1g x <或()3g x >即321x-<或323x->所以1x <或3log 5x >;由()2g x <得322x-<即34x<所以3log 4x <故(,1)MN =-∞二、填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应位置· (11)首项为1,公比为2的等比数列的前4项和4S = 【答案】:15【解析】:44121512S -==- 【考点定位】本题考查等比数列的前n 项和公式(12)函数()()(4)f x x a x =+- 为偶函数,则实数a =(13)设△ABC 的内角A B C 、、 的对边分别为a b c 、、,且1cos 4a b C ==1,=2,,则sin B =【答案】(14)设P 为直线3b y x a =与双曲线22221(0,0)x y a b a b-=>> 左支的交点,1F 是左焦点,1PF 垂直于x 轴,则双曲线的离心率e =(15)某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其它三门艺术课各1节,则在课表上的相邻两节文化课之间至少间隔1节艺术课的概率为 (用数字作答)· 【答案】:15三、解答题:本大题共6小题,共75分·解答应写出文字说明、证明过程或演算步骤· 16.(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分))已知{}n a 为等差数列,且13248,12,a a a a +=+=(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)记{}n a 的前n 项和为n S ,若12,,k k a a S +成等比数列,求正整数k 的值· 【答案】:(Ⅰ)n a =2n (Ⅱ)6k =【解析】::(Ⅰ)设数列{}n a 的公差为d,由题意知112282412a d a d +=⎧⎨+=⎩ 解得12,2a d ==所以1(1)22(1)2n a a n d n n =+-=+-= (Ⅱ)由(Ⅰ)可得1()(22)(1)22n n a a n n nS n n ++===+ 因12,,k k a a S + 成等比数列,所以212k k a a S += 从而2(2)2(2)(3)k k k =++ ,即 2560k k --=解得6k = 或1k =-(舍去),因此6k = ·17.(本小题满分13分)已知函数3()f x ax bx c =++在2x =处取得极值为16c - (1)求a 、b 的值;(2)若()f x 有极大值28,求()f x 在[3,3]-上的最大值. 【答案】:(Ⅰ)1327(Ⅱ)427【解析】::(Ⅰ)因3()f x ax bx c =++ 故2()3f x ax b '=+ 由于()f x 在点2x = 处取得极值故有(2)0(2)16f f c '=⎧⎨=-⎩即1208216a b a b c c +=⎧⎨++=-⎩ ,化简得12048a b a b +=⎧⎨+=-⎩解得112a b =⎧⎨=-⎩(Ⅱ)由(Ⅰ)知 3()12f x x x c =-+,2()312f x x '=-令()0f x '= ,得122,2x x =-=当(,2)x ∈-∞-时,()0f x '>故()f x 在(,2)-∞-上为增函数; 当(2,2)x ∈- 时,()0f x '< 故()f x 在(2,2)- 上为减函数 当(2,)x ∈+∞ 时()0f x '> ,故()f x 在(2,)+∞ 上为增函数·由此可知()f x 在12x =- 处取得极大值(2)16f c -=+,()f x 在22x = 处取得极小值(2)16f c =-由题设条件知1628c += 得12c =此时(3)921,(3)9f c f c -=+==-+=,(2)164f c =-=-因此()f x 上[3,3]-的最小值为(2)4f =-【考点定位】本题主要考查函数的导数与极值,最值之间的关系,属于导数的应用.(1)先对函数()f x 进行求导,根据(2)0f '==0,(2)16f c =-,求出a ,b 的值.(1)根据函数()f x =x3-3ax2+2bx 在x=1处有极小值-1先求出函数中的参数a ,b 的值,再令导数等于0,求出极值点,判断极值点左右两侧导数的正负,当左正右负时有极大值,当左负右正时有极小值.再代入原函数求出极大值和极小值.(2)列表比较函数的极值与端点函数值的大小,端点函数值与极大值中最大的为函数的最大值,端点函数值与极小值中最小的为函数的最小值.18.(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分)甲、乙两人轮流投篮,每人每次投一球,约定甲先投且先投中者获胜,一直每人都已投球3次时投篮结束,设甲每次投篮投中的概率为13,乙每次投篮投中的概率为12,且各次投篮互不影响·(Ⅰ)求乙获胜的概率;(Ⅱ)求投篮结束时乙只投了2个球的概率· 【答案】:(Ⅰ)1327(Ⅱ)427独立事件同时发生的概率计算公式知112211223()()()p D p A B A B p A B A B A =+112211223()()()()()()()()()p A p B P A P B p A p B P A P B p A =+2222212114()()()()3232327=+=19.(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)设函数()sin()f x A x ωϕ=+(其中0,0,A ωπϕπ>>-<< )在6x π=处取得最大值2,其图象与轴的相邻两个交点的距离为2π(I )求()f x 的解析式; (II )求函数426cos sin 1()()6x x g x f x π--=+的值域·【答案】:(Ⅰ)6πϕ=(Ⅱ)775[1,)(,]4422231cos 1(cos )22x x =+≠因2cos [0,1]x ∈,且21cos 2x ≠故()g x 的值域为775[1,)(,]442(20)(本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分)已知直三棱柱111ABC A B C -中,4AB =,3AC BC ==,D 为AB 的中点·(Ⅰ)求异面直线1CC 和AB 的距离;(Ⅱ)若11AB AC ⊥,求二面角11A CD B --的平面角的余弦值· 【答案】:(Ⅰ)(Ⅱ)13【解析】:(Ⅰ)如答(20)图1,因AC=BC , D 为AB 的中点,故CD ⊥AB ·又直三棱柱中,1CC ⊥ 面ABC ,故1CD CC ⊥ ,所以异面直线1CC 和AB的距离为(Ⅱ):由1CD ,CD ,AB BB ⊥⊥故CD ⊥ 面11A ABB ,从而1CD DA ⊥ ,1CD DB ⊥故11A DB ∠ 为所求的二面角11A CD B --的平面角·因1A D 是1AC 在面11A ABB 上的射影,又已知11C,AB A ⊥ 由三垂线定理的逆定理得11D,AB A ⊥从而11A AB ∠,1A DA ∠都与1B AB ∠互余,因此111A AB A DA ∠=∠,所以1Rt A AD ≌11Rt B A A ,因此1111AA A B AD AA =得21118AA AD A B =⋅=从而111A D B D A D ===所以在11A DB 中,由余弦定理得222111111111cos 23A D DB A B A DB A D DB +-==⋅ (21)(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分) 已知椭圆的中心为原点O ,长轴在x 轴上,上顶点为A ,左、右焦点分别为12,F F ,线段12,OF OF 的中点分别为12,B B ,且△12AB B 是面积为4的直角三角形·(Ⅰ)求该椭圆的离心率和标准方程;(Ⅱ)过1B 作直线交椭圆于,P Q ,22PB QB ⊥,求△2PB Q 的面积【答案】:(Ⅰ)220x +24y =1(Ⅱ)9,12|OA B B ⊥(*)设1122(,),(,),P x y Q x y 则12,y y 是上面方程的两根,因此1224,5my y m +=+ 122165y y m -⋅=+ 又111222(2,),(2,)B P x y B P x y =-=-,所以1212(2)(2)B P B P x x ⋅=-- 12y y +1212(4)(4)my my y y =--+212(1)m y y =+124()16m y y -++222216(1)161655m m m m -+=-+++ 2216645m m -=-+由22PB QB ⊥ ,知220B P B Q ⋅= ,即216640m -= ,解得2m =± 当2m = 时,方程(*)化为:298160y y --=故12y y == ,12||y y -=2PB Q 的面积12121||||29S B B y y =-= 当2m =- 时,同理可得(或由对称性可得)2PB Q的面积9S = 综上所述,2PB Q 的面积为9·。
2012年全国新课标高考文科数学真题及答案(Word版)

绝密*启用前2012年普通高等学校招生全国统一考试 文科数学 注息事项:1. 本试卷分第I 卷(选择题)和第n 卷 号填写在本试卷和答题卡相应位置上。
2. 问答第I 卷时。
选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动 擦干净后,再选涂其它答案标号。
写在本试卷上无效3.回答第n 卷时。
将答案写在答题卡上 .写在本试卷上无效•4. 考试结束后.将本试卷和答且卡一并交回。
1y i ) (i=1,2,…,n)都在直线y=2x+1上,则这组样本数据的样本相关系数为x 2 y 2 3aF 2是椭圆E :耸+ y^= 1(a>b>0)的左、右焦点,P 为直线x=3a 上一点,△ F 1PF 2是底角为30°a b 2 的等腰三角形,则 E 的离心率为()(A) 1 ( B ) 2 (C ) 4( D ) 4 5、已知正三角形 ABC 的顶点A(1,1),B(1,3),顶点C 在第一象限,若点(x ,丫)在厶ABC 内部,贝U z= —x+y 的取值范围是 (A ) (1 — 3, 2) ( B ) (0, 2)( C ) ( 3— 1, 2)( D ) (0,1+ 3)(6)如果执行右边的程序框图,输入正整数 N(N >2)和实数a 1,a 2,…,a N ,输出A,B ,则(A)A+B 为 a 1,a 2,…,a N 的和 A + B(B)—2 —为a1,a 2,…,a N 的算术平均数(A )— 1(B) 0 (D) 1(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证.用橡皮 、选择题: 本大题共 12小题, 每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
1、已知集合 A={ x|x 2— x — 2<0}, B={ x|— 1<x<1},(A) A B(B ) B A (C ) A=B(D ) A n B=(2)复数 z =—的共轭复数是2+i(A) 2+i( B ) 2 — i(C )— 1+i (D )— 1— i3、在一组样本数据(X 1, y 1), (x 2, y 2),…,(x n .y n ) ( n > 2, X 1,x 2,…,X n 不全相等)的散点图中,若所有样本点(X i ,(4)设 F 1、(C) A和B分别是a i,a2,…,a N中最大的数和最小的数(D) A和B分别是a i,a2,…,a N中最小的数和最大的数(7) 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为(A) 6(B) 9(C) 12(D)18(8) 平面a截球0的球面所得圆的半径为1球心O到平面a的距离为,2,则此球的体积为(A) 6n ( B) 4 3n (C) 4 6n (D) 6 3n(9) 已知3>0, 0< o <n直线x=4和x=5^函数f(x)=sin( ®x+妨图像的两条相邻的对称轴,贝Un n n 3 n(A ) 4 (B) 3 ( C) 2 ( D) G(10) 等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=l6x的准线交于A , B两点, 则C的实轴长为(A ) 2 (B) 2 2 (C) 4 ( D) 8(11) 当0<x< 2时,4x<|og a x,贝y a的取值范围是(A ) (0,子) (B)(今,1) (C) (1 , 2) ( D) (.2, 2)(12) 数列{a n}满足a n+1 + (- 1)n a n = 2n- 1,则{a n}的前60项和为(A) 3690 ( B) 3660 (C) 1845 ( D) 1830本卷包括必考题和选考题两部分。
2012年高考数学真题高清版(全国卷文科数学)

页。
考试结束后,将本卷和答题卡x (1x =+(sin 3x j (A)2p(B)23p (C)32p (D)53p 35=,则2425- 1225- (C) 1225 (D) 2425x=-4,则该则该椭圆的方程为椭圆的方程为 (A)1612+=(B) 128+=(C) 84+=(D) 124+=32ç÷èø23ç÷èø(D) 112n -位选手依次演讲,其中选手甲不再第一个也不再最后一个演讲,则不同的演讲次序22,(B) 3 (C) 29、△ABC 中,AB 边的高为CD, CB = a ,CA = b ,0×=a b ,1=a ,2=b ,则AD =(A) 1133-a b (B) 2233-a b (C) 3355-a b (D) 4455-a b10、已知1F 、2F 为双曲线为双曲线 C :222x y -=的左、右焦点,点P 在C 上,122PF PF =,则12cos F PF Ð=(A)14 (B) 35 (C) 34 (D) 4511、已知ln x p =,5log 2y =, 12z e -=,则,则(A) x y z << (B) z x y << (C) z y x << (D) y z x << 12、正方形ABCD 的边长为1,点E 在边AB 上,点F 在边BC 上,AE=BF=13,动点P 从E 出发沿直线向F 运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,当点P 第一次碰到E 时,P 与正方形的边碰撞的次数为(A) 8 (B) 6 (C) 4 (D) 3 第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.13、 812xx æö+ç÷èø的展开式中2x 的系数为____________. 14、若x 、y 满足约束条件1030330x y x y x y -+³ìï+-£íï+-³î,则z = 3x – y 的最小值为_____________. 15、当函数()sin 3cos 02y x x x p =-£<取得最大值时,x=_____________. 16、已知正方体1111ABCD A B C D -中,E 、F 分别为1BB 、1CC 的中点,那么异面直线AE 与1D F 所成角的余弦值为____________. 三、解答题:本大题共6小题,共70分。
2012年(全国卷II)(含答案)高考文科数学

2012年普通高等学校招生全国统一考试(2全国卷)数学(文)试题一、选择题 ( 本大题 共 12 题, 共计 60 分)1.已知集合A ={x |x 是平行四边形},B ={x |x 是矩形},C ={x |x 是正方形},D ={x |x 是菱形},则( )A .AB B .CB C .DC D .AD2.函数1y x =+x ≥-1)的反函数为( ) A .y =x 2-1(x ≥0) B .y =x 2-1(x ≥1) C .y =x 2+1(x ≥0) D .y =x 2+1(x ≥1) 3.若函数()sin 3x f x ϕ+=(φ∈[0,2π])是偶函数,则φ=( ) A .π2 B .2π3 C .3π2 D .5π34.已知α为第二象限角,3sin 5α=,则sin2α=( ) A .2425-B .1225-C .1225D .2425 5.椭圆的中心在原点,焦距为4,一条准线为x =-4,则该椭圆的方程为( )A .2211612x y += B .221128x y += C .22184x y += D .221124x y += 6.已知数列{a n }的前n 项和为S n ,a 1=1,S n =2a n +1,则S n =( )A .2n -1B .13()2n -C .12()3n -D .112n -7. 6位选手依次演讲,其中选手甲不在第一个也不在最后一个演讲,则不同的演讲次序共有( )A .240种B .360种C .480种D .720种8.已知正四棱柱ABCD -A 1B 1C 1D 1中,AB =2,122CC =E 为CC 1的中点,则直线AC 1与平面BED 的距离为( )A.2 BC .2D.19.△ABC中,AB边的高为CD.若CB =a,CA=b,a·b=0,|a|=1,|b|=2,则AD=()A.1133-a b B.2233-a bC.3355-a b D.4455-a b10.已知F1,F2为双曲线C:x2-y2=2的左、右焦点,点P在C上,|PF1|=2|PF2|,则cos∠F1PF2=()A.14B.35C.34D.4511.已知x=ln π,y=log52,12=ez-,则()A.x<y<z B.z<x<y C.z<y<x D.y<z<x12.正方形ABCD的边长为1,点E在边AB上,点F在边BC上,AE=BF=1 3 .动点P从E出发沿直线向F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当点P第一次碰到E时,P与正方形的边碰撞的次数为()A.8 B.6 C.4 D.3二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.13.(x+12x)8的展开式中x2的系数为__________.14.若x,y满足约束条件10,30,330, x yx yx y-+≥⎧⎪+-≤⎨⎪+-≥⎩则z=3x-y的最小值为__________.15.当函数y=sin x x(0≤x<2π)取得最大值时,x=__________。
(完整word版)2012年全国高考新课标1卷数学文科高考试题
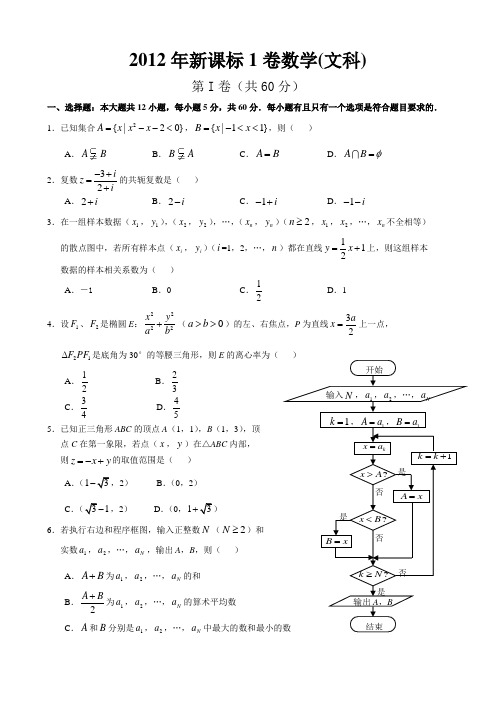
2012年新课标1卷数学(文科)第I 卷(共60分)一、选择题:本大题共12小题,每小题5分,共60分.每小题有且只有一个选项是符合题目要求的. 1.已知集合2{|20}A x x x =--<,{|11}B x x =-<<,则( )A .AB B .B AC .A B =D .A B φ=2.复数32iz i-+=+的共轭复数是( ) A .2i + B .2i -C .1i -+D .1i --3.在一组样本数据(1x ,1y ),(2x ,2y ),…,(n x ,n y )(2n ≥,1x ,2x ,…,n x 不全相等)的散点图中,若所有样本点(i x ,i y )(i =1,2,…,n )都在直线112y x =+上,则这组样本 数据的样本相关系数为( ) A .-1B .0C .12D .14.设1F 、2F 是椭圆E :2222x y a b +(0a b >>)的左、右焦点,P 为直线32ax =上一点,21F PF ∆是底角为30°的等腰三角形,则E 的离心率为( )A .12B .23C .34D .455.已知正三角形ABC 的顶点A (1,1),B (1,3),顶 点C 在第一象限,若点(x ,y )在△ABC 内部, 则z x y =-+的取值范围是( )A .(13-,2)B .(0,2)C .(31-,2)D .(0,13+)6.若执行右边和程序框图,输入正整数N (2N ≥)和 实数1a ,2a ,…,N a ,输出A ,B ,则( )A .AB +为1a ,2a ,…,N a 的和B .2A B +为1a ,2a ,…,N a 的算术平均数C .A 和B 分别是1a ,2a ,…,N a 中最大的数和最小的数否是是1k k =+B x=A x=结束输出A ,B ?k N ≥?x B <kx a =?x A >开始输入N ,1a ,2a ,…,N a1k =,1A a =,1B a =否是 否D .A 和B 分别是1a ,2a ,…,N a 中最小的数和最大的数7.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )A .6B .9C .12D .158.平面α截球O 的球面所得圆的半径为1,球心O 到平面α的 距离为2,则此球的体积为( ) A .6πB .43πC .46πD .63π9.已知0ω>,0ϕπ<<,直线4x π=和54x π=是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴,则ϕ=( ) A .4π B .3πC .2πD .34π 10.等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线216y x =的准线交于A ,B 两点,||43AB =,则C 的实轴长为( )A .2B .22C .4D .811.当102x <≤时,4log xa x <,则a 的取值范围是( ) A .(0,22) B .(22,1) C .(1,2) D .(2,2) 12.数列{n a }满足1(1)21nn n a a n ++-=-,则{n a }的前60项和为( )A .3690B .3660C .1845D .1830第Ⅱ卷(共90分)本试卷包括必考题和选考题两部分。
2012年普通高等学校招生全国统一考试文科数学(重庆卷)

12重庆(文)1.(2012重庆,文1)命题“若p 则q ”的逆命题是( ). A .若q 则pB .若p 则qC .若q 则pD .若p 则qA 根据逆命题的定义,命题“若p 则q ”的逆命题为“若q 则p ”,故选A . 2.(2012重庆,文2)不等式12x x -+<0的解集为( ). A .(1,+∞)B .(-∞,-2)C .(-2,1)D .(-∞,-2)∪(1,+∞)C 不等式12x x -+<0可化为(x -1)(x +2)<0,解不等式得其解集为(-2,1),故选C .3.(2012重庆,文3)设A ,B 为直线y =x 与圆x 2+y 2=1的两个交点,则|AB |=( ).A .1BCD .2D 由已知条件可知直线y =x 过圆x 2+y 2=1的圆心,所以AB 为圆x 2+y 2=1的直径,|AB |=2,故选D . 4.(2012重庆,文4)(1-3x )5的展开式中x 3的系数为( ). A .-270B .-90C .90D .270A (1-3x )5的展开式的通项为T r +1=5C r(-3)r x r ,令r =3,则x 3的系数为35C (-3)3=-270,故选A . 5.(2012重庆,文5)sin47sin17cos30cos17︒-︒︒︒=( ).A B .-12 C .12D C 因为sin 47°=sin (30°+17°)=sin 30°cos 17°+sin 17°cos 30°,所以原式=sin30cos17sin17cos30sin17cos30cos17︒︒+︒︒-︒︒︒=sin 30°=12,故选C .6.(2012重庆,文6)设x ∈R ,向量a =(x ,1),b =(1,-2),且a ⊥b ,则|a +b |=( ).A B C .D .10B 因为a ⊥b ,所以a ·b =x -2=0,解得x =2,a =(2,1),a +b =(3,-1),|a +b 故选B .7.(2012重庆,文7)已知a =log 23+log b =log 29-log c =log 32,则a ,b ,c 的大小关系是( ). A .a =b <c B .a =b >c C .a <b <c D .a >b >cB a =log 23+log log 2b =log 29-log log 2因此a =b ,而log 2log 22=1,log 32<log 33=1,所以a =b >c ,故选B .8.(2012重庆,文8)设函数f (x )在R 上可导,其导函数为f '(x ),且函数f (x )在x =-2处取得极小值,则函数y =xf '(x )的图象可能是( ).C 由题意可得f '(-2)=0,而且当x ∈(-∞,-2)时,f '(x )<0,此时xf '(x )>0;当x ∈(-2,+∞)时,f '(x )>0,此时若x ∈(-2,0),xf '(x )<0,若x ∈(0,+∞),xf '(x )>0,所以函数y =xf '(x )的图象可能是C .9.(2012重庆,文9)设四面体的六条棱的长分别为1,1,1,1a ,且长为a ,则a 的取值范围是( ).A .(0B .(0C .(1D .(1A 四面体如图1所示.设AB =AC =BD =CD =1,ADBC =a ,则a >0,当A ,B ,C ,D 四点共面时,BC如图2所示). 而此时A ,B ,C ,D 不能构成四面体,所以BC故选A.图1 图210.(2012重庆,文10)设函数f (x )=x 2-4x +3,g (x )=3x -2,集合M ={x ∈R |f (g (x ))>0},N ={x ∈R |g (x )<2},则M ∩N 为( ).A .(1,+∞)B .(0,1)C .(-1,1)D .(-∞,1)D 函数f (x )=(x -3)(x -1),令f (x )>0得x >3或x <1,不等式f (g (x ))>0可化为g (x )>3或g (x )<1,即3x -2>3或3x -2<1,分别求解得x >log 35或x <1,即M ={x ∈R |x >log 35或x <1},N ={x ∈R |3x -2<2}={x ∈R |x <log 34},所以M ∩N ={x ∈R |x <1},故选D .11.(2012重庆,文11)首项为1,公比为2的等比数列的前4项和S 4= .15 由等比数列前n 项和公式S n =n1a (1q )1q --得,S 4=41212--=15. 12.(2012重庆,文12)若f (x )=(x +a )(x -4)为偶函数,则实数a = .4 f (x )=x 2+(a -4)x -4a .因为f (x )为偶函数,所以f (-x )=x 2+(4-a )x -4a =x 2+(a -4)x -4a ,a -4=4-a ,a =4.13.(2012重庆,文13)设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且a =1,b =2,cos C =14,则sin B =.由余弦定理得c 2=a 2+b 2-2ab cos C =4,故c =2,而sin C∵b =c ,故sin B =sin C14.(2012重庆,文14)设P 为直线y =b 3ax 与双曲线22x a -22y b =1(a >0,b >0)左支的交点,F 1是左焦点,PF 1垂直于x 轴,则双曲线的离心率e =.因为F 1为左焦点,PF 1垂直于x 轴,所以P 点坐标为bc c,-3a ⎛⎫- ⎪⎝⎭.又因为P 点为直线与双曲线的交点,所以22c a -2222b c 9a b =1,即89e 2=1,所以e15.(2012重庆,文15)某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课各1节,则在课表上的相邻两节文化课之间至少间隔1节艺术课的概率为 (用数字作答).15基本事件总数为66A =720,事件“相邻两节文化课之间至少间隔1节艺术课”所包含的基本事件分两类,一类是相邻两节文化课之间恰好间隔1节艺术课有23333A A =72,一类是相邻两节文化课之间间隔1节或2节艺术课有32223322A C A A =72,由古典概型概率公式得P =15.16.(2012重庆,文16)已知{a n }为等差数列,且a 1+a 3=8,a 2+a 4=12. (1)求{a n }的通项公式;(2)记{a n }的前n 项和为S n ,若a 1,a k ,S k +2成等比数列,求正整数k 的值. 解:(1)设数列{a n }的公差为d ,由题意知112a 2d 8,2a 4d 12.+=⎧⎨+=⎩解得a 1=2,d =2.所以a n =a 1+(n -1)d =2+2(n -1)=2n .(2)由(1)可得S n =1n n(a a )2+=n(22n)2+=n (n +1).因a 1,a k ,S k +2成等比数列,所以2k a =a 1S k +2. 从而(2k )2=2(k +2)(k +3),即k 2-5k -6=0. 解得k =6或k =-1(舍去).因此k =6.17.(2012重庆,文17)已知函数f (x )=ax 3+bx +c 在点x =2处取得极值c -16. (1)求a ,b 的值;(2)若f (x )有极大值28,求f (x )在[-3,3]上的最小值. 解:(1)因f (x )=ax 3+bx +c ,故f '(x )=3ax 2+b ,由于f (x )在点x =2处取得极值c -16,故有f'(2)0,f (2)c 16,=⎧⎨=-⎩即12a b 0,8a 2b c c 16,+=⎧⎨++=-⎩化简得12a b 0,4a b 8,+=⎧⎨+=-⎩解得a =1,b =-12. (2)由(1)知f (x )=x 3-12x +c ; f '(x )=3x 2-12=3(x -2)(x +2).令f '(x )=0,得x 1=-2,x 2=2.当x ∈(-∞,-2)时,f '(x )>0,故f (x )在(-∞,-2)上为增函数; 当x ∈(-2,2)时,f '(x )<0,故f (x )在(-2,2)上为减函数; 当x ∈(2,+∞)时,f '(x )>0,故f (x )在(2,+∞)上为增函数.由此可知f (x )在x 1=-2处取得极大值f (-2)=16+c ,f (x )在x 2=2处取得极小值f (2)=c -16. 由题设条件知16+c =28得c =12.此时f (-3)=9+c =21,f (3)=-9+c =3,f (2)=-16+c =-4, 因此f (x )在[-3,3]上的最小值为f (2)=-4.18.(2012重庆,文18)甲、乙两人轮流投篮,每人每次投一球.约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为13,乙每次投篮投中的概率为12,且各次投篮互不影响.(1)求乙获胜的概率;(2)求投篮结束时乙只投了2个球的概率. 解:设A k ,B k 分别表示甲、乙在第k 次投篮投中,则P (A k )=13,P (B k )=12(k =1,2,3).(1)记“乙获胜”为事件C ,由互斥事件有一个发生的概率与相互独立事件同时发生的概率计算公式知 P (C )=P (1A B 1)+P (112A B A B 2)+P (11223A B A B A B 3)=P (1A )P (B 1)+P (1A )P (1B )P (2A )P (B 2)+P (1A )P (1B )P (2A )P (2B )P (3A )P (B 3)=23×12+222132⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭+332132⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭=1327.(2)记“投篮结束时乙只投了2个球”为事件D ,则由互斥事件有一个发生的概率与相互独立事件同时发生的概率计算公式知P (D )=P (112A B A B 2)+P (1122A B A B A 3)=P (1A )P (1B )P (2A )P (B 2)+P (1A )P (1B )P (2A )P (2B )P (A 3)=222132⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭+22211323⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=427. 19.(2012重庆,文19)设函数f (x )=A sin (ωx +φ)(其中A >0,ω>0,-π<φ≤π)在x =6π处取得最大值2,其图象与x 轴的相邻两个交点的距离为2π.(1)求f (x )的解析式;(2)求函数g (x )=426x x 1f x 6cos sin π--⎛⎫+ ⎪⎝⎭的值域.解:(1)由题设条件知f (x )的周期T =π,即2ωπ=π,解得ω=2.因f (x )在x =6π处取得最大值2,所以A =2.从而sin 2φ6π⎛⎫⨯+ ⎪⎝⎭=1,所以3π+φ=2π+2k π,k ∈Z .又由-π<φ≤π得φ=6π.故f (x )的解析式为f (x )=2sin 2x 6π⎛⎫+ ⎪⎝⎭.(2)g (x )=426x x 122x 2cos sin sin π--⎛⎫+ ⎪⎝⎭=426x x 222x cos cos cos +-=222(2x 1)(3x 2)2(2x 1)cos cos cos -+-=32cos 2x +121x 2cos ⎛⎫≠ ⎪⎝⎭.因cos 2x ∈[0,1],且cos 2x ≠12,故g (x )的值域为7751,,442⎡⎫⎛⎤⎪ ⎢⎥⎣⎭⎝⎦⋃.20.(2012重庆,文20)如图,在直三棱柱ABC -A 1B 1C 1中,AB =4,AC =BC =3,D 为AB 的中点. (1)求异面直线CC 1和AB 的距离;(2)若AB 1⊥A 1C ,求二面角A 1-CD -B 1的平面角的余弦值.解:(1)如图所示,因AC =BC ,D 为AB 的中点,故CD ⊥AB .又直三棱柱中,CC 1⊥面ABC ,故CC 1⊥CD ,所以异面直线CC 1和AB 的距离为CD(2)解法一:由CD ⊥AB ,CD ⊥BB 1,故CD ⊥面A 1ABB 1,从而CD ⊥DA 1,CD ⊥DB 1,故∠A 1DB 1为所求的二面角A 1-CD -B 1的平面角.因A 1D 是A 1C 在面A 1ABB 1上的射影,又已知AB 1⊥A 1C ,由三垂线定理的逆定理得AB 1⊥A 1D ,从而∠A 1AB 1,∠A 1DA 都与∠B 1AB 互余,因此∠A 1AB 1=∠A 1DA ,所以Rt △A 1AD ∽Rt △B 1A 1A .因此1AA AD =111A B AA ,得A 21A =AD ·A 1B 1=8.从而A 1DB 1D =A 1D =所以在△A 1DB 1中,由余弦定理得cos ∠A 1DB 1=222111111A D DB A B 2A D DB +-⋅⋅=13.(2)解法二:如图,过D 作DD 1∥AA 1交A 1B 1于D 1,在直三棱柱中,由(1)知DB ,DC ,DD 1两两垂直.以D 为原点,射线DB ,DC ,DD 1分别为x 轴、y 轴、z 轴的正半轴建立空间直角坐标系D -xyz .设直三棱柱的高为h ,则A (-2,0,0),A 1(-2,0,h ),B 1(2,0,h ),C (00),从而1AB =(4,0,h ),1A C=(2h ). 由11AB A C ⊥ 得1AB ·1A C=0,即8-h 2=0,因此h =故1DA =(-2,0,1DB=(2,0,DC =(00).设平面A 1CD 的法向量为m =(x 1,y 1,z 1),则m ⊥DC ,m ⊥1DA ,即1110,2x 0,⎧=⎪⎨-+=⎪⎩取z 1=1,得m0,1).设平面B 1CD 的法向量为n =(x 2,y 2,z 2),则n ⊥DC ,n ⊥1DB ,即2220,2x 0,⎧=⎪⎨+=⎪⎩取z 2=-1,得n0,-1).所以cos <m ,n >=m n |m ||n |⋅⋅=13.所以二面角A 1-CD -B 1的平面角的余弦值为13.21.(2012重庆,文21)如图,设椭圆的中心为原点O ,长轴在x 轴上,上顶点为A ,左、右焦点分别为F 1,F 2,线段OF 1,OF 2的中点分别为B 1,B 2,且△AB 1B 2是面积为4的直角三角形. (1)求该椭圆的离心率和标准方程;(2)过B 1作直线交椭圆于P ,Q 两点,使PB 2⊥QB 2,求△PB 2Q 的面积.解:(1)设所求椭圆的标准方程为22x a +22y b =1(a >b >0),右焦点为F 2(c ,0).因△AB 1B 2是直角三角形且|AB 1|=|AB 2|,故∠B 1AB 2为直角,从而|OA |=|OB 2|,即b =c 2.结合c 2=a 2-b 2得4b 2=a 2-b 2,故a 2=5b 2,c 2=4b 2,所以离心率e =c a在Rt △AB 1B 2中,OA ⊥B 1B 2,故12AB B S =12·|B 1B 2|·|OA |=|OB 2|·|OA |=c 2·b =b 2, 由题设条件12AB BS =4得b 2=4,从而a 2=5b 2=20.因此所求椭圆的标准方程为 2x 20+2y 4=1. (2)由(1)知B 1(-2,0),B 2(2,0).由题意,直线PQ 的倾斜角不为0,故可设直线PQ 的方程为x =my -2.代入椭圆方程得(m 2+5)y 2-4my -16=0.(*)设P (x 1,y 1),Q (x 2,y 2),则y 1,y 2是上面方程的两根,因此y 1+y 2=24m m 5+,y 1·y 2=216m 5-+.又2B P =(x 1-2,y 1),2B Q=(x 2-2,y 2),所以2B P ·2B Q=(x 1-2)(x 2-2)+y 1y 2 =(my 1-4)(my 2-4)+y 1y 2=(m 2+1)y 1y 2-4m (y 1+y 2)+16=2216(m 1)m 5-++-2216m m 5++16 =-2216m 64m 5-+.由PB 2⊥QB 2,知2B P ·2B Q=0,即16m 2-64=0,解得m =±2. 当m =2时,方程(*)化为9y 2-8y -16=0,故y1y 2y 1-y 2△PB2Q 的面积S =12|B 1B 2|·|y 1-y 2当m =-2时,同理可得(或由对称性可得)△PB 2Q 的面积S 综上所述,△PB2Q。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年普通高等学校招生全国统一考试(重庆卷)
数学(文)
1.命题“若p 则q ”的逆命题是
A. 若q 则p
B. 若﹃p 则﹃q
C. 若﹃q 则﹃p
D. 若p 则﹃q
2.不等式的解集为
A.(1,+∞)
B.(- ∞,-2)
C.(-2,1)
D.(- ∞,-2)∪(1,+∞)
3.设A ,B 为直线y=x 与圆x 2+y 2=1的两个交点,则|AB|=
A.1
C. D.2
4.(1-3x )5的展开式中x 3的系数为
A.-270
B.-90
C.90
D.270
(5)
-
A.- B-12 C. 12
D. (6)设x ∈R,向量a=(x,1),b=(1,-2),且a ⊥b,则|a+b|=
A. B. C. D.10
(7)已知a=
,b=,c=log 32,则a ,b ,c 的大小关系是 (A )a=b <c (B )a=b >c
(C )a <b <c (D )a >b >c
(8)设函数f (x )在R 上可导,其导函数为f ′(x ),且函数f (x )在x=-2处取得极小值,则函数y=xf ′(x )的图像可能是
(9)设四面体的六条棱的长分别为1,1,1,1和a,且长为a a 的取值范围是
(A)(B)(C)(D)
(10)设函数f(x)=x²-4x+3,g(x)=3x-2,集合M={x∈R|f(g(x))>0},N={x∈R g(x)g(x)<2},则M∩N为
(A)(1,﹢∞)(B)(0,1)(C)(-1,1)(D)(-∞,1)
(11)首项为1,公比为2的等比数列的前4项和S4=__________________
(12)若f(x)=(x+a)(x-4)为偶函数,则实数a=___________________
(13)设△ABC的内角A,B,C的对边分别为a,b,c,且a=1,b=2,,则sinB=________
(14)设P为直线与双曲线(a>0,b>0)左支的交点,F1是左焦点,
PF1垂直于x轴,则双曲线的离心率e=___________
(15)某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其它三门艺术课各1节,则在课表上的相邻两节文化课之间至少间隔1节艺术课的概率为____________(用数字作答)(16)(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分。
)
已知{a n}为等差数列,且a1+a3=8,a2+a4=12.
(17)(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分。
)
已知函数f(x)=ax3+bx+c在点x=2处取得极值c-16。
(Ⅰ)求a,b的值;
(Ⅱ)若f(x)有极大值28,求f(x)在[﹣3,3]上的最小值。
(18)(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分。
)
甲、乙两人轮流投篮,每人每次投一球。
约定甲先投且先投中者获胜,一直到有人获胜或每人都
已投球三次时投篮结束。
设甲每次投篮投中的概率为,乙每次投篮投中的概率为,且各次投篮互不影响。
(Ⅰ)求乙获胜的概率;
(Ⅱ)求投篮结束时乙只投了2个球的概率。
(19)(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分。
)
设函数f (x )=Asin ()(其中A >0,>0,-π<≤π)在x=6π处取得最大值2,其图像与x 轴的相邻两个交点的距离为
2
π。
(Ⅰ)求f (x )的解析式; (Ⅱ)求函数g (x )=的值域。
20.(本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分)
如图(20),在直三棱柱ABC-A 1B 1C 1中,AB=4,AC=BC=3,D 为AB 的中点。
(Ⅰ)求异面直线CC 1和AB 的距离;
(Ⅱ)若AB 1⊥A 1C ,求二面角A 1—CD —B 1的平面角的余弦值。
21. (本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)
如题(21)图,设椭圆的中心为原点O ,长轴在x 轴上,上顶点为A ,左、右焦点分别为F 1,F 2,线段OF 1,OF 2的中点分别为B 1,B 2,且△AB 1B 2是面积为4的直角三角形。
(Ⅰ)求该椭圆的离心率和标准方程;
(Ⅱ)过B1作直线交椭圆于P,Q两点,使PB2⊥QB2,求△PB2Q的面积。
