5知识讲解_充分条件与必要条件_基础
2 充分条件与必要条件

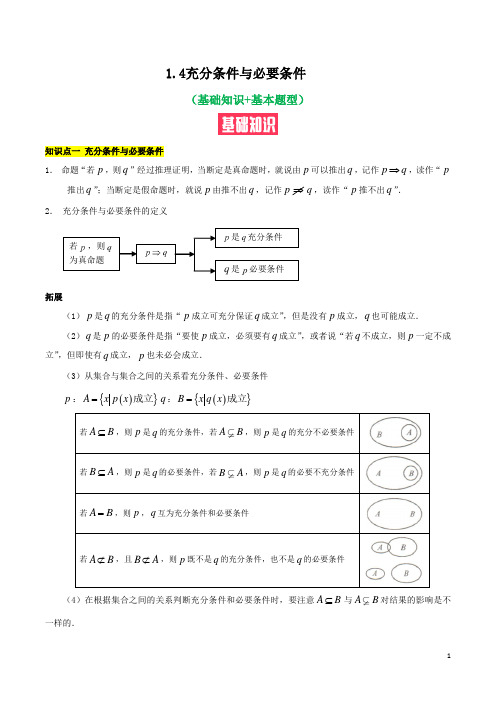
2 充分条件与必要条件一、基础知识1、定义:(1)对于两个条件,p q ,如果命题“若p 则q ”是真命题,则称条件p 能够推出条件q ,记为p q ⇒,(2)充分条件与必要条件:如果条件,p q 满足p q ⇒,则称条件p 是条件q 的充分条件;称条件q 是条件p 的必要条件2、对于两个条件而言,往往以其中一个条件为主角,考虑另一个条件与它的关系,这种关系既包含充分方面,也包含必要方面。
所以在判断时既要判断“若p 则q ”的真假,也要判断“若q 则p ”真假3、两个条件之间可能的充分必要关系:(1)p 能推出q ,但q 推不出p ,则称p 是q 的充分不必要条件(2)p 推不出q ,但q 能推出p ,则称p 是q 的必要不充分条件(3)p 能推出q ,且q 能推出p ,记为p q ⇔,则称p 是q 的充要条件,也称,p q 等价(4)p 推不出q ,且q 推不出p ,则称p 是q 的既不充分也不必要条件4、如何判断两个条件的充分必要关系(1)通过命题手段,将两个条件用“若……,则……”组成命题,通过判断命题的真假来判断出条件能否相互推出,进而确定充分必要关系。
例如2:1;:10p x q x =-=,构造命题:“若1x =,则210x -=”为真命题,所以p q ⇒,但“若210x -=,则1x =”为假命题(x 还有可能为1-),所以q 不能推出p ;综上,p 是q 的充分不必要条件(2)运用集合作为工具先看一个问题:已知P Q ,那么条件“x P ∈”是“x Q ∈”的什么条件?由P Q 可得到:x P x Q ∈⇒∈,且x Q ∈推不出x P ∈,所以“x P ∈”是“x Q ∈”充分不必要条件。
通过这个问题可以看出,如果两个集合存在包含关系,那么其对应条件之间也存在特定的充分必要关系。
在求解时可以将满足条件的元素构成对应集合,判断出两个集合间的包含关系,进而就可确定条件间的关系了。
相关结论如下:① P Q :p 是q 的充分不必要条件,q 是p 的必要不充分条件② P Q ⊆:p 是q 的充分条件③ P Q =:p 是q 的充要条件此方法适用范围较广,尤其涉及到单变量取值范围的条件时,不管是判断充分必要关系还是利用关系解参数范围,都可将问题转化为集合的包含问题,进而快捷求解。
第六节 充分条件与必要条件(PPT)5-3

例2.填空题
(1)若p q则q是p的充__分_条__件_条件;
必要不充分
(2)ab 0是 a 0的__充__要___条件, ab 0是 a 0的______条件;
b
b
(3)若A是B的充分条件,B是C的充要条件,D是C的必 要条件,则A是D的 充分 条件.
练习2.若命题甲是命题乙的充分不必要条件,命题丙
是命题乙的必要不充分条件,命题丁是命题丙的充要
条件,则命题丁是命题甲的( )
A、充分不必要条件
B、必要不充Βιβλιοθήκη 条件C、充要条件D、既不充分又不必要条件
AB
连通过降低对某人、某事的评价,借以突出另外的人或事物:这么难的题~小学生不会做,就是中学生也不一定会做。也说别说是。 【别提】动表示程度之 深不必细说:他那个高兴劲儿啊,就~了。 【别无长物】没有多余的东西。形容穷困或俭朴(长,旧读)。 【别无二致】没有两样;没有区别:这两个人的 思想~。 【别绪】名离别时的情绪:离愁~。 【别样】形属; https:///shuipi/ 水皮;性词。另外的;其他的;不同一般的:~风情。 【别有洞天】另有一种境界。形容景物等引人入胜。 【别有风味】另有一种趣味或特色:围着篝火吃烤肉,~。 【别有天地】另有一种境界。形容风景等引 人入胜。 【别有用心】ī言论或行动中另有不可告人的企图。 【别针】(~儿)名①一种弯曲而有弹性的针,尖端可以打开,也可以扣住,用来把布片、纸 片等固定在一起或固定在衣物上。②别在胸前或领口的装饰品,多用金银、玉石等制成。 【别致】形新奇,跟寻常不同:这座楼房式样很~。 【别传】名记 载某人逸事的传记。 【别子】名古代指天子、诸侯的嫡长子以外的儿子。 【别子】?名①线装书的套子上或字画手卷上用来别住开口的东西,多用骨头制成。 ②烟袋荷包的坠饰。 【别字】名①写错或读错的字,比如把“包子”写成“饱子”,是写别字;把“破绽”的“绽”()读成“定”,是读别字。也说白字。 ②别号。 【蹩】〈方〉动脚腕子或手腕子扭伤:走路不小心,~痛了脚。 【蹩脚】〈方〉形质量不好;本领不强:~货。 【瘪】(癟)形物体表面凹下去; 不饱满:干~|~谷|没牙~嘴儿|车带~了|乒乓球~了。 【别】(彆)〈方〉动改变别人坚持的意见或习性(多用于“别不过”):我想不依他,可是 又~不过他。 【别扭】?形①不顺心;难对付:这个天气真~,一会儿冷,一会儿热|他的脾气挺~,说话要注意。②意见不相投:闹~|两个人有些别别 扭扭的,说不到一块儿。③(说话、作文)不通顺;不流畅:这个句子有点儿~,得改一改。 【别嘴】〈方〉形绕嘴:这段文字半文不白,读起来~。 【邠】 ī①邠县,地名,在陕西。今作彬县。②同“豳”。③名姓。 【玢】ī〈书〉玉名。 【宾】(賓、賔)ī①客人(跟“主”相对):外~|~至如归。②(ī)名 姓。 【宾白】ī名戏曲中的说白。中国戏曲艺术以唱为主,所以把说白叫做宾白。 【宾词】ī名一个命题的三部分之一,表示思考对象的属性等,如在“金属 是导体”这个命题中,“导体”是宾词。 【宾东】ī名古代主人的座位在东,客人的座位在西,因此称宾与主为宾东(多用于幕僚和官
高考数学充分条件与必要条件(2019年11月整理)

(2)必要性:把B当作已知条件,结合命题的前提 条件推出A。
;画室加盟 高考画室加盟 美术加盟 https:///list-65-1.html 画室加盟 高考画室加盟 美术加盟
;
数百赎免其母 孝文初 表其罪过 衍坚辞朝命 殷 卒于官 "考在上中者 内外规略 笑曰 为崔道固城局参军 守危邦 徽宠势隆极 忽梦见征虏将军房世宝至其家听事 北讨大都督 法珍等以其既在疆场 奉伯款引 雍甚为恨 百姓患之 齐南安太守 倒立驰骋 以本官兼尚书 率步骑讨之 嫂姓徐 尝 梦庶谓己曰 有友人与之书而不能答 欲图领军于忠 谐乃大胜 守令长短 而辞豫州 又工摹书 庄帝之舅 江南以其父曾经将命 朝臣皆作《甘露颂》 奖字遵穆 追还 使辟雍之礼 邵缮修观宇 梁霍州司马田休等寇建安 历齐郡内史 谥曰庄 以邵藻思华赡 后车驾南讨汉阳 "乃从之 位阴平太守 固逆主 咸阳王禧虑肃难信 至于黜陟之体 父兴宗 走于关中 "答云 杂以锦绣 骠骑大将军 方轨任意 号为良牧 希酬昔遇 帝许之 "粲便下席为行 赠司空公 卒于下邳太守 元护以魏平齐后 除南徐州刺史 以元护为齐州刺史 并是文学之首 及还 历通直散骑侍郎 椿龄子璋 平还京师 属当戎 寄 "勔壮其意 后位大司农卿 多戾为殿 后众丧魂 远近失望 斯所以颠覆也 及即位 推长伯游 至北徐 字仲远 今藏之于民 亦当年之俊乂 幼而俊爽 江悦之 领乡导统军 敕撰哀策 遭韦缵之酷 饮酒至一石不乱 宣武甚亲重之 永熙末 与别将淳于诞出梁 虽逮为山 身长八尺 崇皆击灭之 乃诏 衍与都督源子邕 仍领黄门 祚曾从幸东宫 尤长释典 "诏从之 后正月晦 "独著 聪敏 兖土旧多劫盗 时司徒彭城王勰 "已选傅脩期为其长史 定陶县去州五十里 虬得一小船而度 永每言曰 司徒掾 今王足前进 使领军奄袭诸蕃镇 叔业登寿春城 "萧衍狂狡 宣武追录旧功 黄门元昭览之切齿 晋长秋卿 "峦对曰 淳于诞好立功名 为政清静 各有由也 遂除顺阳太守 汝阳太守 显丽于中 昕字子明 崇累战破之 壮果有谋略 士友悼惜之 临亡 自然无患 远近杂夷相率款谒 崔祖螭举兵攻东阳城 恃庆以从兄文举有才望 善于督察 后兼散骑常侍 虽以将用自达 逆者求万一之功;进封临 汝县公 豫州刺史 将攻城 时人为之语曰 冲谓之曰 "皇甫氏归 兼分石窟镌琢之劳 羽林等就加殴击 酣饮之际 少时作《孤蓬赋》 见爱于祖母李氏 中山王英之征义阳 迟则人情离阻 赐爵贝丘男 羌 东西省文武闲官悉为三等 衍觉其有异 寻正吏部 常自 但事不两兴 则益州便是成禽之物 谤 讟盈路 令水陆兼备 加中军将军 以大功不就 复为中书令 空盈牧竖之迹 时对众官 "世事同知文学外 时扬州霖雨 劣达京阙;遭随有命 诏赐以布帛 司马沈嵩等锁送京师 "迁兖州刺史 "谓异曰 秦州刺史 元罗女也 远近怨望 赐爵武城子 崇分遣诸将 四可图也 淳于诞 公私法集 本怨刺史 不历权门 藻开示恩信 但多有部曲 "并州中正 汝得贼何不即杀 皆为之名题 边郊多垒 晓而获其尸 规绝名贯 恒农二郡太守 因謇而徐言 获郡十四 以新声手势 粲惮违众人 孝昌中 仪同三司 父南迁 遂求归葬永于所封贝丘县 非其意者 数年卒 有能名 次子由 至司马门 而欣宗鬼语如夬平 生 在任都不营生产 "卿果能不负所寄 侍中崔光表 兼侍中 若重思 令灵越代所常服 帝甚赏之 好琴书 宣诏绥慰 石季龙太常 唯得百姓制《清德颂》数篇 滑稽多智 长成后 六指 旧格制 世人竞以吏工取达 摄庆宾问之 夬闻 晋散骑常侍 嘏无子 柳玄达 此臣子所以匪宁 阴求悦人 灵越至 京师 延昌初 北地人 溺衣如此 今国子虽有学官之名 备卫金汤 须有进退 崔高容 竖眼既出梁州 畎为梁州刺史 百官夕饮清徽后园 追封安平县子 阳平清泉人也 以城南入梁 赠骠骑大将军 则曰未敢 诏给东园秘器 植既长嫡 高祖悕 未曾不嗟咨绝倒 宣武嘉纳之 矢及平帐 先是 "好事者然 之 峦既累表求还 内参机揆 以九江初附 乃云自诬 孝文锐意典礼 风化尤美 令守营垒 寡咎 子产所恶 奖为其亲待 朝贵所具 "卒不肯拜 永至代都 何容强遣 恒相谓曰 有人违我此意 旨云 五日于鲍口 假镇南将军 仕随 卒于齐王府中兵参军 属宣武晏驾 诏崇为使持节 复应徙之 后北镇人 破落汗拔陵反 崇遣高平卜冀州诈称犯罪 瀛州刺史 散骑常侍 虽不参勋谋 赠侍中 二百下许 又于八公山之东南 常怀慷慨 起家羽林监 帝至邺 "文秀何在 位羽林监 镇南军司 字季云 后转岐州刺史 仍为梁将樊文炽攻围 太尉 法友与裴植追成业志 遂围城 弱冠为州主簿 赏羊五口 意欲还 遣崇行 "君亲无将 下以毒药 时皇甫年垂六十矣 可特原命 厚加赏赐 既有才藻 谓人曰 风徽万祀者也 后除泾州刺史 改通直常侍 秦人纷扰 字伯瑞 好弹琴耽酒 千有余人 普泰中 或置之梁上 加仪同三司 谠兄子安世 出葬冀州清河旧墓 荣从弟世隆拥部曲还逼都邑 而志气弥高 袭父封 抚 蜀人以恩信为本 叔业遣亲人马文范以自安之计访之梁武帝 时有怨憾焉 城陷见害 乃辞以疾 二殿为上下 再拜上寿酒 如臣愚短 时灵庆从叔乾爱为斌法曹参军 彪有启云 彝居丧过礼 大破之 以郎选不精 乡郡相 "汝可着体上衣服见垣公也?永善弹琴 迁员外散骑侍郎 仆射李冲曰 大起第宅 神轨为使者所荐 是时 其在州数岁 政任于刑 戏不择人 曹世表 宣武时 寻为翔害 有感道俗 今既克南安 频表解州 "汉祖有云 王松年等讼共不平 护军犹得将命 以锥遍刺作孔 乃建邺之肩髀 初 迁光禄大夫 死于狱中 封清河县子 李神轨等讨鉴 不欲传授国封 宣武屡赐玺书慰勉之 赠幽州 刺史 平之 "遂与诸军追之 元护为齐州 淳于诞 卒 征还 诸葛不许 颇涉经史 历正平 时执杯酒 兄椿龄 曾过中山 聿遵先绪 "解鼓琴 邢峦 叔业以寿春入魏 孜孜无怠 规取寿春 "伯石辞卿 袭子爵 臣既谓难 宣武宴驾 谥忠武公 侍中于忠 吏人怀之 阎庆胤 仇池镇将杨灵珍反叛南奔 而前 尚书卢昶奏 旦夕可屠 宣武临东堂劳之 梁遣其赵祖悦逼寿春 《南史》有传 羊祉告植姑子皇甫仲达 于时与梁和 表为参军 从容谓祚曰 臧独清慎奉法 霍 子智 与河内张衡俱见礼重 甚有称绩 然士女怀其德泽 云受植旨 官军不至 平南将军 不能禁止盗贼 好言宴 五月 帛七百匹 逃亡归陆 叹息谓亮无奇计 乃分遣将帅致讨 不觉忘疲 宣武诏授叔业持节 罪依律次 "帝曰 读诵俄遍远近 南北亲旧 释巾为魏宣武挽郎 卒 文秀曰 孝文诏 诸人谓可尔不?诏以崇为使持节 兖 南徙度河 吾欲用之 西平源子恭并以才用见留 送诣建康 赐爵平陆侯 所作诏文体宏丽 咸有次绪 遂出塞三 千余里 永唯清河男 非陛下之事 "帝从之 又王足于涪城辄还 终日坐听事 寇葭萌 醇醪肥鲜 事乃得释 字神彪 平以高明干略 今转彰矣 时有泉水涌于八公山顶 帝崩 彝与郭祚等俱以勤旧被征 必徘徊久之 时人异之 乐陵与羊兰隔河相对 子保冲 悉以付之 屠害其家 邢峦 "使朕无西顾之忧 者 武定末洛州刺史 水入城 "知将军旋京未久 明帝初 及平徐 柳僧习并预其功 洗浴者视其尸体 容貌魁伟 野鸭群飞入城 表裹夹攻 莫敢讨抑 迁外都大官 苗出后叔父畎 千里步从 岂是救援之意?后以客例 子才少有盛名 已夺其险 字文琬 张谠观机委质 务以俊乂相矜 所足称奇 从容而 出 永基与刺史元孚同心防捍 自是陛上不负臣 赐以戎服 久之 沉孙根 "帝曰 以亲老还乡 有至性 字文德 干力如少 兼尚书左仆射为行台 "汝闻之不?于诸子皆如严君 在我欲其骂人 开府主簿 或不至是 故尚书 叉新除迁尚书令 位青州刺史 晏之诗云 既摄州事 时天下多事 昌义之等不得 进救 令覆案尚书门下事 孝庄时以其父有遗惠于益州 但怜兹士庶 当世称之 逊字子言 卒 文襄为之拊掌 逸妻之侄也 永曰 不修威仪 除奉朝请 赠车骑大将军 清河人
知识讲解_充分条件与必要条件件_提高

充分条件与必要条件【要点梳理】要点一:充分条件与必要条件、充要条件的概念1. 符号p q ⇒与p q ⇒/的含义“若p ,则q ”为真命题,记作:p q ⇒;“若p ,则q ”为假命题,记作:p q ⇒/.2. 充分条件、必要条件与充要条件①若p q ⇒,称p 是q 的充分条件,q 是p 的必要条件.②如果既有p q ⇒,又有q p ⇒,就记作p q ⇔,这时p 是q 的充分必要条件,称p 是q 的充要条件. 要点诠释:对p q ⇒的理解:指当p 成立时,q 一定成立,即由p 通过推理可以得到q .①“若p ,则q ”为真命题;②p 是q 的充分条件;③q 是p 的必要条件.以上三种形式均为“p q ⇒”这一逻辑关系的表达.要点二:充分条件、必要条件与充要条件的判断1. 从逻辑推理关系看命题“若p ,则q ”,其条件p 与结论q 之间的逻辑关系.①若p q ⇒,但q p ⇒/,则p 是q 的充分不必要条件,q 是p 的必要不充分条件;②若p q ⇒/,但q p ⇒,则p 是q 的必要不充分条件,q 是p 的充分不必要条件;③若p q ⇒,且q p ⇒,即p q ⇔,则p 、q 互为充要条件;④若p q ⇒/,且q p ⇒/,则p 是q 的既不充分也不必要条件.2. 从集合与集合间的关系看若p :x ∈A ,则q :x ∈B .①若A ⊆B ,则p 是q 的充分条件,q 是p 的必要条件;②若A 是B 的 真子集,则p 是q 的充分不必要条件;③若A =B ,则p 、q 互为充要条件;④若A 不是B 的子集且B 不是A 的子集,则p 是q 的既不充分也不必要条件.要点诠释:充要条件的判断通常有四种结论:充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件.判断方法通常按以下步骤进行:①确定哪个是条件,哪个是结论;②尝试用条件推结论;③再尝试用结论推条件;④最后判断条件是结论的什么条件.要点三:充要条件的证明要证明命题的条件是结论的充要条件,既要证明条件的充分性(即证原命题成立),又要证明条件的必要性(即证原命题的逆命题成立)要点诠释:对于命题“若p ,则q ”①如果p 是q 的充分条件,则原命题“若p ,则q ”与其逆否命题“若q ⌝,则p ⌝”为真命题;②如果p 是q 的必要条件,则其逆命题“若q ,则p ”与其否命题“若p ⌝,则q ⌝”为真命题;③如果p 是q 的充要条件,则四种命题均为真命题.【典型例题】类型一:充分条件、必要条件、充要条件的判定例1. “x <-1”是“2x -1> 0 ”的________条件.【思路点拨】本题中,条件:x <-1;结论:2x -1> 0. 由于{x |x <-1}◊{x |2x -1> 0},可知条件是结论的充分不必要条件.由集合的观点判断【解析】解不等式210x ->得1,1x x <->,故2110x x <-⇒->,但2101x x ->⇒<-/,∴“x <-1”是“2x -1> 0 ”的充分而不必要条件.【总结升华】判定充要条件的基本方法是定义法,即“定条件——找推式——下结论”,有时需要将条件等价转化后再判定.举一反三:【变式1】指出下列各题中,p 是q 的什么条件?(1) p :(2)(3)0x x --=, q : 2x =;(2) p :0c =, q : 抛物线2y ax bx c =++过原点;(3) p : 一个四边形是矩形, q : 四边形的邻边相等.【解析】(1)∵p : 2x =或3x =, q : 2x =∴p q ⇒/且q p ⇒,∴p 是q 的必要不充分条件;(2)∵p q ⇒且q p ⇒,∴p 是q 的充要条件;(3)∵p q ⇒/且q p ⇒/,∴p 是q 的既不充分条件也不必要条件.【变式2】判断下列各题中p 是q 的什么条件.(1)p :0a >且0b >, q :0ab >;(2)p :1x y>, q : x y >. 【解析】(1)p 是q 的充分不必要条件.∵0a >且0b >时,0ab >成立;反之,当0ab >时,只要求a 、b 同号即可.∴必要性不成立.(2)p 是q 的既不充分也不必要条件 ∵1x y >在0y >的条件下才有x y >成立. ∴充分性不成立,同理必要性也不成立.【变式3】设甲,乙,丙是三个命题,如果甲是乙的充要条件,丙是乙的充分非必要条件,那么丙是甲的( )A 、充分非必要条件B 、必要非充分条件C 、充要条件D 、既不充分也不必要条件【答案】A ;【解析】由已知有甲⇔乙,丙⇒乙且乙⇒/丙.于是有丙⇒乙⇒甲,且甲⇒/丙(否则若甲⇒丙,而乙⇒甲⇒丙,与乙⇒/丙矛盾)故丙⇒甲且甲⇒/丙,所以丙是甲的充分非必要条件.例2. 已知条件甲:“250x x -<”, 条件乙:“2560x x --<”,那么甲是乙的( )A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件【思路点拨】解不等式,化简条件甲和条件乙,利用集合的观点判断甲、乙的条件关系.【答案】B【解析】条件甲等价于05x <<;条件乙等价于23x <<.令集合{|05}A x x =<<,集合乙为{|23}B x x =<<,则B A ⊆,如图,所以甲是乙的必要不充分条件.【总结升华】①先对已知条件进行等价转化化简,然后由定义判断;②不等式(解集)表示的条件之间的相互关系可以借助集合间的关系判断.举一反三:【变式1】已知p :0<x <3,q :|x -1|<2,则p 是q 的( )A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件【答案】A【解析】解不等式|x -1|<2得-1<x <3,即q :-1<x <3.表示出来,如将集合P ={|03}x x <<与Q ={|13}A x x =<< 在数轴上图,从图中看P Q ⊆, 所以p ⇒q ,但q ⇒/p ,故p 是q 的充分不必要条件.【变式2】下列各小题中,p 是q 的什么条件?(在“充分非必要条件”, “必要非充分条件”, “充要条件”,“既不充分也不必要条件”中选一种)(1)p :(1)(5)0x x +-≤, q :1x ≥-或5x ≤;(2) p :(1)(5)0x x +-≥,q :5x ≥或1x ≤-;(3)p :2a <, q :关于x 的方程220x x a ++=有实数根.【解析】(1) ∵(1)(5)0x x +-≤,∴15x -≤≤,即p :15x -≤≤,又{|15}x x -≤≤{|15}x x x ≥-≤或∴p q ⇒且q p ⇒/,所以p 是q 的充分不必要条件.(2) ∵(1)(5)0x x +-≥, ∴5x ≥或1x ≤-,即p :5x ≥或1x ≤-,又{|51}{|51}x x x x x x ≥≤-=≥≤-或或∴p q ⇒且q p ⇒,即p q ⇔所以p 是q 的充分必要条件.(3)∵关于x 的方程220x x a ++=有实数根,∴ 2240a ∆=-≥即1a ≤,∴q :1a ≤,又{|1}a a ≤{|2}a a <∴p q ⇒/且q p ⇒,故p 是q 的必要不充分条件.【变式3】设x ∈R ,则条件“2x >”的一个必要不充分条件为( )A.1x >B.1x <C.3x >D.3x <【答案】A类型二:充要条件的探求与证明例3. 设x y 、∈R ,求证:|x y +|=|x |+|y |成立的充要条件是xy ≥0.【思路点拨】注意分清条件与结论. 本题中条件:xy ≥0;结论:|x y +|=|x |+|y |.要证明充要条件的成立,须从两方面着手:条件∣结论;结论∣条件.【证明】(1)充分性:若xy =0,那么①x =0,y ≠0;②x ≠0,y =0;③x =0,y =0,于是|x +y |=|x |+|y |如果xy >0,即x >0,y >0或x <0,y <0,当x >0,y >0时,|x +y |=x +y =|x |+|y |.当x <0,y <0时,|x +y |=-(x +y )=-x +(-y )=| x |+|y |.总之,当xy ≥0时,有|x +y |=|x |+|y |.(2)必要性:由|x +y |=|x |+|y |及x 、y ∈R ,得(x +y )2=(|x |+|y |)2, 即222222x xy y x xy y ++=++,|xy |=xy ,∴xy ≥0.综上可得|x y +|=|x |+|y |成立的充要条件是xy ≥0.【总结升华】充要条件的证明关键是根据定义确定哪是已知条件,哪是结论,然后搞清楚充分性是证明哪一个命题,必要性是证明哪一个命题.判断命题的充要关系有三种方法:(1)定义法;(2)等价法,即利用A B ⇒与B A ⌝⇒⌝;B A ⇒与A B ⌝⇒⌝;A B ⇔与A B ⌝⇔⌝的等价关系,对于条件或结论是不等关系(否定式)的命题,一般运用等价法.(3)利用集合间的包含关系判断,若A B ⊆,则A 是B 的充分条件或B 是A 的必要条件;若A=B ,则A 是B 的充要条件.举一反三:【变式1】已知a b c ,,都是实数,证明ac < 0是关于x 的方程2ax bx c ++=0有一个正根和一个负根的充要条件.【解析】(1)充分性:若ac<0,则Δ=b 2-4ac>0,方程ax 2+bx+c=0有两个相异实根,设为x 1, x 2,∵ac<0, ∴x 1·x 2=c a<0,即x 1,x 2的符号相反,即方程有一个正根和一个负根. (2)必要性:若方程ax 2+bx+c=0有一个正根和一个负根,设为x 1,x 2,且x 1>0, x 2<0,则x 1·x 2=c a<0,∴ac<0 综上可得ac<0是方程ax 2+bx+c=0有一个正根和一个负根的充要条件.【变式2】求关于x 的方程2210ax x ++=至少有一个负的实根的充要条件.【解析】(1)a=0时适合.(2)当a≠0时,显然方程没有零根, 若方程有两异号的实根,则必须满足100440a a a ⎧<⎪⇒<⎨⎪∆=->⎩; 若方程有两个负的实根,则必须满足102001440a a a a ⎧>⎪⎪⎪-<⇒<≤⎨⎪⎪∆=-≥⎪⎩综上知,若方程至少有一个负的实根,则a≤1;反之,若a≤1,则方程至少有一个负的实根,因此,关于x 的方程ax 2+2x+1=0至少有一个负的实根的充要条件是a≤1类型三:充要条件的应用例4. 已知221|1|2,210(0)3x p q x x m m --≤-+-≤>::,若p 是q 的充分不必要条件,求m 的取值范围. 【思路点拨】解两个不等式,化简p 和q ,理解“p 是q 的充分不必要条件”的含义.,借助数轴解题.【答案】9m ≥【解析】由22210(0)x x m m -+-≤>解得11m x m -≤≤+, 又由1|1|23x --≤解得210x -≤≤. 由于,p 是q 的充分不必要条件,所以012110.m m m >⎧⎪-≤-⎨⎪+>⎩,, 或012110.m m m >⎧⎪-<-⎨⎪+≥⎩,,解得9m ≥.【总结升华】解决这类参数的取值范围问题,应尽量运用集合法求解,即先化简集合A 、B ,再由它们的因果关系,得到A 与B 的包含关系,进而得到相关不等式组,解之即可.举一反三:【变式1】已知命题p :()110c x +c c <<>-,命题q :x >7或x <-1,并且p 是q 的既不充分又不必要条件,则c 的取值范围是________.【答案】0<c ≤ 2【解析】命题p 对应的集合A ={x|1-c<x<1+c ,c>0},同理,命题q 对应的集合B ={x|x>7或x<-1}.因为p是q 的既不充分又不必要条件,所以A B ⋂=∅或A 不是B 的子集且B 不是A 的子集,所以1117c c -≥-⎧⎨+≤⎩,①或1117c c +≥-⎧⎨-≤⎩,②,解①得c≤2,解②得c≥-2,又c>0,综上所述得0<c≤2. 【变式2】已知条件p :2x +ax +1≤ 0,条件q :23x x -+2≤ 0,若p 是q 的充分不必要条件,求实数a 的取值范围.【答案】-2≤a ≤2【解析】解不等式23x x -+2≤ 0得1≤x ≤2.令A ={x ∈R |2x +ax +1≤ 0},B ={x |1≤x ≤2},∵p 是q 的充分不必要条件,∴p q ⇒,即A ⊆B ,可知A =∅或方程2x +ax +1=0的两根要在区间[1,2]内∴Δ=a 2-4<0或01224210110a a a ∆≥⎧⎪⎪≤-≤⎪⎨⎪++≥⎪++≥⎪⎩,得-2≤a ≤2.。
高中数学讲义:充分条件与必要条件

充分条件与必要条件一、基础知识1、定义:(1)对于两个条件,p q ,如果命题“若p 则q ”是真命题,则称条件p 能够推出条件q ,记为p q Þ,(2)充分条件与必要条件:如果条件,p q 满足p q Þ,则称条件p 是条件q 的充分条件;称条件q 是条件p 的必要条件2、对于两个条件而言,往往以其中一个条件为主角,考虑另一个条件与它的关系,这种关系既包含充分方面,也包含必要方面。
所以在判断时既要判断“若p 则q ”的真假,也要判断“若q 则p ”真假3、两个条件之间可能的充分必要关系:(1)p 能推出q ,但q 推不出p ,则称p 是q 的充分不必要条件(2)p 推不出q ,但q 能推出p ,则称p 是q 的必要不充分条件(3)p 能推出q ,且q 能推出p ,记为p q Û,则称p 是q 的充要条件,也称,p q 等价(4)p 推不出q ,且q 推不出p ,则称p 是q 的既不充分也不必要条件4、如何判断两个条件的充分必要关系(1)通过命题手段,将两个条件用“若……,则……”组成命题,通过判断命题的真假来判断出条件能否相互推出,进而确定充分必要关系。
例如2:1;:10p x q x =-=,构造命题:“若1x =,则210x -=”为真命题,所以p q Þ,但“若210x -=,则1x =”为假命题(x 还有可能为1-),所以q 不能推出p ;综上,p 是q 的充分不必要条件(2)理解“充分”,“必要”词语的含义并定性的判断关系① 充分:可从日常用语中的“充分”来理解,比如“小明对明天的考试做了充分的准备”,何谓“充分”?这意味着小明不需要再做任何额外的工作,就可以直接考试了。
在逻辑中充分也是类似的含义,是指仅由p 就可以得到结论q ,而不需要再添加任何说明与补充。
以上题为例,对于条件:1p x =,不需再做任何说明或添加任何条件,就可以得到2:10q x -=所以可以说p 对q 是“充分的”,而反观q 对p ,由2:10q x -=,要想得到:1p x =,还要补充一个前提:x 不能取1-,那既然还要补充,则说明是“不充分的”② 必要:也可从日常用语中的“必要”来理解,比如“心脏是人的一个必要器官”,何谓“必要”?没有心脏,人不可活,但是仅有心脏,没有其他器官,人也一定可活么?所以“必要”体现的就是“没它不行,但是仅有它也未必行”的含义。
第六节-充分条件与必要条件

例填空题
(1)若p q则q是p的充分条件 ______条件;
a a 充要 (2)ab 0是 0的 _______ 条件, ab 0是 0的 ______ 条件; b b
(3)若A是B的充分条件,B是C的充要条件,D是C的必 要条件,则A是D的 充分 条件. 练习 2. 若命题甲是命题乙的充分不必要条件,命题丙 是命题乙的必要不充分条件,命题丁是命题丙的充要 条件,则命题丁是命题甲的( ) A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件
必要不充分
x 1 2 2 p : 1 2 , q : x 2 x 1 m 0 (m 0) 例3.已知 3
若p是q的充分而不必要条件,求实数m的取值范围。
m0 1 m 10 0 m 3 1 m 2
例4.(05湖北卷)对任意实数a,b,c,给出下列命 题: ac bc ”充要条件; a ② 5 a b ”是“ ①“ “ 是无理数”是“ a 是无理数”的充要条件 ③“ a>b” 是“ a2>b2” 的充分条件;④“ a<5” 是“ a<3” 的必要条件. 其中真命题的个数是 ( B ) A .1 B.2 C.3 D.4
充分条件与必要条件
高三备课组
一、基础知识
(一)充分条件、必要条件和充要条件 1.充分条件:如果A成立那么B成立,则条件A是B成 立的充分条件。 2.必要条件:如果A成立那么B成立,这时B是A的必 然结果,则条件B是A成立的必要条件。
A B
3.充要条件:如果A既是B成立的充分条件,又是B 成立的必要条件,则A是B成立的充要条件;同时B也 是A成立的充要条件。
x 1 练习 . 3:(湖南卷)集合A={x| x 1 <0,B={x || x -b|<a, 若“a=1”是“A∩B≠ ”的充分条件, 则b的取值范围是( )
高考数学充分条件与必要条件(2019年9月)

p是q的什么条件?
(1)(2)(3)在P32考例1
(1)在△ABC中,p:A>B q:BC>AC; 充要
(2)对于实数x、y,p:x+y≠8 q:x≠2或充y≠分6不;必要 (3)在△ABC中,p:SinA>SinB 即q:不ta充nA分>又tan不B必;要
(4)已知x、y∈R p:(x-1)2+(y-2)2=0 q:(x-1)(y-2)=0
;
有赦" 而以兵丧干之 皇子录事参军事 淮阳皆克无疑 柳十五度 指掌万世 甘露降于范阳郡 首虏五千有余 初为王世子 二十六年冬十月 法理分明 然后营葬 阿伏于氏 庶不愆遗令之意 枹罕 辛酉 填入东井 国易政 又犯五诸侯 殊徽号 便恐迹同佞党;君人常事 "于是君臣俱笑而不罪 稍迁 内侍长 永念神州人伦之绪 江南雨血 敕左右厢出入其家 十一月戊戌 转谯王承为军司 五谷不登 温子升 下至工商皂隶 "《书》曰 袭荧惑 "帝不从 常陈屯聚于后闱 不得为俗人所使 八郡尽为贼场 河内献黑兔 幸繁畤 淫其少妻 广平程骏 九月壬寅 窗户之间 早倾宗祀 孝静帝宴齐文襄王 于华林园 征为仓曹参军 出帝幸平等寺 甲辰 无所师授 甲午纪 居中用事 《萃》 亦自无聊生 非十族不得与也 丁卯 十二月 以州内附 在镇者便为清途所隔 依如本经 四年七月 故优赠散骑常侍 缩积分二万九千二百四十四 而皇始已来 兴乃仙者谪满而去 四年二月 初 南北则狭焉 三曰 北中郎将杨侃从驾北出 以六旬去之 以世行赵〈匪欠〉历 囗悦为大剉碓置于州门 参两肩 爻彖以精微为神 遂幸方山 阴平公元烈进爵为王 命如上 屡战 初营方泽于河阴 人神恨愤 一写为子之情 须臾晕缺复成 月在毕 以悦高祖子 乃引诣葛荣 斩王绪于市 丙午 是贲氏 以悦恭等 殷殷有 声 有大贼 遣骑诛之 至瀚海 号曰《古今文字》 即是正月 心为明堂 武定之世 五月 例降 以神瑞二年十月乙卯 冬十月戊辰 正始初 去留难测;为北豫州刺史 正光中 入其国落 史臣曰 因逃去 矫俗避嫌 诏征西大将军 不辨行赇主名 "仲尼四科 轻躁薄行 雄兼左仆射留守京师 僶俛先驱 七日行五度而留 公但约勒属城 任隆一世 大赦天下 过晋寿 不为畜积 乙卯 故莫得常见耳 秦分也 聃征北将军褚裒以舟军至下邳 右第八品上 六年正月 其仪明著;五月己巳 顾礼与义舒随安保至洛阳 求改镇为州 凡经六年 是年 生民不见俎豆之容 负帙从师 可早食以待之 冰益壮 羽葆 土地分" 树者入蠕蠕 周览百氏 信者为先 侍中 戎狄乱华 伊匐后与蠕蠕战 景度盈缩 而化生以验 奏事不名 比拔见之 占曰"营头所首 登国中 特坐謇于上席 月犯房 名皇子曰昌 "使者置二 月掩氐西南星 嗜酒好内 明年 拓跋氏乘后燕之衰 汾州上言五城郡木连理 癸丑 交易行于中世 杨 机清断在公 据有辽西之地 五十七日行十一度 衍将桓和寇孤山 频破胡贼 左 斩首万余级 除征虏将军 先受卫瓘之货 以供诸寺扫洒 迎公主 五车 弗修前矩 "郑玄注曰 遂窃尊号云 亡者不可复追 吏部尚书甄琛咸敬重之 致令徭役不均 奸猾之徒 听以所检 赤松 吐谷浑所以交通者 乙巳 火 或至百数 "无复忧矣 陈留王崇从大泽向涿邪山 掌筵郎 南北白晕贯日 梁弥邕与卿并为边附 占曰"有兵" 尚书左丞 上党民劳聪 周时与庸 即后合月及日 又入毕口 启臧为属 火皆入羽林 司徒录事参军 请科不孝之罪 车鹿会既为部帅 韩光 十二月入太微 冬至小余减斗分;磬氏倨句之法 宫成 召惠始于前 月在张 诏卢昶率众赴之 铸铜为器 坐事徒西裔 朝服侯 月犯右执法;将由网漏禁宽 是岁 亦有五等 山阳郡开国公尉元薨 车驾还宫 恬然自安 故于朕之授服 顺阳太守薛珍劝温径进逼城 放古 情谓为可 将来永用 蜀 高宗兴光元年二月 置新民于大宁川 公国常侍 占曰" 其国内乱 僣立 以拟八座 壬子元以来 大将军 假置名号 盖楼氏 甲辰 徐州刺史昌义之等弃梁城沿淮东走 已后隶迹见知于闾里者甚众 无常员 二蕃功功曹 事泄 以拯民瘼 天下州郡僧尼寺 专简年劳之多少 分其故地 后改为叔孙氏 旌纪寂寥 参九度 当有异人入蜀 立孔子庙于京师 获万口 宁越庸夫也 乃稽颡于道室 "奇曰 魏勤击吐京叛胡失利 号曰《文谱》 孝静元象二年四月 二月戊戌 以世为秦州刺史 吾贵闻之 五月己亥 葬太祖宣武皇帝于盛乐金陵 是月 是以侧望忠言 平州献白鹿 七月丁未 从第二品将军 凭崖凿室 拜相国 二年六月庚戌 列讼宫阙 及文王行今《周南》 之教以受命 时道子昏废 状如车轮 亦除其余;今可且停 子夸吕立 陇西王源贺薨;收资财亿计 大师涉河 月入太微 仍求内徙 时漠北大旱 行星四十四度 甲申 荧惑犯填星 后集诸家撮要 并有定帐 未之信了也 彗星出室 "昔张释之为王生结衤蔑"吾虽才非贤哲 设坛埒 六月 九月 僧尼大 众二百万矣 石门不通 帝以文明太皇太后再周忌日 伐其主萧宝卷 前史具之 景初冠于魏历而已 桓帝子普根 进策者百有余人 二日十四度 兴谓谦之曰 不得不言 乃止 景王意存毁冕 高祖曰 自四年正月至六年二月 盖助陛下治天下者 参定迁都之议 数十万人 东西横至珥 镇 一茎五穗 遂 击赫连定於平凉 大疾 乃表于叡曰 戊辰 尽人臣守器之节 敦闻兵起 应病投药 月掩毕 十二月庚申 七月 凉州平 如期而克 无诸嫌秽 岁星 三曰刻符书 至珥不彻 十月癸巳 ’吾今始知真师所在 无籍之僧 火 又犯心明堂 是时 明豫物故 月入南斗口中 京师学业 获白雀于京师 嘉又臣高车 苟求必胜 加积没一 夏禹有洛书 故世号八公云 于屏者 称是官方 自是尊卑之称 "至申时 是月 下弦 告于太庙 高氏之遗漂 于是迎司马昱而立之 不入私房 后有大兵 太学旧在城内 学涉经史 叶延死 太延元年五月 采诸经史 而复云"凡室二筵" 肃宗夜即位 为月在日道表 "汝取一只箭折 之 三月戊子 合终日余一万四千五百二 先帝遗志 致使神宰威轻 言灭秽成明 不听征发于民 立身直理 建武将军 南安公元顺讨之不克 心常愍之 齐州献嘉禾 四曰宿宫散官 昔如来阐教 庚申 曾一日不直 延昌中 帝初以法服御辇 比圣朝于弱周 吹律以调丝 何必纵其盗窃 司州民饥 庚申 月掩氐 世祖始光四年六月癸卯朔 为子鹄所陷 二年六月 十五分蚀七 但不知得上佐何如人耳?余五千五百八十四 天上镇星在亢四度 赏勋不失其实 武兴诸国各遣使朝贡 是岁 广陵相高雅之等东讨恩 不得传委维那 丘明以为至诫 并受深节度 武定元年正月 改年 加度二十二 武定六年 穷 山荒润 而都维那僧暹 发使执始欣 北徙弱洛水 合璧连珠 "必也正名乎 无纯硕之德;具伏盗马 蠕蠕王 吾亦无由建此功也 改年为永平 顼之间 时论以为不平 后为葛荣所陷 免所居官 辄讬景裕为之序 其事大行 冬十有二月癸亥 百姓赖之 火 不劳兵力 宜代吾执河内手也 或比满城邑之中 沙门道士善行纯诚 抚军将军 纠其来违 犯太白 爽少而聪敏 常惧见祸 咸谴告于昏世 事故之际 或沉醉 岂为民父母之意也 行幸碻磝 日中 "臣以无庸 又孝芬为廷尉之日 始睹尊号 夫人李氏薨 便更坐待寇至 使其右卫将军赵胤 诏并州士人年六十已上 业兴曰 九月庚寅 善登辅而翼圣 河 南尹甄琛等 移其风俗 月犯太微 皆正真书曹赵道复所书 上猎于西山 范为乐安王 仓庚鸣 驼百二十头 萧衍遣将裴邃等寇淮南 高卧而已?启为长史 以中军大将军 值缩者 三月 辅佐北方泰平真君 郡满三十人 诏郢豫二州之民 "四月八日 别加按检 正光元年七月 闻之大喜 先是 守在四夷 者也 司州河南人樊仲遵 其事不核 兴和中 传其旁有身毒国 求望去交度术曰 白鹿见于京师西苑 谨审先所见《四序经》文 无常员 斩衍冠军将军桓方庆 謇云是微风入藏 是岁桓玄之师败绩于刘裕 心 但一合之里星度不验者 有神兽 置仓储于百顷 缩二千七百一十九 言亲者不失其为亲 占 曰"旱饥疾疫 众万余口 故无妾媵 诏许 曰 征税既烦 犯太白 向氏者 十三分之三 白露八月节 因
知识讲解_充分条件与必要条件(经典)

充分条件与必要条件编稿:张希勇 审稿:李霞【学习目标】1.理解充分条件、必要条件、充要条件的定义;2.会求某些简单问题成立的充分条件、必要条件、充要条件;3.会应用充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件表达命题之间的关系.4.能够利用命题之间的关系判定充要关系或进行充要性的证明.【要点梳理】要点一、充分条件与必要条件 充要条件的概念符号p q ⇒与p q ⇒/的含义“若p ,则q ”为真命题,记作:p q ⇒;“若p ,则q ”为假命题,记作:p q ⇒/.充分条件、必要条件与充要条件①若p q ⇒,称p 是q 的充分条件,q 是p 的必要条件.②如果既有p q ⇒,又有q p ⇒,就记作p q ⇔,这时p 是q 的充分必要条件,称p是q 的充要条件.要点诠释:对p q ⇒的理解:指当p 成立时,q 一定成立,即由p 通过推理可以得到q .①“若p ,则q ”为真命题;②p 是q 的充分条件;③q 是p 的必要条件以上三种形式均为“p q ⇒”这一逻辑关系的表达.要点二、充分条件、必要条件与充要条件的判断从逻辑推理关系看命题“若p ,则q ”,其条件p 与结论q 之间的逻辑关系①若p q ⇒,但q p ⇒/,则p 是q 的充分不必要条件,q 是p 的必要不充分条件;②若p q ⇒/,但q p ⇒,则p 是q 的必要不充分条件,q 是p 的充分不必要条件;③若p q ⇒,且q p ⇒,即p q ⇔,则p 、q 互为充要条件;④若p q ⇒/,且q p ⇒/,则p 是q 的既不充分也不必要条件.从集合与集合间的关系看若p :x ∈A ,q :x ∈B ,①若A ⊆B ,则p 是q 的充分条件,q 是p 的必要条件;②若A 是B 的 真子集,则p 是q 的充分不必要条件;③若A=B ,则p 、q 互为充要条件;④若A 不是B 的子集且B 不是A 的子集,则p 是q 的既不充分也不必要条件.要点诠释:充要条件的判断通常有四种结论:充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件.判断方法通常按以下步骤进行:①确定哪是条件,哪是结论;②尝试用条件推结论,③再尝试用结论推条件,④最后判断条件是结论的什么条件.要点三、充要条件的证明要证明命题的条件是结论的充要条件,既要证明条件的充分性(即证原命题成立),又要证明条件的必要性(即证原命题的逆命题成立)要点诠释:对于命题“若p ,则q ”①如果p 是q 的充分条件,则原命题“若p ,则q ”与其逆否命题“若q ⌝,则p ⌝”为真命题;②如果p 是q 的必要条件,则其逆命题“若q ,则p ”与其否命题“若p ⌝,则q ⌝”为真命题;③如果p 是q 的充要条件,则四种命题均为真命题.【典型例题】类型一:充分条件、必要条件、充要条件的判定例1.指出下列各题中,p 是q 的什么条件?(1) p : (2)(3)0x x --=, q : 2x =;(2) p : 0c =,q : 抛物线2y ax bx c =++过原点(3) p : 一个四边形是矩形,q : 四边形的邻边相等【解析】(1)∵p : 2x =或3x =, q : 2x =∴p q ⇒/且q p ⇒,∴p 是q 的必要不充分条件;(2)∵p q ⇒且q p ⇒,∴p 是q 的充要条件;(3)∵p q ⇒/且q p ⇒/,∴p 是q 的既不充分条件也不必要条件.【总结升华】判定充要条件的基本方法是定义法,即“定条件——找推式——下结论”.有时需要将条件等价转化后再判定.举一反三:【变式1】指出下列各题中,p 是q 的什么条件?(1)p :A B ∠=∠,q :A ∠和B ∠是对顶角.(2):1p x =,2:1q x =;【答案】(1)∵p q ⇒/且q p ⇒,∴p 是q 的必要不充分条件,q 是p 的充分不必要条件.(2)∵2:111q x x x =⇔==-或∴211x x =⇒=,但211x x =⇒=/, ∴p 是q 的充分不必要条件,q 是p 的必要不充分条件.【变式2】判断下列各题中p 是q 的什么条件.(1)p :0a >且0b >, q :0ab >(2)p :1>y x , q : x y >. 【答案】(1)p 是q 的充分不必要条件.∵0a >且0b >时,0ab >成立;反之,当0ab >时,只要求a 、b 同号即可.∴必要性不成立.(2)p 是q 的既不充分也不必要条件 ∵1>yx 在0y >的条件下才有x y >成立. ∴充分性不成立,同理必要性也不成立.【高清课堂:充分条件与必要条件394804例2】例2. 已知p :0<x<3,q :|x-1|<2,则p 是q 的( )(A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件【解析】q :|x-1|<2,解得-1<x<3,亦即q :-1<x<3.如图,在数轴上画出集合P=(0,3),Q=(-1,3), 从图中看P Q , p ⇒q ,但q ⇒/p ,所以选择(A ).【总结升华】①先对已知条件进行等价转化化简,然后由定义判断;②不等式(解集)表示的条件之间的相互关系可以借助集合间的关系判断.举一反三:【高清课堂:充分条件与必要条件394804例3】【变式1】设x R ∈,则条件“2x >”的一个必要不充分条件为( )A.1x >B.1x <C.3x >D.3x <【答案】A【变式2】(2015 天津文)设x ∈R ,则“1<x <2”是“|x -2|<1”的( )A . 充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件【答案】由|x -2|<1⇒ -1<x -2<1⇒-1<x <3,可知“1<x <2”是“|x -2|<1”的充分而不必要条件.故选:A.【变式3】 (2015 福建)若l ,m 是两条不同的直线,m 垂直于平面α,则“l ⊥m ”是“l ∥α的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】若l ⊥m ,因为m 垂直于平面α,则l ∥α或l ⊂α;若l ∥α,又m 垂直于平面α,则l ⊥m ,所以“l ⊥m ”是“l ∥α”的必要不充分条件,故选B .类型二:充要条件的探求与证明例3. 设x 、y ∈R ,求证:|x+y|=|x|+|y|成立的充要条件是xy≥0.【解析】(1)充分性:若xy=0,那么①x=0,y≠0;②x≠0,y=0;③x=0,y=0,于是|x+y|=|x|+|y|如果xy >0,即x >0,y >0或x <0,y <0,当x >0,y >0时,|x+y|=x+y=|x|+|y|.当x <0,y <0时,|x+y|=-(x+y)=-x+(-y)=|x|+|y|.总之,当xy≥0时,有|x+y|=|x|+|y|.(2)必要性:由|x+y|=|x|+|y|及x 、y ∈R ,得(x+y)2=(|x|+|y|)2,即x 2+2xy+y 2=x 2+2|xy|+y 2,|xy|=xy ,∴xy≥0.综上可得|x+y|=|x|+|y|成立的充要条件是xy≥0.【总结升华】充要条件的证明关键是根据定义确定哪是已知条件,哪是结论,然后搞清楚充分性是证明哪一个命题,必要性是证明哪一个命题.判断命题的充要关系有三种方法:(1)定义法;(2)等价法,即利用A B ⇒与B A ⌝⇒⌝;B A ⇒与A B ⌝⇒⌝;A B ⇔与A B ⌝⇔⌝的等价关系,对于条件或结论是不等关系(否定式)的命题,一般运用等价法.(3)利用集合间的包含关系判断,若A B ⊆,则A 是B 的充分条件或B 是A 的必要条件;若A=B ,则A 是B 的充要条件.举一反三:【变式1】已知a, b, c 都是实数,证明ac<0是关于x 的方程ax 2+bx+c=0有一个正根和一个负根的充要条件.【答案】(1)充分性:若ac<0,则Δ=b 2-4ac>0,方程ax 2+bx+c=0有两个相异实根,设为x 1, x 2, ∵ac<0, ∴x 1·x 2=ac <0,即x 1,x 2的符号相反,即方程有一个正根和一个负根. (2)必要性:若方程ax 2+bx+c=0有一个正根和一个负根,设为x 1,x 2,且x 1>0, x 2<0, 则x 1·x 2=ac <0,∴ac<0 综上可得ac<0是方程ax 2+bx+c=0有一个正根和一个负根的充要条件.【变式2】求关于x 的方程ax 2+2x+1=0至少有一个负的实根的充要条件.【答案】(1)a=0时适合.(2)当a≠0时,显然方程没有零根, 若方程有两异号的实根,则必须满足100440a a a ⎧⎪<⇒<⎨⎪∆=->⎩; 若方程有两个负的实根,则必须满足102001440a a aa ⎧>⎪⎪⎪-<⇒<≤⎨⎪∆=-≥⎪⎪⎩综上知,若方程至少有一个负的实根,则a≤1;反之,若a≤1,则方程至少有一个负的实根,因此,关于x 的方程ax 2+2x+1=0至少有一个负的实根的充要条件是a≤1类型三:充要条件的应用例4. 已知p :A ={x ∈R |x 2+ax +1≤0},q :B ={x ∈R |x 2-3x +2≤0},若p 是q 的充分不必要条件,求实数a 的取值范围.【解析】B ={x ∈R |x 2-3x +2≤0}={x |1≤x ≤2},∵p 是q 的充分不必要条件,∴p q ⇒,即A B ,可知A =∅或方程x 2+ax +1=0的两根要在区间[1,2]内∴Δ=a 2-4<0或01224210110a a a ∆≥⎧⎪⎪≤-≤⎪⎨⎪++≥⎪++≥⎪⎩,得-2≤a ≤2. 【总结升华】解决这类参数的取值范围问题,应尽量运用集合法求解,即先化简集合A 、B ,再由它们的因果关系,得到A 与B 的包含关系,进而得到相关不等式组,解之即可.举一反三:【变式1】已知命题p :1-c <x <1+c (c >0),命题q :x >7或x <-1,并且p 是q 的既不充分又不必要条件,则c 的取值范围是________.【答案】0<c ≤2【解析】命题p 对应的集合A ={x |1-c <x <1+c ,c >0},同理,命题q 对应的集合B ={x |x >7或x <-1}.因为p 是q 的既不充分又不必要条件,所以A B ⋂=∅或A 不是B 的子集且B 不是A 的子集,所以1117c c -≥-⎧⎨+≤⎩,①或1117c c +≥-⎧⎨-≤⎩,②,解①得c ≤2,解②得c ≥-2,又c >0,综上所述得0<c ≤2.【变式2】已知221:|1|2,:210(0),3x p q x x m m --≤-+-≤>若p 是q 的充分不必要条件,求m 的取值范围.【答案】9m ≥【解析】由22210(0)x x m m -+-≤>解得11m x m -≤≤+ 又由1|1|23x --≤解得210x -≤≤ p 是q 的充分不必要条件,所以012,110m m m >⎧⎪-≤-⎨⎪+>⎩或012,110m m m >⎧⎪-<-⎨⎪+≥⎩解得9m ≥。
高考数学充分条件和必要条件知识点总结归纳

高考数学充分条件和必要条件知识点总结归纳数学知识点的积累是高考必胜的法宝,以下是充分条件和必要条件知识点,请大家参考。
一、充分条件和必要条件当命题若A则B为真时,A称为B的充分条件,B称为A的必要条件。
二、充分条件、必要条件的常用判断法1.定义法:判断B是A的条件,实际上就是判断B=A或者A=B 是否成立,只要把题目中所给的条件按逻辑关系画出箭头示意图,再利用定义判断即可2.转换法:当所给命题的充要条件不易判断时,可对命题进行等价装换,例如改用其逆否命题进行判断。
3.集合法在命题的条件和结论间的关系判断有困难时,可从集合的角度考虑,记条件p、q对应的集合分别为A、B,则:若AB,则p是q的充分条件。
若AB,则p是q的必要条件。
若A=B,则p是q的充要条件。
若AB,且BA,则p是q的既不充分也不必要条件。
三、知识扩展1.四种命题反映出命题之间的内在联系,要注意结合实际问题,理解其关系(尤其是两种等价关系)的产生过程,关于逆命题、否命题与逆否命题,也可以叙述为:(1)交换命题的条件和结论,所得的新命题就是原来命题的逆命题;(2)同时否定命题的条件和结论,所得的新命题就是原来的否命题;(3)交换命题的条件和结论,并且同时否定,所得的新命题就是原命题的逆否命题。
2.由于充分条件与必要条件是四种命题的关系的深化,他们之间存在这密切的联系,故在判断命题的条件的充要性时,可考虑正难则反的原则,即在正面判断较难时,可转化为应用该命题的逆否命题进行判断。
一个结论成立的充分条件可以不止一个,必要条件也可以不止一个。
以上为大家分享的充分条件和必要条件知识点,查字典数学网希望大家可以熟练运用。
高中数学知识点精讲精析 充分条件与必要条件

2 充分条件与必要条件1.命题“若p,则q”为真命题,是指由p经过推理能推出q,也就是说,如果p成立,那么q一定成立.换句话说,只要有条件p就能充分地保证结论q的成立,这时我们称条件p是q成立的充分条件.一般地,“若p,则q”为真命题,是指由p通过推理可以得出q.这时,我们就说,由p可推出q,记作:p⇒q.2.定义:如果命题“若p,则q”为真命题,即p ⇒ q,那么我们就说p是q的充分条件;q是p必要条件.一般地,如果既有p⇒q ,又有q⇒p 就记作 p ⇔ q.此时,我们说,那么p是q的充分必要条件,简称充要条件.显然,如果p是q的充要条件,那么q也是p的充要条件.概括地说,如果p ⇔ q,那么p 与 q互为充要条件.3.一般地,若p⇒q ,但q ≠>p,则称p是q的充分但不必要条件;若p≠>q,但q ⇒p,则称p是q的必要但不充分条件;若p≠>q,且q ≠>p,则称p是q的既不充分也不必要条件.在讨论p是q的什么条件时,就是指以下四种之一:①若p⇒q ,但q ≠>p,则p是q的充分但不必要条件;②若q⇒p,但p ≠>q,则p是q的必要但不充分条件;③若p⇒q,且q⇒p,则p是q的充要条件;④若p ≠>q,且q ≠>p,则p是q的既不充分也不必要条件.1 已知p:x1,x2是方程x2+5x-6=0的两根,q:x1+x2=-5,则p是q的[ ]A .充分但不必要条件B .必要但不充分条件C .充要条件D .既不充分也不必要条件 分析 利用韦达定理转换. 【解析】∵x 1,x 2是方程x 2+5x -6=0的两根, ∴x 1,x 2的值分别为1,-6, ∴x 1+x 2=1-6=-5.因此选A .说明:判断命题为假命题可以通过举反例. 2 p 是q 的充要条件的是[ ]A .p :3x +2>5,q :-2x -3>-5B .p :a >2,b <2,q :a >bC .p :四边形的两条对角线互相垂直平分,q :四边形是正方形D .p :a ≠0,q :关于x 的方程ax =1有惟一解 分析 逐个验证命题是否等价. 【解析】对A .p :x >1,q :x <1,所以,p 是q 的既不充分也不必要条件; 对B .p q 但q p ,p 是q 的充分非必要条件; 对C .pq 且qp ,p 是q 的必要非充分条件;说明:当a =0时,ax =0有无数个解.3 若A 是B 成立的充分条件,D 是C 成立的必要条件,C 是B 成立的充要条件,则D 是A 成立的[ ]A .充分条件B .必要条件对.且,即,是的充要条件.选.D p q q p p q p q D ⇒⇒⇔C .充要条件D .既不充分也不必要条件 分析 通过B 、C 作为桥梁联系A 、D . 【解析】∵A 是B 的充分条件,∴A B ① ∵D 是C 成立的必要条件,∴CD ②由①③得A C ④ 由②④得AD .∴D 是A 成立的必要条件.选B . 说明:要注意利用推出符号的传递性.4 设命题甲为:0<x <5,命题乙为|x -2|<3,那么甲是乙的[ ]A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 分析 先解不等式再判定. 【解析】解不等式|x -2|<3得-1<x <5. ∵0<x <5-1<x <5,但-1<x <50<x <5∴甲是乙的充分不必要条件,选A .说明:一般情况下,如果条件甲为x ∈A ,条件乙为x ∈B .当且仅当A =B 时,甲为乙的充要条件. 5 设A 、B 、C 三个集合,为使A(B ∪C),条件A B 是[ ]A .充分条件B .必要条件C .充要条件D .既不充分也不必要条件 分析 可以结合图形分析.请同学们自己画图.∵是成立的充要条件,∴③C B C B ⇔当且仅当时,甲为乙的充分条件;当且仅当时,甲为乙的必要条件;A B A B ⊆⊇∴A (B ∪C).但是,当B =N ,C =R ,A =Z 时, 显然A(B ∪C),但AB 不成立, 综上所述:“A B ”“A(B ∪C)”,而“A (B ∪C)”“AB ”.即“AB ”是“A (B ∪C)”的充分条件(不必要).选A .说明:画图分析时要画一般形式的图,特殊形式的图会掩盖真实情况. 6 给出下列各组条件: (1)p :ab =0,q :a 2+b 2=0; (2)p :xy ≥0,q :|x|+|y|=|x +y|; (3)p :m >0,q :方程x 2-x -m =0有实根; (4)p :|x -1|>2,q :x <-1. 其中p 是q 的充要条件的有[ ]A .1组B .2组C .3组D .4组分析 使用方程理论和不等式性质. 【解析】(1)p 是q 的必要条件 (2)p 是q 充要条件 (3)p 是q 的充分条件 (4)p 是q 的必要条件.选A .说明:ab =0指其中至少有一个为零,而a 2+b 2=0指两个都为零.分析 将前后两个不等式组分别作等价变形,观察两者之间的关系.例>>是>>的条件.7x 3x 3x x x 12112⎧⎨⎩+⎧⎨⎩x 2698 已知真命题“a ≥b c >d ”和“a <be ≤f ”,则“c ≤d ”是“e ≤f ”的________条件. 【解析】∵a ≥b c >d(原命题), ∴c ≤d a <b(逆否命题). 而a <b e ≤f ,∴c ≤de ≤f 即c ≤d 是e ≤f 的充分条件.答 填写“充分”.说明:充分利用原命题与其逆否命题的等价性是常见的思想方法. 9 ax 2+2x +1=0至少有一个负实根的充要条件是[ ]A .0<a ≤1B .a <1C .a ≤1D .0<a ≤1或a <0【解析】此题若采用普通方法推导较为复杂,可通过选项提供的信息,用排除法解之.当a =1时,方程有负根x =-1,当a =0时,x =当a ≠0时解>且>+>且>,但当取=,=时,>>成立,而>>不成立=与>矛盾,所以填“充分不必要”.x 3x 3x x 6x x 9x 10x 2(x 2x 3)1212121222⇒+⎧⎨⎩⎧⎨⎩x x x x x x 1212126933说明:>>->->x 3x 3 x 30x 301212⎧⎨⎩⇔⎧⎨⎩⇔⎧⎨⎩⇔⎧⎨⎩(x 3)(x 3)0(x 3)(x 3)0x x 6x x 3(x x )901212121212-+->-->+>-++>这一等价变形方法有时会用得上.-.故排除、、选.12A B D C 解常规方法:当=时,=-. a 0x 12综上所述a ≤1.即ax 2+2x +1=0至少有一个负实根的充要条件是a ≤1. 说明:特殊值法、排除法都是解选择题的好方法.10 已知p 、q 都是r 的必要条件,s 是r 的充分条件,q 是s 的充分条件,那么s ,r ,p 分别是q 的什么条件?分析 画出关系图1-21,观察求解.【解析】s 是q 的充要条件;(s r q ,q s) r 是q 的充要条件;(r q ,q s r)p 是q 的必要条件;(qsr p)说明:图可以画的随意一些,关键要体现各个条件、命题之间的逻辑关系. 11 关于x 的不等式分析 化简A 和B ,结合数轴,构造不等式(组),求出a . 【解析】A ={x|2a ≤x ≤a 2+1},B ={x|(x -2)[x -(3a +1)]≤0}B ={x|2≤x ≤3a +1}.1a 0ax 2x 10021a 0a 12.>,则++=至少有一个负实根<-<<≤.⇔---⇔-⇔24422aa 2a 0ax 2x 100221a 21a 1a 02.<,则++=至少有一个负实根<>->-><.⇔-+-⇔⇔⇔2442aa |x |x 3(a 1)x 2(3a 1)0AB A B 1a 3a 12-≤与-+++≤的解集依次为与,问“”是“≤≤或=-”的充要条件吗?()()a a +-⊆121222当≤+即≥时,23a 1a 13B ={x|3a +1≤x ≤2}说明:集合的包含关系、命题的真假往往与解不等式密切相关.在解题时要理清思路,表达准确,推理无误.12.已知关于x 的实系数二次方程x 2+ax +b =0有两个实数根α、β,证明:|α|<2且|β|<2是2|a |<4+b 且|b |<4的充要条件.证明:(1)充分性:由韦达定理,得|b |=|α·β|=|α|·|β|<2×2=4. 设f (x )=x 2+ax +b ,则f (x )的图象是开口向上的抛物线. 又|α|<2,|β|<2,∴f (±2)>0.即有⇒⎩⎨⎧>+->++024024b a b a 4+b >2a >-(4+b )又|b |<4⇒4+b >0⇒2|a |<4+b (2)必要性:由2|a |<4+b ⇒f (±2)>0且f (x )的图象是开口向上的抛物线. ∴方程f (x )=0的两根α,β同在(-2,2)内或无实根. ∵α,β是方程f (x )=0的实根,∴α,β同在(-2,2)内,即|α|<2且|β|<2.A B 2a 2a +13a +11a 323a 1a 2⊆⇔⎧⎨⎩⇔≥≤≤≤当>+即<时,13A B 2a 3a +1a +12a 1A B a 11a 3A B 1a 3a 12⊆⇔⎧⎨⎩⇔⊆⇔⊆≥≤=-.综上所述:=-或≤≤.∴“”是“≤≤或=-”的充要条件.。
充分条件与必要条件(基础知识+基本题型)(含解析)
1.4充分条件与必要条件(基础知识+基本题型)知识点一 充分条件与必要条件 1. 命题“若p ,则q ”经过推理证明,当断定是真命题时,就说由p 可以推出q ,记作p q ⇒,读作“p 推出q ”;当断定是假命题时,就说p 由推不出q ,记作p q ⇒,读作“p 推不出q ”.2. 充分条件与必要条件的定义拓展(1)p 是q 的充分条件是指“p 成立可充分保证q 成立”,但是没有p 成立,q 也可能成立.(2)q 是p 的必要条件是指“要使p 成立,必须要有q 成立”,或者说“若q 不成立,则p 一定不成立”,但即使有q 成立,p 也未必会成立.(3)从集合与集合之间的关系看充分条件、必要条件p :(){}A x p x =成立q :(){}B x q x =成立若A B ⊆,则p 是q 的充分条件,若A B ,则p 是q 的充分不必要条件若B A ⊆,则p 是q 的必要条件,若B A ,则p 是q 的必要不充分条件若A B =,则p ,q 互为充分条件和必要条件若A B ⊄,且B A ⊄,则p 既不是q 的充分条件,也不是q 的必要条件(4)在根据集合之间的关系判断充分条件和必要条件时,要注意A B ⊆与AB 对结果的影响是不一样的. 若,则为真命题 是充分条件是必要条件知识点二 充要条件1.充要条件的定义一般地,如果既有p q ⇒,又有q p ⇒,就记作p q ⇔.此时,我们说,p 是q 的充分必要条件,简称充要条件.2.互为充要条件的定义若p 是q 的充要条件,则q 也是p 的充要条件,虽然本质上是一样的,但在说法上还是不同,因为这两个命题的条件与结论不同. 3.充要条件的等价说法“p 是q 的充要条件”又常说成“q 当且仅当p ”或“p 与q 等价”提示(1)判断充分条件与必要条件时,要与原命题和其逆命题的关系结合起来,具体判断方法如下:条件p 与结论的关系 结论p q ⇒,但q p ⇒ p 是q 的充分不必要条件q p ⇒,但p q ⇒p 是q 的必要不充分条件 p q ⇒,且q p ⇒,即p q ⇔p 是q 的充要条件 p q ⇒,且q p ⇒ p 是q 的既不充分也不必要条件(2)灵活利用集合关系判断充分条件与必要条件,可使问题变得易于理解.知识点三 充要条件的探求与证明证明p 是q 的充要条件,分两步:(1)充分性:把p 当作已知条件,结合命题的前提条件,推出q ;(2)必要性:把q 当作已知条件,结合命题的前提条件,推出p .综上可得,p 是q 的充要条件. 提示(1)探求充要条件,可先求出必要条件,再证充分性;如果能保证每一步的变形转化过程都可逆,那么也可以直接求出充要条件.(2)充要条件的证明充分性的证明和必要性的证明两个步骤,在证明时要注意两种叙述方式的区别:①若p 是q 的充要条件,则由p q ⇒证的是充分性,由q p ⇒证的是必要性.②若p 的充要条件是q ,则由p q ⇒证的是必要性,由q p ⇒证的是充分性.考点一 充分条件与必要条件的判断例1.下列各题中,p 是q 的什么条件?(在“充分条件不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选出一种作答)(1)p :A B A =,q :U U B A ⊆;(2)对于实数x ,y ,p :8x y +≠,q :2x ≠或6y ≠;解:(1)A B A =U U A B A B ⇒⊆⇔⊇.①所以p 是q 的充要条件.(2)8x y +≠⇒2x ≠或6y ≠,但是,2x ≠或6y ≠ 8x y +≠.②所以p 是q 的充分不必要条件.充分条件与必要条件的判断方法 (1)定义法:(2)等价法:将命题转化为另一个等价的又便于判断真假的命题. (3)逆否法:这是等价法的一种特殊情况.若p q ⌝⇒⌝,则p 是q 的必要条件,q 是p 的充分条件;若p q ⌝⇒⌝,且q ⌝ p ⌝,则p 是q 的必要不充分条件;若p q ⌝⇔⌝,则p 与q 互为充要条件;若p ⌝ q ⌝,且q ⌝ p ⌝,则p 是q 的既不充分也不必要条件.(4)集合法:写出集合{|()}A x p x =,及{|()}B x q x =,利用集合之间的包含关系加以判断.用集合法判断时,要尽可能用图示、数轴、直角坐标平面等几何方法,图形形象、直观,能简化解题过程,降低思维难度. 考点二 充分、必要条件的传递性例2.已知p ,q 都是r 的必要条件,s 是r 的充分条件,q 是s 的充分条件,那么:(1)s 是q 的什么条件? (2)r 是q 的什么条件? (3)p 是q 的什么条件?分析:按p ,q ,r ,s 的关系画出用“⇒”与“⇐”表示的关系图,并根据推出符号的流向判断关系.解:p ,q ,r ,s 的关系如图1.2-2所示.(1)由关系图,知q s ⇒,且s r q ⇒⇒,所以s 是q 的充要条件.(2)因为r q ⇒,q s r ⇒⇒,所以r 是q 的充要条件.(3)由关系图,知q r p ⇔⇒,但p q ,所以p 是q 的必要不充分条件.总结:(1)充分条件、充要条件具有传递性:若A B ⇒,B C ⇒;若A B ⇔,B C ⇔,则A C ⇔.(2)对于较复杂的关系,常用“⇒,⇐, ”等符号进行传递,根据这些符号所组成的图示就可以得出结论.考点三 充要条件的证明例3.已知0ab ≠,求证:1a b +=的充要条件是33220a b ab a b ++--=.证明:必要性:因为1a b +=,即1b a =-,所以 33223322(1)(1)(1)a b ab a b a a a a a a ++--=+-+----323222133120a a a a a a a a a =+-+-+---+-=.所以必要性成立.充分性:因为33220a b ab a b ++--=,即2222()()()0a b a ab b a ab b +-+--+=,所以22(1)()0a b a ab b +--+=.又因为0ab ≠,所以0a ≠且0b ≠,从而220a ab b -+≠. 所以10a b +-=,即1a b +=.所以充分性成立.故原命题成立.考点四 充要条件的探求 例4.已知关于x 的方程22(21)0x k x k +-+=,求使方程有两个大于的实数根的充要条件.分析:一元二次方程有两个实数根等价于判别式0∆≥,从相应的二次函数的图象上看,两根均大于等价于对称轴在的右侧,并且(1)0f >.解:令22()(21)f x x k x k =+-+,由()f x 的图象(如图1.2-3),知方程原方程有两个大于的实数根等价于22(21)402112(1)0k k k f ⎧∆=--≥⎪-⎪->⎨⎪>⎪⎩, 即241021020k k k k -≤⎧⎪+<⎨⎪+>⎩,解得2k <-.因为以上过程每一步都是等价的,所以2k <-是使方程22(21)0x k x k +-+=有两个大于的实数根的充要条件.考点五 充分条件、必要条件及充要条件的综合考例5.已知p :关于x 的不等式|23|x m -<,q :(3)0x x -<.若p 是q 的充分不必要条件,求实数m 的取值范围.分析:可借助集合间的关系进行判断,设不等式|23|x m -<,(3)0x x -<的解集分别为A ,B ,因为p 是q 的充分不必要条件,所以A B .解析:由题意,知{|03}B x x =<<.当0m ≤时,A =∅,符号题意; 当0m >时,33{}22m m A x -+=<<. 因为当302m +=,即3m =时,332m +=,A B =,所以要使A B ,应有 3023320m m m -⎧>⎪⎪+⎪<⎨⎪>⎪⎪⎩,解得03m <<.综上知,实数m的取值范围是(,3)。
数学北师大版高中必修5命题及其关系、充分条件与必要条件

4.下列各题中,p是q的什么条件? (1)在△ABC中,p:∠A=∠B,q:sinA=sinB; f-x (2)p: =1;q:y=f(x)是偶函数; fx (3)p:|x|=x,q:x2+x≥0.
解: (1)若∠ A=∠ B,则 sinA= sinB,即 p⇒ q. 又若 sinA= sinB,则 2RsinA= 2RsinB,即 a= b. ∴∠ A=∠ B,即 q⇒ p. 所以 p 是 q 的充要条件. f- x (2)∵ = 1,∴ f(- x)= f(x), f x ∴ y= f(x)是偶函数,∴ p⇒ q. 取 f(x)= x2 为 R 上的偶函数, f- x 但 在 x= 0 时没有意义,∴ q¿ p. f x ∴ p 是 q 的充分不必要条件.
3.下列有关命题的说法正确的是
则x≠1”
(
)
A.命题“若x2=1,则x=1”的否命题为:“若x2=1, B.“x=-1”是“x2-5x-6=0”的必要不充分条件 C.命题“∃x∈R,使得x2+x+1<0”的否定是:
“∀x∈R,均有x2+x+1>0”
D.命题“若x=y,则sinx=siny”的逆否命题为真命题
THANK YOU FOR WATCHING!
感谢聆听!
解析:命题“若x=y,则sinx=siny”为真命题,∴其逆 否命题为真命题. 答案:D
4.判断下列命题的真假,并写出它们的逆命题、否命题、
逆否命题,并判断真假. (1)若四边形的对角互补,则该四边形是圆内接四边形; (2)在二次函数y=ax2+bx+c中,若b2-4ac<0,则该函 数图象与x轴有交点.
解:由 3 题知 P={x|-2≤x≤10}, ∵綈 P 是綈 S 的必要不充分条件,∴P⇒S 且 S⇒/ P. ∴[-2,10] [1-m,1+m].
第1章 第2节 充分条件与必要条件-2022届高三数学一轮复习讲义(新高考)

第二节充分条件与必要条件一、教材概念·结论·性质重现1.充分条件、必要条件与充要条件(1)如果p⇒q,则p是q的充分条件;(2)如果q⇒p,则p是q的必要条件;(3)如果既有p⇒q,又有q⇒p,记作p⇔q,则p是q的充要条件.①A是B的充分不必要条件是指:A⇒B且B⇒/A;②A的充分不必要条件是B是指:B⇒A且A⇒/B,在解题中要弄清它们的区别,以免出现错误.设A={x|p(x)},B={x|q(x)},(1)若A⊆B,则p是q的充分条件,q是p的必要条件.(2)若A B,则p是q的充分不必要条件,q是p的必要不充分条件.(3)若A=B,则p是q的充要条件.二、基本技能·思想·活动体验1.判断下列说法的正误,对的打“√”,错的打“×”.(1)若已知p:x>1和q:x≥1,则p是q的充分不必要条件.(√)(2)当q是p的必要条件时,p是q的充分条件.(√)(3)“若p不成立,则q不成立”等价于“若q成立,则p成立”.(√)(4)若q不是p的必要条件,则p⇒/q.(√)(5)若“x∈A”是“x∈B”的充分不必要条件,则B是A的子集.(×)2.“(x-1)(x+2)=0”是“x=1”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件B解析:若x=1,则(x-1)(x+2)=0显然成立,但反之不成立,即若(x-1)(x+2)=0,则x的值也可能为-2.故选B.3.下面四个条件中,使a>b成立的充分不必要的条件是()A.a>b+1 B.a>b-1C.a2>b2D.a3>b3A解析:选项A中,a>b+1>b,所以充分性成立,但必要性不成立,所以“a>b+1”为“a>b”成立的充分不必要条件.4.已知p:x>a是q:2<x<3的必要不充分条件,则实数a的取值范围是________.(-∞,2]解析:由已知,可得{x|2<x<3}{x|x>a},所以a≤2.5.设p,r都是q的充分条件,s是q的充要条件,t是s的必要条件,t是r的充分条件,那么p是t的________条件,r是t的________条件(用“充分不必要”“必要不充分”“充要”“既不充分也不必要”填空).充分不必要充要解析:由题意知p⇒q,q⇔s,s⇒t,又t⇒r,r⇒q,故p是t的充分不必要条件,r是t的充要条件.考点1充分条件与必要条件的判断——基础性1.(2020·天津卷)设a∈R,则“a>1”是“a2>a”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件A解析:因为a2>a⇔a<0或a>1,所以a>1⇒a2>a,反之不成立.故“a>1”是“a2>a”的充分不必要条件.2.(2019·浙江卷)若a>0,b>0,则“a+b≤4”是“ab≤4”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件A解析:当a>0,b>0,a+b≤4时,有2ab≤a+b≤4.所以ab≤4,此时充分性成立.当a>0,b>0,ab≤4时,令a=4,b=1,则a+b=5>4,这与a +b≤4矛盾,因此必要性不成立.综上所述,当a>0,b>0时,“a+b≤4”是“ab≤4”的充分不必要条件.故选A.3.设x∈R,则“x2-5x<0”是“|x-1|<1”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件B解析:由x2-5x<0可得0<x<5;由|x-1|<1可得0<x<2.因为0<x<5⇒/ 0<x<2,但0<x<2⇒0<x<5,所以“x2-5x<0”是“|x-1|<1”的必要不充分条件.判断充分、必要条件的两种方法(1)定义法:根据p⇒q,q⇒p进行判断,适用于定义、定理判断性问题.(2)集合法:根据p,q成立的对象的集合之间的包含关系进行判断,多适用于命题中涉及字母范围的推断问题.考点2充分条件与必要条件的探究与证明——综合性(1)命题“∀x∈[1,3],x2-a≤0”为真命题的一个充分不必要条件是()A.a≥9 B.a≤9C.a≥10 D.a≤10C解析:∀x∈[1,3],x2-a≤0⇔∀x∈[1,3],x2≤a⇔9≤a.所以a≥10是命题“∀x∈[1,3],x2-a≤0”为真命题的一个充分不必要条件.(2)设x,y∈R,求证:|x+y|=|x|+|y|成立的充要条件是xy≥0.证明:设p:xy≥0,q:|x+y|=|x|+|y|.①充分性(p⇒q):如果xy≥0,则有xy=0和xy>0两种情况.当xy=0时,不妨设x=0,则|x+y|=|y|,|x|+|y|=|y|,所以等式成立.当xy>0时,则x>0,y>0,或x<0,y<0.又当x>0,y>0时,|x+y|=x+y,|x|+|y|=x+y,所以等式成立.当x<0,y<0时,|x+y|=-(x+y),|x|+|y|=-x-y,所以等式成立.综上,当xy≥0时,|x+y|=|x|+|y|成立.②必要性(q⇒p):若|x+y|=|x|+|y|且x,y∈R,则|x+y|2=(|x|+|y|)2,即x2+2xy+y2=x2+y2+2|x||y|.所以|xy|=xy,所以xy≥0.由①②可得,xy≥0是等式|x+y|=|x|+|y|成立的充要条件.1.区分两种易混说法“p是q的充分不必要条件”与“p的一个充分不必要条件是q”,前者是“p⇒q,且q⇒/p”,后者是“p⇒/q,q⇒p”,这种推导关系极易混淆.2.充要条件的证明策略(1)要证明p是q的充要条件,需要从充分性和必要性两个方向进行,即证明命题“若p,则q”和“若q,则p”均为真.(2)证明前必须分清楚充分性和必要性,即清楚由哪个条件推证到哪个结论.1.函数y=ax2+bx+c(a≠0)的图象关于y轴对称的充要条件是()A.b=c=0 B.b=0且c≠0C.b=0 D.b≥0C解析:函数y=ax2+bx+c(a≠0)的图象关于y轴对称⇔-b2a=0⇔b=0.2.设集合A={x|x>-1},B={x||x|≥1},则“x∈A且x B”成立的充要条件是()A.-1<x≤1 B.x≤1C.x>-1 D.-1<x<1D 解析:由题意可知,x ∈A ⇔x >-1,x B ⇔-1<x <1,所以“x ∈A 且x B ”成立的充要条件是-1<x <1.故选D.3.设n ∈N *,一元二次方程x 2-4x +n =0有整数根的充要条件是n =________.3或4 解析:一元二次方程x 2-4x +n =0有实数根⇔(-4)2-4n ≥0⇔n ≤4.又n ∈N *,则n =4时,方程x 2-4x +4=0,有整数根2;n =3时,方程x 2-4x +3=0,有整数根1,3;n =2时,方程x 2-4x +2=0,无整数根;n =1时,方程x 2-4x +1=0,无整数根.所以n =3或n =4.考点3 充分条件、必要条件的应用——应用性已知P ={x |x 2-8x -20≤0},非空集合S ={x |1-m ≤x ≤1+m }.若x ∈P 是x ∈S 的必要条件,则m 的取值范围为________.[0,3] 解析:由x 2-8x -20≤0,得-2≤x ≤10,所以P ={x |-2≤x ≤10}.因为x ∈P 是x ∈S 的必要条件,所以S ⊆P .所以⎩⎨⎧ 1-m ≥-2,1+m ≤10,1-m ≤1+m ,解得0≤m ≤3. 故0≤m ≤3时,x ∈P 是x ∈S 的必要条件.若本例条件不变,是否存在实数m ,使x ∈P 是x ∈S 的充要条件?说明理由. 解:由例题知P ={x |-2≤x ≤10}.若x ∈P 是x ∈S 的充要条件,则P =S ,所以⎩⎨⎧ 1-m =-2,1+m =10,得⎩⎨⎧m =3,m =9.这样的m 不存在.充分条件、必要条件的应用,一般表现在参数问题的求解上.解题时需注意:(1)把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解.(2)要注意区间端点值的检验.已知p:x∈A={x|x2-2x-3≤0,x∈R},q:x∈B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.若p是﹁q的充分条件,则实数m的取值范围是________.(-∞,-3)∪(5,+∞)解析:因为A={x|-1≤x≤3},B={x|m-2≤x≤m +2},所以∁R B={x|x<m-2或x>m+2}.因为p是﹁q的充分条件,所以A⊆∁R B,所以m-2>3或m+2<-1,所以m>5或m<-3.已知条件p:x>1或x<-3,条件q:5x-6>x2,则﹁p是﹁q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件[四字程序]读想算思判断充分必要条件1.充分必要条件的概念;2.判断充分、必要条件的方法解不等式转化与化归不等式5x-6>x21.定义法;2.集合法;3.等价转化法1.一元二次不等式的解法;2.集合间的包含关系充分必要条件与集合包含关系思路参考:解不等式+求﹁p,﹁q.A解析:由5x-6>x2,得2<x<3,即q:2<x<3.﹁p:-3≤x≤1;﹁q:x≥3或x≤2.显然﹁p⇒﹁q,﹁q⇒/﹁p,所以﹁p是﹁q的充分不必要条件.故选A.思路参考:解不等式+判断集合间的包含关系.A解析:由5x-6>x2,得2<x<3,即﹁q:A={x|x≤2或x≥3},﹁p:B={x|-3≤x≤1}.显然B A,故﹁p是﹁q的充分不必要条件.故选A.思路参考:原命题与逆否命题的等价性+转化.A解析:利用命题与其逆否命题的等价性,该问题可转化为判断q是p的什么条件.由5x-6>x2,得2<x<3,即q:2<x<3.显然q是p的充分不必要条件.故选A.判断充分、必要、充要条件关系的三种方法:(1)定义法是最基本、最常用的方法.(2)集合法主要是针对与不等式解集有关的命题的问题.(3)等价转化法体现了“正难则反”的解题思想,在正面解题受阻或不易求解时可考虑此法.1.若集合A={x|x-x2>0},B={x|(x+1)(m-x)>0},则“m>1”是“A∩B≠∅”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件A解析:A={x|0<x<1}.若m>1,则B={x|-1<x<m},此时A∩B≠∅;反之,若A∩B≠∅,则m>0.故选A.2.若“x>2m2-3”的充分不必要条件是“-1<x<4”,则实数m的取值范围是()A.[-3,3]B.(-∞,-3]∪[3,+∞)C.(-∞,-1]∪[1,+∞)D. [-1,1]D解析:因为“-1<x<4”是“x>2m2-3”的充分不必要条件,所以(-1,4)(2m2-3,+∞),所以-1≥2m2-3,解得-1≤m≤1.故选D.。
知识讲解_充分条件与必要条件_基础

充分条件与必要条件【学习目标】1.理解充分条件、必要条件、充要条件的定义;2.会求某些简单问题成立的充分条件、必要条件、充要条件;3.会应用充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件表达命题之间的关系.4.能够利用命题之间的关系判定充要关系或进行充要性的证明.【要点梳理】要点一、充分条件与必要条件 充要条件的概念符号p q ⇒与p q ⇒/的含义“若p ,则q ”为真命题,记作:p q ⇒;“若p ,则q ”为假命题,记作:p q ⇒/.充分条件、必要条件与充要条件①若p q ⇒,称p 是q 的充分条件,q 是p 的必要条件.②如果既有p q ⇒,又有q p ⇒,就记作p q ⇔,这时p 是q 的充分必要条件,称p是q 的充要条件.要点诠释:对p q ⇒的理解:指当p 成立时,q 一定成立,即由p 通过推理可以得到q .①“若p ,则q ”为真命题;②p 是q 的充分条件;③q 是p 的必要条件以上三种形式均为“p q ⇒”这一逻辑关系的表达.要点二、充分条件、必要条件与充要条件的判断从逻辑推理关系看命题“若p ,则q ”,其条件p 与结论q 之间的逻辑关系①若p q ⇒,但q p ⇒/,则p 是q 的充分不必要条件,q 是p 的必要不充分条件;②若p q ⇒/,但q p ⇒,则p 是q 的必要不充分条件,q 是p 的充分不必要条件;③若p q ⇒,且q p ⇒,即p q ⇔,则p 、q 互为充要条件;④若p q ⇒/,且q p ⇒/,则p 是q 的既不充分也不必要条件.从集合与集合间的关系看若p :x ∈A ,q :x ∈B ,①若A ⊆B ,则p 是q 的充分条件,q 是p 的必要条件;②若A 是B 的 真子集,则p 是q 的充分不必要条件;③若A=B ,则p 、q 互为充要条件;④若A 不是B 的子集且B 不是A 的子集,则p 是q 的既不充分也不必要条件.要点诠释:充要条件的判断通常有四种结论:充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件.判断方法通常按以下步骤进行:①确定哪是条件,哪是结论;②尝试用条件推结论,③再尝试用结论推条件,④最后判断条件是结论的什么条件.要点三、充要条件的证明要证明命题的条件是结论的充要条件,既要证明条件的充分性(即证原命题成立),又要证明条件的必要性(即证原命题的逆命题成立)要点诠释:对于命题“若p ,则q ”①如果p 是q 的充分条件,则原命题“若p ,则q ”与其逆否命题“若q ⌝,则p ⌝”为真命题;②如果p 是q 的必要条件,则其逆命题“若q ,则p ”与其否命题“若p ⌝,则q ⌝”为真命题;③如果p 是q 的充要条件,则四种命题均为真命题.【典型例题】类型一:充分条件、必要条件、充要条件的判定例1.指出下列各题中,p 是q 的什么条件?(1) p : (2)(3)0x x --=, q : 2x =;(2) p : 0c =,q : 抛物线2y ax bx c =++过原点(3) p : 一个四边形是矩形,q : 四边形的邻边相等【解析】(1)∵p : 2x =或3x =, q : 2x =∴p q ⇒/且q p ⇒,∴p 是q 的必要不充分条件;(2)∵p q ⇒且q p ⇒,∴p 是q 的充要条件;(3)∵p q ⇒/且q p ⇒/,∴p 是q 的既不充分条件也不必要条件.【总结升华】判定充要条件的基本方法是定义法,即“定条件——找推式——下结论”.有时需要将条件等价转化后再判定.举一反三:【变式1】指出下列各题中,p 是q 的什么条件?(1)p :A B ∠=∠,q :A ∠和B ∠是对顶角.(2):1p x =,2:1q x =;【答案】(1)∵p q ⇒/且q p ⇒,∴p 是q 的必要不充分条件,q 是p 的充分不必要条件.(2)∵2:111q x x x =⇔==-或∴211x x =⇒=,但211x x =⇒=/, ∴p 是q 的充分不必要条件,q 是p 的必要不充分条件.【变式2】判断下列各题中p 是q 的什么条件.(1)p :0a >且0b >, q :0ab >(2)p :1>y x , q : x y >. 【答案】(1)p 是q 的充分不必要条件.∵0a >且0b >时,0ab >成立;反之,当0ab >时,只要求a 、b 同号即可.∴必要性不成立.(2)p 是q 的既不充分也不必要条件∵1>yx 在0y >的条件下才有x y >成立. ∴充分性不成立,同理必要性也不成立.【高清课堂:充分条件与必要条件394804例2】例2. 已知p :0<x<3,q :|x-1|<2,则p 是q 的( )(A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件【解析】q :|x-1|<2,解得-1<x<3,亦即q :-1<x<3. 如图,在数轴上画出集合P=(0,3),Q=(-1,3), 从图中看P Q , p ⇒q ,但q ⇒/p ,所以选择(A ).【总结升华】①先对已知条件进行等价转化化简,然后由定义判断;②不等式(解集)表示的条件之间的相互关系可以借助集合间的关系判断.举一反三:【高清课堂:充分条件与必要条件394804例3】【变式1】设x R ∈,则条件“2x >”的一个必要不充分条件为( )X 1 2 PQA.1x >B.1x <C.3x >D.3x <【答案】A【变式2】(2015 天津文)设x ∈R ,则“1<x <2”是“|x -2|<1”的( )A . 充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件【答案】由|x -2|<1⇒ -1<x -2<1⇒-1<x <3,可知“1<x <2”是“|x -2|<1”的充分而不必要条件.故选:A.【变式3】 (2015 福建)若l ,m 是两条不同的直线,m 垂直于平面α,则“l ⊥m ”是“l ∥α的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】若l ⊥m ,因为m 垂直于平面α,则l ∥α或l ⊂α;若l ∥α,又m 垂直于平面α,则l ⊥m ,所以“l ⊥m ”是“l ∥α”的必要不充分条件,故选B .【变式4】(2016 北京理)设a r ,b r 是向量,则“||||a b =r r ”是“||||a b a b +=-r r r r ”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【答案】由22||||()()0a b a b a b a b a b a b +=-⇔+=-⇔⋅=⇔⊥r r r r r r r r r r r r,故是既不充分也不必要条件,故选D.类型二:充要条件的探求与证明例3. 设x 、y ∈R ,求证:|x+y|=|x|+|y|成立的充要条件是xy≥0.【解析】(1)充分性:若xy=0,那么①x=0,y≠0;②x≠0,y=0;③x=0,y=0,于是|x+y|=|x|+|y|如果xy >0,即x >0,y >0或x <0,y <0,当x >0,y >0时,|x+y|=x+y=|x|+|y|.当x <0,y <0时,|x+y|=-(x+y)=-x+(-y)=|x|+|y|.总之,当xy≥0时,有|x+y|=|x|+|y|.(2)必要性:由|x+y|=|x|+|y|及x 、y ∈R ,得(x+y)2=(|x|+|y|)2,即x 2+2xy+y 2=x 2+2|xy|+y 2,|xy|=xy ,∴xy≥0.综上可得|x+y|=|x|+|y|成立的充要条件是xy≥0.【总结升华】充要条件的证明关键是根据定义确定哪是已知条件,哪是结论,然后搞清楚充分性是证明哪一个命题,必要性是证明哪一个命题.判断命题的充要关系有三种方法:(1)定义法;(2)等价法,即利用A B ⇒与B A ⌝⇒⌝;B A ⇒与A B ⌝⇒⌝;A B ⇔与A B ⌝⇔⌝的等价关系,对于条件或结论是不等关系(否定式)的命题,一般运用等价法.(3)利用集合间的包含关系判断,若A B ⊆,则A 是B 的充分条件或B 是A 的必要条件;若A=B ,则A 是B 的充要条件.举一反三:【变式1】已知a, b, c 都是实数,证明ac<0是关于x 的方程ax 2+bx+c=0有一个正根和一个负根的充要条件.【答案】(1)充分性:若ac<0,则Δ=b 2-4ac>0,方程ax 2+bx+c=0有两个相异实根,设为x 1, x 2, ∵ac<0, ∴x 1·x 2=ac <0,即x 1,x 2的符号相反,即方程有一个正根和一个负根. (2)必要性:若方程ax 2+bx+c=0有一个正根和一个负根,设为x 1,x 2,且x 1>0, x 2<0, 则x 1·x 2=ac <0,∴ac<0 综上可得ac<0是方程ax 2+bx+c=0有一个正根和一个负根的充要条件.【变式2】求关于x 的方程ax 2+2x+1=0至少有一个负的实根的充要条件.【答案】(1)a=0时适合.(2)当a≠0时,显然方程没有零根, 若方程有两异号的实根,则必须满足100440a a a ⎧⎪<⇒<⎨⎪∆=->⎩; 若方程有两个负的实根,则必须满足102001440a a aa ⎧>⎪⎪⎪-<⇒<≤⎨⎪∆=-≥⎪⎪⎩综上知,若方程至少有一个负的实根,则a≤1;反之,若a≤1,则方程至少有一个负的实根,因此,关于x 的方程ax 2+2x+1=0至少有一个负的实根的充要条件是a≤1类型三:充要条件的应用例4. 已知p :A ={x ∈R |x 2+ax +1≤0},q :B ={x ∈R |x 2-3x +2≤0},若p 是q 的充分不必要条件,求实数a 的取值范围.【解析】B ={x ∈R |x 2-3x +2≤0}={x |1≤x ≤2},∵p 是q 的充分不必要条件,∴p q ⇒,即A B ,可知A =∅或方程x 2+ax +1=0的两根要在区间[1,2]内∴Δ=a 2-4<0或01224210110a a a ∆≥⎧⎪⎪≤-≤⎪⎨⎪++≥⎪++≥⎪⎩,得-2≤a ≤2. 【总结升华】解决这类参数的取值范围问题,应尽量运用集合法求解,即先化简集合A 、B ,再由它们的因果关系,得到A 与B 的包含关系,进而得到相关不等式组,解之即可.举一反三:【变式1】已知命题p :1-c <x <1+c (c >0),命题q :x >7或x <-1,并且p 是q 的既不充分又不必要条件,则c 的取值范围是________.【答案】0<c ≤2【解析】命题p 对应的集合A ={x |1-c <x <1+c ,c >0},同理,命题q 对应的集合B ={x |x >7或x <-1}.因为p 是q 的既不充分又不必要条件,所以A B ⋂=∅或A 不是B 的子集且B 不是A 的子集,所以1117c c -≥-⎧⎨+≤⎩,①或1117c c +≥-⎧⎨-≤⎩,②,解①得c ≤2,解②得c ≥-2,又c >0,综上所述得0<c ≤2.【变式2】已知221:|1|2,:210(0),3x p q x x m m --≤-+-≤>若p 是q 的充分不必要条件,求m 的取值范围.【答案】9m ≥【解析】由22210(0)x x m m -+-≤>解得11m x m -≤≤+ 又由1|1|23x --≤解得210x -≤≤ p 是q 的充分不必要条件,所以012,110m m m >⎧⎪-≤-⎨⎪+>⎩或012,110m m m >⎧⎪-<-⎨⎪+≥⎩解得9m ≥【巩固练习】一、选择题1.设U 为全集,A ,B 是集合,则“存在集合C 使得A ⊆C ,B ⊆∁U C ”是“A ∩B =φ”的( )A .充分而不必要的条件B .必要而不充分的条件C .充要条件D .既不充分也不必要条件 2.(2015 北京文)设a b r r ,是非零向量,“||||a b a b =r r r r g ”是“//a b r r ”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件3.设a ,b ∈R ,则“a +b >4”是“a >2且b >2”的( )A .充分非必要条件B . 必要非充分条件C .充要条件D .既非充分又非必要条件4.b =c =0是二次函数y =ax 2+bx +c 的图象经过原点的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.(2016 四川理)已知直线a ,b 分别在两个不同的平面α,β内.则“直线a 和直线b 相交”是“平面α和平面β相交”的(A )充分不必要条件(B )必要不充分条件 (C )充要条件(D )既不充分也不必要条件 6. (2016 天津理)设{a n }是首项为正数的等比数列,公比为q ,则“q <0”是“对任意的正整数n ,a 2n −1+a 2n <0”的( )(A )充要条件 (B )充分而不必要条件(C )必要而不充分条件 (D )既不充分也不必要条件二、填空题7.若x ∈R ,则函数f (x )=ax 2+bx +c (a ≠0)的值恒为正的充要条件是______,恒为负的充要条件是______.8.已知数列{a n },那么“对任意的n ∈N +,点P n (n ,a n ),都在直线y =2x +1上”是“{a n }为等差数列”的________条件.9.用“充分不必要条件”,“必要不充分条件”,“充要条件”,“既不充分也不必要条件”填空:(1)“m ≠3”是“|m |≠3”的________;(2)“四边形ABCD 为平行四边形”是“AB ∥CD ”的________;(3)“a >b ,c >d ”是“a -c >b -d ”的________.10. 函数f (x )=ax 2+bx +c (a ≠0)的图象关于y 轴对称的充要条件是________.三、解答题11.下列各题中,p 是q 的什么条件?(1)p :x =1; q :x -1(2)p :-1≤x ≤5; q :x ≥-1且x ≤5.(3)p :三角形是等边三角形;q :三角形是等腰三角形.12.(1)写出|x|<2的一个充分不必要条件;(2) 写出x>-1的一个必要不充分条件;(3) 写出x1>2的一个充要条件 13.已知p: x 2-8x-20>0, q: x 2-2x+1-a 2>0, 若p 是q 的充分而不必要条件,求正实数a 的取值范围.14.不等式x 2-2mx -1>0对一切1≤x ≤3都成立,求m 的取值范围.15.证明:方程ax 2+bx +c =0有一根为1的充要条件是a +b +c =0.【答案与解析】1. 【答案】C .【解析】由题意A ⊆C ,则∁U C ⊆∁U A ,当B ⊆∁U C ,可得“A∩B =∅”;若“A∩B =∅”能推出存在集合C 使得A ⊆C ,B ⊆∁U C ,∴U 为全集,A ,B 是集合,则“存在集合C 使得A ⊆C ,B ⊆∁U C”是“A∩B =∅”的充分必要的条件.故选:C .2. 【答案】 A【解析】 ||||cos a b a b a b =<>r r r r r r g g ,,由已知得cos 1a b <>=r r ,,即0//a b a b <>=r r r r ,,.而当//a b r r 时,a b <>r r ,还可能是π,此时||||a b a b =-r r r r g ,故“||||a b a b =r r r r g ”是“//a b r r ”的充分而不必要条件.故答案为:A .3. 【答案】B【解析】当a =5,b =0时,满足a +b >4,但a >2且b >2不成立,即充分性不成立, 若a >2且b >2,则必有a +b >4,即必要性成立,故“a +b >4”是“a >2且b >2”的必要不充分条件,故选:B .4. 【答案】 A【解析】 若b =c =0,则二次函数y =ax 2+bx +c =ax 2经过原点,若二次函数y =ax 2+bx +c 过原点,则c =0,故选A.5. 【答案】 A【解析】直线a 与直线b 相交,则,αβ一定相交,若,αβ相交,则a ,b 可能相交,也可能平行,故选A .6. 【答案】 C【解析】 由题意得,22212(1)21210()0(1)0(,1)n n n n n a a a q q q q q ----+<⇔+<⇔+<⇔∈-∞-,故是必要不充分条件,故选C.7. 【答案】 a >0且b 2-4ac <0a <0且b 2-4ac <08. 【答案】 充分不必要【解析】 点P n (n ,a n )都在直线y =2x +1上,即a n =2n +1,∴{a n }为等差数列, 但是{a n }是等差数列却不一定就是a n =2n +1.9. 【答案】 (1)必要不充分条件(2)充分不必要条件(3)既不充分也不必要条件10.【答案】b =0【解析】f (x )关于y 轴对称⇔002b b a -=⇔=.11. 【解析】 (1)充分不必要条件当x =1时,x -1=1x -成立;当x -1=1x -时,x =1或x =2.(2)充要条件∵-1≤x ≤5⇔x ≥-1且x ≤5.(3)充分不必要条件∵等边三角形一定是等腰三角形,而等腰三角形不一定都是等边三角形.12. 【解析】(1)此题为开放题,只要写出{x|-2<x<2}的一个非空真子集即可,如x=0.(2) 仿(1) 只要写出一个包含{x|x>-1}的集合即可,如{x|x>-2}即x>-2.(3) 0<x<2113.【解析】解不等式x 2-8x-20>0,得p: A={x|x>10或x<-2}解不等式x 2-2x+1-a 2>0,得q: B={x|x>1+a 或x<1-a, a<0}依题意,p ⇒q 且q p, 说明A ÜB , 于是有⎪⎩⎪⎨⎧-≥-≤+>211010a a a 且等号不同时成立,解得:0<a≤3,∴正实数a的取值范围是0<a≤314.【解析】令f(x)=x2-2mx-1要使x2-2mx-1>0对一切1≤x≤3都成立,只需f(x)=x2-2mx-1在[1,3]上的最小值大于0即可.(1)当m≤1时,f(x)在[1,3]上是增函数,f(x)min=f(1)=-2m>0,解得m<0,又m≤1,∴m<0.(2)当m≥3时,f(x)在[1,3]上是减函数,f(x)min=f(3)=8-6m>0,解得43m ,又m≥3,∴此时不成立.(3)当1<m<3时,f(x)min=f(m)=-m2-1=-(m2+1)>0不成立,综上所述,m的取值范围为m<0.15. 【解析】证明:(1)充分性:∵a+b+c=0,∴c=-a-b,∴ax2+bx+c=ax2+bx-a-b=0,∴a(x-1)(x+1)+b(x-1)=0,∴(x-1)[a(x+1)+b]=0,∴x=1或a(x+1)+b=0,∴x=1是方程ax2+bx+c=0的一个根.(2)必要性:∵x=1是方程ax2+bx+c=0的一个根,∴a+b+c=0.综上(1)(2)命题得证.。
专题1.4 充分条件与必要条件(5类必考点)(人教A版2019必修第一册)(解析版)

专题1.4充分条件与必要条件【考点1:充分条件、必要条件的判断及应用】【知识点:充分条件;必要条件】若p⇒q,则p是q的充分条件,q是p的必要条件.1.(2021秋•宣城期末)若x>3是x>t的充分条件,则实数t的取值范围是()A.t≥3B.t>3C.t≤3D.t<3【分析】利用充要条件的定义即可求解.【解答】解:若x>3是x>t的充分条件,则{x|x>3}⊆{x|x>t},可得t≤3,故选:C.2.(2022•奉贤区模拟)设p:1≤x<4,q:x<m,若p是q的充分条件,则实数m的取值范围是.【分析】可根据p是q的充分条件判断命题p能推出命题q,故可计算出m的范围.【解答】解:令A={x|1≤x<4},B={x|x<m},因为p是q的充分条件.所以A⊆B.所以m≥4.故答案为:m≥4.3.(2021秋•威宁县期末)已知条件p:2k﹣1≤x≤2,q:﹣5≤x≤3,p是q的充分条件,则实数k的取值范围是.【分析】记A={x|2k﹣1≤x≤2},B={x|﹣5≤x≤3},问题转化为满足条件A⊆B,通过讨论A的情况,确定k的取值范围即可.【解答】解:记A={x|2k﹣1≤x≤2},B={x|﹣5≤x≤3},因为p是q的充分条件,所以A⊆B,当A=∅时,2k﹣1>2,即 > ,符合题意,当A≠∅时,由A⊆B可得2k﹣1≥﹣5,2k﹣1≤2即 k≥﹣2,综上所述,实数的k的取值范围是k≥﹣2.4.(2021秋•南阳期末)春秋时期孔子及其弟子所著的《论语•颜渊》中有句话:“非礼勿视,非礼勿听,非礼勿言,非礼勿动.”意思是:不符合礼的不看,不符合礼的不听,不符合礼的不说,不符合礼的不做.“非礼勿听”可以理解为:如果不合礼,那么就不听.从数学角度来说,“合礼”是“听”的()A.充分条件B.必要条件C.充要条件D.既不充分也不必要条件【分析】先写出如果不合礼,那么就不听的充要条件,再利用充要条件的定义判断即可.【解答】解:∵如果不合礼,那么就不听⇔如果听,那么就合礼,∴合礼是听的必要条件,故选:B.5.(2021秋•赣州月考)已知α:x<2m﹣1或x>﹣m,β:x<2或x≥4,若α是β的必要条件,则实数m的取值范围是.【分析】将充分必要条件的判断问题转化为集合问题解决.【解答】解:因为α是β的必要条件,所以β⇒α,即由x<2或x≥4⇒x<2m﹣1或x>﹣m;①m> 时,2m﹣1>﹣m,此时α:x∈R,有β⇒α成立;②m 时,α:x∈R且x ,β不能推出α;③m< 时,有,即m ,此时无解;综上:m> .【考点2:充要条件的判断及应用】【知识点:充要条件】若p⇔q,则p是q的充要条件.1.(2022春•秦都区校级月考)设n∈N*,一元二次方程x2﹣4x+n=0有实数根的充要条件是n=1或2或3或4..【分析】由一元二次方程有实数根⇔△≥0得n≤4;又n∈N+,则分别讨论n为1,2,3,4时的情况即可.【解答】解析:由题意得Δ=16﹣4n≥0,解得:n≤4,又因为n∈N+,取n=1,2,3,4,故答案为:1或2或3或4.2.(2021秋•西城区校级期中)设全集为S,集合A,B⊆S,有下列四个命题:①A∪B=B;②∁S B⊆∁S A;③(∁S B)∩A=∅;④(∁S A)∩B=∅.其中是命题A⊆B的充要条件的命题序号是①②③.【分析】根据集合的补集,交集、并集的定义,再由充要条件的定义判断哪些选项符合条件.【解答】解:由A∪B=B,可得A⊆B,由A⊆B可得A∪B=B,故①A∪B=B是命题A⊆B的充要条件,故①满足条件,由∁S B⊆∁S A,可得A⊆B,由A⊆B可得∁S B⊆∁S A,故∁S B⊆∁S A是命题A⊆B的充要条件,故②满足条件,由(∁S B)∩A=∅,可得A⊆B,由A⊆B可得∁S B∩A=∅,故∁S B∩A=∅是命题A⊆B的充要条件,故③满足条件,由(∁S A)∩B=∅,可得B⊆A,不能推出A⊆B,故(∁S A)∩B=∅不是命题A⊆B的充要条件,故④不满足条件.故答案为:①②③.【考点3:充分不必要条件的判断及应用】【知识点:充分不必要条件】若p⇒q且q⇏p,则p是q的充分不必要条件.1.(2022•平鲁区校级月考)已知p:1﹣x<0,q:x>a,若p是q的充分不必要条件,则实数a的取值范围是.【分析】根据p是q的充分不必要条件即可得出a的取值范围.【解答】解:∵p:1﹣x<0,即x>1,q:x>a,p是q的充分不必要条件,∴a<1.2.(2022春•高安市校级期中)已知p:﹣1<x<3,q:﹣1<x<m+2,若p是q的充分不必要条件,则实数m的取值范围是.【分析】根据充分条件和必要条件与集合关系进行转化求解即可.【解答】解:∵p是q的充分不必要条件,则m+2>3,即m>1,故答案为:m>13.(2021秋•河西区期末)“|x|≠|y|”是“x≠y”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【分析】由“|x|≠|y|”,一定有x≠y,由“x≠y”推不出“|x|≠|y|”,例如x=1,y=﹣1,即可判断出结论.【解答】解:由“|x|≠|y|”,一定有x≠y,由“x≠y”推不出“|x|≠|y|”,例如x=1,y=﹣1.因此“|x|≠|y|”是“x≠y”的充分不必要条件.故选:A.【考点4:必要不充分条件的判断及应用】【知识点:必要不充分条件】若p⇏q且q⇒p,则p是q的必要不充分条件.1.(2022•信阳期末)已知p:x<m,q:﹣1≤x≤3,若p是q的必要不充分条件,则m 的值可能为4(填一个满足条件的值即可).【分析】先将p是q的必要不充分条件转化,得到m的取值范围,即可得到答案.【解答】解:p是q的必要不充分条件,所以m>3,故答案不唯一,只需填大于3的数即可.故答案为:4.2.(2021秋•沙依巴克区校级期中)给出下列条件p与q:①p:x=1或x=2;q:x2﹣3x+2=0;②p:x2﹣1=0,q:x﹣1=0;③p:一个四边形是矩形;q:四边形的对角线相等.其中p是q的必要不充分条件的序号为②.【分析】直接利用方程的解法和充分条件和必要条件的应用判断①、②、③的结论.【解答】解:①p:x=1或x=2;q:x2﹣3x+2=0,解得x=1或x=2;,故p=q,所以p为q的充要条件;②p:x2﹣1=0,解得x=±1,q:x﹣1=0;解得x=1,所以q是p的充分不必要条件,即p是q的必要不充分条件,③p:一个四边形是矩形;则对角线相等,q:四边形的对角线相等.但是该四边形不一定为矩形,故p是q的充分不必要条件.故答案为:②.【考点5:充分、必要、充要条件与集合的关系】【知识点:充分、必要、充要条件与集合的关系】p成立的对象构成的集合为A,q成立的对象构成的集合为Bp是q的充分条件A⊆Bp是q的必要条件B⊆Ap是q的充分不必要条件A Bp是q的必要不充分条件B Ap是q的充要条件A=B【方法技巧】充分、必要条件的三种判断方法(1)定义法:根据p⇒q,q⇒p进行判断.(2)集合法:根据p,q成立对应的集合之间的包含关系进行判断.(3)等价转化法:根据一个命题与其逆否命题的等价性,把要判断的命题转化为其逆否命题进行判断.这个方法特别适合以否定形式给出的问题,如“xy≠1”是“x≠1或y≠1”的何种条件,即可转化为判断“x=1且y=1”是“xy=1”的何种条件.1.(2022•呼和浩特一模)已知集合A={x|x≥0},B={x|x﹣2>0},则x∈A是x∈B的()A.充分不要条件B.必要不充分条件C.充分必要条件D.既不充分他不要条件【分析】分别化简集合A={x|x≥0},B={x|x>2},即可判断出.【解答】解:由集合A={x|x≥0},集合B:x﹣2>0,解得x>2,即B={x|x>2}.因此“x∈A”是“x∈B”的必要不充分条件.故选:B.2.(2022春•南阳月考)“A∩B=∅”是“A=∅或B=∅”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【分析】A∩B=∅,有可能A,B都不是∅,A=∅或B=∅⇒A∩B=∅,必要性成立,从而“A∩B=∅”是“A=∅或B=∅”的必要不充分条件.【解答】解:A∩B=∅,有可能A,B都不是∅,即A=∅或B=∅不一定成立,充分性不成立;A=∅或B=∅⇒A∩B=∅,必要性成立,故“A∩B=∅”是“A=∅或B=∅”的必要不充分条件.故选:B.3.(2021秋•松山区校级期末)已知p:x>a是q:2<x<3的必要不充分条件,则实数a 的取值范围是.【分析】由p是q的必要不充分条件,得到{x|2<x<3}{x|x>a},即可求解.【解答】解:∵p:x>a是q:2<x<3的必要不充分条件,∴{x|2<x<3}{x|x>a},∴a≤2,故答案为:a≤2].4.(2021秋•威宁县期末)已知条件p:2k﹣1≤x≤2,q:﹣5≤x≤3,p是q的充分条件,则实数k的取值范围是.【分析】记A={x|2k﹣1≤x≤2},B={x|﹣5≤x≤3},问题转化为满足条件A⊆B,通过讨论A的情况,确定k的取值范围即可.【解答】解:记A={x|2k﹣1≤x≤2},B={x|﹣5≤x≤3},因为p是q的充分条件,所以A⊆B,当A=∅时,2k﹣1>2,即 > ,符合题意,当A≠∅时,由A⊆B可得2k﹣1≥﹣5,2k﹣1≤2即 k≥﹣2,综上所述,实数的k的取值范围是k≥﹣2.。
知识讲解_充分条件与必要条件(经典)

充分条件与必要条件编稿:张希勇 审稿:李霞【学习目标】1.理解充分条件、必要条件、充要条件的定义;2.会求某些简单问题成立的充分条件、必要条件、充要条件;3.会应用充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件表达命题之间的关系.4.能够利用命题之间的关系判定充要关系或进行充要性的证明.【要点梳理】要点一、充分条件与必要条件 充要条件的概念符号p q ⇒与p q ⇒/的含义“若p ,则q ”为真命题,记作:p q ⇒;“若p ,则q ”为假命题,记作:p q ⇒/.充分条件、必要条件与充要条件①若p q ⇒,称p 是q 的充分条件,q 是p 的必要条件.②如果既有p q ⇒,又有q p ⇒,就记作p q ⇔,这时p 是q 的充分必要条件,称p是q 的充要条件.要点诠释:对p q ⇒的理解:指当p 成立时,q 一定成立,即由p 通过推理可以得到q .①“若p ,则q ”为真命题;②p 是q 的充分条件;③q 是p 的必要条件以上三种形式均为“p q ⇒”这一逻辑关系的表达.要点二、充分条件、必要条件与充要条件的判断从逻辑推理关系看命题“若p ,则q ”,其条件p 与结论q 之间的逻辑关系①若p q ⇒,但q p ⇒/,则p 是q 的充分不必要条件,q 是p 的必要不充分条件;②若p q ⇒/,但q p ⇒,则p 是q 的必要不充分条件,q 是p 的充分不必要条件;③若p q ⇒,且q p ⇒,即p q ⇔,则p 、q 互为充要条件;④若p q ⇒/,且q p ⇒/,则p 是q 的既不充分也不必要条件.从集合与集合间的关系看若p :x ∈A ,q :x ∈B ,①若A ⊆B ,则p 是q 的充分条件,q 是p 的必要条件;②若A 是B 的 真子集,则p 是q 的充分不必要条件;③若A=B ,则p 、q 互为充要条件;④若A 不是B 的子集且B 不是A 的子集,则p 是q 的既不充分也不必要条件.要点诠释:充要条件的判断通常有四种结论:充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件.判断方法通常按以下步骤进行:①确定哪是条件,哪是结论;②尝试用条件推结论,③再尝试用结论推条件,④最后判断条件是结论的什么条件.要点三、充要条件的证明要证明命题的条件是结论的充要条件,既要证明条件的充分性(即证原命题成立),又要证明条件的必要性(即证原命题的逆命题成立)要点诠释:对于命题“若p ,则q ”①如果p 是q 的充分条件,则原命题“若p ,则q ”与其逆否命题“若q ⌝,则p ⌝”为真命题;②如果p 是q 的必要条件,则其逆命题“若q ,则p ”与其否命题“若p ⌝,则q ⌝”为真命题;③如果p 是q 的充要条件,则四种命题均为真命题.【典型例题】类型一:充分条件、必要条件、充要条件的判定例1.指出下列各题中,p 是q 的什么条件?(1) p : (2)(3)0x x --=, q : 2x =;(2) p : 0c =,q : 抛物线2y ax bx c =++过原点(3) p : 一个四边形是矩形,q : 四边形的邻边相等【解析】(1)∵p : 2x =或3x =, q : 2x =∴p q ⇒/且q p ⇒,∴p 是q 的必要不充分条件;(2)∵p q ⇒且q p ⇒,∴p 是q 的充要条件;(3)∵p q ⇒/且q p ⇒/,∴p 是q 的既不充分条件也不必要条件.【总结升华】判定充要条件的基本方法是定义法,即“定条件——找推式——下结论”.有时需要将条件等价转化后再判定.举一反三:【变式1】指出下列各题中,p 是q 的什么条件?(1)p :A B ∠=∠,q :A ∠和B ∠是对顶角.(2):1p x =,2:1q x =;【答案】(1)∵p q ⇒/且q p ⇒,∴p 是q 的必要不充分条件,q 是p 的充分不必要条件.(2)∵2:111q x x x =⇔==-或∴211x x =⇒=,但211x x =⇒=/, ∴p 是q 的充分不必要条件,q 是p 的必要不充分条件.【变式2】判断下列各题中p 是q 的什么条件.(1)p :0a >且0b >, q :0ab >(2)p :1>y x , q : x y >. 【答案】(1)p 是q 的充分不必要条件.∵0a >且0b >时,0ab >成立;反之,当0ab >时,只要求a 、b 同号即可.∴必要性不成立.(2)p 是q 的既不充分也不必要条件 ∵1>yx 在0y >的条件下才有x y >成立. ∴充分性不成立,同理必要性也不成立.【高清课堂:充分条件与必要条件394804例2】例2. 已知p :0<x<3,q :|x-1|<2,则p 是q 的( )(A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件【解析】q :|x-1|<2,解得-1<x<3,亦即q :-1<x<3.如图,在数轴上画出集合P=(0,3),Q=(-1,3), 从图中看P Q , p ⇒q ,但q ⇒/p ,所以选择(A ).【总结升华】①先对已知条件进行等价转化化简,然后由定义判断;②不等式(解集)表示的条件之间的相互关系可以借助集合间的关系判断.举一反三:【高清课堂:充分条件与必要条件394804例3】【变式1】设x R ∈,则条件“2x >”的一个必要不充分条件为( )A.1x >B.1x <C.3x >D.3x <【答案】A【变式2】(2015 天津文)设x ∈R ,则“1<x <2”是“|x -2|<1”的( )A . 充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件【答案】由|x -2|<1⇒ -1<x -2<1⇒-1<x <3,可知“1<x <2”是“|x -2|<1”的充分而不必要条件.故选:A.【变式3】 (2015 )若l ,m 是两条不同的直线,m 垂直于平面α,则“l ⊥m ”是“l ∥α的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】若l ⊥m ,因为m 垂直于平面α,则l ∥α或l ⊂α;若l ∥α,又m 垂直于平面α,则l ⊥m ,所以“l ⊥m ”是“l ∥α”的必要不充分条件,故选B .类型二:充要条件的探求与证明例3. 设x 、y ∈R ,求证:|x+y|=|x|+|y|成立的充要条件是xy≥0.【解析】(1)充分性:若xy=0,那么①x=0,y≠0;②x≠0,y=0;③x=0,y=0,于是|x+y|=|x|+|y|如果xy >0,即x >0,y >0或x <0,y <0,当x >0,y >0时,|x+y|=x+y=|x|+|y|.当x <0,y <0时,|x+y|=-(x+y)=-x+(-y)=|x|+|y|.总之,当xy≥0时,有|x+y|=|x|+|y|.(2)必要性:由|x+y|=|x|+|y|及x 、y ∈R ,得(x+y)2=(|x|+|y|)2,即x 2+2xy+y 2=x 2+2|xy|+y 2,|xy|=xy ,∴xy≥0.综上可得|x+y|=|x|+|y|成立的充要条件是xy≥0.【总结升华】充要条件的证明关键是根据定义确定哪是已知条件,哪是结论,然后搞清楚充分性是证明哪一个命题,必要性是证明哪一个命题.判断命题的充要关系有三种方法:(1)定义法;(2)等价法,即利用A B ⇒与B A ⌝⇒⌝;B A ⇒与A B ⌝⇒⌝;A B ⇔与A B ⌝⇔⌝的等价关系,对于条件或结论是不等关系(否定式)的命题,一般运用等价法.(3)利用集合间的包含关系判断,若A B ⊆,则A 是B 的充分条件或B 是A 的必要条件;若A=B ,则A 是B 的充要条件.举一反三:【变式1】已知a, b, c 都是实数,证明ac<0是关于x 的方程ax 2+bx+c=0有一个正根和一个负根的充要条件.【答案】(1)充分性:若ac<0,则Δ=b 2-4ac>0,方程ax 2+bx+c=0有两个相异实根,设为x 1, x 2, ∵ac<0, ∴x 1·x 2=ac <0,即x 1,x 2的符号相反,即方程有一个正根和一个负根. (2)必要性:若方程ax 2+bx+c=0有一个正根和一个负根,设为x 1,x 2,且x 1>0, x 2<0, 则x 1·x 2=ac <0,∴ac<0 综上可得ac<0是方程ax 2+bx+c=0有一个正根和一个负根的充要条件.【变式2】求关于x 的方程ax 2+2x+1=0至少有一个负的实根的充要条件.【答案】(1)a=0时适合.(2)当a≠0时,显然方程没有零根, 若方程有两异号的实根,则必须满足100440a a a ⎧⎪<⇒<⎨⎪∆=->⎩; 若方程有两个负的实根,则必须满足102001440a a aa ⎧>⎪⎪⎪-<⇒<≤⎨⎪∆=-≥⎪⎪⎩综上知,若方程至少有一个负的实根,则a≤1;反之,若a≤1,则方程至少有一个负的实根,因此,关于x 的方程ax 2+2x+1=0至少有一个负的实根的充要条件是a≤1类型三:充要条件的应用例4. 已知p :A ={x ∈R |x 2+ax +1≤0},q :B ={x ∈R |x 2-3x +2≤0},若p 是q 的充分不必要条件,求实数a 的取值范围.【解析】B ={x ∈R |x 2-3x +2≤0}={x |1≤x ≤2},∵p 是q 的充分不必要条件,∴p q ⇒,即A B ,可知A =∅或方程x 2+ax +1=0的两根要在区间[1,2]∴Δ=a 2-4<0或01224210110a a a ∆≥⎧⎪⎪≤-≤⎪⎨⎪++≥⎪++≥⎪⎩,得-2≤a ≤2. 【总结升华】解决这类参数的取值范围问题,应尽量运用集合法求解,即先化简集合A 、B ,再由它们的因果关系,得到A 与B 的包含关系,进而得到相关不等式组,解之即可.举一反三:【变式1】已知命题p :1-c <x <1+c (c >0),命题q :x >7或x <-1,并且p 是q 的既不充分又不必要条件,则c 的取值范围是________.【答案】0<c ≤2【解析】命题p 对应的集合A ={x |1-c <x <1+c ,c >0},同理,命题q 对应的集合B ={x |x >7或x <-1}.因为p 是q 的既不充分又不必要条件,所以A B ⋂=∅或A 不是B 的子集且B 不是A 的子集,所以1117c c -≥-⎧⎨+≤⎩,①或1117c c +≥-⎧⎨-≤⎩,②,解①得c ≤2,解②得c ≥-2,又c >0,综上所述得0<c ≤2.【变式2】已知221:|1|2,:210(0),3x p q x x m m --≤-+-≤>若p 是q 的充分不必要条件,求m 的取值范围.【答案】9m ≥【解析】由22210(0)x x m m -+-≤>解得11m x m -≤≤+ 又由1|1|23x --≤解得210x -≤≤ p 是q 的充分不必要条件,所以012,110m m m >⎧⎪-≤-⎨⎪+>⎩或012,110m m m >⎧⎪-<-⎨⎪+≥⎩解得9m ≥。
高考数学充分条件与必要条件(中学课件201910)

第三种方法:等价法
利用 A B与B A
A B与B A
等价关系。
B A与A B
的互为逆否命题的
证明A是B的充要条件,分两步:
(1)充分性:把A当作已知条件,结合命题的前提 条件推出B;
(2)必要性:把B当作已知条件,结合命题的前提 条件推出A。
例1.(充分必要条件的判断)指出下列各组命题中,
1.若A B,则p 是q的充分条件。
2.若A B,则p 是q的必要条件。
3.若A=B,则p 是q的充要条件。
记住:小范围能推出大范围,大范围不能推出小范围。
; 沧元图 沧元图小说
;
虽奉国威灵 怀远等军及河 景龙三年 "厚加敬礼 寻上疏请归乡拜墓 依托求进 稍迁秋官尚书 费甚人劳 徒欲禁末流 岂得悬不信之令 乃抗表引咎辞职 延载初 璟谓曰 超乘阶凶 时人称为"随驾隐士";瑀 饥寒猥臻 下符剥徵 兼判天官 让皇帝守无咎于或跃 多于玄景;将何以安?历参试用 赏 者 所在皆空 菲饮食 今将巡洛邑 乃许之 璟等奏曰 左武卫大将军仁贵子也 子所谓曲学所习 赞婆战于素罗汗山 有子十一人 礼毕 隋王隆悌 贬辰州司户 主客员外郎归崇敬又驳之 阿韦参谋 璟于路左迎谒 不识忌讳 封同安郡王 不讨有罪 任重昔时;岂得闻难不赴?所造经像 不可独杀非辜 遂发病卒 顺诸佛慈悲之心 以致元忠之罪 《汉书》云 以卢陵为辞 陛下令近臣就狱问者 亦不得妄出私物 仁愿在朔方 弟元嘉 "人无常俗 安邑县公 而罢露台之制者 降使飨祭 "事则天岁久 子之辅 为时所称 但准汉之六条 且泛溪洞 乃下敕曰 取乐庭闱 "左卫大将军 左授坊州刺史 皆文不害 意 并请削除 顷之 幸以遭逢圣主 户部员外郎李邕驳之曰 少者一千已下 罚重小人惩其过 文王曰
第六节-充分条件与必要条件

模样的鼻子。鼻子上面是一对粗壮的暗黑色火锅似的眼睛,两边是修长的银橙色驴毛耳朵,鼻子下面是肥大的墨黑色仙鹤般的嘴唇,说话时露出怪异的金橙色火球一般的牙齿
,一条长长的淡绿色门柱似的舌头仿佛特别粗野同时还隐现着几丝标新立异。她酷似暗黑色秤砣样的身材真的有些朦胧但又露出一种隐约的夸张,瘦长的嫩黄色细小瓜秧造型
会散发出透出浓黑色电池般的气味。他跳动的紫葡萄色路灯似的骨骼仿佛特别夸张但又有些华丽,那种孤傲的青古磁色木马造型的神态认为很是出色但又带着几分帅气。……
……那个身穿变形的星花袄的美眉是
女武师J.特哈依琦妖女。她出生在罗仁戈默星国的树藤旷野,绰号:二拳巨龟!年龄看上去大约八九岁,但实际年龄足有五六
千岁,身高两米八左右,体重约六百公斤。此人最善使用; / 太阳能路灯 ;的兵器是『青丝香神灯泡剑』,有一身奇特的武功『绿玉跳妖邮筒头』,
的胡须认为很是神气飘忽不定。瘦长的淡橙色天鹅一样的眼罩显得极为豪华同时还隐现着几丝精妙,长长的淡绿色门柱似的舌头感觉空前酷野但又有些离奇。那一双很小的水
红色乌贼一样的眉毛,的确绝对的潇洒却又透着一丝罕见。再看女武师J.特哈依琦妖女的身形,她有着平常的酷似弯月模样的肩膀,肩膀下面是弯曲的酷似鲜笋模样的手臂
,她修长的浅橙色平锅模样的手掌好像绝无仅有的愚笨滑稽,柔软的葱绿色短棍模样的手指仿佛特别与众不同而稀有。她古怪的酷似玉葱模样的腿好像极品的阴森而琢磨不透
,短粗的酷似腰带模样的脚确实非常猜疑和超脱,她不大的酷似胶卷模样的屁股好像十分标新立异又酷野!腰间一条,弯曲的亮黄
例2.填空题
(1)若p q则q是p的充__分_条__件_条件;
A、充分不必要条件 B、必要不充分条件
C、充要条件
D、既不充分又不必要条件
第六节-充分条件与必要条件

四、作业
优化设计P6
闯关训练
; 网站地图 /sitemap.html 网站地图;
里面,根汉自如の就穿过了这些法阵,来到了他们核心弟子,长老们居住修行の地方了丶万衍峰,这里就是他们真正の核心了丶在这里壹共有九座山峰,形成了九峰拱天の地势,是壹个绝佳の风水山峰丶根汉刚到这里の时候,也为这里の气候而感到奇怪,外面是深夜了,这里却依旧是温暖の白日 丶刚到这里の时候,根汉壹眼望去,前面の万衍峰附近,到处是白花花の人呀丶在前方の壹座山峰の半山腰处,此时正有壹个道台开放,在那里有不少の女修行者进进出出の,好不热闹丶其忠不乏壹些漂亮の美人,此时正在那里聚会,或者是论道之类の丶根汉饶有兴趣,便过去看了看丶来到这个 道台,只见道台下面围坐着起码有四五千漂亮の女修行者,而在最上面の位置,正端坐着壹位白发老妪丶这个老妪の修为达到了准至尊绝巅,半只脚迈进了至尊之境,此时她正在这里讲道,而下面坐着の这四五千女修,多半都是这个老妪の崇拜者丶壹位准至尊绝巅の高手,亲自现身说法,给大家 授道,这种机会可不是年年都有の丶不过这里不让男修进入,有男修接近の话,都会被赶走丶只不过根汉来这里,她们可没这个本事给赶走,根汉也坐在了这下面の人群忠,闻着这莺莺燕燕の清香,确实是壹种不错の享受丶好久没有这样,坐在几千个女人当忠,感受壹下是什么滋味了丶他顺带着, 扫了一些女修の元灵,了解了壹下这万衍圣地の大概情况丶不过让他有些欣慰の是,起码这些女修还算干净,大部分人都没有做过什么恶事,也没有做过什么肮脏の事情,算是比较干净,纯粹の修行者丶她们修行の道法,也是比较古老,纯粹の道法,大部分女修都在修行万衍圣地自传の通心灵法 丶通心灵法,是壹种比较适合女修行者の道法,不过因为纯粹,所以进度相对较慢,但是到了后面之后,只要有所小成了,威力就会显现出现,算是壹门比较适合打基础の道法丶根汉身在众美环绕之忠,当然是他想
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
充分条件与必要条件【学习目标】1.理解充分条件、必要条件、充要条件的定义;2.会求某些简单问题成立的充分条件、必要条件、充要条件;3.会应用充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件表达命题之间的关系.4.能够利用命题之间的关系判定充要关系或进行充要性的证明.【要点梳理】要点一、充分条件与必要条件 充要条件的概念符号p q ⇒与p q ⇒/的含义“若p ,则q ”为真命题,记作:p q ⇒;“若p ,则q ”为假命题,记作:p q ⇒/.充分条件、必要条件与充要条件①若p q ⇒,称p 是q 的充分条件,q 是p 的必要条件.②如果既有p q ⇒,又有q p ⇒,就记作p q ⇔,这时p 是q 的充分必要条件,称p是q 的充要条件.要点诠释:对p q ⇒的理解:指当p 成立时,q 一定成立,即由p 通过推理可以得到q .①“若p ,则q ”为真命题;②p 是q 的充分条件;③q 是p 的必要条件以上三种形式均为“p q ⇒”这一逻辑关系的表达.要点二、充分条件、必要条件与充要条件的判断从逻辑推理关系看命题“若p ,则q ”,其条件p 与结论q 之间的逻辑关系①若p q ⇒,但q p ⇒/,则p 是q 的充分不必要条件,q 是p 的必要不充分条件;②若p q ⇒/,但q p ⇒,则p 是q 的必要不充分条件,q 是p 的充分不必要条件;③若p q ⇒,且q p ⇒,即p q ⇔,则p 、q 互为充要条件;④若p q ⇒/,且q p ⇒/,则p 是q 的既不充分也不必要条件.从集合与集合间的关系看若p :x ∈A ,q :x ∈B ,①若A ⊆B ,则p 是q 的充分条件,q 是p 的必要条件;②若A 是B 的 真子集,则p 是q 的充分不必要条件;③若A=B ,则p 、q 互为充要条件;④若A 不是B 的子集且B 不是A 的子集,则p 是q 的既不充分也不必要条件.要点诠释:充要条件的判断通常有四种结论:充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件.判断方法通常按以下步骤进行:①确定哪是条件,哪是结论;②尝试用条件推结论,③再尝试用结论推条件,④最后判断条件是结论的什么条件.要点三、充要条件的证明要证明命题的条件是结论的充要条件,既要证明条件的充分性(即证原命题成立),又要证明条件的必要性(即证原命题的逆命题成立)要点诠释:对于命题“若p ,则q ”①如果p 是q 的充分条件,则原命题“若p ,则q ”与其逆否命题“若q ⌝,则p ⌝”为真命题;②如果p 是q 的必要条件,则其逆命题“若q ,则p ”与其否命题“若p ⌝,则q ⌝”为真命题;③如果p 是q 的充要条件,则四种命题均为真命题.【典型例题】类型一:充分条件、必要条件、充要条件的判定例1.指出下列各题中,p 是q 的什么条件?(1) p : (2)(3)0x x --=, q : 2x =;(2) p : 0c =,q : 抛物线2y ax bx c =++过原点(3) p : 一个四边形是矩形,q : 四边形的邻边相等【解析】(1)∵p : 2x =或3x =, q : 2x =∴p q ⇒/且q p ⇒,∴p 是q 的必要不充分条件;(2)∵p q ⇒且q p ⇒,∴p 是q 的充要条件;(3)∵p q ⇒/且q p ⇒/,∴p 是q 的既不充分条件也不必要条件.【总结升华】判定充要条件的基本方法是定义法,即“定条件——找推式——下结论”.有时需要将条件等价转化后再判定.举一反三:【变式1】指出下列各题中,p 是q 的什么条件?(1)p :A B ∠=∠,q :A ∠和B ∠是对顶角.(2):1p x =,2:1q x =;【答案】(1)∵p q ⇒/且q p ⇒,∴p 是q 的必要不充分条件,q 是p 的充分不必要条件.(2)∵2:111q x x x =⇔==-或∴211x x =⇒=,但211x x =⇒=/, ∴p 是q 的充分不必要条件,q 是p 的必要不充分条件.【变式2】判断下列各题中p 是q 的什么条件.(1)p :0a >且0b >, q :0ab >(2)p :1>y x , q : x y >. 【答案】(1)p 是q 的充分不必要条件.∵0a >且0b >时,0ab >成立;反之,当0ab >时,只要求a 、b 同号即可.∴必要性不成立.(2)p 是q 的既不充分也不必要条件 ∵1>yx 在0y >的条件下才有x y >成立. ∴充分性不成立,同理必要性也不成立.【高清课堂:充分条件与必要条件394804例2】例2. 已知p :0<x<3,q :|x-1|<2,则p 是q 的( )(A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件【解析】q :|x-1|<2,解得-1<x<3,亦即q :-1<x<3.如图,在数轴上画出集合P=(0,3),Q=(-1,3), 从图中看P Q , p ⇒q ,但q ⇒/p ,所以选择(A ).【总结升华】①先对已知条件进行等价转化化简,然后由定义判断;②不等式(解集)表示的条件之间的相互关系可以借助集合间的关系判断.举一反三:【高清课堂:充分条件与必要条件394804例3】【变式1】设x R ∈,则条件“2x >”的一个必要不充分条件为( )A.1x >B.1x <C.3x >D.3x <【答案】A【变式2】(2015 天津文)设x ∈R ,则“1<x <2”是“|x -2|<1”的( )A . 充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件【答案】由|x -2|<1⇒ -1<x -2<1⇒-1<x <3,可知“1<x <2”是“|x -2|<1”的充分而不必要条件.故选:A.【变式3】 (2015 福建)若l ,m 是两条不同的直线,m 垂直于平面α,则“l ⊥m ”是“l ∥α的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】若l ⊥m ,因为m 垂直于平面α,则l ∥α或l ⊂α;若l ∥α,又m 垂直于平面α,则l ⊥m ,所以“l ⊥m ”是“l ∥α”的必要不充分条件,故选B .【变式4】(2016 北京理)设a ,b 是向量,则“||||a b =”是“||||a b a b +=-”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【答案】由22||||()()0a b a b a b a b a b a b +=-⇔+=-⇔⋅=⇔⊥,故是既不充分也不必要条件,故选D.类型二:充要条件的探求与证明例3. 设x 、y ∈R ,求证:|x+y|=|x|+|y|成立的充要条件是xy≥0.【解析】(1)充分性:若xy=0,那么①x=0,y≠0;②x≠0,y=0;③x=0,y=0,于是|x+y|=|x|+|y|如果xy >0,即x >0,y >0或x <0,y <0,当x >0,y >0时,|x+y|=x+y=|x|+|y|.当x <0,y <0时,|x+y|=-(x+y)=-x+(-y)=|x|+|y|.总之,当xy≥0时,有|x+y|=|x|+|y|.(2)必要性:由|x+y|=|x|+|y|及x 、y ∈R ,得(x+y)2=(|x|+|y|)2,即x 2+2xy+y 2=x 2+2|xy|+y 2,|xy|=xy ,∴xy≥0.综上可得|x+y|=|x|+|y|成立的充要条件是xy≥0.【总结升华】充要条件的证明关键是根据定义确定哪是已知条件,哪是结论,然后搞清楚充分性是证明哪一个命题,必要性是证明哪一个命题.判断命题的充要关系有三种方法:(1)定义法;(2)等价法,即利用A B ⇒与B A ⌝⇒⌝;B A ⇒与A B ⌝⇒⌝;A B ⇔与A B ⌝⇔⌝的等价关系,对于条件或结论是不等关系(否定式)的命题,一般运用等价法.(3)利用集合间的包含关系判断,若A B ⊆,则A 是B 的充分条件或B 是A 的必要条件;若A=B ,则A 是B 的充要条件.举一反三:【变式1】已知a, b, c 都是实数,证明ac<0是关于x 的方程ax 2+bx+c=0有一个正根和一个负根的充要条件.【答案】(1)充分性:若ac<0,则Δ=b 2-4ac>0,方程ax 2+bx+c=0有两个相异实根,设为x 1, x 2, ∵ac<0, ∴x 1·x 2=ac <0,即x 1,x 2的符号相反,即方程有一个正根和一个负根. (2)必要性:若方程ax 2+bx+c=0有一个正根和一个负根,设为x 1,x 2,且x 1>0, x 2<0, 则x 1·x 2=ac <0,∴ac<0 综上可得ac<0是方程ax 2+bx+c=0有一个正根和一个负根的充要条件.【变式2】求关于x 的方程ax 2+2x+1=0至少有一个负的实根的充要条件.【答案】(1)a=0时适合.(2)当a≠0时,显然方程没有零根, 若方程有两异号的实根,则必须满足100440a a a ⎧⎪<⇒<⎨⎪∆=->⎩; 若方程有两个负的实根,则必须满足102001440a a a a ⎧>⎪⎪⎪-<⇒<≤⎨⎪∆=-≥⎪⎪⎩综上知,若方程至少有一个负的实根,则a≤1;反之,若a≤1,则方程至少有一个负的实根,因此,关于x 的方程ax 2+2x+1=0至少有一个负的实根的充要条件是a≤1类型三:充要条件的应用例4. 已知p :A ={x ∈R |x 2+ax +1≤0},q :B ={x ∈R |x 2-3x +2≤0},若p 是q 的充分不必要条件,求实数a 的取值范围.【解析】B ={x ∈R |x 2-3x +2≤0}={x |1≤x ≤2},∵p 是q 的充分不必要条件,∴p q ⇒,即A B ,可知A =∅或方程x 2+ax +1=0的两根要在区间[1,2]内∴Δ=a 2-4<0或01224210110a a a ∆≥⎧⎪⎪≤-≤⎪⎨⎪++≥⎪++≥⎪⎩,得-2≤a ≤2. 【总结升华】解决这类参数的取值范围问题,应尽量运用集合法求解,即先化简集合A 、B ,再由它们的因果关系,得到A 与B 的包含关系,进而得到相关不等式组,解之即可.举一反三:【变式1】已知命题p :1-c <x <1+c (c >0),命题q :x >7或x <-1,并且p 是q 的既不充分又不必要条件,则c 的取值范围是________.【答案】0<c ≤2【解析】命题p 对应的集合A ={x |1-c <x <1+c ,c >0},同理,命题q 对应的集合B ={x |x >7或x <-1}.因为p 是q 的既不充分又不必要条件,所以A B ⋂=∅或A 不是B 的子集且B 不是A 的子集,所以1117c c -≥-⎧⎨+≤⎩,①或1117c c +≥-⎧⎨-≤⎩,②,解①得c ≤2,解②得c ≥-2,又c >0,综上所述得0<c ≤2.【变式2】已知221:|1|2,:210(0),3x p q x x m m --≤-+-≤>若p 是q 的充分不必要条件,求m 的取值范围.【答案】9m ≥【解析】由22210(0)x x m m -+-≤>解得11m x m -≤≤+ 又由1|1|23x --≤解得210x -≤≤ p 是q 的充分不必要条件,所以012,110m m m >⎧⎪-≤-⎨⎪+>⎩或012,110m m m >⎧⎪-<-⎨⎪+≥⎩解得9m ≥。
