matlab程序大全答案
MATLAB编程练习(含答案很好的)

001双峰曲线图:z=peaks(40);mesh(z);surf(z)002解方程:A=[3,4,-2;6,2,-3;45,5,4];>> B=[14;4;23];>> root=inv(A)*B003傅里叶变换load mtlb ;subplot(2,1,1);plot(mtlb);>> title('原始语音信息');>> y=fft(mtlb);>> subplot(2,1,2);>> yy=abs(y);>> plot(yy);>> title('傅里叶变换')004输入函数:a=input('How many apples\n','s')005输出函数a=[1 2 3 4 ;5 6 7 8;12 23 34 45;34 435 23 34]a =1 2 3 45 6 7 812 23 34 4534 435 23 34disp(a)a =1 2 3 45 6 7 812 23 34 4534 435 23 34b=input('how many people\n' ,'s')how many peopletwo peopleb =two people>> disp(b)two people>>006求一元二次方程的根a=1;b=2;c=3;d=sqrt(b^2-4*a*c);x1=(-b+d)/(2*a)x1 =-1.0000 + 1.4142i>> x2=(-b-d)/(2*a)x2 =-1.0000 - 1.4142i007求矩阵的相乘、转置、存盘、读入数据A=[1 3 5 ;2 4 6;-1 0 -2;-3 0 0];>> B=[-1 3;-2 2;2 1];>> C=A*BC =3 142 20-3 -53 -9>> C=C'C =3 2 -3 314 20 -5 -9>> save mydat C>> clear>> load mydat C008编写数学计算公式:A=2.1;B=-4.5;C=6;D=3.5;E=-5;K=atan(((2*pi*A)+E/(2*pi*B*C))/D) K =1.3121009A=[1 0 -1;2 4 1;-2 0 5];>> B=[0 -1 0;2 1 3;1 1 2];>> H=2*A+BH =2 -1 -26 9 5-3 1 12>> M=A^2-3*BM =3 3 -62 13 -2-15 -3 21>> Y=A*BY =-1 -2 -29 3 145 7 10>> R=B*AR =-2 -4 -1-2 4 14-1 4 10>> E=A.*BE =0 0 04 4 3-2 0 10>> W=A\BW =0.3333 -1.3333 0.66670.2500 1.0000 0.25000.3333 -0.3333 0.6667 >> P=A/BP =-2.0000 3.0000 -5.0000-5.0000 3.0000 -4.00007.0000 -9.0000 16.0000>> Z=A.\BWarning: Divide by zero.Z =0 -Inf 01.0000 0.2500 3.0000-0.5000 Inf 0.4000>> D=A./BWarning: Divide by zero.D =Inf 0 -Inf1.0000 4.0000 0.3333-2.0000 0 2.5000010a=4.96;b=8.11;>> M=exp(a+b)/log10(a+b)M =4.2507e+005011求三角形面积:a=9.6;b=13.7;c=19.4;>> s=(a+b+c)/2;>> area=sqrt(s*(s-a)*(s-b)*(s-c))area =61.1739012逻辑运算A=[-1 0 -6 8;-9 4 0 12.3;0 0 -5.1 -2;0 -23 0 -7]; >> B=A(:,1:2)B =-1 0-9 40 00 -23>> C=A(1:2,:)C =-1.0000 0 -6.0000 8.0000 -9.0000 4.0000 0 12.3000>> D=B'D =-1 -9 0 00 4 0 -23>> A*Bans =1.0000 -184.0000-27.0000 -266.90000 46.0000 207.0000 69.0000>> C<Dans =0 0 1 01 0 0 0>> C&Dans =1 0 0 00 1 0 1>> C|Dans =1 1 1 11 1 0 1>> ~C|~Dans =0 1 1 11 0 1 0013矩阵运算练习:A=[8 9 5;36 -7 11;21 -8 5]A =8 9 536 -7 1121 -8 5>> BB =-1 3 -22 0 3-3 1 9>> RT=A*BRT =-5 29 56-83 119 6-52 68 -21>> QW=A.*BQW =-8 27 -1072 0 33-63 -8 45>> ER=A^3ER =6272 3342 294415714 -856 52608142 -1906 2390 >> BF=A.^3BF =512 729 12546656 -343 13319261 -512 125 >> A/Bans =3.13414.9634 -0.4024-1.2561 12.5244 -3.2317-1.9878 6.4512 -2.0366>> EKV=B\AEKV =10.7195 -1.2683 3.52449.4756 1.5854 3.71954.8537 -1.4878 1.3171>> KDK=[A,B]KDK =8 9 5 -1 3 -236 -7 11 2 0 321 -8 5 -3 1 9 >> ERI=[A;B]ERI =8 9 536 -7 1121 -8 5-1 3 -22 0 3-3 1 9014一般函数的调用:A=[2 34 88 390 848 939];>> S=sum(A)S =2301>> min(A)ans =2>> EE=mean(A)EE =383.5000>> QQ=std(A)QQ =419.3794>> AO=sort(A)AO =2 34 88 390 848 939 >> yr=norm(A)yr =1.3273e+003>> RT=prod(A)RT =1.8583e+012>> gradient(A)ans =32.0000 43.0000 178.0000 380.0000 274.5000 91.0000 >> max(A)ans =939>> median(A)ans =239>> diff(A)ans =32 54 302 458 91>> length(A)ans =6>> sum(A)ans =2301>> cov(A)ans =1.7588e+005>>015矩阵变换:A=[34 44 23;8 34 23;34 55 2]A =34 44 238 34 2334 55 2>> tril(A)ans =34 0 08 34 034 55 2>> triu(A)ans =34 44 230 34 230 0 2>> diag(A)ans =34342norm(A)ans =94.5106>> rank(A)ans =3>> det(A)ans =-23462>> trace(A)ans =70>> null(A)ans =Empty matrix: 3-by-0>> eig(A)ans =80.158712.7671-22.9257>> poly(A)ans =1.0e+004 *0.0001 -0.0070 -0.1107 2.3462>> logm(A)Warning: Principal matrix logarithm is not defined for A with nonpositive real eigenvalues. A non-principal matrixlogarithm is returned.> In funm at 153In logm at 27ans =3.1909 + 0.1314i 1.2707 + 0.1437i 0.5011 - 0.2538i0.4648 + 0.4974i 3.3955 + 0.5438i 0.1504 - 0.9608i0.2935 - 1.2769i 0.8069 - 1.3960i 3.4768 + 2.4663i>> fumn(A)Undefined command/function 'fumn'.>> inv(A)ans =0.0510 -0.0502 -0.0098-0.0326 0.0304 0.02550.0305 0.0159 -0.0343>> cond(A)ans =8.5072>> chol(A)Error using ==> cholMatrix must be positive definite.>> lu(A)ans =34.0000 44.0000 23.00000.2353 23.6471 17.58821.0000 0.4652 -29.1816>> pinv(A)ans =0.0510 -0.0502 -0.0098-0.0326 0.0304 0.02550.0305 0.0159 -0.0343>> svd(A)ans =94.510622.345611.1095>> expm(A)ans =1.0e+034 *2.1897 4.3968 1.93821.31542.6412 1.16431.8782 3.7712 1.6625>> sqrtm(A)ans =5.2379 + 0.2003i 3.4795 + 0.2190i 1.8946 - 0.3869i0.5241 + 0.7581i 5.1429 + 0.8288i 2.0575 - 1.4644i3.0084 - 1.9461i4.7123 - 2.1276i 2.1454 + 3.7589i >>016多项式的计算:A=[34 44 23;8 34 23;34 55 2]A =34 44 238 34 2334 55 2>> P=poly(A)P =1.0e+004 *0.0001 -0.0070 -0.1107 2.3462>> PPA=poly2str(P,'X')PPA =X^3 - 70 X^2 - 1107 X + 23462017多项式的运算:p=[2 6 8 3];w=[32 56 0 2];>> m=conv(p,w)m =64 304 592 548 180 16 6 >> [q,r]=deconv(w,p)q =16r =0 -40 -128 -46>> dp=polyder(w)dp =96 112 0>> [num,den]=polyder(w,p)num =80 512 724 312 -16den =4 24 68 108 100 48 9>> b=polyfit(p,w,4)Warning: Polynomial is not unique; degree >= number of data points. > In polyfit at 74b =-0.6704 9.2037 -32.2593 0 98.1333>> r=roots(p)r =-1.2119 + 1.0652i-1.2119 - 1.0652i-0.5761018求多项式的商和余p=conv([1 0 2],conv([1 4],[1 1]))p =1 5 6 10 8>> q=[1 0 1 1]q =1 0 1 1>> [w,m]=deconv(p,q)w =1 5m =0 0 5 4 3>> cq=w;cr=m;>> disp([cr,poly2str(m,'x')])5 x^2 + 4 x + 3>> disp([cq,poly2str(w,'x')])x + 5019将分式分解a=[1 5 6];b=[1];>> [r,p,k]=residue(b,a)r =-1.00001.0000p =-3.0000-2.0000k =[]020计算多项式:a=[1 2 3;4 5 6;7 8 9];>> p=[3 0 2 3];>> q=[2 3];>> x=2;>> r=roots(p)r =0.3911 + 1.0609i0.3911 - 1.0609i-0.7822>> p1=conv(p,q)p1 =6 9 4 12 9>> p2=poly(a)p2 =1.0000 -15.0000 -18.0000 -0.0000 >> p3=polyder(p)p3 =9 0 2>> p4=polyval(p,x)p4 =31021求除式和余项:[q,r]=deconv(conv([1 0 2],[1 4]),[1 1 1])022字符串的书写格式:s='student's =student>> name='mary';>> s1=[name s]s1 =marystudent>> s3=[name blanks(3);s]s3 =marystudent>>023交换两个数:clearclca=[1 2 3 4 5];b=[6 7 8 9 10];c=a;a=b;b=c;ab24If语句n=input('enter a number,n=');if n<10nend025 if 双分支结构a=input('enter a number ,a=');b=input('enter a number ,b=');if a>bmax=a;elsemax=b;endmax026三个数按照由大到小的顺序排列:A=15;B=24;C=45;if A<BT=A;A=B;B=T;elseif A<CT=A;A=C;C=T;elseif B<CT=B;B=C;C=T;endABC027建立一个收费优惠系统:price=input('please jinput the price : price=') switch fix(price/100)case[0,1]rate =0;case[2,3,4]rate =3/100;case num2cell(5:9)rate=5/100;case num2cell(10:24)rate=8/100;case num2cell(25:49)rate=10/100;otherwiserate=14/100;endprice=price*(1-rate)028:while循环语句i=0;s=0;while i<=1212s=s+i;i=i+1;ends029,用for循环体语句:sum=0;for i=1:1.5:100;sum=sum+i;endsum030循环的嵌套s=0;for i=1:1:6;for j=1:1:8;s=s+i^j;end;end;s031continue 语句的使用:for i=100:120;if rem(i,7)~=0;continue;end;iend032x=input ('输入X的值x=')if x<1y=x^2;elseif x>1&x<2y=x^2-1;elsey=x^2-2*x+1;endy033求阶乘的累加和sum=0;temp=1;for n=1:10;temp=temp*n;sum=sum+temp;endsum034对角线元素之和sum=0;a=[1 2 3 4;5 6 7 8;9 10 11 12;13 14 15 16]; for i=1:4;sum=sum+a(i,i);endsum035用拟合点绘图A=[12 15.3 16 18 25];B=[50 80 118 125 150.8];plot(A,B)036绘制正玄曲线:x=0:0.05:4*pi;y=sin(x);plot(x,y)037绘制向量x=[1 2 3 4 5 6;7 8 9 10 11 12;13 14 15 16 17 18] plot(x)x=[0 0.2 0.5 0.7 0.6 0.7 1.2 1.5 1.6 1.9 2.3]plot(x)x=0:0.2:2*piy=sin(x)plot(x,y,'m:p')038在正弦函数上加标注:t=0:0.05:2*pi;plot(t,sin(t))set(gca,'xtick',[0 1.4 3.14 56.28])xlabel('t(deg)')ylabel('magnitude(v)')title('this is a example ()\rightarrow 2\pi')text(3.14,sin(3.14),'\leftarrow this zero for\pi')039添加线条标注x=0:0.2:12;plot(x,sin(x),'-',x,1.5*cos(x),':');legend('First','Second',1)040使用hold on 函数x=0:0.2:12;plot(x,sin(x),'-');hold onplot(x,1.5*cos(x),':');041一界面多幅图x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(221);plot(x,y1);title('sin(x)')subplot(222);plot(x,y2);title('cos(x)')subplot(223);plot(x,y3);title('sin(2x)')subplot(224);plot(x,y4);title('cos(2x)')042染色效果图x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(221);plot(x,y1);title('sin(x)');fill(x,y1,'r') subplot(222);plot(x,y2);title('cos(x)');fill(x,y2,'b') subplot(223);plot(x,y3);title('sin(2x)');fill(x,y3,'k') subplot(224);plot(x,y4);title('cos(2x)');fill(x,y4,'g')043特殊坐标图clcy=[0,0.55,2.5,6.1,8.5,12.1,14.6,17,20,22,22.1] subplot(221);plot(y);title('线性坐标图');subplot(222);semilogx(y);title('x轴对数坐标图');subplot(223);semilogx(y);title('y轴对数坐标图');subplot(224);loglog(y);title('双对数坐标图')t=0:0.01:2*pi;r=2*cos(2*(t-pi/8));polar(t,r)044特殊函数绘图:fplot('cos(tan(pi*x))',[-0.4,1.4])fplot('sin(exp(pi*x))',[-0.4,1.4])045饼形图与条形图:x=[8 20 36 24 12];subplot(221);pie(x,[1 0 0 0 1]);title('饼图');subplot(222);bar(x,'group');title('垂直条形图');subplot(223);bar(x,'stack');title('累加值为纵坐标的垂直条形图'); subplot(224);barh(x,'group');title('水平条形图');046梯形图与正弦函数x=0:0.1:10;y=sin(x);subplot(121);stairs(x);subplot(122);stairs(x,y);047概率图x=randn(1,1000);y=-2:0.1:2;hist(x,y)048向量图:x=[-2+3j,3+4j,1-7j];subplot(121);compass(x);rea=[-2 3 1];imag=[3 4 -7];subplot(122);feather(rea,imag);049绘制三维曲线图:z=0:pi/50:10*pi;x=sin(z);y=cos(z);plot3(x,y,z)x=-10:0.5:10;y=-8:0.5:8;[x,y]=meshgrid(x,y);z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2); subplot(221);mesh(x,y,z);title('普通一维网格曲面');subplot(222);meshc(x,y,z);title('带等高线的三维网格曲面'); subplot(223);meshz(x,y,z);title('带底座的三维网格曲面'); subplot(224);surf(x,y,z);title('充填颜色的三维网格面')050 带网格二维图x=0:pi/10:2*pi;y1=sin(x);y2=cos(x);plot(x,y1,'r+-',x,y2,'k*:')grid onxlabel('Independent Variable x') ylabel('Dependent Variable y1&y2') text(1.5,0.5,'cos(x)')051各种统计图y=[18 5 28 17;24 12 36 14;15 6 30 9]; subplot(221);bar(y)x=[4,6,8];subplot(222);bar3(x,y)subplot(223);bar(x,y,'grouped') subplot(224);bar(x,y,'stack')052曲面图x=-2:0.4:2;y=-1:0.2:1;[x,y]=meshgrid(x,y);z=sqrt(4-x.^2/9-y.^2/4); surf(x,y,z)grid on053创建符号矩阵e=[1 3 5;2 4 6;7 9 11];m=sym(e)符号表达式的计算问题因式分解:syms xf=factor(x^3-1)s=sym('sin(a+b)'); expand(s)syms x tf=x*(x*(x-8)+6)*t; collect(f)syms xf=sin(x)^2+cos(x)^2; simplify(f)syms xs=(4*x^2+8*x+3)/(2*x+1); simplify(s)通分syms x yf=x/y-y/x;[m,n]=numden(f)嵌套重写syms xf=x^4+3*x^3-7*x^2+12; horner(f)054求极限syms x a;limit(exp(-x),x,0,'left')求导数syms xdiff(x^9+x^6)diff(x^9+x^6,4)055求不定积分与定积分syms x ys=(4-3*x^2)^2;int(s)int(x/(x+y),x)int(x^2/(x+2),x,1,3) double(ans)056函数的变换:syms x ty=exp(-x^2);Ft=fourier(y,x,t)fx=ifourier(Ft,t,x)057求解方程syms a b c xs=a*x^2+b*x+c;solve(s)syms x y zs1=2*x^2+y^2-3*z-4;s2=y+z-3;s3=x-2*y-3*z;[x,y,z]=solve(s1,s2,s3)058求微分方程:y=dsolve('Dy-(t^2+y^2)/t^2/2','t')059求级数和syms x ksymsum(k)symsum(k^2-3,0,10)symsum(x^k/k,k,1,inf)060泰勒展开式syms xs=(1-x+x^2)/(1+x+x^2);taylor(s)taylor(s,9)taylor(s,x,12)taylor(s,x,12,5)061练习syms x a;s1=sin(2*x)/sin(5*x);limit(s1,x,0)s2=(1+1/x)^(2*x);limit(s2,x,inf)syms xs=x*cos(x);diff(s)diff(s,2)diff(s,12)syms xs1=x^4/(1+x^2);int(s1)s2=3*x^2-x+1int(s2,0,2)syms x y zs1=5*x+6*y+7*z-16;s2=4*x-5*y+z-7;s3=x+y+2*z-2;[x,y,z]=solve(s1,s2,s3)syms x yy=dsolve('Dy=exp(2*x-y)','x')y=dsolve('Dy=exp(2*x-y)','y(0)=0','x')n=sym('n');s=symsum(1/n^2,n,1,inf)x=sym('x');f=sqrt(1-2*x+x^3)-(1-3*x+x^2)^(1/3);taylor(f,6)062求于矩阵相关的值a=[2 2 -1 1;4 3 -1 2;8 5 -3 4;3 3 -2 2]adet=det(a)atrace=trace(a)anorm=norm(a)acond=cond(a)arank=rank(a)eiga=eig(a)063矩阵计算A=[0.1389 0.6038 0.0153 0.9318;0.2028 0.2772 0.7468 0.4660;0.1987 0.1988 0.4451 0.4186]B=var(A)C=std(A)D=range(A)E=cov(A)F=corrcoef(A)064求根及求代数式的值P=[4 -3 2 5];x=roots(P)x=[3 3.6];F=polyval(P,x)065多项式的和差积商运算:f=[1 2 -4 3 -1]g=[1 0 1]g1=[0 0 1 0 1]f+g1f-g1conv(f,g)[q,r]=deconv(f,g)polyder(f)066各种插值运算:X=0:0.1:pi/2;Y=sin(X);interp1(X,Y,pi/4)interp1(X,Y,pi/4,'nearest')interp1(X,Y,pi/4,'spline')interp1(X,Y,pi/4,'cubic')067曲线的拟合:X=0:0.1:2*pi;Y=cos(X);[p,s]=polyfit(X,Y,4)plot(X,Y,'K*',X,polyval(p,X),'r-')068求函数的最值与0点x=2:0.1:2;[x,y]=fminbnd('x.^3-2*x+1',-1,1) [x,y]=fzero('x.^3-2*x+1',1)069求多项式的表达式、值、及图像y=[1 3 5 7 19]t=poly(y)x=-4:0.5:8yx=polyval(t,x)plot(x,yx)070数据的拟合与绘图x=0:0.1:2*pi;y=sin(x);p=polyfit(x,y,5);y1=polyval(p,x)plot(x,y,'b',x,y1,'r')071求代数式的极限:syms xf=sym('log(1+2*x)/sin(3*x)');b=limit(f,x,0)072求导数与微分syms xf=sym('x/(cos(x))^2');y1=diff(f)y2=int(f,0,1)078划分网格函数[x,y]=meshgrid(-2:0.01:2,-3:0.01:5); t=x.*exp(-x.^2-y.^2);[px,py]=gradient(t,0.05,0.1);td=sqrt(px.^2+py.^2);subplot(221)imagesc(t)subplot(222)imagesc(td)colormap('gray')079求多次多项方程组的解:syms x1 x2 a ;eq1=sym('x1^2+x2=a')eq2=sym('x1-a*x2=0')[x1 x2]=solve(eq1,eq2,x1,x2)v=solve(eq1,eq2)v.x1v.x2an1=x1(1),an2=x1(2)an3=x2(1),an4=x2(2)080求解微分方程:[y]=dsolve('Dy=-y^2+6*y','y(0)=1','x')s=dsolve('Dy=-y^2+6*y','y(0)=1','x')[u]=dsolve('Du=-u^2+6*u','u(0)=1')w=dsolve('Du=-u^2+6*u','z')[u,w]=dsolve('Du=-w^2+6*w,Dw=sin(z)','u(0)=1,w(0)=0','z') v=dsolve('Du=-w^2+6*w,Dw=sin(z)','u(0)=1,w(0)=0','z')081各种显现隐含函数绘图:f=sym('x^2+1')subplot(221)ezplot(f,[-2,2])subplot(222)ezplot('y^2-x^6-1',[-2,2],[0,10])x=sym('cos(t)')y=sym('sin(t)')subplot(223)ezplot(x,y)z=sym('t^2')subplot(224)ezplot3(x,y,z,[0,8*pi])082极坐标图:r=sym('4*sin(3*x)')ezpolar(r,[0,6*pi])083多函数在一个坐标系内:x=0:0.1:8;y1=sin(x);subplot(221)plot(x,y1)subplot(222)plot(x,y1,x,y2)w=[2 3;3 1;4 6]subplot(223)plot(w)q=[4 6:3 5:1 2]subplot(224)plot(w,q)084调整刻度图像:x=0:0.1:10;y1=sin(x);y2=exp(x);y3=exp(x).*sin(x);subplot(221)plot(x,y2)subplot(222)loglog(x,y2)subplot(223)plotyy(x,y1,x,y2)085等高线等图形,三维图:t=0:pi/50:10*pi;subplot(2,3,1)plot3(t.*sin(t),t.*cos(t),t.^2) grid on[x,y]=meshgrid([-2:0.1:2])z=x.*exp(-x.^2-y.^2)subplot(2,3,2)plot3(x,y,z)box offsubplot(2,3,3)meshz(x,y,z)subplot(2,3,4)surf(x,y,z)contour(x,y,z)subplot(2,3,6)surf(x,y,z)subplot(2,3,5)contour(x,y,z)box offsubplot(2,3,6)contour3(x,y,z)axis off086统计图Y=[5 2 1;8 7 3;9 8 6;5 5 5;4 3 2]subplot(221)bar(Y)box offsubplot(222)bar3(Y)subplot(223)barh(Y)subplot(224)bar3h(Y)087面积图Y=[5 1 2;8 3 7;9 6 8;5 5 5;4 2 3];subplot(221)area(Y)grid onset(gca,'Layer','top','XTick',1:5)sales=[51.6 82.4 90.8 59.1 47.0];x=90:94;profits=[19.3 34.2 61.4 50.5 29.4];subplot(222)area(x,sales,'facecolor',[0.5 0.9 0.6], 'edgecolor','b','linewidth',2) hold onarea(x,profits,'facecolor',[0.9 0.85 0.7], 'edgecolor','y','linewidth',2) hold offset(gca,'Xtick',[90:94])set(gca,'layer','top')gtext('\leftarrow 销售量') gtext('利润')gtext('费用')xlabel('年','fontsize',14)088函数的插值:x=0:2*pi;y=sin(x);xi=0:0.1:8;yi1=interp1(x,y,xi,'linear')yi2=interp1(x,y,xi,'nearest') yi3=interp1(x,y,xi,'spline')yi4=interp1(x,y,xi,'cublic')p=polyfit(x,y,3)yy=polyval(p,xi)subplot(3,2,1)plot(x,y,'o')subplot(3,2,2)plot(x,y,'o',xi,yy)subplot(3,2,3)plot(x,y,'o',xi,yi1)subplot(3,2,4)plot(x,y,'o',xi,yi2)subplot(3,2,5)plot(x,y,'o',xi,yi3)subplot(3,2,6)plot(x,y,'o',xi,yi4)089二维插值计算:[x,y]=meshgrid(-3:0.5:3);z=peaks(x,y);[xi,yi]=meshgrid(-3:0.1:3); zi=interp2(x,y,z,xi,yi,'spline') plot3(x,y,z)hold onmesh(xi,yi,zi+15)hold offaxis tight090函数表达式;function f=exlin(x)if x<0f=-1;elseif x<1f=x;elseif x<2f=2-x;elsef=0;end091:硬循环语句:n=5;for i=1:nfor j=1:nif i==ja(i,j)=2;elsea(i,j)=0;endendendwhile 循环语句:n=1;while prod(1:n)<99^99;n=n+1endn:092 switch开关语句a=input('a=?')switch acase 1disp('It is raning') case 0disp('It do not know')case -1disp('It is not ranging')otherwisedisp('It is raning ?')end093画曲面函数:x1=linspace(-3,3,30)y1=linspace(-3,13,34)[x,y]=meshgrid(x1,y1);z=x.^4+3*x.^2-2*x+6-2*y.*x.^2+y.^2-2*y; surf(x,y,z)。
matlab 部分答案

课
D=A.*B
后
答
MATLAB: A=[1,4,8,13; -3,6,-5,-9; 2,-7,-12,-8];
案
网
8 13 ⎤ ⎡ 5 4 3 −2 ⎤ ⎡1 4 ⎥ ⎢ ⎥ 10. 设 A = ⎢ −3 6 −5 −9 ⎥ , B = ⎢ ⎢ 6 −2 3 − 8 ⎥ ⎢ ⎢ ⎣ −1 3 −9 7 ⎥ ⎦ ⎣ 2 −7 −12 −8⎥ ⎦
2
+ y2 )
,求定义域 x = [−2, 2] , y = [−2, 2] 内的 z 值(网格取 0.1 见方) ,并绘制
15.设 x = cos(t ) , y = sin( Nt + α ) ,若 N = 2 , α = 0, π / 3, π / 2, π ,在 4 个子图中分别画出其
MATLAB: t=0:0.01:3; N=2;
4. 用三点公式计算 y=f(x)在 x=1.0,1.2 处的导数值, f(x)值由下表给出; x f(x)
5
1.0 0.25
4
1.1
ww w
1.2
2
.k
1.3 0.1890 1.4 0.1736
后
7. 求解下列线性常微分方程的解析解。
答
6.设方程的根为 x = [−3, −5, −8, −9] ,求它们对应的 x 多项式的系数。
π
2π
课
=∫
0
17.设 ( X , Y ) 的概率密度为
网
⎧ d 2 x dy + − x = et ⎪ ⎪ dt 2 dt ⎨ 2 ⎪ d y + dx + y = 0 ⎪ ⎩ dt 2 dt
dy 。 dx
2π
MATLAB全部实验及答案

MATLAB全部实验及答案实验一、MATLAB基本操作实验内容及步骤1、命令窗口的简单使用(1)简单矩阵的输入(2)求[12+2×(7-4)]÷32的算术运算结果2、有关向量、矩阵或数组的一些运算(1)设A=15;B=20;求C=A+B与c=a+b?(2)设A=[1 2 3;4 5 6;7 8 9],B=[9 8 7;6 5 4;3 2 1];求A*B与A.*B?A*B就是线代里面的矩阵相乘 A.*B是对应位置的元素相乘(3)设a=10,b=20;求i=a/b=0.5与j=a\b=2?(4)设a=[1 -2 3;4 5 -4;5 -6 7]请设计出程序,分别找出小于0的矩阵元素及其位置(单下标、全下标的形式),并将其单下标转换成全下标。
clear,clca=[1 -2 3;4 5 -4;5 -6 7];[x,y]=find(a<0);c=[];for i=1:length(x)c(i,1)=a(x(i),y(i));c(i,2)=x(i);c(i,3)=y(i);c(i,4)=(y(i)-1)*size(a,2)+x(i);endc(5)在MATLAB命令行窗口运行A=[1,2;3,4]+i*[5,6;7,8];看结果如何?如果改成运行A=[1,2;3,4]+i[5,6;7,8],结果又如何?前面那个是虚数矩阵,后面那个出错(6)请写出完成下列计算的指令:a=[1 2 3;3 4 2;5 2 3],求a^2=?,a.^2=?a^2= 22 16 1625 26 2326 24 28a.^2=1 4 99 16 425 4 9(7)有一段指令如下,请思考并说明运行结果及其原因clearX=[1 2;8 9;3 6];X( : ) 转化为列向量(8)使用三元组方法,创建下列稀疏矩阵2 0 8 00 0 0 10 4 0 06 0 0 0方法一:clear,clcdata=[2 8 1 4 6];ir=[1 1 2 3 4 ];jc=[1 3 4 2 1];s=sparse(ir,jc,data,4,4);full(s)方法二:不用三元组法clear,clca=zeros(4,4);a(1,[1,3])=[2,8];a(2,4)=1;a(3,2)=4;a(4,1)=6;a(9) 写出下列指令的运行结果>> A = [ 1 2 3 ]; B = [ 4 5 6 ];>> C = 3.^A>> D = A.^B3、 已知⎪⎭⎫ ⎝⎛+⋅=-334sin 234πt e y t 若需要计算t ∈[-1,1],取间隔为0.01,试计算出相对应的y 值。
matlab程序设计例题及答案

matlab程序设计例题及答案1.编写程序:计算1/3+2/5+3/7+……+10/21法一: s=0;for i=1:10s=s+i/(2*i+1); end ss =法二:sum((1:10)./(3:2:21)) ans =2.编写程序:计算1~100中即能被3整除,又能被7整除的所有数之和。
s=0;for i=1:100if mod(i,3)==0&&mod(i,7)==0 s=s+i; end,end ss =2103.画出y=n!的图,阶乘的函数自己编写,禁用MATLAB 自带的阶乘函数。
x=1:10; for i=1:10try y(i)=y(i-1)*i; catch y(i)=1; end,end plot(x,y)106123456789104.一个数恰好等于它的因子之和,这个数就称为完数。
例如,6的因子为1,2,3,而6=1+2+3,因此6就是一个完数。
编程找出20XX以内的所有完数。
g=;for n=2:20XX s=0;for r=1:n-1if mod(n,r)==0 s=s+r; end endif s==ng=[g n]; end end gg =6 28 4965.编写一个函数,模拟numel函数的功能,函数中调用size函数。
function y=numelnumel(x) m=size(x); y=m(1)*m(2);numelnumel([1 2 3;4 5 6])ans =66. 编写一个函数,模拟length函数的功能,函数中调用size函数。
function y=lengthlength(x) m=size(x);y=max(m(1),m(2));lengthlength([1 2 3;4 5 6])ans =37.求矩阵rand的所有元素和及各行平均值,各列平均值。
s=rand(5);sum=sum(sum(s)) mean2=mean(s,2) mean1=mean(s)sum =mean2 =mean1 =8.编程判断1001,1003,1007,1009,1011为素数,若不是,输出其约数。
matlab课后习题答案(1-9章)

1 数字1.5e2,1.5e3 中的哪个与1500相同吗?1.5e32 请指出如下5个变量名中,哪些是合法的?abcd-2xyz_33chan a 变量ABCDefgh 2、5是合法的。
3 在MATLAB 环境中,比1大的最小数是多少? 1+eps4 设 a = -8 , 运行以下三条指令,问运行结果相同吗?为什么?w1=a^(2/3) w2=(a^2)^(1/3) w3=(a^(1/3))^2w1 = -2.0000 + 3.4641i ;w2 = 4.0000 ;w3 =-2.0000 + 3.4641i 5 指令clear, clf, clc 各有什么用处?clear 清除工作空间中所有的变量。
clf 清除当前图形。
clc 清除命令窗口中所有显示。
第二章1 说出以下四条指令产生的结果各属于哪种数据类型,是“双精度”对象,还是“符号”符号对象?3/7+0.1双; sym(3/7+0.1)符; sym('3/7+0.1') 符;; vpa(sym(3/7+0.1)) 符;2 在不加专门指定的情况下,以下符号表达式中的哪一个变量被认为是自由符号变量. sym('sin(w*t)'),sym('a*exp(-X)'),sym('z*exp(j*th)') symvar(sym('sin(w*t)'),1) w a z3 (1)试写出求三阶方程05.443=-x 正实根的程序。
注意:只要正实根,不要出现其他根。
(2)试求二阶方程022=+-a ax x 在0>a 时的根。
(1)reset(symengine)syms x positive solve(x^3-44.5) ans =(2^(2/3)*89^(1/3))/2(2)求五阶方程022=+-a ax x 的实根 syms a positive %注意:关于x 的假设没有去除 solve(x^2-a*x+a^2)Warning: Explicit solution could not be found. > In solve at 83 ans =[ empty sym ]syms x clear syms a positivesolve(x^2-a*x+a^2) ans =a/2 + (3^(1/2)*a*i)/2 a/2 - (3^(1/2)*a*i)/24 观察一个数(在此用@记述)在以下四条不同指令作用下的异同。
MATLAB课后习题集附标准答案

MATLAB课后习题集附标准答案第2 章 MATLAB 概论1、与其他计算机语言相比较,MA TLAB 语言突出的特点是什么?答:起点高、人机界面适合科技人员、强大而简易的作图功能、智能化程度高、功能丰富,可扩展性强.2、MA TLAB 系统由那些部分组成?答:开发环境、MATLAB数学函数库、MATLAB语言、图形功能、应用程序接口3、安装MATLAB 时,在选择组件窗口中哪些部分必须勾选,没有勾选的部分以后如何补安装?答:在安装MATLAB时,安装内容由选择组件窗口中各复选框是否被勾选来决定,可以根据自己的需要选择安装内容,但基本平台(即MATLAB选项)必须安装 . 第一次安装没有选择的内容在补安装时只需按照安装的过程进行,只是在选择组件时只勾选要补装的组件或工具箱即可. 矚慫润厲钐瘗睞枥庑赖。
4、MATLAB 操作桌面有几个窗口?如何使某个窗口脱离桌面成为独立窗口?又如何将脱离出去的窗口重新放置到桌面上?聞創沟燴鐺險爱氇谴净。
答:在MATLAB操作桌面上有五个窗口,在每个窗口的右下角有两个小按钮,一个是关闭窗口的Close 按钮,一个是可以使窗口称为独立的Undock 按钮,点击 Undock 按钮就可以使该窗口脱离桌面称为独立窗口,在独立窗口的 view 菜单中选择 Dock ,菜单项就可以将独立的窗口重新防止的桌面上.残骛楼諍锩瀨濟溆塹籟。
5、如何启动 M 文件编辑 /调试器?答:在操作桌面上选择“建立新文件”或“打开文件”操作时,M 文件编辑 /调试器将被启动 .在命令窗口中键入 edit 命令时也可以启动酽锕极額閉镇桧猪訣锥。
M 文件编辑 /调试器 .6、存储在工作空间中的数组能编辑吗?如何操作?答:存储在工作空间的数组可以通过数组编辑器进行编辑:在工作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输入修改内容即可.彈贸摄尔霁毙攬砖卤庑。
7、命令历史窗口除了可以观察前面键入的命令外,还有什么用途?答:命令历史窗口除了用于查询以前键入的命令外,还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中 . 謀荞抟箧飆鐸怼类蒋薔。
matlab简单编程21个题目及答案
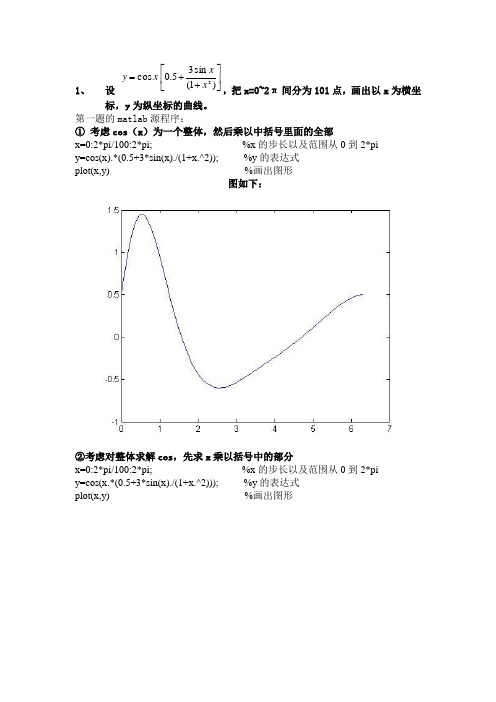
1、设⎥⎦⎤⎢⎣⎡++=)1(sin35.0cos2xxxy,把x=0~2π间分为101点,画出以x为横坐标,y为纵坐标的曲线。
第一题的matlab源程序:①考虑cos(x)为一个整体,然后乘以中括号里面的全部x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x).*(0.5+3*sin(x)./(1+x.^2)); %y的表达式plot(x,y)%画出图形图如下:②考虑对整体求解cos,先求x乘以括号中的部分x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x.*(0.5+3*sin(x)./(1+x.^2))); %y的表达式plot(x,y) %画出图形图如下:2、产生8×6阶的正态分布随机数矩阵R1, 求其各列的平均值和均方差。
并求该矩阵全体数的平均值和均方差。
第二题的matlab源程序如下:R1=randn(8,6) %产生正态分布随机矩阵R1 =1.0933 -0.7697 1.5442 -0.1924 1.4193 0.21571.1093 0.3714 0.0859 0.8886 0.2916 -1.1658-0.8637 -0.2256 -1.4916 -0.7648 0.1978 -1.14800.0774 1.1174 -0.7423 -1.4023 1.5877 0.1049-1.2141 -1.0891 -1.0616 -1.4224 -0.8045 0.7223-1.1135 0.0326 2.3505 0.4882 0.6966 2.5855-0.0068 0.5525 -0.6156 -0.1774 0.8351 -0.66691.5326 1.1006 0.7481 -0.1961 -0.2437 0.1873aver=(sum(R1(1:end,1:end)))./8 %产生各行的平均值aver =0.0768 0.1363 0.1022 -0.3473 0.4975 0.1044a=std(R1(1:end,1:end)) %产生各行的均方差也就是标准差a =1.0819 0.8093 1.3456 0.8233 0.8079 1.2150aver1=(sum(R1(:)))./48 %全体数的平均值aver1 =0.0950b=std(R1(:)) %全体数的均方差即标准差b =1.01033、设x=rcost+3t,y=rsint+3,分别令r=2,3,4,画出参数t=0~10区间生成的x~y 曲线。
Matlab习题答案

参考答案: (1) >> (3-5*i)*(4+2*i) ans =
22.0000 -14.0000i
(2) >> sin(2-8*i) ans =
1.3553e+003 +6.2026e+002i
5.判断下面语句的运算结果。 (1) 4 < 20 (2) 4 <= 20 (3) 4 == 20 (4) 4 ~= 20 (5) 'b'<'B' 参考答案: (1) >> 4<20 ans =
y_nearest(i)=interp1(x,y,scalar_x(i),'nearest'); y_linear(i) =interp1(x,y,scalar_x(i),'linear'); y_spline(i) =interp1(x,y,scalar_x(i),'spline'); y_cubic(i) =interp1(x,y,scalar_x(i),'cubic'); end subplot(2,2,1),plot(x,y,'*'),hold on,plot(scalar_x,y_nearest),title('method=nearest'); subplot(2,2,2),plot(x,y,'*'),hold on,plot(scalar_x,y_linear),title('method=linear'); subplot(2,2,3),plot(x,y,'*'),hold on,plot(scalar_x,y_spline),title('method=spline'); subplot(2,2,4),plot(x,y,'*'),hold on,plot(scalar_x,y_cubic),title('method=cubic'); 得到结果为:
MATLAB程序设计教程(第二版)课后答案

MATLAB第二版课后答案unit3-8 unit3实验指导1、n=i nput('请输入一个三位数:');a=fix (n/100);b=fix(( n-a*100)/10);c=n-a*100-b*10;d=c*100+b*10+a2 (1)n=input('请输入成绩');switch ncase num2cell(90:100)p='A';case num2cell(80:89)p='B';case num2cell(70:79)p='C';case num2cell(60:69)p='D';otherwisep='E';end price二p(2)n=input('请输入成绩'); if n>=90&n <=100 p='A:elseif n>=80&n v=89p='B';elseif n>=70&n v=79p='C';elseif n>=60&n v=69p='D';elsep='E';endprice=p(3)tryn;catchprice二'erroe'end3n二[1,5,56,4,3,476,45,6,3,76,45,6,4,3,6,4,23,76,908,6]; a=n(1);b=n (1);for m=2:20if n(m )>aa=n( m);elseif n(m)<bb=n( m);endendmax=amin=b法2n二[1,5,56,4,3,476,45,6,3,76,45,6,4,3,6,4,23,76,908,6]; mi n=mi n(n)max二max (n)4b二[-3.0:0.130];for n=1:61a=b( n);y(n )=(exp(0.3*a)-exp(-0.3*a))/2*si n(a+0.3)+log((0.3+a)/2);5y1=0;y2=1;n=input('请输入n的值:');for i=1: ny1=y1+1/i A2;y2二y2*((4*i*i)/((2*i-1)*(2*i+1)));endyiy26A=[1,1,1,1,1,1;2,2,2,2,2,2;3,3,3,3,3,3;4,4,4,4,4,4;5,5,5,5,5,5;6,6,6,6,6,6]; n=input('请输入n的值:');if n<=5&n>=0disp(A([n],:));elseif n<0disp(lasterr);else disp(A([6],:));disp(lasterr);endf=[];for n=1:40f(n )=n+10*log( n^2+5);endy=f(40)/(f(30)+f(20))(2)f=[];a=0;for n=1:40f(n )=a+n*( n+1);a=f(n);endy=f(40)/(f(30)+f(20))8y=0;m=input('输入m 的值:');n=input('输入n 值:');for i=1: ny=y+i A m;end************************************************************fun cti on s=shi8_1( n,m)s=0;for i=1: ns=s+i A m;end************************************************************ shi8_1(100,1)+shi8_1(50,2)+shi8_1(10,1/2)思考练习2N=[1,2,3,4,5];2.*NN./21./N1./N.A23s=fix(100*ra nd(1,20)*9/10+10)y=sum(s)/20j=0;for i=1:20if s(i)vy&rem(s(i),2)==0j=j+1;A(j)=s(i);else con ti nue;endendA4y1=0;y2=0;n=input('请输入n的值:'); for i=1: n y1=y1+-(-1)A i/(2*i-1); y2=y2+1/4A i; endyiy2unit4实验指导1 (1)x=-10:0.05:10;y=x-x.A3./6;Plot(x,y)(2)x=-10:0.5:10;ezplot('x A2+2*y A2-64',[-8,8]);grid on;2t=-pi:pi/10:pi;y=1./(1+exp(-t)); subplot(2,2,1);bar(t,y); title('条形图(t,y)');axis([-pi,pi,0,1]); subplot(2,2,2);stairs(t,y,'b');title('阶梯图(t,y)');axis([-pi,pi,0,1]); subplot(2,2,3);stem(t,y,'k');title('杆图(t,y)');axis([-pi,pi,0,1]); subplot(2,2,4);loglog(t,y,'y');title('对数坐标图(t,y)');3 (1)t=0:pi/50:2*pi;r=5.*cos(t)+4;polar(t,r);title('\rho=5*cos\theta+4');(2)t=-pi/3:pi/50:pi/3;r=5.*((si n( t)).A2)./cos(t);polar(t,r);4 (1)t=0:pi/50:2*pi;x=exp(-t./20).*cos(t);y=exp(-t./20).*si n( t);z=t;plot3(x,y,z);grid on;(2)[x,y]=meshgrid(-5:5); z=zeros(11)+5; mesh(x,y,z); shad ing in terp;5[x,y,z]=sphere(20);surf(x,y,z);axis off;shad ing in terp;m=movie in( 20);axis([-i,i,-i,i,-i,i])m(:,i)=getframe;endmovie(m,4);思考练习2 (1)x=-5:0.1:5;y=(1./(2*pi)).*exp((-(x“2))/2); plot(x,y);(2)t=-2*pi:0.1:2*pi;x=t.*si n( t);y=t.*cos(t);grid on;3t=O:pi/1OOO:pi;x=si n( 3.*t).*cos(t);y1=si n(3.*t).*si n( t);y2=2.*x-0.5;plot(x,y1,'k',x,y2);hold on;k二fin d(abs(y1-y2)<1e-2); x1=x(k);y3=2.*x1-0.5;plot(x1,y3,'rp');4x=-2:0.01:2;y=s in (1./x);subplot(2,1,1);plot(x,y);subplot(2,1,2);fplot('si n(1./x)',[-2,2],1e-4);5 (1)i=-4*pi:0.1:10;j=12./sqrt(i);polar(ij);title('{\rho}=12/sqrt(\theta)')(2)a=-pi/6:0.01:pi/6;b=3.*asi n( a).*cos (a) ./((s in (a)).八3+(cos(a)).八3); polar(a,b);6 (1)[u,v]=meshgrid(-4:0.1:4);x=3.*u.*s in (v);y=2.*u.*cos(v);z=4.*u.A2;subplot(2,1,1);mesh(x,y,z);subplot(2,1,2);surf(x,y,z);(2)[x,y]=meshgrid(-3:0.2:3);z=-5./(1+x.A2+y.A2);subplot(1,2,1);mesh(x,y,z);subplot(1,2,2); surf(x,y,z);unit5实验指导1A=ra ndn (10,5)x=mea n(A)y=std(A)Max二max(max(A))Min二min( mi n( A))Sumha ng二sum(A,2) SumA=sum(Sumha ng) B=sort(A); C=sort(B,2,'desce nd'); C2 (1)a=0:15:90;b=a./180.*pi;s=s in(b)c=0:15:75;d二c./180.*pi;t=ta n(d)e=i nput('请输入想计算的值:');S=si n( e/180*pi)T=ta n(e/180*pi)S1=i nterp1(a,s,e,'spli ne')T1二in terp1(c,t,e,'spli ne')P1=polyfit(a,s,5);P2=polyfit(c,t,5);S2=polyval(P1,e)T2=polyval(P2,e)(2)n二[1,9,16,25,36,49,64,81,100]; N=sqrt (n);x=in put('ji sua n zhi :');in terp1( n,N,x,'cubic')3N=64;T=5;t=li nspace(0,T,N);h=exp(-t);dt=t( 2)-t(1);f=1/dt;X=fft(t);F=X(1:N/2+1);f=f*(0:N/2)/N;plot(f,abs(F),'-*')4P=[2,-3,0,5,13];Q=[1,5,8];p=polyder(P)q=polyder(P,Q)[a,b]=polyder(P,Q)5P仁[1,2,4,0,5];P2=[0,1,2];P3=[1,2,3];P=P1+co nv(P2,P3)X=roots(P)A二[-1,1.2,-1.4;0.75,2,3.5;0,5,2.5]; p=polyval(P,A)思考练习A=ra nd(1,30000);a=mea n(A)b二std(A)Max二max(A)Min 二mi n(A)n=0;for i=1:30000if(A(i)>0.5)n=n+1;endendny=n/300005p二[45,74,54,55,14;78,98,45,74,12;87,98,85,52,65] [M,S]=max(p)[N,H]=mi n(p)jun zhi=mea n( p,1)fan gcha=std(p,1,1)zon g=sum(p,2);[Max,wei]=max(z ong)[Mi n, wei]=mi n(zong)[zcj,xsxh]=sort(z on g,'desce nd')6x=[1:10:101];y二[0,1.0414,1.3222,1.4914,1.6128,1.7076,1.7853,1.8513,1.9085,1.9590,2.0043]; [p,s]=polyfit(x,y,5)a=1:5:101;y1=polyval(p,a);plot(x,y,':o',a,y1,'-*')unit6实验指导1A二[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6];p二[0.95,0.67,0.52]';x=A\pA=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6];p二[0.95,0.67,0.53]';x=A\pcon d(A)2 (1)x1二fzero(@fu nx1,-1) fun cti on fx二fun x1(x) fx=x A41+x A3+1;(2)x2=fzero(@fu nx2,0.5)fun cti on fx二fun x2(x)fx=x-si n( x)/x;(3)optio ns=optimset('Display','off); x=fsolve(@fu n3,[1,1,1]',optio ns) q=fu n3(x) fun cti on q二fun 3(p)x=p(1);y=p (2);z=p (3);q(1)=si n(x)+yA2+log (z)-7;q(2)=3*x+2Ay-zA3+1; q(3)=x+y+z-5;3 (1)t0=0;tf=5;yO=1;[t,y]=ode23(@fu n4 ,[tO,tf],yO); t'y'fun cti on yp二fu n4 (t,y)yp=-(1.2+si n(1O*t))*y;(2)t0=0;tf=5;y0=1;[t,y]=ode23(@fu n5,[t0,tf],y0); t'y'fun cti on yp二fu n5(t,y)yp=cos(t)-y/(1+t A2);4x=fm inbn d(@m ymin, 0,2);-mymi n(x)fun cti on fx=mymi n(x)fx=-(1+x.A2)/(1+x.A4);5optio ns=optimset('Display','off);[x,fval]=fmi neon (@fu n6,[0,0,0],[],[],a,b,lb,ub)-fvalfun eti on f二fun 6(x)f=-(sqrt(x(1))+(400-x(1))*1.1+(sqrt(x (2))+(400-x(1))*1.1-x (2))*1.1+sqrt(3)+(((400- x(1))*1.1-x(2))*1.1-x(3))*1.1+sqrt(x(x4)));思考练习1 (1)A=[2,3,5;3,7,4;1,-7,1];B=[10,3,5]';C1=i nv(A)*BC2=A\B[L,U]=lu(A);x=U\(L\B)(2)A=[6,5,-2,5;9,-1,4,-1;3,4,2,-2;3,-9,0,2]; B二[-4,13,1,11]';C1=i nv(A)*BC2=A\B[L,U]=lu(A);x=U\(L\B)2 (1)x1二fzero(@fu nx1,1.5)fun cti on fx二fun x1(x)fx=3*x+si n(x)-exp(x);(2)x1=fzero(@fu nx2,1)fun cti on fx二fun x2(x) fx=x-1/x+5;(3)optio ns=optimset('Display','off); x=fsolve(@fu n3,[3,0]',optio ns) q=fu n3(x) fun cti on q二fun 3(p)x=p(1);y=p (2);q(1)=x A2+y A2-9;q(2)=x+y-1;3 (1)t0=0;tf=5;yo=[o,i];[t,y]=ode45(@vdpol,[t0,tf],y0);[t,y]fun cti on ydot二vdpol(t,y);ydot(1)=(2-3* y(2)-2*t*y(1))./(1+t A2);ydot(2)=y(1);ydot=ydot';(2)t0=0;tf=5;y0=[i;0;2];[t,y]=ode45(@vdpoll,[t0,tf],y0);[t,y]fun cti on ydot二vdpoll(t,y);ydot(1)=cos(t)-y(3)./(3+si n( t))+5*y(1).*cos(2*t)/((t+1)A2)-y(2); ydot(2)=y(1);ydot(3)=y(2);ydot=ydot';4x=fmi nbn d(@mymi n,0,pi);-mymi n(x)fun cti on fx=mymi n(x)fx=-si n(x)-cos(x.A2);5[x,y1]=fmi nbn d(@mymax,0,1.5);-yifun cti on fx=mymax(x);fx=-(9*x+4*x.A3-12*x.A2);unit7实验指导1 (1)format longfx二in li ne('s in( x)./x');[I, n ]=quadl(fx,0,2,1e-10)(2)format longfx=i nlin e('1./((x-0.3)A2+0.01)-1./((x-0.9)A2+0.04)-6'); [l,n ]=quad(fx,0,1,1e-10)2 (1)global ki;ki=0;l=dblquad(@fxy,0,1,0,1)ki(2)f=in li ne('abs(cos(x+y))','x','y');匸dblquad(f,O,pi,O,pi)3X=0.3:0.2:1.5;F二[0.3895,0.6598,0.9147,1.1611,1.3971,1.6212,1.8325]; trapz(X,F)4p=0:pi/5:2*pi;for n=1:3DX=diff(s in (p), n)end5f=inlin e('si n(x)./(x+cos(2.*x))');g=i nlin e('(cos(x).*(x+cos(2*x))-si n(x).*(1-2.*si n(2*x)))/(x+cos(2.*x)).八2'); x=-pi:0.01:pi;p=polyfit(x,f(x),5);dp=polyder(p);dpx=polyval(dp,x); %求dp在假设点的函数值dx=diff(f([x,3.01]))/0.01; %直接对f(x)求数值导数gx=g(x); %求函数f的导函数g在假设点的导数plot(x,dpx,x,dx,'.',x,gx,'-'); %作图思考练习2format longfx=i nlin e('1./(1+x.A2)');[I, n]二quad(fx,-l nf,ln f,1e-10)[I, n]=quadl(fx,-I nf,ln f,1e-10) x=-100000:100000;y=1./(1+x.A2);trapz(x,y)format short3(1)format longfx=i nli ne('log(1+x).心+x.A2)');[l,n ]=quad(fx,0,1,1e-10)⑵format longfx=i nli ne('sqrt(cos(t.A2)+4*s in ((2吐).八2)+1)'); [I, n]=quad(fx,0,2*pi,1e-10)4f=in li ne('4.*x.*z.*exp(-z.A2.*y-x.A2)');匸triplequad(f,0,pi,0,pi,0,1)5f=in li ne('s in( x)');g=i nli ne('cos(x)');x=0:0.01:2*pi;p=polyfit(x,f(x),5);dp二polyder(p);dpx=polyval(dp,x);dx二diff(f([x,2*pi+0.01]))/0.01;plot(x,dpx,x,dx,'.',x,gx,'-') unit8实验指导1syms x y;s=x A4-y A4;factor(s)factor(5135)2syms x;f=(x-2)/(xA2-4);Iimit(f,x,2)sym x;f=(sqrt(pi)-sqrt(acos(x)))/sqrt(x+1); limit(f,x,-1,'right')3sym x;f=si n(1/x);diff(f,'x')diff(f,'x',2)f=(1-cos(2*x))/x;diff(f,'x')diff(f,'x',2)4sym x;f=sqrt(exp(x)+1);in t(f,'x')syms x y;f=x/(x+y);in t(f,'y')sym x;f=exp(x)*(1+exp(x))八2;in t(f,'x',0,log(2))sym x;f=x*log(x);in t(f,'x',1,exp(1))5sym x;s=symsum((-1)八(x+1)/x,1,l nf) sym y;z=symsum(y A(2*y-1)/(2*y-1),1,I nf)6sym x;f1=(exp(x)+exp(-x))/2;f2=sqrt(xA3-2*x+1);(f1,x,5,0)(f2,x,6,0)7syms x y a;x=solve('xA3+a*x+1=0','x')x=solve('si n( x)+2*cos(x)-sqrt(x)=0','x')[x y]=solve('log(x/y)=9','exp(x+y)=3','x','y')syms n;[x,y]=dsolve('x*(D2y)+(1-n)*(Dy)+y=O','y(O)=O','Dy(O)=O','x') 思考练习2syms x B1 B2 a bs1=2*((cos(x))A2)-(si n(x))八2;s2=si n(B1)*cos(B2)-cos(B1)*si n(B2);s3二sqrt((a+sqrt(aA2-b))/2)+sqrt((a-sqrt(aA2-b))/2);s4=(4*xA2+8*x+3)/(2*x+1);h1=simplify(s1)h2=simplify(s2)h3=simplify(s3)h4=simplify(s4)3syms x a;f=abs(x)/x;limit(f,x,0,'left')f=(x+a/x)Ax;limit(f,x, inf)4syms x y m f=sqrt(x+sqrt(x+sqrt(x))); m=diff(f,'x') diff(m,'x') syms x y; f=x+y-sqrt(x A2+y A2);z1=diff(f,x)z2=diff(f,y)5syms x y; f=x+y-sqrt(xA2+yA2);z1=diff(f,x)z2=diff(f,y)sym x;f=1/(asi n(xF2*(1-xA2)A(1/2)); int(f)6syms xf=1/(1+x);in t(f,0,4)sym x;f=x A3*si n(xF2/(xA6+2*x%+1);in t(f,-1,1)sym x;f=xA3*si n(xF2/(xA6+2*xA4+1); in t(f,-1,1)7syms ns=symsum(1/4A n,1,i nf)sym n;s=symsum((( n+1)/n)A(1/2),1,i nf) eval(y)8syms xf=ta n( x);(f,x,3,0)syms xf=si n( x)A2;(f,x,5,0)9syms xx=solve('log(1+x)-5/(1+si n(x))=2','x')syms x y z[x yz]=solve('4*x A2/(4*x A2+1)=y','4*y A2/(4*y A2+1)=z','4*z A2/(4*z A2+1)=x','x','y','z')10[x ,y]=dsolve('Dx=3*x+4*y','Dy=5*x-7*y','x(0)=0','y(0)=1','t')。
MATLAB第1-8章答案

第1章一、思考题4. (1) B=A(2:5,1:2:5)(2)A(7)=[](3) A=A+30(4)size(A)(5) t(find(t==0))=eps(6)t=reshape(x,3,4)(7)abs('matlab')(8)char(93)5. A=[97,67,34,10;-78,75,65,5;32,5,-23,-59;0,-12,54,7](1) B=A(1:3,:)C=A(:,1:2)D=A(2:4,3:4)E=B*C(2)A(find(A>=50 & A<=100))二、实验题1.x=-74/180*pi;y=-27/180*pi;sin(x*x+y*y)/sqrt(tan(abs(x+y)))+pi2.a=-3.0:0.1:3.0;exp(-0.3*a).*sin(a+0.3)3.x=[2,4;-0.45,5];log(x+sqrt(1+x.*x))/24. A=[3,54,2;34,-45,7;87,90,15];B=[1,-2,67;2,8,74;9,3,0]; (1)A*Bans =129 432 41977 -407 -1052402 591 12489A.*Bans =3 -108 13468 -360 518783 270 0(2) A^3ans =-28917 240246 -4368137883 -259101 27669171333 252504 38673A.^3ans =27 157464 839304 -91125 343658503 729000 3375(3)A/Bans =-5.8845 5.3549 -0.20286.3554 -5.6596 4.3293-6.6325 6.2078 9.0241B/Aans =30.2855 19.2643 -8.561433.4394 21.1547 -9.3974-0.7443 -0.3938 0.2830(4)[A,B]ans =3 54 2 1 -2 6734 -45 7 2 8 7487 90 15 9 3 0[A([1,3],:);B^2]ans =3 54 287 90 15600 183 -81684 282 72615 6 8255.a=1+2i;b=3+4i;c=exp(pi*i/6)c =0.8660 + 0.5000ic+a*b/(a+b)ans =1.6353 + 1.8462i第2章一、思考题3.s=0;for n=0:63s=s+2^n;enddisp(s)n=0:63;s=sum(2.^n)二、实验题1.x=input('输入一个四位整数:');y=[fix(x/1000),mod(fix(x/100),10),mod(fix(x/10),10),mod(x,10)] z=mod((y+7),10)x=z(3)*1000+z(4)*100+z(1)*10+z(2)2.gh=input('输入工号');h=input('输入工时');dj=84;if h>120gz=dj*120+1.15*dj*(h-120);elseif h<60gz=dj*h-700;elsegz=dj*h;endformat bank;display([gh,gz])3.循环结构n=input('input n:');s=0;for k=1:ns=s+1/k^2;enddisplay(sqrt(s*6))向量运算n=input('input n:');k=1:n;display(sqrt(sum(1./k.^2)*6))4.y=0;k=0;while y<3k=k+1;y=y+1/(2*k-1);enddisplay([k-1,y-1/(2*k-1)])5.x0=0;x=1;k=0;a=input('a=');b=input('b=');while abs(x-x0)>=1e-5 && k<500x0=x;x=a/(b+x0);k=k+1;enddisplay([k,x]);display([(-b+sqrt(b^2+4*a))/2,(-b-sqrt(b^2+4*a))/2]);6.y=fun(40)/(fun(30)+fun(20))(1)函数文件fun.mfunction f=fun(n)f=n+log(n^2+5);(2)函数文件fun.mfunction f=fun(n)a=1:n;f=sum(a.*(a+1));第3章一、思考题4.t=0:0.01:1.5;y=sqrt(3)/2*exp(-4*t).*sin(4*sqrt(3)*t+pi/3);5.x=-10:0.01:10;y=linspace(-6,6,size(x,2))z=x.^3+3*x.*y.^2;plot3(x,y,z)6.x=100:100:400;y=100:100:400;z=[636,697,624,478;698,712,630,478;680,674,598,412;662,626,552,334]; [X,Y]=meshgrid(x,y);mesh(X,Y,z)二、实验题1.(1)x=-10:0.01:10;plot(x,x-x.^3/3/2)(2)plot(x,exp(-x.*x/2)/2/pi)(3)x=-8:0.01:8;plot(x,sqrt((64-x.*x)/2))(4)t=0:pi/100:6*pi;plot(t.*sin(t),t.*cos(t))2. (1)x1=linspace(0,1,100);y1=2*x1-0.5;t=linspace(0,pi,100);x=sin(3*t).*cos(t);y=sin(3*t).*sin(t);plot(x1,y1,'r-',x,y,'b:');text(0.4,1,'y=2x-0.5');text(-0.4,0.5,'x=sin(3t)cos(t)');text(-0.4,0.3,'y=sin(3t)sin(t)');(2)subplot(1,2,1);scatter(x1,y1,10)title('y=2x-0.5');subplot(1,2,2);scatter(x,y,10)3.subplot(1,21);x=1:1:100; y=sin(1./x);plot(x,y)subplot(1,2,2);fplot('sin(1/x)',[1,100])4.subplot(2,2,1);bar(t,y);subplot(2,2,2);stairs(t,y);subplot(2,2,3);stem(t,y)subplot(2,2,4);semilogy(t,y);5.theta=linspace(-pi,pi,100);ro=5.*cos(theta)+4;polar(theta,ro);fi=linspace(0,2*pi,100);a=1r=a.*(1+cos(fi));polar(fi,r);6.t=0:pi/20:2*pi;x=exp(-t./20).*cos(t);y=exp(-t./20).*sin(t);z=t; plot3(x,y,z);t=0:0.01:1;x=t;y=t.^2;z=t.^3;plot3(x,y,z);7.x=-30:0.1:0;y=0:0.1:30;[x,y]=meshgrid(x,y);z=10.*sin(sqrt(x.^2+y.^2))./sqrt(1+x.^2+y.^2); meshc(x,y,z);8.x=linspace(-3,3,100);y=linspace(-3,3,100);[x y]=meshgrid(x,y);fxy=-5./(1+x.^2+y.^2);i=find(abs(x)<=0.8 & abs(y)<=0.5);fxy(i)=NaN;surf(x,y,fxy)9.u=linspace(1,10,100);v=linspace(-pi,pi,100);[u,v]=meshgrid(u,v);x=3.*u.*sin(v);y=2.*u.*cos(v);z=4*u.^2;x=3*u.*sin(v);y=2*u.*cos(v);z=4*u.^2;surf(x,y,z);shading interp;light('position',[1,0,1]);10.t=0:pi/100:2*pi;y=sin(t);comet(t,y)第4章一、思考题5.(1)A=eye(3);(2)C=100+(200-100)*rand(5,6);(3)D=1+sqrt(0.2)*randn(1,500);(4)E=ones(size(A));(5)A=A+30*eye(size(A));(6)B=diag(diag(A))二、实验题1.P=pascal(5);H=hilb(5);Dp=det(P);Dh=det(H);Kp=cond(P);Kh=cond(H);P矩阵的性能更好,因为Kp较小2.A=[1,-1,2,3;0,9,3,3;7,-5,0,2;23,6,8,3]B=[3,pi/2,45;32,-76,sqrt(37);5,72,4.5e-4;exp(2),0,97]A1=diag(A);B1=diag(B);A2=triu(A);B2=triu(B);A3=tril(A);B3=tril(B);rA=rank(A);rB=rank(B);nA=norm(A);nb=norm(B);cA=cond(A);cB=cond(B);3.A=[31,1,0;-4,-1,0;4,-8,-2];[V,D]=eig(A);4.A=diag([-1,-1,-1,-1],-1)+diag([-1,-1,-1,-1],1)+diag([2,2,2,2,2]) b=[1,0,0,0,0]';x1=inv(A)*b;x2=A\b;[L,U]=lu(A);x3=U\(L\b);[Q,R]=qr(a);[Q,R]=qr(A);x4=R\(Q\b)R=chol(A);x5=R\(R'\b)5.B=sparse(A);x1=inv(B)*b;x2=B\b;[L,U]=lu(B);x3=U\(L\b);第5章一、思考题3.A=randn(10,5);mean(A)std(A)max(max(A))min(min(A))sum(A,2)sum(sum(A))sort(A,1)sort(A,2,'descend')二、实验题1.A=rand(1,30000);mean(A)std(A)max(A)min(A)size(find(A>0.5))/size(A)2.h=[466,715,950,1422,1635];w=[7.04,4.28,3.40,2.52,2.13];hh=[500,900,1500];ww=interp1(h,w,hh,'spline')3.x=linspace(1,10,50);y=log(x);f=polyfit(x,y,5);yy=polyval(f,x);plot(x,y,'r-',x,yy,'g.')4.N=64; % 采样点数T=5; % 采样时间终点t=linspace(0,T,N); % 给出N个采样时间ti(I=1:N) x=3*exp(-t); % 求各采样点样本值xdt=t(2)-t(1); % 采样周期f=1/dt; % 采样频率(Hz)X=fft(x); % 计算x的快速傅立叶变换XF=X(1:N/2+1); % F(k)=X(k)(k=1:N/2+1) f=f*(0:N/2)/N; % 使频率轴f从零开始plot(f,abs(F),'-*') % 绘制振幅-频率图xlabel('Frequency');ylabel('|F(k)|')5.(1)p1=[1 2 0 0 7];p2=[1 -2];p3=[1 0 0 5 1];p12=conv(p1,p2);p=p12+[zeros(1,size(p12,2)-size(p3,2)),p3];roots(p)(2)A=[-1,4,3;2,1,5;0,5,6];Px=polyval(p,A)Pxm=polyvalm(p,A)6.(1)z=fzero('3*x-sin(x)+1',0)(2)建立函数文件myfun.mfunction F=myfun(X)x=X(1);y=X(2);F(1)=x*x+y*y-9;F(2)=x+y-1;在命令窗口中输入以下命令:x=fsolve(@myfun,[3,0]',optimset('Display','off')) 第6章一、思考题2.fx=inline('1./(1+x.^2)');[I,n]=quad(fx,-100000,100000,1e-3);[I,n]=quadl(fx,-100000,100000,1e-3);x=-100000:0.01:100000;y=1./(1+x.*x);trapz(x,y);3.(1)fx=inline('-2*y+2*x*x+2*x');[t,y]=ode23(fx,[0,0.5],1)(2)fx=inline('y-exp(x)*cos(x)');[t,y]=ode23(fx,[0,3],1)二、实验题1.for x=1:3fx=[x,x^2,x^3;1,2*x,3*x;0,2,6*x];diff(fx)end2.(1)x=0:0.01:1;y=x.^10+10.^x+1./log10(x);dy=diff(y)/0.01;(2)x=0:0.01:1;y=log(1+x);dy=diff(y,2)/0.01;plot(x(1:99),dy)3.(1)fx=inline('x.^2.*sqrt(2*x.*x+3)');quad(fx,1,5)(2)fx=inline('x./sin(x).^2');quad(fx,pi/4,pi/3)(3)fx=inline('abs(cos(x+y))');dblquad(fx,0,pi,0,pi)(4)syms x y ;fx=x*y;int(int(fx,y^2,y+2),-1,2)x 的积分区间为【0,2】时fx=inline('x.*y');dblquad(fx,0,2,-1,2)4.x=0.3:0.2:1.5;y=[0.3895,0.6598,0.9147,1.1611,1.3971,1.6212,1.8325]; trapz(x,y)5.(1)yp=inline('-(1.2+sin(10*x))*y');[t,y]=ode23(yp,[0,5],1);(2)令''3,,21y x y x y x ='==,则可写出原方程的状态方程形式:123233221sin 31)1(2cos 5cos x tx x t t t x x x x x +--++='='='⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+-+-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'''t x x x t t t x x x cos 00)1(2cos 51sin 311000103212321 建立函数文件ztfun.mfunction y=ztfun(t,x)b=[0;0;cos(t)];y=[0,1,0;0,0,1;-1/(3+sin(t)),-1,5*cos(2*t)/(t+1)^2]*x+b; 解微分方程组[t,y]=ode23(@ztfun,[0,5],[1;0;2]);6.建立函数文件ztfun.mfunction yy=ztfun(t,y)yy=[y(2)*y(3);-y(1)*y(3);-0.51*y(1)*y(2)];解微分方程组[t,y]=ode23(@ztfun,[0,5],[0;1;1])第7章一、思考题3.(1)数值积分fx=inline('exp(x).*(1+exp(x)).^2');quad(fx,0,log(2))符号积分f=sym('exp(x)*(1+exp(x))^2');v=int(f,0,log(2));eval(v)(2)略二、实验题1.A=sym('[1,2,3;x,y,z;3,2,1]')rank(A)inv(A)det(A)2.(1) y=sym('sqrt(x+sqrt(x+sqrt(x)))');y1=diff(y)y2=diff(y,'x',2)(2) syms x y;fxy=sin(x^2*y)*exp(-x^2-y);diff(diff(fxy,x),y)3.(1) syms xint(1/(1+x^4))(2) syms x tint((-2*x*x+1)/(2*x*x-3*x+1)^2,x,cos(t),exp(2*t)) 4.syms n xsymsum(1/(2*n+1)/(2*x+1)^(2*n+1),n,0,inf)symsum(1/(2*n+1)/(2*x+1)^(2*n+1),n,0,5)5.(1) syms xtaylor((exp(x)+exp(-x))/2,5,0)(2) syms a xtaylor(exp(-5*x)*sin(3*x+pi/3),5,a)6.(1)x=solve(sym('x^3+a*x+1=0'))(2) [x y]=solve(sym('sqrt(x^2+y^2)-100=0,3*x+5*y-8=0'))7. 方程转化为: π21'11't y y y y -=+=⎩⎨⎧符号解[y1,y11]=dsolve('Dy=y1,Dy1+y=1-t^2/pi','y(-2)=5,y1(-2)=5','t') 数值解编写函数文件ztfun.mfunction yy=ztfun(t,y)yy=[y(2);1-t^2/pi-y(1)];在命令窗口输入以下命令[t,y]=ode45(@ztfun,[-2,7],[-5;5]);t=linspace(-2,7,49)y2=y8.[x,y]=dsolve('Dx=3*x+4*y,Dy=-4*x+3*y','x(0)=0,y(0)=1')。
matlab课后答案完整版

matlab课后答案完整版ones表⽰1矩阵zeros表⽰0矩阵ones(4)表⽰4x4的1矩阵zeros(4)表⽰4x4的0矩阵zeros(4,5)表⽰4x5的矩阵eye(10,10)表⽰10x10的单位矩阵rand(4,5)表⽰4x5的伴随矩阵det(a)表⽰计算a的⾏列式inv(a)表⽰计算a的逆矩阵Jordan(a)表⽰求a矩阵的约当标准块rank(a)表⽰求矩阵a的秩[v,d]=eig(a)对⾓矩阵b=a’表⽰求a矩阵的转置矩阵sqrt表⽰求平⽅根exp表⽰⾃然指数函数log⾃然对数函数abs绝对值第⼀章⼀、5(1)b=[97 67 34 10;-78 75 65 5;32 5 -23 -59]; >> c=[97 67;-78 75;32 5;0 -12]; >> d=[65 5;-23 -59;54 7];>> e=b*ce =5271 11574-11336 6641978 3112(2)a=50:1:100⼆、1 、x=-74;y=-27;z=(sin(x.^2+y.^2))/(sqrt(tan(abs(x+y)))+pi) z =-0.09012、a=-3.0:0.1:3.0;>> b=exp(-0.3*a).*sin(a+0.3)y =0.7218 1.0474-0.2180 1.15624、a*b表⽰a矩阵和b矩阵相乘a.*b表⽰a矩阵和b矩阵单个元素相乘A(m,n)表⽰取a矩阵第m⾏,第n列A(m,:)表⽰取a矩阵第m⾏的全部元素A(:,n)表⽰取a矩阵的第n列全部元素A./B表⽰a矩阵除以b矩阵的对应元素,B.\A等价于A./BA.^B表⽰两个矩阵对应元素进⾏乘⽅运算A.^2表⽰a中的每个元素的平⽅A^2表⽰A*A例:x=[1,2,3];y=[4,5,6];z=x.^yz=1 32 729指数可以是标量(如y=2).底数也可以是标量(如x=2)5、a=1+2i;>> b=3+4i;>> c=exp((pi*i)/6)c =0.8660 + 0.5000id=c+a*b/(a+b)d =1.6353 + 1.8462i第⼆章⼆、4、(1)y=0;k=0;>> while y<3k=k+1;>> display([k-1,y-1/(2*k-1)])ans =56.0000 2.9944第三章⼆1(1) x=0:pi/10:2*pi; >> y=x-x.^3/6; >> plot(x,y)1234567-40-35-30-25-20-15-10-505(2)x=0:pi/10:2*pi; y=(exp(-x.^2/2))/2*pi;plot(x,y)012345670.20.40.60.811.21.41.6(3)x=-8:0.01:8; y=sqrt((64-x.^2)/2);plot(x,y)-8-6-4-2024680123456(4)t=0:0.1:8*pi; >> x=t.*sin(t); >> y=t.*cos(t);-25-20-15-10-50510152025-30-20-10102030例3.4x=0:pi/100:2*pi; y1=exp(-0.5*x);y2=exp(-0.5*x).*sin(2*x); plot(x,y1,x,y2)>> title('x from 0 to 2{\pi} '); >> xlabel('variable x'); >> ylabel('variable y'); >> text(1.5,0.5,'曲线y1=e^(-0.5x)'); >> text(3,0.1,'曲线y2=cos(4{\pi}x)e^{-0.5x}'); >> legend('y1','y2')1234567-0.4-0.20.20.40.60.81x from 0 to 2πvariable xv a r i a b l e y曲线y1=e (-0.5x)曲线y2=cos(4πx)e -0.5xy1y22、(1)y1=2*x-0.5;t=linspace(0,pi,100); x=sin(3*t).*cos(t); y=sin(3*t).*sin(t);>> k=find(abs(y-x)<1e-2); >> t1=t(k) t1 =0 0.7933 1.04722.0944>> z=sin(3.*(t1)).*cos(t1) z =0 0.4841 0.0000 0.0000 -0.0000>> plot(t,x,t,y,'k:',t1,z,'bp');0.511.522.533.5-1-0.8-0.6-0.4-0.200.20.40.60.81(2)subplot(1,2,1); >> scatter(x1,y1,10); >> title('y=2x-0.5'); >> subplot(1,2,2); >> scatter(x,y,10)-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.63、subplot(1,2,1); x=0:0.01:pi; y=sin(1./x); plot(x,y)subplot(1,2,2);fplot('sin(1./x)',[1,100])1234-1-0.8-0.6-0.4-0.200.20.40.60.81204060801000.10.20.30.44、t=0:pi:2*pi; y=1./(1+exp(-t));subplot(2,2,1);%图形窗⼝的分割bar(t,'group'); %绘制柱形图(分组) subplot(2,2,2);barh(t,'stack');%绘制柱形图(堆积) subplot(2,2,3);loglog(t,y); %函数使⽤全对数坐标,x,y 均采⽤常⽤对数刻度 subplot(2,2,4); semilogy(t,y); %函数使⽤半对数坐标,y 轴为常⽤对数刻度,x 轴仍为线性刻度1230246802468123100.5100.710-0.01810-0.0010246810-0.310-0.210-0.15、(1)theta=linspace(-pi,pi,100); ro=5.*cos(theta)+4; polar(theta,ro); (2)x=linspace(0,2*pi,100);a=1>> r=a.*(1+cos(x)); polar(x,r);3021060240902701203001503301806、(1)t=0:pi/10:2*pi;>> x=exp((-t)/20).*cos(t); >> y=exp((-t)/20).*sin(t); >> z=t; >> plot3(x,y,z);-1-0.50.51-1-0.50.5102468(2)t=0:0.01:1; x=t;>> y=t.^2; >> z=t.^3;>> plot3(x,y,z);0.20.40.60.800.20.40.60.817、x=-30:0.1:0; >> y=0:0.1:30;>> [x,y]=meshgrid(x,y); >>z=10.*sin(sqrt(x.^2+y.^2))./sqrt(1+x.^2+y.^2);>> meshc(x,y,z);绘制曲⾯图和等⾼线-30-20-10102030-4-202468、x=linspace(-3,3,100); >> y=linspace(-3,3,100); >> [x y]=meshgrid(x,y); %可以将向量转化为矩阵 >> fxy=-5./(1+x.^2+y.^2); >> i=find(abs(x)<=0.8 & abs(y)<=0.5); >> fxy(i)=NaN; >>surf(x,y,fxy) %绘制三维曲⾯图-4-224-4-224-4-3-2-19、u=linspace(1,10,100); v=linspace(-pi,pi,100);[u v]=meshgrid(u,v); x=3.*u.*sin(v); y=2.*u.*cos(v); z=4*u.^2; surf(x,y,z); shading interp;-40-20-1010200100200300400第五章⼆1、a=rand(1,30000);mean(a) %求平均数 ans =0.5010 >>b=std(a) %求标准差 b =0.2882 >> c=max(a) c =0.9999 >> d=min(a) d =3.5706e-005size(find(a>0.5))/size(a) %求⼤于0.5的随机数个数占总数的百分⽐ans =0.50322、h=[466,715,950,1422,1635]; >> w=[7.04,4.28,3.40,2.52,2.13]; >> hh=[500,900,1500]; >> ww=interp1(h,w,hh,'spline')ww =6.4903 3.5226 2.3845 3、x=linspace(1,10,50); y=log(x);f=polyfit(x,y,5); %求曲线的拟合 >> yy=polyval(f,x); >> plot(x,y,'r-',x,yy,'g.') 123456789100.511.522.55、(1)、(2) p1=[1,2,0,7]; p2=[1,-2]; p3=[1,0,5,1]; p12=conv(p1,p2); >>p=p12+[zeros(1,size(p12,2)-size(p3,2)),p3]; >> roots(p) ans =-3.4656 0.6128 + 1.6278i 0.6128 - 1.6278i 1.2400-29 291 95 19 -3 697 -13 697 1427 >>y2=polyvalm(p,a)%以矩阵a 为⾃变量 y2 =391 2084 3273 502 2693 4207 720 3775 5892 6、(1)z=fzero('3*x-sin(x)+1',0) %求x=0时附近的根 z =-0.4903 第⼋章⼆、2t=0:pi/20:2*pi; x=sin(t); y=cos(t); x1=sin(7*t); y1=cos(7*t);h=plot(x,y,x1,y1);set(h,'marker','x','linewidth',2); set(gca,'xtick',-1:0.1:1); title('篮筐')-1-0.9-0.8-0.7-0.6-0.5-0.4-0.3-0.2-0.100.10.20.30.40.50.60.70.80.91 -1-0.8-0.6-0.4-0.200.20.40.60.81篮筐3、x=0:pi/10:5*pi;y=exp(-0.2*x).*cos(x)+2; h=plot(x,y);set(gca,'color','red','linestyle','-','linewidth',3);text(5,2.4,'y=exp(-0.2*x).*cos(x)+2');02468101214161.41.61.822.22.42.62.83y=exp(-0.2*x).*cos(x)+24、t=-pi:pi/100:pi; x=cos(t); y=sin(t); z=t;h=plot(t,x,t,y,t,z);set(h,'linestyle','-','linewidth',3);-4-3-2-101234-4-3-2-101234字符串例ch='Welcome to Beijing';subch=ch(12:18) 选12~18个字符串(空格也算)ans =WELCOME TO BEIJING >> length(k)统计⼩写字母的个数ans = 14 例:已知y=1-1/2+1/3-1/4.........-1/100求y 的值y=0; >> n=100; >> for i=1:100; y=y+(-1)^(i-1)/i; end>> disp(y)0.6882绘制⼆维曲线图x=0:pi/100:2*pi; >> y1=0.2*exp(-0.5*x).*cos(4*pi*x); >> y2=1.5*exp(-0.5*x).*cos(pi*x); >> plotyy(x,y1,x,y2); 7-0.20.20123456-202绘制三维图像例:x=sint+tcost y=cost-tsint z=tt=0:pi/10:10*pi; x=sin(t)+t.*cos(t); y=cos(t)-t.*sin(t); z=t; plot3(x,y,z); axis([-30 30 -30 30 0 35]); 坐标轴的最⼤值与最⼩值title('line in 3-D space'); 图形的题⽬ >> xlabel('x');ylabel('y');zlabel('z'); 标注坐标>> grid on; 加⽹格线 -30-20-10102030-20205101520253035xline in 3-D spaceyz三维例]2/,0[],,0[,cos sin 22ππ∈∈+=y x y x z [x,y]=meshgrid(0:pi/100:pi,0:pi/100:pi/2);>> z=sin(x.^2)+cos(y.^2);>> mesh(x,y,z);>> axis([0 4 0 1.8 -1.5 1.5]); 012340.511.5-1.5-1-0.500.511.5例3.16t=0:pi/20:2*pi; subplot(1,2,1);[x,y,z]=cylinder(sin(t),30);surf(x,y,z); 绘制三维曲⾯图subplot(1,2,2);>> [x,y,z]=peaks(100);>> mesh(x,y,z); 绘制三维⽹格图-11-10100.20.40.60.81-55-505-10-5510多项式求导例:f(x)=1/x^2+5 p=[1];>> q=[1,0,5];>> [p,q]=polyder(p,q)注:c=conv(a,b) 表⽰a 多项式与b 多项式乘积[p,r]=deconv(a,b) 表⽰a 多项式与b 多项式相除其中p 为商向量 r 为余数向量p=polyder(p) 表⽰求p 的导数 p=poleder(p,q) 表⽰求p 乘以q 的导数[p,q]=poleder(p,q) 表⽰p 除以q 的导数多项式求根例:f(x)=2x^4-12x^3+3x^2+5 p=[2,-12,3,0,5]; >> x=roots(p); >> p=[2,-12,3,0,5]; x=roots(p) 求⽅程f(x)=0的根 x =5.7246 0.8997 -0.3122 + 0.6229i -0.3122 - 0.6229i>> g=poly(x) 已知多项式的根求多项式 g =1.0000 -6.0000 1.5000 -0.00002.5000符号求导例7.3x=a(t-tsint)y=b(1-cost) 求y 对x 的⼀阶导数 syms x y a b t;>> f21=a*(t-sin(t)); >> f22=b*(1-cos(t));>> diff(f22)/diff(f21) 求y 对x 的⼀阶导数ans =b*sin(t)/a/(1-cos(t))注:diff(f1,x,2) 表⽰f1对x 的⼆阶导数diff (f3,x )表⽰z 对x 的偏导 diff (f3,y )表⽰z 对y 的偏导求不定积分int(f) 求f 的不定积分 f1=int(f,a,b) 求f 在a ,b 之间的定积分eval (f1)计算积分值符号求极限例7.2 syms x h>> f=(sin(x+h)-sin(x))/h;>> limit(f,h,0) h 趋向于0ans =cos(x)例2f=sym('(1+t/x)^x');limit(f,inf) f趋向于⽆穷ans =exp(t)例3f=sym('x*(sqrt(x^2+1)-x)');limit(f,sym('x'),inf,'left') x 趋向于正⽆穷ans =1/2⼤⼩写ch='Welcome to Beijing';subch=ch(12:18)subch =Beijing>> k=find(ch>='A'&ch<='Z'); ch(k)=ch(k)-('A'-'a');>> char(ch)ans =welcome to beijing>> length(k)ans =2。
matlab习题及答案

matlab习题及答案《Matlab习题及答案:提升编程技能,解决实际问题》Matlab是一种强大的数值计算和数据分析工具,它被广泛应用于工程、科学和其他领域的计算和模拟。
为了帮助大家提升编程技能,解决实际问题,我们为大家准备了一些Matlab习题及答案,希望能够帮助大家更好地掌握Matlab的使用。
1. 习题一:编写一个Matlab程序,计算斐波那契数列的前20个数字,并将结果打印出来。
答案:下面是一个简单的Matlab程序,用于计算斐波那契数列的前20个数字。
```matlaba = 0;b = 1;fib = zeros(1, 20);fib(1) = a;fib(2) = b;for i = 3:20fib(i) = fib(i-1) + fib(i-2);enddisp(fib);```2. 习题二:编写一个Matlab程序,求解一个二次方程ax^2 + bx + c = 0的根。
答案:下面是一个简单的Matlab程序,用于求解二次方程的根。
```matlaba = 1;b = -3;c = 2;delta = b^2 - 4*a*c;if delta > 0x1 = (-b + sqrt(delta))/(2*a);x2 = (-b - sqrt(delta))/(2*a);disp(['The roots are ', num2str(x1), ' and ', num2str(x2)]);elseif delta == 0x = -b/(2*a);disp(['The root is ', num2str(x)]);elsedisp('The equation has no real roots');end```通过以上两个习题及答案的示例,我们可以看到Matlab的强大功能和灵活性。
通过练习这些习题,我们可以更好地掌握Matlab的基本语法和常用函数,从而在实际问题中更快更准确地解决数值计算和数据分析的挑战。
matlab程序设计与应用习题答案

matlab程序设计与应用习题答案Matlab程序设计与应用习题答案Matlab是一种强大的数学软件,被广泛应用于科学计算、数据分析和工程模拟等领域。
无论是学术界还是工业界,Matlab都扮演着重要的角色。
在学习和应用Matlab时,我们常常会遇到一些习题,下面我将为大家提供一些常见习题的解答。
习题一:编写一个Matlab程序,计算一个数列的和。
数列的定义如下:a(1) = 1, a(n) = a(n-1) + 2*n, 其中n大于等于2。
解答一:```matlabfunction sum = calculate_sum(n)a = zeros(1, n);a(1) = 1;for i = 2:na(i) = a(i-1) + 2*i;endsum = sum(a);end```习题二:编写一个Matlab程序,求解一个线性方程组。
方程组的定义如下:2x + 3y + z = 7, 3x - 2y + 2z = 5, x + y - z = 3。
解答二:```matlabfunction [x, y, z] = solve_equations()A = [2, 3, 1; 3, -2, 2; 1, 1, -1];b = [7; 5; 3];solution = A\b;x = solution(1);y = solution(2);z = solution(3);end```习题三:编写一个Matlab程序,实现矩阵的转置操作。
解答三:```matlabfunction transposed_matrix = transpose_matrix(matrix) [m, n] = size(matrix);transposed_matrix = zeros(n, m);for i = 1:mfor j = 1:ntransposed_matrix(j, i) = matrix(i, j);endendend```习题四:编写一个Matlab程序,实现矩阵的相乘操作。
MATLAB 课后部分答案

P77 第2章1、>> x=2;>> y=power(x,3)+(x-0.98).^2./(x+1.35).^3-5*(x+1./x)>> x=4;>> y=power(x,3)+(x-0.98).^2./(x+1.35).^3-5*(x+1./x)7、>> mat=rand(4,5);>> m=1;>> for i=1:2for j=1:5if mat(i,j)>0.3b(m)=mat(i,j);m=m+1;endendend>> b8、>> V=inv(A)>> A=rand(5,5);10、>> A=[1 4 8 13;-3 6 -5 -9;2 -7 -12 -8];B=[5 4 3 -2;6 -2 3 -8;-1 3 -9 7]; >> C=A*B??? Error using ==> mtimesInner matrix dimensions must agree.>> C=A.*BC =5 16 24 -26-18 -12 -15 72-2 -21 108 -5611、>> x=linspace(0,2*pi,125);>> y=cos((x).*(0.5+3*sin(x)./(1+x.^2)));>> plot(x,y)13、>> x=-2:0.1:2;y=-2:0.1:2;>> [X,Y]=meshgrid(x,y);>> Z=X.^2.*exp(-X.^2-Y.^2);>> mesh(Z)建立一个M函数文件mycos.m,程序如下:function y=mycos(x)clear allx=input('请输入x的值')y=1./((x-2).^2+0.1)+1./((x-3).^3+0.01)在命令窗口输入:mycosP123 第3章1、>> x=[446 714 950 1422 1634];y=[7.04 4.28 3.40 2.54 2.13];>> xi=500:500:1500;>> yi=interp1(x,y,xi,'linear')4、>> p=[3 4 7 2 9 12];>> roots(p)8、>> a=[2 4 9;4 2 4;9 4 18];>> [V,D]=eig(a) %V的列向量是相应的特征向量,对角阵D的对角元素为a的特征值10、>> p1=[-1 4 0];p2=[-1 -4 0];>> A=polyder(p1);B=polyder(p2);>> A1=roots(A);B1=roots(B);>> y=4*A1-4*B1-A1.^2-B1.^213、>> syms x y>> Ex=int(int(x.*12.*y.^2,y,0,x),x,0,1)>> Ey=int(int(y.*12.*y.^2,x,y,1),y,0,1)>> Exy=Ex.*Ey14、>> A=rand(4,4);>> [L,U]=lu(A)>> [Q,R]=qr(A)P183 第4章1、>> n=-2*pi:0.01:2*pi;>> N=12;x=cos(n*pi./6);>> X=fft(x,N)>> nx=((n>=0)&(n<=11)); hx=((n>=0)&(n<=5)); >> xn=0.8*nx;hn=hx;>> y=conv(xn,hn)4、>> n=0:11;h=0:5;>> nx=((n>=0)&(n<=11)); hx=((n>=0)&(n<=5)); >> xn=0.8*nx;hn=hx;>> M=length(xn);N=length(hn);>> L=pow2(nextpow2(M+N-1));>> Xk=fft(xn,L);Hk=fft(hn,L);>> Yk=Xk.*Hk;>> yn=ifft(Yk,L)5、>> num=[2 3 0];den=[1 0.4 1];>> [z,p,k]=tf2zp(num,den)6、>> num=[4 15.6 6 2.4 -6.4];den=[3 2.4 6.3 -11.4 6]; >> [z,p,k]=tf2zp(num,den)>> zplane(z,p)7、>> num=[18 0 0 0];den=[18 3 -4 -1];>> [r,p,k]=residuez(num,den)9、建立一个M函数文件,程序如下:clear allN=10;[z,p,k]=buttap(N);[A,B,C,D]=zp2ss(z,p,k);wc1=100;wc2=200;[At,Bt,Ct,Dt]=lp2bp(A,B,C,D,wc1,wc2);[num1,den1]=ss2tf(At,Bt,Ct,Dt);[num2,den2]=impinvar(num1,den1);dimpulse(num2,den2)10、建立一个M函数文件,程序如下:clear allwp=100*2*pi;ws=200*2*pi;Rp=2;Rs=15;Fs=500;[N,Wc]=buttord(wp,ws,Rp,Rs,'s'); %选择滤波器的最小阶数[z,p,k]=buttap(N);[B,A]=zp2tf(z,p,k);[num,den]=bilinear(B,A,Fs); %模拟滤波器的传递函数转换为数字滤波器的传递函数freqz(num,den)11、建立一个M函数文件,程序如下:clear allN=48;w=[0.35,0.65];B=fir1(N,w,'bandpass'); %返回一个N阶的带通滤波器freqz(B) %绘制滤波器的频率响应曲线12、建立一个M函数文件,程序如下:clear allN=37;wc=0.3*pi;B=fir1(N,wc);freqz(B) %绘制滤波器的频率响应曲线13、建立一个M函数文件,程序如下:clear allN=55;F=[0:1/55:1];A=[ones(1,28),zeros(1,N-27)];B=fir2(N,F,A);freqz(B) %绘制滤波器的频率响应曲线15、建立一个M函数文件,程序如下:clear allwc=0.4*pi/(2*pi);N=12;[B,A]=butter(N,wc);%设计N阶截止频率为wc的Butterworth低通数字滤波器的传递函数模型m=dimpulse(B,A,101);stem(m,'.')P277 第6章2、建立一个M函数文件,程序如下:function [h,l]=huffmancode(P)if length(find(P<0))~=0,error('Not a prod.vector')endif abs(sum(P)-1)>10e-10error('Not a prod.vector')endn=length(P);for i=1:n-1for j=i:nif P(i)<=P(j)p=P(i);P(i)=P(j);P(j)=p;endendenddisp('概率分布'),PQ=P;m=zeros(n-1,n);for i=1:n-1[Q,l]=sort(Q);m(i,:)=[l(1:n-i+1),zeros(1,i-1)];Q=[Q(1)+Q(2),Q(3:n),1];endfor i=1:nc(i,:)=blanks(n*n);endc(n-1,n)='0';c(n-1,2*n)='1';for i=2:n-1c(n-i,1:n-1)=c(n-i+1,n*(find(m(n-i+1,:)==1))-(n-2):n*(find(m(n-i+1,:)==1)));c(n-1,n)='0';c(n-i,n+1:2*n-1)=c(n-i,1:n-1);c(n-i,2*n)='1';for j=1:i-1c(n-i,(j+1)*n+1:(j+2)*n)=c(n-i+1,n*(find(m(n-i+1,:)==j+1)-1)+1:n*find(m(n-i+1,:)==j+1));endendfor i=1:nh(i,1:n)=c(1,n*(find(m(1,:)==i)-1)+1:find(m(1,:)==i)*n);ll(i)=length(find(abs(h(i,:))~=32));endl=sum(P.*ll); %计算平均码长在命令窗口中输入:>> P=[0.20 0.15 0.13 0.12 0.1 0.09 0.08 0.07 0.06];>> [h,l]=huffmancode(P)3、建立一个M函数文件,程序如下:function[sqnr,a_quan,code]=u_pcm(a,n)% U_PCM 一个序列均匀的PCM编码.% n=量化级数的数目(偶数).% sqnr=输入信号量化噪声比(偶数)。
matlab答案

大于0.5的元素的全下标
行号1 3 2 3 3 2 3 1 2
列号1 1 2 2 3 4 4 5 5
大于0.5的元素的单下标
1 3 5 6 9 11 12 13 14
25.在使用123作为rand随机数发生器的初始化状态的情况下,写出产生长度为1000的“等概率双位(即取-1,+1)取值的随机码”程序指令,并给出-1码的数目。
a
ans =
z
4.求符号矩阵 的行列式值和逆,所得结果应采用“子表达式置换”简洁化。
〖答案〗
A =
[ a11, a12, a13]
[ a21, a22, a23]
[ a31, a32, a33]
DA =
a11*a22*a33-a11*a23*a32-a21*a12*a33+a21*a13*a32+a31*a12*a23-a31*a13*a22
for k=10:-1:1
A=reshape(1:10*k,k,10);
Sa(k,:)=sum(A);
end
Sa
习题
31.根据题给的模拟实际测量数据的一组 和 试用数值差分diff或数值梯度gradient指令计算 ,然后把 和 曲线绘制在同一张图上,观察数值求导的后果。(模拟数据从prob_data401.mat获得)
f =
exp(3*t)*sin(4*t)
g =
exp(3*t)*cos(4*t)
习题
23.要求在闭区间 上产生具有10个等距采样点的一维数组。试用两种不同的指令实现。
24.由指令rand('state',0),A=rand(3,5)生成二维数组A,试求该数组中所有大于0.5的元素的位置,分别求出它们的“全下标”和“单下标”。
(完整版)第4章MATLAB程序流程控制_习题答案

第4章 MATLAB程序流程控制习题4一、选择题1.下列关于脚本文件和函数文件的描述中不正确的是()。
AA.函数文件可以在命令行窗口直接运行B.去掉函数文件第一行的定义行可转变成脚本文件C.脚本文件可以调用函数文件D.函数文件中的第一行必须以function开始2.下列程序的输出结果是()。
Dy=10;if y==10y=20;elseif y>0y=30enddisp(y)A.1 B.30 C.10 D.203.有以下语句:a=eye(5);for n=a(2:end,:)for循环的循环次数是()。
CA.3 B.4 C.5 D.104.设有程序段k=10;while kk=k-1end则下面描述中正确的是()。
AA.while循环执行10次B.循环是无限循环C.循环体语句一次也不执行D.循环体语句执行一次5.有以下程序段:x=reshape(1:12,3,4);m=0;n=0;for k=1:4if x(:,k)<=6m=m+1;elsen=n+1;endend则m和n的值分别是()。
CA.6 6 B.2 1 C.2 2 D.1 26.调用函数时,如果函数文件名与函数名不一致,则使用()。
A A.函数文件名B.函数名C.函数文件名或函数名均可D.@函数名7.如果有函数声明行为“function [x,y,z]=f1(a,b,c)”,则下述函数调用格式中错误的是()。
BA.x=f1(a,b,c) B.[x,y,z,w]=f1(a,b,c)C.[x,b,z]=f1(a,y,c) D.[a,b]=f1(x,y,z)8.执行语句“fn=@(x) 10*x;”,则fn是()。
AA.匿名函数B.函数句柄C.字符串D.普通函数9.执行下列语句后,变量A的值是()。
D>> f=@(x,y) log(exp(x+y));>> A=f(22,3);A.22,3B.22 C.3 D.2510.程序调试时用于设置断点的函数是()。
matlab课后习题参考答案

Matlab课后习题部分参考答案习题二2.student=struct('name',{'zhang','wang','li'},'age',{18,21,[] },'email',{['zh ang@','zhang@'],'',''})5、a=[1 0 0;1 1 0;0 0 1];b=[2 3 4;5 6 7;8 9 10];c=[a b]d=[a;b]c =1 0 023 41 1 0 5 6 70 0 1 8 9 10d =1 0 01 1 00 0 12 3 45 6 78 9 1010、reshape(c,2,9)1 0 1 0 1 5 3 9 71 0 0 02 8 6 4 10 reshape(d,2,9)ans =1 0 5 0 0 6 0 1 71 2 8 1 3 9 0 4 10 (注意:重新排列矩阵,是将原来的矩阵按列排序)11、a.’12、a+b a.*ba\b (即inv(a)*b,考试时,要求能自己手算出a的逆)ans =2 3 43 3 38 9 1013、c=4*ones(3);a>=cb>=c14.strcat('The picture is ','very good')a=['The picture is ','very good']18.double('very good')1.norm(A),det(A),rank(A)2.b=[1 1 1 1 1];c=b';a=[17,24,1,8,50;23,5,7,14,49;4,6,13,20,43;10,12,19,21,62;11,18,25,2,56]; x=a\c习题四1、a=14*rand(1,10)-5;for i=1:9max=i;for j=i+1:10if a(j)>a(max)max=j;endendtemp=a(i);a(i)=a(max);a(max)=temp;enda将上述脚本保存为script41.m2、function y=function42(n)3*randn(1,n)+3;for i=1:n-1max=i;for j=i+1:nif a(j)>a(max)max=j;endendtemp=a(i);a(i)=a(max);a(max)=temp;endy=a;将上述函数保存为function42.m 3、r=input(‘please input 1/2: ’);if r= =1script41;elsen=input(‘please input the length: ’);y=funtion42(n);end4.function f=function1(x,y)if y==1f=sin(x);elseif y==2f=cos(x);elsef=sin(x).*cos(x);end在命令窗口调用函数f=function1(1,3) 5.function result=function3(x,n)result=0;for i=1:nresult=result+sin(x.*i)+(-1).^i.*cos(i.*x); endfunction result=function4(n,t)result=0;A=[1 2 3;0 1 2;0 0 1];for i=1:nresult=result+A*i.*exp(A*i.*t);end习题五3.x1=-2:0.01:2;x2=-2:0.01:2;y1=x1.*sin(x2);y2=x2.*cos(x1);plot3(x1,x2,y 1,'-d',x1,x2,y2,'-d')14、x=8*rand(1,100)-2;y=reshape(x,10,10);save mydata.mat yclearclcload mydatak=y>ones(10);totel=0;for i=1:100if k(i)==1totel=totel+1;endend15、x=rand(5); %生成5*5均匀分布的随机矩阵(该处只作举例,未按题目要求)fid=fopen(‘text.txt’,’w’);count=fwrite(fid,x,’int32’); closestatus=fclose(fid);清除内存,关闭所有窗口fid=fopen(‘text.txt’,’r’);x=fread(fid,[5,5],’int32’); closestatus=fclose(fid); inv(x)16.随便生成一个矩阵,x1=-1:0.2:0.8;x2=-1:0.2:0.8;y1=x1.*sin(x2);y2=x2.*cos(x1);a=reshape([y1;y2],10,10);fid=fopen('table.txt','w'); fprintf (fid,‘%f’,a); fclose(fid) ;清除内存,关闭所有窗口a=fscanf('table.txt','%f') ; exp(a) ;fclose(fid) ;习题六1.c=ploy2str(A);B=[2,0,0,1,3,5];2.x=1:10;B=ployval(A,x);。
MATLAB课后习题集附标准答案

第2章MATLAB概论1、与其他计算机语言相比较,MA TLAB 语言突出的特点是什么?答:起点高、人机界面适合科技人员、强大而简易的作图功能、智能化程度高、功能丰富,可扩展性强.2、MA TLAB 系统由那些部分组成?答:开发环境、MATLAB数学函数库、MATLAB语言、图形功能、应用程序接口3、安装MATLAB 时,在选择组件窗口中哪些部分必须勾选,没有勾选的部分以后如何补安装?答:在安装MATLAB时,安装内容由选择组件窗口中各复选框是否被勾选来决定,可以根据自己的需要选择安装内容,但基本平台(即MATLAB选项)必须安装. 第一次安装没有选择的内容在补安装时只需按照安装的过程进行,只是在选择组件时只勾选要补装的组件或工具箱即可. 矚慫润厲钐瘗睞枥庑赖。
4、MATLAB 操作桌面有几个窗口?如何使某个窗口脱离桌面成为独立窗口?又如何将脱离出去的窗口重新放置到桌面上?聞創沟燴鐺險爱氇谴净。
答:在MATLAB 操作桌面上有五个窗口,在每个窗口的右下角有两个小按钮,一个是关闭窗口的Close 按钮,一个是可以使窗口称为独立的Undock 按钮,点击Undock 按钮就可以使该窗口脱离桌面称为独立窗口,在独立窗口的view 菜单中选择Dock,菜单项就可以将独立的窗口重新防止的桌面上.残骛楼諍锩瀨濟溆塹籟。
5、如何启动M 文件编辑/调试器?答:在操作桌面上选择“建立新文件”或“打开文件”操作时,M 文件编辑/调试器将被启动.在命令窗口中键入edit 命令时也可以启动M 文件编辑/调试器.酽锕极額閉镇桧猪訣锥。
6、存储在工作空间中的数组能编辑吗?如何操作?答:存储在工作空间的数组可以通过数组编辑器进行编辑:在工作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输入修改内容即可.彈贸摄尔霁毙攬砖卤庑。
7、命令历史窗口除了可以观察前面键入的命令外,还有什么用途?答:命令历史窗口除了用于查询以前键入的命令外,还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中. 謀荞抟箧飆鐸怼类蒋薔。
MATLAB习题参考答案(胡良剑

第一章 MATLAB 入门4、求近似解解:>> x=-2:0.05:2;y=x.^4-2.^x两个近似解:y1=f(-0.85)= -0.0328; y2=f(1.250)= 0.0630第二章 MATLAB 编程与作图1、 设x 是数组,求均值和方差解:函数文件如下:function [xx,s]=func1(x)n=length(x);xx=sum(x)/n;s=sqrt((sum(x.^2)-n*xx^2)/(n-1));命令窗口:>> x=[1 2 3 4 5];[xx,s]=func1(x)2、求满足的最小m 值 100)1ln(0>+∑=m n n s=0;n=0;while(s<=100)s=s+log(1+n);n=n+1;endn,s3、用循环语句形成Fibonacci 数列,....4,3,,12121=+===−−k F F F F F k k k 。
并验证极限2511+→−k k F F (提示:计算至两边误差小于精度1e-8为止) 解: 求Fibonacci 数列的函数文件:function f=fun(n)if n<=2f=1;elsef=fun(n-1)+fun(n-2);end验证极限的函数文件:function [k,a]=funTest(e)a=abs(1-(1+sqrt(5))/2);k=2;while(a>e)k=k+1;a=abs(fun(k)/fun(k-1)-(1+sqrt(5))/2);end命令行:>> [k,a]=funTest(10^-8)k =21a =9.7719e-009或者M 文件如下:clear; F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1; F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1);enda,x,k4、分别用for 和while 循环结构编写程序,求出∑==610123i i K ,并考虑一种避免循环语句的程序设计,比较各种算法的运行时间。
MATLAB答案整理(1)

a=b;b=temp;2 a=input('a=');b=input('b=');if a>=bfprintf('较大的数是a,a=%g\n',a)elsefprintf('较大的数是b,b=%g\n',b)end3 function [x1,x2 ] = xunlian24_3( a,b,c)p=b*b-4*a*c;x1=(-b+sqrt(p))/2*a;x2=(-b-sqrt(p))/2*a;disp(x1)disp(x2)end4 %函数文件function [s c]=xunlian24_4(r)r=input('请输入圆的半径r=');s=pi*r*r;c=2*pi*r;fprintf('面积是s=%.4f\n',s)fprintf('周长是c=%.4f\n',c)end%脚本文件r=input('r=');s=pi*r*r;c=2*pi*r;fprintf('s=%.4f\n',s)fprintf('c=%.4f\n',c)5function xunlian24_5(t)s=0;for ii=1:ts=s+digui(ii);%把ii放到下面那个累乘的函数,累乘完后相加ends %相加后输出sfunction [ y ] =digui( n )if n==1elsey=digui(n-1)*n; %对比它小一的数再用一次函数,达到累乘的效果endendend6 x=input('输入x:');if x<1p=x^2;elseif x>=1&x<2p=x^2-1;elsep=x^2-2*x-1;endfprintf('p=%g\n',p);switch pcase 1y=x^2;case 2y=x^2-1;otherwisey=x^2-2*x-1;endfprintf('y=%g\n',y);7 function [ y ] = xunlian24_7( x )%UNTITLED12 Summary of this function goes here% Detailed explanation goes herex=input('x=')if x<2y=2*e*(x^-1);elsey=log(x^2-1);end8 ch=input('输入一个字符:','s');if ch>='A'&ch<='Z'ch=ch+1;if ch=='Z'+1ch='A';endfprintf('为大写字母,后继字符为:%s\n',ch); %s 输出字符串elseif ch>='a'&ch<='z'ch=ch-1;if ch=='a'-1ch='z';endfprintf('为小写字母,前导字符为:%s\n',ch); %s 输出字符串elseif ch>='0'&ch<='9'fprintf('为数字,其ASCII码为:%d\n',ch);%d 十进制有符号整数elsefprintf('为其他字符,原样输出:%s\n',ch)end9 % x=input('总价是');% if x<=500&x>0% x=x% elseif x>500&x<=1000%% elseif x>1000&x<=3000% x=0.9*x% elseif x>3000&x<=5000% x=0.85*x% elseif x>5000% x=0.8*x% else x<=0% x=('输入错误')% end% fprintf('实际总价=%.2f/',x);a=input('原来总价是');x=floor(a/100);switch xcase {0,1,2,3,4}x=x;case {5,6,7,8,9}x=0.95*x;endfprintf('实际总价=%f\n',x)10 x=input('打折前价格');if x<500&x>=200x=0.97*xelseif x>=500&x<1000x=0.95*xelseif x>=1000&x<2500x=0.92*xelseif x>=2500&x<5000x=0.9*xelseif x>=5000x=0.86*xelse x<200x=xendfprintf('打折后价格%.2f/',x);11 x=input( '成绩=');if x>=90,y='优秀';elseif x>=80,y='良好';elseif x>=70,y='中等';elseif x>=60,y='及格';else y='不及格';endfprintf('成绩=%g\n等级为%s\n',x,y); 13 function [ ] = xunlian24_13(x)num=length(x);solu=[];count=1;disp(' 数据组个数');for ii=1:num-1if x(ii)==x(ii+1);count=count+1;continue;%继续看下一个数据endsolu=[solu;x(ii) count];count=1;end14 s=0;for i=1:100s=s+i;endfprintf(' for型循环,结果是%g\n',s); i=1;s=0;while i<=100s=s+i;i=i+1;endfprintf('while型循环,结果是%g',s);15 A=fix(rand(20,10)*100)disp(' 每行的和为')R1=0;for a=1:20for b=1:10R1=R1+A(a,b);if b==10disp(R1)R1=0;endendenddisp(' 每列的和为')R2=0;for m=1:10for n=1:20R2=R2+A(n,m);if n==20disp(R2)R2=0;endendend16 yy1=[];A=rand(20,10);for m=1:20s1=0;for n=1:10s2=s1+A(m,n);ends3=s2/10;yy1=[yy1,s3];y1=[y1,s2];endq=[y1' yy1'];disp('每行的和为每行的平均值为') disp(q)y2=[];yy2=[];B=rand(20,10);for n=1:10s4=0;for m=1:20s5=s4+B(m,n);ends6=s5/10;yy2=[yy2,s6];y2=[y2,s5];endp=[y2' yy2'];disp('每列的和为每列的平均值为')disp(p)17 B=[];A=fix((rand(20,10))*100)for n=1:10;s=0;for m=1:20s=s+A(m,n);endif s==0B(:,n)=0;else B(:,n)=A(:,n)/s;endendB18 s=0;for a=1:10;s=s+1^a+2^a+3^a;endfprintf('结果是%g\n',s)19 disp('水仙花数有:')for m=100:999m1=fix(m/100); %求m的百位数字m2=mod(fix(m/10),10); %求m的十位数字m3=mod(m,10); %求m的个位数字if m==m1^3+m2^3+m3^3fprintf('%g \n',m)endend20 for i=100:200if mod(i,21)==0breakendenddisp('第一个能被21整除的数为')disp(i)21 m=ceil(rand(1)*100);for i=1:7x=input('玩家猜的数是:');if x>mdisp('High');elseif x<mdisp('Low');else x==m;disp('You won');breakendif i==7disp('bye bye')endend22 a=input('输入a=');b=input('输入b=');yy1=[];yy2=[];for n=1:10y1=(a+b)^n;y2=(a-b)^n;yy1=[yy1,y1];yy2=[yy2,y2];enddisp('(a+b)^n (a-b)^n')yy3=[yy1' yy2']23 n=input('请输入任意正整数');while 1while 1if mod(n,2)~=0break%是奇数跳出循环,跳出第一个whileelse n=n/2endend %循环结束,由于while 1一直成立,可以一直执行n到变成奇数if n==1break %结果是1跳出循环,输出结果,跳出最外层的while elsen=n*3+1 %是奇数但不是1,做题目要求的操作endend%最外层while的end 但只有满足n=1是才能跳出循环disp(n)24 disp('200内的素数有:')y=[];for i=2:200for jj=2:iif mod(i,jj)==0if jj>=iy=[y,i];elsebreakendendendenddisp(y')25 y1=[];for m=2:100;for n=2:m;if mod(m,n)==0;if n>=my1=[y1,m];elsebreak;endendendendy2=[];i=length(y1);disp('100以下相差为2的素数对有');for p=1:i-1if y1(p)+2==y1(p+1)%y2=[y2 y1(p+1)];disp([y1(p) y1(p+1)]);endend26 disp('99以内的完全数有:')for i=1:99k=i^2;if k<100if mod(k,10)==ifprintf('%5d%5d\n',i,k);endelseif mod(k,100)==ifprintf('%5d%5d\n',i,k);endendend27 %冒泡排序function N=xunlian24_27(P)N=P;for i=1:numel(P)for j=2:numel(P)if N(j-1)>N(j)Q=N(j-1);N(j-1)=N(j);N(j)=Q;endendendend28 %选择排序function S = xunlian24_28( A ) %定义函数,输入为A,输出为SS = zeros(size(A));%初始化S的大小for i = 1:numel(A)%给S的每一个数赋值,第一个为A中最小的,第二个为第二小的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
频率特性类题目1 一个系统的开环传递函数为 ,试绘制其当K=5、30时系统的开环频率特性Nyquist 图,并判断系统的稳定性。
w=linspace(0.5,5,1000)*pi; sys1=zpk([],[0 -10 -2],100) sys2=zpk([],[0 -10 -2],600) figure(1)nyquist(sys1,w)title('system nyquist charts with k=5') figure(2)nyquist(sys2,w)title('system nyquist charts with k=30')由图可知K=5时,开环Nyquist 曲线没有包围(-1,j0)点,所以系统稳定。
K=30时,开环Nyquist 曲线包围(-1,j0)点,所以系统不稳定。
2系统开环传递函数为 ,建立其零极点增益模型,然后分别绘制当K=5、K=30时系统的开环频率特性Bode 图,并判断系统的稳定性。
sys1=zpk([],[0 -10 -2],100) sys2=zpk([],[0 -10 -2],600) figure(1)[Gm1,Pm1,Wcg1,Wcp1]=margin(sys1) bode(sys1)title('system bode charts with k=5'),grid figure(2)[Gm2,Pm2,Wcg2,Wcp2]=margin(sys2) bode(sys2)title('system bode charts with k=30'),grid 因为K=5时,Wcg>Wcp,所以系统稳定。
K=10时,Wcg<Wcp,系统不稳定。
3 系统开环传递函数为 ,计算K=5和K=30时系统的幅值裕度与相位裕度。
sys1=zpk([],[0 -10 -2],100) sys2=zpk([],[0 -10 -2],600)[Gm1,Pm1,Wcg1,Wcp1]=margin(sys1) [Gm2,Pm2,Wcg2,Wcp2]=margin(sys2)4 已知某系统的闭环传递函数()s Φ如下,试用roots ()命令来判断系统的稳定性。
)5.01)(1.01()(s s s k s G ++=)5.01)(1.01()(s s s ks G ++=)5.01)(1.01()(s s s ks G ++=25432325()24576s s s s s s s s ++Φ=+++++num=[0 0 0 3 2 5]; den=[1 2 4 5 7 6]; D=num+den; roots(D)5 某单位负反馈系统的开环控制系统的传递函数为2k (0.80.64)()(0.05)(5)(40)K s s G s s s s s ++=+++ (1)绘制系统的根轨迹;num=[1 0.8 0.64]; x=[0 -0.05 -5 -40]; den=poly(x); rlocus(num,den)(2)当10K =时,绘制系统的Bode 图,判断系统的稳定性,并且求出幅值裕度和相角裕度。
num=[1 0.8 0.64]; x=[0 -0.05 -5 -40]; den=poly(x); sys=tf(num,den) bode(sys),grid[Gm,Pm,Wcg,Wcp]=margin(sys)6 已知系统的状态空间模型如下:⎢⎣⎡=11x⎥⎦⎤-31x + ⎥⎦⎤⎢⎣⎡01u [1=y ]1x(1)绘制系统的Bode 图和nyquist 图; (2)求系统的幅值裕度和相位裕度;A=[1,-1;1,3];B=[1,0]'; C=[1,1];D=0;w=linspace(0.5,5,1000)*pi; sys=ss(A,B,C,D)figure(1),bode(sys),grid figure(2),nyquist(sys,w)[Gm,Pm,Wcg,Wcp]=margin(sys)7 已知单位负反馈系统的开环传递函数为)1(12++s s s ,试绘制系统的单位阶跃响应、开环Bode 图和Nyquist 曲线,并求系统的幅值裕度和相位裕度。
sys=zpk(-1,[0 0 -1],1)sys1=feedback(sys,1,-1)figure(3)step(sys1)figure(1)bode(sys),gridfigure(2)nyquist(sys),grid[Gm,Pm,Wcg,Wcp]=margin(sys)编写程序题1 编写两个m文件,分别使用for和while循环语句计算20031kk=∑。
y=0;for k=1:200y=y+k^3;endyy=0;k=1;while k<=200y=y+k^3;k=k+1;endy2 一个三位整数各位数字的立方和等于该数本身则称该数为水仙花数,编写M 文件,输出全部水仙花数。
for m=100:999m1=fix(m/100);m2=fix((m-100*m1)/10);m3=fix(m-100*m1-10*m2);if m==m1^3+m2^3+m3^3disp(m)endend3 编写M文件,实现以下功能:从键盘输入若干个数,当输入0时结束输入,求这些数的平均值和它们之和。
i=1;x=[];sum=0;a=input('请输入任意一个数,输0回车结束');while (a~=0)x(i)=a;i=i+1;sum=sum+a;mea=(sum/(i-1));a=input('请输入任意一个数,输0回车结束');endsummea4 编写M脚本文件,使得运行该文件后能求出[100,200]之间第一个能被21整除的整数。
for i=100:200if mod(i,21)==0breakendendi5 先编写一个函数文件,文件名为tran,使得该函数文件实现直角坐标(x,y)与极坐标(ρ,θ)之间的转换。
然后编写脚本文件,文件名为main1,在脚本文件中实现如下功能:要求用户从键盘输入直角坐标X和Y,调用函数文件实现直角坐标到极坐标的转换,输出极坐标的值。
tran.m :function [rho,theta]=tran(x,y)rho=sqrt(x*x+y*y);theta=atan(y/x);main1.m :x=input('Please input x=:')y=input('Please input y=:')[rho,theta]=tran(x,y);rhotheta6 猜数游戏。
首先由计算机产生[1,100]之间的随机整数,然后由用户猜测所产生的随机数。
根据用户猜测的情况给出不同提示,如猜测的数大于产生的数,则显示“High”,小于则显示“Low”,等于则显示“You won”,同时退出游戏。
用户最多可以猜7次。
x=fix(100*rand(1));i=1while i<=7y=input('')if x==ydisp('You won') break; elseif x>ydisp('Low') else disp('High') end i=i+1; end7 编写M 脚本文件,分别使用for 和 while 循环语句计算∑==101i i i sum 的值,并且显示出sum 的结果。
sum=0;for i=1:10 sum=sum+i^i; end sum sum=0; while i<=10 sum=sum+i^i; i=i+1; end sum8 用筛选法求某自然数范围内的全部素数。
素数是大于1,且除了1和它本身以外,不能被其他任何整数所整除的整数。
用筛选法求素数的基本思想是:要找出2~m 之间的全部素数,首先在2~m 中划去2的倍数(不包括2),然后划去3的倍数(不包括3),由于4已被划去,再找5的倍数 (不包括5),…,直到再划去不超过的数的倍数,剩下的数都是素数。
function y=sushu(x) y=2:x; n=2:x; for j=2:x m=j*n;y=setdiff(y,m); end9 已知 ∑=-=nk k y 1121,当n=100时,求y 的值。
y=0;n=100;for k=1:ny=y+(1/(2*k-1)); k=k+1;end y10 利用for 循环计算1!+2!+3!+….. +20!的值。
sum=0; for i=1:20 y=1; for n=1:i y=y*n; endsum=sum+y; end sum11 用while 循环来实现求1+2+……+100的值。
y=0;n=1; while n<=100 y=y+n; n=n+1; end y12 编一函数计算以下分段函数值。
232(0)21(01)321(1)xx x x x x x <⎧⎪+<⎨⎪++⎩≤≥ function y=f(x);if x<0 y=x;elseif x>=0&x<1 y=2*x^2+1;else y=3*x^3+2*x^2+1; end13 我国新税法规定:个体工商户的生产、经营所得和对企事业单位的承包经营、承租经营所得应缴纳的个人所得税为全年收入中应缴纳所得税部分 税率/% (1) 不超过5000元的 5 (2) 超过5000元至10000元的部分 10 (3) 超过10000元至30000元的部分 20 (4) 超过30000元至50000元的部分 30 (5) 超过50000元的部分 35 试编程加以计算。
x=input('x=') if x<=5000 y=0.05*x;elseif x>5000&x<=10000 y=0.1*x;elseif x>10000&x<=30000y=0.2*x;elseif x>30000&x<=50000y=0.3*x;else y=0.35*x;endy14 矩阵乘法运算要求两矩阵的维数相容,否则会出错。
设两个矩阵为A=[1,2; 5,6]; B=[7,9;20,11];先求两矩阵的乘积,若出错,则自动转去求两矩阵的点乘。
A=[1,2;5,6];B=[7,9;20,11];tryC=A*B;catchC=A.*B;endC15 编制M脚本文件,要求从键盘逐个输入数值(input),然后判断输入的数是大于0还是小于0,并输出提示(使用disp命令)是正数(positive one)还是负数(negative one),同时记录输入的正数、负数的个数。
