2014年四川省高考理科数学压轴卷(含解析)

合集下载

2014四川高考真题数学理(含解析)

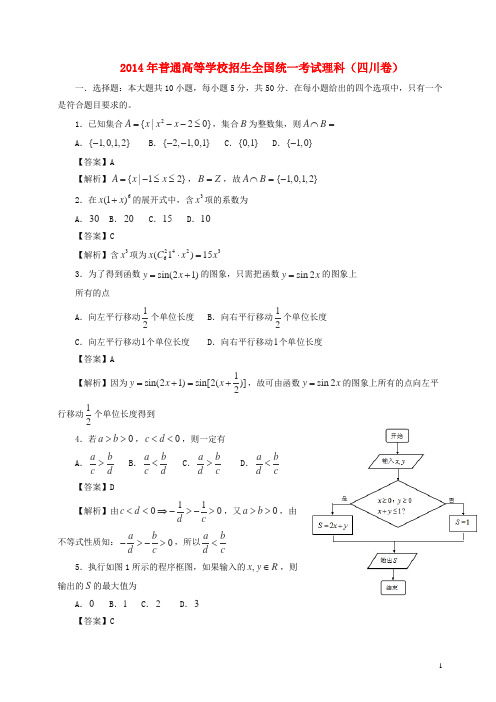
2014 年普通高等学校招生全国统一考试（四川卷）数学（理工类）一、选择题：本大题共10 小题，每小题5 分，共50 分．在每小题给出的四个选项中，只有一个是符合题目要求的．1．已知集合A ={x | x2 -x - 2 ，集合B 为整数集，则A （）．A．{-1, 0,1, 2} B．{-2,-1, 0,1} C．{0, 1} D．{-1, 0}2．在x(1+x)6 的展开式中，含x3 项的系数为（）．A．30 B．20 C．15 D．103．为了得到函数y = sin(2x +1) 的图象，只需把函数y = sin 2x 的图象上所有的点（）．A．向左平行移动12个单位长度B．向右平行移动12个单位长度C．向左平行移动1个单位长度D．向右平行移动1个单位长度4．若a >b > 0，c <d < 0，则一定有（）．A．a b>B．a <b C．a b>D．c d c d d ca b<d c5．执行如图 1 所示的程序框图，如果输入的x, y ∈R ，则输出的S的最大值为（）．A．0 B．1 C．2 D．36．六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有（）．A．192种B．216 种C．240 种D．288 种7．平面向量a = (1, 2)，b = (4, 2)，c =m a +b（m∈R ），且c 与a 的夹角等于c 与b 的夹角，则m =（）．A．-2 B．-1 C．1 D．28．如图，在正方体ABCD -A1B1C1D1 中，点O 为线段BD的中点．设点P 在线段CC 上，直线OP1与平面A1BD 所成的角为α，则sinα的取值范围是（）．A．[ 3 ,1]3 B．[ 6 ,1]3C．[ 6 , 2 2 ]3 3D．[2 2 ,1]39．已知f (x) = ln(1+x) - ln(1-x) ，x∈(-1, 1) ．现有下列命题：（）．①f (-x) =-f (x) ；②2xf ( ) = 2 f (x)x 1；③| f (x) |≥ 2 | x | ．其中的所2有正确命题的序号是A．①②③B．②③C．①③D．①②1/ 1510．已知F 是抛物线y =x 的焦点，点A ，B 在该抛物线上且位于x 轴的两侧，OA⋅OB = 2（其中2O 为坐标原点），则△ABO 与△AFO 面积之和的最小值是（）．17 28A．2 B．3 C．D．10二、填空题：本大题共5 小题，每小题5 分，共25 分．11．复数2 2i-=1+i．12．设f (x) 是定义在R 上的周期为2 的函数，当x∈[-1, 1) 时，f (x)⎧- 2 +-≤<4x 2, 1 x 0, =⎨x, 0 ≤x <1,⎩，则3f ( ) =．213．如图，从气球 A 上测得正前方的河流的两岸 B，C 的俯角分别为67 ，30 ，此时气球的高是46m ，则河流的宽度 BC 约等于m ．（用46m30°67°四舍五入法将结果精确到个位．参考数据：s i n 6 7≈0 . ，cos 67 ≈ 0.39，sin 37 ≈ 0.60 ，cos 37 ≈ 0.80 ， 3 ≈1.73）B C14．设m∈R，过定点A的动直线x +my = 0 和过定点B的动直线mx -y -m + 3 = 0交于点P(x, y) ，则| PA|⋅| PB |的最大值是．15．以A 表示值域为 R 的函数组成的集合，B 表示具有如下性质的函数ϕ(x) 组成的集合：对于函数ϕ，存在一个正数M ，使得函数ϕ(x) 的值域包含于区间[-M,M ] ．例如，当ϕ=，(x) 1(x) x3 ϕ=时，ϕ1(x)∈A， 2 (x) B2(x) sin xϕ∈．现有如下命题：①设函数f (x) 的定义域为D ，则“f (x)∈A”的充要条件是“∀b∈R，∃a∈D，f (a) =b ”；②函数f (x)∈B 的充要条件是f (x) 有最大值和最小值；③若函数f (x) ，g(x) 的定义域相同，且f (x)∈A，g(x)∈B ，则f (x) +g(x)∉B ；④若函数f (x) =a ln(x + 2) +x（x >-2，a∈R ）有最大值，则f (x)∈B ．x +12其中的真命题有．（写出所有真命题的序号）三、解答题：本大题共6 小题，共75 分．解答须写出文字说明，证明过程或演算步骤．16．已知函数πf (x) = sin(3x +) ．4（1）求f (x) 的单调递增区间；（2）若α是第二象限角，(α ) = 4 cos(α+π) cos 2αf3 5 4，求cosα-sinα的值．2/ 1517．一款击鼓小游戏的规则如下：每盘游戏都需要击鼓三次，每次击鼓要么出现一次音乐，要么不出现音乐；每盘游戏击鼓三次后，出现一次音乐获得 10 分，出现两次音乐获得 20 分，出现三次音乐获得 100 分，没有出现音乐则扣除 200 分（即获得 200分）．设每次击鼓出现音乐的概率为且各次击鼓出现音乐相互独立．（1）设每盘游戏获得的分数为X ，求X 的分布列；（2）玩三盘游戏，至少有一盘出现音乐的概率是多少？12，（3）玩过这款游戏的许多人都发现，若干盘游戏后，与最初的分数相比，分数没有增加反而减少了．请运用概率统计的相关知识分析分数减少的原因．3/ 1518．三棱锥A-BCD及其侧视图、俯视图如图所示．设M ，N 分别为线段AD ，AB 的中点，P 为线段BC 上的点，且MN ⊥NP ．（1）证明：P 为线段BC 的中点；（2）求二面角A-NP-M 的余弦值．4/ 1519．设等差数列{a }的公差为d ，点(a ,b )在函数f (x) = 2x 的图象上（n∈N* ）．n n n（1）若a1 =-2 ，点(a ,4b ) 在函数f (x) 的图象上，求数列{a }的前n 项和8 7 n S ；n(a ,b ) 处的切线在x 轴上的截距为2 1（2）若a1 =1，函数f (x) 的图象在点a-，求数列{ n } 2 2b ln 2n 的前n 项和T ．n5/ 15x y2 2+=（a >b > 0）的焦距为 4，其短轴的两个端点与长轴的一个端点构成正20．已知椭圆C： 2 2 1a b三角形．（1）求椭圆C 的标准方程；（2）设F 为椭圆C 的左焦点，T 为直线x =-3上任意一点，过F 作TF 的垂线交椭圆C 于点P，Q．（i）证明：OT 平分线段PQ（其中O 为坐标原点）；（ii）当|TF || PQ |最小时，求点T 的坐标．6/ 1521．已知函数f (x) = e x -ax2 -bx -1，其中a,b∈R ，e = 2.71828 为自然对数的底数．（1）设g(x) 是函数f (x) 的导函数，求函数g(x) 在区间[0,1]上的最小值；（2）若f (1) = 0，函数f (x) 在区间(0,1) 内有零点，求a 的取值范围．7/ 152014 年普通高等学校招生全国统一考试（四川卷理科）答案解析一、选择题：本大题共10 小题，每小题5 分，共50 分．在每小题给出的四个选项中，只有一个是符合题目要求的．1．A【解析】A ={x -1 ，所以A , 0,1, 2}2．C【解析】x(1+x)6 =x(1+6x+15x2 +20x3 +15x4 +6x5 +x6)，所以含x 项的系数为 1533．Ay =x +=x +，所以只需把y = sin 2x 的图像上所有的点向左平移1sin(2 1) sin 2( )1【解析】2 2个单位4．D∴->->，又a >b > 0， a b 01 1 ∴->->， a b【解析】0 ，∴-c >-d > 0 ，∴<d c d c d c 5．C⎧x⎪⎨y【解析】该程序执行以下运算，已知⎪+x y⎩，求S=2x y+的最大值，作出⎧x⎪⎨y⎪+x y⎩表示的区域如图所示，由图可知，当⎧x =1⎨=⎩y 0时，S = 2 x+y的取最大值，最大值为S = 26．B【解析】最左端排甲，有A5 =种排法，最左端排乙，有4A4 = 96种排法，共有120+96 = 216 种5 1204排法7．D【解析】由题意得c ⋅a c ⋅b a b +8 8m+ 20=⇒m = 5 2 528．B【解析】设正方体的棱长为 1，AC =，1 12 AC =，1 3A O =OC =+=， 11 OC =，1 31 12 2 2 8/ 153 3+- 2 12 2cos∠AOC ==所以 1 13 32⨯2 ，sin3 1+-3 32 2 2 2cos∠AOC ==-AOC =， 11 13 332⨯2，sin6AOC =，所以sinα的范围为13⎡⎤6⎢,1⎥3⎣⎦9．C【解析】①f (-x) = ln(1-x) - ln(1+x) =-f (x) ，成立②左边的x可以取任意值，而右边的x ∈ (-1,1) ，故不成立③作出图像易知成立10．B【解析】依题意，1F ( ,0) ，设4A(x , y )，1 1B x y ，则 2 1 2 1 2 2( , ) x =y ， 2x =y ，y2 y2 +y y =，得2 2 1 1 2 2y y =-或1 2 2 y y =，因为A ，B 位于x 轴两侧所以，1 2 1y y =-两面积之和为1 2 21 1 12 1 2 9 S =x y -x y +⨯⨯y =+y +⨯y =+y1 2 2 1 1 1 1 12 2 4 y 8 y 81 1二、填空题：本大题共5 小题，每小题5 分，共25 分．11．-2i【解析】2-2i 2(1-i)2= =-2i 1+i (1+i)(1-i)12． 1【解析】3 1 1f ( ) =f (-) =-4⨯+ 2 =12 2 413．60【解析】AC = 92，14．546AB =，cos 67AB =BC ，AB sin 37 60BC =≈sin 30 sin 37 sin 309/ 15【解析】易得A(0, 0) ，B(1, 3) ，设P(x,y) ，则消去m得：x2 +y2 -x-3y =0，所以点P 在以AB为直径的圆上，PA ⊥PB，所以PA ⨯PB AB22515．①③④【解析】①若对任意的b∈R ，都有∃a∈D，使得f (a) =b ，则f (x) 的值域必为R ；反之f (x) 的值域为，则对任意的R ，b∈R，都有∃a∈D，使得f (a) =b ；②比如函数f (x) =x(-1 <x < 1) 属于B ，但是它既无最大值也无最小值，故错误；③正确；④正确三、解答题：本大题共6 小题，共75 分．解答须写出文字说明，证明过程或演算步骤．π16．已知函数f (x) = sin(3x +) ．4（1）求f (x) 的单调递增区间；（2）若α是第二象限角，(α ) = 4 cos(α+π ) cos 2αf3 5 4，求cosα-sinα的值．πππ解：（1）2kπ-k ∈Z2 4 23ππ2kπ-,4 42 2kπ-πkππ,3 4 3 12∴求f (x) 的单调递增区间为⎡2kπ-π2kπ+π⎤∈，，k Z ．⎢⎥⎣ 3 4 3 12⎦（2）fα=α+π=α+πα,4( ) sin( ) cos( )cos 2 3 4 5 42 4 2( s i n c o s ) ( c o s s i n ) ( c o s α+α=⋅α-α2 α+α, 2 5 22 5(cos sin )α-α=, α是第二象限角，4∴sinα> cosα5∴cosα-sinα=-．217．一款击鼓小游戏的规则如下：每盘游戏都需要击鼓三次，每次击鼓要么出现一次音乐，要么不出现音乐；每盘游戏击鼓三次后，出现一次音乐获得 10 分，出现两次音乐获得 20 分，出现三次音乐获得 100 分，没有出现音乐则扣除 200 分（即获得-200分）．设每次击鼓出现音乐的概率为各次击鼓出现音乐相互独立．（1）设每盘游戏获得的分数为X ，求X 的分布列；（2）玩三盘游戏，至少有一盘出现音乐的概率是多少？12，且10/ 15（3）玩过这款游戏的许多人都发现，若干盘游戏后，与最初的分数相比，分数没有增加反而减少了．请运用概率统计的相关知识分析分数减少的原因．解：X 可取 10,20,100,-200．1 2⎛ 1 ⎫⎛ 1 ⎫ 3P(X 10) C 1== ⎪ -⎪=13⎝ 2 ⎭⎝ 2 ⎭82 1⎛ 1 ⎫⎛ 1 ⎫ 3P(X = 20) = C ⎪ 1-⎪=23⎝ 2 ⎭⎝ 2 ⎭83 0⎛ 1 ⎫⎛ 1 ⎫ 1P(X =100) = C ⎪ 1-⎪=33⎝ 2 ⎭⎝ 2 ⎭80 3⎛ 1 ⎫⎛ 1 ⎫ 1P(X 200) C 1=-=0 ⎪ -⎪=3⎝ 2 ⎭⎝ 2 ⎭8X 10 20 100 -200P 3 3 1 18 8 8 8 （2）设至少有一盘出现音乐为事件A ．一盘中不出现音乐的概率为1 P =P(X =-200) =．83P =P A =-⎛⎪⎫=( ) 11 511⎝ 8 ⎭512．（3）每一盘游戏的期望为：10E(X ) =10⋅P(X =10) + 20⋅P(X = 20) +100⋅P(X =100) + (-200)⋅P(X =-200) =-8 这说明每盘游戏得分是负分，由概率统计的知识可知：若干盘游戏后，与最初的分数相比，分数没有增加反而减少了．18．三棱锥A-BCD及其侧视图、俯视图如图所示．设M ，N 分别为线段AD ，AB 的中点，P 为线段BC 上的点，且MN ⊥NP ．（1）证明：P 为线段BC 的中点；（2）求二面角A-NP-M 的余弦值．解：（1）由三棱锥A-BCD及其侧视图、俯视图可知，在三棱锥中，平面ABD ⊥平面CBD， AB =AD =BD =CD =CB = 2，设O 为BD的中点，连接OA，OC ，于是OA ⊥BD ，OC ⊥BD ，所以BD ⊥平面OAC ⇒BD ⊥AC，因为M ，N 分别为线段AD ，AB 的中点，所以MN//BD ，11/ 15又 MN ⊥ NP ，故 BD ⊥ NP ，假设 P 不是线段 BC 的中点，则直线 NP 与直线 AC 是平面 ABC 内相交直线，从而 BD ⊥平面 ABC ，这与 ∠DBC = 60 矛盾，所以 P 是线段 BC 的中点（2）以O 为坐标原点，OB 、OC 、OA 分别为 x 、 y 、 z 轴建立空间直角坐标系，则 A (0, 0, 3) ， B，C (0,1, 0) ， M (- 1 ,0, 3)， (1 ,0, 3)(1, 0, 0)N， 22221 3 P ( , ,0)2 2于是 AN = ( ,0,- 3) ， (0, 3 , 3)PN = - ， MN = (1, 0, 0) 2 2 2 2设平面 ANP 和平面 NPM 的法向量分别为 m = (x , y , z ) 和 111n = (x , y , z )222由⎧ 1 3 x - z = 0⎪⎧⎪ ⇒ ⎪ ⎨⎨1 12 2 ⎪⎪PN ⋅m = 0 33 ⎩- + =yz ⎪ ⎩ 2211，设 y 1 =1，则 m = ( 3 ,1,1)由 ⎧x = 0 ⎧⎪ ⇒ ⎪ ⎨ ⎨332⎩⎩ PN n ⋅ = 0 - y +z =⎪ ⎪212 2，设 y 2 =1，则 n = (0,1,1) 0 cos2 10 m ⋅n == ⋅ 5m n5 2，所以二面角 A - NP -M 的余弦值 10 5 19．设等差数列{ }a 的公差为 d ，点(a ,b )在函数 f (x ) = 2x 的图象上（ n ∈ N * ）．nnn（1）若 a 1 = -2 ，点(a ,4b ) 在函数 f (x ) 的图象上，求数列{a }的前 n 项和87nS ；n(a ,b ) 处的切线在 x 轴上的截距为 21a（2）若a1 =1，函数f (x) 的图象在点-，求数列{ n } 2 2b ln 2n 的前n 项和T ．nb =，又等差数列{} 【解析】（1）点(a ,b )在函数f (x) = 2x 的图像上，所以 2a 的公差为d ，所ann n n n以b 1 2 2an+1n+==d b 2ann因为点(a8,4b7 ) 在函数f (x) 的图像上，所以b4b = 2a =b ，所以8 d2d == 4 ⇒= 2 ，又87 8 b7a =-，1 2所以n(n -1)S =na + d =-2n +n -n =n -3n2 2n 12（ 2 ）由 f (x) = 2x ，得到 f '(x ) = x2 l n，函数f (x) 的图像在点(a ,b ) 处的切线方程为2 2by -b2 = (2 ln 2)(x -a2 ) ，所以切线在x 轴上的截距为a a -，得22a=，从而222 2a ln 22 a =n ，b = 2n ，n n得到anbn1=n⋅( )2n1 1 1T =⋅+⋅ 2 +①，1 2 ( ) )nn2 2 212/ 151 1 1 1 1T =⋅+⋅+⋅+n⋅+②，1 ( )2 ( ) ) ( ) ( )2 3 n n 1 n2 2 2 2 2①-②，得1 1 1 1 1 1T =++-n⋅+=-n ++( ) ( ) 1 ( 2)( )2 n 1 n 1 n2 2 2 2 2 21T =-n ++2 ( 2)( )n 1故n2x y2 2+=（a >b > 0）的焦距为 4，其短轴的两个端点与长轴的一个端点构20．已知椭圆 C： 2 2 1a b成正三角形．（1）求椭圆 C 的标准方程；（2）设 F 为椭圆 C 的左焦点，T 为直线x =-3上任意一点，过 F 作 TF 的垂线交椭圆 C 于点 P，Q．（i）证明：OT 平分线段 PQ（其中 O 为坐标原点）；（ii）当|TF || PQ |最小时，求点 T 的坐标．解：（1）2c = 4,c = 2a =b, a2 = 3b2 = 4 +b23∴b2 = 2,a2 = 6∴椭圆C 的标准方程：x +y =．2 216 2（2）（i）m - 0 1F(-2, 0), T(-3,m),k ==-m,∴k =FT PQ-3+ 2 m．P Q: y1 (x )m∴=+m⎧=+1() y x m ⎪⎪m ,⎛+⎫++-=3 12 121 x x 6 02⎪⎝m ⎭m m2 2 2, ()m2 + 3 x2 +12x +12 - 6m2 = 0⎨ xy22⎪ += 1⎪⎩ 6 2 ∆ > 0 x + x =P Q12 - 6m2x ⋅ x =PQm2-12 m 2+11144m ()() ()y + y =x + 2 + x + 2 = x + x += PQPQPQ+mmmm m 32PQ 中点⎛ -m ⎫m6 2 ，O T : y = -x + + ⎪ ⎝ m 3 m 3⎭322-6 ⋅⎛- ⎫⎪= 2 m mm 3 3 m 32 + ⎝ ⎭ 2 +∴OT 平分 PQ （ii）TF =-2 + 3 + 0 - m = m +1,222PQ()1 2 6 m m +122 6 m +1 2= 1+=mm3m3 22+2+13 / 15tTF m + 32==PQ m +2 6 12t 2 =()()()2 2m2 m2 m2 m2+ 3 +1 +4 +1 +4 +1 1 1 1 1 1 = = + + + = ()()()24 m +1 24 m +1 24 6 6 m +1 144 6 32 2 2m2 +1 1=当且仅当()24 6 2 1m +时取到等于号，∴(+)，m2 +1=2 ，m2 =1，∴T(-3,±1)．2m2 1 =421．已知函数f (x) =e x -ax2 -bx -1，其中a,b∈R ，e = 2.71828 为自然对数的底数．（1）设g(x) 是函数f (x) 的导函数，求函数g(x) 在区间[0,1]上的最小值；（2）若f (1) = 0，函数f (x) 在区间(0,1) 内有零点，求a 的取值范围．解：（1）g (x)=f '(x)=e - 2ax -b , g'(x)=e - 2a ．因为x∈[0,1],1 ,所以x x①若1a 则2a 所以函数g (x)在区间[0，1]上单增，2g (x)=g ()=-min 0 1 b②若'()()[][]gx=e 1 e<<则1< 2a <e, 于是当0 <x < ln(2a)时，() 2 0,a ,g'x =e x - a <当ln(2a)<x <1时，2 2x-2a>0,ln(2a)ln(2a)1gx，，所以函数在区间上单减，在区间上单增，g x =g ⎣⎡ a ⎦⎤= a - a a -min ln 2 2 2 ln(2 ) b()()③若ea 则2a ()x 2g'x =e - a 所以函数g (x)在区间[0，1]上单减，2g (x)=g ()=e - a -min 1 2 b⎧ -1 1 ba⎪ 2⎪ ⎪1e综上：函数 g (x )在区间[0，1]上的最小值为( )= ⎨ -- < <gx 2a 2a ln(2a ) b a,min2 2 ⎪ ⎪--ee 2a ba ⎪ ⎩2（2）由 f (1)= 0,e - a -b -1= 0,b = e - a -1, 又 f (0) = 0若函数 f (x ) 在区间 (0,1) 内有零点，则函数 f (x ) 在区间(0,1) 内至少有三个单调区间．1由（1）知当 a 或ea函数 f (x ) 在区间(0,1) 上单调，不可能满足条件．若11 ' = - ( ) h x x ln 0,由( )' = - > ⇒ < h x1 e 3< < g (x ) = g ⎡⎣ ( a )⎤⎦ = a - a a - ，令 ( ) ( ) a , min ln 2 2 2 ln(2 ) b h x = x - x ln x -e -1 1< x < e , 2 2 2 ln 2 2xxe14/ 15所以函数h(x) 在区间(1, e)上单增，在区间( e，e) 上单减．3h x =h e = e - e e -e -<即()()()ln 1 0g min x < 0 恒成立．max2于是，函数f (x) 在区间(0,1) 内至少有三个单调区间⎧(0)= 2 -+> 0 ⎧>- 2⎪g e a a e⇔⎨⇒⎨,g (1)=-a +1> 0 a <1⎪⎩⎩又1 e<a <,所以e-2 <a <1．2 2综上，a 的取值范围为(e - 2，1)．15/ 15。

2014年四川高考数学试卷(理科)(含答案解析)

2014年四川省高考数学试卷（理科）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给处的四个选项中，只有一项是符合题目要求的．1．（5分）（2014•四川）已知集合A={x|x2﹣x﹣2≤0}，集合B为整数集，则A∩B=（）A．{﹣1，0，1，2} B．{﹣2，﹣1，0，1} C．{0，1} D．{﹣1，0}2．（5分）（2014•四川）在x（1+x）6的展开式中，含x3项的系数为（）A．30 B．20 C．15 D．103．（5分）（2014•四川）为了得到函数y=sin（2x+1）的图象，只需把y=sin2x的图象上所有的点（）A．向左平行移动个单位长度B．向右平行移动个单位长度C．向左平行移动1个单位长度D．向右平行一定1个单位长度4．（5分）（2014•四川）若a＞b＞0，c＜d＜0，则一定有（）A．＞B．＜C．＞D．＜5．（5分）（2014•四川）执行如图所示的程序框图，若输入的x，y∈R，那么输出的S的最大值为（）A．0B．1C．2D．36．（5分）（2014•四川）六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有（）A．192种B．216种C．240种D．288种7．（5分）（2014•四川）平面向量=（1，2），=（4，2），=m+（m∈R），且与的夹角等于与的夹角，则m=（）A．﹣2 B．﹣1 C．1D．28．（5分）（2014•四川）如图，在正方体ABCD﹣A1B1C1D1中，点O为线段BD的中点，设点P在线段CC1上，直线OP与平面A1BD所成的角为α，则sinα的取值范围是（）A．[，1]B．[，1]C．[，]D．[，1]9．（5分）（2014•四川）已知f（x）=ln（1+x）﹣ln（1﹣x），x∈（﹣1，1）．现有下列命题：①f（﹣x）=﹣f（x）；②f（）=2f（x）③|f（x）|≥2|x|其中的所有正确命题的序号是（）A．①②③B．②③C．①③D．①②10．（5分）（2014•四川）已知F为抛物线y2=x的焦点，点A，B在该抛物线上且位于x轴的两侧，•=2（其中O为坐标原点），则△ABO与△AFO面积之和的最小值是（）A．2B．3C．D．二、填空题：本大题共5小题，每小题5分，共25分11．（5分）（2014•四川）复数=_________．12．（5分）（2014•四川）设f（x）是定义在R上的周期为2的函数，当x∈[﹣1，1）时，f（x）=，则f（）=_________．13．（5分）（2014•四川）如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为67°，30°，此时气球的高是46m，则河流的宽度BC约等于_________m．（用四舍五入法将结果精确到个位．参考数据：sin67°≈0.92，cos67°≈0.39，sin37°≈0.60，cos37°≈0.80，≈1.73）14．（5分）（2014•四川）设m∈R，过定点A的动直线x+my=0和过定点B的动直线mx﹣y﹣m+3=0交于点P（x，y）．则|PA|•|PB|的最大值是_________．15．（5分）（2014•四川）以A表示值域为R的函数组成的集合，B表示具有如下性质的函数φ（x）组成的集合：对于函数φ（x），存在一个正数M，使得函数φ（x）的值域包含于区间[﹣M，M]．例如，当φ1（x）=x3，φ2（x）=sinx时，φ1（x）∈A，φ2（x）∈B．现有如下命题：①设函数f（x）的定义域为D，则“f（x）∈A”的充要条件是“∀b∈R，∃a∈D，f（a）=b”；②函数f（x）∈B的充要条件是f（x）有最大值和最小值；③若函数f（x），g（x）的定义域相同，且f（x）∈A，g（x）∈B，则f（x）+g（x）∉B．④若函数f（x）=aln（x+2）+（x＞﹣2，a∈R）有最大值，则f（x）∈B．其中的真命题有_________．（写出所有真命题的序号）三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．16．（12分）（2014•四川）已知函数f（x）=sin（3x+）．（1）求f（x）的单调递增区间；（2）若α是第二象限角，f（）=cos（α+）cos2α，求cosα﹣sinα的值．17．（12分）（2014•四川）一款击鼓小游戏的规则如下：每盘游戏都需要击鼓三次，每次击鼓要么出现一次音乐，要么不出现音乐：每盘游戏击鼓三次后，出现一次音乐获得10分，出现两次音乐获得20分，出现三次音乐获得100分，没有出现音乐则扣除200分（即获得﹣200分）．设每次击鼓出现音乐的概率为，且各次击鼓出现音乐相互独立．（1）设每盘游戏获得的分数为X，求X的分布列；（2）玩三盘游戏，至少有一盘出现音乐的概率是多少？（3）玩过这款游戏的许多人都发现．若干盘游戏后，与最初分数相比，分数没有增加反而减少了．请运用概率统计的相关知识分析分数减少的原因．18．（12分）（2014•四川）三棱锥A﹣BCD及其侧视图、俯视图如图所示，设M，N分别为线段AD，AB的中点，P为线段BC上的点，且MN⊥NP．（1）证明：P是线段BC的中点；（2）求二面角A﹣NP﹣M的余弦值．19．（12分）（2014•四川）设等差数列{a n}的公差为d，点（a n，b n）在函数f（x）=2x的图象上（n∈N*）．（1）若a1=﹣2，点（a8，4b7）在函数f（x）的图象上，求数列{a n}的前n项和S n；（2）若a1=1，函数f（x）的图象在点（a2，b2）处的切线在x轴上的截距为2﹣，求数列{}的前n项和T n．20．（13分）（2014•四川）已知椭圆C：+=1（a＞b＞0）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形．（1）求椭圆C的标准方程；（2）设F为椭圆C的左焦点，T为直线x=﹣3上任意一点，过F作TF的垂线交椭圆C于点P，Q．①证明：OT平分线段PQ（其中O为坐标原点）；②当最小时，求点T的坐标．21．（14分）（2014•四川）已知函数f（x）=e x﹣ax2﹣bx﹣1，其中a，b∈R，e=2.71828…为自然对数的底数．（1）设g（x）是函数f（x）的导函数，求函数g（x）在区间[0，1]上的最小值；（2）若f（1）=0，函数f（x）在区间（0，1）内有零点，求a的取值范围．2014年四川省高考数学试卷（理科）参考答案与试题解析一、选择题：本大题共10小题，每小题5分，共50分．在每小题给处的四个选项中，只有一项是符合题目要求的．1．（5分）（2014•四川）已知集合A={x|x2﹣x﹣2≤0}，集合B为整数集，则A∩B=（）A．{﹣1，0，1，2} B．{﹣2，﹣1，0，1} C．{0，1} D．{﹣1，0}考点：交集及其运算．专题：计算题．分析：计算集合A中x的取值范围，再由交集的概念，计算可得．解答：解：A={x|﹣1≤x≤2}，B=Z，∴A∩B={﹣1，0，1，2}．故选：A．点评：本题属于容易题，集合知识是高中部分的基础知识，也是基础工具，高考中涉及到对集合的基本考查题，一般都比较容易，且会在选择题的前几题，考生只要够细心，一般都能拿到分．2．（5分）（2014•四川）在x（1+x）6的展开式中，含x3项的系数为（）A．30 B．20 C．15 D．10考点：二项式系数的性质．专题：二项式定理．分析：利用二项展开式的通项公式求出（1+x）6的第r+1项，令x的指数为2求出展开式中x2的系数．然后求解即可．解答：解：（1+x）6展开式中通项T r+1=C6r x r，令r=2可得，T3=C62x2=15x2，∴（1+x）6展开式中x2项的系数为15，在x（1+x）6的展开式中，含x3项的系数为：15．故选：C．点评：本题考查二项展开式的通项的简单直接应用．牢记公式是基础，计算准确是关键．3．（5分）（2014•四川）为了得到函数y=sin（2x+1）的图象，只需把y=sin2x的图象上所有的点（）A．向左平行移动个单位长度B．向右平行移动个单位长度C．向左平行移动1个单位长度D．向右平行一定1个单位长度考点：函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质．分析：根据y=sin（2x+1）=sin2（x+），利用函数y=Asin（ωx+φ）的图象变换规律，得出结论．解答：解：∵y=sin（2x+1）=sin2（x+），∴把y=sin2x的图象上所有的点向左平行移动个单位长度，即可得到函数y=sin（2x+1）的图象，故选：A．点评：本题主要考查函数y=Asin（ωx+φ）的图象变换规律，属于基础题．4．（5分）（2014•四川）若a＞b＞0，c＜d＜0，则一定有（）A．＞B．＜C．＞D．＜考点：不等式比较大小；不等关系与不等式．专题：不等式的解法及应用．分析：利用特例法，判断选项即可．解答：解：不妨令a=3，b=1，c=﹣3，d=﹣1，则，，∴A、B不正确；，=﹣，∴C不正确，D正确．故选：D．点评：本题考查不等式比较大小，特值法有效，导数计算正确．5．（5分）（2014•四川）执行如图所示的程序框图，若输入的x，y∈R，那么输出的S的最大值为（）A．0B．1C．2D．3考点：程序框图．专题：计算题；算法和程序框图．分析：算法的功能是求可行域内，目标还是S=2x+y的最大值，画出可行域，求得取得最大值的点的坐标，求出最大值．解答：解：由程序框图知：算法的功能是求可行域内，目标还是S=2x+y的最大值，画出可行域如图：当时，S=2x+y的值最大，且最大值为2．故选：C．点评：本题借助选择结构的程序框图考查了线性规划问题的解法，根据框图的流程判断算法的功能是解题的关键．6．（5分）（2014•四川）六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有（）A．192种B．216种C．240种D．288种考点：排列、组合及简单计数问题．专题：应用题；排列组合．分析：分类讨论，最左端排甲；最左端只排乙，最右端不能排甲，根据加法原理可得结论．解答：解：最左端排甲，共有=120种，最左端只排乙，最右端不能排甲，有=96种，根据加法原理可得，共有120+96=216种．故选：B．点评：本题考查排列、组合及简单计数问题，考查学生的计算能力，属于基础题．7．（5分）（2014•四川）平面向量=（1，2），=（4，2），=m+（m∈R），且与的夹角等于与的夹角，则m=（）A．﹣2 B．﹣1 C．1D．2考点：数量积表示两个向量的夹角．专题：平面向量及应用．分析：由已知求出向量的坐标，再根据与的夹角等于与的夹角，代入夹角公式，构造关于m的方程，解方程可得答案．解答：解：∵向量=（1，2），=（4，2），∴=m+=（m+4，2m+2），又∵与的夹角等于与的夹角，∴=，∴=，∴=，解得m=2，故选：D点评：本题考查的知识点是数量积表示两个向量的夹角，难度中档．8．（5分）（2014•四川）如图，在正方体ABCD﹣A1B1C1D1中，点O为线段BD的中点，设点P在线段CC1上，直线OP与平面A1BD所成的角为α，则sinα的取值范围是（）A．[，1]B．[，1]C．[，]D．[，1]考点：直线与平面所成的角．专题：空间角．分析：由题意可得：直线OP于平面A1BD所成的角α的取值范围是∪．再利用正方体的性质和直角三角形的边角关系即可得出．解答：解：由题意可得：直线OP于平面A1BD所成的角α的取值范围是∪．不妨取AB=2．在Rt△AOA1中，==．sin∠C1OA1=sin（π﹣2∠AOA1）=sin2∠AOA1=2sin∠AOA1cos∠AOA1=，=1．∴sinα的取值范围是．故选：B．点评：本题考查了正方体的性质和直角三角形的边角关系即可、线面角的求法，考查了推理能力，属于中档题．9．（5分）（2014•四川）已知f（x）=ln（1+x）﹣ln（1﹣x），x∈（﹣1，1）．现有下列命题：①f（﹣x）=﹣f（x）；②f（）=2f（x）③|f（x）|≥2|x|其中的所有正确命题的序号是（）A．①②③B．②③C．①③D．①②考点：命题的真假判断与应用．专题：函数的性质及应用．分析：根据已知中函数的解析式，结合对数的运算性质，分别判断三个结论的真假，最后综合判断结果，可得答案．解答：解：∵f（x）=ln（1+x）﹣ln（1﹣x），x∈（﹣1，1），∴f（﹣x）=ln（1﹣x）﹣ln（1+x）=﹣f（x），即①正确；f（）=ln（1+）﹣ln（1﹣）=ln（）﹣ln（）=ln（）=ln[（）2]=2ln（）=2[ln（1+x）﹣ln（1﹣x）]=2f（x），故②正确；当x∈[0，1）时，|f（x）|≥2|x|⇔f（x）﹣2x≥0，令g（x）=f（x）﹣2x=ln（1+x）﹣ln（1﹣x）﹣2x（x∈[0，1））∵g′（x）=+﹣2=≥0，∴g（x）在[0，1）单调递增，g（x）=f（x）﹣2x≥g（0）=0，又f（x）≥2x，又f（x）与y=2x为奇函数，所以丨f（x）丨≥2丨x丨成立，故③正确；故正确的命题有①②③，故选：A点评：本题以命题的真假判断为载体，考查了对数的运算性质，代入法求函数的解析式等知识点，难度中档．10．（5分）（2014•四川）已知F为抛物线y2=x的焦点，点A，B在该抛物线上且位于x轴的两侧，•=2（其中O为坐标原点），则△ABO与△AFO面积之和的最小值是（）A．2B．3C．D．考点：直线与圆锥曲线的关系．专题：圆锥曲线中的最值与范围问题．分析：可先设直线方程和点的坐标，联立直线与抛物线的方程得到一个一元二次方程，再利用韦达定理及•=2消元，最后将面积之和表示出来，探求最值问题．解答：解：设直线AB的方程为：x=ty+m，点A（x1，y1），B（x2，y2），直线AB与x轴的交点为M（（0，m），由⇒y2﹣ty﹣m=0，根据韦达定理有y1•y2=﹣m，∵•=2，∴x1•x2+y1•y2=2，从而，∵点A，B位于x轴的两侧，∴y1•y2=﹣2，故m=2．不妨令点A在x轴上方，则y1＞0，又，∴S△ABO+S△AFO==．当且仅当，即时，取“=”号，∴△ABO与△AFO面积之和的最小值是3，故选B．点评：求解本题时，应考虑以下几个要点：1、联立直线与抛物线的方程，消x或y后建立一元二次方程，利用韦达定理与已知条件消元，这是处理此类问题的常见模式．2、求三角形面积时，为使面积的表达式简单，常根据图形的特征选择适当的底与高．3、利用基本不等式时，应注意“一正，二定，三相等”．二、填空题：本大题共5小题，每小题5分，共25分11．（5分）（2014•四川）复数=﹣2i．考点：复数代数形式的乘除运算．专题：数系的扩充和复数．分析：利用两个复数代数形式的乘除法法则化简所给的复数，可得结果．解答：解：复数===﹣2i，故答案为：﹣2i．点评：本题主要考查两个复数代数形式的乘除法法则的应用，属于基础题．12．（5分）（2014•四川）设f（x）是定义在R上的周期为2的函数，当x∈[﹣1，1）时，f（x）=，则f（）=1．考点：函数的值．专题：计算题．分析：由函数的周期性f（x+2）=f（x），将求f（）的值转化成求f（）的值．解答：解：∵f（x）是定义在R上的周期为2的函数，∴=1．故答案为：1．点评：本题属于容易题，是考查函数周期性的简单考查，学生在计算时只要计算正确，往往都能把握住，在高考中，属于“送分题”．13．（5分）（2014•四川）如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为67°，30°，此时气球的高是46m，则河流的宽度BC约等于60m．（用四舍五入法将结果精确到个位．参考数据：sin67°≈0.92，cos67°≈0.39，sin37°≈0.60，cos37°≈0.80，≈1.73）考点：余弦定理的应用；正弦定理；正弦定理的应用．专题：应用题；解三角形．分析：过A点作AD垂直于CB的延长线，垂足为D，分别在Rt△ACD、Rt△ABD中利用三角函数的定义，算出CD、BD的长，从而可得BC，即为河流在B、C两地的宽度．解答：解：过A点作AD垂直于CB的延长线，垂足为D，则Rt△ACD中，∠C=30°，AD=46m∴CD==46≈79.58m．又∵Rt△ABD中，∠ABD=67°，可得BD==≈19.5m∴BC=CD﹣BD=79.58﹣19.5=60.08≈60m故答案为：60m点评：本题给出实际应用问题，求河流在B、C两地的宽度，着重考查了三角函数的定义、正余弦定理解三角形的知识，属于中档题．14．（5分）（2014•四川）设m∈R，过定点A的动直线x+my=0和过定点B的动直线mx﹣y﹣m+3=0交于点P（x，y）．则|PA|•|PB|的最大值是5．考点：点到直线的距离公式．专题：直线与圆．分析：先计算出两条动直线经过的定点，即A和B，注意到两条动直线相互垂直的特点，则有PA⊥PB；再利用基本不等式放缩即可得出|PA|•|PB|的最大值．解答：解：有题意可知，动直线x+my=0经过定点A（0，0），动直线mx﹣y﹣m+3=0即m（x﹣1）﹣y+3=0，经过点定点B（1，3），注意到动直线x+my=0和动直线mx﹣y﹣m+3=0始终垂直，P又是两条直线的交点，则有PA⊥PB，∴|PA|2+|PB|2=|AB|2=10．故|PA|•|PB|≤=5（当且仅当时取“=”）故答案为：5点评：本题是直线和不等式的综合考查，特别是“两条直线相互垂直”这一特征是本题解答的突破口，从而有|PA|2+|PB|2是个定值，再由基本不等式求解得出．直线位置关系和不等式相结合，不容易想到，是个灵活的好题．15．（5分）（2014•四川）以A表示值域为R的函数组成的集合，B表示具有如下性质的函数φ（x）组成的集合：对于函数φ（x），存在一个正数M，使得函数φ（x）的值域包含于区间[﹣M，M]．例如，当φ1（x）=x3，φ2（x）=sinx时，φ1（x）∈A，φ2（x）∈B．现有如下命题：①设函数f（x）的定义域为D，则“f（x）∈A”的充要条件是“∀b∈R，∃a∈D，f（a）=b”；②函数f（x）∈B的充要条件是f（x）有最大值和最小值；③若函数f（x），g（x）的定义域相同，且f（x）∈A，g（x）∈B，则f（x）+g（x）∉B．④若函数f（x）=aln（x+2）+（x＞﹣2，a∈R）有最大值，则f（x）∈B．其中的真命题有①③④．（写出所有真命题的序号）考点：命题的真假判断与应用；充要条件；函数的值域．专题：新定义；极限思想；函数的性质及应用；不等式的解法及应用．分析：根据题中的新定义，结合函数值域的概念，可判断出命题①②③是否正确，再利用导数研究命题④中函数的值域，可得到其真假情况，从而得到本题的结论．解答：解：（1）对于命题①“f（x）∈A”即函数f（x）值域为R，“∀b∈R，∃a∈D，f（a）=b”表示的是函数可以在R中任意取值，故有：设函数f（x）的定义域为D，则“f（x）∈A”的充要条件是“∀b∈R，∃a∈D，f（a）=b”∴命题①是真命题；（2）对于命题②若函数f（x）∈B，即存在一个正数M，使得函数f（x）的值域包含于区间[﹣M，M]．∴﹣M≤f（x）≤M．例如：函数f（x）满足﹣2＜f（x）＜5，则有﹣5≤f（x）≤5，此时，f（x）无最大值，无最小值．∴命题②“函数f（x）∈B的充要条件是f（x）有最大值和最小值．”是假命题；（3）对于命题③若函数f（x），g（x）的定义域相同，且f（x）∈A，g（x）∈B，则f（x）值域为R，f（x）∈（﹣∞，+∞），并且存在一个正数M，使得﹣M≤g（x）≤M．∴f（x）+g（x）∈R．则f（x）+g（x）∉B．∴命题③是真命题．（4）对于命题④∵函数f（x）=aln（x+2）+（x＞﹣2，a∈R）有最大值，∴假设a＞0，当x→+∞时，→0，ln（x+2）→+∞，∴aln（x+2）→+∞，则f（x）→+∞．与题意不符；假设a＜0，当x→﹣2时，→，ln（x+2）→﹣∞，∴aln（x+2）→+∞，则f（x）→+∞．与题意不符．∴a=0．即函数f（x）=（x＞﹣2）当x＞0时，，∴，即；当x=0时，f（x）=0；当x＜0时，，∴，即．∴．即f（x）∈B．故命题④是真命题．故答案为①③④．点评：本题考查了函数值域的概念、基本不等式、充要条件，还考查了新定义概念的应用和极限思想．本题计算量较大，也有一定的思维难度，属于难题．三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．16．（12分）（2014•四川）已知函数f（x）=sin（3x+）．（1）求f（x）的单调递增区间；（2）若α是第二象限角，f（）=cos（α+）cos2α，求cosα﹣sinα的值．考点：两角和与差的余弦函数；正弦函数的单调性．专题：三角函数的求值．分析：（1）令2kπ﹣≤3x+≤2kπ+，k∈z，求得x的范围，可得函数的增区间．（2）由函数的解析式可得f（）=sin（α+），又f（）=cos（α+）cos2α，可得sin（α+）=cos（α+）cos2α，化简可得（cosα﹣sinα）2=．再由α是第二象限角，cosα﹣sinα＜0，从而求得cosα﹣sinα的值．解答：解：（1）∵函数f（x）=sin（3x+），令2kπ﹣≤3x+≤2kπ+，k∈z，求得﹣≤x≤+，故函数的增区间为[﹣，+]，k∈z．（2）由函数的解析式可得f（）=sin（α+），又f（）=cos（α+）cos2α，∴sin（α+）=cos（α+）cos2α，即sin（α+）=cos（α+）（cos2α﹣sin2α），∴sinαcos+cosαsin=（cos2α﹣sin2α）（sinα+cosα）．又∵α是第二象限角，∴cosα﹣sinα＜0，当sinα+cosα=0时，此时cosα﹣sinα=﹣．当sinα+cosα≠0时，此时cosα﹣sinα=﹣．综上所述：cosα﹣sinα=﹣或﹣．点评：本题主要考查正弦函数的单调性，三角函数的恒等变换，属于中档题．17．（12分）（2014•四川）一款击鼓小游戏的规则如下：每盘游戏都需要击鼓三次，每次击鼓要么出现一次音乐，要么不出现音乐：每盘游戏击鼓三次后，出现一次音乐获得10分，出现两次音乐获得20分，出现三次音乐获得100分，没有出现音乐则扣除200分（即获得﹣200分）．设每次击鼓出现音乐的概率为，且各次击鼓出现音乐相互独立．（1）设每盘游戏获得的分数为X，求X的分布列；（2）玩三盘游戏，至少有一盘出现音乐的概率是多少？（3）玩过这款游戏的许多人都发现．若干盘游戏后，与最初分数相比，分数没有增加反而减少了．请运用概率统计的相关知识分析分数减少的原因．考点：离散型随机变量及其分布列；离散型随机变量的期望与方差．专题：概率与统计．分析：（1）设每盘游戏获得的分数为X，求出对应的概率，即可求X的分布列；（2）求出有一盘出现音乐的概率，独立重复试验的概率公式即可得到结论．（3）计算出随机变量的期望，根据统计与概率的知识进行分析即可．解答：解：（1）X可能取值有﹣200，10，20，100．则P（X=﹣200）=，P（X=10）==P（X=20）==，P（X=100）==，故分布列为：X ﹣200 10 20 100P由（1）知，每盘游戏出现音乐的概率是p=+=，则至少有一盘出现音乐的概率p=1﹣．由（1）知，每盘游戏或得的分数为X的数学期望是E（X）=（﹣200）×+10×+20××100=﹣=．这说明每盘游戏平均得分是负分，由概率统计的相关知识可知：许多人经过若干盘游戏后，入最初的分数相比，分数没有增加反而会减少．点评：本题主要考查概率的计算，以及离散型分布列的计算，以及利用期望的计算，考查学生的计算能力．18．（12分）（2014•四川）三棱锥A﹣BCD及其侧视图、俯视图如图所示，设M，N分别为线段AD，AB的中点，P为线段BC上的点，且MN⊥NP．（1）证明：P是线段BC的中点；（2）求二面角A﹣NP﹣M的余弦值．考点：二面角的平面角及求法；直线与平面平行的判定；用空间向量求平面间的夹角．专题：空间向量及应用．分析：（1）用线面垂直的性质和反证法推出结论，（2）先建空间直角坐标系，再求平面的法向量，即可求出二面角A﹣NP﹣M的余弦值．解答：解：（1）由三棱锥A﹣BCD及其侧视图、俯视图可知，在三棱锥A﹣BCD中：平面ABD⊥平面CBD，AB=AD=BD=CD=CB=2设O为BD的中点，连接OA，OC于是OA⊥BD，OC⊥BD 所以BD⊥平面OAC⇒BD⊥AC因为M，N分别为线段AD，AB的中点，所以MN∥BD，MN∥NP，故BD⊥NP假设P不是线段BC的中点，则直线NP与直线AC是平面ABC内相交直线从而BD⊥平面ABC，这与∠DBC=60°矛盾，所以P为线段BC的中点（2）以O为坐标原点，OB，OC，OA分别为x，y，z轴建立空间直角坐标系，则A（0，0，），M（，O，），N（，0，），P（，，0）于是，，设平面ANP和平面NPM的法向量分别为和由，则，设z1=1，则由，则，设z2=1，则cos===所以二面角A﹣NP﹣M的余弦值点评：本题考查线线的位置关系，考查二面角知识的应用，解题的关键是掌握用向量的方法求二面角大小的步骤，属于中档题．19．（12分）（2014•四川）设等差数列{a n}的公差为d，点（a n，b n）在函数f（x）=2x的图象上（n∈N*）．（1）若a1=﹣2，点（a8，4b7）在函数f（x）的图象上，求数列{a n}的前n项和S n；（2）若a1=1，函数f（x）的图象在点（a2，b2）处的切线在x轴上的截距为2﹣，求数列{}的前n项和T n．考点：数列的求和；数列与函数的综合．专题：函数的性质及应用；等差数列与等比数列．分析：（1）由于点（a8，4b7）在函数f（x）=2x的图象上，可得，又等差数列{a n}的公差为d，利用等差数列的通项公式可得=2d．由于点（a8，4b7）在函数f（x）的图象上，可得=b8，进而得到=4=2d，解得d．再利用等差数列的前n项和公式即可得出．（2）利用导数的几何意义可得函数f（x）的图象在点（a2，b2）处的切线方程，即可解得a2．进而得到a n，b n．再利用“错位相减法”即可得出．解答：解：（1）∵点（a8，4b7）在函数f（x）=2x的图象上，∴，又等差数列{a n}的公差为d，∴==2d，∵点（a8，4b7）在函数f（x）的图象上，∴=b8，∴=4=2d，解得d=2．又a1=﹣2，∴S n==﹣2n+=n2﹣3n．（2）由f（x）=2x，∴f′（x）=2x ln2，∴函数f（x）的图象在点（a2，b2）处的切线方程为，又，令y=0可得x=，∴，解得a2=2．∴d=a2﹣a1=2﹣1=1．∴a n=a1+（n﹣1）d=1+（n﹣1）×1=n，∴b n=2n．∴．∴T n=+…++，∴2T n=1+++…+，两式相减得T n=1++…+﹣=﹣==．点评：本题综合考查了指数函数的运算性质、导数的几何意义、等差数列与等比数列的通项公式及其前n项和公式等基础知识与基本技能方法，考查了推理能力、计算能力、“错位相减法”，属于难题．20．（13分）（2014•四川）已知椭圆C：+=1（a＞b＞0）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形．（1）求椭圆C的标准方程；（2）设F为椭圆C的左焦点，T为直线x=﹣3上任意一点，过F作TF的垂线交椭圆C于点P，Q．①证明：OT平分线段PQ（其中O为坐标原点）；②当最小时，求点T的坐标．考点：直线与圆锥曲线的关系；椭圆的标准方程．专题：圆锥曲线中的最值与范围问题．分析：第（1）问中，由正三角形底边与高的关系，a2=b2+c2及焦距2c=4建立方程组求得a2，b2；第（2）问中，先设点的坐标及直线PQ的方程，利用两点间距离公式及弦长公式将表示出来，由取最小值时的条件获得等量关系，从而确定点T的坐标．解答：解：（1）依题意有解得所以椭圆C的标准方程为+=1．（2）设T（﹣3，m），P（x1，y1），Q（x2，y2），PQ的中点为N（x0，y0），①证明：由F（﹣2，0），可设直线PQ的方程为x=my﹣2，由⇒（m2+3）y2﹣4my﹣2=0，所以于是，从而，即，则，所以O，N，T三点共线，从而OT平分线段PQ，故得证．②由两点间距离公式得，由弦长公式得==，所以，令，则（当且仅当x2=2时，取“=”号），所以当最小时，由x2=2=m2+1，得m=1或m=﹣1，此时点T的坐标为（﹣3，1）或（﹣3，﹣1）．点评：本题属相交弦问题，应注意考虑这几个方面：1、设交点坐标，设直线方程；2、联立直线与椭圆方程，消去y或x，得到一个关于x或y一元二次方程，利用韦达定理；3、利用基本不等式或函数的单调性探求最值问题．21．（14分）（2014•四川）已知函数f（x）=e x﹣ax2﹣bx﹣1，其中a，b∈R，e=2.71828…为自然对数的底数．（1）设g（x）是函数f（x）的导函数，求函数g（x）在区间[0，1]上的最小值；（2）若f（1）=0，函数f（x）在区间（0，1）内有零点，求a的取值范围．考点：导数在最大值、最小值问题中的应用；函数的零点．专题：导数的综合应用．分析：（1）求出f（x）的导数得g（x），再求出g（x）的导数，对它进行讨论，从而判断g（x）的单调性，求出g（x）的最小值；（2）利用等价转换，若函数f（x）在区间（0，1）内有零点，则函数f（x）在区间（0，1）内至少有三个单调区间，所以g（x）在（0，1）上应有两个不同的零点．解答：解：∵f（x）=e x﹣ax2﹣bx﹣1，∴g（x）=f′（x）=e x﹣2ax﹣b，又g′（x）=e x﹣2a，x∈[0，1]，∴1≤e x≤e，∴①当时，则2a≤1，g′（x）=e x﹣2a≥0，∴函数g（x）在区间[0，1]上单调递增，g（x）min=g（0）=1﹣b；②当，则1＜2a＜e，∴当0＜x＜ln（2a）时，g′（x）=e x﹣2a＜0，当ln（2a）＜x＜1时，g′（x）=e x﹣2a＞0，∴函数g（x）在区间[0，ln（2a）]上单调递减，在区间[ln（2a），1]上单调递增，g（x）min=g[ln（2a）]=2a﹣2aln（2a）﹣b；③当时，则2a≥e，g′（x）=e x﹣2a≤0，∴函数g（x）在区间[0，1]上单调递减，g（x）min=g（1）=e﹣2a﹣b，综上：函数g（x）在区间[0，1]上的最小值为；（2）由f（1）=0，⇒e﹣a﹣b﹣1=0⇒b=e﹣a﹣1，又f（0）=0，若函数f（x）在区间（0，1）内有零点，则函数f（x）在区间（0，1）内至少有三个单调区间，由（1）知当a≤或a≥时，函数g（x）在区间[0，1]上单调，不可能满足“函数f（x）在区间（0，1）内至少有三个单调区间”这一要求．若，则g min（x）=2a﹣2aln（2a）﹣b=3a﹣2aln（2a）﹣e+1令h（x）=（1＜x＜e）则．由＞0⇒x＜∴h（x）在区间（1，）上单调递增，在区间（，e）上单调递减，=+＜0，即g min（x）＜0 恒成立，∴函数f（x）在区间（0，1）内至少有三个单调区间⇔⇒，又，所以e﹣2＜a＜1，综上得：e﹣2＜a＜1．点评：本题考查了，利用导数求函数的单调区间，分类讨论思想，等价转换思想，函数的零点等知识点．是一道导数的综合题，难度较大．参与本试卷答题和审题的老师有：任老师；王老师；孙佑中；刘长柏；qiss；尹伟云；翔宇老师；szjzl；caoqz；清风慕竹；静定禅心；maths（排名不分先后）菁优网2014年6月24日。

2014年四川高考理科数学试题逐题详细讲解(纯word解析版)

2014年高考理科数学试题逐题详解（纯word 解析版）一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一个是符合题目要求的。

[2014年卷（理01）]已知集合2{|20}A x x x =--≤，集合B 为整数集，则A B ⋂=A ．{1,0,1,2}-B ．{2,1,0,1}--C ．{0,1}D ．{1,0}- [答案]A[解析]{|12}A x x =-≤≤，B Z =，故A B ⋂={1,0,1,2}-[2014年卷（理02）]在6(1)x x +的展开式中，含3x 项的系数为A ．30B ．20C ．15D ．10 [答案]C[解析]含3x 项为24236(1)15x C x x ⋅=[2014年卷（理03）]为了得到函数sin(21)y x =+的图象，只需把函数sin 2y x =的图象上所有的点A ．向左平行移动12个单位长度 B ．向右平行移动12个单位长度 C ．向左平行移动1个单位长度 D ．向右平行移动1个单位长度 [答案]A[解析]因为1sin(21)sin[2()]2y x x =+=+，故可由函数sin 2y x =的图象上所有的点向左平行移动12个单位长度得到[2014年卷（理04）]若0a b >>，0c d <<，则一定有A ．a b c d >B ．a b c d <C ．a b d c >D ．a b d c< [答案]D[解析]由1100c d d c<<⇒->->，又0a b >>，由不等式性质知：0a b d c ->->，所以a bd c<[2014年卷（理05）]执行如图1所示的程序框图，如果输入的,x y R ∈，则输出的S 的最大值为A ．0B ．1C ．2D ．3 [答案]C[解析]当001x y x y ≥⎧⎪≥⎨⎪+≤⎩时，函数2S x y =+的最大值为2.[2014年卷（理06）]六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有A ．192种B ．216种C ．240种D ．288种 [答案]B[解析]当最左端为甲时，不同的排法共有55A 种；当最左端为乙时，不同的排法共有14C 44A 种。

四川省2014高考数学压轴卷理(含解析)

2014四川省高考压轴卷数学〔理工类〕本试卷分第1卷〔选择题〕和第2卷〔非选择题〕。

第1卷1至2页，第2卷3至4页。

考生作答时，须将答案答在答题卡上，在本试题卷、草稿纸上答题无效。

总分为150分。

考试时间120分钟，考试完毕后，将本试题卷和答题卡一并收回。

第1卷〔选择题共50分〕须知事项：必须使用2B 铅笔在答题卡上将所选答案的标号涂黑。

一、选择题：本大题共10小题，每一小题5分，共50分。

在每一小题给出的四个选项中，只有一项为哪一项符合题目要求的。

1.集合M={|ln(1)x y x =-}，集合N={|,xy y e x R =∈}，(e 为自然对数的底数) 如此M N =〔〕A ．{|1x x <}B ．{|1x x >}C ．{|01x x <<}D ．∅ 2．复数131iZ i-=+的实部是〔〕 A ． 2 B ． 1C ．1- D ．4-3. 函数 y=log 2(x 2＋2x －3)的单调递减区间为〔〕A ．〔－∞，－3〕B ．〔－∞，－1〕C ．(1，+∞)D ．(－3，－1)4.在等差数列{}n a 中，1315310a a a ++=，如此5a 的值为〔〕 A ．2 B ．3 C ．4 D ．55.函数x x y sin =在[]ππ,-上的图象是〔〕6. 运行右图所示框图的相应程序,假设输入,a b 的值分别为2log 3和3log 2,如此输出M 的值是〔〕A.0B.1C. 2D. －17.不重合的直线m 、l 和平面αβ、，且m α⊥，l β⊂．给出如下命题： ①假设//αβ，如此m l ⊥；②假设αβ⊥，如此//m l ；③假设m l ⊥，如此//αβ；④假设//m l ，如此αβ⊥，其中正确命题的个数是〔〕 A ．1 B ．2 C ．3 D ．48.双曲线1C 的中心在原点，焦点在x 轴上，假设1C 的一个焦点与抛物线2C ：212y x =的焦点重合，且抛物线2C 的准线交双曲线1C 所得的弦长为43，如此双曲线1C 的实轴长为〔〕A ．6B ．26C ．3D ．239.我国第一艘航母“辽宁舰〞在某次舰载机起降飞行训练中，有5架歼一15飞机准备着舰，如果甲、乙两机必须相邻着舰，而丙、丁两机不能相邻着舰，那么不同的着舰方法种数为〔〕A. 12 B ．18 C ．24 D.4810.定义域为R 的函数()f x 满足(2)2()f x f x +=，当[0,2)x ∈时，23||2,[0,1),()1(),[1,2),2x x x x f x x -⎧-∈⎪=⎨-∈⎪⎩假设当[4,2)x ∈--时，函数21()42t f x t ≥-+恒成立，如此实数t 的取值范围为( )(A)23t ≤≤(B)13t ≤≤ (C)14t ≤≤(D)24t ≤≤ 第2卷〔非选择题共100分〕须知事项：必须使用0.5毫米黑色签字笔在答题卡上题目指示的答题区域内作答。

2014四川高考数学试卷(理工类)及部分参考答案

2x 2 f x ; 2 1 x
3 f x 2 x . ○
其中的所有正确命题的序号是（
C
） 1
诗蜀博士特教育
预祝四川学子金榜题名
2 ○ 3 （B）○ 1 ○ 3 （C）○ 1 ○ 2 （D）○
1 ○ 2 ○ 3 （A）○
10、已知 F 为抛物线 y 2 x 的焦点，点 A,B 在该抛物线上且位于 x 轴的两侧， OA OB 2 （其中 O 为坐标原点），则△ ABO 与△ AFO 面积之和的最小值是（（A）2 （B）3 （C）第Ⅱ卷
6 ,1 3
（C）
6 2 2 , 3 3
（D）
2 2 ,1 3
第8题图
9、已知 f x ln 1 x ln 1 x ,x 1,1 ，现有下列命题：
1 f x f x ; ○ 2 f ○
诗蜀博士特教育
预祝四川学子金榜题名
2014 年全国普通高等学校招生统一考试数
第Ⅰ卷（选择题共 50 分）注意事项：必须使用 2B 铅笔在答题卡上将所选答案对应的标号涂黑。一、选择题. 1、已知集合 A {x x x 2 0} ，集合 B 为整数集，则 A
2
学（四川卷理工类）
(ii)
当
TF 最小时，求点 T 的坐标. PQ
21．（本小题满分 14 分）已知函数 f x e ax bx 1 其中 a,b R,e 2.71828
x 2
为自然对数的底数．
（Ⅰ）设 g x 是函数 f x 的导函数，求函数 g x 在区间 0 ,1 上的最小值；（Ⅱ）若 f 1 0 ，函数 f ( x) 在区间 0,1 内有零点，求 a 的取值范围．

2014年普通高等学校招生全国统一考试四川理科数学试题及答案解析(Word版)

2014年普通高等学校招生全国统一考试（四川卷）数学（理工类）一. 选择题1. 已知集合2{|20},A x x x B =--≤集合为整数集，则A B =（ A ）A ．{-1,0,1,2} B.{-2,-1,0,1} C.{0,1} D.{-1,0} 2.在6(1)x x +的展开式中，含3x 的系数的为（ C ） A ．30 B.20 C.15 D.10 解析：即求6226(1)15x x C +=中的系数为.3.为了得到函数sin(21)y x =+的图像，只需把函数sin 2y x =的图像上所有的点（ A ）A.向左平移12个单位长度 B.向右平移12个单位长度C.向左平移1个单位长度D.向右平移1个单位长度解析：1sin(21)=sin 2()2y x x =++，将sin 2y x =向左平移12个单位长度. 4.若0,0,a b c d >><<则一定有（ D ）A.a b c d > B. a b c d < C. a b d c > D. a b d c<解析：（1）特殊值法：取2,1,2,1a b c d ===-=-即可；（2）利用不等式的性质：110,0,c d c d d c<<∴->->->- 又0,0,a b a ba b d c d c >>∴->->∴<5.执行如图的程序框图，如果输入的,x y R ∈，那么输出的S 的最大值为（ C ） A ．0 B.1C ．2 D.3解析：本题将程序框图和线性规划结合起来，有一定的新颖性，摆脱了传统的线性规划考题模式，关键是能够理解程序框图表达的含义，将原题转化为：已知001x y x y ≥⎧⎪≥⎨⎪+≤⎩，求解2S x y =+的最大值. 作图易知，S 在(1,0)处取得最大值2.6.六个人从左自右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法有（ B ） A ．192种 B. 216种 C ．240种 D.288种解析：由甲，乙的位置分两种情况：（1）最左端排甲，有5!120=种；（2）最左端排乙，有44!96⨯=种. 共120+96=216种. 7.平面向量(1,2),(4,2),a b c ma b ===+，且c a c b 与的夹角等于与的夹角，则m=（ D ） A.-2 B.-1 C.1 D.2 解析：==a cb cc a c b a b⋅⋅⇔与的夹角与的夹角 8.在正方体1111ABCD A BC D -中，点O 为线段BD 的中点，设点P 在线段1CC 上，直线OP 与平面1A BDαα的夹角为，则sin 的取值范围是（ B ）A.3B. 3C.3D. [,1]3结束输出S S=1S=2x+y否是x≥0，y≥0,x+y≤1？输入x,y开始C解析：设棱长为1，则11111AC AC AO OC OC =====所以1111111cos ,sin 333AOC AOC AOC AOC ====. 9.已知()ln(1)ln(1),(1,1)f x x x x =+--∈-. 现有下列命题： ①()()f x f x -=-；②22()2()1xf f x x=+；③()2f x x ≥ 其中所有的正确命题序号是（ C ）A. ①②③B. ②③C. ①③D. ①② 解析：①()()f x f x -=-显然成立；②左边22()1xf x+中的x 只是不能为1，右边()f x 中的(1,1)x ∈-，故不对；③由于左右两边均为偶函数，只需判断()2,(0,1)f x x x ≥∈即可，记()()2,(0,1)g x f x x x =-∈，则22'()20,(0,1)1g x x x =->∈-，故()(0)0g x g >=，于是③成立.10.已知F 为抛物线2y x =的焦点，点,A B 在该抛物线上且位于x 轴的两侧，2OA OB ⋅=. 则ABO AFO ∆∆与面积之和的最小值是 A ．2 B.3D.10 解析：由题意得22112211221(,0),(,),(,),,,4F A x y B x y y x y x ==设则由2OA OB ⋅=得，22121212122x x y y y y y y +=+=，于是1221y y =-或，又点,A B 位于x 轴的两侧，故122y y =-. 所以2212211122111111122428ABO AFO S S x y x y y y y y y y ∆∆+=⨯-+⨯⨯=-+12111111121293888y y y y y y y y =-+=++=+≥. 注：已知原点1122,(,),(,)O A x y B x y ，设过点A ，B 的直线斜率为k ，则直线AB 为211121()y y y x x y x x -=-+-，所以1112122122111222ABOx y S x x y x yx y ∆=-=-=. 二．填空题11.复数221ii-=+2i-12.设()f x是定义在R上的周期为2的函数，当[1,1)x∈-时，242,10,(),01,x xf xx x⎧-+-≤<=⎨≤<⎩则3()2f=113.从气球A上测得正前方的河流的两岸B，C的府角分别是67,30，此时气球的高度是46m，则河流的宽度BC约等于60 m(四舍五入将结果精确到个位.参考数据：sin670.92,cos670.39,sin370.60,cos37 1.73≈≈≈≈≈) 解析：解三角形的实际问题，利用正弦定理即可.14.设m R∈，过定点A的动直线0x my+=和过定点B的动直线30mx y m--+=交于点(,)P x y，则PA PB⋅的最大值是 5解析：由题意得(0,0),(1,3)A B，消去m得P点方程为：2230x y x y+--=上，所以点P 在以AB为直径的圆上，且PA PB⊥，故222522PA PB ABPA PB+⋅≤==.15.以A表示值域为R的函数组成的集合，B表示具有如下性质的函数()xϕ组成的集合：对于函数()xϕ，存在一个正数M，使得函数()xϕ的值域包含于区间[,]M M-. 例如，当312(),()sinx x x xϕϕ==时，12(),()x A x Bϕϕ∈∈. 现有如下命题①设函数()f x的定义域为D，则“()f x A∈”的充要条件是“,,()b R a D f a b∀∈∃∈=”；②函数()f x B∈的充要条件是()f x有最大值和最小值；③若函数(),()f xg x的定义域相同，且(),(),f x Ag x B∈∈则()()f xg x B+∉；④若函数2()ln(2)(2,)1xf x a x x a R x =++>-∈+有最大值，则()f x B ∈. 其中证明题有_________________________解析：①集合A 的特点是：函数是满射；②()x ϕ一定有上下确界，不一定有最值； ③正确；④要使函数()f x 取到最大值，则必有0a =，故2()1xx B x =∈+. 三．解答题16.已知函数()sin(3)4f x x π=+（1）求()f x 的单调递增区间；（2）若α是第二象限角，4()cos()cos 2,cos sin 354f απαααα=+-求的值. 解：（1）由232242k x k πππππ-≤+≤+得()f x 的单调递增区间为：22[,],34312k k k Z ππππ-+∈；（2）由4()cos()cos 2354f απαα=+得4sin()cos()cos 2454ππααα+=+整理得25(cos sin )4αα-=，又α是第二象限角，所以cos sin 0αα-<，故cos sin 2αα-=-. 17.击鼓游戏规则如下，每盘游戏都需要击鼓三次，没次击鼓要么出现一次音乐，要么不出现音乐：每盘游戏击鼓三次后，出现一次音乐获10分，出现2次音乐获20分，出现三次音乐获100分，没有出现音乐则扣除200分（即获得-200分）. 设每次击鼓出现音乐的概率为12，且各次击鼓出现音乐相互独立. (1)设每盘游戏获得的分数为X ，求X 的分布列；（2）玩三盘游戏，至少有一盘出现音乐的概率是多少？（3）玩过这款游戏的许多人都发. 若干盘游戏后，与最初的分数相比，分数没有增加反而减少. 请运用概率统的相关知识分析分数减少的原因.解析：（1）X 的可能取值为-200，10，20，100，所以X 的分布列为(2) 至少有一盘出现音乐的概率是311()8-=511512；（3）54EX =-，说明获得分数X 的均值为负，因此多次游戏后分数减少的可能性更大. 18.三棱锥A BCD -及其侧视图，俯视图如图所示. 设,M N 分别为线段,AD AB 的中点，P 为线段BC 上的点，且MN NP ⊥.俯视图11侧视图1BC（1）证明：P 是线段BC 的中点；（2）求二面角A NP M --的余弦值.519.设等差数列{}n a 的公差为d,点(,)n n a b 在函数()2xf x =的图像上（*n N ∈）（1）若12a =-，点87(,4)a b 在函数()f x 的图像上，求数列{}n a 的前n 项和n S ；（2）若11a =，函数()f x 的图像在点22(,)a b 处的切线在x 轴上的截距为12ln 2-，求数列{}n nab 的前n 项和n T . 解析：点(,)n n a b 在函数()2xf x =的图像上，∴ 2n an b =（1）点87(,4)a b 在函数()f x 的图像上，∴8742ab =，即872722a a b -==，所以87872,2a a d a a -==-=，故{}22n a -是首项为，公差为的等差数列.因此，2(1)2232n n n S n n n -=-+⨯=-；（2）由'()2ln 2xf x =得，函数()f x 的图像在点22(,)a b 处的切线为：2222ln 2()a y x a b =-+，其在x 轴上的截距为：22221122ln 2ln 2ln 2a b a a -=-=-，所以22a =，故{}11n a 是首项为，公差为的等差数列，=,2n n n a n b =由=2n n n a nb 得，12311231++++22222n n n n n T --=⋅⋅⋅+ ①234111231++++222222n n n n nT +-=⋅⋅⋅+ ② ①-②得，12311111[1()]11111222++12222222212n n n n n n n n n T +++-+=+⋅⋅⋅+-=-=-- 所以222n n nT +=-.20.已知椭圆2222:1(0)x y C a b a b+=>>的焦距为4，其短轴的两个端点与长轴的的一个端点构成正三角形，（1）求椭圆C 的标准方程；（2）设F 是椭圆C 的左焦点， T 为直线x=-3上任意一点，过F 做TF 的垂线交椭圆C 于点P ，Q ，（i ）证明：OT 平分线段PQ ；（ii ）当TP PQ最小时，求点T 的坐标.解析：（1）由题意得24,c a ==，解得a b ==所以椭圆C 的标准方程为：22162x y +=；21.已知函数2()1x f x e ax bx =---，其中,a b R ∈（1）设()g x 是函数()f x 的导函数，求函数()g x 在区间[0,1]的最小值；（2）若(1)0f =，函数()f x 在区间（0,1）内有零点，求a 的取值范围. 解：（1）()'()2,[0,1],'()2xxg x f x e ax b x g x e a ==--∈=-则当0a ≤时，'()0g x >，min ()(0)1g x g b ==-；当0a >时，令'()0g x =得ln 2x a =,(i)当10ln 202a a <≤≤时，，()g x 在[0,1]上单调递增， min ()(0)1g x g b ==-；（ii ）当1ln 2122ea a <<<<时，0，()g x 在[0,ln 2]a 上单调递减，在[ln 2,1]a 上单调递增，所以min ()(ln 2)2(ln 2)g x g a ab a a ==--；（iii ）当ln 212ea a ≥≥时，，()g x 在[0,1]上单调递减，所以 min ()(1)2g x g e a b ==--.综上所述，min11,21()2(ln 2),222,2b a e g x a b a a a e e a b a ⎧-≤⎪⎪⎪=--<<⎨⎪⎪--≥⎪⎩（2）由(1)0f =得，1b e a =--注意到(0)(1)0f f ==，()f x 在区间[0,1]内连续， (i)当102a <≤时，min ()120g x b a e =-=+-<；。

2014年高考真题(理科数学)四川卷纯Word版解析可编辑

2014·四川卷(理科数学)1．[2014·四川卷] 已知集合A ＝{x |x 2－x －2≤0}，集合B 为整数集，则A ∩B ＝( ) A ．{－1，0，1，2} B ．{－2，－1，0，1} C ．{0，1} D ．{－1，0} 1．A [解析] 由题意可知，集合A ＝{x |－1≤x ≤2}，其中的整数有－1，0，1，2，故A ∩B ＝{－1，0，1，2}，故选A.2．[2014·四川卷] 在x (1＋x )6的展开式中，含x 3项的系数为( ) A ．30 B ．20 C ．15 D ．102．C [解析] x (1＋x )6的展开式中x 3项的系数与(1＋x )6的展开式中x 2项的系数相同，故其系数为C 26＝15.3．[2014·四川卷] 为了得到函数y ＝sin (2x ＋1)的图像，只需把函数y ＝sin 2x 的图像上所有的点( )A ．向左平行移动12个单位长度B ．向右平行移动12个单位长度C ．向左平行移动1个单位长度D ．向右平行移动1个单位长度3．A [解析] 因为y ＝sin(2x ＋1)＝sin2⎝⎛⎭⎫x ＋12，所以为得到函数y ＝sin(2x ＋1)的图像，只需要将y ＝sin 2x 的图像向左平行移动12个单位长度．4．[2014·四川卷] 若a >b >0，c <d <0，则一定有( ) A.a c >b d B.a c <b d C.a d >b c D.a d <b c4．D [解析] 因为c ＜d ＜0，所以1d <1c ＜0，即－1d >－1c ＞0，与a ＞b ＞0对应相乘得，－a d >－b c ＞0，所以a d <bc.故选D. 5．，[2014·四川卷] 执行如图1-1所示的程序框图，如果输入的x ，y ∈R ，那么输出的S 的最大值为( )图1-1A ．0B ．1C ．2D ．35．C [解析] 题中程序输出的是在⎩⎪⎨⎪⎧x ＋y ≤1，x ≥0，y ≥0的条件下S ＝2x ＋y 的最大值与1中较大的数．结合图像可得，当x ＝1，y ＝0时，S ＝2x ＋y 取得最大值2，2>1，故选C.6．[2014·四川卷] 六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有( )A ．192种B ．216种C ．240种D ．288种6．B [解析] 当甲在最左端时，有A 55＝120(种)排法；当甲不在最左端时，乙必须在最左端，且甲也不在最右端，有A 11A 14A 44＝4×24＝96(种)排法，共计120＋96＝216(种)排法．故选B.7．[2014·四川卷] 平面向量a ＝(1，2)，b ＝(4，2)，c ＝m a ＋b (m ∈R )，且c 与a 的夹角等于c 与b 的夹角，则m ＝( )A ．－2B ．－1C ．1D ．27．2 [解析] c ＝m a ＋b ＝(m ＋4，2m ＋2)，由题意知a ·c |a |·|c |＝b ·c |b |·|c |，即（1，2）·（m ＋4，2m ＋2）12＋22＝（4，2）·（m ＋4，2m ＋2）42＋22，即5m ＋8＝8m ＋202，解得m ＝2.图1-28．[2014·四川卷] 如图1-2，在正方体ABCD - A 1B 1C 1D 1中，点O 为线段BD 的中点，设点P 在线段CC 1上，直线OP 与平面A 1BD 所成的角为α，则sin α的取值范围是( )A.⎣⎡⎦⎤33，1B.⎣⎡⎦⎤63，1 C.⎣⎡⎦⎤63，223 D.⎣⎡⎦⎤223，1 8．B [解析] 连接A 1O ，OP 和P A 1，不难知∠POA 1就是直线OP 与平面A 1BD 所成的角(或其补角)设正方体棱长为2，则A 1O ＝ 6.(1)当P 点与C 点重合时，PO ＝2，A 1P ＝23，且cos α＝6＋2－122×6×2＝－33，此时α＝∠A 1OP 为钝角，sin α＝1－cos 2α＝63； (2)当P 点与C 1点重合时，PO ＝A 1O ＝6，A 1P ＝22，且cos α＝6＋6－82×6×6＝13，此时α＝∠A 1OP 为锐角，sin α＝1－cos 2 α＝223；(3)在α从钝角到锐角逐渐变化的过程中，CC 1上一定存在一点P ，使得α＝∠A 1OP ＝90°.又因为63＜223，故sin α的取值范围是⎣⎡⎦⎤63，1，故选B. 9．[2014·四川卷] 已知f (x )＝ln(1＋x )－ln(1－x )，x ∈(－1，1)．现有下列命题： ①f (－x )＝－f (x )；②f ⎝⎛⎭⎫2x1＋x 2＝2f (x )；③|f (x )|≥2|x |.其中的所有正确命题的序号是( )A ．①②③B ．②③C ．①③D ．①② 9．A [解析] f (－x )＝ln(1－x )－ln(1＋x ) ＝ln1－x 1＋x ＝－ln 1＋x1－x＝－[]ln （1＋x ）－ln （1－x ）＝－f (x )，故①正确；当x ∈(－1，1)时，2x 1＋x 2∈(－1，1)，且f ⎝⎛⎭⎫2x 1＋x 2＝ln ⎝⎛⎭⎫1＋2x 1＋x 2－ln ⎝⎛⎭⎫1－2x 1＋x 2＝ln 1＋2x1＋x 21－2x 1＋x 2＝ln 1＋x 2＋2x 1＋x 2－2x ＝ln ⎝ ⎛⎭⎪⎫1＋x 1－x 2＝2ln 1＋x 1－x ＝2[ln(1＋x )－ln(1－x )]＝2f (x )，故②正确；由①知，f (x )为奇函数，所以|f (x )|为偶函数，则只需判断当x ∈[0，1)时，f (x )与2x 的大小关系即可．记g (x )＝f (x )－2x ，0≤x ＜1，即g (x )＝ln(1＋x )－ln(1－x )－2x ，0≤x <1，g ′(x )＝11＋x ＋11－x －2＝2x 21－x 2，0≤x ＜1.当0≤x ＜1时，g ′(x )≥0，即g (x )在[0，1)上为增函数，且g (0)＝0，所以g (x )≥0，即f (x )－2x ≥0，x ∈[0，1)，于是|f (x )|≥2|x |正确．综上可知，①②③都为真命题，故选A. 10．，[2014·四川卷] 已知F 为抛物线y 2＝x 的焦点，点A ，B 在该抛物线上且位于x 轴的两侧，OA →·OB →＝2(其中O 为坐标原点)，则△ABO 与△AFO 面积之和的最小值是( )A ．2B ．3 C.1728D.1010．B [解析] 由题意可知，F ⎝⎛⎭⎫14，0.设A (y 21，y 1)，B (y 22，y 2)，∴OA →·OB →＝y 1y 2＋y 21y 22＝2，解得y 1y 2＝1或y 1y 2＝－2.又因为A ，B 两点位于x 轴两侧，所以y 1y 2＜0，即y 1y 2＝－2. 当y 21≠y 22时，AB 所在直线方程为y －y 1＝y 1－y 2y 21－y 22(x －y 21)＝ 1y 1＋y 2(x －y 21)，令y ＝0，得x ＝－y 1y 2＝2，即直线AB 过定点C (2，0)．于是S △ABO ＋S △AFO ＝S △ACO ＋S △BCO ＋S △AFO ＝12×2|y 1|＋12×2|y 2|＋12×14|y 1|＝18(9|y 1|＋8|y 2|)≥18×29|y 1|×8|y 2|＝3，当且仅当9|y 1|＝8|y 2|且y 1y 2＝－2时，等号成立．当y 21＝y 22时，取y 1＝2，y 2＝－2，则AB 所在直线的方程为x ＝2，此时求得S △ABO ＋S △AFO ＝2×12×2×2＋12×14×2＝1728，而1728>3，故选B. 11．[2014·四川卷] 复数2－2i1＋i ＝________．11．－2i [解析] 2－2i 1＋i ＝2（1－i ）2（1＋i ）（1－i ）＝－2i.12．[2014·四川卷] 设f (x )是定义在R 上的周期为2的函数，当x ∈[－1，1)时，f (x )＝⎩⎪⎨⎪⎧－4x 2＋2，－1≤x <0，x ， 0≤x <1，则f ⎝⎛⎭⎫32＝________． 12．1 [解析] 由题意可知，f ⎝⎛⎭⎫32＝f ⎝⎛⎭⎫2－12＝f ⎝⎛⎭⎫－12＝－4⎝⎛⎭⎫－122＋2＝1. 13．，[2014·四川卷] 如图1-3所示，从气球A 上测得正前方的河流的两岸B ，C 的俯角分别为67°，30°，此时气球的高度是46 m ，则河流的宽度BC 约等于________m ．(用四舍五入法将结果精确到个位．参考数据：sin 67°≈0.92，cos 67°≈0.39，sin 37°≈0.60，cos 37°≈0.80，3≈1.73)图1-313．60 [解析] 过A 点向地面作垂线，记垂足为D ，则在Rt △ADB 中，∠ABD ＝67°，AD ＝46 m ，∴AB ＝AD sin 67°＝460.92＝50(m)，在△ABC 中，∠ACB ＝30°，∠BAC ＝67°－30°＝37°，AB ＝50 m ，由正弦定理得，BC ＝AB sin 37°sin 30°＝60 (m)，故河流的宽度BC 约为60 m. 14．，[2014·四川卷] 设m ∈R ，过定点A 的动直线x ＋my ＝0和过定点B 的动直线mx －y －m ＋3＝0交于点P (x ，y )，则|P A |·|PB |的最大值是________．14．5 [解析] 由题意可知，定点A (0，0)，B (1，3)，且两条直线互相垂直，则其交点P (x ，y )落在以AB 为直径的圆周上，所以|P A |2＋|PB |2＝|AB |2＝10.∴|P A ||PB |≤|P A |2＋|PB |22＝5，当且仅当|P A |＝|PB |时等号成立． 15．，[2014·四川卷] 以A 表示值域为R 的函数组成的集合，B 表示具有如下性质的函数φ(x )组成的集合：对于函数φ(x )，存在一个正数M ，使得函数φ(x )的值域包含于区间[－M ，M ]．例如，当φ1(x )＝x 3，φ2(x )＝sin x 时，φ1(x )∈A ，φ2(x )∈B .现有如下命题：①设函数f (x )的定义域为D ，则“f (x )∈A ”的充要条件是“∀b ∈R ，∃a ∈D ，f (a )＝b ”； ②函数f (x )∈B 的充要条件是f (x )有最大值和最小值；③若函数f (x )，g (x )的定义域相同，且f (x )∈A ，g (x )∈B ，则f (x )＋g (x )∉B ；④若函数f (x )＝a ln(x ＋2)＋xx 2＋1(x >－2，a ∈R )有最大值，则f (x )∈B .其中的真命题有________．(写出所有真命题的序号)15．①③④ [解析] 若f (x )∈A ，则f (x )的值域为R ，于是，对任意的b ∈R ，一定存在a ∈D ，使得f (a )＝b ，故①正确．取函数f (x )＝x (－1＜x ＜1)，其值域为(－1，1)，于是，存在M ＝1，使得f (x )的值域包含于[－M ，M ]＝[－1，1]，但此时f (x )没有最大值和最小值，故②错误．当f (x )∈A 时，由①可知，对任意的b ∈R ，存在a ∈D ，使得f (a )＝b ，所以，当g (x )∈B 时，对于函数f (x )＋g (x )，如果存在一个正数M ，使得f (x )＋g (x )的值域包含于[－M ，M ]，那么对于该区间外的某一个b 0∈R ，一定存在一个a 0∈D ，使得f (a 0)＝b －g (a 0)，即f (a 0)＋g (a 0)＝b 0∉[－M ，M ]，故③正确．对于f (x )＝a ln(x ＋2)＋xx 2＋1 (x ＞－2)，当a ＞0或a ＜0时，函数f (x )都没有最大值．要使得函数f (x )有最大值，只有a ＝0，此时f (x )＝xx 2＋1(x ＞－2)．易知f (x )∈⎣⎡⎦⎤－12，12，所以存在正数M ＝12，使得f (x )∈[－M ，M ]，故④正确． 16．，，，[2014·四川卷] 已知函数f (x )＝sin ⎝⎛⎭⎫3x ＋π4.(1)求f (x )的单调递增区间；(2)若α是第二象限角，f ⎝⎛⎭⎫α3＝45cos ⎝⎛⎭⎫α＋π4cos 2α，求cos α－sin α的值．16．解：(1)因为函数y ＝sin x 的单调递增区间为⎣⎡⎦⎤－π2＋2k π，π2＋2k π，k ∈Z ，由－π2＋2k π≤3x ＋π4≤π2＋2k π，k ∈Z ，得－π4＋2k π3≤x ≤π12＋2k π3，k ∈Z .所以，函数f (x )的单调递增区间为⎣⎡⎦⎤－π4＋2k π3，π12＋2k π3，k ∈Z . (2)由已知，得sin ⎝⎛⎭⎫α＋π4＝45cos ⎝⎛⎭⎫α＋π4(cos 2α－sin 2α)，所以sin αcos π4＋cos αsin π4＝45⎝⎛⎭⎫cos α cos π4－sin αsin π4(cos 2 α－sin 2 α)，即sin α＋cos α＝45(cos α－sin α)2(sin α＋cos α)．当sin α＋cos α＝0时，由α是第二象限角，得α＝3π4＋2k π，k ∈Z ，此时，cos α－sin α＝－ 2.当sin α＋cos α≠0时，(cos α－sin α)2＝54.由α是第二象限角，得cos α－sin α<0，此时cos α－sin α＝－52. 综上所述，cos α－sin α＝－2或－52. 17．，，，[2014·四川卷] 一款击鼓小游戏的规则如下：每盘游戏都需击鼓三次，每次击鼓要么出现一次音乐，要么不出现音乐；每盘游戏击鼓三次后，出现一次音乐获得10分，出现两次音乐获得20分，出现三次音乐获得100分，没有出现音乐则扣除200分(即获得－200分)．设每次击鼓出现音乐的概率为12，且各次击鼓出现音乐相互独立．(1)设每盘游戏获得的分数为X ，求X 的分布列．(2)玩三盘游戏，至少有一盘出现音乐的概率是多少？(3)玩过这款游戏的许多人都发现，若干盘游戏后，与最初的分数相比，分数没有增加反而减少了．请运用概率统计的相关知识分析分数减少的原因．17．解：(1)X 可能的取值为10，20，100，－200. 根据题意，有P (X ＝10)＝C 13×⎝⎛⎭⎫121×⎝⎛⎭⎫1－122＝38，P (X ＝20)＝C 23×⎝⎛⎭⎫122×⎝⎛⎭⎫1－121＝38， P (X ＝100)＝C 33×⎝⎛⎭⎫123×⎝⎛⎭⎫1－120＝18， P (X ＝－200)＝C 03×⎝⎛⎭⎫120×⎝⎛⎭⎫1－123＝18. 所以X 的分布列为：X 10 20 100 －200 P38381818(2)设“第i 盘游戏没有出现音乐”为事件A i (i ＝1，2，3)，则 P (A 1)＝P (A 2)＝P (A 3)＝P (X ＝－200)＝18.所以“三盘游戏中至少有一盘出现音乐”的概率为1－P (A 1A 2A 3)＝1－⎝⎛⎭⎫183＝1－1512＝511512.因此，玩三盘游戏至少有一盘出现音乐的概率是511512.(3)由(1)知，X 的数学期望为EX ＝10×38＋20×38＋100×18－200×18＝－54.这表明，获得分数X 的均值为负．因此，多次游戏之后分数减少的可能性更大． 18．，，，[2014·四川卷] 三棱锥A - BCD 及其侧视图、俯视图如图1-4所示．设M ，N 分别为线段AD ，AB 的中点，P 为线段BC 上的点，且MN ⊥NP .(1)证明：P 是线段BC 的中点； (2)求二面角A - NP - M 的余弦值．图1-418．解：(1)如图所示，取BD 的中点O ，连接AO ，CO . 由侧视图及俯视图知，△ABD ，△BCD 为正三角形，所以AO ⊥BD ，OC ⊥BD .因为AO ，OC ⊂平面AOC ，且AO ∩OC ＝O ，所以BD ⊥平面AOC .又因为AC ⊂平面AOC ，所以BD ⊥AC . 取BO 的中点H ，连接NH ，PH .又M ，N ，H 分别为线段AD ，AB ，BO 的中点，所以MN ∥BD ，NH ∥AO ，因为AO ⊥BD ，所以NH ⊥BD . 因为MN ⊥NP ，所以NP ⊥BD .因为NH ，NP ⊂平面NHP ，且NH ∩NP ＝N ，所以BD ⊥平面NHP . 又因为HP ⊂平面NHP ，所以BD ⊥HP .又OC ⊥BD ，HP ⊂平面BCD ，OC ⊂平面BCD ，所以HP ∥OC . 因为H 为BO 的中点，所以P 为BC 的中点．(2)方法一：如图所示，作NQ ⊥AC 于Q ，连接MQ .由(1)知，NP ∥AC ，所以NQ ⊥NP .因为MN ⊥NP ，所以∠MNQ 为二面角A - NP - M 的一个平面角．由(1)知，△ABD ，△BCD 为边长为2的正三角形，所以AO ＝OC ＝ 3. 由俯视图可知，AO ⊥平面BCD .因为OC ⊂平面BCD ，所以AO ⊥OC ，因此在等腰直角△AOC 中，AC ＝ 6. 作BR ⊥AC 于R因为在△ABC 中，AB ＝BC ，所以R 为AC 的中点，所以BR ＝AB 2－⎝⎛⎭⎫AC 22＝102.因为在平面ABC 内，NQ ⊥AC ，BR ⊥AC ，所以NQ ∥BR .又因为N 为AB 的中点，所以Q 为AR 的中点，所以NQ ＝BR 2＝104.同理，可得MQ ＝104. 故△MNQ 为等腰三角形，所以在等腰△MNQ 中， cos ∠MNQ ＝MN 2NQ ＝BD 4NQ ＝105.故二面角A - NP - M 的余弦值是105. 方法二：由俯视图及(1)可知，AO ⊥平面BCD .因为OC ，OB ⊂平面BCD ，所以AO ⊥OC ，AO ⊥OB . 又OC ⊥OB ，所以直线OA ，OB ，OC 两两垂直．如图所示，以O 为坐标原点，以OB ，OC ，OA 的方向为x 轴，y 轴，z 轴的正方向，建立空间直角坐标系O -xyz .则A (0，0，3)，B (1，0，0)，C (0，3，0)，D (－1，0，0)．因为M ，N 分别为线段AD ，AB 的中点，又由(1)知，P 为线段BC 的中点，所以M ⎝⎛⎭⎫－12，0，32，N ⎝⎛⎭⎫12，0，32，P ⎝⎛⎭⎫12，32，0，于是AB ＝(1，0，－3)，BC ＝(－1，3，0)，MN ＝(1，0，0)，NP ＝⎝⎛⎭⎫0，32，－32. 设平面ABC 的一个法向量n 1＝(x 1，y 1，z 1)，由⎩⎪⎨⎪⎧n 1⊥AB ，n 1⊥BC ，得⎩⎪⎨⎪⎧n 1·AB ＝0，n 1·BC ＝0，即⎩⎨⎧（x 1，y 1，z 1）·（1，0，－3）＝0，（x 1，y 1，z 1）·（－1，3，0）＝0，从而⎩⎨⎧x 1－3z 1＝0，－x 1＋3y 1＝0.取z 1＝1，则x 1＝3，y 1＝1，所以n 1＝(3，1，1)．设平面MNP 的一个法向量n 2＝(x 2，y 2，z 2)，由，⎩⎪⎨⎪⎧n 2⊥MN ，n 2⊥NP ，得⎩⎪⎨⎪⎧n 2·MN ＝0，n 2·NP ＝0，即⎩⎪⎨⎪⎧（x 2，y 2，z 2）·（1，0，0）＝0，（x 2，y 2，z 2）·⎝⎛⎭⎫0，32，－32＝0，从而⎩⎪⎨⎪⎧x 2＝0，32y 2－32z 2＝0. 取z 2＝1，则y 2＝1，x 2＝0，所以n 2＝(0，1，1)．设二面角A - NP - M 的大小为θ，则cos θ＝⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|＝⎪⎪⎪⎪⎪⎪（3，1，1）·（0，1，1）5×2＝105. 故二面角A -NP -M 的余弦值是105. 19．，[2014·四川卷] 设等差数列{a n }的公差为d ，点(a n ，b n )在函数f (x )＝2x 的图像上(n ∈N *)．(1)若a 1＝－2，点(a 8，4b 7)在函数f (x )的图像上，求数列{a n }的前n 项和S n ；(2)若a 1＝1，函数f (x )的图像在点(a 2，b 2)处的切线在x 轴上的截距为2－1ln 2，求数列⎩⎨⎧⎭⎬⎫a nb n 的前n 项和T n .19．解：(1)由已知得，b 7＝2a 7，b 8＝2a 8＝4b 7，所以 2a 8＝4×2a 7＝2a 7＋2，解得d ＝a 8－a 7＝2，所以S n ＝na 1＋n （n －1）2d ＝－2n ＋n (n －1)＝n 2－3n .(2)函数f (x )＝2x 在点(a 2，b 2)处的切线方程为y －2a 2＝(2a 2ln 2)(x －a 2)，其在x 轴上的截距为a 2－1ln 2.由题意有a 2－1ln 2＝2－1ln 2，解得a 2＝2.所以d ＝a 2－a 1＝1.从而a n ＝n ，b n ＝2n ，所以数列{a n b n }的通项公式为a n b n ＝n2n ，所以T n ＝12＋222＋323＋…＋n －12n －1＋n 2n ，2T n ＝11＋22＋322＋…＋n2n －1，因此，2T n －T n ＝1＋12＋122＋…＋12n －1－n 2n ＝2－12n －1－n 2n ＝2n ＋1－n －22n .所以，T n ＝2n ＋1－n －22n.20．，，[2014·四川卷] 已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形．(1)求椭圆C 的标准方程．(2)设F 为椭圆C 的左焦点，T 为直线x ＝－3上任意一点，过F 作TF 的垂线交椭圆C 于点P ，Q .①证明：OT 平分线段PQ (其中O 为坐标原点)；②当|TF ||PQ |最小时，求点T 的坐标．20．解：(1)由已知可得⎩⎨⎧a 2＋b 2＝2b ，2c ＝2a 2－b 2＝4，解得a 2＝6，b 2＝2，所以椭圆C 的标准方程是x 26＋y 22＝1.(2)①证明：由(1)可得，F 的坐标是(－2，0)，设T 点的坐标为(－3，m )，则直线TF 的斜率k TF ＝m －0－3－（－2）＝－m .当m ≠0时，直线PQ 的斜率k PQ ＝1m .直线PQ 的方程是x ＝my －2.当m ＝0时，直线PQ 的方程是x ＝－2，也符合x ＝my －2的形式．设P (x 1，y 1)，Q (x 2，y 2)，将直线PQ 的方程与椭圆C 的方程联立，得⎩⎪⎨⎪⎧x ＝my －2，x 26＋y 22＝1.消去x ，得(m 2＋3)y 2－4my －2＝0，其判别式Δ＝16m 2＋8(m 2＋3)>0. 所以y 1＋y 2＝4mm 2＋3，y 1y 2＝－2m 2＋3，x 1＋x 2＝m (y 1＋y 2)－4＝－12m 2＋3.设M 为PQ 的中点，则M 点的坐标为⎝ ⎛⎭⎪⎫－6m 2＋3，2m m 2＋3.所以直线OM 的斜率k OM ＝－m3，又直线OT 的斜率k OT ＝－m3，所以点M 在直线OT 上，因此OT 平分线段PQ .②由①可得，|TF |＝m 2＋1，|PQ |＝（x 1－x 2）2＋（y 1－y 2）2＝（m 2＋1）[（y 1＋y 2）2－4y 1y 2]＝（m 2＋1）⎣⎢⎡⎦⎥⎤⎝⎛⎭⎫4m m 2＋32－4·－2m 2＋3 ＝24（m 2＋1）m 2＋3. 所以|TF ||PQ |＝124·（m 2＋3）2m 2＋1＝ 124⎝⎛⎭⎫m 2＋1＋4m 2＋1＋4≥124（4＋4）＝33. 当且仅当m 2＋1＝4m 2＋1，即m ＝±1时，等号成立，此时|TF ||PQ |取得最小值．故当|TF ||PQ |最小时，T 点的坐标是(－3，1)或(－3，－1)． 21．，[2014·四川卷] 已知函数f (x )＝e x －ax 2－bx －1，其中a ，b ∈R ，e ＝2.718 28…为自然对数的底数．(1)设g (x )是函数f (x )的导函数，求函数g (x )在区间[0，1]上的最小值；(2)若f (1)＝0，函数f (x )在区间(0，1)内有零点，求a 的取值范围．21．解：(1)由f (x )＝e x －ax 2－bx －1，得g (x )＝f ′(x )＝e x －2ax －b .所以g ′(x )＝e x －2a .当x ∈[0，1]时，g ′(x )∈[1－2a ，e －2a ]．当a ≤12时，g ′(x )≥0，所以g (x )在[0，1]上单调递增，因此g (x )在[0，1]上的最小值是g (0)＝1－b ；当a ≥e 2时，g ′(x )≤0，所以g (x )在[0，1]上单调递减，因此g (x )在[0，1]上的最小值是g (1)＝e －2a －b ；当12<a <e 2时，令g ′(x )＝0，得x ＝ln(2a )∈(0，1)，所以函数g (x )在区间[0，ln(2a )]上单调递减，在区间(ln(2a )，1]上单调递增，于是，g (x )在[0，1]上的最小值是g (ln(2a ))＝2a －2a ln(2a )－b .综上所述，当a ≤12时，g (x )在[0，1]上的最小值是g (0)＝1－b ；当12<a <e 2时，g (x )在[0，1]上的最小值是g (ln(2a ))＝2a －2a ln(2a )－b ；当a ≥e 2时，g (x )在[0，1]上的最小值是g (1)＝e －2a －b . (2)设x 0为f (x )在区间(0，1)内的一个零点，则由f (0)＝f (x 0)＝0可知，f (x )在区间(0，x 0)上不可能单调递增，也不可能单调递减．则g (x )不可能恒为正，也不可能恒为负．故g (x )在区间(0，x 0)内存在零点x 1.同理g (x )在区间(x 0，1)内存在零点x 2.故g (x )在区间(0，1)内至少有两个零点．由(1)知，当a ≤12时，g (x )在[0，1]上单调递增，故g (x )在(0，1)内至多有一个零点；当a ≥e 2时，g (x )在[0，1]上单调递减，故g (x )在(0，1)内至多有一个零点，都不合题意．所以12<a <e 2. 此时g (x )在区间[0，ln(2a )]上单调递减，在区间(ln(2a )，1]上单调递增．因此x 1∈(0，ln(2a )]，x 2∈(ln(2a )，1)，必有g (0)＝1－b >0，g (1)＝e －2a －b >0.由f (1)＝0得a ＋b ＝e －1<2，则g (0)＝a －e ＋2>0，g (1)＝1－a >0，解得e －2<a <1.当e －2<a <1时，g (x )在区间[0，1]内有最小值g (ln(2a ))．若g (ln(2a ))≥0，则g (x )≥0(x ∈[0，1])，从而f (x )在区间[0，1]内单调递增，这与f (0)＝f (1)＝0矛盾，所以g (ln(2a ))<0. 又g (0)＝a －e ＋2>0，g (1)＝1－a >0.故此时g (x )在(0，ln(2a ))和(ln(2a )，1)内各只有一个零点x 1和x 2.由此可知f (x )在[0，x 1]上单调递增，在(x 1，x 2)上单调递减，在[x 2，1]上单调递增．所以f (x 1)>f (0)＝0，f (x 2)<f (1)＝0，故f (x )在(x 1，x 2)内有零点．综上可知，a 的取值范围是(e －2，1)．。

2014年普通高等学校招生全国统一考试数学理试题(四川卷,含答案)

2014年普通高等学校招生全国统一考试理科（四川卷）一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一个是符合题目要求的。

1．已知集合2{|20}A x x x =--≤，集合B 为整数集，则A B ⋂= A ．{1,0,1,2}- B ．{2,1,0,1}-- C ．{0,1} D ．{1,0}- 【答案】A【解析】{|12}A x x =-≤≤，B Z =，故A B ⋂={1,0,1,2}- 2．在6(1)x x +的展开式中，含3x 项的系数为 A ．30 B ．20 C ．15 D ．10 【答案】C【解析】含3x 项为24236(1)15x C x x ⋅=3．为了得到函数sin(21)y x =+的图象，只需把函数sin 2y x =的图象上所有的点 A ．向左平行移动12个单位长度 B ．向右平行移动12个单位长度 C ．向左平行移动1个单位长度 D ．向右平行移动1个单位长度【答案】A【解析】因为1sin(21)sin[2()]2y x x =+=+，故可由函数sin 2y x =的图象上所有的点向左平行移动12个单位长度得到4．若0a b >>，0c d <<，则一定有 A ．a b c d > B ．a b c d < C ．a b d c > D ．a b d c< 【答案】D【解析】由1100c d d c<<⇒->->，又0a b >>，由不等式性质知：0a b d c ->->，所以a bd c< 5．执行如图1所示的程序框图，如果输入的,x y R ∈，则输出的S 的最大值为A ．0B ．1C ．2D ．3 【答案】C【解析】当001x y x y ≥⎧⎪≥⎨⎪+≤⎩时，函数2S x y =+的最大值为2.6．六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有 A ．192种 B ．216种 C ．240种 D ．288种【答案】B【解析】当最左端为甲时，不同的排法共有55A 种；当最左端为乙时，不同的排法共有14C 44A 种。

2014年四川高考理科数学试题含答案(Word版)

| PA |2 | PB |2 5 （当且仅当 | PA || PB | 5 时取“ ” ） 2 15．以 A 表示值域为 R 的函数组成的集合， B 表示具有如下性质的函数 ( x) 组成的集合：对于函数 ( x) ，存在一个正数 M ，使得函数 ( x) 的值域包含于区间 [ M , M ] 。例如，当
x （ x 2 ， a R ）有最大值，则 f ( x) B 。 x 1
2
。（写出所有真命题的序号）
三．解答题：本大题共 6 小题，共 75 分。解答须写出文字说明，证明过程或演算步骤。 16．已知函数 f ( x) sin(3 x

4
)。
（1）求 f ( x) 的单调递增区间；
4 x 2 2, 1 x 0, 3 f ( x) ，则 f ( ) 2 0 x 1, x, 【答案】 1 3 1 1 【解析】 f ( ) f ( ) 4 ( ) 2 2 1 2 2 2
。
13．如图，从气球 A 上测得正前方的河流的两岸 B，C 的俯角分别为 67 ， m。（用 30 ，此时气球的高是 46m ，则河流的宽度 BC 约等于四舍五入法将结果精确到个位。参考数据： sin 67 0.92 ，
5 1 4 9 24 216 种共有 A5 + C4 A4
7．平面向量 a (1, 2) ， b (4, 2) ， c ma b （ m R ），且 c 与 a 的夹角等于 c 与 b 的夹角，则 m
-1-

A． 2 【答案】D
B． 1

2014年高考理科数学四川卷答案及解析(word版)

2014四川理科卷一、选择题1. 答案：A解析：{|12},{1,0,1,2}A x x AB =-≤≤∴=-，选A.【考点定位】集合的基本运算.2. 答案：C 解析：623456(1)(161520156)x x x x x x x x x +=++++++，所以含3x 项的系数为15.选C【考点定位】二项式定理.3. 答案：A 解析：1sin(21)sin 2()2y x x =+=+，所以只需把sin 2y x =的图象上所有的点向左平移12个单位.选A. 【考点定位】三角函数图象的变换.4. 答案：D 解析：110,0,0c d c d d c <<∴->->->->，又0,0,a b a b a b d c d c>>∴->->∴<.选D 【考点定位】不等式的基本性质.5. 答案：C解析：该程序执行以下运算：已知001x y x y ≥⎧⎪≥⎨⎪+≤⎩，求2S x y =+的最大值.作出001x y x y ≥⎧⎪≥⎨⎪+≤⎩表示的区域如图所示，由图可知，当10x y =⎧⎨=⎩时，2S x y =+最大，最大值为202S =+=.选C.【考点定位】线性规划6. 答案：B解析：最左端排甲，有5!120=种排法；最左端排乙，有44!96⨯=种排法，共有12096216+=种排法.选B.【考点定位】排列组合.7. 答案： D.解析：由题意得：25c ac bc ac bm c a c b a b ⋅⋅⋅⋅=⇒=⇒=⇒=⋅⋅，选D.【考点定位】向量的夹角及向量的坐标运算.8. 答案：B解析：设正方体的棱长为1，则11111,,A C A C A O OC ==，所以1111332122cos ,sin 3322AOC AOC +-∠==∠=⨯，11313cos AOC AOC +-∠==∠=.所以sin α的范围为3，选B. 【考点定位】空间直线与平面所成的角.9. 答案：C解析：对①，()ln(1)ln(1)()f x x x f x -=--+=-，成立；对②，左边的x 可以取任意值，而右边的(1,1)x ∈-，故不成立；对③，作出图易知③成立【考点定位】1、函数的奇偶性；2、对数运算；3、函数与不等式.10. 答案：B 解析：据题意得1(,0)4F ，设1122(,),(,)A x y B x y ，则221122,x y x y ==，221212122,2y y y y y y +==-或121y y =，因为,A B 位于x 轴两侧所以.所以122y y =-两面积之和为12211111224S x y x y y =-+⨯⨯111218y y y =++⨯112938y y =+≥. 【考点定位】1、抛物线；2、三角形的面积；3、重要不等式.二、填空题11. 答案：2i -. 解析：2222(1)21(1)(1)i i i i i i --==-++-. 【考点定位】复数的基本运算.12. 答案：1 解析：311()()421224f f =-=-⨯+=. 【考点定位】周期函数及分段函数.13. 答案：60解析：92AC =，46cos 67AB =，sin 37,60sin 30sin 37sin 30AB BC AB BC =∴=≈. 【考点定位】解三角形.14. 答案：解析：易得(0,0),(1,3)A B .设(,)P x y ，则消去m 得：2230x y x y +--=，所以点P 在以AB 为直径的圆上，PA PB ⊥，所以2||||||52AB PA PB ⨯≤=. 法二、因为两直线的斜率互为负倒数，所以PA PB ⊥，点P 的轨迹是以AB 为直径的圆.以下同法一.【考点定位】1、直线与圆；2、重要不等式.15. 答案：①③④解析：对①，若对任意的b R ∈，都a D ∃∈，使得()f a b =，则()f x 的值域必为R ；反之，()f x 的值域为R ，则对任意的b R ∈，都a D ∃∈，使得()f a b =.故正确.对②，比如函数()(11)f x x x =-<<属于B ，但是它既无最大值也无最小值.故错误. 对③正确，对④正确.【考点定位】命题判断。

2014年四川高考理科数学试卷(带详解)

14四川理第I 卷(选择题共50分)一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一个是符合题目要求的.1.已知集合2{|20}A x x x =--…，集合B 为整数集，则A B = ( ) A.{1,0,1,2}- B.{2,1,0,1}-- C.{0,1} D.{1,0}-【测量目标】集合的基本运算(交集),一元二次不等式.【考查方式】综合考查一元二次不等式的求解和交集运算. 【难易程度】容易. 【参考答案】A【试题解析】由题意可知，集合{|12}A x x ＝－剟，其中的整数有－1，0，1，2，故A B ＝{－1，0，1，2}，故选A.2.在6(1)x x +的展开式中，含3x 项的系数为( )A.30B.20C.15D.10 【测量目标】二项式定理.【考查方式】考查二项式定理的某项指数为定值时，此项的系数. 【难易程度】容易. 【参考答案】C【试题解析】6(1)x x ＋的展开式中3x 项的系数与6(1)x ＋的展开式中2x 项的系数相同，故其系数为26C 15=.故选C.3.为了得到函数sin(21)y x =+的图象，只需把函数sin 2y x =的图象上所有的点( )A.向左平行移动12个单位长度 B.向右平行移动12个单位长度 C.向左平行移动1个单位长度 D.向右平行移动1个单位长度【测量目标】函数图像的变换.【考查方式】考查为了达到目标函数的图像，需要将原图像所做的变换.. 【难易程度】容易. 【参考答案】A【试题解析】因为1=sin(2+1)=sin22y x x ⎛⎫+ ⎪⎝⎭，所以为得到函数sin(21)y x ＝＋的图像，只需要将sin 2y x ＝的图像向左平行移动12个单位长度,故选A.4.若0a b >>，0c d <<，则一定有( ) A.a b c d > B.a b c d < C.a b d c > D.a b d c< 【测量目标】分式不等式.【考查方式】由已知不等关系判断分式不等式是否成立. 【难易程度】容易. 【参考答案】D【试题解析】因为0c d ＜＜，所以11<<0d c ，即11>>0d c --，与0a b ＞＞对应相乘得，>>0a bd c--，所以<a bd c.故选D. 5.执行如图1所示的程序框图，如果输入的,x y ∈R ，则输出的S 的最大值为( ) A.0 B.1 C.2 D.3第5题图 SCL01【测量目标】程序框图，判断语句，选择语句,线性规划. 【考查方式】当输入值不确定时，求最大的输出值. 【难易程度】容易. 【参考答案】C【试题解析】题中程序输出的是在100x y x y +⎧⎪⎨⎪⎩………的条件下2S x y ＝＋的最大值与1中较大的数.结合图像可得，当1x ＝，0y ＝时，2S x y ＝＋取得最大值2，2>1，故选C.6.六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有( ) A.192种 B.216种 C.240种 D.288种【测量目标】排列组合.【考查方式】考查将特殊元素优先排列的排列组合思想. 【难易程度】容易. 【参考答案】B【试题解析】当甲在最左端时，有55A =120 (种)排法；当甲不在最左端时，乙必须在最左端，且甲也不在最右端，有114144A A A =424=96⨯ (种)排法，共计120＋96＝216(种)排法.故选B.7.平面向量a =(1,2)， b =(4,2), c ma b =+ (m ∈R )，且c 与a 的夹角等于c 与b的夹角，则m =( )A.2-B.1-C.1D.2 【测量目标】向量的运算.【考查方式】通过中间参数夹角的公式将夹角联系在一起，解出未知数. 【难易程度】容易. 【参考答案】D【试题解析】c ma b =+ ＝(m ＋4，2m ＋2)，由题意知a c b ca cb c，即221(4)2(22)12m m ++++ 224(4)2(22)42m m +++=+ ，即8205+8=2m m +，解得m ＝2,故选D. 8.如图，在正方体1111ABCD A B C D -中，点O 为线段BD 的中点.设点P 在线段1CC 上，直线OP 与平面1A BD 所成的角为α，则sin α的取值范围是( ) A.3[,1]3 B.6[,1]3 C.622[,]33 D.22[,1]3第8题图SCL02【测量目标】直线与平面的夹角.【考查方式】考查分类讨论思想和三角函数. 【难易程度】容易. 【参考答案】B【试题解析】连接1A O ，OP 和1PA ，不难知1POA ∠就是直线OP 与平面1A BD 所成的角(或其补角)设正方体棱长为2，则1=6A O .(1)当P 点与C 点重合时，2PO =，123A P =，且66123c o s =3262α+-=-⨯⨯，此时1AOP α∠＝为钝角26sin = 1cos 3αα-=；(2)当P 点与1C 点重合时，16PO AO ==，122A P =，且6681cos =3266α+-=⨯⨯，此时1AOP α∠＝为锐角，222sin = 1cos 3αα-=；(3)在α从钝角到锐角逐渐变化的过程中，1CC 上一定存在一点P ，使得190A OP α∠︒＝＝.又因为62233α<<，故sin α的取值范围是6,13⎡⎤⎢⎥⎣⎦，故选B. 9.已知()ln(1)ln(1)f x x x =+--，(1,1)x ∈-.现有下列命题：①()()f x f x -=-； ②22()2()1xf f x x =+；③|()|2||f x x ….其中的所有正确命题的序号是( ) A.①②③ B.②③ C.①③ D.①② 【测量目标】函数的奇偶性，对数函数.【考查方式】考查判断函数可能具有的某些性质的方法. 【难易程度】中等. 【参考答案】A【试题解析】()=ln(1)ln(1+)=f x x x ---1ln =1x x -+[]1ln =ln(1)ln(1)=()1xx x f x x +--+----，故①正确；当x ∈(－1，1)时，221+x x ∈(－1，1)，且222222=ln 1+ln 11+1+1x x x f x x x ⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭-=222221121ln =ln 21211xx x x x x x x +++++--+ =211ln =2ln 11x x x x ++⎛⎫⎪--⎝⎭()2[ln(1)ln(1)]2x x f x ＝＋－－＝，故②正确；由①知，f (x )为奇函数，所以()f x 为偶函数，则只需判断当x ∈ [0，1)时，f (x )与2x 的大小关系即可.记g (x )＝f (x )－2x ，01x <…，即()ln(1)ln(1)2g x x x x ＝＋－－－，01x <…，22112()=+21+11x g x x x x '-=--，01x <….当0≤x ＜1时，()g x '≥0，即g (x )在[0，1)上为增函数，且g (0)＝0，所以g (x )≥0，即f (x )－2x ≥0，x ∈[0，1)，于是()2f x x …正确.综上可知，①②③都为真命题，故选A.10.已知F 是抛物线2y x =的焦点，点A ，B 在该抛物线上且位于x 轴的两侧，2OA OB ⋅=(其中O 为坐标原点)，则ABO △与AFO △面积之和的最小值是( )A.2B.3C.1728D.10 【测量目标】向量的运算，最小值问题.【考查方式】考察向量的数量积，点到直线距离等，围成图形的面积等. 【难易程度】中等. 【参考答案】B【试题解析】设直线AB 的方程为：x =ty +m ，点A (1x ，1y )，B (2x ，2y )，直线AB 与x 轴的交点为M (m ，0)，由2x ty my x =+⎧⎨=⎩⇒2y -ty -m =0，根据韦达定理有1y •2y =-m ，∵OA •OB =2，∴1x •2x +1y •2y =2，从而()212y y ⋅+1y •2y −2＝0，∵点A ，B 位于x 轴的两侧，∴1y •2y =-2，故m =2．不妨令点A 在x 轴上方，则1y ＞0，又F (14，0)， ∴ABO S +AFO S =12×2×(1y −2y )+12×14×1y =198y +12y ≥119228y y ⋅＝3．当且仅当198y =12y ，即1y ＝43时，取“=”号，∴△ABO 与△AFO 面积之和的最小值是3，故选B. 第II 卷(非选择题共100分)二、填空题：本大题共5小题，每小题5分，共25分.11.复数22i1i-=+ .【测量目标】含有分式的复数基本运算.【考查方式】考查带有分式的复数的分母实数化. 【难易程度】容易. 【参考答案】-2i 【试题解析】原式=2(22i)(1i)(1i)2i (1i)(1i)--=-=-+-12.设()f x 是定义在R 上的周期为2的函数，当[1,1)x ∈-时，242,10,(),01,x x f x x x ⎧-+-<=⎨<⎩……，则3()2f = . 【测量目标】分段函数和周期函数.【考查方式】给出分段函数的表示形式和某些性质，求在某点的函数值. 【难易程度】容易. 【参考答案】1【试题解析】由已知得，2311()()4()2 1.222f f =-=--+=13.如图，从气球A 上测得正前方的河流的两岸B ，C 的俯角分别为67 ，30 ，此时气球的高是46m ，则河流的宽度BC 约等于 m .(用四舍五入法将结果精确到个位.参考数据：sin 670.92≈ ，cos 670.39≈ ，sin 370.60≈ ，cos370.80≈ ，3 1.73≈)第13题图SCL03【测量目标】三角函数，正弦定理.【考查方式】考察对三角函数和正弦定理的应用以及利用公共边求解未知数. 【难易程度】容易. 【参考答案】60【试题解析】过A 点向地面作垂线，记垂足为D ，则在Rt ADB △中，ABD ∠＝67°，AD ＝46 m ，∴46AB==50sin670.92AD =(m)，在ABC △中，30ACB ∠︒＝，673037BAC ∠︒︒︒＝－＝，AB ＝50 m ，由正弦定理得，sin37==60sin30AB BC(m)，故河流的宽度BC 约为60 m.14.设m ∈R ，过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(,)P x y ，则||||PA PB ⋅的最大值是 .【测量目标】线段长度乘积的最值问题.【考查方式】考察了动直线的定点，两直线关系的判定以及均值不等式的应用. 【难易程度】中等. 【参考答案】5【试题解析】由题意可知，定点A (0，0)，B (1，3)，且两条直线互相垂直，则其交点P (x ，y )落在以AB 为直径的圆周上，所以22210PA PB AB ＋＝＝，∴22||+|||PA||PB|=52PA PB …，当且仅当|PA PB ＝|时等号成立.15.以A 表示值域为R 的函数组成的集合，B 表示具有如下性质的函数()x ϕ组成的集合：对于函数()x ϕ，存在一个正数M ，使得函数()x ϕ的值域包含于区间[,]M M -.例如，当31()x x ϕ=，2()sin x x ϕ=时，1()x A ϕ∈，2()x B ϕ∈.现有如下命题：①设函数()f x 的定义域为D ，则“()f x A ∈”的充要条件是“b R ∀∈，a D ∃∈，()f a b =”；②函数()f x B ∈的充要条件是()f x 有最大值和最小值；③若函数()f x ，()g x 的定义域相同，且()f x A ∈，()g x B ∈，则()()f x g x B +∉；④若函数2()ln(2)1xf x a x x =+++(2x >-，a ∈R )有最大值，则()f x B ∈.其中的真命题有 .(写出所有真命题的序号)【测量目标】充要条件，最值，定义域，复合函数，真假命题. 【考查方式】综合考查函数和简单逻辑用语. 【难易程度】中等. 【参考答案】①③④【试题解析】若()f x A ∈，则f (x )的值域为R ，于是，对任意的b ∈R ，一定存在a ∈D ，使得f (a )＝b ，故①正确.取函数f (x )＝x (－1<x <1)，其值域为(－1，1)，于是，存在M ＝1，使得f (x )的值域包含于[－M ，M ]＝[－1，1]，但此时f (x )没有最大值和最小值，故②错误.当f (x )∈A 时，由①可知，对任意的b ∈R ，存在a ∈D ，使得f (a )＝b ，所以，当g (x )∈B 时，对于函数f (x )＋g (x )，如果存在一个正数M ，使得f (x )＋g (x )的值域包含于[－M ，M ]，那么对于该区间外的某一个0b ∈R ，一定存在一个0a ∈D ，使得f (0a )＝b －g (0a )，即f (0a )＋g (0a )∈ [-M ，M ]，故③正确.对于2()=ln(+2)++1xf x a x x (x >－2)，当a >0或a<0时，函数f (x )都没有最大值.要使得函数f (x )有最大值，只有a ＝0，此时2()=+1xf x x (x ＞－2).易知f (x )∈11,22⎡⎤-⎢⎥⎣⎦，所以存在正数M ＝12，使得f (x )∈[－M ，M ]，故④正确.三、解答题：本大题共6小题，共 75分.解答应写出文字说明、证明过程或演算步骤.16.(本小题满分12分)已知函数()sin(3)4f x x π=+.(1)求()f x 的单调递增区间；(2)若α是第二象限角，4()cos()cos 235f ααα=+π4，求cos sin αα-的值.【测量目标】正弦函数的性质，三角恒等变换.【考查方式】考查正弦型函数的性质，简单的三角恒等变换等基础知识，考察运算求解能力，考察分类与整合，化归与转化等数学思想. 【难易程度】中等.【试题解析】(1)由πππ2π32π242k x k -++剟⇒2ππ2ππ34312k k x -+剟,所以()f x 的单调递增区间为2ππ2ππ[,]34312k k -+(k ∈Z ).(2)由4π()cos()cos 2354f ααα=+⇒4πsin()cos()cos 2454αααπ+=+,因为πcos 2sin(2)sin[2()]24πααα=+=+ππ2sin()cos()44αα=++,所以2π8ππsin()cos ()sin()4544ααα+=++,又α是第二象限角，所以πsin()04α+=或2π5cos ()48α+=.①由πsin()04α+=⇒π3π2ππ2π44k k αα+=+⇒=+(k ∈Z ),所以33cos sin cos sin 244ππαα-=-=-;②由2π5π5cos ()cos()48422αα+=⇒+=-15(cos sin )222αα⇒-=-,所以5cos sin 2αα-=-;综上，cos sin 2αα-=-或5cos sin 2αα-=-. 17.一款击鼓小游戏的规则如下：每盘游戏都需要击鼓三次，每次击鼓要么出现一次音乐，要么不出现音乐；每盘游戏击鼓三次后，出现一次音乐获得10分，出现两次音乐获得20分，出现三次音乐获得100分，没有出现音乐则扣除200分(即获得200-分).设每次击鼓出现音乐的概率为12，且各次击鼓出现音乐相互独立.(1)设每盘游戏获得的分数为X ，求X 的分布列； (2)玩三盘游戏，至少有一盘出现音乐的概率是多少？(3)玩过这款游戏的许多人都发现，若干盘游戏后，与最初的分数相比，分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.【测量目标】排列组合，古典概型，分布列，用期望分析问题. 【考查方式】考查排列组合，古典概型，分布列的综合运用. 【难易程度】中等.【试题解析】(1)X 可能取值有-200，10，20，100,0033111(200)C ()(1)228P X =-=-=，1123113(10)C ()(1)228P X ==-=，2213113(20)C ()(1)228P X ==-=，3303111(100)C ()(1)228P X ==-=,故分布列为: X-2001020100P1838 38 18 (2)由(1)知：每盘游戏出现音乐的概率是33178888p =++=,则玩三盘游戏，至少有一盘出现音乐的概率是00313775111C ()(1)88512p =--=.(3)由(1)知，每盘游戏获得的分数为X 的数学期望是133110()(200)102010088888E X =-⨯+⨯+⨯+⨯=-分.这说明每盘游戏平均得分是负分，由概率统计的相关知识可知：许多人经过若干盘游戏后，与最初的分数相比，分数没有增加反而会减少.18.三棱锥A BCD -及其侧视图、俯视图如图所示.设M ，N 分别为线段AD ，AB 的中点，P 为线段BC 上的点，且MN NP ⊥. (1)证明：P 为线段BC 的中点； (2)求二面角A NP M --的余弦值.第18题图SCL04【测量目标】三视图，二面角的余弦值，证明题.【考查方式】考查了几何体的三视图，由三视图求出几何体尺寸，建立立体坐标系求二面角. 【难易程度】中等. 【试题解析】(1)由三棱锥A BCD -及其侧视图、俯视图可知，在三棱锥A BCD -中：平面ABD ⊥平面CBD ，2AB AD BD CD CB =====,设O 为BD 的中点，连接OA ，OC ,于是OA BD ⊥，OC BD ⊥ 所以BD ⊥平面OAC ⇒BD AC ⊥,因为M ，N 分别为线段AD ，AB 的中点，所以//MN BD ，又MN NP ⊥，故BD NP ⊥,假设P 不是线段BC 的中点，则直线NP 与直线AC 是平面ABC 内相交直线,从而BD ⊥平面ABC ，这与60DBC ∠= 矛盾,所以P 为线段BC 的中点.(2)以O为坐标原点，OB 、OC 、OA 分别为x 、y 、z 轴建立空间直角坐标系，则(0,0,3)A ，13(,0,)22M -，13(,0,)22N ，13(,,0)22P ,于是13(,0,)22AN =- ，33(0,,)22PN =- ，(1,0,0)MN = ,设平面ANP 和平面NPM 的法向量分别为111(,,)m x y z = 和222(,,)n x y z =,由00AN m PN m ⎧⋅=⎪⎨⋅=⎪⎩⇒11111302233022x z y z ⎧-=⎪⎪⎨⎪-+=⎪⎩，设11z =，则(3,1,1)m = ,由00MN n PN n ⎧⋅=⎪⎨⋅=⎪⎩ ⇒222033022x y z =⎧⎪⎨-+=⎪⎩，设21z =，则(0,1,1)n = , 210cos ,5||||52m n m n m n ⋅===⋅⋅,所以二面角A NP M --的余弦值105. 19.设等差数列{}n a 的公差为d ，点(,)n n a b 在函数()2xf x =的图象上(*n ∈N ).(1)若12a =-，点87(,4)a b 在函数()f x 的图象上，求数列{}n a 的前n 项和n S ； (2)若11a =，函数()f x 的图象在点22(,)a b 处的切线在x 轴上的截距为12ln 2-，求数列{}n na b 的前n 项和n T .【测量目标】等数数列，导函数的应用，复合数列前n 项和的求解. 【考查方式】数列和函数综合考查. 【难易程度】较难.【试题解析】(1)点(,)n n a b 在函数()2xf x =的图象上，所以2n an b =，又等差数列{}n a 的公差为d ,所以1112222n n n n a a a d n a n b b ++-+===,因为点87(,4)a b 在函数()f x 的图象上，所以87842a b b ==，所以8724d b b ==2d ⇒=,又12a =-，所以221(1)232n n n S na d n n n n n -=+=-+-=-.(2)由()2()2ln 2x x f x f x '=⇒=,函数()f x 的图象在点22(,)a b 处的切线方程为222(2ln 2)()a y b x a -=-,所以切线在x 轴上的截距为21ln 2a -，从而2112ln 2ln 2a -=-，故22a =,从而n a n =，2n nb =，2n n n a nb =,231232222n n n T =++++ ,2341112322222n n n T +=++++ ,所以23411111112222222n n n n T +=+++++- 111211222n n n n n +++=--=-,故222n n n T +=-. 20.已知椭圆C ：22221x y a b+=(0a b >>)的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形.(1)求椭圆C 的标准方程；(2)设F 为椭圆C 的左焦点，T 为直线3x =-上任意一点，过F 作TF 的垂线交椭圆C 于点P ，Q . (i)证明：OT 平分线段PQ (其中O 为坐标原点)； (ii)当||||TF PQ 最小时，求点T 的坐标. 【测量目标】椭圆的方程，椭圆和直线的关系，均值不等式.【考查方式】考查数形结合思想，几何条件和代数关系的相互转化，曲线和直线联立求解的方法，均值不等式的应用. 【难易程度】较难.【试题解析】(1)依条件2222226324c a a b b a b c =⎧⎧=⎪⎪=⇒⎨⎨=⎪⎩⎪-==⎩,所以椭圆C 的标准方程为22162x y +=.(2)设(3,)T m -，11(,)P x y ，22(,)Q x y ，又设PQ 中点为00(,)N x y .(i)因为(2,0)F -，所以直线PQ 的方程为：2x my =-,22222(3)420162x my m y my x y =-⎧⎪⇒+--=⎨+=⎪⎩,所以222122122168(3)24(1)04323m m m m y y m y y m ⎧⎪∆=++=+>⎪⎪+=⎨+⎪-⎪=⎪+⎩,于是1202223y y m y m +==+， 20022262233m x my m m -=-=-=++,所以2262(,)33m N m m -++.因为3OT ON mk k =-=,所以O ，N ，T三点共线,即OT 平分线段PQ (其中O 为坐标原点).(ii)2||1TF m =+，22212224(1)||||113m PQ y y m m m +=-+=++, 所以222222||13||24(1)24(1)13TF m m PQ m m m m ++==++++，令21m x +=(1x …), 则2||2123()||32626TF x x PQ x x +==+…(当且仅当22x =时取“=”), 所以当||||TF PQ 最小时，22x =即1m =或1-，此时点T 的坐标为(3,1)-或(3,1)--.21.已知函数2()1x f x e ax bx =---，其中,a b ∈R ， 2.71828e = 为自然对数的底数. (1)设()g x 是函数()f x 的导函数，求函数()g x 在区间[0,1]上的最小值； (2)若(1)0f =，函数()f x 在区间(0,1)内有零点，求a 的取值范围【测量目标】函数的导函数，极值，最值，函数的零点.【考查方式】考查函数的求导，单调区间的确定，分类讨论思想，数形结合思想的应用. 【难易程度】较难.【试题解析】(1)因为2()1xf x e ax bx =--- 所以()()2xg x f x e ax b '==-- 又()2xg x e a '=-,因为[0,1]x ∈，1xee 剟,所以：①若12a …，则21a …，()20xg x e a '=-…，所以函数()g x 在区间[0,1]上单增，min ()(0)1g x g b ==-;②若122ea <<，则12a e <<，于是当0ln(2)x a <<时()20x g x e a '=-<，当ln(2)1a x <<时()20x g x e a '=->，所以函数()g x 在区间[0,ln(2)]a 上单减，在区间[ln(2),1]a 上单增，min ()[ln(2)]22ln(2)g x g a a a a b ==--;③若2ea …，则2a e …，()20x g x e a '=-…,所以函数()g x 在区间[0,1]上单减，min ()(1)2g x g e a b ==--;综上：()g x 在区间[0,1]上的最小值为min 11,,21()22ln(2),222,,2b a e g x a a a b a e e a b a ⎧-⎪⎪⎪=--<<⎨⎪⎪--⎪⎩…….(2)由(1)0f =⇒10e a b ---=⇒1b e a =--，又(0)0f =,若函数()f x 在区间(0,1)内有零点，则函数()f x 在区间(0,1)内至少有三个单调区间,由(1)知当12a …或2ea …时，函数()g x 即()f x '在区间[0,1]上单调，不可能满足“函数()f x 在区间(0,1)内至少有三个单调区间”这一要求.若122ea <<，则min ()22ln(2)32ln(2)1g x a a ab a a a e =--=--+, 令3()ln 12h x x x x e =--+(1x e <<),则1()ln 2h x x '=-.由1()ln 02h x x x e '=->⇒<,所以()h x 在区间(1,)e 上单增，在区间(,)e e 上单减,max 3()()ln 1102h x h e e e e e e e ==--+=-+<即min ()0g x <恒成立,于是，函数()f x 在区间(0,1)内至少有三个单调区间⇔(0)20(1)10g e a g a =-+>⎧⎨=-+>⎩21a e a >-⎧⇒⎨<⎩,又122ea <<, 所以21e a -<<,综上，a 的取值范围为(2,1)e -.。

2014 年高考四川卷理科压轴题的解法研究及赏析

2014 年高考四川卷理科压轴题的解法研究及赏析2014年四川高考理科压轴题的解析和评价2014年四川卷理科第21题：已知函数$f(x)=e^{-ax-bx}-1$，其中$a,b\in R$，$e$为自然对数的底数。

（Ⅰ）设$g(x)$是函数$f(x)$的导函数，求函数$g(x)$在区间$[0,1]$上的最小值。

（Ⅱ）若$f(1)=0$，函数$f(x)$在区间$(0,1)$内有零点，求$a$的取值范围。

试题分析与评价：本题以指数函数和二次函数作为知识背景，以推理论证能力、运算求解能力、创新意识立意设计，试题的解答入手容易深入难。

试题具有“平和自然，落落大方；亮点纷呈，不落俗套；情理之中，意料之外”的特点，既利于中学教学，也利于高校选拔。

第（Ⅰ）题要求考生求函数$g(x)=e^{-2ax-b}$（其中$a,b\in R$）在$[0,1]$上的最小值，属于典型的常规问题。

第（Ⅱ）题作为全卷的压轴题，看似平和，但问题全面考查学生的数学素养，需要学生会灵活运用数形结合思想、化归与转化思想方能较好解决问题，尤其是对代数的抽象思维、“数的严谨与形的直观的关系”的处理、推理的严谨性和深刻性等，有很高要求。

今年的这道压轴题主要考察导数的运算、导数在研究函数中的应用、函数的零点等基础知识，考查推理论证能力、运算求解能力、创新意识、函数与方程、数形结合、分类与整合、化归与转化等数学思想，并考查思维的严谨性。

题目只设置两问，精炼清晰。

文字简短，表述自然平和，不拒人于千里之外，给人以亲切感，让考生紧张的情绪得到一定的舒缓，给予考生一种人文情怀又易于激发考生解决问题的潜能。

该题紧扣《2014年四川高考数学考试说明》，不超纲，不怪异。

既有对中学数学“双基”的考核，更有对考生数学思维的灵活性和创新能力的考查。

试题层次分明，梯度适宜，信度和效度极好，是一道优秀的高考压轴题，有利于正确引导高考数学方向；同时考题贴近学生的学情，为新课程的推进起到指明航向的作用，值得广大一线教师深入研究和发扬光大。

2014年普通高等学校招生全国统一考试数学卷(四川.理)含详解

绝密★启用前2014年普通高等学校招生全国统一考试(四川卷)数学(理工类)本试卷分第一部分(选择题)和第二部分(非选择题)。

第一部分1至2页，第二部分3至4页，共4页．考生作答时，须将答案答在答题卡上及试题卷，草稿纸上答题无效，满分150分，考试时间120分钟。

考试结束后，将本试卷和答题卡一并交回. 参考公式：如果事件A 、B 互斥，那么球的表面积公式 P(A+B) =P(A)+P(B) 24s R π= 如果事件A 、B 相互独立，那么其中R 表示球的半径 P(A·B)=P(A)·P(B) 球的体积公式如果事件A 在一次试验中发生的概率是p ，那么243v R π=在n 次独立重复试验中事件A 恰好发生k 次的概率其中R 表示球的半径n ()(1)(0,1,2,...)k k n kn P k C p p k n -=-= 第一部分（选择题共60分）注意事项：1.选择题必须使用2B 铅笔将答案标号填涂在答题卡上对应题目标号的位置上。

2.本部分共12小题，每小题5分，共60分。

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1、有一个容量为66的样本，数据的分组及各组的频数如下：[11.5，15.5) 2 [15.5,19.5) 4 [19.5，23．5) 9 [23.5,27.5) 18 [27.5，31.5) 1l [31.5，35.5) 12 [35.5．39.5) 7 [39.5,43.5) 3 根据样本的频率分布估计，数据落在[31.5，43.5)的概率约是 (A)16 (B)13 (C)12 （D ）23答案：B解析：从31.5到43.5共有22，所以221663P ==。

2、复数1i i-+=(A)2i - （B ）12i （C ）0 （D ）2i 答案：A解析：12i i i i i-+=--=- 3、1l ，2l ，3l 是空间三条不同的直线，则下列命题正确的是(A)12l l ⊥，23l l ⊥13l l ⇒ （B ）12l l ⊥，23l l ⇒13l l ⊥ (C)233l l l ⇒ 1l ，2l ，3l 共面（D ）1l ，2l ，3l 共点⇒1l ，2l ，3l 共面答案：B解析：A 答案还有异面或者相交，C 、D 不一定 4、如图，正六边形ABCDEF 中，BA CD EF ++=(A)0 (B)BE (C)AD (D)CF答案D 解析：B AC ++=+5、5函数，()f x 在点0x x =处有定义是()f x 在点0x x =处连续的(A)充分而不必要的条件 (B)必要而不充分的条件 (C)充要条件 (D)既不充分也不必要的条件答案：B解析：连续必定有定义，有定义不一定连续。

2014年高考真题——理科数学(四川卷)解析版(部分) Word版含解析

2014年普通高等学校招生全国统一考试（四川卷）数学（理工类）本试题卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）。

第Ⅰ卷1至2页，第Ⅱ卷3至4页，共4页。

考生作答时，须将答案答在答题卡上，在本试题卷、草稿纸上大题无效。

满分150分。

考试时间120分钟。

考试结束后，将本试题卷和答题卡上一并交回。

第Ⅰ卷（选择题共50分）注意事项：必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑。

一、选择题.1、已知集合2{20}A x x x =--≤，集合B 为整数集，则AB =（）（A ）{1,0,1,2}- （B ）{2,1,0,1}-- （C ）{0,1} （D ）{1,0}-2、在6(1)x x +的展开式中，含3x 的系数为（）（A ）30 （B ）20 （C ）15 （D ）103、为了得到函数sin(21)y x =+的图象，只需把函数sin 2y x =的图像上所有的点（）（A ）向左平行移动12个单位长度（B ）向右平行移动12个单位长度（C ）向左平行移动1个单位长度（D ）向右平行移动1个单位长度4、若设0,0a b c d >><<，则一定有（）（A ）a b c d > （B ）a b c d < （C ）a b d c > （D ）a b d c<5、执行如右图的程序框图，如果输入的,x y R ∈，那么输出的S 的最大值为（）（A ）0 （B ）1 （C ）2 （D ）36、六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有（）（A ）192 （B ）216 （C ）240 （D ）2887、平面向量(1,2),(4,2),()c m m R ===+∈a b a b ，且c 与a 的夹角等于c 与b 的夹角，则m =（A ）2- （B ）1- （C ）1 （D ）28、如图，在正方体1111ABCD A B C D -中，点O 为线段BD 的中点，设点P 在线段1CC 上，直线OP 与平面1A BD 所成的角为α，则sin α的取值范围是（）（A ）1⎤⎥⎦ （B ）1⎤⎥⎦ （C ）（D ）1,⎤⎥⎦9、已知()()()()1111f x ln x ln x ,x ,=+--∈-，现有下列命题：○1()()f x f x ;-=- ○2()2221x f f x ;x ⎛⎫=⎪+⎝⎭○3()2f x x .≥ 其中的所有正确命题的序号是（）（A ）○1○2○3 （B ）○2○3 （C ）○1○3 （D ）○1○210、已知F 为抛物线2y x =的焦点，点A,B 在该抛物线上且位于x 轴的两侧，2OA OB =（其中O 为坐标原点），则△ABO 与△AFO 面积之和的最小值是（）（A ）2 （B ）3 （C （D第Ⅱ卷（非选择题共100分）注意事项：必须使用0.5毫米黑色签字笔在答题卡上题目所指示的答题区域内作答。

2014年四川高考数学试卷(理科)(含答案解析)

2014年四川高考数学试卷(理科)(含答案解析)2014年四川省高考数学试卷（理科）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给处的四个选项中，只有一项是符合题目要求的． 1．（5分）（2014•四川）已知集合A={x|x 2﹣x ﹣2≤0}，集合B 为整数集，则A ∩B=（） A ． {﹣1，0，1，2} B ． {﹣2，﹣1，0，1}C ． {0，1}D ． {﹣1，0}2．（5分）（2014•四川）在x （1+x ）6的展开式中，含x 3项的系数为（） A ． 30 B ． 20C ． 15D ． 103．（5分）（2014•四川）为了得到函数y=sin （2x+1）的图象，只需把y=sin2x 的图象上所有的点（） A ．向左平行移动个单位长度 B ．向右平行移动个单位长度 C ．向左平行移动1个单位长度 D ．向右平行一定1个单位长度4．（5分）（2014•四川）若a ＞b ＞0，c ＜d ＜0，则一定有（） A ．＞ B ．＜ C ．＞ D ．＜5．（5分）（2014•四川）执行如图所示的程序框图，若输入的x，y∈R，那么输出的S的最大值为（）A．0B．1C．2D．36．（5分）（2014•四川）六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有（）A．192种B．216种C．240种D．288种7．（5分）（2014•四川）平面向量=（1，2），=（4，2），=m+（m∈R），且与的夹角等于与的夹角，则m=（）A．﹣2 B．﹣1 C．1D．28．（5分）（2014•四川）如图，在正方体ABCD﹣A1B1C1D1中，点O为线段BD的中点，设点P在线段CC1上，直线OP与平面A1BD所成的角为α，则sinα的取值范围是（）A．[，1]B．[，1]C．[，]D．[，1]9．（5分）（2014•四川）已知f（x）=ln（1+x）﹣ln（1﹣x），x∈（﹣1，1）．现有下列命题：①f（﹣x）=﹣f（x）；②f（）=2f（x）③|f（x）|≥2|x|其中的所有正确命题的序号是（）A．①②③B．②③C．①③D．①②10．（5分）（2014•四川）已知F为抛物线y2=x的焦点，点A，B在该抛物线上且位于x轴的两侧，•=2（其中O为坐标原点），则△ABO与△AFO面积之和的最小值是（）A．2B．3C．D．二、填空题：本大题共5小题，每小题5分，共25分11．（5分）（2014•四川）复数=_________．12．（5分）（2014•四川）设f（x）是定义在R上的周期为2的函数，当x∈[﹣1，1）时，f（x）=，则f（）=_________．13．（5分）（2014•四川）如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为67°，30°，此时气球的高是46m，则河流的宽度BC约等于_________m．（用四舍五入法将结果精确到个位．参考数据：sin67°≈0.92，cos67°≈0.39，sin37°≈0.60，cos37°≈0.80，≈1.73）14．（5分）（2014•四川）设m∈R，过定点A的动直线x+my=0和过定点B的动直线mx﹣y﹣m+3=0交于点P（x，y）．则|PA|•|PB|的最大值是_________．15．（5分）（2014•四川）以A表示值域为R的函数组成的集合，B表示具有如下性质的函数φ（x）组成的集合：对于函数φ（x），存在一个正数M，使得函数φ（x）的值域包含于区间[﹣M，M]．例如，当φ1（x）=x3，φ2（x）=sinx 时，φ1（x）∈A，φ2（x）∈B．现有如下命题：①设函数f（x）的定义域为D，则“f（x）∈A”的充要条件是“∀b∈R，∃a∈D，f（a）=b”；②函数f（x）∈B的充要条件是f（x）有最大值和最小值；③若函数f（x），g（x）的定义域相同，且f（x）∈A，g（x）∈B，则f（x）+g（x）∉B．④若函数f（x）=aln（x+2）+（x＞﹣2，a∈R）有最大值，则f（x）∈B．其中的真命题有_________．（写出所有真命题的序号）三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．16．（12分）（2014•四川）已知函数f（x）=sin（3x+）．（1）求f（x）的单调递增区间；（2）若α是第二象限角，f（）=cos（α+）cos2α，求cosα﹣sinα的值．17．（12分）（2014•四川）一款击鼓小游戏的规则如下：每盘游戏都需要击鼓三次，每次击鼓要么出现一次音乐，要么不出现音乐：每盘游戏击鼓三次后，出现一次音乐获得10分，出现两次音乐获得20分，出现三次音乐获得100分，没有出现音乐则扣除200分（即获得﹣200分）．设每次击鼓出现音乐的概率为，且各次击鼓出现音乐相互独立．（1）设每盘游戏获得的分数为X，求X的分布列；（2）玩三盘游戏，至少有一盘出现音乐的概率是多少？（3）玩过这款游戏的许多人都发现．若干盘游戏后，与最初分数相比，分数没有增加反而减少了．请运用概率统计的相关知识分析分数减少的原因．18．（12分）（2014•四川）三棱锥A﹣BCD及其侧视图、俯视图如图所示，设M，N分别为线段AD，AB的中点，P为线段BC上的点，且MN⊥NP．（1）证明：P是线段BC的中点；（2）求二面角A﹣NP﹣M的余弦值．19．（12分）（2014•四川）设等差数列{a n}的公差为d，点（a n，b n）在函数f（x）=2x的图象上（n∈N*）．（1）若a1=﹣2，点（a8，4b7）在函数f（x）的图象上，求数列{a n}的前n项和S n；（2）若a1=1，函数f（x）的图象在点（a2，b2）处的切线在x轴上的截距为2﹣，求数列{}的前n项和T n．20．（13分）（2014•四川）已知椭圆C：+=1（a＞b＞0）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形．（1）求椭圆C的标准方程；（2）设F为椭圆C的左焦点，T为直线x=﹣3上任意一点，过F作TF的垂线交椭圆C于点P，Q．①证明：OT平分线段PQ（其中O为坐标原点）；②当最小时，求点T的坐标．21．（14分）（2014•四川）已知函数f（x）=e x﹣ax2﹣bx﹣1，其中a，b∈R，e=2.71828…为自然对数的底数．（1）设g（x）是函数f（x）的导函数，求函数g（x）在区间[0，1]上的最小值；（2）若f（1）=0，函数f（x）在区间（0，1）内有零点，求a的取值范围．2014年四川省高考数学试卷（理科）参考答案与试题解析一、选择题：本大题共10小题，每小题5分，共50分．在每小题给处的四个选项中，只有一项是符合题目要求的． 1．（5分）（2014•四川）已知集合A={x|x 2﹣x ﹣2≤0}，集合B 为整数集，则A ∩B=（） A ． {﹣1，0，1，2} B ． {﹣2，﹣1，0，1}C ． {0，1}D ． {﹣1，0}考点：交集及其运算．专题：计算题．分析：计算集合A 中x 的取值范围，再由交集的概念，计算可得．解答：解：A={x|﹣1≤x ≤2}，B=Z ， ∴A ∩B={﹣1，0，1，2}．故选：A ．点评：本题属于容易题，集合知识是高中部分的基础知识，也是基础工具，高考中涉及到对集合的基本考查题，一般都比较容易，且会在选择题的前几题，考生只要够细心，一般都能拿到分．2．（5分）（2014•四川）在x（1+x）6的展开式中，含x3项的系数为（）A．30 B．20 C．15 D．10考点：二项式系数的性质．专题：二项式定理．分析：利用二项展开式的通项公式求出（1+x）6的第r+1项，令x的指数为2求出展开式中x2的系数．然后求解即可．解答：解：（1+x）6展开式中通项T r+1=C6r x r，令r=2可得，T3=C62x2=15x2，∴（1+x）6展开式中x2项的系数为15，在x（1+x）6的展开式中，含x3项的系数为：15．故选：C．点评：本题考查二项展开式的通项的简单直接应用．牢记公式是基础，计算准确是关键．3．（5分）（2014•四川）为了得到函数y=sin（2x+1）的图象，只需把y=sin2x的图象上所有的点（）A．向左平行移动个单位长度B．向右平行移动个单位长度C．向左平行移动1个单位长D．向右平行一定1个单位长度度考点：函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质．分析：根据y=sin（2x+1）=sin2（x+），利用函数y=Asin （ωx+φ）的图象变换规律，得出结论．解答：解：∵y=sin（2x+1）=sin2（x+），∴把y=sin2x的图象上所有的点向左平行移动个单位长度，即可得到函数y=sin（2x+1）的图象，故选：A ．点评：本题主要考查函数y=Asin （ωx+φ）的图象变换规律，属于基础题．4．（5分）（2014•四川）若a＞b＞0，c＜d＜0，则一定有（）A．＞B．＜C．＞D．＜考点：不等式比较大小；不等关系与不等式．专题：不等式的解法及应用．分析：利用特例法，判断选项即可．解答：解：不妨令a=3，b=1，c=﹣3，d=﹣1，则，，∴A、B不正确；，=﹣，∴C不正确，D正确．故选：D．点评：本题考查不等式比较大小，特值法有效，导数计算正确．5．（5分）（2014•四川）执行如图所示的程序框图，若输入的x，y∈R，那么输出的S的最大值为（）A．0B．1C．2D．3考点：程序框图．专题：计算题；算法和程序框图．分析：算法的功能是求可行域内，目标还是S=2x+y的最大值，画出可行域，求得取得最大值的点的坐标，求出最大值．解答：解：由程序框图知：算法的功能是求可行域内，目标还是S=2x+y的最大值，画出可行域如图：当时，S=2x+y的值最大，且最大值为2．故选：C．点评：本题借助选择结构的程序框图考查了线性规划问题的解法，根据框图的流程判断算法的功能是解题的关键．6．（5分）（2014•四川）六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有（）A．192种B．216种C．240种D．288种考点：排列、组合及简单计数问题．专题：应用题；排列组合．分分类讨论，最左端排甲；最左端只排乙，最右端不能排析：甲，根据加法原理可得结论．解答：解：最左端排甲，共有=120种，最左端只排乙，最右端不能排甲，有=96种，根据加法原理可得，共有120+96=216种．故选：B．点评：本题考查排列、组合及简单计数问题，考查学生的计算能力，属于基础题．7．（5分）（2014•四川）平面向量=（1，2），=（4，2），=m+（m∈R），且与的夹角等于与的夹角，则m=（）A．﹣2 B．﹣1 C．1D．2考点：数量积表示两个向量的夹角．专题：平面向量及应用．分析：由已知求出向量的坐标，再根据与的夹角等于与的夹角，代入夹角公式，构造关于m的方程，解方程可得答案．解答：解：∵向量=（1，2），=（4，2），∴=m +=（m+4，2m+2），又∵与的夹角等于与的夹角，∴=，∴=，∴=，解得m=2，故选：D点评：本题考查的知识点是数量积表示两个向量的夹角，难度中档．8．（5分）（2014•四川）如图，在正方体ABCD﹣A1B1C1D1中，点O为线段BD的中点，设点P在线段CC1上，直线OP与平面A1BD所成的角为α，则sinα的取值范围是（）A．[，1]B ．[，1]C ．[，]D．[，1]考点：直线与平面所成的角．专题：空间角．分析：由题意可得：直线OP于平面A1BD所成的角α的取值范围是∪．再利用正方体的性质和直角三角形的边角关系即可得出．解答：解：由题意可得：直线OP 于平面A 1BD 所成的角α的取值范围是∪．不妨取AB=2．在Rt△AOA1中，==．sin∠C1OA 1=sin（π﹣2∠AOA1）=sin2∠AOA1=2sin∠AOA 1cos∠AOA1=，=1．∴sinα的取值范围是．故选：B．点评：本题考查了正方体的性质和直角三角形的边角关系即可、线面角的求法，考查了推理能力，属于中档题．9．（5分）（2014•四川）已知f（x）=ln（1+x）﹣ln（1﹣x），x ∈（﹣1，1）．现有下列命题：①f（﹣x）=﹣f（x）；②f（）=2f（x）③|f（x）|≥2|x|其中的所有正确命题的序号是（）A．①②③B．②③C．①③D．①②考点：命题的真假判断与应用．专题：函数的性质及应用．分析：根据已知中函数的解析式，结合对数的运算性质，分别判断三个结论的真假，最后综合判断结果，可得答案．解答：解：∵f（x）=ln（1+x）﹣ln（1﹣x），x∈（﹣1，1），∴f（﹣x）=ln（1﹣x）﹣ln（1+x）=﹣f（x），即①正确；f（）=ln（1+）﹣ln（1﹣）=ln（）﹣ln（）=ln（）=ln[（）2]=2ln（）=2[ln （1+x）﹣ln（1﹣x）]=2f（x），故②正确；当x∈[0，1）时，|f（x）|≥2|x|⇔f（x）﹣2x≥0，令g （x）=f（x）﹣2x=ln（1+x）﹣ln（1﹣x）﹣2x（x∈[0，1））∵g′（x）=+﹣2=≥0，∴g（x）在[0，1）单调递增，g（x）=f（x）﹣2x≥g（0）=0，又f（x）≥2x，又f（x）与y=2x为奇函数，所以丨f （x）丨≥2丨x丨成立，故③正确；故正确的命题有①②③，故选：A点评：本题以命题的真假判断为载体，考查了对数的运算性质，代入法求函数的解析式等知识点，难度中档．10．（5分）（2014•四川）已知F为抛物线y2=x的焦点，点A，B在该抛物线上且位于x轴的两侧，•=2（其中O为坐标原点），则△ABO与△AFO面积之和的最小值是（）A．2B ．3C．D．考点：直线与圆锥曲线的关系．专题：圆锥曲线中的最值与范围问题．分析：可先设直线方程和点的坐标，联立直线与抛物线的方程得到一个一元二次方程，再利用韦达定理及•=2消元，最后将面积之和表示出来，探求最值问题．解答：解：设直线AB 的方程为：x=ty+m，点A（x1，y1），B （x2，y2），直线AB与x轴的交点为M（（0，m），由⇒y 2﹣ty﹣m=0，根据韦达定理有y1•y2=﹣m，∵•=2，∴x1•x2+y1•y 2=2，从而，∵点A，B位于x轴的两侧，∴y1•y 2=﹣2，故m=2．不妨令点A在x轴上方，则y1＞0，又，∴S△ABO+S△AFO==．当且仅当，即时，取“=”号，∴△ABO与△AFO面积之和的最小值是3，故选B．点评：求解本题时，应考虑以下几个要点：1、联立直线与抛物线的方程，消x或y后建立一元二次方程，利用韦达定理与已知条件消元，这是处理此类问题的常见模式．2、求三角形面积时，为使面积的表达式简单，常根据图形的特征选择适当的底与高．3、利用基本不等式时，应注意“一正，二定，三相等”．二、填空题：本大题共5小题，每小题5分，共25分11．（5分）（2014•四川）复数=﹣2i．考点：复数代数形式的乘除运算．专题：数系的扩充和复数．分析：利用两个复数代数形式的乘除法法则化简所给的复数，可得结果．解答：解：复数===﹣2i，故答案为：﹣2i．点评：本题主要考查两个复数代数形式的乘除法法则的应用，属于基础题．12．（5分）（2014•四川）设f（x）是定义在R上的周期为2的函数，当x∈[﹣1，1）时，f（x）=，则f（）=1．考点：函数的值．专题：计算题．分析：由函数的周期性f（x+2）=f（x），将求f（）的值转化成求f（）的值．解答：解：∵f（x）是定义在R上的周期为2的函数，∴=1．故答案为：1．点评：本题属于容易题，是考查函数周期性的简单考查，学生在计算时只要计算正确，往往都能把握住，在高考中，属于“送分题”．13．（5分）（2014•四川）如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为67°，30°，此时气球的高是46m，则河流的宽度BC约等于60m．（用四舍五入法将结果精确到个位．参考数据：sin67°≈0.92，cos67°≈0.39，sin37°≈0.60，cos37°≈0.80，≈1.73）考点：余弦定理的应用；正弦定理；正弦定理的应用．专题：应用题；解三角形．分析：过A点作AD垂直于CB的延长线，垂足为D，分别在Rt△ACD、Rt△ABD中利用三角函数的定义，算出CD、BD的长，从而可得BC，即为河流在B、C两地的宽度．解答：解：过A点作AD垂直于CB的延长线，垂足为D，则Rt △ACD中，∠C=30°，AD=46m∴CD==46≈79.58m．又∵Rt△ABD中，∠ABD=67°，可得BD==≈19.5m∴BC=CD﹣BD=79.58﹣19.5=60.08≈60m故答案为：60m点评：本题给出实际应用问题，求河流在B、C两地的宽度，着重考查了三角函数的定义、正余弦定理解三角形的知识，属于中档题．14．（5分）（2014•四川）设m∈R，过定点A的动直线x+my=0和过定点B的动直线mx﹣y﹣m+3=0交于点P（x，y）．则|PA|•|PB|的最大值是5．考点：点到直线的距离公式．专题：直线与圆．分析：先计算出两条动直线经过的定点，即A和B，注意到两条动直线相互垂直的特点，则有PA⊥PB；再利用基本不等式放缩即可得出|PA|•|PB|的最大值．解答：解：有题意可知，动直线x+my=0经过定点A（0，0），动直线mx﹣y﹣m+3=0即m（x﹣1）﹣y+3=0，经过点定点B（1，3），注意到动直线x+my=0和动直线mx﹣y﹣m+3=0始终垂直，P又是两条直线的交点，则有PA⊥PB，∴|PA|2+|PB|2=|AB|2=10．故|PA|•|PB|≤=5（当且仅当时取“=”）故答案为：5点评：本题是直线和不等式的综合考查，特别是“两条直线相互垂直”这一特征是本题解答的突破口，从而有|PA|2+|PB|2是个定值，再由基本不等式求解得出．直线位置关系和不等式相结合，不容易想到，是个灵活的好题．15．（5分）（2014•四川）以A表示值域为R的函数组成的集合，B表示具有如下性质的函数φ（x）组成的集合：对于函数φ（x），存在一个正数M，使得函数φ（x）的值域包含于区间[﹣M，M]．例如，当φ1（x）=x3，φ2（x）=sinx 时，φ1（x）∈A，φ2（x）∈B．现有如下命题：①设函数f（x）的定义域为D，则“f（x）∈A”的充要条件是“∀b∈R，∃a∈D，f（a）=b”；②函数f（x）∈B的充要条件是f（x）有最大值和最小值；③若函数f（x），g（x）的定义域相同，且f（x）∈A，g（x）∈B，则f（x）+g（x）∉B．④若函数f（x）=aln（x+2）+（x＞﹣2，a∈R）有最大值，则f（x）∈B．其中的真命题有①③④．（写出所有真命题的序号）考点：命题的真假判断与应用；充要条件；函数的值域．专题：新定义；极限思想；函数的性质及应用；不等式的解法及应用．分析：根据题中的新定义，结合函数值域的概念，可判断出命题①②③是否正确，再利用导数研究命题④中函数的值域，可得到其真假情况，从而得到本题的结论．解答：解：（1）对于命题①“f（x）∈A”即函数f（x）值域为R，“∀b∈R，∃a∈D，f（a）=b”表示的是函数可以在R中任意取值，故有：设函数f（x）的定义域为D，则“f（x）∈A”的充要条件是“∀b∈R，∃a∈D，f（a）=b”∴命题①是真命题；（2）对于命题②若函数f（x）∈B，即存在一个正数M，使得函数f（x）的值域包含于区间[﹣M，M]．∴﹣M≤f（x）≤M．例如：函数f（x）满足﹣2＜f（x）＜5，则有﹣5≤f（x）≤5，此时，f（x）无最大值，无最小值．∴命题②“函数f（x）∈B的充要条件是f（x）有最大值和最小值．”是假命题；（3）对于命题③若函数f（x），g（x）的定义域相同，且f（x）∈A，g （x）∈B，则f（x）值域为R，f（x）∈（﹣∞，+∞），并且存在一个正数M，使得﹣M≤g（x）≤M．∴f（x）+g（x）∈R．则f（x）+g（x）∉B．∴命题③是真命题．（4）对于命题④∵函数f（x）=aln（x+2）+（x＞﹣2，a∈R）有最大值，∴假设a＞0，当x→+∞时，→0，ln（x+2）→+∞，∴aln（x+2）→+∞，则f（x）→+∞．与题意不符；假设a＜0，当x→﹣2时，→，ln（x+2）→﹣∞，∴aln（x+2）→+∞，则f（x）→+∞．与题意不符．∴a=0．即函数f（x）=（x＞﹣2）当x＞0时，，∴，即；当x=0时，f（x）=0；当x＜0时，，∴，即．∴．即f（x）∈B．故命题④是真命题．故答案为①③④．点评：本题考查了函数值域的概念、基本不等式、充要条件，还考查了新定义概念的应用和极限思想．本题计算量较大，也有一定的思维难度，属于难题．三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．16．（12分）（2014•四川）已知函数f（x）=sin（3x+）．（1）求f（x）的单调递增区间；（2）若α是第二象限角，f（）=cos（α+）cos2α，求cosα﹣sinα的值．考点：两角和与差的余弦函数；正弦函数的单调性．专题：三角函数的求值．分析：（1）令2k π﹣≤3x+≤2kπ+，k∈z ，求得x的范围，可得函数的增区间．（2）由函数的解析式可得f （）=sin （α+），又f（）=cos（α+）cos2α，可得sin（α+）=cos（α+）cos2α，化简可得（cosα﹣sinα）2=．再由α是第二象限角，cosα﹣sinα＜0，从而求得cos α﹣sinα的值．解答：解：（1）∵函数f（x）=sin（3x+），令2k π﹣≤3x+≤2kπ+，k∈z，求得﹣≤x≤+，故函数的增区间为[﹣，+]，k∈z．（2）由函数的解析式可得f（）=sin（α+），又f（）=cos（α+）cos2α，∴sin（α+）=cos（α+）cos2α，即sin（α+）=cos（α+）（cos2α﹣sin2α），∴sinαcos+cosαsin=（cos2α﹣sin2α）（sinα+cosα）．又∵α是第二象限角，∴cosα﹣sinα＜0，当sinα+cosα=0时，此时cosα﹣sin α=﹣．当sinα+cosα≠0时，此时cosα﹣sinα=﹣．综上所述：cosα﹣sinα=﹣或﹣．点评：本题主要考查正弦函数的单调性，三角函数的恒等变换，属于中档题．17．（12分）（2014•四川）一款击鼓小游戏的规则如下：每盘游戏都需要击鼓三次，每次击鼓要么出现一次音乐，要么不出现音乐：每盘游戏击鼓三次后，出现一次音乐获得10分，出现两次音乐获得20分，出现三次音乐获得100分，没有出现音乐则扣除200分（即获得﹣200分）．设每次击鼓出现音乐的概率为，且各次击鼓出现音乐相互独立．（1）设每盘游戏获得的分数为X，求X的分布列；（2）玩三盘游戏，至少有一盘出现音乐的概率是多少？（3）玩过这款游戏的许多人都发现．若干盘游戏后，与最初分数相比，分数没有增加反而减少了．请运用概率统计的相关知识分析分数减少的原因．考点：离散型随机变量及其分布列；离散型随机变量的期望与方差．专题：概率与统计．分（1）设每盘游戏获得的分数为X，求出对应的概率，即析：可求X的分布列；（2）求出有一盘出现音乐的概率，独立重复试验的概率公式即可得到结论．（3）计算出随机变量的期望，根据统计与概率的知识进行分析即可．解答：解：（1）X可能取值有﹣200，10，20，100．则P （X=﹣200）=，P （X=10）==P（X=20）==，P（X=100）==，故分布列为：X ﹣200 10 20 100P由（1）知，每盘游戏出现音乐的概率是p=+=，则至少有一盘出现音乐的概率p=1﹣．由（1）知，每盘游戏或得的分数为X的数学期望是E （X）=（﹣200）×+10×+20××100=﹣=．这说明每盘游戏平均得分是负分，由概率统计的相关知识可知：许多人经过若干盘游戏后，入最初的分数相比，分数没有增加反而会减少．点评：本题主要考查概率的计算，以及离散型分布列的计算，以及利用期望的计算，考查学生的计算能力．18．（12分）（2014•四川）三棱锥A﹣BCD及其侧视图、俯视图如图所示，设M，N分别为线段AD，AB的中点，P为线段BC上的点，且MN⊥NP．（1）证明：P是线段BC的中点；（2）求二面角A﹣NP﹣M的余弦值．考点：二面角的平面角及求法；直线与平面平行的判定；用空间向量求平面间的夹角．专题：空间向量及应用．分析：（1）用线面垂直的性质和反证法推出结论，（2）先建空间直角坐标系，再求平面的法向量，即可求出二面角A﹣NP﹣M的余弦值．解答：解：（1）由三棱锥A﹣BCD及其侧视图、俯视图可知，在三棱锥A﹣BCD中：平面ABD⊥平面CBD，AB=AD=BD=CD=CB=2设O为BD的中点，连接OA，OC于是OA⊥BD，OC⊥BD 所以BD⊥平面OAC⇒BD⊥AC因为M，N分别为线段AD，AB的中点，所以MN∥BD，MN∥NP，故BD ⊥NP假设P 不是线段BC的中点，则直线NP 与直线AC是平面ABC内相交直线从而BD ⊥平面ABC，这与∠DBC=60°矛盾，所以P 为线段BC的中点（2）以O为坐标原点，OB，OC ，OA分别为x，y ，z 轴建立空间直角坐标系，则A（0，0，），M （，O，），N（，0，），P （，，0）于是，，设平面ANP和平面NPM的法向量分别为和由，则，设z1=1，则由，则，设z2=1，则cos===所以二面角A﹣NP﹣M的余弦值点评：本题考查线线的位置关系，考查二面角知识的应用，解题的关键是掌握用向量的方法求二面角大小的步骤，属于中档题．19．（12分）（2014•四川）设等差数列{a n}的公差为d，点（a n，b n）在函数f（x）=2x的图象上（n∈N*）．（1）若a1=﹣2，点（a8，4b7）在函数f（x）的图象上，求数列{a n}的前n项和S n；（2）若a1=1，函数f（x）的图象在点（a2，b2）处的切线在x轴上的截距为2﹣，求数列{}的前n项和T n．考点：数列的求和；数列与函数的综合．专题：函数的性质及应用；等差数列与等比数列．分析：（1）由于点（a8，4b7）在函数f（x）=2x的图象上，可得，又等差数列{a n}的公差为d，利用等差数列的通项公式可得=2d．由于点（a8，4b7）在函数f（x）的图象上，可得=b8，进而得到=4=2d，解得d．再利用等差数列的前n项和公式即可得出．（2）利用导数的几何意义可得函数f（x）的图象在点（a2，b2）处的切线方程，即可解得a2．进而得到a n，b n．再利用“错位相减法”即可得出．解答：解：（1）∵点（a8，4b7）在函数f（x）=2x的图象上，∴，又等差数列{a n}的公差为d，∴==2d，∵点（a8，4b7）在函数f（x）的图象上，∴=b8，∴=4=2d，解得d=2．又a1=﹣2，∴S n==﹣2n+=n2﹣3n．（2）由f（x）=2x，∴f′（x）=2x ln2，∴函数f（x）的图象在点（a2，b2）处的切线方程为，又，令y=0可得x=，∴，解得a2=2．∴d=a2﹣a1=2﹣1=1．∴a n=a1+（n﹣1）d=1+（n﹣1）×1=n，∴b n=2n．∴．∴T n=+…++，∴2T n=1+++…+，两式相减得T n=1++…+﹣=﹣==．点评：本题综合考查了指数函数的运算性质、导数的几何意义、等差数列与等比数列的通项公式及其前n项和公式等基础知识与基本技能方法，考查了推理能力、计算能力、“错位相减法”，属于难题．20．（13分）（2014•四川）已知椭圆C：+=1（a＞b＞0）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形．（1）求椭圆C的标准方程；（2）设F为椭圆C的左焦点，T为直线x=﹣3上任意一点，过F作TF的垂线交椭圆C于点P，Q．①证明：OT平分线段PQ（其中O为坐标原点）；②当最小时，求点T的坐标．考点：直线与圆锥曲线的关系；椭圆的标准方程．专题：圆锥曲线中的最值与范围问题．分析：第（1）问中，由正三角形底边与高的关系，a2=b2+c2及焦距2c=4建立方程组求得a 2，b2；第（2）问中，先设点的坐标及直线PQ的方程，利用两点间距离公式及弦长公式将表示出来，由取最小值时的条件获得等量关系，从而确定点T的坐标．解解：（1）依题意有解得答：所以椭圆C的标准方程为+=1．（2）设T（﹣3，m），P（x1，y1），Q（x2，y2），PQ的中点为N（x0，y0），①证明：由F（﹣2，0），可设直线PQ的方程为x=my﹣2，由⇒（m2+3）y2﹣4my﹣2=0，所以于是，从而，即，则，所以O，N，T三点共线，从而OT平分线段PQ，故得证．②由两点间距离公式得，由弦长公式得==，所以，令，则（当且仅当x2=2时，取“=”号），所以当最小时，由x2=2=m2+1，得m=1或m=﹣1，此时点T的坐标为（﹣3，1）或（﹣3，﹣1）．点评：本题属相交弦问题，应注意考虑这几个方面：1、设交点坐标，设直线方程；2、联立直线与椭圆方程，消去y或x，得到一个关于x 或y一元二次方程，利用韦达定理；3、利用基本不等式或函数的单调性探求最值问题．21．（14分）（2014•四川）已知函数f（x）=e x﹣ax2﹣bx﹣1，其中a，b∈R，e=2.71828…为自然对数的底数．（1）设g（x）是函数f（x）的导函数，求函数g（x）在区间[0，1]上的最小值；（2）若f（1）=0，函数f（x）在区间（0，1）内有零点，求a的取值范围．考点：导数在最大值、最小值问题中的应用；函数的零点．专题：导数的综合应用．分析：（1）求出f（x）的导数得g（x），再求出g（x）的导数，对它进行讨论，从而判断g（x）的单调性，求出g（x）的最小值；（2）利用等价转换，若函数f（x）在区间（0，1）内有零点，则函数f（x）在区间（0，1）内至少有三个单调区间，所以g（x）在（0，1）上应有两个不同的零点．解答：解：∵f（x）=e x﹣ax2﹣bx﹣1，∴g（x）=f′（x）=e x﹣2ax﹣b，又g′（x）=e x﹣2a，x∈[0，1]，∴1≤e x≤e，∴①当时，则2a≤1，g′（x）=e x﹣2a≥0，∴函数g（x）在区间[0，1]上单调递增，g（x）min=g （0）=1﹣b；②当，则1＜2a＜e，∴当0＜x＜ln（2a）时，g′（x）=e x﹣2a＜0，当ln（2a）＜x＜1时，g′（x ）=e x﹣2a＞0，∴函数g（x）在区间[0，ln（2a）]上单调递减，在区间[ln（2a），1]上单调递增，g（x）min=g[ln（2a）]=2a﹣2aln（2a）﹣b；③当时，则2a≥e，g′（x）=e x﹣2a≤0，∴函数g（x）在区间[0，1]上单调递减，g（x）min=g（1）=e﹣2a﹣b，综上：函数g（x）在区间[0，1]上的最小值为；（2）由f（1）=0，⇒e﹣a﹣b﹣1=0⇒b=e﹣a﹣1，又f（0）=0，若函数f（x）在区间（0，1）内有零点，则函数f （x）在区间（0，1）内至少有三个单调区间，由（1）知当a≤或a≥时，函数g（x）在区间[0，1]上单调，不可能满足“函数f（x）在区间（0，1）内至少有三个单调区间”这一要求．若，则g min（x）=2a ﹣2aln（2a）﹣b=3a﹣2aln（2a）﹣e+1令h（x）=（1＜x＜e）则．由＞0⇒x＜∴h（x）在区间（1，）上单调递增，在区间（，e）上单调递减，=+＜0，即g min（x）＜0 恒成立，∴函数f（x）在区间（0，1）内至少有三个单调区间⇔⇒，又，所以e﹣2＜a＜1，综上得：e﹣2＜a＜1．点评：本题考查了，利用导数求函数的单调区间，分类讨论思想，等价转换思想，函数的零点等知识点．是一道导数的综合题，难度较大．参与本试卷答题和审题的老师有：任老师；王老师；孙佑中；刘长柏；qiss；尹伟云；翔宇老师；szjzl；caoqz；清风慕竹；静定禅心；maths（排名不分先后）菁优网2014年6月24日。

(新课标Ⅱ)2014高考数学压轴卷理(含解析)

2014新课标II 高考压轴卷理科数学选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.的共轭复数为（3. 由y=f （x ）的图象向左平移个单位，再把所得图象上所有点的横坐标伸长到原来的2倍得到y=2sin 的图象，则 f （x ）为（） 2sin4.已知函数，则的值是（）D5. 设随机变量~X N (3，1)，若(4)P X p >=，，则P(2<X<4)= ( A)12p + ( B)l —p (C)l-2p (D)12p - 6. 6．运行右面框图输出的S 是254，则①应为(A) n ≤5 (B) n ≤6 (C)n ≤7 (D) n ≤8 7. 若曲线在点（a ，f （a ））处的切线与两条坐标轴围成的三角形的面积为18，则a=（）8.已知A 、B是圆22:1O x y +=上的两个点，P 是AB 线段上的动点，当AOB ∆的面积最大时，则AO AP ⋅-2AP 的最大值是（）A.1-B.0C.81D.219.一个四面体的四个顶点在空间直角坐标系xyz O -中的坐标分别是（0，0，0），（1，2，0），（0，2，2），（3，0，1），则该四面体中以yOz 平面为投影面的正视图的面积为 A ．3 B ．25 C ．2 D ．2710. .已知函数2()cos()f n n n π=，且()(1)n a f n f n =++，则123100a a a a ++++=A ． 0B ．100-C ．100D ．1020011．设x ，y 满足约束条件，若目标函数z=ax+by （a ＞0，b ＞0）的最大值为12，则+的最小值为（）C 12．设双曲线﹣=1（a ＞0，b ＞0）的右焦点为F ，过点F 作与x 轴垂直的直线l 交两渐近线于A 、B 两点，且与双曲线在第一象限的交点为P ，设O 为坐标原点，若=λ+μ（λ，μ∈R ），λμ=，则该双曲线的离心率为（）BCD二、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡的相应位置． 13.某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间[5，40]中，其频率分布直方图如图所示．从抽样的100根棉花纤维中任意抽取一根，则其棉花纤维的长度小于20mm 的概率为．14.已知1cos21sin cos ααα-=，1tan()3βα-=-，则tan(2)βα-的值为．15.函数43y x x =++(3)x >-的最小值是．16.已知函数f(x)＝x 3＋x ，对任意的m ∈[－2,2]，f(mx －2)＋f(x)<0恒成立，则x 的取值范围为________．三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．解答写在答题卡上的指定区域内．17.已知函数3cos 32cos sin 2)(2-+=x x x x f ，R ∈x ．（Ⅰ）求函数(3)1y f x =-+的最小正周期和单调递减区间；（Ⅱ）已知ABC ∆中的三个内角,,A B C 所对的边分别为,,a b c ，若锐角A 满足()26A f π-=7a =，sin sin 14B C +=，求ABC ∆的面积． 18.随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明，得到如下列联表：⑴根据以上列联表进行独立性检验，能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系？⑵从被询问的16名不读营养说明的大学生中，随机抽取2名学生，求抽到男生人数ξ的分布列及其均值（即数学期望）．（注：))()()(()(22d b c a d c b a bc ad n K ++++-=，其中d c b a n +++=为样本容量．）19.已知正四棱柱1111-ABCD A B C D 中，12,4==AB AA . （Ⅰ）求证：1BD AC ⊥；（Ⅱ）求二面角11--A AC D 的余弦值；（Ⅲ）在线段1CC 上是否存在点P ，使得平面11ACD ⊥平面PBD ，若存在，求出1CPPC 的值；若不存在，请说明理由.20.已知动圆P 与圆221:(3)81F x y ++=相切，且与圆222:(3)1F x y -+=相内切，记圆心P 的轨迹为曲线C ；设Q 为曲线C 上的一个不在x 轴上的动点，O 为坐标原点，过点2F 作OQ的平行线交曲线C 于,M N 两个不同的点. （Ⅰ）求曲线C 的方程；（Ⅱ）试探究||MN 和2||OQ 的比值能否为一个常数？若能，求出这个常数，若不能，请说明理由；（Ⅲ）记2QF M ∆的面积为1S ，2OF N ∆的面积为2S ，令12S S S =+，求S 的最大值. 21.已知0t >，函数()3x tf x x t-=+. (1)1t =时，写出()f x 的增区间；(2)记()f x 在区间[0,6]上的最大值为()g t ，求()g t 的表达式；(3)是否存在t ，使函数()y f x =在区间(0,6)内的图象上存在两点，在该两点处的切线互相垂直？若存在，求t 的取值范围；若不存在，请说明理由．请考生在第22、23、24题中任选一题作答，如果多做，则按所做的第一题计分.作答时请写清题号.22.选修4﹣1：几何证明选讲如图，AB 是⊙O 的直径，AC 是弦，直线CE 和⊙O 切于点C ，AD 丄CE ，垂足为D ．（I ）求证：AC 平分∠BAD；（II ）若AB=4AD ，求∠BAD 的大小．23.选修4﹣4：坐标系与参数方程将圆x2+y2=4上各点的纵坐标压缩至原来的，所得曲线记作C；将直线3x﹣2y﹣8=0绕原点逆时针旋转90°所得直线记作l．（I）求直线l与曲线C的方程；（II）求C上的点到直线l的最大距离．24. 选修4﹣5：不等式选讲设函数，f（x）=|x﹣1|+|x﹣2|．（I）求证f（x）≥1；（II）若f（x）=成立，求x的取值范围．2014新课标II高考压轴卷理科数学参考答案1. 【答案】A.【解析】由A={0，1，2}，B={x|x=2a，a∈A}={0，2，4}，所以A∩B={0，1，2}∩{0，2，4}={0，2}．所以A∩B中元素的个数为2．故选C．2. 【答案】A.【解析】由z•i=2﹣i，得，∴．故选：A．3. 【答案】B.【解析】由题意可得y=2sin的图象上各个点的横坐标变为原来的，可得函数y=2sin（6x﹣）的图象．再把函数y=2sin （6x ﹣）的图象向右平移个单位，即可得到f （x ）=2sin[6（x ﹣）﹣）]=2sin （6x ﹣2π﹣）=2sin的图象，故选B ．4. 【答案】C. 【解析】=f （log 2）=f （log 22﹣2）=f （﹣2）=3﹣2=，故选C ．5. 【答案】C.【解析】因为(4)(2)P X P X p >=<=，所以P(2<X<4)= 1(4)(2)12P X P X p ->-<=-，选C. 6. 【答案】C.【解析】本程序计算的是212(12)2222212n nn S +-=+++==--，由122254n +-=，得12256n +=，解得7n =。

2014年四川省高考理科数学压轴卷(含解析)

2014四川高考真题数学理(含解析)

2014年四川高考数学试卷(理科)(含答案解析)

2014年四川高考理科数学试题逐题详细讲解(纯word解析版)

四川省2014高考数学压轴卷 理(含解析)

2014四川高考数学试卷(理工类)及部分参考答案

2014年普通高等学校招生全国统一考试四川理科数学试题及答案解析(Word版)

2014年高考真题(理科数学)四川卷 纯Word版解析可编辑

2014年普通高等学校招生全国统一考试数学理试题(四川卷,含答案)

2014年四川高考理科数学试题含答案(Word版)

2014年高考理科数学四川卷答案及解析(word版)

2014年四川高考理科数学试卷(带详解)

2014 年高考四川卷理科压轴题的解法研究及赏析

2014年普通高等学校招生全国统一考试数学卷(四川.理)含详解

2014年高考真题——理科数学(四川卷)解析版(部分) Word版含解析

2014年四川高考数学试卷(理科)(含答案解析)

(新课标Ⅱ)2014高考数学压轴卷 理(含解析)

四川省2014高考数学压轴卷理(含解析)

2014年高考真题(理科数学)四川卷纯Word版解析可编辑

(新课标Ⅱ)2014高考数学压轴卷理(含解析)