9种谱校正方法
9种谱校正方法及matlab代码

9种谱校正方法及matlab 程序代码采样间隔归一化成1T ∆=,采样长度为N .这样FFT 离散谱线为0,1)i X i N =-(,相应的频率分辨率2/(1/)N f N ωπ∆=∆=. 设FFT 离散谱线局部极高谱线为m (为了数学上简洁,假定从0开始,注意在MATLAB 环境下数组实际操作的是从1开始),记频偏量δωδω=∆. 我们需要使用谱线m 和与之相邻一条次高谱线,记这连续两条谱线中左边一条序号为M (当次高谱线在m 左侧时1M m =-,反之M m =).下面列出若干算法的δ计算公式1. 加矩形窗的精确谱校正[1]i i i X U jV =+111()sin()()cos()M M M M opt M MV V M U U M K U U ωω+++-∆+-∆=- 1211cos()sin()cos()sin()opt M M opt M M K M Z V U M K M Z V U M ωωωωωω++-∆⎡⎤=+⎢⎥∆⎣⎦-∆+∆⎡⎤=+⎢⎥∆+∆⎣⎦ 2121cos()cos()()Z M Z M M m Z Z ωωωδ∆+∆-∆=+-- 2. 加矩形窗情形,采用解析单频模型的幅值比校正[1, 2]11||()||||M M M X M m X X δ++=+-+ 3. 加汉宁窗情形,采用解析单频模型的幅值比校正[1, 2]112||||()||||M M M M X X M m X X δ++-=+-+ 4. 加矩形窗情形,采用解析单频模型的复比值校正[3]11Re ()M M M X M m X X δ++⎛⎫=+- ⎪-⎝⎭5. 加汉宁窗情形,采用解析单频模型的复比值校正[3]112()M M M MX X M m X X δ+++=+-- 6. 加矩形窗情形,采用解析单频模型的复合复比值校正[3]11Re ()M m M M X M m X X δ++⎛⎫=+- ⎪-⎝⎭ 11m R m mX X X δ++=-,1111m m L m m m m X X X X X X δ---=-=-- 0.5)0.5)m L m R δδδδδ=-++((7. 加汉宁窗情形,采用解析单频模型的复合复比值校正[3]112Re ()M M m M M X X M m X X δ++⎛⎫+=+-⎪-⎝⎭ 112m m R m mX X X X δ+++=-,1111221m m m m L m m m m X X X X X X X X δ----++=-=-- 0.5)0.5)m L m R δδδδδ=-++((8. 加矩形窗,Quin 校正[4]11Re()Re(),Re()Re()m m L R m m X X X X αα-+== 11L R L R L Rααδδαα==---,, 00 R R L R δδδδδ>>⎧=⎨⎩当且其它9. 加汉宁窗,Quin 校正[4]11Re()Re(),Re()Re()m m L R m m X X X X αα-+== 212111L RL R L Rααδδαα++==---,,00 R R L R δδδδδ>>⎧=⎨⎩当且其它References1. Schoukens, J., R. Pintelon,H. Van Hamme. The interpolated fast Fourier transform: Acomparative study . IEEE Transactions on Instrumentation and Measurement. 1992, 41(2):226-232.2. 谢明,丁康. 频谱分析的校正方法.振动工程学报. 1994, 7(2): 172-179.3. 陈奎孚, 王建立,张森文. 频谱校正的复比值法.振动工程学报(已投). 2007.4. Quinn, B.G. Estimating frequency by interpolation using Fourier coefficients.IEEETransactions on Signal Processing. 1994, 42(5): 1264-1268.%========================这是调用调试==================DT=1;N=1024;PHI=pi/3;Ampl=1;CiR=11.9; %cycles in recordFreq=CiR/(DT*N); %frequencyTV=[0:N-1];DatVec=Ampl*cos(Freq*TV*2*pi+PHI);FV=fft(DatVec);figuresubplot(2,1,1);plot(TV,DatV ec);subplot(2,1,2);plot(abs(FV(1:round(N/2.56))));grid on[MV,MI]=max(abs(FV));%加矩形窗的解析校正--1FreqShift=SpecCorr(FV,MI,N,1);%加矩形窗的解析单频模型校正--2FreqShift=SpecCorr(FV,MI,N,2);%加汉宁窗的解析单频模型校正--3HanDat=DatVec.*hanning(N,'periodic')';FV=fft(HanDat);FreqShift=SpecCorr(FV,MI,N,3);%加矩形窗的解析单频模型校正+复比值法--4FV=fft(DatVec);FreqShift=SpecCorr(FV,MI,N,4);%加汉宁窗的解析单频模型校正+复比值法--5HanDat=DatVec.*hanning(N,'periodic')';FV=fft(HanDat);FreqShift=SpecCorr(FV,MI,N,5);%加矩形窗的解析单频模型校正+复比值法+左右平均--6FV=fft(DatVec);FreqShift=SpecCorr(FV,MI,N,6);%加汉宁窗的解析单频模型校正+复比值法+左右平均--7HanDat=DatVec.*hanning(N,'periodic')';FV=fft(HanDat);FreqShift=SpecCorr(FV,MI,N,7);%加矩形窗的解析单频模型校正+Quinn算法--8FV=fft(DatVec);FreqShift=SpecCorr(FV,MI,N,8);%加汉宁窗的解析单频模型校正+Quinn算法--9HanDat=DatVec.*hanning(N,'periodic')';FV=fft(HanDat);FreqShift=SpecCorr(FV,MI,N,9);===========这是子程序======================%spectrum correction assemble% the sampling interval is 1 s (or unitary)%Input: SpecVec--Discrte Fourier Spectrum from FFT% PeakIdx--the peak index, noting the matrix in MatLab start from 1% TL--the length (or the point number) of the FFT% method--correction method% output: PeakShift-- the corrected peak shifting from the peak in discrete% spectrumfunction PeakShift=SpecCorr(SpecVec,PeakIdx,TL,method)% picking up the second highest spectrum lineif(abs(SpecVec(PeakIdx-1))>abs(SpecVec(PeakIdx+1)))IP=[PeakIdx-1,PeakIdx];ShiftCorr=-1; %shift aligning with the PeakIdxelseIP=[PeakIdx,PeakIdx+1];ShiftCorr=0; %shift aligning with the PeakIdxendII=IP(1)-1; % noting that the index of a matrix in MATLAB starts from 1, not zero if(method==1) %an analyitic solution for rectangular windowU=real(SpecVec(IP));V=imag(SpecVec(IP));DW=2*pi/TL;KOPT=(sin(II*DW)*(V(2)-V(1))+cos(II*DW)*(U(2)-U(1)))/(U(2)-U(1));Z=V.*(KOPT-cos((IP-1)*DW))./(sin(DW*(IP-1)))+U;Tmp1=(Z(2)*cos(DW*(II+1))-Z(1)*cos(DW*II))/(Z(2)-Z(1));PeakPos=acos(Tmp1)/DW;PeakShift=PeakPos-(PeakIdx-1);elseif(method==2) %based on the analytical-single-tone model for rectangular window PeakShift=abs(SpecVec(IP(2)))/(abs(SpecVec(IP(2)))+abs(SpecVec(IP(1))));PeakShift=PeakShift+ShiftCorr; %shift aligning with the PeakIdxelseif(method==3) %based on the analytical-single-tone model for Hanning windowPeakShift=(2*abs(SpecVec(IP(2)))-abs(SpecV ec(IP(1))))/(abs(SpecV ec(IP(2)))+abs(SpecVec(IP(1 ))));PeakShift=PeakShift+ShiftCorr; %shift aligning with the PeakIdxelseif(method==4) %based on the analytical-single-tone model for rectangular window with complex correctionPeakShift=real(SpecVec(IP(2))/(SpecVec(IP(2))-SpecVec(IP(1))));PeakShift=PeakShift+ShiftCorr; %shift aligning with the PeakIdxelseif(method==5) %based on the analytical-single-tone model for Hanning window with complex correctionPeakShift=(2*SpecVec(IP(2))+SpecVec(IP(1)))/(SpecVec(IP(2))-SpecVec(IP(1)));PeakShift=real(PeakShift)+ShiftCorr; %shift aligning with the PeakIdx elseif(method==6) %based on the analytical-single-tone model for rectangular window with complex correction+averagePeakShift=real(SpecVec(IP(2))/(SpecVec(IP(2))-SpecVec(IP(1))));MaxPeakShift=PeakShift+ShiftCorr; %shift aligning with the PeakIdxLeftShift=real(SpecVec(PeakIdx)/(SpecVec(PeakIdx)-SpecVec(PeakIdx-1)))-1;RightShift=real(SpecVec(PeakIdx+1)/(SpecVec(PeakIdx+1)-SpecVec(PeakIdx)));%averagePeakShift=(0.5-MaxPeakShift)*LeftShift+(0.5+MaxPeakShift)*RightShift;elseif(method==7) %based on the analytical-single-tone model for Hanning window with complex correction+average,????PeakShift=(2*SpecVec(IP(2))+SpecVec(IP(1)))/(SpecVec(IP(2))-SpecVec(IP(1)));MaxPeakShift=real(PeakShift)+ShiftCorr; %shift aligning with the PeakIdxLeftShift=(2*SpecVec(PeakIdx)+SpecV ec(PeakIdx-1))/(SpecVec(PeakIdx)-SpecVec(PeakIdx-1))-1;RightShift=(2*SpecVec(PeakIdx+1)+SpecV ec(PeakIdx))/(SpecVec(PeakIdx+1)-SpecVec(PeakIdx ));%averagePeakShift=(0.5-MaxPeakShift)*LeftShift+(0.5+MaxPeakShift)*RightShift;elseif(method==8) %Quinn method for the rectangular windowa1 = real(SpecV ec(PeakIdx-1)/SpecVec(PeakIdx)); %lefta2 = real(SpecV ec(PeakIdx+1)/SpecVec(PeakIdx)); %rightLeftShift = a1/(1-a1);RightShift = -a2/(1-a2);if (LeftShift>0 & RightShift>0)PeakShift = RightShift;elsePeakShift = LeftShift;endelseif(method==9) %Quinn method for the Hanning windowa1 = real(SpecV ec(PeakIdx-1)/SpecVec(PeakIdx)); %lefta2 = real(SpecV ec(PeakIdx+1)/SpecVec(PeakIdx)); %rightLeftShift = (2*a1+1)/(1-a1);RightShift = -(2*a2+1)/(1-a2);if (LeftShift>0 & RightShift>0)PeakShift = RightShift;elsePeakShift = LeftShift;endendend。
第9章 紫外吸收光谱分析

讨论:
(1) 转动能级间的能量差Δ Ε r:0.005~0.050eV,跃迁 产生吸收光谱位于远红外区。远红外光谱或分子转动光谱; (2) 振动能级的能量差Δ Ε v约为:0.05~1eV,跃迁产 生的吸收光谱位于红外区,红外光谱或分子振动光谱; (3) 电子能级的能量差Δ Ε e较大1~20eV,电子跃迁产生 的吸收光谱在紫外—可见光区,紫外—可见光谱或分子的电 子光谱;
p → p*跃迁:红移; ;e
pp np
max(正己烷)
230 329
max(氯仿)
238 315
max(甲醇)
237 309
max(水)
243 305
溶剂的影响
苯
1
1:乙醚
酰
丙
2:水
酮
2
极性溶剂使精细结构 消失;
250 300
非极性 → 极性 n → p*跃迁:兰移; ;e p → p*跃迁:红移; ;e
(2)共轭烯烃中的 p → p*
p*
p*₃
p*
p p*
165nm 217nm p₂
(HOMO LVMO) p
p₁
p
max
共轭烯烃(不多于四个双键)p p*跃迁吸收峰位置可由伍德
沃德——菲泽 规则估算。 max= 基+nii
基-----是由非环或六环共轭二烯母体决定的基准值; 无环、非稠环二烯母体: max=217 nm
红移与蓝移
有机化合物的吸收谱带 常常因引入取代基或改变溶 剂使最大吸收波长λmax和吸 收强度发生变化:
λmax向长波方向移动称为 红移,向短波方向移动称为 蓝移 (或紫移)。吸收强度即 摩尔吸光系数ε增大或减小的 现象分别称为增色效应或减 色效应,如图所示。
化学杀虫剂中9种拟除虫菊酯检测方法

化学杀虫剂中9种拟除虫菊酯检测方法作者:孙长恩等来源:《江苏农业科学》2014年第04期摘要:采用HP-5MS毛细管柱和FID检测器,建立了同时测定农药杀虫剂中隐性成分四氟苯菊酯、烯丙菊酯、氯氟醚菊酯、联苯菊酯、高效氯氟氰菊酯、氯菊酯、高效氯氰菊酯、S-氰戊菊酯、溴氰菊酯等9种拟除虫菊酯的气相色谱分析方法。
9种拟除虫菊酯的标准偏差均小于0.03,变异系数小于3.0%,线性相关系数均大于0.999;9种拟除虫菊酯成分5个水平的添加回收率为95.5%~107.5%。
该法分离效果好、准确度高、重现性好且操作简单快速。
关键词:拟除虫菊酯;隐性成分;气相色谱中图分类号: S482.3+5 文献标志码: A 文章编号:1002-1302(2014)04-0273-02收稿日期:2013-08-13作者简介:孙长恩(1970—),男,江苏徐州人,硕士,高级工程师,从事农药产品质量检验及全分析工作。
Tel:(025)84470312;E-mail:**********************。
近年来,一些农药生产企业为了尽快使自制产品在同类产品中脱颖而出,获得更高效益,随意添加隐性成分现象比较严重。
生产商根据不同产品,针对不同使用目的,添加不同隐性成分,使其产品在防止同类害虫时,显示出比未添加隐性成分产品的“良好效果”[1]。
部分农药生产企业在农药中以增效剂名义加入另外一种农药的违规现象,特别是在全面禁止使用甲胺磷等高毒农药后出现一个较为突出的新问题,它可能成为现在或将来农产品安全重大隐患和农药管理的一个盲点[2]。
在农药中任意添加其他农药成分,不但违反了《农药管理条例》,更有可能对农业生产安全和病虫害治理产生重大隐患,甚至严重干扰我国农业重大生物灾害的防控行动。
为了维护广大消费者利益,保持农药杀虫剂可持续发展,近两年国家有关部门在实施农药国家监督抽查时对农药中隐性成分进行了检测,发现部分企业违规添加隐性成分。
光谱 校准 奇异值分解

光谱校准奇异值分解光谱校准是光谱分析中的一个关键环节,通过对光谱数据进行校准,可以提高光谱分析的准确性和可靠性。
其中,奇异值分解(Singular Value Decomposition, SVD)是常用的光谱校准方法之一。
本文将以简体中文介绍光谱校准和奇异值分解的原理、方法及其在光谱分析中的应用。
光谱是指在不同波长的电磁辐射下,物体所发射、吸收或散射的光的强度分布。
光谱分析是一种常用的分析手段,可以通过测量物体在不同波长下的光谱信息,来获取物质的结构、组成和性质等信息。
然而,光谱数据受到很多因素的影响,如仪器漂移、噪声、非线性等,这些影响会导致光谱数据的失真和偏差,从而影响光谱分析的准确性。
为了解决这些问题,光谱校准应运而生。
光谱校准是一种通过数学方法对光谱数据进行修正和优化的过程,主要目的是消除或减小仪器误差、噪声和其他影响因素对光谱数据的影响,从而提高光谱分析的准确性和可靠性。
奇异值分解是一种常用的矩阵分解方法,可以将一个矩阵分解为三个矩阵的乘积,其中一个矩阵是奇异值矩阵,另外两个矩阵是正交矩阵。
在光谱校准中,可以将光谱数据矩阵进行奇异值分解,通过对奇异值矩阵的处理,实现对光谱数据的校准和优化。
具体而言,光谱校准中的奇异值分解主要包括以下几个步骤:1.构建光谱数据矩阵:将采集到的光谱数据按照一定的格式组织成矩阵形式,其中每一行代表一个光谱样本,每一列代表一个波长点的光强值。
2.进行奇异值分解:对光谱数据矩阵进行奇异值分解,得到三个矩阵U、S和VT,其中U和VT是正交矩阵,S是奇异值矩阵。
3.选择合适的奇异值并修正:根据奇异值的大小来选择前几个重要的奇异值,并对其进行修正。
通常情况下,前几个奇异值代表了光谱数据中最重要的信息,因此可以选择这些奇异值进行修正。
4.重建光谱数据矩阵:通过修正后的奇异值和原始的正交矩阵U 和VT,重建光谱数据矩阵。
这样得到的重建矩阵可以更好地反映光谱数据的真实情况,消除了仪器漂移、噪声和非线性等因素的影响。
谱方法在计算流体力学中的应用研究

西北工业大学硕士学位论文谱方法在计算流体力学中的应用研究姓名:王建瑜申请学位级别:硕士专业:计算数学指导教师:欧阳洁200703013.3谱近似(a)右端函数(b)精确解图3.1右端函数与精确解3.3.1ChebyshevTau方法应用谱方法数值求解问题(3.1)式,首先要确定展开基函数。
根据第二章中关于基函数的介绍,选择Chebyshev多项式(同样可以选择Legendre多项式)作为基函数,其表达式为丸。
(x,Y)=乙(x)瓦∽其中乙(x)为m次Chebyshev多项式。
根据2.2.2小节中关于Chebyshev多项式的介绍,由于基函数不满足问题(3一1)式的边界条件,应用Tau方法来逼近。
为使基函数和权函数满足单位正交关系,选权函数为‰(x,力=最(x)6(y)其中删=石2再1獬铲∽冀此时有如下两种单位正交关系成立虬舭朋心y蚴={:!富剧硼£~鹕∽出={:!等“。
ⅣO,_y)=∑∑口射如(x,y)(3·8)将近似解(3-8)式代入问题(3—1)式的微分方程,并对余量进行加权积分眦等+等Mw)蛐=“m蒯_伽少,k,l=0,1,--.,N由权函数和基函数的正交性,得a£’o’+4眢’2’=厶,||},,=0,1,…,Ⅳ(3.9)(3-9)式中厶=£l£lj;f,盯(训),(x,y)dxdy,k,l=0,1,…,N而且(3.6)式和(3-7)式依然成立,应用这两个关系式代替函数关于两个空问变量的二阶偏导数的展开系数,则方程组(3-9)式等价于下列方程组去耋p2_k2h+去”p2_12ZP(Pk21y,PCP12‰=1‘1鼽似y№y)dxdy÷)%+■)%=rI∥甜(w),(而q;i:妊戢“pp+f为=l+2儡敢k,,=0,1,…,N(3一12)求解代数方程组(3-12)式,即可得(3.8)式所表示的近似解。
3.3.3结果分析首先研究右端函数基于经典Chebyshev多项式的展开。
九种常见的家谱格式

九种常见的家谱格式
1. 血簪家谱:
血簪家谱是最常见的家谱格式,通常按照祖孙正序排列,以男性为主,女性则标注婚配的夫家姓氏。
2. 家族谱:
家族谱是按照同一个祖宗的后代进行排列,包括所有后代的姓名、出
生日期、配偶、孩子等信息。
3. 地区谱:
地区谱是按照某一个地区的所有家族进行排列,其中包括这些家族的
发展历史、族谱、文化特点等内容。
4. 世系谱:
世系谱是按照一个家族的世系关系排列,主要是为了记录家族树的延
伸和发展情况。
5. 改元谱:
改元谱是按照某一位祖先的改元年号进行排列,以记录家族世代的延
续和变化。
6. 分支谱:
分支谱是指将同一个家族的后代按照分支进行排列,主要是为了记录家族在不同地区的分支发展情况。
7. 家谱图:
家谱图是将家族树的图像化表现,以方便人们更加清晰地了解家族发展的历程和世系关系。
8. 纪念录:
纪念录是一种较为简略的家谱,包括主要的家族成员信息以及重要事件、文化传承、家族口传历史等内容。
9. 家训:
家训是对家族的传统、文化和价值观进行总结和归纳,以指导后代继承和发扬家族优良传统和文化精神。
火花源原子发射光谱法测定线材中9种元素

A理但is骚-但字分册PTCA(PART B:CHEM.ANAL.)I工作简报DOI:10.11973lhjy-h\202l03012火花源原子发射光谱法测定线材中9种元素杨再军,刁正斌,王娟,羊绍松(攀枝花钢饥有限公司制造部.攀枝花617000)摘要:建立了火花源原子发射光谱法测定直径为8〜12mm的小规格线材中的碳、硅、猛、磷、硫、鎳l、珞、铜和筑等9种元素含量的方法。
试样经切割和打磨后.按规格及钢种选择对应的自制夹具固定.垂直于磨样机打磨试样的端面。
用随V型板专用的定位夹具将样晶定位在火花源原子发射光谱仪激发孔中心位置.使试样支架中心和电极中心对齐。
盖好顶盖.用氫气吹扫火花室5s.采用能量为0.2J、频率为100Hz激发光激发样品。
在优化的仪器工作条件下,试样中9种元素可在10min内完成测定。
采用块状光谱国家标准样品制作校准曲线.用校正公式消除了共存元素的干扰及由标准试样和实际试样形状差异带来的系统偏差。
结果显示:9种元素的质量分数均在一定范围内与其对应的响应值呈线性关系.检出限(3s)为1.5〜18.1“g•g1;用此方法分析实际样品.所得测定值与参考文献使用的其他方法的基本一致.测定值的相对标准偏差("=11)均在5%以内。
关键词:自制夹具;火花源原子发射光谱法;元素;小规格线材中图分类号:0657.31文献标志码:A文章编号:1001-4020(2021)03-0258-06热轧带肋钢筋等线材产品的国家标准要求分析其中的碳、硅、猛、磷、硫、镰、锯、铜和帆等9种元素'.因此.建立一种可以快速、准确地测定钢筋钢中化学成分的方法.对生产工艺及产品质量的控制具有重要意义。
通常采用国家标准方法湿法测定线材中的元素反。
对于直径为8〜12mm的线材,需要先用专用工具钻取装置钻取屑样.然后针对其中的碳、硫两元素采用高频感应燃烧-红外吸收光谱法进行测定.其余元素采用电感耦合等离子体原子发射光谱法(ICP-AES)进行测定'.该方法试样前处理流程复杂•分析周期长,难以满足线材产品大批量检验的需求。
等离子体质谱法测定Nb、Ta、Zr、Hf等9种元素量
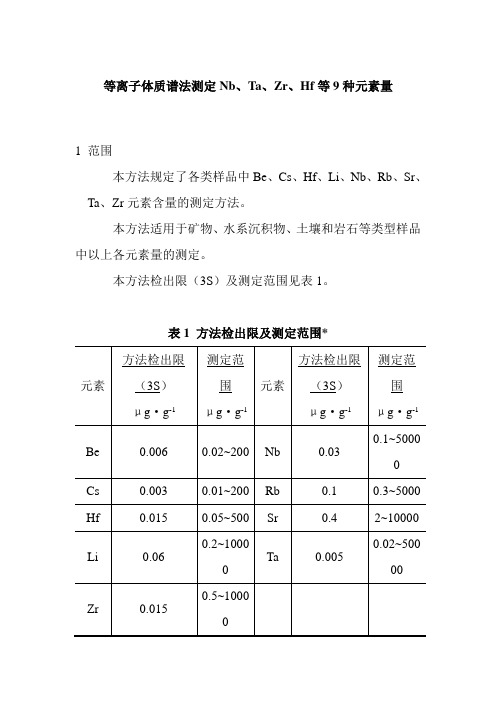
等离子体质谱法测定Nb、Ta、Zr、Hf等9种元素量1 范围本方法规定了各类样品中Be、Cs、Hf、Li、Nb、Rb、Sr、Ta、Zr元素含量的测定方法。
本方法适用于矿物、水系沉积物、土壤和岩石等类型样品中以上各元素量的测定。
本方法检出限(3S)及测定范围见表1。
表1 方法检出限及测定范围*元素方法检出限(3S)μg·g-1测定范围μg·g-1元素方法检出限(3S)μg·g-1测定范围μg·g-1Be 0.006 0.02~200 Nb 0.03 0.1~5000Cs 0.003 0.01~200 Rb 0.1 0.3~5000 Hf 0.015 0.05~500 Sr 0.4 2~10000Li 0.06 0.2~1000Ta 0.0050.02~50000Zr 0.015 0.5~1000*可根据含量确定称样量及稀释倍数扩大测定范围上限。
2 规范性引用文件下列文件中的条款通过本方法的本部分的引用而成为本部分的条款:下列不注日期的引用文件,其最新版本适用于本方法。
GB/T20001.4 标准编写规则第4部分:化学分析方法。
GB/T14505 岩石和矿石化学分析方法总则及一般规定。
GB6379 测试方法的精密度通过实验室间试验确定标准测试方法的重复性和再现性。
GB/T14496-93 地球化学勘查术语。
3 方法提要试料用氢氟酸、硝酸、高氯酸分解并赶尽高氯酸,用王水溶解后,移至聚乙烯试管中,定容,摇匀。
分取部分澄清溶液,用硝酸(3+97)稀释至1000倍(指试料总稀释系数为1000)后,在等离子体质谱仪上测定。
4 试剂除非另有说明,在分析中仅使用确认为优级纯的试剂和去离子水。
在空白试验(6.2)中,若已检测到所用优级纯试剂中含有大于以上元素方法检出限的含量,并确认已经影响试料中以上元素低量的测定,应净化试剂。
4.1 盐酸(1.19g/mL)4.2 硝酸(1.40g/mL)4.3 氢氟酸(1.13g/mL)4.4 高氯酸(1.67g/mL)4.5 硝酸(3+97)4.6 王水750mL盐酸(4.1)与250mL硝酸(4.2)混合,摇匀。
2020版《中国药典》9种有机氯类农药残留量测定法

《中国药典》2020版已经正式实施,关于农残检测有很大变化,主要是增加了第五法禁用农药的检测方法,不过今天小编要说的是药典中多年未变的2341通则第一法中“9种有机氯类农药残留量测定法”,新版药典要求下,甘草和黄芪两种样品还是按照第一法检测五氯硝基苯的含量,而“9种有机氯类农药残留量测定法”中有个关于系统适应性的要求一直是困扰很多小伙伴的问题,如下图所示,标准中要求理论塔板数按α-BHC(α-六六六)计算应不低于1×106,两个峰的分离度应大于1.5。
今天小编为大家介绍三种在不偏离药典气相通则规定条件下能够满足这个系统适应性要求的方法。
《中国药典2020版》四部通则2341方法一仪器:安捷伦7890A;色谱柱:CNW CD-1701(30m*0.32mm*0.25um);进样口:230℃;进样量:1μL;不分流进样;载气流速:初始流速0.8 mL /min,保持13min,以1mL/min2的速率升至1.5mL/min,保持12.75min;升温程序:初始100℃,10℃/min 升至220℃,8℃/min升至250℃,保持10min;ECD检测器温度:300℃,尾吹气(N2)流量50mL/min。
该方法下的谱图和实验结果见下图:方法二仪器:安捷伦7890A;色谱柱:CNW CD-1701(30m*0.25mm*0.25um);进样口:230℃;进样量:1μL;不分流进样;载气流速:1.0mL/min;升温程序:初始100℃,10℃/min 升至220℃,8℃/min升至250℃,保持10min;ECD检测器温度:300℃,尾吹气(N2)流量50mL/min。
该方法下的谱图和实验结果见下图:方法三仪器:安捷伦7890A;色谱柱:CNW CD-1701(30m*0.32mm*0.25um);进样口:230℃;进样量:1μL;不分流进样;载气流速:1.0mL/min;升温程序:初始70℃,10℃/min 升至220℃,8℃/min升至250℃,保持10min;ECD检测器温度:300℃,尾吹气(N2)流量50mL/min。
色谱定性和定量分析方法

Identification
2019/9/22
二、 色谱定量分析方法 1. 峰面积的测量
(1)峰高(h)乘半峰宽(Y 1/2)法:近似将色谱峰当作等腰三角形。此法算 出的面积是实际峰面积的0.94倍:
A = 1.064 h·Y1/2 (2)峰高乘平均峰宽法:当峰形不对称时,可在峰高0.15和0.85处分别测定峰 宽,由下式计算峰面积:
fi' Ai
f
' s
AS
ci
%
mi W
100
ms
fi' Ai
f
' s
AS
W
100
ms W
fi' Ai
f
' s
AS
100
2019/9/22
内标法特点
(1) 内标法的准确性较高,操作条件和进样量的稍许变动对定量结果的影响 不大。
(2) 每个试样的分析,都要进行两次称量,不适合大批量试样的快速分析。 (3)若将内标法中的试样取样量和内标物加入量固定,则:
Ai Ai
)
100
i 1
特点及要求: 归一化法简便、准确; 进样量的准确性和操作条件的变动对测定结果影响不大; 仅适用于试样中所有组分全出峰的情况。
2019/9/22
(2)外标法
外标法也称为标准曲线法。 特点及要求: 外标法不使用校正因子,准确性较高, 操作条件变化对结果准确性影响较大。 对进样量的准确性控制要求较高,适用于大批量试样的快速分析。
1.0 DEG/MI N
HEWLET PTACKAR
5972A
D
Mass Selectiv eDetecto r
光谱白版校正原理

光谱白版校正原理
光谱白版校正是一种常用的光谱仪器校准方法,用于消除由于光源、光路、检测器等因素引入的误差,提高仪器的测量精度和稳定性。
光谱仪器在进行测量时,会受到多种因素的影响,如光源的强度分布、光路的透过率、检测器的响应等。
这些因素会导致测量结果的偏差,因此需要进行校准以消除这些误差。
光谱白版校正的原理是利用白色反射板的特性进行校准。
白色反射板具有较高的反射率,并且在可见光和近红外光谱范围内反射率相对稳定。
因此,将白色反射板作为标准样品,通过测量其反射光谱,可以得到光源、光路和检测器的综合响应。
在进行光谱白版校正时,首先需要将白色反射板放置在仪器的样品位置,并进行扫描测量。
在测量过程中,仪器会记录下反射率、背景和暗信号等数据。
然后,将这些数据与样品扫描时的数据进行对比和修正。
修正的过程通常包括以下几个步骤:
扣除背景信号:从测量数据中扣除背景信号,以消除环境光和仪器本身对测量结果的影响。
归一化处理:将测量数据归一化到相同的尺度上,以便进行比较和修正。
线性化校正:根据白色反射板的反射率数据,对仪器的
响应进行线性化校正,以消除非线性误差。
稳定性校正:根据多次测量的结果,对仪器的稳定性进行校正,以提高测量的重复性。
通过光谱白版校正,可以有效地消除由于光源、光路、检测器等因素引入的误差,提高仪器的测量精度和稳定性。
同时,白版校正还可以用于监测仪器的性能变化,及时发现并解决问题,确保测量结果的准确性和可靠性。
五线谱与简谱对应的9种基本节奏型.

五线谱与简谱对应的9种基本节奏型.
五线谱和简谱都是看谱子的方式,五线谱看起来没有简谱直观,数字简谱以可动唱名法为基础,用1、2、3、4、5、6、7代表音阶中的7个基本音级,读音为do、re、mi、fa、sol、la、si,休止以O表示。
每一个数字的时值名相当于五线谱的4分音符。
五线谱的每根线以及线与线之间的空间,自下而上分别称为第1线、第2线、第3线、第4线、第5线和第1间、第2间、第3间、第4间。
线和间如不够使用,可在五线谱上方或下方增加线和间。
加线及加间各分别称为上加第1线、上加第1间;下加第1线、下加第1间等,各代表1个音级。
这些音级的固定高度根据所用的谱号来决定。
谱号有3种:高音谱号,亦称G谱号;低音谱号,亦称F谱号;中音谱号,亦称C谱号。
光谱反射比校准方法

光谱反射比校准方法
1. 标准样品校准,使用已知反射率的标准样品进行校准。
这些
标准样品通常由国际标准组织或相关行业组织制定,并具有已知的
光谱反射率。
通过将仪器测量的数据与标准样品的数据进行比较,
可以进行校准。
2. 参考光源校准,使用已知光谱反射率的参考光源进行校准。
这种方法通过将光源照射到参考反射标准上,然后测量光谱反射率,以确保光源的稳定性和一致性。
3. 零点校准,在进行光谱反射测量之前,将仪器设置为零反射率。
这可以通过遮挡光源或将探测器置于零反射率的表面上来实现。
这种方法可以消除仪器本身的系统误差。
4. 仪器响应校准,定期检查和校准光谱仪器的响应。
这包括检
查探测器的线性响应、波长校准和灵敏度校准,以确保仪器能够准
确地测量光谱反射率。
5. 数据处理校准,在进行光谱反射测量后,对数据进行后处理
校准。
这包括校正仪器漂移、噪声和其他干扰因素,以确保最终的
光谱反射率数据准确可靠。
总的来说,光谱反射比校准方法是一个系统工程,需要从标准
样品、光源、仪器响应和数据处理等多个方面进行全面考虑和实施,以确保光谱反射测量结果的准确性和可靠性。
这些方法的正确应用
可以提高光谱反射测量的精度和可重复性,对于科研、工程和实验
室应用具有重要意义。
211133766_标准曲线和单点校正定量方法的结果比较

标准曲线和单点校正定量方法的结果比较胡嘉敏(鹤山市农产品质量监督检验测试中心,广东鹤山 529700)摘 要:本文采用气相色谱-质谱联用的检测方法,以冬瓜为基质,对添加浓度为0.05 mg·kg-1、0.10 mg·kg-1、0.12 mg·kg-1的腐霉利、甲基对硫磷、甲氰菊酯、三唑酮、氧乐果进行测定,采用标准曲线法和单点校正法两种方法进行定量分析,对定量结果进行可重复双因素方差分析。
结果表明,不同的添加浓度、不同农药种类采用标准曲线法和单点校正法两种方法进行定量的结果之间没有显著差异(P>0.05)。
当数据分析中出现标准曲线相关系数不符合要求的情况,可以选择采用单点校正法来进行定量,以减少误差。
关键词:气相色谱-质谱联用仪;可重复双因素分析;标准曲线法;单点校正法Comparison of Results for the Standard Curve Quantitation Method and the Single Point Calibration MethodHU Jiamin(Supervision and Testing Center for Agricultural Products Quality of Heshan, Heshan 529700, China)Abstract: The test method of gas chromatography tandem mass spectrometry (GC-MS/MS) was used to determine the concentration of procymidone, parathion-methyl, fenpropathrin, triadimefon and omethoate added at 0.05 mg·kg-1, 0.10 mg·kg-1 and 0.12 mg·kg-1, using wax gourd as the matrix, the standard curve quantitation method and single point calibration method were used for quantitative analysis, and the results were analyzed by repeatable two-factor variance analysis. The results showed that there was no significant difference between the quantitative results of standard curve quantitation method and single point calibration method for different added concentrations and different pesticide types (P>0.05). When the correlation coefficient of the standard curve does not meet the requirements, the single point calibration method can be selected for quantification to reduce errors.Keywords: gas chromatography tandem mass spectrometry; repeatable two-factor analysis; standard curve quantitation method; single point calibration method蔬菜和水果在人们的膳食结构中占据非常重要的位置,其为人们的生存提供了必需的营养物质[1],在水果和蔬菜的种植过程中,为了得到最大的经济效益,农民往往会使用各种不同种类的农药和化肥促进生长,消灭或预防病虫害[2]。
拉曼光谱是研究分子振动的一种光谱方法

拉曼光谱是研究分子振动的一种光谱方法 ,它的原理和机制都与红外光谱不同 ,但它提供的结构信息却是类似的 ,都是关于分子内部各种简正振动频率及有关振动能级的情况 ,从而可以用来鉴定分子中存在的官能团。
分子偶极矩变化是红外光谱产生的原因 ,而拉曼光谱是分子极化率变化诱导的 ,它的谱线强度取决于相应的简正振动过程中极化率的变化的大小。
在分子结构分析中 ,拉曼光谱与红外光谱是相互补充的。
例如:电荷分布中心对称的键 ,如 C-C、N=N、S-S 等 ,红外吸收很弱 ,而拉曼散射却很强 ,因此 ,一些在红外光谱仪无法检测的信息在拉曼光谱能很好地表现出来。
喇曼效应起源于分子振动(和点阵振动)与转动,因此从喇曼光谱中可以得到分子振动能级(点阵振动能级)与转动能级结构的知识。
用虚的上能级概念可以说明了喇曼效应:设散射物分子原来处于基电子态,振动能级如图所示。
当受到入射光照射时,激发光与此分子的作用引起的极化可以看作为虚的吸收,表述为电子跃迁到虚态(Virtual state),虚能级上的电子立即跃迁到下能级而发光,即为散射光。
设仍回到初始的电子态,则有如图所示的三种情况。
因而散射光中既有与入射光频率相同的谱线,也有与入射光频率不同的谱线,前者称为瑞利线,后者称为喇曼线。
在喇曼线中,又把频率小于入射光频率的谱线称为斯托克斯线,而把频率大于入射光频率的谱线称为反斯托克斯线。
附加频率值与振动能级有关的称作大拉曼位移,与同一振动能级内的转动能级有关的称作小拉曼位移:大拉曼位移:v=v0+v',v= v-v' (v'为振动能级带频率)小拉曼位移:v~= v~±(6+4J)B,J=0,1,2… (其中B为转动常数)简单推导小拉曼位移:利用转动常数 B=h/4πIc转动能级Ej=J(J+1)h2/2I=J(J+1)hcB能级的选择定则为:△J=±2所以有E-E0=±(6+4J)hcB即v~=v~±(6+4J)B,J=0,1,2…谱线特征拉曼散射光谱具有以下明显的特征:b.在以波数为变量的拉曼光谱图上,斯托克斯线和反斯托克斯线对称地分布在瑞利散射线两侧,这是由于在上述两种情况下分别相应于得到或失去了一个振动量子的能量。
光谱峰位微调

光谱峰位微调
光谱峰位微调是一种技术,用于对光谱中的峰位进行微调,以达到更准确的分析和识别。
这种微调可以通过多种方法实现,例如改变光谱仪的参数、调整样品的位置或改变光源的波长等。
具体来说,光谱峰位微调的方法可能包括以下几个步骤:
收集光谱数据:使用光谱仪收集待测样品的光谱数据。
分析光谱数据:对收集到的光谱数据进行处理和分析,确定需要微调的峰位。
调整光谱仪参数:根据分析结果,微调光谱仪的参数,例如扫描速度、分辨率、滤波器等,以获得更准确的光谱数据。
微调样品位置:通过微调样品的位置或角度,改变光线的入射角度和路径长度,从而微调光谱中的峰位。
改变光源波长:通过改变光源的波长,可以获得更广泛的光谱范围,并进一步微调光谱中的峰位。
在进行光谱峰位微调时,需要注意以下几点:
确保光谱仪的稳定性和准确性,以获得可靠的光谱数据。
根据待测样品的特性和分析需求,选择合适的微调方法和参数。
在微调过程中保持谨慎和耐心,以避免误操作或损坏设备。
总之,光谱峰位微调是一种重要的光谱分析技术,可以帮助我们
更准确地识别和分析光谱中的峰位信息。
9种最常见的原料药晶型检测方法

9种最常见的原料药晶型检测⽅法写在前⾯药物晶型研究和药物固态研发在制药业具有举⾜轻重的意义。
研究药物晶型的⼿段有很多种,今天咱们就其中的⼏种进⾏探讨。
药物分⼦通常有不同的固体形态,包括盐类,多晶,共晶,⽆定形,⽔合物和溶剂合物;同⼀药物分⼦的不同晶型,在晶体结构,稳定性,可⽣产性和⽣物利⽤度等性质⽅⾯可能会有显著差异,从⽽直接影响药物的疗效以及可开发性。
如果没有很好的评估并选择最佳的药物晶型进⾏研发,可能会在临床后期发⽣晶型的变化,从⽽导致药物延期上市⽽蒙受巨⼤的经济损失,如果上市后因为晶型变化⽽导致药物被迫撤市,损失就更为惨重。
因此,药物晶型研究和药物固态研发在制药业具有举⾜轻重的意义。
X-射线衍射法(X-ray diffraction)X-射线衍射是研究药物晶型的主要⼿段,该⽅法可⽤于区别晶态和⾮晶态,鉴别晶体的品种,区别混合物和化合物,测定药物晶型结构,测定晶胞参数(如原⼦间的距离、环平⾯的距离、双⾯夹⾓等),还可⽤于不同晶型的⽐较。
X-射线衍射法⼜分为粉末衍射和单晶衍射两种,前者主要⽤于结晶物质的鉴别及纯度检查,后者主要⽤于分⼦量和晶体结构的测定。
1单晶衍射单晶衍射是国际上公认的确证多晶型的最可靠⽅法,利⽤该⽅法可获得对晶体的各晶胞参数,进⽽确定结晶构型和分⼦排列,达到对晶型的深度认知。
⽽且该⽅法还可⽤于结晶⽔/溶剂的测定,以及对成盐药物碱基、酸根间成键关系的确认。
然⽽,由于较难得到⾜够⼤⼩和纯度的单晶,因此该⽅法在实际操作中存在⼀定困难。
2粉末衍射粉末衍射是研究药物多晶型的最常⽤的⽅法。
粉末法研究的对象不是单晶体,⽽是众多取向随机的⼩晶体的总和。
每⼀种晶体的粉末X-射线衍射图谱就如同⼈的指纹,利⽤该⽅法所测得的每⼀种晶体的衍射线强度和分布都有着特殊的规律,以此利⽤所测得的图谱,可获得出晶型变化、结晶度、晶构状态、是否有混晶等信息。
该⽅法不必制备单晶,使得实验过程更为简便,但在应⽤该⽅法时,应注意粉末的细度,⽽且在制备样品时需特别注意研磨过筛时不可发⽣晶型的转变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9种谱校正方法及matlab 程序代码采样间隔归一化成1T ∆=,采样长度为N .这样FFT 离散谱线为0,1)i X i N =-(,相应的频率分辨率2/(1/)N f N ωπ∆=∆=. 设FFT 离散谱线局部极高谱线为m (为了数学上简洁,假定从0开始,注意在MA TLAB 环境下数组实际操作的是从1开始),记频偏量δωδω=∆. 我们需要使用谱线m 和与之相邻一条次高谱线,记这连续两条谱线中左边一条序号为M (当次高谱线在m 左侧时1M m =-,反之M m =).下面列出若干算法的δ计算公式1. 加矩形窗的精确谱校正[1]i i i X U jV =+111()sin()()cos()M M M M opt M MV V M U U M K U U ωω+++-∆+-∆=- 1211cos()sin()cos()sin()opt M M opt M M K M Z V U M K M Z V U M ωωωωωω++-∆⎡⎤=+⎢⎥∆⎣⎦-∆+∆⎡⎤=+⎢⎥∆+∆⎣⎦ 2121cos()cos()()Z M Z M M m Z Z ωωωδ∆+∆-∆=+-- 2. 加矩形窗情形,采用解析单频模型的幅值比校正[1, 2]11||()||||M M M X M m X X δ++=+-+ 3. 加汉宁窗情形,采用解析单频模型的幅值比校正[1, 2]112||||()||||M M M M X X M m X X δ++-=+-+ 4. 加矩形窗情形,采用解析单频模型的复比值校正[3]11Re ()M M M X M m X X δ++⎛⎫=+- ⎪-⎝⎭5. 加汉宁窗情形,采用解析单频模型的复比值校正[3]112()M M M MX X M m X X δ+++=+-- 6. 加矩形窗情形,采用解析单频模型的复合复比值校正[3]11Re ()M m M M X M m X X δ++⎛⎫=+- ⎪-⎝⎭ 11m R m mX X X δ++=-,1111m m L m m m m X X X X X X δ---=-=-- 0.5)0.5)m L m R δδδδδ=-++((7. 加汉宁窗情形,采用解析单频模型的复合复比值校正[3]112Re ()M M m M M X X M m X X δ++⎛⎫+=+-⎪-⎝⎭ 112m m R m mX X X X δ+++=-,1111221m m m m L m m m m X X X X X X X X δ----++=-=-- 0.5)0.5)m L m R δδδδδ=-++((8. 加矩形窗,Quin 校正[4]11Re()Re(),Re()Re()m m L R m m X X X X αα-+== 11L R L R L Rααδδαα==---,, 00 R R L R δδδδδ>>⎧=⎨⎩当且其它9. 加汉宁窗,Quin 校正[4]11Re()Re(),Re()Re()m m L R m m X X X X αα-+== 212111L RL R L Rααδδαα++==---,,00 R R L R δδδδδ>>⎧=⎨⎩当且其它References1. Schoukens, J., R. Pintelon,H. Van Hamme. The interpolated fast Fourier transform: Acomparative study . IEEE Transactions on Instrumentation and Measurement. 1992, 41(2):226-232.2. 谢明,丁康. 频谱分析的校正方法.振动工程学报. 1994, 7(2): 172-179.3. 陈奎孚, 王建立,张森文. 频谱校正的复比值法.振动工程学报(已投). 2007.4. Quinn, B.G. Estimating frequency by interpolation using Fourier coefficients.IEEETransactions on Signal Processing. 1994, 42(5): 1264-1268.%========================这是调用调试==================DT=1;N=1024;PHI=pi/3;Ampl=1;CiR=11.9; %cycles in recordFreq=CiR/(DT*N); %frequencyTV=[0:N-1];DatVec=Ampl*cos(Freq*TV*2*pi+PHI);FV=fft(DatVec);figuresubplot(2,1,1);plot(TV,DatV ec);subplot(2,1,2);plot(abs(FV(1:round(N/2.56))));grid on[MV,MI]=max(abs(FV));%加矩形窗的解析校正--1FreqShift=SpecCorr(FV,MI,N,1);%加矩形窗的解析单频模型校正--2FreqShift=SpecCorr(FV,MI,N,2);%加汉宁窗的解析单频模型校正--3HanDat=DatVec.*hanning(N,'periodic')';FV=fft(HanDat);FreqShift=SpecCorr(FV,MI,N,3);%加矩形窗的解析单频模型校正+复比值法--4FV=fft(DatVec);FreqShift=SpecCorr(FV,MI,N,4);%加汉宁窗的解析单频模型校正+复比值法--5HanDat=DatVec.*hanning(N,'periodic')';FV=fft(HanDat);FreqShift=SpecCorr(FV,MI,N,5);%加矩形窗的解析单频模型校正+复比值法+左右平均--6FV=fft(DatVec);FreqShift=SpecCorr(FV,MI,N,6);%加汉宁窗的解析单频模型校正+复比值法+左右平均--7HanDat=DatVec.*hanning(N,'periodic')';FV=fft(HanDat);FreqShift=SpecCorr(FV,MI,N,7);%加矩形窗的解析单频模型校正+Quinn算法--8FV=fft(DatVec);FreqShift=SpecCorr(FV,MI,N,8);%加汉宁窗的解析单频模型校正+Quinn算法--9HanDat=DatVec.*hanning(N,'periodic')';FV=fft(HanDat);FreqShift=SpecCorr(FV,MI,N,9);===========这是子程序======================%spectrum correction assemble% the sampling interval is 1 s (or unitary)%Input: SpecVec--Discrte Fourier Spectrum from FFT% PeakIdx--the peak index, noting the matrix in MatLab start from 1% TL--the length (or the point number) of the FFT% method--correction method% output: PeakShift-- the corrected peak shifting from the peak in discrete% spectrumfunction PeakShift=SpecCorr(SpecVec,PeakIdx,TL,method)% picking up the second highest spectrum lineif(abs(SpecVec(PeakIdx-1))>abs(SpecVec(PeakIdx+1)))IP=[PeakIdx-1,PeakIdx];ShiftCorr=-1; %shift aligning with the PeakIdxelseIP=[PeakIdx,PeakIdx+1];ShiftCorr=0; %shift aligning with the PeakIdxendII=IP(1)-1; % noting that the index of a matrix in MATLAB starts from 1, not zero if(method==1) %an analyitic solution for rectangular windowU=real(SpecVec(IP));V=imag(SpecVec(IP));DW=2*pi/TL;KOPT=(sin(II*DW)*(V(2)-V(1))+cos(II*DW)*(U(2)-U(1)))/(U(2)-U(1));Z=V.*(KOPT-cos((IP-1)*DW))./(sin(DW*(IP-1)))+U;Tmp1=(Z(2)*cos(DW*(II+1))-Z(1)*cos(DW*II))/(Z(2)-Z(1));PeakPos=acos(Tmp1)/DW;PeakShift=PeakPos-(PeakIdx-1);elseif(method==2) %based on the analytical-single-tone model for rectangular window PeakShift=abs(SpecVec(IP(2)))/(abs(SpecVec(IP(2)))+abs(SpecVec(IP(1))));PeakShift=PeakShift+ShiftCorr; %shift aligning with the PeakIdxelseif(method==3) %based on the analytical-single-tone model for Hanning windowPeakShift=(2*abs(SpecVec(IP(2)))-abs(SpecV ec(IP(1))))/(abs(SpecV ec(IP(2)))+abs(SpecVec(IP(1 ))));PeakShift=PeakShift+ShiftCorr; %shift aligning with the PeakIdxelseif(method==4) %based on the analytical-single-tone model for rectangular window with complex correctionPeakShift=real(SpecVec(IP(2))/(SpecVec(IP(2))-SpecVec(IP(1))));PeakShift=PeakShift+ShiftCorr; %shift aligning with the PeakIdxelseif(method==5) %based on the analytical-single-tone model for Hanning window with complex correctionPeakShift=(2*SpecVec(IP(2))+SpecVec(IP(1)))/(SpecVec(IP(2))-SpecVec(IP(1)));PeakShift=real(PeakShift)+ShiftCorr; %shift aligning with the PeakIdx elseif(method==6) %based on the analytical-single-tone model for rectangular window with complex correction+averagePeakShift=real(SpecVec(IP(2))/(SpecVec(IP(2))-SpecVec(IP(1))));MaxPeakShift=PeakShift+ShiftCorr; %shift aligning with the PeakIdxLeftShift=real(SpecVec(PeakIdx)/(SpecVec(PeakIdx)-SpecVec(PeakIdx-1)))-1;RightShift=real(SpecVec(PeakIdx+1)/(SpecVec(PeakIdx+1)-SpecVec(PeakIdx)));%averagePeakShift=(0.5-MaxPeakShift)*LeftShift+(0.5+MaxPeakShift)*RightShift;elseif(method==7) %based on the analytical-single-tone model for Hanning window with complex correction+average,????PeakShift=(2*SpecVec(IP(2))+SpecVec(IP(1)))/(SpecVec(IP(2))-SpecVec(IP(1)));MaxPeakShift=real(PeakShift)+ShiftCorr; %shift aligning with the PeakIdxLeftShift=(2*SpecVec(PeakIdx)+SpecV ec(PeakIdx-1))/(SpecVec(PeakIdx)-SpecVec(PeakIdx-1))-1;RightShift=(2*SpecVec(PeakIdx+1)+SpecV ec(PeakIdx))/(SpecVec(PeakIdx+1)-SpecVec(PeakIdx ));%averagePeakShift=(0.5-MaxPeakShift)*LeftShift+(0.5+MaxPeakShift)*RightShift;elseif(method==8) %Quinn method for the rectangular windowa1 = real(SpecV ec(PeakIdx-1)/SpecVec(PeakIdx)); %lefta2 = real(SpecV ec(PeakIdx+1)/SpecVec(PeakIdx)); %rightLeftShift = a1/(1-a1);RightShift = -a2/(1-a2);if (LeftShift>0 & RightShift>0)PeakShift = RightShift;elsePeakShift = LeftShift;endelseif(method==9) %Quinn method for the Hanning windowa1 = real(SpecV ec(PeakIdx-1)/SpecVec(PeakIdx)); %lefta2 = real(SpecV ec(PeakIdx+1)/SpecVec(PeakIdx)); %rightLeftShift = (2*a1+1)/(1-a1);RightShift = -(2*a2+1)/(1-a2);if (LeftShift>0 & RightShift>0)PeakShift = RightShift;elsePeakShift = LeftShift;endendend。
