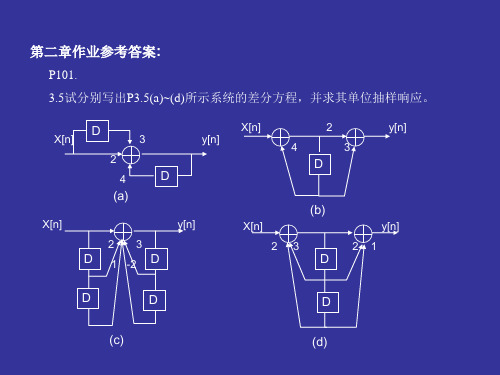
信号与系统作业作业答案
北交20春《信号与系统》在线作业二_答案

(单选题)1: 当输入信号的复频率等于系统函数的零点时,系统的强迫响应分量为()。
A: 无穷大
B: 不为零的常数
C: 0
D: 随输入信号而定
正确答案: C
(单选题)2: 满足傅氏级数收敛条件时,周期信号f(t)的平均功率()。
A: 大于各谐波分量平均功率之和
B: 不等于各谐波分量平均功率之和
C: 小于各谐波分量平均功率之和
D: 等于各谐波分量平均功率之和
正确答案: D
(单选题)3: 卷积δ(t)*f(t)*δ(t)的结果为()。
A: δ(t)
B: δ(2t)
C: f(t)
D: f(2t)
正确答案: C
(单选题)4: 信号的时宽与信号的频宽之间呈()。
A: 正比关系
B: 反比关系
C: 平方关系
D: 没有关系
正确答案: B
(单选题)5: 设一个矩形脉冲的面积为S,则矩形脉冲的傅氏变换在原点处的函数值等于()。
A: S/2
B: S/3
C: S/4
D: S
正确答案: D
(单选题)6: 线性系统具有()。
A: 分解特性
B: 零状态线性
C: 零输入线性
D: 以上全对
正确答案: D
(单选题)7: 如果一连续时间二阶系统的系统函数H(s)的共轭极点在虚轴上,则它的h(t)应是()。
信号与系统习题与答案

【填空题】(为任意值)是________ (填连续信号或离散信号),若是离散信号,该信号____(填是或不是)数字信号。
【填空题】是________ (填连续信号或离散信号),若是离散信号,该信号____(填是或不是)数字信号。
【填空题】信号________ (填是或不是),若是周期信号,周期为__pi/5__。
【填空题】系统为____(填线性或非线性)系统、____(填时变或非时变)系统、____(填因果或非因果)系统。
【填空题】系统为____(填线性或非线性)系统、____(填时变或非时变)系统、____(填因果或非因果)系统。
【简答题】判断下图波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号。
连续时间信号【简答题】判断下图波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号。
离散时间信号且为数字信号【简答题】判断信号是功率信号还是能量信号,若是功率信号,平均功率是多少?若是能量信号,能量为多少?功率信号平均功率为4.5【简答题】线性时不变系统具有哪些特性?均匀性、叠加性、时不变性、微分性、因果性。
【填空题】的函数值为____。
2【填空题】的函数值为____。
【填空题】假设,的函数值为____。
1【填空题】假设,的函数值为____。
【填空题】的函数值为____。
我的答案:第一空:e^2-26【填空题】已知,将____(填左移或右移)____可得。
右移个单位7【简答题】计算的微分与积分。
8【简答题】什么是奇异信号?我的答案:奇异信号是指函数本身或其导数或高阶导数具有不连续点(跳变点)。
9【简答题】写出如下波形的函数表达式。
我的答案:f(t)=u(t)+u(t-1)+u(t-2)10【简答题】已知信号的图形如图所示,画出的波形。
我的答案:【简答题】信号微分运算具有什么特点?举一个应用实例。
特点:微分凸显了信号的变化部分。
微分方程(包括偏微分方程和积分方程)把函数和代数结合起来,级数和积分变换解决数值计算问题。
信号与系统课后习题参考答案

1试分别指出以下波形是属于哪种信号?题图1-11-2 试写出题1-1 图中信号的函数表达式。
1-3 已知信号x1(t)与x2(t)波形如题图1-3 中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴x1(t2)⑵ x1(1 t)⑶ x1(2t 2)⑷ x2(t 3)⑸ x2(t 2) ⑹x2(1 2t)2⑺x1(t) x2( t)⑻x1(1 t)x2(t 1)⑼x1(2 t) x2(t 4)21- 4 已知信号x1(n)与x2 (n)波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴x1(2n 1) ⑵ x1(4 n)⑶ x1(n)2⑷ x2 (2 n)⑸ x2(n 2) ⑹ x2(n 2) x2( n 1)⑺x1(n 2) x2(1 2n)⑻x1(1 n) x2(n 4)⑼ x1(n 1) x2(n 3)1- 5 已知信号x(5 2t )的波形如题图1-5 所示,试作出信号x(t)的波形图,并加以标注。
题图1-51- 6 试画出下列信号的波形图:1⑴ x(t) sin( t) sin(8 t)⑵ x(t) [1 sin( t )] sin(8 t)21⑶x(t) [1 sin( t)] sin(8 t)⑷ x(t) sin( 2t )1-7 试画出下列信号的波形图:⑴ x(t)1 e t u(t) ⑵ x(t) e t cos10 t[u(t 1) u(t 2)]⑶ x(t)(2 e t)u(t)⑷ x(t) e (t 1)u(t)⑸ x(t)u(t22 9) ⑹ x(t)(t2 4)1-8 试求出以下复变函数的模与幅角,并画出模与幅角的波形图1j2 ⑴ X (j ) (1 e j2)⑵ X( j1 e j4⑶ X (j ) 11 ee j ⑷ X( j )试作出下列波形的奇分量、偶分量和非零区间上的平均分量与交流分量。
题图 1-10形图。
题图 1-141-15 已知系统的信号流图如下,试写出各自系统的输入输出方程。
信号与系统 于敏慧(第二版)第二周作业答案

y0(t)
1
t
0
2
4
(6) x(t) = dx0 (t) , h(t) = dh0 (t) 。
dt
dt
x(t) * h(t) = dx0 (t) * dh0 (t) = d 2 y0 (t)
dt dt
dt 2
x(t) ∗ h(t) = 0.5δ(t) − 0.5δ(t − 2)
2.10 求 y[n] = x1[n]* x2[n]* x3[n] 。 其 中 x1[n] = (0.5)n u[n] , x2[n] = u[n + 3] 和
(2)利用(1)的结果,求系统的逆系统的单位样值(脉冲)响应。
(3)利用(2)的结果,结合卷积性质,求一信号 x[n],使之满足
x[n]* h[n] = 2n (u[n] − u[n − 4])
解:(1) h[n] − Ah[n −1] = δ [n],其中 h[n] = (1 )n u[n] , 2
(通项: an = a1q n−1 )
n
∑ 此题: a1 = 1, q = 2 ; x[n]* h[n] = 2nu[n]*u[n] = ( 2k )u[n] = (2n+1 −1)u[n] k =0
2.6 计算图 2-45(b)与(c)所示信号 x(n)与 h(n)的卷积和,注意:N=4。 解:(b)利用脉冲信号δ(n)的卷积性质以及卷积的延时性质计算:
k =−∞
+ 3] =
u[n + 3] 0.5k
k =0
;
= 2(1 − 0.5n+4 )u[n + 3]
(2) x1[n]* x2[n]* x3[n] = 2(1 − 0.5n+4 )u[n + 3]* (δ [n] − δ [n −1]) ; = 2(1 − 0.5n+4 )u[n + 3] − 2(1 − 0.5n+3 )u[n + 2]
信号与系统习题解答 (9)

0 7Ω 9Ω
ω
2Aj
2Aj /
3
2Aj /
由X
4 ()
2A 2
X1()
F{sin
10t}
得x4 (t)
F
1{X
4 ()}
4A
x1(t) sin
10t
x4(t)
(b)可取
x5(t) ( / 2A)sin 10t
则
x6 (t) x4 (t)x5 (t)
2x1(t)
sin
2
10t
2x1
10)
X 1 (
10)]
2A 2
X 1 ( )
F{sin
10t}
X1( 30)
2 Aj
…
2 Aj 3 9
-29Ω -27Ω
-33Ω -31Ω 2Aj
2 Aj 9
3
X1( 10)
2Aj /
2 Aj
3
-9Ω -7Ω
-13Ω -11Ω
0
2Aj /
X1( 10)
2Aj /
2 Aj
3
11Ω 13Ω
]
X 3() F{x1(t)x2 (t)} X1() X 2 () / 2
4 Aj 2
X1()
k 1
1 [ 2k 1
(
(2k
1)0 )
(
(2k
1)0 ]
2 Aj
k 1
1 2k
1
[
X1
(
(2k
1)0 )
X 1 (
(2k
1)0 ]
k 1
2 Aj (2k
1)
[
X
1
(
(2k
北理工-信号与系统-第三版-第三章-作业参考答案
k
| u[k ] | ,有界
是非稳定系统
(e) 显然n<0时,h[n]=0,所以是因果系统;
k
| h[k ] | | u[k ] / n | ,无界
k
是非稳定系统
(f) 显然n<0时,h[n]=0,所以是因果系统;
| h[k ] |
(d)
y[n] x[n] h[n]
k
[k n ] [n k n ]
1 2
[n n1 n2 ]
3.11在LTI离散时间系统中 已知x[n]=u[n]时的零状态响应(单位阶跃响应)为s[n],求单位抽样响应h[n]; 已知h[n],求s[n].
y[n] - 4y[n-1] =2x[n]+3x[n-1];
令x[n]=δ[n],则有 h[n] – 4h[n-1] =2 δ[n]+3 δ[n-1];当n<0时,h[n]=0,得h[0]=2,h[1]=11,
特征方程为 λ-4=0, 得λ=4,
h[n]=c(4)nu[n],由h[1]=4c=11,c=11/4得 h[n]=(11/4)(4)nu[n-1]=11 (4)n-1u[n-1],考虑h[0]=2=2 δ[n],得 h[n]=2 δ[n]+11 (4)n-1u[n-1]。(n>0的解) (b).据图有同(a)一样的结果…。 (c).据图 y[n]=3y[n-1]- 2y[n-2]+ x[n]+2x[n-1]+x[n-2] ,即差分方程为 y[n] -3y[n-1]+2y[n-2] = x[n]+2x[n-1]+x[n-2], 先求
第三章作业答案_1-7

a2 N =
1 1 T 1 T − j (4 N π / T ) t 2 x t e dt = x(t )e− j (4 Nπ / T )t dt + ∫T x(t )e− j (4 Nπ / T )t dt ( ) ∫ ∫ T T T 0 T 2 =
T 1 T T ( ∫ 2 x(t )e − j (4 Nπ / T )t dt + ∫T − x(t − )e− j (4 Nπ / T )t dt ) T 0 2 2 T 1 T ( ∫ 2 x(t )e − j (4 Nπ / T ) t dt + ∫ 2 − x(t )e− j (4 Nπ / T )t dt ) = 0 0 T 0
+∞
e − j 2ω (答案) 2 + jω
+∞ +∞ −∞
X ( jϖ ) = ∫ x(t )e − jωt dt = ∫ e −2 ( t − 2) u (t − 2)e − jωt dt = ∫ e −2 ( t − 2) e − jωt dt
−∞ 2
= ∫ e −( 2+ jω )t + 4 dt =
jkπt
,由已知条件 k ≤ 4 时,H(jw)不为零,而 k ≥ 5 ,H(jw)=0
jkπt
故响应为: y k (t ) = H ( jkπ ) a k e 当 k > 5 时,激励 x k (t ) = a k e 此有 y (t ) =
= (1 −
k 5
)a k e jkπt , k ≤ 4
(2) 由于系统的单位冲激响应 h(t)已知,可以据此而求出其频谱。因为 h(t)是方波脉冲,直 接由典型信号的频谱得:
FT h(t ) ←→ H ( jω ) =
信号与系统课后答案(第二版)+曾禹村+第二章作业参考答案

i1(t) = i2 (t) + i3 (t) , i2 (t) R2 − L 有 8i2 `(t) + 3i2 (t) = 2e`(t) ˆ ˆ 由 h`(t) + 3h(t) = 2δ (t)
0
h
(−1) t 3
T
t
t 3E − τ E (t) = ∫ δ (τ )dτ − ∫ e 8 u(τ )dτ −∞ 4 −∞ 32
x(t)
1
2 t
yx(t)
1 2 3 4 t
0
1
0
Qh(0) = 0, t ≤ 0, 有 0 ≤ t <1 , h(t) + h(t −1) + h(t − 2) = h(t) = t 时 1≤ t < 2时 h(t) + h(t −1) + h(t − 2) = h(t) + h(t −1) =1 , h(t) =1− h(t −1) =1− (t −1) = 2 −t 2 ≤ t < 3 , h(t) + h(t −1) + h(t − 2) =1 时 h(t) =1− h(t −1) − h(t − 2) =1− (2 − (t −1)) − (t − 2) = 0 3 ≤ t < 4时 h(t) = 4 − t − h(t −1) − h(t − 2) =4 −t − 0 − (2 − (t − 2)) = 0 , t, 0 ≤ t < 1 ∴h(t) = 2 − t, 1 ≤ t ≤ 2 0, t < 0,2 < t
解: (e) 特征方程为 λ2+4λ+4=0 得 λ1=-2, λ2=-2。 则 h(t)= (c1eλ1 t+ c2eλ2t)u(t)=( c1e- 3 t+ c2e-2 t)u(t) h`(t)= (c1+ c2)δ(t)+(-3c1e- 3 t-2c2e- 2t)u(t) h``(t)= (c1+ c2)δ`(t)+(-3c1-2c2) δ(t)+ (9c1e- 3 t+4c2e- 2t)u(t) 将x(t)= δ(t), y(t)=h(t)代入原方程得:
信号与系统课后答案第三章作业答案

初始为 0, C2 -4
y f (t) -4e3tu(t) 4e2tu(t)
全响应= yx (t)+y f (t) 4e2tu(t)-2e3tu(t)
3-2 描述某 LTI 系统的微分方程为
d2 y(t) dt 2
3dy(t) dt来自2y(t)
df (t) dt
6
1
1
(2e1 e1 et ) u(t)
e1(2 et ) u(t)
(2)
f
(t)
a[u(t
s) 2
u(t
2)]
h(t) b[u(t 2) u(t 3)]
f
(t)
h(t)
ab[(t
1 2
)
u(t
1 2
)
(t
1 2
)
u(t
1) 2
tu(t)
1 4
(et
e3t
)u(t)
1 2
t
e3tu(t)
[
1 4
et
(
1 2
t
1 4
)e3t
]u
(t)
3-19 一 个 LTI 系 统 , 初 始 状 态 不 祥 。 当 激 励 为 f (t) 时 其 全 响 应 为
(2e3t sin 2t)u(t) ;当激励为 2 f (t) 时其全响应为 (e3t 2sin 2t)u(t) 。求
(1) 初始状态不变,当激励为 f (t 1) 时的全响应,并求出零输入相应、
零状态响应; (2) 初始状态是原来的两倍、激励为 2 f (t) 时系统的全响应。
第二次信号与系统作业答案

下半年信号与系统作业1一、判断题:1.拉普拉斯变换满足线性性。
正确2.拉普拉斯变换是连续时间系统进行分析的一种方法。
正确 3.冲击信号的拉氏变换结果是一个常数。
正确 4.单位阶跃响应的拉氏变换称为传递函数。
错误二、填空题1.如果一个系统的幅频响应是常数,那么这个系统就称为 全通系统 。
2.单位冲击信号的拉氏变换结果是 ( 1 ) 。
3.单位阶跃信号的拉氏变换结果是 (1 / s) 。
4.系统的频率响应和系统的传递函数之间的关系是把传递函数中的s 因子用j ω 代替后的数学表达式。
5.从数学定义式上可以看出,当双边拉氏变换的因子s=j ω时,双边拉氏变换的就变成了傅立叶变换的定义式,所以双边拉氏变换又称为 广义傅立叶变换 。
6、单边拉普拉斯变换(LT)的定义式是:.7、双边拉普拉斯变换(LT)的定义式是:.三、计算题 1. 求出以下传递函数的原函数 1)F (s )=1/s 解:f (t)=u(t) 2)F(s)=11+s 解:f (t)=e -tu(t)3)F(s)=)1(12-s s解:F(S)=)1(12-s s =)1)(1(1+-s s s =)1(5.0-s +)1(5.0+s -s1F(t)=0.5e-tu(t)+ 0.5e -t u(t)-U(t)2.根据定义求取单位冲击函数和单位阶跃函数的拉氏变换。
解:L[δ(t)]= ⎰+∞∞-δ(t) e -st dt=1L[u(t)]= ⎰+∞∞-u(t) e -stdt=⎰+∞∞- e -st dt=s13、已知信号)(t f 是因果信号其拉氏变换为F (s )=21s,试求)0(f =? )0(f =lim 0→t )(t f =lim ∞→s S ·F(s)=lim∞→s 2ss =0 4、已知信号)(t f 是因果信号其拉氏变换为F (s )=)100010()10)(2(2++++s s s s s ,试求)(∞f =? 由终值定理)(∞f =lim 0→s SF(s)=lim→s s)100010()10)(2(2++++s s s s s =0.025、求)()(3t u t t f =的拉氏变换答:L[)(t f ]=46s(Re(s)>0)一、判断题(1)如果x(n)是偶对称序列,则X(z)=X(z -1)。
电子科技大学14秋《信号与系统》在线作业3答案

B.虚偶函数的傅里叶级数中不包含正弦项,只可能包含直流项和余弦项
C.实奇函数的傅里叶技术中不包含余弦项和直流项,只可能包含正弦项
D.实奇谐函数的傅里叶级数中只可能包含基波和奇次谐波的正弦、余弦项,而不包含偶次谐波项
?
正确答案:ACD
4.题目及选项如下:
A.若H(z)的全部极点落在单位圆内,则系统稳定
B.若H(z)的全部极点落在单位圆外,则系统稳定
C.若H(z)有极点落于单位圆外,或在单位圆上具有二阶以上的极点,则系统不稳定
D.若H(z)在单位圆上有一阶极点,但其他极点均在单位圆内,则系统临界稳定。
?
正确答案:ACD
3.对于函数的时域对称性与傅里叶系数的关系,下列说法正确的有()。
A.
B.
C.
D.
?
正确答案:B
7.题目及选项如下:
A.
B.
C.
D.
?
正确答案:A
8.对于一个三阶常系数线性微分方程描述的连续时间系统进行系统的时域模拟时,所需积分器数目最少是( )个。
A. 2
B. 3
C. 4
D. 5
?
正确答案:B
9.离散信号f(n)是指()。
A. n的取值是连续的,而f(n)的取值是任意的信号
14秋《信号与系统》在线作业3
一,单选题
1.题目及选项如下:
A.
B.
C.
D.
?
正确答案:B
2.题目及选项如下:
A.
B.
C.
D.
?
正确答案:D
3.题目及选项如下:
A.
B.
信号与系统 于敏慧(第二版)第八周作业答案

n=−∞ 3
m=0
1− 3z z − 1
3
3
∑ ∑ ∑ ∑ (6)x[n]是左边序列, X (z) =
∞
x[n]z −n =
0
(1 n)z −n
∞
=−
(1 m)z m = − 1
∞
mz m
n=−∞
n=−∞ 2
m=0 2
2 m=0
∑ 有多种方法可得
∞
mz m =
z −1
,
m=0
(1 − z −1 )2
z
>a
#############################################
第八周作业 2
7.4; 7.9 (2)、(4); 7.11; 7.14 (2); 7.19; 7.20;7.22
7.4 用长除法、留数定理、部分分式法求以下 X(z)的 Z 反变换。
1 − 1 z −1 (1) 2 ,
1 + 1 z −1
2
4
8
16
2
x[n] = {1,− 1 , 1 ,− 1 ,+ 1 − } = (− 1 )n u[n] 2 4 8 16 2
法二:留数定理:
x[n]
=
{Re
s{X
(
z)
z
n−1}
z
=−
1
u[n]
=
{(
z
+
2
1) 2
z ⋅ z n−1
z+
1
} z=−
1
2
= (− 1 )n u[n] 2
(2) z < 0.5 对应的左边序列
x[n] = Z −1{ z − z } = [−0.5n + 2n ]u[−n −1] z − 0.5 z − 2
[信号与系统作业解答]第一章
![[信号与系统作业解答]第一章](https://img.taocdn.com/s3/m/9bc4ece8f8c75fbfc77db2da.png)
1-3、分别求下列各周期信号的周期 T 1) cos(10 t ) cos(30 t) ; 2) e j 10 t ; 4)
(1)n[u(t nT ) u(t nT T )]
n 0
n
(1) [u(t nT ) u(t nT T )]
图(b)表达式为:
f ( t ) u( t ) u( t 1) 2[u( t 1) u( t 2)] 3u( t 2) ; u( t ) u( t 1) u( t 2)
图(c)表达式为: f ( t ) sin
t [u( t ) u( t T )] ; T
C1e1 (t ) C2e2 (t ) sin[C1e1 (t ) C2e2 (t )]u(t ) C1r1 (t ) C2r2 (t )
由于
所以系统是非线性的。
e( t ) r (t ) sin[e( t )]u(t )
而
e(t t0 ) sin[e(t t0 )]u(t ) r (t t0 ) sin[e(t t0 )]u(t t0 )
5)由于 e1 (t ) r1 (t ) e1 (2t ) , e2 (t ) r2 (t ) e2 (2t ) , 而
C1e1 (t ) C2e2 (t ) C1e1 (2t ) C2e2 (2t ) C1r1 (t ) C2r2 (t )
由于
所以系统是线性的。
C1e1 ( t ) C 2e2 ( t ) C1e1 (t ) C 2e2 (t ) C1r1 (t ) C 2r2 (t )
由于
2
所以系统是非线性的。
信号与系统作业答案郑君里版

信号与系统作业答案郑君里版1.1 1.2 1.3画出信号f(t)sin a(t t0) 的波形。
a(t t0)已知信号f(t) (t 1) u(t 1) u(t 2) ,画出f( 2t 3)的波形。
已知信号f(t) (t 1) u(t 1) u(t 2) ,试求它的直流分量。
答案:01.4 已知信号f(t) (t 1) u(t 1) u(t 2) ,试求它的奇分量和偶分量。
答案:偶分量:0.5(1 t) u(t 2) u(t 1) u(t 1) u(t 1) 0.5(t 1) u(t 1) u(t 2)奇分量:0.5(t 1) u(t 2) u(t 1) t u(t 1) u(t 1) 0.5(t 1) u(t 1) u(t 2)1.5 信号f(t)2 tt 0是否是奇异信号。
t 0答案:二阶以上导数不连续,是奇异信号。
1.6 已知f(t)是有界信号,且当t 时f(t) 0,试问f(t)是否是能量有限信号。
答案:不一定。
1.7 对一连续三角信号进行抽样,每周期抽样8点,求抽样所得离散三角序列的离散角频率。
答案:/41.8 以Ts 0.5s的抽样间隔对下列两个三角信号抽样,写出抽样所得离散序列的表达式,画出它们的波形。
比较和说明两波形的差别,为什么?(1)f1(t) cos4t (2)f2(t) cos15t 4答案:两个离散序列是相同的。
1.9 判断下列信号是否是周期信号。
如果是周期信号,试确定其周期。
(1)f(t) Asin4t Bcos7t Ccos9t 答案:是周期函数,周期T 2 。
(2)fd(n) ejn8答案:是周期信号,周期N 161.10 求下列表达式的函数值(1)(2)(3)(4)(5)(6)(7)f(t t0) (t)dt;答案:f( t0)f(t0 t) (t)dt;答案:f(t0)(t t0)u(t t02)dt;答案:当t0 0时为1;当t0 0时为0 (t t0)u(t 2t0)dt;答案:当t0 0时为1;当t0 0时为0(e t t) (t 2)dt;答案:e2 2 (t sint) (t 6)dt;答案:/6 1/2e j t (2t) (t t0) dt;答案:1/2 e j t01.11 判断下列系统是否线性、时不变和因果de(t);答案:线性,时不变,因果dt(2)r(t) e(t)u(t);答案:线性,时变,因果(1)r(t)(3)r(t) sin e(t) u(t);答案:非线性,时变,因果(4)r(t) e(1 t);答案:线性,时变,非因果(5)r(t) e(2t);答案:线性,时变,非因果(6)r(r) e2(t);答案:非线性,时不变,因果1.12 试证明:f(t) '(t) f(0) '(t) f'(0) (t)。
信号与系统习题解答 (4)

(h) 由1 Re{s} 0, x(t)应为双边信号
x(t )
L -1 X
(s)
L
-1
s(s
s 1 1)( s
2)
L
-1
1/2
s
1/2 s2
1 2
u (t )
1 2
e 2t u (t )
7.11 已知因果系统的系统函数 入x(t)的零状态响应。
H
(s)
s2
s,1求系统对于下列输
(e) (f)
L {teatu(t)}sin
0 (t
)u(t)}
e e e e j0 j0t
j0 j0t
L{
2j
u(t)}
e e j0 j0t
e e j0 j0t
L{
u(t)} L {
u(t)}
2j
2j
e j0
1
e j0
1
s sin 0 0 cos0
X (s) (s 3) y(0) y`(0)
Y (s) s2 3s 2
s2 3s 2
Yx (s)
s2
X (s) 3s
2
s2
1 3s
2
2 s
1 s
2 s 1
s
1
2
yx (t) 1 2et e2t u(t)
1) 5s
6
L
-1
(s
(s 1) 2)(s
3)
L
-1
(
1 s 2)
(s
2
3)
e 2t u (t )
2e 3t u (t )
(f) 由0 Re{s} 1, x(t)应为双边信号
x(t )
西南大学21春[1073]《信号与系统》作业答案
![西南大学21春[1073]《信号与系统》作业答案](https://img.taocdn.com/s3/m/d03a7839d15abe23492f4d9e.png)
1073 20211单项选择题1、设是信号的傅里叶变换,的波形如图所示,则等于()。
1.4pi2.2pi3.6pi4.02、完整表示对理想滤波器的逼近,可以采用()1.误差容限图2.阻带最小衰减3.对模拟与数字滤波器要区别对待4.通带内最大误差3、冲激函数的单边(下限规定为从0-时刻开始)拉氏变换为1.js2.03.s4.14、下列滤波器中,通带最平坦的是()1.巴特沃思2.贝塞尔滤波器3.椭圆滤波器4.切比雪夫5、等于()1. F. 12.03.e^-54.e^-16、()1.f(-1)2.f(1)3.04.f(0)7、已知信号x(t)的傅里叶变换为,则信号y(t)的频谱为()。
1.R(w)cos(w)2.R(w)/23.R(w/2)4.R(w)8、关于抽样,下列说法错误的是()1. E. 理想的冲激采样可表示零阶保持抽样,二者的频谱变化是一致的。
2.时域抽样,频域会产生周期延拓3.频域抽样,时域会产生周期延拓4.由时域抽样可知,序列的频谱是周期连续的频谱9、已知,则等于()1.2pi2.03.1/24.110、周期信号的波形如图所示,则其傅里叶级数中含有()。
1.正弦分量与余弦分量2.直流分量与正弦分量3.奇次谐波分量4.直流分量与余弦分量11、从S域到Z域的映射中,为保证映射前后滤波器的稳定性不变,则应满足()1.s域左半平面映射到z域的单位圆内,虚轴到单位圆外2.s域左半平面映射到z域的单位圆外,虚轴到单位圆内3.s域左半平面映射到z域的单位圆外部,虚轴到单位圆4.s域左半平面映射到z域的单位圆内,虚轴到单位圆12、关于傅里叶变换,时域做虚指数加权,频域()1.左移2.尺度3.右移4.平移13、已知二端口网络如下图所示,则该系统为()。
1.带阻2.带通3.低通4.高通判断题14、抽样函数可简写为Sa(t)=sin(t)/t,是偶对称的函数。
1. A.√2. B.×15、连续信号的移位、翻转、尺度等运算,都是针对独立变量t而言。
奥鹏2020年6月福师《信号与系统》在线作业一_3.doc

1.信号f(t)=Sa(100t)的最低抽样率等于( )。
A.100/πB.π/100C.100D.1/100【参考答案】: A2.下列描述正确的是()。
A.信号f(t)反折,则其相应的频谱F(jω)也反折B.信号f(t)在时间轴上扩展2倍,则其相应的频谱在ω轴上也扩展2倍C.信号f(t)在时间轴上平移2,则其相应的频谱在ω轴上也平移2D.信号f(t)为时限信号,则其相应的频谱也是频带有限的【参考答案】: A3.函数f(s)=1/s+1/(s+1)逆变换的初值等于( )。
A.0B.1C.2D.3【参考答案】: C4.单位序列响应h(n)=2u(n)的系统是( )系统。
A.因果及稳定B.非因果及稳定C.因果及非稳定D.非因果及非稳定【参考答案】: C5.单位序列响应h(n)=u(n)/n的系统是( )系统。
A.因果及稳定B.非因果及稳定C.因果及非稳定D.非因果及非稳定【参考答案】: C6.在一个周期内绝对可积是周期信号频谱存在的( )条件。
A.充分B.必要C.充要D.以上答案都不正确【参考答案】: B7.一个矩形脉冲信号,当脉冲幅度提高一倍,脉冲宽度扩大一倍,则其频带宽度较原来频带宽度()。
A.缩小一倍B.扩大一倍C.不变D.不能确定【参考答案】: A8.函数f(s)=(s+6)/[(s+2)*(s+5)]逆变换的初值等于( )。
A.1B.0C.6D.2【参考答案】: A9.信号f(t)=Asin(500πt)cos(2000πt)的归一化功率等于( )。
A.A*A/2B.A*A/4C.1/4D.以上答案都不正确【参考答案】: B10.零输入响应是( )。
A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差【参考答案】: B11.信号f(t)=Acos(200πt)cos(2000πt)的归一化功率等于( )。
A.A*A/2B.A*A/4C.1/4D.以上答案都不正确【参考答案】: B12.单位序列响应h(n)是指离散系统的激励为( ) 时,系统的零状态响应。
[答案][北京交通大学]《信号与系统》在线作业二
![[答案][北京交通大学]《信号与系统》在线作业二](https://img.taocdn.com/s3/m/4b1e6c6f65ce05087732133a.png)
1.在工程上,从抽样信号恢复原始信号时需要通过的滤波器是()。
[答案:B]A.高通滤波器B.低通滤波器C.带通滤波器D.带阻滤波器2.当输入信号的复频率等于系统函数的零点时,系统的强迫响应分量为()。
[答案:C]A.无穷大B.不为零的常数C.0D.随输入信号而定3.信号的时宽与信号的频宽之间呈()。
[答案:B]A.正比关系B.反比关系C.平方关系D.没有关系4.离散时间单位延迟器D的单位序列响应为()。
[答案:C]A.δ(k)B.δ(k+1)C.δ(k-1)D.15.信号f(t)=3cos(4t+π/3)的周期是()。
[答案:C]A.2πB.πC.π/2D.π/46.线性系统具有()。
[答案:D]A.分解特性B.零状态线性C.零输入线性D.以上全对7.零输入响应是()。
[答案:B]A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差8.Sa[π(t-4)]δ(t-4)等于()。
[答案:A]A.δ(t-4)B.sinπ(t-4)C.1D.09.欲使信号通过系统后只产生相位变化,则该系统一定是()。
[答案:C]A.高通滤波网络B.带通滤波网络C.全通网络D.最小相移网络10.设系统零状态响应与激励的关系是:yzs(t)=|f(t)|,则以下表述不对的是()。
[答案:A]A.系统是线性的B.系统是时不变的C.系统是因果的D.系统是稳定的11.若一个连续LTI系统是因果系统,它一定是一个稳定系统。
()[答案:A]A.错误B.正确12.稳定系统的H(s)极点一定在s平面的左半平面。
()[答案:A]A.错误B.正确13.一个因果的稳定系统的系统函数所有的零、极点必须都在s平面的左半平面内。
()[答案:A]A.错误B.正确14.对连续周期信号取样所得的离散时间序列也是周期信号。
()[答案:A]A.错误B.正确15.两个非线性系统的级联构成的系统也是非线性的。
()[答案:A]A.错误B.正确16.两个线性时不变系统的级联构成的系统是线性时不变的。
奥鹏地大21年春季 《信号与系统》在线作业一.doc

1.f(k)=sin3k是()。
A.周期信号B.非周期信号C.不能表示信号D.以上都不对【参考答案】: B2.以线性常系数微分方程表示的连续时间系统的自由响应取决于()A.系统函数极点B.系统函数零点C.激励极点D.激励零点【参考答案】: A3.某系统的输入为f(t),输出为y(t),且y(t)=3f(t),则该系统是()A.线性非时变系统B.线性时变系统C.非线性非时变系统D.非线性时变系统【参考答案】: B4.信号f(4-3t)是()A.f(3t)右移4B.f(3t)左移4/3C.f(-3t)左移4D.f(-3t)右移4/3【参考答案】: D5.离散线性时不变系统的单位序列响应h(n)为()A.输入为单位冲激信号的零状态响应B.输入为单位阶跃信号的响应C.系统的自由响应D.系统的强迫响应【参考答案】: A6.函数f(s)=(s+6)/[(s+2)*(s+5)]逆变换的终值等于( )。
A.1B.0C.6D.2【参考答案】: B7.信号f(t)与δ(t)的卷积等于( )。
A.f(t)B.δ(t)C.f(t)δ(t)D.0【参考答案】: A8.信号的时宽与频宽之间的关系是()。
A.正比关系B.反比关系C.平方关系D.没有关系【参考答案】: B9.在一个周期内绝对可积是周期信号频谱存在的( )条件。
A.充分B.必要C.充要D.以上都不对【参考答案】: B10.某系统的系统函数为H(s),若同时存在频响函数H(jw),则该系统必须满足条件()。
A.时不变系统B.因果系统C.稳定系统D.线性系统【参考答案】: C11.模拟离散系统的三种基本部件是什么()。
A.加法器B.乘法器C.积分器D.减法器【参考答案】: ABC12.下列系统中,()不是可逆系统。
A.y[n]=nx[n]B.y[n]=x[n]x[n-1]C.y(t)=x(t-4)D.y(t)=cos[x(t) ]【参考答案】: ABD13.时域是实偶函数,其傅氏变换不可能是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与系统作业作业答案Document serial number【UU89WT-UU98YT-UU8CB-UUUT-第二章 作业答案2–1 已知描述某LTI 连续系统的微分方程和系统的初始状态如下,试求此系统的零输入响应。
(1))()(2)(2)(3)(t e t e t y t y t y +'=+'+''2)0(=-y ,1)0(-='-y解:根据微分方程,可知特征方程为:0)2)(1(0232=++⇒=++λλλλ所以,其特征根为: 1,221-=-=λλ 所以,零输入响应可设为:0)(221≥+=--t e C e C t y tt zi又因为 ⎩⎨⎧=-=⇒⎩⎨⎧-=--='=+=--3112)0(2)0(212121C C C C y C C y 所以,03)(2≥-=--t e e t y tt zi(2))(2)()(6)(5)(t e t e t y t y t y -'=+'+''1)0()0(=='--y y 。
解:根据微分方程,可知特征方程为:0)3)(2(0652=++⇒=++λλλλ所以,其特征根为: 3,221-=-=λλ 所以,零输入响应可设为:0)(3221≥+=--t e C e C t y tt zi又因为 ⎩⎨⎧-==⇒⎩⎨⎧=--='=+=--34132)0(1)0(212121C C C C y C C y 所以,034)(32≥-=--t e e t y tt zi2–2 某LTI 连续系统的微分方程为)(3)()(2)(3)(t e t e t y t y t y +'=+'+''已知1)0(=-y ,2)0(='-y ,试求:(1) 系统的零输入响应)(t y zi ;(2) 输入)()(t t e ε=时,系统的零状态响应)(t y zs 和全响应)(t y 。
解:(1)根据微分方程,可知特征方程为:0)2)(1(0232=++⇒=++λλλλ所以,其特征根为: 1,221-=-=λλ 所以,零输入响应可设为:0)(221≥+=--t e C e C t y t t zi又因为 ⎩⎨⎧=-=⇒⎩⎨⎧=--='=+=--4322)0(1)0(212121C C C C y C C y所以,034)(2≥-=--t e e t y tt zi(2) 可设零状态响应为:0)(221>++=--t p e C e C t y t x t x zs其中p 为特解,由激励信号和系统方程确定。
因为)()(t t e ε= 所以,p 为常数,根据系统方程可知,23=p 。
于是,零状态响应可设为为:023)(221>++=--t e C e C t y t x t x zs将上式代入原方程中,比较方程两边的系数,可得到⎪⎩⎪⎨⎧-==22121C C 所以,023221)(2>+-=--t e e t y t t zs全响应为 )()()(t y t y t y zs zi +=0)23221()34()(22>+-+-=----t e e e e t y t t t t zs0)23252()(2>+-=--t e e t y t t zs2–3 试求下列各LTI 系统的冲激响应和阶跃响应。
(1))(2)()(3)(4)(t e t e t y t y t y +'=+'+'' 解:根据 在激励信号为)(t δ的条件下,求解系统的零状态响应可得())(21)(3t e e t h t tε⋅+=-- 因为,单位阶跃响应⎰-⋅=td h t g 0)()(ττ所以,()⎰-⋅+=--td e e t g 0321)(τττ0),1(61)1(2161216030>-+-=--=------t e e e e t t t t ττ0,6121326>--=--t e e tt(2))(2)(2)()(2)(3)("t e t e t e t y t y t y +'+''=+'+ 解:可先求系统 )()(2)(3)("t e t y t y t y =+'+ 的冲激励响应)(0t h ,则,原系统的冲激响应为)(2)(2)()(0'0"0t h t h t h t h ++=。
因为)()(2)(3)("t e t y t y t y =+'+的特征根为:1,221-=-=λλ 所以,可设冲激响应为:)()()(2210t e C e C t h t t ε⋅+=-- 将)(0t h 代入系统方程,并确定待定系数后,可得:)()()(20t e e t h t t ε⋅-=--因为,)(2)(2)()(0'0"0t h t h t h t h ++= 又因为,)()2()(2'0t e e t h t t ε⋅-=--,)()4()()(2"t e e t t h t t εδ⋅--=-- 所以,[])()(2)()2(2)()4()()(222t e e t e e t e e t t h t t t t t t εεεδ⋅-⋅+⋅-⋅+⋅--=------)()2()(2t e e t t t εδ⋅--=--因为,单位阶跃响应⎰-⋅=td h t g 0)()(ττ所以,[]⎰-⋅--=--t t t d t e e t t g 02)()(2)()(τεδ())(212tee ttε⋅-+=--2–4 各信号的波形如题2–4图所示,试计算下列卷积,并画出其波形。
(1))()(21tftf*(2))()(31tftf*(3))()(24tftf*(4))()(34tftf*题2–4 图解:根据)()()(ttftttf-=-*δ,可方便地得到此题的卷积结果。
(1)(2))(3(4h和各激励信号)(t e的波图所示,试求此系统对激励信号的零状态响应。
形如题2–5题2–5图解:因为,)()()(thtetyzs*=所以,[][])2()()2()()(--*--=tttttyzsεεεε)2()2()2()()()2()()(-*-+-*-*--*=ttttttttεεεεεεεε)4()4()2()2(2)(--+---=ttttttεεε2–6 题2–6图所示系统是由几个子系统组合而成的,各子系统的冲激响应分别为)()(1tthε=,)1()(2-=tthδ,)1()(3-=tthε试求总系统的冲激响应)(th并画出其波形。
题2–6图解:根据系统框图,可得:[])()()()()(1321ththththth**+=[])()1()1()(ttttεεδε*-*--=[])()2()(tttεεε*--=)2()2()(-⋅--=ttttεε此系统的单位冲激响应的波形为:2–7 题2–7图所示系统是由几个子系统组合而成,各子系统的冲激响应分别为)1()(1-=t t h δ,)3()1()(2---=t t t h εε试求总系统的冲激响应)(th 并画出其波形。
题2–7图解:根据系统框图,可得:[])()()()()()(2111t h t h t h t h t t h **++=δ[][])3()1()1()1()1()(---*-*-+-+=t t t t t t εεδδδδ [][])3()1()2()1()(---*-+-+=t t t t t εεδδδ[][][])5()3()4()2()3()1(---+---+---=t t t t t t εεεεεε )5()4()2()1(-----+-=t t t t εεεε此系统的单位冲激响应的波形为:。
