2016年北京市朝阳区初三数学二模试题答案
【人教版】北京朝阳初三数学二模试题及答案

下面1-8题均有四个选项,其中符合题意的选项只有..一个. 1.若代数式3x x的值为零,则实数x 的值为( ) (A ) x =0 (B )x ≠0 (C )x =3 (D )x ≠3 2.如图,左面的平面图形绕直线l 旋转一周,可以得到的立体图形是( )3.中国传统扇文化有着深厚的底蕴,下列扇面图形既是轴对称图形又是中心对称图形的是( )4.如图,在数轴上有点O ,A ,B ,C 对应的数分别是0,a ,b ,c ,AO =2,OB =1,BC =2,则下列结论正确的是( ) 一、选择题(本题共16分,每小题2分)数学试卷北京市朝阳区九年级综合练习(二)(A )a c = (B )ab >0 (C )a +c =1 (D )b -a=1 5.⊙O 是一个正n 边形的外接圆,若⊙O 的半径与这个正n 边形的边长相等,则n 的值为( )(A )3 (B )4 (C )5 (D )6 6.已知a a 252=-,代数式)1(2)2(2++-a a 的值为( ) (A )-11 (B )-1 (C ) 1 (D )117.小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了直方图.根据图中信息,下列说法:①这栋居民楼共有居民140人28~35次的人数最多 35~42次 21次的有15人 其中正确的是( )(A )①② (B )②③ (C )③④ (D )④8.如图,矩形ABCD 中,AB =4,BC =3,F 是AB 中点,以点A 为圆心,AD 为半径作弧交AB 于点E ,以点B 为圆心,BF 为半径作弧交BC 于点G ,则图中阴影部分面积的差S 1-S 2为( ) (A )41312π-(B )4912π-(C )4136π+ (D )6二、填空题(本题共16分,每小题2分)9. 写出一个比2大且比5小的有理数: .10.直线AB ,BC ,CA 的位置关系如图所示,则下列语句:①点A 在直线上BC ;②直线AB 经过点C ;③直线AB ,BC ,CA 两两相交;④点B 是直线AB ,BC ,CA 的公共点,正确的有 (只填写序号).第10题图 第11题图 第12题图 11. 2017年5月5日我国自主研发的大型飞机C919成功首飞,如图给出了一种机翼的示意图,用含有m 、n 的式子表示AB 的长为 .12.如图,△ABC 内接于⊙O ,AB 是⊙O 的直径,点D 在圆O 上,BD =CD ,AB=10,AC =6,连接OD 交BC 于点E ,DE = . 13.鼓励科技创新、技术发明,北京市2012-2017年专利授权量如图所示. 根据统计图中提供信息,预估2018年北京市专利授权量约______件,你的预估理由是_______.第13题图 第14题图14.如图,在平面直角坐标系xOy 中,四边形OABC 是正方形,点C (0,4),D 是OA 中点,将△CDO 以C 为旋转中心逆时针旋转90°后,再将得到的三角形平移,使点C 与点O 重合,写出此时点D 的对应点的坐标: . 15.下列对于随机事件的概率的描述: ①抛掷一枚均匀的硬币,因为“正面朝上”的概率是0.5,所以抛掷该硬币100次时,就会有50次“正面朝上”;②一个不透明的袋子里装有4个黑球,1个白球,这些球除了颜色外无其他差别.从中随机摸出一个球,恰好是白球的概率是0.2; ③测试某射击运动员在同一条件下的成绩,随着射击次数的增加,“射中9环以上”的频率总是在0.85附近摆动,显示出一定的稳定性,可以估计该运动员“射中9环以上”的概率是0.85。
北京市朝阳区普通中学2016届九年级3月中考模拟(二)考试数学试题解析(原卷版)

北京市朝阳区普通中学2016届九年级3月中考模拟(二)考试数学试题一.选择题1.下列运算中,正确的是()A.x3•x3=x6B.3x2+2x3=5x5C.(x2)3=x5D.(x+y2)2=x2+y42.若0<a<1,则点M(a﹣1,a)在第()象限.A.一B.二C.三D.四3.某地连续10天的最高气温统计如下表:则这组数据的中位数和平均数分别为()A.24.5,24.6 B.25,26 C.26,25 D.24,264.如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=()A.12 B.8 C.4 D.35.抛物线y=2x2﹣3x+l的顶点坐标为()A.(﹣34,18)B.(34,﹣18)C.(34,18)D.(﹣34,﹣18)6.下面等式中,对于任意实数,使各式都有意义的实数a总能成立的个数为()(1)|a﹣1|=a﹣1(2(3a=(4)(1﹣a)2=(a﹣1)2.A.4 B.3 C.2 D.17.在直角△ABC ,∠C=90°,sinA=35,BC=8,则AB 的长为( ) A .10 B .403 C .245D .12 8.如图,P 1、P 2、P 3是双曲线上的三点.过这三点分别作y 轴的垂线,得到三个三角形P 1A 10,P 2A 20,P 3A 30,设它们的面积分别是S 1、S 2、S 3,则( )A .S 1<S 2<S 3B .S 2<S 1<S 3C .S 1<S 3<S 2D .S 1=S 2=S 3二.填空题9.﹣3的相反数是 ;的绝对值是 .10.不等式组2311x x -<⎧⎨>-⎩的解集是 .11.如图所示,正方形ABCD 的边长为1,点E 为AB 的中点,以E 为圆心,1为半径作圆,分别交AD ,BC 于M ,N 两点,与DC 切于点P ,则图中阴影部分面积是 .12.已知圆锥的母线长OA=8,底面圆的半径r=2,若一只小虫从点A 出发,绕圆锥的侧面爬行一周后又回到A 点,则小虫爬行的最短路线的长是 (结果保留根号).三.解答题.13.计算:0-21+3(π()9tan30°14.解方程:2631x 13x -=-- 15.如图,是某公园“六一”前新增设的一架滑梯,该滑梯高度AC=2cm ,滑梯着地点B 与梯架之间的距离BC=4cm .(1)求滑梯AB 的长.(2)若规定滑梯倾斜面(∠ABC )不超过45度属于安全范围,通过计算说明这架滑梯的倾斜角是否符合要求?16.某产品每件成本10元,试销阶段每件产品的销售价x (元)与产品的日销售量y (件)之间的关系如下表:若日销售量y 是销售价x 的一次函数.(1)求出日销售量y (件)是销售价x (元)的函数关系式; (2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日的销售利润是多少元? 17.在直角坐标平面中,O 为坐标原点,二次函数y=x 2+bx +c 的图象与x 轴的负半轴相交于点C (如图),点C 的坐标为(0,﹣3),且BO=CO(1)求这个二次函数的解析式;(2)设这个二次函数的图象的顶点为M ,求AM 的长.18.如图,在△ABC 中,AB=AC ,若将△ABC 绕点C 顺时针旋转180°,得到△FEC(1)猜想AE 与BF 有何关系,说明理由.(2)若△ABC的面积为3cm2,求四边形ABFE的面积.(3)当∠ACB为多少度时,四边形ABFE为矩形?19.如图,AO是△ABC的中线,⊙O与AB边相切于点D.(1)要使⊙O与AC边也相切,应增加条件(任写一个);(2)增加条件后,请你说明⊙O与AC边相切的理由.20.在直角坐标系中,⊙C过原点O,交x轴于点A(2,0),交y轴于点B(0,.(1)求圆心C的坐标.(2)抛物线y=ax2+bx+c过O,A两点,且顶点在正比例函数(3)过圆心C作平行于x轴的直线DE,交⊙C于D,E两点,试判断D,E两点是否在(2)中的抛物线上.(4)若(2)中的抛物线上存在点P(x0,y0),满足∠APB为钝角,求x0的取值范围.。
3.2016-2017朝阳初三数学二模试题及答案

北京市朝阳区九年级综合练习(二)数学试卷 2017.6下面各题均有四个选项,其中只有一个是符合题意的.1.中国海军第一艘国产航母001A 型航母在2017年4月26日下水,该航母的飞行甲板长约300米,宽约70米,总面积约21000平方米.将21000用科学记数法表示应为 A .42.110⨯B .50.2110⨯C .32110⨯D .52.110⨯2. 实数a ,b 在数轴上的对应点的位置如图所示,则正确的结论是A .a <-2B .b >-1C .-a <-b D .a > b3. 如图所示,用量角器度量∠AOB ,可以读出∠AOB 的度数为 A .45° B .55° C .135° D .145°4.内角和与外角和相等的多边形是A B C D5.在一个不透明的袋子里装有2个红球、3个黄球和5个蓝球,这些球除颜色外,没有任何区别. 现从这个袋子中随机摸出一个球,摸到红球的概率是 A .110 B .15 C .310D .126. 下列图标中,是轴对称的是A B C D7.中国象棋是中华民族的文化瑰宝,它渊远流长,趣味浓厚.如图,在某平面直角坐标系中,○炮所在位置的坐标为(-3, 1),○相所在位置的坐标为(2,-1), 那么, ○帅所在位置的坐标为A .(0,1)B .(4,0)C .(-1,0)D .(0,-1)8.抛物线263y x x =-+的顶点坐标为A .(3,–6)B .(3,12)C .(–3,-9)D .(–3,–6)9.如图,⊙O 的半径OC 垂直于弦AB ,垂足为D ,OA=, ∠B =22.5°,AB 的长为A .2B .4 C. D.10. 甲、乙、丙三名射箭运动员在某次测试中各射箭8次,三人的测试成绩如下表:s 2甲、s 2乙、s 2丙分别表示甲、乙、丙三名运动员这次测试成绩的方差,下面各式中正确的是A .s 2甲>s 2乙>s 2丙B .s 2乙>s 2甲>s 2丙C .s2丙>s 2甲>s 2乙 D .s 2丙>s 2乙>s 2甲二、填空题(本题共18分,每小题3分)11.在函数y =中,自变量x 的取值范围是 . 12. 分解因式:ax 2-4ay 2= .13. 写出一个图象经过点(1,1)的函数的表达式,所写的函数的表达式为 .14.在某一时刻,测得一根高为1.2m 的竹竿的影长为3m ,同时测得一栋楼的影长为45m ,那么这栋楼的高度为 m .15.在一段时间内,小军骑自行车上学和乘坐公共汽车上学的次数基本相同,他随机记录了其中某些天上学所用的时间,整理如下表:①平均来说,乘坐公共汽车上学所需的时间较短 ②骑自行车上学所需的时间比较容易预计③如果小军想在上学路上花的时间更少,他应该更多地乘坐公共汽车 ④如果小军一定要在16 min 内到达学校,他应该乘坐公共汽车 其中合理的是 (填序号).16.阅读下面材料:数学课上,老师提出如下问题:小强的作法如下:老师表扬了小强的作法是对的.请回答:小强这样作图的主要依据是 .三、解答题(本题共72分,第17-26题,每小题5分,第27题7分,第28题7分,第29题8分)尺规作图:经过直线外一点作这条直线的平行线.已知:直线l 和直线l 外一点A . 求作:直线l 的平行线,使它经过点A .如图,(1)过点A 作直线m 交直线l 于点B ;(2)以点A 为圆心,AB 长为半径作弧,交直线m 于点C ; (3)在直线l 上取点D (不与点B 重合),连接CD ; (4)作线段CD 的垂直平分线n ,交线段CD 于点E ; (5)作直线AE . 所以直线AE 即为所求.17.计算:201()(4cos 452π---︒.18. 已知2310x x +-=,求代数式()239x x x--÷的值.19. 解不等式2133x x --<,并把它的解集在数轴上表示出来.20.如图,在△ABC 中,AB =AC ,AD 是BC 边上的高, 过点C 作CE ∥AB 交AD 的延长线于点E. 求证:CE =AB21.已知关于x 的一元二次方程24210x x m -+-=有两个不相等的实数根. (1)求m 的取值范围;(2)若m 为正整数,且该方程的根都是整数,求m 的值.22.调查作业:了解你所在学校学生本学期社会实践活动的情况.小明、小亮和小天三位同学在同一所学校上学.该学校共有三个年级,每个年级都有6个班,每个班的人数在30~40之间.为了了解该校学生本学期社会实践活动的情况,他们各自设计了如下的调查方案: 小明:我给每个班学号分别为1、2、11、12、21、22的同学各发一份问卷,一两天就可以得到结果.小亮:我把要调查的问题放在某两个班的微信群里,这样群里的大部分人就可以完成调 查的问题,并很快就可以反馈给我.小天:我给每个班发一份问卷,一两天也就可以得到结果了. 根据以上材料回答问题:小明、小亮和小天三人中,哪一位同学的调查方案能较好地获得该校学生本学期社会实践活动的情况,并简要说明其他两位同学调查方案的不足之处.23. 如图,在ABCDY中,BC=2AB,E,F分别是BC,AD的中点,AE,BF交于点O,连接EF,OC.(1)求证:四边形ABEF是菱形;(2)若BC=8,60∠=︒,求OC的长.ABC24.阅读下列材料:自2011年以来,朝阳区统筹推进稳增长、调结构、促改革、惠民生等各项工作,经济转型发展不断加快,全区经济实力不断迈上新台阶.2011年,朝阳区生产总值3272.2 亿元.2012年,朝阳区生产总值3632.1 亿元,比上年增长359.9亿元.2013年,朝阳区生产总值4030.6 亿元,比上年增长398.5亿元.2014年,朝阳区生产总值4337.3 亿元,比上年增长7.6%.2015年,朝阳区生产总值4640.2 亿元,比上年增长7.0%,其中,第一产业1.2 亿元,第二产业358.0 亿元,第三产业4281.0 亿元.2016年,朝阳区生产总值4942.0亿元,比上年增长6.5%,居民人均可支配收入达到59886元,比上年增长8%.根据以上材料解答下列问题:(1)用折线图将2011-2016年朝阳区生产总值表示出来,并在图中标明相应数据;(2)根据绘制的折线图中提供的信息,预估2017年朝阳区生产总值约亿元,你的预估理由是.25.如图,△ABC中,∠A=45°,D是AC边上一点,⊙O过D、A、B三点,OD∥BC.(1)求证:直线BC是⊙O的切线;(2)OD,AB相交于点E,若AB=AC,OD=r,写出求AE长的思路.26. 下面是小东的探究学习过程,请补充完整:(1)探究函数22222x x y x +-=-(x <1)的图象与性质.小东根据学习函数的经验,对函数22222x x y x +-=-(x <1)的图象与性质进行了探究.①下表是y 与x 的几组对应值.求m 的值;②如下图,在平面直角坐标系xOy 中,描出以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;③进一步探究发现,该函数图象的最高点的坐标是(0,1),结合函数的图象,写出该函数的其他性质(一条即可): _____;(2)小东在(1)的基础上继续探究:他将函数22222x x y x +-=-(x <1)的图象向上平移1个单位长度,再向右平移1个单位长度后得到函数22724x x y x +-=-(x <2)的图象,请写出函数22724x x y x +-=-(x <2)的一条性质:_____.27.在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.(1)求点A,B的坐标;(2)点C,D在x轴上(点C在点D的左侧),且与点B的距离都为2,若该抛物线与线段CD有两个公共点,结合函数的图象,求m的取值范围.28.在△ABC中,∠ACB=90°,以AB为斜边作等腰直角三角形ABD,且点D与点C在直线AB的两侧,连接CD.(1) 如图1,若∠ABC=30°,则∠CAD的度数为.(2)已知AC=1,BC=3.①依题意将图2补全;②求CD的长;小聪通过观察、实验、提出猜想,与同学们进行交流,通过讨论,形成了求CD长的几种想法:想法1:延长CB,在CB延长线上截取BE=AC,连接DE.要求CD的长,需证明△ACD≌△BED,△CDE为等腰直角三角形.想法2:过点D作DH⊥BC于点H,DG⊥CA,交CA的延长线于点G,要求CD的长,需证明△BDH≌△ADG,△CHD为等腰直角三角形.……请参考上面的想法,帮助小聪求出CD的长(一种方法即可).(3)用等式表示线段AC,BC,CD之间的数量关系(直接写出即可).图2图129. 在平面直角坐标系xOy中,对于半径为r(r>0)的⊙O和点P,给出如下定义:若r≤PO≤32r,则称P为⊙O的“近外点”.(1)当⊙O的半径为2时,点A(4,0),B (52-,0),C(0,3),D (1,-1) 中,⊙O的“近外点”是;(2)若点E(3,4)是⊙O的“近外点”,求⊙O的半径r的取值范围;(3)当⊙O的半径为2时,直线y b=+(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“近外点”,直接写出b的取值范围.北京市朝阳区九年级综合练习(二)数学试卷评分标准及参考答案 2017.6一、选择题(本题共30分,每小题3分)11. x ≥2.12. (2)(2)a x y x y +-.13. 答案不惟一 ,如:y =x . 14. 18. 15.①②③.16. 同圆半径相等;线段垂直平分线的定义;三角形的中位线平行于第三边.三、解答题(本题共72分,第17-26题,每小题5分,第27题7分,第28题7分,第29题8分)17.解:原式=4142-+⨯ =3. 18.解:()239x x x--÷=(3)(3)3xx x x +-⋅- =23x x +. 2310,x x +-=∴原式=1.19.解: 去分母,得 2193x x --<. 移项,得 2391x x ++<. 合并,得 510x <. 系数化1,得 2x <. 不等式的解集是在数轴上表示如下 :20.证明:∵,AB AC AD BC =是边上的高, ∴∠BAE =∠CAE . ∵CE ∥AB , ∴∠E =∠BAE . ∴∠E =∠CAE .∴CE =AC . ∵AB =AC ,∴CE =AB .21.解:(1)依题意,得∆=16-4(2m -1)>0.∴ m <52. (2)∵m 为正整数, ∴m =1或2.当m=1时,方程为2410x x -+=的根2x = 当m=2时,方程为2430x x -+=的根121,3x x ==,都是整数. 综上所述,m =2.22.答:小明的调查方案能较好地获得该校学生本学期社会实践活动的情况.小亮的调查方案的不足之处:抽样调查所抽取的样本的代表性不够好. 小天的调查方案的不足之处:抽样调查所抽取的学生数量太少.23. (1) 证明:∵四边形ABCD 是平行四边形,∴BC ∥AD ,BC =AD . ∵E ,F 分别是BC ,AD 的中点, ∴11,22BE BC AF AD ==.∴BE =AF .∴四边形ABEF 是平行四边形.∵BC =2AB , ∴AB =BE .∴ ABEF 是菱形.(2)解:过点O 作OG ⊥BC 于点G . ∵E 是BC 的中点,BC =8,∴BE =CE =4.∵四边形ABEF 是菱形,∠ABC =60°,∴∠OBE =30,∠BOE =90°.∴OE =2,∠OEB =60°.∴GE =1,∴GC =5.∴OC =24.解: (1) 2011—2016年朝阳区生产总值折现统计图(2)预估理由须包含折线图中提供的信息,且支撑预估的数据.25.(1)证明:连接OB .∵∠A =45°,∴∠DOB =90°.∵OD ∥BC ,∴∠DOB +∠CBO =180°.∴∠CBO =90°.∴ 直线BC 是⊙O 的切线.(2)求解思路如下:如图,延长BO 交⊙O 于点F ,连接AF .①由AB =AC ,∠BAC =45°,可得∠ABC =67.5°,∠ABF =22.5°;②在Rt △EOB 中,由OB =r ,可求BE 的长;③由BF 是直径,可得∠F AB =90°,在Rt △F AB 中,由BF =2r ,可求AB 的长,进而可求AE 的长.26.解: (1)①当x =12时,y =34. ∴34m .②该函数的图象如下图所示:③答案不惟一,如:当x <0时,y 随x 的增大而增大.(2)答案不惟一,如:函数图象的最高点坐标为(1,2).27.解:(1)由题意,当x =0时,y =2.∴A (0,2).∵2222(1)2y mx mx m x m =-+=-+-,∴对称轴为直线x =1.∴B (1,0).(2)由题意,C (-1,0),D (3,0).①当m >0时,结合函数图象可知,满足题意的抛物线的顶点须在x 轴下方,即2-m <0.∴m >2.②当m <0时,过C (-1,0)的抛物线的顶点为E (1,83). 结合函数图象可知,满足条件的抛物线的顶点须在点E 上方或与点E 重合,即2-m ≥83. ∴m ≤23-. 综上所述,m 的取值范围为m >2或m ≤23-.28.解:(1)105°.(2)①补全图形,如图所示.②想法1:如图,∵∠ACB=∠ADB =90°,∴∠CAD+∠CBD==180°.∵∠DBE+∠CBD==180°,∴∠CAD=∠DBE.∵DA=DB,AC=BE,∴△ACD≌△BED.∴DC=DE,∠ADC=∠BDE.∴∠CDE =90°.∴△CDE为等腰直角三角形.∵AC=1,BC=3,∴CE=4.∴CD=想法2:如图,∵∠ACB=∠ADB =90°,∴∠CAD+∠CBD==180°.∵∠DAG+∠CAD==180°,∴∠CBD=∠DAG.∵DA=DB,∠DGA=∠DHB=90°,∴△BDH≌△ADG.∴DH=DG,BH=AG.∴∠DCH=∠DCG=45°.∴△CHD为等腰直角三角形.∵AC=1,BC=3,∴CH=2.∴CD=(3)AC BC+=.29.解:(1)B,C.(2)∵E(3,4)∴EO=5.∴5, 35. 2rr≤⎧⎪⎨≥⎪⎩∴105 3r≤≤.(3b b≤≤≤≤说明:各解答题的其他正确解法请参照以上标准给分.。
2015-2016学年北京市朝阳区初三毕业考试数学试题.docx

北京市朝阳区 2016 年初中毕业考试数学试卷2016.4考1.考试时间为 90 分钟,满分 100 分;生2.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(填空题、解答题)两部分,共8 页,须第 8 页为草稿纸;知3.认真填写密封线内学校、班级、姓名.第Ⅰ卷(共 30 分)一、选择题(共 10 道小题,每小题 3 分,共 30 分)下列各题均有四个选项,其中只有一个是符合题意的.请用铅笔把“机读答题卡”上对应题目答案的相应字母处涂黑.1.在下列各数中,绝对值最大的数是A . 1B .- 2C.1D.1 232. 2015 年 10 月 16 日,新一期全球超级计算机500强榜单在美国公布,中国“天河二号”超级计算机以每秒338600000 亿次浮点运算速度连续第六度称雄.将 338600000用科学记数法表示为A . 3. 386 ×107B . 0.3386 ×109 C. 3. 386 ×108 D . 0.3386 ×1083.右图是某个几何体的三视图,则这个几何体是A.圆柱B.圆锥C.三棱柱D.三棱锥4.阿仁是一名非常爱读书的学生.他制作了五张材质和外观完全一样的书签,每张书签上写有一本书的名称和作者,分别是:《海底两万里》(作者:凡尔纳,法国)、《三国演义》(作者:罗贯中)、《西游记》(作者:吴承恩)、《骆驼祥子》(作者:老舍)、《钢铁是怎样炼成的》(作者:尼·奥斯特洛夫斯基,前苏联),从这五张书签中随机抽取一张,则抽到的书签上的作者是中国人的概率是1234A .B.C.D.55555.下列运算正确的是A .x 2x3x6B.x63x2C.4x32x22 x D.x32x6x6.一次函数y kx b的图象如右图所示,则 k,b 应满足的条件是A .k 0, b 0B.k 0, b 0k 0, b 0k 0, b 07.如图,将一块含有45°的直角三角板的两个顶点放在直尺的对边上,如果∠1=20 °,则∠2 的度数是A . 15°B. 20°C.25°D. 30°8.如图,⊙ O 的半径为10, AB 是弦, OC⊥ AB 于点 C,若 AB=12,则 OC 的长为OA . 2B.22C C.6D. 8A B9.某闭合电路中,电源电压为定值,电流I(A) 与电阻 R( Ω)成反比例,右图表示的是该电路中电流I 与电阻 R 之间函数关系的图象,则电流 I 关于电阻 R 的函数关系式为6B .I 632A .I C.IR D .IR R RA'10.如图,把正方形 ABCD 绕它的中心O 顺时针旋转,得到A E F D正方形 A’B’C’D’,旋转角大于 0°小于90°.△ A’EF 的面积为 S,线段 AE 的长度为 x,那么 S 关于 x 的函数的图象可能是B'O D'SB CS S SC'O x O x O x O nA B C D第Ⅱ卷(共 70 分)二、填空题(共 6 道小题,每小题 3 分,共 18 分)11.分解因式:ax2ay2___________.12.某校在进行―阳光体育活动‖中,统计了7 位原来偏胖的学生的情况,他们的体重分别降低了 5, 9, 3, 10,6, 8, 5(单位: kg),则这组数据的中位数是__________.第 13 题图第14题图13.如图,若在象棋棋盘上建立直角坐标系,使―帥‖位于点(-3,-2),“炮”位于点(-2.0),14.如图,“吃豆小人”是一个经典的游戏形象,它的形状是一个扇形,开口∠1=60°,半径为,则这个“吃豆小人” (阴影图形)的面积为.15.若关于x 的一元二次方程kx 24x 2 0 有两个不相等的实数根,则k 的取值范围是_________________.16.阅读下面材料 :在数学课上,老师提出如下问题 :尺规作图:作一个角等于已知角.已知:∠ AOB.O BA求作:∠ A′O′,B′使∠ A′O′=B′∠ AOB .小义同学作法如下:①作射线O′A;′②以点 O 为圆心,以任意长为半径作弧,交OA 于 C,交 OB 于 D ;③以点 O′为圆心,以 OC 长为半径作弧,交O′A于′ C′;④以点 C′为圆心,以 CD 为半径作弧,交③中所画弧于D′;⑤经过点D′作射线 O′B,′∠ A′O′就B′是所求的角.B B'D D'O A A'C O'C'老师说 : “小义的作法正确. ”请回答 :小义的作图依据是______________________________________________________ .三、解答题(共 10 道小题, 17-24 题每小题 5 分, 25-26 题每小题 6 分,共 52 分)17.(本小题 5 分)120161计算: 1- 2 -2sin45 .318.(本小题 5 分)2 x1解不等式 x 1,并写出不等式的正整数解.319.(本小题 5 分)如图,△ AFD 和△ BEC 中,点 A、 E、 F、 C 在同一条直线上.有下面四个关系式:(1) AD = CB,( 2) AD∥ BC,( 3)∠ B=∠ D,( 4) AE= CF .请用其中三个作为已知条件,余下一个作为求证的结论,写出你的已知和求证,并证明.已知:A D求证:证明:EFB C1x22xy y220.(本小题 5 分)先化简,再求值:,其中 x 3 y .x y x 2 y21.(本小题 5 分)某城市 2015 年约有初中生10 万人, 2016 年初中生人数还会略有增长.该市青少年活动中心对初中生阅读情况进行了统计,绘制的统计图表如下:2015 年某市喜爱阅读的初中生的2012-2015 年某市阅读首选类别喜爱阅读的初中生人数年份喜爱阅读的初中生人数(万人)2012 1.02013 2.22014 3.52015 5.0根据以上信息解答下列问题:( 1)扇形统计图中m 的值为;( 2) 2015 年,在该市喜爱阅读的初中生中,首选阅读科普读物的人数为万;( 3)请你结合对数据的分析,预估2016 年该市喜爱阅读的初中生人数,并简单说明理由.22.(本小题5 分)在“校园文化”建设中,某校用8 000 元购进一批绿植,种植在礼堂前的空地处 . 根据建设方案的要求,该校又用7500 元购进第二批绿植 .两次所买绿植盆数相同,且第二批每盆的价格比第一批的少10 元 . 请问第二批绿植每盆多少元?23.(本小题 5 分)如图,△ ABC 和△ CDE 都是直角三角形, 点 B 、C 、D 在同一条直线上, ∠B=∠ D=∠ ACE=90 °,BC1AB 1 , CD4 .2( 1)求 DE 的长;( 2)连接 AE .求证:四边形 ABDE 是矩形.A EB CD24.(本小题 5 分)如图,以△ ABC 的一边 BC 为直径的⊙ O ,交 AB 于点 D ,连接 CD , OD ,已知∠ A+ 1∠ 1=90°.2( 1)求证: AC 是⊙ O 的切线;( 2)若∠ B=30°, AD=2,求⊙ O 的半径.ADC1 BO25.(本小题 6 分)在平面直角坐标系中,已知抛物线y x22mx 与 x 轴的一个交点为A( 4,0).( 1)求抛物线的表达式及顶点 B 的坐标;( 2)将0 x 5时函数的图象记为G,点 P 为 G 上一动点,求P 点纵坐标 n 的取值范围;( 3)在( 2)的条件下,若经过点C( 4, -4)的直线y kx b k 0 与图象G有两个公共点,结合图象直接写出 b 的取值范围.26.(本小题6 分)在一节数学活动课上,老师和同学们一起研究不同等腰三角形形状差异问题,老师提出我们可以规定一个“正度” ,“正度” 应满足三个条件:①可以用来衡量等腰三角形与正三角形的接近程度;②相似的等腰三角形的“正度”相等;③“正度”的值是非负数.经过讨论后,有两个组给出了答案:小智组提出:设等腰三角形的底和腰分别为a,b,可用式子a b 来表示“正度”, a b 的值越小,表示等腰三角形越接近正三角形;小信组提出:设等腰三角形的底角和顶角分别为α和β,可用式子来表示“正度” ,的值越小,表示等腰三角形越接近正三角形.⑴他们的方案哪个较为合理,为什么?⑵请再写出一种可以衡量“正度”的表达式.北京市朝阳区2016 年初中毕业考试数学试卷评分标准及参考答案2016.4一、 (每小 3 分,共 30 分)1. B 2. C 3. B4.C 5. D 6. A7.C8. D9. A10. B二、填空 (每小 3 分,共18 分)11. a x y x y12. 613.(5 , 1) 14. 5π 15. k 2 且 k 016.三 分 相等的两个三角形全等;全等三角形 角相等(写出其中一个即可). 三、解答 ( 17— 24 每小5 分, 25—26 每小6 分,共 52 分)17.解:原式132 22 分⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯42=4. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分 518.解: 3x3 2x1 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分3x 2x 3 1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分x2 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分∴原不等式的所有正整数解 1,2. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分19.已知: AD = CB , AD ∥ CB ,∠ D =∠ B . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分求 : AE = CF .明:∵ AD ∥ CB ,∴∠ A =∠ C.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分∵AD = CB ,∠ D =∠ B,∴△ ADF ≌△ CBE ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分∴AF =CE. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分∴AE =CF.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分1x 220.解:原式y分x y x⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯32 yx y ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分 4x 2 y当 x 3y ,原式3 y y 2 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 分3y 2 y21. 解:( 1) 8.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分( 2) 0.75. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分( 3)答案依据数据 明,合理即可.如:6.6 万人,因 市喜 的初中生人数逐年增 ,且增 快. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分22. 解: 第二批 植每盆 x 元. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分依 意,得80007500 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分x10x解得 x 150. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分, x =150 是原方程的解,且符合 意.⋯⋯⋯⋯⋯ 4 分答:第二批 植每盆150 元. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分23.( 1)解:∵∠ B=∠ ACE=90 °,∴∠ A+∠ ACB=90°,∠ ECD+∠ ACB=90°.∴∠ A=∠ ECD . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分∵∠ B=∠ D=90°,∴△ ABC ∽△ CDE . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分∴ BCAB . DECD∵ BC1AB 1 , CD 4 ,2∴ DE2 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分( 2) 明:∵∠ B=∠ D=90°, ∴∠B+∠ D=180°.∴ AB ∥ DE . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分 ∵ AB=DE=2,∴四 形 ABDE 是平行四 形. ∵∠B=90°,∴平行四 形 ABDE 是矩形. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 分24.( 1) 明:依 意,得∠B= 1∠1. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分2∵∠ A+ 1∠1=90°,2∴∠ A+∠ B=90°. ∴∠ ACB=90°. ∴ AC ⊥ BC.∵ BC 是⊙ O 的直径,∴ AC 是⊙ O 的切 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分 ( 2)解:∵ BC 是⊙ O 的直径,∴∠ CDB =∠ ADC=90°. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分∵∠ B=30°,∴∠ A=60°,∠ ACD=30°.∴ AC=2AD =4. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分AC 4 3 .∴ BCtan B∴⊙ O 的半径 23 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 分25.解:( 1)∵ A ( 4, 0)在抛物 y x 2 2mx 上,∴16 8m 0 .解得m 2 .∴ y x2 4 x .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分即 y x2 24 .∴ 点坐 B 2, 4 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分(2)当x2,y有最小–4;当x 5 ,y有最大 5.∴点 P 坐的n 的取范是 4 n 5 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分(3) 4 b 0 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分26.解:( 1)小信的方案合理.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分因的越小,两个角越接近60°,等腰三角形就越接近正三角形,且保相似三角形的正度相等.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分小智的方案不合理.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分因不能保相似的等腰三角形的正度相等,如三分4、 4、 2 和 8、 8、 4,4 2 8 4 |.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分(2)60 (+120 ,b1 , 1 ,⋯)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分a明:各解答的其他正确解法参照以上准分.。
朝阳中考数学二模试题及答案

北京市朝阳区九年级综合练习(二)数学试卷学校 班级 姓名一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的. 1.??的绝对值是A .?2B .12-C .12D .22.我国质检总局规定,针织内衣等直接接触皮肤的制品,每千克的衣物上甲醛含量应在千克以下.将用科学记数法表示为A .57.510´ B.57.510-´C .40.7510-´ D.67510-´ 3.如图,在△ABC 中,DE ∥BC ,如果AD =3,BD =5,那么DEBC的值是 A. 35 B. 925 C. 38D.584.从分别标有1到9数字的9张卡片中任意抽取一张,抽到所标数字是3的倍数的概率为A .19B .18C .29D .135.如图,圆锥的底面半径OA 为2,母线AB 为3,则这个圆锥的侧面积为 π B. 6π C. 12πD. 18π6.如图,下列水平放置的几何体中,主视图不是..长方形的是7. 某校篮球课外活动小组21名同学的身高如下表则该篮球课外活动小组21名同学身高的众数和中位数分别是 A .176,176 B .176,177 C .176,178 D .184,1788.图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第 3格、第4格、第5格,此时这个正方体朝上..一面的字是 A .我 B .的 C .梦 D .中二、填空题(本题共16分,每小题4分) 9.在函数y =x 的取值范围是 .10.分解因式:32242x x x -+= .11.如图,在⊙O 中,直径CD ⊥弦AB 于点E ,点F 在弧AC 上,若∠BCD =32°,则∠AFD 的度数为 .12.如图,在平面直角坐标系xOy 中,直线AB 与x 、y 轴分别交于点A 、B ,且A(-2,0),B (0,1),在直线 AB 上截取BB 1=AB ,过点B 1分别作x 、y 轴的垂线,垂足分别为点A 1 、C 1,得到矩形OA 1B 1C 1;在直线AB 上截取B 1B 2= BB 1,过点B 2分别作x 、y 轴的垂线,垂足分别为点A 2 、C 2,得到矩形OA 2B 2C 2;在直线 AB 上截取B 2B 3= B 1B 2,过点B 3分别作x 、y 轴的垂线,垂足分别为点A 3 、C 3,得到矩形OA 3B 3C 3;……则第3个矩形OA 3B 3C 3的面积是 ;第n 个矩形OA n B n C n 的面积是 (用含n 的式子表示,n 是正整数).三、解答题(本题共30分,每小题5分)13.计算:)214452-⎛⎫︒ ⎪⎝⎭.14.计算:2312()111x x x -÷-+- .15.如图,为了测量楼AB 的高度,小明在点C 处测得楼AB 的顶端A 的仰角为30o ,又向前走了20米后到达点D ,点B 、D 、C 在同一条直线上,并在点D 测得楼AB 的顶端A 的仰角为60o ,求楼AB 的高.16.已知:如图,E 、F 为BC 上的点,BF=CE ,点A 、D 分别在BC 的两侧,且AE ∥DF ,AE =DF .求证:AB ∥CD .17.如图,在平面直角坐标系xOy 中,一次函数y kx =-2的图象与x 、y 轴分别交于点A 、B ,与反比例函数32y x =-(x <0)的图象交于点3()2M n -,. (1)求A 、B 两点的坐标;(2)设点P 是一次函数y kx =-2图象上的一点,且满足△APO 的面积是△ABO 的面积的2倍,直接写出点P 的坐标.18.某新建小区要铺设一条全长为2200米的污水排放管道,为了尽量减少施工对周边居民所造成的影响,实际施工时,每天铺设的管道比原计划增加10%,结果提前5天完成这一任务,原计划每天铺设多少米管道?B四、解答题(本题共20分,每小题5分)19.如图,在平行四边形ABCD 中,AD = 4,∠B =105o ,E 是BC 边的中点,∠BAE =30o ,将△ABE 沿AE 翻折,点B 落在点F 处,连接FC ,求四边形ABCF 的周长.20.如图,在△ABC 中,AC=BC ,D 是BC 上的一点,且满足∠BAD =12∠C ,以AD 为直径的⊙O 与AB 、AC 分别相交于点E 、F . (1)求证:直线BC 是⊙O 的切线; (2)连接EF ,若tan ∠AEF =43,AD =4,求BD 的长.21.今年“五一”假期,小翔参加了学校团委组织的一项社会调查活动,了解他所在小区家庭的教育支出情况.调查中,小翔从他所在小区的500户家庭中,随机调查了40个家庭,并将调查结果制成了部分统计图表.(注:每组数据含最小值,不含最大值)根据以上提供的信息,解答下列问题: (1)频数分布表中的a = ,b = ; (2)补全频数分布直方图;(3)请你估计该小区家庭中,教育支出不足1500元的家庭大约有多少户?B (元)教育支出频数分布表 教育支出频数分布直方图22.阅读下列材料:小华遇到这样一个问题,如图1, △ABC 中,∠ACB =30o ,BC =6,AC =5,在△ABC 内部有一点P ,连接P A 、PB 、PC ,求P A +PB +PC 的最小值.小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折、旋转、平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC 绕点C 顺时针旋转60o ,得到△EDC ,连接PD 、BE ,则BE 的长即为所求.(1)请你写出图2中,P A +PB +PC 的最小值为 ; (2)参考小华的思考问题的方法,解决下列问题:①如图3,菱形ABCD 中,∠ABC =60o ,在菱形ABCD 内部有一点P ,请在图3中画出并指明长度等于P A +PB +PC 最小值的线段(保留画图痕迹,画出一条即可);②若①中菱形ABCD 的边长为4,请直接写出当P A +PB +PC 值最小时PB 的长.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知关于x 的一元二次方程x 2?(4?m )x ?1?m = 0.(1)求证:无论m 取何值,此方程总有两个不相等的实数根;(2)此方程有一个根是?3,在平面直角坐标系xOy 中,将抛物线y ?x 2?(4?m )x ?1?m向右平移3个单位,得到一个新的抛物线,当直线y ?x ?b 与这个新抛物线有且只有一个公共点时,求b 的值.24.如图,在平面直角坐标系xOy 中,抛物线y ? ax 2?bx ?4与x 轴交于点A (?2,0)、B (6,0),与y 轴交于点C ,直线CD ∥x 轴,且与抛物线交于点D ,P 是抛物线上一动 点.B图2B图3C B 图1(1)求抛物线的解析式; (2)过点P 作PQ ⊥CD 于点Q ,将△CPQ 绕点C 顺时针旋转,旋转角为α(0o ﹤α﹤90o ),当cos α=35,且旋转后点P 的对应点'P 恰好落在x 轴上时,求点P 的坐标.25. 在□ABCD 中,E 是AD 上一点,AE =AB ,过点E 作直线EF ,在EF 上取一点G ,使得∠EGB =∠EAB ,连接AG .(1)如图1,当EF 与AB 相交时,若∠EAB =60°,求证:EG =AG +BG ; (2)如图2,当EF 与AB 相交时,若∠EAB = α(0o ﹤α﹤90o ),请你直接写出线段EG 、AG 、BG 之间的数量关系(用含α的式子表示);(3)如图3,当EF 与CD 相交时,且∠EAB =90°,请你写出线段EG 、AG 、BG 之间的数量关系,并证明你的结论.北京市朝阳区九年级综合练习(二)数学试卷参考答案一、选择题(本题共32分,每小题4分) 二、填空题(本题共16分,每小题4分) 9. x ≥23 10. 22(1)x x - 11. 32° ,2n 2+2n图3图2 F 图1 F三、解答题(本题共30分,每小题5分)13.解:)214452-⎛⎫︒ ⎪⎝⎭4312=-+-……………………………………………………4分 1=. ………………………………………………………………………5分 14. 解:2312111x x x 骣÷ç-?÷ç÷ç桫-+- ()()3(1)11(1)1(1)x x x x x x ⎡⎤++=-⎢⎥+-+-⎣⎦221x ¸-………………………………2分 ()()2242111x x x x +=÷+--…………………………………………………………………3分()()()()1124112x x x x x +-+=⋅+-…………………………………………………………4分 2x =+.……………………………………………………………………………………5分15. 解: 由题意可知∠ACB =30°,∠ADB =60°,CD =20,在Rt △ABC 中,()tan 30=20AB BC BD =⋅︒+.………………………………1分 在Rt △ABD中,tan 60=AB BD BD =⋅︒………………………………………2分∴()20BD BD +…………………………………………………………3分 ∴10BD =.…………………………………………………………………………4分∴AB =.……………… ……………………………………………………5分16. 证明:∵AE ∥DF ,∴∠AEB =∠DFC . ………………………………………………………………1分 ∵BF =CE ,∴BF +EF =CE +EF .即BE =CF . ………………………………………………………………………2分 在△ABE 和△DCF 中,AE DF AEB DFC BE CFì=ïïï??íïï=ïïî∴△ABE ≌△DCF . … ……………………………………………………………3分 ∴∠B =∠C . ………………………………………………………………………4分 ∴AB ∥CD . … ……………………………………………………………………5分17. 解:(1)∵点3()2M n -,在反比例函数32y x=-(x <0)的图象上, ∴1n =.…………………………………………………………………………1分∴3()2M -,1.∵一次函数y kx =-2的图象经过点3()2M -,1, ∴3122k =--. ∴2k =-.∴一次函数的解析式为22y x =--.∴A (?1,0),B (0,?2) . ………………………………………………………3分 (2)P 1(?3,4),P 2(1,?4) . ………………………………………………………5分18. 解:设原计划每天铺设x 米管道.…………………………………………………1分由题意,得220022005(110%)x x=++ ……………………………………………3分解得 40x =. ……………………………………………………………4分经检验40x =是原方程的根. …………………………………………………5分答:原计划每天铺设40米管道.四、解答题(本题共20分,每小题5分) 19.解:作BG ⊥AE ,垂足为点G , ∴∠BGA =∠BGE =90o.在平行四边形ABCD 中,AD = 4, ∵E 是BC 边的中点,∴11 2.22BE EC BC AD ====……………………………………………………1分 ∵∠BAE =30o ,∠ABC =105o , ∴∠BEG =45o.由已知得△ABE ≌△AFE .∴AB =AF ,BE =FE ,∠BEF =90o.在Rt △BGE 中,BG =GE……… ………………………………………………………………2分 在Rt △ABG 中,∴AB =AF=………………………………………………………………………3分 在Rt △ECF 中,FC = ………………………………………………… ……4分 ∴四边形ABCF的周长4+……………………………………………………5分20. (1)证明:在△ABC 中,∵AC=BC ,∴∠ CAB = ∠B .∵∠ CAB +∠B +∠C =180o , ∴2∠B +∠C =180o. ∴12BC ??=90o. ……………………………………………………1分∵∠BAD =12∠C , ∴B BAD ??=90o.∴∠ADB =90o. ∴AD ⊥BC.∵AD 为⊙O 直径的,∴直线BC 是⊙O 的切线. …………………………………………………2分(2)解:如图,连接DF ,∵AD 是⊙O 的直径,∴∠AFD = 90o. ……………………………………………………………………3分 ∵∠ADC =90o ,∴∠ADF +∠FDC =∠CD +∠FDC =90o.∴∠ADF =∠C . …………………………………………………………………4分∵∠ADF =∠AEF ,tan ∠AEF =43, ∴tan ∠C =tan ∠ADF =43. 在Rt △ACD 中,设AD =4x ,则CD =3x .∴5.AC x ==∴BC =5x ,BD =2x .∵AD =4,∴x =1.∴BD =2. …………………………………………………………………………5分21.解:(1)a =3,b =; ……………………………………………………………2分 (2)…………………………3分B(3)500(0.050.15)100⨯+=.所以该小区家庭中,教育支出不足1500元的家庭大约有100户.…………5分21.解:(11分(2)①如图,…………………………………………2分BD;……………………………………………………………………………3分(3. …………………………………………………………………………5分五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23. (1)证明:∵△=()()2441m m---.………………………………………………1分=2412m m-+=()228m-+…………………………………………………………2分∴△>0.…………………………………………………………………3分∴无论m取何值,方程总有两个不相等的实数根.(2)把x=-3代入原方程,解得m=1.…………………………………………………4分∴23y x x=+.即23924y x⎛⎫=+-⎪⎝⎭.依题意,可知新的抛物线的解析式为239'24y x⎛⎫=--⎪⎝⎭. ………………………5分即2'3y x x=+∵抛物线'y与直线y x b=+只有一个公共点,∴23x x x b-=+..…………………………………………………………………6分即240x x b--=.∵△=0.∴()()2440b--⨯-=.解得b= -4. ……………………………………………………………………7分24. 解:(1)根据题意得424036640a ba b-+=⎧⎨++=⎩,.…………………………………………………………1分解得1343ab⎧=-⎪⎪⎨⎪=⎪⎩,.B所以抛物线的解析式为214433y x x =-++.………………………………2分(2)如图1,过点Q 的对应点'Q 作EF ⊥CD 于点E ,交x 轴于点F .设P (x ,y ),则CQ = x ,PQ =4- y .由题意可知'CQ = CQ = x ,''P Q =PQ =4- y ,∠CQP =∠C ''Q P =90°. ∴'''''QCQ CQ E P Q F CQ E ∠+∠=∠+∠=90°.∴'''P Q F QCQ α∠=∠=.……………………………………………………3分 又∵cos α=35, ∴4'5EQ x = ,3'(4)5FQ y =-. ∴43(4)455x y +-=. ∵214433y x x =-++,整理可得2145x =.∴1x =2x =-.∴P .………………………………………………………………5分如图2,过点Q 的对应点'Q 作EF ⊥CD 于点E ,交x 轴于点F . 设P (x ,y ),则CQ =- x ,PQ =4- y .可得'''P Q F QCQ α∠=∠=.……………………………………………………6分又∵cos α=35,∴4'5EQ x =- ,3'(4)5FQ y =-.∴434(4)55x y -+=-.∵214433y x x =-++, 整理可得2145x =.∴1x =,2x =-∴(P -.……………………………………………………………7分∴P或(P -.25. 解:(1)证明:如图,作∠GAH =∠EAB 交GE 于点H .∴∠GAB =∠HAE . ………………………………………………………………1分∵∠EAB =∠EGB ,∠APE =∠BPG ,∴∠ABG =∠AEH .∵又AB =AE ,∴△ABG ≌△AEH . ………………2分 ∴BG =EH ,AG =AH .∵∠GAH =∠EAB =60°, ∴△AGH 是等边三角形. ∴AG =HG .∴EG =AG +BG . …………………………………………………………………3分(2) 2sin.2EG AG BG α=+…………………………………………………………5分(3).EG BG =-……………………………………………………………6分如图,作∠GAH =∠EAB 交GE 于点H .∴∠GAB =∠HAE . ∵∠EGB =∠EAB =90°,∴∠ABG +∠AEG =∠AEG +∠AEH =180°.∴∠ABG =∠AEH .∵又AB =AE ,∴△ABG ≌△AEH . ………………7分∴BG =EH ,AG =AH .∵∠GAH =∠EAB =90°, ∴△AGH 是等腰直角三角形.=HG .∴.EG BG -…………………………………………………………8分说明:各解答题其它正确解法请参照给分.F。
5.北京2016初三中考二模数学word版答案-东城
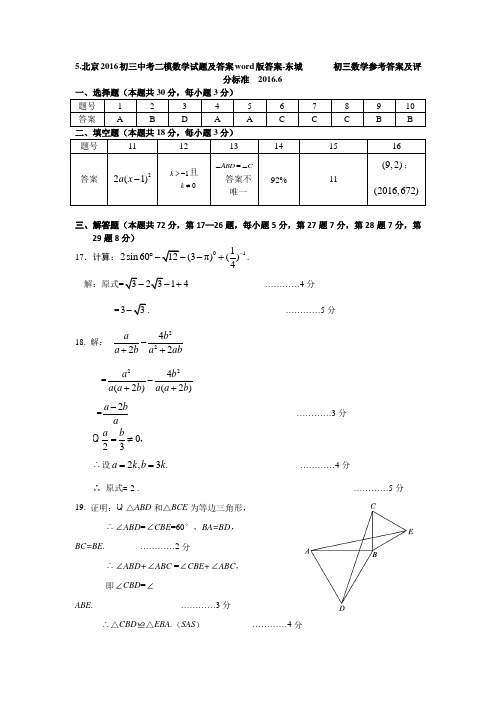
5.北京2016初三中考二模数学试题及答案word 版答案-东城 初三数学参考答案及评分标准 2016.6二、填空题(本题共18分,每小题3分)三、解答题(本题共72分,第17—26题,每小题5分,第27题7分,第28题7分,第29题8分) 17.计算:0112sin 60(3π)()4-︒-+.解:原式14+ …………4分 =3 …………5分18. 解: 22422a b a b a ab-++=224(2)(2)a b a a b a a b -++ =2a ba - …………3分 023a b=≠ , ∴设2,3.a k b k == …………4分∴ 原式=-2 . …………5分 19. 证明: △ABD 和△BCE 为等边三角形, ∴∠ABD =∠CBE =60°,BA=BD ,BC=BE. …………2分∴∠ABD+∠ABC =∠CBE+∠ABC ,即∠CBD =∠ABE. …………3分∴△CBD ≌△EBA.(SAS ) …………4分∴AE=CD. …………5分20.解:设打折前一件商品A 的价格为x 元,一件商品B 的价格为y 元. …………1分依据题意,得631083494x y x y +=⎧⎨+=⎩. …………3分 解得:1016x y =⎧⎨=⎩. …………4分 所以5×10+4×16-86=28(元) 答:比打折前节省了28元. …………5分 21. 满足条件的所有图形如图所示:…………5分注意:画出一个给2分,二个给4分,三个给5分. 22.解:(1)∵矩形ABCD ,∴∠B =∠BAC =90°.∵EF ⊥AM ,∴∠AFE =∠B =∠BAD =90°.∴∠BAM +∠EAF =∠AEF+∠EAF =90°. ∴∠BAM =∠AEF . …………2分 (2)在Rt △ABM 中,∠B =90°,AB =4,cos ∠BAM =45, ∴AM =5.∵F 为AM 中点, ∴AF =52. ∵∠BAM =∠AEF , ∴cos ∠BAM = cos ∠AEF =45. ∴sin ∠AEF =35.在Rt △AEF 中, ∠AFE =90°,AF =52,sin ∠AEF =35, ∴AE =256. ∴DE=AC-AE =6-256=116. …………5分 23.解:(1)∵四边形ABCD 是平行四边形,点(10)(31)(33)A B C ,,,,,,∴BC =2.∴D (1,2). ∵反比例函数my x=的图象经过点D , ∴21m =. ∴2m =.∴2y x=. …………3分(2)233p x <<. …………5分 24.解:(1)172;133. …………2分25.(1)证明:连结BD .∵AB 是O 的直径, ∴90ADB ∠=︒.∴90DAB DBA ∠+∠=︒. ∵AB AC =,∴2ABD ABC ∠=∠,12AD AC =. ∵AF 为⊙O 的切线, ∴∠F AB =90°.∴90FAC CAB ∠+∠=︒. ∴FAC ABD ∠=∠.∴2.ABC CAF ∠=∠ …………2分⑵ 解:连接AE.∴∠AEB =∠AEC =90°.∵sin CAF ABD CAF CBD CAE ∠=∠=∠=∠=∠,∴sin sin ABD CAF ∠=∠=.∵90ABD AC ∠=︒=,∴AD 10sin ADAB ABD==∠=BC .∵90AEC AC ∠=︒=, ∴sin 2CE AC CAE =⋅∠=.∴1028BE BC CE =-=-=. …………5分26.解:(1)sin α=13, sin2α…………2分 (2)∵AC = cos α,BC =sin α,∴CD =AC BCAB⨯=sin cos αα⋅.∵∠DCB =∠A ,∴在Rt △BCD 中,BD =sin 2α.∴OD =12- sin 2α. ∴tan2α=CD OD =22sin cos 2sin cos 112sin sin 2αααααα⋅⋅=--. …………5分 27.解:(1)∵21:C y x bx c =++的图象过点A (-1,2),B (4,7),∴217164.b c b c =-+⎧⎨=++⎩,∴21.b c =-⎧⎨=-⎩,∴221y x x =--. …………2分(2)∵二次函数2C 与1C 的图象关于x 轴对称,∴22:21C y x x =-++. ∴2C 的顶点为(1,2). ∵A (-1,2),B (4,7),∴过A 、B 两点的直线的解析式:3y x =+. 令x =1,则y =4.∴2C 的顶点不在直线AB 上. …………4分(3)414m <≤或4m =-. …………7分28.解:【探究发现】:相等. …………1分 【数学思考】证明:在AC 上截取CG=CE ,连接GE. ∵∠ACB =90°,∴∠CGE =∠CEG =45°.∵AE ⊥EF ,AB ⊥BF ,∴∠AEF =∠ABF =∠ACB =90°,∴∠FEB +∠AEF =∠AEB =∠EAC +∠ACB. ∴∠FEB =∠EAC. ∵CA=CB ,∴AG=BE ,∠CBA =∠CAB =45°. ∴∠AGE =∠EBF =135°. ∴△AGE ≌△EBF .∴AE=EF . …………5分 【拓展应用】ABC S △:AEF S △=1:(222n n ++) …………7分29.解:(1)图象略;是. …………2分 (2)①2. …………4分②M (3,3). …………6分…………8分。
2016朝阳二模初三数学与答案

市区九年级综合练习(二)数 学 试 卷 2016.6考生须知1.本试卷共8页,共三道大题,29道小题,满分120分.考试时间120分钟. 2.在试卷和答题卡上认真填写学校名称、和号. 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效. 4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答. 5.考试结束,请将本试卷、答题卡一并交回. 一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的.1.2015年6月国家主席和比利时国王菲利普,在人民大会堂共同见证了两国公司在集成电路方面进行合作研发的签约仪式,两国将共同着力研发14纳米量产技术,这标志 着我国芯片制造能力将进入国际顶尖水平.14纳米为0.000 000 014米,将0.000 000 014 用科学记数法表示应为A .70.1410-⨯ B .81.410-⨯ C .60.01410-⨯ D .91410-⨯ 2.如图,在单位长度为1的数轴上,点A 、B 表示的两个数互为相反数,那么点A 表示的 数是A .2B .-2C . 3D .-3 3.在中国有很多吉祥的图案深受大家喜爱,人们会用这些图案来装饰生活,祈求平安. 比如下列图案分别表示“福”、“禄”、“寿”、“喜”,其中是.轴对称图形,不是..中心 对称图形的为A B C D4.一个袋子中只装有黑、白两种颜色的球,这些球的形状、质地等完全相同,其中白色球有2个, 黑色球有n 个.在看不到球的条件下,随机地从袋子中摸出一个球,记录下颜色后,放回袋子 中并摇匀.同学们进行了大量重复试验,发现摸出白球的频率稳定在0.4附近,则n 的值为 A .2 B .3 C .4 D .55.如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF 的半径是23cm , 则这个正六边形的周长是A .63cmB .12 cmC .123cmD .36 cm6.某篮球队12名队员的年龄统计如图所示,则该队队员年龄的众数和中位数分别是A .16,15B .15,15.5C .15,17D .15,16 7.一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图所示,搜救船位于图中 圆心O 处,事故船位于距O 点40海里的A 处,雷达操作员要用方位角...把事故船相对于搜救船 的位置汇报给船长,以便调整航向,下列四种表述方式中正确的为A .事故船在搜救船的北偏东60°方向B .事故船在搜救船的北偏东30°方向C .事故船在搜救船的北偏西60°方向D .事故船在搜救船的南偏东30°方向8.现有A 、B 两种商品,买3件A 商品和2件B 商品用了160元,买2件A 商品和3件B 商品用 了190元.如果准备购买A 、B 两种商品共10件,下列方案中费用最低的为 A .A 商品7件和B 商品3件 B .A 商品6件和B 商品4件 C .A 商品5件和B 商品5件 D .A 商品4件和B 商品6件9.把图1所示的正方体的展开图围成正方体(文字露在外面),再将这个正方体按照图2,依次 翻滚..到第1格,第2格,第 3格,第4格,此时正方体朝上一面的文字为 A .富 B .强 C .文 D .民10.如图,ABC ∆为等边三角形,点O 在过点A 且平行于BC 的直线上运动,以ABC ∆的高为半径的⊙O 分别交线段AB 、AC 于点E 、F ,则所对的圆周角的度数 A .从︒0到︒30变化 B .从︒30到︒60变化 C .总等于︒30 D .总等于︒60第7题图第5题图图1第9题图图2 第6题图FEOCB A 第10题图二、填空题(本题共18分,每小题3分) 11.分解因式:2312=a -________. 12.函数121y x x =++的自变量x 的取值围是________. 13.请写出一个开口向下,并且与y 轴交于点(0,2)的抛物线的表达式,y =________.14.将一元二次方程0562=+-x x 化成2()x a b -=的形式,则ab =________.15.如图,在⊙O 中,AB 为⊙O 的弦,半径OC ⊥AB 于点D ,若OB 的长为10,4sin 5BOD ∠=, 则AB 的长为________. 16.在数学活动课上,老师说有人根据如下的证明过程,得到“1=2”的结论.大家经过认真讨论,发现上述证明过程中从某一步开始出现错误,这一步是________ (填入编号),造成错误的原因是________.三、解答题(本题共72分,第17-26题,每小题5分,第27题7分,第28题7分,第29题8分)1711|5|()2tan 602----︒.18.解方程组212x y x y +=⎧⎨-=⎩,.19.已知2220a a --=,求代数式22111a a a -÷-+的值. 20.如图,在Rt △ABC 中,∠BAC = 90º,AD 是BC 边上的中线,ED BC ⊥于D ,交BA 延长线于点E ,若∠E =35°, 求∠BDA 的度数.EBA21.每年的4月23日,是“世界读书日”.据统计,“幸福家园小区”1号楼的住户一年共阅读纸质图书460本,2号楼的住户一年共阅读纸质图书184本,1号楼住户的人数比2号楼住户人数的2倍多20人,且两栋楼的住户一年人均阅读纸质图书的数量相同.求这两栋楼的住户一年人均阅读纸质图书的数量是多少本?22.如图,四边形ABCD中,AB∥DC,∠B = 90º,F为DC上一点,且FC = AB,E为AD上一点,EC交AF于点G.(1)求证:四边形ABCF是矩形;(2)若ED = EC,求证:EA = EG.23.如图,在平面直角坐标系xOy中,反比例函数4yx的图象与正比例函数y=kx的图象的一个交点为M(1,b).(1)求正比例函数y=kx的表达式;(2)若点N在直线OM上,且满足MN=2OM,直接写出点N的坐标.24.如图,O是∠MAN的边AN上一点,以OA为半径作⊙O,交∠MAN的平分线于点D,DE⊥AM于E.(1)求证:DE是⊙O的切线;(2)连接OE,若∠EDA=30º,AE=1,求OE的长.前四天每天接待的观众人数统计图图15月3日观看各种戏剧人数分布统计图图225.为弘扬中国传统文化,2016年4月30日“戏曲文化周”在园博园开始举行,活动期间开展了丰富多样的戏曲文化互动体验活动,同时也推出了好戏连台园博看大戏的活动,主办方统计了前几天观看戏剧情况的部分相关数据,绘制统计图表如下:(1)m =_______;(2)若5月3日当天看豫剧的人数为93人,请你补全图1;(3)请你根据前四天接待观众人数,估计“戏曲文化周”活动在5月4日接待观众约为 ________人.5月4日的戏曲活动,分别演出 “京剧”、“曲剧”、“沪剧”、“腔”、“粤剧”. 通过对100名观众的调查发现, 有12人喜欢“沪剧”,5人喜 欢“腔”,8人喜欢“粤剧”.主办方希望把“沪剧”、“腔”、“粤剧”三种戏剧安排到以下五个园(如下表)中的三个园进行演出.请你结合下表为这三种戏剧选择 合适的演出地点,并说明理由.园中可以容纳人数园 130人 园 100人 岭南园 70人 园 60人 晋中园30人26.(1)如图,在平面直角坐标系xOy 中,直线132y x =+与抛物线y = x 2相交于点A 、B , 与x 轴交于点C ,A 点横坐标为x 1,B 点横坐标为x 2(x 1 < x 2),C 点横坐标为x 3. 请你计算1211x x +与31x 的值,并判断它们的数量关系.xyx 3x 1x 2CBA O(2)在数学的世界里,有很多结论的形式是统一的,这也体现了数学的美.请你在下列两组 条件中选择一组....,证明1211x x +与31x 仍具有(1)中的数量关系. ①如图,∠APC =120º,PB 平分∠APC ,直线l 与P A 、PB 、PC 分别交于点A 、B 、C , P A =x 1,PC =x 2,PB =x 3.②如图,在平面直角坐标系xOy 中,过点A (x 1,0)、B (0,x 2)作直线l ,与直线y =x 交于 点C ,点C 横坐标为x 3.27.在平面直角坐标系xOy 中,抛物线22(9)6y x m x =-++-的对称轴是2x =.(1)求抛物线表达式和顶点坐标;(2)将该抛物线向右平移1个单位,平移后的抛物线与原抛物线相交于点A ,求点A 的坐标; (3)抛物线22(9)6y x m x =-++-与y 轴交于点C ,点A 关于平移后抛物线的对称轴的对称点为点B ,两条抛物线在点A 、C 和点A 、B 之间的部分(包含点A 、B 、C ) 记 为图象M .将直线22y x =-向下平移b (b >0)个单位,在平移过程中直线与图象M 始终有两个公共点,请你写出b 的取值围_________.llCBAPxy x 3x 1x 2CABO28.在ABC ∆中,点D 、E 分别在AB 、AC 上,BE 、CD 相交于点O ,且A EBC DCB ∠=∠=∠21. (1)如图1,若AB =AC ,则BD 与CE 的数量关系是______________;(2)如图2,若AC AB ≠,请你补全图2,思考BD 与CE 是否仍然具有(1)中的数量关系, 并说明理由;(3)如图3,︒=∠105BDC ,BD = 3,且BE 平分∠ABC ,请写出求BE 长的思路. (不用写出计算结果)29.P 是⊙O 一点,过点P 作⊙O 的任意一条弦AB ,我们把PA PB ⋅的值称为点P 关于⊙O 的“幂值”.(1)⊙O 的半径为5,OP = 3.①如图1,若点P 恰为弦AB 的中点,则点P 关于⊙O 的“幂值”为________; ②判断当弦AB 的位置改变时,点P 关于⊙O 的“幂值”是否为定值,若是定值,证明你的结论;若不是定值,求点P 关于⊙O 的“幂值”的取值围.(2)若⊙O 的半径为r ,OP = d ,请参考(1)的思路,用含r 、d 的式子表示点P 关于⊙O 的“幂值”或“幂值”的取值围________;(3)在平面直角坐标系xOy 中,⊙O 的半径为4,若在直线33y x b =+上存在点P ,使得 点P 关于⊙O 的“幂值”为13,请写出b 的取值围________.图1图3图1POBAO备用图图2市区九年级综合练习(二)数学试卷评分标准及参考答案 2016.6一、选择题(本题共30分,每小题3分)二、填空题(本题共18分,每小题3分)三、解答题(本题共72分,第17~26题,每小题5分,第27题7分,第28题7分, 第29题8分)17.解:原式=52-- ..................................................................4分 =3. (5)分18.解:21,2.x y x y +=⎧⎨-=⎩①+②,得33x =,1x =.………………………………………………………2分 把1x =代入②,得12y -=,1y =-.……………………………………………………4分所以这个方程组的解是1,1.x y =⎧⎨=-⎩ …………………………………………………5分19.解:原式()()21111a a a a +=⋅+-- ……………………………………………………1分()22=1a - ……………………………………………………………………3分22=21a a -+.∵2220a a --=,∴222a a -=.……………………………………………………………4分 ∴ 原式23=.………………………………………………………………5分 ①②20.解:∵ED BC ⊥,35E ∠=︒,∴55B ∠=︒. …………………………………………1分∵在Rt △ABC 中,∠BAC = 90º,AD 是BC 边上的中线, ∴AD BD =. …………………………………………3分∴55BAD B ∠=∠=︒ .………………………………4分∴70BDA ∠=︒.…………………………………………………………………5分21.解:设这两栋楼的住户一年人均阅读纸质图书的数量为x 本.……………………1分 由题意,得460218420x x⨯=+. …………………………………………3分 解得 4.6x =. ……………………………………………………4分 经检验, 4.6x =是原方程的解,且符合题意.……………………………5分 答:这两栋楼的住户一年人均阅读纸质图书的数量为4.6本. 22.证明:(1)∵AB ∥DC ,FC=AB ,∴四边形A B C F 是平行四边形.…………………………………………1分∵90B ∠=︒,∴四边形A B C F 是矩形.…………………………………………………2分(2)由(1)可得,90AFC ∠=︒,∴90DAF D ∠=︒-∠,90CGF ECD ∠=︒-∠. ………………3分 ∵ED EC =,∴D ECD ∠=∠.…………………………4分 ∴DAF CGF ∠=∠.∵EGA CGF ∠=∠, ∴EAG EGA ∠=∠.∴EA EG =.………………………………………………………5分 23.解:(1)∵双曲线4y x=过点M (1,b ), ∴4b =.……………………………………………………………………1分 ∵正比例函数y kx =的图象过点M (1,4),∴4k =.……………………………………………………………………2分 ∴正比例函数的表达式为4y x =.………………………………………3分 (2)(-1,-4),(3,12). …………………………………………………5分E CBA24.(1)证明:连接OD .∵AD 平分MAN ∠, ∴EAD OAD ∠=∠. ∵OA OD =, ∴ODA OAD ∠=∠.∴EAD ODA ∠=∠.……………………………1分 ∵DE AM ⊥于E , ∴90AED ∠=︒. ∴90EAD EDA ∠+∠=︒, ∴90ODA EDA ∠+∠=︒.∴OD ED ⊥.∴DE 是⊙O 的切线. ………………2分 (2)解:∵30EDA ∠=︒,∴60ODA ∠=︒. ∵OA OD =,∴△ADO 为等边三角形.…………………………………………………3分在Rt △AED 中,1AE =,可得2AD =,3ED =.………………4分 ∴2OD AD ==.在Rt △ODE 中,由勾股定理可得7OE =. ………………………5分25.解:(1)41. ……………………………………………………………………… ……1分 (2)补全图1,如图所示. ……………………………………………… ………2分(3)801; ………………………………………………………………3分答:预计观看“沪剧”、“腔”、“粤剧”的人数分别约为96、40、64,…………4分所以演出应分别安排在园、园、岭南园.………………………………5分前四天每天接待的观众人数统计图图126.(1)解: 由题意可得2132x x =+. ∵12x x <,∴132x =-,22x =. …………………………………………………1分 ∴121116x x +=-. ∵直线132y x =+与x 轴交于点C ,C 点横坐标为3x ,∴36x =-.………………………………………………………………2分∴3116x =-. ∴123111x x x +=.…………………………………………………………3分 (2)①证明:如图,过点B 作BE ∥PA 交PC 于点E .∴△BEC ∽△APC .…………………………………………………4分 由PB 平分APC ∠,120APC ∠=︒,可得△PBE 是等边三角形.∴3BE PE PB x ===.∴23EC x x =-.∵BE ECAP PC =, ∴32312x x x x x -=.∴231312x x x x x x +=. ∴123111x x x +=.…………………………………………………………5分 ②解:过点C 作CD ⊥x 轴于点D ,CE ⊥y 轴于点E .∵点C 在直线y x =上,且横坐标为3x , ∴点C (3x ,3x ).∴3CE CD x ==.……………………………4分 ∵BOC AOC AOB S S S ∆∆∆+=,∴231312111222x x x x x x +=. ∴123111x x x +=.…………………………………………………………5分 lxy E Dx 3x 1x 2C A BO l图 2 27.解:(1)∵抛物线()2296y x m x =-++-的对称轴是2x =,∴922(2)m +-=⨯-.∴1m =-. ……………………………………………………………1分∴抛物线的表达式为2286y x x =-+-.…………………………………2分 ∴22(2)2y x =--+.∴顶点坐标为(2,2).………………………………………………3分 (2)由题意得,平移后抛物线表达式为 ()2232y x =--+……………………4分 ∵()()222223x x --=--,∴52x =. ∴A (52,32).………………………5分(3)702b <≤. ……………………………7分28.(1)BD CE =;………………………………………1分(2)补全图形.………………………………………2分证明:如图2,在BE 上截取BF CD =,连接CF .∵12DCB EBC A ∠=∠=∠, ∴△DCB ≌△FBC .………………………3分 ∴BD CF =,FCB DBC ∠=∠.∴CFE FBC FCB FBC ABE ∠=∠+∠=∠+∠2.∵CEF A ABE ∠=∠+∠.∴CFE CEF ∠=∠.………………………………………………………4分 ∴CF CE =.∴BD CE =.………………………………………………………5分(3)求解思路如下:a .如图3,过点E 作EM BC ⊥于M ;b .由BE 平分ABC ∠,可得ABC A ∠=∠;c .由BDC ∠=︒105,可得EBC ∠=︒25,50A ∠=︒,80ACB ∠=︒;………………………………………………………6分 d .由(2)知CE BD ==3,在Rt △CEM 中,可求EM 的长度;e .在Rt △BEM 中,由EBM ∠的度数和的EM 的长度,可求BE 的长度.…7分图3ADBMCE29.(1)①16.………………………………………………………………………………1分②当弦AB 的位置改变时,点P 关于⊙O 的“幂值”为定值.………………2分 证明:如图,AB 为⊙O 中过点P 的任意一条弦,且不与OP 垂直. 过点P 作⊙O 的弦''A B ⊥OP ,连接'AA 、'BB . ∵在⊙O 中,''AA P B BP ∠=∠,''APA BPB ∠=∠,∴△'APA ∽△'B PB .…………………………………………………3分∴''PA PA PB PB=. ∴''PA PB PA PB ⋅=⋅.…………………………4分∵OP ⊥''A B ,3OP =,⊙O 半径为5. ∴''4A P B P ==.∴16PA PB ⋅=.…………………………………………………………5分 ∴当弦AB 的位置改变时,点P 关于⊙O 的“幂值”为定值.(2)22r d -. …………………………………………………………………………6分 (3)22b -≤≤. …………………………………………………………………8分说明:各解答题的其他正确解法请参照以上标准给分.。
2016北京市各区初三数学二模-第26题汇编包含答案

8 3
3
2
0
3 2
n…
求 m,n 的值;
(3)如下图,在平面直角坐标系 xOy xOy 中,描出了以上表中各对 y
对应值为坐标的点. 根据描出的点,画出该函数的图象;
5
4
(4)结合函数的图象,写出该函数的性质
3
(一条即可):________________.
2 1
-3
-2
-1
O -1
12 345
x
-2
C
C 点横坐标为 x3.请你计算 1 1 与 1 的值,并判断
x3
x1 x2 x3
它们的数量关系.
y
B A
x1 O
x2 x
(2)在数学的世界里,有很多结论的形式是统一的,这也体现了数学的美.请你在下列两
组条件中选.择.一.组.,证明
1 x1
1 x2
与
1 x3
仍具有(1)中的数量关系.
①如图,∠APC=120º,PB 平分∠APC,直线 l 与 PA、
则 cosA A的邻边 AC
斜边
AB
3 2
.
类似的,可以在等腰三角形中建立边角之间的联系,我们定
义:等腰三角形中底边与腰的比叫做顶角的正对. 如图 2,在△ ABC 中,AB=AC,顶角 A 的
正对记作 sadA,这时,sadA= 底边 BC . 容易知道一个角的大小与这个角的正对值也是相 腰 AB
26.(1)解: 由题意可得 x2 1 x 3 . 2
∵ x1 x2 ,
∴
x1
3 2
,
x
2 2
.
…………………………………………………1 分
∴ 1 1 1.
2016北京市各区初三数学二模 双曲线与直线综合问题归纳整理含答案

2016北京市各区初三数学二模 双曲线与直线综合问题归纳整理(西城2016二模) 23.在平面直角坐标系xOy 中,反比例函数xky =1的图象与一次函数2y ax b =+的图象交于点A (1,3)和(3)B m -,. (1)求反比例函数xky =1和一次函数2y ax b =+的表达式; (2)点C 是坐标平面内一点,BC ∥x 轴,AD ⊥BC 交直线BC 于点D ,连接AC .若AC ,求点C 的坐标. 23.解:(1)∵反比例函数xky =1的图象与一次函数2y ax b =+的图象交于点A (1,3)和(3)B m -,.∴点A (1,3)在反比例函数xky =1的图象上, ∴3k =.∴反比例函数的表达式为13y x=.…………………………………………1分 ∵点(3)B m -,在反比例函数13y x=的图象上, ∴1m =-.……………………………………………………………………2分 ∵点A (1,3)和点(31)B --,在一次函数2y ax b =+的图象上,∴3,3 1.a b a b +=⎧⎨-+=-⎩解得1,2.a b =⎧⎨=⎩∴一次函数的表达式为22y x =+.…………………………………………3分(2)如图.∵BC ∥x 轴,∴点C 的纵坐标为1-.∵AD ⊥BC 于点D , ∴∠ADC =90°,点D 的坐标为(1,1-). ∴AD =4. ∵在Rt △ACD 中,222AC AD CD =+,且AC ,∴222)4CD =+. 解得2CD =.∴点C 1的坐标为(3,1-),点C 2的坐标为(1-,1-).……………5分 综上可得,点C 的坐标为(3,1-)或(1-,1-).评述:考点:考查双曲线以及直线的解析式,利用两点间的距离关系,逆向求点C 的坐标 方法:勾股定理,注意分类讨论思想. 问题:没有分类讨论.这类题目的考查比前几年难度加大,条件不直接,需要自己画图,是一道区分度较大的题目.(2016海淀二模)23.在平面直角坐标系xOy 中,直线1l :12y x b =+与双曲线6y x =的一个交点为(,1)A m .(1)求m 和b 的值;(2)过(1,3)B 的直线交1l 于点D ,交y 轴于点E .若2BD BE =,求点D 的坐标. 23.解:(1)∵点)1,(m A 在双曲线xy 6=上, ∴6=m .………………………1分 ∵点)1,6(A 在直线b x y +=21上, ∴2-=b .………………………2分 (2)当点B 在线段DE 上时,如图1,过点D 作DP ⊥y 轴于P ,过点B 作BQ ⊥y 轴于Q .可得EQB △∽EPD △. ∵BE BD 2=, ∴13BQ BE DP DE ==. ∵1BQ =, ∴3DP =. ∵点D 在直线1l 上,∴)213(-,的坐标为点D .………………4分 当点B 在线段DE 的延长线上时,如图2, 同理,由BE BD 2=,可得点D 的坐标为图15(1)2--,.综上所述,点D 的坐标为)213(-,或5(1)2--,.…………… 5分(2016朝阳二模)23.如图,在平面直角坐标系xOy 中,反比例函数4y x=的图象 与正比例函数y =kx 的图象的一个交点为M (1,b ). (1)求正比例函数y =kx 的表达式;(2)若点N 在直线OM 上,且满足MN=2OM , 直接写出点N 的坐标. 23.解:(1)∵双曲线4y x=过点M (1,b ), ∴4b =.……………………………………………………………………1分 ∵正比例函数y kx =的图象过点M (1,4),∴4k =.……………………………………………………………………2分 ∴正比例函数的表达式为4y x =.………………………………………3分 (2)(-1,-4),(3,12).…………………………………………………5分 (2016顺义二模)23.在平面直角坐标系xOy 中,一次函数y x k =-+的图象与反比例函数4y x=-的图象交于点A (-4,n )和点B .(1)求k 的值和点B 的坐标;(2)若P 是x 轴上一点,且=AP AB ,直接写出点P 的坐标.23. 解:(1)把A (-4,n )代入4y x=-中,得1n =, …………………....….1分把A (-4,1)代入y x k =-+中,得3k =- ……………….….…….2分解方程组3,4.y x y x =--⎧⎪⎨=-⎪⎩得4,1.x y =-⎧⎨=⎩ , 1,4.x y =⎧⎨=-⎩∴点B 的坐标是(1,4)- ……………………………………….…...…3分 (2)点P 的是坐标(3,0)或(11,0)- ……………………………….…...…5分(2016丰台二模)23. 已知反比例函数y =xk(k ≠0)的图象经过点A (-1,6). (1)求k 的值;(2)过点A 作直线AC 与函数y =xk的图象交于点B ,与x 轴交于点C , 且AB =2BC ,求点B 的坐标.(2016通州二模)22. 如图。
北京市2016年各区中考二模汇编:四边形

北京市2016年各区中考二模汇编四边形一、四边形与三角形1. 【2016年西城二模,第10题】一级管道如图1所示,其中四边形是矩形,是是中点,管道由组成,在的中点处放置了一台定位仪器.一个机器人在管道内匀速行进,对管道进行检测.设机器人行进的时间为,机人与定位仪器之间的距离为,表示与的函数关系的图象大致如图2所示,则机器人的行进路线可能为图1 图2A. B. C. D.2. 【2016年房山二模,第14题】如图,在正方形网格中,每个小正方形的边长均为1,△ABC 的三个顶点均在格点上,则△A BC 的面积为 .3. 【2016年昌平二模,第10题】如图1,四边形ABCD 是菱形,对角线AC ,BD 相交于点O ,AB =2厘米,∠BAD =60°.P ,Q 两点同时从点O 出发,以1厘米/秒的速度在菱形的对角线及边上运动. 设运动的时间为x 秒,P ,Q 间的距离为y 厘米,y 与x 的函数关系的图象大致如图2所示,则P ,Q 的运动路线可能为ABCD O AC ,,,,,,,AB BC CD DA OA OB OC OD BC M x y yx A O D →→B O D →→A B O -→→A D O →→ABCA. 点P : O —A —D —C ,点Q : O —C —D —OB. 点P : O —A —D —O ,点Q : O —C —B —OC. 点P : O —A —B —C ,点Q : O —C —D —OD. 点P : O —A —D —O ,点Q : O — C —D —O4. 【2016年通州二模,第23题】如图,四边形ABCD 中,∠A=∠ABC=90°,AD=1,BC=3,E 是边CD 的中点,连接BE 并延长与AD 的延长线相较于点F.连接CF. (1)求证:四边形BDFC 是平行四边形; (2)已知CB=CD ,求四边形BDFC 的面积。
5. 【2016年通州二模,第28题】已知,在菱形ABCD 中,∠ADC=60°,点F 为CD 上任意一点(不与C 、D 重合),过点F 作CD 的垂线,交BD 于点E ,连接AE. (1)①依愿意补全图1;②线段EF 、CF 、AE 之间的等量关系是 。
2016朝阳二模数学答案

一、选择题(每小题3分,共30分)
1. 【答案】B
2. 【答案】D
3. 【答案】C
4. 【答案】B 5. 【答案】C 6. 【答案】D
康 智 爱
7. 【答案】B
8. 【答案】A
9. 【答案】A
10. 【答案】C
二、填空题(每题3分,共18分.)
11. 【答案】3(a + 2)(a − 2)
25. 【
1
1
1
26. 【答案】(1) + =
x1
x2
x3
(2)证明见解析.
康 27.
【答案】(1)抛物线的表达式为y
2 = −2x +
8x − 6
,顶点坐标为(2, 2)
.
53
(2)A ( , )
22
7
(3)0 < b ⩽
2
智 爱
28. 【答案】(1)BD = CE (2)仍有(1)中的数量关系. (3)见解析.
x=1
18. 【答案】{
y = −1
2
19. 【答案】 .
3
20. 【答案】70∘
康 智 爱
21. 【答案】这两栋楼的住户一年内人均阅读纸质图书的数量为4.6 本.
22. 【答案】(1)证明见解析. (2)证明见解析.
23. 【答案】(1)y = 4x (2) , (−1, −4) (3, 12)
24. 【答案】(1)证明见解析. (2)OE = √7 .
12. 【答案】x ≠ −1 13. 【答案】−x2 + 2 (答案不唯一)
14. 【答案】12
15. 【答案】16
16. 【答案】1.④ 2.等式两边除以值为零的式子,不符合等式性质.
朝阳区二模数学答案
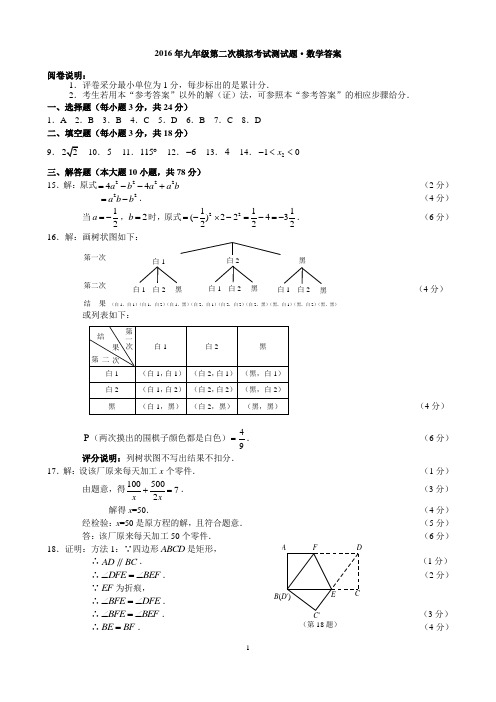
2016年九年级第二次模拟考试测试题·数学答案阅卷说明:1.评卷采分最小单位为1分,每步标出的是累计分.2.考生若用本“参考答案”以外的解(证)法,可参照本“参考答案”的相应步骤给分. 一、选择题(每小题3分,共24分)1.A 2.B 3.B 4.C 5.D 6.B 7.C 8.D 二、填空题(每小题3分,共18分)9. 10.5 11.115︒ 12.6- 13.4 14.210x -<< 三、解答题(本大题10小题,共78分)15.解:原式222244a b a a b =--+ (2分)22a b b =-. (4分)当12a =-,2b =时,原式22111()2243222=-⨯-=-=-. (6分)16.解:画树状图如下:(4分)或列表如下:(4分)P (两次摸出的围棋子颜色都是白色)49=. (6分)评分说明:列树状图不写出结果不扣分.17.解:设该厂原来每天加工x 个零件. (1分)由题意,得72500100=+xx . (3分)解得x =50. (4分) 经检验:x =50是原方程的解,且符合题意. (5分) 答:该厂原来每天加工50个零件. (6分)18.证明:方法1:∵四边形ABCD 是矩形,∴AD BC . (1分) ∴DFE BEF ∠=∠. (2分) ∵EF 为折痕,∴BFE DFE ∠=∠.∴BFE BEF ∠=∠. (3分) ∴BE BF =. (4分)A B (D')C D F E C'(第18题) 第一次 第二次 白1 白1 白2 黑 白2 白1 白2 黑 黑 白1 白2 黑结 果 (白1,白1)(白1,白2)(白1,黑)(白2,白1)(白2,白2)(白2,黑)(黑,白1)(黑,白2)(黑,黑)∵,BF DF BE DE ==, (5分) ∴BF DF BE DE ===. (6分) ∴四边形BEDF 是菱形. (7分) 方法2:∵四边形ABCD 是矩形,∴AD BC . (1分) ∴DFE BEF ∠=∠. (2分) ∵EF 为折痕,∴BFE DFE ∠=∠,BF DF =.∴BFE BEF ∠=∠. (3分) ∴BE BF =. (4分) ∴,DF BE DF BE =, (5分) ∴四边形BEDF 是平行四边形. (6分) ∵BF DF =.∴平行四边形BEDF 是菱形. (7分) 方法3:∵四边形ABCD 是矩形,∴90,ABC ADC AB CD ∠=∠=︒=. (2分) ∵EF 为折痕, ∴EBF EDF ∠=∠.∴ABE CDE ∠=∠. (3分) ∴ABF ∆≌CDE ∆. (4分) ∴BF DE =. (5分) ∵,BF DF BE DE ==,∴BF DF BE DE ===. (6分) ∴四边形BEDF 是菱形. (7分)19.解:(1)10012301840m =---=. (1分)如图.(3分) (2)1.5 (5分)(3)被调查同学的平均劳动时间为1(0.512130 1.540218) 1.32100⨯+⨯+⨯+⨯=小时. (7分)评分说明:条形统计图画线不标40或只标40不画线,均可得分.20.解:过点A 作直线BC 的垂线,垂足为点D . (1分)由题意,得45CAD ∠=°,23BAD ∠=°,180CD =. (2分) ∴45CAD ACD ∠=∠=°.∴180CD AD ==. (4分) 在Rt ABD △中,90BDA ∠=°tan 0.42BDBAD AD∠==. (5分)∴0.4218075.6BD =⨯=. (6分) ∴18075.6104.4104m BC CD BD =-=-=≈. (7分) 答:这栋大楼的高约为104m . (第20题)(第19题) 人数/评分说明:(1)计算过程和结果中写成“=”或“≈”均不扣分.(2)计算过程加单位不扣分,结果不写单位不扣分.21.解:(1)甲车的速度是180 1.8100km/h ÷=. (2分) (2)乙车的速度是18010080km /h -=. 18080 2.25a =÷=. (3分) 方法1:设y 与x 之间的函数关系式为y kx b =+.由题意,得 1.8144,2.25180.k b k b +=⎧⎨+=⎩ (4分)解得80,0.k b =⎧⎨=⎩(5分)甲车到达A 地后y 与x 之间的函数关系式为80(1.8 2.25)y x x =≤≤. (6分)方法2:14480( 1.8)y x =+-.甲车到达A 地后y 与x 之间的函数关系式为80(1.8 2.25)y x x =≤≤. (6分)(3)当160y =时,80160x =. (7分) 解得2x =. (8分) 答:两车相距160km 时货车行驶了2h .评分说明:第(2)问列出方程组给1分,解对给1分,写出函数关系式给1分,不写自变量取值范围不扣分.22.猜想:5 (2分) 探究:∵四边形ABCD 是菱形,∴ADBC ,AO CO =,142BO BD ==. (3分)∴OAE OCF ∠=∠,OEA OFC ∠=∠. (4分) ∴AOE ∆≌COF ∆. (5分) ∵AC BD ⊥,∴1144822ABC ABFE S S AC BO ∆==⋅=⨯⨯=四形边. (6分)应用:12 (9分) 23.解:(1)∵PQN ∆与ABC ∆都是等边三角形,∴当点N 落在边BC 上时,点Q 与点B 重合. ∴23t =.解得32t =. (2分) (2)∵当点N 到点A 、B 的距离相等时,点N 在边AB 的中线上,∴PD DQ =.∴62t t =-. 解得2t =. (4分) (3)如图①,当3t <≤时,2PQMN S S ==菱形. (6分)M如图②,当335t <≤时,223)24PQMN MEF S S S t ∆=-=--菱形.2S =. (8分) (4)1t =或157t =. (10分)评分说明:(1)第(1)问若直接写出32t =不扣分.第(2)问直接写出2t =不扣分.(2)第(3)问的取值范围写0t =扣1分,第二段取值范围32t =带不带均不扣分.24.解:(1)4m -+ (1分)2143m m --+ (2分)(2)∵四边形BCDE 是矩形,∴DE y 轴.∵2CD =,∴当2x =时,2y =.∴DE 与AB 的交点坐标为(2,2). (3分) ∴当点P 在矩形BCDE 的边DE 上时,抛物线的顶点坐标为(2,2).∴抛物线对应的函数表达式为21(2)23y x =--+. (4分)(3)∵直线3y x =-+与y 轴交于点B ,∴点B 的坐标是(0,4).当点B 与点C 重合时,21443m m --+=. 解得120, 3m m ==-.当3m <-或0m >时,如图①、②,22114(4)33BC m m m m =---+=+.22122(2)2433d m m m m =++=++.(6分)②当30m -<<时,如图③,2211(4)433BCm m m m =--+-=--.22122(2)2433d mm m m =--+=--+.(8分) 图② 图③(4)1m =、1m =-、m 、m . (12分) 评分说明:(1)第(1)问每空1分,共2分,第2个空填上点的坐标不给分. (2)第(3)问的取值范围均不带等号.若将3m <-或0m >写成点B 在点C 的上方,将30m -<<写成点B 在点C 的下方,不扣分.(3)第(4)问答对1个值给1分.若答对4个,多答1个或多个答案时扣1分.。
2016北京11区初三二模汇编---圆

2016北京各区初三二模汇编 圆朝阳 24.如图,O 是∠MAN 的边AN 上一点,以OA 为半径作⊙O ,交∠MAN 的平分线于点D ,DE ⊥AM 于E . (1)求证:DE 是⊙O 的切线;(2)连接OE ,若∠EDA =30º,AE =1,求OE 的长.昌平 25. 如图,以△ABC 的边AB 为直径作⊙O ,与BC交于点D ,点E 是弧BD 的中点,连接AE 交BC 于点F ,2ACB BAE ∠=∠.(1)求证:AC 是⊙O 的切线;(2)若2sin 3B =,BD=5,求BF 的长. 西城 24.如图,四边形ABCD 内接于⊙O ,点E 在CB 的延长线上,连接AC ,AE ,∠ACD =∠BAE =45°(1)求证:AE 是⊙O 的切线;(2)若 AB=AD ,AC,tan ∠ADC =3,求 CD 的长.石景山 25.如图,在Rt △ACB 中,∠C =90°,D 是AB 上一点,以BD 为直径的⊙O 切AC于点E ,交BC 于点F ,连接DF . (1)求证:DF=2CE ;(2)若BC =3,sin B =54,求线段BF 的长.海淀 24.如图,在△ABC 中,∠C =90°,点E 在AB 上,以AE为直径的⊙O 切BC 于点D ,连接AD . (1)求证:AD 平分∠BAC ; (2)若⊙O 的半径为5,sin ∠DAC=5,求BD 的长通州 26.如图,△ABC 是⊙O 的内接三角形,∠ACB =45°,∠AOC =150°,过点C 作⊙O 的切线交AB 的延长线于点D . (1)求证:CD =CB ;(2)如果⊙OAC 的长.顺义 24.已知:如图,在ABC ∆中,以AB 为直径的⊙O 分别交AC 、BC 于点D 、E ,且AD DC =. (1)求证:AB BC =;(2)过点B 作⊙O 的切线,交AC 的延长线于点F ,且CF DC =,求sin CAE ∠的值. 东城 25. 如图,在△ABC 中,BA =BC ,以AB 为直径的⊙O 分别交AC ,BC 于点D ,E ,BC 的延长线与⊙O 的切线AF 交于点F . (1)求证:∠ABC =2∠CAF ;(2)若AC=,sin CAF ∠=,求BE 的长.丰台 24. 如图,AB 是⊙O 的直径,BD 交⊙O 于点C ,E 为 BC ⌒的中点,连接AE 交BD房山 26.如图,△ABC 中,AB =AC ,以AB 为直径的⊙O 与BC 相交于点D ,与CA 的延长线相交于点E ,DF 过点D 作⊙O 的切线交AC 于点F . (1)求证:DF ⊥AC ;(2)如果33sin =C ,AE 的长为2.求⊙O 的半径.2016 圆答案朝阳24.(1)证明:连接OD . ∵AD 平分MAN ∠, ∴EAD OAD ∠=∠. ∵OA OD =, ∴ODA OAD ∠=∠.∴EAD ODA ∠=∠.……………………………1分 ∵DE AM ⊥于E , ∴90AED ∠=︒. ∴90EAD EDA ∠+∠=︒, ∴90ODA EDA ∠+∠=︒.∴OD ED ⊥.∴DE 是⊙O 的切线. ………………2分 (2)解:∵30EDA ∠=︒,∴60ODA ∠=︒. ∵OA OD =,∴△ADO 为等边三角形.…………………………………………………3分 在Rt △AED 中,1AE =,可得2AD =,ED =.………………4分∴2OD AD ==.在Rt △ODE中,由勾股定理可得OE = ………………………5分昌平25.(1)证明:连接AD .∵ E 是弧BD 的中点,∴弧BE = 弧ED , ∴∠1=∠2. ∴∠BAD = 2∠1.∵∠ACB = 2∠1,∴∠C =∠BAD . ……………………………………………………………1分∵AB 为⊙O 直径,∴∠ADB =∠ADC =90°. ∴∠DAC +∠C =90°.∵∠C =∠BAD ,∴∠DAC+∠BAD=90°.∴∠BAC=90°.即AB⊥AC.又∵AC过半径外端,∴AC是⊙O的切线. ……………………………………………………………2分(2)解:过点F作FG⊥AB于点G.在Rt△ABD中,∠ADB=90°,2 sin3ADBAB==,设AD=2m,则AB=3m,利用勾股定理求得BD∵BD=5,∴m∴AD=, AB=. …………………………………………………………3分∵∠1=∠2,∠ADB=90°,∴FG=FD. ……………………………………………………………4分设BF =x,则FG =FD =5- x.在Rt△BGF中,∠BGF=90°,2sin3B=,∴523xx-=.解得,x=3.∴BF=3.石景山25.(1)证明:连接OE交DF于G,∵AC切⊙O于E,∴∠CEO=90°.又∵BD为⊙O的直径,∴∠DFC=∠DFB=90°.∵∠C=90°,∴四边形CEGF为矩形.∴CE=GF,∠EGF=90°…………………1分∴DF=2CE.………………………………2分(2)解:在Rt△ABC中,∠C=90°,∵BC=3,4sin5B=,∴AB=5.…………………………………3分设OE=x,∵OE//BC,∴△AOE∽△ABC.∴OE AOBC AB=,∴535x x-=,∴158x=.………………………4分∴BD=154.在Rt △BDF 中,∠DFB =90°,∴BF =94…… 海淀24. (1)证明:连接OD .………………………1分∵⊙O 切BC 于点D , 90C ∠=︒, ∴90ODB C ∠=∠=︒. ∴OD ∥AC . ∴DAC ODA ∠=∠. ∵OD OA =, ∴OAD ODA ∠=∠. ∴DAC OAD ∠=∠.∴AD 平分BAC ∠.………………………2分(2)解:连接DE . ∵AE 为直径, ∴︒=∠90ADE .∵OAD DAC ∠=∠,sin 5DAC ∠=, ∴sinOAD ∠=. ∵5OA =, ∴10AE =.∴AD =.………………………3分 ∴4CD =,8AC =. ∵OD ∥AC ,∴BOD BAC △∽△.………………………4分∴OD BDAC BC =. 即584BD BD =+. ∴203BD =.通州26.如图,△ABC 是⊙O 的内接三角形,∠ACB =45°,∠AOC =150°,过点C 作⊙O 的切线交AB 的延长线于点D . (1)求证:CD =CB ;(2)如果⊙OAC 的长. (1)证明:连结OB .∵»»AB AB =,∠ACB =45°,∴290AOB ACB ∠=∠=︒, ………………… 1分;∵OA=OB ,∴45OAB OBA ∠=∠=︒ ∵∠AOC =150°,∴60COB ∠=︒ ∵OC=OB ,∴△OCB 是等边三角形, ………………… 2分; ∴60OCB OBC ∠=∠=︒, ∴75CBD ∠=︒, ∵CD 是⊙O 的切线,∴90OCD OCB BCD ∠=∠+∠=︒, ∴30BCD ∠=︒, ∴75D CBD ∠=∠=︒,∴CD =CB . ………………… 3分;(2)解:过点B 作BE ⊥AC 于点E ,∵△OCB 是等边三角形,∴BC OC ==∵∠ACB =45°,∴1CE BE ==, ………………… 4分;∵»»BCBC =,∠BOC =60°, ∴1302EAB BOC ∠=∠=︒, ∴tan BEEAB AE∠=,∴13AE=,∴AE =∴1AC AE CE =+=, 顺义24.(1)证明:∵AB 为⊙O 的直径,∴90ADB ∠=︒.………………………………………………………………………..……1分又∵AD DC =,∴AB BC =.…………………………………………………………………………………2分 (2)解:∵BF 切⊙O 于点B ,∴90ABF ∠=︒.…………………………………………………………………………………………………..…………3分 ∴90BAF F ∠+∠=︒.又∵90BAF ABD ∠+∠=︒, ∴ABD F ∠=∠, ∴△ABD ∽△BFD , ∴AD BDBD DF=, ∴2BD AD DF =⋅. 又∵CF DC =, ∴CF DC AD ==,设=CF DC AD k ==,则2222BD AD DF k k k =⋅=⋅=,∴BD .在RT △BCD 中,BC ,sin3CBD ∠==, 又∵CBD CAE ∠=∠,……………………..………………………………………………………………….……4分∴sin CAE ∠=.…………………………………………………………..…………5分 东城25.(1)证明:连结BD .∵AB 是O 的直径, ∴90ADB ∠=︒.∴90DAB DBA ∠+∠=︒. ∵AB AC =,∴2ABD ABC ∠=∠,12AD AC =. ∵AF 为⊙O 的切线, ∴∠F AB =90°.∴90FAC CAB ∠+∠=︒. ∴FAC ABD ∠=∠.∴2.ABC CAF ∠=∠ …………2分⑵ 解:连接AE.∴∠AEB =∠AEC =90°.∵sin CAF ABD CAF CBD CAE ∠=∠=∠=∠=∠,∴sin sin ABD CAF ∠=∠.∵90ABD AC ∠=︒=,∴AD 10sin ADAB ABD==∠=BC .∵90AEC AC ∠=︒=, ∴sin 2CE AC CAE =⋅∠=.∴. FG … 房山26.(1)证明:连接OD .∵DF 是⊙O 的切线,∴ OD ⊥DF .------------1分 ∵ OB =OD ,∴ ∠B =∠ODB . ∵AB =AC .∴ ∠B =∠C . ∴ ∠ODB =∠C∴ OD ∥AC . --------------------------2分 ∴DF ⊥AC , --------------------------3分 (2)解:连结BE ,AD .∵ AB 是直径, ∴ ∠ADB =∠AEB =90° ∵ AB =AC ,∴BD =CD . ∵ DF ⊥AC ∴FD ∥BE ∴可得点F 是CE 的中点.∴sin ∠ABD= sin ∠ACB= sin ∠ADF=33 设⊙O 的半径为r,则AB=2r,AC=2r∴AD =r 332,AF =r-1 ∵sin ∠ADF==AD AF33=rr 3321-----------------------------------------4分 ∴r=3∴⊙O 的半径为3.。
2016年北京初三一模二模各城区16题汇总

16.阅读下面材料:在数学课上,老师提出如下问题: 小云的作法如下:老师说:“小云的作法正确.”请回答:小云的作图依据是________________________________________. 16.阅读下面材料:数学课上,老师提出如下问题:小艾的作法如下:老师表扬了小艾的作法是对的.请回答:小艾这样作图的依据是____________. 16.阅读下面材料:在数学课上,老师提出如下问题:如图,(1)在直线AB 上取一点D ,使点D 与点C 不重合,以点C 为圆心,CD 长为半径作弧,交AB 于D ,E 两点;(2)分别以点D 和点E 为圆心,大于12DE 长为半径作弧,两弧相交于点F ; (3)作直线CF .所以直线CF 就是所求作的垂线.尺规作图:经过已知直线上一点作这条直线的垂线.已知:直线AB 和AB 上一点C .求作:AB 的垂线,使它经过点C .如图,已知△ABC ,AB <BC ,用尺规作图的方法在BC 上取一点P ,使得P A +PC =BC .甲同学的作法:如图甲:以点B 为圆心,BA 长为半径画弧,交BC 于点P ,则点P 就是所求的点. 乙同学的作法:如图乙:作线段AC 的垂直平分线交BC 于点P ,则点P 就是所求的点.丙同学的作法:如图丙:以点C 为圆心,CA 长为半径画弧,交BC 于点P ,则点P 就是所求的点. 丁同学的作法:如图丁:作线段AB 的垂直平分线交BC 于点P ,则点P 就是所求的点.请你判断哪位同学的作法正确 ; 这位同学作图的依据是 . 16.如图,已知∠AOB . 小明按如下步骤作图:①以点O 为圆心,任意长为半径画弧,交OA 于点D ,交OB 于点E . ②分别以D ,E 为圆心,大于12DE 长为半径画弧,在∠AOB 的内部两弧交于点C . ③ 画射线OC .所以射线OC 为所求∠AOB 的平分线.根据上述作图步骤,回答下列问题:(1)写出一个正确的结论:________________________. (2)如果在OC 上任取一点M ,那么点M 到OA 、OB 的距离相等. 依据是:_______________________________________________________.16. 小明同学用配方法推导关于x 的一元二次方程ax 2 + bx + c = 0的求根公式时,对于b 2-4ac >0的情况,他是这样做的:小明的解法从第步开始出现错误;这一步的运算依据应是.16.在数学课上,老师提出如下问题:如图,将锐角三角形纸片ABC(BC >AC)经过两次折叠,得到边AB ,BC ,CA 上的点D,E,F .使得四边形DECF 恰好为菱形. 小明的折叠方法如下:老师说:“小明的作法正确.”请回答:小明这样折叠的依据是_________________________. 16.阅读下面材料:解:CBA老师说:“小明作法正确.” 请回答:(1)小明的作图依据是;(2)他所画的痕迹弧MN 是以点为圆心,为半径的弧.16.阅读下面材料:在数学课上,老师提出如下问题:请回答:小米的作图依据是_________________________.16.阅读下面材料:在数学课上,老师请同学思考如下问题:已知:在△ABC 中,∠A =90°. 求作:⊙P ,使得点P 在边AC 上,且⊙P 与AB ,BC 都相切.小轩的主要作法如下: 如图,(1)作∠ABC 的平分线BF ,与AC 交于点P ;(2)以点P 为圆心,AP 长为半径作⊙P .所以⊙P 即为所求. 老师说:“小轩的作法正确.”请回答:⊙P 与BC 相切的依据是____________________________________. 16.数学课上,同学们兴致勃勃地尝试着利用不同画图工具画一个角的平分线. 小明用直尺画角平分线的方法如下: (1)用直尺的一边贴在∠AOB 的OA上,沿着直尺的另一条边画直线m ; (2)再用直尺的一边贴在∠AOB 的边上,沿着直尺的另一条边画直线n 直线m 与直线n 交于点P ;(3)作射线OP .射线OP 是∠AOB 的平分线.请回答:小明的画图依据是.15.在学习“用直尺和圆规作射线OC 作法:(1)以O (2)分别以D ,E 为圆心,以大于2DE 的同样长为半径作弧,两弧交于点C ; (3)作射线OC .C BAFPCBA则OC 就是所求作的射线.小明同学想知道为什么这样做,所得到射线OC 就是∠AOB 的平分线.小华的思路是连接DC 、EC ,可证△ODC ≌△OEC ,就能得到∠AOC =∠BOC . 其中证明△ODC ≌△OEC 的理由是_______________________________________.14.已知O e ,如图所示.(1)求作O e 的内接正方形(要求尺规作图,保留作图痕迹,不写作法); (2)若O e 的半径为4,则它的内接正方形的边长为_______________. 15.阅读下面材料:如图,C 是以点O 为圆心,AB 为直径的半圆上一点,且CO AB ⊥,在OC 两侧分别作矩形OGHI 和正方形ODEF ,且点I ,F 在OC 上,点H ,E 在半圆上,求证:IG FD =.小云发现连接已知点得到两条线段,便可证明IG FD =.请回答:小云所作的两条线段分别是__________和___________,证明IG FD =的依据是___________________________.9.用直尺和圆规作一个角等于已知角,如图,能得出A O B AOB '''∠=∠的依据是 A .(SAS ) B .(SSS ) C .(AAS ) D .(ASA )16.阅读下面材料:小敏的作法如下: 老师说:“小敏的作法正确.” 请回答:小敏的作图依据是 .1、【西城】16.在平面直角坐标系xOy 中,点A 的坐标为(1,0),P 是第一象限内任意一点,连接PO ,PA ,若∠POA =m °,∠PAO =n °,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的 “双角坐标”为(45°,90°). (1)点的“双角坐标”为 ;(2)若点P 到x 轴的距离为12,则m +n 的最小值为 .2、【海淀】16.阅读下面材料:实际生活中,有时会遇到一些“不能接近的角”,如图中的P ∠,我们可以采用下面的方法作一条直线平分P ∠.如图,(1)作直线l 与P ∠的两边分别交于点A ,B ,分别作PAB ∠和PBA ∠的角平分线,两条角平分线相交于点M ;(2)作直线k 与P ∠的两边分别交于点C ,D ,分别作PCD ∠和PDC ∠的角平分 线,两条角平分线相交于点N ; (3)作直线 MN . 所以,直线MN 平分P ∠. 请回答:上面作图方法的依据是_.3、【丰台】16. 如图,在棋盘中建立直角坐标系xOy ,三颗棋子A ,O ,B 别是(-1,1),(0,0)和(1,0).如果在其他格点位置添加一颗棋子C ,使A ,O B ,C 四颗棋子成为一个轴对称图形,请写出所有满足条件的棋子C4、【石景山】16.为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y (mg)与时间x (分钟)的函数关系如图所示.已知,药物燃烧阶段,y 与x 成正比例,燃完后y 与x 成反比例.现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg .当每立方米空气中含药量低于1.6mg 时,对人体才能无毒害作用.那么从消毒开始,经过分钟后教室内的空气才能达到安全要求.5、【朝阳】16.在数学活动课上,老师说有人根据如下的证明过程,得到“1=2”的结论.大家经过认真讨论,发现上述证明过程中从某一步开始出现错误,这一步是________ (填入编号),造成错误的原因是________.y6、【东城】16.在平面直角坐标系中,小明玩走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位,…,依此类推,第n 步的走法是:当n 能被3整除时,则向上走1个单位;当n 被3除,余数为1时,则向右走1个单位;当n 被3除,余数为2时,则向右走2个单位,当走完第8步时,棋子所处位置的坐标是;当走完第2016步时,棋子所处位置的坐标是. 7、【房山】16.如图,在平面直角坐标系中,点A 、B 、C 的坐标分别为(1,0),(0,1),(﹣1,0).一个电动玩具从坐标原点O 出发,第一次跳跃到点P 1,使得点P 1与点O 关于点A 成中心对称;第二次跳跃到点P 2,使得点P 2与点P 1关于点B 成中心对称;第三次跳跃到点P 3,使得点P 3与点P 2关于点C 成中心对称;第四次跳跃到点P 4,使得点P 4与点P 3关于点A 成中心对称;第五次跳跃到点P 5,使得点P 5与点P 4关于点B 成中心对称;……照此规律重复下去,则点P 5的坐标为,点P 2016的坐标为.8、【通州】16.在数学课上,老师提出如下问题:小明的作法如下:如图:(1)以点C 为圆心,AB 长为半径孤弧; (2)以点A 为圆心,BC 长为半径面弧;(3)两弧在BC 上方交于点D ,连接AD ,CD ,四边形ABCD 为所求作平行四边形 老师说:“小明的作法正确。
4.北京2016初三中考二模数学word版答案-顺义

4.北京2016初三中考二模数学试题及答案word 版答案-顺义数学答案及评分参考一、选择题(本题共30分,每小题3分)二、填空题(本题共18分,每小题3分)11.3; 12.>; 13.21; 14.70︒; 15.4y x =-+(不唯一); 16.BCE ∠和线段BC ;思路:①在Rt BCE ∆中,由tan BEBCE BC∠=,求出tan BE BC BCE =⋅∠, ②由13AE AB =,可求23BE AB =,求得33tan 22AB BE BC BCE ==⋅∠.三、解答题(本题共72分,第17-26题,每小题5分,第27题7分,第28题7分,第29题8分)17.解:1112cos453-⎛⎫++-︒ ⎪⎝⎭312=+…………………………..…………………...………4分2=+ …….…………………………………………………….……….….…5分18.解:解不等式532x x -< ,得1x <. …….…………….…….……….…1分 解不等式7332x x +> ,得3x >- ..……………….…….……….…2分 ∴原不等式组的解集为31x -<< . ………….…………….…4分 ∴原不等式组的所有整数解为2-、1-、0 . ……….………….….…5分 19. 解:原式=2(1)(1)11(1)12x x x x x x +-+⋅+-++ ……………….…….……….…1分=1112x x x ++-+ ……………………………………….………2分 =2(1)(1)(1)(2)(1)(2)x x x x x x x +-++-+-+ ………………….……….….…3分=2212x x x x +++- ……………………………………….……….…4分∵ 230x x +-= ∴ 23x x +=∴原式=221314232x x x x +++==+-- ………………….………….….…5分 20. 证明:∵AB AC =,AD 是BC 边上的中线,∴90ADC ∠=︒.………………………………………………………………………….….1分 又∵E 是AC 的中点,∴AE DE =,………………………..…………………………………………………….….2分 ∴=90ADE EAD C ∠=∠-∠.………………………………………………………..…..3分 ∵BF CA ⊥延长线于点F ,∴=90CBF C ∠-∠.……………………………………………………………………….4分 ∴CBF ADE ∠=∠.……………………………………………………………………..….5分21.解:设甲工程队整治了x 米的河道,则乙工程队整治了(360)x -米的河道. …….………………………………1分 根据题意得:360202416x x -+= ……………………………………….…...…3分 解得:120x = ………………………………………….….….…4分 ∴360240x -=答:甲工程队整治了120米的河道,乙工程队整治了240米的河道 ….………..5分 22.(1)证明:∵AC BD ⊥,AE AC ⊥,∴AE ∥BD ,……………………………………………………………………..………….1分 ∵AB ∥DC , ∴AB ∥DE .∴四边形ABDE 为平行四边形.……………………………………………..…………..….2分 (2)解:∵四边形ABDE 为平行四边形,∴BD AE =,E ABD ∠=∠.………………………………………………………...….3分 ∵4sin 5ABD ∠=, ∴4sin 5E ∠=.……………………………………………………………….………....….4分 在RT △EAC 中,8AC =, ∴10CE =,6AE =,∴6BD =.………………………………………………………………………..…...….5分23. 解:(1)把A (-4,n )代入4y x=-中,得1n =, …………………....….1分把A (-4,1)代入y x k =-+中,得3k =- ……………….….…….2分解方程组3,4.y x y x =--⎧⎪⎨=-⎪⎩得4,1.x y =-⎧⎨=⎩ , 1,4.x y =⎧⎨=-⎩∴点B 的坐标是(1,4)- ……………………………………….…...…3分 (2)点P 的是坐标(3,0)或(11,0)- ……………………………….…...…5分24. (1)证明:∵AB 为⊙O 的直径,∴90ADB ∠=︒.………………………………………………………………………..……1分又∵AD DC =,∴AB BC =.…………………………………………………………………………………2分 (2)解:∵BF 切⊙O 于点B ,∴90ABF ∠=︒.…………………………………………………………………………………………………..…………3分 ∴90BAF F ∠+∠=︒.又∵90BAF ABD ∠+∠=︒, ∴ABD F ∠=∠, ∴△ABD ∽△BFD , ∴AD BDBD DF=, ∴2BD AD DF =⋅.又∵CF DC =, ∴CF DC AD ==,设=CF DC AD k ==,则2222BD AD DF k k k =⋅=⋅=,∴BD .在RT △BCD中,BC,sin 3CBD ∠==, 又∵CBD CAE ∠=∠,……………………..………………………………………………………………….……4分∴sin 3CAE ∠=.…………………………………………………………..…………5分 25. 解:(1)18,0.18;…………………………………..…………………………….……2分 (2)…………………………..………3分(3)80-90;…………………………………..…………………………………………4分(4)3500.30105⨯=(人)…………………………………..………………..……5分答:约有105人. 26. 解:(1) 结论:点是四边形在边上的相似点.……….…1分证明:∵50A B DEC ∠=∠=∠=︒, ∴1+2=130∠∠︒,1+3=130∠∠︒,∴2=3∠∠,………………………………………………..……2分 ∴△AED ∽△BCE ,∴点是四边形在边上的相似点.…………….…3分 (2)E ABCD AB E ABCD AB 321ABCDE 成绩/分9080706050010084频数或BA D CEE CD AB……………………………………………………………………5分27. 解:(1)[]22224(21)42441(21)b ac m m m m m ∆=-=-+-⨯=-+=- -----1分∵不论m 为任何实数时 ,总有2(21)0m ∆=-≥,∴该方程总有两个实数根 . --------------------------------------------------2分(2)(21)(21)2m m x +±-==∴12x m =, 21x = ………………………………………………….… 4分 不妨设点(1,0)B ,依题意则点(3,0)A - ∴ 32m =-∴ 抛物线的表达式为223y x x =+- …………….…………………5分 (3)134b >……………………………………………...………………….…7分 28.(1)①……………………….…………………1分②证明:∵90ACD ∠=︒, 又∵CE CB ⊥, ∴90=ECB ACD ∠=︒∠, ∴1=2∠∠.∵DB MN ⊥于点B , ∴90ABD ∠=︒, ∴180BAC D ∠+∠=︒.E12NMABCD又∵180BAC EAC ∠+∠=︒,∴D EAC ∠=∠.……………………………………………….…..……2分 ∴△CAE ≌△CDB ,∴CE CB =.………………………………………………………..……3分BD AB =+.……………………………………………....….4分(2AB BD =-BD AB =-.……………….…………6分(31.…………………………………………………..……7分 29.解:(1)① 在点M ,N ,E ,F 中,⊙O 的关联点是M ,N ; ….………..2分② ∵过点F 作直线l 交y 于点G ,使30GFO ∠=︒,点F∴OF = 2OG =∴ 点G 的坐标是(0 ,2) ----------------------------------------------------3分设直线l 的表达式为y kx b =+,又直线l 过点点F 和点(0,2)G∴ 直线l 的表达式为23y x =-+ ----------------------------------------4分 ∵ 直线l 上的点(,)P m n 是⊙O 的关联点∴直线l 上的点(,)P m n 满足2OP ≤的所有点都是⊙O 的关联点∴当2OP =时, 224m n +=,即 22(2)4m ++= --------5分∴ 10m = ,2m =∴m 的取值范围是0m ≤ ------------------------------------------------6分 (2) 2r ≥ --------------------------------------------------------------------------------8分。
北京初三数学二模几何综合压轴十年汇编2016

海澱28.(7分)已知:AB=BC,∠ABC=90°.將線段AB繞點A逆時針旋轉α(0°<α<90°)得到線段AD.點C關於直線BD的對稱點為E,連接AE,CE.(1)如圖,①補全圖形;②求∠AEC的度數;(2)若AE=,CE=﹣1,請寫出求α度數的思路.(可以不寫出計算結果)西城28.(7分)在等腰直角三角形ABC中,AB=AC,∠BAC=90°.點P為直線AB上一個動點(點P不與點A,B重合),連接PC,點D在直線BC上,且PD=PC.過點P作PE⊥PC,點D,E在直線AC的同側,且PE=PC,連接BE.(1)情況一:當點P在線段AB上時,圖形如圖1 所示;情況二:如圖2,當點P在BA的延長線上,且AP<AB時,請依題意補全圖2;.(2)請從問題(1)的兩種情況中,任選一種情況,完成下列問題:①求證:∠ACP=∠DPB;②用等式表示線段BC,BP,BE之間的數量關係,並證明.28.(7分)【問題】在△ABC中,AC=BC,∠ACB=90°,點E在直線BC上(B,C除外),分別經過點E和點B作AE和AB的垂線,兩條垂線交於點F,研究AE和EF的數量關係.【探究發現】某數學興趣小組在探究AE,EF的關係時,運用“從特殊到一般”的數學思想,他們發現當點E是BC的中點時,只需要取AC邊的中點G(如圖1),通過推理證明就可以得到AE 和EF的數量關係,請你按照這種思路直接寫出AE和EF的數量關係;【數學思考】那麼當點E是直線BC上(B,C除外)(其它條件不變),上面得到的結論是否仍然成立呢?請你從“點E在線段BC上”;“點E在線段BC的延長線”;“點E在線段BC的反向延長線上”三種情況中,任選一種情況,在圖2中畫出圖形,並證明你的結論;【拓展應用】當點E在線段CB的延長線上時,若BE=nBC(0<n<1),請直接寫出S△ABC:S△AEF的值.28.(7分)在△ABC中,點D、E分別在AB、AC上,BE、CD相交於點O,且∠DCB=∠EBC=∠A(1)如圖1,若AB=AC,則BD與CE的數量關係是;(2)如圖2,若AB≠AC,請你補全圖2,思考BD與CE是否仍然具有(1)中的數量關係,並說明理由;(3)如圖3,∠BDC=105°,BD=3,且BE平分∠ABC,請寫出求BE長的思路.(不用寫出計算結果)房山28.(7分)在△ABC中,BD平分∠ABC(∠ABC<60°)(1)如圖1,當點D在AC邊上時,若∠ABC=42°,∠ACB=32°,請直接寫出AB,DC和BC之間的數量關係.(2)如圖2,當點D在△ABC內部,且∠ACD=30°時,①若∠BDC=150°,直接寫出AB,AD和BC之間的數量關係,並寫出結論成立的思路.②若∠ABC=2α,∠ACB=60°﹣α,請直接寫出∠ADB的度數(用含α的式子表示).28.(7分)在△ABC中,AC=BC,∠ACB=90°.點D為AC的中點.將線段DE繞點D逆時針旋轉90°得到線段DF,連接EF,CF.過點F作FH⊥FC,交直線AB於點H.(1)若點E在線段DC上,如圖1,①依題意補全圖1;②判斷FH與FC的數量關係並加以證明.(2)若E為線段DC的延長線上一點,如圖2,且CE=,∠CFE=15°,請求出△FCH的面積.28.(7分)如圖,在矩形ABCD中,E是AD的中點,點A關於BE的對稱點為G(G在矩形ABCD內部),連接BG並延長交CD於F.(1)如圖1,當AB=AD時,①根據題意將圖1補全;②直接寫出DF和GF之間的數量關係.(2)如圖2,當AB≠AD時,如果點F恰好為DC的中點,求的值.(3)如圖3,當AB≠AD時,如果DC=nDF,寫出求的值的思路(不必寫出計算結果).燕山28.(5分)如圖,△ABC中,已知∠BAC=45°,AD⊥BC於D,BD=4,DC=6,求AD的長.小萍同學靈活運用軸對稱知識,將圖形進行翻折變換,巧妙地解答了此題.請按照小萍的思路,探究並解答下列問題:(1)分別以AB、AC為對稱軸,畫出△ABD、△ACD的軸對稱圖形,D點的對稱點為E、F,延長EB、FC相交於G點,證明四邊形AEGF是正方形;(2)設AD=x,利用畢氏定理,建立關於x的方程模型,求出x的值.28.(7分)已知∠ABC=90°,D是直線AB上的點,AD=BC.(1)如圖1,過點A作AF⊥AB,並截取AF=BD(點C,F在直線AB的兩側),連接DC,DF,CF.①依題意補全圖1;②判斷△CDF的形狀並證明;(2)如圖2,E是直線BC上的一點,直線AE,CD相交於點P,且∠APD=45°.求證:BD =CE.28.(7分)如圖,正方形ABCD,G為BC延長線上一點,E為射線BC上一點,連接AE.(1)若E為BC的中點,將線段EA繞著點E順時針旋轉90°,得到線段EF,連接CF.①請補全圖形;②求證:∠DCF=∠FCG;(2)若點E在BC的延長線上,過點E作AE的垂線交∠DCG的平分線於點M,判斷AE 與EM的數量關係並證明你的結論.28.(7分)已知,在菱形ABCD中,∠ADC=60°,點F為CD上任意一點(不與C、D重合),過點F作CD的垂線,交BD於點E,連接AE.(1)①依題意補全圖1;②線段EF、CF、AE之間的等量關係是.(2)在圖1中將△DEF繞點D逆時針旋轉,當點F、E、C在一條直線上(如圖2).線段EF、CE、AE之間的等量關係是.寫出判斷線段EF、CE、AE之間的等量關係的思路(可以不寫出證明過程)28.(7分)在△ABC中,∠ABC=90°,D為△ABC內一動點,BD=a,CD=b(其中a,b 為常數,且a<b).將△CDB沿CB翻折,得到△CEB.連接AE.(1)請在圖(1)中補全圖形;(2)若∠ACB=α,AE⊥CE,則∠AEB=;(3)在(2)的條件下,用含a,b,α的式子表示AE的長.28.(7分)已知:如圖,∠ACD=90°,MN是過點A的直線,AC=DC,DB⊥MN於點B.(1)在圖1中,過點C作CE⊥CB,與直線MN於點E,①依題意補全圖形;②求證:△BCE是等腰直角三角形;③圖1中,線段BD、AB、CB滿足的數量關係是;(2)當MN繞A旋轉到如圖(2)和圖(3)兩個位置時,其它條件不變.在圖2中,線段BD、AB、CB滿足的數量關係是;在圖3中,線段BD、AB、CB滿足的數量關係是;(3)MN在繞點A旋轉過程中,當∠BCD=30°,BD=時,則CB=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市朝阳区九年级综合练习(二)数学试卷评分标准及参考答案 2016.6一、选择题(本题共30分,每小题3分)二、填空题(本题共18分,每小题3分)三、解答题(本题共72分,第17~26题,每小题5分,第27题7分,第28题7分, 第29题8分)17.解:原式=52--…………………………………………………………4分 =3.…………………………………………………………………5分18.解:21,2.x y x y +=⎧⎨-=⎩①+②,得33x =,1x =.………………………………………………………2分 把1x =代入②,得12y -=,1y =-.……………………………………………………4分 所以这个方程组的解是1,1.x y =⎧⎨=-⎩ …………………………………………………5分19.解:原式()()21111a a a a +=⋅+-- ……………………………………………………1分()22=1a - ……………………………………………………………………3分22=21a a -+.∵2220a a --=,∴222a a -=.……………………………………………………………4分 ∴ 原式23=.………………………………………………………………5分 ①②20.解:∵ED BC ⊥,35E ∠=︒,∴55B ∠=︒. …………………………………………1分∵在Rt △ABC 中,∠BAC = 90º,AD 是BC 边上的中线, ∴AD BD =. …………………………………………3分∴55BAD B ∠=∠=︒ .………………………………4分 ∴70BDA ∠=︒.…………………………………………………………………5分21.解:设这两栋楼的住户一年内人均阅读纸质图书的数量为x 本.……………………1分 由题意,得460218420x x⨯=+. …………………………………………3分 解得 4.6x =. ……………………………………………………4分 经检验, 4.6x =是原方程的解,且符合题意.……………………………5分 答:这两栋楼的住户一年内人均阅读纸质图书的数量为4.6本. 22.证明:(1)∵AB ∥DC ,FC=AB ,∴四边形ABCF 是平行四边形.…………………………………………1分∵90B ∠=︒,∴四边形ABCF 是矩形.…………………………………………………2分(2)由(1)可得,90AFC ∠=︒,∴90DAF D ∠=︒-∠,90CGF ECD ∠=︒-∠. ………………3分 ∵ED EC =,∴D ECD ∠=∠.…………………………4分 ∴DAF CGF ∠=∠.∵EGA CGF ∠=∠, ∴EAG EGA ∠=∠.∴EA EG =.………………………………………………………5分 23.解:(1)∵双曲线4y x=过点M (1,b ), ∴4b =.……………………………………………………………………1分 ∵正比例函数y kx =的图象过点M (1,4),∴4k =.……………………………………………………………………2分 ∴正比例函数的表达式为4y x =.………………………………………3分 (2)(-1,-4),(3,12). …………………………………………………5分E CBA24.(1)证明:连接OD .∵AD 平分MAN ∠, ∴EAD OAD ∠=∠. ∵OA OD =, ∴ODA OAD ∠=∠.∴EAD ODA ∠=∠.……………………………1分 ∵DE AM ⊥于E , ∴90AED ∠=︒. ∴90EAD EDA ∠+∠=︒, ∴90ODA EDA ∠+∠=︒.∴OD ED ⊥.∴DE 是⊙O 的切线. ………………2分 (2)解:∵30EDA ∠=︒,∴60ODA ∠=︒. ∵OA OD =,∴△ADO 为等边三角形.…………………………………………………3分 在Rt △AED 中,1AE =,可得2AD =,ED =.………………4分 ∴2OD AD ==.在Rt △ODE中,由勾股定理可得OE = ………………………5分25.解:(1)41. ……………………………………………………………………… ……1分 (2)补全图1,如图所示. ……………………………………………… ………2分(3)801; ………………………………………………………………3分答:预计观看“沪剧”、“秦腔”、“粤剧”的人数分别约为96、40、64,…………4分所以演出应分别安排在江苏园、福建园、岭南园.………………………………5分前四天每天接待的观众人数统计图图126.(1)解: 由题意可得2132x x =+. ∵12x x <,∴132x =-,22x =. …………………………………………………1分 ∴121116x x +=-.∵直线132y x =+与x 轴交于点C ,C 点横坐标为3x ,∴36x =-.………………………………………………………………2分∴3116x =-.∴123111x x x +=.…………………………………………………………3分(2)①证明:如图,过点B 作BE ∥PA 交PC 于点E .∴△BEC ∽△APC .…………………………………………………4分 由PB 平分APC ∠,120APC ∠=︒,可得△PBE 是等边三角形.∴3BE PE PB x ===.∴23EC x x =-.∵BE ECAP PC =, ∴32312x x x x x -=.∴231312x x x x x x +=. ∴123111x x x +=.…………………………………………………………5分②解:过点C 作CD ⊥x 轴于点D ,CE ⊥y 轴于点E .∵点C 在直线y x =上,且横坐标为3x , ∴点C (3x ,3x ).∴3CE CD x ==.……………………………4分 ∵BOC AOC AOB S S S ∆∆∆+=,∴231312111222x x x x x x +=. ∴123111x x x +=.…………………………………………………………5分 lxy E Dx 3x 1x 2C A BO l图 2 27.解:(1)∵抛物线()2296y x m x =-++-的对称轴是2x =,∴922(2)m +-=⨯-.∴1m =-. ……………………………………………………………1分∴抛物线的表达式为2286y x x =-+-.…………………………………2分 ∴22(2)2y x =--+.∴顶点坐标为(2,2).………………………………………………3分 (2)由题意得,平移后抛物线表达式为 ()2232y x =--+……………………4分 ∵()()222223x x --=--,∴52x =. ∴A (52,32).………………………5分(3)702b <≤. ……………………………7分28.(1)BD CE =;………………………………………1分(2)补全图形.………………………………………2分 证明:如图2,在BE 上截取BF CD =,连接CF .∵12DCB EBC A ∠=∠=∠, ∴△DCB ≌△FBC .………………………3分 ∴BD CF =,FCB DBC ∠=∠.∴CFE FBC FCB FBC ABE ∠=∠+∠=∠+∠2.∵CEF A ABE ∠=∠+∠.∴CFE CEF ∠=∠.………………………………………………………4分 ∴CF CE =.∴BD CE =.………………………………………………………5分(3)求解思路如下:a .如图3,过点E 作EM BC ⊥于M ;b .由BE 平分ABC ∠,可得ABC A ∠=∠;c .由BDC ∠=︒105,可得EBC ∠=︒25,50A ∠=︒,80ACB ∠=︒;………………………………………………………6分d .由(2)知CE BD ==3,在Rt △CEM 中,可求EM 的长度;e .在Rt △BEM 中,由EBM ∠的度数和的EM 的长度,可求BE 的长度.…7分图3ADBM CE29.(1)①16.………………………………………………………………………………1分②当弦AB 的位置改变时,点P 关于⊙O 的“幂值”为定值.………………2分 证明:如图,AB 为⊙O 中过点P 的任意一条弦,且不与OP 垂直. 过点P 作⊙O 的弦''A B ⊥OP ,连接'AA 、'BB . ∵在⊙O 中,''AA P B BP ∠=∠,''APA BPB ∠=∠,∴△'APA ∽△'B PB .…………………………………………………3分∴''PA PA PB PB=. ∴''PA PB PA PB ⋅=⋅.…………………………4分∵OP ⊥''A B ,3OP =,⊙O 半径为5. ∴''4A P B P ==.∴16PA PB ⋅=.…………………………………………………………5分 ∴当弦AB 的位置改变时,点P 关于⊙O 的“幂值”为定值.(2)22r d -. …………………………………………………………………………6分 (3)22b -≤≤. …………………………………………………………………8分说明:各解答题的其他正确解法请参照以上标准给分.。
