平行线能力提高训练题
第七章 平行线的证明(能力提升)(原卷版)

第七章平行线的证明能力提升卷班级___________ 姓名___________ 学号____________ 分数____________(考试时间:60分钟试卷满分:100分)注意事项:1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
答卷前,考生务必将自己的班级、姓名、学号填写在试卷上。
2.回答第I卷时,选出每小题答案后,将答案填在选择题上方的答题表中。
3.回答第II卷时,将答案直接写在试卷上。
第Ⅰ卷(选择题共30分)一、选择题:本题共10个小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(本题3分)如图,直线AB∥CD,则下列结论正确的是()A.∠1=∠2 B.∠3=∠4 C.∠1+∠3=180°D.∠3+∠4=180°2.(本题3分)如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于()A.112°B.110°C.108°D.106°3.(本题3分)已知直线a∥b,将一块含45°角的直角三角板(∠C=90°)按如图所示的位置摆放,若∠1=55°,则∠2的度数为()A.80°B.70°C.85°D.75°4.(本题3分)如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于()A.132°B.134°C.136°D.138°5.(本题3分)如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于()A.40°B.45°C.50°D.55°6.(本题3分)如图,在△AB C中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC 于点E,若∠A=54°,∠B=48°,则∠CDE的大小为()A.44°B.40°C.39°D.38°7.(本题3分)下列说法不正确的是()A.过任意一点可作已知直线的一条平行线 B.在同一平面内两条不相交的直线是平行线C.在同一平面内,过直线外一点只能画一条直线与已知直线垂直 D.直线外一点与直线上各点连接的所有线段中,垂线段最短8.(本题3分)如图,下列能判定AB∥EF的条件有( )①∠B+∠BFE=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.A.1个B.2个C.3个D.4个9.(本题3分)下列条件中不能判定AB∥CD的是( )A.∠1=∠4 B.∠2=∠3 C.∠5=∠B D.∠BAD+∠D=180°10.(本题3分)①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180°;④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )A.、1个B.2个C.3个D.4个第II卷(非选择题)二、填空题(共15分)11.(本题3分)如图,DA⊥CE于点A,CD∥AB,∠1=30°,则∠D=_____.12.(本题3分)如图,A、B、C表示三位同学所站位置,C同学在A同学的北偏东50方∠=______.向,在B同学的北偏西60方向,那么C同学看A、B两位同学的视角ACB13.(本题3分)如图,m∥n,∠1=110°,∠2=100°,则∠3=_______°.14.(本题3分)如图,在△AB C中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=20°,则∠B=_____.15.(本题3分)如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°,∠BCD =40°,则∠BED的度数为_____.三、解答题(共55分)16.(本题7分)已知:如图,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥BF.17.(本题8分)已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.(1)求证:AB∥CD;(2)求∠C的度数.18.(本题9分)如图,在Rt△AB C中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.(1)求∠CBE的度数;(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.19.(本题9分)如图,已知四边形ABC D中,BC⊥AB,CF平分∠DCB,∠DCF+∠BAE=90°,试判断AE与CF的位置关系,并说明理由.20.(本题10分)如图所示,在△AB C中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=78°,求∠DAC的度数.21.(本题12分)已知△ABC中,∠A=60°,∠ACB=40°,D为BC边延长线上一点,BM 平分∠ABC,E为射线BM上一点.(1)如图1,连接CE,①若CE∥AB,求∠BEC的度数;②若CE平分∠ACD,求∠BEC的度数.(2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.。
(完整版)平行线与相交线提高训练
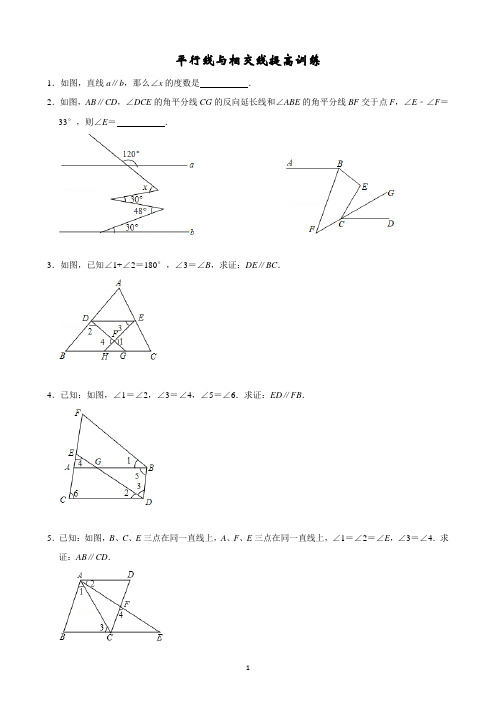
平行线与相交线提高训练1.如图,直线a∥b,那么∠x的度数是.2.如图,AB∥CD,∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F,∠E﹣∠F=33°,则∠E=.3.如图,已知∠1+∠2=180°,∠3=∠B,求证:DE∥BC.4.已知:如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.5.已知:如图,B、C、E三点在同一直线上,A、F、E三点在同一直线上,∠1=∠2=∠E,∠3=∠4.求证:AB∥CD.6.已知,如图,AE∥BD,∠1=3∠2,∠2=26°,求∠C.7.直线l1∥l2,∠A=125°,∠B=105°,求∠1+∠2的度数(提示:要作辅助线哟!)8.已知:射线OP∥AE(1)如图1,∠AOP的角平分线交射线AE与点B,若∠BOP=58°,求∠A的度数.(2)如图2,若点C在射线AE上,OB平分∠AOC交AE于点B,OD平分∠COP交AE于点D,∠ADO=39°,求∠ABO﹣∠AOB的度数.(3)如图3,若∠A=m,依次作出∠AOP的角平分线OB,∠BOP的角平分线OB1,∠B1OP的角平分线OB2,∠B n﹣1OP的角平分线OB n,其中点B,B1,B2,…,B n﹣1,B n都在射线AE上,试求∠AB n O 的度数.9.数学思考:(1)如图1,已知AB∥CD,探究下面图形中∠APC和∠P AB、∠PCD的关系,并证明你的结论推广延伸:(2)①如图2,已知AA1∥BA1,请你猜想∠A1,∠B1,∠B2,∠A2、∠A3的关系,并证明你的猜想;②如图3,已知AA1∥BA n,直接写出∠A1,∠B1,∠B2,∠A2、…∠B n﹣1、∠A n的关系拓展应用:(3)①如图4所示,若AB∥EF,用含α,β,γ的式子表示x,应为A.180°+α+β﹣γB.180°﹣α﹣γ+βC.β+γ﹣αD.α+β+γ②如图5,AB∥CD,且∠AFE=40°,∠FGH=90°,∠HMN=30°,∠CNP=50°,请你根据上述结论直接写出∠GHM的度数是.10.已知,直线AB∥DC,点P为平面上一点,连接AP与CP.(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC 之间的数量关系,并说明理由.(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.11.如图,已知AM∥BN,∠A=80°,点P是射线AM上动点(与A不重合),BC、BD分别平分∠ABP 和∠PBN,交射线AM于C、D.(1)求∠CBD的度数;(2)当点P运动时,那么∠APB:∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.12.如图1,AB∥CD,直线EF交AB于点E,交CD于点F,点G在CD上,点P在直线EF左侧、且在直线AB和CD之间,连接PE、PG.(1)求证:∠EPG=∠AEP+∠PGC;(2)连接EG,若EG平分∠PEF,∠AEP+∠PGE=110°,∠PGC=∠EFC,求∠AEP的度数;(3)如图2,若EF平分∠PEB,∠PGC的平分线所在的直线与EF相交于点H,则∠EPG与∠EHG 之间的数量关系为.13.已知E、D分别在∠AOB的边OA、OB上,C为平面内一点,DE、DF分别是∠CDO、∠CDB的平分线.(1)如图1,若点C在OA上,且FD∥AO,求证:DE⊥AO;(2)如图2,若点C在∠AOB的内部,且∠DEO=∠DEC,请猜想∠DCE、∠AEC、∠CDB之间的数量关系,并证明;(3)若点C在∠AOB的外部,且∠DEO=∠DEC,请根据图3、图4分别写出∠DCE、∠AEC、∠CDB 之间的数量关系(不需证明).14.已知,AB∥CD,点E为射线FG上一点.(1)如图1,若∠EAF=30°,∠EDG=40°,则∠AED=°;(2)如图2,当点E在FG延长线上时,此时CD与AE交于点H,则∠AED、∠EAF、∠EDG之间满足怎样的关系,请说明你的结论;(3)如图3,DI平分∠EDC,交AE于点K,交AI于点I,且∠EAI:∠BAI=1:2,∠AED=22°,∠I=20°,求∠EKD的度数.15.长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a﹣3b|+(a+b﹣4)2=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°(1)求a、b的值;(2)若灯B射线先转动20秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?(3)如图,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ 于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.16.已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE与射线AF交于点G.(1)若OE平分∠BOA,AF平分∠BAD,∠OBA=42°,则∠OGA=;(2)若∠GOA=∠BOA,∠GAD=∠BAD,∠OBA=42°,则∠OGA=;(3)将(2)中的“∠OBA=42°”改为“∠OBA=α”,其它条件不变,求∠OGA的度数.(用含α的代数式表示)(4)若OE将∠BOA分成1:2两部分,AF平分∠BAD,∠ABO=α(30°<α<90°),求∠OGA的度数.(用含α的代数式表示)17.已知直线AB∥CD,E是直线AB的上方一点,连接AE、EC(1)如图1,求证:∠AEC+∠EAB=∠ECD(2)如图2,AF平分∠BAE,CF平分∠DCE,且∠AFC比∠AEC的倍少40°,直接写出∠AEC的度数18.直线MN与直线PQ相交于O,点A在射线OP上运动,点B在射线OM上运动.(1)如图1,若∠AOB=80°,已知AE、BE分别是∠BAO和∠ABO的角平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.(2)如图2,若∠AOB=80°,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,AD、BC的延长线交于点F,点A、B在运动的过程中,∠F=;DE、CE又分别是∠ADC和∠BCD 的角平分线,点A、B在运动的过程中,∠CED的大小也不发生变化,其大小为:∠CED=.(3)如图3,若∠AOB=90°,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F,则∠EAF=;(4)如图3,若AF,AE分别是∠GAO,∠BAO的角平分线,∠AOB=90°,在△AEF中,如果有一个角是另一个角的4倍,则∠ABO的度数=.20.如图,点D、点E分别在△ABC边AB,AC上,∠CBD=∠CDB,DE∥BC,∠CDE的平分线交AC 于F点.(1)求证:∠DBF+∠DFB=90°;(2)如图②,如果∠ACD的平分线与AB交于G点,∠BGC=50°,求∠DEC的度数.(3)如图③,如果H点是BC边上的一个动点(不与B、C重合),AH交DC于M点,∠CAH的平分线AI交DF于N点,当H点在BC上运动时,的值是否发生变化?如果变化,说明理由;如果不变,试求出其值.。
(完整版)平行线与相交线提高训练

平行线与相交线提高训练1如图,直线a // b,那么/ x的度数是________________ .2.如图,AB// CD,/ DCE的角平分线CG的反向延长线和/ ABE的角平分线BF交于点F,/ E -/ F =3.如图,已知/ 1 + / 2= 180°,/ 3=/ B,求证: DE // BC.C/ 3 =/ 4,/ 5=/ 6.求证:ED // FB.5.已知:如图,B、C、E三点在同一直线上,A、F、E三点在同一直线上, / 1 = / 2 = / E, / 3=/ 4.求证:AB // CD .6.已知,如图, AE // BD ,/ 1 = 3/ 2,/ 2 = 26°,求一(3)如图3,若Z A = m ,依次作出Z AOP 的角平分线 OB , Z BOP 的角平分线 OB 1 ,Z B 1OP 的角平分 线OB 2,Z B n - 1OP 的角平分线 OB n ,其中点 B , B 1, B 2,…,B n -1, B n 都在射线AE 上,试求Z AB n O 的度数.,求/ 1 + / 2的度数(提示:要作辅助线哟!/ AOP 的角平分线交射线 AE 与点B ,若/ BOP = 58°,求/ A 的度数.(2)如图 2, 若点C 在射线AE 上,OB 平分/ AOC 交AE 于点B , OD 平分/ COP 交AE 于点D ,/ADO = 39° ,求/ ABO -Z AOB 的度数./ B = 105 (1)如图 1,9. 数学思考:(1)如图1,已知AB // CD ,探究下面图形中/ APC 和/ PAB 、/ PCD 的关系,并证明你的 结论推广延伸:(2)①如图2,已知AA i / BA 1,请你猜想/ A 1,/ B 1,/ B 2,/ A 2、/ A 3的关系,并证明你的猜想;②如图3,已知AA 1 / BA n ,直接写出/ A 1,/ B 1,/ B 2,/ A 2、…/ B n -1、/ A n 的关系拓展应用:(3)①如图4所示,若AB // EF ,用含a, 3, 丫的式子表示X ,应为 _________________A.180° + a + 3- YB.180 °_ a _ Y +3 C .供丫― a D . a + 3+ 丫②如图 5, AB / CD ,且/ AFE = 40°,/ FGH = 90°,/ HMN = 30°,/ CNP = 50°,请你根据上述结论直接写出/ GHM 的度数是(2) 如图2,点P 在直线AB 、CD 之间,/ BAP 与/ DCP 的角平分线相交于点之间的数量关系,并说明理由.(3) 如图3,点P 落在CD 夕卜,/ BAP 与/ DCP 的角平分线相交于点 K , / AKC 与/ APC 有何数量关 系?并说明理由.10. 已知,直线 AB / DC ,点P 为平面上一点,连接 AP 与 CP .(1) 如图1,点P 在直线AB 、CD 之间,当/BAP = 60°,/ DCP = 20° 时,求/ APC .K ,写出/ AKC 与/ APC11. 如图,已知 AM II BN ,/ A = 80。
七下数学第一章:平行线能力提升测试题答案

七下数学第一章:平行线能力提升测试题答案一.选择题:(本题共10小题,每小题3分,共30分)温馨提示:每一题的四个答案中只有一个是正确的,请将正确的答案选择出来!1.答案:C解析:A、∵∠1=∠2,∴EF∥AC,故A不符合题意;B、∵∠4=∠C,∴EF∥AC,故B不符合题意;C、∵∠1+∠3=180°,∴DE∥BC,故C符合题意;D、∵∠3+∠C=180°,∴EF∥AC,故D不符合题意.故选择:C.2.答案:B解析:由平移可知AF=CE=2cm,∵AE=7cm,∴FC=AE-AF-CE=3cm.故选择:B.3.答案:C解析:∵∠1=∠2,∴l1l2,故A不符合题意;∵∠3=∠4∴l1l2,故B不符合题意;∠4与∠6不是两条直线被第三条直线所截形成的角,所以即使∠4=∠6,也不能判定l1l2,故C符合题意;∵∠2+∠5=180°,∴l1l2,故D不符合题意;故选择:C.4.答案:C解析:∵l1∥l2∥l3,∴∠1=∠2+∠4,∠4+∠3=180°,∴∠1﹣∠2+∠3=180°,故选择:C.5.答案:B解析“如图,将围巾展开,则∠ADM =∠ADF,∠KCB=∠BCN设∠ABC = x,则∠DAB=x+8°∵CDIlAB∴∠ADM=∠DAB=x+8°= ∠ADF∵DFlICG∴∠FDC=∠KCG=2x∵∠FDC + ∠FDM = 180°∴2x +2(x+ 8°) = 180°解得 x=41°∴∠DAB+2∠ABC=(x+ 8°)+2x= 131°故选择:B.6.答案:B解析:∵AB∥EF,∴∠α=∠BOF,∵CD∥EF,∴∠γ+∠COF=180°,∵∠BOF=∠COF+∠β,∴∠γ+∠α﹣∠β=180°,故选择:B.7.答案:B解析:根据题意得:图1中,AD∥BC,∴∠DEF=∠EFB,设∠DEF=∠EFB=α,图2中,CF∥DE,AE∥BG,∴∠GFC=∠BGD=∠AEG=180°-2∠EFB=180°-2α,图3中,∠CFE=∠GFC-∠EFG=180°-2α-α=120°,解得α=20°.即∠DEF=20°,故选择:B.8.答案:C解析:如图1,∵AB∥EF,∴∠3=∠2,∵BC∥DE,∴∠3=∠1,∴∠1=∠2.如图2,∵AB∥EF,∴∠3+∠2=180°,∵BC∥DE,∴∠3=∠1,∴∠1+∠2=180°∴如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.设另一个角为x,则这一个角为4x﹣30°,(1)两个角相等,则x=4x﹣30°,解得x=10°,4x﹣30°=4×10°﹣30°=10°;(2)两个角互补,则x+(4x﹣30°)=180°,解得x=42°,4x﹣30°=4×42°﹣30°=138°.所以这两个角是42°、138°或10°、10°.故选:C.9.答案:D解析:如图,作HP∥AB,取AB与FG的交点为Q,设∠BEN=x,∠CGH=y,则∠FEN = 2x,∠FGH = 2y,∵AB∥CD,∴AB∥HP∥CD,∴∠PHN=∠BEN ,∠PHG=∠CGH ,∠FQE=∠FGD , ∴∠H=∠PHN+∠CGH=∠BEN+∠CGH = x+y ,∴∠F=∠FEB-∠FQE=∠FEB-∠FGD=∠FEB-(180° -∠FGC)= 3x- (180° - 3y) = 3(x+y)- 180° =3∠H-180°, ∴3∠H-∠F= 180°, 故选择:D.10.答案:C解析:①∵AM ∥BN ,∴∠ACB =∠CBN (两直线平行,内错角相等),故①对; ②∵AM ∥BN ,∠A =64°,∴∠ABN =180°﹣∠A =180°﹣64°=116°; ∵BC 、BD 分别平分∠ABP 和∠PBN , ∴∠CBD =∠CBP +∠DBP =21(∠NBP +∠ABP )=21×∠ABN =21×116°=58°,故②错; ③∵BC 、BD 分别平分∠ABP 和∠PBN , ∴∠ABC =∠PBC ,∠PBD =∠NBD ,∵∠ACB =∠ABD (已知),∠ACB =∠CBN (已证), ∴∠ABD =∠CBN ,则∠ABC =∠NBD , ∴∠ABC =∠PBC =∠PBD =∠NBD , ∴∠ABC =41∠ABN =29°,故③对; ④∵AM ∥BN ,∴∠APB =∠PBN ,∠ADB =∠DBN , ∵BD 分别平分∠PBN , ∴∠PBN :∠DBN =2:1, ∴∠APB :∠ADB =2:1,故④对, 故选择:C .二.填空题(本题共6小题,每题4分,共24分) 温馨提示:填空题必须是最简洁最正确的答案!11.答案:∠1+∠2=∠3. 解析:∵AB ∥CD ∥EF∴∠1=∠BCD ,∠3=∠DCE , 又∵∠DCE=∠2+∠BCD ∴∠1+∠2=∠3故答案为:∠1+∠2=∠3.12.答案:12解析:由题意可得,阴影部分是矩形,长=6﹣2=4,宽=4﹣1=3, ∴阴影部分的面积=4×3=12, 故答案为:12.13.答案:①④解析:①∵∠1=∠3, ∴AD ∥BC ,故本选项符合题意; ②∵∠2=∠4, ∴AB ∥CD ,故本选项不符合题意; ③∵∠DAB =∠EDC , ∴AB ∥CD ,故本选项不符合题意; ④∵∠DAB +∠B =180°,∴AD ∥BC ,本选项符合题意, 则正确的选项为①④. 故答案为:①④.14.答案221∠=∠解析:如图,过P 作AB PH //, ∵AB//CD , ∴AB//CD//PH ,∴EPH BEP FPH ∠=∠∠=∠,2, ∴0902=∠=∠+∠EPF BEP , ∴2900∠-=∠BEP . ∵GEP BEP ∠=∠又,∴()222902*********∠=∠--=∠-=∠BEP , 即.221∠=∠ 故答案为:221∠=∠15.答案:540解析:如图,把两条”之”字路平移到长方形地块的最上边和最左边,则余下部分是矩形.∵30232=-=CF (米),18220=-=CG (米), ∴矩形EFCG 的面积5401830=⨯=(平方米). 答:绿化的面积为2540m . 故答案为540.16.答案:①②③④ 解析://AB CD ,//CD EF ,//AB EF ∴,故①正确;AE 平分BAC ∠,21BAC ∴∠=∠, //AB CD , 2180BAC ∴∠+∠=︒, 212180∴∠+∠=︒(1), AC CE ⊥,2490∴∠+∠=︒(2),∠-∠=︒,故②正确;∴(1)-(2)得,21490AB EF,//BAE∴∠+∠=︒,3180AE平分BAC∠,∴∠=∠,1BAE13180∴∠+∠=︒,∴∠+∠=︒(3),2123360212180∠+∠=︒(1),(3)-(1)得,232180∠-∠=︒,故③正确;//CD EF,∴∠+∠=︒,4180CEF∴∠+∠+∠=︒,AEC34180⊥,AC CE190∴∠+∠=︒,AECAEC∴∠=︒-∠,901∴∠+∠-∠=︒,34190∠-∠=︒,214901∴∠=︒+∠,145421∴∠+∠=︒,故④正确.341352故正确的结论有:①②③④.故答案为:①②③④.三.解答题(共6题,共66分)温馨提示:解答题应将必要的解答过程呈现出来!17.解析:(1)∵AD∥BE,∴∠D=∠DCE.∵∠B=∠D,∴∠DCE=∠B,∴AB∥CD.(2)∵∠BAE=∠2=60°, ∵∠BAC=3∠EAC ,∴∠BAE=∠BAC+3∠EAC=4∠EAC=60°, ∴∠EAC=15°,∴∠BAC=3∠EAC=45°,∴∠B=180°-∠BAC-∠1=180°-45°-60°=75°.18.解析:(1)AD ∥EC , 理由是:∵AB ∥CD , ∴∠1=∠ADC , ∵∠1+∠2=180°, ∴∠2+∠ADC =180°, ∴AD ∥EC ;(2)∵AD ∥EC ,CE ⊥AE , ∴AD ⊥AE , ∴∠FAD =90°,∵∠1+∠2=180°,∠2=140°, ∴∠1=40°,∴∠FAB =∠FAD ﹣∠1=90°﹣40°=50°.19.解析:4∠=∠FAB , 理由如下: ∵EF AC //, ∴018031=∠+∠, ∴32∠=∠ ∴CD FA //, ∴4∠=∠FAB ;(2)∵AC 平分FAB ∠, ∴CAD ∠=∠2, ∵32∠=∠ ,3∠=∠∴CAD , CAD ∠+∠=∠3403978214213=⨯=∠=∠∴ EF AC BE BF //,⊥ BE AC ⊥∴ 090=∠∴ACB0051390=∠-=∠∴BCD20.解析:(1)平行;理由如下: //AC BD ,//MN AC , //MN BD ∴;(2)//AC BD ,//MN BD ,1PBD ∴∠=∠,2PAC ∠=∠,12APB PBD PAC ∴∠=∠+∠=∠+∠.(3)答:不成立.它们的关系是APB PBD PAC ∠=∠-∠. 理由是:如图2,过点P 作//PQ AC , //AC BD ,////PQ AC BD ∴,PAC APQ ∴∠=∠,PBD BPQ ∠=∠, APB BPQ APQ PBD PAC ∴∠=∠-∠=∠-∠.21.解析:(1)AB ∥DE ,理由如下: ∵MN ∥BC ,∠1=60°, ∴∠ABC =∠1=60°, 又∵∠1=∠2, ∴∠ABC =∠2, ∴AB ∥DE ; (2)∵MN ∥BC , ∴∠NDE +∠2=180°,∴∠NDE =180°﹣∠2=180°﹣60°=120°, ∵DC 是∠NDE 的角平分线, ∴∠EDC =∠NDC =21∠NDE =60°, ∵MN ∥BC ,∴∠C =∠NDC =60°, ∴∠ABC =∠C ;(3)∵∠ADC +∠NDC =180°,∠NDC =60°, ∴∠ADC =180°﹣∠NDC =180°﹣60°=120°, ∵BD ⊥DC , ∴∠BDC =90°,∴∠ADB =∠ADC ﹣∠BDC =120°﹣90°=30°, ∵MN ∥BC ,∴∠DBC =∠ADB =30°, ∵∠ABC =∠C =60°, ∴∠ABD =30°.22.解析:(1)证明:如图1,延长DE 交AB 于点F ,∵∠ACB =∠CED ,∴AC ∥DF ,∴∠A =∠DFB ,∵∠A =∠D ,∴∠DFB =∠D ,∴AB ∥CD ;(2)解:如图2,作EM ∥CD ,HN ∥CD ,∵AB ∥CD ,∴AB ∥EM ∥HN ∥CD ,∴∠1+∠EDF =180°,∠MEB =∠ABE ,∵BG 平分∠ABE ,∴∠ABG =21∠ABE , ∵AB ∥HN ,∴∠2=∠ABG ,∵CF ∥HN ,∴∠2+∠β=∠3,∴21∠ABE+∠β=∠3, ∵DH 平分∠EDF ,∴∠3=21∠EDF , ∴21∠ABE+∠β=21∠EDF , ∴∠EDF ﹣∠ABE =2∠β,设∠DEB =∠α,∵∠α=∠1+∠MEB =180°﹣∠EDF+∠ABE =180°﹣(∠EDF ﹣∠ABE )=180°﹣2∠β, ∵∠DEB 比∠DHB 大60°,∴∠α﹣60°=∠β,∴∠α=180°﹣2(∠α﹣60°),解得:∠α=100°,∴∠DEB 的度数为100°;(3)解:∠PBM 的度数不变,理由如下:如图3,过点E 作ES ∥CD ,设直线DF 和直线BP 相交于点G ,∵BM 平分∠EBK ,DN 平分∠CDE ,∴∠EBM =∠MBK =21∠EBK ,∠CDN =∠EDN =21∠CDE , ∵ES ∥CD ,AB ∥CD ,∴ES ∥AB ∥CD ,∴∠DES =∠CDE ,∠BES =∠ABE =180°﹣∠EBK ,∠G =∠PBK ,由(2)可知:∠DEB =100°,∴∠CDE+180°﹣∠EBK =100°,∴∠EBK ﹣∠CDE =80°,∵BP ∥DN ,∴∠CDN =∠G ,∴∠PBK =∠G =∠CDN =21∠CDE , ∴∠PBM =∠MBK ﹣∠PBK =21∠EBK ﹣21∠CDE =21(∠EBK ﹣∠CDE )=21× 80°=40°. ∴∠PBM 的度数不改变.23.解析:(1)如图1,①∵∠MON =36°,OE 平分∠MON ,∴∠AOB =∠BON =18°,∵AB ∥ON ,∴∠ABO =18°;②当∠BAD =∠ABD 时,∠BAD =18°,∵∠AOB +∠ABO +∠OAB =180°,∴∠OAC =180°﹣18°×3=126°;③当∠BAD =∠BDA 时,∵∠ABO =18°,∴∠BAD =81°,∠AOB =18°,∵∠AOB +∠ABO +∠OAB =180°,∴∠OAC =180°﹣18°﹣18°﹣81°=63°,故答案为:①18°;②126°;③63°;(2)如图2,存在这样的x 的值,使得△ADB 中有两个相等的角.∵AB ⊥OM ,∠MON =36°,OE 平分∠MON ,∴∠AOB =18°,∠ABO =72°,若∠BAD =∠ABD =72°,则∠OAC =90°﹣72°=18°;若∠BAD =∠BDA =(180°﹣72°)÷2=54°,则∠OAC =90°﹣54°=36°; 若∠ADB =∠ABD =72°,则∠BAD =36°,故∠OAC =90°﹣36°=54°;综上所述,当x =18、36、54时,△ADB 中有两个相等的角.。
平行线 同步提升训练(解析版)

1.1平行线同步提升训练一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2021秋•鼓楼区校级期末)下列说法正确的是()A.不相交的两条直线叫做平行线B.同一平面内,过一点有且仅有一条直线与已知直线垂直C.平角是一条直线D.过同一平面内三点中任意两点,只能画出3条直线【分析】根据平行线、垂线的性质,角和直线的概念逐一判断可求解.【解答】解:A.应强调在同一平面内,错误;B.同一平面内,过一点有且仅有一条直线与已知直线垂直,正确;C.直线与角是不同的两个概念,错误;D.过同一平面内三点中任意两点,能画出3条直线或1条直线,故错误.故选:B.2.(2022•南京模拟)在同一个平面内,不重合的两条直线的位置关系是()A.平行B.相交C.平行或相交D.无法确定【分析】根据在同一平面内两条不重合的直线的位置关系得出即可.【解答】解:在同一平面内两条不重合的直线的位置关系是平行和相交.故选:C.3.(2020秋•苏州期末)下列说法正确的是()A.具有公共顶点的两个角是对顶角B.A、B两点之间的距离就是线段ABC.两点之间,线段最短D.不相交的两条直线叫做平行线【分析】依据对顶角、两点的距离,线段的性质,平行线,即可得出结论.【解答】解:A.具有公共顶点的两个角不一定是对顶角,故本选项错误;B.A、B两点之间的距离就是线段AB的长,故本选项错误;C.两点之间,线段最短,故本选项正确;D.在同一平面内,不相交的两条直线叫做平行线,故本选项错误;故选:C.4.(2021春•和平区校级月考)下列语句正确的有()个①任意两条直线的位置关系不是相交就是平行②过一点有且只有一条直线和已知直线平行③过两条直线a,b外一点P,画直线c,使c∥a,且c∥b④若直线a∥b,b∥c,则c∥a.A.4B.3C.2D.1【分析】根据同一平面内,任意两条直线的位置关系是相交、平行;过直线外一点有且只有一条直线和已知直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行进行分析即可.【解答】解:①任意两条直线的位置关系不是相交就是平行,说法错误,应为根据同一平面内,任意两条直线的位置关系不是相交就是平行;②过一点有且只有一条直线和已知直线平行,说法错误,应为过直线外一点有且只有一条直线和已知直线平行;③过两条直线a,b外一点P,画直线c,使c∥a,且c∥b,说法错误;④若直线a∥b,b∥c,则c∥a,说法正确;故选:D.5.(2021春•沙河市期末)观察如图所示的长方体,与棱AB平行的棱有几条()A.4B.3C.2D.1【分析】根据长方体即平行线的性质解答.【解答】解:图中与AB平行的棱有:EF、CD、GH.共有3条.故选:B.6.(2021秋•江阴市期末)有下列说法:①两条不相交的直线叫平行线;②同一平面内,过一点有且只有一条直线与已知直线垂直;③两条直线相交所成的四个角中,如果有两个角相等,那么这两条直线互相垂直;④有公共顶点的两个角是对顶角.其中说法正确的个数是()A.1B.2C.3D.4【分析】依据平行线的定义、对顶角的定义、垂线进行判断,即可得出结论.【解答】解:①同一平面内,两条不相交的直线叫平行线;故不符合题意;②同一平面内,过一点有且只有一条直线与已知直线垂直;故符合题意;③两条直线相交所成的四个角中,如果有两个角相等,那么这两条直线不一定互相垂直;故不符合题意;④有公共顶点,两边互为反向延长线的两个角是对顶角;故不符合题意;故其中说法正确的个数是1,故选:A.7.(2021春•梁山县期中)若a、b、c是同一平面内三条不重合的直线,则它们的交点可以有()A.1个或2个或3个B.0个或1个或2个或3个C.1个或2个D.以上都不对【分析】根据平行线的定义,相交线的定义,可得答案.【解答】解:当三条直线互相平行,交点是个0;当两条直线平行,与第三条直线相交,交点是2个;当三条直线两两相交交于同一点,交点个数是1个;当三条直线两两相交且不交于同一点,交点个数是3个;故选:B.8.(2017秋•连云区期末)下列说法:①用两根钉子固定一根木条,体现数学事实是两点之间线段最短;②射线AB 与射线BA表示同一条射线;③若AB=BC,则B为线段AC的中点;④不相交的两条直线叫做平行线;⑤过一点有且只有一条直线与已知直线垂直,其中正确的有()A.0个B.1个C.2个D.3个【分析】根据平行线、相交线等相关知识解答.【解答】解:①用两根钉子固定一根木条,体现数学事实是两点确定一条直线,此结论错误;②射线AB与射线BA的起点不同、方向不同,不是同一射线,此结论错误;③若AB=BC,则B不一定是线段AC的中点,此结论错误;④同一平面内不相交的两条直线叫做平行线,此结论错误;⑤同一平面内,过一点有且只有一条直线与已知直线垂直,此结论错误;故选:A.9.(2015春•丰台区期末)在同一平面内有2014条直线a1,a2,…,a2014,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,依此类推,那么a1与a2014的位置关系是()A.垂直B.平行C.垂直或平行D.重合【分析】根据观察发现规律,以四次为一个循环,⊥,⊥,∥,∥,根据此规律即可解决问题.【解答】解:∵a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,∴a1⊥a2,a1⊥a3,a1∥a4,a1∥a5…以四次为一个循环,⊥,⊥,∥,∥规律:下标除以4余数为2或3垂直,下标除以4余数为0或1平行,2014÷4的余数为2,∴a1⊥a2014,所以直线a1与a2014的位置关系是:a1⊥a2014.故选:A.二、填空题(本大题共6小题,每小题4分,共24分)请把答案直接填写在横线上10.(2021春•松江区校级期末)如图,在长方体ABCD﹣EFGH中,与棱FG异面并且与棱FB平行的棱有HD 和AE.【分析】根据平行、异面的定义解决此题.【解答】解:根据题意得,与棱FG异面并与FB平行的棱有HD和AE.故答案为:HD和AE.11.(2021春•浦东新区校级期末)在如图的长方体中,既与平面ABCD垂直,又与平面ABB1A1平行的平面是面CDD1C1.【分析】根据平行线的定义解决此题.【解答】解:既与平面ABCD垂直,又与平面ABB1A1平行的平面是面CDD1C1.故答案为:CDD1C1.12.(2022春•赵县月考)在同一平面内,直线a,b相交于P,若a∥c,则b与c的位置关系是相交.【分析】根据同一平面内,一条直线与两条平行线中的一条相交,则必与另一条直线也相交.解答即可.【解答】解:因为a∥c,直线a,b相交,所以直线b与c也有交点;故答案为:相交.13.(2022春•东平县期末)在同一平面内,直线a、b、c中,若a⊥b,b∥c,则a、c的位置关系是c⊥a.【分析】根据b∥c,则得到同旁内角互补,然后利用a⊥b即可得到a与c的夹角为90度,则可判断a⊥c.【解答】解:∵c∥b,a⊥b,∴c⊥a.故答案为c⊥a14.(2018春•雁塔区校级月考)平面上不重合的四条直线,可能产生交点的个数为0,1,3,4,5,6个.【分析】从平行线的角度考虑,先考虑四条直线都平行,再考虑三条、两条直至都不平行,作出草图即可看出.【解答】解:(1)当四条直线平行时,无交点;(2)当三条平行,另一条与这三条不平行时,有三个交点;(3)当两两直线平行时,有4个交点;(4)当有两条直线平行,而另两条不平行时,有5个交点;(5)当四条直线同交于一点时,只有一个交点;(6)当四条直线两两相交,且不过同一点时,有6个交点;(7)当有两条直线平行,而另两条不平行并且交点在平行线上时,有3个交点.故答案为:0,1,3,4,5,6.15.(2016秋•淮安期末)下列说法中:①棱柱的上、下底面的形状相同;②若AB=BC,则点B为线段AC的中点;③相等的两个角一定是对顶角;④在同一平面内,不相交的两条直线叫做平行线;⑤直线外一点与直线上各点连接的所有线段中,垂线段最短.正确的有①④⑤.(只填序号)【分析】分别根据棱柱的特征以及对顶角和垂线段的性质得出答案即可.【解答】解:①棱柱的上、下底面的形状相同,正确;②若AB=BC,则点B为线段AC的中点,A,B,C不一定在一条直线上,故错误;③相等的两个角一定是对顶角,角的顶点不一定在一个位置,故此选项错误;④在同一平面内,不相交的两条直线叫做平行线,正确;⑤直线外一点与直线上各点连接的所有线段中,垂线段最短,正确.故答案为:①④⑤.三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)16.如图所示,哪些线段是互相平行的?用“∥”表示出来.【分析】根据网格即可判断哪些线段是互相平行的.【解答】解:根据网格可知:线段DE和FG都是2×2格对角线,而且方向相同,∴DE∥FG;∵线段HI和AB都1×4格对角线,而且方向相同,∴HI∥AB.17.在同一平面内,任意三条直线有哪几种不同的位置关系?你能画图说明吗?下面是小明的解题过程:解:有两种位置关系,如图:你认为小明的解答正确吗?如果不正确,请你给出正确的解答.【分析】根据同一平面内的两条直线有相交、平行两种关系画出图形即可解答.【解答】解:不正确,如图所示,故在同一平面内,任意三条直线有四种不同的位置关系.18.如图所示,马路上的斑马线,运动场上的双杠这些都给我们平行线的形象.请分别在图中标出字母;(1)并用不同字母表示各组平行线;(2)在双杠中哪些线是互相垂直关系?【分析】(1)根据直线的表示方法,用一个小写字母表示出即可;(2)根据图形写出互相垂直的直线即可.【解答】解:(1)如图,a∥b∥c∥d,e∥f,g∥h∥m∥n;(2)e⊥m,e⊥n,f⊥g,f⊥h.19.如图的长方体中,与AA′平行的棱有哪几条?与AB平行的棱有哪几条?分别用符号把它们表示出来.【分析】根据平行的定义,结合图形直接找出和棱AB平行的棱,与棱AA′平行的棱即可.【解答】解:由图可知,和棱AB平行的棱有CD,A′B′,C′D′;与棱AA′平行的棱有DD′,BB′,CC′.20.试说出在同一平面内三条直线的交点情况并画出图形.【分析】分三条直线互相平行,两条直线互相平行,三条直线都不平行作出图形解答.【解答】解:如图,三条直线有0或1或2或3个交点.21.如图,在同一平面内,一组互相平行的直线共n条(n为大于1的正整数),它们和两条平行线a、b相交,构成若干个“♯”字形.设构成的“♯”字形个数为x.请填写下表:n2345……nx13610n(n﹣1)【分析】观察图形,根据平行线的性质,可得一组互相平行的直线共n条,构成的“♯”字形个数为n(n﹣1),依此即可求解.【解答】解:一组互相平行的直线共n条,构成的“♯”字形个数为n(n﹣1),n=2时,×2×(2﹣1)=1;n=3时,×3×(3﹣1)=3;n=4时,×4×(4﹣1)=6;n=5时,×5×(5﹣1)=10;填表如下:n2345……nx13610n(n﹣1)故答案为:1,3,6,10,n(n﹣1).22.根据下列语句,画出图形:(1)过顶点C,画MN∥AB;(2)过AB中点D,画平行于AC的直线,交BC于点E;(3)过点B画AC的垂线,交AC于点F.【分析】(1)利用三角板作出平行线即可.(2)首先确定AB中点D,然后利用三角板作出平行线;(3)依题意利用直角三角板过点B画AC的垂线即可.【解答】解:如图所示:23.(2021秋•内乡县期末)如图所示,在∠AOB内有一点P.(1)过P画l1∥OA;(2)过P画l2∥OB;(3)用量角器量一量l1与l2相交的角与∠O的大小有怎样关系?【分析】用两个三角板,根据同位角相等,两直线平行来画平行线,然后用量角器量一量l1与l2相交的角与∠O 的关系为:相等或互补.【解答】解:(1)(2)如图所示,(3)l1与l2夹角有两个:∠1,∠2;∠1=∠O,∠2+∠O=180°,所以l1和l2的夹角与∠O相等或互补.。
浙教版七下数学第一章:平行线能力提升测试试题答案

第一章:平行线能力提升测试试题答案一.选择题:(本题共10小题,每小题3分,共30分)温馨提示:每一题的四个答案中只有一个是正确的,请将正确的答案选择出来!1.答案:D解析:0140,180=∠=∠+∠CDE CDA CDE , ∴040140180=-=∠CDA , ∵CD AB //,∴040=∠=∠CDA A ,故选择D2.答案:C解析:A 、∵∠1=∠2,∴a ∥b ,因此A 不符合题意; B 、∵∠1=∠3,∴a ∥b ,因此B 不符合题意;C 、∠1+∠4=180° ,∠1与∠4是邻补角,不能证明a ∥b ,因此C 符合题意;D 、∵∠2+∠4=180°,∴a ∥b ,因此D 不符合题意; 故答案为:C3.答案:B解析:图中与AB 平行的棱有:EF 、CD 、GH .共有3条. 故选:B .4.答案:C解析:过E 作CD AB EH ////, ∴,230=∠=∠B HEB ∴042=∠=∠D HED , ∴0654223=+=∠BED , 故选择C5.答案:D解析:∵CD ∥EF ,AB ∥EF ∴∠C=∠CFE ,∠A=∠AFE ∵FC 平分∠AFE ∴∠AFE=50°, 即∠A=50° 故答案为:D 。
6.答案:C 解析:∵DE ∥BC ,∴∠DCB =∠1,∠AED =∠ACB ,(2)正确; ∵∠1=∠2, ∴∠2=∠DCB , ∴FG ∥DC ,(1)正确; ∴∠BFG =∠BDC , (5)正确;正确的个数有3个,故选:C .7.答案:D解析:∵MN F '∆是由BMN ∆沿MN 折叠而成, ∴BNM NM F BMN MN F ∠='∠∠='∠,, ∵AD M F //',0100=∠='∠∴A MB F , ∵CD N F //',∴070=∠='∠C F BN ,∴()00857010021=+=∠+∠BNMBMN,∴009585180=-=∠B,故选择D8.答案:C解析:∵21∠=∠,∴1∠的对顶角等于2∠,∴21//ll,∴4∠的补角等于0553=∠,∴00125551804=-=∠,故选择C9.答案:D解析:如图:过C作nmCH////,∴0201,3=∠=∠∠=∠HCBACH,∵060=∠ACB,∴0403=∠∵090=∠BAC,∴09032=∠+∠,∴0502=∠,故选择DH310.答案:C解析:∵∠1=∠2,∴AC∥DE,故①正确;∵AC⊥BC,CD⊥AB,∴∠ACB=∠CDB=90°,∴∠A+∠B=90°,∠3+∠B=90°,∴∠A=∠3,故②正确;∵AC∥DE,AC⊥BC,∴DE⊥BC,∴∠DEC=∠CDB=90°,∴∠3+∠2=90°(∠2和∠3互余),∠2+∠EDB=90°,∴∠3=∠EDB,故③正确,④错误;∵AC⊥BC,CD⊥AB,∴∠ACB=∠CDA=90°,∴∠A+∠B=90°,∠1+∠A=90°,∴∠1=∠B,故⑤正确;即正确的个数是4个,故选择C二.填空题(本题共6小题,每题4分,共24分)温馨提示:填空题必须是最简洁最正确的答案!11.答案:EF∥CG,AB∥CD.解析:∵∠2=∠C,∴EF∥CG,又∵∠1=∠2,∴∠1=∠C,∴AB∥CD.故答案为EF∥CG,AB∥CD.12.答案:12解析:∵将Rt△ABC沿射线BC方向平移得到△DEF,∴DE=AB=5,∵DH=2,∴HE=DE﹣DH=3,∵∠B=90°,∴四边形ABEH是梯形,S 阴影=S △DEF ﹣S △CEH =S △ABC ﹣S △CEH =S 梯形ABEH=21(AB +HE )•BE =21×(5+3)×3=1213.答案:6解:∵AB ∥EF ∥CD ,∴∠AGE =∠GEP =∠H ,又∵GE ∥BC ,∴∠AGE =∠ABP =∠BPF =∠CPE =∠DCP , ∴图中与∠AGE 相等的角(不含∠AGE )共有6个,14.答案:0140 解析:如图:∵21//l l , ∴∴0401=∠=∠ECA , ∵βα∠=∠, ∴DE AC //,∴01802=∠+∠ACE , ∴00140401802=-=∠15.答案:DPC ABP ∠=∠ 解析:∵CD AB //,∴0180=∠+∠DCB ABC , ∵PB 和PC 均为角平分线, ∴090=∠+∠PCB PBC , ∴090=∠BPC ,∴090=∠+∠DPC APB , ∵AB AD ⊥, ∴090=∠PAB , ∴090=∠+∠APB ABP , ∴DPC ABP ∠=∠16.答案:36°或37°解析:如图,过E 作EG ∥AB , ∵AB ∥CD , ∴GE ∥CD ,∴∠BAE=∠AEG ,∠DFE=∠GEF , ∴∠AEF=∠BAE+∠DFE , 设∠CEF=x ,则∠AEC=2x , ∴x+2x=∠BAE+60°, ∴∠BAE=3x ﹣60°, 又∵6°<∠BAE <15°, ∴6°<3x ﹣60°<15°, 解得22°<x <25°,又∵∠DFE 是△CEF 的外角,∠C 的度数为整数, ∴∠C=60°﹣23°=37°或∠C=60°﹣24°=36°, 故答案为:36°或37°.三.解答题(共6题,共66分)温馨提示:解答题应将必要的解答过程呈现出来!17.解析:如图所示:18.解析:∵AE⊥BC,FG⊥BC,∴AE∥FG,∴∠2=∠CFG.∵∠1=∠2,∴∠CFG=∠1,∴AB∥CD.19.解析:结论:AB∥DG.理由:∵AD⊥BC于D,EF⊥BC于F,∴AD∥EF,∴∠1=∠BAD,∵∠1=∠2,∴∠BAD=∠2,∴AB∥DG.20.解析:∵AD∥BC,∴∠1=∠BF C' =α,∵∠C'FC+∠BF C'=180°∴∠C'FC=180°-∠BF C'=180°-α∵EF 为折痕, ∴∠C 'FE =∠CFE =21∠C 'FC =90°-21α,∵AD ∥BC , ∴∠2=∠CFE =90°-21α.21.解:(1):∵∠BAD +∠ADC =180°,∴AB ∥CD ,∴∠DCG =∠B =86°; (2)AD ∥BC ;理由如下: ∵AB ∥CD ,∴∠BAF =∠CFE ,∵AE 平分∠BAD ,∴∠BAF =∠FAD ,∴∠DAF =∠CFE , ∵∠CFE =∠AEB ,∴∠DAF =∠AEB , ∴AD ∥BC ;(3)α=2β时,AE ∥DG ;理由如下: ∵AD ∥BC ,∴∠DAF =∠AEB ,∵AE 平分∠BAD ,∴∠DAB =2∠DAF =2∠AEB , 当AE ∥DG , ∴∠AEB =∠G , ∴α=2β.22.解析:(1)①∵∠A =60°,∠ACB =40°, ∴∠ABC =80°, ∵BM 平分∠ABC , ∴∠AB E =21AB C =40°,∵CE ∥AB ,∴∠BEC =∠ABE =40°; ②∵∠A =60°,∠ACB =40°,∴∠ABC =80°,∠ACD =180°﹣∠ACB =140°, ∵BM 平分∠ABC ,CE 平分∠ACD , ∴∠CBE =21ABC =40°,∠ECD =21∠ACD =70°, ∴∠BEC =∠ECD ﹣∠CBE =30°; (2)①如图1,当CE ⊥BC 时, ∵∠CBE =40°, ∴∠BEC =50°;②如图2,当CE ⊥AB 于F 时, ∵∠ABE =40°,∴∠BEC =90°+40°=130°, ③如图3,当CE ⊥AC 时, ∵∠CBE =40°,∠ACB =40°,∴∠BEC =180°﹣40°﹣40°﹣90°=10°.23.解析:(1)∵AB ∥CD , ∴∠AMN +∠CNM =180°,∵ME ,NE 分别是∠AMN 与∠CNM 的平分线, ∴∠EMN =21∠AMN ,∠ENM =21∠MNC , ∴∠EMN +∠ENM =90°,即∠MEN =90°, 又∵NG ⊥EN ,∴∠MEN +∠ENH =180°, ∴EM ∥NG ;(2)设∠HEG=x,则∠HGE=∠MEG=x,∠NEH=90°﹣2x,∵EP平分∠FEH,∴∠FEH=2∠PEH=2(∠PEG+x),又∵∠FEH+∠HEN=180°,∴2(∠PEG+x)+90°﹣2x=180°,解得∠PEG=45°.中小学教育资源及组卷应用平台21世纪教育网()。
平行线的性质 同步提升训练(解析版)

1.4平行线的性质同步提升训练一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2022秋•临洮县期中)将直尺和三角板按如图所示的位置放置.若∠1=50°,则∠2度数是()A.60°B.50°C.40°D.70°【分析】先根据平行线的性质求出∠3的度数,再由三角形内角和定理求出∠2的度数即可.【解答】解:∵直尺的两条边互相平行,∠1=50°,∴∠3=∠1=50°,∵∠4=60°,∴∠2=180°﹣∠4﹣∠3=180°﹣60°﹣50°=70°.故选:D.2.(2022秋•碑林区校级月考)如图,a∥b.∠1=58°,则∠2的度数为()A.58°B.112°C.120°D.132°【分析】根据平行线性质得出∠1=∠3,根据对顶角相等即可得出答案.【解答】解:如图,∵a∥b,∠1=58°,∴∠3=∠1=58°,∴∠2=∠3=58°,故选:A.3.(2022秋•龙岗区期末)如图,已知AB∥CD,BC平分∠ACD,∠B=35°,E是CA延长线上一点,则∠BAE的度数是()A.35°B.60°C.65°D.70°【分析】由平行线的性质可得∠BCD=∠B=35°,∠BAE=∠DCE,再由角平分线的定义求得∠DCE=2∠BCD,即可求∠BAE的度数.【解答】解:∵AB∥CD,∠B=35°,∴∠BCD=∠B=35°,∠BAE=∠DCE,∵BC平分∠ACD,∴∠DCE=2∠BCD=70°,∴∠BAE=70°.故选:D.4.(2022秋•宜兴市月考)如图,将长方形ABCD沿线段OG折叠到OB'C'G的位置,∠OGC'等于100°,则∠DGC'的度数为()A.20°B.25°C.30°D.40°【分析】根据折叠得出∠OGC=∠OGC′=100°,求出∠OGD,即可求出答案.【解答】解:∵将长方形ABCD沿线段OG折叠到OB'C'G的位置,∠OGC'等于100°,∴∠OGC=∠OGC′=100°,∴∠OGD=180°﹣∠OGC=80°,∴∠DGC'=∠OGC′﹣∠OGD=20°,故选:A.5.(2022•项城市校级模拟)如图,AB∥CD,∠MNC=138°,MP平分∠BMN,则∠MPN的度数为()A.59°B.48°C.54°D.69°【分析】首先根据AB∥CD,∠MNC=138°,求出∠MNC=∠BMN=138°,再根据MP平分∠BMN,求出∠BNP的度数.【解答】解:∵AB∥CD,∠MNC=138°,∴∠MNC=∠BMN=138°,∵MP平分∠BMN,∴∠BNP=BMN=69°,∵AB∥CD,∴∠BMP=∠MPN=69°.故选:D.6.(2022•博望区校级一模)如图是一款手推车的平面示意图,其中AB∥CD,∠1=24°,∠2=76°,则∠3的度数为()A.104°B.128°C.138°D.156°【分析】先根据平行线性质求出∠A,再根据邻补角的定义求出∠4,最后根据三角形外角性质得出∠3=∠4+∠A.【解答】解:如图:∵AB∥CD,∠1=24°,∴∠A=∠1=24°,∵∠2=76°,∠2+∠4=180°,∴∠4=180°﹣∠2=180°﹣76°=104°,∴∠3=∠4+∠A=104°+24°=128°.故选:B.7.(2022秋•南岗区校级期中)如图,AB∥CD∥EF,则下列各式中正确的是()A.∠1+∠2+∠3=180°B.∠1+∠2=180°+∠3C.∠1+∠3=180°+∠2D.∠2+∠3=180°+∠1【分析】根据两直线平行,同旁内角互补可得∠2+∠BDC=180°,再根据两直线平行,内错角相等可得∠3=∠CDE,而∠CDE=∠1+∠BDC,整理可得∠2+∠3﹣∠1=180°.【解答】解:∵AB∥CD∥EF,∴∠2+∠BDC=180°,∠3=∠CDE,又∠BDC=∠CDE﹣∠1,∴∠2+∠3﹣∠1=180°.故选:D.8.(2021秋•盐湖区校级期末)如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转()A.10°B.20°C.30°D.40°【分析】由平行线的判定“同位角相等,两直线平行”可知,∠EGB=∠EHD时,AB∥CD,即∠EGB需要变小20°,即将木棒AB绕点G逆时针旋转20°即可.【解答】解:当∠EGB=∠EHD时,AB∥CD,∵∠EGB=100°,∠EHD=80°,∴∠EGB需要变小20°,即将木棒AB绕点G逆时针旋转20°.故选:B.9.(2021秋•霍州市期末)如图,如果AB∥EF、EF∥CD,若∠1=50°,则∠2+∠3的和是()A.200°B.210°C.220°D.230°【分析】由平行线的性质可用∠2、∠3分别表示出∠BOE和∠COF,再由平角的定义可得出答案.【解答】解:∵AB∥EF,∴∠2+∠BOE=180°,∴∠BOE=180°﹣∠2,同理可得∠COF=180°﹣∠3,∵O在EF上,∴∠BOE+∠1+∠COF=180°,∴180°﹣∠2+∠1+180°﹣∠3=180°,∴∠2+∠3=180°+∠1=180°+50°=230°,故选:D.10.(2021秋•晋中期末)如图,已知AB∥CD,点F,G分别在直线AB,CD上,∠BFE的平分线FQ所在直线与∠CGE的平分线相交于点P,若∠BFE=50°,∠CGE=140°,则∠GPQ的度数为()A.30°B.40°C.45°D.50°【分析】根据平行线的性质可得∠BMG=∠CGP,根据角平分线的定义得:∠BFQ=∠BFE,∠CGP=∠CGE,由三角形的外角的性质得:∠GPQ=∠GMF﹣∠PFM=∠CGP﹣∠BFQ,代入计算即可得到答案.【解答】解:如图:∵AB∥CD,∴∠BMG=∠CGP,∵FQ平分∠BFE,GP平分∠CGE,∠BFE=50°,∠CGE=140°,∴∠BFQ=∠BFE=25°,∠CGP=∠CGE=70°,∴∠GPQ=∠BMG﹣∠PFM=∠CGP﹣∠BFQ=70°﹣25°=45°.故选:C.二、填空题(本大题共6小题,每小题4分,共24分)请把答案直接填写在横线上11.(2021秋•赣县区期末)如图,AB∥CD,∠B=42°,∠A+10°=∠1,则∠ACD=64°.【分析】利用平行线的性质解答即可.【解答】解:∵AB∥CD,∵∠DCB+∠B=180°,∵∠B=42°,∴∠DCB=138°,即∠DCA+∠1=138°.∴∠1=138°﹣∠DCA.∵AB∥CD,∴∠DCA=∠A,∴∠1=138°﹣∠A.∵∠A+10°=∠1,∴∠A+10°=138°﹣∠A,∴∠A=64°,∴∠ACD=∠A=64°.故答案为:64°.12.(2021秋•社旗县期末)如图,已知AB∥CD,∠A=30°,∠B=71°,则∠BEF的度数是101°.【分析】利用平行线的性质求出∠AEC,再由对顶角相等得到∠DEF,从而可计算∠BEF.【解答】解:∵AB∥CD,∴∠AEC=∠A=30°,∠BED=∠B=71°,∴∠DEF=∠AEC=30°,∴∠BEF=∠BED+∠DEF=71°+30°=101°.故答案为:101°.13.(2021秋•叙州区期末)如图,AB∥CD,MF与AB、CD分别交于点E、F,∠CFE的平分线FG交AB于点G,若∠MEG=140°,则∠EGF的度数为70°.【分析】根据两直线平行同位角相等可得∠CFE=140°,根据角平分线的定义可得∠CFG=70°,再根据两直线平行内错角相等可得∠EGF=70°.【解答】解:∵FG平分∠CFE,∴∠CFG=∠EFG,∵AB∥CD,∴∠CFE=∠MEG,∵∠MEG=140°,∴∠CFE=140°,∴∠CFG=∠EFG=70°,∵AB∥CD,∴∠EGF=∠CFG=70°.故答案为:70°.14.(2022秋•肇源县期中)如图,已知AB∥CD,∠1=∠2,∠E=50°,则∠F的度数50°.【分析】连接BC,由平行线的性质得∠ABC=∠BCD,由∠1=∠2得∠EBC=∠BCF,根据内错角相等,两直线平行可得EB∥CF,再根据两直线平行,内错角相等即可求解.【解答】解:连接BC,∵AB∥CD,∴∠ABC=∠BCD,∵∠1=∠2,∴∠EBC=∠BCF,∴EB∥CF,∴∠F=∠E=50°.故答案为:50°.15.(2022秋•香坊区校级期中)若∠1和∠2的两边互相平行,且∠1比∠2的3倍少36度,则∠2=18°或54°.【分析】由∠1和∠2的两边互相平行,可得此两角互补或相等,然后设∠2的度数为x,分别从两角相等或互补去分析,由∠1比∠2的3倍少36度列方程求解即可求得答案.【解答】解:∵∠1和∠2的两边互相平行,∴∠1和∠2互补或相等,设∠2的度数为x,则∠1=3x﹣36°,①当∠1和∠2相等时,则x=3x﹣36°,解得:x=18°,②当∠1和∠2互补时,则x+3x﹣36°=180°,解得:x=54°,综上,∠2=18°或54°,故答案为:18°或54°.16.(2021秋•盘州市期末)如图,已知AB∥CD,易得∠1+∠2+∠3=360°,∠1+∠2+∠3+∠4=540°,根据以上的规律求∠1+∠2+∠3+…+∠n=(n﹣1)×180°.【分析】由∠1+∠2+∠3=2×180°=360°,∠1+∠2+∠3+∠4=3×180°=540°,可得一般规律为∠1+∠2+∠3+…+∠n=(n﹣1)×180°.【解答】解:∵∠1+∠2+∠3=360°,∠1+∠2+∠3+∠4=540°,∴∠1+∠2+∠3=2×180°=360°,∠1+∠2+∠3+∠4=3×180°=540°,∴∠1+∠2+∠3+…+∠n=(n﹣1)×180°,故答案为:(n﹣1)×180°.三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)17.(2022秋•黄岛区校级期末)如图,点E、F分别在AB、CD上,AF⊥CE于点O,∠1=∠B,∠A+∠2=90°,求证:AB∥CD.请填空.证明:∵AF⊥CE(已知)∴∠AOE=90°(垂直的定义)又,∵∠1=∠B(已知)∴CE∥BF(同位角相等,两直线平行)∴∠AFB=∠AOE(两直线平行,同位角相等)∴∠AFB=90°(等量代换)又,∵∠AFC+∠AFB+∠2=180°(平角的定义)∴∠AFC+∠2=(90)°又∵∠A+∠2=90°(已知)∴∠A=∠AFC(同角的余角相等)∴AB∥CD.(内错角相等,两直线平行)【分析】先证CE∥BF得∠AOE=∠AFB,由AF⊥CE得∠AOE=∠AFB=90°,利用平角定义得出∠AFC+∠2=90°,结合∠A+∠2=90°可以得出∠AFC=∠A,从而得证.【解答】证明:∵AF⊥CE(已知),∴∠AOE=90°(垂直的定义).又∵∠1=∠B(已知),∴CE∥BF(同位角相等,两直线平行),∴∠AFB=∠AOE(两直线平行,同位角相等),∴∠AFB=90°(等量代换).又∵∠AFC+∠AFB+∠2=180°(平角的定义),又∵∠A+∠2=90°(已知),∴∠A=∠AFC(同角的余角相等),∴AB∥CD(内错角相等,两直线平行).故答案为:垂直的定义;CE∥BF;已知;两直线平行,同位角相等;等量代换;90;同角的余角相等.18.(2022秋•李沧区期末)如图,AB∥CD,直线EF分别与直线AB、直线CD相交于点E,F,点G在CD上,EG平分∠BEF.若∠EGC=58°,求∠EFD的度数.【分析】根据两直线平行,内错角相等求出∠BEG的度数,再根据角平分线的定义得到∠FEG,然后利用平行线的性质可得解.【解答】解:∵AB∥CD,∠EGC=58°,∴∠BEG=∠EGC=58°,∵EG平分∠BEF,∴∠BEF=2∠BEG=116°,∵AB∥CD,∴∠EFD=180°﹣∠BEF=180°﹣116°=64°.19.(2022秋•福田区期末)如图,已知点D是△ABC中BC边上的一点,DE⊥AC于点E,∠AGF=∠ABC,∠1+∠2=180°.(1)求证:DE∥BF;(2)若AF=3,AB=4,求BF的长.【分析】(1)根据平行线的判定方法可得FG∥CB,由平行线的性质即可得出∠1=∠3,再根据∠1+∠2=180°,即可得到∠2+∠3=180°,进而判定DE∥BF;(2)根据平行线的性质可得∠BFC=∠DEC=90°,再根据勾股定理计算即可.【解答】(1)证明:∵∠AGF=∠ABC,∴FG∥CB,∴∠1=∠3,又∵∠1+∠2=180°,∴DE∥BF;(2)解:∵DE⊥AC,∴∠DEA=90°,∵DE∥BF,∴∠BF A=∠DEA=90°,∵AF=3,AB=4,∴BF===.20.(2022•杭州模拟)已知:如图,AE⊥BC,FG⊥BC,∠CEA=∠FGB,∠D=∠ABC+50°,∠CBD=70°.(1)求证:AB∥CD;(2)求∠C的度数.【分析】(1)先证明AE∥GF,可得∠EAB=∠FGB,再证明∠CEA=∠EAB,从而可得答案;(2)由AB∥CD,可得∠D+∠CBD+∠ABC=180°,再把∠D=∠ABC+50°,∠CBD=70°代入进行计算即可.【解答】(1)证明:∵AE⊥BC,FG⊥BC,∴AE∥GF,∴∠EAB=∠FGB,∵∠CEA=∠FGB,∴∠CEA=∠EAB,∴AB∥CD;(2)解:由(1)得,AB∥CD,∴∠D+∠CBD+∠ABC=180°,∵∠D=∠ABC+50°,∠CBD=70°,∴∠ABC+70°+∠ABC+50°=180°,∴∠ABC=30°,∴∠C=∠ABC=30°.21.(2021秋•略阳县期末)如图,在三角形ABC中,点D,E分别在AB,BC上,且DE∥AC,∠1=∠2.(1)AF与BC平行吗?为什么?(2)若AC平分∠BAF,∠B=36°,求∠1的度数.【分析】(1)由平行线的性质可得∠1=∠C,从而可求得∠2=∠C,即可判定AF∥BC;(2)由平行线的性质可得∠B+∠BAF=180°,从而可求得∠BAF=144°,再由角平分线的定义求得∠2=72°,即可求∠1.【解答】解:(1)AF∥BC,理由如下:∵DE∥AC,∴∠1=∠C,∵∠1=∠2,∴∠C=∠2,∴AF∥BC;(2)∵AF∥BC,∴∠B+∠BAF=180°,∵∠B=36°,∴∠BAF=144°,∵AC平分∠BAF,∴,∵∠1=∠2,∴∠1=72°.22.(2021秋•镇巴县期末)如图1,直线MN与直线AB、CD分别交于点E、F,∠1+∠2=180°.(1)试判断直线AB与直线CD的位置关系,并说明理由;(2)如图2,∠BEF与∠EFD的角平分线交于点P,延长EP交CD于点C,点H是MN上一点,且GH⊥EG,过点P作PQ∥AB,则PF与GH平行吗?为什么?【分析】(1)由对顶角相等可求∠1=∠AEF,∠2=∠CFE,结合条件可得∠AEF+∠CFE=180°,由同旁内角互补,两直线平行可以证明结论;(2)由(1)得AB∥CD,则有∠BEF+∠EFD=180°,根据角平分线的定义可得∠BEP=∠BEF,∠PFD=∠EFD,根据平行线的判定和性质可得∠EPF=∠EPQ+∠FPQ=(∠BEF+∠EFD)=90°,根据垂直的定义可得EG⊥PF,由GH⊥EG可得PF∥GH.【解答】解:(1)AB∥CD,理由如下:∵∠1=∠AEF,∠2=∠CFE,∠1+∠2=180°,∴∠AEF+∠CFE=180°,∴AB∥CD;(2)PF∥GH,理由如下:由(1)知AB∥CD,∴∠BEF+∠EFD=180°,∵∠BEF与∠EFD的角平分线交于点P,∴∠BEP=∠FEP=∠BEF,∠PFD=∠EFP=∠EFD,∵AB∥CD,PQ∥AB,∴PQ∥CD,∴∠EPQ=∠BEP=∠BEF,∴∠FPQ=∠PFD=∠EFD,∴∠EPQ+∠FPQ=(∠BEF+∠EFD),∴∠EPF=90°,即EG⊥PF,∵GH⊥EG,∴PF∥GH.23.(2022春•西安月考)如图,射线PE分别与直线AB,CD相交于E,F两点,∠PFD的平分线与直线AB相交于点M,射线PM交CD于点N,且∠PFM=∠EMF.(1)求证:AB∥CD;(2)点G为射线MA(不与M重合)上一点,H为射线MF(不与M,F重合)上一点,且∠MGH=∠PNF,试找出∠FMN与∠GHF之间存在的数量关系,并证明你的结论.【分析】(1)因为FM平分∠PFN,可得∠EMF=∠MFN,利用内错角相等,两直线平行可得结论;(2)分H在线段MF上和H在MF的延长线上两种情形解答即可.【解答】(1)证明:∵FM平分∠PFN,∴∠PFM=∠MFN,∵∠PFM=∠EMF,∴∠MFN=∠EMF,∴AB∥CD;②当H在线段MF上时,∠GHF+∠FMN=180°;当H在线段MF的延长线上时,∠GHF=∠FMN,证明如下:∵AB∥CD,∴∠PNF=∠PME.∵∠MGH=∠PNF,∴∠MGH=∠PME.∴GH∥PN.如图,当H在线段MF上时,∵GH∥PN,∴∠GHM=∠FMN,∵∠GHF+∠GHM=180°,∴∠GHF+∠FMN=180°;如图,当H在线段MF的延长线上时,∵GH∥PN,∴∠GHM=∠FMN,∴∠GHF=∠FMN.。
(完整版)平行线与相交线提高训练.docx
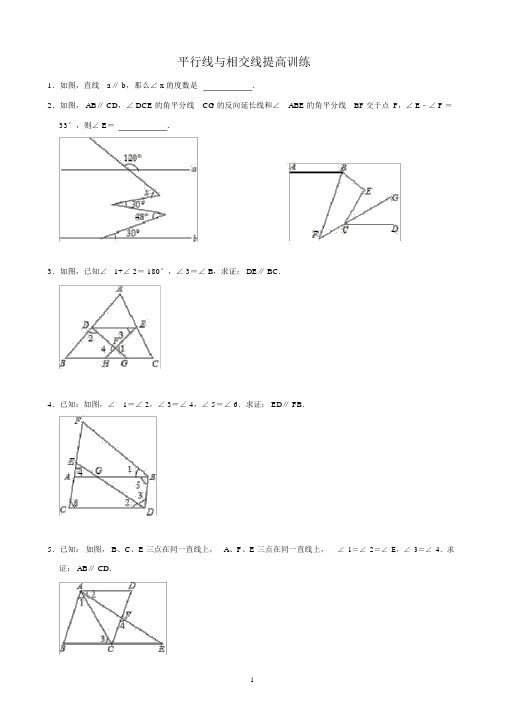
平行线与相交线提高训练1.如图,直线a∥ b,那么∠ x 的度数是.2.如图, AB∥ CD,∠ DCE 的角平分线CG 的反向延长线和∠ABE 的角平分线BF 交于点 F,∠ E﹣∠ F =33°,则∠ E=.3.如图,已知∠1+∠ 2= 180°,∠ 3=∠ B,求证: DE∥ BC.4.已知:如图,∠1=∠ 2,∠ 3=∠ 4,∠ 5=∠ 6.求证: ED∥ FB.5.已知:如图, B、C、E 三点在同一直线上,A、F、E 三点在同一直线上,∠ 1=∠ 2=∠ E,∠ 3=∠ 4.求证: AB∥ CD.6.已知,如,AE∥ BD,∠ 1= 3∠2,∠ 2=26°,求∠ C.7.直 l1∥ l2,∠ A= 125°,∠ B= 105°,求∠ 1+∠2 的度数(提示:要作助!)8.已知:射OP∥ AE(1)如 1,∠ AOP 的角平分交射 AE 与点 B,若∠ BOP= 58°,求∠ A 的度数.(2)如 2,若点 C 在射 AE 上, OB 平分∠ AOC 交 AE 于点 B, OD 平分∠ COP 交 AE 于点 D,∠ADO= 39°,求∠ ABO ∠ AOB 的度数.(3)如 3,若∠ A= m,依次作出∠ AOP 的角平分 OB,∠ BOP 的角平分 OB1,∠ B1OP 的角平分OB2,∠ B n﹣1OP 的角平分 OB n,其中点 B, B1, B2,⋯, B n﹣1, B n都在射 AE 上,求∠ AB n O的度数.9.数学思考:( 1)如 1,已知 AB ∥CD,探究下面形中∠ APC 和∠ PAB、∠ PCD 的关系,并明你的推广延伸:( 2)① 如 2,已知 AA1∥ BA1,你猜想∠ A1,∠ B1,∠ B2,∠ A2、∠ A3的关系,并明你的猜想;②如 3,已知 AA1n1122n﹣ 1n∥BA,直接写出∠ A ,∠ B,∠ B ,∠ A、⋯∠ B 、∠ A的关系拓展用:( 3)① 如 4所示,若 AB∥ EF ,用含α,β,γ的式子表示 x,A.180° +α+β γB.180° α γ+βC.β+γ αD.α+β+γ②如 5, AB∥ CD ,且∠ AFE = 40°,∠ FGH = 90°,∠ HMN = 30°,∠ CNP= 50°,你根据上述直接写出∠ GHM 的度数是.10.已知,直AB∥ DC,点 P 平面上一点,接AP 与 CP.( 1)如 1,点 P 在直 AB、 CD 之,当∠ BAP= 60°,∠ DCP =20° ,求∠ APC.( 2)如 2,点 P 在直 AB、CD 之,∠ BAP 与∠ DCP 的角平分相交于点 K ,写出∠ AKC 与∠ APC 之的数量关系,并明理由.( 3)如 3,点 P 落在 CD 外,∠ BAP 与∠ DCP 的角平分相交于点 K,∠ AKC 与∠ APC 有何数量关系?并明理由.11.如图,已知AM ∥ BN,∠ A= 80°,点 P 是射线 AM 上动点(与 A 不重合), BC、 BD 分别平分∠ ABP 和∠ PBN,交射线 AM 于 C、 D.(1)求∠ CBD 的度数;(2)当点 P 运动时,那么∠ APB:∠ ADB 的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;(3)当点 P 运动到使∠ ACB=∠ ABD 时,求∠ ABC 的度数.12.如图 1,AB∥ CD,直线 EF 交 AB 于点 E,交 CD 于点 F ,点 G 在 CD 上,点 P 在直线 EF 左侧、且在直线AB 和 CD 之间,连接 PE、 PG.(1)求证:∠ EPG=∠ AEP+∠ PGC;( 2)连接 EG,若 EG 平分∠ PEF ,∠ AEP+∠PGE= 110°,∠ PGC=∠ EFC,求∠ AEP的度数;( 3)如图 2,若 EF 平分∠ PEB,∠ PGC 的平分线所在的直线与EF 相交于点H ,则∠ EPG 与∠ EHG之间的数量关系为.13.已知 E、D 分别在∠ AOB 的边 OA、OB 上, C 为平面内一点,DE、DF 分别是∠ CDO 、∠ CDB 的平分线.(1)如图 1,若点 C 在 OA 上,且 FD ∥ AO,求证: DE⊥ AO;(2)如图 2,若点 C 在∠ AOB 的内部,且∠ DEO =∠ DEC ,请猜想∠ DCE、∠ AEC、∠ CDB 之间的数量关系,并证明;(3)若点 C 在∠ AOB 的外部,且∠ DEO=∠ DEC,请根据图 3、图 4 分别写出∠ DCE 、∠ AEC、∠ CDB 之间的数量关系(不需证明).14.已知, AB ∥CD ,点 E 为射线 FG 上一点.( 1)如图 1,若∠ EAF = 30°,∠ EDG = 40°,则∠ AED=°;( 2)如图 2,当点 E 在 FG 延长线上时,此时CD 与 AE 交于点 H,则∠ AED 、∠ EAF、∠ EDG 之间满足怎样的关系,请说明你的结论;(3)如图 3, DI 平分∠ EDC ,交 AE 于点 K,交 AI 于点 I,且∠ EAI :∠ BAI = 1: 2,∠ AED = 22°,∠I = 20°,求∠ EKD 的度数.15.长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯 A 射线自 AM 顺时针旋转至AN 便立即回转,灯 B 射线自 BP 顺时针旋转至BQ 便立即回转,两灯不停交叉照射巡视.若灯 A 转动的速度是a°/秒,灯 B 转动的速度是b° /秒,且 a、b 满足 |a﹣3b|+( a+b﹣ 4)2= 0.假定这一带长江两岸河堤是平行的,即PQ∥ MN ,且∠ BAN= 45°( 1)求 a、 b 的值;( 2)若灯 B 射线先转动20 秒,灯 A 射线才开始转动,在灯 B 射线到达BQ 之前, A 灯转动几秒,两灯的光束互相平行?( 3)如图,两灯同时转动,在灯 A 射线到达 AN 之前.若射出的光束交于点C,过 C 作 CD⊥ AC 交 PQ 于点 D,则在转动过程中,∠BAC 与∠ BCD 的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.16.已知如图,∠ COD =90°,直线 AB 与 OC 交于点 B,与 OD 交于点 A,射线 OE 与射线 AF 交于点 G.( 1)若 OE 平分∠ BOA, AF 平分∠ BAD ,∠ OBA= 42°,则∠ OGA=;( 2)若∠ GOA =∠BOA,∠ GAD=∠ BAD,∠ OBA=42°,则∠ OGA=;( 3)将( 2)中的“∠ OBA = 42°”改为“∠ OBA=α”,其它条件不变,求∠OGA 的度数.(用含α的代数式表示)(4)若 OE 将∠ BOA 分成 1: 2 两部分, AF 平分∠ BAD ,∠ ABO=α(30°<α< 90°),求∠ OGA 的度数.(用含α的代数式表示)17.已知直线AB∥ CD ,E 是直线 AB 的上方一点,连接AE、 EC( 1)如图 1,求证:∠ AEC+∠ EAB=∠ ECD( 2)如图 2, AF 平分∠ BAE, CF 平分∠ DCE ,且∠ AFC 比∠ AEC 的倍少40°,直接写出∠AEC 的度数18.直线 MN 与直线 PQ 相交于 O,点 A 在射线 OP 上运动,点 B 在射线 OM 上运动.( 1)如图 1,若∠ AOB= 80°,已知AE、 BE 分别是∠ BAO 和∠ ABO 的角平分线,点A、 B 在运动的过程中,∠ AEB 的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB 的大小.( 2)如图 2,若∠ AOB= 80°,已知 AB 不平行 CD,AD 、BC 分别是∠ BAP 和∠ ABM 的角平分线, AD 、BC 的延长线交于点F,点 A、 B 在运动的过程中,∠ F =;DE、CE又分别是∠ ADC和∠ BCD 的角平分线,点A、 B 在运动的过程中,∠CED 的大小也不发生变化,其大小为:∠CED =.( 3)如图 3,若∠ AOB= 90°,延长BA 至 G,已知∠ BAO、∠ OAG 的角平分线与∠BOQ 的角平分线及其延长线相交于E、F ,则∠ EAF =;( 4)如图 3,若 AF, AE 分别是∠ GAO,∠ BAO 的角平分线,∠AOB=90°,在△ AEF 中,如果有一个角是另一个角的 4 倍,则∠ ABO 的度数=.20.如图,点 D 、点 E 分别在△ ABC 边 AB, AC 上,∠ CBD =∠ CDB , DE∥BC ,∠ CDE 的平分线交AC 于 F 点.(1)求证:∠ DBF +∠ DFB = 90°;(2)如图②,如果∠ ACD 的平分线与 AB 交于 G 点,∠ BGC= 50°,求∠ DEC 的度数.( 3)如图③,如果 H 点是 BC 边上的一个动点(不与B、C 重合),AH 交 DC 于 M 点,∠ CAH 的平分线 AI 交 DF 于 N 点,当 H 点在 BC 上运动时,的值是否发生变化?如果变化,说明理由;如果不变,试求出其值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行线能力提高训练题
1.填空:如图,已知:AD ⊥BC 于D ,EG ⊥BC 于G ,∠E=∠3,
求证:AD 平分∠BAC . 证明:∵AD ⊥BC ,( ) ∴∠ADG=90°( ) ∵EG ⊥BC ,( )
∴∠EGC=90°,( )
∴∠ADC=∠EGC=90°,( ) ∴EG ∥AD ,( ) ∴∠1=∠E ,( ) ∠2=∠3,( ) ∵∠E=∠3,( ) ∴∠1=∠2,( ) 即AD 平分∠BAC
2.如图,点B 、E 、C 、F 在一条直线上,并且AB ∥DE ,∠A=∠D ,AC ⊥BF ,求证:DF ⊥BF 。
3.如图,∠BAF = 50°,∠ACE = 140°,CD ⊥CE ,则有:DC ∥AB ,试说明理由。
4.如图,已知∠D = 90°,∠1 = ∠2,EF ⊥CD ,问:∠B 与∠AEF 是否相等?若相等,请说明理由。
5.如图,已知∠ADE =∠B ,FG ⊥AB ,∠EDC =∠GFB ,问:CD 与AB 是否垂直?若垂直,请说明理由。
6.已知:∠BAP+∠APD=180°,∠BAF=∠CPE ,求证:∠E=∠F .
7.如图,已知AB ∥CD ,分别探究下面四个图形中∠APC 和∠PAB 、∠PCD 的关系,并从所得的四个关系中任选一个加以说明,证明所探究的结论的正确性。
结论⑴ ⑵
⑶ ⑷ 选择结论 ,说明理由是什么。
A B C D E
G 1
23。
