北京邮电大学602量子力学2017年考研真题试卷

合集下载

大学物理试卷参考答案(对应北京邮电大学版)

物理试卷参考答案1解：理想气体分子的能量RT i E 2υ=平动动能 3=t 5.373930031.823=⨯⨯=t E J 转动动能 2=r249330031.822=⨯⨯=r E内能5=i 5.623230031.825=⨯⨯=i E J 2解： ∵ xv v t x x v t v ad d d d d d d d ===分离变量： x x adx d )62(d 2+==υυ两边积分得c x x v ++=322221 由题知，0=x时，100=v ,∴50=c∴ 13s m 252-⋅++=x x v3.解：∵ t tva 34d d +==分离变量，得 t t v d )34(d +=积分，得 12234c t t v ++=由题知，0=t,00=v ,∴01=c故 2234t t v +=又因为 2234d d t t t x v +== 分离变量， t t t x d )234(d 2+=积分得 232212c t t x ++=由题知 0=t,50=x ,∴52=c故 521232++=t t x所以s 10=t 时m70551021102s m 190102310432101210=+⨯+⨯=⋅=⨯+⨯=-x v4. )由题知，0=t时，00=φ，t t =时 3,0,20πφ=<+=t v A x 故且 ∴ s 322/3==∆=ππωφt 5)222υυ+=u 52202=+=υυu m/s=4.47υυθ00)90tan(=-2142== 6）由图知，0=t时，0,2<-=P P v A y ，∴34πφ-=P (P 点的位相应落后于0点，故取负值) ∴P 点振动方程为)3410cos(1.0ππ-=t y p∵ πππ34|3)10(100-=+-=t x t ∴解得 67.135==x m Y=-1/2M 7) 解： bt v tsv -==0d dRbt v R v a b tva n 202)(d d -==-==τ则 240222)(R bt v b a a a n-+=+=τ8）又 11x k F A∆= 22x k F B ∆=Mg F F B A ==弹性势能之比为12222211121212k kx k x k E E p p =∆∆=二．填空题答案1）解: m 从M 上下滑的过程中，机械能守恒，以m ，M ，地球为系统，以最低点为重力势能零点，则有222121MV mv mgR +=又下滑过程，动量守恒，以m ,M 为系统则在m 脱离M 瞬间，水平方向有0=-MV mv联立，以上两式，得()M m MgRv +=22）正比3）v v nf d )(：表示分布在速率v 附近、速率区间dv 内的分子数密度 4)⎰21d )(v v v v Nf ：表示分布在21~v v 区间内的分子数5) 卡诺热机效率121T T -=η%7010003001=-=η6）W E Q+∆=7) E=1/2KA 2 8）书P144 三．计算题解：设人到船之间绳的长度为l ，此时绳与水面成θ角，由图可知 222s h l+=将上式对时间t 求导，得tss t l l dd 2d d 2= 题1-4图根据速度的定义，并注意到l ,s 是随t 减少的，∴ ts v v t l v d d ,d d 0-==-=船绳即 θcos d d d d 00v v s lt l s l t s v ==-=-=船或 sv s h s lv v 02/1220)(+==船将船v 再对t 求导，即得船的加速度322d d sv h t v a ==船2）解：由题图(a)，∵0=t时，s 2,cm 10,,23,0,0000===∴>=T A v x 又πφ即 1s rad 2-⋅==ππωT故 m )23cos(1.0ππ+=t x a由题4-8图(b)∵0=t 时，35,0,2000πφ=∴>=v A x 01=t 时，22,0,0111ππφ+=∴<=v x又 ππωφ253511=+⨯=∴ πω65=故 m t x b )3565cos(1.0ππ+= 3）解: (1)射入的过程对O 轴的角动量守恒ωθ2000)(sin R m m v m R +=∴ Rm m v m )(sin 000+=θω(2)020*********sin 21])(sin ][)[(210m m m v m R m m v m R m m E E k k +=++=θθ4）解：由abc 过程可求出b 态和a 态的内能之差 W E Q+∆=224126350=-=-=∆W Q E Jabd过程，系统作功42=WJ26642224=+=+∆=W E Q J 系统吸收热量ba 过程，外界对系统作功84-=A J30884224-=--=+∆=W E Q J 系统放热5）解：(1)从图上可得分布函数表达式⎪⎩⎪⎨⎧≥=≤≤=≤≤=)2(0)()2()()0(/)(00000v v v Nf v v v a v Nf v v v av v Nf ⎪⎩⎪⎨⎧≥≤≤≤≤=)2(0)2(/)0(/)(00000v v v v v Na v v Nv av v f )(v f 满足归一化条件，但这里纵坐标是)(v Nf 而不是)(v f 故曲线下的总面积为N，(2)由归一化条件可得⎰⎰==+0002032d d v v v v N a Nv a N v v avN(3)可通过面积计算 N v v a N 31)5.12(00=-=∆(4) N 个粒子平均速率⎰⎰⎰⎰+===∞∞00202d d d )(1d )(v v v v av v v av v v vNf Nv v vf v02020911)2331(1v av av N v =+=(5)05.0v 到01v 区间内粒子平均速率⎰⎰==0005.0115.0d d v v v v NNv N N N Nv v ⎰⎰==00005.05.00211d d )(v v v v v Nv av N N v v vf N N 2471)243(1d 12103003015.002100av N v av v av N v v av N v v v =-==⎰ 05.0v 到01v 区间内粒子数N av v v a a N 4183)5.0)(5.0(210001==-+=9767020v N av v ==6）解: (1)如题5-11图(a)，则波动方程为])(cos[0φω+-+=uxu l t A y 如图(b)，则波动方程为])(cos[0φω++=uxt A y(2) 如题5-11图(a)，则Q 点的振动方程为])(cos[0φω+-=ubt A A Q如题5-11图(b)，则Q 点的振动方程为])(cos[0φω++=ubt A A Q。

《量子力学》22套考研自测题+答案

⎜⎝ 0 3λ 3 + 2λ ⎟⎠ 的本征值至 λ 的二次项，本征矢至 λ 的一次
项。
五、（10 分）一体系由三个全同的玻色子组成, 玻色子之间无相互作
用. 玻色子只有两个可能的单粒子态. 问体系可能的状态有几
个? 它们的波函数怎样用单粒子波函数构成?
QQ：704999167
QQ：704999167
En
=
−
Z 2e2 2a
， ψ 100 =
1
⎜⎛
Z
⎟⎞ 3 /
2
− Zr
ea
π ⎝a⎠
，计算时，可利用积分公式
∫∞ xe−2ax dx = 1 。
0
4α 2
五、（本题 20 分）
设一维谐振子的能量本征函数为ψ n (x) ，求：
QQ：704999167
HY制作
HY制作
HY制作
量子力学自测题（5）
一、填空题（本题 20 分）
1．Planck 的量子假说揭示了微观粒子
特性，Einstein 的光
量子假说揭示了光的
性。Bohr 的氢原子理论解决了经典
考研自测题精美汇总
电磁场理论和原子的
之间的矛盾，解决了原子的
的起源问题。
2．力学量算符必须是
10. n 为 Lz 的本征态，本征值为 n 。求在 L z 的本征态 n 下， Lx
和 Ly 的平均值。
11. 氢原子处于状态
⎜⎛
ψ
(r
,
s
z
)
=
⎜ ⎜
⎜− ⎝
1 2
R
21
Y 11
3 2 R 21 Y10
⎟⎞ ⎟ ⎟ ⎟
=

北京邮电大学通信原理考研真题试题2017年——2019年

考试科目：801通信原理
第 1 页共 8 页北京邮电大学
2017年硕士研究生入学考试试题
考试科目：通信原理
请考生注意：①所有答案(包括选择题)一律写在答题纸上，否则不计
成绩。

②不允许使用计算器
一.单项选择题（每空1.5分，共54分）
按下面的格式在答题纸．．．上填写最佳．．答案．．
(11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (31) (32) (33)
(34) (35) (36) (37) (38) (39) (40) 设有AM 信号,1+m(t)-cos 2πf c t ，其中基带调制信号m(t)的带宽是250Hz 、平均功率是m 2(t)=0.25W 、最大幅度是|m (t )|max =1V 。

此AM 信号的带宽是(1)kHz ，调制指数是(2)，调制效率是(3)。

所有答案一律写在答题纸上，否则不计成绩！所有答案一律写在答题纸上，否则不计成绩！。

量子力学试题含答案

一、填空题：（每题 4 分，共 40 分）1. 微观粒子具有波粒二象性。

2．德布罗意关系是粒子能量E 、动量P 与频率ν、波长λ之间的关系，其表达式为：E=h ν, p=/h λ 。

3．根据波函数的统计解释，dx t x 2),(ψ的物理意义为：粒子在x —dx 范围内的几率。

4．量子力学中力学量用厄米算符表示。

5．坐标的x 分量算符和动量的x 分量算符x p 的对易关系为：[],x p i = 。

6．量子力学关于测量的假设认为：当体系处于波函数ψ(x)所描写的状态时，测量某力学量F 所得的数值，必定是算符Fˆ的本征值。

7．定态波函数的形式为： t E in n ex t x-=)(),(ϕψ。

8．一个力学量A 为守恒量的条件是：A 不显含时间，且与哈密顿算符对易。

9．根据全同性原理，全同粒子体系的波函数具有一定的交换对称性，费米子体系的波函数是_反对称的_____________,玻色子体系的波函数是_对称的_______ _。

10．每个电子具有自旋角动量S ，它在空间任何方向上的投影只能取两个数值为： 2± 。

二、证明题：（每题10分，共20分）1、（10分）利用坐标和动量算符的对易关系，证明轨道角动量算符的对易关系：证明：zy x L i L L ˆ]ˆ,ˆ[ =]ˆˆ,ˆˆ[]ˆ,ˆ[z x y z yx p x p z p z p y L L --=2、（10分）由Schr ödinger 方程证明几率守恒：其中几率密度几率流密度证明：考虑 Schr ödinger 方程及其共轭式：2|),(|),(),(),(t r t r t r t rψ=ψψ=*ω22(,)[()](,)2i r t V r r t t μ∂ψ=-∇+ψ∂0=∙∇+∂∂J tω][2ψ∇ψ-ψ∇ψ=**μi J ]ˆˆ,ˆ[]ˆˆ,ˆ[z x y z x z p x p z p z p x p z py ---=]ˆ,ˆ[]ˆ,ˆ[]ˆ,ˆ[]ˆ,ˆ[z y x y z z x z p x p z p z p z p x p y p z py +--=]ˆ,ˆ[]ˆ,ˆ[z y x z p x p z p z py +=y z z y z x x z p p x z p x p z p p z y p z py ˆ]ˆ,[]ˆ,ˆ[ˆ]ˆ,[]ˆ,ˆ[+++=y z x z p p x z p z py ˆ]ˆ,[]ˆ,ˆ[+=y z y z x z x z p p x z p p z x p z p y p pyz ˆˆ],[ˆ]ˆ,[ˆ],ˆ[]ˆ,ˆ[+++=y x p i x pi y ˆ)(ˆ)( +-=]ˆˆ[x y p y px i -= zL i ˆ =在空间闭区域τ中将上式积分，则有：三、计算题：（共40分）1、（10分）设氢原子处于状态),()(23),()(21),,(11211021ϕθϕθϕθψ--=Y r R Y r R r 求氢原子能量E 、角动量平方L 2、角动量Z 分量L Z 的可能值及这些可能值出现的几率。

北京科技大学期末真题量子力学2015-2016考研876量子力学参考

U(x)
的电场可视为匀强电场，其电势能 H与 x 成正比。
参照求跃迁几率的公式计算其跃迁选择定则。
( sin sin 1 [cos( ) cos( )] )
a
2
8. 用玻恩近似法求高能粒子在势场 U (r) U0er/a (a 0) 中散射的微分散射截面。
2
量子力学试题答案
1．20 分
E E2 / 4 3E3 / 4 7e4 / 96 2, L2 2 2 1/ 4 6 2 3/ 4 5 2.
Lz ,
sz / 2 1/ 4 / 2 3/ 4 / 4.
1
(2) 4 分
j
l
1 2
,
j | m | .
l
=1
时，
m
3 2
,
j
1
1 2
3 2
.
l
=2
时，
m
1 2
,
j
表示任意波函数，并由此确定该力学量的取值几率。
(3)
Hˆ
与时间无关
，
(r, t )
1 (2 )3/ 2
ei(p
rEt ) /
.
(4)微观粒子的物理量取值一般不唯一，各取值都是该物理量算符的本征值，且各有相应的取值几率。这些都是与宏观粒子不同的。把 ψ 表示为 Ô 的本征函数的迭加，各迭加系数绝对值的平方就对应于 Ô 的各取值概率。
(5) 动量 p，| (p,t) |2 dp 是动量处于 p→p +dp 的几率。
(6)定态微扰处理波函数和能量的近似计算(波函数和能量的修正)问题，含时微扰处理跃迁问题。跃迁由微扰引起。
(7) q(,) 是入射粒子流密度 N = 1 时，单位时间内在 (, ) 方向的单位立

北京邮电大学大学物理学习题答案10

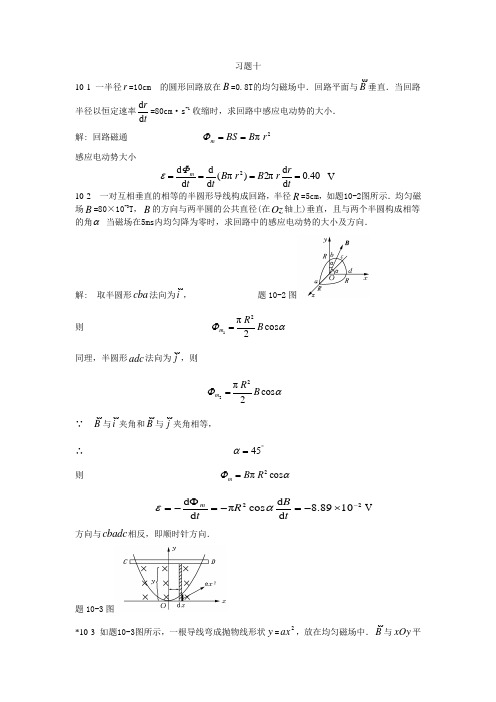
习题十10-1 一半径r =10cm 的圆形回路放在B =0.8T 的均匀磁场中．回路平面与B垂直．当回路半径以恒定速率tr d d =80cm ·s -1 收缩时，求回路中感应电动势的大小．解: 回路磁通 2πr B BS m ==Φ 感应电动势大小40.0d d π2)π(d d d d 2====tr rB r B ttm Φε V10-2 一对互相垂直的相等的半圆形导线构成回路，半径R =5cm ，如题10-2图所示．均匀磁场B =80×10-3T ，B 的方向与两半圆的公共直径(在Oz 轴上)垂直，且与两个半圆构成相等的角α 当磁场在5ms 内均匀降为零时，求回路中的感应电动势的大小及方向．解: 取半圆形cba 法向为i，题10-2图则 αΦcos 2π21B R m =同理，半圆形adc 法向为j，则αΦcos 2π22B R m =∵ B 与i夹角和B 与j 夹角相等，∴ ︒=45α则 αΦcos π2R B m =221089.8d d cos πd d -⨯-=-=Φ-=tB RtmαεV方向与cbadc 相反，即顺时针方向．题10-3图*10-3 如题10-3图所示，一根导线弯成抛物线形状y =2ax ，放在均匀磁场中．B与xOy 平面垂直，细杆CD 平行于x 轴并以加速度a 从抛物线的底部向开口处作平动．求CD 距O 点为y 处时回路中产生的感应电动势．解: 计算抛物线与CD 组成的面积内的磁通量⎰⎰=-==aym y B x x y B S B 0232322d )(2d 2ααΦ∴ v y Bty y Btm 21212d d d d ααε-=-=Φ-=∵ ay v 22=∴ 212y a v =则 ααεaByy a yBi 8222121-=-= i ε实际方向沿ODC ．题10-4图10-4 如题10-4图所示，载有电流I 的长直导线附近，放一导体半圆环MeN 与长直导线共面，且端点MN 的连线与长直导线垂直．半圆环的半径为b ，环心O 与导线相距a ．设半圆环以速度v 平行导线平移．求半圆环内感应电动势的大小和方向及MN 两端的电压NM UU -．解: 作辅助线MN ，则在MeNM 回路中，沿v方向运动时0d =m Φ ∴ 0=MeNM ε 即 MN MeN εε=又∵ ⎰+-<+-==ba ba MN ba b a Ivl vB 0ln2d cos 0πμπε所以MeN ε沿NeM 方向，大小为ba b a Iv-+ln20πμM 点电势高于N 点电势，即ba b a IvU U N M -+=-ln20πμ题10-5图10-5如题10-5所示，在两平行载流的无限长直导线的平面内有一矩形线圈．两导线中的电流方向相反、大小相等，且电流以tI d d 的变化率增大，求：(1)任一时刻线圈内所通过的磁通量； (2)线圈中的感应电动势．解: 以向外磁通为正则 (1) ]ln[lnπ2d π2d π2000da db ab Ilr l r Ir l r Iab b ad d m +-+=-=⎰⎰++μμμΦ(2) tIb a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε 10-6 如题10-6图所示，用一根硬导线弯成半径为r 的一个半圆．令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转．整个电路的电阻为R ．求：感应电流的最大值．题10-6图解: )cos(2π02ϕωΦ+=⋅=t r B S B m∴Bfr f r B r B t r B tm m i 222202ππ22π2π)sin(2πd d ===+=-=ωεϕωωΦε∴ RBf r RI m 22π==ε10-7 如题10-7图所示，长直导线通以电流I =5A ，在其右方放一长方形线圈，两者共面．线圈长b =0.06m ，宽a =0.04m ，线圈以速度v =0.03m ·s -1垂直于直线平移远离．求：d =0.05m 时线圈中感应电动势的大小和方向．题10-7图解: AB 、CD 运动速度v方向与磁力线平行，不产生感应电动势． DA 产生电动势⎰==⋅⨯=A D Ivb vBb l B v d2d )(01πμεBC 产生电动势)(π2d )(02d a I vbl B v CB+-=⋅⨯=⎰με∴回路中总感应电动势8021106.1)11(π2-⨯=+-=+=ad dIbvμεεεV方向沿顺时针．10-8 长度为l 的金属杆ab 以速率v 在导电轨道abcd 上平行移动．已知导轨处于均匀磁场B中，B 的方向与回路的法线成60°角(如题10-8图所示)，B的大小为B =kt (k 为正常)．设t =0时杆位于cd 处，求：任一时刻t 导线回路中感应电动势的大小和方向．解: ⎰==︒=⋅=22212160cos d klvt lv kt Blvt S B m Φ∴ klvt tm -=-=d d Φε即沿abcd 方向顺时针方向．题10-8图10-9 一矩形导线框以恒定的加速度向右穿过一均匀磁场区，B的方向如题10-9图所示．取逆时针方向为电流正方向，画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0)．解: 如图逆时针为矩形导线框正向，则进入时0d d <Φt,0>ε；题10-9图(a)题10-9图(b)在磁场中时0d d =tΦ,0=ε；出场时0d d >tΦ，0<ε，故t I -曲线如题10-9图(b)所示.题10-10图10-10 导线ab 长为l ，绕过O 点的垂直轴以匀角速ω转动，aO =3l 磁感应强度B 平行于转轴，如图10-10所示．试求：（1）ab 两端的电势差；（2）b a ,两端哪一点电势高? 解: (1)在Ob 上取dr r r +→一小段则 ⎰==320292d lOb l B r rB ωωε同理 ⎰==32181d lOa l B r rB ωωε∴ 2261)92181(l B l B Ob aO ab ωωεεε=+-=+=(2)∵ 0>ab ε 即0<-b a U U ∴b 点电势高．题10-11图10-11 如题10-11图所示，长度为b 2的金属杆位于两无限长直导线所在平面的正中间，并以速度v平行于两直导线运动．两直导线通以大小相等、方向相反的电流I ，两导线相距2a ．试求：金属杆两端的电势差及其方向．解：在金属杆上取r d 距左边直导线为r ，则 ba b a Ivr ra rIv l B v ba ba BAAB -+-=-+-=⋅⨯=⎰⎰+-lnd )211(2d )(00πμπμε∵ 0<AB ε ∴实际上感应电动势方向从A B →，即从图中从右向左，∴ ba ba Iv U AB -+=ln 0πμ题10-12图10-12 磁感应强度为B的均匀磁场充满一半径为R 的圆柱形空间，一金属杆放在题10-12图中位置，杆长为2R ，其中一半位于磁场内、另一半在磁场外．当tB d d ＞0时，求：杆两端的感应电动势的大小和方向．解： ∵ bc ab ac εεε+=tB R B R ttab d d 43]43[d d d d 21=--=-=Φε=-=tab d d 2ΦεtB R B R td d 12π]12π[d d 22=--∴ tB R R ac d d ]12π43[22+=ε∵0d d >tB∴ 0>ac ε即ε从c a → 10-13 半径为R 的直螺线管中，有dtdB ＞0的磁场，一任意闭合导线abca ，一部分在螺线管内绷直成ab 弦，a ,b 两点与螺线管绝缘，如题10-13图所示．设ab =R ，试求：闭合导线中的感应电动势．解：如图，闭合导线abca 内磁通量)436π(22R R B S B m-=⋅= Φ∴ tB R R i d d )436π(22--=ε∵ 0d d >tB∴0<i ε，即感应电动势沿acba ，逆时针方向．题10-13图题10-14图10-14 如题10-14图所示，在垂直于直螺线管管轴的平面上放置导体ab 于直径位置，另一导体cd 在一弦上，导体均与螺线管绝缘．当螺线管接通电源的一瞬间管内磁场如题10-14图示方向．试求：（1）ab 两端的电势差；（2）cd 两点电势高低的情况．解：由⎰⎰⋅-=⋅l S t Bl Ed d d d 旋知，此时旋E 以O 为中心沿逆时针方向．(1)∵ab 是直径，在ab 上处处旋E与ab 垂直 ∴ ⎰=⋅ll 0d旋∴0=ab ε,有b a U U =(2)同理， 0d >⋅=⎰l Ecddc旋ε∴ 0<-c d U U 即d c U U >题10-15图10-15 一无限长的直导线和一正方形的线圈如题10-15图所示放置(导线与线圈接触处绝缘)．求：线圈与导线间的互感系数．解：设长直电流为I ，其磁场通过正方形线圈的互感磁通为⎰==32300122ln π2d π2aa Ia r rIa μμΦ∴ 2ln π2012aIM μΦ==10-16 一矩形线圈长为a =20cm ，宽为b =10cm ，由100匝表面绝缘的导线绕成，放在一无限长导线的旁边且与线圈共面．求：题10-16图中(a)和(b)两种情况下，线圈与长直导线间的互感．解：(a)见题10-16图(a)，设长直电流为I ，它产生的磁场通过矩形线圈的磁通为2ln π2d 2πd 020)(12Iarr Ia S B bbS μμΦ⎰⎰==⋅=∴ 6012108.22ln π2-⨯===aNIN M μΦ H(b)∵长直电流磁场通过矩形线圈的磁通012=Φ，见题10-16图(b) ∴ 0=M题10-16图题10-17图10-17 两根平行长直导线，横截面的半径都是a ，中心相距为d ，两导线属于同一回路．设两导线内部的磁通可忽略不计，证明：这样一对导线长度为l 的一段自感为πμl L 0=Inaa d -．解：如图10-17图所示，取r l S d d = 则 ⎰⎰-----=--=-+=ad aad aad d aa d Il r r rIl r l r I r πI )ln(ln2πd )d11(π2d ))d (π22(0000μμμμΦaa d Il-=lnπ0μ∴ aa d lI L -==lnπ0μΦ10-18 两线圈顺串联后总自感为1.0H ，在它们的形状和位置都不变的情况下，反串联后总自感为0.4H ．试求：它们之间的互感．解： ∵顺串时 M L L L 221++= 反串联时M L L L 221-+='∴ M L L 4='-15.04='-=L L M H10-19图10-19 一矩形截面的螺绕环如题10-19图所示，共有N 匝．试求： (1)此螺线环的自感系数；(2)若导线内通有电流I ，环内磁能为多少? 解：如题10-19图示 (1)通过横截面的磁通为 ⎰==baab NIhr h r NIlnπ2d π200μμΦ磁链 ab Ih N N ln π220μΦψ==∴ ab h N IL lnπ220μψ==(2)∵ 221LIW m =∴ ab hI N W m ln π4220μ=10-20 一无限长圆柱形直导线，其截面各处的电流密度相等，总电流为I ．求：导线内部单位长度上所储存的磁能．解：在R r <时 20π2RI B rμ=∴ 4222002π82RrI Bw m μμ==取 r r V d π2d =(∵导线长1=l ) 则 ⎰⎰===RRm I Rr r I r r w W 0204320π16π4d d 2μμπ。

2017年硕士学位研究生入学考试大学物理试题北京市联合命题

2017年攻读硕士学位研究生入学考试北京市联合命题大学物理试题（请将答案写在答题纸上，写在试题上的答案无效）一、选择题（每题4分，共60分）1．质点作曲线运动，r 表示位矢，s 表示路程，υ 表示速度，υ表示速率，a表示加速度，t a表示切向加速度。

则以下表达式中正确的是(A) υ=t r d d； (B) υ=t s d d ； (C) a t=d d υ； (D) t d d a t =υ。

2．以下物理量中，是矢量的是(A) 转动惯量； (B) 重力势能； (C) 电流密度； (D) 电位移通量。

3．下列说法中错误的是 (A) 质点作匀速率圆周运动时，其加速度为零； (B) 质点系总动量的改变与内力无关； (C) 质点系总动能的改变与内力有关； (D) 质点系机械能的改变与保守内力无关。

4．一人站在转盘中央，两臂侧平举，人和转盘的转动惯量为I 。

当整个系统绕转轴以某一角速度匀速旋转时，系统的转动动能为E k 。

这时此人将两臂收回，使得系统的转动惯量变为I /3，则此时系统的转动动能变为 (A) 9E k ；(B) 3E k ；(C) √3 E k ；(D) E k 。

5．密闭容器中的理想气体，当其温度升高时，下列表述中错误的是 (A) 分子的热运动变得剧烈； (B) 分子的无规则运动变得剧烈； (C) 分子的平均平动动能增大； (D) 分子间的相互作用势能增加。

6．下列说法中正确的是(A) 功可以全部变为热，但热不能全部变为功；(B) 可逆过程就是可以向相反方向进行的准静态过程；(C) 不可逆过程就是不能向相反方向进行的准静态过程； (D) 系统某一状态的熵值是其所对应的宏观状态的无序性的量度。

7．下列说法中正确的是(A) 电势为零处，场强一定为零； (B) 场强为零处，电势一定为零；(C) 通过闭合曲面的电通量仅由该曲面内的电荷决定；(D) 点电荷在电场中某点受力的方向，即为该点的电场强度的方向。

《中科院量子力学考研真题及答案详解(1990—2010共40套真题)》

ˆ和J ˆ 间夹角的可能值，并画出 L ˆ和S ˆ, S ˆ 的矢量模型图。 (3) 确定（2）中 L 五、求在一维常虚势场 iV (V E ) 中运动粒子的波函数，计算几率流密度，并证明虚势代表粒子的吸收，求吸收系数（用 V 表示）。
试题名称：1990 量子力学（实验型）第1页共1页
试题名称：1992 量子力学（理论型）
第1页
共1页
6
中国科学院－中国科技大学 1992 年招收攻读硕士学位研究生入学试卷
试题名称：量子力学（实验型）
说明：共五道大题，无选择题，计分在题尾标出，满分 100 分。
一、简单回答下列问题： (1) 举出一个实验事实说明微观粒子具有波粒二象性。 (2) 量子力学的波函数与经典的波场有何本质的区别？ (3) 如图所示，一个光子入射到半透半反镜面 M , P 1和P 2 为光电探测器，试分别按照经典与量子的观点说明 P 1和P 是否能同时接收到光信号（ l1 l2 ）。
E
n

n
E0 n x 0
2
常数
ˆ2 ˆ p 这里 En 是哈密顿量 H V ( x) 的本征能量，相应的本征态为 n 。求出该常数。 2m 三、设一质量为的粒子在球对称势 V (r ) kr (k 0) 中运动。利用测不准关系估算其基态的能量。四、电子偶素（ e e 束缚态）类似于氢原子，只是用一个正电子代替质子作为核，在非相对论极限下，其能量和波函数与氢原子类似。今设在电子偶素的基态里，存在一 ˆ 和M ˆ 8 M ˆ M ˆ 其中 M ˆ 是电子和正电子的自旋磁矩种接触型自旋交换作用 H e p e p 3 ˆ , q e) 。利用一级微扰论，计算此基态中自旋单态与三重态之间的能 ˆ q S (M mc 量差，决定哪一个能量更低。对普通的氢原子，基态波函数： 1 r a e2 1 2 100 e , a , 3 2 me a c 137

(完整版)量子力学期末考试题及解答

一、波函数及薛定谔方程1.推导概率（粒子数）守恒的微分表达式;()(),,w r t J r t o t∂+∇•=∂解答：由波函数的概率波解释可知，当(),r t ψ已经归一化时，坐标的取值概率密度为()()()()2,,,,w r t r t r t r t ψψψ*== （1）将上式的两端分别对时间t 求偏微商，得到()()()()(),,,,,w r t r t r t r t r t t t tψψψψ**∂∂∂=+∂∂∂ （2）若位势为实数，即()()V r V r *=，则薛定谔方程及其复共轭方程可以分别改写如下形式()()()()2,,,2r t ih ir t V r r t t m h ψψψ∂=∇-∂ （3）()()()()2,,,2r t ih ir t V r r t t m hψψψ***∂=-∇+∂ （4）将上述两式代入（2）式，得到()()()()()22,,,,,2r t ih r t r t r t r t t mψψψψψ**∂⎡⎤=∇-∇⎣⎦∂ ()()()(),,,,2ihr t r t r t r t mψψψψ**⎡⎤=∇•∇-∇⎣⎦ （5）若令()()()()(),,,,,2ih J r t r t r t r t r t mψψψψ**⎡⎤=∇-∇⎣⎦ （6）有()(),,0w r t J r t t∂+∇•=∂ （7）此即概率（粒子数）守恒的微分表达式。

2.若线性谐振子处于第一激发态()2211exp 2x C x α⎛⎫ψ=- ⎪⎝⎭求其坐标取值概率密度最大的位置，其中实常数0α>。

解答：欲求取值概率必须先将波函数归一化，由波函数的归一化条件可知()()222221exp 1x dx Cx x dx ψα∞∞-∞-∞=-=⎰⎰（1）利用积分公示())2221121!!exp 2n n n n x x dx αα∞++--=⎰ （2）可以得到归一化常数为C = （3）坐标的取值概率密度为 ()()()322221exp w x x x x ψα==- （4）由坐标概率密度取极值的条件())()3232222exp 0d w x x x x dx αα=--= （5）知()w x 有五个极值点，它们分别是 10,,x α=±±∞（6）为了确定极大值，需要计算()w x 的二阶导数()()()232222322226222exp d w x x x x x x dx αααα⎤=----⎦)()32244222104exp x x x ααα=-+- （7）于是有()23200x d w x dx ==> 取极小值（8）()220x d w x dx =±∞= 取极小值（9）()23120x d w x dx α=±=< 取极大值（10）最后得到坐标概率密度的最大值为2111w x x ψαα⎛⎫⎛⎫=±==±= ⎪ ⎪⎝⎭⎝⎭（11）3.半壁无限高势垒的位势为()()()()000x v x x a v x a ∞<⎧⎪=≤≤⎨⎪>⎩求粒子能量E 在00E v <<范围内的解。

北京邮电大学2020年《602量子力学》考研专业课真题试卷

（动2=
5. 对于氢原子，不考虑电子自旋，则能级简并度为
考虑电子自旋，
但不考虑自旋与轨道角动量的耦合，则能级简并度为
。
二、计算题(20分）
＾
旷 dz
质量为m的粒子只能沿圆环（半径为R)运动，能量算符为H= 2mR2 d矿，其中。
为旋转角。求能级(En )和归一化波函数(lf/n), 并讨论各能级的简并度。
五、计算题(25 分）
设算符A, B不对易，[A,B]=C, 但C和A、B对易，即[A,C]=0, [B,C]=0,
请计算l、[A,B勹，
2、[A, e勹， 3、[A,e,1,8 ] (n为正整数，儿为参变量）。
六、计算题(25 分）测量一个电子（处于自由空间）自旋的z分量，发现是－h2 。
A=
' 粒子出现概率密度最大的位置x=
a 2. 一维谐振子的升、降算符矿和的对易关系为
一维谐振子哈密顿量表示为升降算符的形式为 3. 坐标算符与动量算符的x分量，文和九之间的对易关系为
二者满足的不确定关系表示为
。
4. 对于泡利算符6冲y ' 可以定义：立= Ux 土 ;a-y , 则［妇 a--1=
北京邮电大学 2020年硕士研究生招生考试试题
考试科目： 602量子力学请考生注意：切所有答案（包括选择题和填空题）一律写在答题纸上，否则不计成绩。
＠不允许使用计算器。
一、填空题（每个空4分，每小题8分，共40分）
1. 粒子处千态叭x)=Axe一气(O<x<ao), A为常数，A为归一化常数。则归一化常数
第 2页共2 页
l、接着测量自旋的x分量，可能得到什么结果？得到这些结果的儿率是什么？期望值是多少？

北京邮电大学2018年《602量子力学》考研专业课真题试卷

北京邮电大学
2018年硕士研究生入学考试试题
考试科目：量子力学
请考生注意：＠所有答案（包括选择题和填空题）一律写在答题纸上，否则不计成绩。

＠不允许使用计算器。

一、选择填空题（共25分）
(1)质量为m的粒子在宽度为a的一维无限深方势阱中运动，当该粒子从第一激发态跃迁至基态，所放出光子在真空中的波长为。

(2)算符0=九x+x九厄米算符（填“是”或“不是＂）。

()对易关系[l x,l] =
(4)若体系所处的状态用球谐函数Y心(0,<p)描写，则关千角动量的平均值I=，互＝
二、计算题(30分）
质量为m的粒子沿x轴运动，描写其运动的某个定态波函数是：
叭x)=A x2e-lxl l a
其中a为已知的正值实常量，A为归一化常数。

(1)求在何处最容易发现粒子？
(2)规定无穷远处(x_.,土00)为势能零点，求粒子在此状态的能量E,以及势能V(x)的表达式。

三、计算题(20分）
求一维线性谐振子的坐标X,动量P以及哈密顿量H在能量表象中的矩阵表示。

考试科目：602最子力学第1页共2页。

821设计基础-2017 北京邮电大学硕士研究生考研真题

北京邮电大学2017年硕士研究生入学考试试题考试科目：设计基础请考生注意：①所有答案(包括选择题和填空题)一律写在答题纸上，否则不计成绩。

②不允许使用计算器一、选择题（每小题 2 分，共 20分）1、下图中运用的主要构成手法是：（）A渐变 B对称 C重复 D发射2、下图用的最重要的构成手法是：（）A 变异B 共形 C重复 D发射3、下面图片中运用的典型设计风格是？（）A达达主义 B解构主义 C现代主义 D立体主义4、下图用的是何种形式美原则？（）A 渐变B 重复C 起伏 D节奏5、下图是由一个正方形和一个圆形进行了（）之后形成的。

A结合 B减缺 C 差叠 D 透叠6、下图是由一个正方形和一个圆形进行了（）之后形成的。

A结合 B覆叠 C 差叠 D 透叠7、色光的三原色是（）A红绿蓝 B红黄蓝 C 红紫绿 D蓝紫黄8、可见光中波长最短的色光是：（）A红色 B黄色 C 绿色 D紫色9、点、线、面、体四个构成元素中相对最灵活的是（）A点 B线 C 面 D体10、“一道残阳铺水中，半江瑟瑟半江红”中提到的“瑟瑟”是形容一种颜色，这种颜色与“红色”形成了什么对比关系？（）A类似色对比 B中差色对比 C对比色对比 D互补色对比二、分析题（每小题 25，共 50分）1、从设计的角度分析一下微信支付与支付宝的异同点，可以从产品的设计定位、交互框架的设计定位，界面风格的设计定位等方面进行分析。

（25分）2、下图是微软公司2016年10月发布Surface Studio，请简要分析其外观工业设计，以及其对微软产品线的意义。

（25分）三、创意题（每小题 25分共 50分）1、以方形、圆形、三角形为设计元素，设计一套五个天气符号（包括晴、雨、雪、雾、风等）。

（25分）2、请设计两组造型分别表现“上升”和“下降”的概念，其中每组造型由三个直棱体构成，分别代表主导物体、次要物体和附属物体。

（25分）要求：整体造型中主导、次要和附属等造型要素的关系恰当、合理。

量子力学-卷一(第三版)答案-井孝功

量子力学-卷一(第三版)答案-井孝功第一章量子力学的诞生1.1设质量为m 的粒子在谐振子势2221)(x m x V ω=中运动，用量子化条件求粒子能量E 的可能取值。

提示：利用 )]([2,,2,1,x V E m p n nh x d p -===⋅⎰Λ)(x V 解：能量为E 的粒子在谐振子势中的活动范围为ax ≤（1）其中a由下式决定：2221)(a m x V E a x ω===。

a- 0 a x由此得2/2ωm E a = ，（2）ax ±=即为粒子运动的转折点。

有量子化条件hn a m a m dx x a m dx x m E m dx p aaa a==⋅=-=-=⋅⎰⎰⎰+-+-222222222)21(22πωπωωω得ωωπm nm nh aη22==（3）代入（2），解出Λη,3,2,1,==n n E nω （4）积分公式： cau a u a u du u a ++-=-⎰arcsin 22222221.2设粒子限制在长、宽、高分别为cb a ,,的箱内运动，试用量子化条件求粒子能量的可能取值。

解：除了与箱壁碰撞外，粒子在箱内作自由运动。

假设粒子与箱壁碰撞不引起内部激发，则碰撞为弹性碰撞。

动量大小不改变，仅方向反向。

选箱的长、宽、高三个方向为z y x ,,轴方向，把粒子沿z y x ,,轴三个方向的运动分开处理。

利用量子化条件，对于x 方向，有()⎰==⋅Λ,3,2,1,x x xn h n dx p即hn a p x x =⋅2 （a 2：一来一回为一个周期）ah n p x x 2/=∴,同理可得， bh n p y y 2/=,ch n p z z 2/=, Λ,3,2,1,,=z y x n n n粒子能量⎪⎪⎭⎫ ⎝⎛++=++=222222222222)(21c n b n a n mp p p m E z y x z y x n n n zy x ηπΛ,3,2,1,,=z y x n n n1.3设一个平面转子的转动惯量为I ，求能量的可能取值。