INTERVAL ARITHMETIC A Fortran 90 module for an interval data type
Scalarizing fortran 90 array syntax

1.2
Scalarization Dependence Matrix
In their early work on the subject, Allen and Kennedy [3] observed that the scalarized code is correct only if the generated loop nest carries no true dependence. We assume readers are familiar with the concept of true, anti-, output and input dependences, and with loop-carried and loop-independent dependences. Allen and Kennedy have defined the dependence matrix for a loop nest to be a matrix in which each row is a dependence vector for some dependence in the nest and every such direction vector is included as a row. Note that nothing is lost if there is only one row per distinct direction vector—that is no row is duplicated. In this paper, all algorithms are based on the scalarization dependence matrix, which is the dependence matrix for the naively scalarized loop nest. Note that, in nests generated from Fortran 90 assignments, there cannot be any carried output dependences. Since there are only loop-carried true dependences and antidependences, the type information associated with each dependence vector in ordinary dependence matrix is omitted. We distinguish true dependences from antidependences by whether the leftmost non-= direction is “<” (for true dependence) or “>” (for antidependence). For a scalarization to be correct, the scalarized loop nest cannot carry any true dependences. Therefore, in the corresponding scalarization dependence matrix, the first non-“=” entries of all dependence vectors have to be “>”, such a matrix is called valid scalarization dependence matrix. Note that we consider the dependences caused by the original left-hand-side array only, excluding dependences introduced by the temporary arrays the algorithms may generate.
F90第三章

3.下划线:_ 下划线: 4.特殊字符:空格 + - * / ( ) , . ‘ : ! “ % & ; < > ? $ =
90基础知识 第三章 FORTRAN 90基础知识
3.2 名称
概述 语法描述 作用域
名称( 标识符) 名称 ( 标识符 ) 在程序中用来标识有关实 变量、命名常量、 函数、过程、 体 ( 如 : 变量 、 命名常量 、 函数 、 过程 、 程序 单元、公用块、和哑元等) 单元、公用块、和哑元等)。
3.3 关键字/分类 关键字/
! 按顺序指定参数 ! 按变元关键字指定参数 ! 按变元关键字指定参数
MOD(a 21, 10) MOD(a=21,p=10) MOD(p 10, 21) MOD(p=10,a=21)
如何察看内部函数和过程的变元关键字形式? 如何察看内部函数和过程的变元关键字形式? 内部函数和过程的变元关键字形式
3.5 语句/排列次序 语句/
90基础知识 第三章 FORTRAN 90基础知识
3.5 语句
概述 排列次序 排列次序 受限使用
对语句的使用范围有具体规定, F90对语句的使用范围有具体规定 , 即 90 对语句的使用范围有具体规定 给出了F90受限语 语句的受限使用。 语句的受限使用 。 表 3-3 给出了 F90 受限语 句及使用的程序单元范围。 句及使用的程序单元范围。
3.4 程序单元
90基础知识 第三章 FORTRAN 90基础知识
3.4 程序单元
四种类型程序单元
概述 分类 描述 示例
主程序单元:程序运行的入口点, 1. 主程序单元:程序运行的入口点,其它程序 单元执行的启动器。由PROGRAM语句开始, 单元执行的启动器。 PROGRAM语句开始, 语句开始 可缺省。 可缺省。 外部子程序单元: 2. 外部子程序单元 : 不包含在其它单元中的 函数或子例行子程序所构成的程序单元, 函数或子例行子程序所构成的程序单元,能 够 被 其 它 程 序 单 元 调 用 。 由 FUNCTION 或 SUBROUTINE语句开始。 SUBROUTINE语句开始。 语句开始
FORTRAN90

FORTRAN90 程序设计复习资料(2)一、选择题1.FORTRAN 90规定,变量类型声明的优先顺序是。
A.隐含约定(I-N规则)、IMPLICIT声明、类型声明B.类型声明、隐含约定(I-N规则)、IMPLICIT声明C.类型声明、IMPLICIT声明、隐含约定(I-N规则)D.IMPLICIT声明、类型声明、隐含约定(I-N规则)2.表达式15/4/2.0的值是。
A.整数2 B.实数1.5 C.实数2.25 D.实数1. 33.数组声明语句为:INTEGER,DIMENSION(-5:-1,-3:3,11:15) ::num ,数组共有个元素。
A.175 B.150 C.120 D.174.下列语句函数声明中,正确的是。
A.F1(I,I)=5*I-10*I**2 B. F2(MAT(5),A)=5*A+MAT(5)C. F3(X,Y,5.0)=X**2+Y**2+5.0**2D.F4(X,Y)=SQRT(X**2+Y**2+5.0**2)5.下列关于子程序的有关说法中,不正确的是。
A.对于无参子例行程序,调用时子例行程序名后的括号可取消B.对于无参函数子程序,调用时函数名后括号可取消C.对于有参子程序,形式参数可以是子程序名对于有参子程序,形式参数可以是星号“*”6.下列关于外部子程序的说法中,正确的是。
A.外部子程序可与主程序单元放在一个源程序文件中,但必须放在PROGRAM语句之前B.外部子程序可与主程序单元放在一个源程序文件中,但必须放在END语句之后C.外部子程序允许单独放在一个源程序文件中,并与主程序分别编译D.外部子程序允许单独放在一个源程序文件中,并与主程序单元一起编译7.关于FORTRAN90的派生(即自定义)类型,以下四种说法中错误的是。
A.派生类型定义从“TYPE 派生类型名”开始到“END TYPE'’结束B.派生类型名不得和系统内定类型同名,在同一程序单位内也不得重复定义 C.派生类型的分量(或称成员)不能是派生类型名,即派生类型不允许嵌套定义D.引用派生类型变量的成员可用“%”号或“.”号,例如abc%a,或abc.a均可8.指针声明语句为:INTEGER,POINTER ::A1,A2目标变量声明语句为:INTEGER,TARGET ::M=20,N=30下列语句执行后,M、N的值分别为。
Fortran90 第2章

Selected_int_kind送回
表示十进制幂的范围由内在函数range送回的
在FORTRAN90中,也可以表示二进制、八进制、
十六进制形式的无符号整数。其形式如下:
二进制数:B‟101101‟ 或 B”101101” 八进制数:O‟76210‟ 或 O”76210” 十六进制数:Z‟1FA2‟ 或 Z”1FA2”
§2.2 FORTRA90源程序基本结构
例[2-1]: 见书P16页例题:已知华氏温度与摄氏温度之间的换 算公式为: 5
TC 9 (Th 32)
现输入某一华氏温度Th,请计算出相应的摄氏温度Tc。 PROGRAM H_TO_C
!Given the Fahrenheit temprature ,to caculate the Centigrade
2、主程序结构 [program 程序名称] IMPLICIT NONE [声明(说明)语句部分] [执行语句部分] END [program [程序名称]]
§2.3 语言元素
2.3.1 FORTRAN90字符集:
编写Fortran90程序时,允许使用的所有字符及符号。 ⑴ A~Z(a~z)程序中不区分大小写 26个
非0; 例:0.7436E-12,而 21.835E5、0.0023E4 × 2.数字部分有且仅有一位非零的整数。
例:7.123E24,而 345.2E7 ×
可以说明种别类型参数值:
REAL,PARAMETER::LONG=SELECTED_REAL_KIND(8,88) 说明的符号常量LONG提供了至少8位的精度,以及 -10
对于逻辑型数据,系统同样提供不同的种
别类型参数。表示方法的种别类型参数值 由函数KIND得到;
Fortran90编程
字。以关键词end type结束。
派生类型的声明和使用
n 声明: n 赋值: n 引用结构成员:
例一:派生数据类型
模块(Module)
n 是一种不能直接执行的程序单元,但可以包含
数据声明和过程
n
使不同的过程实现过程和数据的共享 n 可以实现对自定义数据类型的封装
n 相对于program,function,subroutine,是一种特
例三:数据类型的范围
定义符号常量
n 符号常量在程序中不可以改变其值 n 定义符号常量可以增强程序的可读性和可维护
性 n 定义方法:加上parameter属性
real (8) ,parameter :: pi=3.1415926535_8
例四:定义符号常量
三、控制结构
n if语句:if then elseif else endif
n
在Compaq Visual Fortran中调用 CXML
n 第一种方法:在工程中加入cxml.lib
n 第二种方法:使用include
PROGRAM example INCLUDE 'CXML_INCLUDE.F90’
在Compaq Visual Fortran中调用 Intel MKL
n 添加库函数路径 n 在工程中加入mkl_s.lib
总结:Fortran90的新特性
n n n n n n n n
高级的表达能力:数组运算 (例如, X(1:N)=R(1:N)*COS(A(1:N))) 动态存储分配 (ALLOCATE, DEALLOCATE, ...) 导出类型(derived types)与操作符重载(operator overloading) 更好的变量声明方式(parameterized types),提高移植性 模块 更多的现代控制结构 (SELECT CASE,END SELECT,DO, END DO,EXIT...) 更多的内部函数 (date, precision, arrays, ...) 新的源程序书写格式-自由格式(free format) 指针
FORTRAN_90_复习

FORTRAN 90 基础知识第三章基本知识,如:字符集、名称、关键字、程序单元、书写格式、数据类型。
名称:①名称只能由英文字母、数字、下划线符“_”和美元符号“$”组成。
②名称第一个字符必须是英文字母。
③名称不能超过31个字符。
合法名称: Number,Max, PrOgRaM, FIND_IT, read, x, a3b7, china, total, x$y$z 。
非法名称:X-Y-Z, 8q, a.5, _wrong,U.S.A., DR.WANG,$abcd,r a t e 。
书写格式:自由格式,固定格式3个通用标志符:注释标志符“!”、语句分隔标志符“;”和续行标志符“&”。
数据类型第四章 内部数据类型常量和变量:语法描述; 精度(kind 值)和取值范围 整型常量:整数(10进制)。
实型常量:实数。
复型常量:复数。
字符型常量:字符串。
逻辑型常量:逻辑值,布尔值。
.true. .false.变量的申明。
表达式算术表达式:算术运算符的优先级和结合规则;操作数的类型转换FORTRAN 90 数据类型内部数据类型派生类型(记录类型)数组类型指针类型 公用区类型类型整数类型 实数类型 复数类型字符类型 逻辑类型运算符 含义 结合顺序 优先级 运算速度 说明 ( ) 最高 ** 乘方 左←右 高 慢 两个**之间不能出现空格 * / 乘 除 左→右 ↑ ↑ 数学符号× ÷为非法字符,用*和/代替 + - 加(二元加) 减(二元减) 左→右 ↓ ↓ + - 正(一元加) 负(一元减) 低 快不同优先级运算符,“先高后低”结合先乘方、后乘除、再加减,括号最优先相同优先级运算符,“从左向右”结合,如9-4+12/3*2**3 = ?乘方算符,“从右向左”结合,如2**3**2 = ?尽量多地使用( ),以使意义明确,避免出现歧义和产生错误转换规则“由低级向高级转换”①数据类型和KIND相同的两个算术操作数,计算时不转换,运算结果的类型和KIND与原数据相同。
F90第一章

《FORTRAN90程序设计》课多媒体课件
第一章 程序设计概述
1. 2. 3. 4.
程序设计语言 程序与程序设计 算法的基本概念和特征 程序设计方法
《FORTRAN90程序设计》课多媒体课件
1.1 程序设计语言
概述 分类
概念
描述
程序设计语言是人与计算机进行交 流的工具。 计算机系统按照某种程序设计语言 编写出的程序进行工作 , 人类通过程序 来指挥和控制计算机系统。
sum+I=>sum
N
I+1=>I 输出sum 结束
第一章 程序设计概述
1.4 程序设计方法
概述 模块化方法
结构化方法
面向对象方法
要求设计出的程序具有正确性、 可靠性、可读性、可理解性、可 修改性和可维护性 程序设计方法:面向过程(模块 化、结构化)、面向对象。
1.4 程序设计方法/概述
概述 模块化方法
结构化方法
面向对象方法
传统程序设计方法以功能和操作作为 驱动,数据从属于操作,不利于有效 的分析问题;算法和程序结构与求解 的实际问题不完全一致,降低了程序 的可读性、可维护性和可修改性。
面向对象方法针对具体问题进行分析, 对数据实体进行类定义,对其中的数 据和操作进行封装和隐蔽处理,创建 对象实例。运行对象实例可完成问题 的求解。
第一章 程序设计概述
1.4 程序设计方法
概述 模块化方法
结构化程序设计强调程序设计风格 和程序结构的规范化。
结构化方法
面向对象方法
两大特征:一是使用三种基本控制 结构;二是采用自顶向下和逐步求 精方法。
intel visual fortran 在visual studio中如何正常的使用openmp并行程序
write ( *, '(a)' ) ' '
write ( *, '(a,i8,a)' ) ' Call OMP_SET_NUM_THREADS, and request ', &
nthreads, ' threads.'
call omp_set_num_threads ( nthreads )
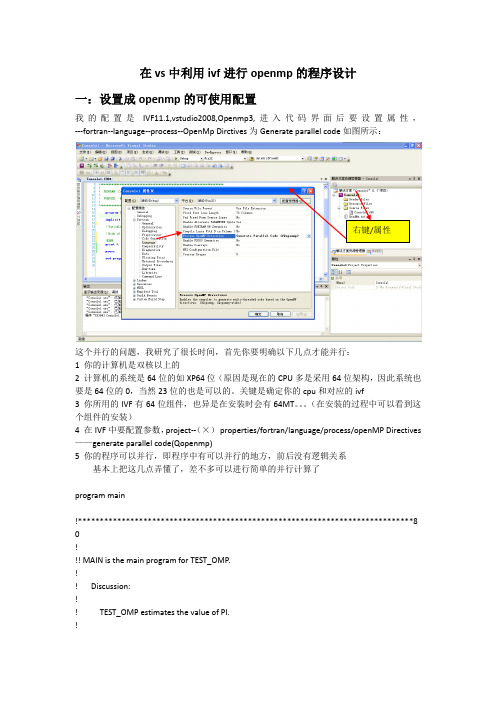
在vs中利用ivf进行openmp的程序设计
一:设置成openmp的可使用配置
我的配置是IVF11.1,vstudio2008,Openmp3,进入代码界面后要设置属性,---fortran--language--process--OpenMp Dirctives为Generate parallel code如图所示:
write ( *, '(a)' ) ' N = number of terms computed and added;'
write ( *, '(a)' ) ' '
write ( *, '(a)' ) ' ESTIMATE = the computed estimate of PI;'
write ( *, '(a)' ) ' '
write ( *, '(a,i3)' ) ' This is proபைடு நூலகம்ess ', id
if ( id == 0 ) then
write ( *, '(a)' ) ' '
write ( *, '(a)' ) ' Calling OMP_GET_NUM_THREADS inside a '
FORTRAN 90

FORTRAN 90第一章绪论一、特点在FORTRAN 77的基础上增添了许多具有现代特性的功能、递归、数组直接运算、派生类型、指针和过程。
二、与FORTRAN 77的区别1、不区分书写格式2、不赞成语句标号3、不使用BLOCK DATA 数据块子程序、语句函数4、主程序以PROGRAM 开头,以END PROGRAM为结尾函数子程序:区分函数名与函数值5、不使用GOTO 10、STOP、PAUSE语句6、不使用DO 10 I=1,3,而以DO与END DO 匹配使用。
7、不使用:I-N规则、双精度、DATA语句、多条RETURN语句。
而使用REAL ::A=0,B=2.58、不使用COMMON语句,而用模块MODULE9、用假定形状数组取代假定大小数组10、DIMENSION A(10)在FORTRAN 90中不再定义数组11、FORMAT 语句不再使用第二章F ORTRAN 90 基础知识第2.1节语言元素一、字符集1、A-Z (26个)2、0-9 (10个)3、_(下划线)(1个)4、特殊符号(21个):空格、等号、加号、减号、*、/、(、)、,、.、’、:、!、”、%、&、;、<、>、?、$二、数据类型本身:INTEGER real complex character logical派生类型种别参数:对可移值数据精度和范围进行选择的机制,他提供了对每种内部数据类型的不同机器表示进行选择的参数化方式,种别参数均为整数。
用法:KIND=种别参数。
函数KIND(X)表示返回X的种别参数。
1、常量(字符型:双、单引号表示)常数的种别标示:例15_2 14.36_3 .false._4 5_’ang’带种别参数的常量的运算:15_2+14.36_3=29.36_3定义常量:REAL(KIND=2),PARAMETER::N=52、变量(1)变量名(程序名、常量、虚参、派生类型)命名规则:长度小于等于31个字符、须以字母开头、由字母、数字、下划线构成,其中不出现空格。
intelvisualfortran在visualstudio中如何正常的使用openmp并行程序

intelvisualfortran在visualstudio中如何正常的使⽤openmp并⾏程序在vs中利⽤ivf进⾏openmp的程序设计⼀:设置成openmp的可使⽤配置我的配置是IVF11.1,vstudio2008,Openmp3,进⼊代码界⾯后要设置属性,---fortran--language--process--OpenMp Dirctives为Generate parallel code如图所⽰:右键/属性这个并⾏的问题,我研究了很长时间,⾸先你要明确以下⼏点才能并⾏:1 你的计算机是双核以上的2 计算机的系统是64位的如XP64位(原因是现在的CPU多是采⽤64位架构,因此系统也要是64位的0,当然23位的也是可以的。
关键是确定你的cpu和对应的ivf3 你所⽤的IVF有64位组件,也异是在安装时会有64MT。
(在安装的过程中可以看到这个组件的安装)4 在IVF中要配置参数,project--(×)properties/fortran/language/process/openMP Directives ——generate parallelcode(Qopenmp)5 你的程序可以并⾏,即程序中有可以并⾏的地⽅,前后没有逻辑关系基本上把这⼏点弄懂了,差不多可以进⾏简单的并⾏计算了program main!*****************************************************************************8 0!!! MAIN is the main program for TEST_OMP.!! Discussion:!! TEST_OMP estimates the value of PI.!! This program uses Open MP parallelization directives.!! It should run properly whether parallelization is used or not.!! However, the parallel version computes the sum in a different! order than the serial version; some of the quantities added are! quite small, and so this will affect the accuracy of the results.!! Modified:! Author:!! John Burkardt!! A FORTRAN 90 module may be available:!! use omp_lib!! A FORTRAN 77 include file may be available:!! include 'omp_lib.h'!implicit noneinteger, parameter :: r4_logn_max = 9integer idinteger nthreadsinteger omp_get_num_procsinteger omp_get_num_threadsinteger omp_get_thread_numcall timestamp ( )write ( *, '(a)' ) ' 'write ( *, '(a)' ) 'TEST_OMP'write ( *, '(a)' ) ' FORTRAN90 version'write ( *, '(a)' ) ' 'write ( *, '(a)' ) ' Estimate the value of PI by summing a series.'write ( *, '(a)' ) ' 'write ( *, '(a)' ) ' This program includes Open MP directives, which' write ( *, '(a)' ) ' may be used to run the program in parallel.' write ( *, '(a)' ) ' 'write ( *, '(a)' ) ' The number of processors available:'write ( *, '(a,i8)' ) ' OMP_GET_NUM_PROCS () = ', omp_get_num_procs ( ) nthreads = 4write ( *, '(a)' ) ' 'write ( *, '(a,i8,a)' ) ' Call OMP_SET_NUM_THREADS, and request ', &nthreads, ' threads.'! Note that the call to OMP_GET_NUM_THREADS will always return 1! if called outside a parallel region!!!$OMP parallel private ( id )id = omp_get_thread_num ( )write ( *, '(a,i3)' ) ' This is process ', idif ( id == 0 ) thenwrite ( *, '(a)' ) ' 'write ( *, '(a)' ) ' Calling OMP_GET_NUM_THREADS inside a 'write ( *, '(a)' ) ' parallel region, we get the number of'write ( *, '(a,i3)' ) ' threads is ', omp_get_num_threads ( )write ( *, '(a)' ) ' 'end if!$OMP end parallelcall r4_test ( r4_logn_max )write ( *, '(a)' ) ' 'write ( *, '(a)' ) 'TEST_OMP'write ( *, '(a)' ) ' Normal end of execution.'write ( *, '(a)' ) ' 'call timestamp ( )stopendsubroutine r4_test ( logn_max )!*****************************************************************************8 0!!! R4_TEST estimates the value of PI using single precision.!! Discussion:!! PI is estimated using N terms. N is increased from 10^2 to 10^LOGN_MAX.! The calculation is repeated using both sequential and Open MP enabled code. ! Wall clock time is measured by calling SYSTEM_CLOCK.!! 06 January 2003!! Author:!! John Burkardt!implicit noneinteger clock_maxinteger clock_rateinteger clock_startinteger clock_stopreal errorreal estimateinteger logninteger logn_maxcharacter ( len = 3 ) modeinteger nreal r4_pireal timewrite ( *, '(a)' ) ' 'write ( *, '(a)' ) 'R4_TEST:'write ( *, '(a)' ) ' Estimate the value of PI,'write ( *, '(a)' ) ' using single precision arithmetic.'write ( *, '(a)' ) ' 'write ( *, '(a)' ) ' N = number of terms computed and added;' write ( *, '(a)' ) ' 'write ( *, '(a)' ) ' ESTIMATE = the computed estimate of PI;' write ( *, '(a)' ) ' 'write ( *, '(a)' ) ' ERROR = ( the computed estimate - PI );'write ( *, '(a)' ) ' 'write ( *, '(a)' ) ' TIME = elapsed wall clock time;'write ( *, '(a)' ) ' 'write ( *, '(a)' ) ' Note that you can''t increase N forever, because:'write ( *, '(a)' ) ' B) maximum integer size is a problem.'write ( *, '(a)' ) ' 'write ( *, '(a,i12)' ) ' The maximum integer:' , huge ( n )write ( *, '(a)' ) ' 'write ( *, '(a)' ) ' 'write ( *, '(a)' ) ' N Mode Estimate Error Time' write ( *, '(a)' ) ' 'n = 1do logn = 2, logn_maxmode = 'OMP'call system_clock ( clock_start, clock_rate, clock_max )call r4_pi_est_omp ( n, estimate )call system_clock ( clock_stop, clock_rate, clock_max )time = real ( clock_stop - clock_start ) / real ( clock_rate )error = abs ( estimate - r4_pi ( ) )write ( *, '( i12, 2x, a3, 2x, f14.10, 2x, g14.6, 2x, g14.6 )' ) &n, mode, estimate, error, timen = n * 10end doreturnendsubroutine r4_pi_est_omp ( n, estimate )!*****************************************************************************8 0 !!! R4_PI_EST_OMP estimates the value of PI, using Open MP.!! Discussion:!! The calculation is based on the formula for the indefinite integral:!! Integral 1 / ( 1 + X**2 ) dx = Arctan ( X )!! Hence, the definite integral!! Integral ( 0 <= X <= 1 ) 1 / ( 1 + X**2 ) dx!! A standard way to approximate an integral uses the midpoint rule.! If we create N equally spaced intervals of width 1/N, then the! midpoint of the I-th interval is!! X(I) = (2*I-1)/(2*N).!! The approximation for the integral is then:!! Sum ( 1 <= I <= N ) (1/N) * 1 / ( 1 + X(I)**2 )!! In order to compute PI, we multiply this by 4; we also can pull out! the factor of 1/N, so that the formula you see in the program looks like: !! ( 4 / N ) * Sum ( 1 <= I <= N ) 1 / ( 1 + X(I)**2 )!! Until roundoff becomes an issue, greater accuracy can be achieved by ! increasing the value of N. !! Modified:!! 06 January 2003!! Author:!! John Burkardt!! Parameters:!! Input, integer N, the number of terms to add up.!! Output, real ESTIMATE, the estimated value of pi.!implicit nonereal hinteger nreal sum2real xh = 1.0E+00 / real ( 2 * n )sum2 = 0.0E+00!!$OMP parallel do private(x) shared(h) reduction(+: sum2)!do i = 1, nx = h * real ( 2 * i - 1 )sum2 = sum2 + 1.0E+00 / ( 1.0E+00 + x**2 )end doestimate = 4.0E+00 * sum2 / real ( n )returnendfunction r4_pi ( )!*****************************************************************************8 0 !!! R4_PI returns the value of pi.!! Modified:!! 02 February 2000!! Author:!! John Burkardt!! Parameters:!! Output, real R4_PI, the value of pi.!implicit noner4_pi = 3.14159265358979323846264338327950288419716939937510E+00 returnendsubroutine timestamp ( )!*****************************************************************************8 0!!! TIMESTAMP prints the current YMDHMS date as a time stamp.!! Example:!! May 31 2001 9:45:54.872 AM!! Modified:!! 31 May 2001!! Author:!! John Burkardt!! Parameters:!! None!implicit nonecharacter ( len = 8 ) ampminteger dcharacter ( len = 8 ) dateinteger hinteger minteger mmcharacter ( len = 9 ), parameter, dimension(12) :: month = (/ &'January ', 'February ', 'March ', 'April ', &'May ', 'June ', 'July ', 'August ', &integer ninteger scharacter ( len = 10 ) timeinteger values(8)integer ycharacter ( len = 5 ) zonecall date_and_time ( date, time, zone, values ) y = values(1)m = values(2)d = values(3)h = values(5)n = values(6)s = values(7)mm = values(8)if ( h < 12 ) thenampm = 'AM'else if ( h == 12 ) thenif ( n == 0 .and. s == 0 ) thenampm = 'Noon'elseampm = 'PM'end ifelseh = h - 12if ( h < 12 ) thenampm = 'PM'else if ( h == 12 ) thenif ( n == 0 .and. s == 0 ) thenampm = 'Midnight'elseampm = 'AM'end ifend ifend iftrim ( month(m) ), d, y, h, ':', n, ':', s, '.', mm, trim ( ampm ) returnend!===================================== COPY上⾯的程序,可以完全运⾏成功,运⾏界⾯如下:。
Fortran90

1、定义:系统函数,FORTRAN90系统已经定义了的函数
2、种类与函数调用写法: 函数名 ( 函数参数 ) |x| : ABS(X) e:
x
x
EXP(x) SQRT(X)
Real(x)
INT(x)取整数部分
NINT(x)最靠近的整数 CMPLX(两种) DBLE(x) Max(a,b,c,……)
Cosx COS(X)
3、名字的命名规则: 字母、数字、下划线组成 字母开头 长度1~31 名字中不能含有空格 错例 3A 、 x-3 、3.14
S_p_r , waiter_ , b123 , a是正确的
字符的大小写没有要求 ,最好遵循“见名知意”的准则
在FORTRAN90标准中,并没有规定保留字,因此完全可以使用其中 的函数名或关键字作为变量名。但为了避免混淆,建议不要使用 FORTRAN90中已有的具有特定意义的名字作为变量名。
例
1/2*2值为0
8/5+2.0*5/2值为6.0
(注意在计算过程中逐步转化、实数有效位7位) FORTRAN90允许不同类型的数值型数据类型之间 进行算术运算,但不允许在数值型数据类型与非数 值型数据类型之间进行算术运算
例:
1、 2 sin( 4) 3
(sin 4 cos10)e2.5 2、 2 ax ln(3 * 5)
Fortran Manual

Tanja van Mourik Chemistry Department University College London Copyright: Tanja van MourikFortran 90/95 Programming ManualBrief History of FortranThe first FORTRAN (which stands for Formula Translation) compiler was developed in 1957 at IBM. In 1966 the American Standards Association (later the America National Standards Institute, ANSI) released the first standard version of FORTRAN, which later became known as FORTRAN 66. The standard aimed at providing a standardised, portable language, which could easily be transferred from one computer system to the other. In 1977, a revised version of FORTRAN, FORTRAN 77, was completed (the standard was published in 1978). The next version is Fortran 90, which is a major advance over FORTRAN 77. It contains many new features; however, it also contains all of FORTRAN 77. Thus, a standard-conforming FORTRAN 77 program is also a standard-conforming Fortran 90 program. Some of FORTRAN 77’s features were identified as “obsolescent”, but they were not deleted. Obsolescent features are candidates for deletion in the next standard, and should thus be avoided. The latest standard is Fortran 95. Fortran 95 contains only minor changes to Fortran 90; however, a few of the obsolescent features identified in Fortran 90 were deleted.Because of the requirement that all of FORTRAN 77’s features must be contained in Fortran 90, there are often several ways to do the same thing, which may lead to confusion. For example, an integer-type variable can be declared in FORTRAN 77 format:integer ior in Fortran 90 format:integer :: iIn addition, as a legacy from FORTRAN 77, Fortran 90 contains features that are considered bad or unsafe programming practice, but they are not deleted in order to keep the language “backward compatible”.To remedy these problems, a small group of programmers developed the F language. This is basically a subset of Fortran 90, designed to be highly regular and reliable to use. It is much more compact than Fortran 90 (because it does not contain all of FORTRAN 77’s features).There will be a new standard soon, which will be called Fortran 2003 (even though the final international standard will not come out before late 2004). There will be new features in Fortran 2003 (such as support for exception handling, object-oriented programming, and improved interoperability with the C language), but the difference between Fortran 90/95 and Fortran 2000 will not be as large as that between FORTRAN 77 and Fortran 90.Introduction to the courseThis course intends to teach Fortran 90/95, but from the point of view of the F language. Thus, many of the old FORTRAN 77 features will not be discussed, and should not be used in the programs.It is assumed that you have access to a computer with a Fortran 90 or Fortran 95 compiler. It is strongly recommended to switch on the compiler flag that warns when the compiler encounters source code that does not conform to the Fortran 90 standard, and the flag that shows warning messages. For example:Silicon Graphics: f90 –ansi –w2 –o executable-name sourcefile.f90Or even better:f90 –ansi –fullwarn –o executable-name sourcefile.f90–ansiSun: f90You can check these flags by typing “man f90” or “man f95” (on a Unix system). You may ask someone in your group for help how to use the compiler and editor on the computer you use.If you have access to emacs or xemacs, and know how to use it (or are willing to invest a bit of time in learning how to use it), it is recommended to use this editor. It will pay off (emacs can format the source code for you, and thus detect program mistakes early on). BibliographyFortran 95 Handbook, complete ISO/ANSI ReferenceJ.C. Adams, W.S. Brainerd, B.T. Smith, J.L. Wagener, The MIT Press, 1997The F programming languageM. Metcalf and J. Reid, Oxford University Press, 1996Programming in Fortran 90I.M. Smith, John Wiley and Sons, 1995Migrating to Fortran 90J.F. Kerrigan, O’Reilly & Associates, Inc., 1993CONTENTSChapter 1 Gettingstarted 4 Chapter 2Types, Variables, Constants, Operators 4Chapter 3 ControlConstructs 15 Chapter 4 Procedures 23 Chapter 5More on Arrays 35Chapter 6 Modules 43 Chapter 7More on I/O 49Chapter 8 Pointers 55 Chapter 9 NumericPrecision 61 Chapter 10Scope and Lifetime of Variables 62Chapter 11 Debugging 651.Getting startedType, compile and run the following program (call the file hello.f90): program hello! this programs prints "hello world!" to the screenimplicit noneprint*, "Hello world!"end program helloNote the following:••••••a program starts with program program_nameit ends with end program program_nameprint*displays data (in this case, the character string “Hello, world!”) on the screen.all characters after the exclamation mark (!) (except in a character string) are ignored by the compiler. It is good programming practice to include comments. Comments can also start after a statement, for example:print*, “Hello world!” ! this line prints the message “Hello world!”Note the indentation. Indentation is essential to keep a program readable. Additionally, empty lines are allowed and can help to make the program readable. Fortran 90 allows both upper and lowercase letters (unlike FORTRAN 77, in which only uppercase was allowed).2.Types, Variables, Constants, OperatorsNames in Fortran 90A name or “identifier” in Fortran must adhere to fixed rules. They cannot be longer than31 characters, must be composed of alphanumeric characters (all the letters of the alphabet, and the digits 0 to 9) and underscores ( _ ), and the first character must be a letter. Identifiers are case-insensitive (except in character strings like “Hello world!” in the example above); Thus, PRINT and print are completely identical.TypesA variable is a data object whose value can be defined and redefined (in contrast to constants, see below). Variables and constants have a type, which can be one of the five intrinsic types, or a derived type. Intrinsic types are part of the Fortran language. There are five different intrinsic types. In Fortran 90, there is additionally the possibility of defining derived types, which are defined by the user (see below). The five intrinsic types are:Integer TypeFor integer values (like 1, 2, 3, 0, -1, -2, …).Real TypeFor real numbers (such as 3.14, -100.876, 1.0 etc.). A processor must provide two different real types: The default real type and a type of higher precision, with the name double precision. Also this is a legacy of FORTRAN 77. Fortran 90 gives much more control over the precision of real and integer variables (through the kind specifier), see chapter on Numeric Precision, and there is therefore no need to use double precision. However, you will see double precision often used in older programs. For most of the exercises and examples in this manual the real type suffices. In the real word however, double precision is often required.For now, if you prefer to use double precision in your programs, use:real (kind=kind(1.0d0)) :: variable_nameComplex TypeFor complex numbers. A complex value consists of two real numbers, the real part and the imaginary part. Thus, the complex number (2.0, -1.0) is equal to 2.0 – 1.0i. Logical TypeThere are only two logical values: .true. and .false. (note the dots around the words true and false).Character TypeData objects of the character type include characters and strings (a string is a sequence of characters). The length of the string can be specified by len (see the examples below). If no length is specified, it is 1.ConstantsA constant is a data object whose value cannot be changed.A literal constant is a constant value without a name, such as 3.14 (a real constant), “Tanja” (a character constant), 300 (an integer constant), (3.0, -3.0) (a complex constant), .true. or .false. (logical constants. These two are the only logical constants available).A named constant is a constant value with a name. Named constants and variables must be declared at the beginning of a program (or subprogram – see Chapter 4), in a so-called type declaration statement. The type declaration statement indicates the type and name of the variable or constant (note the two colons between the type and the name of the variable or constant). Named constants must be declared with the parameter attribute: real, parameter :: pi = 3.1415927VariablesLike named constants, variables must be declared at the beginning of a program (or subprogram) in a type declaration statement:integer :: totalreal :: average1, average2 ! this declares 2 real valuescx::complexlogical :: donecharacter(len=80) :: line ! a string consisting of 80 charactersThese can be used in statements such as:total = 6.7average1 = average2done = .true.line = “this is a line”Note that a character string is enclosed in double quotes (“).Constants can be assigned trivially to the complex number cx:cx = (1.0, 2.0) ! cx = 1.0 + 2.0iIf you need to assign variables to cx, you need to use cmplx:cx = cmplx (1.0/2.0, -3.0) ! cx = 0.5 – 3.0icx = cmplx (x, y) ! cx = x + yiThe function cmplx is one of the intrinsic functions (see below).ArraysA series of variables of the same type can be collected in an array. Arrays can be one-dimensional (like vectors in mathematics), two-dimensional (comparable to matrices), up to 7-dimensional. Arrays are declared with the dimension attribute.Examples:real, dimension(5) :: vector ! 1-dim. real array containing 5 elements integer, dimension (3, 3) :: matrix ! 2-dim. integer arrayThe individual elements of arrays can be referenced by specifying their subscripts. Thus, the first element of the array vector, vector(1), has a subscript of one. The array vector contains the real variables vector(1), vector(2), vector(3), vector(4), and vector(5). The array matrix contains the integer variables matrix(1,1), matrix(2,1), matrix(3,1),matrix(1,2), ..., matrix(3,3):The array vector could also have been declared with explicit lower bounds: real, dimension (1:5) :: vectorAll the following type declaration statements are legal:real, dimension (-10:8) :: a1 ! 1-dim array with 19 elementsinteger, dimension (-3:3, -20:0, 1:2, 6, 2, 5:6, 2) :: grid1 ! 7-dim array The number of elements of the integer array grid1 is 7 x 21 x 2 x 6 x 2 x 2 x 2 = 14112. You may not be able to use arrays with more than 7 dimensions. The standard requires that a compiler supports up to 7-dimensional arrays. A compiler may allow more than 7 dimensions, but it does not have to.Character stringsThe elements of a character string can be referenced individually or in groups.With:character (len=80) :: namename = “Tanja”Thenname(1:3) would yield the substring “Tan”A single character must be referenced in a similar way:name(2:2) yields the character “a”If the lower subscript is omitted, it is assumed to be one, and if the upper subscript is omitted, it is supposed to be the length of the string.Thus:name (:3)! yields “Tan”name (3:)! yields “nja”name (:)! yields “Tanja”Implicit typingFortran allows implicit typing, which means that variables do not have to be declared. If a variable is not declared, the first letter of its name determines its type: if the name of the variable starts with i, j, k, l, m, or n, it is considered to be an integer, in all other cases it is considered to be a real. However, it is good programming practice to declare all variables at the beginning of the program. The statementimplicit noneturns off implicit typing. All programs should start with this statement. (Implicit typing is not allowed in the F language).Derived data typesWe have seen that the Fortran language contains 5 intrinsic types (integer, real, complex, logical, and character). In addition to these, the user can define derived types, which can consist of data objects of different type.An example of a derived data type:type :: atomcharacter (len=2) :: labelreal :: x, y, zend type atomThis type can hold a 2-character atom name, as well as the atom’s xyz coordinates.An object of a derived data type is called a structure. A structure of type atom can be created in a type declaration statement like:::carbon1type(atom)The components of the structure can be accessed using the component selector character (%):carbon1%label = “C”carbon1%x = 0.0000carbon1%y = 1.3567carbon1%z = 2.5000Note that no spaces are allowed before and after the %!One can also make arrays of a derived type:type(atom), dimension (10) :: moleculeand use it likemolecule(1)%type = “C”Arithmetic operatorsThe intrinsic arithmetic operators available in Fortran 90 are:======================** exponentiation======================* multiplication/division======================addition+− subtraction======================These are grouped in order of precedence, thus, * has a higher precedence than +. The precedence can be overridden by using parentheses. For example:3 * 2 + 1yields 7, but3 * (2+1)yields 9.For operators of equal strength the precedence is from left to right. For example:a *b / cIn this statement, first a and b are multiplied, after which the results is divided by c. The exception to this rule is exponentiation:2**2**3is evaluated as 2**8, and not as 4**3.Numeric expressionsAn expression using any of the arithmetic operators (**, *, /, +, -), like the examples in the previous section, is called a numeric expression.Be careful with integer divisions! The result of an integer division, i.e., a division in which the numerator and denominator are both integers, is an integer, and may therefore have to be truncated. The direction of the truncation is towards zero (the result is the integer value equal or just less than the exact result):3/2 yields1–1-3/2 yields93**2 yields3**(-2) equals1/3**2, which yields 0Sometimes this is what you want. However, if you do not want the result to be truncated, you can use the real function. This function converts its argument to type real. Thus, real(2) yields a result of type real, with the value 2.0.With the examples from above:1.5real(2)/3 yields1.52/real(3) yields–1.5-2/real(3) yieldsreal(3)**-2yields 0.1111111111 (which is 1/9)However:real(2/3)yields 0 (the integer division is performed first, yielding 0, which is then converted to a real.)Note that the function real can have 2 arguments (see the table in the section on intrinsic functions, below). The second argument, an integer specifying the precision (kind value) of the result, is however optional. If not specified, the conversion will be to default precision. Kind values will be discussed later.Numeric expressions can contain operands of different type (integer, real, complex). If this is the case, the type of the “weaker” operand will be first converted to the “stronger” type. (The order of the types, from strong to weak, is complex, real, integer.) The result will also be of the stronger type.If we consider the examples above again, inreal(2)/3The integer 3 is first converted to a real number 3.0 before the division is performed, and the result of the division is a real number (as we have seen).Logical operatorsThe type logical can have only two different values: .true. and .false. (note the dots around the words true and false). Logical variables can be operated upon by logical operators. These are (listed in decreasing order of precedence):==================.not..and..or..eqv. and .neqv.==================The .and. is “exclusive”: the result of a .and. b is .true. only if the expressions a and b are both true. The .or. is “inclusive”: the result of a .or. b is .false. only if the expressions a and b are both false. Thus, if we have the logical constants:parameter :: on = .true.logical,logical,parameter :: off = .false.Then:.not. on ! equals .false..not. off ! equals .true.on .and. on ! equals .true.on .and. off ! equals .false.off .and. off ! equals .false.on .or. on ! equals .true.on .or. off ! equals .true.off .or. off !equals .false.on .eqv. on ! equals .true.on .eqv. off ! equals .false.off .eqv. off ! equals .true.on .neqv. on !equals .false.on .neqv. off ! equals .true.off .neqv. off ! equals .false.Relational operatorsRelational operators are operators that are placed between expressions and that compare the results of the expressions. The relational operators in Fortran 90 are:==============================than< less<=less than or equal tothan> greater>=greater than or equal toto== equalto/= notequal==============================Logical expressionsExpressions that use the relational operators are logical expressions. The values of logical expressions can be either .true. or .false. Note that the range of numerical numbers in Fortran ranges from the largest negative number to the largest positive number (thus, -100.0 is smaller than 0.5).A few examples:real :: val1, val2logical :: resultval1 = -3.5val2 = 2.0result = val1 < val2 ! result equals .true.result = val1 >= val2 ! result equals .false.result = val1 < (val2 – 2.0) ! result equals .true.Be careful though with comparing real numbers. Reals are represented with finite accuracy. Thus:print*, 2 * 3.2may give as output: 6.4000001. So instead of comparing two real variables a and b like: a== bit is safer to compare their difference:real, parameter :: delta = 0.000001abs(a-b) < delta ! equals .true. if a and b are numerically identical The function abs returns the absolute value of (a-b).Intrinsic functionsIntrinsic functions are functions that are part of the language. Fortran, as a scientific language aimed at numerical applications, contains a large number of mathematical functions.The mathematical functions are:============================================inverse cosine (arc cosine) function(x)acosasin (x)inverse sine (arc sine) function(x) inverse tangent (arc tangent) functionatanatan2 (x)arc tangent for complex numbersfunctioncos (x) cosinecosh (x)hyperbolic cosine functionfunctionexp (x) exponentiallog (x)natural logarithm functionlog10 (x)common logarithm functionfunctionsin (x) sinesinh (x)hyperbolic sine functionsqrt (x)square root functionfunctiontan (x) tangenttanh (x)hyperbolic tangent function============================================Some other useful intrinsic functions are:=============================================================== abs (x)absolute value of the numerical argument xcomplx (x,y [, ikind])convert to complex. The ikind argument is optional. Ifnot specified, the conversion is to default precision.floor (x) greatest integer less than or equal to x. Examples: floor(3.4) equals 3, floor (-3.4) equals –4.int (x)convert to integer. If abs (x < 1), the result is 0. If abs(x) >= 1, the result is the largest integer not exceeding x(keeping the sign of x). Examples: int(0.3) equals 0, int (-0.3) equals 0, int (4.9) equals 4, int (-4.9) equals –4.nint (x [, ikind])rounds to nearest integer.real (x [, ikind]) convert to real. The ikind argument is optional. If notspecified, the conversion is to default precision.mod (a,p)remainder function. Result is a – int (a/p) * p. Thearguments a and p must be of the same type (real orinteger).modulo (a,p) modulo function. Result is a – floor (a/p) * p. Thearguments a and p must be of the same type (real orinteger).============================================================== Simple in- and outputAs we have seen in the hello.f90 program above, characters can be displayed on the screen by the print* statement. Data can be transferred into the program by the read* statement. This is the simplest form of input/output (I/O), called list-directedinput/output. As an example, with pi being declared as in the previous section, the statementprint*, “The number pi = “, pimight appear on the screen asThe number pi = 3.141590The exact format is dependent on the computer system used. Later we will see a more sophisticated form of I/O, using read and write, which gives the programmer more control over the format.The following read statement (with x, y, and z being declared as variables of type real) read*, x, y, zexpects three numbers to be typed, separated by a comma, one or more spaces, or a slash (/). The variable x will have the value of the first number typed, y will have the value of the second number typed, and z of the third number typed.CommentsWe have already seen the exclamation mark (!). All characters after the exclamationmark are ignored. Comments can be used for descriptive purposes, or for “commenting out” a line of code.Continuation linesThe maximum length of a Fortran statement is 132 characters. Sometimes statements are so long that they don’t fit on one line. The continuation mark (&), placed at the end ofthe line, allows the statement to continue on the next line. Fortran 90 allows a maximumof 39 continuation lines.Thus, the following codecos (alpha) = b*b + c*c – &2*b*c*cos (gamma)is identical tocos (alpha) = b*b + c*c – 2*b*c*cos (gamma)Summary• A program starts with program program_name and ends with end program program_name.•The first statement should always be implicit none.•We have learned the different types of variables and constants in Fortran: integer, real, complex, logical and character, and how to declare them in typedeclaration statements.•The arithmetic operators: **, *, /, + and -.•The logical operators: .not., .and., .or., .eqv., and .neqv.•The relational operators: <, <=, >, >=, == and /=.•We learned the mathematical functions, and a selection of other intrinsic functions.•We learned how to read in variables and how to write to the screen.Exercises1.Which of the following are valid names in Fortran 90:a.this_is_a_variableb.3dimc.axis1d.y(x)f.DotComg.z axis2.Write a program that reads in a number, and computes the area of a circle that has adiameter of that size.3.Find out, for your compiler, what the compiler flags are for displaying warningmessages, and for issuing a warning when the compiler encounters non-standard source code.4.Write a program that reads in a time in seconds, and computes how many hours andminutes it contains. Thus, 3700 should yield: 1 hour, 1 minute, and 40 seconds.(Hint: use the mod function).3.Control ConstructsControl ConstructsA program can consist of several statements, which are executed one after the other:program program_nameimplicit nonestatement1statement2statement3statement4program_nameendHowever, this rigid sequence may not suit the formulation of the problem very well. For example, one may need to execute the same group of statements many times, or two different parts of the program may need to be executed, depending on the value of a variable. For this, Fortran 90 has several constructs that alter the flow through the statements. These include if constructs, do loops, and case constructs.If constructs:The simplest form of an if construct is:if (logical expression) thenstatementifendas in:if (x < y) thenx = yifendThe statement x = y is only executed if x is smaller than y.Several statements may appear after the logical expression. The if block can also be given a name, so the more general form of the if construct is:[name:] if (logical expression) then! various statements...end if [name]Both endif and end if are allowed. The name preceding the if is optional (but if it is specified, the name after the endif must be the same).The block if statement can also contain an else block:[name:] if (logical expression) then! various statements...else! some more statements...end if [name]Block if statements can be nested:[name:] if (logical expression 1) then! block 1else if (logical expression 2) then! block 2else if (logical expression 3) then! block 3else! block 4end if [name]Example (try to follow the logic in this example):if ( optimisation ) thenprint*, "Geometry optimisation: "if ( converged ) thenprint*, "Converged energy is ", energyelseprint*, "Energy not converged. Last value: ", energyend ifelse if (singlepoint ) thenprint*, "Single point calculation: "print*, "Energy is ", energyelseprint*, "No energy calculated."end ifIndentation is optional, but highly recommended: a consistent indentation style helps to keep track of which if, else if, and end if belong together (i.e., have the same “if level”). Do loopsA program often needs to repeat the same statement many times. For example, you may need to sum all elements of an array.You could write:real, dimension (5) :: array1real :: sum! here some code that fills array1 with numbers...sum = array1(1)sum = sum + array1(2)sum = sum + array1(3)sum = sum + array1(4)sum = sum + array1(5)But that gets obviously very tedious to write, particularly if array1 has many elements. Additionally, you may not know beforehand how many times the statement or statements need to be executed. Thus, Fortran has a programming structure, the do loop, which enables a statement, or a series of statements, to be carried out iteratively.For the above problem, the do loop would take the following form:real, dimension (5) :: array1real :: suminteger :: i ! i is the “control variable” or counter! here some code that fills array1 with numbers...sum = 0.0 ! sum needs to be initialised to zerodo i = 1, 5sum = sum + array1(i)doendBoth enddo and end do are allowed.It is possible to specify a name for the do loop, like in the next example. This loop prints the odd elements of array2 to the screen. The name (print_odd_nums in this case) is optional. The increment 2 specifies that the counter i is incremented with steps of 2, and therefore, only the odd elements are printed to the screen. If no increment is specified, it is 1.real, dimension (100) :: array2integer :: i! here some code that fills array2 with numbers...print_odd_nums:do i = 1, 100, 2print*, array2(i)end do print_odd_numsDo loops can be nested (one do loop can contain another one), as in the following example:real, dimension (10,10) :: a, b, c ! matricesinteger :: i, j, k! here some code to fill the matrices a and b...! now perform matrix multiplication: c = a + bdo i = 1, 10do j = 1, 10c(i, j) = 0.0do k = 1, 10c(i, j) = c(i, j) + a(i, k) + b(k, j)end doend dodoendNote the indentation, which makes the code more readable.Endless DoThe endless do loop takes the following form:do[doname:]! various statementsexit [doname]! more statementsend do [doname]Note the absence of the control variable (counter). As before, the name of the do loop is optional (as indicated by the square brackets).To prevent the loop from being really “endless”, an exit statement is needed. If the exit statement is executed, the loop is exited, and the execution of the program continues at the first executable statement after the end do.The exit statement usually takes the formif (expression) thenexitend if。
Fortran 90标准库函数

FORTRAN90标准库函数
符号约定:
l I代表整型;R代表实型;C代表复型;CH代表字符型;S代表字符串;L代表逻辑型;A代表数组;P代表指针;T代表派生类型;AT为任意类型。
l s:P表示s类型为P类型(任意kind值)。
s:P(k)表示s类型为P类型(kind值=k)。
l […]表示可选参数。
l *表示常用函数。
表1 数值和类型转换函数
表2 三角函数
注:三角函数名前有C、D的函数为复数、双精度型函数。
表3 指数、平方根和对数函数
注:指数函数名、平方根函数名、对数函数名前有C、D的函数为复数、双精度型函数。
表4 参数查询函数
表5 实数检测和控制函数
表6 字符处理函数
表7 二进制位操作函数
表8 数组运算、查询和处理函数
注: 参数m指逻辑型掩码数组,指明允许操作的数组元素。
缺省掩码数组指对数组所有元素进行操作。
Fortran90-marc必备

REM 让marc自定义子程序支持f90REM 请将本run_marc.bat文件copy到marc安装目录下tools文件夹REM 作者:阚前华REM *.bat清单:REM######################################################################## @echo offsetlocalfor %%i in (%0) do set DIR=%%~dpiif exist "%DIR%\..\tools\include.bat" goto full_pathfor %%i in (run_marc.bat) do set DIR=%%~dp$PATH:i:full_pathREM if edited in here by user, the path must include the drive letterset DIR=%DIR%..CALL "%DIR%\tools\include.bat"REMREM ######################################################################### REMREM run_marc - run a marc jobREM -------------------------REMREM usage: run_marc -j jid { options }REMREM where options are:REMREM -j jid job id number.REM -pr prog program name (saved user subroutine executable)REM -r rid restart file job id.REM -si sid substructure file id.REM -pi post post file job id.REMREM -u user user subroutine.REM -sa y|n do or do not save load module: defaults to noREM -au y|n use auto restart feature: defaults to noREM Auto restart control stops the analysis, runsREM a mesher to remesh and restarts the analysisREM Windows NT only. Used for DCOM server support.REM -nprocd number of tasks for domain decomposition.REM -nthread number of threads per task.REM -itree message passing tree for domain decomposition.REM -de defaults file.REM -vf viewfactor file.REM -host host file: defaults to localREM -me manual remeshing controlREM -ma maxall parameter. overrides value given in include fileREM -pc remote computer name: defaults to local. Windows NT only.REM Used for DCOM server support.REM -dir sets the current directory. this is where the jobREM i/o takes place. defaults to current directoryREM -sdir sets the scratch directory. this is where scratchREM files for the job are created. defaults to currentREM directoryREM -dcoup contact decoupling used for Superform problem withREM deformable toolsREMREM -alloc only perform memory allocation test, no analysisREMREM -dytran flag to switch from Dytran to MarcREM dytran = 0,program will run without Marc-Dytran switch.REM = 1,program will restart Marc after Dytran run.REM >= 2,Not supported yet.REM -dytran is not supported for MSC.Marc2003REMREM ######################################################################## REM V ariables for the MARC environmentSET EXITMSG=%DIR%\tools\MESSAGESSET AFMATDAT=%DIR%\AF_flowmat\rem: define path to global unified material databaseSET MATFILE=REM set PATH to include Patran mesh dynamic librarySET PA TH=%DIR%\lib;%PATH%REM defaultsset prog=marcset jid=set pid=set rid=set sid=set did=set vid=set dirjid=set dirpid=set dirrid=set dirsid=set dirdid=set dirvid=set user=set userdir=set qid=yrem set priority=set att=set pid=set prgsav=nset error=set nprocd=0set nthread=0set itree=0set iam=set nthreadmax=0set marclink=set nauto=0set ndcoup=0set ndytran=0set host=set userhost=set cpinput=yset cpresults=yset dist=nset mesh=0set mach=set cmdline=set jidlog=set dcomserver=set dotdat=.datset dirscrset=rem initialize dirjob and dirscr to current directoryfor /f "delims== " %%i in ( 'cd' ) do set curdir=%%iset dirjob=%curdir%if exist "%dir%\bin\run_marc_read.exe" goto run_marc_readecho error, programecho %dir%\bin\run_marc_read.exeecho which reads the command line options does not existgoto end_of_file:run_marc_readrem first run %dirjob%\ through run_marc_read with -j as dummy rem argument to strip off backslash in case job is run in for instance c:\call "%dir%\bin\run_marc_read.exe" -j "%dirjob%"\ > .\run_marc_read.batcall .\run_marc_read.batset dirjob=%value2%set dirscr=%dirjob%rem scratch directory can be specified via environmental variablerem MARCSCRATCHif "%MARCSCRATCH%"=="" goto nomarcscratchif exist %MARCSCRA TCH% goto marcscratchexistsecho.echo error, scratch directory "%MARCSCRATCH%"echo specified via environmental variable MARCSCRATCH does not existgoto end_of_file:marcscratchexistsset dirscr=%MARCSCRATCH%:nomarcscratchREM########################################################################### REM parse input - arguments always come in pairs # REM###########################################################################set arg=%1if not "%arg%"=="" goto no_arg_endset error=no input parameters specifiedgoto read_arg_error:no_arg_endset cmdline=%1:read_arg_begshiftset cmdline=%cmdline% %1if "%arg%"=="-al" goto al_end1if not "%arg%"=="-alloc" goto al_end:al_end1rem just run marc with -alloc option"%BINDIR%\marc.exe" -alloc 1goto end_of_file:al_endset value=%1if "%arg%" =="" goto read_arg_endif not "%error%"=="" goto read_arg_errorcall "%dir%\bin\run_marc_read.exe" %arg% %value% > .\run_marc_read.bat call .\run_marc_read.batif not "%arg%"=="-pr" goto pr_endset prog=%value%goto read_new:pr_endif not "%arg%"=="-j" goto j_endset jid=%value%set dirjid=%value2%if "%dirjid%"=="" set dirjid=%curdir%goto read_new:j_endif not "%arg%"=="-pi" goto pi_endset pid=%value%set dirpid=%value2%if "%dirpid%"=="" set dirpid=%curdir%goto read_new:pi_endif not "%arg%"=="-r" goto r_endset rid=%value%set dirrid=%value2%if "%dirrid%"=="" set dirrid=%curdir%goto read_new:r_endif not "%arg%"=="-si" goto si_endset sid=%value%set dirsid=%value2%if "%dirsid%"=="" set dirsid=%curdir%goto read_new:si_endif not "%arg%"=="-de" goto de_endset did=%value%set dirdid=%value2%if "%dirdid%"=="" set dirdid=%curdir% goto read_new:de_endif not "%arg%"=="-vf" goto vf_end set vid=%value%set dirvid=%value2%if "%dirvid%"=="" set dirvid=%curdir% goto read_new:vf_endif not "%arg%"=="-u" goto u_end set user=%value%set userdir=%value2%goto read_new:u_endif not "%arg%"=="-sa" goto sa_end set prgsav=%value%goto read_new:sa_endif not "%arg%"=="-np" goto np_end set nprocd=%value%goto read_new:np_endif not "%arg%"=="-nt" goto nt_end set nthread=%value%goto read_new:nt_endif not "%arg%"=="-ia" goto iam_end set iam=%value%goto read_new:iam_endif not "%arg%"=="-it" goto it_end set itree=%value%goto read_new:it_endif not "%arg%"=="-b" goto b_endset qid=%value%rem qid is checked and reset belowgoto read_new:b_endif not "%arg%"=="-ho" goto ho_end set host=%value%set userhost=%value%goto read_new:ho_endif not "%arg%"=="-au" goto au_end set nauto=%value%goto read_new:au_endif not "%arg%"=="-dcoup" goto dcoup_end set ndcoup=%value%goto read_new:dcoup_endif not "%arg%"=="-me" goto me_end set mesh=%value%goto read_new:me_endif not "%arg%"=="-ma" goto ma_end set maxsize=%value%goto read_new:ma_endif not "%arg%"=="-ci" goto ci_end set cpinput=%value%goto read_new:ci_endif not "%arg%"=="-cr" goto cr_end set cpresults=%value%goto read_new:cr_endif not "%arg%"=="-di" goto di_end set dirjob=%1if "%dirscrset%"=="" set dirscr=%dirjob%goto read_new:di_endif not "%arg%"=="-sd" goto sd_endset dirscr=%1set dirscrset=yesgoto read_new:sd_endif not "%arg%"=="-pc" goto pc_endset mach=%1set qid=ngoto read_new:pc_endif not "%arg%"=="-dy" goto dytran_endset ndytran=%value%goto read_new:dytran_endREM -server option only set by the marcsvr.exe program if not "%arg%"=="-se" goto se_endset dcomserver=%1set qid=%value%goto read_new:se_endif "%arg%"=="-v" goto read_newif "%arg%"=="-ve" goto read_newif "%arg%"=="-co" goto read_newif "%arg%"=="-q" goto read_newset error=no such option: %arg% or input value: %value% goto read_arg_error:read_newshiftset arg=%1set cmdline=%cmdline% %1goto read_arg_beg:read_arg_endif "%nprocd%"=="1" set nprocd=0set nthreadmax=%nthread%if not "%nthreadmax%"=="0" goto nthreadmax_endset nthreadmax=1if not "%nprocd%"=="0" set nthreadmax=%nprocd%:nthreadmax_endREM ########################################################################## REM check parameter validity # REM ########################################################################## REMREM check for input file existenceREMif not "%mach%" == "" goto run_dcomrem if "%nprocd%"=="0" goto host_endif "%host%"=="" goto host_endif not exist "%host%" goto host_not_existREM Count the number of cpus. If only one, thenREM this is the DCOM server host to connect with.set /A MCOUNT=0for /f "tokens=1,2 delims= " %%i in (%host%) do (set mach=%%iset /A MCOUNT+=%%j)if not %MCOUNT% == 1 goto host_endgoto run_dcomrem if exist "%host%" goto host_end:host_not_existset error=file %host% does not existgoto read_arg_error:host_endset testfile=%dirjid%\%jid%%dotdat%if not "%nprocd%"=="0" set testfile=%dirjid%\1%jid%%dotdat%if exist "%testfile%" goto dat_endset error=file "%testfile%" does not existgoto read_arg_error:dat_endREMREM assume that "program" is a program in the users local directory REMset MDSRCLIB=mdsrc.libset bd=%BINDIR%\if not "%prog%"=="marc" goto marc_endset program=marc.exeset prefix=if not "%nprocd%"=="0" set prefix=1if not "%nprocd%"=="0" goto parallelrem check if single processor executable existsif exist %bd%\marcs.exe set program=marcs.exeif exist %bd%\marcs.exe set MDSRCLIB=mdsrcs.lib:parallelif "%pid%"=="" goto mt16_endif exist "%dirpid%\%pid%.t16" goto mt16_endif exist "%dirpid%\%pid%.t19" goto mt16_endset error=file %dirpid%\%pid%.t16/t19 does not existgoto read_arg_error:mt16_endif "%rid%"=="" goto mt08_endif exist "%dirrid%\%rid%.t08" goto mt08_endset error=file %dirrid%\%rid%.t08 does not existgoto read_arg_error:mt08_endif "%did%"=="" goto mt49_endif exist "%dirdid%\%prefix%%did%%dotdat%" goto mt49_end set error=file %dirdid%\%prefix%%did%%dotdat% does not exist goto read_arg_error:mt49_endif "%vid%"=="" goto mt50_endif exist "%dirvid%\%prefix%%vid%.vfs" goto mt50_endset error=file %dirvid%\%prefix%%vid%.vfs does not existgoto read_arg_error:mt50_endif "%user%"=="" goto param_val_endif exist "%userdir%\%user%.f90" goto param_val_endif exist "%userdir%\%user%.f" goto param_val_endset error=user routine %userdir%\%user% does not existgoto read_arg_error:marc_endset program=%prog%.exeset bd=set prefix=if not "%nprocd%"=="0" set prefix=1if "%rid%"=="" goto prt08_endif exist "%dirrid%\%rid%.t08" goto prt08_endset error=file %dirrid%\%rid%.t08 does not existgoto read_arg_error:prt08_endif "%pid%"=="" goto prt16_endif exist "%dirpid%\%prefix%%pid%.t16" goto prt16_endif exist "%dirpid%\%prefix%%pid%.t19" goto prt16_endset error=file %dirpid%\%prefix%%pid%.t16/t19 does not existgoto read_arg_error:prt16_endif "%did%"=="" goto prt49_endif exist "%dirdid%\%prefix%%did%%dotdat%" goto prt49_endset error=file %dirdid%\%prefix%%did%%dotdat% does not existgoto read_arg_error:prt49_endif "%vid%"=="" goto prt50_endif exist "%dirvid%\%prefix%%vid%.vfs" goto prt50_endset error=file %dirvid%\%prefix%%vid%.vfs does not existgoto read_arg_error:prt50_endif exist "%bd%%prog%.exe" goto param_val_endset error=user program %bd%%prog%.exe does not existgoto read_arg_error:param_val_endREM #########################################################################REM check argument integrity # REM #########################################################################if exist "%dirjob%" goto dirjob_existsecho.echo error, run directory "%dirjob%"echo does not existgoto end_of_file:dirjob_existsif exist "%dirscr%" goto dirscr_existsecho.echo error, scratch directory "%dirscr%"echo does not existgoto end_of_file:dirscr_existsif not "%jid%"=="" goto jid_endset error=job id requiredgoto read_arg_error:jid_endif not "%qid%"=="n" goto qid_yesset qid=foregroundgoto qid_end:qid_yesif not "%qid%"=="y" goto qid_noneset qid=backgroundgoto qid_end:qid_noneset error=bad value for background option; valid options are "yes" and "no"goto read_arg_error:qid_endif not "%prgsav%"=="n" goto prgsave_yesset prgsav=nogoto prgsave_end:prgsave_yesif not "%prgsav%"=="y" goto prgsave_noneset prgsav=yesgoto prgsave_end:prgsave_noneset error=bad value for save option; valid options are "yes" and "no"goto read_arg_error:prgsave_endif not "%dist%"=="y" goto dist_noset dist=yesgoto dist_end:dist_noif not "%dist%"=="n" goto dist_noneset dist=goto dist_end:dist_noneset error=bad value for distributed option; valid options are "yes" and "no"goto read_arg_error:dist_endrem check that jobname and restart job name are not the sameif "%rid%"=="" goto rid_endif not "%rid%"=="%jid%" goto rid_endset error=job id is the same as restart job idgoto read_arg_error:rid_endgoto print_beg:read_arg_errorecho read error: %error%goto run_marc_exitREM ######################################################################### REM print informationREM #########################################################################:print_begset jidlog=%jid%.logif "%dcomserver%" == "y" set jidlog=%dirjid%\%jid%.logif exist "%jidlog%" erase "%jidlog%"if "%qid%"=="background" goto printbackecho MSC.Marc %REVISION% %MACHINE% versionecho --------------------------------echo :echo Program name : %prog%echo Job ID : %jid%echo User subroutine name : %user%echo Restart file job ID : %rid%echo Substructure file ID : %sid%echo Post file job ID : %pid%echo Defaults file ID : %did%echo View factor file ID : %vid%echo Save generated module: %prgsav%echo Auto restart : %nauto%echo Contact decoupling : %ndcoup%REM echo Marc-Dytran Switch : %ndytran%echo Number of tasks : %nprocd%echo Host file : %host%echo Distributed i/o : %dist%echo Run directory : %dirjob%echo Scratch directory : %dirscr%echo Default bin directory: %BINDIR%echo Material database : %afmatdat%echo :goto printend:printbackecho MSC.Marc %REVISION% %MACHINE% version >> %jidlog% echo -------------------------------- >> %jidlog%echo : >> %jidlog%echo Program name : %prog% >> %jidlog%echo Job ID : %jid% >> %jidlog%echo User subroutine name : %user% >> %jidlog%echo Restart file job ID : %rid% >> %jidlog%echo Substructure file ID : %sid% >> %jidlog%echo Post file job ID : %pid% >> %jidlog%echo Defaults file ID : %did% >> %jidlog%echo View factor file ID : %vid% >> %jidlog%echo Save generated module: %prgsav% >> %jidlog%echo Auto restart : %nauto% >> %jidlog%echo Contact decoupling : %ndcoup% >> %jidlog%REM echo Marc-Dytran Switch : %ndytran% >> %jidlog%echo Number of tasks : %nprocd% >> %jidlog%echo Host file : %host% >> %jidlog%echo Distributed i/o : %dist% >> %jidlog%echo Run directory : %dirjob% >> %jidlog%echo Scratch directory : %dirscr% >> %jidlog%echo Default bin directory: %BINDIR% >> %jidlog%echo Material database : %afmatdat% >> %jidlog%echo : >> %jidlog%:printendREMREM user subroutine usedREMif "%user%"=="" goto user_program_endset program=%user%.exeset bd=set marclink=yes:user_program_endif "%prog%"=="marc" goto program_endset bd=:program_endREMREM set executable nameREMset execnm=%bd%%program%if "%nprocd%"=="0" goto hostfile_endREMREM make reasonable attempt to create UNC informationREM if tools\ file does not exist. if UNC namesREM cannot be created, create network drive information.REM put UNC and drive information into marc.drive file.REMif "%host%"=="" goto netinfo_endset run_marc_path=if exist "%dirjob%\" set run_marc_path=%dirjob%\ if exist "%dir%\tools\" set run_marc_path=%dir%\tools\ if exist "%run_marc_path%" goto netinfo_endnet share > "%dirjob%\"if exist "%dirjob%\" set run_marc_path=%dirjob%\if exist "%run_marc_path%" goto netinfo_endrem echo error: check that marc installation directory is sharedrem echo error: check that tools\ file is currentrem goto run_marc_exit:netinfo_endREMREM create marc.drive to contain plus network driveREM information.REMif "%host%"=="" goto netuse_endtype "%run_marc_path%" > "%dirjob%\marc.drive"net use >> "%dirjob%\marc.drive"if exist "%dirjob%\marc.drive" set run_marc_path=%dirjob%\marc.drive:netuse_endREMREM find sharename of executable path based onif "%host%"=="" goto defaultsh_endif exist run_marc_unc.bat erase run_marc_unc.batif "%prog%"=="marc" set execnm=%dir%if not "%prog%"=="marc" set execnm=%dirjob%if not "%user%"=="" set execnm=%dirjob%set execshare=%execnm%call "%dir%\bin\run_marc_unc.exe" "%run_marc_path%" "run_marc_unc.bat" "%execnm%" "%hostname%" "execshare" "1"if exist run_marc_unc.bat call .\run_marc_unc.bat:defaultsh_endREMREM find sharename of input files if current path is standard pathREM or network drive based.REM if UNC or network drive name not find, use default working directory.REMif "%host%"=="" goto dirshare_endif "%dist%"=="yes" goto dirshare_endif exist run_marc_unc.bat erase run_marc_unc.batcall "%dir%\bin\run_marc_unc.exe" "%run_marc_path%" "run_marc_unc.bat" "%dirjob%" "%hostname%" "dirjob" "1"if exist run_marc_unc.bat call .\run_marc_unc.batREM dirjidif exist run_marc_unc.bat erase run_marc_unc.batcall "%dir%\bin\run_marc_unc.exe" "%run_marc_path%" "run_marc_unc.bat" "%dirjid%" "%hostname%" "dirjid" "1"if exist run_marc_unc.bat call .\run_marc_unc.batREM dirpidif "%dirpid%"=="" goto end_unc_pidif exist run_marc_unc.bat erase run_marc_unc.batcall "%dir%\bin\run_marc_unc.exe" "%run_marc_path%" "run_marc_unc.bat" "%dirpid%" "%hostname%" "dirpid" "1"if exist run_marc_unc.bat call .\run_marc_unc.bat:end_unc_pidREM dirridif "%dirrid%"=="" goto end_unc_ridif exist run_marc_unc.bat erase run_marc_unc.batcall "%dir%\bin\run_marc_unc.exe" "%run_marc_path%" "run_marc_unc.bat" "%dirrid%" "%hostname%" "dirrid" "1"if exist run_marc_unc.bat call .\run_marc_unc.bat:end_unc_ridREM dirsidif "%dirsid%"=="" goto end_unc_sidif exist run_marc_unc.bat erase run_marc_unc.batcall "%dir%\bin\run_marc_unc.exe" "%run_marc_path%" "run_marc_unc.bat" "%dirsid%" "%hostname%" "dirsid" "1"if exist run_marc_unc.bat call .\run_marc_unc.bat:end_unc_sidREM dirdidif "%dirdid%"=="" goto end_unc_didif exist run_marc_unc.bat erase run_marc_unc.batcall "%dir%\bin\run_marc_unc.exe" "%run_marc_path%" "run_marc_unc.bat" "%dirdid%" "%hostname%" "dirdid" "1"if exist run_marc_unc.bat call .\run_marc_unc.bat:end_unc_didREM dirvidif "%dirdid%"=="" goto end_unc_vidif exist run_marc_unc.bat erase run_marc_unc.batcall "%dir%\bin\run_marc_unc.exe" "%run_marc_path%" "run_marc_unc.bat" "%dirvid%" "%hostname%" "dirvid" "1"if exist run_marc_unc.bat call .\run_marc_unc.bat:end_unc_vid:dirshare_endremrem read user host file to see if working directory specifiedrem in host file. translate user hostfile.remif "%host%"=="" goto userhost_endif "%prog%"=="marc" set execnm=%execshare%\bin\marc.exe & set usub=0if not "%prog%"=="marc" set execnm=%execshare%\%program% & set usub=1if not "%user%"=="" set execnm=%execshare%\%program% & set usub=1if exist "%jid%.host" erase "%jid%.host"if %MPITYPE%==patent call "%dir%\bin\run_marc_host.exe" "%nprocd%" "%host%" "%jid%.host" "%execnm%" "%hostname%" "%program%" "%usub%" "%dirjob%"if %MPITYPE%==mpich call "%dir%\bin\run_marc_mpich.exe" "%nprocd%" "%host%" "%jid%.host" "%execnm%" "%hostname%" "%program%" "%usub%" "%dirjob%"if %MPITYPE%==mpipro call "%dir%\bin\run_marc_mach.exe" "%nprocd%" "%host%" "%jid%.host" "%execnm%" "%hostname%" "%program%" "%usub%" "%dirjob%"if %MPITYPE%==nt-mpich call "%dir%\bin\run_marc_mach.exe" "%nprocd%" "%host%" "%jid%.host" "%execnm%" "%hostname%" "%program%" "%usub%" "%dirjob%"if exist "%jid%.host" set host=%jid%.host & goto defaulthost_endif not exist "%jid%.host" goto run_marc_exit:userhost_endREMREM write default hostfile or machinefileREMif not "%host%"=="" goto defaulthost_endset /a ntmp1=%nprocd%-1if %MPITYPE%==patent echo local %ntmp1% > %dirjob%\%jid%.hostif %MPITYPE%==mpipro echo %hostname% > %dirjob%\%jid%.hostif %MPITYPE%==nt-mpich echo %hostname% > %dirjob%\%jid%.hostset jid2=%jid%for %%i in (%jid2%) do set jid2=%%~nxiset host=%jid2%.host:defaulthost_endset host=%dirjob%\%host%if not "%userhost%"=="" set dirscr=%dirjob%:hostfile_endREM ######################################################################### REM construct run stream (Marc only)REM #########################################################################if "%nprocd%"=="0" goto single_begif "%userhost%"=="" goto host_endif %MPITYPE%==mpich set run_job=%run_job1% "%host%" -sharemem %sharemem% -jid %jid% -nprocd %nprocd% -maxnum %maxnum% -maxsize %maxsize% -itree %itree% -nthread %nthread% -dirjob "%dirjob%"goto mpich_end:host_endif %MPITYPE%==mpich set run_job=%run_job1% -np %nprocd% "%execnm%"-sharemem %sharemem% -jid %jid% -nprocd %nprocd% -maxnum %maxnum% -maxsize %maxsize% -itree %itree% -nthread %nthread% -dirjob "%dirjob%":mpich_endif %MPITYPE%==patent set run_job=%run_job1% "%execnm%" -sharemem %sharemem% -p4pg "%host%" -jid %jid% -nprocd %nprocd% -maxnum %maxnum% -maxsize %maxsize% -itree %itree% -nthread %nthread% -prog "%execnm%" -dirjob "%dirjob%"if %MPITYPE%==mpipro set run_job=%run_job1% -wd "%dirjob%" -np %nprocd% -mach_file "%host%" "%execnm%" -jid %jid% -nprocd %nprocd% -maxnum %maxnum% -maxsize %maxsize% -itree %itree% -nthread %nthread% -prog "%execnm%" -dirjob "%dirjob%"if %MPITYPE%==nt-mpich set run_job=%run_job1% -n %nprocd% -machinefile "%host%" -- "%execnm%" -jid %jid% -nprocd %nprocd% -maxnum %maxnum% -maxsize %maxsize% -itree %itree% -nthread %nthread% -dirjob "%dirjob%"for %%i in (%userhost%) do set fullpath=%%~fiif not "%userhost%"=="" set run_job=%run_job% -mhost "%fullpath%"if not "%dirjid%"=="%dirjob%" set run_job=%run_job% -dirjid "%dirjid%"goto rid_add_beg:single_begif "%nauto%"=="1" goto auto_begif "%nauto%"=="2" goto auto_begif "%ndcoup%"=="1" goto auto_begif "%ndcoup%"=="2" goto auto_begset run_job=%run_job0% "%execnm%" -jid %jid% -maxnum %maxnum% -maxsize %maxsize% -nthread %nthread% -prog %program% -dirjob "%dirjob%" -dirjid "%dirjid%" -me "%mesh%" goto auto_end:auto_begrem only use the C program exe_auto to start a job if auto restart is usedset run_job="%BINDIR%\exe_auto" %run_job0% "%execnm%" -jid %jid% -maxnum %maxnum% -maxsize %maxsize% -nthread %nthread% -prog %program% -dirjob "%dirjob%" -dirjid "%dirjid%" -me "%mesh%":auto_end:rid_add_begif "%rid%"=="" goto pid_add_begset run_job=%run_job% -rid %rid%if not "%dirrid%"=="%dirjob%" set run_job=%run_job% -dirrid "%dirrid%":pid_add_begif "%pid%"=="" goto sid_add_begset run_job=%run_job% -pid %pid%。
Fortran90数值计算chap4f9

Sample page from NUMERICAL RECIPES IN FORTRAN 90: THE Art of PARALLEL Scientific Computing (ISBN 0-521-57439-0)Copyright (C) 1986-1996 by Cambridge University Press.Programs Copyright (C) 1986-1996 by Numerical Recipes Software. Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copying of machine-readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website or call 1-800-872-7423 (North America only),or send email to directcustserv@ (outside North America).Chapter B4.Integration of Functions SUBROUTINE trapzd(func,a,b,s,n)USE nrtype;USE nrutil,ONLY:arth IMPLICIT NONE REAL(SP),INTENT(IN)::a,b REAL(SP),INTENT(INOUT)::s INTEGER(I4B),INTENT(IN)::n INTERFACE FUNCTION func(x)USE nrtype REAL(SP),DIMENSION(:),INTENT(IN)::x REAL(SP),DIMENSION(size(x))::func END FUNCTION func END INTERFACE This routine computes the n th stage of refinement of an extended trapezoidal rule.func is input as the name of the function to be integrated between limits a and b,also input.When called with n=1,the routine returns as s the crudest estimate of b a f(x)dx.Subsequent calls with n=2,3,...(in that sequential order)will improve the accuracy of s by adding2n-2additional interior points.s should not be modified between sequential calls.REAL(SP)::del,fsum INTEGER(I4B)::it if(n==1)then s=0.5_sp*(b-a)*sum(func((/a,b/)))else it=2**(n-2)del=(b-a)/it This is the spacing of the points to be added.fsum=sum(func(arth(a+0.5_sp*del,del,it)))s=0.5_sp*(s+del*fsum)This replaces s by its refined value.end if END SUBROUTINE trapzd f90While most of the quadrature routines in this chapter are coded as functions,trapzd is a subroutine because the argument s that returns the function value must also be supplied as an input parameter.We could change the subroutine into a function by declaring s to be a local variable with the SAVE attribute.However,this would prevent us from being able to use the routine recursively to do multidimensional quadrature(see quad3d on p.1065).When s is left as an argument,a fresh copy is created on each recursive call.As a SAVE’d variable,by contrast,its value would get overwritten on each call,and the code would not be properly“re-entrant.”s=0.5_sp*(b-a)*sum(func((/a,b/)))Note how we use the(/.../)con-struct to supply a set of scalar arguments to a vector function.1052Chapter B4.Integration of Functions1053 Sample page from NUMERICAL RECIPES IN FORTRAN 90: THE Art of PARALLEL Scientific Computing (ISBN 0-521-57439-0)Copyright (C) 1986-1996 by Cambridge University Press.Programs Copyright (C) 1986-1996 by Numerical Recipes Software. Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copying of machine-readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website or call 1-800-872-7423 (North America only),or send email to directcustserv@ (outside North America).FUNCTION qtrap(func,a,b)USE nrtype;USE nrutil,ONLY:nrerror USE nr,ONLY:trapzd IMPLICIT NONE REAL(SP),INTENT(IN)::a,b REAL(SP)::qtrap INTERFACE FUNCTION func(x)USE nrtype REAL(SP),DIMENSION(:),INTENT(IN)::x REAL(SP),DIMENSION(size(x))::func END FUNCTION func END INTERFACE INTEGER(I4B),PARAMETER::JMAX=20REAL(SP),PARAMETER::EPS=1.0e-6_sp Returns the integral of the function func from a to b.The parameter EPS should be set to the desired fractional accuracy and JMAX so that2to the power JMAX-1is the maximum allowed number of steps.Integration is performed by the trapezoidal rule.REAL(SP)::olds INTEGER(I4B)::j olds=0.0Initial value of olds is arbitrary.do j=1,JMAX call trapzd(func,a,b,qtrap,j)if(j>5)then Avoid spurious early convergence.if(abs(qtrap-olds)<EPS*abs(olds).or.&(qtrap==0.0.and.olds==0.0))RETURN end if olds=qtrap end do call nrerror(’qtrap:too many steps’)END FUNCTION qtrap FUNCTION qsimp(func,a,b)USE nrtype;USE nrutil,ONLY:nrerror USE nr,ONLY:trapzd IMPLICIT NONE REAL(SP),INTENT(IN)::a,b REAL(SP)::qsimp INTERFACE FUNCTION func(x)USE nrtype REAL(SP),DIMENSION(:),INTENT(IN)::x REAL(SP),DIMENSION(size(x))::func END FUNCTION func END INTERFACE INTEGER(I4B),PARAMETER::JMAX=20REAL(SP),PARAMETER::EPS=1.0e-6_sp Returns the integral of the function func from a to b.The parameter EPS should be set to the desired fractional accuracy and JMAX so that2to the power JMAX-1is the maximum allowed number of steps.Integration is performed by Simpson’s rule.INTEGER(I4B)::j REAL(SP)::os,ost,st ost=0.0os=0.0do j=1,JMAXcall trapzd(func,a,b,st,j)qsimp=(4.0_sp*st-ost)/3.0_sp Compare equation(4.2.4).if(j>5)then Avoid spurious early convergence.if(abs(qsimp-os)<EPS*abs(os).or.&(qsimp==0.0.and.os==0.0))RETURNend ifos=qsimp1054Chapter B4.Integration of Functions Sample page from NUMERICAL RECIPES IN FORTRAN 90: THE Art of PARALLEL Scientific Computing (ISBN 0-521-57439-0)Copyright (C) 1986-1996 by Cambridge University Press.Programs Copyright (C) 1986-1996 by Numerical Recipes Software. Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copying of machine-readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website or call 1-800-872-7423 (North America only),or send email to directcustserv@ (outside North America).ost=st end do call nrerror(’qsimp:too many steps’)END FUNCTION qsimp FUNCTION qromb(func,a,b)USE nrtype;USE nrutil,ONLY:nrerror USE nr,ONLY:polint,trapzd IMPLICIT NONE REAL(SP),INTENT(IN)::a,b REAL(SP)::qromb INTERFACE FUNCTION func(x)USE nrtype REAL(SP),DIMENSION(:),INTENT(IN)::x REAL(SP),DIMENSION(size(x))::func END FUNCTION func END INTERFACE INTEGER(I4B),PARAMETER::JMAX=20,JMAXP=JMAX+1,K=5,KM=K-1REAL(SP),PARAMETER::EPS=1.0e-6_sp Returns the integral of the function func from a to b.Integration is performed by Romberg’s method of order2K,where,e.g.,K=2is Simpson’s rule.Parameters:EPS is the fractional accuracy desired,as determined by the extrapolation er-ror estimate;JMAX limits the total number of steps;K is the number of points used in the extrapolation.REAL(SP),DIMENSION(JMAXP)::h,s These store the successive trapezoidal ap-proximations and their relative stepsizes.REAL(SP)::dqromb INTEGER(I4B)::j h(1)=1.0do j=1,JMAX call trapzd(func,a,b,s(j),j)if(j>=K)then call polint(h(j-KM:j),s(j-KM:j),0.0_sp,qromb,dqromb)if(abs(dqromb)<=EPS*abs(qromb))RETURN end if s(j+1)=s(j)h(j+1)=0.25_sp*h(j)This is a key step:The factor is0.25even though the stepsize is decreased by only0.5.This makes the extrapolation a poly-nomial in h2as allowed by equation(4.2.1),not just a polynomial in h.end do call nrerror(’qromb:too many steps’)END FUNCTION qromb SUBROUTINE midpnt(func,a,b,s,n)USE nrtype;USE nrutil,ONLY:arth IMPLICIT NONE REAL(SP),INTENT(IN)::a,b REAL(SP),INTENT(INOUT)::s INTEGER(I4B),INTENT(IN)::n INTERFACEFUNCTION func(x)USE nrtypeREAL(SP),DIMENSION(:),INTENT(IN)::xREAL(SP),DIMENSION(size(x))::funcEND FUNCTION funcEND INTERFACEThis routine computes the n th stage of refinement of an extended midpoint rule.func is input as the name of the function to be integrated between limits a and b,also input.WhenChapter B4.Integration of Functions1055 Sample page from NUMERICAL RECIPES IN FORTRAN 90: THE Art of PARALLEL Scientific Computing (ISBN 0-521-57439-0)Copyright (C) 1986-1996 by Cambridge University Press.Programs Copyright (C) 1986-1996 by Numerical Recipes Software. Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copying of machine-readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website or call 1-800-872-7423 (North America only),or send email to directcustserv@ (outside North America).called with n=1,the routine returns as s the crudest estimate of b a f(x)dx.Subsequent calls with n=2,3,...(in that sequential order)will improve the accuracy of s by adding(2/3)×3n-1additional interior points.s should not be modified between sequential calls.REAL(SP)::del INTEGER(I4B)::it REAL(SP),DIMENSION(2*3**(n-2))::x if(n==1)then s=(b-a)*sum(func((/0.5_sp*(a+b)/)))else it=3**(n-2)del=(b-a)/(3.0_sp*it)The added points alternate in spacing between del and2*del.x(1:2*it-1:2)=arth(a+0.5_sp*del,3.0_sp*del,it)x(2:2*it:2)=x(1:2*it-1:2)+2.0_sp*del s=s/3.0_sp+del*sum(func(x))The new sum is combined with the old integral to give a refined integral.end if END SUBROUTINE midpnt f90midpnt is a subroutine and not a function for the same reasons as trapzd.This is also true for the other mid...routines below.s=(b-a)*sum(func((/0.5_sp*(a+b)/)))Here we use(/.../)to pass a single scalar argument to a vector function. FUNCTION qromo(func,a,b,choose)USE nrtype;USE nrutil,ONLY:nrerror USE nr,ONLY:polint IMPLICIT NONE REAL(SP),INTENT(IN)::a,b REAL(SP)::qromo INTERFACE FUNCTION func(x)USE nrtype IMPLICIT NONE REAL(SP),DIMENSION(:),INTENT(IN)::x REAL(SP),DIMENSION(size(x))::func END FUNCTION func SUBROUTINE choose(funk,aa,bb,s,n)USE nrtype IMPLICIT NONE REAL(SP),INTENT(IN)::aa,bb REAL(SP),INTENT(INOUT)::s INTEGER(I4B),INTENT(IN)::n INTERFACE FUNCTION funk(x)USE nrtype IMPLICIT NONE REAL(SP),DIMENSION(:),INTENT(IN)::x REAL(SP),DIMENSION(size(x))::funk END FUNCTION funk END INTERFACEEND SUBROUTINE chooseEND INTERFACEINTEGER(I4B),PARAMETER::JMAX=14,JMAXP=JMAX+1,K=5,KM=K-1REAL(SP),PARAMETER::EPS=1.0e-6Romberg integration on an open interval.Returns the integral of the function func from a to b,using any specified integrating subroutine choose and Romberg’s method.Normally choose will be an open formula,not evaluating the function at the endpoints.It is assumed that choose triples the number of steps on each call,and that its error series contains only1056Chapter B4.Integration of Functions Sample page from NUMERICAL RECIPES IN FORTRAN 90: THE Art of PARALLEL Scientific Computing (ISBN 0-521-57439-0)Copyright (C) 1986-1996 by Cambridge University Press.Programs Copyright (C) 1986-1996 by Numerical Recipes Software. Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copying of machine-readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website or call 1-800-872-7423 (North America only),or send email to directcustserv@ (outside North America).even powers of the number of steps.The routines midpnt,midinf,midsql,midsqu,and midexp are possible choices for choose.The parameters have the same meaning as in qromb.REAL(SP),DIMENSION(JMAXP)::h,s REAL(SP)::dqromo INTEGER(I4B)::j h(1)=1.0do j=1,JMAX call choose(func,a,b,s(j),j)if(j>=K)then call polint(h(j-KM:j),s(j-KM:j),0.0_sp,qromo,dqromo)if(abs(dqromo)<=EPS*abs(qromo))RETURN end if s(j+1)=s(j)h(j+1)=h(j)/9.0_sp This is where the assumption of step tripling and an even error series is used.end do call nrerror(’qromo:too many steps’)END FUNCTION qromo SUBROUTINE midinf(funk,aa,bb,s,n)USE nrtype;USE nrutil,ONLY:arth,assert IMPLICIT NONE REAL(SP),INTENT(IN)::aa,bb REAL(SP),INTENT(INOUT)::s INTEGER(I4B),INTENT(IN)::n INTERFACE FUNCTION funk(x)USE nrtype REAL(SP),DIMENSION(:),INTENT(IN)::x REAL(SP),DIMENSION(size(x))::funk END FUNCTION funk END INTERFACE This routine is an exact replacement for midpnt,i.e.,returns as s the n th stage of refinement of the integral of funk from aa to bb,except that the function is evaluated at evenly spaced points in1/x rather than in x.This allows the upper limit bb to be as large and positive as the computer allows,or the lower limit aa to be as large and negative,but not both.aa and bb must have the same sign.REAL(SP)::a,b,del INTEGER(I4B)::it REAL(SP),DIMENSION(2*3**(n-2))::x call assert(aa*bb>0.0,’midinf args’)b=1.0_sp/aa These two statements change the limits of integration ac-cordingly.a=1.0_sp/bb if(n==1)then From this point on,the routine is exactly identical to midpnt.s=(b-a)*sum(func((/0.5_sp*(a+b)/)))else it=3**(n-2)del=(b-a)/(3.0_sp*it)x(1:2*it-1:2)=arth(a+0.5_sp*del,3.0_sp*del,it)x(2:2*it:2)=x(1:2*it-1:2)+2.0_sp*del s=s/3.0_sp+del*sum(func(x))end if CONTAINSFUNCTION func(x)This internal function effects the change of variable.REAL(SP),DIMENSION(:),INTENT(IN)::xREAL(SP),DIMENSION(size(x))::funcfunc=funk(1.0_sp/x)/x**2END FUNCTION funcEND SUBROUTINE midinfChapter B4.Integration of Functions1057 Sample page from NUMERICAL RECIPES IN FORTRAN 90: THE Art of PARALLEL Scientific Computing (ISBN 0-521-57439-0)Copyright (C) 1986-1996 by Cambridge University Press.Programs Copyright (C) 1986-1996 by Numerical Recipes Software. Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copying of machine-readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website or call 1-800-872-7423 (North America only),or send email to directcustserv@ (outside North America).f90FUNCTION func(x)The change of variable could have been effected by a statement function in midinf itself.However,the statement function is a Fortran77feature that is deprecated in Fortran90because it does not allow the benefits of having an explicit interface,i.e.,a complete set of specification statements.Statement functions can always be coded as internal subprograms instead.SUBROUTINE midsql(funk,aa,bb,s,n)USE nrtype;USE nrutil,ONLY:arth IMPLICIT NONE REAL(SP),INTENT(IN)::aa,bb REAL(SP),INTENT(INOUT)::s INTEGER(I4B),INTENT(IN)::n INTERFACE FUNCTION funk(x)USE nrtype REAL(SP),DIMENSION(:),INTENT(IN)::x REAL(SP),DIMENSION(size(x))::funk END FUNCTION funk END INTERFACE This routine is an exact replacement for midpnt,i.e.,returns as s the n th stage of refinement of the integral of funk from aa to bb,except that it allows for an inverse square-root singularity in the integrand at the lower limit aa.REAL(SP)::a,b,del INTEGER(I4B)::it REAL(SP),DIMENSION(2*3**(n-2))::x b=sqrt(bb-aa)These two statements change the limits of integration ac-cordingly.a=0.0if(n==1)then From this point on,the routine is exactly identical to midpnt.s=(b-a)*sum(func((/0.5_sp*(a+b)/)))else it=3**(n-2)del=(b-a)/(3.0_sp*it)x(1:2*it-1:2)=arth(a+0.5_sp*del,3.0_sp*del,it)x(2:2*it:2)=x(1:2*it-1:2)+2.0_sp*del s=s/3.0_sp+del*sum(func(x))end if CONTAINS FUNCTION func(x)This internal function effects the change of variable.REAL(SP),DIMENSION(:),INTENT(IN)::x REAL(SP),DIMENSION(size(x))::func func=2.0_sp*x*funk(aa+x**2)END FUNCTION func END SUBROUTINE midsql SUBROUTINE midsqu(funk,aa,bb,s,n)USE nrtype;USE nrutil,ONLY:arth IMPLICIT NONE REAL(SP),INTENT(IN)::aa,bb REAL(SP),INTENT(INOUT)::s INTEGER(I4B),INTENT(IN)::n INTERFACE FUNCTION funk(x)USE nrtypeREAL(SP),DIMENSION(:),INTENT(IN)::xREAL(SP),DIMENSION(size(x))::funkEND FUNCTION funkEND INTERFACEThis routine is an exact replacement for midpnt,i.e.,returns as s the n th stage of refinement of the integral of funk from aa to bb,except that it allows for an inverse square-root singularity in the integrand at the upper limit bb.REAL(SP)::a,b,del1058Chapter B4.Integration of Functions Sample page from NUMERICAL RECIPES IN FORTRAN 90: THE Art of PARALLEL Scientific Computing (ISBN 0-521-57439-0)Copyright (C) 1986-1996 by Cambridge University Press.Programs Copyright (C) 1986-1996 by Numerical Recipes Software. Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copying of machine-readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website or call 1-800-872-7423 (North America only),or send email to directcustserv@ (outside North America).INTEGER(I4B)::it REAL(SP),DIMENSION(2*3**(n-2))::x b=sqrt(bb-aa)These two statements change the limits of integration ac-cordingly.a=0.0if(n==1)then From this point on,the routine is exactly identical to midpnt.s=(b-a)*sum(func((/0.5_sp*(a+b)/)))else it=3**(n-2)del=(b-a)/(3.0_sp*it)x(1:2*it-1:2)=arth(a+0.5_sp*del,3.0_sp*del,it)x(2:2*it:2)=x(1:2*it-1:2)+2.0_sp*del s=s/3.0_sp+del*sum(func(x))end if CONTAINS FUNCTION func(x)This internal function effects the change of variable.REAL(SP),DIMENSION(:),INTENT(IN)::x REAL(SP),DIMENSION(size(x))::func func=2.0_sp*x*funk(bb-x**2)END FUNCTION func END SUBROUTINE midsqu SUBROUTINE midexp(funk,aa,bb,s,n)USE nrtype;USE nrutil,ONLY:arth IMPLICIT NONE REAL(SP),INTENT(IN)::aa,bb REAL(SP),INTENT(INOUT)::s INTEGER(I4B),INTENT(IN)::n INTERFACE FUNCTION funk(x)USE nrtype REAL(SP),DIMENSION(:),INTENT(IN)::x REAL(SP),DIMENSION(size(x))::funk END FUNCTION funk END INTERFACE This routine is an exact replacement for midpnt,i.e.,returns as s the n th stage of refinement of the integral of funk from aa to bb,except that bb is assumed to be infinite(value passed not actually used).It is assumed that the function funk decreases exponentially rapidly at infinity.REAL(SP)::a,b,del INTEGER(I4B)::it REAL(SP),DIMENSION(2*3**(n-2))::x b=exp(-aa)These two statements change the limits of integration ac-cordingly.a=0.0if(n==1)then From this point on,the routine is exactly identical to midpnt.s=(b-a)*sum(func((/0.5_sp*(a+b)/)))else it=3**(n-2)del=(b-a)/(3.0_sp*it)x(1:2*it-1:2)=arth(a+0.5_sp*del,3.0_sp*del,it)x(2:2*it:2)=x(1:2*it-1:2)+2.0_sp*del s=s/3.0_sp+del*sum(func(x))end if CONTAINS FUNCTION func(x)This internal function effects the change of variable.REAL(SP),DIMENSION(:),INTENT(IN)::xREAL(SP),DIMENSION(size(x))::funcfunc=funk(-log(x))/xEND FUNCTION funcEND SUBROUTINE midexpChapter B4.Integration of Functions1059 Sample page from NUMERICAL RECIPES IN FORTRAN 90: THE Art of PARALLEL Scientific Computing (ISBN 0-521-57439-0)Copyright (C) 1986-1996 by Cambridge University Press.Programs Copyright (C) 1986-1996 by Numerical Recipes Software. Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copying of machine-readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website or call 1-800-872-7423 (North America only),or send email to directcustserv@ (outside North America).SUBROUTINE gauleg(x1,x2,x,w)USE nrtype;USE nrutil,ONLY:arth,assert_eq,nrerror IMPLICIT NONE REAL(SP),INTENT(IN)::x1,x2REAL(SP),DIMENSION(:),INTENT(OUT)::x,w REAL(DP),PARAMETER::EPS=3.0e-14_dp Given the lower and upper limits of integration x1and x2,this routine returns arrays x and w of length N containing the abscissas and weights of the Gauss-Legendre N-point quadrature formula.The parameter EPS is the relative precision.Note that internal computations are done in double precision.INTEGER(I4B)::its,j,m,n INTEGER(I4B),PARAMETER::MAXIT=10REAL(DP)::xl,xm REAL(DP),DIMENSION((size(x)+1)/2)::p1,p2,p3,pp,z,z1LOGICAL(LGT),DIMENSION((size(x)+1)/2)::unfinished n=assert_eq(size(x),size(w),’gauleg’)m=(n+1)/2The roots are symmetric in the interval,so we only have tofind half of them.xm=0.5_dp*(x2+x1)xl=0.5_dp*(x2-x1)z=cos(PI_D*(arth(1,1,m)-0.25_dp)/(n+0.5_dp))Initial approximations to the roots.unfinished=.true.do its=1,MAXIT Newton’s method carried out simultane-ously on the roots.where(unfinished)p1=1.0p2=0.0end where do j=1,n Loop up the recurrence relation to get the Legendre polynomials evaluated at z.where(unfinished)p3=p2p2=p1p1=((2.0_dp*j-1.0_dp)*z*p2-(j-1.0_dp)*p3)/j end where end do p1now contains the desired Legendre polynomials.We next compute pp,the derivatives,by a standard relation involving also p2,the polynomials of one lower order.where(unfinished)pp=n*(z*p1-p2)/(z*z-1.0_dp)z1=z z=z1-p1/pp Newton’s method.unfinished=(abs(z-z1)>EPS)end where if(.not.any(unfinished))exit end do if(its==MAXIT+1)call nrerror(’too many iterations in gauleg’)x(1:m)=xm-xl*z Scale the root to the desired interval,x(n:n-m+1:-1)=xm+xl*z and put in its symmetric counterpart.w(1:m)=2.0_dp*xl/((1.0_dp-z**2)*pp**2)Compute the weight w(n:n-m+1:-1)=w(1:m)and its symmetric counterpart.END SUBROUTINE gauleg f90Often we have an iterative procedure that has to be applied until all components of a vector have satisfied a convergence criterion.Some components of the vector might converge sooner than others,and it isinefficient on a small-scale parallel(SSP)machine to continue iterating on those components.The general structure we use for such an iteration is exemplified by the following lines from gauleg:LOGICAL(LGT),DIMENSION((size(x)+1)/2)::unfinished...unfinished=.true.do its=1,MAXIT1060Chapter B4.Integration of Functions Sample page from NUMERICAL RECIPES IN FORTRAN 90: THE Art of PARALLEL Scientific Computing (ISBN 0-521-57439-0)Copyright (C) 1986-1996 by Cambridge University Press.Programs Copyright (C) 1986-1996 by Numerical Recipes Software. Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copying of machine-readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website or call 1-800-872-7423 (North America only),or send email to directcustserv@ (outside North America).where(unfinished)...unfinished=(abs(z-z1)>EPS)end where if(.not.any(unfinished))exit end do if(its==MAXIT+1)call nrerror(’too many iterations in gauleg’)We use the logical mask unfinished to control which vector components are processed inside the where.The mask gets updated on each iteration by testing whether any further vector components have converged.When all have converged,we exit the iteration loop.Finally,we check the value of its to see whether the maximum allowed number of iterations was exceeded before all components converged.The logical expression controlling the where block(in this case unfinished)gets evaluated completely on entry into the where,and it is then perfectlyfine to modify it inside the block.The modification affects only the next execution of the where.On a strictly serial machine,there is of course some penalty associated with the above scheme:after a vector component converges,its corresponding component in unfinished is redundantly tested on each further iteration,until the slowest-converging component is done.If the number of iterations required does not vary too greatly from component to component,this is a minor,often negligible,penalty.However,one should be on the alert against algorithms whose worst-case convergence could differ from typical convergence by orders of magnitude.For these,one would need to implement a more complicated packing-unpacking scheme.(See discussion in Chapter B6,especially introduction,p.1083,and notes for factrl,p.1087.)SUBROUTINE gaulag(x,w,alf)USE nrtype;USE nrutil,ONLY:arth,assert_eq,nrerror USE nr,ONLY:gammln IMPLICIT NONE REAL(SP),INTENT(IN)::alf REAL(SP),DIMENSION(:),INTENT(OUT)::x,w REAL(DP),PARAMETER::EPS=3.0e-13_dp Given alf,the parameterαof the Laguerre polynomials,this routine returns arrays x and w of length N containing the abscissas and weights of the N-point Gauss-Laguerre quadrature formula.The abscissas are returned in ascending order.The parameter EPS is the relative precision.Note that internal computations are done in double precision.INTEGER(I4B)::its,j,n INTEGER(I4B),PARAMETER::MAXIT=10REAL(SP)::anu REAL(SP),PARAMETER::C1=9.084064e-01_sp,C2=5.214976e-02_sp,&C3=2.579930e-03_sp,C4=3.986126e-03_sp REAL(SP),DIMENSION(size(x))::rhs,r2,r3,theta REAL(DP),DIMENSION(size(x))::p1,p2,p3,pp,z,z1LOGICAL(LGT),DIMENSION(size(x))::unfinished n=assert_eq(size(x),size(w),’gaulag’)anu=4.0_sp*n+2.0_sp*alf+2.0_sp Initial approximations to the roots go into z.rhs=arth(4*n-1,-4,n)*PI/anur3=rhs**(1.0_sp/3.0_sp)r2=r3**2theta=r3*(C1+r2*(C2+r2*(C3+r2*C4)))z=anu*cos(theta)**2unfinished=.true.do its=1,MAXIT Newton’s method carried out simultaneously on where(unfinished)the roots.p1=1.0Chapter B4.Integration of Functions1061 Sample page from NUMERICAL RECIPES IN FORTRAN 90: THE Art of PARALLEL Scientific Computing (ISBN 0-521-57439-0)Copyright (C) 1986-1996 by Cambridge University Press.Programs Copyright (C) 1986-1996 by Numerical Recipes Software. Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copying of machine-readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website or call 1-800-872-7423 (North America only),or send email to directcustserv@ (outside North America).p2=0.0end where do j=1,n Loop up the recurrence relation to get the La-guerre polynomials evaluated at z.where(unfinished)p3=p2p2=p1p1=((2.0_dp*j-1.0_dp+alf-z)*p2-(j-1.0_dp+alf)*p3)/j end where end do p1now contains the desired Laguerre polynomials.We next compute pp,the derivatives,by a standard relation involving also p2,the polynomials of one lower order.where(unfinished)pp=(n*p1-(n+alf)*p2)/z z1=z z=z1-p1/pp Newton’s formula.unfinished=(abs(z-z1)>EPS*z)end where if(.not.any(unfinished))exit end do if(its==MAXIT+1)call nrerror(’too many iterations in gaulag’)x=z Store the root and the weight.w=-exp(gammln(alf+n)-gammln(real(n,sp)))/(pp*n*p2)END SUBROUTINE gaulag The key difficulty in parallelizing this routine starting from the Fortran77version is that the initial guesses for the roots of the Laguerre polynomials were given in terms of previously determined roots.This prevents one fromfinding all the roots simultaneously.The solution is to come up with a new approximation to the roots that is a simple explicit formula,like the formula we used for the Legendre roots in gauleg.We start with the approximation to Lαn(x)given in equation(10.15.8)of[1].We keep only thefirst term and ask when it is zero.This gives the following prescription for the k th root x k of Lαn(x):Solve forθthe equation2θ−sin2θ=4n−4k+34n+2α+2π(B4.1)Since1≤k≤n andα>−1,we can alwaysfind a value such that0<θ<π/2.Then the approximation to the root is x k=(4n+2α+2)cos2θ(B4.2)This typically gives3-digit accuracy,more than enough for the Newton iteration to be able to refine the root.Unfortunately equation(B4.1)is not an explicit formula forθ.(You may recognize it as being of the same form as Kepler’s equation in mechanics.)If we call the right-hand side of(B4.1)y,then we can get an explicit formula by working out the power series for y1/3nearθ=0(using a computeralgebra program).Next invert the series to giveθas a function of y1/3.Finally, economize the series(see§5.11).The result is the concise approximation θ=0.9084064y1/3+5.214976×10−2y+2.579930×10−3y5/3+3.986126×10−3y7/3(B4.3)Once again we need an explicit approximation for the polynomial roots, this time for H n(x).We can use the same approximation scheme as for Lαn(x),sinceH2m(x)∝L−1/2m (x2),H2m+1(x)∝xL1/2m(x2)(B4.4)Sample page from NUMERICAL RECIPES IN FORTRAN 90: THE Art of PARALLEL Scientific Computing (ISBN 0-521-57439-0)Copyright (C) 1986-1996 by Cambridge University Press.Programs Copyright (C) 1986-1996 by Numerical Recipes Software. Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copying of machine-readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website or call 1-800-872-7423 (North America only),or send email to directcustserv@ (outside North America).SUBROUTINE gauher(x,w)USE nrtype;USE nrutil,ONLY:arth,assert_eq,nrerror IMPLICIT NONE REAL(SP),DIMENSION(:),INTENT(OUT)::x,w REAL(DP),PARAMETER::EPS=3.0e-13_dp,PIM4=0.7511255444649425_dp This routine returns arrays x and w of length N containing the abscissas and weights of the N-point Gauss-Hermite quadrature formula.The abscissas are returned in descending order.Note that internal computations are done in double precision.Parameters:EPS is the relative precision,PIM4=1/π1/4.INTEGER(I4B)::its,j,m,n INTEGER(I4B),PARAMETER::MAXIT=10REAL(SP)::anu REAL(SP),PARAMETER::C1=9.084064e-01_sp,C2=5.214976e-02_sp,&C3=2.579930e-03_sp,C4=3.986126e-03_sp REAL(SP),DIMENSION((size(x)+1)/2)::rhs,r2,r3,theta REAL(DP),DIMENSION((size(x)+1)/2)::p1,p2,p3,pp,z,z1LOGICAL(LGT),DIMENSION((size(x)+1)/2)::unfinished n=assert_eq(size(x),size(w),’gauher’)m=(n+1)/2The roots are symmetric about the origin,so we have tofind only half of them.anu=2.0_sp*n+1.0_sp rhs=arth(3,4,m)*PI/anu r3=rhs**(1.0_sp/3.0_sp)r2=r3**2theta=r3*(C1+r2*(C2+r2*(C3+r2*C4)))z=sqrt(anu)*cos(theta)Initial approximations to the roots.unfinished=.true.do its=1,MAXIT Newton’s method carried out simultaneously on the roots.where(unfinished)p1=PIM4p2=0.0end where do j=1,n Loop up the recurrence relation to get the Hermite poly-nomials evaluated at z.where(unfinished)p3=p2p2=p1p1=z*sqrt(2.0_dp/j)*p2-sqrt(real(j-1,dp)/real(j,dp))*p3end where end do p1now contains the desired Hermite polynomials.We next compute pp,the derivatives,by the relation(4.5.21)using p2,the polynomials of one lower order.where(unfinished)pp=sqrt(2.0_dp*n)*p2z1=z z=z1-p1/pp Newton’s formula.unfinished=(abs(z-z1)>EPS)end where if(.not.any(unfinished))exit end do if(its==MAXIT+1)call nrerror(’too many iterations in gauher’)x(1:m)=z Store the root x(n:n-m+1:-1)=-z and its symmetric counterpart.w(1:m)=2.0_dp/pp**2Compute the weight w(n:n-m+1:-1)=w(1:m)and its symmetric counterpart.END SUBROUTINE gauher。
FORTRAN90习题

,A(2,2)的值是
,A(3,1)的值是
。
,第二行是
,A(2)的值是
n-1 n
。 之和的外部函数
+…+anT 表示x ,S 表示多项式之和。 FUNCTION p(A,N,x) RESULT(r_p) S= T=1.0 DO I=1,N T= S=S+A(I)*T PRINT*,'S=',S END 8. 用选择法,将 N 个整数按从小到大排列。 PARAMETER(numl=500) INTEGER num(numl) READ*,N,(num(I), ) DO I=1,N-1 min=I DO J= (22) IF(num(min) .GT. num(J)) ENDDO IF(min .NE. I)THEN it=num(I) num(I)=num(min) ENDIF ENDDO PRINT*,(num(I),I=1,N) END 9. 以下程序是通过超载赋值(=)运算符,实现将字符的 ASCII 码赋给整型变量的功能. SUBROUTINE CTOI(I,C) INTEGER ,INTENT(OUT):: I CHARACTER ,INTENT(IN):: C I= END SUBROUTINE PROGRAMMAIN INTERFACE ASSIGNMENT(=) SUBROUTINE INTEGER ,INTENT(OUT):: I CHARACTER ,INTENT(IN):: C ENDSUBROUTINE INTEGER I CHARACTER:: C='A' I=C PRINT*,C,I END PROGRAMMAIN 10.求 N!。 PRINT*,'Input N?' READ *,N
,第三行是
FORTRAN90写的雅克比和高斯赛德尔迭代程序

!JACOBI迭代求解方程组program jacobiimplicit noneinteger :: i,jinteger :: k !迭代次数旗标save kreal,parameter :: e=0.001integer,parameter :: n=4real :: x(n),y(n),b(n)data b /1.38,-0.34,0.67,1.52/real :: Dreal :: a(n,n)!!!千万千万要注意Fortran的数据存放是按照列来存放的,如果变成还按照习惯的数组存放方式输入数据,会导致错误!!!data a /2.52,0.39,0.55,0.23,0.95,1.69,-1.25,-1.15,1.25,-0.45,1.96,-0.45,-0.85,0.49,-0.98,2.31/ write(*,*)"*********矩阵A的形式为*********"write(*,"(1x,4f6.2,/)")aforall(i=1:n)x(i)=0end forallk=1100 D=0do i=1,ny(i)=b(i)do j=1,nif(i/=j) y(i)=y(i)-a(i,j)*x(j)end doy(i)=y(i)/a(i,i)end dodo j=1,nD=abs(x(j)-y(j))end doforall(i=1:n)x(i)=y(i)end forallif(D>=e) thenk=k+1write(*,*)"迭代次数为:",kgoto 100elsegoto 200end if200 write(*,*)"*************************************"write(*,*)"用jacobi方法解得的结果X[t]为:"write(*,"(1x,4f6.2,/)")x(:)stopend program*******************************************************************************!GAUSS-SEIDEL迭代求解方程组program jacobiimplicit noneinteger :: i,jinteger :: k !迭代次数旗标save kreal,parameter :: e=0.001integer,parameter :: n=4real :: x(n),y(n),b(n)data b /1.38,-0.34,0.67,1.52/real :: Dreal :: a(n,n)!!!千万千万要注意Fortran的数据存放是按照列来存放的,如果变成还按照习惯的数组存放方式输入数据,会导致错误!!!data a /2.52,0.39,0.55,0.23,0.95,1.69,-1.25,-1.15,1.25,-0.45,1.96,-0.45,-0.85,0.49,-0.98,2.31/ write(*,*)"*********矩阵A的形式为*********"write(*,"(1x,4f6.2,/)")aforall(i=1:n)x(i)=0end forallk=1100 D=0do i=1,ny(i)=b(i)do j=1,nif(i<j) y(i)=y(i)-a(i,j)*x(j)if(i>j) y(i)=y(i)-a(i,j)*y(j)end doy(i)=y(i)/a(i,i)end dodo j=1,nD=abs(x(j)-y(j))end doforall(i=1:n)x(i)=y(i)end forallif(D>=e) thenk=k+1write(*,*)"迭代次数为:",kgoto 100elsegoto 200end if200 write(*,*)"*************************************"write(*,*)"用Gauss-seidel方法解得的结果X[t]为:"write(*,"(1x,4f6.2,/)")x(:)write(*,*)"由运行结果可以看出,运算量G-S比JACOBI少至少一倍"stopend programimplicit nonesubroutine gauss(a,b,n,x,l,js)dimension a(n,n),x(n),b(n),js(n) double precision a,b,x,t l=1do k=1,n-1 d=0.0do i=k,ndo j=k,nif(abs(a(i,j)).gt.d)then d=abs(a(i,j)) js(k)=j is=iEndifend doif(d+1.0.eq.1.0)then l=0else if(js(k).ne.k)thendo i=k,n t=a(i,k) a(i,k)=a(i,js(k)) a(i,js(k))=tend doendifif(is.ne.k)thendo j=k,n t=a(k,j) a(k,j)=a(is,j) a(is,j)=tend do t=b(k) b(k)=b(is) b(is)=tendifendifif(l.eq.0)then write(*,100)endifdo j=k+1,n a(k,j)=a(k,j)/a(k,k)end do b(k)=b(k)/a(k,k)do i=k+1,ndo j=k+1,n a(i,j)=a(i,j)-a(i,k)*a(j,k)end do b(i)=b(i)-a(i,k)*b(k)end doend do if(abs(a(n,n))+1.0.eq.1.0)then l=0 write(*,100)end if x(n)=b(n)/a(n,n)do i=n-1,1,-1 t=0.0do j=i+1,n t=t+a(i,j)*x(j)end do x(i)=b(i)-tend do 100 format(1x,'fall') js(n)=ndo k=n,1,-1if(js(k).ne.k)then t=x(k) x(k)=x(js(k)) x(js(k))=t end if end doend do。
fortran90-知识点整理

Fortran90关于变量说明的新功能:1.在变量说明的同时,可以给变量赋初值。
INTEGER::I=5,J=126REAL::X=7.2,Z,W=774.22.在说明变量的同时也可说明其种别REAL(KIND=4)::X,Y 或REAL(4)::X,Y3.在说明变量的同时,还可说明变量的属性INTEGER,PARAMETER::I=5,J=123Ps :PARAMETER 属性(1)功能:用一个符号代表一个常量,称为符号常量(常数)(2)写法:Real,Parameter ::G=9.8 &&说明类型时赋值(3)位置:位于可执行语句之前REAL,DIMENSION(1:10)::A2.3.6 派生数据类型根据需要而由基本数据类型定义新的数据类型。
在一个派生类型中可包含多个基本类型。
如:TYPE STUDENT (定义开始)CHARACTER(LEN=20)::DEPARTMENTCHARACTER(LEN=10)::CLASSCHARACTER(LEN=15)::NAMEINTEGER::NUMBER (成员定义)END TYPE STUDENT (定义结束)派生类型变量的定义:TYPE(STUDENT)::PERSON变量的赋值:PERSON=(”COMPUTER”,”92_2”,”LI LIN”,21)成员的表示:PERSON%CLASS=“92_2”PERSON%NAME=“LI LIN”主程序其他限制主程序的可执行部分不能包含有RETURN语句或者ENTRY语句。
程序名对可执行程序是全局的,而且不得于该可执行程序中的任何其它程序单元名、外部过程名或公用块名相同,也不得于主程序内的任何局部名相同。
在主程序的作用范围内的说明不得包含OPTIONAL语句、INTENT语句、PUBLIC语句或它们的等价属性,在主程序内SAVE语句不起作用。
主程序内的任何内部过程的定义必须跟在CONTAINS语句之后。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
INTERVAL ARITHMETIC:A Fortran90Module for an Interval Data TypeR.BAKER KEARFOTTDepartment of MathematicsUniversity of Southwestern LouisianaInterval arithmetic is useful in automatically verified computations,that is,in computations in which the algorithm itself rigorously proves that the answer must lie within certain bounds.In addition to rigor,interval arithmetic also provides a simple and sometimes sharp method of bounding ranges of functions for global optimization and other tasks.Convenient use of interval arithmetic requires an interval data type in the programming lan-guage.Although various packages supply such a data type,previous ones are machine-specific, obsolete and unsupported,for languages other than Fortran,or commercial.The Fortran90mod-ule INTERVAL ARITHMETIC provides a portable interval data type in Fortran90.This data type is based on two double precision real Fortran storage units.Module INTERVAL ARITHMETIC uses the FORTRAN77library INTLIB(ACM TOMS Algorithm737)as supporting library.The module has been employed extensively in the author’s own research.Categories and Subject Descriptors:G1.0[Numerical Analysis]:General—Computer arith-metic;Error analysis;Numerical AlgorithmsGeneral Terms:Programming Languages,PortabilityAdditional Key Words and Phrases:Interval arithmetic,operator overloading1.INTRODUCTION AND SYNOPSISInterval arithmetic,when practical,allows rigor in scientific computations,and can provide tests of correctness of hardware,compilers,and function libraries for floating point computations.Interval arithmetic can also be useful in sensitivity analysis.Additionally,since interval arithmetic provides rigorous bounds on the ranges of functions,it is appropriate in applications in which Lipschitz constants or bounds on moduli of continuity are required.In fact,interval arithmetic is a convenient,and sometimes the sharpest,means of obtaining such information in algorithms.For example,evaluation of f(x)=x4+x3+x over the interval[1,2] results in[1,16]+[1,8]+[1,2]=[3,26],which happens to be the range1of f over 1Conditions under which the interval value is the range can be found in discussions of the properties of interval arithmetic,such as in[Neumaier1990].In general,interval values are just bounds on the range.Author’s address:R. B.Kearfott,Department of Mathematics,University of Southwestern Louisiana,USL Box4-1010,Lafayette,LA70504-1010USA.Email:rbk@This work was supported in part by National Science Foundation grant CCR-9203730. Permission to copy without fee all or part of this material is granted provided that the copies are not made or distributed for direct commercial advantage,the ACM copyright notice and the title of the publication and its date appear,and notice is given that copying is by permission of the Association for Computing Machinery.To copy otherwise,or to republish,requires a fee and/or specific permission.2·R.B.KearfottC This standard FORTRAN-77routine uses INTLIB directly.PROGRAM TEST_INTLIBC Intervals are represented as double precision arraysC with two elements--DOUBLE PRECISION X(2),F(2)DOUBLE PRECISION TMP2(2),TMP3(2)C Initialize machine constants and interval constants used inC the standard functions--CALL SIMINIC The range over[1,2]will be computed--X(1)=1D0X(2)=2D0C Round out in case the decimal-to-binary conversion isC not exact--CALL RNDOUT(X,.TRUE.,.TRUE.)C Compute X**4+X**3+X--CALL POWER(X,4,TMP2)CALL POWER(X,3,TMP3)CALL ADD(TMP2,TMP3,TMP2)CALL ADD(TMP2,X,F)WRITE(6,*)F(1),F(2)ENDFig.1.Interval evaluation in FORTRAN77using INTLIB[1,2].The INTLIB package,ACM TOMS Algorithm737,consists of a portable FOR-TRAN77library for interval arithmetic and standard functions,so that interval values can be obtained for most functions that can be calculated as Fortran sub-routines.However,direct use of INTLIB is cumbersome.For example,an interval computation of f([1,2])for f(x)=x4+x3+x,using INTLIB directly,would require a program similar to that in Figure1.Fortunately,operator overloading in Fortran90allows a computation equivalent to Figure1to be expressed in simple syntax.With module INTERVAL ARITHMETIC, the computation can be expressed as in Figure2.The actual machine operations corresponding to Figure2will consist of a series of calls to INTLIB routines as in Figure1,with the order of these calls depending on the particular compiler. There are numerous previous packages for interval arithmetic,including those based on the operator overloading technique here;the oldest is the Augment pre-compiler[Crary1976]in conjunction with a FORTRAN66,somewhat transportable interval library[Yohe1979].More recently,several C++packages,including the package mentioned in[Leclerc1993],the package of[Kn¨u ppel1994],and C-XSCINTERVAL ARITHMETIC:An Interval Data Type·3 PROGRAM EVALUATE_EXAMPLE!This standard Fortran90routine!evaluates X**4+X**3+X over[1,2].USE INTERVAL_ARITHMETICTYPE(INTERVAL)X,FCALL SIMINIX=INTERVAL(1,2)F=X**4+X**3+XWRITE(6,*)FEND PROGRAM EVALUATE_EXAMPLEFig.2.Fortran90Interval evaluation with module INTERVAL ARITHMETIC [Klatte et al.1993]have been developed.C-XSC,as well as Pascal-XSC[Hammer et al.1993],are commercial languages available on a variety of machines.An exten-sion of FORTRAN77,ACRITH-XSC[Walter1993a]is an IBM product running under the VM operating system.The preprocessor TPX[Husung1989]translates to Turbo-Pascal,and an alternate set of Fortran90modules[Walter1993b]is under development.However,our module INTERVAL ARITHMETIC,based on a minimalist philosophy,is thefirst polished,publicly available and portable access to an interval data type.It is reasonably efficient and practical in a variety of applications,and is simple to maintain and extend.INTERVAL ARITHMETIC is the most universally useful portion of the package de-scribed in[Kearfott1995].In module INTERVAL ARITHMETIC,the endpoints of the interval are represented as double precision Fortran variables.The module should be useful to persons requiring portable interval arithmetic in standard Fortran90,with reasonable,but not optimal,accuracy and efficiency.2.SYNTAX DEFINED IN INTERVAL ARITHMETICThe module INTERVAL ARITHMETIC defines the four elementary operations(+,−,∗, and/),as well as negation(i.e.unary minus),on interval data types.Mixed-mode operations are allowed only between intervals and double precision,or between intervals and integer numbers2.Exponentiation∗∗is defined for interval-to-interval, interval-to-integer,double precision-to-interval,interval-to-double precision,and integer-to-interval.The module defines the generic namesACOS,ACOT,ASIN,ATAN,COS,COT,EXP,LOG,SIN,(1)SINH,SQRT,and TAN,2This is because intervals are stored and rounded out as double precision numbers.Arithmetic between a single-length real and interval wouldfirst involve converting the single-length real to double precision,then rounding according to the double precision machine epsilon.However,the single-precision value may be only accurate to single precision,so the rounded interval would not contain the theoretical value.Rigor would thus be sacrificed.4·R.B.KearfottTable I.Special interval functions in module INTERVAL ARITHMETICfunctionSyntax CorrespondingINTLIB routineZ=ABS(X)IVLABS z←{|x|,x∈x}R=WID(X)IWID r←x−xR=MID(X)IMID r←(x−x)/2R=MAG(X)INTABS r←max{|x|,|x|}Z=MAX(X,Y)−z←[max{x,y},max{x,y}]Z=MIN(X,Y)−z←[min{x,y},min{x,y}]R=MIG(X)IMIG“mignitude:”r←min{|x|,|x|}if0∈x,and r←0otherwiseeach of which returns bounds on the range,to within roundout error,of the cor-responding point-valued function.In each case,a corresponding INTLIB routine [Kearfott et al.1994]is used,with TAN and COT employing the INTLIB routines ISIN and ICOS.(Here,“roundout error”is the excess width of the interval result caused by rounding the lower endpoint down and the upper endpoint up after each operation in a series of interval computations.)Additionally,the special interval functions in Table I are defined3.The defini-tions of ABS and MAG vary slightly from those in ACRITH-XSC[Walter1993a]and other languages with interval data types:the function ABS in ACRITH-XSC cor-responds to the INTERVAL ARITHMETIC function MAG,and is consistent with use of |◦|throughout the literature on interval computations.However,when coding objective functions for interval branch and bound algorithms,it is more natural for ABS to return the range of|◦|.Finally,INTERVAL ARITHMETIC defines the operators exhibited in Table II.The binary operations in Table II that correspond to Fortran intrinsic relational oper-ators on default data types(i.e..LT.,.GT.,.LE.,.GE.,.NE.,and.EQ.)admit mixed mode operations between intervals and double precision or integers,while either or both arguments of.CH.may be double precision.Also,note that,in stan-dard Fortran90,the relational operations may be given either by.LT.,.GT.,.LE., .GE.,.NE.,and.EQ.or by<,<=,>,>=,/=,and==,respectively.For example,the expression“A<B”,where A and B are intervals,is equivalent to“A.LT.B”.With the exception of ABS and MAG,the operators and functions in the list(1) and Tables I and II act similarly to those in ACRITH-XSC.The interval data type in module INTERVAL ARITHMETIC is a user-defined se-quenced structure with two components(e.g.the interval X has components X%LOWER and X%UPPER).In contrast,the interval data type in INTLIB consists of a singly-dimensioned array with two elements,e.g.the lower bound X(1)and the upper bound X(2).In a non-portable version of INTERVAL ARITHMETIC,the Fortran90in-terval data type was associated directly and efficiently with corresponding INTLIB intervals through subroutine calls.This technique worked,since the storage se-quence of the Fortran90data type is the same as the storage sequence of an inter-val in INTLIB.However,this implicit equivalencing is non-standard,and cannot be expected to be possible on all systems,i.e.,it cannot be assumed that an interval3In Table I,the Fortran90interval variables X,Y and Z are identified with intervals x=[x,x], y=[y,y]and z=[z,z],while r is identified with the double precision variable R.INTERVAL ARITHMETIC:An Interval Data Type·5 Table II.Relational operators defined in module INTERVAL ARITHMETICfunctionSyntax CorrespondingINTLIB routineZ=X.IS.Y ICAP z←x∩yZ=X.CH.Y IHULL z←[min{x,y},max{x,y}]X.SB.Y IILEI.TRUE.if x⊆yX.SP.Y IILEI.TRUE.if x⊇yX.DJ.Y IDISJ.TRUE.if x∩y=∅R.IN.X IRLEI.TRUE.if r∈xY.IN.X IRLEI.TRUE.if y is in the interior of xY.LT.X−.TRUE.if y<xY.GT.X−.TRUE.if y>xY.LE.X−.TRUE.if y≥xY.GE.X−.TRUE.if y≥xY.NE.X−.TRUE.if y=x(set inequality)Y.EQ.X−.TRUE.if y=x(set equality)as defined by INTERVAL ARITHMETIC can be passed directly as an actual argument to an INTLIB routine.For this reason,the module INTERVAL ARITHMETIC uses the(less efficient)technique of actually moving the data between the data types. (INTERVAL ARITHMETIC also contains Fortran90versions of some low-level INTLIB routines,for efficiency.)Assignment of interval values can be done using the default Fortran90assign-ment to structures,e.g.X=INTERVAL(.3D0,.3D0).However,this scheme is not recommended,since the values may not be properly rounded when converted from character strings tofloating point numbers.The function IVL,which accepts ei-ther one or two double precision or integer arguments,causes the internally-stored result to be rigorously rounded4.Also,the module INTERVAL ARITHMETIC over-loads assignment(=),so that,when an integer or double precision number is as-signed to an interval,the result is properly rounded.For example,X=IVL(.3D0), X=IVL(.3D0,.3D0),and X=.3D0each5cause a properly rounded inclusion of the number.3to be stored in the interval variable X.The left and right endpoints of an interval X are double precision numbers ac-cessed as X%LOWER and X%UPPER,respectively.These expressions may occur on either side of an assignment statement.The lower and upper endpoints of an inter-val may also be accessed in an expression(but not on the left side of an assignment statement)with INF(X)and SUP(X),respectively.Implicit conversion between in-tervals and other data types is not allowed:conversions are done with INF,SUP, and MID.3.INSTALLATION AND USEThe system consists of the following components.4assuming that INTLIB has been installed properly to take account of the conversion errors;see [Kearfott et al.1994].5IVL also accepts integer arguments,such as X=IVL(3),X=IVL(3,3D0),or X=3,where X is an interval variable.However,many machines can store small integers exactly infloating point formats;for such machines,outward rounding is not necessary,and X=INTERVAL(3,3)would be more logical.6·R.B.KearfottIVL DEF:a small Fortran90module that defines the intervaldata type;INTERVAL ARITHMETIC:the Fortran90module,approximately866lines,thatdefines the syntax of§2;TEST INTERVAL ARITHMETIC:a short program to test proper installation of the sys-tem;TEST INTERVAL SYSTEM:a lengthier program for more extensive testing6of theinstallation.SAMPLE.OUT:sample output from TEST INTERVAL SYSTEM. TINYSMPL.OUT sample output from TEST INTERVAL ARITHMETIC INTLIB:the FORTRAN77library that provides the actualelementary operations and standard functions[Kear-fott et al.1994].D1MACH:a portable,Fortran90version of this SLATEC rou-tine,that can replace the version in INTLIB. Installation of the system is in the following order.(1)Install INTLIB according to the instructions of[Kearfott et al.1994].(2)Compile IVL DEF in the directory for Fortran90modules.(3)Compile INTERVAL ARITHMETIC in the directory for Fortran90modules,makingsure the compiler has access to the module IVL DEF.(4)Compile and link TEST INTERVAL ARITHMETIC,making sure the compiler hasaccess to the modules IVL DEF and INTERVAL ARITHMETIC;the linker should have access to the object code for IVL DEF and INTERVAL ARITHMETIC,as well as to the object library for INTLIB.(5)Run TEST INTERVAL ARITHMETIC(or TEST INTERVAL SYSTEM)to check properinstallation.The program TEST INTERVAL ARITHMETIC provides a template for use of the sys-tem.The syntax is as in§2.The program TEST INTERVAL SYSTEM provides a somewhat more exhaustive test of module INTERVAL ARITHMETIC.The program TEST INTERVAL SYSTEM causes each executable statement in module INTERVAL ARITHMETIC to be executed,and checks that operators and functions give the proper results.Since most of the results are intervals with integer endpoints,the exact results are input explicitly as integer constants,then converted,e.g.[1,2]is input as INTERVAL(1,2).The computed results are compared to the exact results so input,and an error isflagged if the computed results do not contain the exact results.If no errors areflagged,then a message stating that module INTERVAL ARITHMETIC appears to be installed cor-rectly is printed at the end of the output.Output,to thefile INTARITH.OUT,also includes printouts of the results of the explicit conversion routine IVL,results of rounding out near the underflow threshold,and results of precipitating two types of errors that INTLIB catches.Examining the less significant digits in the printed 6Note that INTLIB comes with its own set of tests,for the arithmetic itself.The tests provided with the module INTERVAL ARITHMETIC check the syntax defined in INTERVAL ARITHMETIC.INTERVAL ARITHMETIC:An Interval Data Type·7 results of IVL and the rounding out may help the installer to determine that the simulated directed rounding is operating correctly.The output should correspond roughly to the samplefile SAMPLE.OUT that is supplied with the algorithm,ex-cept that the endpoints may differ slightly depending on the characteristics of the arithmetic and on the details of the particular implementation of binary-to-decimal conversion for formatted output.This should not be a problem,assuming INTLIB, and,in particular,D1MACH,have been installed correctly.Correct simulated directed rounding is important for mathematical rigor in the computations.If some of the tests in TEST INTERVAL SYSTEM fail,it can be due to inaccurate conversion of the character strings representing integer and decimalfloating point constants,either in the program TEST INTERVAL SYSTEM or in the INTLIB routine SIMINI.It is assumed in TEST INTERVAL SYSTEM that such conversions give the closest machine number to the decimal string representation,and it is assumed in INTLIB that such conversions are of the same accuracy as the four basic arithmetic operations.Failure of the tests in TEST INTERVAL SYSTEM can also be due to an insufficient number of decimal digits in the representation,if DOUBLE PRECISION on the target machine corresponds to more than30digits.Sample output to the less exhaustive test program TEST INTERVAL ARITHMETIC is in thefile TINYSMPL.OUT,while running TEST INTERVAL ARITHMETIC produces thefile TEST F90INTARITH.OUT.The output to TEST INTERVAL ARITHMETIC will be the same on many systems.The source code to INTERVAL ARITHMETIC is meant to be readable and modifiable by the user,although a conservative approach to modifications is recommended.In particular,it is hoped that this module will provide a basis for standardization of syntax for interval computations in Fortran.4.ADDITIONAL ASSUMPTIONS AND COMMENTSIn addition to the assumptions for which INTLIB is rigorous,it is assumed that 0and1are represented exactly in double precision,and that conversion from in-teger to double precision(e.g.with DBLE(I))yields an exact representation.The integer-to-double conversions are used in the mixed mode binary operations;if such conversions are not exact,then the conversion should be done explicitly using the function IVL.Representations of0and1are assigned explicitly in the module to the parameter variables ZERO and ONE.The four elementary operations,unary negation,and the routine RNDOUT were re-defined in this module(i.e.the corresponding INTLIB routines are not always used) for a combination of portability and efficiency considerations.The corresponding INTLIB routines were used as templates.Finally,as with INTLIB,the author has a non-portable version,using assembler language for the directed rounding as in[Kn¨u ppel1994],available for Sun Sparc systems,that runs roughly twice as fast on those systems.ACKNOWLEDGMENTSI wish to thank my students Kaisheng Du,Xiaofa Shi and Shiying Ning,as well as Claire Adjiman and George Corliss,who have used the system over a period of several years,and have provided valuable suggestions.I also wish to thank John8·R.B.KearfottReid for the extensive help he gave.Finally,I thank the referee,whose extensive comments led to substantial changes.REFERENCESCrary,F.1976.The AUGMENT precompiler.Technical Report1470,MRC,University of Wisconsin,Madison.Hammer,R.,Neaga,M.,and Ratz, D.1993.PASCAL-XSC,New concepts for scientific computation and numerical data processing.In Adams,E.and Kulisch-U.(Ed.),Scientific computing with automatic result verification,New York,etc.,pp.15–44.Academic Press.Husung,D.1989.Precompiler for scientific computation(TPX).Technical Report91.1,Inst.for Comp.Sci.III,Technical University Hamburg–Harburg.Kearfott,R.B.1995.A Fortran90environment for research and prototyping of enclosure algorithms for constrained and unconstrained nonlinear equations.ACM Trans.Math.Soft-ware21,1(March),63–78.Kearfott,R.B.,Dawande,M.,Du,K.-S.,and Hu,C.-Y.1994.Algorithm737:INTLIB:A portable FORTRAN77interval standard function library.ACM Trans.Math.Soft-ware20,4(December),447–459.Klatte,R.,Kulisch,U.,Wiethoff,A.,Lawo,C.,and Rauch,M.1993.C-XSC A C++ Class Library for Extended Scientific Computing.Springer-Verlag,New York.Kn¨u ppel,O.1994.PROFIL/BIAS—A fast interval puting53,277–287.Leclerc,A.1993.Parallel interval global optimization in C++.Interval Computations1993,3, 148–163.Neumaier,A.1990.Interval Methods for Systems of Equations.Cambridge University Press, Cambridge,England.Walter,W.V.1993a.ACRITH-XSC:A Fortran-like language for verified scientific comput-ing.In Adams,E.and Kulisch,U.(Ed.),Scientific Computing with Automatic Result Verification,New York,etc.,pp.45–70.Academic Press.Walter,W.V.1993b.FORTRAN-XSC:A portable Fortran90module library for accurate and reliable scientific puting(Suppl.)9,265–286.Yohe,J.M.1979.Software for interval arithmetic:A reasonably portable package.ACM Trans.Math.Software5,1(March),50–53.。
