1.1.2弧度制2010.3.4
1.1.2弧度制及弧度制与角度制的换算(技术总结

的所对的圆心
角的大小;
(3) 弧度制是十进制 , 它的表示是用一个实 数表示 ,而角度制是六十进制;
(4) 以弧度和度为单位的角 ,都是一个与 半径无关的定值。
4. 弧度制与角度制的换算
① 用角度制和弧度制度量角 ,零角既是0º 角 , 又是0 rad角 , 同一个非零角的度数和 弧度数是不同的.
②平角 、周角的弧度数: 平角= rad 、周角=2 rad.
③ ∵ 360 =2 rad , ∴180 = rad ∴1 = 1 rad
例3. 填写下表:
角度 0 ° 30° 45° 60° 90° 120°
弧度 0
角度 135° 150° 180° 210° 225° 240°
弧度
π
角度 270° 300° 315° 330° 360°
注: 今后在用弧度制表示角的时候 , 弧度二字 或rad可以略去不写。
3. 弧度制与角度制相比:
(1) 弧度制是以“弧度 ”为单位的度量角的 单位制 , 角度制是以“度 ”为单位来度量角 的单位制; 1弧度≠1º ;
(2) 1弧度是 弧 长 等 于 半 径 长 的 圆 弧 所 对 的 圆
心角的大小 ,而1度是圆周
弧度
2π
5. 用弧度制表示弧长及扇形面积公式: ① 弧长公式:
由公式:
比公式
简单.
弧长等于弧所对的圆心角(的弧度数) 的绝对值与半径的积. ②扇形面积公式
其中l 是扇形弧长 ,R是圆的半径。
例1
【解析】 根据角度 、弧度的定义 ,可知无论角 度制还是弧度制 , 角的大小都与圆的半径长短无 关 ,而与弧长与半径的比值有关 ,所以D错误 . 【m , 当它的半径和圆心角
1.1.2_弧度制

例 、已知A {/2k 2k 1 ,k Z} B {/ - 4 4}求A B 1 ( ) ,
变: A {x/y 36 - x },B {/2k 2
3
2k
3
, k Z}求A B
例2、M / (2k 1) , k Z , N / (4k 1) , k Z , 求M、N关系
取“-”表示终边在y轴的负半轴上的角的集合
A 提示: { | k
(B) A B (D)以上都不对。
y
o y o
x 取+ x 取-
, k Z}
k取奇数
另解:只要将k取几个连续整数就能快速求解,不信?你可 试一试。
(2)已知集合 A | 2k (2k 1) , k Z, B | 4 4 则 A B 等于( D )
| n | | n | r l 2 r 360 180
| n | r 2 | n | S r2 360 360
弧度制
l R
1 S lR 2
说明: ① 弧度制下的公式要显得简洁的多了; ② 以上公式中的必须为弧度单位.
例题讲解
例4 如果一扇形的周长为20cm,问扇形的半径和圆 心角各取什么值时,才能使扇形的面积最大?
设扇形的中心角为 , 半径为r, 则
20 2r 2r r 20, r 1 2 1 20 2r 2 r (10 r )r 10r r 2 S 扇形 r 2 r 2 10 当r 5时, S扇形 25, 此时 2 max 2 (1) 答 : 扇形的半径为 cm,圆心角为 rad时, 扇形面积最大 5 2
1.1.2弧度制课件

导出关系
∴平角的弧度数= RR= 同理,弧是整圆,圆心角是周角, 周角的弧度数为2
360°=2 rad 180°= rad
1°= 180 rad 0.01745 rad
1
rad=
180
57.30=57°18′
(1)设一个角的弧度数为 rad
则
(180)o
rad =
(2)设一个角的角度数为no
则 no = n rad
解:∵
6730
=
135
2
6730' = rad 135 = 3 rad
180
28
例2 把 3.14 rad化成度.(精确到0.001)
180 = 3.14 = 3.14 (180) 179.909
1 = rad
180
1rad
=
180
写出一些特殊角的弧度数
角 度
0 30 45 60 90 120135150180 270 360
弧长与半径的比值是唯一 确定的,与半径大小无关
弧长等于半径长度的弧所对的圆心角为 1弧度的角
单位:弧度,单位符号:rad, 读作弧度.
B
l =r
Oo r A
AOB=1rad
C这种以l 弧= 2度r 作为单位来A
r
度量O角o的单 位制叫做弧 度制。
AOC=2rad
角度制与弧度制的比较
单位 1
角度制
解 : 设扇形半径为 r,弧长为l,则由
2r l = 8 1 lr = 4 2
l
r
解得 R = 2 l = 4
故该扇形的圆心角的弧度数为
= l =4 =2
1.1.2弧度制

0
π π 6 4
π π 3 2
2π 3π 5π 3 4 时候,“弧度” 二字或者“rad”通常省略不写,而只写这个角 。 所对应的弧度数.但如果以度( )为 单位表 。 示角时,度( )不能省略.
1 例1:利用弧度制证明扇形面积公式 S = lR 2
其中是l扇形弧长,R是圆的半径。
π rad=0.01745 rad 1°= 180
课堂练习
1、-300°化为弧度是( B )
A. - 4π
3
B.- 5π
3
C.- 7π
4
D.- 7π
6
2、计算
tan1.5
解: 1.5rad = 57.30按 1.5 = 85.95 = 85 57'
所以 tan1.5 = tan 85 57 ' = 14.12
周角的弧度数是2π,而在角度制 下的度数是360。 ∴ 360°= 2πrad; 180°= πrad.
π 1= rad ≈ 0.01745rad 180
°
180°= πrad
180 ° 1rad = ( )≈ 57.30° π
角 度 弧 度
0
30 45 60 90 120 135 150 270 360 180
3 、不论是以“弧度”还是以“度”为单位 的角的大小都是一个与圆的半径大小无关的 定值.
一般地,我们规定:
正角的弧度数是正数。 负角的弧度数是负数。
零角的弧度数是0。
弧度数的绝对值公式 角的弧度数的绝对值
l (l为弧长,r为半径) r
l |α|= r
r r
其中 : 1、l是以角α作为圆心角时所对弧的长,r是半径; 2、正角的弧度数是一个正数,负角的弧度数是 一个负数,零角的弧度数是0; 2 πr 3、圆心角θ为周角时,l = 2πr,则θ = = 2 π; r πr 4、圆心角θ为半角时,l = πr,则θ = = π。 r
1.1.2弧度制

例3
写出满足下列条件的角的集合(用弧度制):
1、 终边与X轴正半轴重合;
2、 终边与X轴负半轴重合; 3、 终边与X轴重合;
| = 2 ( ) | = 2 ( )
| 2 2 2 7、第一象限内的角; | 2 2 8、第二象限内的角; 2 3 | 2 2 2 9、第三象限内的角; 3 | 2 2 2 10、第四象限内的角; 2
o
终边相同的角的表示:
(1)用角度表示
与终边相同的角可以表示为: k 360 ,k Z
它们构成一个集合: S = | = k 360 , k Z (2)用弧度表示
与终边相同的角可以表示为: 2k,k Z
它们构成一个集合: S = | = 2k , k Z
弧度制 : 定义: 我们把长度等于半径长的弧所对的 圆心角叫做1弧度的角,即用弧度制度量时, 这样的圆心角等于1rad。 单位符号 :rad B
l =r O
读作弧度 C
l = 2r
2 rad O r
o
1rad r
A
A
o
AOB=1rad
AOC=2rad
思考:为什么可以用弧长与其半径的比值来度 量角的大小呢?即这个比值是否与所取的圆 的半径大小无关呢? AB AB = =定值? 设α =nº, AB 弧长为l,半径OA为r,
1 1 2 ② 扇形面积公式 S = lR = R . 2 2
其中l是扇形弧长,R是圆的半径。 证明:设扇形所对的圆心角为nº (αrad),则
n 1 2 S =R = R 360 2
【人教版】高中数学必修四第一章《1.1.2弧度制》精品课件

下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
(单击进入电子文档)
首
பைடு நூலகம்
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
课件1:1.1.2 弧度制和弧度制与角度制的换算

是多少?
答案
半径R=10㎝时,扇形的面积最大,最大值为
100㎝²。此时圆心角为2rad
题型三
自行车大链轮有48个齿,小链轮有20个齿,彼此
由链条连接,当大链轮转过一周时,小链轮转过
的角是多少度?多少弧度?(三维)
题型三
解:由于大链轮与小链轮在相同时间内转过的
式可得解。
解析(1)因为α=120°=2/3πrad, R=6
所以,AB的弧长为 l=2/3π×6=4π
(2)因为S扇形OAB=1/2lr=1/2×4π×6=12π
S
=1/2R²×sin2/3π=1/2×6²×√3/2=9√3
三角形ABO
S弓形OAB=S扇形OAB-S三角形OAB=12π-9√3
已知一扇形的周长为 ,当它的半径和圆心角
式中。
考点分析:
1、弧度制与实数的集合之间建立一种一一对
应的关系。
2、一些特殊角的度数与弧度数的对应值应
该记住。但值得注意的是,用“度”为单位度
量时,“度”不能省略。
3、今后在具体运算时,“弧度”二字和单位
符号“rad”可以省略 如:3表示3rad 。sinπ表
示πrad角的正弦。
总结提炼
(1)
式有诸多优越性,但是如果已知的角是以“度”
为单位,则必须先把它化成弧度后再计算,这
样可避免计算过程或结果出错。
要点阐释
3.与 终边相同的角的一般形式为
+ ∗ º, ∈
注意以下四点:
① k∈Z;②是任意角;
③ k·360º与之间是“+”号,如k·360º-30º,应看成
k·360º+(-30º);
1.1.2弧度制(一)

②整圆所对的圆心角为 2 r 2 .
r ③正角的弧度数是一个正数.
④负角的弧度数是一个负数.
⑤零角的弧度数是零.
⑥角的弧度数的绝对值||= l .
r
角度与弧度之间的转换 ①将角度化为弧度:
角度与弧度之间的转换 ①将角度化为弧度:
角度与弧度之间的转换 ①将角度化为弧度:
角度与弧度之间的转换 ①将角度化为弧度:
角 度
0o
30o
45o
60o
90o 120o
弧 度
0
6
角 度
135o
150o
180o
270o
360o
弧 度
特殊角的弧度
角 度
0o
30o
45o
60o
90o 120o
弧 度
0
6
4
角 度
135o
150o
180o
270o
360o
弧 度
特殊角的弧度
角 度
0o
30o
45o
60o
90o 120o
弧 度
0
6
4
3
弧度制定义 我们规定,长度等于半径的弧所
对的圆心角叫做1弧度的角; 用弧度来度量角的单位制叫做弧
度制.
讲授新课
弧度制定义 我们规定,长度等于半径的弧所
对的圆心角叫做1弧度的角; 用弧度来度量角的单位制叫做弧
度制. 在弧度制下,1弧度记做1rad.
讲授新课
弧度制定义 我们规定,长度等于半径的弧所
对的圆心角叫做1弧度的角; 用弧度来度量角的单位制叫做弧
r
②整圆所对的圆心角为 2 r 2 .
r ③正角的弧度数是一个正数.
1.1,2弧度制

①
②
解得 R1 =1,R 2 =4
2.一条弦的长度等于圆的半径,则这条弦所对 的圆心角的弧度数是( A)
A.
3
B.
6
C.1 D.
3.圆的半径变为原来的2倍,而弧长也增大到 原来的2倍,则( B ) A.扇形的面积不变 B.扇形的圆心角不变 C.扇形的面积增大到原来的2倍 D.扇形的圆心角增大到原来的2倍
4.已知半径为120mm的圆上,有一条弧的长 为144mm,求该弧所对的圆心角的弧度数。
R R
l=R
r r
l=r
弧度角的大小也与所取圆的半径大小无关。
若l=2r,
若l=3 r,
l = 2 弧度 则∠AOB= l r 则∠AOB= = 3弧度 r
B
2弧度
l=2r
A
3r
3rad
O r
r
若圆心角∠AOB表示一个负角,且它所对 的弧的长为3r,则∠AOB的弧度数是多少?
∠AOB的弧度数绝对值=
一、弧度制的定义:
用弧度做单位来度量角的制度叫做 弧度制
1.定义:把长度等于半径长的弧 所对的圆心角叫做1弧度的角. 记作1弧度 ,或1 rad ,或1
B r O
l=r
1rad
A
r
做一做:课本P10 习题1.1 A组 6
作半径不等的甲、乙两圆,在每个圆上作出 等于其半径的弧长,连结圆心与弧的两个端点, 得到两个角,将乙图移到甲图上,两个角有什么 样的关系?
其中 R是半径 , l是弧长 , (0 2 )为圆心角 , S是扇形的面积 .
1 1 2 (1)l R; (2) S lR. (3) S R ; 2 2 B
人教版数学必修4第一章1.1.2弧度制课件

(二)弧度制的绝对值公式
完成下列表格,你能得出哪些结论?
弧AB的长 OB旋转的方向 AOB 的弧度数 AOB 的度数
r
逆时针方向
2 r 逆时针方向
r
逆时针方向
1
2r
顺时针方向
-2
顺时针方向
未旋转
0
逆时针方向
180
逆时针方向
运用新知
根据度与弧度的换算关系,下表中各特殊角对应 的弧度数分别是多少?
注意:用弧度制表示角时,“弧度”二字或 “rad”通常略去不写,而只写该角所对应的弧 度数.如α=2表示α是2rad的角.
随堂练习: 1.根据条件完成下列度和弧度的转化;
(1)把 - 35 化成弧度;
(2)把 - 弧度化成度; 2.把下列角化成 0 到 2 的角加上 2 k 的形式;
4.在半径为r的圆中,n°的圆心角所对的圆弧长 如何计算?
l 2r n nr
360 180
5. 圆心角的大小是否与圆半径的大小有关?
探究新知
(一)弧度制的概念
讨论:角除了以度为单位,还有分和秒,他们 是六十进制的,计算不方便,角的度量是否也 能用不同的单位制?(类比长度的度量单位)
新知1:弧度制的定义
3.正角的弧度数是一个正数,负角的弧度数是一 个负数,零角的弧度数是0.
4.如果半径为R的圆的圆心角 所对弧的长为l,
那么,角的弧度数的绝对值是 l.
r
5.角度制与弧度制换算 :180°=π rad
运用新知
例1按照下列要求,把67°30′化成弧度:
(1)精确值;
(2)精确到0.001的近似值.
1.1.2弧度制

AOB的度数
r
2r
2
1 2
180 360
180 360
r
2r
逆时针
顺时针 顺时针
不旋转 顺时针
r
0 2r
0
180 0
360
2
B
O
1rad
“弧度”不是弧长,它 r 注: A 是一个比值,与半径大 小无关,值有正负.
正实数 零 负实数 实数集R
对应角的 弧度数
作业
金太阳导学测评 (二)来自0π 6 4
π 2 π 3 π 5 3 2 3 4 6
3π 2 2
例3 利用弧度制证明下列关于扇形公式:
1 l R
1 2 2 S R 2
1 3 S lR 2
其中R是半径,l是弧长,α(0<α<2π)为圆心角,S 是扇形面积.
l 证明:由公式 = 得l=αR (0<α<2π) r
1.1.2弧度制
复习:
任 意 角 正角:按逆时针方向旋转形成的角
负角:按顺时针方向旋转形成的角
零角:射线不做旋转时形成的角
象限角: 角的终边(除端点外)在第几象限就说这个角是第几象限角。
所有与角α终边相同的角,连同角α在内可构成一个集合
S={β|β= α + k· 360°,k∈Z}
即任一与角α终边相同的角,都可以表示成α与整数个周 角的和.
π 135 3 67 30 rad π rad 180 2 8
例1 按照下列要求,把67°30′化成弧度: (2)精确到0.001的近似值.
(2)利用计算器
MODE MODE °′″
1.1.2 弧度制
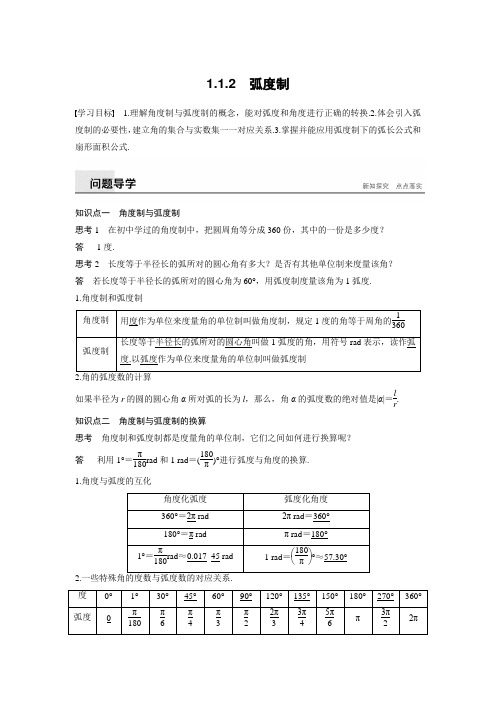
1.1.2弧度制学习目标 1.理解角度制与弧度制的概念,能对弧度和角度进行正确的转换.2.体会引入弧度制的必要性,建立角的集合与实数集一一对应关系.3.掌握并能应用弧度制下的弧长公式和扇形面积公式.知识点一角度制与弧度制思考1在初中学过的角度制中,把圆周角等分成360份,其中的一份是多少度?答1度.思考2长度等于半径长的弧所对的圆心角有多大?是否有其他单位制来度量该角?答若长度等于半径长的弧所对的圆心角为60°,用弧度制度量该角为1弧度.1.角度制和弧度制角度制用度作为单位来度量角的单位制叫做角度制,规定1度的角等于周角的1 360弧度制长度等于半径长的弧所对的圆心角叫做1弧度的角,用符号rad表示,读作弧度.以弧度作为单位来度量角的单位制叫做弧度制如果半径为r的圆的圆心角α所对弧的长为l,那么,角α的弧度数的绝对值是|α|=l r.知识点二角度制与弧度制的换算思考角度制和弧度制都是度量角的单位制,它们之间如何进行换算呢?答利用1°=π180rad和1 rad=(180π)°进行弧度与角度的换算.1.角度与弧度的互化角度化弧度弧度化角度360°=2π rad2π rad=360°180°=π radπ rad=180°1°=π180rad≈0.017_45 rad 1 rad=⎝⎛⎭⎫180π°≈57.30°2.度0°1°30°45°60°90°120°135°150°180°270°360°弧度0π180π6π4π3π22π33π45π6π3π22π知识点三 扇形的弧长及面积公式思考 扇形的面积与弧长公式用弧度怎么表示? 设扇形的半径为R ,弧长为l ,α为其圆心角,则α为度数 α为弧度数 扇形的弧长 l =απR180°l =αR 扇形的面积S =απR 2360°S =12lR =12αR 2类型一 角度与弧度的互化 例1 将下列角度与弧度进行互化. (1)20°;(2)-15°;(3)7π12;(4)-11π5.解 (1)20°=20π180=π9.(2)-15°=-15π180=-π12.(3)7π12=712×180°=105°. (4)-11π5=-115×180°=-396°.反思与感悟 (1)进行角度与弧度换算时,要抓住关系:π rad =180°.(2)熟记特殊角的度数与弧度数的对应值.跟踪训练1 (1)把112°30′化成弧度; (2)把-5π12化成度.解 (1)112°30′=⎝⎛⎭⎫2252°=2252×π180=5π8. (2)-5π12=-⎝⎛⎭⎫5π12×180π°=-75°. 类型二 利用弧度制表示终边相同的角例2 把下列各角化成2k π+α (0≤α<2π,k ∈Z )的形式,并指出是第几象限角: (1)-1 500°; (2)23π6; (3)-4.解 (1)∵-1 500°=-1 800°+300°=-5×360°+300°.∴-1 500°可化成-10π+5π3,是第四象限角.(2)∵23π6=2π+11π6,∴23π6与11π6终边相同,是第四象限角.(3)∵-4=-2π+(2π-4),π2<2π-4<π.∴-4与2π-4终边相同,是第二象限角.反思与感悟 用弧度制表示终边相同的角2k π+α(k ∈Z )时,其中2k π是π的偶数倍,而不是整数倍,还要注意角度制与弧度制不能混用.跟踪训练2 设α1=-570°,α2=750°,β1=3π5,β2=-π3.(1)将α1,α2用弧度制表示出来,并指出它们各自的终边所在的象限;(2)将β1,β2用角度制表示出来,并在[-720°,0°)范围内找出与它们终边相同的所有角. 解 (1)∵180°=π rad ,∴α1=-570°=-570π180=-19π6=-2×2π+5π6,α2=750°=750π180=25π6=2×2π+π6.∴α1的终边在第二象限,α2的终边在第一象限. (2)β1=35π=35×180°=108°,设θ=108°+k ·360°(k ∈Z ),则由-720°≤θ<0°,即-720°≤108°+k ·360°<0°, 得k =-2,或k =-1.故在[-720°,0°)范围内,与β1终边相同的角是-612°和-252°. β2=-π3=-60°,设θ=-60°+k ·360°(k ∈Z ),则由-720°≤θ<0°,即-720°≤-60°+k ·360°<0°, 得k =-1或k =0.故在[-720°,0°)范围内,与β2终边相同的角是-420°和-60°.类型三 扇形的弧长及面积公式的应用例3 已知一个扇形的周长为a ,求当扇形的圆心角多大时,扇形的面积最大,并求这个最大值.解 设扇形的弧长为l ,半径为r ,圆心角为α,面积为S .由已知,2r +l =a ,即l =a -2r . ∴S =12l ·r =12(a -2r )·r =-r 2+a 2r=-⎝⎛⎭⎫r -a 42+a 216. ∵r >0,l =a -2r >0,∴0<r <a 2,∴当r =a 4时,S max =a 216.此时,l =a -2·a 4=a2,∴α=lr=2.故当扇形的圆心角为2 rad 时,扇形的面积最大,最大值为a 216.反思与感悟 (1)联系半径、弧长和圆心角的有两个公式:一是S =12lr =12|α|r 2,二是l =|α|r ,如果已知其中两个,就可以求出另一个.(2)当扇形周长一定时,其面积有最大值,最大值的求法是把面积S 转化为r 的函数. 跟踪训练3 一个扇形的面积为1,周长为4,求圆心角的弧度数. 解 设扇形的半径为R ,弧长为l ,则2R +l =4, ∴l =4-2R ,根据扇形面积公式S =12lR ,得1=12(4-2R )·R ,∴R =1,∴l =2,∴α=l R =21=2,即扇形的圆心角为2 rad.1.时针经过一小时,时针转过了( ) A.π6radB.-π6radC.π12 radD.-π12rad答案 B解析 时针经过一小时,转过-30°, 又-30°=-π6 rad ,故选B.2.若θ=-5,则角θ的终边在( ) A.第四象限 B.第三象限 C.第二象限D.第一象限答案 D解析 2π-5与-5的终边相同, ∵2π-5∈(0,π2),∴2π-5是第一象限角,则-5也是第一象限角.3.已知扇形的周长是6 cm ,面积是2 cm 2,则扇形的圆心角的弧度数是( ) A.1B.4C.1或4D.2或4答案 C解析 设扇形半径为r ,圆心角弧度数为α,则由题意得⎩⎪⎨⎪⎧ 2r +αr =6,12αr 2=2,∴⎩⎪⎨⎪⎧ r =1,α=4或⎩⎪⎨⎪⎧r =2,α=1.4.已知两角的和是1弧度,两角的差是1°,则这两个角分别为____________. 答案 12+π360,12-π360解析 设这两个角为α,β弧度,不妨设α>β,则⎩⎪⎨⎪⎧α+β=1,α-β=π180,解得α=12+π360,β=12-π360.5.将-1 485°化成2k π+α,(0≤α<2π,k ∈Z )的形式为________. 答案 -10π+74π解析 因为-1 485°=-4×360°-45°=-4×360°+(-360°+315°) =-5×360°+315°, 所以-1 485°=-10π+74π.1.角的概念推广后,在弧度制下,角的集合与实数集R 之间建立起一一对应的关系:每一个角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应.2.解答角度与弧度的互化问题的关键在于充分利用“180°=π rad ”这一关系式. 易知:度数×π180rad =弧度数,弧度数×⎝⎛⎭⎫180π°=度数. 3.在弧度制下,扇形的弧长公式及面积公式都得到了简化,具体应用时,要注意角的单位取弧度.一、选择题1.-300°化为弧度是( ) A.-43πB.-53πC.-74πD.-76π答案 B解析 -300°=-300×π180=-53π.2.下列转化结果错误的是( ) A.60°化成弧度是π3B.-103π化成度是-600°C.-150°化成弧度是-76πD.π12化成度是15° 答案 C解析 C 项中-150°=-150×π180=-56π.3.若α=-10,则α为( ) A.第一象限角 B.第二象限角 C.第三象限角D.第四象限角答案 B解析 ∵-4π<-10<-2π, ∴-10=-4π+(4π-10). 又π2<4π-10<π, ∴4π-10为第二象限角, 则-10也是第二象限角.4.集合A =⎩⎨⎧⎭⎬⎫α|α=k π+π2,k ∈Z 与集合B ={α|α=2k π±π2,k ∈Z }的关系是( )A.A =BB.A ⊆BC.B ⊆AD.以上都不对 答案 A5.下列与9π4的终边相同的角的表达式中,正确的是( )A.2k π+45°(k ∈Z )B.k ·360°+9π4(k ∈Z )C.k ·360°-315°(k ∈Z )D.k π+5π4(k ∈Z )答案 C解析 A ,B 中弧度与角度混用,不正确. 94π=2π+π4,所以94π与π4终边相同. -315°=-360°+45°,所以-315°也与45°终边相同.故选C.6.已知2弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长是( ) A.2B.sin 2C.2sin 1D.2sin 1答案 C解析 ∵r =1sin 1,∴l =|α|r =2sin 1. 7.把-114π表示成θ+2k π(k ∈Z )的形式,使|θ|最小的θ值是( )A.-34π B.-2π C.π D.-π答案 A解析 ∵-114π=-2π+⎝⎛⎭⎫-34π =2×(-1)π+⎝⎛⎭⎫-34π, ∴θ=-34π.二、填空题8.已知集合A ={x |2k π≤x ≤2k π+π,k ∈Z },集合B ={x |-4≤x ≤4},则A ∩B =______________.答案 [-4,-π]∪[0,π] 解析 如图所示,∴A ∩B =[-4,-π]∪[0,π].9.如果圆心角为2π3的扇形所对的弦长为23,则扇形的面积为________.答案4π3解析 如图,作BF ⊥AC .已知AC =23,∠ABC =2π3,则AF =3,∠ABF =π3.∴AB =AFsin ∠ABF =2,即R =2.∴弧长l =|α|R =4π3,∴S =12lR =4π3.10.如果一扇形的弧长变为原来的32倍,半径变为原来的一半,则该扇形的面积为原扇形面积的________. 答案 34解析 由于S =12lR ,若l ′=32l ,R ′=12R ,则S ′=12l ′R ′=12×32l ×12R =34S .三、解答题11. 如图所示,半径为1的圆的圆心位于坐标原点,点P 从点A (1,0)出发,依逆时针方向等速沿单位圆圆周旋转,已知P 点在1 s 内转过的角度为θ (0<θ<π),经过2 s 达到第三象限,经过14 s 后又回到了出发点A 处,求θ.解 因为0<θ<π,且2k π+π<2θ<2k π+3π2(k ∈Z ),则必有k =0,于是π2<θ<3π4,又14θ=2n π(n ∈Z ),所以θ=n π7(n ∈Z ),从而π2<n π7<3π4(n ∈Z ),即72<n <214(n ∈Z ),所以n =4或5,故θ=4π7或5π7.12.已知一扇形的圆心角是α,所在圆的半径是R .(1)若α=60°,R =10 cm ,求扇形的弧长及该弧所在的弓形面积; (2)若扇形的周长是30,当α为多少弧度时,该扇形有最大面积? 解 (1)设弧长为l ,弓形面积为S 弓,∵α=60°=π3,R =10(cm),∴l =αR =10π3(cm).S 弓=S 扇-S △=12×10π3×10-2×12×10×sin π6×10×cos π6=50⎝⎛⎭⎫π3-32 (cm 2).(2)有l +2R =30,∴l =30-2R , 从而S =12·l ·R =12(30-2R )·R=-R 2+15R =-⎝⎛⎭⎫R -1522+2254. ∴当半径R =152 cm 时,l =30-2×152=15 cm ,扇形面积的最大值是2254 cm 2,这时α=lR=2 rad.∴当扇形的圆心角为2 rad ,半径为152 cm 时,面积最大,为2254 cm 2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在平面几何中研究角的度量,当时是用度做 在平面几何中研究角的度量, 单位来度量角, 的角是如何定义的? 单位来度量角,1 的角是如何定义的?
我们把用度做单位来度量角的制度叫做 角度制, 角度制,在数学和其他许多科学研究中还要 经常用到一种度量角的制度—弧度制 弧度制, 经常用到一种度量角的制度 弧度制,它是 如何定义呢? 如何定义呢?
写出一些特殊角的弧度数
角 度 弧 度
0
30 45 60 90 120 135 150 180 270 360
0
π π 6 4
3π π π 2π 3π 5π π π 2 2π 3 2 3 4 6
正角 零角 负角 正实数 零 负实数
练习3:用弧度表示: 练习 :用弧度表示: (1)终边在 轴上的角的集合 终边在x轴上的角的集合 终边在 轴上的角的集合;
1 360
所对的圆心角(或该弧) 所对的圆心角(或该弧)
小结
π ( 2)"角化弧"时,n 乘以 ) 角化弧" 将 180 180
将 α乘以 (3)弧长公式:l = a r )弧长公式: (1) 180 ) 弧度; = π 弧度; ;"弧化角"时, 弧化角"
π
;
1 1 2 扇形面积公式: 扇形面积公式: = lr = r α(其中 l为圆心角α 所 S 2 2
例1把67°30′化成弧度. (1)精确值 (2)精确到0.001 的近似值
例2 把 3.14 rad化成 度.(精确到0.001)
练习1:把下列角度化为弧度: 练习 :把下列角度化为弧度: (1)22030'; (2)-2100
练习2: 把下列弧度化为度: π 4π (1) ; (2) 12 3
是半径, 是弧长, 0 其中R是半径, l是弧长, α( < α < 2π) 为圆心角, 为圆心角, S是扇形面积.
角度制与弧度制的比较
①弧度制是以"弧度"为单位度量角的制度,角度制 弧度制是以"弧度"为单位度量角的制度, 是以" 为单位度量角的制度; 是以"度"为单位度量角的制度; ②1弧度是等于半径长的圆弧所对的圆心角(或该弧) 弧度是等于半径长的圆弧所对的圆心角( 弧度是等于半径长的圆弧所对的圆心角 或该弧) 的大小, 的大小,而 1 是圆的 的大小; 的大小; 不论是以"弧度"还是以" ③不论是以"弧度"还是以"度"为单位的角的大小都是 一 个与半径大小无关的定值. 个与半径大小无关的定值.
弧度制定义
我们把等于半径长 我们把等于半径长 圆弧所对的 所对的圆心 的圆弧所对的圆心 叫做1弧度的角 的角. 角叫做1弧度的角.
为什么可以用弧长与 其半径的比值来度量 角的大小呢? 角的大小呢?即这个 比值是否与所取的圆 的半径大小无关呢? 的半径大小无关呢?
弧度制—— 弧度制
一种新的度量角的单位制
B
2r=AB B
A O A
B
2r=AB 2r=AB2r=AB=AB 2r
B
B
2r=AB
r
O
O
A
A O
O A O
AO
A O
A
O
O A
A
A
AБайду номын сангаас
角度制与弧度制的换算
正角的弧度数是一个正数, 正角的弧度数是一个正数,负角 数是一个负数, 的弧度 数是一个负数,零角的弧 度数是0. 度数是0.
l α= r 正负
l | α |= r
角度制与弧度制的换算
用"弧度"与"度"去度量每一个角 弧度" 除了零角以外, 时,除了零角以外,所得到的量数都 是不同的, 是不同的,但它们既然是度量同一个 角的结果,二者就可以相互换算. 角的结果,二者就可以相互换算.
若弧是一个整圆,它的圆心角是周角,其弧 若弧是一个整圆,它的圆心角是周角, 度数是 2π ,而在角度制里它是360 , 因此 360 = 2π rad .
{α α = kπ , k ∈ Z }
(2)终边在 轴上的角的集合. 终边在y轴上的角的集合 终边在 轴上的角的集合.
{α α =
π
2
+ kπ , k ∈ Z }
例3.利用弧度制证明下列关于扇形的 利用弧度制证明下列关于扇形的 公式: 公式:
(1)l = αR; 1 2 ( 2 ) S = αR ; 2 1 ( 3 )S = lR. 2
对的弧长, 为圆心角的弧度数, 对的弧长,α 为圆心角的弧度数, 为圆半径.) r 为圆半径.)
�
B
定义: r 定义:长度等于半 r r r r r=ABr=AB r r=ABr rr r r=AB r=AB 径长的弧长所对 2rad r=AB 1rad r r rr rA r r O r r r Or r r 的圆心角为1 的圆心角为1弧度 的角. 的角.
r r
B B B B B
B
r=AB
O
B
