用分层法和D值法求解框架在竖向荷载作用下的内力_吴珊瑚
框架施工图—内力分析及侧移计算(建筑构造)

(2) 侧移刚度d的确定 侧移刚度d表示柱上下两端有单位侧移时在柱中产生的 剪力。根据假定(1),梁柱线刚度之比无穷大,则各 柱端转角为零,由结构力学的两端无转角但有单位水平 位移时杆件的杆端剪力方程,柱的侧移刚度d可写成:
V 12 i
d= =
c
D
h2
EI
i=
c
h
内力分析及侧移计算
(3)同层各柱剪力的确定
(5
柱端弯矩确定以后,根据节点平衡条件可确定梁的弯矩。
对于边柱节点(图(a)),有Mb=Mc1+Mc2 对于中柱节点(图1(b))
Mb1=ib1/(ib1+ib2)(Mc1+Mc2 Mb2=ib2/(ib1+ib2)(Mc1+Mc2)
内力分析及侧移计算
如图所示,从框架中任取一柱AB,根据转角位移方
内力分析及侧移计算
分层法
认为某层框架梁上的荷载只给本层梁及与本层梁相连的框架产 生剪力和弯矩
进行弯矩分配后叠加,叠加后的不平衡弯矩再分配但不传递
内力分析及侧移计算
2 框架在水平荷载作用下内力的近似计算——反弯点法和D值法
A 反弯点法 反弯点法基本假定: (1) 在进行各柱间的剪力分配时,假定梁与柱的线
(2) 在确定各柱的反弯点位置时,假定除底层柱以
多层多跨框架所受水平荷载主要是风荷载及水平 地震作用。一般可简化为作用在框架节点上的集中 荷载,其弯矩图如图(a)所示。它的特点是,各杆的 弯矩图都是直线形,每杆都有一个零弯矩点,称为 反弯点。框架在水平荷载作用下的变形情况如图(b) 所示
内力分析及侧移计算
程,柱两端剪力为:
V
=
12ic h2
6ic h
《钢筋混凝土结构》练习册及答案

第一讲绪论和混凝土材料一、填空:1、钢筋和混凝土相结合并能共同工作的三个基本条件是(两者相近的线膨胀系数);(有可靠的粘结力、钢筋在混凝土中有可靠的锚固);(混凝土对钢筋的保护作用)。
2、反映钢筋塑性性能的指标有(伸长率)和(冷弯性能)。
3、不同强度等级的混凝土,其σ–ε曲线不同。
一般混凝土强度等级越高,其极限抗压强度越(高),延性越(差)。
4、混凝土徐变的特性与其作用的初应力大小有关,当初应力σ/ƒc≤0.5时,产生(线性)徐变;当初应力σ/ƒc>0.5时,产生(非线性)徐变。
5、混凝土强度等级是以尺寸这为(150mm×150mm×150mm)的标准试件,在(28)天龄期准试验准试验方法测得的具有( 95% )保证率的抗压强度。
6、二、选择题:1、我国《混凝土结构设计规范》中,混凝土强度等级是按(C)确定的。
A、立方体抗压强度平均值;B、圆柱体抗压强度平均值;C、立方体抗压强度标准值;D、棱柱体抗压强度标准值。
2、对于混凝土的徐变和收缩,论述正确的是(A)。
A、混凝土在不变应力作用下,随时间的延续沿应力作用方向而增长的应变,称为混凝土的徐变;B、混凝土在不变应力作用下,随时间的延续沿应力作用方向而减小的应变,称为混凝土的收缩;C、混凝土在空气中结硬时,由于蒸发而失去水分,其体积缩小,称为混凝土的徐变;D、混凝土的徐变和收缩对钢筋混凝土结构只产生不利影响。
3、混凝土的变形模量是指(D)。
A、应力与塑性应变的比值;B、应力应变曲线切线的斜率dσ/dε;C、应力应变曲线原点切线的斜率;D、应力应变曲线上某一点的应力与总应变的比值。
4、混凝土的弹性系数是指(B)。
A、塑性应变与总应变的比值;B、弹性应变与总应变的比值;C、塑性应变与弹性应变的比值;D、变形模量与切线模量的比值。
5、三、简答题:1、在混凝土立方体强度试验中,尺寸效应是如何影响试件强度的?P62、什么是混凝土的徐变现象?徐变的性质与哪些因素有关?徐变对结构的影响有哪些?P15-16。
框架在竖向荷载作用下内力计算

A2
q1=10kN/m
B2
ic2 1
ib 0.777 ic2 1
A1
B1
8000
A 2
B 2
ic2 1
ic2 1
q 1 = 8 k N / m
A 1
B 1
ib 0.777
ic1 0.801
ic1 0.801
A 0
8 0 0 0
B 0
3、用力矩分配法计算第二层开口框架
(1)计算分配系数:
➢ 根据算得的各杆端弯矩值,作最后的弯矩图并求得 相应的剪力图和轴力图。
例题:
1882 12
42.667kNgm
(3)循环过程:A1
B1
用力矩分配法计算顶层开口框架
(1)计算分配系数:
A 2结 点
S A 2 A1 4 (0 .9 ic 2 )
S A 2 B 2 4 ib
S 4 (0 .9 ic 2 ib ) 4 1 .6 7 7
A2
A 2 A 1
S A 2 A1 S
6、计算梁跨中弯矩,计算梁剪力,绘制框架M、V图
例题:
用分层法计算 图示框架的内力
1、计算梁柱线刚度
Ic
bh3 12
1 12
0.4 0.553
1 12
0.0666
Ib
bh3 12
1 12
0.3
0 .7 3
1 12
0 .1 0 2 9
ic1
EIc H1
1 1 5 12
0.0666 E
1 12
1 2
,以作校核;
' ik
1 2
iik iik
(i)
➢ 计算荷载作用下各杆端产生的固端弯矩MFik,并写在相 应的各杆端部,求出汇交于每一节点的各杆固端弯矩之 和MFi,把它写在该节点的内框中;
框架结构在竖向荷载作用下的内力计算

框架结构在竖向荷载作用下的内力计算
框架结构在竖向荷载作用下的内力计算可近似地采用分层法.
在进行竖向荷载作用下的内力分析时,可假定:(1)作用在某一层框架梁上的竖向荷载对其他楼层的框架梁的影响不计,而仅在本楼层的框架梁以及与本层框架梁相连的框架柱产生弯矩和剪力.(2)在竖向荷载作用下,不考虑框架的侧移.
计算过程可如下:
(1)分层:分层框架柱子的上下端均假定为固定端支承,
(2)计算各个独立刚架单元:用弯矩分配法或迭代法进行计算各个独立刚架单元.而分层计算所得的各层梁的内力,即为原框架结构中相应层次的梁的内力.
(3)叠加:在求得各独立刚架中的结构内力以后,则可将相邻两个独立刚架中同层同柱号的柱内力叠加,作为原框架结构中柱的内力.
叠加后为原框架的近似弯距图,由于框架柱节点处的弯矩为柱上下两层之和因此叠加后的弯距图,在框架节点处常常不平衡.这是由于分层计算单元与实际结构不符所带来的误差.若欲提高精度,可对节点,特别是边节点不平衡弯矩再作一次分配,予以修正.。
框架柱竖向荷载作用下分层法

框架柱竖向荷载作用下分层法在工程建设中,框架结构是常见的一种结构形式,其承载能力主要通过竖向的荷载来传递。
为了更好地分析和计算框架结构的承载能力,就需要采用合理的设计方法。
分层法是一种常用的框架结构设计方法,本文将详细介绍框架柱竖向荷载作用下分层法的相关内容。
框架结构是由柱子和梁连接组成的,承载能力主要依赖于柱子的受力特性。
在柱子竖向荷载作用下,分层法是一种常用的计算方法。
根据力学原理,柱子受力的方式可以分为压力和拉力两种情况。
分层法的基本思路是将框架分成若干个水平分层,将荷载沿着结构的垂直方向分层作用,然后分析每一层的受力情况,最终得到整个框架结构的受力状态。
分层法的具体步骤如下:1.确定分层:首先,在进行分析之前需要将框架结构按照楼层进行分层。
每一层的高度可以根据实际情况来确定,一般可以按照楼层高度进行划分。
2.计算荷载:确定了分层之后,就需要计算每一层受到的荷载大小和作用位置。
荷载可以是静态荷载,如自重和楼层荷载,也可以是动态荷载,如地震荷载和风荷载。
根据实际情况,确定每一层的荷载大小和作用位置。
3.计算受力:在确定了荷载之后,就可以根据力学原理和分层的特点,计算每一层的受力情况。
对于柱子来说,根据受力情况将柱子分为压力区和拉力区,然后进行受力计算。
4.总结受力:在计算了每一层的受力情况之后,就可以将所有层的受力情况进行总结。
根据每一层的受力情况和柱子的承载能力,确定整个框架结构的受力状态和承载能力。
分层法的优点是能够较为直观地反映框架结构受力的状态,适用于对框架结构进行初步分析和估算。
然而,分层法也有其局限性,它忽略了框架结构的横向荷载作用和柱子的弯矩效应,只是一种粗略的计算方法。
在实际工程设计中,还需要结合其他分析方法进行综合计算和验证。
综上所述,框架柱竖向荷载作用下的分层法是一种常用的计算方法。
通过将框架结构按照楼层分层,计算每一层的受力情况,然后总结整个框架结构的受力状态,可以初步了解框架结构的承载能力。
框架结构竖向荷载作用下的内力计算

框架结构竖向荷载作用下的内力计算框架结构是由梁柱等构件组成的,在受到竖向荷载作用下,会引起构件内力的产生。
了解框架结构竖向荷载作用下的内力计算对于结构的设计和分析非常重要。
下面将详细介绍框架结构竖向荷载作用下的内力计算方法。
首先,通过建立结构模型来描述框架结构。
结构模型中包括构件、节点和连接关系。
构件可以是梁或柱,节点是构件之间的连接点,连接关系表示构件之间的刚性约束。
在竖向荷载作用下,框架结构的内力主要有两种情况:梁内力和柱内力。
1.梁内力计算:在竖向荷载作用下,梁会产生弯矩和剪力。
根据梁的基本理论,可以得出计算弯矩和剪力的公式。
-弯矩计算:弯矩是由竖向荷载作用在梁上引起的。
根据弯矩的定义,弯矩M等于施加在梁上的力乘以力臂。
当梁需要承受重力荷载时,弯矩的计算公式为M=w*l^2/8,其中w为荷载大小,l为梁的跨度。
-剪力计算:剪力是由竖向荷载作用在梁上引起的。
根据剪力的定义,剪力V等于施加在梁上的力。
当梁需要承受重力荷载时,剪力的计算公式为V=w*l/2,其中w为荷载大小,l为梁的跨度。
2.柱内力计算:在竖向荷载作用下,柱会产生压力和拉力。
根据柱的基本理论,可以得出计算压力和拉力的公式。
-压力计算:压力是由竖向荷载作用在柱上引起的。
根据力学平衡原理,压力P等于施加在柱上的荷载之和。
当柱需要承受多个重力荷载时,压力的计算公式为P=∑w,其中w为荷载大小。
-拉力计算:拉力是由竖向荷载作用在柱上引起的。
和压力类似,拉力T等于施加在柱上的荷载之和。
在实际计算过程中,需要考虑梁和柱的截面形状和材料性质,以及节点和连接部位的刚性约束等因素。
同时,还需要考虑结构的整体平衡条件和节点处的力的平衡条件。
在计算过程中,可以使用静力平衡原理和弹性力学理论来进行分析。
通过平衡方程和应变-位移关系等基本原理,可以建立结构方程组,并通过求解方程组得到内力的值。
总结起来,框架结构竖向荷载作用下的内力计算是一个复杂的过程,需要考虑多个因素和使用多种方法。
竖向荷载下内力计算方法(1)分层法

高层建筑结构是一个高次超静定结构,目前已有许多计 算机程序供内力、位移计算和截面设计。尽管如此,作为初 学者,应该学习和掌握一些简单的手算方法。
通过手算,不但可以了解各类高层建筑结构的受力特点, 还可以对电算结果的正确与否有一个基本的判别力。除此之 外,手算方法在初步设计中作为快速估算结构的内力和变形 也十分有用。
节点区混凝土灌注不密实等原因,节点容易产生变 形而达不到绝对刚性,框架梁端的实际弯短比弹性 计算值要小,因此,弯矩调幅系数允许取得低一
些,一般取0.7-0.8。
注意:
竖向荷载作用下பைடு நூலகம்框架
梁跨中计算所得的弯矩
1. M A M A0, 弯矩调幅系数 值小于按简支梁计算的
M B M B0 , =0.8 �����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
框架在竖向荷载作用下内力计算ppt课件

q2l 2
1 12
10 82
53.333kN gm
(3)循环过程B2
A2
19
20
4、还原-叠加、结点不平衡弯矩再分配一次
21
6、计算框架梁其他截面的弯矩 计算框架梁截面的剪力 计算框架柱的轴力
绘出弯矩图、剪力图
22
(2)迭代法
不考虑框架侧移时
基本步骤: ➢ 绘出结构的计算简图,在每个节点上绘两个框;
2
(1)分层法
▪ 分层法计算框架的内力的思路
以求解框架梁端与柱端弯矩为目标进行的,在求出 框架梁端和柱端弯矩后,即可求出梁其他截面的弯矩; 然后再求出梁的剪力和柱的轴力。
▪ 基本假定:
➢ 忽略垂直荷载作用下框架结构的侧移; ➢ 每层梁上的荷载只在本层梁及与其相连的上、下层柱
产生内力,不在其他层梁和其他层柱上产生内力。
多层与高层房屋结构设计
多层与高层框架结构设计
Multi-story Frame Structures and Tall Frame Structures
第五讲
——框架在竖向荷载作用下内力的近似计算方法
1
竖向荷载下的内力计算的弹性分析方法
在竖向荷载(vertical load)作用下,多、高层框架结构的 内力可用力法、位移法等结构力学方法计算。工程设计中,如 采用手算,可采用分层法、迭代法、力矩分配法、弯矩二次分 配法及系数法等近似方法计算
Mi'k
' M F
ik
i
M ' ki
i
式中,
M
' ki
——汇交于节点i各杆的远端转角弯矩
i
之和,最初可假定为0。
注:按上述公式计算时,一般选择不平衡弯矩较大的节点开始计 算循环若干轮,直到全部节点的弯矩值达到要求的精度为2止4 。
第六章-框架在竖向荷载作用下的内力分析
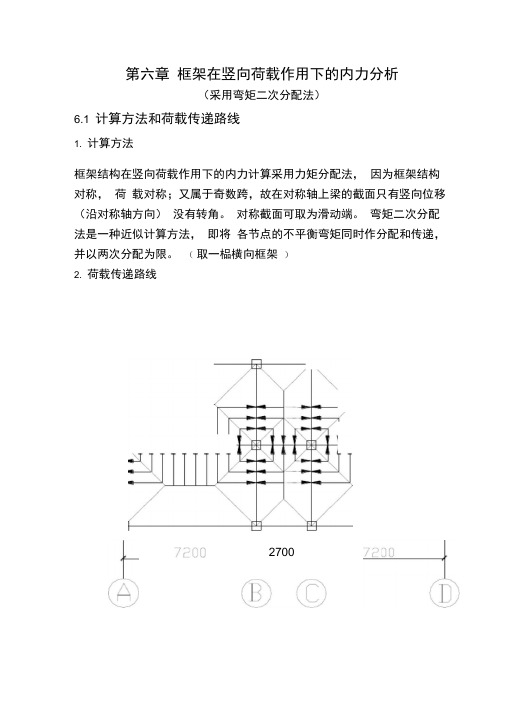
第六章框架在竖向荷载作用下的内力分析(采用弯矩二次分配法)6.1 计算方法和荷载传递路线1. 计算方法框架结构在竖向荷载作用下的内力计算采用力矩分配法,因为框架结构对称,荷载对称;又属于奇数跨,故在对称轴上梁的截面只有竖向位移(沿对称轴方向)没有转角。
对称截面可取为滑动端。
弯矩二次分配法是一种近似计算方法,即将各节点的不平衡弯矩同时作分配和传递,并以两次分配为限。
(取一榀横向框架)2. 荷载传递路线2700对于边跨板,为7.2 m×4.5m,由于7.2/4.5<3.0 所以按双向板计算对于中跨板,为 4.5m×2. 7m,由于 4.5/2.7 〈3.0 所以按双向板计算6.2 竖向荷载计算5.2.1 A-B(C-D) 轴间框架梁板传至梁上的三角形或梯形荷载等效为均布荷载。
1. 屋面板传载恒载: 5.0 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=18.85kN/m活载:0.5 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=1.89kN/m2. 楼面板传荷载恒载: 3.99 ×4.5/2 ×(1-2 × 0.31 2+0.31 3) ×2=15.08kN/m活载: 2.0 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=7.56kN/m3. 梁自重: 5.46 kN/mA-B(C-D) 轴间框架梁均布荷载为:屋面梁:恒载=梁自重+板传荷载=5.46 kN/m+18.85 kN/m=24.31 kN/m 活载=板传荷载=1.89 kN/m楼面梁:恒载=梁自重+板传荷载=5.46 kN/m+15.08 kN/m=20.54 kN/m 活载=板传荷载=7.56 kN/m5.2.2 B-C 轴间框架梁1. 屋面板传载恒载: 5.0 ×2.4/2 ×5/8 ×2=8.44kN/m活载:0.5 ×2.7/2 ×5/8 ×2=0.84kN/m2. 楼面板传荷载恒载: 3.99 ×2.7/2 ×5/8 ×2=6.73kN/m活载: 2.0 ×2.7/2 ×5/8 ×2=4.22kN/m3. 梁自重: 3.9kN/mB-C 轴间框架梁均布荷载为:屋面梁:恒载=梁自重+板传荷载=3.9 kN/m+8.44kN/m=12.34kN/m 活载=板传荷载=0.84kN/m楼面梁:恒载=梁自重+板传荷载=3.9 kN/m+6.73kN/m=10.63kN/m 活载=板传荷载=4.22kN/m6.3 框架计算简图g=24.31KN/m g=12.34KN/m g=24.31KN/m(q=1.89KN/m)2700框架计算简图6.4. 梁固端弯矩梁端弯矩以绕杆端顺时针为正,反之为负。
竖向荷载作用下框架结构采用分层法进行内力计算举例

竖向荷载作用下框架结构采用分层法进行内力计算举例
例,某8层框架,底层层高5.0m ,其余层层高3.2 m ,各层横梁竖向均布荷载为12kN/m ,各层梁柱的相对线刚度如下图所示,用分层法计算此框架在竖向荷载作用下的弯矩。
梁柱相对线刚度图
解:分层法采用力矩分配法计算,具体过程见以下各图,各杆的分配系数写在方框内。
带*号的数值是固端弯矩,各结点均分配两次,次序为先两边结点,后中间结点。
固端弯矩分配时要变号,弯矩传递不变号。
梁端弯矩传递系数为1/2,顶层和中间层各柱远端弯矩等于各柱近梁端弯矩的1/3(即传递系数为1/3),底层各柱远端弯矩等于各柱近梁端弯矩的1/2(即传递系数为1/2)。
最下一行数字为分配后各杆端弯矩。
12
-2
ql M =均载固, Fe M -=集中荷载固, 集中荷载均载梁固端M M M +=
顶层框架力矩分配过程
顶层弯矩图
中间层框架力矩分配过程
中间层弯矩图
底层框架力矩分配过程
底层弯矩图
各层柱端弯矩叠加,不平衡弯矩可再进行一次分配,得到框架弯矩总图(略)。
梁剪力可采用结构力学取脱离体的方法。
某框架顶层受荷图
完成顶层框架力矩分配过程。
分层法D值法课件

(
M
u c
M
d c
)Mr b源自ibr ibl ibr(M
u c
M
d c
)
二、水平荷载作用下的 D 值法
1.反弯点法存在的问题
(1)由于框架各层节点转角不可能相等, 故柱的反弯点位置也不可能 都在 柱中点;
(2)由于梁柱线刚度之比不可能为无穷大, 故柱的抗侧移刚度也不完全取 决于柱本身, 还与梁的刚度由关。
12 14.3 计算方法
第十四章 多层框架结构
2.修正后的柱抗侧移刚度 考虑柱上下端节点的弹性约束作用后,
柱的抗侧移刚度为:
D
12ic h2
13 14.3 计算方法
第十四章 多层框架结构
推导的基本假定为:
(1)柱AB及与其上下相邻的柱的线刚度均为ic; (2) 柱AB及与其上下相邻的柱的层间位移均为Δuj
7 14.3 计算方法
第十四章 多层框架结构
二、水平荷载作用下的反弯点法 P.160
8 14.3 计算方法
第十四章 多层框架结构
基本假定: (1)求各柱剪力时, 假定各柱上下端都不发生角位移, 即认为 梁的线刚度与柱线刚度之比为无限大;(柱按两端嵌固考虑, 因此各柱的抗剪刚度只与柱本身有关)
(2)确定柱反弯点位置时, 假定除底层以外的各层柱的上下端 节点转角均相同, 则除底层外各层框架柱的反弯点均位于柱高 的中点;对于底层柱, 则假定其反弯点距底支座2/3柱高处。 (柱反弯点位置是定值) (3)梁端弯矩可由节点平衡条件求出, 按节点左右梁的线刚度进 行分配。
第十四章 多层框架结构
作业:
P.202: 习题13-1
23
第十四章 多层框架结构
四、框架结构侧移计算及限值
框架结构的内力和位移计算分享

令
k
2k
D 12ic
h2
K ——为梁柱刚度比
——柱刚度修正系数(表示梁柱线刚度比对柱刚度的
影响)
2019/10/14
30
D 值法
梁柱刚度比K 中柱:(梁线刚度不同)
k i1 i2 i3 i4 2ic
边柱:( i1 i3 0 或 i3 i4 0 )
第j层总剪力 V pj
Vpj V1 j V2 j Vmj
2019/10/14
23
反弯点法
第j层各柱剪力为
V1 j
d1 j
m
V pj
dij
i 1
V2 j
d2 j
m
V pj
dij
i 1
Vij
d ij
m
V pj
dij
i1
2019/10/14
24
反弯点法
任意水平荷载下柱轴向变形产生的第j层处侧移 把框架连续化,根据单位荷载法:
Nj
2
Hj 0
(NN
/ EA)dz
N (H j z) / B
N——q(z)对坐标z处的力矩M(z)引起的边柱轴力 N——为单位集中力作用在j处时在边柱产生的轴力 Hj——j层楼板距底面高度
2019/10/14
2019/10/14
3
步骤七:内力组合、确定最不利内力
步骤八:截面尺寸验算 步骤九:延性设计调整 步骤十:构件截面设计
(抗弯、剪、扭、压等承载力计算)
步骤十一:构造要求
步骤十二:施工图绘制
2019/10/14
4
空间结构分析:TBSA、TAT、广厦 平面结构分析:
计算竖向荷载作用下的框架结构的方法

计算竖向荷载作用下的框架结构的方法框架结构是一种常见的建筑结构,它由柱子和梁组成。
竖向荷载是作用在结构的垂直方向上的力,包括自重、楼层荷载、雨水荷载、雪荷载等。
为了确保框架结构的安全性和承载能力,需要进行竖向荷载的计算和分析。
在计算竖向荷载作用下的框架结构时,一般采用结构分析的方法,包括静力分析和动力分析。
静力分析是指在结构不考虑振动和位移的情况下进行的力学分析。
它主要采用受力平衡方程来计算结构的内力和变形。
对框架结构来说,可以采用刚度法、位移法和力法等方法进行分析。
1. 刚度法:刚度法是一种常用的静力分析方法。
它基于结构刚度和受力平衡原理,将结构划分为单元,通过计算单元的刚度矩阵和节点位移来求解结构的内力和变形。
刚度法适用于简单框架结构的分析,通过构建刚度方程组,可以求解出结构的内力和位移。
2. 位移法:位移法是一种将结构的位移作为主要未知量的静力分析方法。
它基于受力平衡原理和位移相容条件,将结构划分为单元,在每个单元内根据位移的连续性和力的平衡关系建立方程。
通过求解位移方程组,可以得到结构的内力和位移。
3. 力法:力法是一种以力作为主要未知量的静力分析方法。
它基于受力平衡原理和材料力学性质,通过构建力的平衡方程组和力的变形关系式,求解出结构的内力和位移。
力法适用于结构相对复杂,难以直接建立刚度方程的情况。
动力分析是指考虑结构的振动和变形对受力和稳定性的影响进行分析。
在竖向荷载作用下的框架结构中,垂直地震荷载是最常见且重要的动力荷载。
动力分析一般分为静态分析和动态分析。
1. 静态分析:静态分析是指在地震作用下无需考虑结构的动力响应,主要考虑的是结构的受力和变形。
通过采用静态等效荷载法,将地震荷载转化为与之等效的静态荷载进行分析。
静态分析适用于低层次、简单结构,不涉及结构的动力特性。
2. 动态分析:动态分析是指考虑结构的动力响应,对地震荷载进行全面分析。
动态分析可以细分为线性动力分析和非线性动力分析。
用分层法和D值法求解框架在竖向荷载作用下的内力_吴珊瑚

MDB 7.83 7.35 6.10 9.18 17.20
MBD 5.40 3.68 31.90 5.92 9.60
References:
[ 1] ZHOUYun.Structuraldesignoftallbuilding[ M] .Wuhan:PressofWuhanUniversityofTechnology, 2006.(inChinese) [ 2] FANGE-hua, QIAN Jia-ru, YELie-ping.Structuraldesignoftallbuilding[ M] .Beijing:ChinaArchitecture& Building
1 问题的提出
框架在竖向荷载作用下内力的近似计算一般 采用分层法 [ 1 -2] .分层法的基本假定 :①忽略竖向 荷载作用下框架的侧移及由侧移 引起的弯矩 ;② 每层梁上的竖向荷载仅对本层梁及与本层梁相连 的柱的内力产生影响 , 而对其它层梁 、柱的内力影 响忽略不计 ;③忽略梁 、柱的 轴向变 形及剪 切变 形 .对于结构和荷载都接近对称的框架而言 , 框架 在竖向荷载作用下的侧移很小 , 因此 , 由假定 ①所 带来的内力误差也很小 .但是 , 当框架结构严重不 对称 , 或各跨框架梁上的荷载变化较大时 , 框架在 竖向荷载作用下的侧移就会较大 , 仅用分层法计 算的框架内力将产生较大的误差 [ 3] .D值法 [ 4 -5]
参考文献 :
[ 1] 周云 .高层建筑结构设计 [ M] .武汉 :武汉理工大学出版社 , 2006. [ 2] 方鄂华 , 钱稼茹 , 叶列平 .高层建筑结构设计 [ M] .北京 :中国建筑工业出版社 , 2003. [ 3] 周俐俐 .竖向荷载作用下框架内力计算方法的对比分析 [ J] .绵阳经济技术高等专科学校学报 , 2001, 18(3):19-21. [ 4] 廉为江 .水平荷载作用下框架内力手算方法评判 [ J] .中外建筑 , 2005, 11(1):90-91. [ 5] 沈蒲生 .高层建筑结构设计 [ M] .北京 :中国建筑工业出版社 , 2006. [ 6] 阎兴华 .混凝土结构设计 [ M] .北京 :科学出版社 , 2005. [ 7] 李汝庚 , 张季超 .混凝土 结构设计 [ M] .北京 :中国环境科学 出版社 , 2003. [ 8] 龙驭球 , 包世华 .结构力 学教程 (I)[ M] .北京 :高等教育出版社 , 2002. [ 9] 袁驷 , 叶康生 , 袁征 .《结构力学求解器 》的算法与性能 [ J] .工程力学 , 2001, A01:174-180. [ 10] 肖启扬 .框架结构计算例题的结构力学求解器分析 [ J] .黎明职业大学学报 , 2007, 19(3):61-64.
分层法和D值法

(2)除底层柱外,其余各层柱的弯矩传递系数取为1/3,底层取为1/2。
2. 力学知识回顾
1)转动刚度——杆端对转动的抵抗能力。以S表示。等于杆端产生单位转 角时需要施加的力矩。
线刚度: i EI / l
计算各层梁上竖向荷载值和梁的固端弯矩;
➢ 计算方法
1. D值——修正柱抗侧移刚度的计算
水平荷载作用下,框架不仅有侧移,且各结点有转角,设
杆端有相对位移 ,转角 1 、 2 ,转角位移方程为:
V
12ic h2
6ic h
(1
2)
令
DV
(D值的物理意义同d相同——单位位移下柱的剪力) D值计算假定:
(1)各层层高相等; (2)各层梁柱节点转角相等; (3)各层层间位移相等
第四章
框架结构设计(二)
——框架结构内力与位移计算
(二) 框架结构内力与位移计算
空间结构分析:TBSA、TAT、广厦 平面结构分析:
(1)结构力学方法计算:弯矩分配法 (2)近似计算方法:
<a> 竖向荷载下框架内力计算:分层法 <b> 水平荷载下框架内力计算:反弯点法
D值法 手算优点:容易理解结构受力性能的基本概念,掌握结构分析的基本方法 手算缺点:繁杂、耗时
③ 计算梁、柱弯矩分配系数和传递系数(上层柱的弯矩传递系数取为1/3, 底层取为1/2);
④ 计算各层梁上竖向荷载值和梁的固端弯矩;
⑤ 按力矩分配法计算单层梁、柱弯矩(次序为先两边结点,然后中间结点)
⑥ 分层计算的梁端弯矩为最终弯矩;
⑦ 分层计算的上下层所得同一根柱子内力叠加,得到柱得最终弯矩;
⑧ 节点会不平衡,误差不大。如误差较大,可将节点不平衡弯矩再进行一 次分配
水平荷载作用下框架内力的计算——D值法资料讲解

水平荷载作用下框架内力的计算——D值法资料讲解D值法是一种常用于计算框架结构在水平荷载作用下的内力的方法。
下面是对D值法进行详细讲解的资料。
一、D值法的基本概念D值法是一种近似计算框架结构内力的方法,其基本思想是通过估算框架结构在水平荷载作用下的刚度来计算内力。
具体而言,D值法通过假设结构刚度的变化与结构的变形呈线性正比关系,将结构的刚度表示为一个D值,再通过对结构的初始刚度和变形的估计,计算出结构在水平荷载作用下的内力。
二、D值的计算步骤(一)计算结构的初始刚度1.根据结构的几何形状和材料特性,计算出结构在初始状态下的刚度矩阵。
2.对刚度矩阵进行变换,得到初始刚度矩阵。
(二)估算结构的变形1.假设结构受到线性弹性变形的影响。
2.估计结构的位移和转角。
(三)计算D值1.根据估算的位移和转角,计算出结构的变形矩阵。
2.根据初始刚度矩阵和变形矩阵,计算出结构的刚度矩阵。
3.将刚度矩阵转化为D值,即刚度指数。
(四)计算内力1.根据D值和水平荷载的大小,计算出结构的内力。
2.对结构的各个部位进行内力平衡计算,得到各个构件的内力。
三、D值法的优缺点D值法在计算框架结构内力时具有一定的优势和局限性。
(一)优点1.简洁易行:D值法不需要进行繁琐的矩阵计算,计算步骤相对简单。
2.适用范围广:D值法适用于一般的框架结构,包括多层和复杂形状的结构。
3.结果可靠:在合理的假设和估计前提下,D值法可以得到较为准确的内力计算结果。
(二)缺点1.假设过于理想化:D值法假设结构的变形与刚度呈线性正比关系,这在实际情况下不一定成立。
2.忽略非线性效应:D值法无法考虑结构中的非线性效应,如材料的非线性和连接件的滑动、屈曲等。
3.精度受限:由于D值法是一种近似计算方法,其精度相对有限,不适用于对结构内力要求较高的情况。
四、D值法的应用领域D值法在实际工程中被广泛应用,特别是在简化计算和快速评估结构内力的情况下。
1.结构抗震设计:D值法常用于抗震设计中,通过快速计算内力,进行结构的抗震性能评估。
竖向荷载作用下的近似计算方法分层法

分层法计算要点
(3)用无侧移框架的计算方法(如弯矩分配法)计算各敞口 框架的杆端弯矩,由此所得的梁端弯矩即为其最后的弯矩值; 因每一柱属于上、下两层,所以每一柱端的最终弯矩值需将 上、下层计算所得的弯矩值相加。在上、下层柱端弯矩值相 加后,将引起新的节点不平衡弯矩,如欲进一步修正,可对 这些不平衡弯矩再作一次弯矩分配。 如用弯矩分配法计算各敞口框架的杆端弯矩,在计算每 个节点周围各杆件的弯矩分配系数时,应采用修正后的柱线 刚度计算;并且底层柱和各层梁的传递系数均取1/2,其他各 层柱的传递系数改用1/3。
竖向荷载作用下内力的近似计算方法 ——分层法
主讲:范凌燕
竖向荷载作用下的内力近似计算
在竖向荷载(vertical load)作用下,多、 高层框架结构的内力可用力法、位移法等结构 力学方法计算。工程设计中,如采用手算,可 采用迭代法、分层法、弯矩二次分配法及系数 法等近似方法计算。
常用方法——分层法
指结构的几何形状、约束、刚度和荷载具有对 称性(正对称或反对称)。正对称简称对称。 当结构承受正对称或反对称荷载时,也可以只 截取结构的一半进行计算,又称为半刚架法。
对称结构在对称荷载作用下变形是对称的,其内力图的特点是:
I2
I1 I1
M Q N
对称结构在反对称荷载作用下变形是反对称的,其内力图的特点是:
(4)在杆端弯矩求出后,可用静力平衡条件计算梁端剪力及 梁跨中弯矩;由逐层叠加柱上的竖向荷载(包括节点集中力、 柱自重等)和与之相连的梁端剪力,即得柱的轴力。
分层法的适用范围
分层法一般用于结构与荷载沿 高度分布比较均匀的多层框架的内 力计算,对于侧移较大或不规则的 多层框架不宜采用
力学补充知识:对称性的利用
层三跨框架结构内力计算任务书

五层三跨框架构造内力计算任务书学院:土木匠程与力学学院教师:戴萍科目:构造力学班级:土木0901 班姓名:许和平学号: U2目录1.计算任务⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ .32.计算构造的根本数据⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ ..33.水平荷载计算⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ (5)反弯矩法⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5反弯矩法弯矩⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ (8)反弯矩法剪力⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9反弯矩法力⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ (10)D 值法⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯..11法弯矩⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12.D法剪力⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ (13)D法力⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ (14)构造力学求解器⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ (15)构弯矩⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯..15构剪力⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯..16构力⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯..17计算结果比较⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ (17)4.竖直荷载计算⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 18.分层法⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯.18.分法弯矩⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯..20分法剪力⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯..21分法力⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯..22构造力学求解器⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯..23构弯矩⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯..23构剪力⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯..24构力⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯..25计算结果比较⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ (26)一、任务1、计算多层多跨框架构造在荷载作用下的内力,画出内力争。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 分层法的计算要点
用分层法计算图 1(b)的内力 , 其计算要点如 下 [ 1 -2] :
(1)将框架分成 n个 (n为层数 )独立的单层 无侧移框架 , 用力矩分配法进行计算 , 求得各单层 框架的弯矩后再进行叠加 , 从而得到框架各杆端 的弯矩 ;
(2)用力矩 分配法计 算时 , 除底层外 的各层 柱 , 线刚度乘以 0.9的折减系数 , 弯矩传递系数取 1 /3;
5 D值法的计算要点
用 D值法 计 算 图 1 (c)的 内 力 , 其 计 算 要 点[ 5] :①分别取各层柱反弯点处以上部分作为 分 离体 , 根据分离体的平衡条件求出各层剪力 ;②层 剪力按各柱的抗侧刚度 D在该层总抗侧刚度中所 占比例分配到各柱 ;③根据框架的层数 、柱所在的 位置 、梁柱线刚度比 、上下层梁刚度及层高的变化 情况 、荷载形式等确定各柱的反弯点高度 ;④根据 各柱的剪力大小及反弯点高度求出各柱端弯矩 , 并根据各节点平衡条件 求出各梁端弯矩 ;⑤梁 剪 力和柱轴力可根据杆件平衡条件求得 .
取第 i层以上框架结构为分离体如图 2(b)所
示 , 根据平衡条件得
n
n
∑ ∑ Ri =Vi1 +Vi2 - Rk =Vi - Rk (2)
k=i+1
k=i+1
7 结 论
联合应用分层法和 D值法来求解框架在竖向 荷载作用下的内力 , 由于考虑了框架的侧移 , 所以 计算精度肯定比仅采用分层法计算时要高 .需要 指出的是 , 由于分层法和 D值法都是近似计算方 法 , 因此 , 误差的存在是不可避免的 .当框架结构 的梁柱线刚度比越 大时 , 本文提出的计算方法 计 算的结果误差越小 .
表 1为算例按分层法 、联合运用 分层法和 D 值法以及结构力学求解器计算所得的杆端弯矩比 较 , 显然易见 , 分层法与 D值法联合应用所得结果 误差较分层法要小得多 .
图 2 不动铰支座反力计算 Fig.2 Hypothesissupportingforcescalculat、Vn2 为顶 层第 1和第 2根柱的剪力 ;Vn为顶层各柱的剪力和 .
杆端弯矩 结构力学求解器
MEF 17.70
分层法
弯矩 /(kN· m) 20.28
误差 /% 14.60
分层法与 D 弯矩 /(kN· m) 16.30
值法联合应用 误差 /% 7.90
MFE 17.60 12.75 27.60 16.73 4.90
MCD 25.20 29.98 19.00 24.89 1.20
(3)梁剪力 、柱剪力和轴力可根据杆件平衡条 件求得 .
4 不动铰支座反力 Ri的计算
由分层法求出图 1(b)的内力后 , 可根据力的
平衡条件 , 按下述方 法分别求出各不动铰支座的
反力 Ri.取顶层的分离体如图 2(a)所示 , 根据平
衡条件得
Rn =Vn1 +Vn2 =Vn
(1)
式中 , Ri为第 i层不动铰支座反力 ;Vi1 、Vi2 为 第 i层第 1和第 2根柱的剪力 ;Rk为第 k层不动铰 支座反力 ;Vi为第 i层各柱的剪力和 .
第 5期
吴珊瑚等 :用分层法和 D值法求解框架在竖向荷载作用下的内力
3 7
图 3 算例 Fig.3 Illustrationofthemethod
表 1 算例中各计算方法杆端弯矩比较 Table1 Comparisonofmomentsatrodendsbydifferentcalculatingmethods
第 9卷
到原受力状态 (即在竖向荷载作用下各层柱顶产 生侧移 Δi).即图 1(a)是图 1(b)和图 1(c)的叠 加 .叠加图 1(b)和图 1(c)的内力 , 即可得到图 1 (a)框架的内力 .
联合运用分层法和 D值法求解 , 即用分层法求 解图 1(b)的内力 , 用 D值法求解图 1(c)的内力 .
第20 910卷年 第105月期
广州大学学报 (自然科学版 )
JournalofGuangzhouUniversity(NaturalScienceEdition)
文章编号 :1671-4229(2010)05-0035-04
Vol.9 No.5 Oct. 2 010
用分层法和 D值法求解框架在竖向荷载作用下的内力
Architecture, 2005, 11(1):90-91.(inChinese) [ 5] SHENPu-sheng.Structuraldesignoftallbuilding[ M] .Beijing:ChinaArchitecture& BuildingPress, 2006.(inChinese) [ 6] YANXing-hua.Designofconcretestructure[ M] .Beijing:SciencePress, 2005.(inChinese) [ 7] LIRu-geng, ZHANGJi-chao.Designofconcretestructure[ M] .Beijing:ChinaEnvironmentSciencePress, 2003.(inChi-
Press, 2003.(inChinese) [ 3] ZHOULi-li.Acomparativeanalysisofcalculationofframeinternalforceunderverticalloads[ J] .JournalofMianyangCol-
legeofEconomyandTechnology, 2001, 18(3):19-21.(inChinese) [ 4] LIANWei-jiang.Adiscussiononthemanualcalculationofframeinternalforceofhorizontalloads[ J] .ChineseandOverseas
图 1 计算原 理 Fig.1 Calculationprinciple
收稿日期 :2010 -02 -26; 修回日期 :2010 -04 -11 作者简介 :吴珊瑚 (1963 -)女, 副教授 , 一级注册结构工程师 .E-mail:wushanhu5@
36
广州大学学报 (自然科学版 )
MDC 23.32 17.61 24.50 22.70 2.70
MCE 15.39 17.21 11.80 13.95 9.40
MDF 15.49 10.26 33.80 13.52 12.70
MCA 9.81 12.77 30.20 10.94 11.50
MAC 3.42 6.39 86.80 4.15 21.30
吴珊瑚 , 张季超 , 陈 原
(广州大学 土木工程学院 , 广东 广州 510006)
摘 要 :分层法是计算框架在竖向荷载作用下内力的一种近似方法 , 该方法简单 , 计算 量少 , 故常用于手算 .但 对于结构不对称或荷载 变化较大的有侧移框架 , 仅用 分层法计 算内力 往往会 造成较 大的误 差 .文 章提出 了联 合应用分层法和 D值法求解该类框架内力的方法 , 并以一个 两层框 架为例进 行了对 比分析 .由于 该方法 考虑 了侧移对框架内力的影 响 , 所以使计算精度有较大的提高 . 关键词 :框架 ;竖向荷载 ;侧移 ;分层法 ;D值法 中图分类号 :TU323.5 文献标志码 :A
1 问题的提出
框架在竖向荷载作用下内力的近似计算一般 采用分层法 [ 1 -2] .分层法的基本假定 :①忽略竖向 荷载作用下框架的侧移及由侧移 引起的弯矩 ;② 每层梁上的竖向荷载仅对本层梁及与本层梁相连 的柱的内力产生影响 , 而对其它层梁 、柱的内力影 响忽略不计 ;③忽略梁 、柱的 轴向变 形及剪 切变 形 .对于结构和荷载都接近对称的框架而言 , 框架 在竖向荷载作用下的侧移很小 , 因此 , 由假定 ①所 带来的内力误差也很小 .但是 , 当框架结构严重不 对称 , 或各跨框架梁上的荷载变化较大时 , 框架在 竖向荷载作用下的侧移就会较大 , 仅用分层法计 算的框架内力将产生较大的误差 [ 3] .D值法 [ 4 -5]
6 算 例
图 3为一计 算实例 , 框架的 计算简图 如图 3 (a).用分层法计算的弯矩图和剪力图分别如图 3 (b)、图 3(c)所示 ;由图 3(c)可得不动铰支座反 力 R2 =12.5 -7.67 =4.83 kN, R1 =6.39 -3.68 = -2.12 kN;把 R1 、R2 反向作用于框 架上 (如图 3 (d)所示 ), 用 D值法算得的弯矩图如图 3(e);叠 加图 3(b)和图 3(e), 得所求框架的弯矩图如图 3 (f).图 3(g)为用结构力学求解器 [ 8 -10] 计算所得 的弯矩图 .
nese) [ 8] LONGYu-qiu, BAOShi-hua.Structuralmechanics(I)[ M] .Beijing:HigherEducationPress, 2002.(inChinese)
38
广州大学学报 (自然科学版 )
第 9卷
[ 9] YUANSi, YEKang-sheng, YUAN Zeng.CalculationmethodsandperformanceofSM solverforwindows[ J] .Engineering Mechanics, 2001, A01:174-180.(inChinese)
[ 10] XIAOQi-yang.AnanalysisonframestructurecalculationexerciseofSM solverforwindows[ J] .JournalofLimingVocationalUniversity, 2007, 19(3):61-64.(inChinese)
参考文献 :
[ 1] 周云 .高层建筑结构设计 [ M] .武汉 :武汉理工大学出版社 , 2006. [ 2] 方鄂华 , 钱稼茹 , 叶列平 .高层建筑结构设计 [ M] .北京 :中国建筑工业出版社 , 2003. [ 3] 周俐俐 .竖向荷载作用下框架内力计算方法的对比分析 [ J] .绵阳经济技术高等专科学校学报 , 2001, 18(3):19-21. [ 4] 廉为江 .水平荷载作用下框架内力手算方法评判 [ J] .中外建筑 , 2005, 11(1):90-91. [ 5] 沈蒲生 .高层建筑结构设计 [ M] .北京 :中国建筑工业出版社 , 2006. [ 6] 阎兴华 .混凝土结构设计 [ M] .北京 :科学出版社 , 2005. [ 7] 李汝庚 , 张季超 .混凝土 结构设计 [ M] .北京 :中国环境科学 出版社 , 2003. [ 8] 龙驭球 , 包世华 .结构力 学教程 (I)[ M] .北京 :高等教育出版社 , 2002. [ 9] 袁驷 , 叶康生 , 袁征 .《结构力学求解器 》的算法与性能 [ J] .工程力学 , 2001, A01:174-180. [ 10] 肖启扬 .框架结构计算例题的结构力学求解器分析 [ J] .黎明职业大学学报 , 2007, 19(3):61-64.
