专题复习：高考中“球”的计算问题

合集下载

高考满分数学压轴题13 与球相关的外接与内切问题(可编辑可打印)

一．方法综述如果一个多面体的各个顶点都在同一个球面上，那么称这个多面体是球的内接多面体，这个球称为多面体的外接球.有关多面体外接球的问题，是立体几何的一个重点，也是高考考查的一个热点. 考查学生的空间想象能力以及化归能力。

研究球与多面体的接、切问题主要考虑以下几个方面的问题：（1）多面体外接球半径的求法，当三棱锥有三条棱垂直或棱长相等时，可构造长方体或正方体. （2）与球的外切问题，解答时首先要找准切点，可通过作截面来解决. （3）球自身的对称性与多面体的对称性；二．解题策略类型一柱体与球【例1】（2020·河南高三（理））已知长方体1111ABCD A B C D -的表面积为208，118AB BC AA ++=，则该长方体的外接球的表面积为（） A ．116π B ．106πC ．56πD ．53π【答案】A 【解析】【分析】由题意得出11118104AB BC AA AB BC BC AA AB AA ++=⎧⎨⋅+⋅+⋅=⎩，由这两个等式计算出2221AB BC AA ++，可求出长方体外接球的半径，再利用球体表面积公式可计算出结果.【详解】依题意，118AB BC AA ++=，11104AB BC BC AA AB AA ⋅+⋅+⋅=，所以，()()222211112116AB BC AA AB BC AA AB BC BC AA AB AA ++=++-⋅+⋅+⋅=，故外接球半径r ==，因此，所求长方体的外接球表面积24116S r ππ==.故选：A.【点睛】本题考查长方体外接球表面积的计算，解题的关键就是利用长方体的棱长来表示外接球的半径. 【举一反三】1.（2020·2，若与球相关的外接与内切问题该棱柱的顶点都在一个球面上，则该球的表面积为（） A ．73π B ．113π C ．5π D ．8π【答案】D【解析】根据条件可知该三棱柱是正三棱柱，上下底面中心连线的中点就是球心，如图，则其外接球的半径22221123222sin 60R OB OO BO ⎛⎫ ⎪⎛⎫==+=+= ⎪ ⎪︒⎝⎭⎝⎭，外接球的表面积428S ππ=⨯=.故选：D【指点迷津】直棱柱的外接球的球心在上、下底面的外接圆的圆心的连线上，确定球心，用球心、一底面的外接圆的圆心，一顶点构成一个直角三角形，用勾股定理得关于外接球半径的关系式，可球的半径. 2.（2020·安徽高三（理））已知一个正方体的各顶点都在同一球面上，现用一个平面去截这个球和正方体，得到的截面图形恰好是一个圆及内接正三角形，若此正三角形的边长为a ，则这个球的表面积为（）． A ．234a π B ．23a π C ．26a πD ．232a π【答案】D【解析】由已知作出截面图形如图1，可知正三角形的边长等于正方体的面对角线长，正方体与其外接球的位置关系如图2所示，可知外接球的直径等于正方体的体对角线长，设正方体的棱长为m ,外接球的半径为R ，则2a m =，23R m =，所以64R a =，所以外接球的表面积为222634442a S R a πππ⎛⎫==⨯= ⎪ ⎪⎝⎭，故选：D .【点睛】本题考查正方体的外接球、正方体的截面和空间想象能力，分析出外接球的半径与正三角形的边长的关系是本题的关键，3．（2020·河南高三（理））有一圆柱状有盖铁皮桶（铁皮厚度忽略不计），底面直径为20cm ，高度为100cm ，现往里面装直径为10cm 的球，在能盖住盖子的情况下，最多能装（）（附：2 1.414,3 1.732,5 2.236≈≈≈） A ．22个 B ．24个C ．26个D ．28个【答案】C【解析】由题意，若要装更多的球，需要让球和铁皮桶侧面相切，且相邻四个球两两相切，这样，相邻的四个球的球心连线构成棱长为10cm 的正面体，易求正四面体相对棱的距离为52cm ，每装两个球称为“一层”，这样装n 层球，则最上层球面上的点距离桶底最远为()()10521n +-cm ，若想要盖上盖子，则需要满足()10521100n +-≤，解得19213.726n ≤+≈，所以最多可以装13层球，即最多可以装26个球．故选：C 类型二锥体与球【例2】5．已知球O 的半径为102，以球心O 为中心的正四面体Γ的各条棱均在球O 的外部，若球O 的球面被Γ的四个面截得的曲线的长度之和为8π，则正四面体Γ的体积为_________．【来源】重庆市2021届高三下学期二模数学试题【答案】182【解析】由题知，正四面体截球面所得曲线为四个半径相同的圆，每个圆的周长为2π，半径为1，故球心O 到正四面体各面的距离为2106122⎛⎫-=⎪⎝⎭，设正四面体棱长为a ，如图所示，则斜高332AE EF a ==，体高63=AF a ，在Rt AEF 和R t AGO 中，13OG EF AO AE ==，即61236632a =-，∴6a =，∴231362618234312V a a =⋅⋅=⋅=．【举一反三】1.（2020四川省德阳一诊）正四面体ABCD 的体积为，则正四面体ABCD 的外接球的体积为______．【答案】【解析】如图，设正四面体ABCD 的棱长为，过A 作AD ⊥BC ，设等边三角形ABC 的中心为O ，则，，，即．再设正四面体ABCD 的外接球球心为G ，连接GA ，则，即．∴正四面体ABCD 的外接球的体积为.故答案为：．2．（2020·宁夏育才中学）《九章算术》是我国古代的数学名著,其中有很多对几何体体积的研究,已知某囤积粮食的容器的下面是一个底面积为32π,高为h 的圆柱,上面是一个底面积为32π,高为h 的圆锥,若该容器有外接球,则外接球的体积为【答案】288π【解析】如图所示，根据圆柱与圆锥和球的对称性知，其外接球的直径是23R h =，设圆柱的底面圆半径为r ，母线长为l h =，则232r ππ=，解得42r =222(2)(3)l r h +=， 222(82)9h h ∴+=，解得4h =，∴外接球的半径为3462R =⨯=，∴外接球的体积为3344628833R V πππ⨯===．3．（2020·贵阳高三（理））在四棱锥P ABCD -中，底面ABCD 是边长为4的正方形，PAD ∆是一个正三角形，若平面PAD ⊥平面ABCD ，则该四棱锥的外接球的表面积为（） A ．143πB ．283πC ．563πD ．1123π【答案】D 【解析】【分析】过P 作PF AD ⊥，交AD 于F ，取BC 的中点G ，连接,PG FG ，取PF 的三等分点H （2PH HF =），取GF 的中点E ，在平面PFG 过,E F 分别作,GF PF 的垂线，交于点O ，可证O 为外接球的球心，利用解直角三角形可计算PO ．【详解】如图，过P 作PF AD ⊥，交AD 于F ，取BC 的中点G ，连接,PG FG ，在PF 的三等分点H （2PH HF =），取GF 的中点E ，在平面PFG 过,E F 分别作,GF PF 的垂线，交于点O ．因为PAD ∆为等边三角形，AF FD =，所以PF ⊥AD ．因为平面PAD ⊥平面ABCD ，平面PAD平面ABCD AD =，PF ⊂平面PAD ，所以PF ⊥平面ABCD ，因GF ⊂平面ABCD ，故PF GF ⊥．又因为四边形ABCD 为正方形，而,G F 为,BC AD 的中点，故FG CD ，故GF AD ⊥，因ADPF F =，故PF ⊥平面PAD ．在Rt PGF ∆中，因,OE GF PF GF ⊥⊥，故OE PF ，故OE ⊥平面ABCD ，同理OH ⊥平面PAD ．因E 为正方形ABCD 的中心，故球心在直线OE 上，因H 为PAD ∆的中心，故球心在直线OH 上，故O 为球心，OP 为球的半径．在Rt PGF ∆中，2234343323PH PF ==⨯⨯=，2OH EF ==，故16282214333OP =+==，所以球的表面积为28112433ππ⨯=．类型三构造法（补形法）【例3】已知三棱锥P ABC -的各个顶点都在球O 的表面上，PA ⊥底面ABC ，AB AC ⊥，6AB =，8AC =，D 是线段AB 上一点，且2AD DB =.过点D 作球O 的截面，若所得截面圆面积的最大值与最小值之差为25π，则球O 的表面积为（） A ．128π B ．132πC ．144πD ．156π【答案】B【解析】PA ⊥平面ABC ，AB AC ⊥，将三棱锥P ABC -补成长方体PQMN ABEC -，如下图所示：设AE BC F =，连接OF 、DF 、OD ，可知点O 为PE 的中点，因为四边形ABEC 为矩形，AE BC F =，则F 为AE 的中点，所以，//OF PA 且12OF PA =，设2PA x =，且2210AE AB BE =+=，222225PE PA AE x ∴+=+所以，球O 的半径为21252R PE x ==+，在Rt ABE △中，2ABE π∠=，6AB =，10AE =，3cos 5AB BAE AE ∠==，在ADF 中，243AD AB ==，5AF =，由余弦定理可得222cos 17DF AD AF AD AF BAE =+-⋅∠=，PA ⊥平面ABCD ，OF ∴⊥平面ABCD ，DF ⊂平面ABCD ，则OF DF ⊥，12OF PA x ==，22217OD OF DF x ∴=+=+，设过点D 的球O 的截面圆的半径为r ，设球心O 到截面圆的距离为d ，设OD 与截面圆所在平面所成的角为θ，则22sin d OD R r θ==-.当0θ=时，即截面圆过球心O 时，d 取最小值，此时r 取最大值，即2max 25r R x ==+；当2πθ=时，即OD 与截面圆所在平面垂直时，d 取最大值，即2max 17d OD x ==+，此时，r 取最小值，即()22min max 22r R d =-=. 由题意可得()()()222max min 1725r r x πππ⎡⎤-=+=⎣⎦，0x，解得22x =.所以，33R =，因此，球O 的表面积为24132S R ππ==.故选：B.【举一反三】1.（2020宁夏石嘴山模拟）三棱锥中，侧棱与底面垂直，，，且，则三棱锥的外接球的表面积等于．【答案】【解析】把三棱锥，放到长方体里,如下图:,因此长方体的外接球的直径为,所以半径,则三棱锥的外接球的表面积为.2.（2020菏泽高三模拟）已知直三棱柱的底面为直角三角形，且两直角边长分别为1和，此三棱柱的高为，则该三棱柱的外接球的体积为A．B．C．D．【答案】C【解析】如图所示，将直三棱柱补充为长方体，则该长方体的体对角线为，设长方体的外接球的半径为，则，,所以该长方体的外接球的体积，故选C.3．（2020·贵州高三月考（理））某几何体的三视图如图所示，则该几何体的体积为（）A．43B．53C．83D．163【答案】A【解析】【分析】如图所示画出几何体，再计算体积得到答案.【详解】由三视图知该几何体是一个四棱锥，可将该几何体放在一个正方体内，如图所示：在棱长为2的正方体1111ABCD A B C D -中，取棱11,,,,B C DA AB BC CD 的中点分别为,,,,E M N P Q ，则该几何体为四棱锥E MNPQ -，其体积为()2142233⨯⨯=.故选：A 类型四与球体相关的最值问题【例4】（2020·福建高三期末（理））在外接球半径为4的正三棱锥中，体积最大的正三棱锥的高h =（） A ．143B ．134C ．72D ．163【答案】D 【解析】【分析】设正三棱锥底面的边长为a ，高为h ，由勾股定理可得22234(4)3h a ⎛⎫=-+ ⎪ ⎪⎝⎭，则22183h h a -=，三棱锥的体积()23384V h h =-，对其求导，分析其单调性与最值即可得解. 【详解】解：设正三棱锥底面的边长为a ，高为h ，根据图形可知22234(4)3h a ⎛⎫=-+ ⎪ ⎪⎝⎭，则22180,3h h a -=>08h ∴<<. 又正三棱锥的体积21334V a h =⨯()2384h h h =-()23384h h =-，则()231634V h h '=-，令0V '=，则163h =或0h =（舍去）， ∴函数()23384V h h =-在160,3⎛⎫ ⎪⎝⎭上单调递增，在16,83⎛⎫⎪⎝⎭上单调递减，∴当163h =时，V 取得最大值，故选：D. 【点睛】本题考查球与多面体的最值问题，常常由几何体的体积公式、借助几何性质，不等式、导数等进行解决，对考生的综合应用，空间想象能力及运算求解能力要求较高. 【举一反三】1.（2020·广东高三（理））我国古代数学名著《九章算术》中有这样一些数学用语，“堑堵”意指底面为直角三角形，且侧棱垂直于底面的三棱柱，而“阳马”指底面为矩形，且有一侧棱垂直于底面的四棱锥.现有一如图所示的堑堵，AC BC ⊥，若12AA AB ==，当阳马11B A ACC -体积最大时，则堑堵111ABC A B C -的外接球体积为（）A ．22πB ．823C ．23D ．2π【答案】B【解析】依题意可知BC ⊥平面11ACC A .设,AC a BC b ==，则2224a b AB +==.111111323B A ACC V AC AA BC AC BC -=⨯⨯⨯⨯=⨯⨯22114232323AC BC +≤⨯=⨯=，当且仅当2AC BC ==时取得最大值.依题意可知1111,,A BC A BA A BB ∆∆∆是以1A B 为斜边的直角三角形，所以堑堵111ABC A B C -外接球的直径为1A B ，故半径221111222OB A B AA AB ==⨯+=.所以外接球的体积为()34π82π233⋅=. 特别说明：由于BC ⊥平面11ACC A ，1111,,A BC A BA A BB ∆∆∆是以1A B 为斜边的直角三角形，所以堑堵111ABC A B C -外接球的直径为1A B 为定值，即无论阳马11B A ACC -体积是否取得最大值，堑堵111ABC A B C -外接球保持不变，所以可以直接由直径1A B 的长，计算出外接球的半径，进而求得外接球的体积.故选：B2．（2020·遵义市南白中学高三期末）已知A ，B ，C ，D 四点在同一个球的球面上，6AB BC ==，90ABC ∠=︒，若四面体ABCD 体积的最大值为3，则这个球的表面积为（）A ．4πB ．8πC ．16πD ．32π【答案】C 【解析】根据6AB BC ==可得直角三角形ABC ∆的面积为3,其所在球的小圆的圆心在斜边AC 的中点上,设小圆的圆心为Q , 由于底面积ABC S ∆不变,高最大时体积最大,所以DQ 与面ABC 垂直时体积最大，最大值为为133ABC S DQ ∆⨯=，即133,33DQ DQ ⨯⨯=∴=,如图, 设球心为O ,半径为R ，则在直角AQO ∆中,即222(3)(3,)2R R R =∴+=-, 则这个球的表面积为24216S ππ=⨯=,故选C.3．（2020·河南高三（理））菱形ABCD 的边长为2，∠ABC ＝60°，沿对角线AC 将三角形ACD 折起，当三棱锥D －ABC 体积最大时，其外接球表面积为（） A ．153π B ．2153π C ．209π D ．203π 【答案】D 【解析】【分析】当平面ACD 与平面ABC 垂直时体积最大，如图所示，利用勾股定理得到2223(3)()3R OG =-+和22223()3R OG =+，计算得到答案. 【详解】易知：当平面ACD 与平面ABC 垂直时体积最大. 如图所示：E 为AC 中点，连接,DE BE ，外接球球心O 的投影为G 是ABC ∆中心，在BE 上 3BE =，3DE =，33EG =，233BG =设半径为R ，则2223(3)()3R OG =-+，22223()3R OG =+ 解得：153R =，表面积22043S R ππ== 故选：D三．强化训练一、选择题1．（2020·广西高三期末）棱长为a 的正四面体ABCD 与正三棱锥E BCD -的底面重合，若由它们构成的多面体ABCDE 的顶点均在一球的球面上，则正三棱锥E BCD -的表面积为（） A ．2334a + B ．2336a + C ．2336a - D ．2334a - 【答案】A【解析】由题意，多面体ABCDE 的外接球即正四面体ABCD 的外接球，由题意可知AE ⊥面BCD 交于F ，连接CF ，则233323CF a a =⋅= 且其外接球的直径为AE ，易求正四面体ABCD 的高为223633a a a ⎛⎫ ⎪ ⎪=⎝⎭-. 设外接球的半径为R ，由2226333R a R a ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭=⎭-⎝-得64R a =. 设正三棱锥E BCD -的高为h ，因为6623AE a a h ==+，所以66h a =. 因为底面BCD ∆的边长为a ，所以2222EB EC ED CF h a ===+=，则正三棱锥E BCD -的三条侧棱两两垂直.即正三棱锥E BCD -的表面积222121333322224S a a a ⎛⎫+=⨯⨯+⨯= ⎪ ⎪⎝⎭，故选：A .2、（2020辽宁省师范大学附属中学高三）在三棱锥中，，则三棱锥外接球的表面积为（）A．B．C．D．【答案】C【解析】如图，把三棱锥补形为长方体，设长方体的长、宽、高分别为，则，∴三棱锥外接球的半径∴三棱锥外接球的表面积为．故选：C．3．（2020·安徽高三期末）如果一个凸多面体的每个面都是全等的正多边形，而且每个顶点都引出相同数目的棱，那么这个凸多面体叫做正多面体.古希腊数学家欧几里得在其著作《几何原本》的卷13中系统地研究了正多面体的作图，并证明了每个正多面体都有外接球.若正四面体、正方体、正八面体的外接球半径相同，则它们的棱长之比为（）A23B．223C．22D．223【答案】Ba b c R【解析】设正四面体、正方体、正八面体的棱长以及外接球半径分别为,,,则2223,23,22R a R b R c =⨯==, 即222,,2::2:2:333R R a b c R a b c ===∴=故选：B 4．（2020·北京人大附中高三）如图，在四棱锥S ABCD -中，四边形ABCD 为矩形，23AB =，2AD =，120ASB ∠=︒，SA AD ⊥，则四棱锥外接球的表面积为（）A ．16πB ．20πC ．80πD ．100π 【答案】B【解析】由四边形ABCD 为矩形，得AB AD ⊥，又SA AD ⊥，且SA AB A ⋂=，∴AD ⊥平面SAB ，则平面SAB ⊥平面ABCD ，设三角形SAB 的外心为G ，则23322sin 2sin12032AB GA ASB ====∠︒. 过G 作GO ⊥底面SAB ，且1GO =，则22215OS =+=.即四棱锥外接球的半径为5． ∴四棱锥外接球的表面积为24(5)20S ππ=⨯=.故选B ．5．（2020河南省郑州市一中高三）在三棱锥中，平面，M 是线段上一动点，线段长度最小值为，则三棱锥的外接球的表面积是（） A ． B ．C ．D ．【答案】C【解析】解：如图所示：三棱锥中，平面，M是线段上一动点，线段长度最小值为，则：当时，线段达到最小值，由于：平面，所以：，解得：，所以：，则：，由于：，所以：则：为等腰三角形．所以，在中，设外接圆的直径为，则：，所以外接球的半径，则：，故选：C．6、（2020河南省天一大联考）某多面体的三视图如图所示，其中正视图是一个直角边为2的等腰直角三角形，侧视图是两直角边分别为2和1的直角三角形，俯视图为一矩形，则该多面体的外接球的表面积为（）A．B．C．D．【答案】C【解析】由三视图可得，该几何体为一个三棱锥，放在长、宽、高分别为2，1，2的长方体中，此三棱锥和长方体的外接球是同一个，长方体的外接球的球心在体对角线的中点处，易得其外接球的直径为，从而外接球的表面积为.故答案为：C.7．（2020·江西高三期末（理））如图，三棱锥P ABC -的体积为24，又90PBC ABC ∠=∠=︒，3BC =，4AB =，410PB =，且二面角P BC A --为锐角，则该三棱锥的外接球的表面积为（）A ．169πB ．144πC ．185πD ．80π【答案】A【解析】因90PBC ABC ∠=∠=︒，所以BC ⊥平面PAB ，且PBA ∠为二面角P BC A --的平面角，又3BC =，4AB =，410PB =，由勾股定理可得13PC =，5AC =，因为1sin 8102PAB S PB AB PBA PBA ∆⋅=⋅∠=∠，所以三棱锥的体积1181032433PAB V S BC PBA ∆=⋅=⨯∠⨯=，解得310sin PBA ∠=，又PBA ∠为锐角，所以10cos 10PBA ∠=，在PAB ∆中，由余弦定理得2101601624410144PA =+-⨯⨯=，即12PA =，则222PB PA AB =+，故PA AB ⊥，由BC ⊥平面PAB 得BC PA ⊥，故PA ⊥平面ABC ，即PA AC ⊥，取PC 中点O ，在直角PAC ∆和直角PBC ∆中，易得OP OC OA OB ===，故O 为外接球球心，外接圆半径11322R PC ==，故外接球的表面积24169S R ππ==.故选：A. 8．（2019·湖南长沙一中高三）在如图所示的空间几何体中，下面的长方体1111ABCD A B C D -的三条棱长4AB AD ==，12AA =，上面的四棱锥1111P A B C D -中11D E C E =，1111PE A B C D ⊥平面，1PE =，则过五点A 、B 、C 、D 、P 的外接球的表面积为（）A ．311π9B ．311π18C ．313π9D ．313π18【答案】C【解析】问题转化为求四棱锥P ABCD -的外接球的表面积．4913PC =+=，∴3sin 13PCD ∠=．所以PCD ∆外接圆的半径为131336213r ==⨯，由于PE ⊥平面1111D C B A ，则PE ⊥平面ABCD ，PE ⊂平面PCD ，所以平面PCD ⊥平面ABCD ，所以外接球的222169313243636R r =+=+=．所以2313π4π9S R ==球表面积．9．三棱锥P —ABC 中，底面ABC 满足BA=BC ，，点P 在底面ABC 的射影为AC 的中点，且该三棱锥的体积为，当其外接球的表面积最小时，P 到底面ABC 的距离为（） A ．3 B ．C ．D ．【答案】B【解析】设外接球半径为，P 到底面ABC 的距离为，，则，因为，所以，因为，所以当时，，当时，，因此当时，取最小值，外接球的表面积取最小值，选B.10．（2019·河北高三月考）在平面四边形ABCD 中，AB ⊥BD ，∠BCD =30°，2246AB BD +=，若将△ABD 沿BD 折成直二面角A -BD -C ，则三棱锥A-BDC 外接球的表面积是( ) A ．4π B ．5πC ．6πD ．8π【答案】C【解析】取,AD BD 中点,E F ，设BCD ∆的外心为M ，连,,MB MF EF ，则01,30,22MF BD BMF DMB BCD BM BF BD ⊥∠=∠=∠=∴== 分别过,E M 作,MF EF 的平行线，交于O 点，即//,//OE MF OM EF ，,BD AB E ⊥∴为ABD ∆的外心，平面ABD ⊥平面BCD ，AB ⊥平面BCD ，//,EF AB EF ∴⊥平面BCD ，OM ∴⊥平面BCD ，同理OE ⊥平面ABD ，,E M 分别为ABD ∆，BCD ∆外心，O ∴为三棱锥的外接球的球心，OB 为其半径, 22222221342OB BM OM BD EF BD AB =+=+=+=， 246S OB ππ=⨯=球.故选:C11．（2020·梅河口市第五中学高三期末（理））设三棱锥P ABC -的每个顶点都在球O 的球面上，PAB ∆是面积为3的等边三角形，45ACB ∠=︒，则当三棱锥P ABC -的体积最大时，球O 的表面积为（） A ．283π B ．10πC ．323π D ．12π【答案】A【解析】如图，由题意得2334AB =，解得2AB =.记,,AB c BC a AC b ===， 12sin 24ABC S ab C ab ∆==，由余弦定理2222cos c a b ab C =+-，得224222a b ab ab ab =+-≥-，42(22)22ab ≤=+-，当且仅当a b =时取等号．所以CA CB =且平面PAB ⊥底面ABC 时，三棱锥P ABC -的体积最大.分别过PAB ∆和ABC ∆的外心作对应三角形所在平面的垂线，垂线的交点即球心O ，设PAB ∆和ABC ∆的外接圆半径分别为1r ，2r ，球O 的半径为R ，则123r =，21222sin 45r =⨯=︒.故222211172233R r r ⎛⎫=+=+= ⎪⎝⎭，球O 的表面积为22843R ππ=.故选：A.12.（2020四川省成都外国语学校模拟）已知正方形ABCD 的边长为4，E ，F 分别是BC ，CD 的中点，沿AE ，EF ，AF 折成一个三棱锥P-AEF （使B ，C ，D 重合于P ），三棱锥P-AEF 的外接球表面积为（）A ．B ．C ．D ．【答案】C 【解析】如图，由题意可得，三棱锥P-AEF 的三条侧棱PA ，PE ，PF 两两互相垂直，且，，把三棱锥P-AEF 补形为长方体，则长方体的体对角线长为，则三棱锥P-AEF 的外接球的半径为，外接球的表面积为．故选：C ．13．已知球O 夹在一个二面角l αβ--之间，与两个半平面分别相切于点,A B .若2AB =，球心O 到该二面角的棱l 的距离为2，则球O 的表面积为（） A ．8πB ．6πC ．4πD ．2π【来源】江西省萍乡市2021届高三二模考试数学（文）试题【答案】A【解析】过,,O A B 三点作球的截面，如图：设该截面与棱l 交于D ，则OA l ⊥，OB l ⊥，又OA OB O =，所以l ⊥平面AOB ，所以OD l ⊥，所以||2OD =，依题意得,OA AD OB BD ⊥⊥，所以,,,O A D B 四点共圆，且OD 为该圆的直径，因为||2||AB OD ==，所以AB 也是该圆的直径，所以四边形OADB 的对角线AB 与OD 的长度相等且互相平分，所以四边形OADB 为矩形，又||||OA OB =，所以该矩形为正方形，所以2||||22OA AB ==，即圆O 的半径为2，所以圆O 的表面积为24(2)8ππ⨯=. 故选：A14．已知点,,A B C 在半径为2的球面上，满足1AB AC ==，3BC =，若S 是球面上任意一点，则三棱锥S ABC -体积的最大值为（） A ．32312+ B ．3236+ C ．23312+ D ．3312+ 【答案】A【解析】设ABC 外接圆圆心为O '，三棱锥S ABC -外接球的球心为O ，1AB AC ==，设D 为BC 中点，连AD ，如图，则AD BC ⊥，且O '在AD 上，221()22BC AD AB =-=，设ABC 外接圆半径为r ，222231()()()242BC r AD r r =+-=+-，解得1r =， 22||23OO r '∴=-=要使S ABC -体积的最大，需S 到平面ABC 距离最大，即S 为O O '32，所以三棱锥S ABC -体积的最大值为11112)2)3322ABCS ⨯=⨯⨯⨯=故选：A15．已知半球O 与圆台OO '有公共的底面，圆台上底面圆周在半球面上，半球的半径为1，则圆台侧面积取最大值时，圆台母线与底面所成角的余弦值为（）A B C ．6D 【答案】D【解析】如图1所示，设BC x =，CO r '=，作CF AB ⊥于点F ，延长OO '交球面于点E ，则1BF r =-，OO CF '===2得CO O D ''⋅=()()11O E O H OO OO ''''⋅=+⋅-，即((211r =+⋅，解得212x r =-，则圆台侧面积(2π1102x S x x ⎛⎫=⋅+-⋅<< ⎪⎝⎭，则'2322S x ππ=-，令'0S =，则3x =或x =，当0x <<时，'0S >x <<'0S <，所以函数2π112x S x ⎛⎫=⋅+-⋅ ⎪⎝⎭在⎛ ⎝⎭上递增，在⎝上递减，所以当3x =时，S 取得最大值．当3x BC ==时，21123x r =-=，则213BF r =-=．在轴截面中，OBC ∠为圆台母线与底面所成的角，在Rt CFB △中可得cos 3BF OBC BC ∠==故选：D ．16．（2020·重庆八中高三）圆柱的侧面展开图是一个面积为216π的正方形，该圆柱内有一个体积为V 的球，则V 的最大值为【答案】323π【解析】设圆柱的底面直径为2r ，高为l ，则222π16πr l l =⎧⎨=⎩，解得24πr l =⎧⎨=⎩.故圆柱的底面直径为4，高为4π，所以圆柱内最大球的直径为4，半径为2，其体积为34π32π233⨯=. 17．（2020·江西高三）半正多面体(semiregular solid )亦称“阿基米德多面体”，如图所示，是由边数不全相同的正多边形为面的多面体，体现了数学的对称美．将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，如此共可截去八个三棱锥，得到一个有十四个面的半正多面体，它们的边长都相等，其中八个为正三角形，六个为正方形，称这样的半正多面体为二十四等边体.若二十四等边体的棱长为2，则该二十四等边体外接球的表面积为【答案】8π【解析】2，侧棱长为2的正四棱柱的外接球，2222(2)(2)(2)2R ∴=++,2R ∴,∴该二十四等边体的外接球的表面积24πS R =24π(2)8π=⨯=.18．（2020·福建高三期末（理））在棱长为4的正方体1111ABCD A B C D -中，E ，F 分别为1AA ，BC 的中点，点M 在棱11B C 上，11114B M BC =，若平面FEM 交11A B 于点N ，四棱锥11N BDD B -的五个顶点都在球O 的球面上，则球O 半径为【答案】2293【解析】如图1，2,,B M F 三点共线，连结22,B E B MF ∈从而2B ∈平面FEM ，则2B E 与11A B 的交点即为点N ，又12Rt B B N ∆与1Rt A EN ∆相似，所以1112112A E A NB B NB ==；如图2，设11B D N ∆的外接圆圆心为1O ，半径为r ，球半径为R ，在11B D N ∆中，111445,103NB D D N ︒∠==，由正弦定理得453r =，所以1853D P =，在1Rt DD P ∆中，解得4293DP =，即42293R =，所以所求的球的半径为2293.19．（2020·黑龙江高三（理））设,,,A B C D 是同一个半径为4的球的球面上四点，在ABC 中，6BC =,60BAC ∠=︒,则三棱锥D ABC -体积的最大值为【答案】183【解析】ABC 中，6BC =,60BAC ∠=︒，则643223sin sin 60a r r A ===∴=︒，22max 6h R r R =-=，222222cos 36a b c bc A b c bc bc bc =+-=+-≥∴≤ ，1sin 932S bc A =≤ 当6a b c ===时等号成立，此时11833V Sh ==20．（2020·河北承德第一中学高三）正三棱锥S －ABC 的外接球半径为2，底边长AB ＝3，则此棱锥的体积为【答案】934或334【解析】设正三棱锥的高为h ，球心在正三棱锥的高所在的直线上，H 为底面正三棱锥的中心因为底面边长AB=3，所以2222333332AH AD ⎛⎫==-= ⎪⎝⎭当顶点S 与球心在底面ABC 的同侧时，如下图此时有222AH OH OA += ，即()()222322h +-=，可解得h=3因而棱柱的体积113393333224S ABC V -=⨯⨯⨯⨯=当顶点S 与球心在底面ABC 的异侧时，如下图有222AH OH OA +=，即()222322h +-=，可解得h=1所以113333313224S ABC V -=⨯⨯⨯⨯=9333421．（2020·江西高三（理））已知P,A,B,C 是半径为2的球面上的点，PA=PB=PC=2，90ABC ∠=︒，点B 在AC 上的射影为D ，则三棱锥P ABD -体积的最大值为【答案】338【解析】如下图，由题意，2PA PB PC ===，90ABC ∠=︒，取AC 的中点为G ，则G 为三角形ABC 的外心，且为P 在平面ABC 上的射影，所以球心在PG 的延长线上，设PG h =，则2OG h =-，所以2222OB OG PB PG -=-，即22424h h --=-，所以1h =. 故G CG 3A ==，过B 作BD AC ⊥于D ，设AD x =(023x <<)，则23CD x =-,设(03)BD m m =<≤，则~ABD BCD ，故23m xx m-=，所以()223m x x =-，则()23m x x =-，所以ABD 的面积()3112322S xm x x ==-，令()()323f x x x =-，则()2'634f x x x =-（），因为20x >，所以当3032x <<时，()'0f x >，即()f x 此时单调递增；当33232x ≤<时，()'0f x ≤，此时()f x 单调递减．所以当332x =时，()f x 取到最大值为24316，即ABD 的面积最大值为1243932168=．当ABD 的面积最大时，三棱锥P ABD -体积取得最大值为19333388⨯=.22．已知H 是球O 的直径AB 上一点，:1:3AH HB =，AB ⊥平面α，H 为垂足，α截球O 所得截面的面积为π，则球O 的表面积为__________.【来源】宁夏固原市第五中学2021届高三年级期末考试数学（文）试题【答案】163π【解析】如下图所示，设AH x =，可得出3HB x =，则球O 的直径为4AB x =，球O 的半径为2x ，设截面圆H 的半径为r ，可得2r ππ=，1r ∴=，由勾股定理可得()2222OH r x +=，即()22214x AH x -+=，即2214x x +=，33x ∴=，所以球O 的半径为2323x =，则球O 的表面积为22316433S ππ⎛⎫=⨯= ⎪ ⎪⎝⎭. 23．如图，在三棱锥P ABC -中，PA ⊥平面ABC ，AB BC ⊥，2PA AB ==，22AC =，M 是BC 的中点，则过点M 的平面截三棱锥P ABC -的外接球所得截面的面积最小值为___【答案】π 【解析】PA ⊥平面ABC ，AB BC ⊥，将三棱锥P ABC -补成长方体ABCD PEFN -，则三棱锥P ABC -的外接球直径为22222223R PC PA AB AD PA AC ==++=+=，所以，3R =，设球心为点O ，则O 为PC 的中点，连接OM ，O 、M 分别为PC 、BC 的中点，则//OM PB ，且2211222OM PB PA AB ==+=，设过点M 的平面为α，设球心O 到平面α的距离为d . ①当OM α⊥时，2d OM ==；②当OM 不与平面α垂直时，2d OM <=. 综上，2d OM ≤=.设过点M 的平面截三棱锥P ABC -的外接球所得截面圆的半径为r ，则221r R d =-≥，因此，所求截面圆的面积的最小值为2r ππ=.24．若正四棱锥P ABCD -的底面边长和高均为8，M 为侧棱PA 的中点，则四棱锥M ABCD -外接球的表面积为___________.【来源】山西省运城市2021届高三上学期期末数学（文）试题【答案】132π【解析】在正四棱锥P ABCD -中M 为侧楼PA 中点,∴四棱锥M ABCD -外接球即为棱台MNEF ABCD -的外接球，如图，四棱锥P ABCD -的底面边长和高均为8，1214,42AB O N O M ===∴ 212242AO MO ==∴设球心为O ，则图中12,OO A OMO △△均为直角三角形，设1OO h =，222(42)OA h ∴=+，222(22)(4)OM h =++，A , M 都在球面上，222O O M R A =∴=,解得21,33h R =∴=,24132S R ππ∴==球25．已知P 为球O 球面上一点，点M 满足2OM MP =，过点M 与OP 成30的平面截球O ，截面的面积为16π，则球O 的表面积为________.【来源】广西钦州市2021届高三第二次模拟考试数学（理）试题【答案】72π 【解析】如图所示：设截面圆心为1O ，依题意得130OMO ∠=，设1OO h =，则2OM h =，又2OM MP =，所以3OP h =，即球的半径为3h ，所以3ON h =，又截面的面积为16π，所以()2116O N ππ=，解得14O N =，在1Rt OO N 中，()22316h h =+，解得2h =，所以球的半径为32，所以球的表面积是()243272S ππ==，故答案为： 72π 26．如图是数学家GeminadDandelin 用来证明一个平面截圆锥得到的截面是椭圆的模型(称为丹德林双球模型)：在圆锥内放两个大小不同的小球，使得它们分别与圆锥侧面､截面相切，设图中球1O 和球2O 的半径分别为1和3，128O O =，截面分别与球1O 和球2O 切于点E 和F ，则此椭圆的长轴长为___________.【来源】江苏省盐城市阜宁县2020-2021学年高三上学期期末数学试题【答案】15【解析】如图，圆锥面与其内切球12,O O 分别相切与,B A ，连接12,O B O A ，则12,O B AB O A AB ⊥⊥，过1O 作12O D O A 于D ，连接12,,O F O E EF 交12O O 于点C ，设圆锥母线与轴的夹角为α，截面与轴的夹角为β，在Rt △12O O D 中,2312DO ,22182215O D11221515cos 84O D O O α===128O O = , 218CO O C =-,△2EO C △1FO C ,11218O C O C EO O F -= 解得12O C =,26O C = 222211213CF O C FO ∴=-=-= ,即13cos 2CFO C , 所以椭圆离心率为cos 25cos 5c e aβα=== 在△2EO C 中223cos cos 2EC ECO O C β=∠== 解得33EC =,432EF c ==2325155a a =⇒= 2215a ∴=故答案为：21527．在长方体1111ABCD A B C D -中，13AB =，5AD =，112AA =，过点A 且与直线CD 平行的平面α将长方体分成两部分.现同时将两个球分别放入这两部分几何体内，则在平面α变化的过程中，这两个球的半径之和的最大值为___________.【来源】江苏省六校2021届高三下学期第四次适应性联考数学试题【答案】16538【解析】如图所示：平面ABMN 将长方体分成两部分，MN 有可能在平面11CDD C 上或平面1111A D C B 上，根据对称性知，两球半径和的最大值是相同的，故仅考虑在平面11CDD C 上的情况，延长11B C 与BM 交于点P ，作1O Q BC ⊥于Q 点，设1CBP BPB α∠=∠=，圆1O 对应的半径为1r ，根据三角形内切圆的性质，在1Rt O QB 中，12QBO α∠=，15BQ BC CQ r =-=-，111tan 25O Q r BQ r α==-，则15tan5251tan 1tan 22r ααα==-++，又当BP 与1BC 重合时，1r 取得最大值，由内切圆等面积法求得1512251213r ⨯≤=++，则2tan 23α≤ 设圆2O 对应的半径为2r ，同理可得266tan2r α=-，又252r ≤，解得7tan 212α≥. 故1255566tan 176(1tan )221tan 1tan 22r r αααα+=-+-=--+++，72tan 1223α≤≤，设1tan 2x α=+，则195[,]123x ∈，()5176f x x x=--，由对号函数性质易知195[,]123x ∈，函数()f x 单减，则19519165()()1761912123812f x f ≤=--⨯=，即最大值为16538 故答案为：16538 28．设A B C D ，，，是同一个半径为4的球的球面上四点，ABC 为等边三角形且其面积为93，则三棱锥D ABC -体积的最大值为___________.【来源】江苏省南京市秦淮中学2021届高三下学期期初学情调研数学试题【答案】183【解析】ABC 为等边三角形且其面积为93，则23934ABC SAB ==，6AB ∴=，如图所示，设点M 为ABC 的重心，E 为AC 中点，当点D 在平面ABC 上的射影为M 时，三棱锥D ABC -的体积最大，此时，4OD OB R ===，点M 为三角形ABC 的重心，2233BM BE ∴==， Rt OMB ∴中，有222OM OB BM =-=，426DM OD OM ∴=+=+=，所以三棱锥D ABC -体积的最大值19361833D ABC V -=⨯=29．已知四面体ABCD 的棱长均为6,,EF 分别为棱,BC BD 上靠近点B 的三等分点，过,,A E F 三点的平面与四面体ABCD 的外接球O 的球面相交,得圆'O ，则球O 的半径为___________，圆'O 的面积为__________．【来源】河南省九师联盟2021届高三下学期3月联考理科数学试题【答案】3 8π【解析】。

【高考数学培优专题】第12讲立体几何中球的综合问题

【高考数学培优专题】第十二讲立体几何中球的综合问题A 组一、选择题1．(2018年高考全国卷Ⅰ)已知圆柱的上、下底面的中心分别为1O ，2O ，过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为（） A ．122πB ．12πC ．82πD ．10π【答案】B【解析】∵过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形，所以圆柱的高为22，底面圆的直径为22，所以该圆柱的表面积为22(2)222212πππ⨯⨯+⨯=．故选B ．2．三棱柱111ABC A B C -的各个顶点都在球O 的球面上，且11,2,AB AC BC CC ===⊥平面ABC 。

若球O 的表面积为3π，则这个三棱柱的体积是（）A ．16B ．13 C ．12D ．1【答案】C 【解析】11,2,,AB AC BC AB AC CC ===∴⊥⊥平面ABC ,三棱柱111ABC A B C -内接球O ,O ∴为距形11BCC B 的中心, 设球O 半径为r ,则2343,r r ππ=∴=,即3OC r ==,∴三棱柱的高221212h r BC ⎛⎫=-= ⎪⎝⎭,∴三棱柱的体积1111122ABC V S h ∆==⨯⨯⨯=,故选C 。

3．球O 的球面上有四点,,,S A B C ，其中,,,O A B C 四点共面，ABC ∆是边长为2的正三角形，面SAB ⊥面ABC ，则棱锥S ABC -的体积的最大值为（） A ．3B ．3C ．23D ．4 【答案】A【解析】设球心和ABC ∆的外心为O ，延长CO 交AB 于点P ，则由球的对称性可知AB PD ⊥，继而由面SAB ⊥面ABC 可得⊥PD ABC ∆所在的平面，所以PD 是三棱锥的高；再由,,,O A B C 四点共面可知O 是ABC ∆的中心，故332,33==R OP ，当三棱锥的体积最大时，其高为1)33()332(22=-=PD ，故三棱锥的体积的最大值为331243312=⨯⨯⨯，应选A 。

高考数学复习考点题型专题讲解17 球的切、接、截问题

高考数学复习考点题型专题讲解专题17 球的切、接、截问题1.球的切接问题(1)长方体的外接球①球心：体对角线的交点；②半径：r＝a2＋b2＋c22(a，b，c为长方体的长、宽、高).(2)正方体的外接球、内切球及与各条棱相切的球(a为正方体的棱长)①外接球：球心是正方体中心，半径r＝32a，直径等于体对角线长；②内切球：球心是正方体中心，半径r＝a2，直径等于正方体棱长；③与各条棱都相切的球：球心是正方体中心，半径r＝22a，直径等于面对角线长.(3)正四面体的外接球与内切球(正四面体可以看作是正方体的一部分，a为正四面体的棱长)①外接球：球心是正四面体的中心，半径r＝64a；②内切球：球心是正四面体的中心，半径r＝612a.2.平面截球平面截球面得圆.截面圆的圆心与球心的连线与截面圆圆面垂直且R2＝d2＋r2(R为球半径，r为截面圆半径，d为球心到截面圆的距离).类型一外接球问题考向1 墙角模型墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型，用构造法(构造长方体)解决，外接球的直径等于长方体的体对角线长.长方体同一顶点的三条棱长分别为a，b，c，外接球半径为R.则(2R)2＝a2＋b2＋c2，即2R＝a2＋b2＋c2.常见的有以下三种类型：例1 已知三棱锥P－ABC的四个顶点在球O的球面上，PA＝PB＝PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF＝90°，则球O的体积为( )A.86πB.46πC.26πD.6π答案 D解析因为点E，F分别为PA，AB的中点，所以EF∥PB.因为∠CEF＝90°，所以EF⊥CE，所以PB⊥CE.取AC的中点D，连接BD，PD，易证AC⊥平面BDP，所以PB⊥AC，又AC∩CE＝C，AC，CE⊂平面PAC，所以PB⊥平面PAC，所以PB⊥PA，PB⊥PC，因为PA＝PB＝PC，△ABC为正三角形，所以PA⊥PC，即PA，PB，PC两两垂直，将三棱锥P－ABC放在正方体中如图所示. 因为AB＝2，所以该正方体的棱长为2，所以该正方体的体对角线长为6，所以三棱锥P－ABC的外接球的半径R＝6 2，所以球O的体积V＝43πR3＝43π⎝⎛⎭⎪⎫623＝6π，故选D.考向2 对棱相等模型对棱相等模型是三棱锥的三组对棱长分别相等模型，用构造法(构造长方体)解决，外接球的直径等于长方体的体对角线长，如图所示，(2R)2＝a2＋b2＋c2(长方体的长、宽高分别为a，b，c)，即R2＝18(x2＋y2＋z2)，如图.例2 在三棱锥A －BCD 中，AB ＝CD ＝2，AD ＝BC ＝3，AC ＝BD ＝4，则三棱锥A －BCD 外接球的表面积为________. 答案29π2解析构造长方体，三个长度为三对面的对角线长，设长方体的长宽高分别为a ，b ，c ，则a 2＋b 2＝9，b 2＋c 2＝4，c 2＋a 2＝16，所以2(a 2＋b 2＋c 2)＝9＋4＋16＝29，即a 2＋b 2＋c 2＝4R 2＝292，则外接球的表面积为S ＝4πR 2＝29π2.考向3 汉堡模型汉堡模型是直三棱柱、圆柱的外接球模型，模型如下，由对称性可知，球心O 的位置是△ABC 的外心O 1与△A 1B 1C 1的外心O 2的连线的中点，算出小圆O 1的半径AO 1＝r ，OO 1＝h2，所以R 2＝r 2＋h 24.例3(2022·金华调研)在三棱柱ABC －A 1B 1C 1中，AB ＝BC ＝AC ，侧棱AA 1⊥底面ABC ，若该三棱柱的所有顶点都在同一个球O 的表面上，且球O 的表面积的最小值为4π，则该三棱柱的侧面积为( ) A.63B.3 3 C.32D.3 答案 B解析如图，设三棱柱上、下底面中心分别为O 1，O 2，则O 1O 2的中点为O ，设球O 的半径为R ，则OA ＝R ，设AB ＝BC ＝AC ＝a ，AA 1＝h ，则OO 2＝12h ，O 2A ＝23×32AB ＝33a .在Rt△OO 2A 中，R 2＝OA 2＝OO 22＋O 2A 2＝14h 2＋13a 2≥2×12h ×33a ＝33ah ，当且仅当h ＝233a 时，等号成立，所以S 球＝4πR 2≥4π×33ah ，所以43π3ah ＝4π，所以ah ＝3，所以该三棱柱的侧面积为3ah＝3 3.考向4 垂面模型垂面模型是有一条侧棱垂直底面的棱锥模型，可补为直棱柱内接于球；如图所示，由对称性可知球心O的位置是△CBD的外心O1与△AB2D2的外心O2连线的中点，算出小圆O1的半径CO1＝r，OO1＝h2，则R＝r2＋h24.例4(2022·广州模拟)已知四棱锥S－ABCD的所有顶点都在球O的球面上，SD⊥平面ABCD，底面ABCD是等腰梯形，AB∥CD且满足AB＝2AD＝2DC＝2，且∠DAB＝π3，SC＝2，则球O的表面积是( ) A.5π B.4πC.3πD.2π答案 A解析依题意，得AB＝2AD＝2，∠DAB＝π3，由余弦定理可得BD＝3，则AD2＋DB2＝AB2，则∠ADB＝π2.又四边形ABCD是等腰梯形，故四边形ABCD的外接圆直径为AB，半径r＝AB2＝1，设AB的中点为O1，球的半径为R，因为SD ⊥平面ABCD ，所以SD ＝SC 2－CD 2＝1， R 2＝12＋⎝ ⎛⎭⎪⎫SD 22＝54，则S ＝4πR 2＝5π. 考向5 切瓜模型切瓜模型是有一侧面垂直底面的棱锥模型，常见的是两个互相垂直的面都是特殊三角形，在三棱锥A －BCD 中，侧面ABC ⊥底面BCD ，设三棱锥的高为h ，外接球的半径为R ，球心为O ，△BCD 的外心为O 1，O 1到BC 的距离为d ，O 与O 1的距离为m ，△BCD 和△ABC 外接圆的半径分别为r 1，r 2，则⎩⎨⎧R 2＝r 21＋m 2，R 2＝d 2＋（h －m ）2，解得R ，可得R ＝r 21＋r 22－l 24(l 为两个面的交线段长).例5(2022·济宁模拟)在边长为6的菱形ABCD 中，∠A ＝π3，现将△ABD 沿BD 折起，当三棱锥A －BCD 的体积最大时，三棱锥A －BCD 的外接球的表面积为________. 答案 60π解析边长为6的菱形ABCD ，在折叠的过程中，当平面ABD ⊥平面BCD 时，三棱锥的体积最大；由于AB ＝AD ＝CD ＝BC ＝6， ∠C ＝∠A ＝π3.所以△ABD 和△CBD 均为正三角形，设△ABD 和△CBD 的外接圆半径为r ，则2r ＝BDsin C，所以r ＝2 3.△ABD 和△CBD 的交线段为BD ，且BD ＝6. 所以三棱锥A －BCD 的外接球的半径R ＝（23）2＋（23）2－624＝15.故S 球＝4·π(15)2＝60π.训练1 (1)(2022·青岛一模)设三棱柱的侧棱垂直于底面，所有棱的长都为1，顶点都在一个球面上，则该球的表面积为( ) A.5π B.π C.113π D.73π (2)在三棱锥P －ABC 中，平面PAB ⊥平面ABC ，平面PAC ⊥平面ABC ，且PA ＝4，底面△ABC 的外接圆的半径为3，则三棱锥P －ABC 的外接球的表面积为________. 答案 (1)D (2)52π解析 (1)由三棱柱所有棱的长a ＝1，可知底面为正三角形，底面三角形的外接圆直径2r ＝1sin 60°＝233，所以r ＝33，设外接球的半径为R ，则有R 2＝r 2＋⎝ ⎛⎭⎪⎫a 22＝13＋14＝712，所以该球的表面积S ＝4πR 2＝73π，故选D.(2)因为平面PAB ⊥平面ABC ，平面PAC ⊥平面ABC ，所以PA ⊥平面ABC .设三棱锥P －ABC 的外接球的半径为R ，结合底面△ABC 的外接圆的半径r ＝3，可得R 2＝⎝ ⎛⎭⎪⎫PA 22＋r 2＝22＋33＝13，所以三棱锥P －ABC 的外接球的表面积为S 表＝4πR 2＝52π. 类型二内切球问题内切球问题的解法(以三棱锥为例)第一步：先求出四个表面的面积和整个锥体的体积；第二步：设内切球的半径为r ，建立等式V P －ABC ＝V O －ABC ＋V O －PAB ＋V O －PAC ＋V O －PBC ⇒V P －ABC ＝13S △ABC ·r ＋13S △PAB ·r ＋13S △PAC ·r ＋13S PBC ·r ＝13(S △ABC ＋S △PAB ＋S △PAC ＋S △PBC )r ；第三步：解出r ＝3V P －ABCS △ABC ＋S △PAB ＋S △PAC ＋S △PBC.例6 (1)(2022·成都石室中学三诊)《九章算术》中将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P －ABC 为鳖臑，PA ⊥平面ABC ，PA ＝BC ＝4，AB ＝3，AB ⊥BC ，若三棱锥P －ABC 有一个内切球O ，则球O 的体积为( ) A.9π2B.9π4 C.9π16D.9π (2)在直三棱柱ABC －A 1B 1C 1中，AA 1＝AB ＝6，BC ＝8，AC ＝10，则该三棱柱内能放置的最大球的表面积是( ) A.16π B.24π C.36π D.64π答案(1)C (2)A解析(1)设球O的半径为r，则三棱锥P－ABC的体积V＝13×12×3×4×4＝13×(12×3×4＋12×4×3＋12×5×4＋12×4×5)×r，解得r＝34，所以球O的体积V＝43πr3＝9π16，故选C.(2)由题意，球的半径为底面三角形内切圆的半径r，因为底面三角形的边长分别为6，8，10，所以底面三角形为直角三角形，r＝AB＋BC－AC2＝6＋8－102＝2.又因为AA1＝6，2r＝4<6，所以该三棱柱内能放置的最大球半径为2，此时S表面积＝4πr2＝4π×22＝16π.训练 2 已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为________.答案2 3π解析圆锥内半径最大的球即为圆锥的内切球，设其半径为r.作出圆锥的轴截面PAB，如图所示，则△PAB的内切圆为圆锥的内切球的大圆.在△PAB中，PA＝PB＝3，D为AB的中点，AB＝2，E为切点，则PD＝22，△PEO∽△PDB，故PO PB ＝OE DB ，即22－r 3＝r 1，解得r ＝22，故内切球的体积为43π⎝ ⎛⎭⎪⎫223＝23π.类型三球的截面问题解决球的截面问题抓住以下几个方面：(1)球心到截面圆的距离；(2)截面圆的半径；(3)直角三角形(球心到截面圆的距离、截面圆的半径、球的半径构成的直角三角形).例7(2022·杭州质检)在正三棱锥P －ABC 中，Q 为BC 中点，PA ＝2，AB ＝2，过点Q 的平面截三棱锥P －ABC 的外接球所得截面面积的取值范围为________. 答案⎣⎢⎡⎦⎥⎤π，3π2解析因为正三棱锥P －ABC 中，PB ＝PC ＝PA ＝2，AC ＝BC ＝AB ＝2，所以PB 2＋PA 2＝AB 2，即PB ⊥PA ，同理PB ⊥PC ，PC ⊥PA ，因此正三棱锥P －ABC 可看作正方体的一角，如图.记正方体的体对角线的中点为O ，由正方体结构特征可得，点O 即是正方体的外接球球心，所以点O 也是正三棱锥P －ABC 外接球的球心，记外接球半径为R ，则R ＝122＋2＋2＝62，因为球的最大截面圆为过球心的圆，所以过点Q 的平面截三棱锥P －ABC 的外接球所得截面的面积最大为S max ＝πR 2＝3π2. 又Q 为BC 中点，由正方体结构特征可得OQ ＝12PA ＝22；由球的结构特征可知，当OQ 垂直于过点Q 的截面时，截面圆半径最小为r ＝R 2－OQ 2＝1，所以S min ＝πr 2＝π.因此，过Q 的平面截三棱锥P －ABC 的外接球所得截面面积的取值范围为⎣⎢⎡⎦⎥⎤π，3π2. 训练3 (1)设球O 是棱长为4的正方体的外接球，过该正方体棱的中点作球O 的截面，则最小截面的面积为( ) A.3π B.4π C.5π D.6π(2)(2022·武汉质检)已知棱长为2的正方体ABCD －A 1B 1C 1D 1，球O 与该正方体的各个面相切，则平面ACB 1截此球所得的截面的面积为________. 答案 (1)B (2)2π3解析 (1)当球O 到截面圆心连线与截面圆垂直时，截面圆的面积最小，由题意，正方体棱的中点与O 的距离为22，球的半径为23， ∴最小截面圆的半径为12－8＝2， ∴最小截面面积为π·22＝4π.(2)∵正方体ABCD －A 1B 1C 1D 1的棱长为2，球O 与该正方体的各个面相切，则球O 的半径为1，设E ，F ，G 分别为球O 与平面ABCD 、平面BB 1C 1C 、平面AA 1B 1B 的切点，则等边三角形EFG 为平面ACB 1截此球所得的截面圆的内接三角形，由已知可得EF ＝EG ＝GF ＝2， ∴平面ACB 1截此球所得的截面圆的半径r ＝22sin 60°＝63，∴截面的面积为π×⎝ ⎛⎭⎪⎫632＝2π3.一、基本技能练1.已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( ) A.π B.3π4C.π2D.π4 答案 B解析如图画出圆柱的轴截面ABCD ，O 为球心.球的半径R ＝OA＝1，球心到底面圆的距离为OM ＝12.∴底面圆半径r ＝OA 2－OM 2＝32故圆柱体积V ＝π·r 2·h ＝π·⎝ ⎛⎭⎪⎫322×1＝3π4.2.若棱长为23的正方体的顶点都在同一球面上，则该球的表面积为( ) A.12π B.24π C.36π D.144π 答案 C解析由题意知球的直径2R ＝（23）2＋（23）2＋（23）2＝6， ∴R ＝3，∴S 球＝4πR 2＝36π.故选C.3.一个四面体的所有棱长都为2，四个顶点在同一球面上，则此球的表面积为( ) A.3π B.4π C.33π D.6π 答案 A解析构造棱长为1的正方体，该四面体的外接球也是棱长为1的正方体的外接球，所以外接球半径R ＝32，所以外接球表面积为S ＝4πR 2＝3π.4.已知直三棱柱ABC －A 1B 1C 1的6个顶点都在球O 的球面上，若AB ＝3，AC ＝4，AB ⊥AC ，AA 1＝12，则球O 的半径为( )A.3172B.210C.132D.310 答案 C解析将直三棱柱补为长方体ABEC －A 1B 1E 1C 1，则球O 是长方体ABEC －A 1B 1E 1C 1的外接球. ∴体对角线BC 1的长为球O 的直径. 因此2R ＝32＋42＋122＝13，则R ＝132.5.(2022·南阳二模)已知边长为2的等边三角形ABC ，D 为BC 的中点，以AD 为折痕进行折叠，使折后的∠BDC ＝π2，则过A ，B ，C ，D 四点的球的表面积为( )A.3πB.4πC.5πD.6π 答案 C解析折后的几何体构成以D 为顶点的三棱锥，且三条侧棱互相垂直，可构造长方体，其对角线即为球的直径，三条棱长分别为1，1，3，所以2R ＝1＋1＋3＝5，球的表面积S ＝4π⎝ ⎛⎭⎪⎫522＝5π.6.(2022·青岛模拟)如图是一个由6个正方形和8个正三角形围成的十四面体，其所有顶点都在球O 的球面上，若十四面体的棱长为1，则球O 的表面积为( )A.2πB.4πC.6πD.8π 答案 B解析根据图形可知，该十四面体是由一个正方体切去八个角得到的，如图所示，十四面体的外接球球心与正方体的外接球球心相同，建立空间直角坐标系，∵该十四面体的棱长为1，故正方体的棱长为2， ∴该正方体的外接球球心的坐标为O ⎝ ⎛⎭⎪⎫22，22，22，设十四面体上一顶点为D ，则D ⎝ ⎛⎭⎪⎫2，22，0，所以十四面体的外接球半径R ＝OD ＝⎝ ⎛⎭⎪⎫2－222＋⎝ ⎛⎭⎪⎫22－222＋⎝ ⎛⎭⎪⎫0－222＝1，故外接球的表面积为S ＝4πR 2＝4π.故选B.7.四面体ABCD 的四个顶点都在球O 上且AB ＝AC ＝BC ＝BD ＝CD ＝4，AD ＝26，则球O 的表面积为( )A.70π3B.80π3C.30πD.40π答案 B解析如图，取BC的中点M，连接AM，DM，由题意可知，△ABC和△BCD都是边长为4的等边三角形. ∵M为BC的中点，∴AM⊥BC，且AM＝DM＝23，又∵AD＝26，∴AM2＋DM2＝AD2，∴AM⊥DM，∵BC∩DM＝M，BC，DM⊂平面BCD，∴AM⊥平面BCD，∵AM⊂平面ABC，∴平面ABC⊥平面BCD，△ABC与△BCD外接圆半径r＝23DM＝433，又△ABC与△BCD的交线段BC＝4. 所以四面体外接球半径R ＝⎝ ⎛⎭⎪⎫4332＋⎝ ⎛⎭⎪⎫4332－424＝2153，四面体ABCD 的外接球的表面积为4π×R 2＝803π. 8.已知三棱锥P －ABC 的棱AP ，AB ，AC 两两垂直，且长度都为3，以顶点P 为球心，2为半径作一个球，则球面与三棱锥的表面相交所得到的四段弧长之和等于( ) A.2π3B.5π6C.πD.3π2答案 D解析如图，∠APC ＝π4，AP ＝3，AN ＝1，∠APN ＝π6，∠NPM ＝π12，MN ︵＝π12×2＝π6，同理GH ︵＝π6，HN ︵＝π2，GM ︵＝2π3，故四段弧长之和为π6＋π6＋π2＋2π3＝3π2.9.(多选)(2022·石家庄调研)已知一个正方体的外接球和内切球上各有一个动点M 和N ，若线段MN 长的最小值为3－1，则( ) A.该正方体的外接球的表面积为12π B.该正方体的内切球的体积为π3C.该正方体的棱长为1D.线段MN长的最大值为3＋1 答案AD解析设该正方体的棱长为a，则其外接球的半径R＝32a，内切球的半径R′＝a2，该正方体的外接球与内切球上各有一个动点M，N，由于两球球心相同，可得MN的最小值为3a2－a2＝3－1，解得a＝2，故C错误；所以外接球的半径R＝3，表面积为4π×3＝12π，故A正确；内切球的半径R′＝1，体积为43π，故B错误；MN的最大值为R＋R′＝3＋1，故D正确.故选AD.10.(多选)设圆锥的顶点为A，BC为圆锥底面圆O的直径，点P为圆O上的一点(异于B，C)，若BC＝43，三棱锥A－PBC的外接球表面积为64π，则圆锥的体积为( ) A.4π B.8πC.16πD.24π答案BD解析如图，设圆锥AO的外接球球心为M，半径为r，则M在直线AO上，4πr2＝64π，解得r＝4.由勾股定理得BM2＝OM2＋OB2，即42＝(23)2＋OM2，可得OM＝2，即OM＝|AO－r|＝|AO－4|＝2，解得AO＝6或AO＝2.当AO＝6时，圆锥AO的体积为V＝13π×(23)2×6＝24π；当AO＝2时，圆锥AO的体积为V＝13π×(23)2×2＝8π.故选BD.11.在三棱锥A－BCD中，△BCD和△ABD均是边长为1的等边三角形，AC＝2，则该三棱锥外接球的表面积为________.答案2π解析取AC的中点O，连接OB，OD，在△ABC中，AB＝BC＝1，AC＝2，所以∠ABC＝90°，所以OA＝OB＝OC＝2 2，同理得OD＝22，故点O为该三棱锥外接球的球心，所以球O的半径r＝22，S球＝4πr2＝2π.12.如图，已知球O是棱长为3的正方体ABCD－A1B1C1D1的内切球，则平面ACD1截球O的截面面积为________.答案3π2解析根据题意知，平面ACD 1是边长为9＋9＝32的正三角形，且所求截面的面积是该正三角形的内切圆的面积，则由图得，△ACD 1内切圆的半径r ＝13（32）2－⎝⎛⎭⎪⎫3222＝62，所以平面ACD 1截球O 的截面面积为 S ＝π×⎝ ⎛⎭⎪⎫622＝3π2.二、创新拓展练13.(多选)(2022·华大新高考联考)已知三棱锥S －ABC 中，SA ⊥平面ABC ，SA ＝AB ＝BC ＝2，AC ＝2，点E ，F 分别是线段AB ，BC 的中点，直线AF ，CE 相交于G ，则过点G 的平面α截三棱锥S －ABC 的外接球O 所得截面面积可以是( ) A.23π B.89π C.π D.32π答案 BCD解析因为AB 2＋BC 2＝AC 2，故AB ⊥BC ，故三棱锥S －ABC 的外接球O的半径R ＝2＋2＋22＝62，取AC 的中点D ，连接BD 必过G ，因为AB ＝BC ＝2，故DG ＝13BD ＝13，因为OD ＝22，故OG 2＝⎝ ⎛⎭⎪⎫222＋⎝ ⎛⎭⎪⎫132＝1118，则过点G 的平面截球O 所得截面圆的最小半径r 2＝⎝ ⎛⎭⎪⎫622－1118＝89，故截面面积的最小值为89π，最大值为πR 2＝32π，故选BCD.14.(多选)(2022·济南模拟)已知三棱锥P －ABC 的四个顶点都在球O 上，AB ＝BC ＝AC ＝1，∠APC ＝π6，平面PAC ⊥平面ABC ，则( )A.直线OA 与直线BC 垂直B.点P 到平面ABC 的距离的最大值为1＋32C.球O 的表面积为13π3D.三棱锥O －ABC 的体积为18答案 ACD解析设△ABC 外接圆的圆心为O 1，连接OO 1，O 1A . 因为O 为三棱锥P －ABC 外接球的球心，所以OO 1⊥平面ABC ，所以OO 1⊥BC ，因为AB ＝BC ＝AC ＝1，所以O 1A ⊥BC ，所以BC ⊥平面OO 1A ，所以OA ⊥BC ，故A 选项正确；设△PAC 外接圆的圆心为O 2，AC 的中点为D ，连接O 2D ，由于AC ＝1，∠APC ＝π6，所以圆O 2的半径r 2＝12×1sinπ6＝1，则易知O 2D ＝32，所以点P 到平面ABC 的距离的最大值为1＋32(此时P ，O 2，D 三点共线)，故B 选项错误；由于AB ＝BC ＝AC ＝1，平面PAC ⊥平面ABC ，平面PAC ∩平面ABC ＝AC ，所以圆O 1的半径r 1＝12×1sin π3＝33，圆O 2的半径r 2＝1，△ABC 与△PAC 的交线段AC ＝1，所以三棱锥P －ABC 外接球半径R 2＝⎝ ⎛⎭⎪⎫332＋12－14＝1312.故球O 的表面积S ＝4π×1312＝13π3，故C 选项正确；由于OO 1⊥平面ABC ，且OO 1＝O 2D ＝32，S △ABC ＝34，所以三棱锥O－ABC的体积为13×OO1×S△ABC＝13×32×34＝18，故D选项正确，故选ACD.15.(多选)(2022·湖州调研)已知正四面体ABCD的棱长为3，其外接球的球心为O.点E 满足AE→＝λAB→(0<λ<1)，过点E作平面α平行于AC和BD，设α分别与该正四面体的棱BC，CD，DA相交于点F，G，H，则( )A.四边形EFGH的周长为定值B.当λ＝12时，四边形EFGH为正方形C.当λ＝13时，平面α截球O所得截面的周长为13π4D.四棱锥A－EFGH的体积的最大值为22 3答案ABD解析将正四面体ABCD放入正方体中.因为正四面体ABCD的棱长为3，所以正方体的棱长为322.如图所示，过点E作平面α平行于AC和BD，平面α与正方体的棱交于M，N，P，Q四点.因为AE→＝λAB→，故AH→＝λAD→，即有EH＝λBD，同理FG＝λBD，EF＝(1－λ)AC，HG＝(1－λ)AC，且EH∥BD，EF∥AC，故四边形EFGH 为平行四边形.因为AC ⊥BD ，故EF ⊥EH ，则四边形EFGH 为矩形.对于A ，四边形EFGH 的周长为2(EF ＋EH )＝2[(1－λ)AC ＋λBD ]＝2[(1－λ)AC ＋λAC ]＝2AC ＝6，为定值，故A 选项正确；对于B ，当λ＝12时，E 为AB 的中点，故EF ＝EH ，所以四边形EFGH 为正方形，故B 选项正确；对于C ，当λ＝13时，球心O 到平面EFGH 的距离即球心到平面MNPQ 的距离，即BC 中点到MF 的距离，经计算为24，球半径为322×32＝364，故截面圆的半径为⎝ ⎛⎭⎪⎫3642－⎝ ⎛⎭⎪⎫242＝132，所以截面圆的周长为132×2π＝13π，故C 选项错误；对于D ，四棱锥A －EFGH 的高为AQ ，所以其体积V ＝13×322λ×3(1－λ)×3λ＝922λ2(1－λ)，0<λ<1，令f (λ)＝922λ2(1－λ)，则f ′(λ)＝922(2λ－3λ2)，令f ′(λ)＝0得λ＝23，故当λ＝23时，四棱锥A －EFGH 的体积最大，最大值为922×49×13＝223，故D 选项正确，故选ABD.16.(多选)(2022·嘉兴测试)如图，在等腰梯形ABCD 中，AB ＝2AD ＝2BC ＝2CD ＝4.现将△DAC沿对角线AC所在的直线翻折成△D′AC，记二面角D′－AC－B的大小为α(0<α<π)，则( )A.存在α，使得D′A⊥BCB.存在α，使得D′A⊥平面D′BCC.存在α，使得三棱锥D′－ABC的体积为3 3D.存在α＝π2，使得三棱锥D′－ABC的外接球的表面积为20π答案ACD解析如图1，取AB的中点E，连接DE交AC于点F.因为AB＝2CD，所以CD＝EB＝AE，所以四边形AECD为菱形，四边形EBCD为菱形，所以△AED，△DEC，△EBC均为等边三角形，所以AC⊥ED，∠DAC＝∠BAC＝π6，∠ACB＝π2，在翻折过程中，如图2，AC⊥D′F，AC⊥FE，所以∠D′FE为二面角D′－AC－B的平面角，所以∠D′FE＝α.对于A，当α＝π2时，平面D′AC⊥平面ABC.因为BC⊥AC，所以BC⊥平面D′AC.又因为D′A⊂平面D′AC，所以D′A⊥BC，所以存在α，使得D′A⊥BC，故A选项正确；对于B，假设存在α，使得D′A⊥平面D′BC.因为D′C⊂平面D′BC，所以D′A⊥D′C，与∠AD′C＝2π3矛盾，故B选项不正确；对于C，由分析可得，D′F＝12DE＝12AD＝1，AC＝2AF＝2×32×AD＝2 3.设D′到平面ABC的距离为d，则V三棱锥D′－ABC＝13×S△ABC×d＝13×12×AC×BC×d＝13×12×23×2×d＝33，解得d＝1 2，所以sin α＝dD′F＝12，所以α＝π6或5π6，故C选项正确；对于D，当α＝π2时，平面D′AC⊥平面ABC，所以BC⊥平面D′AC，D′F⊥平面ABC.如图2所示，因为E，F分别为AB，AC的中点，所以EF∥BC，且EF＝12BC＝1，所以EF⊥平面D′AC.设△D′AC外接圆圆心为O1，则O1A＝O1D′＝AD′＝2.因为E是Rt△ABC斜边的中点，所以E为Rt△ABC的外心.过O1作平面D′AC的垂线，过点E作平面ABC的垂线，则两垂线的交点O即为三棱锥D′－ABC外接球的球心，显然四边形EFO1O是矩形，所以OO1＝EF＝1.设三棱锥D′－ABC的外接球半径为R，则在Rt△OO1D′中，R＝OD′＝O1O2＋O1D′2＝1＋4＝5，所以三棱锥D′－ABC的外接球的表面积S＝4πR2＝20π，故D选项正确.综上所述，故选ACD.17.在菱形ABCD中，AB＝23，∠ABC＝60°，若将菱形ABCD沿对角线AC折成大小为60°的二面角B－AC－D，则四面体DABC的外接球球O的体积为________.答案5239π27解析如图，设M，N分别为△ABC，△ACD的外心，E为AC的中点，则EN＝EM＝13BE＝1，在平面BDE内过点M作BE的垂线与过点N作DE的垂线交于点O. ∵BE⊥AC，DE⊥AC，BE∩DE＝E，∴AC⊥平面BDE.∵OM⊂平面BDE，∴OM⊥AC，∵OM⊥BE，BE∩AC＝E，∴OM⊥平面ABC，同理可得ON⊥平面ACD，则O为四面体DABC的外接球的球心，连接OE，∵EM＝EN，OE＝OE，∠OME＝∠ONE＝90°，∴△OME≌△ONE，∴∠OEM＝30°，∴OE＝EMcos 30°＝233.∵AC⊥平面BDE，OE⊂平面BDE，∴OE⊥AC，∴OA＝OE2＋AE2＝39 3，即球O的半径R＝39 3.故球O的体积V＝43πR3＝5239π27.18.(2022·湖南三湘名校联考)在直三棱柱ABC－A1B1C1中，AB⊥BC，AB＝BC＝AA1＝4，M 为棱AB的中点，N是棱BC的中点，O是三棱柱外接球的球心，则平面MNB1截球O所得截面的面积为________.答案8π解析如图1，将直三棱柱补形成正方体ABCD－A1B1C1D1，连接BD1，则直三棱柱的外接球也是正方体的外接球，球心O是BD1的中点，半径R＝2 3. 连接BD交MN于点E，连接B1E交BD1于点F，过点O作OO1⊥B1E于点O1，连接B1D1，因为MN∥AC，AC⊥平面BB1D1D，所以MN⊥平面BB1D1D，所以OO1⊥MN，所以OO1⊥平面MNB1.如图2，31 / 31 在矩形BB 1D 1D 中，BF FD 1＝BE B 1D 1＝14，所以BF OF ＝23，过点B 作BG ⊥B 1E 于点G ，则BG ＝BE ·BB 1B 1E ＝43，BGOO 1＝BF OF ＝23，所以OO 1＝2，设截面圆的半径为r ，则r 2＝R 2－OO 21＝(23)2－22＝8，所以截面的面积为8π.。

高考必考题—几何体中与球有关的切、接问题(含解析)

几何体中与球有关的切、接问题球的截面的性质(1)球的任何截面是圆面；(2)球心和截面(不过球心)圆心的连线垂直于截面；(3)球心到截面的距离d 与球的半径R 及截面的半径r 的关系为r ＝R 2－d 2几个与球有关的切、接常用结论(1)正方体的棱长为a ，球的半径为R ，①若球为正方体的外接球，则2R ＝3a ；②若球为正方体的内切球，则2R ＝a ；③若球与正方体的各棱相切，则2R ＝2a .(2)若长方体的同一顶点的三条棱长分别为a ，b ，c ，外接球的半径为R ，则2R ＝a 2＋b 2＋c 2. (3)正四面体的外接球与内切球的半径之比为3∶1. 一、题型选讲题型一、几何体的外接球解决多面体的外接球问题，关键是确定球心的位置，方法是先选择多面体中的一面，确定此面外接圆的圆心，再过圆心作垂直此面的垂线，则球心一定在此垂线上，最后根据其他顶点确定球心的准确位置．对于特殊的多面体还可采用补成正方体或长方体的方法找到球心位置．例1、【2020年高考全国Ⅰ卷理数】已知,,A B C 为球O 的球面上的三个点，⊙1O 为ABC △的外接圆，若⊙1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为 A ．64π B ．48πC ．36πD ．32π例2、【2020年高考天津】若棱长为 A ．12π B ．24π C ．36πD ．144π例3、（2020届山东省潍坊市高三上学期统考）已知边长为2的等边三角形ABC ，D 为BC 的中点，以AD 为折痕进行折叠，使折后的2BDC π∠=，则过A ，B ，C ，D 四点的球的表面积为（）A ．3πB ．4πC ．5πD ．6π例4、（2020届山东省日照市高三上期末联考）已知四棱锥P ABCD -的体积是ABCD 是正方形，PAB ∆是等边三角形，平面PAB ⊥平面ABCD ，则四棱锥P ABCD -外接球体积为（）A ．BCD ．例5、（2020届山东省德州市高三上期末）中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就，书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑，如图为一个阳马与一个鳖臑的组合体，已知PA ⊥平面ABCE ，四边形ABCD 为正方形，AD =ED =P ADE -的外接球的体积为，则阳马P ABCD -的外接球的表面积等于______.题型二、几何体的内切球求解多面体的内切球的问题，一般是将多面体分割为以球心为顶点，多面体的各面为底面的棱锥，利用多面体的体积等于各棱锥的体积之和求内切球的半径．例6、【2020年高考全国Ⅲ卷理数】已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为_________．例7、（2020届山东省潍坊市高三上期中）如图，平行四边形形状的纸片是由六个边长为1的正三角形构成的，将它沿虚线折起来，可以得到如图所示粽子形状的六面体，则该六面体的表面积为__________；若该六面体内有一小球，则小球的最大体积为___________．二、达标训练1、（2020届山东省泰安市高三上期末）已知正三棱锥S ABC -的侧棱长为6，则该正三棱锥外接球的表面积是（） A ．16πB ．20πC ．32πD ．64π2、【2020年高考全国II 卷理数】已知△ABC O 的球面上.若球O 的表面积为16π，则O 到平面ABC 的距离为A B ．32C ．1D 3、【2019年高考全国Ⅰ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上，PA =PB =PC ，△ABC 是边长为2的正三角形，E ，F 分别是PA ，AB 的中点，∠CEF =90°，则球O 的体积为A ．B ．C ．D4、【2018年高考全国Ⅰ卷理数】设A B C D ，，，是同一个半径为4的球的球面上四点，ABC △为等边三角形且其面积为D ABC -体积的最大值为A ．B ．C ．D ．5、【2020年新高考全国Ⅰ卷】已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2，∠BAD =60°．以1D 半径的球面与侧面BCC 1B 1的交线长为________．6、（2020届山东省滨州市三校高三上学期联考）已知三棱锥S ABC -，SA ⊥平面ABC ，6ABC π∠=，3SA =，1BC =，直线SB 和平面ABC 所成的角大小为3π.若三棱锥S ABC -的四个顶点都在同一球面上，则该球的表面积为________.7、（2020届山东省枣庄、滕州市高三上期末）如图，在三棱锥P -ABC 中，,PA AB ⊥PC BC ⊥，,AB BC ⊥22,AB BC ==PC =，则PA 与平面ABC 所成角的大小为________；三棱锥P -ABC 外接球的表面积是________.8、（2020届山东省烟台市高三上期末）已知三棱锥P ABC -的四个顶点都在球O 的表面上，PA ⊥平面ABC，6PA =，AB =2AC =，4BC =，则：（1）球O 的表面积为__________；（2）若D 是BC 的中点，过点D 作球O 的截面，则截面面积的最小值是__________．9、（2020届山东省滨州市高三上期末）在四面体S ABC -中，2SA SB ==，且SA SB ⊥，BC =，AC=________，该四面体外接球的表面积为________.10、（2020届山东省济宁市高三上期末）下图是两个腰长均为10cm的等腰直角三角形拼成的一个四边形-的外接球的体积为ABCD，现将四边形ABCD沿BD折成直二面角A BD C--，则三棱锥A BCDcm．__________3一、题型选讲题型一、几何体的外接球解决多面体的外接球问题，关键是确定球心的位置，方法是先选择多面体中的一面，确定此面外接圆的圆心，再过圆心作垂直此面的垂线，则球心一定在此垂线上，最后根据其他顶点确定球心的准确位置．对于特殊的多面体还可采用补成正方体或长方体的方法找到球心位置．例1、【2020年高考全国Ⅰ卷理数】已知,,A B C 为球O 的球面上的三个点，⊙1O 为ABC △的外接圆，若⊙1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为 A ．64π B ．48πC ．36πD ．32π【答案】A【解析】设圆1O 半径为r ，球的半径为R ，依题意，得24,2r r π=π=∴，ABC 为等边三角形，由正弦定理可得2sin 60AB r =︒=，1OO AB ∴==1OO ⊥平面ABC ，11,4OO O A R OA ∴⊥====， ∴球O 的表面积2464S R ππ==.故选：A.本题考查球的表面积，应用球的截面性质是解题的关键，考查计算求解能力，属于基础题.例2、【2020年高考天津】若棱长为 A ．12π B ．24πC ．36πD ．144π【答案】C【解析】这个球是正方体的外接球，其半径等于正方体的体对角线的一半，即3R ==，所以，这个球的表面积为2244336S R πππ==⨯=. 故选：C ．本题考查正方体的外接球的表面积的求法，求出外接球的半径是本题的解题关键，属于基础题.求多面体的外接球的面积和体积问题，常用方法有：（1）三条棱两两互相垂直时，可恢复为长方体，利用长方体的体对角线为外接球的直径，求出球的半径；（2）直棱柱的外接球可利用棱柱的上下底面平行，借助球的对称性，球心为上下底面外接圆的圆心连线的中点，再根据勾股定理求球的半径；（3）如果设计几何体有两个面相交，可过两个面的外心分别作两个面的垂线，垂线的交点为几何体的球心. 例3、（2020届山东省潍坊市高三上学期统考）已知边长为2的等边三角形ABC ，D 为BC 的中点，以AD 为折痕进行折叠，使折后的2BDC π∠=，则过A ，B ，C ，D 四点的球的表面积为（）A ．3πB ．4πC ．5πD ．6π【答案】C【解析】边长为2的等边三角形ABC ，D 为BC 的中点，以AD 为折痕进行折叠，使折后的2BDC π∠=，构成以D 为顶点的三棱锥，且三条侧棱互相垂直，可构造以其为长宽高的长方体，其对角线即为球的直径，三条棱长分别为1,12R ==2452S ππ==，故选C.例4、（2020届山东省日照市高三上期末联考）已知四棱锥P ABCD -的体积是ABCD 是正方形，PAB ∆是等边三角形，平面PAB ⊥平面ABCD ，则四棱锥P ABCD -外接球体积为（）A ．BCD ．【答案】A【解析】设AB 的中点为Q ，因为PAB ∆是等边三角形，所以PQ AB ⊥，而平面PAB ⊥平面ABCD ，平面PAB ⋂平面ABCD AB =，所以PQ ⊥平面ABCD ，四棱锥P ABCD -的体积是13AB AB PQ =⨯⨯⨯13AB AB AB =⨯⨯，所以边长6AB =，PQ =OH x =，OM x =，()(222222R OA OM AM x==+=+，2222223R OP OH PH x ==+=+，x =2212321R =+=343V R π==球.故选：A.例5、（2020届山东省德州市高三上期末）中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就，书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑，如图为一个阳马与一个鳖臑的组合体，已知PA ⊥平面ABCE ，四边形ABCD 为正方形，AD =ED =P ADE -的外接球的体积为，则阳马P ABCD -的外接球的表面积等于______.【答案】20π 【解析】四边形ABCD 是正方形，AD CD ∴⊥，即AD CE ⊥，且AD =ED =，所以，ADE ∆的外接圆半径为122AE r ===设鳖臑P ADE -的外接球的半径1R ，则3143R π=，解得12R =.PA ⊥平面ADE ，1R ∴=2PA ==PA ∴=正方形ABCD 的外接圆直径为22r AC ==22r ∴=，PA ⊥平面ABCD ，所以，阳马P ABCD -的外接球半径2R ==因此，阳马P ABCD -的外接球的表面积为22420R ππ=.故答案为：20π. 题型二、几何体的内切球求解多面体的内切球的问题，一般是将多面体分割为以球心为顶点，多面体的各面为底面的棱锥，利用多面体的体积等于各棱锥的体积之和求内切球的半径．例6、【2020年高考全国Ⅲ卷理数】已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为_________．【解析】易知半径最大球为圆锥的内切球，球与圆锥内切时的轴截面如图所示，其中2,3BC AB AC ===，且点M 为BC 边上的中点，设内切圆的圆心为O ，由于AM ==122S =⨯⨯=△ABC 设内切圆半径为r ，则：ABC AOB BOC AOC S S S S =++△△△△111222AB r BC r AC r =⨯⨯+⨯⨯+⨯⨯()13322r =⨯++⨯=解得：2r，其体积：343V r =π=.故答案为：3. 与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.例7、（2020届山东省潍坊市高三上期中）如图，平行四边形形状的纸片是由六个边长为1的正三角形构成的，将它沿虚线折起来，可以得到如图所示粽子形状的六面体，则该六面体的表面积为__________；若该六面体内有一小球，则小球的最大体积为___________．【解析】（1）因为16(12S =⨯⨯=. （2）由图形的对称性得，小球的体积要达到最大，即球与六个面都相切时，每个三角形面积是4，六面体体积是正四面体的2倍，所以六面体体积是6. 由于图像的对称性，内部的小球要是体积最大，就是球要和六个面相切，连接球心和五个顶点，把六面体分成了六个三棱锥，设球的半径为R ，所以16()6349R R =⨯⨯⨯⇒=，所以球的体积334433V R ππ===.故答案为：. 二、达标训练1、（2020届山东省泰安市高三上期末）已知正三棱锥S ABC -的侧棱长为6，则该正三棱锥外接球的表面积是（） A ．16π B ．20πC ．32πD ．64π【答案】D【解析】如图所示，因为正三棱锥S ABC -的侧棱长为6，则263AE ==6SE ===, 又由球心O 到四个顶点的距离相等，在直角三角形AOE 中，,6AO R OE SE SO R ==-=-，又由222OA AE OE =+，即222(6)R R =+-，解得4R =，所以球的表面积为2464S R ππ==，故选D.2、【2020年高考全国II 卷理数】已知△ABC O 的球面上.若球O 的表面积为16π，则O 到平面ABC 的距离为A B ．32C ．1D 【答案】C【解析】设球O 的半径为R ，则2416R π=π，解得：2R =.设ABC △外接圆半径为r ，边长为a ，ABC △21224a ∴⨯=，解得：3a =，2233r ∴===，∴球心O 到平面ABC 的距离1d ==.故选：C ．本题考查球的相关问题的求解，涉及到球的表面积公式和三角形面积公式的应用；解题关键是明确球的性质，即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.3、【2019年高考全国Ⅰ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上，PA =PB =PC ，△ABC 是边长为2的正三角形，E ，F 分别是PA ，AB 的中点，∠CEF =90°，则球O 的体积为A ．B ．C ．D【答案】D 【解析】解法一：,PA PB PC ABC ==△为边长为2的等边三角形，P ABC ∴-为正三棱锥，PB AC ∴⊥，又E ，F 分别为PA ，AB 的中点，EF PB ∴∥，EF AC ∴⊥，又EF CE ⊥，,CEAC C EF =∴⊥平面PAC ，∴PB ⊥平面PAC ，APB PA PB PC ∴∠=90︒,∴===P ABC ∴-为正方体的一部分，2R ==即344π33R V R =∴=π==，故选D ．解法二：设2PA PB PC x ===，,E F 分别为,PA AB 的中点，EF PB ∴∥，且12EF PB x ==，ABC △为边长为2的等边三角形，CF ∴=又90CEF ∠=︒，12CE AE PA x ∴===， AEC △中，由余弦定理可得()2243cos 22x x EAC x+--∠=⨯⨯，作PD AC ⊥于D ，PA PC =，D 为AC 的中点，1cos 2AD EAC PA x ∠==，2243142x x x x+-+∴=，22121222x x x ∴+=∴==，，，PA PB PC ∴=== 又===2AB BC AC ，,,PA PB PC ∴两两垂直，2R ∴==R ∴=，34433V R ∴=π==，故选D.本题主要考查学生的空间想象能力，补体法解决外接球问题．可通过线面垂直定理，得到三棱两两互相垂直关系，快速得到侧棱长，进而补体成正方体解决．4、【2018年高考全国Ⅰ卷理数】设A B C D ，，，是同一个半径为4的球的球面上四点，ABC △为等边三角形且其面积为D ABC -体积的最大值为 A． B ． C．D ．【答案】B【解析】如图所示，设点M 为三角形ABC 的重心，E 为AC 中点，当点D 在平面ABC 上的射影为M 时，三棱锥D ABC -的体积最大，此时，4OD OB R ===，2ABC S AB ==△，6AB ∴=,点M 为三角形ABC 的重心，23BM BE ∴==，Rt OBM ∴△中，有2OM ==，426DM OD OM ∴=+=+=，()max 163D ABC V -∴=⨯= B.5、【2020年新高考全国Ⅰ卷】已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2，∠BAD =60°．以1D 半径的球面与侧面BCC 1B 1的交线长为________．【答案】2. 【解析】如图：取11B C 的中点为E ，1BB 的中点为F ，1CC 的中点为G ，因为BAD ∠=60°，直四棱柱1111ABCD A B C D -的棱长均为2，所以△111D B C 为等边三角形，所以1D E=111D E B C ⊥，又四棱柱1111ABCD A B C D -为直四棱柱，所以1BB ⊥平面1111D C B A ，所以111BB B C ⊥，因为1111BB B C B =，所以1D E ⊥侧面11B C CB ，设P 为侧面11B C CB 与球面的交线上的点，则1D E EP ⊥，1D E =，所以||EP ===所以侧面11B C CB 与球面的交线上的点到E ，因为||||EF EG ==11B C CB 与球面的交线是扇形EFG 的弧FG ，因为114B EFC EG π∠=∠=，所以2FEG π∠=，所以根据弧长公式可得22FG π==.. 6、（2020届山东省滨州市三校高三上学期联考）已知三棱锥S ABC -，SA ⊥平面ABC ，6ABC π∠=，3SA =，1BC =，直线SB 和平面ABC 所成的角大小为3π.若三棱锥S ABC -的四个顶点都在同一球面上，则该球的表面积为________. 【答案】13π【解析】如图：SA ⊥平面ABC ，则SBA ∠为直线SB 和平面ABC 所成的角，即3SBA π∠=在Rt SAB ∆中：tan3SA AB π=== 如图，设O 为三棱锥S ABC -外接球的球心，G 为ABC ∆外接圆圆心，连结,,,,OA OB GA GB OG ，则必有OG ⊥面ABC 在ABC ∆，2222cos 312162AC AB BC AB BC π=+-⋅⋅=+-=，则1AC = 其外接圆半径122,1sin sin 6AC r r ABC π====∠，又1322OG SA ==，所以三棱锥S ABC -外接球半径为R ===该球的表面积为21344134S R πππ==⨯=, 故答案为：13π.7、（2020届山东省枣庄、滕州市高三上期末）如图，在三棱锥P -ABC 中，,PA AB ⊥PC BC ⊥，,AB BC ⊥22,AB BC ==PC =，则PA 与平面ABC 所成角的大小为________；三棱锥P -ABC 外接球的表面积是________.【答案】45︒ 6π【解析】如图，作平行四边形ABCD ，连接PD ，由AB BC ⊥，则平行四边形ABCD 是矩形．由BC CD ⊥，BC PC ⊥，PCCD C =，∴BC ⊥平面PCD ，而PD ⊂平面PCD ，∴BC PD ⊥，同理可得AB PD ⊥，又AB BC B ⋂=，∴PD ⊥平面ABCD ．,PD CD PD AD ⊥⊥，PAD ∠是PA 与平面ABC 所成角．由2,CD AB PC ===1PD =，又1AD BC ==，∴45PAD ∠=︒．∴PA 与平面ABC 所成角是45︒．由,PA AB ⊥PC BC ⊥知PB 的中点到,,,A B C P 的距离相等，PB 是三棱锥P -ABC 外接球的直径．由BC ⊥平面PCD 得BC PC ⊥，PB ===24()62PB S ππ==．故答案为：45︒；6π．8、（2020届山东省烟台市高三上期末）已知三棱锥P ABC -的四个顶点都在球O 的表面上，PA ⊥平面ABC，6PA =，AB =2AC =，4BC =，则：（1）球O 的表面积为__________；（2）若D 是BC 的中点，过点D 作球O 的截面，则截面面积的最小值是__________．【答案】52π 4π【解析】（1）由题,根据勾股定理可得AC AB ⊥,则可将三棱锥P ABC -可放入以,,AP AC AB 为长方体的长,宽,高的长方体中,则体对角线为外接球直径,即2r ==则r =,所以球的表面积为224452r πππ=⨯=；（2）由题,因为Rt ABC ,所以D 为底面ABC 的外接圆圆心,当DO ⊥截面时,截面面积最小,即截面为平面ABC ,则外接圆半径为2,故截面面积为224ππ⨯=故答案为：（1）52π；（2）4π9、（2020届山东省滨州市高三上期末）在四面体S ABC -中，2SA SB ==，且SA SB ⊥，BC =，AC =________，该四面体外接球的表面积为________.【答案】68π【解析】因为2SA SB ==，且SA SB ⊥，BC =，AC =AB ==，因此222BC AC AB +=，则AC BC ⊥；取AB 中点为O ，连接OS ，OC ，则OA OB OC OS ====，所以该四面体的外接球的球心为O ，半径为OC=所以该四面体外接球的表面积为248S ππ=⋅=；又因为SA SB =，所以SO AB ⊥；因为底面三角形ABC 的面积为定值122AC BC ⋅=，SO ，因此，当SO ⊥平面ABC 时，四面体的体积最大，为136ABC V S SO =⋅=.故答案为：(1).6(2). 8π10、（2020届山东省济宁市高三上期末）下图是两个腰长均为10cm 的等腰直角三角形拼成的一个四边形ABCD ，现将四边形ABCD 沿BD 折成直二面角A BD C --，则三棱锥A BCD -的外接球的体积为__________3cm ．【答案】【解析】由题设可将该三棱锥拓展成如图所示的正方体，则该正方体的外接球就是三棱锥的外接球，由于正方体的对角线长为2l R ==即球的半径R =该球的体积343V R π==，应填答案．。

高考数学球体截面有关的计算问题(解析版)

专题10 与球体截面有关的计算问题【母题来源一】【2020年高考全国Ⅰ卷理数】已知,,A B C 为球O 的球面上的三个点，⊙1O 为ABC 的外接圆，若⊙1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为 A. 64π B. 48πC. 36πD. 32π【答案】A【解析】设圆1O 半径为r ，球的半径为R ，依题意，得24,2r r ππ=∴=，ABC 为等边三角形，由正弦定理可得2sin 60AB r =︒=，1OO AB ∴==，根据球的截面性质1OO ⊥平面ABC ，11,4OO O A R OA ∴⊥====，∴球O 的表面积2464S R ππ==.故选：A【名师点睛】本题考查球的表面积，应用球的截面性质是解题的关键，考查计算求解能力，属于基础题. 【母题来源二】【2019年高考全国Ⅰ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上，P A =PB =PC ，△ABC 是边长为2的正三角形，E ，F 分别是P A ，AB 的中点，∠CEF =90°，则球O 的体积为A ．B ．C ．D【答案】D 【解析】解法一：,PA PB PC ABC ==△为边长为2的等边三角形，P ABC ∴-为正三棱锥，PB AC ∴⊥，又E ，F 分别为PA ，AB 的中点，EF PB ∴∥，EF AC ∴⊥，又EF CE ⊥，,CEAC C EF =∴⊥平面PAC ，∴PB ⊥平面PAC ，APB PA PB PC ∴∠=90︒,∴===P ABC ∴-为正方体的一部分，则2R ==R =344π338V R ∴=π=⨯=.故选D ．解法二：设2PA PB PC x ===，,E F 分别为,PA AB 的中点，EF PB ∴∥，且12EF PB x ==，ABC △为边长为2的等边三角形，CF ∴=，又90CEF ∠=︒，12CE AE PA x ∴===，在AEC △中，由余弦定理可得()2243cos 22x x EAC x+--∠=⨯⨯，作PD AC ⊥于D ，PA PC =，D 为AC 的中点，1cos 2AD EAC PA x∠==， 2243142x x x x +-+∴=，22121222x x x ∴+=∴==，，，PA PB PC ∴======2AB BC AC ，,,PA PB PC ∴两两垂直，2R ∴==2R ∴=，344338V R ∴=π=π⨯=.故选D.【名师点睛】本题主要考查学生的空间想象能力，补体法解决外接球问题．可通过线面垂直定理，得到三棱两两互相垂直关系，快速得到侧棱长，进而补体成正方体解决．【命题意图】高考对本部分内容重点考查球的几何性质及体积与表面积的计算.考查直观想象、数学运算和逻辑推理的核心素养.【命题规律】本部分是高考考查的重点内容，考查的主要角度有两种：一是由球体截面的性质计算体积与表面积；二是球与多面体的切与接问题.命题形式以选择题与填空题为主，涉及空间几何体的结构特征、三视图等内容，要求考生要有较强的空间想象能力和计算能力，能用转化与化归的思想解题.【答题模板】解答本类题目，一般考虑如下三步：第一步：确定球心；第二步：运用球体的性质求出球的半径；第三步：根据公式计算.【方法总结】1．解决球与其他几何体的切、接问题，关键在于仔细观察、分析，弄清相关元素的关系和数量关系，选准最佳角度作出截面(要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系)，达到空间问题平面化的目的．2．记住几个常用的结论：（1）正方体的棱长为a，球的半径为R.①对于正方体的外接球，2R；②对于正方体的内切球，2R＝a；③对于球与正方体的各棱相切，2R.（2）在长方体的同一顶点的三条棱长分别为a，b，c，球的半径为R，则2R=（3）正四面体的外接球与内切球的半径之比为3∶1.3．构造法在定几何体外接球球心中的应用（1）正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥，可将三棱锥补形成长方体或正方体；（2）同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥，可将三棱锥补形成长方体或正方体；（3）若已知棱锥含有线面垂直关系，则可将棱锥补形成长方体或正方体；（4）若三棱锥的三个侧面两两垂直，则可将三棱锥补形成长方体或正方体．【好题训练】1．【2020广西南宁高三三模】已知过球面上三点,,A B C 的截面到球心距离等于球半径的一半，且ABC 是边长为6的等边三角形，则球表面积为 A ．42π B ．48πC ．64πD ．60π【答案】C【解析】取AB 的中点D ，连接CD ，由题意可得△ABC 的外心O '在线段CD 上，由ABC 是边长为6的等边三角形可得CD =23O C CD '== 设球的球心为O ，半径为R ，连接OC 、OO '，如图：由球的性质可得OC R =，OO '⊥平面ABC ，即2ROO '=，所以OO O C ''⊥，在Rt OO C '△中，222O O O C OC ''+=即(2222R R ⎛⎫+= ⎪⎝⎭，解得4R =或4R =-（舍去），所以该球的表面积2464S R ππ==.故选：C.【名师点睛】本题考查了球的几何特征的应用及表面积的求解，考查了空间思维能力与运算求解能力，属于基础题.2．【2020安徽合肥一六八中学高三模拟】球面上有三点,,A B C 组成这个球的一个截面的内接三角形的三个顶点，其中18AB =，24BC =，30AC =，球心到这个截面的距离为球半径的一半，则该球的表面积为 A ．1200π B ．1400πC ．1600πD ．1800π【答案】A【解析】设所求球的球心为O ，半径为,R AC 中点为1O ，连1,OO OA ，18AB =，24BC =，30AC =，222,AB BC AC AB BC ∴+=∴⊥，1O ∴为过,,A B C 三点截面圆的圆心，1OO ∴⊥平面1,ABC OO AC ∴⊥，在1Rt OO A ∆中，22222211154R AO R OO AO ==+=+，解得2300R =，球O 的表面积为241200R ππ=.故选：A.【名师点睛】本题考查球的表面积，利用球的性质是解题的关键，属于中档题.3．【2020广东佛山高三调研】如图，有一个水平放置的透明无盖的正方体容器，容器高8cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm ，如果不计容器的厚度，则球的体积为A ．3500cm 3πB ．3866cm 3πC ．31372cm 3πD ．32048cm 3π【答案】A【解析】设球的半径为R cm ，根据已知条件知，正方体的上底面与球相交所得截面圆的半径为4cm ，球心到截面圆的距离为()2R -cm ，所以由()22242R R +-=，得5R =，所以球的体积为()333445005cm 333V R πππ==⨯=．故选：A ．【名师点睛】本题主要考查球的体积公式的应用，以及球的结构特征的应用，属于基础题．4．【2020重庆八中高三三模】用一根长为18cm 的铁丝围成正三角形框架，其顶点为,,A B C ，将半径为2cm 的球放置在这个框架上（如图）.若M 是球上任意一点，则四面体MABC 体积的最大值为A ．34cm B 3 C ．3 D ．3【答案】D【解析】设球的圆心为O ，半径为R ，ABC 内切圆圆心为1O ，由题意知ABC 三边长为6cm ，则ABC 内切圆半径1cos303r AB =⋅⋅︒=，则11OO ==，所以四面体MABC 的高max 13h OO R =+=.因为22ABCS AB ==，所以四面体MABC 体积的最大值3max max 13ABCV S h =⋅=.故选:D.【名师点睛】本题考查了三棱锥体积的求解.本题的难点是求出球心到三角形所在平面的距离.5．【2020湖北宜昌高三二模】已知正方体1111ABCD A B C D -的棱长为2，点M 为棱1DD 的中点，则平面ACM 截该正方体的内切球所得截面面积为A ．3πB ．23π C ．πD ．43π 【答案】A【解析】如图所示：设内切球球心为O ，O 到平面ACM 的距离为d ，截面圆的半径为r ，因为内切球的半径等于正方体棱长的一半，所以球的半径为1，又因为O AMC M AOC V V --=，所以123AMCAOCd SS ⨯⨯=⨯，又因为()()1122526,221222AMCAOCSS=⨯⨯-==⨯⨯=，所以1233d ⨯=，所以d =，所以截面圆的半径r ==23S ππ=⋅=⎝⎭.故选：A. 【名师点睛】本题考查正方体的内切球的特点以及球的截面面积的计算，难度一般.任何一个平面去截球，得到的截面一定是圆面，截面圆的半径可通过球的半径以及球心到截面的距离去计算.6．【2020湖南省长郡中学高三模拟】已知长方体1111ABCD A B C D -各个顶点都在球面上，8AB AD ==，16AA =，过棱AB 作该球的截面，则当截面面积最小时，球心到截面的距离为A ．3B ．4C ．5D ．6【答案】C【解析】过棱AB 作该球的截面，则当截面面积最小时，截面的直径为8AB =，长方体1111ABCD A B C D -各个顶点都在球面上，8AB AD ==，16AA =，∴，∴5=．故选：C. 【名师点睛】本题考查求球心到截面的距离，考查学生的计算能力，确定当截面面积最小时，截面的直径为8AB =是关键，是基础题．7．【2020四川南充高三三模】已知圆锥1SO 的顶点和底面圆周均在球O 的球面上，且该圆锥的高为8，母线12SA =，点B 在SA 上，且3SB BA =，则过点B 的平面被该球O 截得的截面面积的最小值为 A ．27π B ．36πC ．54πD ．81π【答案】A【解析】如图所示：设球的球心为O ，半径为R ，则8,,SM OA R AM ====，所以222OA OM AM =+，即()(2228RR =-+，解得9R =，取SA 的中点N ，则3BN =，所以ON ==，OB ==设点C 为截面圆周上一点，若截面面积最小，则 OB ⊥截面，此时截面圆半径为 r BC ===，所以截面面积的最小值为227r ππ=.故选：A【名师点睛】本题主要考查球的截面面积的求法以及截面的性质，还考查了空间想象和运算求解的能力，属于中档题.8．【2020福建泉州高三调研】在直四棱柱1111ABCD A B C D -中，底面ABCD 是边长为6的正方形，点E 在线段AD 上，且满足2AE ED =，过点E 作直四棱柱1111ABCD A B C D -外接球的截面，所得的截面面积的最大值与最小值之差为19π，则直四棱柱1111ABCD A B C D -外接球的半径为A B ．C ．D ．【答案】C【解析】因为四棱柱1111ABCD A B C D -是直棱柱，且底面是正方形，所以其外接球的球心位于直四棱柱的中心，记作O ，过点O 向底面ABCD 作垂线，垂足为G ，则112OG AA =，连接BD ，因为底面ABCD 是边长为6的正方形，所以点G 为BD 的中点，取AD 中点为F ，连接OF ，OE ，OB ，设12AA a =，则OG a =，所以外接球的半径为R OB === 因为点E 在线段AD 上，且满足2AE ED =，则116EF DF DE AB =-==，又132FG AB ==，所以OF 因为直四棱柱中，AB ⊥侧面11ADD A ，//FG AB ，所以FG ⊥侧面11ADD A ，所以FG AD ⊥，又OG ⊥底面ABCD ，所以OG AD ⊥，又FG OG G ⋂=，所以OF AD ⊥，则OE =根据球的特征，过点E 作直四棱柱1111ABCD A B C D -外接球的截面，当截面过球心时，截面圆面积最大，此时截面面积为2S R π=；当OE ⊥，所以此时截面圆面积为()2221S R OE ππ==-；又截面面积的最大值与最小值之差为19π，所以()2222119S S R R OEOEππππ-=--=⋅=，因此21019a +=，即29a =，所以R ==.故选：C.【名师点睛】本题主要考查求几何体外接球的半径，熟记直四棱柱以及球的结构特征即可，考查空间想象能力，属于常考题型.9．【2020山西师大附中高三质检】设直线l 与球O 有且只有一个公共点P ，从直线l 出发的两个半平面,αβ截球O 的两个截面圆的半分别为1l αβ--的平面角为150︒，则球O 的表面积为 A ．112π B ．28πC ．16πD ．4π【答案】A【解析】过P 与O 作直线l 的垂面如图所示，设球的半径为r ，,OE QP OF PM ⊥⊥，垂足为,E F，则有1,EP PF ==设5,6OPE OPF απα∠=∴∠=-，所以有cos sin 5cos()6r r αααπα⋅=⇒=⋅-，而22sin cos 1αα+=，所以21cos 28α=，所以228r =，因此球O 的表面积等于：24112r ππ=.故选：A【名师点睛】本题考查了二面角的有关知识，考查了球的表面积公式，考查了空间想象能力.10．【2020广东惠州高三三模】已知正四棱锥P ABCD -的所有顶点都在球O 的球面上，该四棱锥的五个面所在的平面截球面所得的圆大小相同，若正四棱锥P ABCD -的高为2，则球O 的表面积为 A ．8π B ．9πC ．12πD ．16π【答案】A【解析】如图所示，圆O '是正方形ABCD 和等腰△P AB 的外接圆，设圆O '的半径为r ,则,O E AE BE O P r ''====，所以12PE r ⎛=+ ⎝⎭所以2222(2AP AE PE r =+=+设点O 是四棱锥P - ABCD 的外接球的球心，F 为正方形ABCD 的中心，如图，则PF ⊥平面ABCD ，所以在Rt AFP 中有2222(24AF AP PF r =-=+-又因为AF 的长度为圆O '的半径r ,所以22(24r r +-=所以221)AF r === 设四棱锥P - ABCD 的外接球的半径为R ,在Rt AFO 中，222OF OA AF =-，所以221)OF R =-，因为OF PF OP =-，所以22(2)OF R =-所以221)(2)R R -=-解得R =所以四棱锥P - ABCD 的外接球的表面积为248S R ππ==，故选：A【名师点睛】本题主要考查了四棱锥的外接球，球的性质，三角形、正方形外接圆的性质,考查了空间想象力，属于难题.。

高考中关于“球”的计算问题分类解读

截面）的面积是（
Ａ．Ｂ．
）
Ｃ．Ｄ．
提示：显然正六棱锥ＰＡＢＥＦ的底面的外ＬＣＤ接圆是球的一个大圆，于是可求得底面长为２又，
正六棱锥
可求得６７ √．
Ｃｊ的高依题意可得为２依此Ｄｌ晒，
３２０．（０６年高考山东卷）如图，等晨梯形在ＡＢＤ中，Ｂ＝２ＣＡＤＣ＝２＝６＂Ｅ为．Ｂ的ＺＤ０，Ａ
詈，ｏ，Ａｃ等詈，＝Ｃ，两则Ｂ０都于ＡＡ，ｃＢＢ
点球距离的面是号， ∞＝Ｂ＝，作Ｂ号，Ｃ１过Ｂ
ＢＤ上Ａ０，足为Ｄ，接Ｃ则ＣｌＡ则垂连Ｄ，Ｄ－Ｄ，－／ＢＤＣ是二面角ＢＯＣ的平面角，Ｄ＝Ｃ－Ａ－ＢＤ＝
提示：易证所得三棱锥为正四面体，它的梭长
几何体的表面积、体积、角等问题的关键是寻找几
何体的边长与球半径之间的关系，这往往需要作出
相应的辅助线。
．
为，外球径，接的积号ｃ１接半为外球体为，故
（）譬ｃ。＝
・
练习题：
１２０．（０６年高考北京卷）已知Ａ，Ｃ三点在Ｂ，
【作者单位：湖北省黄石实验高中ｌ
音任垃ｌ奉君Ｉ．
ｌ一一
锥的侧面积是— —
．
Ｐ
２，．ＺＢＣ・Ｄ＝吾，．二面角ＢＡＣ的大小是－－Ｏ
罢，ｃ选
【５（０６高考湖南卷）棱长为２的正例】２０年四面体的四个顶点都在同一个球面上，若过该球球

高考物理计算题复习《竖直上抛运动》(解析版)

《竖直上抛运动》一、计算题1.如图甲所示，将一小球从地面上方ℎ=0.8m处以v0=3m/s的速度竖直上抛，不计空气阻力，上升和下降过程中加速度不变，g取10m/s2，求：(1)小球从抛出到上升至最高点所需的时间t1；(2)小球从抛出到落地所需的时间t；(3)在图乙中画出小球从抛出到落地过程中的v−t图象。

2.在竖直井的井底，将一物块以v0=15m/s的速度竖直向上抛出，物块在上升过程中做加速度大小a=10m/s2的匀减速直线运动，物块上升到井口时被人接住，在被人接住前1s内物块的位移x1=6m.求：(1)物块从抛出到被人接住所经历的时间；(2)此竖直井的深度．3.原地纵跳摸高是篮球和羽毛球重要的训练项目。

已知质量m=60kg的运动员原地摸高为2.05米，比赛过程中，该运动员先下蹲，重心下降0.5米，经过充分调整后，发力跳起摸到了2.85米的高度。

假设运动员起跳过程为匀加速运动，忽略空气阻力影响，g取10m/s2.求：(1)该运动员离开地面时的速度大小为多少；(2)起跳过程中运动员对地面的压力；(3)从开始起跳到双脚落地需要多少时间？4.气球以10m/s的速度匀速上升，当它上升到离地面40m高处，从气球上落下一个物体．不计空气阻力，求(1)物体落到地面需要的时间；(2)落到地面时速度的大小．(g=10m/s2).5.小运动员用力将铅球以v0=10m/s的速度沿与水平方向成37°方向推出，已知铅球出手点到地面的高度为ℎ=1.4m，求：(1)铅球出手后运动到最高点所需时间t1；(2)铅球运动的最高点距地面的高度H；(3)铅球落地时到运动员投出点的水平距离x．6.气球下挂一重物，以v0=10m/s的速度匀速上升，当到达离地高度ℎ=175m处时，悬挂重物的绳子突然断裂，(空气阻力不计，g取10m/s2.)则求：(1)绳断后物体还能向上运动多高？(2)绳断后物体再经过多长时间落到地面。

(3)落地时的速度多大？7.气球下挂一重物，以v0=10m/s的速度匀速上升，当到达离地高度ℎ=175m处时，悬挂重物的绳子突然断裂，那么重物经多长时间落到地面？落地时的速度多大？空气阻力不计，g取10m/s2。

高考球的外接、内接球问题

途径3：若已知棱锥含有线面垂直关系，则可将棱锥补成长方体或正方体或直棱柱．
途径4：若三棱锥的三个侧面两两垂直，则可将三棱锥补成长方体或正方体．
途径1：正四面体、三条侧棱两两垂直的正三棱锥、四个面都是是直角三角形的三棱锥都分别可构造正方体．
例1、如下图所示，在等腰梯形ABCD中，AB=2CD=2，DAB 60
.
途径3：若已知棱锥含有线面垂直关系，则可将棱锥补成长方体或正方体或直棱柱．
例3、在三棱锥中A-BCD中，AB 平面BCD ，CD BC ,
AB=3,BC=4,CD=5, 则三棱锥A-BCD外接球的表面
积
. 50
途径3：若已知棱锥含有线面垂直关系，则可将棱锥补成长方体或正方体或直棱柱．
.( 1)6
结论2：正棱柱的外接球的球心是上下底面中心的连线的中点．
例2、一个六棱柱的底面是正六边形，其侧棱垂直于底面，已知该
正六棱柱的顶点都在同一个球面上，且该六棱柱的体积为 9 ，底
面周长为３，则这个球的体积为 4 .
8
3
结论3：直三棱柱的外接球的球心是上下底面三角形外心的连线的中点．
（1）截面图为正方形的内切圆EFGH，得
；
（2）与正方体各棱相切的球：球与正方体的各棱相切，切点为各棱的中点，
如图4作截面图，圆o为正方形EFGH的外接圆，易得
。
（3）正方体的外接球：正方体的八个顶点都在球面上，如图5，以对角面AA1
作截面图得，圆O为矩形AA1C1C的外接圆，易得
。
图3
图4
图5
2.棱锥的内切球（分割法）
.
4
3
结论5：若棱锥的顶点可构成共斜边的直角三角形，则公共
斜边的中点就是其外接球的球心．

高考数学中的内切球和外接球问题---专题复习

高考数学中的内切球和外接球问题---专题复习高考数学：内切球和外接球问题多面体的顶点都在同一球面上时，称该多面体为球的内接多面体，该球为多面体的外接球。

多面体外接球问题是立体几何的重点，也是高考的热点，考查学生的空间想象能力和化归能力。

解决该问题需要运用多面体和球的知识，并特别注意多面体的几何元素与球的半径之间的关系。

多面体外接球半径的求法在解题中往往起到至关重要的作用。

一、直接法（公式法）1、求正方体的外接球的有关问题例1：若正方体的棱长为3且顶点都在同一球面上，求该球的表面积。

解析：要求球的表面积，只需知道球的半径。

由于正方体内接于球，所以它的体对角线正好为球的直径，因此求球的半径可转化为先求正方体的体对角线长，再计算半径。

故表面积为27π。

例2：一个正方体的各顶点均在同一球的球面上，若该正方体的表面积为24，则该球的体积为多少？解析：要求球的体积，还需先求出球的半径。

由正方体表面积可求出棱长，从而求出正方体的体对角线长为3√3.因此，该球的半径为3，故该球的体积为36π。

2、求长方体的外接球的有关问题例1：一个长方体的各顶点均在同一球面上，且一个顶点上的三条棱长分别为1、2、3，则该球的表面积为多少？解析：关键是求出球的半径，因为长方体内接于球，所以它的体对角线正好为球的直径。

长方体体对角线长为√14，故球的表面积为14π。

例2：已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则该球的表面积为多少？解析：正四棱柱也是长方体。

由长方体的体积16及高4可以求出长方体的底面边长为2，因此，长方体的长、宽、高分别为2、2、4.故该球的表面积为24π。

3、求多面体的外接球的有关问题例：一个底面为正六边形的六棱柱，侧棱垂直于底面，已知该六棱柱的顶点都在同一球面上，且该六棱柱的体积为8，底面周长为3，则该球的体积为多少？解析：设正六棱柱的底面边长为x，高为h。

由底面周长可得x=3/6=1/2，由体积可得h=4/3.因此，正六棱柱的底面圆的半径为√3/2，外接球的半径为√13/2.故该球的体积为(52/3)π。

高考数学二轮专题复习——浅谈球有关问题的难点突破

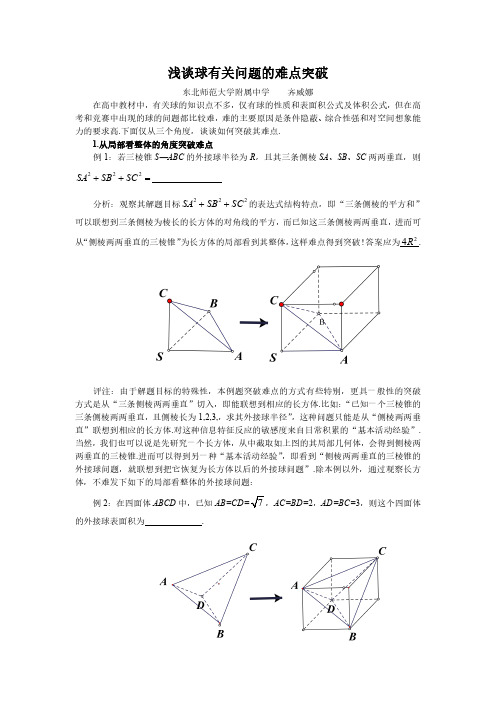
浅谈球有关问题的难点突破东北师范大学附属中学齐威娜在高中教材中，有关球的知识点不多，仅有球的性质和表面积公式及体积公式，但在高考和竞赛中出现的球的问题都比较难，难的主要原因是条件隐蔽、综合性强和对空间想象能力的要求高.下面仅从三个角度，谈谈如何突破其难点.1.从局部看整体的角度突破难点例1：若三棱锥S —ABC 的外接球半径为R ，且其三条侧棱SA 、SB 、SC 两两垂直，则222SA SB SC ++=分析：观察其解题目标222SA SB SC ++的表达式结构特点，即“三条侧棱的平方和”可以联想到三条侧棱为棱长的长方体的对角线的平方，而已知这三条侧棱两两垂直，进而可从“侧棱两两垂直的三棱锥”为长方体的局部看到其整体，这样难点得到突破！答案应为24R .评注：由于解题目标的特殊性，本例题突破难点的方式有些特别，更具一般性的突破方式是从“三条侧棱两两垂直”切入，即能联想到相应的长方体.比如：“已知一个三棱锥的三条侧棱两两垂直，且侧棱长为1,2,3,，求其外接球半径”，这种问题只能是从“侧棱两两垂直”联想到相应的长方体.对这种信息特征反应的敏感度来自日常积累的“基本活动经验”.当然，我们也可以说是先研究一个长方体，从中截取如上图的其局部几何体，会得到侧棱两两垂直的三棱锥.进而可以得到另一种“基本活动经验”，即看到“侧棱两两垂直的三棱锥的外接球问题，就联想到把它恢复为长方体以后的外接球问题”.除本例以外，通过观察长方体，不难发下如下的局部看整体的外接球问题：例2：在四面体ABCD 中，已知，AC=BD=2，AD=BC=3，则这个四面体的外接球表面积为.分析：根据上面提到的通过观察长方体的局部得到一种“基本活动经验”，即“长方体两个相对的面中，各找一条对角线，使之互相异面（比如AC 与BD ），就可以以它们的四个端点为顶点构成“对棱都相互相等的”四面体ABCD ”，也就是看到对棱都相互相等四面体的外接球问题时，我们会联想到与之相关的长方体的外接球，进而难点得到突破.这种难点突破途径是依据“基本活动经验”，那么如何从四面体切入寻求突破难点的方式呢？根据四面体的“对棱都相等”这个条件，我们可以进行如下的“补形”的过程，同样可以把“局部”（四面体）转化为“整体”（长方体）.根据AC=BD=2，取两条棱的中点作对棱的平行线，就可以构成如图所示的两个矩形（所在的两个平面平行），然后得到的两个矩形的八个顶点自然形成我们要得到的长方体，但这种思维方式比起前面提到的方法更难一些.求解过程如下：设长方体的长，宽，高分别为,,x y z ，则根据题设，可得如下的三个等式：222222222(7),2,3x y z y x z +=+=+=，三个等式相加得到22210x y z ++=，所以此四面体的外接球表面积为10π.2.从整体看局部的角度突破难点在上面的“从局部看整体的角度突破难点”中，也已经展示了“从整体看局部突破难点”方法，其原因是“割补思想方法”中，“割”与“补”是互逆的思维方式，自然就可以从“分析”和“综合”的角度，两种突破难点的方式经常是都可以解决相同的球的问题.但除此之外，关于球的另外一些组合体问题中也需要研究突破难点的方法.难点就是问题中不提供图形，就是提供图形，也很难从原图中直接找出突破难点的方法.所以需要依靠空间想象发现球的组合体的本质特征，再通过画出能解决问题的局部图形来突破难点，也就是我们常说的转化为等效的局部图形．．．．．．．.例3：侧棱长为3，底面边长为2的正三棱锥的外接球半径R =，其内切球半径r =.分析：图1中的几何体是求外接球半径的局部图形，从中又可以简化为右侧的平面图形，其中AB 是其外接球的直径，O 是球心，E 底面的中心，易知,AC BC CE AB⊥⊥进而得出2CE AE EB=⋅其中0243232sin 6033CE CE ==⇒=所以2223693()33AE =-=，所以2236969()(2)333R =-解得96946R =由于有前面的铺垫，求内切球半径可以用“等体积法”去求得.下面再通过转化为“等效局部图形”的方法求其内切球半径.图2右侧的平面图形中，不难看出点E 、H 是球的切点，P 是内切球的球心，通过相似三角形的性质得到的比例式为r AP EM AM=其中223,3122,3EM AM ==-=693AP AE r r =-=-，代入求得6466969r -=评注：对于解决正三棱锥的外接球、内切球半径问题，体现了“空间问题平面化”的立体几何中的转化思想，这种转化也起到了突破难点的作用.但正四面体作为特殊的正三棱锥，我们要懂得其性质，这样在解决有有关正四面体的问题时，其几何图形甚至可以不画.比如：正四面体的外接球和内切球的球心是重合的，同时球心将高四等分，其中外接球半径为高的四分之三，内切球半径为高的四分之一，且棱长为a 的正四面体的高为63a h =.例4：将6个半径为r 的球中的5个球放入由一个半径大于2r 的球面和这个球的内接正四面体的四个面分割成的五个空间内，且此正四面体的棱长为26，另一个球放入棱长为x 的正八面体内，当r 取得最大值时，x 的最小值为分析：此小题考查正四面体、正八面体和球的性质以及空间想象能力和转化思想。

高考中与内切球和外接球相关的几个问题

问题２（０３年全国１一个四面体的所有棱长都为２０２）
数学学习与研究
２１．０２１
臻
专题研究
婚豢
。
●一Ｉ－， ●
●
解析由正四面体的图像的对称性可知，内切球的球心必为正四面体的中心，与各棱相切，切点必为各棱中球其点，查三组对棱中点的连线交于一点，为内切球的球考即心，以每组对棱间的距离即为内切球的直径，是有：所于
正三角形的边长为 √ ．于这个２由
正三棱锥的侧棱两两垂直，能故将它补成长方体．然，个正三显这棱锥与补成的长方体有同一个外一
点，ＡＰＰＰ，Ｂ，ｃ两两垂直，Ｐ且Ａ＝ＰＢ：ＰＣ＝ｌ求球的体积，
问题３（北黄冈麻城博达学校２０湖０８届三月综合测试）三棱锥Ｐ— Ｂ的三条侧棱两两垂直，这个正三棱正ＡＣ则锥Ｐ— Ｂ的内切球与外接球的半径之比为（ＡＣ）．
Ⅱ，ＯＢ＝ｂ，ＯＣ＝ｃ则：，
，
ｒ：，ｎ２Ｔ＝．
质：
于是ｒｒ＝： √ ｒ３１
应用１（９５年全国４正方体的全面积是ａ，的１９）它
顶点都在球面上，个球的表面积是（这

高考数学一轮复习与球有关的切与接问题

体的棱长为2，则半球的表面积为
A.10π
B.12π
（
）
C.15π
D.18π
解析：D 因为正方体的一个面在半球的底面圆内，所以过正方
体体对角线的轴截面如图所示，又正方体的棱长为2，所以FG＝
2，EF＝2 2，则OF＝ 2（O为半球的球心），OG＝
2 + 2 ＝ 6，即半球的半径为 6，所以半球的表面积为
π
4
α×4sin α＝8πsin 2α，当且仅当α＝，sin 2α＝1时，圆柱的侧面积
最大，∴圆柱的侧面积的最大值为8π.
2.已知三棱锥P－ABC的顶点都在球O的球面上，△ABC是边长为2的等边三角
64
9
形，球O的表面积为 π，则三棱锥P－ABC的体积的最大值为
A.2 3
C.
4 3
3
2 3
B.
3
2
3 2
1
2
－ABC的内切球的半径为R，则由VP－ABC＝ SR＝9R＝6，解得R＝，所以三棱锥
3
3
4π 3 4π
2 3 32π
P－ABC的内切球的体积V＝ R ＝ ×
＝ .
3
3
3
81
答案
32π
81
｜解题技法｜
“切”的问题的处理规律
（1）找准切点，通过作过球心的截面来解决；
（2）体积分割是求内切球半径的通用方法.
果是外接球，球心到接点的距离相等且为半径；②作截面：选准最佳角度作出
截面，达到空间问题平面化的目的.
（2）代数法：找出问题中的代数关系，建立目标函数，利用代数方法求目标函
数的最值.解题途径很多，在函数建成后，可用一次函数的端点法，二次函数的

高考球的问题

高考球的问题典型例题1——球的截面例 1 球面上有三点A 、B 、C 组成这个球的一个截面的内接三角形三个顶点，其中18=AB ，24=BC 、30=AC ，球心到这个截面的距离为球半径的一半，求球的表面积．【练习】过球O 表面上一点A 引三条长度相等的弦AB 、AC 、AD ，且两两夹角都为︒60，若球半径为R ，求弦AB 的长度．典型例题2——球面距离例2 过球面上两点作球的大圆，可能的个数是（）．A ．有且只有一个B ．一个或无穷多个C ．无数个D ．以上均不正确例3 球面上有3个点，其中任意两点的球面距离都等于大圆周长的61，经过3个点的小圆的周长为π4，求这个球的半径．例4 A 、B 是半径为R 的球O 的球面上两点，它们的球面距离为R 2π，求过A 、B 的平面中，与球心的最大距离是多少？典型例题3——其它问题例5．自半径为R 的球面上一点M ，引球的三条两两垂直的弦MC MB MA ,,，求222MC MB MA ++的值．例6．试比较等体积的球与正方体的表面积的大小．典型例题4——球与几何体的切、接问题例7 一个倒圆锥形容器，它的轴截面是正三角形，在容器内注入水，并放入一个半径为r 的铁球，这时水面恰好和球面相切．问将球从圆锥内取出后，圆锥内水平面的高是多少？例8．设正四面体中，第一个球是它的内切球，第二个球是它的外接球，求这两个球的表面积之比及体积之比．例9．把四个半径都是1的球中的三个放在桌面上，使它两两外切，然后在它们上面放上第四个球，使它与前三个都相切，求第四个球的最高点与桌面的距离．例10．如图1所示，在棱长为1的正方体内有两个球相外切且又分别与正方体内切．（1）求两球半径之和；（2）球的半径为多少时，两球体积之和最小．作业1. 正三棱锥的高为1，底面边长为62，正三棱锥内有一个球与其四个面相切．求球的表面积与体积．2. 求球与它的外切圆柱、外切等边圆锥的体积之比．3 在球心同侧有相距cm 9的两个平行截面，它们的面积分别为249cm π和2400cm π．求球的表面积．高考球的问题（教师）典型例题1——球的截面例 1 球面上有三点A 、B 、C 组成这个球的一个截面的内接三角形三个顶点，其中18=AB ，24=BC 、30=AC ，球心到这个截面的距离为球半径的一半，求球的表面积．分析：求球的表面积的关键是求球的半径，本题的条件涉及球的截面，ABC ∆是截面的内接三角形，由此可利用三角形求截面圆的半径，球心到截面的距离为球半径的一半，从而可由关系式222d R r -=求出球半径R ．解：∵18=AB ，24=BC ，30=AC ，∴222AC BC AB =+，ABC ∆是以AC 为斜边的直角三角形． ∴ABC ∆的外接圆的半径为15，即截面圆的半径15=r ，又球心到截面的距离为R d 21=，∴22215)21(=-R R ，得310=R ． ∴球的表面积为πππ1200)310(4422===R S ．说明：涉及到球的截面的问题，总是使用关系式22d R r -=解题，我们可以通过两个量求第三个量，也可能是抓三个量之间的其它关系，求三个量．【练习】过球O 表面上一点A 引三条长度相等的弦AB 、AC 、AD ，且两两夹角都为︒60，若球半径为R ，求弦AB 的长度．由条件可抓住BCD A -是正四面体，A 、B 、C 、D 为球上四点，则球心在正四面体中心，设a AB =，则截面BCD 与球心的距离R a d -=36，过点B 、C 、D 的截面圆半径a r 33=，所以222)36()33(R a R a --=得R a 362=．典型例题2——球面距离例2 过球面上两点作球的大圆，可能的个数是（）．A ．有且只有一个B ．一个或无穷多个C ．无数个D ．以上均不正确分析：对球面上两点及球心这三点的位置关系进行讨论．当三点不共线时，可以作一个大圆；当三点共线时，可作无数个大圆，故选B ．例3 球面上有3个点，其中任意两点的球面距离都等于大圆周长的61，经过3个点的小圆的周长为π4，求这个球的半径．分析：利用球的概念性质和球面距离的知识求解．设球的半径为R ，小圆的半径为r ，则ππ42=r ，∴2=r ．如图所示，设三点A 、B 、C ，O 为球心，362ππ==∠=∠=∠COA BOC AOB ．又∵OB OA =，∴AOB ∆是等边三角形，同样，BOC ∆、COA ∆都是等边三角形，得ABC ∆为等边三角形，边长等于球半径R ．r 为ABC ∆的外接圆半径，R AB r 3333==，3233==r R ．说明：本题是近年来球这部分所出的最为综合全面的一道题，除了考查常规的与多面体综合外，还考查了球面距离，几乎涵盖了球这部分所有的主要知识点，是一道不可多得的好题．例4 A 、B 是半径为R 的球O 的球面上两点，它们的球面距离为R 2π，求过A 、B 的平面中，与球心的最大距离是多少？分析：A 、B 是球面上两点，球面距离为R 2π，转化为球心角2π=∠AOB ，从而R AB 2=，由关系式222d R r -=，r 越小，d 越大，r 是过A 、B 的球的截面圆的半径，所以AB 为圆的直径，r 最小．解：∵球面上A 、B 两点的球面的距离为R 2π． ∴2π=∠AOB ，∴R AB 2=．当AB 成为圆的直径时，r 取最小值，此时R AB r 2221==，d 取最大值， R r R d 2222=-=，即球心与过A 、B 的截面圆距离最大值为R 22．说明：利用关系式222d R r -=不仅可以知二求一，而且可以借此分析截面的半径r 与球心到截面的距离d 之间的变化规律．此外本题还涉及到球面距离的使用，球面距离直接与两点的球心角AOB ∠有关，而球心角AOB ∠又直接与AB 长度发生联系，这是使用或者求球面距离的一条基本线索．典型例题3——其它问题例5．自半径为R 的球面上一点M ，引球的三条两两垂直的弦MC MB MA ,,，求222MCMB MA ++的值．分析：此题欲计算所求值，应首先把它们放在一个封闭的图形内进行计算，所以应引导学生构造熟悉的几何体并与球有密切的关系，便于将球的条件与之相联．解：以MC MB MA ,,为从一个顶点出发的三条棱，将三棱锥ABC M -补成一个长方体，则另外四个顶点必在球面上，故长方体是球的内接长方体，则长方体的对角线长是球的直径．∴222MC MB MA ++=224)2(R R =．说明：此题突出构造法的使用，以及渗透利用分割补形的方法解决立体几何中体积计算．例6．试比较等体积的球与正方体的表面积的大小．分析：首先抓好球与正方体的基本量半径和棱长，找出等量关系，再转化为其面积的大小关系．解：设球的半径为r ，正方体的棱长为a ，它们的体积均为V ，则由ππ43,3433V r V r ==，343πV r =，由,3V a =得3V a =． 322324)43(44V V r S ππππ===球． 32322322166)(66V V V a S ====正方体． ∴<2164π <324V π32216V ，即正方体球S S <．典型例题4——球与几何体的切、接问题例7 一个倒圆锥形容器，它的轴截面是正三角形，在容器内注入水，并放入一个半径为r 的铁球，这时水面恰好和球面相切．问将球从圆锥内取出后，圆锥内水平面的高是多少？分析：先作出轴截面，弄清楚圆锥和球相切时的位置特征，利用铁球取出后，锥内下降部分(圆台)的体积等于球的体积，列式求解．解：如图作轴截面，设球未取出时水面高h PC =，球取出后，水面高x PH =∵r AC 3=，r PC 3=，则以AB 为底面直径的圆锥容积为PC AC V ⋅⋅=231π圆锥3233)3(31r r r ππ=⋅=，球取出后水面下降到EF ，水体积为32291)30tan (3131x PH PH PH EH V πππ=︒=⋅⋅=水．又球圆锥水V V V -=，则33334391r r x πππ-=，解得r x 315=．例8．设正四面体中，第一个球是它的内切球，第二个球是它的外接球，求这两个球的表面积之比及体积之比．分析：此题求解的第一个关键是搞清两个球的半径与正四面体的关系，第二个关键是两个球的半径之间的关系，依靠体积分割的方法来解决的．解：如图，正四面体ABCD 的中心为O ，BCD ∆的中心为1O ，则第一个球半径为正四面体的中心到各面的距离，第二个球的半径为正四面体中心到顶点的距离．设R OA r OO ==,1，正四面体的一个面的面积为S ．依题意得)(31r R S V BCD A +=-，又S r V V BCD O BCD A ⋅⨯==--3144 r r R 4=+∴即r R 3=．所以914422==R r ππ外接球的表面积内切球的表面积．271343433==R r ππ外接球的体积内切球的体积．说明：正四面体与球的接切问题，可通过线面关系证出，内切球和外接球的两个球心是重合的，为正四面体高的四等分点，即定有内切球的半径h r 41=(h 为正四面体的高)，且外接球的半径r R 3=．例9．把四个半径都是1的球中的三个放在桌面上，使它两两外切，然后在它们上面放上第四个球，使它与前三个都相切，求第四个球的最高点与桌面的距离．分析：关键在于能根据要求构造出相应的几何体，由于四个球半径相等，故四个球一定组成正四面体的四个顶点且正四面体的棱长为两球半径之和2．解：四球心组成棱长为2的正四面体的四个顶点，则正四面体的高362)332(222=⋅-=h ．而第四个球的最高点到第四个球的球心距离为求的半径1，且三个球心到桌面的距离都为1，故第四个球的最高点与桌面的距离为3622+．例10．如图1所示，在棱长为1的正方体内有两个球相外切且又分别与正方体内切．（1）求两球半径之和；（2）球的半径为多少时，两球体积之和最小．分析：此题的关键在于作截面，一个球在正方体内，学生一般知道作对角面，而两个球的球心连线也应在正方体的体对角线上，故仍需作正方体的对角面，得如图2的截面图，在图2中，观察R 与r 和棱长间的关系即可．解：如图2，球心1O 和2O 在AC 上，过1O ，2O 分别作BC AD ,的垂线交于F E ,．则由3,1==AC AB 得R CO r AO 3,321==．3)(3=+++∴R r R r ， 233133-=+=+∴r R ．（1）设两球体积之和为V ，则))((34)(342233r Rr R R r r R V +-+=+=ππ =[]=-+rR r R 3)(233342π⎥⎦⎤⎢⎣⎡--)233(3)233(233342R R π =⎥⎦⎤⎢⎣⎡-+--22)233(2)33(3323334R R π当433-=R 时，V 有最小值．∴当433-==r R 时，体积之和有最小值．作业1. 正三棱锥的高为1，底面边长为62，正三棱锥内有一个球与其四个面相切．求球的表面积与体积．解：如图，球O 是正三棱锥ABC P -的内切球，O 到正三棱锥四个面的距离都是球的半径R ．PH 是正三棱锥的高，即1=PH ．E 是BC 边中点，H 在AE 上，图2ABC ∆的边长为62，∴26263=⨯=HE ． ∴3=PE 可以得到2321=⋅===∆∆∆PE BC S S S PBC PAC PAB ． 36)62(432==∆ABC S 由等体积法，ABC O PBC O PAC O PAB O ABC P V V V V V -----+++= ∴R R ⨯⨯+⨯⨯⨯=⨯⨯36313233113631得：2633232-=+=R ， ∴πππ)625(8)26(4422-=-==R S 球． ∴33)26(3434-==ππR V 球．说明：球心是决定球的位置关键点，本题利用球心到正三棱锥四个面的距离相等且为球半径R 来求出R ，以球心的位置特点来抓球的基本量，这是解决球有关问题常用的方法．2. 求球与它的外切圆柱、外切等边圆锥的体积之比．分析：首先画出球及它的外切圆柱、等边圆锥，它们公共的轴截面，然后寻找几何体与几何体之间元素的关系．解：如图，等边SAB ∆为圆锥的轴截面，此截面截圆柱得正方形11CDD C ，截球面得球的大圆圆1O ．设球的半径R OO =1，则它的外切圆柱的高为R 2，底面半径为R ；R O O OB 330cot 1=︒⋅=， R R OB SO 33360tan =⋅=︒⋅=，∴334R V π=球，3222R R R V ππ=⋅=柱， 3233)3(31R R R V ππ=⋅⋅=锥， ∴964∶∶∶∶锥柱球=V V V ．3 在球心同侧有相距cm 9的两个平行截面，它们的面积分别为249cm π和2400cm π．求球的表面积．分析：可画出球的轴截面，利用球的截面性质，求球的半径．解：如图为球的轴截面，由球的截面性质知，21//BO AO ，且若1O 、2O 分别为两截面圆的圆心，则11AO OO ⊥，22BO OO ⊥．设球的半径为R ．∵ππ4922=⋅B O ，∴)(72cm B O = 同理ππ40021=⋅A O ，∴)(201cm A O = 设xcm OO =1，则cm x OO )9(2+=．在A OO Rt 1∆中，22220+=x R ；在B OO Rt 2∆中，2227)9(++=x R ，∴222)9(720++=+x x ，解得15=x ， ∴22222520=+=x R ，∴25=R ∴)(2500422cm R S ππ==球． ∴球的表面积为22500cm π．。

高考球的问题总结

高考球的问题总结在高考数学中，球的问题是一个重要的考点，涵盖了多个方面的知识点。

本文将对高考中涉及的球的问题进行总结，主要包含球的表面积、球的体积、球与内切圆、球的切线问题、球的旋转体问题、球与多面体的关系、球的几何变换、球的物理属性及应用、球在数学问题中的应用等方面。

一、球的表面积球的表面积公式为4πr^2，其中r为球的半径。

在高考中，涉及球的表面积的问题主要考查学生对于公式的理解和应用，以及如何利用已知条件计算球的表面积。

二、球的体积球的体积公式为(4/3)πr^3，其中r为球的半径。

涉及球的体积的问题同样需要学生掌握公式的应用，以及如何利用已知条件计算球的体积。

三、球与内切圆球的内切圆半径可以通过球的体积和表面积的公式求得，内切圆半径为r=3V/S，其中V为球的体积，S为球的表面积。

在高考中，考查学生对于内切圆半径的理解和应用。

四、球的切线问题球的切线问题是球的问题中的一个重要考点，主要考查学生对于切线的性质和判定方法的理解和应用。

在解决这类问题时，学生需要利用球心到切点的连线与切线垂直的性质，结合几何知识进行证明和计算。

五、球的旋转体问题球的旋转体问题主要考查学生对于旋转体的性质和判定方法的理解和应用。

在解决这类问题时，学生需要利用旋转体的性质和几何知识进行证明和计算。

六、球与多面体的关系球与多面体的关系主要考查学生对于多面体和球之间的关系的理解，以及如何利用已知条件计算球的半径和多面体的边长等参数。

在解决这类问题时，学生需要利用几何知识进行证明和计算。

七、球的几何变换球的几何变换主要考查学生对于球的各种变换的理解和应用，如旋转、平移、对称等。

在解决这类问题时，学生需要利用几何知识进行证明和计算。

八、球的物理属性及应用球的物理属性及应用主要考查学生对于球在物理中的各种属性的理解和应用，如重力加速度、转动惯量等。

在解决这类问题时，学生需要利用物理知识和几何知识进行证明和计算。

九、球在数学问题中的应用球在数学问题中的应用非常广泛，如几何、代数、概率统计等领域都可以涉及到球的问题。

高考中”球“中的最值问题

最值一、球心到某个面距离固定1. 已知A,B 是球O 的球面上两点，∠AOB=90,C 为该球面上的动点，若三棱锥O-ABC 体积的最大值为36，则球O 的表面积为A. 36πB.64πC.144πD.256π2. 三棱锥P －ABC 的四个顶点都在体积为500π3的球的表面上，△ABC 所在的小圆面积为16π，则该三棱锥的高的最大值为A. 7 B ．7.5 C ．8 D ．93. 球O 的球面上有4个点C B A S ,,,，其中C B A O ,,,四点共面，ABC ∆是边长为2的正三角形，面⊥SAB 面ABC ，则ABC S -的体积的最大值A. 3B. 31 C. 23 D. 33 二、有定值，利用不等式1. 正三棱柱内接于一个半径为2的球，则正三棱柱的侧面积取最大值时，底面边长为AA. B. C. D. 22. 如果长方体的顶点都在半径为9的球面上，求长方体的表面积的最大值三、找出特殊情况1. 有一棱长为a 的正方体骨架，其内放置一气球，使其充气且尽可能地大（仍保持为球的形状），则气球表面积的最大值为___2. 在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球，若AB ⊥BC ，AB =6，BC =8，AA 1=3，则V 的最大值是A. 4πB. 92πC. 6πD. 323π 3. 球的半径是R ，距球心4R 处有一光源，光源能照到的地方用平面去截取，则截面的最大面积是A. 2R πB. 21615R πC. 2169R πD. 221R π 4. 半径为R 的球内有一内接正三棱锥，它的底面三个顶点恰好都在同一个大圆上，一个动点从三棱锥的一个顶点出发沿球面运动，经过其余三点后返回，则经过的最短路程是A. R π2B. R π37C. R π38D. R π67 5. 已知正三角形ABC 的三个顶点都在半径为2的球面上，且三棱锥ABC O -的高位1（O 为球心），点D 是线段BC 的中点，过点D 作球的截面，则截面面积最小值？6. 已知球O 的半径为5，球内有一点A ，且A 到球心的距离为3，则过A 的截面中，面积最大值为7. 四面体的一条棱长为x ，其余棱长为3，当该四面体体积最大时，经过这个四面体所有顶点的球的表面积为A. 272π B ．92π C ．152π D ．15π 8. 已知在半径为2的球面上有A 、B 、C 、D 四点，若AB=CD=2，则四面体ABCD 的体积的最大值为A. (C) (D) 9. 把半径为r 的四只小球全部放入一个大球内，则大球半径的最小值为10. 把四个半径都是1的球中的三个放在桌面上，使它两两外切，然后在它们上面放上第四个球，使它与前三个都相切，求第四个球的最高点与桌面的距离。

体面于“心”——高考数学中与球相关问题的分析

突破重难点Җ㊀安徽㊀汪庭斌㊀蔡㊀赫㊀㊀立体几何是高考数学的考查模块之一,每年的分值相对稳定,一般是２２分,包括一道解答题和两道客观题．而在小题的考查当中,外接球与内切球的体积与面积问题几乎在每年的全国卷中都有涉及,难度属于中等偏上,有时以压轴小题的形式出现．对于这类问题,很多空间想象力不够的学生对此一筹莫展,无法拿分．另外,由于各地的教学水平和条件限制,大部分地区对这部分知识无法进行直观讲解．本文对外接球与内切球的体积与面积问题进行一些剖析与归纳,希望能为广大师生提供一些帮助．笔者查阅了五年的高考全国卷,现将涉及的相关问题汇总如下(如表１)．表１年份试卷题目位置考查内容２０１６全国卷Ⅲ理１０求柱体内切球体积的最值２０１６全国卷Ⅲ文１１求柱体内切球体积的最值２０１７全国卷Ⅰ文１６求锥体外接球的表面积２０１７全国卷Ⅱ文１５求柱体外接球的表面积２０１７全国卷Ⅲ文９求球内柱体的体积２０１８全国卷Ⅲ理１０求球内锥体体积的最值２０１８全国卷Ⅲ文１２求球内锥体体积的最值２０１９全国卷Ⅰ理１２求锥体外接球的体积２０２０全国卷Ⅰ理１０求锥体外接球的表面积２０２０全国卷Ⅱ理１１求球心到平面的距离２０２０全国卷Ⅲ理１５求锥体内切球体积的最值２０２０全国卷Ⅰ文１２求锥体外接球的表面积２０２０全国卷Ⅱ文１１求球心到平面的距离２０２０全国卷Ⅲ文１６求锥体内切球体积的最值㊀㊀从表１可以看出全国卷对和球相关的问题考查力度有加大趋势,特别是２０２０年,６套全国卷中均考查了相关内容,因此有必要引起重视．本文将从柱体和锥体的外接球以及多面体的内切球三种类型入手,着重分析球心位置的确定和球体半径的求解,并从中归纳出一些模型．首先对涉及球的基本概念和性质进行一些说明．球中的大圆:过球心的平面截球面形成的圆．球中的小圆:不过球心的平面截球面形成的圆㊀㊀图１垂径定理:球心与小圆圆心的连线垂直于小圆(此定理基本可以解决绝大多数体积和表面积问题,其中寻找直角三角形是解决球相关问题的关键)．如图１所示,在以O 为球心的球中,O １是球中一个小圆的圆心,点A 在小圆上,则有O O １ʅ圆O １,并且在R t әO O １A 中有O O ２１＋O １A ２＝O A ２．１㊀柱体的外接球问题对于这类问题,有两种解题策略．１)寻找球心位置,再求球的半径,在具体的问题中,一般采取的策略是先易再难．由于球心到各个顶点距离相等,那么球心在各个面的每个投影点到相对应面的各个顶点距离也相等．也就是说这些投影点都是外心,球心在过外心垂直于此面的直线上,所以不妨先寻找柱体的某个特殊面的外接圆圆心,再利用垂径定理和勾股定理求解．２)将柱体通过切割或者增补,将其转化成长方体或正方体,而长方体㊁正方体外接球的球心位置是其体对角线的中点,这样就将问题难度大大降低了．但是这种转化过程有时会有一些难度,需要一定的直观想象和逻辑推理能力．例１㊀已知直三棱柱A B C ＧA １B １C １的６个顶点都在球O 的球面上,若A B ＝３,A C ＝４,A A １＝１２,且有A B ʅA C ,则球O 的半径为．㊀㊀图２解法１㊀确定球心位置,球心O 到６个顶点距离相等,因此球心在上㊁下面的投影点是上㊁下面的外接圆的圆心．如图２所示,由条件可知әA B C 为直角三角形,斜边为B C ,故其外接圆圆心为B C 的中点O １,则球心O 与O １的连线O O １与底面A B C 垂直．同理,取B １C １中点O ２,则O O ２ʅ平面A １B １C １,再由上㊁下面平行,可知O １,O ,O ２三点共线,要使得O 到上㊁下６个顶点距离相等,则O 为O １O ２的中点．在R t әO O １C 中,O C 为球的半径R ,O １C ＝１２B C ＝５２,O O １＝１２O １O ２＝１２A A １＝６,４突破重难点则R ＝O O ２１＋O １C ２＝１３２．㊀㊀图３解法２㊀凑长方体模型,利用割补法．由解法１的分析知O １,O ,O ２三点共线,则O １O ２ʅ平面A B C ,O １B O ２B １,故四边形O １B B １O ２为平行四边形,则O １O ２ʊB B １,B B １ʅ平面A B C ,所以此三棱柱是底面为直角三角形的直三棱柱,将这个三棱柱补成长方体,如图３所示．此长方体的长㊁宽㊁高分别为４,３,１２,则其对角线长即为球的直径,因此有２R ＝３２＋４２＋１２２＝１３,故球的半径为１３２．问题总结㊀解决柱体外接球问题,为寻找球心,可以将其模型化．最常用的就是长方体模型,将给的柱体凑成长方体,则这个长方体的体对角线即为其外接球的直径,对角线的中点即为球心位置．设长方体的长㊁宽㊁高分别为a ,b ,c ,则可直接用公式２R ＝a ２＋b ２＋c２求出R ．２㊀锥体的外接球问题锥体的外接球问题解决方法和柱体类似．１)确定球心位置,同样是先易后难 ,先寻找某个特殊面的外接圆圆心和半径(优先考虑直角三角形㊁等边三角形和等腰三角形所在的面)．若是这个锥体的面都不是特殊的面,则可以借助正弦定理求出某个面的外接圆半径,将圆心设出,则球心同样在过这个面的外接圆圆心与此面垂直的直线上,再设出球心,利用垂径定理和勾股定理求解．２)将题目所给的锥体放到某个特殊的棱柱体中(优先考虑长方体㊁正方体和一些直棱柱),利用这些特殊的棱柱体辅助寻找球心和半径．这涉及转化与化归的数学思想,对学生的思维要求较高．㊀㊀图４例２㊀(２０１９年全国卷Ⅰ理１２)已知三棱锥P ＧA B C 的四个顶点在球O 的球面上,P A ＝P B ＝P C ,әA B C 是边长为２的正三角形,E ,F 分别是P A ,A B的中点,øC E F ＝９０ʎ,则球O 的体积为(㊀㊀)．A．８６π㊀B ．４６πC ．２６π㊀D．６π解法１㊀如图４所示,因为P A ＝P B ＝P C ,әA B C 是边长为２的等边三角形,所以三棱锥P ＧA B C 为正三棱锥,所以P B ʅA C ．又因为E ,F 分别为P A ,A B 的中点,所以E F ʊP B ,所以E F ʅA C ,又E F ʅC E ,C E ɘA C ＝C ,所以E F ʅ平面P A C ,P B ʅ平面P A C ,øA P B ＝９０ʎ,所以P A ＝P B ＝P C ＝２,所以三棱锥P ＧA B C 为正方体的一部分,２R ＝２＋２＋２＝６,即R ＝６２,所以V ＝４３πR ３＝６π．故选D．㊀图５解法２㊀如图５所示,设P A ＝P B ＝P C ＝２x ,因为E ,F 分别为P A ,A B 的中点,所以E F ʊP B ,且E F ＝１２P B ＝x ．因为әA B C 为边长为２的等边三角形,所以C F ＝３,又因为øC E F ＝９０ʎ,所以C E ＝３－x ２,A E ＝１２P A ＝x ．在әA E C中,由余弦定理知c o s øE A C ＝x ２＋４－(３－x ２)２ˑ２ˑx＝２x ２＋１４x．作P D ʅA C 于D ,因为P A ＝P C ,所以D 为A C 中点,c o s øE A C ＝A D P A ＝１２x ,所以２x ２＋１４x ＝１２x ,则２x ２＋１＝２,解得x ＝２２,所以P A ＝P B ＝P C ＝２．又因为A B ＝B C ＝A C ＝２,所以P A ,P B ,P C 两两垂直,所以２R ＝２＋２＋２＝６,即R ＝６２,所以V ＝４３πR ３＝６π．故选D ．问题总结㊀通过上述例题不难发现,球体的相关计算和球心位置的确定有很大关系,但也不是必须画出具体图形．根据球体的性质,尤其是垂径定理和勾股定理的拓展应用,可以将问题转化为平面几何的相关运算,但是这需要学生具备一定的理论基础和空间想象力,最终形成解题模型．最基本的模型是长方体外接球模型,长方体对角线即为外接球直径,除此之外还有一类常见模型,对棱相等模型．四面体A ＧB C D 中,三组对棱分别相等,即A B ＝C D ,A D ＝B C ,A C ＝B D ,求这个四面体外接球的半径,可以构造这样一个模型．如图６所示,取一个长方体上㊁下两个面的异面直线A D 和B C ,这个四面体的５突破重难点㊀㊀图６三组对棱分别相等,设长方体长㊁宽㊁高分别为a ,b ,c ,A D ＝B C ＝x ,A B ＝C D ＝y ,A C ＝B D ＝z ,列出方程组a ２＋b ２＝x ２,b ２＋c ２＝y ２,c ２＋a ２＝z ２,ìîíïïïï三者相加可以得到a ２＋b ２＋c ２＝x ２＋y ２＋z ２２,根据长方体对角线公式２R ＝a ２＋b ２＋c ２＝x ２＋y ２＋z ２２,求出R ．例３㊀平行四边形A B C D 中,әA B D 是腰长为２的等腰直角三角形,øA B D ＝９０ʎ,现将әA B D 沿B D 折起,使二面角A ＧB D ＧC 大小为２π３,若A ,B ,C ,D 四点在同一球面上,则该球的表面积为．㊀㊀图７如图７所示,取A D ,BC 的中点分别为O １,O ２,过O １作平面A B D 的垂线,过O ２作平面B C D 的垂线,两垂线交点O 即为所求外接球的球心．取B D 中点E ,连接O １E ,O ２E ,则øO １E O ２即为二面角A ＧB D ＧC 的平面角．又知O １E ＝O ２E ＝１,连接O E ,在R t әO １O E 中,则O １O ＝３．在R t әO １O A 中,O １A ＝２,则O A ＝５,即球的半径为R ＝O A ＝５,所以球的表面积为S ＝４πR ２＝２０π．㊀图３㊀空间几何体内切球问题一般来说内切球的球心非常不容易确定,内切球的相关问题常用等体积法来求．首先将内切球球心与空间几何体各个顶点相连,再将整个几何体分割成若干个高为内切球半径的小几何体,这些小几何体的体积之和就是整个几何体的体积,因此求解的关键在于求出几何体的体积,而求几何体体积的关键在于高的确定．如图８所示,以正四面体为例,球O 与它的四个面均相切,设其半径为r ,则球O 将这个正四面体分割成四个小三棱锥,四个小三棱锥的底面对应这个正四面体的四个面,高是内切球的半径．设这个正四面体的棱长为a ,则其体积为２１２a ３,利用等体积法,四个小三棱锥的体积之和为３３a ２r ＝２１２a ３,则可计算出r ＝６１２a ．㊀㊀图９例４㊀在三棱锥A ＧB C D 中,A B ＝C D ＝６,其余各棱长均为５,则三棱锥内切球半径为．如图９所示,取C D 中点E ,连接A E ,B E ,则有A E ʅC D ,B E ʅC D ,且B E ɘA E ＝E ,故C D ʅ平面A B E ,在平面A B E 内,过A 作B E的垂线交B E 于F ,则A F ʅ平面B C D ,即A F 为这个三棱锥的高．根据题中所给数据可得A E ＝B E ＝４,在әA B E 中,将A B 作为底边,则高为４２－３２＝７,则әA B E 面积为１２A B ˑ７＝１２B E ˑA F ,解得A F ＝３７２．这个三棱锥四个面的面积均为１２ˑ６ˑ４＝１２,设内切球半径为r ,由等体积法则有V A ＧB C D ＝１３S әB C D ˑA F ＝４ˑ１３ˑ１２ˑr ,即r ＝３７８．问题总结㊀对于内切球问题,等体积法的使用并不困难,关键在于求出原几何体的体积,最为关键的是求出高,在求高过程中往往涉及线面和面面垂直定理的使用,知识的综合性较强．在解决与几何体的外接㊁内切相关问题时,基本都涉及球心这个关键因素．而球心的位置确定,常利用割补法,将所给图形向特殊的几何体模型(长方体㊁正方体㊁正四面体等)进行转化,这些特殊的几何体的球心位置很好确定．在无法转化为特殊模型时,需要通过球心及几何体中的特殊点(如切点或切线)作截面把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或画内切㊁外接的几何体的直观图．弄清球的半径(直径)与该几何体已知量的关系,列方程组求解,在解题过程中不断进行转化化归,将立体几何问题转化为平面几何问题,再将其转化为解三角形的问题．这可谓:球心位置哪里寻,特殊模型寻突破,立几问题化平几,勾股三角来辅助．(作者单位:安徽省宁国中学)６。

高考试题中球类问题的探讨

高考试题中球类问题的探讨
高考球类问题较为常见，其中主要包括物理学方面和数学方面的探讨。

在物理学方面，首先可以涉及到运动物理学中的弹道学，主要涉及到
动量定律，加速度原理，以及改变运动轨迹的各种力的作用，比如杨氏力
等等。

由此可以推导出许多球运动的物理规则，如释放角，角速度，旋转
抛物线等。

在数学方面，可以涉及到微积分方面的内容，比如可以利用坐标变换
方法来求解抛物线的解析式，来求解球运动的位置；可以利用向量论去解
决三维球运动的问题；利用几何方法来求解障碍物之间的反弹效果，以及
反射，折射等方面的数学解决方案。

因此从物理学和数学的角度来看，解决球类高考题目，既可以利用物
理学的力学原理，也可以利用数学的几何，微积分等知识来求解。

高考数学球知识点

高考数学球知识点在高考数学考试中，球是一个常见的几何图形，对于球的相关知识点了解和掌握是非常重要的。

本文将从球的定义、球的性质以及球的应用等方面，对高考数学中与球相关的知识点进行详细的介绍。

一、球的定义球是由空间中的一点（球心）到该点距离小于等于一定数值（半径）的全部点的集合。

球的形状呈现出圆心对称性，球的表面则是由无数个点组成。

二、球的性质1. 球的半径：球的半径是从球心到球上任意一点的距离，通常用字母r表示。

2. 球面积：球面积指的是球的表面积，用字母S表示。

球的表面积公式为S = 4πr²，其中π取近似值3.14。

3. 球体积：球体积指的是球内部空间的容积，用字母V表示。

球的体积公式为V = (4/3)πr³。

4. 球的切线与切平面：过球上任意点可以作出两个相切的切线，而通过球心也可以作出一个与切线平行的切平面。

三、球的应用球的相关知识点在数学中有着广泛的应用，下面列举几个重要的应用场景：1. 球的测量：对于实际生活中的球形物体，如篮球、足球等，我们可以通过测量半径或直径来计算出其体积或表面积。

2. 球体积与体积比较：在解决实际问题中，常常需要比较两个球的体积大小，运用球的体积公式可以快速求解。

3. 球与圆柱、圆锥等的相交问题：通过运用球与其他几何图形的相交关系，可以解决球与圆柱、圆锥等的相交过程中的相关问题。

4. 空间几何解析：在三维空间几何解析中，球的方程是一个常见的形式，需要掌握方程化简和应用技巧。

综上所述，球作为数学中的一个重要几何图形，具有其独特的性质和广泛的应用。

在高考数学中，理解和掌握球的相关知识点，将有助于更好地解决与球相关的问题，提高数学成绩。

通过不断的练习和巩固，相信大家一定能够在高考中取得优异的成绩！。