期末模拟试卷E

合集下载

2022-2023学年八年级(上)期末数学模拟试卷(三)

2022-2023学年八年级（上）期末数学模拟试卷（三）一、选择题（本大题共12小题，每小题3分，共36分。

在每小题所给的四个选项中，有且只有一项是符合题目要求的）1．（3分）下列体育运动图标中，是轴对称图形的是（）A．B．C．D．2．（3分）如图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，使其不变形，这种做法的根据是（）A．三角形的稳定性B．长方形的对称性C．长方形的四个角都是直角D．两点之间线段最短3．（3分）光刻机采用类似照片冲印的技术，把掩膜版上的精细图形通过光线的曝光印制到硅片上，是制造芯片的核心装备．ArF准分子激光是光刻机常用光源之一，其波长为0.000000193米，该光源波长用科学记数法表示为（）A．193×106米B．193×10﹣9米C．1.93×10﹣7米D．1.93×10﹣9米4．（3分）如图，用直尺和圆规作一个三角形O1A1B1，使得△O1A1B1≌△OAB 的示意图，依据（）定理可以判定两个三角形全等．A．SSS B．SAS C．ASA D．AAS5．（3分）下列由左边到右边的变形中，是因式分解的为（）A．10x2y3＝5xy2•2xy B．m2﹣n2＝（m+n）（m﹣n）C．3m（R+r）＝3mR+3mr D．x2﹣x﹣5＝（x+2）（x﹣3）+1 6．（3分）已知一个正多边形的每个外角的度数都是60°，则该多边形的对角线条数为（）A．6B．9C．12D．187．（3分）如图，AE，BE，CE分别平分∠BAC，∠ABC，∠ACB，ED⊥BC于点D，ED＝3，△ABC的周长为24，则△ABC的面积为（）A．18B．24C．36D．728．（3分）随着快递业务的增加，某快递公司为快递员更换了快捷的交通工具，公司投递快件的能力由每周3000件提高到4200件，平均每人每周比原来多投递80件，若快递公司的快递员人数不变，求原来平均每人每周投递快件多少件？设原来平均每人每周投递快件x件，根据题意可列方程为（）A．＝B．+80＝C．＝﹣80D．＝9．（3分）如图，点D为△ABC的边BC上一点，且满足AD＝DC，作BE⊥AD 于点E，若∠BAC＝70°，∠C＝40°，AB＝6，则BE的长为（）A．2B．3C．4D．510．（3分）下列说法：①三角形中至少有一个内角不小于60°；②三角形的重心是三角形三条中线的交点；③周长相等的两个圆是全等图形；④到三角形的三条边距离相等的点是三角形三条高的交点．其中正确说法的个数是（）A．1B．2C．3D．411．（3分）如图，由4个全等的小长方形与1个小正方形密铺成正方形图案，该图案的面积为49，小正方形的面积为4，若分别用x，y（x＞y）表示小长方形的长和宽，则下列关系式中不正确的是（）A．x2+2xy+y2＝49B．x2﹣2xy+y2＝4C．x2+y2＝25D．x2﹣y2＝1412．（3分）如图，已知∠ABC＝120°，BD平分∠ABC，∠DAC＝60°，若AB ＝2，BC＝3，则BD的长是（）A．5B．7C．8D．9二、填空题（本大题共4小题，每小题4分，共16分）13．（4分）当x＝时，分式的值为0．14．（4分）已知点P（4，2a﹣3）关于x轴对称的点在第一象限，则a的取值范围是．15．（4分）已知a＝+2021，b＝+2022，c＝+2023，则代数式2（a2+b2+c2﹣ab﹣bc﹣ac）的值为．16．（4分）如图，△ABC中，BF是高，延长CB至点D，使BD＝BA，连接AD，过点D作DE⊥AB交AB的延长线于点E，当AF＝BE，∠CAD＝96°时，∠C＝．三、解答题（本大题共9小题，共98分。

2022-2023学年北师大版九年级上册数学期末模拟试卷+(1)

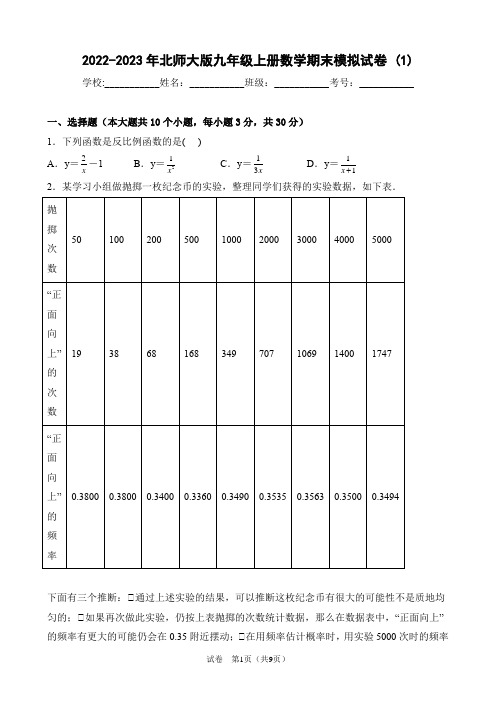
2022-2023年北师大版九年级上册数学期末模拟试卷 (1) 学校:___________姓名：___________班级：___________考号：___________一、选择题（本大题共10个小题，每小题3分，共30分）1．下列函数是反比例函数的是()A．y＝2x －1B．y＝21xC．y＝13xD．y＝11x2．某学习小组做抛掷一枚纪念币的实验，整理同学们获得的实验数据，如下表．抛掷次数5010020050010002000300040005000“正面向上”的次数193868168349707106914001747“正面向上”的频率0.38000.38000.34000.33600.34900.35350.35630.35000.3494下面有三个推断：①通过上述实验的结果，可以推断这枚纪念币有很大的可能性不是质地均匀的；①如果再次做此实验，仍按上表抛掷的次数统计数据，那么在数据表中，“正面向上”的频率有更大的可能仍会在0.35附近摆动；①在用频率估计概率时，用实验5000次时的频率0.3494一定比用实验4000次时的频率0.3500更准确．其中正确的是（）A．①①B．①①C．①①D．①①①3．下列几何体中，主视图是长方形的是（）A．B．C．D．4．如图，①DEF和①ABC是位似图形点O是位似中心，点D，E，F，分别是OA，OB，OC 的中点，若①ABC的面积是8，①DEF的面积是()A．2B．4C．6D．85．把抛物线y＝x2+1向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为（）A．y＝（x+3）2+1B．y＝（x+1）2+3C．y＝（x﹣1）2+4D．y＝（x+1）2+46．为了方便行人推车过某天桥,市政府在10m高的天桥一侧修建了40m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是()A．B．C．D ．7．如图，已知：AB 是O 的直径，O 的半径为1，3BD sin C ∠的值等于（）A ．12B 3C 3D 2 8．已知关于x 的一元二次方程2(1)410a x x ---=有两个实数根，则a 的取值范围是（） A ．4a ≥- B ．3a >- C ．3a ≥-且1a ≠ D ．3a >-且1a ≠9．已知：如图，菱形ABCD 的周长为20cm ，对角线AC =8cm ，直线l 从点A 出发，以1c m/s 的速度沿AC 向右运动，直到过点C 为止在运动过程中，直线l 始终垂直于AC ，若平移过程中直线l 扫过的面积为S （cm 2），直线l 的运动时间为t （s ），则下列最能反映S 与t 之间函数关系的图象是（）A ．B ．C ．D ．10．下列计算错误的是（）A 236=B 236C 1232=D 822=二、填空题（本大题共5个小题，每小题3分，共15分）11．当2x =时，函数21y x =-+的值是______． 12．-1a b a b a b a a a a---=--=( ) 13．已知一个直角三角形的两条直角边的长恰好是方程x 2﹣6x=8（x ﹣6）的两个实数根，那么这个直角三角形的内切圆半径为_____．14．二次函数y=x 2+bx 图象的对称轴为直线x=1，若关于x 的一元二次方程x 2+bx ﹣t=0（t 为实数）在﹣1≤x≤2的范围内有解，则t 的取值范围是_____．15．如图，G 、H 分别是四边形ABCD 的边AD 、A B 上的点，①GCH =45°，CD =CB =2，①D =①DCB =①B =90°，则△AGH 的周长为_______．三、解答题（一）(本大题共3个小题，每小题8分，共24分)16.(本题8分)解下列方程(1)x 2－4x －1＝0（配方法）(2)3x （x －1）＝2－2x （因式分解法）17.(本题8分)如果四边形ABCD 的四个顶点坐标分别是A(2,1),B(4,3),C(6,2),D(3,-1). 试将此四边形缩小为原来的12 ．18.(本题8分)如图，ABC 为等边三角形，BD AC ⊥交AC 于点D ，DE BC ∥交AB 于点E ．(1)求证：ADE 是等边三角形．(2)求证：12AE AB =．四、解答题（二）(本大题共3个小题，每小题9分，共27分)19.(本题9分)学校图书馆去年年底有图书5万册，预计到明年年底增加到7.2万册．求这两年的年平均增长率．20.(本题9分)春节期间甲乙两商场搞促销活动.甲商场的方案是：在一个不透明的箱子里放4个完全相同的小球，球上分别标“0元”、“20元”、“30元”、“50元”，顾客每消费满300元，就可从箱子里不放回地摸出2个球，根据两个小球所标金额之和可获相应价格的礼品.乙商场的方案是：在一个不透明的箱子里放2个完全相同的小球，球上分别标“5元”、“30元”，顾客每消费满100元，就可从箱子里不放回地摸出1个球，根据两个小球所标金额之和可获相应价格的礼品. 某顾客准备消费300元，(1)若该顾客在甲商场消费，至少可得价值_________元的礼品，至多可得价值_________元的礼品；(2)请用画树状图或列表法，说明该顾客去哪个商场消费，获得礼品的总价值不低于50元的概率大.21.(本题9分)y=x+1x 是一种类似于反比例函数的对勾函数，形如y=ax+bx．其函数图像形状酷似双勾，故称“对勾函数”，也称“勾勾函数”、“海鸥函数”．y=x+1x函数图像如下图所示．根据y=x+1x 图像对函数y=|x|+1x的图像和性质进行了探究．(1)绘制函数图像：y=|x|+1 x列表：下表是x与y的几组对应值x………-3-2-1-12-131312123………y (10)35225210310352252103………描点：根据表中各组对应值，在平面直角坐标系中描出各点；连线：用平滑的曲线顺次连接各点，请你在平面直角坐标系中将y=|x|+1x图像补充完整；(2)观察发现：①写出函数y=|x|+1x的一条性质_________①函数图像与直线y=2有_________个交点，所以对应的方程|x|+120x-=有_________个实数根．(3)分析思考：①方程的|x-1|+11x--2=0的解为_________①不等式|x|+1x-52＜0，x的取值范围为_________(4)延伸探究：①当x＞0时，直线y=kx+3与y=|x|+1x只有一个交点，求k的值？五、解答题（三）(本大题共2个小题，每小题12分，共24分)22.(本题12分)综合与实践折纸是同学们喜欢的手工活动之一，通过折纸我们既可以得到许多美丽的图形，同时折纸的过程还蕴含着丰富的数学知识．折一折：把边长为4的正方形纸片ABCD对折，使边AB与CD 重合，展开后得到折痕EF．如图①：点M为CF上一点，将正方形纸片ABCD沿直线DM折叠，使点C落在EF上的点N处，展开后连接DN，MN，AN，如图①图①图①（一）填一填，做一做：（1）图①中，CMD∠=_______．线段NF=_______．（2）图①中，试判断AND∆的形状，并给出证明．剪一剪、折一折：将图①中的AND∆剪下来，将其沿直线GH折叠，使点A落在点A'处，分别得到图①、图①．（二）填一填图① 图①（3）图①中阴影部分的周长为_______．（4）图①中，若80A GN '∠=︒，则A HD '∠=_______°．（5）图①中的相似三角形（包括全等三角形）共有_______对；（6）如图①点A '落在边ND 上，若A N m A D n '='_______，则AG AH=_______用含m ，n 的代数式表示）．23.(本题12分)如图，在Rt①ABC 中，①C=90°，AB=10cm,BC=6cm ，点P 、Q 同时从点C 出发，分别沿C→A 和 C→B 的方向运动，速度分别为2cm/s 和1cm/s.过点P 作PM①AC 交AB 于M ，分别连接PQ 、PM ．当点Q 运动到B 时，两点都停止．设运动时间为t 秒．(1)当t= s 时，PQ①QM ？(2)将①PQM 沿PM 翻折，得到①PMQ /．①当t= s 时,点Q /恰好落在AB 上；①设①PMQ /与①ABC 重叠部分的面积为Scm 2，求：S 与t 的函数关系式，并指出t 的取值范围．。

2022-2023学年人教版七年级英语上册期末模拟试卷含答案

2022-2023学年七年级英语上册期末模拟试卷时量：120分钟满分：120分第一部分听力 (共两节,满分20分)第一节 (共5小题；每小题1分,满分5分)听下面5段对话。

每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。

听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话读两遍。

1．What's the boy's last name？A.Mike．B．Jack．C．Smith.2．Where's Mary's key？A．In the box．B．On the desk．C．Under the desk．3．What is the girl's favorite subject？A．Music．B．Science．C．Art．4．When is the girl's mother's birthday？A．On July 2nd．B．On December 2nd．C．On October 2nd．5．Who's the boy on the right in the photo？A．He's the girl's cousin．B．He's Andy's cousin．C．He's the girl's brother．第二节 (共15小题；每小题1分,满分15分)听下面6段对话或独白。

每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。

听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟；听完后,各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第六段对话,回答第6、7小题。

6. What's the new classmate's name?A.Lucy.B.Sally.C.Jenny.7.How old is she?A.Thirteen.B. Twelve.C. Fourteen.听第七段对话,回答第8、9小题。

专题07 八年级下册期末模拟试卷一(解析版)-2020-2021学年八年级数学期末复习特训(人教版)

专题07 八年级下册期末模拟试卷一（解析版）一．选择题（共10小题，满分30分，每小题3分）1．（3分）在▱ABCD中，AB＝6，AD＝4，则▱ABCD的周长为（）A．10B．20C．24D．12【解答】解：∵四边形ABCD是平行四边形，∴AB＝CD＝6，AD＝BC＝4，∴▱ABCD的周长为：2×（AB+AD）＝2×（6+4）＝20，故选：B．2．（3分）下列二次根式中，是最简二次根式的是（）A．B．C．D．【解答】解：A.，故本选项不合题意；B.，故本选项不合题意；C.是最简二次根式，故本选项符合题意；D.，故本选项不合题意．故选：C．3．（3分）若甲、乙、丙、丁四人参加跳远比赛，经过几轮初赛，他们的平均成绩相同，方差分别是：＝0.34，S乙2＝0.21，S丙2＝0.4，S丁2＝0.45．你认为最应该派去的是（）A．甲B．乙C．丙D．丁【解答】解：∵＝0.34，S乙2＝0.21，S丙2＝0.4，S丁2＝0.45，∴S乙2＜＜S丙2＜S丁2，∴乙的成绩更加稳定，故选：B．4．（3分）下列计算正确的是（）A．÷＝B．﹣＝C．+＝D．×＝【解答】解：A、原式＝＝，所以A选项错误；B、与不能合并，所以B选项错误；C、与不能合并，所以C选项错误；D、原式＝＝，所以D选项正确．故选：D．5．（3分）下列线段不能构成直角三角形的是（）A．5，12，13B．2，3，C．4，7，5D．1，，【解答】解：A、52+122＝169＝132，故是直角三角形，不符合题意；B、22+（）2＝9＝32，故是直角三角形，不符合题意；C、42+52＝41≠72，故不是直角三角形，符合题意；C、12+（）2＝（）2，故是直角三角形，不符合题意．故选：C．6．（3分）下列各曲线中不能表示y是x的函数的是（）A．B．C．D．【解答】解：当x取一个值时，y有唯一的值与其对应，就说y是x的函数，x是自变量．选项A中的曲线，当x取一个值时，y的值可能有2个，不满足对于自变量的每一个确定的值，函数值有且只有一个值与之对．故A中曲线不能表示y是x的函数，故选：A．7．（3分）数学老师为了判断小颖的数学成绩是否稳定，对小颖在中考前的6次模拟考试中的成绩进行了统计，老师应最关注小颖这6次数学成绩的（）A．方差B．中位数C．平均数D．众数【解答】解：由于方差反映数据的波动大小，故老师最关注小颖这6次数学成绩的稳定性，就是关注这6次数学成绩的方差．故选：A．8．（3分）在下列给出的条件中，能判定四边形ABCD是平行四边形的是（）A．AB∥CD，AD＝BC B．∠A＝∠B，∠C＝∠DC．AD∥BC，AD＝BC D．AB＝AD，CD＝BC【解答】解：A．由AB∥CD，AD＝BC，不能判定四边形ABCD是平行四边形，故本选项不合题意；B．由∠A＝∠B，∠C＝∠D，不能判定四边形ABCD是平行四边形，故本选项不合题意；C．由AD∥BC，AD＝BC，能判定四边形ABCD是平行四边形，故本选项符合题意；D．由AB＝AD，CD＝BC，不能判定四边形ABCD是平行四边形，故本选项不合题意；故选：C．9．（3分）如图，一次函数y1＝x+b与一次函数y2＝kx+4的图象相交于点P（2，﹣2），则关于x的不等式x+b＞kx+4的解集是（）A．x＞﹣2B．x＜﹣2C．x＜2D．x＞2【解答】解：∵一次函数y1＝x+b与一次函数y2＝kx+4的图象相交于点P（2，﹣2），∴当x＞2时，x+b＞kx+4，即关于x的不等式x+b＞kx+4的解集是x＞2．故选：D．10．（3分）将一张正方形纸片按如图的步骤，通过折叠得到④，再沿虚线剪去一个角，展开平铺后得到⑤，其中FM、GN为折痕，若正方形EFGH与五边形MCNGF的面积之比为4：5，则的值为（）A．B．C．D．【解答】解：如图，连接HF，直线HF与AD交于点P，∵正方形EFGH与五边形MCNGF的面积之比为4：5，设正方形EFGH与五边形MCNGF的面积为4x2，5x2，∴GF2＝4x2，∴GF＝2x，∴HF＝＝2x，由折叠可知：正方形ABCD的面积为：4x2+4×5x2＝24x2，∴PM2＝24x2，∴PM＝2x，∴FM＝PH＝（PM﹣HF）＝（2x﹣2x）＝（﹣）x，∴＝＝．故选：A．二．填空题（共6小题，满分18分，每小题3分）11．（3分）若二次根式有意义，则x的取值范围是x≥．【解答】解：∵二次根式有意义，∴2x﹣1≥0，解得：x≥．故答案为：x≥．12．（3分）如图，在校园内有两棵树相距12米，一棵树高14米，另一棵树高9米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞13米．【解答】解：如图所示，AB，CD为树，且AB＝14米，CD＝9米，BD为两树距离12米，过C作CE⊥AB于E，则CE＝BD＝12，AE＝AB﹣CD＝5，在直角三角形AEC中，AC＝＝＝13．答：小鸟至少要飞13米．故答案为：13．13．（3分）已知a，b，c，d的平均数是3，则2a﹣1，2b﹣1，2c﹣1，2d﹣1的平均数是5．【解答】解：∵a，b，c，d的平均数是3，∴a+b+c+d＝12，∴[（2a﹣1）+（2b﹣1）+（2c﹣1）+（2d﹣1）]÷4＝（2a﹣1+2b﹣1+2c﹣1+2d﹣1）÷4＝[2（a+b+c+d）﹣4]×＝﹣1＝﹣1＝6﹣1＝5，故答案为：5．14．（3分）如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A、B、C、D的面积分别是3、5、2、3，则正方形E的边长是．【解答】解：设中间两个正方形的边长分别为x、y，正方形E的边长为z，则由勾股定理得：x2＝3+5＝8，y2＝2+3＝5，z2＝x2+y2＝13；即最大正方形E的面积为：z2＝13．则正方形E的边长是．故答案为：．15．（3分）已知直线y＝kx+b，若k+b+kb＝0，且kb＞0，那么该直线不经过第一象限．【解答】解：∵k+b+kb＝0，且kb＞0，∴k+b＝﹣kb＜0，k和b同号，∴k＜0，b＜0，∴直线y＝kx+b经过第二、三、四象限，不经过第一象限，故答案为：一．16．（3分）已知三角形一边上的中线，与三角形三边有如下数量关系：三角形两边的平方和等于第三边一半的平方与第三边中线平方之和的2倍．即：如图1，在△ABC中，AD是BC边上的中线，则有AB2+AC2＝2（BD2+AD2）．请运用上述结论，解答下面问题：如图2，点P为矩形ABCD外部一点，已知P A＝PC＝3，若PD＝1，则AC的取值范围为﹣1≤AC＜2．【解答】解：如图，连接BD交AC于O，连接PO，∵四边形ABCD是矩形，∴AC＝BD，AO＝CO＝BO＝DO，∵PO是△ACP的中线，也是△PBD的中线，∴P A2+PC2＝2（AO2+PO2），PB2+PD2＝2（PO2+OD2），∴P A2+PC2＝PB2+PD2，∴9+9＝1+PB2，∴PB＝，在△PBD中，﹣1≤BD≤+1，∴﹣1≤AC≤+1，当点P在AD上时，CD＝＝＝2，∴AC＝＝＝2，故答案为：﹣1≤AC＜2．三．解答题（共8小题，满分72分）17．（6分）计算：（1）﹣+；（2）（+1）（﹣1）+÷．【解答】解：（1）原式＝3﹣4+＝0；（2）原式＝（）2﹣1+＝2﹣1+＝1+．18．（8分）如图，在△ABC中，点D、E、F分别是BC、AC、AB边上的中点．（1）求证：四边形BDEF是平行四边形；（2）若AB＝BC，连接BE、DF．请判断BE与DF的位置关系，并说明理由．【解答】（1）证明：∵D、E、F分别是BC、AC、AB的中点，∴DE是△CAB的中位线，EF是△ABC的中位线，∴DE∥AB，EF∥BC，∴四边形BDEF是平行四边形；（2）解：BE与DF的位置关系为：BE⊥DF，如图所示，理由如下：由（1）得：DE是△CAB的中位线，EF是△ABC的中位线，∴DE＝AB，EF＝BC，∵AB＝BC，∴DE＝EF，∵四边形BDEF是平行四边形，∴四边形BDEF是菱形，∴BE⊥DF．19．（8分）已知一次函数y＝（m﹣3）x+m+1的图象经过点（1，2）．（1）求此一次函数解析式，并画出函数图象；（2）求此一次函数图象与坐标轴围成图形的面积．【解答】解：（1）把x＝1，y＝2代入一次函数解析式，得（m﹣3）+m+1＝2．解得m＝2．所以一次函数解析式为：y＝﹣x+3．函数图象见右图．（2）当x＝0时，y＝3；当y＝0时，x＝﹣3．所以直线和x、y轴围成的三角形的面积为：×3×3＝．20．（8分）某校九年级的一次数学小测试由20道选择题构成，每题5分．共100分．为了了解本次测试中同学们的成绩情况，某调查小组从中随机调查了部分同学，并根据调查结果绘制了如下尚不完整的统计图：请根据以上信息解答下列问题：（1）本次调查的学生人数为50人；（2）调查的学生中，该次测试成绩的中位数是90分；（3）调查的学生中，该次测试成绩的众数为95分；（4）补全条形统计图；（5）若测试成绩80分或80分以上为“优秀”，则估计该校九年级800名学生中，本次测试成绩达到“优秀”的人数是多少？【解答】解：（1）本次调查的学生有：5÷10%＝50（人），故答案为：50；（2）∵3+18＝21，21+12＝33，∴这组数据的中位数是（90+90）÷2＝90（分），故答案为：90；（3）85分的学生有50﹣（2+5+12+18+3）＝10（人），故这组数据的众数是95分，故答案为：95；（4）由（3）知，85分的学生有10人，补全的条形统计图如右图所示；（5）800×＝768（人），即该校九年级800名学生中，本次测试成绩达到“优秀”的人数是768人．21．（8分）如图，在Rt△ABC中，∠ABC＝90°，AB＝6，BC＝8，将△DCE沿DE翻折，使点C落在点A处．（1）设BD＝x，在Rt△ABC中，根据勾股定理，可得关于x的方程62+x2＝（8﹣x）2；（2）分别求DC、DE的长．【解答】解：（1）∵将△DCE沿DE翻折，使点C落在点A处．∴AD＝CD，AE＝EC，设BD＝x，则DC＝AD＝8﹣x，∵AB2+BD2＝AD2，∴62+x2＝（8﹣x）2，故答案为：62+x2＝（8﹣x）2；（2）由（1）得62+x2＝（8﹣x）2，解得x＝，∴BD＝，∴DC＝BC﹣BD＝8﹣＝．∵AB＝6，BC＝8，∴AC＝＝＝，∴CE＝AC＝5，∴DE＝＝＝．22．（10分）甲、乙两名同学沿直线进行登山，甲、乙沿相同的路线同时从山脚出发到达山顶．甲同学到达山顶休息1小时后再沿原路下山．他们离山脚的距离S（千米）随时间t（小时）变化的图象如图所示．根据图象中的有关信息回答下列问题：（1）分别求出甲、乙两名同学上山过程中S与t的函数解析式；（2）若甲同学下山时在点F处与乙同学相遇，此时点F与山顶的距离为0.75千米；①求甲同学下山过程中S与t的函数解析式；②相遇后甲、乙两名同学各自继续下山和上山，求当乙到山顶时，甲离乙的距离是多少千米？【解答】解：（1）设甲、乙两同学登山过程中，路程s（千米）与时间t（时）的函数解析式分别为S甲＝k1t，S＝k2t乙由题意，得2＝4k1，2＝6k2∴k1＝，k2＝，∴解析式分别为S甲＝t，S乙＝t；（2）①当y＝4﹣0.75时，，解得t＝，∴点F（，），甲到山顶所用时间为：4＝8（小时）由题意可知，点D坐标为（9，4），设甲同学下山过程中S与t的函数解析式为s＝kt+b，则：，解答，∴甲同学下山过程中S与t的函数解析式为s＝﹣t+13；②乙到山顶所用时间为：（小时），当x＝12时，s＝﹣12+13＝1，当乙到山顶时，甲离乙的距离是：4﹣1＝3（千米）．23．（12分）已知菱形ABCD的边长为2，∠ABC＝60°，对角线AC、BD相交于点O．点M从点B向点C运动（到点C时停止），点N为CD上一点，且∠MAN＝60°，连接AM交BD于点P．（1）求菱形ABCD的面积；（2）如图1，过点D作DG⊥AN于点G，若BM＝4﹣2，求NG的长；（3）如图2，点E是AN上一点，且AE＝AP，连接BE、OE．试判断：在运动过程中，BE+OE是否存在最小值？若存在，请求出；若不存在，请说明理由．【解答】解：（1）如图1中，∵四边形ABCD是菱形，∴AB＝BC＝CD＝AD＝2，∠ABC＝∠ADC＝60°，AC⊥BD，∴△ABC，△ACD都是等边三角形，∵∠AOB＝90°，∠ABO＝∠CBO＝30°，∴OA＝AB＝1，OB＝OA＝，∴AC＝2AO＝2，BD＝2OB＝2，∴S菱形ABCD＝•BD•AC＝×2×2＝2．（2）如图1中，过点A作AT⊥CD于T．∵△ABC，△ACD都是等边三角形，∴∠ACN＝∠ABM＝60°，AB＝AC，∵∠MAN＝∠BAC＝60°，∴∠BAM＝∠CAN，∴△BAM≌△ACN（ASA），∴BM＝CN＝4﹣2，∵AC＝AD，AT⊥CD，∴CT＝DT＝1，AT＝，∴TN＝CT﹣CN＝1﹣（4﹣2）＝2﹣3，∴AN＝＝＝3﹣，∵S△ADN＝•AN•DG＝•DN•AT，∴DG＝＝，∴GN＝＝＝2﹣．（3）如图2中，取CD的中点G，连接BG，CE，EG，过点G作GH⊥BD于H．∵∠BAC＝∠P AE＝60°，∴∠BAP＝∠CAE，∵AB＝AC，AP＝AE，∴△BAP≌△CAE（SAS），∴∠ABP＝∠ACE＝30°，∵∠ACD＝60°，∴∠OCE＝∠GCE，∵∠COD＝90°，∠ODC＝∠ADC＝30°，∴CD＝2OC，∵CG＝GD，∴OC＝CG，∵CE＝CE，∴△OCE≌△GCE（SAS），∴OE＝EG，∴BE+OE＝BE+EG≥BG，在Rt△BGH中，∵∠GHB＝90°，GH＝DG＝，BH＝，∴BG＝＝＝，∴BE+OE≥，∴BE+OE的最小值为．24．（12分）如图，在平面直角坐标系xOy中，已知直线l1：y＝x﹣2和直线l2：y＝2x﹣4相交于点A．（1）已知点P（1﹣t，9﹣3t），求证：无论t为何值，点P总在直线y＝3x+6上；（2）直线y＝3x+6分别与x轴、y轴交于B、C两点，平移线段BC，使点B、C的对应点M、N分别落在直线l1和l2上，请你判断四边形BMNC的形状，并说明理由；（3）在（2）问的条件下，已知直线y＝mx﹣6m+8 把四边形BMNC的面积分成1：3两部分，求m的值．【解答】（1）证明：对于直线y＝3x+6，当x＝1﹣t时，y＝3（1﹣t）+6＝﹣3t+9，∴P（1﹣t，9﹣3t）在直线y＝3x+6上．（2）解：∵直线y＝3x+6分别与x轴、y轴交于B、C两点，∴B（﹣2，0），C（0，6），∵线段MN是由线段BC平移得到，∴可以假设M（t，t﹣2），N（t+2，t﹣2+6），即N（t+2，t+4），∵N（t+2，t+4）在直线y＝2x﹣4上，∴t+4＝2（t+2）﹣4，解得t＝4，∴M（4，2），N（6，8），∴BM＝＝2，BC＝＝2，∴BM＝BC，∵BC＝MN，BC∥MN，∴四边形BMNC是平行四边形，∵BC＝BM，∴四边形BMNC是菱形．（3）∵直线y＝mx﹣6m+8，∴x＝6时，y＝8，∴直线y＝mx﹣6m+8经过定点（6，8），∴直线y＝mx﹣6m+8经过点N（6，8），∵直线y＝mx﹣6m+8把四边形BMNC的面积分成1：3两部分，∴直线y＝mx﹣6m+8经过BC的中点G或经过BM的中点H，∵G是BC的中点，H是BM的中点，∴G（﹣1，3），H（1，1），把G（﹣1，3）代入y＝mx﹣6m+8得到m＝，把H（1，1）代入y＝mx﹣6m+8得到m＝，综上所述，满足条件的m的值为或．。

2022-2023学年冀教版七年级数学上册期末模拟试卷含答案

2022-2023学年冀教版七年级数学上册期末模拟试卷一．选择题（共16小题，满分32分，每小题2分）1．下列四个有理数中，其中最小的数是（）A．﹣3B．﹣1C．0D．12．如图的几何体由5个相同的小正方体搭成．从正面看，这个几何体的形状是（）A．B．C．D．3．下列各式中，代数式有（）个（1）a+b＝b+a（2）1 （3）2x﹣1 （4）（5）s＝πr2（6）A．2B．3C．4D．54．下列各组单项式属于同类项的是（）A．与B．﹣m3与m2C．a2b与2ab2D．2a2与3a25．已知M＝﹣x+1，N＝x﹣5，若M+N＝20，则x的值为（）A．﹣30B．﹣48C．48D．306．下列语句正确的有（）①射线AB与射线BA是同一条射线②两点之间的所有连线中，线段最短③连接两点的线段叫做这两点的距离④欲将一根木棍固定在墙上，至少需要2个钉子A．1个B．2个C．3个D．4个7．若2x3y m与﹣x n y2是同类项，则m﹣n的值是（）A．1B．﹣1C．5D．﹣58．若关于x的方程（m﹣3）x|m﹣2|﹣3＝0是一元一次方程，则m值是（）A．1或2B．1或3C．1D．39．下面的图形中，不是平面图形的是（）A．角B．圆柱C．直线D．圆10．某商品原价为a元，因销量下滑，经营者连续两次降价，每次降价10%，后因供不应求，又一次提高20%，问现在这种商品的价格是（）A．1.08a元B．0.88a元C．0.972a元D．0.968 a元11．对于有理数a、b，定义一种新运算“※”，规定：a※b＝|a|﹣|b|﹣|a﹣b|，则2※（﹣3）等于（）A．﹣2B．﹣6C．0D．212．如图，点C是AB的中点，点D是BC的中点，则下列等式中成立的有（）①CD＝AD﹣BD；②CD＝AD﹣BC；③2CD＝2AD﹣AB；④CD＝ABA．①②B．②③C．①③D．②④13．甲、乙两水池共储水100吨，若甲池注进水20吨，乙池用去水30吨后，两池所储水量相等，设甲池原来有水x吨，则可列方程如下正确的是（）A．x+20＝（100﹣x）+30B．x﹣20＝（100﹣x）﹣30C．x+20＝（100﹣x）﹣30D．x﹣20＝（100﹣x）+3014．数轴上，点A、B分别表示﹣1、7，则线段AB的中点C表示的数是（）A．2B．3C．4D．515．代数式a2+2a+7的值是6，则4a2+8a+7的值是（）A．3B．﹣3C．13D．﹣1316．已知甲、乙两地相距65km，小红从甲地先坐公交车出发，公交车以40km/h的速度行驶了1.5h，然后小红步行，共花了2.5h到达乙地，则小红步行速度是（）A．2km/h B．3km/h C．4km/h D．5km/h二．填空题（共4小题，满分12分，每小题3分）17．若x＝﹣1是关于x的一元一次方程1﹣2x＝3m的解，则m的值是．18．一张正方形纸片ABCD按如图所示的方式折叠，AE、AF为折痕，若∠B′AD′＝20°，则∠EAF＝．19．已知a，b表示两个有理数，规定一种新运算：a*b＝2（a﹣b），则（﹣5）*（﹣2）的值是．20．观察下列一组数的排列规律：，，，，，，，，，，，，，，，…那么，这一组数的第2019个数是．三．解答题（共6小题，满分56分）21．（8分）计算：（1）（2）22．（10分）解方程：﹣x＝+．23．（8分）已知：A＝x4﹣x3+x2﹣3x+1，B＝﹣2﹣x+x2，求2A﹣[B﹣（B﹣A）]．24．（10分）如图，∠AOB＝90°，OC在∠AOB的内部，分别作∠AOC、∠BOC的平分线OM、ON．（1）若∠BOC＝30°，求∠MON的度数；（2）若将OC绕点O顺时针旋转，使OC在∠AOB的外部且锐角∠BOC＝2x°，仍然分别作∠AOC、∠BOC的平分线OM、ON，画出示意图，你能求出∠MON的度数吗？若能，求出其值，若不能，试说明理由；（3）若将OC绕点O逆时针旋转，使OC在∠AOB的外部且锐角∠AOC＝2y°，仍然分别作∠AOC、∠BOC的平分线OM、ON，画出示意图，你还能求出∠MON的度数吗？若能，求出其值，若不能，说明理由．25．（10分）某市居民使用自来水按如下标准收费（水费按月缴纳）户月用水量单价不超过12m3的部分2元/m3超过12m3但不超过20m3的部分3元/m3超过20m3的部分4元/m3（1）某用户一个月用了14m3水，求该用户这个月应缴纳的水费（2）某户月用水量为n立方米（12＜n≤20），该用户缴纳的水费是39元，列方程求n 的值（3）甲、乙两用户一个月共用水40m3，设甲用户用水量为xm3，且12＜x≤28①当12＜x≤20时，甲、乙两用户一个月共缴纳的水费为元（用含x的整式表示）②当20＜x≤28时，甲、乙两用户一个月共缴纳的水费为元（用含x的整式表示）26．（10分）如图，在长方形ABCD中，AB＝8cm，BC＝6cm，点E是CD的中点，动点P 从A点出发，以每秒2cm的速度沿A→B→C→E运动，最终到达点E．若设点P运动的时间是t秒，那么当t取何值时，△APE的面积会等于10？参考答案与试题解析一．选择题（共16小题，满分32分，每小题2分）1．解：﹣3＜﹣1＜0＜1，故选：A．2．解：从正面看第一层是三个小正方形，第二层中间一个小正方形，故选：A．3．解：（1）a+b＝b+a，是等式，不是代数式；（2）1，是单项式，是代数式；（3）2x﹣1，是多项式，是代数式；（4），是分式，是代数式；（5）s＝πr2，是等式，不是代数式；（6）﹣，是单项式，是代数式；所以代数式有4个，故选：C．4．解：2a2与3a2属于同类项，故选：D．5．解：∵M＝﹣x+1，N＝x﹣5，M+N＝20，∴﹣x+1+x﹣5＝20，去分母得：﹣4x+6+x﹣30＝120，移项合并得：﹣3x＝144，解得：x＝﹣48．故选：B．6．解：①因为射线只有一个端点和一个方向，不可度量，所以射线AB与射线BA不是同一条射线，①说法不正确，故①不符合题意；②因为两点的所有连线中，可以有无数种连法，如折线、曲线、线段等，这些所有的线中，线段最短．所以②说法正确，故②符合题意；③因为连接两点间的线段的长度叫两点间的距离．所以③说法不正确，故③不符合题意；④因为经过两点有且只有一条直线，所以④说法正确，故④符合题意．所以正确的有②④共2个．故选：B．7．解：根据题意得：m＝2，n＝3，则m﹣n＝2﹣3＝﹣1．故选：B．8．解：∵关于x的方程（m﹣3）x|m﹣2|﹣3＝0是一元一次方程，∴|m﹣2|＝1且m﹣3≠0，解得m＝1．故选：C．9．解：根据平面图形的定义可得，B圆柱不是平面图形．故选：B．10．解：根据题意，得a（1﹣10%）2（1+20%）＝0.972a故选：C．11．解：∵a※b＝|a|﹣|b|﹣|a﹣b|，∴2※（﹣3）＝|2|﹣|﹣3|﹣|2﹣（﹣3）|＝2﹣3﹣|2+3|＝2﹣3﹣5＝﹣6，故选：B．12．解：∵点C是AB的中点，点D是BC的中点，∴AC＝BC＝AB，CD＝BD＝BC，则CD＝AD﹣AC＝AD﹣BC，①不符合题意；②符合题意；2AD﹣AB＝2AC+2CD﹣AB＝2CD，③符合题意；CD＝AB，④不符合题意；故选：B．13．解：设甲池原来有水x吨，则x+20＝（100﹣x）﹣30．故选：C．14．解：线段AB的中点C表示的数为：＝3，故选：B．15．解：∵a2+2a+7＝6，∴a2+2a＝﹣1，∴4a2+8a+7＝4（a2+2a）+7＝﹣1×4+7＝3．故选：A．16．解：坐公交车行驶的路程+步行行驶的路程＝甲、乙两地距离．设小红步行速度为xkm/h，得40×1.5+2.5x＝65，解得x＝2，小红步行速度为2km/h，故答案为：A．二．填空题（共4小题，满分12分，每小题3分）17．解：∵x＝﹣1是关于x的一元一次方程1﹣2x＝3m的解，∴1﹣2×（﹣1）＝3m，∴3m＝3，解得m＝1．故答案为：1．18．解：∵AF、AE为折痕，∠B′AD′＝20°，∴∠DAF＝∠D′AF＝∠FAB′+∠B′AD′＝∠FAB′+20°，∠BAE＝∠EAD′+∠B′AD′＝∠EAD′+20°，∵四边形ABCD为正方形，∴∠BAD＝90°，∴∠DAF+∠BAE+∠EAF＝∠FAB′+20°+∠EAD′+20°+∠FAB′+20°+∠EAD′＝90°，∴∠FAB′+∠EAD′＝15°，∴∠EAF＝∴∠FAB′+∠EAD′+∠B′AD′＝15°+20°＝35°．故答案为：35°．19．解：根据题中的新定义得：原式＝2×（﹣5+2）＝2×（﹣3）＝﹣6．故答案为：﹣6．20．解：一列数为：，，，，，，，，，，，，，，，，…则这列数也可变为：，，，，，，，，，，，，，，，…由上列数字可知，第一个数的分母是1+21＝3，这样的数有1个；第二个数的分母是1+22＝5，这样的数有2个；第三个数的分母是1+23＝9，这样的数有3个；…，∵1+2+3+…+63＝2016＜2019，∴这一组数的第2019个数是：，故答案为：．三．解答题（共6小题，满分56分）21．解：（1）原式＝﹣＝；（2）原式＝÷＝×＝．22．解：﹣x＝+，﹣x＝+﹣，﹣x＝﹣，x＝．23．解：∵A＝x4﹣x3+x2﹣3x+1，B＝﹣2﹣x+x2，∴原式＝2A﹣B+B﹣A＝A＝x4﹣x3+x2﹣3x+1．24．解：（1）∵OM平分∠AOC，ON平分∠BOC，∴∠MOC＝∠AOC，∠CON＝∠COB，∴∠MON＝∠MOC+∠CON＝∠AOC+∠COB＝（∠AOC+∠COB），∵∠AOC+∠COB＝∠AOB＝90°，∴∠MON＝（∠AOC+∠COB）＝×90°＝45°，∴∠MON的度数为45°；（2）如图所示，能，理由如下：∵OM平分∠AOC，ON平分∠BOC，∴∠MOC＝∠AOC，∠CON＝∠BOC，∵∠AOC＝∠AOB+∠BOC，∠AOB＝90°，∠BOC＝2x°，∴∠MOC＝（90°+2x°）＝45°+x°，∠CON＝×2x°＝x°，∴∠MON＝∠MOC﹣∠CON＝45°+x°﹣x°＝45°，∴∠MON的度数为45°；（3）如图所示，能，理由如下：∵OM平分∠AOC，ON平分∠BOC，∴∠COM＝∠AOC，∠CON＝∠COB，∵∠AOC＝2y°，∠AOB＝90°，∠COB＝∠AOC+∠AOB，∴∠CON＝×2y°，∠CON＝×（2y°+90°）＝y°+45°，∴∠MON＝∠CON﹣∠COM＝y°+45°﹣y°＝45°，∴∠MON的度数为45°．25．解：（1）由题意可得：2×12+3×（14﹣12）＝30元，答：该用户这个月应缴纳30元水费．（2）由题意可得，2×12+3（n﹣12）＝39，解得n＝17；（3）①∵12＜x≤20，∴乙用户用水量20≤40﹣x＜28，∴12×2+3（x﹣12）+12×2+3×8+4（40﹣x﹣20）＝（116﹣x）元；②∵20＜x≤28，∴乙用户用水量12≤40﹣x＜20，∴12×2+3×8+4（x﹣20）+12×2+3（40﹣x﹣12）＝（x+76）元；故答案为（116﹣x）元，（x+76）元．26．解：如图1，当点P在AB上，即0＜t≤4时，∵四边形ABCD是矩形，∴AD＝BC＝6，AB＝CD＝8．∵AP＝2t，∴S△APE＝×2t×6＝10，∴t＝．如图2，当点P在BC上，即4＜t≤7时，∵E是DC的中点，∴DE＝CE＝4．∵BP＝2t﹣8，PC＝6﹣（2t﹣8）＝14﹣2t．∴S＝（4+8）×6﹣×（2t﹣8）×8﹣（14﹣2t）×4＝10，解得：t＝7.5＞7舍去；当点P在EC上，即7＜t≤9时，PE＝18﹣2t．∴S△APE＝（18﹣2t）×6＝10，解得：t＝．总上所述，当t＝或时△APE的面积会等于10．。

2022-2023学年八年级(上)期末数学模拟试卷(一)

2022-2023学年八年级（上）期末数学模拟试卷（一）一、选择题（本大题10小题，每小题3分，共30分）每小题给出四个选项中只有一个是正确的，请把答题卡上对应题目所选的选项涂黑.1．（3分）生活垃圾处理是关系民生的基础性公益事业，加强生活垃圾管理，维护公共环境和节约资源是全社会共同的责任．下列四个垃圾分类标识中的图形是轴对称图形的是（）A．B．C．D．2．（3分）下列长度的三条线段（单位：cm），能组成三角形的是（）A．4，5，9B．8，8，15C．5，5，11D．3，6，9 3．（3分）下列运算正确的是（）A．（m+1）（m﹣1）＝m2﹣1B．（﹣3a2）2＝6a4C．a2⋅a3＝a6D．4．（3分）华为麒麟990芯片采用了最新的0.000000007米的工艺制程，数0.000000007用科学记数法表示为（）A．7×10﹣9B．7×10﹣8C．0.7×10﹣9D．0.7×10﹣8 5．（3分）若一个多边形的内角和是540°，则该多边形的边数为（）A．4B．5C．6D．76．（3分）如图，已知AB＝AC，添加下列条件仍不能使△ABD≌△ACD的是（）A．∠B＝∠C＝90°B．AD平分∠BAC C．AD平分∠BDCD．BD＝CD7．（3分）如图，△ABC中，AB＝AC，D是BC中点，下列结论中不正确的是（）A．∠B＝∠C B．AD⊥BC C．AD平分∠BAC D．AB＝2BD 8．（3分）如图，把一张长方形纸片沿对角线BD折叠，∠CBD＝25°，则∠ABF 的度数是（）A．25°B．30°C．40°D．50°9．（3分）在△ABC中，AC＜BC，用尺规作图的方法在BC上确定一点D，使AD+CD＝BC．根据作图痕迹判断，符合要求的是（）A．B．C．D．10．（3分）如图，在△ABC中，∠ACB＝90°，AC＞BC，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多可画（）A．9个B．7个C．6个D．5个二、填空题（本大题7小题，每小题4分，共28分）请将下列各题的正确答案填写在答题卡相应的位置上．14题图11．（4分）要使分式有意义，则x的取值范围为．12．（4分）分解因式：3y2﹣12＝．13．（4分）计算：＝．14．（4分）如图是两个边长分别为2a，a的正方形，则△ABC的面积是．15．（4分）全国最长、珠海最美的板障山慢行隧道自开通以来迅速成为网红打卡点，隧道全长约为1200米，小海慢跑的速度是a米/秒（a＞0），小东骑车的速度是小海慢跑速度的3倍，两人匀速通过隧道，那么小海花的时间比小东花的时间多秒（用含字母a的式子表示）．16．（4分）如图，Rt△ABC中，∠ABC＝90°，AB＝6，BC＝8，BD为△ABC 的角平分线，则点D到边AB的距离为．17．（4分）对于两个不相等的实数a，b，我们规定符号Min{a，b}表示a，b中的较小的值，如Min{2，4}＝2，按照这个规定，方程Min（其中x≠0）的解为．三.解答题（一）（本大题3小题，每小题6分，共18分）18．（6分）化简：2x（x﹣3y）+（5xy2﹣2x2y）÷y．19．（6分）如图，在△ABC中，AN是∠BAC的角平分线，∠B＝50°，∠ANC ＝80°．求∠C的度数．20．（6分）先化简再求值：，其中x＝1．四、解答题（二）（本大题3小题，每小题8分，共24分）21．（8分）如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．（1）在图中画出△ABC关于y轴对称的图形△A1B1C1，并写出点A1的坐标；（2）求△ABC的面积；（3）在x轴上有一点P使得P A+PB的值最小，则点P的坐标是．22．（8分）为了帮助湖北省武汉市防控新冠肺炎，某爱心组织筹集了部分资金，计划购买甲、乙两种救灾物资共2000件送往灾区，已知每件甲种物资的价格比每件乙种物资的价格贵10元，用350元购买甲种物资的件数恰好与用300元购买乙种物资的件数相同．（1）求甲、乙两种救灾物资每件的价格各是多少元？（2）经调查，灾区对甲种物资的需求量不少于乙种物资的1.5倍，该爱心组织共需要购买2000件物资，请问乙种物资最多能购买多少件？23．（8分）如图，△ABC，△ADE均是等边三角形，点B，D，E三点共线，连接CD，CE，且CD⊥BE．（1）求证：BD＝CE；（2）若线段DE＝3，求线段BD的长．五、解答题（三）（本大题2小题，每小题10分，共20分）24．（10分）已知（x+a）（x+b）＝x2+mx+n．（1）若a＝﹣3，b＝2，则m＝，n＝；（2）若m＝﹣2，，求的值；（3）若n＝﹣1，当时，求m的值．25．（10分）如图，在平面直角坐标系中，△ABC的顶点A在y轴上，顶点C 在x轴上，∠BAC＝90°，AB＝AC，点E为边AC上一点，连接BE交y轴于点F，交x轴于点G，作CD⊥BE交BE延长线于点D，且CD＝BF，连接AD，CF．（1）求证：△ABF≌△ACD；（2）若∠ACF＝2∠CBF，求证：∠ACO＝∠FCO；（3）在（2）的条件下，若点A的坐标为（0，2），求OC的长．2022-2023学年八年级（上）期末数学模拟试卷（一）参考答案与试题解析一、选择题（本大题10小题，每小题3分，共30分）每小题给出四个选项中只有一个是正确的，请把答题卡上对应题目所选的选项涂黑.1．（3分）生活垃圾处理是关系民生的基础性公益事业，加强生活垃圾管理，维护公共环境和节约资源是全社会共同的责任．下列四个垃圾分类标识中的图形是轴对称图形的是（）A．B．C．D．【解答】解：A、不是轴对称图形，故本选项不合题意；B、不是轴对称图形，故本选项不合题意；C、不是轴对称图形，故本选项不合题意；D、是轴对称图形，故本选项符合题意．故选：D．2．（3分）下列长度的三条线段（单位：cm），能组成三角形的是（）A．4，5，9B．8，8，15C．5，5，11D．3，6，9【解答】解：A、4+5＝9，不能构成三角形；B、8+8＞15，能构成三角形；C、5+5＜11，不能够组成三角形；D、3+6＝9，不能构成三角形．故选：B．3．（3分）下列运算正确的是（）A．（m+1）（m﹣1）＝m2﹣1B．（﹣3a2）2＝6a4C．a2⋅a3＝a6D．【解答】解：（m+1）（m﹣1）＝m2﹣1，故选项A正确；（﹣3a2）2＝9a4，故选项B错误；a2⋅a3＝a5，故选项C错误；2ab•（﹣ab）＝﹣a2b2，故选项D错误；故选：A．4．（3分）华为麒麟990芯片采用了最新的0.000000007米的工艺制程，数0.000000007用科学记数法表示为（）A．7×10﹣9B．7×10﹣8C．0.7×10﹣9D．0.7×10﹣8【解答】解：数0.00 000 0007用科学记数法表示为7×10﹣9．故选：A．5．（3分）若一个多边形的内角和是540°，则该多边形的边数为（）A．4B．5C．6D．7【解答】解：设多边形的边数是n，则（n﹣2）•180°＝540°，解得n＝5．故选：B．6．（3分）如图，已知AB＝AC，添加下列条件仍不能使△ABD≌△ACD的是（）A．∠B＝∠C＝90°B．AD平分∠BAC C．AD平分∠BDCD．BD＝CD【解答】解：A、符合HL定理，能推出△ABD≌△ACD，故本选项错误；B、符合SAS定理，能推出△ABD≌△ACD，故本选项错误；C、不符合全等三角形的判定定理，不能推出△ABD≌△ACD，故本选项正确；D、符合SSS定理，能推出△ABD≌△ACD，故本选项错误；故选：C．7．（3分）如图，△ABC中，AB＝AC，D是BC中点，下列结论中不正确的是（）A．∠B＝∠C B．AD⊥BC C．AD平分∠BAC D．AB＝2BD 【解答】解：∵△ABC中，AB＝AC，D是BC中点∴∠B＝∠C，（故A正确）AD⊥BC，（故B正确）∠BAD＝∠CAD（故C正确）无法得到AB＝2BD，（故D不正确）．故选：D．8．（3分）如图，把一张长方形纸片沿对角线BD折叠，∠CBD＝25°，则∠ABF 的度数是（）A．25°B．30°C．40°D．50°【解答】解：由折叠可得：∠CBD＝∠EBD＝25°，则∠EBC＝∠CBD+∠EBD＝50°．∵四边形ABCD是长方形，∴∠ABC＝90°，∴∠ABF＝90°﹣∠EBC＝40°．故选：C．9．（3分）在△ABC中，AC＜BC，用尺规作图的方法在BC上确定一点D，使AD+CD＝BC．根据作图痕迹判断，符合要求的是（）A．B．C．D．【解答】解：A、BD＝BA，不能得到AD+CD＝BC，所以A选项错误；B、DA＝DC，AD+CD＝2CD，所以B选项错误；C、CD＝CA，不能得到AD+CD＝BC，所以C选项错误；D、BD＝AD，则AD+CD＝BD+CD＝BC，所以D选项正确．故选：D．10．（3分）如图，在△ABC中，∠ACB＝90°，AC＞BC，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多可画（）A．9个B．7个C．6个D．5个【解答】解：如图：①以B为圆心，BC长为半径画弧，交AB于点D，△BCD 就是等腰三角形；②以A为圆心，AC长为半径画弧，交AB于点E，△ACE 就是等腰三角形；③以C为圆心，BC长为半径画弧，交AC于点F，交AB 于H，△BCF，△BCH就是等腰三角形；④分别作AB，BC，AC的垂直平分线，也可以得到三个分别以AB，BC，AC为底的等腰三角形．所以一共有1+1+2+3＝7（个）三角形．故选：B．二、填空题（本大题7小题，每小题4分，共28分）请将下列各题的正确答案填写在答题卡相应的位置上．14题图11．（4分）要使分式有意义，则x的取值范围为x≠﹣2．【解答】解：由题意可知：x+2≠0，∴x≠﹣2故答案为：x≠﹣212．（4分）分解因式：3y2﹣12＝3（y+2）（y﹣2）．【解答】解：3y2﹣12＝3（y2﹣4）＝3（y+2）（y﹣2），故答案为：3（y+2）（y﹣2）．13．（4分）计算：＝4．【解答】解：原式＝3+1＝4，故答案为：4．14．（4分）如图是两个边长分别为2a，a的正方形，则△ABC的面积是．【解答】解：∵两个正方形的边长分别为2a，a，∴△ABC的高为：2a+a，底边为：BC＝a，∴△ABC的面积是：（2a+a）•a＝a2．故答案为：a2．15．（4分）全国最长、珠海最美的板障山慢行隧道自开通以来迅速成为网红打卡点，隧道全长约为1200米，小海慢跑的速度是a米/秒（a＞0），小东骑车的速度是小海慢跑速度的3倍，两人匀速通过隧道，那么小海花的时间比小东花的时间多秒（用含字母a的式子表示）．【解答】解：小海慢跑的速度是a米/秒（a＞0），则小东骑车的速度是3a米/秒，小海花的时间比小东花的时间多：﹣＝＝（秒）；故答案为：． 16．（4分）如图，Rt △ABC 中，∠ABC ＝90°，AB ＝6，BC ＝8，BD 为△ABC 的角平分线，则点D 到边AB 的距离为．【解答】解：过D 作DE ⊥AB 于E ，DF ⊥BC 于F ，∵BD 为△ABC 的角平分线，∴DE ＝DF ，设DE ＝DF ＝R ，∵∠ABC ＝90°，AB ＝6，BC ＝8，∴S △ABC ＝＝＝24， ∴S △ABD +S △DBC ＝24，∵AB ＝6，BC ＝8，∴R +＝24，解得：R ＝，即DF ＝，∴点D 到边AB 的距离是，故答案为：．17．（4分）对于两个不相等的实数a ，b ，我们规定符号Min {a ，b }表示a ，b 中的较小的值，如Min {2，4}＝2，按照这个规定，方程Min（其中x ≠0）的解为 4 ．【解答】解：（1）x＞0时，∵Min（其中x≠0），∴﹣＝﹣1，∴＝1，解得：x＝4．（2）x＜0时，∵Min（其中x≠0），∴＝﹣1，∴＝1，解得：x＝2，∵2＞0，∴x＝2不符合题意．综上，可得：方程Min（其中x≠0）的解为4．故答案为：4．三.解答题（一）（本大题3小题，每小题6分，共18分）18．（6分）化简：2x（x﹣3y）+（5xy2﹣2x2y）÷y．【解答】解：原式＝2x2﹣6xy+5xy﹣2x2＝﹣xy．19．（6分）如图，在△ABC中，AN是∠BAC的角平分线，∠B＝50°，∠ANC ＝80°．求∠C的度数．【解答】解：∵∠ANC＝∠B+∠BAN，∴∠BAN＝∠ANC﹣∠B＝80°﹣50°＝30°，∵AN是∠BAC角平分线，∴∠BAC＝2∠BAN＝60°，在△ABC中，∠C＝180°﹣∠B﹣∠BAC＝70°．20．（6分）先化简再求值：，其中x＝1．【解答】解：原式＝（﹣）×＝×＝，当x＝1时，原式＝＝﹣．四、解答题（二）（本大题3小题，每小题8分，共24分）21．（8分）如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．（1）在图中画出△ABC关于y轴对称的图形△A1B1C1，并写出点A1的坐标；（2）求△ABC的面积；（3）在x轴上有一点P使得P A+PB的值最小，则点P的坐标是（2，0）．【解答】解：（1）如图所示，△A1B1C1即为所求，点A1（﹣1，1）．（2）S＝3×3﹣×1×2﹣×1×3﹣×2×3＝．△ABC（3）如图，点P即为所求作，P（2，0）．22．（8分）为了帮助湖北省武汉市防控新冠肺炎，某爱心组织筹集了部分资金，计划购买甲、乙两种救灾物资共2000件送往灾区，已知每件甲种物资的价格比每件乙种物资的价格贵10元，用350元购买甲种物资的件数恰好与用300元购买乙种物资的件数相同．（1）求甲、乙两种救灾物资每件的价格各是多少元？（2）经调查，灾区对甲种物资的需求量不少于乙种物资的1.5倍，该爱心组织共需要购买2000件物资，请问乙种物资最多能购买多少件？【解答】解（1）设每件乙种物品的价格是x元，则每件甲种物品的价格是（x+10）元，根据题意得：＝，解得：x＝60，经检验，x＝60是原方程的解，∴x+10＝60+10＝70，答：甲、乙两种救灾物资每件的价格分别为70元、60元；（2）设购买乙种物品件数为m件，根据题意得：2000﹣m≥1.5m，解得：m≤800，∴乙种物资最多能购买800件．答：乙种物资最多能购买800件．23．（8分）如图，△ABC，△ADE均是等边三角形，点B，D，E三点共线，连接CD，CE，且CD⊥BE．（1）求证：BD＝CE；（2）若线段DE＝3，求线段BD的长．【解答】证明：（1）∵△ABC、△ADE是等边三角形，∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝60°，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，∴∠BAD＝∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴BD＝CE；（2）∵△ADE是等边三角形，∴∠ADE＝∠AED＝60°，∴∠ADB＝120°，∵△ABD≌△ACE，∴∠AEC＝∠ADB＝120°，∴∠CED＝∠AEC﹣∠AED＝60°，∵CD⊥BE，∴∠CDE＝90°，∴∠DCE＝30°，∴BD＝CE＝2DE＝6．五、解答题（三）（本大题2小题，每小题10分，共20分）24．（10分）已知（x+a）（x+b）＝x2+mx+n．（1）若a＝﹣3，b＝2，则m＝﹣1，n＝﹣6；（2）若m＝﹣2，，求的值；（3）若n＝﹣1，当时，求m的值．【解答】解：（1）将a＝﹣3，b＝2代入（x+a）（x+b）得：（x+a）（x+b）＝（x﹣3）（x+2）＝x2﹣x﹣6＝x2+mx+n，∴m＝﹣1，n＝﹣6．故答案为：﹣1，﹣6．（2）∵（x+a）（x+b）＝x2+（a+b）x+ab＝x2+mx+n．∴，∴+＝＝＝＝﹣4．（3）∵a+b＝m，ab＝n＝﹣1，，∴，∴，∴，∴m2﹣2×（﹣1）+4m+2＝0，∴m2+4m+4＝0，∴（m+2）2＝0，∴m＝﹣2．25．（10分）如图，在平面直角坐标系中，△ABC的顶点A在y轴上，顶点C 在x轴上，∠BAC＝90°，AB＝AC，点E为边AC上一点，连接BE交y轴于点F，交x轴于点G，作CD⊥BE交BE延长线于点D，且CD＝BF，连接AD，CF．（1）求证：△ABF≌△ACD；（2）若∠ACF＝2∠CBF，求证：∠ACO＝∠FCO；（3）在（2）的条件下，若点A的坐标为（0，2），求OC的长．【解答】解（1）证明：∵CD⊥BE，∴∠CDE＝∠BAC＝90°，∵∠CED＝∠AEB，∴∠DCE＝∠ABF，在△ABF和△ACD中，，∴△ABF≌△ACD（SAS）；（2）∵△ABF≌△ACD，∴AF＝AD，∠BAF＝∠CAD，∴∠BAC＝∠F AD＝90°，∴∠ADF＝45°，∵∠ACB＝∠ADB＝45°，∠AED＝∠BEC，∴∠DAE＝∠CBE，∵∠DAF＝∠COF＝90°，∴AD∥OC，∴∠DAE＝∠ACO，∴∠CBE＝∠ACO，∵∠ACF＝2∠CBF，∴∠ACF＝2∠ACO，∴∠FCO＝∠ACO．（3）过点D作DH⊥OC交OC于点H，∵∠AOC＝∠COF＝90°，∠ACO＝∠FCO，∴∠OAC＝∠OFC，∴AC＝CF，∵CA＝CF，CO⊥AF，∴OA＝OF＝2，∴AD＝AF＝4，∵AD∥OC，∴AO＝DH＝2，∵DH⊥OC，∠DCG＝45°，∴DH＝HC＝2，∴OC＝OH+HC＝6．。

【苏科版】初一数学下期末模拟试卷(附答案)

一、选择题1．如图，按下面的程序进行运算，规定：程序运行到“判断结果是否大于28”为一次运算，若运算进行了3次才停止，则x 的取值范围是（）A ．24x <≤B ．24x ≤<C ．24x <<D ．24x ≤≤2．如果方程组54356x y k x y -=⎧⎨+=⎩的解中的x 与y 互为相反数，则k 的值为（） A ．1 B ．1或1- C ．27- D ．5-3．把方程23x y -=改写成用含x 的式子表示y 的形式，正确的是（）A ．23x y =+B ．32y x +=C ．23y x =-D ．32y x =- 4．二元一次方程组7317x y x y +=⎧⎨+=⎩的解是（） A ．52x y =⎧⎨=⎩ B ．25x y =⎧⎨=⎩ C ．61x y =⎧⎨=⎩ D ．16x y =⎧⎨=⎩5．不等式组10,{360x x -≤-<的解集在数轴上表示正确的是（） A ．B ．C ．D ．6．已知关于x 、y 方程组734521x y x y m +=⎧⎨-=-⎩的解能使等式4x ﹣3y ＝7成立，则m 的值为（）A ．8B ．0C ．4D ．﹣2 7．如图，点A 的坐标是()3,1-将四边形ABCD 先向左平移3个单位，再向上平移2个单位，那么点A 的对应点A '的坐标是（）A ．()0,1B ．()6,1C ．()0,3-D ．()6,3- 8．如图，线段OA ，OB 分别从与x 轴和y 轴重合的位置出发，绕着原点O 顺时针转动，已知OA 每秒转动45︒，OB 的转动速度是每秒转动30，则第2020秒时，OA 与OB 之间的夹角的度数为（）A ．90︒B ．145︒C ．150︒D ．165︒ 9．和数轴上的点一一对应的数是（）A ．自然数B ．有理数C ．无理数D ．实数 10．下列命题中，属于假命题的是（）A ．如果三角形三个内角的度数比是1:2:3，那么这个三角形是直角三角形B ．内错角不一定相等C ．平行于同一直线的两条直线平行D ．若数a 使得a a >-，则a 一定小于0 11．不等式组32153x x ->⎧⎨-<-⎩的解集在数轴上的表示是（） A ． B ．C ．D ．12．若不等式组11x x m->⎧⎨<⎩无解，那么m 的取值范围是（） A ．2m > B ．2m < C ．2m ≥ D ．2m ≤二、填空题13．某超市促销活动，将车厘子、波罗蜜、山竹三种水果采用三种不同方式搭配成礼盒，分别是蒸蒸日上礼盒、独占鳌头礼盒、吉祥如意礼盒，将礼盒进行销售，每盒的总成本为盒中车厘子、波罗蜜、山竹三种水果成本之和，盒子成本忽略不计，蒸蒸日上每盒分别装有车厘子、波罗蜜、山竹三种水果8千克，4千克，3千克；独占鳌头每盒装有车厘子、波罗蜜、山竹三种水果3千克，8千克，6千克；蒸蒸日上每盒的总成本是每千克车厘子水果成本的14倍，每盒蒸蒸日上的销售利润是60%，每盒独占鳌头的售价是成本的43倍，每盒吉祥如意在成本上提高60%标价后打八折出售，获利为每千克车厘子水果成本的2.8倍，当销售蒸蒸日上、独占鳌头、吉祥如意三种礼盒的数量之比为5:2:5，则销售的总利润率为______．14．若关于x ，y 的方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解为46x y =⎧⎨=⎩，则方程组111222435435a x b y c a x b y c +=⎧⎨+=⎩的解为______．15．若点A （m +2，﹣3）与点B （﹣4，n +5）在二四象限角平分线上，则m +n ＝_____． 16．如图，正方形ABCD 的各边分别平行于x 轴或y 轴，蚂蚁甲和蚂蚁乙都由点E （3，0）出发，同时沿正方形ABCD 的边逆时针匀速运动，蚂蚁甲的速度为3个单位长度/秒，蚂蚁乙的速度为1个单位长度/秒，则两只蚂蚁出发后，蚂蚁甲第3次追上蚂蚁乙的坐标是_____．17．对于有理数,a b ，我们规定*a b b ab =-（1）求(2)*1-的值．（2）若有理数x 满足(2)*36x -=，求x 的值．18．如图，CB ∥OA ，∠B ＝∠A ＝100°，E 、F 在CB 上，且满足∠FOC ＝∠AOC ，OE 平分∠BOF ，若平行移动AC ，当∠OCA 的度数为_____时，可以使∠OEB ＝∠OCA ．19．关于x 的不等式组460930x x ->⎧⎨-≥⎩的所有整数解的积是__________．20．关于x 、y 的二元一次方程组3234x y a x y a +=+⎧⎨+=-⎩的解满足x+y ＞2，则a 的取值范围为__________．三、解答题21．解不等式：()3157x x +≤+，并把它的解集在数轴上表示出来．22．某市出租车的计费标准如下：行程3km 以内（含3km ），收费7元．行程超过3km ，如果往返乘同一出租车并且中间等候时间不超过3min ，超过3km 的部分按每千米1.6元计费，另加收1.6元等候费；如果返程时不再乘坐此车，超过3km 的部分按每千米2.4元计费．小文等4人从A 处到B 处办事，在B 处停留时间在3min 之内，然后返回A 处．现在有两种往返方案：方案一：去时4人同乘一辆出租车，返回都乘公交车（公交车票为每人2元）；方案二：4人乘同一辆出租车往返．（1）若A ，B 两地相距1.2km ，方案一付费_____元，方案二付费______元；（2）若A ，B 两地相距2.5km ，方案一付费_____元，方案二付费______元；（3）设A ，B 两地相距x km （x ＜12），请问选择那种方案更省钱？23．解方程组：22432x y x y +=⎧⎨+=⎩①②． 24．在平面直角坐标系中，点A 从原点O 出发，沿x 轴正方向按半圆形弧线不断向前运动，其移动路线如图所示，其中半圆的半径为1个单位长度，这时点1234,,,A A A A 的坐标分别为()()()()12340,0,1,12,03,1A A A A -，按照这个规律解决下列问题：()1写出点5678,,,,A A A A 的坐标；()2点2018A 的位置在_____________(填“x 轴上方”“x 轴下方”或“x 轴上”)；()3试写出点n A 的坐标(n 是正整数)．25．“比差法”是数学中常用的比较两个数大小的方法，即0,0,0,a b a b a b a b a b a b ->>⎧⎪-==⎨⎪-<<⎩则则则 192与2的大小；1922194--=-，161925<<，则4195<<，19221940∴--=->，1922∴->．请根据上述方法解答以下问题：（1）比较大小：329_______3；（2）比较223-与3-的大小，并说明理由．26．利用网格画图，每个小正方形边长均为1（1）过点C画AB的平行线CD；（2）仅用直尺,过点C画AB的垂线，垂足为E；（3）连接CA、CB，在线段CA、CB、CE中，线段______最短，理由___________．（4）直接写出△ABC的面积为 _________．【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】根据程序运算进行了3次才停止，即可得出关于x的一元一次不等式组：()()33222833322228xx⎧--≤⎪⎨⎡⎤--->⎪⎣⎦⎩，解之即可得出x的取值范围．【详解】解：依题意，得：()()33222833322228xx⎧--≤⎪⎨⎡⎤--->⎪⎣⎦⎩①②，由①得：936x≤4x ∴≤，由②得：()398x -＞30，98x ∴-＞10，x ＞2，所以不等式组的解集为：24x <≤．故选：A ．【点睛】本题考查了程序框图中的一元一次不等式组的应用，找准不等关系，正确列出一元一次不等式组是解题的关键．2．C解析：C【分析】根据x 与y 互为相反数，得到y=-x ，代入方程组求出k 的值即可．【详解】解：由题意得：y=-x ，代入方程组得：926x k x ⎧⎨-⎩＝＝， ∴x=-3解得：k=-27．故选：C ．【点睛】此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．3．C解析：C【分析】将x 看做常数移项求出y 即可得．【详解】由2x-y=3知2x-3=y ，即y=2x-3，故选C ．【点睛】此题考查了解二元一次方程，解题的关键是将x 看做已知数求出y ．4．A解析：A【分析】方程组利用加减消元法求出解即可．【详解】解：7317x y x y +=⎧⎨+=⎩①②， ②﹣①得：2x ＝10，解得：x ＝5，把x ＝5代入①得：y ＝2，则方程组的解为52x y =⎧⎨=⎩．故选：A ．【点睛】本题考查了二元一次方程组的解法以及二元一次方程组的解的定义：一般地，二元一次方程组的两个方程的公共解，叫做二元一次方程组的解．本题还可以利用代入法求解． 5．D解析：D【解析】试题分析：10{360x x -≤-<①②，由①得：x≥1，由②得：x ＜2，在数轴上表示不等式的解集是：，故选D ．考点：1．在数轴上表示不等式的解集；2．解一元一次不等式组．6．A解析：A【分析】先利用加减消元法求出方程组734437x y x y +=⎧⎨-=⎩的解，再代入方程521x y m -=-即可得．【详解】由题意得：方程组734437x y x y +=⎧⎨-=⎩①②的解能使等式521x y m -=-成立，由①+②得：1111x =，解得1x =，将1x =代入①得：734y +=，解得1y =-，将1,1x y ==-代入521x y m -=-得：()5211m -⨯-=-，解得8m =，故选：A ．【点睛】本题考查了利用加减消元法解二元一次方程组，熟练掌握方程组的解法是解题关键．7．A解析：A【分析】四边形ABCD与点A平移相同，据此即可得到点A′的坐标．【详解】四边形ABCD先向左平移3个单位，再向上平移2个单位，因此点A(3,−1) 也先向左平移3个单位，再向上平移2个单位，故A′坐标为（0，1）．故选：A．【点睛】本题考查了坐标与图形的变化−−平移，本题本题考查了坐标系中点、线段的平移规律，在平面直角坐标系中，图形的平移与图形上某点的平移相同．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．8．C解析：C【分析】先求出线段OA、OB第2020秒时旋转的度数，再除以360︒得到余几，确定最终状态时OA、OB的位置，再求夹角度数．【详解】⨯︒=︒，解：第2020秒时，线段OA旋转度数=20204590900⨯︒=︒，线段OB旋转度数=20203060600︒÷︒=︒，90900360252180︒÷︒=︒，60600360168120此时OA、OB的位置如图所示，︒-︒=︒．OA与OB之间的夹角度数=270120150故选：C．【点睛】本题考查线段的旋转，解题的关键是利用周期问题的方法确定最终状态时OA、OB所在位置．9．D解析：D【分析】根据实数与数轴上的点是一一对应关系，即可得出．【详解】解：根据实数与数轴上的点是一一对应关系．故选：D．【点睛】本题考查了实数与数轴的对应关系，任意一个实数都可以用数轴上的点表示；反之，数轴上的任意一个点都表示一个实数．10．D解析：D【分析】利用三角形内角和对A进行判断；根据内错角的定义对B进行判断；根据平行线的判定方法对C进行判断；根据绝对值的意义对D进行判断．【详解】解：A、如果三角形三个内角的度数比是1：2：3，则三个角的度数分别为30°，60°，90°，所以这个三角形是直角三角形，所以A选项为真命题；B、内错角不一定相等，所以B选项为真命题；C、平行于同一直线的两条直线平行，所以C选项为真命题；D、若数a使得|a|＞-a，则a为不等于0的实数，所以D选项为假命题．故选：D．【点睛】本题考查了命题与定理：命题的“真”“假”是就命题的内容而言．任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．11．C解析：C【分析】先解不等式组求出其解集，然后根据不等式的解集在数轴上的表示方法进行判断即可．【详解】解：对不等式组32153 xx->⎧⎨-<-⎩，解不等式3x－2＞1，得x＞1，解不等式x－5＜﹣3，得x＜2，∴不等式组的解集是1＜x＜2，不等式组的解集在数轴上表示为：．故选：C．【点睛】本题考查了一元一次不等式组的解法和不等式的解集在数轴上的表示，属于基础题目，熟练掌握解一元一次不等式组的方法是解题的关键．12．D解析：D【分析】先求出11x ->的解，再根据不等式组无解，可得关于m 的不等式，根据解不等式，可得答案．【详解】解：解11x ->得2x >．∵不等式组11x x m ->⎧⎨<⎩无解， ∴2m ≤，故选：D ．【点睛】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．二、填空题13．44【分析】分别设每千克车厘子菠萝蜜山竹三种水果的成本价分别为xyz 再由题意分别求出每一种礼盒的成本利润则可求解【详解】设设每千克车厘子菠萝蜜山竹三种水果的成本价分别为xyz 由题意可得：∴蒸蒸日上的解析：44%【分析】分别设每千克车厘子、菠萝蜜、山竹三种水果的成本价分别为x 、y 、z ，再由题意分别求出每一种礼盒的成本、利润则可求解．【详解】设设每千克车厘子、菠萝蜜、山竹三种水果的成本价分别为x 、y 、z ，由题意可得：84314x y z x ++=∴436y z x +=蒸蒸日上的总成本为：84314x y z x ++=，每盒的利润是：342(843)55x y z x ++=；独占鳌头的总成本为：38632615x y z x x x ++=+⨯=，每盒的售价是：4(386)3x y z ++，每盒的利润是：()()41(386)386386533x y z x y z x y z x ++-++=++= 每盒吉祥如意的销售利润是2.8x ，则成本为：()2.810160%80%1x x =+⨯-，当销售蒸蒸日上、独占鳌头、吉祥如意三种礼盒的数量之比为5:2:5，总成本是：51425510150x x x x ⨯+⨯+⨯=，总利润是：425255 2.8665x x x x ⨯+⨯+⨯= ∴总利润是6644%150x x= 故答案为：44%【点睛】本题考查了三元一次方程的应用；理解题意，能够通过所给的量之间的关系列出正确的方程是解题的关键．14．【分析】利用换元法解二元一次方程组即可得【详解】方程组可变形为令则方程组可化为由题意得：此方程组的解为因此有解得即所求方程组的解为故答案为：【点睛】本题考查了二元一次方程组的特殊解法观察两个方程组正解析：510x y =⎧⎨=⎩【分析】利用换元法解二元一次方程组即可得．【详解】方程组111222435435a x b y c a x b y c +=⎧⎨+=⎩可变形为11122243554355a x b y c a x b y c ⎧+=⎪⎪⎨⎪+=⎪⎩，令43,55m x n y ==，则方程组可化为111222a m b n c a m b n c +=⎧⎨+=⎩，由题意得：此方程组的解为46m n =⎧⎨=⎩，因此有445365x y ⎧=⎪⎪⎨⎪=⎪⎩，解得510x y =⎧⎨=⎩，即所求方程组的解为510 xy=⎧⎨=⎩，故答案为：510 xy=⎧⎨=⎩．【点睛】本题考查了二元一次方程组的特殊解法，观察两个方程组，正确换元是解题关键．15．【分析】根据二四象限角平分线上点的特征解答【详解】∵A（m+2﹣3）在二四象限角平分线上∴m+2＝3解得m＝1∵点B（﹣4n+5）在二四象限角平分线上∴n+5＝4解得n＝﹣1∴m+n＝1﹣1＝0故答解析：【分析】根据二四象限角平分线上点的特征解答．【详解】∵A（m+2，﹣3）在二四象限角平分线上，∴m+2＝3，解得m＝1，∵点B（﹣4，n+5）在二四象限角平分线上，∴n+5＝4，解得n＝﹣1，∴m+n＝1﹣1＝0．故答案为：0．【点睛】本题考查坐标与图形的关系，熟练掌握二四象限角平分线上点的特征是解题关键．16．（﹣10）【分析】由图可知正方形的边长为4故正方形的周长为16因为蚂蚁甲和蚂蚁乙的速度分别为3个和1个单位所以用正方形的周长除以（3−1）可得蚂蚁甲第1次追上蚂蚁乙时间从而算出蚂蚁乙所走过的路程则第解析：（﹣1，0）．【分析】由图可知，正方形的边长为4，故正方形的周长为16，因为蚂蚁甲和蚂蚁乙的速度分别为3个和1个单位，所以用正方形的周长除以（3−1），可得蚂蚁甲第1次追上蚂蚁乙时间，从而算出蚂蚁乙所走过的路程，则第二次和第三次相遇过程中蚂蚁乙所走过的路程和第一次是相同的，从而结合图形可求得蚂蚁甲第3次追上蚂蚁乙的坐标．【详解】解：由图可知，正方形的边长为4，故正方形的周长为16∴蚂蚁甲第1次追上蚂蚁乙时间：16÷（3﹣1）＝8（秒）蚂蚁乙走的路程为：1×8＝8，∴此时相遇点的坐标为：（﹣1，0），因为蚂蚁甲和蚂蚁乙的速度比为3：1，∴再经过16秒蚂蚁甲和蚂蚁乙第三次相遇，相遇点坐标为：（﹣1，0），故答案为：（﹣1，0）．【点睛】本题考查了物体在平面直角坐标系中运动的规律问题，明确相遇问题的计算公式及多次相遇中物体所走路程的规律是解题的关键．17．（1）3；（2）【分析】（1）由新定义的运算法则进行计算即可得到答案；（2）由新定义列出方程解方程即可得到答案【详解】解：∵∴；（2）由题意则∵∴解得：【点睛】本题考查了一元一次方程新定义的运算法则解析：（1）3；（2）1x =．【分析】（1）由新定义的运算法则进行计算，即可得到答案；（2）由新定义列出方程，解方程即可得到答案．【详解】解：∵*a b b ab =-，∴(2)*11(2)1123-=--⨯=+=；（2）由题意，则∵(2)*36x -=，∴(2)*333(2)6x x -=--=，解得：1x =．【点睛】本题考查了一元一次方程，新定义的运算法则，解题的关键是掌握运算法则进行解题． 18．60°【分析】设∠OCA=a ∠AOC=x 利用三角形外角内角和定理平行线定理即可解答【详解】解：设∠OCA=a ∠AOC=x 已知CB ∥OA ∠B=∠A=100°即a+x=80°又因为∠OEB=∠EOC+∠解析：60°【分析】设∠OCA=a,∠AOC=x,利用三角形外角，内角和定理，平行线定理即可解答.【详解】解：设∠OCA=a,∠AOC=x,已知CB ∥OA ，∠B=∠A=100°，即a+x=80°，又因为∠OEB=∠EOC+∠ECO=40°+x.当∠OEB=∠OCA ，a=80°-x,40°+x=a,解得∠OCA=60°.【点睛】本题考查角度变换和平行线定理的综合运用，熟悉掌握是解题关键.19．6【分析】分别解出两不等式的解集再求其公共解然后求得整数解进行相乘即可【详解】解：由①得；由②得∴不等式组的解集为∴不等式组的解集中所有整数解有：23∴故答案为：6【点睛】此题考查了一元一次不等式组解析：6【分析】分别解出两不等式的解集，再求其公共解，然后求得整数解进行相乘即可．【详解】解：460930->⎧⎨-≥⎩①②x x 由①得32x >；由②得3x ≤ ∴不等式组的解集为332x <≤， ∴不等式组的解集中所有整数解有：2，3，∴23=6⨯ ，故答案为：6．【点睛】此题考查了一元一次不等式组的整数解．解题的关键在于正确解得不等式组或不等式的解集，然后再根据题目中对于解集的限制得到下一步所需要的条件，再根据得到的条件进而求得不等式组的整数解．20．a ＜-2【解析】试题解析：a ＜-2．【解析】试题32{34x y a x y a +=++=-①②由①-②×3，解得2138a x +=-；由①×3-②，解得678a y +=； ∴由x+y ＞2，得2136788a a ++-+＞2，解得，a ＜-2．考点：1解一元一次不等式；2．解二元一次方程组．三、解答题21．2x ≥-，在数轴上表示见解析【分析】利用不等式的性质解一元一次不等式的解集，然后将解集表示在数轴上即可．【详解】解：3(1)57x x +≤+，去括号，得： 3357x x +≤+，移项、合并同类项，得：24x -≤ ，化系数为1，得：2x ≥- ，∴不等式的解集为2x ≥-，不等式的解集在数轴上表示为：【点睛】本题考查解一元一次不等式、在数轴上表示不等式的解集，熟练掌握一元一次不等式的解法步骤，会在数轴上表示不等式的解集是解答的关键，特别注意不等号的方向和端点的空（实）心．22．（1）15,8.6；（2）15,11.8；（3）当0＜x ＜5时，方案二更省；当x=5时，方案一、二一样；当5＜x ＜12时，方案一更省．【分析】（1）根据题意分别列出表示两种方案费用的代数式，进行计算即可得到答案；（2）根据题意分别列出表示两种方案费用的代数式，进行计算即可得到答案；（3）当0＜x≤1.5时，得到方案一：15元；方案二：8.6元，于是得到方案二更省钱；当1.5＜x≤3时，求得方案一：15元；方案二：()7 1.623 1.6 3.2 3.8x x +-+=+，即当x=3，有最大费用13.4元，13.4＜15，于是得到方案二更省钱；当x ＞3时；求得方案一：7+2.4（x-3）+8=2.4x+7.8；方案二：7+1.6（2x-3）+1.6=3.2x+3.8；列方程或不等式，再讨论即可得到结论．【详解】解：（1） 1.2＜3，∴ 方案一：7+42=7+8=15⨯（元），方案二：7+1.6=8.6（元），故答案为：15,8.6.（2）∵2.5＜3，∴方案一付费：7+4×2=15元，方案二付费：()7+53 1.6 1.611.8-⨯+=，故答案为：15,11.8.（3）当0＜x≤1.5时，方案一：7+42=7+8=15⨯元；方案二：7+1.6=8.6元，∴方案二更省钱；当1.5＜x≤3时，方案一：7+42=7+8=15⨯元；方案二：()7 1.623 1.6 3.2 3.8x x +-+=+，即当x=3，最大费用为：13.4元，方案二：13.4＜15∴方案二更省钱；当x ＞3时；方案一：()7 2.438 2.47.8x x +-+=+；方案二：()7 1.623 1.6 3.2 3.8x x +-+=+；当2.47.8 3.2 3.8x x +=+时，解得：5x =；∴当x=5时，两者均可，当2.47.8x +＜3.2 3.8x +时，0.8x ∴-＜4-，∴x ＞5，所以x ＞5时方案一更省，当2.47.8x +＞3.2 3.8x +时，0.8x ∴-＞4-，∴x ＜5，所以x ＜5时，方案二更省；综上可得：当0＜x ＜5时，方案二更省；当x=5时，方案一、二一样；当5＜x ＜12 时，方案一更省．【点睛】本题考查了列代数式，一元一次方程的应用，一元一次不等式的应用，最优化选择问题，解答本题的关键是根据题目所示的收费标准，列出x 的关系式，再计算与比较．23．22x y =⎧⎨=-⎩．【分析】根据自己的特长,选择代入消元法或加减消元法求解即可.【详解】由22432x y x y +=⎧⎨+=⎩①②解法1：①×3-②，得24=x ，解得：2x =，把2x =代入①，解得2y =-，∴原方程组的解是22x y =⎧⎨=-⎩；解法2：由①得：22y x =-③把③代入②得，43(22)2x x +-=解得：2x =，把2x =代入③，得2y =-，∴原方程组的解是22x y =⎧⎨=-⎩．解法3：由①×2得：424x y +=③，由②-③得，2y =-把2y =-代入①，解得2x =，∴原方程组的解是22x y =⎧⎨=-⎩．【点睛】本题考查了二元一次方程组的解法，灵活运用代入消元法或加减消元法是解题的关键. 24．()()514,0A ，()65,1A ，()76,0A ，()87,1A -；()2x 轴上方；()3 A （n-1,0）或()1,1A n -或()1,0A n -或()1,1A n --【分析】()1可根据点在图形中的位置及前4点坐标直接求解；()2根据图形可知点的位置每4个数一个循环，20184504...2÷=，进而判断2018A 与2A 的纵坐标相同在x 轴上方，即可求解；()3根据点的坐标规律可分4种情况分别写出坐标即可求解．【详解】解：（1）由数轴可得：()54,0A ，()65,1A ，()76,0A ，()87,1A -；（2）根据图形可知点的位置每4个数一个循环，20184504...2÷=，2018A ∴与2A 的纵坐标相同，在x 轴上方，故答案为：x 轴上方；（3）根据图形可知点的位置每4个数一个循环，每个点的横坐标为序数减1，纵坐标为0、1、0、-1循环，∴点n A 的坐标(n 是正整数)为A （n-1,0）或()1,1A n -或()1,0A n -或()1,1A n --．【点睛】本题主要考查找点的坐标规律，点的坐标的确定，方法，根据已知点的坐标及图形总结点坐标的变化规律，并运用规律解决问题是解题的关键．25．（1）＞；（2）3-＜223-．【分析】（1）由327＜329＜364，可得：3＜329＜4，从而可得答案；（2）由16＜23＜25，可得4＜23＜5，从而可得：0＜523-，即0＜()2233---，从而可得答案．【详解】解：（1）327＜329＜364，3∴＜329＜4，故答案为：＞．（2）16＜23＜25，4∴＜23＜5，0∴＜523-，0∴＜3+223-，0∴＜()2233---，∴ 3-＜223-．【点睛】本题考查的是实数的大小比较，掌握实数的大小比较的方法是解题的关键．26．（1）见详解；（2）见详解；（3）CE ，垂线段最短；（4）8．【分析】(1)取点D 作直线CD 即可;(2)取点F 作直线CF 交AB 与E 即可;(3)根据垂线段最短即可解决问题;(4)用割补法，大长方形的面积减去三个小三角形的面积即可;【详解】解：（1）直线CD即为所求；（2）直线CE即为所求；（3）在线段CA、CB、CE中，线段CE最短，理由：垂线段最短；故答案为CE，垂线段最短；（4） S△ABC=18﹣12×1×5﹣12×1×3﹣12×2×6=8，∴△ABC的面积为8.【点睛】本题主要考查垂线、平行线及其做图，注意作图的准确性.。

黑龙江省大庆市第六十九中学2022-2023学年数学九年级第一学期期末经典模拟试题含解析

2022-2023学年九上数学期末模拟试卷注意事项1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题（每题4分，共48分）1．如图，路灯距离地面8米，若身高1.6米的小明在距离路灯的底部（点O ）20米的A 处，则小明的影子AM 的长为（）A ．1.25米B ．5米C ．6米D ．4米2．方程3x 2－4x －1＝0的二次项系数和一次项系数分别为（）A ．3和4B ．3和－4C ．3和－1D ．3和13．小明在太阳光下观察矩形木板的影子，不可能是（）A ．平行四边形B ．矩形C ．线段D ．梯形4．如图，在ABC ∆中，90ACB ∠=，30B ∠=，AD 平分BAC ∠，E 是AD 的中点，若8AB =，则CE 的长为（）A ．4B ．33C 3D ．2335．已知e 是单位向量，且2,4a e b e =-=，那么下列说法错误的是（）A ．a ∥bB ．|a |=2C ．|b |=﹣2|a |D ．a =﹣12b 6．有一等腰三角形纸片ABC ，AB ＝AC ，裁剪方式及相关数据如图所示，则得到的甲、乙、丙、丁四张纸片中，面积最大的是（）A．甲B．乙C．丙D．丁7．如图所示的几何体的左视图为（）A．B．C．D．8．抛物线y＝4x2﹣3的顶点坐标是（）A．(0，3) B．(0，﹣3) C．(﹣3，0) D．(4，﹣3)9．如图，AB是⊙O的直径，弦CD⊥AB于点M，若CD＝8 cm，MB＝2 cm，则直径AB的长为（）A．9 cm B．10 cm C．11 cm D．12 cm10．已知一组数据：-1，0，1，2，3是它的一个样本，则这组数据的平均值大约是（）A．5 B．1 C．-1 D．011．据有关部门统计，2019年“五一小长假”期间，广东各大景点共接待游客约14400000人次，将数14400000用科学记数法表示为（）A．71.4410⨯B．70.14410⨯C．81.4410⨯D．80.14410⨯12．袋中装有5个白球，3个黑球，除颜色外均相同，从中一次任摸出一个球，则摸到黑球的概率是（）A．35B．38C．58D．34二、填空题（每题4分，共24分）13．如图所示，在平面直角坐标系中，A （4，0），B （0，2），AC 由AB 绕点A 顺时针旋转90°而得，则AC 所在直线的解析式是_____．14．一个口袋中装有2个完全相同的小球，它们分别标有数字1，2，从口袋中随机摸出一个小球记下数字后放回，摇匀后再随机摸出一个小球，则两次摸出小球的数字和为偶数的概率是．15．已知二次函数222(1)22y x m x m m =--+--(m 为常数)，若对于一切实数m 和均有y ≥k ，则k 的最大值为____________.16．如图是抛物线21(0)y ax bx c a =++≠图象的一部分，抛物线的顶点坐标为(1,3)A ，与x 轴的一个交点为(4,0)B ，点A 和点B 均在直线2(0)y mx n m =+≠上.①20a b +=；②>0abc ；③抛物线与x 轴的另一个交点时(4,0)-；④方程23ax bx c ++=-有两个不相等的实数根；⑤4a b c m n -+<+；⑥不等式2mx n ax bx c +>++的解集为14x <<.上述六个结论中，其中正确的结论是_____________.（填写序号即可）17．下面是“用三角板画圆的切线”的画图过程．如图1，已知圆上一点A ，画过A 点的圆的切线．画法：（1）如图2，将三角板的直角顶点放在圆上任一点C（与点A不重合）处，使其一直角边经过点A，另一条直角边与圆交于B点，连接AB；（2）如图3，将三角板的直角顶点与点A重合，使一条直角边经过点B，画出另一条直角边所在的直线AD．所以直线AD就是过点A的圆的切线．请回答：该画图的依据是______________________________________．18．如图，在△ABC中，AB＝AC＝1，点D、E在直线BC上运动，设BD＝x，CE＝y.如果∠BAC＝30°，∠DAE＝105°，则y与x之间的函数关系式为________________.三、解答题（共78分）19．（8分）如图，CD是⊙O的切线，点C在直径AB的延长线上．（1）求证：∠CAD=∠BDC；（2）若BD=23AD，AC=3，求CD的长．20．（8分）济南国际滑雪自建成以来，吸引大批滑雪爱好者，一滑雪者从山坡滑下，测得滑行距离y（单位：m）与滑行时间x（单位：s）之间的关系可以近似的用二次函数来表示．滑行时间x/s 0 1 2 3 …滑行距离y/m 0 4 12 24 …（1）根据表中数据求出二次函数的表达式．现测量出滑雪者的出发点与终点的距离大约840m，他需要多少时间才能到达终点？（2）将得到的二次函数图象补充完整后，向左平移2个单位，再向下平移5个单位，求平移后的函数表达式．21．（8分）在平面直角坐标系xOy中，已知抛物线G：y＝ax2﹣2ax+4（a≠0）．（1）当a＝1时，①抛物线G的对称轴为x＝；②若在抛物线G上有两点（2，y1），（m，y2），且y2＞y1，则m的取值范围是；（2）抛物线G的对称轴与x轴交于点M，点M与点A关于y轴对称，将点M向右平移3个单位得到点B，若抛物线G与线段AB恰有一个公共点，结合图象，求a的取值范围．22．（10分）如图，身高1.6米的小明站在距路灯底部O点10米的点A处，他的身高（线段AB）在路灯下的影子为线段AM，已知路灯灯杆OQ垂直于路面．（1）在OQ上画出表示路灯灯泡位置的点P；（2）小明沿AO方向前进到点C，请画出此时表示小明影子的线段CN；（3）若AM=2.5米，求路灯灯泡P到地面的距离．23．（10分）如图，在平面直角坐标系中，点A，C分别在x轴，y轴上，四边形ABCO为矩形，AB＝16，点D与点A关于y轴对称，tan∠ACB＝43，点E、F分别是线段AD、AC上的动点，（点E不与点A，D重合），且∠CEF＝∠ACB．（1）求AC的长和点D的坐标；（2）求证：FE AE EC DC=；（3）当△EFC 为等腰三角形时，求点E 的坐标．24．（10分）如图，已知抛物线y=ax 2+bx+c （a≠0）的对称轴为直线x=﹣1，求抛物线经过A （1，0），C （0，3）两点，与x 轴交于A 、B 两点．（1）若直线y=mx+n 经过B 、C 两点，求直线BC 和抛物线的解析式；（2）在该抛物线的对称轴x=﹣1上找一点M ，使点M 到点A 的距离与到点C 的距离之和最小，求出点M 的坐标；（3）设点P 为该抛物线的对称轴x=﹣1上的一个动点，直接写出使△BPC 为直角三角形的点P 的坐标．（提示：若平面直角坐标系内有两点P （x 1，y 1）、Q （x 2，y 2），则线段PQ 的长度221212()()x x y y -+-．25．（12分）已知：在同一平面直角坐标系中，一次函数4y x =-与二次函数22y xx c =-++的图象交于点(1,)A m -.（1）求m ，c 的值；（2）求二次函数图象的对称轴和顶点坐标.26．解方程：（1）x 2+2x ﹣3＝0；（2）x （x+1）＝2（x+1）．参考答案一、选择题（每题4分，共48分）1、B【分析】易得：△ABM ∽△OCM ，利用相似三角形对应边成比例可得出小明的影子AM 的长．【详解】如图，根据题意，易得△MBA ∽△MCO ，根据相似三角形的性质可知AB AM OC OA AM =+ ，即1.6820AM AM=+，解得AM=5m ．则小明的影子AM 的长为5米．故选：B ．【点睛】此题考查相似三角形的应用，利用相似三角形对应边成比例列出比例式是解题的关键．2、B【详解】方程3x 2－4x －1＝0的二次项系数是3，和一次项系数是-4.故选B.3、D【分析】根据平行投影的特点可确定矩形木板与地面平行且与光线垂直时所成的投影为矩形；当矩形木板与光线方向平行且与地面垂直时所成的投影为一条线段；除以上两种情况矩形在地面上所形成的投影均为平行四边形，据此逐一判断即可得答案.【详解】A.将木框倾斜放置形成的影子为平行四边形，故该选项不符合题意，B.将矩形木框与地面平行放置时，形成的影子为矩形，故该选项不符合题意，C.将矩形木框立起与地面垂直放置时，形成的影子为线段，D.∵由物体同一时刻物高与影长成比例，且矩形对边相等，梯形两底不相等，∴得到投影不可能是梯形，故该选项符合题意，故选：D.【点睛】本题考查了平行投影特点：在同一时刻，不同物体的物高和影长成比例，平行物体的影子仍旧平行或重合．灵活运用平行投影的性质是解题的关键．4、B【分析】首先证明AD BD =，然后再根据在直角三角形中，斜边上的中线等于斜边的一半，即12CE AD =. 【详解】解：90,30,ACB B ∠=︒∠=︒60.CAB ∴∠=︒AD CAB ∠又平分30CAD DAB ∴∠=∠=︒DAB B ∴∠=∠.AD BD ∴=1.2Rt ACD CD AD =在中，设,AD BD x == 则12CD x =, 142AC AB == 在Rt ACD 中，222AC CD AD += 即222142x x ⎛⎫+= ⎪⎝⎭解得x = E 为AD 中点， 12CE AD ∴== 故选B【点睛】本题主要考查了角平分线的性质、直角三角形斜边上的中线，含30度角的直角三角形.5、C【详解】解：∵e 是单位向量，且2a e =-，4b e =，∴//a b ，2a =， 4b = ， 12a b =-，故C 选项错误，故选C.6、D【分析】根据相似三角形的性质求得甲的面积和丙的面积，进一步求得乙和丁的面积，比较即可求得．【详解】解：如图：∵AD ⊥BC ，AB ＝AC ，∴BD ＝CD ＝5+2＝7，∵AD ＝2+1＝3，∴S △ABD ＝S △ACD ＝1732⨯⨯＝212 ∵EF ∥AD ，∴△EBF ∽△ABD ， ∴ABD S S 甲＝（57）2＝2549， ∴S 甲＝7514， ∴S 乙＝2175362147-=，同理ACD S S ∆丙＝（23）2＝49， ∴S 丙＝143， ∴S 丁＝212﹣143＝356， ∵3575361461473>>>， ∴面积最大的是丁，故选：D ．【点睛】本题考查了三角形相似的判定和性质，相似三角形面积的比等于相似比的平方．解题的关键是熟练掌握相似三角形的判定和性质进行解题.7、D【解析】根据左视图是从几何体左面看得到的图形，认真观察实物，可得这个几何体的左视图为长方形，据此观察选项即可得.【详解】观察实物，可知这个几何体的左视图为长方形，只有D 选项符合题意，故选D.【详解】本题考查了几何体的左视图，明确几何体的左视图是从几何体的左面看得到的图形是解题的关键.注意错误的选项B 、C.8、B【分析】根据抛物线2y ax b =+的顶点坐标为(0，b)，可以直接写出该抛物线的顶点坐标，【详解】解：抛物线243y x =-， ∴该抛物线的顶点坐标为()0,3-，故选：B ．【点睛】本题考查二次函数的性质，解答本题的关键是明确题意，利用二次函数的性质解答．9、B【分析】由CD ⊥AB ，可得DM=1．设半径OD=Rcm ，则可求得OM 的长，连接OD ，在直角三角形DMO 中，由勾股定理可求得OD 的长，继而求得答案．【详解】解：连接OD ，设⊙O 半径OD 为R,∵AB 是⊙O 的直径，弦CD ⊥AB 于点M ，∴DM=12CD=1cm ，OM=R-2, 在RT △OMD 中，OD²=DM²+OM²即R²=1²+(R-2)², 解得：R=5,∴直径AB 的长为:2×5=10cm ．故选B ．【点睛】本题考查了垂径定理以及勾股定理．注意掌握辅助线的作法及数形结合思想的应用．10、B【分析】根据平均数的定义计算即可．【详解】这组数据的平均数为(﹣1+0+1+2+3)÷5=1．故选：B．【点睛】本题考查了平均数．掌握平均数的求法是解答本题的关键．11、A【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同；当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【详解】14400000=1.44×1．故选：A．【点睛】本题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．12、B【解析】先求出球的总个数，根据概率公式解答即可．【详解】因为白球5个，黑球3个一共是8个球，所以从中随机摸出1个球，则摸出黑球的概率是38．故选B．【点睛】本题考查了概率公式，明确概率的意义是解答问题的关键，用到的知识点为：概率=所求情况数与总情况数之比．二、填空题（每题4分，共24分）13、y＝2x﹣1【分析】过点C作CD⊥x轴于点D，易知△ACD≌△BAO（AAS），已知A（4，0），B（0，2），从而求得点C坐标，设直线AC的解析式为y＝kx+b，将点A，点C坐标代入求得k和b，从而得解．【详解】解：∵A（4，0），B（0，2），∴OA＝4，OB＝2，过点C作CD⊥x轴于点D，∵∠ABO +∠BAO ＝∠BAO +∠CAD ， ∴∠ABO ＝∠CAD ，在△ACD 和△BAO 中ABO CAD AOB CDA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△ACD ≌△BAO （AAS ） ∴AD ＝OB ＝2，CD ＝OA ＝4， ∴C （6，4）设直线AC 的解析式为y ＝kx +b ，将点A ，点C 坐标代入得4064k b k b +=⎧⎨+=⎩， ∴28k b =⎧⎨=-⎩∴直线AC 的解析式为y ＝2x ﹣1．故答案为：y ＝2x ﹣1．【点睛】本题是几何图形旋转的性质与待定系数法求一次函数解析式的综合题，求得C 的坐标是解题的关键，难度中等． 14、12．【解析】试题分析：如图所示，∵共有4种结果，两次摸出小球的数字和为偶数的有2次，∴两次摸出小球的数字和为偶数的概率=24=12．故答案为12．考点：列表法与树状图法． 15、134-【分析】因为二次函数系数大于0，先用含有m 的代数式表示出函数y 的最小值，得出min y 23m m =+-，再求出于m 的函数23M m m =+-的最小值即可得出结果.【详解】解： 222(1)22y x m x m m =--+--, 22min41(22)4(1)41m m m y ⨯⨯----=⨯23m m =+-,关于m 的函数为23M m m =+-, 2min 41(3)113=414M ⨯⨯--=-⨯,∴134k -≥,∴k 的最大值为134-. 【点睛】本题考查二次函数的最值问题，先将函数化为顶点式，即可得出最值. 16、①④【分析】①由对称轴x=1判断；②根据图象确定a 、b 、c 的符号；③根据对称轴以及B 点坐标，通过对称性得出结果；③根据23ax bx c ++=-的判别式的符号确定；④比较x=1时得出y 1的值与x=4时得出y 2值的大小即可；⑤由图象得出，抛物线总在直线的下面，即y 2＞y 1时x 的取值范围即可．【详解】解：①因为抛物线的顶点坐标A （1，3），所以对称轴为：x=1，则-2ba=1，2a+b=0，故①正确； ②∵抛物线开口向下，∴a ＜0，∵对称轴在y 轴右侧，∴b ＞0，∵抛物线与y 轴交于正半轴，∴c ＞0，∴abc ＜0，故②不正确；③∵抛物线对称轴为x=1,抛物线与x 轴的交点B 的坐标为（4,0），∴根据对称性可得，抛物线与x 轴的另一个交点坐标为（-2,0），故③不正确；④∵抛物线与x 轴有两个交点，∴b 2-4ac ＞0，∴23ax bx c ++=-的判别式，∆=b 2-4a （c+3）= b 2-4ac-12a,又a ＜0，∴-12a ＞0，∴∆= b 2-4ac-12a ＞0，故④正确；⑤当x=-1时，y 1=a-b+c ＞0;当x=4时，y 2=4m+n=0,∴a-b+c ＞4m+n,故⑤不正确； ⑥由图象得：2mx n ax bx c +>++的解集为x ＜1或x ＞4；故⑥不正确；则其中正确的有：①④．故答案为：①④．【点睛】本题选项较多，比较容易出错，因此要认真理解题意，明确以下几点是关键：①通常2a+b 的值都是利用抛物线的对称轴来确定；②抛物线与x 轴的交点个数确定其△的值，即b 2-4ac 的值：△=b 2-4ac ＞0时，抛物线与x 轴有2个交点；△=b 2-4ac=0时，抛物线与x 轴有1个交点；△=b 2-4ac ＜0时，抛物线与x 轴没有交点；③知道对称轴和抛物线的一个交点，利用对称性可以求与x 轴的另一交点．17、90°的圆周角所对的弦是直径，经过半径外端并且垂直于这条半径的直线是圆的切线【详解】解：利用90°的圆周角所对的弦是直径可得到AB为直径，根据经过半径外端并且垂直于这条半径的直线是圆的切线可判断直线AD就是过点A的圆的切线．故答案为90°的圆周角所对的弦是直径，经过半径外端并且垂直于这条半径的直线是圆的切线．点睛：本题考查了复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．18、1 yx =【解析】∵∠BAC=30°， AB=AC，∴∠ACB=∠ABC=18030752-=，∴∠ACE=∠ABD=180°-75°=105°，∵∠DAE=105°，∠BAC=30°，∴∠DAB+∠CAE=105°-30°=75°，又∵∠DAB+∠ADB=∠ABC=75°，∴∠ADB=∠CAE.∴△ADB∽△EAC，∴CE ACAB DB=，即11yx=，∴1 yx =.故答案为1 yx =.三、解答题（共78分）19、（1）证明见解析；（1）CD=1．【解析】分析：（1）连接OD，由OB=OD可得出∠OBD=∠ODB，根据切线的性质及直径所对的圆周角等于180°，利用等角的余角相等，即可证出∠CAD=∠BDC；（1）由∠C=∠C、∠CAD=∠CDB可得出△CDB∽△CAD，根据相似三角形的性质结合BD=23AD、AC=3，即可求出CD的长．详（1）证明：连接OD，如图所示．∵OB=OD，∴∠OBD=∠ODB．∵CD是⊙O的切线，OD是⊙O的半径，∴∠ODB+∠BDC=90°．∵AB是⊙O的直径，∴∠ADB=90°，∴∠OBD+∠CAD=90°，∴∠CAD=∠BDC．（1）∵∠C=∠C，∠CAD=∠CDB，∴△CDB∽△CAD，∴BD CD AD AC=．∵BD=23 AD，∴23 BDAD=，∴2=3 CDAC，又∵AC=3，∴CD=1．点睛：本题考查了相似三角形的判定与性质、圆周角定义以及切线的性质，解题的关键是：（1）利用等角的余角相等证出∠CAD=∠BDC；（1）利用相似三角形的性质找出2=3 CDAC．20、（1）20s；（2）2511 222 y x⎛⎫=+-⎪⎝⎭【解析】（1）利用待定系数法求出函数解析式，再求出y＝840时x的值即可得；（2）根据“上加下减，左加右减”的原则进行解答即可．【详解】解：（1）∵该抛物线过点（0，0），∴设抛物线解析式为y＝ax2+bx，将（1，4）、（2，12）代入，得：44212a b a b +=⎧⎨+=⎩，解得：22a b =⎧⎨=⎩，所以抛物线的解析式为y ＝2x 2+2x ，当y ＝840时，2x 2+2x ＝840，解得：x ＝20（负值舍去），即他需要20s 才能到达终点；（2）∵y ＝2x 2+2x ＝2（x +12）2﹣12， ∴向左平移2个单位，再向下平移5个单位后函数解析式为y ＝2（x +2+12）2﹣12﹣5＝2（x +52）2﹣112．【点睛】本题主要考查二次函数的应用，解题的关键是掌握待定系数法求函数解析式及函数图象平移的规律． 21、（1）①1；②m ＞2或m ＜0；（2）﹣43＜a ≤﹣12或a ＝1．【分析】（1）当a ＝1时，①根据二次函数一般式对称轴公式2bx a=-，即可求得抛物线G 的对称轴； ②根据抛物线的对称性求得()12,y 关于对称轴1x =的对称点为()10y ,，再利用二次函数图像的增减性即可求得答案；（2）根据平移的性质得出()1,0A -、()4,0B ，由题意根据函数图象分三种情况进行讨论，即可得解．【详解】解：（1）①∵当a ＝1时，抛物线G ：y ＝ax 2﹣2ax +1（a ≠0）为：224y x x =-+ ∴抛物线G 的对称轴为2122b x a -=-=-=； ②画出函数图象：∵在抛物线G 上有两点（2，y 1），（m ，y 2），且y 2＞y 1，10a =>，∴①当1x >时，y 随x 的增大而增大，此时有2m >；②当1x <时，y 随x 的增大而减小，抛物线G 上点()12,y 关于对称轴1x =的对称点为()10y ,，此时有0m <． ∴m 的取值范围是2m >或0m <；（2）∵抛物线G ：y ＝ax 2﹣2ax +1（a ≠0的对称轴为x ＝1，且对称轴与x 轴交于点M ∴点M 的坐标为（1，0） ∵点M 与点A 关于y 轴对称 ∴点A 的坐标为（﹣1，0） ∵点M 右移3个单位得到点B ∴点B 的坐标为（1，0）依题意，抛物线G 与线段AB 恰有一个公共点把点A （﹣1，0）代入y ＝ax 2﹣2ax +1，可得43a =-；把点B （1，0）代入y ＝ax 2﹣2ax +1，可得12a =-；把点M （1，0）代入y ＝ax 2﹣2ax +1，可得a ＝1．根据所画图象可知抛物线G 与线段AB 恰有一个公共点时可得：4132a -<≤-或4a =．故答案是：（1）①1；②m ＞2或m ＜0；（2）4132a -<≤-或4a = 【点睛】本题考查了二次函数图像的性质、二次函数图象上的点的坐标特征以及坐标平移，解决本题的关键是综合利用二次函数图象的性质．22、（1）见解析；（2）见解析；（3）8米【解析】【试题分析】（1）点B 在地面上的投影为M ．故连接MB ，并延长交OP 于点P.点P 即为所求；（2）连接PD ，并延长交OM 于点即为所求；（3）根据相似三角形的性质，易得：AB AM OP OM ∴=，即1.6 2.510 2.5OP =+，解得8OP =．从而得求. 【试题解析】()1如图：()2如图：()3//AB OP ，MAB ∴∽MOP ，AB AM OP OM ∴=，即1.6 2.510 2.5OP =+，解得8OP =．即路灯灯泡P 到地面的距离是8米．【方法点睛】本题目是一道关于中心投影的问题，涉及到如何确定点光源，相似三角形的判定，相似三角形的性质，难度中等.23、（1）AC =20，D （12，0）；（2）见解析；（3）（8，0）或(143，0)．【分析】（1）在Rt △ABC 中，利用三角函数和勾股定理即可求出BC 、AC 的长度，从而得到A 点坐标，由点D 与点A 关于y 轴对称，进而得到D 点的坐标；（2）欲证FE AEEC DC=，只需证明△AEF 与△DCE 相似，只需要证明两个对应角相等即可．在△AEF 与△DCE 中，易知∠CAO ＝∠CDE ，再利用三角形的外角性质证得∠AEF ＝∠DCE ，问题即得解决；（3）当△EFC为等腰三角形时，有三种情况，需要分类讨论：①当CE＝EF时，此时△AEF与△DCE相似比为1，则有AE＝CD，即可求出E点坐标；②当EF＝FC时，利用等腰三角形的性质和解直角三角形的知识易求得CE65EF=，再利用（2）题的结论即可求出AE的长，进而可求出E点坐标；③当CE＝CF时，可得E点与D点重合，这与已知条件矛盾，故此种情况不存在．【详解】解：（1）∵四边形ABCO为矩形，∴∠B=90°，∵AB＝16，tan∠ACB＝43，∴4163ABBC BC==，解得：BC＝12=AO，∴AC＝22AB BC+=20，A点坐标为（﹣12，0），∵点D与点A关于y轴对称，∴D（12，0）；（2）∵点D与点A关于y轴对称，∴∠CAO＝∠CDE，∵∠CEF＝∠ACB，∠ACB＝∠CAO，∴∠CDE＝∠CEF，又∵∠AEC＝∠AEF+∠CEF＝∠CDE+∠DCE，∴∠AEF＝∠DCE，∴△AEF∽△DCE．∴FE AE EC DC=；（3）当△EFC为等腰三角形时，有以下三种情况：①当CE＝EF时，∵△AEF∽△DCE，∴△AEF≌△DCE，∴AE＝CD＝20，∴OE＝AE﹣OA＝20﹣12＝8，∴E（8，0）；②当EF＝FC时，如图1所示，过点F作FM⊥CE于M，则点M为CE中点，∴CE＝2ME＝2EF•cos∠CEF＝2EF•cos∠ACB＝1262205EF EF⨯=．∵△AEF∽△DCE，∴EF AECE CD=，即：6205EF AEEF=，解得：AE＝503，∴OE＝AE﹣OA＝143，∴E(143，0)．③当CE＝CF时，则有∠CFE＝∠CEF，∵∠CEF＝∠ACB＝∠CAO，∴∠CFE＝∠CAO，即此时F点与A点重合，E点与D点重合，这与已知条件矛盾．所以此种情况的点E不存在，综上，当△EFC为等腰三角形时，点E的坐标是（8，0）或(143，0)．【点睛】本题综合考查了矩形的性质、等腰三角形的性质、勾股定理、相似三角形的判定和性质、轴对称的性质、三角形的外角性质以及解直角三角形等知识，熟练掌握相似三角形的判定与性质是解题关键．难点在于第（3）问，当△EFC为等腰三角形时，有三种情况，需要分类讨论，注意不要漏解.24、（1）y=x+3；y=﹣x2﹣2x+3；（2）M的坐标是（﹣1，2）；（3）P的坐标是（﹣1317+1317-或（﹣1，4）或（﹣1，﹣2）．【分析】（1）用待定系数法即可求出直线BC和抛物线的解析式；（2）设直线BC与对称轴x＝−1的交点为M，则此时MA＋MC的值最小．把x＝−1代入直线y＝x＋3得y的值，即可求出点M坐标；（3）设P（−1，t），又因为B（−3，0），C（0，3），所以可得BC2＝18，PB2＝（−1＋3）2＋t2＝4＋t2，PC2＝（−1）2＋（t−3）2＝t2−6t＋10，再分三种情况分别讨论求出符合题意t值即可求出点P的坐标．【详解】（1）A（1，0）关于x=﹣1的对称点是（﹣3，0），则B的坐标是（﹣3，0）根据题意得：303m nn-+=⎧⎨=⎩解得13 mn=⎧⎨=⎩则直线的解析式是y=x+3；根据题意得：解得：93003a b c a b c c -+=⎧⎪++=⎨⎪=⎩则抛物线的解析式是y=﹣x 2﹣2x+3（2）设直线BC 与对称轴x ＝−1的交点为M ，则此时MA ＋MC 的值最小．把x ＝−1代入直线y ＝x ＋3得，y ＝−1＋3＝2，∴M （−1，2），即当点M 到点A 的距离与到点C 的距离之和最小时M 的坐标为（−1，2）；（3）如图，设P （−1，t ），又∵B （−3，0），C （0，3），∴BC 2＝18，PB 2＝（−1＋3）2＋t 2＝4＋t 2，PC 2＝（−1）2＋（t −3）2＝t 2−6t ＋10，①若点B 为直角顶点，则BC 2＋PB 2＝PC 2即：18＋4＋t 2＝t 2−6t ＋10解之得：t ＝−2；②若点C 为直角顶点，则BC 2＋PC 2＝PB 2即：18＋t 2−6t ＋10＝4＋t 2解之得：t ＝4，③若点P 为直角顶点，则PB 2＋PC 2＝BC 2即：4＋t 2＋t 2−6t ＋10＝18解之得：t 1＝3172+，t 2＝3172-； ∴P 的坐标是（﹣1，3172+）或（﹣1，3172-）或（﹣1，4）或（﹣1，﹣2）．【点睛】本题是二次函数的综合题，考查了二次函数的图象与性质，待定系数法求函数的解析式，利用轴对称性质确定线段的最小长度，两点间的距离公式的运用，直角三角形的性质等知识点，熟练掌握二次函数的性质是解题的关键．25、（1）5m =-，2c =-;（2）对称轴为直线1x =，顶点坐标(1,1)-.【分析】（1）把A 点坐标代入一次函数解析式可求得m 的值，得出A 点坐标，再代入二次函数解析式可得c ；（2）将（1）中得出的二次函数的解析式化为顶点式可求得其顶点坐标和对称轴．【详解】解：（1）∵点A 在一次函数图象上，∴m=-1-4=-5，∵点A 在二次函数图象上，∴-5=-1-2+c ，解得c=-2；（2）由（1）可知二次函数的解析式为：()22y 2211x x x =-+-=---，∴二次函数图象的对称轴为直线x=1，顶点坐标为(1,-1)．【点睛】本题考查的知识点是一次函数的性质以及二次函数的性质，熟记各知识点是解此题的关键．26、（1）x 1＝－3，x 2＝1；（2）x 1＝－1，x 2＝2【分析】（1）利用“十字相乘法”对等式的左边进行因式分解；又可以利用公式法解方程；（2）利用因式分解法解方程．【详解】（1）解一：（x+3）（x ﹣1）=0解得：x 1=﹣3，x 2=1解二：a=1，b=2，c=﹣3解得：即x 1=﹣3，x 2=1．（2）x （x+1）﹣2（x+1）=0（x+1）（x ﹣2）=0x 1=﹣1，x 2=2点睛: 本题主要考查了因式分解法和公式法解一元二次方程的知识，解题的关键是掌握因式分解法解方程的步骤以及熟记求根公式．。

人教PEP版2022-2023学年四年级英语上册期末模拟试卷(附答案和音频)

人教PEP版2022-2023学年四年级英语上册期末模拟试卷（附答案和音频）★听力部分一、听音，选择听到的内容（10分）1．听录音，选出你所听到的单词，并将其标号填入题前括号内。

每题读两遍。

2．听录音，根据问句选择相应答句。

( ) 1). A．I’d like some chicken. B．She is in the kitchen.( ) 2). A．It’s in the bag.B．Some story books.( ) 3). A．It’s blue and white.B．It’s a teacher’s desk.( ) 4). A．They are in the door.B．Yes, they are.( ) 5). A．She is a nurse.B．There are four.二、听音判断（5分）3．听录音判断下列句子与所听到的句子是(T) 否(F) 一致。

() 1). The picture is near the door.() 2). My cousin is short and thin.() 3). My friend has black shoes.() 4). Mike is in the bedroom.() 5). I’d like some beef for dinner.三、听音排序（5分）4．听录音，你将听到五段对话，根据对话内容给下列图片排序。

★笔试部分四、词汇选择题（5分）选出下列单词中不同类的一项。

5．( )A．father B．teacher C．doctor 6．( )A．noodles B．bed C．rice7．( )A．Chinese B．English C．book8．( )A．quiet B．apple C．friendly 9．( )A．uncle B．aunt C．bowl 五、单选题（20分）10．—______ people are there in your family? () —Six.A．What B．Where’s C．How many11．______ name is Amy. She’s a girl. ()A．Her B．She C．His12．—Is he your brother? ()—______A．Yes, it is.B．No, he isn’t.C．No , they aren’t. 13．How many ______ are there in the zoo? () A．a tiger B．tiger C．tigers14．—What’s his mother’s jo b? ()—______A．Yes, she is.B．She’s 30.C．She’s a doctor. 15．I’d like ________ rice and soup. ()A．a B．an C．some16．—______ my English book? ()—It’s in the desk.A．Where’s B．What’s C．How’s17．My uncle ________ a football player. ( )A．am B．is C．are18．—Who is that boy? ()—______A．He’s in the living room.B．He’s a boy.C．He’s my baby brother. 19．—Are the pictures near the window? ()—No, ______.A．it is B．they are C．they aren’t六、情景选择（10分）20．你想表达“让我们尝尝吧！”，你应该说：()A．Let’s go and see!B．Let’s try it!C．I’d like to go!21．如果Jim找到了你丢失的书包，你应该对他说：()A．You’re right.B．OK.C．Thank you so much.22．家里来了客人，你招呼别人吃东西，应该说：( )A．Eat, please.B．Help yourself.C．I don’t know.23．你想表达“我的家有四口人”，你应该说：()A．My family have five people.B．My family has four people.C．My family is four people.24．如果你想询问别人姑姑的工作是什么，你应该问：()A．What’s your job?B．What’s your uncle’s job?C．What’s your aunt’s job?七、选词/短语填空（5分）八、句子匹配（5分）30．What would you like? () 31．Is this Tom’s aunt? ()32．Are they on the fridge? ()33．Would you like some beef?()34．Is Amy in the study? ()九、连词成句（10分）35．the, in, kitchen, She’s (!)_________________________________ 36．job, What’s, sister’s, your (?)______________________________________ 37．people, in, many, there, are, How, family, his (?) ______________________________________ 38．you, lunch, What, like, would, for (?)__________________________39．table they Are the on(?)______________________________________十、选内容补全对话/短文（5分）A: Dad, I can’t find my notebook.B: ___40___A: Thank you!B: ___41___A: It’s blue.B: ___42___A: No, it isn’t.B: ___43___A: Some storybooks.B: Oh! It’s in your hand!A: ___44___ Silly me!B: Haha!A．Yes, it is.B．Let me help you.C．Is it in your schoolbag?D．What colour is it?E．What’s in your schoolbag?十一、阅读选择（10分）My name is Jam. I am from the USA．My Chinese teacher is Wang Mei. She is a good teacher. I have many friends at school. Jimmy is my best friend. He is from Canada. He is tall and he has brown hair. He likes tigers very much. Mary is a short girl. She likes elephants. Sarah is from UK. She has long brown hair. She likes monkeys. Wang Dong is from China. He has short black hair. He speaks English well.45．Wang Mei is Jam’s ______. ()A．teacher B．friend C．mother46．______ is from Canada. ()A．Wang Dong B．Jimmy C．Sarah47．______ has long brown hair and likes monkeys. ()A．Mary B．Sarah C．Wang Dong48．Wang Dong speaks ______ well. ()A．Japanese B．China C．English49．How many friends does Jam have? () A．Three.B．Four.C．Five.十二、阅读判断（10分）50．It has 7 rooms in the house. ( ) 51．The sofa is in the study. ( ) 52．The table is in the kitchen. ( ) 53．It’s 1500 yuan a month for rent. ( ) 54．The house is on Quancheng Road. ( )参考答案1．C A A B C【详解】1). Turn on the computer.2). Write the letters f-r-i.3). The key is yellow.4). Read the letters b-d-p-q.5). Drive the taxi.2．B B A A A【详解】1). Where is Amy?2). What’s in your school bag?3). What colour is it?4). Where are the keys?5). What’s your sister’s job?3．T F F T F【详解】1). The picture is near the door.2). My cousin is tall and strong.3). My friend has brown shoes.4). Mike is in the bedroom.5). I’d like some bread for dinner.4．2315 4【详解】1). A: Would you like a knife and fork?B: Yes, please.2). A: What’s your aunt’s job.B: She’s a nurse.3). A: Where are the toys?B: They’re o n the sofa.4). A: Would you like some juice?B: No, thanks. I’d like some milk.5). A: Where is Amy? Is she in the living room?B: Yes, she is.5．A6．B7．C8．B9．C【解析】5．A爸爸，B老师，C医生，BC都是职业，A是家庭称谓。

高二数学2022-2023学年第二学期期末模拟卷(含答案)

2022-2023学年高二下学期期末模拟试卷(时间：120分钟，分值：150分，范围：必修二第5章——必修三第6、7、8章)一、单项选择题：本题共8小题，每小题5分，共40分.在每个小题绐岀的四个选项中，只有一项是符合题目要求的.1．下列说法，正确的是（）A ．对分类变量X 与Y 的独立性检验的统计量2χ来说，2χ值越小，判断“X 与Y 有关系”的把握性越大B ．在残差图中，残差点分布在以取值是0的横轴为对称轴的水平带状区域越窄，说明模型的拟合精度越高C ．若一组样本数据(),i i x y （1i =，2，…，n ）的对应样本点都在直线23y x =-+上，则这组样本数据的相关系数r 为1D ．数据－1，1，2，4，5，6，8，9的第25百分位数是22．某校有演讲社团､篮球社团､乒乓球社团､羽毛球社团､独唱社团共五个社团，甲､乙､丙､丁､戊五名同学分别从五个社团中选择一个报名，记事件A 为“五名同学所选项目各不相同”，事件B 为“只有甲同学选篮球”，则()P A B =（）A ．332B ．316C ．34D ．253．82x x ⎛⎫+ ⎪ ⎪⎝⎭展开式中，二项式系数最大的项是（）A ．第3项B ．第4顶C ．第5项D ．第6项4．将7个人从左到右排成一排，若甲、乙、丙3人中至多有2人相邻，则不同的站法有（）A ．1440种B ．2880种C ．4320种D ．3600种5．2023年春，为了解开学后大学生的身体健康状况，寒假开学后，学校医疗部门抽取部分学生检查后，发现大学生的舒张压呈正态分布()270.8,7.02X N ~（单位：mm /Hg ），且()82.80.1P X >=，若任意抽查该校大学生6人，恰好有k 人的舒张压落在()58.8,82.8内的概率最大，则k =（）A ．3B ．4C ．5D ．66．抛掷三枚质地均匀的硬币一次，在有一枚正面朝上的条件下，另外两枚也正面朝上的概率是（）A ．18B ．78C ．17D ．677．三名男生和三名女生站成一排照相，男生甲与男生乙相邻，且三名女生中恰好有两名女生相邻，则不同的站法共有A ．72种B ．108种C ．36种D ．144种8．若不等式222e ln e ln 2e xaa x x a -+-≥-在[1,2]x ∈-有解，则实数a 的取值范围是（）A ．21,e 2e ⎡⎤⎢⎥⎣⎦B ．221,e e ⎡⎤⎢⎥⎣⎦C ．421,e e ⎡⎤⎢⎥⎣⎦D ．41,e e ⎡⎤⎢⎥⎣⎦二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9．已知21nx x ⎛⎝的展开式中二项式系数之和为1024，则下列说法正确的（）A ．展开式中奇数项的二项式系数和为256B ．展开式的各项系数之和为1024C ．展开式中常数项为45D ．展开式中含15x 项的系数为4510．下列说法正确的是（）A ．在一个2×2列联表中，计算得到2χ的值，则2χ的值越接近1，可以判断两个变量相关的把握性越大B ．随机变量()2~,N ξμσ，若函数()()2f x P x x ξ=≤≤+为偶函数，则1μ=C ．若回归直线方程为ˆ 1.22yx =+，则样本点的中心不可能为(5,7)D ．若甲、乙两组数据的相关系数分别为0.91-和0.89，则甲组数据的线性相关性更强11．一个袋子中有编号分别为1,2,3,4的4个球，除编号外没有其它差异.每次摸球后放回，从中任意摸球两次，每次摸出一个球.设“第一次摸到的球的编号为2”为事件A ，“第二次摸到的球的编号为奇数”为事件B ，“两次摸到的球的编号之和能被3整除”为事件C ，则下列说法正确的是（）A ．()516P C =B ．事件B 与事件C 相互独立C ．()12P CA =∣D ．事件A 与事件B 互为对立事件12．下列不等关系中正确的是（）A 32ln 3<B 344ln 3>C ．sin 33sin1cos1<D ．sin 33sin1cos1>三、填空题：本题共4小题，每小题5分，共计20分.13．2023年五一节到来之前，某市物价部门对本市5家商场的某种商品一天的销售量及其价格进行调查，5家商场这种商品的售价x （单位：元）与销售量y （单位：件）之间的一组数据如下表所示：价格x 89.5m 10.512销售量y1610865经分析知，销售量y 件与价格x 元之间有较强的线性关系，其线性回归直线方程为 3.544y x =-+，则m =________．14．某城市休闲公园管理人员拟对一块圆环区域进行改造封闭式种植鲜花，该圆环区域被等分为5个部分，每个部分从红、黄、紫三种颜色的鲜花中选取一种进行栽植．要求相邻区域不能用同种颜色的鲜花，总的栽植方案有_________种．15．假设有两箱零件，第一箱内装有10件，其中有3件次品；第二箱内装有20件，其中有2件次品．现从两箱中随意挑选一箱，然后从该箱中随机取1个零件，已知取出的是次品，则它是从第一箱取出的概率为__________．16．已知函数()ln 20()a x x a f x =-≠，若不等式222e ()e cos(())a x x x f x f x ≥+对0x >恒成立，则实数a 的取值范围为__________.四、解答题：本题共6小题，共计70分．解答时应写出文字说明、证明过程或演算步骤.17．（10分）为了解学生对党的“二十大”精神的学习情况，学校开展了“二十大”相关知识的竞赛活动，全校共有1000名学生参加，其中男生450名，采用分层抽样的方法抽取100人，将他们的比赛成绩（满分为100分），分为6组：[40,50)，[50,60)，[60,70)，[70,80)，[80,90)，[90,100]，得到如图所示的频率分布直方图．其中成绩不低于80分为“优秀”，低于80分为“非优秀”．(1)求实数a 的值，并估算全校1000名学生中成绩优秀的人数；(2)完成下列22⨯列联表，判断是否有95%的把握认为比赛成绩优秀与性别有关．优秀非优秀合计男女10合计附：22()()()()()n ad bc a b c d a c b d χ-=++++，其中n a b c d =+++．2()P k αχ=≥0.100.050.0100.0050.001k2.7063.8416.6357.87910.82818．（12分）已知()()52601261(1)(1)m x x a a x a x a x +=+-+-++- ，其中R m ∈，且13564a a a ++=，(1)求m 的值；(2)求4a 的值.19．（12分）已知0a >，函数()()2ln ln f x x a a x x e =-+-，其中e 是自然对数的底数.(1)当1a =时，求曲线()y f x =在点()()1,1f 处的切线方程；(2)当a e =时，求函数()f x 的单调区间；(3)求证：函数()f x 存在极值点，并求极值点0x 的最小值.20．（12分）某校20名学生的数学成绩(1,2,,20)i x i = 和知识竞赛成绩(1,2,,20)i y i = 如下表：学生编号i 12345678910数学成绩i x 100999693908885838077知识竞赛成绩iy 29016022020065709010060270学生编号i 11121314151617181920数学成绩i x 75747270686660503935知识竞赛成绩iy 4535405025302015105计算可得数学成绩的平均值是75x =，知识竞赛成绩的平均值是90y =，并且()20216464i i x x =-=∑，()2021149450ii yy =-=∑，()()20121650i i i x x y y =--=∑．(1)求这组学生的数学成绩和知识竞赛成绩的样本相关系数（精确到0.01）．(2)设*N N ∈，变量x 和变量y 的一组样本数据为(){},|1,2,,i i x y i N = ，其中(1,2,,)i x i N = 两两不相同，(1,2,,)i y i N = 两两不相同．记i x 在{},2|1,,n x n N = 中的排名是第i R 位，i y 在{},2|1,,n y n N = 中的排名是第i S 位，1,2,,i N = ．定义变量x 和变量y 的“斯皮尔曼相关系数”（记为ρ）为变量x 的排名和变量y 的排名的样本相关系数．（i ）记i i i d R S =-，1,2,,i N = ．证明：()221611Ni i d N N ρ==--∑．（ii ）用（i ）的公式求这组学生的数学成绩和知识竞赛成绩的“斯皮尔曼相关系数”（精确到0.01）．(3)比较（1）和（2）（ii ）的计算结果，简述“斯皮尔曼相关系数”在分析线性相关性时的优势．注：参考公式与参考数据．()()niix x y y r --=∑21(1)(21)6nk n n n k =++=∑31000≈．21．（12分）某商场拟在周年店庆进行促销活动，对一次性消费超过200元的顾客，特别推出“玩游戏，送礼券”的活动，游戏规则如下：每轮游戏都抛掷一枚质地均匀的骰子，若向上点数不超过4点，获得1分，否则获得2分，进行若干轮游戏，若累计得分为9分，则游戏结束，可得到200元礼券，若累计得分为10分，则游戏结束，可得到纪念品一份，最多进行9轮游戏.(1)当进行完3轮游戏时，总分为X ，求X 的分布列和数学期望；(2)若累计得分为i 的概率为()1,2,,9i p i =⋅⋅⋅，初始分数为0分，记01p =（i ）证明：数列{}()11,2,,9i i p p i --=⋅⋅⋅是等比数列；（ii ）求活动参与者得到纪念品的概率.22．（12分）已知函数()e ln xf x x a x =-在1x =处的切线方程为()()21,R y e x b a b =+-∈(1)求实数a ，b 的值；(2)设函数()()23xg x f x e x =--+，当1,12x ⎡⎤∈⎢⎥⎣⎦时，()g x 的值域为区间()(),,Z m n m n ∈的子集，求n m -的最小值．2022-2023学年高二下学期期末模拟试卷(时间：120分钟，分值：150分，范围：必修二第5章——必修三第6、7、8章)一、单项选择题：本题共8小题，每小题5分，共40分.在每个小题绐岀的四个选项中，只有一项是符合题目要求的.1．下列说法，正确的是（）A ．对分类变量X 与Y 的独立性检验的统计量2χ来说，2χ值越小，判断“X 与Y 有关系”的把握性越大B ．在残差图中，残差点分布在以取值是0的横轴为对称轴的水平带状区域越窄，说明模型的拟合精度越高C ．若一组样本数据(),i i x y （1i =，2，…，n ）的对应样本点都在直线23y x =-+上，则这组样本数据的相关系数r 为1D ．数据－1，1，2，4，5，6，8，9的第25百分位数是2【答案】B【分析】对选项A ，根据独立性检验的定义即可判断A 错误，对选项B ，根据残差图的性质即可判断B 正确，对选项C ，根据题意得到相关系数为1-，故C 错误，对选项D ，根据计算得到第25百分位数是32，即可判断D 错误.【详解】对于A ，由独立性检验可知，2χ值越大，判断“X 与Y 有关系”的把握性越大，故A 错误；对于B ，在残差图中，残差点分布的水平带状区域越窄，说明波动越小，即模型的拟合精度越高，故B 正确；对于C ，样本点都在直线23y x =-+上，说明是负相关，相关系数为1-，故C 错误；对于D ，8个数据从小到大排列，由于80.252⨯=，所以第25百分位数应该是第二个与第三个的平均数12322+=，故D 错误，故选：B 2．某校有演讲社团､篮球社团､乒乓球社团､羽毛球社团､独唱社团共五个社团，甲､乙､丙､丁､戊五名同学分别从五个社团中选择一个报名，记事件A 为“五名同学所选项目各不相同”，事件B 为“只有甲同学选篮球”，则()P A B =（）A ．332B ．316C ．34D ．25【答案】A【分析】分别求出事件AB 、事件B 的可能的种数，代入条件概率公式()()()P AB P A B P B =即可求解.【详解】事件AB ：甲同学选篮球且五名同学所选项目各不相同，所以其他4名同学排列在其他4个项目，且互不相同为44A ，事件B ：甲同学选篮球，所以其他4名同学排列在其他4个项目，可以安排在相同项目为44，故()()()44545A 354325P AB P A B P B ===.故选:A .3．8x x ⎛⎫+ ⎪ ⎪⎝⎭展开式中，二项式系数最大的项是（）A ．第3项B ．第4顶C ．第5项D ．第6项【答案】C【分析】根据二项式确定展开式中二项式系数最大的项即可.【详解】由题设，展开式中二项式1r T +对应二项式系数为8C r ，所以，二项式系数最大的项为4r =，即5T ：第5项.故选：C4．将7个人从左到右排成一排，若甲、乙、丙3人中至多有2人相邻，则不同的站法有（）A ．1440种B ．2880种C ．4320种D ．3600种【答案】C【分析】采用间接法，先求出没有限制的所有站法，再排除不满足条件的站法可求解.【详解】7个人从左到右排成一排，共有77A 5040=种不同的站法，其中甲、乙、丙3个都相邻有3535A A 720=种不同的站法，故甲、乙、丙3人中至多有2人相邻的不同站法有50407204320-=种不同的站法.故选：C5．2023年春，为了解开学后大学生的身体健康状况，寒假开学后，学校医疗部门抽取部分学生检查后，发现大学生的舒张压呈正态分布()270.8,7.02X N ~（单位：mm /Hg ），且()82.80.1P X >=，若任意抽查该校大学生6人，恰好有k 人的舒张压落在()58.8,82.8内的概率最大，则k =（）A ．3B ．4C ．5D ．6【答案】C【分析】利用正态分布计算出()58.882.8P X <<，然后利用二项分布概率最大可得出关于k 的不等式组，解之即可.【详解】因为()270.8,7.02X N ~，则()()58.882.81282.80.8P X P X <<=->=，由题意知：抽查该校大学生6人，恰好有k 人的舒张压落在()58.8,82.8内的概率为()()()66C 0.20.81,2,,5kkk k -⋅⋅= ，要使此式的值最大，由6171666151664141C C55554141C C 5555kkk kk k kkk kk k -----+-+⎧⎛⎫⎛⎫⎛⎫⎛⎫⋅⋅≥⋅⋅⎪ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎨⎛⎫⎛⎫⎛⎫⎛⎫⎪⋅⋅≥⋅⋅ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎩，即()()()()()()6176156!416!41!6!551!7!556!416!41!6!551!5!55k kk kk kk kk k k k k k k k ----+-⎧⎛⎫⎛⎫⎛⎫⎛⎫⋅⋅≥⋅⋅⎪⎪ ⎪ ⎪ ⎪⋅--⋅-⎝⎭⎝⎭⎝⎭⎝⎭⎪⎨⎛⎫⎛⎫⎛⎫⎛⎫⎪⋅⋅≥⋅⋅ ⎪ ⎪ ⎪ ⎪⎪⋅-+⋅-⎝⎭⎝⎭⎝⎭⎝⎭⎩，解得232855k ≤≤，{}1,2,3,4,5k ∈ ，所以，5k =.故选：C.6．抛掷三枚质地均匀的硬币一次，在有一枚正面朝上的条件下，另外两枚也正面朝上的概率是（）A ．18B ．78C ．17D ．67【答案】C【分析】由题可知，抛掷三枚硬币，则基本事件共有8个，其中有一枚正面朝上的基本事件有7个，分别求出“有一枚正面朝上”和“三枚都正面朝上”的概率，最后根据条件概率的计算公式，即可求出结果.【详解】解：根据题意，可知抛掷三枚硬币，则基本事件共有8个，其中有一枚正面朝上的基本事件有7个，记事件A 为“有一枚正面朝上”，则()78P A =，记事件B 为“另外两枚也正面朝上”，则AB 为“三枚都正面朝上”，故()18P AB =，故()()()118778P AB P B A P A ===.即在有一枚正面朝上的条件下，另外两枚也正面朝上的概率是17.故选：C.【点睛】本题考查条件概率的计算公式的应用，考查分析和计算能力．7．三名男生和三名女生站成一排照相，男生甲与男生乙相邻，且三名女生中恰好有两名女生相邻，则不同的站法共有A ．72种B ．108种C ．36种D ．144种【答案】D【分析】根据题意，利用捆绑法和插空法，再利用分布乘法原理，即可求出结果．【详解】解：先将男生甲与男生乙“捆绑”，有22A 种方法，再与另一个男生排列，则有22A 种方法，三名女生任选两名“捆绑”，有23A 种方法，再将两组女生插空，插入男生3个空位中，则有23A 种方法，利用分步乘法原理，共有22222233144A A A A =种.故选：D ．【点睛】本题考查乘法原理的运用和排列知识，还运用了捆绑法和插空法解决相邻和不相邻问题，考查学生分析解决问题的能力．8．若不等式222e ln e ln 2e xaa x x a -+-≥-在[1,2]x ∈-有解，则实数a 的取值范围是（）A ．21,e 2e ⎡⎤⎢⎥⎣⎦B ．221,e e ⎡⎤⎢⎥⎣⎦C ．421,e e ⎡⎤⎢⎥⎣⎦D ．41,e e ⎡⎤⎢⎥⎣⎦【答案】D【分析】先得到0a >，不等式变形得到()22e ln 21e exx a a ⎛⎫≥- -⎪⎝⎭，换元后令()()21ln 22e f t t t =--+，问题转化为存在2,e e t a a ⎡⎤∈⎢⎥⎣⎦，使得()0f t ≥，求导后得到()f t 的单调性，结合()()21e 0f f ==，得到当21e t ≤≤时，()0f t ≥，比较端点值得到答案.【详解】由ln a 有意义可知，0a >，222e ln e ln 2e x a a x x a -+-≥-变形为()()22e ln 2e1x aa x --≥-，即()22e ln 21eexx a a⎛⎫≥- -⎪⎝⎭，令e xt a =，即有()2e 1ln 220t t --+≥，因为[1,2]x ∈-，所以2,e e e x t a a a ⎡=⎤∈⎢⎥⎣⎦，令()()21ln 22e f t t t =--+，问题转化为存在2,e e t a a ⎡⎤∈⎢⎥⎣⎦，使得()0f t ≥，因为()22e 1212e t f t t t---'=-=，令()0f t '<，即20e 21t --<，解得2e 12t ->，令()0f t '>，即20e 21t -->，解得2e 102t -<<，所以()f t 在2e 10,2⎛⎫- ⎪⎝⎭上单调递增，在2e 1,2⎛⎫-+∞ ⎪⎝⎭上单调递减，又()()()222210,e e 1ln e 2e 20f f ==--+=，而221e e 1<2-<，所以当21e t ≤≤时，()0f t ≥，若存在2,e e t a a ⎡⎤∈⎢⎥⎣⎦，使得()0f t ≥成立，只需22e e a ≤且e 1a ≥，解得4e 1e ,a ⎡⎤∈⎢⎥⎣⎦.故选：D【点睛】对于求不等式成立时的参数范围问题，一般有三个方法，一是分离参数法,使不等式一端是含有参数的式子，另一端是一个区间上具体的函数，通过对具体函数的研究确定含参式子满足的条件.二是讨论分析法，根据参数取值情况分类讨论，三是数形结合法，将不等式转化为两个函数，通过两个函数图像确定条件.二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9．已知21nx x ⎛⎝的展开式中二项式系数之和为1024，则下列说法正确的（）A ．展开式中奇数项的二项式系数和为256B ．展开式的各项系数之和为1024C ．展开式中常数项为45D ．展开式中含15x 项的系数为45【答案】BCD【分析】先由已知条件得21024n =求出n 的值，然后求出二项式展开式的通项公式，再逐个分析判断即可【详解】解：因为2nx x ⎛⎝的展开式中二项式系数之和为1024，所以21024n =，得10n =，所以二项式展开式的通项公式为5202102110101()rr rrr r T C x C xx --+==⋅，对于A ，展开式中奇数项的二项式系数和为110245122⨯=，所以A 错误，对于B ，因为2nx x ⎛⎝的展开式中二项式系数之和与展开式的各项系数之和相等，所以展开式的各项系数之和为1024，所以B 正确，对于C ，令52002r -=，解得8r =，所以展开式中常数项为81045C =，所以C 正确，对于D ，令520152r -=，解得2r =，所以展开式中含15x 项的系数为21045C =，所以D 正确，故选：BCD10．下列说法正确的是（）A ．在一个2×2列联表中，计算得到2χ的值，则2χ的值越接近1，可以判断两个变量相关的把握性越大B ．随机变量()2~,N ξμσ，若函数()()2f x P x x ξ=≤≤+为偶函数，则1μ=C ．若回归直线方程为ˆ 1.22yx =+，则样本点的中心不可能为(5,7)D ．若甲、乙两组数据的相关系数分别为0.91-和0.89，则甲组数据的线性相关性更强【答案】BCD【分析】由独立性检验的相关知识可判断A ；根据偶函数的对称性可判断B ；根据回归直线过样本点的中心可判断C ；根据线性相关性与相关系数的关系可判断D.【详解】对于A ，在一个2×2列联表中，由计算得2χ的值（可大于1），2χ的值越大，两个变量相关的把握越大，故A 错误；对于B ，()()2f x P x x ξ=≤≤+为偶函数，则()()f x f x -=，即()()22P x x P x x ξξ-≤≤-+=≤≤+，故可得212x x μ-++==，故B 正确；对于C ，7 1.252≠⨯+，所以样本点的中心不可能为()5,7，C 正确；对于D ，具有线性相关关系的两个变量x ，y 的相关系数为r ，则r 越接近于1，x 和y 之间的线性相关程度越强，D 正确．故选：BCD.11．一个袋子中有编号分别为1,2,3,4的4个球，除编号外没有其它差异.每次摸球后放回，从中任意摸球两次，每次摸出一个球.设“第一次摸到的球的编号为2”为事件A ，“第二次摸到的球的编号为奇数”为事件B ，“两次摸到的球的编号之和能被3整除”为事件C ，则下列说法正确的是（）A ．()516P C =B ．事件B 与事件C 相互独立C ．()12P CA =∣D ．事件A 与事件B 互为对立事件【答案】AC【分析】对于选项A ，由古典概型的概率公式得()516P C =，所以该选项正确；对于选项B ，由题得()()()P BC P B P C ≠⋅，事件B 与事件C 不相互独立，所以该选项错误；对于选项C,()12P C A =∣，所以该选项正确；对于选项D,举例说明事件A 与事件B 不是对立事件，所以该选项错误.【详解】对于选项A ，两次摸到的球的编号之和能被3整除的基本事件有(1,2),(2,1),(2,4),(4,2),(3,3)，共5个，由古典概型的概率公式得()554416P C ==⨯，所以该选项正确；对于选项B ，由题得241()442P B ⨯==⨯,21()448P BC ==⨯,所以()()()P BC P B P C ≠⋅，事件B 与事件C 不相互独立，所以该选项错误；对于选项C,()()21()142P AC P CA P A ===⨯∣，所以该选项正确；对于选项D,如果第一次摸到编号为1的球，第二次摸到编号为4的球，则事件A 和B 都没有发生，所以事件A 与事件B 不是对立事件，所以该选项错误.故选：AC12．下列不等关系中正确的是（）A 2ln 3<B 4>C ．sin 33sin1cos1<D ．sin 33sin1cos1>【答案】BC【分析】根据函数值的特征，构造函数()ln xf x x=，求出其导数，判断函数的单调性，可判断AB ；同理构造函数()sin xg x x=，判断CD.【详解】令()ln x f x x=，则()21ln xf x x -'=，当0e x <<时，()0f x ¢>，当e x >时，()0f x '<所以函数()f x 在()0,e 上单调递增，在()e,+∞上单调递减，所以()2f f>，即ln22>2ln 3>=，故A 错误，又ln 42ln 2=，所以ln 4ln242=>44ln >B 正确；令()sin x g x x =，π()0,x ∈，则2cos sin ()x x xg x x -'=，令()cos sin u x x x x =-，则()cos sin u x x x x =--'cos sin 0x x x =-<在(0,π)上恒成立，所以()u x 在(0,π)上单调递减，所以()(0)0u x u <=，所以()0g x '<在(0,π)上恒成立，所以()g x 在(0,π)上单调递减，所以(2)(3)g g >，即sin 2sin 323>，即3sin 2sin 32<=3sin1cos1，故C 正确，D 错误，故选：BC ．【点睛】关键点点睛：构造函数()ln xf x x=和()sin x g x x =，π()0,x ∈，是解决本题的关键.三、填空题：本题共4小题，每小题5分，共计20分.13．2023年五一节到来之前，某市物价部门对本市5家商场的某种商品一天的销售量及其价格进行调查，5家商场这种商品的售价x （单位：元）与销售量y （单位：件）之间的一组数据如下表所示：价格x 89.5m 10.512销售量y1610865经分析知，销售量y 件与价格x 元之间有较强的线性关系，其线性回归直线方程为 3.544y x =-+，则m =________．【答案】10【分析】计算变量的平均值,x y ，根据变量y 与x 之间有较强的线性关系，结合回归直线的性质即可求得m 的值.【详解】变量x 的平均值为89.510.512855m m x ++++==+，变量y 的平均值为161086595y ++++==，又销售量y 件与价格x 元之间有较强的线性关系，所以其线性回归直线方程 3.544y x =-+经过点(),x y ，所以9 3.58445m ⎛⎫=-⨯++ ⎪⎝⎭，解得10m =.故答案为：10.14．某城市休闲公园管理人员拟对一块圆环区域进行改造封闭式种植鲜花，该圆环区域被等分为5个部分，每个部分从红、黄、紫三种颜色的鲜花中选取一种进行栽植．要求相邻区域不能用同种颜色的鲜花，总的栽植方案有_________种．【答案】30【分析】依颜色为出发点，分析可得必用3种颜色的鲜花，先安排1，2位置，再讨论第三种颜色的可能位置，分析运算即可.【详解】若只用两种颜色的鲜花，则1，3位置的颜色相同，2，4位置的颜色相同，即可得1，4位置的颜色不同，则5位置无颜色可选，不合题意；故必用3种颜色的鲜花，则1，2的栽植方案有23A 6=种，已用两种颜色，第三种颜色可能在3，4，5，可得：（i ）若第三种颜色在3或5，有如下两种可能：①3，5的颜色相同，则4的颜色有两种可能，栽植方案有12C 2=种；②3，5的颜色不相同，则4的颜色必和1的颜色相同，栽植方案有12C 2=种；栽植方案共有224+=种；（ⅱ）若第三种颜色在4，则3的颜色必和1的颜色相同，5的颜色必和2的颜色相同，栽植方案共有1种；综上所述：总的栽植方案有()64130⨯+=种.故答案为：30.15．假设有两箱零件，第一箱内装有10件，其中有3件次品；第二箱内装有20件，其中有2件次品．现从两箱中随意挑选一箱，然后从该箱中随机取1个零件，已知取出的是次品，则它是从第一箱取出的概率为__________．【答案】0.75/34【分析】利用条件概率求取出的是次品，求它是从第一箱取出的概率.【详解】设事件i A 表示从第(1,2)i i =箱中取一个零件，事件B 表示取出的零件是次品，则121122()()()()(|)()(|)P B P A B P A B P A P B A P A P B A =+=⋅+⋅131241*********=⨯+==,所以已知取出的是次品，求它是从第一箱取出的概率为1113()3210(|)4()420P A B P A B P B ⨯===.故答案为：34.16．已知函数()ln 20()a x x a f x =-≠，若不等式222e ()e cos(())a x x x f x f x ≥+对0x >恒成立，则实数a 的取值范围为__________.【答案】(0,2e]【分析】将不等式等价转化，构造函数()e 2cos t g t t t =--，并探讨其性质，再利用导数分类讨论()t f x =的值域即可求解作答.【详解】ln 2()22()cos[()]e 2()cos[()]0e 2()cos[()]0eaa x x f x x x f x f x f x f x f x f x --≥⇔--≥⇔--≥，令()t f x =，则()e 2cos t g t t t =--，()e 2sin t g t t '=-+，设()e 2sin t h t t =-+，则()e cos t h t t '=+，当0t ≤时,e 1,sin 1t t ≤≤，且等号不同时成立，则()0g t '<恒成立，当0t >时，e 1,cos 1t t >≥-，则()0h t '>恒成立，则()g t '在(0,)+∞上单调递增，又因为(0)1,(1)e 2sin10g g ''=-=-+>，因此存在0(0,1)t ∈，使得()00g t '=，当00t t <<时，()0g t '<，当0t t >时,()0g t '>，所以函数()g t 在()0,t -∞上单调递减，在(0t ,)∞+上单调递增,又(0)0g =，作出函数()g t的图像如下：函数()ln 2(0)f x a x x a =-≠定义域为(0,)+∞，求导得2()2a a x f x x x-'=-=，①当a<0时，()0f x '<，函数()f x 的单调递减区间为(0,)+∞，当01x <<时，ln y a x =的取值集合为(0,)+∞，而2y x =-取值集合为(2,0)-，因此函数()f x 在(0,1)上的值域包含(0,)+∞，当1x ≥时，ln y a x =的取值集合为(,0]-∞，而2y x =-取值集合为(,2)-∞-，因此函数()f x 在[1,)+∞上无最小值，从而函数()f x 的值域为R ，即()R t f x =∈，()00g t <，不合题意，②当0a >时，由()0f x '<得2a x >，由()0f x '<得02a x <<，函数()f x 在(0,)2a上单调递增，在(,)2a +∞上单调递减，max ()()ln 22a af x f a a ==-，当01x <≤时，ln y a x =的取值集合为(,0]-∞，而2y x =-取值集合为(2,0]-，因此函数()f x 在(0,1]上的值域包含(,0]-∞，此时函数()f x 的值域为(,ln ]2aa a -∞-，即()(,ln ]2a t f x a a =∈-∞-，当ln 02aa a -≤时，即当02e a <≤时，()0g t ≥恒成立，符合题意，当ln02a a a ->时，即当2e a >时，10min ln ,2a t a a t ⎧⎫=-⎨⎬⎩⎭，结合图象可知，()10g t <，不合题意，所以实数a 的取值范围为(0,2e].故答案为：(0,2e]【点睛】关键点睛：函数不等式恒成立求参数范围问题，结合已知，利用换元法构造新函数，用导数探讨函数的性质，借助数形结合的思想推理求解.四、解答题：本题共6小题，共计70分．解答时应写出文字说明、证明过程或演算步骤.17．（10分）为了解学生对党的“二十大”精神的学习情况，学校开展了“二十大”相关知识的竞赛活动，全校共有1000名学生参加，其中男生450名，采用分层抽样的方法抽取100人，将他们的比赛成绩（满分为100分），分为6组：[40,50)，[50,60)，[60,70)，[70,80)，[80,90)，[90,100]，得到如图所示的频率分布直方图．其中成绩不低于80分为“优秀”，低于80分为“非优秀”．(1)求实数a 的值，并估算全校1000名学生中成绩优秀的人数；(2)完成下列22⨯列联表，判断是否有95%的把握认为比赛成绩优秀与性别有关．优秀非优秀合计男女10合计附：22()()()()()n ad bc a b c d a c b d χ-=++++，其中n a b c d =+++．2()P k αχ=≥0.100.050.0100.0050.001k2.7063.8416.6357.87910.828【答案】(1)0.020a =，250（人）(2)填表见解析；没有【分析】（1）根据频率和为1求得a ，进而根据频率估计成绩优秀的人数；（2）根据题意结合分层抽样完善列联表，求2χ，并与临界值对比分析.【详解】（1）由题意可得：(0.0050.0150.0300.0250.005)101a +++++⨯=，解得0.020a =，样本中成绩优秀的频率为：0.0200.0051025(.)0+⨯=，以样本估计总体，全校1000名学生中成绩优秀的人数为：0.251000250⨯=（人）.（2）由题意，采用分层抽样，男生抽取人数450100451000⨯=人，女生抽取1004555-=人，且样本中优秀的人数为1000.2525⨯=人，故22⨯列联表如下：优秀非优秀合计男153045女104555合计2575100可得22100(15453010)1003.0304555257533χ⨯⨯-⨯==≈⨯⨯⨯，因为3.030 3.841<，故没有95%的把握认为比赛成绩优秀与性别有关18．已知()()52601261(1)(1)m x x a a x a x a x +=+-+-++- ，其中R m ∈，且13564a a a ++=，(1)求m 的值；(2)求4a 的值.【答案】(1)2(2)25【分析】（1）分别令0x =，2x =，然后两式相减求结合13564a a a ++=即可得解；（2）()52x x +化为()()53111x x ⎡⎤⎡⎤+--+⎣⎦⎣⎦，求出()511x ⎡⎤-+⎣⎦展开式的通项，令()1x -的指数等于4和3即可得解.【详解】（1）当0x =时，()012345600m a a a a a a a +⋅=-+-+-+，①当2x =时，()5012345622m a a a a a a a +⋅=++++++，②②-①得，()()5135222m a a a +⋅=++，因为13564a a a ++=，所以()()5135222128m a a a +⋅=++=，解得2m =；（2）()()()5523111x x x x ⎡⎤⎡⎤+=+--+⎣⎦⎣⎦，()511x ⎡⎤-+⎣⎦展开式的通项为()515C 1kk k T x -+=-，令54k -=，则1k =，令53k -=，则2k =，所以124553C C 25a =+=.19．已知0a >，函数()()2ln ln e f x x a a x x =-+-，其中e 是自然对数的底数.(1)当1a =时，求曲线()y f x =在点()()1,1f 处的切线方程；(2)当e a =时，求函数()f x 的单调区间；(3)求证：函数()f x 存在极值点，并求极值点0x 的最小值.【答案】(1)()212e e 0x y --+=(2)单调增区间为(e,)+∞，单调减区间为(0,e)(3)证明见解析，0x 的最小值是e ．【分析】（1）先求()f x 的导函数,再点斜式求曲线()y f x =在点()()1,1f 处的切线方程（2）先求()f x 的导函数，根据()f x '的正负判定函数的增减即可；（3）根据导数的分母正，需要分子有变号零点，转变为双变量函数的恒成立和有解问题，利用导数再次确定新函数单调性和最值即可求解.【详解】（1）当1a =时，()()2ln e f x x x =-+-,()()()221ln11e 1e f ==-+--,()()12e f x x x'=-+-,()()1121e 12e f '=-+-=-,曲线()y f x =在点()()1,1f 处的切线方程()()()21e 12e 1y x --=--,切线方程()212e e 0x y --+=.（2）当e a =时，2()eln (e)f x x x x =-+-，则2e 2(12e)e (21)(e)()12(e),(0)x x x x f x x x x x x+--+-+-='=-=>令()0f x '>，得e x >；令()0f x '<，得e x <；所以，函数()y g x =的单调增区间为(e,)+∞，单调减区间为(0,e)．（3）22(ln 2e)()ln 2(e)a x a x af x a x x x+--=-+'-=令2()2(ln 2e)0t x x a x a =+--=，因为2(ln 2e)80a a ∆=-+>，所以方程22(ln 2e)0x a x a +--=，有两个不相等的实根()1212,x x x x <，又因为1202ax x =-<，所以120x x <<，令02x x =，列表如下:x ()00,x 0x ()0,x +∞()f x '-0+()f x 减极小值增所以()f x 存在极值点0x .所以存在0x 使得2002(ln 2e)0x a x a +--=成立，所以存在0x 使得200022e ln x x a x a -=-，所以存在0x 使得2000ln 22e a x a x x -=-对任意的0a >有解，因此需要讨论等式左边的关于a 的函数，记0()ln u t t x t =-，所以0()1x u t t=-'，当00t x <<时，()0,()u t u t <'单调递减；当0t x >时，()0,()u t u t >'单调递增．所以当0t x =时，0()ln u t t x t =-的最小值为()0000ln u x x x x =-．所以需要200000022e ln ln x x a x a x x x -=-≥-，即需要200002(2e 1)ln 0x x x x -++≥，即需要002(2e 1)ln 0x x -++≥，即需要002ln (2e 1)0x x -+≥+因为()2ln (2e 1)v t t t =+-+在(0,)+∞上单调递增，且()0()0v x v e ≥=，所以需要0e x ≥，故0x 的最小值是e ．20．某校20名学生的数学成绩(1,2,,20)i x i = 和知识竞赛成绩(1,2,,20)i y i = 如下表：学生编号i 12345678910数学成绩i x 100999693908885838077知识竞赛成绩iy 29016022020065709010060270学生编号i 11121314151617181920数学成绩i x 75747270686660503935知识竞赛成绩iy 4535405025302015105计算可得数学成绩的平均值是75x =，知识竞赛成绩的平均值是90y =，并且()20216464i i x x =-=∑，()2021149450ii yy =-=∑，()()20121650i i i x x y y =--=∑．(1)求这组学生的数学成绩和知识竞赛成绩的样本相关系数（精确到0.01）．(2)设*N N ∈，变量x 和变量y 的一组样本数据为(){},|1,2,,i i x y i N = ，其中(1,2,,)i x i N = 两两不相同，(1,2,,)i y i N = 两两不相同．记i x 在{},2|1,,n x n N = 中的排名是第i R 位，i y 在{},2|1,,n y n N = 中的排名是第i S 位，1,2,,i N = ．定义变量x 和变量y 的“斯皮尔曼相关系数”（记为ρ）为变量x 的排名和变量y 的排名的样本相关系数．。

福建上杭县第一中学2022-2023学年高一上数学期末学业水平测试模拟试题含解析

；②
（2）若函数的定义域为 D，且具有性质，则“ 存在零点”是“
，
.
”的___________条件，说明理由；（横
线上填“充分而不必要”、“必要而不充分”、“充分必要”、“既不充分也不必要”）
（3）若存在唯一的实数 a，使得函数
，
具有性质，求实数 t 的值.
参考答案
一、选择题：本大题共 10 小题，每小题 5 分，共 50 分。在每个小题给出的四个选项中，恰有一项是符合题目要求的
【点睛】本题主要考查了幂函数和对数函数的图像特征，属于基础题. 6、B 【解析】根据交集定义运算即可
【详解】因为
M
{x
|
0
x
4}, N
{x
|
1 3
x
5} ，所以
M
N
x|
1 3
x
4 ,
故选：B. 【点睛】本题考查集合的运算，属基础题，在高考中要求不高，掌握集合的交并补的基本概念即可求解.
7、C 【解析】
根据函数 y 3cos(2x ) 的图像关于点 ( 4 , 0) 中心对称，由 cos(8 ) 0 求出的表达式即可.
3
3
【详解】因为函数 y 3cos(2x ) 的图像关于点 ( 4 , 0) 中心对称， 3
所以 cos(8 ) 0 ， 3
所以 8 k ，
3
2
解得 k 13 , k Z ， 6
【解析】若 m⊂α，α∥β，则 m∥β；
若 m⊥α，α∥β，则 m⊥β
故答案为（1）③⑤（2）②⑤
9、B
【解析】由图可知， 3 T 5 ( ) ，所以T 4 2 ，所以 3 ，又当
46 6
3

中医内科学期末模拟试卷(卷4)

中医内科学试题及答案1、肾气虚证者，若出现尿频较甚及小便失禁，应加用的药物是A.黄芪.党参.白术B.沙参.五味子.百合C.肉豆蔻.补骨脂D.补骨脂.五味子.蛤蚧E.菟丝子.五味子.益智仁【答案】E2、外感咳嗽其病尚浅而易治，但燥与哪个邪气二者较为缠绵A.湿B.风C.寒D.火E.暑【答案】A3、聚证可能出现的变证有A.胸痹B.中风C.水肿D.积证E.关格【答案】A B C D E4、肺痿的主症是A.咳吐腥臭脓痰B.咳吐腥臭痰血C.咳吐浊唾涎沫D.咳嗽喉间痰鸣E.咳吐黄绿色痰【答案】C5、肝阳上亢型眩晕的临床表现A.耳鸣B.口苦C.急躁D.脉弦E.头重如蒙【答案】A B C D6、下列属于少阴病的临床表现的有A.畏寒蜷卧，四肢逆冷B.精神萎靡，似睡非睡C.下利清谷，小便清长D.心烦不得眠E.心中疼热，饥不欲食【答案】A B C D7、下面属于寒凝心脉时的临床表现的是A.心痛如绞B.手足不温C.情志不遂诱发D.时欲太息E.胸闷气短【答案】A B E8、患者眩晕，动则加剧，劳则即发，面色㿠白，唇甲不华，心悸少寐，神疲懒言，饮食减少，舌质淡，脉细弱。

其治法是A.健脾益气，益肾温中B.温补脾肾，通络宁心C.健脾益肾，活血化瘀D.补益肝肾，化瘀通络E.补益气血，调养心脾【答案】E9、风寒袭肺型咳嗽的治则是A.疏风散寒，宣肺止咳B.疏风散寒，化痰止咳C.疏风清热，宣肺止咳D.疏风清肺，润燥止咳E.以上都不是【答案】A10、下列哪项不是眩晕肝阳上亢证的主症A.头晕而痛B.心烦少寐C.面色潮红D.口苦便秘E.肢软乏力【答案】E11、痢疾的治疗方法是A.初痢宜通B.久痢宜涩C.大便赤多重用血药D.大便白多重用气药E.宜利小便【答案】A B C D12、患者久病体虑，四肢微弱肌肉瘦削，手足麻木不仁，四肢青筋显露，伴有肌肉活动时引痛不适，舌痿不能伸缩，舌质暗淡有瘀点，脉细涩。

此属A.痿证湿热浸淫型B.痿证肺热津伤型C.痿证脾胃虚弱型D.痿证肝肾亏损型E.痿证脉络瘀阻证【答案】E13、下列各项中哪一项不是引起劳淋的病因A.诸淋日久B.过服寒凉C.久病体虚D.劳伤过度E.情志失调【答案】B14、痰与饮的区别，下列正确的是A.痰质地较稠，饮质地较稀B.痰流动性大，饮流动性小C.痰致病广泛，饮致病局限D.痰性有寒热，饮性多偏寒E.饮可凝为痰，痰难化为饮【答案】A C D E15、胃痛应与哪些病证相鉴别A.胃痞B.真心痛C.胁痛D.腹痛E.呕吐【答案】B C D16、积证在历代医籍中亦称为A.癥积B.痃癖C.癖块D.伏梁E.肥气【答案】A B C D E17、肺痨的发展变化可累及哪些脏腑A.肝B.心C.脾D.肺E.肾【答案】A B C D E18、治疗便秘的基本法则是A.补中益气B.滋阴增液C.顺气导滞D.润肠通便E.温里散寒【答案】D19、症见腹中气聚，攻窜胀痛，时聚时散，苔白脉弦，治法为A.理气化浊B.理气活血C.疏肝解郁D.行气消聚E.祛瘀活血【答案】C D20、黄疸的各种病理因素中，最重要的是A.湿邪B.热邪C.寒邪D.疫毒E.气滞【答案】A21、最先明确提出“内伤发热”这病名的中医书籍的是A.《内经》B.《太平圣惠方》C.《症因脉治》D.《证治汇补》E.《内外伤辨惑论》【答案】C22、中风的表现A.缓慢起病B.突发半身不遂C.口舌歪斜D.言语謇涩E.神志昏蒙【答案】B C D E23、下列哪项不是聚证的主要特征A.腹中气聚B.聚散无常C.痛有定处D.时作时止E.病情较轻【答案】C24、下列各项，属于癌病病因的是A.六淫邪毒B.内伤七情C.饮食失调D.素体内虚E.误治失治【答案】A B C D E25、患者不寐，性情急躁易怒，不思饮食，口渴喜饮，目赤口苦，小便黄赤，大便秘结，舌红苔黄，脉弦而数。

中医内科学期末模拟试卷(卷8)

中医内科学试题及答案1、瘀血停滞之胃痛，痛甚者常加何药A.木香.陈皮B.桃仁.红花C.川楝子.元胡D.三棱.莪术E.元胡.木香.郁金【答案】E2、李某，男，33岁。

病起发热，热后突然出现肢体软弱无力，肌肉瘦削，皮肤干燥，心烦口渴，咳呛少痰，咽干不利者，宜选用A.桑杏汤B.六味地黄丸C.虎潜丸D.加味二妙散E.清燥救肺汤【答案】E3、聚证的基本治则是A.疏肝理气，行气消聚B.活血化瘀，软坚散结C.行气导滞，通腑泻实D.理气活血，祛痰消积E.攻补兼施，补虚消积【答案】A4、刘某，78岁。

哮喘病史20余年，近1周，咳吐涎沫，不渴，短期不足以息，头眩，神疲乏力，食少，形寒，小便数，咳嗽时尿失禁，舌质淡，脉虚弱。

治宜选用A.麦门冬汤B.甘草干姜汤C.生姜甘草汤D.清燥救肺汤E.真武汤【答案】B C5、腹痛中虚脏寒证可选用的方剂是A.大建中汤B.小建中汤C.附子理中汤D.良附丸E.枳实导滞丸【答案】A B C6、肺痨的治疗大法以A.滋阴益气B.治痨杀虫C.化痰通络D.温肺止咳E.补虚培元【答案】B E7、厥之虚证的特点有A.眩晕昏厥B.面色苍白C.声低息微D.口开手撒E.舌胖或淡【答案】A B C D E8、水肿湿毒浸淫证，疮痍湿盛糜烂者，应加用A.麻黄.杏仁B.苏子.葶苈子C.白鲜皮.地肤子D.苦参.茯苓E.茯苓.泽泻9、痢疾的病位在A.肝B.脾C.肾D.肠E.心【答案】D10、湿热下注扰动精室之遗精应选用A.龙胆泻肝汤B.苍术二陈汤C.程氏萆薢分清饮D.八正散E.知柏地黄丸【答案】C11、症见腹中气聚，攻窜胀痛，时聚时散，苔白脉弦，治法为A.理气化浊B.理气活血C.疏肝解郁E.祛瘀活血【答案】C D12、以下何项症状为胃痞之主症A.胃脘疼痛B.胃脘满闷C.胸脘痞闷D.满闷不舒E.胸脘闷痛【答案】B13、下列哪些为感冒的特征A.恶寒发热B.鼻塞声重C.周身疼痛D.喷嚏流涕E.咳喘痰多【答案】A B C D14、李某，男性，56岁。

2023届四川省资阳市高中(物理高二下期末教学质量检测模拟试题含解析

2022-2023学年高二下物理期末模拟试卷注意事项1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、单项选择题：本题共6小题，每小题4分，共24分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、23290Th经过一系列α衰变和β衰变后变成20882Pb，则20882Pb比23290Th少A．16个中子，8个质子B．8个中子，16个质子C．24个中子，8个质子D．8个中子，24个质子2、下列四幅图是交流电的图象，其中能正确反映我国居民日常生活所用交流电的是（）A．B．C．D．3、如图，一重为25N的球固定在弹性杆AB的上端，现用测力计沿与水平方向成37°角斜向右上方拉球，使杆发生弯曲，此时测力计的示数为15N，已知sin37°=0.6，cos37°=0.8则杆AB对球作用力的大小为A．40NB．25NC．20ND．15N4、如图所示，两块相互垂直的光滑挡板OP、OQ，OP竖直放置，小球a、b固定在轻弹簧的两端，并斜靠在OP、OQ 挡板上．现有一个水平向左的推力F作用于b上，使a、b紧靠挡板处于静止状态．现保证b球不动，使竖直挡板OP 向右缓慢平移一小段距离，则（）A．b对挡板OQ的压力变大B．挡板OP对a的弹力不变C．推力F变大D．弹簧长度变长5、用同一实验装置如图甲研究光电效应现象，分别用A、B、C三束光照射光电管阴极，得到光电管两端电压与相应的光电流的关系如图乙所示，其中A、C两束光照射时对应的遏止电压相同，均为U c1，下列论述正确的是A．B光束光子的能量最小B．A、C两束光的波长相同，且比B光的波长短C．三个光束中B光束照射时单位时间内产生的光电子数量最多D．三个光束中B光束照射时光电管发出的光电子最大初动能最大6、如图所示，使一个水平铜盘绕过其圆心的竖直轴OO 转动，且假设摩擦等阻力不计，转动是匀速的.现把一个蹄形磁铁水平向左移近铜盘，则A．铜盘转动将变快B．铜盘转动将变慢C．铜盘仍以原来的转速转动D．因磁极方向未知，无法确定二、多项选择题：本题共4小题，每小题5分，共20分。