40、中国科学技术大学2019-2020学年第一学期数学分析(B1)期中考试(9页 文字版)
中国科学技术大学数学系本科生计算四年课程安排一览
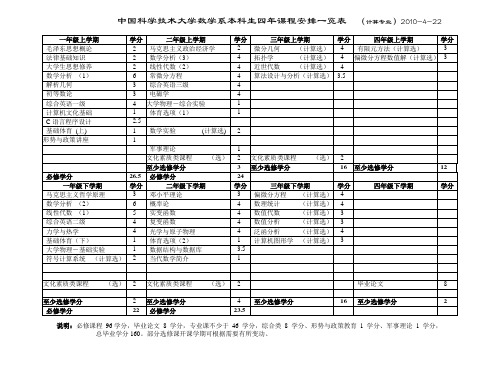
至少选修学分
4
至少选修学分
16
至少选修学分
2
必修学分
22
必修学分
23.5
说明:必修课程96学分,毕业论文8学分,专业课不少于46学分,综合类8学分、形势与政策教育1学分、军事理论1学分,
总毕业学分160。部分选修课开课学期可根据需要有所变动。
3
综合英语二级
4
复变函数
4
数值分析(计算选)
3
力学与热学
4
光学与原子物理
4
泛函分析(计算选)
4
基础体育(下)
1
体育选项(2)
1
计算机图形学(计算选)
3
大学物理-基础实验
1
数据结构与数据库(选)
3.5
符号计算系统(计算选)
2
当代数学简介
1
文化素质类课程(选)
2
文化素质类课程(选)
2
毕业论文
8
至少选修学分
2
文化素质类课程(选)
2
至少选修学分
3
至少选修学分
16
至少选修学分
12
必修学分
26.5
必修学分
24
一年级下学期
学分
二年级下学期
学分
三年级下学期
学分
四年级下学期
学分
马克思主义哲学原理
3
邓小平理论
3
偏微分方程(计算选)
4
数ቤተ መጻሕፍቲ ባይዱ分析(2)
6
概率论
4
数理统计(计算选)
4
线性代数(1)
5
实变函数
4
数值代数(计算选)
2
线性代数(2)
中科大数学分析(B1) 期中考试

f (x)
f (0) = 0, f (x) > 0, (x > 0).
1
2
{a2n}
:
:
( x = y,
15 ) f (x)
[0, 1]
0 f (x) 1.
|f (x) − f (y)| < |x − y|.
x, y ∈ [0, 1],
x0 ∈ (0, 1]
f (x0)
=
. 1−x0 x0
g(x) = 1−xf (x)−x. g(x) [0, 1]
h2(x) = 0, (x 0). f (x)
g (x) = 0, x ∈ (−∞, +∞). 2
g(x) (......... 10 )
2
2
1. lim ln2(n 1) ln2 n ; n
3.
x
lim
1 2
x x
x
;
2. lim 3 n2(3 n 1 3 n) ;
n
4.
x
lim
x
1
1 x
x
e .
三、(本题 16 分, 每小题 4 分) 计算下面的导数:
1.
ln
tan
x 2
;
2.
arcsin
1 1
x x
2 2
;
3. ( 1 x 2 ) ;
4. (xex )(n) .
四、(本题 15 分)
设 a1
1, an1
1 1 ,n an
1, 2, .
求证:
数列 {an } 收敛,
并求其极限.
五、(本题 15 分) 求证: sin x x x 3 , (x 0) . 6
六、(本题 15 分) 设 f (x) 在区间[0,1] 上连续且 0 f (x) 1 . 若对一切 x,y [0,1], x y , 有
中科大数学分析历年期末考试卷

:
(3)
2
1
大学生数学竞赛及考研:122307834
7.
15
a, b ax, −π < x < 0; bx, 0 ≤ x < π.
f (x) =
(1) (2)
f (x) f (x) (a)
Fourier Fourier
∞ ∑ (−1)n , 2 n + 1 n=0
(b)
∞ ∑ n=0
0 0
π 2 π 2
n=1 n = 1.
3.
x = sin t. ∫ 1 √ ∫ 2 2 x 1 − x dx = 2
−1
1
x
π 2
2
sin2 t cos2 t dt
1 = 2 4. ∫
0 +∞ √
∫
0
0
1 sin 2t dt = 4
2
1 (1 − cos 4t) dt = . 8 ∫ +
e dt − x
n+1
n→+∞ n
sin x dx x
n→+∞ 0
e x dx
x n
n→∞
lim
1 1 1 + + ··· + n+1 n+2 n+n
)
n→∞
lim ∫
n! n ( 5 ) 2. ∫ 1− x2 dx (x + y )dx + xdy = 0.
∞ ∑ (√ n=1
√
1
∫
x ln x dx
3.
ex xn ≤ exn , x ∈ [0, 1],
n→∞ 0
∫1 e 0 ≤ 0 ex xn dx ≤ n+1 . ∫ 1 lim ex xn dx = 0.
数学分析2019-2020期中考试卷及答案

数学分析2019-2020期中考试卷及答案(考试时间:120分钟)科目:数学分析I (期中卷)专业 本、专科 年级 班 姓名 学号我承诺,遵守《上海师范大学考场规则》,诚信考试. 签名:________________一. 判断题(对的打√, 错的打×, ''21020⨯=)1. ( × ) 设a 为有理数,x 为无理数,则ax 一定是无理数.2. ( × ) 设数列{},{}n n a b 满足:对任何自然数n , 有n n a b >, 且n n a ∞→lim 和n n b ∞→lim 都存在,则lim lim n n n n a b →∞→∞>.3. ( √ ) 单调数列{}n a 如果含有一个收敛的子列, 则{}n a 本身一定也收敛.4. ( × ) 设{}n a 是无穷小数列, n {b }是无穷大数列, 则n n {a b }是无穷大数列.5. ( × ) 任何数列都存在收敛的子列.6. ( × ) 设{},{}n n a b 均为无界数列, 则{}n n b a 一定为无界数列.7. ( √ ) 设函数()f x 在某00()U x 内有定义, 且()f x 在0x 点的左右极限都存在且相等, 则()f x 在0x 极限存在.8. ( × ) 设0,lim ()lim ()x x x x f x g x b →→∞==, 则0lim ()()x x f x g x →=∞.9. ( √ ) 如果对任何以0x 为极限的递减数列00{}()n x U x +⊂, 都有lim ()n n f x A ∞→=,则有0lim ()x x f x A +→=.10. ( × ) 若00,0,εδ∃>∃> 总可找到00',''(,),x x U x δ∈使得0|(')('')|f x f x ε-≥,则0lim ()x x f x →不存在.二.叙述题(''842=⨯)1. 叙述极限0lim ()x f x →存在的柯西准则.答: 设函数()f x 在0(0,)U δ内有定义. 0lim ()x f x →存在的充要条件是:0ε∀>,0δ∃>,(2分) 使得对0),,'(0U x x δ∀∈有()(')f x f x ε-<.(2分) 2. 叙述集合S 上确界的分析定义.设S 是R 中的一个数集,若数η满足以下两条:(1) 对一切x S ∈ 有x η≤,即η是数集S 的上界;(2分) (2) 对任何αη<存在0x S ∈使得(即η是S 的最小上界)(2分) 则称数η为数集S 的上确界. 三.计算题(本大题满分24', 每小题'4)1. 求⎪⎪⎭⎫⎝⎛++⋅⋅⋅+⋅+⋅∞→)1(1321211lim n n n 2. 求02lim x x → 解: 111lim()1223(1)n n n→∞+++⋅⋅⋅+ 解: 021lim 4x x x →→===11111lim(1)223(1)n n n →∞-+-++-+ =1lim(1)1n n →∞-+=1 3. 求0sin 2lim ln(1)x xx →+ 4. x x x cos 111lim 20--+→解: 00sin 22limlim 2ln(1)x x x xx x →→==+ 解:)11(2sin )2(2)11(2sin 211lim 2222220++=++-+→x x x x x x x1=。
2019-2020学年度第一学期七年级期中联考数学科答案和参考评分标准

'''5 43124 41673 4161825 -=+--=+-+-=解:原式2019-2020学年度第一学期七年级期中联考数学科试卷答案第一部分(共36分)1. C2. D3. A4. B5. D6. D7. D8. D9. B 10. C 11. B 12. B第二部分(各3分,共12分)15.16.【解析】时,,时,, 时,, 时,,依此类推,三角形的边上有 枚棋子时,S=3n —3第三部分17.(各5分,共10分)(1) (2)18.(6分)当时,19. (6分)(1) 第二组人数:62a ⎛⎫+ ⎪⎝⎭人.(2) 第三组人数: 3(6)2a+人. (3) 第四组人数:(人). (4) 时,第四组有 人(答案不唯一).'''5 134 2730-161 36-43-36-6536-94- =+=⨯⨯+⨯=)()()()(解:原式……2分 ……4分 ……6分……1分……2分……4分……6分92290)]5()3(810[5190=+=-+-++++20. (6分)克,答:抽样检测的袋食品的平均质量是克.(列式4分+正确结论2分)21. 三视图如下:(每个2分共6分)22.(8分)解:因为10>8>0>—3>—5所以第3的计为0分,小明的90分计为0分其余的分数分别是90+10=100分,90+8=98分,90-3=87分,90-5=85分平均分是:23.(10分)(1),,,都是负数或其中一个为负数,另两个为正数,……1分①当,,都是负数,即,,时,则……3分②,,有一个为负数,另两个为正数时,设,,,则.……5分因此的值为或.……6分(2),,且,,,……8分则.……10分……1分……2分……4分……6分……8分。
中国科学技术大学数学分析历年考试真题

an n
=
0,证明: lim n→∞
1 n
max {ak}
1kn
=
0.
5
中国科学技术大学2012-2013学年第一学期 数学分析(B1)第二次测验
1. (35分)计算.
(1)x2ex的n阶导数.
(2)已知sin(xy) + y2 = x,求 dy . (用x, y的函数表示)
dx
1 − cos x2
在x = 1处连续,证明f (x)为常值函数.
5.
(12分)设α
>
1,x1
>
0,xn+1
=
α(1 + xn) (n α + xn
=
1, 2, · · ·).
求
n
(−1)k−1 k
,判断数列{an}的收敛性.
k=1
7.
(8分)设数列{an}满足 lim n→∞
(3)若f : [−2, 2] → [−1, 1]连续,则存在x0 ∈ [−2, 2]使得f (x0) = x0; (4)若f : R → R一致连续,则f 有界.
2. (32分)计算下列极限.
(1) lim
1 1+
1 n
n→∞
n
x + 3 2x (3) lim
x→+∞ x + 1
1
(2) lim n − (n − 1) 1 −
n→∞
√
n
tan x( 1 + sin x − 1)
(4) lim
x→0 1 − cos (sin x)
3. (10分)设f (x) = lim 1 + x2enx . 求f (x),并研究其连续性. n→∞ x + enx
中国科学技术大学考试试卷集(五)

设是区间[0,1]上的黎曼可积函数,且在 = 0连续。定义函数列 如下:
() = ∫ ( ) , ∈ [0,1], = 1,2, ⋯.
0
(1)求函数列{ }的极限(不需要证明)
;
(2)证明函数列{ }一致收敛.
5.(15 分)
设{ }是一个有界数列,是它的极限点集。若 lim (+1 − ) = 0,证明是一个闭区
(3’)
(3) 求 H 的每个不可约复特征标 χ 的诱导复特征标 χG ;
(7’)
(4) 在 (2) 的基础上利用行列正交关系求 G 的复特征标表.
(7’)
4. 设 A 是有限维 F -代数。
(1) 证明下述命题等价:
(14’)
(a) A 是半单代数 (即左正则 A-模 A A 是半单模);
(b) 任一左 A-模是半单模;
四(9 分)设 = [0,1] × [0,1], 上连续函数列{ }关于单调递减趋于 0,,求证
lim ∫
→∞
= 0.
五(15 分)令() = 0 + , 0 , ∈ ℝ3为固定向量,|| = 1。令
(, ) = | − ()| − , ≥ 0
1. 设 (V, ρ) 为群 G 的 F -表示。令 V ∗ := HomF (V, F ) 为 V 的对偶空间。考虑
映射 ρ∗ : G → GL(V ∗ ), 其中 ρ∗ (g)(f )(v) := f (g −1 v), ∀g ∈ G, f ∈ V ∗ , v ∈ V . 证
明:
(1) (V ∗ , ρ∗ ) 为 G 的 F -表示,称为 (V, ρ) 的对偶表示; (4’)
R1
中国科学技术大学2018年数学分析考研试题及解答

证明: ak = o(k2), k → +∞.
2. 设 Φ(x) 为周期为 1 的黎曼函数.
(1) 求 Φ(x) 的连续点和间断点的类型.
(2) 计算积分
1 0
Φ(x)
dx.
3. 已知 Ω 为 R3 中的有界域, ⃗n 为单位向量. 求证: 存在以 ⃗n 为法向量的平面平分 Ω 的体积.
4. 已知 f (x) 为周期等于 2π 的奇函数, 当 x ∈ (0, π) 时, f (x) = −1. 试利用 f 的 Fourier 级数计算
t
2−t
=2
(f ′(x − t))2 + (g′(x + t))2 dx.
t
dF (t) dt = −2
(f ′(2 − 2t))2 + (g′(x))2
−2
(f ′(0))2 + (g′(2t))2
2−t
+2
−2f ′(x − t)f ′′(x − t) + 2g′(x + t)g′′(x + t) dx
7. 已知 Dt = {(x, y) ∈ R2 : (x − t)2 + (y − t)2 ⩽ 1, y ⩾ t} , f (t) = Dt x2 + y2 dx dy, 计算 f ′(0). 8. 已知 u(x) ∈ C[0, 1], u(x) ∈ C2(0, 1), u′′(x) ⩾ 0, 令 v(x) = u(x) + εx2, ε > 0.
t
= −4 (g′(2t))2 − 4 (f ′(2 − 2t))2 ⩽ 0.
计算上述积分时会用到
f ′(x)f ′′(x) dx =
f ′(x) df ′(x)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、(本题 18 分,
每小题 6 分)
设 为实数,
函数 f (x)
x 0,
sin
1 x
,
x x
0. 0
解答下列问题:
(1)问当且仅当 取何值时, f (x) 在 x 0 处连续, 但不可导(需说明理由)?
(2)问当且仅当 取何值时, f (x) 在 x 0 处可导, 但导函数 f (x) 在 x 0 处不连续(需说明理由)?
b2
(*)
(1 a2) 3 2ab 2 b2
lim
x
x2
x x 2 3x 2 ax b
x2
x2
0
因为
第 2 页, 共 9 页
x
lim
x2
3x x2
2
ax x2
b
0
x
lim
(1
a
2
)
3 2ab x
2
b2 x2
1 a2
0
a
1.
其中已用到a 0 . 将a 1 代入式(*), 得:
2g(0) 2
dx 2
dx 2 x 0
说明 注意反函数的求导法则: df 1(x)
1
而不是 1 .
dx
f (f 1(x))
f (x)
三、(本题 18 分,
每小题 6 分)
设 为实数,
函数 f (x)
x 0,
sin
1 x
,
x x
0. 0
解答下列问题:
(1)问当且仅当 取何值时, f (x) 在 x 0 处连续, 但不可导(需说明理由)?
1 n2
.
解 记 Sn a1 a2 an , 则 {Sn } 单调递增.
①若 {Sn } 无界, 则 Sn (n ) , 又 M 0, an M , 故
0
an
M
a1 a2 an Sn
由 lim M 0 及两边夹法则知, n Sn
lim
an
0.
n a1 a2 an
6. 求极限 lim cos(sin x) cos x .
x 0
x4
二、(本题 12 分) 设函数 f (x) 在 x 0 处二阶可导, 满足 f (0) 0, f (0) 1 , 并且 f (x) 有反函数 g(x), 求
f (x 2)和 g(x 2) 在 x 0 处的关于 x 的二阶导数的值.
lim
f (x0) f (x)
(1)
xx0 f (x0)(f (x) f (x0)) (x x0)f (x0))
f (x) f (x0)
lim
x x0
f
(x 0 )
f (x) x
x
x0 f (x0) x0
f
(x 0 )
f (x0) (2) 2(f (x0))2
说明 上式(1)用到 L’Hospital 法则, (2)运用的是导数的定义. 错解 (1)运用带 Lagrange 余项的 Taylor 定理; (2)直接运用两次 L’Hospital 法则. 出现上述错误的原因是, f (x) 在 x0 处二阶可导只能说明 f (x) 在 x0 附近存在一阶导数, 但在 x0 附近不 一定存在二阶导数.
3x
2
x
3 2
(a
1)x
b
3 2
0
注意到,
x
lim
x2
Hale Waihona Puke 3x2x3 2
lim
x
1
4
0
x 2 3x 2 x 3
2
从而,
x
lim
(a
1)x
b
3 2
0
ab
1 3 2
0 0
ab
1 3
2
故a 1, b 3 . 2
解(3) 由带 Peano 余项的 Taylor 定理,
x 2 3x 2 x
d dt
dy dx
dt dx
2(1 t2)
5. 设函数 f (x) x 2 ln(1 x 2) , 求当 n 2 时, f (n)(0) 的值.
提示 运用 Leibniz 公式.
解 由 Leibniz 公式,
n
(fg)(n)
n k
f (k )g(nk )
k 0
(ln(1 x 2))(n) (ln(1 x) ln(1 x))(n) (1)n1(n 1)!(1 x)n (n 1)!(1 x)n
3.
设 f (x) 在 x0 处二阶可导,
且 f (x0)
0,
求
lim
x x0
f
(x
)
1
f
(x0
)
(x
x
1 0 )f
(x
0
)
.
4.
设由参数方程 yx
arctan t ln(1 t2) 确定 y 是 x 的函数,
求 dy , d2y dx dx 2
.
5. 设函数 f (x) x 2 ln(1 x 2) , 求当 n 2 时, f (n)(0) 的值.
4.
设由参数方程 yx
arctan t ln(1 t2) 确定 y 是 x 的函数,
求 dy , d2y dx dx 2
.
解 由题意得,
dx 1 , dy 2t dt 1 t2 dt 1 t2
故
dy dy dt 2t (1 t2) 2t dx dt dx 1 t2
d2y dx 2
f (x0)
(x
1 x 0 )f
(x0)
f (x0) 2(f (x0))2
.
解(2) 由 L’Hospital 法则,
lim
x x0
1
f (x)
f (x0)
(x
1
x0)f (x0)
lim (x x0)f (x0) (f (x) f (x0)) x x0 (f (x ) f (x0))(x x0)f (x0)
解 由题意得,
df (x 2) 2xf (x 2), d2f (x 2) 2f (x 2) 4x 2f (x 2) d2f (x 2)
2f (0) 2
dx
dx 2
dx 2 x 0
由于 g(x) 是 f (x) 的反函数,
g(0) 0, g(0)
f
1 (0)
1,
故
d2g(x 2) 2g(x 2) 4x 2g(x 2) d2g(x 2)
(2)运用 Taylor 定理, 其中 50%的同学在展开时错了, 一部分同学算得 1 后算错了. 3!
第 5 页, 共 9 页
二、(本题 12 分) 设函数 f (x) 在 x 0 处二阶可导, 满足 f (0) 0, f (0) 1 , 并且 f (x) 有反函数 g(x), 求
f (x 2)和 g(x 2) 在 x 0 处的关于 x 的二阶导数的值.
一、(本题 36 分, 每小题 6 分) 计算题(给出必要的计算步骤)
1.
设数列 {an } 为正的有界数列,
求 lim n a1
an a2 an
.
提示 考虑如下几个数列:
(1) an
1;
(2) an
10,,
n n
2k 2k
; 1
(3) an
1; n
(4) an
1; n(n 1)
(5) an
第 4 页, 共 9 页
f (n)(0) x 2(ln(1 x 2))(n)
n 1
2x(ln(1 x 2))(n1)
n 2
2(ln(1 x 2))(n2)
x 0
n(n 1)(n 3)!((1)n3 1)
2n
2 0,
! n
,
n n
2k 2k
2 (k 1
*
)
注意 运用 Leibniz 公式时, 不要遗漏二项式系数.
(*) lim
x
(3 2b) 2 b2 x
3 2b 0 3 2b 0 b 3 .
x 2 3x 2 x b
2
2
x
x
经检验, a 1, b 3 时, 原式成立, 故a 1, b 3 .
2
2
解(2)
lim
x
x 2 3x 2 ax b
x
lim
x2
6. 求极限 lim cos(sin x) cos x .
x 0
x4
解(1) 由带 Peano 余项的 Taylor 定理,
sin x x 1 x 3 o(x 3) (x 0) 3!
cos x 1 1 x 2 1 x 4 o(x 4 ) (x 0) 2! 4!
cos(sin x)
2. 设 f (x) 在[0,) 上二阶可导, f (0) 1, f (0) 1, f (x) f (x) , 证明: 当 x 0 时, f (x) ex .
第 1 页, 共 9 页
中国科学技术大学 2019~2020 学年第一学期
数学分析(B1) 期中考试 参考答案
2019 年 11 月 16 日
(2)问当且仅当 取何值时, f (x) 在 x 0 处可导, 但导函数 f (x) 在 x 0 处不连续(需说明理由)?
(3)问当且仅当 取何值时, f (x) 在 x 0 处可导, 且导函数 f (x) 在 x 0 处连续(需说明理由)?
1 3 2 x x2
x
1
1 2
3 x
2 x2
o
3 x
2 x2
x
3 o(1) (x 2
)
lim x
x 2 3x 2 ax b
x
lim
