木渎实验中学综合练习四(满分65分)

合集下载

江苏省苏州吴中区木渎实验中学2014-2015学年八年级上学期期中考试物理试卷(含答案)

2014.11本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共三大题，31小题。

满分100分，考试用时100分钟。

第Ⅰ卷（选择题共24分）一、选择题（每小题2分，共24分。

下列各题中每小题只有一个选项是正确的，把正确答案的序号填在答题卡相应的空格中。

）１．夏天的早晨，苏州市区自来水龙头流出水的温度最接近于A ．0℃B ．25℃C ．50℃D ．75℃2．能说明“液体可以传播声音”的事例是A ．我们听到雨滴打在雨伞上的“嗒嗒”声 B.我们听到树枝上小鸟的“唧唧”声C ．将要上钩的鱼被岸边的说话声吓跑D.人在小溪边听到“哗哗”的流水声3．CCTV 3·15晚会曝光黄金造假：个别不法商贩为牟取暴利，在黄金中掺入少量金属铱颗粒，已知黄金的熔点是1064.6℃，铱的熔点是2443.0℃，可以有效检测黄金制品中有无铱颗粒的手段是A ．加热至1064.0℃并观察有无铱颗粒B ．加热至1065.0℃并观察有无铱颗粒C ．加热至2444.0℃并观察有无铱颗粒D ．加热至3507.6℃并观察有无铱颗粒4．如图所示的现象中，由光折射形成的是5．关于光的反射，下列说法正确的是A ．当入射光线与镜面的夹角是20°时，反射角也是20°B ．入射角增大5°时，反射光线与入射光线的夹角也增大5°C ．镜面反射遵循光的反射定律，漫反射不遵循光的反射定律D ．入射光线靠近法线时，反射光线也靠近法线6．下列几种说法中，正确的是A ．给冰加热，冰的温度一定升高B ．把5℃的水放入-5℃的房间，水马上会结冰C ．把糖放入水中，水变甜是熔化现象D ．夏天，室外的自来水管外会有湿润现象，这是空气中水蒸气液化形成的7．体育比赛中运动员一旦受伤，医生会对着受伤部位喷射一种叫氯乙烷的药液，该药液会在皮肤表而迅速汽化，使受伤部位表层骤然变冷而暂时失去痛感。

这说明氯乙烷具有较低的A ．沸点B ．熔点C ．凝固点D ．温度8．在探究平面镜成像特点的过程中，小明把四个模型分别面对玻璃直立在桌面上，用于研究像与物左右位A ．日食美景B ．天空彩虹C ．耀眼幕墙D ．林间光柱置的关系，其中能够达到实验目的的是9．如图所示，将一束太阳光投射到玻璃三棱镜上，在棱镜后侧光屏上的AB范围内观察到了不同颜色的光，则A．A处应是紫光B．只有AB之间有光C．将照相底片放到AB范围B的外侧，底片会感光D．将温度计放到AB范围A的外侧温度不会升高10．自然界中的云、雨、雪、雾、露、霜等现象，都是水的物态发生变化形成的，图中描述的物理现象理解正确的是11．如图是对冰加热时其温度随时间变化的图像，由图可知A．BC段是一个放热过程B．BC段处于冰水混合状态C．CD段该物质处于气态D．DE段表示冰的熔化过程12．如图所示，一只小鸭浮在平静的湖面上。

苏州木渎实验初级中学数学新初一分班试卷含答案

苏州木渎实验初级中学数学新初一分班试卷含答案一、选择题1．在一张图纸上有400：1这样的一个比例．这个比例告诉我们的是( )．A．图上距离是实际距离的1 400B．实际距离是图上距离的400倍C．这张图纸是将实物放大到400倍画出来的2．如图所示是一个正方体展开图，和这个展开图对应的正方体是（）A．B．C．D．3．7路公共汽车的行驶路线全长8 km，每相邻两站的距离是1 km．一共有几个车站？正确的算式是()A．7÷1＋1 B．7÷1－1C．8÷1＋1 D．8÷1－14．一个直角三角形，两个锐角的度数比是1∶8，这个三角形中最小的锐角是（）。

A．40°B．20°C．10°5．如果x是一个大于0的数，那么x＋79和x×79比较的结果是（）。

A．x×79大B．x＋79大C．无法确定6．下面四个立体图形，从右面看形状相同的是( )。

A．①和③B．①和④C．③和④D．①③和④7．一项工程，甲队单独做需要10天完成，乙队单独做需要12天完成。

下面说法有错误的是（）。

A．甲每天可以完成这项工程的110B．两队合作每天可以完成这项工程的11 1012C．甲的工作效率比乙的工作效率低D．甲乙两队合作一共需要60 11天8．如果正方体、圆柱、圆锥的底面积相等，高也相等。

下面说法正确的是（）。

A ．圆柱的体积比正方体的体积小B ．圆柱和正方体的表面积相同C ．圆柱的体积是圆锥的13D ．圆锥的体积是正方体的139．小亮13岁，身高170厘米，体重84千克。

根据下边的体重分类标准，他的体重符合（）。

少年儿童（7～16岁）体重（千克）分类标准标准体重＝（身高－100）×0.9 轻度肥胖：超过标准体重13~510中度肥胖：超过标准体重31~102重度肥胖；超过标准体重12以上 A ．轻度肥胖B ．中度肥胖C ．重度肥胖10．观察下面的点阵图规律，第（10）个点阵图中点的个数是（）A ．30个B ．33 个C ．36个D ．39 个二、填空题11．三峡水电站平均发电八百四十七亿六千万千瓦时，横线上的数写作（______），改写成“亿”作单位的数是（______）。

江苏省苏州吴中区木渎实验中学七年级语文上学期期中试题苏教版

江苏省苏州吴中区木渎实验中学2014-2015学年七年级语文上学期期中试题注意事项：1．本试卷共三部分。

考生作答时，将答案答在规定的答题纸范围内，答在本试卷上无效。

2．答题时使用0.5毫米黑色中性（签字）笔书写，字体工整，笔迹清楚。

第一部分（24分）1．根据汉语拼音写出汉字。

（4分）①惊 ( xiàn) ▲② (xiāo) ▲洒③(pin) ▲请④(yā) ▲雀无声2．下面一段话中有四个错别字，请把它们找出来填入表中，然后改正。

（4分）一切都那么的宁静与安祥。

夜色在老树粼峋的枝丫上缠绵着，枝丫的剪影在月色里摇恍。

我低头看着脚下的路，不知道它还能沿伸多少。

我多希望一直走下去，走到晨曦微露的明天。

3．默写古诗文名句，并在括号内的横线上填写相应的作家、篇名。

（8分）①▲，风正一帆悬。

（王湾《次北固山下》）②中庭地白树栖鸦，▲。

（王建《十五夜望月》）③东风不与周郎便，▲。

（▲《赤壁》）④谁道人生无再少？门前流水尚能西，▲。

（苏轼《▲》）⑤四面湖山归眼底，▲。

（湖南岳阳楼上的楹联）⑥但愿人长久，▲。

（苏轼《水调歌头》4．阅读《汤姆·索亚历险记》，回答下列问题。

（5分）他始终穿着大人遗弃的旧衣服，上面一年四季全是洞，破布条条随风飘舞。

他头戴一顶又大又破的帽子，半圈月牙形的帽檐耷拉下来。

他只要有上装可穿，那上装准是差不多拖到脚跟，背部两侧的纽扣一直扣到臀部下面。

裤子只有一根背带吊着，裤裆松松垮垮像条口袋似的，看上去空荡荡的。

①这段文字描述的是汤姆的哪个朋友？除了他和汤姆，还有谁和他们一起去杰克逊岛当“海盗”？（2分）②在岛上当海盗时，始终困扰他们的最大的问题是什么？汤姆为了留住伙伴，用了哪些办法？（3分）5．下面划线的句子中，有三处语病，请按要求进行修改。

（3分）①我的身体分为笔芯、笔帽和笔杆三部分。

笔帽的上方有一小挂钩，那是我的手。

②你可别见笑我这小小的“独臂，”有了它，我就能紧紧攀伏在主人的衣兜上，随主人到处工作。

苏州木渎实验初级中学运动和力单元综合训练

苏州木渎实验初级中学运动和力单元综合训练一、选择题1．如图甲所示，水平地面上的一个物体受到水平推力F的作用，物体的速度v与时间t的关系如图乙所示。

下列说法中正确的是（）A．0~2s，推力小于摩擦力B．2~4s，物体做匀速运动C．4~6s，推力等于摩擦力D．0~6s，推力的大小始终不变2．一只木箱，静止放在水平地面上，下列说法中正确的是（）A．木箱所受的重力和木箱对地面的压力为一对平衡力B．木箱所受的重力和地面对木箱的支持力为一对平衡力C．木箱对地面的压力和地面对木箱的支持力为一对平衡力D．木箱所受的重力和木箱对地球的吸引力为一对平衡力3．中央电视台《是真的吗》某期节目中，有这样一个实验：将一根绳子穿过内壁和端口光滑的空心圆筒，绳子上端系一个金属球，下端与装有皮球的网袋连接。

转动空心圆筒，使金属球转动(如图)。

随着转速加大，网袋由静止开始向上运动。

下列判断正确的是（）A．金属球转动速度越大，惯性越大B．金属球转动过程中，运动状态保持不变C．网袋静止时，它对绳子的拉力和绳子对它的拉力是一对平衡力D．网袋开始向上运动，说明所受到的拉力大于它的重力4．如图甲所示，小球从某高度处由静止下落到竖直放置的轻弹簧上并压缩弹簧.从小球刚接触弹簧到将弹簧压缩到最短的过程中，得到小球的速度和弹簧被压缩的长度△L之间的关系图像，如图乙所示，其中b为曲线最高点.不计空气阻力，弹簧在整个过程中始终发生弹性形变，则小球（）A．在a处弹簧的弹力最大B．在b处弹簧的弹性势能最大C．从a到c过程中，小球的速度逐渐减小D．在b处小球受到的弹力与它所受的重力满足二力平衡的条件5．茶杯放在水平桌面上处于静止状态，下列说法正确的是（）A．桌面受到杯子的压力就是杯子的重力B．杯子受到的重力和桌面对杯子的支持力是一对平衡力C．桌子受到的重力与地面对桌子的支持力是一对平衡力D．杯子受到的重力和桌面对杯子的支持力是一对相互作用力6．下列关于生活中几个事例的说法，正确的是A．一辆汽车在平衡力的作用下，一定做匀速直线运动B．若跳高运动员竖直向下蹬地的力大于他的重力，运动员就能从地上跳起来C．鸡蛋掉到地面上破裂，是因为地面对蛋壳的作用力大于蛋壳对地面的作用力D．一袋重500N的米放在地面上，用300N的力竖直向上提它，这袋米受到的合力为200N 7．如图所示，昆明公共自行车绿色标志由人、自行车和道路三个元素组成，寓意绿色出行，以下关于摩擦力的说法正确的是（）A．骑行过程中，人受到了路面的摩擦力B．摩擦力大小不受路面粗糙程度的影响C．轮胎的表面做得凹凸不平是为了减小摩擦力D．刹车时用力捏闸柄，通过增大闸皮对车圈的压力来增大摩擦力8．汽车在平直公路上匀速行驶时，下列属于平衡力的是（）A．汽车受到的牵引力和阻力B．汽车受到的支持力和地面受到的压力C．汽车受到的牵引力和重力D．汽车受到的牵引力和地面受到的压力9．一只手握住甲、乙两个核桃，逐渐增大握力，发现甲核桃碎裂时乙核桃完好，下列有关两核桃相互挤压时的说法正确的是（）A．甲对乙的作用力小于乙对甲的作用力B．甲对乙的作用力没有使乙核桃发生形变C．甲对乙的作用力与乙对甲的作用力都是弹力D．甲对乙的作用力与乙对甲的作用力是一对平衡力10．下列情景中，处于平衡状态的是（）A．绕地球匀速运行的卫星B．加速追赶猎物的猎豹C．下落的苹果D．匀速下降的跳伞运动员二、填空题11．如图所示，长木板放在水平桌面上，木块放在长木板上，砝码放在木块上．现用4N 的拉力F水平拉木块，木块、砝码和长木板均保持静止，在静止状态下，木块对砝码的摩擦力为_______N，长木板对木块的摩擦力为_______N，桌面对长木板的摩擦力为_______N。

江苏省苏州市木渎实验中学2020-2021学年高二数学文测试题含解析

江苏省苏州市木渎实验中学2020-2021学年高二数学文测试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 定义：离心率的椭圆为“黄金椭圆”，对于椭圆E：，c为椭圆的半焦距，如果不成等比数列，则椭圆E（）A．一定是“黄金椭圆” B．一定不是“黄金椭圆”C．可能是“黄金椭圆” D．可能不是“黄金椭圆”参考答案：B略2. 已知一个平面，那么对于空间内的任意一条直线，在平面内一定存在一条直线，使得直线与直线（ )A．平行B．相交C．异面D．垂直参考答案：D【知识点】点线面的位置关系【试题解析】因为当直线垂直于平面时，直线与平面内任一条直线垂直，直线不垂直于平面时，作在平面内的射影，在平面内一定存在一条直线，使得直线的射影与直线垂直所以，故答案为：D3. 设，则此函数在区间和内分别（）A. 单调递增，单调递减B. 单调递减，单调递增C. 单调递增，单调递增D. 单调递减，单调递减参考答案：B【分析】对函数求导，判断导函数在区间和内的符号，即可确定函数的单调性。

【详解】，当时，，函数在上单调递减；当时，，函数在上单调递增；故答案选B【点睛】本题考查利用导数研究函数的单调性，注意导数符号与原函数的单调区间之间的关系，以及函数的定义域，属于基础题。

4. 过抛物线y2＝8x的焦点F作倾斜角为135°的直线交抛物线于A，B两点，则弦AB的长为（）A、4B、8C、12D、16参考答案：D5. 在等比数列中，，，，则项数为（）A. 3B. 4C. 5D. 6参考答案：C略6. 一个直角三角形的两条直角边长为满足不等式，则这个直角三角形的斜边长为（）A．5 B． C．6 D．参考答案：B解析：原不等式化为，而，所以．于是，斜边长为．7. 设双曲线的一条渐近线与抛物线y=x+1 只有一个公共点，则双曲线的离心率为( ).A. B. 5 C. D.参考答案：D双曲线的一条渐近线为,由方程组,消去y,得有唯一解,所以△=,所以,,故选D.8. 函数的定义域为( )A. B. C. D.参考答案：C9. 抛物线的焦点到准线的距离为( )A. B. C.8 D.2参考答案：D10. 设x,y满足约束条件,则z=2x-3y的最小值是（***）A．B．-6 C．D．-3参考答案：B略二、填空题:本大题共7小题,每小题4分,共28分11. 设,是纯虚数,其中是虚数单位,则.参考答案：-2试题分析：由题意，考点：纯虚数的概念，复数相等的条件12. 在平面内，三角形的面积为S，周长为C，则它的内切圆的半径．在空间中，三棱锥的体积为V，表面积为S，利用类比推理的方法，可得三棱锥的内切球（球面与三棱锥的各个面均相切）的半径R=__________．参考答案：试题分析：若三棱锥表面积为S，体积为V，则其内切球半径”证明如下：设三棱锥的四个面积分别为：，由于内切球到各面的距离等于内切球的半径∴∴内切球半径考点：类比推理13. 已知扇形的圆心角为（定值），半径为（定值），分别按图一、二作扇形的内接矩形，若按图一作出的矩形面积的最大值为，则按图二作出的矩形面积的最大值为▲．参考答案：14. 已知关于的不等式，它的解集是[1，3 ]，则实数的值是参考答案：-215. 设，且，则的最小值是▲．参考答案：3略16. 某地区有荒山2200亩,从2009年开始每年年初在荒山上植树造林,第一年植树100亩,以后每年比上一年多植树50亩.如图,某同学设计了一个程序框图计算到哪一年可以将荒山全部绿化(假定所植树全部成活),则程序框图中A处应填上____________.参考答案：略17. 函数f（x）=﹣x﹣cosx在[0，]上的最大值为________．参考答案：-1【考点】利用导数求闭区间上函数的最值【解答】解：f′（x）=﹣+sinx，∵x∈[0，]，∴sinx∈[0，]，∴f′（x）＜0，f（x）在[0，]递减，故f（x）max=f（0）=﹣1，故答案为：﹣1．【分析】求出函数的导数，得到函数f（x）的单调性，求出函数的最大值即可．三、解答题：本大题共5小题，共72分。

苏州吴中区木渎实验中学2011-2012学年九年级数学上学期第一次月考(常用版)

苏州吴中区木渎实验中学2011-2012学年九年级数学上学期第一次月考（常用版）(可以直接使用，可编辑完整版资料，欢迎下载）2021—2021学年第一学期木渎实验中学阶段性测试卷九年级数学注意事项：1．本试卷满分130分，考试时间120分钟；2．答卷前将密封线内的项目填写清楚，所有解答均须写在答题卷上，在本试卷上答题无效．一、选择题（本大题共10小题，每小题3分，共30分．每小题只有一个选项是正确的，把正确选项前的字母填在答题卷相应位置上．）1（） A ．4B． C ．2D2.x 的取值范围是（）A ． 2x ≥B ．2x >C ．2x <D ．2x ≤3.在下列方程中是一元二次方程的是（）A ．x2－2xy+y2=0B ．x(x+3)=x2－1C ．x2－2x=3D ．x+1x =04.一元二次方程x x 22=的根是（） A ．2=x B ．0=x C ．2,021==x x D ．2,021-==x x 5.（）ABCD6.（） A ．2 B ．3 C ．4 D ．57.方程2x2－3x+1=0经过配方化为(x+a)2=b 的形式，正确的是（）A ．23(x-)=162 B ．2312(x-)=416 C ．231(x-)=416 D ．231(x-)=216 8.关于x 的一元二次方程2620x x k -+=有两个不相等的实数根，则实数k 的取值范围是（）A ．92k ≤B ．92k <C ． 92k ≥D ．92k >9.若一组数：1，3，5，x 的极差是7，则x 的值为（）A ．4B ．8C ．9D ．8或－22021.1010.已知0xy >，化简二次根式的正确结果为（）A．．．二、填空题（本大题共8小题，每小题3分，共24分．把答案填在答题卷相应位置上．） 11.计算：2(= _______________． 12.设1x ，2x 是一元二次方程2320x x --=的两个实数根，则12x x += ．13.一组数据2，-2，0，4的方差是．14.已知：21571y x x =++，22915y x x =--，则当x = 时，12.y y = 15.若,x y为实数，且20x +=，则2010()x y +的值为____ _______．16.b ，则b 1= ．17.已知关于x 的一元二次方程01)12=++-x x m （有实数根，则m 的取值范围是．18.已知：2,则yx ＝．三、解答题（本大题共10题，共76分．解答时应写出文字说明、证明过程或演算步骤．） 19．计算：（每小题4分，共16分.）（1）（2）3⎛ ⎝（a>0，b>0）（3）01)4) （4）21418122-+-20．解下列关于x 的方程：（每小题4分，共12分.）(1) 2540x x -+=；（2） x2－x-3＝0(3) (21)(3)4x x -+=21．（本题4分）已知：132-=x ，求221x x -+的值.22．（本题5分）先化简，再求值：()22111a a a ⎛⎫-+÷+ ⎪+⎝⎭，其中1a =．23. （本题5分）已知2是关于x 的一元二次方程x2＋4x －p ＝0的一个根，求实数p 的值以及该方程的另一个根．24．（本题6分）一次期中考试中，A 、B 、C 、D 、E 五位同学的数学、英语成绩等有关信息如下表所示：（单位：分）（1）填写表格中的空档；（2）为了比较不同学科考试成绩的好与差，采用标准分是一个合理的选择，标准分的计算公式是：标准分＝（个人成绩－平均成绩）÷成绩标准差。

苏州木渎实验初级中学浮力单元综合训练

苏州木渎实验初级中学浮力单元综合训练一、选择题1．如图所示，两个底面积相同的薄壁容器甲乙分别装有密度为ρa，ρb的液体，放置在水平桌面上，现将同一物块（密度为ρ）分别放入两容器中，物块静止时两容器中液面等高。

下列说法正确的是（）A．液体密度与物体密度的关系为ρa<ρb<ρB．放入物块前，甲容器底受到液体的压强较大C．放入物块后，甲容器对桌面的压强增加量较大D．放入物块后与放入前相比，甲容器底受到液体的压力增加量较大2．如图甲所示，木块A的重力为10N，将合金块B放在木块A上方，木块A恰好有五分之四的体积浸入水中；若将合金块B取下放到水中，如图乙所示，B沉底，木块A露出水面的体积为自身体积的二分之一，此时B受到容器底部的支持力为2N，下列说法正确的是（）A．木块A的密度为0.8×103kg/m3B．图乙中水对A底部的压力为2NC．合金B的密度为1×103kg/m3D．从图甲到图乙水对容器底部压力的变化了8N3．两块完全相同的冰分别漂浮在甲、乙两种液体中，这两种液体的密度分别为ρ甲、ρ乙，当冰块熔化后，甲液体液面高度不变，乙液体液面高度升高。

下列说法中正确的是（）A．ρ冰>ρ甲B．ρ乙<ρ冰C．ρ甲>ρ冰D．ρ乙<ρ甲4．质量相等的甲、乙两实心小球，密度之比ρ甲:ρ乙＝3:2，将它们分别放入水中静止时，两球所受的浮力之比F甲:F乙＝4：5，设水的密度为ρ水。

则甲球的密度为（）A．43ρ水B．54ρ水C．32ρ水D．35ρ水5．春天到了，农村还有人让老母鸡来孵小鸡。

逐渐发育的小鸡会把鸡蛋内的营养成分消耗掉，总质量变小，来实现自己的成长。

利用这个原理，孵过一段时间后，人们会把鸡蛋拿出来放入盆中加水，来检验孵化是否成功，这时会发现有的鸡蛋沉底，有的鸡蛋则浮出水面，假设最初挑选的是大小完全相同的鸡蛋，那么（）A ．浮出水面的鸡蛋受到的浮力大B ．下沉的鸡蛋是孵化成功的鸡蛋C ．无论哪种，鸡蛋的密度都不变D ．上浮鸡蛋孵化成功，密度变小6．如图是a 、b 两种物质的质量与体积关系图，分别用a 、b 两种物质制成两个规则的体积相同的实心长方体甲和乙，并将甲乙两物块用细线捆在一起放入密度为0.83g cm 的溶液中，请问捆绑后的物体在溶液中（）A ．漂浮B ．悬浮C ．沉底D ．无法判断7．如图所示，水平桌面上放置一底面积为S 2的轻质圆柱形容器，容器足够深：在容器中放入底面积为S1，质量为m 的圆柱形木块，在容器中缓慢加入水，当木块对容器底部的压力恰好为零时，容器对桌面的压力大小为（）A ．21S mg SB ．211S S mg S ﹣C ．121S mg S S ﹣D ．221S mg S S ﹣ 8．如图所示，在装有一定深度水的玻璃水槽中放入一正方体木块，再在水槽口下方安装固定的水平金属网（水能倒入但木块不能穿过）。

苏州木渎实验初级中学简单机械单元综合训练

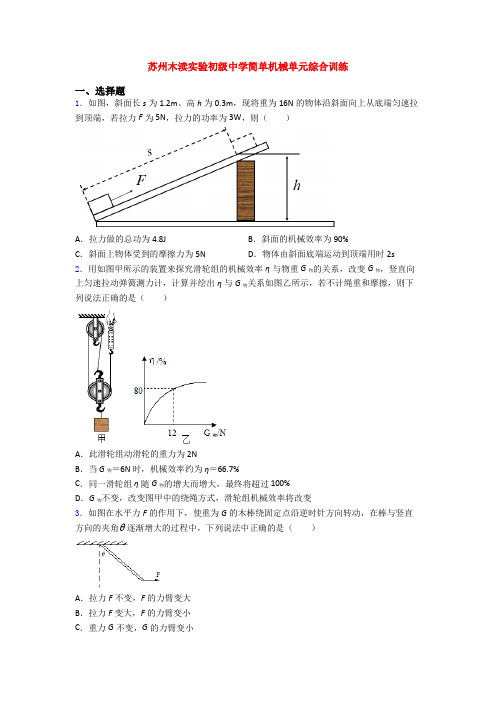
苏州木渎实验初级中学简单机械单元综合训练一、选择题1．如图，斜面长s为1.2m、高h为0.3m，现将重为16N的物体沿斜面向上从底端匀速拉到顶端，若拉力F为5N，拉力的功率为3W，则（）A．拉力做的总功为4.8J B．斜面的机械效率为90%C．斜面上物体受到的摩擦力为5N D．物体由斜面底端运动到顶端用时2s 2．用如图甲所示的装置来探究滑轮组的机械效率η与物重G物的关系，改变G物，竖直向上匀速拉动弹簧测力计，计算并绘出η与G物关系如图乙所示，若不计绳重和摩擦，则下列说法正确的是（）A．此滑轮组动滑轮的重力为 2NB．当G物＝6N 时，机械效率约为η＝66.7%C．同一滑轮组η随G物的增大而增大，最终将超过 100%D．G物不变，改变图甲中的绕绳方式，滑轮组机械效率将改变3．如图在水平力F的作用下，使重为G的木棒绕固定点沿逆时针方向转动，在棒与竖直方向的夹角逐渐增大的过程中，下列说法中正确的是（）A．拉力F不变，F的力臂变大B．拉力F变大，F的力臂变小C．重力G不变，G的力臂变小D．重力G变小，G的力臂变大4．如图所示，用甲、乙滑轮组在相同时间分别将A、B物体匀速提升相同高度，已知物体受到的重力G A＞G B，滑轮组的机械效率η甲＜η乙（忽略绳重和摩擦）．下列判断正确的是（）A．两滑轮组绳端移动的距离相等B．甲滑轮组的有用功比乙的少C．甲滑轮组的总功率比乙的小D．甲滑轮组的动滑轮比乙的重5．关于定滑轮、动滑轮，以下说法不正确的是A．使用定滑轮虽然不省力，但可以改变力的方向B．定滑轮实质是等臂杠杆，而动滑轮实质是不等臂杠杆C．又省力又少移动距离的动滑轮是无法实现的D．使用一个定滑轮和一个动滑轮组成的滑轮组，只能省一半力6．用4只完全相同的滑轮和2根相同的绳子组成如图所示的甲、乙两个滑轮组，在绳的自由端用大小分别为F1和F2的拉力，将同一重物在相同的时间内，匀速提升相同的高度，两滑轮组绳子的自由端移动的速度分别为v1和v2．若不计绳重和摩擦，下列说法正确的是A．甲乙滑轮组绳子自由端移动的距离相同B．F1大于F2C．v1大于v2D．F1和F2做的功不相等7．如图所示，一根直硬棒被细绳系在O点吊起．A处挂一实心金属块甲，B处挂一石块乙时恰好能使硬棒在水平位置平衡．不计硬棒与悬挂的细绳质量，下列推断合理的是A．甲的质量和密度都比乙大B．O点绳子拉力一定等于甲、乙重力之和C．如果甲浸没在水中，硬棒会逆时针转动D．如果甲浸没在水中，要使硬棒水平平衡，可将乙向右移动8．如图所示，杠杆处于平衡状态，下列说法中正确的是A．将支点两侧钩码都向右移动一格，杠杆仍平衡B．在支点两边的钩码下各增加一个钩码，杠杆仍平衡C．将支点左边加上二个钩码，右边加上一个钩码，杠杆仍平衡D．将支点左边的钩码向左移动两格，将支点右侧的钩码向右移动一格，杠杆仍平衡9．如图，质量分别为m1、m2、m3（m1＞m2）的物体通过轻绳和弹簧连接起来，三个物体均处于静止状态．不计弹簧自重、绳重和摩擦，关于此装置的说法错误的是（）A．绳子对m2的拉力大小为m2gB．绳子对m1的拉力大小为m1gC．弹簧中拉力大小为（m1-m2）gD．地面对m3的支持力大小为（m2+m3-m1）g10．如图所示，重20N的物体A放在水平桌面上，（不计绳重及绳子与轮的摩擦）动滑轮重6N，滑轮下面悬挂一个物体B，当物体B重8N时，恰能匀速下落，若用一个水平向左的力F A作用在物体A，使物体A向左做匀速直线运动，则此拉力F A的大小为A．F A＝8NB．F A＝20NC．F A＝14ND．F A＝7N11．如图所示，在水平拉力F的作用下重100 N的物体A，沿水平桌面做匀速直线运动，弹簧测力计B的示数为10 N，则拉力F的大小及物体A与水平桌面的摩擦力大小分别为( )A．200 N，10 N B．200 N，20 NC．20 N，10 N D．20 N，20 N12．如图所示，粗细均匀的直尺AB，将中点O支起来，在B端放一支蜡烛，在AO的中点C放两支与B端完全相同的蜡烛，此时直尺AB恰好在水平位置平衡，如果将三支蜡烛同时点燃，且它们的燃烧速度相同，那么在蜡烛的燃烧过程中，直尺AB将（）A．A端将逐渐上升B．始终保持平衡C．B端将逐渐上升D．不能保持平衡，待两边蜡烛燃烧完了以后，才能恢复平衡二、填空题13．如图是一种轮式垃圾桶，拖动时它相当于一个______（选填“省力”或“费力”）杠杆。

苏州木渎实验初级中学功和机械能单元综合训练

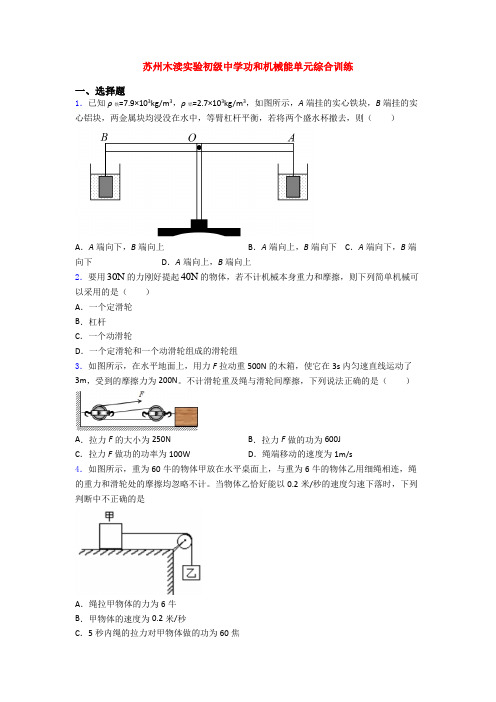
苏州木渎实验初级中学功和机械能单元综合训练一、选择题1．已知ρ铁=7.9×103kg/m3，ρ铝=2.7×103kg/m3，如图所示，A端挂的实心铁块，B端挂的实心铝块，两金属块均浸没在水中，等臂杠杆平衡，若将两个盛水杯撤去，则（）A．A端向下，B端向上B．A端向上，B端向下C．A端向下，B端向下D．A端向上，B端向上2．要用30N的力刚好提起40N的物体，若不计机械本身重力和摩擦，则下列简单机械可以采用的是（）A．一个定滑轮B．杠杆C．一个动滑轮D．一个定滑轮和一个动滑轮组成的滑轮组3．如图所示，在水平地面上，用力F拉动重500N的木箱，使它在3s内匀速直线运动了3m，受到的摩擦力为200N。

不计滑轮重及绳与滑轮间摩擦，下列说法正确的是（）A．拉力F的大小为250N B．拉力F做的功为600JC．拉力F做功的功率为100W D．绳端移动的速度为1m/s4．如图所示，重为60牛的物体甲放在水平桌面上，与重为6牛的物体乙用细绳相连，绳的重力和滑轮处的摩擦均忽略不计。

当物体乙恰好能以0.2米/秒的速度匀速下落时，下列判断中不正确的是A．绳拉甲物体的力为6牛B．甲物体的速度为0.2米/秒C．5秒内绳的拉力对甲物体做的功为60焦D．绳的拉力做功的功率为1.2W5．某同学自制了一架天平，由于制作粗糙，天平两侧长度不同．当将一物体放在天平的左盘时，右侧砝码的质量为m1，恰好平衡；当将该物体放在天平的右盘时，左侧砝码的质量为m2，天平才平衡．则该物体的质量应为：（）A．B．C．D．无法确定6．工人师傅用拉力F1将重物匀速搬运到h高处，对重物做的功是W1；若工人改用动滑轮将该重物匀速提升到h高处，拉力为F2，对重物做的功是W2（滑轮、绳的重力及摩擦力可忽略不计），则下列说法正确的是A．F1=F2B．F1<F2C．W2>W1D．W2=W17．如图所示杠杆，力F方向始终竖直向上，当此杠杆在动力F作用下，将一个由细绳系的物体由图中位置逆时针匀速转动到水平位置时，则A．F大小始终不变B．F先变大后变小C．F先变小后变大D．无法判断F大小的变化8．通过测量滑轮组机械效率的实验，可得出下列各措施中能提高机械效率的是( )A．增加动滑轮，减小拉力 B．改用质量小的定滑轮C．减少提升高度，减少做功 D．增加提升重物重力，增大有用功9．如图为一健身器材模型，杠杆AB可绕O点在竖直平面内转动，OA∶OB＝1∶4，质量为60 kg的小明站在水平放置的体重计上，通过该杠杆提起吊篮中的重物，吊篮重80 N．当棱长为20 cm的正方体重物甲刚被提起时，体重计示数为43 kg；当棱长为40 cm的正方体重物乙刚被提起时，体重计示数为18 kg．杠杆始终在水平位置保持平衡，A、B两端绳子拉力保持竖直．不计绳重、杠杆自重及摩擦， g取10 N/kg，则重物甲与重物乙的密度之比为( )A．1∶3 B．2∶3 C．3∶2 D．3∶110．分别用如图所示的两个滑轮组，将同一物体提升到相同高度．若物体受到的重力为100N，动滑轮的重力为20N．在把物体匀速提升1m的过程中，（不计绳重和摩擦）下列说法正确的是A．甲、乙两滑轮组所做的有用功都是100JB．甲滑轮组所做的有用功为200J ，乙滑轮组所做的有用功为300JC．甲、乙滑轮组中绳子的自由端的拉力相等D．甲、乙两滑轮组的机械效率不相等11．一个原来处于平衡状态的杠杆，如果再作用一个力后，杠杆仍处于平衡状态，则此力（）A．必须作用于动力的作用点上 B．必须作用在支点上C．必须作用在阻力的作用点上 D．可以作用在杠杆任一点上，但必须使力的作用线通过支点12．用同种材料制成的物体A和B，分别挂在杠杆的两端，且G A＞G B，此时杠杆平衡，如图（a）所示，若将两物体全部浸入水中，如图（b）所示，杠杆将会（）A．A物体下移，B物体上移B．A物体上移，B物体下移C．仍将保持平衡D．无法判断二、填空题13．如图，重力不计的一长木板AB可绕O点无摩擦转动，且OA=1m，OB=4m。

2020-2021学年苏州木渎实验中学高三语文第一次联考试题及参考答案

2020-2021学年苏州木渎实验中学高三语文第一次联考试题及参考答案一、现代文阅读（36分）(一)现代文阅读I(9分)阅读下面的文字，完成各题。

回家过年赵长春心里的花，带你回家，感受我家乡的文化，看看我的老爹老妈，让他们也看看你这朵美好的花！德昌高兴地哼着改了的歌词，握着九月的手，车速时急时缓。

再翻过前面的岗坡，一路下去，不过二三里地，就可以安全进村了。

疫情随时播报，一路上还算顺利，被拦着量了几次体温，都正常。

刚才几个发小还高兴地相约，晚上就见，好好喝酒好好说话……手机响起。

“是我爹，快接。

”德昌想让九月多给爹说话，就握好方向盘，把手机递给九月。

“……爹，好。

”九月脸色有些红，“哦，德昌说马上过东大岗……，好，好。

”九月将手机递回德昌，德昌接了，爹的声音迟疑，“你们下岗后，先停那里，我在那等，还有你妈，你婶……”没关闭手机，德昌就又冲九月眨眼睛，“几辈子没有当过公公婆婆。

爹妈他们出村接咱了，还有大娘，二婶，小妹……”说着，车子下了东岗，往村子方向驶去：心里的花，带你回家……岗坡下，爹，妈，远远冲着车子来的方向挥手、摆手。

一辆三轮车横在路中央，车把上一张红纸：欢迎回老家，防疫不防人。

停车。

七八米远，有道简易限高杆，上横一道标语：疫情紧急，禁止进村！九月张大了嘴巴，德昌也愣住了。

看见爹拿着手机冲他示意，德昌拿起了手机，“娃儿，别怪爹，不让你们进村，上头统一规定，防堵肺炎，都这样……”德昌点点头，看见妈在抹眼泪，就握紧九月的手，“出去一下，叫妈看看你。

”两人出了车，寒风有些凉意。

德昌想往前走，妈挥了挥手，“小昌，小月，别往前走了。

”旁边的二婶头一拧，“嫂子，就叫俩孩儿回家怕啥？大过年的，妮儿还是头一回来，又不发烧，自己孩儿们！”爹往前跨了一大步，“听我的，先不回来。

给你们啥都预备好了，米、面、油，就在三轮车上，正准备往东头农场里送。

那里给你们收拾了一间房，装了空调……”“哥，嫂子！我给你们铺好的床铺，还贴好了对联，大红喜字、福字！”一直拍照的婶家妹子抢了一句话，冲德昌和九月挥挥手，“三轮车，上有饺子馅，炸货，零食，够你们过年的……”大娘和二婶也赶紧接话头，“九月，真漂亮！给你的红包就在三轮车里，拿好！不准交给德昌……哈哈！”笑声中，暮色苍茫，妈又擦眼睛，“钥匙就在妈给的红包里。

江苏省木渎实验中学~第一学期九年级物理第一次阶段测试试卷(有答案)苏科版

木渎实验中学初三第一次阶段练习物理试卷（满分100分，考试时间80分钟）（同学们，欢迎你参加练习！这是你进入初三后的第一次重要练习，相信你能成功!请认真审题，按照要求将答案填在答题纸上，考试结束只交答题纸，试题卷保管好。

）第Ⅰ卷选择题（30分）一、选择题（本大题共15小题，每小题2分，共30分。

每小题给出的四个选项中只有一个符合题意。

请将答案标号填在答题纸上）1．2008年 8月17日下午，北京奥运会赛艇女子四人双桨的决赛在顺义奥林匹克水上公园进行,我国选手唐宾、金紫薇、奚爱华、张杨杨最终以6分16秒06的成绩,夺得该项目金牌。

赛艇的桨可看成一个杠杆。

若把杠杆按省力杠杆、等臂杠杆和费力杠杆进行分类，赛艇的桨属于A.省力杠杆B.费力杠杆C.等臂杠杆D.无法确定 2．下列现象中，力没有．．对物体做功的是 A ．人提着水桶在水平路面上行走 B ．将书包背上楼 C ．骑自行车匀速前进 D ．用力将铅球掷出3.园艺师傅使用如图所示的剪刀修剪树枝时，常把树枝尽量往剪刀轴O 靠近，这样做的目的是为了A ．增大阻力臂，减小动力移动的距离B ．减小动力臂，减小动力移动的距离C ．增大动力臂，省力D ．减小阻力臂，省力4. 下列机械中，能省功的机械是A ．扳手B ．天平C ．剪刀D ．以上三个均不省功 5．下列关于力F1力臂的作图中，正确的是( )6．学校国旗的旗杆下有一个滑轮，升旗时往下拉动绳子，国旗就会上升，对该滑轮的说法，正确的是A ．这是一个动滑轮，可省力B ．这是一个定滑轮，可改变力的方向C ．这是一个动滑轮，可改变力的方向D ．这是一个定滑轮，可省力7．王小虎同学听到上课铃响了，他一口气从一楼跑到三楼，所用时间为10秒。

那么他上楼过程中，克服自己重力做功的功率最接近下面哪个值A ．3WB ．30WC ．300WD ．3000W 8．林雨将掉在地上的物理课本捡回桌面，所做的功最接近于 A ．0．02J B ．O ．2J C ．2J D ．20J 9．下列关于功率的说法中，正确的是A ．物体做功越快，功率越大B ．物体做功时间越短，功率越大C ．物体做功越多，功率越大D ．物体做功时间越长，功率越大 10．如图所示，粗略测量小明同学引体向上运动的功率时，下列物理量不需要测量的是A .小明的质量B .单杠的高度C .每次身体上升的高度D .做引体向上的时间 11．如图，O 为支点，在A 端施加一个力使杠杆在水平位置平衡，则这个杠杆为A.一定省力B.一定费力C.不省力也不费力D.都有可能12．如图所示，小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼，用甲滑轮所做的总功为W 1，机械效率为η1；用乙滑轮所做的总功为W 2，机械效率为η2。

苏州木渎实验初级中学七年级下册数学期末试卷检测（Word版含答案）

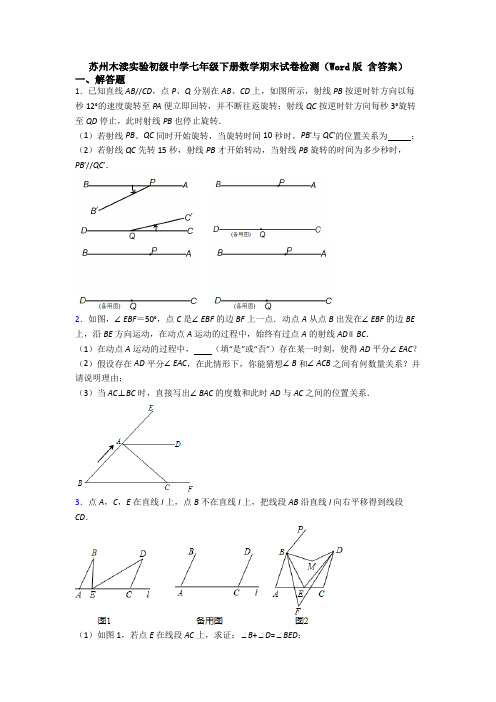
苏州木渎实验初级中学七年级下册数学期末试卷检测（Word版含答案）一、解答题1．已知直线AB//CD，点P、Q分别在AB、CD上，如图所示，射线PB按逆时针方向以每秒12°的速度旋转至PA便立即回转，并不断往返旋转；射线QC按逆时针方向每秒3°旋转至QD停止，此时射线PB也停止旋转．（1）若射线PB、QC同时开始旋转，当旋转时间10秒时，PB'与QC'的位置关系为；（2）若射线QC先转15秒，射线PB才开始转动，当射线PB旋转的时间为多少秒时，PB′//QC′．2．如图，∠EBF＝50°，点C是∠EBF的边BF上一点．动点A从点B出发在∠EBF的边BE 上，沿BE方向运动，在动点A运动的过程中，始终有过点A的射线AD∥BC．（1）在动点A运动的过程中，（填“是”或“否”）存在某一时刻，使得AD平分∠EAC？（2）假设存在AD平分∠EAC，在此情形下，你能猜想∠B和∠ACB之间有何数量关系？并请说明理由；（3）当AC⊥BC时，直接写出∠BAC的度数和此时AD与AC之间的位置关系．3．点A，C，E在直线l上，点B不在直线l上，把线段AB沿直线l向右平移得到线段CD．（1）如图1，若点E在线段AC上，求证：∠B+∠D=∠BED；（2）若点E不在线段AC上，试猜想并证明∠B，∠D，∠BED之间的等量关系；（3）在（1）的条件下，如图2所示，过点B作PB//ED，在直线BP，ED之间有点M，使得∠ABE=∠EBM，∠CDE=∠EDM，同时点F使得∠ABE=n∠EBF，∠CDE=n∠EDF，其中n≥1，设∠BMD=m，利用（1)中的结论求∠BFD的度数（用含m，n的代数式表示）．4．汛期即将来临，防汛指挥部在某水域一危险地带两岸各安置了一探照灯，便于夜间查看河水及两岸河堤的情况．如图1，灯A射出的光束自AM顺时针旋转至AN便立即回转，灯B射出的光束自BP顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视．若灯A射出的光束转动的速度是a︒/秒，灯B射出的光束转动的速度是b︒/秒，且a、b满足20)34(a b a b-++-=．假定这一带水域两岸河堤是平行的，即//PQ MN，且45BAN∠=︒．（1）求a、b的值；（2）如图2，两灯同时转动，在灯A射出的光束到达AN之前，若两灯射出的光束交于点C，过C作CD AC⊥交PQ于点D，若20BCD∠=︒，求BAC∠的度数；（3）若灯B射线先转动30秒，灯A射出的光束才开始转动，在灯B射出的光束到达BQ 之前，A灯转动几秒，两灯的光束互相平行?5．已知AB∥CD，∠ABE与∠CDE的角分线相交于点F．（1）如图1，若BM、DM分别是∠ABF和∠CDF的角平分线，且∠BED＝100°，求∠M的度数；（2）如图2，若∠ABM＝13∠ABF，∠CDM＝13∠CDF，∠BED＝α°，求∠M的度数；（3）若∠ABM＝1n∠ABF，∠CDM＝1n∠CDF，请直接写出∠M与∠BED之间的数量关系二、解答题6．（1）光线从空气中射入水中会产生折射现象，同时光线从水中射入空气中也会产生折射现象，如图1，光线a从空气中射入水中，再从水中射入空气中，形成光线b，根据光学知识有12,34∠=∠∠=∠，请判断光线a与光线b是否平行，并说明理由．（2）光线照射到镜面会产生反射现象，由光学知识，入射光线与镜面的夹角与反射光线与镜面的夹角相等，如图2有一口井，已知入射光线α与水平线OC 的夹角为40︒，问如何放置平面镜MN ，可使反射光线b 正好垂直照射到井底?（即求MN 与水平线的夹角）（3）如图3，直线EF 上有两点A 、C ，分别引两条射线AB 、CD ．105BAF ∠=︒，65DCF ∠=︒，射线AB 、CD 分别绕A 点，C 点以1度/秒和3度/秒的速度同时顺时针转动，设时间为t ，在射线CD 转动一周的时间内，是否存在某时刻，使得CD 与AB 平行？若存在，求出所有满足条件的时间t ．7．如图1，//AB CD ，E 是AB 、CD 之间的一点．（1）判定BAE ∠，CDE ∠与AED ∠之间的数量关系，并证明你的结论；（2）如图2，若BAE ∠、CDE ∠的两条平分线交于点F ．直接写出AFD ∠与AED ∠之间的数量关系；（3）将图2中的射线DC 沿DE 翻折交AF 于点G 得图3，若AGD ∠的余角等于2E ∠的补角，求BAE ∠的大小．8．已知射线//AB 射线CD ，P 为一动点，AE 平分PAB ∠，CE 平分PCD ∠，且AE 与CE 相交于点E ．（注意：此题不允许使用三角形，四边形内角和进行解答）（1）在图1中，当点P 运动到线段AC 上时，180APC ∠=︒．直接写出AEC ∠的度数；（2）当点P 运动到图2的位置时，猜想AEC ∠与APC ∠之间的关系，并加以说明；（3）当点P 运动到图3的位置时，（2）中的结论是否还成立？若成立，请说明理由：若不成立，请写出AEC ∠与APC ∠之间的关系，并加以证明．9．已知//a b ，直角ABC 的边与直线a 分别相交于O 、G 两点，与直线b 分别交于E 、F 点，90ACB ∠=．（1）将直角ABC 如图1位置摆放，如果46AOG ∠=，则CEF ∠=______；（2）将直角ABC 如图2位置摆放，N 为AC 上一点，180NEF CEF ︒∠+∠=，请写出NEF ∠与AOG ∠之间的等量关系，并说明理由．（3）将直角ABC 如图3位置摆放，若140GOC ∠=，延长AC 交直线b 于点Q ，点P 是射线GF 上一动点，探究POQ ∠，OPQ ∠与PQF ∠的数量关系，请直接写出结论． 10．如图，两个形状，大小完全相同的含有30°、60°的三角板如图放置，PA 、PB 与直线MN 重合，且三角板PAC ，三角板PBD 均可以绕点P 逆时针旋转．（1）①如图1，∠DPC ＝度．②我们规定，如果两个三角形只要有一组边平行，我们就称这两个三角形为“孪生三角形”，如图1，三角板BPD 不动，三角板PAC 从图示位置开始每秒10°逆时针旋转一周（0°<旋转<360°），问旋转时间t 为多少时，这两个三角形是“孪生三角形”．（2）如图3，若三角板PAC 的边PA 从PN 处开始绕点P 逆时针旋转，转速3°/秒，同时三角板PBD 的边PB 从PM 处开始绕点P 逆时针旋转，转速2°/秒，在两个三角板旋转过程中，（PC 转到与PM 重合时，两三角板都停止转动）．设两个三角板旋转时间为t 秒，以下两个结论：①CPD BPN∠∠为定值；②∠BPN +∠CPD 为定值，请选择你认为对的结论加以证明．三、解答题11．阅读下列材料并解答问题：在一个三角形中，如果一个内角的度数是另一个内角度数的3倍，那么这样的三角形我们称为“梦想三角形”例如：一个三角形三个内角的度数分别是120°，40°，20°，这个三角形就是一个“梦想三角形”．反之，若一个三角形是“梦想三角形”，那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍．（1）如果一个“梦想三角形”有一个角为108°，那么这个“梦想三角形”的最小内角的度数为__________（2）如图1，已知∠MON＝60°，在射线OM上取一点A，过点A作AB⊥OM交ON于点B，以A为端点作射线AD，交线段OB于点C（点C不与O、B重合），若∠ACB=80°．判定△AOB、△AOC是否是“梦想三角形”，为什么？（3）如图2，点D在△ABC的边上，连接DC，作∠ADC的平分线交AC于点E，在DC上取一点F，使得∠EFC+∠BDC＝180°，∠DEF＝∠B．若△BCD是“梦想三角形”，求∠B的度数．12．（生活常识）射到平面镜上的光线（入射光线）和变向后的光线（反射光线）与平面镜所夹的角相等．如图 1，MN 是平面镜，若入射光线AO 与水平镜面夹角为∠1，反射光线OB 与水平镜面夹角为∠2，则∠1=∠2 .（现象解释）如图 2，有两块平面镜OM，ON，且OM⊥ON，入射光线AB 经过两次反射，得到反射光线CD.求证AB∥CD.（尝试探究）如图 3，有两块平面镜OM，ON，且∠MON =55 ，入射光线AB 经过两次反射，得到反射光线CD，光线AB 与CD 相交于点E，求∠BEC 的大小.（深入思考）如图 4，有两块平面镜 OM ，ON ，且∠MON = α ，入射光线 AB 经过两次反射，得到反射光线 CD ，光线 AB 与 CD 所在的直线相交于点 E ，∠BED =β , α 与 β 之间满足的等量关系是 .（直接写出结果）13．如图，在ABC 中，ABC ∠与ACB ∠的角平分线交于O 点.（1）若40A ∠=︒，则BOC ∠= ︒；（2）若A n ∠=︒，则BOC ∠= ︒；（3）若A n ∠=︒，ABC ∠与ACB ∠的角平分线交于O 点，ABO ∠的平分线与ACO ∠的平分线交于点1O ，，2016O BD ∠的平分线与2016O CE ∠的平分线交于点2017O ，则2017O ∠=︒.14．Rt △ABC 中，∠C=90°，点D 、E 分别是△ABC 边AC 、BC 上的点，点P 是一动点.令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α.（1）若点P 在线段AB 上，如图（1）所示，且∠α=50°，则∠1+∠2= °；（2）若点P 在边AB 上运动，如图（2）所示，则∠α、∠1、∠2之间的关系为：；（3）若点P运动到边AB的延长线上，如图（3）所示，则∠α、∠1、∠2之间有何关系？猜想并说明理由.（4）若点P运动到△ABC形外，如图（4）所示，则∠α、∠1、∠2之间的关系为：. 15．直线MN与直线PQ垂直相交于O，点A在射线OP上运动，点B在射线OM上运动,A、B不与点O重合，如图1，已知AC、BC分别是∠BAP和∠ABM角的平分线，（1）点A、B在运动的过程中，∠ACB的大小是否发生变化？若发生变化，请说明理由；若不发生变化，试求出∠ACB的大小.（2）如图2，将△ABC沿直线AB折叠，若点C落在直线PQ上，则∠ABO＝________,如图3，将△ABC沿直线AB折叠，若点C落在直线MN上，则∠ABO＝________（3）如图4，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其反向延长线交于E、F，则∠EAF＝；在△AEF中，如果有一个角是另一个角的32倍，求∠ABO的度数.【参考答案】一、解答题1．（1）PB′⊥QC′；（2）当射线PB旋转的时间为5秒或25秒或45秒时，PB′∥QC′【分析】（1）求出旋转10秒时，∠BPB′和∠CQC′的度数，设PB′与QC′交于O，过O作OE∥AB，根解析：（1）PB′⊥QC′；（2）当射线PB旋转的时间为5秒或25秒或45秒时，PB′∥QC′【分析】（1）求出旋转10秒时，∠BPB′和∠CQC′的度数，设PB′与QC′交于O，过O作OE∥AB，根据平行线的性质求得∠POE和∠QOE的度数，进而得结论；（2）分三种情况：①当0＜t≤15时，②当15＜t≤30时，③当30＜t＜45时，根据平行线的性质，得出角的关系，列出t的方程便可求得旋转时间．【详解】解：（1）如图1，当旋转时间30秒时，由已知得∠BPB′＝10°×12＝120°，∠CQC′＝3°×10=30°，过O作OE∥AB，∵AB∥CD，∴AB∥OE∥CD，∴∠POE＝180°﹣∠BPB′＝60°，∠QOE＝∠CQC′＝30°，∴∠POQ＝90°，∴PB′⊥QC′，故答案为：PB′⊥QC′；（2）①当0＜t≤15时，如图，则∠BPB′＝12t°，∠CQC′＝45°+3t°，∵AB∥CD，PB′∥QC′，∴∠BPB′＝∠PEC＝∠CQC′，即12t＝45+3t，解得，t＝5；②当15＜t≤30时，如图，则∠APB′＝12t﹣180°，∠CQC'＝3t+45°，∵AB∥CD，PB′∥QC′，∴∠BPB′＝∠BEQ＝∠CQC′，即12t﹣180＝45+3t，解得，t＝25；③当30＜t≤45时，如图，则∠BPB′＝12t﹣360°，∠CQC′＝3t+45°，∵AB∥CD，PB′∥QC′，∴∠BPB′＝∠BEQ＝∠CQC′，即12t﹣360＝45+3t，解得，t＝45；综上，当射线PB旋转的时间为5秒或25秒或45秒时，PB′∥QC′．【点睛】本题主要考查了平行线的性质，第（1）题关键是作平行线，第（2）题关键是分情况讨论，运用方程思想解决几何问题．2．（1）是；（2）∠B＝∠ACB，证明见解析；（3）∠BAC＝40°，AC⊥AD．【分析】（1）要使AD平分∠EAC，则要求∠EAD＝∠CAD，由平行线的性质可得∠B＝∠EAD，∠ACB＝∠CAD解析：（1）是；（2）∠B＝∠ACB，证明见解析；（3）∠BAC＝40°，AC⊥AD．【分析】（1）要使AD平分∠EAC，则要求∠EAD＝∠CAD，由平行线的性质可得∠B＝∠EAD，∠ACB＝∠CAD，则当∠ACB＝∠B时，有AD平分∠EAC；（2）根据角平分线可得∠EAD＝∠CAD，由平行线的性质可得∠B＝∠EAD，∠ACB＝∠CAD，则有∠ACB＝∠B；（3）由AC⊥BC，有∠ACB＝90°，则可求∠BAC＝40°，由平行线的性质可得AC⊥AD．【详解】解：（1）是，理由如下：要使AD平分∠EAC，则要求∠EAD＝∠CAD，由平行线的性质可得∠B＝∠EAD，∠ACB＝∠CAD，则当∠ACB＝∠B时，有AD平分∠EAC；故答案为：是；（2）∠B＝∠ACB，理由如下：∵AD平分∠EAC，∴∠EAD＝∠CAD，∵AD∥BC，∴∠B＝∠EAD，∠ACB＝∠CAD，∴∠B＝∠ACB．（3）∵AC⊥BC，∴∠ACB＝90°，∵∠EBF＝50°，∴∠BAC＝40°，∵AD∥BC，∴AD⊥AC．【点睛】此题考查了角平分线和平行线的性质，熟练掌握角平分线和平行线的有关性质是解题的关键．3．（1）见解析；（2）当点E在CA的延长线上时，∠BED=∠D-∠B；当点E 在AC的延长线上时，∠BED=∠BET-∠DET=∠B-∠D；（3）【分析】（1）如图1中，过点E作ET∥AB．利用平行解析：（1）见解析；（2）当点E在CA的延长线上时，∠BED=∠D-∠B；当点E在AC的延长线上时，∠BED=∠BET-∠DET=∠B-∠D；（3）()12m nn-【分析】（1）如图1中，过点E作ET∥A B．利用平行线的性质解决问题．（2）分两种情形：如图2-1中，当点E在CA的延长线上时，如图2-2中，当点E在AC的延长线上时，构造平行线，利用平行线的性质求解即可．（3）利用（1）中结论，可得∠BMD=∠ABM+∠CDM，∠BFD=∠ABF+∠CDF，由此解决问题即可．【详解】解：（1）证明：如图1中，过点E作ET∥A B．由平移可得AB∥CD，∵AB∥ET，AB∥CD，∴ET∥CD∥AB，∴∠B=∠BET，∠TED=∠D，∴∠BED=∠BET+∠DET=∠B+∠D．（2）如图2-1中，当点E在CA的延长线上时，过点E作ET∥A B．∵AB∥ET，AB∥CD，∴ET∥CD∥AB，∴∠B=∠BET，∠TED=∠D，∴∠BED=∠DET-∠BET=∠D-∠B．如图2-2中，当点E在AC的延长线上时，过点E作ET∥A B．∵AB∥ET，AB∥CD，∴ET∥CD∥AB，∴∠B=∠BET，∠TED=∠D，∴∠BED=∠BET-∠DET=∠B-∠D．（3）如图，设∠ABE=∠EBM=x，∠CDE=∠EDM=y，∵AB ∥CD ，∴∠BMD =∠ABM +∠CDM ，∴m =2x +2y ，∴x +y =12m ，∵∠BFD =∠ABF +∠CDF ，∠ABE =n ∠EBF ，∠CDE =n ∠EDF ，∴∠BFD =()111n n n x y x y n n n ---+=+=112n m n -⨯=()12m n n -．【点睛】本题属于几何变换综合题，考查了平行线的性质，角平分线的定义等知识，解题的关键是学会条件常用辅助线，构造平行线解决问题，属于中考常考题型． 4．（1），；（2）30°；（3）15秒或82.5秒【分析】（1）解出式子即可；（2）根据，用含t 的式子表示出，根据（2）中给出的条件得出方程式，求出 t 的值，进而求出的度数；（3）根据灯B 的解析：（1）3a =，1b =；（2）30°；（3）15秒或82.5秒【分析】（1）解出式子()2340a b a b -++-=即可；（2）根据//PQ MN ，用含t 的式子表示出BCA ∠，根据（2）中给出的条件得出方程式 ()()9090180229020⎡⎤∠=︒-∠=︒-︒-︒=︒-︒=︒⎣⎦BCD BCA t t ，求出 t 的值，进而求出BAC ∠的度数；（3）根据灯B 的要求，t <150，在这个时间段内A 可以转3次，分情况讨论．【详解】解：（1）2|3|(4)0a b a b -++-=．又|3|0a b -≥，2(4)0a b +-≥．3a ∴=，1b =；（2）设A 灯转动时间为t 秒，如图，作//CE PQ ，而//,PQ MN////,PQ CE MN ∴1803ACE CAN t ∴∠=∠=︒-︒，BCE CBD t ∠=∠=︒，()()18031802∴∠=∠+∠=︒+︒-︒=︒-︒BCA CBD CAN t t t ，90ACD ∠=︒，[]9090180(2)(2)9020∴∠=︒-∠=︒-︒-︒=︒-︒=︒BCD BCA t t ，55∴=t()1803∠=︒-︒CAN t ，()()451803313516513530∴∠=︒-︒-︒=︒-︒=︒-︒=︒⎡⎤⎣⎦BAC t t（3）设A 灯转动t 秒，两灯的光束互相平行．依题意得0150t <<①当060t <<时，两河岸平行，所以()233t ∠=∠=︒ 两光线平行，所以2130t ∠=∠=+︒所以，13∠=∠即：330=+t t ，解得15t =；②当60120t <<时，两光束平行，所以()2330t ∠=∠=+︒两河岸平行，所以12180∠+∠=︒13180t ∠=-︒所以，318030180-++=t t ，解得82.5t =；③当120150t <<时，图大概如①所示336030t t -=+，解得195150t =>（不合题意）综上所述，当15t =秒或82.5秒时，两灯的光束互相平行．【点睛】这道题考察的是平行线的性质和一元一次方程的应用．根据平行线的性质找到对应角列出方程是解题的关键．5．（1）65°；（2）；（3）2n ∠M+∠BED=360°【分析】（1）首先作EG ∥AB ，FH ∥AB ，连结MF ，利用平行线的性质可得∠ABE+∠CDE=260°，再利用角平分线的定义得到∠ABF+解析：（1）65°；（2）3606α︒-︒；（3）2n ∠M +∠BED =360° 【分析】（1）首先作EG ∥AB ，FH ∥AB ，连结MF ，利用平行线的性质可得∠ABE +∠CDE =260°，再利用角平分线的定义得到∠ABF +∠CDF =130°，从而得到∠BFD 的度数，再根据角平分线的定义和三角形外角的性质可求∠M 的度数；（2）先由已知得到∠ABE =6∠ABM ，∠CDE =6∠CDM ，由（1）得∠ABE +∠CDE =360°-∠BED ，∠M =∠ABM +∠CDM ，等量代换即可求解；（3）由（2）的方法可得到2n ∠M +∠BED =360°．【详解】解：（1）如图1，作//EG AB ，//FH AB ，连结MF ，//AB CD ，//////EG AB FH CD ∴，ABF BFH ∴∠=∠，CDF DFH ∠=∠，180ABE BEG ∠+∠=︒，180GED CDE ∠+∠=︒， 360ABE BEG GED CDE ∴∠+∠+∠+∠=︒，100BED BEG DEG ∠=∠+∠=︒，260ABE CDE ∴∠+∠=︒，ABE ∠和CDE ∠的角平分线相交于E ，130ABF CDF ∴∠+∠=︒，130BFD BFH DFH ∴∠=∠+∠=︒，BM 、DM 分别是ABF ∠和CDF ∠的角平分线，12MBF ABF ∴∠=∠，12MDF CDF ∠=∠， 65MBF MDF ∴∠+∠=︒，1306565BMD ∴∠=︒-︒=︒；（2）如图1，13ABM ABF ∠=∠，13CDM CDF ∠=∠， 3ABF ABM ∴∠=∠，3CDF CDM ∠=∠，ABE ∠与CDE ∠两个角的角平分线相交于点F ，6ABE ABM ∴∠=∠，6CDE CDM ∠=∠，66360ABM CDM BED ∴∠+∠+∠=︒，BMD ABM CDM ∠=∠+∠，6360BMD BED ∴∠+∠=︒，3606BMD α︒-︒∴∠=；（3）由（2）结论可得，22360n ABM n CDM E ∠+∠+∠=︒，M ABM CDM ∠=∠+∠，则2360n M BED ∠+∠=︒．【点睛】本题主要考查了平行线的性质和四边形的内角和，关键在于掌握两直线平行同位角相等，内错角相等，同旁内角互补的性质．二、解答题6．（1）平行，理由见解析；（2）65°；（3）5秒或95秒【分析】（1）根据等角的补角相等求出∠3与∠4的补角相等，再根据内错角相等，两直线平行即可判定a ∥b ；（2）根据入射光线与镜面的夹角与反解析：（1）平行，理由见解析；（2）65°；（3）5秒或95秒【分析】（1）根据等角的补角相等求出∠3与∠4的补角相等，再根据内错角相等，两直线平行即可判定a ∥b ；（2）根据入射光线与镜面的夹角与反射光线与镜面的夹角相等可得∠1=∠2，然后根据平角等于180°求出∠1的度数，再加上40°即可得解；（3）分①AB 与CD 在EF 的两侧，分别表示出∠ACD 与∠BAC ，然后根据两直线平行，内错角相等列式计算即可得解；②CD 旋转到与AB 都在EF 的右侧，分别表示出∠DCF 与∠BAC ，然后根据两直线平行，同位角相等列式计算即可得解；③CD 旋转到与AB 都在EF 的左侧，分别表示出∠DCF 与∠BAC ，然后根据两直线平行，同位角相等列式计算即可得解．【详解】解：（1）平行．理由如下：如图1，∵∠3=∠4，∴∠5=∠6，∵∠1=∠2，∴∠1+∠5=∠2+∠6，∴a∥b(内错角相等，两直线平行）；（2）如图2：∵入射光线与镜面的夹角与反射光线与镜面的夹角相等，∴∠1=∠2，∵入射光线a与水平线OC的夹角为40°，b垂直照射到井底，∴∠1+∠2=180°-40°-90°=50°，∴∠1＝1×50°=25°，2∴MN与水平线的夹角为：25°+40°=65°，即MN与水平线的夹角为65°，可使反射光线b正好垂直照射到井底；（3）存在．如图①，AB与CD在EF的两侧时，∵∠BAF=105°，∠DCF=65°，∴∠ACD=180°-65°-3t°=115°-3t°，∠BAC=105°-t°，要使AB∥CD，则∠ACD=∠BAC，即115-3t=105-t，解得t=5；如图②，CD旋转到与AB都在EF的右侧时，∵∠BAF=105°，∠DCF=65°，∴∠DCF=360°-3t°-65°=295°-3t°，∠BAC=105°-t°，要使AB∥CD，则∠DCF=∠BAC，即295-3t=105-t，解得t=95；如图③，CD旋转到与AB都在EF的左侧时，∵∠BAF=105°，∠DCF=65°，∴∠DCF=3t°-（180°-65°+180°）=3t°-295°，∠BAC=t°-105°，要使AB∥CD，则∠DCF=∠BAC，即3t-295=t-105，解得t=95，此时t＞105，∴此情况不存在．综上所述，t为5秒或95秒时，CD与AB平行．【点睛】本题考查了平行线的判定与性质，光学原理，读懂题意并熟练掌握平行线的判定方法与性质是解题的关键，（3）要注意分情况讨论．7．（1），见解析；（2）；（3）60°【分析】（1）作EF//AB ，如图1，则EF//CD ，利用平行线的性质得∠1＝∠BAE ，∠2＝∠CDE ，从而得到∠BAE ＋∠CDE ＝∠AED ；（2）如图2，解析：（1）BAE CDE AED ∠+∠=∠，见解析；（2）12AFD AED ∠=∠；（3）60° 【分析】（1）作EF //AB ，如图1，则EF //CD ，利用平行线的性质得∠1＝∠BAE ，∠2＝∠CDE ，从而得到∠BAE ＋∠CDE ＝∠AED ；（2）如图2，由（1）的结论得∠AFD ＝∠BAF ＋∠CDF ，根据角平分线的定义得到∠BAF ＝12∠BAE ，∠CDF ＝12∠CDE ，则∠AFD ＝12（∠BAE ＋∠CDE ），加上（1）的结论得到∠AFD ＝12∠AED ；（3）由（1）的结论得∠AGD ＝∠BAF ＋∠CDG ，利用折叠性质得∠CDG ＝4∠CDF ，再利用等量代换得到∠AGD ＝2∠AED －32∠BAE ，加上90°－∠AGD ＝180°－2∠AED ，从而可计算出∠BAE 的度数．【详解】解：（1）BAE CDE AED ∠+∠=∠理由如下：作//EF AB ，如图1，//AB CD ，//EF CD ∴．1BAE ∴∠=∠，2CDE ∠=∠，BAE CDE AED ∴∠+∠=∠；（2）如图2，由（1）的结论得AFD BAF CDF ∠=∠+∠，BAE ∠、CDE ∠的两条平分线交于点F ，12BAF BAE ∴∠=∠，12CDF CDE ∠=∠， 1()2AFD BAE CDE ∴∠=∠+∠，BAE CDE AED ∠+∠=∠，12AFD AED ∴∠=∠；（3）由（1）的结论得AGD BAF CDG ∠=∠+∠，而射线DC 沿DE 翻折交AF 于点G ，4CDG CDF ∴∠=∠，11422()22AGD BAF CDF BAE CDE BAE AED BAE ∴∠=∠+∠=∠+∠=∠+∠-∠= 322AED BAE ∠-∠， 901802AGD AED ︒-∠=︒-∠，390218022AED BAE AED ∴︒-∠+∠=︒-∠， 60BAE ∴∠=︒．【点睛】本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．8．（1）；（2），证明见解析；（3），证明见解析．【分析】（1）过点作，先根据平行线的性质、平行公理推论可得，从而可得，再根据平行线的性质可得，然后根据角平分线的定义可得，最后根据角的和差即可得；解析：（1）90︒；（2）2APC AEC ∠=∠，证明见解析；（3）2360APC AEC ∠+∠=︒，证明见解析．【分析】（1）过点E 作//EF AB ，先根据平行线的性质、平行公理推论可得,AEF BAE CEF DCE ∠=∠∠=∠，从而可得AEC BAE DCE ∠=∠+∠，再根据平行线的性质可得180PAB PCD ∠+∠=︒，然后根据角平分线的定义可得11,22BAE PAB DCE PCD ∠=∠∠=∠，最后根据角的和差即可得；（2）过点E 作//EF AB ，过点P 作//PQ AB ，先根据（1）可得1()2AEC BAE DCE PAB PCD ∠=∠+∠=∠+∠，再根据（1）同样的方法可得APC PAB PCD ∠=∠+∠，由此即可得出结论；（3）过点E 作//EF AB ，过点P 作//PQ AB ，先根据（1）可得2PAB PCD AEC ∠+∠=∠，再根据平行线的性质、平行公理推论可得180,180APQ PAB CPQ PCD ∠=︒-∠∠=︒-∠，然后根据角的和差、等量代换即可得出结论．【详解】解：（1）如图，过点E 作//EF AB ，AEF BAE ∴∠=∠，//AB CD ，//EF CD ∴，CEF DCE ∴∠=∠，AEC AEF CEF BAE DCE ∴∠=∠+∠=∠+∠，又//AB CD ，且点P 运动到线段AC 上，180PAB PCD ∴∠+∠=︒，AE ∵平分PAB ∠，CE 平分PCD ∠， 11,22BAE PAB DCE PCD ∴∠=∠∠=∠， 111()90222AEC PAB PCD PAB PCD ∴∠=∠+∠=∠+∠=︒；（2）猜想2APC AEC ∠=∠，证明如下：如图，过点E 作//EF AB ，过点P 作//PQ AB ，由（1）已得：1()2AEC BAE DCE PAB PCD ∠=∠+∠=∠+∠，同理可得：APC PAB PCD ∠=∠+∠，2APC AEC ∴∠=∠；（3）2360APC AEC ∠+∠=︒，证明如下：如图，过点E 作//EF AB ，过点P 作//PQ AB ，由（1）已得：1()2AEC BAE DCE PAB PCD ∠=∠+∠=∠+∠，即2PAB PCD AEC ∠+∠=∠，//PQ AB ，180APQ PAB ∴∠+∠=︒，即180APQ PAB ∠=︒-∠，//AB CD ，//PQ CD ∴，180CPQ PCD ∴∠+∠=︒，即180CPQ PCD ∠=︒-∠，APC APQ CPQ ∴∠=∠+∠，180180PAB PCD =︒-∠+︒-∠，()360PAB PCD =︒-∠+∠，3602AEC =︒-∠，即2360APC AEC ∠+∠=︒．【点睛】本题考查了平行线的性质、平行公理推论、角平分线的定义等知识点，熟练掌握平行线的性质是解题关键．9．（1）136°；（2）∠AOG+∠NEF ＝90°，理由见解析；（3）当点P 在GF 上时，∠OPQ ＝140°﹣∠POQ+∠PQF ；当点P 在线段GF 的延长线上时，140°﹣∠POQ ＝∠OPQ+∠PQF ．解析：（1）136°；（2）∠AOG +∠NEF ＝90°，理由见解析；（3）当点P 在GF 上时，∠OPQ ＝140°﹣∠POQ +∠PQF ；当点P 在线段GF 的延长线上时，140°﹣∠POQ ＝∠OPQ +∠PQF ．【分析】（1）如图1，作CP ∥a ，则CP ∥a ∥b ，根据平行线的性质可得∠AOG ＝∠ACP ，∠BCP +∠CEF ＝180°，然后利用∠ACP +∠BCP ＝90°即可求得答案；（2）如图2，作CP ∥a ，则CP ∥a ∥b ，根据平行线的性质可得∠AOG ＝∠ACP ，∠BCP +∠CEF ＝180°，然后结合已知条件可得∠BCP ＝∠NEF ，然后利用∠ACP +∠BCP ＝90°即可得到结论；（3）分两种情况，如图3，当点P 在GF 上时，过点P 作PN ∥OG ，则NP ∥OG ∥EF ，根据平行线的性质可推出∠OPQ ＝∠GOP +∠PQF ，进一步可得结论；如图4，当点P 在线段GF 的延长线上时，同上面方法利用平行线的性质解答即可．【详解】解：（1）如图1，作CP ∥a ，∵//a b ，∴CP ∥a ∥b ，∴∠AOG＝∠ACP，∠BCP+∠CEF＝180°，∴∠BCP＝180°﹣∠CEF，∵∠ACP+∠BCP＝90°，∴∠AOG+180°﹣∠CEF＝90°，∵∠AOG＝46°，∴∠CEF＝136°，故答案为136°；（2）∠AOG+∠NEF＝90°．理由如下：如图2，作CP∥a，则CP∥a∥b，∴∠AOG＝∠ACP，∠BCP+∠CEF＝180°，而∠NEF+∠CEF＝180°，∴∠BCP＝∠NEF，∵∠ACP+∠BCP＝90°，∴∠AOG+∠NEF＝90°；（3）如图3，当点P在GF上时，过点P作PN∥OG，∴NP∥OG∥EF，∴∠GOP＝∠OPN，∠PQF＝∠NPQ，∴∠OPQ＝∠GOP+∠PQF，∴∠OPQ＝140°﹣∠POQ+∠PQF；如图4，当点P在线段GF的延长线上时，过点P作PN∥OG，∴NP ∥OG ∥EF ，∴∠GOP ＝∠OPN ，∠PQF ＝∠NPQ ，∵∠OPN ＝∠OPQ +∠QPN ，∴∠GOP ＝∠OPQ +∠PQF ，∴140°﹣∠POQ ＝∠OPQ +∠PQF ．【点睛】本题考查了平行线的性质以及平行公理的推论等知识，属于常考题型，正确添加辅助线、灵活应用平行线的判定和性质是解题的关键．10．（1）①90；②t 为或或或或或或；（2）①正确，②错误，证明见解析．【分析】（1）①由平角的定义，结合已知条件可得：从而可得答案；②当时，有两种情况，画出符合题意的图形，利用平行线的性质与角的和解析：（1）①90；②t 为3s 或6s 或9s 或18s 或21s 或24s 或27s ；（2）①正确，②错误，证明见解析．【分析】（1）①由平角的定义，结合已知条件可得：180,DPC CPA DPB ∠=︒-∠-∠从而可得答案；②当//BD PC 时，有两种情况，画出符合题意的图形，利用平行线的性质与角的和差求解旋转角，可得旋转时间；当//PA BD 时，有两种情况，画出符合题意的图形，利用平行线的性质与角的和差关系求解旋转角，可得旋转时间；当//AC DP 时，有两种情况，画出符合题意的图形，利用平行线的性质与角的和差关系求解旋转角，可得旋转时间；当//AC BD 时，画出符合题意的图形，利用平行线的性质与角的和差关系求解旋转角，可得旋转时间；当//AC BP 时的旋转时间与//PA BD 相同；（2）分两种情况讨论：当PD 在MN 上方时，当PD 在MN 下方时，①分别用含t 的代数式表示,CPD BPN ∠∠，从而可得CPD BPN∠∠的值；②分别用含t 的代数式表示,CPD BPN ∠∠，得到BPN CPD ∠+∠是一个含t 的代数式，从而可得答案．【详解】解：（1）①∵∠DPC ＝180°﹣∠CPA ﹣∠DPB ，∠CPA ＝60°，∠DPB ＝30°，∴∠DPC ＝180﹣30﹣60＝90°，故答案为90；②如图1﹣1，当BD∥PC时，∵PC∥BD，∠DBP＝90°，∴∠CPN＝∠DBP＝90°，∵∠CPA＝60°，∴∠APN＝30°，∵转速为10°/秒，∴旋转时间为3秒；如图1﹣2，当PC∥BD时，PC BD∠PBD＝90°，∵//,∴∠CPB＝∠DBP＝90°，∵∠CPA＝60°，∴∠APM＝30°，∵三角板PAC绕点P逆时针旋转的角度为180°+30°＝210°，∵转速为10°/秒，∴旋转时间为21秒，如图1﹣3，当PA∥BD时，即点D与点C重合，此时∠ACP＝∠BPD＝30°，则AC∥BP，∵PA∥BD，∴∠DBP＝∠APN＝90°，∴三角板PAC绕点P逆时针旋转的角度为90°，∵转速为10°/秒，∴旋转时间为9秒，如图1﹣4，当PA∥BD时，∵∠DPB＝∠ACP＝30°，∴AC∥BP，∵PA∥BD，∴∠DBP＝∠BPA＝90°，∴三角板PAC绕点P逆时针旋转的角度为90°+180°＝270°，∵转速为10°/秒，∴旋转时间为27秒，如图1﹣5，当AC∥DP时，∵AC∥DP，∴∠C＝∠DPC＝30°，∴∠APN＝180°﹣30°﹣30°﹣60°＝60°，∴三角板PAC绕点P逆时针旋转的角度为60°，∵转速为10°/秒，∴旋转时间为6秒，AC DP时，如图1﹣6，当////AC DP，∴∠=∠=︒，90DPA PAC1803090240DPN DPA ∠+∠=︒-︒+︒=︒，∴三角板PAC 绕点P 逆时针旋转的角度为240︒，∵转速为10°/秒，∴旋转时间为24秒，如图1﹣7，当AC ∥BD 时，∵AC ∥BD ，∴∠DBP ＝∠BAC ＝90°，∴点A 在MN 上，∴三角板PAC 绕点P 逆时针旋转的角度为180°，∵转速为10°/秒，∴旋转时间为18秒，当//AC BP 时，如图1-3，1-4，旋转时间分别为：9s ，27s ．综上所述：当t 为3s 或6s 或9s 或18s 或21s 或24s 或27s 时，这两个三角形是“孪生三角形”；（2）如图，当PD 在MN 上方时，①正确，理由如下：设运动时间为t 秒，则∠BPM ＝2t ，∴∠BPN ＝180°﹣2t ，∠DPM ＝30°﹣2t ，∠APN ＝3t ．∴∠CPD ＝180°﹣∠DPM ﹣∠CPA ﹣∠APN ＝90°﹣t ，21802,BPN CPD t ∴∠=∠=︒- ∴1.2CPD BPN ∠=∠ ②∠BPN +∠CPD ＝180°﹣2t +90°﹣t ＝270°﹣3t ，可以看出∠BPN +∠CPD 随着时间在变化，不为定值，结论错误．当PD 在MN 下方时，如图，①正确，理由如下：设运动时间为t 秒，则∠BPM ＝2t ，∴∠BPN ＝180°﹣2t ，∠DPM ＝230,t -︒ ∠APN ＝3t ．∴∠CPD ＝360CPA APN DPB BPN ︒-∠-∠-∠-∠()360603301802t t =︒-︒--︒-︒-=90t ︒-21802,BPN CPD t ∴∠=∠=︒- ∴1.2CPD BPN ∠=∠ ②∠BPN +∠CPD ＝180°﹣2t +90°﹣t ＝270°﹣3t ，可以看出∠BPN +∠CPD 随着时间在变化，不为定值，结论错误．综上：①正确，②错误．【点睛】本题考查的是角的和差倍分关系，平行线的性质与判定，角的动态定义（旋转角）的理解，掌握分类讨论的思想是解题的关键．三、解答题11．（1）36°或18°；（2）△AOB 、△AOC 都是“梦想三角形”，证明详见解析；（3）∠B ＝36°或∠B ＝．【分析】（1）根据三角形内角和等于180°，如果一个“梦想三角形”有一个角为108°，解析：（1）36°或18°；（2）△AOB 、△AOC 都是“梦想三角形”，证明详见解析；（3）∠B ＝36°或∠B ＝5407︒（）．【分析】（1）根据三角形内角和等于180°，如果一个“梦想三角形”有一个角为108°，可得另两个角的和为72°，由三角形中一个内角是另一个内角的3倍时，可以分别求得最小角为180°﹣108°﹣108÷3°＝36°，72°÷（1＋3）＝18°，由此比较得出答案即可；（2）根据垂直的定义、三角形内角和定理求出∠ABO 、∠OAC 的度数，根据“梦想三角形”的定义判断即可；（3）根据同角的补角相等得到∠EFC ＝∠ADC ，根据平行线的性质得到∠DEF ＝∠ADE ，推出DE ∥BC ，得到∠CDE ＝∠BCD ，根据角平分线的定义得到∠ADE ＝∠CDE ，求得∠B ＝∠BCD ，根据“梦想三角形”的定义求解即可．【详解】解：当108°的角是另一个内角的3倍时，最小角为180°﹣108°﹣108÷3°＝36°，当180°﹣108°＝72°的角是另一个内角的3倍时，最小角为72°÷（1＋3）＝18°，因此，这个“梦想三角形”的最小内角的度数为36°或18°．故答案为：18°或36°．（2）△AOB、△AOC都是“梦想三角形”证明：∵AB⊥OM，∴∠OAB＝90°，∴∠ABO＝90°﹣∠MON＝30°，∴∠OAB＝3∠ABO，∴△AOB为“梦想三角形”，∵∠MON＝60°，∠ACB＝80°，∠ACB＝∠OAC＋∠MON，∴∠OAC＝80°﹣60°＝20°，∴∠AOB＝3∠OAC，∴△AOC是“梦想三角形”．（3）解：∵∠EFC＋∠BDC＝180°，∠ADC＋∠BDC＝180°，∴∠EFC＝∠ADC，∴AD∥EF，∴∠DEF＝∠ADE，∵∠DEF＝∠B，∴∠B＝∠ADE，∴DE∥BC，∴∠CDE＝∠BCD，∵AE平分∠ADC，∴∠ADE＝∠CDE，∴∠B＝∠BCD，∵△BCD是“梦想三角形”，∴∠BDC＝3∠B，或∠B＝3∠BDC，∵∠BDC＋∠BCD＋∠B＝180°，∴∠B＝36°或∠B＝5407（）．【点睛】本题考查的是三角形内角和定理、“梦想三角形”的概念，用分类讨论的思想解决问题是解本题的关键．12．【现象解释】见解析；【尝试探究】BEC 70；【深入思考】2.【分析】[现象解释]根据平面镜反射光线的规律得∠1=∠2，∠3=∠4，再利用∠2+∠3=90°得出∠1+∠2+∠解析：【现象解释】见解析；【尝试探究】∠BEC = 70︒；【深入思考】β= 2α.【分析】[现象解释]根据平面镜反射光线的规律得∠1=∠2，∠3=∠4，再利用∠2+∠3=90°得出∠1+∠2+∠3+∠4=180°，即可得出∠DCB+∠ABC=180°，即可证得AB∥CD；[尝试探究]根据三角形内角和定理求得∠2+∠3=125°，根据平面镜反射光线的规律得∠1=∠2，∠3=∠4，再利用平角的定义得出∠1+∠2+∠EBC+∠3+∠4+∠BCE=360°，即可得出∠EBC+BCE=360°-250°=110°，根据三角形内角和定理即可得出∠BEC=180°-110°=70°；[深入思考]利用平角的定义得出∠ABC=180°-2∠2，∠BCD=180°-2∠3，利用外角的性质∠BED=∠ABC-∠BCD=（180°-2∠2）-（180°-2∠3）=2（∠3-∠2）=β，而∠BOC=∠3-∠2=α，即可证得β=2α．【详解】[现象解释]如图2，∵OM⊥ON，∴∠CON=90°，∴∠2+∠3=90°∵∠1=∠2，∠3=∠4，∴∠1+∠2+∠3+∠4=180°，∴∠DCB+∠ABC=180°，∴AB∥CD；【尝试探究】如图3，在△OBC中，∵∠COB=55°，∴∠2+∠3=125°，∵∠1=∠2，∠3=∠4，∴∠1+∠2+∠3+∠4=250°，∵∠1+∠2+∠EBC+∠3+∠4+∠BCE=360°，∴∠EBC+BCE=360°-250°=110°，∴∠BEC=180°-110°=70°；【深入思考】如图4，β=2α，理由如下：∵∠1=∠2，∠3=∠4，∴∠ABC=180°-2∠2，∠BCD=180°-2∠3，∴∠BED=∠ABC-∠BCD=（180°-2∠2）-（180°-2∠3）=2（∠3-∠2）=β，∵∠BOC=∠3-∠2=α，∴β=2α．【点睛】本题考查了平行线的判定，三角形外角的性质以及三角形内角和定理，熟练掌握三角形的性质是解题的关键．13．（1）110（2）（90 +n）（3）×90°+n°【分析】（1）根据角平分线的性质，结合三角形的内角和定理可得到角之间的关系，然后求解即可；（2）根据BO、CO分别是∠ABC与∠ACB的角平解析：（1）110（2）（90 +12n）（3）201712×90°+20182018212n°【分析】（1）根据角平分线的性质，结合三角形的内角和定理可得到角之间的关系，然后求解即可；（2）根据BO、CO分别是∠ABC与∠ACB的角平分线，用n°的代数式表示出∠OBC与∠OCB的和，再根据三角形的内角和定理求出∠BOC的度数；（3）根据规律直接计算即可.【详解】解：（1）∵∠A=40°，∴∠ABC+∠ACB=140°，∵点O 是∠AB 故答案为：110°；C 与∠ACB 的角平分线的交点，∴∠OBC+∠OCB=70°，∴∠BOC=110°．（2）∵∠A=n°，∴∠ABC+∠ACB=180°-n°，∵BO 、CO 分别是∠ABC 与∠ACB 的角平分线，∴∠OBC +∠OCB ＝12∠ABC +12∠ACB ＝12（∠ABC +∠ACB ）＝12（180°﹣n °）＝90°﹣12n °，∴∠BOC ＝180°﹣（∠OBC +∠OCB ）＝90°+12n °．故答案为：（90+12n ）；（3）由（2）得∠O ＝90°+12n °，∵∠ABO 的平分线与∠ACO 的平分线交于点O 1， ∴∠O 1BC ＝34∠ABC ，∠O 1CB ＝34∠ACB ， ∴∠O 1＝180°﹣34（∠ABC +∠ACB ）＝180°﹣34（180°﹣∠A ）＝14×180°+34n °，同理，∠O 2＝18×180°+78n °， ∴∠O n ＝112n +×180°+11212n n ++- n °， ∴∠O 2017＝201812×180°+20182018212-n °，故答案为：201712×90°+20182018212-n °．【点睛】本题考查了三角形内角和定理，角平分线定义的应用，注意：三角形的内角和等于180°． 14．（1）140°；（2）∠1+∠2=90°+α；（3）∠1=90°+∠2+α,理由见解析;(4)∠2=90°+∠1﹣α．【详解】试题分析：（1）根据四边形内角和定理以及邻补角的定义，得出∠1+∠2 解析：（1）140°；（2）∠1+∠2=90°+α；（3）∠1=90°+∠2+α,理由见解析;(4)∠2=90°+∠1﹣α．【详解】试题分析：（1）根据四边形内角和定理以及邻补角的定义，得出∠1+∠2=∠C+∠α，进而得出即可；。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

木渎实验中学综合练习四(满分65分)
班级姓名
一、选择题(每小题2分，共24分.每小题只有一个选项是正确的.)
（）1．最先用实验证实电磁波存在的科学家是
A．麦克斯韦B．莫尔斯C．赫兹D．贝尔
（）2．口技演员能惟妙惟肖地模仿一些动物和乐器的声音，他主要是模仿声音的A．音色B．响度C．音调D．乐音
（）3．如图所示的四种事例中，应用了光的折射规律的是
（）4．在我国“三星堆遗址”的出土文物中，发现了用极薄的金箔贴饰的精美“金器”，黄金可以被做成极薄的金箔，主要是因为黄金的
A．延展性好B．硬度大C．弹性好D．密度大
（）5．当温度降低到很低时，某些金属的电阻会突然消失，这种现象称为超导现象，假如所有导体都没有了电阻，当用电器通电时，下列说法正确的是
A．白炽灯仍能发光B．电动机仍能转动
C．电饭锅仍能煮饭D．电熨斗仍能熨衣服
（）6．小明用托盘天平称一块橡皮的质量，正确使用天平时称得橡皮质量为m1．在托盘天平未调平衡(当指针静止时，还偏在分度盘中央刻度线的右边)就去称量，称得橡皮质量为m2．则m1和m2的大小关系是m2
A．m1= m2B．m1＜m2C．m1＞m2D．无法确定
（）7．关于能量和能源的利用，下列说法中正确的是
A人类大量使用太阳能会导致温室效应
B．因为能量是守恒的，所以不存在能源危机
C．核能的利用会造成放射性污染，所以应该关闭核电站
D．现在人类社会使用的主要能源是煤、石油和天然气
（）8．目前，科学家正任研究太空电站，即地球同步轨道
上的太阳能电站，其示意图如图所示．下列说法中错误
．．是
A．太阳能来自太阳内部的核聚变
B．太阳能恢集板将太阳能转化为电能
C．利用微波传输，实现了无缆输电
D．以地面接收站为参照物，太阳能电站是运动的
（）9．物体放在凸透镜前某一位置，在透镜的另一侧离透镜10cm的光屏上成一倒立缩小的像．当物体移至距透镜10cm处时，所成的是
A．倒立缩小的实像B．倒立放大的实像
C．正立放大的虚像D．以上都有可能
（）10．下列四幅图中能说明电动机的工作原理的是
（）11．下图为核电站发电流程图．在核电站的发电过程中，从核能到电能，图中所示的能量转化顺序正确的是
A．核能，化学能，机械能，电能B．核能，内能，化学能，电能
C．核能，机械能，内能，电能D．核能，内能，机械能，电能
（）12．用电器R1和R2上都标有“6V”字样，它们的电流随电
压变化关系如图所示．若把R1和R2串联在电源电压为6V的电
路中工作，则用电器R2的实际功率是
A．0．2W B．0．4W
C．0．6W D．1．8W
二、填空(每空1分，共20分)
13．古诗《小儿垂钓》中有“路人借问遥招手，怕得鱼惊不应人”．这个钓鱼的小儿面对路人的询问，只是招招手却默不作声．这是因为他知道声音能在______中传播；小儿招手________(选填“会”或“不会”)产生振动，鱼儿听不见的原因是__________．14．昆山阳澄湖面积120平方公里，螃蟹远近闻名．(1)阳澄湖对周围气温起到很好的调节作用，这是由于水的比热容较______．(2)在湖面上划船时，船相对于岸是______ (选填：“运动”或“静止”)的．(3)漫步在湖边林荫道上，树荫是由于光的______形成的．
15．我国是世界上手机用户最多的国家，手机间是通过___________传递信息的．若把一手机放在真空罩中，再用另一手机拨打罩内的手机号码，结果发现罩内手机彩灯闪烁，但却听不到手机的铃声，这是因为_______________．
16．获取核能有两条途径──重核的裂变和
轻核的聚变．如图所示，甲图属于核
______变；乙图属于核______变．
17．根据电流表和电压表的知识推断，图示
的仪表，指针所指示的物理量的大小是_________，此仪器
的刻度与电流表、电压表的区别是(写出一点即
可)________________．
18．王老师在课堂上，看近处课本时要戴上眼镜，观察远处同学
时又摘下眼镜，这样戴上摘下，非常不方便．王老师的眼睛是
______(填：“近”或“远”)视眼，可以用_____透镜来矫正．小军将一
种新型眼镜送给了老师，如图所示，镜片A区厚度相同，B区可以矫正
视力，现在王老师可以通过_____区看书，通过_______区看同学，再不
需要频繁戴上摘下眼镜．
19．以汽油为燃料的助动车，由于燃烧不充分和对环境造成污染等原因，已逐步被电动自行车取代．请写出电瓶车在下列过程中的能量转化，电瓶充电：电能转化为______能；电瓶放电：化学能转化为______能；电瓶车行驶过程中：电能转化为______能．经转化后，可利用的能量只会减少，不会增加，表明能量的转化和转移是有______的．
三、作图与实验( 共6+5=11分)
20．如图，一束光线垂直射向玻璃棱镜，请在图中画出光通过三棱镜折
射的大致路径．
21．如图所示，MN是凸透镜的主光轴，P、Q、S是在
主光轴上顺次的三个位置．把一物点放在P处，像成在Q处；
如把该物点放在Q处，凸透镜位置不变，像成在S处．则
可以判断凸透镜的位置应该在( ) .
A．P的左边B．PQ之间C．QS之间D．S的右边
22．在实验室里，小明利用一个水平气垫导轨(气垫导轨可以看成光滑轨道)研究物体的运动．他将物体A和物体B分别放在轨道的一端和中间位置，使轨道一端的物体A先运动起来，然后撞击物体B．他根据实验数据绘制了物体A撞击物体B前、后路程随时间变化的图像，如图所示．由图像可以看出：在0-5s内物体A的速度大小为________m／s；
物体A撞击物体B后，是作_________运动(选填“减速”、“匀速”或“加速”)．
23．如上图是“探究导体在磁场中运动时产生感应电流的条件”实验装置．闭合开关后，铜棒AB、电流表、开关组成闭合电路．
(1)要使电流表指针发生偏转，一种可行的操作是________ _ __．
(2)使铜棒彻上下运动，电流表指针能否发生偏转?______ ______．
(3)要使电流表指针偏转方向发生改变，可以采取两种方法．
方法一：__________ ____方法二：________ ______．
(4)感应电流的大小除了与铜棒运动速度有关以外，还和___ _____有关．
四、计算(共8分)
24.右表是LG微波炉的部分技术参数．请根据表中信息完成
下列问题．
(1)求该微波炉在使用微波档工作时的额定电流．
(2)若使用微波档工作时，做一道菜需用15min，则消耗
的电能是多少度?
(3)该微波炉在使用烧烤档工作时的效率为多少?
(4)使用微波档和烧烤档都可以用来加热食物，但它们
加热的方式是不同的，前者采用微波加热，后者采用
热传递的方式(红外线)加热．请猜测“振荡频率”
是针对微波炉哪种工作状态而言的?
五、应用（(共2分)
25．如图所示，B是一个被销钉锁住的活塞，气缸A密封有压缩空气，C是一支温度计。

若活塞与气缸壁之间没有摩擦，当把销钉K拔出
后，将观察到活赛向右移动，温度计的读数________．(选填“变
大”、“变小”或不变),原因是。