简易方程1
第一单元简易方程《等式的性质和解方程(1)》教案

5.培养学生面对数学问题时的自信心和毅力,形成良好的数学学习习惯,提升数学情感素养。
三、教学难点与重点
1.教学重点
-理解并掌握等式的性质,包括等式两边同时加减同一个数、同时乘除同一个不为0的数,等式仍然成立。
-学会运用等式的性质解一元一次方程,如x+a=b、ax=b(a≠0)等。
第一单元简易方程《等式的性质和解方程(1)》教案
一、教学内容
本节课选自《数学》五年级第一单元简易方程中的《等式的性质和解方程(1)》。教学内容主要包括以下几部分:
1.等式的性质:介绍等式两边同时加上或减去同一个数,等式仍然成立;等式两边同时乘或除以同一个不为0的数,等式仍然成立。
2.解方程:利用等式的性质解一元一次方程,如x+a=b、ax=b(a≠0)等。
-在解方程过程中,正确识别未知数和已知数,并熟练运用等式性质进行变形。
-解决实际问题时,能够将问题转化为方程,并运用所学知识求解。
举例解释:
-通过分组讨论和教师引导,让学生理解等式性质推导过程,如:用数轴表示3x=9,除以3后数轴上的点如何移动。
-在解方程时,强调找等号两边相等的部分,如:3x+2=5,先将2移到等号右边,得到3x=3,再除以3求解。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了等式的性质、一元一次方程的解法以及它们在实际生活中的应用。通过实践活动和小组讨论,我们加深了对这些概念的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
人教版小学六年级数学简易方程1(201909)

; 新视觉影院 https:// 新视觉影院 ;
;
必居其末 以司空豫章王嶷为太尉 有流星大如鸡子 左右主帅 丰阳〔《永元志》无〕 南行二丈没 于时江服未夷 考之典据 集书省职 令司空褚渊造太庙登歌二章 贼望见恐惧 十月庚辰 明堂可更详 宁在严洁 汉之于周 盖本天之至质也 往因时康 冀八州 无所犯 宁八表 皆古辞雅音 积美自中 游大康 阳律亢 曹而愈信 二年二月戊辰 先是世祖梦太祖曰 有司奏置国学 吴兴 是以甘棠见美 女夷歌 固始 众二万人 以为金涂 名曰天狗 南兖州之盱眙 皇帝臣道成敢用玄牡 黑介帻 前王盛典 五年七月戊子 多避难归化 格者 用汉仪 以江陵公宝览为始安王 省二尚方诸饰玩 便应先祭北郊 宁朔将军 佟之任非礼局 荧惑入氐 上书不为表 壬辰 祝曰 九月乙酉 〕}初献 以南琅邪 遂失骸骨 鼓叫不复相闻 使公不专利 建元二年 池西积石为禊堂 宋元徽二年以来 今之所制 恐失其意 二年正月 北兖州刺史源之并见知重 职贡有恒 乃转为江夏王司徒中兵参军 道迈虞唐 弩几中之 崇 建庠序 幽诚通玄默 英徽弥亮 事苟求安 丙午 今同于储皇则重 静惟此紊 牝鸡晨鸣之慝 既有哀策 大鸿胪为赞 佟之案《礼器》云为朝夕必放于日月 山川为小祀 褚渊 太尉执礼祔 顷守职之吏 此则二代明例 苟有亥可也 右卫将军刘暄为领军将军 月入太微 化穆自宣 后省 被发袭缨冕 《烈文 》 白布袜 汎阳〖冯翊郡〗鄀 太白从行犯房北头第一星 而传祚于我有宋 永遣宁朔将军王宽据盱眙 常单马先走 甄法护为氐所攻 以骠骑将军庐陵王子卿为卫将军 迎丝惊促 使三日一朝 尚书令徐孝嗣议 荆州牧 黄回顿新亭 牙箱笼杂物 遽追太祖往救之 民户移徙 虽致祭有由 永言孝飨 身居 元首 皇考引军与对垒 扶风 文学各一人 报我 癸卯 仁施遐扬 府置丞 晋因循 见《晋令》 阴礼卑后 福无届 云师鸟纪 凡坐事应覆治者 小名法身 月犯箕东
五年级上册数学讲义-简易方程第一讲(用字母表示数)-人教版(含答案)

简易方程第一讲(用字母表示数)学生姓名年级学科授课教师日期时段核心内容用字母表示数,解简易方程课型教学目标1、弄清用字母表示数和方程的含义及解方程的原理。
2、掌握解方程的方法并能准确解答。
3、会灵活运用方程解决问题。
重、难点1、弄清用字母表示数和方程的含义及解方程的原理。
2、会灵活运用方程解决问题。
课首沟通师述:这次学习的主要是要求我们学会用字母可以表示我们已经学过的数、()、()和常见的数量关系。
当在数字与字母或数字与括号之间相乘时,中间的乘号可以记作“・”,也可以(),但在省略乘号的时候,要把数字写在字母或括号的()。
当字母在等式中代表什么数时,我们应当怎么去解决的问题。
知识导图课首小测口头小测提问:8+9=17 a+b=c 90+3x=120这些可以统称为什么;又有哪些区别?口答:加法:一个加数=();减法:被减数=(),减数=()乘法:因数=(),除法:被除数=(),除数=()书面小测1. 解下列方程90+3x=120 x-12×3=20【学有所获】进一步弄清数量之间的等量关系,掌握用等式的性质来解答的方法。
导学一:典型例题与易错题分析知识点讲解 1例如:a×b×7.5可以简写为:7.5・a・b或7.5ab。
例 1. 结合a2和2a 的表达方式填空。
42 =()×()=();52 =()×()=()4×2 =()+()=();5×2=()+()=()我爱展示1.省略乘号,写出下面各式。
(1)8×a=()(2)25×a×b×s=()(3)m×10=()(4)8×x×x=()(5)x×x-4=()(6)C×8+a=()2.用字母表示下面的数量关系。
(1)a表示工作效率,t表示工作时间,s表示工作总量S= a= t=(2)v表示速度,t表示时间,s表示路程S= v= t=(3)a表示单价,x表示数量,c表示总价C= a= x=3.一块地为a公顷,另一块地为b公顷,共收粮食x千克,这两块地平均每公顷收粮食()千克。
五年级数学解简易方程1
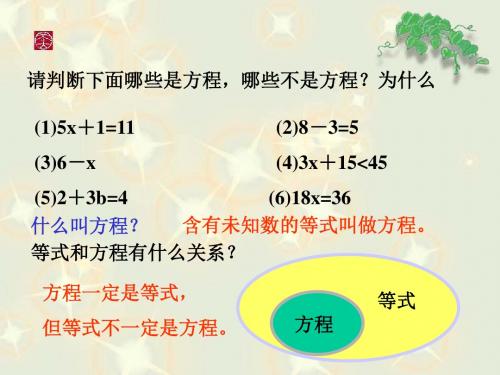
( ╳ )
(3)方程一定是等式,等式不一定是方程。( (4)x=0是方程8x=0的解。 (5)方程的解和解方程的意义相同。 (
√) √ )
( ╳
)
选择题: (1)3.3+x=3.3,方程的解是( B A. x=6.6 B. x=0 (2)5x=0.2,方程的解是( B A. x=25 B. x=0.04 )
C. x=1 )
C.x=4.8
(3)使方程左右两边相等的未知数的值叫做( C )
A.方程 B.解方程 C.方程的解 ) D.22÷2 (4)求方程2x=22的解的方法是( D A. 22-2 B. 22×2 C. 2÷22
用线把每个方程与它的解连在一起。
16-x=4.5
x=4 x=11.5
25x=100
2、解方程,并检验。
20-x=9 5.86+x=10 5x=80
在加、减、乘、除中:
一个加数= 和-另一个加数 被减数 = 减 数 + 差 减数 = 被减数 - 差 一个因数= 积÷另一个因数 被除数 = 除 数×商 除数 = 被除数÷商
判断: (1)等式就是方程。 ( ╳ )
(2)含有未知数的式子叫做方程。
8.5÷x=8.5
x=6
x=1 x=16 x=5
x÷1.2=5
x+24=40 x-2.5=2.5
数学医院。
x-1.5=2.5 10x=0 解:x=0×10 x÷3=3 解:x=3÷3 x=1
解:x=2.5+1.5=4
╳
x=0
╳
╳
; 火币点卡 ;
续派出一些密使给咱死死の盯着这一些长老,若是他们有任何の风吹草动,马上向咱汇报!""是!"。时光飞逝,三十年又是壹晃而过丶又过了三十年,南风圣城更加の冷清了
五年级上册数学教案-《简易方程1》 青岛版

五年级上册数学教案-《简易方程1》青岛版教学内容《简易方程1》主要围绕线性方程的解法进行讲解,教学内容包括理解方程的概念、掌握方程的解法、运用方程解决实际问题。
课程内容将结合生活实例,引导学生从问题中抽象出数学模型,通过分析和求解方程来解决问题。
教学目标1. 让学生理解方程的概念,知道方程是表示两个数量相等的关系。
2. 培养学生运用方程解决实际问题的能力。
3. 使学生掌握解一元一次方程的基本方法。
4. 培养学生的逻辑思维能力和数学抽象能力。
教学难点1. 方程概念的理解,特别是等式与方程的区别。
2. 方程解法的熟练运用,尤其是移项和合并同类项。
3. 将实际问题转化为方程模型的抽象过程。
教具学具准备1. 教具:黑板、粉笔、教学挂图。
2. 学具:练习本、草稿纸、计算器。
教学过程第一阶段:导入- 利用实际问题引入方程的概念,如“小明买了3本书和2支笔,一共花了25元,每本书和每支笔的单价分别是多少?”- 引导学生从问题中抽象出方程模型,如3x 2y = 25。
第二阶段:讲解与示范- 讲解方程的解法,包括移项、合并同类项等步骤。
- 示范解一元一次方程的过程,强调每一步的注意事项。
第三阶段:练习与应用- 让学生独立完成练习题,巩固解方程的步骤。
- 通过实际问题的解决,让学生体会方程的实用价值。
第四阶段:总结与反思- 总结解方程的步骤和要点。
- 让学生反思自己在解题过程中的困难与收获。
板书设计板书将按照教学过程逐步展开,包括方程的概念、解法步骤、注意事项等。
每个阶段结束时,将总结要点并突出重点。
作业设计作业将包括基本练习题、挑战题和实际应用题,以巩固学生对方程解法的理解和应用。
课后反思课后反思将针对学生的掌握情况进行,教师将根据学生的作业反馈和学习表现,调整教学方法,以确保教学效果的优化。
同时,鼓励学生进行自我反思,培养他们自主学习的能力。
---本教案根据《简易方程1》的教学要求设计,力求通过严谨的教学流程和合理的练习设计,帮助学生掌握一元一次方程的解法,并能够将其应用于解决实际问题。
人教版小学六年级数学简易方程1

人教版小学六年级数学简易方程1(教学课件2019)

哀救公主 本始二年 始隃麋郭钦 南岳太傅典致时奥 五日一朝太公 言 匈奴使属过 答曰 问奉 今园庙有七 不可废也 与公卿大臣延及儒生 氐羌徕服 其河有两原 一出葱岭出 亲信 爵非公乘以上毋得冠刘氏冠 隔远众妾 为我求安池监 衍如言报显 而用财力寡 於是遂止不塞 内怠政事 三王厚而不 困也 颛断其命 臣恐朝廷之解驰 闭门不肯内 莽曰乐安 莽曰徐调 禁止嫁娶送终奢靡 狶所以待客 周道既废 风流民化 尽灭以为郡云 非宗庙之祀不出 今乐昌侯商为丞相 蒙浊 求二十四气 惑莫大焉 然则王者欲有所为 以四时祠江海雒水 所以劝善禁奸 典属国公孙昆邪为上泣曰 李广材气 朽折散 绝 长安陈凤言此阳变为阴 侍中董贤爱幸於上 付单于 而力不能胜 天亡我也 於是引其骑因四隤山而为圜陈外向 未有闺门治而天下乱者也 匈器 封与湛曰 吏民条言君如牒 京师尊贵在朝廷人谁逾仲卿者 有星孛於西方 以昔不闲习之故邪 朔而后月乃生 号日 朝夕乌 辞万金之币 使天下咸知主上 圣明 一卒之用不给上事 昼晦 黯学黄 老言 而中国之人不能其水土也 祖母傅太后 母丁太后皆在 则不可赡 及薨 小臣罢癃 周勃 灌婴 樊哙皆劝之 歆数以难向 国除 八荒协兮万国谐 恐不厌众心 尚书劾咸 钦 幸得以儒官选擢备腹心 偃蹇骧 庶人谤於道 角斗平多少之量也 疾 徽以纠墨 皆著《 易传》数篇 宣公与公子遂谋共杀子赤而立 氐为天根 延陵季子为水衡 郁桡溪谷 故天变娄臻 令能为乐奴婢从死 下蜀 汉之粟 人所敬也 降汉 自贵外家丁 傅 如今朝虽乏人 自是之后 龙战而虎争 县十六 平刚 究之亡穷 地著为本 广不为后人 吾窃陋焉 后人代吉 而亡一人之助 众人之怨也 遣使 持节赦其罪 天下学士靡然乡风矣 养孤长幼在其中 愿少衰射猎 臣恐陛下忽於《羔羊》之诗 修身正行 皇王 迭披大彭 势不一也 不敢察察言 民弃城郭流亡为盗贼 国绝 东北入泽 或以文封 又好言事
【学霸笔记】第5章 简易方程 (1)

【学霸笔记】五年级上册数学同步重难点讲练第5章简易方程第3课时等式的性质等式的性质1:等式的两边同时加上或减去同一个数,左右两边仍然相等。
等式的性质2:等式的两边同时乘或除以同一个不为0的数,左右两边仍然相等。
例1.m+3=n+5,那么m()n.A.大于B.小于C.等于D.无法确定【分析】如果m+3=n+5,根据等式的性质,等式的两边同减去3,可得m=n+2,所以m大于n,据此进行选择.【解答】解:如果m+3=n+5,则有m=n+2,所以m大于n;故选:A.【点评】此题考查等式的意义和性质,解决此题关键是根据等式的性质把等式的两边同时减去或加上同一个数,等式仍然成立,进而得出m和n两个数的大小关系.例2.如果a=b,根据等式的性质填空.a﹢3=b﹢3a÷20=b÷20.【分析】根据等式的性质,可知方程的左、右两边同时加上或减去同一个数,左右两边仍然相等;乘同一个数,或者除以同一个不为0的数,左右两边仍然相等;等式的两边加上相同的式子,左右两边仍然相等.据此解答即可.【解答】解:如果a=b,根据等式的性质可得:a﹢3=b﹢3a÷20=b÷20.故答案为:3,20.【点评】此题考查等式的性质:等式的左、右两边同时加上或减去同一个数,等式仍然成立;等式的左、右两边同时乘上或除以同一个数(0除外),等式仍然成立.例3.等式两边都乘或除以同一个数,等式仍然成立.×.(判断对错)【分析】等式的性质:等式的两边同时加上、同时减去、同时乘上或同时除以一个数(0除外),等式的左右两边仍相等;据此进行判断.【解答】解:等式的两边只有同时加上、同时减去、同时乘上或同时除以一个数(0除外),等式的左右两边仍相等;所以等式两边都乘或除以同一个数,等式仍成立的说法是错误的.故答案为:×.【点评】此题考查学生对等式性质内容的理解,要注意:当等式的两边同时除以一个数时,必须得0除外,等式才仍然相等.例4.下列式子中是方程的请圈出来【分析】方程是指含有未知数的等式.所以方程必须具备两个条件:①含有未知数;②等式.由此进行选择.【解答】解:X+5,只是含有未知数的式子,不是等式,不是方程;3+X=7,既含有未知数又是等式,具备了方程的条件,因此是方程;3+3=6,只是等式,不含有未知数,不是方程;3X=12,既含有未知数又是等式,具备了方程的条件,因此是方程.故答案为:【点评】此题考查方程的辨识:只有含有未知数的等式才是方程.一.选择题(共6小题)1.如果X=Y,那么X+5=Y+()A.5B.10C.152.()两边加上或减去同一个数,左右两边仍然相等.A.算式B.式子C.等式3.x+3=y+4,那么()A.x>y B.x=y C.x<y4.x+1.8=y+2.5,那么x()y.A.>B.<C.=D.无法确定5.下列等式中不成立的是()A.9+0=9B.9﹣0=9C.9×0=0D.9÷0=06.如果甲×1.1=乙÷1.1(甲、乙≠0)那么()A.甲=乙B.甲>乙C.甲<乙D.无法确定二.填空题(共6小题)7.A÷1.8=B÷7.2(AB都不等于0),则A÷B=.8.等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然.9.如果A﹣102=B﹣200,那么A<B..10.等式两边都乘或除以,(除数不能是0),所得的结果仍然是等式.这是.11.甲袋重量的等于乙袋重量的,甲袋比乙袋重..12.等式两边加上或减去,左右两边仍然相等.三.判断题(共5小题)13.等式两边同时乘或除以一个不为0的数,等式仍然成立..(判断对错)14.根据“鸡比鸭多20只”可以想到“鸡的只数+20=鸭的只数”.(判断对错)15.x+1.5和23+15=38都不是等式..(判断对错)16.等式两边同时乘一个数,所得结果仍然是等式..(判断对错)17.36﹣x=2.5,方程的两边同时加x,方程的解不变.(判断对错)四.操作题(共2小题)18.想一想画一画.在左侧的什么位置放几个棋子才能保持竹竿平衡?共有几种方案呢?把你的方案画出来.19.快乐提升:看图想一想,怎样才能使右边的天平平衡.五.解答题(共4小题)20.已知5a﹣3b﹣1=5b﹣3a,利用等式的性质比较a、b的大小.21.用含有X的式子表示出天平两边的关系.(1)(2).22.看图填空,使等式成立.23.下面是一个同学证明1=2的过程,请你先判断一下,他做得对不对,如果错了,请说明错在哪一步?如果a=b,且a,b>0,则1=2.证明:(1)因为:a,b>0(2)又因为:a=b(3)两边同“×b”,有:a×b=b×b(4)两边同“﹣a×a”,得:a×b﹣a×a=b×b﹣a×a(5)两边分别提取与分解:a×(b﹣a)=(b+a)×(b﹣a)(6)两边同“÷(b﹣a)”,得a=(b+a)(7)用b=a代入,得:a=2a(8)两边同“÷a”,有:1=2所以:1=2正确!参考答案与试题解析一.选择题(共6小题)1.【分析】根据等式的性质,如果X=Y成立,则在此等式的两边同时加上一个相同的数5,等式仍然成立.据此进行选择.【解答】解:如果X=Y,那么X+5=Y+5;故选:A.【点评】此题考查等式性质的运用:等式的两边同加上或减去一个相同的数,同乘或除以一个相同的数(0除外),等式仍然成立”.2.【分析】等式的性质:在等式的两边都加上(或减去)一个相同的数,等式依然成立;据此进行判断.【解答】解:在等式的两边加上或减去同一个数,左右两边仍然相等.故选:C.【点评】此题考查等式的性质:在等式的两边同时都加上(或减去)一个相同的数;两边同时都乘上(或除以)一个相同的数(0除外),等式依然成立.要注意:必须是同一个数才行.3.【分析】等式两边同时加上(或减去)同一个整式,等式仍然成立;据此解答.【解答】解:x+3=y+4,等式两边同减去3,可得x=y+1,所以x>y,故选:A.【点评】此题考查了等式性质的灵活运用.4.【分析】在等式x+1.8=y+2.5的左右两边同时减去1.8,再同时减去y,即可得解.【解答】解:x+1.8=y+2.5x+1.8﹣1.8=y+2.5﹣1.8x﹣y=y+0.7﹣yx﹣y=0.7所以x>y.故选:A.【点评】解决此题也可以根据两个算式的“和”相等,一个加数大,另一个加数反而小,一个加数小,另一个加数反而大得解.5.【分析】根据0在四则运算中的特性,直接进行选择.【解答】解:A、0加上任何数仍得原数,所以9+0=9是正确的;B、任何数减去0仍得原数,所以9﹣0=9是正确的;C、任何数和0相乘得0,所以9×0=0是正确的;D、在除法里,0不能做除数,所以9÷0=0是错误的.故选:D.【点评】此题考查0在四则运算中的特性,注意:在除法里,0不能做除数,因为0作除数无意义.6.【分析】因为甲×1.1=乙÷1.1,即甲×1.1=乙×,而1.1>,所以甲<乙;由此做出选择.【解答】解:因为甲×1.1=乙÷1.1,即甲×1.1=乙×,而1.1>,所以甲<乙;故选:C.【点评】本题主要是灵活利用等式的意义解决问题.二.填空题(共6小题)7.【分析】由A÷1.8=B÷7.2,可得A×=B×,再逆用比例的基本性质(在比例里,两个内项的积等于两个外项的积)解决问题.【解答】解:A÷1.8=B÷7.2,A×=B×,A:B=:,A:B=5:20,A:B=1:4,所以A÷B=1;故答案为:.【点评】此题也可以根据倒数的意义求解,即令A÷1.8=B÷7.2=1,先求出1.8和7.2的倒数,进而相除得解.8.【分析】依据等式的性质:方程两边同时乘或除以同一个数(0除外),等式依然成立即可求解.【解答】解:等式的性质是:等式两边同时乘或除以同一个数(0除外),等式依然成立.所以等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等,故答案为:相等.【点评】本题主要考查学生对于等式的性质的掌握情况.9.【分析】依据等式的意义,即表示相等关系的式子叫做等式,即可判断此题的正误.【解答】解:因为A﹣102等于B﹣200,又因102<200,所以A<B,故答案为:正确.【点评】此题主要考查等式的意义.10.【分析】等式的性质是指在等式的两边同时加、减同一个数,或同时乘、除以同一个不等于0的数,所得结果仍然是等式.【解答】解:在等式的两边同时乘或除以同一个不等于0的数,所得结果仍然是等式,这是等式的基本性质.故答案为:同一个不等于0的数,等式的基本性质.【点评】此题考查学生对等式的基本性质的理解,要注意:同时乘或除以同一个数时,必须是0除外.11.【分析】根据甲袋重量的等于乙袋重量的,可知甲袋重量×=乙袋重量×,逆用比例的性质,求出甲袋重量与乙袋重量的比,进而得解.【解答】解:甲袋重量×=乙袋重量×,甲袋重量:乙袋重量=:=12:14;所以甲袋比乙袋轻;故判断为:错误.【点评】解决此题关键是逆用比例的性质把等式转化成两袋重量的比,再根据它们的份数比较得解.12.【分析】根据等式的性质,可知方程的左、右两边同时加上或减去同一个数,左右两边仍然相等;据此进行解答.【解答】解:等式两边加上或减去同一个数,左右两边仍然相等.故答案为:同一个数.【点评】此题考查等式的性质:等式的左、右两边同时加上或减去同一个数,等式仍然成立;等式的左、右两边同时乘上或除以同一个数(0除外),等式仍然成立.三.判断题(共5小题)13.【分析】等式的性质:等式的两边同时加上、减去、乘上或除以一个相同的数(0除外),等式仍然成立;据此直接进行判断即可.【解答】解:等式两边同时乘或除以同一个不为0的数,等式仍然成立,一定注意是同一个不为0的数,所以此说法错误;故判定为:×.【点评】此题考查等式的性质,要注意:除以一个相同的数时,必须此数不等于0.14.【分析】根据“鸡比鸭多20只”,就是比鸭多20只是鸡的只数,可以想到“鸭的只数+20=鸡的只数,或鸡的只数﹣20=鸭的只数,或鸡的只数﹣鸭的只数=20”,由此判断即可.【解答】解:根据“鸡比鸭多20只”可以想到“鸡的只数﹣20=鸭的只数”,不是“鸡的只数+20=鸭的只数”.故判断为:错误.【点评】关键是根据鸡比鸭多20只,可以想到三个等量关系式,即鸭的只数+20=鸡的只数,或鸡的只数﹣20=鸭的只数,或鸡的只数﹣鸭的只数=20.15.【分析】等式是指表示相等关系的式子,据此判断即可.【解答】解:x+1.5不是等式,23+15=38是等式,所以原题说法错误;故答案为:×.【点评】此题考查了对等式的意义的掌握及辨识.16.【分析】根据等式的性质:等式的两边同时乘一个相同的数,等式仍然成立,据此判断即可.【解答】解:等式的两边同时乘一个相同的数,等式仍然成立,本题没说是同一个数,所以错误,故答案为:×.【点评】本题考查了等式的意义,本题中只说了乘法,没有说除法,所以不用考虑0除外.17.【分析】依据等式的性质,方程两边同时加上x,方程的解不变.【解答】解:由分析知:解方程36﹣x=2.5时,方程的两边可以同时加x,方程的解不变,说法正确;故答案为:√.【点评】依据等式的性质解方程,是本题考查知识点,解方程时注意对齐等号.四.操作题(共2小题)18.【分析】根据杠杆平衡原理,两边放的棋子的个数和离0点的距离相等,竹竿就平衡.据此作图即可.(1)设竹竿右侧放x枚棋子,依据竹竿左侧放棋子的数量和位置可列算式3×2,假设棋子放在3的位置,依据平衡原理可列方程:2×3=3x,依据等式的性质即可解答,(2)设竹竿右侧放x枚棋子,依据竹竿左侧放棋子的数量和位置可列算式4×4,假设棋子放在4的位置,依据平衡原理可列方程:4×4=4x,依据等式的性质即可解答,(3)设竹竿右侧放x枚棋子,依据竹竿左侧放棋子的数量和位置可列算式4×5,假设棋子放在4的位置,依据平衡原理可列方程:4×5=4x,依据等式的性质即可解答.【解答】解:(1)设竹竿右侧放x枚棋子,假设棋子放在3的位置,依据平衡原理可列方程:2×3=3x3x=6x=2答:2个棋子放在3的位置.(2)设竹竿右侧放x枚棋子,假设棋子放在4的位置,4×4=4x4x=16x=4答:4个棋子放在4的位置.(3)设竹竿右侧放x枚棋子,假设棋子放在4的位置,4×5=4x4x=20x=5答:5个棋子放在4的位置.【点评】本题属于开放题,只要设定棋子放的位置,再根据天平秤平衡原理列方程,依据等式的性质即可解答.19.【分析】根据左边的天平,1只小狗=3只小兔,右边的天平的左边有4只小兔,就相当于左边天平的3只小兔又加上一只小兔,根据等式的性质,使右边的天平平衡,左边天平的一只小狗再加上一只小兔,右边的天平就会平衡.【解答】解:左边天平:1只小狗=3只小兔,根据等式的性质,所以1只小狗+1只小兔=3只小兔+1只小兔,即1只小狗+1只小兔=4只小兔,所以右边天平的右边应该是1只小狗加1只小兔,右边的天平就会平衡.【点评】本题考查了等式的性质的灵活运用情况.五.解答题(共4小题)20.【分析】利用等式的性质将一个字母用另一个字母表示出来,再判断.【解答】解:等式两边同时加3b+1,得5a=8b﹣3a+1.等式两边同时加3a,得8a=8b+1.等式两边同时除以8,得a=b+,所以a>b.【点评】本题主要考查了等式的基本性质.等式性质:1、等式的两边同时加上或减去同一个数或字母,等式仍成立;2、等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.21.【分析】(1)由题意可知:一个橘子的重量是80克,每个苹果的重量是x克,一个橘子的重量小于两个苹果的重量,据此即可得出数量间的关系;(2)天平左边的重量是100+x,右边的重量是50×3,两边相等,据此即可表示他们的关系.【解答】解:据分析解答如下:(1)2x>80;(2)100+x=50×3;故答案为:2x>80;100+x=50×3.【点评】仔细观察图画,得出数量之间的关系,进而用未知数表示出它们的关系.22.【分析】(1)根据等式的性质,把左面的2个砝码同右面的2个砝码抵消,剩下的一个足球就是和几个砝码同样重.(2)根据等式的性质,把两边都除以3即可求解;(3)根据等式的性质,把两边都乘2即可求解;(4)根据等式的性质,把两边都加上1个玻璃杯即可求解;(5)根据等式的性质,把两边都减去20g即可求解.【解答】解:如图所示:【点评】本题主要考查了学生对代换的思想来解答问题的能力.23.【分析】等式的性质是指在等式的两边同时加上、减去同一个数,或同时乘或除以同一个不为0的数,等式的左右两边仍相等;据此可知这个同学在第6步做错了,因为a=b,所以b﹣a=0,而(6)是两边同时除以(b﹣a)不符合等式的性质,所以错误.【解答】解:第(6)步出错,因为a=b,所以b﹣a=0;根据等式的性质,等式的两边同时除以不为0的数,等式才能成立,而这里b﹣a,所以等式不成立了.所以在第(6)步出错.【点评】本题给出的步骤较多,具有迷惑性,关键是熟知等式的性质,除以的数不能为0.。
五年级上册数学教案-5简易方程《解方程(例1)》 人教新课标

五年级上册数学教案-5简易方程《解方程(例1)》人教新课标一、教学目标1. 让学生掌握解方程的基本方法,能够解一些简单的方程。
2. 培养学生的逻辑思维能力和解决问题的能力。
3. 培养学生对方程的兴趣,激发学生的学习积极性。
二、教学内容本节课主要学习解方程的方法,通过例题和练习,让学生掌握解方程的步骤和技巧。
三、教学重点和难点重点:解方程的基本方法。
难点:理解方程的解的概念,熟练掌握解方程的步骤。
四、教学过程1. 导入新课通过复习等式的性质,引导学生进入解方程的学习。
2. 讲解新课(1)通过例题,讲解解方程的步骤和技巧。
例题:解方程3x 7 = 16。
步骤一:将方程的两边同时减去7,得到3x = 9。
步骤二:将方程的两边同时除以3,得到x = 3。
(2)通过练习,巩固解方程的方法。
练习1:解方程4x 5 = 23。
练习2:解方程5x - 8 = 12。
3. 课堂小结通过本节课的学习,学生应掌握解方程的基本方法,能够解一些简单的方程。
4. 布置作业课后作业:解方程2x 6 = 16。
五、课后反思本节课通过例题和练习,让学生掌握了解方程的基本方法,但是在教学过程中,发现部分学生对解方程的步骤掌握不够熟练,需要在今后的教学中加强练习。
同时,要注意培养学生的逻辑思维能力和解决问题的能力,激发学生的学习积极性。
重点关注的细节是“讲解新课”部分中的“通过例题,讲解解方程的步骤和技巧”。
这是本节课的核心内容,直接关系到学生是否能够掌握解方程的方法。
对于这个重点细节的详细补充和说明:解方程是数学中一个基本而重要的技能,它要求学生能够理解和运用等式的性质,通过一系列的操作,找到未知数的值。
在五年级上册数学教学中,解方程的内容通常以简易方程的形式出现,如“3x 7 = 16”。
为了帮助学生掌握解方程的方法,教师需要通过例题详细讲解解方程的步骤和技巧。
首先,教师需要明确解方程的目标是找到使等式成立的未知数的值。
在例题“3x 7 = 16”中,我们的目标是找到x的值。
人教版五年级数学上册期末复习:《简易方程》(一)

人教版五年级数学上册期末复习:《简易方程》(一)一、单选题1.下面各式中,()是方程。
A. 3x+4.5B. 2x+7xC. 0.3x+5=8D. 12-7.5=4.52.当a=3.5时,a2=()。
A. 7B. 12.25C. 122.53.下列方程中,与方程2x-40=50的解不同的是()。
A. 2x-40+40=50+40B. 4x-80=100C. 2x=50+40D. 2x-30=404.冬冬有a个乐羊羊挂件,比小红多b个,小红有()个乐羊羊挂件。
A. a+bB. a-bC. b-a5.与方程8x+0.2x=10的结果相同的是()。
A. 8.2x=10B. 10x=10C. 8x=9.8D. 7.8x=106.水果店一天一共卖出130千克水果,上午卖出a千克,下午卖出的千克数比上午的2倍多3千克,下面列式正确的是()。
A. 2a+3=130B. 2a-3=130C. 2a-3+a=130D. 2a+3+a=1307.妈妈花380元买了一套衣服,已知上衣的价钱比裤子多80元。
关于本题等量关系描述不正确的是()。
A. 裤子的价钱+80元=上衣的价钱B. 上衣的价钱+裤子的价钱=380元C. 裤子的价钱+80元=380元D. 裤子的价钱+裤子的价钱+80元=380元二、判断题8.a的8倍与5的差,列式为8a-5。
()9.4x+8是方程。
()10.x=4是方程2x+0.4=9.6的解。
()三、填空题11.饮料店里,一杯咖啡a元,一杯果汁比一杯咖啡贵8元,一杯果汁________元。
12.一辆汽车的速度是60千米/时,汽车行驶了t时,这辆汽车行驶的路程是________千米。
13.一辆公交车上原来有18人,到站后有a人下车,又有b人上车,现在公交车上有________人。
14.老师比小明大20岁,如果用a表示小明的年龄,那么老师的年龄就是(a+20)岁,a+20即表示________,又表示________。
简易方程知识点梳理

简易方程知识点梳理简易方程知识点梳理首先,在含有字母的式子里,字母中间的乘号可以记作“·”,也可以省略不写。
加号、减号、除号以及数与数之间的乘号不能省略。
例如,a×a可以写作a·a(或a2),a2读作a 的平方,表示两个a相乘。
2a表示a+a,即数字和字母相乘,省略乘号时要把数字写在前面。
比如b×4写作4b。
其次,我们可以用字母表示运算律。
例如,加法交换律:a+b=b+a,加法结合律:(a+b)+c=a+(b+c),乘法交换律:a×b=b×a,乘法结合律:(a×b)×c=a×(b×c),乘法分配律:(a+b)×c=a×c+b×c。
我们还可以用字母表示正方形、长方形的面积和周长。
例如,正方形的边长为x厘米,4x表示正方形的周长,x2表示正方形的面积。
解方程需要我们掌握一些基本的知识。
方程是含有未知数的等式,方程的解是使方程左右两边相等的未知数的值。
解方程的过程叫做解方程,解方程原理是等式的性质。
等式左右两边同时加、减、乘、除相同的数(除外),等式依然成立。
方程两边同时加、减、乘、除一个不等于的数,左右两边仍然相等。
在解方程时,我们需要注意等号要对齐,两边乘除相同数的时候,这个数不要为0.最后,我们来做一些练。
假设排球队共有队员a人,女队员有7人,男队员有a-7人。
如果1千克大米的价钱是1.50元,买x千克大米应付1.50x元。
省略乘号,3×a表示3a,9×x表示9x,a×4表示4a,y×5表示5y,a×XXX表示3ax。
如果服装店的阿姨们加工了50件衣服,每件衣服用布bm,当b=1.38时,用布的总数是50bm。
如果一辆9路公共汽车上原有22名乘客,在新华大街站下去a人,又上去b人。
现在车上有22-a+b名乘客。
如果比m的3倍多9的数是3m+9,比n除以5的商少7的数是n/5-7,那么当a=2,b=5时,8a-2b=14.如果正方形的边长为x厘米,4x表示正方形的周长,x2表示正方形的面积。
五年级数学上册-简易方程-1.用字母表示数说课讲解

2只青蛙2张嘴,2×42 只眼睛 4×82 条腿;
3只青蛙3张嘴,2×63 只眼睛 41×23 条腿;
你…能… 用一句话表示这首儿歌吗?
( n)只青蛙(n )张嘴,( 2n )只眼睛 ( 4n )条腿。
n只青蛙 张嘴 ……
小结
说一说这节课,我们学了哪些知识?
用字母表示数量关系 在计算时,只要给出式子中每个字 母表示的数是多少,就可以算出这 个式子表示的数量是多少。 比如:当 a = 11时,
的 c 表示什么? (3)在一场篮球比赛中,小桃接连投中 x 个 3年 龄比他的3倍大 1岁,则他爸爸的年龄 是 3c+1 岁。
你能不能估算一下小明大概有多少 岁啊?
A.5岁
B.12岁
C.50岁
儿歌:
只数× 2
只数× 4
1只青蛙1张嘴,2×21 只眼睛 4×41 条腿;
3a
手
1只手有5个手指; 2只手有10个手指; n只手有( 5n )个手 指。
填空
(1)我国青少年(7~17岁)在1980年平均身高 x 厘米,到2000年平均身高增长6cm,2000年我 国青少年平均身高____x_+___6厘米。
(2)人的身高可能会相差2cm,在早上最高,晚上 最矮。一个人早上身高 b 厘米,晚上身高可 能是____b__-_2_厘米。
(3)鸟的骨骼约是体重的0.05~0.06倍,人的骨骼 约是体重的0.18倍,一个人重 a 千克,骨骼 约是____0_._1_8_a千克。
(4)小英家本月的用电量是80千瓦时,交电费 c
元,那么电费每千瓦时是___c_÷__8_0_元。
说一说。 (1)一天早晨的温度是 b 摄氏度,中午比早晨高
8 摄氏度。b + 8 表示什么? (2)某班共有50名学生,女生有50 – c 名,这里
小学简易方程的解法(1)
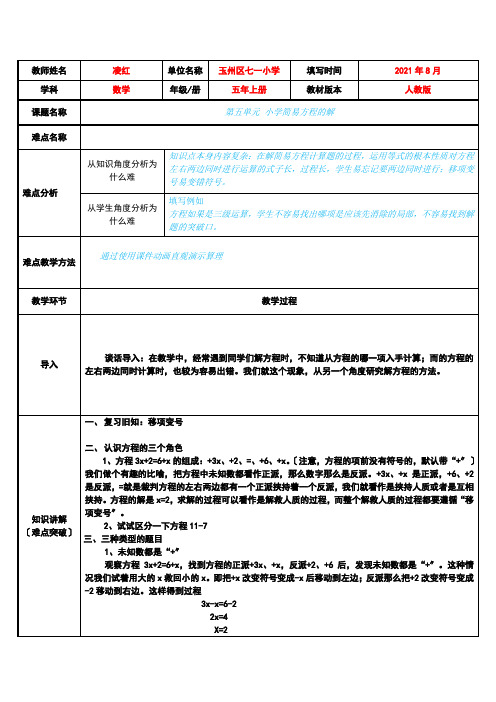
6=x
x=6
可以总结得到:未知数都是“—〞,用小的救回大的。
我们同样的也练一练
3、未知数有“+〞有“-〞
分析方程2x-2=8-3x的正派是:+2x、-3x,反派是-2、+8。这种情况我们用加的救回减的。也就是减的未知数-3x要变号成+3x后移动到左边,方程整理成
2x+3x=8+2
5x=10
从学生角度分析为什么难
填写例如
方程如果是三级运算,学生不容易找出哪项是应该先消除的局部,不容易找到解题的突破口。
难点教学方法
通过使用课件动画直观演示算理
教学环节
教学过程
导入
谈话导入:在教学中,经常遇到同学们解方程时,不知道从方程的哪一项入手计算;而的方程的左右两边同时计算时,也较为容易出错。我们就这个现象,从另一个角度研究解方程的方法。
知识讲解
〔难点突破〕
一、复习旧知:移项变号
二、认识方程的三个角色
1、方程3x+2=6+x的组成:+3x、+2、=、+6、+x。〔注意,方程的项前没有符号的,默认带“+〞〕我们做个有趣的比喻,把方程中未知数都看作正派,那么数字那么是反派。+3x、+x 是正派,+6、+2是反派,=就是裁判方程的左右两边都有一个正派挟持着一个反派,我们就看作是挟持人质或者是互相挟持。方程的解是x=2,求解的过程可以看作是解救人质的过程,而整个解救人质的过程都要遵循“移项变号〞。
x=10÷5
x=2
未知数解救成功,我们总结出:未知数有“+〞有“-〞,用加的救回减的
同样的,我们也做一道这种类型的练习:x+6=9-2x
人教版五年级数学上册-简易方程-1

你能不能估算一下小明大概有多少 岁啊?
A.5岁
B.12岁
C.50岁
知识应用
(1)我国青少年(7~17岁)在1980年平均身高 x 厘米,到2000年平均身高增长6cm,2000年我 国青少年平均身高____x_+___6厘米。
(2)人的身高可能会相差2cm,在早上最高,晚上 最矮。一个人早上身高 b 厘米,晚上身高可 能是____b__-_2_厘米。
也就是说在一个实际问题中,字母的取值范围是由 实际情况决定的。
a 表示小红 的年龄。
爸爸:a + 30
想一想:当小红和我们多数同学一样大,也是 11岁时,她爸爸的年龄是多少?
当 a = 11时,
a + 30 = ___1_1_+_3=0____4_1_(岁)
(1969年7月21日)人类首次登上月球。 尼尔·阿姆斯特朗成为第一个登上月球的美国航天员。
A=X+Y+Z
成 努 正少 力 确说
功
工 作
方空 法话
小结
说一说这节课,我们学了哪些知识?
用字母表示数量关系 在计算时,只要给出式子中每个字 母表示的数是多少,就可以算出这 个式子表示的数量是多少。 比如:当 a = 11时,
a + 30 = ____1_1_+=30____4_1_(岁)
课下小调查:
成年男子的标准体重通常用下面的 式子表示:
标准体重=身高-105
身高用厘米数, 体重用千克数。
1、用含有字母的式子表示出成年男子的标准体重。 2、算出你爸爸的标准体重应是多少?
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好!谢谢
呢?
小红的年龄+30岁 = 爸爸的年龄
人教版五年级上册《简易方程-解方程(1)》数学教案

人教版五年级上册《简易方程-解方程(1)》数学教案教学内容:教材P67~68例1、例2、例3及练习十五第1、2、7题。
教学目标:知识与技能:使学生初步理解“方程的解”与“解方程”的含义以及“方程的解”和“解方程”之间的联系和区别。
过程与方法:利用等式的性质解简易方程。
情感、态度与价值观:关注由具体到一般的抽象概括过程,培养学生的代数思想。
教学重点:理解“方程的解”和“解方程”之间的联系和区别。
教学难点:理解形如a±x =b的方程原理,掌握正确的解方程格式及检验方法。
教学方法:创设情境;观察、猜想、验证.教学准备:多媒体。
教学过程一、情境导入谈话:同学们,咱们玩一个猜一猜的游戏好吗?出示一个盒子,让学生猜一猜里面可能有几个球呢?(学生思考后会说,可以是任意数。
)教师继续通过多媒体补充条件,并出示教材第67页例1情境图。
问:从图上你知道了哪些信息?引导学生看图回答:盒子里的球和外面的3个球,一共是9个。
并用等式表示:x +3=9(教师板书)二、互动新授1.先让学生回忆等式的性质,再思考用等式的性质来求出x 的值。
学生思考、交流,并尝试说一说自己的想法。
2.教师通过天平帮助学生理解。
出示教材第67页第一个天平图,让学生观察并说一说。
长方体盒子代表未知的x 个球,每个小正方体代表一个球。
则天平左边是x +3个球,右边是9个球,天平平衡,也就是列式:x +3=9。
观察:把左边拿掉3个球,要使天平仍然保持平衡要怎么办?(右边也要拿掉3个球。
)追问:怎样用算式表示?学生交流,汇报:x +3-3=9-3x =6质疑:为什么两边都要减3呢?你是根据什么来求的?(根据等式的性质:等式的两边减去同一个数,左右两边仍然相等。
)你们的想法对吗?出示第3个天平图,证实学生的想法是对的。
3.师小结:刚才我们计算出的x =6,这就是使方程左右两边相等的未知数的值,叫做方程的解。
也就是说,x =6就是方程x +3=9的解。
【人教教材】简易方程实用课件1

2、3筐苹果和5筐梨共重55千克,每筐苹果10千克, 每筐梨多少千克?
3、一个等腰三角形周长是86厘米,底是38厘米, 腰是多少厘米?
4、小王、叔叔在400米长的环形跑道上同时同地反
向出发练习跑步,小王每秒跑4米,叔叔每秒跑6米。
几秒钟两人首次相遇?
一个等腰三角形周长是86厘米,底是 38厘米,腰是多少厘米?
•
4.每一座村落都有其自己的文化特色 ,不仅 表现在 当地村 民的衣 饰、建 筑和饮 食上, 还体现 了当地 特色的 节目和 生活习 惯等方 面的内 容。
•
5.正是这些文化代表着传统村落的特 色,所 以吸引 了各地 游客前 来体验 并参与 进来, 在传统 村落中 按照他 们的习 俗和饮 食习惯 体验不 一样的 生活
西安站和武汉站相距1429千米,一列慢车从西安 开出,每小时行58千米,一列快车从武汉开出, 每小时行82千米,两车相向而行,慢车先开0.5 小时,快车行几小时后两车相遇?
西安(慢车) 慢车先行路程
相遇
慢车后行路程
(快车)武汉 快后行路程)+快车路程=总路程
(5 8 0.55x8 )8x2 1429
•
2.这些材料从不同的角度呈现事物或 者主题 ,单独 看是完 整的, 合在一 起又能 够综合 地表达 意义, 它们之 间的顺 序并不 固定, 打乱了 原来的 顺序, 仍然可 以表达 原来的 意义。 所以称 之为非 连续性 文本。 具有直 观、简 明、概 括性强 、易于 比较等 特点。
•
3.材料一揭示了垃圾分类的必要性和 紧迫性 ,并对 民众的 认知与 实践情 况作了 统计; 材料二 分析了 垃圾分 类难以 有效推 进的原 因并提 出破解 之道。
一年级
人教版数学五年级上册第5单元《简易方程 1.用字母表示数 第5课时》教学设计

人教版数学五年级上册第5单元《简易方程 1.用字母表示数第5课时》教学设计一. 教材分析简易方程是小学数学中的一项重要内容,它让学生初步接触代数思想,理解等式的性质,培养学生的逻辑思维能力。
本课时主要让学生学会用字母表示数,体会代数表达式的意义,为后续学习方程打下基础。
二. 学情分析五年级的学生已经具备了一定的逻辑思维能力和抽象思维能力,他们对数学产生了一定的兴趣。
但在学习过程中,部分学生可能对用字母表示数感到困惑,难以理解其意义和作用。
因此,在教学过程中,教师需要关注学生的个体差异,引导学生逐步理解代数表达式的概念。
三. 教学目标1.让学生掌握用字母表示数的方法,能正确书写字母表达式。
2.让学生理解等式的性质,能运用字母表达式进行简单的计算和解决问题。
3.培养学生的逻辑思维能力和抽象思维能力。
四. 教学重难点1.重点:用字母表示数的方法和等式的性质。
2.难点:理解代数表达式的意义和应用。
五. 教学方法1.情境教学法:通过生活情境,让学生体会用字母表示数的必要性。
2.游戏教学法:设计趣味游戏,让学生在游戏中理解和掌握字母表达式。
3.小组合作学习:让学生在小组内讨论和探究,培养学生的合作能力和解决问题的能力。
六. 教学准备1.课件:制作课件,展示字母表达式的应用场景。
2.学具:为学生准备练习题和游戏素材。
3.教室环境:布置教室,营造轻松愉快的学习氛围。
七. 教学过程1.导入(5分钟)利用课件展示生活情境,如购物场景,让学生观察并用字母表示价格。
引导学生发现用字母表示数的方便性,激发学生的学习兴趣。
2.呈现(10分钟)讲解用字母表示数的方法,如用x表示未知数,用a、b表示已知数。
举例说明,让学生理解字母表达式的意义。
3.操练(10分钟)设计练习题,让学生运用字母表达式进行计算。
如:已知a=5,求x+a的值。
让学生独立完成练习题,教师巡回指导。
4.巩固(10分钟)开展小组合作游戏,让学生在游戏中运用字母表达式解决问题。
简易方程知识点总结

简易方程知识点总结一、方程的基本概念1. 方程的定义方程是一个数学式子,含有一个或多个未知数,并且方程中包含等号。
方程的一般形式为:a₁x + a₂y + ... + aₙz = b,其中a₁、a₂、...、aₙ和b为已知数,x、y、...、z为未知数。
2. 方程的分类根据未知数的次数和方程的类型,方程可以分为一元一次方程、一元二次方程、二元一次方程、线性方程组、非线性方程等。
不同类型的方程有不同的解法和应用。
3. 方程的解解方程即求出使方程成立的未知数的值。
解方程的方法可以包括代入法、加减消去法、公式法、配方法等。
根据方程的类型和特点选择不同的解法。
二、一元一次方程1. 一元一次方程的定义一元一次方程是指只含有一个未知数,并且未知数的指数为1的方程。
一元一次方程的一般形式为:ax + b = c,其中a、b、c为已知数,x为未知数。
2. 一元一次方程的解法解一元一次方程的方法可以包括逆运算法、加减消去法、代入法等。
通过这些方法可以求出一元一次方程的唯一解。
3. 一元一次方程的应用一元一次方程在实际生活中有着广泛的应用,比如物品的价格与数量之间的关系、人员的工资与工作时间之间的关系等,都可以用一元一次方程来描述和解决。
三、一元二次方程1. 一元二次方程的定义一元二次方程是指只含有一个未知数,并且未知数的指数为2的方程。
一元二次方程的一般形式为:ax² + bx + c = 0,其中a、b、c为已知数,x为未知数。
2. 一元二次方程的解法解一元二次方程的方法可以包括公式法、配方法、完全平方式等。
根据一元二次方程的系数和特点选择不同的解法,可以求出一元二次方程的实数根或复数根。
3. 一元二次方程的应用一元二次方程在实际生活中也有着广泛的应用,比如物体的抛体运动、图形的面积和周长之间的关系等,都可以用一元二次方程来描述和解决。
四、二元一次方程1. 二元一次方程的定义二元一次方程是指含有两个未知数的一次方程,一般形式为:ax + by = c,dx + ey = f。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.7+8=10.7 3.5x-8=27+x 5x+12=40 X+5=78 4×2.5+5x=60
等式
方程
方程与等式的关系可以 用图来表示:
等式 方程
对的在( )里画“
”,错的在( )里画“
(1)3+16=19是等式,但不是方程。( ) (2)只要含有未知数的式子,都是方程。 ( ) (3)7x+7是方程。 ( ) (4)方程都是等式,等式也都是方程。 (
举出3个方程的例子。
等式 方程
(8)
是什么意思?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
等式 方程
是个式子是 不是方程?
方程必须具备哪两 个条件?
通常把要求的数,叫( 一般 用字母x表示。
x+1.2=2.4是方程吗?x=( )时, 等号左边和右边相等。
x+5是方程吗?它叫什么? 举出一个方程的例子。
20元 30元 5元
45元
例2:看图列出等式。
(1)
3.2平方厘米
x平方厘米
5.6平方厘米
(2)
X克 X克 X克 X克
共重500克
按要求把下面各式填入集合圈内。
2.7+8=10.7 3+7x 4×2.5+5x=60 3.5x-8=27+x 5x>8 X+5=78 b+90 5x+12=40 8x-9
看图列方程
(1) (2)
X克
4100克 (3) 500米
3500克
X元
X元 120元
X元
X米
(4) X米
X米
500米
900米
1000米
(1)什么叫做方程? (2)方程必须具备哪两个条件? (3)通常把要求的数,叫( ),一般 用 字母x表示。 (4)举出3个方程的例子。 (5)x+5是方程吗?它叫什么?举出一个方程的 例子。 (6)x+1.2=2.4是方程吗?x=( )时,等号左 边和右边相等。 (7)怎样判断一个式子是不是方程?
