高数课件chapter03微分中值定理与导数的应用
高等数学第三章中值定理与导数的应用
1 0. 当 x 0 时 0 , 因此由上式得 cos
0? 问是否可由此得出 lim cos 1 x
x0
不能 !
因为 ( x) 是依赖于 x 的一个特殊的函数.
x 0 表示 x 从右侧以任意方式趋于 0 .
备用题 1. 设 f ( x) 在 [0,1] 连续, (0 ,1) 可导,且 f (1) 0 ,
f ( x0 ) 0, 即方程有小于 1 的正根
2) 唯一性 .
f ( x) 在以 x0 , x1 为端点的区间满足罗尔定理条件 , 在 x0 , x1 之间
至少存在一点
假设另有
但
矛盾, 故假设不真!
二、拉格朗日中值定理
满足: (1) 在区间 [ a , b ] 上连续
y
y f ( x)
使
f ( x) sin ln x ,
F ( x) ln x
则 f (x) , F(x) 在 [ 1 , e ] 上满足柯西中值定理条件, f (e) f (1) f ( ) , (1, e ) 因此 F (e) F (1) F ( ) 1 cos ln 即
1
分析:
例5. 试证至少存在一点 法2 令 f ( x) sin ln x sin1 ln x
使
则 f (x) 在 [ 1 , e ] 上满足罗尔中值定理条件, 因此存在 使
1 1 f ( x) cos ln x sin1 x x
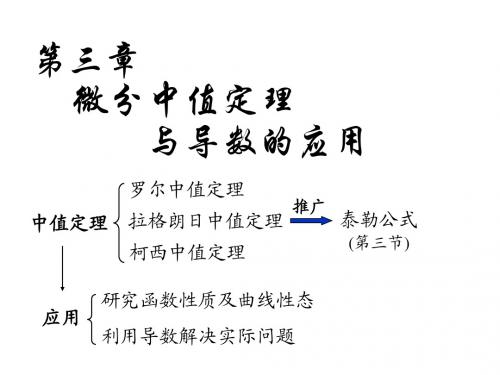
内容小结
1. 微分中值定理的条件、结论及关系
3 15 4 . _____
方程
有 3 个根 , 它们分别在区间 (1, 2) , (2 , 3) , (3 , 4) 上.
高等数学 第3章 第一节 中值定理

(函数
即
6
,
y
5
6
ln sin x
是 y
是初等函数, 且当
x
6
ln sin x 定义域内的一部分;
,
5
6
时,cossixn
y'
sin x
x
0,
cot x.)
且ln s in
lnsin 5
ln 1 .
6
62
令 y' cos x cot x 0, sin x
得 x , 5 .
F(b) F(a)
( x) 满足罗尔定理的全部条件,且:
'(x) f '(x) f (b) f (a) F '(x)
F(b) F(a)
Y F , f Fb, f b
C•
•B
由罗尔定理,至少存在一点 ∈(a,b) ,
即:
使
f
'( )
'( ) 0,
f (b) f (a) F '( ) 0
即 1、 2、 3都是方程 f 'x 0 的根。 注意到 f ' x 0 为三次方程, 它最多有三个根。
我们已经找到它的三个实根
1、 2、 3 ,
所以这三个根就是方程
f 'x 0 的全部根。
14
例3 证明当x 0时, x ln1 x x
1 x
证 设f x ln1 x, 显然,函数 f x 在 0, x 上满足
f (b) f (a)
O a
bx
结论等价于: f f b f a
ba
或: f f b f a 0
ba
AB的方程为:
第三章中值定理与导数的应用课件
f (b) f (a) f ' ( ) 成立 F (b) F (a) F ' ( )
例1:验证罗尔定理对函数y ln sin x在区间
[
6
,
5
6
]的正确性
解:y ln sin x在[ , 5 ]上连续
66
y ln sin x在( , 5 )上可导
66
lim 2 cos3x 3 1 x0 3 cos2x 2
例6:求
lim
x
xn ex
(n 0, 0)
解:lim xn lim n xn1 lim n (n 1) xn2
e e x x x
x x
2 ex
lim n! 0
x n ex
例7:求 lim x sin x
且f ( ) ln 1 f (5 )
6
2
6
又
y'
c os x
ctgx
令
0
x
(
, 5 )sin x源自2 662罗尔定理正确
例2:证明arctgx arcctgx
2
证 : (arctgx arcctgx)' 1 1 0 1 x2 1 x2
arctgx arcctgx c
取x 1 c c
若f (x)是一般的函数,且它存在直到n 1 阶的导数,那么
n
f (x)
f (k) (a) (xa)k ?
k 0 k!
泰勒(Taylor)中值定理
泰勒(Taylor)中值定理 如果函数 f ( x)在含有 x0 的某个开区间(a, b)内具有直到(n 1)阶的导数,则
当 x在(a, b)内时, f ( x)可以表示为( x x0 )的一个
大一高数上_1完整_第三章ppt课件

在[1,3]上连,续 在 (1,3)内可导 , 且 f( 1 ) f(3 ) 0 ,
f(x ) 2 (x 1 )取 , 精 选1 课,件(1 ( 1 ,3 ))f()0. 2Biblioteka 几何解释:yC
yf(x)
若连续曲线弧的两个
端点的纵坐标相等,
且除去两个端点外处 o a 处有不垂直于横轴的
f(x2)f(x1)。 因此 f(x)在区间I上是一个常数。
精选课件
10
例 2 . 证 明 当 x > 0 时 , x l 1 x ) n x 。 ( 1 x
证明:设f(x)ln(1x),显然f(x)在区间[0, x]上满足
拉格朗日中值定理的条件,根据定理,就有
f(x)f(0)f ()(x0),0<<x。
在闭区间[a, b]上连续,在开区间(a, b)内可导,且F ' ( x)
在(a, b)内每一点处均不为零,那么在(a, b)内至少
有一点(a b),使等式
f F
(a) (a)
f (b) F (b)
f F
' ()成立. ' ()
Cauchy定理又称为广义微分中值定理
精选课件
12
结构图
特例
推广
lim xn 0.
n x 0
精选课件
21
2. 型
步骤: 11 0 0 . 0 0 00
例8 求lim ( 1 1). x0 sinx x
()
解 原式 lim xsin xlim1coxs x 0 xsin x x 0sin xxcoxs
lim sinx
0.
x0 2cosxxsinx
高等数学 微分中值定理与导数的应用

注意 : 与罗尔定理相比条件中去掉了 f (a) f (b). 结论亦可写成 f (b) f (a) f (). ba
f (b) f (a) f ( )
ba
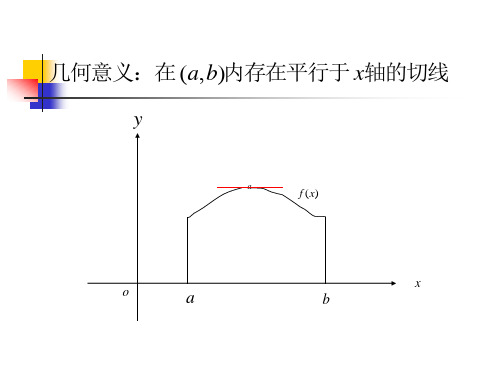
y 几何解释:
在曲线弧 AB 上至少有
一点 C ,在该点处的切
A
C
y f (x)
有一点(a b),使等式
f (a) F (a)
f (b) F (b)
f F
' () 成立. ' ()
Cauchy定理又称为广义微分中值定理
结构图
特例
推广
Rolle定理
Lagrange定理
Cauchy定理
拉格朗日中值定理又称微分中值定理.
第二节 洛必达法则
一、0 型及 型未定式解法: 洛必达法则 0
且除去两个端点外处 o a 处有不垂直于横轴的
1
2 b x
切线,在曲线弧AB上至少有一点C ,在该点处的
切线是水平的.
注① Rolle定理有三个条件:闭区间连续;开区间可导
区间端点处的函数值相等; 这三个条件只是充分条件,而非必要条件
如:y=x2在[-1,2]上满足(1),(2),不满足(3) 却在(-1,2)内有一点 x=0 使
第三章 微分中值定理与导数的应用
§3. 1 微分中值定理
一、罗尔(Rolle)定理
定理(Rolle) 若函数f ( x ) 满足 (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 (3)在区间端点处的函数值相等f(a)=f(b)
则在(a,b)内至少存在一点 , (a,b)使得函数 f ( x)在该点的导数为零,即 f ( ) 0
第三章 微分中值定理与导数的应用

第三章 微分中值定理与导数的应用§1 微 分 中 值 定 理一、 罗尔定理1. 费马定理:设f (x )在U (x 0)内有定义,且在x 0处可导,若∀x 0∈U (x 0),有f (x )≤f (x 0)[或f (x )≥f (x 0)], 则 f ′(x 0)=0.证明:不妨设x ∈U (x 0)时,有f (x )≤f (x 0).则对x 0+∆x ∈U (x 0),有f (x 0+∆x )≤f (x 0)即 当∆x >0时,xx f x x f ∆-∆+)()(00≤0; 当∆x <0时,xx f x x f ∆-∆+)()(00≥0;从而:f ′(x 0)= f ′+(x 0)=+→∆0limx xx f x x f ∆-∆+)()(00≤0;f ′(x 0)= f ′-(x 0)=+-→∆0limx xx f x x f ∆-∆+)()(00≥0;于是 f ′(x 0)= 0定义:称满足f ′(x )=0的点为驻点(或稳定点,或临界点). 2. 罗尔定理:如果函数y =f (x )满足:1) f (x )∈C [a ,b ] 2) f (x )∈D(a ,b ) 3) f (a )=f (b )那么在(a ,b )内至少存在一点ξ (a <ξ<b ),使得: f ′(ξ)=0.证明:因为f (x )∈C [a ,b ],所以f (x )在[a ,b ]内存在最大值M 和最小值m . 以下分两种情形讨论: 1) M =m .此时f (x )在[a ,b ]上必然取得相同的值f (x )=M .此时有f ′(x )=0,即 对∀ξ∈(a ,b ),有f ′(ξ)=0. 2) M >m .由于f (a )=f (b ),所以M 和m 中至少有一个不等于f (x )在[a ,b ]上的函数值.不妨设:M ≠f (a ).则在(a ,b )内必有ξ使得f (ξ)=M . 即∀x ∈[a ,b],有f (x )≤f (ξ). 有费马定理得: f ′(ξ)=0.例1. 验证罗尔定理对函数y =lnsin x 在区间[π/6,5π/6]上的正确性.证明:显然函数在区间[π/6,5π/6]上连续,在(π/6,5π/6)上可导,且有:y (π/6)=y (5π/6)=ln1/2.令y ′=cot x =0,则有:x =π/2,因此存在ξ=π/2∈(π/6,5π/6),使得y ′(ξ)=0.例2. 不求函数f (x )=(x -1)(x -2)(x -3)(x -4)的导数,说明方程f ′(x )=0的根的个数,并指出根所在的区间.解:由于f (1)=f (2)=0,且f (x )在[1,2]上连续,可导,且当x ∈(1,2)时f (x )≠0从而存在点ξ1∈[1,2]使得f ′(ξ1)=0;同理存在ξ2∈[2,3],ξ3∈[3,4]使得f ′(ξ2)= f ′(ξ3)=0.例3. 证明无论C 为何实数值,方程x 3-3x +C =0在[0,1]上至多有一个实数根.证明:(反证法)假设方程x 3-3x +C =0在[0,1]上有两个实数根ξ1,ξ2,且ξ1<ξ2.则f (x )= x 3-3x +C 在[0,1]上连续,可导且f (ξ1)=f (ξ2)=0,于是 f (x )在[ξ1,ξ2]上满足罗尔定理的条件, 从而存在ξ∈(ξ1,ξ2)⊂(0,1)使得f ′(ξ)=0.但f ′(x )=3(x -1)(x +1)=0只有两个根-1和1,且此两个根显然不在(ξ1,ξ2)⊂(0,1)内,矛盾.所以原命题正确. 二、 拉格朗日中值定理 拉格朗日定理: 如果函数y =f (x )1) f (x )∈C [a ,b ] 2) f (x )∈D(a ,b )那么在(a ,b )内至少存在一点ξ (a <ξ<b ),成立等式:f (b )-f (a )=f ′(ξ)(b -a )此公式称为拉格朗日中值公式.此公式称为拉格朗日中值公式. 定理的几何解释:ab a f b f --)()(为弦AB 的斜率.f ′(ξ)为曲线点C 处的斜率.几何意义:如果曲线y =f (x )在弧AB 上除端点外处处具有不垂直于x 轴的切线,那么在这弧上至少存在一点C ,使曲线在C 点处的切线平行于弦AB . 辅助函数的建立:有向线段NM 的值是x 的函数,记为φ(x ),则显然有φ(a )=φ(b )=0. 由于直线AB 的方程为:L (x )=f (a )+ab a f b f --)()((x -a )又点N 、M 的纵坐标分别为L (x )、f (x ),因此有向线段NM 的值的函数为:φ(x )=f (x )-L (x )=f (x )-f (a )-ab a f b f --)()((x -a )此函数满足罗尔定理的全部条件.证明:作辅助函数: φ(x )=f (x )-L (x )=f (x )-f (a )-ab a f b f --)()((x -a )则该函数在[a ,b ]内满足罗尔定理的条件,从而在(a ,b )内存在一点ξ,使得φ′(ξ)=0. 又φ′(x )=f ′(x ) -ab a f b f --)()(所以:f ′(ξ)=ab a f b f --)()(.注:拉格朗日公式对a >b 也成立. 拉格朗日公式的其它形式:当x ,x +Δx ∈[a ,b ]时,则在区间[x ,x +Δx ](x >0)或区间[x +Δx ,x ](Δx <0)上有:f (x +Δx )-f (x )=f ′(x +θΔx )·Δx (0<θ<1).或 Δy = f ′(x +θΔx )·Δx (0<θ<1).此公式表明当Δx 有限时,Δy 有精确值,定理也称为有限增量定理.定理: 如果函数f (x )在区间I 上的导数恒为零,那么f (x )在区间I 上时一个常数.证明:在区间I 上任取x 1,x 2 (x 1<x 2),则有:f (x 2)-f (x 1)=f ′(ξ)( x 2-x 1) (x 1<ξ<x 2)由假定:f ′(ξ)=0,所以: f (x 2)-f (x 1)=0.即: f (x 2)=f (x 1).例4. 证明等式:arcsin x +arccos x =π/2.证明:设f (x )= arcsin x +arccos x ,则f ′(x )=0,从而f (x )=C =f (0)=π/2.例5. 验证拉格朗日定理对函数y =4x 3-5x 2+x -2在区间[0,1]上的正确性.证明:函数在[0,1]上显然连续可导.令y ′=12x 2-10x +1=0,得:x =12135-∈(0,1).例6. 证明:当x >0时,xx +1<ln(1+x )<x .证明:设f (x )=ln(1+x ),则f (x )在[0,x ]上满足拉格朗日中值定理的条件,于是有: f (x )-f (0)=f ′(ξ)(x -0), (0<ξ<x ). 由于f (0)=0,f ′(x )=x+11, 所以上式为:ln(1+x )=ξ+1x又 0<ξ<x ,所以: xx +1<ξ+1x<x .即:xx +1<ln(1+x )<x .例7.设a >b >0,证明:ab a -< ba ln <bb a -.证明:设f (x )=ln x ,则f (x )在[b ,a ]上满足拉格朗日定理的条件,从而 ∃ξ∈(b ,a ) 使得:ba b a --ln ln =ξ1,由于a1<ξ1<b1,所以结论成立.三、 柯西中值定理:柯西中值定理:如果函数f (x )和F (x )满足 1) f (x ),F (x )∈[a ,b ]2) f (x ),F (x )∈(a ,b ),且F ′(x )≠0,∀x ∈(a ,b )则在(a ,b )内至少存在一点ξ,成立等式:)()()()(a F b F a f b f --=)()(ξξF f ''.分析:在参数方程:⎩⎨⎧==)()(x f Y x F X (a ≤x ≤b )表示的曲线上,弦AB 的斜率为:)()()()(a F b F a f b f --.曲线上点(X ,Y )处的切线的斜率为: dXdY =)()(x F x f ''.当x =ξ时,则点C 处的切线平行于弦AB . 证明:因为F (b )-F (a )=F ′(η)(b -a ) (a <η<b ), 由假设:F ′(η)≠0,所以F (b )-F (a )≠0. 所以AB 的方程为:Y -f (a )=)()()()(a F b F a f b f --[F (x )-F (a )].于是:N 点的纵坐标为:Y =f (a )+)()()()(a F b F a f b f --[F (x )-F (a )],M 的纵坐标为f (x ).于是:NM 的方程为:φ(x )=f (x )-f (a )-)()()()(a F b F a f b f --[F (x )-F (a )]此函数满足罗尔定理的条件,即:存在ξ∈(a ,b ),使得:f ′(ξ)-)()()()(a F b F a f b f --F ′(ξ)=0.即:)()()()(a F b F a f b f --=)()(ξξF f ''.当F (x )=x 时,即为拉格朗日中值定理.例8. 设函数y =f (x )在x =0的某邻域内具有n 阶导数,且f (0)=f ′(0)=…=f(n -1)(0)=0.证明:nxx f )(=!)()(n x fn θ(0<θ<1)证明:设F (x )=x n ,则f (x )和F (x )在[0,x ](或[x ,0])上满足柯西中值定理.即: ∃θ1∈(0,x ),使得nxx f )(=)0()(--nx f x f =111)(-'n n f θθ.在[0,θ1]上,函数f ′(θ1)和n θ1n -1满足柯西中值定理,即:∃θ2∈(0,θ1)使得111)(-'n n f θθ=)0()(111-'-'-n n f f θθ=212)1()(--''n n n f θθ同理:nxx f )(=nn n n fθθ!)()(.由于θn =θx ,(0<θ<1)所以:nxx f )(=!)()(n x fn θ(0<θ<1)§2 洛必达法则当x →a (或x →∞)时,f (x ),F (x )→0(或f (x ),F (x )→∞), 称极限)()(lim )(x F x f x ax ∞→→为未定式.记为:00或∞∞.一、未定式00或∞∞的求法.定理:设1) x →a 时,f (x )和F (x )→0;2) 在点a 的某个去心邻域内,f ′(x )和F ′(x )存在,且F ′(x )≠0;3) ax →lim)()(x F x f ''存在(或为∞).那么ax →lim)()(x F x f =ax →lim)()(x F x f ''.证明:定义f (a )=F (a )=0.则f (x )和F (x )在[x ,a ]或[a ,x ]上满足柯西中值定理的条件,于是)()(x F x f =)()()()(a F x F a f x f --=)()(ξξF f '' (ξ在a 与x 之间).令x →a ,则有ξ→a ,于是: ax →lim)()(x F x f =ax →lim)()(x F x f ''.当f ′(x )和F ′(x )满足定理的条件时,可以继续使用.即:ax →lim)()(x F x f =ax →lim)()(x F x f ''=ax →lim)()(x F x f ''''.对x →∞时的未定式00及x →a 或x →∞时的未定式∞∞,有相应的结论.例1. 求下列极限:1)lim→x bxax sin sin (b ≠0)解:原式=0lim →x bxb ax a cos cos =ba 2)1lim→x123233+--+-x x x x x解:原式=1lim→x 1233322---x x x =1lim→x 266-x x =233)lim→x 3sin xx x - 解:原式=0lim →x 23cos 1xx -=0lim→x xx 6sin =0lim→x 6cos x =614)+∞→x limx (xarctan 2-π)解:原式=+∞→x limxx 1arctan 2-π=+∞→x lim22111xx -+-=+∞→x lim221xx+=1.5)+∞→x limnxx ln (n >0)解:原式=+∞→x lim 11-n nxx =+∞→x limnnx1=0.6)+∞→x limxnex λ(n 为正整数,λ>0)解:原式=+∞→x limxn enxλλ1-=…=+∞→x limxn en λλ!=0.7)2limπ→x2)2(sin ln x x -π解: 原式=2lim π→x )2(4cot x x --π=2lim π→x 8csc 2x-=-818)lim→x xx x cos sec )1ln(2-+解:原式=0lim→x x x x x xsin tan sec 122++=0lim→x )1)(1(secsin 222x x x x++=19)1lim→x 13)1()1()1)(1(-----n nx x x x解:原式=1lim→x xx--11•1lim→x x x--113•…•1lim→x x xn--11=1lim→x 121--x•1lim→x 13132---x •…•1lim→x 111----nn xn=!1n二、 未定式0·∞;∞- ∞; 00; 1∞; ∞0的求法. 例2. 求下列极限: 1)lim+→x x n ln x (n >0)解:原式=0lim +→x nxx 1ln =0lim+→x 111+-n xnx =0lim +→x -nxn=02)2limπ→x (sec x -t a n x );解: 原式=2lim π→x xx cos sin 1-=2lim π→x xx sin cos --=03)lim+→x x x ;解:原式=0lim +→x xx eln =xx x e1ln lim+→=211limxx x e-+→=14)lim→x x x x x sin tan 2-解:原式=0lim→x 3tan xxx -=0lim→x 2231secxx -=0lim→x xx x 222cos 3cos 1-=315)0lim →x 21arctan xx x ⎪⎭⎫ ⎝⎛ 解:设y =21arctan xx x ⎪⎭⎫ ⎝⎛则ln y =xxxarctan ln12=2ln arctan ln xxx -由于0lim →x 2ln arctan ln x x x -=0lim →x xx x x 21arctan 112-+=0lim→x xxxx 21arctan )1(12-+=0lim→x xx x x x x arctan )1(2arctan )1(222++-=0lim→x 211x+•0lim→x 322arctan )1(xxx x +-=0lim→x 222611)1(arctan 21xxx x x ++--=0lim→x 2262xx -=-31所以,原式=31-e .6)lim +→x )1(-xx x解:设y =)1(-xx x⇒ln y =(x x -1)ln x由于0lim +→x x ln x =0lim +→x xx 1ln =0lim+→x 2/1/1xx -=0所以当x →0时,e x ln x -1~x ln x ,从而lim+→x (x x -1)ln x =0lim +→x x ln x •ln x ==0lim+→x xx1ln2=0lim+→x 2/11ln 2xx x -∙=0lim +→x -2xx 1ln =0. 即: 0lim +→x )1(-xxx =1例3. 求常数a 和n ,使当x →0时,ax n 与ln(1-x 3)+x 3为等价无穷小.解:0lim→x naxx x )1ln(33-+=0lim→x 1322133---+n naxxx x =0lim →x -)1(136x naxn --6=n当n =6时, 0lim→x naxx x )1ln(33-+=-a61例4. 求下列极限:1) ∞→n lim nn解:xx=xxe ln 1 由于 +∞→x limxx ln =+∞→x limx1=0; 所以+∞→x limxx=+∞→x lim xxe ln 1=1从而 ∞→n limnn=11)∞→n lim nnnnc b a ⎪⎪⎭⎫⎝⎛++3(a ,b ,c 均为正数)解:n nnnc b a ⎪⎪⎭⎫ ⎝⎛++3=)3ln(111nn n c b a n e++因为:+∞→x lim )3ln(111xx xc b ax ++t x=1+→0lim t tc b a tt t 3ln )ln(-++=+→0limt tt t tttcb a cc b b a a ++++ln ln ln =3)ln(abc所以∞→n lim )3ln(111nnncban ++=3)ln(abc即:∞→n lim nnnnc b a ⎪⎪⎭⎫⎝⎛++3=3)ln(abc e =3abc例5. 求下列极限:1) 0lim→x xx x sin 1sin2解:此题不能用洛必塔法则,因为0lim→x xx x x cos 1cos1sin2-不存在原式=0lim →x )1sin (sin x x x x ∙=0lim→x x xsin •0lim →x x x 1sin =0 2) +∞→x lim xxx cos -解:此题也不能用洛必塔法则,因为:+∞→x lim 1sin 1x-不存在原式=+∞→x lim (1-xxcos )=1例6. 讨论函数f (x )=⎪⎪⎩⎪⎪⎨⎧≤>+-0,0,])1([2111x e x ex x x 在x =0处的连续性. 解:当x >0时,ln f (x )=ln x xex 11])1([+=x1·[x1ln(1+x )-ln e ]=2)1ln(xxx -+所以0lim +→x ln f (x )=0lim+→x 2)1ln(xxx -+=0lim +→x xx2111-+=0lim+→x )1(21x +-=-1/2.从而: 0lim +→x f (x )=e -1/2.由0lim -→x f (x )=f (0)=e -1/2=0lim +→x f (x ),所以函数在x =0处连续.例7. 设f ′′(x 0)存在,证明20000)(2)()(limhx f h x f h x f h --++→=f ′′(x 0).解: 0lim→h 2000)(2)()(h x f h x f h x f --++=0lim→h hh x f h x f 2)()(00-'-+'= f ′′(x 0).§3 泰 勒 公 式一、 泰勒公式设函数f (x )在x 0处可导,则由微分公式有:f (x )=f (x 0)+f ′(x 0)(x -x 0)+o (x -x 0)这表明在x 0处f (x )可以用一个一次多项式来近似表示.但这种表示存在缺陷:函数的表示不够精确,且误差不易估计.为了解决此问题,用一个高次多项式来近似表示函数,且使其误差容易估计,这就是泰勒公式.设函数f (x )在含有x 0的开区间内具有直到(n +1)阶导数, 下面找出(x -x 0)的n 次多项式:p n (x )=a 0+a 1(x -x 0)+ a 2(x -x 0)2+...+ a n (x -x 0)n (1)使其近似表示f (x ),要求1) p n (x )与f (x )之差是比(x -x 0)n 高阶的无穷小; 2) 给出误差|f (x )-p n (x )|的具体表达式.假设p n (x )在x 0处的函数值及n 阶导数在x 0处的值满足:p n (x 0)=f (x 0), p ′n (x 0)= f ′(x 0), p n ′′(x 0)=f ′′(x 0),… ,p n (n )(x 0)=f (n )(x 0). 下面确定多项式的系数a 0,a 1,a 2 …,a n 为此, 对(1)式求各阶导数,然后分别代入以上等式,得:a 0=f (x 0),a 1=f ′(x 0), 2!a 2=f ′′(x 0),…, n ! a n =f (n )(x 0),即得:a 0=f (x 0), a 1=f ′(x 0), a 2=!21f ′′(x 0),… a n =!n 1f (n )(x 0).从而p n (x )= f (x 0)+f ′(x 0)(x -x 0)+!2)(0x f '' (x -x 0)2+…+!)(0)(n x fn (x -x 0)n .泰勒中值定理:如果函数f (x )在含有x 0的某个开区间(a ,b )内具有直到(n +1)阶的导数,则∀x ∈(a ,b ),f (x )可以表示为关于(x -x 0)的一个n 次多项式与p n (x )一个余项R n (x )之和:f (x )=f (x 0)+f ′(x 0)(x -x 0)+!2)(0x f '' (x -x 0)2+…!)(0)(n x fn (x -x 0)n +R n (x ). (2)其中R n (x )=)!1()()1(++n fn ξ (x -x 0)n +1, (3)这里ξ是x 0与x 之间的某个值.证:记 R n (x )=f (x )-p n (x ).只需证明R n (x )=)!1()()1(++n fn ξ(x -x 0)n +1,(ξ在x 0与x 之间).由假设可知,R n (x )在(a ,b )内具有直到(n +1)阶导数,且R n (x 0)=R n ′(x 0)=R n ′′(x 0)=…=R n (n )(x 0)=0.则R n (x )和(x -x 0)n +1在[x 0,x ]或[x ,x 0]满足柯西中值定理,即有:10)()(+-n n x x x R =0)()()(100---+n n n x x x R x R =nnx n R ))(1()(011-+'ξξ (ξ1在x 0与x 之间),同样函数R n ′(x )与(n +1)(x -x 0)n 在[x 0,x ]或[x ,x 0]满足柯西中值定理,即:nnx n R ))(1()(011-+'ξξ=))(1()()(0101--+'-'x n x R R n nξξ=1022))(1()(--+''n nx n n R ξξ(ξ2在x 0与ξ1之间).余此经过n +1次后,得:10)()(+-n n x x x R =)!1()()1(++n R n nξ,(ξ在x 0与ξn 之间,从而在x 0与ξ之间) 由于R n (n +1)(x )=f (n +1)(x ) ;[因为p n (n +1)(x )=0]所以R n (x )=)!1()()1(++n fn ξ (x -x 0)n +1, 这里ξ是x 0与x 之间的某个值.(2)称为泰勒公式,余项(3)称为拉格朗日余项.对某个固定的n 值,如果∃M >0,使得|f (n +1)(x )|≤M ,则有余项估计式:|R n (x )|=|)!1()()1(++n fn ξ (x -x 0)n +1|≤)!1(+n M |x -x 0|n +1.且limx x →10)()(+-n n x x x R =0, 因此R n (x )=o [(x -x 0)(n )].特别当n =0时,有:f (x )=f (x 0)+f ′(ξ)(x -x 0) (ξ在x 与x 0之间)此为拉格朗日中值定理.当不需要余项的精确表达式时,则n 阶泰勒公式为:f (x )=f (x 0)+f ′(x 0)(x -x 0)+!2)(0x f '' (x -x 0)2+…!)(0)(n x fn (x -x 0)n +o [(x -x 0)(n )].此式称为Peano 公式R n (x )= o [(x -x 0)(n )] 称为Peano 余项公式 特别当x 0=0时,即为麦克劳林公式:f (x )=f (0)+f ′(0)x +!2)0(f '' x 2+…+!)0()(n fn x n+)!1()()1(++n x fn θx n +1. (0<θ<1).或 f (x )=f (0)+f ′(0)x +!2)0(f '' x 2+…+!)0()(n fn x n+o (x n ). 于是 f (x )≈f (0)+f ′(0)x +!2)0(f '' x 2+…+!)0()(n fn x n.且|R n (x )|≤)!1(+n M|x |n +1.二、 求函数的泰勒公式: 例1. 求函数f (x )=e x 的n 阶麦克劳林公式.解: 由于 f ′(x )=f ′′(x )=…=f (n )(x )=e x . 所以f (0)=f ′(0)=f ′′(0)=…=f (n )(0)=1.|R n (x )|=|)!1(+n exθxn +1|<|)!1(||+n ex |x |n +1.当x =1时,则有: e =1+1+!21+…+!n 1其中|R n (1)|=|)!1(+n eθ|<|)!1(3+n .例2. 求函数f (x )=sin x 的n 阶麦克劳林公式.解: 由于 f (n )(x )=sin(x +n π/2). 所以 f (0)=0, f ′(0)=1, f ′′(0)=0, f ′′′(0)=-1, f (4)(0)=0, 即有: f (2m )(0)=0, f (2m -1)(0)=(-1)m -1. m =0,1,2,…. 因此:其中R 2m (x )=)!12(]2)12(sin[+++m m x πθx 2m +1.(0<θ<1).当m =1时, sin x ≈y =x , |R 2|=|!3)23sin(πθ+x x 3|≤|x |3/6.当m =2时,sin x ≈y =x -!33x,|R 4|≤|x |5/5!.当m =2时, sin x ≈y =x -!33x +!55x|R 6|≤|x |7/7!例3.求函数f (x )=cos x 的麦克劳林公式.π解:其中R 2n +1(x )=)!22(])1(cos[+++n n x πθx 2n +2.例4.其中: R n (x )=11)1)(1()1(++++-n n nxx n θ (0<θ<1)其中: R n (x )=)!1())(1()1(+-+--n n n αααα (1+θx )α-n -1x n +1 (0<θ<1)例5.求函数f (x )=t a n x 的二阶麦克劳林公式. 解:f (0)=0,f ′(0)=sec 2x |x =0=1;f ′′(0)=2sec 2x tan x |x =0=0. f ′′′(x )=4sec 2x tan 2x +2sec 4x =2·xx42cos sin21+所以 tan x =x +!32)(cos )(sin 2142x x θθ+x 3=x +)(cos 3)(sin 2142x x θθ+x 3 (0<θ<1).例6. 用Talor 公式求极限1)+∞→x lim(3233x x +-4342x x -)解:3233xx +=331x x +=x [1+x 331∙+2)3(!2)131(31x-∙+2)3(x o ]=x +1-x 1+)1(x o 4342x x -=421x x -=x [1-x 241∙+2)2(!2)141(41x--∙+2)2(x o ]=x -21-x 83+)1(x o3233x x +-4342x x -= x +1-x1+)1(xo -[ x -21-x 83+)1(xo ]=23-x85+)1(xo+∞→x lim(3233x x +-4342x x -)=+∞→x lim [23-x85+)1(xo ]=232)lim→x xe x xx xsin )(cos 1211222-+-+解:21x +=1+221x +4!2)121(21x -+o (x 4);221211xx +-+=481x +o (x 4);cos x =1-!21x 2+!41x 4+o (x 4);2xe=1+x 2+4!21x+ o (x 4);cos x -2xe =-23x 2-42411x + o (x 4); 0lim→x xe x xx xsin )(cos 1211222-+-+=0lim→x )](241123[)(81442244x o x x x x o x +--+=0lim→x )](23)(814444x o x x o x +-+=-121§4 函数的单调性与曲线的凹凸性一、 函数单调性的判定法定理:(函数单调性的判定法) 设函数y =f (x )∈C [a ,b ], f (x )∈D (a ,b ).1) 如果:∀x ∈(a ,b ),f ′(x )>0, 则y =f (x )在[a ,b ]上单调增加; 2) 如果:∀x ∈(a ,b ),f ′(x )<0, 则y =f (x )在[a ,b ]上单调减少.yf ′(x )>0,图形上升图 f ′(x )<0图形下降证明1)由于f (x )∈C [a ,b ],f (x )∈D (a ,b ),在(a ,b )内任取两点x 1、x 2(x 1<x 2),由拉格朗日中值定理,得f (x 2)-f (x 1)=f ′(ξ)(x 2-x 1) (x 1<ξ<x 2)由于x 2-x 1>0,且f ′(x )>0,从而有f ′(ξ)>0,于是f (x 2)-f (x 1)=f ′(ξ)(x 2-x 1)>0, 即 f (x 2)>f (x 1).例1. 判定函数y =x -sin x 在[0,2π]上的单调性. 解: 因为在(0,2π)内y ′=1-cos x >0,所以函数y =sin x 在[0.2π]上单调增加. 例2. 讨论函数y =e x -x -1的单调性. 解: y ′=e x -1.y =e x -x -1的定义域为(-∞,+∞),因为在(-∞,0)内y ′<0,所以函数y =e x -x -1在(-∞,0)上单调减少; 因为在(0,+∞)内y ′>0,所以函数y =e x -x -1在[0,+∞]上单调增加.例3. 讨论函数y =32x 的单调性.解 这函数的定义域为(-∞,+∞).当x ≠0时,这函数的导数为y ′=332x,当x =0时,函数的导数不存在,∀x ∈(-∞,0), y ′<0, 函数y =32x 在(-∞,0)上单调减少,∀x ∈(0,+∞), y ′>0,函数y =32x 在[0,+∞]上单调增加.例4. 确定函数f (x )=2x 3-9x 2+12x -3的单调区间.解:函数的定义域为(-∞,+∞), 函数的导数为:f ′(x )=6x 2-18x +12=6(x -1)(x -2).令f ′(x )=0,即解6(x -1)(x -2)=0.得x 1=1、x 2=2,这两个根把(-∞,+∞)分成三个部分区间(-∞,1)、[1,2]及(2,+∞).∀x ∈(-∞,1)U (2,+∞), f ′(x )>0, 函数单调上升; ∀x ∈(1,2), f ′(x )<0, 函数单调下降.例5. 讨论函数y =x 3的单调性.解: 函数定义域为(-∞,+∞).且y ′=3x 2≥0,函数单调上升. 例6. 证明:当x >1时,2x >3-x1证: 令f (x )=2x -(3-x 1),则 f ′(x )=-x 121x=21x(x x -1).f (x )∈C [1,+∞],∀x ∈(1,+∞),f ′(x )>0, f (x )在 [1,+∞]上单调增加,从而 当x >1时, f (x )>f (1)=0. 即: 2x -(3-x1)>0,亦即2x >3-x 1(x >1).例7. 证明当0<x <π/2时,t a n x >x +x 3/3. 证: 设f (x )=x +x 3/3-t a n x .则f ′(x )=1+x 2-sec 2x =x 2-t a n 2x =(x -t a n x )(x +t a n x )<0. 所以 f (x )<f (0)=0. 即: t a n x >x +x 3/3. [这里用了:x <t a n x ].例8. 讨论方程ln x =ax (其中a >0)有几个实根? 解:设f (x )=ln x -ax ,则令f ′(x )=x 1-a =0得: x =1/a .当0<x <a 时, f ′(x )>0, 函数单调上升, 当a <x <+∞时, f ′(x )<0, 函数单调下降. 又+→0lim x f (x )=-∞, +∞→x lim f (x )=+∞→x lim x [xx ln -a ]=-∞.因此f (1/a )=-ln a -1为函数的最大值. 当 f (1/a )=-ln a -1>0,即0<a <1/e 时, 在(-∞,1/a )内存在唯一点ξ1,使f (ξ1)=0. 在(1/a ,+∞)内,存在唯一点ξ2,使f (ξ2)=0,此时函数f (x )有两个零点,从而方程有两个根. 当f (1/a )=-ln a -1=0,即a =1/e 时,此时x =1/a 为函数的唯一零点,从而方程只有唯一根. 当f (1/a )=-ln a -1<0时,即:1/e <a <+∞时 函数无零点,从而方程没有根.y=lnx-ax (a=1/e) y=lnx-ax(0<a<1/e)y=lnx-ax(a>1/e)例9. 设α>β>e ,证明αβ<βα. 证明:设f (x )=xx ln ,(x ≥e )则f ′(x )=2ln 1xx -<0.因此函数在(e ,+∞)上单调下降.从而当α>β时,f (α)<f (β),即:ααln <ββln ,于是βln α<αln β,从而有: αβ<βα.例10.比较e π和πe 的大小.解: 由于πe =e e ln π.于是只要比较e π和e e ln π的大小.从而只要比较π和e ln π的大小. 设 f (x )=x -e ln x (x >1)令f ′(x )=1-e x 1=0得:x =e .当1<x <e 时,f ′(x )<0,函数单调下降, 当e <x <+∞时,f ′(x )>0,函数单调上升.所以f (e )=0为函数的最小值.从而f (π)>f (e )=0.即:π-e ln π>0. 从而: e π>πe .二、 曲线的凹凸性与拐点定义:设f (x )在区间I 上连续,如果对I 上的任意两点x 1和x 2有:)2(21x x f +<2)()(21x f x f +称f (x )在I 上的图形是向上凹的(或凹弧); )2(21x x f +>2)()(21x f x f +称f (x )在I 上的图形是向上凸的(或凸弧);另一定义为:定义:设f (x )在区间I 上连续,如果对∀x 1,x 2∈I 及实数t (0<t <1)有:f [tx 1+(1-t )x 2]<tf (x 1)+(1-t )f (x 2),称f (x )在I 上的图形是向上凹的(或凹弧); f [tx 1+(1-t )x 2]>tf (x 1)+(1-t )f (x 2),称f (x )在I 上的图形是向上凸的(或凸弧); 凹凸性的判断定理:定理:设f (x )∈C [a ,b ],在(a ,b )内具有连续的一阶和二阶导数,则: 1) 若在(a ,b )内有f ′′(x )>0,则f (x )在[a ,b ]上的图形是向上凹的; 2) 若在(a ,b )内有f ′′(x )<0,则f (x )在[a ,b ]上的图形是向上凸的; 证明:1)∀x 1,x 2∈[a ,b ],记x 0=(x 1+x 2)/2.则由泰勒公式有:f (x )=f (x 0)+f ′(x 0)(x -x 0)+f ′′(ξ1)(x -x 0)2/2< f (x 0)+f ′(x 0)(x -x 0)(ξ1在x 与x 0之间)从而: f (x 1)< f (x 0)+f ′(x 0)(x 1-x 0); f (x 2)< f (x 0)+f ′(x 0)(x 2-x 0); 所以: f (x 1)+f (x 2)<2 f (x 0)+f ′(x 0)(x 1+x 2-x 0)=2f (x 0). 同理可证明2).例11. 判断函数y =ln x 的凹凸性.解:由于y ′=1/x ,y ′′=-1/x 2<0 (x >0),所以函数在(0,+∞)内是向上凸的. 例12. 判断函数y =x 3的凹凸性 解:由于:y ′=3x 2,y ′′=6x ,当x ∈(-∞,0)时,y ′′<0,曲线在(-∞,0)内是向上凸的, 当x ∈(0,+∞)时,y ′′>0,曲线在(0,+∞)内是向上凹的. 拐点的定义:定义:曲线由凹变凸(或由凸变凹)的分界点称为曲线的拐点. 连续曲线上凹弧与凸弧的分界点为曲线的拐点. 例13. 判断函数y =3x 的凹凸性. 解:y ′=3231x;y ′′=-3292xx.当x ∈(-∞,0)时, ,y ′′<0,曲线在(-∞,0)内是向上凸的, 当x ∈(0,+∞)时,y ′′>0,曲线在(0,+∞)内是向上凹的.函数在x =0处的一阶和二阶导数不存在,但(0,0)为函数图形的拐点. 例14. 判断函数y =x 4的凹凸性.解:由于y ′′=12x 2>0 ,∀x ∈(-∞,+∞),所以函数在(-∞,+∞)内是向上凹的. 这里y ′′(0)=0,但(0,0)不是曲线的拐点. 拐点的求法:1) 求f ′′(x )=0的根;2) 求f ′′(x )不存在的点;3) 对上面求出的每一个点x 0,判断f ′′(x )在点(x 0,f (x 0))的左右两侧的符号,当两侧符号相反时,点(x 0,f (x 0))为拐点,当两侧的符号相同时,点(x 0,f (x 0))不是拐点. 例15. 求函数y =(x -1)3x 的凹凸区间和拐点. 解:函数的定义区间为:(-∞,+∞).y ′=32313134--xx, y ′′=35329294--+xx=359)12(2x x +当x例16. 证明曲线y =112+-x x 有三个拐点在同一直线上. 解: y ′=222)1(12+++-x x x ,y ′′=3223)1(2662++--x x x x =32)1()32)(32)(1(2+--+--x x x x可以判断点A (-1,-1)、B (2-3,)32(431--)、C (2+3,)32(431++)为拐点.k AB =)1(32)1()32(431-------=41=k AC .例17. 试确定k 的值,使曲线y =k (x 2-3)2的拐点处的法线通过原点. 解:由于 y ′=2k (x 2-3)2x =4kx 3-12kx , y ′′=12k (x -1)(x +1). 显然x 1=-1和x 2=1为拐点的横坐标. 当x 1=-1时,y 1=4k ,点(-1,4k )处有: y ′(-1)=8k , 所以法线方程为:y -4k =-k81(x +1).由法线通过原点有:32k 2=1,即: k =±82.当x 2=1时, y 1=4k ,点(1,4k )处有:y ′(1)=-8k , 所以法线方程为:y -4k =k81(x -1).由法线通过原点有:32k 2=1,即: k =±82.因此当k =±82时,曲线在拐点处的法线通过原点.例18. 设y =f (x )在x =x 0的某一邻域内具有三阶连续的导数,如果f ′(x 0)=0, f ′′(x 0)=0而f ′′′(x 0)≠0,问x =x 0是否为极值点?(x 0, f (x 0))是否为拐点?为什么?解:由f ′′′(x 0)≠0,不妨设f ′′′(x 0)>0.由于f ′′′(x )在U (x 0)内连续,从而存在区间I ⊂U (x 0),对∀x ∈I ,有f ′′′(x )>0.于是由泰勒公式有: f (x )= f (x 0)+f ′(x 0)(x -x 0)+!21f ′′(x 0)(x -x 0)2+!31f ′′′(ξ)(x -x 0)3 ,ξ在x 与x 0之间.即: f (x )- f (x 0)=!31f ′′′(ξ)(x -x 0)3 ,由于f ′′′(ξ)>0,所以当x >x 0时,有f (x )>f (x 0); 当x <x 0时,有f (x )<f (x 0);从而x 0非极值点. 又f ′′(x )-f ′′(x 0)=f ′′′(ξ1)(x -x 0), ξ1在x 与x 0之间.即: f ′′(x )=f ′′′(ξ1)(x -x 0),所以当x <x 0时,有f ′′(x )<0, 当x >x 0时,有f ′′(x )>0. 所以点(x 0,f (x 0))为拐点.一般地:如果f (x )在U (x 0)内具有n 阶连续的导数,且f ′(x 0)= f ′′(x 0)=…= f (n -1)(x 0)=0,f (n )(x 0)≠0,当n 为奇数时,x =x 0为曲线拐点的横坐标; 当n 为偶数时,x =x 0为极值点,且当f (n )(x 0)>0时x =x 0为极小值点; 当f (n )(x 0)<0时x =x 0为极大值点. 例19. 证明不等式:1)21(x n +y n )>ny x)2(+ (x >0,y >0,x ≠y ,n >1).2) x ln x +y ln y >(x +y )ln2y x +(x >0,y >0,x ≠y ).证明:1)设f (x )=x n (x >0,n >1).则f ′′(x )=n (n -1)x n -2>0.从而f (x )在(0,+∞)内是向上凹的,于是对∀x ≠y ∈(0,+∞)有:21(x n +y n )>ny x)2(+2)设f (x )=x ln x ,则f ′(x )=1+ln x ,f ′′(x )=1/x >0.从而f (x )在(0,+∞)内是向上凹的,于是对∀x ≠y ∈(0,+∞)有:21(x ln x +y ln y )>21(x +y )ln2y x +,即: x ln x +y ln y >(x +y )ln 2y x+.§5 函数的极值与最大值最小值一、 极值及求法1. 定义: 设函数f (x )在区间(a ,b )内有定义, x 0是(a ,b )内的一个点,如果存在点x 0的一个去心邻域Ů(x 0,δ),对于∀x ∈Ů(x 0,δ),有f (x )<f (x 0), 称f (x 0)是函数f (x )的一个极大值;∀x ∈Ů(x 0,δ),有f (x )>f (x 0),称f (x 0)是函数f (x )的一个极小值. 2. 极值存在的必要条件:定理(必要条件)设f (x )在点x 0处可导,且在x 0处取得极值,则 f ′(x 0)=0. 证明:设函数f (x )在x 0处取得极大值f (x 0).由于f ′(x 0)=00)()(limx x x f x f x x ---→≥0; f ′(x 0)=00)()(limx x x f x f x x --+→≤0.所以f ′(x 0)=0.驻点: 方程f ′(x )=0的点 (或导数为零的点). 3. 驻点与极值点的关系:可导函数的极值点必为驻点,但驻点不一定是极值点. 例如y =x 3有驻点x =0,但不是极值点. 4. 极值存在的充分条件定理(第一种充分条件)设函数f (x )在x 0连续,在Ů(x 0,δ)可导,且f ′(x 0)=0. 1) 若∀x ∈(x 0-δ,x 0),f ′(x )>0, ∀x ∈(x 0,x 0+δ),f ′(x )<0, f (x )在x 0处取极大值; 2) 若∀x ∈(x 0-δ,x 0),f ′(x )<0, ∀x ∈(x 0,x 0+δ),f ′(x )>0, f (x )在x 0处取极小值; 3) 若∀x ∈ Ů(x 0,δ) f ′(x )不变号,则 f (x )在x 0处没有极值. 证明:1) 当∀x ∈(x 0-δ,x 0),f ′(x )>0 函数是单调上升的;当∀x ∈(x 0,x 0+δ),f ′(x )<0 函数是单调下降的; 所以f (x 0)为函数的极大值. 同理可证明2)和3). 5. 求极值的方法:如果函数f (x )在定义区间内可导,则求极值步骤为: 1) 求函数的导数f ′(x );2) 求出f ′(x )=0的全部实根(即函数的所有驻点);3) 对每个驻点讨论f ′(x )在其左、右两边的符号,确定是否为极值. 例1. 求函数f (x )=x 3-3x 2-9x +5的极值.解:f ′(x )=3x 2-6x -9=3(x +1)(x -3); 令f ′(x )=0得 驻点:x 1=-1 ;x 2=3.当x <-1时,f ′(x )>0,当-1<x <3时,f ′(x )<0,所以x 1=-1为函数的极大值点; 当x >3时,f ′(x )>0,从而x 2=3为函数的极小值点; 所以函数的极大值为:f (-1)=10;极小值为f (3)=-22. 当函数在驻点处的二阶导数存在且不为零时,有定理3(第二充分条件)设函数f (x )在点x 0处具有二阶导数且f ′(x )=0, f ′′(x )≠0, 那末1) f ′′(x 0)<0时,函数f (x )在x 0处取得极大值; 2) f ′′(x 0)>0时,函数f (x )在x 0处取得极小值.证明:1)由于f ′′(x 0)=0limx x →00)()(x x x f x f -'-'<0.由保号性定理,存在Ů(x 0,δ),对x ∈Ů(x 0,δ),有00)()(x x x f x f -'-'=0)(x x x f -'<0.即f ′(x )与x -x 0异号.所以在Ů(x 0,δ)内, 当x <x 0时,f ′(x )>0;当x >x 0时,f ′(x )<0,由第一充分条件得f (x 0)为函数的极大值.同理可证2).注:当f ′′(x 0)=0时,f (x )在x 0处可能有极值,也可能没有极值.例如y =x 3和y =x 4在x =0处有f ′(0)=f ′′(0)=0,但x =0不是y =x 3的极值点,而x =0是y =x 4的极小值点.例2. 求函数f (x )=(x 2-1)3+1的极值.解:由于:f ′(x )=6x (x 2-1)2=6x (x -1)2(x +1)2, 所以驻点: x 1=-1, x 2=0, x 3=1. 又 f ′′(x )=6(x 2-1)(5x 2-1)f ′′(0)=6>0,所以x =0为函数的极小值点,极小值为f (0)=0. 而f ′′(-1)=f ′′(1)=0.不能用第二充分条件判断.但当x <-1时,f ′(x )<0,当-1<x <0时,f ′(x )<0,所以x =-1不是极值点. 同理x =1也不是极值点.例3. 求函数f (x )=1-(x -2)2/3的极值.解:当x ≠2时,f ′(x )=-3232-x .当x <2时, f ′(x )>0, 当x >2时,f ′(x )<0,所以x =2为函数的极大值点,且极大值为f (2)=1.注:函数在x =2处不可导.函数的极值可能在导数不存在的点处取得. 但导数不存在的点处函数也可能没有极值,例如函数y =3x 在x =0处不可导,函数在x =0处没有极值.由此可得求函数极值的方法如下:1) 求出函数的所有驻点和导数不存在的点;2) 对上述每一个点讨论其左、右两边f ′(x )的符号,判断是否为极值点. 3) 求出极值. 例4.求函数f (x )=⎩⎨⎧≤+>0,202x x x x x ,的极值.解:当x >0时, f ′(x )=2x 2x (1+ln x ); 当x <0时, f ′(x )=1. f ′+(0)=+→0limx xxx22-=-∞;f ′-(0)=-→0limx xx 22-+=0所以函数在x =0处不可导.令f ′(x )=0得驻点:x =1/e .当0<x <1/e 时,f ′(x )<0,当1/e <x <+∞时,f ′(x )>0,所以f (1/e )=e -2/e 为函数的极小值.当x =0时,由于f (0-0)=2=f (0);f (0+0)=+→0lim x x 2x =+→0lim x e 2x ln x =1,所以函数在x =0处间断.由于f (0+0)=1,所以对ε=1/2,存在δ>0,当0<x <δ时,有|f (x )-1|<1/2,即有f (x )<f (0)=2.而当x <0时,f ′(x )=1>0,所以f (x )<f (0)=2,于是f (0)=2为函数的极大值. 例5. 求函数f (x )=x 2/3-(x 2-1)1/3极值.解:f (x )的定义域为(-∞,+∞).f ′(x )=xx x2)1(313232231∙----=3223134322)1()1(32---x x x x令f ′(x )=0得驻点x 1=-1/2,x 2=1/2.设函数f (x )∈C [a ,b ],则在[a ,b ]上f (x )有最大值和最小值,求法如下: 1) 求出函数在[a ,b ]上的驻点x 1,x 2,…,x n .2) 求出函数在[a ,b ]上的导数不存在的点y 1,y 2,…,y m .3) 求出函数值:f (x 1), f (x 2),…f (x n ), f (y 1), f (y 2),…, f (y n ), f (a ),f (b ). 4) m =min{ f (x 1), f (x 2),…f (x n ), f (y 1), f (y 2),…, f (y n ), f (a ),f (b )} M =m ax { f (x 1), f (x 2),…f (x n ), f (y 1), f (y 2),…, f (y n ), f (a ),f (b )} 特别情形:1) 当函数在一个区间(有限或无限,开或闭)内可导且只有一个驻点x 0,且此驻点x 0为函数的极值点,那么当f (x 0)为极小值时,则它为最小值;当f (x 0)为极大值时,它为最大值.2) 由实际问题可以断言函数的最值存在并在区间的内部取得,且只有唯一的一个驻点时,可以不必判断此驻点是否为极值,直接断定f (x 0)是最大值或最小值.例6. 求函数y =2x 3-6x 2-18x -7(1≤x ≤4)的最大值和最小值. 解:令 y ′=6x 2-12x -18=6(x +1)(x -3)=0 得驻点 x =3. 又 y (1)=-29; y (3)=-61,y (4)=81.例7. 如图,从南到北的铁路干线经过A ,B 两城,两城之间的距离为150公里,某工厂位于B 城正西20公里处,今要从A 城把货物运往工厂C ,已知。
第三章 微分中值定理、导数的应用资料

只需证明 x f (x) f (x) x 0, 只需证明 x f (x) (x) f (x) x 0,
xf (x) (x) f (x)
只需证明
当 x 0时,则在(x,0) 内至少存在一点 ,使
F(0) F(x) F ( )
0x
ex (1 x) x F( ) x (e 1) 0 ex 1 x
综上可得:当 x 0 ,有 e x 1 x .
四、柯西(Cauchy)中值定理 如果函数 f (x) 和 F(x) 满足: (1)在[a,b] 上连续; (2)在(a,b) 内可导且 F(x) 0. 则在 (a,b) 内至少存在一点 , 使
提示: f (x) 0, f (x) 在 x 0处可导, f (x) 在 x 0处
连续, f (0) lim f (x) x0
lim x f (x) lim x lim f (x)
x0
x
x x0 x0
0.
f (0) lim f (x) f (0) lim f (x) 1.
f (x) . F (x)
【例】计算:(1) lim x x cosx x0 x sin x
提示:原式 lim 1 cosx xsin x lim sin x sin x x cosx
1 4
满足定理的结论.
推论 1:若在(a,b) 内 f (x) 0, 则在 (a,b) 内 f (x) 为一常数.
推论2:若在(a,b) 内 f (x) g(x), 则 f (x) g(x) C. (常数).
微分中值定理及导数的应用

积分因子法
通过引入一个积分因子,将微分方程转化为可解的一 阶线性方程组。
感谢您的观看
THANKS
微分中值定理及导数的应用
目录
• 微分中值定理 • 导数的定义与性质 • 导数在函数中的应用 • 导数在实际问题中的应用 • 导数的进一步研究
01
微分中值定理
微分中值定理的定义
微分中值定理
若函数$f(x)$在闭区间$[a, b]$上连续,在开区间$(a, b)$上可 导,则存在$c in (a, b)$,使得$f'(c) = frac{f(b) - f(a)}{b - a}$。
导数与积分的关系
牛顿-莱布尼兹公式
用导数和积分相互转化的方式,将定积分转化为求和的 形式,从而简化计算。
微积分基本定理
定积分可以表示为被积函数的一个原函数在积分上下限 的函数值的差,即牛顿-莱布尼兹公式的特殊形式。
导数与微分方程
微分方程
描述一个变量关于另一个变量的导数等于某个给定函 数的方程。
初值问题
导数在科学计算中的应用
数值分析
导数在数值分析中有着广泛的应用,例如在求解微分方程、 积分方程和线性代数方程时,导数可以帮助我们找到近似 解。
图像处理
在图像处理中,导数可以帮助我们进行边缘检测、图像滤 波和图像增强等操作,从而提高图像的清晰度和质量。
信号处理
在信号处理中,导数可以用来分析信号的变化趋势和频率 特征,例如在音频处理和图像处理中,导数可以帮助我们 提取信号中的重要信息。
详细描述
如果一个函数在某区间的导数大于0, 则该函数在此区间单调递增;如果导 数小于0,则函数单调递减。
第三章 中值定理与导数的应用(1-6节)

证明:不妨设
证毕
4
二、罗尔定理( R - Th)
若f ( x)满足
1在a,b上连续
2在a,b内可导 3 f a f b 则至少一点 a,b f 0
5
R-Th 的几何意义:
y
A
B
0
x
6
证:∵ f (x) 在 闭区间[ a, b ]上连续, ∴f (x)在[ a, b ]上必有最大值M及最小值m, 有两种情况: (1) M = m ; (2) M > m . (1) 若 M = m , 则 m = f (x) = M ,
且a b 0
由R Th至少一点 a,b,使 0
f
f F
b b
f F
a a
F
0
36
注 : 在C Th中令F( x) x即为L Th, 可见C Th是L Th的推广, 或L Th是C Th的一个特例.
其逆命题成立
若f ( x)在(a, b)上恒为常数,则f ( x) 0
19
推论2 若 f ( x) 和 g( x) 在区间I 上有 f ( x) g( x) 则 f (x)与 g(x) 在 I上相差一个常数
证:令F( x) f ( x) g( x) F ( x) 0 由推论1 F( x) C 即 f ( x) g( x) C
第三章 微分中值定理与导数的应用
1
罗尔定理、拉格朗日中值定理、柯西中值定理 统称微分学中值定理,它们在理论上和应用上都有 着重大意义,尤其是拉格朗日中值定理,它刻划了 函数在整个区间上的变化与导数概念的局部性之间 的联系,是研究函数性质的理论依据。
高等数学》课件4.微分中值定理与导数的应用

思考题
1. 将拉格朗日中值定理中的条件 f (x) “在 闭区间[a,b]上连续”换为“在开区(a,b) 内连续” 后,定理是否还成立?试举例(只需画图)说明.
2. 罗尔(Rolle)中值定理是微分中值定理中一 个最基本的定理.仔细阅读下面给出的罗尔中值定理 的条件与结论,并回答所列问题.
罗尔(Rolle)中值定理 若 f (x)满足如下 3 条: (1) 在闭区间[a,b]上连续; (2) 在开区间(a,b)内可导; (3) 在 区 间 [a,b] 端 点 出 的 函 数 值 相 等 , 即
例1
求
lim
x1
x3 x3 x
3x 2
x
2
. 1
解
lim
x 1
x3 x3 x
3x 2
x
2
1
=
lim
x 1
3x2 3x2
3 2x
1
= lim 6x = 6 = 3 .
x1 6x 2
4
2
例 2 求lim1 cos x . xπ tan x
解 lim1 cos x = lim sin x = 0.
推 论 2 如 果 对 (a,b) 内 任 意 x , 均 有 f (x) g(x),则在(a,b) 内 f (x)与 g(x)之间只差一个 常数,即 f (x) g(x) C (C 为常数).
证 令F (x) f (x) g(x),则F(x) 0,由推论 1 知 , F(x) 在 (a,b) 内 为 一 常 数 C , 即 f (x) g(x) C, x (a,b),证毕.
f (a) f (b),则在开区间(a,b) 内至少存在一点 ,使 得 f ( ) 0.
需回答的问题: (1) 罗尔中值定理与拉格朗日中值定理的联系与
高数)第3章:微分中值定理与导数的应用共91页

在(2, 3)内至少存在一点 2,使f (2)0,2也是f (x)
的一个零点。 f (x) 是二次多项式,只能有两个零点,分别在区间
(1, 2)及(2, 3)内。
可导函数的两个零点之间必有其导数的零点。
9
3.将拉罗 格尔 朗日定(L理ag条 ran件 gfe(中 )a中)去 值f(定b掉 )理,得到
第一节 微分中值定理
微分中值定理的核心是拉格朗日(Lagrange) 中值定理,费马定理是它的预备定理,罗尔定理 是它的特例,柯西定理是它的推广。
1. 预备定理——费马(Fermat)定理
若函f数 (x)在(a,b)内一x0取 点得 最值 且f(x)在x点 0可 导 , f(x则 0)0.
费马(Fermat,1601-1665),法国人,与笛卡尔共 同创立解析几何。因提出费马大、小定理而著名于世。
1
2
y
几何解释:
曲线在最高点和最低点 显然有水平切线,其斜
率为 0,当切线沿曲线连 o
续滑动时,就必然经过 位于水平位置的那一点 .
yf(x)
1
2
x
3
证明: 只就f (x)在x0达到最大值证明。
由f于 (x)在 x0达到最大值x, 0所 x在 (以 a,b)内 只 , 要
就f有 (x0x)f(x0), 即 f(x 0 x ) f(x 0 ) 0 ,
从f(而 x 0 x )f(x 0)0 ,当 x0 时 ; x
f(x0 x)f(x0)0,当 x0时 ; x
这 f(x 样 0 0 ) lx 0 im f(x 0 x x ) f(x 0 ) 0 f(x 0 0 ) lx i0 m f(x 0 x x )f(x 0) 0 .
《高等数学(上册)》 第三章

证明 设 f (x) arcsin x arccos x ,则
f (x) 1 1 0 , x (1,1) , 1 x2 1 x2
所以 f (x) C , x (1,1) .
又因为 f (0) arcsin 0 arccos0 0 ,所以 f (x) f (0) ,结论得证.
又因为
H (x) F(x)[G(b) G(a)] G(x)[F(b) F(a)] ,
所以
H ( ) F( )[G(b) G(a)] G( )[F(b) F(a)] 0 .
又因为 x (a ,b) 时,G(x) 0 ,则 G( ) 0 ,G(b) G(a) 0( G(x) 在[a ,b] 上
设
F ( x)
,
G(x)
是
x
x0
时的无穷小量,即
lim
x x0
F ( x)
lim
xx0
G(x)
0
,且
F (x) , G(x) 在 (x0 ,x) (或 (x ,x0 ) )内可导,且 G(x) 0 ,令 F(x0 ) 0 ,
G(x0 ) 0 ,则由柯西中值定理可知
lim
x x0
F (x) G(x)
f (x2 ) f (x1) f ( )(x2 x1) (x1 x2 ) . 假设 f ( ) 0 ,所以 f (x2 ) f (x1) 0 ,而 x1 , x2 在区间 I 上的选取是任意 的,因此 f (x) 在区间 I 上是一个常数.
3.1.2 拉格朗日中值定理
例 4 证明 arcsin x arccos x , x (1,1) . 2
例 2 证明 f (x) x(x 2)(x 4)(x 6) 1的导函数 f (x) 有 3 个零点分别位 于区间 (0 ,2) , (2 ,4) , (4 ,6)
第三章 中值定理和导数的应用

三、柯西定理 Cauchy, 1789~1857
定理3(柯西定理) 设f (x)及g (x)满足:(i)在[a, b]上连续;
(ii)在(a, b)内可导,且g (x) 0 , 则至少存在一点 (a, b),使 f ( ) f (b) f (a)
1 x2
1 x2
f (x) arcsin x arccos x c (c为常数)(1 x 1)
令x 0, 得 0 c ,
2
所以 arcsin x arccosx , (1 x 1)
又
x 1时,
arcsin
x
2 arccos
一. 未定式 0 型的极限
定理 3.2.1
0
设函数
f
(x)
和g(x)
在点
x
0的某一去心邻域内有
定义,且满足
10 lim f (x) 0 xx0
lim g(x) 0
xx0
20. f ( x) 和 g( x)
g( x) 0
在 x的0 某一去心邻域内存在,且
30 lim f (x) A(或) xx0 g( x)
则在曲线上至少有一点C,在该点处切线水平.
若定理条件不满足,则结论不一定成立.
y f (a) y f (x) f (b)
区间内有不可导的点
0a
x0 b
xy
f (b)
两端点的函数值不相等
f (a)
y
y f (x)
f (a)
f (b)
0a b
x
区间内有不连续的点
0a
x0 b
x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
罗尔中值定理
定理 1 (费马引理) 已知 f (x) 在 x0 处可导, 若在 x0 附近有 f (x) ≤ f (x0 ) (或f (x) ≥ f (x0 )), 则 f ′ (x0 ) = 0. 证明: 仅证明 f (x) ≤ f (x0 ) 的情形. 给 x0 以增量 ∆x, 则有 f (x0 + ∆x) ≤ f (x0 + ∆x) − f (x0 ) ≤ 0, ∆x f (x0 + ∆x) − f (x0 ) ≤ 0. ∆x f (x0 + ∆x) − f (x0 ) ≥ 0. ∆x
显然, F (x) 在 [a, b] 上连续, 在 (a, b) 内可导, 且 bf (a) − af (b) 1 f (a) f (a) − f (b) − = , b−a a a b−a f (a) − f (b) bf (a) − af (b) 1 f (b) − = . F (b) = b−a b b b−a F (a) = 因此, 由罗尔中值定理知, 至少存在一点 ξ ∈ (a, b), 使得
x=ξ
= e−ξ f ′ (ξ ) − 3ξ 2 f (ξ ) = 0.
3
6
未定式的极限, 洛比达法则
未定式极限的分类
1
在自变量 x 的同一变化过程中, 若 f (x) 和 g (x) 都是无穷小量或无穷大量, 则 0 (x) lim f 可能存在, 也可能不存在 (或者为无穷大). 这两种极限我们称之为 型和 g (x) 0 ∞ 型未定式的极限. 同样的情形, 也有 ∞ − ∞, 0 · ∞, 00 , 1∞ 和 ∞0 等共 7 种未定 ∞ 式的极限. 大致可以分为以下 3 类: 0 ∞ 1. , 型, 0 ∞ 2. ∞ − ∞, 0 · ∞ 型, 3. 00 , 1∞ , ∞0 型. 以下给出的求解方法洛比达法则, 只是针对第 1 类的情形, 所以对于第 2, 3 类 的未定式的极限, 必须先转换为第 1 类情形之后, 才可以利用洛比达法则.
证明: 构造函数 f (x) = ln(1 + x), 则有 1 1 f (ξ ) = . = 1 + x x=ξ 1 + ξ
′
所以, ln(1 + x) = ln(1 + x) − ln(1 + 0) =f (x) − f (0) =f ′ (ξ )(x − 0) = 其中 0 < ξ < x. 又注意到 1 1 < < 1, 1+x 1+ξ 所以 x < ln(1 + x) < x. 1+x 例 2 假设 a > b > 0, n > 1, 则 nbn−1 (a − b) < an − bn < nan−1 (a − b). 3 1 x, 1+ξ
f (a) − f (b) g ′ (ξ ) = g (a) − g (b) f ′ (ξ ),
即
f (a) − f (b) g (ξ ) − g (a) − g (b) f ′ (ξ ) = 0.
′
为此, 构造函数 F (x) = f (a) − f (b) g (x) − g (a) − g (b) f (x). 显然, F (x) 在 [a, b] 上连续, 在 (a, b) 内可导, 且 F (a) = f (a) − f (b) g (a) − g (a) − g (b) f (a) = f (a)g (b) − f (b)g (a), F (b) = f (a) − f (b) g (b) − g (a) − g (b) f (b) = f (a)g (b) − f (b)g (a). 因此, 由罗尔中值定理知, 至少存在一点 ξ, 使得 F ′ (ξ ) = f (a) − f (b) g ′ (ξ ) − g (a) − g (b) f ′ (ξ ) = 0. 结论成立. 4
ξ2
b
x
证明: 只需证明 f (a) − f (b) = f ′ (ξ )(a − b), 即 f (a) − f (b) − f ′ (ξ )(a − b) = 0. 构造函数 F (x) = f (a) − f (b) x − f (x)(a − b). 则显然, F (x) 在 [a, b] 上连续, 在 (a, b) 内可导, 且 F (a) = (f (a) − f (b))a − f (a)(a − b) = bf (a) − af (b), F (b) = (f (a) − f (b))b − f (b)(a − b) = bf (a) − af (b). 2
2
第 1 类未定式的极限
以下定理对于自变量的其他变化过程也同样成立. 定理 1 (洛比达法则 ( 0 型)) 设函数 f (x) 和 g (x) 满足以下条件: 0 (1) lim f (x) = lim g (x) = 0,
x →x 0 x→x0
(2)在x0 的某个去心邻域内, f ′ (x), g ′ (x)存在, 且g ′ (x) ̸= 0, (3) xlim →x 则
x→x0
0
f ′ (x) 存在(或者为无穷大). g ′ (x) f ′ (x) f (x) = lim ′ . g (x) x→x0 g (x) 与 f (x0 ), g (x0 ) 是否有定义无关, 所以我们可
lim
证明: 由于我们考察的 lim 以做如下定义:
因此, 由罗尔中值定理知, 至少存在点 ξ ∈ (a, b), 使得 F ′ (ξ ) = 0, 即 f (a) − f (b) − f ′ (ξ )(a − b) = 0. 结论成立. 推论 1 若 f (x) 在区间 I 上的导数恒为 0, 则 f (x) 在区间 I 上恒为常数. 证明: 任取 x1 , x2 ∈ I, 则由拉格朗日中值定理得 f (x1 ) − f (x2 ) = f ′ (ξ )(x1 − x2 ) = 0, 即 f (x1 ) = f (x2 ). 例 1 求证 x < ln(1 + x) < x, 1+x x > 0.
e−x f (x)
3
′
= e−x f ′ (x) + f (e 因此, 只需证明
−x3
f (x)
′
x=ξ
= e−ξ f ′ (ξ ) − 3ξ 2 f (ξ ) .
3
e 即可. 为此, 构造函数
−x3
f (x)
′
1
f (x0 ). 则当 ∆x > 0 时,
所以,
′ f+ (x0 ) = lim + ∆x→0
同理,
′ f− (x0 ) = lim − ∆x→0
因为
′ ′ f ′ (x0 ) = f− (x0 ) = f+ (x0 ),
所以,
f ′ (x0 ) = 0.
定义 1 若 f ′ (x0 ) = 0, 则称 x0 为 f (x) 的驻点. 定理 2 若 f (x) 满足: (1) f (x) 在 [a, b] 上连续, (2) f (x) 在 (a, b) 内可导, (3) f (a) = f (b). 则至少存在一点 ξ ∈ (a, b), 使得 f ′ (ξ ) = 0. 证明: 首先, 由闭区间上连续函数的性质 知, 函数 f (x) 在 [a, b] 上有最大值和 最小值. 不妨设最大值和最小值分别为 M, m.
O a ξ b x
2
拉格朗日中值定理
定理 3 (拉格朗日中值定理) 若 f (x) 满足: (1) f (x) 在 [a, b] 上
y
连续, (2) f (x) 在 (a, b) 内可导, 则至少 存在一点 ξ ∈ (a, b), 使得
f ′ (ξ ) =
f (a) − f (b) . a−b
O
a
ξ1
F ′ (ξ ) = 结论成立.
bf (a) − af (b) 1 f (x) − b−a x x
′
= 0.
x=ξ
5
例 6 已知 f (x) 在 [a, b] 上连续, 在 (a, b) 内可导, 且 f (a) = f (b) = 0. 则至少 存在一点 ξ ∈ (a, b), 使得 f ′ (ξ ) = 3ξ 2 f (ξ ). 证明: 显然, 只需证明 f ′ (ξ ) − 3ξ 2 f (ξ ) = 0 即可. 注意到
1
(1) 若 M = m, 则函数 f (x) 在 [a, b] 上是常数, 则 f ′ (x) = 0, x ∈ (a, b). 结论成立.
使得 f (ξ ) = M (或者 f (ξ ) = m). 进而 由费马引理得 f ′ (ξ ) = 0.
y
(2) 若 M ̸= m, 则有 M ̸= f (a) = f (b) 和 m ̸= f (a) = f (b) 至少有一 个成立. 若 M ̸= f (a) = f (b)(或者 m ̸= f (a) = f (b) ) 成立, 则有 ξ ∈ (a, b), 注: 以上定理中的 3 个条件缺一不可.
其中 ξ ∈ (b, a). 进而结论成立.
3
柯西中值定理
定理 4 若 f (x), g (x) 满足: (1) f (x), g (x) 在 [a, b] 上连续, (2) f (x), g (x) 在
(a, b) 内可导, (3) g ′ (x) ̸= 0, ∀x ∈ (a, b). 则至少存在一点 ξ ∈ (a, b), 使得 f ′ (ξ ) f (b) − f (a) = ′ . g (b) − g (a) g (ξ ) 证明: 首先, 由 g (a) − g (b) = g ′ (ξ )(a − b) 知 g (a) ̸= g (b). 显然, 只需证明
