第二教学楼平面示意图(修改后)
三年级下册数学课件-2. 简单的平面图(人教版)(共16张PPT)

Hale Waihona Puke 课堂小结今天主要认识了简单的平面图。 为了便于交流,地图通常按 上北下南,左西右东绘制。
基础练习
1.填一填。
天安门
人民大会堂
中国国家 博物馆
基础练习
2、按平面图上的方向描述物体的位置。
东 南
北
北 东 西
基础练习
3、小兔、小羊、小马和小狗要搬进下面的新家了。请你给它们安排好房 间,并说一说它们分别住在小鹿家的什么方向。
探究新知
2.感悟平面图按“上北下南,左西右东”绘制的必要性。
相这
同四
点 和 不 同
幅 示
意 图 有
点什
?么
探究新知
为了便于交流,地图通常按上北下 南,左西右东绘制。
探究新知
3.认识平面图上的方向。
示意图的下面、左面和右面分别表示的是什 么方向呢?
上北下南、左西右东。
探究新知
3.认识平面图上的方向。
85.人生的游戏不在于拿了一副好牌,而在于怎样去打好坏牌,世上没有常胜将军,勇于超越自我者才能得到最后的奖杯。 86.在成功的领奖台上,有人到得早,有人到得晚,但他们都比中途放弃的人多了一份坚持。87.你可以不够强大,但你 不能没有梦想。如果你没有梦想,你只能为别人的梦想打工筑路。这一路你可以哭,但一定88.胆量不够大,能力再强都是小人物;魄力不够大,努力一生都是小成就;在成长的路上,我们突破的不是现实,而是自己。在人生的跑道上,战胜 对手,只是赛场的赢家,战胜自己,才是命运的强者。89.任何时候任何理由,都不是你不努力工作的理由,人一旦停止追求,你的人生将从此失去变得更好的资本!90.生活可以是甜的,也可以是苦的,但不能是没味的。你可以胜利,也可 以失败,但你不能屈服。
北京交通大学校区平面图
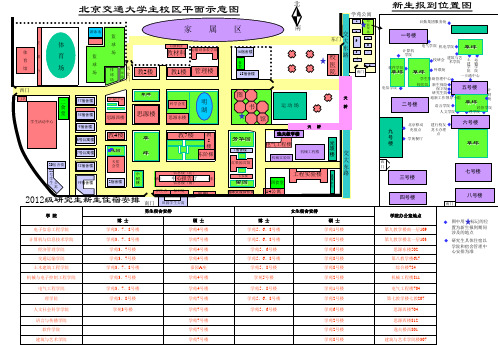
女生宿舍安排 学院办公室地点 硕 士 学苑1号楼 学苑2号楼 学苑6号楼 学苑8号楼 学苑8号楼 学苑2号楼 学苑1号楼 学苑2号楼 学苑6号楼 学苑2号楼 学苑2号楼 学苑8号楼 第九教学楼南一层109 第九教学楼北一层103 思源东楼502 第八教学楼617 综合楼724 机械工程楼811 电气工程楼704 第七教学楼七教207 思源西楼704 思源西楼812 逸夫楼西801 建筑与艺术学院楼307 图中用 标记的位 置为新生报到期间 涉及的地点 研究生具体住宿以 学院和宿舍管理中 心安排为准
运动场
桥
二号楼
语言学院 人文学院
草坪
六号楼
计 财 处
15宿舍楼 9宿舍楼 8号公寓楼 7号公寓楼
思源西楼
思源楼
经管学院 理学院
思源东楼
教4楼
花园
天佑 会堂 小 树 林
草 坪
教7楼
教 5 楼 东阶梯
芳华园
1宿舍楼
逸夫教学楼
电气工程楼
机械工程楼 机械实验馆
光 波 楼
九 号 楼
北京移动 充值点 学苑餐厅
建行校友 龙卡办理 点
运输设备教学馆
台
排 球 场
西 北 门
教2楼
教1楼
管理楼
校 医 院
东 路
草坪
土 运 建 输 学 学 院 院 一卡通中心
南门
草坪
草坪
外联处
西门
门卫
电信学院
二 食 堂
学生活动中心
17宿舍楼
计算中心
草坪
科学会堂
图 明 湖 书 馆
天 桥
学生资助管理中心 校医院、新生保险 保卫处 研究生院
五号楼
天
小学数学三年级下册(人教版)1位置与方向(一)简单的平面示意图 课件

简单的平面示意图
知识回顾 夜晚,当你面向北极星, 前面是( 北 ), 后面是( 南 ), 左面是( 西 ), 右面是( 东 )。
北极星在天空的北方。
下面是我们学校的示意图。 北
西
地图通常是按 上北下南,左 西右东绘制的。
东
南 指的是什么方向?
指的方向是北 。
下面是我们学校的示意图。 北
答案不唯一
王小红
北
刘帅
我
赵强
张一萌
3 做一做,根据下面的描述标明天安门地区示意图中的建筑物。
(1)天安门城楼在国旗的北面。 (2)人民大会堂在人民英雄纪 念碑的西面。 (3)中国国家博物馆在人民英 雄纪念碑的东面。
天安门城楼
人民大会堂
中国国家 博物馆
4 (1)书店在学校的(西 )面。
(2)体育馆在学校的( 南)面。
1
(1)邮局在公园的( 东 )面,学校在公园的(北)面。 (2)小娟家在学校的(南)面,小娟家在小峰家的(东)面。 (3)体育馆在博物馆的(北)面,体育馆在学校的(西)面。
2 恒山
华山
泰山 嵩山
衡山
我国有五座名山,合称“五 岳”。它们分别是中岳嵩山、 东岳泰山、南岳衡山、西岳 华山、北岳恒山。
你能在地图上 找到它们吗?
(3)学校的东面是(科技城 ),
学校的北面是(明明家)。
(4)书店在科技城的( 西)面。
书店
(5)明明家和学校都在体育馆
的( 北 )面。
北
明明家
学校
科技城
体育馆
1.地图通常是按上北下南,左西右东绘制的。
2.辨认地图或平面图上的方向:根据“上北下南,左西右东” 确定方向。
新人教版三下数学第2课时 简单的平面示意图

新人教版三年级下册数学第1单元位置与方向(一)第2课时简单的平面示意图【教学内容】教材第4页例2及“做一做”,练习一第3~6题。
【教学目标】1.会辨认地图上的东、南、西、北方位,能看懂平面图的方向,能识别简单的示意图。
2.培养辨认方向的意识,进一步发展空间观念。
【教学重难点】重点:会辨认地图上的东、南、西、北方位,能看懂平面图的方向。
难点:在平面图或地图上辨认方向。
【教学过程】一、故事引入淘气的喜羊羊到森林里采蘑菇,回家时不小心迷路了,谁能想办法告诉喜羊羊怎样才能回到家?(引出课题:认识平面图上的东、南、西、北)二、探究新知1.教学例2。
(1)介绍方向标。
师:在画平面图或地图时,一般要画一个“”,上面写个“北”字,表示这幅平面图或地图是按“上北、下南、左西、右东”的规则绘制的。
(2)学生根据绘制的学校示意图说说大门、教学楼和体育馆分别在操场的什么方向。
(3)同桌互相交流,全班汇报。
(4)师:根据学校示意图还可以提出什么问题呢?出示例2中余下的问题。
学生独立思考后,全班反馈。
2.绘制校园的示意图。
(1)看一看、说一说,学校操场的东、南、西、北面各有什么建筑物?(2)在学生描述的基础上,确定操场四个方向的主要建筑物,并让每个学生完成下面的校园示意图。
长方形中填写主要建筑物,正方形中填写相应建筑物所在的方向,学生可以面向东、南、西、北的任一方向填写。
3.反馈练习。
(1)课件出示中国地图。
师:这是一副中国地图,地图和平面图一样,也是按照“上北、下南、左西、右东”的要求绘制的。
(2)找出我们生活的城市。
位于中国的什么方向?北京、海南位于中国的什么方向?如果你到北京旅游要往哪个方向走?(3)完成练习一第4题。
4.小结。
师:说说在平面图和地图上辨别方向的方法。
三、巩固拓展1.完成第4页“做一做”。
2.完成练习一第3、5、6题。
四、课堂小结同学们,学完这节课你们有什么收获?【板书设计】认识平面图上的东、南、西、北地图通常按照上北、下南、左西、右东绘制的。
水施-六安皋城中学南山校区项目,教学楼 图文信息中心CAD图.dwg

校区平面示意图

532471
北区第五教学楼四楼
5403
772
北区第五教学楼四楼
5405
773
北区第五教学楼四楼
5407
774
北区第五教学楼四楼
5409
775
北区第五教学楼四楼
5411
776
北区第五教学楼四楼
5413
777
北区第五教学楼四楼
5402
778
北区第五教学楼四楼
5404
779
北区第五教学楼四楼
5421
780
北区第五教学楼四楼
5423
781
北区第五教学楼四楼
5422
782
北区第五教学楼四楼
5424
783
北区第五教学楼五楼
5501
784
北区第五教学楼五楼
5503
785
北区第五教学楼五楼
5505
786
北区第五教学楼五楼
5507
787
北区第五教学楼五楼
5509
788
5121
741
北区第五教学楼一楼
5123
742
北区第五教学楼一楼
5122
743
北区第五教学楼一楼
5124
744
北区第五教学楼二楼
5201
745
北区第五教学楼二楼
5203
746
北区第五教学楼二楼
5205
747
北区第五教学楼二楼
5207
748
北区第五教学楼二楼
5209
749
北区第五教学楼二楼
5211
750
北区第五教学楼二楼
5213
人教版八年级第一学期期中数学试卷及答案六

人教版八年级第一学期期中数学试卷及答案一、选择题(3分×10=30分)1.下列各数中,无理数是()A.B.C.D.3.14159262.满足下列条件的△ABC不是直角三角形的是()A.∠A:∠B:∠C=2:3:4B.a2+b2﹣c2=0C.∠A﹣∠B=∠C D.BC=3,AC=4,AB=53.下列计算正确的是()A.=±4B.=8C.D.=34.如图所示的是一所学校的平面示意图,若用(3,2)表示教学楼,(4,0)表示旗杆,则实验楼的位置可表示成()A.(1,﹣2)B.(﹣2,1)C.(﹣3,2)D.(2,﹣3)5.下列所描述的四个变化过程中,变量之间的关系不能看成函数关系的是()A.小车在下滑过程中下滑时间t和支撑物的高度h之间的关系B.三角形一边上的高一定时,三角形的面积s与这边的长度x之间的关系C.骆驼某日的体温T随着这天时间t的变化曲线所确定的温度T与时间t的关系D.一个正数x的平方根是y,y随着这个数x的变化而变化,y与x之间的关系6.利用估算判断大小正确的是()A.<3.8B.>2C.﹣3>0D.7.对于一次函数y=﹣2x+4,下列结论正确的有()①函数的图象不经过第三象限;②函数的图象与x轴的交点坐标是(2,0);③函数的图象向下平移4个单位长度得y=﹣2x的图象;④若两点A(1,y1),B(3,y2)在该函数图象上,则y1<y2.A.1个B.2个C.3个D.4个8.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A'D为1.5米,则小巷的宽为()A.2.5米B.2.6米C.2.7米D.2.8米9.在同一平面直角坐标系中,函数y=kx与y=x+3﹣k的图象不可能是()A.B.C.D.10.如图,一个粒子在第一象限内及x轴、y轴上运动,在第一分钟,它从原点运动到点(1,0),第二分钟,它从点(1,0)运动到点(1,1),而后它接着按图中箭头所示在与x轴,y轴平行的方向上来回运动,且每分钟移动1个单位长度,那么在第2022分钟时,这个粒子所在位置的坐标是()A.(44,4)B.(44,3)C.(44,2)D.(44,1)二、填空题(每小题3分,共15分)11.的算术平方根是.12.若x,y为实数,且满足|x﹣3|+=0,则()2022的值是.13.如图,△ABC是直角三角形,点C表示﹣2,且AC=3,AB=1,若以点C为圆心,CB为半径画弧交数轴于点M,则A,M两点间的距离为.14.已知点A的坐标为(1,2),直线AB∥x轴,且AB=5,则点B坐标为.15.如图,直线AB的解析式为y=﹣x+b分别与x,y轴交于A,B两点,点A的坐标为(3,0),过点B的直线交x轴负半轴于点C,且OB:OC=3:1.在x轴上方存在点D,使以点A,B,D为顶点的三角形与△ABC全等,则点D的坐标为.三、解答题(7题,共75分)16.(10分)计算:(1);(2).17.(9分)已知,点A(﹣2,1)和点B(4,3).(1)在坐标平面内描出点A和点B的位置.(2)连接AB并计算AB的长度.(3)若点C(a﹣1,2b+3)与点B(4,3)关于x轴对称,求a﹣b的值.18.(10分)勾股定理是初中数学学习的重要定理之一,这个定理的验证方法有很多,你能验证它吗?请你根据所给图形选择一种方法画出验证勾股定理的方法并写出验证过程.19.(10分)我们知道,是一个无理数,将这个数减去整数部分,差就是小数部分,即的整数部分是1,小数部分是﹣1,请回答以下问题:(1)的小数部分是,5﹣的小数部分是.(2)若a是的整数部分,b是的小数部分,求a+b﹣+1的平方根.20.(10分)如图,AC是将长方形纸片ABCD沿对角线BD折叠后得到的.(1)试判断三角形BDE的形状,并说明理由;(2)若CD=8,BC=16,求三角形BDE的面积.21.(11分)请根据函数相关知识,对函数y=2|x﹣3|﹣1的图象与性质进行探究,并解决相关问题.①列表;②描点;③连线.x…01234567…y…5m1﹣113n7…(1)表格中:m=,n=.(2)在直角坐标系中画出该函数图象.(3)观察图象:①根据函数图象可得,该函数的最小值是;②观察函数y=2|x﹣3|﹣1的图象,写出该图象的一条性质.③进一步探究函数图象发现:函数图象与x轴有个交点,所以对应的方程2|x﹣3|﹣1=0有个解.22.(15分)甲、乙两人参加从A地到B地的长跑比赛,两人在比赛时所跑的路程y(米)与时间x(分钟)之间的函数关系如图所示,请你根据图象,回答下列问题:(1)先到达终点(填“甲”或“乙”);(2)根据图象,求出甲的函数表达式;(3)求何时甲乙相遇?(4)根据图象,直接写出何时甲与乙相距250米.参考答案与试题解析一、选择题(3分×10=30分)1.下列各数中,无理数是()A.B.C.D.3.1415926【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.据此解答即可.【解答】解:是有理数;=4是有理数;是无理数,3.1415926是有理数.故选:C.2.满足下列条件的△ABC不是直角三角形的是()A.∠A:∠B:∠C=2:3:4B.a2+b2﹣c2=0C.∠A﹣∠B=∠C D.BC=3,AC=4,AB=5【分析】根据勾股定理的逆定理,三角形内角和定理,进行逐一判断即可.【解答】解:∵∠A:∠B:∠C=2:3:4,∠A+∠B+∠C=180°,∴∠C=180°×=80°,∴△ABC不是直角三角形,故选项A符合题意;∵a2+b2﹣c2=0,∴a2+b2=c2,∴△ABC是直角三角形,故选项B不符合题意;∵∠A﹣∠B=∠C,∴∠A=∠C+∠B,∵∠A+∠B+∠C=180°,∴2∠A=180°,∴∠A=90°,∴△ABC是直角三角形,故选项C不符合题意;∵BC=3,AC=4,AB=5,∴BC2+AC2=32+42=25,AB2=52=25,∴BC2+AC2=AB2,∴△ABC是直角三角形,故选项D不符合题意;综上所述,符合题意的选项为A.故选:A.3.下列计算正确的是()A.=±4B.=8C.D.=3【分析】A、C、D直接根据算术平方根的性质解答即可;B根据立方根的概念解答即可.【解答】解:=4,故A选项不合题意;=4,故B选项不合题意;=,故C选项符合题意;﹣无意义,故D选项不合题意.故选:C.4.如图所示的是一所学校的平面示意图,若用(3,2)表示教学楼,(4,0)表示旗杆,则实验楼的位置可表示成()A.(1,﹣2)B.(﹣2,1)C.(﹣3,2)D.(2,﹣3)【分析】直接利用已知点坐标得出原点位置进而得出答案.【解答】解:如图所示:实验楼的位置可表示成(2,﹣3).故选:D.5.下列所描述的四个变化过程中,变量之间的关系不能看成函数关系的是()A.小车在下滑过程中下滑时间t和支撑物的高度h之间的关系B.三角形一边上的高一定时,三角形的面积s与这边的长度x之间的关系C.骆驼某日的体温T随着这天时间t的变化曲线所确定的温度T与时间t的关系D.一个正数x的平方根是y,y随着这个数x的变化而变化,y与x之间的关系【分析】利用函数的定义:设在一个变化过程中有两个变量x与y,对于x的每一个确定的值,y都有唯一的值与其对应,那么就说y是x的函数,x是自变量,进而得出答案.【解答】解:A、小车下滑过程中下滑时间t与支撑物高度h之间的关系,两个变量之间的关系被看成函数关系,故此选项不符合题意;B、三角形一边上的高一定时,三角形面积S与该边的长度x之间的关系,两个变量之间的关系被看成函数关系,故此选项不符合题意;C、骆驼某日体温随时间的变化曲线所确定的温度与时间的关系,两个变量之间的关系被看成函数关系,故此选项不符合题意;D、y表示一个正数x的平方根,x对应两个y的值,两个变量之间的关系不能看成函数关系,故此选项符合题意.故选:D.6.利用估算判断大小正确的是()A.<3.8B.>2C.﹣3>0D.【分析】求出3.82=14.44,再判断选项A即可;求出2=,再判断选项B即可;估算出2<3,再判断选项C即可;先求出﹣,再比较大小即可.【解答】解:A.∵3.82=14.44<15,∴>3.8,故本选项不符合题意;B.∵2==,∴<2,故本选项不符合题意;C.∵2<3,∴﹣3<0,故本选项不符合题意;D.∵﹣==,∵<9,∴﹣<0,∴<,故本选项符合题意;故选:D.7.对于一次函数y=﹣2x+4,下列结论正确的有()①函数的图象不经过第三象限;②函数的图象与x轴的交点坐标是(2,0);③函数的图象向下平移4个单位长度得y=﹣2x的图象;④若两点A(1,y1),B(3,y2)在该函数图象上,则y1<y2.A.1个B.2个C.3个D.4个【分析】根据一次函数的性质k与b的符号,来判断是否正确.【解答】解:由y=﹣2x+4可知k=﹣2<0,b=4>0,∴直线过一,二,四象限,故①正确;当x=2时,y=﹣2×2+4=0,故②正确;直线y=﹣2x+4向下平移4个单位长度得,y=﹣2x+4﹣4得y=﹣2x,故③正确;∵k=﹣2<0,∴y随x的增大而减小,故④错.故选:C.8.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A'D为1.5米,则小巷的宽为()A.2.5米B.2.6米C.2.7米D.2.8米【分析】在Rt△ABC中,利用勾股定理计算出AB长,再在Rt△A′BD中利用勾股定理计算出BD长,然后可得CD的长.【解答】解:在Rt△ABC中,AB===2.5(米),∴A′B=2.5米,在Rt△A′BD中,BD===2(米),∴BC+BD=2+0.7=2.7(米),故选:C.9.在同一平面直角坐标系中,函数y=kx与y=x+3﹣k的图象不可能是()A.B.C.D.【分析】根据题目中的函数解析式和一次函数的性质、正比例函数的性质,可以判断哪个选项正确,本题得以解决.【解答】解:当k>3时,函数y=kx的图象经过第一、三象限且过原点,y=x+3﹣k的图象经过第一、三、四象限,当0<k<3时,函数y=kx的图象经过第一、三象限且过原点,y=x+3﹣k的图象经过第一、二、三象限;当k<0时,函数y=kx的图象经过第二、四象限且过原点,y=x+3﹣k的图象经过第一、二、三象限,由上可得,选项A不可能;故选:A.10.如图,一个粒子在第一象限内及x轴、y轴上运动,在第一分钟,它从原点运动到点(1,0),第二分钟,它从点(1,0)运动到点(1,1),而后它接着按图中箭头所示在与x轴,y轴平行的方向上来回运动,且每分钟移动1个单位长度,那么在第2022分钟时,这个粒子所在位置的坐标是()A.(44,4)B.(44,3)C.(44,2)D.(44,1)【分析】找出粒子运动规律和坐标之间的关系即可解题.【解答】解:由题知(0,0)表示粒子运动了0分钟,(1,1)表示粒子运动了2=1×2(分钟),将向左运动,(2,2)表示粒子运动了6=2×3(分钟),将向下运动,(3,3)表示粒子运动了12=3×4(分钟),将向左运动,…,于是会出现:(44,44)点粒子运动了44×45=1980(分钟),此时粒子将会向下运动,∴在第2022分钟时,粒子又向下移动了2022﹣1980=42个单位长度,∴粒子的位置为(44,2),故选:C.二、填空题(每小题3分,共15分)11.的算术平方根是.【分析】根据算术平方根的定义进行化简,再根据算术平方根的定义求解即可.【解答】解:∵52=25,∴=5,∴的算术平方根是.故答案为:.12.若x,y为实数,且满足|x﹣3|+=0,则()2022的值是1.【分析】利用非负数的性质求出x,y的值,代入计算.【解答】解:∵|x﹣3|+=0,∴x﹣3=0,x+y﹣6=0,∴x=3,y=3.∴()2022==1.故答案为:1.13.如图,△ABC是直角三角形,点C表示﹣2,且AC=3,AB=1,若以点C为圆心,CB为半径画弧交数轴于点M,则A,M两点间的距离为﹣3.【分析】AC=3,AB=1,根据勾股定理,求出BC的长,AM=CM,进而可得AM的距离.【解答】解:根据勾股定理可得,BC===,∵CM=BC=,AC=3,∴AM=CM﹣AC=﹣3,∴A,M两点间的距离为﹣3.故答案为:﹣3.14.已知点A的坐标为(1,2),直线AB∥x轴,且AB=5,则点B坐标为(﹣4,2)或(6,2).【分析】根据平行于x轴的直线是上的点的纵坐标相等求出点B的纵坐标,再分点B在点A的左边与右边两种情况求出点B的横坐标,即可得解.【解答】解:∵AB∥x轴,点A的坐标为(1,2),∴点B的纵坐标为2,∵AB=5,∴点B在点A的左边时,横坐标为1﹣5=﹣4,点B在点A的右边时,横坐标为1+5=6,∴点B的坐标为(﹣4,2)或(6,2).故答案为(﹣4,2)或(6,2).15.如图,直线AB的解析式为y=﹣x+b分别与x,y轴交于A,B两点,点A的坐标为(3,0),过点B的直线交x轴负半轴于点C,且OB:OC=3:1.在x轴上方存在点D,使以点A,B,D为顶点的三角形与△ABC全等,则点D的坐标为(4,3)或(3,4).【分析】求出B(0,3)、点C(﹣1,0),分当BD平行x轴、BD不平行x轴两种情况,分别求解即可.【解答】解:将点A的坐标代入函数表达式得:0=﹣3+b,解得:b=3,故直线AB的表达式为:y=﹣x+3,则点B(0,3),OB:OC=3:1,则OC=1,即点C(﹣1,0);①如图,当BD平行x轴时,点A,B,D为顶点的三角形与△ABC全等,则四边形BDAC为平行四边形,则BD=AC=1+3=4,则点D(4,3),②当BD不平行x轴时,则S△ABD=S△ABD′,则点D、D′到AB的距离相等,则直线DD′∥AB,设:直线DD′的表达式为:y=﹣x+n,将点D的坐标代入上式并解得:n=7,直线DD′的表达式为:y=﹣x+7,设点D′(n,7﹣n),A,B,D为顶点的三角形与△ABC全等,则BD′=BC==,解得:n=3,故点D′(3,4);故答案为:(4,3)或(3,4).三、解答题(7题,共75分)16.(10分)计算:(1);(2).【分析】(1)根据二次根式的运算法则进行即可;(2)注意的是完全平方式的展开式是三项.【解答】解:(1)﹣4=﹣4=10﹣4,(2)×+6=(3﹣4+4)×+2=(7﹣4)×2+2=14﹣24+2=16﹣24.17.(9分)已知,点A(﹣2,1)和点B(4,3).(1)在坐标平面内描出点A和点B的位置.(2)连接AB并计算AB的长度.(3)若点C(a﹣1,2b+3)与点B(4,3)关于x轴对称,求a﹣b的值.【分析】(1)根据点的坐标在坐标平面内描出点A和点B即可;(2)根据勾股定理即可得到结论;(3)根据轴对称的性质求出a、b的值即可.【解答】解:(1)如图所示;(2)AB==2;(3)∵点C(a﹣1,2b+3)与点B(4,3)关于x轴对称,∴a﹣1=4,2b+3=﹣3,∴a=5,b=﹣3,∴a﹣b=8.18.(10分)勾股定理是初中数学学习的重要定理之一,这个定理的验证方法有很多,你能验证它吗?请你根据所给图形选择一种方法画出验证勾股定理的方法并写出验证过程.【分析】根据正方形的面积等于四个直角三角形的面积与正方形面积的即可得出结论【解答】解:则由图形可知:(a+b)2﹣4×ab=a2+b2+2ab﹣4×ab=c2,整理得:a2+b2=c2.答案不唯一.19.(10分)我们知道,是一个无理数,将这个数减去整数部分,差就是小数部分,即的整数部分是1,小数部分是﹣1,请回答以下问题:(1)的小数部分是﹣3,5﹣的小数部分是4﹣.(2)若a是的整数部分,b是的小数部分,求a+b﹣+1的平方根.【分析】(1)估算无理数的近似数,减去整数部分,即为小数部分.(2)估算,的整数部分,得到a,b代入代数式求值.【解答】解:(1)∵3<<4,∴整数部分为3,小数部分为﹣3;∵3<<4,∴5﹣的整数部分为1,小数部分为5﹣﹣1=4﹣;故答案为:﹣3;4﹣.(2)∵9<<10,∴的整数部分为9,即a=9;∵1<<2,∴的整数部分为1,小数部分为﹣1,即b=﹣1;a+b﹣+1=9+(﹣1)﹣+1=9+﹣1﹣+1=9.∵±=±3.∴a+b﹣+1的平方根为±3.20.(10分)如图,AC是将长方形纸片ABCD沿对角线BD折叠后得到的.(1)试判断三角形BDE的形状,并说明理由;(2)若CD=8,BC=16,求三角形BDE的面积.【分析】(1)由折叠的性质可得DC=DC',∠C=∠C'=90°,∠CBD=∠C'BD,由平行线的性质可得∠EDB =∠CBD=∠EBD,可得结论;(2)由勾股定理可求DE的长,由三角形的面积公式可求解.【解答】解:(1)△EBD为等腰三角形,理由如下:由题意得:△BCD≌△BC'D,∴DC=DC',∠C=∠C'=90°,∠CBD=∠C'BD,又∵四边形ABCD为长方形,∴DE∥BC,∴∠EDB=∠CBD,∴∠EDB=∠EBD,∴EB=ED,∴△EBD为等腰三角形;(2)∵四边形ABCD是长方形,∴AD=BC=16,AB=CD=8,∴∠A=90°,设DE=BE=x,则AE=16﹣x,在Rt△ABE中,BE2=AE2+AB2,∴x2=82+(16﹣x)2,∴x=10,∴DE=10,∴.21.(11分)请根据函数相关知识,对函数y=2|x﹣3|﹣1的图象与性质进行探究,并解决相关问题.①列表;②描点;③连线.x…01234567…y…5m1﹣113n7…(1)表格中:m=3,n=5.(2)在直角坐标系中画出该函数图象.(3)观察图象:①根据函数图象可得,该函数的最小值是﹣1;②观察函数y=2|x﹣3|﹣1的图象,写出该图象的一条性质.③进一步探究函数图象发现:函数图象与x轴有2个交点,所以对应的方程2|x﹣3|﹣1=0有2个解.【分析】(1)分别将x=1,x=6代入函数的解析式,即可求m、n的值;(2)利用描点法画出函数图象即可;(3)①通过观察图象直接可求解;②通过观察函数的图象写出符合函数图象的性质即可;③通过观察图象直接求解即可.【解答】解:(1)当x=1时,y=2|1﹣3|﹣1=3,当x=6时,y=2|6﹣3|﹣1=5,故答案为:3,5;(2)(3)①当x=3时,y有最小值﹣1,故答案为:﹣1;②当x≥3时,y随x值的增大而增大;当x≤3时,y最x值的增大而减小;③函数图象与x轴有2个交点,2|x﹣3|﹣1=0有两个解,分别是x=或x=,故答案为:2,2.22.(15分)甲、乙两人参加从A地到B地的长跑比赛,两人在比赛时所跑的路程y(米)与时间x(分钟)之间的函数关系如图所示,请你根据图象,回答下列问题:(1)乙先到达终点(填“甲”或“乙”);(2)根据图象,求出甲的函数表达式;(3)求何时甲乙相遇?(4)根据图象,直接写出何时甲与乙相距250米.【分析】(1)依据函数图象可得到两人跑完全程所用的时间,从而可知道谁先到达终点;(2)甲的图像是正比例函数,直线经过点(20,5000),可求出解析式;(3)当10<x<16 时,甲乙两相遇,求得乙的路程与时间的函数关系式,再求得两个函数图象交点坐标即可;(4)根据题意列方程解答即可.【解答】解:(1)由函数图象可知甲跑完全程需要20分钟,乙跑完全程需要16分钟,所以乙先到达终点,故答案为:乙;(2)设甲跑的路程y(米)与时间x(分钟)之间的函数关系式为y=kx,经过点(20,5000)根据图象,可得y=x=250x,∴甲的函数表达式为y=250x;(3)设甲乙相遇后(即10<x<16 ),乙跑的路程y(米)与时间x(分钟)之间的函数关系式为:y=kx+b,经过点(10,2000),(16,5000),联立方程可得:,解得,∴y=500x﹣3000,再联立方程:,解得:,∴甲与乙在12分钟时相遇;(4)设此时起跑了x分钟,根据题意得或250x=3000﹣250,解得x=5或x=11.∴在甲、乙相遇之前,5分钟或11分钟时甲与乙相距250米.。
提升卷-【难度分层期中卷】2022-2023学年七年级地理上学期期中测试卷(湘教版)(解析版)

【难度分层·期中卷】2022-2023学年七年级地理上学期期中测试卷(湘教版)提升卷【考试范围:七年级上册第一章至第二章】一、单项选择题:本题共25小题,每小题2分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
阅读常德市某中学平面分布图(下图),结合所学知识完成下面1-3题。
1.贝贝同学下课后从主教学楼前往食堂吃饭,前进的主要方向是()A.向东B.向南C.向西D.向北2.A为学校艺术中心,玲玲发现春分日琴房①上午洒满阳光,琴房②正午阳光普照,琴房③下午阳光比其他两处更多,造成这种现象的原因是()A.地球自转B.地球公转C.地球形状D.地球大小3.主教学楼下建有地下停车场,近年来学校为了保障学生安全,实现人车分流,车辆从④处简易门出入,据图测算从简易门到地下停车场入口的距离约为()A.200米B.300米C.400米D.500米【答案】1.D2.A3.B【解析】1.读图可知,贝贝同学下课后从主教学楼前往食堂吃饭,根据图中的指向标,前进的主要方向是向北,D正确,ABC错误,故选D2.A为学校艺术中心,玲玲发现春分日琴房①上午洒满阳光,琴房②正午阳光普照,琴房③下午阳光比其他两处更多,造成这种现象的原因是由于地球自转产生的日月星辰的东升西落,A正确。
跟地球的公转、形状和大小无关,BCD错误,故选A。
3.主教学楼下建有地下停车场,近年来学校为了保障学生安全,实现人车分流,车辆从④处简易门出入,据图中的比例尺,图中1厘米代表实际距离150米,测算从简易门到地下停车场入口的图上距离为2厘米,实际距离约为300米,B正确,ACD错误,故选B。
4.2022年北京冬奥会花样滑冰比赛在首都体育馆举行。
家住北京的丽丽要去现场观看比赛,如需查阅地图,可参考()A.北京地形图B.中国人口分布图C.中国气候类型分布图D.北京城市交通图【答案】D【详解】在庞大的地图家族中,有自然地图和社会经济地图。
人教新课标三年级下册数学课件-1位置与方向(一)简单的平面示意图 (共21张PPT)

司南
古代罗盘
指南针
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子 像桃子一样甜蜜。21.3.1321.3.13Saturday, March 13, 2021
• 10、人的志向通常和他们的能力成正比例。13:48:4513:48:4513:483/13/2021 1:48:45 PM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。21.3.1313:48:4513:48Mar-2113-Mar-21 • 12、越是无能的人,越喜欢挑剔别人的错儿。13:48:4513:48:4513:48Saturday, March 13, 2021 • 13、志不立,天下无可成之事。21.3.1321.3.1313:48:4513:48:45March 13, 2021
2.辨认地图或平面图上的方向:根据“上北下南,左西右东” 确定方向。
3.根据确定点观察方向:首先看确定点和要观察点 的范围是在左右方向(即东西方向),还是上下 方向(即南北方向),再确定具体的方向。
1
(1)邮局在公园的( 东 )面,学校在公园的(北)面。 (2)小娟家在学校的(南)面,小娟家在小峰家的(东)面。 (3)体育馆在博物馆的(北)面,体育馆在学校的(西)面。
17、一个人如果不到最高峰,他就没有片刻的安宁,他也就不会感到生命的恬静和光荣。下午1时48分45秒下午1时48分13:48:452
1.3.13
I wouldn't have known my way about.
。2021年3月13日星期六下午1时48分45秒13:48:4521.3.13
• 15、会当凌绝顶,一览众山小。2021年3月下午1时48分21.3.1313:48March 13, 2021
【新课标】三年级上册道德与法治第4课《说说我们的学校》教案教学设计(第二课时)

三年级上册道德与法治第4课《说说我们的学校》第二课时教学设计都十分的熟悉。
在学校生活中,我们会遇到各种各样的事情。
你知道遇到下面的问题后,该找哪个部门吗?2.图片+文本学习:遇到困难怎么办(1)我刚当上班级小记者,写完的广播稿送到哪里去呢?(2)应该交给广播站的老师3.图片+文本学习:遇到困难怎么办(1)教室的门锁坏了,找谁来修理呢?(2)教室门锁坏了,可以找后勤部的负责老师来维修。
4.文本学习:遇到困难怎么办(1)如果同学手指弄破了,到哪里去包扎呢?(2)对学校午餐有好建议,该到哪里反映呢?(3)我想借几本书看,去哪里借?(4)我在操场上捡到一件外套,该交给谁?……医务室、后勤部、图书馆、广播站5.文本学习:你有没有遇到问题却不知道找哪个部门的情况?6.表格+文本学习:你是如何应对的呢?一起交流一下。
(1)我遇到的问题(2)我是这样做的教学环节二:解决困难有办法1.图片+文本学习:知道怎样才能解决问题吗?有经思考问题回答问题指名回答观看图片学习文本了解文本感悟文本观看图片学习文本了解文本感悟文本学习文本了解文本思考回答指名回答补充回答学习文本思考回答学习文本了解文本思考文本独立填写交流汇报指名汇报学习文本了解文本思考文本独立填写交流汇报指名汇报观看图片思考在学校遇到事情后该找哪个部门处理。
这一页两张图是两个具体的情境。
主持人的提问是引导学生说一说自己的经历,为过渡到下一教学内容做好铺垫。
教学不必拘泥于教材,可以根据本班最近发生的具体事例让学生说说可以找什么部门解决。
如果学生确实有遇到问题不知道找哪个部门解决的经历,可以组织其他同学一起出主意,也可以启发学生思考:怎样才能找到合适的部门?图文说明教学中验的同学介绍一下吧。
(1)办公室门口都挂着牌子,要做会观察的有心人。
(2)学会看校园示意图或指示牌很重要。
(3)询问老师或同学,他们都乐意帮忙。
2.文本学习:我们来调查一下,学校有哪些部门,这些部门帮我们解决哪些问题。
三年级下册数学课件1.2位置与方向《简单的平面示意图》人教版

巩 三、按要求做一做。
固
北
练 科技楼
操场
生物园
习
食堂
体育馆
宿舍楼
办公楼
教学楼
图书馆
巩 固
四、根据生活经验填方向。
练
习
树的年轮较密的一
边向着(北 )面,较疏 的一边向着(南 )面。
谢谢观看
练
习 (1)天安门城楼在国旗的北面。
天安门城楼
(2)人民大会堂在人民英雄纪念 碑的西面。
(3)中国国家博物馆在人民英雄 纪念碑的东面。
人民大会堂
ቤተ መጻሕፍቲ ባይዱ
中国国家 博物馆
巩 固 二、想一想,填一填。 练 习 乐乐家在学校的( 东 )面。
美美家在学校的( 西 )面。
邮局在科技馆的( 北 )面。 美美家在乐乐家的(西 )面。
以大门为观测点
大门在教学楼的( 南 )面。
以教学楼为观测点
发 现
操场怎么在图书馆 的西面?又在体育馆 的东面?
你还有什 么发现吗?
参照物体不同,描 述的方位会有不同。
教学楼在大门的北面, 大门在教学楼的南面。
小
结
根据确定点观察方向:先确 定观测点,然后画十字交叉确
定周围事物在观测点的什么方
向。
巩 固 一、 根据下面的描述标明天安门地区示意图中的建筑物。
位置与方向(一)
简单的平面示意图
复 填一填
习
新
知
傍晚,两人相约看落
日,此时,他们的前面
是( 西),后面是( ),
左面东是( ),右面是
( 南)。
北
复
习
新 知
面东背西,左北右南;
关于教学楼设计说明

关于教学楼设计说明教学楼设计说明1 一、目的要求为配合《房屋建筑学》第一至第四章理论教学,进行一次建筑方案设计,培养学生综合运用建筑设计原理去分析问题和解决问题,从中了解方案设计的方法和步骤。
二、设计条件1.修建地点:本建筑位于中小城市或工矿区新建的职工住宅区内,地段情况可参考提供的地形图,亦可自己另选地段。
2.房间名称及使用面积3.建筑标准:(1)建筑层数:1~4层(2)层高:教学用房3.6~3.9m办公用房3.0~3.4m(3)结构:混合结构或钢筋混凝土框架结构(4)门窗:木门、铝合金窗(或塑钢窗)(5)装修:根据当地社会经济状况,自行确定。
(6)走道宽(轴线尺寸):2.4~3.0m(中间走道),1.8~2.1m(单面走道)。
(7)采光:教室窗地比为1/4,其他用房为1/6~1/8。
(8)卫生:设室内厕所(蹲式大便器、小便槽或小便斗),数量按男女学生各半计算。
男厕所:40~50人一个大便器,两个小便斗(或1m长小便槽)。
女厕所:20~25人一个大便器。
三、设计内容及深度本设计按方案设计深度要求进行,2#图纸两张。
完成下列内容:1.平面图:各层平面,比例1:100~1:200(1)底层各入口要画出踏步、花池、台阶等。
(2)尺寸标注为两道,即总尺寸与轴线尺寸。
(3)确定门窗位置、大小(按比例画,不注尺寸)及门的开启方向。
(4)楼梯要按比例尺寸画出梯段、平台及踏步,并标出上下行箭头。
(5)标出剖面线及编号。
(6)注明房间名称。
(7)标图名及比例。
2.立面图:入口立面及侧立面,比例1:100~1:200。
(1)外轮廓线画中粗线,地坪线画粗实线,其余画细实线。
(2)注明图名及比例。
3.剖面图:1~2个剖面,比例1:100。
(1)剖切部分用粗实线,看见部分用细实线;地坪为粗实线,并表示出室内外地坪高差。
(2)尺寸标两道,即各层层高及建筑总高。
(3)标高:标注各层标高,室内外标高。
(4)标图名及比例。
4.主要技术经济指标:总建筑面积、平均建筑面积(校舍总面积/学生总人数)、平面系数K(使用面积/建筑面积)等。
房屋建筑学课程设计某中学教学楼方案设计

《房屋建筑学》课程设计题目某中学教学楼方案设计系别土木工程学院专业土木工程班级10级土木7班学号110206010640学生姓名刘八平起讫日期2012.5.21~2012.5. 25指导教师刘汉职称助教教研室主任吉中亮日期2012.5.25江西科技学院教务处印制目录1课程设计任务书 (1)1.1 题目 (1)1.2 设计目的及要求 (1)1.3 设计条件及内容 (1)1.4 设计成果 (1)1.5 图纸要求 (2)1.5.1 平面图 (2)1.5.2 立面图 (2)1.5.3 剖面图 (2)1.5.4 屋顶平面图 (2)1.5.5 详图 (2)2、施工图设计方案 (2)2.1 设计总说明 (2)2.1.1 工程概述 (2)2.1.2 建筑部分 (3)2.1.2.1 标高 (3)2.1.2.2 建筑做法 (3)2.1.2.3 室外工程 (3)2.1.3 其他 (3)2.2 图纸目录 (3)2.3 门窗表 (4)3、建筑设计及计算 (4)3.1 建筑总平面设计 (4)3.2 建筑方案设计 (4)3.3 建筑平面设计及计算 (5)3.3.1 建筑平面设计 (5)3.3.2 建筑平面计算 (5)3.4 建筑立面设计及计算 (5)3.4.1 建筑立面设计 (5)3.4.2 建筑立面计算 (5)3.5 建筑剖面设计 (6)3.5.1 建筑剖面设计 (6)3.6 卫生间及辅助用房设计 (6)3.6.1 卫生间详图设计 (6)3.6.2 走廊、楼梯、大厅 (6)3.6.3 楼梯详图尺度设计及计算 (6)3.7 屋顶设计 (6)4、参考文献 (6)5、附录 (7)附表一教学楼所需房间名称及所需面积 (7)附表二教学楼各房间尺寸设计和面积表 (7)附表三门窗表 (8)一、课程设计任务书1.1 题目26班某中学教学楼设计1.2 目的和要求为了巩固《房屋建筑学》所学知识,培养学生运用建筑设计原理去分析和解决实际问题的能力,从中学会建筑设计的方法和步骤,并通过设计提高学生绘图的基本功底。
小学数学三年级下册简单的平面图
教学楼在操场的( )面北 图书馆在体育馆的( )面 东 大门在教学楼的( )面南
教学楼在大门的( )面北 操场在图书馆的( )面西 操场在体育馆的( )面东
二、探究新知
4. 我来当导游。
天安门城楼
(1)根据描述标明天安门地区 示意图中的建筑物。
人民大会 堂
中国国家 博物馆
(2)用所学的东、南、西、北知 识和了解的天安门地区建筑物知识, 当导游进行介绍。
向哦!
西
东
南
如果要将图中的操场、图书馆、大门、体育馆和教学楼用示意图表 示出来,该怎么绘制?
二、探究新知
2.感悟平面图按“上北下南,左西右东”绘制的必要性。
图书馆 东
体育馆
教
学
操场
楼
大 门
体育馆
大 门
操场
图书馆
大门
图 书 操场 馆
教学楼
南
体 育 馆
教学楼
体
育
操场
馆
大门
这四幅示意图有什么相同点和不同点?
四、课堂小结
这节课你有什么收获? 怎样在地图上辩认东、西、南、北?
第一单元 位置与方向
简单的平面图
初稿:项 萍(安徽省黄山市黄山区甘棠小学) 修改:高娟娟(安徽省黄山市教科院) 统稿:齐胜利(安徽省黄山市黄山区教研室)
一、复习导入 北
西
你知道校园东、南、西、北四个方向各有 东
什么?
南
你能说一说图中的标志物所在 的方向吗?
二、探究新知
1.用示意图表示例1情境图中的北标志物。 要注意建筑物所在的实际方
二、探究新知
3.认识平面图上的方向。
大 体门 育在馆操在场操的场什的么什方么向方?向? 示意图中,大体门育在馆操在场操的 场下 的面 左, 面就 ,是 就在 是操 在场 操 的场南的面西。面。
西安某大学教学楼设计cad全套建施图

- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
说明:1.机房2间共91台电脑;阅览室(共藏本) 2.第五层为女生宿舍楼层 3.各行政部门办公室共13间 4.本栋楼建筑面积为m2
说明:1本栋楼共有教室21间;教师办公室3间;学生生活超市1间 2.本栋楼建筑面积为 m 2
说明:1.本栋楼共五层,每层六间宿舍,每间宿舍住6人/间;其中105号宿舍住8人/间;共住190人。
2.本栋楼共建筑面积为:M2
说明:1.本栋楼层共五层,每层21间宿舍,共105间;其中6人间15*5=75间;8人间计5*3=15间;10人间计5*3=15间;共可容纳人数为720人
2.本栋楼建筑面积为:M2
汽车实训中心一楼示意图
学生食堂示意图
2.食堂餐位共个,可同时容纳人就餐;。
