5.2 刚体定轴转动定律
合集下载
5-刚体的定轴转动

L1 L2
刚体定轴转动的角动量 L=?
z
v
ri mi
O
刚体 定轴
L Li mirivi
m iri(ri) ( miri2)
J M=0的原因,可能
1)F=0(不受外力) 2)外力作用于转轴上 3)外力作用线通过转轴
4)外力作用线与转轴平行
刚体定轴转动的角动量守恒
L1 L2
J11J22
位置,求它由此下摆角时的角速度。
解:如图建立坐标
x
杆受到的重力矩为:
O
M = gxd g m xdm
X
dm
据质心x定 d= m 义 mCx MmgxC
xc
1l 2
cos
M1mgclos
2
dmg
MJJdJ d d J d M dJd
dt d dt d
0 1 2mc go lds 0 Jd
mglsin
端点 o 且与桌面垂直的固定光滑轴转动,另有 一水平运动的质量 m2为的小滑块,从侧面垂直 与杆的另一端 A 相碰撞,设碰撞时间极短,已知 小滑块在碰撞前后的速度分别为 v1 和 v2 ,方 向如图所示,求碰撞后从细杆开始转动到停止 转动过程所需时间,(已知杆绕点 o 的转动惯 量 J= ml2/ 3 )
dLR J2J0m0d2 其中 Jo 12moR2
J J1J2 1 3m LL 21 2m oR 2m o(LR )2
2.对薄平板刚体的正交轴定理
z
Jz miri2
yi
xi
ri
y
m i(x2y2) m ix 2 m iy 2
x
Δmi
Jz JxJy
z
应用
例:已知圆盘
大学物理第5章刚体的定轴转动

d ctdt
对上式两边积分得
d c td t
0 0
t
1 2 ct 2
2 2 600π π 3 rad s 由给定条件, c 2 t 300 2 75
d π 2 由角速度的定义,则任意 t 时刻的角速度可写为: d t 150
得到: 转子转数:
A M d E K
a b
动能定理
动量定理
A F ds E K
动能定理 角动量定理 角动量 守恒
t 0Fdt P
t
动量守恒
F 0, P 0
t 0 M z dt Lz
t
M 0, L 0
§5.1 刚体、刚体运动
一、一般运动 二、刚体的定轴转动 三、解决刚体动力学问题的一般方法
基本方法: 加
质点系运动定理 刚体特性 平动:动量定理
刚体定轴转动的 动能定理 角动量定理
F mac
可以解决刚体的一般运动(平动加转动)
一、一般运动
1. 刚体 特殊的质点系, 形状和体积不变化 —— 理想化模型 在力作用下,组成物体的所有质点间的距离始终保持不变 2. 自由度 确定物体的位置所需要的独立坐标数 —— 物体的自由度数 z
刚体平面运动可看做刚体的平动与定轴转动的合成。 例如:车轮的滚动可以看成车轮随轮 轴的平动与绕轮轴的转动的组合。 描述刚体平面运动的自由度:3个
定点转动 刚体运动时,刚体上的一点固定不动,刚体绕过定点的一 瞬时转轴的转动,称作定点转动。
描述定点转动的自由度:3个
刚体的一般运动 质心的平动
+
绕质心的转动
z
描述刚体绕定轴转动的角量: 角坐标
大学物理 刚体的定轴转动

⑶ t =6 ·0 s 时转过的角度为
6s
0
6s
d t 0
0(1et)dt
0 [te t]6 0 s 9 [6 ( 2 0 0) 5 (0 2 )]369rad
则 t =6 ·0 s
时电动机转过的圈数
N 587圈 2
5.2 5.4 刚体的转动定律及应用
5.2.1力对转轴的力矩
转轴
§5.1 刚体的运动的描述 §5.2 刚体定轴转动 §5.3 转动惯量的计算 §5.4 转动定律应用 §5.5 角动量守恒 §5.6 定轴转动中的功和能
5.1 刚体的运动的描述
•刚体(rigid body)
任何情况下形状和体积都不改变的物体(理想化模型)。 刚体是特殊的质点系。 刚体可以看作是由许多质点组成,每一个质点叫做 刚体的一个质元,刚体这个质点系的特点是,在外 力作用下各质元之间的相对位置保持不变。
2、刚体定轴转动的转动定律
M d(J )dL J
dt dt
刚体绕定轴转动时,它的角加速度与作用于刚体上的 合外力矩成正比,与刚体对转轴的转动惯量成反比。
刚体定轴转动的转动定律
M=J 与 F ma地位相当 m反映质点的平动惯性,J 反映刚体的转动惯性
力矩是使刚体转动状态发生改变而产生角加速度的原因。力
ri
即 F itfitΔ m iri
则刚体转动定律为
变形有 F ir tifir tiΔm iri2
M J
对所有质元求和:
F ir ti fir ti (m ir i2 ) 上式表明:
这里 FitriM i M外
刚体绕定轴转动时,刚
fitri 0 定义 JΔmiri2 叫转动惯量
体的角加速度与它所 受的合外力矩成正比.
刚体的转动

动平面。
自由度S 3
1
3
3
6
引言2: 刚体角速度的特征
刚体角速度指的是自转角速度,与单质点的绕轴角 速度(单质点体积为零,没有自转)完全不同。
B
●
o p ●A
质点由A点运动到B点,对o轴的
角 位 移 是
,角速度
是 是
d
dt
; 对p
,角速度是
轴的角位移 d 。可见质
dt
点的绕轴角速度依赖于转轴的选
定义刚体对z轴的转动惯量:
z
ri
riz
J z ri 2mi
对质量连续分布的i刚体,Jz r 2dV
对于刚体,Jz 是常量。动力学方 程成为
Mz
dLz dt
Jz
d
dt
J z
转动惯量是转动问题中系统惯性的
量度。上式可简写成:
M J
此称刚体定轴转动的转动定律。它
mi
2
2ri2
它与平动动能
Ek
m 2
2
2
mi ri2
i
v2 对应。
J 2
2
§5.2.1 几种典型刚体的转动惯量
1.均匀圆环对于中心垂直轴
选取质量元 dm
dm dl m Rd m d
R dm
2 R
2
d
dJ R2dm R2 m d
2
J 2 R2 m d mR 2
转轴光滑,初态静止,求下摆到θ角时的角 加速度,角速度。
解:非保守力 不作功,杆机 械能守恒。
势能零点
0
mg
自由度S 3
1
3
3
6
引言2: 刚体角速度的特征
刚体角速度指的是自转角速度,与单质点的绕轴角 速度(单质点体积为零,没有自转)完全不同。
B
●
o p ●A
质点由A点运动到B点,对o轴的
角 位 移 是
,角速度
是 是
d
dt
; 对p
,角速度是
轴的角位移 d 。可见质
dt
点的绕轴角速度依赖于转轴的选
定义刚体对z轴的转动惯量:
z
ri
riz
J z ri 2mi
对质量连续分布的i刚体,Jz r 2dV
对于刚体,Jz 是常量。动力学方 程成为
Mz
dLz dt
Jz
d
dt
J z
转动惯量是转动问题中系统惯性的
量度。上式可简写成:
M J
此称刚体定轴转动的转动定律。它
mi
2
2ri2
它与平动动能
Ek
m 2
2
2
mi ri2
i
v2 对应。
J 2
2
§5.2.1 几种典型刚体的转动惯量
1.均匀圆环对于中心垂直轴
选取质量元 dm
dm dl m Rd m d
R dm
2 R
2
d
dJ R2dm R2 m d
2
J 2 R2 m d mR 2
转轴光滑,初态静止,求下摆到θ角时的角 加速度,角速度。
解:非保守力 不作功,杆机 械能守恒。
势能零点
0
mg
大学物理教程-刚体的定轴转动

刚体最简单的运动形式是: 平动和定轴转动。
大学物理教程
哈尔滨工业大学(威海)
5.1 刚体的运动 Harbin Institute of Technology at Weihai
1.平动:
刚体在平动时,在任意一段时间内,刚体
中所有质点的位移都是相同的。而且在任何
时刻,各个质点的速度和加速度也都是相同
5.2.1 对轴的力矩
M ro F (r rz ) F
M z (r F ) z r (F Fz )z r F
M z rF sin r F rF
➢ 说明: ① 只有垂直于轴的分量(或在转动平面内的分量)
才能产生沿轴方向的力矩! ② 作用点到轴的垂直距离决定对轴的力矩
大学物理教程
例3. 圆环绕中心轴旋转的转动惯量。
解: 选圆环上dl长度质量微元dm,
设线密度为 m 2 R
dl
m R
Jz R2 d m R2 d l
O
R22 R
mR2
大学物理教程
延伸:
薄壁圆筒: J mR2
哈尔滨工业大学(威海)
5.2 刚体定轴转动定律 Harbin Institute of Technology at Weihai
(A)
(B)
解: (A)
M J
FR 1 mR2
2F mR
2
2F
mR
a R 2F / m
R
R
m
m
(B) m1g T m1a
TR J 1 mR2
2
a R
m1
g
m1
1 2
m
R
a
m1
g
m1
1 2
m
恒力 F
大学物理教程
哈尔滨工业大学(威海)
5.1 刚体的运动 Harbin Institute of Technology at Weihai
1.平动:
刚体在平动时,在任意一段时间内,刚体
中所有质点的位移都是相同的。而且在任何
时刻,各个质点的速度和加速度也都是相同
5.2.1 对轴的力矩
M ro F (r rz ) F
M z (r F ) z r (F Fz )z r F
M z rF sin r F rF
➢ 说明: ① 只有垂直于轴的分量(或在转动平面内的分量)
才能产生沿轴方向的力矩! ② 作用点到轴的垂直距离决定对轴的力矩
大学物理教程
例3. 圆环绕中心轴旋转的转动惯量。
解: 选圆环上dl长度质量微元dm,
设线密度为 m 2 R
dl
m R
Jz R2 d m R2 d l
O
R22 R
mR2
大学物理教程
延伸:
薄壁圆筒: J mR2
哈尔滨工业大学(威海)
5.2 刚体定轴转动定律 Harbin Institute of Technology at Weihai
(A)
(B)
解: (A)
M J
FR 1 mR2
2F mR
2
2F
mR
a R 2F / m
R
R
m
m
(B) m1g T m1a
TR J 1 mR2
2
a R
m1
g
m1
1 2
m
R
a
m1
g
m1
1 2
m
恒力 F
刚体的定轴转动定律

物体2这边的张力为
T2、 T2’(T2’= T2)
T1
T2
T1
T2
am
a
1
a
m
m1
m1g 2
m2
m2g
因m2>m1,物体1向上运动,物体2向下运动,滑轮以
顺时针方向旋转,Mr的指向如图所示。可列出下列方
程
T1 G1 m1a
G2 T2 m2a
T2r T1r M J
式中是滑轮的角加速度,a是物体的加速度。滑轮
t 0
方向:
t dt
右手螺旋方向
z (t)
x
参考平面
参考轴
刚体定轴转动(一
维转动)的转动方向可
以用角速度的正负来表
示.
角加速度
d
dt
定轴转动的特点
z
>0
z
<0
1) 2)
每一质点均作圆周运动,圆面为转动平面;
任一质点运动
,
,
均相同,但
v,
a不同;
3) 运动描述仅需一个坐标 .
三、 匀变速转动公式
轴的力矩 Mzk
r
F
z
F
k
O rFz
F
M z rF sin
z
Байду номын сангаас
F
M
O
r P
d
五. 定轴转动刚体的转动定律:
Fit
Fi
fit
•
ri
fi
mi• fin
Fin
O
•
j
d
fij
fji
i
Fit ri (miri2 )
I miri2
i
T2、 T2’(T2’= T2)
T1
T2
T1
T2
am
a
1
a
m
m1
m1g 2
m2
m2g
因m2>m1,物体1向上运动,物体2向下运动,滑轮以
顺时针方向旋转,Mr的指向如图所示。可列出下列方
程
T1 G1 m1a
G2 T2 m2a
T2r T1r M J
式中是滑轮的角加速度,a是物体的加速度。滑轮
t 0
方向:
t dt
右手螺旋方向
z (t)
x
参考平面
参考轴
刚体定轴转动(一
维转动)的转动方向可
以用角速度的正负来表
示.
角加速度
d
dt
定轴转动的特点
z
>0
z
<0
1) 2)
每一质点均作圆周运动,圆面为转动平面;
任一质点运动
,
,
均相同,但
v,
a不同;
3) 运动描述仅需一个坐标 .
三、 匀变速转动公式
轴的力矩 Mzk
r
F
z
F
k
O rFz
F
M z rF sin
z
Байду номын сангаас
F
M
O
r P
d
五. 定轴转动刚体的转动定律:
Fit
Fi
fit
•
ri
fi
mi• fin
Fin
O
•
j
d
fij
fji
i
Fit ri (miri2 )
I miri2
i
第五章 刚体的定轴转动

单位: 单位:rad / s 角速度
刚体定轴转动
ω
v 的方向按右手螺旋法则确定. 的方向按右手螺旋法则确定.
在定轴转动中, 在定轴转动中,角速度的方向 沿转轴方向. 沿转轴方向.
角加速度α 角加速度
v ω
2
ω dω d θ = = 2 α = lim t →0 t dt dt
单位: 单位:rad /s 2 角加速度也是矢量, 角加速度也是矢量,方向与角速度增量 的极限方向相同,在定轴转动中, 与 同向 的极限方向相同,在定轴转动中,α与ω同向 或反向. 或反向. 刚体的转动其转轴是可以改变的, 刚体的转动其转轴是可以改变的,为反映瞬时轴的方 向及其变化情况,引入角速度矢量和角加速度矢量. 向及其变化情况,引入角速度矢量和角加速度矢量. 注意 退化为代数量. :定轴转动时, ω,α退化为代数量. 定轴转动时, 退化为代数量
刚体的一般运动都可认为是平动和转动的结合. 刚体的一般运动都可认为是平动和转动的结合.
1. 用角量描述转动 (1) 角位移 θ : ) 时间内刚体转动角度. 在 t 时间内刚体转动角度. 单位: 单位:rad (2)角速度 ω : )
z θ
B A
θ dθ ω = lim = t →0 t dt
●
r2
转动惯量的定义: 转动惯量的定义:
J = ∑mi ri
2
对质量连续分布的刚体, 对质量连续分布的刚体,上式可写成积分形式
J = ∫ r dm
2
dm—质元的质量 质元的质量 r—质元到转轴的距离 质元到转轴的距离
线分布 dm = λdx 面分布 dm = σds 体分布 dm = ρdV
λ 是质量的线密度
F iz
ri = roi sinθ
刚体定轴转动
ω
v 的方向按右手螺旋法则确定. 的方向按右手螺旋法则确定.
在定轴转动中, 在定轴转动中,角速度的方向 沿转轴方向. 沿转轴方向.
角加速度α 角加速度
v ω
2
ω dω d θ = = 2 α = lim t →0 t dt dt
单位: 单位:rad /s 2 角加速度也是矢量, 角加速度也是矢量,方向与角速度增量 的极限方向相同,在定轴转动中, 与 同向 的极限方向相同,在定轴转动中,α与ω同向 或反向. 或反向. 刚体的转动其转轴是可以改变的, 刚体的转动其转轴是可以改变的,为反映瞬时轴的方 向及其变化情况,引入角速度矢量和角加速度矢量. 向及其变化情况,引入角速度矢量和角加速度矢量. 注意 退化为代数量. :定轴转动时, ω,α退化为代数量. 定轴转动时, 退化为代数量
刚体的一般运动都可认为是平动和转动的结合. 刚体的一般运动都可认为是平动和转动的结合.
1. 用角量描述转动 (1) 角位移 θ : ) 时间内刚体转动角度. 在 t 时间内刚体转动角度. 单位: 单位:rad (2)角速度 ω : )
z θ
B A
θ dθ ω = lim = t →0 t dt
●
r2
转动惯量的定义: 转动惯量的定义:
J = ∑mi ri
2
对质量连续分布的刚体, 对质量连续分布的刚体,上式可写成积分形式
J = ∫ r dm
2
dm—质元的质量 质元的质量 r—质元到转轴的距离 质元到转轴的距离
线分布 dm = λdx 面分布 dm = σds 体分布 dm = ρdV
λ 是质量的线密度
F iz
ri = roi sinθ
第五章刚体的转动

38
§5.5 刚体定轴转动的角动量定理 和角动量守恒定律
讨论力矩对时间的积累效应。
质点系: 对点:
M外
dL dt
, t2 t1
M
外
dt
L2
L1
对轴:
M t2
t1 外z
dt
L2z
L1z
刚体: Lz J z
M t2
t1 外z
dt
J z2
J z1
——刚体定轴转动的角动量定理 39
z
mC a
mD
a
l
24
§5.4 转动定律应用举例
M
J
d
J
dt
刚体定轴转动的两类问题:
(t) (t) (t) J M
用求导的方法
M J (t) (t) (t) 积分加初始条件
25
例1.
R· 定轴
已知:R = 0.2m,m =1kg,v0= 0, h =1.5m, 绳轮间无相对
r P
a
r
dv d
r
r
d
r
r
刚体基点O×
dt dt
dt
r
v
瞬时轴
旋转加速度 向轴加速度 9
2.定转轴轴转固动定(,rota和tion
about a fixed axis)
退化为代数量 和
。
z ,
第五章 刚体的转动
(Rotation of Rigid Body about a Fixed Axis)
§5.5 刚体定轴转动的角动量定理 和角动量守恒定律
讨论力矩对时间的积累效应。
质点系: 对点:
M外
dL dt
, t2 t1
M
外
dt
L2
L1
对轴:
M t2
t1 外z
dt
L2z
L1z
刚体: Lz J z
M t2
t1 外z
dt
J z2
J z1
——刚体定轴转动的角动量定理 39
z
mC a
mD
a
l
24
§5.4 转动定律应用举例
M
J
d
J
dt
刚体定轴转动的两类问题:
(t) (t) (t) J M
用求导的方法
M J (t) (t) (t) 积分加初始条件
25
例1.
R· 定轴
已知:R = 0.2m,m =1kg,v0= 0, h =1.5m, 绳轮间无相对
r P
a
r
dv d
r
r
d
r
r
刚体基点O×
dt dt
dt
r
v
瞬时轴
旋转加速度 向轴加速度 9
2.定转轴轴转固动定(,rota和tion
about a fixed axis)
退化为代数量 和
。
z ,
第五章 刚体的转动
(Rotation of Rigid Body about a Fixed Axis)
第5章 刚体

5.3.1 力矩对时间的积累效应 角动量守恒定理
1. 刚体的角动量
L
对于定点转动而言:
Lrp
r mv
描述物体转动状态的量
r
O
r sin
p mv
m
对于绕固定轴Oz的转
动的质元
m而i 言:
Li ri mivi
miri2k
对于绕固定轴Oz 转动 的整个刚体而言:
z
L
vi
mi
O ri
L N miri2 J
m1
Mr r
F’T1 FT1
a m1
a
m2 G1
m2
F’T2 FT2
a
G2
因m2>m1,物体1向上运动,物体2向下运动,滑轮以顺 时针方向旋转,Mr的指向如图所示。可列出下列方程:
FT1 G1 m1a G2 FT2 m2a
FT2r FT1r M r J
式中是滑轮的角加速度,a是物体的加速度。滑轮
现在将这些方法用于刚体的研究。
第5章 刚体
5.1 刚体运动学 5.2 刚体定轴转动定律 转动惯量 5.3 力矩对时间和空间的累积效应
5.1 刚体运动学
刚体:在外力的作用下,大小和形状都不变的物体 ----物体内任意两点的距离不变。
刚体运动研究的基础:刚体是由无数个连续分布的 质点组成的质点系,每个质点称为刚体的一个质量 元dm。每个质点运动都服从质点力学规律。刚体的 运动是这些质量元运动的总和。
一般的力学分析方法可归纳为:
(1)突出主要矛盾,撇开次要因素,建立理想模型; (2)将质点系化整为零,以质点或质元为研究对象,
作为突破口; (3)根据受力情况,正确画出受力图; (4)根据已知条件或初始条件,选用所需的基本原
力学.第5章.刚体的转动_778107259(1)

瞬时轴 旋转加速度 向轴加速度
四. 定轴转动 r r 对定轴转动, 都沿定轴, 对定轴转动, ω 和 α 都沿定轴,但两者方 向不一定相同,都退化为代数量 代数量。 向不一定相同,都退化为代数量。
7
z ω, α
r v
v = r⊥ω
dv dω at = = r⊥ = r⊥α dt dt
刚体
O×
r r⊥ P θ r r
猫从树枝和手的下落
26
J1 O1 r1
ω10
ω20
J2 O2 r2
【例1】如图两轮磨合问题, 】如图两轮磨合问题, 已知:初始参量( 已知:初始参量(J1, ω10, r1) 和(J2, ω20, r2), 求:接触达稳定后的 ω′1和ω′2
解:此系统角动量并不守恒,因为 1和O2处的 此系统角动量并不守恒,因为O 轴力产生的力矩和不为零。 轴力产生的力矩和不为零。 应对每个轮作隔离分析,用角动量定理求解。 应对每个轮作隔离分析,用角动量定理求解。 f1 设摩擦力方向如图示, 设摩擦力方向如图示,有:
3
2. 转动 — 基本的运动形式之二 一点固定不动, 定点转动: 刚体只有一点固定不动 定点转动: 刚体只有一点固定不动,整体 绕通过该点的瞬时轴转动。 瞬时轴转动 绕通过该点的瞬时轴转动。 定轴转动: 定点转动的瞬时轴成固定轴。 定轴转动: 定点转动的瞬时轴成固定轴。 3. 平面运动:刚体各点运动都平行于某固定 平面运动: 平面,各点轨道面平行或重合。 平面,各点轨道面平行或重合。 4. 一般运动:不受任何限制的自由运动, 一般运动:不受任何限制的自由运动, 是下面两种运动的组合: 是下面两种运动的组合: 随基点 O(可任选)的平动 (可任选) 的瞬时轴的定点转动 绕通过基点 O 的瞬时轴的定点转动
四. 定轴转动 r r 对定轴转动, 都沿定轴, 对定轴转动, ω 和 α 都沿定轴,但两者方 向不一定相同,都退化为代数量 代数量。 向不一定相同,都退化为代数量。
7
z ω, α
r v
v = r⊥ω
dv dω at = = r⊥ = r⊥α dt dt
刚体
O×
r r⊥ P θ r r
猫从树枝和手的下落
26
J1 O1 r1
ω10
ω20
J2 O2 r2
【例1】如图两轮磨合问题, 】如图两轮磨合问题, 已知:初始参量( 已知:初始参量(J1, ω10, r1) 和(J2, ω20, r2), 求:接触达稳定后的 ω′1和ω′2
解:此系统角动量并不守恒,因为 1和O2处的 此系统角动量并不守恒,因为O 轴力产生的力矩和不为零。 轴力产生的力矩和不为零。 应对每个轮作隔离分析,用角动量定理求解。 应对每个轮作隔离分析,用角动量定理求解。 f1 设摩擦力方向如图示, 设摩擦力方向如图示,有:
3
2. 转动 — 基本的运动形式之二 一点固定不动, 定点转动: 刚体只有一点固定不动 定点转动: 刚体只有一点固定不动,整体 绕通过该点的瞬时轴转动。 瞬时轴转动 绕通过该点的瞬时轴转动。 定轴转动: 定点转动的瞬时轴成固定轴。 定轴转动: 定点转动的瞬时轴成固定轴。 3. 平面运动:刚体各点运动都平行于某固定 平面运动: 平面,各点轨道面平行或重合。 平面,各点轨道面平行或重合。 4. 一般运动:不受任何限制的自由运动, 一般运动:不受任何限制的自由运动, 是下面两种运动的组合: 是下面两种运动的组合: 随基点 O(可任选)的平动 (可任选) 的瞬时轴的定点转动 绕通过基点 O 的瞬时轴的定点转动
刚体定轴转动定律

于 180°的夹角 θ 转向 F 时,拇指所指的方向就是力矩的方向。
可见,力矩的方向与转轴的方向平行,只有两个可能的方向,因此,可用 M 的正负表示力矩的方向。 一般可按力矩的作用来判断其正负:由转轴 Oz 正向俯视,若力矩的作用使刚体逆时针转动,则力矩为 正,否则为负。
刚体定轴转动定律 1.1 力矩
可加性
• 对同一转轴而言,刚体各部分转动惯量之 和等于整个刚体的转动惯量。
平行轴定理
• 设有两个彼此平行的转轴,一个通过刚体 的质心,另一个不通过质心。两平行轴之 间的距离为d,刚体的质量为m。
如果此刚体对通过质心转轴的转动惯量为 Jc ,则对另一 转轴的转动惯量 J 为 J Jc md 2
刚体定轴转动定律
刚体定轴转动定律Βιβλιοθήκη , ,,,
例题讲解 2
如图所示,一轻绳跨过一轴承光滑的定滑轮。绳两边分别悬有质量为 m1 和 m2 的两个物体 A,B。已知 m1
小于 m2 ,滑轮可看作质量均匀分布的等厚圆盘,其质量为 m,半径为 r,设绳与滑轮间无相对滑动。求:① 物
体的加速度;② 滑轮的角加速度;③ 绳的张力。
i 1
n
用 M 表示,即 M (Δmiri2 ) β
i 1
n
n
式中的 (Δmiri2 ) 称为转动惯量,用 J 表示,即 J (Δmiri2 )
i 1
i 1
于是,式可写为 M Jβ
刚体定轴转动定律 1.2 转动定律
转动定律:刚体定轴转动时,刚体的角加速度与刚体所受的合外力矩成正比,与刚体的转动惯量 成反比。
r 2 dm
Ω
式中 r ——质元 dm 到转轴的距离(m)。 在国际单位制中,转动惯量的单位为 kg m2 。
可见,力矩的方向与转轴的方向平行,只有两个可能的方向,因此,可用 M 的正负表示力矩的方向。 一般可按力矩的作用来判断其正负:由转轴 Oz 正向俯视,若力矩的作用使刚体逆时针转动,则力矩为 正,否则为负。
刚体定轴转动定律 1.1 力矩
可加性
• 对同一转轴而言,刚体各部分转动惯量之 和等于整个刚体的转动惯量。
平行轴定理
• 设有两个彼此平行的转轴,一个通过刚体 的质心,另一个不通过质心。两平行轴之 间的距离为d,刚体的质量为m。
如果此刚体对通过质心转轴的转动惯量为 Jc ,则对另一 转轴的转动惯量 J 为 J Jc md 2
刚体定轴转动定律
刚体定轴转动定律Βιβλιοθήκη , ,,,
例题讲解 2
如图所示,一轻绳跨过一轴承光滑的定滑轮。绳两边分别悬有质量为 m1 和 m2 的两个物体 A,B。已知 m1
小于 m2 ,滑轮可看作质量均匀分布的等厚圆盘,其质量为 m,半径为 r,设绳与滑轮间无相对滑动。求:① 物
体的加速度;② 滑轮的角加速度;③ 绳的张力。
i 1
n
用 M 表示,即 M (Δmiri2 ) β
i 1
n
n
式中的 (Δmiri2 ) 称为转动惯量,用 J 表示,即 J (Δmiri2 )
i 1
i 1
于是,式可写为 M Jβ
刚体定轴转动定律 1.2 转动定律
转动定律:刚体定轴转动时,刚体的角加速度与刚体所受的合外力矩成正比,与刚体的转动惯量 成反比。
r 2 dm
Ω
式中 r ——质元 dm 到转轴的距离(m)。 在国际单位制中,转动惯量的单位为 kg m2 。
刚体定轴转动定律公式

刚体定轴转动定律公式
刚体定轴转动定律是描述刚体绕定轴转动的物理规律。
其中,定轴转动指围绕一个固定轴心旋转,而刚体则指形状不变的物体。
该定律的公式可以表示为:
τ= Iα
其中,τ表示刚体所受的力矩,I表示刚体的转动惯量,α表示刚体的角加速度。
转动惯量是描述刚体绕定轴转动惯性的物理量,具体定义为:
I = ∫r2dm
其中,r表示离定轴的距离,dm表示质量元素。
这个公式的意义是,刚体所受到的力矩与刚体的转动惯量和角加速度成正比。
因此,当转动惯量越大或角加速度越大时,刚体所受到的力矩也相应增大。
需要注意的是,该公式适用于定轴转动的刚体,而对于非定轴转动的刚体,需要使用更为复杂的公式来描述其运动规律。
《大学物理》第五章刚体的定轴转动

偏转角为30°。问子弹的初速度为多少。
o
解: 角动量守恒:
30°
mva 1 Ml 2 ma 2
la
3
v
机械能守恒:
1 1 Ml 2 ma 2 2 mga1 cos 30 Mg l 1 cos 30
23
2
v 1 g 2 3 Ml 2ma Ml 2 3ma 2 ma 6
刚体可以看成是很多质元组成的质点系,且在外力 作用下,各个质元的相对位置保持不变。 因此,刚体的运动规律,可通过把牛顿运动定律应 用到这种特殊的质点系上得到。
3
2.刚体的运动
平动:刚体在运动过程中,其上任意两点的连线 始终保持平行。
刚体的平动可看做刚体质心 的运动。
转动:刚体中所有的点都绕同一直线做圆周运动. 转动又分定轴转动和非定轴转动 .
r2dm
L
r2 dl
L
(线质量分布)
12
3 平行轴定理
如果刚体的一个轴与过质 心轴平行并相距d,则质量 为 m 的刚体绕该轴的转动 惯量,等于刚体绕过质心 轴的转动惯量与 md2 之和:
J z Jc md 2
请同学们自己证明平行轴定理的。
提示:利用余弦定理 ri2 ri '2 d 2 2dxi 13
hc hi
若A外+ A内非=0
Ep=0
则Ek +Ep =常量。
例13 一均质细杆可绕一水平轴旋转,开始时处于 水平位置,然后让它自由下落。求: ( )
解 方法一 动能定理
M mg L cos
2
W
Md
mg
L cosd
0
0
2
mg L sin
2
θ
5刚体的定轴转动

2J
yc
m(R
l )2 2
R
l
R
m
m
2( 2 mR2 mR2 mlR ml2 )
5 14 mR2 2mlR ml2
4
(2)J //
2J y//
2
2 5
mR2
5
2
4 mR2
5
39
例4:从一个半径为R的均匀薄板上挖去一个直径为R的
圆板,所形成的圆洞中心在距薄板中心R/2处,所剩薄
▲ 定点转动:运动中刚体上只有一点固定不动, 整个刚体绕过该定点的某一瞬时轴线转动。
6
7
三、 刚体的定轴转动
定轴转动:
刚体上各点都绕同一转轴作不同半径的圆周运 动,且在相同时间内转过相同的角度。
角位移,角速度和角加速度均相同; 特点: 质点在垂直转轴的平面内运动,且作圆周
运动。
角位移
角速度
at
解 (1)设初角度为0方向如图所示,
11
量值为0=21500/60=50 rad/s,对于匀
变速转动,可以应用以角量表示的运动方程,在
t=50S 时刻 =0 ,代入方程=0+αt 得
0 50 rad / s2
t
50
3.14 rad / s2
从开始制动到静止,飞轮的角位移 及转数
N 分别为
板的质量为m,求此时薄板对于通过原中心而与板面垂
直的轴的转动惯量。
JO
J DO
J dO
1 2
MR 2
1
2
md
R 2
2
md
(
R )2 2
1 2
MR 2
3 2
md
R 2
刚体定轴转动定律

F ma
(2) 列方程: 对于刚体:定轴转动定律 M J
线量与角量的关系:at R
(3) 解方程.
例题. 一轻绳跨过一轴承光滑的定滑轮,滑轮可视为
圆 盘 , 绳 的 两 端 分 别 悬 有 质 量 为 m1 和 m2 的 物 块 , 且 m1<m2. 设滑轮的质量为M,半径为R,绳与轮之间无 相对滑动,求物块的加速度和绳中张力.
本次课所讲知识点是刚体力学这部分内容的重点, 希望大家课后好好复习,多多练习,熟练掌握。
切向分量式: Fit fit miait
ait ri Fit fit miri
ri
作圆周运动. z
o
f Fit
i fit
ri mi
Fir
Fi
上式两端同乘以ri再对所有质点求和:
Fit ri fit ri miri2
i
i
i
合外力矩M 内力矩之和 =0 转动惯量J
M J
刚体所受的对某一固定转轴的合外力矩等于刚体 对此转轴的转动惯量与刚体在此合外力矩作用下所 获得的角加速度的乘积.
二、 刚体定轴转动定律与牛顿第二定律的比较
定律方程
牛顿第二定律 F ma
促使运动状态发 生变化的因素
合外力:F
阻碍运动状态发 生变化的因素
产生的物理量
质量:m
加速度:a
刚体定轴转动定律
M J
合外力矩:M
ห้องสมุดไป่ตู้转动惯量:J
角加速度:
三、 刚体定轴转动定律的应用
解题思路:
(1) 受力分析;
对于质点:牛顿第二定律
刚体定轴转动定律
一、 刚体定轴转动定律的证明
刚体可看成是由n个质点组成的连续质点系.
§5.2-力矩---刚体绕定轴转动微分方程
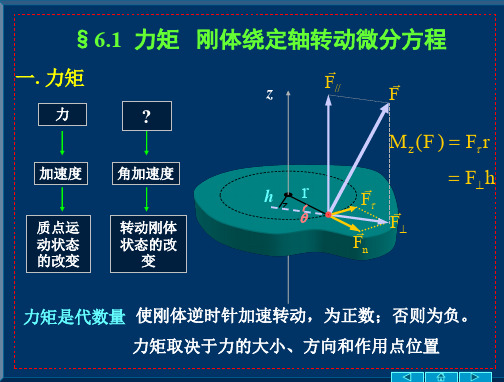
F f m a i i
的切向加速度,质元沿
法向运动的科里奥里加
i
i
速度(定轴转动刚体没 有这种运动)
圆周轨迹切线投影
Fi fi miai
同乘以 ri
Fi ri fi ri miai ri miri2β ai=ri
对所有质元求和
Fi ri fi ri ( miri2 )β
根据牛顿第二定律,第 i 个质元
外内
力 Fi
力 fi
miai
圆周轨迹切线投影
同乘以 ri
Fi fi miai Fi ri fi ri miai ri miri2β
ai=ri
对所有质元求和
Fi ri fi ri ( miri2 )β
§6.1 力矩
一. 力矩
力
?
加速度 角加速度
质点运 动状态 的改变
转动刚体 状态的改
变
刚体绕定轴转动微分方程
z
F//
F
hr
M z (F ) F r
F F Fn
Fh
力矩是代数量 使刚体逆时针加速转动,为正数;否则为负。 力矩取决于力的大小、方向和作用点位置
二. 刚体定轴转动微分方程
它在水平位置
求 它由此下摆 角时的 解 dm 质元 dm m dx
l
dm 重力矩 dM gdm x cos
O
ml
x
M
dM
1 2
mgl cos
gdm
重力对整个棒的合力矩等于重力全部 集中于质心所产生的力矩
转动定律 M
J J 1 ml2
3
的切向加速度,质元沿
法向运动的科里奥里加
i
i
速度(定轴转动刚体没 有这种运动)
圆周轨迹切线投影
Fi fi miai
同乘以 ri
Fi ri fi ri miai ri miri2β ai=ri
对所有质元求和
Fi ri fi ri ( miri2 )β
根据牛顿第二定律,第 i 个质元
外内
力 Fi
力 fi
miai
圆周轨迹切线投影
同乘以 ri
Fi fi miai Fi ri fi ri miai ri miri2β
ai=ri
对所有质元求和
Fi ri fi ri ( miri2 )β
§6.1 力矩
一. 力矩
力
?
加速度 角加速度
质点运 动状态 的改变
转动刚体 状态的改
变
刚体绕定轴转动微分方程
z
F//
F
hr
M z (F ) F r
F F Fn
Fh
力矩是代数量 使刚体逆时针加速转动,为正数;否则为负。 力矩取决于力的大小、方向和作用点位置
二. 刚体定轴转动微分方程
它在水平位置
求 它由此下摆 角时的 解 dm 质元 dm m dx
l
dm 重力矩 dM gdm x cos
O
ml
x
M
dM
1 2
mgl cos
gdm
重力对整个棒的合力矩等于重力全部 集中于质心所产生的力矩
转动定律 M
J J 1 ml2
3
52--定轴转动定律

dt
Mdt d(J) 刚体定轴转动角动量定理微分形式
t
J
Mdt
t0
J00 d(J) J J00
刚体定轴转动角动量定理积分形式
4
L (miviri ) (miri2 ) ( miri 2 ) J
J miri 2 称为刚体对转轴的转动惯量
3
L J
于是有 M d(J) J d J
dt
dt
刚体定轴转动定理: M J
F ma
对 M d (J) 进行处理得到:
大小:M Fr sin
M
F
Or
d
Pr
z
F∥
or
F θ F⊥
转轴
转动平面 2
二、刚体定轴转动定理
在以角速度ω作定轴转动的刚体
内取一质点 mi ,则其对OZ轴
的角动量为:
o ri
v
P
Li miviri
对于整个刚体,各质点对定轴的角动量都具有相同的 方向。则定轴转动刚体的角动量就是对组成刚体的所 有质点的角动量求和。
刚体转动定律
1
一、作用于定轴刚体的外力矩
1 .力对固定点的矩
M
rF
2 .力对固定轴的矩
(1)力直于转轴
这种情况相当于质点绕固 定点O转动的情形。
(2)力与转轴不垂直 可以把力分解为平行于转轴
的分量和垂直于转轴的分量。
平行转轴的力不产生转动效果,
该力对转轴的 力矩 为零。 M r F
Mdt d(J) 刚体定轴转动角动量定理微分形式
t
J
Mdt
t0
J00 d(J) J J00
刚体定轴转动角动量定理积分形式
4
L (miviri ) (miri2 ) ( miri 2 ) J
J miri 2 称为刚体对转轴的转动惯量
3
L J
于是有 M d(J) J d J
dt
dt
刚体定轴转动定理: M J
F ma
对 M d (J) 进行处理得到:
大小:M Fr sin
M
F
Or
d
Pr
z
F∥
or
F θ F⊥
转轴
转动平面 2
二、刚体定轴转动定理
在以角速度ω作定轴转动的刚体
内取一质点 mi ,则其对OZ轴
的角动量为:
o ri
v
P
Li miviri
对于整个刚体,各质点对定轴的角动量都具有相同的 方向。则定轴转动刚体的角动量就是对组成刚体的所 有质点的角动量求和。
刚体转动定律
1
一、作用于定轴刚体的外力矩
1 .力对固定点的矩
M
rF
2 .力对固定轴的矩
(1)力直于转轴
这种情况相当于质点绕固 定点O转动的情形。
(2)力与转轴不垂直 可以把力分解为平行于转轴
的分量和垂直于转轴的分量。
平行转轴的力不产生转动效果,
该力对转轴的 力矩 为零。 M r F
5.2 力矩 刚体绕定轴转动微分方程解析
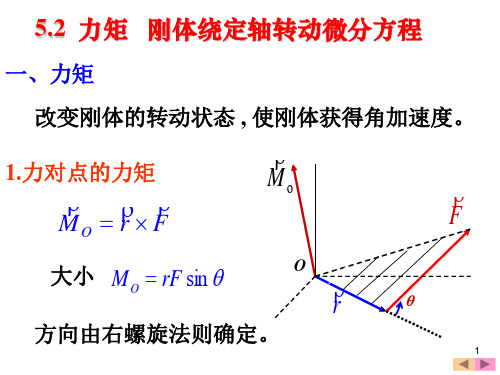
m
R
0
2m 3 m 2 r dr R 2 R 2
10
例3 求质量为m、半径为R、厚为h 的均匀圆盘 的转动惯量。轴与盘平面垂直并通过盘心。 解: 取半径为r宽为dr 的薄圆环: 圆环质量:
R
h
dm 2πrdr h
圆环转动惯量:
r
dJ r dm 2πhr dr
z
mk ak Fk f k
o
vk
在圆轨迹切线方向 投影: mk ak mk rk Fk f k 两边乘以rk,得:m
2 k k
mk
r Fk rk fk rk
对整个刚体求和,得:
( m r ) Fk rk f k rk
力不在转动平面内时:
h θ
r
A
F Fn F//
F F
M F r sin F h Fτ r
z z
r
F
F
矢量形式: M r F
方向由右螺旋法则确定。
h θ
A
Fn
F
2
二、刚体绕定轴的转动微分方程 作用在 mk 上的合外力 Fk ,合内力 f k
L
0
1 2 2 x dx mL 3
2
O
m
dx C
L
x
1 2 J C x dx mL L /2 12
L /2
m
O
2
L dx
x
1 2 L J D J C mL J C m 此关系具有普遍意义 4 2
13
平行轴定理
J D J C mL
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因为各质元角动量方向相同, 因为各质元角动量方向相同, 所以合矢量的大小就是分矢量 大小的直接相加 因为 L = L = rmυ S
mi
α r P
r
i
i i
υi = riω
L = ω(∑ mi ri2 )
i
定义刚体对定轴 定义刚体对定轴 J = 的转动惯量
3
∑m r
i
2
i i
r r L = Jω
对于转轴z,
r ri α
A
r F τ
r r r M z = ri × F⊥
不产生对z轴的力矩
α
Fn
r r F ⊥
M z = ri F⊥ sin α = F⊥ h
F ——平行于z轴 平行于 //
在转动平面内 F ——在转动平面内 产生对z轴的力矩 ⊥
r rz
O
r r
α
r F ⊥
y
x
力对任意点的力矩, 力对任意点的力矩,在通过该点的任一轴上的投影 等于该力对该轴的力矩
2 第5章 刚体的定轴转动
质点对定点 的动量矩 角动量) 质点对定点o的动量矩 角动量 定点 的动量矩(角动量
r r r r r L = r × P = r × mv = Lx x + Ly y + Lz z
2. 任一质量元的定轴角动量大小为
对z轴的 轴的 动量矩
r LO
Liz = ri miυi
§5.2 刚体绕定轴转动
(质点系角动量定理微分形式的简化) 质点系角动量定理微分形式的简化) 质点系角动量定理微分形式: 质点系角动量定理微分形式:
r z Fz
r F
r r dL M = dt
r 1. 力 F 对 O点的力矩
r r r Mo = r × F = Mx x + M y y + Mz z
4 第5章 刚体的定轴转动
刚体对定轴的角动量
第5章 刚体的定轴转动
刚体对定轴的转动惯量 刚体对定轴的角动量
J = ∑ mi ri 2
i
r r L = Jω
3. 刚体定轴转动的转动定律
r r r dL dω M = =J dt dt
r v M = Jβ
r r F = ma
定轴转动定律在转动问题中的地位相当于平动的牛顿第二定律 应用转动定律解题步骤与牛顿第二定律时完全相同。 应用转动定律解题步骤与牛顿第二定律时完全相同。
O
对于过O点Z 轴,力矩可分解为两个分量
A
r F ⊥
r r
r F ⊥
y
r r r r r r M O = Mz + M⊥ = r ×(F⊥ + Fz )
1 第5章 刚体的定轴转动
x
r r r r r r MO = Mz + M⊥ = r ×(F⊥ + Fz )
r z Fz
Oi h
r F
r r r r = (ri + rz ) × ( F⊥ + Fz ) r r r r r r = (ri × F⊥ ) + (rz × F⊥ + ri × Fz )
mi
α r P
r
i
i i
υi = riω
L = ω(∑ mi ri2 )
i
定义刚体对定轴 定义刚体对定轴 J = 的转动惯量
3
∑m r
i
2
i i
r r L = Jω
对于转轴z,
r ri α
A
r F τ
r r r M z = ri × F⊥
不产生对z轴的力矩
α
Fn
r r F ⊥
M z = ri F⊥ sin α = F⊥ h
F ——平行于z轴 平行于 //
在转动平面内 F ——在转动平面内 产生对z轴的力矩 ⊥
r rz
O
r r
α
r F ⊥
y
x
力对任意点的力矩, 力对任意点的力矩,在通过该点的任一轴上的投影 等于该力对该轴的力矩
2 第5章 刚体的定轴转动
质点对定点 的动量矩 角动量) 质点对定点o的动量矩 角动量 定点 的动量矩(角动量
r r r r r L = r × P = r × mv = Lx x + Ly y + Lz z
2. 任一质量元的定轴角动量大小为
对z轴的 轴的 动量矩
r LO
Liz = ri miυi
§5.2 刚体绕定轴转动
(质点系角动量定理微分形式的简化) 质点系角动量定理微分形式的简化) 质点系角动量定理微分形式: 质点系角动量定理微分形式:
r z Fz
r F
r r dL M = dt
r 1. 力 F 对 O点的力矩
r r r Mo = r × F = Mx x + M y y + Mz z
4 第5章 刚体的定轴转动
刚体对定轴的角动量
第5章 刚体的定轴转动
刚体对定轴的转动惯量 刚体对定轴的角动量
J = ∑ mi ri 2
i
r r L = Jω
3. 刚体定轴转动的转动定律
r r r dL dω M = =J dt dt
r v M = Jβ
r r F = ma
定轴转动定律在转动问题中的地位相当于平动的牛顿第二定律 应用转动定律解题步骤与牛顿第二定律时完全相同。 应用转动定律解题步骤与牛顿第二定律时完全相同。
O
对于过O点Z 轴,力矩可分解为两个分量
A
r F ⊥
r r
r F ⊥
y
r r r r r r M O = Mz + M⊥ = r ×(F⊥ + Fz )
1 第5章 刚体的定轴转动
x
r r r r r r MO = Mz + M⊥ = r ×(F⊥ + Fz )
r z Fz
Oi h
r F
r r r r = (ri + rz ) × ( F⊥ + Fz ) r r r r r r = (ri × F⊥ ) + (rz × F⊥ + ri × Fz )
