电磁学梁灿彬习题选解
梁彬灿电磁学第三章习题解答

代入数据得
此值低于玻璃的击穿场强,说明玻璃不会被击穿。因
此值高于空气的击穿场强,说明空气被击穿。
若取出玻璃,则
此值低于空气的击穿场强,说明空气不会被击穿。
3.4.4
解答:
如附图所示,法线单位矢 向下,因是均匀电介质,故 。在界面处作一底面积为 的柱面,被包围导体面上的自由电荷的电荷量为 ,根据高斯定理,自由电荷在介质中激发的电场为
而极化电荷面密度为
极化电荷在介质中激发的电场为
自由电荷和极化电荷在介质中激发的总电场为
3.4.5
解答:
(1)根据电容器的定义并代入数据,得
3.5.6
解答:
(1)图3.5.6(a)和图3.5.6(b)是题图的等效电路,“+”、“—”符号标在相应的图上。
(2)两个电容器的电容值为
3.5.7
证明:
在介质中的电位移矢量 ,因此,电场强度 ,按题意
介质中离球心为r处的电势为
3.5.8
解答:
设玻璃的电场强度为 ,空气的电场强度为 ,当两极板间加上电压U后Hale Waihona Puke 有3.2.1解答:
(1)如图3.2.1所示,偶极子的电荷量 和 所受的电场力分别为 和 ,大小相等,合力为0,但所受的力矩为
当且仅当 和 时,电偶极子受的力矩为0,达到平衡状态,但在 的情况下稍受微扰,电偶极子将受到回复力矩回到平衡位置上,因此, 时,是稳定平衡;但在 的情况下稍受微扰,电偶极子受到的力矩将使电偶极子“倾覆”到达 情况,因此, 的情况是不稳定平衡。
所受的电场力为
偶极子 受到的合力为
令 , , ,则 ,故
因 ,对 和 在 处展开后,略去高次项
梁灿彬《电磁学》考研核心题库之填空题精编

梁灿彬《电磁学》考研核心题库之填空题精编电磁学作为物理学的重要分支,在考研中占据着不可忽视的地位。
梁灿彬老师的《电磁学》更是众多考生备考的重要参考资料。
为了帮助广大考生更好地掌握这门学科,提高解题能力,以下精心整理了一系列填空题,涵盖了电磁学的核心知识点。
在静电场部分,我们首先要了解电场强度的定义。
电场中某点的电场强度等于置于该点的单位正电荷所受到的电场力。
例如,真空中一个点电荷 q 产生的电场中,距离该点电荷r 处的电场强度大小为_____。
库仑定律描述了两个静止点电荷之间的相互作用力,其表达式为_____。
对于电场的高斯定理,通过任意闭合曲面的电通量等于该闭合曲面所包围的电荷代数和除以_____。
在均匀电场中,电场强度与电势梯度的关系为_____。
在导体和电介质的相关内容中,导体处于静电平衡时,导体内部的电场强度为_____,导体表面附近的电场强度方向与导体表面_____。
电介质在电场中的极化会产生极化电荷,极化强度与极化电荷面密度的关系为_____。
接着是磁场部分。
磁感应强度的定义是描述磁场强弱和方向的物理量,一个运动电荷在磁场中受到的洛伦兹力为_____。
毕奥萨伐尔定律给出了电流元产生磁场的规律,其表达式为_____。
磁场的高斯定理表明,通过任意闭合曲面的磁通量恒为_____。
安培环路定理则指出,在稳恒磁场中,磁感应强度沿任意闭合回路的环流等于穿过该回路所包围面积的电流代数和的_____倍。
电磁感应是电磁学中的重要内容。
法拉第电磁感应定律指出,闭合回路中的感应电动势大小与穿过回路的磁通量的变化率成正比,其表达式为_____。
动生电动势的产生是由于导体在磁场中运动,其计算公式为_____。
麦克斯韦方程组是电磁学的核心理论,它包含四个方程。
其中,描述电场的高斯定律为_____;描述磁场的高斯定律为_____;描述变化的磁场产生电场的方程为_____;描述变化的电场产生磁场的方程为_____。
梁彬灿电磁学第五章习题解答

///5.1.1 解答:(1) 质子所受洛伦兹力的方向向东(2) 质子的电荷量191.610q C -=⨯,质子所受洛伦兹力大小为163.210F qvB N -==⨯质子的质量271.6710m kg -=⨯,质子所受洛伦兹力与受到的地球引力相比较:101.9510F qvB F mg==⨯洛重 5.2.1 解答:O 点的磁场B 可看作两条半无限长直载流导线产生的磁场1B 、2B 和MN 部分阶段1/4圆周载流导线产生的磁场3B 的合成。
由于磁场方向均垂直纸面向外,所以直接求出它们大小并相加即可0012cos0cos 424I IB B R Rμμπππ⎛⎫==-=⎪⎝⎭ 40032448I IB Rd R Rππμμαπ-==⎰0123124I B B B B R μππ⎛⎫=++=+ ⎪⎝⎭方向垂直纸面向外 5.2.2 解答:(a )延长线通过圆心的直长载流导线在O 点产生磁场为1B ,其大小为0;另一直长载流导线在O 点产生的磁场为2B ,方向垂直纸面向里;圆弧部分载流导线在O 点产生的磁场为3B ,方向垂直纸面向里。
故O 点的合磁场大小为0001233314842I I I B B B B R R R μμμπππ⎛⎫=++=+=+ ⎪⎝⎭方向垂直纸面向里(b )两半直长载流导线在O 点产生的磁场分别为1B 、2B ,方向均垂直纸面向里;圆弧部分载流导线在O 点产生的磁场为3B ,方向垂直纸面向里。
故O 点的合磁场大小为()000012324444I I I IB B B B R R R Rμμμμππππ=++=++=+ 方向垂直纸面向里 5.2.3 解答:(a )因为两直长载流导线延长线均通过圆心,所以对O 点的磁场没有贡献,故只需要考虑两个圆弧载流导线在O 点产生的磁场,它们所激发的磁场分别为1B 、2B ,方向均垂直纸面向里,故O 点的合磁场大小为00123312248I I B B B a b a b ππμμπ⎛⎫⎪⎛⎫=+=+=+ ⎪ ⎪⎝⎭ ⎪⎝⎭方向均垂直纸面向里(b )两延长线的直长载流导线对O 点的磁场没有贡献,只需要考虑两长度为b 的直长载流导线对O 点的磁场1B 、2B 和圆弧载流导线对O 点的磁场3B ,方向均垂直纸面向里,其合磁场大小为()0001232332cos90cos13524442a I I I B B B B b a b a πμμμππππ⎛⎫⎛⎫⎪=++=-⨯+=+ ⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭方向均垂直纸面向里。
梁灿斌电磁学习题

梁灿斌电磁学习题第一章(共35题)§2 库伦定律两类6题(1)数值计算:1.2.1~1.2.4(建议:不留为作业)(2)证明:1.2.5~1.2.6§3 静电场的场强三类9题(1)匀强场中的带电粒子运动:1.3.1~1.3.4(建议:不留为作业)(2)点电荷的电场(叠加原理—类似于偶极子):1.3.5(建议:作业)(3)连续分布电荷的电场:1.3.6~1.3.9(其中:1.3.6和1.3.7可作为例题,1.3.8和1.3.9可作为作业)§4 高斯定理两类10题(1)高斯定理基础练习(通量计算):1.4.1~1.4.2(建议:作业)(2)三种对称类型(建议:作业)①线与柱对称:1.4.3、1.4.4、1.4.9、1.4.10②面对称:1.4.5、1.4.7③球对称:1.4.6、1.4.8(其中1.4.8用到类似于“负质量法”的叠加原理)§5电场线一类2题(建议:均偏难,不留为作业)§6 电势两类8题(1)点电荷的电势(基础练习):1.6.1~1.6.3(建议:作业)(2)两种对称类型①球对称:1.6.4~1.6.6(建议:留1题为作业)②线与柱对称:1.6.7~1.6.8(建议:留1题为作业)第二章(共23题)§1 静电场中的导体三类6题(1)球对称:2.1.1(建议:作业)(2)板:2.1.2~2.1.4(其中:2.1.3为基本题,务必令学生掌握)(建议:作业)(3)拓展:2.1.5~2.1.6(建议:不留为作业)§2封闭金属壳内外的静电场二类5题(1)球对称:2.2.1~2.1.4(其中:2.2.1和2.2.3为基本题,务必令学生掌握)(建议:作业)(2)柱对称:2.2.5(建议:作业)§3 电容器和电容两类8题(1)电容基础练习:2.3.1~2.3.4(建议:作业)(2)电容器的串并联:2.3.5~2.3.8(建议:可不留作业)§5带电体系的静电能两类5题(1)电容器串并联的电能(基础练习):2.5.1(建议:作业)(2)拓展:2.5.2~2.5.4(建议:酌情可留为作业)第三章(共27题)§2 偶极子两类4题(1)偶极子受力和力矩:3.2.1.~3.2.3(建议:可将3.2.2和3.2.3为作业)(2)偶极子的静电能:3.3.4(建议:不留为作业)§4 极化电荷两类6题(1)极化电荷与极化强度:3.4.1~3.4.3(建议:可将3.4.2和3.4.3为作业)(2)介质对电容器的影响:3.4.4~3.4.5(板)3.4.6(球)(建议:作业)§5有电介质时的高斯定理三种对称类型11题(1)板:3.5.1~3.5.6、3.5.8、3.5.11(其中3.5.1~3.5.6为基本题,3.5.8为击穿场强,3.5.11为拓展)(建议:3.5.1~3.5.6为作业)(2)球:3.5.7(建议:作业)(3)柱:3.5.9~3.5.10(建议:作业)§6有电介质时的静电场方程两类4题(1)基本题:3.6.1(建议:作业)(2)拓展题:3.6.2~3.6.4(建议:均偏难,不留为作业)§7 电场的能量2题均为基础练习:3.7.1~3.7.2(建议:作业)第四章(共30题)§1恒定电流1题偏重于积分运算§2直流电路3题均为电阻的串并联问题(建议:可忽略)§3欧姆定律和焦耳定律两类8题(1)基本题:4.3.1~4.3.4(建议:作业)(2)应用题:4.3.5~4.3.8(建议:忽略)§4电源和电动势11题§5 基尔霍夫方程组7题。
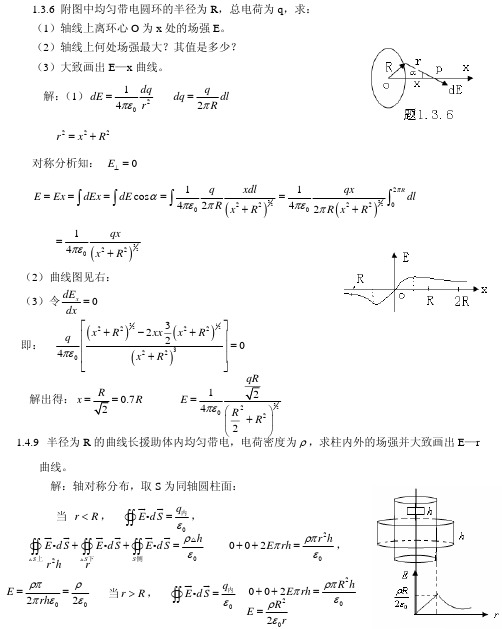
梁彬灿电磁学第三章习题解答

3.2.1 解答:(1)如图3.2.1所示,偶极子的电荷量q 和q -所受的电场力分别为qE 和qE -,大小相等,合力为0,但所受的力矩为M P E =⨯当且仅当0θ=和θπ=时,电偶极子受的力矩为0,达到平衡状态,但在0θ=的情况下稍受微扰,电偶极子将受到回复力矩回到平衡位置上,因此,0θ=时,是稳定平衡;但在θπ=的情况下稍受微扰,电偶极子受到的力矩将使电偶极子“倾覆”到达0θ=情况,因此,θπ=的情况是不稳定平衡。
(2)若E 不均匀,一般情况下,偶极子的电荷量q 和q -所受的电场力不为0,电场力将使偶极子转向至偶极矩P 与场强E 平行的情况,由于电场不均匀,偶极子所受的合力不为0.因此,电偶极子不能达到平衡状态。
3.2.2 解答:(1)如图3.2.2所示,偶极子1P 和2P 中的2q -处激发的电场为13222p E kl r -=⎛⎫- ⎪⎝⎭2q -所受的电场力为2123222q p F q E kl r ---=-=⎛⎫- ⎪⎝⎭偶极子1P 和2P 中的2q 处激发的电场为13222p E kl r +=⎛⎫+ ⎪⎝⎭2q 所受的电场力为2123222q p F q E kl r ++==⎛⎫+ ⎪⎝⎭偶极子2P 受到的合力为()332221222l l F F F k q p r r --+-⎡⎤⎛⎫⎛⎫=+=+--⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦令22l x ≡,()()3f x r x -≡+,()()3g x r x -≡-,则()()330,0f r g r --==,故()()()()()()4444'3,'3,'03,'03f x r x g x r x f r g r ----=-+=-=-=因22l r >>,对22l r ⎛⎫+ ⎪⎝⎭和22l r ⎛⎫- ⎪⎝⎭在0r =处展开后,略去高次项 ()()()()()()3434'003,0'03f x f x f r r x g x g g x r r x ----≈+=-=+=+()()46f x g x xr --=-所以()42121221440033(2)62q p l p p F k q p xr r rπεπε--=-=-= 其大小为124032p p F r πε=以上是1P 和2P 同向的情况,反向时大小不变,受力方向相反。
电磁学(梁灿彬)第二章导体周围的静电场

电像法可以用来求解导体周围的静电场,并给出导体表面的电荷分布和电场强度。
静电场中的高斯定理和环路定理
CATALOGUE
03
环路定理表明在静电场中,电场强度沿任意闭合路径的线积分等于零,也就是说,电场线没有起点也没有终点,它们形成闭合的曲线或直线。
总结词
环路定理是静电场的另一重要定理,它表明在静电场中,电场强度沿任意闭合路径的线积分等于零。这意味着电场线没有起点也没有终点,它们形成闭合的曲线或直线。这个定理可以用公式表示为:∮E·dl = 0。
电场强度与导体表面的电荷密度成正比
02
导体表面的电场线与导体表面垂直,并且从导体内部指向导体外部。
电场线与导体表面垂直
03
随着距离的增加,电场强度逐渐减小。
电场强度随距离的增加而减小
电像法是一种通过引入虚拟电荷来描述静电场的数学方法。
在电像法中,虚拟电荷的位置和大小是根据静电平衡条件和电场线与导体表面垂直的条件来确定的。
CATALOGUE
02
导体内部无电荷
导体内部任意位置均无电荷分布,电荷只分布在导体的表面。
电场线与导体表面垂直
导体表面的电场线与导体表面垂直,并且从导体内部指向导体外部。
导体表面电场强度与导体表面的电荷密度成正比
导体表面的电荷密度越大,导体表面的电场强度越大。
01
导体表面的电荷密度越大,导体表面的电场强度越大。
01
电子设备中的隔直、旁路和耦合作用
电容器在电子设备中可以起到隔离直流信号的作用,同时也可以旁路掉不需要的交流信号,实现不同电路之间的耦合。
02
调谐和滤波
利用电容器的充放电特性,可以调整电路的频率响应,从而实现调谐和滤波的功能。
电磁学(梁灿彬)第三章

V
S
二. ’ 与 P 的关系
全部在 V 内/外的偶极子对 V 内的 q’ 无贡献 仅与 V 的边界面 S 相截的偶极子才有贡献
V
S
计算 q’ 与 ’
在 S 上取 dS = dS nˆ 附近 p = ql || P
l/2 P nˆ
作斜柱体:l 为母线,dSdS 相截)
荷就穿出界面dS外边,则穿出dS外面的正电荷为:
nql dS np dS P dS
由于介质是电中性的,由V内通过界面S 穿出的正电荷量等于V内净余的负电荷量
V 'dV
P dS S
注:
(1)线性均匀介质中,极化迁出的电荷与迁入的电 荷相等,不出现极化电荷分布。
(2)不均匀介质或由多种不同结构物质混合而成的 介质,可出现极化电荷。
例题 2
平行导体板间充满均匀电介质 r = +1= 3.0 ,板间
距 d = 5.0 mm,介质内 E = 10 6 V/m。求 0 和
’ 。
解:由高斯定理
E 0 ' 0
' P nˆ 0E nˆ 0E
nˆ
0
’
-’
( E与 nˆ 反 向)
-0
0E 0 ' 0 0E
解得 0 0 (1 )E 0 r E
7
3、各向异性介质
• p, E 的关系与 E的方向有关。同一大
小的场强如果方向不同引起的 p 的
大小,方向也会不同。
• 一般是张量,不是常量, 个3n分
量。
8
1、极化强度
pi p
P np
定义:宏观电偶极矩用电极化
强度矢量P描述,它等于物理
小体积ΔV内的总电偶极矩与
《电磁学》梁灿彬课后部分答案
解:(1)解法一:在两电容器中,
C1
=
ε0s d1
, C2
=
d
ε0s −t −
d1
得:
ε0s . ε0s
C
=
C1C2 C1 + C2
=
d1 ε0s
d +
− t − d1 ε0s
= ε0s d −t
d1 d − t − d1
解法二:设板上自由电荷 Q,电荷分布如图,
由 E= σ 得: ε0
U=
σ ε0
B
=
u0 2π r
⋅ π
I R12
⋅π r2
=
u0 I 2π R12
r
B = u0I 当R1< r < R2时: 2π r
当R2
<
r
<R3时:
B
=
u0 2π r
[I
−
π
I (R32 −
R22 )
⋅π
(r2
−
R22 )]
=
u0 I 2π r
⋅
R32 R32
− r2 − R22
B = u0I (I − I ) = 0
B
=
μ0 μ rH
=
μ0μrN L
I
(2) 线圆电流 I0 产生的磁场为 B0
∫ ∑ L B0 ⋅ dl = μ0 Ii
B0 ⋅l = μ0 NI ,
B0
=
μ0 N l
I
磁化电流在匀质中产生的磁场为 B′
B′
=
B−
B0
=
μ0μr N l
I
−
μ0 N l
I
=
μ0 N I l
(完整版)电磁学(梁灿彬)第五章稳恒电流的磁场

§1 基本磁现象概述 (summary of basic magnetic phenomenon)
一、磁的基本现象
对磁现象的认识很早 最早发现的磁现象:天然磁石吸铁, 我国远在春秋战国时期(公元前六、七世 纪)的古书中已有记载
电磁学讲义
Electromagnetism Teaching materials
CH5 稳恒电流的磁场
2010级物理学专业
前言(Preface)
一、本章的基本内容及研究思路
静止电荷的周围存在着电场 运动电荷周围,不仅有电场,而且还有磁场。 不随时间变化的磁场称为稳恒磁场,有时也 称为“静磁场”。 稳恒电流激发的磁场就是一种稳恒磁场。 运动的电荷(或电流)要产生磁场,磁场又 会对其他的运动电荷(或电流)有作用力。 本章就是从这两个方面来研究磁场的。
大量实验证明,电现象和磁现象存在相互联系。 我们知道,电的作用是“近距”的,磁极或电 流之间的相互作用也是这样的,不过它通过另 外一种场—磁场来传递的。
用磁场的观点,可以把上述关于磁铁和磁铁, 磁铁和电流,以及电流和电流之间相互作用的各 个实验统一起来,概括成这样一个图示:
磁铁 电流
磁场
磁铁 电流
安培认为,任何物质的分子都存在环形电流, 称为分子电流,分子电流产生的磁场在轴线上的 方向可以用右手定则来判断,每一个分子电流相 当于一个小磁体。当物质中的分子电流排列得毫 无规则时,他们的磁场互相抵消,整个物体不显 磁性,但是,在一定条件下,这些分子电流比较 有规则的定向排列起来,他们的磁场互相加强, 整个物体就会显示出磁性。
安培的分子电流的想法基本上是正确的,近 代物理学证实,分子电流是由原子中的各个电子 自旋和电子的轨道运动合成的结果。
电磁学第二版梁灿彬 课后答案

f = 2k
Qq 0.2 i = 3.22 × 10−7 ( N ) 2 2 2 0.1 + 0.2 0.1 + 0.2
2
方向:水平向右
1.2.5 在正方形的顶点上各放一个电荷为 q 的同行点带电体。
1 2 )q 解之得: Q = ( + 4 2
(Q 应为负点电荷)
1.2.6 两个量值相等的同性点电荷相距为 2a,在两者连线的中垂面上置一试点电荷 q0,求 q0 受力最
大的点的轨迹。 解:∵
f = 2k
又∵
2kqq′r qq′ r = 2 2 3 2 (a + r ) (a 2 + r 2 ) (a + r ) 2
第一章
静电场的基本规律
1.1
判断下列说法是否正确, 说明理由。
(1)一点的场强方向就是该点的试探点电荷所受电场力的方向。 (2)场强的方向可由 E=F/q 确定,其中 q 可正可负。 (3)在以点电荷为心的球面上,由该点电荷产生的场强处处相等。 答案: (1) ×,正的试探电荷; 1.2 1.3 (2) √ ; (3)× 在无外场是,球面上 E 大小相等。
1 q1q2 可以得到: 4πε 0 r 2
1.6 =
4q12 4πε 0 (5 ×10−2 ) 2 1
解之得: q1 = 0.33 × 10−6 ,
q2 = 4q1 = 1.33 ×10−6
∴ 当 r=0.1 时,所受排斥力为:
F=
q1q2 =0.4(N) 4πε 0 (0.1) 2
电磁学》梁灿斌习题答案大全集

1.5 附图中 A 和 B 为两个均匀点电体,S 为与 A 同心的球面,试问: (1)S 面的通量与 B 的位置及电荷是否有关? (2)S 面上某点的电场强度与 B 的位置及电荷是否有关? (3)可否用高斯定理求出 S 面上一点的场强?为什么?
答案:(1)无关 (2) 有关 (3)不能(导体球)、可以(介质球)。 场强叠加原理应用到有导体的问题时,要注意,带电导体单独存在时,有一种电荷分布,它
1.2.1 真空中有两个点电荷,其中一个的量值是另一个的 4 倍。她们相距 5.0×10-2 m 时相互排斥力
为 1.6N。问: (1)她们的电荷各为多少? (2)她们相距 0.1m 时排斥力的多少?
解:设一个电量为 q1 ,则 q2
=
4q1 ,由公式
F
=
1 4πε 0
q1q2 r2
可以得到:
1.6
=
q 4πε 0 r 2
不变,
被气球表面掠过的点
,E
发生跃变,由
E
=
q 4πε0r 2
→0。
1.8 附图中 S1、S2 是四个闭曲面,以 E1、E2、E3 分别代表由 q1、q2、q3 激发的静电场强,试判断 下列各等式的对错
∫∫ (1)
s1
E1
⋅
d
s
=
q1 ε0
∫∫ (2)
s2
E3
⋅
d
s
=
q3 ε0
满足什么条件时内球电势为正?满足什么条件时内球电势为零?满足什么条件时内球电势为负?
(参考点选在无远。)
答案:U1
=
q1 4πε 0 R1
+
q2 4πε0 2R1
梁彬灿电磁学第二章习题解答

在导体球壳内场强和电势分别为
球壳外的电场由壳外壁电荷激发,壳外的电势为
场强大小E和电势V的分布如图2.2.1(a)和(b)中 曲线和 曲线所示。
2.2.2
解答:
球形金属腔内壁感应电荷的电荷量为 ,由于点电荷q位于偏心位置,所以腔内壁电荷面密度分布 不均匀,球形金属腔外壁的电荷量为 ,腔外壁电荷面密度 均匀分布。根据电势叠加原理,O点的电势为
可表示为
2.3.1
解答:
孤立导体球的电容为
C=
代入数据得
2.3.2
解答:
(1)平行放置一厚度为x的中性金属板后,在金属板上、下将出现等值异号的感应电荷,电场仅在电容器极板与金属板之间,设电荷密度为 ,电场为
A、B间电压为
A、B间电容C为
(2)金属板离极板的远近对电容C没有影响
(3)设未放金属板时电容器的电容为
(4)根扰前几题的分析,只有答案(b)是正确的,即 是除 外所有电荷(包括2上的电荷)激发的场强(方向垂直导体表面),也是1上位于A的面元 在C点激发的电场。
2.5
解答:
不可能,用反证法证明。假定出现图中所示的情况,设 是M表面上某个 的面元,则由它发出的电场线只有两种可能的“归宿”:一是终止于N的负电荷;二是终止于无穷远处。
2.7
解答:
用反证法,假定A带正电而又不是电势最高者,则说明导体A上有的地方电荷面密度为负,从而有电场线终止于导体A上,这些电场线或来自于壳M,或来自于B的正电荷,则说明 ,但因为导体B为中性导体,所以在它上面必有负电荷,终止于这些负电荷上的电场线,显然不能来自导体B自身,只可能来自壳M上的正电荷,因而有 。但由于导体A所带的电荷量为正,所以A上的正电荷必发出电场线,但是这些电场线却没有去处:既不能终止于导体B,又不能终止于壳上,参看图2.7(a)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电磁学习题解答
1.2.2 两个同号点电荷所带电荷量之和为Q 。
在两者距离一定的前提下,它们带电荷量各为多少时相互作用力最大?
解答:
设一个点电荷的电荷量为1q q =,另一个点电荷的电荷量为
2()q Q q =-,两者距离为r ,则由库仑定律求得两个点电荷之间的作用力为
2
0()
4q Q q F r πε-=
令力F 对电荷量q 的一队导数为零,即
20()04dF Q q q
dq r
πε--== 得
122
Q
q q ==
即取 122
Q
q q ==
时力F 为极值,而 22
2
02
204Q q d F dq r
πε==
<
故当122
Q
q q ==
时,F 取最大值。
1.2.3 两个相距为L 的点电荷所带电荷量分别为2q 和q ,将第三个点电荷放在何处时,它所受的合力为零?
解答:
要求第三个电荷Q 所受的合力为零,只可能放在两个电荷的连线中间,设它与电荷q 的距离为了x ,如图1.2.3所示。
电荷Q 所受的两个电场力方向相反,但大小相等,即
22
00204()4qQ qQ
L x x
πεπε-=- 得 22
20x Lx L +-=
舍去0x <的解,得
1)x L =- 1.3.8解答:
A
E 3
x
∞
(c)
(b)
(a)
(1)先求竖直无限长段带电线在O 点产生的场强1E ϖ
,由习题1.3.7
(2)可知 104x E R
η
πε=
仿习题1.3.7解答过程,得
12
223/2
1223/20sin ()0()4y y dl
ldl
dE k
k
r R l ldl E k R l R
ηηαη
ηπε==-+∞=-=-
+⎰
故 10ˆˆ()4E i j R
ηπε=
-v
同理,水平无限长段带电线在O 点产生的场强
20ˆˆ()4E i j R
ηπε=
-+v 对于圆弧段带电线在O 点产生的场强3E ϖ
,参看图1.3.8(b ),得
32
30cos cos /2cos 04x x dl
d dE k
k
R
R
k E d R R
ηηα
αα
πηηααπε====⎰
同理得 304y E R
η
πε=
故 30ˆˆ()4E i j R
ηπε=
+v
解得
12330ˆˆ()4E E E E E i j R
ηπε=++==
+v v v v v (2)利用(1)中的结论,参看习题1.3.8图(b ),A -∞的带电直线在O 点的场强为
=
0ˆˆ()4A E i j R
ηπε--v
B -∞的带电直线在O 点产生的场强为
0ˆˆ()4B E i j R
ηπε=
-+v 根据对称性,圆弧带电线在O 点产生的场强仅有x 分量,即
0/2ˆˆˆcos /22AB ABx k E E i d i i R R
πηηααππε===-⎰v v 故带电线在O 点产生的总场强为。
