分析力学五一
分析力学PPT课件

x 2 y 2 z 2 (R0 bt)2
f (x, y, z,t) x 2 y 2 z 2 (R0 bt)2 0
(3)可解约束和不可解约束 a 可解约束:只从一侧限制系统运动的约束,
即单方向约束 如甲虫在气球内(或外)但可飞离球面 x2 y2 z2 R2 或 x2 y2 z2 R2
1、广义坐标定义 任何 f 个可以完全确定(刻化)系统(f 个
自由度)位置的变量 q1, q2 , q f 称为该系统的广
义坐标,其对时间的导数则称广义速度。 (1)对完整约束,广义坐标数目与自由度数
目相等; (2)广义坐标的选择不是唯一的,并且是任
意的,长度、角度、面积、能量、电量、电流, 电极化强度 P ,磁化强度 M 等都可以作广义坐标;
2、问题的提出:导出理论的思路 实际问题是每个质点受到的作用力中还包括由
于维持约束而出现的约束力(或约束反力),这些 力都是未知的,而且与体系的运动有关,这使问题 更为复杂。分析力学把这类力的存在当做处理难点 来建立力学理论。
还是从质点组出发,但用一个受有约束的质点 组可以概括广泛的力学研究对象——非自由体系。
反映约束条件的方程称其约束方程
2、约束力:为维持约束而加于系统的力称为约 束力(也称约束反力)
(1)约束力可以是物体间相互接触而产生的力 (如桌面对其上物体的支持力),也可以是物体内 各部分的相互作用力(刚体内各质点间的作用力) (2)约束力在动力学问题未解出之前一般是未知 的 (特 殊 情 况 为 已 知 如 桌 面 对 物 体 的 支 撑 力 为 mg ),约束的存在并没有因事先知道了部分运动 情况而使求解变得简单,常常反而使问题变得更复 杂了
(3)约束力的大小和方向与约束有关,还与 外力及运动状态有关,可按约束运动的需要自动 调节,是一种因运动,外力而变化的被动力
《分析力学总结》课件

总结
重要性
作为物理学的核心学科之一, 分析力学主要研究物体运动和 相互作用力,具有广泛应用价 值。
应用广泛性
分析力学不仅涉及到结构、机 械、工程和控制等多个领域, 而且可以帮助解决设计和优化 的问题。
发展和前景
分析力学的研究和应用将助力 世界各地的工程学家和科学家, 成就更析力学诞生于18世纪末19世纪初,随着科学技术的不断进步,分析力学得到了长足的 发展。
2 研究现状
分析力学在计算机科学等多学科领域的崛起,为分析力学理论的研究和工程实践的应用 奠定了坚实的基础。
3 未来发展趋势
随着人类对宇宙和微观世界的了解的不断深入,分析力学将在科学发现和工程实践中继 续发挥着至关重要的作用。
共轭动量和泊松括号是研究动力学系统和守恒定律
分析力学应用
1
刚体动力学
2
分析刚体运动和受外力之后的角动量变
化。
3
实际问题求解
4
用数学模型,计算和解决现实工程问题, 如桥梁结构分析和控制系统设计等。
刚体运动学
研究刚体的运动状态和运动轨迹。
建立分析模型
将分析力学理论,应用于现实情况下的 工程问题。
分析力学在工程中的应用
分析力学总结
分析力学是研究物体运动和相互作用力的学科。本PPT将全面介绍分析力学的 基本概念、理论基础、应用场景、发展历程和未来趋势。
什么是分析力学?
基本概念
分析力学是研究力学系统中,物体的动力学特 性和运动的规律性的科学。它广泛用于描述和 预测机械结构及控制系统的运动和状态。
特点和应用
分析力学有高度的数学抽象性和广泛的实际应 用价值,如在航空、汽车、机械制造、船舶和 建筑工程等领域中。
分析力学

M
v0
drt dr′
dr
M′
为 dr ,则
drt
dr = drt + dr′
δ r1
M
δ r2
• 物块 M的虚位移可以是沿斜
面向上的 δ r1 ,也可以是沿斜 面向下的 δ r2,因为 δ r1 和 δ r2 都是约束所允许的 .
可见,不稳定约束下,质点系无限小的实位移并不是 其虚位移之一 .
青岛科技大学数理学院
∂x ∂y ∂z
∵ δ r = δ xi + δ yj + δ zk
∂f i + ∂f j + ∂f k = n ∂x ∂y ∂z
∴ n⋅δr = 0
非自由质点的虚位移垂直于曲面上该点处的法线,即虚 位移必在通过该点的曲面的切平面上 .
青岛科技大学数理学院
19
¾ 质点在直角坐标中的虚位移与广义坐标中的虚位移之 间的关系:
面向上的 δ r1 ,也可以是沿斜 面向下的 δ r2,因为 δ r1 和 δ r2 都是约束所允许的 .
可见,稳定约束下,质点系无限小的实位移是其虚位 移之一 .
青岛科技大学数理学院
17
物块 M置于以速度 v0 移动的斜面上,则斜面对物块M 的
约束为不稳定约束 .
• dt 时间内,斜面位移为 drt dt 时间内,物块的实位移
为 s = 3n − k .
¾ 选广义坐标 q1, q2,……, qs ,则各质点的坐标
⎧ ⎪ ⎨
xi yi
= =
xi (q1, q2,……, qs ) yi (q1, q2,……, qs )
⎪⎩zi = zi (q1, q2,……, qs )
i = (1, 2,……, n)
§1.1分析力学

第一章分析力学到现在为止,我们所研究的力学问题,基本上是用牛顿运动定律来求解的。
但用牛顿运动运动定律来求质点组的运动问题时,常常需要求解大量的微分方程组。
如果质点组受到约束,则因约束反力都是未知的,所以并不能因此而减少,甚至是增加了问题的复杂性。
十八、十九世纪,随着工业革命的迅速发展,在工程技术上迫切需要解决的又正好是这一类问题。
因此迫切需要寻求另外的方法来处理这一问题。
1788年,拉格朗日写了一本大型著作《分析力学》,在这一本著作中,完全用数学分析的方法来解决所有的力学问题,而无需借助以往常用的几何方法,全书一张图也没有。
在此基础上逐步发展成为一系列处理力学问题的新方法,称之为分析力学。
分析力学以拉格朗日和哈密顿等所建立的变分原理为基础,将力学的基本定律表示为分析数学的形式。
通过分析的方法来解决任意力学体系的运动问题,它所涉及的量是标量。
而牛顿力学涉及的量如力、速度、加速度等多为矢量。
由此看来,分析力学和牛顿力学只是同一个力学领域应用不同的数学描述而已。
对于自由质点和简单问题,两种方法无优劣(lie)之分,对复杂问题,分析力学的优越性就体现出来了。
分析力学是从能量的观点来研究力学问题,因而具有更广泛的应用价值。
它广泛的应用于结构分析、机器动力学与振动、航天力学、多刚体系统、机器人动力学以及各种工程技术领域,也可推广应用于连续介质力学和相对论力学。
许多新兴学科,如量子力学、相对论、电动力学、连续介质力学、天体力学、统计力学等等,都可以用到分析力学的理论和方法。
但是,由于分析力学中的数学推理较多,在历史上也发生过一些不良倾向,容易使人忘记力学的物理实质,对此我们应当引以为戒。
§1.1 广义坐标一、基本概念1、力学体系n 个相互作用着的质点构成的集合体。
2、 位形质点系各质点在空间的位置的有序集合,它决定了质点的位置和形状,也就是位形是质点系在空间的位置状态。
3、约束限制质点自由运动的条件。
15.分析静力学

7
第十一章 分析静力学基础 §11–1 分析力学基本概念 虚位移、虚功、 §11–2 虚位移、虚功、理想约束 §11–3 虚位移原理 §11–4 以广义坐标表示的虚位移原理 、广义力 §11–5 保守系统平衡的稳定性
8
§11-1
一、约束和约束方程
分析力学基本概念
限制质点或质点系运动的各种条件称为约束。 限制质点或质点系运动的各种条件称为约束。 将约束的限制条件以数学方程来表示,则称为约束方程。 将约束的限制条件以数学方程来表示,则称为约束方程。 例如: 例如
曲柄连杆机构 平面单摆
x2 + y2 = l 2
x A2 + y A2 = r 2
( xB − x A ) 2 + ( y B − y A ) 2 = l 2 , y B = 0
9
y A = x A tan ωt zA = 0
yA = 0 zA = 0
2 ( x B − vt ) 2 + y B = l 2
ri = ri (q1 , q2 ...qk , t )
(i = 1,2, L, n)
§11-2
一、虚位移 1.概念
虚位移 虚功 理想约束
在质点系运动过程的某瞬时 某瞬时,质点或质点系为约束所允 某瞬时 为约束所允 许的、假想的 任意微小的位移。 假想的、任意微小的 许的 假想的 任意微小的 虚位移可以是线位移,也可以是角位移。通常用变分符 虚位移可以是线位移,也可以是角位移。 号δ 表示虚位移。 例如
16
、广义坐标 一般地,质点系的自由度
k =3n − s
通常, 很大而k 很小。 通常,n 与 s 很大而 很小。为了确定质点系的位置,用 适当选择的k 个参数(相互独立),要比用3n个直角坐标和s个 约束方程方便得多。 用来确定质点系位置的独立参数,称为广义坐标 广义坐标。 广义坐标 广义坐标的选择不是唯一的。广义坐标可以取线位移(x, y, z, s 等)也可以取角位移(如α , β, γ, ϕ 等)。在完整约束情 况下,广义坐标的数目就等于自由度数目。
第六章_分析力学

本章难点: 本章难点:
掌握虚位移、虚功、简正坐标、哈密顿函数、 掌握虚位移、虚功、简正坐标、哈密顿函数、 虚位移 泊松括号、 泊松括号、变分等概念 掌握虚功原理、拉格朗日方程、哈密顿正则方程、 掌握虚功原理、拉格朗日方程、哈密顿正则方程、 虚功原理 哈密顿原理、 哈密顿原理、泊松定理
4
理论力学
第六章 分析力学
xi = xi (q1 , q2 ,..., qs ; t ) ,其中 (i = 1, 2,...,3n)
例如质点限制在半径为R的圆槽中时, 例如质点限制在半径为 的圆槽中时, 的圆槽中时 个坐标参量: 有3个坐标参量: x, y, z ,只有 个独立坐标参量 个坐标参量 只有1个独立坐标参量 个几何约束方程: 有2个几何约束方程:z = 0, x 2 + y 2 = R 2 个几何约束方程
3
理论力学
第六章 分析力学
本章重点: 本章重点:
掌握约束、理想约束、虚位移、虚功、广义坐标、 掌握约束、理想约束、虚位移、虚功、广义坐标、 约束 自由度、广义动量、广义角动量、简正坐标、 自由度、广义动量、广义角动量、简正坐标、 哈密顿函数、泊松括号、 哈密顿函数、泊松括号、变分等概念 掌握约束分类、虚功原理、 变换、 掌握约束分类、虚功原理、 Legendre变换、泊松定理、 约束分类 变换 泊松定理、 拉格朗日方程、哈密顿正则方程、 拉格朗日方程、哈密顿正则方程、哈密顿原理
7
理论力学
第六章 分析力学
2、稳定约束和不稳定约束 、 稳定约束的约束方程中不显含时间t 稳定约束的约束方程中不显含时间 不稳定约束的约束方程中显含时间t 不稳定约束的约束方程中显含时间 有的书叫(不 稳定约束为 稳定约束为(非 定常约束 有的书叫 不)稳定约束为 非)定常约束 3、可解约束和不可解约束 、 可解约束指在力学体系运动过程中, 可解约束指在力学体系运动过程中,某些约束可以被解除 r 约束方程为不等式,有时也称单侧(面 约束 约束方程为不等式,有时也称单侧 面)约束 f ( r ) ≤ 0 不可解约束指在力学体系运动过程中, 不可解约束指在力学体系运动过程中,始终不能被解除 r f ( r) = 0 约束方程为等式,有时也称双侧(面 约束 约束方程为等式,有时也称双侧 面)约束
第一章 分析力学基础

y = f (x) (x, y R)
在闭区间a, b上的连续函数A(x),积分
b
I = a A(x)dx
设定义在 a, b上的所有连续函数组成的集合为 ,则
上式给出了集合 到数域R的一个映射关系,称之为泛函 数,记为
I (A) (I R,A )
n个质点组成的质点系,任一瞬时这n个质点在空间中 位置的集合称为该质点系的位形。
所有满足约束条件的质点系的位形的集合称为该质点 系位形空间 。可以证明,对于完整约束系统,位形空间为 线性空间。
对于保守系统,位形空间的每一个元素(即质点系的 每一个位形),都有唯一的势能值与之对应,因此,质点 系的势能可以看成是定义在位形空间的一个泛函数。
n
δWF δWFi i 1
n
i 1
( Fix
N k 1
xi qk
δqk
Fiy
N k 1
yi qk
δqk
Fiz
N k 1
zi qk
δqk )
N n (Fix
k 1 i1
xi qk
Fiy
yi qk
Fiz
zi qk
)δqk 0 Nhomakorabea令Qk
n
( Fix
i 1
xi qk
Fiy
yi qk
势能变分的定义
设y=f(x)是定义在数域R上的可微函数,当自变量x发生 微小变化dx时,对应函数值的微小变化称为函数的微分,记 作
dy = f (x + dx) - f (x) = f (x)dx
设 I (A) 是定义在集合 上的泛函数,当自变量A发 生微小变化 A 时,对应泛函数值的微小变化称为泛函数的 变分
分析力学知识点总结

分析力学知识点总结在分析力学知识中,有一些重要的概念和原理,接下来我们将对其进行详细分析和总结。
一、广义坐标和广义速度在分析力学中,广义坐标和广义速度是非常重要的概念。
广义坐标是用来描述系统中每个自由度的变化的参数,而广义速度则是描述系统各自由度变化率的参数。
广义坐标和广义速度并不是系统中每个粒子的坐标和速度,而是用来描述整个系统运动规律的一组参数。
对于一个具有N个自由度的系统,可以找到N个独立的广义坐标和广义速度来描述系统的状态。
通过广义坐标和广义速度,可以建立系统的运动方程,进而研究系统的运动规律。
二、拉格朗日方程拉格朗日方程是分析力学的重要原理之一,它是用来描述系统运动规律的一种方法。
拉格朗日方程是通过系统的动能和势能函数来建立的,它可以描述系统在广义坐标变化下的运动规律。
对于一个N个自由度的系统,其拉格朗日方程可以写为:d/dt(∂L/∂q_i) - ∂L/∂q_i = Q_i其中,L是系统的拉格朗日函数,q_i表示系统的广义坐标,Q_i表示系统的广义力。
通过拉格朗日方程,可以得到系统的运动方程,进而研究系统的运动规律。
三、哈密顿方程哈密顿方程也是分析力学的一个重要原理,它是通过系统的哈密顿函数来描述系统的运动规律的一种方法。
哈密顿函数是系统的广义坐标和广义动量的函数,通过哈密顿函数可以得到系统的哈密顿方程。
对于一个N个自由度的系统,其哈密顿方程可以写为:dq_i/dt = ∂H/∂p_idp_i/dt = -∂H/∂q_i其中,H是系统的哈密顿函数,q_i表示系统的广义坐标,p_i表示系统的广义动量。
通过哈密顿方程,可以得到系统的运动方程,进而研究系统的运动规律。
四、刚体运动在分析力学中,刚体运动是一个重要的研究对象。
刚体是一个在运动中保持形状不变的物体,它的运动规律可以通过刚体力学来描述。
刚体力学包括了刚体的运动方程、角动量定理、动能、角速度等内容,通过这些内容可以研究刚体的运动规律。
第五章 分析力学ppt课件

或
不可解约束以等式表示,可解约束则同时以等式和 不等式表示。
5.1
约束与广义坐标
第5章 分析力
③几何约束(完整约束)与运动约束(微分约束)
某些约束仅对力学系统的空间位置加以限制,而对各质点的速
度没有限制, 这种约束称为几何约束 (geometrical constraint )。可 表示为
f r , r , r , , t 0 1 2 3
§5.0
引言
第5章 分析力
5 提出新的力学原理代替牛顿定律
牛顿力学 矢量力学 力学第一原理 拉格朗日方程 拉格朗日力学 (相当于“几何公理” ) 哈密顿力学 哈密顿原理
三者本质上相同,可以相互证明 利用无穷小计算原理对抽象数学及应用数学的应用,使用拉格 郞日和哈密顿方法给以力学问题抽象的数学处理,即把物理世 界事物属性翻译成数学关系式,中间不考虑物理意义,只在讨 论计算结果时再翻译转化到真实物理世界上去。
或
f r , r , r , , r ; r , r , r , , r 0 1 2 3 n 1 2 3 n
或
f r , r , r , , r ; r , r , r , , r , t 0 1 2 3 n 1 2 3 n f r , r , r , , r ; r , r , r , , r , t 0 1 2 3 n 1 2 3 n
或
f r , r , r , , r ; r , r , r , , r , t 0 1 2 3 n 1 2 3 n
5.1
约束与广义坐标
分析力学-总结

• 分析力学概述 • 牛顿运动定律与动量守恒 • 经典力学中的拉格朗日力学 • 相对论力学与量子力学 • 分析力学的应用领域 • 分析力学的未来发展与挑战
01
分析力学概述
定义与特点
定义
分析力学是经典力学的一个分支 ,主要研究质点和刚体的运动以 及它们之间的相互作用。
特点
分析力学以数学分析为工具,通 过建立数学模型来描述物理现象 ,具有高度的理论性和抽象性。
变。
表达式
L = r × p = constant,其中L为 角动量,r为位置矢量,p为动Байду номын сангаас。
应用领域
在旋转运动中广泛应用,如行星 运动、陀螺仪等。
03
经典力学中的拉格朗日力学
拉格朗日方程
拉格朗日方程是分析力学中的基本方程,它描述了系统的运动状态和变化规律。
拉格朗日方程基于拉格朗日函数L,该函数由系统的动能T和势能V组成,并定义了 系统在给定时间内的运动状态。
相对论与量子力学的进一步发展
相对论力学
相对论力学是经典力学在高速运动和强 引力场条件下的扩展。相对论力学的进 一步发展需要深入研究相对论效应对物 质运动和相互作用的影响,以及在宇宙 学、天体物理等领域的应用。
VS
量子力学
量子力学是描述微观世界物质运动规律的 学科。随着纳米科技、量子计算等领域的 快速发展,量子力学在材料科学、信息科 技等领域的应用越来越广泛。进一步发展 量子力学需要解决如何将量子力学的原理 应用于实际工程中的问题,以及如何实现 量子技术的商业化应用。
THANKS
感谢观看
通过分析力学,研究卫星在地球引力、太阳辐射压和其他力作用下 的运动轨迹,确保卫星能够稳定运行和有效通信。
理论力学-第五章分析力学1-wcx

(1)使用范围:理想约束 (2)范围的扩展:对于有摩檫的约束,可将其视为主动力 (3)优点:去掉约束力,仅得到主动力平衡方程
局限性:无法求约束力
F Fx i Fy j Fz k 【例1】自由质点受外力作用保持平衡,所受外力为:
试由虚功原理求其平衡方程。
2、广义坐标形式的虚功原理
约束力不出现在方程中
方程形式与坐标系的选择无关
方程形式与研究对象无关
完全用数学分析的方法来处理力学问题
第一节 约束与广义坐标
一、约束 1、约束的概念:限制质点自由运动的条件 2、约束与自由度的关系:s 3n k 3、约束的分类 (1)稳定约束和非稳定约束
f ( x, y, z ) 0 稳定约束(定常约束) 约束方程 束) f ( x, y, z; t ) 0 非稳定约束(非定常约 v
a 2 sin cos l 2 a 2 sin 2
1
Q M Fa sin F
a 2 sin cos l a 何约束 f ( x, y, z; t ) 0 微分约束
, y , z ; t ) 0 f ( x, y, z; x
可以积分 不可积分
完整约束 非完整约束
可解约束
(2)完整系:只受完整约束的力学体系;
不完整系:受到不完整约束的力学体系
x
s
y
F
虚位移的大小: s l
x s cos l cos 分量形式: y s sin l sin
(2)变分运算法
先写出质点的笛卡尔坐标,找到其与广义坐标之间的关系,再 利用变分计算出对应的虚位移
周衍柏著理论力学——第五章分析力学 pdf讲义

3
不可解约束:质点始终不能脱离的约束。如质点始终被曲面 约束,即存在约束方程
f ( x, y , z ) = 0 或 f ( x, y , z , t ) = 0 (5.1.3)
约束又可分为几何约束和运动约束。 几何约束又叫做完整约束,它只限制质点在空间的位置,因 而表现为质点坐标的函数,如
f ( x, y , z ) = 0 或 f ( x, y , z , t ) = 0 (5.1.3)
dr P
δr
7
8
9
三、虚功原理 以下讨论只限于不可解约束的情况,设体系在 k 个几何约束 下处于平衡状态。由于体系处于平衡状态,所以体系中每一 个质点都处于平衡状态。 因此任一质点 Pi ,受到主动力的合力 Fi 与约束反力的合力 Ri 满足: (i = 1,2, L , n ) (5.2.3) Fi + Ri = 0 让每一质点在平衡位置发生一虚位移 δr ,则有 Fi ⋅ δr + Ri ⋅ δr = 0 (i = 1,2, L , n ) 上式对各质点求和得:
1
第一节 约束与广义坐标
一、约束的概念和分类 1、力学体系:质点的集合,且质点间存在相互作用,每一 个质点的运动都和其它质点的位置及运动有关,简称体系。 若有 n 个质点,则描述所有质点位置的坐标有 3n 个。 2、约束:限制质点自由运动的条件叫做的约束。 约束一般可表示成质点位置、速度和时间的方程。如:
理论力学第五章分析力学

P x1 , y1 1 P2 x2 , y2 B x3 , y3
1 1 Pl1 cos P2l1 cos Fl1 sin P2l2 cos Fl2 sin 0 1 2 2
ri ri q 0 Fi q mi ri q 1 i 1
s n
ri ri q 0 Fi q mi ri q 1 i 1
xi xi q1 , q2 ,...qs , t
i i
1
2
s
i 1, 2,..., n, s 3n
i
i
1
2
s
或
ri ri q1 , q2 ,...qs , t
i 1, 2,..., n, s 3n
这s个独立参数就叫广义坐标
§5.2 虚功原理
1.实位移和虚位移
第五章 分析力学
分析力学是拉格朗日等人在十八世纪在牛顿力学 基础上建立的经典力学的一个体系,因为所用的方法 完全是数学分析,称之为分析力学。建立分析力学的 目的是为了 用数学方法解决复杂的力学问题,后来的 研究发现,分析力学的体系和方法不局限于力学,对 物理学的其他领域也非常有用。其原因是将物理规律 抽象为数学原理和定理,揭示了物理规律背后更普遍 的性质,掌握这些对今后的学习很重要。 这一章的重点是拉格朗日方程,哈密顿正则方程 和正则变换在统计物理中有重要应用,泊松括号的概 念在量子力学中非常重要。
若拉氏函数不显含
分析力学教学课件

v0
drr
dr M'
dr = dre + drr = MM‘ dre = v0dt ---牵连位移 drr ---物块相对斜面的位移
dre
δr2
M
δr1
物块M的虚位移可以是沿斜面向下的 δr1,也可以是沿斜面向上的δr2,因为 δr1,δr2都是约束所容许的。
f(x,y,z)0 ——约束方程
f(x x ,y y ,z z ) 0
因此: 平面图形上任意一点B的运动可用合成运动的概念进行
分析,其速度可用速度合成定理求解。
2. 速度投影定理
定理: 同一瞬时,平面图形上任意两点的 速度在这两点连线上的投影相等。
反映了刚体不变形的特性:
因刚体上任意两点间的距离应保持不变,所以刚体上任意两点的速度在 这两点连线上的投影应该相等,否则,这两点间的距离不是伸长,就要缩短, 这将与刚体的性质相矛盾。因此,速度投影定理不仅适用于刚体作平面运动, 而且也适用于刚体的一般运动。
• 实现这些约束条件的物体称为约束体。 受到约束条件限制的物体叫做被约束体。习惯
上,把约束体简称为约束,将被约束体简称为物体 。
• 主动力和约束力(或约束反力)
• 约束力(或约束反力)——把约束对物体的作用 力称为约束力。
• 主动力——作用于被约束物体上的除了约束以外的 力统称为主动力,如重力,结构承受的风力和水压 力、机械结构中的弹簧力以及电磁力等等。
l2 cos2 l2 sin2
对于有n个质点的质点系,若有s个完整约束组成,则其自由
度N = 3n- s,可选N个广义坐标 q1, q2 ,…,qN。
则各质点的坐标可由广义坐标表示为:
xi yi
xyii((qq11,,qq22,, ,,qqNN))
第一章 分析力学的基本概念

应用力学研究所 李永强
第15页
§1.1 分析力学的研究对象&约束
几何约束&运动约束 几何约束
在质点系中,只能限制各质点在空间位置或质点系的位 形的约束称为几何约束或位置约束。 约束方程:
f ri , t 0 i 1,2, ,n i质点的个数
或 f xi , yi , zi ,t 0
应用力学研究所 李永强
第4页
§1.1 分析力学的研究对象&约束
分析力学的研究对象 约束&约束的分类 几何约束&运动约束 完整约束&非完整约束 完整系统&非完整系统 线性运动约束可积分条件简介(Pfaff(伐夫) 型微分方程的可积条件)
应用力学研究所 李永强
第5页
§1.1 分析力学的研究对象&约束
约束方程对时间求一阶导数(全导数的形式):
n i 1
f ri
ri
f t
0
其中:
ri
xii
yi j
zi k
f ri
f xi
i
f
yi
j
f
zi
k
可得:
i
n 1
f xi
xi
f yi
yi
f zi
zi
f t
0
应用力学研究所 李永强
第29页
§1.1 分析力学的研究对象&约束
完整约束&非完整约束:
应用力学研究所 李永强
第11页
§1.1 分析力学的研究对象&约束
分析力学的研究对象__ 分析力学的发展史
1788年:法国学者 Lagrange出版“分析力学”(Mécanique Analylique) 引入广义坐标,建立力学最重要的动力学方程;
华中师范大学分析力学4(共4)

¨ 其中 U0 为分子势能在平衡位置的二阶导数,它只与分子中原子 的种类以及带电量有关,与原子的质量无关。 方程(1)的解为一种简谐振动,振动频率为
ω2 =
所以
ω0 2 (ω)
2U0 m
=
m1 m2 (m0 +m0 ) 1 2 0 m0 (m +m ) m1 2 1 2
质量为 m 的穿孔小球可以自由的在一根光滑直杆上滑动,如 图所示。将一根弹簧系在此球上,弹簧的另一端固定在离杆 l 的钉子上。平衡时弹簧的拉力为 F 。求此球在平衡位置附近做 微小振动的频率。 解:这个球只有一个自由度,取为小球离开平衡 位置的距离 x 。那么小球的拉格朗日可以写成:
ml 12
2
0
ml2 12
0 0
mR2 4
0
(c)
0 0 ⎠ 0
⎞
(b)
(d)
⎜ I=⎝+ 0 0 Nhomakorabea+ 0 0
mh2 12
⎜ I=⎝
2
⎛
2ma2 5
0
2ma 5
2
0 0
⎞ ⎟ ⎠ ⎞ ⎟ ⎠
0 0
2ma2 5
⎞ ⎟ ⎠
0
mR 4
2
0 + 0
mh 12
0 0
mR2 2
⎜ I=⎝
mb2 12
mc2 12
带入拉格朗日方程可得
µ (m1 + m2 )l1 (g − l1 w2 ) −m2 l1 l2 w2 −m2 l1 l2 w2 m2 l2 (g − l2 w2 )
¶µ
u1 u2
¶
=0
上式有非零解的条件是
¯ ¯ (m1 + m2 )l1 (g − l1 w2 ) ¯ ¯ −m2 l1 l2 w2 ¯ −m2 l1 l2 w2 ¯ ¯ 2 ¯ = 0 m2 l2 (g − l2 w )
1.1分析力学基本概念
⑦ 1843年,哈密顿提出哈密顿原理。
分析力学的特点
牛顿力学 1、真实空间、一般坐标 2、侧重“力”,“加速 度” 3、以牛顿三定律为基础 分析力学 1、数学空间、广义坐标 2、能量(L函数、H函数) 3、哈密顿原理(公理)为基础
4、运用微积分
4、运用变分
几何约束方程的一般形式为
2 2 xA yA r 2 OA,AB距离一定 2 2 2 ( xB x A ) ( y B y A ) l yB 0
f r ( x1 , y1 , z1 , , xn , yn , zn ) 0
y
B( xB , yB ) v r B
x x A A
yA yA zA 0 xB xA l sin q cos yB y A l sin q sin z l cosq
B
广义坐标对时间的导数称为与该广义坐标对应的广义速度, 写成
a dqa dt q
7.位形空间:
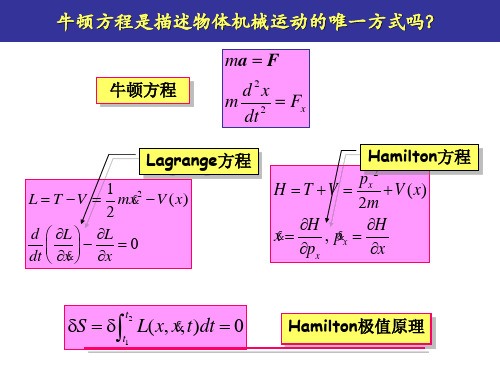
牛顿方程是描述物体机械运动的唯一方式吗?
ma F
牛顿方程
d 2x m 2 Fx dt
Hamilton方程 px 2 H T V V ( x) 2m H H x , px px x
Lagrange方程
L T V 1 2 mx V ( x) 2 d L L 0 dt x x
三、双面约束与单面约束 同时限制质点某方向及相反方向运动的约束称为双面约束(不可解约束)。 只能限制质点某方向的运动,而不能限制相反方向运动的约束称为单面约束 (可解约束)。并非约束面是单面还是双面。约束是对运动方向而言的。
此方向不受限制,可缩短
分析力学

分析力学分析力学是理论力学的一个分支,它通过用广义坐标为描述质点系的变数,以牛顿运动定律为基础,运用数学分析的方法,研究宏观现象中的力学问题。
分析力学是适合于研究宏观现象的力学体系,它的研究对象是质点系。
质点系可视为宏观物体组成的力学系统的理想模型,例如刚体、弹性体、流体以及它们的综合体都可看作质点系,质点数可由一到无穷。
又如太阳系可看作自由质点系,星体间的相互作用是万有引力,研究太阳系中行星和卫星运动的天体力学,同分析力学密切相关,在方法上互相促进;工程上的力学问题大多数是约束的质点系,由于约束方程类型的不同,就形成了不同的力学系统。
例如,完整系统、非完整系统、定常系统、非定常系统等。
不同的系统所遵循的运动微分方程不同;研究大量粒子的系统需用统计力学;量子效应不能忽略的过程需用量子力学研究。
但分析力学知识在统计力学和量子力学中仍起着重要作用。
分析力学对于具有约束的质点系的求解更为优越,因为有了约束方程,系统的自由度就可减少,运动微分方程组的阶数陆之降低,更易于求解。
分析力学的发源1788年拉格朗日出版的《分析力学》是世界上最早的一本分析力学的著作。
分析力学是建立在虚功原理和达朗贝尔原理的基础上。
两者结合,可得到动力学普遍方程,从而导出分析力学各种系统的动力方程。
1760~1761年,拉格朗日用这两个原理和理想约束结合,得到了动力学的普遍方程,几乎所有的分析力学的动力学方程都是从这个方程直接或间接导出的。
1834年,汉密尔顿推得用广义坐标和广义动量联合表示的动力学方程,称为正则方程。
汉密尔顿体系在多维空间中,可用代表一个系统的点的路径积分的变分原理研究完整系统的力学问题。
从1861年有人导出球在水平面上作无滑动的滚动方程开始,到1899年阿佩尔在《理性力学》中提出阿佩尔方程为止,基本上已完成了线性非完整约束的理论。
20世纪分析力学对非线性、不定常、变质量等力学系统作了进一步研究,对于运动的稳定性问题作了广泛的研究。
分析静力学

解:由虚位移原理
FQxB Fpxx A Fpyy A 0
用解析法求各虚位移之间的关系
取 为广义坐标,有
xB 2l1 cos xA 2l1 cos (l1 l2 ) cos (l1 l2 ) cos yA (l1 l2 ) sin FPx Fp sin, FPy Fp cos
xB 2l1 sin xA (l1 l2 ) sin yA (l1 l2 ) cos
FQ 2l1 sin FP sin (l1 l2 ) sin FP cos (l1 l2 ) cos 0
FP 2l1 sin FQ l2 l1 cos 2
例5 多跨静定梁, 求支座B处反力。
理论力学
分析力学概述
牛顿力学以力、位移、速度、加速度等矢量为基本量。 故又称矢量力学。牛顿力学一般取单个质点或刚体为研究对 象,以建立坐标、矢量在坐标轴上投影的方法求解。
这种求解方法对质点或刚体个数少的不甚复杂的力学系统 可以得到满意的结果,且直观性较强。但对于质点或刚体个 数较多的复杂系统的力学问题,取单个物体为研究对象就会 出现约束力多、方程多、求解困难的问题。
即 rB rC
由虚位移原理
FS5rB cos30 FPrC cos30 0
得
FS5 FP
课堂练习 一、 滑套D套在光滑直杆AB上,并带
动杆CD在铅直滑道上滑动。已知=0o
时,弹簧等于原长,弹簧刚度系数为
5(kN/m),求在任意位置( 角)平衡
时,加在AB杆上的力偶矩M ? 解:这是一个已知系统平衡,求作用于系统上主动力之间关
系的问题。将弹簧力计入主动力,系统简化为理想约束系统, 故可以用虚位移原理求解。
34
选择AB杆、CD杆和滑套D的系统为研究对象。
分析力学发展历程

近代分析力学
分析力学近代发展的重要表现在于它的现代 化.近二十年来分析力学发生了根本变化,促 进这种变化的主要因素有两个.一个是微分几 何的进步,用以得到更几何更本质的观点.这 种观点充满物理学(如规范场论),特别是力 学.另一因素是数学分析以及流形上泛函分析 的近代发展.荷兰著名力学家Koiter说得 好:“为使力学得到进一步的发展,我们一定 要逐步应用更加抽象和更加精密的数学”。
Company Logo
近代分析力学
近代分析力学也可以叫作“几何动力学”, 系指用近代微分几何(如流形、微分流形、辛 流形等)观点研究分析力学的原理和方 法.1982年6月在意大利都灵召开的分析力学 近代发展讨论会上,许多力学家、数学家和 物理学家介绍了他们在几何动力学方面的研 究成果.法国人在用近代微分几何方法研究天 体力学、刚体力学、动力系统的结构等方面 取得重要进展;意大利人在分析力学中的辛关 系上贡献突出
中国分析力学的发展方向
5
约束系统 非线性动 力学的研 究
6
数学问 题的力 学化求 解方法
7
分析力学 与工程科 学、高新 技术的结 合
Company Logo
LOGO
Company Logo
近代分析力学的主要内容
流形与 lagrange 力学
辛sympletic 流形与 hamilton力 学
KAM定理
Company Logo
流形与lagrange力学
Lagrange力学用位形(configuration)空间 描述力学系统的运动.力学系统的位形空间具 有微分流形结构,其同胚群作用在此结构 上.Lagrange力学的基本思想和定理相对此 群是不变的. 一个Lagrange力学系统用一流形(位形空间) 和在流形的切丛上的函数(Lagrange函数)给 出。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t 实际上,I ⋅ ω = I ω 就是前面讲的本征值方程,即
∑I ω
j=1 ij
3
(a) j
= Iaω
(a) i
(i =1 ,2,3)
,2,3), 由上式可解出相互垂直的本征方向 ω(a) (a =1
即角动量与角速度共线的方向或惯量主轴。 在三个相互垂直的惯量主轴 ω(a) (a =1 ,2,3) 上, 以三个本征值 Ia为半轴作出的椭球,称为刚体的惯量 椭球。它就是转动惯量矩阵的本征椭球。
ψ 定义 ϕ, θ,ψ 为欧勒角( ϕ, θ :确定自转轴位置, :确
定绕自转轴转动的角度)
z, z '
y'
O
ϕ
y
ϕ
x
N, x '
刚体的基本运动形式:平动、转动 平动规律:质量集中在质心上的单质点运动规律 重点:转动 转动的特点:绕不同轴的转动之间有相互关联
§1.5.1 刚体的角速度、角动量与转动能量 一、不同转轴转动之间的关联
r →T∆ϕ1T∆ϕ2 r = (1+∆ϕ1×)(1+∆ϕ2×)r = (1+∆ϕ1×)(r +∆ϕ2 ×r) v v v v = r +∆ϕ2 ×r +∆ϕ1 ×r +∆ϕ1 ×(∆ϕ2 ×r)
两者之差:
v
v
v
v
(T∆ϕ1T∆ϕ2 −T∆ϕ2T∆ϕ1 )r = (∆ϕ1 ×∆ϕ2 ) ×r
对于无限小转动: ∆ϕ1 →0, ∆ϕ2 →0
设:刚体绕通过o点的轴线转动了一个微小角度 ∆ϕ 。
v ∆ 沿轴线方向作一有向线段: ϕ ,∆ϕ = ∆ϕ。这一
v v 则: r →r +∆r = r +∆ϕ ×r = (1+∆ϕ×)r (转动 ∆ϕ 后)
转动:空间变换 转动变换的数学表示: T∆ϕ =1+∆ϕ × 设:∆ϕ1, ∆ϕ2 ——绕两个不同轴的转动 v v ∆ϕ2 时,r 变为 1. 先转 ∆ϕ1 ,后转
第五章
刚体的运动
刚体:特殊的质点组——任何两个质点之间的距离保持 不变 刚体的形状和大小都不变化(自由度降低) 引入两套坐标系,确定刚体在空间的位置,即
Ox0 y0z0 : 静止坐标系
ox1x2x3 : 固连在刚体中的坐标系(参与刚体的全部运动),
它的原点在静止坐标系中的位矢为 R0 。 注:下图中oxyz为从静止坐标系过渡动坐标系的坐标系
⇒
ω' = ω
——角速度不因转动中心(坐标系)的选择而变 通常,以刚体的质心作为运动坐标系的原点, 此时,V0——质心的速度。
三、角动量矢量与转动惯量张量
1 . 刚体平动:单个质点的运动 P =M V 2 . 定轴转动:L = I ω 3. 刚体绕o点的转动:刚体——质点组,对o点的总角动量
L = ∑ra ×pa =∑mara × va
a=1 N a=1 a=1 a=1
N
N
N
+[∑m r e ⋅ e3 − ∑ma xara ⋅ e3]ωz
a=1 2 a a 1 a=1
N
2 = [∑(mara2 − ma xa )]ωx +[−∑ma xa ya ]ωy +[−∑ma xa za ]ωz a=1 a=1 a=1
N
N
N
=[∑m( y2 + z2 )]ωx +[−∑mxy]ωy +[−∑mxz]ωz
a=1 a=1
N
N
va =ω×ra
⇒
2 L = ∑mara × (ω× ra ) = ∑ma [ra ω− (ra ⋅ω ra ] ) a=1 a=1
N
N
又
ω = ∑eiωi = ∑ei ( ei ⋅ω = ∑[ei ei ]⋅ω )
i=1 i=1 i=1
3
3
3
[ei ei ] —并矢
同理,有
(ra ⋅ω ra = ra (ra ⋅ω = [rara ]⋅ω ) )
若选相互垂直的三个惯量主轴作坐标轴,则:所 有的惯量积都为零 (为什么?)。此时,转动惯量张量 具有对角形式
I1 0 I = 0 I2 0 0
在这一坐标系中,L = i
0 0 I3
j
∑I ω
j =1 ij
3
成为
L = I1ω , L2 = I2ω2, L3 = I3ω3 1 1
——关于ωx , ωy , ωz的线性齐次方程组
I xx − I
非零解条件
I xy I yy − I I zy
I xz I yz = 0 I zz − I
I yx I zx
I 有三个正实根:Ia (a=1、2、3)
由 Ia 的三组解
(a)
ω
(a)
(a =1 2、 、 3)
三组解 ω 的方向决定了角动量与角速度共线的 三个方向。这三个方向称为刚体的惯量主轴。 Ia :沿主轴方向的转动惯量。
I xy , I yz , I zx为惯量积。
质量连续分布:
dm = ρdτ ,
∑→∫
⇒
I xx = ∫ ( y2 + z 2 )ρdτ, I xy = −∫ xyρdτ L
四、惯量主轴
定义了转动惯量、惯量积后,得到
Lx = Ixxωx + Ixyωy + Ixzωz Ly = I yxωx + I yyωy + I yzωz Lz = Izxωx + Izyωy + Izzωz
线位移:沿不同方向彼此独立 A+B=B+A——平行四边形法则
角速度矢量
但:对转动,绕不同轴的转动,彼此之间互相关联。 例子:书的大角度转动。 显然:绕不同轴转动有限角度,与先后次序有关,并不 独立。 结论:两个有限转动的合成不服从平行四边形法则 不 结论 两个有限转动的合成不服从平行四边形法则,不 两个有限转动的合成不服从平行四边形法则 能看成矢量。 能看成矢量 注意:矢量——有大小、方向,且满足平行四边形法则 的量。 无限小角位移是矢量。 然而可证明:无限小角位移是矢量 无限小角位移是矢量
d R0 dR V= 固定坐标系: P点速度 V = ;o点速度 0 P dt dt
v
Vp = V + ω×rop 0
( ω 是以o点为中心的角速度)
对另一点o',且oo' = a,同理有
V ' = V +ω×oo' = V +ω×a o 0 0
现设:o' 为转动中心,以o' 为原点的坐标系中,P点 r' 的矢径为r'op 则 rop= r'op+ a
= [∑m r
a=1
N
2 a a
∑δ
i=1
3
1,i i
e − ∑ma xara ]⋅ (ωxe1 +ωye2 +ωze3 )
a=1
N
= [∑m r e − ∑ma xara ]⋅ (ωxe1 +ωye2 +ωze3 )
a=1
N
N
N
2 a a 1
a=1
=[∑mara2 −∑ma xara ⋅e1]ωx +[∑mara2e1 ⋅ e2 −∑ma xara ⋅ e2 ]ωy
同理,有
Ly =[−∑myx]ωx +[∑m(z2 + x2 )]ωy +[−∑myz]ωz
Lz =[−∑mzx]ωx +[−∑mzy]ωy +[∑m(x2 + y2 )]ωz
2 2 Lx ∑m( y + z ) ⇒ Ly = − ∑myx L − mzx ∑ z
2 L = ∑[mara ∑(ei ei ) ⋅ ω− marara ⋅ ω] a=1 N i=1 3 N 3
= ∑[m r
a=1
2 a a
∑e e −m r r ]⋅ω
i=1 i i a a a
比较:L = Iω——定轴转动,即
L//ω,L和 ω共线
定点转动:转动惯量不再是常数,而是一个并矢
3 t N 2 I = ∑[mara ∑ei ei − marara ] a=1 i=1
v
v
v
v
略去二阶小量 (∆ϕ1 ×∆ϕ2 )×r
v
v
(∆ϕ1 ×∆ϕ2 体现关联: ϕ1, ∆ϕ2 顺序不一样,结果不一样) ∆
则
v
v
v
v
T∆ϕ1T∆ϕ2 r = T∆ϕ2 T∆ϕ1 r
即
r + (∆ϕ2 +∆ϕ1)×r = r + (∆ϕ1 +∆ϕ2 )×r v v v v (r:任意) ∆ϕ2 +∆ϕ1 =∆ϕ1 +∆ϕ2
− ∑mxy m(z2 + x2 ) ∑ − ∑mzy
− ∑mxz ωx − ∑myz ωy m(x2 + y2 ) ωz ∑
t 上式为 L = I ⋅ω 的矩阵形式 t ⇒ 并矢 I 有九个分量
t I 的矩阵形式
∑m( y2 + z2 ) I = −∑myx −∑mzx 2 2 ∑m(z + x ) −∑myz −∑mzy m(x2 + y2 ) ∑ −∑mxy −∑mxz
—— 两个无穷小转动与次序无关:两个无 两个无穷小转动与次序无关: 穷小角位移相加服从平行四穷小角位移是矢量。 无穷小角位移是矢量。 无穷小角位移是矢量
二、角速度矢量
定义:
∆ϕ dϕ lim = = ω ——瞬时角速度(矢量) ∆t →0 ∆ t dt
v
v
