必修2第一单元典型例题汇编
(完整)高一物理必修二经典例题带答案

高一物理必修 2 复习第一章 曲线运动1、 曲线运动中速度的方向不停变化,因此曲线运动必然是一个变速运动。
2、物体做曲线运动的条件:当力 F 与速度 V 的方向不共线时,速度的方向必然发生变化,物体将做曲线运动。
注意两点: 第一,曲线运动中的某段时间内的位移方向与某时辰的速度方向不一样。
位移方向是由开端地点指向末地点的有向线段。
速度方向则是沿轨迹上该点的切线方向。
第二,曲线运动中的行程和位移的大小一般不一样。
3、 平抛运动:将物体以某一初速度沿水平方向抛出,不考虑空气阻力,物体所做的运动。
平抛运动的规律: ( 1)水平方向上是个匀速运动( 2)竖直方向上是自由落体运动位移公式: x0t; y1 gt2 速度公式: v xv 0 ;v y gt2合速度的大小为: vv x 2v y 2; 方向,与水平方向的夹角为: tanv y v 01. 对于质点的曲线运动,以下说法中不正确的选项是( )A .曲线运动必定是一种变速运动B .变速运动必然是曲线运动C .曲线运动能够是速率不变的运动D .曲线运动能够是加快度不变的运动2、某人骑自行车以 4m/s 的速度向正东方向行驶, 天气预告报告当时是正寒风, 风速也是 4m/s , 则骑车人感觉的风速方向和大小( )A. 西寒风,风速 4m/sB. 西寒风,风速 4 2 m/sC. 东寒风,风速 4m/sD. 东寒风,风速 42 m/s3、有一小船正在渡河,离对岸50m 时,已知在下游 120m 处有一危险区。
假定河水流速为5 m s ,为了使小船不经过危险区而抵达对岸,则小船自此时起相对静水速度起码为()A 、 2.08 m sB 、 1.92 m sC 、 1.58 m sD 、 1.42 m s 4. 在竖直上抛运动中, 当物体抵达最高点时()A. 速度为零, 加快度也为零B. 速度为零, 加快度不为零C. 加快度为零,有向下的速度 D.有向下的速度和加快度5.如下图,一架飞机水平川匀速飞翔,飞机上每隔1s 开释一个铁球,先后共开释 4 个 , 若不计空气阻力,则落地前四个铁球在空中的摆列状况是( )6、做平抛运动的物体,每秒的速度增量老是: ()A .大小相等,方向同样B .大小不等,方向不一样C .大小相等,方向不一样D .大小不等,方向同样7.一小球从某高处以初速度为v 0 被水平抛出,落地时与水平川面夹角为45 ,抛出点距地面的高度为 () A .v 02B . 2v 02C .v 02D .条件不足没法确立gg 2g8、如下图, 以 9.8m/s 的水平初速度 v 0 抛出的物体,飞翔一段时间后,垂直 地撞在倾角 θ为 30°的斜面上,可知物体达成这段飞翔的时间是( )A . 3sB .2 3sC . 3 sD .2s33第二章 圆周运动物体做匀速圆周运动时: 线速度、 向心力、 向心加快度的方向时辰变化, 但大小不变; 速率、角速度、周期、转速不变。
人教版必修二第一章测试题汇编
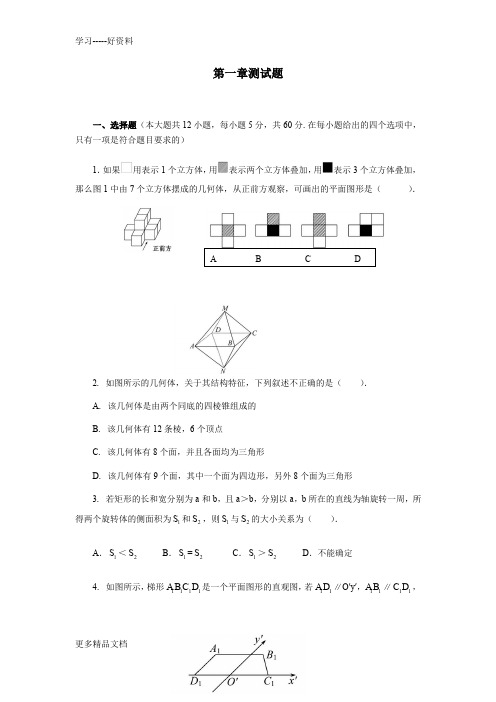
第一章测试题一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.如果用表示1个立方体,用表示两个立方体叠加,用表示3个立方体叠加,那么图1中由7个立方体摆成的几何体,从正前方观察,可画出的平面图形是( ).2. 如图所示的几何体,关于其结构特征,下列叙述不正确的是( ). A . 该几何体是由两个同底的四棱锥组成的 B . 该几何体有12条棱,6个顶点C . 该几何体有8个面,并且各面均为三角形D . 该几何体有9个面,其中一个面为四边形,另外8个面为三角形3. 若矩形的长和宽分别为a 和b ,且a >b ,分别以a ,b 所在的直线为轴旋转一周,所得两个旋转体的侧面积为1S 和2S ,则1S 与2S 的大小关系为( ).A .1S <2SB .1S =2SC .1S >2SD .不能确定4. 如图所示,梯形1111A B C D 是一个平面图形的直观图,若11A D ∥O′y′,11A B ∥11C D,11A B =11C D =2,11A D =1,则原图形的面积是( ).A . 10B . 5C . 5D . 105. 下列几何体中,正视图、侧视图、俯视图都相同的几何体的序号是( ). A .(1)(2)B .(2)(3)C .(3)(4)D .(1)(4)6. 某人用如图所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( ).A . 快、新、乐B . 乐、新、快C . 新、乐、快D . 乐、快、新7. 已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是 ( ).A . 16πB . 20πC . 24πD . 32π8. 圆锥的表面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为 ( ). A . 120° B . 150° C . 180°D . 240°9. 把3个半径为R 的铁球熔成一个底面半径为R 的圆柱,则圆柱的高为( ). A . RB . 2RC . 3RD . 4R10. 表面积为则此球的体积为( ).A .B .C .D .11. 下列几何体中是棱柱的有( ).A . 1个B . 2个C . 3个D . 4个12. 如下图为一个几何体的三视图,尺寸如图所示,则该几何体的表面积为( ).(不考虑接触点)A .π B .4π C . 32π+ D .18+π二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上) 13. 一个立方体的六个面上分别标有字母A ,B ,C ,D ,E ,F ,如图是此立方体的两种不同的摆放方式,则与D 相对的字母是 ______.正 视侧视俯视14.一个水平放置的平面图形的斜二测直观图是一个底角为45°腰和上底边为1的等腰梯形的面积是.15.一个正四棱锥的底面边长为2,侧棱长为3,五个顶点都在同一个球面上,则此球的表面积为.16.图3中实线围成的部分是长方体(图2)的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是14,则此长方体的体积是.三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10法)18.(12分)在长方体ABCD-A1B l C l D l中,AB=3,AD=2,CC l=1,一条绳子从点A 沿表面拉到点C l,求绳子的最短长度.19.(12分)设圆台的高为3,其轴截面(过圆台轴的截面)如图,母线AA1与底面圆直径AB的夹角为60°,轴截面中的一条对角线A1B垂直于腰A1A,求圆台的体积.20(12分)已知四棱锥P-ABCD,其三视图和直观图如图,求该四棱锥的体积.21.(12分)如图所示,三棱锥P—ABC侧棱的长度均为1,且侧棱间的夹角均为40°,动点M在棱PB上移动,动点N在棱PC上移动,求AM+MN+NA的最小值.22.(12分)如图,BD是正方形ABCD的对角线,弧BD的圆心是A,半径为AB,正方形ABCD以AB所在直线为轴旋转,求图中Ⅰ、Ⅱ、Ⅲ三部分旋转所得旋转体的体积之比.参考答案一、选择题1. 选B .画出该几何体的正视图为,其上层有两个立方体,下层中间有三个立方体,两侧各一个立方体,故B 项满足条件.2. 选D . 结合多面体的相关概念知,该几何体共有8个三角形面,12条棱,6个顶点,它可以看成有两个“同底”的四棱锥组合而成,故D 项不正确.3. 选B . 由圆柱的侧面积公式可得,1S =2πab , 2S=2πba ,∴1S =2S .4. 选B .将直观图还原为平面图形,如图, AB =2,CD =3,AD =2, 所以S 梯形ABCD =12×(2+3)×2=5. 5. 选D .正方体与球的正视图、侧视图、俯视图都相同.6. 选A . 将纸片折起,自上向下看逆时针方向“新年快乐”,故②为“新”,①为“快”,③为“乐”.7. 选C . 设正四棱柱的底边长为a ,则V =2a ·h ,∴16=2a ×4,∴a =2.由球和正四棱柱的性质可知,球的直径为正四棱柱的对角线.∴R ==∴S =4π2R =24π. 8. 选C . 设圆锥底半径为R ,母线长为L ,由题意,π2R +πRL=3 π2R ,∴L=2R , 圆锥的底面圆周长l =2πR ,展开成扇形后,设扇形圆心角为n°,扇形的弧长l =ππ2180180n L n R=,∴2πR=π2180n R,∴n=180, 即展开后扇形的圆心角为180°. 9. 选D . 设圆柱的高为h ,由三个铁球的体积与圆柱的体积相等,可得324π3π3R R h ⨯=⨯,所以h=4R .10.选C.因为表面积为,所以棱长为2.11.选C.由棱柱的结构特征可知①③④是棱柱.12.选D.该几何体由正三棱柱和球组成,正三棱柱的表面积为18+球的表面积为π,所以该几何体的表面积为18π+.二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13. B.做出正方体模型观察可得,与D相对的字母是B.14.2.由斜二测画法可知,该平面图形是一个直角梯形,其上底为1,下底为1,直角边长为2,所以该平面图形的面积为111)222⨯+⨯.15. 9π 易求得:球的半径为32,所以球的表面积为9π.16. 3.向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是14,设长方体的高为x,则()()42122214xx x+=++,所以3x=,所以长方体的体积为3.三、解答题17.直观图如下图所示.(1)画轴:在直观图中画出x′轴,y′轴,使∠x′O′y′=45°.(2)确定A′,B′,C′三点,在x′轴上取B′使O′B′=4.过(2,0),(4,0)两点作y′轴的平行线,过(0,2),(0,-1)两点作x′轴的平行线,得交点A′,C′.(3)顺次连接O ′A ′,A ′B ′,B ′C ′,C′O′并擦去辅助线,就得到四边形OABC 的直观图O′A′B′C ′.18.若把绳子沿表面A A 1BB l 和BB l C l C 从点A 拉到点C l ,如图所示,则绳子的最短长度为A C l ==同理,若把绳子沿表面AA 1BB l 和A 1B l C l D l 从点A 拉到点C l ,如图所示,则绳子的最短长度为AC l ==同理,若把绳子沿表面AA 1D l D 和A 1D l C l B 1从点A 拉到点C l ,如图所示,则绳子的最短长度为AC l =522)31(22=++.比较三种路径,知道绳子的最短长度为19. 设圆台的上下底面半径和高分别为r 、R 、h .过A 1作A 1D ⊥AB 于D ,则A 1D =3,∠A 1AB =60°. 又因为∠AA 1B =90°, 所以∠BA 1D =60°. 所以AD =A 1D cot60°=3⨯33=3. R +r =A 1D tan60°=33. 易得R =23,r=3. 而h =3,所以圆台的体积为()221π3V h R Rr r =++=221π3]3⨯⨯+=21π. 20.由三视图知底面ABCD 为矩形,AB =2,BC =4,顶点P 在面ABCD 内的射影为BC 中点E ,即棱锥的高为2,则体积V P-ABCD = 13S ABCD ×PE=13×2×4×2=163. .21. 三棱锥P —ABC 的展开图如图所示,则AM +MN +NA =A 1M +MN +AN .又∵A 1M +MN +AN ≥ AA 1,∴当A ,M ,N 三点共线时,取到最小值. 在图中,∵∠A1PB =∠BPC =∠CP A =40°,∴在图中∠AP A 1=120°.在△AP A 1中,AA 1A 1M +MN +NA 的最小值为,即AM +MN +NA .22. 图中Ⅰ绕AB 所在直线旋转形成一个圆锥,Ⅱ绕AB 所在直线旋转形成的几何体为半球挖去一个圆锥,Ⅲ绕AB 所在直线旋转形成一个圆柱挖去一个半球.把图中Ⅰ、Ⅱ、Ⅲ三部分分别绕AB 所在直线旋转所得旋转体体积分别记为V Ⅰ、V Ⅱ、V Ⅲ,并设正方形的边长为a ,因此,23111ππ,33V a a a =⋅= 331141ππ,233V a V a II =⋅-=3311ππ,3V a V V a III II =--=所以1::1:1:1V V V II III =.。
(人教版最新)高中英语必修第二册 Unit 1单元测试01

Unit 1 单元测试一、阅读理解(共两节,满分35分)第一节(共10小题,每小题2.5分,满分25分)阅读下列短文,从每题所给的A、B、C和D四个选项中,选出最佳选项。
AFrom early times, man has been interested in art. People have often worked together to collect and save the world’s art treasures. Fine art treasures from many countries are kept in an art museum called the Louvre in Paris, France. The works of art have been collected by the people of France over many centuries. It is one of the biggest art museums in the world.The Louvre has not always been a museum. The first building was a fort(堡垒). In 1190, it was the king’s castle with high walls and a round tower. It had a moat(护城河)to keep out the enemies. Over the years, the number of buildings around the castle grew. By 1350, the castle no longer needed a fort. The Louvre became a palace home for French kings and queens.During the time of peace, new treasures were brought in. During the days of war, many treasures were stolen, and the buildings were damaged.When Francis I became the King of France in 1515, he brought in many artists from other countries. One of the artists was Leonardo da Vinci from Italy. Da Vinci’s Mona Lisa is the best known painting in the museum today.In 1793, the Louvre became a public museum. It is a place where art treasures are kept for everyone to enjoy. Every year millions of people from all over the world come to the Louvre to see the masterpieces.1. Most of works of art in the Louvre have been collected probably by ________.A. the French peopleB. Francis IC. Leonardo da VinciD. people of the world2. Why is it good for the works of art to be kept in public museums?A. The works of art will not be stolen.B. The works of art will not be damaged.C. Artists can study the works of art.D. Everyone has a chance to enjoy the works of art.3. According to the passage, which of the following statements is TRUE?A. The Louvre is always a museum since it was built.B. All the art treasures in the Louvre have been destroyed in the war.C. The Louvre was once the king’s castle in history.D. There is still a fort near the Louvre now.BWhat killed King Tut? Historians and scientists have long believed that ancient Egypt’smost famous king was probably murdered. But a recent scientific study claims to have found adifferent answer to this more than 3,300-year-old mystery. A team of researchers now say thatKing Tut, the boy ruler, died of complications (并发症)from a broken leg.Tut’s full name was Tutankhamun. He was just 9 years old when he became the ruler ofEgypt in 1333 BC. His treasure-filled tomb was discovered almost a century ago. It was filled with royal riches, including a solid-gold coffin, a gold mask, and piles of jewelry.Unfortunately Tut died at the age of 19. Many experts have thought that Tut was killed by one of his advisers, named Ay, who wanted to be king. But thanks to a major modern science project, it seems Ay is innocent.Researchers set out to solve the mystery of King Tut’s death by using the tools of science, including DNA tests and electronic scans of his mummy(木乃伊). Scientist Carsten Pusch carried out the tests on Tut for the new study. He thinks a broken leg led to the young king’s death. More than 100 walking sticks were found in King Tut’s tomb. This supports the team’s findings. But how could a person die from a simple broken leg?Pusch also found DNA evidence in Tut’s body that shows he had malaria, a disease carried by mosquitoes. Malaria seriously weakens the immune system(免疫系统).Pusch and his fellow researchers believe the malaria and the bone disease together caused the king’s fracture (骨折)to become deadly. Finally, the young king was just too weak to recover. So effects of the disease combined with the bad luck of a broken bone —not a jealous adviser —are likely the real, causes of King Tut’s death.4. It has long been believed by historians and scientists that ________.A. King Tut was the youngest ruler in the world historyB. King Tut was the richest ruler in the history of EgyptC. King Tut was murdered by one of his advisersD. King Tut was poisoned by one of his servants.5. With the help of modern technology, the new study discovered that the king ________.A. died directly of a disease called malariaB. died of complications from a broken legC. died of a simple cut in the broken legD. was bitten to death by deadly mosquitoes6. Researchers uncovered the mystery of King Tut’s death by ________.A. testing the King’s immune systemB. studying the walking sticks found in the tombC. performing experiments on mosquitoesD. applying DNA tests and electronic scan technology7. The passage mainly tells us about ________.A. a different answer to King Tut’s deathB. a famous boy king in ancient EgyptC. a treasure-filled tomb discovered in EgyptD. a team of researchers studying ancient tombsCIn the 1960s, while studying the volcanic history of Yellowstone National Park, Bob Christiansen became puzzled about something that, oddly, had not troubled anyone before: he couldn’t find the park’s volcano. It had been known for a long time that Yellowstone was volcanic in nature —that’s what accounted for all its hot springs and other steamy features. But Christiansen couldn’t find the Yellowstone volcano anywhere.Most of us, when we talk about volcanoes, think of the classic cone(圆锥体)shapes of a Fuji or Kilimanjaro, which are created when erupting magma(岩浆)piles up. These can form remarkably quickly. In 1943, a Mexican farmer was surprised to see smoke rising from a small part of his land. In one week he was the confused owner of acone five hundred feet high. Within two years it had topped out at almost fourteen hundred feet and was more than half a mile across. Altogether there are some ten thousand of these volcanoes on Earth, all but a few hundred of them extinct. There is, however, a second less known type of volcano that doesn’t involve mountain building. These are volcanoes so explosive that they burst open in a single big crack, leaving behind a vast hole, the caldera. Yellowstone obviously was of this second type, but Christiansen couldn’t find the caldera anywhere.Just at this time NASA decided to test some new high-altitude cameras by taking photographs of Yellowstone.A thoughtful official passed on some of the copies to the park authorities on the assumption that they might make a nice blow-up for one of the visitors’ centers. As soon as Christiansen saw the photos, he realized why he had failed to spot the caldera: almost the whole park —2.2 million acres —was caldera. The explosion had left a hole more than forty miles across —much too huge to be seen from anywhere at ground level. At some time in the past Yellowstone must have blown up with a violence far beyond the scale of anything known to humans.8. What puzzled Christiansen when he was studying Yellowstone?A. Its complicated geographical features.B. Its ever-lasting influence on tourism.C. The mysterious history of the park.D. The exact location of the volcano.9. What does the second paragraph mainly talk about?A. The shapes of volcanoes.B. The impacts of volcanoes.C. The activities of volcanoes.D. The heights of volcanoes.10. What does the underlined word “blow-up” in the last paragraph most probably mean?A. Hot-air balloon.B. Digital camera.C. Big photograph.D. Bird’s view.第二节(共5小题;每小题2分,满分10分)根据短文内容,从短文后的选项中选出能填入空白处的最佳选项。
(典型题)高中数学必修二第一章《立体几何初步》检测题(答案解析)

一、选择题1.如下图所示,在正方体1111ABCD A B C D -中,E 是平面11ADD A 的中心,M 、N 、F 分别是11B C 、1CC 、AB 的中点,则下列说法正确的是( )A .12MN EF =,且MN 与EF 平行B .12MN EF ≠,且MN 与EF 平行 C .12MN EF =,且MN 与EF 异面 D .12MN EF ≠,且MN 与EF 异面 2.在正方体1111ABCD A B C D -中,点,E F 分别是梭BC ,CD 的中点,则1A F 与1C E 所成角的余弦值为( )A .5B .25C .5D .25 3.如图,在正四棱锥P ABCD -中,设直线PB 与直线DC 、平面ABCD 所成的角分别为α、β,二面角P CD B --的大小为γ,则( )A .,αβγβ>>B .,αβγβ><C .,αβγβ<>D .,αβγβ<< 4.已知三棱锥A BCD -的各棱长都相等,E 为BC 中点,则异面直线AB 与DE 所成角的余弦值为( )A 13B 3C 33D 115.已知正三棱柱111ABC A B C -中,1AB AA =,M 是1CC 的中点,则异面直线AM 与1A B 所成角的大小为( )A .π6B .π4C .π3D .π2 6.如图,正三棱柱111ABC A B C -的高为4,底面边长为43,D 是11B C 的中点,P 是线段1A D 上的动点,过BC 作截面AP α⊥于E ,则三棱锥P BCE -体积的最小值为( )A .3B .23C .43D .127.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是( )A .24B .30C .47D .7 8.一个底面为正三角形的棱柱的三视图如图所示,若在该棱柱内部放置一个球,则该球的最大体积为( )A .6πB .12πC .43πD .83π 9.一个正方体的平面展开图及该正方体的直观图如图所示,在正方体中,设BC 的中点为M ,GH 的中点为N ,下列结论正确的是( )A .//MN 平面ABEB .//MN 平面ADEC .//MN 平面BDHD .//MN 平面CDE10.如图是某个四面体的三视图,则下列结论正确的是( )A.该四面体外接球的体积为48πB.该四面体内切球的体积为2 3πC.该四面体外接球的表面积为323πD.该四面体内切球的表面积为2π11.某几何体的三视图如图所示,该几何体的体积为V,该几何体所有棱的棱长之和为L,则()A.8,14253V L==+B.8,1425V L==+C.8,16253V L==+D.8,1625V L==+12.某三棱锥的三视图如图所示,则该三棱锥的体积为()A .16B .13C .23D .2二、填空题13.在边长为3的菱形ABCD 中,对角线3AC =,将三角形ABC 沿AC 折起,使得二面角B AC D --的大小为2π,则三棱锥B ACD -外接球的体积是_________________.14.已知三棱锥P ABC -的外接球O 的表面积为12π,PA ⊥平面ABC ,BA AC ⊥,2PA =,则ABC 面积的最大值为__________.15.已知四棱锥P ABCD -的底面ABCD 为矩形,且所有顶点都在球O 的表面上,侧面PAB ⊥底面ABCD ,23PA PB ==,120APB ∠=︒,4=AD ,则球O 的表面积为_______.16.在如图棱长为2的正方体中,点M 、N 在棱AB 、BC 上,且1AM BN ==,P 在棱1AA 上,α为过M 、N 、P 三点的平面,则下列说法正确的是__________.①存在无数个点P ,使面α与正方体的截面为五边形;②当11A P =时,面α与正方体的截面面积为33③只有一个点P ,使面α与正方体的截面为四边形;④当面α交棱1CC 于点H ,则PM 、HN 、1BB 三条直线交于一点.17.已知长方体1234ABCD A B C D -,底面是边长为4的正方形,高为2,点O 是底面ABCD 的中心,点P 在以O 为球心,半径为1的球面上,设二面角111P A B C --的平面角为θ,则tan θ的取值范围是________.18.如图,矩形ABCD 中,2AB AD =,E 为边AB 的中点,将ADE 沿直线DE 翻折成1A DE △.若M 为线段1A C 的中点,则在ADE 翻折过程中,下面四个选项中正确的是______(填写所有的正确选项)(1)BM 是定值(2)点M 在某个球面上运动(3)存在某个位置,使1DE A C ⊥(4)存在某个位置,使//MB 平面1A DE19.如图,在长方体1111ABCDA B C D ﹣中,O 是11B D 的中点,P 是线段AC 上一点,且直线1PA 交平面11AB D 于点M .给出下列结论:①A ,M ,O 三点共线;②A ,M ,O ,1A 不共面;③A ,M ,C ,O 共面;④B ,1B ,O ,M 共面.其中正确结论的序号为______.20.如图,已知正四面体P ABC -的棱长为2,动点M 在四面体侧面PAC 上运动,并且总保持MB PA ⊥,则动点M 的轨迹的长度为__________.三、解答题21.如图,三棱柱111ABC A B C -中,122AB BC AC BB ===,1B 在底面ABC 上的射影恰好是点A ,E 是11A C 的中点.(1)证明:1//A B 平面1B CE ;(2)求1A B 与平面11BCC B 所成角的正弦值.22.如图,在直三棱柱111ABC A B C -中,底面ABC 为正三角形,1AB 与1A B 交于点O ,E ,F 是棱1CC 上的两点,且满足112EF CC =.(1)证明://OF 平面ABE ;(2)当1CE C F =,且12AA AB =,求直线OF 与平面ABC 所成角的余弦值. 23.如图所示,在长方体1111ABCD A B C D -中,11,2AD AA AB ===,点E 是AB 的中点.(1)证明:1//BD 平面1A DE ;(2)证明:11D E A D ⊥;(3)求二面角1D EC D --的正切值.24.如图,已知三棱锥P ABC -﹐PC AB ⊥,ABC 是边长为23的正三角形,43PB =﹐60PBC ∠=,点F 为线段AP 的中点.(1)证明:PC ⊥平面ABC ;(2)求直线BF 与平面PAC 所成角的大小.25.在四棱锥P ABCD -中,90ABC ACD ∠=∠=,60BAC CAD ∠=∠=,PA ⊥平面ABCD ,E 为PD 的中点,M 为AD 的中点,24PA AB ==.(1)取PC 中点F ,证明:PC ⊥平面AEF ;(2)求点D 到平面ACE 的距离.26.如图,ABC 中,2AC BC AB ==,ABED 是边长为1的正方形,平面ABED ⊥平面ABC ,若G 、F 分别是EC 、BD 的中点.(1)求证://GF 平面ABC ;(2)求证:AC ⊥平面EBC .【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】设正方体1111ABCD A B C D -的棱长为2,利用正方体性质可求得2MN =,3EF =知12MN EF ≠,再利用三角形中位线性质知1//MN B C ,从而//MN ED ,又EF 与ED 相交,可知MN 与EF 异面,即可选出答案.【详解】设正方体1111ABCD A B C D -的棱长为2,则22112MN MC C N =+=作E 点在平面ABCD 的投影点G ,即EG ⊥平面ABCD ,连接,EG GF ,在直角EGF △中,1EG =,222GF AG AF =+=2222123EF EG GF =+=+=以12MN EF ≠,故排除A 、C 连接DE ,由E 是平面11ADD A 的中心,得112DE A D = 又M N 、分别是11B C 、1CC 的中点,所以1//MN B C又11//A D B C ,所以//MN ED ,又EF ED E ⋂=,所以MN 与EF 异面故选:D.【点睛】关键点睛:本题考查正方体中的线面关系,线线平行的关系,及判断异面直线,解题的关键是熟记正方体的性质,考查学生的逻辑推理能力,属于基础题.2.D解析:D【分析】延长DA 至G ,使AG CE =,可证11//A G C E ,得1GA F ∠是异面直线1A F 与1C E 所成的角(或其补角).在1AGF △中,由余弦定理可得结论. 【详解】延长DA 至G ,使AG CE =,连接1,GE GA ,GF ,11,AC A C ,又//AG CE 所以AGEC 是平行四边形,//,GE AC GE AC =,又正方体中1111//,AC AC AC AC =,所以1111//,AC DE AC DE =,所以11AC EG 是平行四边形,则11//A G C E ,所以1GA F ∠是异面直线1A F 与1C E 所成的角(或其补角).设正方体棱长为2,在正方体中易得15AG =10GF =22222112(21)3A F AA AF =+=++=,1AGF △中,2221111125cos 2253AG A F GF GA F AG A F +-∠===⋅⨯⨯. 故选:D .【点睛】方法点睛:本题考查空间向量法求异面直线所成的角,求异面直线所成角的方法: (1)定义法:根据定义作出异面直线所成的角并证明,然后解三角形得结论; (2)建立空间直角坐标系,由两异面直线的方向向量的夹角得异面直线所成的角.3.A解析:A 【分析】连接AC 、BD 交于O ,连PO ,取CD 的中点E ,连,OE PE ,根据正棱锥的性质可知,PCE α∠=,PCO β∠=,PEO γ∠=,再比较三个角的正弦值可得结果. 【详解】连接AC 、BD 交于O ,连PO ,取CD 的中点E ,连,OE PE ,如图:因为//AB CD ,所以PBA α∠=,又因为四棱锥P ABCD -为正四棱锥,所以PCE α∠=,由正四棱锥的性质可知,PO ⊥平面ABCD ,所以PCO β∠=, 易得OE CD ⊥,PE CD ⊥,所以PEO γ∠=, 因为sin PE PC α=,sin POPC β=,且PE PO >,所以sin sin αβ>,又,αβ都是锐角,所以αβ>, 因为sin PO PE γ=,sin POPCβ=,且PC PE >,所以sin sin γβ>,因为,βγ都是锐角,所以γβ>. 故选:A 【点睛】关键点点睛:根据正棱锥的性质,利用异面直线所成角、直线与平面所成角、二面角的平面角的定义得到这三个角是解题关键,属于中档题.4.B解析:B 【分析】取AC 中点F ,连接,EF DF ,证明FED ∠是异面直线AB 与DE 所成角(或其补角),然后在三角形中求得其余弦值即可得. 【详解】取AC 中点F ,连接,EF DF ,∵E 是BC 中点,∴//EF AB ,12EF AB =, 则FED ∠是异面直线AB 与DE 所成角(或其补角), 设1AB =,则12EF =,32DE DF ==, ∴在等腰三角形DEF 中,11324cos 63EFFED DE ∠===.所以异面直线AB 与DE 所成角的余弦值为36. 故选:B .【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下: (1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.5.D解析:D 【分析】取AC 中点E ,连接1,A E BE ,先通过BE ⊥平面11ACC A 可得BE AM ⊥,再由1ACM A AE ≅可得1AM A E ⊥,即可得出AM ⊥平面1A BE ,即1AM A B ⊥.【详解】取AC 中点E ,连接1,A E BE ,ABC 为正三角形,BE AC ∴⊥,正三棱柱111ABC A B C -中,1CC ⊥平面ABC ,BE ⊂平面ABC ,1CC BE ∴⊥,1ACCC C =,BE ∴⊥平面11ACC A ,AM ⊂平面11ACC A ,BE AM ∴⊥,在直角三角形ACM 和直角三角形1A AE 中,1,AC A A CM AE ==,1ACM A AE ∴≅, 1CAM AA E ∴∠=∠,12CAM A EA π∴∴∠+∠=,则1AM A E ⊥,1BE A E E ⋂=,AM ∴⊥平面1A BE ,1A B ⊂平面1A BE ,1AM A B ∴⊥,故异面直线AM 与1A B 所成角的大小为2π.【点睛】本题考查异面直线所成角的求解,解题的关键是通过证明AM ⊥平面1A BE 判断出1AM A B ⊥.6.C解析:C 【分析】因为P BCE P ABC E ABC V V V ---=-则当E ABC V -取最大值时,三棱锥P BCE -体积有最小值,建立坐标系求得当点E 的高为3时,问题得解.【详解】以点O 为原点,,,OA OD OB 分别为,,x y z 轴建立空间直角坐标系,如图所示:设点(),0,E x z ,依题意得()6,0,0A ,则()6,0,AE x z =- ,(),0,OE x z = 因为过BC 作截面AP α⊥于E ,所以AE OE ⊥则0AE OE ⋅=, 故()2600x x z -++= 所以()6z x x =-3x =时max 3z =又()143P BCE P ABC E ABC ABCV V V S z ---=-=-因为max 3z =所以三棱锥P BCE -体积的最小值()1114343643332P BCE ABC V S-=-=⋅⋅=故选:C 【点睛】关键点点晴:本题的解题关键是将问题转化为求E ABC V -的最大值,通过建系求得三棱锥E ABC -的高的最大值即可.7.D解析:D 【分析】先找到几何体的原图,再求出几何体的高,再求几何体的体积得解. 【详解】由三视图可知几何体为图中的四棱锥1P CDD E -, 由题得22437AD =-7 所以几何体的体积为11(24)676732⋅+⋅=. 故选:D 【点睛】方法点睛:通过三视图找几何体原图常用的方法有:(1)直接法;(2)拼凑法;(3)模型法.本题利用的就是模型法.要根据已知条件灵活选择方法求解.8.C解析:C 【分析】先由三视图计算底面正三角形内切圆的半径,内切圆的直径和三棱柱的高比较大小,确定球的半径的最大值,计算球的最大体积. 【详解】由三视图知该直三棱柱的高为4,底面正三角形的高为33半径为高的三分之一,即3r =234<,所以该棱柱内部可放置球的半径的最大3343433V ππ==.故选:C 【点睛】关键点点睛:本题的第一个关键是由三视图确定底面三角形的高是33定球的最大半径.9.C解析:C 【分析】根据题意,得到正方体的直观图及其各点的标记字母,取FH 的中点O ,连接ON ,BO ,可以证明MN ‖BO ,利用BO 与平面ABE 的关系可以判定MN 与平面ABE 的关系,进而对选择支A作出判定;根据MN 与平面BCF 的关系,利用面面平行的性质可以判定MN 与平面ADE 的关系,进而对选择支B 作出判定;利用线面平行的判定定理可以证明MN 与平面BDE 的平行关系,进而判定C ;利用M ,N 在平面CDEF 的两侧,可以判定MN 与平面CDE 的关系,进而对D 作出判定. 【详解】根据题意,得到正方体的直观图及其各点的标记字母如图所示,取FH 的中点O ,连接ON ,BO ,易知ON 与BM 平行且相等,∴四边形ONMB 为平行四边形,∴MN ‖BO , ∵BO 与平面ABE (即平面ABFE )相交,故MN 与平面ABE 相交,故A 错误; ∵平面ADE ‖平面BCF ,MN ∩平面BCF =M ,∴MN 与平面ADE 相交,故B 错误; ∵BO ⊂平面BDHF ,即BO ‖平面BDH ,MN ‖BO ,MN ⊄平面BDHF ,∴MN ‖平面BDH ,故C 正确; 显然M ,N 在平面CDEF 的两侧,所以MN 与平面CDEF 相交,故D 错误. 故选:C.【点睛】本题考查从面面平行的判定与性质,涉及正方体的性质,面面平行,线面平行的性质,属于小综合题,关键是正确将正方体的表面展开图还原,得到正方体的直观图及其各顶点的标记字母,并利用平行四边形的判定与性质找到MN 的平行线BO .10.D解析:D 【分析】先找到几何体原图,再求出几何体的外接球的半径和内切球的半径,再判断每一个选项得解. 【详解】由三视图得几何体为下图中的三棱锥A BCD -,AB ⊥平面BCD ,42AB =2CE DE ==,2BE =,由题得2CBD π∠=.设外接球的球心为,O 外接球的半径为R ,则OE ⊥平面BCD , 连接,OB OA ,取AB 中点F ,连接OF .由题得1222OE BF AB ===,所以222(22)2,23R R =+∴=, 所以外接球的体积为34(23)3233ππ⨯=,所以选项A 错误; 所以外接球的表面积为24(23)48ππ⨯=,所以选项C 错误; 由题得22(42)(22)210AC AD ==+=, 所以△ACD △的高为24026-=, 设内切球的半径为r ,则1111111(422242222446)24423222232r ⨯⨯+⨯⨯+⨯⨯+⨯⨯=⨯⨯⨯⨯ 所以22r, 所以内切球的体积为3422)323ππ⨯=(,所以选项B 错误; 所以内切球的表面积为224()22ππ⨯=,所以选项D 正确. 故选:D【点睛】方法点睛:求几何体外接球的半径一般有两种方法:模型法和解三角形法.模型法就是把几何体放在长方体中,使几何体的顶点和长方体的若干个顶点重合,则几何体的外接球和长方体的外接球是重合的,长方体的外接球的半径22212r a b c =++几何体的外接球半径.如果已知中有多个垂直关系,可以考虑用此种方法.解三角形法就是找到球心O 和截面圆的圆心O ',找到OO '、球的半径OA 、截面圆的半径O A '确定的Rt OO A '△,再解Rt OO A '△求出球的半径OA .11.A解析:A【分析】由三视图还原几何体,由棱锥的体积公式可得选项. 【详解】在如图所示的正方体1111ABCD A B C D -中,P ,E 分别为11,B C BC 的中点,该几何体为四棱锥P ABCD -,且PE ⊥平面ABCD . 由三视图可知2AB =,则5,3PCPB PD PA ====,则21825681425,2233L V =++=+=⨯⨯=. 故选:A.【点睛】方法点睛:三视图问题的常见类型及解题策略:(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.12.C解析:C 【分析】根据题中所给的几何体的三视图还原几何体,得到相应的三棱锥,之后利用椎体体积公式求得结果. 【详解】根据题中所给的几何体的三视图还原几何体如图所示:该三棱锥满足底面BCD△是等腰三角形,且底边和底边上的高线都是2;且侧棱AD⊥底面BCD,1AD=,所以112 =221=323V⨯⨯⨯⨯,故选:C.【点睛】方法点睛:该题考查的是有关根据所给几何体三视图求几何体体积的问题,解题方法如下:(1)应注意把握三个视图的尺寸关系:主视图与俯视图长应对正(简称长对正),主视图与左视图高度保持平齐(简称高平齐),左视图与俯视图宽度应相等(简称宽相等),若不按顺序放置和不全时,则应注意三个视图名称;(2)根据三视图还原几何体;(3)利用椎体体积公式求解即可.二、填空题13.;【分析】分析菱形的特点结合其翻折的程度判断其外接球球心的位置放到相应三角形中利用勾股定理求得半径利用球的体积公式求得外接球的体积【详解】根据题意画出图形根据长为的菱形中对角线所以和都是正三角形又因解析:56π;【分析】分析菱形的特点,结合其翻折的程度,判断其外接球球心的位置,放到相应三角形中,利用勾股定理求得半径,利用球的体积公式求得外接球的体积.【详解】根据题意,画出图形,3的菱形ABCD 中,对角线3AC = 所以ABC 和DBC △都是正三角形, 又因为二面角B AC D --的大小为2π, 所以分别从两个正三角形的中心做面的垂线,交于O , 则O 是棱锥B ACD -外接球的球心,且11,2GD OG GE ===, 所以球的半径2252R GD OG =+=, 所以其体积为3344555(33V R ππ==⋅=, 55π. 【点睛】思路点睛:该题考查的是有关几何体外接球的问题,解题思路如下: (1)根据题中所给的条件,判断菱形的特征,得到两个三角形的形状;(2)根据直二面角,得到两面垂直,近一倍可以确定其外接球的球心所在的位置; (3)利用勾股定理求得半径; (4)利用球的体积公式求得结果;(5)要熟知常见几何体的外接球的半径的求解方法.14.2【分析】由球的表面积可求出半径取的中点可得设由基本不等式可得即可求出面积的最大值【详解】因为球的表面积为所以球的半径取的中点则为的外接圆圆心平面设由得因为所以当且仅当时取等因为的面积为所以面积的最解析:2 【分析】由球的表面积可求出半径3R =,取BC 的中点D ,可得1OD =,设AB x =,AC y =,由基本不等式可得4xy ≤,即可求出ABC 面积的最大值.【详解】因为球O 的表面积为12π,所以球O 的半径3R =. 取BC 的中点D ,则D 为ABC 的外接圆圆心,PA ⊥平面ABC ,112OD PA ∴==, 设AB x =,AC y =,由2222134+==+=+=x y R OC CD OD ,得228x y +=. 因为222x y xy +≥,所以4xy ≤,当且仅当2x y ==时取等.因为ABC 的面积为1122⋅=AB AC xy ,所以ABC 面积的最大值为2. 故答案为:2.【点睛】本题考查几何体的外接球问题,解题的关键是是建立勾股关系,利用基本不等式求出4xy ≤.15.【分析】首先利用垂直关系和底面和侧面外接圆的圆心作出四棱锥外接球的球心再计算外接球的半径以及球的表面积【详解】连结交于点取中点连结并延长于点点是外接圆的圆心侧面底面侧面底面平面过点作平面侧面所以点是 解析:64π【分析】首先利用垂直关系和底面ABCD 和侧面ABCD 外接圆的圆心,作出四棱锥P ABCD -外接球的球心,再计算外接球的半径,以及球O 的表面积. 【详解】连结,AC BD ,交于点M ,取AB 中点N 连结AN ,MN ,并延长于点E ,点E 是PAB △外接圆的圆心,侧面PAB ⊥底面ABCD ,侧面PAB 底面ABCD AB =,MN AB ⊥ MN ∴⊥平面PAB ,过点M 作MO ⊥平面ABCD ,//EO MN ,EO ∴⊥侧面PAB ,所以点O 是四棱锥P ABCD -外接球的球心, 可知四边形MNEO 是矩形,右图,23PA PB ==,120APB ∠=,2cos306AB PB ∴==, 点E 是PAB △外接圆的圆心,sin 303PN PB ∴==,PBE △是等边三角形,23PE =, 2333NE ∴=-=,3MO ∴=,2211641322MC AC ==+=, 223134R OC MO MC ∴==+=+=,∴球O 的表面积2464S R ππ==故答案为:64π 【点睛】本题考查了球与几何体的综合问题,考查空间想象能力以及化归和计算能力,(1)当三棱锥的三条侧棱两两垂直时,并且侧棱长为,,a b c ,那么外接球的直径2222R a b c =++2)当有一条侧棱垂直于底面时,先找底面外接圆的圆心,过圆心做底面的垂线,球心在垂线上,根据垂直关系建立R 的方程.(3)而本题类型,需要过两个平面外接圆的圆心作面的垂线,垂线的交点就是球心.16.①②④【分析】让从开始逐渐向运动变化观察所得的截面从而可得正确的选项【详解】由题设可得为所在棱的中点当时如图(1)直线分别交与连接并延长于连接交于则与正方体的截面为五边形故①正确当如图(2)此时与正解析:①②④ 【分析】让P 从A 开始逐渐向1A 运动变化,观察所得的截面,从而可得正确的选项. 【详解】由题设可得,M N 为所在棱的中点. 当203AP <<时,如图(1),直线MN 分别交,AD DC 与,T S ,连接TP 并延长1DD 于G , 连接GS 交1CC 于H ,则α与正方体的截面为五边形,故①正确.当11A P =,如图(2),此时α2, 其面积为2362=33B 正确.当,A P 重合或1,A P 重合时,如图(3),α与正方体的截面均为四边形,故③错误.如图(4),在平面α内,设PM HN S ⋂=,则S PM ∈,而PM ⊂平面11A B BA , 故S ∈平面11A B BA ,同理S ∈平面11C B BC ,故S ∈平面11A B BA ⋂平面111C B BC BB =即PM 、HN 、1BB 三条直线交于一点. 故答案为:①②④. 【点睛】思路点睛:平面的性质有3个公理及其推理,注意各个公理的作用,其中公理2可用来证明三点共线或三线共点,公理3及其推理可用来证明点共面或线共面,作截面图时用利用公理2来处理.17.【分析】根据题意画出相应的图形结合题意找出什么情况下取最大值什么情况下取最小值利用和差角正切公式求得最值得到结果【详解】根据题意如图所示:取的中点过点作球的切线切点分别为可以判断为的最小值为的最大值解析:4747,⎡⎤-+⎢⎥⎣⎦【分析】根据题意,画出相应的图形,结合题意,找出什么情况下取最大值,什么情况下取最小值,利用和差角正切公式求得最值,得到结果. 【详解】根据题意,如图所示:取11A B 的中点H ,过H 点作球O 的切线,切点分别为,M N , 可以判断1O HN ∠为θ的最小值,1O HM ∠为θ的最大值, 且1112tan 12OO O HO HO ∠===, 22,1OH OM ON ===,所以7HM HN ==tan tan 7NHO OHM ∠=∠=, 11171827477tan tan()7117O HN O HO NHO ----∠=∠-∠====++ 11171827477tan tan()7117O HM O HO OHM ++++∠=∠+∠====- 所以tan θ的取值范围是4747,33⎡+⎢⎣⎦, 故答案为:4747-+⎣⎦.【点睛】方法点睛:该题考查的是有关二面角的求解问题,解题方法如下: (1)先根据题意画图;(2)结合题意,找出在什么情况下取最大值和最小值; (3)结合图形求得相应角的正切值; (4)利用和差角正切公式求得结果.18.(1)(2)(4)【分析】首先取中点连结先判断(4)是否正确再根据平行关系以及等角定理和余弦定理判断(1)再判断(2)假设成立根据直线与平面垂直的性质及判定可得矛盾来判断(3)【详解】取中点连结则平解析:(1)(2)(4) 【分析】首先取CD 中点Q ,连结MQ ,BQ ,先判断(4)是否正确,再根据平行关系,以及等角定理和余弦定理判断(1),再判断(2),假设1DE A C ⊥成立,根据直线与平面垂直的性质及判定,可得11DA A E ⊥矛盾来判断(3). 【详解】取CD 中点Q ,连结MQ ,BQ ,则1//MQ DA ,//BQ DE ,∴平面//MBQ 平面1A DE ,又MB ⊂平面MBQ ,//MB ∴平面1A DE ,故(4)正确;由1A DE MQB ∠=∠,112MQ A D ==定值,QB DE ==定值, 由余弦定理可得2222cos MB MQ QB MQ QB MQB =+-⋅⋅∠ 所以MB 是定值,故(1)正确;B 是定点,M ∴是在以B 为球心,MB 为半径的球面上,故(2)正确;145A DE ADE ∠=∠=,45CDE ∠=,且设1AD =,2AB =,则2DE CE ==若存在某个位置,使1DE A C ⊥,则因为222DE CE CD +=,即CE DE ⊥,因为1AC CE C =,则DE ⊥平面1A CE ,所以1DE A E ⊥,与11DA A E ⊥矛盾,故(3)不正确.故答案为:(1)(2)(4) 【点睛】关键点点睛:本题考查线线,线面位置关系时,首先判断(4)是否正确,其他选项就迎刃而解,而判断线面平行时,可根据面面平行证明线面平行.19.①③【分析】由公理1判断①正确;由公理2判断②错误③正确用反证法可得④错误【详解】∵连接∵是的中点∴平面与平面有公共点与则平面平面对于①平面则平面又平面则即三点共线故①正确;对于②在平面内由①知∴平解析:①③ 【分析】由公理1判断①正确;由公理2判断②错误③正确,用反证法可得④错误. 【详解】∵连接11A C ,∵O 是11B D 的中点,∴11O A C ∈. 平面11AB D 与平面11AAC C 有公共点A 与O , 则平面11AAC C平面11AB D AO =.对于①,1M PA ∈,1PA ⊂平面11AAC C ,则M ∈平面11AAC C , 又M ∈平面11AB D ,则M AO ∈,即A ,M ,O 三点共线,故①正确; 对于②,A ,O ,1A 在平面11AAC C 内,由①知M AO ∈,∴O ∈平面11AAC C , 即A ,M ,O ,1A 共面,故②错误;对于③,A ,O ,C 在平面11AAC C 内,由①知M AO ∈,∴O ∈平面11AA C CA , 则A ,M ,C ,O 共面11AAC C ,故③正确;对于④,连接BD ,则B ,1B ,O 都在平面11BB D D 上,若M ∈平面11BB D D ,则直线OM ⊂平面11BB D D ,∴A ∈面11BB D D ,显然A ∉面11BB D D 的,故④错误. ∴正确命题的序号是①③. 故答案为:①③.【点睛】本题考查命题的真假判断与应用,考查空间中的直线与平面、平面与平面的位置关系,考查空间想象能力与思维能力,是中档题.20.【分析】取PA 的中点E 连接EBEC 推出PA ⊥平面BCE 故点M 的轨迹为线段CE 解出即可【详解】取PA 的中点E 连接EBEC 因为几何体是正四面体P ﹣ABC 所以BE ⊥PAEC ⊥PAEB∩EC =E ∴PA ⊥平面 解析:3【分析】取PA 的中点E ,连接EB ,EC ,推出PA ⊥平面BCE ,故点M 的轨迹为线段CE ,解出即可. 【详解】取PA 的中点E ,连接EB ,EC ,因为几何体是正四面体P ﹣ABC ,所以BE ⊥PA ,EC ⊥PA ,EB ∩EC =E ,∴PA ⊥平面BCE ,且动点M 在正四面体侧面PAC 上运动,总保持MB PA ⊥,∴点M 的轨迹为线段CE ,正四面体P ﹣ABC 的棱长为2,在等边三角形PAC 中求得CE =3232⨯=. 故答案为:3【点睛】本题考查了正四面体的性质和线面垂直与线线垂直的判定,判断轨迹是解题的关键,属于中档题.三、解答题21.(1)证明见解析;(2105. 【分析】(1)连接1BC 与1B C 相交于M ,连接EM ,证明1//EM A B ,再由线面平行的判定定理证明即可;(2)证明平面1AB F ⊥平面11BCC B ,得出NO ⊥平面11BCC B ,结合线面角的定义得出OBN ∠即为1A B 与平面11BCC B 所成角,再由相似三角形、勾股定理、直角三角形边角关系得出1A B 与平面11BCC B 所成角的正弦值. 【详解】(1)连接1BC 与1B C 相交于M ,连接EM由于E ,M 分别是11A C ,1BC 的中点,则1//EM A B因为EM ⊂平面1B CE ,1A B ⊄平面1B CE ,所以1//A B 平面1B CE .(2)取BC 中点F ,连接AF ,1B F ,则AF BC ⊥ 因为1B A ⊥平面ABC ,所以1B A BC ⊥又1,AF B A ⊂平面1AB F ,1AF B A A ⋂=,所以BC ⊥平面1AB F又BC ⊂平面11BCC B ,所以平面1AB F ⊥平面11BCC B ,过N 作1NO B F ⊥于O 因为NO ⊂平面1AB F ,平面1AB F ⋂平面111BCC B B F =所以NO ⊥平面11BCC B ,连接OB ,则OBN ∠即为1A B 与平面11BCC B 所成角 设12BB =,易知2211022BN AN AB =+=+=,6AF =,1142B F = 由11ONB AFB △△,114214B N ON AF B F =⋅= 所以105sin 35ON OBN BN ∠==. 【点睛】关键点睛:解决第一问的关键在于由中位线定理证明线线平行,再由线面平行的判定定理证明线面平行;解决第二问的关键在于由线面垂直找出线面角,再由直角三角形边角关系求出正弦值.22.(1)证明见解析;(23【分析】(1)取AB 中点G ,连结OG 、EG ,可证明四边形OGEF 为平行四边形,则 OF EG ∥,由线面平行的判定定理即可求证;(2)由(1)可知,OF EG ∥,则直线OF 与平面ABC 所成角即为直线EG 与平面ABC 所成角,EC ⊥平面ABC ,则EGC ∠即为直线EG 与平面ABC 所成的角,在EGC 中即可求EGC ∠的余弦值. 【详解】(1)取AB 中点G ,连结OG 、EG ,在直三棱柱111ABC A B C -中,1OG BB ∥,则OG EF ∥, 又112EF CC =,则OG EF =, 所以四边形OGEF 为平行四边形,则 OF EG ∥, 又EG ⊂平面ABE ,OF ⊄平面ABE , 故//OF 平面ABE .(2)由(1)可知,OF EG ∥,则直线OF 与平面ABC 所成角即为直线EG 与平面ABC 所成角,连接CG ,由直三棱柱111ABC A B C -可得EC ⊥平面ABC , 则EGC ∠即为直线EG 与平面ABC 所成的角, 设2AB =,则114AA CC ==, 又1CE C F =,则1CE =,3CG =2EG =,所以,直线EG 与平面ABC 所成角的余弦值为32, 故直线OF 与平面ABC 3 【点睛】方法点睛:证明直线与平面平行的常用方法(1)定义法:证明直线与平面没有公共点,通常要借助于反证法来证明;(2)判定定理:在利用判断定理时,关键找到平面内与已知直线平行的直线,常考虑利用三角形中位线、平行四边形的对边平行或过已知直线作一平面,找其交线进行证明; (3)利用面面平行的性质定理:直线在一平面内,由两平面平行,推得线面平行;直线在两平行平面外,且与其中一平面平行,这这条直线与另一个平行.。
人教版新课标高一必修2Unit1Culturalrelics单元测试题.doc

Unitl单元测试题第二部分:阅读理解(共两节,满分40分)第一节(共15小题;每小题2分,满分30分)阅读下列短文,从每题所给的四个选项(A、B、C和D)中,选出最佳选项。
Insects (昆虫)are a very healthy food. They have almost as much protein (蛋口质)as meat from a pig or cow and are low in fat. Eating insects is also very good for the environment since they need less land and water than larger animals.Marcel Dicke, who studies insects, explained in a talk how insects also produce more meat from the food they eat. For example, imagine a farmer feeds a cow 10 pounds of food・ Those 10 pounds of food produce about 1 pound of meat for people to eat. However, imagine the farmer gives a certain number of insects 10 pounds of food. Those 10 pounds of food produce 9 pounds of meat for people to eat!Eating more insects can also help people in poor areas. Many people can raise and sell insects, which can provide jobs and food.But insects will not replace (替彳弋)animal meat very quickly. First, people in some countries would have to change how they think about eating insects. Many people in North America and Europe eat a lot of meat like beef and pork・ But they do not traditionally cat insects. In fact, for many people in the west, eating insects sounds crazy! They believe insects are dirty and dangerous. Insects make them feel uncomfortable ・Some people are trying to deal with this problem. For example, David George Gordon wrote a book named "The Eat-A-Bug Cookbook”,which tries to show people that insects can be delicious. Other insect experts travel around telling people about the benefits (好处)of eating insects. But they still have a lot of work to do.21.Eating insects _____ .A.is not healthyB.makes people put on fatC・ helps protect large animalsD. is environmentally friendly22.The example of Marcel Dicke is given to show ____ .A.the high cost of food productionB.it's quite easy for farmers to raise insectsC・ raising insects is a good choice for formersD. the different ways of feeding cows and insects23.The long way eating insects has to go mainly results from _____ .C・ family traditions D. eating methods24.We can infer from David and other insect experts that ____A.people can make a lot of money from insectsB.insects should be better protectedC.people should eat more insectsD.it,s dangerous to eat insectsBKhan Academy is a website providing a free education for any person• The website includes more than 4,000 short teaching videos about many different subjects. Every month, over 7 million people go to the Khan Academy website to watch its videos.Khan Academy began with one man named Salman Khan. As a young man, Khan got a degree from Harvard Business School and began to work in business.In 2006, Khan used the Internet to help his young cousins, who lived far away, with their mathematics schoolwork. He drew numbers and pictures on the website to teach them. After a time, he put his videos onto the website YouTube, where his cousins could watch them any time they wanted. But KJian noticed that other people were also watching his videos on YouTube.By 2009, the number of people watching his videos on YouTube was getting very large・ Khan decided to make the videos his job instead・ So he officially began Khan Academy, providing videos on mathematics and other school subjects.People did not have to pay to watch the videos. But they could give Khan money if they wanted to support (支持)his work. Some people did give Khan small amounts of money, but he was still having a hard time. Later, a woman told Khan that Bill Gates uses Khan Academy for his kids. After that, the Bill and Melinda Gates Foundation began giving money to Khan Academy・ In 2010 Google gave the website money too, wanting Khan to translate his videos into the worlds most common languages. Today, people can see Khan's videos in many different languages.Some people think that Khan Academy will be the way more and more people learn in the future. Teachers can use it in their classrooms. Khan believes that Khan Academy will never, and should never, replace a school. But he believes teachers and students can use it to make schools better.25.What can one get from Klian Academy?A.Video-making methods.B.Free learning information.C.Any help with the schoolwork.D.A good number of beautiful pictures.26.Salman KJian started Khan Academy ____ •A.in 2006B・ as a studentC.to satisfy the needs of learnersD.under the influence of his cousins27.What docs Salman Khan think of Khan Academy?A.It will play an active role in school teaching.B.It can replace teachers in classrooms.C.It can replace a teaching school.D.It's the future of education.The Tower of London, not a single tower but a large group, was built to guard London.Besides William and Henry VIII, the tower's history has other famous names in British history. In 1389 a clerk of works (现场监工员)named Geoffrey Chaucer 一author of The Canterbury Tales一oversaw (监督)the building of the Tower Wharf. In 1671Colonel Blood tried to steal the crown jewels (皇冠上镶的宝石)after overpowering the elderly Jewel House keeper・(Blood was caught but later pardoned.) Today the jewels remain in the tower as they have since BloocTs day.For six centuries this place was also home to a group of animals from elephants to big cats• It stopped being used as an animals9 home in 1835 and its animals were moved to the London Zoo.Today visitors can walk the walls, visit guard towers and see the crown jewels- Guards at the tower, popularly known as beefeaters, not only guard the tower but also give interesting tours that arc among the most popular parts of any visit.How to Get ThereTrains and the Dockland Light Railway stop near the tower. Buses 15, 42, 78 and 100 reach the tower, and riverboats stop at Tower Pier. Taxis, bicycles, and foot power are also good ways to reach the tower. Driving is a less attractive choice because of the expensive parking.When to GoThe tower is open all year round, except during the Christmas holidays (December 24 to 26) and January 1. School holidays and summertime are the busiest times.How to VisitAs expected at a place that has seen so much history, there is enough of interest at the Tower of London to keep visitors busy for days. Stop at the Welcome Center for visitor information on everything from the crown jewels to family fun activities.2& The underlined sentence in Paragraph 2 shows ____ .A.the tower was built by famous peopleB.some famous people caused trouble thereC.there were many famous people in British historyD.there were many interesting stories connected to the tower29・ Beefeaters at the tower ___ .A.have two rolesB. like to eat beefC.seem very serious D・ often joke with visitors30.According to the text, the Tower of London is ____ •A.easy to reachB. full of parked carsC. busy all year roundD. a perfect place for a one-day tourDQuite a few years ago, as I celebrated my 25th birthday with a party, I was surprised to receive an unusual present. The gift-giver smiled widely and said loudly, “It's a nice, strong plant, so even you carf t kill it."I was well known in my circle of friends as an "anti-gardener^ — how was I going to care for this piece of greenery?For four years the plant received little care. I felt guilty (内疚的)just looking at it!As a non-gardener, my offers to look after friends' houses were met with laughter: "We appreciate (感激)the offer but, really, we don't want to come home to a dead garden!" It didn't occur to (想至0) them that I just had no interest in having a garden. It was a choice, not a failing.Some time later my husband accepted a job in Belgium. Because I couldn't throwaway a gift, I decided to ask my neighbor to care for my plant.Our lovely house in Belgium had a beautiful garden. Slowly gardening became a part of my daily life, teaching me to slow down and to be happy in the silence of the garden. It was with regret that I left that garden to return to Sydney some months laterBack home life soon went back to normal. Then one day, it occurred to me that I could start my own little garden. So, I went to collect my unwanted plant from my neighbor・ I took the plant home, watered it and watched as its leaves turned from a lifeless yellow to a rich green within weeks・ Many years on, I still don't know the name of my first plant, but I do know that as it grows, so do I. It symbolises a change in me when I stopped listening to the voices around me and started to believe in myself.31.When the author received a plant as a birthday gift, she felt _____ .A.funnyB. guiltyC. excitedD. displeased32.What did the author's friends think of her?A. Her anti-gardening was a weakness.B.She was bored with gardening.C・ She was a good housekeeper.D.Her dead garden was ugly.33.How did the author deal with the plant before moving away?A.She threw it away.B.She asked for help.C.She left it in the house.D.She gave it to a neighbor as a gift.34.The author's stay in Belgium made her _____ •A.miss her days back in SydneyB.feel sorry for her first plantC.fall in love with gardeningD.become strangely silent35.What does the author want to tell us from her experience?A.We should try to be perfect.B.Doit be afraid of making mistakes.C.We should learn to make clear choices.D.Don't refuse something yoifve never tried.第二节(共5小题;每小题2分,满分10分)根据短文内容,从短文后的选项屮选出能填入空白处的最佳选项。
人教A版高中数学必修2第一章单元测试题(含详细解析)

………外………○…………线____………内………○…………线人教A 版高中数学必修2第一章单元测试题(含解析) 第I 卷(选择题) 一、单选题 1.如图,在多面体ABCDEF 中,已知ABCD 是边长为1的正方形,且ADE ∆,BCF ∆是正三角形,//EF AB ,2EF =,则该多面体的体积为( )A B .3 C D .2 2.边长为6的两个等边ABC V ,CBD V 所在的平面互相垂直,则四面体ABCD 的外接球的体积为( ). A . B . C .20π3 D . 3.已知ABC V 的三个顶点在以O 为球心的球面上,且2AB =,4AC =,BC =三棱锥O ABC -的体积为43,则球O 的表面积为( ) A .22π B .743π C .24π D .36π 4.圆锥的高缩小为原来的13,底面半径扩大为原来的2倍,则它的体积是原来体积的( ) A .23 B .32 C .43 D .34 5,则三棱锥的外接球的表面积为( ) A .1129π B .1123π C .289π D………外…………○…装…………○……订…………○…※※※要※※在※※装※※※※内※※答※※题※※ ………内…………○…装…………○……订…………○…6.某圆锥的侧面展开图是面积为3π,圆心角为23π的扇形,则该圆锥的母线与底面所成的角的余弦值为( ) A .12 B .13 C .14 D .15 7.三棱锥P ABC -的所有顶点都在半径为2的球O 的球面上.若PAC ∆是等边三角形,平面PAC ⊥平面ABC ,AB BC ⊥,则三棱锥P ABC -体积的最大值为( ) A .2 B .3 C .D .8.某几何体的三视图如图所示,则该几何体的表面积为( )A .48+B .40+C .48+D .44+ 9.某几何体的三视图如图,其中侧视图为半圆,则该几何体的表面积为A .64π+B .63π+C .94π+D .93π+10.已知一个简单几何体的三视图如图所示,若该几何体的体积为24π+48,则r =( )A .2B .4C .1D .311.如图,为一圆柱切削后的几何体及其正视图,则相应的侧视图可以是( )…………外…………○………○…………订线…………○……学校:__________班级:___________考…………内…………○………○…………订线…………○…… A . B . C . D . 12.已知四面体P ABC - 中,AP ⊥平面ABC ,4PA = ,PC =AB =BC=则四面体P ABC -的外接球的表面积为( )A .32πB .3C .3D .64π 二、填空题 13.如图,三棱锥A BCD -中,E 是AC 中点,F 在AD 上,且2AF FD =,若三棱锥A BEF -的体积是2,则四棱锥B ECDF -的体积为____. 14.已知正方体1111ABCD A B C D -的棱长为1,点E 是棱1B B 的中点,则三棱锥1B ADE -的体积为______. 15.如图,第一排的图形绕虚线旋转一周能形成第二排中的某个几何体.请写出第一排、第二排中相应的图形的对应关系________. A . B . C . D . 16.如图,正方体1111ABCD A B C D -的棱长为2,P 为BC 的中点,Q 为线段1CC 上的…………○………○…………订…线…………※※请※装※※订※※线※※内…………○………○…………订…线…………动点,过点A ,P ,Q 的平面截该正方体所得的截面记为S ,则下列命题正确的是______(写出所有正确命题的编号). ①当01CQ <<时,S 为四边形;②当1CQ =时,S 为等腰梯形;③当32CQ =时,S 与11C D 的交点R 满足123D R =;④当322CQ <<时,S 为五边形;⑤当2CQ =时,S.三、解答题17.如图,正三棱柱111ABC A B C -底面三角形的周长为6,侧棱长1AA 长为3.(1)求正三棱柱111ABC A B C -的体积;(2)求异面直线1A C 与AB 所成角的大小.18.如图,直三棱柱1111=42,ABC A BC CC AB BC AC -===中,,,点M 是棱1AA ,上不同于1,A A 的动点.(I)证明:1BC B M ⊥;(Ⅱ)若1=90CMB o∠,判断点M 的位置并求出此时平面1MB C 把此棱柱分成的两部分几何体的体积之比.19.如图,已知点E 是圆心为1O 半径为2的半圆弧上从点B 数起的第一个三等分点,外…………○…………………订…………线………学校:______________________考号:内…………○…………………订…………线………点F 是圆心为2O 半径为1的半圆弧的中点,AB 、CD 分别是两个半圆的直径,122O O =,直线12O O 与两个半圆所在的平面均垂直,直线AB 、DC 共面.(1)求三棱锥D ABE -的体积; (2)求直线AF 与BE 所成角的余弦值. 20.(1)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中俯视图由两个半圆和两条线段组成,求该几何体的表面积. (2)圆台的较小底面半径为1,母线长为2,一条母线和底面的一条半径有交点且成60o ,求圆台的侧面积. 21.如图所示,在四棱锥P ABCD -中,四边形ABCD 为矩形,PAD ∆为等腰三角形,APD 90︒∠=,平面PAD ⊥平面ABCD ,且1,2,,AB AD E F ==分别为,PC BD 的中点. (1)证明://EF 平面PAD ; (2)证明:平面PDC ⊥平面PAD ; (3)求三棱锥E ABD -的体积.参考答案1.B【解析】【分析】该几何体是一个直三棱柱截去两个四棱锥,先计算出三棱柱的底面积和高,得到其体积,再计算出四棱锥的体积,相减即为该多面体的体积.【详解】将多面体补齐为一个直三棱柱,则该直三棱柱的底面三角形的底为1因为BCF ∆为正三角形,且边长为1,所以其高为2,2=,所以直三棱柱的体积为112222⨯⨯=.割去的一个四棱锥的体积为:11132212⨯⨯⨯=,2= 故选:B.【点睛】本题考查空间想象能力,割补法求几何体的体积,求棱柱和棱锥的体积,属于简单题. 2.B【解析】根据外接球的性质先找到球心位置,再由球和圆的性质用勾股定理求出半径,即可求出外接球体积.【详解】如图所示:1OO 为三角形CBD 过中心1O 且垂直平面CBD 的直线,2OO 为三角形ABC 过中心2O 且垂直平面ABC 的直线,1OO 与2OO 相交于O 点.由球的性质知:四面体ABCD 的外接球球心为O 点.因为AE ==2O 为ABC 的中心,所以213O E AE ==因为21O E OO =,所以1OO .又因为123DO DE ==R OD ====故外接球的体积为334433R ππ==. 故选:B【点睛】本题主要考查多面体的外接球,利用外接球球心到多面体顶点的距离相等的性质找到球心是解决本题的关键,属于难题.3.C【解析】【分析】由已知可得三角形ABC 为直角三角形,斜边BC 的中点O '就是ABC V 的外接圆圆心,利用三棱锥O ABC -的体积,求出O 到底面的距离,可求出球的半径,然后代入球的表面积【详解】在ABC V 中,∵2AB =,4AC =,BC =AB AC ⊥,则斜边BC 的中点O '就是ABC V 的外接圆的圆心,∵三棱锥O ABC -的体积为43, 11424323OO '⨯⨯⨯⨯=,解得1OO '=,R == 球O 的表面积为2424R ππ=.故选C .【点睛】本题考查球的表面积的求法,考查锥体体积公式的应用,考查空间想象能力和计算能力,属于基础题.4.C【解析】【分析】先求得圆锥原来的体积,再求得变换后圆锥的体积,由此求得新圆锥体积和原来体积的关系,从而得出正确选项.【详解】设一个圆锥的底面半径为r ,高为h ,则其体积213V r h π=; 圆锥的高缩小为原来的13,底面半径扩大为原来的2倍,则所得圆锥的底面半径为2r ,高为13h ,体积为()2211142339V r h r h ππ=⋅⋅=.∴212449133r h V V r h ππ==.∴它的体积是原来体积的43. 故选:C.【点睛】本小题主要考查圆锥体积计算,考查运算求解能力,属于基础题.5.A【解析】【分析】通过三视图还原几何体的直观图是有相邻两个侧面互相垂直的三棱锥,找出这两个面的外心,利用勾股定理构造出关于外接球半径OA 的方程.【详解】根据几何体的三视图,还原几何体的直观图为三棱锥A BCD -,设O 为三棱锥外接球的球心,1O 为ABD ∆的外心,2O 为BCD ∆的外心,E 为BD 中点,则四边形12OO O E为矩形,因为2224cos 25AB AD BD BAD AB AD +-∠===⋅, 所以3sin 5BAD ∠=,所以ABD ∆的外接圆半径为152sin 3BD AO BAD ==⋅∠, 因为BCD ∆是边长为2的正三角形,所以213O E OO ==, 所以2222211528()()339OA OO AO =+=+=, 所以三棱锥的外接球的表面积28112499S ππ=⋅=.【点睛】三棱锥与球的切接问题,找到球心是解题的关键,其步骤是,一找两相邻面的外心12,O O ,二是假设球心为O ,三是连结12,O O O O 得到这两个面的垂线,再从中寻找直角三角形,构造关于球半径的方程.6.B【解析】【分析】根据已知计算出圆锥的母线长和底面半径,可得答案.【详解】Q 圆锥的侧面展开图是面积为3π,圆心角为23π的扇形, 则圆锥的母线l 满足:2133l ππ⋅=故圆锥的母线长为3, 又由232r l ππ= 可得圆锥的底面半径为1, 故该圆锥的母线与底面所成的角的余弦值为13.故选B. 【点睛】本题考查的知识点是旋转体,熟练掌握圆锥的几何特征,是解答的关键.7.B【解析】【分析】由题意求得PA AC PC ===1PO AC ⊥且13PO =, 又由平面PAC ⊥平面ABC ,可得1PO ⊥平面ABC ,即三棱锥P ABC -的高3h =,在ABC ∆中,利用基本不等式求得面积的最大值,进而可得三棱锥体积的最大值,得到答案.【详解】由题意知,三棱锥P ABC -的所有顶点都在半径为2的球O 的球面上,若PAC ∆是等边三角形,如图所示,可得PA AC PC ===,则1PO AC ⊥且13PO =,又由平面PAC ⊥平面ABC ,所以1PO ⊥平面ABC ,即三棱锥P ABC -的高3h =, 又由在ABC ∆中,AB BC ⊥,设,AB a BC b ==,则22212a b AC +==, 所以22111()3222ABC S ab a b ∆=≤⋅+=,当且仅当a b =时取等号,即ABC S ∆的最大值为3, 所以三棱锥P ABC -体积的最大值为max 11()33333ABC V S h ∆=⋅=⨯⨯=, 故选B.【点睛】本题主要考查了有关球的内接组合体的性质,以及三棱锥的体积的计算问题,其中解答中充分认识组合体的结构特征,合理计算三棱锥的高和底面面积的最大值是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题.8.C【解析】【分析】由三视图知,该几何体的直观图为多面体EFGD CBA -,其中四边形ABCD 是边长为4的正方形,四边形EBAF 和GDAF 为全等的直角梯形,四边形ECGF 是菱形,其对角线长分别为.【详解】由三视图知,该几何体的直观图为多面体EFGD CBA -,如图所示其中四边形ABCD 是边长为4的正方形,所以16ABCD S =,四边形EBAF 和GDAF 为全等的直角梯形,所以244122EBAF S +=⨯=,4BCE DCG S S ∆∆==,四边形ECGF 是菱形,其对角线长分别为所以12ECGF S =⨯=所以该几何体的表面积为421621248⨯++⨯+=+C .【点睛】本题考查了几何体的三视图及体积的计算,在由三视图还原为空间几何体的实际形状时,要根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线在三视图中为虚线,求解以三视图为载体的空间几何体的表面积与体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应公式求解.9.A【解析】【分析】根据三视图知该几何体是半圆柱体,结合图中数据计算该几何体的表面积即可.【详解】根据三视图知,该几何体是半圆柱体,画出图形如图所示;结合图中数据,计算该几何体的表面积为:S =212⨯π•1212+⨯2π•1•3+2×3=4π+6. 故选:A .【点睛】本题考查了利用三视图求几何体表面积的应用问题,是基础题.10.A【解析】【分析】由题意,直观图为14圆锥与三棱锥的组合体,利用几何体的体积求出r,再求出该几何体的表面积.【详解】由题意,直观图为14圆锥与三棱锥的组合体,该几何体的体积为14×13×π×9r2×4r+13×12×3r×3r×4r=24π+48,∴r=2.故选:A.【点睛】本题考查由三视图求面积、体积,考查学生的计算能力,确定直观图的形状是关键.11.B【解析】【分析】三视图是对一个物体从一个三个不同的侧面进行正投影得到的,三个视图间存在长对正,高平齐,宽相等的对应关系,在三视图中不可见的轮廓用虚线表示.【详解】根据题意以及已知图形:由主视图得出主视方向,左视图应该是从实物图的左边进行正投影,右边的轮廓为不可见轮廓,所以要用虚线表示,故B正确.故选:B.【点睛】考查正投影,以及三视图的作图知识,本题属于中档题.12.A【解析】【分析】先求得三角形ABC 外接圆的半径r ,然后则球的半径2222AP R r ⎛⎫=+ ⎪⎝⎭,由此求得球的表面积.【详解】由于AP ⊥平面ABC ,故三角形PAB 和三角形PAC 为直角三角形,所以AC ==ABC 为等边三角形,在等边三角形ABC中,由正弦定理得42sin 2BC r BAC ===∠,其中r 为三角形ABC 外接圆的半径,则2r =.又由于AP ⊥平面ABC ,球心在三角形ABC 外接圆圆心的正上方,则球的半径2222AP R r ⎛⎫=+ ⎪⎝⎭8=,故外接球的表面积为24π32πR =. 【点睛】本小题主要考查几何体的外接球半径的求解方法,考查球的表面积公式和正弦定理的应用,属于中档题.13.10【解析】【分析】根据题中条件先求出三棱锥A BEF -与三棱锥C ABD -的体积比,进而得到三棱锥C ABD -的体积,利用两个三棱锥的体积之差可得四棱锥B ECDF -的体积.【详解】设ABF ∆的面积为S ,∵2AF FD =,∴ABD ∆的面积为3S .设点E 到平面ABD 的距离为d ,则点C 到平面ABD 的距离为2d ,则有123A BEF E ABF V V Sd --===, ∴1(3)(2)123A BCD C ABD V V S d --==⋅⋅=, ∴四棱锥B ECDF -的体积为12210C ABDE ABF V V ---=-=.故答案为:10【点睛】解答本题的关键是由题意得到三棱锥A BEF -与三棱锥C ABD -的体积比,考查锥体体积的求法和转化思想方法的运用,同时也考查计算能力,属于中档题.14.112【解析】【分析】由题意,三棱锥B 1﹣ADE 的体积=三棱锥D ﹣B 1AE 的体积,即可得出结论.【详解】由题意,三棱锥B 1﹣ADE 的体积=三棱锥D ﹣B 1AE 的体积11111132212=⨯⨯⨯⨯=. 故答案为:112.【点睛】本题考查三棱锥体积的求法,正确转换底面是关键,属于基础题.15.(1)~C ,(2)~B ,(3)~D ,(4)~A【解析】【分析】根据旋转体的几何性质,判断出对应关系.【详解】对于(1),旋转所得是半球,对应C;对于(2)旋转所得是两个圆锥,对应B;对于(3)旋转所得是一个圆锥和一个圆柱,对应D;对于(4)旋转所得是圆锥,对应A.故填:(1)~C,(2)~B,(3)~D,(4)~A.【点睛】本小题主要考查旋转体的几何性质,考查空间想象能力,属于基础题.16.①②④【解析】【分析】利用空间几何元素的位置关系和截面的性质逐一分析推理判断每一个命题的真假得解. 【详解】对于①,由图1知,当点Q向C移动时,满足0<CQ<1,只需在DD1上取点M,且满足AM∥PQ,则截面图形为四边形APQM,∴①正确;对于②,当CQ=1时,即Q为CC1中点,此时可得PQ∥AD1,AP=QD1可得截面APQD1为等腰梯形,∴②正确;对于③,当CQ=32时,如图2所示,延长DD 1至N ,使D 1N=1,连接AN 交A 1D 1于S ,连接NQ 交C 1D 1于R ,连接SR , 可证AN ∥PQ ,由△NRD 1∽△QRC 1,可得C 1R :D 1R=C 1Q :D 1N=1:2,可得C 1R=23,D 1R=43,∴③错误; 对于④,当322CQ <<时,只需点Q 上移,此时的截面形状仍然上图所示的APQRS ,是五边形,④正确;对于⑤,当CQ=2时,Q 与C 1重合,取A 1D 1的中点F ,连接AF ,可证PC 1∥AF ,且PC 1=AF ,可知截面为APC 1F 为菱形,且面积为12AC 1•PF ,⑤错误; 综上可得:正确命题的序号为①②④.故答案为①②④.【点睛】本题主要考查空间几何体的性质和截面的性质,意在考查学生对这些知识的理解掌握水平和分析推理能力.17.(1)2【解析】【分析】 (1)由已知求得三棱柱底面边长,得到底面积,再由棱柱体积公式求解;(2)以C 为坐标原点,以过C 且垂直于AB 的直线为x 轴,以过C 且平行于AB 的直线为y 轴,以CC 1所在直线为z 轴建立空间直角坐标系,利用空间向量求解.【详解】解:(1)∵正三棱柱ABC ﹣A 1B 1C 1底面三角形的周长为6,∴边长为2,则AB∴122ABC S =⨯=n 又侧棱长AA 1长为3,则正三棱柱ABC ﹣A 1B 1C 1的体积V=1ABC S AA ⋅=V(2)以C 为坐标原点,以过C 且垂直于AB 的直线为x 轴,以过C 且平行于AB 的直线为y 轴,以CC 1所在直线为z 轴建立空间直角坐标系,则C (0,0,0),A)1,0-,B )0,,A1)12-,, ())10,2,01,2AB CA ==-u u u r u u u r ,, ∴cos 1CA AB u u u r u u u r ,=11CA AB CA AB ⋅⋅u u u r u u u r u u u r u u u r4=-. ∴异面直线A 1C 与AB所成角的大小为4.【点睛】本题考查多面体体积的求法,训练了利用空间向量求解异面直线所成角,考查运算求解能力,考查数形结合思想,是中档题.18.(Ⅰ)见证明;(Ⅱ)1:1.【解析】【分析】(I )证明BC ⊥平面ABB 1A 1,即可得出BC ⊥B 1M ;(II )求出棱锥C ﹣ABB 1M 和棱柱的体积即可得出结论.【详解】(Ⅰ)在ABC V 中,2228AB BC AC +==Q ,90,ABC BC AB ∴∠=︒∴⊥,又11,BC BB BB AB B ⊥⋂=Q ,BC ∴⊥平面11ABB A ,又1B M ⊂面11ABB A ,1BC B M ∴⊥.(Ⅱ)当190CMB ∠=︒时,设()04AM t t =<<,14A M t ∴=-,则在Rt MAC V 中,228CM t =+,同理:()2221144,16420B M t B C =-+=+=,据()2222211,84420B C MB MC t t =+∴++-+=,整理得,2440,2t t t -+=∴=故M 为1AA 的中点此时平面1MB C 把此棱柱分成两个几何体为:四棱锥1C ABB M -和四棱锥111B A MCC - 由(Ⅰ)知四棱锥1C ABB M -的高为BC=2, 124262ABB M S +=⨯=梯形, 116243C ABB M V -∴=⨯⨯=锥,又=24=8V ⨯柱, 111844B A MCC V -∴=-=锥,故两部分几何体的体积之比为1:1.【点睛】本题考查了线面垂直的判定与性质,棱锥的体积计算,属于中档题.19.(1;(2【解析】【分析】(1)由题意得出160BO E ∠=o ,可得出1BO E ∆为等边三角形,由此求出BE 、AE 的长度,并计算出ABE ∆的面积,易知三棱锥D ABE -的高等于12O O ,再由锥体体积公式可得出三棱锥D ABE -的体积;(2)以点1O 为坐标原点,1O B uuu r 、2O F uuu u r 、12O O u u u u u r 分别为x 、y 、z 轴的正方向建立空间直角坐标系,利用空间向量法计算出AF u u u r 与BE u u u r所成角的余弦值,从而可得出异面直线AF 与BE 所成角的余弦值.【详解】(1)由于点E 是圆心为1O 半径为2的半圆弧上从点B 数起的第一个三等分点,则160BO E ∠=o ,1BO E ∴∆是边长为2的等边三角形,2BE ∴=,且4AB =,E Q 是以AB 为直径的半圆1O 上的一点,则90AEB ∠=o ,AE ∴==,ABE ∴∆的面积为11222ABE S AE BE ∆=⋅=⨯= 易知三棱锥D ABE -的高等于12O O ,则三棱锥D ABE -的体积为12133D ABE ABE V S O O -∆=⋅=; (2)以点1O 为坐标原点,1O B uuu r 、2OF uuu u r 、12O O u u u u u r 分别为x 、y 、z 轴的正方向建立空间直角坐标系,则()2,0,0A -、()2,0,0B 、()E 、()0,1,2F .于是()2,1,2AF =uu u r ,()BE =-uur .由于22cos ,326AF BE AF BE AF BE⋅===⨯⋅uu u r uur uu u r uur uu u r uur , 因此,直线AF 与BE所成角的余弦值为26-【点睛】本题考查锥体体积和异面直线所成角的余弦值的计算,在求解异面直线所成角的余弦值时,可利用建立空间直角坐标系的方法,转化为空间向量来进行计算,考查运算求解能力,属于中等题.20.(1)1220π+(2)6π【解析】【分析】(1)根据三视图可复原几何体,该几何体为半个圆柱中挖去半个圆柱,根据公式可算计算其表面积.(2)在圆台的轴截面中,可计算出底面半径,根据公式可求其侧面积.【详解】(1)三视图对应的几何体如图所示:其表面积为()22112233121323312+2022S ππππ=⨯⨯+⨯-+⨯⨯⨯⨯+⨯⨯⨯⨯=. (2)圆台的轴截面如图所示:由题设可知:2,2NQ NR ==,过N 作OP 的垂线,垂足为S ,则1RS =,故224RP =+=,故底面的半径为2,故圆台的侧面积为()()121226S r r l πππ=+=⨯+⨯=.【点睛】本题(1)考查三视图及其几何体的复原,注意根据复原前后对应的点、线、面的位置关系,(2)考查圆台的基本量的计算,注意利用轴截面来实现各基本量关系的转化.21.(1)证明见解析;(2)证明见解析;(3)23. 【解析】【分析】(1)在平面PAD 中找EF 的平行线;(2)转化为CD ⊥平面PAD ;(3)以四边形ABCD 为底面,P 与AD 中点的连线为高求体积.【详解】(1)证明:取PD 的中点G ,连结,AG GE ,∵PAD ∆中,,G E 分别为,PD PC 的中点,∴//GE CD ,12GE CD =, ∵,E F 分别为,PC AB 的中点,∴ //AF CD ,12AF CD =, ∴ //AF GE ,AF GE =,∴ AEFG 为平行四边形,∴ //EF GA ,∵ EF ⊂平面PAD ,PA ⊄平面PAD ,∴ //EF 平面PAD ;(2)证明:∵ 平面PAD ⊥平面ABCD ,CD AD ⊥,平面PAD I 平面ABCD AD =, ∴ CD ⊥平面PAD ,∵ CD ⊂平面PDC∴平面PDC ⊥平面PAD(3)取AD 中点O ,连结PO ,∵平面PAD ⊥平面ABCD 及PAD ∆为等腰直角三角形,∴PO ⊥平面ABCD , 即PO 为四棱锥P ABCD -的高,∵2AD =,∴1PO =, ∴1233V PO AB AD =⨯⨯⨯=. 【点睛】本题考查线面平行和面面垂直的证明;以及锥体体积的计算.。
(典型题)高中数学必修二第一章《立体几何初步》测试卷(含答案解析)

一、选择题1.已知正方体1111ABCD A B C D -,E 、F 分别是正方形1111D C B A 和11ADD A 的中心,则EF 和BD 所成的角的大小是( ) A .30B .45C .60D .902.已知AB 是平面α外的一条直线,则下列命题中真命题的个数是( ) ①在α内存在无数多条直线与直线AB 平行; ②在α内存在无数多条直线与直线AB 垂直; ③在α内存在无数多条直线与直线AB 异面; ④一定存在过AB 且与α垂直的平面β. A .1个B .2个C .3个D .4个3.如图,在长方体1111ABCD A B C D -中,1AB AD ==,12AA =,M 为棱1DD 上的一点.当1A M MC +取得最小值时,1B M 的长为( )A 3B 6C .23D .264.已知三棱柱111ABC A B C -的所有顶点都在球O 的表面上,侧棱1AA ⊥底面111A B C ,底面111A B C △是正三角形,1AB 与底面111A B C 所成的角是45°.若正三棱柱111ABC A B C -的体积是3O 的表面积是( ) A .28π3B .14π3C .56π3D .7π 35.正方体1111ABCD A B C D -的棱长为2,E 是1CC 的中点,则点1C 到平面EBD 的距离为( ) A .34B 6C 5D 226.在棱长为2的正方体ABCD ﹣A 1B 1C 1D 1中,点E ,F 分别是棱C 1D 1,B 1C 1的中点,P 是上底面A 1B 1C 1D 1内一点,若AP ∥平面BDEF ,则线段AP 长度的取值范围是( )A .[322,5] B .[5,22]C .[324,6] D .[6,22]7.如图为某几何体的三视图,正视图、左视图和俯视图均为等腰直角三角形,则该几何体的表面积是( )A .23+B .223+C .63+D .6 8.三个平面将空间分成n 个部分,则n 不可能是( )A .5B .6C .7D .89.如图,正方体1111ABCD A B C D -中,P 为线段1A B 上的动点,则下列结论错误的是( )A .1DC PC ⊥B .异面直线AD 与PC 不可能垂直 C .1D PC ∠不可能是直角或者钝角 D .1APD ∠的取值范围是,62ππ⎛⎫⎪⎝⎭ 10.已知四面体ABCD 中,二面角A BC D --的大小为60,且2AB =,4CD =,120CBD ∠=,则四面体ABCD 体积的最大值是( )A 43B 23C .83D .4311.已知长方体1111ABCD A B C D -的顶点A ,B ,C ,D ,在球O 的表面上,顶点1A ,1B ,1C ,1D ,在过球心O 的一个平面上,若6AB =,8AD =,14AA =,则球O 的表面积为( ) A .169πB .161πC .164πD .265π12.如图,长、宽、高分别为2、1、1的长方体木块上有一只小虫从顶点A 出发沿着长方体的外表面爬到顶点B ,则它爬行的最短路程是( )A .10B .5C .22D .3二、填空题13.在三棱锥P ABC -中,PA ⊥平面ABC ,22AB =,3BC =,4PA =,4ABC π∠=,则该三棱锥的外接球体积为___________.14.如图,在三棱台111ABC A B C -中,11190,4,22ACB AC BC A B CC ∠=︒====,平面11AA B B ⊥平面ABC ,则该三棱台外接球的表面积为___________.15.在正三棱锥A BCD -中,5AB AC AD ===,6BC BD CD ===.点M 是线段BC 上的点,且2BM MC =.点P 是棱AC 上的动点,直线PM 与平面BCD 所成角为θ,则sin θ的最大值为______.16.如图,在长方体1111ABCDA B C D ﹣中,O 是11B D 的中点,P 是线段AC 上一点,且直线1PA 交平面11AB D 于点M .给出下列结论:①A ,M ,O 三点共线;②A ,M ,O ,1A 不共面;③A ,M ,C ,O 共面;④B ,1B ,O ,M 共面.其中正确结论的序号为______.17.如下图所示,三棱锥P ABC -外接球的半径为1,且PA 过球心,PAB △围绕棱PA 旋转60︒后恰好与PAC △重合.若3PB =,则三棱锥P ABC -的体积为_____________.18.如图在长方形ABCD 中,AB 6=,BC 2=.E 为线段DC 上一动点,现将△AED 沿AE 折起.使点D 在面ABC 上的射影K 在直线AE 上,当E 从D 运动到C .则K 所形成轨迹的长度为_____.19.若三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形,23AB =,7SA SB SC ===,则该三棱锥的外接球的表面积为__________. 20.棱长为a 的正四面体的外接球的表面积为______.三、解答题21.如图,四棱锥P ABCD -的底面ABCD 是边长为2的菱形,60BCD ∠=,已知2PB PD ==,6PA =,E 为PA 的中点.(1)求证:PC BD ⊥;(2)求二面角B PC E --的余弦值; (3)求三棱锥P BCE -的体积.22.将棱长为2的正方体1111ABCD A B C D -沿平面11A BCD 截去一半(如图1所示)得到如图2所示的几何体,点E ,F 分别是BC ,DC 的中点.(Ⅰ)证明:EF ⊥平面1A AC ; (Ⅱ)求三棱锥1A D EF -的体积.23.如图,在四棱锥P ABCD -中,底面ABCD 为菱形,平面PAD ⊥平面ABCD ,PA PD ⊥,PA PD =,3BAD π∠=,E 是线段AD 的中点,连结BE .(1)求证:BE PA ⊥;(2)求二面角A PD C --的余弦值;(3)在线段PB 上是否存在点F ,使得//EF 平面PCD ?若存在,求出PFPB的值;若不存在,说明理由.24.如图,已知三棱锥P ABC -﹐PC AB ⊥,ABC 是边长为33PB =60PBC ∠=,点F 为线段AP 的中点.(1)证明:PC ⊥平面ABC ;(2)求直线BF 与平面PAC 所成角的大小.25.如图,在直角梯形ABED 中,//BE AD ,DE AD ⊥,BC AD ⊥,4AB =,23BE =.将矩形BEDC 沿BC 翻折,使得平面ABC ⊥平面BCDE .(1)若BC BE =,证明:平面ABD ⊥平面ACE ;(2)当三棱锥A BCE -的体积最大时,求平面ADE 与平面ABC 所成的锐二面角的余弦值.26.我市论语广场准备设置一些多面体形或球形的石凳供市民休息,如图(1)的多面体石凳是由图(2)的正方体石块截去八个相同的四面体得到,且该石凳的体积是3160dm 3.(Ⅰ)求正方体石块的棱长;(Ⅱ)若将图(2)的正方体石块打磨成一个球形的石凳,求此球形石凳的最大体积.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】作出图形,连接1AD 、11B D 、1AB ,推导出1//EF AB ,11//BD B D ,可得出异面直线EF 和BD 所成的角为11AB D ∠,分析11AB D 的形状,即可得出结果. 【详解】如下图所示,连接1AD 、11B D 、1AB ,设正方体1111ABCD A B C D -的棱长为1,则11112AD AB B D ===, 所以,11AB D 为等边三角形,则1160AB D ∠=,因为E 、F 分别是正方形1111D C B A 和11ADD A 的中心,则E 、F 分别是11B D 、1AD 的中点,所以,1//EF AB ,在正方体1111ABCD A B C D -中,11//BB DD 且11BB DD =, 所以,四边形11BB D D 为平行四边形,则11//BD B D , 所以,异面直线EF 和BD 所成的角为1160AB D ∠=. 故选:C. 【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下: (1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.2.C解析:C 【分析】根据线面平行,线面垂直,异面直线等有关结论和定义即可判断. 【详解】对于A ,若直线AB 与平面α相交,则在α内不存在直线与直线AB 平行,错误; 对于B ,若直线AB 与平面α相交且不垂直,设AB M α=,过平面α外直线AB 上一点P 作PC α⊥,垂足为C ,则在平面α内过点C 一定可以作一条直线CD ,使得CD CM ⊥,所以CD AB ⊥,而在平面α内,与直线CD 平行的直线有无数条,所以在α内存在无数多条直线与直线AB 垂直,若直线AB 与平面α垂直,显然在α内存在无数多条直线与直线AB 垂直,当直线AB 与平面α平行时,显然可知在α内存在无数多条直线与直线AB 垂直,正确;对于C ,若直线AB 与平面α相交,设AB M α=,根据异面直线的判定定理,在平面α内,不过点M 的直线与直线AB 异面,所以在α内存在无数多条直线与直线AB 异面,当直线AB 与平面α平行时,显然可知在α内存在无数多条直线与直线AB 异面,正确; 对于D ,若直线AB 与平面α相交且不垂直,设AB M α=,过平面α外直线AB 上一点P 作PC α⊥,垂足为C ,所以平面ABC 与平面α垂直,若直线AB 与平面α垂直,则过直线AB 的所有平面都与平面α垂直,当直线AB 与平面α平行时,在直线AB 上取一点P 作PC α⊥,垂足为C ,所以平面ABC 与平面α垂直,正确. 故真命题的个数是3个. 故选:C . 【点睛】本题主要考查线面平行,线面垂直,异面直线等有关结论和定义的理解和应用,熟记定义,定理和有关结论是解题的关键,属于中档题.3.A解析:A 【分析】本题首先可通过将侧面11CDD C 绕1DD 逆时针转90展开得出当1A 、M 、2C 共线时1A M MC +取得最小值,此时M 为1DD 的中点,然后根据11B A ⊥平面11A D DA 得出111B A A M ⊥,最后根据1M B =即可得出结果.【详解】如图,将侧面11CDD C 绕1DD 逆时针转90展开,与侧面11ADD A 共面,连接12A C ,易知当1A 、M 、2C 共线时,1A M MC +取得最小值, 因为1AB AD ==,12AA =,所以M 为1DD 的中点,12A M = 因为11B A ⊥平面11A D DA ,1A M ⊂平面11A D DA ,所以111B A A M ⊥, 则222211111(2)3M B A A M B =+=+=故选:A. 【点睛】关键点点睛:本题考查根据线面垂直判断线线垂直,能否根据题意得出当M 为1DD 的中点时1A M MC +取得最小值是解决本题的关键,考查计算能力,考查数形结合思想,是中档题.4.A解析:A 【分析】首先得到11AB A ∠是1AB 与底面111A B C 所成的角,再通过三棱柱的体积得到三棱柱的底面等边三角形的边长,最后通过球的半径,球心到底面距离,底面外接圆半径的关系计算. 【详解】因为侧棱1AA ⊥底面111A B C ,则11AB A ∠是1AB 与底面111A B C 所成的角,则1145AB A ∠=︒. 故由11111tan tan 451AA AB A A B ∠=︒==,得111AA A B =. 设111AA A B a ==,则111313323224ABC A B C a V a a -=⨯⨯⨯==三棱柱 解得2a =.所以球O 的半径22232722233R ⎛⎫⎛⎫+⨯⨯= ⎪ ⎪ ⎪⎝⎭⎝=⎭,所以球O 的表面积22728π4π4π33S R ⎛⎫==⨯= ⎪ ⎪⎝⎭. 故选:A . 【点睛】解决球与其他几何体的切、接问题,关键在于仔细观察、分析,弄清相关元素的关系和数量关系,选准最佳角度作出截面(要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系),达到空间问题平面化的目的.5.B解析:B 【分析】利用等体积法11C EBD D C EB V V --=,设点1C 到平面EBD 的距离为d ,利用三棱锥的体积公式代入面积即求得d . 【详解】如图,利用等体积法,11C EBD D C EB V V --=,设点1C 到平面EBD 的距离为d ,正方体1111ABCD A B C D -的棱长为2,故22,5BD BE ED ===,如图,2215232h ED BD ⎛⎫=-=-= ⎪⎝⎭11223622EBDSBD h =⨯⨯=⨯= 又点D 到平面1C EB 的距离,即D 到平面11C CBB 的距离,为CD =2,111212EBC S=⨯⨯=, 由11C EBD D C EB V V --=得,1161233d =⨯⨯,故636d ==. 故选:B.【点睛】方法点睛:空间中求点到平面的距离的常见方法:(1)定义法:直接作垂线,求垂线段长;(2)等体积法:利用三棱锥换底求体积,结合两个面积和另一个高求未知高,即得距离;(3)向量法:过点的一个斜线段对应的向量a,平面法向量n,则a n dn⋅=.6.A解析:A【分析】分别取棱A1B1、A1D1的中点M、N,连接MN,可证平面AMN∥平面BDEF,得P点在线段MN上.由此可判断当P在MN的中点时,AP最小;当P与M或N重合时,AP最大.然后求解直角三角形得答案.【详解】如图所示,分别取棱A1B1、A1D1的中点M、N,连接MN,连接B1D1,∵M、N、E、F为所在棱的中点,∴MN∥B1D1,EF∥B1D1,∴MN∥EF,又MN⊄平面BDEF,EF⊂平面BDEF,∴MN∥平面BDEF;连接NF,由NF∥A1B1,NF=A1B1,A1B1∥AB,A1B1=AB,可得NF∥AB,NF=AB,则四边形ANFB为平行四边形,则AN∥FB,而AN⊄平面BDEF,FB⊂平面BDEF,则AN∥平面BDEF.又AN∩NM=N,∴平面AMN∥平面BDEF.又P是上底面A1B1C1D1内一点,且AP∥平面BDEF,∴P点在线段MN上.在Rt△AA1M中,AM===同理,在Rt△AA1N中,求得AN=△AMN为等腰三角形.当P在MN的中点时,AP,当P与M或N重合时,AP∴线段AP长度的取值范围是2⎡⎢⎣.故选:A.【点睛】本题主要考查了空间中点、线、面间的距离问题,其中解答中通过构造平行平面寻找得到点P 的位置是解答的关键,意在考查空间想象能力与运算能力,属于中档试题.7.A解析:A 【分析】由三视图可知原几何体是三棱锥,平面ACD ⊥平面ABC ,ACD ACB ≅底面是等腰直角三角形,底为2AC =,高为1BE =,ABD BCD ≅是边长为2的等边三角形,计算四个三角形面积之和即可求解. 【详解】由三视图可知原几何体是三棱锥:底面ACB △是等腰直角三角形,底2AC =,高1BE =,平面ACD ⊥平面ABC ,ACD ACB ≅,由三视图知ACB △中,2AC =,ACB △是等腰直角三角形,所以2AB BC ==ACD △是等腰直角三角形,2AD CD ==,2AC =,222BD BE DE =+=所以等腰直角三角形ACB △的面积为12112⨯⨯=, 等腰直角三角形ACD △的面积为12112⨯⨯=,等边ABD △的面积为()233242⨯=, 等边BCD △的面积为()2332⨯=, 所以该几何体的表面积是331123+++=+, 故选:A.8.A解析:A 【分析】三个平面不重合,先按其中平行的平面的个数分类:三个平面两两平行,两个平面平行,没有平行的平面(两两相交),对两两相交的情况,再根据三条交线互相平行,重合,交于一点,分别讨论. 【详解】按照三个平面中平行的个数来分类:(1)三个平面两两平行,如图1,可将空间分成4部分;(2)两个平面平行,第三个平面与这两个平行平面相交,如图2,可将空间分成6部分;(3)三个平面中没有平行的平面:(i )三个平面两两相交且交线互相平行,如图3,可将空间分成7部分; (ii )三个平面两两相交且三条交线交于一点,如图4,可将空间分成8部分.(iii )三个平面两两相交且交线重合,如图5,可将空间分成6部分;综上,可以为4,6,7,8部分,不能为5部分, 故选:A.9.D解析:D 【分析】在正方体中根据线面垂直可判断A ,根据异面直线所成角可判断B ,由余弦定理可判断CD. 【详解】 如图,设正方体棱长为2,在正方体中易知1DC ⊥平面11A BCD ,P 为线段1A B 上的动点,则PC ⊂平面11A BCD ,所以1DC PC ⊥,故A 正确;因为异面直线AD 与PC 所成的角即为BC 与PC 所成的角,在Rt PBC 中不可能BC 与PC 垂直,所以异面直线AD 与PC 不可能垂直,故B 正确;由正方体棱长为2,则222222211114480D P PC D C A P BP A P BP +-=+++-=+>,所以由余弦定理知1cos 0D PC ∠>,即1D PC ∠不可能是直角或者钝角,故C 正确;设1(0A P x x =≤≤,则2214D P x =+,222422cos44AP x x x π=+-⨯=+-,由余弦定理,2222111112cos =22AP D P AD x AP D P A PD P AP D ∠=+--⋅⋅,当x <1cos 0APD ∠<,所以1APD ∠为钝角,故D 错误.故选:D 【点睛】关键点点睛:判断正方体中的角的范围时,可选择合适三角形,利用正方体中数量关系,位置关系,使用余弦定理,即可判断三角形形状或角的范围,属于中档题.10.D解析:D 【分析】在BCD △中,利用余弦定理和基本不等式可得163BC BD ⋅≤,由三角形的面积公式可得3BCDS≤,由二面角A BC D --的大小为60,可得A 到平面BCD 的最大距离为2sin 603h ==ABCD 体积的最大值.【详解】在BCD △中,由余弦定理可得2222cos120CD BC BD BC BD =+-⋅22BC BD BC BD =++⋅因为222BC BD BC BD +≥,所以23CD BC BD ≥⋅, 所以163BC BD ⋅≤,当且仅当BC BD =时等号成立,1116sin1202232BCDSBC BD =⋅≤⨯⨯= 因为二面角A BC D --的大小为60,所以点A 到平面BCD的最大距离为2sin603h == 所以114333A BCD BCDV S h -=⋅≤=,所以四面体ABCD 体积的最大值是43, 故选:D 【点睛】关键点点睛:本题解题的关键点是利用余弦定理和基本不等式、三角形面积公式求出BCD S △最大值,再由二面角求出高的最大值.11.C解析:C 【分析】把两个这样的长方体叠放在一起,构成一个长宽高分别为6,8,8的长方体,则球O 就是该长方体的外接球,根据长方体外接球的直径等于体对角线的长,求出直径,即可得出球的表面积. 【详解】 如下图所示:把两个这样的长方体叠放在一起,构成一个长宽高分别为6,8,8的长方体,则球O 就是该长方体的外接球,根据长方体的结构特征可得,其外接球直径等于体对角线的长, 所以球O 的半径R 满足2222688164R =++=, 所以球O 的表面积24164S R ππ==. 故选:C.【点睛】关键点点睛:本题主要考查几何体外接球的表面积,熟记长方体结构特征,其外接球的球心和半径与长方体的关系,以及球的表面积公式,是解决此类问题的关键.12.C解析:C 【分析】小虫有两种爬法,一种是从点A 沿着侧面ACGF 和上底面BHFG 爬行,另一种是从点A 沿着侧面ACGF 和侧面BDCG 爬行,将两种情况下的两个面延展为一个面,计算出平面图形的对角线长,比较大小后可得结果. 【详解】由于长方体ACDE FGBH -的长、宽、高分别为2、1、1,则小虫从点A 沿着侧面AEHF 和上底面FHBG 爬行,以及小虫从点A 沿着侧面ACGF 和侧面BDCG 爬行,这两条线路的最短路程相等.①若小虫从点A 沿着侧面ACGF 和上底面BHFG 爬行,将侧面ACGF 和上底面BHFG 延展为一个平面,如下图所示:则2AC BC ==,最短路程为2222AB AC BC =+=;②若小虫从点A 沿着侧面ACGF 和侧面BDCG 爬行,将面ACGF 和侧面BDCG 延展为一个平面,如下图所示:则3AD AC CD =+=,1BD =,最短路程为2210AB AD BD =+.因为2210<,因此,小虫爬行的最短路程为22 故选:C. 【点睛】方法点睛:(1)计算多面体或旋转体的表面上折线段的最值问题时,一般采用转化的方法进行,即将侧面展开化为平面图形,即“化折为直”或“化曲为直”来解决,要熟练掌握多面体与旋转体的侧面展开图的形状;(2)对于几何体内部折线段长的最值,可采用转化法,转化为两点间的距离,结合勾股定理求解.二、填空题13.【分析】利用余弦定理求得利用正弦定理计算出的外接圆直径可计算出三棱锥的外接球半径然后利用球体体积公式可求得结果【详解】如下图所示圆柱的底面圆直径为圆柱的母线长为则的中点到圆柱底面圆上每点的距离都相等解析:13263π【分析】利用余弦定理求得AC,利用正弦定理计算出ABC的外接圆直径2r,可计算出三棱锥P ABC-的外接球半径R,然后利用球体体积公式可求得结果.【详解】如下图所示,圆柱12O O的底面圆直径为2r,圆柱的母线长为h,则12O O的中点O到圆柱底面圆上每点的距离都相等,所以,圆柱12O O的外接球直径为()2222R r h=+.本题中,作出ABC的外接圆2O,由于PA⊥平面ABC,可将三棱锥P ABC-放在圆柱12O O中,在ABC中,22AB=3BC=,4ABCπ∠=,由余弦定理可得222cos5AC AB BC AB BC ABC+-⋅∠=,由正弦定理可知,ABC的外接圆直径为5210sin2ACrABC===∠则三棱锥P ABC-的外接球直径为()222226R PA r=+=262R=,因此,三棱锥P ABC -的外接球的体积为334433V R ππ==⨯=⎝⎭.故答案为:3. 【点睛】方法点睛:求空间多面体的外接球半径的常用方法:①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径; ③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.14.【分析】取与中点根据平面平面可知平面球心必在直线上设球心为D 则可求得球心恰好为点O 从而求得外接球的半径代入球的表面积公式计算【详解】在三棱台中可得都是等腰三角形四边形为等腰梯形即如图取与中点连接则可 解析:32π【分析】取AB 与11A B 中点,O O ',根据平面11AA B B ⊥平面ABC ,可知'⊥O O 平面ABC ,球心必在直线O O '上,设球心为D ,则()22221O D O O OC O D O C ''''-+=+,可求得球心恰好为点O ,从而求得外接球的半径R ,代入球的表面积公式计算. 【详解】在三棱台111ABC A B C -中,11190,4,ACB AC BC A B CC ∠=︒====111,A A C C B B 都是等腰三角形,11112A C B C ==,四边形11A ABB 为等腰梯形即11AA BB =,如图,取AB 与11A B 中点,O O ',连接1,,CO OO C O '',则可得1CO C O '==O O AB '⊥,又平面11AA B B ⊥平面ABC ,两面交线为AB ,所以'⊥O O 平面ABC .因为OA OB OC ==,111O A O B O C '''==,面//ABC 面111A B C ,所以球心必在直线O O '上.所以在直角梯形1C O OC '中可求得O O '=由题意可知,该三棱台外接球的外接球的球心必在直线O O '上,设球的半径为R ,球心为D ,则()22221O D O O OC O D O C ''''-+=+,得O D '=O ,所以球的半径为2432ππ=. 故答案为:32π【点睛】方法点睛:定义法:到各个顶点距离均相等的点为外接球的球心,借助面面垂直的性质,找到线面垂直,则球心一定在垂线上,再根据到其他顶点距离也是半径,列关系求解即可.15.【分析】证明直线与平面所成角中当此为二面角的平面角时最大即可得【详解】先证一个命题:平面内所有直线与平面所成的角中当此角为二面角的平面角时最大如图平面于点于是上任一点则而则平面又平面∴是二面角的平面 13 【分析】证明直线PM 与平面BCD 所成角中当此为二面角的平面角时最大即可得. 【详解】先证一个命题:平面ABC 内所有直线与平面BCD 所成的角中,当此角为二面角的平面角时最大.如图AO ⊥平面BCD 于点O ,OE BC ⊥于E ,Q 是BC 上任一点, 则AO BC ⊥,而AOOE O =,则BC ⊥平面OAE ,又AE ⊂平面OAE ,∴AEO∠是二面角A BC D --的平面角,而AQO 是直线AQ 与平面ABCD 所成的角,显然sin AOAEO AE∠=,sin AO AQO AQ ∠=,又AQ AE ≥,∴sin sin sin AQO AEO ∠≤∠,,AEO AQO ∠∠都是锐角,∴AQO AEO ∠≤∠,,Q E 重合时等号成立.由此可知平面ABC 内所有直线与平面BCD 所成的角中,当此角为二面角的平面角时最大. 由已知3636EO ==22534AE -=,2213AO AE EO - 13sin 4AEO ∠=, ∴直线PM 与平面BCD 所成角最大值等于AEO ∠, ∴sin θ13.故答案为:134. 【点睛】结论点睛:在二面角A BC D --(为锐二面角)中,AEO ∠是A BC D --二面角的平面角,Q 是棱BC 上任一点,则AQ 与平面BCD 所成角中最大值为二面角的平面角,AQ 与平面BCD 内过Q 点的直线(实际上是所有直线)所成角中最大值为直线AQ 与平面BCD 所成的角.16.①③【分析】由公理1判断①正确;由公理2判断②错误③正确用反证法可得④错误【详解】∵连接∵是的中点∴平面与平面有公共点与则平面平面对于①平面则平面又平面则即三点共线故①正确;对于②在平面内由①知∴平解析:①③【分析】由公理1判断①正确;由公理2判断②错误③正确,用反证法可得④错误.【详解】∵连接11A C ,∵O 是11B D 的中点,∴11O A C ∈.平面11AB D 与平面11AAC C 有公共点A 与O ,则平面11AAC C 平面11AB D AO =.对于①,1M PA ∈,1PA ⊂平面11AAC C ,则M ∈平面11AAC C ,又M ∈平面11AB D ,则M AO ∈,即A ,M ,O 三点共线,故①正确;对于②,A ,O ,1A 在平面11AAC C 内,由①知M AO ∈,∴O ∈平面11AAC C , 即A ,M ,O ,1A 共面,故②错误;对于③,A ,O ,C 在平面11AAC C 内,由①知M AO ∈,∴O ∈平面11AA C CA , 则A ,M ,C ,O 共面11AAC C ,故③正确;对于④,连接BD ,则B ,1B ,O 都在平面11BB D D 上,若M ∈平面11BB D D ,则直线OM ⊂平面11BB D D ,∴A ∈面11BB D D ,显然A ∉面11BB D D 的,故④错误.∴正确命题的序号是①③.故答案为:①③.【点睛】本题考查命题的真假判断与应用,考查空间中的直线与平面、平面与平面的位置关系,考查空间想象能力与思维能力,是中档题.17.【分析】作于可证得平面得得等边三角形利用是球的直径得然后计算出再应用棱锥体积公式计算体积【详解】∵围绕棱旋转后恰好与重合∴作于连接则∴又过球心∴而∴同理由得平面∴故答案为:【点睛】易错点睛:本题考查 解析:38【分析】作BH PA ⊥于H ,可证得PA ⊥平面BCH ,得60BHC ∠=︒,得等边三角形BCH ,利用PA 是球的直径,得PB AB ⊥,然后计算出BH ,再应用棱锥体积公式计算体积.【详解】∵PAB △围绕棱PA 旋转60︒后恰好与PAC △重合,∴PAB PAC ≅△△,作BH PA ⊥于H ,连接CH ,则,CH PA CH BH ⊥=,60BHC ∠=︒,∴BC BH CH ==.又PA 过球心,∴PB AB ⊥,而2,3PA PB ==,∴1AB =,同理1AC =,313PB AB BH PA ⋅⨯===,223333344216BCH S BH ⎛⎫=== ⎪ ⎪⎝⎭△, 由BH PA ⊥,CH PA ⊥,CHBH H =,得PA ⊥平面BCH , ∴11333233168P ABC BCH V S PA -=⋅=⨯⨯=△ 故答案为:38.【点睛】易错点睛:本题考查求棱锥的体积,解题关键是作BH PA ⊥于H ,利用旋转重合,得PA ⊥平面BCH ,这样只要计算出BCH 的面积,即可得体积,这样作图可以得出60BHC ∠=︒,为旋转所形成的二面角的平面角,这里容易出错在误认为旋转60︒,即为60CAB ∠=︒.旋转60︒是旋转形成的二面角为60︒.应用作出二面角的平面角. 18.【分析】由题意分析可得可知K 所形成轨迹为一个圆弧求出圆心角再求弧长即可【详解】由题意D′K ⊥AE 所以K 的轨迹是以AD′为直径的一段圆弧D′K 设AD′的中点为O ∵长方形ABCD′中ABBC ∴∠D′AC 解析:23π 【分析】 由题意分析可得DK AE ⊥可知K 所形成轨迹为一个圆弧,求出圆心角再求弧长即可.【详解】由题意,D ′K ⊥AE ,所以K 的轨迹是以AD ′为直径的一段圆弧D ′K ,设AD ′的中点为O , ∵长方形ABCD ′中,AB 6=,BC 2=, ∴∠D ′AC =60°,∴∠D ′OK =120°23π=, ∴K 所形成轨迹的长度为2223ππ⨯=,2 【点睛】 本题主要考查了空间中的轨迹问题,主要是找到定量关系分析轨迹,属于中等题型. 19.【详解】取的中点由题意可得:所以面ABC 所以球心在直线上所以得所以解析:494π 【详解】取AB 的中点,由题意可得:2222,3,SD DC SD DC SC ==+=,所以,SD AB SD DC ⊥⊥,SD ⊥面ABC. 所以球心在直线SD 上,所以()2232R R =+-,得74R =, 所以24944S R ππ==. 20.【分析】由正四面体性质可知球心在棱锥高线上利用勾股定理可求出半径R 即可求出球的面积【详解】正四面体的棱长为:底面三角形的高:棱锥的高为:设外接球半径为R 解得所以外接球的表面积为:;故答案为:【点睛】 解析:232a π 【分析】由正四面体性质可知,球心在棱锥高线上,利用勾股定理可求出半径R ,即可求出球的面积.【详解】正四面体的棱长为:a , 底面三角形的高:3322a a =, 22236()323a a a -⨯⨯=, 设外接球半径为R ,222)()33R a R a =-+,解得4R a =,所以外接球的表面积为:22342a ππ⎫⨯=⎪⎪⎝⎭; 故答案为:232a π. 【点睛】本题考查球的表面积的求法,解题的关键是根据球心的位置,在正四面体中求出球的半径. 三、解答题21.(1)证明见解析;(2;(3)12. 【分析】(1)连接AC 交BD 于点O ,连接PO ,推导出BD ⊥平面PAC ,进而可得出PC BD ⊥;(2)过点O 在平面PAC 内作OF PC ⊥,垂足为点F ,连接BF ,推导出OFB ∠为二面角B PC E --的平面角,计算出OF 、BF ,可计算出cos OFB ∠,即可得解; (3)计算出PCE 的面积,利用锥体的体积公式可得出13P BCE B PCE PCE V V S OB --==⋅△,即可得解. 【详解】证明:(1)连接AC 交BD 于O 点,连接PO ,∵四边形ABCD 是菱形,AC BD ∴⊥,则O 是BD 的中点,PB PD =,PO BD ∴⊥,又AC PO O =,AC 、OP ⊂平面PAC ,BD ∴⊥平面PAC ,又PC ⊂平面PAC ,PC BD ∴⊥;(2)由(1)知BO ⊥平面PAC ,PC ⊂平面PAC ,则OB PC ⊥,过O 在平面PAC 内作OF PC ⊥于F ,连接BF ,由OB OF O ⋂=,则PC ⊥平面OBF ,BF ⊂平面OBF ,得BF PC ⊥,故OFB ∠为二面角B PC E --的平面角, 四边形ABCD 是菱形,60BAD ∠=,ABD ∴为等边三角形,2BD AB AD ∴===,112OB BD ∴==,223OC OA AB OB ==-= OB ⊥平面PAC ,OP ⊂平面PAC ,OP OB ∴⊥,223OP PB OB ∴-= 3OA =3OP =6PA =222OP PA OA +∴=,即OA OP ⊥,即PO AC ⊥,3366PO OC OF PC ⋅⨯∴===,222261012BF BO OF ⎛⎫=+=+= ⎪ ⎪⎝⎭, 故615cos 510OF OFB BF ∠===,即二面角B PC E --的余弦值是155; (3)E 为PA 的中点,11333222PCE PAC POA S S S ∴====△△△, 又OB ⊥平面PAC ,113113322P BCE B PCE PCE V V S OB --∴==⋅=⨯⨯=△. 【点睛】方法点睛:求二面角常用的方法:(1)几何法:二面角的大小常用它的平面角来度量,平面角的作法常见的有: ①定义法;②垂面法,注意利用等腰三角形的性质;(2)空间向量法:分别求出两个平面的法向量,然后通过两个平面法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求二面角是锐角还是钝角.22.(Ⅰ)证明见解析;(Ⅱ)1.【分析】(Ⅰ)由BD AC ⊥和1A A BD ⊥,利用线面垂直的判定定理证得BD ⊥平面1A AC ,然后再由//BD EF 证明.(Ⅱ)由1D D ⊥平面ABCD ,则1D D 是三棱锥1D AEF -在平面AEF 上的高,然后利用等体积法11A D EF D AEF V V --=求解.【详解】(Ⅰ)如图所示:连接BD ,易知BD AC ⊥,因为1A A ⊥平面ABCD ,BD ⊂平面ABCD ,所以1A A BD ⊥,又1A AAC A =, 所以BD ⊥平面1A AC .在CBD 中,点E ,F 分别是BC ,DC 的中点,所以//BD EF .所以EF ⊥平面1A AC .(Ⅱ)∵1D D ⊥平面ABCD ,∴1D D 是三棱锥1D AEF -在平面AEF 上的高,且12D D =.∵点E ,F 分别是BC ,DC 的中点,∴1DF CF CE BE ====. ∴2111322222AEF S AD DF CF CE AB BE =-⋅⋅-⋅⋅-⋅⋅=△. ∴11111321332A D EFD AEF AEF V V S D D --==⋅⋅=⨯⨯=△. 【点睛】方法点睛:(1)证明直线和平面垂直的常用方法:①线面垂直的定义;②判定定理;③垂直于平面的传递性(a ∥b ,a ⊥α⇒b ⊥α);④面面平行的性质(a ⊥α,α∥β⇒a ⊥β);⑤面面垂直的性质.(2)证明线面垂直的核心是证线线垂直,而证明线线垂直则需借助线面垂直的性质.因此,判定定理与性质定理的合理转化是证明线面垂直的基本思想.23.(1)证明见解析;(2)77-;(3)存在;12PF PB =. 【分析】(1)首先证明BE AD ⊥,再由面面垂直的性质定理可得BE ⊥平面PAD ,即证.(2)连结PE ,以E 为坐标原点,EP ,EA ,EB 为,,x y z 轴,建立空间直角坐标系,。
(典型题)高中数学必修二第一章《立体几何初步》测试卷(包含答案解析)

一、选择题1.已知正方体1111ABCD A B C D -,E 、F 分别是正方形1111D C B A 和11ADD A 的中心,则EF 和BD 所成的角的大小是( ) A .30B .45C .60D .902.大摆锤是一种大型游乐设备(如图),游客坐在圆形的座舱中,面向外,通常大摆锤以压肩作为安全束缚,配以安全带作为二次保险,座舱旋转的同时,悬挂座舱的主轴在电机的驱动下做单摆运动.假设小明坐在点A 处,“大摆锤”启动后,主轴OB 在平面α内绕点O 左右摆动,平面α与水平地面垂直,OB 摆动的过程中,点A 在平面β内绕点B 作圆周运动,并且始终保持OB β⊥,B β∈.设4OB AB =,在“大摆锤”启动后,下列结论错误的是( )A .点A 在某个定球面上运动;B .β与水平地面所成锐角记为θ,直线OB 与水平地面所成角记为δ,则θδ+为定值;C .可能在某个时刻,AB//α;D .直线OA 与平面α所成角的正弦值的最大值为17. 3.如图,在正四棱锥P ABCD -中,设直线PB 与直线DC 、平面ABCD 所成的角分别为α、β,二面角P CD B --的大小为γ,则( )A .,αβγβ>>B .,αβγβ><C .,αβγβ<>D .,αβγβ<<4.某几何体的三视图如图所示,其中网格纸的小正方形的边长是1,则该几何体外接球的体积为( )A .323πB .48πC .32327π D .643π 5.如图,正三棱柱111ABC A B C -的高为4,底面边长为43,D 是11B C 的中点,P 是线段1A D 上的动点,过BC 作截面AP α⊥于E ,则三棱锥P BCE -体积的最小值为( )A .3B .23C .43D .126.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是( )A .24B .30C .47D .677.如图所示,A ,B 为正方体的两个顶点,M ,N 为其所在棱的中点,则异面直线AB 与MN 所成角的大小为( )A .30°B .45°C .60°D .90°8.如图正三棱柱111ABC A B C 的所有棱长均相等,O 是1AA 中点,P 是ABC 所在平面内的一个动点且满足//OP 平面11A BC ,则直线OP 与平面ABC 所成角正弦值的最大值为( )A .22B .255C .3 D .2779.下图中小正方形的边长为1,粗线画出的是某四棱锥的三视图,则该四棱锥的体积为( )A .64B .48C .32D .1610.某三棱锥的三视图如图所示, 则该三棱锥的体积为( )A .16B .13C .23D .211.已知直线a 、b 都不在平面α内,则下列命题错误的是( ) A .若//a b ,//a α,则//b α B .若//a b ,a α⊥,则b α⊥ C .若a b ⊥,//a α,则b α⊥D .若a b ⊥,a α⊥,则//b α12.已知在底面为菱形的直四棱柱1111ABCD A B C D -中,14,42AB BD ==,若60BAD ︒∠=,则异面直线1B C 与1AD 所成的角为( )A .90︒B .60︒C .45︒D .30︒二、填空题13.如图,已知直四棱柱1111ABCD A B C D -的所有棱长均相等,3BAD π∠=,E 是棱AB的中点,设平面α经过直线1A E ,且α平面111,B BCC l α=⋂平面112C CDD l =,若α⊥平面11A ACC ,则异面直线1l 与2l 所成的角的余弦值为_______.14.已知H 是球O 的直径AB 上一点,:1:3AH HB =,AB ⊥平面α,H 为垂足,α截球O 所得截面的面积为π,则球O 的表面积为__________.15.已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为24,则这个球的体积为____________.16.已知一个圆锥内接于球O (圆锥的底面圆周及顶点均在同一球面上),圆锥的高是底面半径的3倍,圆锥的侧面积为910π,则球O 的表面积为________. 17.已知等腰直角三角形ABC 中,2C π∠=,22CA =,D 为AB 的中点,将它沿CD 翻折,使点A 与点B 间的距离为22,此时三棱锥C ABD -的外接球的表面积为____.18.在三棱锥-P ABC 中,侧面PBC 和底面ABC 都是边长为2的正三角形,若3PA =,则侧棱PA 与底面ABC 所成的角的大小是___________.19.如图,在长方体1111ABCDA B C D ﹣中,O 是11B D 的中点,P 是线段AC 上一点,且直线1PA 交平面11AB D 于点M .给出下列结论:①A ,M ,O 三点共线;②A ,M ,O ,1A 不共面;③A ,M ,C ,O 共面;④B ,1B ,O ,M 共面.其中正确结论的序号为______.20.正四棱台的上、下两底面边长分别是方程x 2-9x +18=0的两根,其侧面积等于两底面面积之和,则其侧面梯形的高为________.三、解答题21.在所有棱长均为2的直棱柱1111ABCD A B C D -中,底面ABCD 是菱形,且60BAD ∠=︒,O ,M 分别为1,BD B C 的中点.(Ⅰ)求证:直线//OM 平面11DB C ; (Ⅱ)求二面角1D AC D --的余弦值.22.如图,正四棱锥P ABCD -中,底面ABCD 的边长为4,4PD =,E 为PA 的中点.(1)求证://PC 平面EBD . (2)求三棱锥E ABD -的体积.23.如图,在四棱锥P ABCD -中,底面ABCD 是边长为1的正方形,PA ⊥底面ABCD ,PA AB =,点M 是棱PD 的中点.(1)求证://PB 平面ACM ; (2)求三棱锥P ACM -的体积.24.如图,四棱锥P ABCD -的底面ABCD 是边长为2的菱形,60BCD ∠=,已知2PB PD ==,6PA E 为PA 的中点.(1)求证:PC BD ⊥;(2)求二面角B PC E --的余弦值; (3)求三棱锥P BCE -的体积.25.如图,在多面体ABCDEF 中,底面ABCD 为菱形,且∠DAB =π3,AB =2,EF //AC ,EA =ED =3,BE =5.(1)求证:平面EAD ⊥平面ABCD ; (2)求三棱锥F -BCD 的体积.26.如图,四边形ABCD 为梯形,//,60,2,3,6AB CD C AB BC CD ∠=︒===,点M 在边CD 上,且13CM CD =.现沿AM 将ADM △折起至AQM 的位置,使3QB =.(Ⅰ)求证:QB ⊥平面ABCM ;(Ⅱ)求直线BM 与平面AQM 所成角的正弦值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】作出图形,连接1AD 、11B D 、1AB ,推导出1//EF AB ,11//BD B D ,可得出异面直线EF 和BD 所成的角为11AB D ∠,分析11AB D 的形状,即可得出结果. 【详解】如下图所示,连接1AD 、11B D 、1AB ,设正方体1111ABCD A B C D -的棱长为1,则11112AD AB B D ===, 所以,11AB D 为等边三角形,则1160AB D ∠=,因为E 、F 分别是正方形1111D C B A 和11ADD A 的中心,则E 、F 分别是11B D 、1AD 的中点,所以,1//EF AB ,在正方体1111ABCD A B C D -中,11//BB DD 且11BB DD =, 所以,四边形11BB D D 为平行四边形,则11//BD B D , 所以,异面直线EF 和BD 所成的角为1160AB D ∠=. 故选:C. 【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下: (1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.2.C解析:C 【分析】利用已知条件确定OA 是定值,即得A 选项正确;作模型的简图,即得B 正确;依题意点B 在平面α内,不可能AB//α,得C 错误;设AB a ,结合题意知AB α⊥时,直线OA 与平面α所成角最大,计算此时正弦值,即得D 正确. 【详解】因为点A 在平面β内绕点B 作圆周运动,并且始终保持OB β⊥,所22OA OB AB =+,又因为OB ,AB 为定值,所以OA 也是定值,所以点A 在某个定球面上运动,故A 正确;作出简图如下,OB l ⊥,所以2πδθ+=,故B 正确;因为B α∈,所以不可能有AB//α,故C 不正确; 设AB a ,则4OB a =,2217OA AB OB a =+,当AB α⊥时,直线OA 与平面α所成角最大,此时直线OA 与平面α171717a =,故D 正确. 故选:C. 【点睛】本题解题关键在于认真读题、通过直观想象,以实际问题为背景构建立体几何关系,再运用立体几何知识突破难点.3.A解析:A 【分析】连接AC 、BD 交于O ,连PO ,取CD 的中点E ,连,OE PE ,根据正棱锥的性质可知,PCE α∠=,PCO β∠=,PEO γ∠=,再比较三个角的正弦值可得结果. 【详解】连接AC 、BD 交于O ,连PO ,取CD 的中点E ,连,OE PE ,如图:因为//AB CD ,所以PBA α∠=,又因为四棱锥P ABCD -为正四棱锥,所以PCE α∠=,由正四棱锥的性质可知,PO ⊥平面ABCD ,所以PCO β∠=, 易得OE CD ⊥,PE CD ⊥,所以PEO γ∠=, 因为sin PE PC α=,sin POPCβ=,且PE PO >,所以sin sin αβ>,又,αβ都是锐角,所以αβ>,因为sin PO PE γ=,sin POPCβ=,且PC PE >,所以sin sin γβ>,因为,βγ都是锐角,所以γβ>.故选:A 【点睛】关键点点睛:根据正棱锥的性质,利用异面直线所成角、直线与平面所成角、二面角的平面角的定义得到这三个角是解题关键,属于中档题.4.A解析:A 【分析】由三视图可知,该几何体是四棱锥,其中四棱锥底面是边长为4的正方形,将四棱锥补成棱长为4的正方体,则该几何体的外接球就是正方体的外接球,进而可得答案. 【详解】由三视图可知,该几何体是如图所示的四棱锥P ABCD -, 其中四棱锥底面是边长为4的正方形,四棱锥的一条侧棱与底面垂直,四棱锥的高为4, 将四棱锥补成棱长为4的正方体, 则该几何体的外接球就是正方体的外接球, 外接球的直径2R 等于正方体的对角线长, 即24323R R =⇒=所以该几何体外接球的体积为(34233π⨯=323π,故选:A.【点睛】方法点睛:三视图问题是考查学生空间想象能力最常见题型,也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键,不但要注意三视图的三要素“高平齐,长对正,宽相等”,还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响,对简单组合体三视图问题,先看俯视图确定底面的形状,根据正视图和侧视图,确定组合体的形状.5.C解析:C 【分析】因为P BCE P ABC E ABC V V V ---=-则当E ABC V -取最大值时,三棱锥P BCE -体积有最小值,建立坐标系求得当点E 的高为3时,问题得解. 【详解】以点O 为原点,,,OA OD OB 分别为,,x y z 轴建立空间直角坐标系,如图所示:设点(),0,E x z ,依题意得()6,0,0A ,则()6,0,AE x z =- ,(),0,OE x z = 因为过BC 作截面AP α⊥于E ,所以AE OE ⊥则0AE OE ⋅=, 故()2600x x z -++= 所以()6z x x =-3x =时max 3z =又()143P BCE P ABC E ABC ABCV V V S z ---=-=-因为max 3z =所以三棱锥P BCE -体积的最小值()1114343643332P BCE ABC V S-=-=⋅⋅⋅= 故选:C 【点睛】关键点点晴:本题的解题关键是将问题转化为求E ABC V -的最大值,通过建系求得三棱锥E ABC -的高的最大值即可.6.D解析:D 【分析】先找到几何体的原图,再求出几何体的高,再求几何体的体积得解. 【详解】由三视图可知几何体为图中的四棱锥1P CDD E -, 由题得22437AD =-7 所以几何体的体积为11(24)676732⋅+⋅=. 故选:D 【点睛】方法点睛:通过三视图找几何体原图常用的方法有:(1)直接法;(2)拼凑法;(3)模型法.本题利用的就是模型法.要根据已知条件灵活选择方法求解.7.C解析:C 【分析】由MN 与正方体的面对角线平行,可得异面直线所成的角,此角是正三角形的内角,由此可得. 【详解】作如图所示的辅助线,由于M ,N 为其所在棱的中点,所以//MN PQ ,又因为//AC PQ ,所以//AC MN ,所以CAB ∠即为异面直线AB 与MN 所成的角(或补角),易得AB AC BC ==,所以60CAB ∠=︒. 故选:C .8.D解析:D 【分析】先找到与平面11A BC 平行的平面OEFG ,确定点P 在直线FG 上,作出线面角,求出正弦,转化为求AP 的最小值. 【详解】分别取1,,CC BC BA 的中点,连接,,,OE EF FG GO ,并延长FG ,如图,由中位线性质可知11//OE A C , 1//EF BC ,且OE EF E =,故平面11//A BC 平面OGFE ,又P 是ABC 所在平面内的一个动点且满足//OP 平面11A BC 则点P 在直线FG 上,OA ⊥平面ABC ,OPA ∴∠是直线OP 与平面ABC 所成角,sin OAOPA OP∴∠=,OA 为定值,∴当OP 最小时,正弦值最大,而22OP OA AP =+,所以当AP 最小时,sin OPA ∠最大, 故当AP FG ⊥时,sin OPA ∠最大, 设棱长为2, 则1212AG =⨯=,而30GAP ∠=︒, 32AP ∴=, 又1212OA =⨯=, 222sin 773()12OAOPA OP∴∠===+故选:D 【点睛】关键点点睛:由P 是ABC 所在平面内的一个动点且满足//OP 平面11A BC ,转化为找过O 的平面与平面11A BC 平行,P 在所找平面与平面ABC 的交线上,从而容易确定出线面角,是本题解题的关键所在.9.C解析:C 【分析】在长方体中还原三视图后,利用体积公式求体积. 【详解】根据三视图还原后可知,该四棱锥为镶嵌在长方体中的四棱锥P -ABCD (补形法) 且该长方体的长、宽、高分别为6、4、4, 故该四棱锥的体积为1(64)4323V =⨯⨯⨯=. 故选C .(1)根据三视图画直观图,可以按下面步骤进行:①、首先看俯视图,根据俯视图画出几何体地面的直观图;②、观察正视图和侧视图找到几何体前、后、左、右的高度;③、画出整体,让后再根据三视图进行调整;(2)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解.10.C解析:C【分析】根据题中所给的几何体的三视图还原几何体,得到相应的三棱锥,之后利用椎体体积公式求得结果.【详解】根据题中所给的几何体的三视图还原几何体如图所示:该三棱锥满足底面BCD△是等腰三角形,且底边和底边上的高线都是2;且侧棱AD⊥底面BCD,1AD=,所以112 =221=323V⨯⨯⨯⨯,故选:C.【点睛】方法点睛:该题考查的是有关根据所给几何体三视图求几何体体积的问题,解题方法如下:(1)应注意把握三个视图的尺寸关系:主视图与俯视图长应对正(简称长对正),主视图与左视图高度保持平齐(简称高平齐),左视图与俯视图宽度应相等(简称宽相等),若不按顺序放置和不全时,则应注意三个视图名称;(2)根据三视图还原几何体;(3)利用椎体体积公式求解即可.11.C解析:C利用线面平行的性质和判定定理可判断A 选项的正误;由线面垂直的定义可判断B 选项的正误;根据已知条件判断b 与α的位置关系,可判断C 选项的正误;根据已知条件判断b 与α的位置关系,可判断D 选项的正误. 【详解】由于直线a 、b 都不在平面α内.在A 中,若//a α,过直线a 的平面β与α的交线m 与a 平行,因为//a b ,可得//b m ,b α⊄,m α⊂,所以,//b α,A 选项正确;在B 中,若a α⊥,则a 垂直于平面α内所有直线,//a b ,则b 垂直于平面α内所有直线,故b α⊥,B 选项正确; 在C 中,若a b ⊥,//a α,则b 与α相交或平行,C 选项错误;在D 中,若a b ⊥,a α⊥,则//b α或b α⊂,b α⊄,//b α∴,D 选项正确.故选:C. 【点睛】方法点睛:对于空间线面位置关系的组合判断题,解决的方法是“推理论证加反例推断”,即正确的结论需要根据空间线面位置关系的相关定理进行证明,错误的结论需要通过举出反例说明其错误,在解题中可以以常见的空间几何体(如正方体、正四面体等)为模型进行推理或者反驳.12.A解析:A 【分析】把1AD 平移到1BC ,把异面直线所成的角转化为相交直线的夹角. 【详解】 连接1,BD BC ,∵四边形ABCD 为菱形, 60,4BAD AB ︒∠==,4BD ∴=.又1BDD 为直角三角形,22211BD BD DD ∴=+,得14DD =,∴四边形11BCC B 为正方形.连接1BC 交1B C 于点O 11//BC AD ,BOC ∴∠(或其补角)为异面直线1B C 与1AD 所成的角,由于11BCC B 为正方形, 90BOC ︒∴∠=,故异面直线1B C 与1AD 所成的角为90°.【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下: (1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.二、填空题13.【分析】取的中点连接证明平面平面平面即平面然后分别取的中点证明平面平面可得可得异面直线与所成的角即与所成的角由余弦定理可得答案【详解】由直四棱柱的所有棱长均相等所以是菱形连接且所以因为平面平面所以且解析:910【分析】 取AD 的中点F ,连接1A F ,证明平面1A EF ⊥平面11A ACC ,平面1A EF 即平面α,然后分别取1111B C D C 、的中点M N 、,证明平面1//A EF 平面MNC ,可得//CM 1l ,//CN 2l ,可得异面直线1l 与2l 所成的角即CM 与CN 所成的角,由余弦定理可得答案.【详解】由直四棱柱1111ABCD A B C D -的所有棱长均相等,3BAD π∠=,所以ABCD 是菱形,连接AC BD 、,1111AC B D 、,且ACBD O =,11111A C B D O ⋂=,所以BD AC ⊥,1111B D A C ⊥,因为1AA ⊥平面ABCD ,BD ⊂平面ABCD , 所以1AA BD ⊥,且1AA AC A =,所以BD ⊥平面11A ACC ,取AD 的中点F ,连接1A F ,连接EF 交AC 与G ,所以//EF BD ,且G 是AO 的中点,所以EF ⊥平面11A ACC ,所以平面1A EF ⊥平面11A ACC , 又1A E ⊂平面1A EF ,所以平面1A EF 即平面α,分别取1111B C D C 、的中点M N 、,连接MN 交11A C 与H 点,H 即为11O C 的中点, 所以1A H GC =,且1//A H GC ,所以四边形1A HCG 是平行四边形,所以1//A G HC ,1AG ⊄平面CMN ,CH ⊂平面CMN ,所以//A G 平面CMN , 又因为11//////EF BD B D MN ,EF ⊄平面CMN ,MN ⊂平面CMN , 所以//MN 平面CMN ,又1AG EF G =,所以平面1//A EF 平面MNC ,且平面11B C CB ⋂平面MNC MC =, 平面11D C CD平面MNC NC =,所以//CM 1l ,//CN 2l ,所以异面直线1l 与2l 所成的角即CM 与CN 所成的角,设2AB =, 则直四棱柱1111ABCD A B C D -的所有棱长均为2,由3BAD π∠=,所以112BD AB B D ===,11112MN D B ==, 且2211415CM CN CC C M ==+=+=,由余弦定理得222551922510CM CN MN MCN CM CN +-+-∠===⨯⨯.故答案为:910. 【点睛】本题考查了异面直线所成的角,关键点是作出平面α及找出异面直线所成的角,考查了学生分析问题、解决问题的能力及空间想象力.14.【分析】求出截面圆的半径设可得出从而可知球的半径为根据勾股定理求出的值可得出球的半径进而可求得球的表面积【详解】如下图所示设可得出则球的直径为球的半径为设截面圆的半径为可得由勾股定理可得即即所以球的 解析:163π【分析】求出截面圆H 的半径,设AH x =,可得出3HB x =,从而可知,球O 的半径为2x ,根据勾股定理求出x 的值,可得出球O 的半径,进而可求得球O 的表面积. 【详解】如下图所示,设AH x =,可得出3HB x =,则球O 的直径为4AB x =,球O 的半径为2x ,设截面圆H 的半径为r ,可得2r ππ=,1r ∴=,由勾股定理可得()2222OH r x +=,即()22214x AH x -+=,即2214x x +=,3x ∴=, 所以,球O 的半径为232x =,则球O 的表面积为22316433S ππ⎛⎫=⨯= ⎪ ⎪⎝⎭. 故答案为:163π. 【点睛】方法点睛:在求解有关球的截面圆的问题时,一般利用球的半径、截面圆的半径以及球心到截面圆的距离三者之间满足勾股定理来求解.15.【分析】根据正方体的表面积可得正方体边长然后计算外接球的半径利用球的体积的公式可得结果【详解】设正方体边长正方体外接球的半径为R 由正方体的表面积为24所以则又所以所以外接球的体积为:故答案为:【点睛 解析:3π【分析】根据正方体的表面积,可得正方体边长a ,然后计算外接球的半径3R =,利用球的体积的公式,可得结果. 【详解】设正方体边长a ,正方体外接球的半径为R , 由正方体的表面积为24,所以2624a =, 则2a =,又3R =,所以3R , 所以外接球的体积为:(334434333R πππ==.故答案为:3π.【点睛】方法点睛:求多面体的外接球的表面积和体积问题关键是要求出外接球的半径,常用方法有:(1)三条棱两两互相垂直时,可恢复为长方体,利用长方体的体对角线为外接球的直径,求出球的半径;(2)直棱柱的外接球可利用棱柱的上下底面平行,借助球的对称性,球心为上下底面外接圆的圆心连线的中点,再根据勾股定理求球的半径;(3)如果设计几何体有两个面相交,可过两个面的外心分别作两个面的垂线,垂线的交点为几何体的球心.16.【分析】设圆锥的底面半径为球的半径为根据勾股定理可得根据圆锥的侧面积公式可得再根据球的表面积公式可得结果【详解】设圆锥的底面半径为球的半径为则圆锥的高为则球心到圆锥的底面的距离为根据勾股定理可得化简 解析:100π【分析】设圆锥的底面半径为r ,球O 的半径为R ,根据勾股定理可得53R r =,根据圆锥的侧面积公式可得3,5r R ==,再根据球的表面积公式可得结果. 【详解】设圆锥的底面半径为r ,球O 的半径为R ,则圆锥的高为3r , 则球心O 到圆锥的底面的距离为3r R -, 根据勾股定理可得()2223R r r R =+-,化简得53R r =,因为圆锥的高为3r =,所以圆锥的侧面积为2r r π=,2r =,解得r =3,所以5353R =⨯=, 所以球O 的表面积为24425100R πππ=⨯=. 故答案为:100π 【点睛】关键点点睛:利用圆锥的侧面积公式和球的表面积公式求解是解题关键.17.12【分析】根据题意可判断出两两垂直即可求出外接球半径得出表面积【详解】等腰直角三角形中为的中点满足两两垂直设外接球的半径为则即三棱锥的外接球的表面积为故答案为:【点睛】本题考查三棱锥外接球问题解题 解析:12π【分析】根据题意可判断出,,DC DA DB 两两垂直,即可求出外接球半径,得出表面积. 【详解】等腰直角三角形ABC 中,2C π∠=,CA CB ==D 为AB 的中点,2CD AD BD ∴===,,CD AD CD BD ∴⊥⊥, 22AB =,满足222AD BD AB +=,AD BD ∴⊥,,,DC DA DB ∴两两垂直,设外接球的半径为R ,则222222223R =++=,即3R =,∴三棱锥C ABD -的外接球的表面积为2412R ππ=.故答案为:12π.【点睛】本题考查三棱锥外接球问题,解题的关键是得出,,DC DA DB 两两垂直.18.【分析】先画出直观图证明平面平面然后侧棱与底面ABC 所成的角即为根据题目中的数据算出即可【详解】如图作的中点连结因为侧面PBC 和底面ABC 都是边长为2的正三角形而为的中点所以又所以平面同时平面所以平 解析:o 60.【分析】先画出直观图,证明平面PAD ⊥平面ABC ,然后侧棱PA 与底面ABC 所成的角即为PAD ∠,根据题目中的数据算出即可.【详解】如图,作BC 的中点D ,连结AD 、PD因为侧面PBC 和底面ABC 都是边长为2的正三角形而D 为BC 的中点,所以BC PD ⊥,BC AD ⊥,又PD AD D ⋂=,所以BC ⊥平面PAD ,同时BC ⊂平面ABC所以平面PAD ⊥平面ABC ,所以PAD ∠即为侧棱PA 与底面ABC 所成的角由侧面PBC 和底面ABC 都是边长为2的正三角形得AD PD ==PA =所以PAD ∆为等边三角形,则=PAD ∠o 60即侧棱PA 与底面ABC 所成的角为o 60故答案为:o 60【点睛】本题主要考查空间直线与平面所成角的计算,较简单.19.①③【分析】由公理1判断①正确;由公理2判断②错误③正确用反证法可得④错误【详解】∵连接∵是的中点∴平面与平面有公共点与则平面平面对于①平面则平面又平面则即三点共线故①正确;对于②在平面内由①知∴平解析:①③【分析】由公理1判断①正确;由公理2判断②错误③正确,用反证法可得④错误.【详解】∵连接11A C ,∵O 是11B D 的中点,∴11O A C ∈.平面11AB D 与平面11AAC C 有公共点A 与O ,则平面11AAC C 平面11AB D AO =.对于①,1M PA ∈,1PA ⊂平面11AAC C ,则M ∈平面11AAC C ,又M ∈平面11AB D ,则M AO ∈,即A ,M ,O 三点共线,故①正确;对于②,A ,O ,1A 在平面11AAC C 内,由①知M AO ∈,∴O ∈平面11AAC C , 即A ,M ,O ,1A 共面,故②错误;对于③,A ,O ,C 在平面11AAC C 内,由①知M AO ∈,∴O ∈平面11AA C CA , 则A ,M ,C ,O 共面11AAC C ,故③正确;对于④,连接BD ,则B ,1B ,O 都在平面11BB D D 上,若M ∈平面11BB D D ,则直线OM ⊂平面11BB D D ,∴A ∈面11BB D D ,显然A ∉面11BB D D 的,故④错误.∴正确命题的序号是①③.故答案为:①③.【点睛】本题考查命题的真假判断与应用,考查空间中的直线与平面、平面与平面的位置关系,考查空间想象能力与思维能力,是中档题.20.【分析】】解方程得出棱台的上下底面边长根据面积关系和比例关系求出棱台的高和小棱锥的高【详解】解方程x2-9x +18=0得x=3或x=6∴棱台的上下底面边长分别为36设棱台的斜高为h 则∴h=即答案为【 解析:52【分析】】解方程得出棱台的上下底面边长,根据面积关系和比例关系求出棱台的高和小棱锥的高.【详解】解方程x 2-9x +18=0得x=3或x=6,∴棱台的上下底面边长分别为3,6.设棱台的斜高为h ,, 则22143636452h ⨯⨯+=+=() , ∴h=52. 即答案为52. 【点睛】本题考查了棱台的结构特征,画出草图帮助观察各线段的关系比较重要.三、解答题21.(Ⅰ)证明见解析;(Ⅱ5 【分析】(Ⅰ)由中位线定理证明1//OM C D ,即可得线面平行;(Ⅱ)连1D O ,证明1D OD ∠为二面角1D AC D --的平面角, 在直角1D DO △中计算可得.【详解】解:(Ⅰ)连1BC ,则M 也为1BC 的中点,又M 为BD 的中点,所以1//OM C D ,因为OM ⊄平面11DB C ,1C D ⊂平面11DC B ,所以直线//OM 平面11DB C ;(Ⅱ)连1D O ,因为ABCD 是菱形,所以DO AC ⊥,又1111ABCD A B C D -为直棱柱,底面为菱形,所以11D A D C =,而O 为AC 中点,所以1D O AC ⊥,所以1D OD ∠为二面角1D AC D --的平面角,因为ABCD 是边长为2的菱形,且60BAD ∠=︒,所以1DO =,又12DD =, 由直棱柱知1DD DO ⊥,所以15DO =,所以115cos DO D OD D O ∠==.【点睛】方法点睛:本题考查证明线面平行,考查求二面角角,求二面角常用方法:(1)定义法:作出二面角的平面角并证明,然后在三角形中计算可得;(2)向量法:建立空间直角坐标系,求出两个平面的法向量夹角的余弦即可得二面角的余弦(注意判断二面角是锐角还是钝角).22.(1)证明见解析;(2)823. 【分析】(1)连接AC 交BD 于点O ,连接EO ,利用三角形中位线定理可得//EO PC ,再由线面平行的判定定理可得结论;(2)先证明PO ⊥面ABCD ,由E 是PA 的中点,可得E 到面ABCD 的距离12PO =,再利用棱锥的体积公式可得答案.【详解】(1)连接AC 交BD 于点O ,连接EO .四边形ABCD 为正方形,所以O 为AC 中点,又E 为PA 中点, //EO PC ∴,又EO ⊂面EBD ,PC ⊄面EBD ,//PC ∴面EBD .(2)正四棱锥P ABCD -中,PA PC =,O 是AC 的中点PO AC ∴⊥,PD PB =,O 是BD 的中点PO BD ∴⊥,又AC 与BD 在平面ABCD 内相交,所以PO ⊥面ABCD E 是PA 的中点,E ∴到面ABCD 的距离12PO =, 221822,2ABD S AB AD PO PD DO ∆=⋅⋅==-= 182323E ABD ABD PO V S -∆=⋅⋅= 【点睛】方法点睛:证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面.23.(1)证明见解析;(2)23. 【分析】(1)连接BD 交AC 于点O ,由中位线定理得//OM PB ,从而得证线面平行; (2)由M 是PD 中点,得12M ACD P ACD V V --=,求出三棱锥P ACD -的体积后可得. 【详解】(1)如图,连接BD 交AC 于点O ,连接OM ,则O 是BD 中点,又M 是PD 中点, ∴//OM PB ,又PB ⊄平面ACM ,OM ⊂平面ACM ,所以//PB 平面ACM ;(2)由已知12222ACD S =⨯⨯=,11422333P ACD ACD V S PA -=⋅=⨯⨯=△,又M 是PD 中点,所以1223M ACD P ACD V V --==, 所以23P ACM P ACD M ACD V V V ---=-=.【点睛】思路点睛:本题考查证明线面平行,求三棱锥的体积.求三棱锥的体积除掌握体积公式外,还需要注意割补法,不易求体积的三棱锥(或一个不规则的几何体)的体积可通过几个规则的几何体(柱、锥、台等)的体积加减求得.三棱锥的体积还可通过转化顶点,转移底面利用等体积法转化为求其他三棱锥的体积,从而得出结论.24.(1)证明见解析;(2)155;(3)12. 【分析】(1)连接AC 交BD 于点O ,连接PO ,推导出BD ⊥平面PAC ,进而可得出PC BD ⊥;(2)过点O 在平面PAC 内作OF PC ⊥,垂足为点F ,连接BF ,推导出OFB ∠为二面角B PC E --的平面角,计算出OF 、BF ,可计算出cos OFB ∠,即可得解; (3)计算出PCE 的面积,利用锥体的体积公式可得出13P BCE B PCE PCE V V S OB --==⋅△,即可得解. 【详解】证明:(1)连接AC 交BD 于O 点,连接PO ,∵四边形ABCD 是菱形,AC BD ∴⊥,则O 是BD 的中点,PB PD =,PO BD ∴⊥,又AC PO O =,AC 、OP ⊂平面PAC ,BD ∴⊥平面PAC ,又PC ⊂平面PAC ,PC BD ∴⊥;(2)由(1)知BO ⊥平面PAC ,PC ⊂平面PAC ,则OB PC ⊥,过O 在平面PAC 内作OF PC ⊥于F ,连接BF ,。
(典型题)高中数学必修二第一章《立体几何初步》检测题(包含答案解析)(1)

一、选择题1.如图,在长方体1111ABCD A B C D -中,1AB AD ==,12AA =,M 为棱1DD 上的一点.当1A M MC +取得最小值时,1B M 的长为( )A .3B .6C .23D .262.在三棱锥P ABC -中,PA ⊥平面ABC ,120224BAC AP AB AC ∠====,,则三棱锥P ABC -的外接球的表面积是( ) A .18πB .36πC .40πD .72π3.在正方体1111ABCD A B C D -,中,M ,N ,P ,Q 分别为1A B ,1B D ,1A D ,1CD 的中点,则异面直线MN 与PQ 所成角的大小是( )A .6π B .4π C .3π D .2π4.如图,在四棱锥E ABCD -中,底面ABCD 是正方形,且平面ABCD ⊥平面AEB ,则( )A .DEC ∠可能为90︒B .若AEB △是等边三角形,则DEC 也是等边三角形C .若AEB △是等边三角形,则异面直线DE 和AB 2D .若AEB △是直角三角形,则BE ⊥平面ADE5.已知α、β是平面,m 、n 是直线,下列命题中不正确的是( ) A .若//m α,n αβ=,则//m n B .若//m n ,m α⊥,则n α⊥ C .若m α⊥,m β⊥,则//αβD .若m α⊥,m β⊂,则αβ⊥6.已知平面图形PABCD ,ABCD 为矩形,4AB =,是以P 为顶点的等腰直角三角形,如图所示,将PAD △沿着AD 翻折至P AD '△,当四棱锥P ABCD '-体积的最大值为163,此时四棱锥P ABCD '-外接球的表面积为( )A .12πB .16πC .24πD .32π7.如图,在四棱锥P ABCD -中,底面ABCD 是矩形.其中3AB =,2AD =,PAD △是以A ∠为直角的等腰直角三角形,若60PAB ∠=︒,则异面直线PC 与AD 所成角的余弦值是( )A .2211B .22C .77D .11118.已知一个正三棱锥的四个顶点都在一个球的球面上,且这个正三棱锥的所有棱长都为2,求这个球的表面积( )A .4πB .8πC .12πD .24π9.在长方体1111ABCD A B C D -中,2AB =,1AD =,12AA =,点E 为11C D 的中点,则二面角11B A B E --的余弦值为( ) A .3B .3 C .33D .3210.在三棱锥S ABC -中,SA ⊥底面ABC ,且22AB AC ==,30C ∠=,2SA =,则该三棱锥外接球的表面积为( )A .20πB .12πC .8πD .4π11.平行六面体1111ABCD A B C D -的六个面都是菱形,那么点1A 在面11AB D 上的射影一定是11AB D 的________心,点1A 在面1BC D 上的射影一定是1BC D 的________心( )A .外心、重心B .内心、垂心C .外心、垂心D .内心、重心12.已知四面体ABCD ,AB ⊥平面BCD ,1AB BC CD BD ====,若该四面体的四个顶点都在球O 的表面上,则球O 的表面积为( ) A .73π B .7π C .712π D .79π 二、填空题13.在直三棱柱111ABC A B C -中,90ABC ∠=︒,13AA =,设其外接球的球心为O ,已知三棱锥O ABC -的体积为3,则球O 表面积的最小值为______.14.如图,在四棱柱1111ABCD A B C D -中,底面ABCD 是正方形,1AA ⊥平面ABCD ,且2AB BC ==,13AA =,经过顶点A 作一个平面α,使得//α平面11CB D ,若α平面1ABCD l =,α平面112ABB A l =,则异面直线1l 与2l 所成的角的余弦值为___________.15.点A 、B 、C 、D 在同一个球的球面上,3AB BC AC ===,若四面体ABCD 体积3______.16.如图,四边形ABCD 是矩形,且有2AB BC =,沿AC 将ADC 翻折成AD C ',当二面角D AC B '--的大小为3π时,则异面直线D C '与AB 所成角余弦值是______.17.一个三棱锥的三视图如图所示,该三棱锥中最长棱的长度为_______.18.在三棱锥-P ABC 中,侧面PBC 和底面ABC 都是边长为2的正三角形,若3PA =,则侧棱PA 与底面ABC 所成的角的大小是___________.19.已知四面体P ﹣ABC 的外接球的球心O 在AB 上,且PO ⊥平面ABC ,2AC 3=AB ,若四面体P ﹣ABC 的体积为32,则该球的体积为_____. 20.将底面直径为8,高为23的圆锥体石块打磨成一个圆柱,则该圆柱侧面积的最大值为______.三、解答题21.如图,在长方体1111ABCD A B C D -中,12AB BC AA ==,1O 是底面1111D C B A 的中心.(Ⅰ)求证:1//O B 平面1ACD ;(Ⅱ)求二面角1D AC D --的平面角的余弦值.22.将棱长为2的正方体1111ABCD A B C D -沿平面11A BCD 截去一半(如图1所示)得到如图2所示的几何体,点E ,F 分别是BC ,DC 的中点.(Ⅰ)证明:EF ⊥平面1A AC ; (Ⅱ)求三棱锥1A D EF -的体积.23.在三棱柱111ABC A B C -中,侧面11BCC B 为矩形,AC ⊥平面11BCC B ,D ,E 分别是棱1AA ,1BB 的中点.(1)求证://AE 平面11B C D ; (2)求证:1CC ⊥平面ABC ;(3)若12AC BC AA ===,求直线AB 与平面11B C D 所成角的正弦值. 24.如图,在四棱锥P ABCD -中,底面ABCD 为菱形,M 是棱PD 的中点.(1)求证://PB 平面AMC ;(2)若PD ⊥平面ABCD ,2AD PD ==,3BAD π∠=,求点B 到平面AMC 的距离.25.在四棱台1111ABCD A B C D -中,1AA ⊥平面ABCD ,//AB CD ,90ACD ∠=︒,26BC AC ==,1CD =,1AM CC ⊥,垂足为M .(1)证明:平面ABM ⊥平面11CDD C ; (2)若二面角B AM D --正弦值为217,求直线AC 与平面11CDD C 所成角的余弦. 26.如图,在直角梯形ABED 中,//BE AD ,DE AD ⊥,BC AD ⊥,4AB =,23BE =.将矩形BEDC 沿BC 翻折,使得平面ABC ⊥平面BCDE .(1)若BC BE =,证明:平面ABD ⊥平面ACE ;(2)当三棱锥A BCE -的体积最大时,求平面ADE 与平面ABC 所成的锐二面角的余弦值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【分析】本题首先可通过将侧面11CDD C 绕1DD 逆时针转90展开得出当1A 、M 、2C 共线时1A M MC +取得最小值,此时M 为1DD 的中点,然后根据11B A ⊥平面11A D DA 得出111B A A M ⊥,最后根据221111M A B B A M =+即可得出结果.【详解】如图,将侧面11CDD C 绕1DD 逆时针转90展开,与侧面11ADD A 共面,连接12A C ,易知当1A 、M 、2C 共线时,1A M MC +取得最小值, 因为1AB AD ==,12AA =,所以M 为1DD 的中点,12A M = 因为11B A ⊥平面11A D DA ,1A M ⊂平面11A D DA ,所以111B A A M ⊥, 则222211111(2)3M B A A M B =+=+=故选:A. 【点睛】关键点点睛:本题考查根据线面垂直判断线线垂直,能否根据题意得出当M 为1DD 的中点时1A M MC +取得最小值是解决本题的关键,考查计算能力,考查数形结合思想,是中档题.2.D解析:D 【分析】先找出ABC 的外接圆的半径,然后取ABC 的外接圆的圆心N ,过N 作平面ABC 的垂线NG ,作PA 的中垂线,交NG 于O ,则O 是外接球球心, OA 为外接球半径,求解半径并求表面积即可. 【详解】如图所示,1204BAC AB AC ∠===,,取BC 中点M ,连接AM 并延长到N 使AM =MN ,则四边形ABNC 是两个等边三角形组成的菱形,AN =BN =CN ,点N 是ABC 的外接圆圆心,过N 作平面ABC 的垂线NG ,则球心一定在垂线NG 上,因为PA ⊥平面ABC ,则PA //NG ,PA 与NG 共面,在面内作PA 的中垂线,交NG 于O ,则O 是外接球球心,半径R =OA ,Rt AON 中,122ON AP ==,4AN =,故()224232R =+=2441872S R πππ==⨯=.故选:D. 【点睛】求空间多面体的外接球半径的常用方法:①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径; ③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.本题就是采用这个方法.本题使用了定义法.3.B解析:B 【分析】由M 也是1A B 的中点,P 也是1AD 中点,得平行线,从而找到异面直线MN 与PQ 所成角,在三角形中可得其大小. 【详解】如图,连接1AD ,1AB ,显然M 也是1A B 的中点,P 也是1AD 中点, 又N 是1B D 中点,Q 是1CD 中点,所以//MN AD ,//PQ AC ,所以CAD ∠是异面直线MN 与PQ 所成角(或补角),大小为4π. 故选:B .【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下: (1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.4.C解析:C 【分析】对A ,直角三角形的斜边大于直角边可判断;对B ,由>=EC EB DC 可判断;对C ,可得CDE ∠即异面直线DE 和AB 所成角,即可求出;对D ,EAB ∠(或EBA ∠)为直角时,BE 与平面ADE 不垂直. 【详解】对A ,由题意,若90DEC ∠=︒,则DC EC >,但EC BC CD >=,故A 不正确; 对B ,若AEB △是等边三角形,显然有>=EC EB DC ,所以DEC 不会是等边三角形,故B 不正确;对C ,若AEB △是等边三角形,设边长为2,则22DE EC ==//AB CD ,则CDE ∠即异面直线DE 和AB 所成角,易求2cos 422CDE ∠==,故C 正确; 对D ,当AEB △是以AEB ∠为直角的直角三角形时,BE ⊥平面ADE ,当AEB △是以EAB ∠(或EBA ∠)为直角的直角三角形时,BE 与平面ADE 不垂直,故D 不正确.故选:C. 【点睛】本题考查四棱锥的有关位置关系的判断,解题的关键是正确理解长度关系,正确理解位置关系的变化.5.A解析:A 【分析】根据已知条件判断直线m 、n 的位置关系,可判断A 选项的正误;利用线面垂直的性质可判断BC 选项的正误;利用面面垂直的判定定理可判断D 选项的正误. 【详解】对于A 选项,若//m α,则直线m 与平面α内的直线平行或异面, 由于n αβ=,则直线m 、n 平行或异面,A 选项错误;对于B 选项,若//m n ,m α⊥,则n α⊥,B 选项正确; 对于C 选项,若m α⊥,m β⊥,则//αβ,C 选项正确;对于D 选项,若m α⊥,m β⊂,由面面垂直的判定定理可知αβ⊥,D 选项正确. 故选:A. 【点睛】方法点睛:对于空间线面位置关系的组合判断题,解决的方法是“推理论证加反例推断”,即正确的结论需要根据空间线面位置关系的相关定理进行证明,错误的结论需要通过举出反例说明其错误,在解题中可以以常见的空间几何体(如正方体、正四面体等)为模型进行推理或者反驳.6.C解析:C 【分析】分析出当平面P AD '⊥平面ABCD 时,四棱锥P ABCD '-的体积取最大值,求出AD 、P A '的长,然后将四棱锥P ABCD '-补成长方体P AMD QBNC '-,计算出该长方体的体对角线长,即为外接球的直径,进而可求得外接球的表面积. 【详解】取AD 的中点E ,连接P E ',由于P AD '△是以P '为顶点的等腰直角三角形,则P E AD '⊥,设AD x =,则1122P E AD x '==, 设二面角P AD B '--的平面角为θ,则四棱锥P ABCD '-的高为1sin 2h x θ=, 当90θ=时,max 12h x =, 矩形ABCD 的面积为4S AB AD x =⋅=,2111216433233P ABCD V Sh x x x '-=≤⨯⨯==,解得22x =.将四棱锥P ABCD '-补成长方体P AMD QBNC '-, 所以,四棱锥P ABCD '-的外接球直径为22222226R P N P A P D P Q AD AB ''''==++=+=,则6R =,因此,四棱锥P ABCD '-的外接球的表面积为2424R ππ=. 故选:C.【点睛】方法点睛:求空间多面体的外接球半径的常用方法:①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径; ③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.7.D解析:D 【分析】在图形中找到(并证明)异面直线所成的角,然后在三角形中计算. 【详解】因为//AD BC ,所以PCB ∠是异面直线PC 与AD 所成角(或其补角), 又PA AD ⊥,所以PA BC ⊥,因为AB BC ⊥,AB PA A ⋂=,,AB PA ⊂平面PAB ,所以BC ⊥平面PAB , 又PB ⊂平面PAB ,所以PB BC ⊥. 由已知2PA AD ==,所以22222cos 23223cos607PB PA AB PA AB PAB =+-⋅∠=+-⨯⨯︒= 22211cos 11(7)2BC PCB PC ∠===+,所以异面直线PC 与AD 所成角的余弦值为21111. 故选:D . 【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下: (1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.8.C解析:C 【分析】将正三棱锥补成一个正方体,计算出正方体的棱长,可得出正方体的体对角线长,即为外接球的直径,进而可求得这个球的表面积. 【详解】设该正三棱锥为A BCD -,将三棱锥A BCD -补成正方体AEBF GCHD -,如下图所示:则正方体AEBF GCHD -2222=,该正方体的体对角线长为23 所以,正三棱锥A BCD -的外接球直径为23R =3R =, 该球的表面积为2412S R ππ==. 故选:C. 【点睛】方法点睛:求空间多面体的外接球半径的常用方法:①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径; ③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.9.C解析:C 【分析】取11A B 的中点F ,过F 作1FG A B ⊥,垂足为G ,连EG ,可证EGF ∠为二面角11B A B E --的平面角,通过计算可得结果.【详解】取11A B 的中点F ,过F 作1FG A B ⊥,垂足为G ,连EG ,因为,E F 分别为1111,C D A B 的中点,所以11//EF A D ,在长方体1111ABCD A B C D -中,因为11A D ⊥平面11ABB A ,所以EF ⊥平面11ABB A , 因为1A B ⊂平面11ABB A ,所以1EF A B ⊥,因为1FG A B ⊥,且FGEF F =,所以1A B ⊥平面EFG ,因为EG ⊂平面EFG ,所以1A B EG ⊥,所以EGF ∠为二面角11B A B E --的平面角,因为12AB AA ==,所以14FAG π∠=,因为11A F =,所以12222FG A F ==, 在直角三角形EFG 中,2216122EG EF FG =+=+=, 所以cos FGEGF EG ∠==2326=. 所以二面角11B A B E --的余弦值为33. 故选:C 【点睛】关键点点睛:根据二面角的定义作出其中一个平面角是解题关键.10.A解析:A【分析】利用正弦定理求出ABC 的外接圆直径2r ,利用公式()2222R r SA =+可计算得出三棱锥S ABC -的外接球直径,然后利用球体的表面积公式可求得结果. 【详解】如下图所示,设圆柱的底面半径为r ,母线长为h ,圆柱的外接球半径为R ,取圆柱的轴截面,则该圆柱的轴截面矩形的对角线的中点O 到圆柱底面圆上每个点的距离都等于R ,则O 为圆柱的外接球球心,由勾股定理可得()()22222r h R +=.本题中,SA ⊥平面ABC ,设ABC 的外接圆为圆1O ,可将三棱锥S ABC -内接于圆柱12O O ,如下图所示:设ABC 的外接圆直径为2r ,2SA h ==, 由正弦定理可得24sin ABr C==∠,,该三棱锥的外接球直径为2R ,则()222225R r h =+=.因此,三棱锥S ABC -的外接球的表面积为()224220R R πππ=⨯=. 故选:A. 【点睛】方法点睛:求空间多面体的外接球半径的常用方法:①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径; ③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.11.C解析:C 【分析】将三棱锥111A AB D -、三棱锥11A BC D -分离出来单独分析,根据线段长度以及线线关系证明1A 的射影点分别是11AB D 和1BC D 的哪一种心. 【详解】三棱锥111A AB D -如下图所示:记1A 在面11AB D 上的射影点为O ,连接11,,AO B O D O ,因为11111AA A D A B ==,又1A O ⊥平面11AB D , 所以2222221111111111,,AA AO AO A D AO OD A B AO OB =+=+=+, 所以11AO OB OD ==,所以O 为11AB D 的外心;三棱锥11A BC D -如下图所示:记1A 在面1BC D 上的射影点为1O ,连接1111,,BO C O DO ,因为11//BC AD ,且四边形11ADD A 是菱形,所以11AD A D ⊥,所以11BC A D ⊥, 又因为11A O ⊥平面1BC D ,所以1111111,AO BC AO A D A ⊥=,所以1BC ⊥平面11AO D ,又因为1DO ⊂平面11AO D ,所以11DO BC ⊥, 同理可知:1111,BO DC C O DB ⊥⊥,所以1O 为1BC D 的垂心,故选:C. 【点睛】关键点点睛:解答本题的关键是通过1A 的射影点去证明线段长度的关系、线段位置的关系,借助线面垂直的定义和判定定理去分析解答问题.12.A解析:A 【分析】本题首先可根据题意将四面体ABCD 看作底面是等边三角形的直三棱柱的一部分,然后求出直三棱柱的外接球的半径,最后根据球的表面积计算公式即可得出结果. 【详解】因为AB ⊥平面BCD ,1AB BC CD BD ====,所以可将四面体ABCD 看作底面是等边三角形的直三棱柱的一部分,如图所示:则四面体ABCD 的外接球即直三棱柱的外接球,因为底面三角形BCD 的外心到三角形BCD 的顶点的长度为222131323, 所以直三棱柱的外接球的半径221372312r, 则球O 的表面积277π4π4π123S r ,故选:A. 【点睛】关键点点睛:本题考查四面体的外接球的表面积的计算,能否将四面体ABCD 看作底面是等边三角形的直三棱柱的一部分是解决本题的关键,考查直三棱柱的外接球的半径的计算,是中档题.二、填空题13.【分析】设球的半径为连接交于点取中点连接即为三棱柱外接球球心根据三棱锥体积可得间关系表示出根据基本不等式可求得的最小值从而得到球的表面积的最小值【详解】如图因为三棱柱是且设球的半径为连接交于点取中点 解析:27π【分析】设AB a ,BC b =,球的半径为r ,连接1AC ,1A C 交于点O ,取AC 中点D ,连接BD ,即O 为三棱柱外接球球心,根据三棱锥体积可得a b ,间关系,表示出r ,根据基本不等式可求得r 的最小值,从而得到球的表面积的最小值. 【详解】如图,因为三棱柱111ABC A B C -是 ,且90ABC ∠=︒,设AB a ,BC b =,球的半径为r ,连接1AC ,1A C 交于点O ,取AC 中点D ,连接BD ,则O 到三棱柱六个定点的距离相等,即O 为三棱柱外接球球心,11322OD AA ==, 又因为三棱锥O ABC -3 即1133322ab ⨯⨯=,即12ab =, 所以222222313332224a b r AD OD ab ⎛⎫⎛⎫+=+=+≥+=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 当且仅当a b =时等号成立,所以球O 的表面积最小值为2427S r ππ==, 故答案为:27π. 【点睛】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.14.【分析】先利用线面平行的性质定理和平面扩展得到异面直线所成角即BD 与所成的角再结合长方体棱长的条件在中求其余弦值即可【详解】如图设平面平面平面平面因为平面所以故异面直线与所成的角即与所成的角延长AD 解析:26 【分析】先利用线面平行的性质定理和平面扩展,得到异面直线所成角即BD 与1A B 所成的角1A BD ∠,再结合长方体棱长的条件在1A BD 中求其余弦值即可.【详解】如图,设平面11CB D ⋂平面1ABCD l '=,平面11CB D ⋂平面112ABB A l '=,因为//α平面11CB D ,所以1122//,//l l l l '',故异面直线1l 与2l 所成的角,即1l '与2l '所成的角.延长AD 至E ,使AD DE =,连接CE ,则易见BD 与CE 平行且相等,又BD 与11B D 平行且相等,故BD 与11B D 平行且相等,即四边形11D B CE 是平行四边形,CE 就是交线1l '. 同理可知1B F 就是交线2l '.又知BD //CE ,11//B F A B ,故1l '与2l '所成的角,即BD 与1A B 所成的角1A BD ∠,依题意可知,2AB BC ==,13AA =,故1A BD 中,1113,22A B A D BD ===, 故1112262cos 1313BDA BD AB ∠===. 故答案为:26. 【点睛】 方法点睛:求空间角的常用方法:(1)定义法,由异面直线所成角、线面角、二面角的定义,结合图形,作出所求空间角,再结合题中条件,解对应三角形,即可求出结果;(2)向量法:建立适当的空间直角坐标系,通过计算向量夹角(直线方向向量与直线方向向量、直线方向向量与平面法向量,平面法向量与平面法向量)余弦值,即可求出结果.15.【分析】先由题意得到的面积以及外接圆的半径记的外接圆圆心为为使四面体体积最大只需与面垂直由此求出设球心为半径为根据为直角三角形由勾股定理列出等式求出球的半径即可得出结果【详解】根据题意知是一个等边三 解析:254π【分析】先由题意,得到ABC 的面积,以及ABC 外接圆的半径,记ABC 的外接圆圆心为Q ,为使四面体ABCD 体积最大,只需DQ 与面ABC 垂直,由此求出2DQ =,设球心为O ,半径为R ,根据AQO 为直角三角形,由勾股定理列出等式,求出球的半径,即可得出结果. 【详解】根据题意知,ABC 是一个等边三角形,其面积为()22133333224S ⎛⎫=-= ⎪ ⎪⎝⎭,ABC 外接圆的半径为131260r ==,记ABC 的外接圆圆心为Q ,则1AQ r ==;由于底面积ABCS不变,高最大时体积最大,所以DQ 与面ABC 垂直时体积最大,最大值为13ABCS DQ ⋅=,2DQ ∴=, 设球心为O ,半径为R ,则在直角AQO 中,222OA AQ OQ =+,即2221(2)R R =+-,54R ∴=, 则这个球的表面积为:2525444S ππ⎛⎫== ⎪⎝⎭.故答案为:254π. 【点睛】 思路点睛:求解几何体与球外接问题时,一般需要先确定底面外接圆的圆心位置,求出底面外接圆的半径,根据球的性质,结合题中条件确定球心位置,求出球的半径,进而即可求解.16.【分析】作于于可得等于二面角的平面角从而可得然后求得而因此可得是异面直线与所成角(或补角)这样在求解可得【详解】如图作于于则连接根据二面角平面角的定义知与的夹角等于二面角的平面角所以因为所以设则在矩解析:12. 【分析】作DM AC ⊥于M ,BN AC ⊥于N ,可得,MD NB '<>等于二面角D AC B '--的平面角,从而可得DMD '∠,然后求得DD ',而//AB CD ,因此可得D CD '∠是异面直线D C '与AB 所成角(或补角).这样在DCD '求解可得.【详解】如图,作DM AC ⊥于M ,BN AC ⊥于N ,则//DM BN ,连接,D M DD '', 根据二面角平面角的定义知MD '与NB 的夹角等于二面角D AC B '--的平面角, 所以,3MD NB π'<>=,因为//DM BN ,所以23DMD π'∠=,设1BC =,则AB ==ABCD 中,AC =DM ==,3D M DM '==, 则222222666612cos 2232DD DM D M DM D M π⎛⎫⎛⎫⎛⎫'''=+-⋅=+-⨯⨯⨯-= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 所以2DD '=,因为//AB CD ,所以D CD '∠是异面直线D C '与AB 所成角(或补角).DCD '是正三角形,3D CD π'∠=,1cos 2D CD '∠=. 所以异面直线D C '与AB 所成角余弦值是12. 故答案为:12.【点睛】关键点点睛:本题考查求异面直线所成的角,解题方法根据异面直线所成角定义作出它们所成的角,然后解三角形可得,解题关键是利用图中MD '与NB 的夹角等于二面角D AC B '--的平面角,从而求得DMD '∠,只要设1BC =,可求得DD ',从而求得结论.17.【分析】由三视图还原几何体得到三棱锥P-ABC 分别计算其棱长可得答案【详解】由三视图还原几何体得到三棱锥P-ABC 可将此三棱锥放入棱长为2的正方体内如下图所示所以:BC=所以该三棱锥最长棱的长度为故解析:3【分析】由三视图还原几何体得到三棱锥P -ABC ,分别计算其棱长,可得答案.【详解】由三视图还原几何体得到三棱锥P -ABC ,可将此三棱锥放入棱长为2的正方体内,如下图所示,所以:2AB =,BC =2,22,23BP AC PC AP ====所以该三棱锥最长棱的长度为3故答案为:3【点睛】方法点睛:三视图问题的常见类型及解题策略:(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.18.【分析】先画出直观图证明平面平面然后侧棱与底面ABC 所成的角即为根据题目中的数据算出即可【详解】如图作的中点连结因为侧面PBC 和底面ABC 都是边长为2的正三角形而为的中点所以又所以平面同时平面所以平 解析:o 60.【分析】先画出直观图,证明平面PAD ⊥平面ABC ,然后侧棱PA 与底面ABC 所成的角即为PAD ∠,根据题目中的数据算出即可.【详解】如图,作BC 的中点D ,连结AD 、PD因为侧面PBC 和底面ABC 都是边长为2的正三角形而D 为BC 的中点,所以BC PD ⊥,BC AD ⊥,又PD AD D ⋂=,所以BC ⊥平面PAD ,同时BC ⊂平面ABC所以平面PAD ⊥平面ABC ,所以PAD ∠即为侧棱PA 与底面ABC 所成的角由侧面PBC 和底面ABC 都是边长为2的正三角形得AD PD ==PA =所以PAD ∆为等边三角形,则=PAD ∠o 60即侧棱PA 与底面ABC 所成的角为o 60故答案为:o 60【点睛】本题主要考查空间直线与平面所成角的计算,较简单.19.【分析】根据四面体是球的内接四面体结合位置关系可得棱锥的形状以及棱长之间的关系利用体积公式即可代值计算【详解】设该球的半径为R 则AB =2R2ACAB2R ∴ACR 由于AB 是球的直径所以△ABC 在大圆所解析:【分析】根据四面体是球的内接四面体,结合位置关系,可得棱锥的形状,以及棱长之间的关系,利用体积公式即可代值计算.【详解】设该球的半径为R ,则AB =2R ,2AC ==2R ,∴AC=,由于AB 是球的直径,所以△ABC 在大圆所在平面内且有AC ⊥BC ,在Rt △ABC 中,由勾股定理,得:BC 2=AB 2﹣AC 2=R 2,所以R t △ABC 面积S 12=⨯BC ×AC =2, 又PO ⊥平面ABC ,且PO =R ,四面体P ﹣ABC 的体积为32,∴VP ﹣ABC 13=⨯R 2⨯R 232=3=9,R 3=所以:球的体积V 43=⨯πR 343=⨯=.故答案为:.【点睛】本题考查三棱锥外接球体积的计算,属基础题;本题的重点是要根据球心的位置去推导四面体的几何形态,从而解决问题.20.【分析】欲使圆柱侧面积最大需使圆柱内接于圆锥设圆柱的高为h 底面半径为r 用r 表示h 从而求出圆柱侧面积的最大值【详解】欲使圆柱侧面积最大需使圆柱内接于圆锥;设圆柱的高为h 底面半径为r 则解得;所以;当时取解析:【分析】欲使圆柱侧面积最大,需使圆柱内接于圆锥,设圆柱的高为h ,底面半径为r ,用r 表示h ,从而求出圆柱侧面积的最大值.【详解】欲使圆柱侧面积最大,需使圆柱内接于圆锥;设圆柱的高为h ,底面半径为r , 23423h r -=,解得33h r =; 所以()23222334S rh r r r πππ⎛⎫===- ⎪ ⎪⎝⎭圆柱侧; 当2r 时,S 圆柱侧取得最大值为43π 故答案为:3π.【点睛】本题考查了求圆柱侧面积的最值,考查空间想象能力,将问题转化为函数求最值,属于中档题.三、解答题21.(Ⅰ)证明见解析;(Ⅱ)63. 【分析】(Ⅰ)连接BD 交AC 于点O ,连接1D O ,连接11B D ,可证11//O B D O ,即可得证; (Ⅱ)依题意可得1D OD ∠是二面角1D AC D --的平面角,再根据锐角三角函数计算可得;【详解】(Ⅰ)证明:连接BD 交AC 于点O ,连接1D O ,连接11B D ,由长方体的性质知11BO O D =,且11//BO O D ,故四边形11BO D O 是平行四边形,所以11//O B D O .又因为1D O ⊂平面1ACD ,1O B ⊄平面1ACD ,所以1//O B 平面1ACD .(Ⅱ)解:设122AB BC AA ===,由长方体底面ABCD 是正方形,得DO AC ⊥. 因为11D A D C =,O 是AC 的中点,所以1D O AC ⊥,所以1D OD ∠是二面角1D AC D --的平面角.在直角三角形1D DO 中,190D DO ∠=︒,易得11=D D ,221122222DO BD ==+=,()()222211523D O D C OC =-=-= 得116cos DO D OD D O ∠== 所以二面角1D AC D --6. 【点睛】作二面角的平面角可以通过垂线法进行,在一个半平面内找一点作另一个半平面的垂线,再过垂足作二面角的棱的垂线,两条垂线确定的平面和二面角的棱垂直,由此可得二面角的平面角.22.(Ⅰ)证明见解析;(Ⅱ)1.【分析】(Ⅰ)由BD AC ⊥和1A A BD ⊥,利用线面垂直的判定定理证得BD ⊥平面1A AC ,然后再由//BD EF 证明.(Ⅱ)由1D D ⊥平面ABCD ,则1D D 是三棱锥1D AEF -在平面AEF 上的高,然后利用等体积法11A D EF D AEF V V --=求解.【详解】(Ⅰ)如图所示:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.下列说法中正确的是( )A .元素周期表的七个周期永远不会改变B .元素周期表有九个横行,分为七个周期C .元素周期表有十八个纵行,分为十六个族D .元素周期表有十八个纵行,分为十八个族2.国际无机化学命名委员会将长式周期表原先的主、副族族号取消,从左往右改为18列,碱金属为第1列,稀有气体为第18列,按这个规定,下列说法不正确的是( )A .不仅有第2列元素的原子最外层有2个电子B .第14列元素形成化合物种类最多C .第3列元素种类最多D .第16、17列元素都是非金属元素3.下列各表中的数字代表的是元素的原子序数。
表中数字所对应的元素与它们在周期表中的位置相符的是( )4.甲、乙是周期表中同一主族的两种元素,若甲的原子序数为x ,则乙的原子序数不可能是( )A .x +2B .x +4C .x +34D .x +265.已知A 为ⅡA 族元素,B 为ⅢA 族元素,它们的原子序数分别为m 和n ,且A 、B 为同一周期元素。
下列关系一定错误的是( )A .n =m +1B .n =m +11C .n =m +25D .n =m +106.原子序数为x 的元素位于第ⅡA 族,则原子序数x +1的元素不可能为( ).A .第ⅢA 族B .第ⅠA 族C .镧系元素D .第ⅢB 族7.2007年3月21日,全国科学技术名词审定委员会公布111号元素(符号为Rg)的中文名称为钅仑,该元素所在周期是( )A .第七周期B .第五周期C .第六周期D .第四周期8.由长周期元素和短周期元素共同构成的族是( )①0族 ②主族 ③副族 ④第Ⅷ族A .①②B .①③C .②③D .③④9.有 a 、b 、c 、d 四种主族元素,已知a 、b 的阳离子和c 、d 的阴离子都具有相同的电子层结构,阳离子所带正电荷a<b ;阴离子所带的负电荷c >d ,则四种元素的原子序数关系是( )A .a >b >c >dB .b >a >d >cC .c >b >a >dD .b >a >c >d10. 短周期元素A 、B 、C 在元素周期表中的位置如图所示,已知B 、C 两元素原子的最外层电子数之和等于A 元素原子最外层电子数的2倍,B 、C两元素的原子序数之和是A 元素原子序数的4倍,A 、B 、C 三元素应分别为( )A .C 、Al 、PB .O 、P 、ClC .N 、Si 、SD .F 、S 、Ar11. A 、B 、C 为短周期元素,在周期表中所处的位置如图所示。
A 、C 两元素的原子核外电子数之和等于B 原子的质子数。
B 原子核内质子数和中子数相等。
(1)写出A 、B 、C 三种元素名称:__________、__________、________。
(2)B 位于周期表中第________周期第________族。
(3)写出A 的气态氢化物与B 的最高价氧化物对应水化物反应的化学方程式____________________________________________。
12.钾的金属活动性比钠强,根本原因是( )A .钾的密度比钠的小B .钾原子的电子层数比钠原子多一层C .钾与水反应比钠与水反应剧烈D .加热时,钾比钠更易气化 13.下列关于碱金属的描述正确的是( )A .碱金属都可以保存在煤油中B .碱金属元素的单质硬度小、熔点低C .在空气中加热均可生成多种氧化物D .碱金属与水反应均漂浮在水面上 14.下列关于碱金属元素的原子结构和性质的叙述不正确的是( ) A .碱金属原子最外层都只有1个电子,在化学反应中容易失去 B .碱金属单质是强还原剂C .碱金属单质都能在氧气里燃烧生成过氧化物D .碱金属单质都能与水反应生成碱15.砹(At)是原子序数最大的卤族元素,对砹及其化合物的叙述,正确的是( )A .与H 2化合的能力:At 2>I 2 B .砹在常温下为白色固体C .砹原子的最外层有7个电子D .砹易溶于水,难溶于四氯化碳 16.在盛有少量氯水的试管中加入过量的溴化钾溶液,再加入少量四氯化碳,振荡静置后可观察到的现象是( )A .溶液呈橙色不分层B .溶液分两层,上层呈橙色C .溶液分两层,下层呈橙色D .溶液呈紫色不分层17.甲、乙、丙三种溶液各含有一种X -(X -为Cl -、Br -、I -中的一种),向甲中加淀粉溶液和新制的氯水变为橙色,将此溶液倒入丙中,颜色无明显变化。
则甲、乙、丙依次含有( )A .Br -、Cl -、I -B .Br -、I -、Cl -C .I -、Br -、Cl -D .Cl -、I -、Br -18.X 、Y 是元素周期表第ⅦA 族中的两种元素,下列叙述中能说明X 的非金属性比Y 强的是( )A .X 原子的电子层数比Y 原子的电子层数多B .X 的氢化物的沸点比Y 的氢化物的沸点低C .X 的气态氢化物比Y 的气态氢化物稳定D .Y 的单质能将X 从NaX 的溶液中置换出来19.镭是元素周期表中第七周期第ⅡA 族元素,关于其叙述不正确的是( ) A .镭的金属性比钙弱 B .单质能与水反应生成氢气 C .在化合物中呈+2价 D .碳酸镭难溶于水 20.卤素单质的性质与F 2>Cl 2>Br 2>I 2的变化规律不相符的是( ) A .与氢气反应的剧烈程度 B .气态氢化物的稳定性 C .单质还原性的强弱 D .与水反应的剧烈程度 21.医生建议患甲状腺肿大的病人多食海带,由于海带含有较丰富的( ) A .碘元素 B .铁元素 C .钾元素 D .锌元素 22.向含有NaBr 和KI 的混合溶液中通入过量的Cl 2充分反应。
将溶液蒸干,并灼烧所得的物质,最后剩余的固体物质是( ) A .NaCl 和KI B .NaCl 、KCl 和I 2C .KCl 和NaBr D .KCl 和NaCl 23.据报道,某些花岗岩会产生具有放射性的氡(222 86Rn),从而对人体造成伤害,该核素核内中子数与质子数之差为( ) A .86 B .136 C .50 D .222 24.R 元素的质量数为A ,R n -的核外电子数为x ,则W g R n -所含中子的物质的量为( ) A .(A -x +n ) mol B .(A -x -n ) mol C.W A (A -x +n ) mol D.W A (A -x -n ) mol25.硼有两种天然同位素10B 和11B ,硼元素的相对原子质量为10.8,则10B与11B 的质量之比为( )A .1∶4 B .5∶22 C .10∶1 D .1∶126.2010年以来我国严格抑制了稀土资源的开发和出口,从而引起了美国等西方国家的不满和恐慌。
下列有关稀土资源14462Sm 和15062Sm 的说法正确的是( ) A. 14462Sm 和15062Sm 互为同位素B. 14462Sm 和15062Sm 的质量数相同C. 14462Sm 和15062Sm 是同一种核素 D. 14462Sm 和15062Sm 的核外电子数和中子数均为6227.11H 、21H 、31H 、H +、H 2是( )A .氢的5种同位素B .5种氢元素C .氢的5种同素异形体D .氢元素的5种不同粒子 28.下列叙述错误的是( )A .13C 和14C 属于同一种元素,它们互为同位素B .1H 和2H 是不同的核素,它们的质子数相等C .14C 和14N 的质量数相等,它们的中子数不等D .6Li 和7Li 的电子数相等,中子数也相等 1.下列微粒中,决定元素种类的是( )A .质子数B .中子数C .质量数D .核外电子数 29.决定核素种类的是( )A .质子数B .中子数C 、原子的最外层电子数D .质子数和中子数 30.下面关于多电子原子的核外电子的运动规律的叙述正确的是( )A .核外电子是分层运动的,像卫星一样有确定的轨道B .所有电子在同一区域里运动C .能量高的电子在离核近的区域运动D .能量低的电子在离核近的区域运动 31.下列叙述中不正确的是( )A .两原子,如果核外电子数相同,则一定属于同种元素B .不存在两种质子数和电子数均相同的阳离子和阴离子C .在多电子的原子里不同电子层的核外电子的能量是不相同的D .两种微粒,若核外电子数相同,则其化学性质一定相同32.在第n 电子层中,当它作为原子的最外电子层时,容纳电子数最多与(n -1)层相同,当它作为原子的次外层时,其电子数比(n +1)层最多能多容纳10个电子,则此电子层是( )A .K 层B .L 层C .M 层D .N 层33.有A 、B 两种原子,A 原子的M 层比B 原子的M 层少3个电子,B 原子的L 层电子数恰好为A 原子L 层电子数的2倍。
则A 、B 分别是( ) A .硅原子和钠原子 B .硼原子和氦原子 C .氯原子和碳原子 D .碳原子和铝原子34.有两种气态单质A m 和B n ,已知2.4 g A m 和2.1 g B n 所含的原子个数相等,而分子数之比为2∶3。
又知A 和B 的原子核内质子数都等于中子数,且A 原子L 层电子数是K 层的3倍,试推断:(1)A 、B 的元素符号分别为____________,____________; (2)A m 中的m 值为________。
35.今有甲、乙、丙、丁四种元素,已知:甲元素是地壳中含量最高的元素;乙元素是金属元素,它的原子核外K 、L 层电子数之和等于M 、N 层电子数之和;丙元素的单质及其化合物的焰色反应都显黄色,氢气在丁元素单质中燃烧火焰呈苍白色。
(1)试推断并写出甲、乙、丙、丁四种元素的名称和符号。
____________________________________________________________ (2)写出上述元素两两化合生成的化合物的化学式。
____________________________________________________________ 36.核电荷数分别是16和4的元素原子相比较,前者的下列数据是后者4倍的是( )①质子数 ②最外层电子数 ③电子层数 ④电子总数 A .①② B .①④ C .②③ D .③④37.两种元素原子的核外电子层数之比与最外层电子数之比相等,则在元素周期表的前10号元素中,满足上述关系的元素共有( ) A .1对 B .2对 C .3对 D .4对 38.根据同主族元素性质的变化规律,下列推断中错误的是( )A .砹是一种有色固体,它的气态氢化物很不稳定B .F 2与水反应比Cl 2与水反应剧烈C .铷的硫酸盐易溶解于水,则其氢氧化物一定是强碱D .氯化氢比溴化氢稳定,HClO 4酸性强于HBrO 439.2007年诺贝尔化学奖得主Gerhard Ert l 对金属Pt 表面催化CO 氧化反应的模型进行了深入研究。
