§1.6 不同参考系中的速度和加速度变换定理简介
物体的速度与加速度

物体的速度与加速度在物理学中,速度(speed)和加速度(acceleration)是描述物体运动和变化的重要概念。
本文将探讨速度和加速度之间的关系以及它们在物体运动中的应用。
一、速度(Speed)速度是描述物体在单位时间内所走过的路程。
通常用符号v来表示速度,其公式为:v = s/t,其中s是物体所走过的路程,t是物体运动所花费的时间。
速度的单位通常为m/s(米每秒)或km/h(千米每小时)。
速度可以分为两种:瞬时速度和平均速度。
瞬时速度指的是物体在某一瞬间的速度,通常用v表示。
平均速度指的是物体在一段时间内的平均速度,通常用V表示。
在物理学中,速度的概念广泛应用于解释物体的运动状态。
通过测量物体的速度,我们可以了解物体的运动方向和运动快慢。
二、加速度(Acceleration)加速度是描述物体在单位时间内速度变化的快慢。
通常用符号a来表示加速度,其公式为:a = (v2 - v1)/t,其中v1是物体的初始速度,v2是物体的末速度,t是物体速度变化所花费的时间。
加速度可以分为两种:正加速度和负加速度。
正加速度表示物体速度的增加,负加速度表示物体速度的减小。
加速度乘以时间即可得到速度的变化量。
加速度在物理学中起着重要的作用。
通过测量物体的加速度,我们可以了解物体的加速度方向和加速度的大小,从而进一步研究物体的运动规律。
三、速度与加速度的关系物体的速度和加速度之间存在一定的关系。
当物体的加速度恒定时,速度与时间呈线性关系。
即速度随时间的推移而按照一定的规律逐渐增加或减小。
此外,物体的速度与加速度的互相作用也影响着物体的运动状态。
当物体的速度与加速度方向一致时,物体的速度会逐渐增加;当物体的速度与加速度方向相反时,物体的速度会逐渐减小。
四、速度、加速度与物体运动物体的速度和加速度在研究物体的运动时起着重要的作用。
通过测量物体的速度和加速度,我们可以了解物体的运动状态、轨迹以及受力情况。
例如,在汽车行驶过程中,通过测量车辆的速度和加速度,我们可以掌握车辆的行驶速度、变速情况以及加速度对车辆的影响。
中国矿业大学(北京)《大学物理》课件 第1章 质点运动学

y 0.22 152 9.115 30 57m
r 66i 57 j
r
的大小
r的方向
r 662 (57)2 87m
arctan y arctan 57 41
x
66
(2) 速度沿坐标轴 x、y 的投影为
vx
dx dt
d dt
(0.31t 2
7.2t
28)
0.62t 7.2
物体平动时可视为质点。 物体上任一点的运动都可以代表物体的运动。
➢ 研究汽车突然刹车“前倾”或转弯 涉及转动问题,汽车各部分运动情况不同,各
车轮受力差异很大,不能把汽车作质点处理。
质点是从客观实际中抽象出的理想模型,研 究质点运动可以使问题简化而又不失客观真实性。
二、确定质点位置的方法
静止和运动是相对的 地心学说被日心说取代,让人们明白,判断物体
求 船的运动方程。
解 取坐标系
v
依题意有
l0
l(t) l0 v t
h l(t)
坐标表示为
O
x
x(t) (l0 v t)2 h2
x(t)
说明
质点运动学的基本问题之一 , 是确定质点运动 学方程。 为正确写出质点运动学方程, 先要选定参 考系、坐标系, 明确起始条件等, 找出质点坐标随时 间变化的函数关系。
x 0.31t2 7.2t 28 y 0.22t 2 9.1t 30
试求 t =15s时小田鼠的 (1)位矢;(2)速度; (3)加速度。
解 (1)根据已知条件,小田鼠的位矢可写成
r
(0.31t
2
7.2t
28)i
(0.22t 2 9.1t 30) j
t = 15s 时
高一物理加速度公式和速度,时间,位移的相关公式解析

高一物理加速度公式和速度,时间,位移的相关公式解析
物理学是一门基础性科学,也是一门极具普遍性的科学。
在高一物理中,学习者将要学习一系列有关物理学概念的知识,掌握加速度、速度、时间和位移的相关公式,并用相关的公式做简单的例题。
一、加速度公式
加速度定义为物体在单位时间内的速度变化率,即物体在某一时刻速度与下一时刻速度之比所取得的结果。
用表达式来表示,加速度可以写成:
加速度a=Δv/Δt
其中,Δv表示物体在某一时刻与下一时刻的速度差,Δt表示这两时刻的时间差;我们可以用加速度来研究物体的运动规律。
二、时间、速度、位移之间的关系
物体的运动特征可以用时间、速度和位移表示,而这三者之间就有着密不可分的联系。
具体来说,时间、速度和位移之间的关系可以用以下公式来表示:
s=vt+at^2/2
v=v_0+at
有了这三个公式,我们可以计算出物体在某一特定时间t内的速度及位移。
三、例题
1.物体按匀加速直线运动,半个周期内它的平均速度是30m/s,则其加速度是多少?
2.物体以恒定速度50m/s行驶,若用时3s,则其行驶的距离是多少?
解:
1.据加速度的定义,得到加速度a=Δv/Δt,原来的半个周期内,物体的速度变化为30m/s,时间的变化为t,即加速度a=30m/s/t;
2.据位移表达式s=vt+at2/2,得到位移
s=50m/s*3s+0*(3s)2/2=150m;
综上所述,本文介绍了高一物理中有关加速度、速度、时间和位移的相关公式,并用两个例题做了详细解释。
只要熟悉这些公式,在处理实际问题的过程中就可以发挥其作用,从而达到求解物体的运动规律的目的。
济南大学大学物理大作业完整答案

济南大学大学物理大作业答案完整版第1章 质点运动学§1.3 用直角坐标表示位移、速度和加速度一.选择题和填空题1. (B)2. (B)3. 8 m10 m4. ()[]t t A t ωβωωωββsin 2cos e 22 +--()ωπ/1221+n (n = 0, 1, 2,…) 5. h 1v /(h 1-h 2)二.计算题1解: (1) 5.0/-==∆∆t x v m/s(2) v = d x /d t = 9t - 6t 2 v (2) =-6 m/s (3) S = |x (1.5)-x (1)| + |x (2)-x (1.5)| = 2.25 m2解: =a d v /d t 4=t ,d v 4=t d t⎰⎰=vv 00d 4d tt tv=2t 2v=dx/dt=2t 2t t x txx d 2d 020⎰⎰=x 2=t 3 /3+x 0 (SI)§1.5 圆周运动的角量描述 角量与线量的关系一.选择题和填空题 1. (D) 2. (C)3. 16R t 24rad /s 24. -c(b -ct )2/R二.计算题1. 解: ct b t S +==d /d v c t a t ==d /d v ()R ct b a n /2+=根据题意: a t = a n 即 ()R ct b c /2+=解得 cbc R t -=§1.6 不同参考系中的速度和加速度变换定理简介一.选择题和填空题1. (C)2. (B)3. (A)4.0321=++v v v二.计算题1.解:选取如图所示的坐标系,以V表示质点的对地速度,其x 、y 方向投影为:u gy u V x x +=+=αcos 2v ,αsin 2gy V y y ==v当y =h 时,V的大小为: ()2cos 222222αgh u gh uy x ++=+=V V V V 的方向与x 轴夹角为γ,ugh gh xy +==--ααγcos 2sin 2tg tg 11V V第2章 牛顿定律§2.3 牛顿运动定律的应用一.选择题和填空题 1. (C) 2. (C) 3. (E)4. l/cos 2θ5. θcos /mgθθcos sin gl二.计算题1. 解:质量为M 的物块作圆周运动的向心力,由它与平台间的摩擦力f和质量为m 的物块对它的拉力F的合力提供.当M 物块有离心趋势时,f 和F 的方向相同,而当M 物块有向心运动趋势时,二者的方向相反.因M 物块相对于转台静止,故有F + f max =M r max ω2 2分 F - f max =M r min ω2 2分m 物块是静止的,因而F = m g 1分 又 f max =μs M g 1分 故2.372max =+=ωμM Mgmg r s mm 2分 4.122min=-=ωμM Mg mg r s mm 2分γ v2. 解:球A 只受法向力N 和重力g m,根据牛顿第二定律法向: R m mg N /cos 2v =-θ ① 1分 切向: t ma mg =θsin ② 1分由①式可得 )/c o s (2R g m N v +=θ 1分 根据牛顿第三定律,球对槽压力大小同上,方向沿半径向外. 1分 由②式得 θsin g a t = 1分三.理论推导与证明题 证:小球受力如图,根据牛顿第二定律tm ma F k mg d d vv ==--t mF k mg d /)(d =--v v初始条件: t = 0, v = 0.⎰⎰=-tt F)/m k mg 00d (d v -v v∴ k F mg mkt /)e1)((/---=v第3章 功和能§3.3 动能定理一.选择题和填空题 1. (B) 2. (C)3. 1.28×104 J4. 18 J 6 m/s二.计算题1. 解:用动能定理,对物体⎰⎰+==-402402d 610d 021x x x F m )(v 3分3210x x +==168解出 v =13 m/s 2分§3.4(1)势能一.选择题和填空题1.(C)2. 20kx2021kx -2021kx3. R GmM 32RG m M 3-4. 保守力的功与路径无关W = -ΔE P二.计算题1. 解:(1) 外力做的功=31 J 1分(2) 设弹力为F ′= 5.34 m/s 1分(3) 此力为保守力,因为其功的值仅与弹簧的始末态有关. 2分§3.4(2)机械能守恒定律一.选择题和填空题1. (C)2.)(mr k )2(r k -二.计算题1. (1)建立如图坐标.某一时刻桌面上全链条长为y ,则摩擦力大小为g lymf μ= 1分 摩擦力的功 ⎰⎰--==00d d a l a l f y gy lmy f W μ 2分=022a l y l mg -μ =2)(2a l lmg--μ 2分 (2)以链条为对象,应用质点的动能定理 ∑W =222121v v m m-其中 ∑W = W P +W f ,v 0 = 0 1分W P =⎰la x P d =la l mg x x l mg la 2)(d 22-=⎰ 2分al -a⎰⎰⋅+==21d )4.388.52(d 2x x xx x xF W ⎰⎰⋅=-==1212d d 21'2x x x x Wx F x F m v 3分3分由上问知 la l mg W f 2)(2--=μ所以222221)(22)(v m a l l mg l a l mg =---μ 得 []21222)()(a l a l lg ---=μv 2分 2. 解:把卸料车视为质点.设弹簧被压缩的最大长度为l ,劲度系数为k .在卸料车由最高点下滑到弹簧压缩最大这一过程中,应用功能原理有h G kl h G 12121sin 2.0-=-α ① 2分对卸料车卸料后回升过程应用功能原理,可得:22221sin 2.0kl h G h G -=-α ② 2分由式①和②联立解得: 372.030sin 2.030sin 21=-︒+︒=G G 1分第4章 冲量和动量§4.2 质点系的动量定理一.选择题和填空题 1. (D) 2. (C)3. 18 N ²s二.计算题1. 解:设在某极短的时间t ∆内落在传送带B 上矿砂的质量为m ,即m=q mt ∆,这时矿砂动量的增量为(参看附图)图1分12v v vm m m -=∆)( 1212221s m kg 98.375cos 2)(-⋅⋅∆=︒-+=∆t q m m m v v v v v 2分设传送带作用在矿砂上的力为F,根据动量定理)(v m t F ∆=∆ 于是 N 2.213.98/)(==∆∆=m q t m F v2分 方向: ︒==︒∆2975θ,sin sin )(θm m 2v v 2分由牛顿第三定律,矿砂作用在传送带B 上的(撞击)力与F大小相等方向相反,即等于2.21 N ,偏离竖直方向1︒,指向前下方. 1分§4.3 质点系动量守恒定律一.选择题和填空题 1. (C)2. 4.33 m/s ;与A 原先运动方向成 -30° 3.二.计算题1. 解:这个问题有两个物理过程:第一过程为木块M 沿光滑的固定斜面下滑,到达B 点时速度的大小为θsin gl 21=v 1分方向:沿斜面向下第二个过程:子弹与木块作完全非弹性碰撞.在斜面方向上,内力的分量远远大于外力,动量近似守恒,以斜面向上为正,则有V v v )(cos M m M m +=-1θ 3分Mm gl M m +-=θθsin cos 2v V 1分2. 解:(1) 因穿透时间极短,故可认为物体未离开平衡位置.因此,作用于子弹、物体系统上的外力均在竖直方向,故系统在水平方向动量守恒.令子弹穿出时物体的水平速度为v '有 m v 0 = m v +M v 'v ' = m (v 0 - v )/M =3.13 m/s 2分 T =Mg+M v 2/l =26.5 N 2分(2) s N 7.40⋅-=-=∆v v m m t f (设0v方向为正方向) 2分负号表示冲量方向与0v方向相反. 2分第5章 刚体力学基础 动量矩§5.2 力矩 刚体绕定轴转动微分方程量一.选择题和填空题 1. (C) 2. (B) 3.(B)4. 6.54 rad / s 24.8 s5. 62.51.67s6. 0.25 kg ²m 2二.计算题1. 解:(1) ∵ mg -T =ma 1分TR =J β 2分 a =R β 1分 ∴ β = mgR / (mR 2+J )()R M m mgMR mR mgR +=+=222122 =81.7 rad/s 2 1分 方向垂直纸面向外. 1分211m m t F +∆22211m t F m m t F ∆∆++(2) ∵βθωω2202-=当ω=0 时, rad 612.0220==βωθ物体上升的高度h = R θ = 6.12³10-2 m 2分(3)==βθω210.0 rad/s方向垂直纸面向外. 2分2. 解:(1) 0=ω 0+β tβ=-ω 0 / t =-0.50 rad ²s -2 2分 (2) M r =ml 2β / 12=-0.25 N ²m 2分 (3) θ10=ω 0t +21β t 2=75 rad 1分§5.3 绕定轴转动刚体的动能 动能定理一.选择题和填空题 1. (D) 2. (A) 3.(D)4. 6π rad/s 237 J5. 角动量gl mM 334二.计算题1.解:选泥团和杆为系统,在打击过程中,系统所受外力对O 轴的合力矩为零,对定轴O 的角动量守恒,设刚打击后两者一起摆起的角速度为ω,则有 1分ωJ lm lm +=v v 110 ① 2分其中 2/l ⋅=ωv ② 1分在泥团、杆上摆过程中,选杆、泥团、地球为系统,有机械能守恒.当杆摆到最大角度θ 时有()()222121cos 121ωθJ m l g m M +=-+v ③ 3分联立解以上三式可得()()⎥⎦⎤⎢⎣⎡++-=-gl M m m M m 4331cos 221v θ 3分2.解:(1) 将转台、砝码、人看作一个系统,过程中人作的功W 等于系统动能之增量: W =∆E k =212210222204)21(214)21(21n ml J n ml J π+-π+2 4分 这里的J 0是没有砝码时系统的转动惯量.(2) 过程中无外力矩作用,系统的动量矩守恒:2π(J 0+2121ml ) n 1 = 2π (J 0+2221ml ) n 2 ∴ ()()1222212102n n n l n l m J --= 4分(3) 将J 0代入W 式,得 ()2221212l l n mn W -π= 2分a§5.4 动量矩和动量矩守恒定律一.选择题和填空题 1. (C) 2. (B) 3.(C) 4.(D)5. 031ω6. ()212m R J m r J ++ω 7. ()l m M /3460+v二.计算题1. 解:将杆与两小球视为一刚体,水平飞来小球与刚体视为一系统.由角动量守恒得 1分ωJ l m lm +-=3223200v v (逆时针为正向) ① 2分 又 22)3(2)32(l m l m J += ② 1分将②代入①得 l230v =ω 1分2. 解:(1) 设当人以速率v 沿相对圆盘转动相反的方向走动时,圆盘对地的绕轴角速度为ω,则人对与地固联的转轴的角速度为R R v v221-=-='ωωω ① 2分 人与盘视为系统,所受对转轴合外力矩为零,系统的角动量守恒. 1分设盘的质量为M ,则人的质量为M / 10,有:ωωω'⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+22022211021211021R M MR R M MR ② 2分 将①式代入②式得:R2120v+=ωω ③ 1分(2) 欲使盘对地静止,则式③必为零.即ω0 +2v / (21R )=0 2分 得: v =-21R ω0 / 2 1分式中负号表示人的走动方向与上一问中人走动的方向相反,即与盘的初始转动方向一致.1分3. 解:(1) 角动量守恒:ω⎪⎭⎫ ⎝⎛'+='2231l m ml l m v 2分∴l m m m ⎪⎭⎫ ⎝⎛'+'=31vω=15.4 rad ²s -1 2分(2) -M r =(231ml +2l m ')β 2分0-ω 2=2βθ 2分∴ rM l m m 23122ωθ⎪⎭⎫ ⎝⎛'+==15.4 rad 2分答案 第六章 振动§6.1-1简谐振动 振幅 周期和频率 相位1-2.BB3. 1.2 s 1分; -20.9 cm/s 2分.4. 0.05 m 2分; -0.205π(或-36.9°)2分.5. )212cos(π-πT t A 2分; )312cos(π+πT t A 2分.二计算题1. 解: (1) v m = ωA ∴ω = v m / A =1.5 s -1∴ T = 2π/ω = 4.19 s 3分(2) a m = ω2A = v m ω = 4.5³10-2m/s 2 2分(3) π=21φ x = 0.02)215.1cos(π+t (SI) 3分 2. 解:(1) 1s 10/-==m k ω 1分, 63.0/2=π=ωT s 1分(2) A = 15 cm ,在 t = 0时,x 0 = 7.5 cm ,v 0 < 0 由 2020)/(ωv +=x A 得 3.12020-=--=x A ωv m/s 2分π=-=-31)/(tg 001x ωφv 或 4π/3 2分;∵ x 0 > 0 ,∴ π=31φ(3) )3110cos(10152π+⨯=-t x (SI) 2分§6.1-2简谐运动的能量1-3:DBD4. b ,f 2分; a ,e 2分.5. 9.90³102 J 3分§9-3旋转矢量1-6:BBBBCA7. π 1分; - π /2 2分; π/3. 2分.8. 10 cm 1分; (π/6) rad/s 1分; π/3 1分. 二.计算题1. 解:旋转矢量如图所示. 图3分由振动方程可得 π21=ω,π=∆31φ 1分667.0/=∆=∆ωφt s 1分2. 解:(1) 设振动方程为 )cos(φω+=t A x-由曲线可知 A = 10 cm , t = 0,φcos 1050=-=x ,0sin 100<-=φωv 解上面两式,可得 φ = 2π/3 2分由图可知质点由位移为 x 0 = -5 cm 和v 0 < 0的状态到x = 0和 v > 0的状态所需时间t = 2 s ,代入振动方程得 )3/22c o s (100π+=ω(SI) 则有2/33/22π=π+ω,∴ ω = 5 π/12 2分 故所求振动方程为:)3/212/5cos(1.0π+π=t x (SI) 1分 3. 解:依题意画出旋转矢量图3分。
物体的运动速度和加速度的关系

物体的运动速度和加速度的关系物体的运动速度是描述物体在某一时刻的位移与时间之比,而加速度则是描述物体在单位时间内速度的变化率。
在物理学中,运动速度和加速度之间存在着密切的关系,这种关系深刻地揭示了物体在运动过程中的特性和规律。
一、匀速直线运动的速度和加速度关系我们首先考虑一个简单的情况,即物体进行匀速直线运动。
在这种情况下,物体的速度保持不变,即运动速度的大小和方向都保持一致。
而根据加速度的定义,加速度为零,表示物体在单位时间内速度不发生变化。
因此,在匀速直线运动中,速度和加速度之间不存在任何关系。
二、匀变速直线运动的速度和加速度关系当物体进行匀变速直线运动时,物体的速度会随着时间的推移而发生改变。
根据牛顿第二定律,物体的加速度与所受合外力成正比,而与物体的质量成反比。
因此,在匀变速直线运动中,物体的加速度与物体的质量以及合外力之间存在一定的关系。
首先,考虑一个简单的例子,以自由下落运动为例。
当物体自由下落时,所受合外力为重力,与物体的质量成正比。
根据牛顿第二定律 F = ma,即合外力等于物体的质量乘以加速度。
因此,加速度 a = F/m,即加速度等于重力除以物体的质量。
然而,对于一般的匀变速直线运动,物体所受合外力不仅仅包括重力,还包括其他力的作用,比如摩擦力、推力等。
在这种情况下,物体的加速度由合外力的大小和方向决定。
根据牛顿第二定律,加速度等于合外力之和除以物体的质量。
三、非直线运动的速度和加速度关系上述讨论主要集中在直线运动中的速度和加速度关系,对于非直线运动,稍有不同。
在非直线运动中,速度和加速度的定义需要进行修正。
对于曲线运动而言,物体的速度是物体在某一时刻的瞬时速度的大小和方向。
而加速度则是物体在该时刻的瞬时加速度的大小和方向。
在非直线运动中,物体的速度和加速度不再保持一致的方向,因此两者之间存在一定的关系。
根据速度和加速度定义的关系,可以推导出速度和加速度之间的关系。
具体而言,速度与加速度之间的关系可以通过速度和加速度的瞬时变化率来表示。
加速度与速度关系

加速度与速度关系在物理学中,速度和加速度是两个常用的概念。
它们之间存在一定的关系,对于我们理解物体运动的规律和特性具有重要意义。
一、速度的定义和计算速度是描述物体运动快慢和方向的物理量。
它可以用公式v = Δs / Δt 来表示,其中 v 表示速度,Δs 表示位移的变化量,Δt 表示时间的变化量。
速度的单位通常使用米每秒(m/s)。
二、加速度的定义和计算加速度是指物体单位时间内速度的变化率。
如果物体的速度随时间的增加而增加,则加速度为正值;如果物体的速度随时间的增加而减小,则加速度为负值。
加速度的计算公式为a = Δv / Δt,其中 a 表示加速度,Δv 表示速度的变化量,Δt 表示时间的变化量。
加速度的单位通常使用米每秒平方(m/s^2)。
三、加速度与速度的关系加速度与速度之间存在着密切的关系。
根据速度的定义公式,我们可以将其改写为 v = s / t,其中 s 表示位移,t 表示时间。
将这个公式代入加速度的计算公式,可以得到 a = (s2 - s1) / (t2 - t1)。
进一步变换得到 a = (v2 - v1) / (t2 - t1),可见加速度与速度的差值和时间差值有关。
根据上述公式可以得出以下几个关系:1. 当加速度为正值时,速度随时间的增加而增加,即物体的运动加速。
2. 当加速度为负值时,速度随时间的增加而减小,即物体的运动减速。
3. 当加速度为零时,速度保持不变,即物体做匀速直线运动。
4. 当加速度的绝对值越大时,速度的变化越明显,物体的运动加速或减速越快。
四、应用实例1. 一辆汽车在高速公路上以恒定的加速度行驶,初始速度为20 m/s,经过 10s 后速度增加到 40 m/s。
求该车的加速度。
根据 a = (v2 - v1) / (t2 - t1) 公式,代入已知数据可得 a = (40 - 20) /10 = 2 m/s^2,所以该车的加速度为 2 m/s^2。
2. 一个自由下落的物体从静止开始,经过 5s 后速度为 50 m/s。
加速度计算与速度规律

加速度计算与速度规律在物理学中,加速度是一个重要的概念,它描述了物体在单位时间内速度的变化情况。
加速度的计算可以帮助我们更好地理解物体的运动规律,进而预测和解释各种现象。
本文将介绍加速度的计算方法,并探讨与速度规律的关系。
一、加速度的定义和计算方法加速度是物体单位时间内速度变化的量度,可以用以下公式表示:加速度(a)= (末速度(v)- 初速度(u))/ 时间(t)其中,末速度是物体在某一时间点的速度,初速度是物体在另一时间点的速度,时间是这两个时间点之间的时间间隔。
为了更好地理解加速度的计算方法,我们可以通过一个例子来说明。
假设一个小球从静止的状态开始向前滚动,经过2秒钟后,它的速度变为10米/秒。
我们可以使用上述公式来计算这个小球的加速度:加速度(a)= (10 - 0)/ 2 = 5米/秒²可以看出,这个小球的加速度是5米/秒²。
这意味着在每秒钟内,小球的速度将增加5米/秒。
二、加速度与速度规律的关系加速度与速度规律之间存在着密切的关系。
根据牛顿第二定律,物体的加速度与作用在物体上的力成正比,与物体的质量成反比。
这一定律可以用以下公式表示:力(F)= 质量(m) ×加速度(a)根据这个公式,我们可以得出以下结论:1. 当施加在物体上的力增加时,物体的加速度也会增加。
这意味着物体的速度将以更快的速度增加。
2. 当物体的质量增加时,物体的加速度减小。
这意味着物体的速度将以更慢的速度增加。
这些规律可以帮助我们理解各种物理现象。
例如,当我们用力推动一辆汽车时,汽车的加速度将增加,从而使汽车的速度增加。
相反,当我们用力拉住一辆滑板车时,滑板车的加速度将减小,从而使滑板车的速度增加的速度变慢。
三、加速度的应用加速度的计算和理解对于许多领域都具有重要意义。
以下是一些加速度应用的例子:1. 运动竞技:在田径比赛中,运动员的加速度决定了他们的速度和成绩。
通过计算加速度,教练和运动员可以确定训练和调整策略,以提高竞技表现。
加速度与速度的关系

加速度与速度的关系加速度和速度是物理学中两个非常重要的概念,它们在描述物体运动过程中起着至关重要的作用。
它们之间存在一种密切的关系,了解这种关系对于我们理解物体运动规律有着重要的意义。
一、速度的定义与计算公式速度是描述物体运动快慢和方向的物理量,它的定义是单位时间内走过的路程与所花时间的比值。
在物理学中,速度的计算公式为:速度 = 位移 / 时间其中,位移指物体从一个位置移动到另一个位置的距离,并且需要考虑位移的方向。
时间则指移动所花费的时间。
二、加速度的定义与计算公式加速度是描述物体速度变化快慢和方向的物理量,它的定义是单位时间内速度变化量与所花时间的比值。
在物理学中,加速度的计算公式为:加速度 = 速度变化量 / 时间其中,速度变化量指物体速度从一个数值变化到另一个数值的差值,并且需要考虑速度变化的方向。
时间则指速度变化所花费的时间。
三、加速度与速度的关系在物理学中,加速度与速度之间存在着一种密切的关系。
速度是加速度的积分,也就是说,如果我们已知一个物体的加速度随时间的变化规律,那么我们就可以通过对加速度关于时间的积分来求解物体的速度随时间的变化规律。
例如,当加速度为常量时,我们可以得到速度的计算公式为:速度 = 初始速度 + 加速度 ×时间这个公式告诉我们,当物体的加速度保持不变时,速度随时间的变化是线性的,与时间成正比。
四、实际应用中的加速度与速度关系加速度与速度的关系在实际应用中有着广泛的应用。
举例来说,当我们在开车行驶时,踩下油门的力量会产生一个加速度,从而使车辆的速度增加。
反之,当我们松开油门时,车辆会减速,即速度会下降。
通过控制加速度的大小和方向,我们可以使车辆的速度实现任意变化。
在物体自由落体运动中,加速度的方向是向下的,大小为9.8m/s²。
根据加速度与速度的关系,我们可以得到自由落体运动物体速度随时间的变化规律:速度 = 初始速度 + 加速度 ×时间当物体从静止状态开始自由下落时,初始速度为0,代入上述公式可得速度与时间的关系公式:速度 = 9.8 ×时间这个公式告诉我们,自由落体运动物体的速度随时间的变化是线性的,与时间成正比,且速度的增加速率为9.8m/s²。
加速度与速度的关系及计算

加速度与速度的关系及计算加速度和速度是物理学中经常使用的两个概念。
它们代表了物体在运动过程中的状态和变化,是研究物体运动的重要参数。
在本文中,将详细讨论加速度和速度之间的关系,并介绍如何计算它们。
一、加速度和速度的定义加速度(a)是物体在单位时间内速度变化的量。
通常用公式表示为:a = Δv / Δt其中,Δv代表速度的变化量,Δt代表时间的变化量。
加速度的单位是米每秒平方(m/s²)。
速度(v)则是物体在单位时间内位移变化的量。
它是位移(Δx)和时间(Δt)的比值,可以表示为:v = Δx/ Δt其中,Δx代表位移的变化量。
速度的单位是米每秒(m/s)。
二、加速度和速度的关系加速度和速度之间的关系可以通过微积分的概念来理解。
速度是位移对时间的导数,而加速度则是速度对时间的导数。
换句话说,加速度表示速度的变化率。
在匀加速直线运动中,加速度保持不变。
如果物体的初始速度为v0,加速度为a,时间为t,则物体在时间t内的速度v可以通过以下公式计算:v = v0 + at其中,v0代表初始速度。
这个公式说明了加速度对速度的影响:如果加速度为正值,速度将随时间增加;如果加速度为负值,速度将随时间减小。
三、加速度和速度的计算示例为了更好地理解加速度和速度的计算,我们来看一个具体的例子。
假设一个车辆以每秒10米的速度起步,每秒增加2米的加速度。
我们想知道在5秒钟后车辆的速度是多少。
首先,我们使用加速度和时间的公式计算出速度的变化量:Δv = a * Δt = (2 m/s²) * (5 s) = 10 m/s根据加速度和速度的关系公式,我们可以得到车辆的最终速度:v = v0 + Δv = (10 m/s) + (10 m/s) = 20 m/s所以,在5秒钟后,车辆的速度将达到20米每秒。
四、总结加速度和速度是描述物体运动状态和变化的重要物理量。
加速度代表单位时间内速度变化的量,速度代表单位时间内位移变化的量。
物体的速度与加速度的关系

物体的速度与加速度的关系物体的速度与加速度是物理学中两个基本概念,它们之间存在着密切的关系。
速度是物体在单位时间内所经过的位移,而加速度是物体在单位时间内速度变化的量。
在本文中,我们将讨论物体的速度与加速度之间的关系以及它们对物体运动的影响。
物体的速度与加速度之间的关系可以通过速度-时间图和加速度-时间图来描述。
首先,我们来看速度-时间图。
速度-时间图以时间为横轴,速度为纵轴,用于表示物体在不同时间点的速度变化情况。
若速度-时间图上的直线斜率为正,即速度随时间逐渐增大,则说明物体正以一定的加速度运动;若斜率为零,则说明物体运动匀速;若斜率为负,则说明物体在减速运动。
因此,速度-时间图能够直观地反映物体的加速度情况。
接下来,我们来看加速度-时间图。
加速度-时间图以时间为横轴,加速度为纵轴,用于表示物体在不同时间点的加速度变化情况。
若加速度-时间图上的曲线呈直线,即加速度保持不变,则说明物体的速度以恒定的加速度变化;若曲线为水平直线,即加速度为零,则说明物体是匀速运动;若曲线呈正斜率,则说明物体以逐渐加速的方式运动;若曲线呈负斜率,则说明物体是逐渐减速的情况。
加速度-时间图能够给我们提供物体加速度变化的更详细信息。
根据以上分析可知,物体的速度与加速度之间的关系可以总结如下:当物体的速度增大时,说明物体在单位时间内的位移增大,即加速度为正;当速度保持不变时,说明物体匀速运动,即加速度为零;当速度减小时,说明物体在单位时间内的位移减小,即加速度为负。
因此,物体的速度与加速度是成正比关系的。
物体的速度与加速度之间的关系对物体的运动产生着重要影响。
首先,加速度的大小决定了物体运动的快慢。
加速度越大,物体在单位时间内速度的变化越快,即物体的移动速度越快;加速度越小,则相应的速度变化较慢,物体的移动速度也较慢。
其次,加速度的正负决定了物体的运动方向。
正加速度表示物体朝着同一方向运动,负加速度则表示物体朝着相反的方向运动。
§1.6 不同参考系中的速度和加速度变换定理简介

a
v 弹对地 = v 弹对机 + v 机对地 v 弹对机 = v 弹对地 v 机对地
连线投影
v 机对地
v 弹对机
v 弹对机r = v 弹对地 v 机对地 cosθ
dt = ∫ v 弹对地 dt ∫ v 机对地 cosθ dt 1 0 0
τ
τ τ
∫v
0
τ
v 弹对地
a
θ
弹对机 r
相对于飞机,导弹在连线方向走过距离为 相对于飞机,导弹在连线方向走过距离为a
若a车对地=0,即两系作匀速直线运动,则测得同一物体的加速度相等 ,即两系作匀速直线运动,
上升, 例 升降机以加速度 1.22 m/s2 上升,有一螺母自升降机的天花 板松落, 板松落,天花板与升降机的底板相距 2.74m . 螺母自天花板落到底板所需的时间. 求 螺母自天花板落到底板所需的时间. 相对升降机,螺母作初速为0的落体运动 运动距离2.74m 的落体运动, 分析 相对升降机,螺母作初速为 的落体运动,运动距离 解 以升降机为参考系
v 车对地
解 根据速度变换关系
h
α
d
v 雨对车 = v 雨对地 + v 地对车
矢量关系如图所示
v 雨对地
v 雨对车
h α = arctan = 63.4° d
v 雨对地 v 地对车 15 = = = 9.3(m/s) cos α cos α
α
v 地对车
船逆流而上,遇一桥时,箱子掉落水中顺水漂流, 例 船逆流而上,遇一桥时,箱子掉落水中顺水漂流,半小时 后发觉,返回追赶, 公里处赶上箱子. 后发觉,返回追赶,在桥下 5 公里处赶上箱子. 求 水流速度
Hale Waihona Puke a物对对 = a物对对 + a地对机
加速度与速度的关系分析

加速度与速度的关系分析引言加速度和速度是物理学中两个重要的概念,它们在描述物体运动过程中起着关键作用。
本文将对加速度与速度的关系进行分析,并探讨它们在日常生活和科学研究中的应用。
加速度的定义和计算方法加速度是指单位时间内速度改变的量。
在物理学中,加速度的计算公式为加速度(a)等于速度(v)的变化量(Δv)除以时间(Δt),即a = Δv / Δt。
加速度的单位通常使用米/秒²。
速度的定义和计算方法速度是指物体在单位时间内移动的距离。
在物理学中,速度的计算公式为速度(v)等于物体的位移(s)除以时间(t),即v = s / t。
速度的单位通常使用米/秒。
加速度与速度的关系根据上述定义和计算方法可以得出结论:加速度是速度的变化率。
换句话说,当速度增加或减少时,物体会产生加速度。
如果速度的变化量较大,那么加速度也会相应增大。
正比例关系当速度的变化量与时间的变化量成正比时,加速度与速度之间存在着正比例关系。
例如,当一个物体动能爆发时,它的速度会迅速增加,这时加速度会变得非常大。
反比例关系当速度的变化量与时间的变化量成反比时,加速度与速度之间存在反比例关系。
例如,当一个物体逐渐减速时,速度的变化量会减小,但加速度会逐渐减小。
实际应用加速度与速度的关系在许多实际应用中起着重要作用。
运动学加速度与速度是运动学中研究物体运动的重要参数。
通过测量加速度和速度的变化,我们可以了解物体在不同时间段内的运动情况,并推断出物体所受的力和物体之间相互作用的性质。
交通工程交通工程领域也广泛应用了加速度与速度的关系。
通过研究车辆的速度和加速度,我们可以优化交通信号、改善道路设计以及预测交通拥堵等问题。
此外,还可以根据车辆的加速度和速度变化来评估驾驶员的驾驶行为。
机械工程在机械工程中,加速度与速度的关系对设计和控制机械系统非常重要。
例如,在机械振动分析中,我们可以通过测量振动物体的加速度和速度来判断系统的稳定性和性能。
加速度与速度的关系

加速度与速度的关系速度和加速度是物理学中非常重要的概念。
在运动学中,速度是描述物体在单位时间内所发生的位置改变,而加速度则是描述物体在单位时间内速度改变的量。
在这篇文章中,我们将探讨加速度和速度之间的关系,以及它们在物理学中的应用。
一、速度和加速度的定义速度是一个矢量量,它包含了物体运动的方向和大小。
速度可以通过单位时间内位移的大小来计算,公式为v=Δx/Δt,其中v表示速度,Δx表示位移的变化量,Δt表示时间的变化量。
加速度是一个矢量量,它描述了物体在单位时间内速度变化的快慢。
加速度可以通过单位时间内速度的变化量来计算,公式为a=Δv/Δt,其中a表示加速度,Δv表示速度的变化量,Δt表示时间的变化量。
从这两个定义可以看出,速度和加速度都与时间有关。
速度描述了物体在单位时间内的位置变化,而加速度描述了物体在单位时间内速度的变化。
因此,速度和加速度之间存在一种密切的关系。
二、加速度对速度的影响1. 匀速直线运动在匀速直线运动中,物体的速度保持不变,即速度的变化率为零。
而加速度的定义为速度的变化率,因此在匀速直线运动中,加速度为零。
直观上来看,加速度为零意味着物体的速度没有发生变化,即物体以一定的速度匀速直线运动。
2. 匀变速直线运动在匀变速直线运动中,物体的速度随着时间的变化而改变,即速度的变化率(即加速度)不为零。
这种情况下,加速度可以是正值也可以是负值。
当加速度为正值时,物体的速度逐渐增大;当加速度为负值时,物体的速度逐渐减小。
例如,当一个物体以匀速直线运动时,它的速度为10 m/s,加速度为0 m/s²;但当一个物体以10 m/s²的加速度匀变速直线运动时,它的速度会随着时间的增加而不断增加。
三、应用实例加速度和速度的关系在物理学中有着广泛的应用。
以下是一些常见的应用实例:1. 自由落体运动在自由落体运动中,物体受到重力的作用,沿着竖直方向以加速度g下落。
重力加速度g的大小约为9.8 m/s²。
加速度和速度的关系及牛顿第三定律

加速度和速度的关系及牛顿第三定律在物理学中,加速度和速度是两个重要概念,它们之间存在着密切的关系。
与此同时,牛顿第三定律也是贯穿整个物理学的一项基本原理。
本文将探讨加速度和速度之间的关系,并解释牛顿第三定律对物体运动的影响。
1. 速度和加速度的定义首先我们来定义速度和加速度。
速度是物体在单位时间内所移动的距离,它是矢量量值,具有大小和方向。
常用的速度单位有米每秒(m/s)和千米每小时(km/h)等。
加速度则是速度变化的速率,它描述了物体在单位时间内速度的改变量。
加速度也是矢量量值,具有大小和方向。
常用的加速度单位有米每平方秒(m/s²)。
2. 加速度与速度的关系加速度和速度之间的关系可以用以下公式表示:加速度(a)= 速度变化量(Δv)/ 时间(t)这个公式表明加速度等于速度变化量除以时间。
如果速度的变化量为正值,表示物体的速度增加;如果速度的变化量为负值,则表示物体的速度减小。
因此,加速度的正负号表征了速度的增加或减小的方向。
3. 牛顿第三定律牛顿第三定律是牛顿力学中的基本原理之一,它表明每一个力都具有相反的作用力。
具体而言,牛顿第三定律可以表述为:“对于任何一个作用在物体上的力,都会有一个与之大小相等、方向相反的反作用力作用在施力物体上”。
这个定律的实质是力的相互作用。
当一个物体施加力于另一个物体时,被施力物体同样会对施力物体施加相等大小、方向相反的力。
这个作用力对于物体的运动来说是至关重要的,它可以改变物体的速度和方向。
4. 加速度与牛顿第三定律的关系加速度和牛顿第三定律之间存在着密切的关系。
牛顿第三定律指出,当一个物体受到外力作用时,会产生一个与之大小相等、方向相反的反作用力。
根据牛顿第二定律 F = ma,其中 F 表示力,m 表示物体的质量,a 表示加速度。
可以看出,反作用力的大小取决于施加力的大小,而加速度与反作用力成正比,即加速度会受到牛顿第三定律的影响。
举例来说明,假设一个人在水中推开一个浮球,他向后施加一个往前的力。
速度与加速度的关系

速度与加速度的关系速度和加速度是物理学中两个重要的概念,它们之间存在着密切的关系。
本文将以科普的方式介绍速度和加速度的概念,以及它们之间的关系。
一、速度速度是物体在单位时间内所移动的距离。
通常用V表示速度,其数值等于位移与时间之比。
如果物体在三秒钟内移动了30米的距离,它的速度就是10米/秒。
速度的方向在物理学中也是重要的,因为它描述了物体移动的路径。
例如,一个运动员以每小时10米的速度向东奔跑,他的速度就是正向的。
二、加速度加速度是物体速度变化的快慢程度,表示单位时间内速度的变化率。
常用a表示加速度,数值等于速度变化量与时间变化量之比。
如果一个物体在2秒钟内速度从10米/秒增加到30米/秒,它的加速度就是10米/秒²。
加速度的方向也是必不可少的,它描述了速度变化的方向。
三、速度和加速度之间存在着一种简单的数学关系:加速度等于速度变化量与时间变化量的比值。
换句话说,加速度是速度随时间变化的导数。
数学上表示为a=dV/dt,其中a表示加速度,dV表示速度的变化量,dt表示时间的变化量。
如果一个物体以匀速运动,即其速度不随时间变化,那么它的加速度将为零。
因为速度不发生改变,加速度的变化率就为零。
这意味着物体保持匀速运动,其速度不会增加或减小。
如果一个物体以变速运动,即其速度随时间变化,那么它的加速度将不为零。
因为速度发生改变,加速度的变化率不为零。
这意味着物体在单位时间内速度的变化量不为零,即加速度存在。
在实际运动中,加速度可以是正值、负值或零。
当速度增加时,加速度为正值;当速度减小时,加速度为负值;当速度不变时,加速度为零。
四、加速度与速度的变化关系速度和加速度之间存在着紧密的联系。
如果一个物体加速度为正值,那么其速度将增加;如果一个物体加速度为负值,那么其速度将减小;如果一个物体加速度为零,那么其速度将保持不变。
根据加速度对速度的影响,我们可以知道当一个物体的加速度不变时,其速度将以固定的速率改变。
物理学中的加速度与速度变化关系

物理学中的加速度与速度变化关系加速度和速度是物理学中的两个关键概念,它们之间存在着密切的联系和相互作用。
本文将从多个角度探讨加速度和速度变化之间的关系,希望能给读者带来一些新的认识和启发。
首先,我们来研究一下加速度的概念。
在物理学中,加速度是指物体的速度变化率。
简单地说,就是物体单位时间内速度的改变量。
通常用符号a表示加速度,它的单位是米每秒平方(m/s²)。
加速度可以是正值,也可以是负值,正值表示速度增加,负值表示速度减小。
那么,加速度和速度之间如何相互影响呢?要理解这个问题,需要引入牛顿第二定律。
牛顿第二定律表明,物体的加速度和外力之间存在着直接的关系。
具体而言,加速度等于物体受到的合外力除以物体的质量。
这个公式可以用数学公式表示为:a = F/m其中,a代表加速度,F代表物体所受的合外力,m代表物体的质量。
这个公式说明了加速度与外力的大小和方向成正比,与物体的质量成反比。
了解了加速度与外力之间的关系,我们再来看加速度与速度变化之间的联系。
从牛顿第二定律的角度来看,速度变化率正是加速度的定义。
即,加速度等于速度的变化量除以时间的变化量。
数学上可以表示为:a = Δv/Δt其中,a代表加速度,Δv代表速度的变化量,Δt代表时间的变化量。
这个公式告诉我们,加速度与速度变化率成正比。
速度变化的时间越短,加速度就越大;速度变化的时间越长,加速度就越小。
除了上述的数学定义和关系,加速度与速度变化之间还存在着一些实际应用。
比如,在自动驾驶汽车中,加速度与速度变化之间的关系是十分重要的。
通过控制汽车的加速度,可以实现车辆在不同速度下的安全行驶和平稳变道。
掌握加速度与速度变化之间的关系,可以更好地控制汽车的行驶状态。
此外,加速度与速度变化之间的关系还可以帮助我们理解物体在做直线运动时的运动规律。
当物体的加速度为恒定值时,根据速度的定义,可以得到物体速度与时间的关系为:v = at + v0其中,v代表物体的速度,a代表物体的加速度,t代表时间,v0代表初始速度。
§1.5 圆周运动的角量§1.6 速度变换定理

总加速度
a an 0
dv at 0 dt
v an 0 R
2
大小不变,方向时刻指向圆心(改变)。 即加速度矢量变,所以是变加速运动。
6
例 一质点作半径为0.1 m 的圆周运动,已知运动学方程为
求 (1) 当t =2s 时,质点运动的 an 和 a 以及aτ的大小
2
dv aτ 16t 8.0 m/s 2 dt
v an 2.0 m/s 2 R
2
a an a 8.25 m/s 2
2 2
8
§1.6 不同参考系中的速度和加速 度变换定理简介
一. 基本概念
一个动点 P (研究对象) 二个参照系
PB
y s s'
A
·
r
P
A'
r A'
运动的合成是在一个参考系中,总能成立;
伽利略速度变换则应用于两个参考系之间,只在
u << c时才成立。
●
a绝对 a相对 a牵连
只适用于两个参考系(S'系和S系)平动的情况
14
v船岸 v船水 v水岸
v机地 v机风 v风地
15
例 一个带篷子的卡车,篷高为h=2 m ,当它停在马路边时, 雨滴可落入车内达 d=1 m ,而当它以15 km/h 的速率运动 时,雨滴恰好不能落入车中。 求 雨滴(对地)的速度矢量。
O
r
P
t : t t : dω d d d 2 k 2 k dt dt dt dt 角加速度的方向与 dω 的方向相同
当 恒矢量时,质点作匀角加速圆周运动。
不同参考系中的速度和加速度变换定理简介.
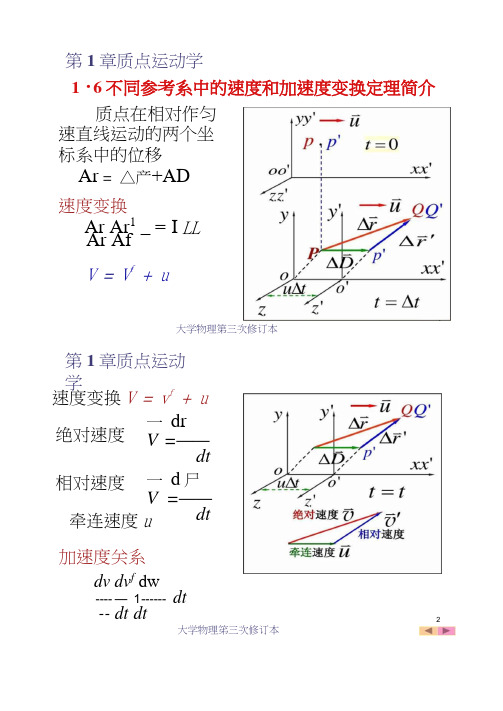
第1章质点运动学1・6不同参考系中的速度和加速度变换定理简介质点在相对作匀速直线运动的两个坐标系中的位移Ar = △产+AD速度变换Ar Ar1 _ = I LLAr AfV = V f + u大学物理第三次修订本第1章质点运动学速度变换V = v f + u绝对速度相对速度一drV=——dt 一d尸V=——dt牵连速度u加速度关系dv dv f dw---- —1 ------ dt-- dt dt2大学物理笫三次修订本4大学物理第三次修订本第1章质点运动学 例一人相对江水以4・0km/h 的速度划船前进,设 江水的流动可以认为是平动。
试问(1)当江水流速为3.5km/h 时,它要从出发处 垂直于江岸而横渡此江,应该如何掌握划行方 向? ⑵如果江宽/=2・0km,他需要多少时间才能横渡到对岸?(3)如果此人顺流划行了 2.0h,他需要多少时间 才能划回到处发出?大学物理第三次修订本第1章质点运动学解以船为研究对象,取如图坐标系,根据己知题条件° 知,牵连速度为的且大小为I 3・5km/h ,方向与水流的方—o f[a -> u X35大学物理第三次修订本相却速度的大小为|绝对速度的大小为。
⑴速度如图所示sin©二=4.0km/hq Ia 吕仝= 0.875 & = 61°|q| 4.o 即人划船时,必须使船身与江岸垂直线间的夹角为61。
,逆流划行。
6大学物理第三次修订本第1章质点运动学(2)由速度三角形,可求出船的绝对速度的大小|y a | = |y r |cos6f以此速度横渡宽为/=2・0km 的江面需要的时间为 11 1二 2,0o -1.03h 4 4.0 x cos 61 (3)顺江滑行时,船的绝对速度的大小为。
=v r +u = 7.5knVhd r经过2・0h,船在离出发点下游的15km 处。
乞=-v r +u = —0.5km/hcl I 以这样的速度匀速划行,必须再经过30h 才能划过15km 回到出发处。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r物对地
A`
r车对地
同除以 t
r物对车
B`
v 物对地 v 物对车 v 车对地
车对地 lim r物对地 r物对车 lim r车对地 lim t 0 t 0 t 0 t t t
Байду номын сангаас
a物对地 a物对车 a车对地
若a车对地=0,即两系作匀速直线运动,则测得同一物体的加速度相等
例 升降机以加速度 1.22 m/s2 上升,有一螺母自升降机的天花 板松落,天花板与升降机的底板相距 2.74m 。 求 螺母自天花板落到底板所需的时间.
分析 相对升降机,螺母作初速为0的落体运动,运动距离2.74m 解 以升降机为参考系
a物对机 a物对地 a地对机
a机对地
9.8 1.22 11.02
1 匀加速运动 h a物对机 t 2 2
2h t 0.7 11.02
h
例 一个带篷子的卡车,篷高为h=2m ,当它停在马路边时,雨 滴可落入车内达 d=1m ,而当它以15km/h 的速率运动时, 雨滴恰好不能落入车中。 求雨滴的速度矢量。
v 地对车
例 船逆流而上,遇一桥时,箱子掉落水中顺水漂流,半小时 后发觉,返回追赶,在桥下 5 公里处赶上箱子。 求 水流速度
5km
解 地面参考系
水流参考系
5km
船速恒定,并且船离开箱子、回追箱子经过路程相同。
所以,船离开箱子、回追箱子所需时间相同。 水流速度 = 5 公里/小时
例 飞机水平匀速飞行,速率为 v机对地。当飞机在导弹正上方
分析 相对车参照系,雨滴作落体运动
v 车对地
h
v 雨对车
d
解 根据速度变换关系 v 雨对车 v 雨对地 v 地对车 矢量关系如图所示
v 雨对地
h arctan 63.4 d
v 雨对地 v 地对车 15 9.3(m/s) cos α cos
且距离为a 时,导弹发射,速率恒定,为 v弹对地 。 求 导弹追上飞机的时间 解
a
v 弹对地 v 弹对机 v 机对地 v 弹对机 v 弹对地 v 机对地
连线投影
v 机对地 v 弹对机
v 弹对机r v 弹对地 v 机对地 cos
dt v 弹对地 dt v 机对地 cos dt 1 0 0
v 机对地
3
τ τ
v
0
τ
v 弹对地
a
弹对机 r
相对于飞机,导弹在连线方向走过距离为a
v
0
弹对机 r
dt a
2
以飞机为参考系
相对于地面,飞机、导弹在水平方向走过距离相同
τ
τ
v 机对地τ v 弹对地 cos dt 0 cos dt v 弹对地 0 av 弹对地 2 v 弹对地 v 2机对地
