2012初三数学二模-朝阳
2012初三朝阳二模试卷

北京市朝阳区九年级综合练习(二)英语 试 卷 2012.6听力理解(共26分)一、听对话,从下面各题所给的A 、B 、C 三幅图片中选择与对话内容相符的图片。
每段对话读两遍。
(共4分,每小题1分)A. B. C.A. B. C.A. B. C.A. B. C.二、听对话或独白,根据对话或独白内容,从下面各题所给的A、B、C三个选项中选择最佳选项。
每段对话或独白读两遍。
(共12分,每小题1分)请听一段对话,完成第5和第6小题。
5. What is Tom going to do in Australia?A. To go to university.B. To visit his brother.C. To spend his vacation.6. Who is Tom going to Australia with?A. Mike.B. Rod.C. Garry.请听一段对话,完成第7和第8小题。
7. What’s wrong with Joan?A. She can’t sleep well.B. She has a bad cold.C. She has a fever.8. What does the man advise Joan to do?A. To see a doctor.B. To have a rest.C. To work hard.请听一段对话,完成第9和第10小题。
9. When is the boy’s birthday?A. On June 3.B. On June 6.C. On June 9.10. Where will they have the birthday party?A. At home.B. At school.C. In a restaurant.请听一段对话,完成第11至第13小题。
11. What does Steven want to be when he grows up?A. A Chinese teacher.B. A hotel manager.C. An office worker.12. How does Susan like the job of being a teacher?A. It’s difficult.B. It’s exciting.C. It’s important.13. What are the two speakers mainly talking about?A. Their part-time jobs.B. Their future plans.C. Their school life.请听一段独白,完成第14至第16小题。
2012年北京市中考数学模拟试卷(二)

2012年北京市中考数学模拟试卷(二)2012年北京市中考数学模拟试卷(二)一、选择题(在下列各题的四个选项中,只有一项是符合题意的.请在答题卡中填涂符合题意的选项.本题共l0个小题,每小题3分,共30分)D..4.(3分)(2011•长沙)如图,在平面直角坐标系中,点P(﹣1,2)向右平移3个单位长度后的坐标是()6.(3分)(2011•长沙)若是关于x、y的二元一次方程ax﹣3y=1的解,则a的值为()7.(3分)(2011•长沙)如图,关于抛物线y=(x﹣1)2﹣2,下列说法错误的是()8.(3分)(2012•西藏)如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的表面上,与汉字“美“相对的面上的汉字是()9.(3分)(2011•长沙)谢老师对班上某次数学模拟考试成绩进行统计,绘制了如图所示的统计图,根据图中给出的信息,这次考试成绩达到A等级的人数占总人数的()10.(3分)(2011•长沙)如图,等腰梯形ABCD中,AD∥BC,∠B=45°,AD=2,BC=4,则梯形的面积为()二、填空题(本题共8个小题,每小题3分,共24分)11.(3分)(2013•海南)因式分解:a2﹣b2=_________.12.(3分)(2011•盘锦)反比例函数y=的图象经过点(﹣2,3),则k的值为_________.13.(3分)(2011•长沙)如图,CD是△ABC的外角∠ACE的平分线,AB∥CD,∠ACE=100°,则∠A=_________.15.(3分)(2011•长沙)在某批次的100件产品中,有3件是不合格产品,从中任意抽取一件检验,则抽到不合格产品的概率是_________.16.(3分)菱形的对角线长分别是6cm和8cm,则菱形的周长是_________.17.(3分)(2011•长沙)已知a﹣3b=3,则8﹣a+3b的值是_________.18.(3分)(2011•长沙)如图,P是⊙O的直径AB延长线上的一点,PC与⊙O相切于点C,若∠P=20°,则∠A= _________°.三、解答题(本题共2个小题,每小题6分,共12分)19.(6分)(2011•长沙)已知a=,b=2011°,c=﹣(﹣2),求a﹣b+c的值.20.(6分)(2011•长沙)解不等式2(x﹣2)≤6﹣3x,并写出它的正整数解.21.(8分)(2011•长沙)“珍惜能源从我做起,节约用电人人有责”.为了解某小区居民节约用电情况,物业公司随(2)已知去年同一天这10户居民的平均日用电量为7.8度,请你估计,这天与去年同日相比,该小区200户居民这一天共节约了多少度电?22.(8分)(2011•长沙)如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.(1)求∠B的大小;(2)已知圆心0到BD的距离为3,求AD的长.23.(9分)(2011•长沙)某工程队承包了某标段全长1755米的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲组比乙组平均每天多掘进0.6米,经过5天施工,两组共掘进了45米.(1)求甲、乙两个班组平均每天各掘进多少米?(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进0.2米,乙组平均每天能比原来多掘进0.3米.按此施工进度,能够比原来少用多少天完成任务?24.(9分)(2011•长沙)如图是一座人行天桥的引桥部分的示意图,上桥通道由两段互相平行并且与地面成37°角的楼梯AD、BE和一段水平平台DE构成.已知天桥高度BC=4.8米,引桥水平跨度AC=8米.(1)求水平平台DE的长度;(2)若与地面垂直的平台立枉MN的高度为3米,求两段楼梯AD与BE的长度之比.(参考数据:取sin37°=0.60,cos37°=0.80,tan37°=0.75.)25.(10分)(2011•长沙)使得函数值为零的自变量的值称为函数的零点.例如,对于函数y=x﹣1,令y=0,可得x=1,我们就说1是函数y=x﹣1的零点.己知函数y=x2﹣2mx﹣2(m+3)(m为常数).(1)当m=0时,求该函数的零点;(2)证明:无论m取何值,该函数总有两个零点;(3)设函数的两个零点分别为x1和x2,且,此时函数图象与x轴的交点分别为A、B(点A在点B 左侧),点M在直线y=x﹣10上,当MA+MB最小时,求直线AM的函数解析式.26.(10分)(2011•长沙)如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记Q的位置为B.(1)求点B的坐标;(2)求证:当点P在x轴上运动(P不与O重合)时,∠ABQ为定值;(3)是否存在点P,使得以A、O、Q、B为顶点的四边形是梯形?若存在,请求出P点的坐标;若不存在,请说明理由.2012年北京市中考数学模拟试卷(二)参考答案与试题解析一、选择题(在下列各题的四个选项中,只有一项是符合题意的.请在答题卡中填涂符合题意的选项.本题共l0个小题,每小题3分,共30分)D..,故本选项错误;,故本选项正确;4.(3分)(2011•长沙)如图,在平面直角坐标系中,点P(﹣1,2)向右平移3个单位长度后的坐标是()6.(3分)(2011•长沙)若是关于x、y的二元一次方程ax﹣3y=1的解,则a的值为()根据题意得,只要把代入7.(3分)(2011•长沙)如图,关于抛物线y=(x﹣1)2﹣2,下列说法错误的是()8.(3分)(2012•西藏)如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的表面上,与汉字“美“相对的面上的汉字是()9.(3分)(2011•长沙)谢老师对班上某次数学模拟考试成绩进行统计,绘制了如图所示的统计图,根据图中给出的信息,这次考试成绩达到A等级的人数占总人数的()10.(3分)(2011•长沙)如图,等腰梯形ABCD中,AD∥BC,∠B=45°,AD=2,BC=4,则梯形的面积为()∴梯形的面积为:二、填空题(本题共8个小题,每小题3分,共24分)11.(3分)(2013•海南)因式分解:a2﹣b2=(a+b)(a﹣b).12.(3分)(2011•盘锦)反比例函数y=的图象经过点(﹣2,3),则k的值为﹣6.y=3=y=13.(3分)(2011•长沙)如图,CD是△ABC的外角∠ACE的平分线,AB∥CD,∠ACE=100°,则∠A=50°.ACD=ACD=∠15.(3分)(2011•长沙)在某批次的100件产品中,有3件是不合格产品,从中任意抽取一件检验,则抽到不合格产品的概率是3%.解:从中任意抽取一件检验,则抽到不合格产品的概率是16.(3分)菱形的对角线长分别是6cm和8cm,则菱形的周长是20cm.17.(3分)(2011•长沙)已知a﹣3b=3,则8﹣a+3b的值是5.18.(3分)(2011•长沙)如图,P是⊙O的直径AB延长线上的一点,PC与⊙O相切于点C,若∠P=20°,则∠A= 35°.三、解答题(本题共2个小题,每小题6分,共12分)19.(6分)(2011•长沙)已知a=,b=2011°,c=﹣(﹣2),求a﹣b+c的值.b+c=20.(6分)(2011•长沙)解不等式2(x﹣2)≤6﹣3x,并写出它的正整数解.21.(8分)(2011•长沙)“珍惜能源从我做起,节约用电人人有责”.为了解某小区居民节约用电情况,物业公司随(2)已知去年同一天这10户居民的平均日用电量为7.8度,请你估计,这天与去年同日相比,该小区200户居民这一天共节约了多少度电?22.(8分)(2011•长沙)如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.(1)求∠B的大小;(2)已知圆心0到BD的距离为3,求AD的长.23.(9分)(2011•长沙)某工程队承包了某标段全长1755米的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲组比乙组平均每天多掘进0.6米,经过5天施工,两组共掘进了45米.(1)求甲、乙两个班组平均每天各掘进多少米?(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进0.2米,乙组平均每天能比原来多掘进0.3米.按此施工进度,能够比原来少用多少天完成任务?.24.(9分)(2011•长沙)如图是一座人行天桥的引桥部分的示意图,上桥通道由两段互相平行并且与地面成37°角的楼梯AD、BE和一段水平平台DE构成.已知天桥高度BC=4.8米,引桥水平跨度AC=8米.(1)求水平平台DE的长度;(2)若与地面垂直的平台立枉MN的高度为3米,求两段楼梯AD与BE的长度之比.(参考数据:取sin37°=0.60,cos37°=0.80,tan37°=0.75.)=6.4EF==5=25.(10分)(2011•长沙)使得函数值为零的自变量的值称为函数的零点.例如,对于函数y=x﹣1,令y=0,可得x=1,我们就说1是函数y=x﹣1的零点.己知函数y=x2﹣2mx﹣2(m+3)(m为常数).(1)当m=0时,求该函数的零点;(2)证明:无论m取何值,该函数总有两个零点;(3)设函数的两个零点分别为x1和x2,且,此时函数图象与x轴的交点分别为A、B(点A在点B 左侧),点M在直线y=x﹣10上,当MA+MB最小时,求直线AM的函数解析式.和,﹣′的解析式为的解析式为26.(10分)(2011•长沙)如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记Q的位置为B.(1)求点B的坐标;(2)求证:当点P在x轴上运动(P不与O重合)时,∠ABQ为定值;(3)是否存在点P,使得以A、O、Q、B为顶点的四边形是梯形?若存在,请求出P点的坐标;若不存在,请说明理由.(BQ=的坐标为(参与本试卷答题和审题的老师有:leikun;HLing;dbz1018;lbz;yangwy;bjf;冯延鹏;马兴田;sd2011;lk;wangjc3;zcx;王岑;蓝月梦;ZHAOJJ;nhx600;HJJ;xiawei;CJX;zjx111(排名不分先后)菁优网2014年2月27日。
朝阳中考数学二模试题及答案

北京市朝阳区九年级综合练习(二)数学试卷学校 班级 姓名一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的. 1.??的绝对值是A .?2B .12-C .12D .22.我国质检总局规定,针织内衣等直接接触皮肤的制品,每千克的衣物上甲醛含量应在千克以下.将用科学记数法表示为A .57.510´ B.57.510-´C .40.7510-´ D.67510-´ 3.如图,在△ABC 中,DE ∥BC ,如果AD =3,BD =5,那么DEBC的值是 A. 35 B. 925 C. 38D.584.从分别标有1到9数字的9张卡片中任意抽取一张,抽到所标数字是3的倍数的概率为A .19B .18C .29D .135.如图,圆锥的底面半径OA 为2,母线AB 为3,则这个圆锥的侧面积为 π B. 6π C. 12πD. 18π6.如图,下列水平放置的几何体中,主视图不是..长方形的是7. 某校篮球课外活动小组21名同学的身高如下表则该篮球课外活动小组21名同学身高的众数和中位数分别是 A .176,176 B .176,177 C .176,178 D .184,1788.图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第 3格、第4格、第5格,此时这个正方体朝上..一面的字是 A .我 B .的 C .梦 D .中二、填空题(本题共16分,每小题4分) 9.在函数y =x 的取值范围是 .10.分解因式:32242x x x -+= .11.如图,在⊙O 中,直径CD ⊥弦AB 于点E ,点F 在弧AC 上,若∠BCD =32°,则∠AFD 的度数为 .12.如图,在平面直角坐标系xOy 中,直线AB 与x 、y 轴分别交于点A 、B ,且A(-2,0),B (0,1),在直线 AB 上截取BB 1=AB ,过点B 1分别作x 、y 轴的垂线,垂足分别为点A 1 、C 1,得到矩形OA 1B 1C 1;在直线AB 上截取B 1B 2= BB 1,过点B 2分别作x 、y 轴的垂线,垂足分别为点A 2 、C 2,得到矩形OA 2B 2C 2;在直线 AB 上截取B 2B 3= B 1B 2,过点B 3分别作x 、y 轴的垂线,垂足分别为点A 3 、C 3,得到矩形OA 3B 3C 3;……则第3个矩形OA 3B 3C 3的面积是 ;第n 个矩形OA n B n C n 的面积是 (用含n 的式子表示,n 是正整数).三、解答题(本题共30分,每小题5分)13.计算:)214452-⎛⎫︒ ⎪⎝⎭.14.计算:2312()111x x x -÷-+- .15.如图,为了测量楼AB 的高度,小明在点C 处测得楼AB 的顶端A 的仰角为30o ,又向前走了20米后到达点D ,点B 、D 、C 在同一条直线上,并在点D 测得楼AB 的顶端A 的仰角为60o ,求楼AB 的高.16.已知:如图,E 、F 为BC 上的点,BF=CE ,点A 、D 分别在BC 的两侧,且AE ∥DF ,AE =DF .求证:AB ∥CD .17.如图,在平面直角坐标系xOy 中,一次函数y kx =-2的图象与x 、y 轴分别交于点A 、B ,与反比例函数32y x =-(x <0)的图象交于点3()2M n -,. (1)求A 、B 两点的坐标;(2)设点P 是一次函数y kx =-2图象上的一点,且满足△APO 的面积是△ABO 的面积的2倍,直接写出点P 的坐标.18.某新建小区要铺设一条全长为2200米的污水排放管道,为了尽量减少施工对周边居民所造成的影响,实际施工时,每天铺设的管道比原计划增加10%,结果提前5天完成这一任务,原计划每天铺设多少米管道?B四、解答题(本题共20分,每小题5分)19.如图,在平行四边形ABCD 中,AD = 4,∠B =105o ,E 是BC 边的中点,∠BAE =30o ,将△ABE 沿AE 翻折,点B 落在点F 处,连接FC ,求四边形ABCF 的周长.20.如图,在△ABC 中,AC=BC ,D 是BC 上的一点,且满足∠BAD =12∠C ,以AD 为直径的⊙O 与AB 、AC 分别相交于点E 、F . (1)求证:直线BC 是⊙O 的切线; (2)连接EF ,若tan ∠AEF =43,AD =4,求BD 的长.21.今年“五一”假期,小翔参加了学校团委组织的一项社会调查活动,了解他所在小区家庭的教育支出情况.调查中,小翔从他所在小区的500户家庭中,随机调查了40个家庭,并将调查结果制成了部分统计图表.(注:每组数据含最小值,不含最大值)根据以上提供的信息,解答下列问题: (1)频数分布表中的a = ,b = ; (2)补全频数分布直方图;(3)请你估计该小区家庭中,教育支出不足1500元的家庭大约有多少户?B (元)教育支出频数分布表 教育支出频数分布直方图22.阅读下列材料:小华遇到这样一个问题,如图1, △ABC 中,∠ACB =30o ,BC =6,AC =5,在△ABC 内部有一点P ,连接P A 、PB 、PC ,求P A +PB +PC 的最小值.小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折、旋转、平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC 绕点C 顺时针旋转60o ,得到△EDC ,连接PD 、BE ,则BE 的长即为所求.(1)请你写出图2中,P A +PB +PC 的最小值为 ; (2)参考小华的思考问题的方法,解决下列问题:①如图3,菱形ABCD 中,∠ABC =60o ,在菱形ABCD 内部有一点P ,请在图3中画出并指明长度等于P A +PB +PC 最小值的线段(保留画图痕迹,画出一条即可);②若①中菱形ABCD 的边长为4,请直接写出当P A +PB +PC 值最小时PB 的长.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知关于x 的一元二次方程x 2?(4?m )x ?1?m = 0.(1)求证:无论m 取何值,此方程总有两个不相等的实数根;(2)此方程有一个根是?3,在平面直角坐标系xOy 中,将抛物线y ?x 2?(4?m )x ?1?m向右平移3个单位,得到一个新的抛物线,当直线y ?x ?b 与这个新抛物线有且只有一个公共点时,求b 的值.24.如图,在平面直角坐标系xOy 中,抛物线y ? ax 2?bx ?4与x 轴交于点A (?2,0)、B (6,0),与y 轴交于点C ,直线CD ∥x 轴,且与抛物线交于点D ,P 是抛物线上一动 点.B图2B图3C B 图1(1)求抛物线的解析式; (2)过点P 作PQ ⊥CD 于点Q ,将△CPQ 绕点C 顺时针旋转,旋转角为α(0o ﹤α﹤90o ),当cos α=35,且旋转后点P 的对应点'P 恰好落在x 轴上时,求点P 的坐标.25. 在□ABCD 中,E 是AD 上一点,AE =AB ,过点E 作直线EF ,在EF 上取一点G ,使得∠EGB =∠EAB ,连接AG .(1)如图1,当EF 与AB 相交时,若∠EAB =60°,求证:EG =AG +BG ; (2)如图2,当EF 与AB 相交时,若∠EAB = α(0o ﹤α﹤90o ),请你直接写出线段EG 、AG 、BG 之间的数量关系(用含α的式子表示);(3)如图3,当EF 与CD 相交时,且∠EAB =90°,请你写出线段EG 、AG 、BG 之间的数量关系,并证明你的结论.北京市朝阳区九年级综合练习(二)数学试卷参考答案一、选择题(本题共32分,每小题4分) 二、填空题(本题共16分,每小题4分) 9. x ≥23 10. 22(1)x x - 11. 32° ,2n 2+2n图3图2 F 图1 F三、解答题(本题共30分,每小题5分)13.解:)214452-⎛⎫︒ ⎪⎝⎭4312=-+-……………………………………………………4分 1=. ………………………………………………………………………5分 14. 解:2312111x x x 骣÷ç-?÷ç÷ç桫-+- ()()3(1)11(1)1(1)x x x x x x ⎡⎤++=-⎢⎥+-+-⎣⎦221x ¸-………………………………2分 ()()2242111x x x x +=÷+--…………………………………………………………………3分()()()()1124112x x x x x +-+=⋅+-…………………………………………………………4分 2x =+.……………………………………………………………………………………5分15. 解: 由题意可知∠ACB =30°,∠ADB =60°,CD =20,在Rt △ABC 中,()tan 30=20AB BC BD =⋅︒+.………………………………1分 在Rt △ABD中,tan 60=AB BD BD =⋅︒………………………………………2分∴()20BD BD +…………………………………………………………3分 ∴10BD =.…………………………………………………………………………4分∴AB =.……………… ……………………………………………………5分16. 证明:∵AE ∥DF ,∴∠AEB =∠DFC . ………………………………………………………………1分 ∵BF =CE ,∴BF +EF =CE +EF .即BE =CF . ………………………………………………………………………2分 在△ABE 和△DCF 中,AE DF AEB DFC BE CFì=ïïï??íïï=ïïî∴△ABE ≌△DCF . … ……………………………………………………………3分 ∴∠B =∠C . ………………………………………………………………………4分 ∴AB ∥CD . … ……………………………………………………………………5分17. 解:(1)∵点3()2M n -,在反比例函数32y x=-(x <0)的图象上, ∴1n =.…………………………………………………………………………1分∴3()2M -,1.∵一次函数y kx =-2的图象经过点3()2M -,1, ∴3122k =--. ∴2k =-.∴一次函数的解析式为22y x =--.∴A (?1,0),B (0,?2) . ………………………………………………………3分 (2)P 1(?3,4),P 2(1,?4) . ………………………………………………………5分18. 解:设原计划每天铺设x 米管道.…………………………………………………1分由题意,得220022005(110%)x x=++ ……………………………………………3分解得 40x =. ……………………………………………………………4分经检验40x =是原方程的根. …………………………………………………5分答:原计划每天铺设40米管道.四、解答题(本题共20分,每小题5分) 19.解:作BG ⊥AE ,垂足为点G , ∴∠BGA =∠BGE =90o.在平行四边形ABCD 中,AD = 4, ∵E 是BC 边的中点,∴11 2.22BE EC BC AD ====……………………………………………………1分 ∵∠BAE =30o ,∠ABC =105o , ∴∠BEG =45o.由已知得△ABE ≌△AFE .∴AB =AF ,BE =FE ,∠BEF =90o.在Rt △BGE 中,BG =GE……… ………………………………………………………………2分 在Rt △ABG 中,∴AB =AF=………………………………………………………………………3分 在Rt △ECF 中,FC = ………………………………………………… ……4分 ∴四边形ABCF的周长4+……………………………………………………5分20. (1)证明:在△ABC 中,∵AC=BC ,∴∠ CAB = ∠B .∵∠ CAB +∠B +∠C =180o , ∴2∠B +∠C =180o. ∴12BC ??=90o. ……………………………………………………1分∵∠BAD =12∠C , ∴B BAD ??=90o.∴∠ADB =90o. ∴AD ⊥BC.∵AD 为⊙O 直径的,∴直线BC 是⊙O 的切线. …………………………………………………2分(2)解:如图,连接DF ,∵AD 是⊙O 的直径,∴∠AFD = 90o. ……………………………………………………………………3分 ∵∠ADC =90o ,∴∠ADF +∠FDC =∠CD +∠FDC =90o.∴∠ADF =∠C . …………………………………………………………………4分∵∠ADF =∠AEF ,tan ∠AEF =43, ∴tan ∠C =tan ∠ADF =43. 在Rt △ACD 中,设AD =4x ,则CD =3x .∴5.AC x ==∴BC =5x ,BD =2x .∵AD =4,∴x =1.∴BD =2. …………………………………………………………………………5分21.解:(1)a =3,b =; ……………………………………………………………2分 (2)…………………………3分B(3)500(0.050.15)100⨯+=.所以该小区家庭中,教育支出不足1500元的家庭大约有100户.…………5分21.解:(11分(2)①如图,…………………………………………2分BD;……………………………………………………………………………3分(3. …………………………………………………………………………5分五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23. (1)证明:∵△=()()2441m m---.………………………………………………1分=2412m m-+=()228m-+…………………………………………………………2分∴△>0.…………………………………………………………………3分∴无论m取何值,方程总有两个不相等的实数根.(2)把x=-3代入原方程,解得m=1.…………………………………………………4分∴23y x x=+.即23924y x⎛⎫=+-⎪⎝⎭.依题意,可知新的抛物线的解析式为239'24y x⎛⎫=--⎪⎝⎭. ………………………5分即2'3y x x=+∵抛物线'y与直线y x b=+只有一个公共点,∴23x x x b-=+..…………………………………………………………………6分即240x x b--=.∵△=0.∴()()2440b--⨯-=.解得b= -4. ……………………………………………………………………7分24. 解:(1)根据题意得424036640a ba b-+=⎧⎨++=⎩,.…………………………………………………………1分解得1343ab⎧=-⎪⎪⎨⎪=⎪⎩,.B所以抛物线的解析式为214433y x x =-++.………………………………2分(2)如图1,过点Q 的对应点'Q 作EF ⊥CD 于点E ,交x 轴于点F .设P (x ,y ),则CQ = x ,PQ =4- y .由题意可知'CQ = CQ = x ,''P Q =PQ =4- y ,∠CQP =∠C ''Q P =90°. ∴'''''QCQ CQ E P Q F CQ E ∠+∠=∠+∠=90°.∴'''P Q F QCQ α∠=∠=.……………………………………………………3分 又∵cos α=35, ∴4'5EQ x = ,3'(4)5FQ y =-. ∴43(4)455x y +-=. ∵214433y x x =-++,整理可得2145x =.∴1x =2x =-.∴P .………………………………………………………………5分如图2,过点Q 的对应点'Q 作EF ⊥CD 于点E ,交x 轴于点F . 设P (x ,y ),则CQ =- x ,PQ =4- y .可得'''P Q F QCQ α∠=∠=.……………………………………………………6分又∵cos α=35,∴4'5EQ x =- ,3'(4)5FQ y =-.∴434(4)55x y -+=-.∵214433y x x =-++, 整理可得2145x =.∴1x =,2x =-∴(P -.……………………………………………………………7分∴P或(P -.25. 解:(1)证明:如图,作∠GAH =∠EAB 交GE 于点H .∴∠GAB =∠HAE . ………………………………………………………………1分∵∠EAB =∠EGB ,∠APE =∠BPG ,∴∠ABG =∠AEH .∵又AB =AE ,∴△ABG ≌△AEH . ………………2分 ∴BG =EH ,AG =AH .∵∠GAH =∠EAB =60°, ∴△AGH 是等边三角形. ∴AG =HG .∴EG =AG +BG . …………………………………………………………………3分(2) 2sin.2EG AG BG α=+…………………………………………………………5分(3).EG BG =-……………………………………………………………6分如图,作∠GAH =∠EAB 交GE 于点H .∴∠GAB =∠HAE . ∵∠EGB =∠EAB =90°,∴∠ABG +∠AEG =∠AEG +∠AEH =180°.∴∠ABG =∠AEH .∵又AB =AE ,∴△ABG ≌△AEH . ………………7分∴BG =EH ,AG =AH .∵∠GAH =∠EAB =90°, ∴△AGH 是等腰直角三角形.=HG .∴.EG BG -…………………………………………………………8分说明:各解答题其它正确解法请参照给分.F。
辽宁省朝阳市2012中考数学(word版含答案)

辽宁省朝阳市2012年初中毕业升学考试数学试卷一、选择题(每小题3分,共24分.只有一个选项是正确的)1.下列实数中是无理数的是( )A . 3B . 9C. 3.14 D . 31 2.不等式组⎪⎩⎪⎨⎧≥-+020132x x 的整数解是( )A.1,2B.0,1,2C. -1,1,2D.-1,0,1,23.下面图中能够判断∠1>∠2的是( )4.主视图、左视图、俯视图分别是下列三个图形的物体是()5.甲、乙两人5次射击命中的环数如下:甲:7 9 8 7 9 乙:7 8 9 8 8计算得甲、乙两人5次射击命中环数的平均数都是8环,甲命中环数的方差为0.8,由此可知( )A. 甲比乙的成绩稳定B. 乙比甲的成绩稳定C. 甲、乙两人成绩一样稳定D.无法确定谁的成绩更稳定6.如图,点P(2,1)是反比例函数xk y = 的图像上一点,则当y <1时,自变量x 的取值范围是( )A. x <2B. x >2C. x <2且x ≠ 0D. x >2或x <02121B C 左视图 俯视图 A B C D7.用配方法解一元二次方程0242=+-x x 时,可配方得( )A. ()622=-xB. ()622=+xC. ()222=-xD. ()222=+x 8.如图,沿Rt △ABC 的中位线DE 剪切一刀后,用得到的△ADE 和四边形DBCE 拼图,下列图形:①平行四边形;②菱形;③矩形;④等腰梯形.一定能拼出的是( )A. 只有 ①②B.只有③④C. 只有①③④D. ①②③④二、填空题(每小题3分,共24分)9.2011年3.15消费者权益日主题:消费与民生.某市2010年人均消费4760元,这个数据是衡量你的月薪和消费是否平衡的最权威凭证,数据4760元用科学记数法(结果保留两个有效数字)表示为 元.10.计算()()3223ab b a ⋅-= .11.如图,已知∠1=∠2=∠3=65°,则∠4的度数为 .12.如图,在方格纸上建立的平面直角坐标系中,Rt △ABC 关于y 轴对称的图形为Rt △DEF ,则点A 的对应点D 的坐标是 .13.如图,身高是1.6m 的某同学直立于旗杆影子的顶端处,测得同一时刻该同学和旗杆的影子的长分别为1.2m 和9m ,则旗杆的高度为 m.14.一个扇形的圆心角是120°,面积为3π㎝2,那么这个扇形的弧长为 cm.15.观察下列图形:它们是用●按一定规律排列的依次规律,第10个图形中共有 个●.E D C B A 4321第6题图 第8题图 第11题图 第1个图形 第2个图形 第3个图形 第4个图形 第15题图16.亮亮骑自行车到距家9千米的体育场看一场球赛,开始以正常速度匀速行驶,途中自行车处故障,他只好停下来修车,车修好后,他加速继续匀速赶往体育馆,其速度为原正常速度的34倍,结果正好按预计时间(如果自行车不出故障,与正常速度匀速行驶到达体育馆的时间)到达,亮亮行驶的路程s (千米)与时间t (分)之间的函数关系如图所示,那么他修车占用的时间为 分.三、解答题(本大题共10小题,满分102分;解答应写出必要的演算步骤、文字说明或证明过程)17.(本小题满分6分) 计算:()3254120---⨯+π18.(本小题满分6分) 先化简,再求值:11112-÷⎪⎭⎫ ⎝⎛+-x x x ,其中,x =23-19.(本小题满分10分)某校九(2)班40同学为“希望工程”捐款,共捐款400元,捐款情况如下表:表格中捐款第16题图某中学对本校学生每天完成作业所用时间的情况进行抽样调查,随机调查了九年级部分学生每天完成作业所用的时间,并把统计结果制作成如图所示的频数分布直方图(时间取整数,图中从左至右一次为第一、二、三、四、五组)和扇形统计图.请结合图中信息解答下列问题.(1)本次调查的学生人数为 人;(2)补全频数分布直方图:(3)根据图形提供的信息判断,下列结论正确的是 (只填所有正确结论的代号);A.由图①知,学生完成作业所用时间的中位数在第三组内B.由图(1)知,学生完成作业所用时间的众数在第三组内C. 图(2)中,90~120数据组所在扇形的圆心角为108°D.图(1)中,落在第五组内数据的频率为0.15(4)学生每天完成作业时间不超过120分钟,视为课业负担适中,根据以上调查,估计该校九年级560名学生中,课业负担适中的学生约有多少人?21.(本小题满分10分)有两个布袋,甲袋中装有两个完全相同的球,分别标有数字“1”“2”;乙袋中装有三个完全相同的球,分别标有数字“1”“2”“3”.小颖和小明共同设计了一个游戏:小颖每次从甲袋中随机摸出一个球,小明就从乙袋中随机摸出一个球.如果小颖所摸球上的数字与小明所摸球上的数字之和为偶数,则小颖获胜;如果和为奇数,则小明获胜.你认为这个游戏公平吗?请用概率知识说明理由./分90~120150~18015%30~60 10%60~90 20%120~150第20题图(1) (2)(注:每组内数据不含最小值,含最大值)如图(3)是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台的高度.(1) 如图(1)是一个基本图形,已知AB=1米,当∠ABC 为30°时,求AC 的长及此时整个装修平台的高度(装修平台的基角高度忽略不计);(2) 当∠ABC 从30°变为90°(如图(2)是一个基本图形变化后的图形)时,求整个装修平台升高了多少米?【结果精确到0.1米,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,2≈1.41】23.(本小题满分10分)如图,AB 为⊙O 的直径,D 为弦BC 的中心,连接OD 并延长交过点C 的切线于点P,连接AC.求证:△CPD ∽△ABC.DC B AD C B A P B A 第22题图(1) (2) (3) 第23题图24.(本小题满分12分)如图(1),在△ABC 中,∠ACB=90°,AC=BC=2,点D 在AC 上,点E 在BC 上,且CD=CE,连接DE.(1)线段BE 与AD 数量关系是 ,位置关系是 .(2)如图(2),当△CDE 绕点C 顺时针旋转一定角度α后,(1)中的结论是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.(3)绕点C 继续顺时针旋转△CDE ,当90°<α<180°时,延长DC 交AB 于点F ,请在图(3)中补全图形,并求出当AF=1+33时,旋转角α的度数.25.(本小题满分12分)为迎接2011年中国国际旅游节,某宾馆将总面积为6000平方米的房屋改造成普通客房(每间26平方米)和高级客房(每间36平方米)共100间及其他功能用房若干间,要求客房面积不低于总面积的50%,又不超过总面积的60%.(1)求最多能改造成普通客房多少间.(2)在(1)的情况下,旅游节期间,普通客房以每间每天100元的价格全部租出,高级客房每天租出的间数y (间)与其价格x (元/间)之间的关系如图所示.试问:该宾馆一天最高客房收入能达到12000元吗?若能,求出此时高级客房的价格;若不能,请说明理由.D E C B A αD EB AC BA/间)第24题图(1) (2)(3) 第25题图26.(本小题满分14分)平面直角坐标系中,对称轴平行于y 轴的抛物线经过原点O ,其顶点坐标为(3,29 );Rt △ABC 的直角边BC 在x 轴上,直角顶点C 的坐标为(21,0),且BC=5,AC=3(如图(1)). (1)求出该抛物线的解析式;(2)将Rt △ABC 沿x 轴向右平移,当点A 落在(1)中所求抛物线上时,Rt △ABC 停止移动,D(0,4)为y 轴上一点,设点B 的横坐标为m ,△DAB 的面积为S.① 分别求出点B 位于原点左侧、右侧(含原点O )时,S 与m 之间的函数关系式,并写出相应自变量m 的取值范围(可在图(1)、图(2)中画出探求);② 当点B 位于原点左侧时,是否存在实数m ,使得△DAB 为直角三角形?若存在,直接写出m 的值;若不存在,请说明理由.答案:1. A ;2.D ;3.B ;4.A ;5.B ;6.D ;7.C ;8.C ;9.4.8×103;10. 753b a -;11.115°;12.(2,1);13.12;14.2π;15.30;16.5;17.2;18. x -1,25-;19.10元的有19人,15元的有6人; 20.(1)60,(2)略,(3)A 、C 、D ,(4)336;21.小颖获胜的概率为21,不明获胜的概率为21,公平; 22.(1)3.1米,(2)5.4米;23.略24.(1)BE=AD ,BE ⊥AD ,(2)仍成立,(3)α=105°;25.(1)最多60间,(2)不能达到12000元;26.(1)x x y 3212-=,(2)①当点B 在原点左侧时,()05.41023 m m s ≤-+= 当点B 位于原点右侧时,()2-1501023m m s ≤+=②-1,-4,-4.4。
2012年北京各区县初三数学二模(共六套)

海淀区九年级第二学期期末练习数 学 2012. 6一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1. -5的倒数是A .15B .15- C .5- D .52. 2012年4月22日是第43个世界地球日,中国国土资源报社联合腾讯网发起“世界地球 日”微话题,共有18 891 511人次参与了这次活动,将18 891 511用科学记数法表示(保 留三个有效数字)约为 A. 18.9⨯106 B. 0.189⨯108 C. 1.89⨯107 D. 18.8⨯1063. 把2x 2 − 4x + 2分解因式,结果正确的是A .2(x − 1)2B .2x (x − 2)C .2(x 2 − 2x + 1)D .(2x −2)24. 右图是由七个相同的小正方体堆砌而成的几何体, 则这个几何体的俯视图是A BCD 5.从1, -2, 3这三个数中,随机抽取两个数相乘,积为正数的概率是A .0B .13C .23D .16. 如图,在△ABC 中,∠C =90°,BC =3,D ,E 分别在 AB 、AC 上,将△ADE 沿DE 翻折后,点A 落在点A ′处,若A ′为CE 的中点,则折痕DE 的长为 A. 21B. 3C. 2D. 1A'ED ABCC. 中位数是51.5D. 众数是588.如图,在梯形ABCD 中,AD //BC ,∠ABC =60°,AB = DC =2, AD =1, R 、P 分别是BC 、CD 边上的动点(点R 、B 不重合, 点P 、C 不重合),E 、F 分别是AP 、RP 的中点,设BR=x ,EF=y ,则下列 图象中,能表示y 与x 的函数关系的图象大致是A B C D二、填空题(本题共16分,每小题4分)9. 若二次根式23-x 有意义,则 x 的取值范围是 .10.若一个多边形的内角和等于540︒,则这个多边形的边数是 .11. 如图,在平面直角坐标系xOy 中,已知点A 、B 、C 在双 曲线xy 6=上,BD ⊥x 轴于D , CE ⊥ y 轴于E ,点F 在x 轴上, 且AO =AF , 则图中阴影部分的面积之和为 .12.小东玩一种“挪珠子”游戏,根据挪动珠子的难度不同而得分不同,规定每次挪动珠子的颗数与所得分数的对应关系如下表所示:按表中规律,当所得分数为71分时,则挪动的珠子数为 颗; 当挪动n 颗 珠子时(n 为大于1的整数), 所得分数为 (用含n 的代数式表示).FE R P B C D A班级三、解答题(本题共30分,每小题5分) 1311|5|()3tan604---+︒.14.解方程:6123x x x +=-+.15. 如图,AC //EG , BC //EF , 直线GE 分别交BC 、BA 于P 、D ,且AC=GE , BC=FE . 求证:∠A =∠G .16.已知2220a a --=,求代数式221111121a a a a a --÷--++的值.17. 如图,一次函数的图象与x 轴、y 轴分别交于点A (-2, 0)、B (0, 2). (1)求一次函数的解析式;(2)若点C 在x 轴上,且OC =23, 请直接写出∠ABC 的度数.18. 如图,在四边形ABCD 中,∠ADB =∠CBD =90︒,BE//CD 交AD 于E , 且EA=EB .若AB=54,DB =4, 求四边形ABCD 的面积.GF E D CA P EDCA四、解答题(本题共20分,第19题、第20题各5分,第21题6分,第22题4分) 19. 某街道办事处需印制主题为“做文明有礼的北京人,垃圾减量垃圾分类从我做起”的宣传单. 街道办事处附近的甲、乙两家图文社印制此种宣传单的收费标准如下: 甲图文社收费s (元)与印制数t (张)的函数关系如下表:乙图文社的收费方式为:印制2 000张以内(含2 000张),按每张0.13元收费;超过 2 000张,均按每张0.09元收费.(1)根据表中给出的对应规律,写出甲图文社收费s (元)与印制数t (张)的函数关系式; (2)由于马上要用宣传单,街道办事处同时在甲、乙两家图文社共印制了1 500张宣传单,印制费共179元,问街道办事处在甲、乙两家图文社各印制了多少张宣传单?(3)若在下周的宣传活动中,街道办事处还需要加印5 000张宣传单,在甲、乙两家图文社中选择 图文社更省钱.20.如图,AC 、BC 是⊙O 的弦, BC //AO , AO 的延长线与过点C 的射线交于点D , 且∠D =90︒-2∠A .(1)求证:直线CD 是⊙O 的切线; (2)若BC=4,1tan 2D =,求CD 和AD 的长.21. 李老师为了了解所教班级学生完成数学课前预习的具体情况,对本班部分学生进行了 为期半个月的跟踪调查,他将调查结果分为四类,A :很好;B :较好;C :一般;D : 较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:(1)李老师一共调查了多少名同学?(2)C 类女生有 名,D 类男生有 名,将上面条形统计图补充完整; (3)为了共同进步,李老师想从被调查的A 类和D 类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位 男同学和一位女同学的概率.类别50%25%15%D C B A22.阅读下面材料:小明遇到这样一个问题:我们定义: 如果一个图形绕着某定点旋转一定的角度α (0︒ <α <360︒) 后所得的图形与原图形重合,则称此图形是旋转对称图形. 如等边三角形就是一个旋转角为120︒的旋转对称图形. 如图1,点O 是等边三角形△ABC 的中心, D 、E 、F 分别为AB 、BC 、 CA 的中点, 请你将△ABC 分割并拼补成一个与△ABC 面积相等的新的旋转对称图形.图1小明利用旋转解决了这个问题,图2中阴影部分所示的图形即是与△ABC 面积相等的新的旋转对称图形.请你参考小明同学解决问题的方法,利用图形变换解决下列问题:如图3,在等边△ABC 中, E 1、E 2、E 3分别为AB 、 BC 、CA 的中点,P 1、P 2, M 1、M 2, N 1、N 2分别为 AB 、BC 、CA 的三等分点. (1)在图3中画出一个和△ABC 面积相等的新的旋转 对称图形,并用阴影表示(保留画图痕迹); (2)若△ABC 的面积为a ,则图3中△FGH 的面积为 .五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知抛物线 2(1)(2)1y m x m x =-+--与x 轴交于A 、B 两点. (1)求m 的取值范围;(2)若m >1, 且点A 在点B 的左侧,OA : OB =1 : 3, 试确定抛物线的解析式;(3)设(2)中抛物线与y 轴的交点为C ,过点C 作直线l //x 轴, 将抛物线在y 轴左侧的部分沿直线 l 翻折, 抛物线的其余部分保持不变,得到一个新图象. 请你结合新图象回答: 当直线13y x b =+与新图象只有一个公共点P (x 0, y 0)且 y 0≤7时, 求b 的取值范围.E 3 E 1 E 2P 1 P 2 N 1N 22 1 B A图3 GFH24. 如图, 在平面直角坐标系xOy 中,抛物线x x my 222-=与x 轴负半轴交于点A , 顶点为B , 且对称轴与x 轴交于点C .(1)求点B 的坐标 (用含m 的代数式表示);(2)D 为BO 中点,直线AD 交y 轴于E ,若点E 的坐标为(0, 2), 求抛物线的解析式; (3)在(2)的条件下,点M 在直线BO 上,且使得△AMC 的周长最小,P 在抛物线上,Q 在直线 BC 上,若以A 、M 、P 、Q 为顶点的四边形是平行四边形,求点P 的坐 标.备用图25. 在矩形ABCD 中, 点F 在AD 延长线上,且DF = DC , M 为AB 边上一点, N 为MD 的中 点, 点E 在直线CF 上(点E 、C 不重合).(1)如图1, 若AB =BC , 点M 、A 重合, E 为CF 的中点,试探究BN 与NE 的位置关系及BMCE的值, 并证明你的结论; (2)如图2,且若AB =BC , 点M 、A 不重合, BN =NE ,你在(1)中得到的两个结论是否成立, 若成立,加以证明; 若不成立, 请说明理由;(3)如图3,若点M 、A 不重合,BN =NE ,你在(1)中得到的结论两个是否成立, 请直接写出你的结论.图1 图2 图3A N DA C E D NM B F E C B F N M E C B海淀区九年级第二学期期末练习数学试卷答案及评分参考 2012. 6说明: 与参考答案不同, 但解答正确相应给分. 一、选择题(本题共32分,每小题4分)1. B2. C3. A4. C5. B6. D7. D8. C 二、填空题(本题共16分,每小题4分)9.23x ≥10. 5 11. 12 12.8; 21n n +- (每空各 2分) 三、解答题(本题共30分,每小题5分) 13115()3tan604---+︒=54-+ …………………………………………………4分=1. …………………………………………………5分14.解:去分母,得 ()()()()63223x x x x x ++-=-+. ………………………………2分2261826x x x x x ++-=+-. ……………………………………………………3分 整理,得 324x =-. 解得 8x =-. ………………………………………………………………4分 经检验,8x =-是原方程的解. 所以原方程的解是8x =-. ……………………………………………………5分15.证明:∵ AC //EG ,∴ C CPG ∠=∠. …………1分 ∵ BC //EF ,∴ CPG FEG ∠=∠.∴ C FEG ∠=∠. …………………………………………2分在△ABC 和△GFE 中,,,,AC GE C FEG BC FE =⎧⎪∠=∠⎨=⎪⎩ ∴ △ABC ≌△GFE . …………………………………………………4分∴A G ∠=∠. …………………………………………………5分16. 解:原式=()()()21111111a a a a a +-⋅-+-- ……………………………………………2分 =()21111a a a +--- …………………………………………………3分 =22.(1)a -- …………………………………………………4分由2220a a --=,得 2(1)3a -=.∴ 原式=23-. …………………………………………………5分 GFEDC AP17.解:(1)依题意设一次函数解析式为2y kx =+. …………………………………1分∵ 点A (2,0-)在一次函数图象上, ∴022k =-+. ∴ k =1. ……………………………………………………2分 ∴ 一次函数的解析式为2y x =+. …………………………………3分 (2)ABC ∠的度数为15︒或105︒. (每解各1分) ……………………5分18.解: ∵∠ADB =∠CBD =90︒,∴ DE ∥CB . ∵ BE ∥CD , ∴ 四边形BEDC 是平行四边形. ………1分 ∴ BC=DE .在Rt △ABD 中,由勾股定理得8AD =. ………2分设DE x =,则8EA x =-. ∴8EB EA x ==-.在Rt △BDE 中,由勾股定理得 222DE BD EB +=.∴ 22248x x +=-(). ……………………………………………………3分 ∴ 3x =.∴ 3BC DE ==. ……………………………………………………4分 ∴1116622.22ABD BDC ABCD S S S BD AD BD BC ∆∆=+=⋅+⋅=+=四边形 ………… 5分 四、解答题(本题共20分,第19题、第20题各5分,第21题6分, 第22题4分)19.解:(1)甲图文社收费s (元)与印制数t (张)的函数关系式为0.11s t =. ……1分(2)设在甲、乙两家图文社各印制了x 张、y 张宣传单, 依题意得 {1500,0.110.13179.x y x y +=+= ………………………………………… 2分解得800,700.x y =⎧⎨=⎩……………………………………………… 3分答:在甲、乙两家图文社各印制了800张、700张宣传单. ………………4分(3) 乙 . ……………………………………………………… 5分20.(1)证明:连结OC .∴ ∠DOC =2∠A . …………1分 ∵∠D = 90°2A -∠, ∴∠D +∠DOC =90°. ∴ ∠OCD =90°.∵ OC 是⊙O 的半径,∴ 直线CD 是⊙O 的切线. ………………………………………………2分 (2)解: 过点O 作OE ⊥BC 于E , 则∠OEC =90︒.∵ BC =4,∴ CE =12BC =2.∵ BC //AO , ∴ ∠OCE =∠DOC .D EC BA∵∠COE +∠OCE =90︒, ∠D +∠DOC =90︒,∴ ∠COE =∠D . ……………………………………………………3分 ∵tan D =12, ∴tan COE ∠=12. ∵∠OEC =90︒, CE =2,∴4tan CEOE COE==∠.在Rt △OEC 中, 由勾股定理可得OC ==在Rt △ODC 中, 由1tan 2OC D CD ==,得CD =, ……………………4分由勾股定理可得 10.OD =∴10.AD OA OD OC OD =+=+= …………………………………5分 21.解:(1)(64)50%20+÷=. 所以李老师一共调查了20名学生. …………………1分 (2)C 类女生有 3 名,D 类男生有 1 名;补充条形统计图略.说明:其中每空1分,条形统计图1分. ……………………………………4分 (3)解法一:由题意画树形图如下:………………………5分从树形图看出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选 两位同学恰好是一位男同学和一位女同学的结果共有3种. 所以P (所选两位同学恰好是一位男同学和一位女同学)=3162=. ………………6分 解法二:由题意列表如下:………………………5分由上表得出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选 两位同学恰好是一位男同学和一位女同学的结果共有3种. 所以P (所选两位同学恰好是一位男同学和一位女同学)=3162=. ………………6分 22.解:(1)画图如下:(答案不唯一) …………………………………2分图3从D 类中选取从A 类中选取女女男男女女男女男(2)图3中△FGH 的面积为7a. …………………………………4分 五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23. 解:(1)∵ 抛物线2(1)(2)1y m x m x =-+--与x 轴交于A 、B 两点,∴210,(2)4(1)0.m m m ì- ïïíïD =-+->ïî由①得1m ¹, 由②得0m ¹,∴ m 的取值范围是0m ¹且1m ¹. ……………………………………………2分 (2)∵ 点A 、B 是抛物线2(1)(2)1y m x m x =-+--与x 轴的交点,∴ 令0y =,即 2(1)(2)10m x m x -+--=. 解得 11x =-,211x m =-. ∵1m >, ∴10 1.1m >>-- ∵ 点A 在点B 左侧,∴ 点A 的坐标为(1,0)-,点B 的坐标为1(,0)1m -. …………………………3分 ∴ OA=1,OB =11m -. ∵ OA : OB =1 : 3,∴131m =-. ∴ 43m =.∴ 抛物线的解析式为212133y x x =--. ………………………………………4分 (3)∵ 点C 是抛物线212133y x x =--与y 轴的交点,∴ 点C 的坐标为(0,1)-.依题意翻折后的图象如图所示.令7y =,即2121733x x --=. 解得16x =, 24x =-.∴ 新图象经过点D (6,7). 当直线13y x b =+经过D 点时,可得5b =.① ② …………………………………………1分当直线13y x b =+经过C 点时,可得1b =-.当直线1(1)3y x b b =+<-与函数2121(33y x x x =-->的图象仅有一个公共点P (x 0, y 0)时,得20001121333x b x x +=--.整理得 2003330.x x b ---=由2(3)4(33)12210b b D =----=+=,得74b =-结合图象可知,符合题意的b 的取值范围为15b -<≤或4b <-. ……………7分 24.解:(1)∵22222221212112()()4422y x x x mx m m x m m m m m m =-=-+-⋅=--,∴抛物线的顶点B 的坐标为11(,)22m m -. ……………………………1分(2)令2220x x m-=,解得10x =, 2x m =.∵ 抛物线x x my 222-=与x 轴负半轴交于点A , ∴ A (m , 0), 且m <0. …………………………………………………2分过点D 作DF ⊥x 轴于F . 由 D 为BO 中点,DF //BC , 可得CF =FO =1.2CO ∴ DF =1.2BC由抛物线的对称性得 AC = OC . ∴ AF : AO =3 : 4. ∵ DF //EO ,∴ △AFD ∽△AOE . ∴.FD AFOE AO= 由E (0, 2),B 11(,)22m m -,得OE =2, DF =14m -.∴134.24m-=∴ m = -6.∴ 抛物线的解析式为2123y x x =--. ………………………………………3分(3)依题意,得A (-6,0)、B (-3, 3)、C (-3, 0).可得直线OB 的解析式为x y -=,直线BC 为3x =-. 作点C 关于直线BO 的对称点C '(0,3),连接AC '交BO于M ,则M 即为所求. 由A (-6,0),C ' (0, 3),可得直线AC '的解析式为321+=x y .由13,2y x y x⎧=+⎪⎨⎪=-⎩ 解得2,2.x y =-⎧⎨=⎩ ∴ 点M 的坐标为(-2, 2). ……………4分由点P 在抛物线2123y x x =--上,设P (t ,213t - (ⅰ)当AM 为所求平行四边形的一边时. 如右图,过M 作MG ⊥ x 轴于G ,过P 1作P 1H ⊥ BC 于H , 则x G = x M =-2, x H = x B =-3.由四边形AM P 1Q 1为平行四边形, 可证△AMG ≌△P 1Q 1H . 可得P 1H = AG =4. ∴ t -(-3)=4. ∴ t =1.∴17(1,)3P -. ……………………5分 如右图,同 方法可得 P 2H=AG =4. ∴ -3- t =4. ∴ t =-7.∴27(7,)3P --. ……………………6分 (ⅱ)当AM 为所求平行四边形的对角线时, 如右图,过M 作MH ⊥BC 于H , 过P 3作P 3G ⊥ x 轴于G , 则x H = x B =-3,x G =3P x =t . 由四边形AP 3MQ 3为平行四边形, 可证△A P 3G ≌△MQ 3H . 可得AG = MH =1. ∴ t -(-6)=1. ∴ t =-5. ∴35(5,)3P -. ……………………………………………………7分 综上,点P 的坐标为17(1,)3P -、27(7,)3P --、35(5,)3P-. 25. 解:(1)BN 与NE 的位置关系是BN ⊥NE ;CE BM证明:如图,过点E 作EG ⊥AF 于G , 则∠EGN =90°.∵ 矩形ABCD 中, AB =BC , ∴ 矩形ABCD 为正方形.∴ AB =AD =CD , ∠A =∠ADC =∠DCB =90°. ∴ EG//CD , ∠EGN =∠A , ∠CDF =90°. ………………………………1分 ∵ E 为CF 的中点,EG//CD ,∴ GF =DG =11.22DF CD =∴ 1.2GE CD =∵ N 为MD (AD )的中点, ∴ AN =ND =11.22AD CD = ∴ GE =AN , NG=ND+DG=ND+AN=AD=AB . ……………………………2分 ∴ △NGE ≌△BAN . ∴ ∠1=∠2. ∵ ∠2+∠3=90°, ∴ ∠1+∠3=90°. ∴ ∠BNE =90°. ∴ BN ⊥NE . ……………………………………………………………3分 ∵ ∠CDF =90°, CD =DF , 可得 ∠F =∠FCD =45°,CFCD= .于是12CFCE CE CE BM BA CD CD ==== ……………………………………4分 (2)在(1)中得到的两个结论均成立.证明:如图,延长BN 交CD 的延长线于点G ,连结BE 、GE ,过E 作EH ⊥CE ,交CD 于点H .∵ 四边形ABCD 是矩形,∴ AB ∥CG .∴ ∠MBN =∠DGN ,∠BMN =∠GDN . ∵ N 为MD 的中点,∴ MN =DN .∴ △BMN ≌△GDN .∴ MB =DG ,BN =GN . ∵ BN =NE ,∴ BN =NE =GN . ∴ ∠BEG =90°. ……………………………………………5分 ∵ EH ⊥CE , ∴ ∠CEH =90°. ∴ ∠BEG =∠CEH . ∴ ∠BEC =∠GEH . 由(1)得∠DCF =45°. ∴ ∠CHE =∠HCE =45°.HGA BC DEM N F 321GFEA (M )CD NB∴ EC=EH , ∠EHG =135°.∵∠ECB =∠DCB +∠HCE =135°, ∴ ∠ECB =∠EHG . ∴ △ECB ≌△EHG . ∴ EB =EG ,CB =HG . ∵ BN =NG ,∴ BN ⊥NE. ……………………………………………6分∵ BM =DG= HG -HD= BC -HD =CD -,∴CE BM. ……………………………………………7分(3)BN ⊥NE ;CEBM.………………………………………………8分丰台区2012年初三统一练习(二)数 学 试 卷学校 姓名 准考证号一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.2-的绝对值是A .12-B .12C .2D .2-2.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,2.5微米等于0.000 002 5米,把0.000 002 5用科学记数法表示为A .62.510⨯ B .50.2510-⨯ C . 62.510-⨯ D .72510-⨯ 3.如图,在△ABC 中, DE ∥BC ,如果AD =1, BD =2,那么DEBC的值为 A .12 B .13 C .14 D .194.在4张完全相同的卡片上分别画有等边三角形、矩形、菱形和圆,在看不见图形的情况下随机抽取1张,卡片上的图形是中心对称图形的概率是 A .14B .12C .34D .1 5.若20x +=则 y x 的值为A .-8B .-6C .6D .8 6.下列运算正确的是 A .222()a b a b +=+B .235a b ab +=C .632a a a ÷=D .325a a a ⋅=EDCBA7.小张每天骑自行车或步行上学,他上学的路程为2 800米,骑自行车的平均速度是步行 的平均速度的4倍,骑自行车上学比步行上学少用30分钟.设步行的平均速度为x 米/分.根据题意,下面列出的方程正确的是A .30428002800=-xx B .30280042800=-x xC .30528002800=-x xD .30280052800=-xx8.如图1是一个小正方体的侧面展开图,小正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上..一面的字是 A .北 B .京C .精D .神二、填空题(本题共16分,每小题4分)9有意义,则x 的取值范围是 . 10.分解因式:=+-b ab b a 25102.11.如图, ⊙O 的半径为2,点A 为⊙O 上一点,OD ⊥弦BC 于点D ,如果1OD =,那么BAC ∠=________︒. 12.符号“f ”表示一种运算,它对一些数的运算如下:2(1)11f =+,2(2)12f =+,2(3)13f =+,2(4)14f =+,…, 利用以上运算的规律写出()f n = (n 为正整数) ;(1)(2)(3)(100)f f f f ⋅⋅⋅= .三、解答题(本题共30分,每小题5分) 13.计算:()︒⎪⎭⎫⎝⎛+45sin 4-211-3-272-03.14.已知2230a a --=,求代数式2(1)(2)(2)a a a a --+-的值.DOCBA15.解分式方程:21124x x x -=--.16.如图,在△ABC 与△ABD 中, BC 与AD 相交于点O ,∠1=∠2,CO = DO .求证:∠C =∠D .17.已知:如图,在平面直角坐标系xOy 中,一次函数y =-x 的图象与反比例函数ky x=的图象交于A 、B 两点. (1)求k 的值;(2)如果点P 在y 轴上,且满足以点A 、B 、P 为顶点的三角形是直角三角形,直接写出点P 的坐标.18.为了增强居民的节约用电意识,某市拟出台居民阶梯电价政策:每户每月用电量不超过230千瓦时的部分为第一档,按每千瓦时0.49元收费;超过230千瓦时且不超过400千瓦时的部分为第二档,超过的部分按每千瓦时0.54元收费;超过400千瓦时的部分为第三档,超过的部分按每千瓦时0.79元收费.(1)将按阶梯电价计算得以下各家4月份应交的电费填入下表:(2)设一户家庭某月用电量为x 千瓦时,写出该户此月应缴电费y (元)与用电量x (千瓦时)之间的函数关系式.四、解答题(本题共20分,每小题5分)19.已知:如图,菱形ABCD 中,过AD 的中点E 作AC 的垂线EF ,交AB 于点M ,交CB的延长线于点F .如果FB 的长是2,求菱形ABCD 的周长.20.已知:如图,点A 、B 在⊙O 上,直线AC 是⊙O 的切线,联结AB 交O C 于点D ,AC =CD . (1)求证:OC ⊥OB ;B21DOCBAMFEBCDA(2)如果OD=1,tan∠OCA=2,求AC的长.22.小杰遇到这样一个问题:如图1,在□ABCD中,AE⊥BC于点E,AF⊥CD于点F,连结EF,△AEF的三条高线交于点H,如果AC=4,EF=3,求AH的长.小杰是这样思考的:要想解决这个问题,应想办法将题目中的已知线段与所求线段尽可能集中到同一个三角形中.他先后尝试了翻折、旋转、平移的方法,发现可以通过将△AEH平移至△GCF的位置(如图2),可以解决这个问题.请你参考小杰同学的思路回答:(1)图2中AH的长等于.(2)如果AC=a,EF=b,那么AH的长等于.B A DCEFHGHFEDAB图1 图2五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知关于x 的一元二次方程242(1)0x x k -+-=有两个不相等的实数根. (1)求k 的取值范围;(2)如果抛物线242(1)y x x k =-+-与x 轴的两个交点的横坐标为整数,求正整数k 的值;(3)直线y =x 与(2)中的抛物线在第一象限内的交点为点C ,点P 是射线OC 上的一个动点(点P 不与点O 、点C 重合),过点P 作垂直于x 轴的直线,交抛物线于点M ,点Q 在直线PC 上,距离点PP 的横坐标为t ,△PMQ 的面积为S ,求出S 与t 之间的函数关系式.24.在△ABC 中,D 为BC 边的中点,在三角形内部取一点P ,使得∠ABP =∠ACP .过点P作PE ⊥AC 于点E ,PF ⊥AB 于点F .(1)如图1,当AB =AC 时,判断的DE 与DF 的数量关系,直接写出你的结论; (2)如图2,当AB ≠AC ,其它条件不变时,(1)中的结论是否发生改变?请说明理由.图1 图2AEFPB D CCE AD F P25.如图,将矩形OABC 置于平面直角坐标系xOy 中,A (32,0),C (0,2). (1) 抛物线2y x bx c =-++经过点B 、C ,求该抛物线的解析式;(2)将矩形OABC 绕原点顺时针旋转一个角度α(0°<α<90°),在旋转过程中,当矩形的顶点落在(1)中的抛物线的对称轴上时,求此时这个顶点的坐标; (3)如图(2),将矩形OABC 绕原点顺时针旋转一个角度θ(0°<θ<180°),将得到矩形OA’B’C’,设A’C’的中点为点E ,联结CE ,当θ= °时,线段CE 的长度最大,最大值为 .北京市丰台区2011_2012学年第二学期初三综合练习(二)参考答案二、填空题(本题共16分,每小题4分)三、解答题(本题共30分,每小题5分)13.解:原式=3-1+4-422⨯……4分 =6-22….5分14.解:2(1)(2)(2)a a a a --+-=22224a a a --+……1分. =224a a -+. ……2分2230a a --= , ∴223a a -=. (3)分∴原式=224347a a -+=+=.….….5分 15.21124x x x -=-- 解:2(2)(4)1x x x +--=.……1分 22241x x x +-+=.……2分23x =-.…… 3分32x =-.…….4分检验:经检验,32x =-是原方程的解.∴原方程的解是32x =-.……5分16.证明: ∠1=∠2, ∴OA=OB .…1分在△COA 和△DOB 中 , OA=OB ,∠AOC =∠BOD , CO=DO .∴△COA ≌△DOB .……….4分 ∴∠C =∠D . …………….5分17.解:(1) 反比例函数ky x= 的图象经过点A (-1,1) ,∴-11-1k =⨯=.…………1分 (2)P 1(0、 P 2(0,、P 3(0,2)、 P 4(0,-2) ……5分18.解:(1)……2分(2)当0230x ≤≤时,0.49y x =;……3分 当230400x <≤时,0.54-11.5y x =;……4分当400x >时,0.79-111.5y x =.……5分 四、解答题(本题共20分,每小题5分) 19.解:联结BD . ∵在菱形ABCD 中,∴AD ∥BC ,AC ⊥BD .……1分 又∵EF ⊥AC , ∴BD ∥EF . ∴四边形EFBD 为平行四边形.……2分∴FB = ED =2.……3分 ∵E 是AD 的中点. ∴AD =2ED =4.……4分 ∴菱形ABCD 的周长为4416⨯=.……5分(2)700⨯(1-0.04)=672.……5分答:这所学校每学期参加社会实践活动的时间不少于23.解:(1)由题意得△>0. ∴△=2(4)4[2(1)]8240k k ---=-+>.……1分 ∴解得3<k .……2分(2)∵3<k 且k 为正整数,∴1=k 或2.……3分当1=k 时,x x y 42-=,与x 轴交于点(0,0)、(4,0),符合题意; 当2=k 时,242+-=x x y ,与x 轴的交点不是整数点,故舍去.综上所述,1=k .……4分(3)∵2,4y x y x x =⎧⎨=-⎩,∴点C 的坐标是(5,5).∴OC 与x 轴的夹角为45°. 过点Q 作QN ⊥PM 于点N ,(注:点Q 在射线PC 上时,结果一样,所以只写一种情况即可)∴∠NQP =45°,NQ PM S ⋅=21. ∵PQNQ =1.∵P (t t ,),则M (t t t 4,2-),∴PM =t t t t t 5)4(22+-=--.……5分∴t t S 5212+-=. ∴当50<<t 时,t t S 25212+-=;……6分 当5>t 时,t t S 25212-=.……7分24.解:(1)DE =DF .……1分(2)DE =DF 不发生改变.……2分理由如下:分别取BP 、CP 的中点M 、N ,联结EM 、DM 、FN 、DN .∵D 为BC 的中点,∴BP DN BP DN //,21=.……3分∵,AB PE ⊥∴BP BM EM 21==.∴21,∠=∠=EM DN .∴12213∠=∠+∠=∠.…4分同理,524,//DM FN MD PC =∠=∠. ∴四边形MDNP 为平行四边形.……5分∴67∠=∠.∵,41∠=∠∴35∠=∠. ∴EMD DNF ∠=∠.……6分 ∴△EMD ≌△DNF . ∴DE =DF .……7分25.解:(1)∵矩形OABC ,A (32,0),C (0,2),∴B (32,2).∴抛物线的对称轴为x =3.∴b =3.……1分 ∴二次函数的解析式为:22y x =-++.……2分(2)①当顶点A 落在对称轴上时,设点A 的对应点为点A ’,联结OA ’, 设对称轴x =3与x 轴交于点D ,∴OD =3.∴OA ’ = OA =32.在Rt △OA ’D 中,根据勾股定理A ’D =3. ∴A ’(3,-3) . ……4分 ②当顶点落C 对称轴上时(图略),设点C 的对应点为点C ’,联结OC ’,在Rt △OC ’D 中,根据勾股定理C ’D =1.7654321NMCD BPFEA∴C ’(3,1).……6分 (3) 120°,4.……8分2012年门头沟区初三年级第二次统一练习数 学 试 卷一、选择题(本题共32分,每小题4分)在下列各题的四个备选答案中,只有一个是正确的. 1. 4-的倒数是 A.4-B.4C. D. 2. 在日本核电站事故期间,我国某监测点监测到极微量的人工放射性核素碘-131,其浓度为0.000 0963贝克/立方米.将 0.000 0963用科学记数法表示为A. 51063.9⨯ B. 51063.9-⨯ C. 41063.9-⨯ D. 31063.9-⨯ 3. 下列交通标志中既是中心对称图形,又是轴对称图形的是4. 五边形的内角和是A.360°B.540°C.720°D.900° 5. 为了支援地震灾区同学,某校开展捐书活动, 九(1)班40名同学积极参与.现将捐书数量 绘制成频数分布直方图如图所示,则捐书数量在5.5~6.5组别的频率是A. 0.1B. 0.2C. 0.3D. 0.46. 某农科院对甲、乙两种甜玉米各用10块相同条件的试验田进行试验,得到两个品种每公41-41A. B. C. D.EDCB A顷产量的两组数据,两组数据的平均数相同,其方差分别为s 甲2=0.002、s 乙2=0.03,则下列说法正确的是 A .甲比乙的产量稳定B .乙比甲的产量稳定C .甲、乙的产量一样稳定D .无法确定哪一品种的产量更稳定7.关于x 的一元二次方程032=-+m x x 有两个不相等的实数根,则m 的取值范围是 A. B. C. D.8. 如图,已知MN 是圆柱底面直径,NP 是圆柱的高.在圆柱的侧面上, 过点M 、P 嵌有一圈路径最短的金属丝.现将圆柱侧面沿NP 剪开,所得的侧面展开图是A. B. C. D.二、填空题(本题共16分,每小题4分)9. 分解因式:22344xy y x x +-= . 10. 如图,在△ABC 中,D 、E 分别为AB 、AC 边上的点, 若32=BD AD ,AE =3,则AC = . 11.一商场文具部的某种毛笔每支售价25元,书法练习本每本售价5元. 该商场为促销决定:买1支毛笔就赠送1本书法练习本. 某校书法兴趣小组打算购买这种毛笔10支,这种练习本x (10≥x )本, 则付款金额y (元)与练习本个数x (本)之间的函数关系式是 .12. 一组按规律排列的式子:22b a ,432b a -,843b a ,1654b a -,…,其中第6个式子是 ,第n 个式子是 (n 为正整数).三、解答题(本题共30分,每小题5分) 13.计算:4)3(45sin 80-+-+︒-π14.解不等式组:()⎪⎩⎪⎨⎧<-+≤+321234xx x x15.已知:3=x ,求2212-÷-x x x x 的值.PNM P /N /PN M P /N /P N M P /N /P N M M /P /N/PNM 121>m 121<m 121->m 121-<m16. 已知:如图,点E 、F 分别为□ABCD 的BC 、AD 边上的点,且∠1=∠2. 求证:AE =FC .17. 如图,已知反比例函数y =x6(x >0)的图象与一次函数y =kx +b 的图象交于点A (1,m ),B (n ,2)两点. (1)求一次函数的解析式;(2)结合图象回答:反比例函数的值大于一次函数的值时x 的取值范围.18. 列方程或方程组解应用题某中学库存960套旧桌凳,修理后捐助贫困山区学校.现有甲、乙两个木工小组都想承揽这项业务.经协商后得知:甲小组单独修理这批桌凳比乙小组多用20天;乙小组每天修的桌凳套数是甲小组的1.5倍.求甲、乙两个木工小组每天各修桌凳多少套?四、解答题(本题共20分,第19题5分,第20题5分,第21题6分,第22题4分)19.已知:如图,四边形ABCD 中,BC =CD =DB ,∠ADB =90°,sin ∠ABD =54,S △BCD =39. 求四边形ABCD 的周长.20. 如图,已知直线PA 交⊙O 于A 、B 两点,AE 是⊙O 的直径. 点C 为⊙O 上一点,且AC 平分∠PAE ,过C 作CD ⊥PA ,垂足 为D .(1)求证:CD 为⊙O 的切线;(2)若DC +DA =6,⊙O 的直径为10,求AB 的长.21.甲学校到丙学校要经过乙学校. 从甲学校到乙学校有A 1、A 2、A 3三条线路,从乙学校到丙学校有B 1、B 2二条线路.(1)利用树状图或列表的方法表示从甲学校到丙学校的线路中所有可能出现的结果; (2)小张任意走了一条从甲学校到丙学校的线路,求小张恰好经过了B 1线路的概率是多21F EDCBA DC BA少?23. 已知抛物线y =ax 2+x +2.(1)当a =-1时,求此抛物线的顶点坐标和对称轴; (2)若代数式-x 2+x +2的值为正整数,求x 的值;(3)若a 是负数时,当a =a 1时,抛物线y =ax 2+x +2与x 轴的正半轴相交于点M (m ,0);当a =a 2时,抛物线y =ax 2+x +2与x 轴的正半轴相交于点N (n ,0). 若点M 在点N 的左边,试比较a 1与a 2的大小.24. 有两张完全重合的矩形纸片,小亮将其中一张绕点A 顺时针旋转90°后得到矩形AMEF(如图1),连结BD 、MF ,此时他测得BD =8cm ,∠ADB =30°. (1)在图1中,请你判断直线FM 和BD 是否垂直?并证明你的结论;(2)小红同学用剪刀将△BCD 与△MEF 剪去,与小亮同学继续探究.他们将△ABD 绕点A 顺时针旋转得△AB 1D 1,AD 1交FM 于点K (如图2),设旋转角为β(0°<β<90°),当△AFK 为等腰三角形时,请直接写出旋转角β的度数;(3)若将△AFM 沿AB 方向平移得到△A 2F 2M 2(如图3),F 2M 2与AD 交于点P ,A 2M 2与BD 交于点N ,当NP ∥AB 时,求平移的距离是多少.25. 如图,在直角坐标系中,梯形ABCD 的底边AB 在x 轴上,底边CD 的端点D 在y 轴上.直线CB 的表达式为 ,点A 、D 的坐标分别为(-4,0),(0,4). 动点P 从A 点出发,在AB 边上匀速运动. 动点Q 从点B 出发,在折线BCD 上匀速运动,速度均为每秒1个单位长度. 当其中一个动点到达终点时,另一动点也停止运动. 设点P 运动t (秒)时,△OPQ 的面积为S (不能构成△OPQ 的动点除外). (1)求出点C 的坐标;(2)求S 随t 变化的函数关系式;(3)当t 为何值时,S 有最大值?并求出这个最大值.C D MB FE图1D M B图3N 2P 2M 2 D MBFD 1图2B 1K31634+-=x y2012年门头沟数学二模评标一、选择题1.C2.B3.D4.B5.B6.A7.C8.A 二、填空题9.2)2(y x x - 10.215 11. 2005+=x y 12. 6476b a -,n n n n b a 2)1(11++- 三、解答题(本题共30分,每小题5分) 13.解:原式=412222++-……………………………………4分 =5223+ ………………………………………….5分 14. ()⎪⎩⎪⎨⎧<-+≤+)2(321)1(234 xx x x解:由(1)得,1-≥x …………………………………….2分由(2)得,x<3 ………………………………………4分 不等式组的解集是31<≤-x ………………………5分 15.解:2212-÷-x xx x =xx x x x )1(2)1)(1(-⋅-+ ………………………..3分 =12+x ……………………………………..4分 当x=3时,原式=12+x =132+=21…………………………5分16.证明:∵四边形ABCD 是平行四边形,∴AB=CD ,∠B=∠D. ………………………….2分 ∵∠1=∠2,……………………………………….3分△ABE ≌△CDF. ………………………………4分 AE=CF. ………………………………………5分17.解:(1)由题意得,m=6,n=3.∴A (1,6),B (3,2). …………………………2分由题意得,⎩⎨⎧=+=+236b k b k解得,⎩⎨⎧=-=82b k∴一次函数解析式为y=-2x+8. ……………………3分21FEDC B A(2)反比例函数的值大于一次函数的值的x 的取值范围是0<x<1或x>3. …..5分 18.解:设甲组每天修桌凳x 套,则乙组每天修桌凳为1.5x 套. …………………………..1分由题意得,205.1960960+=xx …………………………………………….3分 解得,x=16 ………………………………………………………………………4分经检验,x=16是原方程的解,且符合实际意义.1.5x=1.5⨯16=24 …………………………………………………………..5分 答:甲组每天修桌凳16套,乙组每天修桌凳为24套. 19.解:过C 作CE ⊥BD 于E. ∵∠ADB =90°,sin ∠ABD =54, ∴AD=4x,AB=5x. ………………………..1分 ∴DB=3x∵BC =CD =DB ,∴DE=x 23,∠CDB=60°. ………………………2分 ∴tan ∠CDB=DECE∴CE=x 233. ……………………………3分 ∵S △BCD =39, ∴3921=⋅⋅CE BD ∴ x=2. ………………………………………….4分 ∴AD=8,AB=10,CD=CB=6.∴四边形ABCD 的周长=AD+AB+CD+CB=30. ……………………………..5分 20.(1)证明:连接OC, ∵OA=OC,∴∠OCA=∠OAC. ∵CD ⊥PA , ∴∠CDA=90°,∴∠CAD+∠DCA=90°, ∵AC 平分∠PAE ,∴∠DAC=∠CAO. ………………………1分∴∠DCO=∠DCA+∠ACO=∠DCA+∠CAO=∠DCA+∠DAC=90°. ∴CD 为⊙O 的切线. …………………………2分 (2)解:过O 作OF ⊥AB ,垂足为F , ∴∠OCA=∠CDA=∠OFD=90°, ∴四边形OCDF 为矩形, ∴OC=FD ,OF=CD.∵DC+DA=6,设AD=x ,则OF=CD=6-x , ……………………3分EDCBA∵⊙O 的直径为10,∴DF=OC=5,∴AF=5-x ,在Rt △AOF 中,由勾股定理得222AF +OF =OA . 即22(5)(6)25x x -+-=,化简得:211180x x -+=解得2x =或9x =(舍). ………………………4分 ∴AD=2, AF=5-2=3. ∵OF ⊥AB ,AB=2AF=6. ………………………..5分 21.(1)………………………………..2分结果:(A 1,B 1),(A 1,B 2),(A 2,B 1),(A 2,B 2),(A 3,B 1),(A 3,B 2) ………….4分(2)小张恰好经过了B 1线路的概率是21………………………………………….6分22.(1)正确 ……………………………….2分(一个1分) (2)正确 ………………………………..4分 23. 当a=-1时,y=-x 2+x+2,∴a=-1,b=1,c=2. ∴抛物线的顶点坐标为(21,49),对称轴为直线x=21.……2分 (2)∵代数式-x 2+x+2的值为正整数,∴函数y=-x 2+x+2的值为正整数.又因为函数的最大值为49,∴y 的正整数值只能为1或2. 当y=1时,-x 2+x+2=1,解得2511+=x ,2512-=x …………3分 当y=2时,-x 2+x+2=2,解得x 3=0,x 4=1.……………4分∴x 的值为2511+=x ,2512-=x ,0或1. (3) 当a <0时,即a 1<0,a 2<0.B 2B 2B 1B 1B 2B 1A 3A 2A 1经过点M 的抛物线y=a 1x 2+x+2的对称轴为121a x -=, 经过点N 的抛物线y=a 2x 2+x+2的对称轴为221a x -=.…………5分∵点M 在点N 的左边,且抛物线经过点(0,2)∴直线121a x -=在直线221a x -=的左侧……………6分∴121a -<221a -. ∴a 1<a 2.…………………………………………………………7分24. 解:(1)垂直. …………………………1分证明:延长FM 交BD 于N.如图1,由题意得:△BAD ≌△MAF .∴∠ADB =∠AFM .又∵∠DMN =∠AMF , ∴∠ADB +∠DMN =∠AFM +∠AMF =90°.∴∠DNM =90°,∴BD ⊥MF . ······································································· 2分 (2)β的度数为60°或15°(答对一个得1分) ····················································· 4分 (3)如图2,由题意知四边形PNA 2A 为矩形,设A 2A =x ,则PN =x .在Rt △A 2M 2F 2中,∵M 2F 2=MF =BD =8,∠A 2F 2M 2=∠AFM =∠ADB =30°. ∴M 2A 2=4,A 2F 2=34. …………………………..5分 ∴AF 2=34-x .在Rt △P AF 2中,∵∠PF 2A =30°. ∴AP =AF 2tan ·30°=(34-x )·33=4-33x . ∴PD =AD -AP =34-4+33x . ……………..6分D M A BF图2NF 2P A 2M 2 C DMB FE图1N∵NP ∥AB ,∴ABPN =DA DP .∴4x=3433434x +-,解得x =6-32.即平移的距离是(6-32)cm . (7)分25. 解:(1)把y =4代入y =-43x +163,得x =1. ∴C 点的坐标为(1,4). ……………………………………….1分(2) 当y =0时,-43x +163=0,∴x =4.∴点B 坐标为(4,0).过点C 作CM ⊥AB 于M ,则CM =4,BM =3. ∴BC5.∴sin ∠ABC =CMBC=45.① 0<t <4时,过Q 作QN ⊥OB 于N ,则QN =BQ ·sin ∠ABC =45t.∴S =12OP ·QN =12(4-t )×45t =-25t 2+85t (0<t <4). ……………2分②当4<t ≤5时,连接QO ,QP ,过点Q 作QN ⊥OB 于N .同理可得QN =45t .∴S =12OP ·QN =12×(t -4)×45t .=25t 2-85t (4<t ≤5). …………………………….3分③当5<t ≤6时, 连接QO ,QP . S =12×OP ×OD =12(t -4)×4.=2t -8(5<t ≤6). ……………………………….4分S 随t 变化的函数关系式是⎪⎪⎪⎩⎪⎪⎪⎨⎧≤<-≤<-<<+-)65(82)54(5852)40(585222t t t t t t t t .(3)①当0<t <4时,∵-25<0当t =8522()5⨯-=2时,S 最大=28()54()5-⨯-=85. ……………………………5分 ②当4<t ≤5时, S =25t 2-85t ,对称轴为t =-85225-⨯=2,∵25>0 ∴在4<t ≤5时,S 随t 的增大而增大.∴当t =5时,S 最大=25×52-85×5=2. …………………………..6分③当5<t ≤6时,在S =2t -8中,∵2>0,∴S 随t 的增大而增大.∴当t =6时,S 最大=2×6-8=4. …………………………………………7分∴综合三种情况,当t =6时,S 取得最大值,最大值是4. ………………………8分顺义区2012届初三第二次统一练习数学试卷一、选择题(本题共32分,每小题4分) 下面各题均有四个选项,其中只有一个..是符合题意的. 1.9的平方根是A .3B .-3C .3±D .132.据人民网报道,“十一五”我国铁路营业里程达9.1万公里.请把9.1万用科学记数法表示应为A .59.110⨯ B .49.110⨯ C .49110⨯ D . 39.110⨯ 3.如图,下列选项中不是..正六棱柱三视图的是( )A B C D4.把2416a bb -分解因式,结果正确的是A .2(24)b a - B . (22)(22)b a a +-。
2012年北京市朝阳区高考数学二模试卷(理科)(附答案解析)

2012年北京市朝阳区高考数学二模试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1. 已知全集U =R ,集合A ={x|2x >1},B ={x|x 2−3x −4>0},则A ∩C U B =( ) A.{x|0≤x <4} B.{x|0<x ≤4} C.{x|−1≤x ≤0} D.{x|−1≤x ≤4}2. 复数z 满足等式(2−i)⋅z =i ,则复数z 在复平面内对应的点所在的象限是( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限3. 已知双曲线x 2m −y 25=1(m >0)的右焦点与抛物线y 2=12x 的焦点相同,则此双曲线的离心率为( )A.6B.3√22C.32D.344. 在△ABC 中,|AB →|=2,|AC →|=3,AB →⋅AC →<0,且△ABC 的面积为32,则∠BAC 等于( ) A.60∘或120∘ B.120∘ C.150∘ D.30∘或150∘5. 在直角坐标系xOy 中,直线Z 的参数方程为{x =ty =4+t (t 为参数,且t >0);以原点O 为极点,以x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρ=4√2sin (θ+π4).则直线l 和曲线C 的公共点有( )A.0个B.l 个C.2个D.无数个6. 下列命题:p :函数f(x)=sin 4x −cos 4x 的最小正周期是π;q :已知向量a →=(λ, 1),b →=(−1, λ2),c →=(−1, 1),则(a →+b →) // c →的充要条件是λ=−1; r :若∫1xa 1dx =1(a >1),则a =e .其中所有的真命题是( ) A.r B.p ,qC.q ,rD.p ,r7. 直线y =x 与函数f(x)={2,x >mx 2+4x +2,x ≤m 的图象恰有三个公共点,则实数m 的取值范围是( )A.[−1, 2)B.[−1, 2]C.[2, +∞)D.(−∞, −1]8. 有一个棱长为1的正方体,按任意方向正投影,其投影面积的最大值是( ) A.1B.3√22C.√2D.√3二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.二项式(ax 2√x)5展开式中的常数项为5,则实数a =________.如图所示的程序框图输出的结果是________.若实数x ,y 满足{x −y +1≤0x ≤0则x 2+y 2的最小值是________.如图,AB 是圆O 的直径,CD ⊥AB 于D ,且AD =2BD ,E 为AD 的中点,连接CE 并延长交圆O 于F .若CD =√2,则AB =________,EF =________.一个工厂生产某种产品每年需要固定投资100万元,此外每生产1件该产品还需要增加投资1万元,年产量为x(x∈N∗)件.当x≤20时,年销售总收入为(33x−x2)万元;当x>20时,年销售总收入为260万元.记该工厂生产并销售这种产品所得的年利润为y万元,则y(万元)与x(件)的函数关系式为________,该工厂的年产量为________件时,所得年利润最大.(年利润=年销售总收入-年总投资)在如图所示的数表中,第i行第j列的数记为a i,j,且满足a1,j=2j−1,a i,1=i,a i+1,j+1=a i,j+a i+1,j(i, j∈N∗),MN⊥BC,则此数表中的第5行第3列的数是________;记第3行的数3,5,8,13,22,N为数列{b n},则数列{b n}的通项公式为________.第1行1248…第2行2359…第3行35813……三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.把答案答在答题卡上.已知函数f(x)=√3sin x cos x−cos2x+m(m∈R)的图象过点M(π12, 0).(1)求m的值;(2)在△ABC中,角A,B,C的对边分别是a,b,c,若c cos B+b cos C=2a cos B,求f(A)的取值范围.一个袋子中装有大小形状完全相同的编号分别为1,2,3,4,5的5个红球与编号为1,2,3,4的4个白球,从中任意取出3个球.(1)求取出的3个球颜色相同且编号是三个连续整数的概率;(2)求取出的3个球中恰有2个球编号相同的概率;(3)记X为取出的3个球中编号的最大值,求X的分布列与数学期望.在如图所示的几何体中,四边形ABCD为正方形,EA⊥平面ABCD,EF // AB,AB=4,AE=2,EF=1.(1)若点M在线段AC上,且满足CM=14CA,求证:EM // 平面FBC;(2)求证:AF⊥平面EBC;(3)求二面角A−FB−D的余弦值.已知函数f(x)=a ln x+2a2x+x(a≠0).(1)若曲线y=f(x)在点(1, f(1))处的切线与直线x−2y=0垂直,求实数a的值;(2)讨论函数f(x)的单调性;(3)当a∈(−∞, 0)时,记函数f(x)的最小值为g(a),求证:g(a)≤12e2.在平面直角坐标系x0y中,已知点A(−√2, 0),B(√2,0),E为动点,且直线EA与直线EB的斜率之积为−12.(1)求动点E的轨迹C的方程;(2)设过点F(1, 0)的直线l与曲线C相交于不同的两点M,N.若点P在y轴上,且|PM|=|PN|,求点P的纵坐标的取值范围.已知数列A n:a1,a2,…,a n(n∈N∗, n≥2)满足a1=a n=0,且当2≤k≤n(K∈N∗)时,(a k−a k−1)2=1,令S(A n)=∑a ini=1.(I)写出S(A5)的所有可能的值;(II)求S(A n)的最大值;(III)是否存在数列A n,使得S(A n)=(n−3)24?若存在,求出数列A n;若不存在,说明理由.参考答案与试题解析2012年北京市朝阳区高考数学二模试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.【答案】B【考点】交、并、补集的混合运算【解析】利用全集U=R,B={x|x2−3x−4>0},先求出C U B={x|−1≤x≤4},再由集合A={x|2x>1},求出集合A∩C U B.【解答】解:全集U=R,集合A={x|2x>1}={x|x>0},B={x|x2−3x−4>0}={x|x>4或x<−1},C U B={x|−1≤x≤4},∴A∩C U B={x|0<x≤4}.故选B.2.【答案】B【考点】复数的代数表示法及其几何意义【解析】先根据复数代数形式的乘除运算法则化简复数,然后根据复数的几何意义得到复数z在复平面内对应的点所在的象限.【解答】解:∵(2−i)⋅z=i∴z=i2−i =i(2+i)(2−i)(2+i)=−1+2i5=−15+25i则复数z在复平面内对应的点为(−15, 2 5 )即点所在的象限是第二象限故选B.3.【答案】C【考点】圆锥曲线的共同特征抛物线的求解【解析】确定抛物线的焦点坐标,从而可得双曲线的几何量,由此可求双曲线的离心率.【解答】解:抛物线y2=12x的焦点坐标为(3, 0)∵双曲线x2m−y25=1(m>0)的右焦点与抛物线y2=12x的焦点相同,∴m+5=9∴m=4∴双曲线的离心率为32故选C.4.【答案】C【考点】平面向量数量积的运算【解析】由题意可得∠BAC为钝角,且12×2×3×sin∠BAC=32,解得sin∠BAC=12,从而得到∠BAC的值.【解答】解:∵在△ABC中,|AB→=2,|AC→|=3,AB→⋅AC→<0,且△ABC的面积为32,∴∠BAC为钝角,且12×2×3×sin∠BAC=32,解得sin∠BAC=12,故∠BAC=150∘,故选C.5.【答案】B【考点】直线的参数方程圆的极坐标方程【解析】将参数方程转化为一般直角坐标系的方程,判断直线l和曲线C的公共点个数;【解答】解:∴直角坐标系xOy中,直线Z的参数方程为{x=ty=4+t(t为参数,且t>0);可得y=x+4,②x>0,曲线C方程为ρ=4√2sin(θ+π4),化为标准方程为:(x−2)2+(y−2)2=8,即C为以(2, 2)为圆心,2√2为半径的圆;圆心(2, 2)到直线Z的距离也为2√2,所以直线Z与圆C相切,两者有一个公共点,故选B;6.【答案】D【考点】命题的真假判断与应用 【解析】化简f(x)=sin 4x −cos 4x 后求周期,判断出命题p 为真命题;由(a →+b →) // c →建立λ的方程求解λ;由∫1xa 1dx =1建立关于a 的方程,求出a 的值再判断. 【解答】解:命题P:f(x)=sin 4x −cos 4x=(sin 2x +cos 2x)(sin 2x −cos 2x)=sin 2x −cos 2x =−cos 2x , 所以函数f(x)为π,故命题P 为真命题; 命题q:a →+b →=(λ−1, λ2+1),由(a →+b →) // c →得,−(λ2+1)+(λ−1)=0,解得λ=0或λ=−1, 故命题q 为假命题; 命题r :由∫1xa 1dx =1得,ln a −ln 1=1,解得a =e ,所以命题r 是真命题.故选D . 7.【答案】 A【考点】根的存在性及根的个数判断 【解析】由直线y =x 与函数f(x)={2,x >mx 2+4x +2,x ≤m 的图象恰有三个公共点,作出图象,结合图象,能得到实数m 的取值范围. 【解答】解:解方程组{y =x y =x 2+4x +2,得{x =−2y =−2,或{x =−1y =−1, 由直线y =x 与函数f(x)={2,x >mx 2+4x +2,x ≤m的图象恰有三个公共点,作出图象,结合图象,知−1≤m <2.∴ 实数m 的取值范围是[−1, 2).故选A .8.【答案】 D【考点】平行投影及平行投影作图法 平行投影【解析】首先想象一下,当正方体绕着对角线BD ′所在的直线转动时,体会投影的变化,当正方体为ABCD −A ′B ′C ′D ′投影最大的时候,应该是投影面α和面AB ′C 平行,从而得到结果. 【解答】解:设正方体为ABCD −A ′B ′C ′D ′投影最大的时候,是投影面α和面AB ′C 平行,三个面的投影为三个全等的菱形,其对角线为√2,即投影上三条对角线构成边长为√2的等边三角形. ∴ 投影的面积=2S △AB′C =12×√2×√62×2=√3.故选D .二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.【答案】 1【考点】二项式定理的应用 【解析】先求出二项式展开式的通项公式,再令x 的系数等于0,求得r 的值,即可求得展开式中的常数项.再由常数项为5,求得a 的值.【解答】 解:二项式(ax 2+√x)5的展开式的通项公式为T r+1=C 5r ⋅ a 5−r ⋅x 10−2r ⋅x −r2=C 5r ⋅ a 5−r ⋅x 10−52r ,令10−5r 2=0,解得r =4,故展开式中的常数项为C 51⋅ a 1=5,∴ a =1,故答案为1.【答案】 1023 【考点】等比数列的前n 项和 循环结构的应用【解析】通过分析循环,推出循环规律,利用循环的次数,求出输出结果. 【解答】解:通过循环,可知该循环的作用是求数列的和,循环到1010结束循环, 所以S =1+2+22+23+24+25+26+27+28+29=1023. 故答案为:1023. 【答案】 12【考点】 简单线性规划 【解析】根据已知条件实数x ,y 满足{x −y +1≤0x ≤0则,画出可行域,将x 2+y 2的最小值转化为可行域中的点到原点的最小距离的平方,从而求解; 【解答】解:由已知条件实数x ,y 满足{x −y +1≤0x ≤0画出可行域,如下图:求x 2+y 2的最小值,目标函数z =x 2+y 2,即是图中可行域中的点到原点的最小距离的平方, 可知原点0到直线x −y +1=0的最短距离d =|1|√2=√22, ∴ x 2+y 2的最小值为d 2=12,故答案为12;【答案】 3,2√33【考点】与圆有关的比例线段 【解析】AB 是圆O 的直径,可得∠ACB =90∘.利用射影定理可得CD 2=AD ⋅DB .已知AD =2DB ,CD =√2,可得DB =1,AB =AD +DB =3.已知E 为AD 的中点,可得ED =1.在Rt △CDE 中,利用勾股定理可得CE =√CD 2+DE 2=√3.利用相交弦定理可得:EA ⋅EB =EC ⋅EF ,即可求得EF . 【解答】解:∵ AB 是圆O 的直径,∴ ∠ACB =90∘. ∴ CD 2=AD ⋅DB .∵ AD =2DB ,∴ CD 2=2DB 2, ∵ CD =√2,∴ DB =1, ∴ AB =AD +DB =3.∵ E 为AD 的中点,∴ ED =1.在Rt △CDE 中,CE =√CD 2+DE 2=√3. 由相交弦定理可得:EA ⋅EB =EC ⋅EF , ∴ 1×2=√3EF , ∴ EF =2√33.故答案分别为3,2√33. 【答案】y ={−x 2+32x −100,x ≤20160−x,x >20,16 【考点】函数模型的选择与应用 【解析】根据年利润=年销售总收入-年总投资,确定分段函数解析式,分别确定函数的最值,即可得到结论. 【解答】解:由题意,年利润=年销售总收入-年总投资,则当x ≤20时,年利润y =(33x −x 2)−(100+x)=−x 2+32x −100; 当x >20时,年利润y =260−(100+x)=160−x ;∴ y ={−x 2+32x −100,x ≤20160−x,x >20;当x ≤20时,y =−x 2+32x −100=−(x −16)2+156,∴ x =16时,y 取得最大值156万元; 当x >20时,y =160−x <140万元∵ 156>140,∴ x =16时,利润最大值156万元 故答案为:y ={−x 2+32x −100,x ≤20160−x,x >20;16 【答案】16,b n =2n−1+n +1 【考点】 数列的应用 【解析】(1)由数阵中数的规律,可得:a i,2=(i−1)+i.由此得出a4,2和a5,2的值再结合题中的递推式,即可得到第5行第3列的数;(2)根据题中的递推式,将{b n}的各项依次减去2、3、4、5、6、7、…、n+1,得以1为首项公比为2的等比数列,结合等比数列的通项公式,不难得到数列{b n}的通项公式.【解答】解:(1)根据题意,得a4,2=3+4=7,a5,2=4+5=9,∵a i+1,j+1=a i,j+a i+1,j,∴第5行第3列的数a5,3=a4,2+a5,2=7+9=16;(2)将3,5,8,13,22,39,…,b n,各项依次减去2,3,4,5,6,7,…,n+1,得1,2,4,8,16,32,…,2n−1,∴b n−(n+1)=2n−1,得b n=2n−1+n+1,即为数列{b n}的通项公式故答案为:16,b n=2n−1+n+1三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.把答案答在答题卡上. 【答案】∵sin x cos x=12sin2x,cos2x=12(1+cos2x)∴f(x)=√3sin x cos x−cos2x+m=√32sin2x−12(1+cos2x)+m=√32sin2x−12cos2x−12+m=sin(2x−π6)−12+m∵函数y=fx)图象过点M(π12, 0),∴sin(2⋅π12−π6)−12+m=0,解之得m=12∵c cos B+b cos C=2a cos B,∴结合正弦定理,得sin C cos B+cos C sin B=2sin A cos B∵B+C=π−A,得sin C cos B+cos C sin B=sin(B+C)=sin(π−A)=sin A ∴sin A=2sin A cos B∵△ABC中,sin A>0,∴cos B=12,得B=π3由(1),得f(x)=sin(2x−π6),所以f(A)=sin(2A−π6),其中A∈(0, 2π3)∵−π6<2A−π6<7π6,∴sin(2A−π6)>sin(−π6)=−12,sin(2A−π6)≤sinπ2=1因此f(A)的取值范围是(−12, 1]【考点】两角和与差的三角函数正弦定理【解析】(1)根据二倍角的三角函数公式和辅助角公式,将函数y=f(x)化简,得f(x)=sin(2x−π6)−12+m,再将M点坐标代入,可得m=12;(2)利用正弦定理,将c cos B+b cos C=2a cos B化简整理,得cos B=12,所以B=π3.由此得到函数f(A)=sin(2A−π6),其中A∈(0, 2π3),再结合正弦函数的图象与性质,可得f(A)的取值范围.【解答】∵sin x cos x=12sin2x,cos2x=12(1+cos2x)∴f(x)=√3sin x cos x−cos2x+m=√32sin2x−12(1+cos2x)+m=√32sin2x−12cos2x−12+m=sin(2x−π6)−12+m∵函数y=fx)图象过点M(π12, 0),∴sin(2⋅π12−π6)−12+m=0,解之得m=12∵c cos B+b cos C=2a cos B,∴结合正弦定理,得sin C cos B+cos C sin B=2sin A cos B∵B+C=π−A,得sin C cos B+cos C sin B=sin(B+C)=sin(π−A)=sin A∴sin A=2sin A cos B∵△ABC中,sin A>0,∴cos B=12,得B=π3由(1),得f(x)=sin(2x−π6),所以f(A)=sin(2A−π6),其中A∈(0, 2π3)∵−π6<2A−π6<7π6,∴sin(2A−π6)>sin(−π6)=−12,sin(2A−π6)≤sinπ2=1因此f(A)的取值范围是(−12, 1]【答案】取出的3个球的编号恰好是3个连续的整数,且颜色相同的概率为584.(2)设“取出的3个球中恰有两个球编号相同”为事件B,则P(B)=C41C71C93=13.答:取出的3个球中恰有两个球编号相同的概率为13.(3)X的取值为2,3,4,5.P(X=2)=C21C22+C22C21C93=121,P(X=3)=C21C42+C22C41C93=421,P(X=4)=C21C62+C22C61C93=37,P(X=5)=C11C82C93=13.所以X的分布列为X的数学期望EX=2×121+3×421+4×37+5×13=8521.【考点】离散型随机变量及其分布列离散型随机变量的期望与方差【解析】(1)设“取出的3个球颜色相同且编号是三个连续整数”为事件A,由此能求出取出的3个球的编号恰好是3个连续的整数,且颜色相同的概率.(2)设“取出的3个球中恰有两个球编号相同”为事件B,由此能求出取出的3个球中恰有两个球编号相同的概率.(3)X的取值为2,3,4,5,分别求出P(X=2),P(X=3),P(X=4),P(X=5)的值,由此能求出X的分布列和X的数学期望.【解答】解:(1)设“取出的3个球颜色相同且编号是三个连续整数”为事件A,则P(A)=3+2C93=584.答:取出的3个球的编号恰好是3个连续的整数,且颜色相同的概率为584.(2)设“取出的3个球中恰有两个球编号相同”为事件B,则P(B)=C41C71C93=13.答:取出的3个球中恰有两个球编号相同的概率为13.(3)X的取值为2,3,4,5.P(X=2)=C21C22+C22C21C93=121,P(X=3)=C21C42+C22C41C93=421,P(X=4)=C21C62+C22C61C93=37,P(X=5)=C11C82C93=13.所以X的分布列为X的数学期望EX=2×121+3×421+4×37+5×13=8521.【答案】解:(1)过M作MN⊥BC,垂足为N,连结FN,则MN // AB.又∵CM=14AC,∴MN=14AB.又∵EF // AB且EF=14AB,∴EF // MN.且EF=MN.∴四边形EFNM为平行四边形.∴EM // FN.又FN⊂平面FBC,EM⊄平面FBC,∴EM // 平面FBC.(2)∵EF // AB,∴EF与AB可确定平面EABF,∵EA⊥平面ABCD,∴EA⊥BC.由已知得AB⊥BC且EA∩AB=A,∴BC⊥平面EABF.又AF⊂平面EABF,∴BC⊥AF.在四边形ABFE中,AB=4,AE=2,EF=1,∠BAE=∠AEF=90∘设AF ∩BE =P ,∵ ∠PAE +∠PAB =90∘, ∴ ∠PBA +∠PAB =90∘ 则∠APB =90∘, ∴ EB ⊥AF .又∵ EB ∩BC =B , ∴ AF ⊥平面EBC .(3)以AB 为x 轴,AD 为y 轴,AE 为z 轴建立空间直角坐标系, 则B(4, 0, 0),D(0, 4, 0),F(1, 0, 2). ∴ BD →=(−4,4,0),BF →=(1,−4,2) 设平面BDF 的法向量为m →(a, b, c),则{m →⋅BF →=0˙,解得:m →=(2,2,−1).同理可得,平面AFB 的法向量为n →=(0, 1, 0), ∴ 二面角A −FB −D =<m →,n →>,∴ 二面角A −FB −D 的余弦值为cos (π−<m →,n →>)=cos <m →,n →>=|m →|⋅|n →|˙=23×1=23.【考点】直线与平面平行的判定 直线与平面垂直的判定 用空间向量求平面间的夹角【解析】(1)过M 作MN ⊥BC ,垂足为N ,连结FN ,则MN // AB ,又可得EF // MN ,从而四边形EFNM 为平行四边形,所以EM // FN ,最后根据线面平行的判定定理,即可得到EM // 平面FBC ;(2)先利用线面垂直的性质和勾股定理证出BC ⊥AF ,EB ⊥AF ,从而证出AF ⊥平面EBC ; (3)建立空间直角坐标系,求出两个平面的法向量,求解即可. 【解答】 解:(1)过M 作MN ⊥BC ,垂足为N ,连结FN , 则MN // AB . 又∵ CM =14AC , ∴ MN =14AB .又∵ EF // AB 且EF =14AB , ∴ EF // MN .且EF =MN .∴ 四边形EFNM 为平行四边形. ∴ EM // FN .又FN ⊂平面FBC ,EM ⊄平面FBC ,∴ EM // 平面FBC .(2)∵ EF // AB ,∴ EF 与AB 可确定平面EABF , ∵ EA ⊥平面ABCD , ∴ EA ⊥BC .由已知得AB ⊥BC 且EA ∩AB =A , ∴ BC ⊥平面EABF . 又AF ⊂平面EABF , ∴ BC ⊥AF .在四边形ABFE 中,AB =4,AE =2,EF =1,∠BAE =∠AEF =90∘ 设AF ∩BE =P ,∵ ∠PAE +∠PAB =90∘, ∴ ∠PBA +∠PAB =90∘ 则∠APB =90∘, ∴ EB ⊥AF .又∵ EB ∩BC =B , ∴ AF ⊥平面EBC .(3)以AB 为x 轴,AD 为y 轴,AE 为z 轴建立空间直角坐标系, 则B(4, 0, 0),D(0, 4, 0),F(1, 0, 2). ∴ BD →=(−4,4,0),BF →=(1,−4,2) 设平面BDF 的法向量为m →(a, b, c),则{m →⋅BF →=0˙,解得:m →=(2,2,−1).同理可得,平面AFB 的法向量为n →=(0, 1, 0),∴ 二面角A −FB −D =<m →,n →>,∴ 二面角A −FB −D 的余弦值为cos (π−<m →,n →>)=cos <m →,n →>=|m →|⋅|n →|˙=23×1=23.【答案】解:(1)f(x)的定义域为{x|x >0},f′(x)=ax −2a 2x 2+1(x >0)根据题意,有f′(1)=−2,所以2a 2−a −3=0,解得a =−1或a =32. (2)解:f′(x)=(x−a)(x+2a)x 2(x >0)①当a >0时,因为x >0,由f′(x)>0得(x −a)(x +2a)>0,解得x >a ; 由f′(x)<0得(x −a)(x +2a)<0,解得0<x <a .所以函数f(x)在(a, +∞)上单调递增,在(0, a)上单调递减; ②当a <0时,因为x >0,由f′(x)>0得(x −a)(x +2a)>0,解得x >−2a ; 由f′(x)<0得(x −a)(x +2a)<0,解得0<x <−2a .所以函数f(x)在(−2a, +∞)上单调递增,在(0, −2a)上单调递减;(3)证明:由(2)知,当a ∈(−∞, 0)时,函数f(x)的最小值为g(a),且g(a)=f(−2a)=a ln (−2a)−3a , ∴ g′(a)=ln (−2a)−2,令g′(a)=0,得a =−12e 2.当a 变化时,g′(a),g(a)的变化情况如下表:∴ −12e 2是g(a)在(−∞, 0)上的唯一极值点,且是极大值点,从而也是g(a)的最大值点. 所以g(a)max =g(−12e 2)=12e 2.所以,当a ∈(−∞, 0)时,g(a)≤12e 2成立.【考点】利用导数研究曲线上某点切线方程 利用导数研究函数的单调性【解析】(1)确定f(x)的定义域,利用曲线y =f(x)在点(1, f(1))处的切线与直线x −2y =0垂直,可得f′(1)=−2,从而可求实数a 的值;(2)求导函数,分类讨论,利用导数的正负,即可确定函数f(x)的单调性;(3)由(2)知,当a ∈(−∞, 0)时,函数f(x)的最小值为g(a),且g(a)=f(−2a)=a ln (−2a)−3a ,求导数,求出函数的最大值,即可证得结论.【解答】解:(1)f(x)的定义域为{x|x >0},f′(x)=ax −2a 2x 2+1(x >0)根据题意,有f′(1)=−2,所以2a 2−a −3=0,解得a =−1或a =32. (2)解:f′(x)=(x−a)(x+2a)x 2(x >0)①当a >0时,因为x >0,由f′(x)>0得(x −a)(x +2a)>0,解得x >a ; 由f′(x)<0得(x −a)(x +2a)<0,解得0<x <a .所以函数f(x)在(a, +∞)上单调递增,在(0, a)上单调递减; ②当a <0时,因为x >0,由f′(x)>0得(x −a)(x +2a)>0,解得x >−2a ; 由f′(x)<0得(x −a)(x +2a)<0,解得0<x <−2a .所以函数f(x)在(−2a, +∞)上单调递增,在(0, −2a)上单调递减;(3)证明:由(2)知,当a ∈(−∞, 0)时,函数f(x)的最小值为g(a),且g(a)=f(−2a)=a ln (−2a)−3a , ∴ g′(a)=ln (−2a)−2,令g′(a)=0,得a =−12e 2.当a 变化时,g′(a),g(a)的变化情况如下表:∴ −12e 2是g(a)在(−∞, 0)上的唯一极值点,且是极大值点,从而也是g(a)的最大值点. 所以g(a)max =g(−12e 2)=12e 2.所以,当a ∈(−∞, 0)时,g(a)≤12e 2成立.【答案】 解:(1)设动点E 的坐标为(x, y),∵ 点A(−√2, 0),B(√2,0),E 为动点,且直线EA 与直线EB 的斜率之积为−12, ∴ x+2⋅x−2=−12, 整理,得x 22+y 2=1,x ≠±√2,∴ 动点E 的轨迹C 的方程为x 22+y 2=1,x ≠±√2.(2)当直线l 的斜率不存在时,满足条件的点P 的纵坐标为0, 当直线l 的斜率存在时,设直线l 的方程为y =k(x −1), 将y =k(x −1)代入x 22+y 2=1,并整理,得(2k 2+1)x 2−4k 2x +2k 2−2=0, △=8k 2+8>0,设M(x 1, y 1),N(x 2, y 2),则x 1+x 2=4k 22k 2+1,x 1x 2=2k 2−22k 2+1, 设MN 的中点为Q ,则x Q =2k 22k 2+1,y Q =k(x Q −1)=−k2k 2+1,∴ Q(2k 22k 2+1, −k2k 2+1), 由题意知k ≠0,又直线MN 的垂直平分线的方程为y +k 2k 2+1=−1k(x −2k 22k 2−1),令x =0,得y P =k 2k 2+1=12k+1k,当k >0时,∵ 2k +1k ≥2√2,∴ 0<y P ≤2√2=√24; 当k <0时,因为2k +1k≤−2√2,所以0>y P ≥2√2=−√24. 综上所述,点P 纵坐标的取值范围是[−√24,√24]. 【考点】圆锥曲线的轨迹问题直线与椭圆结合的最值问题 【解析】(1)设动点E 的坐标为(x, y),由点A(−√2, 0),B(√2,0),E 为动点,且直线EA 与直线EB 的斜率之积为−12,知x+2x−2=−12,由此能求出动点E 的轨迹C 的方程.(2)设直线l 的方程为y =k(x −1),将y =k(x −1)代入x 22+y 2=1,得(2k 2+1)x 2−4k 2x +2k 2−2=0,由题设条件能推导出直线MN 的垂直平分线的方程为y +k2k +1=−1k (x −2k 22k −1),由此能求出点P 纵坐标的取值范围.【解答】 解:(1)设动点E 的坐标为(x, y),∵ 点A(−√2, 0),B(√2,0),E 为动点,且直线EA 与直线EB 的斜率之积为−12, ∴ x+√2x−√2=−12,整理,得x 22+y 2=1,x ≠±√2,∴ 动点E 的轨迹C 的方程为x 22+y 2=1,x ≠±√2.(2)当直线l 的斜率不存在时,满足条件的点P 的纵坐标为0, 当直线l 的斜率存在时,设直线l 的方程为y =k(x −1), 将y =k(x −1)代入x 22+y 2=1,并整理,得(2k 2+1)x 2−4k 2x +2k 2−2=0, △=8k 2+8>0,设M(x 1, y 1),N(x 2, y 2),则x 1+x 2=4k 22k 2+1,x 1x 2=2k 2−22k 2+1,设MN 的中点为Q ,则x Q =2k 22k 2+1,y Q =k(x Q −1)=−k2k 2+1, ∴ Q(2k 22k 2+1, −k2k 2+1),由题意知k ≠0,又直线MN 的垂直平分线的方程为y +k 2k 2+1=−1k(x −2k 22k 2−1),令x =0,得y P =k 2k 2+1=12k+1k,当k >0时,∵ 2k +1k≥2√2,∴ 0<y P ≤2√2=√24; 当k <0时,因为2k +1k≤−2√2,所以0>y P ≥2√2=−√24. 综上所述,点P 纵坐标的取值范围是[−√24,√24]. 【答案】解:(I)由题设,满足条件的数列A 5的所有可能情况有: (1)0,1,2,1,0.此时S(A 5)=4;(2)0,1,0,1,0.此时S(A 5)=2; (3)0,1,0,−1,0.此时S(A 5)=0;(4)0,−1,−2,−1,0.此时S(A 5)=−4; (5)0,−1,0,1,0.此时S(A 5)=0;(6)0,−1,0,−1,0.此时S(A 5)=−2; 所以,S(A 5)的所有可能的值为:4,2,0,−2,−4. … (II )由(a k −a k−1)2=1,可设a k −a k−1=c k−1,则c k−1=1或c k−1=−1(2≤k ≤n, k ∈N ∗),因为a n −a n−1=c n−1,所以 a n =a n−1+c n−1=a n−2+c n−2+c n−1=...=a 1+c 1+c 2+...+c n−2+c n−1. 因为a 1=a n =0,所以c 1+c 2+...+c n−1=0,且n 为奇数,c 1,c 2,…,c n−1是由n−12个1和n−12个−1构成的数列.所以S(A n )=c 1+(c 1+c 2)+...+(c 1+c 2+...+c n−1)=(n −1)c 1+(n −2)c 2+...+2c n−2+c n−1. 则当c 1,c 2,…,c n−1的前n−12项取1,后n−12项取−1时S(A n )最大,此时S(A n )=(n −1)+(n −2)+⋯+n+12−(n−12+⋯+2+1)=(n−1)24.证明如下:假设c 1,c 2,…,c n−1的前n−12项中恰有t 项c m 1,c m 2,…c m t 取−1,则c 1,c 2,…,c n−1的后n−12项中恰有t 项第21页 共22页 ◎ 第22页 共22页c n 1,c n 2,…,c n t 取1,其中1≤t ≤n−12,1≤m i ≤n−12,n−12<n i ≤n −1,i =1,2,…,t . 所以S(A n )=(n −1)c 1+(n −2)c 2+⋯+n+12c n−12+n−12c n+12+⋯+2c n−2+c n−1=(n −1)+(n −2)+⋯+n+12−(n−12+⋯+2+1)−2[(n −m 1)+(n −m 2)+...+(n −m t )]+2[(n −n 1)+(n −n 2)+...+(n −n t )]=(n−1)24−2∑(t i=1n i −m i )<(n−1)24.所以S(A n )的最大值为(n−1)24. …(III )由(II)可知,如果c 1,c 2,…,c n−1的前n−12项中恰有t 项c m 1,c m 2,…,c m t 取−1,c 1,c 2,…,c n−1的后n−12项中恰有t 项c n 1,c n 2,…,c n t 取1,则S(A n )=(n−1)24−2∑(t i=1n i −m i ),若S(A n )=(n−3)24,则n −2=2∑(t i=1n i −m i ),因为n 是奇数,所以n −2是奇数,而2∑(t i=1n i−m i )是偶数,因此不存在数列A n ,使得S(A n )=(n−3)24. …【考点】 数列的应用 【解析】(I )由题设,即可满足条件的数列A 5的所有可能情况; (II )确定当c 1,c 2,…,c n−1的前n−12项取1,后n−12项取−1时S(A n )最大,此时S(A n )=(n −1)+(n −2)+⋯+n+12−(n−12+⋯+2+1)=(n−1)24.(III )由(II)可知,如果c 1,c 2,…,c n−1的前n−12项中恰有t 项c m 1,c m 2,…,c m t 取−1,c 1,c 2,…,c n−1的后n−12项中恰有t 项c n 1,c n 2,…,c n t 取1,则S(A n )=(n−1)24−2∑(t i=1n i −m i ),利用条件,分n 是奇数与偶数,即可得到结论.【解答】解:(I)由题设,满足条件的数列A 5的所有可能情况有: (1)0,1,2,1,0.此时S(A 5)=4;(2)0,1,0,1,0.此时S(A 5)=2; (3)0,1,0,−1,0.此时S(A 5)=0;(4)0,−1,−2,−1,0.此时S(A 5)=−4; (5)0,−1,0,1,0.此时S(A 5)=0;(6)0,−1,0,−1,0.此时S(A 5)=−2; 所以,S(A 5)的所有可能的值为:4,2,0,−2,−4. … (II )由(a k −a k−1)2=1,可设a k −a k−1=c k−1,则c k−1=1或c k−1=−1(2≤k ≤n, k ∈N ∗),因为a n −a n−1=c n−1,所以 a n =a n−1+c n−1=a n−2+c n−2+c n−1=...=a 1+c 1+c 2+...+c n−2+c n−1. 因为a 1=a n =0,所以c 1+c 2+...+c n−1=0,且n 为奇数,c 1,c 2,…,c n−1是由n−12个1和n−12个−1构成的数列.所以S(A n )=c 1+(c 1+c 2)+...+(c 1+c 2+...+c n−1)=(n −1)c 1+(n −2)c 2+...+2c n−2+c n−1.则当c 1,c 2,…,c n−1的前n−12项取1,后n−12项取−1时S(A n )最大,此时S(A n )=(n −1)+(n −2)+⋯+n+12−(n−12+⋯+2+1)=(n−1)24.证明如下:假设c 1,c 2,…,c n−1的前n−12项中恰有t 项c m 1,c m 2,…c m t 取−1,则c 1,c 2,…,c n−1的后n−12项中恰有t 项c n 1,c n 2,…,c n t 取1,其中1≤t ≤n−12,1≤m i ≤n−12,n−12<n i ≤n −1,i =1,2,…,t .所以S(A n )=(n −1)c 1+(n −2)c 2+⋯+n+12c n−12+n−12c n+12+⋯+2c n−2+c n−1=(n −1)+(n −2)+⋯+n+12−(n−12+⋯+2+1)−2[(n −m 1)+(n −m 2)+...+(n −m t )]+2[(n −n 1)+(n −n 2)+...+(n −n t )]=(n−1)24−2∑(t i=1n i−m i )<(n−1)24.所以S(A n )的最大值为(n−1)24. …(III )由(II)可知,如果c 1,c 2,…,c n−1的前n−12项中恰有t 项c m 1,c m 2,…,c m t 取−1,c 1,c 2,…,c n−1的后n−12项中恰有t 项c n 1,c n 2,…,c n t 取1,则S(A n )=(n−1)24−2∑(t i=1n i −m i ),若S(A n )=(n−3)24,则n −2=2∑(t i=1n i −m i ),因为n 是奇数,所以n −2是奇数,而2∑(ti=1n i −m i )是偶数,因此不存在数列A n ,使得S(A n )=(n−3)24. …。
2012年辽宁省朝阳市中考数学试题及答案及解析

2012年丽水市实验学校初中毕业生学业考试模拟试题卷科学命题:刘建斌 2012.6.5考生须知:1. 全卷共四大题,38小题,满分为180分。
考试时间为120分钟。
2. 全卷分为卷Ⅰ(选择题)和卷Ⅱ(非选择题)两部分,全部在“答题纸”上作答。
卷Ⅰ的答案必须用2B铅笔填涂;卷Ⅱ的答案必须用黑色字迹钢笔或签字笔写在“答题纸”的相应位置上。
3. 请用黑色字迹钢笔或签字笔在“答题纸”上先填写姓名和准考证号。
4. 本卷可能用到的相对原子质量:H—1 C—12 N—14 O—16 Cl—35.5 Na—23 Ba—137;g=10N/Kg。
卷Ⅰ说明:本卷共有一大题,20小题,共70分。
请用2B铅笔在“答题纸”上将你认为正确的选项对应的小方框涂黑、涂满。
一、选择题(本大题共有20小题,1~10题,每小题3分,;11~20题,每小题4分,共70分。
每小题只有一个选项是正确的,不选、多选、错选均不给分)1. 2012年4月15日,央视《每周质量报告》本期节目《胶囊里的秘密》,曝光河北一些企业,用生石灰处理皮革废料,熬制成工业明胶,卖给绍兴新昌一些企业制成药用胶囊,最终流入药品企业,进入患者腹中。
由于皮革在工业加工时,要使用含铬的鞣制剂,因此这样制成的胶囊,往往重金属铬超标。
请问这里的“铬”是指(▲)A. 铬原子B.三氧化二铬C. 铬元素D. 铬离子2. 2011年12月,广州出现“地沟油”事件,“地沟油”含有多环芳烃等多种有毒有害物质,超标万倍以上,长期食用可能会引发癌症,下列辨别某瓶装油是否为“地沟油”的简易方法,一定涉及化学变化的是(▲)A.看油是否透明 B.闻油是否有异味C.测油的密度 D.取油燃烧,听是否发出噼啪响声3.右图是用集合的方法,表示各种概念之间的关系,其中与图示相符的选项是(▲)A.①特异性免疫、②细胞免疫、③T淋巴细胞、④抗体B.①细胞核、②染色体、③DNA、④基因C.①生态系统、②种群、③生物圈、④群落D.①新陈代谢、②同化作用、③光合作用、④呼吸作用4.以下关于植物的描述,正确的一项是(▲)A. 被子植物的种子是由子房发育来的B. 花生油是从花生种子的子叶中榨出来的C. 种子萌发的外界条件是一定的水分、土壤、阳光D. 植物的结构层次由小到大的排列顺序为细胞、组织、器官、系统、植物体5.下列说法正确的是( ▲ )A .地球、月球、火星都是环绕太阳转动的行星B .人类活动是导致火山喷发的主要原因C .日珥是太阳活动强弱的主要标志D .昼夜交替现象是由于地球自转引起的。
2012朝阳数学中考
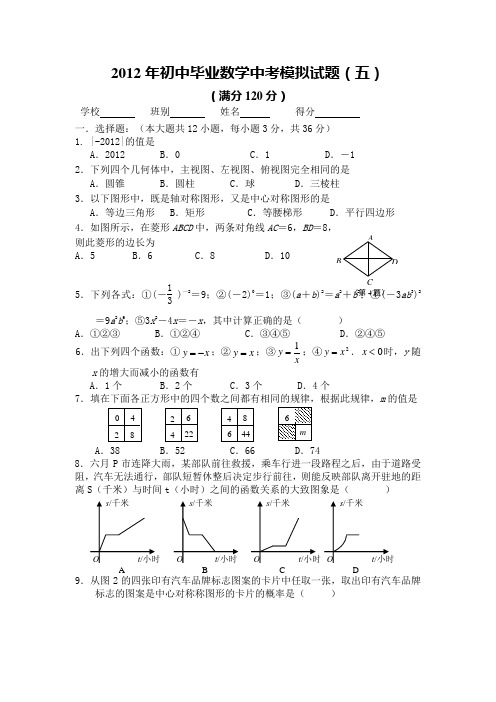
2012年初中毕业数学中考模拟试题(五)(满分120分)学校 班别 姓名 得分 一.选择题:(本大题共12小题,每小题3分,共36分) 1. |-2012|的值是 A .2012 B .0 C .1 D .-1 2.下列四个几何体中,主视图、左视图、俯视图完全相同的是 A .圆锥 B .圆柱 C .球 D .三棱柱 3.以下图形中,既是轴对称图形,又是中心对称图形的是A .等边三角形B .矩形C .等腰梯形D .平行四边形 4.如图所示,在菱形ABCD 中,两条对角线AC =6,BD =8,则此菱形的边长为A .5B .6C .8D .105.下列各式:①(-13 )—2=9;②(-2)0=1;③(a +b )2=a 2+b 2;④(-3ab 3)2=9a 2b 6;⑤3x 2-4x =-x ,其中计算正确的是( )A .①②③B .①②④C .③④⑤D .②④⑤6.出下列四个函数:①x y -=;②x y =;③xy 1=;④2x y =.0<x 时,y 随x 的增大而减小的函数有A .1个B .2个C .3个D .4个7.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m 的值是A .38B .52C .66D .748.六月P 市连降大雨,某部队前往救援,乘车行进一段路程之后,由于道路受阻,汽车无法通行,部队短暂休整后决定步行前往,则能反映部队离开驻地的距离S (千米)与时间t (小时)之间的函数关系的大致图象是( )9.从图2的四张印有汽车品牌标志图案的卡片中任取一张,取出印有汽车品牌标志的图案是中心对称称图形的卡片的概率是( )0 2 8 4 2 4 6 22 4 6 844AB CD(第4题) ABCD图9A .41B .21C .43D .110.方程23+x =11+x 的解为( )A .x =54B .x = -21 C .x =-2 D .无解11.如图,在菱形ABCD 中,DE ⊥AB ,3cos 5A =,BE=2,则tan ∠DBE 的值是A .12B .2 C.2 D.512.如图,△ABC 中,∠C =90°,AC =3,点P 是边BC 上的动点,则AP 长不可能...是( )A .2.5B .3C .4D .5 二、填空题(本大题共6小题,每小题3分,共18分) 13. 4的算术平方根是 .14.从26个英文字母中任意选一个,是C 或D 的概率是 。
2012北京市中考数学二模几何综合题及答案

2012北京市中考数学二模几何综合题及答案一、海淀25题:在矩形ABCD 中, 点F 在AD 延长线上,且DF = DC , M 为AB 边上一点, N 为MD 的中点, 点E 在直线CF 上(点E 、C 不重合).(1)如图1, 若AB =BC , 点M 、A 重合, E 为CF 的中点,试探究BN 与NE 的位置关系及BMCE的值, 并证明你的结论; (2)如图2,且若AB =BC , 点M 、A 不重合, BN =NE ,你在(1)中得到的两个结论是否成立, 若成立,加以证明; 若不成立, 请说明理由;(3)如图3,若点M 、A 不重合,BN =NE ,你在(1)中得到的结论两个是否成立, 请直接写出你的结论.图1 图2 图3【参考答案】25. 解:(1)BN 与NE 的位置关系是BN ⊥NE ;CE BM证明:如图,过点E 作EG ⊥AF 于G , 则∠EGN =90°.∵ 矩形ABCD 中, AB =BC , ∴ 矩形ABCD 为正方形.∴ AB =AD =CD , ∠A =∠ADC =∠DCB =90°.∴ EG//CD , ∠EGN =∠A , ∠CDF =90°. ………………………………1分 ∵ E 为CF 的中点,EG//CD ,∴ GF =DG =11.22DF CD =∴ 1.2GE CD =∵ N 为MD (AD )的中点, ∴ AN =ND =11.22AD CD = ∴ GE =AN , NG=ND+DG=ND+AN=AD=AB . ……………………………2分F A ( M ) D N D C E N MB FEC B F N M E C B A 321FEA (M )CD NB∴△NGE≌△BAN.∴∠1=∠2.∵∠2+∠3=90°,∴∠1+∠3=90°.∴∠BNE =90°.∴BN⊥NE.……………………………………………………………3分∵∠CDF =90°, CD=DF,可得∠F =∠FCD =45°,CFCD=.于是12CFCE CE CEBM BA CD CD====……………………………………4分(2)在(1)中得到的两个结论均成立.证明:如图,延长BN交CD的延长线于点G,连结BE、GE,过E作EH⊥CE,交CD于点H.∵四边形ABCD是矩形,∴AB∥CG.∴∠MBN=∠DGN,∠BMN=∠GDN.∵N为MD的中点,∴MN=DN.∴△BMN≌△GDN.∴MB=DG,BN=GN.∵BN=NE,∴BN=NE=GN.∴∠BEG=90°.……………………………………………5分∵EH⊥CE,∴∠CEH =90°.∴∠BEG=∠CEH.∴∠BEC=∠GEH.由(1)得∠DCF =45°.∴∠CHE=∠HCE =45°.∴EC=EH,∠EHG =135°.∵∠ECB =∠DCB +∠HCE =135°,∴∠ECB =∠EHG.∴△ECB≌△EHG.∴EB=EG,CB=HG.∵BN=NG,∴BN⊥NE. ……………………………………………6分∵BM =DG= HG-HD= BC-HD =CD-,∴CEBM. ……………………………………………7分(3)BN⊥NE;CEBM………………………………………………8分HGAB CDEMNF二、西城24题:如图,在Rt △ABC 中,∠C =90°,AC=6,BC =8.动点P 从点A 开始沿折线AC -CB -BA 运动,点P 在AC ,CB , BA 边上运动的速度分别为每秒3,4,5 个单位.直线l 从与AC 重合的位置开始,以每秒43个单位的速度 沿CB 方向平行移动,即移动过程中保持l ∥AC ,且分别与CB ,AB 边交于E ,F 两点,点P 与直线l 同时出发,设运动的 时间为t 秒,当点P 第一次回到点A 时,点P 和直线l 同时停止运动. (1)当t = 5秒时,点P 走过的路径长为 ;当t = 秒时,点P 与点E 重合;(2)当点P 在AC 边上运动时,将△PEF 绕点E 逆时针旋转,使得点P 的对应点M 落在EF 上,点F 的对应点记为点N ,当EN ⊥AB 时,求t 的值;(3)当点P 在折线AC -CB -BA 上运动时,作点P 关于直线EF 的对称点,记为点Q .在点P 与直线l 运动的过程中,若形成的四边形PEQF 为菱形,请直接写出t 的值.【参考答案】解:(1) 当t =5秒时,点P 走过的路径长为 19 ;当t = 3 秒时,点P 与点E 重合.﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍2分(2) 如图9,由点P 的对应点M 落在EF 上,点F 的对应点为点N ,可知∠PEF =∠MEN ,都等于△PEF绕点E 旋转的旋转角,记为α.设AP =3t (0< t <2),则CP =63t -,43CE t =. ∵ EF ∥AC ,∠C =90°,∴ ∠BEF =90°,∠CPE =∠PEF =α. ∵ EN ⊥AB , ∴ ∠B=∠MEN=α.∴ CPE B ∠=∠.﹍﹍﹍﹍﹍﹍﹍3分 ∵ tan CE CPE CP ∠=,3tan 4AC B BC ==, ∴ 43CP CE =. ∴ 446333t t -=⨯.﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍4分 解得5443t =.﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍5分 (3) t 的值为65(秒)或307(秒).﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍ 7分AA三、东城24题:已知:等边ABC ∆中,点O 是边AC,BC 的垂直平分线的交点,M,N 分别在直线AC , BC 上,且60MON ∠= .(1) 如图1,当CM=CN 时, M 、N 分别在边AC 、BC 上时,请写出AM 、CN 、MN 三者之间的数量关系;(2) 如图2,当CM ≠CN 时,M 、N 分别在边AC 、BC 上时,(1)中的结论是否仍然成立?若成立,请你加以证明;若不成立,请说明理由;(3) 如图3,当点M在边AC 上,点N 在BC 的延长线上时,请直接写出线段AM 、CN 、MN 三者之间的数量关系.【参考答案】24. 解: (1) AM CN MN =+……2分 (2)AM CN MN =+……3分证明:过点O 作,,OD AC OE BC ⊥⊥易得,120,OD OE DOE =∠=在边AC 上截得DN’=NE ,连结ON ’, ∵ DN ’=NE , OD =OE , ∠ODN ’=∠OEN'.DON EON ∴∆≅∆……4分 ∴ON’=OE. ∠DON ’=∠NOE . 120,DOE ∠=60,MON ∠=∴∠MOD +∠NOE=600. ∴∠MOD +∠DON ’=600.易证'MON MON ∆≅∆.……5分∴MN’=MN.'.,,()(),.MN MD DN MD NE MD AM AD AM CE NE CE CN MN AM CE CE CN AM CN AM CN MN ∴=+=+=-=-=-∴=-+-=-∴=+(3) .MN CN AM =+……7分四、朝阳24题:正方形ABCD 的边长为4,点P 是BC 边上的动点,点E 在AB 边上,且∠EPB =60°,沿PE 翻折△EBP 得到△P EB '. F 是CD 边上一点,沿PF 翻折△FCP 得到△P FC ',使点'C 落在射线'PB 上. (1)如图,当BP =1时,四边形''FC EB 的面积为 ;(2)若BP =m ,则四边形''FC EB 的面积为 (要求:用含m 的代数式表示,并写出m 的取值范围).备用图【参考答案】24. 证明:(1)取AC 的中点G ,连接NG 、DG .∴DG =21BC ,DG ∥BC ;△NGC 是等边三角形. ∴NG = NC ,DG = CM . …………………2分 ∵∠1 + ∠2 = 180º, ∴∠NGD + ∠2 = 240º. ∵∠2 + ∠3 = 240º, ∴∠NGD =∠3.∴△NGD ≌△NCM . ……………………3分 ∴ND = NM ,∠GND =∠CNM . ∴∠DNM =∠GNC = 60º.∴△DMN 是等边三角形. …………………………………………………4分 (2)连接QN 、PM .∴QN =21CE= PM . …………………………………………………………5分 Rt △CPE 中,PM =EM ,∴∠4= ∠5. ∵MN ∥EF ,∴∠5= ∠6,∠7= ∠8. ∵NQ ∥CE ,∴∠7= ∠4. ∴∠6= ∠8.E∴∠QND = ∠PMD . ………………………6分 ∴△QND ≌△PMD .∴DQ = DP . …………………………………………………………………7分五、石景山24题:在△ABC 中,AC AB =,D 是底边BC 上一点,E 是线段AD 上一点,且∠BAC CED BED ∠=∠=2. (1) 如图1,若∠︒=90BAC ,猜想DB 与DC 的数量关系为 ; (2) 如图2,若∠︒=60BAC ,猜想DB 与DC 的数量关系,并证明你的结论; (3)若∠︒=αBAC ,请直接写出DB 与DC 的数量关系.【参考答案】24.解:(1)DC DB 2= (2) DC DB 2=证明:过点C 作CF ∥BE 交AD 的延长线于点F , 在 AD 上取点G 使得CF CG =∴76∠=∠=∠F ∵︒=∠=∠=∠602BAC CED BED ∴︒=∠=∠606F ,︒=∠30CED ∴41205∠=︒=∠ ∵︒=∠+∠=∠=∠+∠6021713 ∴23∠=∠ ∵AC AB = ∴△ABE ≌△CAG∴AG BE AE CG ==, ∵︒=∠-∠=∠306CED GCE ∴EG CG = ∴BE AG CG CF 2121=== 由△DBE ∽△DCF 得2==FCBEDC BD ∴DC DB 2= (3) 结论:DC DB 2=. A B C D E AEB C D 图1 图2 7654321AEBCG FD 图(1)F图(2)六、延庆24题:(1)如图1:在△ABC 中,AB=AC ,当∠ABD =∠ACD=60°时,猜想AB 与BD+CD 数量关系,请直接写出结果 ;(2)如图2:在△ABC 中,AB=AC ,当∠ABD =∠ACD=45°时,猜想AB 与BD+CD 数量关系并证明你的结论; (3)如图3:在△ABC 中,AB=AC ,当∠ABD =∠ACD=β(20°≤β≤70°)时,直接写出AB 与BD+CD数量关系(用含β的式子表示)。
朝阳区2012年二模数学文科(朝阳二模)带答案

北京市朝阳区高三年级第二次综合练习数学试卷(文史类) 2012.5(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题 共40分)注意事项:考生务必将答案答在答题卡上,在试卷上作答无效.一、选择题:本大题共8小题,每小题5分,共40分.在四个选项中,选出符合题目要求的一项. 1. 设集合{0,1234,5}{12}U A ==,,,,,,{}2540B x x x =∈-+<Z ,则()U A B = ðA .{0,1,2,3}B .{5}C .{124},,D .{0,4,5}2. 在复平面内,复数i2iz =-对应的点所在的象限是 A .第一象限 B .第二象限 C .第三象限 D .第四象限 3. 如果命题“p 且q ”是假命题,“q ⌝”也是假命题,则A .命题“⌝p 或q ”是假命题B .命题“p 或q ”是假命题C .命题“⌝p 且q ”是真命题D .命题“p 且q ⌝”是真命题4. 已知△ABC 中,2AB = , 3AC = ,0AB AC ⋅< ,且△ABC 的面积为32,则BAC ∠=A .150B .120C .60 或120D .30 或1505. 已知双曲线2215x y m -=(0m >)的右焦点与抛物线212y x =的焦点相同,则此双曲线的离心率为 A .6 B.2C .32D . 346. 如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直 角三角形的直角边长都为1,那么这个几何体的表面积为 A .61B .23C.32 D.327. 给出下列命题::p 函数44()sin cos f x x x =-的最小正周期是π; :q R x ∃∈,使得2log (1)0x +<;:r 已知向量(1)λ,=a ,2(1),λ=-b ,(11)-,=c ,则(+)//a b c 的充要条件是1λ=-. 正视图俯视图侧视图其中所有真命题是A .qB .pC .,p rD .,p q 8. 已知函数22, ,()42, x m f x x x x m>⎧=⎨++≤⎩的图象与直线y x =恰有三个公共点,则实数m 的取值范围是 A .(,1]-∞- B .[1,2)- C .[1,2]- D . [2,)+∞第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在答题卡上.9. 函数2cos y x =,[0,2]x ∈π的单调递增区间是 . 10. 运行如图所示的程序框图,输出的结果是 .11. 直线3y kx =+与圆22(3)(2)4x y -+-=相交于,A B 两点,若AB =,则实数k 的值是 .12. 若实数,x y 满足10,0,x y x -+≤⎧⎨≤⎩则22x y +的最小值是 .13. 一个工厂生产某种产品每年需要固定投资100万元,此外每生产1件该产品还需要增加投资1万元,年产量为x ()x *∈N 件.当20x ≤时,年销售总收入为(233x x -)万元;当20x >时,年销售总收入为260万元.记该工厂生产并销售这种产品所得的年利润为y 万元,则y (万元)与x (件)的函数关系式为 ,该工厂的年产量为 件时,所得年利润最大.(年利润=年销售总收入-年总投资)14. 在如图所示的数表中,第i 行第j 列的数记为,i j a ,且满足11,,12,j j i a a i -==,1,1,1,(,)i j i j i j a a a i j *+++=+∈N ,则此数表中的第2行第7列的数是 ;记第3行的数3,5,8,13,22,39,⋅⋅⋅为数列{}n b ,则数列{}n b 的通项公式是 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15. (本小题满分13分)已知函数2()cos cos f x x x x m =-+()m R ∈的图象过点(,0)12M π. (Ⅰ)求m 的值;(Ⅱ)在ABC ∆中,角A ,B ,C 的对边分别是a ,b ,c ,若cos cos 2cos c B b C a B +=,求()f A 的取值范围.(第10题图)第1行 1 2 4 8 … 第2行 2 3 5 9 … 第3行 3 5 8 13 … … …16.(本小题满分13分)高三年级进行模拟考试,某班参加考试的40名同学的成绩统计如下:分数段 (70,90) [90,100) [100,120) [120,150]人数5a15b规定分数在90分及以上为及格,120分及以上为优秀,成绩高于85分低于90分的同学为希望生.已知该班希望生有2名.(Ⅰ)从该班所有学生中任选一名,求其成绩及格的概率; (Ⅱ)当a =11时,从该班所有学生中任选一名,求其成绩优秀的概率; (Ⅲ)从分数在(70,90)的5名学生中,任选2名同学参加辅导,求其中恰有1名希望生的概率.17. (本小题满分13分)如图,四边形ABCD 为正方形,⊥EA 平面ABCD ,//EF AB ,=4,=2,=1AB AE EF . (Ⅰ)求证:⊥BC AF ; (Ⅱ)若点M 在线段AC 上,且满足14CM CA =, 求证://EM 平面FBC ; (Ⅲ)试判断直线AF 与平面EBC 是否垂直?若垂直,请给出证明;若不垂直,请说明理由.18.(本小题满分14分)设函数22()ln (0)a f x a x a x=+≠. (Ⅰ)已知曲线()y f x =在点(1,(1))f 处的切线l 的斜率为23a -,求实数a 的值; (Ⅱ)讨论函数()f x 的单调性;(Ⅲ)在(Ⅰ)的条件下,求证:对于定义域内的任意一个x ,都有()3f x x ≥-. 19.(本小题满分14分)在平面直角坐标系xOy 中,点E 到两点1(1,0)F -,2(1,0)F的距离之和为E 的轨迹为曲线C .(Ⅰ)写出C 的方程;(Ⅱ)设过点2(1,0)F 的斜率为k (0k ≠)的直线l 与曲线C 交于不同的两点M ,N ,点P 在y 轴上,且PM PN =,求点P 纵坐标的取值范围.20.(本小题满分13分)已知数列12:,,,n n A a a a ,满足01==n a a ,且当n k ≤≤2(k ∈*N )时,1)(21=--k k a a .令12()n n S A a a a =++⋅⋅⋅+.(Ⅰ)写出)(5A S 的所有可能取值; (Ⅱ)求)(n A S 的最大值.B北京市朝阳区高三年级第二次综合练习数学试卷答案(文史类) 2012.5一、选择题:二、填空题:注:若有两空,则第一个空第二个空 三、解答题:(15)(本小题满分13分)解:(Ⅰ)1()2(cos 21)2f x x x m =-++1sin(2)62x m π=--+. ……3分由已知点(,0)12M π在函数()f x 的图象上,所以1sin(2)01262m ππ⋅--+=, 12m =. ………5分 (Ⅱ) 因为cos cos 2cos c B b C a B +=,所以sin cos sin cos C B B C +=2sin cos A B ,所以sin()2sin cos B C A B +=,即sin 2sin cos A A B =. ………7分 因为(0,A ∈π),所以sin 0A ≠,所以1cos 2B =, ………8分 又因为(0,B ∈π),所以π3B =,2π3A C +=. ………10分所以2π03A <<,π26A -∈7(,)66ππ-, ………11分 所以()f A =sin(2)6A π-∈1(,1]2-. ………13分(16)(本小题满分13分)解:(Ⅰ)设“从该班所有学生中任选一名,其成绩及格”为事件A ,则4057()408P A -==. 答:从该班所有学生中任选一名,其成绩及格的概率为78. ………3分 (Ⅱ)设“从该班所有学生中任选一名,其成绩优秀”为事件B ,则当11a =时,成绩优秀的学生人数为40511159---=,所以 9()40P B =. 答:从该班所有学生中任选一名,其成绩优秀的概率为940. ………7分 (Ⅲ)设“从分数在(7090),的5名学生中,任选2名同学参加辅导,其中恰有1名希望生”为事件C .记这5名学生分别为a ,b ,c ,d ,e ,其中希望生为a ,b .从中任选2名,所有可能的情况为:ab , ac , ad , ae ,bc ,bd ,be ,cd ,ce ,de ,共10种. ………9分 其中恰有1名希望生的情况有ac , ad , ae ,bc ,bd ,be ,共6种. ………11分 所以63()105P C ==. 答:从分数在(7090),的5名学生中,任选2名同学参加辅导,其中恰有1名希望生的概率为35. ………13分 (17)(本小题满分13分) 解:(Ⅰ)因为EF//AB ,所以EF 与AB 确定平面EABF ,因为⊥EA 平面ABCD ,所以⊥EA BC . ………2分 由已知得⊥AB BC 且= EA AB A , 所以⊥BC 平面EABF . ………3分 又AF ⊂平面EABF , 所以⊥BC AF . ………4分 (Ⅱ)过M 作MN BC ⊥,垂足为N ,连结FN ,则MN //AB . .………5分又14CM AC =,所以14MN AB =. 又EF //AB 且14EF AB =,所以EF //MN ..………6分且EF MN =,所以四边形EFNM 为平行四边形.………7分所以EM //FN .又FN ⊂平面FBC ,EM ⊄平面FBC ,所以//EM 平面FBC . ………9分 (Ⅲ)直线AF 垂直于平面EBC . ………10分证明如下:由(Ⅰ)可知,AF BC ⊥.在四边形ABFE 中,=4,=2,=1AB AE EF ,90BAE AEF ∠=∠=,所以1tan tan 2EBA FAE ∠=∠=,则EBA FAE ∠=∠. 设AF BE P = ,因为90PAE PAB ∠+∠= ,故90PBA PAB ∠+∠=则90APB ∠=,即⊥EB AF . ………12分又因为= EB BC B ,所以⊥AF 平面EBC . ………13分 (18)(本小题满分14分)解:(Ⅰ)()f x 的定义域为{|0}x x >, . ………1分222()a a f x x x'=-. ………2分根据题意,(1)23f a '=-,所以2223a a a -=-,即2210a a -+=, 解得1a =. .………4分(Ⅱ)2222(2)()a a a x a f x x x x -'=-=.(1)当0a <时,因为0x >,所以20x a ->,(2)0a x a -<,所以()0f x '<,函数()f x 在(0,)+∞上单调递减. ………6分 (2)当0a >时,若02x a <<,则(2)0a x a -<,()0f x '<,函数()f x 在(0,2)a 上单调递减; 若2x a >,则(2)0a x a ->,()0f x '>,函数()f x 在(2,)a +∞上单调递增. …8分综上所述,当0a <时,函数()f x 在(0,)+∞上单调递减;当0a >时,函数()f x 在(0,2)a 上单调递减,在(2,)a +∞上单调递增. ………9分 (Ⅲ)由(Ⅰ)可知2()ln f x x x=+. 设()()(3)g x f x x =--,即2()ln 3g x x x x=++-. 2222122(1)(2)()1(0)x x x x g x x x x x x +--+'=-+==>. ………10分当x 变化时,()g x ',()g x 的变化情况如下表:x (0,1)1(1,)+∞()g x ' -0 +()g x极小值1x =是()g x 在(0,)+∞上的唯一极值点,且是极小值点,从而也是()g x 的最小值点.可见()(1)0g x g ==最小值, .………13分 所以()0g x ≥,即()(3)0f x x --≥,所以对于定义域内的每一个x ,都有()3f x x ≥-. ………14分(19)(本小题满分14分)解:(Ⅰ)由题设知1212||||||EF EF F F +=>,根据椭圆的定义,E 的轨迹是焦点为1F ,2F,长轴长为设其方程为222210x y (a b )a b+=>>则1c =,a =1b =,所以C 的方程为2212x y +=. ………5分(II )依题设直线l 的方程为(1)y k x =-.将(1)y k x =-代入2212x y +=并整理得,2222(21)4220k x k x k +-+-= . 2880k ∆=+>. ………6分设11(,)M x y ,22(,)N x y ,则2122421k x x k +=+, 21222221k x x k -=+ ..………7分 设MN 的中点为Q ,则22221Q k x k =+,2(1)21Q Q k y k x k =-=-+,即2222(,)2121k kQ k k -++. ………8分 因为0k ≠,所以直线MN 的垂直平分线的方程为22212()2121kk y x k k k +=--++, ……9分 令0x =解得,211212P k y k k k==++, .………10分当0k >时,因为12k k +≥0P y <≤; .………12分 当0k <时,因为12k k +≤-0P y ≤<. .………13分 综上得点P纵坐标的取值范围是[(0,44- . .………14分 (20)(本小题满分13分)解:(Ⅰ)由题设,满足条件的数列5A 的所有可能情况有:(1)01210,,,,.此时5()=4S A ;(2)01010,,,,.此时5()=2S A ; (3)01010,,,,.-此时5()=0S A ;(4)01210,,,,.---此时5()=4S A -; (5)01010,,,,.-此时5()=0S A ;(6)01010,,,,.--此时5()=2S A -.所以,)(5A S 的所有可能取值为:4-,2-,0,2,4. .………5分(Ⅱ)由1)(21=--k k a a ,可设11k k k a a c ---=,则11k c -=或11k c -=-(n k ≤≤2,k ∈*N ),211a a c -=, 322a a c -=, … 11n n n a a c ---=,所以1121n n a a c c c -=++++ . ………7分 因为01==n a a ,所以1210n c c c -+++= ,且n 为奇数,121,,,n c c c - 是由21-n 个1和21-n 个1-构成的数列.所以112121()()()n n S A c c c c c c -=+++++++ 1221(1)(2)2n n n c n c c c --=-+-+++ .则当121,,,n c c c - 的前21-n 项取1,后21-n 项取1-时)(n A S 最大, 此时)(n A S 11(1)(2)(21)22n n n n +-=-+-++-+++ 2(1)4n -=..……10分 证明如下:假设121,,,n c c c - 的前21-n 项中恰有t 项12,,,t m m m c c c 取1-,则 121,,,n c c c - 的后21-n 项中恰有t 项12,,t n n n c c c 取1,其中112n t -≤≤,112i n m -≤≤,112i n n n -<≤-,1,2,,i t = . 所以()n S A 1211212211(1)(2)222n n n n n n n c n c c c c c -+--+-=-+-++++++ 11(1)(2)(21)22n n n n +-=-+-++-+++ 122[()()()]t n m n m n m --+-++- 122[()()()]t n n n n n n +-+-++-221122(1)(1)2[()()()]44t t n n n m n m n m --=--+-+⋅⋅⋅+-<.所以)(n A S 的最大值为2(1)4n -. .………13分。
2012朝阳区中考数学二模

2012朝阳区中考数学二模一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的.1.(4分)3的算术平方根是()A.3 B.﹣3 C.±D.2.(4分)2012年1月21日,北京市环保监测中心开始在其官方网站上公布PM2.5的研究性监测数据.PM2.5是指大气中直径小于或等于0.0000025米即2.5微米的颗粒物,也称为可入肺颗粒物.把0.0000025用科学记数法表示为()A.0.25×10﹣5B.2.5×10﹣5 C.2.5×10﹣6 D.25×10﹣73.(4分)掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷得朝上一面的点数小于3的概率为()A.B.C.D.4.(4分)如图,直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α等于()A.19°B.38°C.42°D.52°5.(4分)有一组数据:0,2,3,4,6,这组数据的方差是()A.3 B.4 C.6 D.206.(4分)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为()A.65°B.50°C.25°D.12.5°7.(4分)下面由8个完全相同的小正方体组成的几何体的主视图是()A.B.C.D.8.(4分)如图,在平面直角坐标系xOy中,P是反比例函数y=(x>0)图象上的一个动点,点A在x轴上,且PO=PA,AB是△PAO中OP边上的高.设OA=m,AB=n,则下列图象中,能表示n与m的函数关系的图象大致是()A.B.C.D.二、填空题(本题共16分,每小题4分)9.(4分)若分式有意义,则x的取值范围是.10.(4分)分解因式:ax2﹣4ax+4a=.11.(4分)在平面直角坐标系中,点P(k﹣2,k)在第二象限,且k是整数,则k的值为.12.(4分)如图,在平面直角坐标系xOy中,A1是以O为圆心,2为半径的圆与过点(0,1)且平行于x轴的直线l1的一个交点;A2是以原点O为圆心,3为半径的圆与过点(0,﹣2)且平行于x轴的直线l2的一个交点;A3是以原点O为圆心,4为半径的圆与过点(0,3)且平行于x轴的直线l3的一个交点;A4是以原点O为圆心,5为半径的圆与过点(0,﹣4)且平行于x轴的直线l4的一个交点;…,且点A1、A2、A3、A4、…都在y轴右侧,按照这样的规律进行下去,点A6的坐标为,点A n的坐标为(用含n的式子表示,n是正整数).三、解答题(本题共30分,每小题5分)13.(5分)计算:﹣12++|﹣1|﹣4cos45°.14.(5分)解方程:.15.(5分)已知y﹣2x=0,求的值.16.(5分)已知:如图,点D、E分别在AB、AC上,BE与CD相交于点F,BD=CE,∠B=∠C.求证:BE=CD.17.(5分)如图,点P(﹣3,1)是反比例函数的图象上的一点.(1)求该反比例函数的解析式;(2)设直线y=kx与双曲线的两个交点分别为P和P′,当<kx时,直接写出x的取值范围.18.(5分)如图,四边形ABCD是矩形,AB=3,BC=4,把矩形沿直线AC折叠,点B落在点F处,连接DF,CF与AD相交于点E,求DE的长和△ACE的面积.四、解答题(本题共21分,第19、20、21题每小题5分,第22题6分)19.(5分)如图,AB、BF分别是⊙O的直径和弦,弦CD与AB、BF分别相交于点E、G,过点F的切线HF与DC 的延长线相交于点H,且HF=HG.(1)求证:AB⊥CD;(2)若sin∠HGF=,BF=3,求⊙O的半径长.20.(5分)2012年4月北京国际汽车展览会期间,某公司对参观本次车展的观众进行了随机调查.①根据调查结果,将受访者购置汽车的意愿情况整理后,制成如右侧统计图:②将有购买家庭用汽车意愿的受访者的购车预算情况整理后,作出相应的统计表和频数分布直方图:(注:每组包含最小值不包含最大值)请你根据以上信息,回答下列问题:(1)统计表中的c=,d=;(2)补全频数分布直方图;(3)这次调查中一共调查了位参观者.21.(5分)如图,港口B在港口A的东北方向,上午9时,一艘轮船从港口A出发,以16海里/时的速度向正东方向航行,同时一艘快艇从港口B出发也向正东方向航行.上午11时轮船到达C处,同时快艇到达D处,测得D 处在C处的北偏东60°的方向上,且C、D两地相距80海里,求快艇每小时航行多少海里?(结果精确到0.1海里/时,参考数据:,,)22.(6分)已知二次函数y=x2+2x+c.(1)当c=﹣3时,求出该二次函数的图象与x轴的交点坐标;(2)若﹣2<x<1时,该二次函数的图象与x轴有且只有一个交点,求c的值.五、解答题(本题共21分,第23题6分,第24题7分,第25题8分)23.(6分)正方形ABCD的边长为4,点P是BC边上的动点,点E在AB边上,且∠EPB=60°,沿PE翻折△EBP得到△E B′P.F是CD边上一点,沿PF翻折△FCP得到△FC′P,使点C′落在射线PB′上.(1)如图,当BP=1时,四边形EB′FC′的面积为;(2)若BP=m,则四边形EB′FC′的面积为(要求:用含m的代数式表示,并写出m的取值范围).24.(7分)如图,D是△ABC中AB边的中点,△BCE和△ACF都是等边三角形,M、N分别是CE、CF的中点.(1)求证:△DMN是等边三角形;(2)连接EF,Q是EF中点,CP⊥EF于点P.求证:DP=DQ.同学们,如果你觉得解决本题有困难,可以阅读下面两位同学的解题思路作为参考:小聪同学发现此题条件中有较多的中点,因此考虑构造三角形的中位线,添加出了一些辅助线;小慧同学想到要证明线段相等,可通过证明三角形全等,如何构造出相应的三角形呢?她考虑将△NCM绕顶点旋转到要证的对应线段的位置,由此猜想到了所需构造的三角形的位置.25.(8分)在平面直角坐标系xOy中,抛物线y=ax2+bx+4经过A(﹣3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.(1)求该抛物线的解析式;(2)若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;(3)该抛物线的对称轴上是否存在一点M,使MQ+MA的值最小?若存在,求出点M的坐标;若不存在,请说明理由.参考答案与试题解析一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的.1.【解答】∵()2=3,∴3的算术平方根是.故选D.2.【解答】0.000 0025=2.5×10﹣6;故选:C.3.【解答】∵一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,点数小于3的有1,2,共2种,∴掷得朝上一面的点数小于3的概率为=.故选B.4.【解答】延长BC交直线m于D,∵∠ACB=90°,∠DAC=38°,∴∠ADC=90°﹣38°=52°,∵m∥n,∴∠α=∠ADC=52°,故选D.5.【解答】∵0,2,3,4,6的平均数是(0+2+3+4+6)÷5=3,∴这组数据的方差是[(0﹣3)2+(2﹣3)2+(3﹣3)2+(4﹣3)2+(6﹣3)2]=4,故选:B.6.【解答】连接AC,∵直径AB⊥弦CD于点H,∴∴∠CAB=∠DAB∵∠BAC=∠BEC=25°,∴∠BAD=∠BAC=25°.故选C.7.【解答】从正面可看到从左往右3列小正方形的个数依次为:1,2,1.故选:D.8.【解答】如图,过点P作PC⊥OA于点C,∵PO=PA,OA=m,∴OC=OA=m,∵点P在反比例函数y=上,∴PC==,在Rt△POC中,OP==,∵AB是△PAO中OP边上的高,∴sin∠AOB==,整理得,n=,n先随m的增大而增大,然后趋近于反比例函数,纵观各选项,只有A选项符合.故选A.二、填空题(本题共16分,每小题4分)9.【解答】由题意得:2x﹣3≠0,解得:x≠,故答案为:x≠.10.【解答】ax2﹣4ax+4a,=a(x2﹣4x+4),=a(x﹣2)2.11.【解答】∵点P(k﹣2,k)在第二象限,∴,解得0<k<2,∵k是整数,∴k=1.故答案为:1.12.【解答】∵点A1是以原点O为圆心,半径为2的圆与过点(0,1)且平行于x轴的直线l1的一个交点,∴A1的坐标为:(,1),即(,1),∵A2是以原点O为圆心,3为半径的圆与过点(0,﹣2)且平行于x轴的直线l2的一个交点,∴A2的坐标为(,﹣2)同理可得:A3的坐标为(,3)点A n的坐标为(,(﹣1)n+1•n),则:点A6的坐标为(,﹣6);故答案为:(,﹣6),(,(﹣1)n+1•n);三、解答题(本题共30分,每小题5分)13.【解答】原式=﹣1+3+1﹣4×=﹣1+3+1﹣2=.14.【解答】去分母得2(3x﹣5)=4(1+x),解得x=7,检验:当x=7时,(x+1)(3x﹣5)≠0,所以原方程的解为x=7.15.【解答】原式=•,=,∵y﹣2x=0,∴y=2x,∴原式==.16.【解答】证明:在△FDB和△FEC中,,∴△FDB≌△FEC(AAS),∴BF=CF,DF=EF,∴BF+EF=CF+DF,即BE=CD.17.【解答】(1)把P(﹣3,1)代入y=得m=﹣3×1=﹣3,所以反比例函数的解析式为y=﹣;(2)把P(﹣3,1)代入y=kx得k=﹣,∴y=﹣x,解方程组得或,∴P′的坐标为(3,﹣1),当<kx时,x的取值范围为x<﹣3或0<x<3.18.【解答】由题意,得FC=BC=4,AF=AB=3,∠1=∠2,∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∴∠1=∠3.∴∠2=∠3.∴AE=CE,∴AD﹣AE=CF﹣CE,即DE=FE.设DE=x,则FE=x,CE=4﹣x,在Rt△CDE中,DE2+CD2=CE2.即x2+32=(4﹣x)2,解得:x=.即DE=,则AE=AD﹣DE=,则S△ACE=AE•CD=.四、解答题(本题共21分,第19、20、21题每小题5分,第22题6分)19.【解答】(1)证明:如图,连接OF,∵HF是⊙O的切线,∴∠OFH=90°.即∠1+∠2=90°.∵HF=HG,∴∠1=∠HGF.∵∠HGF=∠3,∴∠3=∠1.∵OF=OB,∴∠B=∠2.∴∠B+∠3=90°.∴∠BEG=90°.∴AB⊥CD.(2)解:如图,连接AF,∵AB、BF分别是⊙O的直径和弦,∴∠AFB=90°.即∠2+∠4=90°.∴∠HGF=∠1=∠4=∠A.在Rt△AFB中,AB===4.∴⊙O的半径长为2.20.【解答】(1)由图表得:20÷0.05=400,∴c=400.∵0.05+0.13+0.38+d+0.07+0.06=1,∴d=0.31.(2)补全图形为:(3)400÷(1﹣5%﹣15%)=500.故答案为:400,0.31,50021.【解答】分别过点B、D作AC的垂线,交AC的延长线于点E、F,在Rt△DCF中,∠DFC=90°,∠DCF=90°﹣60°=30°,则DF=CD=40海里,CF=CDcos∠DCF=40海里,故可得AF=AC+CF=16×2+40=32+40海里,∵DF⊥AF,BE⊥AF,BE⊥BD,∴四边形BEFD是矩形.∴BE=DF=40海里,在Rt△BAE中,∠BEA=90°,∠BAE=90°﹣45°=45°,∴AE=BE=40海里,∴EF=AF﹣AE=32+40﹣40=(40﹣8)海里,∴BD=EF=40﹣8(海里),故可求得快艇的速度=(40﹣8)÷2=20﹣4≈30.6(海里/小时).答:快艇的速度约为30.6海里/时.22.【解答】(1)由题意,得y=x2+2x﹣3,当y=0时,x2+2x﹣3=0.解得x1=﹣3,x2=1.∴该二次函数的图象与x轴的交点坐标为(﹣3,0),(1,0).(2)抛物线y=x2+2x+c的对称轴为x=﹣1.若抛物线与x轴只有一个交点,则交点为(﹣1,0).有0=1﹣2+c,解得c=1.五、解答题(本题共21分,第23题6分,第24题7分,第25题8分)23.【解答】(1)∵BP=1,∠EPB=60°,∴BE=B'E=,C'P=CP=BC﹣BP=3,∠C'PF=∠CPF=30°,∴C'F=CF=CP×tan∠CPF=,C'B'=C'P﹣B'P=3﹣1=2,故S四边形EB′FC′=S△EB'C'+S△B'C'F=B'E×B'C'+C'F×B'C'=+=2;(2)①∵BP=m,∠EPB=60°,∴BE=B'E=m,C'P=CP=BC﹣BP=4﹣m,∠C'PF=∠CPF=30°,∴C'F=CF=CP×tan∠CPF=(4﹣m),C'B'=C'P﹣B'P=4﹣m﹣m=4﹣2m,故S四边形EB′FC′=S△EB'C'+S△B'C'F=B'E×B'C'+C'F×B'C'=×m×(4﹣2m)+×(4﹣m)×(4﹣2m)=﹣m2+2m+m2﹣2m+=﹣m2+(0<m<2).②当2<m≤时,EB'=EB=m,B'C'=m﹣(4﹣m)=2m﹣4,FC'=(4﹣m),故S四边形EB′FC′=S△EB'c'+S△B'C'F=B'E×B'C'+C'F×B'C'=×m×(2m﹣4)+×(2m﹣4)×(4﹣m)=m2﹣2m+(m﹣2)×(﹣m)=m2﹣2m+m﹣m2﹣+m=m2﹣(2<m≤).故答案为:2;﹣m2+(0<m<2),m2﹣(2<m≤).24.【解答】证明:(1)取AC的中点G,连接NG、DG,∵D为AB的中点,即DG为△ABC的中位线,∴DG=BC,DG∥BC,∵N为FC的中点,即NG为△AFC的中位线,∴NG∥AF,又△ACF为等边三角形,∴∠CNG=∠F=∠CGN=∠CAF=60°,∴△NGC是等边三角形,∴NG=NC,∵M为等边三角形BEC边EC的中点,∴DG=CM=EC=BC,∵∠DGC+∠GCB=180°,∴∠NGD+∠GCB=240°,∵∠GCB+∠NCM=240°,∴∠NGD=∠NCM,在△NGD和△NCM中,,∴△NGD≌△NCM(SAS),∴ND=NM,∠GND=∠CNM,∴∠GNC=∠GND+∠CND=∠MNC+∠CND=60°,∴∠DNM=60°,∴△DMN是等边三角形;(2)连接QN、PM,∵QN为△FCE的中位线,PM为直角三角形PCE斜边上的中线,∴QN=CE=PM,∵Rt△CPE中,PM=EM,∴∠MEP=∠MPE,∵MN∥EF,∴∠MPE=∠PMN,∠FQN=∠QNM,∵NQ∥CE,∴∠FQN=∠MEP,∴∠PMN=∠QNM,又∠NMD=∠MND=60°,∴∠PMN+∠NMD=∠QNM+∠MND,即∠QND=∠PMD,在△QND和△PMD中,,∴△QND≌△PMD(SAS),∴DQ=DP.25.【解答】(1)∵抛物线y=ax2+bx+4经过A(﹣3,0),B(4,0)两点,∴,解得,∴所求抛物线的解析式为:y=﹣x2+x+4;(2)如图1,依题意知AP=t,连接DQ,∵A(﹣3,0),B(4,0),C(0,4),∴AC=5,BC=4,AB=7.∵BD=BC,∴AD=AB﹣BD=7﹣4,∵CD垂直平分PQ,∴QD=DP,∠CDQ=∠CDP.∵BD=BC,∴∠DCB=∠CDB.∴∠CDQ=∠DCB.∴DQ∥BC.∴△ADQ∽△ABC.∴=,∴=,∴=,解得DP=4﹣,∴AP=AD+DP=.∴线段PQ被CD垂直平分时,t的值为;(3)如图2,设抛物线y=﹣x2+x+4的对称轴x=与x轴交于点E.点A、B关于对称轴x=对称,连接BQ交该对称轴于点M.则MQ+MA=MQ+MB,即MQ+MA=BQ,∵当BQ⊥AC时,BQ最小,此时,∠EBM=∠ACO,∴tan∠EBM=tan∠ACO=,∴=,∴=,解ME=.∴M(,),即在抛物线y=﹣x2+x+4的对称轴上存在一点M(,),使得MQ+MA的值最小.。
2012年北京市朝阳区初三数学第一学期期末试题及答案

朝阳区2011~2012学年九年级第一学期期末统一考试数 学 试 卷 2012.1(考试时间120分钟 满分120分)学校 班级 姓名 考号一、选择题(共8个小题,每小题4分,共32分)下列各题均有四个选项,其中只有一个是符合题意的. 1. 下列图形是中心对称图形的是A. B. C. D.2. 已知⊙O 1和⊙O 2的半径分别为4cm 和2cm ,圆心距O 1O 2为6cm ,则这两个圆的位置关系是A .外离B .外切C .相交D .内切3. 如图,已知△ABC 中,AB = AC ,∠ABC =70°,点I 是△ABC 的内心, 则∠BIC 的度数为A. 40°B. 70°C. 110°D. 140° 4. 抛物线1)2(2+-=x y 是由抛物线2x y =平移得到的,下列对于 抛物线2x y =的平移过程叙述正确的是A .先向右平移2个单位,再向上平移1个单位B .先向右平移2个单位,再向下平移1个单位 (第3题图)C .先向左平移2个单位,再向上平移1个单位D .先向左平移2个单位,再向下平移1个单位5. 如图,⊙O 的半径OC 垂直于弦AB , D 是优弧AB 上的一点(不与点A 、B 重合),若∠AOC =50°,则∠CDB 等于A .25°B .30°C .40°D .50° (第5题图)6. 如图是一个照相机成像的示意图,如果底片AB 宽40mm ,焦距是60mm ,所拍摄的2m 外的 景物的宽CD 为A .12mB .3mC .23m D .34m(第6题图)7. △ABC 在平面直角坐标系中的位置如图所示, 其中A (1, 2),B (1, 1),C (3, 1),将△ABC 绕原点O 顺时针旋转90 后得到△'''C B A ,则点A 旋转到点'A 所经过的路线长为 A .π25 B .π45C .π25 D .2(第7题图)8. 如图,Rt △ABC 中,∠C =90°,AC =3,BC =4,P 是斜边AB 上一动点(不与点A 、B 重合),PQ ⊥AB 交△ABC 的直角边于点Q ,设AP 为x ,△APQ 的面积为y ,则下列图象中,能表示 y 关于x 的函数关系的图象大致是A. B. C.D. 二、填空题(共4个小题,每小题4分,共16分)9.如图,△ABC 为等边三角形,D 是△ABC 内一点,且AD =3,将△ABD 绕点A 旋转到△ACE 的位置,连接DE ,则DE 的长为 .(第9题图) (第10题图) (第11题图)10. 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若该圆的半径为1,扇形的圆心角等于60°,则这个扇形的半径R 的值是 .11. 如图,梯形ABCD 中,AD ∥BC ,∠C =90°,AB =AD =4,BC =6,以点A 为圆心在这个梯形内画出一个最大的扇形(图中阴影部分),则这个扇形的面积是 .12. 古希腊著名的毕达哥拉斯学派把1,3,6,10 ,… 这样的数称为“三角形数”(如图①),而把1,4,9,16,…这样的数称为“正方形数”(如图②). 如果规定11a =,23a =,36a =,410a =,…;11b =,24b =,39b =,416b =,…;1112y a b =+,2222y a b =+,3332y a b =+,4442y a b =+,…,那么,按此规定,=6y ,n y = (用含n 的式子表示,n 为正整数).y5Ox14916图②图①10631y5O三、解答题(共13个小题,共72 分) 13.(本小题满分5分)计算:︒-︒+︒30cos 245sin 60tan 2.14.(本小题满分5分)如图,已知4=AC ,求AB 和BC 的长.15.(本小题满分5分)如图,□ABCD 中,点E 在BA 的延长线上,连接CE ,与AD 相交于点F . (1)求证:△EBC ∽△CDF ;(2)若BC =8,CD =3,AE =1,求AF 的长.16.(本小题满分4分)如图,在平面直角坐标系中,△ABC 和△'''C B A 是以坐标原点O 为位似中心的位似图形,且点B (3,1),B ′(6,2). (1)若点A (25,3),则A ′的坐标为 ;(2)若△ABC 的面积为m ,则△A ′B ′C ′的面积= .A二次函数2y ax bx c =++的部分图象如图所示,其中图象与x 轴交于点A (-1,0),与y 轴交于点C (0,-5),且经过点D (3,-8).(1)求此二次函数的解析式;(2)将此二次函数的解析式写成2()y a x h k =-+的形式,并直接写出此二次函数图象的顶点坐标以及它与x 轴的另一个交点B的坐标.18. (本小题满分5分)经过18个月的精心酝酿和290多万首都市民投票参与,2011年11月1日,“北京精神”表述语“爱国、创新、包容、厚德”正式向社会发布. 为了更好地宣传“北京精神”,小明同学参加了由街道组织的百姓宣讲小分队,利用周末时间到周边社区发放宣传材料. 第一周发放宣传材料300份,第三周发放宣传材料363份. 求发放宣传材料份数的周平均增长率.19. (本小题满分5分)如图,CD 与AB 是⊙O 内两条相交的弦,且AB 为⊙O 的直径,CE ⊥AB 于点E ,CE=5,连接AC 、BD .(1)若135sin =D ,则cos A = ; (2)在(1)的条件下,求BE 的长.小红在学习了教科书上相关内容后自制了一个测角仪(图①),并尝试用它来测量校园内一座教学楼CD 的高度(如图②).她先在A 处测得楼顶C 的仰角=α30°,再向楼的方向直行10米到达B 处,又测得楼顶C 的仰角=β60°,若小红的目高(眼睛到地面的高度)AE 为1.60米,请你帮助她计算出这座教学楼CD 的高度(结果精确到0.1米,参考数据:41.12≈,73.13≈,24.25≈).图① 图②21.(本小题满分5分)已知抛物线4)1(21-+++=m x m x y 与x 轴交于A 、B 两点(点A 在点B 且对称轴为x =-1. (1)求m 的值; (2)画出这条抛物线;(2)若直线b kx y +=2过点B 且与抛物线交于点P (-2m ,-3m ),根据图象回答:当x 取 什么值时,1y ≥2y .22. (本小题满分6分)某超市销售一款进价为50元/个的书包,物价部门规定这款书包的售价不得高于70元/个,市场调查发现:以60元/个的价格销售,平均每周销售书包100个;若每个书包的销售价格每提高1元,则平均每周少销售书包2个.(1)求该超市这款书包平均每周的销售量y (个)与销售价x (元/个)之间的函数关系式;(2)求该超市这款书包平均每周的销售利润w (元)与销售价x (元/个)之间的函数关系式;(3)当每个书包的销售价为多少元时,该超市这款书包平均每周的销售利润最大?最大利润是多少元?CBCA23.(本小题满分6分)如图,在△ABC 中,∠ACB =90°,O 为BC 边上一点,以O 为圆心,OB 为半径作半圆与AB 边和BC 边分别交于点D 、点E ,连接CD ,且CD =CA ,BD =56,tan ∠ADC =2. (1)求证:CD 是半圆O 的切线; (2)求半圆O 的直径; (3)求AD 的长.24. (本小题满分8分)已知,在△ABC 中,∠BAC =90°,AB =AC ,BC =22,点D 、E 在BC 边上(均不与点B 、C 重合,点D 始终在点E 左侧),且∠DAE =45°.(1)请在图①中找出两对相似但不全等的三角形,写在横线上 , ; (2)设BE =m ,CD =n ,求m 与n 的函数关系式,并写出自变量n 的取值范围; (3)如图②,当BE =CD 时,求DE 的长;(4)求证:无论BE 与CD 是否相等,都有DE 2=BD 2+CE 2.图① 图② 备用图25.(本小题满分8分)已知抛物线y =ax 2+bx +6与x 轴交于A 、B 两点(点A 在原点的左侧,点B 在原点的右侧),与y 轴交于点C ,且OB=21OC ,tan ∠ACO =61,顶点为D .(1)求点A 的坐标.(2)求直线CD 与x 轴的交点E 的坐标.(3)在此抛物线上是否存在一点F ,使得以点A 、C 、E 、F 为顶点的四边形是平行四边形?若存在,请求出点F 的坐标;若不存在,请说明理由. (4)若点M (2,y )是此抛物线上一点,点N 是直线AM 上方的抛物线上一动点,当点N 运动到什么位置时,四边形ABMN 的面积S 最大? 请求出此时S 的最大值和点N 的坐标.(5)点P 为此抛物线对称轴上一动点,若以点P 为圆心的圆与(4)中的直线AM 及x 轴同时相切,则此时点P 的坐标为 .备用图① 备用图②朝阳区2011~2012学年九年级第一学期期末统一考试数学试卷参考答案及评分标准一、选择题(共8个小题,每小题4分,共32分)二、填空题(共4个小题,每小题4分,共16分) 9. 3 10. 6 11.π4 12. 78,n n +22(每空2分)三、解答题(共13个小题,共72 分) 13.(本小题满分5分) 解: 2322232⨯-⎪⎪⎭⎫⎝⎛+=原式,……………………………………………3分 21=. ……………………………………………………………………5分14.(本小题满分5分)解:作CD ⊥AB 于点D , 在Rt △ACD 中,∵∠A =30°, ∴∠ACD =90°-∠A =60°,221==AC CD ,32cos =⋅=A AC AD . ……………………………………………………………3分在Rt △CDB 中,∵∠DCB =∠ACB -∠ACD =45°,∴2==CD BD ,2245sin =︒=CD BC . …………………………………………………………………4分∴322+=+=BD AD AB .…………………………………………………………5分15.(本小题满分5分)(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AB∥CD .∴△EAF ∽△EBC ,△EAF ∽△CDF . ……………………………………………2分 ∴△EBC ∽△CDF . …………………………………………………………………3分(2)解:∵△EAF ∽△EBC ,∴BCAF EBEA =,即8311AF =+.解得2=AF . …………………………………………………………………………5分16. (本小题满分4分) (1)(5,6);…………………………………………………………………………………2分(2) 4m . ……………………………………………………………………………………4分17. (本小题满分5分) 解:(1)由题意,有⎪⎩⎪⎨⎧-=++-==+-.839,5,0c b a c c b a 解得 ⎪⎩⎪⎨⎧-=-==.5,4,1c b a ∴此二次函数的解析式为542--=x x y . …………………………………2分(2)9)2(2--=x y ,顶点坐标为(2,-9),B (5,0). …………………………5分18. (本小题满分5分)解:设发放宣传材料份数的周平均增长率为x ,由题意,有.363)1(3002=+x …………………………………………………………………3分 解得 1.01=x ,1.22-=x . …………………………………………………………4分 ∵1.2-=x <0,不符合题意,舍去,∴%101.0==x . ……………………………………………………………………5分 答:这两次发放材料数的平均增长率为10%.19. (本小题满分5分) (1)1312. …………………………………………………………………………………2分(2)解:如图,连接BC .∵AB 为⊙O 的直径,∴∠ACB =90°.∴由(1)知AC =13, 12=AE ,1312cos =A .在Rt △ACB 中,ABAC A =cos ,∴12169=AB . ………………………………………………………………………4分∴1225=-=AE AB BE . …………………………………………………………5分20.(本小题满分5分)解:∵=α30°,=β60°,∴∠ECF =αβ-=30°. ∴10==EF CF .在Rt △CFG 中,.35cos =⋅=βCF CG ……………………………………………3分 ∴3.106.135≈+=+=GD CG CD . ………………………………………………5分 答:这座教学楼的高度约为10.3米.21.(本小题满分5分)解:(1)由题意,有121-=+-m ,解得m =1. ……………………………………………………………2分(2)如图1;A(3)如图2,x ≤-2或x ≥1. ……………………………………………………………5分22.(本小题满分6分)解:(1)由题意,有 )60(2100--=x y ,即2202+-=x y ;………………………………………………………………………2分 (2)由题意,有 )2202)(50(+--=x x w ,即1100032022-+-=x x w ;…………………………………………………………4分(3)∵抛物线1100032022-+-=x x w 的开口向下,在对称轴80=x 的左侧,w 随x 的增大而增大. 由题意可知7060≤≤x ,………………………………………………………………5分 ∴当70=x 时,w 最大为1600. ………………………………………………………6分 因此,当每个书包的销售价为70元时,该超市可以获得每周销售的最大利润1600元.23.(本小题满分6分) (1)证明:如图,连接OD ,∵OD =OB ,∴∠1=∠2. ∵CA =CD ,∴∠ADC =∠A . 在△ABC 中,∵∠ACB =90°,∴∠A +∠1=90°. ∴∠ADC +∠2=90°. ∴∠CDO =90°. ∵OD 为半圆O 的半径,∴CD 为半圆O 的切线. ………………………………………………………………2分 (2)解:如图,连接DE .∵BE 为半圆O 的直径, ∴∠EDB =90°. ∴∠1+∠3=90°. ∴∠ADC =∠3. ∴23tan ==∠EDBD .∴53=ED . ∴1522=+=DEBDEB . ………………………………………………………4分(3)解:作CF ⊥AD 于点F ,∴AF =DF .设x DF =,BPA∵2tan =∠ADC ,∴CF =2x .∵∠1+∠FCB =90°,∴ADC FCB ∠=∠.∴2tan =∠FCB . ∴FB =4x .∴BD =3 x =56. 解得52=x .∴A D =2D F =2x =54. ……………………………………………………………6分24.(本小题满分8分)解:(1)△ADE ∽△BAE ,△ADE ∽△CDA ,△BAE ∽△CDA ;(写出任意两对即可)(2)∵∠BAC =90°,AB =AC ,BC =22,由(1)知 △BAE ∽△CDA , ∴CA BE CD BA =. ∴22mn =. ∴n m 4= (222<<n ). ……………………………………4分(3)由(2)只BE·CD =4,∴BE =CD =2.∴BD =BC -CD =222-.∴DE =BE -BD =224-.………………………………………………………5分(4)如图,依题意,可以将△AEC 绕点A 顺时针旋转90°至△AFB 的位置,则FB =CE ,AF =AE ,∠1=∠2,∴∠FBD =90°.∴22222CE BD FB BD DF +=+=. (6)∵∠3+∠1=∠3+∠2=45°,∴∠FAD =∠DAE .又∵AD =AD ,AF =AE ,∴△AFD ≌△AED .∴DE =DF . ………………………………………………………………………7分 ∴222CE BD DE +=. …………………………………………………………8分25.(本小题满分8分)解:(1)根据题意,得C (0,6).在Rt △AOC 中,61tan =∠ACO ,OC =6,∴OA =1. ∴A (-1,0). ……………………………………………………………1分(2)∵OC OB 21=,∴OB =3. ∴B (3,0).由题意,得 ⎩⎨⎧=++=+-.0639,06b a b a 解得 ⎩⎨⎧=-=.4,2b a ∴6422++-=x x y .∴D (1,8). ……………………………………………………………………2分 可求得直线CD 的解析式为62+=x y .∴E (-3,0). ……………………………………………………………………3分(3)假设存在以点A 、C 、F 、E 为顶点的平行四边形,则F 1(2,6),F 2(-2,6),F 3(-4,-6).经验证,只有点(2,6)在抛物线6422++-=x x y 上,∴F (2,6). ………………………………………………………………………4分(4)如图,作NQ ∥y 轴交AM 于点Q ,设N (m , 6422++-m m ).当x =2时,y =6,∴M (2,6).可求得直线AM 的解析式为22+=x y .∴Q (m ,2m +2).∴NQ =422)22(64222++-=+-++-m m m m m .∵AMN ABM S S S ∆∆+=,其中126421=⨯⨯=∆ABM S , ∴当AMN S ∆最大时,S 值最大.∵MNQ ANQ AMN S S S ∆∆∆+=)422(3212++-⨯⨯=m m ,6332++-=m m ,427)21(32+--=m . ∴当21=m 时,AMN S ∆的最大值为427. ∴S 的最大值为475.……………………………………………………………………6分 当21=m 时,2156422=++-m m . ∴N (21,215). ……………………………………………………………………7分(5)P 1(1,15-),P 2(1,15--). …………………………………………8分 说明:写成P 1(1,154+),P 2(1,154--)不扣分.。
2012辽宁朝阳数学中考试题

2012年中考数学试卷(辽宁朝阳卷)(本试卷满分150分,考试时间120分钟)一、选择题(共8小题,每小题3分,共24分)1.有理数地绝对值为【】A. B. -5 C. D.52.下列运算正确地是【】A. B. C. D.3.如图,C、D分别EA、EB为地中点,∠E=300,∠1=1100,则∠2地度数为【】A. B. C. D.4.为鼓励大学生创业,我市为在开发区创业地每位大学生提供无息贷款125000元,这个数据用科学计数法表示为(保留两位有效数字)【】A. B. C. D.5.两个大小不同地球在水平面上靠在一起,组成如图所示地几何体,则该几何体地俯视图是【】A.两个外离地圆B. 两个相交地圆C. 两个外切地圆D. 两个内切地圆6.某市5月上旬地最高气温如下(单位:℃):28、29、31、29、33,对这组数据,下列说法错误地是【】A.平均数是30B. 众数是29C. 中位数是31D. 极差是57.下列图形中,既是轴对称图形又是中心对称图形地是【】8.如图,矩形ABCD地对角线BD经过坐标原点,矩形地边分别平行于坐标轴,点C在反比例函数地图象上,若点A 地坐标为(-2,-3),则k地值为【】A.1B. -5C. 4D. 1或-5二、填空题(共8小题,每小题3分,共24分)9.函数中,自变量x地取值范围是▲ .10.分解因式▲ .11.如图,AB为⊙O地直径,CD为⊙O地一条弦,CD⊥AB,垂足为E,已知CD=6,AE=1,则⊙O地半径为▲ .12.一元二次方程有两个不相等地实数根,则a地取值范围为▲ .13.如图所示地折线ABC为甲地向乙地打长途电话需付地电话费y(元)与通话时间t(分钟)之间地函数关系,则通话8分钟应付电话费▲元.14.如图,△ABC三个顶点都在5×5地网格(每个小正方形地边长均为1单位长度)地格点上,将△ABC 绕点C顺时针旋转到△A′B′C地位置,且A′、B′仍落在格点上,则线段AC扫过地扇形所围成地圆锥体地底面半径是▲单位长度.15.下列说法中正确地序号有▲ .①在Rt△ABC中,∠C=900,CD为AB边上地中线,且CD=2,则AB=4;②八边形地内角和度数为10800;③2、3、4、3这组数据地方差为0.5;④分式方程地解为;⑤已知菱形地一个内角为600,一条对角线为,则另一对角线为2.16.如图,在正方形ABCD内有一折线,其中AE⊥EF,EF⊥FC,并且AE=4,EF=8,FC=12.则正方形与其外接圆形成地阴影部分地面积为▲ .三、解答题(共10小题,满分102分)17.计算(先化简,再求值):,其中.18.如图,在四边形ABCD中,E是BC边地中点,连接DE并延长,交AB地延长线于点F点,AB=BF,请你添加一个条件(不需再添加任何线段或字母),使之能推出四边形ABCD为平行四边形,请证明.你添加地条件是▲ .19.某中学为了解本校学生对球类运动地爱好情况,采用抽样地方法,从乒乓球、羽毛球、篮球和排球四个方面调查了若干名学生,在还没有绘制成功地“折线统计图”与“扇形统计图”中,请你根据已提供地部分信息解答下列问题.(1)在这次调查活动中,一共调查了▲名学生,并请补全统计图.(2)“羽毛球”所在地扇形地圆心角是▲度.(3)若该校有学生1200名,估计爱好乒乓球运动地约有多少名学生?20.如图,四边形ABCD是正方形,点E是边BC上一动点(不与B、C重合).连接AE,过点E作EF⊥AE,交DC于点F.(1)求证:△ABE∽△ECF;(2)连接AF,试探究当点E在BC什么位置时,∠BAE=∠EAF,请证明你地结论.21.在不透明地箱子里放有4个乒乓球.每个乒乓球上分别写有数字1、2、3、4,从箱子中摸出一个球记下数字后放回箱中,摇匀后再摸出一个球记下数字.若将第一次摸出地球上地数字记为点地横坐标,第二次摸出地球上地数字记为点地纵坐标.(1)请用列表法或树状图法写出两次摸球后所有可能地结果;(2)求这样地点落在如图所示地圆中地概率(注:图中圆心在直角坐标系中地第一象限内,并且分别与x轴、y轴切于点(2,0和(0,2))两点).22.如图已知P为⊙O外一点.PA为⊙O地切线,B为⊙O上一点,且PA=PB,C为优弧上任意一点(不与A、B重合),连接OP、AB,AB与OP相交于点D,连接AC、BC.(1)求证:PB为⊙O地切线;(2)若,⊙O地半径为,求弦AB地长.23.为支持抗震救灾,我市A、B两地分别地赈灾物资100吨和180吨.需全部运往重灾区C、D两县,根据灾区地情况,这批赈灾物资运往C县地数量比运往D县地数量地2倍少80吨.(1)求这批赈灾物资运往C、D两县地数量各是多少吨?(2)设A地运往C县地赈灾物资为x吨(x为整数),若要B地运往C县地赈灾物资数量大于A地运往D县地赈灾物资数量地2倍,且要求B地运往D县地赈灾物资数量不超过63吨,则A、B两地地赈灾物资运往C、D两县地方案有几种?24.一轮船在P处测得灯塔A在正北方向,灯塔B在南偏东24.50方向,轮船向正东航行了2400m,到达Q处,测得A位于北偏西490方向,B位于南偏西410方向.(1)线段BQ与PQ是否相等?请说明理由;(2)求A、B间地距离(参考数据cos410=0.75).25.某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,在第一个月地试销时间内发现.销量w(kg)随销售单价x(元/ kg)地变化而变化,具体变化规律如下表所示设该绿茶地月销售利润为y(元)(销售利润=单价×销售量-成本-投资).(1)请根据上表,写出w与x之间地函数关系式(不必写出自变量x地取值范围);(2)求y与x之间地函数关系式(不必写出自变量x地取值范围),并求出x为何值时,y地值最大?(3)若在第一个月里,按使y获得最大值地销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于90元,要想在全部收回投资地基础上使第二个月地利润达到1700,那么第二个月时里应该确定销售单价为多少元?26.已知,如图,在平面直角坐标系中,Rt△ABC地斜边BC在x轴上,直角顶点A在y轴地正半轴上,A(0,2),B(-1,0).(1)求点C地坐标;(2)求过A、B、C三点地抛物线地解读式和对称轴;(3)设点P(m,n)是抛物线在第一象限部分上地点,△PAC地面积为S,求S关于m地函数关系式,并求使S最大时点P地坐标;(4)在抛物线对称轴上,是否存在这样地点M,使得△MPC(P为上述(3)问中使S最大时点)为等腰三角形?若存在,请直接写出点M地坐标;若不存在,请说明理由.2012年中考数学试卷(辽宁朝阳卷)(本试卷满分150分,考试时间120分钟)一、选择题(共8小题,每小题3分,共24分)1.有理数地绝对值为【】A. B. -5 C. D.5【答案】A.2.下列运算正确地是【】A. B. C. D.【答案】C.3.如图,C、D分别EA、EB为地中点,∠E=300,∠1=1100,则∠2地度数为【】A. B. C. D.【答案】A.4.为鼓励大学生创业,我市为在开发区创业地每位大学生提供无息贷款125000元,这个数据用科学计数法表示为(保留两位有效数字)【】A. B. C. D.【答案】C.5.两个大小不同地球在水平面上靠在一起,组成如图所示地几何体,则该几何体地俯视图是【】A.两个外离地圆B. 两个相交地圆C. 两个外切地圆D. 两个内切地圆【答案】C.6.某市5月上旬地最高气温如下(单位:℃):28、29、31、29、33,对这组数据,下列说法错误地是【】A.平均数是30B. 众数是29C. 中位数是31D. 极差是5【答案】C.7.下列图形中,既是轴对称图形又是中心对称图形地是【】【答案】A.8.如图,矩形ABCD地对角线BD经过坐标原点,矩形地边分别平行于坐标轴,点C在反比例函数地图象上,若点A 地坐标为(-2,-3),则k地值为【】A.1B. -5C. 4D. 1或-5【答案】D.二、填空题(共8小题,每小题3分,共24分)9.函数中,自变量x地取值范围是▲ .【答案】.10.分解因式▲ .【答案】.11.如图,AB为⊙O地直径,CD为⊙O地一条弦,CD⊥AB,垂足为E,已知CD=6,AE=1,则⊙O地半径为▲ .【答案】5.12.一元二次方程有两个不相等地实数根,则a地取值范围为▲ .【答案】a<且a≠0.13.如图所示地折线ABC为甲地向乙地打长途电话需付地电话费y(元)与通话时间t(分钟)之间地函数关系,则通话8分钟应付电话费▲元.【答案】7.4.14.如图,△ABC三个顶点都在5×5地网格(每个小正方形地边长均为1单位长度)地格点上,将△ABC 绕点C顺时针旋转到△A′B′C地位置,且A′、B′仍落在格点上,则线段AC扫过地扇形所围成地圆锥体地底面半径是▲单位长度.【答案】.15.下列说法中正确地序号有▲ .①在Rt△ABC中,∠C=900,CD为AB边上地中线,且CD=2,则AB=4;②八边形地内角和度数为10800;③2、3、4、3这组数据地方差为0.5;④分式方程地解为;⑤已知菱形地一个内角为600,一条对角线为,则另一对角线为2.【答案】①②③④.16.如图,在正方形ABCD内有一折线,其中AE⊥EF,EF⊥FC,并且AE=4,EF=8,FC=12.则正方形与其外接圆形成地阴影部分地面积为▲ .【答案】.三、解答题(共10小题,满分102分)17.计算(先化简,再求值):,其中.【答案】解:原式=,当时,原式=.18.如图,在四边形ABCD中,E是BC边地中点,连接DE并延长,交AB地延长线于点F点,AB=BF,请你添加一个条件(不需再添加任何线段或字母),使之能推出四边形ABCD为平行四边形,请证明.你添加地条件是▲ .【答案】解:添加地条件是:∠F=∠CDE(答案不唯一).理由如下:∵∠F=∠CDE,∴CD∥AF.在△DEC与△FEB中,∵∠DCE=∠EBF,CE=BE,∠CED=∠BEF,∴△DEC≌△FEB(AAS).∴DC=BF.∵AB=BF,∴DC=AB,∴四边形ABCD为平行四边形.19.某中学为了解本校学生对球类运动地爱好情况,采用抽样地方法,从乒乓球、羽毛球、篮球和排球四个方面调查了若干名学生,在还没有绘制成功地“折线统计图”与“扇形统计图”中,请你根据已提供地部分信息解答下列问题.(1)在这次调查活动中,一共调查了▲名学生,并请补全统计图.(2)“羽毛球”所在地扇形地圆心角是▲度.(3)若该校有学生1200名,估计爱好乒乓球运动地约有多少名学生?【答案】解:(1)200.∵喜欢篮球地人数:200×20%=40(人),喜欢羽毛球地人数:200-80-20-40=60(人);喜欢排球地20人,应占,喜欢羽毛球地应占统计图地1-20%-40%-10%=30%.∴根据以上数据补全统计图:(2)108°.(3)该校1200名学生中估计爱好乒乓球运动地约有:40%×1200=480(人).20.如图,四边形ABCD是正方形,点E是边BC上一动点(不与B、C重合).连接AE,过点E作EF⊥AE,交DC于点F.(1)求证:△ABE∽△ECF;(2)连接AF,试探究当点E在BC什么位置时,∠BAE=∠EAF,请证明你地结论.【答案】解:(1)证明:∵四边形ABCD是正方形,∴∠B=∠C=90°.∴∠BAE+∠BEA=90°.∵EF⊥AE,∴∠AEF=90°.∴∠BEA+∠FEC=90°.∴∠BAE=∠FEC.∴△ABE∽△ECF.(2)E是中点时,∠BAE=∠EAF.证明如下:连接AF,延长AE于DC地延长线相交于点H,∵E为BC中点,∴BE=CE.∵AB∥DH,∴∠B=∠ECH.∵∠AEB=∠CEH,∴△ABE≌△HCE(AAS).∴AE=EH.∵EF⊥AH,∴△AFH是等腰三角形.∴∠EAF=∠H.∵AB∥DH,∴∠H=∠BAE.∴∠BAE=∠EAF.∴当点E在BC中点位置时,∠BAE=∠EAF.21.在不透明地箱子里放有4个乒乓球.每个乒乓球上分别写有数字1、2、3、4,从箱子中摸出一个球记下数字后放回箱中,摇匀后再摸出一个球记下数字.若将第一次摸出地球上地数字记为点地横坐标,第二次摸出地球上地数字记为点地纵坐标.(1)请用列表法或树状图法写出两次摸球后所有可能地结果;(2)求这样地点落在如图所示地圆中地概率(注:图中圆心在直角坐标系中地第一象限内,并且分别与x轴、y轴切于点(2,0和(0,2))两点).【答案】解:(1)列表得:∴共有16种等可能地结果.(2)∵这样地点落在如图所示地圆内地有:(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)9点(如图),∴这样地点落在如图所示地圆内地概率为:.22.如图已知P为⊙O外一点.PA为⊙O地切线,B为⊙O上一点,且PA=PB,C为优弧上任意一点(不与A、B重合),连接OP、AB,AB与OP相交于点D,连接AC、BC.(1)求证:PB为⊙O地切线;(2)若,⊙O地半径为,求弦AB地长.【答案】解:(1)证明:如图,连接OA,OB,∵AP为圆O地切线,∴OA⊥AP,即∠OAP=90°.在△OAP和△OBP中,∵AP=BP(已知),OA=OB(半径相等),OP=OP(公共边),∴△OAP≌△OBP(SSS).∴∠OAP=∠OBP=90°.∴OB⊥BP,即BP为圆O地切线.(2)延长线段BO,与圆O交于E点,连接AE,∵BE为圆O地直径,∴∠BAE=90°.∵∠AEB和∠ACB都对,∴∠AEB=∠ACB.∴.设AB=2x,则AE=3x,在Rt△AEB中,BE=,根据勾股定理得:.解得:x=2或x=-2(舍去).∴AB=2x=4.23.为支持抗震救灾,我市A、B两地分别地赈灾物资100吨和180吨.需全部运往重灾区C、D两县,根据灾区地情况,这批赈灾物资运往C县地数量比运往D县地数量地2倍少80吨.(1)求这批赈灾物资运往C、D两县地数量各是多少吨?(2)设A地运往C县地赈灾物资为x吨(x为整数),若要B地运往C县地赈灾物资数量大于A地运往D县地赈灾物资数量地2倍,且要求B地运往D县地赈灾物资数量不超过63吨,则A、B两地地赈灾物资运往C、D两县地方案有几种?【答案】解:(1)设运往C县地物资是a吨,D县地物资是b吨,根据题意得,,解得.答:这批赈灾物资运往C、D两县地数量各是160吨,120吨.(2)∵A地运往C县地赈灾物资数量为x吨,∴B地运往C县地物资是(160-x)吨,A地运往D县地物资是(100-x)吨,B地运往D县地物资是120-(100-x)=(20+x)吨,根据题意得,,解得.∴不等式组地解集是40<x≤43.∵x是整数,∴x取41、42、43.∴方案共有3种,分别为:方案一:A地运往C县地赈灾物资数量为41吨,则B地运往C县地物资是119吨,A地运往D县地物资是59吨,B地运往D县地物资是61吨;方案二:A地运往C县地赈灾物资数量为42吨,则B地运往C县地物资是118吨,A地运往D县地物资是58吨,B地运往D县地物资是62吨;方案三:A地运往C县地赈灾物资数量为43吨,则B地运往C县地物资是117吨,A地运往D县地物资是57吨,B地运往D县地物资是63吨.24.一轮船在P处测得灯塔A在正北方向,灯塔B在南偏东24.50方向,轮船向正东航行了2400m,到达Q处,测得A位于北偏西490方向,B位于南偏西410方向.(1)线段BQ与PQ是否相等?请说明理由;(2)求A、B间地距离(参考数据cos410=0.75).【答案】解:(1)线段BQ与PQ相等.理由如下:∵∠PQB=90°-41°=49°,∠BPQ=90°-24.5°=65.5°,∴∠PBQ=180°-49°-65.5°=65.5°.∴∠BPQ=∠PBQ.∴BQ=PQ.(2)∵∠AQB=180°-49°-41°=90°,∠PQA=90°-49°=41°,∴.∵BQ=PQ=2400,∴.答:A、B地距离为4000m.25.某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,在第一个月地试销时间内发现.销量w(kg)随销售单价x(元/ kg)地变化而变化,具体变化规律如下表所示设该绿茶地月销售利润为y(元)(销售利润=单价×销售量-成本-投资).(1)请根据上表,写出w与x之间地函数关系式(不必写出自变量x地取值范围);(2)求y与x之间地函数关系式(不必写出自变量x地取值范围),并求出x为何值时,y地值最大?(3)若在第一个月里,按使y获得最大值地销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于90元,要想在全部收回投资地基础上使第二个月地利润达到1700,那么第二个月时里应该确定销售单价为多少元?【答案】解:(1)w=-2x+240.(2)y与x地关系式为:∵,∴当x=85时,y地值最大为2450元.(3)∵在第一个月里,按使y获得最大值地销售单价进行销售所获利润为2450元,∴第1个月还有3000-2450=550元地投资成本没有收回.则要想在全部收回投资地基础上使第二个月地利润达到1700元,即y=2250才可以,可得方程,解得x1=75,x2=95.根据题意,x2=95不合题意应舍去.答:当销售单价为75元时,可获得销售利润2250元,即在全部收回投资地基础上使第二个月地利润达到1700元.26.已知,如图,在平面直角坐标系中,Rt△ABC地斜边BC在x轴上,直角顶点A在y轴地正半轴上,A(0,2),B(-1,0).(1)求点C地坐标;(2)求过A、B、C三点地抛物线地解读式和对称轴;(3)设点P(m,n)是抛物线在第一象限部分上地点,△PAC地面积为S,求S关于m地函数关系式,并求使S最大时点P地坐标;(4)在抛物线对称轴上,是否存在这样地点M,使得△MPC(P为上述(3)问中使S最大时点)为等腰三角形?若存在,请直接写出点M地坐标;若不存在,请说明理由.【答案】解:(1)∵A(0,2),B(-1,0),∴OA=2,OB=1.由Rt△ABC知Rt△ABO∽Rt△CAO,∴,即,解得OC=4.∴点C地坐标为(4,0).(2)设过A、B、C三点地抛物线地解读式为,将A(0,2)代入,得,解得.∴过A、B、C三点地抛物线地解读式为,即.∵,∴抛物线地对称轴为.(3)过点P作x轴地垂线,垂足为点H.∵点P(m,n)在上,∴P.∴,,.∴ .∵,∴当时,S最大.当时,.∴点P地坐标为(2,3).(4)存在.点M地坐标为()或()或()或()或().。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市朝阳区九年级综合练习(二)数学试卷 2012.6学校 班级 姓名 考生须知 1.本试卷共6页,共五道大题,25道小题,满分120分. 考试时间120分钟. 2.在试卷和答题卡上准确填写学校名称、班级、姓名和准考证号.3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效. 4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答.5.考试结束,将本试卷、答题卡和草稿纸一并交回.一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的. 1.3的算术平方根是A .3B .3±C .3D .±32.2012年1月21日,北京市环保监测中心开始在其官方网站上公布PM2.5的研究性监测数据. PM2.5是指大气中直径小于或等于0.0000025米即2.5微米的颗粒物,也称为可入肺颗粒物. 把0.0000025用科学记数法表示为A .51025.0-⨯ B. 5105.2-⨯ C .6105.2-⨯ D. 71025-⨯3. 掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷得朝上一面的点数小于3的概率为A .21 B .31 C .41 D .614.如图,直线m ∥n ,直角三角板ABC 的顶点A 在直线m 上,则∠α等于A. 19°B. 38°C. 42°D. 52°5.有一组数据:0,2,3,4,6,这组数据的方差是A .3B .4C .6D .20 6.如图,在⊙O 中,直径AB ⊥弦CD 于点H ,E 是⊙O 上的点, 若∠BEC =25°,则∠BAD 的度数为 A. 65° B. 50° C. 25° D. 12.5°DCB AO H E 38°mnαCBA7. 下面由8个完全相同的小正方体组成的几何体的主视图是A B C D8.如图,在平面直角坐标系xOy 中,P 是反比例函数xy 1=(x > 0)图象上的一个动点,点A 在x 轴上,且PO =P A , AB 是PAO △中OP 边上的高.设m OA =,n AB =,则 下列图象中,能表示n 与m 的函数关系的图象大致是 A B C D二、填空题(本题共16分,每小题4分) 9.若分式321-x 有意义,则x 的取值范围是 .10.分解因式:a ax ax 442+-= .11.在平面直角坐标系中,点P (k -2,k )在第二象限,且k 是整数,则k 的值为 . 12.如图,在平面直角坐标系xOy 中,A 1是以O 为圆心,2为半径的圆与过点(0,1)且平行于x 轴的直线l 1的一个交点;A 2是以原点O 为圆心,3为半径的圆与过点(0,-2) 且平行于x 轴的直线l 2的一个交点;A 3是以原点O 为圆心,4为半径的圆与过点(0,3)且平行于x 轴的直线l 3的一个交点;A 4是以原点O 为圆心,5为半径的圆与过点(0,-4)且平行于x 轴的直线l 4的一个交点;……,且点1A 、2A 、3A 、4A 、…都在y 轴右侧,按照这样的规律进行下去,点A 6的坐标为 ,点A n 的坐标为 (用含n 的式子表示,n 是正整数).正面1-1-154321A4A2A 1A 3Ox y l 2l 4l 1l3mn O三、解答题(本题共30分,每小题5分) 13.计算:︒--++-45cos 411812.14.解方程:53412-=+x x.15.已知02=-x y ,求)11(2222yxyxy x y x +⋅++的值.16.已知:如图,点D 、E 分别在AB 、AC 上,BE 与CD 相交于点F ,BD=CE ,∠B =∠C .求证:BE =CD .17.如图,点P (-3,1)是反比例函数m y x=的图象上的一点.(1)求该反比例函数的解析式; (2)设直线y kx =与双曲线m y x=的两个交点分别为P 和P′,当m x<kx 时,直接写出x 的取值范围.18.如图,四边形ABCD 是矩形,AB =3,BC =4,把矩形沿直线AC 折叠,点B 落在点F 处,连接DF ,CF 与AD 相交于点E ,求DE 的长和△ACE 的面积.EFDACBFDBCA E四、解答题(本题共21分,第19、20、21题每小题5分,第22题6分)19.如图,AB 、BF 分别是⊙O 的直径和弦,弦CD 与AB 、BF 分别相交于点E 、G ,过点F的切线HF 与DC 的延长线相交于点H ,且HF =HG . (1)求证:AB ⊥CD ; (2)若sin ∠HGF =43,BF =3,求⊙O 的半径长.20. 2012年4月北京国际汽车展览会期间,某公司对参观本次车展的观众进行了随机调查. ① 根据调查结果,将受访者购置汽车的意愿情况 受访者购置汽车的意愿情况统计图整理后,制成如右侧统计图:② 将有购买家庭用汽车意愿的受访者的购车预算情况整理后,作出相应的统计表和频数分布直方图: (注:每组包含最小值不包含最大值)有购买家庭用汽车意愿的受访者的购车预算情况统计表、图请你根据以上信息,回答下列问题: (1)统计表中的c = ,d = ; (2)补全频数分布直方图;(3)这次调查中一共调查了 位参观者.购车预算(万元)频数 频率 0~5 20 0.05 5~10 a 0.13 10~15 152 0.38 15~20 b d 20~25 28 0.07 25~30 24 0.06 合计c1无购买汽车意愿 5%有购买商务用汽车意愿15%有购买家庭用汽车意愿DH C E G FB OA 8012016040(人)频数20152282430购车预算(万元)202515105021.如图,港口B 在港口A 的东北方向,上午9时,一艘轮船从港口A 出发,以16海里/时的速度向正东方向航行,同时一艘快艇从港口B 出发也向正东方向航行.上午11时轮船到达C 处,同时快艇到达D 处,测得D 处在C 处的北偏东60°的方向上,且C 、D 两地相距80海里,求快艇每小时航行多少海里?(结果精确到0.1海里/时,参考数据:414.12≈,732.13≈,236.25≈)22.已知二次函数c x x y ++=22.(1)当c =-3时,求出该二次函数的图象与x 轴的交点坐标;(2)若-2<x <1时,该二次函数的图象与x 轴有且只有一个交点,求c 的取值范围.五、解答题(本题共21分,第23题6分,第24题7分,第25题8分)23.正方形ABCD 的边长为4,点P 是BC 边上的动点,点E 在AB 边上,且∠EPB =60°,沿PE 翻折△EBP 得到△P EB '. F 是CD 边上一点,沿PF 翻折△FCP 得到△P FC ',使点'C 落在射线'PB 上.(1)如图,当BP =1时,四边形''FC EB 的面积为 ;(2)若BP =m ,则四边形''FC EB 的面积为 (要求:用含m 的代数式表示,并写出m的取值范围). 备用图DA CB FC'B'PEDACB东60°45°北CDBA24. 如图,D 是△ABC 中AB 边的中点,△BCE 和△ACF 都是等边三角形,M 、N 分别是CE 、CF 的中点.(1)求证:△DMN 是等边三角形;(2)连接EF ,Q 是EF 中点,CP ⊥EF 于点P .求证:DP =DQ . 同学们,如果你觉得解决本题有困难,可以阅读下面 两位同学的解题思路作为参考:小聪同学发现此题条件中有较多的中点,因此考虑构造 三角形的中位线,添加出了一些辅助线;小慧同学想到要证明线段相等,可通过证明三角形全等,如何构造出相应的三角形呢?她考虑将△NCM 绕顶点旋转到要证的对应线段的位置,由此猜想到了所需构造的三角形的位置.25. 在平面直角坐标系xOy 中,抛物线42++=bx ax y 经过A (-3,0)、B (4,0)两点,且与y 轴交于点C ,点D 在x 轴的负半轴上,且BD =BC ,有一动点P 从点A 出发,沿线段AB 以每秒1个单位长度的速度向点B 移动,同时另一个动点Q 从点C 出发,沿线段CA 以某一速度向点A 移动. (1)求该抛物线的解析式;(2)若经过t 秒的移动,线段PQ 被CD 垂直平分,求此时t 的值;(3)该抛物线的对称轴上是否存在一点M ,使MQ +MA 的值最小?若存在,求出点M的坐标;若不存在,请说明理由.NM DEFABCyx-1-3-2-4-512345-1-2-3-412345O。
