非对称密码体制35页PPT
非对称密码体制课件

• 解决了对称密码的诸多局限性
2020/11/18
非对称密码体制
4
非对称密码基本概念:非对称密码体制
明文
加密器 EK
PK
密钥产生器
密文
解密器 DK
SK
明文
• 密钥—(PK, SK) • PK:俗称公钥(Public Key),通常公钥是公开的,可以被任何实 体通过有效渠道获取; • SK:俗称私钥(Secret Key),通常私钥是保密的,不能被任何实 体通过非法渠道获取;
2020/11/18
非对称密码体制
3
非对称密码基本概念:非对称密码的提出
• 对称密码的局限性 • 密钥管理的困难性问题 • 陌生人间的保密通信问题 • 数字签名问题
非对称密码(1976年由W. Diffie和M. Hellman提出)与对称密码的几点 区别:
• 双钥——双钥密码、公钥密码
• 基于数学函数,而非替换和换位
2020/11/18
非对称密码体制
6
非对称密码基本概念:非对称密码的算法组成
密钥生成KG( ) • 根据输入的安全参数 ,输出公钥和私钥对(PK, SK)
• 加密E( ) • 根据输入的公钥和消息,输出密文。
• 解密D( ) • 根据输入的解密私钥和密文,算法输出消息或输出表示密文不合法的特殊符号“?”
明文
加密器 EK
K
密文
解密器 DK
K
明文
密钥产生器
• 密钥管理:若N个人相互保密通信,每人必须拥有(N-1)个私钥,N很 大时,需要保存的私钥很多。如何解决?
• 可信中心分发:共需要发N*(N-1)/2个私钥:例如N =1000时, 999 *1000/2 = 499500
《非对称密码体制》课件

使用扩展欧几里得算法,计算d, 满足d*e % phi(n) = 1。
2. 计算n
计算n=p*q。
4. 选择公钥
选择一个与phi(n)互质的整数e。
6. 完成
完成后,公钥由n和e组成,私钥由d组成。
RSA算法的解密过程
1. 加密数据
使用公钥(n, e)加密消息M,产生密文C。
2. 计算明文
1
1. 选择素数
选择一个素数q, 以及一个大素数p = kq + 1, 保护q。
2
2. 选取g值
选择一个能提供一个循环群的数g(1 <= g <= p-1)。
3
3. 计算x,y
任意选择一个512位的长整数k,然后计算x = g^k mod p, y = (hash(M) + x*a)/k mod q, hash(M)为M的哈希值。
使用私钥d,计算出原始消息M。M = Cd (mod n)
3. 完成
接收方使用私钥d,根据公式计算出M。
RSA算法的安全性分析
RSA算法显然会受到攻击,但我们认为这个算法还是安全的。攻击者可以使用因子分解算法来破解RSA 算法,但是这需要一个非常长的时间。对于RSA算法安全保护的加强,一般使用扩展和混淆技术。
非对称密码的优势
提高了数据传输的安全性, 避免了密钥管理的麻烦。
小提示
有时候也会将它们结合使 用,来发挥它们的优势。
典型的非对称密码算法
目前最流行的非对称密码算法有:RSA算法、DSA算法、ECC算法等。下图是其概述:
RSA算法
使用65000位的密钥。在加密 时使用一个公钥,但需要一个 私钥才能进行解密。
非对称密码体制
非对称密码体制

ElGamal加密算法
E密lG钥a对ma产l算生法办既法能用于数据加密也能用于数字签名 的 非首对先称选择加一密个算素法数p,两个随机正整数, g 和x,g, x < p,
E计lG算amya=l算gx法m的od安p全,性则依其赖公于钥计为算y,有g 限和域p;上x离是散私对钥数;这g和一p 难可题由。一组用户共享。
Hash算法 摘要1 +时间
加了时 间后的 新摘要
数字 时间戳
用DTS机构的私钥加密
DTS机构
网络安全与电子商务
网络安全与电子商务
非对称密码体制
非对称密码体制
非对称密码体制的特点 非对称密码体制的原理 非对称加密算法
非对称密码体制的应用模型
非对称密码体制的产生和特点
由Diffie 和Hellman 于1976年首次提出了用于对称密钥交换的公钥算法。 1977年Rivest, Shamir & Adleman 提出了著名的RSA公钥算法。 非对称密码体制的特点
ElG美am国a的l加DS密S(过Dig程ital Signature Standard)中的DSA(Digital
S设ig被na加tu密re A信lg息or为ithMm,)算首法先是选经择E一lG个am随al机算数法k演,变k<而p-来1,。计
密钥算对C1产=gk生m办od法p,C2=ykM mod p。
因此,使用非对称加密,明文信息必须转化成足够大的数 才能保证私钥的不可破译。
明文信息
二进制字符串 10进制大数
DOG
010001000100 111101000111
446743
RSA加密算法
择钥大私的钥质对数p的和生q,成并、得加到密n=p以*q及。数(由字于签p名和q。非常大,所以由n几
精品课件-应用密码学-第5章 非对称密码(3)

2020/11/19
15
1155
图5-1 y2≡x3+x+6所表示的曲线 图5-4 y2≡x3+x+6 (mod 11)所表示的曲线
通过比较y2≡x3+x+6在平面的曲线(见图5-1所示)和y2≡x3+x+6 ( mod 11) 在平面上的点(如图5-4所示),直观感觉没有太多的联系。
P +Q+ R1=O。则P+Q =- R1=R,如图5-2。
2020/11/19
2020/11/219020/11/
图5-2 R=P+Q示意图 2020/11/19
8
8 88
点P的倍点定义为:过P点做椭圆曲线的切线,设与椭圆曲线交于R1, 则 P+P+ R1=O, 故2P=- R1=R。如图5-3。
2020/11/19
5
5 55
本章的介绍以第一种椭圆曲线为主,如图5-1是y2≡x3+x+6所表示的曲线,该图 可以用matlab实现。显然该曲线关于x轴对称。
图5-1 y2≡x3+x+6所表示的 曲线
2020/11/19
2020/11/219020/11/
2020/11/19
6
6 66
2.椭圆曲线的加法
2020/11/19
2020/11/19
2020/11/19
20
2200
- ④ 计算点:(x1,y1)=kP - ⑤ 计算点:(x2,y2)=kQ,如果x2=0,则返回第③步 - ⑥ 计算:c=mx2 - ⑦ 传送加密数据(x1,y1,c)给B
(4)解密过程
当实体B解密从A收到的密文(x1,y1,c)时,执行步骤:
非对称加密

非对称加密(公钥加密)指加密和解密使用不同密钥的加密算法,也称为公私钥加密。
假设两个用户要加密交换数据,双方交换公钥,使用时一方用对方的公钥加密,另一方即可用自己的私钥解密。
如果企业中有n个用户,企业需要生成n对密钥,并分发n个公钥。
由于公钥是可以公开的,用户只要保管好自己的私钥即可,因此加密密钥的分发将变得十分简单。
同时,由于每个用户的私钥是唯一的,其他用户除了可以可以通过信息发送者的公钥来验证信息的来源是否真实,还可以确保发送者无法否认曾发送过该信息。
非对称加密的缺点是加解密速度要远远慢于对称加密,在某些极端情况下,甚至能比非对称加密慢上1000倍。
这里非对称加密采用RSA算法为例,具体使用时下面代码中带有说明,C#完整程序代码如下:using System;using System.Collections.Generic;using System.Text;using System.Security.Cryptography;using System.Windows.Forms;using System.Globalization;namespace WindowsApplication12{class RSA{/// <summary>/// generate private key and public key arr[0] for private key arr[1] for public key/// </summary>/// <returns></returns>public static string[] GenerateKeys(){string[] sKeys = new String[2];RSACryptoServiceProvider rsa = new RSACryptoServiceProvider();//从XML文件中读取公钥和私钥sKeys[0] = rsa.ToXmlString(true);sKeys[1] = rsa.ToXmlString(false);return sKeys;}/// <summary>/// RSA Encrypt/// </summary>/// <param name="sSource" >Source string</param>/// <param name="sPublicKey" >public key</param>/// <returns></returns>public static string EncryptString(string sSource, string sPublicKey) {try{RSACryptoServiceProvider rsa = new RSACryptoServiceProvider();string plaintext = sSource;rsa.FromXmlString(sPublicKey);byte[] cipherbytes;byte[] byteEn = rsa.Encrypt(Encoding.UTF8.GetBytes("a"), false); cipherbytes = rsa.Encrypt(Encoding.UTF8.GetBytes(plaintext), false);StringBuilder sbString = new StringBuilder();for (int i = 0; i < cipherbytes.Length; i++){sbString.Append(cipherbytes[i] + ",");}return sbString.ToString();}catch{MessageBox.Show("数据错误");return null;}}/// <summary>/// RSA Decrypt/// </summary>/// <param name="sSource">Source string</param>/// <param name="sPrivateKey">Private Key</param>/// <returns></returns>public static string DecryptString(String sSource, string sPrivateKey) {try{RSACryptoServiceProvider rsa = new RSACryptoServiceProvider();rsa.FromXmlString(sPrivateKey);byte[] byteEn = rsa.Encrypt(Encoding.UTF8.GetBytes("a"), false); string[] sBytes = sSource.Split(',');for (int j = 0; j < sBytes.Length; j++){if (sBytes[j] != ""){byteEn[j] = Byte.Parse(sBytes[j]);}}byte[] plaintbytes = rsa.Decrypt(byteEn, false);return Encoding.UTF8.GetString(plaintbytes);}catch{MessageBox.Show("数据错误");return null;}}}}Hash算法(哈希值)Hash算法特别的地方在于它是一种单向算法,用户可以通过Hash算法对目标信息生成一段特定长度的唯一的Hash值,却不能通过这个Hash值重新获得目标信息。
第5章 非对称密码(1)

2019/8/6
2019/8/6 2019/8/6
2019/8/6
1199
1199
5.1.2 非对称密码体制的设计准则
现在应用的非对称密码体制,其安全是指的计算上是安全的。 以著名的RSA算法所基于的大数分解难题为例,它假定n是两个大素数p 和q的乘积。现在一般认为,p和q的长度都是512比特左右,则n的长度是 1024比特左右。以人们现有的计算能力,在知道n的情况下,在短时间内是 不能分解n的,也就是说,这在计算上是安全的。从理论上讲,如果有足够 的计算能力,是可以分解n的。但如果分解n的时间超过了消息的保密期,或 者投入的物力超过了消息本身的价值,对消息保密的目的就达到了。
第一种方式从时间和代价上来看,都难以符合需要。在非对称密码体制 产生前,对于很多不是很重要的信息,用得较多的解决办法就是第二种方式 ,但效率是比较低的。
2019/8/6
2019/8/6
2019/8/6
3
33
2019/8/6
2019/8/6 2019/8/6
2019/8/6
444
44
5.3.1 非对称密码体制的原理
序列密码都属于对称密码体制。两个用户在用对称密码体制进行保密通信时,必须
要有一个双方共享的加密密钥。那么,如何才能让两个不在同一个地方的用户安全
地拥有共享密钥呢?
我们可能想到的方式包括:
(1)派一个人来把密钥从一方送到另外一方;
(2)通过邮件或快递传递密钥;
(3)电子邮件、电话或电报等方式传递等等。
2019/8/6
2019/8/6
2019/8/6
11
111111
2002年:Ronald L. Rivest,Adi Shamir,Leonard M. Adleman 公钥密码 学(RSA加密算法)
非对称密码体制

非对称密码体制
非对称密码体制的基本概念 非对称密码体制的原理 RSA算法 RSA算法中的计算问题 RSA算法的安全性 非对称密码体制的应用
非对称密码体制的基本概念
非对称密码(公钥密码)与所有以前的密码方法的不同点
基于的基本思想不同 密钥的使用方式不同
公钥密码算法的密钥具有如下特点
是加密密钥与解密密钥是本质上不同的 是大多数公钥密码算法的加密密钥和解密密钥具有互换的性质,即两者是相对的
网络信息安全技术
非对称密码体制
非对称密码体制(Asymmetric CryptoSystem),也称为公钥密码体制(Public Key Cryptosystem),是现代密码学的重要组成部 分。公钥密码的思想在1976年由Diffie和Hellman在 其《密码学新方向》一文中提出。Rivest、Shamir 和Adleman在1978年提出了首个非对称密码体制, 即著名的RSA公钥密码体制。非对称密码体制的发明 是现代密码的具有里程碑意义的重要事件,它的出现 标志着现代密码学的创立。
可以通过加密算法生成密文:
C EPKB (M )
接收方B使用私有密钥容易通过解密算法对密文进行解密,以恢复原来的明文
从公开密钥PKB推出私有密钥SKB,在计算上是不可行的
非对称密码体制的原理
定义 单向陷门函数满足下列条件的函数f:D→V
1)对于任意给定的x∈D,计算y=f(x)是容易的。 2)对于几乎所有任意给定y∈V,计算x∈D使得y=f(x),
RSA算法中的计算问题
即计算(m)cmod N是RSA非对称密码 体制中的主要运算,其计算可以由 c-1次的模乘来实现,然而当比较
(m)c mod N 的有大效时计,算这问不题是一个好的算法,因为
信息安全导论(4-3 密码基础-非对称密码)

作业
RSA算法的练习(选择两个大于30的素数p,q)
两位同学一组,班内序号(1,2), (3,4), … 班内序号为偶数的同学:每人设计一个RSA公钥密码 系统,给出公开钥,保留秘密钥 班内序号为奇数的同学:每人用你同伴的公开钥加密 一个明文信息,将密文交给该同学,由该同学解密 每组同学提交一个算法报告(算法的设计过程、公开 钥、秘密钥、明文、密文、加解密运算过程等)
47
对称密码算法,加/解密速度快,但密钥 分发问题严重 非对称密码算法,加/解密速度较慢,但 密钥分发问题易于解决 为解决每次传送更换密钥的问题,结合 对称加密技术和非对称密钥加密技术的 优点,产生了电子信封技术,用来传输 数据
48
加密技术的使用
49
小结
典型的非对称密码(RSA) 对称密码,非对称密码
52
加密
古典,现代 对称,非对称 分组,序列 消息认证 数字签名 身份认证
53
认证
10
典型的公钥密码算法1:背包算 法
背包系统是1978年Merkle和Hellman 基于求解背包问题的难解性提出的一个 公钥密码系统 背包问题:
11
12
13
例
14
15
加解密运算:
16
17
例
18
19
发送方(加密)
20
பைடு நூலகம்
接收方(解密)
21
典型的公钥密码算法2:RSA
RSA是Rivest、Shamire和Adleman于 1978年在美国麻省理工学院研制的 其安全性建立在“大数分解和素性检测” 这一数论难题基础上
非对称加密与认证PPT课件
2020/10/13
2
谢谢您的指导
THANK YOU FOR YOUR GUIDANCE.
感谢阅读!为了方便学习和使用,本文档的内容可以在下载后随意修改,调整和打印。欢迎下载!
汇报人:XXXX 日期:20XX年XX月XX日
3
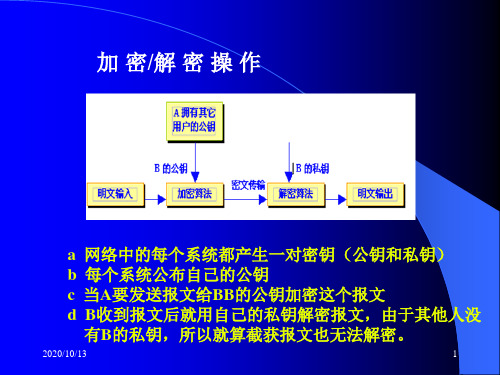
加 密/解 密 操 作
a 网络中的每个系统都产生一对密钥(公钥和私钥) b 每个系统公布自己的公钥 c 当A要发送报文给BB的公钥加密这个报文 d B收到报文后就用自己的私钥解密报文,由于其他人没
有B的私钥,所以就算截获报文也无法解密。
2020/10/13
1
认证操作
a 网络中的每个系统都产生一对密钥(公钥和私钥) b 每个系统公布自己的公钥 c 当A要向B认证自己时,就用A的私钥加密这个报文 d B收到报文后就用A的公钥解密报文,由于其他人没
第5章非对称密码体制与典型算法

算上也是不可行的。
(6)加密和解密函数可以以两个次序中的任何一个来使用: m=dPRb(ePUb(m)) 第5章 m=ePUb(dPRb(m))
7
非对称密码体制与典型算法
三、陷门单向函数
满足下列条件:
• 给定x,容易计算y=f(x) • 给定y =f(x), 难以计算出x • 存在陷门δ,已知δ 时,对给定的 任何y,若相应的x存在,则计 算x使y=f(x)是容易的
明文:
第5章
public
19
非对称密码体制与典型算法
二、RSA算法的实现问题
•如何产生大素数p和q ?
•如何快速计算 am mod
n?
第5章
非对称密码体制与典型算法
20
二、RSA算法的实现问题
1、产生大素数p和q
WITNESS(a,n); a 是基数,判断奇数n是否为素数 将(n-1) 表示为二进制形式bkbk-1…b0; d 1; 返回值 for i k downto 0 do FALSE:n一定不是素数 { TRUE: n可能是素数 x d; d (d d) mod n; if (d = 1) and (x 1) and (x n -1) then return FALSE; if (bi = 1) then d (d a) mod n; } if (d 1) then return FALSE; return TRUE; 第5章 非对称密码体制与典型算法
陷门
第5章
非对称密码体制与典型算法
10
一、RSA算法描述
1、算法描述
• 明文空间P=密文空间C=Zn • 密钥的生成
Lecture05非对称密码体制

62,93,81,88,102,37
加密
明文消息m=011000110101101110 分组m=011000 110101 101110
011000对应93+81=174 110101对应62+93+88+37=280 101110对应62+81+88+102=333
密文为:174 280 333
对公钥密码体制的要求
(1)参与方B容易通过计算产生一对密钥
(公开密钥KUb和私有密钥KRb) (2)对于发送方A,通过计算产生对应的密文:C=EKUb(M) (3)接收方B使用私有密钥解密所得的密文以便恢复原来的报
文:M=DKRb(C)=DKRb(EKUb(M)) (4)敌对方即使知道公开密钥KUb,要确定私有密钥KRb在计
公开密钥密码系统的分析方法
强行攻击。 公开密钥算法本身可能被攻破。 可能报文攻击(对报文本身的强行攻击)。
公钥密码系统的应用类型
加密/解密 数字签名 会话密钥交换
背包问题用于公钥密码学
做法:明文为X,S为密文 奥妙在于有两类背包,一类可以在线性时间
内求解,另一类则不能 把易解的背包问题修改成难解的背包问题
如何计算ab mod n?
要点1:(a x b) mod n = [(a mod n) x (b mod n)] mod n] 要点2:a16=aaaaaaaaaaaaaaaa
=a2, a4,a8, a16
更一般性的问题:am
k
m的二进制表示为bkbk-1…b0, 则 m bi 2i
i0
计算am mod n
由私人密钥产生公开密钥 设私人密钥为(2,3,6,13,27,52),其中 w=31,m=105;那么一般的包序列: 2*31 mod 105=62 3*31 mod 105=93 6*31 mod 105=81 13*31 mod 105=88 27*31 mod 105=102 52*31 mod 105=37 公有密钥为(62,93,81,88,102,37)
应用密码学第5章非对称密码体制

第5章 非对称密码体制
例5-4 此例为判定合数为素数的例子,此处以n=25,
a=7为例。 取n=25,25-1=23*3,即s=3,t=3。 由Miller-Rabin概率检测算法,得 a=73≡18(mod 25),i=0,b2=182≡-1(mod 25) 输出:n是素数。 实际上,25是合数。这时可以通过另选择一个a(1<a<n1),(n,a)=1,如a=2,再次运行算法。
x b (modm ) 2 2 ... x bn (modmn )
第5章 非对称密码体制
的解为:
’ x≡M1M1
b1+
’ M2M2
b2+…+
’ MnMn
bn(modm)
对该定理的理解, 需要注意的是,m=m1m2…mn=miMi, 故 Mi=m/mi。 m1, m2, …,mn 是两两互素的正整数, 故 (Mi, mi) =1, 通过 MiMi’≡1modmi 计算的逆元一定存在。
为在没有共享密钥前,双方只能用明文的方式进行通信,显 然是不安全的;第二种方式的时间需求比较大;第一种方式 从时间和代价上来看,都难以符合需要。在非对称密码体制 产生前,用得较多的解决办法就是第二种方式,但效率是比 较低的。那么如何才能有效地解决这个问题,以用较小的代 价、较高的效率实现通信双方的密钥传递呢?正是由于这个 需求,促使了非对称密码体制的产生。
m=2310,M1=462,M2=385,M3=330,M4=210
利用辗转相除法求得 M1’=-2,M2’=1,M 3’=1,M 4’=1。 所以,x≡1·(-2)· 462+5· 1· 385+ 4· 1· 330+10·1·210≡4421≡2111(mod 2310)
精品课件-应用密码学-9-非对称密码

29 29
RSA算法模幂运算问题
RSA中的计算问题 1. RSA的加密与解密过程
RSA的加密、解密过程都为求一个整数的整数次幂, 再取模。如果按其含义直接计算,则中间结果非常大,有可 能超出计算机所允许的整数取值范围。如上例中解密运算6677 mod 119,先求6677再取模,则中间结果就已远远超出了计算 机允许的整数取值范围。而用模运算的性质: (a×b) mod n=[(a mod n)×(b mod n)] mod n 就可减小中间结果。
即mkφ(n)+1≡m mod n,所以cd mod n≡m.
19 19
RSA保密通信示意图
20
欧拉(Euler)函数 设 (m)为小于或等于m且与m互素的正整数个数,称 (m)为欧拉(Euler)函数。 例如, (3)=2, (5)=4, (8)=4。 显然,当p为素数时, (p)=p-1。
21
证明RSA算法中解密过程的正确性. 证明: 由加密过程知c≡me mod n,所以 cd mod n≡med mod n≡m1 mod φ(n) mod n mod n
≡mkφ(n)+1
17 17
RSA算法
下面分两种情况: ① m与n互素,则由Euler定理得 mφ(n)≡1 mod n,mkφ(n)≡1 mod n,mkφ(n)+1≡m mod n 即cd mod n≡m。 ② gcd(m,n)≠1,先看gcd(m,n)=1的含义,由于n=pq,所以 gcd(m,n)=1意味着m不是p的倍数也不是q的倍数。 因此gcd(m,n)≠1意味着m是p的倍数或q的倍数,不妨设m=tp, 其中t为一正整数。
4第四讲 非对称密码体制

14
四、若干数论基础
原根(primitive root) 离散对数方法基于原根概念 素数p的原根定义:
若a是素数p的原根,0<a<p,当k=1,2,┈,p-1时,分别计算 a k mod p ,可以使1,2, ┈ ,p-1 中的每一种状态都出现一 次。
15
四、若干数论基础
离散对数
对任意的整数b和素数p原根a ,我们可以找到唯一的指数x满足
(The Discrete Logarithm Problem, ElGamal体制)
椭圆曲线上的离散对数问题
(The Elliptic Curve Discrete Logarithm Problem,类比的 ElGamal体制)
10
四、若干数论基础
设a、b为整数,且不全为0,
则gcd(a,b)表示a和b的最大公因子。 如果gcd(a,b)=1,称a和b互为素数(互素)。
A用其私钥加密,得到数字签名,然后,再用B的公钥加密
KU b 提供保密性 KRa 提供鉴别
9
三、公开密钥密码体制
公钥算法的安全性完全建立在计算复杂性理论基础上,或者 说建立在对一个特定的数学难题求解的困难上(NP问题)。
背包问题 又称子集合问题(subsetsum),属于NP问题。 大整数分解问题 (The Integer Factorization Problem, RSA体制) 离散对数问题 有限域的乘法群上的离散对数问题
− 不能用于交换任意信息 − 允许两个用户可以安全地建立一个秘密信息,用于后续的通讯过程 − 该秘密信息仅为两个参与者知道 • 算法的安全性依赖于有限域(素域FP )上计算离散对数的难度。即对任意 x x 正整数x,计算 g 是容易的;但是,已知g和y求x,使y= g ,在计算上几 乎不可能的 • 在美国的专利1997年4月29日到期
