麻省理工化工数值分析第二课
化工数学数值分析

3.14
0.314 101
x1 , x2 ,
, xn = 0 ~ 9,且 x1 0 (最左一位非零字)
n 是正整数,m 是整数。
数值计算中的误差
• 有效数字与相对误差的关系 --- n 位有效数字的近似数 x * 其相对误差: 1 Er ( x) 10 ( n1),且 x1 0(最左一位) 2 x1 --- 相对误差为
课程主要内容
插值方法; 曲线拟合与函数逼近; 数值逼近 数值积分与数值微分; 线性代数方程组数值求解的直接法; 线性代数方程组数值求解的迭代法; 数值代数 非线性方程与方程组数值求解; 常微分方程数值求解。
Matlab 简介
第一章 绪 论
主要内容: 一些常用概念; 数值算法的复杂度与稳定性。 数值计算中的误差; 数值算法设计的若干原则;
3 3
3
3.5 3.5
x x x x
3.5
对于被插函数 f ( x) 和插值函数 P( x)
在节点 xi 处的函数值必然相等
但在节点外 P( x) 的值可能就会偏离 f ( x)
因此 P( x) 近似代替 f ( x) 必然存在着误差 (截断误差)
整体误差的大小反映了插值函数的好坏. 为了使插值函数更方便在计算机上运算,一般 插值函数都使用代数多项式或有理函数.
数值分析研究的对象
科学计算的过程,是从数学模型的提出到上机 计算得出结果的完整过程。(下图表明了其中的 主要步骤和相互关系 ) 实 际 问 题
数学化
数 学 模 型
离散化
数 值 算 法
编 制 程 序
程序化
上 机 运 行
输 出 结 果
麻省理工化工数值分析第六课

⿇省理⼯化⼯数值分析第六课10.34, Numerical Methods Applied to Chemical EngineeringProfessor William H. Green Lecture #6: Modern Methods for Solving Nonlinear Equations.1D-Problemunknown: T of reactor f(x) = 0Q rxn exp(-Ea /RT ) + h(T – T a ) + c(T 4 – T a 4) = 0heat of reaction convection radiation (+) (-) (-)steady state temperatures Make a plot with MATLAB *nethe a t.m* function qdot = netheat(T) % computes the net heating rate of a reactor % qdot = 0 at the steady state qdot = Q.*exp(-Ea/(R.*T)) + h.*(T-Ta) + c.*(T.^4-Ta.^4);Figure 2. Professor Green modified variables Q and c until the plot looked likethe one above. Increased Q and decreased c.T o solve for steady state zerosf(T Figure 1. 1D problem Q = -2e-5; Ea = 5000; R = 1.987; h = 3; Ta = 300; c = 1e-8; Tvec = linspace(300,3000)qdot = netheat(Tvec) plot(Tvec,qdot) Figure 3. Have computer bracket in and find smallrange where plot goes from negative to positive.Bisection10.34 Numerical Methods Applied to Chemical EngineeringLecture 6 Prof. William GreenPage 2 of 4start a,b such that f(a)<0 and f(b) < 0 2b a x +=Figure 4. Funif f(x) · f(a) > 0 a = xelse b = xThis is a problem of TOLERANCEif((b-a) < tol) stopTypes of tolerance Absolute tolerance Relative tolerance atol: has unitsif |f(x)| < atol·f rtol: if(b-a) < rtol*|a| has to be BIG numberIn MATLAB while abs(b-a) > atolx x = (a+b)/2 if f(x)·f(a) > 0 a = x else b = x end *bisect.m* function x = bisect(f,a,b,atolx,rtolx, atolf) %solves f(x) = 0 while abs(b-a) > atolx x = 0.5*(b+a); if((feval(f,x)*feval(f,a))>0) a =x; else b=x; end endCommand Window x = bisect(@netheat,300,2000,0.1,0,0) x = 1.2373e+003CHECK: netheat(1237) = -1.0474 í closeKeep in mind: never get actual solution, but can come closeWe can change tolerances to improve results. ? while(abs(b-a)>atolx)&&(abs(b-a)>(rtolx*abs(a)))x = 0.5*(b+a); AND: must satisfy both conditions if(a bs(fev a l(f,x))x = 1.2363e+003 looser tolerance gives less accurate answerBisection cuts interval by 2 each timeEvery time we cut 3 times, we lose a sig figIn bisection, time grows linearly with the number of significant figures.a < x true < bx true = x soln ± b-a/2Newton’s Method (1-D)evaluates slope of f(x)next guess is the x new that satisfies f(x new)=0for a line from f(x guess) with the slope at f(x guess)Figure 5. Newton’s Method.For a good guess Newton’s method doublesthe number of significant figures after everyiteration; however, we lose robustness ifguess is poorf(x) = f(x0)+f’(x0)*(x-x0)+O(Δx2)0 = f(x guess)+f’(x guess)*(x-x guess)If f’(x guess) ≈ 0 -- doesn’t workx new = x guess – f(x guess)/f’(x guess)Figure 6.NO intersectionAnother drawback is one needs a derivative of the function. Secant Methodsame as Newton’s, but uses f’(x) approximate]1[][]1[][)()()('=kkkkapproxxxxfxfxfBisection method works only for 1D problems, but Newton/Secant can be used for problems with greater dimension 10.34 Numerical Methods Applied to Chemical Engineering Lecture 6 Prof. William Green Page 3 of 4 Broyden’s Method (Multi-dimensional) F(x) = F(x 010.34 Numerical Methods Applied to Chemical EngineeringLecture 6 Prof. William GreenPage 4 of 4f(x) = 0 approx J = B 2][1||||x B BΔ+=+k ][k Outer Product:ΔΔΔΔΔΔ (32221)2312111x F x F x F x F x F x FNewton’s Method (Multi-dimensional)O = F(x 0)+J(x 0)·(x-x 0)J*Δx = -F(x 0) B [k]Δx = -FLU LU [k+1] without redoing factorization Done in detail in homework problem.。
化工数值方法(0_绪论)

第一章 绪论
4.应用工具箱 MATLAB包含两部分内容:基本部分和各种
可选工具箱。基本部分有数百个内部函数。 工具箱分两大类:功能性和学科性工具箱。 功能性工具箱主要用来扩充其符号计算功能、
可视建模仿真功能及文字处理功能等。 学科性工具箱专业性比较强,如控制系统工
具箱、信号处理工具箱、神经网络工具箱、
第一章 绪论
最优化工具箱、金融工具箱等,这些工具箱 都是由该领域内学术水平很高的专家编写的 用户可以直接利用这些工具箱进行相关领域 的科学研究 MATLAB具备很强的开放性。除内部函数外, 所有MATLAB基本文件和各工具箱文件都是 可读可改的源文件,用户可通过对源文件的 修改或加入自己编码的文件去构成新的专用 工具箱。
第一章 绪论
3.图形功能 MATLAB 提供了两个层次的图形命令:一种
是对图形句柄进行的低级图形命令,另一种 是建立在低级图形命令之上的高级图形命令。 高级图形命令可轻易地绘制二维、三维图形, 并可进行图形和坐标的标识、坐标控制、图 形迭绘、视角和光照设计、色彩精细控制等。 利用MATLAB 图形句柄命令,可以随心所欲 地对图形进行各种操作,为用户在图形表现 方面开拓了一个广阔的空间。
第一章 绪论
现代化学及化工发展一个重要标志是模型化
首先根据过程中化学或物理实际现象及 真实过程的物理概念.经过适宜的假设和简 化建立过程的物理模型,然后再经过必要的 归纳和数学推导建立数学模型;最后应用数 学方法求解这些数学模型,再应用这些数学 解来定量地说明实际过程,从而达到定量分 析和预测实际过程的目的。
1.3 MATLAB的几个简单应用实例 求解线性方程组 AX=B,其中
第一章 绪论
解 在MATLAB命令窗口输入命令: a=[l,1.5,2,9,7;0,3.6,0.5,-4,4;7,10, -3,22,33;3,7,8.5,21,6;3,8,0,90,-20] b=[3;-4;20;5;16]; x=a\b
数值分析6.2--牛顿—柯特斯公式市公开课一等奖省赛课获奖PPT课件

n
C
(n k
)
[
f
(
xk
)
~fk ]
k0
n
(b a)
C (n) k
f
(xk )
~ fk
k0
n
(b a)
C (n) k
(b a) .
k0
这表明在b-a>1时,初始误差将会引发计算结果误差
增大,即计算不稳定,故n >7牛顿-柯特斯公式是不
用.
第8页
6.2.2 偶数求积公式代数精度
作为插值型求积公式,n阶牛顿-柯特斯公式最 少含有n次代数精度(推论1). 实际代数精度能否深入 提升呢?
积分中值定理,得辛普森公式余项为
第17页
RS
f (4) ( )
4!
b ( x a)( x c)2 ( x b)dx.
a
(b a) (b a )4 f (4) (),
180 2
(a,b).
关于柯特斯公式积分余项,这里不再详细推导
,仅给出结果以下
若 f(x)C6[a, b],则柯特斯公式余项为
nn
(t j)dt
0 j0, jk
(k=0,1,,n)
则 Ak (b a)Ck(n) , 于是得求积公式
n
In (b a) Ck(n) f ( xk )
k0
称为n 阶牛顿-柯特斯 (Newton-Cotes)公式, Ck(n) 称 为柯特斯系数。
显然, 柯特斯系数与被积函数 f (x) 和积分区间
[a,b]无关, 且为轻易计算多项式积分.
第3页
惯用柯特斯系数表
n
1
1/2
1/2
C(n) k
2
工程数值方法2第二章概论

18
例题
S ( x)
a0
a1x
a2 x2
c1 ( x
x1
)
2
代入xi ,yi( ia1x0 a2x02 y1 a0 a1x1 a2x12 y2 a0 a1x2 a2x22 c1(x2 x1)2
待定常数为n 2个。
14
插值问题的提法
问题1. 给定插值节点xi及相应函数值yi (i 0,1,, n) 和x0 处的导数值y0,求S ( x),使满足 S(x0 ) y0 , S(xi ) yi , (i 0,1,, n) 问题2. 给定插值节点xi及相应导数值yi(i 0,1,, n) 和x0 处的函数值y0,求S ( x),使满足 S(x0 ) y0, S(xi ) yi, (i 0,1,, n)
19
例题
S(x) a1 2a2 x 2c1(x x1) 代入x0 ,y0 y0 a1 2a2 x0
20
例题
y0 a0 a1x0 a2x02 y1 a0 a1x1 a2x12 y2 a0 a1x2 a2x22 c1(x2 x1)2
y0 a1 2a2 x0
21
例题
5
光滑性需要
某些实际应用比如汽车、轮船、飞机等的外形中流线 形设计,不但要求一阶导数连续,而且要求二阶导数 连续。所以一般插值往往不能满足实际需要。
6
样条
所谓“样条”(Spline)是工程绘图中的一种工具,它是 有弹性的细长木条,绘图时,用细木条连接相近的几个 结点,然后再进行拼接,连接全部结点,使之成为一条 光滑曲线,且在结点处具有连续的曲率。样条函数就 是对这样的曲线进行数学模拟得到的。
2
高次插值的缺点-龙格现象
化工问题的建模与数学分析方法化工数学

1940~1950‘s:传递现象,数学模拟
dx 1957 ~1960‘s:化学反应工程
0 r
dr
1970‘s~
:过程系统工程
第一章数学模型——建模方法
化学工程发展史上的几个重要阶段 1 d s dcA
dx ’s:工业化学 dx →化学工程 1901x ~1920
1923~1930‘s:单元操作,化工数学
第一章数学模型——建模方法
例2 管式反应器
衡算对象——微元 化学工程发展史上的几个重要阶段
1901~1920’s:工业化学→化学工程 1923~1930‘s:单元操作,化工数学 v,cAin 1940~1950‘s:传递现象,数学模拟 1957~1960‘s:化学反应工程
0
v,cAL
x
dx
1970‘s~
1化学工程——
研究工业规模的物质转化规律及技术手段
研究对象
质量传递
解决的问题
动量传递
能量传递
化学反应过程 装置放大 流程设计
第一章数学模型——模型有什么用?
1化学工程——
研究工业规模的物质转化规律及技术手段
研究对象
质量传递
解决的问题
动量传递
能量传递
化学反应过程
装置放大
流程设计
第一章数学模型——模型有什么用?
初始与边界条件
t = 0: cA = cA 0
¶ cA x = 0: vcin = vcA - DA ¶x ¶ cA x = 1: = 0 ¶x
第一章数学模型——建模方法
例3 催化剂颗粒
衡算对象——微元,柱坐标与球坐标 化学工程发展史上的几个重要阶段
z 1901~1920’s:工业化学 →化学工程 dr 1923~x1930‘s:单元操作,化工数学 r
计算机在化工中的应用-习题集

J =62.3 lbm / ft 3
1 ft=0.3048m T(o R)=1.8T(K) 1Btu=1055J 1 lbm=0.4536kg
1.8 计算双组分简单精馏塔的理论板数 氯仿-苯双组分精馏系统的气液相平衡数据如下表所示。对氯仿而言,规定:
x f 0.4, xd 0.9, xw 0.15
化率。 提示:等温管式反应器模型为: VR FA0 因此,反应器管长为: L
xA 0 x A dx dx y A0 F0 0 (r ) (rA ) A
x A dx VR 4 y A0 F0 2 2 0 (r ) ( d / 4) d A
然后得到 pA 和 ps 的表达式带入上式中的反应动力学表达式即可。 1.10 等温管式反应器的空时计算 某气相二聚反应 A→3R 在等温恒压管式反应器内进行,反应条件为 T=2150C,
Matlab 在化工中的应用习题集
第一章 化工中的数值分析与求解
1.1. 简单精馏计算(fzero) 简单精馏时,某时刻釜液残液量 F 与低沸点组成 x 之间的关系式为:
ln F0 1 x0 1 x ln ln F 1 x 1 x0
对于苯-甲苯物系,相对挥发度 a=2.5,开始时物系中含苯 60%。试求当蒸馏 至残液量为原加料量的一半时残液中的苯含量。 1.2. 气体状态方程的求解(fzero 或 roots)
6.264×108 111528
B
k3
D k5
k k0 exp( Ea / RT ) 。已知:
k0i Eai 5.7805×1010 124670 3.9232×1012 150386 1.6425×104 77954
C
焊接温度场与应力场的数值分析

本文由Jericho1989贡献pdf文档可能在WAP端浏览体验不佳。
建议您优先选择TXT,或下载源文件到本机查看。
哈尔滨工程大学硕士学位论文焊接温度场与应力场的数值分析姓名:夏培秀申请学位级别:硕士专业:固体力学指导教师:何蕴增 20050201摘要本文用有限元方法研究了温度场和热应力的分布规律。
模拟对象一是开有圆孔的无限大薄板,另一个是两张对接焊的钢板。
文中对开有圆孔的无限大薄板的研究,一是假设材料的机械性能不随温度变化的情况下,计算出了开有圆孔的无限大薄板的稳恒温度场和弹性热应力的解析解。
二是用有限元法对该薄板进行了两种情况下的计算,一种情况是假设材料的机械性能不随温度变化,另一种情况是材料的机械性能随温度变化。
最后将计算结果进行了对比,证明了有限元解的正确性,同时说明了材料的机械性能随温度变化对板中的径向热应力的影响很大。
本文在对两张钢板对接焊的焊接应力的研究中,首先建立了一种计算简化模型;其次用有限元法对钢板的焊接应力进行了计算,计算结果与文献相吻合,钢板在靠近焊缝的区域内出现了拉应力。
并从理论上分析了该结果的合理性。
焊接应力的存在,会直接影响到结构的承载能力,为了保证焊接结构的安全可靠,准确的推断焊接过程中的力学行为和焊接应力是十分重要的课题。
因此本文的研究成果对科学研究和工程设计都具有重要意义。
关键词:热传导;热应力;热应变;有限元法;对接焊钢板ABSTRACTInpresentpaper,thetemperaturefieldandthedistributionofthermalstresswerestudied,SOthattwotypesofmodelswouldbesimulated.Firstmodel,aninfinitesheetwithacircularopening;secondone,twobutt—weldedsteelboards.Inthestudyofformermodel,theanalyticalsolutionsofsteadytemperaturefieldandelasticthermalstressweregivenwiththeassumptionthatthemechanicalpropertiesofthematerialdonltchangewiththetemperature.AlsoFEMwasintroducedtocalculatetwocases.Firstly,themechanicaipropertiescasedon。
化工数学-第2章-数据处理

(2- 11)
lk+1(x) =
(x(xk+ 1 -
xk- 1)(x - xk ) xk- 1)(xk+ 1 - xk )
(2- 12)
2019/9/9
化工数学-第二章-数据处理
得到二次插值多项式
L2 (x) = yk- 1lk- 1(x) + yklk (x) + yk+1lk+1(x)
或者
线性插值基函数的特点是在节点 xk , xk+ 1处满足条件
或
ìï镲 眄 镲 镲 î lk
lk (xk ) = (xk+1) =
1 0
ìï lk+1(xk ) = 0 î lk+1(xk+1) = 1
(2- 7)
lk (xi ) =
ìïïíïïî
1, 0,
i= i¹
k k
(i, k = 0,1)
2019/9/9
化工数学-第二章-数据处理
5
2.1 插值法
2.1.1 概述
像化工物性数据手册、数学手册、热力学手册、腐蚀数
据手册等以列表形式给出的函数值称为列表函数。这些列表
函数的特点是:
① 自变量与函数值一一对应;
② 函数值具有相当可靠的精确度;
③ 自变量与函数间的解析表达式不必知道(复杂?实验值?)。
插值法就是寻求函数近似表达式的一种方法。最简单的
近似表达式是代数多项式。
2019/9/9
化工数学-第二章-数据处理
6
(1)代数插值法
给定函数y=f(x)在区间[a,b]上的n+1个互异点
a ? x0 x1 < < xn ? b 上的函数值 yi = f (xi ) (i = 0,1, , n),建立 一个次数不超过n次的代数多项式
Matlab与化工数值计算ppt

plus
- Plus
+
uplus
- Unary plus
+
minus
- Minus
-
uminus
- Unary minus
-
mtimes
- Matrix multiply
*
times
- Array multiply.*mpower
- Matrix power
^
power
- Array power
.^
本课程的学习目的
学会Matlab的使用,可以利 用Matlab求解较为复杂的化 工数学模型
对于数值分析 的内容不过多 涉及,只注意 数值计算结果 的准确性
Matlab
数值分析
化工数学模型
化工专业知识 作为背景,不 涉及模型的推 导,注重模型 求解过程的方 法与技巧
本课程基本内容
• 第一讲 Matlab简介与基本数学运算 • 第二讲 非线性方程组求解与迭代法 • 第三讲 矩阵操作与线性方程组求解 • 第四讲 插值、拟合与数值微分、积分 • 第五讲 常微分方程数值解 • 第六讲 偏微分方程数值解 • 第七讲 统计初步与最优化方法
含义
正弦值 反正弦值 余弦值 反余弦值 正切 指数运算 自然对数 求平方根 求绝对值 取出复数的虚部 取出复数的实部 复数共轭 四舍五入 求余数 整数x和y的最小公倍数 整数x和y的最大公约数
基本数学函数的使用
计算以下表达式的值: 1) sin(30) 2) sind(30) 3) exp([1 2 3]) 4) log10([10 100 1000]) 5) abs(3+4i) 6) abs(-5)
format命令
化工数值方法(2_预备知识)

第二章 预备知识
第二章 预备知识
第二章 预备知识
1.3.1 截断误差
第二章 预备知识
第二章 预备知识
1.3.2 舍入误差
1.3.3 舍入和舍去
第二章 预备知识
第二章 预备知识
1.3.4 精度损失 设有两个数 p=3.1415926536 和 q=3.1415 957341,二者几乎相等,且都有11位有效数 字精度。它们差为:P - q=-0.0000030806。 由于p和q的前 6 位数相等,所以它们的差别 只有5位数字精度。这种现象称为精度损失或 差额抵消。如果不注意到这一点,最终计算 结果的精度可能会逐渐减少。
第二章 预备知识
研究生课程
化工数值计算方法
第二章 预备知识
1.1 微积分回顾 1.1.1 极限和连续性
第二章 预备知识
第二章 预备知识
第二章 预备知识
第二章 预备知识
第二章 预备知识
1.1.2 微分函数
第二章 预备知识
第二章 预备知识
第二章 预备知识
第二章 预备知识
1.1.3 积分
第二章 预备知识
第二章 预备知识
第二章 预备知识
下例显示的截断泰勒级数有时有助于避免精度损失造成的误差。
第二章 预备知识
第二章 预备知识
对于多项式求值计算,有时可以通过将表达式重新表示为嵌套 乘的形式,以获得较为理想的结果。
第二章 预备知识
1.3.5 数据的不确定性
从真实世界中得到的数据包含一定的不确定性和 误差,这一类型的误差被称为噪声,它将影响任何数 值计算的精度。采用有噪声的数据进行连续的计算并 不能提高精度。因此,如果初始数据有 d 位有效数字 的精度,则计算结果也只具有 d 位有效数字的精度。 例如,设数据 p1=4.152 和 p2=0.07931 都有4位有 效数字的精度,则从计算器上得出的结果(p1+p2= 4.23131) 将被忽略。因为,从有噪声的数据得出的结 果不可能比初始数据具有更多的有效数字位数,因而 正确的答案应该是p1+p2=4.231。
化工数值方法(3-2_非线性方程)

第三章 非线性方程的解法
第三章 非线性方程的解法
2.4.2 被零除错误
第三章 非线性方程的解法来自三章 非线性方程的解法2.4.3 收敛速度
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
2.4.4 缺陷
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
2.4.5 割线法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
2.4.6 加速收敛
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
2.4.7 算法和程序练习
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
研究生课程
化工数值计算方法
第三章 非线性方程的解法
2.4 牛顿拉夫申(Newton-Raphson)法 和割线法
2.4.1 求根的斜率法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
第三章 非线性方程的解法
化工数值计算-5
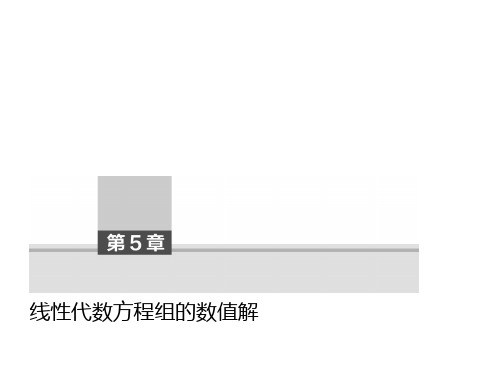
作为保留方程并用它和以下各方程(第k+1、k+2、…、n个)作线性
组合消去它们所含的变元xk,将第k步消xk时用的方程及其系数分别
叫做第k步的主方程和主行,而xk的系数 素。 在消元过程中,若主元素
叫做第k步的主元
为零,则因为零不能作为分母,故计 虽不为零,但其
算程序将在遇到零元素时中止执行。此外,若
存在,则称迭代式是收敛的,这时极限值 (i=1,2,…,n)就是线 性方程组的解。下面来讨论其迭代收敛的条件。
方程组的精确解 与第k+1次迭代近似值
之差为
k+1次迭代近似值的误差为
于是由式(5-6)有
式中
由式(5-7)可得
由此可见,如果L<1,则k→∞,必有ek+1→0,亦即有
经过n-1次消元后可得到上三角形方程组如下:
(2) 回代过程
可以证明,对于线性方程组AX =B,如A为严格对角占优矩阵[即满足 式(5-12)],则用消元法求解时 为零现象。 全不为零。因此在使用消元法 求解线性方程组时,系数矩阵最好是严格对角占优矩阵,防止出现
根据以上讨论,可确定出消元法的通用计算程序框图,如图5-2所示, 包括数据输入、选主元(调用子程序,用于主元消去法)、消元和回
采用赛德尔迭代法求解线性方程组时,最好首先判断方程组的系 数矩阵A是否满足迭代收敛条件,即式(5-12)。如不满足迭代收敛 条件,就必须对方程组进行重新组合。
例5-2
用SEIDEL迭代法解方程组:
解 因为方程组的系数矩阵不属于严格对角占优矩阵,所以需要进行重新 组合处理。 由第一方程的二倍加上第二方程得:
代四部分。其中主要变量的含义如下。
N 线性方程组的变量个数
(整理)化工设备第二章习题答案
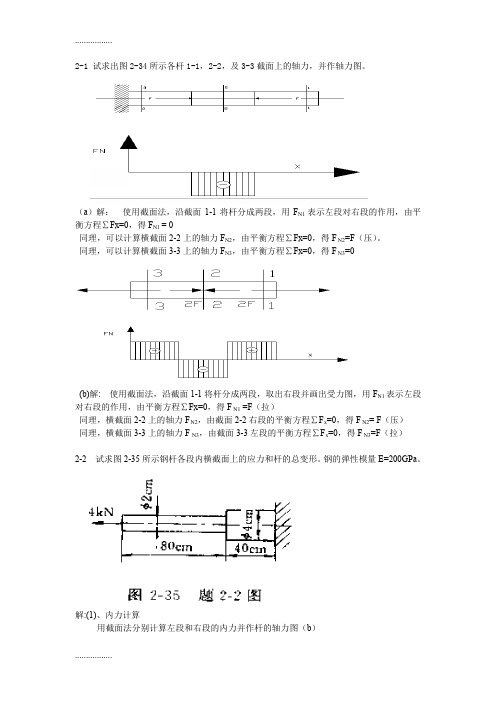
2-1 试求出图2-34所示各杆1-1,2-2,及3-3截面上的轴力,并作轴力图。
(a)解:使用截面法,沿截面1-1将杆分成两段,用F N1表示左段对右段的作用,由平衡方程∑Fx=0,得F N1 = 0同理,可以计算横截面2-2上的轴力F N2,由平衡方程∑Fx=0,得F N2=F(压)。
同理,可以计算横截面3-3上的轴力F N3,由平衡方程∑Fx=0,得F N3=0(b)解: 使用截面法,沿截面1-1将杆分成两段,取出右段并画出受力图,用F N1表示左段对右段的作用,由平衡方程∑Fx=0,得F N1 =F(拉)同理,横截面2-2上的轴力F N2,由截面2-2右段的平衡方程∑F x=0,得F N2= F(压)同理,横截面3-3上的轴力F N3,由截面3-3左段的平衡方程∑F x=0,得F N3=F(拉)2-2 试求图2-35所示钢杆各段内横截面上的应力和杆的总变形。
钢的弹性模量E=200GPa。
解:(1)、内力计算用截面法分别计算左段和右段的内力并作杆的轴力图(b)得 F 左 =4kN (拉) F 右 =4kN (拉)左段:32594F L 4108010L 5.095510m EA 200104104π---⨯⨯⨯∆===⨯⨯⨯⨯⨯左左左左() 右段:32594F L 4104010L 0.63710m EA 2001016104π---⨯⨯⨯∆===⨯⨯⨯⨯⨯右右右右()324F 41012.73MPa A 2104δπ-⨯===⨯⨯左左左324F 410 3.18MPa A 4104δπ-⨯===⨯⨯右右右(2)、各段变形的计算左、右两段的轴力为F 左 、F 右 ,横截面面积A 左、A 右,长度L 左,L 右均不相同,变力计算应力分别进行。
(3)、总变形计算555L L L 5.0955100.63710 5.7310m ---∆=∆+∆=⨯+⨯=⨯左右()计算结果表明,左段伸长5.0955x 10-5m ,右段伸长0.637x 10-5m ,全杆伸长5.73 x10-5m 。
mit化学反应原理

mit化学反应原理MIT化学反应原理引言:MIT化学反应原理是指麻省理工学院(Massachusetts Institute of Technology)在化学反应领域的一系列研究成果和理论原理。
这些原理旨在解释化学反应的机制和动力学过程,为化学工程师和科学家提供理论指导,推动化学反应的发展和应用。
本文将介绍MIT 化学反应原理的几个重要方面,包括速率常数、反应机理和催化剂。
一、速率常数速率常数是描述化学反应速率的物理量,它反映了单位时间内反应物的浓度变化。
MIT化学反应原理研究了速率常数与温度、压力、浓度等因素的关系。
根据Arrhenius方程,速率常数与温度呈指数关系,即随着温度的升高,化学反应速率也会增加。
此外,压力和浓度的增加也会导致速率常数的增加,因为更多的反应物分子之间会发生碰撞,从而增加了反应的可能性。
二、反应机理反应机理是指化学反应过程中各个步骤和中间体的转化关系。
MIT 化学反应原理研究了不同反应机理对反应速率和产物选择性的影响。
一种常见的反应机理是分步反应机理,即反应分为多个连续的步骤。
每个步骤都有自己的速率常数和反应物,通过中间体的转化最终形成产物。
另一种常见的反应机理是并行反应机理,即反应可以同时发生在多个路径上,最终形成不同的产物。
MIT的研究揭示了不同反应机理对反应速率和产物选择性的影响,为化学工程师提供了选择最优反应机理的依据。
三、催化剂催化剂是一种物质,可以在化学反应中降低活化能,加速反应速率,而不参与反应本身。
MIT化学反应原理研究了不同催化剂对反应速率和选择性的影响。
催化剂可以提供新的反应路径,降低反应物之间的反应能垒,从而加速反应速率。
此外,催化剂也可以选择性地促进某些反应路径,从而得到特定的产物。
MIT的研究不仅揭示了催化剂的工作原理,还开发了一系列高效催化剂,为化学工程领域的研究和应用提供了重要支持。
四、应用领域MIT化学反应原理的研究成果在许多领域得到了广泛应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10.34, Numerical Methods Applied to Chemical Engineering
Prof. William Green
Lecture 2: Solving Systems of Linear Equations Sample Function and Computing Tips
function k = rate(T, params)
% computes rate constant given temperature and Arrhenius parameters % Bill Green 9/8/06
% inputs:
% T [=] Kelvin
% params = [A; n; Ea]
% A [=] 1/second
% n unitless exponent
% Ea [=] kj/mole
%
% output:
% k [=] 1/second
%
% unpack params
A=params(1);
N params(2);
Ea=params(3);
R = 8.314; % gas constant J/mole-Kelvin
Ea=1000.*Ea;
K=A.*(T.^n).*exp(-Ea./(R.*T));
One additional feature is to include input/output example at bottom of code:
%Tvec = linspace(300,1200);
%params = [1e9;0.5;82];
%kvec=rate(Tvec,params);
%kvec(3)
%ans = 6.1551e-004
Use a lot of ‘%’ comments for
1)The graders to give you partial credit
2)To help you understand your programs when you review
3)For your classmates if they need to operate your program
TEST your program in pieces!!
Otherwise you write a long program and you have no idea where the problem is. “If you’re going to build a laboratory apparatus, you check the power supply, you check if the tubes leak, if the safety features are in place, etc, before you run experiments. It’s the same thing with software.”
In MATLAB you don’t have to describe the dimension of each array.
This can be used to your advantage by setting up the function as follows: function k = rate(T, params) or using a semi-colon: f(x; p) or f(x; θ)
Matrix Algebra
P-norm of a vector:
p N k p k p v v 11||||||⎥⎥⎦
⎤⎢⎢⎣⎡=∑
= p = 1 city-block norm
p = 2 length, Euclidean norm p = ∞ largest element, useful for error tolerances
Triangle Inequality:
p p p w v w v ||||||||||||+≤+for any p; good for proving bounds
Matrix times a vector:
M * v 1) Weighted sum of cols of M
∑
=col i i M v v M r *
2) Column of dot products
⎟⎟⎟⎟⎟⎠
⎞⎜⎜⎜⎜⎜⎝⎛•••⇒⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛=⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛v M v M v M x x x row n row row n r r M r r r r M M M M M L L L L L L L L L L L L L L L L 2121
3) Rotate and Grow/Shrink 4) Linear Mapping 10.34, Numerical Methods Applied to Chemical Engineering Lecture 1 Prof. William Green Page 2 of 5 Figure 1. A linear map.
All four of these are going on and you can use whichever you want in the current
application.
“I teach little tidbits of information. You have to read the textbook if you want details.”
Reactor System Example
Alcohol + Acid Æ Ester + H2O
R-OH + RCOOH <-> RCOOR + H 2O
4
Figure 2. A reactor for alcohol and acid.
6 streams and four compounds = 24 stream variables (not counting energy balance) Assumptions: Stream 3 has same composition Alcohol/Acid as Stream 4
Set BASIS for stream 1 Unknowns: Compositions for streams 2, 4
m 1,ACID + m 4,ACID = m 2,ACID m 1,ROH + m 4,ROH = m 2,ROH m 1,H2O + m 4,H2O = m 2,H2O IR Analysis of Streams 4 and 2: m ROH / m H2O = 0.43
m 2,ROH /m 2,Acid = 1.4 m 2,tot = 2.1m 1,tot
Set up linear matrix of equations as: -1 1 0 0 0 0 -m 1,Acid 0 0 -1 1 0 0 -m 1,ROH 0 0 0 0 -1 1 (x) = -m 1,H2O 0 0 0 1 0 -.43 0 -1.4 0 1 0 0 0 0
10.34, Numerical Methods Applied to Chemical Engineering Lecture 1 Prof. William Green Page 3 of 5 1 0 1 0 1 0 2.1m 1,tot
10.34, Numerical Methods Applied to Chemical Engineering Lecture 1 earrange equations and use elimination to produce upper triangle matrix U
unknowns
••••••••••x 000000
U v
R x N = v N / U NN gives you value of last element Use backward substitution to solve for other
()⎟⎟⎟⎟⎟⎠
⎞⎜⎜⎜⎜⎜⎝⎛••••=⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛
33
3344444
44321*)(000000*U v x U x v v U v x v x x x x x U new col new
=−===⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛••••+⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛•••+⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛••+⎟⎟⎟⎟⎟⎠
⎞⎜⎜⎜⎜⎜⎝⎛•=r r an permute the rows. Can permute the columns, if you permute the variables in the C x vector.
MATLAB examples
) i; m,m); se of the colon ‘:’
=[1 2 3 4; 5 6 7 8]; ,1:2) silly.m
lly sum + i;
function x = backsub(U,v N = 1: (N-1) for i= m = N+1 – x(m) = v(m)/U( v=v-x(m)*U(: ,m) U
M v1=M(:,1) 1 5 m = M(:m = 1 2 5 6 r loop
fo Save as:function sum = si sum = 0 :4 for i = 2 sum = end。
