2006年湖北省十堰市中考数学试题及标准答案(课改)
湖北十堰中考数学试题版有答案.doc

谢谢聆听
y
A( 1, 4
谢谢聆听
联立
y4 x ,得 ax2 +bx- 4=0,即 ax2 +( 4- a) x- 4=0,
y ax b
方法 1:( x- 1)( ax+4)= 0 ,解得 x1=1或 x=- 4 , a
设直线 AB 交y轴于点 C,则 C( 0, b),即 C( 0, 4-a)
由 S△AOB=S△ AOC+S△ BOC= 1 g(4
②一组邻边相等的平行四边形是正方形
③对角线相等的四边形是矩形
④对角互补的四边形内接于圆
谢谢聆听
谢谢聆听
A .①②
B.②③
C .③④
D .①④
9. (2010
.
堰 ) 方程 x2+2x-1=0 的根可看成函数 y=x+2 与函数 y
断方程 x3+x- 1=0 的实根 x 所在范围为( C )
十
1
的图象交点的横坐标,用此方法可推
3. (2010
.
堰 ) )据人民网 5月 20日电报道:中国森林生态系统年涵养水源量
十 4947.66亿立方米,相当于 12
个三峡水库 2009年蓄水至 175米水位后库容量,将 4947.66亿用科学记数法表示为(
C)
A . 4.94766 ×1013
B. 4.94766 ×1012 C. 4.94766 ×1011 D. 4.94766 ×1010
4. (2010 .十堰 ) 若一个几何体的三视图如图所示,则这个几何体是(
A)
A .三棱柱 B.四棱柱 C .五棱柱 错误 ! 未指定书签。
D .长方体
5. (2010 .十堰 ) 某电脑公司试销同一价位的品牌电脑,一周内销售情况如下表所示:
中考数学规律题

“发现数学规律题”的解题思想相关知识:常见数列的一般公式。
(1)1,2,3,4,…, n (2) 1,4,9,16,…, n2(3)1,3,5,7,9,…, 2n-1. (4) 2,4,6,8,10,…, 2n.(5) 1,3,6,10,15,…, n(n+1)/2.(6) 1,1/2,1/3,1/4,…, 1/n.(7) 1,1/4,1/9,1/16,…, 1/n2. (8) 1/2,1/6,1/12,1/20,…, 1/n(n+1).(9)2,4,8,16,32,…, 2n .典型例题分类解析一、要善于抓主要矛盾有些题目看上去很大、很复杂,实际上,关键性的内容并不多。
对题目做一番认真地分析,去粗取精,取伪存真,把其中主要的、关键的内容抽出来,题目的难度就会大幅度降低,问题也就容易解决了。
例如、观察下列数表:根据数列所反映的规律,第行第列交叉点上的数应为 .总结:数学规律题总是与数相关的问题,所发①首先列出符合要求的数,②然后再寻找其规律还有,邵阳市2006年初中毕业学业考试试题卷(课改区)的数学试题“图中的螺旋形由一系列等腰直角三角形组成,其序号依次为①、②、③、④、⑤……,则第n个等腰直角三角形的斜边长为_____________。
”也可以按照这个思想求解。
二、要抓题目里的变量例如,用同样规格的黑白两种颜色的正方形瓷砖按下图方式铺地板,则第(3)个图形中有黑色瓷砖块,第个图形中需要黑色瓷砖块(用含的代数式表示).(海南省2006年初中毕业升考试数学科试题(课改区))云南省2006年课改实验区高中(中专)招生统一考试也出有类似的题目:“观察图(l)至(4)中小圆圈的摆放规律,并按这样的规律继续摆放,记第n个图中小圆圈的个数为m,则,m=(用含 n 的代数式表示).”三、要善于比较“有比较才有鉴别”。
通过比较,可以发现事物的相同点和不同点,更容易找到事物的变化规律。
找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律。
2006年全国数学题与评析

2006年全国高考数学试题Ⅲ的评析一、2005年高考全国卷数学试题的特点在《2005年高考数学大纲》中明确指出:数学科的考试将会按照“考查基础知识的同时,注重考查能力”的原则,确立以能力立意命题的指导思想,据此,教育部考试中心命制的全国卷1、全国卷2、全国卷3三套试卷,分文、理科共六份试题.试题的设计体现了数学学科的特点,突出了知识的基础性,注意了在知识网络交汇点设题,着力反映了概念性、思辩性、量化的灵活性、解法的多样性及应用的广泛性,在数学思想方法及数学理性思维方面作了比较深入的考查。
试题“温和平缓”,既似曾相识,又推陈出新;既符合考生实际,又符合高考对选拔的要求。
相比之下,“全国卷1”比“全国卷2”和“全国卷3”要难些,但没有使学生望而生畏的题目,新题不难,难题不怪,“纯净淡雅”,平易近人。
既全面的考查了基础知识,又突出了对重点内容的考查;既关注了考查数学的基本方法和技巧,又注重了对能力的考查和思维能力的提升。
所有这些,对中学数学都具有很好的导向作用。
二、全国高考数学试题Ⅲ的评析2005年高考甘肃采用的高考数学试题模版是全国卷Ⅲ,试卷题量与2004年相同。
2005年高考数学试卷总体呈现平稳,没有出现难题、偏题和怪题。
命题凸现了高中数学的主干知识,以“死题”考知识,用“活题”考能力,加强了数学运算能力的考查。
文理科试卷的差异较往年缩小了。
从定量上看,此套试卷继续保持2004年在全国卷Ⅲ在文理差异上的风格,即减少相同题,减少姊妹题增加不同题,但不同题的数量较2004年有所减少,其中,选择题相异的有1道,填空题差异有2道,(而且这3道试题都是因为文理考试知识的不同要求命制的)解答题差异的有2.5道。
总体的感觉是:数学试题整体不难,应该说成绩优秀的学生得高分并不困难。
1、选择题:平淡中考知识,创新中考能力选择题都是容易题和中等题,大多数题属于“一捅就破”的题型,主要考查了数学的基本概念、基本知识和基本的计算、解题方法。
2022年湖北省十堰市中考数学试卷和答案解析

2022年湖北省十堰市中考数学试卷和答案解析一、选择题(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的,请把正确选项的字母填涂在答题卡中相应的格子内.1.(3分)2的相反数是()A.﹣2B.2C.﹣D.2.(3分)下列几何体中,主视图与俯视图的形状不一样的几何体是()A.B.C.D.3.(3分)下列计算正确的是()A.a6÷a3=a2B.a2+2a2=3a2C.(2a)3=6a3D.(a+1)2=a2+14.(3分)如图,工人砌墙时,先在两个墙脚的位置分别插一根木桩,再拉一条直的参照线,就能使砌的砖在一条直线上.这样做应用的数学知识是()A.两点之间,线段最短B.两点确定一条直线C.垂线段最短D.三角形两边之和大于第三边5.(3分)甲、乙两人在相同的条件下,各射击10次,经计算:甲射击成绩的平均数是8环,方差是1.1;乙射击成绩的平均数是8环,方差是1.5.下列说法中不一定正确的是()A.甲、乙的总环数相同B.甲的成绩比乙的成绩稳定C.乙的成绩比甲的成绩波动大D.甲、乙成绩的众数相同6.(3分)我国古代数学名著《张邱建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗.今持粟三斛,得酒五斗,问清、醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清、醑酒各几斗?如果设清酒x斗,那么可列方程为()A.10x+3(5﹣x)=30B.3x+10(5﹣x)=30C.+=5D.+=57.(3分)如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB.如果OA:OC =OB:OD=3,且量得CD=3cm,则零件的厚度x为()A.0.3cm B.0.5cm C.0.7cm D.1cm 8.(3分)如图,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下时,在斜坡上的树影BC长为m,则大树AB的高为()A.m(cosα﹣sinα)B.m(sinα﹣cosα)C.m(cosα﹣tanα)D.﹣9.(3分)如图,⊙O是等边△ABC的外接圆,点D是弧AC上一动点(不与A,C重合),下列结论:①∠ADB=∠BDC;②DA =DC;③当DB最长时,DB=2DC;④DA+DC=DB,其中一定正确的结论有()A.1个B.2个C.3个D.4个10.(3分)如图,正方形ABCD的顶点分别在反比例函数y=(k1>0)和y=(k2>0)的图象上.若BD∥y轴,点D的横坐标为3,则k1+k2=()A.36B.18C.12D.9二、填空题(本题有6个小题,每小题3分,共18分)11.(3分)袁隆平院士被誉为“杂交水稻之父”,经过他带领的团队多年努力,目前我国杂交水稻种植面积约为2.5亿亩.将250000000用科学记数法表示为2.5×10n,则n=.12.(3分)关于x的不等式组中的两个不等式的解集如图所示,则该不等式组的解集为.13.(3分)“美丽乡村”建设使我市农村住宅旧貌变新颜,如图所示为一农村民居侧面截图,屋坡AF,AG分别架在墙体的点B,C 处,且AB=AC,侧面四边形BDEC为矩形.若测得∠FBD=55°,则∠A=°.14.(3分)如图,某链条每节长为2.8cm,每两节链条相连接部分重叠的圆的直径为1cm,按这种连接方式,50节链条总长度为cm.15.(3分)如图,扇形AOB中,∠AOB=90°,OA=2,点C为OB上一点,将扇形AOB沿AC折叠,使点B的对应点B'落在射线AO上,则图中阴影部分的面积为.16.(3分)【阅读材料】如图①,四边形ABCD中,AB=AD,∠B+∠D=180°,点E,F分别在BC,CD上,若∠BAD=2∠EAF,则EF=BE+DF.【解决问题】如图②,在某公园的同一水平面上,四条道路围成四边形ABCD.已知CD=CB=100m,∠D=60°,∠ABC=120°,∠BCD=150°,道路AD,AB上分别有景点M,N,且DM=100m,BN=50(﹣1)m,若在M,N之间修一条直路,则路线M→N 的长比路线M→A→N的长少m(结果取整数,参考数据:≈1.7).三、参考答案题(本题有9个小题,共72分)17.(5分)计算:()﹣1+|2﹣|﹣(﹣1)2022.18.(5分)计算:÷(a+).19.(6分)已知关于x的一元二次方程x2﹣2x﹣3m2=0.(1)求证:方程总有两个不相等的实数根;(2)若方程的两个实数根分别为α,β,且α+2β=5,求m的值.20.(9分)某兴趣小组针对视力情况随机抽取本校部分学生进行调查,将调查结果进行统计分析,绘制成如下不完整的统计图表.抽取的学生视力情况统计表类别调查结人数果A正常4876B轻度近视C中度近60视mD重度近视请根据图表信息参考答案下列问题:(1)填空:m=,n=;(2)该校共有学生1600人,请估算该校学生中“中度近视”的人数;(3)某班有四名重度近视的学生甲、乙、丙、丁,从中随机选择两名学生参加学校组织的“爱眼护眼”座谈会,请用列表或画树状图的方法求同时选中甲和乙的概率.21.(7分)如图,▱ABCD中,AC,BD相交于点O,E,F分别是OA,OC的中点.(1)求证:BE=DF;(2)设=k,当k为何值时,四边形DEBF是矩形?请说明理由.22.(8分)如图,△ABC中,AB=AC,D为AC上一点,以CD 为直径的⊙O与AB相切于点E,交BC于点F,FG⊥AB,垂足为G.(1)求证:FG是⊙O的切线;(2)若BG=1,BF=3,求CF的长.23.(10分)某商户购进一批童装,40天销售完毕.根据所记录的数据发现,日销售量y(件)与销售时间x(天)之间的关系式是y =,销售单价p(元/件)与销售时间x(天)之间的函数关系如图所示.(1)第15天的日销售量为件;(2)0<x≤30时,求日销售额的最大值;(3)在销售过程中,若日销售量不低于48件的时间段为“火热销售期”,则“火热销售期”共有多少天?24.(10分)已知∠ABN=90°,在∠ABN内部作等腰△ABC,AB =AC,∠BAC=α(0°<α≤90°).点D为射线BN上任意一点(与点B不重合),连接AD,将线段AD绕点A逆时针旋转α得到线段AE,连接EC并延长交射线BN于点F.(1)如图1,当α=90°时,线段BF与CF的数量关系是;(2)如图2,当0°<α<90°时,(1)中的结论是否还成立?若成立,请给予证明;若不成立,请说明理由;(3)若α=60°,AB=4,BD=m,过点E作EP⊥BN,垂足为P,请直接写出PD的长(用含有m的式子表示).25.(12分)已知抛物线y=ax2+x+c与x轴交于点A(1,0)和点B两点,与y轴交于点C(0,﹣3).(1)求抛物线的解析式;(2)点P是抛物线上一动点(不与点A,B,C重合),作PD⊥x 轴,垂足为D,连接PC.①如图1,若点P在第三象限,且∠CPD=45°,求点P的坐标;②直线PD交直线BC于点E,当点E关于直线PC的对称点E′落在y轴上时,求四边形PECE′的周长.参考答案与解析一、选择题(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的,请把正确选项的字母填涂在答题卡中相应的格子内.1.【参考答案】解:2的相反数等于﹣2.故选:A.【解析】本题考查了相反数的知识,属于基础题,注意熟练掌握相反数的概念是关键.2.【参考答案】解:A、正方体的主视图与俯视图都是正方形,故A 不符合题意;B、圆柱的主视图与俯视图都是长方形,故B不符合题意;C、圆锥的主视图是等腰三角形,俯视图是一个圆和圆心,故C符合题意;D、球体的主视图与俯视图都是圆形,故D不符合题意;故选:C.【解析】本题考查了简单几何体的三视图,熟练掌握每一个几何体的三种视图是解题的关键.3.【参考答案】解:A、a6÷a3=a3,故A不符合题意;B、a2+2a2=3a2,故B符合题意;C、(2a)3=8a3,故C不符合题意;D、(a+1)2=a2+2a+1,故D不符合题意;故选:B.【解析】本题考查了同底数幂的除法,合并同类项,幂的乘方与积的乘方,完全平方公式,熟练掌握它们的运算法则是解题的关键.4.【参考答案】解:这样做应用的数学知识是两点确定一条直线,故选:B.【解析】本题考查的是三角形的三边关系、两点之间,线段最短、两点确定一条直线、垂线段最短,正确理解它们在实际生活中的应用是解题的关键.5.【参考答案】解:∵各射击10次,甲射击成绩的平均数是8环,乙射击成绩的平均数是8环,∴甲、乙的总环数相同,故A正确,不符合题意;∵甲射击成绩的方差是1.1;乙射击成绩的方差是1.5,∴甲的成绩比乙的成绩稳定,乙的成绩比甲的成绩波动大,故B,C都正确,不符合题意;由已知不能得到甲、乙成绩的众数相同,故D不一定正确,符合题意;故选:D.【解析】本题考查了平均数、方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.6.【参考答案】解:设清酒x斗,则醑酒(5﹣x)斗,由题意可得:10x+3(5﹣x)=30,故选:A.【解析】本题考查由实际问题抽象出一元一次方程,参考答案本题的关键是明确题意,列出相应的方程.7.【参考答案】解:∵OA:OC=OB:OD=3,∠COD=∠AOB,∴△COD∽△AOB,∴AB:CD=3,∵CD=3cm,∴AB=9cm,∵某零件的外径为10cm,∴零件的厚度x为:(10﹣9)÷2=1÷2=0.5(cm),故选:B.【解析】本题考查相似三角形的应用,参考答案本题的关键是求出AB的值.8.【参考答案】解:过点C作水平地面的平行线,交AB的延长线于D,则∠BCD=α,在Rt△BCD中,BC=m,∠BCD=α,则BD=BC•sin∠BCD=msinα,CD=BC•cos∠BCD=mcosα,在Rt△ACD中,∠ACD=45°,则AD=CD=mcosα,∴AB=AD﹣BD=mcosα﹣msinα=m(cosα﹣sinα),故选:A.【解析】本题考查的是解直角三角形的应用—坡度坡角问题,掌握锐角三角函数的定义是解题的关键.9.【参考答案】解:∵△ABC是等边三角形,∴∠BAC=∠ACB=60°,∵=,=,∴∠ADB=∠ACB=60°,∠BDC=∠BAC=60°,∴∠ADB=∠BDC,故①正确;∵点D是弧AC上一动点,∴与不一定相等,∴DA与DC不一定相等,故②错误;当DB最长时,DB为⊙O直径,∴∠BCD=90°,∵∠BDC=60°,∴∠DBC=30°,∴DB=2DC,故③正确;在DB上取一点E,使DE=AD,如图:∵∠ADB=60°,∴△ADE是等边三角形,∴AD=AE,∠DAE=60°,∵∠BAC=60°,∴∠BAE=∠CAD,∵AB=AC,∴△ABE≌△ACD(SAS),∴BE=CD,∴BD=BE+DE=CD+AD,故④正确;∴正确的有①③④,共3个,故选:C.【解析】本题考查等边三角形及外接圆,涉及三角形全等的判定与性质,解题的关键是作辅助线,构造三角形全等解决问题.10.【参考答案】解:连接AC交BD于E,延长BD交x轴于F,连接OD、OB,如图:∵四边形ABCD是正方形,∴AE=BE=CE=DE,设AE=BE=CE=DE=m,D(3,a),∵BD∥y轴,∴B(3,a+2m),A(3+m,a+m),∵A,B都在反比例函数y=(k1>0)的图象上,∴k1=3(a+2m)=(3+m)(a+m),∵m≠0,∴m=3﹣a,∴B(3,6﹣a),∵B(3,6﹣a)在反比例函数y=(k1>0)的图象上,D(3,a)在y=(k2>0)的图象上,∴k1=3(6﹣a)=18﹣3a,k2=3a,∴k1+k2=18﹣3a+3a=18;故选:B.【解析】本题考查反比例函数及应用,涉及正方形性质,解题的关键是用含字母的代数式表示相关点坐标.二、填空题(本题有6个小题,每小题3分,共18分)11.【参考答案】解:∵250000000=2.5×108.∴n=8,故答案为:8.【解析】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.12.【参考答案】解:该不等式组的解集为:0≤x<1.故答案为:0≤x<1.【解析】考查在数轴上表示不等式的解集,关键是读懂数轴上的信息,能正确选用不等号.13.【参考答案】解:∵四边形BDEC为矩形,∴∠DBC=90°,∵∠FBD=55°,∴∠ABC=180°﹣∠DBC﹣∠FBD=35°,∵AB=AC,∴∠ABC=∠ACB=35°,∴∠A=180°﹣∠ABC﹣∠ACB=110°,故答案为:110.【解析】本题考查了矩形的性质,等腰三角形的性质,熟练掌握矩形的性质,以及等腰三角形的性质是解题的关键.14.【参考答案】解:由题意得:1节链条的长度=2.8cm,2节链条的总长度=[2.8+(2.8﹣1)]cm,3节链条的总长度=[2.8+(2.8﹣1)×2]cm,...∴50节链条总长度=[2.8+(2.8﹣1)×49]=91(cm),故答案为:91.【解析】本题考查了规律型:图形的变化类,从数字找规律是解题的关键.15.【参考答案】解:连接AB,∵∠AOB=90°,OA=2,∴OB=OA=2,∴AB==2,设OC=x,则BC=B′C=2﹣x,OB′=2﹣2,则x2+(2﹣2)2=(2﹣x)2,解得x=2﹣2,∴阴影部分的面积是:=π+4﹣4,故答案为:π+4﹣4.【解析】本题考查翻折变换、扇形面积的计算,参考答案本题的关键是求出OC的值,利用数形结合的思想参考答案.16.【参考答案】解:解法一:如图,延长DC,AB交于点G,过点N作NH⊥AD于H,∵∠D=60°,∠ABC=120°,∠BCD=150°,∴∠A=360°﹣60°﹣120°﹣150°=30°,∴∠G=90°,∴AD=2DG,Rt△CGB中,∠BCG=180°﹣150°=30°,∴BG=BC=50,CG=50,∴DG=CD+CG=100+50,∴AD=2DG=200+100,AG=DG=150+100,∵DM=100,∴AM=AD﹣DM=200+100﹣100=100+100,∵BG=50,BN=50(﹣1),∴AN=AG﹣BG﹣BN=150+100﹣50﹣50(﹣1)=150+50,Rt△ANH中,∵∠A=30°,∴NH=AN=75+25,AH=NH=75+75,由勾股定理得:MN===50(+1),∴AM+AN﹣MN=100+100+150+50﹣50(+1)=200+100≈370(m).答:路线M→N的长比路线M→A→N的长少370m.解法二:如图,延长DC,AB交于点G,连接CN,CM,则∠G =90°,∵CD=DM,∠D=60°,∴△BCM是等边三角形,∴∠DCM=60°,由解法一可知:CG=50,GN=BG+BN=50+50(﹣1)=50,∴△CGN是等腰直角三角形,∴∠GCN=45°,∴∠BCN=45°﹣30°=15°,∴∠MCN=150°﹣60°﹣15°=75°=∠BCD,由【阅读材料】的结论得:MN=DM+BN=100+50(﹣1)=50+50,∵AM+AN﹣MN=100+100+150+50﹣50(+1)=200+100≈370(m).答:路线M→N的长比路线M→A→N的长少370m.故答案为:370.【解析】此题重点考查了含30°的直角三角形的性质,勾股定理,二次根式的混合运算等知识与方法,解题的关键是作出所需要的辅助线,构造含30°的直角三角形,再利用线段的和与差进行计算即可.三、参考答案题(本题有9个小题,共72分)17.【参考答案】解:()﹣1+|2﹣|﹣(﹣1)2022=3+﹣2﹣1=.【解析】本题考查了负整数指数幂,有理数的乘方,实数的运算,估算无理数的大小,绝对值,准确熟练地化简各式是解题的关键.18.【参考答案】解:÷(a+)=÷(+)=÷=•=.【解析】本题考查分式的混合运算,明确分式混合运算的步骤是解决问题的关键.19.【参考答案】(1)证明:∵a=1,b=﹣2,c=﹣3m2,∴Δ=(﹣2)2﹣4×1•(﹣3m2)=4+12m2>0,∴方程总有两个不相等的实数根;(2)解:由题意得:,解得:,∵αβ=﹣3m2,∴﹣3m2=﹣3,∴m=±1,∴m的值为±1.【解析】本题考查了根与系数的关系,根的判别式,熟练掌握根的判别式,以及根与系数的关系是解题的关键.20.【参考答案】解:(1)由题意得:48÷24%=200,∴m=200﹣48﹣76﹣60=16,n°=×360°=108°,故答案为:16,108;(2)由题意得:1600×=480(人),∴该校学生中“中度近视”的人数为480人;(3)如图:总共有12种等可能结果,其中同时选中甲和乙的结果有2种,∴P(同时选中甲和乙)==.【解析】本题考查了列表法与树状图,用样本估计总体,扇形统计图,准确熟练地进行计算是解题的关键.21.【参考答案】(1)证明:如图,连接DE,BF,∵四边形ABCD是平行四边形,∴BO=OD,AO=OC,∵E,F分别为AO,OC的中点,∴EO=OA,OF=OC,∴EO=FO,∵BO=OD,EO=FO,∴四边形BFDE是平行四边形,∴BE=DF;(2)解:当k=2时,四边形DEBF是矩形;理由如下:当BD=EF时,四边形DEBF是矩形,∴当OD=OE时,四边形DEBF是矩形,∵AE=OE,∴AC=2BD,∴当k=2时,四边形DEBF是矩形.【解析】本题主要考查了平行四边形的判定与性质,矩形的判定,注意对角线互相平分的四边形是平行四边形.22.【参考答案】(1)证明:如图,连接OF,∵AB=AC,∴∠B=∠C,∵OF=OC,∴∠C=∠OFC,∴∠OFC=∠B,∴OF∥AB,∵FG⊥AB,∴FG⊥OF,又∵OF是半径,∴GF是⊙O的切线;(2)解:如图,连接OE,过点O作OH⊥CF于H,∵BG=1,BF=3,∠BGF=90°,∴FG===2,∵⊙O与AB相切于点E,∴OE⊥AB,又∵AB⊥GF,OF⊥GF,∴四边形GFOE是矩形,∴OE=GF=2,∴OF=OC=2,又∵OH⊥CF,∴CH=FH,∵cosC=cosB=,∴,∴CH=,∴CF=.【解析】本题考查切线的性质和判定,勾股定理,等腰三角形的性质,矩形的判定和性质,锐角三角函数等知识,灵活运用这些性质解决问题是解题的关键.23.【参考答案】解:(1)∵日销售量y(件)与销售时间x(天)之间的关系式是y=,∴第15天的销售量为2×15=30件,故答案为:30;(2)由销售单价p(元/件)与销售时间x(天)之间的函数图象得:p=,①当0<x≤20时,日销售额=40×2x=80x,∵80>0,∴日销售额随x的增大而增大,∴当x=20时,日销售额最大,最大值为80×20=1600(元);②当20<x≤30时,日销售额=(50﹣x)×2x=﹣x2+100x=﹣(x﹣50)2+2500,∵﹣1<0,∴当x<50时,日销售额随x的增大而增大,∴当x=30时,日销售额最大,最大值为2100(元),综上,当0<x≤30时,日销售额的最大值2100元;(3)由题意得:当0<x≤30时,2x≥48,解得:24≤x≤30,当30<x≤40时,﹣6x+240≥48,解得:30<x≤32,∴当24≤x≤32时,日销售量不低于48件,∵x为整数,∴x的整数值有9个,∴“火热销售期”共有9天.【解析】本题主要考查了一次函数的应用,一次函数的性质,二次函数的性质,配方法求函数的极值,正确利用自变量的取值范围确定函数的关系式是解题的关键.24.【参考答案】解:(1)BF=CF;理由如下:连接AF,如图所示:根据旋转可知,∠DAE=α=90°,AE=AD,∵∠BAC=90°,∴∠EAC+∠CAD=90°,∠BAD+∠CAD=90°,∴∠EAC=∠BAD,在△ACE和△ABD中,,∴△ACE≌△ABD(SAS),∴∠ACE=∠ABD=90°,∴∠ACF=90°,在Rt△ABF与Rt△ACF中,,∴Rt△ABF≌Rt△ACF(HL),∴BF=CF,故答案为:BF=CF;(2)成立,理由如下:如图2,连接AF,根据旋转可知,∠DAE=α,AE=AD,∵∠BAC=α,∴∠EAC﹣∠CAD=α,∠BAD﹣∠CAD=α,∴∠EAC=∠BAD,在△ACE和△ABD中,∴△ACE≌△ABD(SAS),∴∠ACE=∠ABD=90°,∴∠ACF=90°,在Rt△ABF与Rt△ACF中,,∴Rt△ABF≌Rt△ACF(HL),∴BF=CF;(3)∵α=60°,AB=AC,∴△ABC为等边三角形,∴∠ABC=∠ACB=∠BAC=60°,AB=AC=BC=4,①当∠BAD<60°时,连接AF,如图所示:∵Rt△ABF≌Rt△ACF,∴∠BAF=∠CAF=∠BAC=30°,在Rt△ABF中,=tan30°,,即CF=BF=4;根据(2)可知,△ACE≌△ABD,∴CE=BD=m,∴EF=CF+CE=4+m,∠FBC=∠FCB=90°﹣60°=30°,∴∠EFP=∠FBC+∠FCB=60°,又∵∠EPF=90°,∴∠FEP=90°﹣60°=30°,∴PF=EF=2+m,∴BP=BF+PF=6+m,∴PD=BP﹣BD=6﹣m;②当∠BAD=60°时,AD与AC重合,如图所示:∵∠DAE=60°,AE=AD,∴△ADE为等边三角形,∴∠ADE=60°,∵∠ADB=90°﹣∠BAC=30°,∴∠ADE=90°,∴此时点P与点D重合,PD=0;③当∠BAD>60°时,连接AF,如图所示:∵Rt△ABF≌Rt△ACF,∴∠BAF=∠CAF=∠BAC=30°,在Rt△ABF中,=tan30°,,即CF=BF=4;根据(2)可知,△ACE≌△ABD,∴CE=BD=m,∴EF=CF+CE=4+m,∠FBC=∠FCB=90°﹣60°=30°,∴∠EFP=∠FBC+∠FCB=60°,又∵∠EPF=90°,∴∠FEP=90°﹣60°=30°,∴PF=EF=2+m,∴BP=BF+PF=6+m,∴PD=BD﹣BP=m﹣6,综上,PD的值为6﹣m或0或m﹣6.【解析】本题考查图形的旋转,等边三角形的性质,全等三角形的判定和性质,理解旋转的性质,注意分类讨论思想解题是关键.25.【参考答案】解:(1)由题意得,,∴,∴y=x2+x﹣3;(2)①如图1,设直线PC交x轴于E,∵PD∥OC,∴∠OCE=∠CPD=45°,∵∠COE=90°,∴∠CEO=90°﹣∠ECO=45°,∴∠CEO=∠OCE,∴OE=OC=3,∴点E(3,0),∴直线PC的解析式为:y=x﹣3,由x2+x﹣3=x﹣3得,∴x1=﹣,x2=0(舍去),当x=﹣时,y=﹣﹣3=﹣,∴P(﹣,﹣);②如图2,设点P(m,m2+m﹣3),四边形PECE′的周长记作l,点P在第三象限时,作EF⊥y轴于F,∵点E与E′关于PC对称,∴∠ECP=∠E′PC,CE=CE′,∵PE∥y轴,∴∠EPC=∠PCE′,∴∠ECP=∠EPC,∴PE=CE,∴PE=CE′,∴四边形PECE′为平行四边形,∴▱PECE′为菱形,∴CE=PE,∵EF∥OA,∴,∴,∴CE=﹣m,∵PE=﹣(﹣)﹣(+﹣3)=﹣﹣3m,∴﹣=﹣m2﹣3m,∴m1=0(舍去),m2=﹣,∴CE=,∴l=4CE=4×=,当点P在第二象限时,同理可得:﹣m=+3m,∴m3=0(舍去),m4=﹣,∴l=4×=,综上所述:四边形PECE′的周长为:或.【解析】本题考查了求一次函数和二次函数的解析式,等腰三角形的判定和性质,相似三角形的判定和性质,菱形的判定和性质,轴对称性质等知识,解决问题的关键是正确分类,作辅助线,表示出线段的数量.。
2017年湖北省十堰市中考数学试卷(含答案)

2017年十堰市初中毕业生升学考试数学试题注意事项:1.本卷共有4页,共有25小题,满分120分,考试时限120分钟.2.答题前,考生先将自己的姓名、准考证号填写在试卷和答题卡指定的位置,并认真核对条形码上的准考证号和姓名,在答题卡规定的位置贴好条形码.3.考生必须保持答题卡的整洁,考试结束后,请将本试卷和答题卡一并上交.一、选择题1.气温由-2℃上升3℃后是( ) ℃.A .1B .3C .5D .-52.如图的几何体,其左视图是( )3.如图,AB ∥DE ,FG ⊥BC 于F ,∠CDE =40º,则∠FGB =( )ºA .40B .50C .60D .70 4.下列运算正确的是( )A .2+3=5B .22×32=62C .8÷2=2D .32-2=3 5.某交警在一个路口统计的某时段来往车辆的车速情况如下表:车速(Km/h) 48 49 50 51 52 车辆数(辆)54821则上述车速的中位数和众数分别是( )A .50,8B .50,50C .49,50D .49,8 6.下列命题错误的是( )A .对角线互相平分的四边形是平行四边形;B .对角线相等的平行四边形是矩形C .一条对角线平分一组对角的四边形是菱形;D .对角线互相垂直的矩形是正方形 7. 甲、乙二人做某种机械零件,甲每小时比乙多做6个,甲做90个所用的时间与做60 个所用的时间相等,设甲每小时做x 个零件,下面所列方程正确的是( )9060906090609060....6666A B C D x x x x x xx x====-+-+ 8.如图,已知圆柱的底面直径BC = 6π,高AB =3,小虫在圆柱表面爬行,从C 点爬到A点,A B C DGBDEA F C然后再沿另一面爬回C 点,则小虫爬行的最短路程为( )A .32B .35C .65D .629. 如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如 ,表示a 1=a 2+a 3,则a 1的最小值为( )A .32B .36C .38D .4010. 如图,直线36y x =-分别交x 轴,y 轴于A ,B ,M 是反比例函数>ky x x=(0)的图象上位于直线上方的一点, MC ∥x 轴交AB 于C , MD ⊥MC 交AB 于D , AC ·BD =43,则k 的值为( )A .-3B .-4C .-5D .-6二、填空题11.某颗粒物的直径是0.0000025米,把0.0000025用科学计数法表示为 . 12.若a -b =1,则代数式2a -2b -1的值为 .13.如图,菱形ABCD 中,AC 交BD 于O ,DE ⊥BC 于E .连接OE ,若∠ABC =140º, 则∠OED = .14.如图,△ABC 内接于⊙O ,∠ACB =90º,∠ACB 的角平分线交⊙O 于D ,若AC =6, BD =52,则BC 的长为 .15.如图,直线y =kx 和y =ax +4交于A (1,k ),则不等式kx -6<ax +4<kx 的解集为 . 16.如图,正方形ABCD 中,BE =EF =FC ,CG =2GD ,BG 分别交AE ,AF 于M ,N . 下列结论:①AF ⊥BG ;②BN = 4 3NF ;③BM MG = 3 8;④S 四边形CGNF = 1 2S 四边形ANGD .其中正确的结论的序号是 .a 1a 3a 2ABCD a 3a 2a 6a 4a 1a 5a 10a 9a 8CABa 7O M xyy=ax +4y =kx AON MG CF E BD O ED AC B O xy ABACD三.解答题17.(5分)计算:20173281-+--(-).18. (5分)化简:222+111a aa a a +--+()÷.19.(7分)如图,海中有一小岛A ,他它周围8海里内 有暗礁,渔船跟踪鱼群由西向东航行,在B 点测得 小岛A 在北偏东60°方向上,航行12海里到达D 点, 这时测得小岛A 在北偏东30°方向上.如果渔船不改 变航线继续向东航行,有没有触礁的危险?20.(9分)某中学艺术节期间,学校向学生征集书画作品,杨老师从全校30个班中随机抽取了4个班 (用A ,B ,C ,D 表示),对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图.请根据以上信息,回答下列问题:(1)杨老师采取的调查方式是 (填“普查”或“抽样调查”); (2)请你将条形统计图补充完整,并估计全校共征集多少件作品?(3)如果全校征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名的两名学生性别相同的概率.ABDN作品数量扇形统计图作品数量条形统计图AB CD90°1210DC B A2468作品(件)次数O21. (7分) 已知关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2.(1)求实数k的取值范围;(2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.22. (8分) 某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱.设每箱牛奶降价x元(x为正整数),每月的销量为y箱.(1)写出y与x之间的函数关系式和自变量x的取值范围;(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?23. (8分)已知AB为半⊙O的直径,BC⊥AB于B,且BC=AB,D为半⊙O上的一点,连接BD并延长交半⊙O的切线AE于E.(1)如图1,若CD=CB,求证:CD是⊙O的切线;(2)如图2,若F点在OB上,且CD⊥DF,求AEAF 的值.图1EDC A O B图2DFC A O B E24. (10分)已知O 为直线MN 上一点,OP ⊥MN ,在等腰Rt △ABO 中,∠BAO =90º,AC ∥OP 交OM 于C ,D 为OB 的中点,DE ⊥DC 交MN 于E .(1) 如图1,若点B 在OP 上,则①AC OE (填“<”,“=”或“>”);②线段CA 、CO 、CD满足的等量关系式是 ; (2) 将图1中的等腰Rt △ABO 绕O 点顺时针旋转α(0º<α<45º),如图2,那么(1)中的结论②是否成立?请说明理由;(3) 将图1中的等腰Rt △ABO 绕O 点顺时针旋转α(45º<α<90º),请你在图3中画出图形,并直接写出线段CA 、CO 、CD 满足的等量关系式 ;图3图2图1O ED CABOE CABODMNPM NPMNP25. (12分)抛物线y =x 2+bx +c 与x 轴交于A (1,0),B (m ,0),与y 轴交于C . (1) 若m =-3,求抛物线的解析式,并写出抛物线的对称轴;(2) 如图1,在(1)的条件下,设抛物线的对称轴交x 轴于D ,在对称轴左侧的抛物线上有一点E ,使S △ACE =10 3S △ACD,求E 点的坐标; (3) 如图2,设F (-1,-4),FG ⊥y 轴于G ,在线段OG 上是否存在点P ,使∠OBP =∠FPG ? 若存在,求m 的取值范围;若不存在,请说明理由.图2图1GFDCBO O AyxAyx十堰2017年中考数学试题参考答案一、选择题:1 2 3 4 5 6 7 8 9 10A B B C B C A D D A二、填空题:11、2.5×10-6;12、1;13、20°;14、8;15、1<x<2.5;16、①③.第16题解析:(1)可证△ABF≌△BCG,得AF⊥BG;(2)32BN BCNF CG==,所以②不正确;(3)设正方形的边长为3,则GH=2,HP=23,得GP=83由GP//BC得△GPM~△BME∴83138 BM BEMG GP==÷=∴③正确.(4)设正方形的边长为3,则S△BCG= S△ABF=1233 2⨯⨯=∴S CGNF=S△ABM=223273()31313ABBG⎛⎫⨯=⨯=⎪⎝⎭∵S ABGD=113= 2+⨯()36∴S ANGD=2751 6-= 1313∴S CGNF:S ANGD=27:51≠1:2∴④不正确.∴正确的选项为①③. 17、解:原式=2-2+1=1;18、解:原式=2221313(1)(1)(1)(1)(1)(1)1a a a a aa a a a a a a a a⎛⎫-+--+⨯=⨯=⎪+-+-+-+⎝⎭;MPHNGFEDCBA19、解析:由∠BAD =∠B =30°可得AD =BD =12∵∠ADC =60°, ∴AC =312=6382⨯> ∴没有触礁的危险.20、解: (1)抽样调查(2)C 班高度为10;24÷4×30=180(件); (3)P =2521、(1)k ≤54; (2)k =-2. 22、(1)y =10x +60,1≤x ≤12,且x 为整数; (2)设利润为W 元,由题意得, w =(36-x -24)(10x +60)整理得,w =-10x 2+60x +720=-10(x -3)2+810 ∵a = -10<0,且1≤x ≤12 ∴当x =3时,w 有最大值810 ∴售价为36-3=33答:当定价为33元/箱时,每月牛奶销售利润最大,最大利润是810元.23、(1)证明:略;(此问简单) (2)连接AD . ∵DF ⊥DC ∴∠1+∠BDF =90° ∵AB 是⊙O 的直径 ∴∠2+∠BDF =90° ∴∠1=∠2又∵∠3+∠ABD =90°, ∠4+∠ABD =90° ∴∠3=∠4 ∴△ADF ~△BCDAF ADBC BD= CD BA4321FOED CBA∵∠3+∠EAD =90°,∠E+∠EAD =90°∴∠3=∠E又∵∠ADE=∠ADB=90° ∴△AD E ~△ABD ∴AE AD AB BD =∴AE AFAB BC = ∴1AE ABAF BC==24、(1)①AC=OE;②CA+CO =2CD;(2)结论②仍然成立. 理由:连接AD.∵△OAB是等腰直角三角形,且D为OB的中点∴AD⊥OB,AD=DO∴∠ADO=90°∴∠ADC+∠CDO=90°∵DE⊥CD∴∠CDE=∠ODE+∠CDO=90°∴∠ADC=∠ODE∵AC⊥MN∴∠ACO=90°∴∠CAD+∠DOC=360°-90°-90°=180°∵∠DOE+∠DOC=180°∴∠CAD=∠DOE在△ACD和△DOE中∠ADC=∠ODE∠DAC=∠DOEAD=DO∴△ACD≌△DOE(ASA)∴AC=OE,CD=DE∵∠CDE=90°∴△CDE是等腰直角三角形∴OE+CO=2CD∴CA+CO=2CD(3)如右图所示,CO-CA=2CD解析:连接AD,先证明△ACD≌△DOF(ASA),得CA=OF,CD=DF;然后证明△CDF是等腰直角三角形,得:CO-OF=2CD,所以CO-CA=2CDECDBANM POFECDBANMP O25、(1)y =x 2+2x -3(2)∵点A (1,0),C (0,-3) ∴直线AC 为y = 3x -3∴过点D (-1,0)且平行于AC 的直线L 1为:y = 3x +3 ∴直线AC 向上平移6个单位得到直线L 1 ∴将直线AC 向上平移106203⨯=个单位得到直线L 2:y =3x +17 联立方程组,y =x 2+2x -3 y =3x +17解得,x 1=-4 x 1=5y 1=5 y 1=32 (不合题意,舍去) ∴点E 坐标为(-4,5)(3)设点P (0,y )①当m <0时,如图所示,易证△POB ~△FPG ,得OB OPPG FG= ∴41m yy --=+ ∴m =y 2+4y =(y +2)2-4 ∵-4<y <0 ∴-4≤m <0②当m >0时,如图所示,易证△POB ~△FPG ,得OB OPPG FG= ∴41m yy -=+ ∴m = -y 2 -4y = -(y +2)2+4 ∵-4<y <0 ∴0<m ≤4综上所述,m 的取值范围是:-4≤m ≤4,且m ≠0.L2L1xyODCBA PGFxyOBAPGFxyOBA。
《二元一次方程组的应用》2006年中考试题集锦

《二元一次方程组的应用》2006年中考试题集锦第1题. (2006 常州课改)小刘同学用10元钱购买两种不同的贺卡共8张,单价分别是1元与2元.设1元的贺卡为x 张,2元的贺卡为y 张,那么x y , 所适合的一个方程组是( )A .1028y x x y ⎧+=⎪⎨⎪+=⎩ B .8210210x y x y ⎧+=⎪⎨⎪+=⎩C .1028x y x y +=⎧⎨+=⎩D .8210x y x y +=⎧⎨+=⎩答案:D第2题. (2006 成都课改)已知代数式1312a x y -与23b a b x y -+-是同类项,那么a b ,的值分别是( ) A .21a b =⎧⎨=-⎩,B .21a b =⎧⎨=⎩,C .21a b =-⎧⎨=-⎩,D .21a b =-⎧⎨=⎩,答案:A第3题. (2006 北京非课改)国外营养学家做了一项研究,甲组同学每天正常进餐,乙组同学每天除正常进餐外,每人还增加六百毫升牛奶.一年后发现,乙组同学平均身高的增长值比甲组同学平均身高的增长值多2.01cm ,甲组同学平均身高的增长值比乙组同学平均身高的增长值的34少0.34cm .求甲、乙两组同学平均身高的增长值.答案:解法一:设甲组同学平均身高的增长值为x cm , 乙组同学平均身高的增长值为y cm .依题意,得 2.0130.34.4y x y x -=⎧⎪⎨-=⎪⎩,解得 4.676.68.x y =⎧⎨=⎩,答:甲、乙两组同学平均身高的增长值分别为4.67cm 和6.68cm .解法二:设甲组同学平均身高的增长值为x cm , 则乙组同学平均身高的增长值为( 2.01)x +cm .依题意,得3( 2.01)0.344x x +-=. 解得 4.67x =. 2.01 6.68x ∴+=.答:甲、乙两组同学平均身高的增长值分别为4.67cm 和6.68cm .第4题. (2006 河北非课改)根据图提供的信息,可知一个杯子的价格是( )共43共94A.51元 B.35元 C.8元 D.7.5元 答案:C第5题. (2006 河北非课改)《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图-1,图-2.图中各行从左到右列出的算筹数分别表示未知数x y ,的系数与相应的常数项.把图-1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是3219423.x y x y +=⎧⎨+=⎩,类似地,图-2所示的算筹图我们可以表述为( )A.2114327.x y x y +=⎧⎨+=⎩, B.2114322.x y x y +=⎧⎨+=⎩, C.3219423.x y x y +=⎧⎨+=⎩, D.264327.x y x y +=⎧⎨+=⎩,答案:A第6题. (2006 济南非课改)某高校共有5个大餐厅和2个小餐厅.经过测试:同时开放1个大餐厅、2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅、1个小餐厅,可供2280名学生就餐. (1)求1个大餐厅、1个小餐厅分别可供多少名学生就餐;(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由.答案:(1)设1个大餐厅可供x 名学生就餐,1个小餐厅可供y 名学生就餐,根据题意,得2168022280.x y x y +=⎧⎨+=⎩,解这个方程组,得960360.x y =⎧⎨=⎩,答:1个大餐厅可供960名学生就餐,1个小餐厅可供360名学生就餐. (2)因为9605360255205300⨯+⨯=>,所以如果同时开放7个餐厅,能够供全校的5300名学生就餐.第7题. (2006 泰州课改)扬子江药业集团生产的某种药品包装盒的侧面展开图如图所示.如果长方体盒子的长比宽多4cm ,求这种药品包装盒的体积.答案:解:设这种药品包装盒的宽为cm x ,高为cm y ,则长为(4)cm x +,图-1 图-2根据题意得,22144213x y x y +=⎧⎨++=⎩解这个方程组得52x y =⎧⎨=⎩故长为9cm ,宽为5cm ,高为2cm . 体积395290(cm )V =⨯⨯=答:这种药品包装盒的体积为390cm .第8题. (2006 广州课改)目前广州市小学和初中在校生共有约128万人,其中小学生在校人数比初中生在校人数的2倍多14万人(数据来源:2005学年度广州市教育统计手册). (1)求目前广州市在校的小学生人数和初中生人数;(2)假设今年小学生每人需交杂费500元,初中生每人需交杂费1000元,而这些费用全部由广州市政府拨款解决,则广州市政府要为此拨款多少?答案:解:(1)方法1: 设目前广州市在校的中学生人数约为x 万,则目前广州市在校的小学生人数约为(214)x + 万,根据题意得:(214)128x x ++=,解这个方程,得38x =.2142381490x +=⨯+=.答:目前广州市在校的小学生人数和初中生人数分别约为:90万和38万. 方法2:设目前广州市在校的小学生人数约为x 万,在校初中生人数约为y 万,根据题意得:128214x y x y +=⎧⎨=+⎩,., 解这个方程组,得9038x y =⎧⎨=⎩,.答:目前广州市在校的小学生人数和初中生人数分别约为:90万和38万.(2)5009010003883000⨯+⨯=(万元). 答:今年,市政府要支出83000万元.第9题. (2006 镇江课改)小刘同学用10元钱购买两种不同的贺卡共8张,单价分别是1元与2元.设1元的贺卡为x 张,2元的贺卡为y 张,那么x y , 所适合的一个方程组是( )A .1028y x x y ⎧+=⎪⎨⎪+=⎩ B .8210210x yx y ⎧+=⎪⎨⎪+=⎩C .1028x y x y +=⎧⎨+=⎩D .8210x y x y +=⎧⎨+=⎩答案:D第10题. (2006 海南非课改)某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和徽章两种奥运商品,根据下图提供的信息,求一盒“福娃”玩具和一枚徽章的价格各是多少元?答案:设一盒“福娃”玩具和一枚徽章的价格分别为x 元和y 元. 依题意,得214523280x y x y +=⎧⎨+=⎩解这个方程组,得12510x y =⎧⎨=⎩答:一盒“福娃”玩具和一枚徽章的价格分别为125元和10元.第11题. (2006 宿迁课改)在2006年德国世界杯足球赛中,32支足球队将分成8个小组进行单循环比赛,小组比赛规则如下:胜一场得3分,平一场得1分,负一场得0分.若小组赛中某队的积分为5分,则该队必是( ) A.两胜一负 B.一胜两平 C.一胜一平一负 D.一胜两负 答案:B第12题. (2006 南昌非课改)一副三角板按如图方式摆放,且1∠的度数比2∠的度数大50,若设1x ∠=,2y ∠= ,则可得到方程组为( )A.50180x y x y =-⎧⎨+=⎩,B.50180x y x y =+⎧⎨+=⎩,C.5090x y x y =-⎧⎨+=⎩,D.5090x y x y =+⎧⎨+=⎩,答案:D第13题. (2006 南京课改)某停车场的收费标准如下:中型汽车的停车费为6元/辆,小型汽车的停车费为4元/辆,现在停车场有50辆中、小型汽车,这些车共缴纳停车费230元,问中、小型汽车各有多少辆? 答案:解法一:设中型汽车有x 辆,小型汽车有y 辆.共计145元 共计280元根据题意,得5064230.x y x y +=⎧⎨+=⎩,解这个方程组,得1535.x y =⎧⎨=⎩,答:中型汽车有15辆,小型汽车有35辆.第14题. (2006 广东非课改)商场销售A B ,两种品牌的衬衣,单价分别为每件30元,50元,一周内共销售出300件;为扩大衬衣的销售量,商场决定调整衬衣的价格,将A 种衬衣降价20%出售,B 种衬衣按原价出售,调整后,一周内A 种衬衣的销售量增加了20件,B 种衬衣销售量没有变,这周内销售额为12880元,求调整前两种品牌的衬衣一周内各销售多少件?答案:解:设A 种品牌的衬衣有x 件,B 种品牌的衬衣有y 件.依题意可得,30030(120%)(20)5012880.x y x y +=⎧⎨⨯-++=⎩,解得,100200.x y =⎧⎨=⎩,答:A 种品牌的衬衣有100件,B 种品牌的衬衣有200件.第15题. (2006 菏泽课改)为迎接“五一”劳动节,菏泽市某中学组织了甲、乙两个义务劳动小组,甲组x 人,乙组y 人,到“中华路”和“青年路”打扫卫生,根据打扫卫生的进度,学校随时调整两组人数,如果从甲组调50人去乙组,则乙组人数为甲组人数的2倍;如果从乙组调m 人去甲组,则甲组人数为乙组人数的3倍.(1)求出x 与m 之间的关系式.(2)问当m 为何值时,甲组人数最少,最少是多少人?答案:解:(1)由题意得方程组()()250503x y x m y m -=+⎧⎪⎨+=-⎪⎩,,整理得215034x y x y m -=⎧⎨-=-⎩,, ① ②3⨯-①②得54504x m =+,4905x m ∴=+(得到54504x m =+或其变形式皆给分). (2)由4905x m =+知x 随m 增大而增大,又因x ,m ,y 均为正整数, 所以当5m =时,x 取得最小值.其最小值为4590945⨯+=,此时38y =适合题意.答:当5m =时,甲组人数最少,最少为94人.第16题. (2006 玉林、防城港课改)商店里把塑料凳整齐地叠放在一起,据图的信息,当有10张塑料凳整齐地叠放在一起时的高度是 cm . 答案:50第17题. (2006 株洲课改)某单位购买甲、乙两种纯净水共用250元,其中甲种水每桶8元,乙种水每桶6元;乙种水的桶数是甲种水桶数的75%.设买甲种水x 桶,买乙种水y 桶,则所列方程组中正确的是( ) A.8625075%x y y x +=⎧⎨=⎩ B.8625075%x y x y +=⎧⎨=⎩ C.6825075%x y y x+=⎧⎨=⎩D.6825075%x y x y+=⎧⎨=⎩答案:A第18题. (2006 鄂尔多斯课改)国家为九年义务教育期间的学生实行“两免一补”政策,下表是我市某中学国家免费提供教科书补助的部分情况.)A.3001109026200x y x y +=⎧⎨+=⎩B.30011090400026200x y x y +=⎧⎨++=⎩C.80300400026200x y x y ++=⎧⎨++=⎩D.8030011090400026200x y x y ++=⎧⎨++=⎩答案:D第19题. (2006 吉林非课改)如图,在33⨯的方格内,填写了一些代数式和数. (1)在图1中各行、各列和对角线上三个数之和都相等,请你求出x ,y 的值; (2)把满足(1)的其它6个数填入图2中的方格内.53x - 4 7 x - 3y 547(图1) (图2)答案:解:由已知条件可得:7343745x y x -=+⎧⎨-=+⎩,.解得23x y =-⎧⎨=⎩,.(本题列方程组具有开放性,只要列、解方程组正确,即得满分.)第20题. (2006 吉林课改)如图,在33⨯的方格内,填写了一些代数式和数. (1)在图1中各行、各列及对角线上三个数之和都相等,请你求出x ,y 的值; (2)把满足(1)的其它6个数填入图2中的方格内.答案:解:由已知条件可得:234345x y y y +=-⎧⎨+=⎩,. 解得11x y =-⎧⎨=⎩,.(本题列方程组具有开放性,只要列、解方程组正确,即给4分).第21题. (2006 泉州课改)某校的一间阶梯教室,第1排的座位数为a ,从第2排开始,每一排都比前一排增加b 个座位.(1(2)已知第4排有18个座位,第15排座位数是第5排座位数的2倍,求第21排有多少个座位?5 4 7 2 96 8 3 10 23- 4y23-(图1) (图2)3 2x y 3 2 3- 3 2- 5 1 0 1- 4答案:解:(1)3a b+(2)依题意得318142(4)a ba b a b+=⎧⎨+=+⎩解得122ab=⎧⎨=⎩1220252+⨯=∴答:第21排有52个座位.第22题. (2006娄底)小英和小强相约一起去某超市购买他们看中的随身听和书包.你能根据他们的对话内容(如图),求出他们看中的随身听和书包单价各是多少元吗?答案:解:设他们看中的书包的单价为x元,随身听的单价为y元.依题意有45248x yy x+=⎧⎨=-⎩解得92360xy=⎧⎨=⎩答:(略)第23题. (2006 湘西自治区)在社会主义新农村建设中,某村积极响应党的号召,大力发动农户扩大烟叶和蔬菜的种植面积,取得了较好的经济效益.今年该村烟叶和蔬菜的种植面积比去年增加了800亩,其中烟叶种植面积增加了20%,蔬菜种植面积增加了30%,从而使该村的烟叶和蔬菜种植面积共达到了4200亩.问该村去年种植烟叶和蔬菜的面积各是多少亩?答案:解:设该村去年种植烟叶和蔬菜面积各为x亩,y亩,根据题意有:420080020%30%800x yx y+=-⎧⎨+=⎩解得:22001200xy=⎧⎨=⎩答:该村去年种植烟叶和蔬菜的面积各是2200亩,1200亩.第24题. (2006 湘西自治区)如图,平行四边形ABCD的周长是48,对角线AC与BD相交于点O,AOD△的周长比AOB △的周长多6,若设AD x =,AB y =,则可用列方程组的方法求AD ,AB 的长,这个方程组可以是:( )A.2()486x y x y +=⎧⎨-=⎩B.2()486x y y x +=⎧⎨-=⎩C.486x y x y +=⎧⎨-=⎩D.486x y y x +=⎧⎨-=⎩答案:A第25题. (2006 岳阳课改)今年五月二十七日,印尼中爪哇省发生强烈地震,给当地人民造成巨大的经济损失.某学校积极组织捐款支援灾区,初三(1)班55名同学共捐款274元,捐款情况如右表.表中捐款2元和5元的人数不小心被墨水污染已看不清楚,请你帮助确定表中数据,并说明理由.答案:解:设捐款2元和5元的学生人数分别为x 人,y 人,依题意得: 556725274670x y x y +=--⎧⎨+=--⎩4225198x y x y ⎛+=⎫⎧ ⎪⎨+=⎩⎝⎭解方程组,得438x y =⎧⎨=⎩答:捐款2元的有4人,捐款5元的有38人.第26题. (2006 张家界课改)我市某生态果园今年收获了15吨李子和8吨桃子,要租用甲、乙两种货车共6辆,及时运往外地,甲种货车可装李子4吨和桃子1吨,乙种货车可装李子1吨和桃子3吨. (1)共有几种租车方案? (2)若甲种货车每辆需付运费1000元,乙种货车每辆需付运费700元,请选出最佳方案,此方案运费是多少.答案:解:(1)设安排甲种货车x 辆,乙种货车(6)x -辆,根据题意,得:4(6)1533(6)85x x x x x x +-⎧⎧⇒⎨⎨+-⎩⎩≥≥≥≤ 35x ∴≤≤x 取整数有:3,4,5,共有三种方案.(2)租车方案及其运费计算如下表.(说明:不列表,用其他形式也可)答:共有三种租车方案,其中第一种方案最佳,运费是5100元.。
湖北省十堰市中考数学试题(含答案)

3.下列运算中,正确的是( )
A. a2 + a3 = a5
B. a6 ¸ a3 = a2
C.(a4 )2 = a6
D. a2 a3 = a5
4.用两块完全相同的长方体摆放成如图所示的几何体,这个几何体的左视图是( )
正面
A.
B.
C.
D.
5.已知关于 x 的一元二次方程 x2+2x-a=0 有两个相等的实数根,则 a 的值是( )
…………………………………2 分
8
4 4
……………………………………5 分
乒 乒 乒 乒 乒 乒 乒 乒 乒 乒乒 乒乒
第二次 第一次
男1
男2
男3
女
男1
男1男2
男1男3
男1 女
男2
男2男1
男2男3
男2 女
男3
男3男1
男3男2
男3 女
女
女男 1
女男 2
女男 3
从上表可以看出,所有可能出现的结果共有 12 种,每种结果出现的可能性均相同,其
=15x+20(100-x) =-5x+2000 …………………………………………………………………………5 分
由题意得:100- x ≤ 3x ,解得:x≥25 ……………………………………………6 分
∵k=-5<0, ∴y 随 x 的增大而减小, ∴当 x=25 时, y 取得最大值:-5×25+2000=1875(元)
1 求反比例函数的解析式;
y
2 观察图象,直接写出正比例函数值大于反比例函数值
时自变量 x 的取值范围;
C
O
x
B
3
A
数学f1初中数学2006年全国中考数学压轴题全解全析(1-14)

本文为自本人珍藏 版权所有 仅供参考 本文为自本人珍藏 版权所有 仅供参考2006年全国中考数学压轴题全解全析1、(北京课改B 卷)我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;(2)探究:当等对角线四边形中两条对角线所夹锐角为60 时,这对60 角所对的两边之和与其中一条对角线的大小关系,并证明你的结论. [解] (1)答案不唯一,如正方形、矩形、等腰梯形等等.(2)结论:等对角线四边形中两条对角线所夹锐角为60 时,这对60 角所对的两边之和大于或等于一条对角线的长.已知:四边形A B C D 中,对角线A C ,B D 交于点O ,A C B D =, 且60AOD ∠= . 求证:B C A D A C +≥.证明:过点D 作D F AC ∥,在D F 上截取D E ,使D E AC =. 连结C E ,B E .故60EDO ∠= ,四边形A C E D 是平行四边形. 所以B D E △是等边三角形,C E A D =. 所以D E B E A C ==.①当B C 与C E 不在同一条直线上时(如图1), 在B C E △中,有B C C E B E +>.所以B C A D A C +>.②当B C 与C E 在同一条直线上时(如图2), 则BC C E BE +=.因此B C A D A C +=.综合①、②,得B C A D A C +≥.即等对角线四边形中两条对角线所夹角为60时,这对60角所对的两边之和大于或等于其中一条对角线的长.[点评]本题是一道探索题,是近年来中考命题的热点问题,在第2小题中要求学生先猜想可能的结论,再进行证明,这对学生的确有较高的能力要求,而在探索结论前可以自己先画几个草图,做到心中有数再去努力求证;很多学生往往会忽略特殊情况没有进行讨论,应当予以关注,总之这是一道新课标形势下的优秀压轴题。
2006中考数学试题分析与2007中考数学命题展
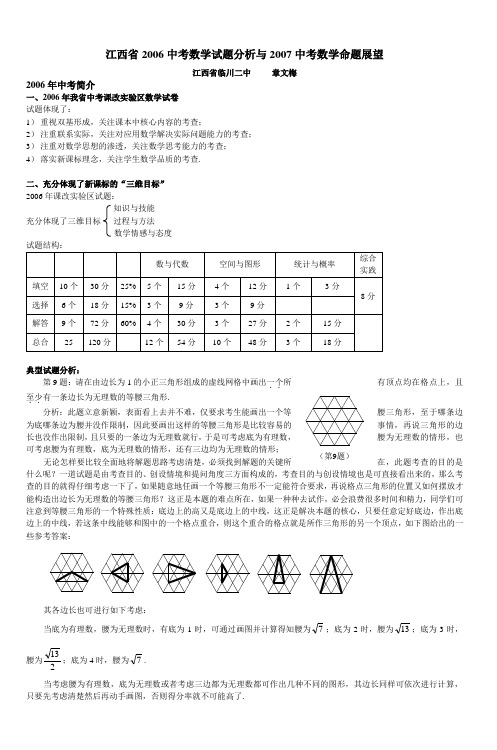
120分
12个
54分
10个
48分
3个
18分
典型试题分析:
第9题:请在由边长为1的小正三角形组成的虚线网格中画出一个所有顶点均在格点上,且至少有一条边长为无理数的等腰三角形.
分析:此题立意新颖,表面看上去并不难,仅要求考生能画出一个等腰三角形,至于哪条边为底哪条边为腰并没作限制,因此要画出这样的等腰三角形是比较容易的事情,再说三角形的边长也没作出限制,且只要的一条边为无理数就行,于是可考虑底为有理数,腰为无理数的情形,也可考虑腰为有理数,底为无理数的情形,还有三边均为无理数的情形;
纵观2006年课改实验区的数学考试题的这些特点,2007年的中考命题将有如下趋势:
(一)数与式部分的试题将不再纯粹地考查记忆的内容,尤其是一些繁、难、偏的计算题目将不再出现,取而代之的是探索数与式的数学意义及与实际生活的联系的问题,在变化的图形或实际问题的背景中观察、概括出一般规律;运用数学模型解决实际问题等.
二、充分体现了新课标的“三维目标”
2006年课改实验区试题:
知识与技能
充分体现了三维目标过程与方法
数学情感与态度
试题结构:
数与代数
空间与图形
统计与概率
综合实践
填空
10个
30分
25%
5个1Leabharlann 分4个12分1个
3分
8分
选择
6个
18分
15%
3个
9分
3个
9分
解答
9个
72分
60%
4个
30分
3个
27分
2个
15分
总合
(二)实间与图形部分的内容与以往相比难度有较大的降低,不会出现繁难的几何论证题目,在填空题和选择题中将重点考查视图、几何体及其平面展开图之间的关系以及初步的空间观念,几何论证题将转为从常见的几何图形中提出问题或猜想,通过对其分析、探索、发现其内在规律并能用简单的逻辑推理来证明命题的正确性,以考查考生的合情推理能力.
初中课改数学试题的剖析和走向经验谈

初中课改数学试题的剖析和走向经验谈摘要:伴随着课程改革的推进,全新的以学生发展为本的教育理念逐渐深入人心,不少学校也根据课程改革对自己的教学方案做出了一系列的调整,并且许多学校使用新课改实验考试试卷,那么新课改数学试题有哪些特点以及它的走向是什么样的呢?下面是对初中数学试题的浅析。
关键词:课改;数学试题;经验一、注重基础知识纵观新课改以来的考试试卷,较容易的基础题占了70%,易中难的比率大概是7∶2∶1左右,并且大多数的基础题在我们的课本中都能找到相类似的题型,是课本例题的类比、延伸和拓展。
随着数学课程改革的发展,中考对数学基础知识进行了重新的认识和定位,在试卷的命题中减少了单纯知识、公式的记忆要求,注重知识的综合性和学科的内在联系,考查了学生是否能熟练运用这些基础知识,也考查了学生对概念的理解。
二、题目贴近生活,重视应用能力新课标倡导在广阔的生活背景下,把握数学学科的结构和应用本质,汲取其中鲜活的、富有生活化的解题原型,从中提炼、构造数学问题。
例如,这样的试题“某鞋店的新款女鞋销售情况如下:经理关注那种鞋号的销售量最大,要通过什么数据来体现?a.平均数。
b.众数。
c.方差。
d.中位数。
”现在的试题对应用性问题的考查,已经渗透到社会生活的各个方面,如,旅游业、商品促销、医疗卫生、生态环境等。
三、注重学生数学思维和综合能力的考查传统的中考试题设计,太过于形式化和验证化,对学生的探究精神的鼓励不够。
很多问题没有探究的表象,只是有着确定的封闭性。
这样的试题结论就是结论,毫无探索精神。
新课改下的数学试题出现了很多,例如将几何和代数结合在一起,答案不唯一,分类讨论等类似的比较难的题型,这些题目需要学生具有数学思维,掌握一些基本的数学方法。
教师要注重培养学生的科学探究能力和综合计算能力,因为这类题型将成为选优拔尖很好的筛选方式,也是试卷中必不可少的一部分。
新课改的中考试题正在进一步成熟,不仅保持了传统数学中考试题的优点,还大胆地尝试了新型探究式的基础试题,试题综合性强,思维容量大,评分标准细致。
轴对称经典中考试题及答案解析二A

图 1DCBA折叠轴对称经典中考试题及答案解析二知识点1 轴对称变换的定义:由一个平面图形得到它的图形叫做轴对称变换.成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对称变换后得到.一个轴对称图形也可以看作以它的一部分为基础,经轴对称变换扩展而成的.【答案】轴对称1.(2006大连)如图1,将矩形沿对称轴折叠,在对称轴处剪下一块,余下部分的展开图为( )【答案】C知识点2作出简单平面图形经过轴对称后的图形.几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的,再这些对应点,就可得到原图形的轴对称图形;对于一些由直线、•线段或射线组成的图形,只要作出图形中的一些(如线段端点)的对应点,连结这些对应点,就可以得到原图形的轴对称图形.【答案】对称点、连结、特殊点。
2.(2005江西) 如图,一轴对称图形画出了它的一半,请你以点画线为对称轴画出它的另一半。
【答案】知识点3坐标表示轴对称:点(x,y)关于x轴对称的点的坐标为,即横坐标相等,纵坐标互为相反数;点(x,y)关于y轴对称的点的坐标为,即横坐标互为相反数,纵坐标相等.利用点关于x轴、y轴对称的点的坐标规律,我们可以很容易地在平面直角坐标系中作出与一个图形关于【答案】(x,-y) (-x,y)3.(2005上海) (1)在图3所示编号为①、②、③、④的四个三角形中,关于y轴对称的两个三角形的编号为;关于坐标原点O对称的两个三角形的编号为;【答案】关于y轴对称的两个三角形的编号为①、②;关于坐标原点O对称的两个三角形的编号为①、③;说明:本部分须罗列本节重要知识点及公式,在对知识点的概念的解释中,可将关键字等重要部分留空,每个知识点下面,节选1~2题考查相应知识点的中考原题,要求此部分所节选的中考题简单、容易,总题量不超过6题。
一、选择题1. (2006山东淄博)4、将一矩形纸片按如图方式折叠,BC 、BD 为折痕,折叠后B E B A ''与与在同一条直线上,则∠CBD 的度数A. 大于90°B.等于90°C. 小于90°D.不能确定 【答案】B2. (2006山东青岛)已知△ABC 在直角坐标系中的位置如图所示,如果△A'B'C' 与△ABC 关于y轴对称,那么点A 的对应点A'的坐标为( ).A .(-4,2)B .(-4,-2)C .(4,-2)D .(4,2)【答案】DAEBDCA 'E '3.(大连课改) 在直角坐标系中,A(1,2)点的横坐标乘以-1,纵坐标不变,得到A’点,则A与A′的关系是()A、关于x轴对称B、关于y轴对称C、关于原点对称D、将A点向x轴负方向平移一个单位【答案】A′的坐标是(-1,2),所以A与A′的关系是关于y轴对称,选B。
初一找规律经典题型(含部分答案)

精心整理图1 图2 图3初一数学规律题应用知识汇总“有比较才有鉴别”。
通过比较,可以发现事物的相同点和不同点,更容易找到事物的变化规律。
找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律。
揭示的规律,常常包含着事物的序列号。
所以,把变量和序列号放在一起加以比较,就比较容易发现其中的奥秘。
初中数学考试中,经常出现数列的找规律题,下面就此类题的解题方法进行探索:一、基本方法——看增幅(一)如增幅相等(实为等差数列):对每个数和它的前一个数进行比较,如增幅相等,则第n 个数可以表示为:a1+(n-1)b ,其中a 为数列的第一位数,b 为增幅,(n-1)b 为第一位数到第n 位的总增幅。
然后再简化代数式a+(n-1)b 。
例:4、10、16、22、28……,求第n 位数。
分析:第二位数起,每位数都比前一位数增加6,增幅都是6,所以,第n 位数是:4+(n-1)6=6n -2例1、已知一个面积为S 的等边三角形,现将其各边n (n 为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如上图所示).(1)当n=5时,共向外作出了个小等边三角形(2)当n=k 时,共向外作出了个小等边三角形(用含k 的式子表示).例2、如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,……,则在第n 个图形中,互不重叠的三角形共有个(用含n 的代数式表示)。
(二)如增幅不相等,但是增幅以同等幅度增加(即增幅的增幅相等,也即增幅为等差数列)。
如增幅分别为3、5、7、9,说明增幅以同等幅度增加。
此种数列第n 位的数也有一种通用求法。
基本思路是:1、求出数列的第n-1位到第n 位的增幅;2、求出第1位到第第n 位的总增幅;3、数列的第1位数加上总增幅即是第n 位数。
此解法虽然较烦,但是此类题的通用解法,当然此题也可用其它技巧,或用分析观察的方法求n=3 n=4 n=5 …出,方法就简单的多了。
2006年初中数学部分篇目索引(112期)范文

2006年初中数学部分篇目索引(1—12期)梅陇中学资料室当前数学课改中的一些问题/章建跃(人民教育出版社中数室)//中学数学教学参考「初中版」(西安).2006,no.1~2-p.l微言数学教师的语言艺术/殷菊桥(湖北省孝感市车站中学)//中学数学教学参考「初中版」(西安).2006,no.1~2-p.5“探索三角形相似的条件”教学设计/张岭(广东省深圳实验学校初中部)//中学数学教学参考「初中版」(西安).2006,no.1~2-p.7课例:圆的面积/刘冬梅(上海市川沙中学华夏西校)//中学数学教学参考「初中版」(西安).2006,no.1~2-p.9点评:敢于放飞——评刘冬梅老师执教的“圆的面积”/马学斌(上海市尚德实验学校)//中学数学教学参考「初中版」(西安).2006,no.1~2-p.11“一元一次不等式和一元一次不等式组”的/张洪波(浙江省宁波市北仓区芦渎中学)//中学数学教学参考「初中版」(西安).2006,no.1~2-p.13“相交线与平行线”教学探讨/朱建良(江苏省太仓市实验中学)//中学数学教学参考「初中版」(西安).2006,no.1~2-p.15数学中考命题的趋势分析(首篇))/罗增儒(陕西师范大学基础教育课程研究中心)//中学数学教学参考「初中版」(西安).2006,no.1~2-p.33对初中生数学学习兴趣的调查/扬素琴(江苏省盐城市教育局初教处)//中学数学教学参考「初中版」(西安).2006,no.1~2-p.l16义务教育初中数学新课标实验教材的研究与编写/田载今李海东(人民教育出版社中学教学室)//中学数学教学参考「初中版」(西安).2006,no.3-p.1-3勾股定理的再发现——一堂数学研究课几个片段的教学与评析/姚志敏(浙江省绍兴市教育局教研室)许芬英(浙江省教育厅教研室)//中学数学教学参考「初中版」(西安).2006,no.3-p.6-8数学中考命题的趋势分析「初中版」(续篇)/罗增儒(陕西师范大学基础教育课程研究中心)//中学数学教学参考「初中版」(西安).2006,no.3-p.20-23中考高频热点新题型系列(一)图象信息类试题/马克(本刊试题研究组)//中学数学教学参考「初中版」(西安).2006,no.3-p.24-26中考高频热点新题型系列(二)阅读理解类试题/马克(本刊试题研究组)//中学数学教学参考「初中版」(西安).2006,no.3-p.27-292006中考热点专题讲练(二)方程「初中版」(组)与不等式「初中版」(组)/方永成(江苏省扬州市汤汪中学)//中学数学教学参考「初中版」(西安).2006,no.3-p.30-422006中考热点专题讲练(三)函数及其图象/张岭(广东省深圳市实验学校初中部)//中学数学教学参考「初中版」(西安).2006,no.3-p.43-51南京市初中数学教师常规教学能力调研分析/李晓明(南京市教学研究室)//中学数学教学参考「初中版」(西安).2006,no.3-p.57-59义务教育初中数学新课标实验教材的研究于编辑(续)田载今,李海东(人民教育出版社中学数学室)//中学数学教学参考「初中版」(西安).2006,no.4-p.1促进学生发展的数学学习评价方式的探析/许盈(西北工业大学附中)//中学数学教学参考「初中版」(西安).2006,no.4-p.3在数据归纳中展开探究——以“格点多边形的面积”为例/范文贵(渤海大学教育学院)罗新兵(陕西师范大学数学与信息科学院)//中学数学教学参考「初中版」(西安).2006,no.4-p.7一道几何题的证明思路及方法/吕建恒(陕西省兴平市教研室)//中学数学教学参考「初中版」(西安).2006,no.4-p.12—道中考题的数形结合分析/罗增儒(陕西师范大学基础教育课程研究中心)//中学数学教学参考「初中版」(西安).2006,no.4-p.17中考高频热点题形系列(三)图形操作类试题/马克,李达等(本刊试题研究组)//中学数学教学参考「初中版」(西安).2006,no.4-p.23中考高频热点题形系列(四)以网格为背景的中考题/刘海宁,施华丽,吴美娜等(本刊试题研究组)//中学数学教学参考「初中版」(西安).2006,no.4-p.262006中考热点专题讲练(三)函数及其图象/张岭(广东省深圳市实验学校初中部)郝锐利(陕西长安师范学校)//中学数学教学参考「初中版」(西安).2006,no.4-p.292006中考热点专题讲练(四)统计与概率/陈锁华(江苏省金坛市华罗庚实验学校)//中学数学教学参考「初中版」(西安).2006,no.4-p.322006中考热点专题讲练(五)图形的认识、全等与证明/贺峰(河北省张家口市高新区东辛庄中学)//中学数学教学参考「初中版」(西安).2006,no.4-p.382006中考热点专题讲练(六)图形的相似/江金海,肖亚冬(江苏海安县李庄中学)//中学数学教学参考「初中版」(西安).2006,no.4-p.52探究——数学文化教育的核心——从一堂数学研究课谈起/张玉华(四川省成都市猛追湾双语学校)//中学数学教学参考「初中版」(西安).2006,no.5-p.6注重解后思考提高解题能力/任国芹(浙江省上虞市实验中学)//中学数学教学参考「初中版」(西安).2006,no.5-p.21初中数学解题的构造性策略与数学美/余德治(湖南常德文理学院)傅世球(湖南怀化学院)//中学数学教学参考「初中版」(西安).2006,no.5-p.23直角坐标系中的图形平移(课标人教版七年级)/钱斌(江苏省包场高级中学)//中学数学教学参考「初中版」(西安).2006,no.5-p.25中考高频热点新题型系列(五:开放探究类试题)/潘红玉武玲(本刊试题研究组)//中学数学教学参考「初中版」(西安).2006,no.5-p.28中考高频热点新题型系列(六:应用类试题)姜宏军张丽敏(本刊试题研究组)//中学数学教学参考「初中版」(西安).2006,no.5-p.322006中考热点专题讲练(七:35勾股定理与直角三角形的边角关系)/江金海(江苏省海安县李庄中学),郭岗田(哈尔滨市教育研究院义务研究部),杨桂美(胶州市第六中学)等//中学数学教学参考「初中版」(西安).2006,no.5-p.352006中考热点专题讲练(八:圆)/徐根林(浙江省湖州市双林二中),赵建平(浙江湖州市吴兴区教研培训中心),吴建丽(浙江省湖州市双林中学)等//中学数学教学参考「初中版」(西安).2006,no.5-p.442006全国初中数学联赛试题讲解/刘康宁(西安铁一中)//中学数学教学参考「初中版」(西安).2006,no.5-p.52初中数学教学中应处理好的六个问题/李昌官(浙江省台州市教育局研究室)//中学数学教学参考「初中版」(西安).2006,no.6-p.1数学课堂教学中的情景设计要注意自然延伸/周南翔,戴海勇(浙江省瑞安市海安中学)//中学数学教学参考「初中版」(西安).2006,no.6-p.8新课程理念下“四边形性质探索”的教学探讨/庞彦福(安徽省临泉县第三中学)//中学数学教学参考「初中版」(西安).2006,no.6-p.31图案设计与欣赏(北师大版七年级)/张洪元(山东省莒南县城关一中)//中学数学教学参考「初中版」(西安).2006,no.6-p.38哪种购货方式合算?(北师大版八年级)/孟坤(山东省枣庄市第二十九中学)//中学数学教学参考「初中版」(西安).2006,no.6-p.39有趣的投镖游戏(华东师大版七年级/王群(广东省东莞市樟木头中学)//中学数学教学参考「初中版」(西安).2006,no.6-p.39乘上等车的学问(华东师大版八年级)/周启东(江苏省扬州市汤汪中学)//中学数学教学参考「初中版」(西安).2006,no.6-p.40初中数学竞赛分级训练:分式/扬宝林(广东省佛山市顺德区均安中学)//中学数学教学参考「初中版」(西安).2006,no.6-p.41英国国家数学课程标准介绍(Ⅰ)——背景、基本思想与框架结构/徐文彬(南京师范大学课程与教学研究所),杨玉东(上海市教育科学研究院教师发展研究中心)//中学数学教学参考「初中版」(西安).2006,no.6-p.53数学新教材中的数学文化/赵菁蕾(浙江省丽水市莲都区花园中学)张维忠(浙江师范大学数理学院)//中学数学教学参考「初中版」(西安).2006,no.7-p.1-3论原型与变式对数学概念学习的影响/李善良(江苏省教研室)//中学数学教学参考「初中版」(西安).2006,no.7-p.4-7让学生在情境学习中建立符号感/陈旭芳(浙江省绍兴市元培中学)//中学数学教学参考「初中版」(西安).2006,no.7-p.8-11新课程数学课堂教学中的应变艺术/俞剑波郑勇(浙江省舟山市普陀二中)//中学数学教学参考「初中版」(西安).2006,no.7-p.14-17中考亮点——课例学习探究型问题/管远镇(浙江省台州市椒江区三甲中学)//中学数学教学参考「初中版」(西安).2006,no.7-p.55-57英国国家数学课程标准介绍(Ⅱ——数学学习计划(1)/徐文彬(南京师范大学课程与教学研究所)杨玉东(上海市教育科学研究院教师发展研究中心)//中学数学教学参考「初中版」(西安).2006,no.7-p.59-63践行理念;和谐试卷放异彩;发掘素材;亮点试题——2006年全国中考课改实验区试题大家评/岳建良,李建民等(本刊试题研究组)//中学数学教学参考「初中版」(西安).2006,no.8-p.1-12例说"情境"中问题设置的改进/李晓明(南京市教学研究室)//中学数学教学参考「初中版」(西安).2006,no.8-p.13-14新课标下初中数学网络化教学的探索/黄桂青(浙江省象山市丹城中学)//中学数学教学参考「初中版」(西安).2006,no.8-p.16-18课例:勾股定理的逆定理/华英姿(上海市尚德实验学校)//中学数学教学参考「初中版」(西安).2006,no.8-p.23-24点评:新课程改革的成功尝试/黄家礼(上海市南汇区教师进修学院)//中学数学教学参考「初中版」(西安).2006,no.8-p.25-25证线段不等的十种方法/刘君,王永会(北华大学理学院数学系)//中学数学教学参考「初中版」(西安).2006,no.8-p.33-35为引导和矫正教与学而考——2006年浙江省台州市中考数学命题探索与实践//李昌官(浙江省台州市教育局教研室)//中学数学教学参考「初中版」(西安).2006,no.8-p.39-42英国国家数学课程标准介绍(Ш——数学学习计划(2)/徐文彬(南京师范大学课程与教学研究所)杨玉东(上海市教育科学研究院教师发展研究中心)//中学数学教学参考「初中版」(西安).2006,no.8-p.56-59坚持改革方向进行适度调整——《数学课程标准(实验稿》评述/张奠宙(华东师范大学数学教育研究所)//中学数学教学参考「初中版」(西安).2006,no.9-p.1捕捉课堂瞬间的美丽/王一杰(浙江省绍兴市元培中学)//中学数学教学参考「初中版」(西安).2006,no.9-p.3例说八年级学生学习函数之困难/范宏业(安徽省马鞍市成功学校)//中学数学教学参考「初中版」(西安).2006,no.9-p.7填空题求解中的“回头望”/李太敏(江苏省灌南县教育局教研室)//中学数学教学参考「初中版」(西安).2006,no.9-p.34英国国家数学课程标准介绍(Ⅳ)——数学学习计划(3)/徐文彬(南京师范大学课程与教学研究所)杨玉东(上海市教育科学院研究院发展中心)//中学数学教学参考「初中版」(西安).2006,no.9-p.58关于一节数学研修课的思考/汪晓玉,李庆社(安徽岳西县城关中学)//中学数学教学参考「初中版」(西安).2006,no.10-p.1“几何画板”特性与教学创新/杨渭清,尚晓青(西安文理学院数学系)//中学数学教学参考「初中版」(西安).2006,no.10-p.4课例《探索三角形全等的条件(第一课时)》大家评——对单个课例的点评:课例(一)点评——数学课堂教学应追求自然与和谐/吴增生(浙江省仙居县教研室),张和平(浙江省仙居县田市中学)//中学数学教学参考「初中版」(西安).2006,no.10-p.9课例(二)点评——一节“以学生为本”的好课/张国英(河北省迁安市建昌营初级中学)//中学数学教学参考「初中版」(西安).2006,no.10-p.15课例(三)点评——学习数学“创造"数学/黄家礼(上海市南汇区教师进修学院),王静鑫(上海市尚德实验学校)//中学数学教学参考「初中版」(西安).2006,no.10-p.19课例(四)点评——一堂建构主义观下的数学课/桂文通(湖北省武汉市第三初级中学)//中学数学教学参考「初中版」(西安).2006,no.10-p.21数学解题中的“模式识别”/罗增儒(陕西师范大学基础教育课程研究中心)//中学数学教学参考「初中版」(西安).2006,no.10-p.262006年中考运动变化类新题展示/李树臣(浙江省沂南教育局)、李学华(河北省威县第二中学)蔡世英(福建省晋江市南岳中学)齐化(山东省济南第十五中学)//中学数学教学参考「初中版」(西安).2006,no.10-p.35考题源于教材方法多姿多彩/殷菊桥湖北省孝感市孝南区车站中学)//中学数学教学参考「初中版」(西安).2006,no.10-p.412006年全国中考新题集锦/本刊试题研究组//中学数学教学参考「初中版」(西安).2006,no.10-p.44关于初中数学教学叙事研究的叙事/李小青(浙江书反大学数理学院教育硕士)//中学数学教学参考「初中版」(西安).2006,no.10-p.54论知识生长点与数学说课/黄晓学(徐州师范大学数学科学学院)//中学数学教学参考「初中版」(西安).2006,no.11-p.1把学习的主动权还给学生/袁政恕(贵州省实验中学)//中学数学教学参考「初中版」(西安).2006,no.11-p.4数学课堂中的认知线索及其运用/吴增生(浙江省仙居县教研室)吴振香(山东省胶州市第二十一中学)//中学数学教学参考「初中版」(西安).2006,no.11-p.7课例《相似多边形的性质(第一课时)》大家评:综合点评——突出过程,注重思维/邝孔秀(湖南师范大学教育科学学院)//中学数学教学参考「初中版」(西安).2006,no.11-p.13课例(一)点评:动态生成尽现风采/潘建明(江苏省金坛市华罗庚实验学校)//中学数学教学参考「初中版」(西安).2006,no.11-p.15课例(二)点评——一堂自然、和谐、实效的生成课/王华民(江苏省无锡市滨湖区教研中心)//中学数学教学参考「初中版」(西安).2006,no.11-p.23数学解题中的“模式识别”(续)/罗增儒(陕西师范大学基础教育课程研究中心)//中学数学教学参考「初中版」(西安).2006,no.11-p.312006年源于生活的中考新题展示/杨通刚(贵州省剑河二中)孙长智(山东省滨州市北镇中学初中部)倪先德(四川省威远县第一初级中学)李文萍(陕西师范大学2004级教育硕士)//中学数学教学参考「初中版」(西安).2006,no.11-p.412006年全国中考新题集锦/本刊试题研究组//中学数学教学参考「初中版」(西安).2006,no.11-p.44新课程背景下区域学科教研初探/雷明生(江苏省溧阳市教育局教研室)//中学数学教学参考「初中版」(西安).2006,no.11-p.54对初中数学实验教材修订的若干建议/周建勋(江苏省无锡市教研中心)//中学数学教学参考「初中版」(西安).2006,no.12-p.7接天莲叶无穷碧——“探索三角形相似的条件”课堂实录与点评/彭玉英(陕西省宝鸡市店子街中学)巨申文(陕西省宝鸡市教学研究室)//中学数学教学参考「初中版」(西安).2006,no.12-p.12谈解题反思的内容与途径/雷明生(江苏省溧阳市教育局教研室)//中学数学教学参考「初中版」(西安).2006,no.12-p.192006年值得商榷的中考题展示/李国凯(安徽省合肥市第四十五中学)林日福(广州省深圳市观澜第二中学)叶慧君(浙江省义乌市苏溪镇中)丁德兴(浙江省东阳市飞华补习学校)//中学数学教学参考「初中版」(西安).2006,no.12-p.23一道中考数学试题的来龙去脉/李桂强(江苏省徐州市王杰中学)//中学数学教学参考「初中版」(西安).2006,no.12-p.272006年全国中考新题集锦/本刊试题研究组//中学数学教学参考「初中版」(西安).2006,no.12-p.33推进上海数学教育的新发展/唐盛昌(上海市上海中学)//数学教学(上海).2006,no.1-p.1几何图形的相似/林磊(四川省巴州区大河初中)//数学教学(上海).2006,no.1-p.17校本数学问题开发的实践与认识/张晓飞,钱立萍,牟锐(北京市北达资源中学)//数学教学(上海).2006,no.1-p.222005年全国各地中考数学压轴题赏析/杨正家(上海市浦东教育发展研究院)//数学教学(上海).2006,no.1-p.38新旧课程理念下数学课堂教学语言对比与思考/曾庆宝(广西富川县民族中学)//数学教学(上海).2006,no.2-p.封二对三道中考题抽样统计引发的思考——兼谈对新教材的几点认识/余立峰(四川省仁寿县教育局教研室)//数学教学(上海).2006,no.2-p.6谈新课导入中情境创设/.钟美玲(浙江省上虞市实验中学)//数学教学(上海).2006,no.2-p.8由海伦公式想到梯形的面积公式/.贺德才(湖北省巴东县一中)//数学教学(上海).2006,no.2-p.14激活试题的裂变效应/./岳荫巍(北京市同仁中学)//数学教学(上海).2006,no.2-p.34一道平面几何题数据的一般化探究/茹双林//数学教学(上海).2006,no.3-p.—13解题教学中的直观性原则/王宽明,宋乃庆//数学教学(上海).2006,no.3-p.16不等式解题常见错误浅析/储红兵//数学教学(上海).2006,no.3-p.27中考几何试题的新特点/罗强//数学教学(上海).2006,no.3-p.32中考数学试题瑕疵举隅/李桂强//数学教学(上海).2006,no.3-p.39趣谈中考中的一类滚动问题/缪月红//数学教学(上海).2006,no.3-p.4l初中数学研究性学习案例的教学实践与思考/王盛裕(浙江省宁波市镇海镇外语实验学校)//数学教学(上海).2006,no.4-p.15应用图形的旋转变换巧解“难题”/严海洪(浙江省宁波市东钱湖中学)//数学教学(上海).2006,no.4-p.28:对初中学生“数形结合”能力的调查研究/邹坚(江苏省苏州市第三十三中学)陈月兰(华东师范大学数学系)//数学教学(上海).2006,no.5-p.15有关排列组合问题的一个算法/吴中才(安徽师范大学附属中学)//数学教学(上海).2006,no.5-p.17由0.00l的差异引发的思考/张闽(上海市第三女子中学)//数学教学(上海).2006,no.5-p.18几何三大难题的不能与“解决”/何莎莎(华东师范大学数学系03级教育硕士)//数学教学(上海).2006,no.5-p.38:近几年中考数学试题“缺陷”剖析/王盛裕(浙江省宁波市镇外语实验学校)//数学教学(上海).2006,no.5-p.40例说“情境”中问题设置的改进/李晓明(江苏省南京市教学研究室)//数学教学(上海).2006,no.7-p.封二函数概念教学的新特点/李桂强(江苏省徐州市第五中学)//数学教学(上海).2006,no.7-p.3概率教学中弱队以少取胜的思考/王红蔚(河南教育学院数学系)//数学教学(上海).2006,no.7-p.6用折纸探究几何问题——初中几何探究型课程的开发一例/孙联荣(上海市新基础教育实验学校)//数学教学(上海).2006,no.8-p.14传统平面几何题的升华/冯德雄(四川省成都大学师范学院)//数学教学(上海).2006,no.8-p.16国外数学中研究性课题一例/顾汉忠,樊亚(江苏省张家港乐余高级中学),黄大龙(江苏省张家港市教育局教研室)//数学教学(上海).2006,no.8-p.35研究一道日本中考试题/岳荫巍(北京市同仁中学)//数学教学(上海).2006,no.8-p.42数学教学中创设现实情境的若干误区/任念兵周心华(上海市育才中学)//数学教学(上海).2006,no.9-p.封二从一堂几何复习课谈提高数学教学的有效性/孙联荣,凌国华(上海市新基础教育实验学校)//数学教学(上海).2006,no.9-p.2谈初中数学“概率’’的教学/王赛英(浙江省象山县丹城中学),潘腊月(浙江省象山县文峰学校)//数学教学(上海).2006,no.9-p.6让学生多角度体验全等变换/彭学军(四川省丹林棱中学)//数学教学(上海).2006,no.9-p.9专家评课:关键还是对数学的理解/陈永明(上海市徐汇区教师进修学院)//数学教学(上海).2006,no.9-p.28新视点:数学与雕塑/袁震东(华东师范大学数学系)//数学教学(上海).2006,no.9-p.30依“标”据“本”命制考题一2006年福建省泉州市课改实验区中考数学试题例析/曾大洋(福建省泉州市教科所)//数学教学(上海).2006,no.9-p.312006年上海市初中毕业生统一学业考试数学试卷//数学教学(上海).2006,no.9-p.39重建三角,全局皆活——中数学课程结构性改革的一个建议/张景中(中国科学院院士)//数学教学(上海).2006,no.10-p.封二让我们来重新认识“三角”——谈数学教育要在数学上下工夫/张奠宙//数学教学(上海).2006,no.10-p.5镶嵌,该教给学生些什么?/章飞(江苏教育学院数学系)//数学教学(上海).2006,no.10-p.12从设计水槽看探索无止境/李发勇(四川省巴中市巴州区大和初中)//数学教学(上海).2006,no.10-p.21专家评课:值得重视的“去数学化”倾向/陈永明(上海市徐汇区教师进修学院)//数学教学(上海).2006,no.10-p.42我们为什么关注美国“课程焦点”/袁震东(华东师范大学数学系)//数学教学(上海).2006,no.11-p.封二美国《学校数学课程和评价标准》及其《课程焦点》/莫由//数学教学(上海).2006,no.11-p.2“数学战”停火,基础获重视//数学教学(上海).2006,no.11-p.5时针分针夹角问题的教学研究/崔雪芳(浙江省宁波教育学院)丁建(浙江省象山中学)//数学教学(上海).2006,no.11-p.18学生解题创新与守旧的行为差异/李广修(江苏省无锡市第一中学)//数学教学(上海).2006,no.11-p.11从一道平面几何寻宝题中“寻宝"/胡芳举(河南省桃江一中)符立平(湖南省桃江县教育局教研室)//数学教学(上海).2006,no.11-p.22从战略上重视数学英才教育——俄罗斯数学物理学校的启示/倪明(华东师范大学出版社)//数学教学(上海).2006,no.12-p.12—封二高效的探究活动需要有效的引导/周..洁(浙江省绍兴市建功中学)//数学教学(上海).2006,no.12-p.12—11在测量中影子分段,怎么办?/一石大浩(江苏省张家港市晨阳学校中学校区)//数学教学(上海).2006,no.12-p.12—20数学教育:这道中考题合适吗?/.宗新//中小学数学「初中教师版」(北京).2006,」no.1~2-p.1教学研究:教学戒文一篇/.甄兰芳(湖北省唐县羊角中学)//中小学数学「初中教师版」(北京).2006,no.1~2-p.3教材研究:体验新教材/高首慧(浙江省绍兴市第三中学)//中小学数学「初中教师版」(北京).2006,no.1~2-p.5百家论坛:关于实数近似计算的争议与思考/.黄承洪(湖北省十堰市第二中学)//中小学数学「初中教师版」(北京).2006,no.1~2-p.11解题研究:一道连续自然数问题的讨论/田大强(安徽省固镇县瓦疃中学)//中小学数学「初中教师版」(北京).2006,no.1~2-p.14研究课:记“垂直”折纸活动实录/贺斐斐(江苏省常州市北郊中学)//中小学数学「初中教师版」(北京).2006,no.1~2-p.19中考研究:从中考题型的变化看今后的初中数学教学——分析2005年河南省中考数学试题有感/.刘国玉(河南省汝南县教研室)//中小学数学「初中教师版」(北京).2006,no.1~2-p.20辅导参考:例析以课本例题为原型的中考题/.古金龙(河北省怀来县桑园中学)//中小学数学「初中教师版」(北京).2006,no.1~2-p.26思路·方法·技巧:圆内角、圆外角与圆心角之间的—个关系曹房兴(湖北省武汉市中国地质大学数学教研室)//中小学数学「初中教师版」(北京).2006,no.1~2-p.36探讨与争鸣:对一个结论的再探讨/李吉箕(山东省平阳县实验中学)//中小学数学「初中教师版」(北京).2006,no.1~2-p.45教学研究:几何教学要重视对学生逻辑思维能力的培养/范宏业(安徽省马鞍山市成功学校)//中小学数学「初中教师版」(北京).2006,no.3-p.1教材研究:让例题教学更加生动活泼/彭林(北京市教育学院宣武分院)//中小学数学「初中教师版」(北京).2006,no.3-p.4教学经验谈:也淡平面几何教学的老经验/沈荣武(浙江省慈溪市慈吉中学)//中小学数学「初中教师版」(北京).2006,no.3-p.4教有特色:—堂函数复习课/.喻鹏(贵州省金沙县沙土镇初级中学)//中小学数学「初中教师版」(北京).2006,no.3-p.10辅导参考:如何让学生正确理解、运用整式算的公式法则/方喜源(浙江省兰溪市诸葛中学)//中小学数学「初中教师版」(北京).2006,no.3-p.14思路·方法·技巧:两正数和为定值,求这两数积的最大值问题/.宋淑敏(黑龙江省海林市第一中学)//中小学数学「初中教师版」(北京).2006,no.3-p.19课本习题研究:制胜的策略在谁手中/.陈冬初(浙江省宁海县梅林中学)//中小学数学「初中教师版」(北京).2006,no.3-p.21探讨与争鸣:对《不能用—元二次方程求路宽吗》的再探讨/陈素萍(江苏省海安县曲塘镇双楼初中)//中小学数学「初中教师版」(北京).2006,no.3-p.28课标与新教材:对用好数学新教材中探究活动内容的反思/.郑燕(广东省贵州省第五十九中学)//中小学数学「初中教师版」(北京).2006,no.3-p.28教学研究:从学生的解题错误透视教师的教学失误——一次质量分析座谈会的记录/顾香才(江苏省高淳高级中学)//中小学数学「初中教师版」(北京).2006,no.4-p.2中考压轴题赏析——思维空间较大的压轴题/傅钧泉(天津市蓟县城关镇中学)//中小学数学「初中教师版」(北京).2006,no.4-p.15中考压轴题赏析——沟通代数与几何关系的好题(浙江省丽水市花园中学)/陈金亮//中小学数学「初中教师版」(北京).2006,no.4-p.16中考研究:例析中考探究性试题/相剑利(浙江省湖州市第八中学)//中小学数学「初中教师版」(北京).2006,no.4-p.17一道中考几何题的多种解法/李俐(山西农业大学附属中学)//中小学数学「初中教师版」(北京).2006,no.4-p.23数学课堂的平衡点——谈谈教学课堂教学中教师主导与学生主体间的互动/童玉泉(浙江省兰溪市游埠初中)//中小学数学「初中教师版」(北京).2006,no.5-p.1使用计算器容易引发的不良现象及教学对策/胡赵云(浙江省衡州市实验学校)//中小学数学「初中教师版」(北京).2006,no.5-p.5纠正一个错误认识/李巧文(陕西师范大学数学与信息科学学院)//中小学数学。
湖北省十堰市2024年中考数学试题(word版-含解析)

湖北省十堰市2024年中考数学试卷参考答案与试题解析一、选择题:(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的,请把正确选项的字母填涂在答题卡中相应的格子内.1.(3分)(2024•十堰)3的倒数是()C.3D.﹣3A.B.﹣考点:倒数.分析:依据倒数的定义可知.解答:解:3的倒数是.故选A.点评:主要考查倒数的定义,要求娴熟驾驭.须要留意的是:倒数的性质:负数的倒数还是负数,正数的倒数是正数,0没有倒数.倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.2.(3分)(2024•十堰)如图,直线m∥n,则∠α为()A.70°B.65°C.50°D.40°考点:平行线的性质.分析:先求出∠1,再依据平行线的性质得出∠α=∠1,代入求出即可.解答:解:∠1=180°﹣130°=50°,∵m∥n,∴∠α=∠1=50°,故选C.点评:本题考查了平行线的性质的应用,留意:两直线平行,同位角相等.3.(3分)(2024•十堰)在下面的四个几何体中,左视图与主视图不相同的几何体是()A.正方体B.长方体C.球D.圆锥考点:简洁几何体的三视图分析:主视图、左视图是分别从物体正面、左面看,所得到的图形.解答:解:A、正方体的左视图与主视图都是正方形,故此选项不合题意;B、长方体的左视图与主视图都是矩形,但是矩形的不一样,故此选项符合题意;C、球的左视图与主视图都是圆,故此选项不合题意;D、圆锥左视图与主视图都是等腰三角形,故此选项不合题意;故选:B.点评:本题考查了几何体的三种视图,驾驭定义是关键.留意全部的看到的棱都应表现在三视图中.4.(3分)(2024•十堰)下列计算正确的是()A.﹣=B.=±2 C.a6÷a2=a3D.(﹣a2)3=﹣a6考点:同底数幂的除法;实数的运算;幂的乘方与积的乘方分析:依据二次根式的运算法则推断,开算术平方根,同底数幂的除法及幂的乘方运算.解答:解:A、不是同类二次根式,不能合并,故选项错误;B、=2≠±2,故选项错误;C、a6÷a2=a4≠a3,故选项错误;D、(﹣a2)3=﹣a6正确.故选:D.点评:本题主要考查了二次根式的运算法则推断,开算术平方根,同底数幂的除法及幂的乘方运算.熟记法则是解题的关键.5.(3分)(2024•十堰)为了调查某小区居民的用水状况,随机抽查了若干户家庭的月用水月用水量(吨)3 4 5 8户数 2 3 4 1A.众数是4 B.平均数是4.6C.调查了10户家庭的月用水量D.中位数是4.5考点:众数;统计表;加权平均数;中位数.分析:依据众数、中位数和平均数的定义分别对每一项进行分析即可.解答:解:A、5出现了4次,出现的次数最多,则众数是5,故本选项错误;B、这组数据的平均数是:(3×2+4×3+5×4+8×1)÷10=4.6,故本选项正确;C、调查的户数是2+3+4+1=10,故本选项正确;D、把这组数据从小到大排列,最中间的两个数的平均数是(4+5)÷2=4.5,则中位数是4.5,故本选项正确;故选A .点评:此题考查了众数、中位数和平均数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数;众数是一组数据中出现次数最多的数.6.(3分)(2024•十堰)如图,在平行四边形ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长是()A.7B.10 C.11 D.12考点:平行四边形的性质;线段垂直平分线的性质.分析:依据线段垂直平分线的性质可得AE=EC,再依据平行四边形的性质可得DC=AB=4,AD=BC=6,进而可以算出△CDE的周长.解答:解:∵AC的垂直平分线交AD于E,∴AE=EC,∵四边形ABCD是平行四边形,∴DC=AB=4,AD=BC=6,∴△CDE的周长为:EC+CD+ED=AD+CD=6+4=10,故选:B.点评:此题主要考查了平行四边形的性质和线段垂直平分线的性质,关键是驾驭平行四边形两组对边分别相等.7.(3分)(2024•十堰)依据如图中箭头的指向规律,从2024到2024再到2024,箭头的方向是以下图示中的()A.B.C.D.考点:规律型:数字的改变类.分析:视察不难发觉,每4个数为一个循环组依次循环,用2024除以4,依据商和余数的状况解答即可.解答:解:由图可知,每4个数为一个循环组依次循环,2024÷4=503…1,∴2024是第504个循环组的第2个数,∴从2024到2024再到2024,箭头的方向是.故选D.点评:本题是对数字改变规律的考查,细致视察图形,发觉每4个数为一个循环组依次循环是解题的关键.8.(3分)(2024•十堰)已知:a2﹣3a+1=0,则a+﹣2的值为()A.+1 B.1C.﹣1 D.﹣5考点:分式的混合运算.专题:计算题.分析:已知等式变形求出a+的值,代入原式计算即可得到结果.解答:解:∵a2﹣3a+1=0,且a≠0,∴a+=3,则原式=3﹣2=1,故选B.点评:此题考查了分式的混合运算,娴熟驾驭运算法则是解本题的关键.9.(3分)(2024•十堰)如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为()A.2B.C.2D.考点:勾股定理;等腰三角形的判定与性质;直角三角形斜边上的中线.分析:依据直角三角形斜边上的中线的性质可得DG=AG,依据等腰三角形的性质可得∠GAD=∠GDA,依据三角形外角的性质可得∠CGD=2∠GAD,再依据平行线的性质和等量关系可得∠ACD=∠CGD,依据等腰三角形的性质可得CD=DG,再依据勾股定理即可求解.解答:解:∵AD∥BC,DE⊥BC,∴DE⊥AD,∠CAD=∠ACB∵点G为AF的中点,∴DG=AG,∴∠GAD=∠GDA,∴∠CGD=2∠CAD,∵∠ACD=2∠ACB,∴∠ACD=∠CGD,∴CD=DG=3,在Rt△CED中,DE==2.故选:C.点评:综合考查了勾股定理,等腰三角形的判定与性质和直角三角形斜边上的中线,解题的关键是证明CD=DG=3.10.(3分)(2024•十堰)已知抛物线y=ax2+bx+c(a≠0)经过点(1,1)和(﹣1,0).下列结论:①a﹣b+c=0;②b2>4ac;③当a<0时,抛物线与x轴必有一个交点在点(1,0)的右侧;④抛物线的对称轴为x=﹣.其中结论正确的个数有()A.4个B.3个C.2个D.1个考点:二次函数图象与系数的关系.分析:将点(﹣1,0)代入y=ax2+bx+c,即可推断①正确;将点(1,1)代入y=ax2+bx+c,得a+b+c=1,又由①得a﹣b+c=0,两式相加,得a+c=,两式相减,得b=.由b2﹣4ac=﹣4a(﹣a)=﹣2a+4a2=(2a﹣)2,当a=时,b2﹣4ac=0,即可推断②错误;③由b2﹣4ac=(2a﹣)2>0,得出抛物线y=ax2+bx+c与x轴有两个交点,设另一个交点的横坐标为x,依据一元二次方程根与系数的关系可得﹣1•x==﹣1,即x=1﹣,再由a<0得出x>1,即可推断③正确;④依据抛物线的对称轴公式为x=﹣,将b=代入即可推断④正确.解答:解:①∵抛物线y=ax2+bx+c(a≠0)经过点(﹣1,0),∴a﹣b+c=0,故①正确;②∵抛物线y=ax2+bx+c(a≠0)经过点(1,1),∴a+b+c=1,又a﹣b+c=0,两式相加,得2(a+c)=1,a+c=,两式相减,得2b=1,b=.∵b2﹣4ac=﹣4a(﹣a)=﹣2a+4a2=(2a﹣)2,当2a﹣=0,即a=时,b2﹣4ac=0,故②错误;③当a<0时,∵b2﹣4ac=(2a﹣)2>0,∴抛物线y=ax2+bx+c与x轴有两个交点,设另一个交点的横坐标为x,则﹣1•x===﹣1,即x=1﹣,∵a<0,∴﹣>0,∴x=1﹣>1,即抛物线与x轴必有一个交点在点(1,0)的右侧,故③正确;④抛物线的对称轴为x=﹣=﹣=﹣,故④正确.故选B.点评:本题考查了二次函数图象上点的坐标特征,二次函数图象与系数的关系,二次函数与一元二次方程的关系,一元二次方程根与系数的关系及二次函数的性质,不等式的性质,难度适中.二、填空题:(本题有6个小题,每小题3分,共18分)11.(3分)(2024•十堰)世界文化遗产长城总长约6700 000m,用科学记数法可表示为6.7×106m.考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的肯定值与小数点移动的位数相同.当原数肯定值>1时,n是正数;当原数的肯定值<1时,n是负数.解答:解:将6700 000m用科学记数法表示为:6.7×106m.故答案为:6.7×106m.点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.12.(3分)(2024•十堰)计算:+(π﹣2)0﹣()﹣1=1.考点:实数的运算;零指数幂;负整数指数幂.分析:本题涉及零指数幂、负指数幂、二次根式化简等考点.针对每个考点分别进行计算,然后依据实数的运算法则求得计算结果.解答:解:原式=2+1﹣=3﹣2=1.故答案为1.点评:本题考查实数的综合运算实力,是各地中考题中常见的计算题型.解决此类题目的关键是驾驭零指数幂、负指数幂、二次根式化简等考点的运算.13.(3分)(2024•十堰)不等式组的解集为﹣1<x≤2.考点:解一元一次不等式组.分析:先求出每个不等式的解集,依据不等式的解集找出不等式组的解集即可.解答:解:∵解不等式x<2x+1得:x>﹣1,解不等式3x﹣2(x﹣1)≤4得:x≤2,∴不等式组的解集是﹣1<x≤2,故答案为:﹣1<x≤2.点评:本题考查了解一元一次不等式和解一元一次不等式组的应用,解此题的关键是能依据不等式的解集找出不等式组的解集.14.(3分)(2024•十堰)如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD 及其延长线上,且DE=DF.给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是①(只填写序号).考点:菱形的判定.分析:首先利用对角线相互平分的四边形是平行四边形判定该四边形为平行四边形,然后结合菱形的判定得到答案即可.解答:解:由题意得:BD=CD,ED=FD,∴四边形EBFC是平行四边形,∵邻边相等或对角线垂直的平行四边形是菱形,∴选择BE⊥EC,故答案为:①.点评:本题考查了菱形的判定,解题的关键是了解菱形的判定定理,难度不是很大.15.(3分)(2024•十堰)如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A 处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是24海里.(结果精确到个位,参考数据:≈1.4,≈1.7,≈2.4)考点:解直角三角形的应用-方向角问题.分析:作BD⊥AC于点D,在直角△ABD中,利用三角函数求得BD的长,然后在直角△BCD中,利用三角函数即可求得BC的长.解答:解:∠CBA=25°+50°=75°.作BD⊥AC于点D.则∠CAB=(90°﹣70°)+(90°﹣50°)=20°+40°=60°,∠ABD=30°,∴∠CBD=75°﹣35°=45°.在直角△ABD中,BD=AB•sin∠CAB=20×sin60°=20×=10.在直角△BCD中,∠CBD=45°,则BC=BD=10×=10≈10×2.4=24(海里).故答案是:24.点评:本题主要考查了方向角含义,正确求得∠CBD以及∠CAB的度数是解决本题的关键.16.(3分)(2024•十堰)如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为2π﹣4.考点:扇形面积的计算;二次函数的最值;勾股定理.分析:由OC=4,点C在上,CD⊥OA,求得DC==,运用S△OCD=OD•,求得OD=2时△OCD的面积最大,运用阴影部分的面积=扇形AOC的面积﹣△OCD的面积求解.解答:解:∵OC=4,点C在上,CD⊥OA,∴DC==∴S△OCD=OD•∴=OD2•(16﹣OD2)=﹣OD4﹣4OD2=﹣(OD2﹣8)2+16∴当OD2=8,即OD=2时△OCD的面积最大,∴DC===2,∴∠COA=45°,∴阴影部分的面积=扇形AOC的面积﹣△OCD的面积=﹣×2×2=2π﹣4,故答案为:2π﹣4.点评:本题主要考查了扇形的面积,勾股定理,解题的关键是求出OD=2时△OCD的面积最大.三、解答题:(本题有9个小题,共72分)17.(6分)(2024•十堰)化简:(x2﹣2x)÷.考点:分式的混合运算.专题:计算题.分析:原式利用除法法则变形,约分即可得到结果.解答:解:原式=x(x﹣2)•=x.点评:此题考查了分式的混合运算,娴熟驾驭运算法则是解本题的关键.18.(6分)(2024•十堰)如图,点D在AB上,点E在AC上,AB=AC,AD=AE.求证:∠B=∠C.考点:全等三角形的判定与性质.专题:证明题.分析:首先依据条件AB=AC,AD=AE,再加上公共角∠A=∠A可利用SAS定理证明△ABE ≌△ACD,进而得到∠B=∠C.解答:证明:在△ABE和△ACD中,,∴△ABE≌△ACD(SAS).∴∠B=∠C.点评:本题主要考查三角形全等的判定方法和性质,关键是驾驭全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.19.(6分)(2024•十堰)甲、乙两人打算整理一批新到的图书,甲单独整理须要40分钟完工;若甲、乙共同整理20分钟后,乙需再单独整理30分钟才能完工.问乙单独整理这批图书须要多少分钟完工?考点:分式方程的应用.分析:将总的工作量看作单位1,依据本工作分两段时间完成列出分式方程解之即可.解答:解:设乙单独整理x分钟完工,依据题意得:+=1,解得x=100,经检验x=100是原分式方程的解.答:乙单独整理100分钟完工.点评:本题考查了分式方程的应用.分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.此题等量关系比较多,主要用到公式:工作总量=工作效率×工作时间.20.(9分)(2024•十堰)据报道,“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会竞赛项目.某校学生会想知道学生对这个提议的了解程度,随机抽取部分学生进行了一次问卷调查,并依据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你依据统计图中所供应的信息解答下列问题:(1)接受问卷调查的学生共有60名,扇形统计图中“基本了解”部分所对应扇形的圆心角为90°;请补全条形统计图;(2)若该校共有学生900人,请依据上述调查结果,估计该校学生中对将“剪刀石头布”作为奥运会竞赛项目的提议达到“了解”和“基本了解”程度的总人数;(3)“剪刀石头布”竞赛时双方每次随意出“剪刀”、“石头”、“布”这三种手势中的一种,规则为:剪刀胜布,布胜石头,石头胜剪刀,若双方出现相同手势,则算打平.若小刚和小明两人只竞赛一局,请用树状图或列表法求两人打平的概率.考点:条形统计图;用样本估计总体;扇形统计图;列表法与树状图法.专题:计算题.分析:(1)由“了解很少”的人数除以占的百分比得出学生总数,求出“基本了解”的学生占的百分比,乘以360得到结果,补全条形统计图即可;(2)求出“了解”和“基本了解”程度的百分比之和,乘以900即可得到结果;(3)列表得出全部等可能的状况数,找出两人打平的状况数,即可求出所求的概率.解答:解:(1)依据题意得:30÷50%=60(名),“了解”人数为60﹣(15+30+10)=5(名),“基本了解”占的百分比为×100%=25%,占的角度为25%×360°=90°,补全条形统计图如图所示:(2)依据题意得:900×=300(人),则估计该校学生中对将“剪刀石头布”作为奥运会竞赛项目的提议达到“了解”和“基本了解”程度的总人数为300人;(3)列表如下:剪石布剪(剪,剪)(石,剪)(布,剪)石(剪,石)(石,石)(布,石)布(剪,布)(石,布)(布,布)全部等可能的状况有9种,其中两人打平的状况有3种,则P==.点评:此题考查了条形统计图,扇形统计图,以及列表法与树状图法,弄清题意是解本题的关键.21.(7分)(2024•十堰)已知关于x的一元二次方程x2+2(m+1)x+m2﹣1=0.(1)若方程有实数根,求实数m的取值范围;(2)若方程两实数根分别为x1,x2,且满意(x1﹣x2)2=16﹣x1x2,求实数m的值.考点:根的判别式;根与系数的关系.分析:(1)若一元二次方程有两实数根,则根的判别式△=b2﹣4ac≥0,建立关于m的不等式,求出m的取值范围;(2)由x1+x2=﹣2(m+1),x1x2=m2﹣1;代入(x1﹣x2)2=16﹣x1x2,建立关于m的方程,据此即可求得m的值.解答:解:(1)由题意有△=[2(m+1)]2﹣4(m2﹣1)≥0,整理得8m+8≥0,解得m≥﹣1,∴实数m的取值范围是m≥﹣1;(2)由两根关系,得x1+x2=﹣(2m+1),x1•x2=m2﹣1,(x1﹣x2)2=16﹣x1x2(x1+x2)2﹣3x1x2﹣16=0,∴[﹣2(m+1)]2﹣3(m2﹣1)﹣16=0,∴m2+8m﹣9=0,解得m=﹣9或m=1∵m≥﹣1∴m=1.点评:本题考查了一元二次方程根的判别式及根与系数关系,利用两根关系得出的结果必需满意△≥0的条件.22.(8分)(2024•十堰)某市政府为了增加城镇居民抵挡大病风险的实力,主动完善城镇医疗费用范围报销比例标准不超过8000元不予报销超过8000元且不超过30000元的部分50%超过30000元且不超过50000元的部分60%超过50000元的部分70%y元.(1)干脆写出x≤50000时,y关于x的函数关系式,并注明自变量x的取值范围;(2)若某居民大病住院医疗费用按标准报销了20000元,问他住院医疗费用是多少元?考点:一次函数的应用;分段函数.分析:(1)首先把握x、y的意义,报销金额y分3段①当x≤8000时,②当8000<x≤30000时,③当30000<x≤50000时分别表示;(2)利用代入法,把y=20000代入第三个函数关系式即可得到x的值.解答:解:(1)由题意得:①当x≤8000时,y=0;②当8000<x≤30000时,y=(x﹣8000)×50%=0.5x﹣4000;③当30000<x≤50000时,y=(30000﹣8000)×50%+(x﹣30000)×60%=0.6x﹣7000;(2)当花费30000元时,报销钱数为:y=0.5×30000﹣4000=11000,∵20000>11000,∴他的住院医疗费用超过30000元,把y=20000代入y=0.6x﹣7000中得:20000=0.6x﹣7000,解得:x=45000.答:他住院医疗费用是45000元.点评:此题主要考查了一次函数的应用,关键是正确理解题意,找出题目中的等量关系,列出函数关系式.23.(8分)(2024•十堰)如图,点B(3,3)在双曲线y=(x>0)上,点D在双曲线y=﹣(x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.(1)求k的值;(2)求点A的坐标.考点:正方形的性质;反比例函数图象上点的坐标特征;全等三角形的判定与性质.分析:(1)把B的坐标代入求出即可;(2)设MD=a,OM=b,求出ab=4,过D作DM⊥x轴于M,过B作BN⊥x轴于N,证△ADM≌△BAN,推出BN=AM=3,MD=AN=a,求出a=b,求出a的值即可.解答:解:(1)∵点B(3,3)在双曲线y=上,∴k=3×3=9;(2)∵B(3,3),∴BN=ON=3,设MD=a,OM=b,∵D在双曲线y=﹣(x<0)上,∴﹣ab=﹣4,即ab=4,过D作DM⊥x轴于M,过B作BN⊥x轴于N,则∠DMA=∠ANB=90°,∵四边形ABCD是正方形,∴∠DAB=90°,A D=AB,∴∠MDA+∠DAM=90°,∠DAM+∠BAN=90°,∴∠ADM=∠BAN,在△ADM和△BAN中,,∴△ADM≌△BAN(AAS),∴BN=AM=3,MD=AN=a,∴0A=3﹣a,即AM=b+3﹣a=3,a=b,∵ab=4,∴a=b=2,∴OA=3﹣2=1,即点A的坐标是(1,0).点评:本题考查了正方形的性质,反比例函数图象上点的坐标特征,全等三角形的性质和判定的应用,主要考查学生运用性质进行推理和计算的实力,题目比较好,难度适中.24.(10分)(2024•十堰)如图1,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.(1)求证:AC平分∠DAB;(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;(3)如图2,连接OD交AC于点G,若=,求sin∠E的值.考点:圆的综合题.专题:计算题.分析:(1)连结OC,如图1,依据切线的性质得OC⊥DE,而AD⊥DE,依据平行线的性质得OC∥AD,所以∠2=∠3,加上∠1=∠3,则∠1=∠2,所以AC平分∠DAB;(2)如图1,由B为OE的中点,AB为直径得到OB=BE=2,OC=2,在Rt△OCE 中,由于OE=2OC,依据含30度的直角三角形三边的关系得∠OEC=30°,则∠COE=60°,由CF⊥AB得∠OFC=90°,所以∠OCF=30°,再依据含30度的直角三角形三边的关系得OF=OC=1,CF=OF=;(3)连结OC,如图2,先证明△OCG∽△DAG,利用相像的性质得==,再证明△ECO∽△EDA,利用相像比得到==,设⊙O的半径为R,OE=x,代入求得OE=3R;最终在Rt△OCE中,依据正弦的定义求解.解答:(1)证明:连结OC,如图1,∵DE与⊙O切于点C,∴OC⊥DE,∵AD⊥DE,∴OC∥AD,∴∠2=∠3,∵OA=OC,∴∠1=∠3,∴∠1=∠2,即AC平分∠DAB;(2)解:如图1,∵直径AB=4,B为OE的中点,∴OB=BE=2,OC=2,在Rt△OCE中,OE=2OC,∴∠OEC=30°,∴∠COE=60°,∵CF⊥AB,∴∠OFC=90°,∴∠OCF=30°,∴OF=OC=1,CF=OF=;(3)解:连结OC,如图2,∵OC∥AD,∴△OCG∽△DAG,∴==,∵OC∥AD,∴△ECO∽△EDA,∴==,设⊙O的半径为R,OE=x,∴=,解得OE=3R,在Rt△OCE中,sin∠E===.点评:本题考查了圆的综合题:娴熟驾驭切线的性质、平行线的性质和锐角三角函数的定义;会依据含30度的直角三角形三边的关系和相像比进行几何计算.25.(12分)(2024•十堰)已知抛物线C1:y=a(x+1)2﹣2的顶点为A,且经过点B(﹣2,﹣1).(1)求A点的坐标和抛物线C1的解析式;(2)如图1,将抛物线C1向下平移2个单位后得到抛物线C2,且抛物线C2与直线AB相交于C,D两点,求S△OAC:S△OAD的值;(3)如图2,若过P(﹣4,0),Q(0,2)的直线为l,点E在(2)中抛物线C2对称轴右侧部分(含顶点)运动,直线m过点C和点E.问:是否存在直线m,使直线l,m与x轴围成的三角形和直线l,m与y轴围成的三角形相像?若存在,求出直线m的解析式;若不存在,说明理由.考点:二次函数综合题;待定系数法求一次函数解析式;待定系数法求二次函数解析式;相像三角形的判定与性质;锐角三角函数的增减性.专题:压轴题;存在型.分析:(1)由抛物线的顶点式易得顶点A坐标,把点B的坐标代入抛物线的解析式即可解决问题.(2)依据平移法则求出抛物线C2的解析式,用待定系数法求出直线AB的解析式,再通过解方程组求出抛物线C2与直线AB的交点C、D的坐标,就可以求出S△OAC:S△OAD的值.(3)设直线m与y轴交于点G,直线l,m与x轴围成的三角形和直线l,m与y轴围成的三角形形态、位置随着点G的改变而改变,故需对点G的位置进行探讨,借助于相像三角形的判定与性质、三角函数的增减性等学问求出符合条件的点G的坐标,从而求出相应的直线m的解析式.解答:解:(1)∵抛物线C1:y=a(x+1)2﹣2的顶点为A,∴点A的坐标为(﹣1,﹣2).∵抛物线C1:y=a(x+1)2﹣2经过点B(﹣2,﹣1),∴a(﹣2+1)2﹣2=﹣1.解得:a=1.∴抛物线C1的解析式为:y=(x+1)2﹣2.(2)∵抛物线C2是由抛物线C1向下平移2个单位所得,∴抛物线C2的解析式为:y=(x+1)2﹣2﹣2=(x+1)2﹣4.设直线AB的解析式为y=kx+b.∵A(﹣1,﹣2),B(﹣2,﹣1),∴解得:∴直线AB的解析式为y=﹣x﹣3.联立解得:或.∴C(﹣3,0),D(0,﹣3).∴OC=3,OD=3.过点A作AE⊥x轴,垂足为E,过点A作AF⊥y轴,垂足为F,∵A(﹣1,﹣2),∴AF=1,AE=2.∴S△OAC:S△OAD=(OC•AE):(OD•AF)=(×3×2):(×3×1)=2.∴S△OAC:S△OAD的值为2.(3)设直线m与y轴交于点G,与直线l交于点H,设点G的坐标为(0,t)当m∥l时,CG∥PQ.∴△OCG∽△OPQ.∴=.∵P(﹣4,0),Q(0,2),∴OP=4,OQ=2,∴=.∴OG=.∴t=时,直线l,m与x轴不能构成三角形.∵t=0时,直线m与x轴重合,∴直线l,m与x轴不能构成三角形.∴t≠0且t≠.①t<0时,如图2①所示.∵∠PHC>∠PQG,∠PHC>∠QGH,∴∠PHC≠∠PQG,∠PHC≠∠QGH.当∠PHC=∠GHQ时,∵∠PHC+∠GHQ=180°,∴∠PHC=∠GHQ=90°.∵∠POQ=90°,∴∠HPC=90°﹣∠PQO=∠HGQ.∴△PHC∽△GHQ.∵∠QPO=∠OGC,∴tan∠QPO=tan∠OGC.∴=.∴=.∴OG=6.∴点G的坐标为(0,﹣6)设直线m的解析式为y=mx+n,∵点C(﹣3,0),点G(0,﹣6)在直线m上,∴.解得:.∴直线m的解析式为y=﹣2x﹣6,联立,解得:或∴E(﹣1,﹣4).此时点E在顶点,符合条件.∴直线m的解析式为y=﹣2x﹣6.②O<t<时,如图2②所示,∵ta n∠GCO==<,tan∠PQO===2,∴tan∠GCO≠tan∠PQO.∴∠GCO≠∠PQO.∵∠GCO=∠PCH,∴∠PCH≠∠PQO.又∵∠HPC>∠PQO,∴△PHC与△GHQ不相像.∴符合条件的直线m不存在.③<t≤2时,如图2③所示.∵tan∠CGO==≥,tan∠QPO===.∴tan∠CGO≠tan∠QPO.∴∠CGO≠∠QPO.∵∠CGO=∠QGH,∴∠QGH≠∠QPO,又∵∠HQG>∠QPO,∴△PHC与△GHQ不相像.∴符合条件的直线m不存在.④t>2时,如图2④所示.此时点E在对称轴的右侧.∵∠PCH>∠CGO,∴∠PCH≠∠CGO.当∠QPC=∠CGO时,∵∠PHC=∠QHG,∠HPC=∠HGQ,∴△PCH∽△GQH.∴符合条件的直线m存在.∵∠QPO=∠CGO,∠POQ=∠GOC=90°,∴△POQ∽△GOC.∴=.∴=.∴OG=6.∴点G的坐标为(0,6).设直线m的解析式为y=px+q∵点C(﹣3,0)、点G(0,6)在直线m上,∴.解得:.∴直线m的解析式为y=2x+6.综上所述:存在直线m,使直线l,m与x轴围成的三角形和直线l,m与y轴围成的三角形相像,此时直线m的解析式为y=﹣2x﹣6和y=2x+6.点评:本题考查了二次函数的有关学问,考查了三角形相像的判定与性质、三角函数的定义及增减性等学问,考查了用待定系数法求二次函数及一次函数的解析式,考查了通过解方程组求两个函数图象的交点,强化了对运算实力、批判意识、分类探讨思想的考查,具有较强的综合性,有肯定的难度.。
2006年湖北十堰初中毕业生学业考试课改试验区

湖北省十堰市2006年课改实验区初中毕业生学业考试数学试题一、精心选一选(本大题共 10小题,每小题都给出代号为A,B,C,D 的四个选项,其中有 且只有一个选项符合题目要求,把符合题目要求的选项的字母代号直接填在答题框内相应的题 号下的方框中,不填、填错或一个方框内填写的代号超过一个,一律得 0分;每小题3分,满分 30分) 1.下列各式中,一定成立的是() A.2222 口 23 2 3 B.3 322D.3x 2y 7,2.—兀一次方程组 2y 5 的解是(( )x 3,x 1,A .y 2By 2 x 4,x 3,c. y 2Dy 13.卜列命题止确的是( )1 ZA BC —ABA.△ABC 中,如果 30 ,那么 2 C. 22 B.如果a b c ,那么线段a , b , c 一定可以围成一个三角形 c.三角形三边垂直平分线的交点有可能在一边上; D.平分弦的直径垂直于弦 4.下列四个数据,精确的是( ) A.小莉班上有 45人; B. 某次地震中,伤亡 10万人; C. 小明测得数学书的长度为 21・°厘米; D. 吐鲁番盆地低于海平面大约 155米5•观察图甲,从左侧正对长方体看到的结果是图乙中的(o角D897) 3个2个4个 A CB) ACBDD. 60D. 1个n rr B C&如图所示,课堂上小亮站在座位上回答数学老师提出的问题,那么数学老师观察小亮身后, 盲区是(题图题图题图A. △ DCEB.四边形ABCD C. △ ABFD. △ABE10.在△ABC 中,/ C 9°°, D 是边AB 上一点(不与点A ,B 重合),过点D 作直线与另一边相交,使所得的三角形与原三角形相似,这样的直线有( 6.学校升旗仪式上,徐徐上升的国旗的高度与时间的关系可以用一幅图近似地刻画, 这幅图是F 图中的(7•如图,将一张长方形纸片对折两次,然后剪下一个角,打开•如果要剪出一个正方形,那么 剪口线与折痕成(9.如图,已知Z 1 Z 2 , AC AD ,增加下列条件:①AB/D ;④/B / E . 其中能使△ABC ◎△ AED 的条件有(A. 22.50角B. 3°o角C. 45°角AE :② BC ED 庖/C第二卷二、耐心填一填(本大题共 6小题,每小题3分,满分18分•把答案直接写在横线上)11 •已知直线I 经过第一、二、四象限,则其解析式可以为 ___________________ (写出一个即可)• 12•用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第 n个图形需 _______________ 根火柴棒.13•学生小颖自制一个无底圆锥形纸帽,圆锥底面圆的半径为5cm ,母线长为16cm ,那么围2成这个纸帽的面积(不计接缝)是 ____________ cm (结果保留三个有效数字). 14.如图,已知 AB 〃 CD , / A 55o , / C 20°,则/ P15•如图,在平面直角坐标系中,请按下列要求分别作出 △ ABC 变换后的图形(图中每个小正方形的边长为1个单位):(1 )向右平移8个单位;(2)关于X 轴对称;(3)绕点O 顺时针方向旋转180° • 16•小亮调查本班同学的身高后,将数据绘制成如下图所示的频数分布直方图(每小组数据包 含最小值,但不包含最大值•比如,第二小组数据x满足:145 < x 150,其它小组的数据类似)•设班上学生身高的平均数为 x ,则x 的取值范围是 _________________________•14 题图15 题图二、细心做一做(本大题共3小题,满分18分)• 2 °sin 45.271 0- 3 2006 6ta n30。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖北省十堰市2006年课改实验区初中毕业生学业考试
数 学 试 题
注意事项:
1.本试题满分120分,考试时间为120分钟; 2.请考生在答题前,先将县(市)、学校、考号和姓名填写在试卷密封线内的矩形方框内; 3.题号 一
二 三 四 五 六 总分 得分 阅卷人 复查人
一、精心选一选(本大题共10小题,每小题都给出代号为A,B,C,D 的四个选项,其中有且只有一个选项符合题目要求,把符合题目要求的选项的字母代号直接填在答题框内相应的题号下的方框中,不填、填错或一个方框内填写的代号超过一个,一律得0分;每小题3分,题号 1 2 3 4 5 6 7 8 9 10 答案
1.下列各式中,一定成立的是( )
A.()2
2
22=-ﻩB.()3
3
22=-ﻩC.2222-=-
D.()()3
3
22-=-
2.二元一次方程组32725x y x y -=⎧⎨+=⎩
,
的解是( )
A.32
x y =⎧⎨
=⎩,ﻩ
B.12
x y =⎧⎨
=⎩,
C .42x y =⎧⎨
=⎩, ﻩﻩD.31
x y =⎧⎨=⎩,
3.下列命题正确的是( )
A .ABC △中,如果30A =∠,那么1
2
BC AB =
; B.如果a b c +>,那么线段a ,b ,c 一定可以围成一个三角形; C.三角形三边垂直平分线的交点有可能在一边上; D.平分弦的直径垂直于弦
4.下列四个数据,精确的是( ) A.小莉班上有45人; ﻩ B.某次地震中,伤亡10万人;
C.小明测得数学书的长度为21.0厘米;ﻩ D.吐鲁番盆地低于海平面大约155米 5.观察图甲,从左侧正对长方体看到的结果是图乙中的( )
(图甲) A. B. C. D.
(图乙)
6.学校升旗仪式上,徐徐上升的国旗的高度与时间的关系可以用一幅图近似地刻画,这幅图是下图中的( )
7.如图,将一张长方形纸片对折两次,然后剪下一个角,打开.如果要剪出一个正方形,那么剪口线与折痕成( ) A .22.5角
ﻩ
B .30角 C.45角
ﻩ
D.60角
8.如图所示,课堂上小亮站在座位上回答数学老师提出的问题,那么数学老师观察小亮身后,盲区是( ) A .DCE △ﻩ B.四边形ABCD C .ABF △ﻩﻩﻩD.ABE △ 9.如图,已知12=∠∠,AC AD =,增加下列条件:①AB AE =;②BC ED =;③C D =∠∠;④B E =∠∠.其中能使ABC AED △≌△的条件有( ) A.4个 ﻩB.3个 ﻩﻩC .2个 D.1个 10.在ABC △中,90C =∠,D 是边AB 上一点(不与点A ,B 重合),过点D 作直线与另一边相交,使所得的三角形与原三角形相似,这样的直线有( ) A.1条ﻩﻩﻩB .2条ﻩ C.3条ﻩﻩ D.4条
二、耐心填一填(本大题共6小题,每小题3分,满分18分.把答案直接写在横线上) 11.已知直线l 经过第一、二、四象限,则其解析式可以为______________(写出一个即可).
12.用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第n 个图形需____________根火柴棒.
13.学生小颖自制一个无底圆锥形纸帽,圆锥底面圆的半径为5cm ,母线长为16cm ,那么围成
O 时间 A. 高度
O 时间 B. 高度 O 时间 C. 高度 O 时间 D.
高度 (第7题图) (第8题图)
(第9题图)
(第一个图形)
(第二个图形) (第三个图形)。
