北航 线性系统第14讲
北京航空航天大学线性代数知识点框架

线性代数知识点框架(一)线性代数的学习切入点:线性方程组。
换言之,可以把线性代数看作是在研究线性方程组这一对象的过程中建立起来的学科。
线性方程组的特点:方程是未知数的一次齐次式,方程组的数目s和未知数的个数n可以相同,也可以不同。
关于线性方程组的解,有三个问题值得讨论:(1)、方程组是否有解,即解的存在性问题;(2)、方程组如何求解,有多少个解;(3)、方程组有不止一个解时,这些不同的解之间有无内在联系,即解的结构问题。
高斯消元法,最基础和最直接的求解线性方程组的方法,其中涉及到三种对方程的同解变换:(1)、把某个方程的k倍加到另外一个方程上去;(2)、交换某两个方程的位置;(3)、用某个常数k乘以某个方程。
我们把这三种变换统称为线性方程组的初等变换。
任意的线性方程组都可以通过初等变换化为阶梯形方程组。
由具体例子可看出,化为阶梯形方程组后,就可以依次解出每个未知数的值,从而求得方程组的解。
对方程组的解起决定性作用的是未知数的系数及其相对位置,所以可以把方程组的所有系数及常数项按原来的位置提取出来,形成一张表,通过研究这张表,就可以判断解的情况。
我们把这样一张由若干个数按某种方式构成的表称为矩阵。
可以用矩阵的形式来表示一个线性方程组,这至少在书写和表达上都更加简洁。
系数矩阵和增广矩阵。
高斯消元法中对线性方程组的初等变换,就对应的是矩阵的初等行变换。
阶梯形方程组,对应的是阶梯形矩阵。
换言之,任意的线性方程组,都可以通过对其增广矩阵做初等行变换化为阶梯形矩阵,求得解。
阶梯形矩阵的特点:左下方的元素全为零,每一行的第一个不为零的元素称为该行的主元。
对不同的线性方程组的具体求解结果进行归纳总结(有唯一解、无解、有无穷多解),再经过严格证明,可得到关于线性方程组解的判别定理:首先是通过初等变换将方程组化为阶梯形,若得到的阶梯形方程组中出现0=d这一项,则方程组无解,若未出现0=d一项,则方程组有解;在方程组有解的情况下,若阶梯形的非零行数目r等于未知量数目n,方程组有唯一解,若r<n,则方程组有无穷多解。
北京航空航天大学 线性代数 课件 空间向量

刘敬伟 博士 jwliu_2005@
机动
目录
上页
下页
返回
结束
相 关 事 宜
学习辅导用书:
《高等代数方法指导》姚幕生编---复旦大学出版社 参考书: 1.《高等代数》第三版,北京大学数学系编—高教出版社 2.《线性代数》第三版,同济大学数学系编—高教出版社 作业规格:16开作业纸,注明姓名、学号 交作业时间:每周四上完《高代》课后 答疑时间:每周三、四、五 19:00---21:00
机动 目录 上页 下页 返回 结束
2. 向量的减法
规定: b a = b + ( a ) 特别地,当 b = a 时
b a = a a = a + ( a ) = 0
a
b b a b + ( a )
a
三角不等式:
ab a b
ab a b
机动 目录 上页 下页 返回 结束
机动 目录 上页 下页 返回 结束
推论2. 向量a, b, c 不共面的充分必要条件是: 由k1a + k2b + k3c = 0 可以推出 k1 = k2 = k3= 0 . 由于上述命题, 使得向量的线性运算可以用 来解决有关点的共线或共面问题以及线段的 定比分割问题. 例2. 设向量a, b, c , 证明 a + b, b + c, c a 共面. 证: 因为 1(a + b) + (1)(b + c) + 1(c a)=0, 且 1, 1, 1 不全为零, 由命题3可知, a + b, b + c, c a 共面.
c=a+b.
机动 目录 上页 下页 返回 结束
自动控制原理(北航)电子教案扰动下对稳态误差及减小稳态误差的措施(第10讲)
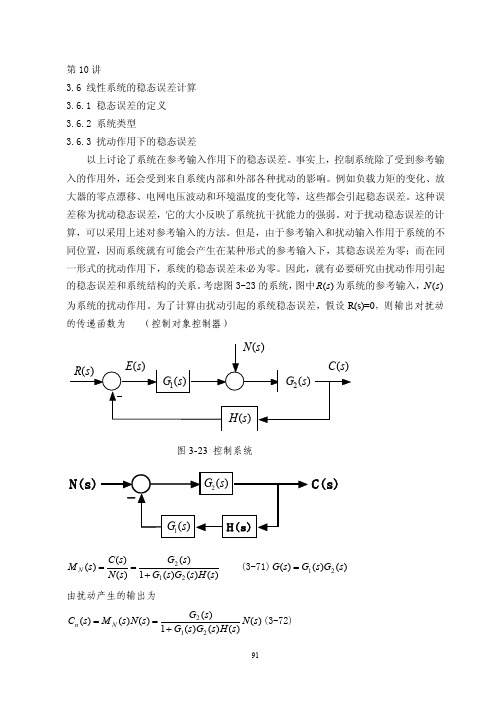
第10讲3.6 线性系统的稳态误差计算3.6.1 稳态误差的定义3.6.2 系统类型3.6.3 扰动作用下的稳态误差以上讨论了系统在参考输入作用下的稳态误差。
事实上,控制系统除了受到参考输入的作用外,还会受到来自系统内部和外部各种扰动的影响。
例如负载力矩的变化、放大器的零点漂移、电网电压波动和环境温度的变化等,这些都会引起稳态误差。
这种误差称为扰动稳态误差,它的大小反映了系统抗干扰能力的强弱。
对于扰动稳态误差的计算,可以采用上述对参考输入的方法。
但是,由于参考输入和扰动输入作用于系统的不同位置,因而系统就有可能会产生在某种形式的参考输入下,其稳态误差为零;而在同一形式的扰动作用下,系统的稳态误差未必为零。
因此,就有必要研究由扰动作用引起的稳态误差和系统结构的关系。
考虑图3-23的系统,图中)(s R 为系统的参考输入,)(s N 为系统的扰动作用。
为了计算由扰动引起的系统稳态误差,假设R(s)=0,则输出对扰动的传递函数为 (控制对象控制器)图3-23 控制系统N(s)C(s))()()(1)()()()(212s H s G s G s G s N s C s M N +== (3-71))()()(21s G s G s G = 由扰动产生的输出为)()()()(1)()()()(212s N s H s G s G s G s N s M s C N n +==(3-72)系统的理想输出为零,故该非单位反馈系统响应扰动的输出端误差信号为)()()()(1)()(0)(212s N s H s G s G s G s C s E n n +-=-=(3-73) 根据终值定理和式(3-73)求得在扰动作用下的稳态误差为)()()()(1)()(lim 2120s N s H s G s G s sG s sE e n s ssn +-==→ (3-74) 若令图3-23中的21)()(,)()(222111ννs s W K s G s s W K s G == (3-75)为讨论方便起见假设1)(=s H 则系统的开环传递函数为νs s W K s W K s G s G s G )()()()()(221121==(3-76)1)0()0(,2121==+=W W ννν。
2019北京航空航天大学线性代数课件第一章行列式的定义-文档资料
朱立永
线性代数
这一讲的主要内容
• 这门课程的主要内容 • 这门课程的特点及考核方式 • 行列式的定义
线性代数
线性代数课程简介
• 英文名字:Linear Algebra • 线性代数是讨论有限维空间中线性关系经 典理论的课程; • 它具有较强的抽象性和逻辑性,是理工科 大学本科各专业的重要基础理论课; • 本课程不仅是学生必须掌握的数学基础, 同时也在现代科学技术的各个领域有着十 分广泛的应用。
2.
线性代数
本门课程的特点
• 具有较强的抽象性和逻辑性
• 各部分内容有紧密的联系
线性代数
课程安排及考核方式
• 总学时:48=36课内学时 + 12学时习题课 课内教师讲授,课外学生自学与作习题 • 考核方式及成绩评定 1. 期末闭卷笔试,占总成绩的90% 2.平时作业占10%
线性代数
其它要注意的几点
线性代数
本章的主要内容
§1.1 n阶行列式 §1.2 行列式的性质 §1.3 行列式的展开与计算 §1.4 克莱姆(Cramer)法则
§1.5 数域
线性代数
§1.1
n阶行列式
1.1.1 排列与逆序 1.1.2 二阶与三阶行列式 1.1.3 n阶行列式的定义
线性代数
1.1.1 排列与逆序
•
定义1.1.1
• 课前一定要做好预习 • 课后要认真完成作业 • 有问题要及时问(/google),(答疑时间 和地点?) 办公室:学院路校区图书馆西配楼519室, Email:
线性代数
第一章 行列式
• 行列式是由解线性方程组引进的,是研究 线性代数的重要工具,它在自然科学的许 多领域有着广泛的应用。
线性系统zy

——状态空间描述
——矩阵分式描述
——系统矩阵描述
线性系统理论研究对象是 (线性的)模型系统,不是 物理系统。
模型
分析
综合(即设计)
模型部分
不同表达领域模型间的转换
• 如何由物理系统得到状态空间表达(传递函数) • 由输入/输出描述得到状态空间表达(SISO)
– 能控规范形描述 – 能观测规范形描述 – 对角形(单极点)
0 (t)
d dt
M
0 (t)
M
2 (t)
A(t)M
1 (t)
d dt
M
1 (t)
则系统在时刻t0∈J完全能控的一
个充分条件为,存在一个有限时
刻t1∈J,t1>t0,,使
r M a 0 ( t 1 ) M n 1 ( , t 1 ) k , M ,n 1 ( t 1 ) n
离散系统:各变量在离散时刻取值,状态空间反映离散时刻的变量组间的
因果关系和变换关系。用k=0,1,2…表示离散时刻。
状态空间描述形式:
X(k1)G(x k)H(u k) Y(k)C(xk)D(u k)
G : 系统矩阵 C : 输出矩阵
H : 输入矩阵
´
D : 传输矩阵
1.3 控制理论分析
表示为:
s
y(t)=L-1[G(s)?U(s)]
m
= L- 1[1?
KÕ(s- zk)
k=1
]
照 s
r
q
(s- pi)? (s2 2djwnjs+wnj2)
i=1
j=1
å Õ =L -1[a s+i= r1s+ bipi+j= q1s2+2 cd js jw + njd s+ j w nj2]
北航自动控制原理-课件(全网八章最完整版)

返回子目录
下面通过具体例子来说明自动控制和自动控制系统 的概念
控制器 气动阀门 流入 Q1 浮子 水箱 H 流出 Q2
水位自动控制系统
•控制任务:
维持水箱内水位恒定;
控制器 气动阀门
•控制装置:
流入 Q1
浮子 水箱
气动阀门、控制器;
•受控对象: 水箱、供水系统; •被控量: 水箱内水位的高度;
H 流出 Q2
北京航空航天大学
返回子目录
于是,建立的动态方程就是非线性微分方程,对其 求解有诸多困难,因此,对非线性问题做线性化处 理确有必要。
对弱非线性的线性化
如上图(a),当输入信号很小时,忽略非线性影 响,近似为放大特性。对(b)和(c),当死区或 间隙很小时(相对于输入信号)同样忽略其影响, 也近似为放大特性,如图中虚线所示。
第一章 自动控制的一般概念
1-1 自动控制的任务 1-2自动控制的基本方式 1-3对控制系统的性能要求
返回主目录
1-1 自动控制的任务
通常,在自动控制技术中,把工作的机器设备 称为被控对象,把表征这些机器设备工作状态 的物理参量称为被控量,而对这些物理参量的 要求值称为给定值或希望值(或参考输入)。 则控制的任务可概括为:使被控对象的被控量 等于给定值。
2 d y (t ) dy(t ) 2 T 2 T y (t ) kF (t ) 2 dt dt
T称为时间常数, 为阻尼比。显然,
上式描述了m-K-f系统的动态关系,它是一个二阶 线性定常微分方程。
北京航空航天大学
2-2 非线性微分方程的线性化
在实际工程中,构成系统的元件都具有不同程 度的非线性,如下图所示。
平衡位置附近的小偏差线性化
北航硕士研究生线性系统课件9

第九讲可控性和可观测性的结构分解不可简约的动态方程定理的证明:下面将说明变换矩阵的构造方法。
1)首先列写出(2-35)的可控性矩阵U ,其秩为n 1;中选个线性关的列向量2)从U 中选取n 1个线性无关的列向量112,,,n q q q 作为变换阵的逆矩阵的前−n 1列,再补充n n 1个n 维的列向量11n n+ q q 得到:11111[]Pn n n −+=q q q q 1−>== n 6112|Im[]Im[]A B B AB A B A <>是不变的。
n q q q 注意:111−+⎡⎤=⎦Pn n n q q q q 11⎣⎡⎤⎦P=: Tp p p p 1111+⎣n n n ⎡T 1⎤⎢⎥ p 即1⎢⎥⎢⎥⎢⎥⎡⎤=P=: T T n p p 111111++⎣⎦⎢⎥⎢⎥n n n Tn p p p p ⎢⎥⎢⎥⎢⎥⎣⎦T n p解 1)计算可控性矩阵⎡1 ra n k ⎢ 1 ⎢ ⎢ ⎣0 0 1 1 −1⎤ −3⎥ = 2 ⎥ −2⎥ ⎦2)现取其中的第1,2列,再补充一个与它们线性无关 T 2 0 1 [ ] 的列向量 。
因此,⎡1 0 P −1 = ⎢ 1 1 ⎢ ⎢ ⎣0 12⎤ 0⎥ ⎥ 1⎥ ⎦2 −2 ⎤ ⎡1 1⎢ P = −1 1 2⎥ ⎥ 3⎢ ⎢ ⎣ 1 −1 1 ⎥ ⎦11再利用变换 x = Px , 可将原系统的动态方程变换为⎡0 ⎢1 x =⎢ ⎢ ⎣0 −1 −2 0 1 ⎤ ⎡1 ⎤ ⎥ x + ⎢0⎥ u −2 ⎥ ⎢ ⎥ ⎢ −1⎥ ⎦ ⎣0⎥ ⎦ y = [1 − 1 − 2 ] x其中二维方程⎡0 −1⎤ ⎡1⎤ x1 = ⎢ x1 + ⎢ ⎥ u ⎥ ⎣1 −2⎦ ⎣ 0⎦是可控的。
y = [1 −1]x112注:若改变基底的顺序,可以得到能控性分解的另 一形式。
令 形式 令P − 1 = [ q n1 +1同的证明方法,有q n q1q n1 ]其中q1, ,q n1仍为U的一组基。
北航线性系统理论答案

2-17 证明:①首先证明()T T T B C A ,,是()s G 的不可简约实现(该题有问题,不是()TT TCB A,,)。
由于()s G 是对称传递函数阵,故有()()T T T C sI B B A sI C 1-1-A --=,所以()TT TBC A,,是()s G 的实现。
又因为()[]n CA CA Crank CA C A C rank n Tn TT T T =⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=1-1- ,其可控; 同理可证其可观,故系统()T T T B C A ,,是可控可观的。
所以其是()s G 的不可简约实现。
②证明P 的对称性。
由题设易知,由于()T T T B C A ,,是()s G 的不可简约实现,则存在非奇异阵P ,使得TT T BCPC PB A PAP===--11,,。
由T T T T T T P P I P P P CP P B C C PB =⇒=⇒==⇒=--11 所以P 是非奇异对称阵。
③证明P 的唯一性。
由T C PB =,很容易知道1-=B C P T ,故知P 是唯一的。
综上可知,命题得证。
2-18 解:[]1 1 3- 4 2301 4 0 2- 3-0 3 2- 6-0 02 0 0 0 0 1 -=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=C B A 。
a.① ><B A |由[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==65 17 5 2 3 3 3 3 00 0 0 1 1 1 1 32B A B A AB B U 所以)53012301(|⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡>=<,span B A 。
② η()⇔⋂=kCAker η064 27 118- 145-16 9 34- 43-4 3 10- 13-1 1 3- 4 032=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⇔=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡x x CACA CA C故)12101301(⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=,span η ③ ><⋂B A |η即任意>⇔<⋂∈B A x |η2153012301x x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=,同时有4312101301x x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=故0--1 1 5 22 3 3 31 0 0 00 1 1 14321=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡x x x x ,有)1301(|⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡>=<⋂span B A η ④ ⊥><⋂B A |η 易知,⇔>∈<⊥B A x |[]065 17 5 2 3 3 3 3 0 0 0 0 1 1 1 1 32=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=T TxB A B A AB B x,即 065 3 0 117 3 0 15 3 0 12 3 0 1=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡x 所以)0103-0010(|⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=><⊥,span B A 同③,可知⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=><⋂⊥0000|B A η⑤ ><⋂⊥B A |η)101-1-0123(⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⊥,span η同③可知⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡>=<⋂⊥0000|B A η⑥ ⊥⊥><⋂B A |η易知)0123(|⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=><⋂⊥⊥span B A η 综上可知,上述空间的维数加起来不等于4,故在上述空间的直和空间中不能取到状态空间的基底。
北航 线性系统第14讲

第十四讲用状态反馈进行极点配置1得以这组给定的复平面上的点为闭环系统极点。
2一、状态反馈对系统可控性、可观测性的影响、、1.状态反馈不改变系统的可控性系统的动态方程如下,(41)x x u y x =+=−A B C 引入线性状态反馈控制律为(42)u v x =+−K 式中的v 是参考输入,K 称为状态反馈增益矩阵,这里它是p ×n 的矩阵。
将(4-1)式和(4-2)式用方块3()()图表示,见图4-1,它是一个闭环系统。
x yB C v x u A∫K 图4-1:闭环系统结构图图4-1所示,引入状态反馈后的闭环系统的状态空间表达式为:u v x =+K (将代入状态方程后得到)()(43)xx u x v y x =+=++=−A B A BK B C 4式中A +BK 为闭环系统的系数矩阵。
,(41)A B C =+=− 前:x x u y x (43) 后(),A BK B C =++=−后:x x v y x 43(41)−⇔−()可控可控。
定理4-1:K,∀证因为明:0I ⎡[][]()I A BK B I A B K I λλ⎤−+=−⎢⎥−⎣⎦n p K ,K,λ∀因此,(44)I A BK B I A B λλ−+=−−rank rank 即状态反馈不影响可控性。
证完。
[][]()()容易得到如下结论:定理状态反馈不能改变不可控的模态即开环的5定理:状态反馈不能改变不可控的模态,即开环的不可控模态在闭环中得到保持。
2. 状态反馈不改变可控子空间1,U 定义状态反馈前的可控性矩阵为即111[]|Im U B AB A B A B U −=⇒<>= n 2,U 定义经状态反馈后的可控性矩阵为即1Im U B A+BK)B A+BK)B A+BK B U −=⇒<>= n 我们有如下结论:22[((]|))定理4-2 :状态反馈不改变可控子空间,即1|(Im )∀<>K A B U ,62|(Im )=<>A +B K B U001|0A B U ⊥∈<>⇒=任取,即T x x 明:证00,0,1,,1A B ==− T i x i n 00(T i x ⇒=(A+BK)B 展开)0|||A+BK B A B A+BK B ⊥⊥⊥⇒∈<>⇒<>⊂<>x ||⊥⊥<>⊃<>A B A+BK B 同理,我们可以证明。
北航线性系统理论完整版答案

1-1 证明:由矩阵 可知A 的特征多项式为nn n n n n n n n n nn n n n a a a a a a a a a a a a a a a a a a a a a a a A I ++++++=+++++=+++=++=+=-+λλλλλλλλλλλλλλλλλλλλλλλ1-3-32-21-11-3-3122-2-1-n 13-n 2-n 21-1n 12-n 1-n 12-n 1-n n1- )1(-)1(- 00 0 1- )1(-)1(- 0 00 1-1 0 1- 0 0 0 1- ΛΛΛMM M ΛΛΛM M M ΛΛΛM M M ΛΛ若i λ是A 的特征值,则所以[]Ti i 1-n i 2 1 λλλΛ是属于i λ的特征向量。
1-7 解:由于()ττ--t e t g =,,可知当τ<t 时,()0≠τ,t g ,所以系统不具有因果性。
又由于()()0 ,,ττ-=t g t g ,所以系统是时不变的。
1-8 解:容易验证该系统满足齐次性与可加性,所以此系统是线性的。
由于()()t 0t ⎩⎨⎧>≤-=-=ααββαβαt u t u P u Q P 而()()⎩⎨⎧+>+≤-=⎩⎨⎧>≤=βαβαβααβαβ t 0 t t 0 t t u t u Q u P Q ,故u P Q u Q P αββα≠,所以系统是时变的。
又因为()()()()()⎩⎨⎧>≤=⎩⎨⎧>≤=ααααα,,T T t u t u P u P P T T min t 0 min t t 0 t 而()()()()()()()⎩⎨⎧>≤=⎩⎨⎧>≤=ααααα,,,,T T t u T T t u P u P P P T T T min t 0 min t min t 0 min t ,故()()u P P P u P P T T T αα=,所以系统具有因果性。
北航学院《大学计算机基础》(社会科学试验班类)课程大纲

北航学院《大学计算机基础》(社会科学试验班类)课程大纲课程基本信息课程编号:B1B061080课程中文名称:大学计算机基础课程英文名称:University Computer Foundation开课学期:春季学分/学时:2.0/40(备注,其中学时按照教务处文件定义(理论学时24课堂及机房授课、实验学时16)课程性质:必修面向大类:社会科学试验班类(法学、经济学、行政管理专业)先修课程:无建议后续课程:无适用专业/开课对象:社会科学试验班类/一年级学生任课教师:欧阳元新,刘禹,吴秀娟团队负责人:曹庆华核准院长:一、课程的性质、目的和任务课程性质:本课程为面向北航学院社会科学试验班类一年级本科生的工程基础类课程,包括法学、经济学、行政管理专业。
本课程着重通过系列课内讲解和上机实践,培养学生以计算思维来解决社会科学数据分析问题的基本思维方法。
因此,课程不仅仅需要熟练掌握常用工具软件,更注重计算思维思想的培养与计算思维方法的训练——如何使用计算机实现数据处理、自动分析和结果展现。
目的和任务:随着信息社会的发展,信息素养和人文素养、科学素养一样,已成为现代人必须具备的核心素养,其代表的是信息获取、信息鉴别和信息利用的意识和能力。
而计算思维是信息素养的核心之一,其在学生综合素质中的位置将越来越重要。
计算思维包含计算机学科领域内的众多概念,在本课程中,以解决社会科学数据分析问题为导向,按照问题求解的方式表述教学内容和实施教学。
通过理论学习和实验环节,使学生理解计算思维的基本概念,掌握使用计算机实现数据处理、自动分析和结果展现的方法,具备通过自学掌握高级编辑和演示工具的能力。
具体教学目标可分解为以下5点:(1)了解计算思维,具备基本的运用计算思维思想解决数据分析问题的能力;(2)理解算法的概念,了解基本的算法控制结构,逐步理解使用计算机求解问题的一般方法;(3)能使用Python语言实现基本的程序设计;(4)能够运用Python语言进行数据自动分析和结果展现;(5)能够使用常用工具软件的基本功能,具备通过自学掌握其他高级功能的能力。
北航最优化教材

例1. 食谱问题
◎ 问题:确定食品数量,满足营养需求,花费最小?
n种食品,m种营养成份; -第 j 种食品的单价 -每单位第 j 种食品所含第 i 种营养的数量 -为了健康,每天必须食用第i 种营养的数量
◎ 变量: -食用第 j 种食品的数量 ◎ 模型:
4
例2. 目标函数中含绝对值的问题
假设: 事实: 转化为:
基本可行解
定义 称
的非负基本解是标准形的基
本可行解(basic feasible solution);
◆ 退化基本可行解:某个或某些基变量取零的基本可行解! 问题:基本可行解与基的对应关系?(见习题2.5)
例. 基本可行解及几何意义
基本可行解的个数不超过
线性规划的基本定理(*****)
考虑线性规划标准形,其中A是秩为m的m×n 矩阵,则以下结论成立:
将 Ax=b 的任一解 x 用非基变量表示为
确定进基变量
◎最优性定理
◎定理:BFS的提高 给定目标值为z0的非退化基本可行解,且假定存
在 j 使得 rj < 0,则 i) 如果用 aj 替换基中某列得到了新的BFS,则新解
处的目标值比 z0 严格小. ii) 如果任何替换都产生不了新的BFS,则问题无界.
基本解
基变量
一般地:
只要有m个单位列
非基变量 即可,次序可以打乱!
8
规范形的转换问题
◎ 替换问题
假设在上述规范形中,想用
⊙ 什么时候可以替换? ⊙ 替换后新规范形是什么?
转轴(pivot)
◎ 当且仅当
,可以替换
◎ 替换后,新规范形的系数
转轴公式
-转轴元(pivot element)
绪论

线性系统理论Linear System Theory 北京理工大学自动化学院学时:54学分:3主讲教师:姚小兰联系电话:68912467Email : yaoxiaolan@ 讲义:《线性系统理论与设计》•第一章绪论1学时•第二章系统的数学描述5学时•第四章线性动态方程和脉冲响应矩阵8学时•第五章线性动态方程的可控性和可观测性8学时•第六章传递函数矩阵的状态空间实现6学时•第七章系统的运动稳定性8学时•第八章线性反馈系统的综合8学时•第九章状态观测器及状态观测器的设计4学时•课堂讨论6学时•根据实际情况,各章所用学时会稍微有所调整。
讲授方式:以课堂讲授为主,适当章节进行自学及讨论。
考核方式:期末闭卷考试80~90%平时10~20%参考书目[1] 陈啟宗[美],王纪文/杜正秋/毛剑琴[译].线性系统理论与设计,科学出版社,1988(英文第三版1999)[2] 郑大鈡. 线性系统理论(第2版),清华大学出版社,2002[3] 段广仁. 线性系统理论(第2版),哈尔滨工业大学出版社,2004[4] 黄琳.系统与控制理论中的线性代数, 科学出版社,1984[5] T.凯拉斯.线性系统,科学出版社,1985[6] (日)须田信英等曹长修译.自动控制中的矩阵理论,科学出版社, 1979何谓控制科学?控制科学是研究各种系统的共同控制规律的科学,是数学与工程学的交叉科学,是自动化系统的核心理论,也是人类改造世界的重要方法。
通俗地说,从现代汽车到航天飞机,都离不开控制理论。
随着计算机和其他高技术的急剧发展,人类需要处理越来越复杂的动态系统,而保持技术和经济竞争优势不断地刺激着追求控制系统的精确性、有效性和可靠性。
航空航天、工业过程、生物医学,社会经济和生态环境等领域出现了大量复杂系统控制问题,对控制科学提出了前所未有的挑战。
一、系统控制理论的研究对象1、系统:由相互关联和相互制约的若干“部分”组成的具有特定功能的一个“整体”。
北航硕士研究生线性系统课件1

线性系统 论 线性系统理论(Linear System Theory)程鹏 教授 编写北京航空航天大学内部讲义参考书:一、矩阵方面: 1.(日)须田信英等,曹长修译 信英等 曹 修 : 《自动控制中的矩阵理论》 科学出版社 1979 2 黄琳 : 2.黄琳 《系统与控制理论中的线性代数》, 科学出版社 1984 3 韩京清,许可康 ,何关钰: 3.韩京清,许可康 《线性系统理论的代数基础》,辽宁科技出版社1987二、线性系统理论方面: 1. T.KAILATH:Linear Systems 1985年有中译本,李清泉等译:凯拉斯: 年有中译本 李清泉等译:凯拉斯:《线性系 统》。
2. C.T.CHEN: Linear System Theory and Design (王纪文、毛剑琴等译 王纪文 毛剑琴等译): 《线性系统理论与设计》,1988年中译本 3. 郑大钟: 《线性系统理论》 清华大学出版社,1992 其余见篇末文献。
课程的地位与目的本课程是控制科学与工程一级学科研究生的公共学 位课和专业基础课。
通过本课程学习,要求学生掌握线性系统的 一般概念和分析研究线性系统的一般方法,为进一 步学习其它控制理论奠定坚实的基础。
步学习其它控制理论奠定坚实的基础 本课程理论性强,用到较多数学工具,因此, 对培养学生的抽象思维、逻辑思维,提高学生运 用数学知识处理控制问题的能力具有重要作用。
一、控制论产生的背景社会背景现代社会的生产和管理对于高度自动化水平的需要社会一旦有技术上的需要,则这种需要就会比十所大学更 能把科学推向前进。
—— 恩格斯直接原因二战期间,维纳参加了火炮控制和电子计算机的研制工作。
1943年,维纳、毕格罗和罗森勃吕特三人共同发表了 年,维纳、毕格罗和罗森勃吕特三人共同发表了《 《行为、 目的和目的论》 目的和目的论 》,首先提出了“控制论”这个概念,第一次把 只属于生物的有目的的行为赋予机器 阐明了控制论的基本思 只属于生物的有目的的行为赋予机器,阐明了控制论的基本思 想。
《线性系统理论讲义》课件

时域分析
卷积积分
学习卷积积分的计算方法,掌握时 域分析的基本方法。
因果性
认识系统因果性的概念,学习如何 判断一个系统是否是因果系统。
冲击响应
了解系统的冲击响应特性,学会如 何使用冲击响应分析系统的动态特 性。
单位脉冲响应
学习单位脉冲响应的计算方法,掌 握时域分析的基本方法。
频域分析
1
傅里叶变换
学习傅里叶变换的基本概念与性质,掌握在频域下分析系统的方法。
本课件内容详细介绍了线性系统的基本概念、信号与系统分析、时域分析、频域分析、线性系统设计和应用实例。 通过本课件的学习,您将掌握线性系统理论的基础知识和应用技能。
学会设计控制系统,实现系统的自动控制。
应用实例
机械控制系统设计
了解机械控制系统的构成和特点, 学会使用线性系统理论设计控制系 统。
自动控制系统设计
认识自动控制系统的概念与分类, 掌握自动控制系统的设计方法。
信号处理应用实例
了解信号处理的基本知识和应用领 域,学会使用线性系统理论进行信 号处理。
总结
线性系统理论讲义PPT课 件
本课程将深入讲解线性系统基础知识和应用技能,介绍系统的数学模型、信 号与系统分析、时域分析、频域分析、线性系统设计等内容。
线性系统基础
1
概念
了解什么是线性系统及其特点。
2
性质
掌握线性函数的性质,了解线性系统的基本概念。
3
数学模型
学习如何使用数学方法描述线性系统的模型。
4
时不变系统
认识时不变系统的概念和特性,掌握时不变系统的分析方法。
信号与系统分析
信号分类及性质
了解信号的种类与性质,熟悉不同种类的信号的特 点。
北航数理统计课程简介
Pre-request Course References
课程的目的 与地位
距离判别,Bayes 判别,Fisher 判别 第八章 相关分析(6 学时) 主成分析,因子分析,典型相关分析
讲授及学习 方法
课堂教学、课后作业及实践性大作业相结合,每周授课 4 学时
考核方式 先修课程
平时考查结合期末闭卷考试 高等数学、线性代数、概率论 作 是 为 校 师 是 者 否 本 教
参 考 书 主 要 参 考 书
名称
作者
出版社
出 版 时间
教材类别
数理统计
孙海燕等
试用版
2012
应用数理统计 数理统计
韩於羹 赵选民等 陈希孺
北京航空航天大 学出版社 科学出版社 科学出版社
1993 2002 1997
否 否 否
数理统计引论
Bickel, P. Mathematical Statistics, Basic J., ay Inc. 1977 Ideas and Selected Topics, Doksum, K.A. 教材类别指是否为“各级精品教材” 、 “全国研究生教学用书” 、 “国防系列教材”或“专著”等等
否
课程简介
课程代码 学时/开课季 节 课程内容关 键词(3 个) 48 / 秋 课程名称 数理统计 B 本课程英 Mathematical Statistics 文名称 估计和检验、回归分析、方差分析和试验 任课教师 设计、相关分析 应用数理统计是全校工科硕士研究生的重要公共基础课,也是一门应用性很广泛的数学 课。通过本课程的学习,使学生掌握数理统计的应用背景、基本原理和研究方法,了解基本 理论,着重培养学生应用数理统计方法分析问题和解决问题的能力,为培养合格的理论和应 用人才服务。 第一章 绪论(4 学时) 1) 数理统计学发展简史及其研究范畴,数据采集和整理 2) 基本概念:总体、样本、统计量及充分统计量 3) 抽样分布 第二章 参数估计(10 学时) 1) 参数的频率替换估计,矩估计和极大似然估计 2) 无偏估计,完全统计量,一致最小方差无偏估计 3) 信息不等式,优效估计,相合估计 4) 区间估计 第三章 假设检验(9 学时) 1) 参数假设检验的基本问题和 Neyman-Pearson 思想简介 2) 单个正态总体和两个正态总体参数的假设检验 课程的主要 章节学时分 配 3) 似然比检验 4) 检验优良性简介 5) Pearson 检验 第四章 回归分析(7 学时) 1) 一元线性回归,最小二乘估计,回归方程和回归系数检验,预测与控制 2) 多元线性回归,回归方程和回归系数检验 3) 多项式回归,一元曲线回归关 第五章 方差分析与正交设计(6 学时) 1) 基本概念,单因素方差分析 2) 双因素方差分析 3) 正交试验设计的直观分析及正交表 4) 正交试验设计的方差分析 第六章 多元正态总统的统计推断(2 学时) 多元正态分布的定义,参数估计与检验理论 第七章 判别分析(4 学时)
“线性系统分析”课程教学实践与改革探索

“线性系统分析”课程教学实践与改革探索王春彦,王佳楠,王丹丹,丁艳(北京理工大学宇航学院,北京100081)[摘要]“线性系统分析”是航空宇航科学与技术学科为一年级研究生开设的专业基础课程之一,是解决航空宇航领域重大科学问题的理论基础,在飞行器导航、制导与控制等研究中占有重要的地位。
通过学习这门课程,可以将自动化的相关知识与航空宇航的应用背景相结合,达到多学科交叉融合的目的。
为提高教学质量,紧跟航空宇航领域的发展趋势,在线性系统分析教学实践的基础上,从教学内容、教学方式和手段、课程考核方式三个方面提出了改革探索方案。
[关键词]线性系统分析;教学实践;改革探索[基金项目]2019年度中国自然科学基金青年项目“基于预估器的时延多智能体系统分布式一致抗干扰研究”(61803032)[作者简介]王春彦(1983—),男,山东曹县人,工学博士,北京理工大学宇航学院特别研究员,博士生导师,主要从事先进控制理论及其在飞行器系统中的应用研究。
[中图分类号]G642.0[文献标识码]A [文章编号]1674-9324(2021)22-0097-04[收稿日期]2021-01-26一、引言“线性系统分析”是控制科学与工程学科的基础理论知识,同时也是航空宇航科学与技术学科的重要理论基础。
该课程一般以“自动控制原理”“现代控制理论”“矩阵分析”等为先修课程,理论性强,涉及多种数理知识,内容抽象晦涩,学习难度较大[1]。
通过本课程的学习,可使研究生系统掌握基于状态变量的控制系统分析和设计方法,为后续学习专业课知识、进行理论研究和参与工程实践打下坚实的理论基础[2]。
“线性系统分析”是北京理工大学宇航学院开设的一门专业基础课程,为飞行器总体设计、飞行动力学与控制、航天器系统与自主技术等专业奠定理论基础,在专业课程体系中占有不可或缺的地位。
根据我校办学定位和人才培养目标,结合《线性系统分析研究生课程教学大纲》的基本要求,在本课程教学实践与改革探索中,坚持“学术为基、育人为本”的培养方针,通过分析总结以往教学实践中存在的问题,不断改进教学方法的手段,科学制定课程教学和考核评价标准,取得良好的教学效果。
航天学院硕士生课程简介

02 航天学院序号:课程编号:02M001课程名称:线性系统理论任课教师:周军刘莹莹英文译名:Linear System Theory先修要求:《线性代数》和《矩阵论》中任一门、《复变函数》内容简介:《线性系统理论》是控制类、系统工程类、电类、计算机类、机电类等许多学科专业硕士研究生的一门公共基础理论课,是控制、信息、系统方面系列理论课程的先行课。
《线性系统理论》是最优估计、最优控制、系统辨识、自适应控制等现代控制理论的基础,系统讲述线性系统的运动规律,揭示系统中固有的结构特性,建立系统的结构、参数与性能之间的定性和定量关系,以及为改善系统性能,满足工程指标要求而采取的各类控制器设计方法。
具体的内容包括:线性系统的状态空间描述、状态空间描述与传递函数描述的关系、线性系统的运动分析、能控性、能观性、稳定性理论、线性反馈系统的状态空间综合方法、线性鲁棒性控制基本理论、线性系统的基本代数理论,以及多变量频域设计方法等。
主要参考书:(1)《线性系统理论》阙志宏主编,西安西北工业大学出版社,1995;(2)《现代控制理论引论》周凤歧等,北京国防工业大学出版社,1988;(3)《线性理论》郑大中编著,北京清华大学出版社;(4)《线性系统理论与设计》[美]陈启宗,科学出版社,1988。
序号:课程编号:02M900课程名称:专业英语任课教师:周军英文译名:Professional English先修要求:专业方面的课程内容简介:本课程作为一种基本的专业英语技能,在阅读和学习与本专业的相关的国外文献资料时,发挥着重要的作用。
因此,主要学习和掌握专业外语的基本语法、句法和结构,通过这门课的学习,期望学生能掌握专业英语的特点;扩大专业英语词汇量,尤其关于本专业有关导弹、航天器、无人机等专业知识方面的英语词汇量;提高专业英语(或科技英语)文章的阅读速度;并进行相应专业英语文献的翻译,在此基础上掌握专业英语的写法,为今后从事工程技术和科学研究工作打下稳固的基础。
线性系统 第14讲

一、最小阶实现问题的提法Hankel矩阵序列寻找最小阶实现1.Markov参数矩阵考虑q×p的正则有理传递函数矩阵G(s),根据定理1-9,存在有限维实现(A,B,C,D),使得G(s)=D+C(s I−A)−1B=G(∞)+H0/s+H1/s2+…(3-62)其中=012)的常量矩阵通常将H i(i=0,1,2…)是q×p的常量矩阵,通常将H i称为G(s)的Markov参数矩阵。
事实上12. 基于矩阵序列{H i}的最小实现问题提法2基于矩阵序列最小实现问题可描述如下:()给定正则有理传递函数矩阵G s⇒求出Markov 矩阵序列{H i} ⇒构造一个三元组(A, B, C),使得H i= CA B,i且(A B C)是可控且可观测的。
, ,3二、由G (s)求{H i }、Hankel 矩阵的构造1. Hankel 矩阵的定义⎡⎤H H 由矩阵序列{H i }可定义矩阵H ij 如下01-112j ⎢⎥H H H H ""23j ij ⎢⎥⎢⎥=⎢⎥H H H ""1-2i i i j −+⎢⎥⎢⎥⎣⎦H H H "H H Hankel 阵序列。
4ij 称为由序列{i }生成的阵序列r−1r−2R1s+R2s+…+R r=(s r+a1s r−1+…+a r−1s+a r)(H0s−1+H1s −2+H2s −3+ …) =H0s r−1+(a1H0+H1)s r−2+(a2H0+a1H1+H2)s r−3(+ ….. +(a r-1H0+a r-2H1+…+a1H r-2+H r-1)s0r-r-−1+(a r H0+a r1H1+…+a1H r1+H r)s+(a r H1+a r-1H2+…+a1H r+H r+1)s−2+(a r H2+a r-1H3+…+a1H r+1+H r+2)s−3 +…… (*)6令s的同次幂系数相等,即有s r−1:H0=R1s r−2:a1H0+H1=R2r−3=s:a2H0+a1H1+H2R3…………s0:a r−1H0+a r−2H1+…+a1H r-2+H r-1=R r++s−(i+1): a r H i+a r−1H i+1+…+a1H r+i−1+H r+i=0,i0,1,2, (367)=0,1,2,….3-67注意:(*)式右边是无穷序列,而左边为有限序列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十四讲
用状态反馈进行
极点配置
1
得以这组给定的复平面上的点为闭环系统极点。
2
一、状态反馈对系统可控性、可观测性的影响、、
1.状态反馈不改变系统的可控性
系统的动态方程如下
,(41)
x x u y x =+=−A B C 引入线性状态反馈控制律为
(42)
u v x =+−K 式中的v 是参考输入,K 称为状态反馈增益矩阵,这里它是p ×n 的矩阵。
将(4-1)式和(4-2)式用方块3
()()图表示,见图4-1,它是一个闭环系统。
x y
B C v x u A
∫
K 图4-1:闭环系统结构图
图4-1所示,引入状态反馈后的闭环系统的状态空间表达式为:
u v x =+K (将代入状态方程后得到)
()(43)
x
x u x v y x =+=++=−A B A BK B C 4式中A +BK 为闭环系统的系数矩阵。
,(41)
A B C =+=− 前:x x u y x (43) 后(),A BK B C =++=−后:x x v y x 43(41)−⇔−()可控可控。
定理4-1:K,
∀证因为明:0I ⎡[][]()I A BK B I A B K I λλ⎤−+=−⎢⎥−⎣
⎦n p K ,K,λ∀因此,(44)I A BK B I A B λλ−+=−−rank rank 即状态反馈不影响可控性。
证完。
[][]()()容易得到如下结论:定理状态反馈不能改变不可控的模态即开环的
5定理:状态反馈不能改变不可控的模态,即开环的不可控模态在闭环中得到保持。
2. 状态反馈不改变可控子空间
1,U 定义状态反馈前的可控性矩阵为即
111
[]|Im U B AB A B A B U −=⇒<>= n 2,U 定义经状态反馈后的可控性矩阵为即1Im U B A+BK)B A+BK)B A+BK B U −=⇒<>= n 我们有如下结论:
22
[((]|))定理4-2 :状态反馈不改变可控子空间,即
1|(Im )
∀<>K A B U ,6
2|(Im )
=<>A +B K B U
001|0A B U ⊥∈<>⇒
=任取,即T x x 明:证00,0,1,,1
A B ==− T i x i n 00(T i x ⇒=(A+BK)B 展开)
0|||A+BK B A B A+BK B ⊥⊥⊥⇒∈<>⇒<>⊂<>
x ||⊥⊥<>⊃<>A B A+BK B 同理,我们可以证明。
因此,我们有
||,
A B A+BK B <>=<>即
完
7
证完。
12Im Im U U =。
3. 状态反馈却可能改变系统的可观测性。
状态反馈是否改变系统的可观测性要进行具体分析是否改变系统的可观测性,要进行具体分析。
例题系统的动态方程如下
[]12110,1x x u y c c x
⎡⎤⎡⎤=+=⎢⎥⎢⎥⎦ 01⎣⎦⎣110⎡⎤⎡⎤ []12,011)=+=⎢⎥⎢⎥⎣⎦⎣⎦
x x u y c c x c 开:[]12(,=++=A bk b x
x v y c x 闭:11⎡8
[]12120,11⎤⎡⎤=+=⎢⎥⎢⎥⎣⎦⎣⎦+ x x v y c c x k k
下表列出了系统c 阵参数、状态增益向量k 和系统可观测性的关系。
[11]闭环系统k 原系统c 2c 1
不可观[0 1]10
可观[1 1] 不可观10
不可观不可观[1 2] 可观11
可观[1 1]11
可观可观任意可观
01上例可观性的变化可以从闭环传递函数的极点变化、9
是否发生零极点对消来说明。
二、单变量系统的极点配置
45x x u =+−A b 开()
环:46k u v x =+−引入状态反馈律:()
()47x x v =++−A bk b (闭)
环:11,,A R b R k R
×××∈∈∈n n n n 定理4-3闭环系统(4-7) 的系数矩阵A +bk 的特征值可以由状态反馈增益阵k 配置到复平面的任意位置(复数共轭成对),其充分必要条件是(4-5)式的系10统可控。
单输入系统
1)当(A, b)可控时,n个方程是未知量k i 的线性方程;
上述方程有解,且解唯一。
对“任意配置”来说,
有解的充要条件就是系统可控。
)
2)可控条件对于任意配置极点是充分必要条件,但
对于某一组指定的特征值进行配置时,系统可控
只是充分条件,而不是必要条件。
推论:给定极点组可用状态反馈达到配置的充分要条件是给定极点含系统的不可控模态
必要条件是给定极点组包含系统的不可控模态。
20
事实上,假设系统是不可控的且已具有可控性分解:11121⎡⎤⎡⎤=+A A b 2200x x u ⎢⎥⎢⎥⎣⎦
⎣⎦A ,u v =+kx 引入状态反馈有
1112111211⎡⎤⎡⎤⎡⎤⎡⎤+A A A A b b []12222200
00+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦+⎡k k k A A 1111122220+⎤=⎢⎥⎣⎦
A b k A k A 1b 显然,由于状态反馈不会改变系统的不可控模态,21故仅当欲配置的极点包含A 22的全部特征值时才是可
行的。
例题系统动态方程为
0011−⎡⎤⎡⎤ 1021x x u ⎢⎥⎢⎥=−+⎢⎥⎢⎥−[]012y x
=−0120⎢⎥⎢⎥⎣⎦⎣⎦给定两组极点,分别为:{−2, −3, −4} 和−1, −2, −3} ,{,,}{,,}问哪组极点可用状态反馈进行配置。
解计算出A 阵的特征值,分别为–1, –0.5±j 0.5√3。
可–1是不可控的其它两个特征值是可控的极点验证–1 是不可控的,其它两个特征值是可控的。
极点组{–1, –2, –3}包含了不可控模态–1,所以可用状态反馈进行配置极点组{234}则不能达到配置
22
馈进行配置;极点组{–2,–3,–4}则不能达到配置。
26
1104++=⎡⎤⎡⎤⎡⎤k k k 121123223211
2319()⎢⎥⎢⎥⎢⎥+++==∇⎢⎥⎢⎥⎢⎥ k k k k 1233()2
1261215⋅=⎢⎥⎢⎥⎢⎥+++=⎣⎦⎣⎦⎣⎦
rank k k k k 上述方程,增广矩阵的秩等于系数矩阵的秩(等于
)有解
2),有解。
方程组的相容条件就是所给极点组应包含不可控模态。
()∇24
由此可见, “任意配置”要求系数矩阵满秩,任意配置要求系数矩阵满秩,系数矩阵满秩的条件是系统可控。
()∇由可解出k 1, k 2, k 3
k 1+ k 2=4 , k 3+ k 2=1
3212123123(2)(232)12(*)s k k s k k k s k k k +++++++++++(*)式又可表成(s +1)[s 2+ (k 1+ k 2+1)s + k 1+ k 3+ 2k 2+1] 将二阶因式与(s +2)(s +3)相比较,可得同样结果。
上式也表明不可控模态是用状态反馈改变不了的25
上式也表明不可控模态是用状态反馈改变不了的。
多变量系统状态反馈极点配置与镇定问题
例子考虑如下系统:3101⎡⎤04⎡⎤×⎡⎤⎢⎥例子,考虑如下系统:
03003⎢⎥⎢⎥⎢⎥=A 00,21⎢⎥⎢⎥⎢⎥=B 1×⎢⎥⎡⎤⎢⎥==⎢⎥b:=B B ρρβ212⎢⎥⎢⎥⎦4320⎢⎥⎢⎥⎢⎥2⎢⎥⎣⎦×⎢⎥⎢⎥ρα0⎢⎥⎣⎣⎦⎣⎦×B 如上所示,其中表示的元讨论中无需用到。
利用ρ)05A B 可控性的若当形判据知,(,为可控的充分必要这表明除ρ00/0.50,)+≠=≠=−=A B 121121条件是=2,2。
这表明除和以外的所有,也即几乎任意的(,为可控。
ρρβρραρρρρρ29
)A B 故一定存在使得(,为可控。
ρρ
例子考虑如下系统:3100⎡⎤04⎡⎤例子,考虑如下系统:03003⎢⎥⎢⎥⎢⎥=A 10,21⎢⎥⎢⎥⎢⎥=B 212⎢⎥⎢⎥⎦4320⎢⎥⎢⎥⎢⎥0⎢⎥⎣⎣⎦
⎡×⎤⎢⎥
×⎢⎥b B B 12ρρρ⎡⎤⎢⎥==×⎢⎥⎢⎥⎣⎦×b:=B 30⎢⎥⎢⎥×⎣⎦
3.由于
1Im ,
b B L R ×∈⇔∃∈p 使得b BL
=故由上式,有
1A BK bk
++11).K
A BK BLk A
B (K Lk =++=++
因此,找状态反馈增益阵K 1是关键。
32。
