5_3树的概念和算法
第八章 图论8.4树及其应用.ppt

⑥ G中每一对结点之间有惟一一条基本通路。(n≥2)
2017/10/10 82-9
定理4.2.1 分析
直接证明这 6 个命题两两等价工作量太大,一 般采用循环论证的方法,即证明
(1) (2) (3) (4) (5) (6) (1) 然后利用传递行,得到结论。
2017/10/10
证明 TG = <VT, ET> 是 G = <V, E> 的生 分析 必要性:假设 必要性由树的定义即得,充分性利用构造性 成树,由定义 4.2.1 , TG 是连通的,于是 G 也是连通的。 方法,具体找出一颗生成树即可
充分性:假设G = <V, E>是连通的。如果G中无回 路, G 本身就是生成树。如果 G 中存在回路 C1 ,可删除 C1中一条边得到图G1,它仍连通且与G有相同的结点集。 如果G1中无回路,G1就是生成树。如果G1仍存在回路C2, 可删除 C2 中一条边,如此继续,直到得到一个无回路 的连通图H为止。因此,H是G的生成树。
2017/10/10 82-22
思考题
1、一个图的生成树是不是唯一的呢?
2、如果不是唯一的,3个顶点的无向完全图有几棵 生成树?4个顶点的无向完全图又有几棵生成树?n 个顶点的无向完全图又有几棵生成树?
完全图是边数最 多的简单无向图
2017/10/10
82-23
定理4.2.3
一个图G = <V, E>存在生成树TG = <VT, ET>的充分 必要条件是G是连通的。
由定理4.2.1(4) 在结点给定的无向图中, 由定理4.2.1(5) 树是边数最多的无回路图 树是边数最少的连通图 由此可知,在无向图G = (n, m)中, 若m<n-1,则G是不连通的 若m>n-1,则G必含回路
图的最小生成树

保证不形成回路
(2)TE=TE+(u0,v0), 边(u0,v0)并入TE (3)U=U+{v0},顶点V0 并入U
特点: 以连通为主、选代价最小的邻接边
说明:Prim算法的起始点(可不写,默认为0)
翻译训练1.学生结合课下注释和工具书自行疏通文义,并画出不解之处。【教学提示】节奏划分与明确文意相辅相成,若能以节奏划分引导学生明确文意最好;若学生理解有限,亦可在解读文意后把握节
奏划分。2.以四人小组为单位,组内互助解疑,并尝试用“直译”与“意译”两种方法译读文章。3.教师选择疑难句或值得翻译的句子,请学生用两种翻译方法进行翻译。翻译示例:若夫日出而林霏开,
【练习】请用kruskal算法找出下图最小生成树。
练习
利用克鲁斯卡尔算法构造最小生成树 算出该最小生成树的代价
最
1
10
小
生
成
21 6
树 19
算
法
33
思
想
5
18
二
1
10
6 Prim算法
2
11
5
6
3
14 6
4
2
11
5
6
3
初始条件
点集合={u0}, TE={φ}。
5
18
4
普里姆(Prim)最小生成树算法
1
③
④
3
42
⑤
6
利用Prim演算法找最小生成树
以A点为起始点
L :A D B C E F T : h c d e a
计算机科学第5章 数据结构与算法

处理步骤2
符合条件
分支条件 不符合条件 符合条件 进入循环
循环条件 不符合条件 循环结束
„
分支1
分支2
循环体
处理步骤N
处理步骤N
处理步骤N
结束
(a)顺序结构
结束
(b)分支结构
结束
(c)循环结构
图 5-3 算法基本结构示意图
5.1 数据结构概述
5.1.2 算法
在大多数情况下,时间和空间因素可以进行相应转换,具体选择时可根
据实际需要和成本因素确定选择什么策略。 另外,需要提醒一点,不是时间复杂度高,算法的数学复杂程序就高。
使用更高级的数学方法,能够以更少的时间和空间代价获取处理结果。
这时,用于算法执行的时间虽然少了,但是用于算法设计的时间会大大 增加。如果设计出的程序有足够多的使用率,代价总体上是值得的。
5.1 数据结构概述
5.1.2 算法
用计算机解决一个复杂的实际问题,大体需要如下的步骤。 (1)将实际问题数学化,即把实际问题抽象为一个带有一般性的数学 问题。这一步要引入一些数学概念,精确地阐述数学问题,弄清问题的 已知条件、所要求的结果、以及在已知条件和所要求的结果之间存在着 的隐式或显式的联系。 (2)对于确定的数学问题,设计其求解的方法,即所谓的算法设计。 这一步要建立问题的求解模型,即确定问题的数据模型并在此模型上定 义一组运算,然后借助于对这组运算的调用和控制,从已知数据出发导 向所要求的结果,形成算法并用自然语言来表述。这种语言还不是程序 设计语言,不能被计算机所接受。 (3)用计算机上的一种程序设计语言来表达已设计好的算法。换句话 说,将非形式自然语言表达的算法转变为一种程序设计语言表达的算法。 这一步叫程序设计或程序编制。 (4)在计算机上编辑、调试和测试编制好的程序,直到输出所要求的 结果。
离散数学7-树

(b)
(a)
V5
2
1
V7
8
9
V2
V4
2
3
V8
5
V1
V1
V4
V5
1
3
V7
V6
8
V4
2
V8
5
6
V1
1
V5
6
V7
V6
8
3
V8
5
6
V7
9
V3
(e)
V3
(f)
(g)
22
V2
V3
(h)
五.应用举例——求最小生成树
例3 用管梅谷算法求下图的最小生成树。
23
五.应用举例——求最小生成树
例3 用管梅谷算法求下图的最小生成树。
成圈。
首先证明T无简单回路。对n作归纳证明。
(i) n=1时,m=n-1=0,显然无简单回路;
(ii)假设顶点数为n-1时无简单回路,现考察顶点数是n的情况:此时至少有一
个顶点v其次数d(v)=1。因为若n个顶点的次数都大于等于2,则不少于n条边,但这与
m=n-1矛盾。
删去v及其关联边得到新图T’,根据归纳假设T’无简单回路,再加回v及其关联
边又得到图T,则T也无简单回路。
再由图的连通性可知,加入任何一边后就会形成圈,且只有一个圈,否则原图
中会含圈。
9
二. 基本定理——证明
证明(4):(3)(4),即证一个无圈图若加入任一边就形成圈,
则该图连通,且其任何一边都是桥。
若图不连通,则存在两个顶点vi和vj,在vi和vj之间没有路,若
加边(vi,vj)不会产生简单回路,但这与假设矛盾。由于T无简单回
考研数据结构图的必背算法及知识点

考研数据结构图的必背算法及知识点Prepared on 22 November 20201.最小生成树:无向连通图的所有生成树中有一棵边的权值总和最小的生成树问题背景:假设要在n个城市之间建立通信联络网,则连通n个城市只需要n—1条线路。
这时,自然会考虑这样一个问题,如何在最节省经费的前提下建立这个通信网。
在每两个城市之间都可以设置一条线路,相应地都要付出一定的经济代价。
n个城市之间,最多可能设置n(n-1)/2条线路,那么,如何在这些可能的线路中选择n-1条,以使总的耗费最少呢分析问题(建立模型):可以用连通网来表示n个城市以及n个城市间可能设置的通信线路,其中网的顶点表示城市,边表示两城市之间的线路,赋于边的权值表示相应的代价。
对于n个顶点的连通网可以建立许多不同的生成树,每一棵生成树都可以是一个通信网。
即无向连通图的生成树不是唯一的。
连通图的一次遍历所经过的边的集合及图中所有顶点的集合就构成了该图的一棵生成树,对连通图的不同遍历,就可能得到不同的生成树。
图G5无向连通图的生成树为(a)、(b)和(c)图所示:G5G5的三棵生成树:可以证明,对于有n个顶点的无向连通图,无论其生成树的形态如何,所有生成树中都有且仅有n-1条边。
最小生成树的定义:如果无向连通图是一个网,那么,它的所有生成树中必有一棵边的权值总和最小的生成树,我们称这棵生成树为最小生成树,简称为最小生成树。
最小生成树的性质:假设N=(V,{E})是个连通网,U是顶点集合V的一个非空子集,若(u,v)是个一条具有最小权值(代价)的边,其中,则必存在一棵包含边(u,v)的最小生成树。
解决方案:两种常用的构造最小生成树的算法:普里姆(Prim)和克鲁斯卡尔(Kruskal)。
他们都利用了最小生成树的性质1.普里姆(Prim)算法:有线到点,适合边稠密。
时间复杂度O(N^2)假设G=(V,E)为连通图,其中V为网图中所有顶点的集合,E为网图中所有带权边的集合。
数据结构第5章课件 中国石油大学(华东)

二叉链表
leftChild
data rightChild
22
二叉树的链表表示(三叉链表)
每个结点增加一个指向双亲的指针parent,使 得查找双亲也很方便。
leftChild data parent rightChild
三叉链表
data
leftChild
27
BinTreeNode *LeftChild (BinTreeNode *current ) { return (current != NULL )? current->leftChild :NULL; } BinTreeNode *RightChild (BinTreeNode *current ) { return ( current!= NULL) ? current->rightChild : NULL; } int Height( ){return Height(root);} int Size( ){return Size(root);} BinTreeNode *GetRoot ( ) const { return root; } void preOrder( ) {preOrder(root);} //前序遍历 void inOrder( ) {inOrder(root);} //中序遍历 void postOrder( ) {postOrder(root);} //后序遍历 void levelOrder( ) ; // 不需要递归,所以直接对外接 口调用即可。层序遍历 28
b
f
c
d
g
6
e
a
b.嵌套集合表示法: b 根据树的集合定义,写出集合划分。 { a, {b,{e},{f}}, {c}, {d,{g}} } e c d
《数据结构与算法设计》第5章 树

5.2.2 二叉树的性质
➢ 满二叉树和完全二叉树
满二叉树是指深度为h且节点数取得最大值2h-1的二叉树。 如果一棵深度为h的二叉树,除第h层外,其他每层的节点数 都达到最大,且最后一层的节点自左而右连续分布,这样的二 叉树称为完全二叉树。
5.2.2 二叉树的性质
5.2.2 二叉树的性质
性质6 对含有n个节点的完全二叉树自上而下、同一层从左往右 对节点编号0,1,2,…,n-1,则节点之间存在以下关系: (1)若i=0,则节点i是根节点,无双亲;若i>0,则其双亲节 点的编号为i/2-1; (2)若2×i +1≤n,则i的左孩子编号为2×i+1; (3)若2×i+2≤n,则i的右孩子编号为2×i+2; (4)若i>1且为偶数,则节点i是其双亲的右孩子,且有编号为 i-1的左兄弟; (5)若i<n-1且为奇数,则节点i是其双亲的左孩子,且有编号 为i+1的右兄弟。
5.3.3 二叉树的二叉链表类模板定义
//根据二叉树的先序遍历序列和中序遍历序列创建以r为根的二叉树
void CreateBinaryTree(BTNode<DataType> * &r, DataType pre[], DataType
in[], int preStart, int preEnd, int inStart, int inEnd); int Height(BTNode<DataType> *r); //求以r为根的二叉树高度 //求以r为根的二叉树中叶子节点数目
5.1.2 树的术语
(9)节点的层次:从根节点开始,根为第一层,根的孩子为 第二层,根的孩子的孩子为第三层,依次类推,树中任一节 点所在的层次是其双亲节点所在的层次数加1。 (10)堂兄弟:双亲在同一层的节点互为堂兄弟。
云大《数据结构》课程教学课件-第6章 树和二叉树(147P)_OK

^d ^ ^ e ^ 三叉链表
3)二叉链表是二叉树最常用的存储结构。还有其它链接方 法,采用何种方法,主要取决于所要实施的各种运算频度。
例:若经常要在二叉树中寻找某结点的双亲时,可在每个结 点上再加一个指向其双亲的指针域parent,称为三叉链表。
lchild data parent rchild
2021/8/16
2021/8/16
9
6.2 二 叉 树
6.2.1 二叉树的概念
一、二叉树的定义: 二叉树(Binary Tree)是n(n>=0)个结点的有限集,它或者是 空集(n=0)或者由一个根结点和两棵互不相交的,分别称 为根的左子树和右子树的二叉树组成。 可以看出,二叉树的定义和树的定义一样,均为递归定 义。
A
集合3
集合1
BCD
EF
G
集合2
2021/8/16
3
2、树的表示方法 1)树形图法
A
BCD
EF
G
2)嵌套集合法
3)广义表形式 ( A(B, C(E,F), D(G) )
4)凹入表示法
2021/8/16
A B
D
CG
EF
A B C E DF G
4
3、 树结构的基本术语
1)结点的度(Degree):为该结点的子树的个数。 2)树的度:为该树中结点的最大度数。
7)路径(Path):若树中存在一个结点序列k1,k2,…,kj,使得ki是 ki+1的双亲(1<=i<j),则称该结点序列是从ki到kj一条路径 (Path)
路径长度:路径的长度为j-1,其为该路径所经过的边的数 目。
A
BCD
EF
G
决策树分类算法

决策树分类算法⼀、决策树原理决策树是⽤样本的属性作为结点,⽤属性的取值作为分⽀的树结构。
决策树的根结点是所有样本中信息量最⼤的属性。
树的中间结点是该结点为根的⼦树所包含的样本⼦集中信息量最⼤的属性。
决策树的叶结点是样本的类别值。
决策树是⼀种知识表⽰形式,它是对所有样本数据的⾼度概括决策树能准确地识别所有样本的类别,也能有效地识别新样本的类别。
决策树算法ID3的基本思想:⾸先找出最有判别⼒的属性,把样例分成多个⼦集,每个⼦集⼜选择最有判别⼒的属性进⾏划分,⼀直进⾏到所有⼦集仅包含同⼀类型的数据为⽌。
最后得到⼀棵决策树。
J.R.Quinlan的⼯作主要是引进了信息论中的信息增益,他将其称为信息增益(information gain),作为属性判别能⼒的度量,设计了构造决策树的递归算法。
举例⼦⽐较容易理解:对于⽓候分类问题,属性为:天⽓(A1) 取值为:晴,多云,⾬⽓温(A2) 取值为:冷,适中,热湿度(A3) 取值为:⾼,正常风 (A4) 取值为:有风,⽆风每个样例属于不同的类别,此例仅有两个类别,分别为P,N。
P类和N类的样例分别称为正例和反例。
将⼀些已知的正例和反例放在⼀起便得到训练集。
由ID3算法得出⼀棵正确分类训练集中每个样例的决策树,见下图。
决策树叶⼦为类别名,即P 或者N。
其它结点由样例的属性组成,每个属性的不同取值对应⼀分枝。
若要对⼀样例分类,从树根开始进⾏测试,按属性的取值分枝向下进⼊下层结点,对该结点进⾏测试,过程⼀直进⾏到叶结点,样例被判为属于该叶结点所标记的类别。
现⽤图来判⼀个具体例⼦,某天早晨⽓候描述为:天⽓:多云⽓温:冷湿度:正常风:⽆风它属于哪类⽓候呢?-------------从图中可判别该样例的类别为P类。
ID3就是要从表的训练集构造图这样的决策树。
实际上,能正确分类训练集的决策树不⽌⼀棵。
Quinlan的ID3算法能得出结点最少的决策树。
ID3算法:⒈对当前例⼦集合,计算各属性的信息增益;⒉选择信息增益最⼤的属性A k;⒊把在A k处取值相同的例⼦归于同⼀⼦集,A k取⼏个值就得⼏个⼦集;⒋对既含正例⼜含反例的⼦集,递归调⽤建树算法;⒌若⼦集仅含正例或反例,对应分枝标上P或N,返回调⽤处。
树及应用实验报告

树及应用实验报告实验目的研究树结构及其应用,了解树的基本概念和常见操作,掌握树在实际问题中的运用。
实验内容1. 树结构的定义和特点2. 常见树的实现方式3. 二叉树及其操作4. 树的遍历算法5. 树在排序和搜索中的应用6. 树在图算法中的应用实验步骤与结果1. 树结构的定义和特点树是一种非线性的数据结构,由节点和边组成。
一个节点可以有多个子节点,但每个节点只有一个父节点。
树具有以下特点:- 树中只有一个根节点,它没有父节点。
- 每个非根节点有且只有一个父节点。
- 除了根节点外,每个节点可以有零个或多个子节点。
- 节点之间通过边连接。
2. 常见树的实现方式树可以通过链表或数组两种方式进行实现。
链表实现的树称为链式树,数组实现的树称为顺序树。
链式树的节点是通过指针进行连接的,每个节点包含数据和指向子节点的指针。
链式树的优点是插入和删除节点方便,缺点是访问节点需要遍历链表。
顺序树将节点存储在一个数组中,通过计算索引值来访问对应位置的节点。
顺序树的优点是访问节点快速,缺点是插入和删除节点困难。
3. 二叉树及其操作二叉树是一种特殊的树结构,每个节点最多有两个子节点。
二叉树的操作包括插入节点、删除节点、查找节点等。
二叉树的插入节点操作如下:1. 如果树为空,则将新节点作为根节点。
2. 如果新节点的值小于当前节点的值,则将新节点插入到当前节点的左子树中。
3. 如果新节点的值大于当前节点的值,则将新节点插入到当前节点的右子树中。
二叉树的删除节点操作如下:1. 如果要删除的节点是叶子节点,则直接删除它。
2. 如果要删除的节点只有一个子节点,则将子节点替代要删除的节点。
3. 如果要删除的节点有两个子节点,则将它的后继节点替代要删除的节点。
4. 树的遍历算法树的遍历算法包括先序遍历、中序遍历和后序遍历。
先序遍历按照根节点、左子树、右子树的顺序遍历树。
中序遍历按照左子树、根节点、右子树的顺序遍历树。
后序遍历按照左子树、右子树、根节点的顺序遍历树。
树的详细介绍

(9)结点的层次(layer):从根开始,树的根结点的层次
(也称层数)定义为1,其余结点的层数等于它的双亲结点 的层数加1,如A结点的层数为1,K结点的层数为4。
(10)树的深度(depth):树中所有结点的最大层数
称为树的深度(也称高度),如树T的高度为4。
(11)有序树和无序树:树T中,如果各子树Ti之间是
有先后次序的,则称为有序树,否则称为无序树。
(12)森林:m (m>0)棵互不相交的树的集合。
一棵树删除根结点所剩子树的集合即为森林。
5.1.3树的基本操作
图5.2树的示例T
树的表示常见的有树状表示法和逻辑表示法 两种,图5.2给出了树状表示法的一个实例。树的 逻辑表示法则给出树中的结点的集合及这个集 合上的关系。如图5.2中的树可描述为T=(N,R)。
其中结点集合N={A,B,C,D,E,F,G,HJ,J,K,L}
N上的关系 R={<A,B>,<A,C>,<A,D>,<B,E>,<B ,F>,<C,G>,
叉树,则返回空值Null。 • (5)Parent(BT,X):返回结点x的双亲结点。当结点x为
根时,返回空值Null。 • (6)LeftChild(BT,x):返回结点x的左孩子.当结点x为
叶子结点或无左孩子时,返回空值Null。 • (7)RightChild(BT,x):返回结点x的右孩子。当结点x
为叶子结点或无右孩子时,返回空值Null。 • (8)TraverseTree(BT):遍历二叉树BT。按某种次序
详解图的应用(最小生成树、拓扑排序、关键路径、最短路径)
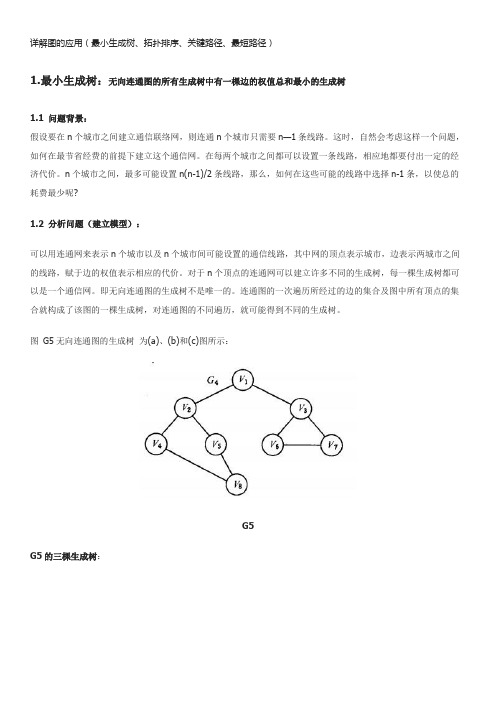
详解图的应用(最小生成树、拓扑排序、关键路径、最短路径)1.最小生成树:无向连通图的所有生成树中有一棵边的权值总和最小的生成树1.1 问题背景:假设要在n个城市之间建立通信联络网,则连通n个城市只需要n—1条线路。
这时,自然会考虑这样一个问题,如何在最节省经费的前提下建立这个通信网。
在每两个城市之间都可以设置一条线路,相应地都要付出一定的经济代价。
n个城市之间,最多可能设置n(n-1)/2条线路,那么,如何在这些可能的线路中选择n-1条,以使总的耗费最少呢?1.2 分析问题(建立模型):可以用连通网来表示n个城市以及n个城市间可能设置的通信线路,其中网的顶点表示城市,边表示两城市之间的线路,赋于边的权值表示相应的代价。
对于n个顶点的连通网可以建立许多不同的生成树,每一棵生成树都可以是一个通信网。
即无向连通图的生成树不是唯一的。
连通图的一次遍历所经过的边的集合及图中所有顶点的集合就构成了该图的一棵生成树,对连通图的不同遍历,就可能得到不同的生成树。
图G5无向连通图的生成树为(a)、(b)和(c)图所示:G5G5的三棵生成树:可以证明,对于有n 个顶点的无向连通图,无论其生成树的形态如何,所有生成树中都有且仅有n-1 条边。
1.3最小生成树的定义:如果无向连通图是一个网,那么,它的所有生成树中必有一棵边的权值总和最小的生成树,我们称这棵生成树为最小生成树,简称为最小生成树。
最小生成树的性质:假设N=(V,{ E}) 是个连通网,U是顶点集合V的一个非空子集,若(u,v)是个一条具有最小权值(代价)的边,其中,则必存在一棵包含边(u,v)的最小生成树。
1.4 解决方案:两种常用的构造最小生成树的算法:普里姆(Prim)和克鲁斯卡尔(Kruskal)。
他们都利用了最小生成树的性质1.普里姆(Prim)算法:有线到点,适合边稠密。
时间复杂度O(N^2)假设G=(V,E)为连通图,其中V 为网图中所有顶点的集合,E 为网图中所有带权边的集合。
《离散数学课件》5树

W(T)等于所有分支点的权之和
36
实例
例 求带权为1, 1, 2, 3, 4, 5的最优树. 解题过程由下图给出,W(T)=38
7,4,5 4,3,4,5 2,2,3,4,5 7,9
37
小结
树与有序树
( m=n1)
无向树及生成树
基本回路与基本回路系统 基本割集与基本割集系统 最小生成树
根树及其应用
23/60
例 求最小生成树
5 1 5 3 6 6 5 1 5 3 6 4 6 6 5 2 3 5 6 4 5 5 1 5 2 5 5 2 5
4
24/60
普里姆(Prim)算法
设置一个集合T,开始图上任选一点u0加入T,图顶点数 为n。重复以下工作n-1次:
• 在满足uT,vT的所有边中选边权w最小的 • 将v加入集合T中 • 输出边u ,v及边上的权 w
6
无向树的性质(续)
定理2 设T 是 n 阶非平凡的无向树,则T中至少 有两片树叶. 证 设T有x片树叶,由握手定理及定理1可知,
2(n 1) d (vi ) x 2(n x)
由上式解出x2.
7
例1 已知一棵树有5个4度顶点,3个3度顶点, 3个2度顶点,问有几个一度顶点?
(a)
(b) 只讨论(b)这样的所谓的“根 树”——有一个根的树。
28/53
根树
设T=(V,E)是一棵有向树,若仅有一个顶点的入度为0, 其余的顶点的入度均为1,这样一棵有向树我们称为 根树。 入度为0的顶点称为树根, 出度为0的顶点称为树叶, 出度不为0的顶点称为分枝点。 例
c d e a b d
有序树: 将根树同层上的顶点规定次序 r元树:根树的每个分支点至多有r个儿子 r元正则树: 根树的每个分支点恰有r个儿子 r元有序树: 有序的r元树 r元正则有序树: 有序的r元正则树
运筹学_树

D A Huffman算法 算法_B 算法
叶子上带权的二叉树, 个叶子的权分别为p 叶子上带权的二叉树 s 个叶子的权分别为 i 根到各叶子 的距离(层次 层次) 二叉树的总权数: 的距离 层次 为l i (i=1,…,s) , 二叉树的总权数: s m (T) = ∑ p i l i i=1 算法) 算法 (D A Huffman算法 算法 例8 s=6, 其权分别为 1.s个叶子按权由小至大排序 个叶子按权由小至大排序 4,3,3,2,2,1, 求最优二 叉树。 叉树。 15 2.最小权的二个叶子合并成 2.最小权的二个叶子合并成 一个分支点, 一个分支点,其权为二者之和 将新分支点作为一个叶子。 将新分支点作为一个叶子。 9 则停; 令s←s-1,若s=1则停;否则转 若 则停 否则转(1). 5 5 6 3 6 3 1 2 2 3 3 4 4 1 2 2 3 3
T
找生成树的两种方法-深探法 深探法 (1) 深探法 在点集V中任取一点 中任取一点v, ① 在点集 中任取一点 给 v 以标号 0 . 在某点u集已得标号 检查一端点为u的各边 集已得标号i 的各边, ②在某点 集已得标号 , 检查一端点为 的各边 另一 端点是否均已标号。 端点是否均已标号。 若有(u, w)边之w未标号, 则给w以标号i+1, 记下边(u, w), 记下边(u, w). 令w代u, 重复②. ② 若这样的边的另一端均已有标号, 就退到标号为i-1的r 0 点, 以r 代u ,重复②. ② 1 直到全部点得到标号为止。 2 3 1 2 8 7 6 4 10 11 7 5 0 3 8 10 13 12 6 9 11 9 12 4 5 13
找生成树的两种方法-广探法 广探法
(2) 广探法 在点集V中任取一点 中任取一点v, ① 在点集 中任取一点 给 v 以标号 0 . 令所有标号为i的点集为 检查[V, V\Vi]中的边端 的点集为V, ②令所有标号为 的点集为 检查 中的边端 点是否均已标号 对所有未标号之点均标以i+1 , 记 标号。 点是否均已标号。对所有未标号之点均标以 下这些边。 下这些边。 对标号i+1的点重复步骤②, 直到全部点得到标号为至 ② 直到全部点得到标号为至. 0 1 1 2 1 1 2 0 2 1 2 4 3 2 1 2
树,二叉树,森林

二叉树
二叉树性质(续) ② 高度为k的二叉树最多有2k-1个结点(k≥1) 证明:
高度为k的二叉树只有在每一层都达到最大结点数时,整个二叉树的结点数 才能达到最大。即当每层的结点数目都达到该层的最大结点数2i-1时(性质 2),对应的二叉树的结点数目取得最大值(等比数列求和) a1(1-qn)/(1-q)
因此如果把完全二叉树的各个结点按编号顺序依次存放到一个一维数组, 对于完全二叉树中任意结点i的双亲结点序号、左孩子结点序号和右孩子 结点序号都可由公式计算得到,具体做法是将n个结点存放到一维数组 a[n+1]中。这便是完全二叉树的顺序存储。
二叉树
带有结点编号的完全二叉树
二叉树
对于非完全二叉树是构造虚结点完成顺序存储
树的基本概念
A B E K L F C G H M D I J
back
树的基本概念
3、树的表示方法 (4种)
树形表示 文氏图表示 凹入表示
嵌套括号表示
A(B,C(D,E))
二叉树
二叉树是树型结构的一个重要类型,许多实际问题抽象 出来的数据结构都是二叉树的形式,此外一般的树也可以 简单的转换为二叉树,因此二叉树是特别重要的一种树结 构。 1、二叉树的定义: 二叉树(Binary Tree)是n(n≥0)个有限结点构成、 每个结点最多有两个孩子且有左右区分的有序树合。 n=0的树称为空二叉树;n>0的二叉树由一个根结点 和两个互不相交的、分别称作左子树和右子树的子二叉树 构成。
树、森林和二叉树的关系
树、森林和二叉树的关系
孩子兄弟表示法(二叉链表表示法): 链表中每个结点设有两个链域,分别指向该结点的第一个孩 子结点和下一个兄弟(右兄弟)结点。
树、森林和二叉树的关系
《认识决策树算法》 说课稿

《认识决策树算法》说课稿尊敬的各位评委、老师:大家好!今天我说课的题目是《认识决策树算法》。
下面我将从教材分析、学情分析、教学目标、教学重难点、教法与学法、教学过程以及教学反思这几个方面来展开我的说课。
一、教材分析本节课选自_____出版社出版的《_____》教材中的第_____章第_____节。
决策树算法是数据挖掘和机器学习领域中一种重要且基础的分类和预测算法。
通过学习决策树算法,学生能够掌握一种有效的数据分析和处理方法,为后续学习更复杂的算法打下坚实的基础。
在教材中,这部分内容首先介绍了决策树的基本概念和原理,然后通过具体的案例展示了如何构建决策树以及如何利用决策树进行分类和预测。
教材内容安排合理,逻辑清晰,注重理论与实践的结合。
二、学情分析本次授课的对象是_____专业的学生,他们已经具备了一定的数学基础和编程能力,对于数据分析和算法有一定的兴趣和好奇心。
然而,由于决策树算法涉及到较多的数学概念和逻辑推理,学生在理解和应用上可能会存在一定的困难。
因此,在教学过程中,需要注重引导学生思考,通过实例帮助学生理解抽象的概念,激发学生的学习积极性。
三、教学目标1、知识与技能目标(1)学生能够理解决策树算法的基本概念和原理,包括信息熵、信息增益等。
(2)学生能够掌握决策树的构建过程,能够使用 Python 等编程语言实现决策树算法。
(3)学生能够运用决策树算法解决实际的分类和预测问题。
2、过程与方法目标(1)通过案例分析和实践操作,培养学生的问题解决能力和动手实践能力。
(2)引导学生进行小组讨论和合作学习,培养学生的团队协作能力和沟通交流能力。
3、情感态度与价值观目标(1)激发学生对数据分析和算法的兴趣,培养学生的创新意识和探索精神。
(2)让学生体会到算法在实际生活中的应用价值,培养学生的应用意识和解决实际问题的能力。
四、教学重难点1、教学重点(1)决策树算法的基本原理和构建过程。
(2)信息熵和信息增益的计算方法。
佛洛伊德算法

佛洛伊德算法摘要:1.引言2.佛洛伊德算法的概念和原理3.佛洛伊德算法的应用领域4.佛洛伊德算法的优缺点5.结论正文:1.引言佛洛伊德算法,是一种经典的图论算法,由奥地利心理学家、精神分析学创始人西格蒙德·佛洛伊德于20 世纪初提出。
该算法主要应用于寻找无向图的最大环、最小生成树、最短路径等问题。
本文将从佛洛伊德算法的概念和原理、应用领域、优缺点等方面进行介绍。
2.佛洛伊德算法的概念和原理佛洛伊德算法是一种基于图的搜索算法,其基本思想是以图的顶点为起点,沿着边的方向进行搜索,不断更新路径,直到找到目标顶点或者无法继续搜索为止。
在搜索过程中,佛洛伊德算法记录下所有可能的路径,以及这些路径的长度。
通过比较这些路径的长度,可以找到最短路径。
3.佛洛伊德算法的应用领域佛洛伊德算法广泛应用于图论的各种问题中,如寻找无向图的最大环、最小生成树、最短路径等。
其中,最短路径问题是佛洛伊德算法应用最为广泛的领域之一。
在实际应用中,佛洛伊德算法可以帮助我们快速找到网络中最短路径,从而提高网络传输效率、降低运输成本等。
4.佛洛伊德算法的优缺点佛洛伊德算法的优点在于其简单易懂、实现简单,且具有一定的效率。
特别是在规模较小的问题中,佛洛伊德算法的性能表现较好。
然而,佛洛伊德算法也存在一些缺点,如算法的复杂度较高,随着图规模的增大,计算时间将显著增加,可能导致算法无法在合理的时间内完成计算。
5.结论总的来说,佛洛伊德算法是一种具有广泛应用价值的图论算法。
尽管存在一些缺点,但在解决一些规模较小的图问题时,佛洛伊德算法仍然具有较高的效率和实用性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定理.1(证明(3)(4))
Ⅱ、增加任何新边,得到一个且仅有一个回路
若在连通图T中加入新的边(ui,uj),则该边与T中ui到 uj的一条路构成一个回路,则该回路必是唯一的。 否则(即回路不唯一),若删去此新边,T中必有回 路,得出矛盾。
综述,T连通且e=v-1则T无回路但增加任何新边,得 到一个且仅有一个回路。
第 7页
定理.1(证明(2)(3))
(2) T无回路 且e=v-1 (3) T连通且e=v-1 证明(2)(3): 证明T连通: (反证法) 假设T有s个连通分支, 则每个连通分支都是连通无 回路即树, 所以 e=e1+e2+…+ es=(v1-1)+(v2-1)+…+(vs-1) =v1+v2+…+vs-s=v-s=v-1, 所以s=1,与s>1矛盾, 所以T连通。
第 6页
定理.1(证明(1)(2))
(1) 无回路的连通图 (2) T无回路且e=v-1 证明(1)(2): e=v-1(归纳法):
v=1时,e=0(平凡树)。 设vk-1时成立,即ek-1=vk-1-1。 当v=k时, 要证ek=vk-1。 因为无回路且连通,故至少有一边其一个端点u的度数为 1,设该边为(u,u*)。删除结点u,得到一个k-1个结点的 连通图T’,T’的边数e’=v’-1=(k-1)-1=k-2,于是将结点u 与边(u,v)加入图T’得到原图T,此时T的边数为e=e’+1=k2+1=k-1, 结点数v=v’+1=(k-1)+1=k,故e=v-1。 综上所述, T无回路且e=v-1。
第12页
定理.1(证明(5)(6))
(5) T连通但删去任一边后便不连通 (6) T中每一对结点之间有且仅有一条路 证明(5)(6): (反证法)
假设T中存在有一对结点之间有两条路。
由连通性知,两个结点有多于一条的路,则T 中必有回路,删去任一边,图仍连通,与(5) 矛盾, 所以T中每一对结点之间有且仅有一条路。
第18页
例题
例2: 已知无向树T有5片树叶, 2度与3度结点各1个, 其余结点的度数均为4。求T的阶数v, 并画出满足 要求的所有非同构的无向树。 解 设T的阶数为v, 则边数e为v1, 4度结点的个数为 v7. 由握手定理得 2e=2(v1)=51+21+31+4(v7) 解出v=8, 4度结点为1个。 T的度数列为1,1,1,1,1,2,3,4 有3棵非同构的无向树
第14页
关于树的不等式的证明
关于树的证明的三个式子 e=v-1 deg(vi)=2e 根据具体的题设条件,进行特殊不等式的改 写(解题关键)
第15页
非平凡树至少有2个树叶
定理.2: 非平凡树至少有2个树叶。 证明方法一:(直接证明) 设T有x个树叶, 由定理.1和握手定理, e=v-1 deg(vi)=2e= 2(v-1) = 2v-2 = vi是树叶deg(vi) + vi是分枝点deg(vi) ≥ x + 2(v-x) = 2v-x, 即2v-2 ≥ 2v-x 所以 x ≥ 2。
第27页
带权图
给定图G=<V,E>(G为无向图或有向图),设W: E→R(R为实数集),对G中任意的边e=(vi,vj) (G为有向图时,e=<vi,vj>)设W(e)=wij,称实 数wij为边e上的权,并将wij标注在边e上,称G为 带权图,此时常将带权图G记作<V,E,W>。 W(G)= ∑W(e)。
第 4页
引理1
设G是至少有一条边的连通图且无回路,则G至少有一 个结点只相邻于另一个结点,即G至少有一个结点的度 数为1。 证明:
因为G至少有一条边,所以,G有一点v1,且v1有相邻 点v2。若v2即为所求,则引理得证。 否则,令v3为v2的不同于v1相邻点,以此类推,即, 对k≥2,或者vk只与vk-1相邻,从而vk即为所求;或者 vk又相邻于vk+1vk-1。于是得v1,v2,…,vk-1,vk, vk+1,…,因为G无回路,故这一串点不能有重复。 上述过程必在有限步内停止。从而引理得证。
e1=v1-1 e2=v2-1 es=vs-1
第 8页
引理1
设G是至少有一条边的连通图且无回路,则G至少有一 个结点只相邻于另一个结点,即G至少有一个结点的 度数为1。 证明:
证明方法二(反证法) 假设对于任意结点u,有deg(u)≥2, 则2e= deg(v)≥2v,所以e≥v,与e=v-1矛盾。 所以,必有一结点的度数为1。
第13页
定理.1(证明(6)(1))
(6) T中每一对结点之间有且仅有一条路 (1) 无回路的连通图 证明:(6)(1): 连通性: u,vV, u,v之间有唯一一条路,则T必连通; 无回路: (反证法)若有回路,则u,v之间的路不唯一, 矛 盾! 所以T无回路。 因此,T是无回路的连通图(即 T是树)。
第21页
注意
余树不一定连通,也不一定不含回路。
第22页
定理.3:连通图G至少有一棵生成树 证明:构造法,不断删除边(破圈法)。 (1)连通图G无回路,则G本身为生成树。 (2)若G至少有一回路,则删去回路上的一边,得 到G1,G1连通并与G有相同的结点集,则若G1无 回路,G1就是生成树。 (3)若G1有回路,再删去回路上的一边,重复上述 步骤,直到得到一连通图T,它没有回路,但与G 有相同结点集,所以T是G的生成树。
第28页
最小生成树(MST)
定义.3 最小生成树(minimal spanning tree): 无 向连通带权图G=<V,E,W>的权最小的生成树 W(T) = eTW(e)
1 2 3 2 1.5 5 6 1 2 3 2 1.5 5 6
3
3
W(T1)=11.5
W(T2)=18
第29页
A Kruskal算法(或避圈法)
第11页
定理.1(证明(4)(5))
(4) T无回路但增加任何新边,得到一个且仅有一 个回路 (5) T连通但删去任一边后便不连通 证明:(4)(5): T连通: (反证法)若T不连通,则存在结点u,vV,在u与 v之间无路,显然增加边(u,v)不会产生回路, 与(4)矛盾,故T连通。 删去任一边后便不连通: 又因为T无回路,所以删去任一边,图 T不连通。 因此,T连通但删去任一边后))
(3) T连通且e=v-1 (4) T无回路但增加任何新边,得到一个且仅有一个回路 证明:(3)(4):(用数学归纳法证明)
① 当v=2时,e=1,即T必无回路,但增加任何新边,得到一 个且仅有一个回路 。 ② 设v=k-1时命题成立。 ③考察v=k时的情况 Ⅰ、T无回路 因为T是连通的,且e=v-1,所以每个结点u有deg(u)≥1, 假设结点u0的度数为1。删去u0及其关联的边,而得到 一个新图T’,由归纳假设知,T’无回路,在T’中加入 u0及关联边又得到T,故T是无回路的。
第23页
连通图的生成树例
例.1:破圈法构造生成树
第24页
定理推论(3个)
推论1: G是v个结点e条边无向连通图 ev-1。 证明:由定理可知,G有生成树,设T为G的一 棵生成树,则e=|E(G)|≥|E(T)|=v-1. 推论2: T是v个结点e条边无向连通图G的生成树 , 则T的余树中含有e-v+1条边。
第 5页
树的等价定义(树的性质)
定理.1: 设T=<V,E>是v个结点e条边无向图,则以 下关于树的定义是等价的,即 (1) 无回路的连通图 (2) T无回路且e=v-1 (3) T连通且e=v-1 (4) T无回路但增加任何新边,得到一个且仅有一 个回路 (5) T连通但删去任一边后便不连通 (6) T中每一对结点之间有且仅有一条路 证明: (1)(2)(3)(4)(5)(6)(1)
第20页
2.生成树(spanning tree)
定义.2 生成树: 若图G的生成子图T是树,则该树称 为图G的生成树。 树枝(tree edge): 属于生成树T的边,共有v-1条。 弦(chord): 图G的不在生成树中的边。 生成树的补: 所有弦组成的集合。 余树: G[E(G)-E(T)]
第17页
例题
例1:已知无向树T中, 有1个3度结点, 2个2度结点, 其 余结点全是树叶。试求树叶数 , 并画出满足要求的 非同构的无向树。 解 用树的性质e=v1和握手定理. 设有x片树叶,于是 v=1+2+x=3+x, 2e=2(v1)=2(2+x)=13+22+x 解出x=3,故T有3片树叶. T的度数列为1, 1, 1, 2, 2, 3 有2棵非同构的无向树, 如图所示。
第25页
定理推论
推论3:简单图是连通的当且仅当它具有生成树。
证明: 必要性:简单图是连通的则它具有生成树。 显然,因为连通图G至少有一棵生成树。 充分性:简单图具有生成树则它是连通的。 设生成树为T,T包含简单图G的所有结点, 因为树为连通的,所以T中任意两个结点有 路。因为T是G的子图,所以G中任意两个 结点都有T中的路,即G连通。
第30页
例 用Kruskal算法求下图的最小树. 在左图中 {e1, e2 ,..., e8}权值 最小的边有 e1, e5 , 任取一条e1, 在 {e2 , e3 ,..., e8} 中选取权值 最小的边 e5 , {e2 , e3 , e4 , e6 , e7 , e8} : 中权值最小边有 e3 , e7, 从中选 任取一条边 e3 ; {e2 , e4 , e6 , e7 , e8} 中选取在中选取 e7 , 在{e2 , e4 , e6 , e8}中选取 e4 , e8 . 但 e4与 e8都 会与已选边构成圈,故停止。
