领先世界的科学技术同步测控优化训练
第17课《先进的科学技术》同步测试7(北师大版历史七上)

第17课先进的科学技术同步测控优化训练自主学习1.造纸术发明以前。
人们通常用或做书写材料。
2.时期,改进了造纸术,后来人们将他改进的纸称为“”。
3.张仲景是时期杰出的医学家,著有《》一书,后世尊称他为“”。
4.华佗擅长和,华佗被人们誉为“”。
5.《》成书于时期,它总结了到的数学成就。
6.下列几位科学家中,对人类文化传播贡献最大的是( )A.张衡B.蔡伦C.张仲景D.华佗基础巩固7.在造纸术发明以前,我国的书写材料主要是( )①羊皮②竹木简③树皮①帛A.①②B.②④C.①④D.②③8.蔡伦改进造纸术的主要突破点是( )A.由笨重改进为携带方便B.简化制作过程C.使造纸原料容易得到而又便宜D.纸张由粗糙改进为精细9.甘肃天水的一座汉墓里出土了一张又薄又软的纸,纸面平整光滑,上面有墨绘的山、川、路等。
据考证,这是西汉早期用麻做的纸,也是目前世界上已知最早的纸。
这充分表明( )①我国人民对世界文化的巨大贡献②经济、实惠、轻便是我国古代造纸所追求的目标③造纸的目的是为了描绘祖国的大好河山④考古发现的纸是宦官蔡伦制造的A.①②B.①②④C.③④D.②③④10.下列表述准确无误的是( )A.西汉宦官蔡伦改进了造纸术B.东汉宦官蔡伦改进了造纸术C.西汉宦官蔡伦发明了造纸术D.东汉宦官蔡伦发明了造纸术11.墨子周游列国时带了三大车竹简,出行不便。
导致这一现象发生根本变化的发明是( )A.丝织技术B.活字印刷术C.雕版印刷术D.造纸术12.东汉末年最著名的两位医学家是( )A.扁鹊与张仲景B.扁鹊与华佗C.张仲景与华佗D.李时珍与华佗13.《伤寒杂病论》的作者被后世尊称为( )A.药王B.医祖C.“医圣”D.炼丹家14.河南省南阳市有一著名景点…“医圣祠”,纪念的是我国古代一位杰出的医学家。
这位医学家是( ) A.张仲景B.华佗C.蔡伦D.孙思邈15.张仲景被称为“医圣”是因为他( )A.采用四诊法B.制成了全身麻醉药C.写出了第一本完整的药物学著作D.奠定了中医治疗学的基础16.下列对华佗的介绍。
新人教数学 8年级上:同步测控优化训练(10.2立方根)

立方根5分钟训练(预习类训练 ,可用于课前)1.以下说法不正确的选项是( )A. -1的立方根是 -1B. -1的平方是1C. -1的平方根是 -1D.1的平方根是±1解析:求某些数的平方根或立方根,常利用其定义来解.答案:C2.以下说法中正确的有( )①±2都是8的立方根 ②x x =33 ③81的立方根是3 ④38-- =2A.1个B.2个C.3个D.4个解析:根据立方根的意义判断.因为8的立方根是2,81的立方根是39,所以说法①③错误,说法②④正确.答案:B3.(1)23 =8,所以_____________是_____________的立方根.(2) ( -5)3 = -125,所以_____________是_____________的立方根.(3) ( )3 = -27,所以 -27的立方根是_____________.(4) ( )3 =4,所以4的立方根是_____________.解析:根据立方根的意义答复.答案: (1)2 8 (2) -5 -125 (3) -3 -3 (4)3434 4.求以下各数的立方根:(1) -27; (2 )1258; (3 ); (4 ) -5. 分析:根据立方根意义可求解.解: (1 )因为 ( -3 )3 = -27,所以 -27的立方根是 -3,即327- = -3;(2 )因为1258)52(3=,所以1258的立方根是52; (3 )因为3 =0.216,所以的立方根是0.6,即3216.0 =0.6;(4 ) -5的立方根是35-.10分钟训练(强化类训练 ,可用于课中)1.立方根等于本身的数是( )A. -1B.0C.±1D.±1或0解析:在实数范围内,一个数的立方根只有一个,并且它们同号.[来源:学科网ZXXK] 答案:D2.以下说法错误的个数是( )①负数没有立方根 ②1的立方根与平方根都是1 ③38的平方根是±2 ④361的立方根是61A.1B.2C.3D.4解析:根据立方根与平方根的意义可知,负数有立方根,1的平方根是±1,38的平方根是±2,361的立方根是3361,所以说法①③④不正确,说法③正确. 答案:C 3.33)6(- =____________,3027.0- = ____________.解析:根据33a =a, 33a a -=-答复.答案:4.估算以下数的大小.(1 )3261 (误差小于1 ); (2 )5.25(误差小于0.1).解析:估算一个根号表示的无理数一般是采用夹逼方法.解: (1 )因为6<3261<7,所以3261≈6或7.(2 )因为5.0<5.25<5.1,所以5.25或5.0.5.用计算器求:(1 )的平方根 (精确到 );(2 )36 -35228 (结果保存四个有效数字 );(3 )39578.0 (精确到 );[来源:学,科,网Z,X,X,K](4 )315786- (精确到 ).解析:用计算器可求得.如果求一个负数的立方根,可以先求它的相反数的立方根,再在结果前加上负号即可.[来源:学科网ZXXK]解:(1)±18.23 =±4.815.[来源:学科网ZXXK](2)3635228-≈541.3. (3)39578.0≈0.986. (4)315786-≈ -25.086.6.某化工厂使用一种球形储气罐储藏气体.现在要造一个新的球形储气罐,如果它的体积是原来的8倍,那么它的半径是原储气罐半径的多少倍?提示:利用球体的体积公式得出变化前后半径的关系式,化简后开立方.解:设原来的球形储气罐的半径为r 1,后来的储气罐的半径为r 2,由球体积公式V =334r π得8×32313434r r ππ=, 所以8r 13 =r 23.[来源:Z +xx +] 所以r 2 =3318r .所以r 2 =2r 1,答:新储气罐的半径是旧储气罐半径的2倍.30分钟训练(稳固类训练 ,可用于课后)1.(甘肃兰州模拟,1)函数y =42113-+-x x 的自变量x 的取值范围是( ) A.x≥1且x≠2 B.x≠2C.x >1且x≠2解析:开立方时被开方数可取任意实数,分母不能为零,所以x≠2.答案:B是 (9- )2的平方根,y 是64的立方根,那么x +y 的值为( )A.3B.7C.3,7D.1,7解析:因为(9-)2 =9,x 是 (9- )2的平方根,所以x =±3.因为y 是64的立方根,所以y =4.当x =3时,x +y =7.当x = -3时,x +y = -3 +4 =1.答案:D3.(1)比拟大小:325_____________25.(2)利用计算器,比拟大小:138____________216-. 解析:(1)因为25 =5,而53 =125>25,所以325<5,即325<25;(2)求出近似值再作比拟.答案:(1)< (2)<4.求以下各式的值: (1)38-;(2)3064.0;(3)31258-;(4)33)9(. 分析:根据立方根性质可求解.解: (1 )333)2(8-=- = -2; (2)333)4.0(064.0= =0.4; (3)52)52(1258333-=--;(4)(39)3 =9.5.求以下各式中的x.(1)8x 3 +125 =0;(2)(x +5)3 = -27.解析:此题实质上是解关于x 的三次方程,两边开立方是解此类题的最|根本方法.第 (1 )小题变形可得x 3 =8125-,所以x 是8125-的立方根;第 (2 )小题中,x +5是 -27的立方根,两边开立方求出x +5后再求x. 解: (1 )∵8x 3 +125 =0,∴x 3 =8125-. ∴x =38125-,即x =25-. (2 )∵(x +5)3 = -27,∴x +5 =327-,即x +5 = -3.∴x = -8.[来源:Z .xx ]6.求满足31-x +1 =x 的x 的值.分析:移项后得31-x =x -1,从而由 "0,1, -1的立方根等于它本身〞可求得x 的值. 解:因为31-x =x -1,[来源:学#科#网Z#X#X#K]所以x -1 = -1或x -1 =0或x -1 =1.所以x =0或x =1或x =2.7.一个正方体木块的体积是125 cm 3,现将它锯成8块同样大小的正方体小木块,求每个小正方体木块的外表积.提示:先根据正方体体积求得正方体木块的边长,再求外表积.解析:设小正方体木块的边长为a,那么a 3 =8125,a =25cm, 所以外表积 =6a 2 =6×(25)2 =275 cm 2.[来源:学|科|网Z|X|X|K] 8.实数x 、y 满足32--y x +(2x -3y -5)2 =0,求x -8y 的平方根和立方根.提示:利用 "如果几个非负数的和等于0,那么这几个非负数都为0”.解析:由题意可知32--y x =0且(2x -3y -5)2 =0,即⎩⎨⎧=--=--,0532,032y x y x 解这个方程组得⎩⎨⎧-==,1,1y x ∴9)1(818±=-⨯-±=-±y x =±3. ∴3398=-y x .9.一个正方体的棱长是5 cm,再做一个正方体,使它的体积是原正方体的体积的2倍,求所做的正方体的棱长(精确到0.1 cm ).解析:正方体的棱长等于体积的立方根.设所做的正方体的棱长为a (a>0 ),那么a3 =2×53,所以a =5×32≈6.3(cm).答:所做的正方体的棱长为6.3 cm.10.任意找一个小于1的正数,利用计算器对它不断进行开立方的运算,其结果如何?根据这个规律,比拟3a和a(0<a<1)的大小.[来源:学#科#网Z#X#X#K]提示:这是一道蕴含极限思想的数学问题,主要是利用计算器去探索规律,并要记住这一规律. 解析:任意找一个小于1的正数,利用计算器对它不断进行开立方的运算,其结果是随着开方次数的增加,运算结果越来越接近于1.[来源:Z,xx,]当0<a<1时,3a>a.。
06-07年同步测控优化训练七年级下数学人教版第5章 本章测评(附答案)
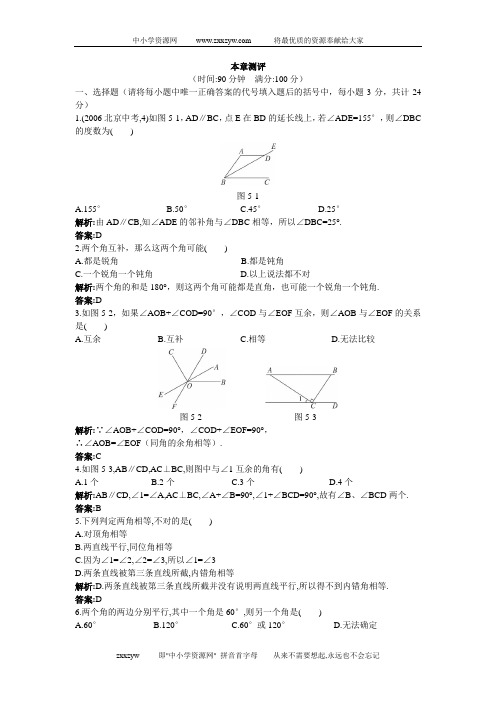
本章测评(时间:90分钟满分:100分)一、选择题(请将每小题中唯一正确答案的代号填入题后的括号中,每小题3分,共计24分)1.(2006北京中考,4)如图5-1,AD∥BC,点E在BD的延长线上,若∠ADE=155°,则∠DBC 的度数为( )图5-1A.155°B.50°C.45°D.25°解析:由AD∥CB,知∠ADE的邻补角与∠DBC相等,所以∠DBC=25°.答案:D2.两个角互补,那么这两个角可能( )A.都是锐角B.都是钝角C.一个锐角一个钝角D.以上说法都不对解析:两个角的和是180°,则这两个角可能都是直角,也可能一个锐角一个钝角.答案:D3.如图5-2,如果∠AOB+∠COD=90°,∠COD与∠EOF互余,则∠AOB与∠EOF的关系是( )A.互余B.互补C.相等D.无法比较图5-2 图5-3解析:∵∠AOB+∠COD=90°,∠COD+∠EOF=90°,∴∠AOB=∠EOF(同角的余角相等).答案:C4.如图5-3,AB∥CD,AC⊥BC,则图中与∠1互余的角有( )A.1个B.2个C.3个D.4个解析:AB∥CD,∠1=∠A,AC⊥BC,∠A+∠B=90°,∠1+∠BCD=90°,故有∠B、∠BCD两个.答案:B5.下列判定两角相等,不对的是( )A.对顶角相等B.两直线平行,同位角相等C.因为∠1=∠2,∠2=∠3,所以∠1=∠3D.两条直线被第三条直线所截,内错角相等解析:D.两条直线被第三条直线所截并没有说明两直线平行,所以得不到内错角相等.答案:D6.两个角的两边分别平行,其中一个角是60°,则另一个角是( )A.60°B.120°C.60°或120°D.无法确定解析:要分两种情况考虑:(1)两角方向相同,此时两角相等;(2)两角方向相反时,两角 互补.答案:C7.如图5-4,∠1=∠B,∠2=∠C,则下列结论不成立的是( )A.AD∥BCB.∠B=∠CC.∠2+∠B=180°D.AB∥CD图5-4 图5-5解析:∠1=∠B,可得AD∥BC.又∠2=∠C,∠B+∠2=180°,所以∠C+∠B=180°.所以AB∥CD.故∠B=∠C是错误的.答案:B8.(2006广东广州中考,2)如图5-5,AB∥CD,若∠2=135°,则∠1的度数是( )A.30°B.45°C.60°D.75°解析:由AB∥CD,知∠1的对顶角与∠2互补,所以∠1=45°.答案:B二、填空题(每小题3分,共计21分)9.∠A的补角比∠A的余角大____________.解析:由题意得(180°-∠A)-(90°-∠A)=180°-∠A-90°+∠A=90°.答案:90°10.如图5-6,AB∥CD,∠1=43°,∠2=47°,则∠B=___________,∠BCE=___________.图5-6 图5-7 图5-8解析:AB∥CD,∠B=∠2=47°,∠DCE=∠1=43°,∠BCE=∠2+∠DCE=90°.答案:47°90°11.如图5-7,有一个与地面成30°角的斜坡,现要在斜坡上竖一电线杆,当电线杆与斜坡成的∠1=___________时,电线杆与地面垂直.解析:可以作辅助线与电线杆平行.如下图,容易得到∠1=60°.答案:60°12.把一张长方形纸条按图58中那样折叠后若得到∠AOB′=70°,则∠B′OG=___________. 解析:利用角平分线与邻补角的定义来求解.∠B′OG=(180°-∠AOB′)÷2=55°.答案:55°13.某灯塔在船的北偏东40°方向上,那么船在灯塔的___________.解析:如下图,由方向的含义及平行线的性质可知船在灯塔的南偏西40°或西偏南50°.答案:南偏西40°或西偏南50°14.如图5-9,直线AB、CD被直线EF、GH所截,且∠1=∠2,求证:∠3+∠4=180°.证明:因为∠1=∠2(___________),又因为∠2=∠5(___________),所以∠1=∠5(___________).所以AB∥CD(___________).所以∠3+∠4=180°(___________).图5-9 图5-10解析:每一步出现的依据要么是已知,要么是以上一步为条件,根据有关的性质得来.答案:已知对顶角相等等量代换同位角相等,两直线平行两直线平行,同旁内角互补15.如图5-1-0所示,△ABC沿射线XY的方向平移一定距离后成为△DEF,找出图中存在的平行且相等的三条线段是________________________.解析:找准对应点,根据平移的性质可得出平行且相等的线段.如题图可知,点A、B、C的对应点分别为点D、E、F,所以AD∥CF,AD=CF=BE.答案:AD∥CF,AD=CF=BE三、解答题(本大题共7小题,共55分)16.(8分)如图5-11,AF平分∠EAC,且AF∥BC,试问∠B与∠C的大小关系如何?请说明理由.图5-11解:∠B=∠C.理由如下:∵AF∥BC,∴∠B=∠EAF,∠C=∠CAF(两直线平行,同位角相等,内错角相等).∵∠EAF=∠CAF,∴∠B=∠C.17.(8分)如图5-12,已知AB、CD、EF三直线相交于一点O,且OE⊥AB,∠COE=20°,OG 平分∠BOD,求∠BOG的度数.图5-12解:因为OE ⊥AB,∠COE=20°(已知),所以∠BOD=180°-90°-20°=70°(邻补角的 定义). 又因为OG 是∠BOD 的角平分线,所以∠BOG=35°(角平分线定义).18.(6分)图5-1-3,∠B=60°,∠ACE=120°,CD 平分∠ACE ,求证:AB ∥CD.图5-13证明:∵CD 平分∠ACE ,∴∠DCE=21∠ACE=60°.∵∠B=60°,∴∠B=∠DCE.∴AB ∥CD.19.(6分)如图5-14,它是由哪个基本图形经过怎样的变化得到的?图5-14解:基本图形是和.是由基本图形向右平移,再向下平移,再向左平移,然后再由基本图形向右平移,再向下平移,再向左平移.20.(6分)你玩过“抓老鼠”的游戏吗?如图5-1-5所示,游戏是:一个小伙伴将照射到室内的太阳光线(图中DO )用平面镜反射到墙上,另一个小伙伴去抓射到墙上的影子(图中OE ),平面镜移动,影子也随之移动,这里的∠1=∠2,它们是对顶角吗?∠1和∠BOC 呢?你能说出图中与∠1相等或互补的角吗?图5-15解:∠1与∠2不是对顶角,∠1与∠BOC 是对顶角.图中与∠1相等的角是∠2、∠BOC ;与∠1互补的角是∠BOD 、∠AOC 、∠AOE.21.(10分)图5-16所示是小明养的小乌龟身体上的一块花纹,DE ∥GF ∥BC ,DC ∥EF ∥AB ,你能知道∠B 和∠F 的关系吗?说说你的理由.图5-16解:∠B=∠F.理由如下:∵DE∥GF,∴∠F+∠E=180°,DC∥EF.∴∠D+∠E=180°.∴∠D=∠F.同理,可证∠D=∠B.∴∠B=∠F.22.(11分)(1)在图5-17甲中,利用已知的辅助线,说明∠A+∠B+∠ACB=180°的道理;(2)如图5-17乙,利用(1)的结论,你能否推导出四边形ABCD的四个角的和等于多少度?图5-17解:(1)过C作CD∥AB,∴∠A=∠ACD,∠B=∠DCE(两直线平行,同位角相等,内错角相等).又∵∠ACD+∠ACB+∠DCE=180°,∴∠A+∠ACB+∠B=180°.(2)连结AC由(1)的结论得∠DAC+∠ACD+∠D=180°,∠CAB+∠ACB+∠B=180°,∴∠DAC+∠ACD+∠D+∠CAB+∠ACB+∠B=360°.∴四边形ABCD的内角和为360°.。
新人教数学 7年级下:同步测控优化训练(6.2坐标方法的简单应用)

精品资料七年级数学复习专用Word精排版,可随意编辑6.2 坐标方法的简单应用5分钟训练(预习类训练,可用于课前)1.如果点A既在x轴的上方,又在y轴的左边,且距离x轴、y轴分别为5、4个单位,那么A 点的坐标为( )A.(5,-4)B.(4,-5)C.(-5,4)D.(-4,5)解析:点A在x轴的上方,则纵坐标大于零;在y轴的左边横坐标小于零.答案:C2.小华若将直角坐标系中的一只猫的图案向左平移了3个单位长度,而猫的形状、大小都不变,则图案上各点的坐标的变化情况为( )A.横坐标加3,纵坐标不变B.纵坐标加3,横坐标不变C.横坐标减小3,纵坐标不变D.纵坐标减小3,横坐标不变解析:若将直角坐标系中的一个图案左、右平移,而图案的形状、大小都不变,只需将原图案的横坐标加或减去一个值,纵坐标不变.答案:C3.若将直角坐标系中的一只鱼的图案向下平移了3个单位长度,而鱼的形状、大小都不变,则图案上各点的坐标的变化情况为( )A.横坐标加3,纵坐标不变B.纵坐标加3,横坐标不变C.横坐标减小3,纵坐标不变D.纵坐标减小3,横坐标不变解析:若将直角坐标系中的一个图案上、下平移,而图案的形状、大小都不变,只需将原图案的纵坐标加或减去一个值,横坐标不变.答案:D4.在平面内,将一个图形沿_____________移动_____________,这样的图形移动称为平移.平移前后两个图形的_____________和_____________不变.答案:某个方向一定的距离形状大小10分钟训练(强化类训练,可用于课中)1.(2010浙江温州模拟,5)点A(1,2)向右平移2个单位得到对应点A′,则点A′的坐标是( )A.(1,4)B.(1,0)C.(-1,2)D.(3,2)解析:向左右平移各点的纵坐标不变,横坐标增加.答案:D2.图6-2-1是画在方格纸上的某行政区简图,(1)地点B,E,H,R的坐标是________________.(2)点(2,4),(5,3),(7,7)所代表的地点分别为点_______________.图6-2-1 图6-2-2解析:根据坐标的定义及画法解题.各点分别向x轴(y轴)作垂线,垂足对应的数字即为横(纵)坐标.答案:(1)B(4,8),E(11,4),H(10,4),R(6,1)(2)M,I,C3.小华、小明、小强、小彬、小亮是很要好的伙伴,正北、正东分别在y轴、x轴的正方向,他们家的位置如图6-2-2所示.比例尺为1∶10 000(1个单位长度,代表10 000 cm). (1)从小华家向____________走____________米到小彬家,再向____________走____________米可到小明家;(2)从小刚家向北走____________米再向____________走____________米到小华家.解析:本题的解题关键是首先要理解坐标的意义及比例尺的计算,如小华与小彬家的距离为5×10 000=50 000(cm)=500(m).答案:(1)东500 北300(2) 200 西4004.(2010湖北十堰模拟,15(1))如图6-2-3,在平面直角坐标系中,请按下列要求分别作出△ABC 变换后的图形(图中每个小正方形的边长为1个单位):向右平移8个单位.图6-2-3解:向右平移8个单位,横坐标加8,各点的纵坐标不变.其图象如下图所示,5.在上一个题目中若△ABC内有一个点M(a,b),平移后其坐标变成什么?解:△ABC向右平移8个单位,点M(a,b)也跟着平移,平移后其坐标变成(a+8,b).6.在直角坐标系中描出下列各点(-1,-2),(0,0),(2,4),并顺次连结各点观察其形状特点,点(1,2)是否在它们的连线上?解:如图所示,是一条直线;点(1,2)在这条直线上.30分钟训练(巩固类训练,可用于课后)1.如果长方形的三个顶点的坐标分别为(-3,2),(3,2),(3,-2),则这个长方形的面积为( )A.32B.24C.6D.8解析:如图所示,长方形的长为6,宽为4,所以面积为24.答案:B2.(1)小明在直角坐标系中画出了一个长方形,他想把这个长方形向右平移3个单位长度,再向上平移2个单位长度,所得图形与原图形相比_______________;(2)若他将此长方形的横坐标都不变,纵坐标变为原来的21,则所得的长方形与原长方形相比_____________.解析:(1)在变化过程中,横坐标分别加3,纵坐标加2即可;(2)若将此长方形的横坐标都不变,纵坐标变为原来的21,则所得的长方形与原长方形相比,图案横向未发生改变,纵向被压缩为原来的一半;答案:(1)横坐标分别加3,纵坐标加2(2)横向未发生改变,纵向压缩为原来的一半3.将一梯形的各顶点的横坐标变为原来的2倍,纵坐标变为原来的21,则所得图形的面积与原来图形的面积_____________.解析:将一梯形的各顶点的横坐标变为原来的2倍,所得的梯形与原梯形相比,图案纵向未发生改变,纵坐标没变,整个图形横向拉长为原来2倍,则面积是原梯形面积的2倍;再将该梯形的各顶点的纵坐标变为原来的21,图案纵向未发生改变,纵向被压缩为原来的一半,即面积又缩小为新梯形的21.综上所述,所得图形的面积与原来图形的面积相等. 答案:相等4.在平面直角坐标系中,(1)将坐标为(0,0),(2,4),(2,0),(4,4)的点用线段依次连结起来形成一个图案.(2)若横坐标保持不变,纵坐标分别加3呢?解:(1)下图虚线即为所求;(2)横坐标保持不变,纵坐标分别加3,相当于把原图案向上平移了3个单位,所以其形状、大小都不发生改变.5.(2010海南模拟,21(2))△ABC 在平面直角坐标系中的位置如图6-2-4所示.将△ABC 向右平移6个单位,作出平移后的△A 2B 2C 2,并写出△A 2B 2C 2各顶点的坐标.图6-2-4分析:△ABC 向右平移6个单位,各点的纵坐标不变,横坐标加6.解:(1)如图所示,(2)△ABC 中点的坐标分别是A (0,4)、B (-2,2)、C (-1,1);所以A 2(6,4),B 2(4,2),C 2(5,1).6.小明头顶上方A 处5 000米的高空有一架飞机飞过,飞机的速度为300米/秒,若飞行方向不变,飞行10秒后来到B 处,用1∶100 000的比例尺,你能否用直角坐标系来表示飞机前后A 、B 的坐标,通过测量试求出小明与B 点的大概距离.解:以小明为原点竖直方向为纵轴,飞行方向为横轴建立如图所示的直角坐标系,则A (0,5),B (3,5).经过测量图中OB 约为5.8 cm ,所以根据公式:比例尺=实际距离图上距离,可求得小明与B 点的大概距离为5.8×100 000=5 800(米).7.(1)在直角坐标系中描出下列各点A (2,1),B (-2,1),C (3,2),D (-3,2);(2)连结AB 、CD 观察它们与y 轴的关系,(3)猜想(a,1)(-a,1)两点的连线是否遵循上述规律.解:(1)描点如图所示;(2)y 轴是AB 、CD 的垂直平分线;(3)已知点的坐标规律是A 与B ,C 与D 的横坐标互为相反数纵坐标相同;点(a,1),(-a,1)具备上述规律,所以y 轴是(a,1)、(-a,1)两点的连线的垂直平分线.8.图6-2-5是游乐城的平面示意图,借助刻度尺、量角器,解决如下问题:图6-2-5(1)建立适当的平面直角坐标系,写出各景点的坐标.(2)用量角器量出海底世界位于入口处的什么方向,在同一方向上还有什么景点?(3)用刻度尺量出球幕电影到入口处的图上距离,并求出它们的实际距离.解:(1)答案不唯一.若以“海底世界”为原点,则入口处(4,-1);童趣花园(4,2);梦幻艺馆(1,3);球幕电影(2,-4);(2)海底世界位于入口处北偏西约76°,在同一方向上还有太空秋千;(3)球幕电影到入口处图上距离约为1.8 cm,实际距离为1.8÷100001=270(米). 9.如图6-2-6所示,在直角坐标系下,图(1)中的图案“A”经过变换分别变成图(2)至图(6)中的相应图案(虚线对应于原图案),试写出图(2)至图(6)中各顶点的坐标,探索每次变换前后图案发生了什么变化,对应点的坐标之间有什么关系.(1) (2) (3)(4) (5) (6)图6-2-6解:由题图可知.由图(1)到图(2)是横坐标变为原来的2倍,纵坐标没变,整个图形横向拉长为原来2倍.由图(1)到图(3)是横坐标都加3,纵坐标不变,整个图形整体向右移动3个单位. 由图(1)到图(4)是横坐标不变,纵坐标都乘以-1,两个图形的大小和形状相同.由图(1)到图(5)是横坐标不变,纵坐标变为原来的2倍,图形被纵向拉长为原来的2倍.由图(1)到图(6)是横坐标、纵坐标都变为原来的2倍,形状不变,大小放大为原来的4倍.。
同步测控优化训练:2.2.1 对数与对数运算

2.2 对数函数 2.2.1 对数与对数运算5分钟训练 (预习类训练,可用于课前) 1.(1)将下列指数式写成对数式: ①210=1 024;②10-3=10001;③0.33=0.027;④e 0=1. (2)将下列对数式写成指数式:①log 0.46.25=-2;②lg2=0.301 0;③log 310=2.095 9;④ln23.14=x. 思路解析:指数式与对数式之间的换算,就是利用log a N=b ⇔a b =N. 解:(1)①log 21 024=10;②lg10001=-3;③log 0.30.027=3;④ln1=0. (2)①0.4-2=6.25;②100.301 0=2;③32.095 9=10;④e x =23.14. 2.计算:log 2487+log 212-21log 242.思路解析:这是几个对数式的加减运算,注意到每个对数式是同底的,则可以利用同底数的对数的运算公式化为一个对数式.当然也可以反其道而行之,即把每个对数的真数写成积或商的形式,再利用积或商的对数的运算性质化为同底对数的和与差,然后进行约简.解法一:原式=21(log 27-log 248)+log 23+2log 22-21(log 27+log 22+log 23) =21log 27-21log 23-21log 216+21log 23+2-21log 27-21=-21. 解法二:原式=log 2[67112347⨯⨯⨯]=-21. 3.求下列各式的值: (1)32log 318-; (2)7lg20×(21)lg0.7; (3)log 2(1+32+)+log 2(1+32-); (4)lg(5353-++); (5)(lg2)3+(lg5)3+3lg2×lg5. 思路解析:(1)32log 318-首先是个指数式,其中底数是8,指数为31-log 23,因为23=8,由幂的运算法则把其化成同底,用对数恒等式Na alog =N 化简计算.(2)通过取对数,先算出对数值,再求值.(3)运用对数运算法则log a M+log a N=log a MN 化成一个对数,然后利用底数与真数的特殊关系求解.(4)运用对数运算法则log a N n =n ×log a N 巧去根号.(5)利用lg2与lg5之间的特殊关系lg2+lg5=lg10=1求解. 解:(1).2722222)2(827log 27log 13log 31)3log 31(33log 3122222=====----(2)设x=7lg20×(21)lg0.7,则lgx=lg20×lg7+lg0.7×lg 21=(lg2+1)×lg7+(lg7-1)×(-lg2)=lg7+lg2=lg14,∴x=14,即7lg20×(21)lg0.7=14. (3)log 2(1+2+3)+log 2(1+2-3) =log 2[(1+2)2-(3)2] =log 222=log 2232=23. (4)lg (5353-++)=21lg (5353-++)2 =21lg (3+5+3-5+259-) =21lg10=21. (5)方法一:运用立方公式.(lg2)3+(lg5)3+3lg2×lg5=(lg2+lg5)(lg 22+lg 25-lg2lg5)+3lg2lg5=lg 22+lg 25+3lg2lg5-lg2lg5=(lg2+lg5)2=1.方法二:利用lg2+lg5=1,用lg5的表达式表示lg2.(lg2)3+(lg5)3+3lg2×lg5=(1-lg5)3+lg 35+3(1-lg5)lg5=1-3lg5+3lg 25-lg 35+lg 35+3lg5-3lg 25=1. 4.已知lg2=0.301 0,lg3=0.477 1,求lg 45.思路解析:解本题的关键是设法将45的常用对数分解为2、3的常用对数代入计算. 解:lg 45=21lg45=21lg 290=21(lg9+lg10-lg2) =21(2lg3+1-lg2) =lg3+21-21lg2=0.477 1+0.5-0.150 5 =0.826 6.10分钟训练 (强化类训练,可用于课中) 1.式子5log 21122+的值为( )A.2+5B.25C.2+25 D.1+25思路解析:考查对数式的运算法则.原式=522252log 5log 122==+.答案:B2.下列四个命题中,真命题是( )A.lg2lg3=lg5B.lg 23=lg9C.若log a M+N=b ,则M+N=a bD.若log 2M+log 3N=log 2N+log 3M ,则M=N 思路解析:解答本题的关键是熟练掌握对数概念及对数运算的有关性质.将选项中提供的答案一一与相关的对数运算性质相对照,不难得出应选D. 答案:D3.设集合A={x|x 2-1>0},B={x|log 2x >0},则A ∩B 等于( ) A.{x|x >1} B.{x|x >0}C.{x|x <-1}D.{x|x <-1或x >1}思路解析:该题考查集合的表示及解不等式.可以先分别求出集合A 、B 中所列不等式的解集,然后再在数轴上求它们的交集. 答案:A4.已知函数f (x )=⎩⎨⎧≤>,0,3,0,log 3x x x x ,则f [f (91)]的值是( )A.9B.91C.-9D.-91思路解析:f (91)=log 391=-2,f (-2)=3-2=91.答案:B5.若函数f (x )(x>0)满足f (yx)=f (x )-f (y ),f (9)=8,则f (3)等于( ) A.2 B.-2 C.1 D.4 思路解析:∵f (3)=f (39)=f (9)-f (3), ∴f (3)=21f (9)=4. 答案:D6.求下列各式中的x : (1)54log x=-21; (2)log x 5=23; (3)log (x-1)(x 2-8x +7)=1. 思路解析:根据式中未知数的位置或直接转化成指数式计算或利用对数性质进行计算.解:(1)原式转化为(21)54-=x ,所以x=25.(2)原式转化为23x =5,所以x=325.(3)由对数性质得⎪⎩⎪⎨⎧>+-≠->--=+-,078,11,01,17822x x x x x x x 解得x=8.7.求下列各式的值:(1)设log b x-log b y=a ,则log b 5x 3-log b 5y 3=_________; (2)设log a (x +y)=3,log a x=1,则log a y=_________; (3)|91log |33=_________.思路解析:利用对数的性质. (1)∵log b x-log b y=a, ∴log b (yx )=a. ∴log b 5x 3-log b 5y 3=log b (3355yx )=log b (y x )3=3log b (yx)=3a. (2)∵log a (x+y)=3,∴3a =x+y.又log a x=1,∴x=a. ∴y=3a -a.从而log a y= log a (3a-a).(3)|3log 2||3log ||91log |3233333-==-=32=9.答案:3a log a (3a -a) 98.已知a=lg (1+71),b=lg (1+491),试用a 、b 的式子表示lg1.4. 思路解析:求以a 、b 表示的lg1.4的式子,实际上是寻找lg 78、lg 4950和lg1.4之间的关系,所以应将三个对数的真数尽量化整并化小(一般把底化成常用对数),便于寻找关系.解:a=lg (1+71)=lg 78=3lg2-lg7, ① b=lg (1+491)=lg 4950=lg 2100-lg72=2-lg2-2lg7. ②由①②得lg2=71(2a-b+2),lg7=71(-a-3b+6),∴lg1.4=lg 1014=lg2+lg7-1=71(a-4b+1).快乐时光刀 法中国、日本、俄罗斯三国武士比赛,只见俄罗斯的武士拔出刀一挥,把裁判放出的苍蝇拦腰砍为两段,裁判给了他80分.这时日本的武士上来,拔刀后,裁判给了他90分,他把苍蝇的翅膀砍下来了!轮到中国的武士了,只见他拿了两把菜刀,一挥,裁判给了他100分.另两个不服就问裁判,裁判把苍蝇捡起来要他们看,说人家中国武士给苍蝇割了个双眼皮! 30分钟训练 (巩固类训练,可用于课后) 1.计算2log 525+3log 264-8log 71的值为( )A.14B.8C.22D.27 思路解析:原式=2×2+3×6-8×0=22. 答案:C2.下列各式中成立的是( )A.log a x 2=2log a xB.log a |xy|= log a |x|+ log a |y|C. log a 3>log a 2D.log ayx= log a x- log a y 思路解析:用对数的运算法则解决问题.A 、D 的错误在于不能保证真数为正,C 的错误在于a 值不定.选B. 答案:B3.设x 、y 为非零实数,a>0且a ≠1,则下列各式中不一定成立的个数是( )①log a x 2=2 log a x ②log a 3> log a 2 ③log a |x ·y|= log a |x|·log a |y| ④log a x 2=2 log a |x| A.1 B.2 C.3 D.4 思路解析:①②③不一定成立,④一定成立. 答案:C4.若log a 2<log b 2<0,则( )A.0<a<b<1B.0<b<a<1C.a>b>1D.b>a>1 解法一:赋值法.取a=21,b=41,则log a 2=-1,log b 2=-21. 解法二:由换底公式可得0log 1log 122<<ba ,∴log 2b<log 2a<0.∴0<b<a<1.解法三:利用函数图象(如图).答案:B5.已知11.2a =1 000,0.011 2b =1 000,那么ba 11-等于( ) A.1 B.2 C.3 D.4 思路解析:本题有两种解题方法.方法一:用指数解.由题意11.2=a11000,0.011 2=b11000,∴两式相除得ba 111000-=0112.02.11=1000.∴ba 11-=1. 方法二:用对数解.由题意,得a ×lg11.2=3,b ×lg0.011 2=3,∴b a 11-=31(lg11.2-lg0.011 2)=1.答案:A6.方程lg (4x +2)=lg2x +lg3的解是_________.思路解析:把方程两边化为同底的对数式,然后比较真数得含有未知数的方程,解之即可. 把两边化成同底的对数式为lg (4x +2)=lg (2x ×3),比较真数,得方程4x +2=2x ×3,利用换元法,解得2x =1或2x =2.所以x=0或x=1. 答案:x 1=0,x 2=1 7.lg5lg8 000+(32lg )2+lg0.06-lg6=_________.思路解析:本题考查对数的运算性质. 原式=lg5(3+3lg2)+3lg 22+lg606.0 =3(1-lg2)(1+lg2)+3lg 22-2=3-2=1. 答案:18.已知log a 2=m ,log a 3=n ,则a 2m-n =_________.思路解析:首先把对数式化为指数式,再进行指数运算.∵log a 2=m ,log a 3=n ,∴a m =2,a n =3. ∴a2m-n=3432)(222===nm n m a a a a . 答案:34 9.计算2lg5+32lg8+lg5·lg20+lg 22的值. 思路解析:考查对数式的化简运算.解:原式=2lg5+2lg2+lg5(2lg2+lg5)+lg 22=lg 25+2lg2·lg5+lg 22+2(lg5+lg2)=(lg5+lg2)2+2(lg5+lg2)=lg 210+2lg10=1+2=3. 10.已知log a x=log a c+b ,求x.思路解析:由于x 是真数,故可直接利用对数定义求解;另外,由于等式右端为两实数和的形式,b 的存在使变形产生困难,故可考虑将log a c 移到等式左端,或者将b 变为对数形式. 解法一:由对数定义可知x=ca alog +b=ca alog ·a b =c ·a b .解法二:由已知移项可得log a x-log a c=b ,即log ac x =b.由对数定义知cx=a b ,∴x=c ·a b . 解法三:∵b=log a a b ,∴log a x=log a c+log a a b =log a c ·a b .∴x=c ·a b .11.(1)已知3a =2,用a 表示log 34-log 36; (2)已知log 32=a ,3b =5,用a 、b 表示log 330. 解:(1)∵3a =2,∴a=log 32. ∴log 34-log 36=log 332=log 32-1=a-1. (2)∵3b =5,∴b=log 35.又∵log 32=a ,∴log 330=21log 3(2×3×5)= 21 (log 32+log 33+log 35)= 21(a+b+1). 12.2005年3月28日在印度尼西亚苏门答腊岛附近发生里氏8.2级地震,日本气象厅测得为里氏8.5级.科学家常以里氏震级为度量地震的强度.若设N 为地震时所散发出来的相对能量程度,那么里氏震级m 可以定义为m=lgN ,试比较8.2级和8.5级地震的相对能量程度.解:设8.2级和8.5级地震的相对能量程度分别为N 1和N 2,由题意得⎩⎨⎧==,lg 5.8,lg 2.821N N 因此lgN 2-lgN 1=0.3,即lg12N N =0.3,∴12N N=100.3≈2.因此,8.5级地震的相对能量程度约为8.2级地震的相对能量程度的2倍.。
新目标人教版九年级上册同步测控优化训练(Unit9Whenwasitinvented)

Unit 9When was it invented?温故知新(课前复习类训练)●Word recycling and grammar reviewing(旧词循环和语法复习)Ⅰ.Write down the correct form of the word according to the request.(根据要求写出单词的相应形式。
)1.phone(完全形式)______________2.leaves(单数形式) ______________3.potato(复数形式) ______________4.good(比较级) ______________5.helpful(最高级) ______________6.think(过去式) ______________7.same(反义词) ______________ 8.mixture(动词) ______________9.healthy(副词) ______________ 10.helpful(名词) ______________答案:1.telephone 2.leaf 3.potatoes 4.better 5.most helpful6.thought7.different8.mix9.healthily10.helpⅡ.Complete the sentence with the right word form.(用单词的适当形式完成句子。
)1.They are used for_________(change) the style of the shoes.ter he decided_________ (taste) the hot mixture.3.This_________ (specially) pen was invented by Zhengjie.4.The_________ (fly) disk was invented by college students.5.Some leaves from a nearby bush fell into the water and_________ (remain) for some time.答案:1.changing介词for后跟动词-ing形式。
21-21年上学期同步测控优化训练高三历史第一章单元测试B卷(附答案)

高三历史同步检测(四)第一章单元测试B卷说明:本试卷分为第Ⅰ、Ⅱ卷两局部,请将第一卷选择题的答案填入题后括号内,第二卷可在各题后直接作答.共100分,测试时间90分钟.第一卷〔选择题共60分〕一、选择题〔每题3分,共60分〕井田制和分封制是奴隶社会典型的制度,是它存在的经济和政治根底.据此答复1~3题. 1.以下引文均出自古代典籍,其中反映井田制实质的是〔〕A.“今大道既隐,天下为家〞B.“富者田连阡陌,贫者无立锥之地〞C.“普天之下,莫非王土〞D.“更名天下田为王田〞解析井田制是一种经济制度,其本质是奴隶制土地国有制,实际上也就是国王所有.答案C2.使西周成为空前强大的奴隶制国家的主要原因是…〔〕A.分封制和井田制的实行B.广阔奴隶创造出大量财富C.农作物品种增多和手工业的开展D.周文王整顿政治和军事解析西周之所以成为强大的奴隶制国家,主要在于西周形成了较为成熟且先进的统治制度,即政治上的分封制和经济上的井田制.答案A3.有网友说:张艺谋在电影?英雄?中宣扬赵国放弃对秦王的对抗就等于抗日战争时期宣扬对日本投降,秦始皇的天下观就是“大东亚共荣圈〞.这种观点根本错在〔〕A.战国诸雄都是华夏族的一员,彼此的征战是内战而不是侵略B.日本人同中国人一样都属于蒙古人种,是一个民族的成员C.古代社会与近代社会没有历史的可比性D.睦邻友好、和平交往是中日两国的历史主流解析此题考查分析历史概念的水平.中华民族内部兄弟民族之间的战争属于内战,它与中华民族和外国之间的战争有本质的区别.答案A4.周文王曾告诫儿子:“山林非时不升斤斧,以成草木之长;川泽非时不入网罟,以成鱼鳖之长;不麛不卵,以成鸟兽之长.〞这反映了〔〕A.统治者已熟悉到“仁政〞的重要性B.周人对环保的重要性有了初步熟悉C.统治者熟悉到因事制宜D.我国古代精神文明的进步解析此题是创新综合题.周文王对自然界的开展规律有了初步的熟悉,并告诫其子要尊重自然规律.答案B5.先秦时期,“我国农业技术史上农用动力的一次革命〞是指〔〕A.磨制石器的使用B.弓箭的创造C.铁农具的使用D.牛耕的运用解析此题考查对历史根底知识的再认再现水平.关键词是“农用动力〞.答案D6.战国时期,不利于商品经济开展的因素有〔〕①诸侯割据混乱②封建城市的兴起③商鞅变法中的农本政策④度量衡混乱A.①②③④B.①③④C.①②④D.②③④解析商品经济的开展需要有充足的商品、统一的市场,也需要有统一的度量衡,故①③④都对,②是商品经济开展的影响,应排除.答案B7.以下最能反映春秋时期社会开展趋势的是…〔〕A.铁器和牛耕用于农业生产B.诸侯争霸C.公田转化为私田D.周王室衰微解析此题实际考查对历史阶段特征的把握.春秋时期是我国奴隶社会的衰落时期,表现为公田转化为私田,奴隶制生产关系开始瓦解.而A项是促使C项出现的原因,不能作为表现.应选C 项.答案C春秋战国时期的争霸,既有大国争雄的一面,也有封建地主反对奴隶主统治的一面.据此答复8~10题.8.以下图中属于齐国都城的是〔〕解析这是一道历史地图题,不仅要熟知历史事实,还要与地理空间知识相结合,这样历史才饱满、鲜活.答案A9.马陵道遗址反映的是哪两国的交战遗址〔〕A.齐国与晋国B.晋国与楚国C.齐国与魏国D.秦国与赵国答案C10.以下关于春秋时期争霸战争的评价,不符合史实的是〔〕A.促进了民族融合B.加速了新旧制度的更替过程C.稳固了周王室的统治地位D.给人民带来了深重灾难解析对春秋争霸要全面分析,D项是其消极影响,A、B两项是客观积极作用,而B项与C项矛盾.故C项不符合史实.答案C春秋战国时期,各国通过变法逐渐实现了向封建社会的过渡,最典型的是秦国.据此答复11~15题.11.最能揭示“废井田,开阡陌〞本质的是〔〕A.铁器的使用,使人类征服自然的水平增强B.随着社会人口的增加,人们迫切需要扩大耕地面积C.为提升生产效率,秦国以大规模的集体耕作取代以往的个体劳动D.反映了秦国奴隶制经济根底的崩溃解析“废井田,开阡陌〞实际上是秦国商鞅变法中破坏井田制、摧毁奴隶制经济根底、奠定封建经济根底的最有效举措.答案D12.据?史记?记载:秦“民勇于公战,怯于私斗.〞这是商鞅哪两项变法举措执行的结果〔〕①废井田,开阡陌②奖励军功,按功受爵③实行连坐之法④重农抑商,奖励耕织A.①②B.③④C.②③D.①④解析此题考查分析水平.由于②,故“民勇于公战〞;由于③,故民“怯于私斗〞.答案C13.商鞅变法的法令中,对社会转型起决定作用的是……〔〕A. “燔诗书而明法令〞B.“为田开阡陌封疆〞C.“连什伍,设告坐之过〞D.“禁游宦之民而显耕战之士〞解析经济决定政治,社会转型中起决定作用的是经济的开展与变化.答案B14商鞅变法的举措中,对当时社会开展具有积极作用的是〔〕①奖励军功②奖励耕织③重农抑商④“燔诗书而明法令〞,实行法治A.①②B.①②③C.①②③④D.③④解析此题的关键词是“当时〞.战国时期,打击奴隶主贵族,增强新兴地主阶级的中央集权制度,促进封建经济开展,实现富国强兵,都符合社会开展趋势,而①②③④都有利于上述情况的出现,应选C项.答案C15.战国时,荀子游访秦国后,在?强国篇?中谈到:秦民风淳朴,官吏忠于职守,士大夫效忠公室,朝廷办事效率高,“故四世(自秦孝公起的四位国君)有胜,非幸也,数也〞.荀子的观点可以说明〔〕A.秦国的四位国君很有作为,秦的强盛是必然的B.秦国军事上的胜利是偶然因素所致C.由于秦国统治政策得当,其强盛成为形势开展的必然D.封建经济开展是秦国强盛的根本原因解析此题属于材料选择题,由荀子的所见可知,“非幸也,数也〞的意思为不是幸运的、偶然的,而是形势开展的必然.答案C16.胡适说:“吾意以为诸子自老聃、孔丘并于韩非,皆忧世之乱而思有以拯救之,故其学皆应时而生.〞胡适对于社会变化与思想状况之间关系的分析是…〔〕A.正确的B.根本错误的C.片面的D.外表的解析春秋战国时期,奴隶制走向衰落,封建社会逐步确立,不同的人站在不同的立场上著书立说,都符合当时形势的需要.答案A17.以下图反映了古代人民的〔〕A.娱乐活动B.农业活动C.狩猎活动D.军事活动解析由图片可知,从左至右人们依次敲乐器、吹奏乐器、舞蹈、击乐等,可判断答案为A项. 答案A18.以下战国时期的各学派中,在物理学方面取得突出成就的是〔〕A.儒家B.法家C.墨家D.道家解析考查对根底史实的再认再现.?墨经?里面有大量的物理学知识,被现代科学家称为“?墨经?光学八条〞.答案C19.公元前8世纪早期至公元前3世纪晚期,我国历史开展的时代特征包括〔〕①由奴隶社会向封建社会过渡②华夏族和周边各族逐步融合③国家由分裂逐渐走向统一④儒家思想成为中华文化的主体A.①②③④B.①②④C.①②③D.①③④解析此题先由时间判断出朝代,时代特征便更清楚了.公元前8世纪早期至公元前3世纪晚期正是我国历史上的春秋战国时期〔公元前770~前221年〕,此时正是社会大变革时期,也是民族融合的时期,更是国家由分裂走向统一的时期,而此时儒家思想还没有成为中华文化的主体.答案C20.原始社会时期,长江流域的农业与黄河流域相媲美,但自战国时期我国南北开展差距拉大,造成战国时期黄河流域经济大规模开展的主要因素是〔〕A.北方政局相对稳定B.北方自然条件更加优越C.铁器得到大力推广D.北方劳动力资源丰富解析战国时期大国争霸,故A项不正确.就农业生产来说,南方自然条件优于北方.战国时期生产力开展的重要原因是铁器的使用.答案C第二卷〔非选择题共40分〕二、非选择题〔每题20分,共40分〕21阅读以下材料:材料一:韩欲疲秦人,使无东伐,乃使水工郑国为间于秦(劝秦开凿水渠).中作而觉,秦人欲杀之.郑国曰:“臣为韩延数年之命,然渠成,亦秦万世之利也.〞(秦王嬴政)乃使卒为之.——?资治通鉴?卷6 材料二:(韩人计策被觉察后)秦宗室大臣皆言秦王(嬴政)曰:“诸侯人来事秦者,大抵为其主游间秦耳,请一切逐客.〞李斯(楚人入秦,时为客卿)议亦在逐中.斯乃上书曰:“……今逐客以资敌国,损民以益仇,内自虚而外树怨于诸侯,求国无危,不可得也.〞秦王乃除逐客之令. ——?史记?卷87请答复:(1)战国时期兴修的都江堰(与青城山一起)为什么能够列入世界文化遗产名录?(2)历史上,秦在泾水流域的北面偏东区域开凿了郑国渠.在材料所反映的事件中,秦王作出了什么决策?秦王的决策导致了什么结果?(3)战国时期还有哪些水利工程以及灌溉工具?(4)这些水利工程的兴修表达了哪派谁的主张?解析此题是对高考题的截取和改造,既联系了当今的生活实际,又考查了阅读分析材料的水平及分析推理水平.第(1)问要从都江堰的作用及该工程表达的人们的智慧两个角度答复.第(2)问从材料中得出信息,如“乃使卒(最终)为之〞“乃除逐客之令〞及李斯的上书等.第(3)问较根底.第(4)问对水利的兴修与应用表达了人们对自然的利用,是荀子主张的表达.参考答案(1)把水患变害为利,使川西平原成为千里沃野;表达了先民的勤劳和智慧.(2)决策:坚持完成郑国渠的开凿;不采纳“逐客〞的建议.结果:郑国渠的开凿使大量田地得到灌溉;留住和吸引了大批人才;秦日益强大,最终灭掉六国.(3)芍陂、西门豹渠(两者答其一即可).桔槔.(4)表达了儒家荀子的“制天命而用之〞的思想.(答“人定胜天〞也可)22.在评价春秋争霸战争时,有人说“春秋无义战〞,有的人引用列宁的一段话作评:“历史上常常有这样的战争,它们虽然像一切战争一样不可防止地带来种种惨祸、暴行、灾难、痛苦,但它们仍然是进步的战争,它们促进了人类的开展,加速地破坏极端有害和反动的制度.〞联系春秋争霸的史实,评述以上观点.解析此题考查分析、评价历史事件和解决历史问题的水平.做这类题的规律是坚持重点论和两点论,分析历史事件,既要看到其积极作用,也应看到其局限性,并能分清以哪方面为主.做这类题还应熟知历史事实,否那么便成无米之炊了.参考答案春秋争霸战争是为了争夺土地、人口和对其他诸侯国的支配权,为了满足奴隶主贵族扩张和掠夺的私欲,因此战争无正义与非正义之分,战争给人民带来了灾难.因此“春秋无义战〞有其合理的一面,但无视了争霸战争的客观进步作用.列宁的话适合对春秋争霸战争的评价,战争虽有破坏性,但在客观上促进了社会进步.①战争给新势力提供了开展条件,要争霸就要富国强兵,因此齐桓公、晋文公、越王勾践等进行改革,开展了社会生产力,同时削弱了旧奴隶主贵族的势力,为封建地主阶级的开展创造了条件.②争霸过程中,大国吞并小国,实现了地区性局部统一,为后来秦的统一提供了前提.③争霸战争中,华夏族建立的国家同其他少数民族建立的国家交战,使得华夏族与其他各族接触频繁,促进了民族融合.。
06-07年上学期同步测控优化训练八年级上生物冀少版期末综合测试(附答案)

期末综合测试一、选择题(每小题2分,共40分)1.谜语“麻屋子,红帐子,里面坐个白胖子”中的白胖子是指()A.果实B.果皮C.胚D.子叶思路解析:此谜语的谜底是花生,麻屋子是果皮,红帐子是种皮,白胖子是胚,包括胚芽、胚轴、胚根和子叶。
平时我们说的豆瓣才是子叶。
答案:C2.以下哪种说法不正确()A.光照可以使种子得到足够的热量,因而有利于种子的萌发B.植物生长发育离不开光合作用,所以种子萌发的必要条件是需要光照C.种子萌发一般不需要光照D.某些种子萌发需要光照思路解析:种子的萌发有的需要光照,有的不需要,虽然植物生长发育离不开光合作用,但是不是所有的种子萌发的必要条件是光照。
种子萌发的必要条件是适量的水分、适宜的温度和充足的氧气。
答案:B3.分生区产生的新细胞有两种去向:下部细胞仍保持分裂能力,上部细胞停止分裂,形成伸长区。
那么,分生区细胞的特点是()A.细胞小,排列紧密、细胞壁薄、细胞核大B.细胞伸长、液泡增大C.细胞大,排列疏松、细胞质浓厚D.细胞排列紧密、整齐,细胞核较小思路解析:分生区细胞具有强大的分裂增生的能力。
它的特点是:细胞小,排列紧密、细胞壁薄、细胞核大。
答案:A4.壮苗先壮根,特别是吸收水分和无机盐的主要部位是()A.根冠B.伸长区C.成熟区D.分生区思路解析:因为根是吸收水分和无机盐的主要器官,根的吸收作用主要在根尖,根尖成熟区是吸收水分和无机盐的主要部位。
答案:C5.种植下列植物中,需要含钾无机盐较多的是()A.芹菜B.苹果C.甘薯D.白菜思路解析:含钾的无机盐的作用是使植物茎秆健壮,促进淀粉的形成和运输。
在所给的选项中,甘薯含淀粉最多,因此应多施含钾无机盐。
答案:C6.以下现象中,与植物根吸收水分和无机盐或能牢牢地抓住土壤等作用无直接关系的是()A.梨树出现小叶病,应补充含锌的无机盐B.莲的新叶呈黄白色是因为光照不足,不能形成叶绿素C.移栽树木时,可让树木的根部带上较大的土块,以减少对幼根和根毛的损伤D.人们在山坡上植树,河堤上种草,其主要目的是保持水土思路解析:本题是考查根的主要作用。
同步测控优化训练(海陆的变迁

绪论:初中地理的学习方法和技巧 一、培养空间概念,学会正确的读图、用图方法 种类繁多、数量巨大的地图是地理课区别于其他学科课程的突出特点,于
是有人说,“没有地图就没有地理学”。只要掌握了正确的读图方法,培养良 好用图习惯,形成基本的地理技能,你就已经掌握了学习地理课的最重要的工 具。
阶段,为不同层次的学生进行相应的辅导,以满足不同层次的学生 的需求,避免了一刀切的弊端,同时加大了后进生的辅导力度。对 后进生的辅导,并不限于学习知识性的辅导,更重要的是学习思想 的辅导,要提高后进生的成绩,首先要解决他们心结,让他们意识 到学习的重要性和必要性,使之对学习萌发兴趣。要通过各种途径 激发他们的求知欲和上进心,让他们意识到学习并不是一项任务, 也不是一件痛苦的事情。而是充满乐趣的。从而自觉的把身心投放 到学习中去。这样,后进生的转化,就由原来的简单粗暴、强制学 习转化到自觉的求知上来。使学习成为他们自我意识力度一部分。 在此基础上,再教给他们学习的方法,提高他们的技能。并认真细 致地做好查漏补缺工作。后进生通常存在很多知识断层,这些都是 后进生转化过程中的拌脚石,在做好后进生的转化工作时,要特别 注意给他们补课,把他们以前学习的知识断层补充完整,这样,他 们就会学得轻松,进步也快,兴趣和求知欲也会随之增加。 (二)经验和体会 1、帮助学生养成良好的学习习惯。 学生的学习习惯不是很好,为了培养良好的学习习惯,本学期 伊始,向学生提出地理教学三步走。预习、学习、复习巩固。效果 不错,学生的学习兴趣和学习热情提高。 2、改变授课风格,运用学习先进的教学模式。用幽默风趣的语 言解决学生课上出现的问题,营造活而不乱的地理课堂。 3、课堂教学应以学生为主体
二、对地理原理,概念的理解要把握住要点、抓住关键。 对地理原理、要领的掌握,并不要求象物理、数学分式、定理那样精确, 只要抓住其中的关键、要点便十分容易地理解并把它们掌握住了。例如:“在自 然界中,对人类有利用价值的阳光、空气、水等都是自然资源”这一对自然资 源概念的理解。我们应该抓住两个要点:第一,自然界中存在的,不是工业产 品。如,汽油,虽然对人类有利用价值,但不是人类从自然界中直接获得的, 它是工业产品。第二,是对人类有利用价值的。没有利用价值的不是,如沙漠 虽然在自然界中存在着,但目前,对人类没有利用价值,也不是自然资源。这 样就可以了。 学习地理有一个正确的方法十分重要,但有一个端正的学习态度对学好地 理同样也十分重要。希望同学们端正学习态度,掌握正确的学习方法,把地理 课学好。 三、学会读书,掌握科学的读书方法 地理教材是我们获取地理知识、提高地理素养的重要途径。怎样才能学好 教材上的地理知识呢?我们应该注意把握以下几个要点。 1.读出书中有什么 2.读出知识网络 3.学会梳理知识 四、要善于把不同的地理事物联系起来。 把不同的地理事物之间建立起联系,首先必须问“为什么?”这样便会养成 由果推因的良好的地理思维习惯。例如:世界雨极是印度的乞拉朋齐,那么,为 什么乞拉朋齐会成为世界的雨极呢?结合地图,根据乞拉朋齐所处的地理位置便 可分析出,乞拉朋齐位于喜马拉雅山的迎风坡,这里有大量的地形雨,这样, 气候便和地形、位置相互联系起来了。 五、培养地理思维能力 培养地理思维能力,是初中地理课程的重要目标,对中学生学好地理非常 重要。组成地理环境的各要素之间是相互联系、互为因果的,任何地理事物的 发生发展都不是由单一的因素造成的,而是由多种因素共同作用造成的。但 是,在这诸多的地理因素中,有某一、两个要素起着关键性的作用。我们应当 学会找出这一关键性的因素,并以此为线索,将其他的各要素联系起来,从而 正确理解各地理要素之间的内在联系。
同步测控优化训练:1.3.1 单调性与最大(小)值

1.3 函数的基本性质1.3.1 单调性与最大(小)值5分钟训练 (预习类训练,可用于课前)1.若函数y=ax 与y=-xb 在(0,+∞)上都是减函数,则函数y=ax 2+bx 在(0,+∞)上是单调递增函数还是单调递减函数?2.如果函数f(x)在[a ,b ]上是增函数,对于任意的x 1、x 2∈[a ,b ](x 1≠x 2),下列结论中不正确的是( ) A.2121)()(x x x f x f -->0 B.(x 1-x 2)[f(x 1)-f(x 2)]>0 C.f(a)<f(x 1)<f(x 2)<f(b) D.)()(2121x f x f x x -->0 3.函数y=1-+x x 的值域为_________.4.证明函数y=x+x 1在(1,+∞)上为增函数. 10分钟训练 (强化类训练,可用于课中)1.已知函数y=f(x)在(-∞,+∞)上是减函数,则y=f(|x +2|)的单调递减区间是( )A.(-∞,+∞)B.[-2,+∞]C.[2,+∞]D.(-∞,-2)2.若函数f(x)=x 2+2(a-1)x +2在区间(-∞,4)上是减函数,则实数a 的取值范围是…( )A.a ≤-3B.a ≥-3C.a ≤5D.a ≥33.设f(x)是定义在A 上的减函数,且f(x)>0,则下列函数中为增函数的个数是( ) ①y=3-f(x) ②y=1+)(2x f ③y=[f(x)]2 ④y=1-)(x fA.1B.2C.3D.44.若函数f(x)在区间[m ,n ]上是增函数,在区间[n ,k ]上也是增函数,则函数f(x)在区间(m ,k)上( )A.必是减函数B.是增函数或减函数C.必是增函数D.未必是增函数或减函数5.若函数y=(2k+1)x+b 在R 上是减函数,则( )A.k >21 B.k <21 C.k >-21 D.k <-21 6.求函数y=x 2-2x+3在x ∈[-1,2]上的最大值、最小值.30分钟训练 (巩固类训练,可用于课后)1.已知f(x)是R 上的增函数,若令F(x)=f(1-x)-f(1+x),则F(x)是R 上的( )A.增函数B.减函数C.先减后增的函数D.先增后减的函数2.函数f(x)在区间(-4,7)上是增函数,则y=f(x-3)的递增区间是( )A.(-2,3)B.(-1,10)C.(-1,7)D.(-4,10)3.在(0,2)上为增函数的是( )A.y=-x+1B.y=xC.y=x 2-4x+5D.y=x2 4.f (x )=x 2+2(a-1)x+2在(-∞,4)上是减函数,则a 的范围是_________.5.函数y=62+--x x 单调递增区间是_________,单调递减区间是_________.6.函数y=f(x)是定义在R 上的减函数,则y=f(|x +2|)的单调减区间是_________.7.已知f(x)=x 3+x(x ∈R ),(1)判断f(x)在(-∞,+∞)上的单调性,并证明;(2)求证:满足f(x)=a(a 为常数)的实数x 至多只有一个.9.函数f (x )=4x 2-4ax+a 2-2a+2在区间[0,2]上有最小值3,求a 的值.。
同步测控优化训练(第七单元课题2 燃料和热量)

课题2 燃料和热量5分钟训练(预习类训练,可用于课前)1.化石燃料包括__________、__________和__________,它们是__________ (填“可再生”或“不可再生”)能源,属于__________ (填“纯净”或“混合”)物。
从石油中炼制出的燃料有多种,举出三例__________、__________、__________;最后一级产品是__________,主要用于__________。
思路解析:本题考查学生对基础知识的认识和掌握,侧重于预习教材。
从课本预习中掌握关键词语(术语),形成基本知识体系。
化石燃料是经过长时间地地质变化得到的燃料。
石油经过炼制得到汽油、煤油等一系列产品后,最后剩余沥青,常用于筑路。
答案:煤石油天然气不可再生混合汽油航空煤油柴油沥青铺路、建筑材料2.甲烷是__________和__________的主要成分,在空气中燃烧的方程式是__________,现象是发出__________,放出__________,生成__________和使澄清石灰水__________气体。
思路解析:本题考查对甲烷燃烧及燃烧产物的掌握,侧重于基础知识的考查。
答案:天然气沼气CH4+2O2−−→−点燃CO2+2H2O蓝色火焰热量水变浑浊的二氧 化碳10分钟训练(强化类训练,可用于课中)1.最早发现和利用石油的国家是( )A.中国B.美国C.日本D.英国思路解析:考查对化学史的把握,激发爱国热情和民族自豪感。
答案:A2.下列物质中不是由煤干馏而得到的是( )A.焦炭B.煤焦油C.煤油D.焦炉气思路解析:煤的干馏得到焦炭、煤焦油、焦炉气等,而煤油是石油分馏的产物。
答案:C3.下列燃料中被称为未来绿色能源的是( )A.煤B.石油C.天然气D.氢气思路解析:煤、石油和天然气都是化石燃料,燃烧产生CO、SO2,污染环境。
而氢气燃烧后得到唯一产物水,故被称为绿色能源。
答案:D4.“西气东输”完成后,很多管道煤气家庭都能用上天然气。
同步测控优化训练(第二单元课题2 氧气)

课题2 氧气5分钟训练 (预习类训练,可用于课前)1.在标准状况下,氧气是一种_____________色、_____________气味的气体。
它的密度比空气_____________,_____________溶于水。
液态氧的颜色是_____________。
思路解析:本题考查氧气的物理性质。
答案:无 没有 略大 不易 淡蓝色2.氧气的化学性质_____________,能与许多物质起反应。
氧气具有_____________,是常用的_____________。
氧气能支持燃烧,带有火星的木条在氧气中能_____________。
思路解析:本题考查氧气的基本化学性质:可以支持燃烧。
答案:比较活泼 氧化性 氧化剂 复燃3.化合反应是由两种或两种以上物质生成_____________的反应,是化学反应中的一种基本反应类型。
氧化反应是物质跟_____________发生的反应,不仅仅是跟氧气。
思路解析:本题考查化合反应和氧化反应的概念。
能够提供氧元素的是氧气或含氧化合物。
答案:另一种物质 氧4.(1)做铁丝在氧气里燃烧的实验时,预先要在集气瓶里装少量水或铺一层细沙,目的是_____________。
(2)写出下列反应的文字表达式①铁丝在氧气中燃烧:_______________________________________;②实验室用加热高锰酸钾的办法制取氧气:_______________________________________; ③蜡烛在空气中燃烧:____________________________________________________。
思路解析:本题考查铝丝在氧气中燃烧,生成氧化铝,放出大量的热。
玻璃容器容易炸裂,必须垫上一层水和细沙;考查氧气的制备和蜡烛燃烧等的反应文字表达式。
答案:(1)防止生成的四氧化三铁炸裂集气瓶(2)①铁+氧气−−→−点燃四氧化三铁 ②高锰酸钾−→−∆锰酸钾+二氧化锰+氧气 ③石蜡−−→−点燃水+二氧化碳 10分钟训练 (强化类训练,可用于课中)1.下列变化中,属于化学变化的是( )A.酒精挥发B.氧气液化C.矿石粉碎D.钢铁生锈思路解析:本题考查物质变化过程和本质。
同步测控优化训练(一)高一英语必修三日常同步测试外研版试题下载

同步测控优化训练(一)试题预览Module 1 Europe(自主测控卷)班级:姓名:得分:测控导航话题世界和环境(The world and the environment)重点单词 1.across prep.&adv. 横过 2.ancient adj.古老的3.architect n.建筑师4.continental adj.&n. 大陆的;欧洲人5.face vt.&vi. 面向6.gallery n. 画廊,戏院ndmark n. 陆标,地界标,里程碑8.locate vt. 使……坐落于,位于9.sculpture v.&n. 雕刻,雕刻品重点短语 1.off the coast 在海面上 2.on the coast 在岸上3.look like 看起来像……4.two thirds 三分之二5.work on从事于,致力于6.in the 1330s 在14世纪30年代7.neither...nor...既不……又不……8.in terms of 根据,按照,在……方面pare...with...把……与……相比 10.on the other hand 另一方面11.little by little 渐渐 12.belong to 属于句型 1.分数作主语时的主谓一致2.倍数的表达方式语法一般现在时和一般过去时的被动语态写作介绍一个地区的地理位置及其他情况共同基础平台(90分钟,100分)基础巩固Ⅰ.单词认识(共10小题;每小题1分,满分10分)1.The people on the European mainland are usually called________.2.When we want to express the idea of “a long time ago”,we usually use the word ________.3.The places where we can appreciate painting,drawings and other valuable art works are called ________.4.The people who design buildings are ________.5.________refers to the art of making shapes and designs on the stone,wood,etc.6.A pigeon can easily find its way home by following the l .7.The 2004 Olympic Games was held in ________ in Greece.8.The white bird is usually a ________of freedom.9.When we find where some place is on the map,we usually say that we have found its ________.10.If a shop is on the other side of the street from your home,you should say the shop is ________to your home.Ⅱ.易混词语(共10小题;每小题0.5分,满分5分)1.across/through/over(1)Don’t run ________the road until you’re sure it is safe.(2)They walked ________the forest without any difficulty.(3)Miss Liu walked ________the office,smiling strangely.(4)The boy was climbing ________the fence at that time.(5)Let’s help push the car ________the bridge.2.work at/work on/work out(1)You will have to ________ ________the weak points if you want to pass the examination.(2)We must ________ ________ a plan acceptable to all as quickly as we can.(3)The medicine the doctor gave him ________ ________his illness(4)You’ll solve this problem if you really ________ ________it.(5)He was ________ ________a report about the harms of smoking when I visited him.Ⅲ.单句改错(共10小题;每小题1分,满分10分)1.India is the second large country in population in the world.2.The oil tanker sank on the coast of Mexico in the hurricane.3.The south of the mountain lies a small village where the villagers lead a peaceful and quiet life.4.Two thirds of the population in Europe is living in cities.5.There was a natural disaster in China in 1960s.6.Shanghai is famous as its advanced technology.7.You have to stay at home until your wife returns,haven’t you?8.It’s well known that Taiwan is belonged to Ch ina.9.The European are not all fond of tea.10.You should have done your homework by this way.Ⅳ.单项填空(共10小题;每小题1分,满分10分)1.A big whale was caught ________the coast by two fishermen.A.alongB.onC.acrossD.off2.In New Zealand,people lives in the houses with their doors ________north.A.faceB.faced to theC.facingD.facing to3.We needn’t have watered the trees.You see,it looks like ________.A.rainsB.to be rainingC.rainD.rained4.We visited the Art Gallery in the morning and an exhibition later,with a hurried lunch________.A.betweenB.inC.amongD.since5.Everyone shouts“Kill it!”when a rat is seen to run________the street.A.alongB.overC.acrossD.cross6.Mr Hiward,a man ________himself Dan came to see you this morning,and left you a message here.A.calledB.callingC.was calledD.calls7.An old friend of mine called me up this morning,but he refused to tell me his present ________.A.homeB.placeC.whereD.whereabouts8.All the teachers are against the idea to ________the new teaching building beside the sports ground.A.findB.setC.locateD.build up9.Many people like white color as it is a ________ of purity.A.symbolB.signC.signalD.example10.There has been a great increase in bicycle sales this year________?A.does thereB.isn’t thereC.hasn’t thereD.isn’t itⅤ.用适当的介词填空(共10小题;每小题0.5分,满分5分)under,between,opposite,above,off,over,across,behind,in front of,along,behind1.The aeroplane is flying ________the village.2.The ship is going ________the bridge.3.The children are swimming________the river.4.Two cats are running________the wall.5.The boy is jumping ________the branch.6.The girl is sitting________her mother and her father.7.The teacher is standing________the blackboard.8.The blackboard is________the teacher.9.The clothes shop is ________the post office.10.The window is well ________the tree.Ⅵ.汉译英(共5小题;每小题2分,满分10分)1.这个国家的60%被森林所覆盖。
22-22年上学期同步测控优化训练高三数学极限(附答案)

高三数学同步检测(六)极限说明:本试卷分为第Ⅰ、Ⅱ卷两局部,请将第一卷选择题的答案填入题后括号内,第二卷可在各题后直接作答.共100分,测试时间90分钟.第一卷(选择题共40分)一、选择题(本大题共10小题,每题4分,共40分)1.以下无穷数列中,极限不存在的数列是( ) A.1,21-,41,81-,n 121·)1(+-n ,… B.3,3,3,3,…,3,… C.3,25,37,…,nn 12+,… D.1,0,-1,0,…,2sin πn ,… 分析 此题考查常见数列的极限.解 ∵∞→n lim (-1)n +1·n 21=0,∞→n lim 3=3, ∞→n lim n n 12+=∞→n lim (n12+)=2, ∴A 、B 、C 存在极限.而D 是一摆动数列,不存在极限.答案 D2.假设∞→n lim a n =3且∞→n lim b n =-1,那么∞→n lim (a n +b n )2等于( ) A.4 B.-4 C.16 D.-16分析 此题考查数列极限的运算法那么,即如果两个数列都有极限,那么它们的和、差、积、商的极限分别等于它们极限的和、差、积、商.解 ∞→n lim (a n +b n )2=∞→n lim (a n 2+2a n b n +b n 2) =∞→n lim a n 2+2∞→n lim a n ·∞→n lim b n +∞→n lim b n 2 =32+2×3×(-1)+(-1)2=4.答案 A3.假设⎪⎩⎪⎨⎧<+=>+=2,,2,,2,)(2x a x x x x b x x f 在x =2处连续,那么实数a 、b 的值是( )A.-1,2B.0,2C.0,-2D.0,0分析 此题考查函数的左、右极限与函数极限的关系、函数连续的概念及它们之间的关系. 解 f (x )在x =2处连续⇔.4)2(lim )(lim 22===-+→→f x f x x ∵-→2lim x f (x )=-→2lim x (x 2+a )=4+a =4,∴a =0.+→2lim x f (x )=+→2lim x (x +b )=2+b =4,∴b =2. 答案 B4.等差数列{a n }、{b n }的前n 项和分别为S n 和T n ,假设,132+=n n T S n n 那么n n n b a ∞→lim 的值等于( )A.1B.36C.32D.94 分析 此题考查当n →∞时数列的极限.解题的关键是把结论中通项的比值用条件中前n 项和的比值表示出来,即把n n b a 转化成关于n 的多项式. 解法一 设S n =k n ·2n ,T n =kn (3n +1)(k 为非零常数).由a n =S n -S n -1(n ≥2),得a n =2kn 2-2k (n -1)2=4kn -2k ,b n =kn (3n +1)-k (n -1)[3(n -1)+1]=6kn -2k . ∴nn n b a ∞→lim ==--∞→k kn k kn n 2624lim .32642624lim ==--∞→n n n 解法二 ∵n n b a =22121121121121----++=++n n n n b b a a b b a a ,2)12(2)12(1212121121----=+⋅-+⋅-=n n n n T S b b n a a n 又∵,132+=n n b S n n ∴.26241)12(3)12(21212--=+--==--n n n n T S b a n n n n ∴.32642624lim lim==--=∞→∞→n n b a n n n n 答案 C5.假设,41121lim 22=--+∞→x x kx x 那么常数k 的值为( ) A.2 B.21 C.-2 D.-21解析 原式=,21121lim 22k x x x k x =--+∞→ ∵,412=k ∴k =21. 答案 B 6.213lim 21-+-→x x x x 的值为( ) A.3 B.-3 C.-2 D.不存在分析 此题考查函数在x →x 0处的极限值.如果把x =x 0代入函数解析式,解析式有意义,那么f (x 0)的值就是函数的极限值.解 .3211113213lim 21-=-+-⨯=-+-→x x x x 答案 B7.函数f (x )= 41624--x x 的不连续点是( ) A.x =2 B.x =-2C.x =2和x =-2D.x =4分析 此题考查函数的连续性.一般地,函数f (x )在点x =x 0处连续必须满足下面三个条件:(1)函数f (x )在点x =x 0处有定义;(2))(lim 0x f x x →存在; (3)),()(lim 00x f x f x x =→,即函数f (x )在点x 0处的极限值等于这一点的函数值. 解 因函数在x =±2时无定义,所以不连续点是x =±2.答案 C 8])13)(23(11071741411[lim +-+⋯+⋅+⋅+⋅∞→n n n 等于( ) A.41 B.31 C.32 D.1 分析 由于“和的极限等于极限的和〞只能用于有限多项相加,因此,对于此题应先求和化为有限项的算式,再运用极限的运算法那么求极限.解 ∵),131231(31)13)(23(1+--=+-n n n n )13)(23(11071741411+-+⋯+⋅+⋅+⋅∴n n.13)1311(31)131231101717141411(31+=+-=+--+⋯+-+-+-=n n n n n ∴原式=.3113lim=+∞→n n n 答案 B9.★一个数列的通项公式为f (n ),n ∈N*,假设7f (n )=f (n -1)(n ≥2)且f (1)=3,那么∞→n lim [f (1)+f (2)+…+f (n )]等于( ) A.27 B.73 C.-7 D.-27 分析 此题考查当n →∞时数列的极限.关键是先求出数列的通项公式f (n ),然后求其前n 项和,把待求极限式化成有限项形式,即化成关于n 的多项式,再求极限.解 ∵f (1)=3≠0,∴.71)1()(=-n f n f ∴数列为首项为3,公比为71的等比数列. ∴f (n )=3·(71)n -1. 由公比不为1的等比数列的前n 项和公式,得S n =].)71(1[27711])71(1[3n n -=-- ∴.27])71(1[27lim )]()2()1([lim =-=+⋯++∞→∞→n n n n f f f 答案 A10.∞→n lim (2x +1)n =0成立的实数x 的范围是( ) A.x =-21 B.-21<x <0 C.-1<x <0 D.-1<x ≤0分析此题考查数列的一个重要极限,即limn →∞an=0时,有|a|<1.解 要使∞→n lim (2x +1)n =0,只需|2x +1|<1,即-1<2x +1<1.解得-1<x <0. 答案 C第二卷(非选择题共60分)二、填空题(本大题共4小题,每题4分,共16分.把答案填在横线上)11.∞→n lim =+-+⋯++++)1121311(222n n n n . 分析 当n 无限增大时, 1)12(3111213112222+-+⋯++=+-+⋯++++n n n n n n 的分子中含无限多项,而“和的极限等于极限的和〞只能用于有限多项相加.因此应先将分子化为只含有限多项的算式,然后再运用极限的运算法那么求极限.解 原式=∞→n lim .11lim 1)12(31222=+=+-+⋯++∞→n n n n n 答案 112.1lim →x =-+-+54222x x x x . 分析 此题考查当x →x 0时函数的极限.假设把x =1代入分子、分母中,分式变成“00〞型,不能直接求极限,因此可把分子、分母分别进行因式分解,约去分子、分母中的“零因式〞,然后再代入求极限.解1lim →x =-+-+54222x x x x 1lim →x =-+-+)1)(5()1)(2(x x x x 1lim →x .216352==++x x 答案 21 13.★一个热气球在第一分钟时间里上升了25米高度,在以后的每一分钟里,它上升的高度都是它在前一分钟里上升高度的80%,这个热气球最多能上升 米.解析 由题意,该热气球在第一分钟,第二分钟,…,上升的高度组成首项为25,公比为54的等比数列,它上升的最大高度S =∞→n lim S n =∞→n lim ).(125541])54(1[25米=--n 答案 12514.∞→n lim =-+-+++11)2(3)2(3n n nn . 分析 此题考查∞→n lim q n =0,|q |<1的应用.由于当n →∞时,构成该式的四项均没有极限,故应将分子、分母同时除以底数最大、次数较高的项3n ,以期转化成每一项都有极限的形式,再运用极限的运算法那么求解.解 .310301)32(23)32(1lim )2(3)2(3lim 11=-+=-⋅--+=-+-+∞→++∞→n n n n n n n n 答案31三、解做题(本大题共5小题,共44分.解容许写出文字说明、证实过程或演算步骤)15.(本小题总分值8分)讨论函数⎩⎨⎧<-->2,)2(2,)(2x x x x x f 在x =2处的左极限、右极限以及在x =2处的极限.分析 此题考查函数在某一点处的极限,左、右极限的定义及其相互关系..)(lim )(lim )(lim 000a x f x f a x f x x x x x x ==⇔=+-→→→ 对于常见函数,可先画出它的图象,观察函数值的变化趋势,利用极限的定义确定各种极限. 解 当x →2-时,函数无限接近于0,即.0)(lim 2=-→x f x 3分 当x →2+时,函数无限接近于2,即.2)(lim 2=+→x f x 综上,可知)(lim 2x f x -→≠)(lim 2x f x +→, 6分 ∴函数f (x )在x =2处极限不存在. 8分16.(本小题总分值8分)数列{a n }中,a n =,)12)(12()2(2+-n n n S n 为其前n 项的和,求n S n n ∞→lim 的值. 分析 由于nS n n ∞→lim 中是无穷项和的极限,必须先求得和的化简式,转化为有限项的极限问题. 而)12)(12()2(2+-=n n n a n 是一类裂项后有明显相消项的数列,所以采用了裂项法.但相消时应注意消去项的规律,即消去了哪些项,保存了哪些项.解 分 3分6.1222)]1211(21[1)]1211215131311(21[1)]121121(1)5131(211)311(211[11,21)121121(1)12)(12(11)2()12)(12()2(22++=+-+=+--+⋯+-+-+=+--++⋯+-++-+=∴⨯+--+=+-+-=+-=n n n n n n n n n n n n S n n n n n n n n n a n n ∴.11212lim lim =++=∞→∞→n n n S n n n 8分 17.(本小题总分值8分)如图,Rt △ABC 中,∠B =90°,tan C =0.5,AB =1,在△ABC 内有一系列正方形,求所有这些正方形面积之和.分析 此题考查等比数列前n 项和的极限.解 设正方形BD 1C 1B 1、D 1D 2C 2B 2、…的边长分别为a 1,a 2,….∵AB =1,tan C =0.5,∴BC =2. 由相似三角形的知识可得11211a a -=, ∴a 1=32.同理,可得a 2=32a 1,…,a n =32a n -1. ∴{a n }是以32为首项,以32为公比的等比数列. 3分 设{S n }是第n 个正方形的面积,那么S n 是以94为首项, 94为公比的等比数列. 4分 ∴∞→n lim (S 1+S 2+…+S n )=∞→n lim ,54])94(1[lim 54941])94(1[94=-=--∞→n n n 即所有这些正方形面积之和为54. 8分 18.★(本小题总分值10分)等差数列{a n }的前三项为a ,4,3a ,前n 项和为S n ,S k =2 550.(1)求a 及k 的值;(2)求∞→n lim )111(21nS S S +⋯++的值. 解 (1)∵a +3a =2×4,∴a =2.∴数列{a n }是首项为2,公差为2的等差数列. 2分 ∵2k +2)1(-k k ×2=2550,∴k =50, 即a 、k 的值分别为2、50. 5分 (2)∵S n =2n +2)1(-n n ×2=n 2+n , ∴分7.111)1(1112+-=+=+=n n n n n n S n ∴.111111312121111121+-=+-+⋯+-+-=+⋯++n n n S S S n ∴.1)111(lim )111(lim 21=+-=+++∞→∞→n S S S n n n 分10 19.★(本小题总分值10分),22lim 22n x mx x x =+++-→求m 、n 的值. 分析 此题考查当x →x 0时,函数的极限.关键是通过极限的运算构造方程组,求m 、n . 由n x mx x x =+++-→22lim 22可知x 2+mx +2含有x +2这一因式,∴x =-2为方程x 2+mx +2=0的根. ∴m =3,代入进而可求得n .也可由,22lim 22n x mx x x =+++-→得 .22)2(lim 2lim 2222+++⋅+=++-→-→x mx x x mx x x x 解出m ,再求n .解法一 ∵,22lim 22n x mx x x =+++-→ ∴x =-2为方程x 2+mx +2=0的根. ∴m =3. 4分 又,1)1(lim 223lim 222-=+=+++-→-→x x x x x x ∴n =-1. 9分∴m =3,n =-1. 10分,0022lim )2(lim 22)2(lim )2(lim 2222222=⋅=+++⋅+=+++⋅+=++-→-→-→-→n x mx x x x mx x x mx x x x x x 解法二 ∴(-2)2+(-2)m +2=0,m =3.同上可得n =-1.。
0607上学期同步测控优化训练高三数学第三章单元检测a卷(附答案)

高三数学同步检测(十一)第三章单元检测(A)说明:本试卷分为第Ⅰ、Ⅱ卷两部分,请将第Ⅰ卷选择题的答案填入题后括号内,第Ⅱ卷可在各题后直接作答.共100分,考试时间90分钟.第Ⅰ卷(选择题共40分)一、选择题(本大题共10小题,每小题4分,共40分)1.设函数f (x )在x =x 0处可导,则hx f h x f h )()(lim 000-+→( ) A.与x 0、h 都有关B.仅与x 0有关,而与h 无关C.仅与h 有关,而与x 0无关D.与x 0、h 均无关解析 本题考查导数的定义.在导数的定义式中,自变量增量可正、可负,但不为0.导数是一个局部概念,它只与函数在某一点及其附近的函数值有关,与自变量增量无关.答案 B2.曲线y =f (x )在点(0,0)处的导数的值是-1,则过该点的切线一定( )A.平行于Ox 轴B.平行于Oy 轴C.平分第一、三象限D.平分第二、四象限分析 本题考查曲线的切线.曲线在某点处的导数,即为该点处切线的斜率.解 因为f (x )在点(0,0)处的导数等于-1,即切线的斜率为-1.根据直线的点斜式方程,可得y -0=-1×(x -0),即y =-x .故它平分第二、四象限.答案 D3.物体自由落体运动方程为s =s (t )=21gt 2,g =9.8 m /s 2,若v =)/()1()1(lim 0s m g ts t s t =∆-∆+→∆,那么说法正确的是( ) A.9.8 m/s 是在0~1 s 这段时间内的速率B.9.8 m/s 是从1 s 到(1+Δt ) s 这段时间内的速率C.9.8 m/s 是物体在t =1 s 这一时刻的速率D.9.8 m/s 是物体从1 s 到(1+Δt ) s 这段时间内的平均速率分析 本题考查导数的物理意义.s (t )在某一时刻的导数为在这一时刻的瞬时速度.解 s ′=tgt t t g t ∆-∆+→∆22021)(21lim ,)(lim )(2)()(2lim 020gt t g gt t t g t gt t t =∆+=∆∆+∆=→∆→∆ ∴s ′|t =1=g ×1=g =9.8(m/s).答案 C4.设在[0,1]上函数f (x )的图象是连续的,且f ′(x )>0,则下列关系一定成立的是( )A.f (0)<0B.f (1)>0C.f (1)>f (0)D.f (1)<f (0)分析 本题主要考查利用函数的导数来研究函数的性质.解 因为f ′(x )>0,所以函数f (x )在区间[0,1]上是增函数.又函数f (x )的图象是连续的,所以f (1)>f (0).但f (0)、f (1)与0的大小是不确定的.答案 C5.设f ′(x )是函数f (x )的导函数,y =f ′(x )的图象如右图所示,则y =f (x )的图象最有可能是( )分析 本题主要考查函数的导数与图象结合处理问题.要求对导数的含义有深刻理解、应用的能力.解 函数的增减性由导数的符号反映出来.由导函数的图象可大略知道函数的图象.由导函数图象知:函数在(-∞,0)上递增,在(0,2)上递减,在(2,+∞)上递增;函数f (x )在x =0处取得极大值,在x =2处取得极小值.答案 C6.一点沿直线运动,若由始点起经过ts 后的路程是s=21t 2+t 1,则速度为0的时刻为 s 末.( )A.0B.2C.3D.1分析 本题主要考查导数的物理意义,即位移对时间的导数是瞬时速度.解 s ′=t -21t ,令s ′=t -21t =0,得t =1. 答案 D7.曲线y =x 3-3x 上切线平行于x 轴的点为( )A.(0,0),(1,3)B.(-1,2),(1,-2)C.(-1,-2),(1,2)D.(-1,3),(1,3)分析 本题主要考查导数的应用.根据与x 轴平行的直线的斜率为零,构造方程f ′(x )=0解得x 的值,进一步求出交点的坐标即可.解 y ′=3x 2-3,令3x 2-3=0,得x =±1.代入曲线方程得⎩⎨⎧=-=⎩⎨⎧-==.2,12,1y x y x 或 答案 B8.函数y =x 3+x3在(0,+∞)上的最小值为( ) A.4 B.5 C.3 D.1分析 本题主要考查应用导数求函数的最值.解 y ′=3x 2-23x ,令y ′=3x 2-23x =0,即x 2-21x=0,解得x =±1.由于x >0,所以x =1.在(0,+∞)上,由于只有一个极小值,所以它也是最小值,从而函数在(0,+∞)上的最小值为y =f (1)=4.答案 A9.函数y =x ln x 在区间(0,1)上是( )A.单调增函数B.单调减函数C.在(0,e 1)上是减函数,在(e1,1)上是增函数 D.在(0,e 1)上是增函数,在(e 1,1)上是减函数分析 本题主要考查利用求导方法判定函数在给定区间上的单调性解 y ′=ln x +1,当y ′>0时,解得x >e1. 又x ∈(0,1),∴e 1<x <1时,函数y =x ln x 为单调增函数.同理,由y ′<0且x ∈(0,1),得0<x <e1,此时函数y =x ln x 为单调减函数.故应选C.答案 C10.若函数y =x 3-3bx +3b 在(0,1)内有极小值,则( )A.0<b <1B.b <1C.b >0D.b <21 分析 本题主要考查应用导数解决有关极值与参数的范围问题.解 对于可导函数而言,极值点是导数为零的点.∵函数在(0,1)内有极小值,∴极值点在(0,1)上.令y ′=3x 2-3b =0,得x 2=b ,显然b >0,∴x =±b .又∵x ∈(0,1),∴0<b <1.∴0<b<1.答案A第Ⅱ卷(非选择题共60分)二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)11.函数y =e x 2的导数是 .分析 本题主要考查指数函数以及复合函数的导数.解 设y =e μ,μ=x 2,则y x ′=y μ′·μx ′=(e u )′·(x 2)′=e μ·2x =2x e x 2.答案 2x e x 2.12.有一长为16 m 的篱笆,要围成一个矩形场地,则矩形场地的最大面积是 m 2.分析 本题考查如何求函数的最值问题,其关键是建立目标函数解 设场地的长为x m ,则宽为(8-x ) m,有S =x (8-x )=-x 2+8x ,x ∈(0,8).令S ′=-2x +8=0,得x =4.∵S 在(0,8)上只有一个极值点,∴它必是最值点,即S max =16.此题也可用配方法、均值不等式法求最值.答案 1613.★过原点作曲线y =2x 的切线,则切点的坐标为 ,切线的斜率为 .分析 本题考查指数函数的导数及导数的几何意义.解 ∵y =2x ,∴y ′=2x ln2.设切点坐标为(x 0,02x ),则过该切点的直线的斜率为02x ln2,直线的方程为y -02x =02xln2(x -x 0).∵直线过原点,∴0-02x =02x ln2(0-x 0).∴02x =x 0·02x ln2.∴x 0=log 2e,即切点坐标为(log 2e,e),斜率为eln2.答案 (log 2e,e) eln2.14.设f (x )、g (x )分别是定义在R 上的奇函数和偶函数,当x <0时,f (x )g ′(x )+f ′(x )g (x )>0且g (-3)=0,则不等式f (x )g (x )<0的解集是 .分析 本题主要考查导数的运算法则及函数的性质.利用f (x )g (x )构造一个新函数φ(x )=f (x )g (x ),利用φ(x )的性质解决问题.解 设φ(x )=f (x )g (x ),则φ′(x )=f (x )g ′(x )+f ′(x )g (x )>0.∴φ(x )在(-∞,0)上是增函数且φ(-3)=0.又∵f (x )为奇函数,g (x )为偶函数,∴φ(x )=f (x )g (x )为奇函数.∴φ(x )在(0,+∞)上也是增函数且φ(3)=0.当x <-3时,φ(x )<φ(-3)=0,即f (x )g (x )<0;当-3<x <0时,φ(x )>φ(-3)=0,即f (x )g (x )>0.同理,当0<x <3时,f (x )g (x )<0;当x >3时,f (x )g (x )>0.∴f (x )g (x )<0的解集为(-∞,-3)∪(0,3).答案 (-∞,-3)∪(0,3)三、解答题(本大题共5小题,共44分.解答应写出文字说明、证明过程或演算步骤)15.(本小题满分8分)过曲线y =x -e x 上某点的切线平行于x 轴,求这点的坐标及切线方程.分析 利用导数的几何意义,先求切点,再求切线的方程.解∵y ′=1-e x , 2分又切线与x 轴平行,∴切线的斜率k =0. 3分∴令y ′=1-e x =0,得x =0. 5分∴切点坐标为(0,-1). 6分∴切线方程为y =-1. 8分16.★(本小题满分8分)已知导函数f ′(x )的下列信息:当1<x <4时,f ′(x )>0;当x >4或x <1时,f ′(x )<0;当x =4或x =1时,f ′(x )=0.试画出函数f (x )图象的大致形状.分析 本题考查函数的单调性、极值与导函数的关系.解 当1<x <4时,f ′(x )>0,可知f (x )在此区间内单调递增; 2分当x >4或x <1时,f ′(x )<0,可知f(x)在这两个区间内单调递减; 4分当x =4或x =1时,f ′(x )=0,是两个极值点. 6分综上,函数f (x )的图象的大致形状如下图所示(注:图象不唯一,只要符合题设条件即可).8分17.(本小题满分8分)设f (x )在x =1处连续,且,21)(lim 1=-→x x f x 求f ′(1). 分析 本题考查抽象函数在某点处的导数.根据f (x )在某点连续的定义及导数的定义求解.解 ∵f (x )在x =1处连续,∴1lim →x f (x )=f (1). 2分 又1lim →x f (x )=1lim →x [(x -1)·1)(-x x f ] =1lim →x (x -1)·1lim →x 1)(-x x f =0·2=0. ∴f (1)=0. 5分根据导数的定义,得f ′(1)=.2)1(lim )1()1(lim 00=∆∆+=∆-∆+→∆→∆xx f x f x f x x 8分 18.(本小题满分10分)设y =f (x )是二次函数,方程f (x )=0有两个相等的实根且f ′(x )=2x +2,求f (x )的表达式.分析 本题主要考查导数运算的逆运用.利用待定系数法设函数解析式,代入条件求解.解 设f (x )=ax 2+bx +c (a ≠0), 2分∴f ′(x )=2ax +b . 3分由条件f ′(x )=2x +2,得a =1,b =2.∴f (x )=x 2+2x +c . 5分∵方程f (x )=0有两个相等实根,∴Δ=4-4c =0,即c =1. 8分∴函数解析式为f (x )=x 2+2x +1. 10分19.(本小题满分10分)如右图,已知曲线C 1:y =x 3(x ≥0)与曲线C 2:y =-2x 3+3x (x ≥0)交于点O 、A ,直线x =t (0<t <1)与曲线C 1、C 2分别相交于点B 、D.(1)写出四边形ABOD 的面积S 与t 的函数关系S =f (t );(2)讨论f (t )的单调性,并求f (t )的最大值.分析 本题主要考查如何以四边形的面积为载体构造目标函数、函数的导数、函数的单调性等基础知识,考查运算能力和利用导数研究函数的单调性,从而确定函数的最值.解 (1)解方程组⎪⎩⎪⎨⎧+-==,32,33x x y x y 得交点O 、A 的坐标分别为(0,0)、(1,1). 2分f (t )=S △ABD +S △OBD =21|BD |·|1-0|=21|BD |=21(-2t 3+3t -t 3)=21(-3t 3+3t ), 即f (t )=-23(t 3-t )(0<t <1). 4分 (2)f ′(t )=-29t 2+23. 6分 令f ′(t)=-29t 2+23=0,得t =33,t=-33(舍去). 当0<t <33时,f ′(t )>0,从而f (t )在区间(0,33)上是增函数; 8分 当33<t <1时,f ′(t )<0,从而f (t )在区间(33,1)上是减函数. 所以当33时,f (t )有最大值f (33)=33. 10分。
06-07年上学期同步测控优化训练高二化学同步检测十一_盐类的水解酸碱中和滴定

一、选择题1.下列有关盐类水解的说法不正确的是( )A.盐类的水解过程破坏了纯水的电离平衡B.盐类的水解是酸碱中和反应的逆反应C.盐类水解的结果使盐溶液不一定显中性D.Na2CO3溶液中c(Na+)是c(CO32-)的2倍2.下列水解离子方程式正确的是( )A.Fe3++3H2OFe(OH)3↓+3H+B.Br-+H2OHBr+OH-C.CO+H2OH2CO3+2OH-D.NH+2H2ONH3〃H2O+H3O+3.向Na2CO3溶液中滴入2滴酚酞,溶液变红,微热后溶液颜色( )A.不变B.变深C.变浅D.褪色4.实验室在配制硫酸铁溶液时,先把硫酸铁晶体溶解在稀硫酸中,再加水稀释至所需浓度,如此操作的目的是( )A.防止硫酸铁分解B.抑制硫酸铁水解C.提高硫酸铁的溶解度D.提高溶液的pH5.25 ℃ 0.1 mol〃L-1某溶液的pH=5,则这溶液可能是( )A.氨水B.NaClC.NH4ClD.盐酸6.现测得某浓度的Na2HPO4溶液的pH为8,以下推测合理的是( )①HPO水解作用大于电离作用②HPO的电离倾向大于其水解作用③溶液中c(HPO)<c(Na+) ④该溶液能与酸反应不与碱反应A.①③B.②③C.①④D.②④7.有一支50 mL酸式滴定管,其中盛有溶液,液面恰好在10.00 mL刻度处。
把滴定管中溶液全部流下排出,承接在量筒中,量筒内溶液的体积( )A.大于40.0 mLB.40.0 mLC.小于40.0 mLD.10.0 mL8.下列有关pH变化的判断正确的是( )A.随着温度的升高,碳酸钠溶液的pH减小B.随着温度的升高,纯水的pH增大C.新制氯水经光照一段时间后,pH减小D.氢氧化钠溶液久臵于空气中,pH增大二、选择题9.下列说法正确的是( )A.HCO在水溶液中只电离,不水解B.硝酸钠溶液水解之后呈中性C.可溶性的铝盐都能发生水解反应D.可溶性的钾盐都不发生水解反应10.下列有关0.1 mol〃L-1 Na2CO3溶液的说法错误的是( )A.其中钠离子的浓度为0.2 mol〃L-1B.溶液中的OH-浓度大于H+浓度,HCO的浓度小于CO 的浓度C.溶液中Na+的浓度等于CO浓度的二倍D.溶液中HCO浓度大于H2CO3浓度11.关于小苏打水溶液的表述正确的是( )①c(Na+)=c(HCO)+c(CO)+c(H2CO3)②c(Na+)+c(H+)=c(HCO)+c(CO)+c(OH-)③HCO的电离程度大于HCO的水解程度④存在的电离有:NaHCO3Na++HCO,HCOH++CO,H2OH++OH-A.①②B.①③C.②③D.①④12.将0.2 mol〃L-1 HCN溶液和0.1 mol〃L-1的NaOH 溶液等体积混合后,溶液显碱性,下列关系式正确的是( )A.c(HCN)<c(CN-)B.c(CN-)>c(Na+)C.c(HCN)-c(CN-)=c(OH-)D.c(HCN)+c(CN-)=0.1 mol〃L-113.盐的水解程度大小可以用―水解度‖来表示。
上学期高同步测控优化训练数学A:极限B卷(附答案)

高中同步测控优化训练(四)第二章极限(B 卷)说明:本试卷分为第i 、n 卷两部分 ,请将第I 卷选择题的答案填入题后括号内 ,第n卷可在各题后直接作答•共100分,考试时间90分钟.第I 卷(选择题共30分)一、选择题(本大题共10小题,每小题3分,共30分)1•设f(x)=『x +b(x 兰0),若lim f(x)存在,则常数b 的值是 e(x >0), T分析:本题考查lim f(x)=a 的充要条件是:X ]X 0lim f(x)= lim f(x)=a.x 「x ()—■'解:T lim (2x+b)=b, lim e x =1,x —0 …x __0 *又条件lim f(x)存在,二b=1.答案:Blim S n 等于n _.■ - lim s n = lim 红=2.n - n▽ - n 亠1 答案:D133. lim ( ~3)等于xi X 1 x 3 1分析:本题考查函数lim f(x)的极限•若把x= — 1代入函数解析式,解析式无意义,故应化简x 0A.0B.1 C. —1D.e2.数列11,1 2 112 312 341 2 3 4 :--- n,…的前n 项和为S n ,则B. 12 分析:本题考查数列极限的求法1A.0 C.1D.2 •要求数列2解:a n =1 +2 +3 +…+n n(n +1)1 1 1 --S n =a 1+a 2+ …+a n =2(1 —+ …+ —2 2 3{a n }的前n 项和,应首先确定它的通项公式1 1=2(—-), n n 1 A.0B. — 1C.1D.不存在函数解析式,约去使它的分母为0的因式,再求解.23x _x 1_3r )= lim厂x 31 x _J (x 1)(x -x 1)=lim (X 忙)=limx7 (x 1)(x -x 1) J 1答案:B3」"一(3」一2」)(n 为奇数),分析:a n =(n 为偶数),答案:C分析:本题考查数学归纳法的应用.解题的关键是分清不等式左边的构成情况,显然它的解:x im 」((x-2) (x 2 _x 1)_1 _2 (-1)2 -(-1) 1 4•若数列{a n }的通项公式是 3』2』•(-1)n(3』_ 2』) a n = ,n=1,2,…,则 lim (ai+a 2+ … + a n )等于A 11A.—B.y 24 C 里 24 D 空242』(n 为奇数),(n 为偶数).—1—3—5--a 1+a 2+ …+a n =(2 +2 +2 + …)+(3即 a n = <.. 2-1]吧2井2+…+咖=百—2—4—6+3 +3 +•••).1 1 -J 9_一.1.1 1- 1 - 4 9 19 241 1 15.设 P(n)=1+ + …+ —— 2 3要添加的项是1A. ~ 2k 1-1 B. 丄 2k1 1 2k 2k 1 -1 1 1D. r k + …+ 2k 2k 12n-1,在用数学归纳法证明 P(n)> -的过程中,从P(k)到P(k+1) 2分母由自变量取k时的第一项1按公差为1依次递增到2k—1共(2k—1)项.故当n =k+1时,它的分母应由1依次递增到2k+1—1共(2k+1—1)项,增加了2k项.解pg 冷宁…*X n — X 1=(—丄)°+(—与 + …+(—丄)2 2 2• •• X n =2 : 1 —(—丄严.3 2•- lim x n = lim — [1 一 (一 — )n-1]=-. — "■ 3 23答案:C7.设函数f(x)= j ig( x) (x 0),贝y 下列结论不正确的是 X(x >0),••• P(k+1)=1 + 1 1 1+ …+ —c — 2 3 2k -11 12k 2k 1 1+ …+ —72k 1 _11 =P (k )+尹 12k 1 +・・・ 1 2k 1 _1答案:D6•用记号“(+)”表示求两个实数 a 与b 的算术平均数的运算,即 列{X n }满足 X 1=0,X 2=1,X n =X n -1®X n -2(n 》3),贝 U lim X n 等于n —j-bc1 2A.OB.—C.—23分析:本题考查数列的极限•此题是信息迁移题,关键是如何求出数列 解:由题意 可知X n = 独 3,即 2X n = X n -1 + X n -2.2整理、变形为 2(X n — X n -1)= —(X n -1 — X n - 2), 令 b n -2=X n —1 — X n -2 贝b n - 1 = X n — X n -1 .•- 2b n - 1= — b n - 2,b 1 = X 2 — X 1=1 — 0=1.••数列{b n }是以1为首项,-丄为公比的等比数列.2 1、n-11、n-1…b n =(— ),即 X n+1— xn =(—).221 0• • x 2 一 x 1=( — _ ),2 1 1X 3— X2=(—),2a (+^b=-^-b .已知数2D.1{X n }的通项公式X n .n —2)将这n -1个等式两边分别相加,得1一(一[)2n —2= 211-(-2)A. lim f(x)=1x ,.10C. lim f(x)=1D. lim f(x)=2x 1 • •x ■分析:本题考查函数的左、右极限 .因为f(x)的图象易得,可根据它的图象求解.其中y= lg( — x)与y=lgx 的图象关于y 轴对称.、 1--a v — 1 或 a > —3 *解法二:本题可利用特殊值代入法,当a=1时成立,排除C 、D. 再令a=i ,vnim ::(1—护0成立八排除A.答案:B分析:本题考查函数lim f(x).当把x=x 0代入函数解析式f(x)有意义时,可采用直接代入法X %B. lim f(x)=0x »0解:由图象可知lim f(x)=0,x 亠而lim f(x)不存在,所以lim f(x)不存在.x )0 • •x _0答案:B8. lim J a )n =0,则a 的取值范围是nr :: 2aA.a=1B.a v — 1 或 1 a> -3C. — 1v a v 13D ・av —3 或 a> 1分析:本题考查极限lim q n =0,|q|v 1.要求a 解法.的范围,可列a 的不等式,要注意分式不等式的解法一 :v lim (! an Y 2an1 - a)=0, P v 1一|1—a|;:4a 2 (1-a)2a = 0a :: -1或 a丄,{39.已知 f(x)=x 2,则 lim A Tf (x x) _ f (x)等于 A xA. xB.2xC.-1D. — x2求极限.f (x+也x)_f (x)_ |im (X "x)2 —X 2 A xZ &2(. :x)x . x 2Zx lim^(2x+ △10. limn —j ::1 22 32 …n 2C2 C3 ...C 2等于A.OB.1C.2分析:本题考查数列的极限•要掌握二项式系数的一个性质:m m 1 m Cn ■ C n= C n -1 .D.3解:•••分子 1+22+32+…+n 2= -n (n+1)(2n+1),6分母 c ; + c 2+…+ c 2 = c 3+c 2+c 2+…+C2322232=c 3 + c 2+c 2+…+ c : = c 3 + c(+…+ c …= u.1=(n 1)n(n 「)2 2.「 1 2 3 --n …lim 222:' n(n 1)(2 n 1) :-=lim n— n(n 1)( n —1) .. 2n 1=lim -------- =2n匸 n -1 答案:C第n 卷(非选择题 共70分)二、填空题(本大题共4小题,每小题4分,共16分•把答案填在横线上) 11.lim (石 _Jn +1 )=n _分析:本— g ”型,应先分子有理化,再求极限.-1=lim=0.n厂.n n 1 答案:0sin2x 12. lim —x _. : cos (二-x)2TTX= —代入函数解析式,解析式无意义,故应化简 2函数解析式,约去使它的分母为 0的因式,再求极限•分析:本题考查函数lim f (x )的极限•若把X r X osin2x2sin xcosx解:lim= lim= — lim 2sinx=— 2.xCOS (M f X )xcosxx -解:lim 之一0答案:B答案:-2分析:本题考查lim f(x)的极限.因为把x=x o 代入分式的分子,分子不为0•又因为lim f(x)x —x ox >x o存在,所以把x=x o 代入分母,分母必不为0•故采用直接代入法即可求极限•解:••• lim x? ;2x -5 J=二x j ax +2a +26 答案:些514.如下图所示,在杨辉三角中,斜线AB 上方的数组成数列1,3,6,10,…,记这个数列前n 项3的和为S n ,则lim — 等于 _____________nY S n12 1 A解法一一 :由 a 2 — a 1=2, a 3 — a 2=3, a 4— a3=4,a n — a n —1 =n.把这n — 1个等式两边分别相加,得a n — a 1=2+3+ — +n. n(n 1) 1 2 1 --a n=1+2+3+…+ n=n n .2 2 21 2 2 2 1…S n = (1 +2 + …+ n )+(1+2+…+ n)2 2n(n 1) _ n(n 1)(2n 1) n(n 1) 2 12 43•'•lim — = limS n n n(n 1)(2n -1) n(n 1)124解法二:由图可知,斜线AB 上方的数分别是二项展开式 (a+b)n .当n =2,3,4,…时的二项式13.已知匹2x _2x _5ax 225- 5,则a 的值为626 …a= .5分析:本题考查数列的极限 本方法求S n .•关键是由数列的前n 项归纳数列的通项公式,然后用求和的基 =丄 X 】n(n+1)(2 n+1)+ - x2 6 2=6.系数c;,c:,c4,…,c:,…,即这些数组成数列的通项公式为c n += “;+1). 以下解法同上. 答案:6三、解答题(本大题共5小题,共54分•解答应写出文字说明、证明过程或演算步骤)•••可设 f(x) — 4x 3=x 2+ax+b(a,b 为待定系数),即 f(x)=4x 3+x 2+ax+b.f (x)=5,即 lim (4x 2+x+a+ — )=5.xxT xa =5得』—,故 f(x)=4x 3+x 2+5x. b = 0.16.(本小题 10 分)已知数列{a n }的前 n 项和为 S n ,a n =5S n — 3(n € N ),求 lim (a 1+a 3+a 5+ …+n — a 2n -1)的值.分析:由式子 a n =5S n — 3,易得到a n 与Sn 的关系式.由a n = S n — S n -1( n 》2),利用此式,再对 n 进行合适的赋值,便可消去S n ,得到{a n }的递推关系式,进而确定数列{a n },再求 lim (a 什a 3+a 5+ …+a 2n —1).n _.解:a 1=$,a n =S n — S n -1(n > 2).又已知a n =5S n — 3, 二an -1 =5S n -1— 3(n》2).两式相减,得 a n — a n - 1=5(S n — S n -1)=5a n (n > 2).. 1八…a n =— 4 a n —1 (n 》2).3 分3由 a 1=5S 1 — 3 及 a 1=S 1,得 a 1=.4可见{a n }是首项为3,公比q= — 1的等比数列.6分 44•- a 1+a 3+a 5+…+a 2n -1是首项为° ,公比为q 2=(—丄)2=丄的等比数列.8分4 4 1615.(本小题8分)f(x)为多项式且lim"xLiimx 2=5,求f(x)的表达式. x分析:本题要求深刻理解函数极限定义 定系数法求解•.根据已知的极限,设出f(x)— 4x 3的表达式,利用待解:••• f(x)是多项式 3f (x) _4x,且 limX 2=1,由于|q2|<1,3•lim(ai+a3+a5+…、a1 4 410分• + a2n—1)= 2.1-q2[ 15n T::1617.(本小题12分)平面内有n条直线,其中任何两条不平行,任何三条不共点,求证:这n条12 / 9直线把平面分成f(n)=-匚2个部分.2分析:用数学归纳法证明几何问题,重难点是处理好当n=k+1时利用归纳假设结合几何知 识证明命题成立.证明:①当n=1时,一条直线将平面分成两个部分,而 12 1 2f(1)==2.2•••命题成立•2分k 2 + k +2②假设当n=k 时,命题成立,即 k 条直线把平面分成f(k)=_—— 个部分•2则当n=k+1时,即增加一条直线I ,因为任何两条直线不平行,所以I 与k 条直线都相交有k 个交点;又因为任何三条不共点 ,所以这k 个交点不同于k 条直线的交点,且k 个交点也互不相同•如此这k 个交点把直线I 分成k+1段,每一段把它所在的平面区域分为两部分 ,故新增加的平面为k+1个部分.k +k +2• f(k+1)=f(k)+k+1=+k+1222k 2k 2 2(k 1) (k 1)2(k 1) 2= 2 = 2• n=k+1时命题成立•由①②知当n € N *时,命题成立•18. (本小题 12 分)已知数列{a n }、{b n },其中 a n =1+3+5+…+(2n+1),b n =2n +4(n > 5),试问是否 存在这样的自然数 n ,使得a n =b n 成立?分析:对n 赋值后,比较几对a n 与b n 的大小,可作出合理猜测,再用数学归纳法予以证明 解:a n =1+3+5+ …+(2 n+1)=( n+1)2,当 n=5 时忌=36, b 5=25+4=36,此时 a 5= b 5; 当 n=6 时卫6=49, b 6=26+4=68,此时 a 6<b 6; 当 n=7 时,a 7=64,b 7=27+4=132,此时 a 7<b 7; 当 n=8 时,a 8=81,b 8=2 +4=260,此时 a 8<b 8. 猜想:当 n 》6时,有a n <b n . 5分下面用数学归纳法证明上述猜想•① 当n=6时,显然不等式成立,• n=6时,不等式a n <b n 成立;② 假设当n=k(k > 6)时,不等式成立,即a k <b k ,也即(k+1)2<2k +4;当n=k+1时, b k+1 =2k+1+4=2(2k+4) - 4>2(k+1)2- 4=2k 2+4k - 2,而(2k 2+4k - 2)- (k+2)2=k 2- 6>0( v k >6,「. k 2> 6), 即 2k 2+4k -2>(k+2)2= :(k+1)+1: 2由不等式的传递性,知b k+1> [(k+1)+1 ] 2=a k+1 • •••当n=k+1时,不等式也成立•11分由①、②可知 对一切n € N ,且n 》6,都有a n <b n .综上所述,可知只有当n=5时,a n =b n ,因此,存在使a n =b n 成立的自然数•12分19. (本小题12分)已知数列{a n }、{b n }都是无穷等差数列,其中a 1=3,b 1=2,b 2是a ?与a ?的11分 12分,且lim a n等差中项n—b n14 / 91 1 1 1求极限lim (川’ 川’ +…+ )的值.n Y a?分析:首先需求出a n、b n的表达式,以确定所求极限的表达式,为此,关键在于求出两个数-”又2给出了另一个等量关系,故可考虑先设出公差用二元方程组求解解:设{a n}、{b n}的公差分别为d1、d2,••• 2b2=a2+a3,即2(2+d2)=(3+d”+(3+2d”,•• 2d2—3d1 =2.又lim a n = lim 3 (n一1)* 二d1n—r b n n》::2 (n -1)d2 d2即d2=2d1, 联立①、②解得d1=2,d2=4.二a n=a1+(n —1)d1=3+(n —1) • 2=2n+1, b n=b1+(n —1)d2=2+(n—1) • 4=4n— 2.1 1 1 1 、( ),(2n 1)(4n —2) 4 2n -1 2n 11 1 ••• lim(----- ----- n . ab1 1 + …+ ------ )= lim| a1b1a2b2a n b n n心4 (1 -2n…12分列的公差,“ b2是a2与a3的等差中项”已给出一个等量关系,“a n与g之比的极限为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第23课领先世界的科学技术同步测控优化训练
自主学习
1.是世界上第一个把圆周率的数值计算到小数点以后第位的人。
2.贾思勰写成《》这部农书,书中内容反映了当时我国方农业生产技术的水平。
3.《》是我国现存的第部完整的农学著作,也是世界史上的优秀著作。
4.在前人所著《水经》的基础上,郦道元写成《》一书。
5.《水经注》既是一部优秀的学著作,同时也具有很高的和价值。
6.2003年,我国“国家最高科学技术奖”的获得者是金怡濂,假设此奖项在中国南朝时就有,则当之无愧的是( )
A.蔡伦B.祖冲之
C.郦道元D.贾思勰
基础巩固
7.世界上第一位把圆周率的数值精确到小数点以后第七位的数学家是( )
A.刘歆B.刘徽
C.何承天D.祖冲之
8.南朝时期的祖冲之已把圆周率推算到小数点后的第七位。
圆周率反映的关系是( ) A.圆的周长与半径
B.圆的半径与直径
C.圆的周长与面积
D.圆的周长与直径
9.祖冲之计算的圆周率数值,比欧洲人早( )
A.800年B.约1000年
C.1800多年D.2000多年
10.1967年,国际天文学家联合会以我国古代祖冲之的名字命名月球上的一座环形山,是因为他( )
A.第一次精确计算出圆周率
B.设计制造出水碓磨
C.造出日行百里的“千里船”
D.对世界科学文化作出巨大贡献
11.我国古代著名的数学家和天文学家祖冲之生活在( )
A.北朝B.西晋时期
C.东晋时期D.南朝
12.农学家贾思勰写的我国现存的第一部完整的农书是( )
A.《缀术》
B.《齐民要术》
C.《水经注》
D.《伤寒杂病论》
13.右图名著的作者是( )
A.郦道元
B.张仲景
C.祖冲之
D.贾思勰
14.《齐民要术》中有这样一句话:“湿耕泽锄,不如归去。
”意思是在太潮湿的地方耕作,肯定会劳而无功。
这一段话反映了贾思勰的什么主张( )
A.因地种植
B.适时耕作
c.注重兴修水利
D.讲究耕作方法
15.世界上最早懂得使用石油资源的国家是( )
A.中国B.英国
C.美国D.加拿大
16.下列著作由北魏人撰写的是( )
①《缀术》②《水经注》③《齐民要术》④《神灭论》
A.①③B.②④
C.②③D.①④
17.《水经注》是一部记载( )
A.全国主要河流的专著
B.全国主要河流发源地的专著
C.江河流经地区地理情况的著作
D.江河流经地区自然地理和人文情况的著作
18.下列关于《水经注》的说法,不正确的是( )
A.是汉魏时期综合性的地理学专著
B.作者参考了古代地理书籍
C.叙述重点是全国的水道系统
D.记述了许多前人没有记述过的河流
19.要想了解我国古代江河流经地区的山川、城镇、物产、矿藏、风光等情况就要阅读( ) A.《肘后备急方》B.《论衡》
C.《三国志》D.《水经注》
20.我国古代杰出的地理学家郦道元生活在( )
A.东晋B.北魏
C.南朝D.西晋
21.下列选项中不属于《齐民要术》内容的是( )
A.农作物栽培方法
B.食品酿造和加工技术
C.介绍渔业生产方法
D.调整产业结构
22.下列搭配没有错误的一项是( )
A.郦道元——《水经注》
B.贾思勰——《兰亭序》
C.祖冲之——《九章算术》
D.顾恺之——《齐民要术》
23.贾思勰是我国古代著名的( )
A.医学家B.数学家
C.文学家D.农学家
24.下列说法错误的是( )
A.祖冲之在数学、天文、机械制造等方面都作出了杰出的贡献
B.贾思勰的《齐民要术》对后世影响很大
C.郦道元是我国古代杰出的农学家
D.上述三人均生活在南北朝时期
25.关于郦道元的《水经注》,下面有一段简短的对话:
陈飞:“一说到《水经注》这部综合性的地理专著,就知道它是关于水系的,与山没有关系。
”
胡翔:“你说得不完全对。
《水经注》以水道系统为纲,以作注的形式,详细介绍了我国当时的主要江河。
由于我国的江河大多发源于山地,长江、黄河等就是如此,所以我们常说‘有山就有水,有水就有山’‘山水相连’‘高山流水’。
我敢肯定地说,《水经注》在介绍水系的同时,会向我们介绍与水系相连的大山。
你怎么能说《水经注》与山没有关系呢?你犯了一个望文生义的错误。
”
请完成:
(1)你认为谁说得对?为什么?
(2)你如何评价《水经注》这部著作?
创新升华
26.阅读下列材料:
强调农业生产要遵循自然规律,农作物必须因地种植,不误农时;还要改革生产技术和工具。
他曾著书总结了我国古代北方劳动人民长期积累的生产经验,介绍了农、林、牧、副、渔业的生产方法。
请完成:
(1)上述材料中的内容反映了哪位科学家的成就?
(2)这位科学家生活在什么朝代?他总结北方人民的生产经验而写的一部著作是什么?
(3)这部著作有何重要价值?
答案:
第23课领先世界的科学技术
自主学习
1.祖冲之七
2.齐民要术北
3.齐民要术一农学
4.水经注
5.地理文学史学
6.B解析:所给选项中,蔡伦是东汉人,郦道元和贾思勰都是北朝人,只有祖冲之生活在南朝。
基础巩固
7.D解析:在总结前人经验的基础上,祖冲之第一次把圆周率的数值精确到小数点以后第七位。
8.D
9.B解析:南朝时期著名的科学家祖冲之,是世界上第一个把圆周率的数值精确到小数点以后第七位的人,比欧洲人早了约100O年。
10.D解析:为了纪念祖冲之对世界科学文化作出的巨大贡献,1967年,国际天文学家联合会把月球上的一座环形山命名为“祖冲之山”。
11.D解析:南朝时期,著名的科学家祖冲之在数学和天文方面取得了重大成就。
12.B解析:北朝时期,我国古代著名的农学家贾思勰写成了我国现存的第一部完整的农书《齐民要术》。
13.D
14.A
15.A解析:从《水经注》中,我们得知中国是世界上最早懂得使用石油资源的国家。
16.C解析:郦道元是北魏时期杰出的地理学家,写成了一部优秀的地理学著作《水经注》;北魏时期,我国古代著名的农学家贾思勰写成了我国现存的第一部完整的农书《齐民要术》。
17.D解析:《水经注》详细地记录了1250多条大河的走向,以及河流沿途的山川和城镇的地理沿革、物产、风土人情等内容。
18.A解析:郦道元是北魏时期杰出的地理学家,写成了一部优秀的地理学著作《水经
注》,该书重点论述了全国的水道系统,记述了许多新河流。
19.D解析:本题主要考查对杰出的地理学著作《水经注》内容的准确认识。
A项属于医学书籍,B项是哲学著作,C项是历史著作。
20.B
21.D解析:《齐民要术》介绍了农作物栽培方法、食品酿造和加工技术、渔业生产方法,反映了当时我国北方农业生产技术的水平.但没有涉及调整产业结构的内容。
22.A
23.D解析:贾思勰是我国古代著名的农学家。
24.C解析:本题主要考查对三国两晋南北朝时期,我国领先世界的科技成就的准确掌握。
郦道元是我国古代杰出的地理学家.不是农学家。
25.参考答案:(1)胡翔是对的。
原因略。
(2)《水经注》既是一部优秀的地理学著作,同时又具有很高的文学和史学价值。
解析:该题重在考查北魏时期杰出的地理学家郦道元的主要成就。
创新升华
26.参考答案:(1)贾思勰。
(2)北魏。
《齐民要术》。
(3)是我国现存的第一部完整的农学著作,也是世界著名的农学著作。
解析:本题主要考查对古代杰出农学家贾思勰及其主要著作《齐民要术》的准确记忆能力。
首先应判断出材料属于《齐民要术》的内容,然后再回答其作者和历史地位。
