成像光学第一章
光学中的光学成像技术

光学中的光学成像技术光学成像技术在我们的日常生活中扮演着重要的角色。
从眼镜到相机再到望远镜,其应用范围非常广泛。
本文将介绍光学中的光学成像技术,从成像原理到应用,为读者提供深入了解这一技术的机会。
第一章成像原理1.1 光的传播光的传播是成像技术的基础。
在真空中,光可以直线传播,但在介质中,光传播会发生一些有趣的现象,如折射和反射。
当光从一种介质传播到另一种介质时,它的速度和方向都会发生改变。
这种现象被称为折射。
反射是另一种现象,当光从一个物体反射到另一个物体时,我们能够看到它。
这是成像技术的关键之一。
1.2 焦点和焦距当光束聚焦在一个点上时,该点被称为“焦点”。
焦点的位置取决于聚集光线的方式,通常需要使用透镜或曲面镜来实现。
此外,焦距是指参照物平面到透镜或镜面的距离。
焦距取决于透镜或曲面的几何形状和折射率。
第二章光学成像设备2.1 显微镜显微镜是一种用于观察显微级物质的光学仪器。
它的基本结构由物镜、目镜和台面组成。
物镜是可移动的,可以设置不同的放大倍数。
显微镜的分辨率越高,放大倍数就越高。
2.2 照相机照相机是一种光学成像设备,可捕捉静态或动态图像。
它由镜头、光圈和感光元件组成。
镜头负责聚焦,光圈控制光线的穿透量,感光元件可将图像转换为数字格式。
2.3 望远镜望远镜是一种用于观测远距离物体的光学仪器。
它由物镜和目镜组成。
物镜负责聚焦并收集有关成像物体的光,目镜使成像得以观测。
第三章光学成像应用3.1 医学成像医学成像旨在提供人体内部结构的视觉呈现,以帮助诊断和治疗疾病。
医学影像学技术包括X射线放射、核磁共振成像(MRI)和计算机断层扫描(CT)等,这些技术基于光学成像学原理。
3.2 遥感成像遥感成像是通过使用各种传感器和设备来获取地球表面信息的技术。
利用遥感技术,我们可以收集和分析海洋和陆地的数据,以获取更全面的环境信息。
这些传感器和设备基于光学成像原理,例如可见光和赤外线。
3.3 装置检测光学成像技术可以用于制造业的装置检测任务。
PPT_第一章—几何光学基本定律与成像概念

光波——光是一种电磁波 波长范围:1mm~10nm 可见光:380~760nm 红外光:波长>760nm 紫外光:波长<400nm 光速: . m/s (真空) 介质中都小于
一、几何光学的基本定律和原理
1. 基本概念
准单色光的获取 可以通过棱镜、光栅、激光器、滤光片由复色光得 到单色光。
7 2013~2014学年《几何光学》课件 yanglp@
一、几何光学的基本定律和原理
2. 几何光学的基本定律
——入射光线; ——入射角 ——反射光线; ——反射角 ——折射光线; ——折射角 ——法线
光的反射定律: ① 入射光线、法线、反射光线在同一平面内; ② 入射光线和反射光线位于法线两侧,且
数学表达——一阶微分为零,即:
理解:实际光路取极值是指与邻近光路相比较取极小(经 平面反射或经平面折射的两点间)、极大(凹球面镜)或 稳定值(完善成象光学系统的物象点之间)
2013~2014学年《几何光学》课件 yanglp@ 20
, ,0
, 0,0
19
2013~2014学年《几何光学》课件
光的折射定律: 入射光线、法线、折射光线在同一平面内; 折射角的正弦与入射角的正弦之比与入射角的大小 无关,只与两种介质的折射率有关。即 sin 或 sin sin sin
9 2013~2014学年《几何光学》课件 yanglp@ 10
由于 ,所以 空气的折射率为 . ,介质相对于空气的折射 率称为相对折射率,简称折射率 光密介质——分界面两边 折射率高的介质 光疏介质——分界面两边 折射率低的介质
全反射棱镜
用以代替平面反射镜,减少反射时的光能损失
工程光学第一章例题

设水深为H,则明亮圆半径为 R H tan Im
4. 观察清澈见底的河床底部的卵石,看来约在水下半 米深处,问实际河水比半米深还是比半米浅?(P10的 1-4)
站在河岸上看水底,由于光在水中较空气中的传播速度慢,光波由一种媒介进入 到另一种媒介会发生折射。如人在河岸向水中看,这时水底在人眼中所成的像为 图中虚线所示,人看到的河底实际上是经光的折射形成的虚像,所以由岸边向水 中看,虚像比实际河底浅。而由水中向岸上看,虚像比实际物体位置高,可形象 地称为“人看鱼浅,鱼看人高”。
2. 证明光线通过平行玻璃平板时,出射光线 与入射光线平行。(P10的1-2)
3. 游泳者在水中向上仰望,能否感觉整个水 面都是亮的?(P10的1-3)
解:本题是全反射现象和光路可逆现象的综合运用。
sin Im
n空 n水
1 1.33
0.75
Im
4836
所以游泳者在水中仰望天 空,不能感觉整个水面都 是明亮的,而只能看到一 个明亮的圆,圆当然的大 小当然与游泳者所在的水 深有关,如图所示。
sin
Im
n2 n1
n0 sin I1 n1 cos Im
n12 n22
7.已知真空中的光速,求光在水(n=1.333)、冕牌玻 璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶 (n=1.526)、金刚石(n=2.417)等介质中的光速。
•
答:根据
nc v
,分别代入数字得:v
c 3108 m / s nn
1)求满足全反射条件的角α
nsin nsin 90
2)求第一折射面的折射角θ1
θ1=180-α-(180-45) =45-α
n=1.51630 n=1.0
第一章_费马原理1-2(10)

§1-3 成像基本原理/近轴成像
2. 单个球面的折射成像
n(−i)n= n′(−−′) M ii
y
S − i′ = φ − u′ −s r n sin(−i) = n′ sin(−i′)
•
− − = −u + φ iu
O
φ
− i′
C
n ′′ n
(2—1)
u
S′
−y
•
s′
主光轴:折射球面的曲率中心与顶点的连线 下面用Fermat原理推导折射成像公式
y
n
i
−s
n′
A′
A
o
i′
C
B′
− y′
s′
由几何关系,得
y − y′ , i′ = i = −s s′
近轴条件下,在入射点 O 处,由折射定律
liyuhong
ni = n′i ′
§1-3 成像基本原理/近轴成像
联立解得:
ny n ′y ′ − =− s s′
定义垂轴放大率为
因此
y′ β = y ns ′ β = n ′s
特殊情况:当等式的两端同时等于零,即
s s′ − 2 =0 2 2 2 n′ (r − s ′) n (r − s) 1 1 − 2 =0 2 n ′ (r − s ′) n (r − s )
2
2
联立解方程,可同时把 s 和
s ′ 定下来,均与 φ 无关
此时的物点和像点是一对特殊的共轭点,称为折射球面的齐 明点或不晕点。对一对齐明点,宽光束经球面折射后仍能严 格成像。显微镜就工作于齐明点。
f′ f + =1 s′ s
s ′ 第一象限 虚物实像
应用光学各章知识点归纳

第一章几何光学基本定律与成像概念波面:某一时刻其振动位相相同的点所构成的等相位面称为波阵面, 为光波波阵面的传播,与波面对应的法线束就是 光束。
波前:某一瞬间波动所到达的位置。
光线的四个传播定律:1)直线传播定律: 在各向冋性的均匀透明介质中,光沿直线传播,相关自然现象有:日月食,小孔成像等。
2)独立传播定律: 从不同的光源发出的互相独立的光线以不同方向相交于空间介质中 的某点时彼此不影响,各光线独立传播。
3) 反射定律:入射光线、法线和反射光线在同一平面内,入射光线和反射光线在法线 的两侧,反射角等于入射角。
4) 折射定律:入射光线、法线和折射光线在同一平面内;入射光线和折射光线在法线 的两侧,入射角和折射角正弦之比等于折射光线所在的介质与入射光线所在的介质的折射率(折射)光线的方向射到媒质表面,必定会逆着原来的入射方 向反射(折射)出媒质的性质。
光程:光在介质中传播的几何路程 S 和介质折射率n 的乘积。
各向同性介质: 光学介质的光学性质不随方向而改变。
各向异性介质:单晶体(双折射现象)马吕斯定律:光束在各向同性的均匀介质中传播时, 始终保持着与波面的正交性,并且入射波面与出射波面对应点之间的光程均为定值。
全反射临界角:C = arcsin 全反射条件:1) 光线从光密介质向光疏介质入射。
2) 入射角大于临界角。
共轴光学系统: 光学系统中各个光学兀件表面曲率中心在一条直线上。
物点/像点:物/像光束的交点。
实物/实像点: 实际光线的汇聚点。
虚物/虚像点: 由光线延长线构成的成像点。
共轭:物经过光学系统后与像的对应关系。
( A , A'的对称性)完善成像:任何一个物点发出的全部光线,通过光学系统后,仍然聚交于同一点。
每一个物之比,即sin Isin In' n简称波面。
光的传播即 光路可逆:光沿着原来的反射 费马原理: 光总是沿光程为极小,极大,或常量的路径传播。
n2ni点都对应唯一的像点。
光学教程第1章_参考答案

忽略玻璃的厚度,则有n1=n2=1,进而有i1=i2=60°,
则
条纹宽度则为 ,
单位长度内的条纹数为
条
即每厘米长度内由10条条纹。
1.10在上题装置中,沿垂直于玻璃片表面的方向看去,看到相邻两条暗纹间距为1.4mm。已知玻璃片长17.9cm,纸厚0.036mm,求光波的波长。
1.14调节一台迈克耳孙干涉仪,使其用波长为500nm的扩展光源照明时会出现同心圆环条纹。若要使圆环中心处相继出现1000条圆环条纹,则必须将移动一臂多远的距离?若中心是亮的,试计算第一暗环的角半径。(提示:圆环是等倾干涉图样。计算第一暗环角半径是可利用 ≈ 及 ≈1- 的关系。)
解:略
1.15用单色光观察牛顿环,测得某一亮环的直径为3mm,在它外边第5个亮环的直径为4.6mm,所用平凸透镜的凸面曲率半径为1.03m,求此单色光的波长。
解:由牛顿环干涉可知
亮环半径满足的条件为 ,即 ,由题意可得
由上面两式得
所以 nm
1.16在反射光中观察某单色光所形成的牛顿环。其第2级亮环与第3级亮环间距为1mm,求第19和20级亮环之间的距离。
解:由牛顿环干涉可知,亮环半径满足的条件为 ,由题意可得 m
m2
mm
即第19级和第20级亮环之间的距离为0.322mm。
解:(1)图(b)中的透镜由A,B两部分胶合而成,这两部分的主轴都不在该光学系统的中心轴线上,A部分的主轴OA 在系统中心线下0.5cm处,B部分的主轴OB 则在中心线上方0.5cm处, 分别为A,B部分透镜的焦点。由于单色点光源P经凸透镜A和B后所成的像是对称的,故仅需考虑P经B的成像位置 即可。
光学成像中的衍射光学技术研究

光学成像中的衍射光学技术研究第一章介绍在今天的现代科技中,光学成像技术无疑是一个不可或缺的领域。
而光学成像领域中的重要技术之一就是衍射光学技术,它是用于光学成像的基础技术之一。
本文将着重介绍衍射光学技术在光学成像中的作用以及其发展历程。
第二章光学成像技术概述在光学成像中,常用的技术有:成像透镜、光栅衍射成像、绕射成像和像散纠正等。
其中,成像透镜是光学成像中最基本的技术。
透镜和像散纠正技术通过检测和纠正透镜的像差来提高光学成像的精度。
而衍射光学技术是利用光的波动性质,通过物体对光的衍射,得到物体图像的一种技术。
第三章光学衍射技术概述衍射光学技术的原理是利用入射光波与物体相互作用产生的衍射现象得到物体的像,这是一种非常有效的图像处理方法。
在衍射光学技术中,常用的衍射模型包括菲涅耳衍射和菲涅尔-富兰克衍射。
另外,光栅衍射是对于纹理复杂度较高的物体进行成像的理想方法,利用光栅网格对入射光产生衍射现象,再通过相应算法进行图像重建。
第四章光学衍射技术的发展历程在光学技术的发展历史中,衍射成像技术不断得到了改进和拓展。
早在19世纪初,感兴趣的科学家就开始研究衍射现象。
20世纪,随着光源以及光学仪器的发展,光学衍射技术逐步走进人们的视野。
并且衍射光学技术不断地发展,衍射光学技术研究成为了一个成熟的研究领域。
第五章光学衍射技术在实际应用中的作用在实际应用中,衍射光学技术已经广泛应用在各个领域中。
例如在医学领域中,衍射光学成像技术被用来观察人体细胞的形态结构;在材料科学领域,利用衍射光学技术可以得到材料的晶体结构等信息;在光学通信领域,衍射光学技术可以被应用于信息传递中等。
第六章总结本文通过概述了光学成像技术和光学衍射技术的发展历程,探讨了衍射光学技术的原理和在实际应用中的作用。
光学衍射技术是光学成像中非常重要的基础技术之一,一直得到各个领域科学家的密切关注和研究。
在未来的发展中,衍射光学技术仍将继续得到拓展和改进,成为光学成像领域中更为重要的一部分。
第一章几何光学基本定律与成像概念

❖ ③ 一个共轴理想光学系统,如果已知两对共轭面的位置 和放大率,或者一对共轭面的位置和放大率,以及轴上的 两对共轭点的位置,则其它一切物点的像点都可以根据这 些已知的共轭面和共轭点来表示。
仪器科学与光电工程学院
基本概念
波面(波阵面):光波向周围传播,在某一瞬时, 其振动相位相同的点所构成的曲面称为波面。光 的传播即为光波波面的传播,即沿着波面法线方 向传播。
平面波(在距发光点无限远处),对应平行光束 波面分: 球面波(以发光点为中心的同心球面),对应同心光束
任意曲面波(像差作用实际光学系统使同心光束不同心)
仪器科学与光电工程学院
几何光学基本定律
❖ 实验证明: (1) 反射光线和折射光线都在入射面内, 它们与入射光分别在法线两侧。
(2)反射角等于入射角。 II
II
(3)折射角的正弦与入射角的正弦比与
入射角无关,仅由两种介质的性质决定。
即 nsiIn nsiIn
当n’=-n时,折射定律就转化为反射定律
。
L2 B’
A1
A
A’
B1
对于L1而言,A1B1是AB的像;
对L2而言,A1B1是物,A’B’是像,则A1B1称为中 间像
仪器科学与光电工程学院
※物所在的空间为物空间,像所在的空间为 像空间,两者的范围都是(-∞,+∞)
※ 通常对于某一光学系统来说,某一位置 上的物会在一个相应的位置成一个清晰的像, 物与像是一一对应的,这种关系称为物与像 的共轭。
仪器科学与光电工程学院
光学第一章 - 费马原理与变折射率光学
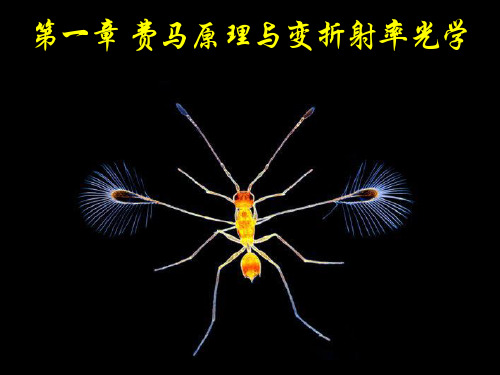
n1 sin i1 n2 sin i2
n1 sin i1 n2 sin i2
临界角 (critical angle)
当光从光密介质射向光疏介质(n1>n2)时, 如果入射角大于(全反射)临界角iC, 入射光将全部返回光密介质,发生全反射 (total internal reflection)。
第一章 费马原理与变折射率光学
第一章 费马原理与变折射率光学
一、惠更斯原理 二、费马原理 三、成像 四、共轴球面光具组傍轴成像 五、薄透镜 六、理想光具组理论 七、矩阵光学 八、光学仪器简介 九、像差 十、光纤及变折射率光学
第一章 费马原理与变折射率光学
一、惠更斯原理 二、费马原理 三、成像 四、共轴球面光具组傍轴成像 五、薄透镜 六、理想光具组理论 七、矩阵光学 八、光学仪器简介 九、像差 十、光纤及变折射率光学
惠更斯原理的不足:
不能回答光振幅或光强的传播问题; 不能回答光位相的传播问题。
惠更斯-菲涅耳原理 光场衍射理论的诞生
惠更斯原理的精华:
次波源的概念。
第一章 费马原理与变折射率光学
一、惠更斯原理 二、费马原理 三、成像 四、共轴球面光具组傍轴成像 五、薄透镜 六、理想光具组理论 七、矩阵光学 八、光学仪器简介 九、像差 十、光纤及变折射率光学
◈折射定律和速度比
光粒子说:
sin i1 v2 const sin i2 v1
1850年傅科和斐索测量了光速, 光波动说又一次得到了证实。
折射率:
In optics the refractive index or index of refraction n of a substance (optical medium) is a dimensionless number that describes how light, or any other radiation, propagates through that medium. It is defined as n=c/v, where c is the speed of light in vacuum and v is the speed of light in the substance.
第一章几何光学基本定律与成像概念

第一章几何光学基本定律与成像概念第一章几何光学基本定律和成像概念1.尝试用折射定律证明光的可逆性原理。
2.尝试用实验证明几何光学的每一个基本定律。
3.弯曲的光纤可以将光从一端传输到另一端。
在均匀介质中,这种光是线性传播的吗这违反法律吗?4.证明当光线穿过几块放置在空气中的平行玻璃板时,出射光和入射光的方向总是相同的平行。
5.试着解释为什么远处的灯光在荡漾的湖面上反射的时间更长。
6.弯曲的光纤可以将光从一端传输到另一端。
在均匀介质中,这种光是线性传播的吗违反法律7.证明当光穿过几块平板玻璃时,出射光和入射光的方向总是平行的。
8.太阳的高度正好使它的光和水平面形成40度角。
询问如何放置镜子来制作镜子阳光直射到井底?9.水的折射率是1.33。
光从空气进入水中的入射角是30度。
问:折射角是多少?诸如如果光连续地从垂直入射变为掠入射,那么折射角会相应地改变多少?10.光线以60度的入射角入射到玻璃板上。
一些光被反射,一些光被折射。
如果反射光玻璃的折射率是多少?11.光从水到某种玻璃的相对折射率是 1.18,从水到甘油的相对折射率是1.11。
从这个玻璃入射到甘油上的光的相对折射率是多少?12.给出了水(折射率为1.33)和玻璃(折射率为1.55)之间的界面,并在水中以45°角计算出一束光。
入射到界面上的透射光的折射角。
如果反向光现在返回到从玻璃沿透射光方向投射的反向界面,则证明折射角为45°。
13.有一个折射率为1.54的等腰直角棱镜。
当找到入射光和棱镜直角边法线之间的角度时,光被斜面反射后,折射光沿斜面射出。
14.空气中有一个折射率为1.5163的玻璃球。
今天,一束光线击中了球的前表面。
如果入射角为60°,计算表面上反射光和折射光之间的角度。
15.折射率n1=1.4、n1’= n2=1.6、N2 = 1的三种介质被两个平行的界面分开,试着寻找第二种介质当物质发生全反射时,光在第一界面上的入射角。
光学第一章习题解答 - 副本概要

2
(3)
I 4 A cos
2 1
0
2
2
1
2
2 1
I 4A
I
p 2
2 1
4
4 cos cos 0.854 I 2 8
2 0
1 cos
4 2 2 2 4
1.3 把折射率n为1.5的玻璃片插入杨氏实验的一 束光路中,光屏上原来第5级亮纹所在的位置。变 为中央亮条纹,求插入玻璃片的厚度。(已知光的 波长为600nm)。
i2 0
2 0
j0
2 1 2
2
(无半波损失)
or : 2d 0 n n sin i1 (2 j 1)
2
5
i1 0
\ d 0 min
5500 × 10 4n 4 × 1.38
7
10 cm
1.9 在两块玻璃片之间一边放一条厚纸,另一边相 互压紧,玻璃片 l 长10cm,纸厚h为0.05mm,从600 的反射角观察波长为500nm的单色光源的象。试问玻 璃片单位长度内能看到的干涉条纹的数目是多少?
0 2 2 2
2 1 1 700 4260 A 考虑半波损失 1.33 1 sin 30 4
0 2 2 2 o
or : 2h n n sin i
2 2 2 2 1 1 2 2 2 2 1 1
2
2h n n sin i (2 j 1) 2 j 1 h n n sin i 4
解:斜面上每一条纹的宽度所对应的空气劈尖的 厚度的变化量为 h h h j 1 j 2 H h x x L n 1
光场成像技术的研究与应用

光场成像技术的研究与应用第一章介绍光学成像技术已经成为科学、医疗、工业等众多领域的基础工具。
近年来,随着计算机科学和数字信号处理技术的不断发展,出现了新兴的光场成像技术。
光场成像技术不仅可以记录物体的各个方向上的光学信息,还可以对物体进行数码焦处理和数码光学变焦。
本文将重点介绍光场成像技术的研究和应用。
第二章光场成像技术的基本原理光场成像技术的基本原理是在微观尺度下,物体这一区域内的每一点都能发射出大量的子光束。
通过记录和处理这些子光束的交叉信息,可以获得物体在三维空间内的光场信息。
光场图像的解密依赖于计算机处理能力和数字信号处理技术。
光场成像技术常用的方法主要包括物体波前捕获和背景光经过规定轨迹后在物体表面形成干涉条纹等。
第三章光场成像技术的应用3.1 医学影像在医学方面,光场成像技术可应用于动态全息术,用于捕捉和传输三维医学图像,如人体器官形态、运动、自发活动和药物传输等生理功能及其内部结构。
采用光场成像技术对疾病的研究有帮助,可提高疾病诊断和治疗效率,成为医学影像领域的一种有前景的方法。
3.2 工业制造在工业制造行业,光场成像技术可以用于检测和测量物体形状、表面和内部结构,以及质量的控制和改进,如半导体工艺、汽车制造、制药和航空航天等领域。
光场成像技术在工业制造中有广泛的应用,是提高生产效率和保证产品质量的重要手段。
3.3 虚拟现实光场成像技术可用于虚拟现实和增强现实技术,如计算机游戏、立体电影等,这些技术通过深度和距离信息感知用户的环境,可以产生增强现实感和超现实的体验。
光场成像技术的应用将为虚拟现实技术带来更丰富、更真实的视觉体验。
第四章光场成像技术的未来发展未来光场成像技术的发展有望在更广阔领域发挥重要作用,特别是随着虚拟现实技术和增强现实技术的发展,光场成像技术将成为这些领域的关键技术。
在医学领域,光场成像技术将有望更广泛地应用于生理学和病理学的研究。
在工业制造领域,光场成像技术将有望提高产品质量、加快设计和生产过程。
光学教程第1章参考答案

1-1波长为500nm的绿光投射在间距〃为0.022cm的双缝上,在距离斥)为180cm处的光屏上形成干涉条纹,求两个亮条纹之间的距离•若改用波长为700nm的红光投射到此双缝上,两个亮条纹之间的距离又为多少?算出这两种光第2级亮纹位置的距离。
解:相邻两个亮条纹之间的距离为△y =畑+ x =字d=180x1() -%500x 10-9 心0.409x 10"2m0.022x10-2若改用700nm的红光照射时,相邻两个亮条纹之间的距离为Av = y M + x =十几a= ⑶)小)x700x10~9 q0.573x 10~2m0.022 x 10~2这两种光第2级亮条纹位置的距离为△)' = >‘21—00””厂==2x N)xl()〒x[(700_500)x 10-y]«3.27x10"加0.022 xW21.2在杨氏实验装置中,光源波长为640nm,两狭缝间距〃为0.4inm,光屏离狭缝的距离心为50cm•试求:(1)光屏上第1亮条纹和中央亮条纹之间的距离;(2)若P点离中央亮条纹O.liniii,问两束光在P点的相位差是多少?(3)求P点的光强度和中央点的强度之比。
解:⑴因为y = J^-2(j=0, l)o所以第1亮条纹和中央亮条纹之间的距离为r 50 x 1[)~2Ay = + 儿=(1 一0)丄2 = --------- r x MO x 10" = 8.0 x 10"加- d 0.4x10」(2)因为,若P点离中央亮纹为0.1mm,贝9这两束光在P点的相位差为. 2. 、2^ yd2龙0.1 xlO'3 x0.4xl0~5兀2 2 zb 640x10-9 50x10- 4⑶山双缝干涉中光强I(p) = 2A J2(/7)[1 + cosA^(/?)],得P点的光强为I(p) = 2A12(/?)[ 1 + cosA^(/?)] = 2A12(p)[l + ^] = A I2(p)[2 + ^2],中央亮纹的光强为1。
八年级物理光学第一章知识点

八年级物理光学第一章知识点一、光的概念及性质光是人们能够直接感知到的一种电磁波辐射,它具有波粒二象性。
光的电磁波理论是最基本的光学理论,它把光视为一种电磁波,它的速度是固定且非常快的。
光的性质有:直线传播、折射、反射、干涉、衍射和偏振。
其中,折射是光线通过介质表面时方向发生改变的现象,反射是指光照射到物体表面时,一部分光线返回原来的方向的现象。
干涉和衍射是光学的现象,后者指光线传播时会弯曲绕过障碍物,前者是指两个或多个波面干涉所产生的互相强化或互相抵消的现象。
光的偏振是指光波中的电场向量只在某个平面内振动的现象。
二、光的传播与光线光的传播是指光从一处到另一处的过程,可以分为直线传播和曲线传播两种形式。
在物理学中,常说的“光线”并不是真正的光线,而是表征光传播方向的一条射线。
光线只是人为的虚构概念,它并不存在于真实光学中。
三、光线的反射与折射光线的反射是指光线照到物体上,并且回弹到原来入射的方向的现象。
在反射光线照到物体表面时,可以得出反射定律。
光线的折射是指光线穿过介质,方向发生了改变的现象。
当光线从一种介质到另一种介质时,可以得出折射定律。
四、光的波动模型光学传统的观点认为光是以波动形式传播的,这种观点依据于被物体表面反射、折射、干涉、衍射和偏振等现象所证明。
在光的波动模型中,光的波长、频率和速度之间存在着一定的关系,即“光速不变理论”。
五、光学仪器光学仪器分为常用光学仪器和专用光学仪器两大类。
常用光学仪器包括显微镜、望远镜、透镜、反射镜、棱镜等;专用光学仪器包括激光器、光电子显微镜、红外光谱仪等。
通过对光学仪器的研究和利用,可以加深对光学的理解和应用。
光学作为应用广泛的一个学科,涉及到工业、医药、通讯、交通等各个领域。
八年级物理光学第一章的知识点涵盖了光的概念、性质、传播、反射、折射、波动模型和光学仪器等方面的内容,是打好光学基础的重要一步。
第一章照相机基础知识
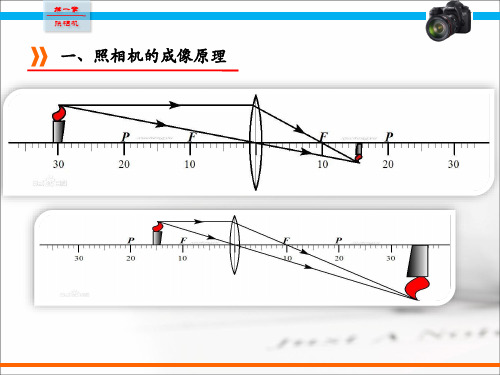
中焦、长焦、远摄镜头:一个镜头的焦距尺寸大于底片
对角线的尺寸,或者说大于标准镜头的焦距,这个镜头就可以被叫做长焦镜 头。但是,习惯上,人们把80mm—135mm的镜头称为中焦镜头,把 135mm—300mm的镜头称作长焦镜头,把300mm以上的镜头称作远摄镜头。
变焦镜头
一般的定焦镜头焦距是固定的,而变焦镜头的焦距可以根据拍摄需要,在一
六、常用摄影附件
1.三脚架和单脚架
2.遮光罩主 要作用:
(2)可在一定 程度上防止尘 土、雨滴、雪 花等进入镜头 表面,造成对 镜面镀膜的破 坏。 (1)防止不必 要的光线进入 镜头从而对底 片画面产生破 坏作用;
3. 反光布: 主要用于拍摄人像 时,人面侧光或背光下对人面 不进行柔性补光;
1、快门。 快门的作用
控制光线进入和停留在感光面上的时间 机械快门、电子快门、机械电子快门 30秒到四千分之一秒,B门、T门
快门的类型
快门时间等级
所谓T门,是指按下快门按钮快门打开,开始曝光,而且快门持续打开,
直至再次按下按钮时快门关闭即停止曝光。
所谓B门,是快门的最慢的一档,你想要多慢就有多慢的一档,按
1,镜头焦距:
焦距,是光学系统中衡量光的聚集或发散的度量方式,指平行镜头焦距光从透镜 的光心到光聚集之焦点的距离。亦是照相机中,从镜片中心到底片或CCD等成像 平面的距离。具有短焦距的光学系统比长焦距的光学系统有更佳聚集光的能力。
2、镜头焦距与视角的关系
焦距越长、视角越短。焦距越短,视角越长
3、镜头分类
焦距 底片尺寸
50mm
75mm 105mm 150mm 300mm
24×36mm
60×60mm 60×90mm 4×5英寸 8×10英寸
光学教程-第一章总结

干涉相消
2
1
k1r1
k2r2 =
2 0
n1r1
2 0
n2r2
(2
j+1)
( j 0,1, 2 )
光程差
n1r1
n2r2
(2
j +1)0
2
( j 0,1, 2 )
等倾干涉
n2 n1
1
L 2
P
i1 D
3
M1 n1 n2
Ai 2 i
C
d
M2 n1
2
B
E
45
光程差
0 2d0
n22 n12 sin2 2d0n2 cos i2
两个同振动方向同频率的振动叠加
E1 A1 cos(t-k1r1 1) E2 A2 cos(t-k2r2 2 )
1 = k1r1 1 2 = k2r2 2
干涉相长
2
1
k1r1
k2r2 =
2 0
n1r1
2 0
n2r2
2
j
( j 0,1, 2 )
光程差
n1r1
n2r2
2
j
0
2
( j 0,1, 2 )
明环半径:
2n
暗环半径: r 2 j R
n2
迈克耳孙干涉仪(Michelson interferometer)
M1与M'2形成空气薄膜层,可产生等倾干涉和等厚干涉。 等倾干涉用扩展光源,等厚干涉用平行光.
等倾干涉
等厚干涉
n1 n2
n2 n1 或者 n2 n1 有半波损失
n1
n1 n2
nn13
n2 n2
或者
nn13
第一章 几何光学基本定律与成像概念

第一章几何光学基本定律与成像概念1.试由折射定律证明光线的可逆性原理。
2.试对几何光学的每条基本定律提出一个实验来证明它。
3.弯曲的光学纤维可以将光线由一端传至另一端,这是否和光在均匀介质中直线传播定律相违背?4.证明光线通过置于空气中的几个平行的玻璃板时,出射光线和入射光线的方向永远平行。
5.试说明,为什么远处灯火在微波荡漾的湖面形成的倒影拉得更长?6.弯曲的光学纤维可以将光线由一端传至另一端,这是否和光在均匀介质中直线传播定律相违背7.证明光线通过几个平面的玻璃板时,出射光线和入射光线的方向永远平行。
8.太阳的高度恰好使它的光线和水平面成40°角,问镜子需怎样放置,才能使反光镜的阳光垂直射入井底?9.水的折射率是1.33,光线从空气射入水中,入射角是30°,问:折射角是多大?如果光线从正入射连续改变到掠入射时,折射角相应地有多大的改变?10.光以60°的入射角射到玻璃板上,一部分光被反射,一部分光被折射,若反射光线和折射光线互成90°,玻璃的折射率是多少?11.光从水射到某种玻璃时的相对折射率是1.18,从水射到甘油时的相对折射率是1.11,光线从这种玻璃入射到甘油时的相对折射率是多少?12.给出水(折射率1.33)和玻璃(折射率1.55)的分界面,求一束光在水中以45°角入射到分界面上时透射光线的折射角,若现在倒过来光线沿此透射光方向返回从玻璃投射倒分界面上,证明其折射角为45°。
13.有一折射率为1.54的等腰直角棱镜,求入射光线与该棱镜直角边法线成什麽角度时,光线经斜面反射后其折射光线沿斜边出射。
14.有一个玻璃球,其折射率为1.5163,处于空气中,今有一光线射到球的前表面,若入射角为60°,求在该表面上此反射光线和折射光线之间的夹角。
15.折射率n1=1.4,n1′=n2=1.6,n2=1的三种介质,被二平行界面分开,试求在第二介质中发生全反射时,光线在第一分界面上的入射角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1同济大学物理系同济大学物理系成像光学2010年9月2同济大学物理系同济大学物理系教材教材:光学原理(第七版上、下册)(德)玻恩(美)沃耳夫(著) |电子工业出版社参考书:•高等光学教程--光学的基本电磁理论季家镕(著) |科学出版社|•物理光学(第3版) 梁铨廷(著) | 电子工业出版社绪论光学几何光学(应用光学)物理光学(波动光学)把光看成沿光线传播,包括直线传播、反射、折射定律等,它是波动光学的极限情况;研究光的物理属性,包括它传播的规律和它与物质之间的相互作用,如光的干涉、衍射和偏振、在介质中的吸收、色散和散射等现象;量子光学电磁理论方法研究光的波粒二象性,而一切微观粒子都具有波粒二象性。
3同济大学物理系同济大学物理系4同济大学物理系同济大学物理系梯度、散度和旋度∇算符:x y ze e e x y z ∂∂∂∇=++∂∂∂ x y ze e e x y z ϕϕϕϕ∂∂∂∇=++∂∂∂ y x zf f f f divf x y z∂∂∂∇⋅==++∂∂∂ xyzxy ze e ef rotf x y z f f f ∂∂∂∇×==∂∂∂ 标量场的梯度:矢量场的散度:矢量场的旋度:5同济大学物理系同济大学物理系矢量场的散度:设闭合曲面s 所包围的体积为ΔV ,则ΔV Æ0时,A 对s 的通量与ΔV 之比的极限称为A 的散度div limsV A dSA A VΔ→⋅=∇⋅=Δ∫K K K Kv 散度的重要性在于,当div A >0时,表示该点有发散通量的正源;当div A <0 ,表示该点有吸收通量的负源;当div A=0 ,表示该点为无源场。
6同济大学物理系同济大学物理系矢量场的旋度:设闭合曲线L 围着的面积为ΔS ,则ΔS Æ0时,A 对L 的环量与ΔS 之比的极限称为A 的旋度沿该面法线的分量()()0rot limlnns A dl A A SΔ→⋅=∇×=Δ∫K K K Kv 旋度的重要性在于,可用以表征矢量在某点附近各方向上环流强弱的程度,如果场中处处rot A =0,称为无旋场。
7同济大学物理系同济大学物理系sA dS AdV⋅=∇⋅∫∫K K K v 高斯定律(Gauss theorem)()LA dl A dS⋅=∇×⋅∫∫K K K K v 斯托克斯定律(Stokes theorem)把一个闭合曲面的面积分转为对该曲面所包围体积的体积分,反之亦然。
把对任意闭合曲线边界的线积分转换为该闭合曲线为界的任意曲面的面积分,反之亦然。
8同济大学物理系同济大学物理系*关于散度和旋度的一些定理(1)标量场的梯度必为无旋场≡∇×∇ϕ令ϕ∇=f()()0 =⎟⎟⎠⎞⎜⎜⎝⎛∂∂∂∂−⎟⎠⎞⎜⎝⎛∂∂∂∂=∂∂−∂∂=×∇=∇×∇y z z y zf y f f yz x xϕϕϕ 同理可证其他分量也为0,因此≡∇×∇ϕ(2)矢量场的旋度必为无源场)(=×∇⋅∇fy yx x z zff ff ff fx y z y z x z x y∇⋅∇×∂∂⎛⎞⎛⎞∂∂∂∂∂∂∂⎛⎞=−+−+−⎜⎟⎜⎟⎜⎟∂∂∂∂∂∂∂∂∂⎝⎠⎝⎠⎝⎠=9同济大学物理系同济大学物理系10同济大学物理系同济大学物理系(3)无旋场必可表示为标量场的梯度(4)无源场必可表示为另一矢量的旋度=×∇f ϕ∇=f0=⋅∇f Af ×∇=11同济大学物理系同济大学物理系* 算符运算公式()()()()()()()()g f g f g f ff f ff f ×∇⋅−⋅×∇=×⋅∇×∇+×∇=×∇⋅∇+⋅∇=⋅∇∇+∇=∇ϕϕϕϕϕϕϕψψϕϕψ注意:∇---微分算符,矢量性质,次序12同济大学物理系同济大学物理系()()()()()()()()()()()()ff f fg f g gf g f g f g f g f fg f g g f22∇−⋅∇∇=×∇×∇∇≡∇⋅∇∇⋅+×∇×+∇⋅+×∇×=⋅∇⋅∇−∇⋅−⋅∇+∇⋅=××∇ϕϕ13同济大学物理系同济大学物理系自从19世纪人们证实了光是一种电磁波后,又经过大量的实验,进一步证实了X 射线、γ射线也都是电磁波。
它们的电磁特性相同,只是频率(或波长)不同而已。
如果按其频率(或波长)的次序排列成谱,称为电磁波谱。
14同济大学物理系同济大学物理系1.1 电磁场-麦克斯韦方程组tD C j CH tB C E B D ∂∂+=×∇∂∂−=×∇=⋅∇=⋅∇14104ππρD, E, B, H 分别称为:电位移矢量,电场强度,磁感应强度和磁场强度,ρ称为电荷密度,j 代表电流密度。
James Clerk Maxwell(1831-1879)15同济大学物理系同济大学物理系4D πρ∇⋅=K电场是有源场磁场是无源场法拉第电磁感应定律安培全电流定律B ∇⋅=K 41D H jC C tπ∂∇×=+∂1B E C t ∂∇×=−∂KK16同济大学物理系同济大学物理系* 微分形式的麦克斯韦方程组tB E ∂∂−=×∇ tD J H ∂∂+=×∇ρ=×∇D 0=×∇B 麦克斯韦方程揭示了电场、磁场的性质及电、磁场之间的联系变化的磁场产生变化的电场:为涡旋场E电流或变化的电场产生变化的磁场为有旋无源场H空间电荷分布决定电场为有源场D没有单独的磁极存在为无源场B17同济大学物理系同济大学物理系* 积分形式的麦克斯韦方程组σd t D J l d H ⋅⎟⎟⎠⎞⎜⎜⎝⎛∂∂+=⋅∫∫∫ΣVd d D ∫∫∫∫∫ΣΩ=⋅ρσ 0=⋅∫∫Σσd B ∫∫∫∑⋅∂∂−=⋅σd t B l d E 高斯定理的数学表示在交变的电磁场中,磁场包含传导电流和位移电流产生的磁场磁场是无源场法拉第电磁感应定律的数学描述:J∑::ρ:Ω表示传导电流密度表示曲面面积表示自由电荷密度表示曲面所包围空间的体积18同济大学物理系同济大学物理系1.1.1 麦克斯韦方程组()4114D H j C C t D j t ππ⎛⎞∂∇⋅∇×=∇⋅+∇⋅⎜⎟∂⎝⎠⎛⎞∂⇒∇⋅=−∇⋅⎜⎟∂⎝⎠4D πρ∇⋅=电流连续性方程:j tρ∂∇⋅+=∂ 电荷守恒定律的微分形式41DH j C C tπ∂∇×=+∂1.1.1 麦克斯韦方程组电流连续性方程:电荷守恒定律的积分形式dj dS dVdtρ⋅+=∫∫KKvS代表了一个闭合曲面,方向朝外法线方向。
第一项代表流入流出该区域V的电流;第二项是区域内的包含的总电荷的变化率。
总的来说:通过界面的流出的电流应该等于区域V内的电量减小率。
19同济大学物理系同济大学物理系20同济大学物理系同济大学物理系1.1.2 物质方程麦克斯韦方程组可用来描述电磁场的变化规律,但在处理实际问题时,电磁场总是在媒质中传播的,媒质的性质对电磁场的传播会带来影响。
描述物质在场作用下特性的关系式称为物质方程。
静止的、各向同性的(物质每一点的物理性质不随方向改变)媒质中的物质方程存在以下关系:E jσ=E D ε=HB μ=σ是电导率ε是介电常数(或电容率)μ是磁导率21同济大学物理系同济大学物理系1.1.2 物质方程E jσ=E D ε=HB μ=σ是电导率ε是介电常数(或电容率)μ是磁导率在各向同性均匀介质中,ε、μ是常数,σ=0。
22120/108542.8mN C ⋅×==−εε2270/104CS N ⋅×==−πμμ在真空中,对于非磁性物质,0μμ≈物质方程的特殊情况:•场强度极大的情况—例如强激光场与物质相互作用;•各向异性材料—例如晶体材料;•材料特性是时间的函数—例如铁磁材料;22同济大学物理系同济大学物理系麦克斯韦方程组使用于连续媒质的空间区域。
但当电磁波由一种介质传播到另一种介质时,电磁场在界面上将是不连续的。
现在来推导场从这种突变面通过时服从的关系式。
图1.1在过渡层T 内,作一小近似圆柱体,T 的法线为柱壁,δA 1和δA 2分别为柱顶和柱底,距离为δh 。
利用麦氏方程和高斯定律可得:23同济大学物理系同济大学物理系图1.1sBdV B dS ∇⋅=⋅=∫∫K K K v 面积分遍及圆柱体表面并方向向外法线,当δh->0时:()112212212100n nB n B n n B B B B ⋅+⋅=⇒⋅−=⇒=K K K KK K K结论:通过突变面磁感应强度法线分量是连续的:()12210n B B ⋅−=K K K24同济大学物理系同济大学物理系图1.1结论:电位移矢量法线分量通过此面时要发生突变,改变量由下面公式给出:对于电场:4D πρ∇⋅=K()11221221ˆ4ˆ4D n D n n D D πρπρ⋅+⋅=⇒⋅−=K K K KK K K()1221ˆ4n D D πρ⋅−=K K K面积分遍及圆柱体表面并方向向外法线,当δh->0时:25同济大学物理系同济大学物理系1l B E dS E dl dS C t∂∇×⋅=⋅=−⋅∂∫∫∫KK K K K K v 对于电场的切向分量:图1.2把突变面换成过渡层T ,并取长方形,令其四边形分别与T 平行和垂直。
由斯托克斯公式:当δh->0时:1122120t tE t E t E E ⋅+⋅=⇒=K K K K 结论:通过突变面时电矢量切线分量是连续的:()12210n E E ×−=K K K1B E C t∂∇×=−∂KK 1.1.3 突变面处的边界条件26同济大学物理系同济大学物理系对于磁场的切向分量:图1.2结论:通过突变面时磁矢量切线分量发生突变:()1122122114ˆ 4ˆContribution D H t H t S j t from ends C t Cn H H jcπδδπ∂⋅+⋅+=⋅+⋅∂⇒×−=KK K K K K K K K Kj 代表线电流密度()12214ˆn H H jcπ×−=K K K K 41D H j C C tπ∂∇×=+∂1.1.3 突变面处的边界条件27同济大学物理系同济大学物理系电磁场是一种物质,它的运动和其它物质运动形式上相互转化,所以就有能量传递。
下面利用电磁场与带电物质相互作用中导出电磁场能量表达式:电荷e 在电磁场(E,B)以速度V 运动时,电荷受到洛仑兹力的作用:如果场对于所有电荷作用一段位移,则场作的总功为:⎟⎠⎞⎜⎝⎛×+=B V C E e F 1v A t v EdV A t j EdVδδρδδ=⋅⇒=⋅∫∫KK K K 其中j v 代表运流电流密度28同济大学物理系同济大学物理系2c v v j EdV j EdV j EdVE dV j EdVσ⋅=⋅+⋅=+⋅∫∫∫∫∫K K KK K K K K 141BE C tD H j C C tπ∂∇×=−∂∂∇×=+∂K K KK K 由麦氏方程可知j=j v +j c ,j v 和j c 分别代表运流电流和传导电流密度,则电场E 对导体总的电荷做功的功率之和为:14C D j E E H C t π⎛⎞∂⎟⎜⎟⋅=⋅∇×−⎜⎟⎜⎟∂⎝⎠KK K K K ()f g g f f g∇⋅×=⋅∇×−⋅∇×K K K K K K()()()144148C D B j E E H E H t t CE H E D H B tππππ⎛⎞∂∂⎟⎜⎟−⋅=∇⋅×+⋅+⋅⎜⎟⎜⎟∂∂⎝⎠⎡⎤∂⎢⎥=∇⋅×+⋅+⋅⎢⎥∂⎣⎦K K K K K K K K K K K K K K 电能密度:磁能密度:坡印亭矢量:电磁场能量定律的微分形式:wj E St∂−⋅=+∇⋅∂K K K 坡印亭矢量:是一个矢量,代表单位时间流过单位面积上的能量。
