选修专项突破01
2020年高考英语语法专项突破训练专题01-冠词(含答案)
专题一冠词重难点分析冠词是一种虚词,没有词义,不能单独使用,放在名词的前面,帮助说明名词的含义。
冠词主要分为定冠词、不定冠词和零冠词。
历年高考试题对冠词的考查涉及到冠词的位置、不定冠词、定冠词、零冠词及固定搭配中的冠词等各个方面。
下面我们以表格的形式对前四个方面进行梳理总结。
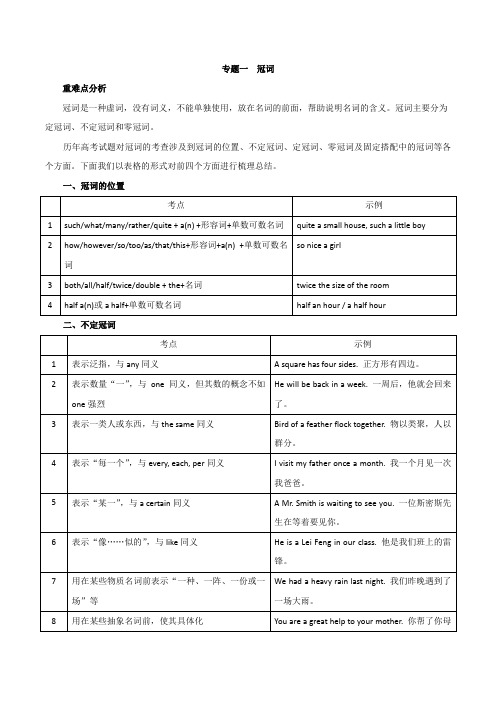
一、冠词的位置考点示例1 such/what/many/rather/quite + a(n) +形容词+单数可数名词quite a small house, such a little boy2 how/however/so/too/as/that/this+形容词+a(n) +单数可数名词so nice a girl3 both/all/half/twice/double + the+名词twice the size of the room4 half a(n)或a half+单数可数名词half an hour / a half hour二、不定冠词考点示例1 表示泛指,与any同义 A square has four sides. 正方形有四边。
2 表示数量“一”,与one同义,但其数的概念不如one强烈He will be back in a week. 一周后,他就会回来了。
3 表示一类人或东西,与the same同义Bird of a feather flock together. 物以类聚,人以群分。
4 表示“每一个”,与every, each, per同义I visit my father once a month. 我一个月见一次我爸爸。
5 表示“某一”,与a certain同义 A Mr. Smith is waiting to see you. 一位斯密斯先生在等着要见你。
6 表示“像……似的”,与like同义He is a Lei Feng in our class. 他是我们班上的雷锋。
7 用在某些物质名词前表示“一种、一阵、一份或一场”等We had a heavy rain last night. 我们昨晚遇到了一场大雨。
高考英语语法词汇专项突破:01重点语法易错易混点(被动语态、by+Ving和情态动词)

高考英语语法词汇专项突破:01重点语法易错易混点(被动语态、by+Ving和情态动词)被动语态、by+Ving和情态动词的用法,现将它们的易错易混点总结如下:【误用1】Our house is being knocking down to make way for a new road.【指正】knocking改为knocked。
现在进行时的被动语态构成是:is/are being done,表示谓语动词动作正在被进行,句子主语与谓语动词之间是动宾关系。
【运用】A meeting on education is being held in Shanghai.【误用2】When the ship sank we had to save ourselves with swimming.【指正】with改为byby doing是“介词by+动名词”形式,表示方式或者手段,在句子中作方式状语。
【运用】He lightened his bag by taking out some books.【误用3】—Can’t you stay a little longer?—It’s getting late. I really may go now. My daughter is home alone.【指正】may改为must或have to。
情态动词may在确定句中表示“可以”,即说话人同意或者许可。
依据“天晚了”和“女儿一个人在家”看出说话人要走,可以理解为认为必需走了,用must,或者由于前后句子提出的事实状况,认为客观状况使得不得不走,用have to。
【运用】She must think rapidly, make a plan, make some use of her knowledge.【误用4】— I’ve prepared all kinds of food for the picnic.—Do you mean we shan’t bring anything with us?【指正】shan’t改为needn't。
高考生物大二轮复习 第02部分 01 选择题专项突破 突破题型02 图解图示类——有效“架桥”破解学案

突破题型2 图解图示类——有效“架桥”破解1.(2016·江苏卷)下图为一种溶质分子跨膜运输的示意图。
下列相关叙述错误的是( )A.载体①逆浓度运输溶质分子B.载体②具有ATP酶活性C.载体①和②转运方式不同D.载体②转运溶质分子的速率比自由扩散快解析:载体①是逆浓度梯度将溶质分子由胞外向胞内转运;载体②是顺浓度梯度将溶质分子由胞内转运到胞外,不需要消耗ATP,载体②不具有ATP酶活性;图中载体①和②分别参与溶质分子逆浓度梯度和顺浓度梯度的运输,前者是主动运输,后者是协助扩散;依赖载体蛋白顺浓度梯度转运溶质分子的速率要比自由扩散快。
答案:B2.(经典高考)细胞的膜蛋白具有物质运输、信息传递、免疫识别等重要生理功能。
下列图中,可正确示意不同细胞的膜蛋白及其相应功能的是( )解析:血红蛋白存在于红细胞内,不是在细胞膜上,A错误;抗原对T淋巴细胞来说是信号分子,通过T淋巴细胞膜上的受体来接受,而不是抗体,B错误;受体具有特异性,胰高血糖素应作用于胰岛B细胞上的胰高血糖素受体,而不是胰岛素的受体,C错误;骨骼肌作为反射弧中的效应器,骨骼肌细胞上有接受神经递质的受体,同时葡萄糖进入细胞也需要载体协助,D正确。
答案:D3.(2016·江苏卷)突变酵母的发酵效率高于野生型,常在酿酒工业发酵中使用。
下图为呼吸链突变酵母呼吸过程,下列相关叙述错误的是(多选)( )A.突变酵母乙醇代谢途径未变B.突变酵母几乎不能产生[H]C.氧气充足时,野生型酵母种群增殖速率大于突变体D.通入氧气后,突变酵母产生ATP的主要部位是线粒体解析:据图分析可知,与野生型酵母相比,突变酵母乙醇代谢途径未变,只是线粒体中的呼吸链中断;分析题图可知,突变酵母可以进行无氧呼吸,在第一阶段能够产生[H];氧气充足时,野生型酵母可进行有氧呼吸,产生能量多,通过出芽生殖快速繁殖后代,而突变酵母不能进行有氧呼吸,产生的能量少,繁殖的速度慢;据图可知,突变酵母的呼吸链中断,通入氧气后,突变酵母产生ATP的部位只有细胞质基质。
2023年中考语文必考12部名著专项突破01《朝花夕拾》(答案带解析)

专题01 《朝花夕拾》中考回应一、选择题1.(2022·吉林·统考中考真题)下面是对《朝花夕拾》主题的理解,请选出不恰当的一项()A.表达对童年自由快乐生活的喜爱。
B.表达对儿童天性被束缚的无奈和厌烦。
C.揭露阿长、庸医、衍太太等人在人性方面的丑陋。
D.批判封建社会不顾人情甚至灭绝人性的所谓“孝道”。
【答案】C【解析】C.阿长主要出现在《阿长与<山海经>》一文中,文中的阿长虽然有着各种不好的习惯,而且还封建迷信,但她却深切关爱着鲁迅,为他买来了《山海经》。
在文中,作者表达了对阿长的感激与怀念之情。
故选C。
2.(2022·广西·统考中考真题)下面对《朝花夕拾》的表述,不正确的一项是()A.鲁迅先生的一部散文集,10篇文章都是“从记忆中抄出来”的“回忆文”,记录了鲁迅从幼年到青年时期的生活经历,是鲁迅作品中最富生活情趣的篇章:这就是作者给集子起名《朝花夕拾》的原因。
B.文中往往呈现出往日和现实两个世界,共存着对往事的温和怜爱和对现实的辛辣批判两种不同情感和温度的文字,表现出作者对人间美好、温暖的爱和对世间无知、冷漠的憎:这种双重性正是《朝花夕拾》的思想价值所在。
C.没有姓名的保姆“长妈妈”,大声朗读古诗文时将头仰起“向后面拗过去,拗过去”的旧学先生,《无常》中在迎神赛会上表演的“活无常”:从《朝花夕拾》中可以窥见旧中国真实的生活面貌。
D.从《琐记》中神往于“老鼠成亲”充满童趣的“我”,到《从百草园到三味书屋》中敢于提问“怪哉”为何物的充满好奇的“我”,再到《父亲的病》中苦苦寻求救国真理的“我”:《朝花夕拾》重温了作者的成长道路。
【答案】D【解析】D.“《父亲的病》中苦苦寻求救国救民真理的‘我’”理解不正确。
《父亲的病》中的“我”批判了庸医这些人巫医不分、故弄玄虚勒索钱财、草菅人命的实质;故选D。
3.(2021·山东烟台·统考中考真题)下列对《朝花夕拾》中的作品说法有误的一项是A.《阿长与<山海经>》一文,前半部分写阿长的粗鄙,是为了突出后半部分阿长对“我”的无私关爱。
高考英语语法词汇专项突破:01聚焦动词及动词短语八大考点+巩固训练答案解析(含高考真题)

高考英语语法词汇专项突破:聚焦动词及动词短语八大考点+巩固训练+答案与解析养成良好的答题习惯,是决定高考英语成败的决定性因素之一。
做题前,要认真阅读题目要求、题干和选项,并对答案内容作出合理预测;答题时,切忌跟着感觉走,最好按照题目序号来做,不会的或存在疑问的,要做好标记,要善于发现,找到题目的题眼所在,规范答题,书写工整;答题完毕时,要认真检查,查漏补缺,纠正错误。
【高考考例展示】【考题1】(2023新高考II卷)And who do they speak English ______?答案与解析:with。
考查动词短语中的“动词+介词”。
句意:他们和谁说英语?分析句子结构可知,这道题的语序可以看成they speak English who,句子中有主语they,speak后有宾语,而who 缺少一个介词,who做介词的宾语,又根据句意可推知,此处强调双向交流,应用固定搭配:speak with sb.意为“与某人交谈”。
故填with。
【考题2】(2022新高考全国I卷)Giant pandas also serve an umbrella species(物种), bringing protection to a host of plants and animals in the southwestern and northwestern parts of China.答案与解析:as。
考查动词短语中的“动词+介词”。
分析句子可知,此处考查固定动词短语serve as,意为“充当”,故空处应填介词as。
故填as。
句意:大熊猫还扮演着保护伞的角色,为中国西南和西北地区的许多动植物带来保护。
【考题3】(2020浙江6月卷)Some time after 10,000 BC,people made the first real attempt to control the world they lived ,through agriculture.答案与解析:考查动词短语中的“动词+介词”。
专项讲解01 热化学方程式的书写与判断-2022-2023学年高二化学同步重难点专项突破

②2S(g) S2(g) ΔH2
反应:2H2S(g) 2H2 (g)+S2(g)可以根据①×2+②得到。
(2)由图可知,第一步热化学反应为H2S(g)+0.5O2(g)===S(s)+
H2O(g) ΔH=-221.19 kJ·mol-1;
第二步反应为S(s)+1.5O2(g)+H2O(g)===2H+(aq)+SO
物质 1 mol 分子中的化学键断裂时需要吸收 的能量(kJ)
H2(g) 436
Br2(g) 200
HBr(g) a
则表中 a=________。
(2)由题中热化学方程式及蒸发 1 mol Br2(l)吸热 30 kJ 可得:H2(g) +Br2(g)===2HBr(g) ΔH=-102 kJ·mol-1,则 436+200-2a=- 102,a=369。
1.热化学方程式中如何表示出能量变化? 提示:在化学方程式的右侧表示出该反应的反应热,以表明反应中的能量 变化。 2.书写热化学方程式的一般步骤有哪些? 提示:①写出配平的化学方程式;②注明物质的聚集状态;③写出ΔH的符 号、数值和单位。
3.同一个化学反应,只有一个与之对应的化学方程式,是否只有一种形式 的热化学方程式?
【典例4】以H2合成尿素CO(NH2)2的有关热化学方程式有: ①N2(g)+3H2(g)===2NH3(g) ΔH1=-92.4 kJ·mol-1 ②NH3(g)+1/2CO2(g)=1/2NH2CO2NH4(s) ΔH2=-79.7 kJ·mol-1 ③NH2CO2NH4(s)===CO(NH2)2(s)+H2O(l) ΔH3=+72.5 kJ·mol-1
压强,若为 25℃、101 kPa,则不用标)
书写热 化学方 程式
第三步:算,依据条件由各种途径(如数据计算、图像分析、 盖斯定律等)得出与方程式中化学计量数相对应的反应热 ΔH,写出 ΔH 的符号、数值、单位 第四步:查,注重细节,从头到尾完整检查
专题01 果酒果醋的制作-高考生物技术实践专项突破(选修1)

真题演练
(18年III卷)2.回答下列与酵母菌有关的问题: (2)酵母菌液体培养时,若通入氧气,可促进___菌__体__快__速__增__殖___(填 “菌体快速增殖”“乙醇产生”或“乳酸产生”);若进行厌氧培养, 可促进___乙__醇_产__生___(填“菌体快速增殖”“乙醇产生”或“乳酸产 生”)。 (3)制作面包时,为使面包松软通常要在面粉中添加一定量的酵母菌, 酵母菌引起面包松软的原因是:
课题1 果酒和果醋的制作
4.什么在葡萄酒的自然发酵中其主要作用? 附着在葡萄皮上的野生型酵母菌
5.为什么葡萄酒呈深红色? 在发酵过程中,随着酒精度数的提高,红葡萄皮的色素也进入发酵液,使葡萄 酒呈现深红色。
6.在发酵过程中,为什么不需要另行消毒或灭菌? 在缺氧、呈酸性的发酵液中,酵母菌可以生长繁殖,而绝大多数其他微生物都 因无法适应这一环境而受到抑制。
课题1 果酒和果醋的制作
1.果酒制作的菌种是?其代谢类型和生殖方式是什么?
菌种:酵母菌(单细胞真菌、真核生物) 代谢类型:异养兼性厌氧性 同化作用类型:异养 异化作用类型:兼性厌氧型 生殖方式:无性生殖(出芽生殖、孢子生殖、分裂生殖)
2.菌种进行有氧呼吸的目的?其方程式是?并写出酒精发酵的方程式:
真题演练
(16年II卷)苹果醋是以苹果汁为原料经发酵而成的,回答下列为题: (1)酵母菌的呼吸代谢途径如图所示。图中过程①和②是苹果醋生产 的第一阶段,在酵母菌细胞的 __细__胞__质__基_质___ 中进行,其产物乙醇与 __重__铬__酸__钾____ 试剂反应呈现灰绿色,这一反应可用于乙醇的检验;过程 ③在酵母菌细胞的 __线__粒__体______ 中进行,与无氧条件相比,在有氧条件 下,酵母菌的增殖速度 __快____ . (2)第二阶段是在醋酸杆菌的作用下将第一阶段产生的乙醇转变为醋 酸的过程,根据醋酸杆菌的呼吸作用类型,该过程需要在 __有__氧__ 条件下 才能完成。 (3)在生产过程中,第一阶段和第二阶段的发酵温度不同,第一阶段 的温度 __低_于___ (填“低于”或“高于”)第二阶段。 (4)醋酸杆菌属于 ___原___ 核生物,其细胞结构中 __不__含__有(填“含有” 或“不含有”)线粒体.
高考物理计算题专项突破专题21之01 匀变速直线运动(解析版)

专题01 匀变速直线运动一、有关匀变速直线运动的基本公式:①速度公式:at v v t +=0;(此公式也可以用来求加速度或者时间) ②位移公式:2021at t v s +=;(注意:当00=v 时,221at s =) ③速度-位移公式:as v v t 2202=-;(公式可以变形为:sv v a t 222-=,从而用于求解加速度)二、匀变速直线运动的常用推论: ①中间时刻瞬时速度公式:tsv v v v t t =+==202; ②位移中点瞬时速度公式:22202tt v v v +=;③两个相邻相等时间间隔内的位移差:2aT s =∆。
(该推论可以用来判断物体是否做匀变速直线运动)在解匀变速直线运动的计算题时,首先要对运动过程进行分析,找出不同运动过程的衔接点,画出运动过程示意图,并在相应的位置上标上已知量和待求量。
其次要根据题干或图形,挖掘隐含条件,明确运动性质,同时抓住三个关系,即:位移关系、速度关系和时间关系。
第三要根据题目和分析结果,选择合适的方法进行解题,在匀变速直线运动的计算题中常用的方法一般有:基本公式法、平均速度法、推论法、比例法以及逆向思维法等。
最后,根据所选择的方法,结合已知量和待求量,列方程求解即可。
1.基本公式法:主要运用速度公式、位移公式以及速度-位移公式这三个公式,在使用时应注意这三个公式都是矢量式,要注意方向性问题。
2.平均速度法:主要运用公式t s v =和220t v v v v =+=,需要注意的是公式tsv =适用于任何性质的运动,而220t v vv v =+=只适用于匀变速直线运动。
3.推论法:主要利用2aT s =∆或者2)(aT n m x x n m -=-,该方法一般在遇到纸带类问题时才使用。
4.比例法:该方法适用于初速度为0的匀加速直线运动或者末速度为0的匀减速直线运动。
5.逆向思维法:把末速度为0的匀减速直线运动看成反向的初速度为0的匀加速直线运动。
高考英语语法词汇专项突破:01表解名词性从句+巩固练习+答案与解析

高考英语语法词汇专项突破:01表解名词性从句+巩固练习+答案与解析【考题呈现】【考例1】(2022年浙江1月)Cobb, for her party, started to ask conference organizers who invited her to speak ______ she could do so remotely.答案与解析:if/whether。
考查名词性从句之宾语从句。
明显ask后面消灭了一个宾语从句,宾语从句句意不完整,whether/if“是否”符合语境,故填whether或if。
句意:对于她的出席,Cobb开头询问邀请她的组织者是否可以远程进行。
【考例2】(2021.6新高考1卷)Going to Mount Huangshan reminds me of the popular Beatle's song "The答案与解析:What。
考查名词性从句之主语从句。
分析题目,空格处无提示词。
分子句子结构可知,_____is so breathing about the experience 作is 的主语,为主语从句。
从句中缺少主语,指代事情;且空格位于句首。
故填What。
【考例3】(2021.3 天津卷)A. whetherB. whyC. whatD. when答案与解析:B。
考查引导表语从句连接词词义辨析。
A. whether是否;B.why为什么;C. what什么;D.when什么时间,当……的时候。
分析成分结构句子,该空需要一个表语从句的连接词。
再结合句意可知,应当是伴侣们不明白Lily 为什么有这么多疯狂的想法。
所以本句为why引导的表语从句。
故选:B。
句意:令Lily的伴侣们感到困扰的是她为什么总是有这么多疯狂的想法。
【考例4】(2021年北京卷)The poor woman wasn't able to give him any information about ________ she lived.答案与解析:where。
小升初英语应试题型专项突破 专题01《填空题》 全国通用版 (word,含答案)

小升初英语应试题型专项突破专题01《填空题》一、填空题Read, think and write.(读一读,想一想下面情况该乘什么交通工具。
)1.My home is near my school. I usually go to school ________.2.The USA is far from China. My father goes there ________.3.I live in Yantai. Yantai and Dalian face(面对)each other across the sea. So I can go to Dalian ________. 4.In Alaska, it snows a lot. Some kids go to school ________.5.My mother has a nice car. She goes to work ________ every day.Read, write and colour.(读一读,根据句意写出单词并写出相应的交通信号颜色。
)6.Look! It’s the________(_____)light, so we must slow down and stop.7.Look! It’s the_______(_____)light, so we must stop and wait.8.Look! It’s the_______(_____)light, so we can go.9.根据汉语意思完成句子:别把故事结尾说出来。
Don’t give away the _______ of the story.10.读一读,填一填:What are you going to do tomorrow?1. I’m going to _________ football tomorrow.2. I’m going to _________ TV tomorrow.3. I’m going to _______ to the park tomorrow.4. I’m going to _________ books tomorrow.5. I’m going to _________ to music tomorrow.6. I’m going to _________ chess tomorrow.7. I’m going to ________ to school tomorrow.用单词的正确形式填空11.There are many _________(child)in the library.12.Look! Little John _________(play)with a dog.13.Today is Jenny’s_________(twelve)birthday.14.His brother is_________ (strong)than he.15.Sam and his brother_________(visit)their grandparents’ house next week.按要求写词语16.happy _________ (反义词)17.big_________ (比较级)18.stop _________ (过去式)19.potato_________(复数)20.we _________(宾格)Read and write.(根据汉语提示完成句子。
高考英语语法词汇专项突破:01表解不定式考点及其时态语态突破(含高考真题)

高考英语语法词汇专项突破:表解不定式考点及其时态语态全突破+巩固训练养成良好的答题习惯,是决定高考英语成败的决定性因素之一。
做题前,要认真阅读题目要求、题干和选项,并对答案内容作出合理预测;答题时,切忌跟着感觉走,最好按照题目序号来做,不会的或存在疑问的,要做好标记,要善于发现,找到题目的题眼所在,规范答题,书写工整;答题完毕时,要认真检查,查漏补缺,纠正错误。
Part 1:不定式考点【高考链接1】【考例1】(2023新高考I卷)Nanxiang aside, the best Xiao long bao have a fine skin, allowing them____ (lift) out of the steamer basket without allowing them tearing or spilling any of their contents.答案与解析:to be lifted。
考查非谓语动词。
句根据搭配allow sb. to do sth.“允许某人做某事”可知,空格需用动词不定式作宾语补足语,补足语lift out与宾语them(指代小笼包)是逻辑上的动宾关系,空格需填动词不定式的被动式to be lifted,故填to be lifted。
意:除了南翔,最好的小笼包有一个精致的,可以让它们从蒸笼篮中拿出来,而不会撕裂或溢出里面的东西。
【考例2】(2022全国甲卷)A visually-challenged man from Beijing recently hiked (徒步) 40 days to Xi’an, as a first step (journey) the Belt and Road route (路线) by foot.答案与解析:to journey。
考查非谓语动词。
step前面有序数词first,应用不定式,作后置定语。
故填to journey。
最新人教A版高中数学选修1-1章末分层突破全套
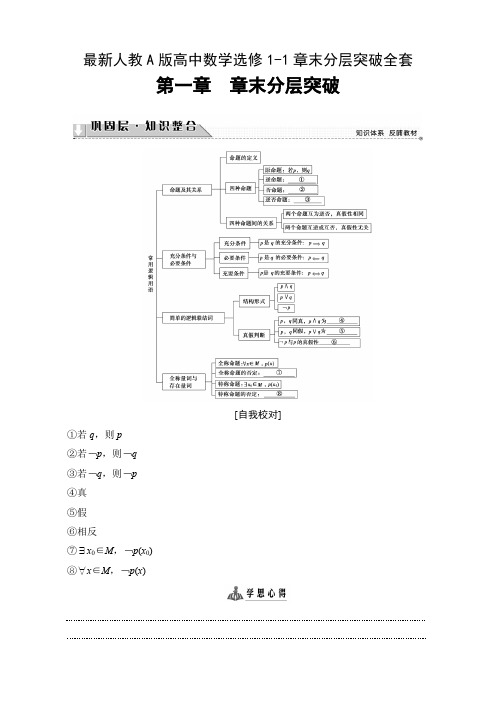
最新人教A版高中数学选修1-1章末分层突破全套第一章章末分层突破[自我校对]①若q,则p②若﹁p,则﹁q③若﹁q,则﹁p④真⑤假⑥相反⑦∃x0∈M,﹁p(x0)⑧∀x∈M,﹁p(x)命题关系及其真假判定(1)命题“若p,则﹁q”;逆否命题为“若﹁q,则﹁p”.书写四种命题应注意:①分清命题的条件与结论,注意大前提不能当作条件来对待.②要注意条件和结论的否定形式.(2)判断命题真假的方法:①直接判断:先确定命题的条件与结论,再判断条件能否推得结论;②利用四种命题的等价关系:互为逆否的两个命题同真同假;③对于“p或q”“p且q”“非p”形式的命题,判断方式可分别简记为:一真即真、一假即假、真假相反.写出下述命题的逆命题、否命题、逆否命题,并判断其真假.(1)若a+b是偶数,则a,b都是偶数;(2)若x=3或x=7,则(x-3)(x-7)=0.【精彩点拨】先明确原命题的条件p与结论q,把原命题写成“若p,则q”的形式,再去构造其他三种命题,对具有大前提的原命题,在写出其他三种命题时,应保留这个大前提.【规范解答】(1)逆命题:若a,b都是偶数,则a+b是偶数,为真.否命题:若a+b不是偶数,则a,b不都是偶数,为真.逆否命题:若a,b不都是偶数,则a+b不是偶数,为假.(2)逆命题:若(x-3)(x-7)=0,则x=3或x=7,为真.否命题:若x≠3且x≠7,则(x-3)(x-7)≠0,为真.逆否命题:若(x-3)(x-7)≠0,则x≠3且x≠7,为真.“都”的否定词是“不都”,而不是“都不”,同理,“全”的否定词是“不全”,而不是“全不”.另外,命题中的“或”,在否命题中要改为“且”.[再练一题]1.有下列命题:①“若x +y >0,则x >0且y >0”的否命题;②“矩形的对角线相等”的否命题;③“若m ≥1,则mx 2-2(m +1)x +m +3>0的解集是R ”的逆命题;④“若a +7是无理数,则a 是无理数”的逆否命题.其中为真命题的是( ) A.①②③ B.②③④ C.①③④D.①④【解析】 ①的逆命题为“若x >0且y >0,则x +y >0”为真,故否命题为真; ②的否命题为“不是矩形的图形对角线不相等”,为假;③的逆命题为“若mx 2-2(m +1)x +m +3>0的解集为R ,则m ≥1”. ∵当m =0时,解集不是R ,∴应有⎩⎪⎨⎪⎧m >0,Δ<0,即m >1.∴③是假命题;④原命题为真,逆否命题也为真. 【答案】 D关于充分条件、必要条件与充要条件的判定,实际上是对命题真假的判定: 若p ⇒q ,且p ⇐/q ,则p 是q 的充分条件,同时q 是p 的必要条件; 若p ⇔q ,则p 是q 的充要条件,同时q 是p 的充要条件;若p ⇔/q ,则p 是q 的既不充分也不必要条件,同时q 是p 的既不充分也不必要条件.已知p :⎩⎨⎧x +2≥0,x -10≤0,q :{x |1-m ≤x ≤1+m ,m >0},若﹁p 是﹁q 的必要条件,求实数m 的取值范围.【精彩点拨】 本题主要考查充分条件、必要条件和充要条件的应用.解答本题应先写出﹁p 和﹁q ,然后由﹁q ⇒﹁p ,且﹁p ⇒/﹁q 求得m 的范围.【规范解答】 法一 由题意,得﹁p :A ={x |x <-2或x >10},﹁q :B ={x |x <1-m 或x >1+m ,m >0},∵﹁p 是﹁q 的必要条件, ∴﹁q ⇒﹁p ,﹁p ⇒/﹁q . ∴BA ,画数轴(略)分析知,BA 的充要条件是⎩⎪⎨⎪⎧m >0,1-m ≤-2,1+m >10或⎩⎪⎨⎪⎧m >0,1-m <-2,1+m ≥10,解得m ≥9.∴m 的取值范围是{m |m ≥9}.法二 ∵﹁p 是﹁q 的必要不充分条件,即﹁q ⇒﹁p , ∴p ⇒q ,即p 是q 的充分不必要条件. 而p :P ={x |-2≤x ≤10}, q :Q ={x |1-m ≤x ≤1+m ,m >0},∴PQ ,即得⎩⎪⎨⎪⎧m >0,1-m <-2,1+m ≥10或⎩⎪⎨⎪⎧m >0,1-m ≤-2,1+m >10.解得m ≥9.∴m 的取值范围是{m |m ≥9}.应用充分条件和必要条件求参数的取值范围,主要是根据集合间的包含关系与充分条件和必要条件的关系,将问题转化为集合之间的关系,建立关于参数的不等式或不等式组求解,注意数形结合思想的应用.[再练一题]2.已知p :x 2-8x -20>0,q :x 2-2x +1-a 2>0,若p 是q 的充分条件,求正实数a 的取值范围.【解】 p :x 2-8x -20>0⇔x <-2或x >10,令A ={x |x <-2或x >10}, ∵a >0,∴q :x <1-a 或x >1+a , 令B ={x |x <1-a 或x >1+a }, 由题意p ⇒q 且pD ⇐/q ,知A B ,应有⎩⎪⎨⎪⎧a >0,1+a <10,1-a ≥-2或⎩⎪⎨⎪⎧a >0,1+a ≤10,解得0<a ≤3,1-a >-2,∴a 的取值范围为(0,3].在解答某些数学问题时,有时会遇到多种情况,需要对各种情况加以分类,并逐类求解,然后综合得解,这就是分类讨论,解含参数的题目时,必须根据参数的不同取值范围进行讨论.已知命题p :x 2+mx +1=0有两个不相等的负根;命题q :4x 2+4(m -2)x +1=0无实根.若p ∨q 为真,p ∧q 为假,求m 的取值范围.【精彩点拨】 本题主要考查根据命题真假求参数的取值范围,由p ∨q 一真全真,p ∧q 一假全假得命题的真假情况.【规范解答】 x 2+mx +1=0有两个不相等的负根⇔⎩⎪⎨⎪⎧m 2-4>0,-m <0⇔m >2.4x 2+4(m -2)x +1=0无实根⇔16(m -2)2-16<0⇔m 2-4m +3<0⇔1<m <3. ∵p ∨q 为真,p ∧q 为假,∴p 和q 一真一假, ∴当p 真q 假时,有⎩⎪⎨⎪⎧m >2,m ≤1或m ≥3,解得m ≥3;当p 假q 真时,有⎩⎪⎨⎪⎧m ≤2,1<m <3,解得1<m ≤2.∴所求m 的取值范围为{m |1<m ≤2,或m ≥3}.若命题“p ∨q ”“p ∧q ”中含有参数,在求解时,可以先等价转化命题p ,q ,直至求出这两个命题为真时参数的取值范围,再依据“p ∨q ”“p ∧q ”的真假情况分类讨论参数的取值范围.[再练一题]3.已知命题p :关于x 的方程x 2-ax +4=0有实根;命题q :关于x 的函数y =2x 2+ax +4在[3,+∞)上是增函数.若“p 或q ”是真命题,“p 且q ”是假命题,求实数a 的取值范围.【解】 p 真:Δ=a 2-4×4≥0,∴a ≤-4或a ≥4.q 真:-a4≤3,∴a ≥-12.由“p 或q ”是真命题,“p 且q ”是假命题,得p ,q 两命题一真一假. 当p 真q 假时,a <-12;当p 假q 真时,-4<a <4. 综上,a 的取值范围为(-∞,-12)∪(-4,4).转化与化归思想就是在研究和解决有关数学问题时采用某种手段将问题通过变换使之转化,进而得到解决的一种方法.对任意x ∈[-1,2],有4x -2x +1+2-a <0恒成立,求实数a 的取值范围. 【精彩点拨】 通过换元,可转化为一元二次不等式的恒成立问题,通过分离参数,又可将恒成立问题转化为求最值的问题.【规范解答】 原不等式化为22x -2·2x +2-a <0,①令t =2x ,因为x ∈[-1,2],所以t ∈⎣⎢⎡⎦⎥⎤12,4,则不等式①化为t 2-2t +2-a <0,即a >t 2-2t +2.所以原命题等价于∀t ∈⎣⎢⎡⎦⎥⎤12,4,a >t 2-2t +2恒成立.令y =t 2-2t +2=(t -1)2+1,因为当t ∈⎣⎢⎡⎦⎥⎤12,4时,y max =10,所以只需a >10即可.故实数a 的取值范围是(10,+∞).在本题的解答过程中,用到了两次化归思想,在第一次通过换元,化归为一元二次不等式恒成立时,要特别注意新元的取值范围.[再练一题]4.已知命题p :“至少存在一个实数x 0∈[1,2],使不等式x 2+2ax +2-a >0成立”为真,试求参数a 的取值范围.【解】 ﹁p :∀x ∈[1,2],x 2+2ax +2-a ≤0,是假命题, 令f (x )=x 2+2ax +2-a ,则⎩⎪⎨⎪⎧ f (1)≤0,f (2)≤0,即⎩⎪⎨⎪⎧1+2a +2-a ≤0,4+4a +2-a ≤0. 解得a ≤-3. 故命题p 中,a >-3.即参数a 的取值范围为(-3,+∞).1.设x >0,y ∈R ,则“x >y ”是“x >|y |”的( ) A.充要条件 B.充分条件 C.必要条件D.既不充分也不必要条件【解析】由x>y推不出x>|y|,由x>|y|能推出x>y,所以“x>y”是“x>|y|”的必要条件.【答案】 C2.已知直线a,b分别在两个不同的平面α,β内,则“直线a和直线b相交”是“平面α和平面β相交”的()A.充分条件B.必要条件C.充要条件D.既不充分也不必要条件【解析】由已知,若直线a,b相交,则平面α,β一定存在公共点,故其一定相交;反之,若平面α与β相交,分别位于这两平面的直线ab未必相交.故为充分条件.【答案】 A3.设m∈R,命题“若m>0,则方程x2+x-m=0有实根”的逆否命题是()A.若方程x2+x-m=0有实根,则m>0B.若方程x2+x-m=0有实根,则m≤0C.若方程x2+x-m=0没有实根,则m>0D.若方程x2+x-m=0没有实根,则m≤0【解析】根据逆否命题的定义,命题“若m>0,则方程x2+x-m=0有实根”的逆否命题是“若方程x2+x-m=0没有实根,则m≤0”.故选D.【答案】 D4.命题“∃x0∈(0,+∞),ln x0=x0-1”的否定是()A.∀x∈(0,+∞),ln x≠x-1B.∀x∉(0,+∞),ln x=x-1C.∃x0∈(0,+∞),ln x0≠x0-1D.∃x0∉(0,+∞),ln x0=x0-1【解析】改变原命题中的三个地方即可得其否定,∃改为∀,x0改为x,否定结论,即ln x≠x-1,故选A.【答案】 A5.设a,b,c是非零向量,已知命题p:若a·b=0,b·c=0,则a·c=0;命题q:若a∥b,b∥c,则a∥c.则下列命题中真命题是()A.p∨qB.p∧qC.(﹁p)∧(﹁q)D.p∨(﹁q)【解析】法一取a=c=(1,0),b=(0,1),显然a·b=0,b·c=0,但a·c=1≠0,∴p 是假命题.a,b,c是非零向量,由a∥b知a=x b,由b∥c知b=y c,∴a=xy c,∴a∥c,∴q是真命题.综上知p∨q是真命题,p∧q是假命题.又∵﹁p为真命题,﹁q为假命题,∴(﹁p)∧(﹁q),p∨(﹁q)都是假命题.法二由于a,b,c都是非零向量,∵a·b=0,∴a⊥b.∵b·c=0,∴b⊥c.如图,则可能a∥c,∴a·c≠0,∴命题p是假命题,∴﹁p是真命题.命题q中,a∥b,则a与b方向相同或相反;b∥c,则b与c方向相同或相反.故a与c方向相同或相反,∴a∥c,即q是真命题,则﹁q是假命题,故p∨q是真命题,p∧q,(﹁p)∧(﹁q),p∨(﹁q)都是假命题.【答案】 A6.下列叙述中正确的是()A.若a,b,c∈R,则“ax2+bx+c≥0”的充分条件是“b2-4ac≤0”B.若a,b,c∈R,则“ab2>cb2”的充要条件是“a>c”C.命题“对任意x∈R,有x2≥0”的否定是“存在x∈R,有x2≥0”D.l是一条直线,α,β是两个不同的平面,若l⊥α,l⊥β,则α∥β【解析】由于“若b2-4ac≤0,则ax2+bx+c≥0”是假命题,所以“ax2+bx+c≥0”的充分条件不是“b2-4ac≤0”,A错;∵ab2>cb2,且b2>0,∴a>c.而a>c时,若b2=0,则ab2>cb2不成立,由此知“ab2>cb2”是“a>c”的充分不必要条件,B错;“对任意x∈R,有x2≥0”的否定是“存在x∈R,有x2<0”,C错;由l⊥α,l⊥β,可得α∥β,理由是:垂直于同一条直线的两个平面平行,D正确.【答案】 D第二章章末分层突破[自我校对]①>②y2a2+x2b2=1(a>b>0)③(0,1)④<⑤y2a2-x2b2=1(a>0,b>0)⑥(1,+∞)⑦1圆锥曲线的定义与性质对于圆锥曲线的有关问题,要有运用圆锥曲线定义解题的意识,“回归定义”是一种重要的解题策略,如:(1)在求轨迹时,若所求轨迹符合某种圆锥曲线的定义,则根据圆锥曲线的方程,写出所求的轨迹方程;(2)涉及椭圆、双曲线上的点与两个焦点构成的三角形问题时,常用定义结合解三角形的知识来解决;(3)在求有关抛物线的最值问题时,常利用定义把到焦点的距离转化为到准线的距离,结合几何图形,利用几何意义去解决.总之,圆锥曲线的定义、性质在解题中有重要作用,要注意灵活运用.(1)F1,F2是椭圆x2a2+y2b2=1(a>b>0)的两焦点,P是椭圆上任一点,从任一焦点引∠F1PF2的外角平分线的垂线,垂足为Q,则点Q的轨迹为()A.圆B.椭圆C.双曲线D.抛物线(2)椭圆x2a2+y25=1(a为定值,且a>5)的左焦点为F,直线x=m与椭圆相交于点A、B,△F AB 的周长的最大值是12,则该椭圆的离心率是________.【规范解答】(1)延长垂线F 1Q 交F 2P 的延长线于点A ,如图所示,则△APF 1是等腰三角形,∴|PF 1|=|AP |,从而|AF 2|=|AP |+|PF 2|=|PF 1|+|PF 2|=2a .由题意知O 是F 1F 2的中点,Q 是AF 1的中点,连接OQ ,则|OQ |=12|AF 2|=a .∴Q 点的轨迹是以原点O 为圆心,半径为a 的圆.故选A.(2)设椭圆的另一个焦点为F ′,则△F AB 的周长|F A |+|AB |+|FB |≤|F A |+|F ′A |+|FB |+|F ′B |=4a ,所以4a =12,a =3,e =a 2-5a =23.【答案】 (1)A (2)231.圆锥曲线的定义是推导标准方程和几何性质的基础,也是解题的重要工具,灵活运用定义,可避免很多复杂的计算,提高解题效率,因此在解决圆锥曲线的有关问题时,要有运用圆锥曲线定义解题的意识,“回归定义”是一种重要的解题策略.2.应用圆锥曲线的性质时,要注意与数形结合、方程等思想结合运用.[再练一题]1.(1)已知双曲线x 2m -y 27=1,直线l 过其左焦点F 1,交双曲线左支于A ,B 两点,且|AB |=4,F 2为双曲线的右焦点,△ABF 2的周长为20,则m 的值为( )A.8B.9C.16D.20(2)如图2-1所示,动圆P 与定圆C :(x -1)2+y 2=1外切且与y 轴相切,则圆心P 的轨迹为________.图2-1【解析】(1)由双曲线的定义可知,|AF2|-|AF1|=2m,|BF2|-|BF1|=2m,所以(|AF2|+|BF2|)-(|AF1|+|BF1|)=4m,|AF2|+|BF2|-|AB|=4m,|AF2|+|BF2|=4+4m.又|AF2|+|BF2|+|AB|=20,即4+4m+4=20,所以m=9.故选B.(2)设P(x,y),动圆P的半径为r.∵两圆外切,∴PC=r+1.又圆P与y轴相切,∴r=|x|(x≠0),即(x-1)2+y2=|x|+1,整理得y2=2(|x|+x).当x>0时,得y2=4x;当x<0时,得y=0.∴点P的轨迹方程是y2=4x(x>0)或y=0(x<0),表示一条抛物线(除去顶点)或x轴的负半轴.【答案】(1)B(2)一条抛物线(除去顶点)或x轴的负半轴直线与圆锥曲线一般有三种位置关系:相交、相切和相离.把直线方程与圆锥曲线方程联立成方程组,消去一个变量后,转化为一元二次方程ax2+bx+c=0.当a≠0时,若Δ>0,直线与圆锥曲线相交,有两个不同的公共点;若Δ=0,直线与圆锥曲线相切,有一个公共点;若Δ<0,直线与圆锥曲线相离,无公共点.当a =0时,即直线平行于双曲线的渐近线时,直线与双曲线相交且只有一个公共点;直线平行于抛物线的对称轴时,直线与抛物线相交且只有一个公共点.已知椭圆x 2a 2+y 2b 2=1(a >b >0)的离心率e =32,连接椭圆的四个顶点得到的菱形的面积为4.(1)求椭圆的方程;(2)设直线l 与椭圆相交于不同的两点A ,B ,已知点A 的坐标为(-a,0). ①若|AB |=425,求直线l 的倾斜角;②若点Q (0,y 0)在线段AB 的垂直平分线上,且QA →·Q B →=4,求y 0的值.【精彩点拨】 (1)建立关于a ,b 的方程组求出a ,b ;(2)构造新方程,综合运用两点间的距离公式、平面向量等知识求解.【规范解答】 (1)由e =c a =32,得3a 2=4c 2. 由c 2=a 2-b 2,得a =2b . 由题意,知12·2a ·2b =4,即ab =2.解方程组⎩⎪⎨⎪⎧a =2b ,ab =2,a >b >0,得⎩⎪⎨⎪⎧a =2,b =1.所以椭圆的方程为x 24+y 2=1.(2)由(1)知,点A 的坐标是(-2,0),设点B 的坐标为(x 1,y 1),直线l 的斜率为k ,则直线l 的方程为y =k (x +2).于是A ,B 两点的坐标满足方程组⎩⎨⎧y =k (x +2),x 24+y 2=1,消去y 并整理,得(1+4k 2)x 2+16k 2x +(16k 2-4)=0.由-2x 1=16k 2-41+4k 2,得x 1=2-8k 21+4k 2,从而y 1=4k 1+4k 2.所以|AB |=⎝ ⎛⎭⎪⎪⎫-2-2-8k 21+4k 22+⎝ ⎛⎭⎪⎫0-4k 1+4k 22=41+k 21+4k 2. ①由|AB |=425,得41+k 21+4k2=425. 整理,得32k 4-9k 2-23=0,即(k 2-1)(32k 2+23)=0, 解得k =±1.所以直线l 的倾斜角为π4或3π4. ②设线段AB 的中点为M ,则点M 的坐标为⎝ ⎛⎭⎪⎫-8k 21+4k 2,2k 1+4k 2. 以下分两种情况:a .当k =0时,点B 的坐标是(2,0),线段AB 的垂直平分线为y 轴,于是QA →=(-2,-y 0), Q B →=(2,-y 0).由QA →·Q B →=4,得y 0=±2 2.b .当k ≠0时,线段AB 的垂直平分线方程为y -2k1+4k2=-1k ⎝ ⎛⎭⎪⎫x +8k 21+4k 2. 令x =0,解得y 0=-6k 1+4k 2.Q A →=(-2,-y 0), Q B →=(x 1,y 1-y 0), Q A →·Q B →=-2x 1-y 0(y 1-y 0)=16k 2-41+4k 2+6k 1+4k 2⎝ ⎛⎭⎪⎫4k 1+4k 2+6k 1+4k 2=4(16k 4+15k 2-1)(1+4k 2)2=4,整理,得7k 2=2,故k =±147.所以y 0=±2145.综上,y 0=±22或y 0=±2145.直线与圆锥曲线的位置关系问题是高考的热点,解题时要注意掌握一些基本的解题规律和技巧,如在研究直线与圆锥曲线的公共点个数问题时,不要仅由判别式Δ来进行判断,还要注意二次项系数是否为0;涉及弦长问题时,利用弦长公式及根与系数的关系求解,而对于焦点弦问题,则结合圆锥曲线的定义求解;解决有关中点弦问题时常常运用“点差法”使运算过程得以简化.[再练一题]2.已知椭圆G :x 2a 2+y 2b 2=1(a >b >0)的离心率为63,右焦点为(22,0).斜率为1的直线l 与椭圆G 交于A ,B 两点,以AB 为底边作等腰三角形,顶点为P (-3,2).(1)求椭圆G 的方程; (2)求△P AB 的面积.【解】 (1)由已知得,c =22,c a =63. 解得a =2 3. 又b 2=a 2-c 2=4,所以椭圆G 的方程为x 212+y 24=1. (2)设直线l 的方程为y =x +m ,由⎩⎨⎧y =x +m ,x 212+y 24=1,得4x 2+6mx +3m 2-12=0.①设A ,B 的坐标分别为(x 1,y 1),(x 2,y 2)(x 1<x 2),AB 中点为E (x 0,y 0),则 x 0=x 1+x 22=-3m 4,y 0=x 0+m =m 4, 因为AB 是等腰△P AB 的底边, 所以PE ⊥AB .所以PE 的斜率k =2-m 4-3+3m 4=-1,解得m =2, 此时方程①为4x 2+12x =0. 解得x 1=-3,x 2=0. 所以y 1=-1,y 2=2. 所以|AB |=3 2.此时,点P (-3,2)到直线AB :x -y +2=0的距离d =|-3-2+2|2=322,所以△P AB 的面积S =12|AB |·d =92.短轴,双曲线的虚轴、实轴,抛物线的焦点等,解决此类问题的主要方法是通过研究直线与曲线的位置关系,把所给问题进行化简,通过计算获得答案;或是从特殊位置出发,确定定值,然后给出一般情况的证明.圆锥曲线中的最值问题,通常有两类:一类是有关长度、面积等最值问题;一类是圆锥曲线中有关几何元素的最值问题,这两类问题的解决往往通过回归定义,结合几何知识,建立目标函数,利用函数的性质或不等式知识,以及数形结合、设参、转化、代换等途径来解决.如图2-2所示,椭圆C :x 2a 2+y 2b 2=1(a >b >0),A 1、A 2为椭圆C 的左、右顶点.图2-2(1)设F 1为椭圆C 的左焦点,证明:当且仅当椭圆C 上的点P 在椭圆的左、右顶点时,|PF 1|取得最小值与最大值;(2)若椭圆C 上的点到焦点距离的最大值为3,最小值为1,求椭圆C 的标准方程; (3)若直线l :y =kx +m 与(2)中所述椭圆C 相交于A 、B 两点(A 、B 不是左、右顶点),且满足AA 2⊥BA 2,求证:直线l 过定点,并求出该定点的坐标.【精彩点拨】 (1)利用函数法,设P (x ,y ),将|PF 1|表示为x 的函数.(3)利用AA 2⊥BA 2得k ,m 的等量关系,从而将直线l 化为只含参数k (或m )的形式. 【规范解答】 (1)证明:设点P 的坐标为(x ,y ), 令f (x )=|PF 1|2=(x +c )2+y 2.又点P 在椭圆C 上,故满足x 2a 2+y 2b 2=1,则y 2=b 2-b2a 2x 2.代入f (x )得,f (x )=(x +c )2+b 2-b 2a 2x 2=c 2a 2x 2+2cx +a 2,则其对称轴方程为x =-a 2c , 由题意,知-a 2c <-a 恒成立, ∴f (x )在区间[-a ,a ]上单调递增.∴当且仅当椭圆C 上的点P 在椭圆的左、右顶点时|PF 1|取得最小值与最大值. (2)由已知与(1)得:a +c =3,a -c =1, ∴a =2,c =1.∴b 2=a 2-c 2=3.∴椭圆C 的标准方程为x 24+y 23=1. (3)证明:如图所示,设A (x 1,y 1),B (x 2,y 2),联立⎩⎨⎧y =kx +m ,x 24+y 23=1,得(3+4k 2)x 2+8mkx +4(m 2-3)=0, 则Δ=64m 2k 2-16(3+4k 2)(m 2-3)>0, 即3+4k 2-m 2>0,x 1+x 2=-8mk3+4k 2,x 1x 2=4(m 2-3)3+4k 2.又y 1y 2=(kx 1+m )(kx 2+m ) =k 2x 1x 2+mk (x 1+x 2)+m 2 =3(m 2-4k 2)3+4k2. ∵椭圆的右顶点为A 2(2,0),AA 2⊥BA 2, ∴(x 1-2)(x 2-2)+y 1y 2=0. ∴y 1y 2+x 1x 2-2(x 1+x 2)+4=0.∴3(m 2-4k 2)3+4k 2+4(m 2-3)3+4k 2+16mk 3+4k 2+4=0. ∴7m 2+16km +4k 2=0,解得m 1=-2k ,m 2=-2k7, 且均满足3+4k 2-m 2>0.当m 1=-2k 时,l 的方程为y =k (x -2), 直线过定点(2,0),与已知矛盾.当m 2=-2k 7时,l 的方程为y =k ⎝ ⎛⎭⎪⎫x -27,直线过定点⎝ ⎛⎭⎪⎫27,0,∴直线l 过定点,定点坐标为⎝ ⎛⎭⎪⎫27,0.解决圆锥曲线中的参数范围问题与求最值问题类似,一般有两种方法:(1)函数法:用其他变量表示该参数,建立函数关系,利用求函数值域的方法求解. (2)不等式法:根据题意建立含参数的不等关系式,通过解不等式求参数范围.[再练一题]3.求抛物线y =-x 2上的点到直线4x +3y -8=0的最小距离. 【解】 法一 设P (t ,-t 2)为抛物线上的点, 它到直线4x +3y -8=0的距离 d =|4t -3t 2-8|5=|3t 2-4t +8|5=15⎪⎪⎪⎪⎪⎪3⎝⎛⎭⎪⎫t -232-43+8 =15⎪⎪⎪⎪⎪⎪3⎝ ⎛⎭⎪⎫t -232+203 =35⎝ ⎛⎭⎪⎫t -232+43. ∴当t =23时,d 有最小值,最小值为43.法二 如图所示,设与直线4x +3y -8=0平行的抛物线的切线方程为4x +3y +m =0,则有方程组⎩⎪⎨⎪⎧y =-x 2,4x +3y +m =0,消去y 得3x 2-4x -m =0, ∴Δ=16+12m =0, ∴m =-43.∴最小距离为⎪⎪⎪⎪⎪⎪-8+435=2035=43.1.直线l 经过椭圆的一个顶点和一个焦点,若椭圆中心到l 的距离为其短轴长的14,则该椭圆的离心率为( )A.13B.12C.23D.34【解析】 不妨设直线l 过椭圆的上顶点(0,b )和左焦点(-c,0),b >0,c >0,则直线l 的方程为bx -cy +bc =0,由已知得bcb 2+c 2=14×2b ,解得b 2=3c 2,又b 2=a 2-c 2,所以c 2a 2=14,即e 2=14,∴e =12.【答案】 B2.设F 为抛物线C :y 2=4x 的焦点,曲线y =kx (k >0)与C 交于点P ,PF ⊥x 轴,则k =( ) A.12 B.1 C.32 D.2【解析】 易知抛物线焦点为F (1,0),设P (x 0,y 0),由PF ⊥x 轴可得x0=1,代入y 2=4x得y 0=2,把P (1,2)代入y =kx 得k =2.【答案】 D3.已知椭圆x 225+y 2m 2=1(m >0)的左焦点为F 1(-4,0),则m =( ) A.2 B.3 C.4 D.9【解析】 由左焦点为F 1(-4,0)知c =4.又a =5,∴25-m 2=16,解得m =3或-3.又m >0,故m =3.【答案】 B4.已知抛物线y 2=2px (p >0)的准线经过点(-1,1),则该抛物线焦点坐标为( ) A.(-1,0) B.(1,0) C.(0,-1)D.(0,1)【解析】 抛物线y 2=2px (p >0)的准线为x =-p 2且过点(-1,1),故-p2=-1,解得p =2.所以抛物线的焦点坐标为(1,0).【答案】 B5.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的一个焦点为F (2,0),且双曲线的渐近线与圆(x -2)2+y 2=3相切,则双曲线的方程为( )A.x 29-y 213=1 B.x 213-y 29=1 C.x 23-y 2=1D.x 2-y 23=1【解析】 由双曲线的渐近线y =±b ax 与圆(x -2)2+y 2=3相切可知⎩⎪⎨⎪⎧⎪⎪⎪⎪⎪⎪±b a ×21+⎝ ⎛⎭⎪⎫b a 2=3,c =2,a 2+b 2=c 2,解得⎩⎪⎨⎪⎧a =1,b = 3.故所求双曲线的方程为x 2-y 23=1.【答案】 D6.已知椭圆E的中心在坐标原点,离心率为12,E的右焦点与抛物线C:y2=8x的焦点重合,A,B是C的准线与E的两个交点,则|AB|=()A.3B.6C.9D.12【解析】抛物线y2=8x的焦点为(2,0),∴椭圆中c=2,又ca=12,∴a=4,b2=a2-c2=12,从而椭圆方程为x216+y212=1.∵抛物线y2=8x的准线为x=-2,∴x A=x B=-2,将x A=-2代入椭圆方程可得|y A|=3,由图象可知|AB|=2|y A|=6.故选B.【答案】 B7.已知双曲线x2a2-y2b2=1(a>0,b>0)的一条渐近线为2x+y=0,一个焦点为(5,0),则a=________,b=________.【解析】由题意知,渐近线方程为y=-2x,故ba=2,由c=5,c2=a2+b2可得b=2,a=1.【答案】1 28.设双曲线x2-y23=1的左、右焦点分别为F1,F2.若点P在双曲线上,且△F1PF2为锐角三角形,则|PF1|+|PF2|的取值范围是________.【解析】∵双曲线x2-y23=1的左、右焦点分别为F1,F2,点P在双曲线上,∴|F1F2|=4,||PF1|-|PF2||=2.若△F1PF2为锐角三角形,则由余弦定理知|PF1|2+|PF2|2-16>0,可化为(|PF1|+|PF2|)2-2|PF1|·|PF2|>16①.由||PF1|-|PF2||=2,得(|PF1|+|PF2|)2-4|PF1||PF2|=4.故2|PF1||PF2|=(|PF1|+|PF2|)2-42,代入不等式①可得(|PF1|+|PF2|)2>28,解得|PF1|+|PF2|>27.不妨设P在左支上,∵|PF1|2+16-|PF2|2>0,即(|PF1|+|PF2|)·(|PF1|-|PF2|)>-16,又|PF1|-|PF2|=-2,∴|PF1|+|PF2|<8.故27<|PF1|+|PF2|<8.【答案】(27,8)第三章章末分层突破[自我校对]①斜率②y-f(x0)=f′(x0)(x-x0)③f′(x)±g′(x)④f′(x)g(x)+f(x)g′(x)⑤f′(x)g(x)-f(x)g′(x)[g(x)]2常见类型有两种:(1)函数y=f(x)“在点x=x0处的切线方程”,这种类型中(x0,f(x0))是曲线上的点,其切线方程为y-f(x0)=f′(x0)(x-x0).(2)函数y=f(x)“过某点的切线方程”,这种类型中,该点不一定是切点,可先设切点Q(x1,y1),则切线斜率为f′(x1),再由切线过点P(x0,y0)得斜率为y1-y0x1-x0,又由y1=f(x1),由上面两个方程可得切点(x1,y1),即求出了过点P(x0,y0)的切线方程.已知函数f(x)=ax3+3x2-6ax-11,g(x)=3x2+6x+12,直线m:y=kx+9,且f′(-1)=0.(1)求a的值;(2)是否存在实数k,使直线m既是曲线y=f(x)的切线,又是y=g(x)的切线?如果存在,求出k的值;如果不存在,说明理由.【精彩点拨】(1)求f′(x)→f′(-1)=0→求得a(2)设直线m与y=g(x)相切→求出相应切线的斜率与切线方程→检验切线是否与y=f(x)相切→得结论【规范解答】(1)因为f′(x)=3ax2+6x-6a,且f′(-1)=0,所以3a-6-6a=0,得a=-2.(2)因为直线m过定点(0,9),先求过点(0,9),且与曲线y=g(x)相切的直线方程.设切点为(x0,3x20+6x0+12),又因为g′(x0)=6x0+6.所以切线方程为y-(3x20+6x0+12)=(6x0+6)(x-x0).将点(0,9)代入,得9-3x20-6x0-12=-6x20-6x0,所以3x20-3=0,得x0=±1.当x0=1时,g′(1)=12,切点坐标为(1,21),所以切线方程为y=12x+9;当x0=-1时,g′(-1)=0,切点坐标为(-1,9),所以切线方程为y=9.下面求曲线y=f(x)的斜率为12和0的切线方程:因为f(x)=-2x3+3x2+12x-11,所以f′(x)=-6x2+6x+12.由f′(x)=12,得-6x2+6x+12=12,解得x=0或x=1.当x=0时,f(0)=-11,此时切线方程为y=12x-11;当x=1时,f(1)=2,此时切线方程为y=12x-10.所以y=12x+9不是公切线.由f′(x)=0,得-6x2+6x+12=0,解得x=-1或x=2.当x=-1时,f(-1)=-18,此时切线方程为y=-18;当x=2时,f(2)=9,此时切线方程为y=9,所以y=9是公切线.综上所述,当k=0时,y=9是两曲线的公切线.此题直线m恒过点(0,9)是解题的突破口,即若m是f(x),g(x)的公切线,则切线必过点(0,9).一般说来,求过定点的两曲线公切线的一般思路是:先求出过定点的一曲线的切线方程,再令斜率值与另一曲线的导数相等,求出可能的切点,得出对应切线方程.若两条直线方程相同,则为公切线;若不同,则不存在公切线.当然,也可能会存在切线斜率不存在的情况.[再练一题]1.已知函数f(x)=x3+x-16.(1)求曲线y=f(x)在点(2,-6)处的切线的方程;(2)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切点坐标;(3)如果曲线y=f(x)的某一切线与直线y=-14x+3垂直,求切点坐标与切线的方程.【解】(1)可判定点(2,-6)在曲线y=f(x)上.∵f(x)=(x3+x-16)′=3x2+1,∴f(x)在点(2,-6)处的切线的斜率为k=f′(2)=13.∴切线的方程为y-(-6)=13(x-2),即y=13x-32.(2)设切点为(x0,y0),则直线l的斜率为f′(x0)=3x20+1,∴直线l的方程为y=(3x20+1)(x-x0)+x30+x0-16.又∵直线l过点(0,0),∴0=(3x20+1)(-x0)+x30+x0-16,整理得,x30=-8,∴x0=-2.∴y0=(-2)3+(-2)-16=-26.k=3×(-2)2+1=13.∴直线l 的方程为y =13x ,切点坐标为(-2,-26). (3)∵切线与直线y =-x4+3垂直, ∴切线的斜率k =4.设切点的坐标为(x 0,y 0),则f ′(x 0)=3x 20+1=4,∴x 0=±1,∴⎩⎪⎨⎪⎧ x 0=1,y 0=-14或⎩⎪⎨⎪⎧x 0=-1,y 0=-18. 即切点坐标为(1,-14)或(-1,-18). 切线方程为y =4(x -1)-14或y =4(x +1)-18. 即y =4x -18或y =4x -14.0,则f (x )在这个区间上为减函数.应注意:在区间内f ′(x )>0[或f ′(x )<0]是f (x )在这个区间上为增函数(或减函数)的充分条件,而不是必要条件.如果f (x )在某个区间上为增函数,那么f ′(x )≥0;如果f (x )在某个区间上为减函数,那么f ′(x )≤0.利用导数研究函数单调性的步骤为: (1)求f ′(x );(2)解不等式f ′(x )>0或f ′(x )<0;(3)确定并指出函数的单调递增区间、递减区间.已知函数f (x )=4x 2-72-x ,x ∈[0,1](1)求f (x )的单调区间和值域;(2)设a ≥1,函数g (x )=x 3-3a 2x -2a ,x ∈[0,1],若对于任意x 1∈[0,1],总存在x 0∈[0,1],使得g (x 0)=f (x 1)成立,求a 的取值范围.【精彩点拨】 (1)求f ′(x ),列表,求单调区间及最值; (2)任意存在型问题,转化为f (x )的值域是g (x )值域的子集.【规范解答】 (1)f ′(x )=-4x 2+16x -7(2-x )2=-(2x -1)(2x -7)(2-x )2,令f ′(x )=0,得x =12或x =72(舍去).当x 变化时,f ′(x ),f (x )的变化情况如下表:∴当x ∈⎝ ⎭⎪⎫0,12时,f (x )是减函数;当x ∈⎝ ⎛⎭⎪⎫12,1时,f (x )是增函数.当x ∈[0,1]时,f (x )的值域为[-4,-3]. (2)对函数g (x )求导,得g ′(x )=3(x 2-a 2). ∵a ≥1,当x ∈[0,1]时,g ′(x )<3(1-a 2)≤0, 且g ′(x )=0的根为有限个. ∴当x ∈[0,1]时,g (x )为减函数. ∴当x ∈[0,1]时,g (x )∈[g (1),g (0)]. 又g (1)=1-2a -3a 2,g (0)=-2a , 即g (x )∈[1-2a -3a 2,-2a ]. 任给x 1∈[0,1],f (x 1)∈[-4,-3]. 存在x 0∈[0,1],使得g (x 0)=-f (x 1), 则[1-2a -3a 2,-2a ][-4,-3],即⎩⎪⎨⎪⎧1-2a -3a 2≤-4, ①-2a ≥-3, ②解①式得a ≥1或a ≤-53,解②式得a ≤32. 又a ≥1,∴a 的取值范围为⎣⎢⎡⎦⎥⎤1,32.1.利用导数求函数的单调区间,也就是求函数定义域内不等式f ′(x )>0或f ′(x )<0的解集.2.已知函数在某个区间上单调,求参数问题,通常是转化为恒成立问题.[再练一题]2.已知a ∈R 函数f (x )=(-x 2+ax )e x (x ∈R ). (1)当a =2时,求函数f (x )的单调区间;(2)若函数f (x )在(-1,1)上单调递增,求a 的取值范围. 【解】 当a =2时,f (x )=(-x 2+2x )e x , f ′(x )=(-x 2+2)e x .当f ′(x )>0时,(-x 2+2)e x >0, 注意到e x >0,所以-x 2+2>0,解得-2<x < 2.所以,函数f (x )的单调递增区间为(-2,2).同理可得,函数f (x )的单调递减区间为(-∞,-2)和(2,+∞).(2)因为函数f (x )在(-1,1)上单调递增,所以f ′(x )≥0在(-1,1)上恒成立. 又f ′(x )=[-x 2+(a -2)x +a ]e x , 即[-x 2+(a -2)x +a ]e x ≥0, 注意到e x >0,因此-x 2+(a -2)x +a ≥0在(-1,1)上恒成立, 也就是a ≥x 2+2x x +1=x +1-1x +1在(-1,1)上恒成立.设y =x +1-1x +1,则y ′=1+1(x +1)2>0,即y =x +1-1x +1在(-1,1)上单调递增, 则y <1+1-11+1=32,故a ≥32.即a 的取值范围为⎣⎢⎡⎭⎪⎫32,+∞.最值与极值的不同.函数的极值表示函数在一点附近的情况,是在局部对函数值比较大小;而最值是在整个区间上对函数值比较大小.函数的极值可以有多个,但最值只能有一个,极值只能在区间内取得,而最值还可以在端点处取得,最值只要不在端点处,必是一个极值.已知函数f (x )=x 3-3ax 2-9a 2x +a 3. (1)设a =1,求函数f (x )的极值;(2)若a >13,且当x ∈[1,4a ]时,f (x )≥a 3-12a 恒成立,试确定a 的取值范围.【规范解答】 (1)当a =1时,f (x )=x 3-3x 2-9x +1且f ′(x )=3x 2-6x -9,由f ′(x )=0得x =-1或x =3.当x <-1时,f ′(x )>0,当-1<x <3时,f ′(x )<0, 因此x =-1是函数的极大值点, 极大值为f (-1)=6;当-1<x <3时,f ′(x )<0,当x >3时,f ′(x )>0, 因此x =3是函数的极小值点,极小值为f (3)=-26. (2)∵f ′(x )=3x 2-6ax -9a 2=3(x +a )(x -3a ),a >13,∴当1≤x <3a 时,f ′(x )<0; 当3a <x ≤4a 时f ′(x )>0.∴x ∈[1,4a ]时,f (x )的最小值为f (3a )=-26a 3. 由f (x )≥a 3-12a 在[1,4a ]上恒成立得-26a 3≥a 3-12a . 解得-23≤a ≤23. 又a >13,∴13<a ≤23. 即a 的取值范围为⎝ ⎛⎦⎥⎤13,23.一般地,已知不等式在某区间上恒成立,求参数的取值范围问题,都可以转化为求函数的最值问题,而导数是解读函数最值问题的有力工具.[再练一题]3.已知函数f (x )=ax 3+bx 2+cx 在点x 0处取得极小值-4,使其导函数f ′(x )>0的x 的取值范围为(1,3).(1)求f (x )的解析式及f (x )的极大值;(2)当x ∈[2,3]时,求g (x )=f ′(x )+6(m -2)x 的最大值.【解】 (1)由题意知f ′(x )=3ax 2+2bx +c =3a (x -1)·(x -3)(由题意f ′(x )>0的x 的范围(1,3)可知a <0),∴在(-∞,1)上f ′(x )<0,f (x )是减函数, 在(1,3)上f ′(x )>0,f (x )是增函数, 在(3,+∞)上f ′(x )<0,f (x )是减函数.因此f (x )在x 0=1处取得极小值-4,在x =3处取得极大值. ∴⎩⎪⎨⎪⎧a +b +c =-4,f ′(1)=3a +2b +c =0,f ′(3)=27a +6b +c =0,解得a =-1,b =6,c =-9, ∴f (x )=-x 3+6x 2-9x .则f (x )在x =3处取得极大值f (3)=0.(2)g (x )=-3x 2+12x -9+6(m -2)x =-3(x 2-2mx +3), g ′(x )=-6x +6m =0,得x =m . ①当2≤m ≤3时, g (x )max =g (m )=3m 2-9;②当m <2时,g (x )在[2,3]上是递减的,g (x )max =g (2)=12m -21; ③当m >3时,g (x )在[2,3]上是递增的,g (x )max =g (3)=18m -36. 因此g (x )max =⎩⎪⎨⎪⎧12m -21, m <2,3m 2-9, 2≤m ≤3,18m -36, m >3.考查求函数的单调区间、函数的极值与最值,参数的取值范围等问题,若以选择题、填空题出现,以中低档题为主;若以解答题形式出现,则难度以中档以上为主,有时也以压轴题的形式出现.考查中常渗透函数、不等式等有关知识,综合性较强.已知函数f (x )=ln x +ke x (k 为常数,e =2.718 28…是自然对数的底数),曲线y =f (x )在点(1,f (1))处的切线与x 轴平行.(1)求k 的值; (2)求f (x )的单调区间;(3)设g (x )=xf ′(x ),其中f ′(x )为f (x )的导函数.证明:对任意x >0,g (x )<1+e -2.【精彩点拨】 (3)中要借助于(2)的结论,构造函数. 【规范解答】 (1)f ′(x )=1x -ln x -ke x,由已知,f ′(1)=1-ke =0,∴k =1. (2)由(1)知,f ′(x )=1x -ln x -1e x.设k (x )=1x -ln x -1,则k ′(x )=-1x 2-1x <0,即k (x )在(0,+∞)上是减函数, 由k (1)=0知,当0<x <1时,k (x )>0,从而f ′(x )>0, 当x >1时,k (x )<0,从而f ′(x )<0.综上可知,f (x )的单调递增区间是(0,1),单调递减区间是(1,+∞).(3)由(2)可知,当x ≥1时,g (x )=xf ′(x )≤0<1+e -2,故只需证明g (x )<1+e -2在0<x <1时成立.当0<x <1时,e x >1,且g (x )>0, ∴g (x )=1-x ln x -xe x <1-x ln x -x .设F (x )=1-x ln x -x ,x ∈(0,1), 则F ′(x )=-(ln x +2), 当x ∈(0,e -2)时,F ′(x )>0, 当x ∈(e -2,1)时,F ′(x )<0,所以当x =e -2时,F (x )取得最大值F (e -2)=1+e -2. 所以g (x )<F (x )≤1+e -2. 综上,对任意x >0,g (x )<1+e -2.利用导数解决不等式问题(如:证明不等式,比较大小等),其实质就是利用求导数的方法研究函数的单调性,而证明不等式(或比较大小)常与函数最值问题有关.因此,解决该类问题通常是构造一个函数,然后判断这个函数的单调性,结合给定的区间和函数在该区间上的最值使问题得以求解.[再练一题]4.已知函数f (x )=12x 2-a ln x (a ∈R ), (1)若f (x )在x =2时取得极值,求a 的值; (2)求f (x )的单调区间;(3)求证:当x >1时,12x 2+ln x <23x 3.【解】 (1)f ′(x )=x -a x ,因为x =2是一个极值点,所以2-a2=0,则a =4.此时f ′(x )=x -4x =(x +2)(x -2)x ,因为f (x )的定义域是(0,+∞),所以当x ∈(0,2)时,f ′(x )<0;当x ∈(2,+∞),f ′(x )>0,所以当a =4时,x =2是一个极小值点,则a =4.(2)因为f ′(x )=x -a x =x 2-ax ,所以当a ≤0时,f (x )的单调递增区间为(0,+∞).当a >0时,f ′(x )=x -a x =x 2-a x =(x +a )(x -a )x,所以函数f (x )的单调递增区间(a ,+∞);递减区间为(0,a ).(3)证明:设g (x )=23x 3-12x 2-ln x ,则g ′(x )=2x 2-x -1x ,因为当x >1时,g ′(x )=(x -1)(2x 2+x +1)x >0,所以g (x )在x ∈(1,+∞)上为增函数,所以g (x )>g (1)=16>0,所以当x >1时,12x 2+ln x <23x 3.些实际问题是函数内容的继续与延伸,这种解决问题的方法使复杂的问题简单化,因而已逐渐成为高考的又一新热点.利用导数求实际问题的最大(小)值时,应注意的问题:(1)求实际问题的最大(小)值时,一定要符合问题的实际意义,不符合实际意义的值应舍去.(2)在实际问题中,由f ′(x )=0常常仅得到一个根,若能判断出函数的最大(小)值在x 的变化区间内部得到,则这个根处的函数值就是所求的最大(小)值.某企业拟建造如图3-1所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为80π3立方米,且l ≥2r .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c (c >3)千元.设该容器的建造费用为y 千元.(1)写出y 关于r 的函数表达式,并求该函数的定义域; (2)求该容器的建造费用最小时的r .图3-1【规范解答】 (1)设容器的容积为V , 由题意知V =πr 2l +43πr 3,又V =80π3, 故l =V -43πr3πr 2=803r 2-43r =43⎝ ⎛⎭⎪⎫20r 2-r .由于l ≥2r ,因此0<r ≤2. 所以建造费用y =2πrl ×3+4πr 2c =2πr ×43⎝ ⎛⎭⎪⎫20r 2-r ×3+4πr 2c ,因此y =4π(c -2)r 2+160πr ,0<r ≤2. (2)由(1)得y ′=8π(c -2)r -160πr 2=8π(c -2)r 2⎝⎛⎭⎪⎫r 3-20c -2,0<r ≤2. 由于c >3,所以c -2>0, 当r 3-20c -2=0时,r =320c -2.令320c -2=m ,则m >0.所以y ′=8π(c -2)r 2(r -m )(r 2+rm +m 2).。
最新高中数学选修1-2:第1章重点突破

高中数学人教A 版选修1-2 重点突破1.(2012·山东寿光中学月考)硕士学位与博士学位的一个随机样本给出了关于所获取学位类 学位性别 硕士 博士 总计男 162 27 189女 143 8 151总计 305 35 340根据以上数据,则( )A .性别与获取学位类别有关B .性别与获取学位类别无关C .性别决定获取学位的类别D .以上都是错误的解析:选A.由表格可得:博士:男性占2735≈77%,女性占835≈23%,相差很大,所以性别与获取学位的类别有关,故选A.2.(2012·泰安一中期中)为预测某种产品的回收率y ,需要研究它和原料有效成分含量x 之间的线性相关关系,现取A.y ^=11.47+2.62xB.y ^=-11.47+2.62xC.y ^=2.62+11.47xD.y ^=11.47-2.62x3.(2012·徐州一中月考)在研究身高和体重的关系时,求得相关指数R 2≈________,可以叙述为“身高解释了56%的体重变化,而随机误差贡献了剩余的44%”,所以身高对体重的效应比随机误差的效应大得多.解析:由相关指数的概念得R 2=0.56,可以叙述为“身高解释了56%的体重变化,而随机误差贡献了剩余的44%”.答案:0.564.(2012·德州一中质量检测)有两个分类变量x 与y ,其一组观测值如下面的2×2列联表所示:y 1 y 2 总计x 1 a 20-a 20x 2 15-a 30+a 45总计 15 50 65其中a ,15-a 均为大于0.1的前提下认为x 与y 之间有关系?解:查表可知,要使在犯错误的概率不超过0.1的前提下认为x 与y 之间有关系,则k ≥2.706,而k =65×[a (30+a )-(20-a )(15-a )]220×45×15×50=65×(65a -300)220×45×15×50=13×(13a -60)260×90. 由k ≥2.706得a ≥7.19或a ≤2.04.又a >5且15-a >5,a ∈Z ,即a =8,9.故a 为8或9时,在犯错误的概率不超过0.1的前提下认为x 与y 之间有关系.。
通用版带答案高中物理选修一综合测试题考点突破

通用版带答案高中物理选修一综合测试题考点突破单选题1、水刀切割具有精度高,无热变形、无毛刺,无需二次加工以及节约材料等特点,因而得到广泛应用。
某水刀切割机床如图所示,若横截面直径为d的圆柱形水流垂直射到要切割的钢板上,碰到钢板后水的速度减为零。
已知水的流量(单位时间流出水的体积)为Q,水的密度为ρ,则钢板受到水的平均冲力大小为()A.4QρB.QρC.16ρQπd2D.4ρQπd2答案:D设t时间内有体积为V的水打在钢板上,则这些水的质量m=ρV=ρSvt=14πd2ρvt以这部分水为研究对象,它受到钢板的作用力为F,以水运动的方向为正方向,由动量定理得Ft=0−mv解得F=−14πd2ρv2水流速度v=QS=4Qπd2得F=−4ρQ2πd2根据牛顿第三定律,钢板受到水的冲力F′=4ρQ2πd2故选D。
2、如图所示,倾角为30°的斜面固定在水平地面上,其底端N与光滑的水平地面平滑连接,N点右侧有一竖直固定挡板。
质量为0.8kg的小物块b静止在地面上,现将质量为0.4kg的小物块a由斜面上的M点静止释放。
已知MN=1.5m,a、b与斜面之间的动摩擦因数均为2√315,a、b碰撞时间极短,碰后黏在一起运动不再分开,a、b 整体与挡板碰撞过程中无机械能损失。
取g=10m/s2,则()A.物块a第一次运动到N点时的动能为3.6JB.a、b碰撞过程中系统损失的机械能为0.6JC.b与挡板第一次碰撞时,挡板对b的冲量大小为1.2N·sD.整个运动过程中,b在斜面上运动的路程为0.25m答案:DA.物块a第一次运动到N点过程,由动能定理m a gMNsin30°−μm a gMNcos30°=E k a=12m a v02带入题中数据可得v0=3m/sE k a=1.8JA错误;B.设a与b碰前速度大小为v0,碰后二者速度为v,由动量守恒m a v0=(m a+m b)v b碰撞过程中系统损失的机械能ΔE损=12m a v02−12(m a+m b)v2解得v=1.0m/sΔE损=1.2JB错误;C.由B分析知,a、b整体与挡板第一次碰撞前的速度即为v=1.5m/s,碰撞过程中无机械能损失,所以碰后整体速度变为向左的1.5m/s,对整体,由动量定理I=Δp=(m a+m b)v−(m a+m b)(−v)=2(m a+m b)v=2.4N⋅s挡板对b的冲量即为对整体的冲量,C错误;D.a、b整体静止在N点,对a、b整体,自碰后至最终停下,由能量守恒1 2(m a+m b)v2=μ(m a+m b)gcosθ⋅s总带入数据解得s总=0.25m D正确。
专题01 成长故事-直击新高考英语 专项突破“读后续写”

专题01直击2022高考英语专项突破“读后续写”--成长故事读后续写“一波三折”:1.情绪------情绪描写。
从原材料中体会作者相应情绪,借助情绪的延续,以此为衔接,续写。
2.细节-----进一步描述。
3.转折----个人的努力或者借助外界的力量,使事情发生转折。
4.转机-----事情似乎有了转机,让人抱有希望,心理能感到安慰。
5.失望----问题仍然没有解决或者又出现了新的问题。
6.想法----面对没有解决的问题或者新问题,突然有了想法或感触。
7.结局-----在想法或感触的影响下,事情有了最后的转折/转机。
8.点题-----呼应前文备注:这八步不是固定的,考生可以根据自己的想法打乱部分顺序,也可以略写个别环节。
此步骤,可让续写有话可说,让情节续写跌宕起伏,前提是要读懂原材料的中心,抓住文章脉络。
每个人都会成长。
在点点滴滴中,在大风大浪中,在自我挣扎中……01阅读下面短文,根据其内容和所给段落开头语续写两段,使之构成一篇完整的短文。
Here’s the story of my growth over the past year. It’s a story of how I found the stren gth to change myself for better and then how I get rid of my fears to be even better. If anyone is inspired by this, that’s wonderful.I’d been stuck as this incredibly insecure, under-confident and just scared individual for years and years. Since childho od I’d been stuck like this. Kids I met for the first time looked at me rudely and unkindly. Even my friends—actually, I had very few friends because I just felt too ashamed and frightened to make some, though I was eager to and felt extremely lonely in the depth of my heart—laughed at me and gave me bad nicknames. I felt terrible, but I’d just resigned to a life where I’d be afraid of everything and be this “introvert” (内向的人) or whatever. I thought I would never be able to change, never, for my whole life.But then it all started changing. Something clicked. I suddenly determined to go on a diet, and lost some weight. It was tough. I felt hungry all the time. I was always tempted by the smell of bread and hamburger, even when I didn’t see them. But the toug hest thing was that even if I had just had my meals, I felt hunger mentally.However, I held on. In over a period of 6 months I finally managed to stick to one of my diets. I didn’t know how. But I did make it.The loss of 90 lbs brought me from overweight straight down to underweight. This isn’t the best part. More importantly and inspiringly, I suddenly found strength in me. I realized I could be totally different. And maybe, I could even be whatever I wanted to be. This taught me that I could change myself.Then I wondered, perhaps, I could also get rid of those of my fears, just like I succeeded in losing my extra pounds. It might not be easy, but it might not be that difficult.注意:1. 续写词数应为150左右:2. 请按如下格式在答题卡的相应位置作答。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
选修专项训练 01命题人: 陈书兰 尚振星 褚加星 审核人: 尚现军 时间 2009-4-21班级 姓名 评价 卷面分1.(8分)[物理—物理3—4] 一根弹性绳沿x 轴方向放置,左端在坐标原点O ,用手握住绳的左端使其沿y 轴方向做周期为1s 的简谐运动,于是在绳上形成一列简谐波。
若从波传到x =1m 处的M 质点时开始计时: (1)经过的时间t 等于多少时,平衡位置在x =4.5m 处的N 质点恰好第一次沿y 轴正向通过平衡位置?(2)在图中准确画出t 时刻弹性绳上的完整波形。
2.(物理3-5模块,8分) 在真空中,原来静止的原子核X ab 在进行α衰变时,放出α粒子的动能为E 0。
假设衰变后产生的新核用字母Y 表示,衰变时产生的能量全部以动能形式释放出来,真空中的光速为c ,原子核的质量之比等于质量数之比,原子核的重力不计。
(1)写出衰变的核反应方程; (2)求衰变过程中总的质量亏损。
3、(苏州市2008届期终考试)(8分)如图,一透明球体置于空气中,球半径R =10cm ,折射率n =2.MN 是一条通过球心的直线,单色细光束AB 平行于MN 射向球体,B 为入射点, AB 与MN 间距为52cm ,CD 为出射光线.①补全光路并求出光从B 点传到C 点的时间; ②求CD 与MN 所成的角α.(需写出求解过程)4.(烟台市2008届第一学期期末考)(8分)在坐标原点O 处有一质点S ,它沿y 轴做频率为10Hz 、振幅为2cm 的简谐运动,形成的波沿x 轴传播,波速为4m/s ,当t =0时,S 从原点开始沿y 轴负方向运动.(1)画出当S 完成第一次全振动时的波形图; (2)经过多长时间x =1m 处的质点第一次出现波峰.5.(青岛市2008年质检)【物理—选修3—4】(8分)在“用双缝干涉测光的波长”的实验中,某同学安装实验装置如图甲所示,调试好后能观察到清晰的干涉条纹。
(1)根据实验装置知,②、③、④依次是 、 、 ;(2)某次实验时,该同学调节分划板的位置,使分划板中心刻线对齐某亮纹的中心,如图乙所示,此时螺旋测微器的读数为 mm 。
转动手轮,使分划线向一侧移动到另一条亮纹的中心位置,再次从螺旋测微器上读数。
若实验测得4条亮纹中心间的距离为△x=0.960mm ,已知双缝间距为d=1.5mm ,双缝到屏的距离为L=1.00m ,则对应的光波波长λ应为多少?6、模块3-4试题(8分)⑴设宇宙射线粒子的能量是其静止能量的k 倍.则粒子运动时的质量等于其静止质量的 倍,粒子运动速度是光速的 倍。
⑵某实验室中悬挂着一弹簧振子和一单摆,弹簧振子的弹簧和小球(球中间有孔)都套在固定的光滑竖直杆上.某次有感地震中观察到静止的振子开始振动4.0 s 后,单摆才开始摆动.此次地震中同一震源产生的地震纵波和横波的波长分别为10 km 和5.0 km ,频率为1.0 Hz .假设该实验室恰好位于震源的正上方,求震源离实验室的距离.选修专项训练参考答案1.解:(1)s m smT v /212==λ…………………………………………………………1分2T v MN t +=…………………………………………………………………………2分=2.25s …………………………………………………………………………………1分 (2)(4分) 2.解。
(1)衰变的核反应方程为:He Y X a b a b 4242+→-- …………2分(2)根据动量守恒定律,反冲核Y 的动量与α粒子的动量大小相等 ……1分 根据公式 m P E k 22= …………1分可知,反冲核Y 的动能为 0144E a E k -=…………1分 衰变时释放出的总能量为 0041E a aE E E k k -=+= ………1分 根据爱因斯坦的质能方程 2c m E k ⋅∆= ………………1分 此衰变过程中总的质量亏损是 20)4(c a aE m -=∆ …………1分 3.解。
①连接BC ,如图 (1分)在B 点光线的入射角、折射角分别 标为i 、r ,Sin i=52/10=2/2, 所以, i =45°(1分)由折射率定律:在B 点有:rin sin sin =(1分) Sin r=1/2 故:r =30° (1分) BC =2R cos r (1分)t = BCn/C =2Rn cos r/C (1分) t/3) ×10-9s (1分)②由几何关系可知︒=∠15cop (1分) ︒=∠135ocp α=30°(2分)4.解:(1)波长m f v 4.0/==λ……………………………………………………①图象如图所示(2)设S 点的振动经t 1传播到s vxt m x 25.0,11===处……………………② 振动传到该质点后又经过43周期该质点才振动到波峰s fT t 075.043432===……………………………………………………③m x 1=∴处的质点第一次出现波峰的时间为21t t t +==0.325s …………④5.(1)滤光片、单缝和双缝。
(每空1分,共3分) (2)螺旋测微器的读数为1.179mm~1.181mm 。
(2分) (3)相邻两条亮(暗)纹间的距离:mm mm n x x 320.014960.01=-=-∆='∆ (1分) mm mm L x d 43108.41000.1320.05.1-⨯=⨯⨯='∆=λ (2分) 6.【解析】⑴k⑵地震纵波传播速度为:v P =f λP 地震横波传播速度为:v S =f λS 震源离实验室距离为s ,有:P s t =v ()S s t t =+∆v 解得:40 km 11sPf ts λλ∆==-选修专项训练 04命题人: 陈书兰 尚振星 褚加星 审核人: 尚现军 时间 2009-5-6班级 姓名 评价 卷面分1.(物理3-4模块,8分) 如图所示,一横波的波源在坐标原点,x 轴为波的传播方向,y 轴为振动方向。
当波源开始振动0.5s 时形成了如图所示的波形(波刚传到图中P 点)。
试求: (1)波的振幅为多少?(2)从图示位置再经多长时间波传到Q 点? (3)Q 点开始振动的方向如何? 2、(1)有以下说法:A .在“探究单摆的周期与摆长的关系”实验中,为减小偶然误差,应测出单摆作n 次全振动的时间t ,利用ntT求出单摆的周期 B .如果质点所受的合外力总是指向平衡位置,质点的运动就是简谐运动C .变化的磁场一定会产生变化的电场D .X 射线是比紫外线频率低的电磁波E .只有波长比障碍物的尺寸小的时候才会发生明显的衍射现象F .在同种均匀介质中传播的声波,频率越高,波长越短 其中正确的是____ ______________________.(2)如图乙所示,一束平行单色光由空气斜射入厚度为h 的玻璃砖,入射光束与玻璃砖上表面夹角为θ,入射光束左边缘与玻璃砖左端距离为b 1,经折射后出射光束左边缘与玻璃砖的左端距离为b 2,可以认为光在空气中的速度等于真空中的光速c .求:光在玻璃砖中的传播速度v .3、(盐城市2008年第二次调研)镭(Ra )是历史上第一个被分离出来的放射性元素,已知Ra22688能自发地放出α粒子而变成新核Rn ,已知Ra22688的质量为M 1=3.7533×10-25kg ,新核Rn 的质量为M 2=3.6867×10-25kg ,α粒子的质量为m=6.6466×10-27kg ,现有一个静止的Ra22688核发生α衰变,衰变后α粒子的速度为3.68×105m/s 。
则:(计算结果保留两位有效数字) ①写出该核反应的方程式。
②此反应过程中放出的能量是多少? ③反应后新核Rn 的速度是多大?4.如图所示,甲车的质量是2kg ,静止在光滑水平面上,上表面光滑,右端放一个质量为1kg 的小物体.乙车质量为4kg ,以5 m/s 的速度向左运动,与甲车碰撞后甲车获得8m/s 的速度,物体滑到乙车上.若乙车足够长,上表面与物体的动摩擦因数为0.2,则物体在乙车上表面滑行多长时间相对乙车静止?(g 取10 m/s 2)5.[ 物理─选修3-4](1)①大海中航行的轮船,受到大风大浪冲击时,为了防止倾覆,应当改变航行方向和 ,使风浪冲击力的频率远离轮船摇摆的 .②光纤通信中,光导纤维递光信号的物理原理是利用光的 现象,要发生这种现象,必须满足的条件是:光从光密介质射向 ,且入射角等于或大于 . (2)如图所示,实线是某时刻的波形图,虚线是0.2s 后的波形图. (1) 若波向左传播,求它传播的最小距离. (2) 若波向右传播,求它的最大周期.6、下列说法正确的是 ( )A .考虑相对论效应,长度、时间的测量结果都随物体与观察者相对运动状态而改变B .一切物理规律在不同的惯性系中是平权的C .圆屏阴影中心的亮斑(泊松亮斑)是光波叠加造成的D .在光的双缝干涉实验中,条纹间距与缝的宽度成正比图乙选修专项训练04参考答案1.(1)根据图象,波的振幅为A=10cm ………………1分(2)根据题意,波的周期为T=0.5s ,波的波长为λ=2m ………………1分波速为v=λ/T=4m/s ………………2分传到Q 点用的时间 s vPQt 5.2==…………2分 (3)Q 点的振动方向就是如图所示的波形中P 点的振动方向,判断可知沿y 轴的负方向。
………………2分 2.解:(1) AF (每个答案2分,共4分)(2)由光的折射定律得 n r i =s i ns i n(1分)又 vcn =(1分) 由几何关系得 θc o s s i n =i (1分)221212)(sin hb b b b r +--=(1分)由以上各式可得 ()θcos )(212212b b h b b c v -+-= (2分)3.①Rn He Ra 222864222688+→ (3分)② J c m M M mc E 122212102.1)(-⨯=--=∆=∆ (2分)③ 220-=M m υυ(2分) 322/ 6.610/∴==⨯m M m s υυ(1分) 4 .乙与甲碰撞动量守恒 m 乙v 乙=m 乙v 乙′+m 甲v 甲′小物体m 在乙上滑动至有共同速度v ,对小物体与乙车运用动量守恒定律得 m 乙v 乙′=(m +m 乙)v对小物体应用牛顿第二定律得a =μg 所以t =v /μg 代入数据得t =0.4 s 5.(1)①速度 频率 ②全反射 光疏介质 临界角 (2) (1)3m ,(2)0.8s解 ① X=3/4λ+n λ 当n 取0时X 最小,则最小位移为X=3m ②右传,t=1/4T+nT 所以T=4t/(1+4n),当n=0时,最大周期为T=0.8s6. ABC图乙。
