五年级春季班第二讲
染色与覆盖
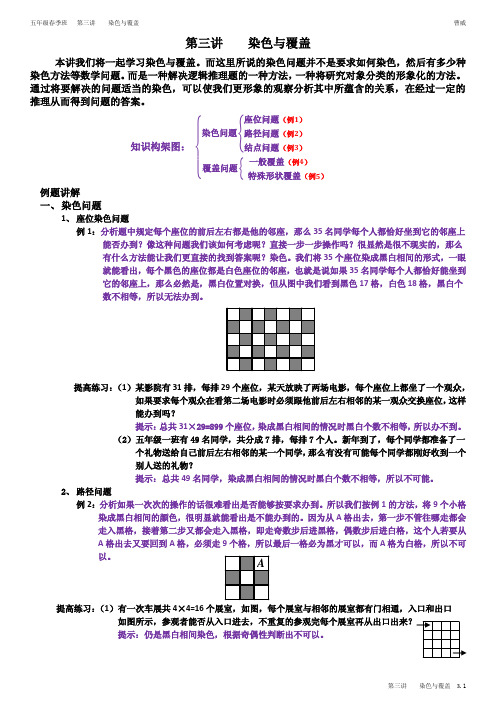
第三讲 染色与覆盖本讲我们将一起学习染色与覆盖。
而这里所说的染色问题并不是要求如何染色,然后有多少种染色方法等数学问题。
而是一种解决逻辑推理题的一种方法,一种将研究对象分类的形象化的方法。
通过将要解决的问题适当的染色,可以使我们更形象的观察分析其中所蕴含的关系,在经过一定的推理从而得到问题的答案。
知识构架图:染色问题 座位问题(例 )路径问题(例 )结点问题(例 )覆盖问题 一般覆盖(例 ) 特殊形状覆盖(例 ) 例题讲解一、 染色问题1、 座位染色问题例1:分析题中规定每个座位的前后左右都是他的邻座,那么35名同学每个人都恰好坐到它的邻座上能否办到?像这种问题我们该如何考虑呢?直接一步一步操作吗?很显然是很不现实的,那么有什么方法能让我们更直接的找到答案呢?染色。
我们将35个座位染成黑白相间的形式,一眼就能看出,每个黑色的座位都是白色座位的邻座,也就是说如果35名同学每个人都恰好能坐到它的邻座上,那么必然是,黑白位置对换,但从图中我们看到黑色17格,白色18格,黑白个数不相等,所以无法办到。
提高练习:(1)某影院有31排,每排29个座位,某天放映了两场电影,每个座位上都坐了一个观众,如果要求每个观众在看第二场电影时必须跟他前后左右相邻的某一观众交换座位,这样能办到吗?提示:总共31×29=899个座位,染成黑白相间的情况时黑白个数不相等,所以办不到。
(2)五年级一班有49名同学,共分成7排,每排7个人。
新年到了,每个同学都准备了一个礼物送给自己前后左右相邻的某一个同学,那么有没有可能每个同学都刚好收到一个别人送的礼物?提示:总共49名同学,染成黑白相间的情况时黑白个数不相等,所以不可能。
2、 路径问题例2:分析如果一次次的操作的话很难看出是否能够按要求办到。
所以我们按例1的方法,将9个小格染成黑白相间的颜色,很明显就能看出是不能办到的。
因为从A 格出去,第一步不管往哪走都会走入黑格,接着第二步又都会走入黑格,即走奇数步后进黑格,偶数步后进白格,这个人若要从A 格出去又要回到A 格,必须走9个格,所以最后一格必为黑才可以,而A 格为白格,所以不可以。
五年级上册奥数培优 第二讲 一般应用题

第二讲一般应用题例1、五年级有6个班,每班人数相等。
从每班选16人参加春季运动会,剩下的同学相当于原来4个班的人数,原来每班有多少人?随堂练习1.5位同学有同样多的存款,若每人拿出16元捐给“希望工程”后,5位同学剩下的钱正好等于原来3人的存款数,原来每人有存款多少元?2.把一堆货物平均分给6个小组运,当每个小组都运68箱时,正好可以运走这堆货物的一半。
这堆货物一共有多少箱?3.老师把一批树苗平均分给4个小队栽,当每队栽6棵时,剩下的树苗总数与每队分得的棵数相同。
这批树苗一共有多少棵?例2、某洗衣液生产厂计划每天加工50箱洗衣液,实际每天生产56箱。
这样,不仅提前3天完成原计划生产的任务,而且还多生产了120箱洗衣液。
这个洗衣液生产厂实际生产了多少箱洗衣液?练一练1星期天楠楠一家开车去旅游,爸爸原计划每小时行50千米实际每小时多行了10千米,这样比原计划提前2小时到达了景点。
楠楠家与景点两地相距多少千米?2.昊昊骑自行车上学,原来每天每分钟行200米,正好准时到达学校,有一天因下雨,他每分钟只能行120米,结果迟到了5分钟。
他家离学校有多远?3.李双骑自行车以320米/分的速度从A地驶向B地,途中因自行车故障推车继续向前步行5分钟到距B地1800米的某地修车,15分钟后以原来速度的1.5倍继续向前驶向B地,到达B地时,比预计时间多用17分钟,则李双推车步行的速度是多少?例3、工程队要铺设一段地下排水管道,用长管子铺需要25根,用短管子铺需要35根。
已知这两种管子的长相差2米,这段排水管道长多少米?练一练1、一班的小朋友在操场上做游戏,每组6人。
玩了一会儿,他们觉得每组人数太少便重新分组,正好每组9人,这样比原来减少了2组。
参加游戏的小朋友一共有多少人?2.甲、乙二人同时从A地到B地,甲经过10小时到达了B 地,比乙多用了4小时。
已知二人的速度差是每小时5千米,求甲、乙二人每小时各行多少千米?3生产一批零件,甲单独生产要用6小时,乙单独生产要用8小时,如果甲每小时比乙多生产10个零件,这批零件一共有多少个?例4、甲、乙两人同时加工一批零件。
K12教育2020春季五年级语文讲义

K12教育2020春季五年级语文讲义第2讲:主题阅读走进西部学易优班次:_________________ 姓名:______________以写景为主的文章,主要是以描写大自然的美丽风光为中心,通过对景物的生动描绘,来抒发作者的某种感情。
阅读此类文章应注意以下几点:一、通读全文,抓住景物的特点景物的特点,就是指景物的姿态、色彩、景物在动态或者静态时的样子等。
了解了景物的特点,可以在我们的脑海中留下一个清晰的印象,有助于进一步理解文章。
二、明确写景的写作顺序写景的文章都是按一定的观察顺序来写的,因此,在阅读时,要明确文章的写作顺序。
写景的文章通常有以下几种顺序:(1)按观察的先后顺序。
也就是以移步换景的方式写景。
(2)按空间顺序。
如从上到下、从远到近、从中间到四周等。
(3)按时间的推移顺序。
如春、夏、秋、冬、早、中、晚等。
三、体会文章的思想感情写景的文章,并不是单纯为写景而写景,而是借助对景物的描绘来抒发作者的思想感情。
阅读时,我们要从字里行间体会作者所流露的思想感情,尽可能融入其中,与作者共同感受大自然的美景。
世界第八奇迹——秦始皇兵马俑,位于今陕西省西安市临潼区秦始皇陵以东1.5千米处的兵马俑坑内。
兵马俑是古代墓葬雕塑的一个类别。
古代实行人殉,奴隶是奴隶主生前的附属品,奴隶主死后奴隶要作为殉葬品为奴隶主陪葬。
兵马俑即制成兵马(战车、战马、士兵)形状的殉葬品。
被列入《世界遗产名录》,并被誉为“世界第八大奇迹”,成为中国古代辉煌文明的一张金字名片,被誉为世界十大古墓稀世珍宝之一。
西双版纳——神奇乐土西双版纳位于云南省最南端,古代傣语为“勐巴拉娜西”,意思是“理想而神奇的乐土”,这里以神奇的热带雨林自然景观和少数民族风情而闻名于世。
每年的泼水节于4月13-15日举行,吸引了众多国内外的游客参与,被誉为“东方狂欢节”。
香格里拉——人间天堂不管你是喜欢自然风光还是人文历史,在香格里拉都会有所收获。
极其多样化的原始自然风光——成片的云杉、冷杉原始森林、留有千年记忆的冰川、古珍稀物种滇金丝猴、花团锦簇的原始高山杜鹃,铭记着横断山脉曾经走过的千万年时光记忆;丰富的人文历史景观——茶马古道上的千年古城独克宗、近四百年历史的“小布达拉宫”松赞林寺……九寨沟——人间仙境九寨沟,以“童话世界”、“人间仙境”而著称,“九寨归来不看水”,是对九寨沟景色真实的诠释。
五年级奥数春季实验班第2讲 组合数学之染色与覆盖

第二讲组合数学之染色与覆盖例1.有一次车展共36个展室,如下图,每个展室与相邻的展室都有门相通,入口和出口如图所示。
参观者(填“能”或“不能”)从人口进去,不重复地参观完每个展室再从出口出来。
解:答:不能;如图将展室黑白相间染色,入口为白色,出口也是白色,而走遍36个展室,从白到黑,再从黑到白,共走了35步,最后应该走到黑格,而出口仍然是白格,矛盾,所以无法完成。
例2.棋盘由下图所示的9个小圆圈排列而成,用1~9编号,在3号和9号的小圆圈中各方一枚棋子,分别代表警察和小偷。
若两个小圆圈之间有线相连,则棋子可以从其中一格走入另一格,现在由警察先走,两人轮流,每人每次走一步,每步可以从一格走到有线相连的临格之中。
如果在6步之内警察走入小偷所在的格子中,就算警察抓住了小偷而立功获胜;如果警察走了6步还没有抓住小偷,就算他失职而失败。
问警察应如何取胜。
解:警察先从3走到1,则小偷从9走到7(或8);第2步,警察走到2,小偷走到6(或9); 第3步,警察走到3,小偷走到7或8;第4步,警察走到4,小偷走到9;第5步,警察6,小偷无论是走到7(或8),警察在第6步一定可以获胜。
例3.空间六点任三点不共线,任四点不共面,成对地连接它们得到十五条线段,用红色或蓝色染这些线段(一条线段只染一种颜色),求证:无论这么染,总存在一个同色的三角形。
解:设六点为A 、B 、C 、D 、E 、F ,从A 点出发的五条线段AB 、AC 、AD 、AE 、AF 中至少有3条是同色的,不妨设AB 、AC 、AD 为红色,我们再看△BCD 的三边,如果都是蓝色,那么存在同为蓝色的△BCD ,若△BCD 中有一条边不是蓝色,而是红色,不妨设BC 是红色,则AB 、AC 、BC 都是红色,这是一个红色三角形。
所以总存在一个同色的三角形。
例4.下图是由14个大小相同的方格组成的图形,试问(“能”或“不能”)剪裁成7个由相邻两个方格组成的长方形。
小学五年级语文讲义11第2讲[1].提高班.教师版
![小学五年级语文讲义11第2讲[1].提高班.教师版](https://img.taocdn.com/s3/m/1274f411360cba1aa811dacf.png)
1.阅读文章,感受文章的中心;2.通过对重点词语、句子的理解、品味,感受作者所表达的感情;3.在全面理解、整体把握文战能够的基础上,读出个人的主观感受。
[成语万花筒]1.请在下面括号内填上适当的动物,使每个成语完整无误。
试一试,你准行。
( )目寸光 ( )鬼蛇神 ( )视眈眈 ( )死狐悲 ( )飞凤舞 ( )蝎心肠( )到成功 ( )肠小道 ( )年马月 ( )毛蒜皮 ( )急跳墙 凤头( )肚【参考答案】鼠目寸光 牛鬼蛇神 虎视眈眈 兔死狐悲 龙飞凤舞 蛇蝎心肠马到成功 羊肠小道 猴年马月 鸡毛蒜皮 狗急跳墙 凤头猪肚2.完成下列与“狗(犬)”有关的成语。
鸡飞狗( ) 鸡鸣狗( ) 鸡犬( )天 猪狗不( ) 鸡犬不( )偷鸡( )狗 兔死狗( ) 狗( )跳墙 狗( )人势 狗( )吕洞宾 【参考答案】鸡飞狗跳 鸡鸣狗盗 鸡犬升天 猪狗不如 鸡犬不宁第2讲我们的童年(下)偷鸡摸狗兔死狗烹狗急跳墙狗仗人势狗咬吕洞宾讲义使用参考[快乐热身]环节重点在积累成语,建议教师在授课的时候可以花几分钟的时间帮助学生积累。
[读文章试身手]环节选用了三篇关于童年的文章。
教师要注意通过提问的方式引导学生讨论、理解文章的中心及作者要表达的情感。
每篇文章后都有[教学思路导引]这个环节,教师参考这些内容,也可以补充其他相关问题。
在授课中,建议先让学生阅读文章,教师提出一系列问题,引导学生分析讨论。
教师在学生讨论中进一步引导,帮助学生得出结论,最后再让学生做文章后的习题,教师讲解方法,订正答案。
(一)朋友小儿今年4年级,每天放学后都忙着呼朋唤友,打打闹闹,互换各类卡片;周末还要组织同学们搞小队活动,上兴趣班,看上去忙得很。
()星期天下雨,搞不成活动,没有小朋友来,他()会拉开窗户朝外面看他养的几盆花草。
冬日的冷雨打在金盏菊小小的花瓣上,花芯里积着一小弯盈盈浅水,他就在作文里马马虎虎地写道:“雨溅在花瓣上,乒乒乓乓像放鞭炮……”我忍不住笑道:“儿子,太夸张了吧。
5五年级数学精品班春季课前练习3

1.三个连续自然数的和是231,这三个数中最大的一个数是()。
2.幼儿园小班的20个小朋友和大班的30个小朋友一起分饼干,小班每人分10个,大班的小朋友每人比大、小班的平均数多2块,那么一共分了()块饼干。
3.一本书共有130页,编写这本书的页码共要用()个数字。
4.为了搞科学试验田,需要将长为75米,宽为60米的长方形土地划分成面积相等的小正方形土地,那么小正方形土地的最大面积是()平方米。
5.54的因数一共有()个。
它所有因数的和是()。
6.已知六位数□2017□能被15整除,这样的六位数最小的是()。
7.四个连续自然数的积为1680,则这四个自然数中最小的一个是()。
8.两个数的和是25,积是156,这两个数的差是()1.有7个数,它们的平均数是18,如果去掉一个数,它们的平均数变成了15,那么去掉的这个数是()。
2.一个口袋里装有红球10颗,黄球3颗,绿球12颗。
从中至少摸出()颗球,才能保证摸出的球中3种球都有。
3.从46写到234,一共写了()个1。
4.两个数的最大公因数是12,最小公倍数是144,其中一个数48,另一个数是()。
5.1~100的自然数中不是5的倍数也不是6的倍数的数有()个。
6.用一个两位数除2015,余数为20,符合条件的两位数中最小的是()。
7.如果两个整数的和是26,这两个数的积可以整除495,那么这两个数的差是()。
1.某校五年级共有475名同学,那么这些同学中至少有()人会在同一个月过生日。
2.每次考试的满分是100分。
小明4次考试的平均成绩是89分,为了使平均成绩尽快达到94分(或更多),他至少再要考()次试。
(1995年奥赛初赛试题)3.五位数4A97A能被3整除,他的最末两位数字组成的数7A又能被6整除,这个五位数是()4.6个空瓶可以换一瓶汽水,某班同学喝了190瓶汽水,其中有一些是用喝了剩下来的空瓶换来的,那么他们至少要买汽水()瓶。
5.有100位学生回答A、B两题都没回答对的有10人,有75人答对A题,有83人答对B题,有()人A、B两题都答对。
2013学而思五年级春季下学期超长123班讲义学案试题(1—7讲)
补充1,2013年华杯赛决赛最后一题第14题.不为零的自然数n既是2010个数字和相同的自然数之和,也是2012个数字和相同的自然数之和,还是2013个数字和相同的自然数之和,那么n最小是多少?
一4.(1)求(5412×852)÷9的余数。
(2)求 ÷9的余数;
(3)有一只猴子摘了一大堆香蕉,他把香蕉平分成3小堆,不多不少。又把其中一小堆再平分成5份,发现多了一根。如果他一开始就把香蕉平分成5堆,会多出几根?
(4)有一只猴子摘了一大堆香蕉,他把香蕉平分成6小堆,多了2根。又把其中一小堆再平分成5份,发现多了4根。如果他一开始就把香蕉平分成5堆,会多出几根?
7.一个半径为1厘米的圆,沿边长为10厘米的正六边形外围滚动一圈,求圆扫过的面积是多少?沿边长为10厘米的正八边形外围滚动一圈,求圆扫过的面积?
8.一个半径为1厘米的圆,沿半径为5厘米的圆外围滚动一圈,求小圆扫过的面积是多少?这次我们继续使用之前几问得到的方法来计算,结果是否仍然正确?
9.一个半径为r的圆,沿着周长为L的任意凸图形外围滚动一周,求圆扫过的面积?
(2)形如1444…4(n>1,n个4)的完全平方数有______个;
三5. + +1(m、n为自然数)能否为平方数?
学案1.称能表示成1+2+3+…+k的形式的自然数为三角数。有一个四位数N,它既是三角数,又是完全平方数,则N=______。
春季班小学五年级家庭作业试题及答案第二讲

第二讲圆与扇形基础班1.如右图,等腰直角三角形ABC的腰为10厘米;以A为圆心,EF为圆弧,组成扇形AEF;阴影部分甲与乙的面积相等。
求扇形所在的圆面积。
解答:等腰三角形的角为45度,则扇形所在圆的面积为扇形面积的8倍。
而扇形面积为等腰三角形面积:S=1/2×10×10=50,则圆的面积为400。
2.求下列各图中阴影部分的面积:解答:如上右图,易得图形面积,(1)25 ;(2)ab 。
【例1】3.以等腰直角三角形的两条直角边为直径画两个半圆弧(见右图),直角边长4厘米,求图中阴影部分的面积。
(π取3)解答:如右下图所示,所求面积等于圆面积减去正方形面积,阴影部分面积=(4÷2)2π-4×4÷2= 4(厘米2)。
4.如右图,ABCD是正方形,且FA=AD=DE=1,求阴影部分的面积。
(取π=3)解答:阴影部分面积=梯形BCEF-三角形BFD-扇形=2-1-3/8=5/8 。
【例2】5.右图中的圆是以O为圆心、半径是10厘米的圆,求阴影部分的面积。
(π取3)解答:100平方厘米。
提高班1.如右图,等腰直角三角形ABC的腰为10厘米;以A为圆心,EF为圆弧,组成扇形AEF;阴影部分甲与乙的面积相等。
求扇形所在的圆面积。
解答:等腰三角形的角为45度,则扇形所在圆的面积为扇形面积的8倍。
而扇形面积为等腰三角形面积:S=1/2×10×10=50,则圆的面积为400。
2.求下列各图中阴影部分的面积:解答:如上右图,易得图形面积,(1)25 ;(2)ab 。
3.以等腰直角三角形的两条直角边为直径画两个半圆弧(见右图),直角边长4厘米,求图中阴影部分的面积。
(π取3)解答:如右下图所示,所求面积等于圆面积减去正方形面积,阴影部分面积=(4÷2)2π-4×4÷2= 4(厘米2)。
4.如右图,ABCD是正方形,且FA=AD=DE=1,求阴影部分的面积。
五年级春季第二讲公因数和公倍数

五年级春季第二讲公因数和公倍数一、公因数与公倍数的定义1、公因数:几个数公有的因数叫做这几个数的公因数,其中最大的一个叫做这几个数的最大公因数。
2、公倍数:几个数公有的倍数叫做这几个数的公倍数,其中最小的一个叫做这几个数的最小公倍数。
3、互质数:只有公因数1的两个数叫做互质数。
二、公因数与公倍数的求法例1. 分别求出下列各组数的公因数与公倍数。
12和18 15和30 5和6 解:(1)12的因数有(1、2、3、4、6、12); 12的倍数有(12、24、36、48、60、72……);18的因数有(1、2、3、6、9、18); 18的倍数有(18、36、54、72、90……);12和18的公因数是(1、2、3、6); 12和18的公倍数是(36、72……);其中最大的公因数是(6)。
其中最小的公倍数是(36)。
三、用短除法求几个数的最大公因数和最小公倍数。
注意:用短除法求最大公因数或最小公倍数时,要除到商的每两个数是互质数为止。
四、两种特殊情况的最大公因数和最小公倍数的求法。
1. 如果两个数成倍数关系,那么较小数就是它们的最大公因数,较大数就是它们的最小公倍数。
2. 如果两个数是互质数,那么它们的最大公因数就是1,最小公倍数就是它们的乘积。
例2. 分别求出下列各组数的最大公因数和最小公倍数。
24和48 17和18 9、18和36 解:(1)因为48是24的倍数,所以24和48的最大公因数是24,最小公倍数是48。
(2)因为17和18是互质数,所以17和18的最大公因数是1,最小公倍数是17×18=306。
(3)因为36是18的倍数,18是9的倍数,所以它们的最大公因数是9,最小公倍数是36。
使学生明确:①因为两个数最大公因数只包含这两个数全部公有质因数,所以只把这两个数全部公有质因数连乘起来,也就是把所有的除数乘起来,就得到它们的最大公因数。
②而两个数的最小公倍数不仅包含这两个数全部公有的质因数,还包含它们各自独有的质因数,所以要把这两个数全部公有的质因数以及各自独有的质因数连乘起来,也就是把所有的除数和商乘起来,就得到它们的最小公倍数。
部编版五年级上册道德与法治 古代技术创造和改变世界的四大发明

2020-2021学年春季部编版(统编)五年级上册《道德与法治》第二课时古代技术创造和改变世界的四大发明教学目标情感态度价值观:让学生知道我国是有几千年历史的文明古国,古代科技的发展达到了世界领先水平,对世界科学技术的伟大贡献。
知识目标:知道古代先进的技术创造和改变世界的四大发明。
过程与方法:让学生知道我国是有几千年历史的文明古国,古代科技的发展达到了世界领先水平,对世界科学技术的伟大贡献。
教学重难点重点:古代先进的技术创造。
难点:改变世界的四大发明。
教法学法教法:讲解法、情景体验法、多媒体教学法。
学法:合作交流、实践法。
教学准备教师准备:准备多媒体课件、素材。
学生准备:了解古代的四大发明。
教学过程教学环节教师活动学生活动个性思考部分一、导入新课1.导入:语文课文《赵州桥》导入。
2.导入语:中国古代劳动让人民的精湛技术和勤劳智慧值得我们引以为豪。
欣赏课文。
【独领风骚的古代技术创造】1.辉煌的古代科技在我国古代,科学技术一直领先世界,出现了许多伟大的科学家,他们的发明和创造,为人类文明和进步留下了宝贵的财富。
2.古代技术创造(1)青铜技术:司母戊鼎(2)丝绸技术:西汉素纱禅衣(3)陶瓷技术:东汉青瓷四系罐(4)工程技术:都江堰、赵州桥3.你还知道哪些中国古代的技术创造?同学们分组搜集资料进行探究,并在班级交流和展示。
同学们查阅相关资料。
全班分成四大组,搜集资料,进行分享展示二、讲授新课【改变世界的四大发明】1.我国古代四大发明:造纸术、印刷术、指南针、火药2.造纸术(1)纸的前世:龟甲、兽骨、青铜器、玉石器、竹木简、丝帛缺点:书写比较麻烦,不易携带、价格昂贵。
(2)书写材料的一次伟大革命公元105年,蔡伦改进了造纸术。
(3)造纸术的外传:751年,唐朝与大食战争,一批唐朝造纸工匠被俘,造纸术传入阿拉伯,后又传入欧洲(14世纪)和北非。
促进了欧洲文化的发展。
3.活字印刷术(1)印刷术的历史:中国约在公元7世纪的初唐时期就已出现采用雕版印刷术印制的书。
五年级奥数:第2讲__质数和合数

北外起航五年级春季班数学第二讲质数和合数教学目标:1.掌握质数、合数的定义和特征。
2.养成准确数学概念、区分概念和灵活运用概念的良好习惯。
知识点拨:概念:一个大于1的整数,如果除了1和它本身以外,不再有别的因数,这个整数就叫做质数(又称为素数)。
一个整数,如果除了1和它本身以外,还有其它的因数,这个整数就叫做合数。
质数特征:①质数只有1和它本身两个约数。
②质数只能表示成1和它本身的乘积,不能表示成任意其它两个整数的积。
③最小的质数是2,2也是唯一的偶数质数,其它所有质数都是奇数。
合数特征:①合数至少有3个约数,至少有1个大于1小于它本身的约数。
②合数可以写成两个大于1的整数的乘积。
③最小的合数是4,大于2的偶数都是合数。
相关知识点:①1既不是质数也不是合数。
②奇数中有质数也有合数。
③在大于零的偶数中只有一个质数2,其它都是合数。
质数的判定:①直接判断:熟记20以内的质数,熟悉100以内的质数;②查看质数表;③试除判断:假设有自然数N、P,且N﹤P2。
可以用小于P的所有质数依次去除N,如果其中某个质数能整除N,则N是合数;如果小于P的所有质数都不能整除N,则N是质数。
例题精讲:例题1:判断437、541是质数还是合数?【解析】:先简单估算一下试除质数的范围。
437﹤212、541﹤242,小于24的质数有:2、3、5、7、11、13、17、19、23。
依次用上面这些质数试除437和541,得:①437÷19=23,所以437是合数;②这些质数都不能整除541,所以541是质数。
例题2:已知A是质数,而且A+4,A+6,A+10都是质数,求符合条件的最小质数A。
【解析】:要求出符合条件的最小质数,可以将所有质数按从小到大的顺序依次尝试,A等于2、3、5时题中三个算式的得数中都有合数出现,只有A等于7时,题中三个算式的得数依次为:11、13、17,都是质数。
所以符合条件的最小质数A是7。
例题3:将1999表示为两个质数之和,1999﹦□+□,在□中填入质数,共有多少种表示法?【解析】:1999是个奇数,拆成两个整数的和,奇数+偶数﹦奇数,这两个整数必然是一个奇数和一个偶数,要使这两个数都是质数,这个偶数只能是2,奇数为(1999-2=)1997。
全国版五年级数学思维(春季)课堂落实
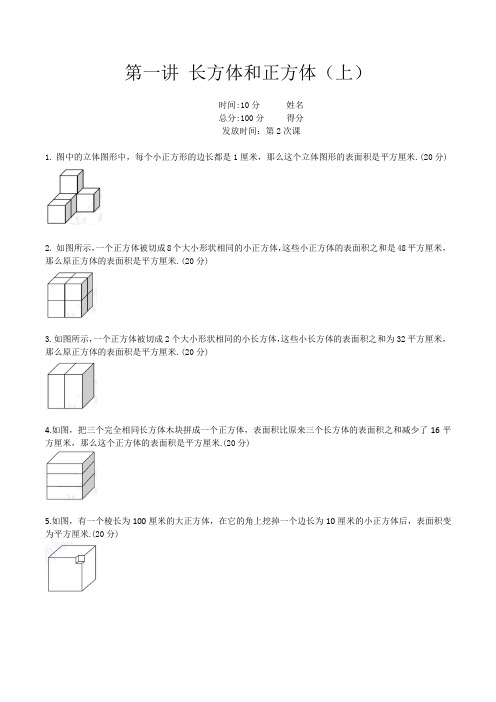
时间:10分姓名总分:100分得分发放时间:第2次课1.图中的立体图形中,每个小正方形的边长都是1厘米,那么这个立体图形的表面积是平方厘米.(20分)2.如图所示,一个正方体被切成8个大小形状相同的小正方体,这些小正方体的表面积之和是48平方厘米,那么原正方体的表面积是平方厘米.(20分)3.如图所示,一个正方体被切成2个大小形状相同的小长方体,这些小长方体的表面积之和为32平方厘米,那么原正方体的表面积是平方厘米.(20分)4.如图,把三个完全相同长方体木块拼成一个正方体,表面积比原来三个长方体的表面积之和减少了16平方厘米,那么这个正方体的表面积是平方厘米.(20分)5.如图,有一个棱长为100厘米的大正方体,在它的角上挖掉一个边长为10厘米的小正方体后,表面积变为平方厘米.(20分)时间:10分姓名总分:100分得分发放时间:第3次课1.有一张边长为10厘米的正方形硬纸片,从四个角各剪去边长为2厘米的正方形,做成一个长方体纸盒.该纸盒的体积是立方厘米.(20分)2.有两个长方体水缸,甲缸长10厘米,宽和高都是5厘米;乙缸长20厘米,宽和高都是10厘米,现在甲缸里面装有一部分水,且水深4厘米,乙缸没有水,如果把甲缸的所有水全部倒入到乙缸,那么乙缸水深厘米.(20分)3.在一个长20厘米、宽10厘米的长方体水箱中,有5厘米深的水。
如果在水中沉入一个棱长为5厘米的正方体铁块,那么水箱中的水面会升高厘米.(20分)4.有一个长方体水箱,从里面量长10分米、宽10分米、高5分米,里面装有水,水深3分米.如果把一块棱长为1分米的正方体铁块完全浸入水中,那么水深会变成分米.(20分)5.一个正方体的棱长是6厘米,在它的表面涂满颜色后,截成棱长是1厘米的小正方体,那么有三个面涂色的小正方体共有个.(20分)第三讲物不知数问题时间:10分姓名总分:100分得分发放时间:第4次课1.一个自然数除以5余2,除以6也余2,这个自然数最小是(20分)2.在小于50的自然数中,某个数除以13与66除以13同余,那么这个数最小是(20分)3.一个自然数除以7余1,除以27余3,这个自然数最小是(20分)4.139和112这两个数除以同一个两位数,得到相同的余数,这个两位数是(20分)5.1987和2012这两个数除以同一个两位数,得到的余数相同,这个两位数是(20分)第四讲1-3将阶段巩固时间:10分姓名总分:100分得分发放时间:第5次课1、如图所示,一个正方体被切了2刀,这些小正方体的表面积之和为100平方厘米,那么原正方体的表面积是多少平方厘米?2、把四个完全相同的长方体木块拼成一个正方体,表面积比原来四个长方体的表面积之和减少了120平方厘米,那么这个正方体的表面积是多少平方厘米?3、有一张边长为50厘米的正方形硬纸片,从四个角各剪去10厘米的正方形,做成一个长方体纸盒,该纸盒的体积是多少立方厘米?4、有一个长方体水箱,从里面量长5分米、宽4分米、高6分米,里面装有水,水深3分米。
五年级春季第二讲分解质因数

第二讲:质数、合数与分解质因数第一天练习题1、从1、7、9这3个数字中选出1个、2个、3个,按任意次序排列,可得到不同的一位数、两位数、三位数,其中哪些是质数?哪些是合数。
2、把下列各数分解质因数。
453602563、如果两个质数的和是58,这两个质数的乘积最大是多少?4、如果两个质数的和是48,这两个质数的乘积可能是多少?请全部写出来。
5、三个连续自然数的积是1716,这三个自然数分别是多少?7、植树节到了,王老师带领同学去植树,学生恰好分成2组,如果师生每人种树一样多,一共种了318棵,这个班共有多少个学生?每人植树多少棵?8、同学们在班主任带领下种树,这个班有60多人,学生恰好分成2组学生?如果师生每人种树一样多,一共种了345棵,这个班共有多少个?每人植树多少棵?9、A是质数,B是奇数,且A×A+B=2017,则B=?第二天练习题1、从1、5、7这3个数字中选出1个、2个、3个,按任意次序排列,可得到不同的一位数、两位数、三位数,其中哪些是质数?哪些是合数。
2、把下列各数分解质因数。
1984505764、如果两个质数的和是32,这两个质数的乘积最大是多少?4、如果两个质数的和是55,这两个质数的乘积可能是多少?请全部写出来。
5、三个连续自然数的积是504,这三个自然数分别是多少?7、植树节到了,王老师带领同学去植树,学生恰好分成6组,如果师生每人种树一样多,一共种了473棵,这个班共有多少个学生?每人植树多少棵?8、同学们在班主任带领下种树,这个班有30多人,学生恰好分成3组学生?如果师生每人种树一样多,一共种了374棵,这个班共有多少个?每人植树多少棵?9、A是质数,B是奇数,且A×A+B=2015,则B=?第二天练习题1、从1、3、6这3个数字中选出1个、2个、3个,按任意次序排列,可得到不同的一位数、两位数、三位数,其中哪些是质数?哪些是合数。
2、把下列各数分解质因数。
五年级春季班第二讲

第 二 讲:巧算分数加、减法 主讲人:孙老师【知识与方法】分数加减混合运算的运算顺序和简算方法与整数加减相同,主要是根据分数的特征结合运算定律和分数性质进行计算。
方法:1、a+b=b+a,(a+b)+c=a+(b+c);2、 a-b-c=a-(b+c), a-(b-c)= a-b+c ;3、ab b a +=a 1+b 1;ab b a -=a 1-b1; 4、代换法;5、裂项法:111)1(1+-=+n n n n ; ⎪⎭⎫ ⎝⎛+-=+k n n k k n n 111)(1; ⎪⎭⎫ ⎝⎛+-=+k n n k n n k 11)(; ⎪⎪⎭⎫ ⎝⎛++-+=++)2)((1)(121)2)((1k n k n k n n k k n k n n ; ⎪⎪⎭⎫ ⎝⎛+++-++=+++)3)(2)((1)2)((131)3)2)((1k n k n k n k n k n n k k n k n k n n (。
【例题精讲】例1:计算 8735-(4312+8720)-412模仿练习(1)97-(21+91)+21 (2)1-0.11+21-0.34+31-0.56+61-0.99例2:计算 21+41+81+161+321+641+1281 思维点拨:此题可用错位相减法或添项去项法解决。
模仿练习(1)21+41+81+161+321+641+1281+……+ 20481(2)32+92+272+812+2432+7292+21872例3:计算211⨯+321⨯+431⨯+……+50491⨯ 思维点拨:此题可以利用这个裂项公式解决:111)1(1+-=+n n n n模仿练习(1)100099911211111101⨯++⨯+⨯(2)21+61+121+201+301+421+561+721+901例4:411⨯+741⨯+1071⨯+13101⨯+16131⨯+19161⨯ 思维点拨:此题可以利用这个裂项公式解决:⎪⎭⎫ ⎝⎛+-=+k n n k k n n 111)(1模仿练习(1)15131131111191971751⨯+⨯+⨯+⨯+⨯(2)1714111141119118158513521⨯+⨯+⨯+⨯+⨯例5:50494816541543143213211⨯⨯++⨯⨯+⨯⨯+⨯⨯+⨯⨯ 思维点拨:此题可以利用这个裂项公式解决:⎪⎪⎭⎫ ⎝⎛++-+=++)2)((1)(121)2)((1k n k n k n n k k n k n n模仿练习(1)100989611086186416421⨯⨯++⨯⨯+⨯⨯+⨯⨯(2)100999826542543243223212⨯⨯++⨯⨯+⨯⨯+⨯⨯+⨯⨯例6:(1+21+31+41)×(21+31+41+51)-(1+21+31+41+51)×(21+31+41) 思维点拨:此题可以利用代换法解决,令21+31+41=A 21+31+41+51=B ,则 原式=(1+ A )×B-(1+ B )×A ……模仿练习(1)(111+211+311+411)×(211+311+411+511)-(111+211+311+411+511)×(211+311+411)(2)(1+21+31+…+20111)×(21+31+…+20121)-(1+21+31+…+20121)×(21+31+…+20111)【巩 固 与 提 高】A 级 (1)501+ 502+503+……+5049 ( 成都嘉祥衔接班招生考试题)(2)1+613+1215+2017+3019+42111+56113+72115+90117( 成都嘉祥外国语学校奖学金考试题)(3)(21+31+41+51+61)+(32+42+52+62)+(43+53+63)+(54+64)+65( 成都嘉祥衔接班招生考试题)(4)1÷(2÷3)÷(3÷4)÷(4÷5)÷……÷(19÷20)( 成都嘉祥6年级衔接班招生考试题)(5)3122⨯+5342⨯+7562⨯+9782⨯+119102⨯+1311122⨯(20XX 年成都七中实验小升初试题)B 级(1)43×54×65×76×……×20092008×20102009(20XX 年成都嘉祥6年级衔接班考试题)(2)(49-81)×81+(46-81)×81+(43-81)×81+……(1--81)×81(20XX 年成都嘉祥奖学金考试题考试题)(3)(1+21+31+…+20071)×(21+31+…+20081)-(1+21+31+…+20081)×(21+31+…+20071) (20XX 年成都实外“德瑞杯”知识竞赛数学试题)(4)21+65+1211+2019+……+97029701+99009899(20XX 年成都实外“德瑞杯”知识竞赛数学试题)C 级(1)(1-5118)+(3-5118×2)+(5-5118×3)+……+(97-5118×49)+(99-5118×50)( 成都嘉祥招生考试题)(2) 20071-20082007200620082007+⨯⨯+ (20XX 年成都实外“德瑞杯”知识竞赛数学试题)(3)2010-23-45-89-1617-3233-6465-128129-256257(20XX 年成都实外“德瑞杯”知识竞赛数学试题)(4)1-)(2112+⨯-)()(321213++⨯+-)()(43213214+++⨯++-……-)()(102192110+⋯⋯++⨯+⋯⋯++ (20XX 年成都实外“德瑞发展基金会”奖学金测试数学B 卷试题)。
五年级春季班第二讲

第 二 讲:巧算分数加、减法主讲人:孙老师[知识与方法]分数加减混合运算的运算顺序和简算方法与整数加减相同,主要是根据分数的特征结合运算定律和分数性质进行计算。
方法:1、a+b=b+a,<a+b>+c=a+<b+c>;2、 a-b-c=a-<b+c>, a-<b-c>= a-b+c ;3、ab b a +=a 1+b 1;ab b a -=a 1-b1; 4、代换法;5、裂项法:111)1(1+-=+n n n n ; ⎪⎭⎫ ⎝⎛+-=+k n n k k n n 111)(1; ⎪⎭⎫ ⎝⎛+-=+k n n k n n k 11)(; ⎪⎪⎭⎫ ⎝⎛++-+=++)2)((1)(121)2)((1k n k n k n n k k n k n n ; ⎪⎪⎭⎫ ⎝⎛+++-++=+++)3)(2)((1)2)((131)3)2)((1k n k n k n k n k n n k k n k n k n n (。
[例题精讲]例1:计算 8735-〔4312+8720〕-412模仿练习〔1〕97-〔21+91〕+21 〔2〕1-0.11+21-0.34+31-0.56+61-0.99例2:计算 21+41+81+161+321+641+1281 思维点拨:此题可用错位相减法或添项去项法解决。
模仿练习〔1〕21+41+81+161+321+641+1281+……+20481〔2〕32+92+272+812+2432+7292+21872例3:计算211⨯+321⨯+431⨯+……+50491⨯ 思维点拨:此题可以利用这个裂项公式解决:111)1(1+-=+n n n n模仿练习〔1〕100099911211111101⨯++⨯+⨯〔2〕21+61+121+201+301+421+561+721+901例4:411⨯+741⨯+1071⨯+13101⨯+16131⨯+19161⨯ 思维点拨:此题可以利用这个裂项公式解决:⎪⎭⎫ ⎝⎛+-=+k n n k k n n 111)(1模仿练习〔1〕15131131111191971751⨯+⨯+⨯+⨯+⨯〔2〕1714111141119118158513521⨯+⨯+⨯+⨯+⨯例5:50494816541543143213211⨯⨯++⨯⨯+⨯⨯+⨯⨯+⨯⨯ 思维点拨:此题可以利用这个裂项公式解决:⎪⎪⎭⎫ ⎝⎛++-+=++)2)((1)(121)2)((1k n k n k n n k k n k n n模仿练习〔1〕100989611086186416421⨯⨯++⨯⨯+⨯⨯+⨯⨯〔2〕100999826542543243223212⨯⨯++⨯⨯+⨯⨯+⨯⨯+⨯⨯例6:<1+21+31+41>×<21+31+41+51>-<1+21+31+41+51>×<21+31+41> 思维点拨:此题可以利用代换法解决,令21+31+41=A 21+31+41+51=B,则 原式=〔1+ A 〕×B-〔1+ B 〕×A ……模仿练习〔1〕<111+211+311+411>×<211+311+411+511>-<111+211+311+411+511>×<211+311+411>〔2〕<1+21+31+…+20111>×<21+31+…+20121>-<1+21+31+…+20121>×<21+31+…+20111>[巩 固 与 提 高]A 级 <1>501+502+503+……+5049 <20####嘉祥衔接班招生考试题>〔2〕1+613+1215+2017+3019+42111+56113+72115+90117〔20####嘉祥外国语学校奖学金考试题〕〔3〕<21+31+41+51+61>+<32+42+52+62>+<43+53+63>+<54+64>+65<20####嘉祥衔接班招生考试题>〔4〕1÷〔2÷3〕÷〔3÷4〕÷〔4÷5〕÷……÷〔19÷20〕<20####嘉祥6年级衔接班招生考试题>〔5〕3122⨯+5342⨯+7562⨯+9782⨯+119102⨯+1311122⨯〔20####七中实验小升初试题〕B 级〔1〕43×54×65×76×……×20092008×20102009〔20####嘉祥6年级衔接班考试题〕〔2〕〔49-81〕×81+〔46-81〕×81+〔43-81〕×81+……〔1--81〕×81〔20####嘉祥奖学金考试题考试题〕〔3〕<1+21+31+…+20071>×<21+31+…+20081>-<1+21+31+…+20081>×<21+31+…+20071> 〔20####实外"德瑞杯"知识竞赛数学试题〕〔4〕21+65+1211+2019+……+97029701+99009899〔20####实外"德瑞杯"知识竞赛数学试题〕C 级<1>〔1-5118〕+〔3-5118×2〕+〔5-5118×3〕+……+〔97-5118×49〕+〔99-5118×50〕〔20####嘉祥招生考试题〕<2> 20071-20082007200620082007+⨯⨯+ 〔20####实外"德瑞杯"知识竞赛数学试题〕〔3〕2010-23-45-89-1617-3233-6465-128129-256257〔20####实外"德瑞杯"知识竞赛数学试题〕〔4〕1-)(2112+⨯-)()(321213++⨯+-)()(43213214+++⨯++-……-)()(102192110+⋯⋯++⨯+⋯⋯++〔20####实外"德瑞发展基金会"奖学金测试数学B 卷试题〕。
数学春季精英版教案 五年级-2 观察物体

第2讲观察物体[教学内容]:《数学》春季精英版,5年级第2讲“观察物体”。
[教学目标]:知识技能:1.学生能根据立体图形,从不同的方向观察,正确的画出平面图。
2.能根据三视图还原立体图形,体会从三个方向观察就能确定立体图形的形状。
3.能根据给定的两个方向观察到的平面图形的形状,确定搭成的这个立体图形所需要的正方体的数量范围。
4.学生能熟练的解决有关几面涂色问题。
数学思考:通过学生自主探索和合作交流,使学生能理解和掌握各类问题的解决方法,培养学生主动获取知识的能力和习惯。
问题解决:学会解决问题的方法,发展空间观念。
情感态度:1.让学生在解决图形问题的过程中,感受数学与实际生活的密切联系。
2.使学生在学习活动中,进一步感受数学学习的挑战性,体验成功的乐趣。
3.培养学生独立探究的好习惯,体验到小组协作学习的重要性。
[教学重点和难点]:教学重点:由平面图还原立体图、立体图形的几面涂色规律。
教学难点:给定的两个方向观察到的平面图形的形状,确定搭成的这个立体图形所需要的正方体的数量范围。
[教学准备]:动画多媒体语言课件第一课时教学过程:教学路径学生活动方案说明一、情境导入旁白(女):据说画家齐白石老先生,五十岁后,花鸟画才逐步有大成,并为世人所公认。
而这和他年青时曾在民间长年习花雕工有关,他那双能随感觉而动的手,经过千百次锤炼,有神奇之力,所作之画,亦称一绝。
课件出示几幅齐白石的画在数学的很多问题中,也需要我们去动手画一画、摆一摆。
今天的数学课堂上,朱老师就想考察一下学生们的动手能力,让我们一起去看看吧!二、呈现问题(一)教学例1课件出示例1:例1: 观察下图,请画出从正面看到的图形。
师:这个图形由两个不同的立体图形组成,你认识它们吗?生:上面的是正方体,下面的是长方体。
师:你能画出从正面看到的形状吗?学生尝试画图课件出示解析:这是一个组合图形,下面的长方体和上面的正方体都要观察。
答案:动画调整视角,出示图形。
染色与覆盖

第三讲 染色与覆盖本讲我们将一起学习染色与覆盖。
而这里所说的染色问题并不是要求如何染色,然后有多少种染色方法等数学问题。
而是一种解决逻辑推理题的一种方法,一种将研究对象分类的形象化的方法。
通过将要解决的问题适当的染色,可以使我们更形象的观察分析其中所蕴含的关系,在经过一定的推理从而得到问题的答案。
知识构架图:染色问题 座位问题(例 )路径问题(例 )结点问题(例 )覆盖问题 一般覆盖(例 ) 特殊形状覆盖(例 ) 例题讲解一、 染色问题1、 座位染色问题例1:分析题中规定每个座位的前后左右都是他的邻座,那么35名同学每个人都恰好坐到它的邻座上能否办到?像这种问题我们该如何考虑呢?直接一步一步操作吗?很显然是很不现实的,那么有什么方法能让我们更直接的找到答案呢?染色。
我们将35个座位染成黑白相间的形式,一眼就能看出,每个黑色的座位都是白色座位的邻座,也就是说如果35名同学每个人都恰好能坐到它的邻座上,那么必然是,黑白位置对换,但从图中我们看到黑色17格,白色18格,黑白个数不相等,所以无法办到。
提高练习:(1)某影院有31排,每排29个座位,某天放映了两场电影,每个座位上都坐了一个观众,如果要求每个观众在看第二场电影时必须跟他前后左右相邻的某一观众交换座位,这样能办到吗?提示:总共31×29=899个座位,染成黑白相间的情况时黑白个数不相等,所以办不到。
(2)五年级一班有49名同学,共分成7排,每排7个人。
新年到了,每个同学都准备了一个礼物送给自己前后左右相邻的某一个同学,那么有没有可能每个同学都刚好收到一个别人送的礼物?提示:总共49名同学,染成黑白相间的情况时黑白个数不相等,所以不可能。
2、 路径问题例2:分析如果一次次的操作的话很难看出是否能够按要求办到。
所以我们按例1的方法,将9个小格染成黑白相间的颜色,很明显就能看出是不能办到的。
因为从A 格出去,第一步不管往哪走都会走入黑格,接着第二步又都会走入黑格,即走奇数步后进黑格,偶数步后进白格,这个人若要从A 格出去又要回到A 格,必须走9个格,所以最后一格必为黑才可以,而A 格为白格,所以不可以。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 二 讲:巧算分数加、减法 主讲人:孙老师
【知识与方法】
分数加减混合运算的运算顺序和简算方法与整数加减相同,主要是根据分数的特征结合运算定律和分数性质进行计算。
方法:1、a+b=b+a,(a+b)+c=a+(b+c);
2、 a-b-c=a-(b+c), a-(b-c)= a-b+c ;
3、
ab
b a +=
a
1+
b
1;
ab
b a -=
a
1-
b
1;
4、代换法;
5、裂项法:
1
11)
1(1+-
=
+n n
n n ;
⎪⎭
⎫ ⎝⎛+-=
+k n n k k n n 111)
(1; ⎪⎭
⎫ ⎝⎛+-=+k n n k n n k
11
)(; ⎪
⎪⎭⎫ ⎝⎛++-+=++)2)((1)(121)2)((1k n k n k n n k k n k n n ;
⎪⎪⎭
⎫ ⎝⎛+++-++=
+++)3)(2)((1)2)((131)
3)2)((1
k n k n k n k n k n n k k n k n k n n (。
【例题精讲】
例1:计算 8
735
-(4
312
+8
720
)-4
12
模仿练习 (1)97
-(
2
1+9
1)+
2
1 (2)1-0.11+
2
1-0.34+3
1-0.56+
6
1-0.99
例2:计算 2
1+
4
1+8
1+
16
1+
32
1+
64
1+
128
1
思维点拨:此题可用错位相减法或添项去项法解决。
模仿练习
(1)21
+
4
1+8
1+
16
1+
32
1+
64
1+
128
1+……+
2048
1
(2)3
2+
9
2+
27
2+
81
2+
243
2+
729
2+
2187
2
例3:计算
2
11⨯+
3
21⨯+
4
31⨯+……+
50
491⨯
思维点拨:此题可以利用这个裂项公式解决:1
11)
1(1+-
=+n n n n
模仿练习
(1)
1000
999112
11111
101⨯+
+⨯+
⨯
(2)21
+
6
1+
12
1+
20
1+
30
1+
42
1+
56
1+
72
1+
90
1
例4:
4
11⨯+
7
41⨯+
10
71⨯+
13
101⨯+
16
131⨯+
19
161⨯
思维点拨:此题可以利用这个裂项公式解决:
⎪⎭
⎫ ⎝⎛+-=
+k n n k k n n 111)
(1
模仿练习
(1)15
13113
11111
919
717
51⨯+
⨯+
⨯+
⨯+
⨯
(2)17
14111
14
1119
11
815
8
513
5
21⨯+⨯+⨯+⨯+⨯
例5:
50
494816
5415
4314
3213
211⨯⨯+
+⨯⨯+
⨯⨯+
⨯⨯+
⨯⨯
思维点拨:此题可以利用这个裂项公式解决:
⎪⎪⎭
⎫ ⎝⎛++-+=
++)2)((1
)(121)
2)((1
k n k n k n n k k n k n n
模仿练习
(1)100
9896110
8618
6416
421⨯⨯+
+⨯⨯+
⨯⨯+
⨯⨯
(2)100
999826
5425
4324
3223
212⨯⨯+
+⨯⨯+
⨯⨯+
⨯⨯+
⨯⨯
例6:(1+
21+3
1+
4
1)×(
2
1+3
1+
4
1+5
1)-(1+
2
1+3
1+
41+51)×(2
1+31+
4
1)
思维点拨:此题可以利用代换法解决,令2
1+31
+
4
1=A 2
1+3
1
+
4
1+5
1
=B ,则
原式=(1+ A )×B-(1+ B )×A ……
模仿练习 (1)(11
1+
21
1+
31
1+
41
1)×(
21
1+
31
1+
41
1+
51
1)-(
11
1+
21
1+
31
1+
41
1+
51
1)×(
21
1+
31
1+
41
1)
(2)(1+21+3
1+…+
2011
1)×(
2
1+3
1+…+
2012
1)-(1+
2
1+3
1+…+
2012
1)×(
2
1+3
1+…+
2011
1)
【巩 固 与 提 高】
A 级
(1)50
1+
50
2+
50
3+……+
50
49 (2007年成都嘉祥衔接班招生考试题)
(2)1+61
3+1215
+20
17
+30
19
+42
111
+56
113
+72
115
+90
117
(2009年成都嘉祥外国语学校奖
学金考试题) (3)(
2
1+3
1+
4
1+5
1+
6
1)+(
3
2+
4
2+
5
2+
6
2)+(
4
3+5
3+
6
3)+(
5
4+
6
4)+
6
5(2007年成都嘉祥衔接班
招生考试题)
(4)1÷(2÷3)÷(3÷接班招生考试题)
(5)
3
12
2
⨯+
5
34
2
⨯+
7
56
2
⨯+
9
78
2
⨯+
11
910
2
⨯+
13
1112
2
⨯(2010年成都七中实验小升初试题)
B 级
(1)43
×
5
4×
6
5×
7
6×……×
2009
2008×
2010
2009(2010年成都嘉祥6年级衔接班考试题)
(2)(49-8
1
)×8
1
+(46-8
1
)×8
1
+(43-8
1
)×8
1
+……(1--8
1
)×8
1
(2010年成都嘉祥
奖学金考试题考试题)
(3)(1+
2
1+3
1+…+
2007
1)×(
2
1+3
1+…+
2008
1)-(1+
2
1+3
1+…+
2008
1)×(
2
1+3
1+…+
2007
1)
(2010年成都实外“德瑞杯”知识竞赛数学试题)
(4)2
1+
6
5+
12
11+
20
19+……+
9702
9701+
9900
9899(2010年成都实外“德瑞杯”知识竞赛数学试题)
C 级
(1)(1-51
18)+(3-
51
18×2)+(5-
51
18×3)+……+(97-
51
18×49)+(99-
51
18×50)(2004
年成都嘉祥招生考试题)
(2) 2007
1
-20082007200620082007+⨯⨯+ (2010年成都实外“德瑞杯”知识竞赛数学试题)
(3)2010-2
3-
4
5-8
9-16
17-
32
33-
64
65-
128
129-
256
257(2010年成都实外“德瑞杯”知识竞赛数学
试题)
(4)1-)
(2112+⨯-
)
()(321213
++⨯+-
)
()(43213214
+++⨯++-……
-)
()(102192110
+⋯⋯++⨯+⋯⋯++ (2010年成都实外“德瑞发展基金会”奖学金测试数学
B 卷试题)。
