第13讲 圆形镜共焦腔、一般稳定球面腔
激光原理与应用答案(陈家壁主编)

思考练习题11. 试计算连续功率均为1W 的两光源,分别发射λ=0.5000μm ,ν=3000MHz 的光,每秒从上能级跃迁到下能级的粒子数各为多少?答:粒子数分别为:188346341105138.21031063.6105.01063.61⨯=⨯⨯⨯⨯=⨯⨯==---λνc h q n 239342100277.51031063.61⨯=⨯⨯⨯==-νh q n2.热平衡时,原子能级E 2的数密度为n 2,下能级E 1的数密度为n 1,设21g g =,求:(1)当原子跃迁时相应频率为ν=3000MHz ,T =300K 时n 2/n 1为若干。
(2)若原子跃迁时发光波长λ=1μ,n 2/n 1=0.1时,则温度T 为多高?答:(1)(//m n E E m m kTn n n g e n g --=)则有:1]3001038.11031063.6exp[2393412≈⨯⨯⨯⨯⨯-==---kT h e n n ν(2)K T Te n n kT h 3623834121026.61.0]1011038.11031063.6exp[⨯=⇒=⨯⨯⨯⨯⨯⨯⨯-==----ν3.已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为1.64×l0-18J ,设火焰(T =2700K)中含有1020个氢原子。
设原子按玻尔兹曼分布,且4g 1=g 2。
求:(1)能级E 2上的原子数n 2为多少?(2)设火焰中每秒发射的光子数为l08 n 2,求光的功率为多少瓦?答:(1)1923181221121011.3]27001038.11064.1exp[4----⨯=⨯⨯⨯-⨯=⇒=⋅⋅n n e g n g n kTh ν且202110=+n n 可求出312≈n(2)功率=W 918810084.51064.13110--⨯=⨯⨯⨯4.(1)普通光源发射λ=0.6000μm 波长时,如受激辐射与自发辐射光功率体密度之比q q 激自1=2000,求此时单色能量密度νρ为若干?(2)在He —Ne 激光器中若34/100.5m s J ⋅⨯=-νρ,λ为0.6328μm ,设μ=1,求q q 激自为若干? 答:(1)3173436333/10857.31063.68)106.0(2000188m s J h h c q q ⋅⨯=⇒⨯⨯⨯=⇒=---ννννρρπρπλρνπ=自激(2)943436333106.71051063.68)106328.0(88⨯=⨯⨯⨯⨯⨯==---πρπλρνπννh h c q q =自激5.在红宝石Q 调制激光器中,有可能将全部Cr 3+(铬离子)激发到激光上能级并产生巨脉冲。
39 一般稳定球面腔的模式特征讲解

2
1
2
0.89( mm)
1
z 2 s 2 ( z2 ) 0 1 2 0.45(mm) f 2 2 0.6328 10 6 3 1.27 10 (rad ) 4 0 3.14 3.2 10
一、一般稳定球面腔与共焦腔的等价性
2. 任一满足稳定性条件的球面腔,唯一地等价于某 一个共焦腔。 由上面三个方程可唯一地解出 一组z1、z2、f(或L):
L( R2 L) z1 2 L R1 R2 L( R1 L) z2 2 L R1 R2 1 2 f L( R1 L)( R2 L )( R1 R2 L ) 2 (2 L R R ) 1 2
1. 任意一个共焦球面腔与无穷多个稳定球面腔等价 设C1、C2为所考虑的共焦腔 的两个等相位面,其曲率半径为 R(z1)、R(z2),如果在这两 个地方放上两个反射镜,它们的 曲率半径分别为R1、R2,且:
f2 R1 R ( z1 ) ( z1 ) z1 f2 R2 R ( z2 ) z2 z2
2 2 1 2 4 2 2 2 1 2 2 1 2 2 2 2
4
2 z1 z2 f z f z f
2 2 1 2 2 2 2 2 z1 z2 z12 z2 2 z12 z2 2 z1 z2 0
2
( z1 z2 ) 2 0
0 (1 上式必成立,所以有: L L )(1 ) 1 ,是稳定腔。 R1 R2
1 2
0.5(m)
二、一般稳定球面腔的计算
解:
(3) f 0
1 2
激光腔

δ d = 1 − e−2α = 1 −
2δΦ = 2 arg 1
对称开腔:
γ
γ
= q ⋅ 2π
四、稳定球面腔中的模结构
• 方形镜共焦腔与圆形镜共焦腔的自再现模 自再现模
镜面上场的振幅和相位分布
共焦腔基模在镜面上的分布 高阶横模(强度花样) 高阶横模(强度花样) 相位分布 单程损耗 单程相移和谐振频率
模的基本特征: (1)电磁场空间分布 (2)模的谐振频率; (3)在腔内往返一次经受的相对功率损耗; (4)与该模相对应的激光束的发散角 纵模:通常将由整数q所表征的腔内纵向光场的分 纵模:通常将由整数 所表征的腔内纵向光场的分 布称为腔的纵模,不同的q相应于不同的纵模 相应于不同的纵模; 布称为腔的纵模,不同的 相应于不同的纵模;达到 谐振时,腔的光学长度应为半波长的整数倍, 谐振时,腔的光学长度应为半波长的整数倍,腔的 谐振频率是分立的,纵模间隔与q无关 谐振频率是分立的,纵模间隔与 无关
共焦腔行波场(共焦场)的特征
振幅分布和光斑尺寸 模体积 等相位面的分布 远场发散角
两镜稳定球面腔。 基于:任意一个共焦腔与无穷多个稳定球面腔等价; 任一满足稳定性条件的球面腔唯一地等价于某一共 焦腔。 “等价”指具有相同的行波场 一般稳定球面腔的两个镜面与其等价共焦腔高斯光 束过轴线上z1、z2两点的等相位面重合(坐标原点在 共焦腔中心)。如果已知稳定球面腔镜面曲率半径 R1、R2和腔长L,则这一关系可描述为
第13讲 圆形镜共焦腔、一般稳定球面腔

L g1 = 1 − R 1 g 2 = 1− L R2
• 当g1=g2=0,L一定时,ωS1、ωS2有 =0, 一定时, 最小值,此时对应对称共焦腔; 最小值,此时对应对称共焦腔; ω 0 = • 当0<g1g2<1时,表达式成立;如果不 <1时 表达式成立; 满足, 为复数; 满足, ωS1与ωS2为复数; ω = • 当g1g2→1或g1g2→0,即稳定球面腔 S1 →0, 趋于稳定条件边界, →∞, 趋于稳定条件边界, ωS1与ωS2 →∞, ω S 2 = 此时高斯近似不再成立。 此时高斯近似不再成立。
z f f2 R( z ) = f + = z + z f z
– 如果在共焦腔的任意两个等相位面上放置两块具有 相应曲率半径的球面反射镜, 相应曲率半径的球面反射镜,则自再现模的行波场 不会受到扰动。 不会受到扰动。
13.2 一般稳定球面腔与对称共焦腔的等价性
• 满足以下条件的无穷多个球面反射镜腔都等价于图中的共 焦腔: 焦腔:
0 0.1 0.3 0.5 0.7 0.9 TEM00
r/a
r/a
13.1 圆形镜共焦腔的模式
• B、等相位面分布: 等相位面分布:
– 圆形镜共焦腔反射镜面本身为场 的等相位面, 的等相位面,即模的等相位面为 球面; 球面;
800 600 400
• C、单程相移
– 模的单程相移与N无关; 模的单程相移与N无关; – 不同横模之间单程相移之差为 /2的整数倍 的整数倍; π/2的整数倍; – n相同而m相差1的各个模相移差为 相同而m相差1 /2, 相同n相差1 π/2,而m相同n相差1的各个模相 移差为π 移差为π; π
激光原理与应用课后题答案 陈家壁版

思考练习题11. 试计算连续功率均为1W 的两光源,分别发射λ=0.5000μm ,ν=3000MHz 的光,每秒从上能级跃迁到下能级的粒子数各为多少?答:粒子数分别为:188346341105138.21031063.6105.01063.61⨯=⨯⨯⨯⨯=⨯⨯==---λνc h qn 239342100277.51031063.61⨯=⨯⨯⨯==-νh q n2.热平衡时,原子能级E 2的数密度为n 2,下能级E 1的数密度为n 1,设21g g =,求:(1)当原子跃迁时相应频率为ν=3000MHz ,T =300K 时n 2/n 1为若干。
(2)若原子跃迁时发光波长λ=1μ,n 2/n 1=0.1时,则温度T 为多高?答:(1)(//m n E E m m kT n n n g e n g --=)则有:1]3001038.11031063.6exp[2393412≈⨯⨯⨯⨯⨯-==---kTh e n n ν(2)K T Te n n kT h 3623834121026.61.0]1011038.11031063.6exp[⨯=⇒=⨯⨯⨯⨯⨯⨯⨯-==----ν3.已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为1.64×l0-18J ,设火焰(T =2700K)中含有1020个氢原子。
设原子按玻尔兹曼分布,且4g 1=g 2。
求:(1)能级E 2上的原子数n 2为多少?(2)设火焰中每秒发射的光子数为l08 n 2,求光的功率为多少瓦?答:(1)1923181221121011.3]27001038.11064.1exp[4----⨯=⨯⨯⨯-⨯=⇒=⋅⋅n n e g n g n kTh ν且202110=+n n 可求出312≈n(2)功率=W 918810084.51064.13110--⨯=⨯⨯⨯4.(1)普通光源发射λ=0.6000μm 波长时,如受激辐射与自发辐射光功率体密度之比q q 激自1=2000,求此时单色能量密度νρ为若干?(2)在He —Ne 激光器中若34/100.5m s J ⋅⨯=-νρ,λ为0.6328μm ,设μ=1,求q q 激自为若干? 答:(1)3173436333/10857.31063.68)106.0(2000188m s J h h c q q ⋅⨯=⇒⨯⨯⨯=⇒=---ννννρρπρπλρνπ=自激(2)943436333106.71051063.68)106328.0(88⨯=⨯⨯⨯⨯⨯==---πρπλρνπννh h c q q =自激5.在红宝石Q 调制激光器中,有可能将全部Cr 3+(铬离子)激发到激光上能级并产生巨脉冲。
激光课后题答案

;是氧乙炔焰的倍。
6.用如图6-18所示的激光脉冲测距方法测量地球到月球之间的准确距 离。若使用调Q技术得到脉宽为10-9S而脉冲峰值功率达到109W的激光 巨脉冲,激光的发散角通过倒置望远镜压缩到0.01毫弧度,光电接收器 最低可以测量的光功率为10-6W,大气层的透过系数为5×10-2,试问, 送上月球的角锥棱镜反射器的通光口径至少要有多大(不考虑角锥棱镜 的角度加工误差)? 答:激光束达到月球上的光斑半径为: 激光束达到月球上的脉冲峰值功率为: 设角锥棱镜的通光口径的直径为a,则有: 激光束达到月球上后再被反射回接收器的总功率为: 这里没有考虑角锥棱镜的角度加工误差,实际上角锥棱镜的角度加工误 差至少要有0.1弧秒,对应返回地球的光束发散角在5×10-8以上,即使
(3)
11.试从(3-81)式出发,证明非均匀增宽激光器最佳输出功率若用 最佳透射率表示有:。 证明:由(3-82)有: 整理上式可得:,式中t即为最佳透射率tm 则最佳输出功率
12.考虑如图(3-18)所示的He-Ne激光器,设谐振腔的腔镜为圆
形镜。试求TEM00和TEM10模之间的频率差。假定TEM00q模的单程衍射 损耗δ00<0.1%,试问:维持该激光器振荡的最小增益系数为多大?
2)假设y轴和z轴的直角有一点偏差,则第三个反射面的法线就变成: 则经过第三次反射后: 则入射光束r1与出射光束r4的夹角θ应满足:
一般稳定球面腔的模式理论
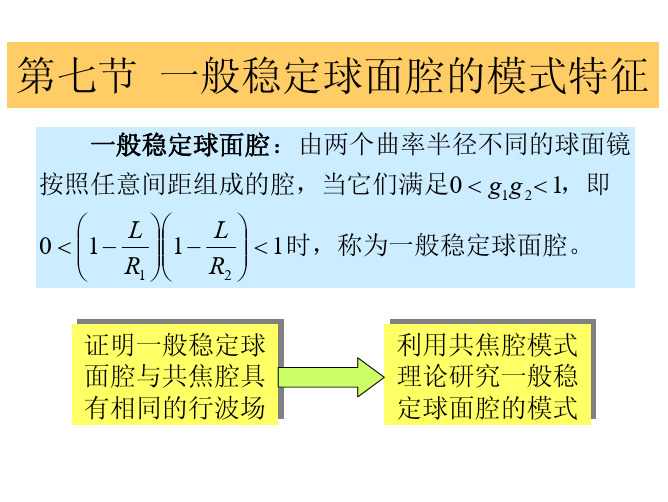
δϕmn = ϕ mn (0,0, z2 ) − ϕ mn (0,0, z1 ) = qπ
得方形镜稳定腔模的谐振频率为
ν mnq
⎛ c ⎡ z2 z1 ⎞ ⎤ 1 q + (m + n + 1)⎜ = − arctg ⎟ arctg ⎢ ⎜ ⎟⎥ f f π 2 L′ ⎣ ⎝ ⎠⎦
z2 z1 令 α = arctg , β = arctg ,并代入 z1、z2 和 f,得 f f
ω (z) = ω0
z 2 [( L − R1 ) + ( L − R2 )]2 1+ L( R1 − L)( R2 − L)( R1 + R2 − L)
其中ω0是基模高斯光束的束腰半径
ω0 =
=
λ ⎧ L(R2 − L )(R1 − L )(R1 + R2 − L ) ⎫ = ⎨ ⎬ 2 π π⎩ [(L − R1 ) + (L − R2 )] ⎭
第七节 一般稳定球面腔的模式特征
一般稳定球面腔 :由两个曲率半径不同的球面镜 按照任意间距组成的腔,当它们满足0 < g1 g 2< 1,即 ⎛ L ⎞⎛ L⎞ 0<⎜ ⎜1 − R ⎟ ⎟⎜ ⎜1 − R ⎟ ⎟ < 1 时,称为一般稳定球面腔。 1 ⎠⎝ 2 ⎠ ⎝
证明一般稳定球 证明一般稳定球 面腔与共焦腔具 面腔与共焦腔具 有相同的行波场 有相同的行波场
tg(α − β ) =
(z2 − z1 ) f
f 2 + z1 z2
=
1 − g1 g 2 g1 g 2
利用三角函数变换公式可得
cos(α − β ) = g1 g 2
因此,方形镜稳定腔的谐振频率为
圆形镜共焦腔、一般稳定球面腔学习笔记

圆形镜共焦腔的模式
• 3、拉盖尔-高斯近似解
• 当N→∞时,积分方程可以求得近似解,即圆形镜共
焦腔的自再现模,为拉盖尔-高斯函数。
• N→∞的物理意义?
对应本征值
ei kL(m2n1) / 2
mn
mn(r
,
)
Cmn
2
r
0S
m
Lnm
2
r2
2 0S
e
r2
2 0
S
e im
其中r,为镜面的极坐标
• 由镜面上的场通过衍射积分方程求出空间场
Emn(r,
)
E
0
0 (z)
2
r
(z)
m
Lnm
2
r2 2(z)
e
r2 2(z)
e e im i (r, , z)
(z) 0
1
z f
2
k
f
(1
)
1
2
r2 2f
m
2n
1
2
R(z)
f
z f
f z
z
f2 z
z腔
z1
z=0
z2
L
'
z2
z1
R1
R2
• 可以证明这无穷多个腔都是稳定腔,即满足条件:
0 1 L'/ R11 L'/ R2 1
• 任意共焦腔,等价于无穷多个稳定球面腔。
一般稳定球面腔与对称共焦腔的等价性
• 2、任一满足稳定条件的球面腔唯一地等价于某
个共焦腔
R1
f
R2
• 如果在共焦腔的任意两个等相位面上放置两块具有相应曲率半径的球面反射镜, 则自再现模的行波场不会受到扰动。
高斯光束基本性质及特征参数

上海大学电子信息科学与技术
TEM11
TEM12
TEM22
TEM34
• 相位分布-与方形镜共焦腔相同,等相位面为镜面
• 单程相移
mn kLm 2n 12 kL mn
上海大学电子信息科学与技术
• 谐振频率
mnq
c 2L
q
1 2
m
2n
1
圆形镜共焦腔模在频率上是高度简并的
同一横模的相邻纵模的频率间隔
z0 0 Rz0 共焦腔中心,波面为垂直腔轴的平面
z0 Rz0 无穷远处,等相位面为平面
z0 z0 R(z0) 相等,共焦腔光束的波面在中心两侧对称分布
z0 f L 2 Rz0 2 f L 波面与共焦腔镜面重合
上海大学电子信息科学与技术
可证明:共焦腔反射镜面是共焦腔中曲率半径最大的等相位面。
z z
圆形镜
将式(2-8-4)中的f ,z1 ,z2 代入上式,并由谐振条件
2r, z 2mn0, z2 mn0, z1 q 2
mnq
c
2L
q
1
m
n
1 arccos
g1
g
2
方形镜
mnq
c
2L
q
1
m
2n 1arccos
g1
g
2
圆形镜
衍射损耗
上海大学电子信息科学与技术
共焦腔菲涅耳数
N
• 只有精确解才能正确描述共焦腔模的损耗特性。每一横 模的损耗由腔的菲涅耳数决定,不同横模的损耗各不相 同。
• 共焦腔的特点:衍射损耗低; 模简并;基模光斑尺寸 沿腔轴以双曲线规律变化; 等相位面近似为球面,在反射 镜处,等相位面与镜面重合。
光学谐振腔的基本知识

2 临界腔
特别是:R1=R2=R=L/2时,为对称共心腔它对应图中B点。如果 R1和R2异号,且R1+R2=L公共中心在腔外,称为虚共心腔。由于 g1>0,g2>0,g1*g2=1,它对应图中第一象限的 g1*g2=1的双曲线。
c) 半共心腔。由一个平面镜和一个凹面镜组成。凹面镜半径 R=L,因而g1=1,g2=0,它对应图中C点和D点。
优点:是可以连续地改变输出光的功率,在某些特 殊情况下能使光的准直性、均匀性比较好。
二、共轴球面腔的稳定图以及分类
3 非稳腔
区分稳定腔与非稳腔在制造和使用激光器时有很重要的实际 意义,由于在稳定腔内傍轴光线能往返传播任意多次而不逸出腔 外,因此这种腔对光的几何损耗(指因反射而引起的损耗)极小。 一般中小功率的气体激光器(由于增益系数G小)常用稳定腔,它 的优点是容易产生激光。
二、共轴球面腔的稳定图以及分类
稳定图来表示共轴球面腔的稳定条件 • 定义参数:
共轴球面谐振腔的稳定性条件(式5.1.1)可改写为
讨论
非稳腔的条件:
临界腔的条件:
(5.1.2) (5.1.3) (5.1.4)
二、共轴球面腔的稳定图以及分类
备 注:
图中没有斜线的部分是谐振腔的稳定工作区, 其中包括坐标原点;
二、共轴球面腔的稳定图以及分类
2 临界腔
a) 平行平面腔。因g1= g2=1,它对应图中的A点。只有 与腔轴平行的光线才能在腔内往返而不逸出腔外。 b) 共心腔。满足条件R1+R2=L的腔称为共心腔。如果,
公共中心在腔内,称为实共心腔。这时:
它对应图中第三象限的g1*g2=1的双曲线
二、共轴球面腔的稳定图以及分类
以下将会看到,整个激光稳定腔的模式理论是建立在对称共 焦腔的基础上的,因此,对称共焦腔是最重要和最有代表性的一 种稳定腔。
方形镜共焦腔与圆形镜共焦腔的自再现模 一般稳定球面腔的模式

0s镜面上基
模的光斑半径
0s
L
0
0 s
2
f L 2
• 腔中不同位置处的光斑大小各不相同。在共焦腔镜 面上, z L 2 f ,此时
0s
r x 2 y 2 L
共焦腔模的场主要集中在镜面中心附近。
2、高阶横模——方形镜的
• TEMmn模在镜面上振幅分布的特点取决于厄 米特多项式与高斯分布函数的乘积,厄米特 多项式的零点决定场的节线,厄米特多项式 的正负交替的变化与高斯函数随着x、y的增 大而单调下降的特性决定着场分布的外形轮 廓。 • m阶厄米特多项式有m个零点, TEMmn模沿x 方向有m条节线,沿y方向有n x, y ) C00e v00 ( r, ) C00e
x2 y2 ( L ) r2
2 0 s
什么 函数?
, 0 s
L
基模在镜面上的分布是高斯型的
• 在离中心的距离为 处场的振幅降 落为中心处的1/e,通常就用半径 r L 的圆 来规定基模光斑的大小,并定义 L 为共 焦腔基模在镜面上的光斑尺寸或光斑半径。 • 共焦腔基模在镜面上的光斑大小与镜的横向 几何尺寸无关,只决定于腔长。 • 举例。
• In particular, the distance which the beam travels from the waist before the beam diameter increases by 2 , or before the beam area doubles, is given simply by the parameter f, called Rayleigh range. The Rayleigh range marks the approximate dividing line between the “near-field” or Fresnel and the “far-field” of Fraunhofer regions for a beam propagating out from a gaussian waist.
陈鹤鸣激光原理习题与思考题3解答

习题与思考题三解答1. 简述光学谐振腔的作用。
2. CO 2激光器的腔长L=100cm ,反射镜直径D=1.5cm ,两镜的光强反射系数分别为r1=0.985,r2=0.8。
求由衍射损耗及输出损耗分别引起的δ,τ。
解答1 衍射损耗:1880107501106102262.).(.a L =⨯⨯⨯=λ=δ-- s ..c L c 881075110318801-⨯=⨯⨯=δ=τ输出损耗:1190809850502121.)..ln(.r r ln =⨯⨯-=-=δ s ..c L c 881078210311901-⨯=⨯⨯=δ=τ解答2:(1)输出损耗由腔镜反射不完全引起。
初始光强为I0在无源腔内往返一次后光强衰减为I1,则:121012011281818861111111ln ln 0.119220.985*0.8100 2.78*100.12*3*10/3*10/222*2.78*10 4.94*1010.6R R R R I I e r r I r r Lcm s c m scm sQ s m δδτδπυτπτπλμ---==⇒==========(2)衍射损耗:腔的菲涅耳数222282862224144*100*10.60.188(1.5)1 1.77*100.188*3*10/2222 3.15*10d R d R R d da D N L L L cm m N D cm L m s c m s cc L L Q c λλλμδτδπυτπτππλλδλδ--==============3. 利用往返矩阵证明共焦腔为稳定腔,即任意近轴光线在其中可以往返无限多次,而且两次往返即自行闭合。
证明如下:(共焦腔的定义——两个反射镜的焦点重合的共轴球面腔为共焦腔。
共焦腔分为实共焦腔和虚共焦腔。
公共焦点在腔内的共 焦腔是实共焦腔,反之是虚共焦腔。
两个反射镜曲率相等的共焦腔称为对称共焦腔,可以证明,对称共焦腔是实双凹腔。
一般稳定球面腔行波场特征.

一般稳定球面镜腔的模式特征
一般稳定球面腔行波场的光斑半径
1.基模的光斑半径
我们知道,共焦腔的两个腔镜关于焦点即原点对称,镜面 上光斑的半径是相同的,但是一般的稳定球面腔换算成与 其等价的共焦腔之后,两个腔镜一般是不对称的,这样, 导致一般稳定球面腔两个腔镜上的光斑半径不再相同,分 别用ωs1、ωs2 来表示。 共焦腔中,行波场基模的光斑半径公式为:
共焦腔中,行波场基模的远场发散角公式为:
0 2 f
代入一般稳定球面腔等价的焦距公式
LR1 L R2 L R1 R2 L f 2 L R1 L R2
2
( g1 g 2 2 g1 g 2 ) 2 得到: 0 2 L g g ( 1 g g ) 1 2 1 2
简单讨论:
g1 g 2 0 , ( g1 g 2 ) 或 g1 g 2 1时,光斑半径 ,
g1 g 2 0 , ( g1 g 2 ) 或 g1 g 2 1时,光斑半径不存在。
2.基模和高阶模的模体积
ws ws 1 V00 L 2 2 g2 L 1 / 2 w1s ( ) [ ]1 / 4 g1 (1 g1 g 2 )
“等价”指具有相同的行波场。具体讲来,如果两个球面腔(R1, R2,L0)与( 腔等价!
激光原理 共轴球面腔的稳定性条件
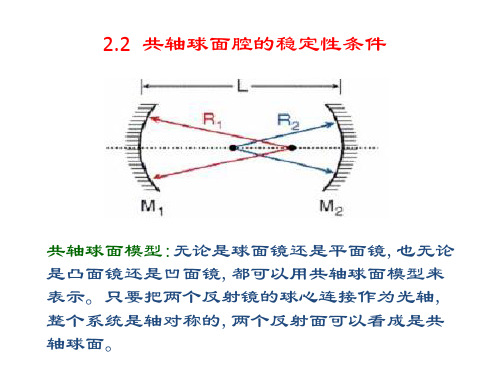
球面反射镜的光学变换矩阵
(r (1) , (1) ) ,经球面反射镜后,达到 (r ( 2) , ( 2) )后, 旁轴光线从
有:
r ( 2) r (1) ( 2) ( (1) 2 ) (1) r (1) R
0 1 r (1) (1)
g g <0
1 2
g g 0
1 2
(一)稳定腔: 0 < g1 g 2 < 1
1.双凹稳定腔:
这种腔的稳定条件有两种情况:
(1)
证明:
R1
R2
R1 > L 且 R2 > L
∵ R1>L
L < <1 ∴ 0 R1
L
L 0 1 <1 < R1
即:0<g1<1 ,同理 0<g2<1
所以:0<g1g2<1
即
g1g2<1
0< g1g2<1
如果 R1=R2 ,则此双凹腔为对称双凹腔,上述的两种稳
定条件可以合并成一个,即: R1=R2=R>L/2
2.平凹稳定腔: 由一个凹面发射镜和一个平面发射镜组成的谐振腔称为平
凹腔。其稳定条件为:R>L
R
L
证明:∵ R1>L , g 1 1
L 0 1 1 <1 <g ∴ R1
经过推导,可以得到稳定性条件 :
1 1 < ( A D) < 1 2
L L 0 < 1 1 R R < 1 1 2
L 引入几何g参数:令 g i 1 Ri
,则上式变为:
0 < g g <1
1 2
几何参数由谐振腔的结构所决定:
L g1 1 R1
激光原理技术稳定球面腔

z f
z
z (m n 1)tg ③附加相移因子 f 谐振腔单程附加相移 mn (m n 1) 2
1
证
z=-f→z=f
(0,0, f ) (0,0, f )
[kf (m n 1)tg
-1
k 2 f (m n 1)
w 2 z2 2 1 2 w0 f
W(Z) w0
-f
②腰斑半径 ③焦参数f
w 0 w (0)
f (腰处z=0)
0 -w0
f
Z
共焦腔反射镜焦距 f=L/2=R/2
w 0s 2w 0
L 2f w 0s 2w 0
④镜面光斑半径与腰斑半径关系
证
f w0
u 20 ( x , y) ( 8x 2)e 2 w 0s
2 x 2 y2 2 w0 s
8x 2 20 2 w 0s
x 1 2 w 0s
例2 方形镜对称共焦腔焦参数f=0.4m,光波长为= 0.314m,求镜面处光斑半径与等相位面曲率半径
解
f 0.314 10 6 0.4 w0 2 10 4 m 3.14
或∵镜面坐标z=f
w (f) w 0
f2 1 2 2w 0 f
(2)横向分布因子 (3)相位因子 e
i ( x , y , z )
2x 2y Hm ( )H n ( )e w (z) w (z)
x 2 y2 - 2 w (z)
反映场振幅的横向分布规律
反映场相位的分布规律
x2 y2 1 z ( x, y, z ) kz k (m n 1)tg 2 R( z ) f
稳定球面腔的光束传播特性

(2)原球面腔镜面的基横模光束有效截面半径
f L R
1
L
R 2
R
1
L
2
R 1
2L
R
2
L
R
z1
L R R
1
2 2
L
z
2 0
R L R
1
2L L
z
2
R
1
R
2
2L )
2
s1 s2
L
[
R1 (R2 L) L(R1 L)(R1 R2 L) R2 (R1 L)
2
2
]
14
L
[
L(R2 L)(R1 R2 L)
]
14
(z)
0
1 (
s s
1
2
非对称
R1
R’
R2
L 共焦腔与稳定球面腔的等价性
3.4.2 稳定球面腔的光束传播特性
一、等效共焦腔的束腰半径和原球面腔镜面的基横模光束有 效截面半径
1、思路:由 R1 , R2 , L
z 0
z 1 f
2
z1 , z2 , f ( 从而知道
s , s
1
0
)
2
非对称 s s
1
2
(1) 等效共焦腔的束腰半径
, z 0 , z 1 m ,f 2 m 1 2
故 R ' R ' L ' 2 f 4 m 1 2
R’1
R1
R2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z f f2 R z f z z f z
1 4
14
13.3 一般稳定球面腔的模式
镜面上的光斑尺寸:
1 2 2 z L 1 S 1 0 1 f L R1 2 R 2 R1 L L S2 L R2 L R1 R2 L
10
13.2 一般稳定球面腔与对称共焦腔的等价性
2、任一满足稳定条件的球面腔唯一地等价于某个共焦腔 以双凹腔为例
R1 z1 f 2 / z1 2 R2 z2 f / z2 L z2 z1
给定满足 0 g1 g2 1的R1 、R2、L的值,可以求出f ,f 必须 为实数,而且z1、z2 必须合理,使共焦腔的中心位置可以求 出。
2
5
13.1 圆形镜共焦腔的模式
振幅分布
基模的振幅分布也是高斯分布, 其1 / e光束半径为 0 S L / , 与方形镜共焦腔一致;
对高阶模式,m代表了方位角 上的极小值数目,n代表了径向
r 上的极小值数目;
相位分布
由于 mn 也是实函数,与方形镜 类似,圆形镜共焦腔自再现模 的等相位面与其腔镜重合。
11
13.2 一般稳定球面腔与对称共焦腔的等价性
L R2 L z 1 R1 L R2 L L R1 L z2 R1 L R2 L 2 L R1 L R2 L R1 R2 L f 2 R1 L R2 L
m n n
r , 为镜面的极坐标
n m ! L 为缔合拉盖尔多项式 k 0 m k ! k ! n k ! Cmn为归一化常数 m L L 2 f 为共焦腔长度 0 1 Lm L 1 1 m 0 S 为镜面上的光斑半径 1 2 Lm 1 m 2 m 2 2 m 2
圆形镜共焦腔中的场更集中在反射镜中心 附近,在镜的边缘部分下降得更低;
振幅分布曲线更光滑; N 越大,镜边缘处的场振幅越小;
0.75 1.0
0 0.1 0.3 0.5 0.7 0.9 TEM00
相 对 振 幅
1.0 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1
r/a
N=0.5
L R R
R12 R2 L
1 1 4
2
L
1 4
g1 1 g2 1
L R1 L R2
1 g1 g2 g1 g2 当g1 g2 0,L一定时, S 1、 S 2 有最小值, 0 g / R g / R 2 1 2 2 1
0.7
1.0
0 0.1 0.3 0.5 0.7 0.9 TEM10
r/a
2
13.1 圆形镜共焦腔的模式
B、等相位面分布:
圆形镜共焦腔反射镜面本身为场的 等相位面,即模的等相位面为球面;
C、单程相移
模的单程相移与N 无关;
不同横模之间单程相移之差为 / 2 的整数倍; n相同而m相差1的各个模相移差为 / 2 m相同n相差1的各个模相移差为
L
z1 0 z2 0
f2 0
有确定 的等价 共焦腔 存在
R 0
1
R
2
L
R
1
L
R
2
L
R1
R2
R1 L, R2 L 或R1 L, R2 L
R1
R2
1
R1 0, R2 0
2
1 2 V00 L0 S 2 2
2 L 1 0 2 其中V00 L0 为腔长L的共焦腔的基模体积; S 2 2 L 0 S = 为其镜面上的光斑尺寸。 0 方形镜 一般稳定腔中 Vmn Vmn 2m 1 2n 1 0 : 的高阶模体积 V00 V00 m 2n 1 圆形镜
如果在共焦腔的任意两个等相位面上放置两块具有相应曲 率半径的球面反射镜,则自再现模的行波场不会受到扰动。
9
13.2 一般稳定球面腔与对称共焦腔的等价性
满足以下条件的无穷多个球面反射镜腔都等价于图中的共焦腔:
f 2 可以证明这无穷多个腔都是稳定腔, R1 R z1 z1 z1 即满足条件: L L 0 1 1 1 2 R1 R2 任意共焦腔, f R2 R z2 z2 等价于无穷多个稳定球面腔。 z 2 L z z 2 1
激光原理与技术
第十三讲 圆形镜共焦腔、一般稳定球面腔
1、积分方程的解
13.1 圆形镜共焦腔的模式 1.0
0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 N=0.5
相 精确解:超椭球函数; 对 数值解:Fox Li利用迭代法得到数值解; 振 近似解:透镜孔径足够大时可以得到近似解; 幅 2、数值解的结论 A、振幅分布:
2 z z 0 1 f r2 k f 1 m 2 n 1 2 2 2 f 1
m
exp im exp i r , , z
此时对应对称共焦腔; 如果不满足, 当0 g1 g2 1时,表达式成立; S1 S 1与 S 2 为复数; 当g1 g2 1或g1 g2 0,即稳定球面腔趋于稳
定条件边界, S 1与 S 2 ,此时高斯近似 不再成立。
1 4
g2 L g1 1 g1 g2
自再现模,为拉盖尔 高斯函数。 m r2 r m r2 mn r , Cmn 2 Ln 2 2 exp 2 exp im 0 S 0 S 0 S 对应的本征值: mn exp i kL m 2n 1 2 k
7
附加相位超前mn与数值计算结果一致。
13.1 圆形镜共焦腔的模式
4、圆形镜共焦腔的行波场
由镜面上的场通过衍射积分方程求出空间场
0 r2 r2 r m E mn r , E0 2 Ln 2 2 exp 2 z z z z
TEM10
TEM00 TEM20
所有模式的损耗随N的增大而迅速 下降;
相应横模的损耗在数量级上要比 平平腔模低得多,但比方形镜共 焦腔的损耗大。
TEM10 TEM00
圆形镜共焦腔
N a /( L )
2
0.6
0.8
1.0
1.2
1.4
4
13.1 圆形镜共焦腔的模式
3、拉盖尔 高斯近似解 当N 时,积分方程可以求得近似解,即圆形镜共焦腔的
2
g1 g2
g2 g1
1 4 1 g1 g2
16
13.3 一般稳定球面腔的模式
3、谐振频率 从反射镜M1 到反射镜M 2的总相移为: mn z2 z1 由前述方形镜行波场的相位部分: r2 f z mn r , z k z kf m n 1 arctg 2R f z 2 可以得到: f z1 f z2 mn kmn z2 z1 m n 1 arctg arctg f z f z 1 2 f z1 f z2 arctg arctg arccos g1 g2 f z1 f z2
z f f2 R z f z 1 2 z f z
1 arctg 1 2z z L f L 0 0 S 2 2 L 2 f
8
13.2 一般稳定球面腔与对称共焦腔的等价性
L R1 R2 L 0
12
13.2 一般稳定球面腔与对称共焦腔的等价性
以上的证明都是在共焦腔的模式能够用厄米 高斯或者 拉盖尔 高斯函数描述时才是正确的, 因为其行波场的
等相位面曲率半径:
f2 R z z z
即本节所有的讨论都是在N 足够大 是在N 足够大时的近似, 的前提下进行的。
6
13.1 圆形镜共焦腔的模式
单程相移
mn arctg
1
mn
kL m 2n 1
2
mn m 2n 1
2
谐振频率 c q 1 m 2n 1 q kL m 2n 1 mnq 2 L 2 2 c c q n m 在腔内,频率是高度简并的。 2 L 4 L 单程衍射损耗 这个结论是必然的,因为近似解是 2 1 在N 的假设下近似得到的,因 mn 1 0 mn 此该分布不能用来研究传输损耗。
1 4
S 2
g1 L g2 1 g1 g2
